Индукционный ток — Какое направление индукционного тока? — Росиндуктор

ИНДУКЦИОННЫЙ ТОК — это электрический ток, возникающий при изменении потока магнитной индукции в замкнутом проводящем контуре. Это явление носит название электромагнитной индукции. Хотите узнать какое направление индукционного тока? Росиндуктор — это торговый информационный портал, где вы найдете информацию про ток.

Содержание

Индукционный ток правило

Определяющее направление индукционного тока правило звучит следующим образом: «Индукционный ток направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван». Правая рука развернута ладонью навстречу магнит¬ным силовым линиям, при этом большой палец направлен в сторону движения проводника, а четыре пальца по-казывают, в каком направлении будет течь индукционный ток. Перемещая проводник, мы перемещаем вместе с проводчиком все электроны, заключенные в нем, а при перемещении в магнитном поле электрических зарядов на них будет действовать сила по правилу левой руки.

Направление индукционного тока

Направление индукционного тока, как и его величина, определяется правилом Ленца, в котором говорится, что направление индукционного тока всегда ослабляет действие фактора, возбудившего ток. При изменении потока магнитного поля через контур направление индукционного тока будет таким, чтобы скомпенсировать эти изменения. Когда магнитное поле возбуждающее ток в контуре создается в другом контуре, направление индукционного тока зависит от характера изменений: при увеличении внешнего тока индукционный ток имеет противоположное направление, при уменьшении — направлен в ту же сторону и стремиться усилить поток.

Индукционный ток в катушке

Катушка с индукционным током имеет два полюса (северный и южный), которые определяются в зависимости от направления тока: индукционные линии выходят из северного полюса. Приближение магнита к катушке вызывает появление тока с направлением, отталкивающим магнит. При удалении магнита ток в катушке имеет направление, способствующее притягиванию магнита.

Индукционный ток возникает

Индукционный ток возникает в замкнутом контуре, находящемся в переменном магнитном поле. Контур может быть как неподвижным (помещенным в изменяющийся поток магнитной индукции), так и движущимся (движение контура вызывает изменение магнитного потока). Возникновение индукционного тока обуславливает вихревое электрическое поле, которое возбуждается под воздействием магнитного поля.

Как создать индукционный ток

О том, как создать кратковременный индукционный ток можно узнать из школьного курса физики.

Для этого есть несколько способов:

• — перемещение постоянного магнита или электромагнита относительно катушки,
• — перемещение сердечника относительно вставленного в катушку электромагнита,
• — замыкание и размыкание цепи,
• — регулирование тока в цепи.

Сила индукционного тока

Основной закон электродинамики (закон Фарадея) гласит, что сила индукционного тока для любого контура равна скорости изменения магнитного потока, проходящего через контур, взятой со знаком минус. Сила индукционного тока носит название электродвижущей силы.

Вопрос 34 Электромагнитная индукция. Самоиндукция.

Электромагнитная индукция.

Электрические токи создают вокруг себя магнитное поле. 1831 г. английский физик М. Фарадей открыл явле­ние электромагнитной индукции (заключа­ющееся в том, что в замкнутом проводя­щем контуре при изменении потока маг­нитной индукции, охватываемого этим контуром, возникает электрический ток, получивший название индукционного). Опытным путем было также установ­лено, что значение индукционного тока совершенно не зависит

от способа измене­ния потока магнитной индукции, а опреде­ляется лишь скоростью его изменения. Открытие явления электромагнитной индукции имело большое значение, так как была доказана возможность получе­ния электрического тока с помощью маг­нитного поля.

Закон Фарадея и его вывод из закона сохранения энергии:

Фарадей пришел к количе­ственному закону электромагнитной ин­дукции. Он показал, что всякий раз, когда происходит изменение сцепленного с кон­туром потока магнитной индукции, в контуре возникает индукционный ток; возник­новение индукционного тока указывает на наличие в цепи электродвижущей силы, называемой

электродвижущей силой элек­тромагнитной индукции. Значение индук­ционного тока, а следовательно, и э. д. с, электромагнитной индукции ξ_i определя­ются только скоростью изменения магнит­ного потока, т. е.

закона электромагнитной индукции Фарадея: какова бы ни была причина изменения потока магнитной индукции, охватыва­емого замкнутым проводящим контуром, возникающая в контуре э.д.с.

Знак минус показывает, что увеличе­ние потока (dФ/dt>0) вызывает э.д.с.

ξξ_i<0, т. е. поле индукционного тока на­правлено навстречу потоку; уменьшение

потока (dФ/dt<0 ) вызывает ξ_i>0,

т. е. направления потока и поля индукци­онного тока совпадают. Знак минус в фор­муле (123.2) является математическим выражением правила Ленца — общего правила для нахождения направления ин­дукционного тока, выведенного в 1833 г.

Правило Ленца: индукционный ток в контуре имеет всегда такое направление, что создаваемое им магнитное поле препятствует изменению магнитного по­тока, вызвавшего этот индукционный ток.

Закон Фарадея э.д.с. ξ_i элек­тромагнитной индукции в контуре числен­но равна и противоположна по знаку ско­рости изменения магнитного потока сквозь поверхность, ограниченную этим конту­ром. Этот закон является универсальным: э.д.с. ξ_i не зависит от способа изменения магнитного потока.

Э.д.с. электромагнитной индукции выражается в вольтах. Действительно, учитывая, что единицей магнитного потока является вебер (Вб), получим

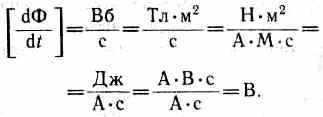
При вращении рамки в ней будет воз­никать переменная э.д.с. индукции (см. (123.2))

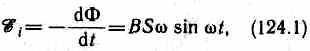
Вихревые токи (токи Фуко)

Индукционный ток возникает не только в линейных проводниках, но и в массивных сплошных проводниках, помещенных в пе­ременное магнитное поле. Эти токи оказы­ваются замкнутыми в толще проводника и поэтому называются вихревыми. Их так­же называют токами Фуко — по имени первого исследователя.

Токи Фуко, как и индукционные токи в линейных проводниках, подчиняются правилу Ленца: их магнитное поле на­правлено так, чтобы противодействовать изменению магнитного потока, индуциру­ющего вихревые токи.

Индуктивность контура. Самоиндукция

Электрический ток, текущий в замкнутом контуре, создает вокруг себя магнитное по­ле, индукция которого, по закону Био — Савара—Лапласа (см. (110.2)), пропор­циональна току. Сцепленный с контуром магнитный поток Ф поэтому пропорциона­лен току I в контуре:

Ф=LI, (126.1)

где коэффициент пропорциональности L называется индуктивностью контура.

При изменении силы тока в контуре будет изменяться также и сцепленный с ним магнитный поток; следовательно, в контуре будет индуцироваться э.д.с. Возникновение э.д.с. индукции в прово­дящем контуре при изменении в нем силы тока называется

самоиндукцией.

Из выражения (126.1) определяется единица индуктивности генри (Гн): 1 Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1 А равен 1 Вб:

1 Гн=1 Вб/А=1В•с/А.

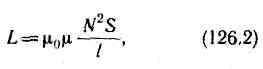
т. е. индуктивность соленоида зависит от числа витков соленоида N, его длины l, площади S и магнитной проницаемости  вещества, из которого изготовлен сердеч­ник соленоида.

Применяя к явлению самоиндукции закон Фарадея (см. (123.2)), получим, что э.д.с. самоиндукции

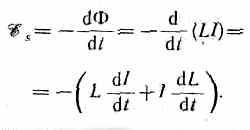
Если контур не деформируется и магнит­ная проницаемость среды не изменяется (в дальнейшем будет показано, что по­следнее условие выполняется не всегда), то L=const и

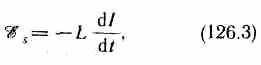
Вопрос №30

Действие магнитного поля на движущийся заряд

Опыт показывает, что магнитное поле дей­ствует не только на проводники с током (см. §111), но и на отдельные заряды, движущиеся в магнитном поле. Сила, дей­ствующая на электрический заряд

Q, дви­жущийся в магнитном поле со скоростью v, называется силой Лоренца и выражает­ся формулой

F=Q[vB], (114.1) где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определя­ется с помощью правила левой руки: если ладонь левой руки расположить так, что­бы в нее входил вектор В, а четыре вы­тянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпада­ют, для Q<0—противоположны), то отогнутый большой палец покажет на­правление силы, действующей на положи­тельный заряд. На рис. 169 показана вза­имная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.

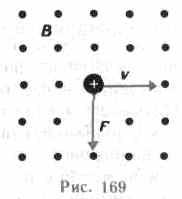
Модуль силы Лоренца (см. (114.1)) равен

F=QvBsin,

где  — угол между v и В.

Отметим еще раз (см. § 109), что маг­нитное поле не действует на покоящийся электрический заряд. В этом существенное отличие магнитного поля от электрическо­го. Магнитное поле действует только на движущиеся в нем заряды.

Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лорен­ца может быть использовано (наравне с другими, см. § 109) для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикуляр­на скорости движения заряженной части­цы, поэтому она изменяет только направ­ление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изме­няется.

Если на движущийся электрический заряд помимо магнитного поля с индук­цией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна век­торной сумме сил — силы, действующей со стороны электрического поля, и силы Ло­ренца:

F=QE + Q[vB].

Это выражение называется формулой Ло­ренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

Движение заряженных частиц в магнитном поле

Выражение для силы Лоренца (114.1) по­зволяет найти ряд закономерностей дви­жения заряженных частиц в магнитном поле. Направление силы Лоренца и на­правление вызываемого ею отклонения за­ряженной частицы в магнитном поле за­висят от знака заряда Q частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле одно­родно и на частицы электрические поля не действуют. Если заряженная частица дви­жется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В ра­вен 0 или . Тогда по формуле (114.1) сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она дви­жется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нор­мальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяет­ся из условия

QvB = mv²/r,

откуда

Период вращения частицы, т. е. вре­мя Т, затрачиваемое ею на один полный оборот,

T = 2nr/v.

Подставив сюда выражение (115.1), по­лучим

т. е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду

(Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)). На этом основано действие цикли­ческих ускорителей заряженных частиц (см. §116).

Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно пред­ставить в виде суперпозиции: 1) равно­мерного прямолинейного движения вдоль поля со скоростью v_||=vcos; 2) равно­мерного движения со скоростью v_┴= vsin по окружности в плоскости, пер­пендикулярной полю. Радиус окружности определяется формулой (115.1) (в данном случае надо заменить v на v_┴=vsin). В результате сложения обоих движений возникает движение по спирали, ось кото­рой параллельна магнитному полю (рис. 170). Шаг винтовой линии

h=v_||T=vTcos.

Подставив в последнее выражение (115.2), получим

h=2mv cos/(BQ).

Направление, в котором закручивается спираль, зависит от знака заряда ча­стицы.

Если скорость v заряженной частицы составляет угол а с направлением векто­ра В неоднородного магнитного поля, ин­дукция которого возрастает в направле­нии движения частицы, то r и h уменьша­ются с ростом В. На этом основана фокусировка заряженных частиц в маг­нитном поле.

Вопрос №31

Ускорителями заряженных частиц назы­ваются устройства, в которых под дей­ствием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (элек­тронов, протонов, мезонов и т.д.).

Любой ускоритель характеризуется типом ускоряемых частиц, энергией, со­общаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пу­чок) и импульсные (из них частицы вы­летают порциями — импульсами). По­следние характеризуются длительностью импульса. По форме траектории и меха­низму ускорения частиц ускорители делят­ся на линейные, циклические и индукци­онные. В линейных ускорителях траекто­рии движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружно­сти или спирали.

Рассмотрим некоторые типы ускорите­лей заряженных частиц.

Циклотрон — циклический резонан­сный ускоритель тяжелых частиц (прото­нов, ионов). Его принципиальная схема приведена на рис. 171. Между полюсами

Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тя­желых заряженных частиц (например, протонов, ионов, -частиц), в котором уп­равляющее магнитное поле постоянно, а частота ускоряющего электрического по­ля медленно изменяется с периодом. Дви­жение частиц в фазотроне, как и в цикло­троне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (огра­ничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).

Синхрофазотрон — циклический ре­зонансный ускоритель тяжелых заряжен­ных частиц (протонов, ионов), в котором объединяются свойства фазотрона и син­хротрона, т. е. управляющее магнитное поле и частота ускоряющего электрическо­го поля одновременно изменяются во вре­мени так, чтобы радиус равновесной орби­ты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.

Вопрос №32

Работа по перемещению проводника и контура с током в магнитном поле

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера (см. §111). Если проводник не закреплен (например, одна из сторон кон­тура изготовлена в виде подвижной пере­мычки, рис. 177), то под действием силы Ампера он будет в магнитном поле переме­щаться. Следовательно, магнитное поле совершает работу по перемещению про­водника с током.

Для определения этой работы рас-

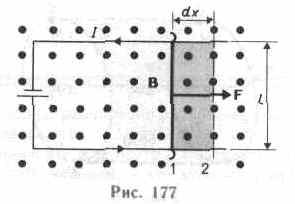
смотрим проводник длиной l с током I (он может свободно перемещаться), помещен­ный в однородное внешнее магнитное по­ле, перпендикулярное плоскости контура. При указанных на рис. 177 направлениях тока и поля сила, направление которой определяется по правилу левой руки, а значение — по закону Ампера (см. (111.2)), равна

F=IBl.

Под действием этой силы проводник пере­местится параллельно самому себе на от­резок Ах из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

dA=Fdx=IBldx =IBdS= IdФ,

так как ldx=dS— площадь, пересекае­мая проводником при его перемещении в магнитном поле, ВdS=dФ — поток век­тора магнитной индукции, пронизываю­щий эту площадь. Таким образом,

dA=IdФ, (121.1)

т. е. работа по перемещению проводника с током в магнитном поле равна произве­дению силы тока на магнитный поток, пересеченный движущимся проводником. Полученная формула справедлива и для произвольного направления вектора В.

Вычислим работу по перемещению за­мкнутого контура с постоянным током I в магнитном поле. Предположим, что кон­тур М перемещается в плоскости чертежа и в результате бесконечно малого переме­щения займет положение М’, изображен­ное на рис. 178 штриховой линией. На­правление тока в контуре (по часовой стрелке) и магнитного поля (перпендику­лярно плоскости чертежа — за чертеж) указано на рисунке. Контур М мысленно

разобьем на два соединенных своими кон­цами проводника: ABC и CDA.

Работа dA, совершаемая силами Ам­пера при рассматриваемом перемещении контура в магнитном поле, равна алгебра­ической сумме работ по перемещению проводников ЛВС (dA₁) и СDA (dА₂), т. е.

dA=dA₁+dA₂. (121.2)

Силы, приложенные к участку CDA контура, образуют с направлением пере­мещения острые углы, поэтому совершае­мая ими работа dA₂>0. Согласно (121.1), эта работа равна произведению силы то­ка I в контуре на пересеченный проводни­ком CDA магнитный поток. Провод­ник CDA пересекает при своем движении поток dФ₀ сквозь поверхность, выполнен­ную в цвете, и поток dФ₂, пронизывающий контур в его конечном положении. Сле­довательно,

dA₂= I(dФ₀+dФ₂). (121.3)

Силы, действующие на участок ЛВС контура, образуют с направлением пе­ремещения тупые углы, поэтому совер­шаемая ими работа dA₁<0. Провод­ник ЛВС пересекает при своем движении поток dФ₀ сквозь поверхность, выполнен­ную в цвете, и поток dФ₁, пронизывающий контур в начальном положении. Следова­тельно,

dA₁=I(dФ₀+dФ₁). (121.4)

Подставляя (121.3) и (121.4) в (121.2), получим выражение для эле­ментарной работы:

dA=I(dФ₂ -dФ₁),

где dФ₂-dФ₁=dФ’— изменение магнит­ного потока через площадь, ограниченную контуром с током. Таким образом,

dA=IdФ’. (121.5)

Проинтегрировав выражение (121.5), оп­ределим работу, совершаемую силами Ам­пера, при конечном произвольном переме­щении контура в магнитном поле:

A=IФ, (121.6)

т. е. работа по перемещению замкнутого

контура с током в магнитном поле равна произведению силы тока в контуре на из­менение магнитного потока, сцепленного

с контуром. Формула (121.6) остается справедливой для контура любой формы в произвольном магнитном поле.

Вопрос№33

Всякое вещество является магнетиком, т. е. оно способно под действием магнитно­го поля приобретать магнитный момент (намагничиваться). Для понимания меха­низма этого явления необходимо рассмот­реть действие магнитного поля на движу­щиеся в атоме электроны.

Ради простоты предположим, что элек­трон в атоме движется по круговой орби­те. Если орбита электрона ориентирована относительно вектора В произвольным об­разом, составляя с ним угол а (рис. 188), то можно доказать, что она приходит в та­кое движение вокруг В, при котором век­тор магнитного момента р_m, сохраняя по­стоянным угол а, вращается вокруг на-

правления В с некоторой угловой скоро­стью. Такое движение в механике на­зывается прецессией. Прецессию вокруг вертикальной оси, проходящей через точку опоры, совершает, например, диск волчка при замедлении движения.

Таким образом, электронные орбиты атома под действием внешнего магнитного поля совершают прецессионное движе­ние, которое эквивалентно круговому то­ку. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется со­ставляющая магнитного поля, направлен­ная противоположно внешнему полю. На­веденные составляющие магнитных полей атомов (молекул) складываются и обра­зуют собственное магнитное поле вещест­ва, ослабляющее внешнее магнитное по­ле. Этот эффект получил название диа­магнитного эффекта, а вещества, на­магничивающиеся во внешнем магнитном поле против направления поля, называют­ся диамагнетиками.

В отсутствие внешнего магнитного по­ля диамагнетик немагнитен, поскольку в данном случае магнитные моменты элек­тронов взаимно компенсируются, и сум­марный магнитный момент атома (он ра­вен векторной сумме магнитных моментов (орбитальных и спиновых) составляющих атом электронов) равен нулю. К диамагнетикам относятся многие металлы (на­пример, Bi, Ag, Au, Cu), большинство органических соединений, смолы, углерод и т. д.

Так как диамагнитный эффект обус­ловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам. Однако наряду с диамагнитными ве­ществами существуют и парамагнитные — вещества, намагничивающиеся во внеш­нем магнитном поле по направлению поля.

У парамагнитных веществ при отсутст­вии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и атомы (молекулы) парамагнети­ков всегда обладают магнитным момен­том. Однако вследствие теплового движе­ния молекул их магнитные моменты ори­ентированы беспорядочно, поэтому пара-

магнитные вещества магнитными свой­ствами не обладают. При внесении пара­магнетика во внешнее магнитное поле устанавливается преимущественная ори­ентация магнитных моментов атомов по полю (полной ориентации препятствует тепловое движение атомов). Таким обра­зом, парамагнетик намагничивается, со­здавая собственное магнитное поле, со­впадающее по направлению с внешним полем и усиливающее его. Этот эффект называется парамагнитным. При ослабле­нии внешнего магнитного поля до нуля ориентация магнитных моментов вследст­вие теплового движения нарушается и па­рамагнетик размагничивается. К парамаг­нетикам относятся редкоземельные эле­менты, Pt, Al и т. д. Диамагнитный эффект наблюдается и в парамагнетиках, но он значительно слабее парамагнитного и по­этому остается незаметным.

Из рассмотрения явления парамагне­тизма следует, что его объяснение совпа­дает с объяснением ориентационной (дипольной) поляризации диэлектриков с по­лярными молекулами (см. §87), только электрический момент атомов в случае поляризации надо заменить магнитным моментом атомов в случае намагничения.

Подводя итог качественному рассмот­рению диа- и парамагнетизма, еще раз отметим, что атомы всех веществ являют­ся носителями диамагнитных свойств. Ес­ли магнитный момент атомов велик, то парамагнитные свойства преобладают над диамагнитными и вещество является па­рамагнетиком; если магнитный момент атомов мал, то преобладают диамагнит­ные свойства и вещество является диамагнетиком.

Подобно тому, как для количественного описания поляризации диэлектриков вво­дилась поляризованность (см. §88), для количественного описания намагничения магнетиков вводят векторную величину — намагниченность, определяемую магнит­ным моментом единицы объема магнетика:

J=p_m/V=p_a/V,

где p_m=р_а— магнитный

Согласно представлениям Вейсса, ферромагнетики при температурах ниже точки Кюри обладают спонтанной намаг­ниченностью независимо от наличия внеш­него намагничивающего поля. Спонтанное намагничение, однако, находится в кажу­щемся противоречии с тем, что многие ферромагнитные материалы даже при тем­пературах ниже точки Кюри не намагниче­ны. Для устранения этого противоречия Вейсс ввел гипотезу, согласно которой ферромагнетик ниже точки Кюри разбива­ется на большое число малых макроскопи­ческих областей — доменов, самопроиз­вольно намагниченных до насыщения.

При отсутствии внешнего магнитного поля магнитные моменты отдельных до­менов ориентированы хаотически и ком­пенсируют друг друга, поэтому результи­рующий магнитный момент ферромагнети­ка равен нулю и ферромагнетик не намагничен. Внешнее магнитное поле ори­ентирует по полю магнитные моменты не отдельных атомов, как это имеет место в случае парамагнетиков, а целых об­ластей спонтанной намагниченности. По­этому с ростом Н намагниченность

J (см. рис. 192) и магнитная индукции В (см. рис. 193) уже в довольно слабых полях растут очень быстро. Этим объясня­ется также увеличение  ферромагнетиков до максимального значения в слабых по­лях (см. рис. 194). Эксперименты показа­ли, что зависимость В от Я не является такой плавной, как показано на рис. 193, а имеет ступенчатый вид. Это свидетель­ствует о том, что внутри ферромагнетика домены поворачиваются по полю скачком.

При ослаблении внешнего магнитного поля до нуля ферромагнетики сохраняют остаточное намагничение, так как тепло­вое движение не в состоянии быстро дезо­риентировать магнитные моменты столь крупных образований, какими являются домены. Поэтому и наблюдается явление магнитного гистерезиса (рис.195). Для того чтобы ферромагнетик размагнитить, необходимо приложить коэрцитивную си­лу; размагничиванию способствуют также встряхивание и нагревание ферромагнети­ка. Точка Кюри оказывается той темпера­турой, выше которой происходит разруше­ние доменной структуры.

Вихревые токи — Википедия

Материал из Википедии — свободной энциклопедии

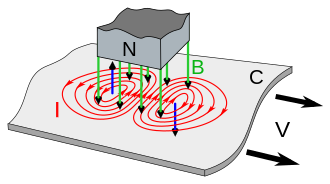Иллюстрация возникновения токов Фуко в движущейся в постоянном магнитном поле проводящей (металлической) пластине C. Вектор магнитной индукции B показан зелеными стрелками, вектор V скорости движения пластин — черными стрелками, силовые линии вектора плотности электрического тока I — красным цветом (эти линии замкнутые, «вихревые»).
Источником магнитного поля является постоянный магнит, его фрагмент показан вверху рисунка серым цветом. Вектор магнитной индукции B направлен от северного (N) полюса магнита, магнитное поле пронизывает пластину. В материале пластины, входящем под магнит, т.е. слева, магнитная индукция изменяется во времени, возрастает (dB_n/dt > 0), и в соответствии с законами Фарадея и Ома в материале пластины возникает (наводится, «индуцируется») замкнутый (вихревой) электрический ток. Этот ток течет против часовой стрелки и, по закону Ампера, создает свое собственное магнитное поле, вектор магнитной индукции которого показан синей стрелкой, направленной перпендикулярно плоскости протекания тока, вверх.
Справа, в материале пластины, удаляющемся от магнита, магнитное поле тоже меняется во времени, однако оно ослабевает, и силовые линии возникающего справа еще одного электрического тока направлены по часовой стрелке.
Точно под магнитом «левый» и «правый» вихри токов направлены в одну и ту же сторону, плотность суммарного электрического тока максимальна. На движущиеся в этой области электрические заряды, поток которых образует электрический ток, в сильном магнитном поле действует сила Лоренца, направленная (по правилу левой руки) против вектора скорости V. Эта сила Лоренца тормозит пластину C. Взаимодействие магнитного поля магнита и магнитного поля индуцированных токов приводит к тому, что результирующее распределение потока магнитного поля в окрестности полюса N магнита отличается от случая неподвижной пластины C (и зависит от скорости V), хотя суммарный поток вектора магнитной индукции остается неизменным (при условии, что материал магнита и пластины C не входит в насыщение). У этого термина существуют и другие значения, см. Ток.

Вихревые токи, или токи Фуко́ (в честь Ж. Б. Л. Фуко) — вихревой^[1] индукционный^[2] объёмный электрический ток^[3], возникающий в электрических проводниках при изменении во времени потока действующего на них магнитного поля.

Впервые вихревые токи были обнаружены французским учёным Д. Ф. Араго (1786—1853) в 1824 г. в медном диске, расположенном на оси под вращающейся магнитной стрелкой. За счёт вихревых токов диск приходил во вращение. Это явление, названное явлением Араго, было объяснено несколько лет спустя M. Фарадеем с позиций открытого им закона электромагнитной индукции: вращаемое магнитное поле наводит в медном диске вихревые токи, которые взаимодействуют с магнитной стрелкой. Вихревые токи были подробно исследованы французским физиком Фуко (1819—1868) и названы его именем. Фуко также открыл явление нагревания металлических тел, вращаемых в магнитном поле, вихревыми токами.

Токи Фуко возникают под действием изменяющегося во времени (переменного) магнитного поля^[4] и по физической природе ничем не отличаются от индукционных токов, возникающих в проводах и вторичных обмотках электрических трансформаторов.

Поскольку электрическое сопротивление массивного^[5] проводника может быть мало, то сила индукционного электрического тока, обусловленного токами Фуко, может достигать чрезвычайно больших значений. В соответствии с правилом Ленца токи Фуко в объеме проводника выбирают такой путь, чтобы в наибольшей мере противодействовать причине, вызывающей их протекание. Поэтому, в частности, движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов Фуко с внешним магнитным полем. Этот эффект используется для демпфирования подвижных частей гальванометров, сейсмографов и других приборов без использования силы трения, а также в некоторых конструкциях тормозных систем железнодорожных поездов.

Тепловое действие токов Фуко используется в индукционных печах, где в катушку, питаемую высокочастотным генератором большой мощности, помещают проводящее тело, в котором возникают вихревые токи, разогревающие его до плавления. Подобным образом работают индукционные плиты, в которых металлическая посуда разогревается вихревыми токами, создаваемыми переменным магнитным полем катушки, расположенной внутри плиты.

С помощью токов Фуко осуществляется прогрев металлических частей вакуумных установок для их дегазации.

В соответствии с правилом Ленца вихревые токи протекают внутри проводника по таким путям и направлениям, чтобы своим действием возможно сильнее противиться причине, которая их вызывает. Вследствие этого при движении в магнитном поле на хорошие проводники действует тормозящая сила, вызываемая взаимодействием вихревых токов с магнитным полем. Этот эффект используется в ряде приборов для демпфирования колебаний их подвижных частей.

Во многих случаях токи Фуко могут быть нежелательными. Для борьбы с ними принимаются специальные меры: с целью предотвращения потерь энергии на нагревание сердечников трансформаторов, эти сердечники набирают из тонких пластин, разделённых изолирующими прослойками (шихтовка). Появление ферритов сделало возможным изготовление этих сердечников сплошными.

Вихретоковый контроль — один из методов неразрушающего контроля изделий из токопроводящих материалов.

1. ↑ Термин вихревой означает, что силовые линии тока замкнуты.
2. ↑ Индукционным называют электрический ток, создаваемый (наводимый) в проводнике за счет взаимодействия проводника с переменным во времени магнитным (электромагнитным) полем, а не за счет действия включенных в разрыв цепи источников тока и ЭДС (гальванических элементов и т.п.).
3. ↑ Часто используется термин токи во множественном числе, поскольку токи Фуко представляют собой электрический ток в объеме проводника, и в отличие от индукционного тока во вторичной обмотке трансформатора затруднительно указать единственную «электрическую цепь» для тока, единственную замкнутую траекторию движения электрических зарядов в толще проводника.
4. ↑ Строго говоря — под действием переменного электромагнитного поля
5. ↑ То есть обладающего большой площадью поперечного току сечения

• Сивухин Д. В.: Общий курс физики, том 3. Электричество. 1977
• Савельев И. В.: Курс общей физики, том 2. Электричество. 1970
• Неразрушающий контроль: справочник: В 7т. Под общ. ред. В. В. Клюева. Т. 2: В 2 кн.-М.:Машиностроение, 2003.-688 с.: ил.

Индукция — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 января 2020; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 января 2020; проверки требует 1 правка.

Инду́кция (из лат. inductio «выведение, наведение») — широко используемый в науке термин.

В логике

• Индуктивное умозаключение — метод рассуждения от частного к общему.
  • Полная индукция — метод доказательства, при котором утверждение доказывается для конечного числа частных случаев, исчерпывающих все возможности.
  • Неполная индукция — наблюдения за отдельными частными случаями наводит на гипотезу, которая нуждается в доказательстве^[1].
• Математическая индукция — метод доказательства для последовательности натуральных чисел либо объектов, однозначно занумерованных натуральными числами.

В философии

В физике

В экономике

• Индукция — это вид обобщения, связанный с предвосхищением результатов наблюдений и экспериментов на основе данных опыта. В индукции данные опыта «наводят» на общее, поэтому индуктивные обобщения рассматриваются обычно как опытные истины или эмпирические законы. Изучая финансово-хозяйственную деятельность ряда типичных российских предприятий, можно делать, например, выводы о закономерностях развития совокупности предприятий.

В юридических науках

• Индуктивный метод — способ исследования и изложения, при котором от наблюдаемых частных фактов переходят к выделению принципов, общих положений теории, установлению закономерностей.

В медицине и биологии

В химии

• Химическая индукция — совместное протекание двух химических реакций, из которых одна обусловливает или ускоряет вторую.

Правило Ленца — Википедия

Материал из Википедии — свободной энциклопедии

Правило Ленца определяет направление индукционного тока и гласит:

Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

— Сивухин Д. В. § 65. Правило Ленца // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 268. — 688 с.

Правило сформулировано в 1833 году Э. Х. Ленцем. Позднее оно было обобщено на все физические явления в работах Ле Шателье (1884 год) и Брауна (1887 год), это обобщение известно как принцип Ле Шателье — Брауна.

Эффектной демонстрацией правила Ленца является опыт Элиу Томсона.

Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока Φ{\displaystyle \Phi }, пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением^[1]:

Eind=−dΦdt,{\displaystyle {\mathcal {E}}^{ind}=-{\frac {d\Phi }{dt}},}

где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.

Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменением величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур.

Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.

1. ↑ Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.

Электромагнитная индукция. Самоиндукция — Мегаобучалка

Как мы уже выяснили, электрический ток способен порождать магнитные поля. Возникает вопрос: может ли магнитное поле вызывать появление электрического тока? Эта задача была решена английским физиком Майклом Фарадеем, открывшим явление электромагнитной индукции в 1831 г.^Свитый в катушку проводник замыкается на гальванометре (рис. 3.19). Если вдвигать в катушку постоянный магнит, то гальванометр покажет наличие тока в течение всего промежутка времени, пока магнит перемещается относительно катушки. При выдергивании магнита из катушки гальванометр показывает наличие тока противоположного направления. Изменения направления тока происходит при изменении вдвигаемого или выдвигаемого полюса магнита.

Аналогичные результаты наблюдались при замене постоянного магнита электромагнитом (катушкой с током). Если обе катушки закрепить неподвижно, но в одной из них менять значение тока, то в этот момент в другой катушке наблюдается индукционный ток.

ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ состоит в возникновении электродвижущей силы (э.д.с.) индукции в проводящем контуре, через который меняется поток вектора магнитной индукции. Если контур является замкнутым, то в нем возникает индукционный ток.

Открытие явления электромагнитной индукции:

1) показало взаимосвязь между электрическим и магнитным полем;

2) предложило способ получения электрического тока с помощью магнитного поля.

Основные свойства индукционного тока:

1. Индукционный ток возникает всегда, когда происходит изменение сцепленного с контуром потока магнитной индукции.

2. Сила индукционного тока не зависит от способа изменения потока магнитной индукции, а определяется лишь скоростью его изменения.

 

Опытами Фарадея было установлено, что величина электродвижущей силы индукции пропорциональна скорости изменения магнитного потока, пронизывающего контур проводника (закон электромагнитной индукции Фарадея)

, или , (3.46)

где (dF) – изменение потока в течении времени (dt).МАГНИТНЫМ ПОТОКОМ или ПОТОКОМ МАГНИТНОЙ ИНДУКЦИИназывается величина, которая определяется на основе следующего соотношения: (магнитный поток через поверхность площадью S): Ф=ВScosα, (3.45), угол a – угол между нормалью к рассматриваемой поверхности и направлением вектора индукции магнитного поля

единица магнитного потока в системе СИ носит название вебер – [Вб=Тл×м²].

Знак «–» в формуле означает, что э.д.с. индукции вызывает индукционный ток, магнитное поле которого противодействует всякому изменению магнитного потока, т.е. при >0 э.д.с. индукции e_И<0 и наоборот.

э.д.с. индукции измеряется в вольтах

 

Для нахождения направления индукционного тока существует правило Ленца (правило установлено в 1833 г.): индукционный ток имеет такое направление, что создаваемое им магнитное поле стремится компенсировать изменение магнитного потока, вызвавшее этот индукционный ток.

Например, если вдвигать северный полюс магнита в катушку, т. е. увеличивать магнитный поток через его витки, в катушке возникает индукционный ток такого направления, что на ближайшем к магниту конце катушки возникает северный полюс (рис.3.20). Итак, магнитное поле индукционного тока стремится нейтрализовать вызвавшее его изменение магнитного потока.

Не только переменное магнитное поле порождает индукционный ток в замкнутом проводнике, но и при движении замкнутого проводника длиной l в постоянном магнитном поле (В) со скоростью v в проводнике возникает эдс:

a (B Ùv) (3.47)

Как вы уже знаете, электродвижущая силав цепи– это результат действия сторонних сил. При движении проводника в магнитном поле роль сторонних сил выполняет сила Лоренца (которая действует со стороны магнитного поля на движущийся электрический заряд). Под действием этой силы происходит разделение зарядов и на концах проводника возникает разность потенциалов. Э.д.с. индукции в проводнике является работой по перемещению единичных зарядов вдоль проводника.

Направление индукционного токаможно определитьпо правилу правой руки:Вектор В входит в ладонь, отведенный большой палец совпадает с направлением скорости проводника, а 4 пальца укажут направление индукционного тока.

Таким образом переменное магнитное поле вызывает появление индуцированного электрического поля. Оно не потенциально( в отличие от электростатического), т.к. работапо перемещению единичного положительного заряда равна э.д.с. индукции, а не нулю.

Такие поля называются вихревыми. Силовые линии вихревогоэлектрического поля – замкнуты сами на себя,в отличие от линий напряженности электростатического поля.

 

Э.д.с. индукции возникает не только в соседних проводниках, но и в самом проводнике при изменении магнитного поля тока, идущего по проводнику. Возникновение э.д.с. в каком-либо проводнике при изменении в нем самом силы тока (следовательно, магнитного потока в проводнике) называется самоиндукцией, а ток, индуцируемый в этом проводнике, – током самоиндукции.

Ток в замкнутом контуре создает в окружающем пространстве магнитное поле, напряженность которого пропорциональна силе тока I. Поэтому магнитный поток Ф, пронизывающий контур, пропорционален силе тока в контуре

Ф=L×I, (3.48).

 

L – коэффициент пропорциональности, который носит название коэффициента самоиндукции, или, просто, индуктивности. Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости среды, окружающей контур.

В этом смысле индуктивность контура — аналогэлектрической емкости уединенного проводника, которая также зависит только от формы проводника, его размеров и диэлектрической проницаемости среды.

Единица индуктивности — генри (Гн): 1Гн — индуктивность такого контура, магнитный поток самоиндукции которого при токе в 1А равен 1Вб (1Гн=1Вб/А=1В·с/А).

Если L=const, то э.д.с. самоиндукции можно представить в следующем виде:

, или , (3.49)

где DI (dI) – изменение тока в цепи, содержащей катушку индуктивности (или контур) L, за время Dt (dt). Знак «–» в этом выражении означает, что э.д.с. самоиндукции препятствует изменению тока (т. е. если ток в замкнутом контуре уменьшается, то э.д.с. самоиндукции приводит к возникновению тока того же направления и наоборот).

 

Одним из проявлений электромагнитной индукции является возникновение замкнутых индукционных токов в сплошных проводящих средах: металлических телах, растворах электролитов, биологических органах и т.д. Такие токи носят название вихревых токов или токов Фуко. Эти токи возникают при перемещении проводящего тела в магнитном поле и/или при изменении со временем индукции поля, в которое помещены тела. Сила токов Фуко зависит от электрического сопротивления тел, а также от скорости изменения магнитного поля.

Токи Фуко также подчиняются правилу Ленца: их магнитное поле направлено так, чтобы противодействовать изменению магнитного потока, индуцирующему вихревые токи.

Поэтому массивные проводники тормозятся в магнитном поле. В электрических машинах, для того чтобы минимизировать влияние токов Фуко, сердечники трансформаторов и магнитные цепи электрических машин собирают из тонких пластин, изолированных друг от друга специальным лаком или окалиной.

Вихревые токи вызывают сильное нагревание проводников. Джоулево тепло, выделяемое токами Фуко, используется в индукционных металлургических печах для плавки металлов, согласно закону Джоуля-Ленца: