СУНЦ УрФУ
Расписание
Электронный журнал
Поступающим
Олимпиады, турниры, конкурсы
Планы работы
Подготовительные курсы
Новости:
22.01.2023
А в общежитии свой Новый год!
Традиционная «Зимняя сказка» прошла в общежитии.
19.01.2023
Этот старый добрый Новый год…
Группа лицеистов отметила праздник на турбазе.
29.12.2022
Успех во Всероссийском конкурсе учебных судов
Команда СУНЦ УрФУ впервые в истории Свердловской области приняла участие в финальном этапе XVI Всероссийского конкурса учебных судов.
24.12.2022
Победа в первом региональном турнире учебных судов
Команда СУНЦ УрФУ одержала победу в первом в истории Свердловской области региональном турнире XVI Всероссийского конкурса учебных судов.
23.12.2022
Долгожданная награда
Награду из рук губернатора Свердловской области получил победитель Всероссийской олимпиады по искусственному интеллекту.
23. 12.2022
12.2022
Волейбол. Итоги
Команды СУНЦ успешно выступили на первенстве Кировского района Екатеринбурга.
Больше новостей
Видеогалерея:
Новогодние поздравления (декабрь 2022)
СУНЦ.АРТ (ноябрь 2022)
«Горнозаводской Урал» (октябрь 2022)
Больше видео
О нас:
Специализированный учебно-научный центр (СУНЦ) — структурное подразделение ФГАОУ ВО «УрФУ имени первого Президента России Б.Н. Ельцина», созданное в 1990 году как нетиповое структурное подразделение вуза, осуществляющее углубленное дифференцированное обучение по программам основного общего и среднего общего образования. Всего в России 10 СУНЦев. До мая 2011 года СУНЦ работал в составе Уральского государственного университета имени А. М. Горького (УрГУ).
В настоящее время СУНЦ имеет в своем составе 8 кафедр, укомплектованных профессорско-преподавательским составом УрФУ и учителями.
Иногородние обучающиеся проживают в уютном общежитии.
Прием производится в 8, 9, 10 и 11 классы. Работают подготовительные курсы.
Подробнее о правилах приема в СУНЦ можно узнать в отделе конкурсного отбора
по телефону +7 343 367-82-22 и в разделе нашего сайта «Поступающим».
Как нас найти:
Данилы Зверева ул., 30, Екатеринбург. N56°52´4˝ E60°39´16˝
Проезд:
- автобусами № 48, 52, 81 до остановки «Фирма Авангард»;
- автобусами № 28, 58 до остановки «Данилы Зверева», далее 7 минут пешком по улице Данилы Зверева;
- троллейбусом № 18 до остановки «Данилы Зверева», далее 14 минут пешком по улицам Сулимова, Данилы Зверева;
- троллейбусами № 4 до остановки «Сулимова», № 19, 32 до остановки «Боровая», далее 15 минут пешком по улицам Боровая, Вилонова, Данилы Зверева.

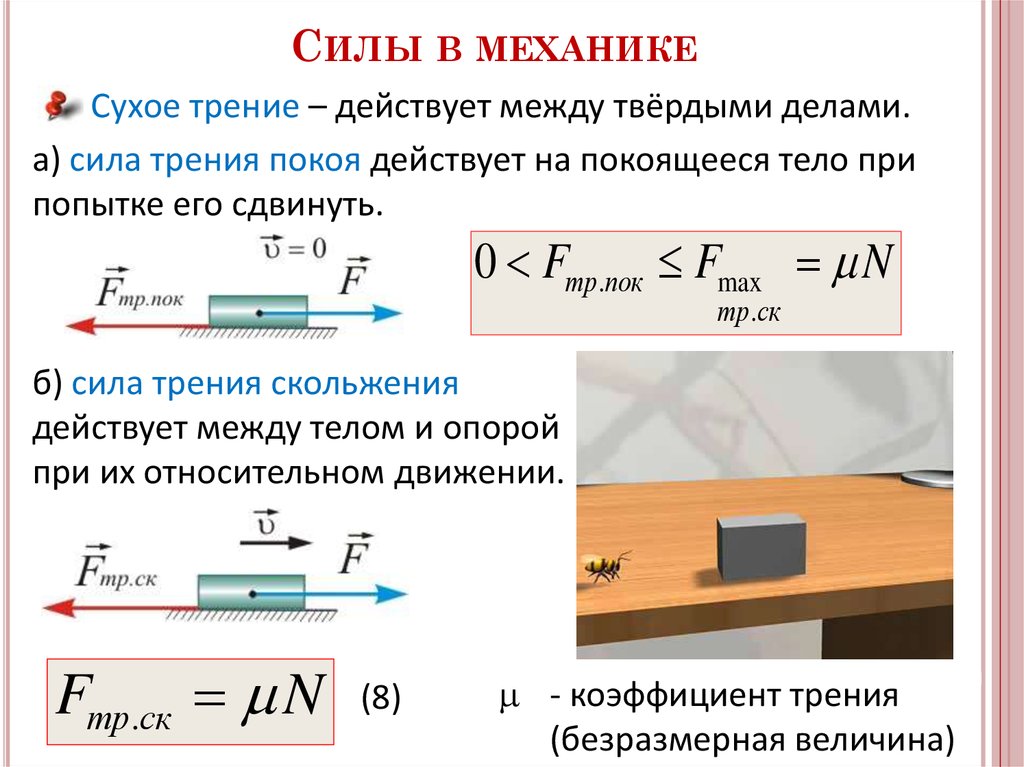
Водородные связи можно изучать с помощью силы трения • Игорь Иванов • Новости науки на «Элементах» • Физика, Химия
Между двумя твердыми поверхностями может образовываться сеть из водородных связей, которая живет по своим особым законам. Измеряя зависимость силы трения от скорости, можно изучать плавление и рекристаллизацию этой сети.
Водородная связь занимает особое место среди всех типов химических связей. Она обеспечивается атомом водорода, расположенным между двумя электроотрицательными ионами (например, атомами кислорода), которые оттягивают на себя электронное облако. Если бы на месте водорода был любой другой атом, то потеря одного электрона не сильно изменила бы его размер. В случае водорода потеря электрона оборачивается катастрофой: вместо атома остается один лишь протон — частица размером в одну стотысячную размера атома. Атом водорода словно исчезает, и поэтому два электроотрицательных атома могут сильно приблизиться друг к другу. Это делает водородные связи, с одной стороны, довольно крепкими, а с другой стороны, очень подвижными и «маневренными»: они легко образуются, легко видоизменяются и восстанавливаются.
Это делает водородные связи, с одной стороны, довольно крепкими, а с другой стороны, очень подвижными и «маневренными»: они легко образуются, легко видоизменяются и восстанавливаются.
Может показаться, что сети из водородных связей должны неизбежно изучаться тонкими методами атомной физики. Тем неожиданнее оказался вывод исследователей из Калифорнийского университета в Беркли. В своей статье J. Chen et al., Physical Review Letters, 96, 236102 (15 June 2006) они утверждают, что многие свойства водородных связей можно изучать чуть ли не в школьной лаборатории, наблюдая за самой обычной силой трения!
На этот вывод авторы работы натолкнулись почти случайно. Их заинтересовал очень простой вопрос: как зависит сила трения между двумя телами от скорости скольжения. В школьном курсе физики говорится, что трение скольжения тела не зависит ни от скорости движения, ни он площади соприкосновения, а только от прижимающей силы и коэффициента трения. На самом деле, этот закон выполняется лишь приближенно. Например, давно известно, что при движении с высокими скоростями коэффициент трения изменяется из-за нагрева поверхности соприкосновения, что приводит к зависимости силы трения от скорости. Однако при скольжении с очень малыми скоростями такие эффекты не должны быть важны.
Например, давно известно, что при движении с высокими скоростями коэффициент трения изменяется из-за нагрева поверхности соприкосновения, что приводит к зависимости силы трения от скорости. Однако при скольжении с очень малыми скоростями такие эффекты не должны быть важны.
Американцы как раз и изучали, зависит ли сила трения от скорости при очень медленном движении (при скоростях от 0,1 до 200 миллиметров в час) и малых нагрузках (эквивалентных весу в доли микрограмма). Нагревом в таких условиях можно пренебречь, и если какая-то зависимость обнаружится, то ее происхождение будет совсем иным.
Зависимость силы трения от скорости действительно наблюдалась, причем в некоторых случаях она уменьшалась, а в некоторых — увеличивалась с увеличением скорости. Пытаясь понять, из-за чего так получается, авторы взглянули на список использованных веществ и поняли простую закономерность. Если в химической формуле веществ есть свободно торчащие островки, способные к образованию водородных связей, например, –OH или –NH2, то сила трения уменьшается с ростом скорости.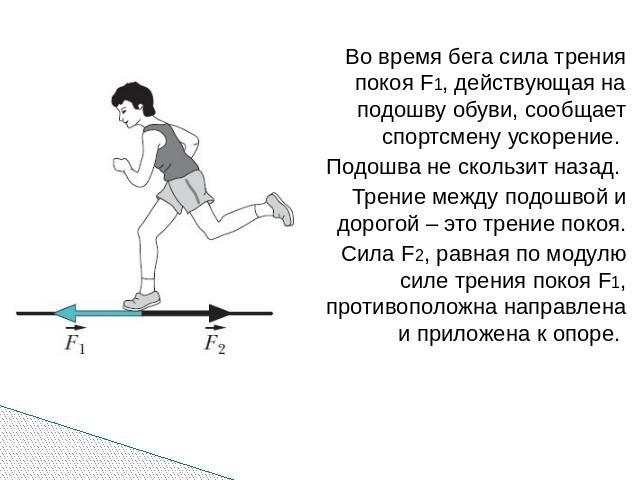 Если же торчащие наружу островки химически насыщены и не могут образовывать водородные связи, то сила трения растет с увеличением скорости.
Если же торчащие наружу островки химически насыщены и не могут образовывать водородные связи, то сила трения растет с увеличением скорости.
Для проверки этого предположения авторы взяли поверхность со свободными группами –NH2 и смазали ее капелькой соляной кислоты, которая привела к образованию химически насыщенных групп –NH3Cl. Водородные связи при скольжении тела по такой поверхности уже не могли образовываться, и зависимость силы трения от скорости послушно изменилась на противоположную.
Почему же водородные связи так влияют на силу трения? Между двумя неподвижными поверхностями образуется густая сеть из таких связей, мелкие детали которой зависят от конкретного расположения двух шероховатых поверхностей. Можно сказать, что в состоянии покоя на границе соприкосновения двух поверхностей возникает «двумерный кристалл» из водородных связей, которые дополнительно удерживают тело от проскальзывания. Если всё же произойдет сдвиг — связи разорвутся, но из-за своей высокой подвижности вскоре воссоединятся вновь. Это можно представить себе как резкое «плавление» кристалла из водородных связей, а затем его рекристаллизацию.
Это можно представить себе как резкое «плавление» кристалла из водородных связей, а затем его рекристаллизацию.
Если два тела скользят очень медленно, меньше скорости, с которой распространяется «волна рекристаллизации», то реорганизация водородных связей поспевает за смещением тела. При повышении скорости движения всё меньшее количество связей будет успевать восстанавливаться при скольжении. Сеть из водородных связей будет похожа уже не на кристалл, а скорее на двумерную жидкость, которая тем «жиже», чем больше скорость скольжения. Всё это приводит к тому, что дополнительная сила трения, возникающая из-за водородных связей, будет уменьшаться.
Полученные экспериментальные данные свидетельствуют о том, что типичная скорость «волны рекристаллизации» водородных связей — порядка нескольких миллиметров в час. Авторы считают, что еще более аккуратное измерение силы трения позволит не только уточнить это число, но и понять в деталях термодинамические свойства этого нового «сорта вещества» — сложной сетки водородных связей.
Игорь Иванов
Кинетическое трение: определение, взаимосвязь и формулы
Вы когда-нибудь задумывались, почему во время дождя дороги становятся скользкими, что затрудняет остановку автомобиля? Оказывается, это прямое следствие кинетической силы трения, так как сухой асфальт обеспечивает лучшее сцепление шины с дорогой, чем мокрый асфальт, что сокращает время остановки автомобиля.
Кинетическое трение — это сила трения, которая почти неизбежна в нашей повседневной жизни. Иногда это остановка, а иногда необходимость. Он присутствует, когда мы играем в футбол, пользуемся смартфонами, гуляем, пишем и занимаемся многими другими обычными делами. В сценариях реальной жизни, когда бы мы ни рассматривали движение, ему всегда будет сопутствовать кинетическое трение. В этой статье мы лучше поймем, что такое кинетическое трение, и применим эти знания к различным примерам задач.
Кинетическое трение Определение
Когда вы пытаетесь толкнуть коробку, вам нужно будет приложить определенное усилие.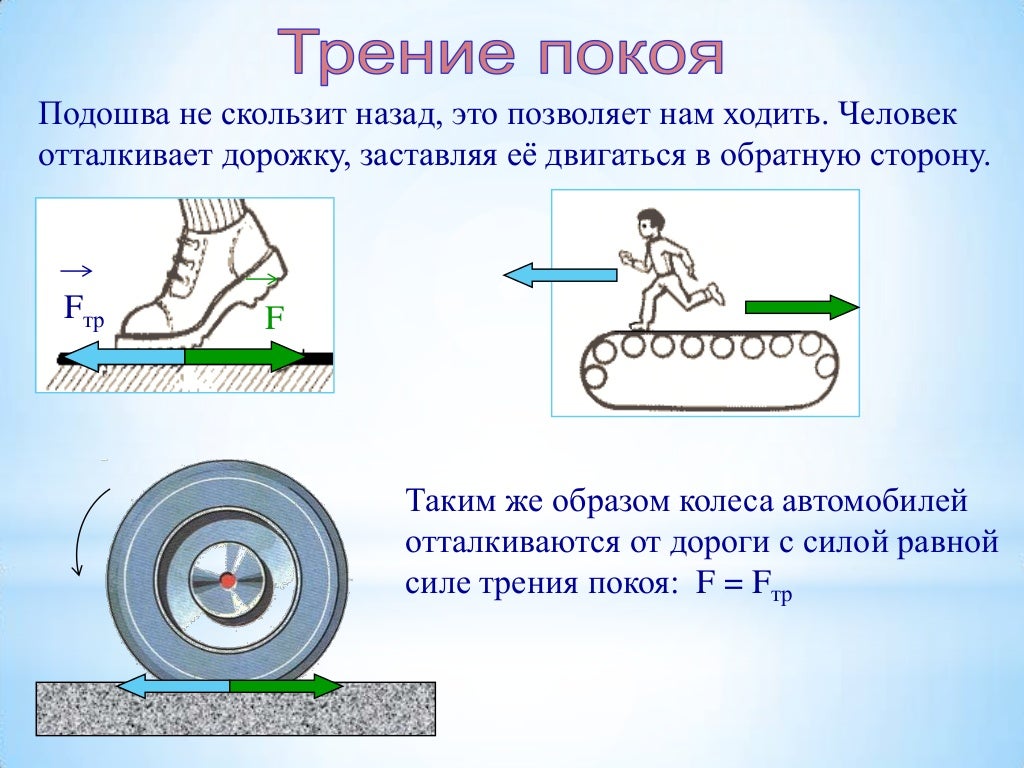 Как только коробка начинает двигаться, легче поддерживать движение. По опыту, чем легче ящик, тем легче его передвигать.
Как только коробка начинает двигаться, легче поддерживать движение. По опыту, чем легче ящик, тем легче его передвигать.
Представим себе тело, лежащее на плоской поверхности. Если одна контактная сила \(\vec{F}\) приложена к телу горизонтально, мы можем определить четыре составляющие силы, перпендикулярные и параллельные поверхности, как показано на рисунке ниже.
Рис. 1 — Если объект положить на горизонтальную поверхность и приложить к нему горизонтальную силу, то кинетическая сила трения возникнет в направлении, противоположном движению, и будет пропорциональна нормальной силе.
Нормальная сила, \(\vec{F_\mathrm{N}}\), перпендикулярна поверхности, а сила трения, \(\vec{F_\mathrm{f}}\),
равна параллельно поверхности. Сила трения направлена против движения.
Кинетическое трение — это тип силы трения, которая действует на движущиеся объекты.
Обозначается \(\vec{F_{\mathrm{f, k}}}\), а его величина пропорциональна величине нормальной силы.
Это отношение пропорциональности интуитивно понятно, как мы знаем из опыта: чем тяжелее объект, тем труднее заставить его двигаться. На микроскопическом уровне большая масса равна большему гравитационному притяжению; поэтому объект будет ближе к поверхности, увеличивая трение между ними.
Формула кинетического трения
Величина кинетической силы трения зависит от безразмерного коэффициента кинетического трения \(\mu_{\mathrm{k}}\) и нормальной силы \(\vec{F_\mathrm{N}} \) измеряется в ньютонах (\(\mathrm{N}\)). Эту связь можно показать математически
$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}.$$
Кинетический коэффициент трения
Отношение кинетической силы трения контактирующих поверхностей к нормальной силе известно как коэффициент кинетического трения . Обозначается \(\mu_{\mathrm{k}}\). Его величина зависит от того, насколько скользкой является поверхность. Поскольку это отношение двух сил, коэффициент кинетического трения безразмерен. В таблице ниже мы можем видеть приблизительные коэффициенты кинетического трения для некоторых распространенных комбинаций материалов.
В таблице ниже мы можем видеть приблизительные коэффициенты кинетического трения для некоторых распространенных комбинаций материалов.
| Материалы | Коэффициент кинетического трения, \(\mu_{\mathrm{k}}\) |
| Сталь по стали | \ (0,57 \) |
| Алюминий на стали | \ (0,47 \) |
| Медная на стали | \ (0,36 \) |
| Glassm41 \ (0,36 \) | |
| Glass. | |
| Copper on glass | \(0.53\) |
| Teflon on Teflon | \(0.04\) |
| Teflon on steel | \(0.04\) |
| Rubber on concrete (dry ) | \(0,80\) |
| Резина на бетоне (мокром) | \(0,25\) |
Теперь, когда мы знаем уравнение для расчета кинетической силы трения и познакомились с коэффициентом кинетического трения, давайте применим это знание к некоторым примерным задачам. !
!
Примеры кинетического трения
Для начала давайте рассмотрим простой случай непосредственного применения уравнения кинетического трения!
Автомобиль движется с постоянной скоростью с нормальной силой \(2000 \, \mathrm{N}\). Если кинетическое трение, приложенное к этому автомобилю, равно \(400 \, \mathrm{N}\). Тогда вычислите коэффициент кинетического трения, связанного с этим?
Решение
В примере даны величины нормальной силы и кинетической силы трения. Итак, \(\vec{F}_{\mathrm{f,k}}=400 \, \mathrm{N}\) и \(F_\mathrm{N}= 2000 \, \mathrm{N}\) . Если мы подставим эти значения в формулу кинетического трения
$$ \vec{F}_{\mathrm{f,k}}=\mu_{\mathrm{k}} \vec{F_\mathrm{N}}, $$
получаем следующее выражение
$$400 \, \mathrm{N} =\mu_{\mathrm{k}} \cdot 2000 \, \mathrm{N}, $$
которое можно преобразовать в найти коэффициент трения 9{\circ}\) к горизонтальной поверхности. Кинетическая сила трения направлена противоположно силе. {\ circ} = F _ {\ mathrm {f, k}} = \ mu _ {\ mathrm {k}} F_ \ mathrm {N}. $ $ 9{\circ}} \\ T &= \frac{0,5000 \cdot 200,0 \, \mathrm{N}}{0,87 + 0,5000 \cdot 0,5} \\ T &= 89,29 \, \mathrm{N}. \end{align}$$
{\ circ} = F _ {\ mathrm {f, k}} = \ mu _ {\ mathrm {k}} F_ \ mathrm {N}. $ $ 9{\circ}} \\ T &= \frac{0,5000 \cdot 200,0 \, \mathrm{N}}{0,87 + 0,5000 \cdot 0,5} \\ T &= 89,29 \, \mathrm{N}. \end{align}$$
Наконец, давайте рассмотрим аналогичный пример, только на этот раз ящик расположен на наклонной плоскости.
Коробка скользит вниз с постоянной скоростью с наклонной плоскости, составляющей угол \(\alpha\) с горизонтом. Поверхность имеет коэффициент кинетического трения \(\mu_{\mathrm{k}}\). Если вес коробки равен \(w\), найдите угол \(\alpha\).
Рис. 4. Коробка, скользящая по наклонной плоскости. Он движется с постоянной скоростью.
Давайте посмотрим на силы, действующие на коробку на рисунке ниже.
Рис. 5 — Все силы, действующие на коробку, скользящую по наклонной плоскости. Мы можем применить новую систему координат, чтобы написать соответствующие уравнения.
Если мы получим новые координаты (\(x\) и \(y\)), то увидим, что в направлении \(x\) действуют кинетическая сила трения и горизонтальная составляющая веса. В направлении \(y\) действуют нормальная сила и вертикальная составляющая веса. Поскольку ящик движется с постоянной скоростью, он находится в равновесии.
В направлении \(y\) действуют нормальная сила и вертикальная составляющая веса. Поскольку ящик движется с постоянной скоростью, он находится в равновесии.
- Для направления \(x\): \(w\cdot\sin\alpha=F_\mathrm{f,k} = \mu_{\mathrm{k}}F_\mathrm{N}\)
- Для \(y\)-направления: \(F_\mathrm{N}=w\cdot\cos\alpha\)
Мы можем вставить второе уравнение в первое уравнение:
$$ \begin{align} w \cdot \sin\alpha & =\mu_\mathrm{k}w \cdot \cos\alpha \\ \cancel{w}\cdot\sin\alpha & =\mu_\mathrm{k} \cancel{w} \cdot \cos\alpha \\ \mu_\mathrm{k} & = \tan\alpha \end{align}$$
Тогда угол \(\alpha\) равен
$$ \alpha = \arctan\mu_\mathrm{k}.$$
Статическое трение и кинетическое трение
В целом коэффициент трения может принимать две формы, одной из которых является кинетическое трение. Другой тип известен как статическое трение . Как мы уже установили, кинетическая сила трения является разновидностью силы трения, действующей на движущиеся объекты. Итак, в чем же разница между статическим трением и кинетическим трением?
Итак, в чем же разница между статическим трением и кинетическим трением?
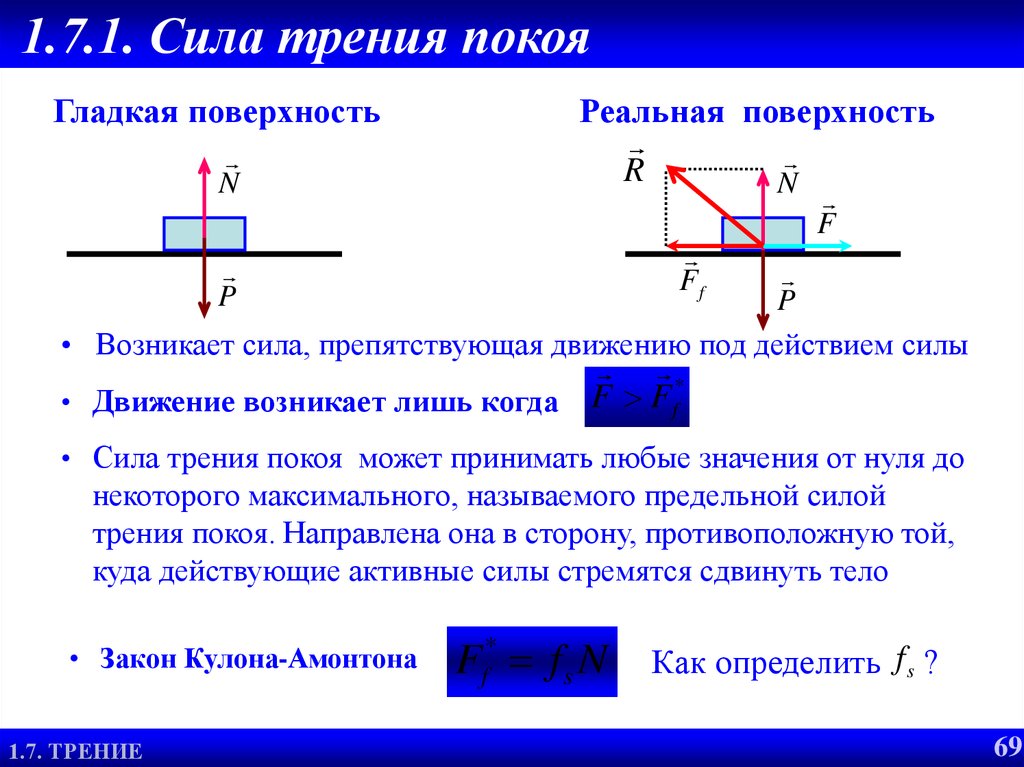
Статическое трение — это сила, обеспечивающая неподвижность объектов, покоящихся друг относительно друга.
Другими словами, кинетическое трение относится к движущимся объектам, тогда как статическое трение относится к неподвижным объектам.
Разницу между двумя типами можно запомнить прямо из словаря. В то время как статика означает отсутствие движения, кинетика означает отношение к движению или его следствие!
Математически статическое трение \(F_\mathrm{f,s}\) очень похоже на кинетическое трение,
$$ F_\mathrm{f,s} = \mu_\mathrm{s}F_\mathrm{N}$$
, где единственным отличием является использование другого коэффициента \(\mu_\mathrm{s} \), который является коэффициентом статического трения.
Давайте рассмотрим пример, когда объект испытывает оба типа трения.
Тяжелая коробка лежит на столе и остается неподвижной до тех пор, пока не будет приложена некоторая сила в горизонтальном направлении, чтобы сдвинуть ее по столу. Поскольку поверхность стола довольно неровная, изначально коробка не движется, несмотря на приложенную силу. В результате коробку толкают еще сильнее, пока, в конце концов, она не начнет двигаться по столу. Объясните различные этапы сил, действующих на коробку, и постройте график зависимости трения от приложенной силы.
Поскольку поверхность стола довольно неровная, изначально коробка не движется, несмотря на приложенную силу. В результате коробку толкают еще сильнее, пока, в конце концов, она не начнет двигаться по столу. Объясните различные этапы сил, действующих на коробку, и постройте график зависимости трения от приложенной силы.
Решение
- Сначала к ящику не приложены никакие силы, поэтому он испытывает только гравитационное притяжение вниз и нормальную силу от стола, толкающую его вверх.
- Затем к коробке горизонтально прикладывается некоторая толкающая сила \(F_\mathrm{p}\). В результате возникнет сопротивление в противоположном направлении, известное как трение \(F_\mathrm{f}\).
- Учитывая, что коробка тяжелая, а поверхность стола неровная, коробка не будет легко скользить, так как обе эти характеристики влияют на трение.
Нормальная сила и шероховатость/гладкость задействованных поверхностей являются основными факторами, влияющими на трение.
- Итак, в зависимости от величины приложенной силы коробка будет оставаться неподвижной за счет трения покоя \(F_\mathrm{f,s}\).
- С увеличением приложенной силы, в конце концов, \(F_\mathrm{p}\) и \(F_\mathrm{f,s}\) будут иметь одинаковую величину. Эта точка известна как порог движения, 9После достижения 0020 и коробка начнет двигаться.
- Как только коробка начнет двигаться, сила трения, влияющая на движение, будет равна кинетическому трению \(F_\mathrm{f,k}\). Поддерживать его движение станет легче, так как коэффициент трения у движущихся объектов обычно меньше, чем у неподвижных.
Графически все эти наблюдения можно увидеть на рисунке ниже.
Рис. 6 – График зависимости трения от приложенной силы.
Кинетическое трение — основные выводы
- Кинетическая сила трения — это тип силы трения, действующей на движущиеся объекты.
- Величина кинетической силы трения зависит от коэффициента кинетического трения и нормальной силы.

- Отношение кинетической силы трения контактирующих поверхностей к нормальной силе называется коэффициентом кинетического трения.
- Для расчета коэффициента трения используется уравнение \(\mu_{\mathrm{k}} = \frac{\vec{F}_{\mathrm{f,k}}}{\vec{F}_ \mathrm{N}}\).
- Коэффициент кинетического трения зависит от того, насколько скользкой является поверхность.
- Нормальная сила не всегда равна весу.
- Статическое трение — тип трения, применяемого к неподвижным объектам.
О влиянии скорости и нормальной силы
На этой странице
АннотацияВведениеРезультатыОбсуждениеВыводыСсылкиАвторское правоСтатьи по теме
С помощью высокоскоростного трибометра были измерены коэффициенты трения бобслеистов в широком диапазоне нагрузок и скоростей. Между 2,8 м/с и 28 м/с (соответствует 10 км/ч и 100 км/ч) измеренные коэффициенты трения показали линейное уменьшение с увеличением скорости. Эксперименты выявили сверхнизкие коэффициенты трения менее 0,01 после превышения скорости скольжения около 20 м/с. При максимальной скорости 28 м/с средний коэффициент трения составил 0,007. Эксперименты помогают преодолеть разрыв между многочисленными тестами на трение на низких скоростях, проведенными другими группами, и тестами, проведенными с бобслеем на реальных трассах. Было показано, что данные о трении, полученные другими группами, и наши измерения могут быть аппроксимированы одной основной кривой. Эта кривая демонстрирует наибольшее уменьшение трения до скорости скольжения около 3 м/с. Дальнейшее увеличение скорости вызывает лишь небольшое уменьшение трения. Кроме того, трение уменьшается с увеличением нагрузки. Снижение прекращается, когда износ льда становится эффективным. Точка нагрузки постоянного трения зависит от радиуса поперечного сечения бегунка. Чем больше радиус, тем выше нагрузка до того, как на льду появятся признаки разрушения. Оказалось, что помимо аэродинамического сопротивления (в данной работе не рассматриваемого) одним из основных ограничивающих скорость факторов является трение об лед.
Эксперименты выявили сверхнизкие коэффициенты трения менее 0,01 после превышения скорости скольжения около 20 м/с. При максимальной скорости 28 м/с средний коэффициент трения составил 0,007. Эксперименты помогают преодолеть разрыв между многочисленными тестами на трение на низких скоростях, проведенными другими группами, и тестами, проведенными с бобслеем на реальных трассах. Было показано, что данные о трении, полученные другими группами, и наши измерения могут быть аппроксимированы одной основной кривой. Эта кривая демонстрирует наибольшее уменьшение трения до скорости скольжения около 3 м/с. Дальнейшее увеличение скорости вызывает лишь небольшое уменьшение трения. Кроме того, трение уменьшается с увеличением нагрузки. Снижение прекращается, когда износ льда становится эффективным. Точка нагрузки постоянного трения зависит от радиуса поперечного сечения бегунка. Чем больше радиус, тем выше нагрузка до того, как на льду появятся признаки разрушения. Оказалось, что помимо аэродинамического сопротивления (в данной работе не рассматриваемого) одним из основных ограничивающих скорость факторов является трение об лед. С точки зрения геометрии полоза, плоский контакт полозья со льдом обеспечивает минимальное трение. Радиус коромысла рабочего колеса имеет большее значение для низкого коэффициента трения, чем радиус поперечного сечения.
С точки зрения геометрии полоза, плоский контакт полозья со льдом обеспечивает минимальное трение. Радиус коромысла рабочего колеса имеет большее значение для низкого коэффициента трения, чем радиус поперечного сечения.
1. Введение
Точное знание коэффициента трения представляет большой интерес для проектировщиков бобслейных трасс, организаторов и техников. Чем быстрее сани могут двигаться на ходу, тем увлекательнее гонка. Но трасса не должна быть слишком быстрой: экипаж еще должен иметь возможность безопасно добраться до дна. Поэтому инженеры должны рассчитать и точно смоделировать, с какой скоростью сани могут двигаться на определенных участках трассы. Расчеты в основном основаны на коэффициенте трения между полозьями и льдом. Вторым важным фактором, влияющим на скорость, является аэродинамическое сопротивление, которое здесь не исследовалось.
Как правило, количество проведенных в прошлом экспериментов по измерению трения в системе сталь-лед ограничено [1, 2]. Большинство данных получено с помощью трибометров (например, [3, 4]) или специальных приборов (например, [1, 5]). В следующем разделе будут рассмотрены результаты, наиболее близкие к системе бегун/лед. Мы концентрируемся на диапазоне температур от -2°C до -12°C.
Большинство данных получено с помощью трибометров (например, [3, 4]) или специальных приборов (например, [1, 5]). В следующем разделе будут рассмотрены результаты, наиболее близкие к системе бегун/лед. Мы концентрируемся на диапазоне температур от -2°C до -12°C.
Эванс и др. определяли коэффициенты низкого трения при скольжении стали по ледяному цилиндру со скоростью скольжения = 1–15 м/с при температуре –11,5°C. колебался от 0,01 до 0,03 [6]. Аналогичные коэффициенты трения около 0,02 были получены при испытаниях возвратно-поступательного трибометра в квазистатических условиях ( = 1,5 × 10 −7 м/с до 7,4 × 10 −3 м/с) при достаточно высоком давлении 270 МПа и температуре льда −10°C [7]. Сани массой 60 кг были сконструированы Итагаки и др. и двигался по льду со скоростью 1,5 м/с. Длина бегунов составляла около 30 см, поэтому можно предположить, что действующее давление было менее 10 МПа. Для гладкого бегунка при = -5°С получен коэффициент трения 0,01 [8]. Основываясь на экспериментах с ледяным трибометром при скорости = 1 м/с и = −2 °C, Хайнцльмайер опубликовал коэффициенты трения порядка 0,05, демонстрирующие умеренное снижение в зависимости от давления (0,5–6,5 МПа) [9].]. Думм провел трибометрические испытания со скоростью 2 м/с и температурой льда -2°C с использованием прямоугольных стальных ползунков (4 мм × 8 мм) и получил коэффициенты трения от 0,01 до 0,02. Диапазон давлений составлял от 1 до 8 МПа [3]. Миллс также провел эксперименты с трибометром и измерил коэффициенты трения от 0,04 до 0,06 для диапазона давлений от 0,1 МПа до 1 МПа при = 2 см/с и = -2°C [4]. Трение уменьшилось до 0,02 при увеличении скорости скольжения до 3,4 м/с. В эксперименте со стальным кольцом, прижатым ко льду, измеряли кручение для определения коэффициента трения. При давлении 0,2 МПа, = 0–3 м/с и = –10°С были получены аналогичные результаты ( = 0,02–0,04) по Тусиме [10].
Основываясь на экспериментах с ледяным трибометром при скорости = 1 м/с и = −2 °C, Хайнцльмайер опубликовал коэффициенты трения порядка 0,05, демонстрирующие умеренное снижение в зависимости от давления (0,5–6,5 МПа) [9].]. Думм провел трибометрические испытания со скоростью 2 м/с и температурой льда -2°C с использованием прямоугольных стальных ползунков (4 мм × 8 мм) и получил коэффициенты трения от 0,01 до 0,02. Диапазон давлений составлял от 1 до 8 МПа [3]. Миллс также провел эксперименты с трибометром и измерил коэффициенты трения от 0,04 до 0,06 для диапазона давлений от 0,1 МПа до 1 МПа при = 2 см/с и = -2°C [4]. Трение уменьшилось до 0,02 при увеличении скорости скольжения до 3,4 м/с. В эксперименте со стальным кольцом, прижатым ко льду, измеряли кручение для определения коэффициента трения. При давлении 0,2 МПа, = 0–3 м/с и = –10°С были получены аналогичные результаты ( = 0,02–0,04) по Тусиме [10].
Данные по сверхнизким коэффициентам трения были опубликованы Нивеном, который измерил трение между ползуном и кольцевым льдом при скорости 0,9 м/с и нашел = 0,002 при = -2°C [11].
Де Конинг и др. анализировали коньки [12]. Средние коэффициенты трения для прямых и кривых составили 0,0046 и 0,0059 соответственно. Аналогичные результаты были получены Федерольфом с сотрудниками [13]. Трение между лезвием хоккея с шайбой и льдом ( = -5,7 ° C и -4,9 ° C, = 1,8 м / с) было в диапазоне 0,0071. Действующее давление не оказывалось. Недавно Пуарье опубликовал данные о трении для бобслея, полученные на основе точного измерения скорости с помощью радара [14]. Усредняя данные для высоких и низких скоростей, мы получили средний коэффициент трения 0,0053. Дополнительные данные можно найти в обзоре Itagaki et al. [1].
Очевидно, что измеренные значения варьируются в широком диапазоне. До сих пор основной проблемой была сложность измерения трения в более широком диапазоне высоких скоростей и реальных нагрузок. Таким образом, собранные данные отражают лишь небольшую часть граничных условий и иногда кажутся довольно далекими от реальности. Поэтому мы представляем новое устройство для высокоскоростных испытаний на трение при реальных нагрузках. Это измерительное устройство позволяет нам установить точный уровень трения между санями и льдом для бобслейных полозьев с различными радиусами поперечного сечения.
Это измерительное устройство позволяет нам установить точный уровень трения между санями и льдом для бобслейных полозьев с различными радиусами поперечного сечения.
2. Эксперименты
2.1. Испытательная камера и подготовка льда
Все испытания проводились на стенде для испытаний шин. Основной частью стенда является большой барабан диаметром 3,8 метра, открытый с одной стороны, расположенный в охлаждаемой камере, см. рис. 1. Внутри барабана находится слой льда, по которому скользят полозья модели. . Гидравлический цилиндр прижимает полозья ко льду, имитируя вес саней и экипажа. При каждом вращении барабана лед выдвигается из-под бегунка, немного смещая его и прикрепленный к нему датчик силы трения. Таким образом, вместо того, чтобы оставаться в самой нижней точке, бегунок немного увлекается вращающимся барабаном. Насколько далеко, зависит от силы трения между бегуном и льдом. Максимальная скорость испытательного стенда составляет 150 км/ч. В нашем исследовании мы ограничили диапазон скоростей до 100 км/ч, чтобы снизить уровень шума и обнаружить ожидаемые сверхнизкие коэффициенты трения.
Охлаждение испытательной камеры и барабана было начато за два дня до проведения измерений. Воздух в камере постоянно циркулировал, а температура поддерживалась постоянной на уровне -5°С. За день до измерения производство льда начинали с подачи дистиллированной воды во вращающийся барабан. Барабан вращался со скоростью 10 км/ч и двигал воду до тех пор, пока не образовывалась постоянная тонкая пленка льда. Добыча льда прекращалась при толщине льда около 3 см. В день испытаний поверхность льда была сглажена в два этапа. Сначала шероховатости убрали стальным лезвием. Затем производилась окончательная полировка гладкой низкопрофильной шиной. Во время этого процесса шина вращалась с постоянной скоростью, а также вращался барабан.
С помощью гидростата к полозью прикладывалась нормальная сила. Нормальный диапазон силы между 100 Н и 500 Н был выбран для имитации бобслея для 2-х мужчин (мужчины и женщины), а также для 4-х мужчин. Например, при выбранной длине полозья модели приложенная нормальная сила около 200 Н соответствовала нагрузке четырехместного бобслейного саня.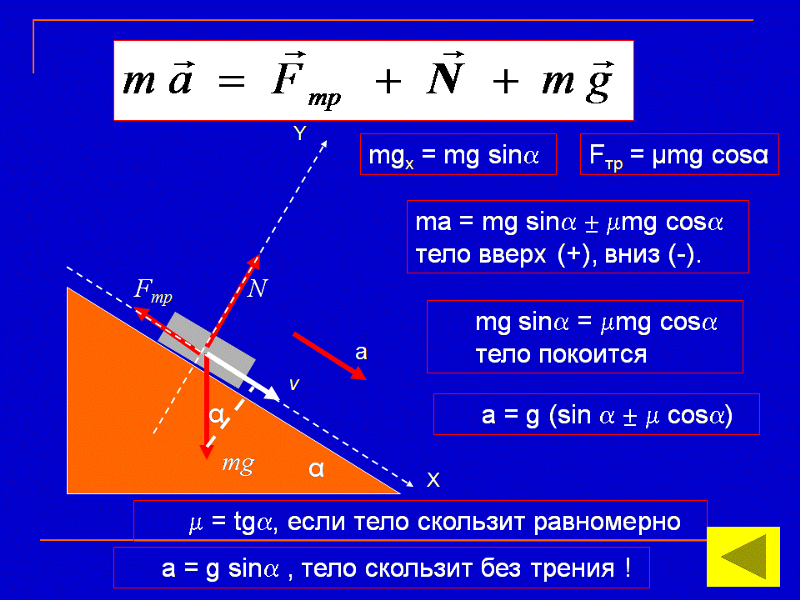 Для моделирования кривых был выбран диапазон силы от 200 Н до 500 Н. Таким образом, с используемой геометрией образца модельного рабочего колеса был перекрыт диапазон давлений от 20 МПа до 64 МПа.
Для моделирования кривых был выбран диапазон силы от 200 Н до 500 Н. Таким образом, с используемой геометрией образца модельного рабочего колеса был перекрыт диапазон давлений от 20 МПа до 64 МПа.
2.2. Подготовка беговых дорожек
Бобовые беговые дорожки изготовлены из ткани F.I.B.T. сталь 1.4057. На рис. 2 представлен чертеж поперечного сечения и фотография бегунка после отделки поверхности. Радиус поперечного сечения бегунка был выбран 4 мм и 8 мм. Для обеспечения плоского контакта с барабаном каждое рабочее колесо было снабжено качающимся радиусом 3,8 м. Все бегуны имели длину 15 см. Оба конца были закруглены, чтобы бегун не поцарапал лед. Таким образом, длина в плоском контакте со льдом составила 10 см.
Полозья изготовлены в соответствии с F.I.B.T. правила в соответствии с процедурой, используемой на соревнованиях. Бегуны были сначала отполированы наждачной бумагой с уменьшающейся зернистостью, а затем обработаны алмазной суспензией. Ни машины, ни специальные шлифовальные жидкости не применялись.
В результате поверхность бегунка показала низкую шероховатость, как показано на рис. 3. Средняя шероховатость составила 9 нм, а шероховатость от пика до впадины – 118 нм.
2.3. Сбор данных
Все данные о силе были измерены с помощью трехосевого датчика (K3D120, ME Messsysteme GmbH, Германия) с максимальной нагрузкой 1000 Н. Датчик очень компактен, имеет поперечные размеры 120 мм × 120 мм и высоту 30 мм. мм. Датчик поставляется со встроенной электроникой, позволяющей отдельно оценивать силы в поперечном ( и ), а также в вертикальном направлении (). Перекрестные помехи от до и при 500 N составляют менее 1%. Перед измерением трения датчик был откалиброван с использованием установленных собственных грузов. Затем датчик был подключен к ПК с помощью USB. Во время всех испытаний как нормальные (), так и тангенциальные силы () регистрировались с частотой дискретизации 1000 Гц. Для устранения шума данные были отфильтрованы и усреднены. Чтобы проверить повторяемость измерений, выбранные точки напряжения, то есть пара скорости и нормальной силы, были протестированы несколько раз для получения планок погрешностей. На диаграммах планки погрешностей всегда были меньше размера символа.
На диаграммах планки погрешностей всегда были меньше размера символа.
Для того, чтобы начать измерения, был приведен в движение барабан и установлена скорость. Затем датчик в сборе медленно опускали до тех пор, пока датчик не показал требуемое нормальное усилие.
3. Результаты
3.1. Трение как функция скорости
Зависимость скорости регистрировалась между 2,8 м/с и 28 м/с (т.е. 10 км/ч и 100 км/ч) с шагом 2,8 м/с при постоянной нагрузке 500 Н, см. рис. 4. Для обоих бегунов было выбрано новое положение на льду и измерено линейное снижение коэффициента трения в зависимости от скорости. При скорости 2,8 м/с трение показывало значения от 0,015 до 0,016. На самой высокой скорости трение колебалось от 0,005 до 0,008. Прямая линия показывает экстраполяцию на более высокие скорости, как будет показано ниже. Принимая во внимание планки погрешностей, обе кривые показывают одинаковое поведение.
3.2. Трение как функция нагрузки
При постоянной скорости 14 м/с ( ≈ 50 км/ч) полозья подвергались 5 различным нагрузкам от 100 Н до 500 Н, см. рисунок 5. Для каждой нормальной силы новая Трек на льду был выбран. Между 100 Н и 300 Н коэффициенты трения значительно уменьшались, но оставались примерно постоянными при более высоких нагрузках. Для нагрузок выше 200 Н коэффициенты трения 4 мм бегунка считались постоянными. Для бегунка диаметром 8 мм постоянное трение появилось при 400 Н. При более высоких нагрузках коэффициенты трения сходятся и показывают значение около 0,011.
рисунок 5. Для каждой нормальной силы новая Трек на льду был выбран. Между 100 Н и 300 Н коэффициенты трения значительно уменьшались, но оставались примерно постоянными при более высоких нагрузках. Для нагрузок выше 200 Н коэффициенты трения 4 мм бегунка считались постоянными. Для бегунка диаметром 8 мм постоянное трение появилось при 400 Н. При более высоких нагрузках коэффициенты трения сходятся и показывают значение около 0,011.
Нормальные силы, указанные стрелками, соответствуют нагрузкам боба 2 (женщины) в 340 кг или боба 4 (630 кг). Это означает, что нормальная сила в лабораторном эксперименте около 130 Н используется для имитации 340 кг, а лабораторная сила 205 Н соответствует 630 кг.
3.3. Разрушение льда
В зависимости от нормальной силы после испытаний на льду были обнаружены следы износа. Из-за неровностей поверхности были обнаружены прерывистые следы износа при небольших нормальных усилиях, см. рис. 6(b). Когда нормальная сила увеличивалась, появлялись сплошные следы износа.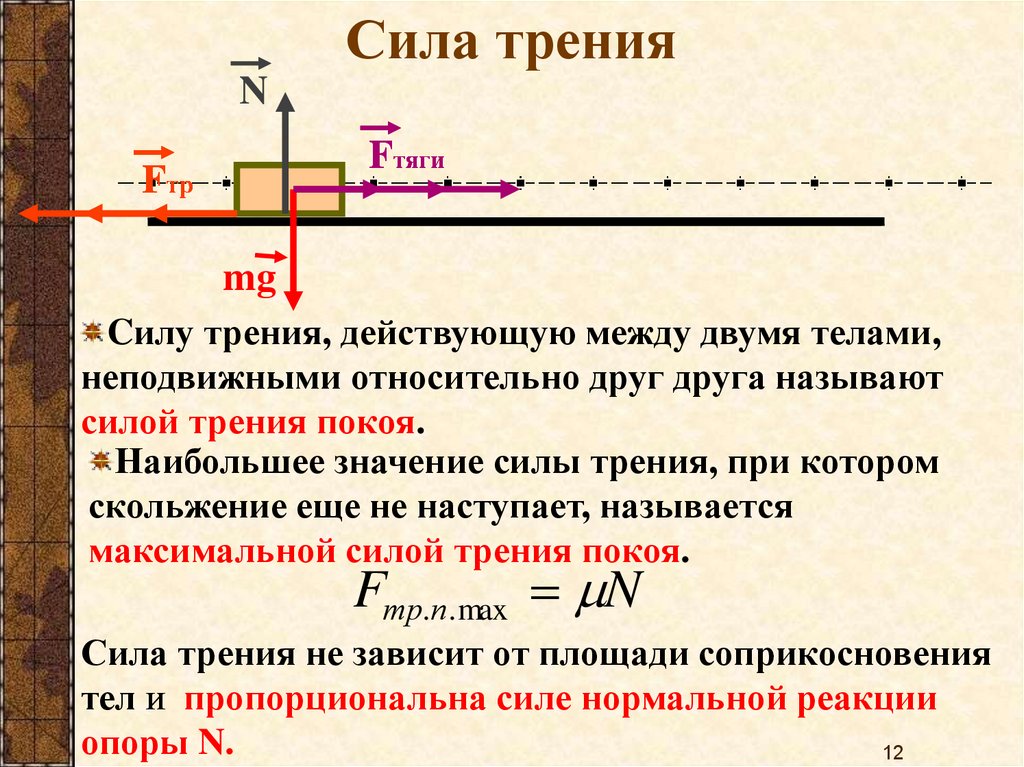 Самая высокая нагрузка в 500 Н привела к самой широкой дорожке износа. Кроме того, были обнаружены обломки льда по бокам бегунка.
Самая высокая нагрузка в 500 Н привела к самой широкой дорожке износа. Кроме того, были обнаружены обломки льда по бокам бегунка.
4. Обсуждение
4.1. Поведение скорости
В экспериментах, анализирующих трение как функцию скорости, самые низкие коэффициенты трения показали среднее значение 0,007 при самой высокой скорости. С ростом скорости увеличивался разброс данных из-за увеличения механического шума. Когда линейная подгонка экстраполируется на скорость 33 м/с (120 км/ч), коэффициент трения уменьшается до значения 0,005. Это значение очень хорошо соответствует измерениям Пуарье [14].
В разделе 1 было показано, что результаты большинства других групп указывают на более высокие коэффициенты трения, чем показано в этой статье. На рисунке 7 показана сводка литературных данных в сочетании с результатами этой работы. Мы используем коэффициенты трения, приведенные в разделе 1, и данные, предоставленные Itagaki et al. [8].
Наши собственные данные представляют собой среднее значение коэффициентов трения, полученных для радиусов поперечного сечения 4 мм и 8 мм. Зарубежные данные в основном получены в результате испытаний в диапазоне давлений от 1 МПа до 10 МПа и температур льда от −2°C до −12°C. Один эксперимент был проведен при 270 МПа. За исключением результатов Нивена [11], все коэффициенты трения могут быть аппроксимированы мастер-кривой. С помощью этой диаграммы можно сделать вывод, что — пока разрушение льда мало — скорость скольжения имеет решающее значение для величины коэффициента трения. Более того, на рисунке 7 показано, что существуют два различных режима трения. До скорости около 3 м/с наблюдается наиболее сильное уменьшение трения. Для более высоких скоростей коэффициент трения уменьшается при постоянном, но значительно меньшем наклоне. Можно предположить, что способность генерировать больше свободной воды с увеличением силы трения достигает предела при более высоких скоростях скольжения. Однако доказательство этого выходит за рамки данной статьи и зарезервировано для будущей работы.
Зарубежные данные в основном получены в результате испытаний в диапазоне давлений от 1 МПа до 10 МПа и температур льда от −2°C до −12°C. Один эксперимент был проведен при 270 МПа. За исключением результатов Нивена [11], все коэффициенты трения могут быть аппроксимированы мастер-кривой. С помощью этой диаграммы можно сделать вывод, что — пока разрушение льда мало — скорость скольжения имеет решающее значение для величины коэффициента трения. Более того, на рисунке 7 показано, что существуют два различных режима трения. До скорости около 3 м/с наблюдается наиболее сильное уменьшение трения. Для более высоких скоростей коэффициент трения уменьшается при постоянном, но значительно меньшем наклоне. Можно предположить, что способность генерировать больше свободной воды с увеличением силы трения достигает предела при более высоких скоростях скольжения. Однако доказательство этого выходит за рамки данной статьи и зарезервировано для будущей работы.
4.2. Поведение при нагрузке
Действующая нагрузка прижимает полоза к льду.
 Влияние напряжения разрушения при сжатии на трение можно увидеть на рис. 5. При определенной нормальной силе, то есть >
Влияние напряжения разрушения при сжатии на трение можно увидеть на рис. 5. При определенной нормальной силе, то есть >
Разрушающее напряжение при сжатии 40 МПа было достигнуто при 200 Н для 4 мм рабочего колеса и для 8 мм рабочего колеса при 400 Н. Это хорошо согласуется с выводами, показанными на рисунке 5. Для более высоких нормальных усилий рисунок 8 теряет смысл, так как следствием являются трещины льда и структурные дефекты льда [20]. Из-за треснувшего льда дорожка износа становится шире, а значит, увеличивается и реальная площадь контакта.
Увеличение нормальной силы, а также увеличение скорости уменьшает силу трения за счет снижения напряжения сдвига из-за образования тонкой пленки воды [21]
Однако с увеличением площади контакта оба влияния уравновешиваются, и трение становится постоянным для нормальных сил выше 200 Н (4 мм бегунок) и выше 400 Н (8 мм бегун). Подробный анализ использования микротрибометра будет предметом будущих исследований.
В то время как коэффициент трения в точке нагрузки четырехместного боба находится на постоянном участке кривой трения на рисунке 5, коэффициент трения в диапазоне нагрузки двухместного боба значительно меняется с нагрузкой.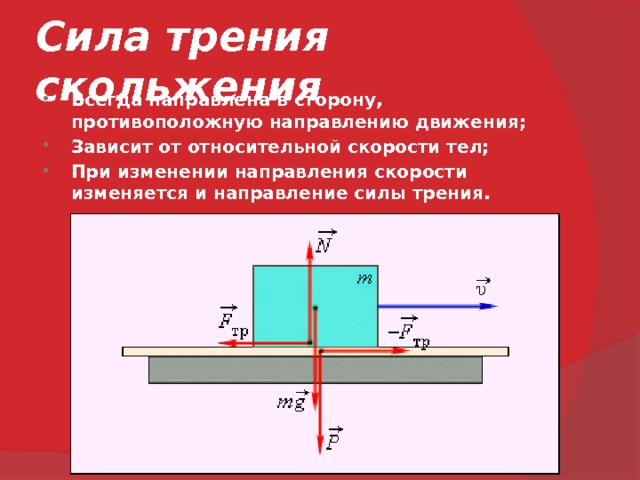
5. Выводы
С помощью высокоскоростного трибометра определены коэффициенты трения при контакте бобслея со льдом. Результаты можно заключить следующим образом. (i) Сверхнизкие коэффициенты трения могут быть получены, когда скорость скольжения выше 3 м / с. При скорости м/с коэффициенты трения становятся меньше 0,01. (ii) Величина трения зависит от контактного давления. При давлениях выше 40 МПа разрушение льда препятствует дальнейшему уменьшению трения. Несмотря на трещины на льду, трение чрезвычайно низкое. (iii) Контактное давление может быть увеличено за счет дополнительных грузов. Эта мера более эффективна для двойных бобов, поскольку кривая трения уменьшается с увеличением нагрузки. Трение начинает становиться постоянным при нагрузке четырехместного боба. (iv) Поскольку действующее давление, особенно на поворотах, почти всегда выше, чем сжимающее разрушающее напряжение льда, радиус коромысла полозья следует тщательно адаптировать.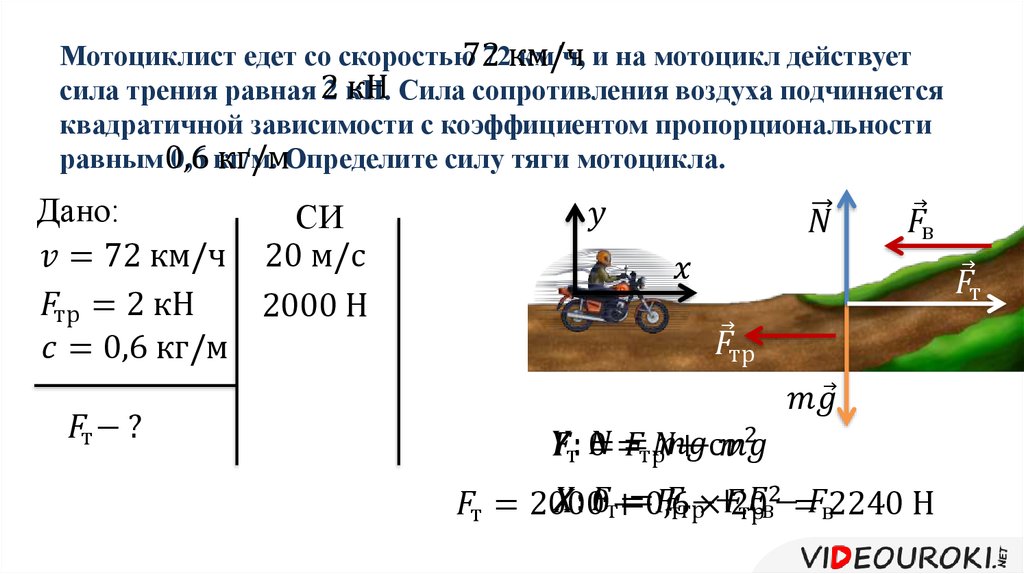 к радиусам кривой дорожки, чтобы реализовать отрегулированный контакт. Точечные контакты следует исключить. (v) Измерения и расчеты показали, что радиус коромысла имеет большее значение для низкого трения, чем радиус поперечного сечения. Этот вывод подтверждается тем фактом, что в данном исследовании моделировался плоский контакт. Радиус коромысла равнялся внутреннему радиусу барабана. Высокие нагрузки вызывают разрушение льда. Уменьшение радиуса коромысла привело бы к точечным контактам с повышенным давлением. Таким образом, трение льда начнется при более низких нормальных силах.
к радиусам кривой дорожки, чтобы реализовать отрегулированный контакт. Точечные контакты следует исключить. (v) Измерения и расчеты показали, что радиус коромысла имеет большее значение для низкого трения, чем радиус поперечного сечения. Этот вывод подтверждается тем фактом, что в данном исследовании моделировался плоский контакт. Радиус коромысла равнялся внутреннему радиусу барабана. Высокие нагрузки вызывают разрушение льда. Уменьшение радиуса коромысла привело бы к точечным контактам с повышенным давлением. Таким образом, трение льда начнется при более низких нормальных силах.
Ссылки
Итагаки К., Хубер Н.П., Лемье Г.Е., Динамическое трение металлического полозка по льду , CRREL Report, 1989.
К. Фонг, С. Моу и П. Монтгомери, «Трение на коньках со льдом: обзор и численная модель — FAST 1.0», в Physics and Chemistry of Ice , F. Wilhelms and WA Kuhs, Eds., pp. 495–504, 2007.
Посмотреть по адресу:
Google Scholar
M.
 Dumm, C. Hainzlmaier, S. Boerboom, and E. Wintermantel, «Влияние давления на трение стали и льда и применение для бобслеистов», в The Engineering of Sport 6 , vol. 3, стр. 103–106, 2006.
Dumm, C. Hainzlmaier, S. Boerboom, and E. Wintermantel, «Влияние давления на трение стали и льда и применение для бобслеистов», в The Engineering of Sport 6 , vol. 3, стр. 103–106, 2006.Посмотреть по адресу:
Google Scholar
А. Миллс, «Коэффициент трения, особенно льда», Physics Education , vol. 43, нет. 4, стр. 392–395, 2008 г.
Посмотреть по адресу:
Сайт издателя | Академия Google
Т. Кобаяши, «Исследования свойств льда на конькобежных катках», Ashrae Journal , vol. 15, нет. 1, pp. 51–56, 1973.
Посмотреть по адресу:
Google Scholar
Д. С. Б. Эванс, Дж. Ф. Най и К. Дж. Чизман, «Кинетическое трение льда», Труды Лондонского королевского общества , том. 347, нет. 1651, pp.
 493–512, 1976.
493–512, 1976.Посмотреть по адресу:
Google Scholar
К. Тусима, «Тренение стального шарика по монокристаллу льда», Журнал гиациологии , том. 19, нет. 81, pp. 225–235, 1977.
Посмотреть по адресу:
Google Scholar
К. Итагаки, Г. Э. Лемье и Н. П. Хубер, «Предварительное исследование трения между льдом и полозьями саней», Journal De Physique , том. 48, нет. 1, pp. 297–301, 1987.
Посмотреть по адресу:
Google Scholar
C. Hainzlmaier, Новый трибологически оптимизированный бобслей [Диссертация] , TU2 M0ünchen.0003
Л. Франссон, А. Патил и Х. Андрен, «Экспериментальное исследование коэффициента трения лабораторного льда», в Трудах 21-й Международной конференции по портовой и морской инженерии в арктических условиях , Монреаль, Канада, 2011.

Просмотр по адресу:
Google Scholar
К. Д. Нивен, «О трении нагретых полозьев саней по льду при высокой нагрузке», Canadian Journal of Technology , vol. 34, стр. 227–231, 1956.
Просмотр по адресу:
Google Scholar
Дж. Дж. Де Конинг, Г. Де Гроот и Г. Дж. В. И. Шенау, «Трение на льду во время конькобежного спорта», Journal of Biomechanics , vol. 25, нет. 6, стр. 565–571, 1992.
Посмотреть по адресу:
Сайт издателя | Google Scholar
П. А. Федерольф, Р. Миллс и Б. Нигг, «Ледяное трение расширяющихся лезвий хоккейных коньков», Journal of Sports Sciences , vol. 26, нет. 11, стр. 1201–1208, 2008.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Л.
 Пуарье, Трение на льду в бобслее [Ph.D. диссертация] , Университет Калгари, 2011.
Пуарье, Трение на льду в бобслее [Ph.D. диссертация] , Университет Калгари, 2011.Е. М. Шульсон, «Хрупкое разрушение льда», Engineering Fracture Mechanics , vol. 68, нет. 17–18, стр. 1839–1887, 2001.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Шазли М., Пракаш В., Лерх Б.А. Поведение льда при высокой скорости деформации при одноосном сжатии // 9.0345 Международный журнал твердых тел и конструкций , том. 46, нет. 6, стр. 1499–1515, 2009.
Посмотреть по адресу:
Сайт издателя | Google Scholar
К. С. Карни, Д. Дж. Бенсон, П. Дюбуа и Р. Ли, «Феноменологическая модель высокой скорости деформации с разрушением льда», International Journal of Solids and Structures , vol. 43, нет. 25–26, стр. 7820–7839, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
H.
 Hertz, «Über die Berührung fester elastischer Körper», Journal Für Die Reine Und Angewandte Mathematik , vol. 92, стр. 156–171, 1881.
Hertz, «Über die Berührung fester elastischer Körper», Journal Für Die Reine Und Angewandte Mathematik , vol. 92, стр. 156–171, 1881.Посмотреть по адресу:
Google Scholar
Дж. Дж. Петрович, «Механические свойства льда и снега», Journal of Materials Science , vol. 38, нет. 1, стр. 1–6, 2003 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Е. М. Шульсон, «Хрупкое разрушение льда при сжатии», Acta Metallurgica Et Materialia , vol. 38, нет. 10, стр. 1963–1976, 1990.
Посмотреть по адресу:
Google Scholar
Ф. П. Боуден и Т. П. Хьюз, «Механика скольжения по льду и снегу», Proceedings of the Royal Society London A , vol. 172, стр. 280–298, 1939.
Посмотреть по адресу:
Google Scholar
Copyright
Copyright © 2013 Matthias Scherge et al.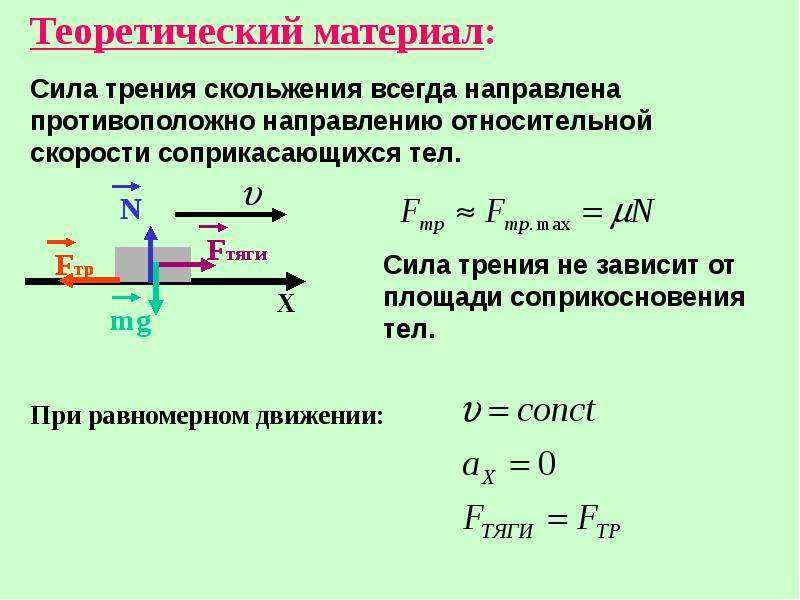




 Dumm, C. Hainzlmaier, S. Boerboom, and E. Wintermantel, «Влияние давления на трение стали и льда и применение для бобслеистов», в The Engineering of Sport 6 , vol. 3, стр. 103–106, 2006.
Dumm, C. Hainzlmaier, S. Boerboom, and E. Wintermantel, «Влияние давления на трение стали и льда и применение для бобслеистов», в The Engineering of Sport 6 , vol. 3, стр. 103–106, 2006. 493–512, 1976.
493–512, 1976.
 Пуарье, Трение на льду в бобслее [Ph.D. диссертация] , Университет Калгари, 2011.
Пуарье, Трение на льду в бобслее [Ph.D. диссертация] , Университет Калгари, 2011. Hertz, «Über die Berührung fester elastischer Körper», Journal Für Die Reine Und Angewandte Mathematik , vol. 92, стр. 156–171, 1881.
Hertz, «Über die Berührung fester elastischer Körper», Journal Für Die Reine Und Angewandte Mathematik , vol. 92, стр. 156–171, 1881.