Формула силы тока в физике
Содержание:
Определение и формула силы тока
Определение
Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
$$I=\frac{d q}{d t}$ (1)$где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).
Некоторые виды силы тока
Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:
$$I=\frac{q}{t}(2)$$Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.
Если переменный ток можно представить как синусоидальный:
$$I=I_{m} \sin \omega t$$то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$где $\varphi_{1}$ —
$\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка,
$\varepsilon$ — ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи. {6}=(30-6)=24$ (Кл)
{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
Слишком сложно?
Формула силы тока не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине) рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении удобно искать в виде:
$dq = UdC (2. {2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Формула силы тока в физике
Содержание:
Определение и формула силы тока
Определение
Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).
Некоторые виды силы тока
Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:
$$I=\frac{q}{t}(2)$$Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.
Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока.
Эффективной величиной силы переменного тока (I
Если переменный ток можно представить как синусоидальный:
$$I=I_{m} \sin \omega t$$то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).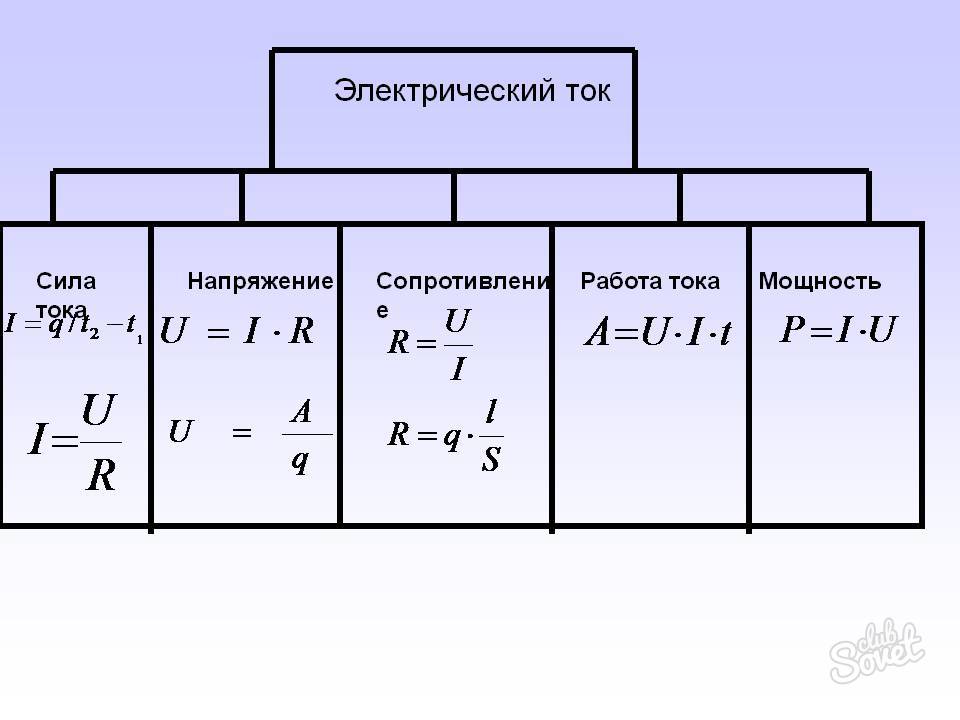
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
$$I=\int_{S} j d S(6)$$где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$где $\varphi_{1}$ —
$\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка,
$\varepsilon$ — ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи. {6}=(30-6)=24$ (Кл)
{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
Слишком сложно?
Формула силы тока не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине) рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении удобно искать в виде:
$dq = UdC (2. {2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Формула силы тока в физике
Содержание:
Определение и формула силы тока
Определение
Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
$$I=\frac{d q}{d t}$ (1)$где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).
Некоторые виды силы тока
Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:
$$I=\frac{q}{t}(2)$$Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.
Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока. Эффективной величиной силы переменного тока (Ieff) называют такую силу постоянного тока, которая выполнит работу равную работе переменного тока в течение одного периода (T):
$$I_{e f f}=\sqrt{\frac{1}{T} \int_{0}^{T} I^{2} d t}(3)$$Если переменный ток можно представить как синусоидальный:
$$I=I_{m} \sin \omega t$$то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
$$I=\int_{S} j d S(6)$$где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$где $\varphi_{1}$ —
$\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка,
$\varepsilon$ — ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи.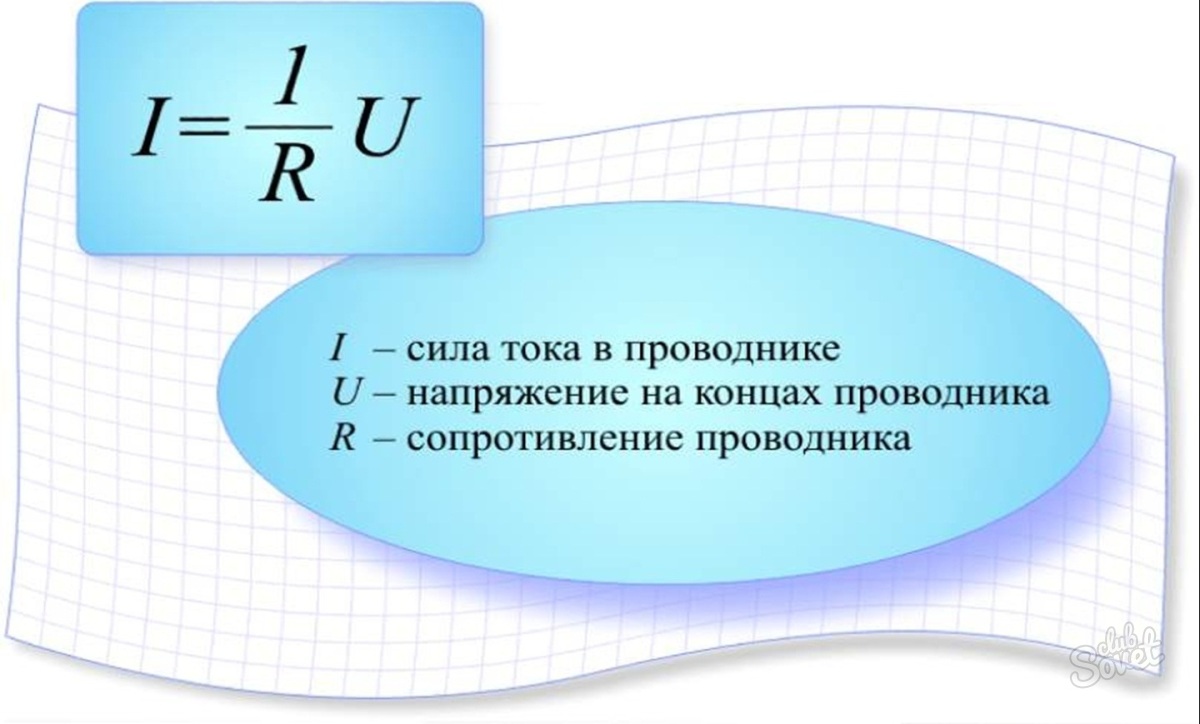 {6}=(30-6)=24$ (Кл)
{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
Слишком сложно?
Формула силы тока не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине) рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении удобно искать в виде:
$dq = UdC (2. {2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Сила тока. Амперметр — урок. Физика, 8 класс.
В процессе своего движения вдоль проводника заряженные частицы (в металлах это электроны) переносят некоторый заряд. Чем больше заряженных частиц, чем быстрее они движутся, тем больший заряд будет ими перенесён за одно и то же время. Электрический заряд, проходящий через поперечное сечение проводника за 1 секунду, определяет силу тока в цепи.
Электрический заряд, проходящий через поперечное сечение проводника за 1 секунду, определяет силу тока в цепи.Сила тока \(I\) — скалярная величина, равная отношению заряда \(q\), прошедшего через поперечное сечение проводника, к промежутку времени \(t\), в течение которого шёл ток.
I=qt, где \(I\) — сила тока, \(q\) — заряд, \(t\) — время.
Единица измерения силы тока в системе СИ — \([I]~=~1~A\) (ампер).
В 1948 г. было предложено в основу определения единицы силы тока положить явление взаимодействия двух проводников с током:
при прохождении тока по двум параллельным проводникам в одном направлении проводники притягиваются, а при прохождении тока по этим же проводникам в противоположных направлениях — отталкиваются.
За единицу силы тока \(1~A\) принимают силу тока, при которой два параллельных проводника длиной \(1\) м, расположенные на расстоянии \(1\) м друг от друга в вакууме, взаимодействуют с силой \(0,0000002\)\(H\).
Андре-Мари Ампер (1775 — 1836) |
А.-М. Ампер ввёл термины: электростатика, электродинамика, соленоид, ЭДС, напряжение, гальванометр, электрический ток.
Ампер — довольно большая сила тока. Например, в электрической сети квартиры через включённую \(100\) Вт лампочку накаливания проходит ток с силой, приблизительно равной \(0,5A\). Ток в электрическом обогревателе может достигать \(10A\), а для работы карманного микрокалькулятора достаточно \(0,001A\).
Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например, миллиампер (мА) и микроампер (мкА):
\(1 мA = 0,001 A\), \(1 мкA = 0,000001 A\), \(1 кA =1000 A\).
То есть \(1 A = 1000 мA\), \(1 A = 1000000 мкA\), \(1 A = 0,001 кA\).
Если электроны перемещаются в одном направлении, т. е. — от одного полюса источника тока к другому, то такой ток называют постоянным.
е. — от одного полюса источника тока к другому, то такой ток называют постоянным.
Переменным называется ток, сила и направление которого периодически изменяются.
В бытовых электросетях используют переменный ток напряжением \(220\) В и частотой \(50\) Гц. Это означает, что ток за \(1\) секунду \(50\) раз движется в одном направлении и \(50\) раз — в другом. У многих приборов имеется блок питания, который преобразует переменный ток в постоянный (у телевизора, компьютера и т.д.).
Силу тока измеряют амперметром. В электрической цепи он обозначается так:
Амперметр включают в цепь последовательно с тем прибором, силу тока в котором нужно измерить.
Обрати внимание!
Амперметр нельзя подсоединять к источнику тока, если в цепь не подключён потребитель!
Измеряемая сила тока не должна превышать максимально допустимую силу тока для измерения амперметром. Поэтому существуют различные амперметры.
Микроамперметр | Миллиамперметр |
Амперметр | Килоамперметр |
Различают амперметры для измерения силы постоянного тока и силы переменного тока.
Обозначения диапазона измерения амперметров:
- «\(~\)» означает, что амперметр предназначен для измерения силы переменного тока;
- «\(—\)» означает, что амперметр предназначен для измерения силы постоянного тока.
Можно обратить внимание на клеммы прибора. Если указана полярность («\(+\)» и «\(-\)»), то это прибор для измерения постоянного тока.
Иногда используют буквы \(AC/DC\). В переводе с английского \(AC\) (alternating current) — переменный ток, а \(DC\) (direct current) — постоянный ток.
Для измерения силы постоянного тока | Для измерения силы переменного тока |
Для измерения силы тока можно использовать и мультиметр. Перед измерением необходимо прочитать инструкцию, чтобы правильно подключить прибор.
Включая амперметр в цепь постоянного тока, необходимо соблюдать полярность (см.схему):
провод, который идёт от положительного полюса источника тока, нужно соединять с клеммой амперметра со знаком «\(+\)»;
провод, который идёт от отрицательного полюса источника тока, нужно соединять с клеммой амперметра со знаком «\(-\)».
В цепь переменного тока включается амперметр для измерения переменного тока. Он полярности не имеет.
Амперметр подключается последовательно к тому прибору, на котором измеряется сила тока.
Значение силы тока до прохождения через лампу равно значению силы тока после прохождения через лампу, значит по всей длине электрической цепи сила тока постоянна (при последовательном соединении).
Обрати внимание!
Безопасным для организма человека можно считать переменный ток силой не выше \(0,05~A\), ток силой более \(0,05\)-\(0,1~A\) опасен и может вызвать смертельный исход.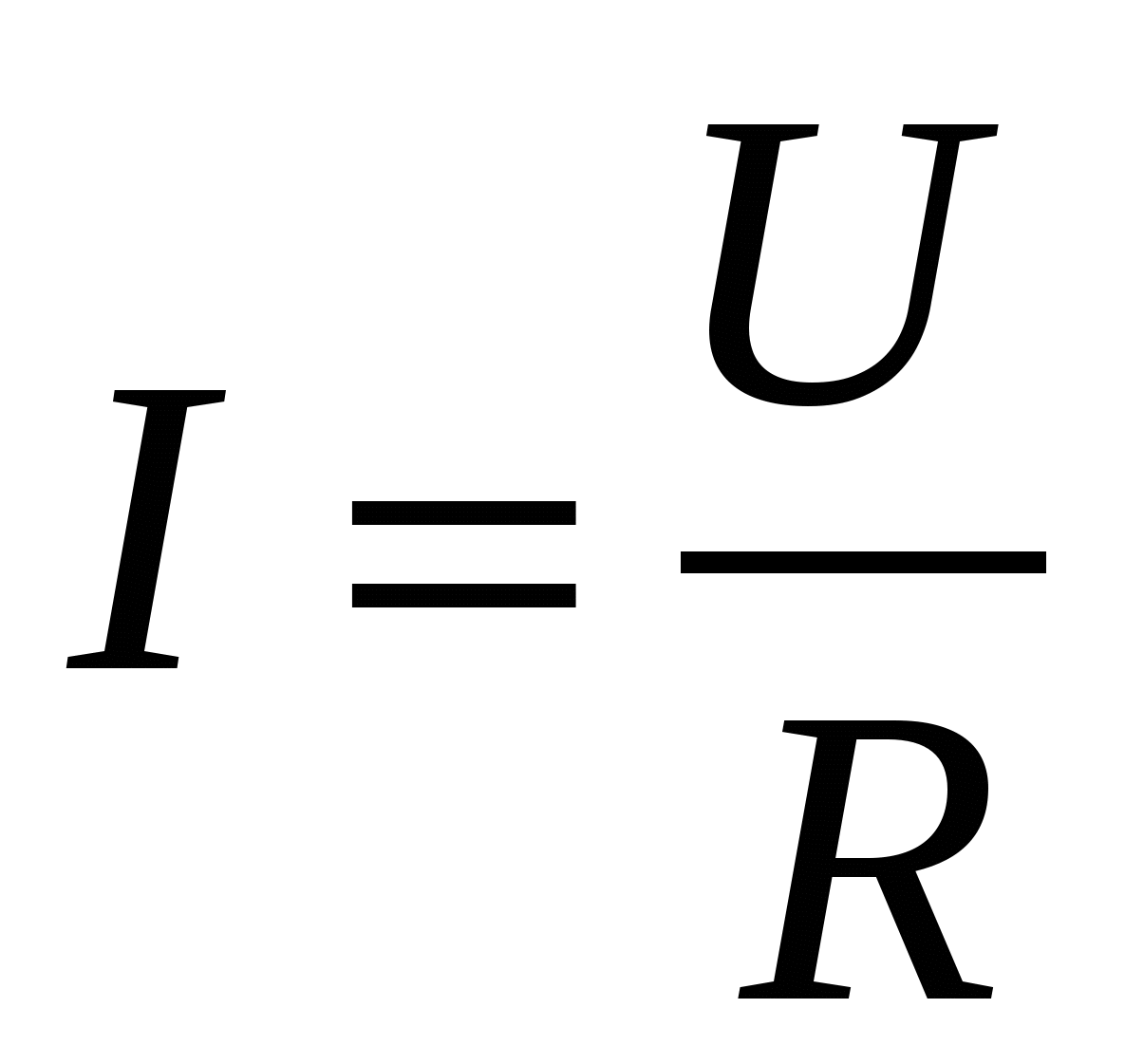
Источники:
http://class-fizika.narod.ru/8_28.htm
http://school.xvatit.com/index.php?title=%D0%A1%D0%B8%D0%BB%D0%B0_%D1%82%D0%BE%D0%BA%D0%B0
http://physics.kgsu.ru/index.php?option=com_content&view=article&id=217&Itemid=72
http://kamenskih3.narod.ru/untitled74.htm
формулы расчета мощности в проводнике
Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.
Электрический ток в проводнике
В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.
От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Зависимость силы тока от электрического заряда
Входящие в формулу величины:
- I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
- Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах. Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
- Время в секундах.
Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:
I = (qnv)cosαS.
Также используется интегрирование по площади поверхности и сечению проводника.
Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.
Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:
Сила тока участка цепи и цепи с источником тока
Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.
В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.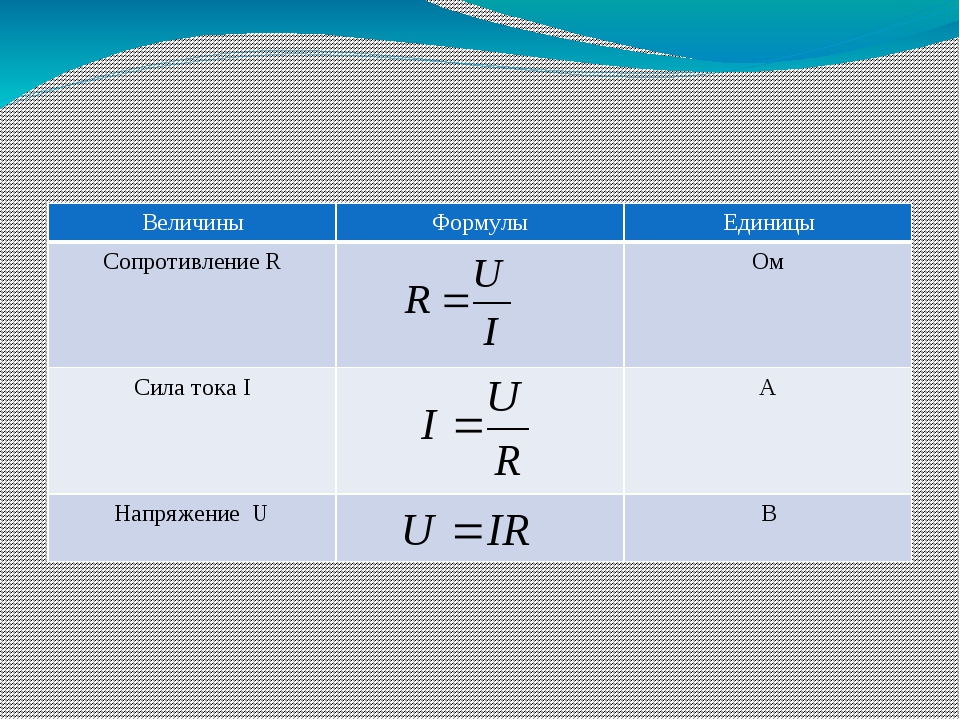
При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.
Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:
RC = 1/ FC.
Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.
Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:
Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.
Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
I = I1 + I2 + I3
Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.
Видео
Оцените статью:Сила тока | Самое простое объяснение, формула, единица измерения
Сила тока с точки зрения гидравлики
Думаю, вы не раз слышали такое словосочетание, как “сила тока“. А для чего нужна сила? Ну как для чего? Чтобы совершать полезную или бесполезную работу. Главное, чтобы что-то делать. Каждый из нас обладает какой-либо силой. У кого-то сила такая, что он может одним ударом разбить кирпич в пух и в прах, а другой не сможет поднять даже соломинку. Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Так вот, дорогие мои читатели, электрический ток тоже обладает силой.
Представьте себе шланг, с помощью которого вы поливаете свой огород
Давайте теперь проведем аналогию. Пусть шланг – это провод, а вода в нем – электрический ток. Мы чуть-чуть приоткрыли краник и вода сразу же побежала по шлангу. Медленно, но все-таки побежала. Сила струи очень слабая.
А давайте теперь откроем краник на полную катушку. В результате струя хлынет с такой силой, что можно даже полить соседский огород.
В обоих случаях диаметр шланга одинаков.
А теперь представьте, что вы наполняете ведро. Напором воды из какого шланга вы его быстрее наполните? Разумеется из зеленого, где напор воды очень сильный. Но почему так происходит? Все дело в том, что объем воды за равный промежуток времени из желтого и зеленого шланга выйдет тоже разный. Или иными словами, из зеленого шланга количество молекул воды выбежит намного больше, чем из желтого за равный период времени.
Разберем еще один интересный пример. Давайте допустим, что у нас есть большая труба, и к ней заварены две другие, но одна в два раза меньше диаметром, чем другая.
Из какой трубы объем воды будет выходить больше за секунду времени? Разумеется с той, которая толще в диаметре, потому что площадь поперечного сечения S2 большой трубы больше, чем площадь поперечного сечения S1 малой трубы. Следовательно, сила потока через большую трубу будет больше, чем через малую, так как объем воды, который протекает через поперечное сечение трубы S2, будет в два раза больше, чем через тонкую трубу.
Что такое сила тока?
Итак, теперь давайте все что мы тут пописали про водичку применим к электронике. Провод – это шланг. Тонкий провод – это тонкий в диаметре шланг, толстый провод – это толстый в диаметре шланг, можно сказать – труба. Молекулы воды – это электроны. Следовательно, толстый провод при одинаковом напряжении можно протащить больше электронов, чем тонкий.
Сила тока – это количество электронов, прошедших через площадь поперечного сечения проводника за какое-либо определенное время.
Все это выглядит примерно вот так. Здесь я нарисовал круглый проводок, “разрезал” его и получил ту самую площадь поперечного сечения. Именно через нее и бегут электроны.
За период времени берут 1 секунду.
Формула силы тока
Формула для чайников будет выглядеть вот так:
где
I – собственно сила тока, Амперы
N – количество электронов
t – период времени, за которое эти электроны пробегут через поперечное сечение проводника, секунды
Более правильная (официальная) формула выглядит вот так:
где
Δq – это заряд за какой-то определенный промежуток времени, Кулон
Δt – тот самый промежуток времени, секунды
I – сила тока, Амперы
В чем прикол этих двух формул? Дело все в том, что электрон обладает зарядом приблизительно 1,6 · 10-19 Кулон.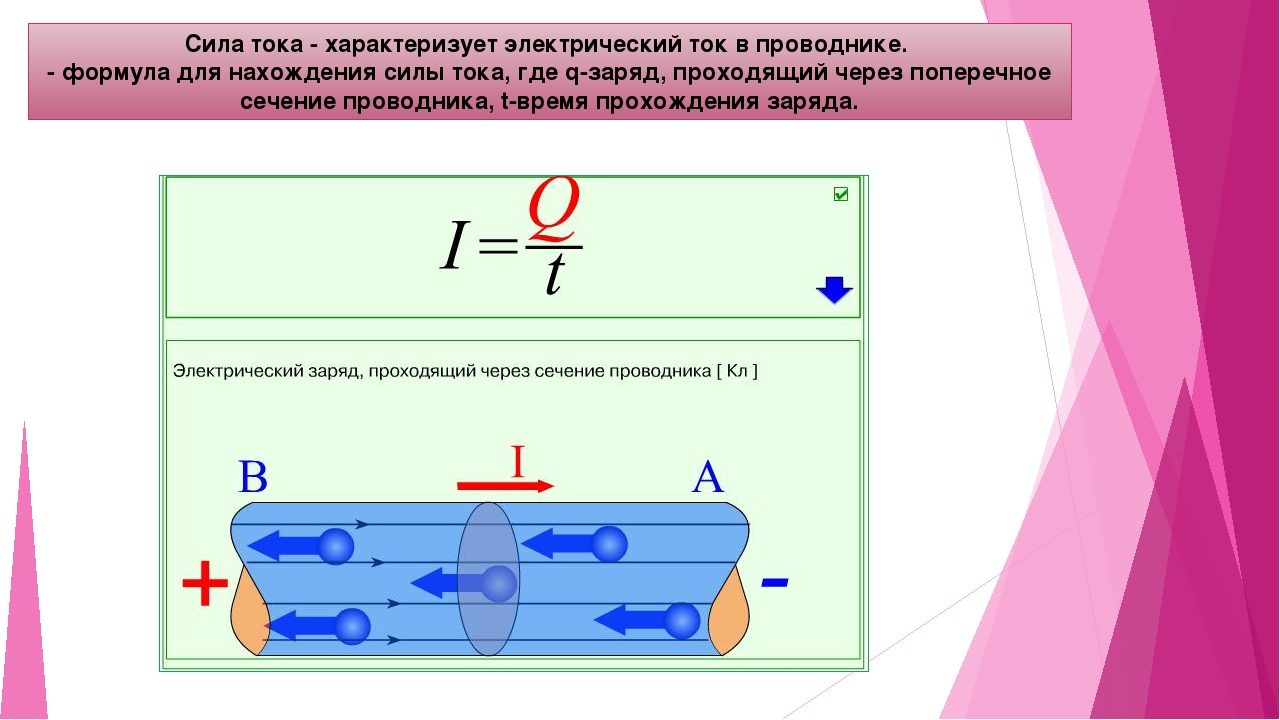 Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅10
Поэтому, чтобы сила тока была в проводе (проводнике) была 1 Ампер, нам надо, чтобы через поперечное сечение прошел заряд в 1 Кулон = 6,24151⋅10
Итак, теперь можно официально сказать, что если через поперечное сечение проводника за 1 секунду пролетят 6,24151⋅1018 электронов, то сила тока в таком проводнике будет равна 1 Ампер! Все! Ничего не надо больше придумывать! Так и скажите своему преподавателю по физике).
Если преподу не понравится ваш ответ, то скажите типа что-то этого:
Сила тока – это физическая величина, равная отношению количества заряда прошедшего через поверхность (читаем как через площадь поперечного сечения) за какое-то время
Сила тока и сопротивление
Давайте еще раз глянем на шланг с водой и зададим себе вопросы.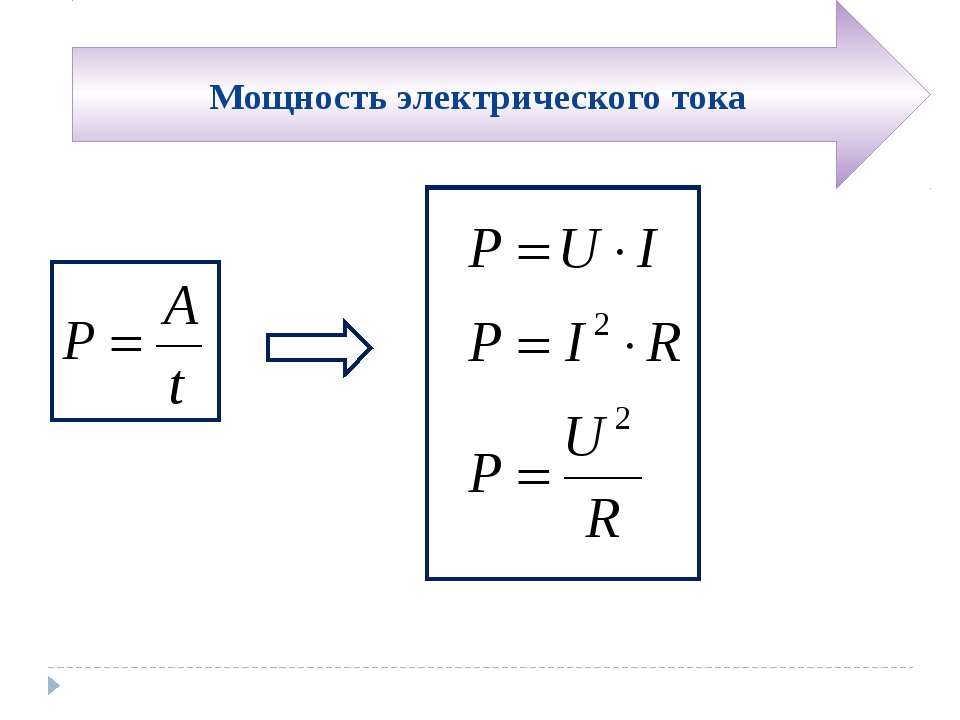 От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
От чего зависит поток воды? Первое, что приходит в голову – это давление. Почему молекулы воды движутся в рисунке ниже слева-направо? Потому, что давление слева, больше чем справа. Чем больше давление, тем быстрее побежит водичка по шлангу – это элементарно.
Теперь такой вопрос: как можно увеличить количество электронов через площадь поперечного сечения?
Первое, что приходит на ум – это увеличить давление. В этом случае скорость потока воды увеличится, но ее много не увеличишь, так как шланг порвется как грелка в пасти Тузика.
Второе – это поставить шланг бОльшим диаметром. В этом случае у нас количество молекул воды через поперечное сечение будет проходить больше, чем в тонком шланге:
Все те же самые умозаключения можно применить и к обыкновенному проводу. Чем он больше в диаметре, тем больше он сможет “протащить” через себя силу тока. Чем меньше в диаметре, то желательно меньше его нагружать, иначе его “порвет”, то есть он тупо сгорит. Именно этот принцип заложен в плавких предохранителях.
Как только сила тока через тонкий проводок предохранителя превысит силу тока, на которую рассчитан предохранитель, то плавкий проводок перегорает и размыкает цепь. Через перегоревший предохранитель ток уже течь не может, так как проводок в предохранителе в обрыве.
сгоревший плавкий предохранительПоэтому, силовые кабели, через которые “бегут” сотни и тысячи ампер, берут большого диаметра и стараются делать из меди, так как ее удельное сопротивление очень мало.
Сила тока в проводнике
Да и вообще, сопротивление проводника рассчитывается по формуле:
формула сопротивления проводникаТаблица с удельным сопротивлением из разных материалов выглядит вот так.
Для того, чтобы найти силу тока в проводнике, мы должны воспользоваться законом Ома для участка цепи. Выглядит он вот так:
Задача
У нас есть медный провод длиной в 1 метр и его площадь поперечного сечения составляет 1 мм2 . Какая сила тока будет течь в этом проводнике (проводе), если на его концы подать напряжение в 1 Вольт?
задача на силу тока в проводникеРешение:
Как измерить силу тока?
Для того, чтобы измерить значение силы тока, мы должны использовать специальные приборы – амперметры. В настоящее время силу тока можно измерить с помощью цифрового мультиметра, который может измерять и силу тока, и напряжение и сопротивление и еще много чего. Для того, чтобы измерить силу тока, мы должны вставить наш прибор в разрыв цепи вот таким образом.
Более подробно как это сделать, можете прочитать в этой статье.
Также советую посмотреть обучающее видео, где очень умный преподаватель объясняет простым языком, что такое “сила тока”.
Сила тока | Физика
Времена, когда ток обнаруживался с помощью личных ощущений ученых, пропускавших его через себя, давно миновали. Теперь для этого применяют специальные приборы, называемые амперметрами.
Амперметр — это прибор, служащий для измерения силы тока. Что понимают под силой тока?
Обратимся к рисунку 21, б. На нем выделено поперечное сечение проводника, через которое проходят заряженные частицы при наличии в проводнике электрического тока. В металлическом проводнике этими частицами являются свободные электроны. В процессе своего движения вдоль проводника электроны переносят некоторый заряд. Чем больше электронов и чем быстрее они движутся, тем больший заряд будет ими перенесен за одно и то же время.
Силой тока называется физическая величина, показывающая, какой заряд проходит через поперечное сечение проводника за 1 с.
Пусть, например, за время t = 2 с через поперечное сечение проводника носители тока переносят заряд q = 4 Кл. Заряд, переносимый ими за 1 с, будет в 2 раза меньше. Разделив 4 Кл на 2 с, получим 2 Кл/с. Это и есть сила тока. Обозначается она буквой I:
I — сила тока.
Итак, чтобы найти силу тока I, надо электрический заряд q, прошедший через поперечное сечение проводника за время t, разделить на это время:
I = q/t (10.1)
Единица силы тока называется ампером (А) в честь французского ученого А. М. Ампера (1775—1836). В основу определения этой единицы положено магнитное действие тока, и мы на нем останавливаться не будем.
Если сила тока I известна, то можно найти заряд q, проходящий через сечение проводника за время t. Для этого надо силу тока умножить на время:
q = It. (10. 2)
2)
Полученное выражение позволяет определить единицу электрического заряда — кулон (Кл):
1 Кл = 1 А · 1 с = 1 А·с.
1 Кл — это заряд, который проходит за 1 с через поперечное сечение проводника при силе тока 1 А.
Помимо ампера на практике часто применяются и другие (кратные и дольные) единицы силы тока, например миллиампер (мА) и микроампер (мкА):
1 мА = 0,001 А, 1 мкА = 0,000001 А.
Как уже говорилось, измеряют силу тока с помощью амперметров (а также милли- и микроамперметров). Демонстрационный гальванометр, о котором упоминалось выше, представляет собой обычный микроамперметр.
Существуют разные конструкции амперметров. Амперметр, предназначенный для демонстрационных опытов в школе, изображен на рисунке 28. На этом же рисунке приведено его условное обозначение (кружок с латинской буквой «А» внутри).
При включении в цепь амперметр, как и всякий другой измерительный прибор, не должен оказывать заметного влияния на измеряемую величину. Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется.
Поэтому амперметр устроен так, что при его включении сила тока в цепи почти не изменяется.
В зависимости от назначения в технике используют амперметры с разной ценой деления. По шкале амперметра видно, на какую наибольшую силу тока он рассчитан. Включать его в цепь с большей силой тока нельзя, так как прибор может испортиться.
Для включения амперметра в цепь ее размыкают и свободные концы проводов присоединяют к клеммам (зажимам) прибора. При этом необходимо соблюдать следующие правила:
1) амперметр включают последовательно с тем элементом цепи, в котором измеряют силу тока;
2) клемму амперметра со знаком «+» следует соединять с тем проводом, который идет от положительного полюса источника тока, а клемму со знаком «–» — с тем проводом, который идет от отрицательного полюса источника тока.
При включении амперметра в цепь не имеет значения, с какой стороны (слева или справа) от исследуемого элемента его подключать. В этом можно убедиться на опыте (рис. 29). Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение.
Как видим, при измерении силы тока, проходящего через лампу, оба амперметра (и тот, что слева, и тот, что справа) показывают одно и то же значение.
??? 1. Что такое сила тока? Какой буквой она обозначается? 2. По какой формуле находится сила тока? 3. Как называется единица силы тока? Как она обозначается? 4. Как называется прибор для измерения силы тока? Как он обозначается на схемах? 5. Какими правилами следует руководствоваться при включении амперметра в цепь? 6. По какой формуле находится электрический заряд, проходящий через поперечное сечение проводника, если известны сила тока и время его прохождения?
электрического тока | Формула и определение
Электрический ток , любое движение носителей электрического заряда, таких как субатомные заряженные частицы (например, электроны с отрицательным зарядом, протоны с положительным зарядом), ионы (атомы, потерявшие или получившие один или несколько электронов), или дырки (недостаток электронов, который можно рассматривать как положительные частицы).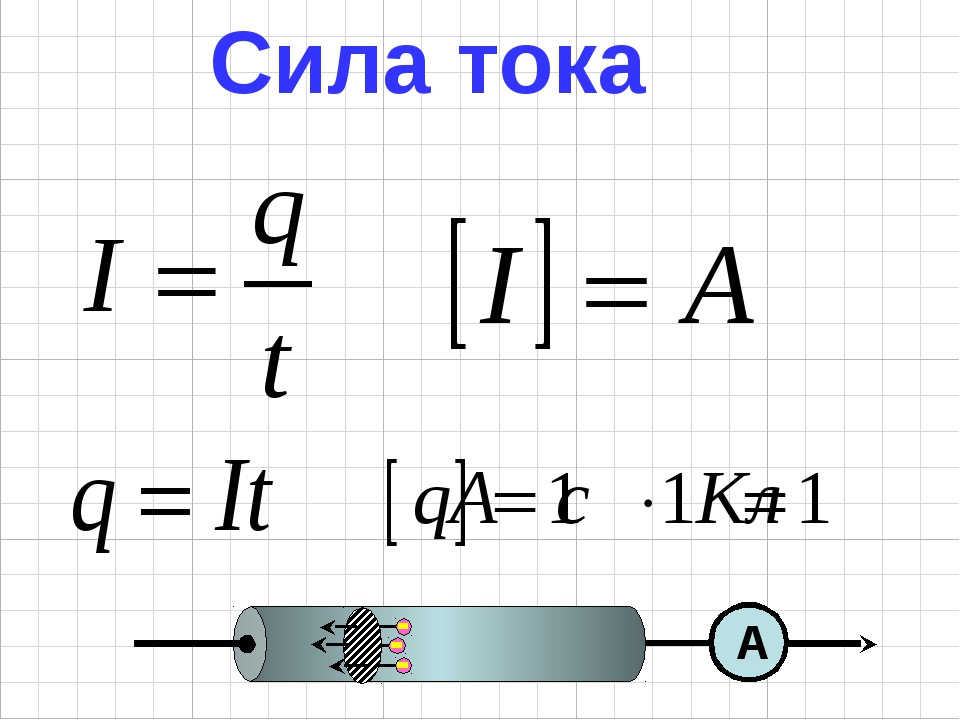
Британская викторина
27 правильных или ложных вопросов из самых сложных викторин «Британника»
Что вы знаете о Марсе? Как насчет энергии? Думаете, будет проще, если вам придется выбирать только истину или ложь? Узнайте, что вы знаете о науке, с помощью этой сложной викторины.
Электрический ток в проводе, носителями заряда которого являются электроны, является мерой количества заряда, проходящего через любую точку провода за единицу времени. В переменном токе движение электрических зарядов периодически меняется на противоположное; в постоянном токе это не так. Во многих контекстах направление тока в электрических цепях принимается за направление потока положительного заряда, направление, противоположное фактическому дрейфу электронов. При таком определении ток называется обычным током.
Узнайте, почему низкое сопротивление меди делает ее отличным проводником электрических токов.
Взаимосвязь между током и сопротивлением в электрической цепи.
Encyclopædia Britannica, Inc. Посмотреть все видео по этой статьеТок обычно обозначается символом I . Закон Ома связывает ток, протекающий по проводнику, с напряжением В и сопротивлением R ; то есть В = I R .Альтернативная формулировка закона Ома: I = V / R .
Ток в газах и жидкостях обычно состоит из потока положительных ионов в одном направлении вместе с потоком отрицательных ионов в противоположном направлении. Чтобы рассматривать общий эффект тока, его направление обычно принимается за направление положительного носителя заряда. Ток отрицательного заряда, движущийся в противоположном направлении, эквивалентен положительному заряду той же величины, движущемуся в обычном направлении, и должен быть включен как вклад в общий ток.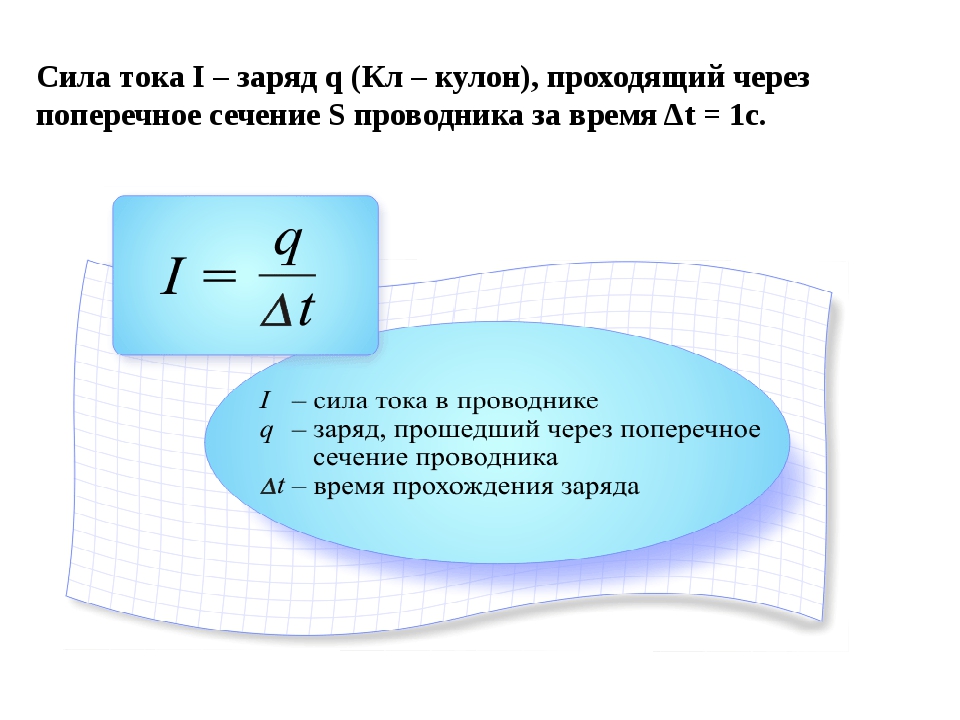 Ток в полупроводниках состоит из движения дырок в обычном направлении и электронов в противоположном направлении.
Ток в полупроводниках состоит из движения дырок в обычном направлении и электронов в противоположном направлении.
Существуют токи многих других видов, такие как пучки протонов, позитронов или заряженных пионов и мюонов в ускорителях частиц.
Электрический ток создает сопутствующее магнитное поле, как в электромагнитах. Когда электрический ток течет во внешнем магнитном поле, он испытывает магнитную силу, как в электродвигателях.Потери тепла или энергия, рассеиваемая электрическим током в проводнике, пропорциональна квадрату тока.
Распространенной единицей электрического тока является ампер, который определяется как поток заряда в один кулон в секунду, или 6,2 × 10 18 электронов в секунду. Единицы тока сантиметр – грамм – секунда — это электростатическая единица заряда (esu) в секунду. Один ампер равен 3 × 10 9 esu в секунду.
Коммерческие линии электропередач обеспечивают ток около 100 ампер в обычном доме; 60-ваттная лампочка потребляет около 0. 5 ампер тока и однокомнатный кондиционер около 15 ампер. (Подробнее об электрическом токе, см. электричество: Постоянный электрический ток и электричество: Переменные электрические токи.)
5 ампер тока и однокомнатный кондиционер около 15 ампер. (Подробнее об электрическом токе, см. электричество: Постоянный электрический ток и электричество: Переменные электрические токи.)
Электрический ток — веб-формулы
Электрический ток определяется по формуле:I = В / R
Соответствующие единицы:
ампер (А) = вольт (В) / Ом (Ом)
Эта формула выводится из закона Ома . Где у нас:
В: напряжение
I: текущий
R: сопротивление
Если электрическая мощность и полное сопротивление известны, то ток можно определить по следующей формуле:
I = √ ( P / R )
Соответствующие единицы:
Ампер (А) = √ (Ватт (Вт) / Ом (Ом))
Где P — электрическая мощность.
Электрический ток
Скорость потока заряда через поперечное сечение некоторой области металлического провода (или электролита) называется током через эту область.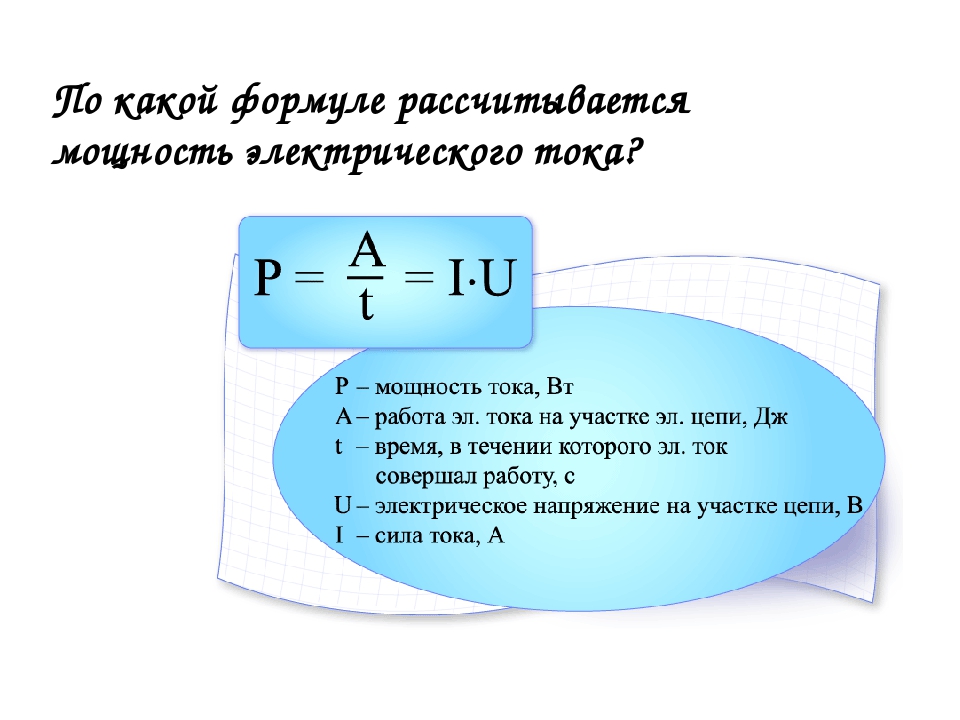
Если скорость потока заряда непостоянна, тогда ток в любой момент задается дифференциальным пределом: I = dQ / dt.
Если заряд Q протекает по цепи в течение времени t, то
I = Q / t.
Единица измерения тока S.I называется ампер (А) (кулон в секунду).
1 ампер = 6,25 × 10 8 электронов / сек
В металлических проводниках ток возникает из-за движения электронов, тогда как в электролитах и ионизированных газах как электроны, так и положительные ионы движутся в противоположном направлении. Направление тока принимается за направление движения положительных зарядов.
В проводимости, хотя ток возникает только за счет электронов, ранее предполагалось, что ток возникает из-за положительных зарядов, протекающих от положительного полюса батареи к отрицательному.Поэтому направление тока считается противоположным потоку электронов.
Если ток постоянный: Δq = I.Δt
функция времени:
Заряд = Площадь под графиком = ½ × t 0 × I 0
To Найти ток в электрической цепи
Для простой цепи или одиночного провода мы имеем:
Для сложной цепи с более чем одним проводом мы можем определить ток с помощью двух законов Кирхгофа
Первый закон: Этот закон основан на принципе сохранения заряда и утверждает, что в электрической цепи (или сети проводов) алгебраическая сумма токов, встречающихся в точке, равна нулю.
Стрелка, отмеченная на схеме, представляет направление обычного тока, то есть направление потока положительного заряда, тогда как направление потока электронов дает направление электронного тока, противоположное направлению обычного тока.
I 1 + I 4 + I 5 = I 3 + I 2 + I 6
Второй закон: Алгебраическая сумма произведения тока и сопротивление в любом замкнутом контуре цепи равно алгебраической сумме электродвижущих сил, действующих в этом контуре.
Математически.
Электродвижущие силы — ЭДС () источника определяется как работа, совершаемая на единицу заряда при прохождении положительного заряда через гнездо ЭДС от конца с низким потенциалом к концу с высоким потенциалом. Таким образом,
𝜖 = w / Q
Когда ток не течет, ЭДС источника точно равна разности потенциалов между его концами. Единица измерения ЭДС и такая же, как у потенциала, то есть вольт.
Средний поток электронов в проводнике, не подключенном к батарее, равен нулю, т.е. количество свободных электронов, пересекающих любой участок проводника слева направо, равно количеству электронов, пересекающих участок проводника справа налево. Таким образом, ток не течет по проводнику, пока он не будет подключен к батарее.
Скорость дрейфа свободных электронов в металлическом проводнике
В отсутствие электрического поля свободные электроны в металле беспорядочно вращаются во всех направлениях, и поэтому их средняя скорость равна нулю.При приложении электрического поля они ускоряются в направлении, противоположном направлению поля, и поэтому имеют общий дрейф в этом направлении. Однако из-за частых столкновений с атомами их средняя скорость очень мала. Эта средняя скорость, с которой электроны движутся в проводнике под действием разности потенциалов, называется дрейфовой скоростью .
Если E — приложенное поле, e — заряд электрона, m — масса электрона и τ — временной интервал между последовательными столкновениями (время релаксации), то ускорение электрона составляет
Поскольку средняя скорость сразу после столкновения равна нулю, а непосредственно перед следующим столкновением это τ, скорость дрейфа должна быть:
Если I — ток через проводник и n — это количество свободных электронов на единицу объема, тогда можно показать, что:
Подвижность µ носителя заряда определяется как скорость дрейфа на единицу электрического поля:
Плотность тока (J)
(i)
(ii) S. I Единица J = Am -2 .
I Единица J = Am -2 .
(iii) Плотность тока — это векторная величина, ее направление — это направление потока положительного заряда в данной точке внутри проводника.
(iv) Размеры плотности тока = [M 0 L -2 T o A 1 ]
Носители тока: заряженные частицы, поток которых в определенном направлении составляет электрический ток, являются носителями тока. . Носители тока могут иметь положительный или отрицательный заряд.Ток переносится электронами в проводниках, ионами в электролитах, электронами и дырками в полупроводниках.
Пример 1: Частица с зарядом q кулонов описывает круговую орбиту. Если радиус орбиты равен R, а частота орбитального движения частиц равна f, то найти ток на орбите.
Решение: Через любой участок орбиты заряд проходит f раз за одну секунду. Следовательно, через этот участок общий заряд, проходящий за одну секунду, равен fq.По определению i = fq.
Пример 2: Ток в проводе изменяется со временем в соответствии с уравнением I = 4 + 2t, где I — в амперах, а t — в секундах. Вычислите количество заряда, прошедшего через поперечное сечение провода за время от t = 2 с до t = 6 с.
Решение: Пусть dq будет изменением, которое произошло за небольшой интервал времени dt.
Тогда dq = I dt = (4 + 2t) dt
Следовательно, общий заряд, прошедший за интервал t = 2 с и t = 6, равен
q = ∫ 6 2 (4 + 2t) dt = 48 кулонов
Пример 3: Дан токоведущий провод неоднородного сечения.Что из следующего является постоянным по всей сети?
(a) Только ток
(b) Ток и скорость дрейфа
(c) Только скорость дрейфа
(d) Ток, скорость дрейфа
Решение : (a)
Пример4 : Когда разность потенциалов на данном медном проводе увеличивается, скорость дрейфа составляет
носители заряда:
(а) Уменьшается
(б) Увеличивается
(в) Остается прежним
(г) Уменьшается до нуля
Решение : (б)
Электрический Current — The Physics Hypertextbook
Обсуждение
определений
текущий
Электрический ток определяется как скорость, с которой заряд проходит через поверхность (например, поперечное сечение провода).Несмотря на то, что оно относится ко многим различным вещам, слово ток часто используется само по себе вместо более длинного, более формального «электрического тока». Прилагательное «электрический» подразумевается контекстом описываемой ситуации. Фраза «ток через тостер», несомненно, относится к потоку электронов через нагревательный элемент, а не к потоку ломтиков хлеба через прорези.
Как и все величины, определяемые как скорость, есть два способа записать определение электрического тока — средний ток для тех, кто заявляет о незнании вычислений…
и мгновенный ток для тех, кто не боится вычислений…
| I = | ∆ к | = | dq | |
| ∆ т | дт |
Единица измерения тока — ампер [А], названная в честь французского ученого Андре-Мари Ампера (1775–1836).В письменных языках без диакритических букв (а именно в английском) принято писать единицу измерения как ампер , а при неформальном общении сокращать это слово до ампер . У меня нет проблем с любым из этих вариантов написания. Только не используйте заглавную букву «А» в начале. Ампер относится к физику, а ампер (или ампер, или ампер) относится к единице.
Поскольку заряд измеряется в кулонах, а время измеряется в секундах, ампер равняется кулону в секунду.
| ⎡ ⎢ ⎣ | А = | С | ⎤ ⎥ ⎦ |
| с |
Элементарный заряд определен как ровно…
e = 1,602176634 × 10 −19 C
Число элементарных зарядов в кулонах будет обратной величине этого числа — повторяющейся десятичной дроби с периодом в 778 716 цифр. Я напишу первые 19 цифр, это максимум, что я могу написать (поскольку произвольных долей элементарного заряда не существует).
C ≈ 6,241,509,074,460,762,607 e
А потом напишу еще раз с более разумным количеством цифр, чтобы было легче читать.
C ≈ 6,2415 × 10 18 e
Ток в один ампер — это передача примерно 6,2415 × 10 18 элементарных зарядов в секунду. Для любителей случайностей это примерно десять микромолей.
плотность тока
Когда я визуализирую ток, я вижу, как что-то движется.Я вижу, как они движутся в определенном направлении. Я вижу вектор. Я вижу не то. Ток не является векторной величиной, несмотря на мою хорошо развитую научную интуицию. Ток — это скаляр. И причина в том … потому что это так.
Но подождите, становится еще страннее. Отношение силы тока к площади для данной поверхности называется плотностью тока.
Единица измерения плотности тока — ампер на квадратный метр , не имеющая специального названия.
| ⎡ ⎢ ⎣ | A | = | A | ⎤ ⎥ ⎦ |
| м 2 | м 2 |
Несмотря на отношение двух скалярных величин, плотность тока является вектором.И причина в том, что это так.
Ну… на самом деле, это потому, что плотность тока определяется как произведение плотности заряда и скорости для любого места в космосе…
Дж = ρ v
Два уравнения эквивалентны по величине, как показано ниже.
| Дж = | ρ | в | ||||||||
| Дж = | кв | DS | = | с | dq | = | 1 | I | ||
| В | дт | sA | дт | А | ||||||
| Дж = | I | |||||||||
| А | ||||||||||
Есть еще кое-что, что нужно учесть.
I = JA = ρ v A
Читатели, знакомые с механикой жидкостей, могли бы узнать правую часть этого уравнения, если бы оно было написано немного иначе.
I = ρ Ср.
Это произведение является величиной, которая остается постоянной в уравнении неразрывности массы .
ρ 1 A 1 v 1 = ρ 2 A 2 v 2
Точно такое же выражение применяется к электрическому току с символом ρ, меняющим значение между контекстами.В механике жидкости ρ обозначает массовую плотность, а в электрическом токе — плотность заряда.
микроскопическое описание
Ток — это поток заряженных частиц. Это дискретные сущности, а значит, их можно сосчитать.
n = N / V
∆ q = нкВ
В = Ad = Av ∆ т
| I = | ∆ к | = | nqAv ∆ т |
| ∆ т | ∆ т |
I = nqAv
Аналогичное выражение можно записать для плотности тока.Вывод начинается в скалярной форме, но в окончательном выражении используются векторы.
Дж = nq v
твердых частиц
Сравнение проводимости и валентных электронов, проводников и изоляторов
Дрейфовое движение, наложенное на тепловое движение
Мостовой текст.
Тепловая скорость электронов в проводе довольно высока и случайным образом изменяется из-за столкновений атомов.Поскольку изменения хаотичны, средняя скорость равна нулю.
Когда провод помещается в электрическое поле, свободные электроны равномерно ускоряются в промежутках между столкновениями. Эти периоды ускорения поднимают среднюю скорость выше нуля. (Эффект на этой диаграмме сильно преувеличен.)
тепловая скорость электрона в меди при комнатной температуре (классическое приближение)…
| ||||
|
ферми-скорость электрона в меди (квантовая величина)…
| ||||
| ||||
|
Скорость дрейфа электрона на 10 м медного провода, подключенного к автомобильному аккумулятору 12 В при комнатной температуре (среднее время свободного пробега между столкновениями при комнатной температуре τ = 3 × 10 −14 с)…
| |||||||||||||||||||
| |||||||||||||||||||
|
Тепловая скорость на несколько порядков превышает скорость дрейфа в обычной проволоке. Время на прохождение круга — около часа.
жидкости
ионы, электролиты
газы
ионов, плазма
- 14:02 — Линии электропередачи разъединяются на юго-западе Огайо
4. Стюарт — Атланта 345 кВ
Эта линия является частью пути передачи из юго-западного Огайо в северный Огайо. Он отключился от системы из-за возгорания кисти под частью линии. Горячие газы от пожара могут ионизировать воздух над линией электропередачи, заставляя воздух проводить электричество и закорачивать проводники.
Источник
исторический
Обозначение I было выбрано для обозначения силы тока французского физика и математика XIX века Андре-Мари Ампера.
Увеличить Pour exprimer en nombre l’intensité d’un courant quelconque, on Concevra qu’on ait choisi un autre courant арбитраж для сравнения терминов…. Désignant donc par i et i ‘ les rapports destensités deux courant donnés à l’intensité du courant pris pour unite…. Чтобы выразить интенсивность тока в виде числа, предположим, что для сравнения выбран другой произвольный ток…. Используем i и i ′ для отношения интенсивностей двух заданных токов к силе опорного тока, взятого за единицу…. Андре-Мари Ампер, 1826 Андре-Мари Ампер, 1826 г. (платная ссылка)
Термин «интенсивность» теперь не имеет никакого отношения к физике. Ток — это скорость, с которой заряд и протекает через поверхность любого размера — например, клеммы аккумулятора или штыри электрической вилки. Интенсивность — это средняя мощность, на единицу площади, передаваемая каким-либо явлением излучения — например, звуком оживленного шоссе, светом Солнца или частицами брызг, испускаемыми радиоактивным источником.Ток и интенсивность теперь — разные величины с разными единицами измерения и разным использованием, поэтому (конечно) они используют одинаковые символы.
| текущий | интенсивность | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
Начало таблицы
- 12 000 А ток через магниты LHC в ЦЕРН
Электрический ток — Практика — Физический гипертекст
Есть два подхода к этой проблеме.Один из них сложнее другого. Давайте сначала воспользуемся базовым методом.
Используйте определение тока и решите для заряда.
Используйте значения для одного импульса и умножьте на количество импульсов.
∆ q = nI ∆ t
∆ q = 95 (3 A) (80 × 10 −6 с)
∆ q = 0,0228 CЭто считается (за неимением точных слов) лот заряда.
Теперь используйте определение тока.
I = I = 0,0228 С 5 с I = 0,00456 A Это не много тока.Вам нужно что-то от 70 до 100 миллиампер, чтобы умереть от удара током. Это даже не 5 мА.
Оба эти ответа вдвое велики. Цифры по этой проблеме взяты из отчета Министерства юстиции США. В отчете цитируется утверждение, что это конкретное «устройство кондуктивной энергии» обеспечивает около 100 микрокулонов заряда за импульс и 2,1 миллиампера среднего тока. Расхождение возникает из-за того, что ток в одном импульсе непостоянен. Представьте себе треугольник с основанием 80 мкс и высотой 3 А.Ток начинается с нуля, достигает пика и возвращается к нулю. Полный доставленный заряд составляет область под этим треугольником.
Вычислите заряд, доставленный за один импульс. Я не буду использовать научные обозначения для этого решения. Я предпочитаю использовать префиксы SI.
∆ q импульс = ½ bh
∆ q импульс = ½ (80 мкс) (3 A)
∆ q импульс = 120 мкКлСогласен с отчетом.Это около 100 микрокулонов. Увеличьте это количество на 95 импульсов, чтобы получить полный заряд за один цикл.
∆ q всего = 95 (120 мкКл)
∆ q всего = 11400 мкКл
∆ q всего = 11,4 мКлЭто все еще считается партией заряда, поэтому это оружие может вызывать невыносимую боль (и почему оно ассоциируется с пытками).
Вернуться к определению тока.
I = I = 11,4 мК 5 с I = 2,28 мА Это значение аналогично значению в отчете.Это все равно не много тока, из-за чего это оружие убивает редко.
Напишите что-нибудь.
Напишите что-нибудь.
Напишите что-нибудь совсем другое.
Электрический ток — Проблемы — Гипертекст по физике
- … батареи
- электрический ток
- электрическое сопротивление…
© 1998–2021 Гленн Элерт
Автор, иллюстратор, веб-мастер
Нет постоянных условий.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Dynamics I: Force
- Сил
- Сила и масса
- Действие-реакция
- Вес
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Код ссылки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые машины
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Динамика вращения
- Статика вращения
- Угловой момент
- Энергия вращения
- Каток
- Вращение в двух измерениях
- Сила Кориолиса
- планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Генератор простых гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа вещества
- Закон о газе
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (световой)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Кондукторы
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- Цепи постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC-цепи
- Цепи RL
- Цепи LC
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Теория относительности
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированное вещество
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика вкусов
- Стандартная модель
- Помимо стандартной модели
- Теория относительности
- Фонды
- шт.
- Международная система единиц
- Гауссова система единиц
- Британо-американская система единиц
- Разные единицы
- Время
- Преобразование единиц
- Измерение
- Значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Векторное умножение
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая таблица элементов
- Люди в физике
- шт.
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- гленнелерт.нас
- Behance
- Твиттер
- YouTube
- Аффилированные сайты
- hypertextbook.com
- midwoodscience.org
- Предисловие
Веб-сайт класса физики
Электрические схемы: обзор набора проблем
Этот набор из 34 задач нацелен на вашу способность определять такие величины цепи, как ток, сопротивление, разность электрических потенциалов, мощность и электрическая энергия, на основе словесных описаний и диаграмм физических ситуаций, относящихся к электрическим цепям.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синим цветом, .
Текущий
Когда заряд течет по проводам электрической цепи , считается, что в проводах присутствует ток. Электрический ток — это измеримое понятие, которое определяется как скорость , с которой заряд проходит через точку в цепи.Его можно определить, измерив количество заряда, протекающего по площади поперечного сечения провода в цепи. Как величина скорости, ток (I) выражается следующим уравнением
I = Q / т
где Q — количество заряда, протекающего через точку за период времени t. Стандартной метрической единицей измерения величины тока является ампер, часто сокращенно Ампер или А. Ток в 1 ампер эквивалентен 1 кулону заряда, протекающему через точку за 1 секунду.Поскольку количество заряда, проходящего через точку в цепи, связано с количеством мобильных носителей заряда (электронов), которые проходят через эту точку, ток также может быть связан с количеством электронов и временем. Чтобы установить связь между током и числом электронов, нужно знать количество заряда на одном электроне.
Q электрон = 1,6 x 10 -19 C
Сопротивление
Когда заряд течет по цепи, он встречает сопротивление или препятствие для его прохождения.Как и ток, сопротивление — это измеримый термин. Величина сопротивления, обеспечиваемого сечением провода, зависит от трех переменных — материала, из которого сделан провод, длины провода и площади поперечного сечения провода. Одним из физических свойств материала является его удельное сопротивление — мера способности этого материала сопротивляться прохождению заряда через него. Значения удельного сопротивления для различных проводящих материалов обычно указаны в учебниках и справочниках. Зная значение удельного сопротивления (ρ) материала, из которого состоит провод, а также его длину (L) и площадь поперечного сечения (A), его сопротивление (R) можно определить с помощью приведенного ниже уравнения.
R = ρ • L / A
Стандартная метрическая единица измерения сопротивления — Ом (сокращенно греческой буквой Ом ).
Основная трудность при использовании приведенного выше уравнения связана с единицами выражения различных величин. Удельное сопротивление (ρ) обычно выражается в Ом • м. Таким образом, длина должна быть выражена в метрах, а площадь поперечного сечения — в метрах 2 . Многие провода круглые и имеют круглое сечение.Таким образом, площадь поперечного сечения в приведенном выше уравнении можно рассчитать, зная радиус или диаметр провода, используя формулу для площади круга.
A = π • R 2 = π • D 2 /4
Соотношение напряжение-ток-сопротивление
Величина тока, протекающего в цепи, зависит от двух переменных. Ток обратно пропорционален общему сопротивлению (R) цепи и прямо пропорционален разности электрических потенциалов, приложенной к цепи.Разность электрических потенциалов (ΔV), приложенная к цепи, — это просто напряжение, подаваемое источником энергии (батареи, розетки и т. Д.). Для домов в США это значение близко к 110–120 вольт. Математическая взаимосвязь между током (I), напряжением и сопротивлением выражается следующим уравнением (которое иногда называют уравнением закона Ома ).
Мощность
Электрические схемы — это энергия.Энергия включается в цепь аккумулятором или коммерческим поставщиком электроэнергии. Элементы схемы (освещение, обогреватели, двигатели, холодильники и даже провода) преобразуют эту электрическую потенциальную энергию в другие формы энергии, такие как световая энергия, звуковая энергия, тепловая энергия и механическая энергия. Мощность означает скорость, с которой энергия передается или преобразуется устройством или цепью. Это скорость, с которой энергия теряется или приобретается в любом заданном месте в цепи.Таким образом, общее уравнение мощности —
.P = ΔE / т
Потеря (или усиление) энергии — это просто произведение разности электрических потенциалов между двумя точками и количества заряда, который перемещается между этими двумя точками за период времени t. Таким образом, потеря (или усиление) энергии равна просто ΔV • Q. Когда это выражение подставляется в вышеприведенное уравнение, уравнение мощности становится
P = ΔV • Q / т
Поскольку отношение Q / t, найденное в приведенном выше уравнении, равно току (I), приведенное выше уравнение также можно записать как
P = ΔV • I
Комбинируя уравнение закона Ома с приведенным выше уравнением, можно получить два других уравнения мощности.Их
| P = I 2 • R | P = ΔV 2 / R |
Стандартная метрическая единица измерения мощности — Вт . В единицах измерения ватт эквивалентен усилителю • Вольт, усилителю 2 • Ом и вольт 2 / Ом.
Затраты на электроэнергию
Коммерческая энергетическая компания взимает с домохозяйств ежемесячную плату за поставленную электроэнергию.В счете за услуги обычно указывается количество энергии, потребленной в течение месяца, в единицах киловатт • часов . Эта единица — единица мощности, умноженная на единицу времени, — это единица энергии. Домохозяйство обычно оплачивает счет на основе количества кВт • ч электроэнергии, потребленной в течение месяца. Таким образом, задача определения стоимости использования конкретного прибора в течение заданного периода времени довольно проста. Сначала необходимо определить мощность и преобразовать ее в киловатты.Затем эту мощность необходимо умножить на время использования в часах, чтобы получить потребляемую энергию в единицах кВт • час. Наконец, это количество энергии должно быть умножено на стоимость электроэнергии в соотношении $ / кВт • час, чтобы определить стоимость в долларах.
Эквивалентное сопротивление
Довольно часто в цепи используется более одного резистора. Хотя каждый резистор имеет собственное индивидуальное значение сопротивления, общее сопротивление цепи отличается от сопротивления отдельных резисторов, составляющих цепь.Величина, известная как эквивалентное сопротивление , указывает полное сопротивление цепи. Концептуально эквивалентное сопротивление — это сопротивление, которое один резистор будет иметь, чтобы оказывать такое же общее влияние на сопротивление, как и комбинация резисторов, которые присутствуют. Таким образом, если в схеме есть три резистора с эквивалентным сопротивлением 25 Ом, то один резистор на 25 Ом может заменить три отдельных резистора и оказать влияние на схему, эквивалентное .Значение эквивалентного сопротивления (R eq ) учитывает индивидуальные значения сопротивления резисторов и способ их подключения.
Есть два основных способа включения резисторов в электрическую цепь. Их можно подключить последовательно или параллельно . Резисторы, которые соединены последовательно, подключаются последовательно, так что весь заряд, который проходит через первый резистор, также проходит через другие резисторы.При последовательном соединении весь заряд, протекающий по цепи, проходит через все отдельные резисторы. Таким образом, эквивалентное сопротивление последовательно соединенных резисторов является суммой значений отдельных сопротивлений этих резисторов.
R экв = R 1 + R 2 + R 3 +… (последовательные соединения)
Параллельно подключенные резисторы подключаются бок о бок, так что заряд, приближающийся к резисторам, разделяется на два или более разных пути.Параллельно подключенные резисторы характеризуются наличием участков разветвления, в которых заряд разветвляется по разным путям. Заряд, который проходит через один резистор, не проходит через другие резисторы. Эквивалентное сопротивление параллельно включенных резисторов меньше значений сопротивлений всех отдельных резисторов в цепи. Хотя это может быть не совсем интуитивно понятным, уравнение эквивалентного сопротивления параллельно соединенных резисторов дается уравнением с несколькими взаимными членами.
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 +… (параллельное соединение)
Анализ последовательной цепи
Некоторые проблемы второй половины этого набора относятся к последовательным цепям. Нередко проблема сопровождается рисунком или схематической диаграммой, показывающей расположение батарей и резисторов. Чертеж и соответствующая принципиальная схема ниже представляют последовательную цепь, питаемую тремя ячейками и имеющую три последовательно соединенных резистора (лампочки).
Если представить себе заряд, покидающий положительный полюс батареи и следующий по своему пути, когда он пересекает полный контур, становится очевидным, что заряд проходит через все резисторы последовательно. Таким образом, он соответствует критериям последовательной цепи. Знание того, что схема является последовательной, позволяет связать общее или эквивалентное сопротивление цепи с отдельными значениями сопротивления с помощью уравнения эквивалентного сопротивления, описанного выше.
R экв = R 1 + R 2 + R 3 +… (последовательные соединения)
Ток последовательной цепи в резисторах такой же, как и в батарее. Поскольку нет ответвлений в местах, где заряд разделяется на пути, можно сказать, что ток в батарее равен току в резисторе 1, равен току в резисторе 2 и равен току в резисторе 3 .. ., В форме уравнения можно записать, что
I аккумулятор = I 1 = I 2 = I 3 =… (последовательные цепи)
Когда заряд проходит через резисторы в последовательной цепи, происходит падение электрического потенциала, когда он проходит через каждый резистор.Это падение электрического потенциала на каждом резисторе определяется током через резистор и сопротивлением резистора. Это согласуется с уравнением закона Ома, описанным выше (ΔV = I • R). Поскольку ток (I) в каждом отдельном резисторе одинаков, логично сделать вывод, что резисторы с наибольшим сопротивлением (R) будут иметь наибольшую разность электрических потенциалов (ΔV), приложенную к ним.
Разность электрических потенциалов на отдельных резисторах цепи часто обозначается как падения напряжения .Эти падения напряжения последовательно соединенных резисторов математически связаны с электрическим потенциалом или номинальным напряжением элементов или батареи, которые питают цепь. Если заряд приобретает 12 В электрического потенциала при прохождении через батарею электрической цепи, то он теряет 12 В при прохождении через внешнюю цепь. Это падение электрического потенциала на 12 В является результатом серии отдельных падений электрического потенциала, проходящих через отдельные резисторы последовательной цепи.Эти отдельные падения напряжения (разность электрических потенциалов) в сумме дают общее падение напряжения в цепи. В форме уравнения можно сказать, что
ΔV аккумулятор = ΔV 1 + ΔV 2 + ΔV 3 +… (последовательные цепи)
где ΔV аккумулятор — это электрический потенциал, накопленный в аккумуляторе, а ΔV 1 , ΔV 2 и ΔV 3 — это падения напряжения (или разности электрических потенциалов) на отдельных резисторах.
Более подробное и исчерпывающее обсуждение последовательных схем и их анализа можно найти в учебном пособии по физике.
Анализ параллельных цепей
Самые последние проблемы в этом наборе относятся к параллельным цепям. Опять же, нет ничего необычного в том, что проблема сопровождается рисунком или схематической диаграммой, показывающей расположение батарей и резисторов.Чертеж и соответствующая принципиальная схема ниже представляют собой параллельную цепь с питанием от трех ячеек и имеющую три параллельно соединенных резистора (лампочки).
Если представить заряд, покидающий положительный полюс батареи и следующий по своему пути, когда он проходит через полный контур, становится очевидным, что заряд достигает места разветвления до достижения резистора. В месте разветвления, которое иногда называют узлом, заряд проходит по одному из трех возможных путей через резисторы.Вместо того, чтобы проходить через каждый резистор, один заряд будет проходить через единственный резистор во время полного цикла вокруг цепи. Таким образом, он соответствует критериям параллельной цепи. Знание того, что схема является параллельной, позволяет связать общее или эквивалентное сопротивление цепи с отдельными значениями сопротивления с помощью уравнения эквивалентного сопротивления, описанного выше.
1 / R eq = 1 / R 1 + 1 / R 2 + 1 / R 3 +… (параллельное соединение)
В месте разветвления заряд разделяется на отдельные пути.Таким образом, ток в отдельных путях будет меньше, чем ток вне путей. Общий ток в цепи и ток в батарее равны сумме тока в отдельных проводящих путях. В форме уравнения можно записать, что
I аккумулятор = I 1 + I 2 + I 3 +… (параллельные цепи)
Текущие значения этих отдельных ветвей контролируются двумя величинами — сопротивлением резистора в ветви и разностью электрических потенциалов (ΔV), приложенной к ветви.В соответствии с уравнением закона Ома, рассмотренным выше, можно сказать, что ток в ветви 1 равен разности электрических потенциалов на ветви 1, деленной на сопротивление ветви 1. Аналогичные утверждения можно сделать и для других ветвей. В форме уравнения можно указать, что
| I 1 = ΔV 1 / R 1 | I 2 = ΔV 2 / R 2 | I 3 = ΔV 3 / R 3 |
Эклектические разности потенциалов (ΔV 1 , ΔV 2 и ΔV 3 ) на отдельных резисторах часто называют падениями напряжения.Подобно последовательным цепям, любой заряд, покидающий батарею, должен испытывать такое же падение напряжения, как и усиление, которое он обнаруживает при прохождении через батарею. Но в отличие от последовательных цепей, в параллельной цепи заряд проходит только через один резистор. Таким образом, падение напряжения на этом резисторе должно равняться разности электрических потенциалов на батарее. В форме уравнения можно указать, что
ΔV аккумулятор = ΔV 1 = ΔV 2 = ΔV 3 +… (параллельные цепи)
где ΔV аккумулятор — это электрический потенциал, накопленный в аккумуляторе, а ΔV 1 , ΔV 2 и ΔV 3 — это падения напряжения (или разности электрических потенциалов) на отдельных резисторах.
Более подробное и исчерпывающее обсуждение параллельных схем и их анализа можно найти в учебном пособии по физике.
Привычки эффективно решать проблемы
Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек. Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки.Эти привычки кратко описаны здесь. Эффективное решение проблем …
- … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
- … идентифицирует известные и неизвестные величины и записывает их в организованном порядке, часто записывая их на самой диаграмме. Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например,г., ΔV = 9,0 В; R = 0,025 Ом; Я = ???).
- … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания принципов физики.
- … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
- … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.
Подробнее …
Дополнительная литература / Учебные пособия:
Следующие страницы Учебного пособия по физике могут быть полезны для того, чтобы помочь вам понять концепции и математику, связанные с этими проблемами.
Набор проблем электрических цепей
Просмотреть набор задач
Электрические схемы Решения с аудиогидом
Просмотрите аудиогид решения проблемы:1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34
Электрический ток: определение, единица, формула, типы (с примерами)
Обновлено 28 декабря 2020 г.
Кевин Бек
Электрический заряд: Какую автоматическую реакцию вызывает эта фраза, когда вы ее читаете? Может быть, ощущение покалывания или образ молнии, раскалывающего небо? Красочный дисплей мигающих огней в таком городе, как Париж или Лас-Вегас? Возможно, даже насекомое, которое каким-то образом светится в темноте, пробираясь через ваш лагерь?
До недавних столетий ученые не только не имели возможности измерить скорость света, но и не знали, какие физические явления лежат в основе того, что сейчас известно как «электричество».В 1800-х годах физики впервые узнали о мельчайших частицах, участвующих в потоке тока (свободные электроны), а также о природе сил, заставляющих их двигаться. Было ясно, что электричество может принести значительную пользу, если оно может быть безопасно «изготовлено» или «захвачено», а электрическая энергия используется для выполнения работы.
Поток электрического заряда легко возникает в веществах, классифицируемых как проводящие материалы , тогда как в изоляторах ему препятствуют.В металлическом проводе, таком как медный провод, например, можно создать разность потенциалов на концах провода, вызывая поток заряда и создавая ток.
Определение электрического тока
Электрический ток — это средняя скорость потока электрического заряда (то есть заряда в единицу времени) через точку в пространстве. Этот заряд переносится электроном, движущимся по проводу в электрической цепи.Чем больше электронов проходит через эту точку за секунду, тем больше величина тока.
Единицей измерения тока в системе СИ является ампер (А), часто неофициально называемый «ампер». Сам электрический заряд измеряется в кулонах (Кл).
- Заряд одного электрона равен -1,60 × 10 -19 Кл, а заряд протона равен по величине, но положительный знак . Это число считается фундаментальным зарядом e .Таким образом, основная единица ампер — кулоны в секунду (Кл / с).
По соглашению, электрический ток течет в направлении, противоположном потоку электронов . Это связано с тем, что направление тока было описано до того, как ученые узнали, какие носители заряда двигались под действием электрического поля. Для всех практических целей положительные заряды, движущиеся в положительном направлении, дают тот же физический (вычислительный) результат, что и отрицательные заряды, движущиеся в отрицательном направлении, когда дело касается электрического тока.
Электроны движутся к положительному выводу в электрической цепи. Таким образом, поток электронов или движущийся заряд находится далеко от отрицательного вывода. Движение электронов в медной проволоке или другом проводящем материале также создает магнитное поле , направление и величина которого определяются направлением электрического тока и, следовательно, движением электронов; это принцип, на котором построен электромагнит .
Формула электрического тока
Для базового сценария обычного тока заряда, движущегося по проводу, формула для тока имеет вид:
I = neAv_d
, где n — количество зарядов на кубический метр (м 3 ), e — основной заряд, A — площадь поперечного сечения провода, а v d — Скорость дрейфа .
Хотя ток имеет и величину, и направление, это скалярная величина, а не векторная величина, поскольку она не подчиняется законам сложения векторов.
Формула закона Ома
Закон Ома дает формулу для определения тока, который будет протекать через проводник:
I- \ frac {V} {R}
, где V — напряжение , или разность электрических потенциалов , измеренная в вольтах, а R — электрическое сопротивление протеканию тока, измеренное в Ом (Ом).
Подумайте о напряжении как о «тянущей силе» (хотя эта «электродвижущая сила» не является буквально силой), специфичной для электрических зарядов. Когда противоположные заряды разделены, они притягиваются друг к другу таким образом, что уменьшается с увеличением расстояния между ними. Это примерно аналог гравитационной потенциальной энергии в классической механике; гравитация «хочет» падения высоких предметов на Землю, а напряжение «хочет», чтобы разделенные (противоположные) заряды столкнулись вместе.
Значение напряжения
Вольт эквивалентно джоулям на кулон, или Дж / Кл.Таким образом, у них есть единицы энергии на единицу заряда. Таким образом, ток, умноженный на напряжение, дает единицы (Кл / с) (Дж / Кл) = (Дж / с), которые переводятся в единицы (в данном случае электрической) мощности:
P = IV
Объединение этого с законом Ома дает переходят к другим полезным математическим соотношениям, связанным с протеканием тока: P = I 2 R и P = V 2 / R. Они показывают, среди прочего, что при фиксированном уровне тока мощность пропорциональна сопротивлению, тогда как при фиксированном напряжении мощность составляет обратно пропорционально сопротивлению .
В то время как движущиеся заряды (ток) индуцируют магнитное поле, магнитное поле само может индуцировать напряжение в проводе.
Типы тока
- Постоянный ток (DC): Это происходит, когда все электроны непрерывно текут в одном направлении. Это тип тока в цепи, подключенной к стандартной батарее. Батареи, конечно, могут поставлять и поставляют лишь исчезающе малое количество энергии, необходимой для питания человеческой цивилизации, хотя постоянно совершенствующиеся технологии в области солнечных элементов сулят более высокий потенциал для хранения энергии.
- Переменный ток (AC): Здесь электроны колеблются взад и вперед (в некотором смысле «покачиваются») очень быстро. Этот тип тока часто легче генерировать на электростанции, и он также приводит к меньшим потерям энергии на большом расстоянии, поэтому он является стандартом, используемым сегодня. Все лампочки и другие электроприборы в стандартном доме начала 21 века питаются от сети переменного тока.
При переменном токе напряжение изменяется синусоидальным образом и задается в любой момент времени t выражением V = V 0 sin (2πft), где V 0 — начальное напряжение, а f — частота или количество полных циклов напряжения (от максимального до минимального обратно к максимальному значению) в каждую секунду.
Измерение тока
Амперметр — это устройство, которое используется для измерения тока, подключая его последовательно, а не параллельно, в электрическую цепь. (Параллельная схема имеет несколько проводов между соединениями — другими словами, у источника питания, конденсаторов и резисторов — в цепи.) Она работает по принципу, согласно которому ток одинаков во всех частях провода между двумя соединениями.
Амперметр имеет известное низкое внутреннее сопротивление и настроен на полное отклонение (FSD) при заданном уровне тока, часто равном 0.015 А или 15 мА. Если вы знаете напряжение и управляете сопротивлением с помощью функции шунтирующего сопротивления амперметра, вы можете определить ток; вы знаете, какое значение тока должно иметь , используя закон Ома.
Примеры электрического тока
1. Вычислите скорость дрейфа электронов в цилиндрическом медном проводе радиусом 1 мм (0,001 м), по которому течет ток 15 А, учитывая, что для меди n = 8,342 × 10 28 э / м 3 .

