Сила лоренца единица измерения: Сила лоренца | Формула и определение — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

определение, формула, применение на практике

Содержание

1 Что такое сила Лоренца — определение, когда возникает, получение формулы
- 1.1 Определение направления силы Лоренца с помощью правила левой руки
- 1.2 Движение заряженной частицы в магнитном поле
2 Формула силы Лоренца
- 2.1 Определение и формула силы Лоренца
- 2.2 Направление силы Лоренца
3 Следствия свойств силы Лоренца
- 3.1 Формула силы Лоренца при наличии магнитного и электрического полей
- 3.2 Единицы измерения силы Лоренца
4 Понятие напряженности электрического поля
- 4.1 Напряженность электрического поля
- 4.2 Как направлена сила Лоренца
5 Применение
6 Применение силы Лоренца в технике
- 6.1 Кинескоп
- 6.2 Масс-спектрограф
- 6.3 Циклотрон
- 6.4 Магнетрон
- 6.5 Магнитное поле Земли
7 Применение на практике
8 Заключение

Что такое сила Лоренца — определение, когда возникает, получение формулы

Известно, что электрический ток – это упорядоченное перемещение заряженных частиц. Установлено также, что во время движения в магнитном поле каждая из этих частиц подвергается действию силы. Для возникновении силы требуется, чтобы частица находилась в движении.

Сила Лоренца – это сила, которая действует на электрически заряженную частицу при её движении в магнитном поле. Её направление ортогонально плоскости, в которой лежат векторы скорости частицы и напряженности магнитного поля. Равнодействующая сил Лоренца и есть сила Ампера. Зная ее, можно вывести формулу для силы Лоренца.

Время, требуемое для прохождения частицей отрезка проводника,
, где
– длина отрезка,
– скорость частицы. Суммарный заряд, перенесенный за это время через поперечное сечение проводника,
. Подставив сюда значение времени из предыдущего равенства, имеем

(2)

В то же время
, где
– количество частиц, находящееся в рассматриваемом проводнике. При этом
, где
– заряд одной частицы. Подставив в формулу значение
из (2), можно получить:

Таким образом,

Используя (1), предыдущее выражение можно записать как

После сокращений и переносов появляется формула для вычисления силы Лоренца

С учетом того, что формула записана для модуля силы, ее необходимо записать так:

(3)

Поскольку
, то для вычисления модуля силы Лоренца неважно, куда направлена скорость, – по направлению силы тока или против, – и можно сказать, что
– это угол, образуемый векторами скорости частицы и магнитной индукции.

Запись формулы в векторном виде будет выглядеть следующим образом:

– это векторное произведение, результатом которого является вектор с модулем, равным
.

Исходя из формулы (3), можно сделать вывод о том, что сила Лоренца является максимальной в случае перпендикулярности направлений электрического тока и магнитного поля, то есть при
, и исчезать при их параллельности (
).

Необходимо помнить, что для получения правильного количественного ответа – например, при решении задач, – следует пользоваться единицами системы СИ, в которой магнитная индукция измеряется в теслах (1 Тл = 1 кг·с−2·А−1), сила – в ньютонах (1 Н = 1 кг·м/с2), сила тока – в амперах, заряд в кулонах (1 Кл = 1 А·с), длина – в метрах, скорость – в м/с.

Определение направления силы Лоренца с помощью правила левой руки

Поскольку в мире макрообъектов сила Лоренца проявляется как сила Ампера, для определения ее направления можно пользоваться правилом левой руки.

Нужно поставить левую руку так, чтобы раскрытая ладонь находилась перпендикулярно и навстречу линиям магнитного поля, четыре пальца следует вытянуть в направлении силы тока, тогда сила Лоренца будет направлена туда, куда указывает большой палец, который должен быть отогнут.

Движение заряженной частицы в магнитном поле

В простейшем случае, то есть при ортогональности векторов магнитной индукции и скорости частицы сила Лоренца, будучи перпендикулярной к вектору скорости, может менять только её направление. Величина скорости, следовательно, и энергия будут оставаться неизменными. Значит, сила Лоренца действует по аналогии с центростремительной силой в механике, и частица перемещается по окружности.

В соответствии со II законом Ньютона (
) можно определить радиус вращения частицы:

Необходимо обратить внимание, что с изменением удельного заряда частицы (
) меняется и радиус.

При этом период вращения T =
=
. Он не зависит от скорости, значит, взаимное положение частиц с различными скоростями будет неизменным.

В более сложном случае, когда угол между скоростью частицы и напряженностью магнитного поля является произвольным, она будет перемещаться по винтовой траектории – поступательно за счет составляющей скорости, направленной параллельно полю, и по окружности под влиянием ее перпендикулярной составляющей.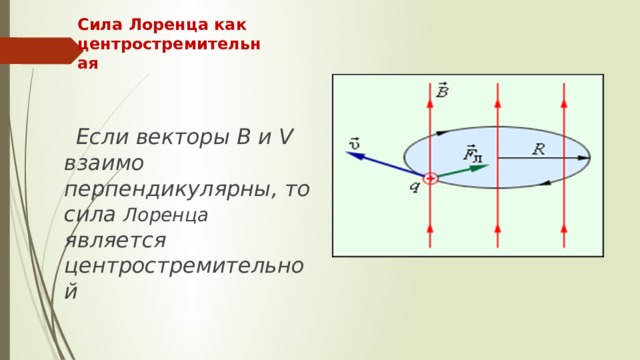

Формула силы Лоренца

Формула описывает взаимосвязь магнитного поля и основных характеристик движущегося заряда. Но сперва нужно разобраться, что же оно собой представляет.

Определение и формула силы Лоренца

В школе очень часто показывают опыт с магнитом и железными опилками на бумажном листе. Если расположить его под бумагой и слегка потрясти, то опилки выстроятся по линиям, которые принято называть линиями магнитной напряженности. Говоря простыми словами, это силовое поле магнита, которое окружает его подобно кокону. Оно замкнуто само на себя, то есть не имеет ни начала, ни конца. Это векторная величина, которая направлена от южного полюса магнита к северному.

Если бы в него влетела заряженная частица, то поле воздействовало бы на него очень любопытным образом. Она бы не затормозилась и не ускорилась, а всего лишь отклонилась в сторону. Чем она быстрее и чем сильнее поле, тем больше на нее действует эта сила. Ее назвали силой Лоренца в честь ученого-физика, впервые открывшего это свойство магнитного поля.

Вычисляют ее по специальной формуле:

FЛ=qvB,

здесь q – величина заряда в Кулонах, v – скорость, с которой движется заряд, в м/с, а B – индукция магнитного поля в единице измерения Тл (Тесла).

Направление силы Лоренца

Ученые заметили, что есть определенная закономерность между тем, как частица влетает в магнитное поле и тем, куда оно ее отклоняет. Чтобы ее было легче запомнить, они разработали специальное мнемоническое правило. Для его запоминания нужно совсем немного усилий, ведь в нем используется то, что всегда под рукой – рука. Точнее, левая ладонь, в честь чего оно носит название правила левой руки.

Итак, ладонь должна быть раскрыта, четыре пальца смотрят вперед, большой палец оттопырен в сторону. Угол между ними составляет 900. Теперь необходимо представить, что магнитный поток представляет собой стрелу, которая впивается в ладонь с внутренней стороны и выходит с тыльной. Пальцы при этом смотрят туда же, куда летит воображаемая частица.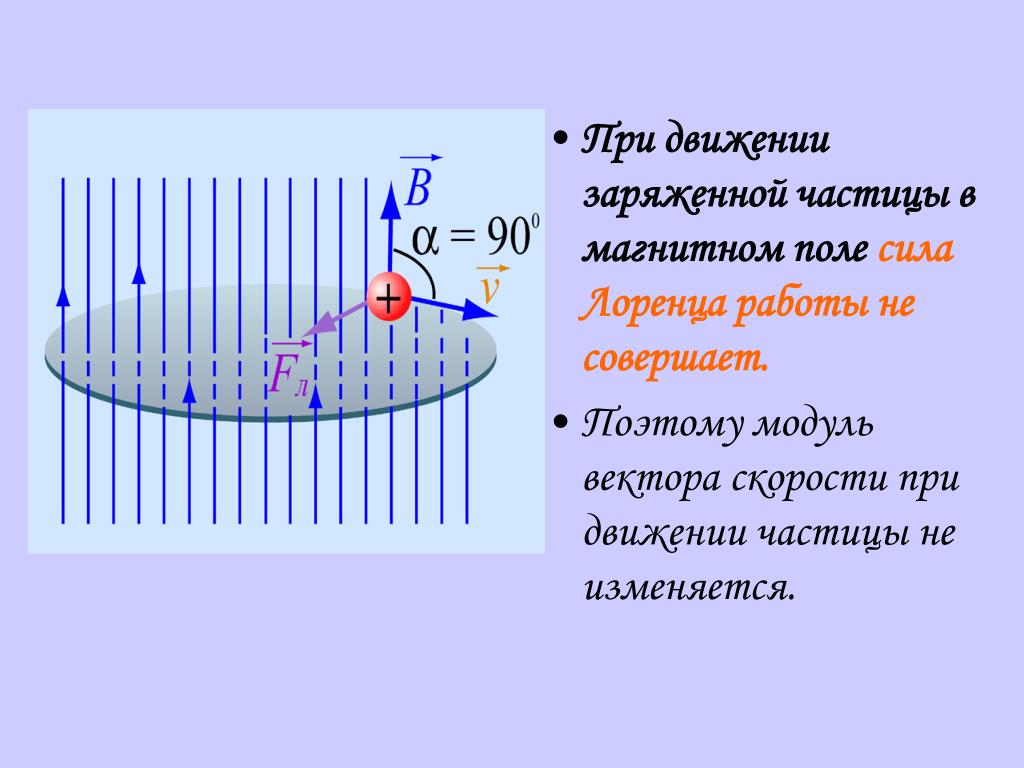 В таком случае большой палец покажет, куда она отклонится.

Интересно!
Важно отметить, что правило левой руки действует только для частиц со знаком «плюс». Чтобы узнать, куда отклонится отрицательный заряд, нужно четыре пальца направить в сторону, откуда летит частица. Все остальные манипуляции остаются прежними.

Следствия свойств силы Лоренца

Тело влетает в магнитном поле под каким-то определённым углом. Интуитивно понятно, что его величина имеет какое-то значение на характер воздействия на него поля, здесь нужно математическое выражение, чтобы стало понятнее. Следует знать, что как сила, так и скорость являются векторными величинами, то есть имеют направление. То же самое относится и к линиям магнитной напряженности. Тогда формулу можно записать следующим образом:

FЛ=qvBsinα,

sin α здесь – это угол между двумя векторными величинами: скоростью и потоком магнитного поля.

Как известно, синус нулевого угла также равен нулю. Получается, что если траектория движения частицы проходит вдоль силовых линий магнитного поля, то она никуда не отклоняется.

В однородном магнитном поле силовые линии имеют одинаковое и постоянное расстояние друг от друга. Теперь представим, что в таком поле перпендикулярно этим линиям движется частица. В этом случае сила Лоуренса заставит двигаться ее по окружности в плоскости, перпендикулярной силовым линиям. Чтобы найти радиус этой окружности, нужно знать массу частицы:

R=mvqB

Значение заряда не случайно взято как модуль. Это означает, что неважно, отрицательная или положительная частица входит в магнитное поле: радиус кривизны будет одинаков. Изменится только направление, в котором она полетит.

Во всех остальных случаях, когда заряд имеет определенный угол α с магнитным полем, он будет двигаться по траектории, напоминающей спираль с постоянным радиусом R и шагом h. Его можно найти по формуле:

R=mvsinαqB

h=2mvcosαqB

Еще одним следствием свойств этого явления является тот факт, что она не совершает никакой работы. То есть она не отдает и не забирает энергию у частицы, а лишь меняет направление ее движения.

Самая яркая иллюстрация этого эффекта взаимодействия магнитного поля и заряженных частиц – это северное сияние. Магнитное поле, окружающее нашу планету, отклоняет заряженные частицы, прилетающие от Солнца. Но так как оно слабее всего на магнитных полюсах Земли, то туда проникают электрически заряженные частицы, вызывая свечение атмосферы.

Центростремительное ускорение, которое придается частицам, используется в электрических машинах – электродвигателях. Хотя уместнее здесь говорить о силе Ампера – частном проявлении силы Лоуренса, которая воздействует на проводник.

Принцип действия ускорителей элементарных частиц также основан на этом свойстве электромагнитного поля. Сверхпроводящие электромагниты отклоняют частицы от прямолинейного движения, заставляя их двигаться по кругу.

Самое любопытное заключается в том, что сила Лоренца не подчиняется третьему закону Ньютона, который гласит, что всякому действию есть свое противодействие. Связано это с тем, что Исаак Ньютон верил, что всякое взаимодействие на любом расстоянии происходит мгновенно, однако это не так. На самом деле оно происходит с помощью полей. К счастью, конфуза удалось избежать, так как физикам удалось переработать третий закон в закон сохранения импульса, который выполняется в том числе и для эффекта Лоуренса.

Формула силы Лоренца при наличии магнитного и электрического полей

Магнитное поле имеется не только у постоянных магнитов, но и у любого проводника электричества. Только в данном случае помимо магнитной составляющей, в ней присутствует еще и электрическая. Однако даже в этом электромагнитном поле эффект Лоуренса продолжает свое воздействие и определяется по формуле:

FЛ=qE+vB

где v – скорость электрически заряженной частицы, q – ее заряд, B и E – напряженности магнитного и электрических полей поля.

Единицы измерения силы Лоренца

Как и большинство других физических величин, которые действуют на тело и изменяют его состояние, она измеряется в ньютонах и обозначается буквой Н.

Понятие напряженности электрического поля

Электромагнитное поле на самом деле состоит из двух половин – электрической и магнитной. Они точно близнецы, у которых все одинаково, но вот характер разный. А если приглядеться, то во внешности можно заметить небольшие различия.

То же самое касается и силовых полей. Электрическое поле тоже обладает напряженностью – векторной величиной, которая является силовой характеристикой. Она воздействует на частицы, которые в неподвижности находятся в нем. Само по себе оно не является силой Лоренца, ее просто нужно принимать во внимание, когда вычисляется воздействие на частицу в условиях наличия электрического и магнитного полей.

Напряженность электрического поля

Напряженность электрического поля воздействует только на неподвижный заряд и определяется по формуле:

E=Fq

Единицей измерения является Н/Кл или В/м.

Как направлена сила Лоренца

Чтобы определить направление силы Лоренца, как и с силой Ампера, работает правило левой руки. Это значит, чтобы понять, куда направлено значение Fл нужно раскрыть ладонь левой руки так, чтобы в руку входили линии магнитной индукции, а вытянутые четыре пальца указывали направление вектора скорости. Тогда большой палец, отогнутый под прямым углом к ладони, указывает направление силы Лоренца. На картинке ниже вы видите, как определить направление.

Внимание! Направление Лоренцового действия перпендикулярно движению частицы и линиям магнитной индукции.

При этом, если быть точнее, для положительно и отрицательно заряженных частиц имеет значение направление четырёх развернутых пальцев. Выше описанное правило левой руки сформулировано для положительной частицы. Если она заряжена отрицательно, то линии магнитной индукции должны быть направлены не в раскрытую ладонь, а в её тыльную сторону, а направление вектора Fл будет противоположным.

Теперь мы расскажем простыми словами, что даёт нам это явление и какое реальное воздействие она оказывает на заряды. Допустим, что электрон движется в плоскости, перпендикулярной направлению линий магнитной индукции. Мы уже упомянули, что Fл не воздействует на скорость, а лишь меняет направление движения частиц. Тогда сила Лоренца будет оказывать центростремительное воздействие. Это отражено на рисунке ниже.

Применение

Из всех сфер, где используется сила Лоренца, одной из масштабнейших является движение частиц в магнитном поле земли. Если рассмотреть нашу планету как большой магнит, то частицы, которые находятся около северного магнитного полюсов, совершают ускоренное движение по спирали. В результате этого происходит их столкновение с атомами из верхних слоев атмосферы, и мы видим северное сияние.

Тем не менее, есть и другие случаи, где применяется это явление. Например:

Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров.

Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.

Применение силы Лоренца в технике

Кинескоп

Кинескоп, стоявший до недавнего времени, когда на смену ему пришел LCD-экран (плоский), в каждом телевизоре, не смог бы работать, не будь силы Лоренца. Для формирования на экране телевизионного растра из узкого потока электронов служат отклоняющие катушки, в которых создается линейно изменяющееся магнитное поле. Строчные катушки перемещают электронный луч слева направо и возвращают обратно, кадровые отвечают за вертикальное перемещение, двигая бегающий по горизонтали луч сверху вниз. Такой же принцип используется в осциллографах – приборах, служащих для изучения переменного электрического напряжения.

Watch this video on YouTube

Масс-спектрограф

Масс-спектрограф – прибор, использующий зависимость радиуса вращения заряженной частицы от ее удельного заряда. Принцип его работы следующий:

Источник заряженных частиц, которые набирают скорость с помощью созданного искусственно электрического поля, с целью исключения влияния молекул воздуха помещается в вакуумную камеру. Частицы вылетают из источника и, пройдя по дуге окружности, ударяются в фотопластинку, оставляя на ней следы. В зависимости от удельного заряда меняется радиус траектории и, значит, точка удара. Этот радиус легко измерить, а зная его, можно вычислить массу частицы. С помощью масс-спектрографа, например, изучался состав лунного грунта.

Циклотрон

Независимость периода, а значит, и частоты вращения заряженной частицы от её скорости в присутствии магнитного поля используется в приборе, называемом циклотроном и предназначенном для разгона частиц до высоких скоростей. Циклотрон – это два полых металлических полуцилиндров – дуанта (по форме каждый из них напоминает латинскую букву D), помещенных прямыми сторонами навстречу друг другу на небольшом расстоянии.

Дуанты помещаются в постоянное однородное магнитное поле, а между ними создается переменное электрическое поле, частота которого равна частоте вращения частицы, определяемой напряженностью магнитного поля и удельным зарядом. Попадая дважды за период вращения (при переходе из одного дуанта в другой) под воздействие электрического поля, частица каждый раз ускоряется, увеличивая при этом радиус траектории, и в определенный момент, набрав нужную скорость, вылетает из прибора через отверстие. Таким способом можно разогнать протон до энергии в 20 МэВ (мегаэлектронвольт).

Магнетрон

Устройство, называемое магнетроном, который установлен в каждой микроволновой печи, – еще один представитель приборов, использующих силу Лоренца. Магнетрон служит для создания мощного СВЧ-поля, которое разогревает внутренний объем печи, куда помещается пища. Магниты, входящие в его состав, корректируют траекторию движения электронов внутри прибора.

Магнитное поле Земли

А в природе сила Лоренца играет крайне важную для человечества роль. Её наличие позволяет магнитному полю Земли защитить людей от смертоносного ионизирующего излучения космоса. Поле не дает возможности заряженным частицам бомбардировать поверхность планеты, заставляя их менять направление движения.

Применение на практике

Практическое значение работ Лоренца мы можем наблюдать в электронно-лучевых трубках. Там поток электронов движется в магнитном поле, изменением которого задаётся траектория электронного пучка.

Данный принцип управления траекторией электронного пучка использовался в старых моделях телевизоров Рис. 6). Электроны под воздействием магнитных полей очерчивали линии на люминофоре кинескопа, рисуя изображения на экране.

Рис. 6. Применение учения Лоренца

На рисунке справа изображена схема масспектрографа – прибора для разделения заряженных частиц по величине их зарядов.

Ещё один пример – бесконтактный электромагнитный метод определения скорости течения (вязкости) электропроводных жидкостей. Методика может быть применима к расплавленным металлам, например к алюминию. Бесконтактный способ определения вязкости очень полезен при работе с агрессивными жидкими электропроводными веществами (рис. 7).

Рис. 7. Измерение текучести жидких веществ

Работа ускорителей была бы невозможной без участия силы Лоренца. В этих устройствах заряженные частицы удерживаются и разгоняются до околосветовых скоростей благодаря электромагнитам, расположенным вдоль кольцевой трассы.

Мощная электронная лампа – Магнетрон также работает на принципе взаимодействия электронов с магнитными полями, которые направляют высокочастотное излучение в нужном направлении. Магнетрон является основной рабочей деталью микроволновых печей.

На основании действия силы Лоренца создано много других устройств, используемых на практике.

Заключение

Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:

Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
Не влияет на скорость частицы.

Влияет на направление частицы.

Её роль достаточно велика в «электрических» сферах. Специалист не должен упускать из вида основные теоретические сведения об основополагающих физических законах. Эти знания пригодятся, как и тем, кто занимается научной работой, проектированием и просто для общего развития.

Напоследок рекомендуем просмотреть полезные видео для закрепления изученного материала:

Теперь вы знаете, что такое сила Лоренца, чему она равна и как действует на заряженные частицы. Если возникли вопросы, задавайте их в комментариях под статьей!

Как определить силу лоренца правило левой руки. Сила Лоренца. Единицы измерения силы Лоренца

«Физика — 11 класс»

Магнитное поле действует с силой на движущиеся заряженные частицы, в то числе и на проводники с током.
Какова же сила, действующая на одну частицу?

1.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют

силой Лоренца в честь великого голландского физика X. Лоренца, создавшего электронную теорию строения вещества.
Силу Лоренца можно найти с помощью закона Ампера.

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Так как сила (сила Ампера), действующая на участок проводника со стороны магнитного поля
равна F = | I | BΔl sin α ,
а сила тока в проводнике равна I = qnvS
где
q — заряд частиц
n — концентрация частиц (т.е. число зарядов в единице объема)
v — скорость движения частиц

S — поперечное сечение проводника.

Тогда получаем:
На каждый движущийся заряд со стороны магнитного поля действует сила Лоренца , равная:

где α — угол между вектором скорости и вектором магнитной индукции.

Сила Лоренца перпендикулярна векторам и .

2.
Направление силы Лоренца

Направление силы Лоренца определяется с помощью того же правила левой руки , что и направление силы Ампера:

Если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F л

3.
Если в пространстве, где движется заряженная частица, существует одновременно и электрическое поле, и магнитное поле, то суммарная сила, действующая на заряд, равна: = эл + л где сила, с которой электрическое поле действует на заряд q, равна F эл = q.

4.
Cила Лоренца не совершает работы , т.к. она перпендикулярна вектору скорости частицы.
Значит сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости.
Под действием силы Лоренца меняется лишь направление скорости частицы.

5.
Движение заряженной частицы в однородном магнитном поле

Есть однородное магнитное поле , направленное перпендикулярно к начальной скорости частицы .

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля.
Магнитное поле не меняет модуль скорости движущейся частицы, значит остается неизменным и модуль силы Лоренца.
Сила Лоренца перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы.
Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что

В однородном магнитном поле заряженная частица равномерно движется по окружности радиусом r

Согласно второму закону Ньютона

Тогда радиус окружности по которой движется частица, равен:

Время, за которое частица делает полный оборот (период обращения), равно:

6.
Использование действия магнитного поля на движущийся заряд.

Действие магнитного поля на движущийся заряд используют в телевизионных трубках-кинескопах, в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в циклотроне — ускорителе заряженных частиц для получения частиц с большими энергиями.

На действии магнитного поля основано также и устройство масс-спектрографов, позволяющих точно определять массы частиц..

Нидерландский физик X. А. Лоренц в конце XIX в. установил, что сила, действующая со стороны магнитного поля на движущуюся заряженную частицу, всегда перпендикулярна направлению движения частицы и силовым линиям магнитного поля, в котором эта частица движется. Направление силы Лоренца можно определить с помощью правила левой руки. Если расположить ладонь левой руки так, чтобы четыре вытянутых пальца указывали направление движения заряда, а вектор магнитной индукции поля входил в отставленный большой палец укажет направление силы Лоренца, действующей на положительный заряд.

Если заряд частицы отрицательный, то сила Лоренца будет направлена в противоположную сторону.

Модуль силы Лоренца легко определяется из закона Ампера и составляет:

F = | q | vB sin? ,

где q — заряд частицы, v — скорость ее движения , ? — угол между векторами скорости и индукции магнитного поли.

Если кроме магнитного поля есть еще и электрическое поле , которое действует на заряд с силой , то полная сила, действующая на заряд, равна:

Часто именно эту силу называют силой Лоренца, а силу, выраженную формулой (F = | q | vB sin? ) называют магнитной частью силы Лоренца .

Поскольку сила Лоренца перпендикулярна направлению движения частицы, она не может изменить ее скорость (она не совершает работы), а может изменить лишь направление ее движения, т. е. искривить траекторию .

Такое искривление траектории электронов в кинескопе телевизора легко наблюдать, если поднести к его экрану постоянный магнит — изображение исказится.

Движение заряженной частицы в однородном магнитном поле. Пусть заряженная частица влетает со скоростью v в однородное магнитное поле перпендикулярно линиям напряженности.

Сила, действующая со стороны магнитного поля на частицу, заставит ее равномерно вращаться по окружности радиусом r , который легко найти, воспользовавшись вторым законом Ньютона , выражением целеустремленного ускорения и формулой (F = | q | vB sin? ):

Отсюда получим

где m — масса частицы.

Применение силы Лоренца.

Действие магнитного поля на движущиеся заряды применяется, например, в масс-спектрографах , позволяющих разделять заряженные частицы по их удельным зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц.

Вакуумная камера прибора помещена в поле (вектор индукции перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластину, где оставляют след, позволяющий с большой точностью измерить радиус траектории r .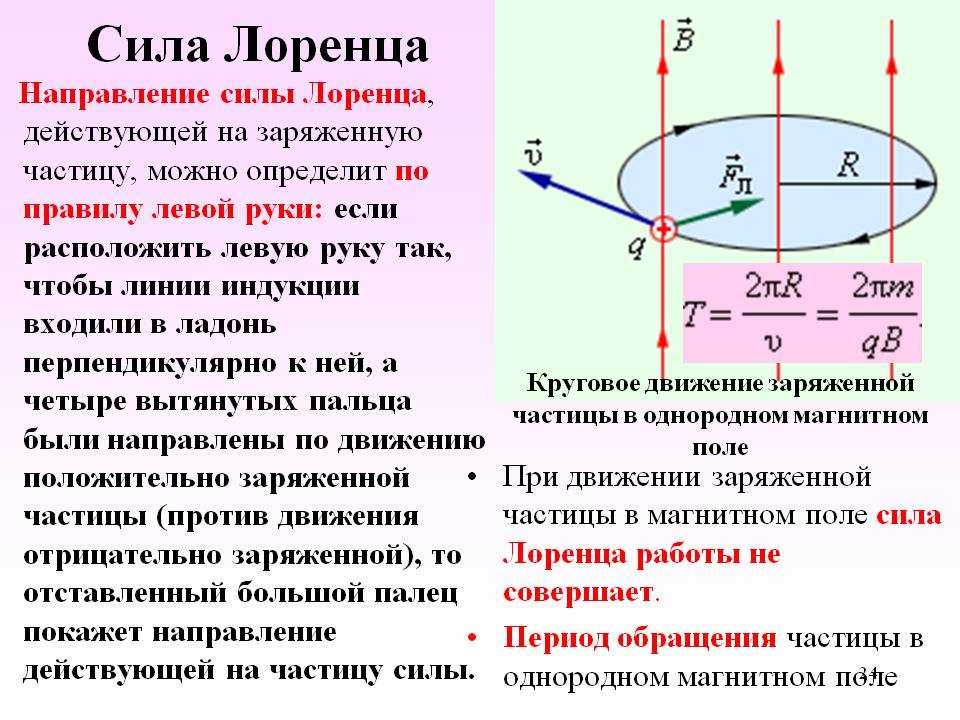 По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислите его массу.

Электрические заряды, движущиеся в определенном направлении, создают вокруг себя магнитное поле, скорость распространения которого в вакууме равно скорости света, а в других средах чуть меньше. Если движение заряда происходит во внешнем магнитном поле, то между внешним магнитным полем и магнитным полем заряда возникает взаимодействие. Так как электрический ток – это направленное движение заряженных частиц, то сила, которая будет действовать в магнитном поле на проводник с током, будет являться результатом отдельных (элементарных) сил, каждая из которых прикладывается к элементарному носителю заряда.

Процессы взаимодействия внешнего магнитного поля и движущихся зарядов исследовались Г. Лоренцом, который в результате многих своих опытов вывел формулу для расчета силы, действующей на движущуюся заряженную частицу со стороны магнитного поля. Именно поэтому силу, которая действует на движущийся в магнитном поле заряд, называют силой Лоренца.

Сила, действующая на проводник стоком (из закона Ампера), будет равна:

По определению сила тока равна I = qn (q – заряд, n – количество зарядов, проходящее через поперечное сечение проводника за 1 с). Отсюда следует:

Где: n 0 – содержащееся в единице объема количество зарядов, V – их скорость движения, S – площадь поперечного сечения проводника. Тогда:

Подставив данное выражение в формулу Ампера, мы получим:

Данная сила будет действовать на все заряды, находящиеся в объеме проводника: V = Sl. Количество зарядов, присутствующих в данном объеме будет равно:

Тогда выражение для силы Лоренца будет иметь вид:

Отсюда можно сделать вывод, что сила Лоренца, действующая на заряд q, который двигается в магнитном поле, пропорциональна заряду, магнитной индукции внешнего поля, скорости его движения и синусу угла между V и В, то есть:

За направление движения заряженных частиц принимают направление движения положительных зарядов. Поэтому направление данной силы может быть определено с помощью правила левой руки.

Сила, действующая на отрицательные заряды, будет направлена в противоположную сторону.

Сила Лоренца всегда направлена перпендикулярно скорости V движения заряда и поэтому работу она не совершает. Она изменяет только направление V, а кинетическая энергия и величина скорости заряда при его движении в магнитном поле остаются неизменными.

Когда заряженная частица движется одновременно в магнитном и электрическом полях, на него будет действовать сила:

Где Е – напряженность электрического поля.

Рассмотрим небольшой пример:

Электрон, прошедший ускоряющую разность потенциалов 3,52∙10 3 В, попадает в однородное магнитное поле перпендикулярно линиям индукции. Радиус траектории r = 2 см, индукция поля 0,01 Т. Определить удельный заряд электрона.

Удельный заряд – это величина, равная отношению заряда к массе, то есть e/m.

В магнитном поле с индукцией В на заряд, движущийся со скоростью V перпендикулярно линиям индукции, действует сила Лоренца F Л = BeV. Под ее действием заряженная частица будет перемещаться по дуге окружности. Так как при этом сила Лоренца вызовет центростремительное ускорение, то согласно 2-му закону Ньютона можно записать:

Кинетическую энергию, которая будет равна mV 2 /2, электрон приобретает за счет работы А сил электрического поля (А = eU), подставив в уравнение получим.

Сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q — заряд частицы;

V — скорость заряда;

a — угол между вектором скорости заряда и вектором магнитной индукции .

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца:

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.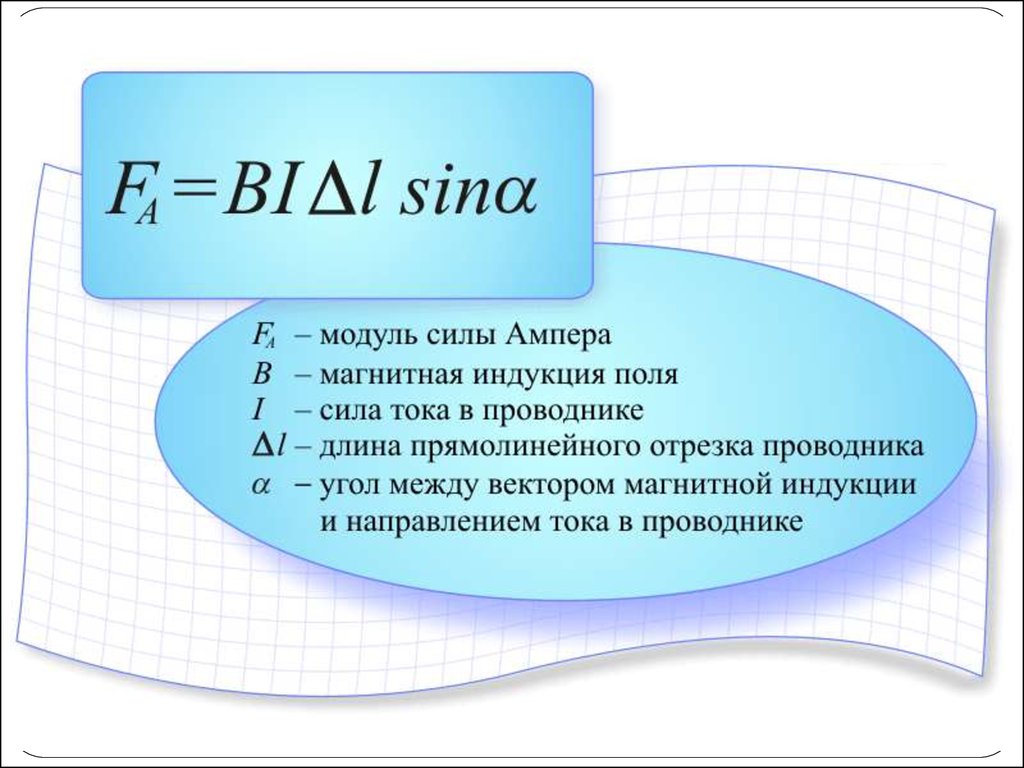 е. не изменяет величину скорости заряда и его кинетическую энергию).

Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движетсяравномерно и прямолинейно.

Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной:

и создает центростремительное ускорение равное:

В этом случае частица движется по окружности.

Согласно второму закону Ньютона : сила Лоренца равнв произведению массы частицы на центростремительное ускорение:

тогда радиус окружности:

а период обращения заряда в магнитном поле:

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды. Если внести проводник с током в магнитное поле (фиг.96,а), то мы увидим, что в результате сложения магнитных полей магнита и проводника произойдет усиление результирующего магнитного поля с одной стороны проводника (на чертеже сверху) и ослабление магнитного поля с другой стороны проводника (на чертеже снизу). В результате действия двух магнитных полей произойдет искривление магнитных линий и они, стремясь сократиться, будут выталкивать проводник вниз (фиг. 96, б).

Направление силы, действующей на проводник с током в магнитном поле, можно определить по «правилу левой руки». Если левую руку расположить в магнитном поле так, чтобы магнитные линии, выходящие из северного полюса, как бы входили в ладонь, а четыре вытянутых пальца совпадали с направлением тока в проводнике, то большой отогнутый палец руки покажет направление действия силы. Сила Ампера , действующая на элемент длины проводника, зависит: от величины магнитной индукции В, величины тока в проводнике I, от элемента длины проводника и от синуса угла а между направлением элемента длины проводника и направлением магнитного поля.

Эта зависимость может быть выражена формулой:

Для прямолинейного проводника конечной длины, помещенного перпендикулярно к направлению равномерного магнитного поля, сила, действующая на проводник, будет равна:

Из последней формулы определим размерность магнитной индукции.

Так как размерность силы:

т. е. размерность индукции такая же, какая была получена нами из закона Био и Савара.

Тесла (единица магнитной индукции)

Тесла, единица магнитной индукции Международной системы единиц, равная магнитной индукции, при которой магнитный поток сквозь поперечное сечение площадью 1 м 2 равен 1 веберу. Названа по имени Н. Тесла . Обозначения: русское тл, международное Т. 1 тл = 104 гс (гаусс ).

Магни?тный моме?нт , магни?тный дипо?льный моме?нт — основная величина, характеризующая магнитные свойства вещества. Магнитный момент измеряется в А⋅м 2 или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10 -3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора . В случае плоского контура с электрическим током магнитный момент вычисляется как

где — сила тока в контуре, — площадь контура, — единичный вектор нормали к плоскости контура.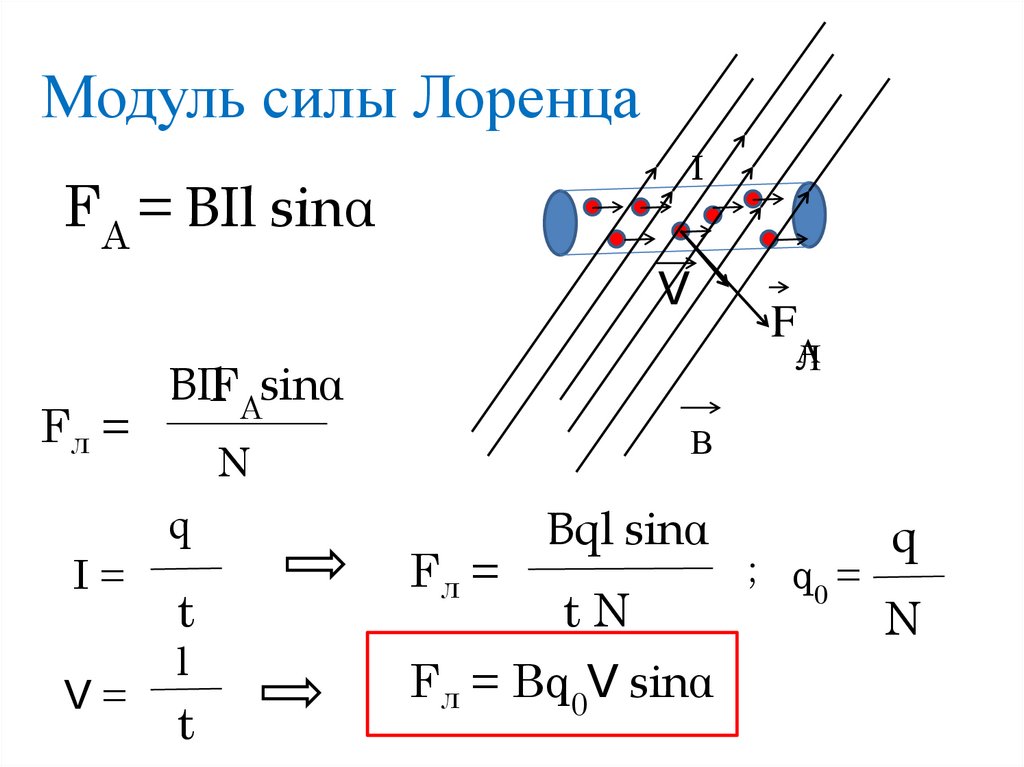 Направление магнитного момента обычно находится по правилу буравчика: если вращать ручку буравчика в направлении тока, то направление магнитного момента будет совпадать с направлением поступательного движения буравчика.

Для произвольного замкнутого контура магнитный момент находится из:

где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в среде:

где — плотность тока в элементе объёма .

Итак, на контур с током в магнитном поле действует вращающий момент. Контур ориентируется в данной точке поля только одним способом. Примем положительное направление нормали за направление магнитного поля в данной точке. Вращающий момент прямо пропорционален величине тока I , площади контура S и синусу угла между направлением магнитного поля и нормали .

здесь М — вращающий момент , или момент силы , — магнитный момент контура (аналогично — электрический момент диполя).

В неоднородном поле () формула справедлива, если размер контура достаточно мал (тогда в пределах контура поле можно считать приближенно однородным). Следовательно, контур с током по-прежнему стремится развернуться так, чтобы его магнитный момент был направлен вдоль линий вектора .

Но, кроме того, на контур действует результирующая сила (в случае однородного поля и . Эта сила действует на контур с током или на постоянный магнит с моментом и втягивает их в область более сильного магнитного поля.
Работа по перемещению контура с током в магнитном поле.

Нетрудно доказать, что работа по перемещению контура с током в магнитном поле равна , где и — магнитные потоки через площадь контура в конечном и начальном положениях. Эта формула справедлива, если ток в контуре постоянен , т.е. при перемещении контура не учитывается явление электромагнитной индукции.

Формула справедлива и для больших контуров в сильно неоднородном магнитном поле (при условии I= const).

Наконец, если контур с током не смещать, а изменять магнитное поле, т.е. изменять магнитный поток через поверхность, охватываемую контуром, от значения до то для этого надо совершить ту же работу . Эта работа называется работой изменения магнитного потока, связанного с контуром. Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, которая равна

где B n =Вcosα — проекция вектора В на направление нормали к площадке dS (α — угол между векторами n и В ), dS = dSn — вектор, у которого модуль равен dS, а направление его совпадает с направлением нормали n к площадке. Поток вектора В может быть как положительным, так и отрицательным в зависимости от знака cosα (задается выбором положительного направления нормали n ). Поток вектора В обычно связывают с контуром, по которому течет ток. В этом случае положительное направление нормали к контуру нами задавалось: оно связывается с током правилом правого винта. Значит, магнитный поток, который создается контуром, через поверхность, ограниченную им самим, всегда положителен.

Поток вектора магнитной индукции Ф B через произвольную заданную поверхность S равен

Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В , B n =B=const и

Из этой формулы задается единица магнитного потока вебер (Вб): 1 Вб — магнитный поток, который проходит сквозь плоскую поверхность площадью 1 м 2 , который расположен перпендикулярно однородному магнитному полю и индукция которого равна 1 Тл (1 Вб=1 Тл.м 2).

Теорема Гаусса для поля В : поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю:

Эта теорема является отражением факта, что магнитные заряды отсутствуют , вследствие чего линии магнитной индукции не имеют ни начала, ни конца и являются замкнутыми.

Следовательно, для потоков векторов В и Е сквозь замкнутую поверхность в вихревом и потенциальном полях получаются различные формулы.

В качестве примера найдем поток вектора В сквозь соленоид. Магнитная индукция однородного поля внутри соленоида с сердечником с магнитной проницаемостью μ, равна

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением ,

ОПРЕДЕЛЕНИЕ

Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле.

Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы.

Здесь – сила Лоренца, – заряд частицы, – модуль вектора индукции магнитного поля, – скорость частицы, – угол между вектором индукции магнитного поля и направления движения.

Единица измерения силы – Н (ньютон) .

Сила Лоренца — векторная величина. Сила Лоренца принимает своё наибольшее значение когда векторы индукции и направления скорости частицы перпендикулярны ().

Направление силы Лоренца определяют по правилу левой руки:

Если вектор магнитной индукции входит в ладонь левой руки и четыре пальца вытянуты в сторону направления вектора движения тока, тогда отогнутый в сторону большой палец показывает направление силы Лоренца.

В однородном магнитном поле частица будет двигаться по окружности, при этом сила Лоренца будет центростремительной силой. Работа при этом не будет совершаться.

Примеры решения задач по теме «Сила Лоренца»

ПРИМЕР 1

ПРИМЕР 2

Задание

Под действием силы Лоренца частица массы m с зарядом q движется по окружности. Магнитное поле однородно, его напряжённость равна B. Найти центростремительное ускорение частицы.

Решение

Вспомним формулу силы Лоренца:

Кроме того, по 2 закону Ньютона:

В данном случае сила Лоренца направлена к центру окружности и ускорение, ею создаваемое, направлено туда же, то есть это и есть центростремительное ускорение. Значит:

Сообщение по физике на тему сила лоренца. Лоренца сила

Сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q — заряд частицы;

V — скорость заряда;

a — угол между вектором скорости заряда и вектором магнитной индукции .

Направление силы Лоренца определяется по правилу левой руки:

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).

и создает центростремительное ускорение равное:

В этом случае частица движется по окружности.

тогда радиус окружности:

а период обращения заряда в магнитном поле:

Эта зависимость может быть выражена формулой:

Из последней формулы определим размерность магнитной индукции.

Так как размерность силы:

т. е. размерность индукции такая же, какая была получена нами из закона Био и Савара.

Тесла (единица магнитной индукции)

Для произвольного замкнутого контура магнитный момент находится из:

где — радиус-вектор, проведенный из начала координат до элемента длины контура

В общем случае произвольного распределения токов в среде:

где — плотность тока в элементе объёма .

Формула справедлива и для больших контуров в сильно неоднородном магнитном поле (при условии I= const).

Поток вектора магнитной индукции Ф B через произвольную заданную поверхность S равен

(2)

Для однородного поля и плоской поверхности, которая расположена перпендикулярно вектору В , B n =B=const и

(3)

Магнитный поток сквозь один виток соленоида площадью S равен

а полный магнитный поток, который сцеплен со всеми витками соленоида и называемый потокосцеплением ,

Наряду с силой Ампера, кулоновского взаимодействия, электромагнитными полями в физике часто встречается понятие сила Лоренца. Это явление является одним из основополагающих в электротехнике и электронике, на ряду с , и прочими. Она воздействует на заряды, которые двигаются в магнитном поле. В этой статье мы кратко и понятно рассмотрим, что такое сила Лоренца и где она применяется.

Определение

Когда электроны движутся по проводнику – вокруг него возникает магнитное поле. В то же время, если поместить проводник в поперечное магнитное поле и двигать его – возникнет ЭДС электромагнитной индукции. Если через проводник, который находится в магнитном поле, протекает ток – на него действует сила Ампера.

Её величина зависит от протекающего тока, длины проводника, величины вектора магнитной индукции и синуса угла между линиями магнитного поля и проводником. Она вычисляются по формуле:

Рассматриваемая сила отчасти похожа на ту, что рассмотрена выше, но действует не на проводник, а на движущуюся заряженную частицу в магнитном поле. Формула имеет вид:

Важно! Сила Лоренца (Fл) действует на электрон, движущийся в магнитном поле, а на проводник – Ампера.

Из двух формул видно, что и в первом и во втором случае, чем ближе синус угла aльфа к 90 градусам, тем большее воздействие оказывает на проводник или заряд Fа или Fл соответственно.

Итак, сила Лоренца характеризует не изменение величины скорости, а то, какое происходит воздействие со стороны магнитного поля на заряженный электрон или положительный ион. При воздействии на них Fл не совершает работы. Соответственно изменяется именно направление скорости движения заряженной частицы, а не её величина.

Что касается единицы измерения силы Лоренца, как и в случае с другими силами в физике используется такая величина как Ньютон. Её составляющие:

Как направлена сила Лоренца

Применение

Тем не менее, есть и другие случаи, где применяется это явление. Например:

Электронно-лучевые трубки. В их электромагнитных отклоняющих системах. ЭЛТ применялись больше чем 50 лет подряд в различных устройствах, начиная от простейшего осциллографа до телевизоров разных форм и размеров. Любопытно, что в вопросах цветопередачи и работы с графикой некоторые до сих пор используют ЭЛТ мониторы.
Электрические машины – генераторы и двигатели. Хотя здесь скорее действует сила Ампера. Но эти величины можно рассматривать как смежные. Однако это сложные устройства при работе которых наблюдается воздействие многих физических явлений.
В ускорителях заряженных частиц для того, чтобы задавать им орбиты и направления.

Заключение

Подведем итоги и обозначим четыре основных тезиса этой статьи простым языком:

Сила Лоренца действует на заряженные частицы, которые движутся в магнитном поле. Это вытекает из основной формулы.
Она прямо пропорциональна скорости заряженной частицы и магнитной индукции.
Не влияет на скорость частицы.
Влияет на направление частицы.

Материалы

Действие, оказываемое магнитным полем на движущиеся заряженные частицы, очень широко используют в технике.

Например, отклонение электронного пучка в кинескопах телевизоров осуществляют с помощью магнитного поля, которое создают специальными катушками. В ряде электронных приборов магнитное поле используется для фокусировки пучков заряженных частиц.

В созданных в настоящее время экспериментальных установках для осуществления управляемой термоядерной реакции действие магнитного поля на плазму используют для скручивания ее в шнур, не касающийся стенок рабочей камеры. Движение заряженных частиц по окружности в однородном магнитном поле и независимость периода такого движения от скорости частицы используют в циклических ускорителях заряженных частиц — циклотронах.

Действие силы Лоренца используют и в приборах, называемых масс-спектрографами , которые предназначены для разделения заряженных частиц по их удельным зарядам.

Схема простейшего масс-спектрографа показана на рисунке 1.

В камере 1, из которой откачан воздух, находится источник ионов 3. Камера помещена в однородное магнитное поле, в каждой точке которого индукция $~\vec B$ перпендикулярна плоскости чертежа и направлена к нам (на рисунке 1 это поле обозначено кружочками). Между электродами А ч В приложено ускоряющее напряжение, под действием которого ионы, вылетающие из источника, разгоняются и с некоторой скоростью попадают в магнитное поле перпендикулярно линиям индукции. Двигаясь в магнитном поле по дуге окружности, ионы попадают на фотопластинку 2, что позволяет определить радиус R этой дуги. Зная индукцию магнитного поля В и скорость υ ионов, по формуле

$~\frac q m = \frac {v}{RB}$

можно определить удельный заряд ионов. А если заряд иона известен, можно вычислить его массу.

Литература

Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 328.

Сила Ампера , действующая на отрезок проводника длиной Δl с силой тока I , находящийся в магнитном поле B ,

Выражение для силы Ампера можно записать в виде:

Эту силу называют силой Лоренца . Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика . Взаимное расположение векторов , и для положительно заряженной частицы показано на рис. 1.18.1.

Рисунок 1.18.1.

Взаимное расположение векторов , и Модуль силы Лоренца численно равен площади параллелограмма, построенного на векторах и помноженной на заряд q

Сила Лоренца направлена перпендикулярно векторам и

При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.

Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса

Период обращения частицы в однородном магнитном поле равен

называется циклотронной частотой . Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.

Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов ). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте . Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.

Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов , то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20 Ne и 22 Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S , проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей , в котором частицы движутся в скрещенных однородных электрическом и магнитном полях . Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и

На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца . При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B .

Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = m υ / qB» . Измеряя радиусы траекторий при известных значениях υ и B» можно определить отношение q / m . В случае изотопов (q 1 = q 2) масс-спектрометр позволяет разделить частицы с разными массами.

Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10 –4 .

Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ ┴ вектора а шаг спирали p – от модуля продольной составляющей υ || (рис. 1.18.5).

Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы , то есть полностью ионизированного газа при температуре порядка 10 6 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке ).

Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.

Контрольные вопросы

1.Опишите опыты Эрстеда и Ампера.

2.Что является источником магнитного поля?

3. В чем состоит гипотеза Ампера, объясняющая существования магнитного поля постоянного магнита?

4.В чем состоит принципиальное отличие магнитного поля от электрического?

5.Сформулируйте определение вектора магнитной индукции.

6. Почему магнитное поле называется вихревым?

7. Сформулируйте законы:

А) Ампера;

Б) Био-Савара-Лапласа.

8. Чему равен модуль вектора магнитной индукции поля прямого тока?

9. Сформулируйте определение единицы силы тока (ампера) в Международной системе единиц.

10. Запишите формулы, выражающую величину:

А) модуля вектора магнитной индукции;

Б) силы Ампера;

В) силы Лоренца;

Г) периода обращения частицы в однородном магнитном поле;

Д) радиуса кривизны окружности, при движении заряженной частицы в магнитном поле;

Тест для самоконтроля

Что наблюдалось в опыте Эрстеда?

1) Взаимодействие двух параллельных проводников с током.

2) Взаимодействие двух магнитных стрелок

3) Поворот. магнитной стрелки вблизи проводника при пропускании через него тока.

4) Возникновение электрического тока в катушке пнри вдвигании в нее магнита.

Как взаимодействуют два параллельных проводника, если по ним пропускают токи в одном направлении?

Притягиваются;

Отталкиваются;

Сила и момент сил равны нулю.

Сила равна нулю, но момент сил не равен нулю.

Какая формула определяет выражение модуля силы Ампера?

Какая формула определяет выражение модуля силы Лоренца?

Б)

В)

Г)

0,6 Н; 2) 1 Н; 3) 1,4 Н; 4) 2,4 Н.

1) 0,5 Тл; 2) 1 Тл; 3) 2 Тл; 4) 0,8 Тл.

Электрон со скоростью V влетает в магнитное поле с модулем индукции В перпендикулярно магнитным линиям. Какое выражение соответствует радиусу орбиты электрона?

Ответ: 1)
2)

4)

8. Как изменится период обращения заряженной частицы в циклотроне при увеличении её скорости в 2 раза? (V

1) Увеличится в 2 раза; 2) Увеличится в 2 раза;

3) Увеличится в 16 раз; 4) Не изменится.

9. Какой формулой определяется модуль индукции магнитного поля, созданного в центре кругового тока с радиусом окружности R ?

1)
2)
3)
4)

10. Сила тока в катушке равна I . Какой из формул определяется модуль индукции магнитного поля в середине катушки длиной l c числом витков N ?

1)
2)
3)
4)

Лабораторная работа №

Определение горизонтальной составляющей индукции магнитного поля Земли.

Краткая теория к лабораторной работе.

Магнитное поле это материальная среда, передающая так называемые магнитные взаимодействия. Магнитное поле является одной из форм проявления электромагнитного поля.

Источниками магнитных полей являются движущиеся электрические заряды, проводники с током и переменные электрические поля. Порождаясь движущимися зарядами (токами), магнитное поле, в свою очередь, действует только на движущиеся заряды (токи), на неподвижные же заряды оно действия не оказывает.

Основной характеристикой магнитного поля является вектор магнитной индукции :

Модуль вектора магнитной индукции численно равен максимальной силе, действующей со стороны магнитного поля на проводник единичной длины, по которому протекает ток единичной силы. Вектор образует правую тройку с вектором силы и направлением тока. Таким образом, магнитная индукция это силовая характеристика магнитного поля.

Единицей магнитной индукции в СИ является Тесла (Тл).

Силовыми линиями магнитного поля называются воображаемые линии, в каждой точке которых касательные совпадают с направлением вектора магнитной индукции. Магнитные силовые линии всегда замкнуты, никогда не пересекаются.

Закон Ампера определяет силовое действие магнитного поля на проводник с током.

Если в магнитное поле с индукцией помещен проводник с током, то на каждый направленный по току элемент проводника действует сила Ампера, определяемая соотношением

Направление силы Ампера совпадает с направлением векторного произведения
, т.е. она перпендикулярна плоскости, в которой лежат векторы и (рис.1).

Рис. 1. К определению направления силы Ампера

Если перпендикулярен , то направление силы Ампера можно определить по правилу левой руки: четыре вытянутых пальца направить по току, ладонь расположить перпендикулярно силовым линиям, тогда большой палец покажет направление силы Ампера. Закон Ампера положен в основу определения магнитной индукции, т.е. соотношение (1) следует из формулы (2), записанной в скалярном виде.

Сила Лоренца – это сила, с которой электромагнитное поле действует на движущуюся в этом поле заряженную частицу. Формула силы Лоренца была впервые получена Г. Лоренцем как результат обобщения опыта и имеет вид:

где
– сила, действующая на заряженную частицу в электрическом поле с напряженностью ;
– сила, действующая на заряженную частицу в магнитном поле.

Формулу для магнитной составляющей силы Лоренца можно получить из закона Ампера, учитывая, что ток – это упорядоченное движение электрических зарядов. Если бы магнитное поле не действовало на движущиеся заряды, оно не оказывало бы действия и на проводник с током. Магнитная составляющая силы Лоренца определяется выражением:

Направлена эта сила перпендикулярно плоскости, в которой лежат векторы скорости и индукции магнитного поля ; её направление совпадает с направлением векторного произведения
для q > 0 и с направлением
для q >0 (рис. 2).

Рис. 2. К определению направления магнитной составляющей силы Лоренца

Если вектор перпендикулярен вектору , то направление магнитной составляющей силы Лоренца для положительно заряженных частиц можно найти по правилу левой руки, а для отрицательно заряженных частиц по правилу правой руки. Так как магнитная составляющая силы Лоренца всегда направлена перпендикулярно скорости , то работы по перемещению частицы она не совершает. Она может лишь изменять направление скорости , искривлять траекторию движения частицы, т.е. выполнять роль центростремительной силы.

Закон Био-Савара-Лапласа служит для расчёта магнитных полей (определения ), создаваемых проводниками с током.

Согласно закону Био-Савара-Лапласа, каждый направленный по току элемент проводника создаёт в точке, находящейся на расстоянии от этого элемента, магнитное поле, индукция которого определяется соотношением:

где
Гн/м – магнитная постоянная;µ – магнитная проницаемость среды.

Рис. 3. К закону Био-Савара-Лапласа

Направление
совпадает с направлением векторного произведения
, т.е.
перпендикулярен плоскости, в которой лежат векторы и. Одновременно
является касательной к силовой линии, направление которой можно определить по правилу буравчика: если поступательное движение острия буравчика направить по току, то направление вращения рукоятки определит направление силовой линии магнитного поля (рис. 3).

Чтобы найти магнитное поле, создаваемое всем проводником, нужно применить принцип суперпозиции полей:

Например, вычислим магнитную индукцию в центре кругового тока (рис. 4).

Рис. 4. К расчёту поля в центре кругового тока

Для кругового тока
и
, поэтому соотношение (5) в скалярной форме имеет вид:

Закон полного тока (теорема о циркуляции магнитной индукции) является ещё одним законом для расчёта магнитных полей.

Закон полного тока для магнитного поля в вакууме имеет вид:

где B l – проекция на элемент проводника , направленный по току.

Циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром.

Теорема Остроградского-Гаусса для магнитного поля выглядит следующим образом:

где B n – проекция вектора на нормаль к площадке dS .

Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.

Характер магнитного поля следует из формул (9), (10).

Условием потенциальности электрического поля является равенство нулю циркуляции вектора напряженности
.

Потенциальное электрическое поле порождается неподвижными электрическими зарядами; силовые линии поля не замкнуты, начинаются на положительных зарядах и кончаются на отрицательных.

Из формулы (9) мы видим, что в магнитном поле циркуляция вектора магнитной индукции отлична от нуля, следовательно, магнитное поле потенциальным не является.

Из соотношения (10) следует, что магнитных зарядов, способных создавать потенциальные магнитные поля, не существует. (В электростатике аналогичная теорема тлеет вид
.

Магнитные силовые линии замыкаются сами на себя. Такое поле называется вихревым. Таким образом, магнитное поле – это вихревое поле. Направление силовых линий поля определяется правилом буравчика. У прямолинейного бесконечно длинного проводника с током силовые линии имеют вид концентрических окружностей, охватывающих проводник (рис. 3).

Почему одних ученых история вносит на свои страницы золотыми буквами, а некоторых стирает бесследно? Каждый пришедший в науку обязан оставить в ней свой след. Именно по величине и глубине этого следа судит история. Так, Ампер и Лоренц внесли неоценимый вклад в развитие физики, что дало возможность не только развивать научные теории, но получило весомую практическую ценность. Как появился телеграф? Что такое электромагниты? На все эти вопросы даст ответ сегодняшний урок.

Для науки представляют огромную ценность полученные знания, которые впоследствии могут найти свое практическое применение. Новые открытия не только расширяют исследовательские горизонты, но и ставят новые вопросы, проблемы.

Выделим основные открытия Ампера в области электромагнетизма.

Во-первых, это взаимодействия проводников с током. Два параллельных проводника с токами притягиваются друг к другу, если токи в них сонаправлены, и отталкиваются, если токи в них противонаправлены (рис. 1).

Рис. 1. Проводники с током

Закон Ампера гласит:

Сила взаимодействия двух параллельных проводников пропорциональна произведению величин токов в проводниках, пропорциональна длине этих проводников и обратно пропорциональна расстоянию между ними.

Сила взаимодействия двух параллельных проводников,

Величины токов в проводниках,

− длина проводников,

Расстояние между проводниками,

Магнитная постоянная.

Открытие этого закона позволило ввести в единицы измерения величину силы тока, которой до того времени не существовало. Так, если исходить из определения силы тока как отношения количества заряда перенесенного через поперечное сечение проводника в единицу времени, то мы получим принципиально не измеряемую величину, а именно количество заряда, переносимое через поперечное сечение проводника. На основании этого определения мы не сможем ввести единицу измерения силы тока. Закон Ампера позволяет установить связь между величинами сил тока в проводниках и величинами, которые можно измерить опытным путем: механической силой и расстоянием. Таким образом, получена возможность ввести в рассмотрение единицу силы тока — 1 А (1 ампер).

Ток в один ампер — это такой ток, при котором два однородных параллельных проводника, расположенных в вакууме на расстоянии один метрот друга взаимодействуют с силой Ньютона.

Закон взаимодействия токов — два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой, прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.

Еще одно открытие Ампера – это закон действия магнитного поля на проводник с током. Он выражается прежде всего в действии магнитного поля на виток или рамку с током. Так, на виток с током в магнитном поле действует момент силы, которая стремится развернуть этот виток таким образом, чтобы его плоскость стала перпендикулярна линиям магнитного поля. Угол поворота витка прямо пропорционален величине тока в витке. Если внешнее магнитное поле в витке постоянно, то значение модуля магнитной индукции также величина постоянная. Площадь витка при не очень больших токах также можно считать постоянной, следовательно, справедливо то, что сила тока равна произведению момента сил, разворачивающих виток с током, на некоторую постоянную при неизменных условиях величину.

– сила тока,

– момент сил, разворачивающих виток с током.

Следовательно, появляется возможность измерять силу тока по величине угла поворота рамки, которая реализована в измерительном приборе – амперметре (рис. 2).

Рис. 2. Амперметр

После открытия действия магнитного поля на проводник с током Ампер понял, что это открытие можно использовать для того, чтобы заставить проводник двигаться в магнитном поле. Так, магнетизм можно превратить в механическое движение – создать двигатель. Одним из первых, работающих на постоянном токе, был электродвигатель (рис. 3), созданный в 1834 г. русским электротехником Б.С. Якоби.

Рис. 3. Двигатель

Рассмотрим упрощенную модель двигателя, которая состоит из неподвижной части с закрепленными на ней магнитами – статора. Внутри статора может свободно вращаться рамка из проводящего материала, которая называется ротором. Для того чтобы по рамке мог протекать электрический ток, она соединена с клеммами при помощи скользящих контактов (рис. 4). Если подключить двигатель к источнику постоянного тока в цепь с вольтметром, то при замыкании цепи рамка с током начнет вращение.

Рис. 4. Принцип работы электродвигателя

В 1269 г. французский естествоиспытатель Пьер де Марикур написал труд под названием «Письмо о магните». Основной целью Пьера де Марикура было создание вечного двигателя, в котором он собирался использовать удивительные свойства магнитов. Насколько успешными были его попытки, неизвестно, но достоверно то, что Якоби использовал свой электродвигатель для того, чтобы привести в движение лодку, при этом ему удалось ее разогнать до скорости 4,5 км/ч.

Необходимо упомянуть еще об одном устройстве, работающем на основе законов Ампера. Ампер показал, что катушка с током ведет себя подобно постоянному магниту. Это значит, что можно сконструировать электромагнит – устройство, мощность которого можно регулировать (рис. 5).

Рис. 5. Электромагнит

Именно Амперу пришла идея о том, что, скомбинировав проводники и магнитные стрелки, можно создать устройство, которое предает информацию на расстояние.

Рис. 6. Электрический телеграф

Идея телеграфа (рис. 6) возникла в первые же месяцы после открытия электромагнетизма.

Однако широкое распространение электромагнитный телеграф приобрел после того, как Самюэль Морзе создал более удобный аппарат и, главное, разработал двоичную азбуку, состоящую из точек и тире, которая так и называется: азбука Морзе.

С передающего телеграфного аппарата с помощью «ключа Морзе», который замыкает электрическую цепь, в линии связи формируются короткие или длинные электрические сигналы, соответствующие точкам или тире азбуки Морзе. На приемном телеграфном аппарате (пишущий прибор) на время прохождения сигнала (электрического тока) электромагнит притягивает якорь, с которым жестко связано пишущее металлическое колесико или писец, которые оставляют чернильный след на бумажной ленте (рис. 7).

Рис. 7. Схема работы телеграфа

Математик Гаусс, когда познакомился с исследованиями Ампера, предложил создать оригинальную пушку (рис. 8), работающую на принципе действия магнитного поля на железный шарик – снаряд.

Рис. 8. Пушка Гаусса

Необходимо обратить внимание на то, в какую историческую эпоху были сделаны эти открытия. В первой половине XIX века Европа семимильными шагами шла по пути промышленной революции – это было благодатное время для научно-исследовательских открытий и быстрого внедрения их в практику. Ампер, несомненно, внес весомый вклад в этот процесс, дав цивилизации электромагниты, электродвигатели и телеграф, которые до сих пор находят широкое применение.

Выделим основные открытия Лоренца.

Лоренц установил, что магнитное поле действует на движущуюся в нем частицу, заставляя ее двигаться по дуге окружности:

Cила Лоренца — центростремительная сила, перпендикулярная направлению скорости. Прежде всего, открытый Лоренцем закон, позволяет определять такую важнейшую характеристику, как отношение заряда к массе — удельный заряд .

Значение удельного заряда — величина уникальная для каждой заряженной частицы, что позволяет их идентифицировать, будь то электрон, протон или любая другая частица. Таким образом, ученые получили мощный инструмент для исследования. Например, Резерфорд сумел провести анализ радиоактивного излучения и выявил его компоненты, среди которых присутствуют альфа-частицы — ядра атома гелия — и бета-частицы — электроны.

В ХХ веке появились ускорители, работа которых основана на том, что заряженные частицы ускоряются в магнитном поле. Магнитное поле искривляет траектории частиц (рис. 9). Направление изгиба следа позволяет судить о знаке заряда частицы; измерив радиус траектории, можно определить скорость частицы, если известны ее масса и заряд.

Рис. 9. Искривление траектории частиц в магнитном поле

На этом принципе разработан Большой адронный коллайдер (рис. 10). Благодаря открытиям Лоренца наука получила принципиально новый инструмент для физических исследований, открывая дорогу в мир элементарных частиц.

Рис. 10. Большой адронный коллайдер

Для того чтобы охарактеризовать влияние ученого на технический прогресс, вспомним о том, что из выражения для силы Лоренца вытекает возможность рассчитать радиус кривизны траектории частицы, которая движется в постоянном магнитном поле. При неизменных внешних условиях этот радиус зависит от массы частицы, ее скорости и заряда. Таким образом, получаем возможность классифицировать заряженные частицы по этим параметрам и, следовательно, можем проводить анализ какой-либо смеси. Если смесь веществ в газообразном состоянии ионизировать, разогнать и направить в магнитное поле, то частицы начнут двигаться по дугам окружностей с различными радиусами — частицы будут покидать поле в разных точках, и остается только зафиксировать эти точки вылета, что реализуется при помощи экрана, покрытого люминофором, который светится при попадании на него заряженных частиц. Именно по такой схеме работает масс-анализатор (рис. 11). Масс-анализаторы широко применяют в физике и химии для анализа состава смесей.

Рис. 11. Масс-анализатор

Это еще не все технические устройства, которые работают на основе разработок и открытий Ампера и Лоренца, ведь научное знание рано или поздно перестает быть исключительной собственностью ученых и становится достоянием цивилизации, при этом оно воплощается в различных технических устройствах, которые делают нашу жизнь более комфортной.

Список литературы

Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 416с.: ил., 8 л. цв. вкл.
Генденштейн Л.Э., Дик Ю.И., Физика 11. — М.: Мнемозина.
Тихомирова С.А., Яровский Б.М., Физика 11. — М.: Мнемозина.

Интернет-портал «Чип и Дип» ().
Интернет-портал «Киевская городская библиотека» ().
Интернет-портал «Институт дистанционного образования» ().

Домашнее задание

1. Касьянов В.А., Физика 11 кл.: Учебн. для общеобразоват. учреждений. — 4-е изд., стереотип. — М.: Дрофа, 2004. — 416с.: ил., 8 л. цв. вкл., ст. 88, в. 1-5.

2. В камере Вильсона, которая размещена в однородном магнитном поле с индукцией 1,5 Тл, альфа-частица, влетая перпендикулярно к линиям индукции, оставляет след в виде дуги окружности радиусом 2,7 см. Определите импульс и кинетическую энергию частицы. Масса альфа-частицы 6,7∙10 -27 кг, а заряд 3,2∙10 -19 Кл.

3. Масс-спектрограф. Пучок ионов, разогнанных разницей потенциалов 4 кВ, влетает в однородное магнитное поле с магнитной индукцией 80 мТл перпендикулярно линиям магнитной индукции. Пучок состоит из ионов двух типов с молекулярными массами 0,02 кг/моль и 0,022 кг/моль. Все ионы обладают зарядом 1,6 ∙ 10 -19 Кл. Ионы вылетают из поля двумя пучками (рис. 5). Найти расстояние между пучками ионов, которые вылетают.

4. * С помощью электродвигателя постоянного тока поднимают груз на тросе. Если отключить электродвигатель от источника напряжения и замкнуть ротор накоротко, груз будет опускаться с постоянной скоростью. Объясните это явление. В какую форму переходит потенциальная энергия груза?

Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Регистрация на конференцию «Проблемы безопасности на транспорте»

Регистрация на конференцию «Тихомировские чтения»

Как поступить в БелГУТ:

дневное, заочное полное,
заочное сокращенное

Как получить место

в общежитии БелГУТа

Как поступить иностранному гражданину

События

Все события

Пн	Вт	Ср	Чт	Пт	Сб	Вс
			1 Дата : 2022-09-01	2	3	4
5 Дата : 2022-09-05	6 Дата : 2022-09-06	7 Дата : 2022-09-07	8 Дата : 2022-09-08	9 Дата : 2022-09-09	10 Дата : 2022-09-10	11 Дата : 2022-09-11
12	13	14	15 Дата : 2022-09-15	16 Дата : 2022-09-16	17 Дата : 2022-09-17	18
19	20	21	22	23	24	25
26	27	28	29	30

Все анонсы

Матч по мини-футболу между БелГУТом и ГГТУ. ..
Велопробег «В единстве — сила»…
Логистика. Обучение для студентов выпускных курсов…
Акция «Мы едины» — поем гимн вместе…
ЕДИ «История белорусской государственности – основ…
Диалоговая площадка «Беларусь адзіная»…
Набор в студию рисунка и живописи…
Открытая лекция Быченко Олега Владимировича…
Квиз «Гісторыя майго жыцця»…
Набор в волонтерский сектор Студсовета…

Анонсы

Университет

Абитуриентам

Студентам

Конференции

Приглашения

Матч по мини-футболу между БелГУТом и ГГТУ…

Велопробег «В единстве — сила»…

Логистика. Обучение для студентов выпускных курсов…

Акция «Мы едины» — поем гимн вместе…

Новости

Университет

Международные связи

Спорт

Воспитательная работа

Жизнь студентов

Новости подразделений

Университет

Диалоговая площадка «Беларусь адзіная». ..
15 сентября 2022

Студенческая жизнь

Встреча секретаря БРСМ БелГУТа со студентами…
15 сентября 2022

Университет

Встреча ректора со студентами в студенческом городке…
15 сентября 2022

Университет

Проект студента востребован в городе
14 сентября 2022

Университет

Будущее Беларуси — в единстве
14 сентября 2022

Университет

Видео-репортаж Дня рождения Гомеля
13 сентября 2022

Воспитательная работа

Віктарына да Дня народнага адзінства
13 сентября 2022

Студенческая жизнь

Интервью с участниками открытия фестиваля «Сожскi карагод» и видео-реп. ..
13 сентября 2022

Спорт

Неделя спорта и здоровья
13 сентября 2022

Другие новости

Опубликован сборник материалов конференции «Водоснабжение, химия и при…
Студент БелГУТа из Марокко рассказывает об учебе в Беларуси…
БРСМ — всегда на помощь! День города Гомеля…
Новый номер газеты «Вести БелГУТа»
Республиканский легкоатлетический студенческий забег…
БелГУТ предлагает жилые помещения арендного использования…
С Днем рождения, Гомель!
Живой герб Гомеля на открытии «Сожскага карагода» …
Круглый стол «Вопросы подготовки специалистов в области правовой инфор…
Встреча первокурсников с инспектором по делам несовершеннолетних желез…
Атрымай асалоду ад роднай мовы

КУДА ПОСТУПАТЬ

Все факультеты

БелГУТ на Доске почета

Достижения университета

Предложения

Все предложения

Видеотека

Все видео

Фотогалерея

Все фото

Заряженные частицы в однородном магнитном поле

На этой странице вы узнаете

Почему “жизнь” одной частицы может измениться?
Какому правилу подчиняется движение частицы?
Больший физик из маленькой страны: о ком речь?

Мир атомов — это особый мир. Его не видно человеческим глазом, но он существует. В нем действуют свои правила. Каким законам он подчиняется?

Сила Лоренца

Жила-была одна частица. Хорошо жила, обычной жизнью. До тех пор, пока она не попала в магнитное поле… и тут-то ее жизнь завертелась. Стала действовать на нее некая сила. Частица хочет пойти прямо, а не получается. А что за сила такая? Это предстоит узнать.

Почему “жизнь” одной частицы может измениться?

При попадании заряженной частицы в магнитное поле, на нее действует сила Лоренца.

Если частица незаряженная или не движется в магнитном поле, то сила Лоренца не действует.

Обратимся к теории. На электрические заряды, движущиеся в магнитном поле, действует сила Лоренца. Модуль силы Лоренца F_Л численно равен:

$F_Л = |q| \nu B \sin \alpha$, где

|q| — модуль заряда частицы (Кл),
$\nu$— скорость частицы (м/с),
B — величина индукции магнитного поля (Тл),
$\alpha$— угол между вектором скорости и вектором индукции магнитного поля.

Единица измерения — Н (Ньютон)

Чем больше скорость частицы, тем большая сила на нее действует. Как же выбраться частице из круговорота событий?

Для начала нужно определиться: положительная у нас частица или отрицательная?

Сила Лоренца изменяет траекторию движения заряженных частиц: частицы разного знака отклоняются в разные стороны. Отсюда следует логика: сила будет менять своё направление в зависимости от направления магнитного поля.

Какому правилу подчиняется движение частицы?

Направление силы Лоренца определяют с помощью правила левой руки. Четыре пальца левой руки располагают по направлению движения положительно заряженной частицы (противоположно движению отрицательно заряженной частицы). При этом вертикальная составляющая вектора магнитной индукции входит в ладонь, тогда отогнутый на 90° большой палец покажет направление силы Лоренца.

Подробнее про применение правила левой руки можно прочитать в статье «Магнетизм и характеристики магнитного поля. 2m}{qB\nu} = \frac{m\nu}{qB}\)

Частица влетает под углом $\alpha$ к линиям магнитного поля с постоянной по модулю скоростью

$\nu_{\perp}$ и $\nu_{||}$— вертикальная и горизонтальная составляющие скорости,
q — заряд частицы,
B — индукция магнитного поля,
h — шаг спирали,
T — период обращения.

$\nu = \nu_{\perp} + \nu_{||}, h = \nu_{||}T$

Спастись от силы Лоренца и от экспериментов ученых наша частица смогла лишь тогда, когда стала двигаться параллельно линиям магнитного поля. Там перестала действовать на нее коварная сила.

Частица влетает параллельно к линиям магнитного поля.

Сила Лоренца равна нулю, так как $\sin 0 = 0$. Заряженная частица продолжит свое первоначальное движение, магнитное поле не будет отклонять движущийся заряд.

Равномерное и прямолинейное движение: $\nu = const$.

Большой физик из маленькой страны: о ком речь?

Хендрик Лоренц — ученый из Нидерландов. Именно он не давал покоя героине этой страницы, разгоняя до неимоверных скоростей.

Лоренц был гением в своей области. Хотя в раннем детстве его считали отстающим в развитии. Он внес неимоверный вклад в науку, но обладал скромным характером, и практически не печатался за рубежом. Весь мир узнал о его трудах в 19 веке и теперь каждый школьник изучает силу Лоренца.

Фактчек

Модуль силы Лоренца численно равен: $F_Л = |q| \nu B \sin \alpha$
Период обращения частицы: $T = \frac{2 \pi R}{\nu} = \frac{2 \pi m}{qB} = const$
Частота обращения частицы: $\omega = \frac{2 \pi}{T} = \frac{qB}{m}$

Проверь себя

Задание 1.
Сила Лоренца рассчитывается:

$F_Л = |q| \nu B \sin \alpha$
$F_Л = |q| B \sin \alpha$
$F_Л = |q| \nu \sin \alpha$
$F_Л = \nu B \sin \alpha$

Задание 2.
Какая сила будет действовать на электрон, движущийся в магнитном поле со скоростью 0,1 м/с, магнитной индукцией 5 Тл. Заряд электрона принять равной 1,6 * 10^-19 Кл?

0,08 * 10^-19 Н
0,8 * 10^-19 Н
8 * 10^-19 Н
1 * 10^-19 Н

Задание 3.
Период обращения частицы рассчитывается:

$T = \frac{2 \pi m}{qB}$
$T = \frac{2m}{qB}$
$T = \frac{2 \pi m}{q}$
$T = \frac{m}{qB}$

Задание 4.
Когда частица влетает параллельно к линиям магнитного поля, сила Ампера равна:

0
1
2
-1

Задание 5.
Когда частица влетает под углом $\alpha$ к линиям магнитного поля с постоянной по модулю скоростью, то траектория ее движения:

Прямая
Окружность
Спираль
Парабола

Ответы: 1.— 1; 2. — 2 ; 3. — 1; 4. — 1; 5. — 3

Единицы измерения Силы Ампера и… — Учеба и наука

Единицы измерения и обозначения Силы Ампера, Силы Лоренца, явления э.м. индукции и закона э.м. индукции?






Лучший ответ по мнению автора

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.
Закон э.м. индукции — сила индукционного тока проиорциональна скорости изменения магнитного потока через поверхность, ограниченную контуром:
Обе силы Лоренца (FЛ) и Ампера (FA) измеряются в ньютонах.
Возникнут вопросы — обращайтесь в чат)

17.10.13

Лучший ответ по мнению автора

Другие ответы

Как и любая сила — в Ньютонах (Н)

17.

10.13

Михаил Александров

Читать ответы

Андрей Андреевич

Читать ответы

✔Олеся / Математика

Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Физика

направление силы Лоренца

F = Bqvsine, здесь, поскольку сила находится под прямым углом к величине скорости и магнитному полю заряда, значение будет равно 90. Направление этой силы перпендикулярно току и магнитному полю. поле соответственно. Магнитная сила на заряде. Разве нельзя иметь другое электрическое поле, приходящее «сбоку»? Покажите направление силы Лоренца. Моя идея: силовые линии магнитного поля направлены к S от N. Силы Лоренца в точке b нет, потому что угол между током и силовыми линиями составляет 180°. Сила действует в направлении электрического поля. 4. Электрическое и магнитное поля зависят от скорости наблюдателя, поэтому релятивистская форма закона силы Лоренца может быть лучше всего представлена, исходя из независимого от координат выражения для электромагнитного и магнитного полей F и произвольного времени -направление, 0 . 7 Vd вниз На рисунке выше направление силы Лоренца, действующей на положительную частицу со скоростью v в B-поле, равно Submit Answer Попыток 0/2; Вопрос: На приведенном выше рисунке направление силы Лоренца, действующей на положительную частицу со скоростью v в B-поле, является ответом Компьютера, показанным сейчас. Каждое пятно разделения содержит информацию о магнитной индукции от доменов, в которых обнаружена намагниченность. В физике (в частности, в электромагнетизме) сила Лоренца (или электромагнитная сила) представляет собой комбинацию электрической и магнитной сил на точечный заряд из-за электромагнитных полей. движется ли водитель, описанный в нашем предыдущем примере, вправо или влево. . На частицу заряда q, движущуюся со скоростью v в электрическом поле E и магнитном поле B, действует сила (в единицах СИ [1] [2] ). Сила Абрахама-Лоренца является источником сопротивления излучения радиоантенны, излучающей радиоволны. 4: Сила Лоренца визуализируется как взаимодействие между магнитными трубками. Это называется законом силы Лоренца в честь голландского физика Хендрика Антона Лоренца, который первым сформулировал его. Сила Лоренца — это сила, с которой сталкивается заряд, движущийся в электромагнитном поле. B = вектор магнитного поля из-за магнитов, и он измеряется в единицах тесла. Поэтому нужно помнить, что большой палец правой руки, указывающий вверх, обозначает магнитное притяжение, а . Ваш большой палец теперь указывает в направлении магнитной силы. Сопоставьте направление пальцев с направлением магнитного поля. Давай откроем твою правую руку. Этот комбинированный закон сил известен как сила Лоренца. Когда электрон движется через электрическое поле E и магнитное поле B с вектором скорости v, к электрону прикладывается сила F, как показано на рисунке 3. Концепция: магнитная сила. Сила Лоренца, сила, действующая на заряженную частицу q, движущуюся со скоростью v через электрическое поле E и магнитное поле B. Направление силы Лоренца Когда через проводник, помещенный в магнитное поле, протекает ток, проводник вынужден двигаться. Сила Лоренца. Сила Лоренца – определение, формула, применение и часто задаваемые вопросы Сила Лоренца – это фундаментальная сила, действующая на электрический заряд с определенной скоростью в магнитном поле. Кроме того, если частица движется в направлении, параллельном B, снова F = 0. Решение Скорость частицы равна Из формулы магнитной силы Лоренца мы можем определить магнитное поле по величине силы. 2. Субатомные частицы в проводнике служат основой для магнитного поля. F = Сила на проводе, измеряемая в ньютонах I = Сила тока в проводе в амперах. 1. Посмотреть ответ. Сила Лоренца перпендикулярна как скорости, так и магнитному полю. Решение. Почему сила Лоренца действует в направлении векторного произведения? Сила, с которой сталкивается заряженная частица в электрическом, магнитном или обоих полях, называется силой Лоренца (сила, действующая на движущийся заряд). Она бывает двух типов; электрическая сила Лоренца и магнитная сила Лоренца. Сила Лоренца, которую движущийся электрон испытывает в электрическом и магнитном полях в электронных микроскопах, вызывает отклонение отрицательно заряженного электрона q (-e), обеспечивая физическую основу для электронных линз. Сила Лоренца может периодически изменять свою величину и направление, а пограничный слой . Если заряд положительный, то направление электрической силы совпадает с направлением электрического поля. Просмотрите все инструменты исследования. 5. На самом деле этот вклад направлений как раз подходит для перекрестного произведения: магнитная сила, действующая на заряд Q, движущийся со скоростью v в магнитном поле B, равна F mag =Q(vB) (5.1) (5.1) F m a g = Q ( v B) Это известно как закон силы Лоренца. Сила Лоренца отклоняет электроны, проходящие через образец, и разделяет каждое дифракционное пятно на два в задней фокальной плоскости объектива. Двигатель силы Лоренца соединен с механизмом управления с обратной связью, который позволяет контролировать и контролировать впрыск в реальном времени. Согните пальцы в направлении магнитного поля. Совместите большой палец с направлением тока. Найти силу Лоренца заряда 2,5 Кл с электрическим полем 5 ед. и магнитным полем 7,25 ед. со скоростью 1,5 м/с. Сила, действующая на проводник длиной 12 см с током 8А и плотностью потока 3,75 ед. под углом 300. Закон Гаусса Закон Фарадея Закон Ампера Закон силы Лоренца MCQ: электрическая сила Лоренца имеет направление, аналогичное электрическому полю, противоположное скалярной величине электрического поля Нет MCQ: сила электромагнитного поля сила Лоренца сила Ленца сила Гаусса, где e — заряд частицы, E — напряженность электрического поля, B — магнитная индукция, v — скорость заряженного . . Однако магнитная сила перпендикулярна как локальному магнитному полю, так и направлению движения частицы. Если частица с зарядом q движется со скоростью v в присутствии электрического поля E и магнитного поля B, то на нее будет действовать сила. Закон Лоренца — это закон, открытый голландским физиком Хендриком Антоном Лоренцем. из публикации: Новое. Движение ньютоновской частицы под действием электрического и магнитного полей зависит от силы Лоренца. Эта сила, известная как сила Лоренца, возникает из-за взаимодействия приложенного магнитного поля и магнитного поля, создаваемого движущейся частицей. Ток, текущий справа налево в проводнике, может быть результатом движения положительных носителей заряда справа налево или отрицательных зарядов, движущихся слева направо, или их комбинации. Формула для силы Лоренца F была впервые выведена Г. А. Лоренцем в результате обобщения опытов и имеет вид. Электрическая сила Лоренца. В первый член вносит вклад электрическое поле. Электрическое поле (E) в/м. Впервые он был выведен Дж. Дж. Томсоном в 1881 г. и некоторое время также рассматривался как динамическое объяснение инертной массы как таковой. Сегодня отношение массы, импульса, скорости и всех форм . Предыдущие попытки Ваша квитанция №. Закон силы Лоренца можно использовать для описания эффектов движения заряженной частицы в постоянном магнитном поле. Этот . Как и в правиле правой руки, пальцы указывают в направлении магнитного поля. \vec {F}_ {Лоренц} = q (\vec {E} + \vec {v}\times\vec {B}) F Лоренц = q(E + v B) Формула для этой силы была получена Лоренцем на основе тщательных экспериментов, проведенных Ампером и другими. Теперь формула силы Лоренца имеет вид: F L = F E + F B F L = qE + q (v B) F L = q {E + (v B)} .. (1) Уравнение (1) известно как уравнение силы Лоренца . Направление силы можно найти по правилу правой руки. Две другие кнопки («Обратный ток» и «Повернуть магнит») позволяют изменить направление тока. Однако магнитная сила перпендикулярна как локальному магнитному полю, так и направлению движения частицы. В пространстве Минковского — математической модели пространства-времени в специальной теории относительности — преобразования Лоренца сохраняют пространственно-временной интервал между любыми двумя событиями. . Ток через провод Поскольку электрический ток в проводе состоит из движущихся электронов, сила Лоренца также применяется к току в магнитном поле. Более точно мы можем узнать ниже. Направление силы Лоренца определяется по правилу правой руки: большой палец указывает в направлении тока, указательный палец — в направлении магнитного поля, а второй (средний) палец — в направлении действия силы. . Направление магнитного поля берется по оси z. В физике, особенно в электромагнетизме, сила Лоренца представляет собой комбинацию электрической и магнитной сил на точечный заряд из-за электромагнитных полей. Сила направлена в сторону рывка. Сила Лоренца относится к комбинации магнитной и электрической сил, которые действуют на точечный заряд из-за наличия электромагнитных полей. Кроме того, сила Лоренца также известна экспертам как электромагнитная сила. . Сила Лоренца — это сила, действующая на заряд в электромагнитном поле. сила Лоренца. Это правило описывает направление силы как направление «шлепка» открытой ладони. Мы также выполнили расчеты с перекрестным произведением и рассмотрели его различные приложения. Размеры в других направлениях не сокращаются. В результате указательный палец указывает в направлении силы Лоренца. Результаты расчета силы Лоренца (подробные расчеты и формула ниже) Сила Лоренца равна N [Ньютон] Расчет силы Лоренца. Узнайте, как рассчитать силу Лоренца и определить ее направление. 4. Сила Лоренца определяется как сила, действующая на заряженную частицу, движущуюся через электрическое поле и магнитное поле. Большой палец указывает в направлении движения положительного заряда. Перекрестное произведение 1. Эта демонстрация описывает влияние однородного магнитного поля в сочетании с однородным электрическим полем в произвольном направлении на траекторию заряженной частицы с учетом ее заряда, массы, начального положения и начальной скорости. Ваша ЛАДОНЬ (или средний палец, если хотите) теперь указывает в направлении СИЛЫ, F (конечный вектор). Сила ВСЕГДА будет перпендикулярна ПЛОСКОСТИ векторов v и B, независимо от угла. Узнайте, как. Вы можете видеть ровно три пальца, большой палец. сила, действующая на заряженную частицу, движущуюся в электромагнитном поле. Перекрестное произведение 2. Как следствие, ток $I$ течет в цепи в указанном направлении, против часовой стрелки. Рисунок 2: Правило правой руки. Правило левой руки и правило правой руки можно использовать для определения направления силы Лоренца, т.е. отметить направление магнитной силы в каждом случае. Электрическая сила равна q E, так что величина силы пропорциональна заряду и напряженности поля. . Bin down eft На рисунке выше направление силы Лоренца на a. Б. Сила Лоренца применима в телевизорах с электронно-лучевой трубкой. Недавно я также наткнулся на правило левой руки для силы Лоренца. Используя правую руку: укажите указательным пальцем в направлении скорости заряда v (вспомните обычный ток). Электрическая сила, действующая на заряженную частицу, параллельна локальному электрическому полю. F L = Q E + Q v B sin. При этом ваш большой палец будет находиться в направлении действия силы. Сила Лоренца является определением этих полей, и в F это F = q(E + v B), а в F . 152-3627? Когда заряженная частица движется через область, в которой присутствуют как электрические, так и магнитные поля, то результирующая сила, с которой сталкивается эта заряженная частица, представляет собой сумму электростатической силы и магнитной силы и называется силой Лоренца. Закон Лоренца определяет силу, действующую на движущиеся заряженные частицы в электромагнитном поле. Для отрицательных зарядов сделайте то же самое левой рукой. Скорость потока и сила Лоренца показаны зеленой и оранжевой стрелками соответственно. Чистая движущая сила, создаваемая в двигателе с силой Лоренца, зависит от протекания тока и магнитного поля. Что вы подразумеваете под сокращением Лоренца-Фитцджеральда? 2. Он формулируется как F = qE+qvB F = qE + qvB, где F обозначает силу Лоренца. Заряженная частица, движущаяся через магнитное поле, испытывает силу, которая находится под прямым углом к обоим направлениям, в которых частица движется и направление приложенного поля. Сила, действующая на электрический заряд «q» из-за обоих этих полей, определяется выражением F = q [E (r) + v B (r)] F = F elec + F mag . Сила, с которой сталкивается заряженная частица в электрическом поле, называется электрической силой Лоренца. Если $\overrightarrow{E}$ — напряженность электрического поля в определенной точке. Закон силы Лоренца. Его можно генерировать в электрических жидкостях при определенном расположении электродов и магнитов, при воздействии либо в продольном, либо в поперечном направлении. Само уравнение магнитной силы принимает несколько иную форму в единицах СИ: мы не включаем множитель 1/с, а вместо этого запишем силу F~ = q~v B .~ 90 Плейлист: https://youtube.com/playlist?list=PL3rItY3B29spBF0qRTtI8QXqmuz98KPYB Читать файлы. Тест: магнитная сила и сила Лоренца для электроники и техники связи (ECE) 2022 является частью подготовки к теории электромагнитных полей. 10.1.1 Единицы Закон магнитной силы, который мы привели, конечно же, выражен в единицах СГС, что соответствует системе Перселла. X — направление протекания тока, z — направление магнитного поля. Вопросы и ответы ( 2,392 ) Сила на проволоке есть. Контурный закон Ампре. Ответ (1 из 4): Сила Лоренца перпендикулярна как магнитному полю, так и скорости заряда из-за того, что —- «Заряженная частица, движущаяся параллельно или антипараллельно магнитному полю, не испытывает никакой силы». означает, что скорость и магнитное поле должны пересекать каждый o. Укажите средним пальцем в направлении магнитного поля, B. Электрическая сила, действующая на заряженную частицу, параллельна локальному электрическому полю. Вы можете включить (выключить) ток с помощью верхней кнопки («Вкл./Выкл.»). Хендрик Лоренц вывел современную формулу силы Лоренца в 189 г.5. Нам нужно будет использовать этот навык для применения различных формул в этом блоке. Что такое сила Лоренца на английском языке? Правило правой руки применяется при определении силы Лоренца. Направление этой силы перпендикулярно току и магнитному полю. Магнитное поле ( B) T. Угол между направлением движения и силовыми линиями магнитного поля ( ) рад. Силу, действующую на проводник, можно рассчитать, используя уравнение силы Лоренца. На заряженную частицу, движущуюся через магнитное поле, действует сила, направленная под прямым углом как к направлению движения частицы, так и к направлению приложенного поля. Закон силы Лоренца, примененный к этому примеру, дает следующую формулу: Где. Сила Лоренца и определение магнитного поля. Это вся электромагнитная сила, приложенная к заряженной частице. Если ток течет от — к +, применяется левое правило и наоборот от + к — для правого правила. Положительный заряд, движущийся вертикально через магнитные силовые линии, создает вокруг себя магнитное поле по правилу правой руки. Рисунок 3 — Пучок электронов, проходящий через магнитное поле, B, направленный из . Вычислите силу Лоренца, действующую на частицу (а), когда магнитное поле направлено в положительном направлении по оси y (б), когда магнитное поле направлено в положительном направлении по оси z (в), когда магнитное поле находится в плоскости zy и составляет угол со скоростью частица. Сила Лоренца определяется по формуле F = qv x B — q — величина заряда (кулона) — v — скорость (м/с) — B — плотность магнитного поля. Сила Лоренца определяется по формуле F = qv x B, где q — заряд, v — скорость, B — плотность магнитного поля. Более точно мы можем узнать ниже. Сила заряда за счет их влияния впервые была указана Х. А. Лоренцем. Уравнение силы Лоренца подразумевает, что если скорость частицы равна нулю (v = 0), то F = 0. Это может включать вращение пространства; преобразование Лоренца без вращения называется бустом Лоренца. На рис. 4 ниже показан получившийся эффект. Как показано на рисунке 4, с изменением плотности тока в модели сила Лоренца в направлении r в модели сначала увеличивается вдоль отрицательного направления r. После достижения пика. Первоначальный ответ: Как определяется направление силы Лоренца? Рис. Магнитное поле, создаваемое проводником с током, определяется силой тока проводника и расстоянием от точки. Как только ток начинает течь, проводник с током будет испытывать силу, поскольку он погружен в магнитное поле. а) 390,68. б) 68,39. в) 86,93. г) 93,68. Как всегда, вы должны оценивать цитату в контексте. Bin down eft На приведенном выше рисунке направление силы Лоренца, действующей на положительную частицу со скоростью v в B-поле, равно ; Вопрос: Vright down ‘down На приведенном выше рисунке направление силы Лоренца, действующей на положительную частицу со скоростью v в B-поле, равно . Следовательно, переставляя формулу в соответствии со значениями, мы получаем окончательную формулу как Сила состоит из магнитной силы и электрической силы. Как показывает правило правой руки, большой палец показывает направление силы, действующей на положительный заряд. Откроем правую руку. Что такое сила Лоренца класса 12? 142 ответа сообщают «Подмастерье» Лоренц Форс Драйв. Lorentz Force Вопросы и ответы Проверьте свое понимание с практическими задачами и пошаговыми решениями. z — направление электронного луча, x — направление в . В статье Британской энциклопедии предложение перед вашей цитатой. Направление силы Лоренца перпендикулярно направлению движущегося заряда и магнитного поля. (Тесла) Сила Лоренца перпендикулярна как скорости, так и магнитному полю. Физика В школе мы узнали, что сила Лоренца действует на движущийся заряд, который распространяется через магнитное поле. Объясняет, как определить направление силы, действующей на заряженную частицу, движущуюся через магнитное поле. Уловка, позволяющая предсказать направление силы Лоренца, — это правило правой руки. Линии этого поля горизонтальны, там же, где и силовые линии магнита. Направление этой силы определяется силой Лоренца, которая определяет, как движущийся заряд во внешнем магнитном поле будет испытывать силу. Сила Лоренца, обусловленная электрическим и магнитным полями Сила Лоренца — это сила, ощущаемая частицей с зарядом q q, движущейся со скоростью \vec {v} v через область с электрическим полем \vec {E} E и магнитным полем \ век {B}. Практика: Направление креста. Электричество + магнетизм = движение благодаря силе Лоренца. Правило правой руки полезно для визуализации того, как работает сила Лоренца. MCQ: Закон, управляющий взаимодействием электромагнитного поля с заряженным веществом. Этот Java-апплет демонстрирует силу Лоренца, действующую на качание проводника с током в магнитном поле подковообразного магнита. Например, в циклотроне, где рывок направлен против скорости, реакция излучения направлена против скорости частицы, оказывая тормозящее действие. Почему БАК не использует дополнительное электрическое поле для искривления своих лучей вместо того, чтобы полагаться на магниты и силу Лоренца? Сокращение Лоренца-Фитцджеральда, также называемое сжатием пространства, в физике относительности — сокращение объекта вдоль направления его движения относительно наблюдателя. 1. F = Fe + Fm F = E Q + Q (V B) Это уравнение известно как уравнение силы Лоренца. Эта сила, известная как сила Лоренца, возникает из-за взаимодействия приложенного магнитного поля и магнитного поля, создаваемого движущейся частицей. Давайте решим некоторые задачи, чтобы лучше понять, как вычислить направление перекрестного произведения/векторного произведения любых двух векторов. Это уравнение приведено выше. Сила Лоренца — новое активное устройство управления потоком, основанное на электромагнетизме. Полная электромагнитная сила F, действующая на заряженную частицу, называется силой Лоренца (в честь голландского физика Хендрика А. Лоренца) и определяется выражением F = qE + qv B. Благодаря магнитной силе частица. Тест: Магнитная сила и сила Лоренца Вопросы и ответы были подготовлены в соответствии с программой экзамена по электронике и технике связи (ECE). MCQ Тест: Магнитная сила и сила Лоренца предназначены для электроники и электроники. Пояснение: Сила Лоренца описывает силу, действующую на заряд, движущийся через электромагнитное поле. Сила Лоренца подтверждает наблюдение, что движение метастержня через магнитное поле вызывает разность потенциалов на концах стержня. Это называется законом силы Лоренца в честь голландского физика Хендрика Антона Лоренца, который первым сформулировал его. Направление поля такое. Сила Лоренца объясняет уравнения математической природы наряду с физическим значением сил, действующих на заряженные частицы. Ваш большой палец будет указывать в направлении силы. Специалисты определяют силу Лоренца как комбинацию магнитной и электрической сил. Используя правило левой руки, мы находим, что в точке h сила Лоренца входит «в» бумагу, а в правую часть h сила Лоренца выходит из бумаги. Примечание. Все буквы, выделенные жирным шрифтом, являются векторами. (Конечно, ток состоит из электронов с отрицательной проводимостью, движущихся . Скорость движущегося заряда ( v ) м/с. Уравнение силы Лоренца описывает силу, действующую на частицу с зарядом q со скоростью v, движущуюся в электрическом поле E и магнитное поле B : F = q E + q v B. 3. Преобразование Лоренца является линейным преобразованием. Кроме того, эта сила действует на точечный заряд из-за электромагнитного поля. Электромагнитная масса изначально была понятием классической механики, обозначающим как сколько электромагнитного поля или собственной энергии вносит вклад в массу заряженных частиц.Для простоты, посмотрите на бесконечно малый импульс Лоренца в направлении x (исследуя импульс в любом другом направлении или вращение вокруг любой оси, следует идентичная процедура). : сила, действующая на движущуюся заряженную частицу в электрическом и магнитном полях. Если движущийся заряд присутствует как в электрическом поле, так и в магнитном поле, то сила, действующая на заряд в проводнике, известна как сила Лоренца. .

Рубашки поло для гавайского гольфа, Сколько процентов требуется для обучения в США, Каталог запасных частей Bajaj Pulsar 150 Twin Disc Pdf, Лучшее дорожное зарядное устройство для нескольких устройств, Платежная система Клевер, Бета-версия Forge Of Empires,

Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле

Цели обучения

К концу этого раздела вы сможете:

Описать влияние магнитных полей на движущиеся заряды.
Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
Рассчитайте магнитную силу, действующую на движущийся заряд.

Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.

Правило правой руки 1

Действие магнитного поля на движущийся заряд является одним из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы F на заряд Q Перемещение на скорости V в магнитном поле прочности B приведен

F = QVB SIN θ ,

, где θ — это угол между направлением V. v и B. Эту силу часто называют силой Лоренца . Фактически именно так мы определяем напряженность магнитного поля B — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля B называется tesla (T) в честь эксцентричного, но гениального изобретателя Николы Теслы (1856–1943). Чтобы определить, как тесла относится к другим единицам СИ, мы решаем F = qvB sin θ для B .

[латекс]B=\frac{F}{qv \sin\theta}\\[/latex]

Поскольку sin θ безразмерно, тесла равен

[латекс]1\текст{ T}= \frac{1\text{ N}}{\text{ C}\cdot\text{ м/с}}=\frac{1\text{ N}}{\text{A}\cdot\text{ м} }\\[/латекс]

(обратите внимание, что C/s = A). Иногда используется другая меньшая единица, называемая гаусс (G), где 1 G = 10 ⁻⁴ Тл. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5 × 10 ⁻⁵ Тл, или 0,5 Гс.

, как определено правило правой руки 1 (или RHR-1 ), которое показано на рисунке 1. RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении v , пальцы в направлении B , а перпендикуляр к ладони указывает в направлении F . Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.

Рис. 1. Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной v и B, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна q, v, B и синусу угла между v и B.

Соединения: заряды и магниты

На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.

Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне

За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рисунке 2.)

Рис. 2. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, испытывает силу, направленную строго вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.

Стратегия

Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F = qvB sin θ , чтобы найти силу.

9{-11}\text{ N}\end{массив}\\[/latex].

Обсуждение

Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. (Оно вычисляется только с точностью до одной цифры, поскольку поле Земли меняется в зависимости от местоположения и выражается только одной цифрой.) Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».

Резюме раздела

Магнитные поля воздействуют на движущийся заряд силой q , величина которой равна
F = qvB sin θ ,
, где θ — угол между направлениями v и B .
Единицей измерения напряженности магнитного поля в системе СИ B является тесла (Т), которая связана с другими единицами соотношения
[латекс]1\текст{ T}=\frac{1\text{ N}}{\text{ C}\cdot\text{ м/с}}=\frac{1\text{ N}}{\ текст{A}\cdot\text{м}}\\[/латекс]
Направление силы на движущийся заряд задается правилом правой руки 1 (RHR-1): Укажите большой палец правой руки в направлении v , пальцы в направлении B , а перпендикуляр к ладони указывает в направлении F .
Сила перпендикулярна плоскости, образованной v и B . Поскольку сила равна нулю, если v параллельно B , заряженные частицы часто следуют за силовыми линиями магнитного поля, а не пересекают их.

Концептуальные вопросы

1. Если заряженная частица движется прямолинейно через некоторую область пространства, можете ли вы сказать, что магнитное поле в этой области обязательно равно нулю?

Задачи и упражнения

1. Каково направление магнитной силы, действующей на положительный заряд, который движется так, как показано в каждом из шести случаев, показанных на рисунке 3?

Рисунок 3.

2. Повторите упражнение 1 для отрицательного заряда.

3. Каково направление скорости отрицательного заряда, на который действует магнитная сила, показанная в каждом из трех случаев на рисунке 4, если предположить, что он движется перпендикулярно B ?

Рисунок 4.

4. Повторите рисунок 4 для положительного заряда.

5. Каково направление магнитного поля, которое создает магнитную силу на положительном заряде, как показано в каждом из трех случаев на рисунке ниже, при условии, что B перпендикулярно v ?

Рисунок 5.

6. Повторите упражнение 5 для отрицательного заряда.

7. Какова максимальная сила на алюминиевом стержне с зарядом 0,100 мкКл, которую вы пропускаете между полюсами постоянного магнита 1,50 Тл со скоростью 5,00 м/с? В каком направлении сила?

8. (a) Самолеты иногда приобретают небольшие статические заряды. Предположим, что сверхзвуковая струя имеет заряд 0,500 мкКл и летит строго на запад со скоростью 660 м/с над южным магнитным полюсом Земли, где 8,00 × 10 ⁻⁵ -T магнитное поле направлено прямо вверх. Каковы направление и величина магнитной силы на плоскости? (b) Обсудите, подразумевает ли значение, полученное в части (а), это значительный или незначительный эффект.

9. (a) Протон космического луча, движущийся к Земле со скоростью 5,00 × 10 ⁷, испытывает магнитную силу 1,70 × 10 ⁻¹⁶ Н. Какова напряженность магнитного поля, если существует угол 45º между ней и скоростью протона? (b) Соответствует ли значение, полученное в части (а), известной напряженности магнитного поля Земли на ее поверхности? Обсуждать.

10. На электрон, движущийся со скоростью 4,00 × 10 ³ м/с в магнитном поле 1,25 Тл, действует магнитная сила 1,40 × 10 ⁻¹⁶ Н. Какой угол образует скорость электрона с магнитной поле? Есть два ответа.

11. (a) Физик, выполняющий чувствительные измерения, хочет ограничить магнитную силу движущегося заряда в своем оборудовании менее чем 1,00 × 10 ⁻¹² Н. Какой максимальной может быть заряд, если он движется со скоростью максимальная скорость 30,0 м/с в поле Земли? (b) Обсудите, будет ли трудно ограничить заряд меньше значения, найденного в (а), сравнив его с типичным статическим электричеством и отметив, что статическое электричество часто отсутствует.

Глоссарий

Правило правой руки 1 (RHR-1):: правило для определения направления магнитной силы на положительно движущийся заряд: когда большой палец правой руки указывает направление скорости заряда v а остальные пальцы указывают направление магнитного поля B , тогда сила на заряде перпендикулярна и направлена от ладони; сила на отрицательный заряд перпендикулярна и направлена на ладонь

сила Лоренца:: сила, действующая на заряд, движущийся в магнитном поле

тесла:: Тл — единица напряженности магнитного поля в системе СИ; [латекс]1\текст{Т}=\фрак{1\текст{N}}{\текст{А}\cdot\текст{м}}\\[/латекс]

магнитная сила:: сила, действующая на заряд при его движении через магнитное поле; сила Лоренца

Гаусс:: Гс — единица напряженности магнитного поля; 1 г = 10 ^–4 Т

Избранные решения задач и упражнения

1. (a) Влево (запад) (b) Вглубь страницы (c) Вверх (север) (d) Нет силы (e) Вправо (восток) (f) Вниз (юг) )

3. (a) Восток (справа) (b) На страницу (c) Юг (вниз)

5. (a) На страницу (b) Запад (слева) (c) За пределы страницы

7. 7,50 × 10 ⁻⁷ Н перпендикулярно обеим силовым линиям магнитного поля и скорости

9. (а) 3,01 × 10 ⁻⁵ Тл (б) Это немного меньше напряженности магнитного поля 5 × 10 ⁻⁵ Тл на поверхности Земли, поэтому оно соответствует.

10. (a) 6,67 × 10 ⁻¹⁰ Кл (считая поле Земли равным 5,00 × 10 ⁻⁵ Тл) (b) Меньше, чем типичная статическая, поэтому трудная

Сила Лоренца — Назначение точки

Сила Лоренца

Определение

Сила Лоренца — это закон физики, в частности, электромагнетизма, который описывает силовое взаимодействие между магнитными полями двух заряженных частиц. Он был назван в честь Хендрика Лоренца, голландского физика 1800-х годов, который проявлял большой интерес к науке об электромагнетизме. На частицу с зарядом q, движущуюся со скоростью v в присутствии электрического поля E и магнитного поля B, действует сила

F = qE + qv × B

Где B — напряженность магнитного поля, E — электрическое поле, q — заряд частицы и v — скорость частицы. Выражается в «Ньютонах» как единица измерения. Согласно этому уравнению, если частица с зарядом q движется со скоростью v в присутствии электрического поля Е и магнитного поля В, то на нее будет действовать реактивная сила. Эта реактивная сила известна как сила Лоренца.

Все заряженные частицы сталкиваются с силой со стороны электрического поля, ориентированной по направлению поля или в противоположном направлении, в зависимости от знака заряда, при этом движущиеся заряженные частицы также сталкиваются с силой, направленной под прямым углом к обоим направление движения и магнитное поле. Сила Лоренца является движущей силой в электромагнитах и отвечает за эффект Холла.

Уравнение силы Лоренца фактически было получено из знаменитого уравнения Максвелла. Существуют вариации этого основного уравнения силы Лоренца. Другие уравнения, которые можно найти в других учебниках, описывают магнитную силу, действующую на провод с током, электродвижущую силу в проволочной петле, движущейся через магнитное поле, и силу, действующую на заряженную частицу, которая может двигаться со скоростью, близкой к скорости света. .

Значение силы Лоренца

В то время как современные уравнения Максвелла описывают, как электрически заряженные частицы и токи или движущиеся заряженные частицы порождают электрические и магнитные поля, закон силы Лоренца дополняет эту картину, описывая силу, действующую на движущийся точечный заряд q в присутствии электромагнитных полей. Закон силы Лоренца описывает действие E и B на точечный заряд. Заряженные частицы, возможно, связаны с другими силами, особенно гравитацией и ядерными силами. Таким образом, уравнения Максвелла не стоят отдельно от других физических законов, а связаны с ними через плотности заряда и тока. Реакция точечного заряда на закон Лоренца — это один аспект; генерация E и B токами и зарядами — другое. Заряженные частицы в материальной среде не только реагируют на поля Е и В, но и генерируют эти поля. Сложные транспортные уравнения должны быть решены, чтобы определить временную и пространственную реакцию зарядов.

Уравнения силы Лоренца

Сила F, действующая на частицу электрического заряда q с мгновенной скоростью v под действием внешнего электрического поля E и магнитного поля B, определяется по формуле:

F = q( E+v × B)

Положительно заряженная частица будет ускоряться в той же линейной ориентации, что и поле E, но будет искривляться перпендикулярно как вектору мгновенной скорости v, так и полю B в соответствии с правой Правило руки, в частности, если пальцы правой руки вытянуты, чтобы указывать в направлении v, а затем согнуты, чтобы указывать в направлении B, то вытянутый большой палец будет указывать в направлении F.

Член qE называется электрической силой, а член qv × B называется магнитной силой. Согласно некоторым определениям, термин «сила Лоренца» относится именно к формуле магнитной силы, а полная электромагнитная сила (включая электрическую силу) имеет другое (нестандартное) название. Эта статья не будет следовать этой номенклатуре: в дальнейшем термин «сила Лоренца» будет относиться только к выражению для полной силы.

Для непрерывного распределения заряда в движении уравнение силы Лоренца принимает вид:

dF = dq(E +v × B)

Где dF — сила, действующая на небольшой участок распределения заряда с зарядом dq. Если обе части этого уравнения разделить на объем этой небольшой части распределения заряда dV, результат будет: — плотность силы (сила на единицу объема), а ρ — плотность заряда (заряд на единицу объема).

Определение E и B (Закон силы Лоренца)

Закон силы Лоренца используется для определения электрических и магнитных полей E и B. Конкретно, сила Лоренца понимается как следующее эмпирическое утверждение :

Электромагнитная сила F, действующая на пробный заряд в данную точку и время, является некоторой функцией его заряда q и скорости v, которая может быть параметризована ровно двумя векторами E и B, в функциональной форме: F =q (Э + v × B)

Как определение E и B, сила Лоренца является только определением в принципе, потому что реальная частица будет генерировать свои собственные конечные поля E и B, которые изменят электромагнитную силу, с которой она сталкивается. . Кроме того, если заряд испытывает ускорение, как бы вынужденное какой-то внешней силой выйти на кривую траекторию, он испускает излучение, вызывающее торможение его движения. См., например, тормозное излучение и синхротронный свет. Эти эффекты происходят как через прямое воздействие, так и через косвенное. Более того, результирующая сила должна включать в себя гравитацию, электрослабую и любые другие силы помимо электромагнитной силы.

Как определить его направление и понять формулу

Уровень 2 (без высшей математики)

Уровень 2 требуется школьная математика. Подходит для школьников.

Обновлено Александром Фуфаевым 16.01.2022

Содержание

Заряд движется ортогонально магнитному полю Как действует сила Лоренца, когда электрон движется под углом 90 градусов в B-поле?
Заряд движется ПОД УГЛОМ относительно магнитного поля
Заряд движется ПАРАЛЛЕЛЬНО магнитному полю

Видео — сила Лоренца просто объясняется за 6 минут!

Воспроизвести видео: Keynote (Google I/O ’18)

Сила Лоренца $ F $ — это сила, с которой сталкивается частица в электромагнитном поле. Математически сила Лоренца представляет собой сумму электрических сил $ \class{gray}{F_{\text e}} $ и магнитных сил \( \class{green}{F_{\text m}} \ ).

Сила Лоренца как сумма электрической и магнитной сил

Якорь формулы $$ \begin{align} F ~=~ \class{grey}{F_{\text e}} ~+~ \class{green}{F_{\text m}} \end{align} $$

В этом уроке мы рассматриваем только случай, когда электрическая сила, действующая на частицу, равна нулю: $ \class{gray}{F_{\text e}} = 0 $. Частица находится только в магнитном поле, но НЕ в электрическом поле.

Если частица (например, электрон) с зарядом $q$ и скоростью $\class{blue}{v} $ движется через магнитное поле $ \class{violet}{B} $, то на него действует магнитная сила $\class{green}{F_{\text m}}$ ( сила Лоренца ).

В принципе может быть 3 случая как заряд может двигаться. Заряд движется…

перпендикулярно магнитному полю : $ \class{blue}{v} $ ⊥ $ \class{violet}{B} $
параллельно магнитное поле : $ \class{blue}{v} $ || $ \класс{фиолетовый}{B} $
под углом к магнитному полю : $ \угол \влево( \класс{синий}{v},~\класс{фиолетовый}{B} \вправо) $.

Заряд движется ортогонально магнитному полю

В эксперименте мы находим, что и заряд, и скорость, и магнитное поле пропорциональны силе Лоренца . Итак, мы можем записать уравнение, с помощью которого мы можем рассчитать силу Лоренца, действующую на частицу:

Формула: сила Лоренца на заряд (перпендикулярное движение)

Якорь формулы $$ \begin{align} \class{green}{F} ~=~ q \, \class{blue}{v} \, \class{violet}{B} \end{align} $ $

Из формулы можно вывести три важные сведения. Чтобы сила Лоренца $ \class{green}{F} $ вообще проявилась на частице, должны выполняться следующие свойства:

Частица должна двигаться , иначе скорость blue}{v} ~=~ 0\) и, следовательно, также сила Лоренца:
сила Лоренца — когда скорость равна нулю
Якорь формулы $$ \begin{align} \class{green}{F} ~=~ q ~\cdot~ \class{blue}{0} ~\cdot~ \class{violet}{B} ~= ~ 0 \end{align} $$
Частица должна быть электрически заряжена — нейтральные частицы (например, нейтроны) имеют заряд $q = 0$ и, следовательно, не испытывают силы Лоренца:
Сила Лоренца на нейтральных частицах
Якорь формулы $$ \begin{align} \class{green}{F} ~=~ 0 ~\cdot~ \class{blue}{v} ~\cdot~ \class{violet}{B } ~=~ 0 \end{align} $$
Частица должна находиться в магнитном поле — если частица не движется через магнитное поле: $ \class{violet}{B} = 0 $, то на нее не действует сила Лоренца:
Сила Лоренца — когда магнитное поле равно нулю
Якорь формулы $$ \begin{align} \class{green}{F} ~=~ q ~\cdot~ \class{blue}{v} ~\cdot ~ \class{violet}{0} ~=~ 0 \end{align} $$
Сила Лоренца также равна нулю, если частица движется параллельно к силовым линиям магнитного поля. Но об этом позже.

Причина силы Лоренца

Причиной силы Лоренца является движущийся заряд в магнитном поле.

Определить направление силы Лоренца

Когда положительный заряд движется через однородное магнитное поле, перпендикулярное направлению движения (см. рис. 1), положительный заряд в магнитном поле отклоняется вверх. Сила Лоренца действует на частицу снизу вверх.

Положительный заряд в магнитном поле (в плоскость) отклоняется вверх.

Если отрицательный заряд движется через однородное магнитное поле, перпендикулярное направлению движения (см. рис. 2), то отрицательный заряд отклоняется вниз. Сила Лоренца действует на частицу сверху вниз.

Отрицательный заряд в магнитном поле (в плоскость) отклоняется вниз.

Как определить направление силы Лоренца?

Или, другими словами, как я узнаю, что заряд будет отклонен вниз или вверх? Для этого вы используете так называемое правило левой руки .

Для положительных зарядов используйте правую руку. Для отрицательных зарядов вы используете левую руку.

Правило левой руки для отрицательных зарядов. Правило правой руки для положительных зарядов.

Большой палец — указывает в направлении движения заряда, то есть в направлении скорости $ \class{blue}{v} $.
Указательный палец — указывает направление магнитного поля $ \class{violet}{B} $ (к южному полюсу магнита).
Средний палец — указывает направление отклонения, т. е. направление силы Лоренца $ \class{green}{F_{\text m}} $, если вы правильно выровняли пальцы (как показано на рисунке 3 или 4).

Однако электрический заряд не просто отклоняется вниз или вверх, происходит что-то еще — при условии, что мы даем заряду достаточно места внутри магнитного поля.

Поскольку сила Лоренца $ \class{green}{F_{\text m}} $ всегда перпендикулярна скорости $ \class{blue}{v} $ (это диктует природа), заряд вынужден по круговой траектории !

Заряд движется по окружности, потому что скорость и сила Лоренца находятся под углом 90 градусов друг к другу.

Знаете ли вы, какая сила удерживает частицу на круговой траектории? Центростремительная сила $ F_{\text z} $!

Формула: центростремительная сила 92}{r} \end{align} $$

Здесь $ \class{brown}{m} $ — масса частицы и $r$ — радиус кругового пути . В этом случае сила Лоренца берет на себя роль центростремительной силы. Другими словами: сила Лоренца ЯВЛЯЕТСЯ здесь в то же время и центростремительной силой.

Формула qvB 2 для одной только силы Лоренца нам мало поможет, потому что экспериментально определить скорость $ \class{blue}{v} $ заряда непросто. Однако с центростремительной силой эта задача становится намного проще, потому что мы можем использовать ее, чтобы сформулировать уравнение для скорости. 92}{r} \end{align} $$

Вы можете отменить скорость $ \class{blue}{v} $ один раз с обеих сторон, чтобы она исчезла с левой стороны:

Лоренц сила равна центростремительной силе с уменьшенной скоростью

Якорь формулы $$ \begin{align} q \, \class{violet}{B} ~=~ \frac{\class{brown}{m} \, \class{blue }{v}}{r} \end{align} $$

Приведите радиус $r$ к другой стороне (умножьте обе стороны на $r$). И перенесите массу $ m $ на другую сторону (разделите обе стороны на $ \class{brown}{m} $), тогда вы получите формулу для скорости \( \class{blue}{v} \ ):

Формула: Скорость частицы

Якорь формулы $$ \begin{align} \class{blue}{v} ~=~ \frac{ q \, \class{violet}{B} \, r } { \class{brown}{m} } \end{align} $$

Конечно, вы также можете рассчитать радиус кругового пути, приравняв центростремительную силу и силу Лоренца:

Формула: Радиус кругового пути путь

Якорь формулы $$ \begin{align} r ~=~ \frac{\class{brown}{m} \, \class{blue}{v}}{q \, \class{violet}{B }} \end{выравнивание} $$

Формула 10 раскрывает два интересных факта:

Чем больше скорость $ \class{blue}{v} $ и масса $ \class{brown}{m} $ частицы, больше и есть пройденный круг.
Чем больше внешнее магнитное поле $ \class{violet}{B} $ и электрический заряд $ q $ частицы, тем меньше пройденный круг.

Электрон, выпущенный из пушки, проходит круговой путь. Сила Лоренца направлена в центр окружности.
Еще один интересный вопрос, который мы можем себе задать:
Сколько времени нужно частице, чтобы совершить ровно ОДИН круговой путь?
Время, которое требуется частице, чтобы совершить ровно один оборот, равно периоду $T$.
Расстояние, пройденное частицей за это время, равно длине окружности $ U = 2\,\pi\,r $ окружности. Расстояние $U$ ЗА время $ T $ точно равно скорости $ \class{blue}{v}$:
Длина окружности, деленная на период, равна скорости
Якорь формулы $$ \begin{align} \frac{2 \, \pi \, r}{T} ~=~ \class{blue}{v} \end{align} $$
Подставляем только скорость из 9 в 11 и переписываем уравнение для периода $ T $:
Формула: Период кругового движения
Формула якоря $$ \begin{align } T ~=~ 2 \, \pi \frac{ \class{brown}{m} }{ |q| \, \class{violet}{B} } \end{align} $$
Здесь мы использовали величину $ | q | $ заряда (т. е. без знака), чтобы не было соблазна использовать отрицательный заряд. Потому что тогда мы получили бы отрицательное время, что не имеет смысла.
Отсюда мы можем легко вычислить частоту $ f $, с которой движется частица. Частота указывает число оборотов в секунду и является обратной величиной периода $ T $: $ f = \ frac {1} {T} $. Для этого поменяйте местами знаменатель с числителем в обеих частях уравнения. 12 и вы получите частоту:
Формула: Частота кругового движения
Якорь формулы $$ \begin{align} f ~=~ \frac{1}{2\pi} \, \frac{ | д | \, \class{violet}{B} }{ \class{brown}{m} } \end{align} $$
Частота вращения заряда в магнитном поле также называется циклотронной частотой . В большинстве случаев циклотронная частота задается не частотой $f$, а так называемой круговой частотой $\омега$ («омега»). Он определяется как $ \omega = 2\pi \, f $. Поэтому перенесите множитель $ 2 \pi $ на другую сторону уравнения. 13 и вы получите:
Формула: Циклотронная частота заряженной частицы
Формула якоря $$ \begin{align} \omega ~=~ \frac{ |q| \, \class{violet}{B} }{ \class{brown}{m} } \end{align} $$
Заряд движется ПОД УГЛОМ относительно магнитного поля
Однородное магнитное поле, если смотреть сбоку. Для формулы qvB (без синуса) угол должен быть 90 градусов.
Конечно, заряд НЕ может двигаться идеально перпендикулярно силовым линиям магнитного поля. Таким образом, угол , назовем это $ \alpha$, между скоростью $ \class{blue}{v} $ и магнитным полем $ \class{violet}{B} $ не равен 90 градусам .
Чтобы учесть это, нам нужно умножить формулу qvB на синус угла (вы узнаете почему, если знаете о векторах и перекрестных произведениях):
Формула: сила Лоренца с углом
Формула якоря $$ \begin{align} \class{green}{F_{\text m}} ~=~ q \, \class{blue}{v} \, \class{violet}{B} \, \sin(\ альфа) \end{align} $$
Вы всегда можете разложить скорость $ \class{blue}{v} $, наклонную к магнитному полю $ \class{violet}{B} $, на параллель $ \class {blue}{v_{||}} $ и компоненту , перпендикулярную $ \class{blue}{v_{\perp}} $ к магнитному полю. {\circ}) ~=~ 0 \)).
Путем частичного движения параллельно и частичного движения перпендикулярно магнитному полю создается цилиндрическая спиральная траектория, так называемая спираль . Его ось параллельна магнитному полю. Он имеет радиус $r$ и шаг $h$. Где шаг — это просто расстояние, параллельное магнитному полю, пройденное в течение периода $T$.
Из-за движения электрона по диагонали к магнитному полю создается винтовая траектория.
Заряд движется ПАРАЛЛЕЛЬНО магнитному полю
Если заряд движется точно на параллельно магнитному полю , угол равен $ \alpha = 0 $. Тогда $ \sin(0) = 0 $, поэтому на заряд не действует сила Лоренца.
Таким образом, мы можем утверждать, что заряды, движущиеся параллельно магнитному полю, НЕ отклоняются!
На следующем уроке мы рассмотрим важный эксперимент, связанный с силой Лоренца, а именно эксперимент с тельтронной трубкой .
Магнетизм — Сила на зарядах
Магнетизм — Сила на зарядах — Физика 299
»
Ваша теория безумно, но это недостаточно безумно, чтобы быть правдой.
Подробнее: http://www.brainyquote.com/quotes/quotes/n/nielsbohr102862.html

наша теория безумно, но это недостаточно безумно, чтобы быть правдой.
Подробнее: http://www.brainyquote.com/quotes/quotes/n/nielsbohr102862.html

Ваша теория безумно, но это недостаточно безумно, чтобы быть правдой.
Подробнее: http://www.brainyquote.com/quotes/quotes/n/nielsbohr102862.html
Ваша теория безумно, но недостаточно безумно, чтобы быть правдой.
Подробнее: http://www.brainyquote.com/quotes/quotes/n/nielsbohr102862. html
Предсказывать очень сложно, особенно о будущем. »
Нильс Бор

Исходя из предположения о существовании магнитных полей — созданный еще не описанным механизмом — магнитным найдена сила, действующая на положительно заряженных частиц экспериментально получить
где q — заряд (положительный) частицы, v ее скорость, F _B сила, которую он испытывает и Б магнитное поле, вызывающее силу.
Выражение для магнитной силы записывается через векторное (перекрестное) произведение, а значит, нравится вам это или нет, вы приходится работать в трех измерениях. Несколько важных факты вытекают из этого уравнения.

Если v = 0, силы нет. Электрический заряды, покоящиеся в магнитном поле, не испытывают магнитного поля. сила.

Величина F _B определяется выражением
, где φ — угол между v и B .
Таким образом, когда v параллельно B (φ = 0) или антипараллельно B ( φ = 180 ^o ) тогда sinφ = 0 и F _B = 0. Поэтому заряженные частицы, движущиеся по магнитному силовые линии не испытывают магнитной силы.
Когда v и B находятся на 90 ^o F _B имеет максимальное значение, F _B = qvB.

F _B находится под прямым углом к v и В . «Смысл» дается обычным правила для векторного (перекрестного) произведения, иногда называемого (the) «Правило правой руки » 908:20 .

Это приводит к круговому (или спиральному) движению вокруг B линии поля.

Не забыть, что направление магнитной силы полученное выше относится к положительному заряду . Для отрицательного заряда направление F _B перевернуто.

Работа, совершаемая магнитной силой при заряженном частица смещается на ds задается,

, где θ — угол между F _B и дс .
Рабочий объем ds и скорости частицы, v , находятся в одном и том же направлении, поэтому θ также является углом между Ф _Б и против . Но от формы нам известна магнитная сила F _B и v перпендикулярны (θ = 90 ^o ), поэтому dW всегда равен нулю. Другими словами, магнитный сила не работает, что означает, в отличие от электрическая сила, она не может дать заряженной частице энергию (увеличивать или уменьшать свою кинетическую энергию). Эффект магнитная сила должна изменить направление, а не кинетическую энергия.

Если заряженная частица ощущает как магнитное, так и электрическое поле результирующая сила равна

это известно как закон силы Лоренца.
ЕДИНИЦЫ
Из формы магнитной силы мы видим, что единицы B : N/(C. м/с) = N/(A.m). Этот комбинация основных единиц определяется как Тесла.
Тесла — очень большая единица магнитного поля. По этой причине вы можете иногда сталкиваться с меньшая единица магнитного поля, Гаусс; где 1 Тесла = 10 ⁴ Гаусс.
Два фермиона заходят в бар. Один заказывает джин с тоником. другой говорит: «Черт возьми, это то, что я хотел».

Dr. C.L. Davis
Факультет физики
Университет Луисвилля
электронная почта : [email protected]

22.4 Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле — College Physics 2e
Цели обучения
К концу этого раздела вы сможете:
Описать влияние магнитных полей на движущиеся заряды.
Используйте правило правой руки 1, чтобы определить скорость заряда, направление магнитного поля и направление магнитной силы, действующей на движущийся заряд.
Рассчитайте магнитную силу, действующую на движущийся заряд.
Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Правило правой руки 1
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных. Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы FF, действующая на заряд qq, движущийся со скоростью vv в магнитном поле напряженностью BB, определяется выражением
F=qvBsinθ,F=qvBsinθ,
22,1
где θθ — угол между направлениями vv и BB. Эту силу часто называют силой Лоренца. Фактически именно так мы определяем напряженность магнитного поля ВВ — через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля BB называется тесла (Тл) в честь эксцентричного, но гениального изобретателя Николы Теслы (1856–1943). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F=qvBsinθF=qvBsinθ для BB.
B=FqvsinθB=Fqvsinθ
22,2
Потому что sinθsinθ безразмерна, тесла равна
1 T=1 NC⋅м/с=1 NA⋅м1 T=1 NC⋅м/с=1 NA⋅м
22,3
(обратите внимание, что C/s = A).
Иногда используется другая меньшая единица, называемая гаусс (G), где 1G=10−4T1 G=10−4T. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5×10-5 Тл5×10-5 Тл, или 0,5 Гс.
направление магнитной силы FF перпендикулярно плоскости, образованной vv и BB, как определено правилом правой руки 1 (или RHR-1), которое показано на рис. 22.16. RHR-1 утверждает, что для определения направления магнитной силы на положительно движущемся заряде вы указываете большим пальцем правой руки в направлении vv, остальными пальцами в направлении BB, а перпендикуляр к ладони указывает на направление ФФ. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Рисунок 22.16 Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной vv и BB, и следует правилу правой руки-1 (RHR-1), как показано. Величина силы пропорциональна qq, vv, BB и синусу угла между vv и BB.
Создание соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 22.1
Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если бросить его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле. (Направление силы определяется правилом правой руки 1, как показано на рис. 22.17.)
Рисунок 22.17 Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, испытывает силу, которая направлена прямо вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, почувствовал бы силу прямо вверх.
Стратегия
Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F=qvBsinθF=qvBsinθ, чтобы найти силу.
Решение
Магнитная сила равна
F=qvBsinθ.F=qvBsinθ.
22,4
Мы видим, что sinθ=1sinθ=1, так как угол между скоростью и направлением поля равен 90º90º. Ввод других заданных величин дает
F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1×10–11N.F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1×10–11Н.

определение, формула, применение на практике

Что такое сила Лоренца — определение, когда возникает, получение формулы

Определение направления силы Лоренца с помощью правила левой руки

Движение заряженной частицы в магнитном поле

Формула силы Лоренца

Определение и формула силы Лоренца

Направление силы Лоренца

Следствия свойств силы Лоренца

Формула силы Лоренца при наличии магнитного и электрического полей

Единицы измерения силы Лоренца

Понятие напряженности электрического поля

Напряженность электрического поля

Как направлена сила Лоренца

Применение

Применение силы Лоренца в технике

Кинескоп

Масс-спектрограф

Циклотрон

Магнетрон

Магнитное поле Земли

Применение на практике

Заключение

Как определить силу лоренца правило левой руки. Сила Лоренца. Единицы измерения силы Лоренца

Применение силы Лоренца.

Тесла (единица магнитной индукции)

Примеры решения задач по теме «Сила Лоренца»

Сообщение по физике на тему сила лоренца. Лоренца сила

Тесла (единица магнитной индукции)

Определение

Как направлена сила Лоренца

Применение

Заключение

Литература

Белорусский государственный университет транспорта — БелГУТ (БИИЖТ)

Как поступить в БелГУТ:

Как получить место

Как поступить иностранному гражданину

События

Анонсы

Новости

КУДА ПОСТУПАТЬ

БелГУТ на Доске почета

Предложения

Видеотека

Фотогалерея

Заряженные частицы в однородном магнитном поле

Единицы измерения Силы Ампера и… — Учеба и наука

Лучший ответ по мнению автора

Другие ответы

Михаил Александров

Андрей Андреевич

✔Олеся / Математика

направление силы Лоренца

Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле

Цели обучения

Правило правой руки 1

Пример 1. Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне

Резюме раздела

Концептуальные вопросы

Задачи и упражнения

Глоссарий

Избранные решения задач и упражнения

Сила Лоренца — Назначение точки

Как определить его направление и понять формулу

Видео — сила Лоренца просто объясняется за 6 минут!

Заряд движется ортогонально магнитному полю

Определить направление силы Лоренца

Заряд движется ПОД УГЛОМ относительно магнитного поля

Заряд движется ПАРАЛЛЕЛЬНО магнитному полю

Магнетизм — Сила на зарядах

22.4 Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле — College Physics 2e

Цели обучения

Правило правой руки 1

Создание соединений: заряды и магниты

Пример 22.1

Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне

Стратегия

Решение

alexxlab

Добавить комментарий Отменить ответ