Катушка индуктивности. Описание, характеристики, формула расчета
Главная » Справочник » Катушка индуктивности. Описание, характеристики, формула расчета
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
Блок питания 0…30В/3A
Набор для сборки регулируемого блока питания…
Подробнее
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково.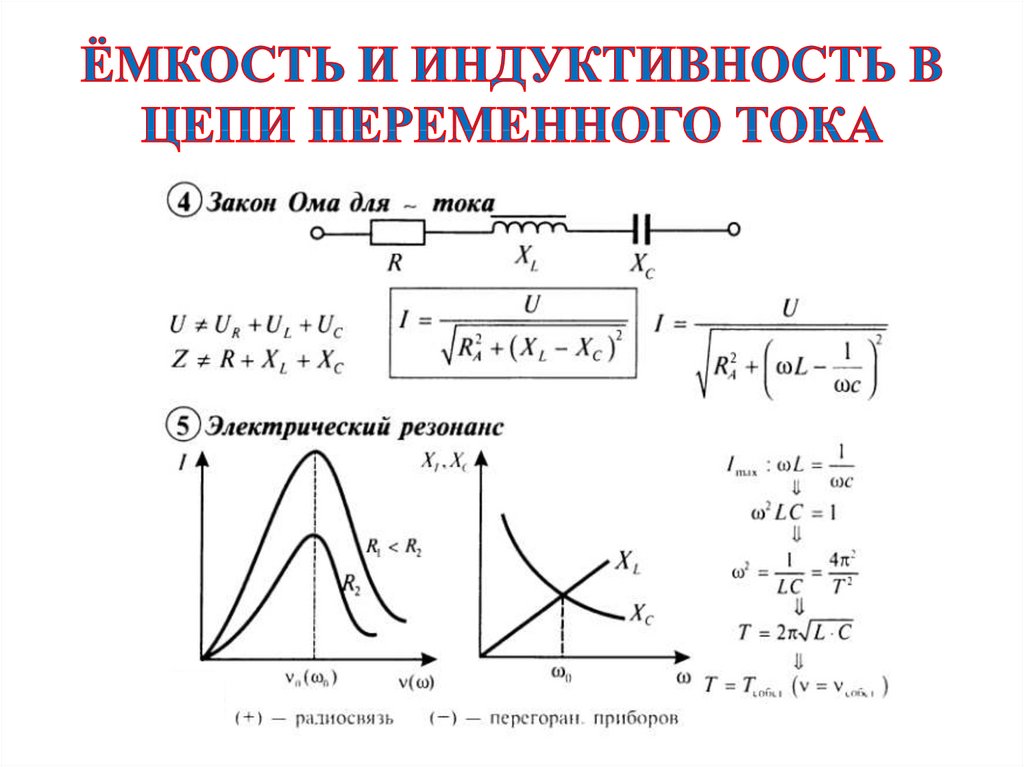 Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Счетчик Гейгера
Высококачественный счетчик Гейгера с высокой чувствительностью для обнаружен…
Подробнее
Катушка индуктивности в цепях переменного тока
Переменный электрический ток:
До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.
Пусть источник тока создает переменное гармоническое напряжение (рис. 194)
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:
где — амплитудное значение силы тока в цепи.
Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.
Величины называются  Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.
Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность которая, в отличие от цепей постоянного тока, изменяется с течением времени.
С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.
Перепишем формулу для мощности по-другому:
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).
Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле
Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.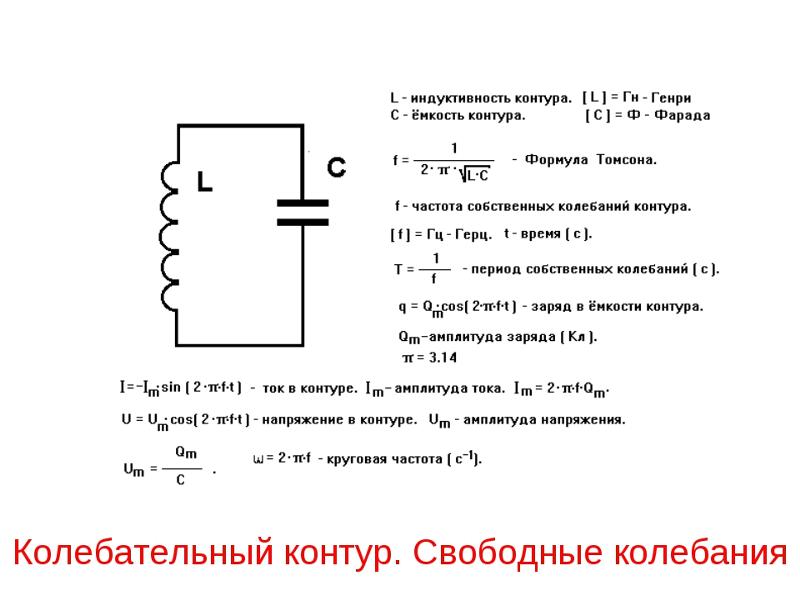
Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока
Аналогично можно ввести действующее значение и для напряжения
Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
 Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.Катушка индуктивности в цепях переменного тока
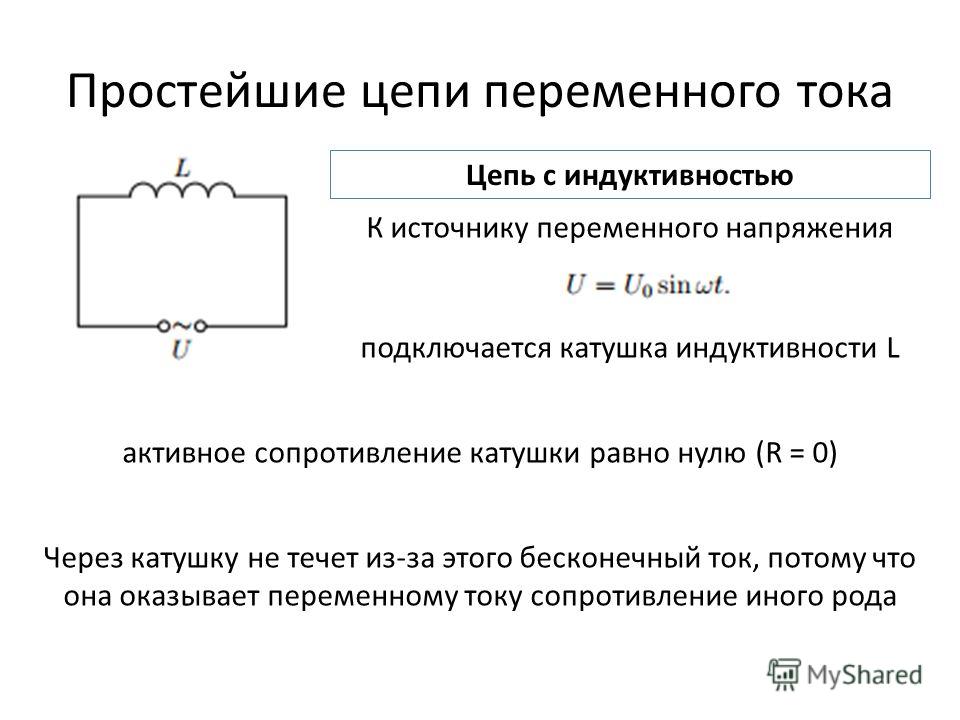
Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.Катушка индуктивности в цепях переменного токаРеальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.
Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.
В катушке индуктивностью L переменный ток вызывает появление ЭДС самоиндукции:
где — амплитудное значение ЭДС самоиндукции (рис. 195).
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи где U(t) напряжение на концах катушки.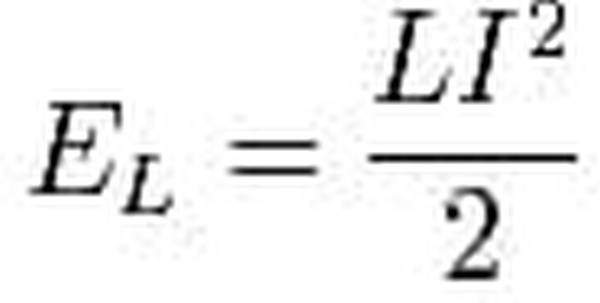
Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде
Величину называют индуктивным сопротивлением катушки. Оно пропорционально индуктивности катушки и частоте переменного тока в цепи
Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока и напряжения так как тогда
Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см.
Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле
Поскольку среднее за период значение функции равно нулю, то и средняя мощность за период также равна нулю:
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.
Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.
Катушка индуктивности что это такое, принцип работы, разновидности катушек
Содержание материала
- Определение и принцип действия
- Видео
- Постоянная времени индуктора
- Зачем используют
- Индуктивность в электрических цепях
- Самоиндукция
- Дроссель
- Виды и типы
- Низкочастотные
- Высокочастотные
- Общие свойства катушек индуктивности
- Конструкция катушки индуктивности
- Обозначение катушек с отводами и начала обмотки
Определение и принцип действия
Читайте также: Что изучает лексика? Зачем нужна эта наука?
Катушка индуктивности — это катушка смотанного в спираль или другую форму изолированного проводника.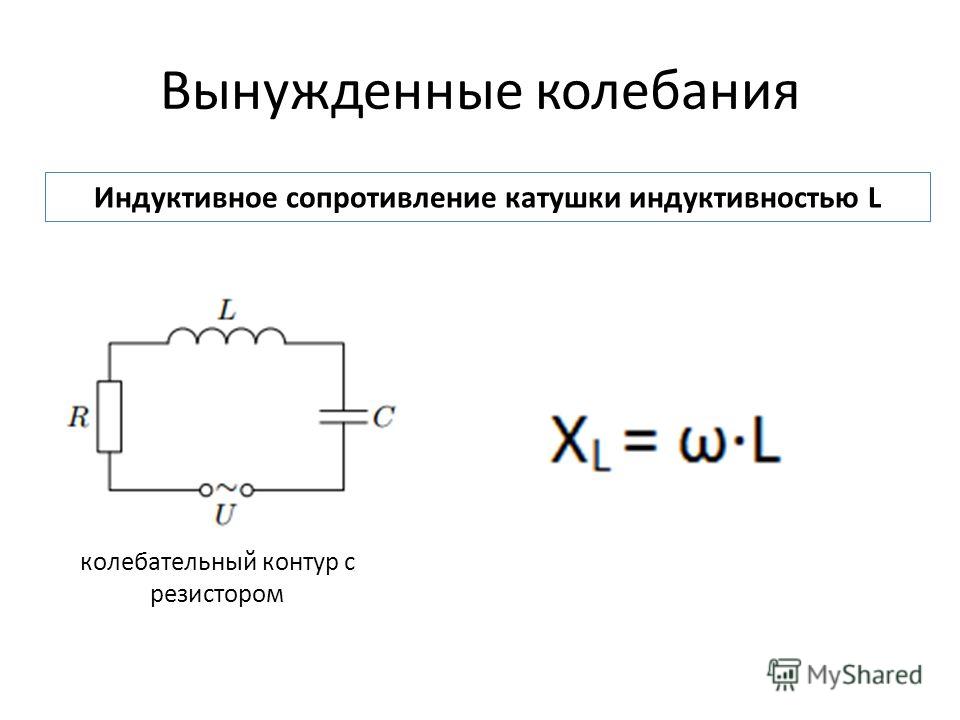 Основные особенности и свойства: высокая индуктивность при низкой ёмкости и активном сопротивлении.
Основные особенности и свойства: высокая индуктивность при низкой ёмкости и активном сопротивлении.
Она накапливает энергию в магнитном поле. На рисунке ниже вы видите её условное графическое обозначение на схеме (УГО) в разных видах и функциональных назначениях.
Читайте также: Уголок безопасности в школе оформление шаблоны
Она может быть с сердечником и без него. При этом с сердечником индуктивность будет в разы больше, чем если его нет. От материала, из которого изготовлен сердечник, также зависит величина индуктивности. Сердечник может быть сплошным или разомкнутым (с зазором).
Напомним один из законов коммутации:
Ток в индуктивности не может измениться мгновенно.
Читайте также: Как взять ипотеку без первоначального взноса в 2021 году
Это значит, что катушка индуктивности — это своего рода инерционный элемент в электрической цепи (реактивное сопротивление).
Давайте поговорим, как работает это устройство? Чем больше индуктивность, тем больше изменение тока будет отставать от изменения напряжения, а в цепях переменного тока — фаза тока отставать от фазы напряжения.
В этом и заключается принцип работы катушек индуктивности – накопление энергии и задерживание фронта нарастания тока в цепи.
Из этого же вытекает и следующий факт: при разрыве в цепи с высокой индуктивностью напряжение на ключе повышается и образуется дуга, если ключ полупроводниковый — происходит его пробой. Для борьбы с этим используются снабберные цепи, чаще всего из резистора и конденсатора, установленного параллельно ключу.
Видео
Постоянная времени индуктора
Теперь мы знаем, что ток не может изменяться мгновенно в индуктивности, потому что для этого ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной di / dt = ∞ , делая индуцированную ЭДС бесконечной, а бесконечного напряжения не существует. Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.
Читайте также: Поздравления с назначением на должность руководителя
Рассмотрим схему индуктора выше. Когда переключатель ( S1 ) разомкнут, ток через катушку индуктивности не течет. Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю. Если скорость изменения тока равна нулю, то в катушке индуктивности нет ЭДС самоиндукции ( V L= 0 ).
Если мы теперь закроем переключатель (t = 0), ток будет проходить через цепь и медленно подниматься до своего максимального значения со скоростью, определяемой индуктивностью индуктора. Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность по Генри, приводит к тому, что на катушке образуется некоторая самоиндуцированная ЭДС с фиксированным значением, определенная уравнением Фарадея V L = Ldi / dt.
Эта самоиндуцированная ЭДС на катушке индуктивности ( V L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто устойчивое состояние. Ток, который сейчас течет через катушку, определяется только постоянным или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, поскольку скорость изменения тока (di / dt) равна нулю в устойчивом состоянии. Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.
Ток, который сейчас течет через катушку, определяется только постоянным или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, поскольку скорость изменения тока (di / dt) равна нулю в устойчивом состоянии. Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.
Аналогичным образом, если переключатель ( S1 ) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается удержать ток в своем прежнем значении, индуцируя напряжение в другом направлении. Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.
Зачем используют
Читайте также: Для чего нужен смеситель?
Как мы уже отмечали в нашей статье, катушки имеют очень широкое применение в электрических приборах. Ниже более подробно расскажем, где и в каких устройствах их используют. Катушка как дроссель. Чаще всего ограничивают ток. Применяют в следующих цепях:
Катушка как дроссель. Чаще всего ограничивают ток. Применяют в следующих цепях:
- В устройстве для разжигания и обеспечения питанием газоразрядной лампы.
- Как фильтры от различных помех. Может фильтровать как электромагнитные помехи, так и акустические помехи. Всё зависит от того, где именно и на каком устройстве задействована катушка. На рисунке ниже катушка задействована для входа блока питания компьютера.
- Как фильтр для частоты. В звуковых системах динамиков и другой акустической аппаратуре.
Как ограничитель токов при коротких замыканиях на линиях электропередач тоже используют катушки в виде ограничивающих ток реакторов. При этом дроссели должны обладать пониженным сопротивлением, чтобы уменьшать нагрев.
Встречаются катушки контурного типа. При этом их применяют в электрических цепях вместе с конденсаторами. Частоты резонансов подбираются по частотам приёма и передач.
Катушка индуктивности как вариометр. Такие устройства можно настраивать.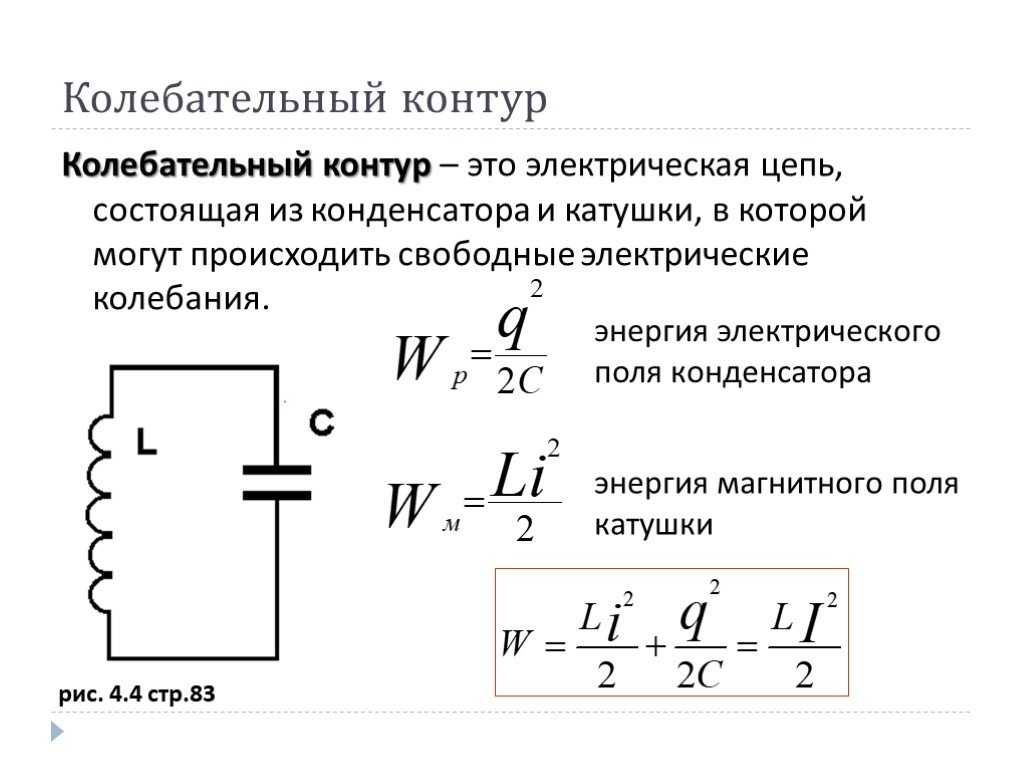 Могут очень точно настроить частоту. Встречаются в контурах колебаний.
Могут очень точно настроить частоту. Встречаются в контурах колебаний.
Катушки индуктивности как соленоиды. Это элементы, которые длиннее своих диаметров. Благодаря этому в них образуются равномерные магнитные поля. Используют в механизмах с поступательным движением. Иногда такую катушку называют «электромагнитом». Более подробно расскажем, где использует такой вид устройства.
Соленоиды имеют широкое распространение. Они активируют замок в автомобиле, где штоки втягиваются, когда на элемент подаётся напряжение.
Они бывают звонками, или устройствами клапанов, магнитами на грузоподъёмных машинах на промышленных предприятиях.
В качестве электромагнитов такие катушки задействованы:
- В реле.
- В контакторах.
- В пускателях.
Обычно в таких ситуациях их называют не соленоидами, а обычными катушками. Используются в качестве рамочной и кольцевой антенны. При этом они передают радиосигнал.
Применяют в машинах, в искателях металла и других устройствах, где передаются сигналы на дистанции.
В качестве нагревателя с индукцией. Данные устройства чаще называют просто «индуктором». В качестве сердечников используется нагревательный элемент, как правило, выполненный из металлических материалов.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов.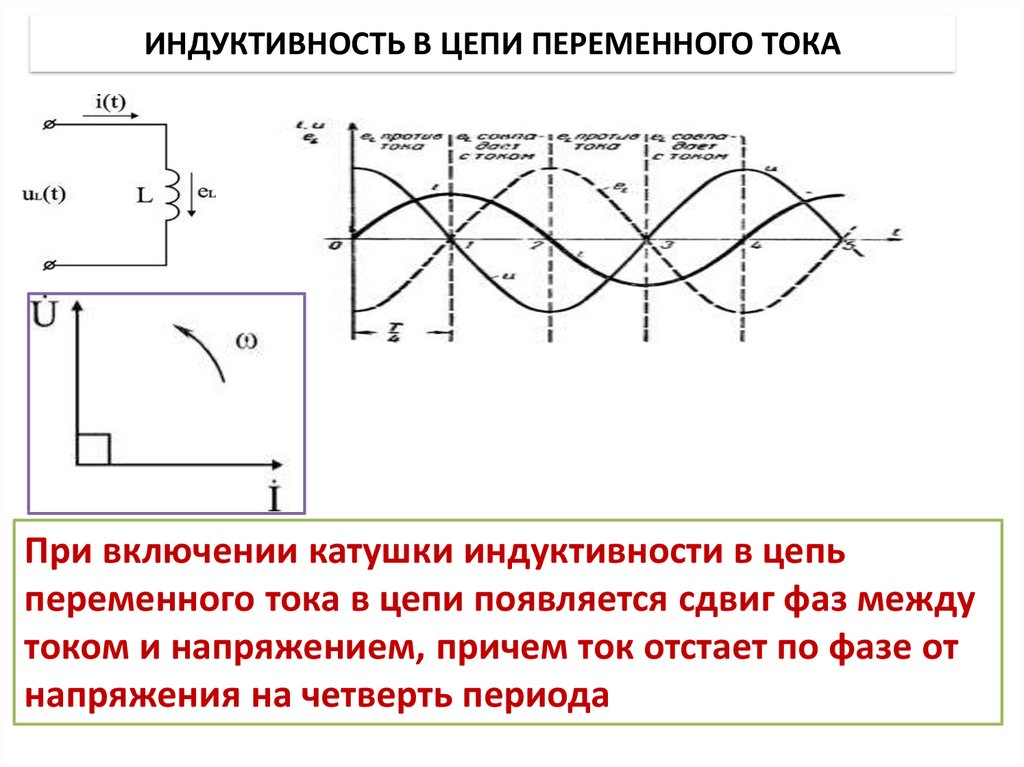 В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
Согласно Закону Ома:
где
I — сила тока в катушке , А
U — напряжение в катушке, В
R — сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
[quads id=1]
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель — это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:
Также существует еще один особый вид дросселей — это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.
Виды и типы
Различают низкочастотные, высокочастотные модели. В отдельную категорию выделяют винтовые, спиральные катушки. Также существуют модификации, которые используются в радиотехнике. Они подходят для защиты конденсатора либо резонансных контуров.
Устройства в радиотехнике
Для трансформаторов годятся катушки с усилителем каскадом. В последнюю категорию выделены вариометры, основное отличие — высокая частота колебательных контуров. Дроссели могут быть одинарными либо сдвоенными. От этого зависит показатель индуктивности и питания системы.
Низкочастотные
Для включения в электрическую цепь, применяется низкочастотная катушка индуктивности. Она предназначена для подавления переменного тока. В формуле учитывается циклическая частота и показатели индуктивности. За основу в устройствах берётся сердечник, который изготавливается из стали. Он может быть с фильтрами либо без них.
Чтобы влиять на частоту, происходит игра с сопротивлением. В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
Когда в цепях повышается напряжение, на каркас оказывается нагрузка. В цепи постоянного тока задействуются непрозрачные проволочные резисторы. Также для этих целей подходят однослойные катушки типа «универсал». Их особенность — использование ферритовых стержней.
Низкочастотная катушка
Высокочастотные
Устройства изготавливаются с различными типами обмотки. Речь идет о наборе преимуществ, которые спасают в той или иной ситуации. Сфера применения элементов широка, учитывается значительная частота модуляции. Таким образом удается бороться с повышенным сопротивлением металлов. У катушек имеется сердечник.
Основная задача — это модуляция частоты генератора. Она происходит за счёт усиления сигнала, и за процессом можно проследить при подключении осциллографа. Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Интересно! Современные товары изготавливаются из алюминия и являются компактными.
Электрикам известны контурные, безконтурные модификации высокой частоты. В зависимости от намотки учитывается стабильность электрических параметров. У моделей высокой частоты могут применяться магниты и провода. Речь идет о порошковых материалах, сделанных из диэлектриков.
Процесс изготовления связан с методом холодного прессования. Индуктивные датчики отличаются по защищенности. На предприятиях элементы могут погружать в раствор либо продевать в трубку. Это делается с целью избежания коротких замыканий. Мировые производители решают проблему путем использование вторичного витка.
Высокочастотная катушка
У моделей значительное сопротивление и есть проблема с концентрацией электролита.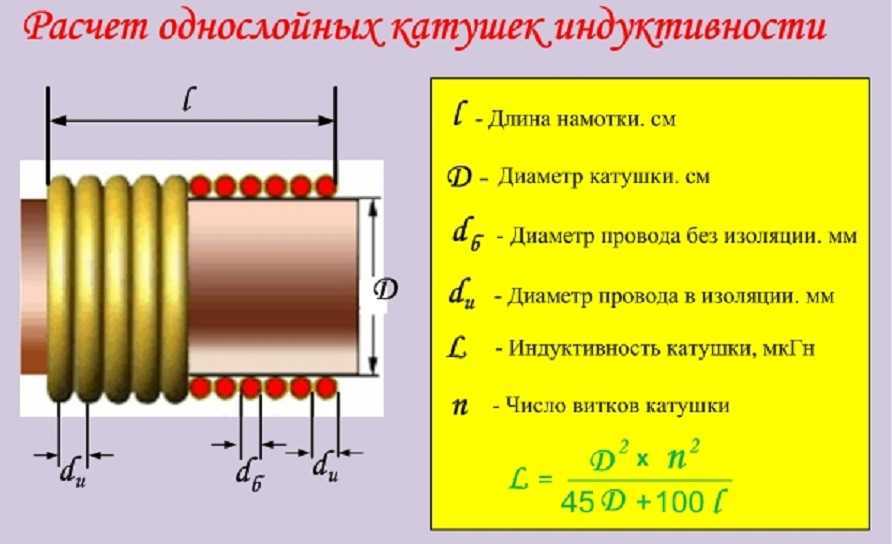 Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.
Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.
Общие свойства катушек индуктивности
В зависимости от требуемой индуктивности и частоты, на которой катушка будет работать, она может иметь самые различные исполнения.
Для высоких частот это может быть простая катушка состоящая из нескольких витков провода или же катушка с сердечником из ферромагнитного материала и иметь индуктивность от нескольких наногенри до нескольких десятков миллигенри. Такие катушки применяются в радиоприемной, передающей, измерительной аппаратуре и т.п.
Катушки, работающие на высоких частотах, можно разделить на катушки контуров, катушки связи и дроссели высокой частоты. В свою очередь катушки контуров могут быть с постоянной индуктивностью и переменной индуктивностью (вариометры).
По конструктивному признаку высокочастотные катушки разделяются на однослойные и многослойные, экранированные и неэкранированные, катушки без сердечников и катушки с магнитными и немагнитными сердечниками, бескаркасные, цилиндрические плоские и печатные.
Для работы в цепи переменного тока низкой частоты, на звуковых частотах, во входных фильтрах блоков питания, в цепях питания осветительного электрооборудования применяются катушки с достаточно большой индуктивностью. Их индуктивность достигает десятки и даже сотни генри, а в обмотках могут создаваться большие напряжения и протекать значительные токи.
Для увеличения индуктивности при изготовлении таких катушек применяют магнитопроводы (сердечники), собранные из отдельных тонких изолированных пластин сделанных из специальных магнитных материалов – электротехнических сталей, пермаллоев и др.
Применение наборных магнитопроводов обусловлено тем, что под действием переменного магнитного поля в сплошном магнитопроводе, который можно рассматривать как множество короткозамкнутых витков, образуются вихревые токи, которые нагревают магнитопровод, бесполезно потребляя часть энергии магнитного поля. Изоляция же между слоями стали оказывается на пути вихревых токов и значительно снижает потери.
Катушки с магнитопроводами из изолированных пластин можно разделить на дроссели и трансформаторы.
Конструкция катушки индуктивности
Вокруг прямолинейного проводника с постоянным током создается круговое магнитное поле. Линии напряженности напоминают спираль. Некто догадался свернуть провод кольцом, чтобы вклад элементарных сегментов сложился в центре. В результате внутри конструкции магнитное поле намного выше, нежели снаружи. Линии визуально наблюдаем на железных опилках. На Ютуб множество роликов, где через индуктивность пропускают ток, демонстрируя упорядоченную ориентацию металлической пыли в момент замыкания контактов. Конструкция способна запасать впрок магнитное поле подобно конденсатору, накапливающему заряд. Катушками называют только индуктивности, содержащие намотку лакированного провода. В микрополосковой технологии напыляемые для запасания магнитного поля элементы логично именовать индуктивностями.
Если в катушке, совсем как в той, что используют швеи, несколько витков провода расположить один за другим бок о бок так, чтобы ось была общей, линии напряженности магнитного поля суммируются. Простейшая индуктивность, способная накапливать энергию магнитного поля. При резком пропадании напряжения образуется явление обратной-ЭДС широко известное технике. Выступает причиной искрения коллекторных двигателей. Используется лакированный (с лаковой изоляцией) медный провод нужного сечения. Количество витков, форма сердечника определяются предварительно расчетами или по имеющемуся образцу.
Простейшая индуктивность, способная накапливать энергию магнитного поля. При резком пропадании напряжения образуется явление обратной-ЭДС широко известное технике. Выступает причиной искрения коллекторных двигателей. Используется лакированный (с лаковой изоляцией) медный провод нужного сечения. Количество витков, форма сердечника определяются предварительно расчетами или по имеющемуся образцу.
Противо-ЭДС является паразитной, для гашения последовательно с катушкой включают емкость размером побольше, пытаясь занизить суммарное реактивное сопротивление. В импеданс индуктивности входят с положительным знаком, емкости – с отрицательным. Тесла изобрел катушку, взял патент. Но конструкция представляла собой плоскую спираль (лабиринт) с двойной намоткой. Ученый показал, индуктивность одновременно характеризуется значительным емкостным сопротивлением, при исчезновении напряжения явления обратной ЭДС никак не проявляет себя.
Бифилярные катушки сегодня широко используются. Что касается обратной ЭДС, служит причиной розжига разрядных ламп (дневного света). Вернемся к конструкции. В первом электромагните проволока оголенная, современные катушки индуктивности наматываются лакированным. Тонкая изоляция при необходимости может быть легко снята (например, токсичной муравьиной кислотой), в исходном состоянии надежно защищает конструкцию против короткого замыкания.
Вернемся к конструкции. В первом электромагните проволока оголенная, современные катушки индуктивности наматываются лакированным. Тонкая изоляция при необходимости может быть легко снята (например, токсичной муравьиной кислотой), в исходном состоянии надежно защищает конструкцию против короткого замыкания.
Внутри катушки находится сердечник из ферромагнитного материала. Форма не важна, сечение лучше брать круглым. На высоких частотах магнитный поток (см. Преобразователь напряжения) выходит на поверхность сердечника, смысл применения ферромагнитных сплавов пропадает, иногда используется латунь (даже композитные материалы, диэлектрики). Снижает индуктивность, на высоких частотах запасаемая за период мощность невелика. Трюк проходит. У многих возникает вопрос – зачем нужен сердечник?
Сердечник катушки индуктивности выступает опорой, долговечным каркасом, усиливая магнитное поле. Индукция связана с напряженностью поля через постоянную магнитной проницаемости среды. У ферромагнитных материалов параметр поистине велик. В тысячи раз больше, нежели воздуха, большинства металлов. С ростом частоты необходимость в сердечнике снижается, возникают некоторые негативные эффекты, два из которых особенно важны:
В тысячи раз больше, нежели воздуха, большинства металлов. С ростом частоты необходимость в сердечнике снижается, возникают некоторые негативные эффекты, два из которых особенно важны:
Линии магнитного поля, сформированные опилками
- Переменное магнитное поле наводит вихревые токи, посредством которых функционируют индукционные плитки. Результат представите сами: какой нагрев сердечника вызовет. Сердечники силовых трансформаторов собираются из специальной электротехнической стали с высоким сопротивлением, разбиваются тонкими листами, изолированными взаимно слоем лака. Шихтование позволит сильно снизить влияние вихревых токов.
- Второй эффект называется перемагничиванием. Отнимает энергию поля, вызывает нагрев материала. Явление характерно для ферромагнитных материалов, устраняется использованием латуни.
В микрополосковой технологии предусмотрено исполнение индуктивностей в виде плоских спиралей: проводящий материал через трафарет напыляется на подложку (возможный метод). Напоминает конструкцию Николы Тесла. Номинал катушка индуктивности имеет весьма малый, иного не надо на частотах СВЧ. Расчет ведется по специальным справочникам, хотя пользуются преимущественно инженеры-конструкторы.
Напоминает конструкцию Николы Тесла. Номинал катушка индуктивности имеет весьма малый, иного не надо на частотах СВЧ. Расчет ведется по специальным справочникам, хотя пользуются преимущественно инженеры-конструкторы.
Для намотки индуктивности изготавливают специальные приспособления, напоминающие катушку спиннинга. На ось одевается сердечник с ограничителем по бокам, вращая ручку, мастер внимательно считает количество оборотов, отмеряет нужную длину. Медленно, по способу челнока рука двигается влево-вправо, витки ровно ложатся последовательно.
Обозначение катушек с отводами и начала обмотки
В радио и электротехнической аппаратуре, например, в приемниках или импульсных преобразователях напряжения, иногда используют не всю индуктивность катушки, а только некоторую ее часть. Для таких случаев катушки изготавливают с отводом или отводами.
При разработке некоторых конструкций иногда необходимо строго соблюсти начало и конец обмотки катушки или трансформатора. Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.
Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.
Для подстройки катушек на частотах свыше 15…20 МГц часто применяют магнитопроводы из немагнитных материалов (меди, алюминия и т.п.). Возникающие в таком магнитопроводе под действием магнитного поля катушки вихревые токи создают свое поле, противодействующее основному, в результате чего индуктивность катушки уменьшается.
Немагнитный магнитопровод-подстроечник обозначают так же, как и ферритовый, но рядом указывают химический символ металла, из которого он изготовлен. На рисунке изображен подстроечник, изготовленный из меди.
Вот и все, что хотел рассказать о катушках индуктивности. Удачи!
Литература: 1. В. А. Волгов «Детали и узлы радиоэлектронной аппаратуры». 2. В. В. Фролов «Язык радиосхем». 3. М. А. Сгут «Условные обозначения и радиосхемы».
Теги
Катушка индуктивности катушка индуктивности Индуктивность катушек индуктивности катушек индуктивности катушка индуктивности Катушка индуктивности представляетТипы катушек индуктивностисоединение катушек индуктивности
добротностьоднойкоэффициентсайтсобственноеграфики
Катушка индуктивности.
 Описание, характеристики, формула расчета
Описание, характеристики, формула расчетаКатушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Паяльный фен YIHUA 8858
Обновленная версия, мощность: 600 Вт, расход воздуха: 240 л/час…
Подробнее
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Теоретика
Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.
Что такое катушка индуктивности
Разнообразие размеров катушек
Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:
- Сглаживание биений;
- Подавление помех;
- Ограничение переменного тока;
- Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.
Дроссели на печатной плате
- Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
- Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.
Соленоид
- Бывают также и цилиндрические катушки индуктивности, называемые соленоидами.
 Длина такого цилиндра в несколько раз превышает его диаметр.
Длина такого цилиндра в несколько раз превышает его диаметр.
Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.
Обмотка с втягивающего реле на стартере
- Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
- Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.
Схема сверхпроводящего индуктивного накопителя
- Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.
Конструкционные особенности
Строение катушки индуктивности
Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса).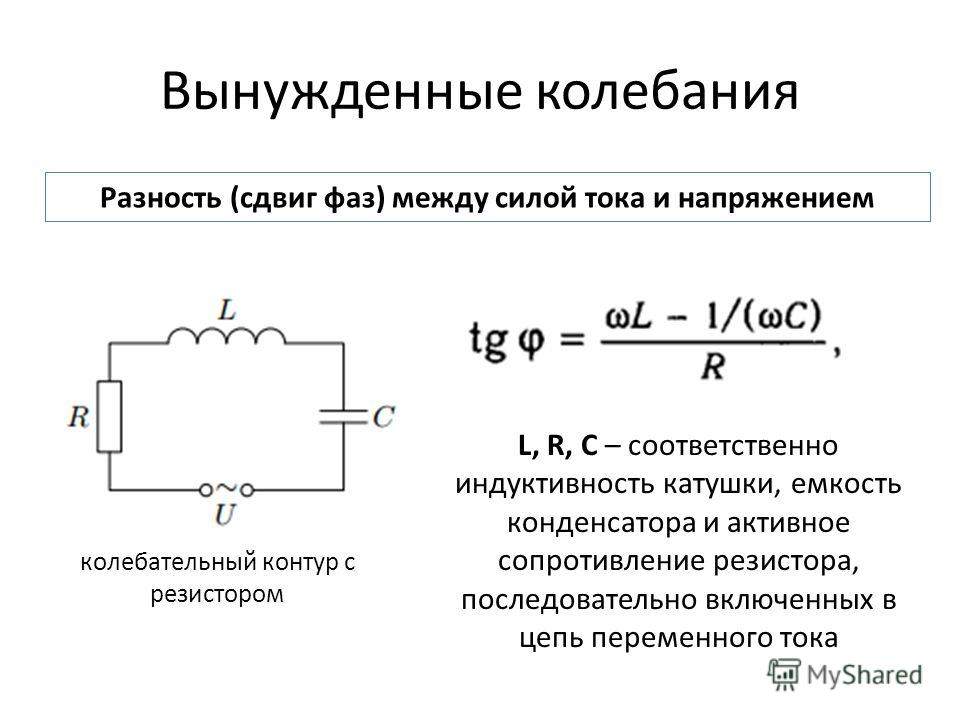 Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.
Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.
Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.
Тороидальная катушка
Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.
Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.
Применение
Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.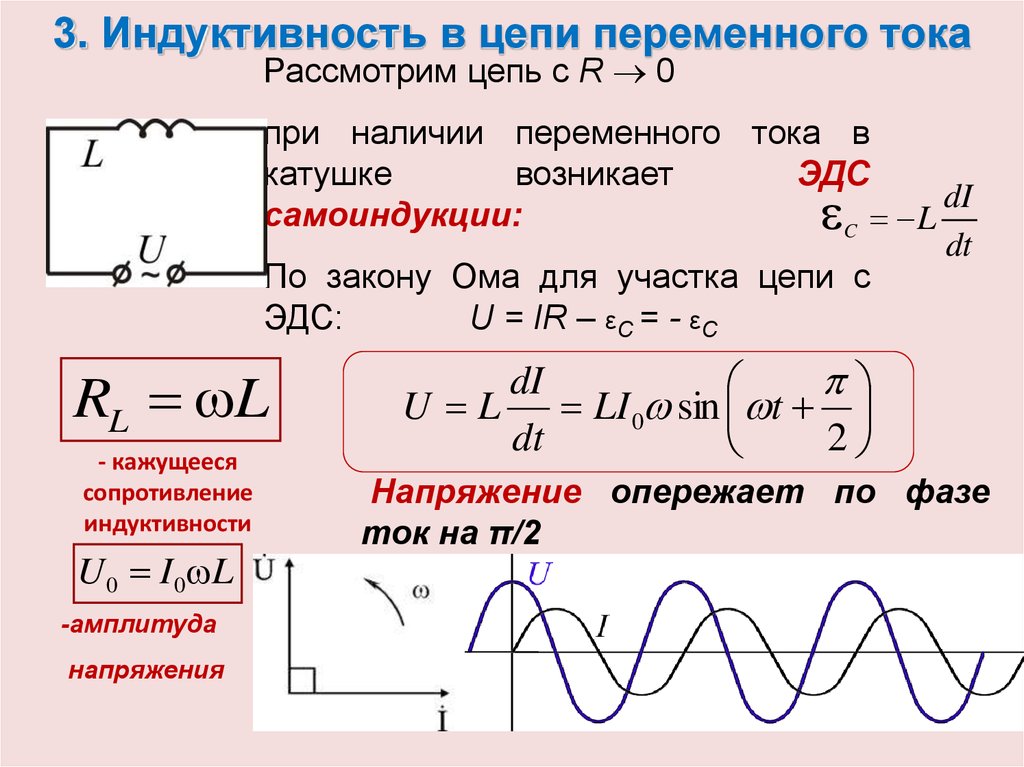
Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.
Строение трансформатора
Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.
Для справки! Трансформаторы способны функционировать только с переменным током.
Основные характеристики катушек индуктивности
Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.
Определение индуктивности: формула
- Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока.
 Измеряется этот параметр в Генри (Гн).
Измеряется этот параметр в Генри (Гн). - Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
- Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.
Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.
Расчет энергии магнитного поля катушки
- Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии.
 Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.
Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.
Гидротурбина
- Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
- Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
- Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.
При последовательном соединении катушек их индуктивность складывается
- Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия.
 Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике. - Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.
Дроссель сварочного аппарата
- Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств.
 Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах. - Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
- С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.
Паразитная емкость катушки индуктивности
- Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
- ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах.
 Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника. - ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Маркировка
При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:
- Серебряный 0,01 мкГн, 10%.
- Золотой 0,1 мкГн, 5%.
- Черный 0,1мкГн, 20%.
- Коричневый 1,1 мкГн.
- Красный 2, 2 мкГн.
- Оранжевый 1 мкГн.
- Желтый 4 мкГн.
- Зеленый 5 мкГн.
- Голубой 6 мкГн.
- Фиолетовый 7мкГн.
- Серый 8 мкГн.
- Белый 9 мкГн.
Маркировка
В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Для чего нужны и какие бывают
В зависимости от того, где применяется катушка индуктивности и её функциональных особенностей, она может называться по-разному: дроссели, соленоиды и прочее. Давайте рассмотрим, какие бывают катушки индуктивности и их сферу применения.
Дроссели. Обычно так называются устройства для ограничения тока, область применения:
- В пускорегулирующей аппаратуре для розжига и питания газоразрядных ламп.
- Для фильтрации помех. В блоках питания — фильтр электромагнитных помех со сдвоенным дросселем на входе компьютерного БП, изображен на фото ниже. Также используется в акустической аппаратуре и прочем.

- Для фильтрации определенных частот или полосы частот, например, в акустических системах (для разделения частот по соответствующим динамикам).
- Основа в импульсных преобразователях — накопитель энергии.
Токоограничивающие реакторы — используются для ограничения токов короткого замыкания на ЛЭП.
Примечание: у дросселей и реакторов должно быть низкое активное сопротивление для уменьшения их нагрева и потерь.
Контурные катушки индуктивности. Используются в паре с конденсатором в колебательном контуре. Резонансная частота подбирается под частоту приема или передачи в радиосвязи. У них должна быть высокая добротность.
Вариометры. Как было сказано — это настраиваемые или переменные катушки индуктивности. Чаще всего используются в тех же колебательных контурах для точной настройки частоты резонанса.
Соленоид — так называется катушка, длина которой значительно больше диаметра. Таким образом внутри соленоида образуется равномерное магнитное поле. Чаще всего соленоиды используются для совершения механической работы — поступательного движения. Такие изделия называют еще электромагнитами.
Чаще всего соленоиды используются для совершения механической работы — поступательного движения. Такие изделия называют еще электромагнитами.
Рассмотрим, где используются соленоиды.
Это может быть активатор замка в автомобиле, шток которого втягивается после подачи на соленоид напряжения, и звонок, и различные исполнительные электромеханические устройства типа клапанов, грузоподъёмные магниты на металлургических производствах.
В реле, контакторах и пускателях соленоид также выполняет функцию электромагнита для привода силовых контактов. Но в этом случае его чаще называют просто катушка или обмотка реле (пускателя, контактора соответственно), как выглядит, на примере малогабаритного реле вы видите ниже.
Рамочные и кольцевые антенны. Их назначение — передача радиосигнала. Используются в иммобилайзерах автомобилей, металлодетекторах и для беспроводной связи.
Индукционные нагреватели, тогда она называется индуктором, вместо сердечника помещают нагреваемое тело (обычно металл).
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Описание устройства
Катушка индуктивности бывает винтовой, спиральной или винтоспиральной, имеющей свернутый изолированный проводник, который обладает значительным показателем индукции при малой емкости с активным сопротивлением. Как следствие, ток протекает через источник тока со значительной инерционностью.
Как следствие, ток протекает через источник тока со значительной инерционностью.
Обратите внимание! Применяется, чтобы подавлять помехи, сглаживать биения, накапливать энергию, ограничивать переменный ток или резонансный/частотно-избирательный контур цепи.
Стоит указать, что ее применение разнообразно. Называется она дросселем, вариометром, соленоидом и токоограничивающим реактором. При этом основные технические характеристики варьируются. Могут отличаться силой тока, сопротивлением потерь, добротностью, емкостью и температурным добротным коэффициентом.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Основные технические параметры
Катушки индуктивности имеют следующие характеристики:
- добротность отклонения;
- эффективность;
- начальная индуктивность;
- температура;
- стабильность;
- предельная емкость;
- номинальная индуктивность.
Стабильность демонстрирует свойства устройства при изменении условий использования. Температура фиксируется вследствие различных причин. Многое зависит от размера каркаса. Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.
Вам это будет интересно Как работает УЗО и что это такое
Температура отслеживается на горячей намотке. В этом плане хорошо себя показали многослойные дроссели с сердечником, которые сделаны из карбонильного железа. Ёмкость отображает количество витков катушки, берется в расчет количество секций и контуров. Высокочастотные модели считаются более емкостными и стабильными.
Высокочастотные модели считаются более емкостными и стабильными.
Емкостные катушки
Номинальная индуктивность — это параметр, который учитывает изменение размеров волны. Измерение происходит в микрогенрах. Если смотреть на формулу, учитывается количество витков, длина намотки, плюс диаметр катушки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
ОБЩАЯ ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА.
 ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
|
Катушка индуктивности
— является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Обозначение катушек с отводами и начала обмотки
В радио и электротехнической аппаратуре, например, в приемниках или импульсных преобразователях напряжения, иногда используют не всю индуктивность катушки, а только некоторую ее часть. Для таких случаев катушки изготавливают с отводом или отводами.
Для таких случаев катушки изготавливают с отводом или отводами.
При разработке некоторых конструкций иногда необходимо строго соблюсти начало и конец обмотки катушки или трансформатора. Чтобы указать, какой из концов обмотки является началом, а какой – концом, у вывода начала обмотки ставят жирную точку.
Для подстройки катушек на частотах свыше 15…20 МГц часто применяют магнитопроводы из немагнитных материалов (меди, алюминия и т.п.). Возникающие в таком магнитопроводе под действием магнитного поля катушки вихревые токи создают свое поле, противодействующее основному, в результате чего индуктивность катушки уменьшается.
Немагнитный магнитопровод-подстроечник обозначают так же, как и ферритовый, но рядом указывают химический символ металла, из которого он изготовлен. На рисунке изображен подстроечник, изготовленный из меди.
Вот и все, что хотел рассказать о катушках индуктивности. Удачи!
Литература: 1. В. А. Волгов «Детали и узлы радиоэлектронной аппаратуры». 2. В. В. Фролов «Язык радиосхем». 3. М. А. Сгут «Условные обозначения и радиосхемы».
2. В. В. Фролов «Язык радиосхем». 3. М. А. Сгут «Условные обозначения и радиосхемы».
Катушка индуктивности. Описание, характеристики, формула расчета
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.
Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:
где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Тестер транзисторов / ESR-метр / генератор
Многофункциональный прибор для проверки транзисторов, диодов, тиристоров…
Подробнее
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Маркировка
При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:
- Серебряный 0,01 мкГн, 10%.
- Золотой 0,1 мкГн, 5%.
- Черный 0,1мкГн, 20%.
- Коричневый 1,1 мкГн.
- Красный 2, 2 мкГн.
- Оранжевый 1 мкГн.
- Желтый 4 мкГн.
- Зеленый 5 мкГн.
- Голубой 6 мкГн.
- Фиолетовый 7мкГн.
- Серый 8 мкГн.
- Белый 9 мкГн.

Маркировка
В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
где ω является угловой частотой резонансной частоты F:
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:
где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
Характеристика элементов
К исключительным параметрам данного устройства относят следующие:
- Обладают высокой индуктивностью;
- Подходят под разные силы тока, на что нужно обращать внимание при использовании в разных устройствах;
- Потеря сопротивления в проводниках, сердечниках, иных элементах;
- Высокая эффективность в использовании;
- Ёмкость витков может быть паразитной;
- Индуктивность и её изменения влияют на температурные коэффициенты устройства;
- Значения добротности могут зависеть от температуры.

Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
Последовательное соединение индуктивностей
Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
где R является собственным сопротивлением обмотки.
Теги
особенности катушки индуктивности. Катушка индуктивностиИндукционная катушка токовая катушка индуктивностиработе катушки фильтрыиндукционная катушка.типа катушки.спиральные катушки.годятся катушки снизкочастотная катушка индуктивности.переменного тока принужна токовая катушкапеременного тока.постоянного тока напряжениепостоянного тока задействуютсяэлектрического тока непроводнику тока вокругпрохождении тока черезрассмотрении катушек индуктивностиразрыва цепи.
самоиндукциистатьяпотеряоченьназываемыеответсхемыисточникипредставляетмоментывсегоэлектромагнитныхсайтграфики
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:
- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:
- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:
- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.
Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Виды и типы
Различают низкочастотные, высокочастотные модели. В отдельную категорию выделяют винтовые, спиральные катушки. Также существуют модификации, которые используются в радиотехнике. Они подходят для защиты конденсатора либо резонансных контуров.
Устройства в радиотехнике
Для трансформаторов годятся катушки с усилителем каскадом. В последнюю категорию выделены вариометры, основное отличие — высокая частота колебательных контуров. Дроссели могут быть одинарными либо сдвоенными. От этого зависит показатель индуктивности и питания системы.
Низкочастотные
Для включения в электрическую цепь, применяется низкочастотная катушка индуктивности. Она предназначена для подавления переменного тока. В формуле учитывается циклическая частота и показатели индуктивности. За основу в устройствах берётся сердечник, который изготавливается из стали. Он может быть с фильтрами либо без них.
Вам это будет интересно Установка УЗО в квартире
Чтобы влиять на частоту, происходит игра с сопротивлением. В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
Когда в цепях повышается напряжение, на каркас оказывается нагрузка. В цепи постоянного тока задействуются непрозрачные проволочные резисторы. Также для этих целей подходят однослойные катушки типа «универсал». Их особенность — использование ферритовых стержней.
Низкочастотная катушка
Высокочастотные
Устройства изготавливаются с различными типами обмотки. Речь идет о наборе преимуществ, которые спасают в той или иной ситуации. Сфера применения элементов широка, учитывается значительная частота модуляции. Таким образом удается бороться с повышенным сопротивлением металлов. У катушек имеется сердечник.
Основная задача — это модуляция частоты генератора. Она происходит за счёт усиления сигнала, и за процессом можно проследить при подключении осциллографа. Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Интересно! Современные товары изготавливаются из алюминия и являются компактными.
Электрикам известны контурные, безконтурные модификации высокой частоты. В зависимости от намотки учитывается стабильность электрических параметров. У моделей высокой частоты могут применяться магниты и провода. Речь идет о порошковых материалах, сделанных из диэлектриков.
Процесс изготовления связан с методом холодного прессования. Индуктивные датчики отличаются по защищенности. На предприятиях элементы могут погружать в раствор либо продевать в трубку. Это делается с целью избежания коротких замыканий. Мировые производители решают проблему путем использование вторичного витка.
Высокочастотная катушка
У моделей значительное сопротивление и есть проблема с концентрацией электролита. Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.
Проводимость раствора падает и повышается частота электромагнитного поля.
Реальная катушка в цепи переменного тока
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
Схема замещения катушки с последовательным соединением элементов
В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.
Активное сопротивление определяется величиной мощности потерь
R = P/I2
а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = Imsinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции eL поэтому ток зависит от действия приложенного напряжения и эдс eL. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:
Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых uR равно падению напряжения в активном сопротивлении, а другое uL уравновешивает эдс самоиндукции.
В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — uR совпадает по фазе с током, UL опережает ток на 90°.
Поэтому:
u = R*Imsinωt + ωLImsin(ωt+π/2).
Векторная диаграмма реальной катушки и полное её сопротивление
Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения
Амплитуды составляющих общего напряжения
UmR = RIm; UmL = ωLIm ,
а действующие величины
UR = RI; UL = XLI .
Вектор общего напряжения
U = UR + UL
Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.
За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.
Вектор UR по направлению совпадает с вектором тока I, а вектор UL направлен перпендикулярно вектору I с положительным углом.
Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях UR и UL :
UR = Ucosφ
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается Ua. Для катушки по схеме рис. 13.9 при Ua = UR
U = Usinφ (13.14)
Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Up. Для катушки Up = UL
Для катушки Up = UL
При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде
U = Umsin(ωt+φ)
Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = UR/I и индуктивное XL = UL/I, сопротивления, а гипотенузой величина Z = U/I.
Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует
Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:
Из треугольников сопротивления и напряжения определяются
cosφ = UR/U = R/Z; sinφ = UL/U = XL/Z; tgφ = UL/UR = XL/R. (13.18)
(13.18)
Мощность реальной катушки
Мгновенная мощность катушки
p = ui = Umsin(ωt+φ) * Imsinωt
Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).
Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).
Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.
Согласно выводам полученных в этих предыдущих (первая, вторая) статьях — в активном сопротивлении P = URI Q = 0; а в индуктивном Р = 0; Q = ULI.
Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении XL. Подставляя значения UR = Ucosφ и UL = Usinφ, определяемые из треугольника напряжений по формулам (13. 18), получим:
18), получим:
P = UIcosφ (13.19)
Q = UIsinφ (13.20)
Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;
S = UI = I2Z (13.21)
Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):
(13.22)
Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить
cosφ = P/S; sinφ = Q/S; tgφ = Q/P. (13.23)
(13.23)
Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).
Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.
Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.
Схема замещения реальной катушки с параллельным соединением элементов
Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной BL проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.
Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством
I = IG + IL (13.24)
Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: IG —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; IL — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.
Вектор тока I и его составляющие IG и IL образуют прямоугольный треугольник, поэтому
Составляющая тока в активном элементе
IG = Icosφ
Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается Iа. Для катушки по схеме на рис. 13.12, б Ia = IG.
Составляющая тока в реактивном элементе
IL = Isinφ
Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки Iр = IL .
Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = IG/U и индуктивная ВL = IL/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.
Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим
Inductance Formula — GeeksforGeeks
Индуктивность — это термин, с которым должен быть знаком каждый студент-физик. Он имеет собственную формулу и часто комбинируется с сопротивлением и емкостью. Оливер Хевисайд впервые придумал эту фразу в 1886 году. Кроме того, мы используем букву L для обозначения катушек индуктивности на принципиальных схемах и индуктивности в уравнениях в честь выдающегося физика Генриха. Давайте узнаем о формуле индуктивности и о том, как ее использовать для определения индуктивности. любой предмет.
Индуктивность
Индуктивность — это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поток электрического тока создает вокруг проводника магнитное поле. Напряженность поля пропорциональна величине тока и не зависит от колебаний тока. Согласно закону индукции Фарадея, любое изменение магнитного поля в цепи создает электродвижущую силу (ЭДС) (напряжение) в проводниках, процесс, известный как электромагнитная индукция.
Согласно закону индукции Фарадея, любое изменение магнитного поля в цепи создает электродвижущую силу (ЭДС) (напряжение) в проводниках, процесс, известный как электромагнитная индукция.
Индуктивность присутствует во многих электрических и электронных системах, а также в цепях. Шестерни доступны в различных формах и размерах, а также различных названиях. Примеры включают катушки, дроссели, трансформаторы, катушки индуктивности и другие детали.
Единицей индуктивности в СИ является генри (Гн) , что может быть представлено в скорости изменения тока и напряжения.
Формула индуктивности
- Ниже приведена формула индуктивности,
L = мкН 2 А/л
Где,
- L = Индуктивность (Гн),
- мк = Проницаемость (Вб/Ам),
- 7 90 число витков18
- Н = Катушка A = Окружность рулона,
- l = Длина рулона (м).
Вывод перепишите приведенное выше уравнение,
E = -N(dϕ/dt)
Предыдущее уравнение изменено для вычисления значения индуктивности.
E = -N(dϕ/dt)
∴ E = -L(di/dt)
N = dΦ = L di
NΦ = Li
Следовательно,
Плотность потока обозначена B, площадь катушки обозначена буквой A.
Li = NΦ = NBA
Hl = Ni
Намагничивающая сила магнитного потока обозначена буквой H. / я = N 2 BA/Ni
N 2 BA/Hl = N 2 μHA/Hl
∴ L = μN 2 A/l
- With an inductance of L, the voltage induced в катушке (В) равно,
В = L × (di/dt)
Где,
- В = напряжение (вольт),
- L = значение индуктивности (Гн),
- i = Ток (А),
- t = Затраченное время (с).
- Реактивное сопротивление индуктивности рассчитывается следующим образом,
X = 2πfL
Где,
- X = реактивное сопротивление (Ом),
- f = частота (Гц),
- L = индуктивность (Гн).
- Если индуктивность последовательно
L = L 1 + L 2 + L 3 . . . . + L n
- Если индуктивность параллельна
1/L = 1/L 1 + 1/L 2 10149 +0147 3 . . . . + 1/L n
Примеры вопросов
Вопрос 1: Определение индуктивности.
Ответ :
Индуктивность – это свойство электрического проводника, которое заставляет его сопротивляться изменениям проходящего через него электрического тока. Поскольку индуктивность имеет N в формуле, это означает, что количество витков в проводнике прямо пропорционально присутствующей индуктивности. Однако интересным фактом является то, что даже прямые проводники несут индуктивность очень мало, чтобы быть значительной.
Вопрос 2: Что такое единица индуктивности в системе СИ?
Ответ:
Единицей индуктивности в системе СИ является генри (Гн).
Открытие индуктивности приписывают Фарадею, однако введение собственной индуктивности для одиночной цепи было впервые введено Генри. Поэтому единица индуктивности посвящена имени ученого.
Вопрос 3: Определите самоиндукцию 210-виткового соленоида с площадью поперечного сечения 17 см 2 и длиной 66,2 см.
Решение:
Дано: μ = 4π × 10 -7 N/A 2 , n = 210 поворотов, A = 17 × 100023 -4 M 2 , L = 66,2 × 10 -2 м
Т.к. -4 ))/(66,2 × 10 -2 )
∴ L = 0,0001422
∴ L = 14,22 × 10 -5 H
Вопрос 4: Каково соответствующее сопротивление при последовательном соединении катушек индуктивности 16H, 10H и 21H?
Решение :
Дано: L 1 = 16 H, L 2 = 10 H, L 3 = 21 H
С.
L 1 + L + L + L + L + L + L + L + L + L + L + L + L + L + L
+2 + L 3
∴ L = 16 + 10 + 21
∴ L = 47 Гн
при условии. рассчитать реактивное сопротивление?
Решение:
Дано: F = 240 Гц, L = 61 H
,
x = 2πfl
∴ x = 2 × 3,14 × 240 × 61
∴ x = o
Вопрос 6: Каково соответствующее сопротивление при параллельном соединении катушек индуктивности 26H, 16H, 21H и 30H?
Решение:
Дано: L 1 = 26 H, L 2 = 16 H, L 3 = 21 H, L 4 = 30 H
Поскольку,
1/л = 1/л 1 + 1/л 2 + 1/л 3 + 1/л 4
1/26 + 1/16 + 1/21 + 1/30
∴ 1/л = 0,03 + 0,06 + 0,04 + 0,03
∴ 1/л = 0,16 Гн
∴ Дл = 6,204 00012 Гн Напряжение переменного тока, приложенное к индуктору: определение, формула и объяснение
Напряжение переменного тока, приложенное к индуктору, подразумевает цепь переменного тока , которая состоит только из индуктора индуктивность л, которая подключена к источнику переменного тока.
Напряжение переменного тока на источнике равно V = V м sin (∏t). Изменение выходного тока источника переменного тока дает обратную ЭДС в катушке, величина которой определяется выражением В L = L d i /d t . Здесь мы узнаем больше о функционировании электрической цепи , где у нас будет индуктор и переменное напряжение V, которое представлено знаком «~».
Read Also: Difference between Resistance and Impedance
Table of Content
- Definition
- AC Voltage applied to an inductor
- Power in AC Circuit
- Важные вопросы
- Вопросы прошлых лет
Ключевые слова: Цепь переменного тока, напряжение переменного тока, цепь постоянного тока, индуктивность, электрическая цепь
Определение
[Нажмите здесь, чтобы просмотреть вопросы за предыдущий год]
Реактор
- В электрическом токе индуктор работает как наиболее мощная электронная схема, хранящая энергию в форме магнитной энергии.
Индуктор также называют дросселем, реактором или катушкой. Катушка индуктивности либо заряжается, либо теряет заряд при каждом использовании для выравнивания тока , протекающего через нее.
- Напряжение катушки индуктивности может измерять величину напряжения, генерируемого для определенной скорости изменения тока.
Подробнее:
Переменное напряжение, подаваемое на катушку индуктивности
[Нажмите здесь, чтобы просмотреть вопросы предыдущего года]
Катушка индуктивности может противодействовать или препятствовать прохождению переменного тока. Есть два способа сделать это: один — подключить индуктор к источнику постоянного тока, а второй — подключить его к источнику переменного тока.
- В цепи постоянного тока лампочка ярко светится, потому что через катушку индуктивности будет протекать постоянный ток.
- В цепи переменного тока лампочка не светится ярко, потому что катушка индуктивности противодействует или блокирует поток переменного тока .
Теперь мы должны использовать закон Ленца, чтобы объяснить противодействие протеканию переменного тока через индуктор:
Закон ЛенцаПеременный ток зависит как от величины, так и от направления. Когда ток увеличивается от нуля до максимального значения в течение временного интервала, ток катушки увеличивается, что означает, что магнитное поле, связанное с катушкой, также увеличивается.
ЭДС определяется законом Ленца как: E = − dΦ/dt
ну и становится нулем.
Итак, индуцированная ЭДС определяется как: E = − Ldt/di
Так как, Φ= L×i
Величина напряжения, требуемая источником переменного тока:
V= L×dt/di
Для поддержания тока генерируемое напряжение должно быть равно обратной ЭДС. Таким образом, напряжение, приложенное к катушка определяется как:
V= L×di/dt
Контрольный вопрос по Полное сопротивление цепи…
Отношение между током и напряжением на катушке
V= L×di/ dt
di/dt= V/L
di/dt= V m sinωt/L….
(1)
Здесь, В м = Максимальное напряжение
ω = Угловая частота
После интегрирования уравнения (1)
i = ∫ В м ×tωt9/Ld0003
i = — V м cosωt/ωL
i = V м sin (ωt- 90)/ ωL
i = i м sin (ωt- 90)
3, 900 Здесь тока
Подробнее: Решения NCERT для 12 класса Физика
Выражение для индуктивного сопротивления
В= В м sinωt
i= i м 02 03148 sin( 02 ωt) i м cosω
i м = V м / ωL
i M = V M /x L
, где, x L = индуктивная реактивность
Индуктивная реактивная реакция x L = ωl
x L = ωl
x L = ωl
x l = ωl
x L = ωl
x L = ωl
x L = ωl
.
Реактивное сопротивление Ом. Индуктивное сопротивление пропорционально угловой частоте. При увеличении частоты значение реактивного сопротивления также увеличивается, а при уменьшении частоты значение реактивного сопротивления также уменьшается. Если значение постоянного тока f = 0, то XL = 0,9.0003
Подробнее: Кинетическая теория 11 класс Физика
Мощность в цепи переменного тока
[Нажмите здесь, чтобы просмотреть вопросы прошлого года]
Потребляемая мощность
Мы знаем, что P = VI. Таким образом, мощность, потребляемая в цепи переменного тока, равна:
P= ( В м × sinωt) × ( 1 м × sin(ωt+Φ ))
Нахождение среднего значения мощности
P среднее = ( В m × sinωt) × ( 1 m × sin(ωt+Φ ) )
Используя тригонометрическое тождество:
2 sin A sin B = cos(A−B)–cos(A+B)
We get:
P avg = Average of V m I m [2⌊cosΦ–cos(2 ωt + Φ )⌋/2
Коэффициент мощности
Коэффициент мощности электрической цепи переменного тока можно определить как отношение реальной мощности, проходящей через цепь, к фактической мощности в цепи.
Коэффициент мощности = кажущаяся мощность/истинная мощность
Коэффициент мощностиПодробнее:
Важные вопросы
- Сопротивление резистора R источника переменного тока в последовательной цепи LCR. …. .[JEE Main 2014]
- Рассмотрим схему LR, показанную на рисунке. Если переключатель S замкнут в момент t=0, то….[ JEE Main 2019]
- Ток в момент времени, когда разность потенциалов на конденсаторе составляет 5 В, составляет… .[ JEE Main 2018]
- Дуговая лампа требует постоянного тока 10 А при 80 В для…. .[JEE Main 2016]
- Синусоидальное напряжение пикового значения 283 В и угловой частоты 320/с подается на.. .[JEE Main 2017]
- Последовательная цепь переменного тока, содержащая катушку индуктивности… Main 2019]
Вопросы прошлых лет
Вопросы с очень коротким ответом
Вопросы: Число витков соленоида увеличивается вдвое без изменения его длины и площади поперечного сечения.
Собственная индуктивность соленоида будет _________ раз. (CBSE 2020)
Ответ. Четыре раза. Исходя из вопроса, количество витков в катушке удваивается без какого-либо изменения индуктивности, приходящейся на катушку. Следовательно, индуктивность катушки увеличивается в четыре раза. Это означает, что собственная индуктивность соленоида увеличивается в четыре раза.
Вопросы: Определите добротность резонанса в последовательном контуре LCR. Какова его единица СИ? (CBSE 2016)
Ответ: Коэффициент качества связывает пиковую или максимальную энергию, запасенную в цепи, т. е. реактивное сопротивление рассеиваемой энергии (сопротивление) во время каждого цикла колебаний.
Коэффициент качества в последовательной цепи LCR выражается как
Q = w o L/R = 1/R √L/C
Коэффициент качества является безразмерным качеством, поэтому он не имеет единицы СИ.
Вопрос: Что такое емкостное сопротивление? Каковы его единицы СИ? (CBSE 2015)
Ответ: При подключении к электрической цепи сопротивление конденсатора называется емкостным реактивным сопротивлением.
В качестве альтернативы
∏ = угловая частота источника
C = емкость конденсатора
Единицей емкостного сопротивления в системе СИ является ом.
Вопросы с краткими ответами
Вопросы: Сопротивление R и конденсатор C соединены последовательно с источником V = V 0 sin \(\Box\)t. Найдите,
a) пиковое значение напряжения на (i) сопротивлении и (ii) конденсаторе
b) разность фаз между приложенным напряжением и током. Кто из них впереди? (CBSE 2020)Ответ:
a) (i) Пиковое значение напряжения на сопротивлении:
Напряжение источника V = V = C
Используя формулу пикового напряжения на сопротивлении
б) Как мы знаем, если есть напряжение на сопротивлении, то напряжение будет в фазе с током.
Опять же, если есть напряжение на емкости, то напряжение должно отставать от тока на 90 или .
Следовательно, напряжение на сопротивлении будет впереди.
Вопрос: Две лампы с номиналами (P 1 , В) и (P 2 , В) подключены (i) последовательно и (ii) параллельно к источнику питания V. Найдите мощность, рассеиваемую в две комбинации с точки зрения P 1 и P 2 . (CBSE 2019)
Отв. Электрическая мощность цепи означает скорость, с которой источник ЭДС совершает работу по поддержанию тока в электрической цепи. Электроэнергия дана, 92}{R}\) (так как V = IR)
Здесь, V = разность потенциалов
I = ток
R = сопротивление
(i) при номинале двух ламп (P 1, V ), (P 2 , В) соединены последовательно
СопротивлениеТок через каждую лампочку одинаков. Если сопротивления двух ламп R1 и R2, то эффективное сопротивление цепи равно
R = R 1 + R 2
Используя соотношение,
(ii) при параллельном подключении двух ламп номиналом (P 1 , В), (P 2 , В)
P 1 + P 2
Вопросы с длинным ответом
Вопрос 1: (a) Нарисуйте схему устройства, которое можно использовать для преобразования высокого переменного напряжения в низкое, и укажите принцип его работы.
Также напишите четыре источника потерь энергии в этом устройстве.
(б) Небольшой город с потребностью в 1200 кВт электроэнергии при напряжении 220 В расположен в 20 км от электростанции, вырабатывающей электроэнергию при напряжении 440 В. Сопротивление двухпроводной линии, по которой передается мощность, составляет 0,5 Ом за км. Город получает электроэнергию от линии через понижающий трансформатор 4000-200 В на подстанции в городах. Оцените потери мощности в линии в виде тепла. (CBSE 2019)Ответ: (a) Трансформатор или понижающий трансформатор — это устройство, которое используется для понижения высокого переменного напряжения до низкого переменного напряжения.
Трансформатор работает по закону электромагнитной индукции Фарадея. Согласно закону электромагнитной индукции, при изменении магнитного потока, связанного с катушкой, в катушке индуцируется ЭДС. Трансформатор состоит из двух катушек, называемых первичной и вторичной обмотками.
ТрансформаторПеременный ток в первичной обмотке изменяет магнитный поток, связанный со вторичной обмоткой, поэтому во вторичной обмотке индуцируется ЭДС.
Источники потерь энергии в трансформаторе,
- Потери в меди: Катушка трансформатора, изготовленная из меди, имеет конечное сопротивление, из-за которого теряется часть энергии в виде тепла.
- Потери в железе: Некоторая часть энергии теряется в массе из-за индуцированных вихревых токов в железном сердечнике.
- Магнитные потери: Происходит некоторая потеря энергии из-за утечки магнитного потока, так как весь магнитный поток в первичной обмотке не проходит через вторичную обмотку.
- Гистерезисные потери: Из-за чередования намагничивания и размагничивания железного сердечника происходит некоторая потеря энергии в виде тепла.
(б) Потребляемая малым городом электрическая мощность, P = 1200 кВт = 1200 x 103 Вт
Напряжение питания, 220 В
Выработка электроэнергии на электростанции, 440 В
0,5 Ом на км
Расстояние от электрогенератора до города, 20 км
Суммарное сопротивление провода
R = 0,5 (20+20) = 20 Ом
Город получает электроэнергию от понижающего трансформатора номинала 4000- 220 В
92 * 20\)= 9 х 10 4 х 20 = 180 х 10 4 = 1800 х 10 3 Вт
Таким образом, потери мощности в виде тепла составляют 1800 кВт.
Вопрос 2: (a) Нарисуйте графики, иллюстрирующие изменение индуктивного и емкостного реактивного сопротивления в зависимости от частоты используемого источника переменного тока.
(b) Нарисуйте векторную диаграмму для последовательной RC-цепи, подключенной к источнику переменного тока.
(c) Переменное напряжение 220 В приложено к устройству X, через которое протекает ток 0,25 А, отстающий по фазе от приложенного напряжения на π/2 радиан. Если такое же напряжение подается на другое устройство Y, то течет тот же ток, но не в фазе с приложенным напряжением.
(i) назвать устройства X и Y
(ii) рассчитать ток, который протекает в цепи, когда одинаковое напряжение приложено к последовательной комбинации X и Y. (CBSE 2018)Ответ : (a) Индуктивное сопротивление
Индуктивное сопротивлениеЕмкостное сопротивление
Емкостное сопротивлениеГде,
Вопрос 3: (a) Нарисуйте маркированную схему генератора переменного тока.
Приведите выражение для ЭДС, индуцируемой во вращающейся катушке из N витков площади поперечного сечения А в каждом при наличии магнитного поля \(\overrightarrow{B}\) .
(b) Горизонтальный проводящий стержень длиной 10 м, вытянутый с востока на запад, падает со скоростью 5,0 мс -1 под прямым углом к горизонтальной составляющей магнитного поля Земли 0,3 x 10 -4 Вбм -2 . Найдите мгновенное значение ЭДС индукции в стержне. (CBSE 2017)Ответ:
ЭДС, индуцированнаяНа основании закона Фарадея об электромагнитной индукции машина, которая преобразует заданную энергию в электрическую, называется генератором. Есть два типа, генератор переменного тока и генератор постоянного тока. Размер генератора постоянного тока сравнительно больше, чем у генераторов переменного тока, потери которых обычно ниже, чем у генератора переменного тока.0011 Генераторы постоянного тока .
Предположим, что t = 0 в данный момент. В направлении магнитного поля плоскость катушки перпендикулярна направлению магнитного поля. Таким образом, поток, проходящий через катушку, максимален.
Катушка через магнитный поток при t = 0
Вращение катушки вокруг оси с постоянной угловой скоростью обозначается ∏.
Катушка, повернутая на угол за время t, равна ∏t.
Поток создан,
Следовательно, e = n∏ba sin ∏t
(b) e = biv sin90 = biv
= 0,3 x 10 — 4 x 10 x 5
= 1,5 мВ
величина ЭДС наведения в стержне 1,5 мВ.
Вопрос 4: Группа учеников, возвращаясь из школы, заметила коробку с надписью «Опасно Х.Т. 2200 В» на подстанции на главной улице. Они не понимали полезности такого высокого напряжения и утверждали, что в сети всего 220 В. На следующий день они задали тот же вопрос своему учителю. Учитель подумал, что это важный вопрос, и поэтому объяснил его всему классу.

Ответьте на следующие вопросы:
(i) Какое устройство используется для понижения высокого напряжения до низкого напряжения переменного тока и укажите принцип его работы.
(ii) Может ли устройство понизить высокое постоянное напряжение до низкого напряжения? Объяснять.
(iii) Запишите значения, отображаемые учениками и учителем. (CBSE 2015)Отв. (i) Устройство, которое используется для понижения высокого напряжения до низкого напряжения переменного тока, называется трансформатором. Трансформатор работает по принципу взаимной индукции двух цепей или обмоток. При изменении тока в одной цепи ЭДС индуцируется в соседней цепи.
(ii) Трансформатор не может снизить высокое постоянное напряжение, поскольку он работает по принципу взаимной индукции. Магнитный поток, связанный со вторичной обмоткой, изменяется при изменении тока, связанного с первичной обмоткой.
Это изменение потока индуцирует ЭДС во вторичной обмотке. Более того, ток останется постоянным, если к первичной обмотке приложить постоянный ток. Следовательно, нет взаимной индукции и, следовательно, ЭДС не индуцируется.
(iii) Учащиеся демонстрируют ценность получения и расширения знаний и интереса к изучению новых вещей. Опять же, учитель продемонстрировал ценность обмена хорошим образованием и развеивания сомнений учеников.
Вопрос 5: (i) Последовательная цепь L-C-R подключена к источнику переменного тока переменной частоты. Нарисуйте диаграмму, чтобы вывести выражения амплитуды тока и фазового угла.
(ii) Получите условие при резонансе. Нарисуйте график, иллюстрирующий изменение тока в зависимости от частоты источника переменного тока для двух сопротивлений R 1 и R2 (R 1 > R2). Отсюда определите добротность Q и укажите ее роль в выключении цепи.(Дели, 2014 г.)
Ответ. (I)
Схема LCR(II)
Давайте предположим, что x L > x C ,
⇒ V L > V C
NUT . = И Р , В Л = IX Л , В С = IX C
Ссылки по теме:
Катушка индуктивности | Накопители энергии
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
Идеальный резистор был полезной аппроксимацией многих практических электрических устройств. Однако в дополнение к сопротивлению, которое всегда рассеивает энергию, электрическая цепь может также иметь емкость и индуктивность, которые служат для накопления и высвобождения энергии, точно так же, как расширительный бак и маховик соответственно действуют в механической системе.
Эти два различных механизма накопления энергии представлены в электрических цепях двумя идеальными элементами схемы: идеальным конденсатором и идеальной катушкой индуктивности, поведение которых приблизительно соответствует реальным дискретным конденсаторам и катушкам индуктивности. Они также аппроксимируют объемные свойства емкости и индуктивности, присутствующие в любой физической системе.
На практике любой элемент электрической цепи обладает некоторым сопротивлением, некоторой индуктивностью и некоторой емкостью, т. е. некоторой способностью рассеивать и накапливать энергию.
Энергия конденсатора хранится в электрическом поле между двумя проводящими пластинами, а энергия катушки индуктивности хранится в магнитном поле проводящей катушки. Оба элемента могут быть заряжены (т. е. накопленная энергия увеличена) или разряжены (т. е. уменьшена запасенная энергия).
Идеальные конденсаторы и катушки индуктивности могут бесконечно накапливать энергию; однако на практике дискретные конденсаторы и катушки индуктивности имеют «утечку», что обычно приводит к постепенному уменьшению накопленной энергии с течением времени.
Все отношения для конденсаторов и индукторов демонстрируют двойственность, что означает, что отношения конденсаторов являются зеркальным отображением отношений индукторов. Примеры двойственности очевидны в Таблица 1.
Таблица 1 Свойства конденсаторов и катушек индуктивности
Идеальный конденсатор
Конденсатор – это устройство, которое может накапливать энергию за счет разделения зарядов. В общем, конденсатор (и, следовательно, емкость) присутствует, когда любые две проводящие поверхности находятся на расстоянии друг от друга.
Простой пример: две параллельные пластины с общей площадью поперечного сечения A, разделенные расстоянием d. Зазор между пластинами может быть вакуумным или заполнен каким-либо диэлектрическим материалом, например воздухом, слюдой или тефлоном. Влияние диэлектрического материала на емкость представлено диэлектрической проницаемостью k.
На рис.
1 изображена типичная конфигурация и символ цепи для конденсатора.
Рисунок 1 Структура плоского конденсатора
Емкость C идеального конденсатора с плоскими пластинами, такого как описанный выше, равна:
\[\begin{matrix}C=\frac{k{{\varepsilon}_{o}}A}{d} & {} & \left( 1 \right) \\\end{matrix}\]
Где ε o = 8,85 × 10 −12 Ф/м — постоянная диэлектрической проницаемости вакуума.
Наличие диэлектрика или вакуума между проводящими пластинами не позволяет заряду переходить напрямую с одной пластины на другую. Однако если приложенное напряжение на конденсаторе изменится, то изменится и накопленный заряд. Таким образом, хотя никакой заряд не может буквально пройти от одной пластины идеального конденсатора непосредственно к другой, изменение напряжения приведет к изменению накопленного заряда, что эквивалентно действию тока через конденсатор.
Всегда разделение зарядов пропорционально приложенному напряжению
$\begin{matrix}{{Q}_{C}}=C{{V}_{C}} & {} & \left( 2 \right) \\\end{matrix}$
где параметр C — емкость и является мерой способности устройства накапливать заряд.
Единицей измерения емкости является кулон на вольт или фарад (Ф). Фарад — непрактично большая единица измерения для многих распространенных электронных приложений; единицы микрофарад (1 мкФ = 10 −6 Ф) и пикофарад (1 пФ = 10 −12 F) на практике встречаются чаще.
Ток через конденсатор определяется как скорость изменения накопленного заряда во времени. То есть
$\begin{matrix}{{i}_{c}}\left( t \right)=\frac{d{{q}_{c}}\left( t \right)}{ dt} & {} & \left( 3 \right) \\\end{matrix}$
Отношение i-v для конденсатора получается из уравнения 3 с использованием уравнения 2 для подстановки для q C (т). Результат:
$\begin{matrix}{{i}_{C}}\left( t \right)=C\frac{d{{v}_{C}}\left( t \right) }{dt} & {} & \left( 4 \right) \\\end{matrix}$ 9{t}{{{i}_{C}}\left( \tau \right)d\tau } & {} & \left( 5 \right) \\\end{matrix}$
Одно непосредственное следствие уравнение 4 заключается в том, что ток через конденсатор в цепи постоянного тока равен нулю.
Почему? Поскольку напряжение на конденсаторе в цепи постоянного тока по определению должно быть постоянным, производная напряжения по времени должна быть равна нулю. Таким образом, уравнение 4 требует, чтобы ток через конденсатор также был равен нулю.
Конденсатор в цепи постоянного тока эквивалентен разомкнутой цепи. 9{t}{{{i}_{C}}\left( \tau \right)d\tau } & t\ge {{t}_{0}} & \left( 6 \right) \\\end {matrix}$
Значение начального напряжения v C (t o ) = V o просто в том, что в момент времени t o некоторый заряд был накоплен в конденсаторе, в результате чего V o , согласно соотношению Q = CV.
Эквивалентная емкость
Точно так же, как резисторы могут быть соединены последовательно и параллельно для получения эквивалентного сопротивления, конденсаторы также могут быть соединены последовательно и параллельно для получения эквивалентной емкости.
Правила расчета приведены ниже.
Для двух конденсаторов, соединенных последовательно и параллельно, эквивалентные емкости равны соответственно:
$\begin{matrix}{{C}_{eq}}=\frac{{{C}_{1}}{{C }_{2}}}{{{C}_{1}}+{{C}_{2}}} & and & {{C}_{eq}}={{C}_{1}} +{{C}_{2}} & \left( 7 \right) \\\end{matrix}$
Обратите внимание, что правило для эквивалентной емкости двух последовательно соединенных конденсаторов представляет собой произведение, деленное на сумму, которая то же правило используется для двух резисторов, включенных параллельно. Точно так же эквивалентная емкость двух параллельно соединенных конденсаторов представляет собой просто сумму двух, что является тем же правилом, которое используется для двух последовательно соединенных резисторов. Более общие правила проиллюстрированы на Рисунок 2.
Рисунок 2 Эквивалентная емкость в цепи
При расчете эквивалентной емкости конденсаторы, соединенные последовательно, объединяются так же, как резисторы, соединенные параллельно, и конденсаторы, соединенные параллельно, объединяются, как резисторы, соединенные последовательно.

Дискретные конденсаторы
Реальные конденсаторы редко состоят из двух параллельных пластин, разделенных воздухом, потому что эта конфигурация либо дает очень низкие значения емкости, либо требует очень больших площадей пластин.
Для увеличения емкости (то есть способности накапливать энергию) физические конденсаторы часто изготавливают из плотно скрученных листов металлической пленки с диэлектриком (например, бумагой или майларом), зажатым между ними.
В таблице 2 приведены типичные значения, материалы, максимальное номинальное напряжение и полезные диапазоны частот для различных типов конденсаторов. Номинальное напряжение важно, потому что любой изолятор выйдет из строя, если к нему будет приложено достаточно высокое напряжение.
Table 2: Capacitors Materials and their Capacities
Material Capacitance range Maximum voltage (V) Frequency range (Hz) Mica 1 pF to 0. 1 µ F
100–600 10 3 −10 10 Ceramic 10 pF to 1 µ F 50–1,000 10 3 −10 10 Mylar 0.001 µ F to 10 µ F 50–500 10 2 −10 8 Paper 1000 PF до 50 мкм F 100–10 000 10 2 -10 8 Electrytic 0411 Electrytic 0411 . 10 4 На практике в реальных конденсаторах наблюдается некоторая утечка между пластинами. Несовершенные методы конструирования неизменно обеспечивают некоторую возможность перехода заряда с одной пластины на другую. Это несовершенство часто представлено эквивалентным сопротивлением параллельно идеальному конденсатору.
Накопление энергии в конденсаторах
Энергия, запасенная в конденсаторе W C (t), может быть легко получена из его определения как интеграла мощности по времени, который является произведением напряжения и тока: 9{2}\left( t \right)$
Идеальный индуктор
Индуктор — это элемент, который может накапливать энергию в магнитном поле внутри и вокруг проводящей катушки.
В общем, индуктор (и, следовательно, индуктивность) присутствует всякий раз, когда проводник превращается в петлю.
Простым примером является соленоид, представляющий собой узкую и плотно намотанную катушку длиной l, площадью поперечного сечения A и N витков. Катушки индуктивности обычно изготавливаются путем намотки проволоки вокруг сердечника, который может быть изолятором или ферромагнитным материалом, как показано на рис. 9.0011 Рисунок 3 . Ток через катушку создает магнитное поле через сердечник и вокруг него. В идеальном индукторе сопротивление провода равно нулю.
Рисунок 3 Индуктивность и практические катушки индуктивности
Индуктивность L определяется следующим соотношением: ]
Где $\Phi $ — магнитный поток через сердечник индуктора, а i L — ток через катушку индуктора. 9{1V-s}/{}_{A} & {} & \left( 10 \right) \\\end{matrix}$
Генри — разумные единицы измерения для практических катушек индуктивности, хотя миллигенри (мГн) очень распространены, а микрогенри (мкГн) встречаются изредка.
Соотношение i-v для индуктора выводится непосредственно из закона индукции Фарадея, но с заменой общего потока $N\Phi $ на Li из определения индуктивности L. Результат:
$\begin{matrix}{{ v}_{L}}\left( t \right)=L\frac{d{{i}_{L}}\left( t \right)}{dt} & {} & \left( 11 \right ) \\\конец{матрица}$ 9{t}{{{V}_{L}}\left( \tau \right)d\tau } & {} & \left( 12 \right) \\\end{matrix}$
Одно непосредственное следствие уравнение 11 заключается в том, что напряжение на катушке индуктивности в цепи постоянного тока равно нулю. Почему? Поскольку ток через катушку индуктивности в цепи постоянного тока по определению должен быть постоянным, производная тока по времени должна быть равна нулю. Таким образом, уравнение 11 требует, чтобы напряжение на катушке индуктивности также было равно нулю.
Катушка индуктивности в цепи постоянного тока эквивалентна короткому замыканию. 9{t}{{{V}_{L}}\left( \tau \right)d\tau } & t\ge {{t}_{0}} & \left( 13 \right) \\\end {matrix}$
Эквивалентная индуктивность
Точно так же, как резисторы могут быть соединены последовательно и параллельно для получения эквивалентного сопротивления, катушки индуктивности также могут быть соединены последовательно и параллельно для получения эквивалентной индуктивности.
Правила расчета приведены ниже.
Для двух катушек индуктивности, соединенных последовательно и параллельно, эквивалентные индуктивности соответственно равны
\[\begin{matrix}{{L}_{eq}}={{L}_{1}}+{{L} _{2}} & и & {{L}_{eq}}=\frac{{{L}_{1}}{{L}_{2}}}{{{L}_{1}} +{{L}_{2}}} & \left( 14 \right) \\\end{matrix}\]
Обратите внимание, что эквивалентная индуктивность двух последовательно соединенных катушек индуктивности представляет собой просто сумму двух, то же правило используется для двух последовательно соединенных резисторов. Точно так же правило эквивалентной индуктивности двух параллельных катушек индуктивности представляет собой произведение, деленное на сумму, что является тем же правилом, которое используется для двух параллельных резисторов. Более общие правила показаны на Рис. 4.
Рис. 40002 При расчете эквивалентной индуктивности индукторы, соединенные последовательно, объединяются так же, как последовательно соединенные резисторы, а параллельно индукторы объединяются, как резисторы, соединенные параллельно.

Двойственность
Все соотношения для конденсаторов и катушек индуктивности демонстрируют двойственность, что означает, что соотношения конденсаторов являются зеркальным отражением соотношений катушек индуктивности. В частности, роли, которые играют напряжение и ток в отношении конденсатора, меняются местами в аналогичном отношении индуктора. Например, отношения i-v для конденсаторов и катушек индуктивности, соответственно, таковы:
\[\begin{matrix}i=C\frac{dv}{dt} & and & v=L\frac{di}{dt } \\\end{matrix}\]
Обратите внимание, что отношение индуктивности получается из отношения конденсаторов заменой i на v и v на i. Также необходимо, конечно, заменить емкость C на индуктивность L. Другой пример двойственности можно найти в соотношениях накопления энергии для конденсаторов и катушек индуктивности.
Двойственность проявляется и в других отношениях, не связанных напрямую с напряжением и током.
Например, рассмотрим правила расчета эквивалентной емкости и эквивалентной индуктивности. Конденсаторы, соединенные последовательно, соединяются параллельно, как катушки индуктивности, в то время как конденсаторы, соединенные параллельно, объединяются, как катушки индуктивности, соединенные последовательно.
Другой пример двойственности можно увидеть в поведении конденсаторов и катушек индуктивности при постоянном токе. В цепи постоянного тока конденсатор действует как разомкнутая цепь, а катушка индуктивности действует как короткое замыкание 9.{2}\left( t \right)$
Еще раз обратите внимание на двойственность выражения для энергии, запасенной в конденсаторе, в уравнении 9 .
Вы нашли apk для андроида? Вы можете найти новые бесплатные игры и приложения для Android.
Расчет напряжения и тока в понижающем дросселе
В этом посте мы попытаемся разобраться в различных параметрах, необходимых для проектирования правильного дросселя понижающего преобразователя, чтобы требуемая выходная мощность позволяла достичь максимальной эффективности.
В нашем предыдущем посте мы изучили основы понижающих преобразователей и осознали важный аспект, касающийся времени включения транзистора по отношению к периодическому времени ШИМ, которое существенно определяет выходное напряжение понижающего преобразователя.
В этом посте мы углубимся и попытаемся оценить взаимосвязь между входным напряжением, временем переключения транзистора, выходным напряжением и током понижающей катушки индуктивности, а также способы их оптимизации при проектировании понижающей катушки индуктивности. .
Содержание
Давайте сначала разберемся с различными параметрами, связанными с понижающим преобразователем:
Пиковый ток дросселя, ( i pk ) = Это максимальное значение тока, которое может накопить дроссель до насыщения. . Здесь термин «насыщенный» означает ситуацию, когда время переключения транзистора настолько велико, что он продолжает оставаться включенным даже после того, как катушка индуктивности преодолела свою максимальную или пиковую емкость накопления тока.
Это нежелательная ситуация, и ее следует избегать.
Минимальный ток индуктора, ( i o ) = Это минимальное значение тока, которое может быть достигнуто индуктором во время разряда индуктора за счет высвобождения накопленной энергии в виде противо-ЭДС .
Это означает, что в процессе, когда транзистор выключен, катушка индуктивности разряжает накопленную энергию на нагрузку, и в ходе этого накопленный ток экспоненциально падает до нуля, однако, прежде чем он достигнет нуля, можно предположить, что транзистор снова включается, и эта точка, в которой транзистор может снова включиться, называется минимальным током дросселя.
Вышеупомянутое состояние также называется непрерывным режимом для конструкции понижающего преобразователя.
Если транзистор не включится обратно до того, как ток катушки индуктивности упадет до нуля, то ситуацию можно назвать прерывистым режимом, что является нежелательным способом работы понижающего преобразователя и может привести к неэффективной работе преобразователя.
система.
Пульсирующий ток, (Δi = i pk — i o ) = Как видно из приведенной формулы, пульсации Δ i представляют собой разницу между пиковым током и минимальным током, индуцируемым в понижающем дросселе.
Конденсатор фильтра на выходе понижающего преобразователя обычно стабилизирует этот пульсирующий ток и помогает сделать его относительно постоянным.
Рабочий цикл, (D = T на /T) = Рабочий цикл рассчитывается путем деления времени включения транзистора на периодическое время.
Периодическое время — это общее время, необходимое для завершения одного цикла ШИМ, то есть время включения + время выключения одного ШИМ, подаваемого на транзистор.
Время включения транзистора ( T на = D/f) = Время включения ШИМ или время «включения» транзистора можно получить, разделив рабочий цикл на частота.
Средний выходной ток или ток нагрузки, ( i ave = Δi / 2 = i нагрузка ) = Получается путем деления тока пульсаций на 2. Это значение представляет собой среднее значение пикового тока и минимального тока, который может быть доступен на нагрузке на выходе понижающего преобразователя.Стоимость среднеквадратичного значения треугольной волны IRM = √ { I O 2 + (ΔI) 2 1 (ΔI) 2 1 (ΔI) 2 1 (ΔI). среднеквадратичное значение всех или любой составляющей треугольной волны, которая может быть связана с понижающим преобразователем.
Итак, выше были различные параметры и выражения, связанные с понижающим преобразователем, которые можно было использовать при расчете понижающего индуктора.
Теперь давайте узнаем, как напряжение и ток могут быть связаны с понижающим индуктором и как их можно правильно определить, исходя из следующих объясненных данных:
Помните, здесь мы предполагаем, что переключение транзистора происходит в непрерывном режиме, то есть транзистор всегда включается до того, как катушка индуктивности сможет полностью разрядить накопленную ЭДС и стать пустой.
На самом деле это достигается путем соответствующего определения времени включения транзистора или рабочего цикла ШИМ в зависимости от емкости катушки индуктивности (количества витков).
Соотношение В и I
Соотношение между напряжением и током в понижающем индукторе можно записать следующим образом:
Приведенную выше формулу можно использовать для расчета выходного тока понижающего преобразователя, и она действительна, когда ШИМ имеет форму экспоненциально нарастающей и затухающей волны или может быть треугольной волной.
Однако, если ШИМ имеет форму прямоугольного сигнала или импульсов, приведенная выше формула может быть записана как:
i = (Vt/L) + i o
Здесь Vt — напряжение на обмотке умножить на время, в течение которого она сохраняется (в микросекундах)
Эта формула становится важной при расчете значения индуктивности L для понижающего индуктора.
Приведенное выше выражение показывает, что выходной ток дросселя индуктивности имеет форму линейной рампы или широких треугольных волн, когда ШИМ имеет форму треугольных волн.
Теперь давайте посмотрим, как можно определить пиковый ток внутри понижающего индуктора, формула для этого:
Расчет пикового тока
Таким образом, приведенное выше выражение можно использовать для расчета пикового нарастания тока внутри катушки индуктивности. понижающий индуктор, пока транзистор находится в фазе включения.
Если выражение io сдвинуть влево, то получим:
i pk — i o = (Vin – Vtrans – Vout)Ton / L
Здесь Vtrans относится к падению напряжения на коллектор/эмиттер транзистора
Напомним, что ток пульсаций также определяется как Δi = ipk — io, поэтому, подставив это в приведенную выше формулу, мы получим:
Δi = (Vin – Vtrans – Vout)Ton / L — ———————————- Уравнение №1
Теперь давайте посмотрим выражение для получения тока в дросселе в течение периода выключения транзистора, его можно определить с помощью следующего уравнения: (Vout – VD)Toff / LОпять же, заменив ipk — io на Δi в приведенном выше выражении, мы получим:
Δi = (Vout – VD)Toff / L ———- ————————— Eq#2
Eq#1 и Eq#2 можно использовать для определения значений пульсаций тока в то время как транзистор подает ток на индуктор, то есть во время его включения.
…. и пока индуктор отводит накопленный ток через нагрузку в периоды выключения транзистора.
В приведенном выше обсуждении мы успешно вывели уравнение для определения коэффициента тока (ампер) в понижающей катушке индуктивности.
Определение напряжения
Теперь попробуем найти выражение, которое может помочь нам определить коэффициент напряжения в понижающем дросселе.
Поскольку Δi является общим как в уравнении № 1, так и в уравнении № 2, мы можем приравнять члены друг к другу, чтобы получить:
(Vin – Vtrans – Vout)Ton / L = (Vout – VD)Toff / L
ВинТон – Втранс – Ввых = VвыхТофф – ВДТофф
Vinton — VTRANS — VOUTTON = VOUTTOFF — VDTOFF
VOUTTON + VOUTTOFF = VDTOFF + VINTON — Vtranston
VOUT = (VDTOFF + VINTON — VTRANSTON) / T . на скважность D в приведенном выше выражении, мы получаем
Vвых = (Vin – Vтранс)D + VD(1 – D)Обрабатывая приведенное выше уравнение дальше, мы получаем:
Vвых + VD = ( Вин – Втранс + ВД)Д
илиD = Vout — VD / (Vin – Vtrans – VD)
Здесь VD относится к падению напряжения на диоде.
Вычисление понижающего напряжения
Если мы игнорируем падения напряжения на транзисторе и диоде (поскольку они могут быть очень незначительными по сравнению с входным напряжением), мы можем уменьшить приведенное выше выражение, как показано ниже:
Vout = DVin
Приведенное выше окончательное уравнение можно использовать для расчета понижающего напряжения, которое может быть получено от конкретной катушки индуктивности при разработке схемы понижающего преобразователя.
Приведенное выше уравнение такое же, как и рассмотренное в примере решения из нашей предыдущей статьи «Как работают понижающие преобразователи».
В следующей статье мы узнаем, как оценить количество витков в понижающем дросселе… .пожалуйста, следите за обновлениями. I определение индуктора
Индуктор (также называемый катушкой или реактором ) представляет собой пассивный электронный компонент, процесс производства которого основан на намотке определенного количества витков проводника на определенную поверхность, например кольцо (которое создает тороидальные индукторы, ролик (соленоиды) или плоскость (спиральные, плоские индукторы).
Кроме того, снаружи/внутри индукторов может быть создан сердечник из магнитного, диамагнитного или ферромагнитного материала .
Символ индуктора
В связи с тем, что индуктор является инерционным элементом, он накапливает энергию в генерируемом магнитном поле. Применение катушки индуктивности с конденсатором в одной цепи приводит к резонансному контуру (являющемуся одной из элементарных электронных схем). индуктор, который питается постоянным током, обычно называют электромагнитом, который используется для создания магнитного поля или его компенсации (уравновешивания, например, при размагничивании). В цепи переменного тока индуктор индуцирует ток, что вызывает запаздывание его напряжения по отношению к фазному напряжению и увеличение общего сопротивления. Катушка индуктивности, размещенная в электрических системах, обладает рядом свойств, например, кроме генерации магнитного поля, она может индуцировать ток, а также влиять на фазу тока и напряжения.
Обозначение индуктора обозначается буквой L – как его индуктивность.
Как работает дроссель
Дроссель в цепях постоянного тока играет роль резистивного элемента (сопротивление зависит от материала, из которого он изготовлен). Однако, когда частота имеет значение больше 0 (ω > 0), сопротивление катушки индуктивности называется электрическим реактивным сопротивлением (обычно обозначается буквой X).
Реактивное сопротивление катушки индуктивностиω – угловая частота
I импеданс индуктораКогда мы имеем дело с идеальным индуктором, импеданс равен произведению его реактивного сопротивления на мнимую единицу: индуктор, маркированный буквой « L» . Он определяется как ток (векторный поток магнитной индукции), протекающий через индуктор. Единицей индуктивности является Генри [Гн] . Формула представлена ниже:
– поток магнитной индукции,i – сила тока, протекающего через индуктор.
Форма катушки индуктивности, толщина провода, используемого в компоненте, и количество витков этого провода имеют прямое влияние на коэффициент k. Индуктивность индуктора также зависит от магнитных свойств сердечника.
Индукционный поток магнитного поля, протекающего через индуктор, описывается формулой:
L – индуктивность индуктора,
i – ток, протекающий через индуктор.Ток заданной силы, протекающий по проводнику, одновременно создает магнитное поле. Энергия этого поля численно равна работе, необходимой для его создания, которая равна:
л – индуктивность индуктора,
л – ток, протекающий через индуктор,
В – магнитная индукция,
В – объем индуктор (фокус индукции В).Электродвижущая сила (ЭДС) , индуцирующая в индукторе, описывается формулой:
Если предположить, что индуктивность катушки индуктивности постоянна (как это справедливо для большинства электрических цепей), приведенная выше формула может быть записана как:
Постоянная катушки индуктивности
Постоянная катушки индуктивности для постоянного тока соответствует индуктивности:
H – напряженность магнитного поля,
I ток индуктора
I – напряженность тока.Мгновенный ток индуктора определяется из уравнения для мгновенного напряжения индуктора. Идеальное преобразование заявленного уравнения приводит к дифференциальному уравнению с разделенными переменными, где одна переменная представляет собой ток индуктора, а другая — напряжение индуктора.
P Катушка индуктивностиКатушка индуктивности способна сохранять энергию в магнитном поле. Формула мощности индуктора возникла из общей формулы энергия/работа. Работа есть интеграл от мгновенной мощности p в момент времени t.→ W=∫p·dt, Принимая во внимание тот факт, что мгновенная мощность является частью мгновенного напряжения, а также мгновенного тока → p=u-i и принимая во внимание формулы, полученные ранее, результатом является формула для энергии, сэкономленной в индукторе. Обратите внимание, что мощность, сохраненная в катушке индуктивности, симметрична току во 2-й степени.
Сопротивление индуктораДля индуктора без ферромагнитного сердечника (воздушный индуктор) его индуктивность постоянна. Для индуктора с ферромагнитным сердечником его индуктивность различна и зависит от типа ферромагнетика, магнитной индукции в сердечнике, а также применения магнитопровода магнитопровода (сердечник с воздушным пространством). Индуктивность катушки индуктивности можно определить напрямую или вычислить с помощью косвенных методов. Для прямого измерения используется измеритель RLC с цифровым считыванием. Из косвенных подходов наиболее часто используется технологический метод определения реактивного сопротивления индуктора XL и, следовательно, его собственной индуктивности L.
Для этой цели индуктор обеспечивается источником переменного тока известной частоты f, а также определяются напряжение U на индукторе, ток I, протекающий через индуктор, и активная мощность P, потребляемая индуктором.Для воздушного индуктора сопротивление, полученное из соотношения:
, практически является сопротивлением провода обмотки индуктора.
Т Постоянная времени индуктораЗависимость от времени тока в цепи при ее отделении от ресурса электродвижущей силы выражается приведенным ниже уравнением.
Результат показывает, что ток в цепи обязательно будет затухать по экспоненциальной зависимости, а скорость вырождения устанавливается пропорцией сопротивления к индуктивности цепи. Обратной величиной этого отношения является постоянная времени цепи RL, которую мы обозначили через τ.
Катушка индуктивности Последовательное и параллельное соединениеКатушки индуктивности можно комбинировать, как резисторы и конденсаторы в последовательной и параллельной конфигурациях и использовать, например, в Системы LC-фильтрации входного напряжения в цифровых схемах («до» микроконтроллеров).
При последовательном соединении одно и то же значение тока проходит через все компоненты. Однако стоит отметить, что каждый из них может иметь разное напряжение.
Катушки последовательного соединенияСуммарная индуктивность такой системы определяется как:
Катушки индуктивности, соединенные параллельным соединением, можно заменить одной с общей индуктивностью, определяемой формулой:
Параллельное соединениеСвойства, показанные выше, применимы только тогда, когда магнитное поле каждой из катушек индуктивности не влияют друг на друга.
Цепи индукторов
Соединительный индуктор
С комбинированным индуктором 2 кабеля намотаны на магнитный сердечник. На этой схеме обратите внимание, что оба провода намотаны на сердечник в противоположных направлениях и также генерируют напряжение одинаковой полярности. Это связано с законом Ленца. Различное магнитное поле, создаваемое током, будет индуцировать ток в противоположных направлениях на связанном индукторе. Генрих Ленц включил отрицательное указание в закон индукции Фарадея.
Здесь ɸB – изменение магнитного потока, а – электродвижущая сила.
Поток внутри магнитного сердечника связанных катушек индуктивности зависит от произведения сердечника
, числа витков провода вокруг сердечника и силы тока.Напряжение на индукторе связано с потоком по числу витков индуктора.
Магнитный поток обязательно будет такой же (как индуцируемый первым индуктором), так же как и получаем формулу общей индуктивности.
Переменная M представляет собой взаимную индуктивность системы в генри. Это зависит от геометрических свойств индукторов, таких как количество витков и радиусы витков каждого индуктора.
Точечное обозначение используется для определения направления обмоток вокруг сердечника. Точки на одних и тех же концах индуктора означают, что индукторы намотаны друг на друга по часовой стрелке-против часовой стрелки. Если точки попадут на противоположные стороны, то катушки индуктивности завернуты параллельно (по часовой стрелке или против часовой стрелки).
Важно помнить, что соглашение о точках соответствует пассивному соглашению. На рисунке показаны напряжения одинаковой полярности, одно из напряжений обязательно будет отрицательным. Точечное соглашение гласит: если ток входит в пунктирную клемму одного индуктора, напряжение будет положительным в точке на 2-м индукторе.
Это напряжение представляет собой напряжение, индуцированное присоединенным током. В трансформатор может поступать ток как от первого, так и от второго индуктора. Напряжение на каждом индукторе, безусловно, будет зависеть от тока через этот индуктор, а также от индуцированного напряжения от другого индуктора. Предположим, что точки находятся на одном и том же конце, и оба тока входят в точки. Напряжения будут.
Если точки будут на противоположных сторонах друг от друга, то напряжения обязательно будут.
Поскольку индукция основана на переменном токе, необходимо использовать связанные катушки индуктивности с переменным током. Это означает, что мы можем оценивать связанные катушки индуктивности в частотной области как векторы.
Переменный индуктор
Переменный индуктор, является компонентом индукционного нагревателя, который определяет эффективность, а также эффективность нагрева платы. Ассортимент наших катушек индуктивности велик; от базовых спиралей, содержащих несколько медных индукторов, окружающих оправку, до точно изготовленных форм, изготовленных из твердых медных изделий, впоследствии сваренных вместе тугоплавким припоем.
Возбудитель предназначен для передачи энергии переменного электромагнитного поля от асинхронного генератора на плату. Электромагнитное поле генерирует ток в заряде, который показывает ток, протекающий в индукторе. Если ток циркулирует через сопротивление заряда, он выделяет тепло в виде потерь по формуле I2R.
Второй фактор для отопления дома связан с явлением гистерезиса, которое характерно для магнитных материалов, таких как углеродистая сталь. Энергия вырабатывается в заряде из-за переменного электромагнитного поля, заставляющего заряд менять полярность (перемагничивать). Гистерезисный нагрев происходит в (магнитных) зарядах примерно на уровне температуры Кюри (750°С для стали), при котором магнитная проницаемость падает до 1,9.0003Ток, протекающий по проводнику, создает электромагнитное поле. Переменный ток создает переменное электромагнитное поле, которое создает переменный ток в дополнительном проводнике (заряде). Ток в заряде пропорционален напряженности поля.
Воздействие трансформатора имеет место, так как ток, наведенный в заряде, симметричен числу витков индуктора, а также является отражением индуктора.
Форма индуктора является основой для производительности, а также производительности процесса индукционного отопления дома. Мы разрабатываем катушки индуктивности в первую очередь для того, чтобы предложить место для обогрева дома. Тепло должно производиться в таком месте и таким образом, чтобы достичь желаемого технического результата.
Индукторы представляют собой медные проводники с водяным охлаждением, изготовленные из медных труб или профилей, которые можно быстро сформировать для необходимой процедуры индукционного отопления дома. Индукторы охлаждаются и также не нагреваются, так как с ними течет вода.
Согласование катушки индуктивности с выходной цепью генератора необходимо для производительности процесса. Это быстро достигается для различных катушек индуктивности благодаря возможности использовать несколько ответвлений на выходном трансформаторе, к которому подключены катушки индуктивности.Дроссельный дроссель
Индукционные дроссели находят широкое применение, особенно в электронике, а также в электротехнике. Они часто используются в приводных системах, где они взаимодействуют с инверторами, т. е. устройствами, преобразующими постоянный ток в переменный с регулируемым напряжением и частотой. Индукционные дроссели также используются в силовых электронных устройствах, где их задачей является уменьшение количества электромагнитных помех, возникающих во время процедуры. Кроме того, эти аспекты используются в выпрямителях, питаемых от электромагнитной сети. В этой ситуации они созданы для подавления пульсаций. В цепях переменного тока индуктивные дроссели используются для уменьшения токов короткого замыкания.
Дроссели являются отличной защитой от помех для цепей переменного тока общеупотребительных устройств. Также стоит понимать, что индуктивный дроссель найдет применение в случае импульсных стабилизаторов, работающих на высоких частотах, т.е. встроенных цепей, питающих поставляемый приемник. Эти стабилизаторы отвечают за генерацию устойчивого выходного напряжения на основе явления самоиндукции. Не менее распространенным применением индуктивного дросселя является его использование для отключения транзисторов регулирования тока в преобразователях с улучшенными тиристорами. Это указывает на то, что дроссель является одним из самых функциональных электрических устройств, а также нельзя недооценивать его значимость в данной цепи.
Конденсатор и катушка индуктивности
- Некоторые различия возникают из-за конструкции самих частных элементов. Конденсатор содержит 2 оболочки, изготовленные из токопроводящего материала, однако между ними находится слой непроводящего диэлектрика. Вывод? Конденсатор не проводит постоянный ток, это просто разрыв в цепи. С переменным же током дело обстоит иначе — конденсатор проводит. Для высоких частот это короткое замыкание – как будто его и не было, т.е. был бы просто кусок провода или дорожка на плате… Как это связано с дросселем? Катушка индуктивности обычно представляет собой правильно сформированный элемент кабеля.
В самых простых терминах. Он проводит постоянный ток. Совсем другая ситуация с переменным током. Проводит, но чем выше частота, тем хуже. Теоретически для очень высоких частот это составляет… разрыв в цепи.
- По первому пункту. Конденсатор образует короткое замыкание для высоких частот, а катушка индуктивности образует разрыв цепи. Это относится к их реактивному сопротивлению (вы знаете, что сопротивление для переменного тока). Емкостное реактивное сопротивление (конденсатор) уменьшается по мере увеличения частоты. Противоположное верно для индуктора. Реактивное сопротивление индуктивности увеличивается с увеличением частоты.
- Катушка индуктивности сопротивляется изменениям тока, индуцируя внутри себя напряжение. Что делает конденсатор? Это делает полную противоположность, если можно так выразиться. Он полностью препятствует регулировке напряжения. Он отвечает на быстрое изменение напряжения столь же быстрым изменением тока.
- Катушки индуктивности и конденсаторы можно размещать в силовых цепях, таких как повышающие преобразователи.
- И дроссель, и конденсатор можно построить своими руками. Вам нужен только кусок кабеля или построить индуктор. Создание конденсатора немного сложнее, однако, опять же, все, что вам нужно, это алюминиевая фольга и пищевая крышка. А также ножницы.
- Катушка индуктивности и конденсатор (а также резистор, помните) являются простыми аспектами. Они не создают электричество, они вызывают потерю мощности.
- Конденсатор накапливает энергию в электрическом поле, а катушка индуктивности — в электромагнитном поле.
- Фундаментальной физической величиной, объясняющей конденсатор, является электрическая емкость, выраженная в фарадах. Для индуктора это индуктивность, выраженная в генри.
Ссылка:
RLC dla początkujących: cewka kontra kondensatorhttps://www.dacpol.eu/pl/grzejnictwo-indukcyjne-wzbudniki/product/ wzbudnik-induktor-grzejnictwo-indukcyjne
https://ocw.nthu.edu.tw/ocw/upload/124/news/[%E9%9B%BB%E5%8B%95%E6%A9%9F%E6%A2%B0L6a%E8% A3%9C%E5%85%85%E6%95%99%E6%9D%90]Maple%20Inc.
_Coupled%20Inductors.pdf
http://if.pw.edu.pl/~wosinska/am2/ w12/segment3/main.htm
http://www.mbmaster.pl/elektrotechnika-cewka-napiecie-prad-energia.html
Михал
Инженер по электронике и телекоммуникациям с дипломом магистра электроэнергетики. Светодизайнер опытный инженер. В настоящее время работает в сфере IT.
Общие сведения о параметрах силового индуктора | Артикул
Sven Spohr
ЗАГРУЗИТЬ PDF
Получайте ценные ресурсы прямо на свой почтовый ящик — рассылка раз в месяц
Подписаться
Мы ценим вашу конфиденциальность потребительские приложения. Для этих приложений требуются силовые катушки индуктивности, в основном для устройств с батарейным питанием, встроенных вычислений и мощных/частотных преобразователей постоянного тока в постоянный. Важно понимать электрические характеристики катушек индуктивности, чтобы проектировать компактные, экономичные, эффективные системы с превосходными тепловыми характеристиками.
Катушки индуктивности представляют собой относительно простые компоненты, состоящие из изолированного провода, намотанного на катушку. Сложность возникает, когда отдельные компоненты объединяются для создания катушки индуктивности с правильными размерами, весом, температурой, частотой и напряжением для удовлетворения целевого применения.
При выборе индуктора важно понимать электрические характеристики, указанные в паспорте индуктора. В этой статье представлены рекомендации по выбору оптимальной катушки индуктивности для решения при прогнозировании характеристик катушки индуктивности при разработке нового преобразователя постоянного тока в постоянный.
Что такое индуктор?
Катушка индуктивности — это компонент электрической цепи, который накапливает энергию в своем магнитном поле. Катушки индуктивности преобразуют электрическую энергию в магнитную, накапливая, а затем подавая энергию в цепь для регулирования тока. Это означает, что если ток увеличивается, магнитное поле увеличивается.
На рис. 1 показана модель индуктора.
Рис. 1: Электрическая модель индуктора
Катушки индуктивности состоят из изолированного провода, намотанного в виде катушки. Катушка может быть разных форм и размеров и может быть намотана с использованием различных материалов сердечника.
Индуктивность зависит от множества факторов, таких как количество витков, размеры сердечника и проницаемость. На рис. 2 показаны основные параметры индуктора.
Рисунок 2: Параметры катушки индуктивности
В таблице 1 показано, как рассчитать индуктивность (L).
Таблица 1: Расчет индуктивности (л)
Уравнение Параметр Параметр Описание $$ мк = мк г мк 0 Проницаемость микро р Относительная проницаемость (керн) µ 0 = 4π10 -7 Константа природы А М Площадь катушки (площадь магнитного поля) И М Длина катушки (длина магнитного поля) µ Количество витков Общие параметры катушки индуктивности более подробно описаны ниже.
ПроницаемостьМагнитная проницаемость — это способность материала реагировать на магнитный поток, а также величина магнитного потока, который может пройти через индуктор в приложенном электромагнитном поле. В таблице 2 показано, как магнитная проницаемость может усиливаться плотностью магнитного потока (В).
Таблица 2: Расчет плотности магнитного потока (B)
Уравнение Параметр Параметр Описание $$B = µ \×H$$ $$µ$$ Проницаемость среды $$H$$ Магнитное поле (зависит от геометрии, числа витков и тока) Исходя из таблицы 2, концентрация магнитного потока зависит от проницаемости и размеров сердечника.
На рис. 3 показана катушка без сердечника.
Рисунок 3: Воздушный змеевик
Проницаемость воздушного змеевика представляет собой постоянную величину (µr воздуха), которая примерно равна 1.
На рис. 4 показан индуктор с сердечником. Обратите внимание, что при использовании сердечника магнитное поле усиливается.
Рис. 4: Катушка индуктивности с сердечником
Типичная проницаемость магнитного сердечника зависит от материалов сердечника. В таблице 3 приведены значения проницаемости трех различных материалов сердечника.
Таблица 3: Проницаемость магнитного сердечника
Материал сердечника Обозначение Проницаемость Железо µ r FE НА ОСНОВЕ от 50 до 150 Никель-цинк µ r NiZn от 40 до 1500 Марганец-цинк µ r MnZn от 300 до 20 000
Индуктивность (л)Индуктивность — это способность катушки индуктивности сохранять наведенную электрическую энергию в виде магнитной энергии.
Катушка индуктивности должна подавать постоянный постоянный ток на выходную нагрузку, управляясь входным напряжением переключения.
В таблице 4 показано соотношение между током и напряжением катушки индуктивности. Обратите внимание, что напряжение на катушке индуктивности пропорционально изменению тока во времени.
Таблица 4: Расчет падения напряжения на дросселе
Уравнение Параметр Параметр Описание $$v = L \times \frac {di}{dt}$$ $$v$$ Падение напряжения на катушке индуктивности $$\frac {di}{dt}$$ Скорость изменения тока Сначала определите диапазон индуктивности для вашей конструкции, учитывая, что индуктивность не является постоянной в зависимости от условий эксплуатации. Индуктивность может изменяться при увеличении частоты, что требует особого внимания для приложений с более высокими частотами переключения.
Сопротивление (R)Производители дросселей обычно проверяют индуктивность на частотах от 100 кГц до 500 кГц, поскольку большинство преобразователей постоянного тока работают в этом диапазоне.
Сопротивление катушки индуктивности по току приводит к рассеиванию тепла, что влияет на КПД. Общие потери в меди состоят из потерь R DC и R AC . R DC является постоянным независимо от частоты, тогда как R AC зависит от частоты. В таблице 5 показано, как рассчитать R DC .
Таблица 5: Расчет Cooper R DC
Уравнение Параметр Параметр Описание $$R_{DC} = ρ \times \frac {I}{A}$$ $$ρ$$ Удельное сопротивление $$I$$ Длина $$A$$ Площадь поперечного сечения Единственный способ уменьшить потери в меди — это увеличить площадь провода либо путем перехода на более толстый провод, либо с помощью плоского провода.
При использовании плоского провода окно обмотки используется полностью, что приводит к снижению RDC. Таблица 6 показывает площадь поперечного сечения круглого провода по сравнению с плоским проводом. 92$$
В таблице 7 сравниваются преимущества круглой и плоской проволоки.
Таблица 7: Круглые и плоские проволоки
Круглая проволока Плоский провод
- Более высокая индуктивность
- Более высокое сопротивление (R DC )
- Нижняя часть поперечного сечения
- Возможно большее количество оборотов
- Меньший ток
- Площадь обмотки ограничена, максимальная индуктивность уменьшена
- Нижнее сопротивление (R DC )
- Заводное окно полностью б/у
- Возможно меньшее количество оборотов
- Высокий ток
Оцените потери в меди постоянного тока катушки индуктивности (P DC ) с помощью уравнения (1):
92_{DC} \times R_{DC}$$Потери в меди (P AC ) основаны на R AC и вызваны близостью и скин-эффектом, который зависит от частоты.
Потери в сердечникеЧем выше частота, тем выше потери в меди P AC .
Как правило, магнитные свойства, необходимые для катушек индуктивности на основе сердечника, могут быть достигнуты с помощью ферромагнитного материала. В зависимости от материала сердечника относительная магнитная проницаемость этого индуктора колеблется от 50 до 20000.
Доменная структура этого материала реагирует на воздействие магнитного поля; без магнитного поля ориентация случайна. Потери в сердечнике возникают при изменении магнитной энергии. Домены ориентируют магнитный момент вдоль направления магнитного поля. По мере расширения и сжатия доменов некоторые из них застревают в кристаллической структуре. Как только застрявшие домены могут вращаться, энергия рассеивается в виде тепла.
Пульсирующий ток (∆I L )Пульсирующий ток (∆I L ) представляет собой величину, на которую ток изменяется во время цикла переключения.
Катушка индуктивности может работать неправильно, если она работает за пределами диапазона пикового тока. Пульсирующий ток катушки индуктивности обычно проектируется так, чтобы он находился в пределах от 30% до 40% от IRMS.
На рис. 5 показана кривая тока катушки индуктивности.
Рис. 5. Форма кривой тока дросселя
Номинальный ток (I DC , I RMS )Номинальный ток относится к постоянному току, необходимому для увеличения температуры катушки индуктивности на заданную величину. Повышение температуры (ΔT) не является стандартным значением, хотя обычно оно составляет от 20 до 40 К.
Номинальный ток измеряется при температуре окружающей среды. Этот ток указан в техническом описании индуктора и является значением, ожидаемым для окончательного применения. Для приложений с более высокими температурами окружающей среды проектировщики должны выбирать индуктор с более высокой температурой самонагрева.
На рис.
6 показано повышение температуры по отношению к номинальному току. Эту кривую можно использовать для определения тока при любом повышении температуры.
Рис. 6. Кривая номинального тока дросселя
Рабочая температура (T OP ) в приложении определяется температурой окружающей среды (T AMB ) и значением самонагрева дросселя (ΔT). T OP можно рассчитать по уравнению (2):
$$T_{OP} = T_{АМБ} + ΔT$$
Данный номинальный ток является хорошим способом оценки повышения температуры катушки индуктивности. На повышение температуры также влияет конструкция схемы, компоновка печатной платы, близость к другим компонентам, а также размеры и толщина дорожек. Дополнительный нагрев также может быть вызван избыточными потерями переменного тока, возникающими в корпусе сердечника индуктора и обмотках.
Используйте индуктор большего размера, если требуется меньший самонагрев.
Ток насыщения (I SAT )Номинальные значения тока насыщения относятся к постоянному току, который индуктор может поддерживать до того, как номинальная индуктивность упадет на определенный процент.
Эталонное падение в процентах уникально для каждого индуктора. Как правило, производители устанавливают это значение в диапазоне от 20% до 35%, что может затруднить сравнение катушек индуктивности. В таблицах данных обычно можно найти кривую, показывающую, как изменяется индуктивность по отношению к постоянному току. Эту кривую можно использовать для оценки всего диапазона индуктивности и того, как он соответствует постоянному току.
Постоянный ток насыщения зависит от температуры, магнитного материала индуктора и структуры его сердечника. Различные конструкции и магнитные сердечники могут влиять на I SAT .
Ферритовые барабанные сердечники являются наиболее распространенными и характеризуются жесткой кривой насыщения (см. рис. 7). Критично ли гарантировать, что индуктор не работает за пределами точки сброса, так как индуктивность значительно падает, а функциональность снижается после этой точки?
Литые индукторы из композитного материала имеют стабильное падение индуктивности при изменении температуры с плавным насыщением.
Мягкое насыщение дает разработчикам большую гибкость и более широкий рабочий диапазон благодаря постепенному падению индуктивности.
На рис. 7 показаны две кривые насыщения. Синяя кривая показывает пример мягкого насыщения с типичным литым индуктором из композитного материала. Красная кривая показывает пример жесткого насыщения с типичным сердечником барабана NiZn/MnZn.
Рисунок 7: Кривая тока насыщения дросселя
Меньшая индуктивность (или больший размер корпуса) позволяет катушкам индуктивности выдерживать более высокие токи насыщения.
Собственная резонансная частота и импедансСобственная резонансная частота (f R ) катушки индуктивности – это самая низкая частота, при которой катушка индуктивности резонирует со своей собственной емкостью. На резонансной частоте полное сопротивление максимально, а эффективная индуктивность равна нулю. На рис. 8 показана схема схемы катушки индуктивности.
Рис. 8. Схема индуктора, модель
Катушка индуктивности имеет индуктивную характеристику (показана синей кривой на рис.
9) вплоть до резонансной частоты (f R ), так как увеличение частоты соответствует более высокому импедансу. На резонансной частоте отрицательное емкостное сопротивление (X C ) равно положительному индуктивному сопротивлению (X L ), оцениваемому по условию уравнения (3):
$$X_L = X_C \to jωL = \frac {1}{jωC}$$
За пределами резонансной частоты (показана красной кривой Рис. 9) катушка индуктивности имеет емкостные характеристики, соответствующие уменьшению импеданса. После этого индуктор не работает должным образом.
На рис. 9 показано соотношение между индуктивностью и частотой.
Рис. 9. Индуктивность в зависимости от частоты
Выбор экономичных и компактных катушек индуктивности
Разработчику несложно выбрать подходящую катушку индуктивности, если он понимает основное значение каждого параметра в техническом описании катушки индуктивности. Однако, если разработчик знает детали каждого параметра, он может выбрать оптимальную катушку индуктивности для преобразователя постоянного тока и предсказать, как система будет работать в различных условиях.
Monolithic Power Systems поставляет широкий спектр силовых катушек индуктивности для различных применений, от источников питания до преобразователей мощности. В частности, индукторы серии MPL-SE представляют собой полуэкранированные индукторы, покрытые внешним магнитным эпоксидным покрытием для улучшения магнитных характеристик.
Серия литых индукторов обеспечивает мягкое насыщение, обеспечивая стабильное поведение при высоких рабочих температурах. Эти литые катушки индуктивности имеют низкое сопротивление постоянному и переменному току и могут выдерживать большие токи. Кроме того, литая конструкция снижает слышимый шум, создаваемый переменным током и частотой пульсовой волны. Выберите оптимальный индуктор, исходя из следующих критериев:
- Выберите низкопрофильную литой серию MPL-AT, если высота является конструктивным ограничением.
- Выберите литые серии MPL-AY, если в приложении требуется высокая сила тока
- Для высокоэффективных применений выберите литые серии MPL-AL.



 Длина такого цилиндра в несколько раз превышает его диаметр.
Длина такого цилиндра в несколько раз превышает его диаметр.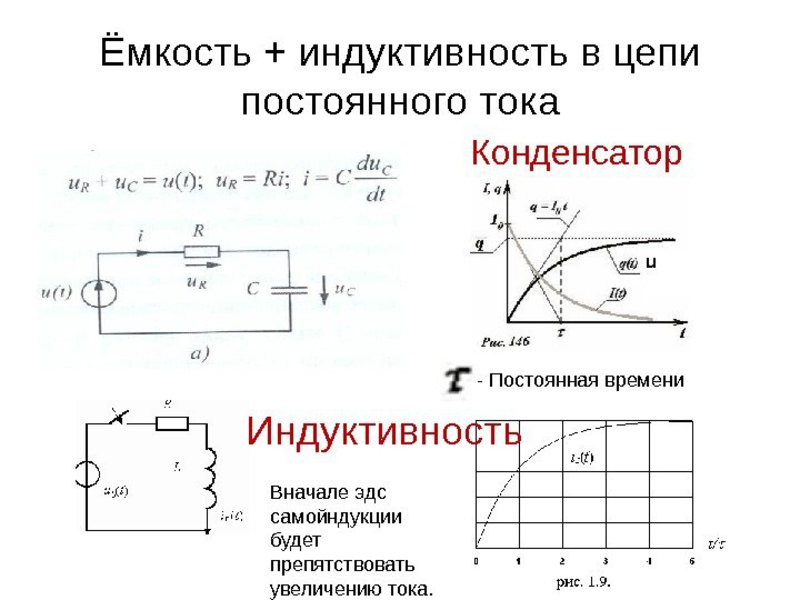 Измеряется этот параметр в Генри (Гн).
Измеряется этот параметр в Генри (Гн). Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.
Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.