Методическая разработка урока по теме «Действие магнитного поля на движущийся заряд. Сила Лоренца «

Министерство образования, науки и молодежной политики

Государственное бюджетное профессиональное образовательное учреждение Краснодарского края

«Курганинский аграрно-технологический техникум»

Методическая разработка

урока по теме « Действие магнитного поля на движущийся заряд. Сила Лоренца «

Из опыта работы преподавателя физики и математики

Ю.А. Спесивцевой.

г. Курганинск, х. Красное Поле, 2017г.

Тема урока: «Действие магнитного поля на движущийся заряд. Сила Лоренца»

Дата проведения: 15.12.2016

Группа: ПК-16 «Программирование в компьютерных системах»

Преподаватель: Спесивцева Ю.А.

Цель урока:  изучить действия магнитного поля на движущийся заряд, ввести понятие силы Лоренца.

Задачи:

Образовательные:

• изучить поведение движущихся электрических зарядов в магнитном поле;

• вывести формулу и правило для определения модуля и направления силы Лоренца.

Развивающие:

Воспитательные:

Тип урока: комбинированный

Метод организации: индивидуальный, фронтальный, групповой.

Материальное обеспечение: Компьютер, проектор, экран (для демонстрации презентации по данному уроку), набор лабораторного оборудования «Электродинамика», презентация по теме: “Сила Лоренца”

Время проведения: 45 минут.

Место проведения: кабинет физики.

Методы обучения:

по источникам знаний: словесные, наглядные, практические;

по степени взаимодействия «Учитель-ученик»:   беседа;

по дидактическим задачам: изучение новой темы.

по характеру познавательной деятельности: частично-поисковый;

по степени расчленения знаний: сравнительный, аналитический, обобщающий;

по характеру движения мысли от незнания к знанию: индуктивный.

Технологии применяемые на уроке:

— технология личностно-ориентированного обучения;

— здоровьесберегающая технология;

— поисково-исследовательской деятельности;

— информационно-коммуникативные технологии.

План урока:

1. Организационный момент: постановка задач и цели урока -1 минута

2. Повторение теоретического материала (фронтальный опрос, работа в парах). — 10 минут

3. Изучение нового материала (мини-лекция с элементами беседы).- 15 минут

4. Закрепление. Первичный контроль усвоения знаний (решение задач) — 15 минут

5. Подведение итогов, домашнее задание, рефлексия – 4 минуты

Ход урока

Организационный момент. (слайд1)

Приветствие студентов. Настрой на урок. Постановка цели и задачи.

Преподаватель: Электрический ток – это упорядоченно движущиеся заряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Действие магнитного поля на движущийся заряд широко используют в современной технике. Например: измерение массы частицы в приборах, позволяющих разделять заряженные частицы по их зарядам. Такие приборы называются масс-спектрограф. В ряде электронных приборов магнитное поле используется для фокусировки пучков заряженных частиц.

Повторение теоретического материала (фронтальный опрос, работа в парах) (слайд 2)

1. Что такое магнитное поле?

2. Какими свойствами обладает магнитное поле?

3. Что понимают под силовыми линиями магнитного поля?

4. Каким образом можно определить направление силовых линий магнитного поля?

5. Что такое сила Ампера?

6. Как рассчитать силу Ампера?

7. Как находят направление силы Ампера?

8. Что такое электрический ток?

Работа в парах по карточкам

Карточка №1: Пользуясь правилом левой руки, определить направление силы Ампера. (рис.1), электрический ток I (рис.2) и магнитное поле (рис.3).

Карточка № 2: Решить задачу.

Как изменится сила Ампера, действующая на прямолинейный проводник с током в однородном магнитном поле при увеличении индукции в 3 раза? Проводник расположен перпендикулярно вектору индукции. (увеличится в 3 раза).

Карточка № 3: Решить расчетную задачу.

Определить силу, с которой однородное магнитное поле действует на проводник длиной 20 см, если сила тока в нем 300 мА, расположенный под углом 45 градусов  к вектору магнитной индукции.  Магнитная индукция составляет 0,5 Тл.

Изучение нового материала

Преподаватель: Так как магнитное поле действует на ток – движущиеся заряженные частицы, то оно действует и на каждую частицу в отдельности. Действие магнитного поля на движущуюся заряженную частицу характеризует сила Лоренца. Запишите тему сегодняшнего урока. (учащиеся записывают дату и тему урока) (слайд 3)

Хендрик Антон Лоренц (1853–1928) выдающийся голландский физик и математик, развил электромагнитную теорию света и электронную теорию материи, а также сформулировал теорию электричества, магнетизма и света, внёс большой вклад в развитие теории относительности, лауреат Нобелевской премии 1902г

Сила, действующая на движущуюся заряженную частицу со стороны магнитного поля, называется силой Лоренца.(слайд 4)

Выведем формулу для расчёта модуля силы Лоренца.(слайд 5)

Рассмотрим движение заряженной частицы под действием силы Лоренца, если α = 90°(слайд 6)

Так как сила, действующая на заряд, оказалась перпендикулярной скорости его движения, то модуль скорости изменяться не будет, а будет меняться направление, т.о. частица будет равномерно двигаться по окружности. Сила, перпендикулярная скорости, вызывает изменение направления движения, т.е. центростремительное ускорение. Зная формулы расчёта центростремительного ускорения и модуля силы Лоренца, которая его вызывает, и, используя второй закон Ньютона, выведите формулу для расчёта радиуса окружности, по которой будет двигаться частица.

r = mV/Bq

Теперь не сложно узнать и период обращения частицы, т.к., где r нами только что найдено. Сделайте вывод: чем определяется период обращения частицы? (слайд 7)

T = 2πmV/BqV=2πm/Bq

(Предполагаемый ответ: магнитной индукцией поля и удельным зарядом частицы, т.е. не зависит от радиуса окружности, по которой частица движется.) (слайд 8)

Эти особенности движения зарядов в магнитном поле нашли практическое применение. (слайд 9)

• Осциллограф

• Кинескоп

• Масс – спектрограф

• Ускорители элементарных частиц (циклотрон, бетатрон, синхрофазотрон)

Преподаватель: Направление силы Лоренца определяется по правилу левой руки с оговоркой, что заряд должен быть положительным, т.к. за направление тока мы принимаем направление движения положительных зарядов. Если же заряд отрицательный, то направление силы меняется на противоположное. (слайд 10)

Если ладонь левой руки расположить так, что четыре вытянутых пальца указывают направление скорости положительного заряда, а вектор магнитной индукции входит в ладонь, то отогнутый на 90° большой палец покажет направление силы, действующей на данный заряд.

Проведение физкультминутки электронные физкультминутки для глаз (с музыкальным сопровождением), кистей пальцев рук, дыхательная гимнастика. (слайд 11)

Решение задач

Преподаватель: давайте попробуем определить направление силы Лоренца на примере. (слайд 12)

Задача (слайд 13)
Определить силу, действующую на заряд 0,005 Кл, движущийся в магнитном поле с индукцией 0,3 Тл со скоростью 200 м/с под углом 45 градусов к вектору магнитной индукции.

Самостоятельная работа для учащихся с целью закрепления полученных знаний, в ходе которой они могут пользоваться своими записями, текстом учебника, консультацией преподавателя. (слайд 14,15)

Подведение итогов (слайд 16)

• Чем характеризуется действие магнитного поля на движущуюся заряженную частицу?

• Какая сила называется силой Лоренца?

• Как рассчитать силу Лоренца?

• Каким образом находят силу Лоренца?

Выставление оценок за участие в уроке

Домашнее задание (слайд 17)

§12.7, сообщение «Определение удельного заряда. Ускорители заряженных частиц»

Рефлексия (слайд 18)

Урок физики «Действие магнитного поля на движущуюся заряженную частицу. Сила Лоренца»

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Использование на уроке наглядности в виде мультимедийной презентации облегчает усвоение учащимися излагаемого материала. Презентация дает возможность компактно излагать учебный материал, что позволяет больше времени уделить закреплению пройденного материала. Применение анимации позволяет показать движение заряда в магнитном поле в динамике. Изучаемый материал связывает полученные теоретические знания с практикой. Разработку и презентацию можно использовать не только в универсальных, но и в профильных классах, так как они содержат материал повышенного уровня сложности.

Цели: изучить новое физическое явление – действие магнитного поля на движущийся заряд, вывести формулу и ввести мнемоническое правило для определения модуля и направления силы Лоренца, показать возможность применения знаний для расчёта периода обращения частицы в магнитном поле, познакомить учащихся с практическим применением действия силы Лоренца в ускорителях.

Оборудование: электронный осциллограф, дугообразный магнит, презентация “Сила Лоренца”, мультимедийный проектор.

Тип урока: формирование новых знаний

Ход урока

Актуализация знаний:

Слайд 1.

• Какими свойствами обладает магнитное поле?
• Что такое сила Ампера?
• Как рассчитать силу Ампера?
• Что такое электрический ток?

Слайд 2.

Учитель: Т.к. магнитное поле действует на ток – движущиеся заряженные частицы, то оно действует и на каждую частицу в отдельности. Действие магнитного поля на движущуюся заряженную частицу характеризует сила Лоренца.

Хендрик Антон Лоренц (1853–1928) выдающийся голландский физик и математик , развил электромагнитную теорию света и электронную теорию материи, а также сформулировал теорию электричества, магнетизма и света, внёс большой вклад в развитие теории относительности, лауреат Нобелевской премии 1902г.

Слайд 3.

, так как является её долей, значит, для определения её направления можно применить то же мнемоническое правило, что и для определения направления сил Ампера – правило левой руки, с оговоркой, что заряд должен быть положительным, т.к. за направление тока мы принимаем направление движения положительных зарядов. Если же заряд отрицательный, то направление силы меняется на противоположное.

Так как сила, действующая на заряд, оказалась перпендикулярной скорости его движения, то модуль скорости изменяться не будет, а будет меняться направление, т.о. частица будет равномерно двигаться по окружности.

Демонстрационный эксперимент: С помощью прибора для демонстрации движения заряженных частиц под действием силы Лоренца или с помощью электронного осциллографа демонстрируется отклонение электронных пучков магнитным полем.

Слайд 4.

Выведем формулу для расчёта модуля силы Лоренца.

Т.к. она является частью силы, действующей на весь отрезок проводника, находящийся в магнитном поле, то её модуль в N раз меньше силы Ампера. Доведите рассуждение до логического завершения: свяжите силу с параметрами заряженной частицы (зарядом и скоростью)

(Ученики завершают вывод формулы в тетрадях, проверяют с помощью анимированного слайда 4.)

Слайд 5.

Движение заряженной частицы под действием силы Лоренца, если α = 90°

Сила, перпендикулярная скорости, вызывает изменение направления движения, т.е. центростремительное ускорение. Зная формулы расчёта центростремительного ускорения и модуля силы Лоренца, которая его вызывает, и, используя второй закон Ньютона, выведите формулу для расчёта радиуса окружности, по которой будет двигаться частица.

(Ученики завершают вывод формулы в тетрадях, проверяют с помощью анимированного слайда 5.)

Слайд 6.

Теперь не сложно узнать и период обращения частицы, т.к. , где r нами только что найдено. Сделайте вывод: чем определяется период обращения частицы?

(Предполагаемый ответ: магнитной индукцией поля и удельным зарядом частицы, т.е. не зависит от радиуса окружности, по которой частица движется.)

Эти особенности движения зарядов в магнитном поле нашли практическое применение.

Слайд 7.

• Осциллограф
• Кинескоп
• Масс – спектрограф
• Ускорители элементарных частиц (циклотрон, бетатрон, синхрофазотрон)

Слайд 8.

Движение заряженной частицы под действием силы Лоренца, если α ≠ 90°

(С помощью анимации на слайде учитель объясняет, как движется заряженная частица, если её скорость не перпендикулярна силовым линиям магнитного поля и совместно с учащимися находит шаг винтовой линии.)

Слайд 10.

Самостоятельная работа для учащихся с целью закрепления полученных знаний, в ходе которой они могут пользоваться своими записями, текстом учебника, консультацией учителя

Слайд 11.

Домашнее задание §6, самостоятельная работа № 31 (“Физика. Самостоятельные и контрольные работы” Л.А.Кирик), достаточный уровень № 1–3, 10

Подведение итогов урока.

Литература и использованные материалы:

1. Г.Я. Мякишев, Б.Б. Буховцев, Н.Н.Сотский “Физика.11”, Просвещение, 2008.
2. Л.А. Кирик “Физика. Самостоятельные и контрольные работы. 10”, Илекса, 2005.
3. Википедия.

« Действие магнитного поля на движущийся заряд. Сила Лоренца»(11 класс)

Конспект урока: « Действие магнитного поля на движущийся заряд. Сила Лоренца»

Цели: изучить новое физическое явление – действие магнитного поля на движущийся заряд, вывести формулу и ввести мнемоническое правило для определения модуля и направления силы Лоренца, показать возможность применения знаний для расчёта периода обращения частицы в магнитном поле, познакомить учащихся с практическим применением действия силы Лоренца в ускорителях.

Ход урока

1.Организационный момент

2.Актуализация знаний:

• Какими свойствами обладает магнитное поле?

• Что такое сила Ампера?

• Как рассчитать силу Ампера?

• Что такое электрический ток?

3.Изучение нового материала

Учитель: Т.к. магнитное поле действует на ток – движущиеся заряженные частицы, то оно действует и на каждую частицу в отдельности. Действие магнитного поля на движущуюся заряженную частицу характеризует сила Лоренца.

Хендрик Антон Лоренц (1853–1928) выдающийся голландский физик и математик , развил электромагнитную теорию света и электронную теорию материи, а также сформулировал теорию электричества, магнетизма и света, внёс большой вклад в развитие теории относительности, лауреат Нобелевской премии 1902г.

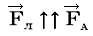, так как является её долей, значит, для определения её направления можно применить то же мнемоническое правило, что и для определения направления сил Ампера – правило левой руки, с оговоркой, что заряд должен быть положительным, т.к. за направление тока мы принимаем направление движения положительных зарядов. Если же заряд отрицательный, то направление силы меняется на противоположное.

Так как сила, действующая на заряд, оказалась перпендикулярной скорости его движения, то модуль скорости изменяться не будет, а будет меняться направление, т.о. частица будет равномерно двигаться по окружности.

Выведем формулу для расчёта модуля силы Лоренца.

Т.к. она является частью силы, действующей на весь отрезок проводника, находящийся в магнитном поле, то её модуль в N раз меньше силы Ампера. Доведите рассуждение до логического завершения: свяжите силу с параметрами заряженной частицы (зарядом и скоростью)

Движение заряженной частицы под действием силы Лоренца, если α = 90°

Сила, перпендикулярная скорости, вызывает изменение направления движения, т.е. центростремительное ускорение. Зная формулы расчёта центростремительного ускорения и модуля силы Лоренца, которая его вызывает, и, используя второй закон Ньютона, выведите формулу для расчёта радиуса окружности, по которой будет двигаться частица.

Теперь не сложно узнать и период обращения частицы, т.к. 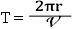 , где r нами только что найдено. Сделайте вывод: чем определяется период обращения частицы?

(Предполагаемый ответ: магнитной индукцией поля и удельным зарядом частицы, т.е. не зависит от радиуса окружности, по которой частица движется.)

Эти особенности движения зарядов в магнитном поле нашли практическое применение.

• Осциллограф

• Кинескоп

• Масс – спектрограф

• Ускорители элементарных частиц (циклотрон, бетатрон, синхрофазотрон)

Движение заряженной частицы под действием силы Лоренца, если α ≠ 90°

4.Закрепление изученного.

Самостоятельная работа для учащихся с целью закрепления полученных знаний, в ходе которой они могут пользоваться своими записями, текстом учебника, консультацией учителя

5.Домашнее задание §6, №851, 855

6.Подведение итогов урока.

ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД — КиберПедия

Сила Лоренца —сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q — заряд частицы;
V — скорость заряда;
B — индукции магнитного поля;
a — угол между вектором скорости заряда и вектором магнитной индукции.

Направление силы Лоренца определяется по правилу левой руки:

Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скоростиотрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

Так как сила Лоренца всегда перпендикулярна скорости заряда, то она не совершает работы (т.е. не изменяет величину скорости заряда и его кинетическую энергию).
Если заряженная частица движется параллельно силовым линиям магнитного поля, то Fл = 0 , и заряд в магнитном поле движется равномерно и прямолинейно.
Если заряженная частица движется перпендикулярно силовым линиям магнитного поля, то сила Лоренца является центростремительной

и создает центростремительное ускорение равное

Согласно второму закону Ньютона: сила Лоренца равнв произведению массы частицы на центростремительное ускорение

тогда радиус окружности

а период обращения заряда в магнитном поле

Так как электрический ток представляет собой упорядоченное движение зарядов, то действие магнитного поля на проводник с током есть результат его действия на отдельные движущиеся заряды.

 

21. Движение заряженной частицы в магнитном поле.

Формула силы Лоренца дает возможность найти ряд закономерностей движения заряженных частиц в магнитном поле. Зная направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле можно найти знак заряда частиц, которые движутся в магнитных полях.
Для вывода общих закономерностей будем полагать, что магнитное поле однородно и на частицы не действуют электрические поля. Если заряженная частица в магнитном поле движется со скоростью v вдоль линий магнитной индукции, то угол α между векторами v иВ равен 0 или π. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
В случае, если заряженная частица движется в магнитном поле со скоростью v, которая перпендикулярна векторуВ, то сила Лоренца F=Q[vB] постоянна по модулю и перпендикулярна к траектории частицы. По второму закону Ньютона, сила Лоренца создает центростремительное ускорение. Значит, что частица будет двигаться по окружности, радиус r которой находится из условия QvB=mv²/r , следовательно

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

т. е. период вращения частицы в однородном магнитном поле задается только величиной, которая обратна удельному заряду (Q/m) частицы, и магнитной индукцией поля, но при этом не зависит от ее скорости (при v<<c). На этом соображении основано действие циклических ускорителей заряженных частиц.
В случае, если скорость v заряженной частицы направлена под углом α к вектору В то ее движение можно задать в виде суперпозиции: 1) прямолинейного равномерного движения вдоль поля со скоростью v_parall=vcosα ; 2) равномерного движения со скоростью v_perpend=vsinα по окружности в плоскости, которая перпендикулярна полю. Радиус окружности задается формулой (1) (в этом случае надо вместо v подставить v_perpend=vsinα). В результате сложения двух данных движений возникает движение по спирали, ось которой параллельна магнитному полю (рис. 1). Шаг винтовой (спиральной) линии

Подставив в данное выражение (2), найдем

Направление, в котором закручивается спираль, определяется знаком заряда частицы.
Если скорость v заряженной частицы составляет угол α с направлением вектораВнеоднородного магнитного поля, у которого индукция возрастает в направлении движения частицы, то r и h уменьшаются с увеличением В. На этом основана фокусировка заряженных частиц в магнитном поле.

 

22. Магнитный поток. Магнитные свойства вещества.

Магнитный поток

По теореме Остроградского-Гаусса в общем случае поток любого вектора через поверхность S численно равен

Индукция — вектор в пространстве, поэтому можно применить понятие потока индукции . Если площадь фигуры, пересекающей силовые линии магнитного поля — площадь контура, по которому протекает ток, тогда — магнитный поток контура с током. Если имеется множество последовательно соединенных контуров, то есть соленоид, то общее количество магнитных силовых линий равно сумме силовых линий, образованных каждым контуром.

. =NФ_витков =Ф .

Магнитные свойства вещества

1. Диамагнетики — µ чуть <1. µ_{висмута}=0,9998 (свинец, цинк, азот и др.).
2. Парамагнетики — µ чуть>1. µ_{алюминия}=1,000023 (кислород, ни­кель и др.).

Для пара- и диамагнетиков намагниченность I прямо пропорциональна индук­ции B₀ магнитного поля в вакууме.

 

 

23. Электромагнитная индукция. Закон электромагнитной индукции. Правило Ленца.

 

Электромагнитная индукция — явление возникновения электрического тока в замкнутом контуре при изменении магнитного потока, проходящего через него.Электромагнитная индукция была открыта Майклом Фарадеем 29 августа 1831 года. Он обнаружил, что электродвижущая сила, возникающая в замкнутом проводящем контуре, пропорциональна скорости изменения магнитного потока через поверхность, ограниченную этим контуром. Величина электродвижущей силы (ЭДС) не зависит от того, что является причиной изменения потока — изменение самого магнитного поля или движение контура (или его части) в магнитном поле. Электрический ток, вызванный этой ЭДС, называется индукционным током.

Закон электромагнитной индукции Фарадея является основным законом электродинамики, касающимся принципов работы трансформаторов, дросселей, многих видов электродвигателей и генераторов.

Правило Ленца — определяет направление пндукц. токов, возникающих в результате электромагнитной индукции; является следствием закона сохранения энергии. Л. п. установлено (1833) Э. X. Ленцем. Индукц. ток в контуре направлен так, что создаваемый им поток магнитной индукции через поверхность, ограниченную контуром, стремится препятствовать тому изменению потока, к-рое вызывает данный ток. Физический энциклопедический словарь. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983.

где Ф=Ф_е+Ф_i — магн. поток через поверхность S, опирающуюся на проводящий контур Л. п. определяет знак правой части

 

24. Самоиндукция. Индуктивность. Электродвижущая сила самоиндукции.

 

Индуктивность – характеристика магнитного поля, точнее проводника, который его образует. Индуктивность — коэффициент самоиндукции (L).

L – индуктивность контура зависит от материала и размеров (формы) контура.

Явление самоиндукции – возникновение ЭДС индукции в цепи в результате изменения силы. Самоиндукция — возникновение ЭДС индукции в замкнутом проводящем контуре при изменении тока, протекающего по контуру.При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

 

25. Энергия магнитного поля.

 

Проводник, c протекающим по нему электрическим ток, всегда окружен магнитным полем, причем магнитное поле исчезает и появляется вместе с исчезновением и появлением тока. Магнитное поле, подобно электрическому, является носителем энергии. Логично предположить, что энергия магнитного поля совпадает с работой, затрачиваемой током на создание этого поля.

Энергию магнитного поля можно рассматривать как функцию величин, которые характеризуют это поле в окружающем пространстве.

 

26. Свободные электромагнитные колебания в контуре.

 

Свободные электромагнитные колебания – колебания, происходящие в контуре за счёт зарядки конденсатора и явления самоиндукции в катушке (внутренняя сила).Если в колебательном контуре внешние э.д.с. отсутствуют, значит колебания в контуре представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре будут гармоническими.

 

 

27. Превращение энергии в колебательном контуре.

 

1. Зарядка конденсатора до q_mи присоединить его к катушке (t=0), то возникновение maxU_m обладает энергией (W)

2. При соединении с катушкой электрический ток, который порождает в катушке магнитное поле – энергия эл. уменьшается, а энергия МП увеличивается.

Со временем уменьшается q иU, но при этом увеличивается Iблагодаря явлению самоиндукции. Когда конденсатор разряжается, МП достигает max

 

3. Перезарядка конденсатора

В момент времени конденсатор заряжается до maxq_m, но с противоположным знаком – U = — U_m

При этом в цепи ток отсутствует

4. Разрядка конденсатора

Постепенно энергия эл. уменьшается, а энергия МП увеличивается – напряжение уменьшается, сила тока увеличивается.

В момент времени конденсатор разряжается

5. В последнее время конденсатор перезаряжается. До q_m– в колебательном контуре происходит преобразование энергии эл. И энергии МП.

28. Собственная частота колебаний в контуре.

 

Если частота собственных колебаний совпадает с частотой вынужденных колебаний, то происходит явление резонанса тока.Свободные электромагнитные колебания в контуре (при R=0) являются гармоническими.

 

29. Затухание электрических колебаний.

 

Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Свободные колебания любого осциллятора рано или поздно затухают и прекращаются. Поэтому на практике обычно имеют дело с затухающими колебаниями. Они характеризуются тем, что амплитуда колебаний является убывающей функцией. Обычно затухание происходит под действием сил сопротивления среды, наиболее часто выражаемых линейной зависимостью от скорости колебаний или её квадрата.Любая система с колебательным контуром при наличии активного сопротивления – пример затухающего колебания. Любые реальные колебания затухающие, если не действует внешняя ЭДС.

 

30. Вынужденные электрические колебания.

 

Вынужденные колебания – колебания, происходящие за счёт внешней периодической силы (перемены ЭДС).

 

31. Переменный ток и его получение. Действующие значения силы тока и напряжения.

 

Переменный ток- электрический ток, который периодически изменяется по модулю и направлению.Переменный ток меняет своё направление с определенной частотой. Согласно гармоническому закону ток и напряжение меняются по закону синуса или косинуса.

Наиболее широкое применение в технике находит не постоянный, а переменный ток, изменяющийся со временем по гармоническому закону с частотой, как правило, равной 50 Герцам.Такой ток создается генераторами переменного тока, в которых электродвижущая сила (ЭДС) возникает в результате процесса электромагнитной индукции.

Величину, равную корню квадратному из среднего за период значения квадрата силы переменного тока, называютдействующим (эффективным) значением переменного тока.

Действующее значение силы переменного тока _{равно силе такого постоянного тока, который выделяет в одном и том же проводнике за одинаковое время то же количество теплоты, что и переменный ток.}

32. Активное, емкостное и индуктивное сопротивления.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии (в тепловую энергию). Реактивное сопротивление — это сопротивление проводников переменного тока с учётом поверхностного эффекта.

Емкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической емкостью цепи (или ее участка).

Индуктивное сопротивление обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности,элемента и частоты, протекающего тока

 

33. Преобразование переменного тока. Трансформатор.

Трансформатор – устройство, которое способно повышать/понижать переменное напряжение.

Элементы трансформатор: железный сердечник, на который помещены 2 катушки ( первичная катушка и вторичная катушка).

Трансформатор характеризуется коэффициентом трансформации

Если N₁ N₂, k — повышающий трансформатор

Если N₁ N₂, k — понижающий трансформатор

Трансформатор работает в 2ух режимах – холодный ход, рабочая нагрузка.

 

34. Передача и распределение электроэнергии.

 

На районной (т.е. приближенной к источникам энергоресурсов) электростанции электроэнергия вырабатывается чаще всего электромашинными генераторами переменного тока. Для уменьшения потерь при ее передаче и распределении напряжение, снимаемое на выходные электрогенератора, повышается трансформаторной подстанцией. Затем электроэнергия передается по высоковольтным линиям электропередачи (ЛЭП) на большие расстояния, которые могут измеряться сотнями километров. КЛЭП подключен ряд распределительных подстанций, отводящих электроэнергию к местным центрам электропотребления. Поскольку далее электроэнергия передается по улицам и населенным районам, на подстанциях напряжение для безопасности еще раз понижается трансформаторами. К понижающим трансформаторам подстанций подключены линии магистральной сети. В удобных точках этой сети устанавливаются пункты ответвления для распределительной сети электропотребителей.

 

35. Открытый колебательный контур как источник электромагнитных волн. Электрический резонанс.

Источником гармонических электромагнитных волн являетсяоткрытый колебательный контур. Герц в своих опытах, уменьшая число витков катушки и площадь пластин конденсатора, а также раздвигая их, совершил переход от закрытого колебательного контура к открытому колебательному контуру (вибратору Герца), представляющему собой два стержня, разделенных искровым промежутком. В открытом контурепеременное электрическое поле заполняет окружающее контур пространство, что существенно повышает интенсивность электромагнитного излучения.

36. Свойства электромагнитных волн.

 

1. ЭМВ представляет поперечную волну

2. Источник ЭМВ должен быть ускоренно движущейся заряженной частицей

3. Основные характеристик ЭМВ являются характеристики механических волн

4. ЭМВ распространяется в любой среде ( + в вакууме)

5. При переходе из одной среды в другую изменяется скорость и длины волны, а частота постоянная.

 

37. Энергия электромагнитного поля волны.

 

Электромагнитная волны как и механическая основывается на том, что передается воздействием на МП на расстоянии без переноса вещества.

ЭМВ – процесс распространения ЭМП в пространстве. ЭМП одновременно взаимодействует с электрическими МП.

 

38. Электромагнитная природа света. Скорость света.

 

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме.Скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

С = 3 10⁸м/с

 

39. Зависимость между длиной волны и частотой электромагнитных колебаний.

ЭМВ характеризуется частотой, периодом, длиной, скоростью.Скорость ЭМВ зависит от длины и частоты ЭМ колебаний

 

 

40. Принцип Гюйгенса.

 

Каждая точка фронта волны – источник вторичных волн, распространяющихся во все стороны со скоростью распространения волны в среде.

Фронт волны – совокупность наиболее отдаленных от источника точек, до которых дошёл процесс распространения волны. Фронтом волны является сфера в однородном пространстве.

 

41. Закон отражения света и закон преломления света.

 

Закон отражения света — устанавливает изменение направления хода светового луча в результате встречи с отражающей (зеркальной) поверхностью: падающий и отражённый лучи лежат в одной плоскости с нормалью к отражающей поверхности в точке падения, и эта нормаль делит угол между лучами на две равные части. Широко распространённая, но менее точная формулировка «угол падения равен углу отражения» не указывает точное направление отражения луча.

Закон преломления света — отношение sin угла падаения к sin угла преломления – величина постоянная для данных сред равная отношению света в средах

 

42. Физический смысл показателя преломления. Полное отражение света.

Угол падения, при котором свет не преломляется в другую среду, а отражается и скользит вдоль раздела двух сред (т.е. угол преломления равен 90⁰), называется предельным углом полного отражения.Полное внутреннее отражение наблюдается при переходе света из среды оптически более плотной в оптически менее плотную среду.

Явление полного отражения можно наблюдать на примере. Если налить в стакан воду и поднять её выше уровня глаз, то поверхность воды при рассмотрении её снизу кажется посеребрённой вследствие полного отражения света.

Если мы попытаемся изпод воды взглянуть на то, что находится в воздухе, то при определённом значении угла, под которым мы смотрим, можно увидеть отражённое от воды дно.

Показатель преломления вещества — величина, равная отношению фазовых скоростейсвета (электромагнитных волн) в вакууме и в данной среде. Также о показателе преломления говорят для любых других волн, например, звуковых.

 

43. Интерференция света, ее проявление в природе и применение в технике.

Интерференция света — перераспределение интенсивности света в результате наложения (суперпозиции) нескольких световых волн. Это явление сопровождается чередующимися в пространстве максимумами и минимумами интенсивности. Её распределение называется интерференционной картиной. На экране интерференция света представлена в виде чередования темных и светлых полос.

Проявление в природе:

— Пятна нефтяного происхождения на воде

— Жирные пятна на стекле

— Мыльные пузыри

— Тонкие крылья насекомых

Применение:

— Контроль, качество поверхности

— Установки для получения колец Ньютона

 

44. Дифракция света. Дифракционная решетка. Дифракционный спектр.

Дифракция света – это отклонение световых лучей от прямолинейного распространения при прохождении сквозь узкие щели, малые отверстия или при огибании малых препятствий. Явление дифракции света доказывает, что свет обладаетволновыми свойствами.
Для наблюдения дифракции можно:
— пропустить свет от источника через очень малое отверстие или расположить экран на большом расстоянии от отверстия. Тогда на экране наблюдается сложная картина из светлых и темных концентрических колец.
— или направить свет на тонкую проволоку, тогда на экране будут наблюдаться светлые и темные полосы, а в случае белого света – радужная полоса.

— наблюдение дифракции света на малом отверстии.

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья. Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки.

Дифракционный спектр образуется при прохождении света через дифракционную решетку. Он зависит от размера ячейки решетки. Чем меньше размер решетки, тем больше преломляется свет и становится более заметен дифракционный спектр, видимое глазом разложение света на основные цвета.

 

45. Понятие о поляризации.

Поляризация волн — явление нарушения симметрии распределения возмущений в поперечной волне (например, напряжённостей электрического или магнитного полей в электромагнитных волнах) относительно направления её распространения. В продольной волне поляризация возникнуть не может, так как возмущения в этом типе волн всегда совпадают с направлением распространения.

Поперечная волна характеризуется двумя направлениями: волновым вектором и вектором амплитуды, всегда перпендикулярным к волновому вектору. Так что в трёхмерном пространстве имеется ещё одна степень свободы — вращение вокруг волнового вектора.

Причиной возникновения поляризации волн может быть:

* несимметричная генерация волн в источнике возмущения;

* анизотропность среды распространения волн;

* преломление и отражение на границе двух сред.

Основными являются два вида поляризации:

* линейная — колебания возмущения происходит в какой-то одной плоскости. В таком случае говорят о «плоско-поляризованной волне»;

* круговая — конец вектора амплитуды описывает окружность в плоскости колебаний. В зависимости от направления вращения вектора может быть правой или левой.

46. Поляроиды, их применение в науке и технике.

Поляроид — название синтетической пластиковой плёнки, используемой для поляризации света. Обычный свет превращается в плоскополяризированный, проходя через пластинки, сделанные из материала, называемого поляроидом, или через кристаллы кальцита (особая кристаллическая форма CaCO3), расположенные таким образом, что они образуют так называемую призму Николя.

Хорошим поляроидом являются кристаллы турмалина. Уже при толщине кристалла турмалина около 1 мм в нём практически полностью поглощается обыкновенный луч. Хорошим поляроидом также является герапатит, в котором уже при толщине 0,1 мм практически полностью поглощается один из лучей.

Если поляроид используется для получения поляризованного света, то он называется поляризатором.

Применение:

— Для съёмки в условиях низкой освещённости

— служит для смягчения или полного уничтожения ярких бликов на раз­личных неметаллических поверхностях: на воде, стекле, пластмассовых из­делиях, полирован­ном дереве, лако­вом покрытии ав­томашин и т. д.

47. Дисперсия света. Разложение белого цвета призмой. Цвета тел.

Дисперсия света (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открытаНьютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее.
Дисперсия света, разная величина преломления света призмой в зависимости от частоты, а белый свет это набор частот. Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному.

48. Виды спектров. Спектральный анализ.

СПЕКТРАЛЬНЫЙ АНАЛИЗ — совокупность методов определения элементного и молекулярного состава и строения веществ по их спектрам. С помощью С. а. определяют как осн. компоненты, составляющие 50- 60% вещества анализируемых объектов, так и незначит. примеси в них.С. а. — наиб. распространённый аналитич. метод, св. 20- 30% всех анализов выполняется с помощью этого метода, в т. ч. контроль состава сплавов в металлургии, автомоб. и авиац. пром-сти, технологии переработки руд, анализ экологич. объектов и материалов высокой чистоты, хим., биол. и мед. исследования. Особо важное значение С. а. имеет при поисках полезных ископаемых.
Линейчатые спектры

Данные спектры образуются от раскалённых и обычных газов под небольшим давлением. При этом все линии наблюдаются одновременно, т.к. энертный газ состоит из множества атомов в разных энергетических состояниях.

Полосатые спектры

Полосатый спектр состоит из отдельных полос, разделенных темными промежутками. С помощью очень хорошего спектрального аппарата можно обнаружить, что каждая полоса представляет собой совокупность большого числа очень тесно расположенных линий. В отличие от линейчатых спектров полосатые спектры создаются не атомами, а молекулами, не связанными или слабо связанными друг с другом.

Сплошной спектр

Дают атомы раскалённых твердых, жидких тел, газов под большим давлением. Чтобы его увидеть можно пропустить свет через призму.

 

49. Эффект Доплера – Физо.

Эффект Доплера — изменение частоты и длины волн, регистрируемых приёмником, вызванное движением их источника и/или движением приёмника.Эффект Доплера легко наблюдать на практике, когда мимо наблюдателя проезжает машина с включённой сиреной.

Для волн (например, звука), распространяющихся в какой-либо среде, нужно принимать во внимание движение, как источника, так и приёмника волн относительно этой среды. Для электромагнитных волн (например, света), для распространения которых не нужна никакая среда, в вакууме имеет значение только относительное движение источника и приёмника.

Опыт Физо — опыт по определению скорости света в движущихся средах (телах), осуществлённый в 1851Луи Физо. Опыт демонстрирует эффект релятивистского сложения скоростей. С именем Физо связан также первый эксперимент по лабораторному определению скорости света.Если — скорость света в вакууме, а — показатель преломления, то скорость света в неподвижной среде равна . Если среда двигается относительно лабораторной системы отсчёта, со скоростью , то скорость света будет равна:

 

50. Электромагнитное излучение в различных диапазонах длин волн: радиоволны, инфракрасное, видимое, ультрафиолетовое и рентгеновское излучение.

Радиоизлучение (радиоволны, радиочастоты) — электромагнитное излучение с длинами волн 5•10−5—1010 метров и частотами, соответственно, от 6•1012 Гц и до нескольких Гц. Радиоволны используются при передаче данных в радиосетях.

Инфракрасное излучение — электромагнитное излучение, занимающее спектральную область между красным концом видимого света (с длиной волны[1] λ = 0,74 мкм) и микроволновым излучением (λ ~ 1—2 мм).

Оптические свойства веществ в инфракрасном излучении значительно отличаются от их свойств в видимом излучении. Инфракрасное излучение составляет большую часть излучения ламп накаливания, газоразрядных ламп, около 50% излучения Солнца; инфракрасное излучение испускают некоторые лазеры. Для его регистрации пользуются тепловыми и фотоэлектрическими приемниками, а также специальными фотоматериалами.

Видимое излучение — электромагнитные волны, воспринимаемые человеческим глазом, которые занимают участок спектра с длиной волны приблизительно от 380 (фиолетовый) до 740 нм (красный). Такие волны занимают частотный диапазон от 400 до 790 терагерц. Электромагнитное излучение с такими длинами волн также называется видимым светом, или просто светом. Наибольшую чувствительность к свету человеческий глаз имеет в области 555 нм (540 ТГц), в зелёной части спектра. В спектре содержатся не все цвета, которые различает человеческий мозг.

Ультрафиолетовое излучение (ультрафиолет, УФ, UV) — электромагнитное излучение, занимающее диапазон между фиолетовой границей видимого излучения и рентгеновским излучением (380 — 10 нм, 7,9•1014 — 3•1016 Герц).

Рентгеновское излучение — электромагнитные волны, энергия фотонов которых лежит на шкале электромагнитных волн между ультрафиолетовым излучением и гамма-излучением, что соответствует длинам волн от 10−2 до 103 Å (от 10−12 до 10−7 м).[1]

 

51. Тепловое излучение. Черное тело.

Абсолютно чёрное тело — физическая идеализация, применяемая в термодинамике, тело, поглощающее всё падающее на него электромагнитное излучение во всех диапазонах и ничего не отражающее. Несмотря на название, абсолютно чёрное тело само может испускать электромагнитное излучение любой частоты и визуально иметь цвет. Спектр излучения абсолютно чёрного тела определяется только его температурой.

Наиболее чёрные реальные вещества, например, сажа, поглощают до 99 % падающего излучения (то есть имеют альбедо, равное 0,01) в видимом диапазоне длин волн, однако инфракрасное излучение поглощается ими значительно хуже.

Тепловое излучение — электромагнитное излучение с непрерывным спектром, испускаемое нагретыми телами за счёт их тепловой энергии.

Примером теплового излучения является свет от лампы накаливания.

Мощность теплового излучения объекта, удовлетворяющего критериям абсолютно чёрного тела, описывается законом Стефана — Больцмана.

Отношение излучательной и поглощательной способностей тел описывается законом излучения Кирхгофа.

Тепловое излучение является одним из трёх элементарных видов переноса тепловой энергии (помимо теплопроводности и конвекции). Равновесное излучение — тепловое излучение, находящееся в термодинамическом равновесии с веществом.

 

52. Распределение энергии в спектре излучения.

Спектральный состав излучения изображается чаще всего графически, в виде кривой спектрального распределения энергии, которую для краткости называют иногда спектром. Такое распределение спектральной плотности потока излучения имеет в науке о цвете наименование спектрального распределения энергии цветового стимула, а сам поток излучения называют просто цветовым стимулом. От рассчитанной спектральной кривой в произвольных единицах легко, конечно, перейти к кривой спектрального распределения энергии в абсолютных единицах, если точно известна излучающая площадь калибрируемой лампы. Разнообразные акустические процессы объединяет то, что для их протекания требуется акустическая энергия с определенным спектральным распределением энергии.

Закон Стефана — Больцмана касается лишь интенсивности интегрального излучения черного тела и ничего не говорит относительно спектрального распределения энергии. Полный излучатель, называемый также абсолютно черным телом или излучателем Планка, является идеальным тепловым излучателем, спектральное распределение энергии которого зависит только от его температуры.

 

53. Квантовая гипотеза Планка. Квантовая природа света.

Квантовая природа света

Квантовая природа света объясняет и такое новое явление, как фотоэффект, а также химическое действие света, играющее большую роль в жизни природы.Фотону, вырывающему электрон из металла, нужно затратить работу на отрыв электрона из поля ядра атома, затем на преодоление сил связи, возникающих на поверхности металла, и, наконец, для придания скорости вылетевшему электрону. Как известно, только в специально поставленных опытах квант света отрывает электрон от ядра атома, в обычном же фотоэффекте, электроны давно обобществлены в полосах проводимости металла и обладают большим запасом кинетической энергии. Добавочная энергия фотона требуется, чтобы совершить работу выхода и дать ускорение электрону. Поэтому красная граница фотоэффекта зависит от природы поверхности металла фотоэлемента.

Гипотеза Планка — гипотеза, выдвинутая 14 декабря1900 годаМаксом Планком и заключающаяся в том, что при тепловом излученииэнергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Каждая такая порция-квант имеет энергию , пропорциональной частотеν излучения:

где h или — коэффициент пропорциональности, названный впоследствии постоянной Планка. На основе этой гипотезы он предложил теоретический вывод соотношения между температурой тела и испускаемым этим телом излучением — формулу Планка. Позднее гипотеза Планка была подтверждена экспериментально. Выдвижение этой гипотезы считается моментом рождения квантовой механики.

54. Энергия и импульс фотонов.

Фотон— элементарная частица, квант электромагнитного излучения (в узком смысле — света). Это безмассовая частица, способная существовать только двигаясь со скоростью света. Электрический заряд фотона также равен нулю. Фотон может находиться только в двух спиновых состояниях с проекцией спина на направление движения (спиральностью) ±1. Этому свойству в классической электродинамике соответствует круговая правая и

Действие магнитного поля на движущийся электрический заряд

Ах, как играет этот Север!

Ах, как пылает надо мной

Разнообразных радуг веер

В его короне ледяной!

Ему, наверно, по натуре

Холодной страсти красота.

Усилием магнитной бури

Преображённая в цвета…

Михаил Александрович Дудин

В данной теме речь пойдёт о том, какое действие оказывает магнитное поле на движущийся электрический заряд.

На любой проводник с током, который будет находиться в магнитном поле, это поле будет действовать с некоторой силой. Силу, действующую на проводник с током в магнитном поле, называют силой Ампера. Направление этой силы определяют по правилу левой руки.

Если бы Ампер знал о природе электрического тока, то, возможно, он бы смог продвинуться дальше в своих исследованиях. Однако, как и многие ученые того времени, Андре Мари Ампер был сторонником «эфирной модели». Т.е. он считал, что ток — это некая электрическая эфирная жидкость (или электрический эфир), которая протекает по проводам, (отсюда и пошло выражение «электрический ток» — то, что течет).

Только в самом конце XIX века – вначале ХХ модели эфиров (или, как их еще называли, «модели невесомых») стали отходить, а на смену им стали появляться новые модели адекватнее отражающие наблюдаемые явления.

Если немножко углубиться в историю, то можно отметить, что развитие классической электродинамики после Максвелла шло по нескольким направлениям, из которых отметим два основных.

Во-первых, совершенствовалась математическая сторона теории Максвелла и были получены некоторые новые результаты. Во-вторых, произошло объединение теории электромагнитного поля с основными идеями теории строения вещества. Последнее направление привело к созданию электронной теории.

Начиная с 70-х годов XIX века разработкой электронной теории занялся Хендрик Антон Лоренц, объяснивший с ее помощью электромагнитные и оптические явления. Он исходил из того, что теория Максвелла нуждается в дополнении, так как в ней не учитывается структура вещества.

В первой половине 90-х годов Лоренц уже выступает в печати с общей теорией электромагнитных и оптических явлений, опирающейся, с одной стороны, на теорию Максвелла, а с другой стороны, на представление о существовании элементарных электрических зарядов, связанных с частицами вещества. Эта теория впоследствии (после открытия электрона) получила название электронной теории.

Вскоре после создания электронной теории была развита электронная теория металлов. Немецкий физик Пауль Друде полагал, что электроны, находящиеся в металле, являются свободными и ведут себя подобно атомам идеального газа. Эта гипотеза дала ему возможность, применив методы кинетической теории газов к электронам внутри металла, построить электронную теорию металлов, которая была далее разработана Лоренцем в 1904—1907 годах.

Согласно этой теории, внутри металла существуют свободные заряды — электроны, которые образуют внутри металла, так называемое, электронное облако или электронный газ. Электроны, в этом облаке движутся хаотически и беспорядочно. Но как только мы подадим разность потенциалов на концы проводника, т.е. создадим электрическое поле внутри проводника, кроме этой хаотической составляющей появляется другая — упорядоченная составляющая или направленное движение. Именно это движение, согласно модели Лоренца, и представляет собой электрический ток.

В магнитном поле на проводник с током действует сила Ампера, направление которой, согласно правилу левой руки, перпендикулярно направлению линий магнитного поля и направлению тока в проводнике.

Возникает вопрос: если электрический ток — это упорядоченное движение отдельных заряженных частиц, то оказывает ли магнитное поле воздействие на эти частицы и, если да, то какое?

Существование этой силы Лоренц объяснил тем, что магнитное поле действует на отдельные движущиеся заряженные частицы в проводнике с током. Силу Ампера можно рассматривать как равнодействующую сил, действующих на все свободные заряженные частицы, движущиеся в проводнике при прохождении в нем тока.

Сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу, называется силой Лоренца.

Ее модуль определяется отношением силы Ампера, действующей на проводник с током в магнитном поле, к числу свободных заряженных частиц в проводнике.

Известно что, сила Ампера определяется произведением силы тока в проводнике, модулем магнитной индукции, длиной проводника и углом, между направлением вектора магнитной индукции и направлением тока в проводнике.

Из курса физики 8 класса известно, что сила тока определяется зарядом, прошедшим через поперечное сечение проводника за единицу времени.

Отношение элемента длины проводника к интервалу времени есть скорость движения заряда.

Тогда, сила Лоренца, действующая на свободную заряженную частицу, будет равна произведению заряда этой частицы, модуля магнитной индукции, модуля скорости заряженной частицы и угла между направлением вектора скорости и вектора магнитной индукции.

 

Направление силы Лоренца, как и направление силы Ампера, можно определить, пользуясь правилом левой руки: если левую руку расположить так, чтобы составляющая магнитной индукции, перпендикулярная к скорости движения заряда, входила в ладонь, а выпрямленные четыре пальца были направлены по движению положительного заряда (или против движения отрицательного), то отогнутый на 90º большой палец покажет направление силы Лоренца.

Поскольку сила Лоренца направлена перпендикулярно к скорости движения заряженной частицы в каждой точке траектории, то работа силы Лоренца при движении заряженной частицы в магнитном поле равна нулю.

Если работа силы Лоренца равна нулю, то, согласно теореме об изменении кинетической энергии, кинетическая энергия изменятся не будет, а значит, заряженная частица движется в магнитном поле с постоянной скоростью. Поэтому сила Лоренца меняет лишь направление вектора скорости заряженной частицы.

Рассмотрим на примере, как будет меняться траектория движения заряженной частицы в магнитном поле.

Задача 1. Протон влетает со скоростью 1000 м/с в однородное магнитное поле. Определите траекторию, по которой будет двигаться протон, и основные характеристики такого движения, если магнитная индукция поля равна 0,01 Тесла.

Задача 2. Протон влетает со скоростью 1000 м/с в однородное магнитное поле под углом 60⁰ к линиям магнитной индукции. Определите траекторию, по которой будет двигаться протон, и основные характеристики такого движения, если магнитная индукция поля равна 0,01 Тл.

Действие магнитного поля на движущиеся заряженные частицы очень широко используют в технике.

Например, отклонение электронного пучка в кинескопах телевизоров осуществляют с помощью магнитного поля, которое создают специальными катушками. В ряде электронных приборов магнитное поле используется для фокусировки пучков заряженных частиц. В созданных в настоящее время экспериментальных установках для осуществления управляемой термоядерной реакции действие магнитного поля на плазму используют для скручивания ее в шнур, не касающийся стенок рабочей камеры. Движение заряженных частиц по окружности в однородном магнитном поле и независимость периода такого движения от скорости частицы используют в циклических ускорителях заряженных частиц — циклотронах. Также действие силы Лоренца используют и в приборах, называемых масс-спектрографами, которые предназначены для разделения заряженных частиц по их удельным зарядам.

Рассмотрим схему простейшего масс-спектрографа.

В камере, из которой откачан воздух, находится источник ионов. Сама камера помещена в однородное магнитное поле, в каждой точке которого индукция перпендикулярна плоскости чертежа и направлена к нам. Между электродами A и B приложено ускоряющее напряжение, под действием которого ионы, вылетающие из источника, разгоняются и с некоторой скоростью попадают в магнитное поле перпендикулярно линиям индукции. Двигаясь в магнитном поле по дуге окружности, ионы попадают на фотопластинку, что позволяет определить радиус этой дуги. Зная индукцию магнитного поля и скорость ионов, можно определить удельный заряд ионов. А если известен и заряд иона, то можно вычислить его массу.

Сила Лоренца, вызывающая отклонение электронов, движущихся в магнитных полях, от их первоначального пути, проявляется и во многих явлениях природы, которые только с помощью этих сил и удается объяснить. Одно из самых красивых и величественных явлений такого рода — это полярные сияния. В местах земного шара, расположенных в сравнительно высоких широтах, преимущественно за северным или южным полярным кругом, во время долгой полярной ночи часто наблюдают на небе явление поразительной красоты: на небе вдруг вспыхивает свечение разнообразной окраски и формы. Иногда оно имеет вид однородной дуги, неподвижной или пульсирующей, иногда как бы состоит из множества лучей разной длины, которые переливаются, свиваются в виде лент или драпировок и т. п. Цвет этого свечения желтовато-зеленый, красный, серо-фиолетовый.

Вот в каких словах описывал это прекрасное явление природы в своём дневнике всемирно известный исследователь Фритьоф Нансен, наблюдавшееся в Арктике в конце 1894 года:

«После полудня было редкостное северное сияние. Когда я вышел в шесть часов, яркая дуга была перекинута над южным краем неба. Долгое время она оставалась спокойной, почти не изменяясь. Затем началось сильное свечение у её верхнего края: с минуту продолжалось пылание, затем вдруг свечение распространилось вдоль дуги на запад, к зениту ото всей ленты метнулись лучи и, не успел я опомниться, вся южная часть неба, от дуги до зенита, оказалась объята светлым пламенем. Оно сверкало и горело, кружилось, словно в вихре ветра, лучи летали взад и вперёд, то красные и красно-фиолетовые, то жёлтые, зелёные и ослепительно белые. То у основания лучи были красные, а наверху жёлтые и зелёные, то наоборот. Выше и выше поднималось пламя: вот оно достигло и северной стороны зенита – на мгновение в нём образовалась великолепная корона; потом всё обратилось в одну крутящуюся огненную массу. Это был точно водоворот огня, красного, жёлтого и зелёного, — глаз ослепляло это зрелище…».

Долгое время природа и происхождение полярных сияний оставались совершенно загадочными, и только сравнительно недавно удалось подойти к решению этой загадки. Была подмечена очень интересная связь между полярными сияниями и рядом других явлений. Полярные сияния не всегда появляются одинаково часто. В одни годы их бывает меньше, в другие больше. Многолетние наблюдения показали, что периоды максимальной частоты полярных сияний регулярно повторяются через 11,5 года.

При наблюдении поверхности Солнца уже давно были замечены на его диске неправильной формы темные пятна, часто изменяющие свой вид и положение на солнечном диске. Оказалось, что число и общая площадь этих пятен изменяются от года к году не случайно, а периодически, с тем же периодом в 11,5 года. При этом в годы максимума солнечных пятен или, как говорят, в годы максимальной солнечной активности, достигает максимума и число полярных сияний, а по мере уменьшения числа пятен ослабевают и полярные сияния.

Сопоставляя эти факты, норвежский ученый Биркеланд высказал предположение, что пятна на Солнце являются теми местами, откуда с огромной скоростью выбрасываются в окружающее пространство потоки заряженных частиц — электронов. Попадая в верхние слои нашей атмосферы, они заставляют светиться составляющие ее газы, подобно тому, как они светятся под влиянием ударов электронов в разрядной трубке.

Но если это так, то почему полярные сияния наблюдаются только в высоких широтах, т. е. в местностях, не очень удаленных от земных полюсов? Ведь солнечные лучи освещают всю Землю. На этот вопрос ответил другой норвежец, Штермер. Заряженные частицы, испускаемые Солнцем, подходя к Земле, попадают в земное магнитное поле. Здесь на них действует сила Лоренца, отклоняющая их от первоначального прямого пути. Штермер произвел сложные математические вычисления и рассчитал пути этих электронов в магнитном поле Земли. Он показал, что, действительно, заряженные частицы, отклоняемые земным магнитным полем, могут попадать только в приполярные области земного шара.

Основные выводы:

– На любую движущуюся заряженную частицу со стороны магнитного поля действует сила Лоренца.

 

– Направление силы Лоренца, как и силы Ампера, можно определить по правилу левой руки.

– Сила Лоренца перпендикулярна вектору магнитной индукции и вектору скорости заряженной частицы. Поэтому она не совершает работы.

13.1. Действие магнитного поля на движущийся заряд. Сила Лоренца.

Естественно предположить, что на каждую частицу действует сила

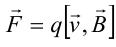
В общем случае, если на движущуюся частицу помимо магнитного поля с индукцией B действует и электрическое поле с напряженностью E , то результирующая сила (сила Лоренца) равна сумме двух составляющихr− электрической и магнитной

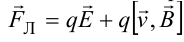
13.2. Движение заряженных частиц в магнитном поле.

Пусть частица с зарядом q и массой m влетает в область, где существует постоянное магнитное поле, под углом α к линиям индукции. Представим скорость v частицы как сумму двух составляющих, − направленную вдоль поля v||=v cos α, и перпендикулярно полю v⊥=v sin α. Тогда силу Лоренца, действующую на частицу, можно представить в виде

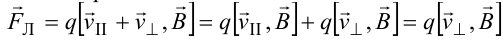
т.е. составляющая скорости, параллельная полю, не вызывает появление магнитной силы.

Направление силы Лоренца перпендикулярно вектору скорости (траектории частицы), следовательно, сила Лоренца может изменять скорость только по направлению, а не по величине.

Следовательно, движение частицы можно представить в виде су перпозиции:

1) равномерного прямолинейного движения частицы вдоль поля со скоростью v||=v cos α;

2) равномерного движения со скоростью v⊥=v sin α по окружности в плоскости, перпендикулярной полю. Радиус окружности может быть найден из соотношений

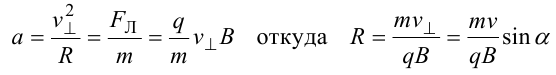
В результате сложения обоих движений возникает движение по спирали, ось которой направлена параллельно магнитному полю. Время одного полного оборота (период)

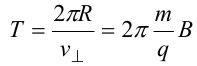
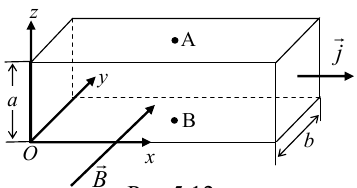
14.1. Эффект Холла.

Эффект Холла (1879 г.) − это возникновение в металле или полупроводнике с током, помещенном в магнитное поле, разности потенциалов в направлении, перпендикулярном движению носителей тока.

Пусть ток с плотностью j в образце в виде прямоугольной пластины обусловлен упорядоченным движением частиц с зарядом q.

Поместим пластину в магнитное поле с индукцией B , перпендикулярное плотности тока j.

На частицу, движущуюся в магнитном поле, действует сила Лоренца 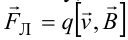. При указанных направлениях тока и магнитного поля сила Лоренца направлена вверх (вдоль положительного направления оси OZ). Под действием силы FЛ частицы будут отклоняться к верхней грани пластины, так что на ней будет накапливаться избыток зарядов того же знака, что и q, а на нижней грани − избыток зарядов противоположного знака. В результате этого в пластине возникнет поперечное электрическое поле, направленное сверху вниз, если q>0, и снизу вверх если q<0. Пусть Е − напряженность образовавшегося электрического поля. Сила qE , действующая на заряд q со стороны поперечного электрического поля, направлена в сторону, противоположную магнитной составляющей FЛ . В случае установившегося состоя-

н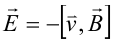ия сила Лоренца равна нулю

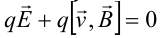
Разность потенциалов между точками А и В на гранях пластины

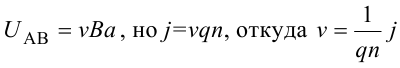
Тогда

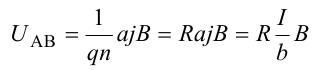
где R=1/(qn) − постоянная Холла.

14.2. Циклотрон

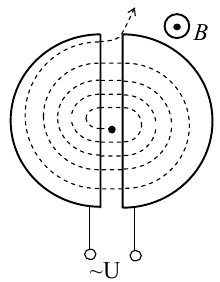Циклотрон − ускоритель тяжелых частиц (протонов, ионов). В основе конструкции циклотрона − два полых электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное (ускоряющее) электрическое поле, и они находятся в вакуумной камере в сильном однородном магнитном поле, перпендикулярном плоскости дуантов.

Заряженные частицы вводятся в центр зазора между дуантами. В зазоре частица ускоряется электрическим и отклоняется магнитным полями. Войдя в дуант, частица описывает полуокружность, радиус которой пропорционален скорости частиц. Очевидно, условием ускорения частицы при каждом проходе зазора является равенство частот ω∼ ускоряющего электрического поля и частоты вращения частицы ωс.

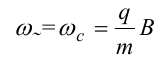
Если амплитуда напряжения между дуантами U0, а число проходов частицы ускоряющей разности потенциалов n, то максимальная энергия, приобретенная частицей, будет

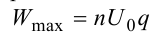
Максимально возможный радиус вращения частицы в магнитном поле (радиус дуантов)

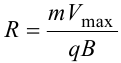
где Vmax − максимальная скорость частицы в циклотроне. Отсюда

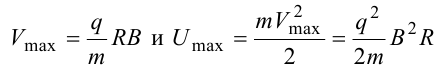
При достижении энергии частиц до максимального значения на последнем витке пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.

Циклотроны позволяют ускорять протоны до энергии ∼20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается.

44. Действие магнитного поля на движущийся заряд. Сила Лоренца.

С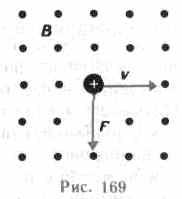ила, дей­ствующая на электрический зарядQ, дви­жущийся в магнитном поле со скоростью v, называется силой Лоренца и выражает­ся формулой F=Q[vB], где В — индукция магнитного поля, в котором заряд движется.

Направление силы Лоренца определя­ется с помощью правила левой руки: если ладонь левой руки расположить так, что­бы в нее входил вектор В, а четыре вы­тянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпада­ют, для Q<0—противоположны), то отогнутый большой палец покажет на­правление силы, действующей на положи­тельный заряд. На рис. 169 показана вза­имная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.

Модуль силы Лоренца равен F=QvBsin, где  — угол между v и В. Магнитное поле действует только на движущиеся в нем заряды. Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лорен­ца может быть использовано для определения вектора магнитной индукции В.

Сила Лоренца всегда перпендикуляр­на скорости движения заряженной части­цы, поэтому она изменяет только направ­ление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изме­няется.

Если на движущийся электрический заряд помимо магнитного поля с индук­цией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна век­торной сумме сил — силы, действующей со стороны электрического поля, и силы Ло­ренца: F=QE + Q[vB]. Это выражение называется формулой Ло­ренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.

45. Движение заряженных частиц в магнитном поле. Ускорители элементарных частиц.

Н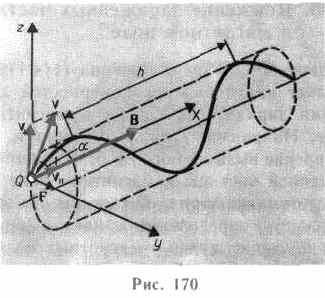аправление силы Лоренца и на­правление вызываемого ею отклонения за­ряженной частицы в магнитном поле за­висят от знака зарядаQ частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле одно­родно и на частицы электрические поля не действуют. Если заряженная частица дви­жется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В ра­вен 0 или . Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она дви­жется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпен­дикулярной вектору В, то сила Лоренца F=Q[vB] постоянна по модулю и нор­мальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус r которой определяет­ся из условия QvB = mv²/r, откуда Период вращения частицы, т. е. 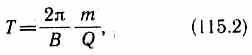вре­мя Т, затрачиваемое ею на один полный оборот, т. е. период вращения частицы в однород­ном магнитном поле определяется только величиной, обратной удельному заряду(Q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v << с)).

Если скорость v заряженной частицы направлена под углом а к вектору В (рис. 170), то ее движение можно пред­ставить в виде суперпозиции: 1) равно­мерного прямолинейного движения вдоль поля со скоростью v_||=vcos; 2) равно­мерного движения со скоростью v_┴= vsin по окружности в плоскости, пер­пендикулярной полю. В результате сложения обоих движений возникает движение по спирали, ось кото­рой параллельна магнитному полю. Шаг винтовой линии h=v_||T=vTcos. Радиус окружности определяется формулой (в данном случае надо заменитьv на v_┴=vsin).

Ускорителями заряженных частиц назы­ваются устройства, в которых под дей­ствием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (элек­тронов, протонов, мезонов и т.д.).

Любой ускоритель характеризуется типом ускоряемых частиц, энергией, со­общаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пу­чок) и импульсные (из них частицы вы­летают порциями — импульсами). По­следние характеризуются длительностью импульса. По форме траектории и меха­низму ускорения частиц ускорители делят­ся на линейные, циклические и индукци­онные. В линейных ускорителях траекто­рии движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружно­сти или спирали.

Рассмотрим некоторые типы ускорите­лей заряженных частиц.

1. Линейный ускоритель. Ускорение частиц осуществляется электростатиче­ским полем, создаваемым, например, вы­соковольтным генератором Ван-де-Граафа. Заряженная частица проходит поле однократно: заряд Q, проходя раз­ность потенциалов ₁-₂, приобретает энергию W=Q(₁-₂). Таким способом частицы ускоряются до 10 МэВ. Их дальнейшее ускорение с помощью источ­ников постоянного напряжения невозмож­но из-за утечки зарядов, пробоев и т. д.

2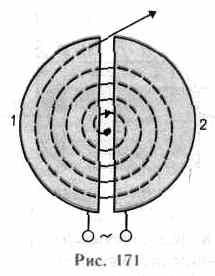. Линейный резонансный ускоритель.Ускорение заряженных частиц осуще­ствляется переменным электрическим по­лем сверхвысокой частоты, синхронно из­меняющимся с движением частиц. Таким способом протоны ускоряются до энергий порядка десятков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.

3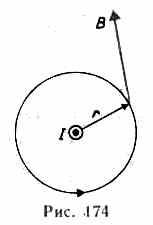. Циклотрон— циклический резонан­сный ускоритель тяжелых частиц (прото­нов, ионов). Между полюсами сильного электромагнита помещается ва­куумная камера, в которой находятся два электрода (1 и 2) в виде полых металличе­ских полуцилиндров, или дуантов. К дуантам приложено переменное электриче­ское поле. Магнитное поле, создаваемое электромагнитом, однородно и перпенди­кулярно плоскости дуантов.

Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус кото­рой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменя­ется (при соответствующем подборе изме­нения напряжения между дуантами), по­этому частица вновь ускоряется и, перехо­дя в дуант 2, описывает там уже полу­окружность большего радиуса и т. д.

Для непрерывного ускорения частицы в циклотроне необходимо выполнить усло­вие синхронизма (условие «резонан­са») — периоды вращения частицы в маг­нитном поле и колебаний электрического поля должны быть равны. При выполне­нии этого условия частица будет двигать­ся по раскручивающейся спирали, полу­чая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус ор­биты доведены до максимально допусти­мых значений, пучок частиц посредством отклоняющего электрического поля выво­дится из циклотрона.

Циклотроны позволяют ускорять про­тоны до энергий примерно 20 МэВ. Даль­нейшее их ускорение в циклотроне ограни­чивается релятивистским возрастанием массы со скоростью, что при­водит к увеличению периода обращения, и синхронизм нарушается. Поэтому цик­лотрон совершенно неприменим для ус­корения электронов (при E=0,5 МэВ m = 2m₀, при E=10 МэВ m=28m₀!).

4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тя­желых заряженных частиц (например, протонов, ионов, -частиц), в котором уп­равляющее магнитное поле постоянно, а частота ускоряющего электрического по­ля медленно изменяется с периодом. Дви­жение частиц в фазотроне, как и в цикло­троне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (огра­ничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).

5. Синхротрон — циклический резо­нансный ускоритель ультрарелятивистских электронов, в котором управляющее маг­нитное поле изменяется во времени, а частота ускоряющего электрического по­ля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.

6. Синхрофазотрон — циклический ре­зонансный ускоритель тяжелых заряжен­ных частиц (протонов, ионов), в котором объединяются свойства фазотрона и син­хротрона, т. е. управляющее магнитное поле и частота ускоряющего электрическо­го поля одновременно изменяются во вре­мени так, чтобы радиус равновесной орби­ты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.

7. Бетатрон — циклический индукци­онный ускоритель электронов, в котором ускорение осуществляется вихревым элек­трическим полем (см. §137), индуцируе­мым переменным магнитным полем, удер­живающим электроны на круговой орбите. В бетатроне в отличие от рассмотренных выше ускорителей не существует пробле­мы синхронизации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W> 100 МэВ режим ускорения в бетатро­не нарушается электромагнитным излуче­нием электронов. Особенно распростране­ны бетатроны на энергии 20—50 МэВ.