Гравитационная сила – формула, определение закона всемирного тяготения кратко

4.6

Средняя оценка: 4.6

Всего получено оценок: 272.

4.6

Средняя оценка: 4.6

Всего получено оценок: 272.

Одним из фундаментальных природных взаимодействий является гравитация. Сила притяжения Земли известна человеку с древности. Однако, точное ее описание появилось лишь в эпоху Возрождения. Рассмотрим особенности этой силы подробнее.

Открытие гравитационных сил

Согласно представлениям Аристотеля, Земля состоит из «абсолютно тяжелого» элемента земли, и находится в геометрическом центре Вселенной. Этот элемент является причиной падения тел, он тянет все тела в центр Вселенной, а поскольку все тела в той или иной степени состоят из него, то все они также испытывают такое же стремление.

Небесные тела никак не связывались с Землей, они совершали движение либо по «хрустальным сферам» либо, в более поздней системе Птолемея по «совершенным» окружностям.

К XVIв стало накапливаться все больше фактов, говорящих о том, что Земля – не единственный объект, обладающий гравитацией. Исследования Н. Коперника, Г. Галилея, И. Кеплера, Р. Декарта подводили к мысли, что причиной непрямолинейного движения планет является существование некоторой силы, постоянно искривляющей траекторию движения, без участия которой планеты бы двигались по прямым.

Законченную форму эти представления обрели в труде И. Ньютона «Математические начала натуральной философии», изданном в 1687 г, где была выведена формула гравитационной силы.

Рис. 1. Книга Ньютона Математические Начала Натуральной Философии.

Согласно Ньютону, любое изменение скорости движения тела – это результат воздействия некоторой силы. Исследовав законы движения планет, открытые Кеплером, Ньютон пришел к выводу, что траектория движения планет – это результат действия гравитационной силы, действующей между планетами и Солнцем. Сила эта пропорциональна массе тел и обратно пропорциональна квадрату расстояния между ними:

$$F_{грав}=G{m_1m_2\over r^2}$$

Заслугой Ньютона явилось то, что он распространил действие гравитации не только на небесные тела, но и на вобще любые тела, обладающие массой, установив, таким образом, Закон Всемирного Тяготения.

Рис. 2. Силы гравитации.

Особенности гравитационной силы

Итак, явление гравитации состоит в том, что между телами существует сила взаимного притяжения, пропорциональная их массам. В чем особенности этой силы ?

• Радиус действия гравитации бесконечен. Величина ее падает пропорционально квадрату расстояния, и эта зависимость неизменна. Таким образом, даже объекты, удаленные на значительные астрономические расстояния, все равно оказывают небольшое гравитационное влияние друг на друга.
• Гравитация – всемирная сила. От поля гравитационной силы укрыться невозможно. В отличие, например, от магнитного поля, которое не проникает в сверхпроводники, гравитация проникает через любые материальные преграды.
• Силы гравитации потенциальны. Это означает, что любой точке пространства соответствует некоторая потенциальная энергия гравитационной силы, и для определения работы гравитации не требуется знать форму траектории, достаточно знать лишь положения начальной и конечной точки пути.

Гравитация – единственная сила, сообщающая всем телам одинаковое ускорение. Ускорение, сообщаемое телу силами любой другой природы, зависит от массы тела. Для гравитационного поля Земли это не так. Еще Галилей показал, что легкая дробинка и тяжелое ядро падают с одинаковым ускорением, несмотря на разницу в весе. Это происходит потому, что хотя масса ядра значительно больше, гравитационная сила для него также больше. В результате ускорение, получаемое ядром, равно ускорению, получаемое дробинкой.

Точность Закона Всемирного Тяготения позволила не только описать движения планет, но и предсказать существование еще неоткрытой планеты – Нептуна. И лишь в XXв появились данные, расходящиеся с ним. Дальнейшее развитие теория гравитации получила в рамках Общей Теории Относительности А.Эйнштейна, для которой гравитация Ньютона является частным случаем.

Рис. 3. Общая теория относительности Эйнштейна.

Что мы узнали?

Согласно теории гравитации И.Ньютона, между любыми телами, имеющими массу, существует сила взаимного притяжения, пропорциональная произведению их масс и обратно пропорциональная квадрату расстояния между ними. Ускорение, сообщаемое гравитацией телам, не зависит от их массы.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.6

Средняя оценка: 4.6

Всего получено оценок: 272.

---

А какая ваша оценка?

понятие и специфические особенности применения формулы для их расчета

Гравитационные силы являются одним из четырех основных видов сил, которые проявляются во всем своем многообразии между различными телами как на Земле, так и за ее пределами. Кроме них еще выделяют электромагнитные, слабые и ядерные (сильные). Вероятно, именно их существование человечество осознало в первую очередь. О силе притяжения со стороны Земли было известно еще с самых древних времен. Однако прошли целые столетия, прежде чем человек догадался, что взаимодействие подобного рода происходит не только между Землей и любым телом, но и между разными объектами. Первым, кто понял, как работают гравитационные силы, был английский физик И. Ньютон. Именно он и вывел всем известный сейчас закон всемирного тяготения.

Формула гравитационной силы

Ньютон решил проанализировать законы, по которым происходит движение планет в системе. В результате он пришел к выводу, что вращение небесных тел вокруг Солнца возможно лишь в том случае, если между ним и самими планетами действуют гравитационные силы. Понимая, что небесные тела от других предметов отличаются всего лишь своими размерами и массой, ученый вывел следующую формулу:

F = f x (m₁ x m₂) / r², где:

• m₁, m₂ – это массы двух тел; 
• r – расстояние между ними по прямой; 
• f – гравитационная постоянная, значение которой равно 6,668 х 10^-8 см³/г х сек².

Таким образом, можно утверждать, что любые два объекта притягиваются друг к другу. Работа гравитационной силы по своей величине прямо пропорциональна массам данных тел и обратно пропорциональна расстоянию между ними, возведенному в квадрат.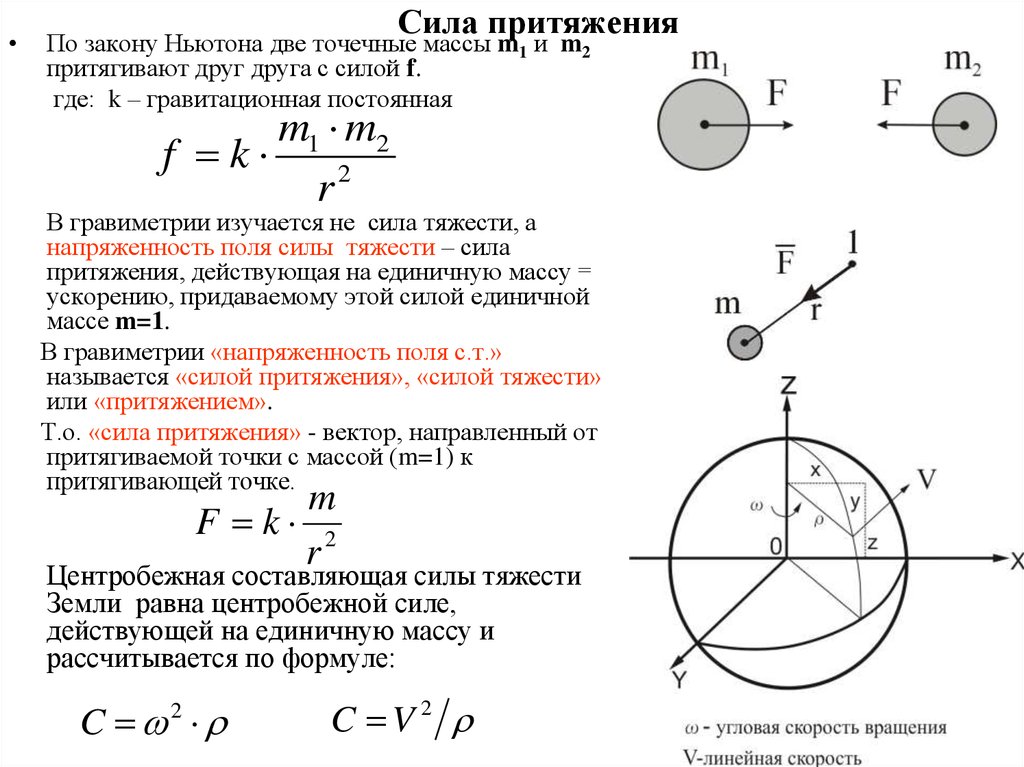

Особенности применения формулы

На первый взгляд, кажется, что пользоваться математическим описанием закона притяжения довольно просто. Однако если поразмыслить, данная формула имеет смысл лишь для двух масс, размеры которых по сравнению с расстоянием между ними ничтожно малы. Причем настолько, что их можно принять за две точки. А как же тогда быть, когда расстояние сопоставимо с размерами тел, а сами они имеют неправильную форму? Разделить их на части, определить гравитационные силы между ними и вычислить равнодействующую? Если так, то сколько точек нужно брать для расчета? Как видите, не все так просто. А если учесть (с точки зрения математики), что точка размеров не имеет, то такое положение и вовсе кажется безвыходным. К счастью, ученые придумали способ, как производить расчеты в таком случае. Они используют аппарат интегрального и дифференциального исчислений. Суть метода в том, что объект разбивается на бесконечное число малых кубиков, массы которых сосредоточены в их центрах. Затем составляется формула для нахождения равнодействующей силы и применяется предельный переход, посредством которого объем каждого составляющего элемента сводится к точке (нулю), а количество таких элементов устремляется в бесконечность. Благодаря данному приему удалось получить некоторые важные выводы.

1. Если тело представляет собой шар (сферу), плотность которого однородна, то оно притягивает к себе любой другой объект так, словно вся его масса сосредоточена в его центре. Поэтому с некоторой погрешностью можно применять этот вывод и для планет.
2. Когда для плотности предмета характерна центральная сферическая симметрия, он взаимодействует с другими объектами так, как будто в точке симметрии находится вся его масса. Таким образом, если взять пустотелый шар (например, футбольный мяч) или несколько вложенных друг в друга шаров (как куклы-матрешки), то они будут притягивать другие тела подобно тому, как это делала бы материальная точка, имеющая их общую массу и расположенная в центре.

Калькулятор гравитационной силы

Создано Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 22 июня 2022 г.

Содержание:

• Определение гравитационной силы
• Что такое уравнение гравитации?
• Как использовать формулу гравитации?

Этот калькулятор гравитационной силы позволяет найти силу между любыми двумя объектами. Читайте дальше, чтобы лучше понять определение гравитационной силы и узнать, как применять формулу гравитации. Обязательно ознакомьтесь с калькулятором скорости убегания!

Определение гравитационной силы

Закон всемирного тяготения Ньютона гласит, что каждый объект с ненулевой массой притягивает любой другой объект во Вселенной. Эта сила притяжения называется гравитацией. Он существует между всеми объектами, хотя это может показаться смешным. Например, пока вы читаете эти слова, между вами и экраном компьютера возникает крошечная сила. Эта сила слишком мала, чтобы вызвать какой-либо видимый эффект, но если вы примените принцип гравитационной силы к планетам или звездам, ее эффекты начнут проявляться.

Одним из наиболее распространенных примеров, иллюстрирующих принцип действия гравитационной силы, является свободное падение.

Что такое уравнение гравитации?

Используйте следующую формулу для расчета гравитационной силы между любыми двумя объектами:

F = GMm/R²

, где:

• F обозначает гравитационную силу. Он измеряется в ньютонах и всегда положителен. Это означает, что два объекта определенной массы всегда притягиваются (и никогда не отталкиваются) друг от друга;
• M и m — массы двух рассматриваемых объектов;
• R — расстояние между центрами этих двух объектов; и
• G — гравитационная постоянная. Он равен 6,674×10 ^-11 Н·м²/кг².

Вы заметили, что это уравнение похоже на формулу закона Кулона? В то время как закон тяготения Ньютона имеет дело с массами, закон Кулона описывает силу притяжения или отталкивания между электрическими зарядами.

Как использовать формулу гравитации?

1. Узнайте массу первого объекта. Выберем Землю — ее масса равна 5,972×10 ²⁴ кг. Вы можете ввести это большое число в калькулятор, набрав 5.972e24 .
2. Узнайте массу второго объекта. Выберем Солнце — оно весит 1,989×10 ³⁰ кг, примерно столько же, сколько 330 000 Земель.
3. Определить расстояние между двумя объектами. Выберем расстояние от Земли до Солнца — около 149600 000 км.
4. Введите все эти значения в калькулятор гравитационной силы. Он будет использовать уравнение гравитации, чтобы найти силу.
5. Теперь вы можете прочитать результат. Например, сила между Землей и Солнцем достигает 3,54×10 ²² Н.
.

Bogna Szyk

F = GMM/R²

МАСС 1 (M)

Масса 2 (M)

Расстояние (R)

Гравитационная сила (F)

Проверьте 83 Классический механик. калькуляторы ⚙️

УскорениеУгол поворота Угол наклона берега… Еще 80

SCIRP Открытый доступ

Издательство научных исследований

Журналы от A до Z

Журналы по темам

• Биомедицинские и медико-биологические науки.
• Бизнес и экономика
• Химия и материаловедение.
• Информатика. и общ.
• Науки о Земле и окружающей среде.
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные науки. и гуманитарные науки

Журналы по теме

• Биомедицина и науки о жизни
• Бизнес и экономика
• Химия и материаловедение
• Информатика и связь
• Науки о Земле и окружающей среде
• Машиностроение
• Медицина и здравоохранение
• Физика и математика
• Социальные и гуманитарные науки

Публикация у нас

• Подача статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Публикуйте у нас  

• Представление статьи
• Информация для авторов
• Ресурсы для экспертной оценки
• Открытые специальные выпуски
• Заявление об открытом доступе
• Часто задаваемые вопросы

Подпишитесь на SCIRP

Свяжитесь с нами

	клиент@scirp. org
	+86 18163351462 (WhatsApp)
	1655362766
	Публикация бумаги WeChat

Недавно опубликованные статьи

Недавно опубликованные статьи

• Эпидемиологические, клинические, параклинические, этиологические и терапевтические аспекты цирроза печени в отделении гепато-гастроэнтерологии больницы Аристид Ле Дантек в Дакаре()

  Мари-Луиза Бассен, Саламата Диалло, Марием Полеле Фолл, Маме Аиссе Тиубу, Тене Сидибе, Кумба Сиссе, Мамаду Нгоне Гуйе

  Открытый журнал гастроэнтерологии Том 12 № 11, 2 ноября 2022 г.

  DOI: 10.4236/ojgas.2022.1211032 5 загрузок  36 просмотров

• Оптимальный размах хвата для измерения максимальной силы хвата у детей дошкольного возраста()

  Такаши Абэ, Рика Сануи, Ариса Сасаки, Аки Исибаши, Нанами Дайкай, Юка Синдо, Акеми Абэ, Джереми П. Лоеннеке

  Международный журнал клинической медицины Том 13 № 11, 2 ноября 2022 г.

  DOI: 10.4236/ijcm.2022.1311035 7 загрузок  50 просмотров

• Подход к лечению боли у пациенток с эндометриозом: систематический обзор литературы ()

  Ванесса Феррейра Диас Дуарте да Кошта, Мария Эдуарда Пазини Модесто Гонсалвеш, Камила душ Сантуш Лейте, Оскар Сезар Пирес

  Journal of Biosciences and Medicines

  Vol. 10 No.11, 2 ноября 2022 г.

  DOI: 10.4236/jbm.2022.1011001 6 загрузок  48 просмотров

• Влияние устных инструкций на оценку боли во время пассивного теста с поднятием прямой ноги у людей с хронической болью в пояснице ()

  Масаэ Икея, Такуми Дзироумару, Хитоми Бунки, Мичио Вачи, Нориюки Кида, Теруо Номура

  Открытый журнал терапии и реабилитации Том 10 №4, 2 ноября 2022 г.

  DOI: 10.4236/ojtr.2022.104014 3 загрузки  32 просмотра

• Импульсный отклик внутренней и внешней процентной ставки в выпуске, цена, модель обменного курса, деконструированный вывод и экономическая калибровка векторной модели коррекции ошибок ()

  Линкай Конг, Юньсинь Чан

  Journal of Mathematical Finance Vol.