Сила электрическая формула: Определение силы тока. Единицы измерения силы тока — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Моделирование силовых линий электрического поля двух точечных зарядов вблизи проводящей плоскости / Хабр

Всегда было интересно как же рисовать линии напряженности не только на интуитивном уровне — от плюсы к минусу, но и на практике. Как на самом деле они выглядят в каждой точке на нашем условном поле? Сейчас и разберемся по ходу дела рассматривать и более сложные системы точек, используя силу языка python.

Теория

Любой заряд создает вокруг себя поле, которое влияет на другие заряды — электрическое поле.

Также в сумме некоторое количество зарядов создает вокруг себя поле, с различным влиянием в каждой точке. Поэтому для обнаружения и исследования электрического поля нам нужен заряд, который называют пробным. Этот заряд мы берем, чтобы «попробовать», существует ли в той или иной точке пространства электрическое поле: если в какой-то точке на этот заряд действует электрическая сила.

Сила с которой взаимодействуют два заряда описывается законом Кулона.

Пусть у нас есть два неподвижных заряда, тогда силой Кулона называется силы, выражаемой формулой:

где радиус векторы первого и второго заряда, а диэлектрическая постоянная. Формула на самом деле очень похожа на формулу гравитационного взаимодействия. Можно сделать такую же аналогию — сила зависит от величины двух объектов и расстояния между ними, помноженную на какую-то константу.

Обобщение на случай распределенного заряда:

Здесь у нас не просто заряд, а какое-то тело. Не вдаваясь в подробности, мы пользуемся аддитивностью силы () и высчитываем силу от заряда до маленькой части тела . Уменьшив размеры части тела и сложив все такие силы, мы получим интеграл.

С помощью пробного заряда можно оценить “силу влияния” какого-то поля — этой величиной называется напряженность электрического поля.

Напряженность в точке пробного заряда пропорциональна силе и обратно пропорциональна заряду —

Соответственно напряженность поля в точке заряда :

Так же как и сила , напряженность электрического поля аддитивна

также это свойство называется принципом суперпозиции.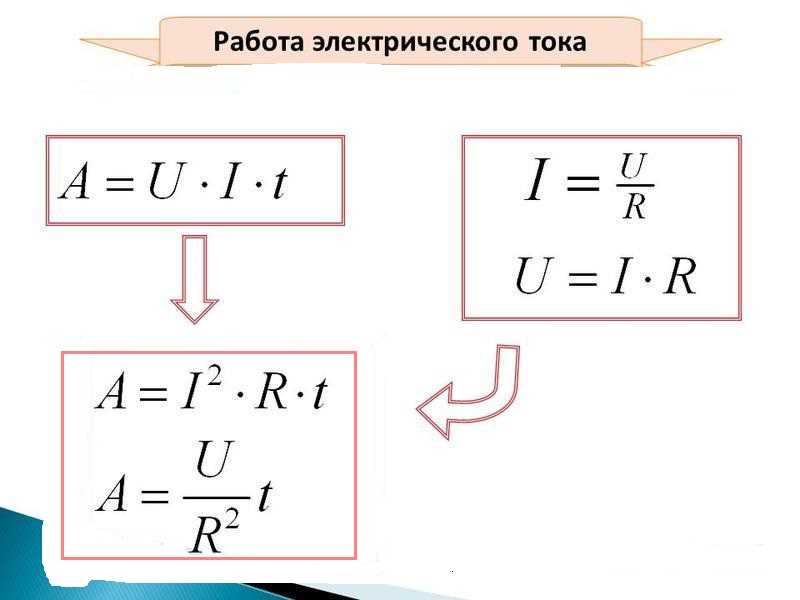 То есть в рассматриваемой нами статье напряженность точки — точка пространства, можно получить сложив напряженность относительно и плоскости:

Моделирование

Для некоторого упрощения понимания результата работы было принято решение смотреть на плоскость — срез — проходящий через две точки и пересекающий перпендикулярно плоскость.

Для моделирования силовых линий электрического поля был использован язык python. В основе реализации лежит класс ElectricField описывающий электрическое поле с конструктором, принимающий на вход все объекты, имеющие заряд.

А именно две точкиPoint(number charge, number x, number y)

и прямую Line(number charge, number[] firstPoint, number[] secondPoint).

Сигнатуру методов указана для упрощения понимания =)

class ElectricField:
    dt0 = 0.01  # The time step for integrations
    def __init__(self, charges):
        #Инициализация поля по вводным объектам
        self. charges = charges
    def vector(self, x):
        #Возвращает все вектора поля
        return np.sum([charge.E(x) for charge in self.charges], axis=0)
    def magnitude(self, x):
        #Возвращает длину вектора
        return norm(self.vector(x))
    def angle(self, x):
        #Возвращает угол от оси абцисс до вектора в радианах
        return np.arctan2(*(self.vector(x).T[::-1]))

Каждый из этих объектов имеет метод, который вычисляет напряженность в какой-то пробной точке по своей специфичной для своего рода объекта формуле.

Например, для класса Point это .

Что примечательно мы не просто так опускаем коэффициент пропорциональности . Дело в том, что этот скаляр влияет лишь на длину всех векторов в поле, поэтому опустив, его мы не упустим наглядности результата. Весь код вы можете найти в дополнительных материалах.

Соответственно, наши объекты будут обладать начальными условиями: Point зарядом и координатами на плоскости, Line зарядом и двумя точками, на длине которой этот заряд определен.

# Создадим объекты и засунем их в поле 
charges = [Line(1, [0, -10], [0, 10]),
        Point(-1, [-1, 0]), 
           Point(1, [1, 0])]
field = ElectricField(charges)

Инициализируем дополнительно наши размеры, массивы размеров ширины и высоты, а далее пройдемся по выделенными нами точкам.

x, y = np.meshgrid(np.linspace(XMIN/ZOOM+XOFFSET, XMAX/ZOOM+XOFFSET, 41),
                      np.linspace(YMIN/ZOOM, YMAX/ZOOM, 31))
u, v = np.zeros_like(x), np.zeros_like(y)
n, m = x.shape
# Вот тут проходим по точкам
for i in range(n):
    for j in range(m):
				# Если точка лежит на прямой Е = 0
        if any(charge.is_close([x[i, j], y[i, j]]) for charge in charges):
            u[i, j] = v[i, j] = None
        else:
						# Находим длину и корректируем ее немного 
            mag = field.magnitude([x[i,j], y[i,j]])**(1/5)
						# Находим угол и суем компоненты вектора в u v массивы
            a = field.angle([x[i,j], y[i,j]])
            u[i, j], v[i, j] = mag*np.cos(a), mag*np.  sin(a)

После чего нам остается кое-что поправить в графике и вывести его функцией pyplot.show()

Примеры

Пусть у нас даны начальные условия двух точек и прямой.

charges = [Line(1, [0, -10], [0, 10]),
        Point(-1, [-1, 0]), 
           Point(1, [1, 0])]

Довольно ожидаемая картина — линии напряженности выходят из положительно заряженных объектов и входят в отрицательно заряженные.

Тогда если изменить заряды на одинаковые:

Отличие лишь в направлении каждого вектора — они поменяли направление из-за знака.

Что если изменить величину зарядов:

Как и ожидалось — более заряженные объекты искривляют электрическое поле больше. Опять же аналогия с гравитационным полем: чем больше масса там больше тело изменяет пространство вокруг себя.

Однако все ли здесь хорошо?

Что происходит? Мне в школе говорили, что одинаково заряженные объекты отталкиваются, а тут получается, что не совсем?

Однако если посмотреть на всю картину, то станет ясно, кто во всем виноват:

Построим более наглядную картину, увеличив отрицательный заряд.

Очень сильно отрицательно заряженная точка искривляет поле так, что влияние этой положительно заряженной линии

Line просто подавляется, но если посмотреть более пристально, то можно увидеть, что длина линий напряженности после прохождения Line немного увеличивается.

При огромном желании эти графики построить можно самому. Этот код я частично позаимствовал у tomduck. Кстати, у него еще больше показательных примеров не только 2-D, но и 3-D графиков. Очень рекомендую посмотреть хотя бы описание библиотеки.

Спасибо, что посмотрели этот пост, который был лишь для защиты проектной лабораторной по физике с моделированием.

Linear Quadrupole with Central Cluster

Работа и мощность электрического тока 10 класс онлайн-подготовка на Ростелеком Лицей

Работа тока

Электрический ток, конечно же, не стал бы так широко использоваться, если бы не одно обстоятельство. Работу тока или же электроэнергию легко преобразовывать в любую нужную нам энергию или работу: тепловую, механическую, магнитную…

Для практического применения тока прежде всего хочется знать, какую работу можно обратить в свою пользу. Выведем формулу для определения работы тока:

Формула для работы электрического поля по перемещению заряда нам уже известна:

Или же

Узнать, какой заряд переместился полем за промежуток времени t можно из определения силы тока:

Отсюда:

Так как все величины, входящие в формулу, можно измерить соответствующими приборами (амперметр, вольтметр, часы), формула является универсальной.

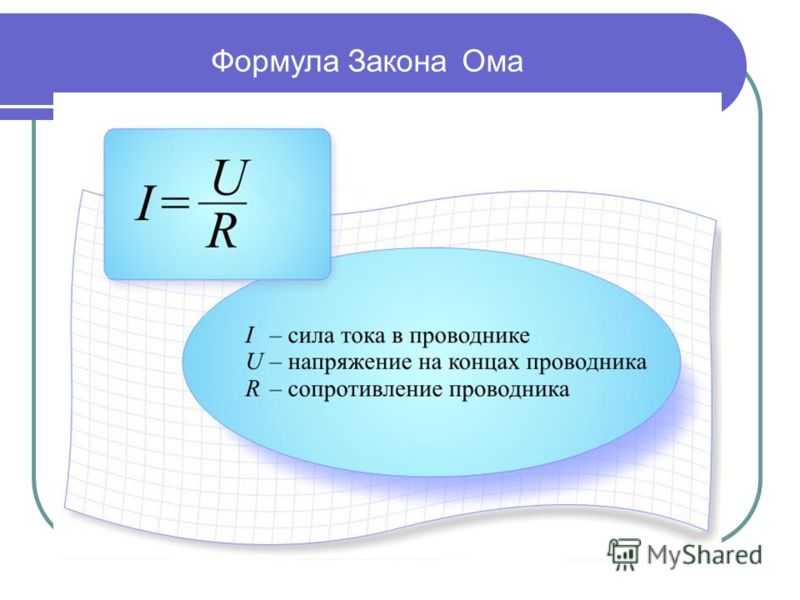
Формулу можно также записать в несколько ином виде, используя закон Ома:

Если в исходную формулу для работы тока подставить силу тока, записанную таким образом, то получим:

Если же из закона Ома выразить напряжение, то тогда:

Использование этих формул удобно, когда в цепи присутствует какое-то одно соединение: параллельное для первого случая и последовательное для второго.

Закон Джоуля-Ленца

Особое внимание следует уделить тепловому действию тока. При прохождении тока через проводник, проводник нагревается.

Почему это происходит? Мы уже затрагивали молекулярное строение проводников в теме о сопротивлении и отмечали, что при протекании тока свободные электроны сталкиваются с узлами кристаллической решетки. При этих столкновениях электроны постоянно придают некоторую скорость узлам решетки (рис. 1).

Рис. 1. Взаимодействие электронов с узлами кристаллической решетки

Так как температура – мера теплового движения, в процессе «расталкивания» температура проводника повышается. В какой-то момент наступает равновесие, когда количество энергии, получаемое проводником вследствие прохождения тока, равно количеству энергии, которое он отдает в окружающую среду.

В том случае, когда работа тока не преобразуется в механическую или же ток не имеет химического действия, работа тока эквивалентна количеству теплоты, высвобождающегося в окружающую среду.

Формулу просчета этого количества теплоты впервые независимо друг от друга открыли двое ученых: русский Эмиль Ленц (рис. 3) и англичанин Джеймс Джоуль (рис. 2).

Закон Джоуля-Ленца:

Как видно, правая часть формулы в точности повторяет одну из форм формулы для работы электрического тока.

Всегда следует помнить, что в случае, когда есть какое-либо другое преобразование энергии тока, формула Джоуля-Ленца не выполняется.


Рис. 2. Джеймс Джоуль (Источник)	Рис. 3. Эмиль Ленц (Источник)

Мощность тока

Наряду с работой тока очень важно отметить мощность тока, так как эта характеристика является ключевой в бытовом использовании электроэнергии (на всех бытовых приборах указано приемлемое напряжение его мощность).

Определение. Мощность – это работа, выполненная за единицу времени (скорость выполнения током работы):

Единица измерения мощности – ватт:

И теперь, используя наши знания о работе тока, мы без труда найдем формулу для мощности тока:

Или же, если использовать другие виды формулы для работы:

На следующем уроке мы разберем тему «Электродвижущая сила».

Список литературы

Тихомирова С. А., Яворский Б. М. Физика (базовый уровень) – М.: Мнемозина, 2012.
Генденштейн Л. Э., Дик Ю. И. Физика 10 класс. – М.: Илекса, 2005.

Мякишев Г. Я., Синяков А. З., Слободсков Б. А. Физика. Электродинамика. – М.: 2010.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал «physics.ru» (Источник)
Интернет-портал «constant-current.narod.ru» (Источник)
Интернет-портал «mugo.narod.ru» (Источник)

Домашнее задание

Стр. 105: № 802–805. Физика. Задачник. 10-11 классы. Рымкевич А. П. – М.: Дрофа, 2013. (Источник)
Как зависит количество теплоты, которое выделяется в проводнике, в случае параллельного соединения проводников?

На фонарике написано «4 В; 1 Вт», а на светильнике – «220 В; 40 Вт». В какой лампе больше сила тока? Сопротивление какой лампы больше и во сколько раз?
* Стальной и медный провода одинаковых размеров присоединили к источнику тока сначала параллельно, а потом последовательно. В каком из проводов в каждом случае выделялось большее количество теплоты?

Расчет электрической мощности

Мы можем рассчитать электрическую мощность, умножив напряжение и силу тока. Когда мы подаем напряжение на электрическую цепь, цепь потребляет ток. Величина электрического тока зависит от напряжения и полного сопротивления цепи.

Закон Ома для определения силы тока

Если мы наблюдаем приведенную выше схему, напряжение и сопротивление цепи известны. Ток, протекающий в электрической цепи, можно определить по закону Ома.

Таким образом, ток в приведенной выше цепи равен;

Теперь мы знаем значение электрического тока. Если мы умножим это значение тока на напряжение, мы получим уравнение мощности , и с помощью этого уравнения мы можем рассчитать электрическую мощность, используя это уравнение мощности. Произведение этих двух величин и есть мощность, потребляемая электрической цепью.

Формула мощности

Формула мощности приведена ниже.

Потребляемая цепью электрическая мощность составляет 36 Вт. Другими словами, эта электрическая мощность представляет собой тепло, которое рассеивается через резистор.

Наблюдение- Мощность, потребляемая цепью, зависит от величины напряжения и сопротивления. Если мы будем поддерживать постоянное сопротивление и изменять напряжение, мощность в цепи будет увеличиваться. Увеличение мощности схемы происходит по двум причинам.

Увеличение напряжения
Увеличение тока из-за увеличения напряжения

Таким образом, напряжение является движущей силой тока, и можно сказать, что причиной увеличения мощности является только напряжение при условии сопротивления цепь постоянная.

Теперь мы обсудим, как увеличивается мощность с увеличением напряжения.

Мощность при увеличении напряжения батареи

При увеличении напряжения ток будет увеличиваться. Здесь мы считаем, что сопротивление цепи не меняется и оно фиксировано.

Снова возьмем тот же случай с батареей, подключенной к резистивной цепи. Мы видели, что мощность схемы составляет 36 Вт при напряжении батареи 12 вольт и силе тока 3 ампера.

Теперь подключаем еще одну батарею 12 вольт последовательно с имеющейся батареей 12 вольт, тогда общее напряжение 24 вольта. Питание 24 вольта подается на такое же сопротивление цепи 4 Ом.

Текущая цепь будет;

Мы можем рассчитать электрическую мощность, используя следующую формулу.

Взаимосвязь между напряжением и мощностью

Теперь мы сведем значения напряжения и мощности в таблицу, чтобы понять увеличение мощности при повышении напряжения батареи.

Напряжение аккумулятора (V)

Power (WATT)

144

напряжение, мощность увеличивается до 4 раза по при фиксированном сопротивлении. Мы можем обосновать эту зависимость с помощью закона Ома.

Из приведенного выше уравнения видно, что мощность, потребляемая цепью, пропорциональна квадрату напряжения при фиксированном сопротивлении.

Теперь вы можете легко рассчитать мощность, используя приведенную выше концепцию. Мощность схемы 36 ватт при напряжении 12 вольт. Теперь посчитаем мощность при напряжении 48 вольт.

Повышение напряжения от исходного значения;

= 48/12 = 4 раза

Увеличение мощности пропорционально квадрату напряжения, поэтому теперь мощность будет;

P= (4) ² X 36
P= 576 Вт

Таблица, показывающая напряжение и соответствующую мощность при фиксированном значении сопротивления.

90070080

Voltage(V)	Power(Watts)
1	0. 25
2	1
3	2.25
4	4
5	6.25
8	16
12	36
24	144
36	324
48	576
72	1296
	2304	2304 9004 9007	2304 9004 9007	2304 9004 9007

Если мы нарисуем график между напряжением и мощностью при постоянном сопротивлении, то график будет таким:

Связь между током и мощностью

Мы можем рассчитать мощность, если известны ток и сопротивление. Связь между током и мощностью можно установить с помощью закона Ома.

Закон Джоуля Против. Закон Ома

Джеймс Прескотт Джоуль впервые обнаружил математическую зависимость между рассеиваемой мощностью и током через сопротивление. Он составил уравнение мощности (P = I2R), которое правильно известно как Закон Джоуля.

Уравнение мощности очень тесно связано с законом Ома.

Уравнения мощности для расчетов электроэнергии

Ниже приведены уравнения мощности.

Электроэнергия

Электрическая мощность в ваттах, связанная с полной электрической цепью или компонентом цепи, представляет скорость, с которой энергия преобразуется из электрической энергии движущихся зарядов в какую-либо другую форму, например, в тепло, механическую энергию или энергию, запасенную в электрических полях.

или магнитные поля. Для резистора в цепи постоянного тока мощность определяется произведением приложенного напряжения и электрического тока:

Р = ВИ Мощность = Напряжение x Ток ватты = вольты х ампер

Введите данные в любые два поля, затем щелкните активный текст для количества, которое вы хотите рассчитать.

Детали блоков следующие:

Мощность резистора

Мощность переменного тока

Пример мощности в последовательной и параллельной цепях

Индекс

Цепи постоянного тока

Гиперфизика***** Электричество и магнетизм

R Ступица

Вернуться

Удобные выражения для мощности, рассеиваемой на резисторе, можно получить, используя закон Ома.

Эти соотношения действительны для приложений переменного тока, даже если напряжения и токи являются действующими или действующими значениями. Резистор представляет собой особый случай, а выражение мощности переменного тока для общего случая включает еще один термин, называемый коэффициентом мощности, который учитывает разность фаз между напряжением и током.

Тот факт, что мощность, рассеиваемая на данном сопротивлении, зависит от квадрата тока, диктует, что для приложений с большой мощностью вы должны минимизировать ток. Это является основанием для преобразования до очень высокого напряжения для распределения электроэнергии по пересеченной местности.