Как найти вектор по точкам? Ответ на webmath.ru
Содержание:
- Формула
- Примеры нахождения координат вектора по точкам
Формула
Чтобы найти координаты вектора $\overline{A B}$ на плоскости, если он задан координатами своих начала $A\left(x_{1} ; y_{1}\right)$ и конца $B\left(x_{2} ; y_{2}\right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть
$$\overline{A B}=\left(x_{2}-x_{1} ; y_{2}-y_{1}\right)$$
Чтобы найти координаты вектора $\overline{A B}$, заданного в пространстве координатами $A\left(x_{1} ; y_{1} ; z_{1}\right)$ и $B\left(x_{2} ; y_{2} ; z_{2}\right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:
$$\overline{A B}=\left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}\right)$$
Примеры нахождения координат вектора по точкам
Пример
Задание. Даны точки $A(4;-1)$ и $B(2;1)$. Найти координаты векторов $\overline{A B}$ и $\overline{B A}$
Решение. Для вектора $\overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $\overline{A B}$ равны
Для вектора $\overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $\overline{A B}$ равны
$$\overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)$$
Для вектора точка $B$ является началом, а точка $A$ — концом. Тогда координаты вектора $\overline{B A}$ равны
$$\overline{B A}=(4-2 ;-1-1)=(2 ;-2)$$
Ответ. $\overline{A B}=(-2 ; 2), \overline{B A}=(2 ;-2)$
Пример
Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов $\overline{A B}$, $\overline{A C}$, $\overline{B C}$
Решение. Для искомого вектора $\overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $\overline{A B}$ соответственно равны:
$$\overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$
Для вектора $\overline{A C}$ точка
$A$ является началом, а точка
$C$ — концом.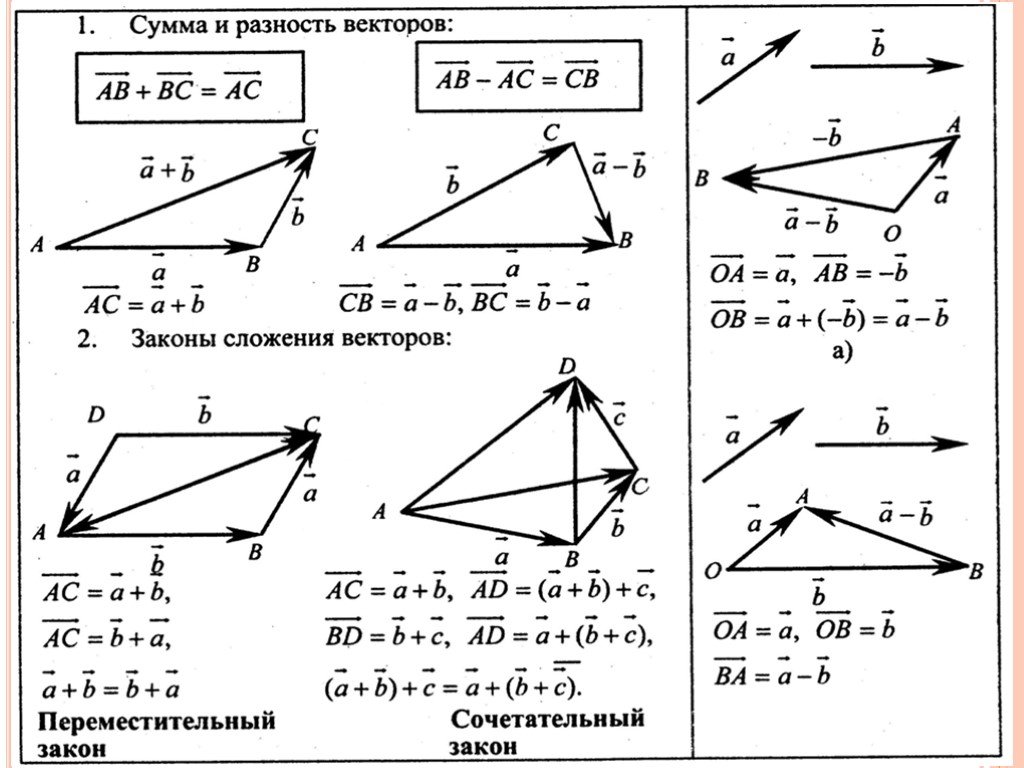 Тогда его координаты соответственно равны
Тогда его координаты соответственно равны
$$\overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)$$
Для вектора $\overline{B C}$ точка $B$ является началом, а точка $C$ — концом. Его координаты равны
$$\overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)$$
Ответ. $\overline{A B}=(2 ; 4 ; 1), \overline{A C}=(-1 ; 1 ; 0,5), \overline{B C}=(-3 ;-3 ;-0,5)$
Читать дальше: как найти сумму векторов.
- Как найти сумму векторов
- Как найти скалярное произведение векторов
- Как найти векторное произведение векторов
- Как найти смешанное произведение векторов
- Как найти вектор коллинеарный вектору
- Как найти вектор перпендикулярный вектору
- Как найти орт вектора
- Как найти разность векторов
- Как найти проекцию вектора
- Как найти длину вектора
- Как найти модуль вектора
- Как найти координаты вектора
- Как найти направляющие косинусы вектора
- Как найти угол между векторами
- Как найти косинус угла между векторами
Как найти разность векторов — интернет энциклопедия для студентов
ФОРМУЛА
Чтобы найти разность векторов\(\
\overline{a}-\overline{b}
\), заданных на плоскости координатами \(\
\overline{a}=\left(a_{x} ; a_{y}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y}\right)
\) , необходимо вычесть из координат первого вектора соответствующие координаты второго, т. е.
е.
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y}\right) \)
Если векторы заданы в пространстве, то есть \(\ \tilde{a}=\left(a_{x} ; a_{y} ; a_{z}\right)\quad{и}\quad \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) \)тогда их различие
\(\ \overline{a}-\overline{b}=\left(a_{x}-b_{x} ; a_{y}-b_{y} ; a_{z}-b_{z}\right) \)
ПРИМЕР
\(\ \overline{a}-\overline{b}-\overline{c}=(2 ;-3 ; 1)-(1 ; 0 ;-2)-(-1 ; 2 ; 3)= \)
\(\ =(2-1-(-1) ;-3-0-2 ; 1-(-2)-3)=(2 ;-5 ; 0) \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Как найти сумму векторов Как найти вектор по точкам Периодические десятичные дроби Понятие десятичной дроби
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Объяснение урока: Сложение и вычитание векторов в 2D
В этом объяснении мы узнаем, как складывать и вычитать векторы в 2D.
Мы знаем, что векторы могут быть представлены отрезками определенной длины (величина) и направление. Мы будем использовать их, чтобы помочь визуализировать сложение векторов и вычитание.
В рамках этого объяснения будут рассматриваться только векторы в двух измерениях; однако описанная методология может быть распространена на переносчиков в трех или более размеры.
Напомним, что единичный вектор — это вектор с величиной, равной 1, и что единичные векторы в 𝑥- и 𝑦-направлениях обозначаются ⃑𝑖 и ⃑𝑗 соответственно.
Любой двумерный вектор можно записать в виде 𝑥⃑𝑖+𝑦⃑𝑗. Они могут альтернативно быть представлено в компонентной форме как (𝑥,𝑦) или 𝑥𝑦.
Определение: Сложение векторов
Сложение векторов — это операция сложения двух или более векторов для нахождения их сумма.
Имея два (или более) вектора в компонентной форме, мы можем найти их сумму по формуле
добавление соответствующих компонентов векторов.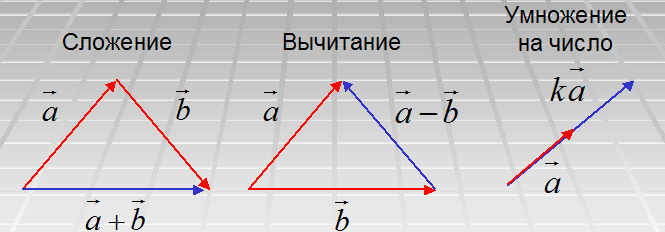
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
Сложение векторов — это операция сложения двух или более векторов вместе в векторная сумма. Сумма двух и более векторов называется равнодействующей.
Сейчас мы рассмотрим пару примеров, где нам нужно сложить векторы в два размеры.
Пример 1. Нахождение суммы двух векторов
Если ⃑𝑎=(3,2) и ⃑𝑏=(4,−1), найти ⃑𝑎+⃑𝑏.
Ответ
Напомним, что в декартовых координатах сложение векторов можно выполнить с помощью добавление соответствующих компонентов векторов.
Если ⃑𝑎=(𝑥,𝑦) и ⃑𝑏=(𝑥,𝑦), тогда ⃑𝑎+⃑𝑏=(𝑥+𝑥,𝑦+𝑦).
В этом вопросе ⃑𝑎=(3,2) и ⃑𝑏=(4,−1).
Итак, ⃑𝑎+⃑𝑏=(3+4,2+(−1))=(7,1).
Таким образом, ⃑𝑎+⃑𝑏=(7,1).
Пример 2. Нахождение компонентов двух векторов и их суммы по диаграмме
На сетке единичных квадратов показаны векторы
⃑𝑢, ⃑𝑣,
и ⃑𝑢+⃑𝑣.
- Из каких компонентов состоит ⃑𝑢?
- Из каких компонентов состоит ⃑𝑣?
- Какие компоненты ⃑𝑢+⃑𝑣?
Ответ
Любой двумерный вектор можно записать через его 𝑥- и 𝑦-компоненты вида (𝑥,𝑦), где 𝑥 — количество единиц в положительное 𝑥-направление, а 𝑦 — количество единиц в положительном 𝑦-направление.
От начальной точки до конечной точки ⃑𝑢 идем на 2 единицы вправо и 1 единица вверх. Это соответствует 2 единицам в 𝑥-направлении и 1 единице в 𝑦-направление.
Итак, ⃑𝑢=(2,1).
От начальной точки до конечной точки ⃑𝑣, проходим 3 единицы осталось и 4 единицы вниз. Это соответствует −3 единицам в 𝑥-направление и −4 единиц в 𝑦-направлении.
Итак, ⃑𝑣=(−3,−4).
Мы знаем, что сумма двух векторов называется равнодействующей и что в
Декартовы координаты, сложение векторов можно выполнить, добавив
соответствующие компоненты векторов.
Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
С ⃑𝑢=(2,1)⃑𝑣=(−3,−4) и затем ⃑𝑢+⃑𝑣=(2+(−3),1+(−4))=(−1,−3).
Мы также можем прочитать эту информацию прямо из векторной диаграммы.
Из начальной точки ⃑𝑢 в конечную точку вектора ⃑𝑣, мы перемещаемся на 1 единицу влево и на 3 единицы вниз. Это соответствует -1 единице в 𝑥-направлении и −3 единицы в 𝑦-направление.
Итак, ⃑𝑢+⃑𝑣=(−1,−3).
Таким образом, ⃑𝑢=(2,1), ⃑𝑣=(−3,−4), и ⃑𝑢+⃑𝑣=(−1,−3).
Вычитание векторов — это процесс нахождения разности векторов; это операция, обратная сложению векторов. Это значит, что ⃑𝑢−⃑𝑣=⃑𝑢+−⃑𝑣. При вычитании ⃑𝑣 из ⃑𝑢, находим равнодействующую ⃑𝑢 и −⃑𝑣.
Определение: вычитание векторов
Вычитание векторов — это операция вычитания двух векторов для нахождения их
разница.
Имея два вектора в компонентной форме, мы можем найти их разность по формуле вычитая соответствующие компоненты векторов.
Например, если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
Стоит отметить, что эффект отрицания ⃑𝑣 является изменением направления. Например, если бы у нас был вектор ⃑𝑣=(5,0), это будет вектор длины 5, параллельный оси 𝑥, указывающей слева направо. Если мы отрицаем ⃑𝑣, мы получаем −⃑𝑣=(−5,0). Величина вектора без изменений; он по-прежнему параллелен оси 𝑥, но его направление изменилось перевернутый; теперь он указывает справа налево.
Теперь мы рассмотрим еще несколько примеров, где мы будем складывать и вычитать векторы в двух измерениях.
Пример 3. Вычитание векторов, выраженных в терминах единичных векторов
При заданных векторах
𝐴𝐵=3⃑𝑖−4⃑𝑗
и 𝐶𝐷=−5⃑𝑖−5⃑𝑗,
рассчитать 𝐴𝐵−𝐶𝐷.
Ответ
Начнем с того, что вспомним, что в декартовых координатах вычитание векторов можно выполнить, вычитая соответствующие компоненты из векторы.
Если ⃑𝑢=𝑎⃑𝑖+𝑏⃑𝑗 и ⃑𝑣=𝑐⃑𝑖+𝑑⃑𝑗, тогда ⃑𝑢−⃑𝑣=(𝑎−𝑐)⃑𝑖+(𝑏−𝑑)⃑𝑗.
Итак, 𝐴𝐵−𝐶𝐷=3⃑𝑖−4⃑𝑗−−5⃑𝑖−5⃑𝑗=(3−(−5))⃑𝑖+(−4−(−5))⃑𝑗=8⃑𝑖+⃑𝑗.
Таким образом, 𝐴𝐵−𝐶𝐷=8⃑𝑖+⃑𝑗.
Пример 4. Сложение и вычитание векторов
Учитывая, что ⃑𝐴=(−2,2), ⃑𝐵=(5,2) и ⃑𝐶=(−3,−2), найти −⃑𝐴+⃑𝐵−⃑𝐶.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Итак, −⃑𝐴+⃑𝐵−⃑𝐶=(−(−2)+5−(−3),−2+2−(−2))=(2+5+3,−2+2+2)=(10, 2).
Таким образом, −⃑𝐴+⃑𝐵−⃑𝐶=(10,2).
Пример 5. Поиск пропущенного вектора по заданному другому вектору и сумме двух векторов
Учитывая, что ⃑𝐴=(−4,5), и
⃑𝐴+⃑𝐵=(2,7),
найти ⃑𝐵.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Поскольку ⃑𝐴=(−4,5) и ⃑𝐴+⃑𝐵=(2,7), тогда (−4,5)+⃑𝐵=(2,7)((−4,5))⃑𝐵=(2,7)−(−4,5)⃑𝐵=(2−(−4),7−5) ⃑𝐵=(6,2).вычитание из обеих сторон
Итак, ⃑𝐵=(6,2).
Пример 6. Нахождение суммы двух векторов по одному из них и разности между ними
Учитывая, что ⃑𝐴=(7,−1) и ⃑𝐴−⃑𝐵=(3,−2), найти ⃑𝐴+⃑𝐵.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵=(𝑥−𝑥,𝑦−𝑦).
Так как ⃑𝐴=(7,−1)
и ⃑𝐴−⃑𝐵=(3,−2), то
(7,−1)−⃑𝐵=(3,−2)⃑𝐵(3,−2)⃑𝐵=(7,−1)−(3,−2)⃑𝐵=(7−3,−1−( −2))⃑𝐵=(4,1). сложение и вычитание из обеих сторон
сложение и вычитание из обеих сторон
Теперь мы вычисляем ⃑𝐴+⃑𝐵.
Если ⃑𝐴=(𝑥,𝑦) и ⃑𝐵=(𝑥,𝑦), тогда ⃑𝐴+⃑𝐵=(𝑥+𝑥,𝑦+𝑦).
Так как ⃑𝐴=(7,−1) и ⃑𝐵=(4,1), тогда ⃑𝐴+⃑𝐵=(7,−1)+(4,1)=(7+4,−1+1)=(11,0).
Итак, ⃑𝐴+⃑𝐵=(11,0).
Пример 7. Нахождение вектора по двум другим векторам и выражению между тремя векторами
Учитывая, что ⃑𝐴=(3,−2), ⃑𝐵=(−5,4), и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), найти ⃑𝐶.
Ответ
Начнем с того, что вспомним, что в декартовых координатах сложение векторов и вычитание может быть выполнено путем добавления или вычитания соответствующего компоненты векторов.
Если ⃑𝐴=(𝑥,𝑦), ⃑𝐵=(𝑥,𝑦), и ⃑𝐶=(𝑥,𝑦), тогда ⃑𝐴−⃑𝐵+⃑𝐶=(𝑥−𝑥+𝑥,𝑦−𝑦+𝑦).
Так как ⃑𝐴=(3,−2),
⃑𝐵=(−5,4),
и ⃑𝐴−⃑𝐵+⃑𝐶=(6,−1), то
(3,−2)−(−5,4)+⃑𝐶=(6,−1)(8,−6)+⃑𝐶=(6,−1)((8,−6))⃑𝐶=(6, −1)−(8,−6)⃑𝐶=(6−8,−1−(−6))⃑𝐶=(−2,5). вычитая из обеих сторон
вычитая из обеих сторон
Итак, ⃑𝐶=(−2,5).
Хотя это выходит за рамки этого объяснения, мы можем представить вектор сложение и вычитание графически с помощью метод параллелограмма или метод метод треугольника .
Мы закончим это объяснение повторением некоторых ключевых моментов.
Ключевые точки
- В декартовых координатах возможно сложение и вычитание векторов. выполняется сложением или вычитанием соответствующих компонент векторов.
- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢+⃑𝑣=(𝑥+𝑥,𝑦+𝑦).
- Если ⃑𝑢=(𝑥,𝑦) и ⃑𝑣=(𝑥,𝑦), тогда ⃑𝑢−⃑𝑣=(𝑥−𝑥,𝑦−𝑦).
векторов — сложение и вычитание
векторов — сложение и вычитаниеВекторыСложение и вычитание вернуться к основному индексу |
Введение Векторы — это сущности, имеющие направление . Однако, когда дело доходит до выполнения определенных математических операций на векторах важно знать, что векторы не являются «бесплатными» но фиксируются в начале системы координат. Например, хотя это делает визуальный смысл, чтобы показать нормаль к поверхности (тип вектора), продолжающуюся прямо из, скажем, полигона, нормаль на самом деле находится не в поверхность «своего» многоугольника, но находится в начале координат система координат, в которой определен полигон, и как таковая следует рассматривать как фиксированных векторов . |
| |
На рис. с = а + б где a, b и c — векторы. |
Фиксированные векторы При рассмотрении некоторых математических операций
на векторах важно знать, что векторы не являются «бесплатными»
но фиксируются в начале системы координат. Например, хотя это делает
визуальный смысл, чтобы показать нормаль к поверхности (тип вектора), продолжающуюся
прямо из, скажем, полигона, нормаль не находится в
поверхность многоугольника, но находится в начале
система координат, в которой определен полигон, и, как таковой, вектор
следует рассматривать как фиксированный вектор . Фиксированные векторы не могут соединяться «хвостом» с «головой».
Когда два вектора, скажем, cx = ax + bx cy = ay + by При вычитании векторов снова получается другой вектор.
Чтобы найти координаты результирующего вектора, соответствующие компоненты
вычитаются, т.е. cx = ax - bx cy = ay - by Всегда имейте в виду, когда дело доходит до арифметики, векторы фиксированы, и поэтому их «хвосты» «привязаны» к началу системы координат. |
© 2002- Малкольм Кессон. Все права защищены.


 и длиной т.е. величина. Как правило, они определяются 2
или 3 значения. Часть путаницы при работе с векторами заключается в том, как
они представлены на иллюстрациях. Часто они представлены
как бесплатных векторов , которые можно перемещать в произвольные места
в зависимости от объясняемой концепции.
и длиной т.е. величина. Как правило, они определяются 2
или 3 значения. Часть путаницы при работе с векторами заключается в том, как
они представлены на иллюстрациях. Часто они представлены
как бесплатных векторов , которые можно перемещать в произвольные места
в зависимости от объясняемой концепции.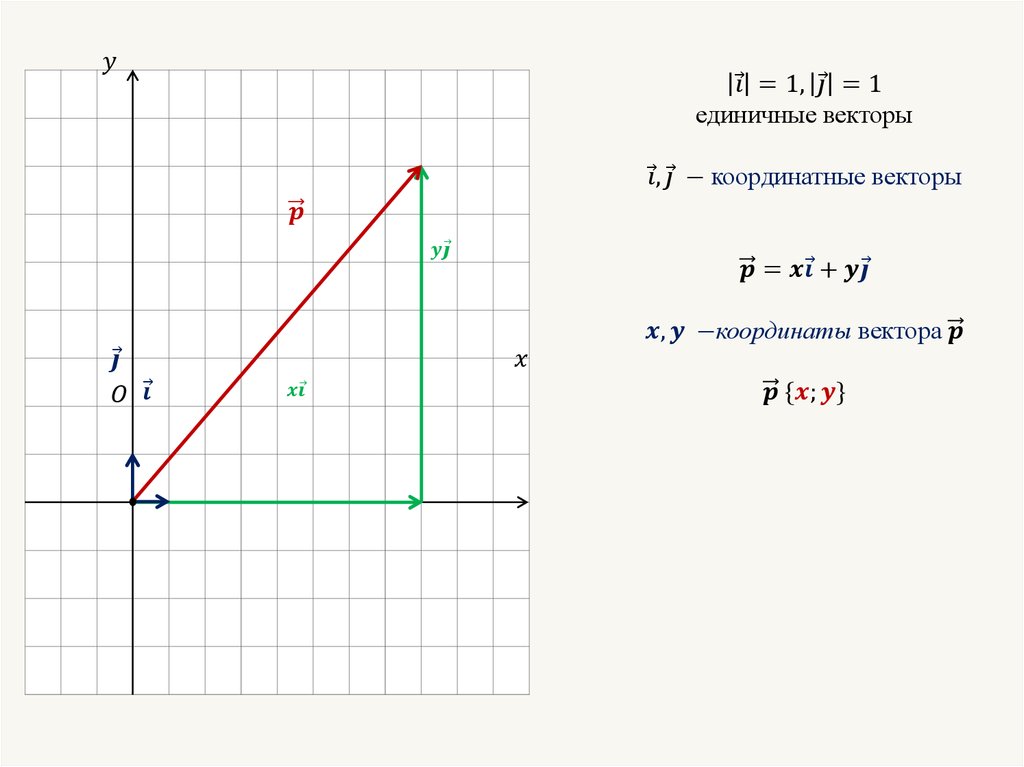 1 показаны два свободных вектора:
1 показаны два свободных вектора: 