Шестнадцатиричная система счисления | это… Что такое Шестнадцатиричная система счисления?
ТолкованиеПеревод
- Шестнадцатиричная система счисления
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 10 до 15.
Содержание
- 1 Применение
- 2 Способы записи
- 2.1 В математике
- 2.2 В языках программирования
- 3 Перевод чисел из одной системы счисления в другую
- 3.1 Перевод чисел из шестнадцатеричной системы в десятичную
- 3.2 Перевод чисел из двоичной системы в шестнадцатеричную
- 3.3 Таблица перевода чисел
- 4 См.
 также
также - 5 Ссылки
Применение
Широко используется в низкоуровневом программировании и вообще в компьютерной документации, поскольку в современных компьютерах минимальной единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, БЭСМ-6) использовали восьмеричную систему.
В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости — с ведущими нулями).
Способы записи
В математике
В языках программирования
В разных языках программирования для записи шестнадцатеричных чисел используют различный синтаксис:
- В Ада и
- В Си и языках схожего синтаксиса, например, в
- В некоторых ассемблерах используют букву «h», которую ставят после числа.
 Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510) - Другие ассемблеры (AT&T, Motorola), а также Паскаль и некоторые версии Бэйсика используют префикс «$». Например, «$5A3».
- Некоторые иные платформы, например ZX Spectrum в своих ассемблерах (MASM, TASM, ALASM, GENS и т.д.) использовали запись #5A3, обычно выровненную до одного или двух байт: #05A3.
- Другие версии Бэйсика используют для указания шестнадцатеричных цифр сочетание «&h». Например, «&h5A3».
- В Unix-подобных операционных системах (и многих языках программирования, имеющих корни в Unix/linux) непечатные символы при выводе/вводе кодируются как \xCC, где CC — шестнадцатеричный код символа.
Перевод чисел из одной системы счисления в другую
Перевод чисел из шестнадцатеричной системы в десятичную
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число 5A3 в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:
5A316=5·162+10·161+3·160
=5·256+10·16+3·1=1280+160+3=144310Перевод чисел из двоичной системы в шестнадцатеричную
Для перевода многозначного двоичного числа в шестнадцатеричную систему нужно разбить его на тетрады справа налево и заменить каждую тетраду соответствующей шестнадцатеричной цифрой.
Например:
101101000112=0101 1010 0011=5A316 Таблица перевода чисел
0hex = 0dec = 0oct 0 0 0 0 1hex = 1dec = 1oct 0 0 0 1 2hex = 2 = 2oct 0 0 1 0 3hex = 3dec = 3oct 0 0 1 1 4hex = 4dec = 4oct 0 1 0 0 5hex = 5dec = 5oct 0 1 0 1 6 = 6dec = 6oct 0 1 1 0 7hex = 7dec = 7oct 0 1 1 1 8hex = 8dec = 10oct 1 0 0 0 9hex = 9dec = 11oct 1 0 0 1 Ahex = 10dec = 12oct 1 0 1 0 Bhex = 11dec = 13oct 1 0 1 1 Chex = 12dec = 14oct 1 1 0 0 Dhex = 13dec = 15oct 1 1 0 1 Ehex = 14dec = 16oct 1 1 1 0 Fhex = 15dec = 17oct 1 1 1 1 См.
 также
также- Система счисления
- Двоичные приставки
- Шестнадцатеричный редактор
Ссылки
- Шестнадцатеричные числа и операции с ними
- Таблица порядков двоичных, шестнадцатеричных и десятичных чисел
- Онлайн калькулятор для перевода чисел из одной системы счисления в другую
Wikimedia Foundation. 2010.
Нужна курсовая?
- Шестиконечная звезда
- Шестнадцатеричные числа
Полезное
Шестнадцатеричная системы счисления примеры. Перевод чисел из одной системы счисления в другую онлайн
Многие пользователи компьютеров понимают, что компьютер работает в двоичной системе счисления. Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния «выключено» и «включено», либо «нет» и «да».
Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2 16), а двоичной 2.
Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.
| Десятичная запись | Шестнадцатеричная запись | Двоичная запись |
|---|---|---|
| 0 | 0 | 0000 |
| 1 | 1 | 0001 |
| 2 | 2 | 0010 |
| 3 | 3 | 0011 |
| 4 | 4 | 0100 |
| 5 | 5 | 0101 |
| 6 | 6 | 0110 |
| 7 | 7 | 0111 |
| 8 | 8 | 1000 |
| 9 | 9 | 1001 |
| 10 | A | 1010 |
| 11 | B | 1011 |
| 12 | C | 1100 |
| 13 | D | 1101 |
| 14 | E | 1110 |
| 15 | F | 1111 |
Записи 10, 11 и т. д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.
д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.
Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10 2 + 2*10 1 + 3*10 0 . Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16 3 + 10*16 2 + 5*16 1 + 14*16 0 = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.
Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16 3 + 10*16 2 + 5*16 1 + 14*16 0 = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.
Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.
Шестнадцатеричная система счисления , на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.
Как следует из названия, основанием данной системы является число шестнадцать 16 или в шестнадцатеричной системе 10 16 .
Чтобы не было путаницы, при записи чисел в системах счисления отличных от десятичных, справа внизу от основной записи числа будем указывать основание системы счисления. Раз основанием системы является число шестнадцать, значит, для изображения чисел нам потребуется шестнадцать цифр.
Первые десять цифр берутся из, привычной нам, десятичной системы (0,1,..,8,9) и еще добавляются шесть букв латинского алфавита (a,b,c,d,e,f) . Например в шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.
Раз основанием системы является число шестнадцать, значит, для изображения чисел нам потребуется шестнадцать цифр.
Первые десять цифр берутся из, привычной нам, десятичной системы (0,1,..,8,9) и еще добавляются шесть букв латинского алфавита (a,b,c,d,e,f) . Например в шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.
Счет в шестнадцатеричной системе происходит аналогично счету в десятичной. Давайте попробуем считать и записывать числа конструируя их из имеющихся шестнадцати цифр:
Ноль — 0 ;
Один — 1 ;
Два — 2 ;
…
и так далее…
…
Восемь — 8 ;
Девять — 9 ;
Десять — a ;
Одиннадцать — b ;
Двенадцать — c ;
Тринадцать — d ;
Четырнадцать — e ;
Пятнадцать — f ;
А что делать дальше? Все цифры кончились. Как же изобразить число Шестнадцать?
Поступим аналогично тому как мы поступали в десятичной системе. Там мы вводили понятие десятка, здесь же введем понятие «шестнадцать»
и скажем, что шестнадцать — это одина «шестнадцать» и ноль единиц. А это уже можно и записать — «10 16 «.
Там мы вводили понятие десятка, здесь же введем понятие «шестнадцать»
и скажем, что шестнадцать — это одина «шестнадцать» и ноль единиц. А это уже можно и записать — «10 16 «.
Итак, Шестнадцать — 10 16 (одна «шестнадцать», ноль единиц)
Семнадцать — 11 16 (одна «шестнадцать», одна единица)
…
и так далее…
…
Двадцать пять — 19 16 (одна «шестнадцать», девять единиц)
Двадцать шесть — 1a 16 (одна «шестнадцать», десять единиц)
Двадцать семь — 1b 16 (одна «шестнадцать», одинадцать единиц)
…
и так далее…
…
Тридцать — 1e 16 (одна «шестнадцать», четырнадцать единиц)
Тридцать один — 1f 16 (одна «шестнадцать», пятнадцать единиц)
Тридцать два — 20 16 (две «шестнадцать», ноль единиц)
Тридцать три — 21 16 (две «шестнадцать», одна единица)
…
и так далее…
…
Двести пятьдесят пять — ff 16 (пятнадцать по «шестнадцать», пятнадцать единиц)
Двести пятьдесят шесть — 100 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», ноль единиц)
Двести пятьдесят семь — 101 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», одна единица)
Двести пятьдесят восемь — 102 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», две единицы)
. ..
..
и так далее…
…
Всегда, когда у нас исчерпался набор цифр для отображения следующего числа, мы вводим более крупные единицы счета (т.е. считаем по «шестнадцать», по «Двести пятьдесят шесть» и т.д.) и записываем число с удлинением на один разряд.
Рассмотрим число 3e2c 16 записанное в шестнадцатиричной системе счисления. Про него можно сказать, что оно содержит: три по четыре тысячи девяносто шесть, «e» (четырнадцать) по двести пятьдесят шесть, два по шестнадцать и «c» (двенадцать) единиц. И получить его значение через входящие в него цифры можно следующим образом.
3e2c 16 = 3 *4096+14 *256+2 *16+12 *1, здесь и далее знак * (звездочка) означает умножение.
Но ряд чисел 4096, 256, 16, 1 есть не что иное, как целые степени числа шестнадцать (основания системы счисления) и поэтому можно записать:
3e2c 16 = 3 *16 3 +14 *16 2 +2 *16 1 +12 *16 0
Подобным образом для шестнадцатиричной дроби (дробного числа) например: 0. 5a2 16 про него можно сказать, что оно содержит: пять шестнадцатых, «a» (десять) двести пятьдесят шестых и две четыретысячи девяносто шестых долей. И его значение можно вычислить следующим образом:
5a2 16 про него можно сказать, что оно содержит: пять шестнадцатых, «a» (десять) двести пятьдесят шестых и две четыретысячи девяносто шестых долей. И его значение можно вычислить следующим образом:
0.5a2 16 = 5 *(1/16) + 10 *(1/256) + 2 *(1/4096)
И здесь ряд чисел 1/16; 1/256 и 1/4096 есть не что иное, как целые степени числа шестнадцать и мы также можем записать:
0.5a2 16 = 5 *16 -1 + 10 *16 -2 + 2 *16 -3
Для смешанного числа 7b2.1f9 аналогичным образом можем записать:
7b2.1f9 = 7 *16 2 +11 *16 1 +2 *16 0 +1 *16 -1 +15 *16 -2 +9 *16 -3
Пронумеруем разряды целой части некоторого шестнадцатиричного числа, справа налево, как 0,1,2…n (нумерация начинается с нуля!). А разряды дробной части, слева направо, как -1,-2,-3…-m, то значение некоторого шестнадцатиричного числа может быть вычислено по формуле:
N = d n 16 n +d n-1 16 n-1 +…+d 1 16 1 +d 0 16 0 +d -1 16 -1 +d -2 16 -2 +…+d -(m-1) 16 -(m-1) +d -m 16 -m
Где: n — количество разрядов в целой части числа минус единица;
m — количество разрядов в дробной части числа
d i — цифра стоящая в i -м разряде
Эта формула называется формулой поразрядного разложения шестнадцатиричного числа, т.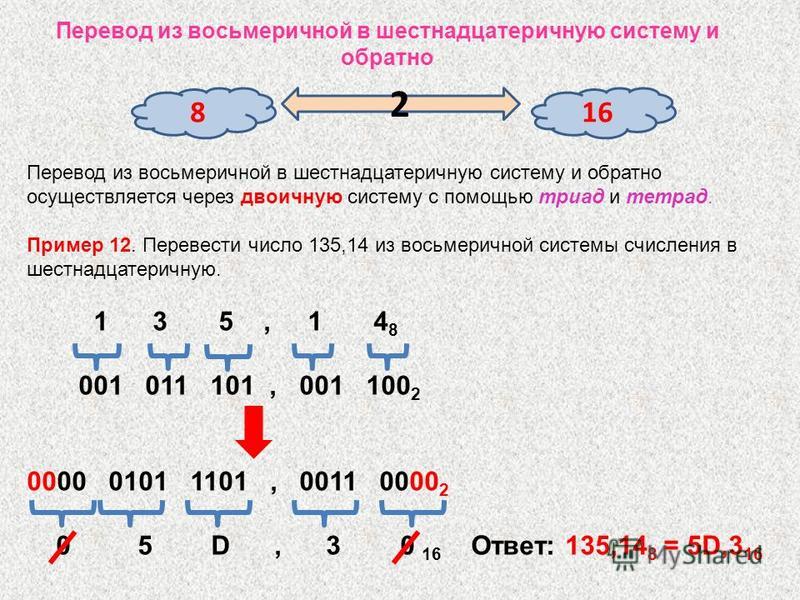 е. числа записанного в шестнадцатиричной системе счисления. Если мы в этой формуле заменим число шестнадцать на некоторое произвольное число q , то получим формулу разложения для числа записанного в q-й системе счисления, т.е. с основанием q :
е. числа записанного в шестнадцатиричной системе счисления. Если мы в этой формуле заменим число шестнадцать на некоторое произвольное число q , то получим формулу разложения для числа записанного в q-й системе счисления, т.е. с основанием q :
N = d n q n +d n-1 q n-1 +…+d 1 q 1 +d 0 q 0 +d -1 q -1 +d -2 q -2 +…+d -(m-1) q -(m-1) +d -m q -m
По этой формуле всегда можно вычислить значение числа записанного в любой позиционной системе счисления с основанием q .
С другими системами счисления можно познакомиться на нашем сайте по следующим ссылкам.
Результат уже получен!
Системы счисления
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15. В таблице Таб.1 представлены числа в разных системах счисления.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111 . Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .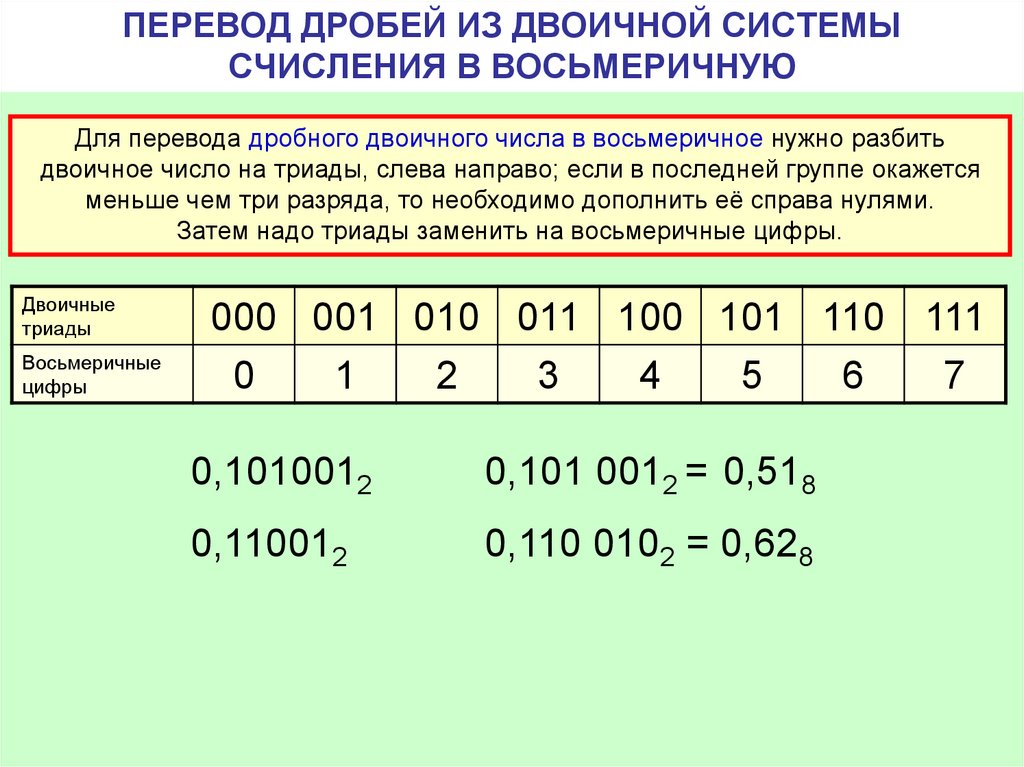
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011 .
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
0. 214 10 =0.36C8B4 16 .
214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример 11 . Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
Шестнадцатеричная система счисления (также — шестнадцатеричный код) является позиционной системой счисления с целочисленным основанием 16. Иногда в литературе также используется термин hex (произносится «хекс», сокращение от англ. hexadecimal). Цифрами данной системы счисления принято использовать арабские цифры 0—9, а также первые символы латинского алфавита A—F. Буквы соответствуют следующим десятичным значениями:
- * A —10;
- * B —11;
- * C —12;
- * D —13;
- * E — 14;
- * F — 15.
Таким образом, десять арабских цифр вкупе с шестью латинскими буквами и составляют шестнадцать цифр системы.
Кстати, на нашем сайте вы можете перевести любой текст в десятичный, шестнадцатеричный, двоичный код воспользовавшись Калькулятором кодов онлайн .
Применение . Шестнадцатеричный код широко применяется в низкоуровневом программировании, а также в различных компьютерных справочных документах. Популярность системы обоснована архитектурными решениями современных компьютеров: в них в качестве минимальной единицы информации установлен байт (состоящий из восьми бит) — а значение байта удобно записывать с помощью двух шестнадцатеричных цифр. Значение байта может ранжироваться с #00 до #FF (от 0 до 255 в десятичной записи) — другими словами, используя шестнадцатеричный код , можно записать любое состояние байта, при этом не остаётся «лишних» не используемых в записи цифр.
В кодировке Юникод для записи номера символа используется четыре шестнадцатеричных цифры. Запись цвета стандарта RGB (Red, Green, Blue — красный, зелёный, синий) также часто использует шестнадцатеричный код (например, #FF0000 — запись ярко-красного цвета).
Способ записи шестнадцатеричного кода.
Математический способ записи . В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В математической записи основание системы записывают в десятичном виде в нижнем индексе справа от числа. Десятичную запись числа 3032 можно записать как 3032 10 , в шестнадцатеричной системе данное число будет иметь запись BD8 16 .
В синтаксисе языков программирования . Синтаксис различных языков программирования по-разному устанавливает формат записи числа, использующего шестнадцатеричный код :
* В синтаксисе некоторых разновидностей языка ассемблера используется латинская буква «h», которая ставится справа от числа, например: 20Dh. Если число начинается с латинской буквы, то перед ним ставится ноль, например: 0A0Bh. Это сделано для того, чтобы отличать от констант значения, использующие шестнадцатеричный код ;
* В прочих разновидностях ассемблера, а также в Pascal (и его разновидностях, таких как Delphi) и некоторых диалектах Basic, применяют префикс «$»: $A15;
* В языке разметки HTML, а также в каскадных файлах CSS, для указания цвета в формате RGB с шестнадцатеричной системой записи, используется префикс «#»: #00DC00.
Как перевести шестнадцатеричный код в другую систему?
Перевод из шестнадцатеричной системы в десятичную. Для совершения операции перевода из шестнадцатеричной системы в десятичную, требуется представить исходное число как сумму произведений цифр в разрядах шестнадцатеричного числа на степень основания.
Двоичная СС | шестнадцатеричная СС |
Например, требуется выполнить перевод шестнадцатеричного числа A14: в нём три цифры. Используя правило, запишем его в виде суммы степеней с основанием 16:
Используя правило, запишем его в виде суммы степеней с основанием 16:
A14 16 = 10.16 2 + 1.16 1 + 4.16 0 = 10.256 + 1.16 + 4.1 = 2560 + 16 + 4 = 2580 10
Перевод чисел из двоичной в шестнадцатеричную систему и наоборот.
Для перевода используется таблица тетрад. Чтобы выполнить перевод числа из двоичной в десятичную систему, необходимо произвести разбиение его на отдельные тетрады справа налево, после чего, используя таблицу, выполнить замену каждой тетрады на соответствующую шестнадцатеричную цифру. При этом, если количество цифр не кратно четырём, то необходимо добавить соответствующее количество нулей справа от числа, для того, чтобы общее число двоичных цифр стало кратно четырём.
Таблица тетрад для перевода.
Для перевода из шестнадцатеричной системы в двоичную, необходимо выполнить обратную операцию: выполнить замену каждой цифры на тетраду из таблицы.
Двоичная СС | Восьмеричная СС |
Пример перевода из шестнадцатеричной системы в двоичную : A5E 16 = 1010 0101 1110 = 101001011110 2
Пример перевода из двоичной системы в шестнадцатеричную : 111100111 2 = 0001 1110 0111 = 1E7 16
В этом примере количество цифр в исходном двоичном числе не было равным четырём (9), поэтому были добавлены незначащие нули — общее число цифр стало 12.
Автоматический перевод . Быстрый перевод из шестнадцатеричной системы счисления в одну из трёх популярных систем (двоичную, восьмеричную и десятичную), как и обратный перевод, можно выполнить, используя стандартный калькулятор из комплекта поставки ОС Windows. Откройте калькулятор, выберите в меню Вид -> Программист. В данном режиме можно устанавливать систему счисления, используемую в данный момент (см. меню слева: Hex, Dec, Oct, Bin). При этом изменение текущей системы счисления автоматически производит перевод.
Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.
Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.
Примеры , стандартная десятичная система счисления — это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.
Шестнадцатеричная система счисления.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.
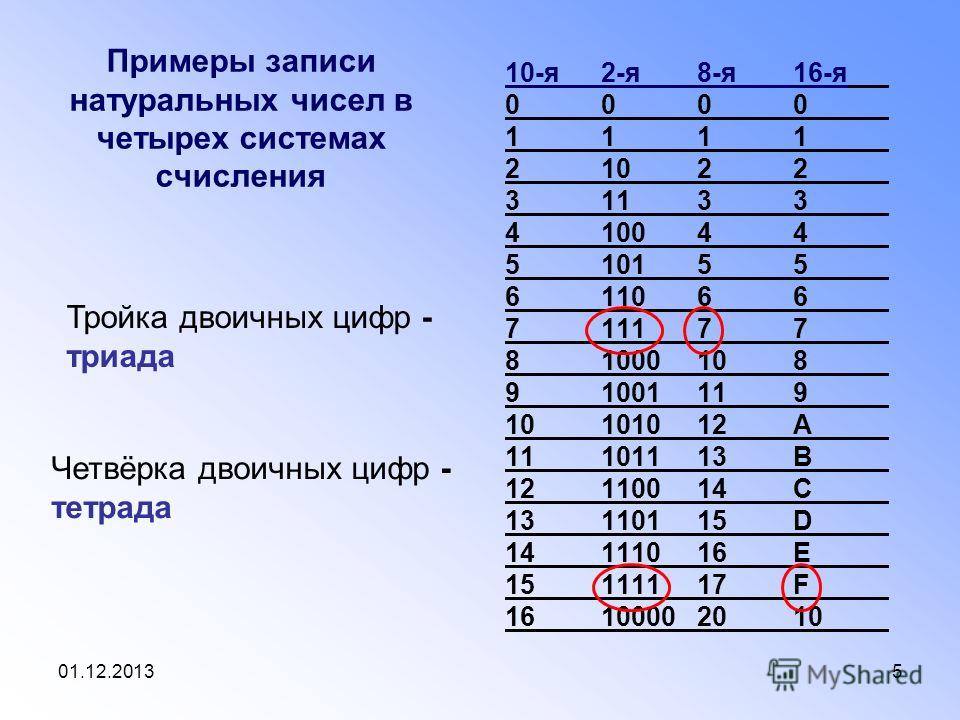
Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.
Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F .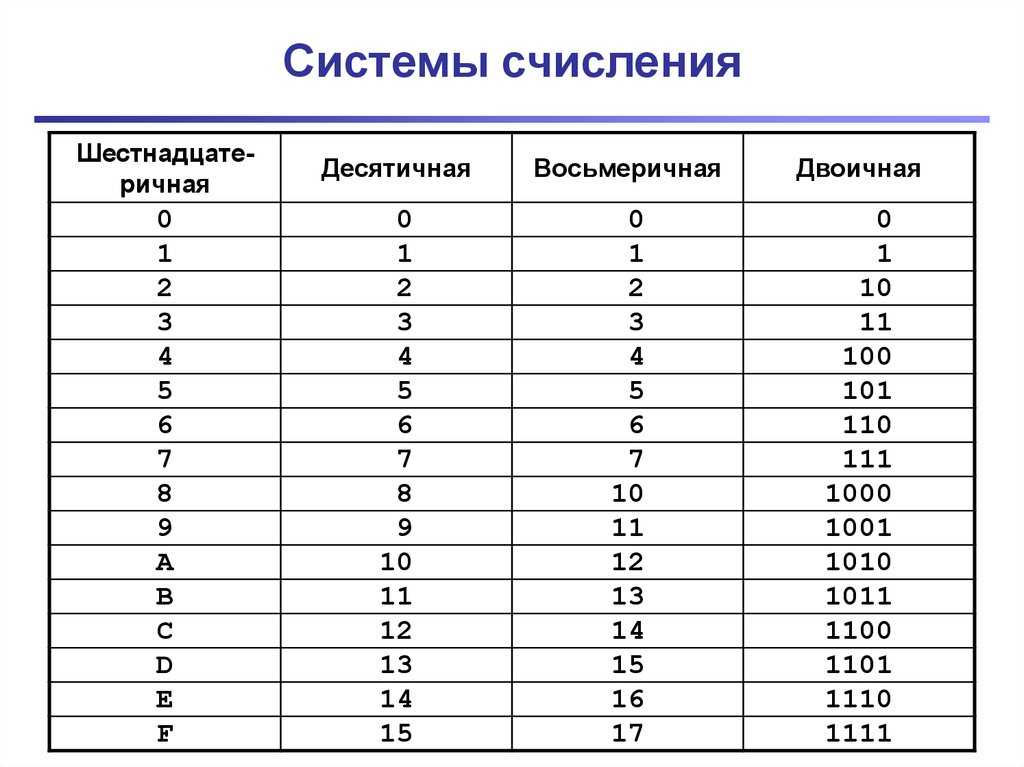 Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.
Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.
Применение шестнадцатеричной системы счисления.
Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.
Перевод чисел из одной системы счисления в другую.
Перевод чисел из шестнадцатеричной системы в десятичную.
Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.
Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:
5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10
Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.
Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.
Например :
010110100011 2 = 0101 1010 0011 = 5A3 16
Таблица перевода чисел.
Алгоритм перевода чисел из одной системы счисления в другую.
1. Из десятичной системы счисления:
- делим число на основание переводимой системы счисления;
- находим остаток от деления целой части числа;
- записываем все остатки от деления в обратном порядке;
2. Из двоичной системы счисления:
- для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
- для перевода числа в восьмеричную разбиваем число на триады.

Например, 1000110 = 1 000 110 = 1068
- для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.
Например, 1000110 = 100 0110 = 4616.
Таблицы для перевода:
Двоичная СС | Шестнадцатеричная СС |
0000 | |
0001 | |
0010 | |
0011 | |
0100 | |
0101 | |
0110 | |
0111 | |
1000 | |
1001 | |
1010 | |
1011 | |
1100 | |
1101 | |
1110 | |
1111 |
Двоичная СС |
1.
 Системы счисления
Системы счисленияТольяттинский государственный университет Автомеханический институт
Кафедра «Компьютерные технологии и обработка материалов давлением»
Ахмедханлы Д.М., Панюкова Е.В.
КУРС ЛЕКЦИЙ
по дисциплине «Информатика»
Тольятти 2007
Содержание |
|
1. Системы счисления……………………………………………………………………………………………………………………………………. | 5 |
Десятичная система счисления…………………………………………………………………………………………………………………. | 6 |
Двоичная система счисления…………………………………………………………………………………………………………………….. | 6 |
Восьмеричная и шестнадцатеричная системы счисления. | 7 |
Перевод чисел из любой системы счисления в десятичную……………………………………………………………………….. | 8 |
Перевод чисел из десятичной системы счисления в любую другую……………………………………………………………. | 8 |
2. Алгебра логики………………………………………………………………………………………………………………………………………… | 10 |
2.1. Логические операции……………………………………………………………………………………………………………………….. | 11 |
Инверсия…………………………………………………………………….. | 13 |
Конъюнкция……………………………………………………………………………………………………………………………………… | 13 |
Дизъюнкция………………………………………………………………………………………………………………………………………. | 13 |
Эквиваленция (равнозначность)…………………………………………………………………………………………………………. | 13 |
Импликация………………………………………………………………………………………………………………………………………. | 14 |
Антиконъюнкция………………………………. | 14 |
Антидизъюнкция ………………………………………………………………………………………………………………………………. | 14 |
2.2. Нормальные формы………………………………………………………………………………………………………………………….. | 16 |
Конъюнктивная нормальная форма……………………………………………………………………………………………………. | 16 |
Дизъюнктивная нормальная форма…………………………………………………………………………………………………….. | 17 |
3. Классические основы построения ЭВМ …………. | 18 |
3.1. Машина Тьюринга……………………………………………………………………………………………………………………………. | 18 |
Основные положения машины Тьюринга…………………………………………………………………………………………… | 18 |
3.2. Автомат Неймана …………………………………………………………………………………………………………………………….. | 19 |
3.3 Архитектура классической ЭВМ……………………………………………………………………………………………………….. | 20 |
4. Применение средств алгебры логики для описания функционирования устройств компьютера. | 22 |
Логические схемы………………………………………………………………………………………………………………………………….. | 27 |
Построение логических схем ………………………………………………………………………………………………………………….. | 27 |
5. Введение в алгоритмизацию…………………………………………………………………………………………………………………….. | 29 |
6. Знакомство со средой Турбо Паскаль……………………………………………………………………………………………………….. | 29 |
6.1. Общие сведения…………………………………………………………………………….. | 29 |
6.2. Запуск Турбо-Паскаля на выполнение………………………………………………………………………………………………. | 30 |
6.3. Назначение функциональных клавиш системы Турбо-Паскаль………………………………………………………….. | 30 |
6.4. Работа с текстовым редактором Турбо-Паскаля ………………………………………………………………………………… | 31 |
Клавиши перемещения курсора …………………………………………………………………………………………………………. | 32 |
Работа с блоками текста…………………………………………………………………………………………………………….. | 32 |
7. Основы алгоритмизации…………………………………………………………………………………………………………………………… | 33 |
7.1. Алгоритм…………………………………………………………………………………………………………………………………………. | 33 |
7.2. Алгоритмические структуры…………………………………………………………………………………………………………….. | 35 |
8. Программирование на языке Pascal…………………………………………………………………………………………………………… | 38 |
8.1. Алфавит языка…………………………………………………………………………………… | 39 |
8.2. Арифметические выражения и правила их записи……………………………………………………………………………… | 39 |
Знаки операций…………………………………………………………………………………………………………………………………. | 39 |
Операции div и mod …………………………………………………………………………………………………………………………… | 40 |
8.3. Типы данных……………………………………………………………………………………………………………………………………. | 40 |
Целые типы …………………………………………………………………….. | 40 |
Логический тип…………………………………………………………………………………………………………………………………. | 41 |
Символьный тип……………………………………………………………………………………………………………………………….. | 41 |
Строковый тип………………………………………………………………………………………………………………………………….. | 41 |
Вещественный тип…………………………………………………………………………………………………………………………….. | 41 |
8.4. Стандартные функции………………………… | 42 |
2
8.5. Структура программы на языке Паскаль …………………………………………………………………………………………… | 43 |
8.6. Описательная часть программы………………………………………………………………………………………………………… | 44 |
8.7. Исполнительная часть программы…………………………………………………………………………………………………….. | 44 |
8.8. Оператор присваивания……………………………………………………………………………………………………………………. | 45 |
8. | 45 |
Оператор ввода …………………………………………………………………………………………………………………………………. | 45 |
Оператор вывода……………………………………………………………………………………………………………………………….. | 45 |
8.10. Комментарии в программе ……………………………………………………………………………………………………………… | 46 |
9. Ветвления………………………………………………………………………………………………………………………………………………… | 47 |
9. | 47 |
Логический оператор…………………………………………………………………………………………………………………………. | 47 |
Операции отношения…………………………………………………………………………………………………………………………. | 48 |
Логические операции ………………………………………………………………………………………………………………………… | 48 |
9.2. Оператор выбора……………………………………………………………………………………………………………………………… | 50 |
10. | 50 |
10.1. Оператор цикла с параметром…………………………………………………………………………………………………………. | 50 |
10.2. Оператор цикла с постусловием ……………………………………………………………………………………………………… | 51 |
10.3. Оператор цикла с предусловием……………………………………………………………………………………………………… | 52 |
10.4. Вложенные циклы………………………………………………………………………………………………………………………….. | 53 |
10. | 53 |
11. Операции с индексированными переменными ………………………………………………………………………………………… | 54 |
11.1. Массивы одномерные …………………………………………………………………………………………………………………….. | 54 |
11.2. Описание массивов…………………………………………………………………………………………………………………………. | 54 |
Ввод элементов массива…………………………………………………………………………………………………………………….. | 55 |
Вывод элементов массива. | 55 |
11.3. Обработка одномерных массивов……………………………………………………………………………………………………. | 55 |
12. Двумерные массивы……………………………………………………………………………………………………………………………….. | 58 |
12.1. Матрицы………………………………………………………………………………………………………………………………………… | 58 |
12.2. Описание двумерного массива………………………………………………………………………………………………………… | 58 |
Ввод элементов двумерного массива. | 60 |
Вывод элементов двумерного массива……………………………………………………………………………………………….. | 60 |
12.3. Обработка двумерных массивов……………………………………………………………………………………………………… | 60 |
13. Подпрограммы ………………………………………………………………………………………………………………………………………. | 66 |
13.1. Функции и процедуры…………………………………………………………………………………………………………………….. | 66 |
Структура программы, содержащей процедуру (функцию). | 66 |
13.2. Процедуры …………………………………………………………………………………………………………………………………….. | 66 |
13.3. Вложенные процедуры …………………………………………………………………………………………………………………… | 67 |
Директива forward……………………………………………………………………………………………………………………………… | 67 |
13.4. Функции………………………………………………………………………………………………………………………………………… | 69 |
14. Обработка строк текста………….. | 70 |
14.1. Символьные переменные………………………………………………………………………………………………………………… | 70 |
Фрагмент таблицы ASCII-кодов букв латинского алфавита………………………………………………………………… | 70 |
Фрагмент таблицы ASCII-кодов букв русского алфавита……………………………………………………………………. | 70 |
14.2. Функции обработки символьных переменных…………………………………………………………………………………. | 71 |
14.3. Строковые переменные………………………………………………………… | 72 |
14.4. Функции обработки строковых переменных……………………………………………………………………………………. | 73 |
14.5. Процедуры обработки строковых переменных………………………………………………………………………………… | 74 |
14.6. Примеры обработки строковых переменных……………………………………………………………………………………. | 74 |
15. Структурированные типы данных…………………………………………………………………………………………………………… | 77 |
15.1. Записи…………………………………………………………………………………………………….. | 77 |
3
УДК 532.5 (533.6)
Курс лекций по дисциплине «Информатика». /Сост. Ахмедханлы Д.М., Панюкова Е.В. –
Тольятти: ТГУ, 2007.
Изложены основы алгебры логики, принципы работы логически-арифметических устройств ЭВМ, рассмотрены принципы перевода чисел из одной системы счисления в другую. Предназначено для студентов технических специальностей по дисциплине «Информатика».
Составитель: Ахмедханлы Д.М., Панюкова Е.В. Научный редактор: Егорова Э.В.
Утверждено редакционно-издательской секцией методического совета института.
© Тольяттинский государственный университет, 2007
4
Информация в ЭВМ хранится и отрабатывается в определенном, закодированном виде. ЭВМ оперируется числами, представленными в некоторой системе счисления.
Системой счисления называется способ представления чисел посредством цифровых знаков.
Системы счисления принято делить на:
•Позиционные.
•Непозиционные.
•Символические.
Всимволических системах каждому числу ставится в соответствие свой символ. Эти системы не находят широкого применения в силу естественной их ограниченности (алхимия, кодированные сообщения) – бесчисленного множества символов, которое требуется для изображения всех возможных чисел.
Впозиционных системах счисления значимости числа зависит от позиции. Позиция – некоторое место, в котором может быть представлен лишь один символ. Примером позиционной системы счисления является десятичная система.
Втаблице 1 показана система представления чисел в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
Всякая система счисления характеризуется основанием – количеством цифр, используемых для изображения чисел.
Система представления чисел в различных системах счисления
|
|
| Таблица 1 | ||
|
|
| Шестнадцатеричная |
|
|
Десятичная | Двоичная | Восьмеричная |
| ||
|
|
| 0 |
|
|
0 | 0000 | 0 |
|
| |
|
|
| 1 |
|
|
1 | 0001 | 1 |
|
| |
|
|
| 2 |
|
|
2 | 0010 | 2 |
|
| |
3 | 0011 | 3 | 3 |
|
|
4 | 0100 | 4 | 4 |
|
|
5 | 0101 | 5 | 5 |
|
|
|
|
| 6 |
|
|
6 | 0110 | 6 |
|
| |
|
|
| 7 |
|
|
7 | 0111 | 7 |
|
| |
|
|
| 8 |
|
|
8 | 1000 | 10 |
|
| |
|
|
| 9 |
|
|
9 | 1001 | 11 |
|
| |
|
|
| А |
|
|
10 | 1010 | 12 |
|
| |
|
|
| B |
|
|
11 | 1011 | 13 |
|
| |
|
|
| C |
|
|
12 | 1100 | 14 |
|
| |
|
|
| D |
|
|
13 | 1101 | 15 |
|
| |
|
|
| E |
|
|
14 | 1110 | 16 |
|
| |
|
|
| F |
|
|
15 | 1111 | 17 |
|
| |
|
|
| 10 |
|
|
16 | 10000 | 20 |
|
| |
|
|
| 11 |
|
|
17 | 10001 | 21 |
|
| |
18 | 10010 | 22 | 12 |
|
|
19 | 10011 | 23 | 13 |
|
|
5
20 | 10100 | 24 | 14 |
Наибольшее распространение для представления чисел в ЭВМ, получили двоичная, восьмеричная и шестнадцатеричная системы счисления.
Десятичная система счисления
В этой системе число представляется в виде полинома n степени, а изображается совокупностью некоторых символов, каждый из которых имеет различный вес в зависимости от позиции, которую он занимает.
Всем позициям приписывается различный вес, который чаще всего выбирается как целая степень основания системы.
Основание системы счисления — число, которое является мощностью множества различных символов, допустимых в каждой позиции числа. Привычная для нас 10-я система счисления использует для записи чисел 10 цифр: 0-9. Это позиционная система счисления, т.е. значение цифры в числе зависит от положения (позиции) (в отличие от римской).
Пример 1. Число 55,5 можно представить: 55,5=5*101+5*100+5*10-1
десятки единицы | десятые доли единицы |
Если g принять за основание системы, то любое число можно представить как
anan−1…a0,a−1…a−m =an gn +an−1 gn−1. ..+a0 g0 +a−1 g−1 +…+a−m g−m
..+a0 g0 +a−1 g−1 +…+a−m g−m
В отличие от системы счета времени, десятичная система является однородной, т.е. одних и тех же десятичных символов достаточно, чтобы изобразить любое число. В то время как в смешанных системах нужно придумывать все новые и новые символы для того, чтобы изобразить следующее по величине число.
Таким образом, однородность – одно из важных свойств позиционных систем.
Двоичная система счисления
В двоичной системе счисления для изображения чисел используют только две цифры 0 и 1.
С помощью двоичных кодов можно кодировать и хранить в памяти ЭВМ любую алфавитноцифровую информацию. Каждому символу присваивается свой код. С помощью кода, состоящего из n- разрядов, можно закодировать (представить) 2n различных символов.
Информация хранится в байтах. 1 байт = 8 бит – т.е. для кодирования используется восьмиразрядный двоичный код.
Основанием двоичной системы является число 2. Пример 2.
101(2)=1*22+0*21+1*20=4+0+1=5(10). 101(2)=>5(10).
101(2)=>5(10).
(Любое число в 0-ой степени равно 1)
Арифметические операции в двоичной системе счисления
Таблица 2
Сложение | Вычитание | Умножение |
6
0+0=0 | 0-0=0 | 0*0=0 |
1+0=1 | 1-0=1 | 1*0=0 |
0+1=1 | 0-1=1 | 0*1=0 |
1+1=10 | 1-1=0 | 1*1=1 |
При сложении двух чисел, равных 1, в данном разряде получается 0, а 1-ца переносится в старший разряд.
Пример 3.
101 + 11
1000 ,
где 101(2)=> 5(10), 11(2)=> 3(10), 1000(2) => 8(10).
Действительно: 5+3=8.
При вычитании из 0 единицы, занимается единица из старшего ближайшего разряда, отличного от 0. При этом, единица занятая в старшем разряде, даёт 2 единицы в младшем разряде и по единице во всех разрядах между старшим и младшим.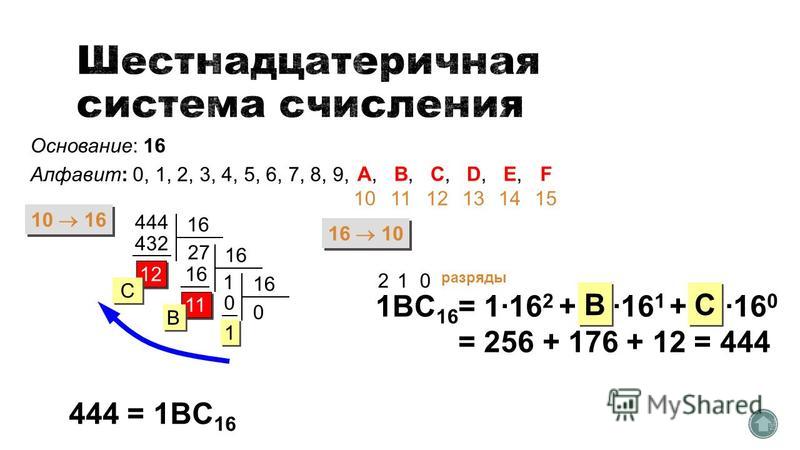
Пример 4.
101 — 11
10 ,
где 101(2)=>5(10), 11(2)=>3(10), 10(2)=>2(10).
Действительно: 5-3=2.
Операция умножения сводится к многократному сдвигу и сложению. Пример 5.
11
*10
00
11
110 ,
где 11(2)=>3(10), 10(2)=>2(10), 110(2)=>6(10).
Действительно: 3*2=6.
Восьмеричная и шестнадцатеричная системы счисления
Запись двоичных чисел достаточно длинна, операции над ними – утомительны. Для краткости записи двоичной информации используются системы с большим основанием. Главным требованием, предъявляемым к этим системам, является то, что перевод из этих систем в двоичную и обратно, должен быть достаточно кратким, т.е. эти системы и двоичная должны быть в некотором смысле эквивалентны. Таковыми являются восьмеричная и шестнадцатеричная системы (см. таблицу 1).
В 8-ой системе для изображения чисел используют 8 цифр: 0-7. Основанием системы являются число 8. Для перевода чисел из 2-ой системы счисления в восьмеричную, достаточно разбить двоичное число на триады (по три) двигаясь влево и вправо от десятичной точки.
Пример 6: 11 110.001 01(2)=36.12(8).
К крайним группам добавляются нули для дополнения их до трех разрядов.
7
8=23 – отсюда триады.
В 16-й с/с для изображения чисел используется 16 символов: 10 цифр и 6 букв латинского алфавита: А, B, C, D, E, F. Основание системы – число 16.
16=24 – для преобразования двоичного числа в 16-ричное, нужно разбить его на тетрады (по четыре), двигаясь влево и вправо от десятичной точки. К крайним группам нули добавляются до 4 разрядов.
Пример 7: 1111 0101.1000 111(2)=F5.8E(16).
и обратно:
6ЕА.4(16)=110 1110 1010.0100(2).
Использование 8-ой или 16-ой систем счисления позволяет уменьшить в 3 или 4 раза количество разрядов для записи чисел.
Перевод чисел из любой системы счисления в десятичную
Для перевода числа из любой системы счисления в десятичную, необходимо разложить это число по степеням основания этой системы.
Пример 8:
1101(2) =1 23 +1 22 +0 21 +1 20 =13(10)
15. 1(8) =1 81 +5 80 +1 8−1 =8 +5 + 18 =13.125(10) A8.2(16) = A 161 +8 160 +2 16−1 =10 161 +8 1+2 161 =
1(8) =1 81 +5 80 +1 8−1 =8 +5 + 18 =13.125(10) A8.2(16) = A 161 +8 160 +2 16−1 =10 161 +8 1+2 161 =
=160 +8 + 18 =168.125(10)
Перевод чисел из десятичной системы счисления в любую другую
Для перевода чисел из десятичной с/с в любую другую, необходимо делить десятичное число на основание системы, в которую переводят, сохраняя при этом остатки от каждого деления.
Результат формируется справа налево. Деление продолжается до тех пор, пока результат деления не станет меньше делителя.
Пример 9. Перевести число 13 из десятичной системы счисления в двоичную систему:
13 | 2 |
|
|
|
|
|
|
| |
12 | 6 |
|
| 2 |
|
|
|
| |
1 |
| 6 |
|
|
|
|
|
| 2 |
|
| 3 |
| ||||||
| 0 | 2 |
|
|
|
| |||
|
|
|
| 1 | |||||
|
|
|
| 1 |
|
|
|
| |
13(10) => 1101(2).
Пример 10. Перевести число 13 из десятичной системы счисления в восьмеричную систему:
8
13 8
8 1
5
13(10) => 15(8).
Пример 11. Перевести число 638 из десятичной системы счисления в шестнадцатеричную систему:
638 |
| 16 |
|
| |
48 |
| 39 |
| 16 | |
158 |
| 32 |
|
| |
| 2 | ||||
144 |
|
| 7 |
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
638(10) => 27E(16).
Остатки записываются в шестнадцатеричном виде (14 => Е). Пример 12. Сложение двоичных чисел:
11011001(2) + 1011101(2) 100110110(2).
Для проверки результата сложения двоичное число нужно разбить на триады, перевести в восьмеричную систему счисления согласно таблице 1, а затем перейти в десятичную систему и осуществить сложение.
11 011 001(2)=331(8)=3*82+3*81+1*80=192+24+1=217(10).
1 011 101(2)=135(8)=1*82+3*81+5*80=64+24+5=93(10).
100 110 110(2)=466(8)=4*82+6*81+6*80=256+48+6=310(10).
Проверка:
217(10)+93(10)=310(10).
Пример 13. Сложение шестнадцатеричных чисел: 8E38C(16)
+ 5D35(16) 940C1(16).
Перед сложением необходимо перейти согласно таблице 1 в 10-ю систему счисления, произвести сложение, затем опять вернуться к 16-ой системе счисления.
C(16)+5(16) => 12(10)+5(10)=17(10) => 11(16). 8(16)+3(16)+1(16)=12(10) => С(16). 3(16)+D(16)=3(10)+13(10)=16(10) => 10(16). E(16)+5(16)+1(16)=14(10)+5(10)+1(10)=20(10) =>14(16).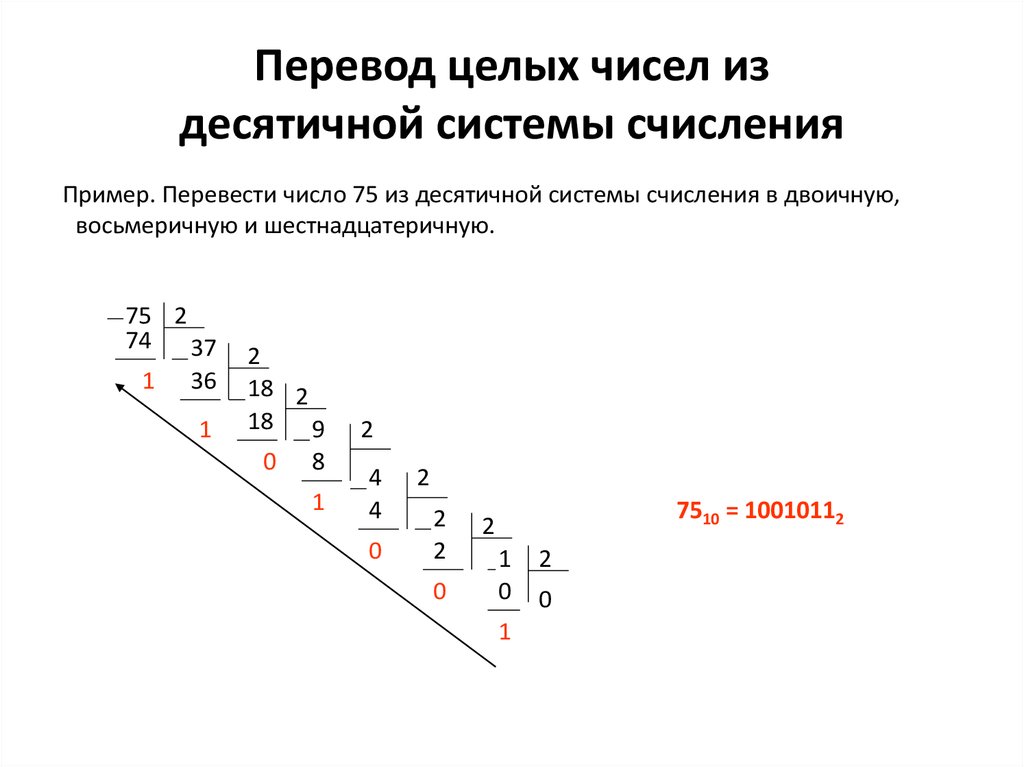 8(16)+1=9(10) => 9(16).
8(16)+1=9(10) => 9(16).
9
Шестнадцатеричное в десятичное — Преобразование, Формула, Метод, Примеры
Шестнадцатеричное в десятичное — это процесс преобразования одного числа в другое в системе счисления. Система счисления представляет собой представление чисел с помощью последовательного использования цифр или других символов. Существует четыре типа систем счисления, а именно: двоичная, восьмеричная, десятичная и шестнадцатеричная. Каждая из них имеет свой уникальный базовый номер, который различает системы. Шестнадцатеричная система счисления имеет базовое число 16, тогда как десятичная система счисления имеет базовое число 10. Давайте узнаем, как преобразовать шестнадцатеричное число в десятичное, таблицу преобразования и решим несколько примеров, чтобы лучше понять концепцию.
| 1. | Что такое преобразование шестнадцатеричных чисел в десятичные? |
| 2. | Как преобразовать шестнадцатеричное число в десятичное? |
3. | Преобразование шестнадцатеричной системы счисления в десятичную Формула |
| 4. | Часто задаваемые вопросы о преобразовании шестнадцатеричной системы счисления в десятичную |
Что такое преобразование шестнадцатеричных чисел в десятичные?
Преобразование шестнадцатеричных чисел в десятичные выполняется с учетом основных чисел каждой из систем счисления. Шестнадцатеричная система счисления работает как с цифрами, так и с символами, особенно для представления двузначных, используются символы. Всего существует 16 обозначений: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9., 10, 11, 12, 13, 14, 15 и 10-15 представлены как A, B, C, D, E, F. Тогда как в десятичной системе счисления 10 обозначений представлены как 0, 1, 2, 3 , 4, 5, 6, 7, 8 и 9. Чтобы преобразовать шестнадцатеричное число в десятичное, мы сначала получаем десятичный эквивалент шестнадцатеричного числа из таблицы преобразования, умножаем как цифру на 16 в степени разрядности и складываем все вместе. Таблица преобразования приведена ниже:
Таблица преобразования приведена ниже:
Определение шестнадцатеричной системы счисления
Шестнадцатеричная система счисления также известна как позиционная система счисления, поскольку каждая цифра имеет вес степени 16. Каждая цифра в 16 раз значительнее предыдущей. . Следовательно, когда мы преобразуем любое шестнадцатеричное число в любую другую систему счисления, мы умножаем цифры по отдельности, учитывая степень числа 16 в соответствии с их положением. Эта система счисления использует шестнадцать цифр/алфавитов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.и A, B, C, D, E, F с базовым числом 16. Например, 7DE 16 , E5F 16 , 9B4A 16 .
Определение десятичной системы счисления
Десятичная система счисления имеет основание 10 с цифрами от 0 до 9. Числа в повседневной жизни обычно представлены в этой форме. Например, 24 10 , 654 10 , 2012 10 .
Как преобразовать шестнадцатеричное число в десятичное?
Преобразование шестнадцатеричного числа в десятичное выполняется с использованием основного числа 16.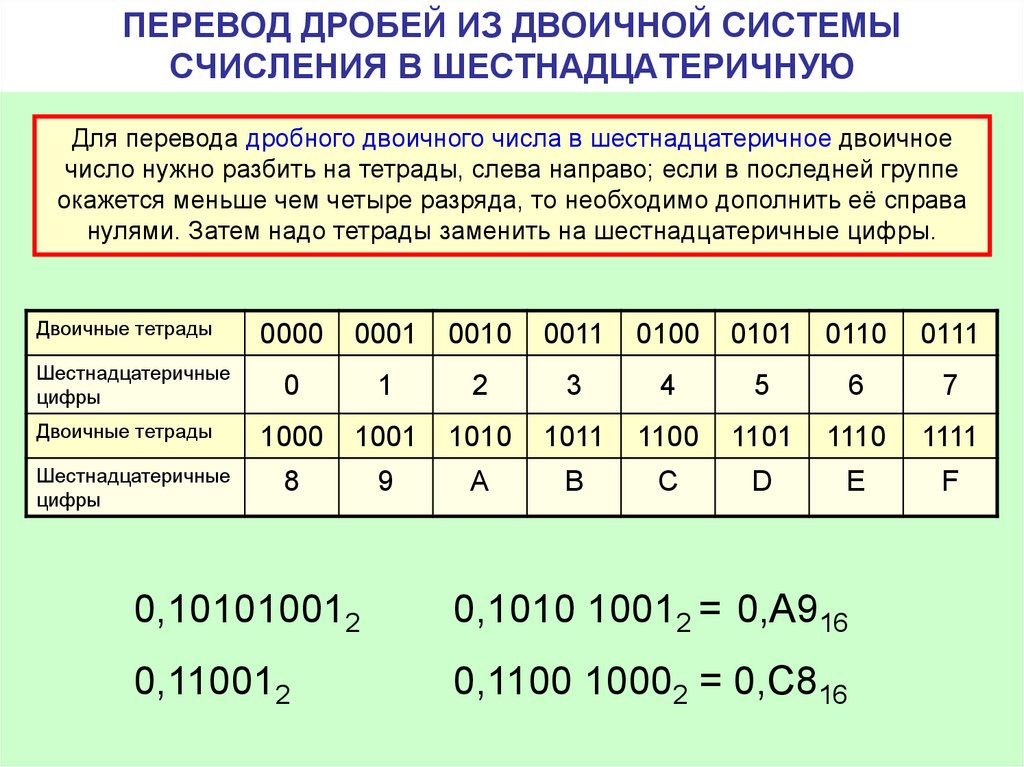 Шестнадцатеричная цифра расширяется, чтобы умножить каждую цифру на степень 16. Степень начинается с 0 справа и движется вперед вправо с увеличением мощности . Для завершения преобразования умноженные числа складываются.
Шестнадцатеричная цифра расширяется, чтобы умножить каждую цифру на степень 16. Степень начинается с 0 справа и движется вперед вправо с увеличением мощности . Для завершения преобразования умноженные числа складываются.
Десятичный номер = d n-1 × 16 r-1 +….+ d 2 × 16 2 + d 1 × 16 4 4 1 0 .
Где,
- n = количество цифр.
- r = размещение цифры.
Шаги для преобразования шестнадцатеричного числа в десятичное:
- Получите десятичный эквивалент шестнадцатеричного числа из таблицы преобразования. (таблица указана выше)
- Умножьте каждую цифру в степени 16, начиная с 0 справа.
- Сложите все числа вместе.
Давайте рассмотрим пример, чтобы лучше понять это.
Например: преобразовать шестнадцатеричное число \((25)_{16}\) в его десятичную форму.
\((25)_{16}\) = 2 × 16 1 + 5 × 16 0
= 2 × 16 + 5 × 1
= 32 + 5
= 37 , \((25)_{16}\) = \((37)_{10}\).
Преобразование шестнадцатеричной системы счисления в десятичную Формула
Преобразование формулы из шестнадцатеричной в десятичную использует следующий метод:
- Основание числа для преобразования здесь равно 16.
- Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени по основанию 16.
- Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз при движении справа налево.
- Мы просто упрощаем каждый из продуктов и добавляем их. 90 \text{(decimal)}\)
☛Связанные темы
Ниже перечислены несколько интересных тем, связанных с преобразованием шестнадцатеричного в десятичное, взгляните.
- Шестнадцатеричный код в двоичный
- Десятичный в восьмеричный
- Восьмеричный в десятичный
- Десятичный в шестнадцатеричный
- Двоичный код в шестнадцатеричный
Часто задаваемые вопросы о шестнадцатеричной системе счисления
Что означает преобразование шестнадцатеричной системы счисления в десятичную?
Преобразование шестнадцатеричных чисел в десятичные выполняется с учетом основных чисел обеих систем счисления.
 При преобразовании шестнадцатеричного в десятичное используется основание числа 16. В шестнадцатеричной системе счисления используется 16 цифр/алфавитов: цифры 0,1, 2, 3, 4, 5, 6, 7, 8, 9 и символы A, B, C, D, E, F, таким образом, имеющие основание 16. , Десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, и поэтому имеет основание 10.
При преобразовании шестнадцатеричного в десятичное используется основание числа 16. В шестнадцатеричной системе счисления используется 16 цифр/алфавитов: цифры 0,1, 2, 3, 4, 5, 6, 7, 8, 9 и символы A, B, C, D, E, F, таким образом, имеющие основание 16. , Десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, и поэтому имеет основание 10.Как преобразовать шестнадцатеричное число в десятичное?
Преобразование шестнадцатеричного в десятичное выполняется с использованием основного числа 16. Шаги следующие:
- Получите десятичный эквивалент шестнадцатеричных символов, обратившись к таблице преобразования.
- Расширьте цифры, чтобы умножить каждую цифру на степень 16, которая начинается с 0 справа налево.
- После завершения процесса умножения найдите сумму.
- Окончательный ответ — десятичное число.
Что такое шестнадцатеричная формула для десятичной?
Формула преобразования шестнадцатеричной системы счисления в десятичную: 90 \текст{(десятичный)}\).

Как использовать формулу преобразования шестнадцатеричной системы счисления в десятичную?
Шестнадцатеричная формула в десятичную помогает преобразовать число, заданное в системе счисления с основанием 16, в системе счисления 10. В этом методе используется формула:
- При необходимости измените символы на цифры с помощью таблицы преобразования.
- Умножьте каждую цифру данного числа, начиная с самой правой цифры, на показатели степени по основанию 16.
- Показатель степени должен начинаться с 0 и увеличиваться на 1 каждый раз при движении справа налево.
- Мы просто упрощаем каждый из продуктов и добавляем их.
Какие существуют четыре типа системы счисления?
В математике существует четыре типа систем счисления, а именно:
- Двоичная система счисления — Основание числа 2
- Восьмеричная система счисления — Основание числа 8
- Десятичная система счисления — Базовое число 10
- Шестнадцатеричная система счисления — Базовое число 16
Преобразование шестнадцатеричной системы счисления в 31 • Конвертер чисел • Распространенные конвертеры единиц измерения • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Этот сайт не будет работать должным образом, так как ваш браузер не поддерживает JavaScript!
Преобразователь случайных чисел
Преобразование шестнадцатеричной системы счисления в основание 31
Преобразователь длины и расстоянияПреобразователь массыСухой объем и общие измерения для приготовления пищиКонвертер площадиКонвертер объема и общего измерения для приготовления пищиПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь мощностиПреобразователь силыПреобразователь силыПреобразователь времениПреобразователь линейной скорости и скоростиПреобразователь углаПреобразователь эффективности использования топлива, расхода топлива и экономии топливаПреобразователь чиселКонвертер единиц информации и Хранение данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер импульсаИмпульс крутящего моментаКонвертер удельной энергии, теплоты сгорания (в расчете на массу)Конвертер удельной энергии, теплоты сгорания (в объеме) Конвертер температуры Конвертер интервала Конвертер коэффициента теплового расширенияКонвертер теплового сопротивленияТеплопровод Конвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплопередачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяженияМодерация проницаемости, проницаемости, паропроницаемости Преобразователь скорости пропускания паровПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической силы (диоптрий) в фокусное расстояниеПреобразователь оптической силы (диоптрий) в увеличение (X)Электрический заряд КонвертерКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаОбъемный заряд De Преобразователь электрического токаПреобразователь линейной плотности токаПреобразователь поверхностной плотности токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электропроводностиПреобразователь емкостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь калибров проводов в СШАПреобразование уровней в дБм, дБВ, Ватт и других единицахПреобразователь силы магнитного поля КонвертерПлотность магнитного потокаМощность поглощенной дозы излучения, Мощность общей дозы ионизирующего излучения КонвертерРадиоактивность.
 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблицаОткуда:
двоично-десятичный шестнадцатеричный base-2base-3base-4base-5base-6base-7base-8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base -23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36
8base-9base-10base-11base-12base-13base-14base-15base-16base-17base-18base-19base-20base-21base-22base-23base-24base-25base-26base-27base-28base-29base-30base-31base-32base-33base-34base-35base-36
Напряженность электрического поля
Знаете ли вы, что ферроэлектрические материалы не содержат железо? Нажмите или коснитесь, чтобы узнать больше о сегнетоэлектриках и других интересных материалах.

Обзор
Различные способы представления чисел
Индо-арабские цифры
Римские
Системы в других культурах
Унарные
Позиционная система
Двоичный
Классификация номеров
Отрицательные номера
Рациональные номера
Натуральные номера
Целевые числа
Комплексные номера
Интересные факты около
Антифрауд Нумерал
Современные обчисления. in Commerce
Группировка цифр
Несчастливые числа
Изучайте технический английский с помощью этого видео!
Обзор
Приложение-калькулятор для iPhone
Число — это абстрактное математическое понятие, представляющее количество. Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем как более абстрактные системы. Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.

Различные способы представления чисел
Некоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания.
Индо-арабские цифры
Индо-арабская система счисления является одной из наиболее широко используемых в современном мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.

Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.
Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне. Он гласит: ANNO : DECIMO : EDWARDI : SEPTIMI : REGIS : VICTORIÆ : REGINÆ : CIVES : GRATISSIMI : MDCCCCX : (На десятом году правления короля Эдуарда VII, королеве Виктории, от самых благодарных граждан, 1910).
Римские
Римские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Roman numerals are based on seven numbers written with the letters of the Latin alphabet:
I 1 V 5 X 10 L 50 С 100 D 500 M 1000 Порядок важен в римской системе, потому что большее количество, за которым следует меньшие средства, которые должны быть добавлены, но меньшее число перед большим означает, что меньшее число вычитается из большего.
 Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.Системы в других культурах
Люди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв. Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа.
В некоторых культурах используются более простые представления, такие как вавилонская система, в которой есть только два клинописных символа: один (немного напоминающий букву «Т») и десять (немного похожий на букву «С»).
 Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.Унарная система счисления. Метки счета в различных культурах
Унарная
Унарная система представляет каждое число с тем же количеством символов, что и его значение. Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства.
 Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему.
Позиционная система
Позиционная система работает с основанием.
 Например, в системе счисления 10 у нас есть следующее:
Например, в системе счисления 10 у нас есть следующее:- Первая позиция предназначена для чисел от нуля до девяти, то есть число в первой позиции должно быть умножено на десять в степени нуля.
- Число во второй позиции умножается на десять в степени один.
- : Число в третьей позиции умножается на десять в степени двойки и так далее, пока числа во всех позициях не будут исчерпаны.
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи.
Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная система счисления
Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2.
 Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:Художественное представление двоичных чисел
- Если число заканчивается нулем, последний ноль заменяется единицей: например, 100 (4) + 1 (1) = 101 (5). Здесь числа с основанием 10 используются в скобках для сравнения.
- Если число оканчивается на единицу, но не на все единицы, то первый ноль справа заменяется единицей, а все последующие за ним справа становятся нулями: 1011 (11) + 1 (1) = 1100.
- Если в исходном числе все единицы, то все они заменяются нулями и впереди добавляется единица: 111 (7) + 1 (1) = 1000 (8).
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию. Например:
11111 (31)
+1011 (11)
———————————
101010 (42)В этом случае, работая справа налево:
- 1+1 дает 0, с одним переносом
- 1+1+1 дает 1, с одним переносом
- 1+1 дает 0, с одним переносом
- 1+1+1 дает 1, с одним переносом
- 1+1 дает 10
Таким образом, складывая это вместе, мы получаем 101010.

Вычитание работает по тому же принципу, только вместо переноса единиц мы «заимствуем» их. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
101 (5)
×10 (2)
———————————
000
101
———————————
1010 (10)Деление и расчет квадратных корней также очень похожи на основание-10.
Классификация номеров
Все номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются.
Долг — отрицательное число
Отрицательные числа
Отрицательные числа — это числа, представляющие отрицательное значение. Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число.
Рациональные числа
Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число.
 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.Натуральные числа
Натуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456.
Целые числа
Целые числа включают нуль, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223.
Комплексные числа
Комплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательного числа.
Простые числа
Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11. 2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге.

Интересные факты о числах
Китайские цифры для защиты от мошенничества
Числительные для защиты от мошенничества
Для предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать путем добавления дополнительных штрихов. Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Современный счет в торговле
Некоторые языки в странах, где в настоящее время используется 10-кратная система счисления, по-прежнему свидетельствуют о том, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов.

Группировка чисел
И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
Несчастливые числа
Леонардо да Винчи. Последний ужин. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия.
В западной традиции число 13 считается несчастливым. Многие считают, что это заимствовано из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году.

В России и многих странах бывшего СССР все четные числа считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как и «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае номер 7 тоже неудачный, потому что он представляет духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов.
 В Японии другое несчастливое число — 9.0230 9 , что имеет то же произношение, что и «страдание».
В Японии другое несчастливое число — 9.0230 9 , что имеет то же произношение, что и «страдание».В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». Это подразумевает, что жизнь окончена, и относится к смерти.
666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или позорным номером, связанным с проституцией.
 Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.Список литературы
Эта статья была написана Kateryna Yuri
Преобразование десятичного десятичного в базу-32
Преобразование восьми в десятичное значение
.
 в 36 с основанием
в 36 с основаниемПреобразовать двоичное в 36 с основанием
Преобразовать десятичное в 3 с основанием
Преобразовать 4 в двоичное с основанием
Вас могут заинтересовать другие преобразователи в группе Общие преобразователи единиц:
Длина и преобразователь расстояния
массовый преобразователь
Объем и общие измерения приготовления
Площадь преобразователя площади
Объем и общий преобразователь измерения приготовления
ТЕМПЕРАТУРА
Давление, напряжение, модульный преобразователь модуля Янга
И трудовой преобразователь
.Преобразователь мощности
Преобразователь силы
Преобразователь времени
Преобразователь линейной скорости и скорости
Преобразователь угла
Конвертер топливной экономичности, расхода топлива и экономии топлива
Конвертер единиц хранения информации и данных
Конвертер метрических префиксов
Конвертер передачи данных
Курсы обмена валют
Размеры мужской одежды и обуви
3 Размеры
Компактный калькулятор Полный калькулятор Определения единиц измерения
У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут вы получите ответ от опытных технических переводчиков.

Общие конвертеры единиц измерения
Длина, масса, объем, площадь, температура, давление, энергия, мощность, скорость и другие популярные конвертеры единиц измерения.
Преобразователь чисел
Позиционное обозначение или разрядное обозначение — это метод представления или кодирования чисел. Позиционное обозначение отличается от других обозначений (таких как римские цифры) использованием одного и того же символа для разных порядков величины (например, «разряд единиц», «разряд десятков», «разряд сотен»). В математических системах счисления основание или основание обычно представляет собой количество уникальных цифр, включая ноль, которые позиционная система счисления использует для представления чисел.
Основание 1 — Унарная система счисления. Это простейшая система счисления для представления натуральных чисел: для представления числа N произвольно выбранный символ, представляющий 1, повторяется N раз.

Основание 2 — Двоичная система счисления. Это позиционная система с основанием 2, в которой числовые значения представлены двумя символами: 0 и 1.
Основание 3 — Троичная (иногда называемая троичной) система счисления. Троичная цифра — это трит (троичная цифра). Он использует цифры 0, 1 и 2 для представления любого действительного числа. Эта система иногда используется в логике и вычислениях для подсчета трех состояний (низкое, высокое, неизвестное или открытое состояние).
Основание 8 — восьмеричная система счисления — это система счисления с основанием 8, в которой используются цифры от 0 до 7. Она используется в цифровом оборудовании.
Основание 10 — Десятичная система счисления (также называемая системой с основанием десять) представляет собой позиционную систему счисления, в основе которой лежит 10. Это числовая база, наиболее широко используемая современными цивилизациями.
Основание 12 — двенадцатеричная система (также известная как основание 12 или дюжина) представляет собой позиционную систему счисления с основанием двенадцать.

Основание 16 — шестнадцатеричная система счисления (также называемая основанием 16 или шестнадцатеричной системой счисления) — это позиционная система счисления с основанием 16. Она используется в современном цифровом оборудовании, информатике и математике.
В системах с основанием менее 36 чаще всего символы 0–9 представляют значения от нуля до девяти, а латинские буквы от A до Z и альтернативно от a до z представляют значения от 10 до 36.
Использование конвертера чисел
Этот онлайн-конвертер единиц измерения позволяет быстро и точно преобразовать множество единиц измерения из одной системы в другую. Страница Unit Conversion предлагает решение для инженеров, переводчиков и всех, чья деятельность требует работы с величинами, измеряемыми в разных единицах. 9», то есть « умножить на десять в степени ». Электронная нотация обычно используется в калькуляторах, а также учеными, математиками и инженерами.
- Выберите единицу измерения для преобразования в левом поле, содержащем список единиц.

- Выберите единицу измерения для преобразования в правом поле, содержащем список единиц измерения.
- Введите значение (например, «15») в левое поле From .
- Результат появится в поле Результат и в 9ящик 0230 — .
- В качестве альтернативы можно ввести значение в правое поле В и прочитать результат преобразования в полях Из и Результат .
Библиотека JavaScript BigInteger
Мы прилагаем все усилия, чтобы результаты, представленные конвертерами и калькуляторами TranslatorsCafe.com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.
Если вы заметили ошибку в тексте или расчетах, или вам нужен другой конвертер, которого вы здесь не нашли, сообщите нам об этом!
TranslatorsCafe.com Конвертер единиц YouTube канал
Hex to Decimal — Конвертер шестнадцатеричных чисел в десятичные
регистр Авторизоваться
РЕКЛАМНОЕ ОБЪЯВЛЕНИЕ
РЕКЛАМНОЕ ОБЪЯВЛЕНИЕ
РЕКЛАМНОЕ ОБЪЯВЛЕНИЕ
Содержание:
- Hex to Decimal
- Что такое шестнадцатеричная система?
- Что такое десятичная система?
Полезен ли этот инструмент?
Да Нет Возможно
Как мы можем это улучшить? Минимальное количество символов 10
Hex to Decimal
Что такое шестнадцатеричная система?Шестнадцатеричная система, или шестнадцатеричная, представляет собой систему счисления с основанием 16.
Что такое десятичная система? Поскольку в десятичной системе всего 10 цифр, дополнительные 6 цифр представлены первыми 6 буквами алфавита. Например, шестнадцатеричное значение B будет представлено в десятичной форме как 11, а двоичное значение — как 1011. Это простой способ выражения двоичных чисел в современных компьютерах, где байт обычно определяется как содержащий восемь двоичных цифр.
Поскольку в десятичной системе всего 10 цифр, дополнительные 6 цифр представлены первыми 6 буквами алфавита. Например, шестнадцатеричное значение B будет представлено в десятичной форме как 11, а двоичное значение — как 1011. Это простой способ выражения двоичных чисел в современных компьютерах, где байт обычно определяется как содержащий восемь двоичных цифр.Десятичная система на сегодняшний день является одной из старейших и наиболее часто используемых систем счисления. Она также известна как нумерация по основанию 10, потому что она основана на 10 однозначных цифрах: 0,1,2,3,4,5,6,7,8,9. Например, десятичное значение 11 будет представлено как шестнадцатеричное значение B или как двоичное значение 1011.
Преобразование шестнадцатеричного числа в десятичноеТеперь, как вручную преобразовать шестнадцатеричное число в десятичное? Во-первых, вы должны знать, что все буквы в шестнадцатеричном коде имеют десятичные эквиваленты, как указано в таблице ниже.
Hexadecimal to Decimal Table
Hex
base 16Decimal
base 10Calculation 0 0 — 1 1 — 2 2 — 3 3 — 4 4 — 4 0007 5 5 — 6 6 — 7 7 — 8 8 — 9 9 — A 10 — B 11 — C 12 — D 0008 13 — E 14 — F 15 — 10 0008 16 1 × 16 19007 100008 160008 1 × 160069 1 701999999 1 × 160069 19007 10 0008 1 × 160069 19007 10 0008 1 × 16009 1 10 0008 1 × 160069 1 10 0008 9 1 × 16009 1 10 9 1, 16 10009119 10 0008 = 16 11 17 1 × 16 1 +1 × 16 0 = 17 12 18 1 × 16969 1 +2 × 169999999. 10007 1 × 16969 1 +2 10069
100699999.1009 00007 1 × 16969 1 +2 18 1 × 16969 1 +2 = 18 13 19 1×16 1 +3×16 0 = 19 14 20 1×16 1 +4×16 0 = 20 15 21 1×16 1 +5×16 0 = 21 16 22 1×16 1 +6×16 0 = 22 17 23 1×16 1 +7×16 0 = 23 18 24 1 × 16 1 +8 × 16 0 = 24 1 25 1 × 16969 1 + 999999 9009 1 × 16969 1 + 999999 1 ° = 25 1A 26 1 × 16 1 +10 × 16 0 = 26 1B 27 1 × 16 1 +110007 1 × 16 1 +1100069 00008 1 × 16 1 +1100099 00008 1 × 16 1 +1100099 1 × 16 1 27 1 × 16 1 27 1 × 16 1 27 1 ° = 27 1С 28 1×16 1 +12 × 16 0 = 28 1D 29 1 × 16 1 +13 × 16 0 = 29 1000 9007 30 9 1.  1 +14×16 0 = 30
1 +14×16 0 = 301F 31 1×16 1 +15×16 0 = 31 20 32 2×16 1 +0×16 0 = 32 30 48 3×16 1 +0×16 0 = 48 40 64 4×16 1 +0×16 0 = 64 50 80 5 × 16 1 +0 × 16 0 = 80 60 6 × 16 1 +0 × 16 0 = 969008 9007 9 9 9007 9007 9007 7 . 112 7×16 1 +0×16 0 = 112 80 128 8 × 16 1 +0 × 16 0 = 128 90 144 9 × 16969 1 +0 × 16 1 +0,1 9 × 160069 1 +0,1 1 +0 00069 1 A0 160 10 × 16 1 +0 × 16 0 = 160 B0 176 11 × 140069 1 +0 × 169009 11 × 160069 1 +0,0 11 × 160069 1 +0,0 11 × 160069 1 +0 00069 11 × 160069 1 +000069 11 × 160069 1 +000069 11000119 1 . 
C0 192 12×16 1 +0×16 0 = 192 D0 208 13×16 1 +0×16 0 = 208 E0 224 14×16 1 +0×16 0 = 224 F0 240 15×16 1 +0×16 0 = 240 100 256 1×16 2 +0×16 1 +0×16 0 = 256 200 512 2×16 2 +0×16 1 +0×16 0 = 512 300 768 3×16 2 +0 ×16 1 +0×16 0 = 768 400 1024 4×16 2 +0×16 1 +0×16 0 = 1024 Существуют и другие таблицы систем счисления с большим количеством значений для восьмеричных, шестнадцатеричных, десятичных и двоичных чисел, но приведенная выше таблица содержит все, что нам нужно, чтобы понять, как преобразовать шестнадцатеричное число в десятичное.
Как вручную преобразовать шестнадцатеричный формат в десятичный?
Чтобы вручную преобразовать шестнадцатеричное число в десятичное, вы должны начать с умножения шестнадцатеричного числа на 16. Затем вы возводите его в степень 0 и каждый раз увеличиваете эту степень на 1 в соответствии с эквивалентным шестнадцатеричным числом.
Мы начинаем справа от шестнадцатеричного числа и идем влево при применении полномочий. Каждый раз, когда вы умножаете число на 16, степень числа 16 увеличивается.
При преобразовании шестнадцатеричной C91) = 192
Тогда мы добавляем результаты
192 + 9 = 201 10 Десятиц Десятиц
. в их десятичные эквиваленты. C равно десятичному числу 12 (см. таблицу выше), а 9 равно десятичному числу 9.
- Затем мы умножили числа 12 и 9, начиная с последнего числа в вопросе, на 16 и его степень. Помните, силы начинаются с нуля. 9) символ представляет собой «возведенный в степень».
 Следовательно, первые члены в скобках читаются как «16 в степени 0». Это означает, что шестнадцать были умножены сами на себя ноль раз. Все, что возведено в нулевую степень, равно 1. Следовательно, 9 умножались на единицу.
Следовательно, первые члены в скобках читаются как «16 в степени 0». Это означает, что шестнадцать были умножены сами на себя ноль раз. Все, что возведено в нулевую степень, равно 1. Следовательно, 9 умножались на единицу.
- Во второй скобке термин читается как «16 в степени 1». Число, возведенное в степень, равно этому числу. Следовательно, 12 умножили на 16. Умножив их, мы получили 192.
- Затем мы сложили результаты, чтобы получить количество десятичных эквивалентов, которое равнялось 201.
Что делать, если вы не хотите вручную преобразовывать шестнадцатеричные значения в десятичные?
Не беспокойтесь! У нас есть конвертер шестнадцатеричных чисел в целые, который поможет вам преобразовать шестнадцатеричные числа в десятичные онлайн. Калькулятор Prepostseo hex to decimal имеет продвинутый и быстрый интерфейс для преобразования шестнадцатеричных чисел в шестнадцатеричные. Кроме того, вы можете конвертировать десятичные числа в шестнадцатеричные с помощью нашего онлайн-конвертера десятичных чисел в шестнадцатеричные.


 также
также Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)
Например, «5A3h». При этом, если число начинается не с десятичной цифры, впереди ставится «0» (ноль): «0FFh» (25510)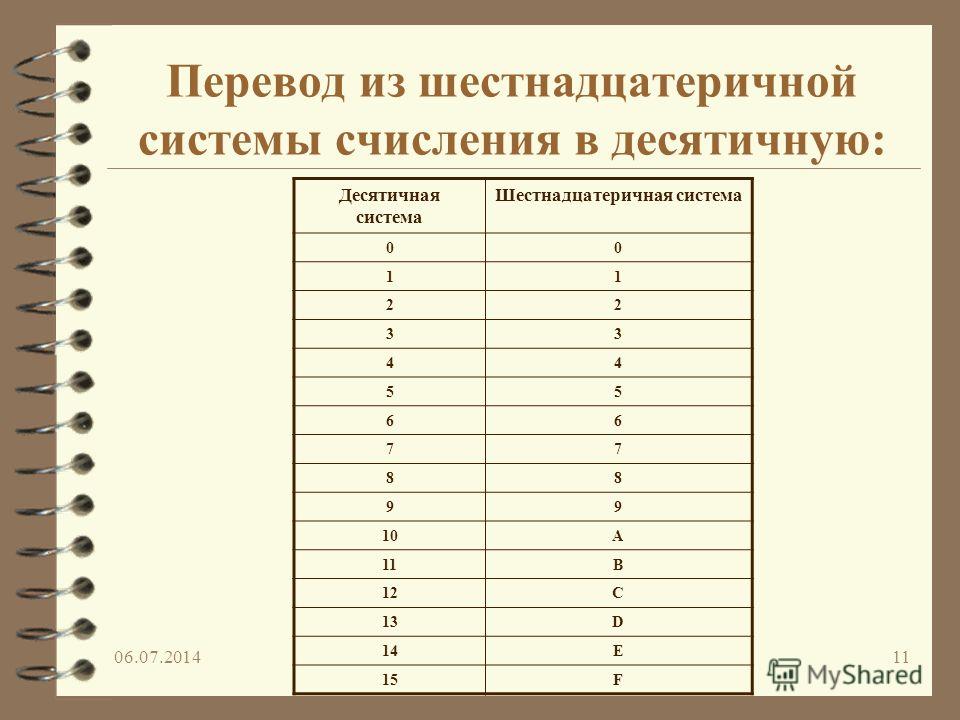
 также
также
 …………………………………………………………………………..
………………………………………………………………………….. …………………………………………………………………….
……………………………………………………………………. ………………………………………………………………………………………………
………………………………………………………………………………………………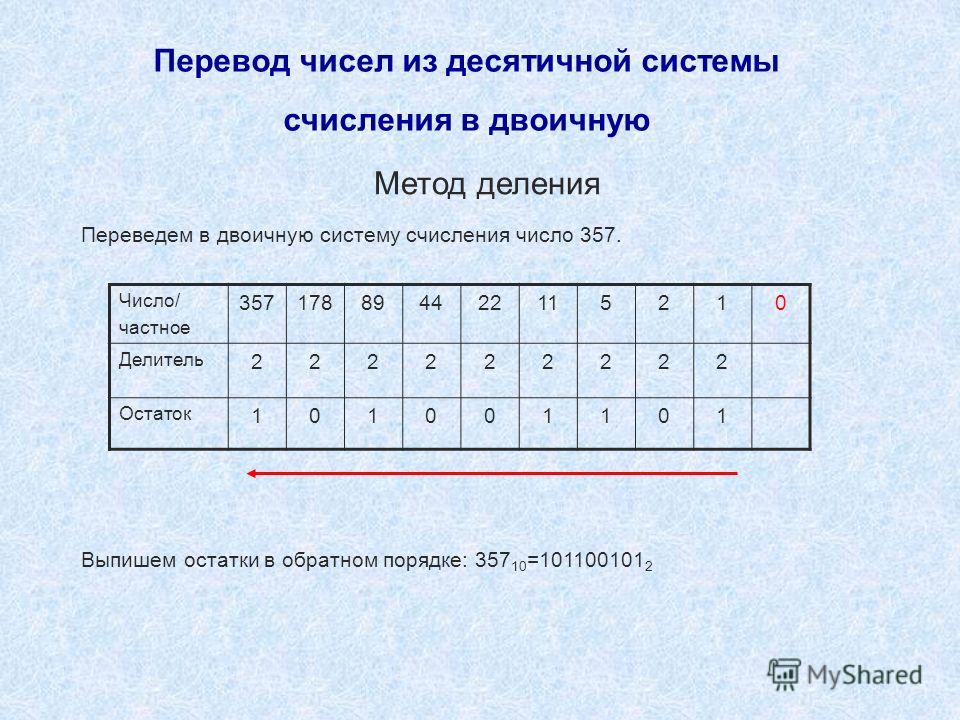 …………………………………………………………………………………………
………………………………………………………………………………………… ………………….
………………….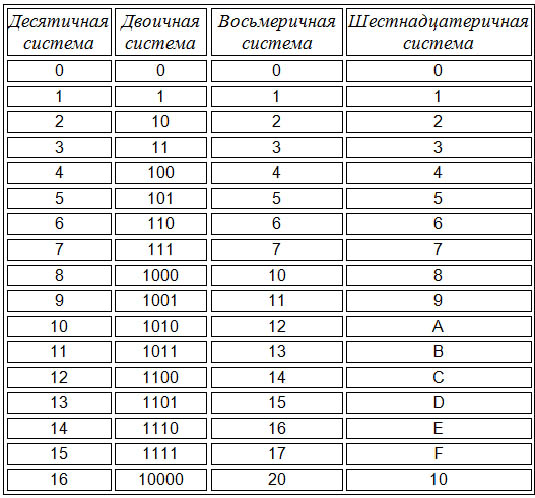 …………………………………………………
…………………………………………………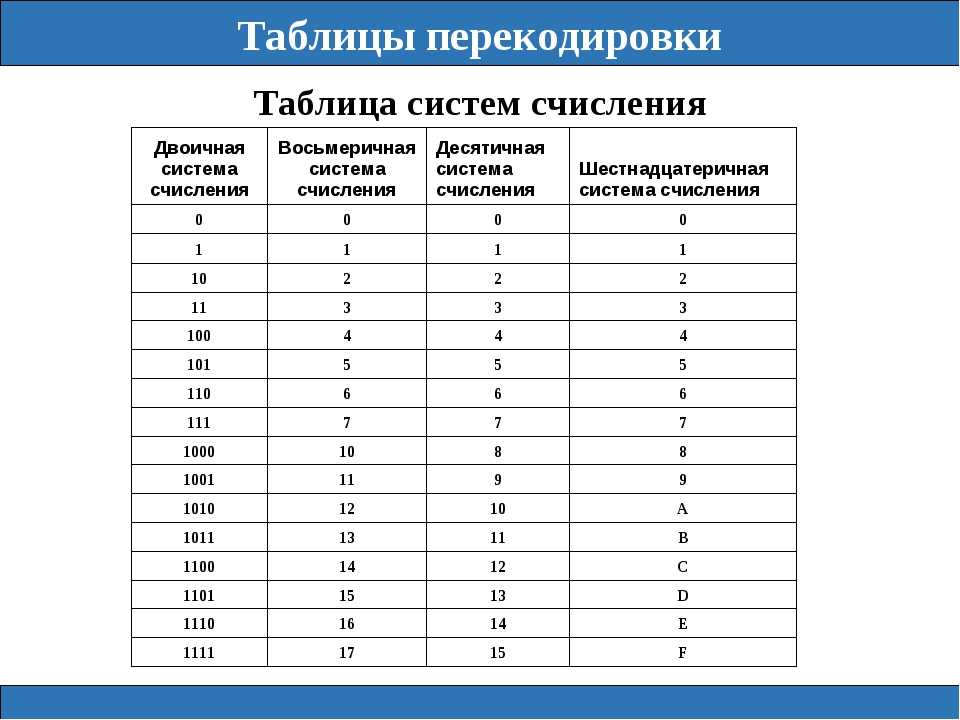 ………
……… …………………………………………….
……………………………………………. ………………………………………………………………..
……………………………………………………………….. …………………………………………………………………………………………….
…………………………………………………………………………………………….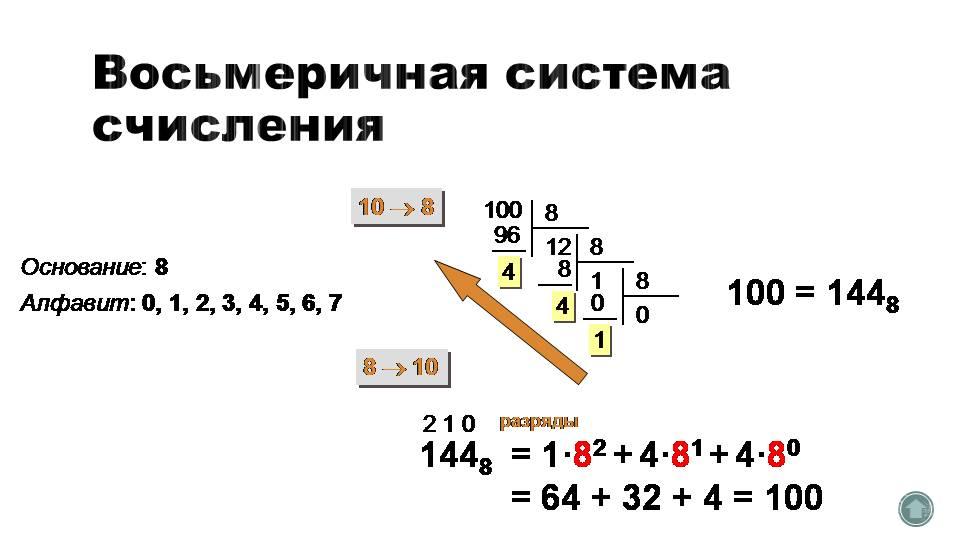 9. Операторы ввода-вывода…………………………………………………………………………………………………………………..
9. Операторы ввода-вывода………………………………………………………………………………………………………………….. 1. Операторы условия и перехода………………………………………………………………………………………………………….
1. Операторы условия и перехода…………………………………………………………………………………………………………. Циклические вычислительные процессы………………………………………………………………………………………………….
Циклические вычислительные процессы…………………………………………………………………………………………………. 5. Оператор прерывания цикла…………………………………………………………………………………………………………….
5. Оператор прерывания цикла…………………………………………………………………………………………………………….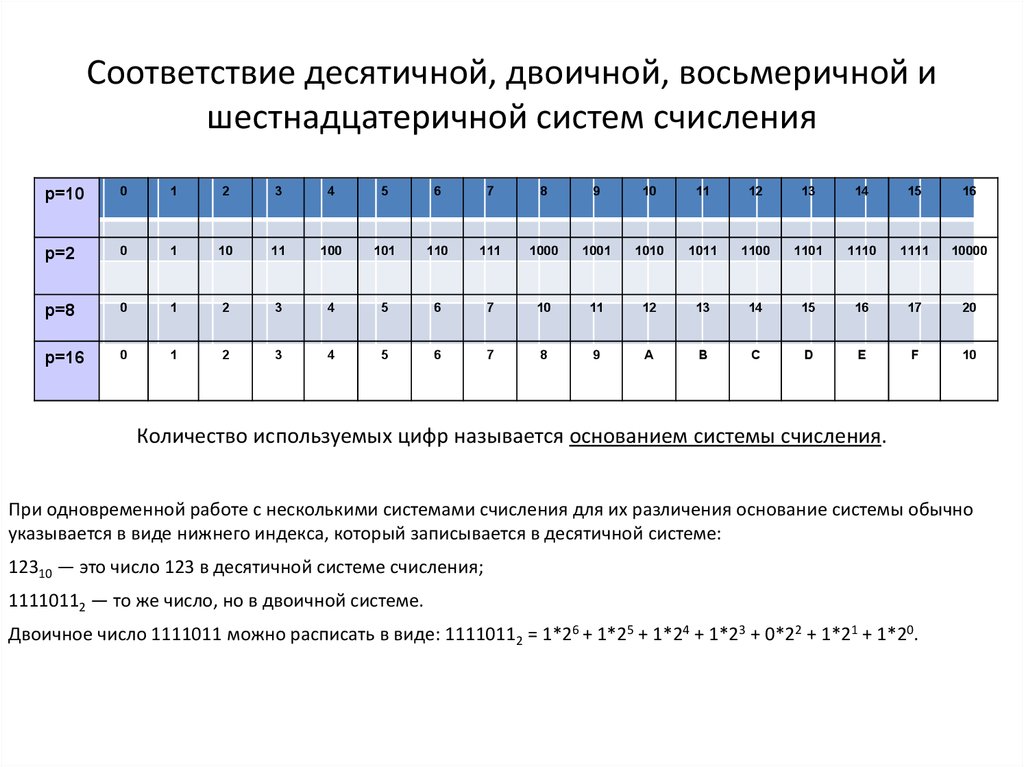 ………………………………………………………………………………………………………………….
…………………………………………………………………………………………………………………. ………………………………………………………………………………………………….
………………………………………………………………………………………………….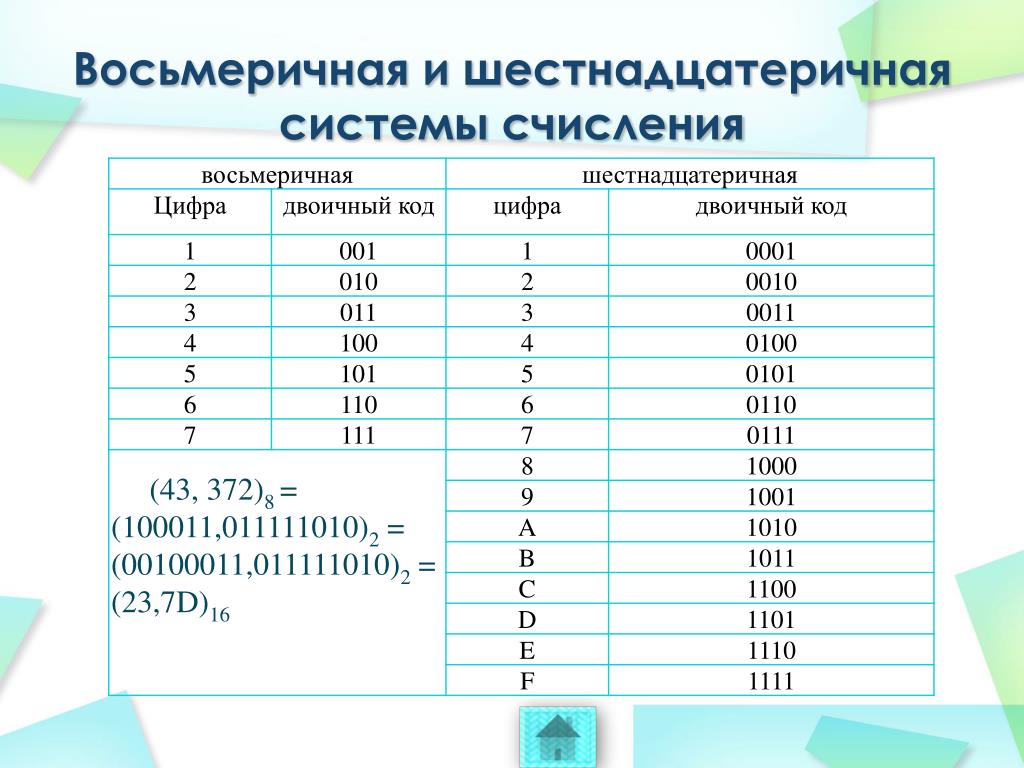 …………………………………………………………………
…………………………………………………………………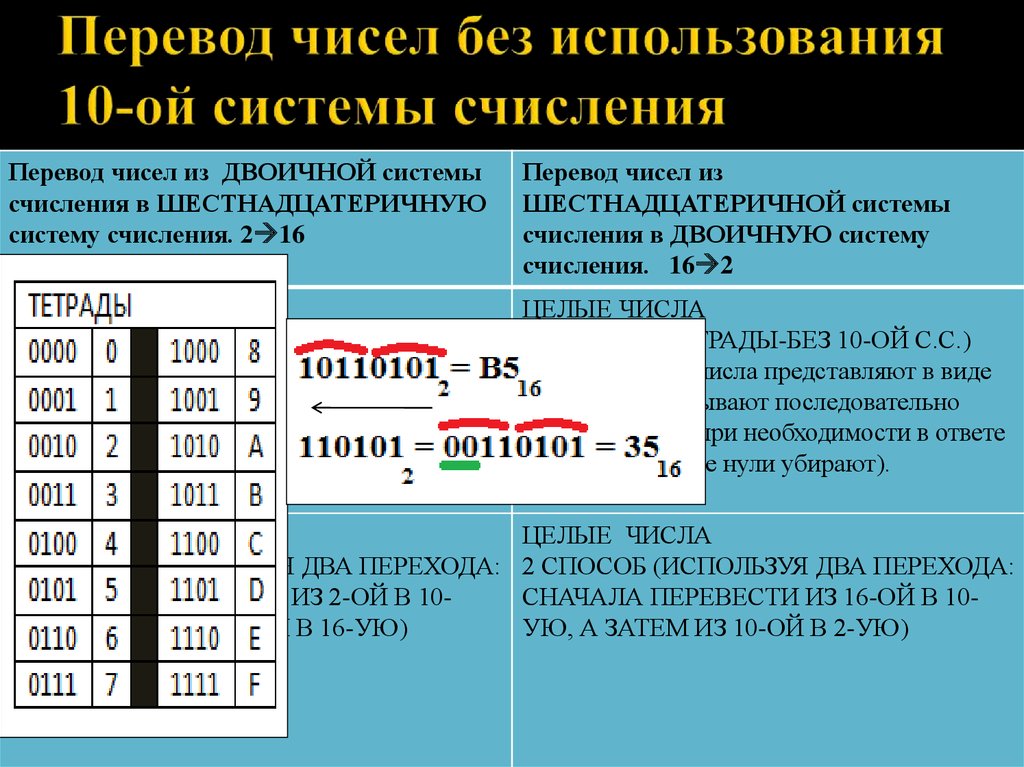 ………………………………………………………………………………………………………………
……………………………………………………………………………………………………………… …………………………………………………………
………………………………………………………… ……………………………………..
……………………………………..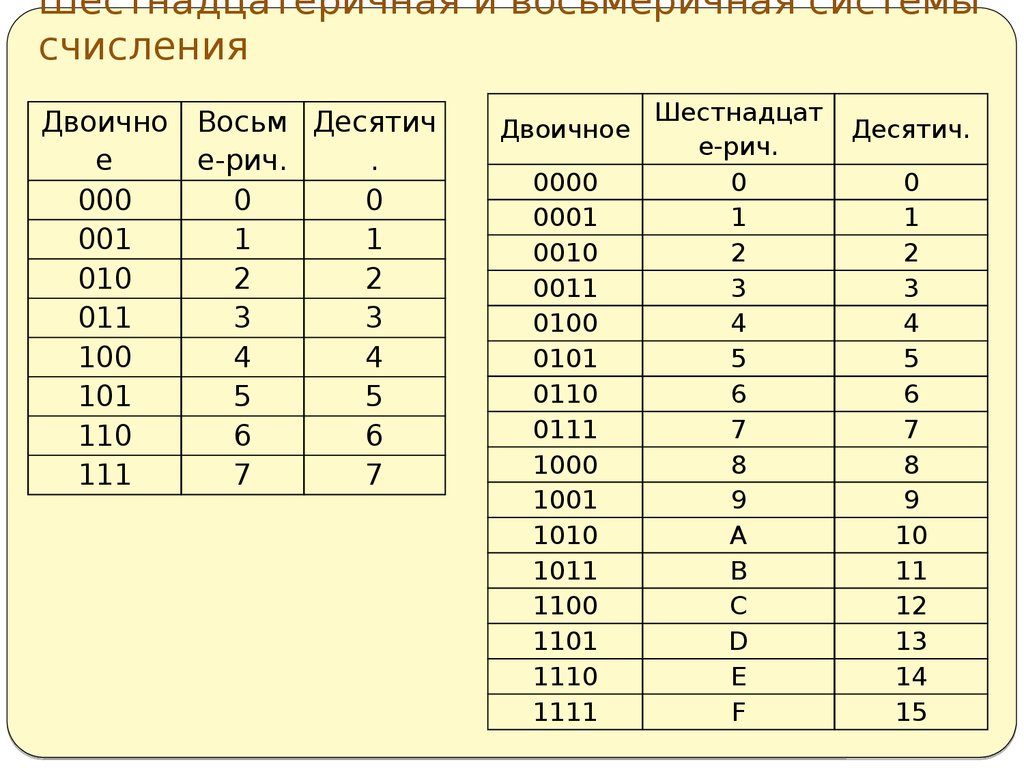 При преобразовании шестнадцатеричного в десятичное используется основание числа 16. В шестнадцатеричной системе счисления используется 16 цифр/алфавитов: цифры 0,1, 2, 3, 4, 5, 6, 7, 8, 9 и символы A, B, C, D, E, F, таким образом, имеющие основание 16. , Десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, и поэтому имеет основание 10.
При преобразовании шестнадцатеричного в десятичное используется основание числа 16. В шестнадцатеричной системе счисления используется 16 цифр/алфавитов: цифры 0,1, 2, 3, 4, 5, 6, 7, 8, 9 и символы A, B, C, D, E, F, таким образом, имеющие основание 16. , Десятичная система счисления использует десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, и поэтому имеет основание 10.
 Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксовКонвертер передачи данныхКонвертер типографских и цифровых изображенийКонвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
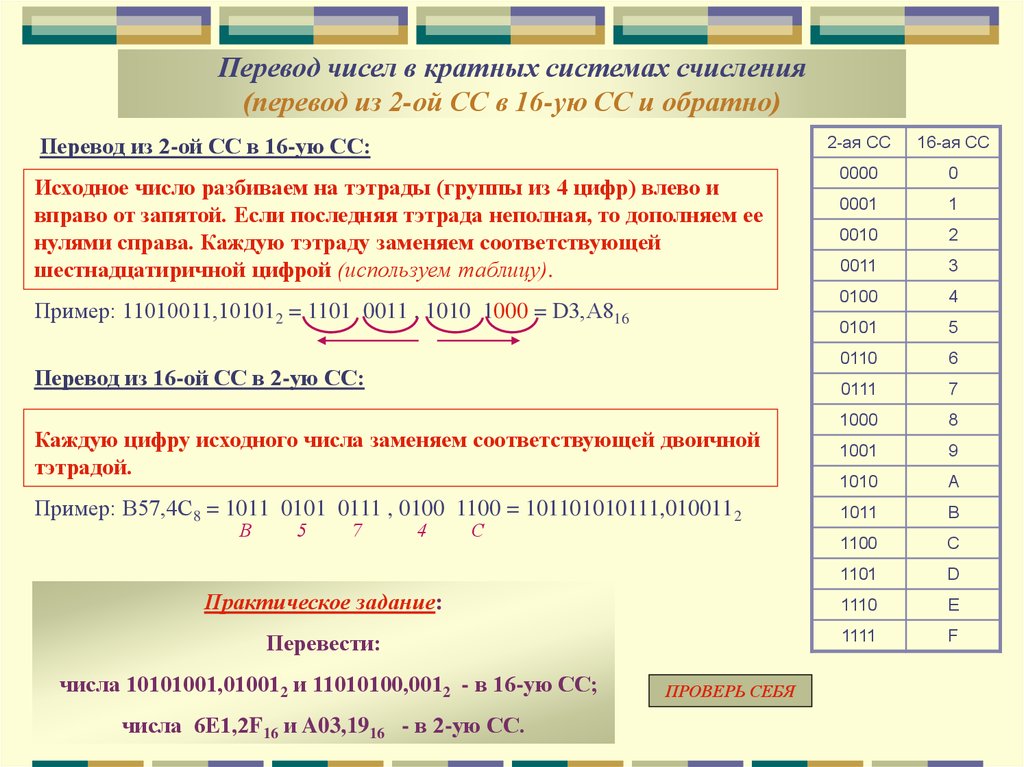
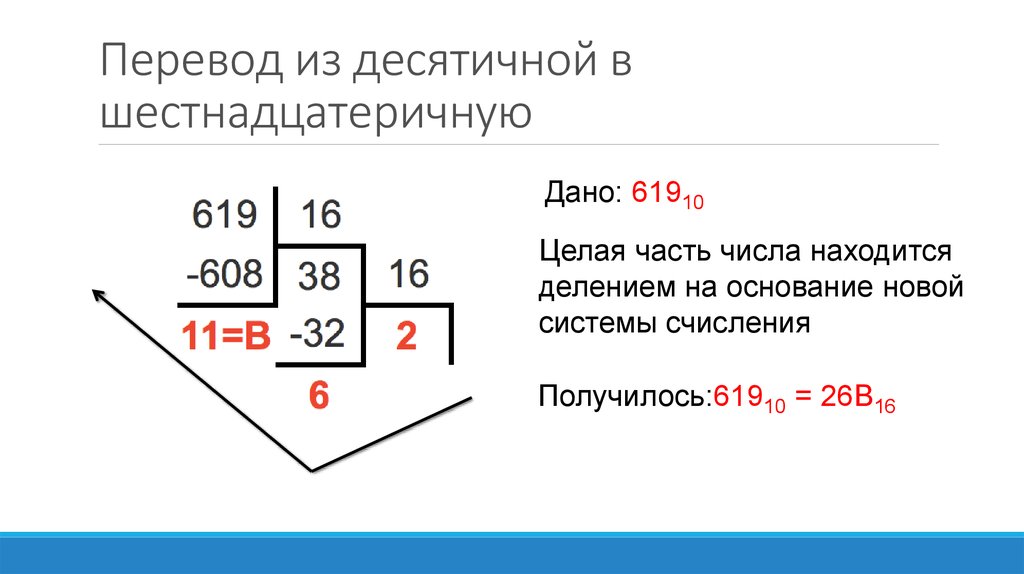
 Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа. Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT. Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.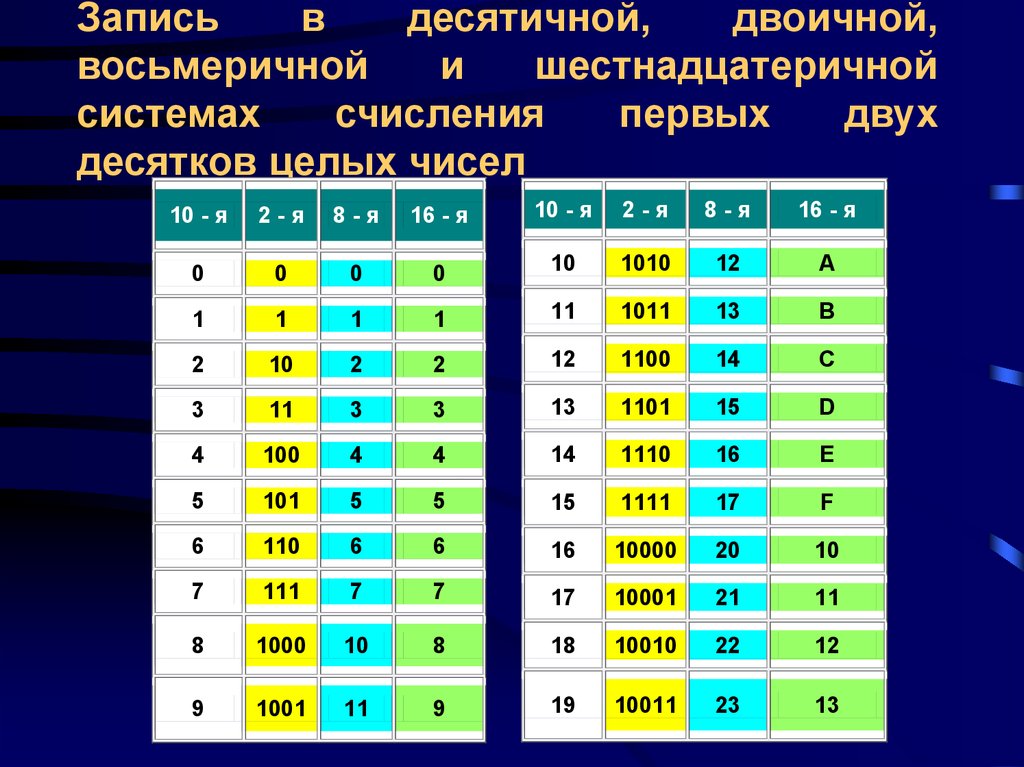 Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс. Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи. Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.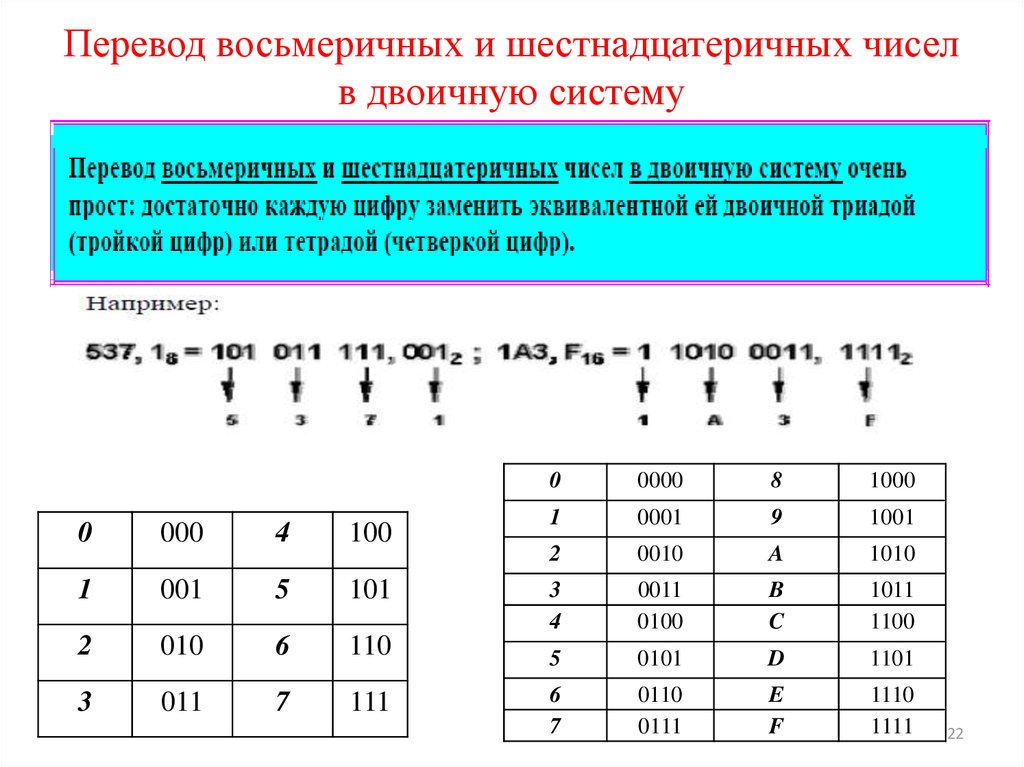 Например, в системе счисления 10 у нас есть следующее:
Например, в системе счисления 10 у нас есть следующее: Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
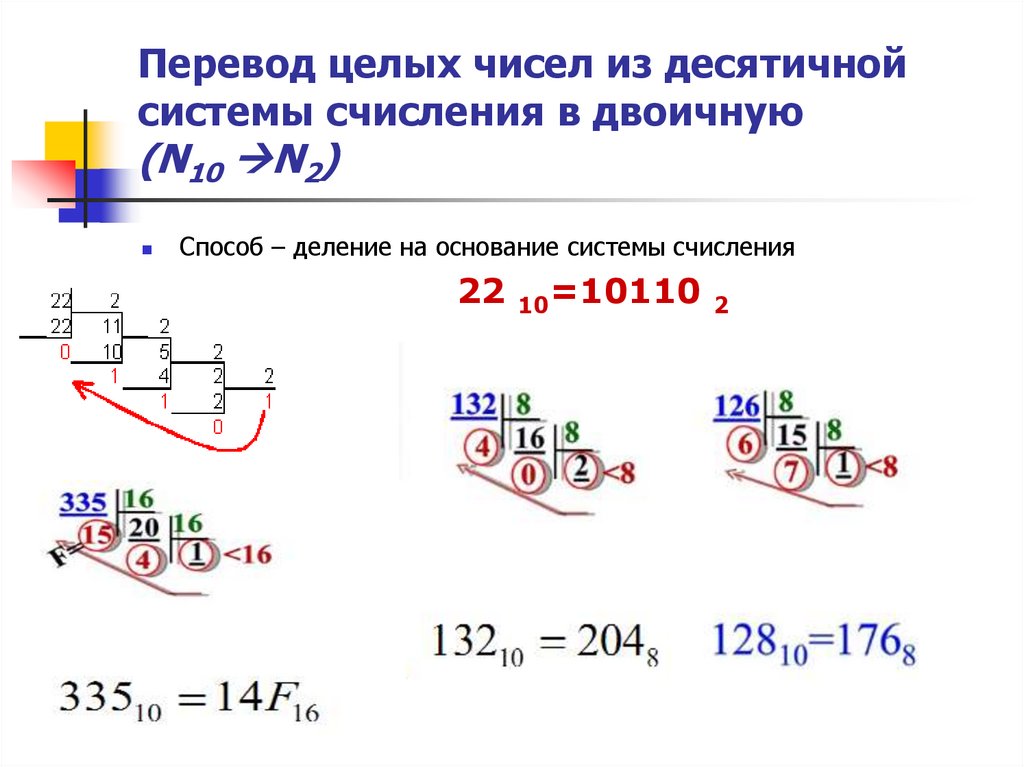 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
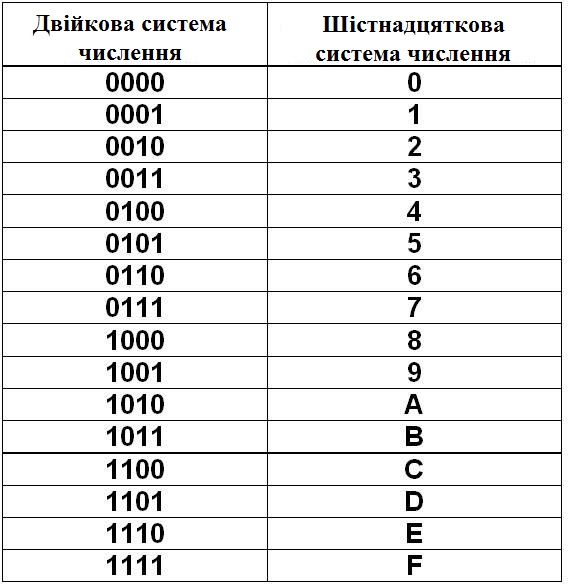

 В Японии другое несчастливое число — 9.0230 9 , что имеет то же произношение, что и «страдание».
В Японии другое несчастливое число — 9.0230 9 , что имеет то же произношение, что и «страдание». Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и иным образом оскорбляют тех, у кого есть 39в их номерном знаке, квартире или номере телефона. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию. Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят. в 36 с основанием
в 36 с основанием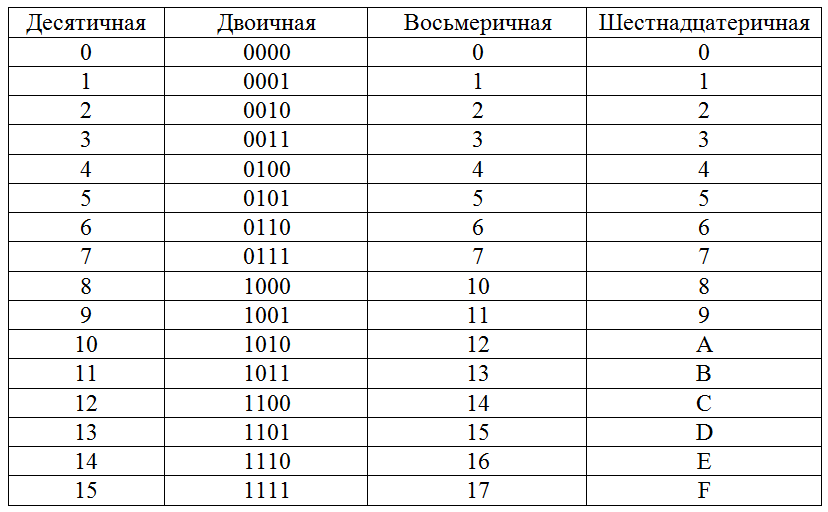



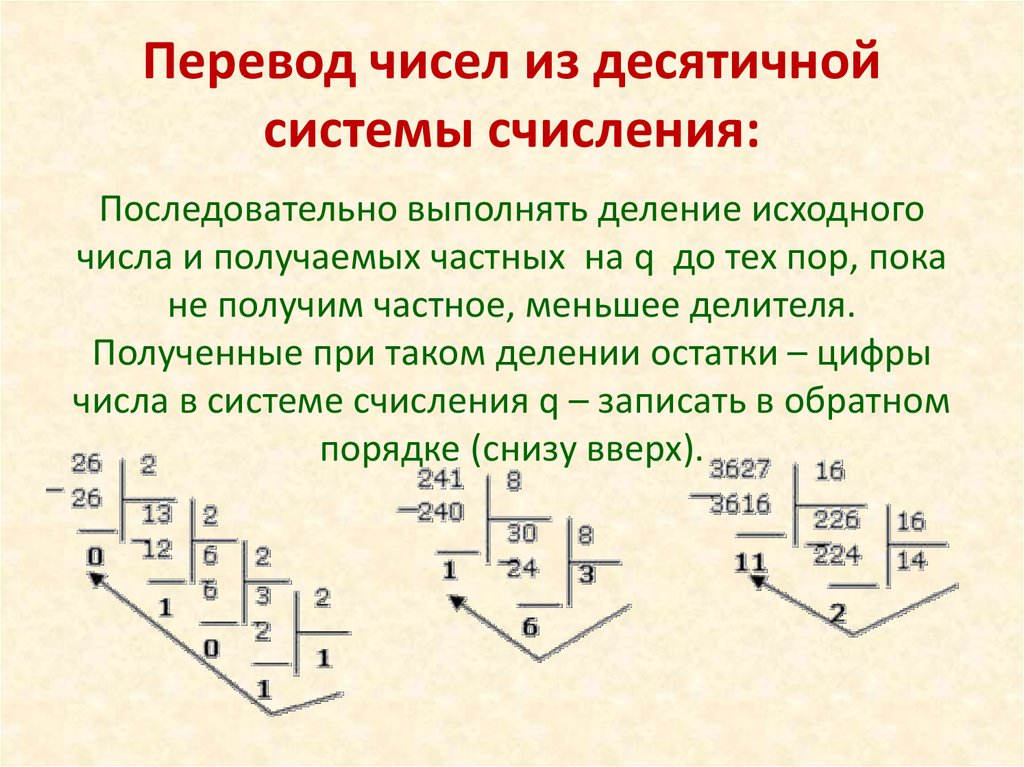 Поскольку в десятичной системе всего 10 цифр, дополнительные 6 цифр представлены первыми 6 буквами алфавита. Например, шестнадцатеричное значение B будет представлено в десятичной форме как 11, а двоичное значение — как 1011. Это простой способ выражения двоичных чисел в современных компьютерах, где байт обычно определяется как содержащий восемь двоичных цифр.
Поскольку в десятичной системе всего 10 цифр, дополнительные 6 цифр представлены первыми 6 буквами алфавита. Например, шестнадцатеричное значение B будет представлено в десятичной форме как 11, а двоичное значение — как 1011. Это простой способ выражения двоичных чисел в современных компьютерах, где байт обычно определяется как содержащий восемь двоичных цифр.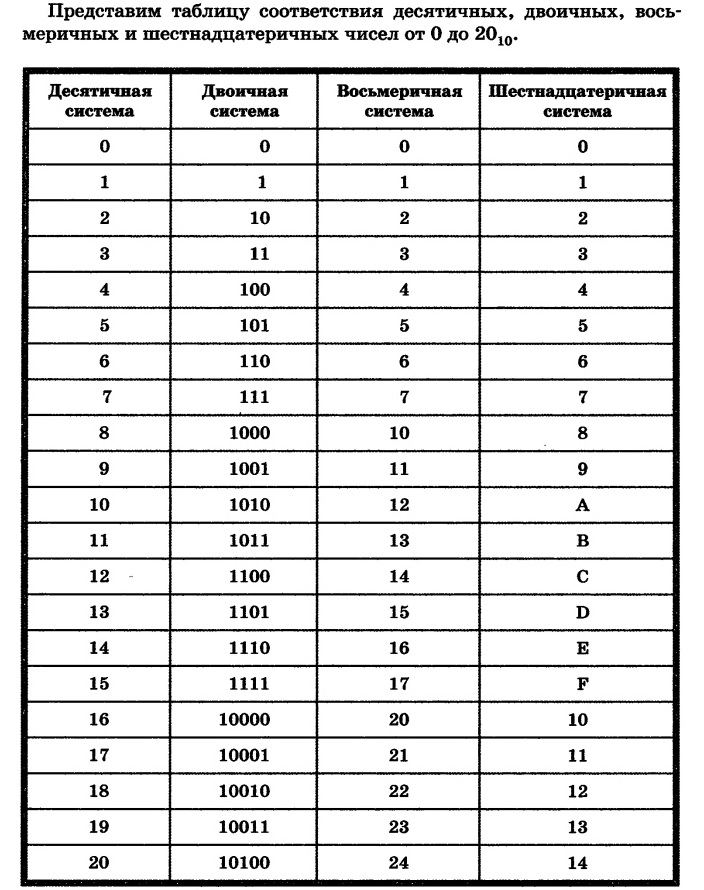
 10069
10069 1 +14×16 0 = 30
1 +14×16 0 = 30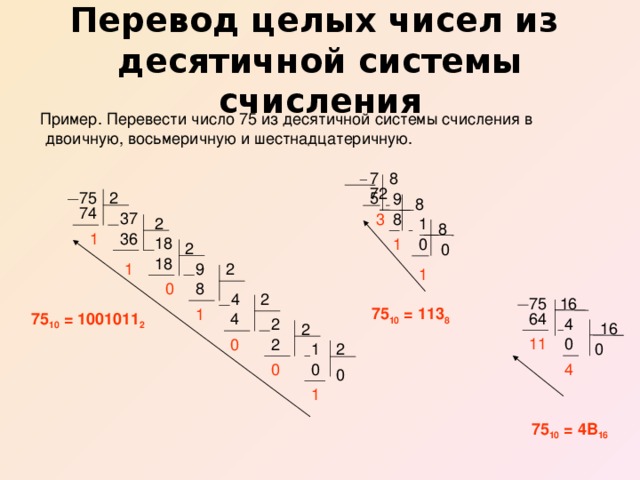

 Следовательно, первые члены в скобках читаются как «16 в степени 0». Это означает, что шестнадцать были умножены сами на себя ноль раз. Все, что возведено в нулевую степень, равно 1. Следовательно, 9 умножались на единицу.
Следовательно, первые члены в скобках читаются как «16 в степени 0». Это означает, что шестнадцать были умножены сами на себя ноль раз. Все, что возведено в нулевую степень, равно 1. Следовательно, 9 умножались на единицу.