Восьмеричная система счисления. Шестнадцатеричная система счисления. Правило перевода целых десятичных чисел в систему счисления с основанием
Для начала вспомним, что такое позиционная система счисления.
Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа.
На этом уроке мы с вами познакомимся с восьмеричной и шестнадцатеричной системами счисления, узнаем правила перевода из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот. Также изучим правило перевода целых десятичных чисел в систему счисления с основание q.
Начнём с восьмеричной системы счисления.
Восьмеричная система счисления – это позиционная система счисления с основанием 8. В алфавит восьмеричной системы счисления входят цифры от 0 до 7 включительно.
Мы с вами уже узнали, как
записывается развёрнутая форма записи числа. Она выглядит следующим образом:
Она выглядит следующим образом:
Из этой формулы можно вывести развёрнутую форму записи целого восьмеричного числа:
Посмотрим, как это выглядит на примере. Нам дано следующее число: 41538. Давайте распишем его по формуле. Ставим равно. Для начала проставим над цифрами степени для восьмёрки справа налево, начиная с нуля.
После равно пишем первую цифру 4 и умножаем её на 83. Ставим плюс. Далее запишем вторую цифру 1, умноженную на 82. Снова ставим плюс. Записываем цифру 5 и умножаем её на 81. И плюс последняя цифра 3, умноженная на 80.
Мы с вами расписали исходное число в развёрнутой форме целого восьмеричного числа.
Правило для перевода из восьмеричной системы счисления в десятичную
Давайте переведём наше
число из восьмеричной системы счисления в десятичную. Оно уже у нас расписано в
развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем
степени числа восемь.
Оно уже у нас расписано в
развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем
степени числа восемь.
Теперь осталось всё посчитать. Ставим равно.
Мы получили число 2 155. Это число представлено в десятичной системе счисления.
А теперь давайте переведём число 125 из десятичной системы счисления в восьмеричную.
Это правило похоже на перевод из десятичной в двоичную систему счисления, но в данном случае мы будем делить на число 8.
Само правило звучит следующим образом: для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего.
Переведём наше число.
Делим его на 8. Получим 15, а в остатке 5. Обведём остаток в кружок.
Теперь число 15 делим на 8. Получим 1. В остатке 7. Снова обведём это число.
1 больше 0. Значит делим число 1 на 8. Получим 0. А в остатке 1. Обводим наш остаток.
Теперь осталось после равно записать все остатки справа налево.
12510 = 1758
Мы перевели число 125 в восьмеричную систему счисления.
А теперь давайте узнаем, что такое шестнадцатеричная система счисления.
Шестнадцатеричная система счисления – это позиционная система счисления с основанием 16. В алфавит этой системы входят цифры от 0 до 9 и буквы А, B, C, D, Е, F. Эти буквы обозначают в десятичной системе числа от 10 до 15 соответственно.
Для представление целого шестнадцатеричного числа в развёрнутой форме записи нужно использовать следующую формулу:
Распишем предоставленное
шестнадцатеричное число A6E
в развёрнутой форме.
Ставим знак равно. Снова проставим степени для шестнадцати над цифрами нашего числа справа налево.
Пишем букву А и умножаем её на 162. Ставим плюс. Пишем цифру 6, умноженную на 161 и прибавляем букву Е, умноженную на 160.
Для перевода целого шестнадцатеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи, заменить буквы на соответствующие им цифры в десятичной системе счисления и вычислить значение получившегося выражения.
Наше число уже записано в развёрнутой форме. Нам осталось заменить буквы на соответствующие им десятичной системе числа и сосчитать. Ставим равно. Буква А соответствует числу 10 в десятичной системе счисления. Запишем число 10 и умножаем его на 162.
Ставим плюс и перепишем число 6, умноженное на 161.
Снова ставим плюс. Букве
Е соответствует число 14 в десятичной системе счисления.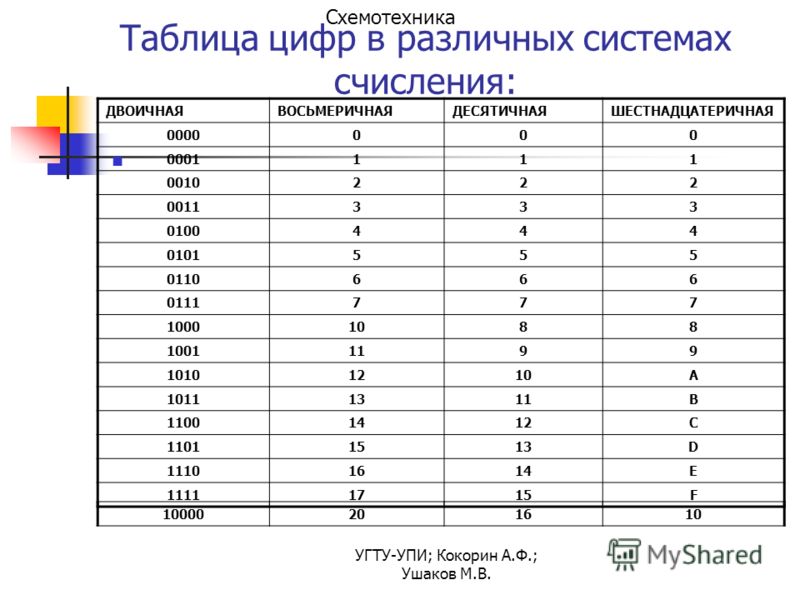
Прежде, чем всё это сосчитать снова обратимся к математике и распишем степени числа шестнадцать.
162 = 256.
162 ·10 = 2 560
Ставим плюс.
161 = 16.
161 · 6 = 96.
Снова ставим плюс.
160 = 1.
160 · 14 = 14.
Ставим равно.
Мы получили 2 670 в десятичной системе счисления.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего, при необходимости, заменяя цифры на соответствующие им буквы в шестнадцатеричной системе счисления.
Переведём число 350 в
шестнадцатеричную систему счисления.
Делим наше число на 16, получим 21, остаток 14. Выделим его.
Делим 21 на 16. Получим 1 и 5 в остатке. Обводим наш остаток.
1 больше 0. Делим 1 на 16, получим 0 и 1 в остатке. И снова выделяем остаток 1.
Теперь запишем все числа справа налево. Записываем следующие цифры: 1, 5.
35010 = 15.
Так как в шестнадцатеричной системе счисления числу 14 соответствует буква Е, то пишем её после 5.
35010 = 15E16.
Мы с вами перевели число 350 в шестнадцатеричную систему счисления.
Вы, наверное, заметили, что все правила перевода целого десятичного числа в любую систему счислению с другим основанием похожи.
Давайте изучим общее правило перевода целых десятичных чисел в любую систему счисления с основание q.
Для того, чтобы перевести целое десятичное число в систему счисления с основанием q нужно:
1. Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
2. Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
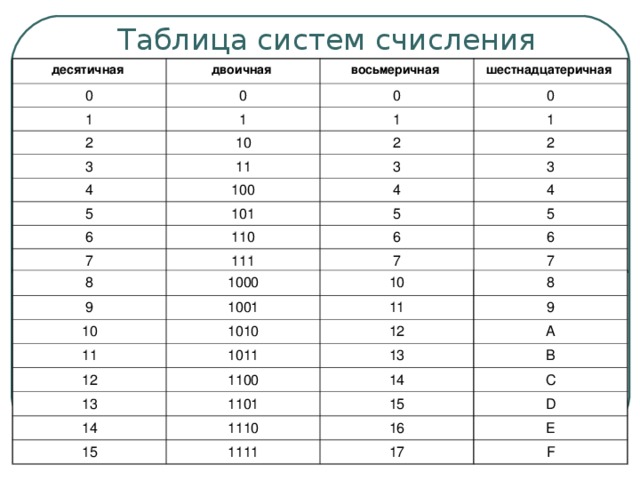
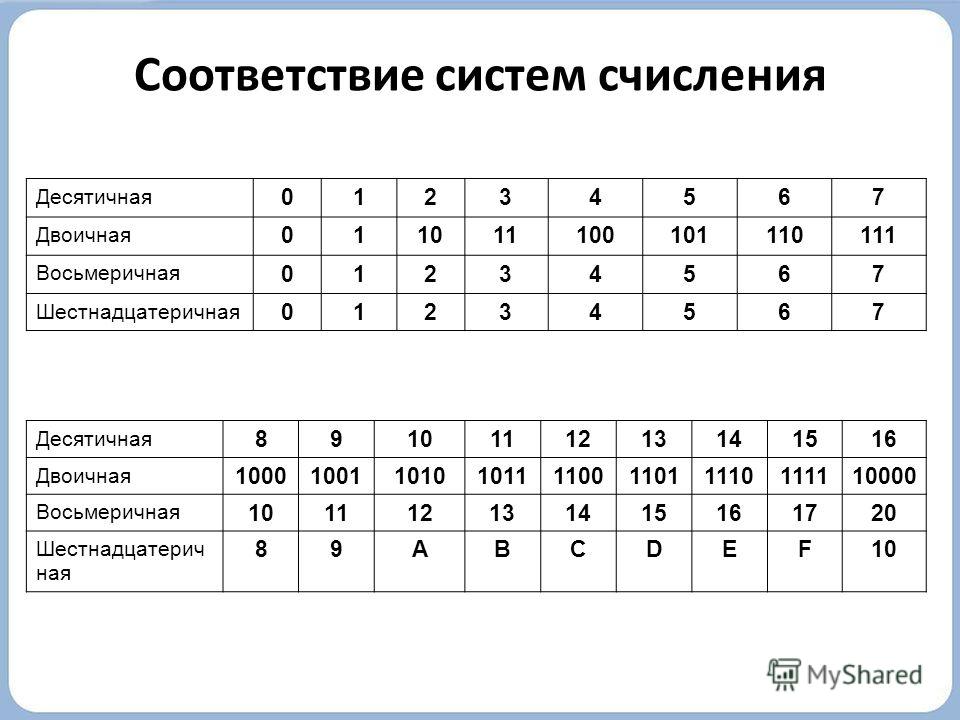
Вам предоставлена таблица соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20. Числа от 0 до 20 подразумевают собой десятичную систему счисления.
А теперь давайте выполним задание.
Переведём одно и то же число 247 в двоичную, восьмеричную и шестнадцатеричную системы счисления и сравним получившиеся числа.
Для начала переведём из
десятичной в двоичную систему счисления. Для этого будем использовать таблицу,
так как число большое. В ней будет две строки. В первую строку первого столбца
запишем наше число.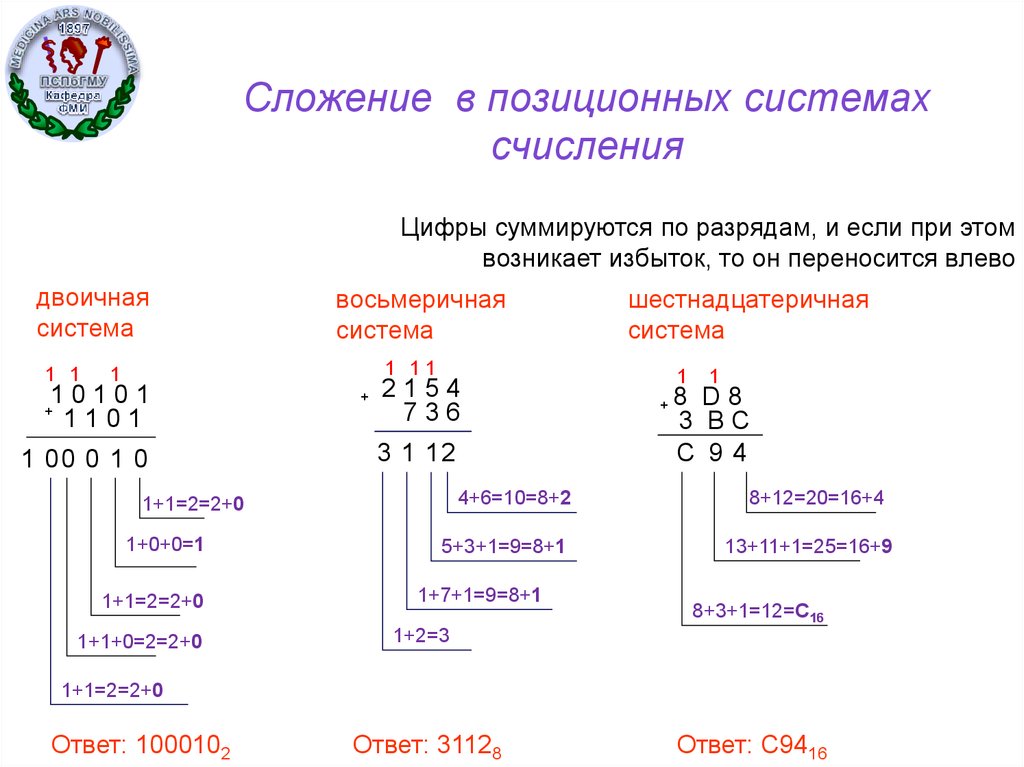
Делим его на 2. Получим 123 и 1 в остатке. 123 запишем во вторую ячейку первой строки, а 1 – в первую ячейку второй строки.
Далее 123 разделить на 2 и получим 61 и 1 в остатке. 61 запишем после числа 123, а остаток один под число 123.
Далее 61 : 2 = 30 и остаток – 1. Запишем их в таблицу.
30 : 2 = 15, а остаток равен 0. Снова запишем их в таблицу в соответствующие ячейки.
При делении 15 на 2 получим 7 и 1 в остатке. Снова заполняем таблицу.
Далее 7 : 2 = 3 и 1 в остатке. Запишем в соответствующие ячейки наши числа.
3 :2 = 1 и 1 в остатке. Занесём данные в таблицу.
И делим 1 на 2, получим 0 и 1 в остатке. 0 писать не будет. Занесём только наш остаток в ячейку.
А теперь соберём все наши цифры в число в двоичной системе. Записываем их поочерёдно справа налево.
24710 = 111101112.
А сейчас переходим к
переводу в восьмеричную систему счисления числа 247.
Делим 247 на 8. Получим 30 и 7 в остатке. Обведём остаток от деления.
Далее 30 делим на 8, получим 3 и 6 в остатке. Выделяем остаток.
3 делим на 8, получаем 0 и 3 в остатке. Обводим остаток.
Теперь запишем все остатки справа налево и получим число в восьмеричной системе счисления.
24710 = 3678.
Нам осталось перевести наше число в шестнадцатеричную систему счисления. Делим 247 на 16. Получим 15 и 7 в остатке. Обведём остаток.
Теперь делим 15 на 16, получим 0. А остаток от деления равен 15. Выделим его.
А сейчас запишем наши цифры справа налево в соответствии с алфавитом шестнадцатеричной системы счисления. Число 15 — это буква F в этой системе счисления. Ставим её на первое место. А затем пишем число 7.
24710 = F716
Задание выполнено. Давайте сравним все наши получившиеся числа.
Как можем видеть – все
они одинаковые, но записаны разными цифрами, потому что они представлены в
различных системах счисления.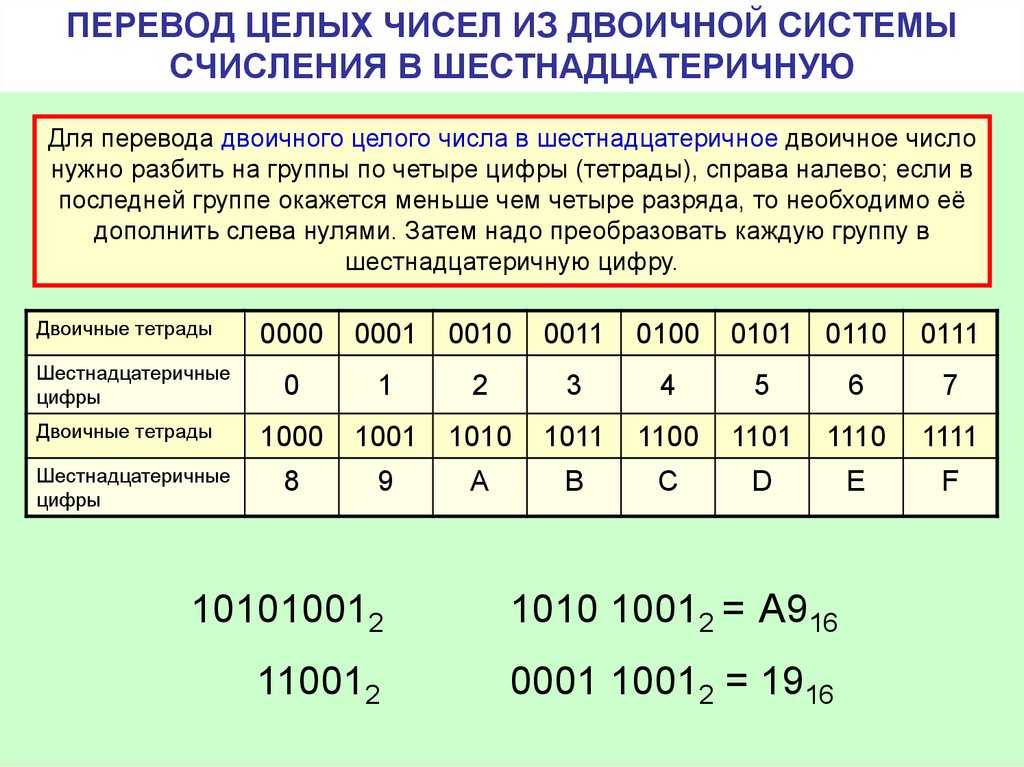 Это можно увидеть, если обратить внимание на
основания чисел.
Это можно увидеть, если обратить внимание на
основания чисел.
А теперь пришла пора довести итоги урока. Сегодня мы узнали, что такое восьмеричная и шестнадцатеричная системы счисления, какие действия нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q.
Также мы сегодня научились переводить числа из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.
Системы счисления: двоичная, восьмеричная, шестнадцатеричная — 8 КЛАСС ► Информатика в школе и дома
Оглавление:
- 1 Урок: Системы счисления: двоичная, восьмеричная, шестнадцатеричная
- 1.1 Общие сведения о системах счисления
- 1.2 Системы счисления: двоичная, восьмеричная, шестнадцатеричная
- 1.3 Рекомендованный список литературы
Want create site? Find Free WordPress Themes and plugins.
Общие сведения о системах счисленияС древних времен в практической деятельности человека часто возникала потребность счета и измерения. Результаты счета предметов выражались вначале весьма примитивно: зарубки на палочках, узелки на веревках и др. С развитием письменности человек начал отображать с помощью знаков (записывать) информацию о количестве предметов на подручных материалах: глиняных табличках, папирусе, бересте и др. Таким образом, для обозначения чисел стали использовать знаки.
Результаты счета предметов выражались вначале весьма примитивно: зарубки на палочках, узелки на веревках и др. С развитием письменности человек начал отображать с помощью знаков (записывать) информацию о количестве предметов на подручных материалах: глиняных табличках, папирусе, бересте и др. Таким образом, для обозначения чисел стали использовать знаки.
Способ записи чисел с помощью письменных знаков называют системой счисления. Знаки, с помощью которых записываются числа, называют цифрами, а их совокупность — алфавитом системы счисления.
Одной из наиболее древних являлась египетская иероглифическая система счисления. В ней числа представлялись в виде отдельных знаков, например:
Так, число означало:
100+10+10+1+1+1=123.
Существовали системы счисления, в которых для записи чисел использовались буквы алфавита, например старославянская система счисления.
Десятичная система счисления зародилась в Индии приблизительно в 5 в. , затем она появилась в арабских рукописях. Из арабских рукописей эта система пришла в Европу в 9-12 вв. Поэтому современную десятичную систему счисления называют арабской.
, затем она появилась в арабских рукописях. Из арабских рукописей эта система пришла в Европу в 9-12 вв. Поэтому современную десятичную систему счисления называют арабской.
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример:
У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, C, D, M.
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
- унарная система;
- непозиционные системы;
- позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления.
В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта.
Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта.
Унарную систему ещё называют системой бирок.
Непозиционными называются такие системы счисления, в которых каждый знак (цифра) в записи любого числа имеет одно и то же значение и не зависит от своего расположения в числе.
В большинстве непозиционных систем счисления числа образуются путём сложения узловых чисел.
В непозиционной римской системе счисления для обозначения чисел используются следующие знаки:
Например, число записанное в римской системе счисления, в десятичной системе счисления означает: 10+10+5+1+1+1=28.
Древнеегипетская и старославянская система также являются непозиционными.
Позиционными называют такие системы счисления, в которых значение каждого знака (цифры) в записи любого числа зависит от расположения (позиции) этого знака в числе.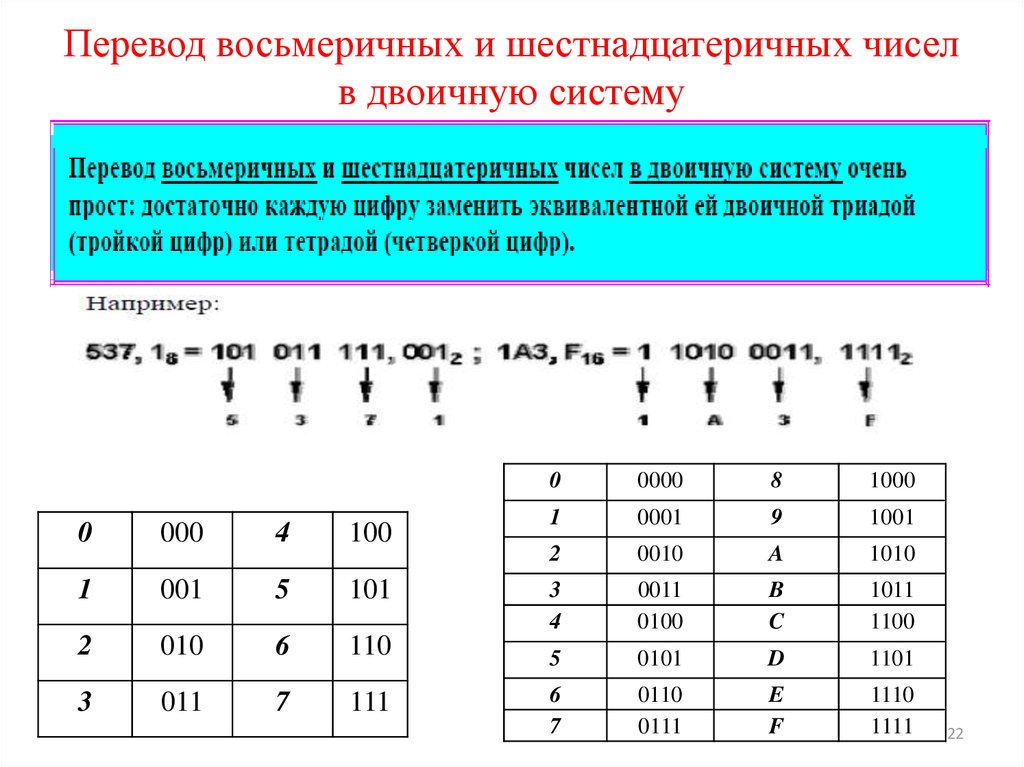 Количество цифр, используемых для записи чисел в позиционной системе счисления, называется ее основанием.
Количество цифр, используемых для записи чисел в позиционной системе счисления, называется ее основанием.
Мы используем позиционную десятичную систему счисления. Основанием этой системы является число 10.
Для записи любого числа в десятичной системе счисления используют десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Комбинируя эти цифры, можно записывать любые числа.
Например, цифры числа 737 в десятичной системе счисления являются коэффициентами его записи в виде суммы степеней числа 10:
737=7⋅102+3⋅101+7⋅100=7⋅100+3⋅10+7⋅1
Из этого примера видно, что цифра 7 в зависимости от своей позиции в этом числе означает и 7 сотен, и 7 единиц, а цифра 3 означает три десятка.
Пример:
Рассмотрим десятичное число 13456,7. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развернутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
1⋅104+3⋅103+4⋅102+5⋅101+6⋅100+7⋅10−1.
Системы счисления: двоичная, восьмеричная, шестнадцатеричнаяДля кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.
Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.
Двоичной системой счисления называется позиционная система счисления с основанием 2.
Для записи чисел в ней использовали только две цифры: 0 и 1.
Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.
Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием 2, например:
1012=1⋅22+0⋅21+1⋅20.
В десятичной системе счисления это число будет выглядеть так:
1012=4+0+1=5.
Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём десятичное число 13 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Получили 1310=11012.
Пример:
Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
224 | 112 | 56 | 28 | 14 | 7 | 3 | 1 |
1 | 1 | 1 |
22410=111000002.
Восьмеричной системой счисления называется позиционная система счисления с основанием 8.
Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в восьмеричной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём восьмеричное число 154368 в десятичную систему счисления.
154368=1⋅84+5⋅83+4⋅82+3⋅81+6⋅80=694210
Пример:
Переведём десятичное число 94 в восьмеричную систему счисления.
9410=1368
Шестнадцатеричной системой счисления называется позиционная система счисления с основанием 16.
Для записи чисел в шестнадцатеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.
Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.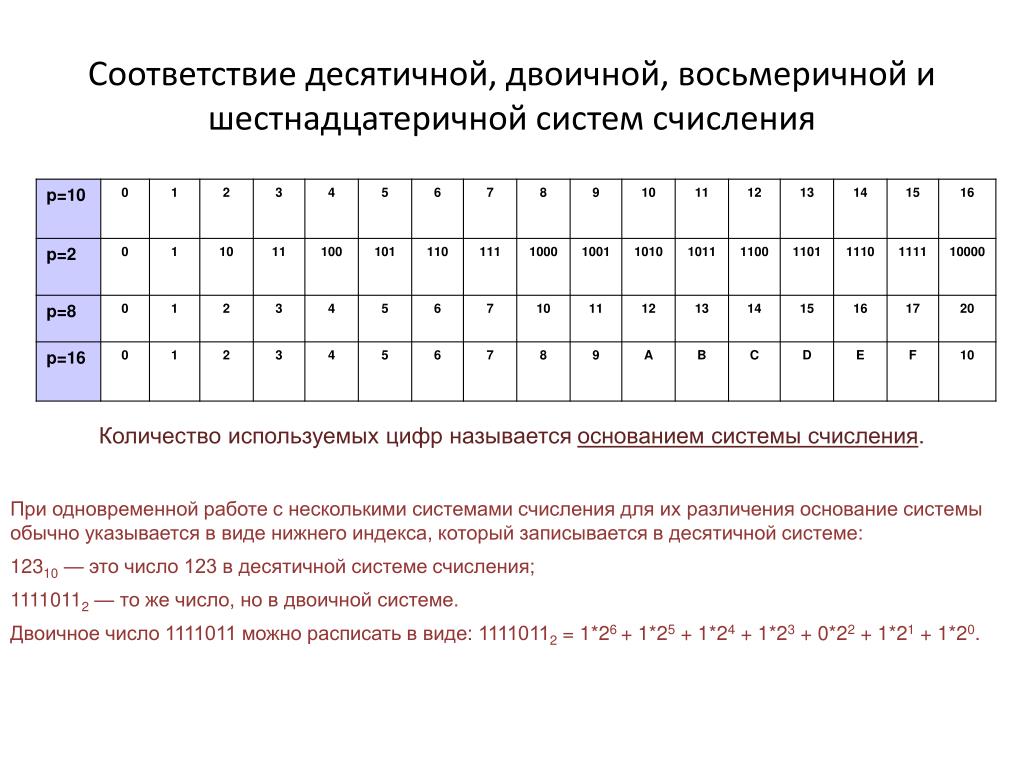
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример:
Переведём шестнадцатеричное число 2A7 в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием 16:
2A716=2⋅162+10⋅161+7⋅160=512+160+7=679.
Пример:
Переведём десятичное число 158 в шестнадцатеричную систему счисления.
15810=9E16.
Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.
Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль.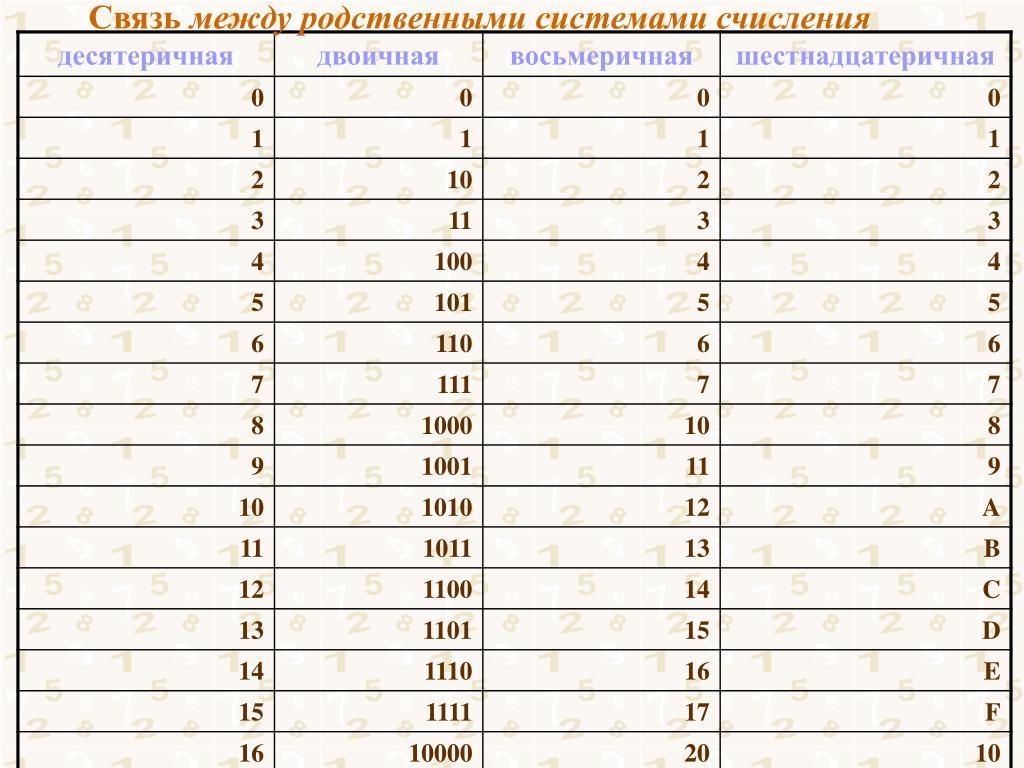 Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
Босова Л.Л. Информатика — Учебник для 8 класса. – М.: БИНОМ. Лаборатория знаний
Did you find apk for android? You can find new Free Android Games and apps.
Метки: МАТЕМАТИЧЕСКИЕ ОСНОВЫ ИНФОРМАТИКИДвоичная, восьмеричная, шестнадцатеричная системы счисления.
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления, числа записываются с помощью двух символов (0 и 1).
Восьмери́чная
систе́ма счисле́ния — позиционная целочисленная система
счисления с основанием 8. Для представления
чисел в ней используются цифры от 0 до
7.
Восьмеричная система часто используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триплеты двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления по целочисленному основанию 16. Обычно в качестве шестнадцатеричных цифр используются десятичные цифры от 0 до 9 и латинские буквы от A до F для обозначения цифр от 1010 до 1510, то есть (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F).
Широко
используется в низкоуровневом
программировании и компьютерной
документации, поскольку в современных
компьютерах минимальной единицей памяти
является 8-битный байт, значения которого
удобно записывать двумя шестнадцатеричными
цифрами. Такое использование началось
с системы IBM/360, где вся документация
использовала шестнадцатеричную систему,
в то время как в документации других
компьютерных систем того времени (даже
с 8-битными символами, как, например,
PDP-11 или БЭСМ-6) использовали восьмеричную
систему.
Такое использование началось
с системы IBM/360, где вся документация
использовала шестнадцатеричную систему,
в то время как в документации других
компьютерных систем того времени (даже
с 8-битными символами, как, например,
PDP-11 или БЭСМ-6) использовали восьмеричную
систему.
Правило деления-умножения
Для преобразования целых чисел используется правило деления, а для преобразования правильных дробей — правило умножения. Для преобразования смешанных чисел используются оба правила соответственно для целой и дробной частей числа.
Проверим, не ошиблись ли мы в процессе преобразования? Для этого преобразуем получившееся двоичное
число в десятичную систему по обычной формуле разложения:1248.
1×82+7×81+4×80=6410+5610+410=124
Таблица
1. Таблица соответствия восьмеричных цифр
и двоичного кода
Таблица соответствия восьмеричных цифр
и двоичного кода
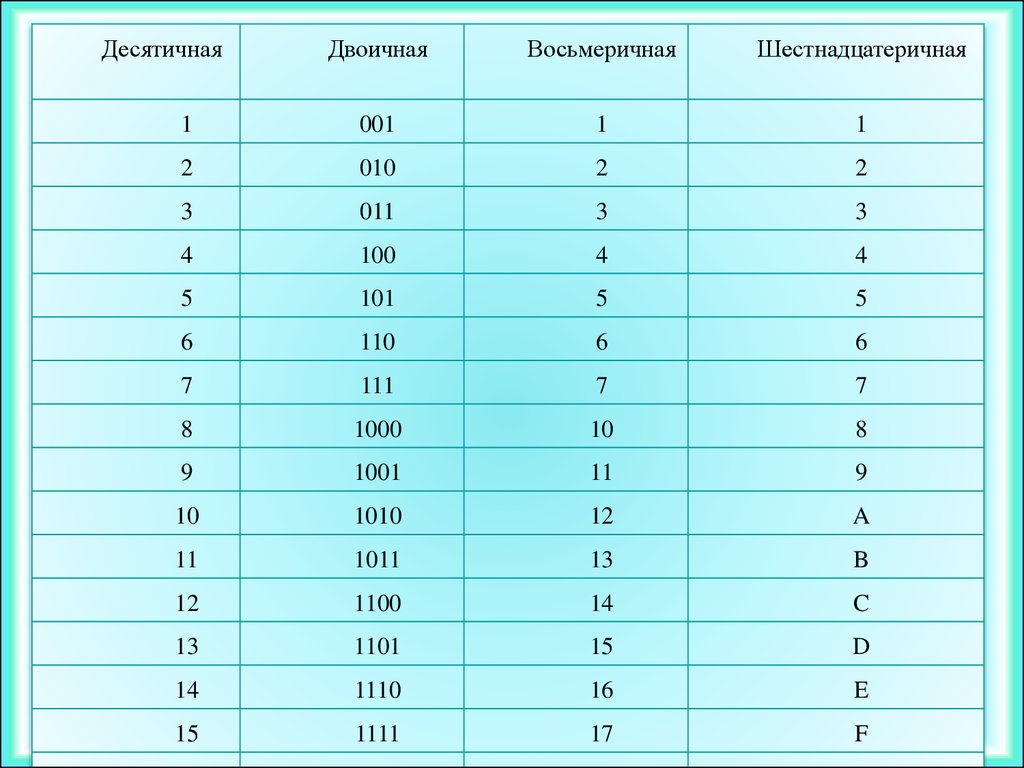
Десятичныйэквивалент | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Двоичныйкод | 0 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Восьмеричнаяцифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Используя
эту таблицу можно просто заменить каждую
восьмеричную цифру тремя двоичными
битами. Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 1748 в двоичную форму при помощи таблицы:
Три двоичных бита обычно называют
триадой или трибитом. Теперь давайте
переведём восьмеричное число 1748 в двоичную форму при помощи таблицы:
Аналогично можно выполнить перевод числа из двоичной системы в восьмеричную. Для этого двоичное число разбивают на триады относительно крайнего правого разряда (или двоичной запятой) и, используя таблицу , каждой триаде ставят в соответствие восьмеричную цифру.
10101001,101112 | 010 | 101 | 001, | 101 | 1102 | =251,568 |
2 | 5 | 1 | 5 | 6 |
Аналогичным
образом можно выполнить перевод числа
из шестнадцатеричной формы в двоичную
и обратно. В этом случае для представления
шестнадцатеричной цифры потребуется
четыре двоичных разряда. Четыре двоичных
разряда обычно называют тетрадой
В этом случае для представления
шестнадцатеричной цифры потребуется
четыре двоичных разряда. Четыре двоичных
разряда обычно называют тетрадой
Таблица 2. Таблица соответствия шестнадцатеричных цифр и двоичного кода
Двоичный код | шестнадцатеричная цифра | Десятичный эквивалент |
0000 | 0 | 0 |
0001 | 1 | 1 |
0010 | 2 | 2 |
0011 | 3 | 3 |
0100 | 4 | 4 |
0101 | 5 | 5 |
0110 | 6 | 6 |
0111 | 7 | 7 |
1000 | 8 | 8 |
1001 | 9 | 9 |
1010 | a | 10 |
1011 | b | 11 |
1100 | c | 12 |
1101 | d | 13 |
1110 | e | 14 |
1111 | f | 15 |
10101001,101112 | 1010 | 1001, | 1011 | 10002 | =A9,B816 | |
A | 9 | B | 8 |
Военно-техническая подготовка
4.
 1. Системы счисления
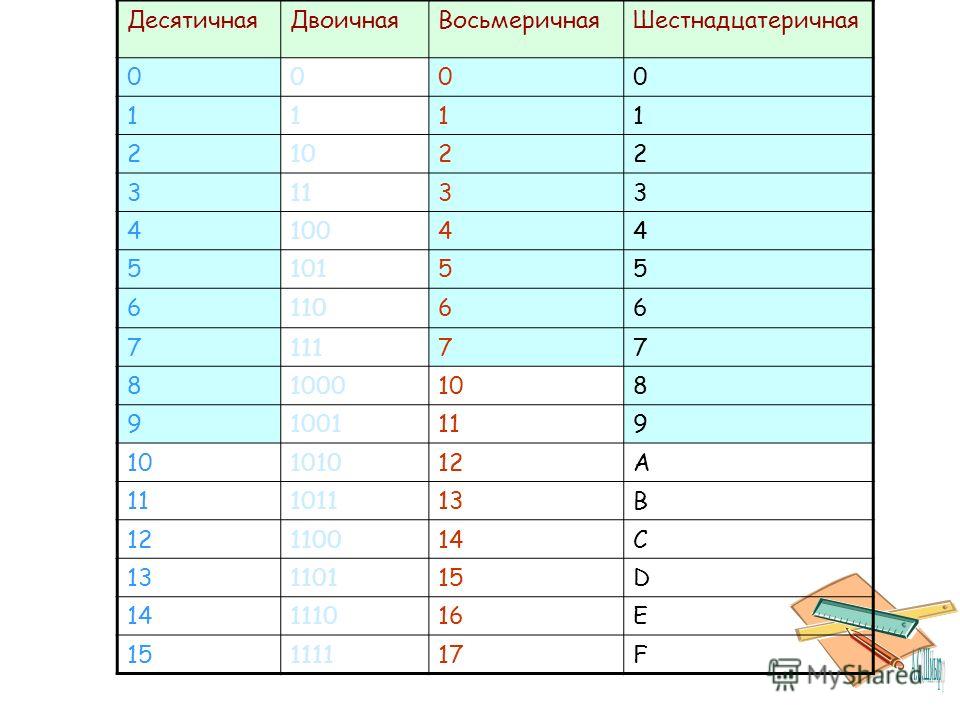
1. Системы счисленияСистема счисления (СС) — это система записи чисел с помощью определенного набора цифр.
4.1.1. Двоичная система счисления
Двоичная система счисления — это система, в которой для записи чисел используются две цифры: 0 и 1. Основанием двоичной системы счисления является число 2.
Двоичный код числа — запись этого числа в двоичной системе счисления. Пример:
- 0=0;
- 1=1;
- 2=10;
- 3=11;
- 7=111;
- 120=1111000;.
4.1.2. Восьмеричная система счисления
Восьмеричная система счисления — это система, в которой для записи чисел используются цифры от 0 до 7.
4.1.3. Десятичная система счисления
Десятичная система счисления — это система, в которой для записи чисел используются цифры от 0 до 9. Это привычная нам система счисления, используемая для записи чисел в повседневной жизни.
4.1.4. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления — это система, в которой для записи чисел используются цифры от 0 до 9 и латинские буквы A, B, C, D, E, F.
Двоичные | Восьмеричные | Десятичные | Шестнадцатеричные |
0 | 0 | 0 | 0 |
1 | 1 | 1 | 1 |
10 | 2 | 2 | 2 |
11 | 3 | 3 | 3 |
100 | 4 | 4 | 4 |
101 | 5 | 5 | 5 |
110 | 6 | 6 | 6 |
111 | 7 | 7 | 7 |
1000 | 10 | 8 | 8 |
1001 | 11 | 9 | 9 |
1010 | 12 | 10 | A |
1011 | 13 | 11 | B |
1100 | 14 | 12 | C |
1101 | 15 | 13 | D |
1110 | 16 | 14 | E |
1111 | 17 | 15 | F |
Таблица представления чисел от 0 до 15 в различных системах счисления.
4.1.5. Элементы булевой алгебры
Булева алгебра — раздел математики, изучающий логические выражения и операции. Логические выражения представляют собой высказывания — некоторые утверждения, которым всегда можно сопоставить одно из двух логических значений: ложь или истина (их можно обозначать как 0 и 1 , false и true).
Основными логическими операциями являются операции отрицания , логического И (конъюнкция) и логического ИЛИ (конъюнкция) . Именно с помощью них наиболее удобно оперировать с логическими выражениями. Производные логические операции могут быть выражены через них.
Отрицание — операция, применяемая к одному операнду, т.е. унарная операция. Выражение не A записывается как ¬A , A ̅ или ! A . Операции отрицания задается следующей таблицей истинности:
| A | ¬ A |
0 | 1 |
1 | 0 |
Логическое И (конъюнкция) — операция, применяемая к двум операндам, т.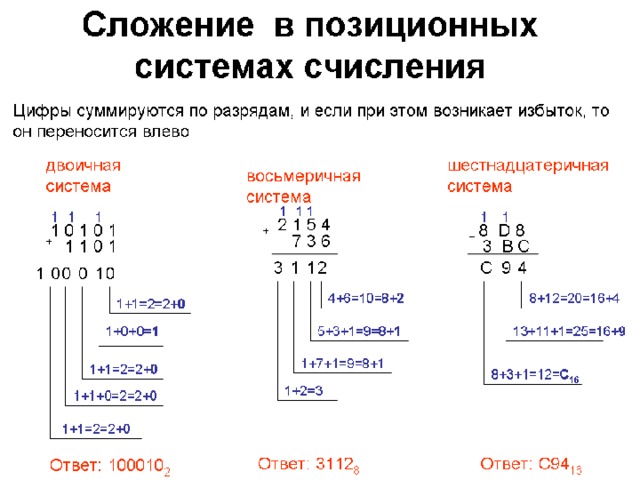 е. бинарная операция. Выражение A и B записывается как A˄B , A ⋅ B или A&&B . Конъюнкция задается следующей таблицей истинности:
е. бинарная операция. Выражение A и B записывается как A˄B , A ⋅ B или A&&B . Конъюнкция задается следующей таблицей истинности:
| A | B | A ˄B |
0 | 0 | 0 |
0 | 1 | 0 |
1 | 0 | 0 |
1 | 1 | 1 |
Логическое ИЛИ (дизъюнкция) — еще одна бинарная операция. Выражение A или B записывается как A˅B , A+B или A||B . Дизъюнкция задается следующей таблицей истинности:
Выражение A или B записывается как A˅B , A+B или A||B . Дизъюнкция задается следующей таблицей истинности:
| A | B | A˅B |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 1 |
Остальные операции булевой алгебры могут быть записаны с использованием лишь этих трех операций. Приоритеты основных логических операций соответствуют приоритетам аналогичных операций в элементарной алгебре.
Приоритеты основных логических операций соответствуют приоритетам аналогичных операций в элементарной алгебре.
- Отрицание.
- Конъюнкция.
- Дизъюнкция.
§ 1.1. Системы счисления
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
- система счисления
- цифра
- алфавит
- позиционная система счисления
- основание
- развёрнутая форма записи числа
- свёрнутая форма записи числа
- двоичная система счисления
- восьмеричная система счисления
- шестнадцатеричная система счисления
1.1.1. Общие сведения о системах счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа (рис. 1.1), называются цифрами, а их совокупность — алфавитом системы счисления.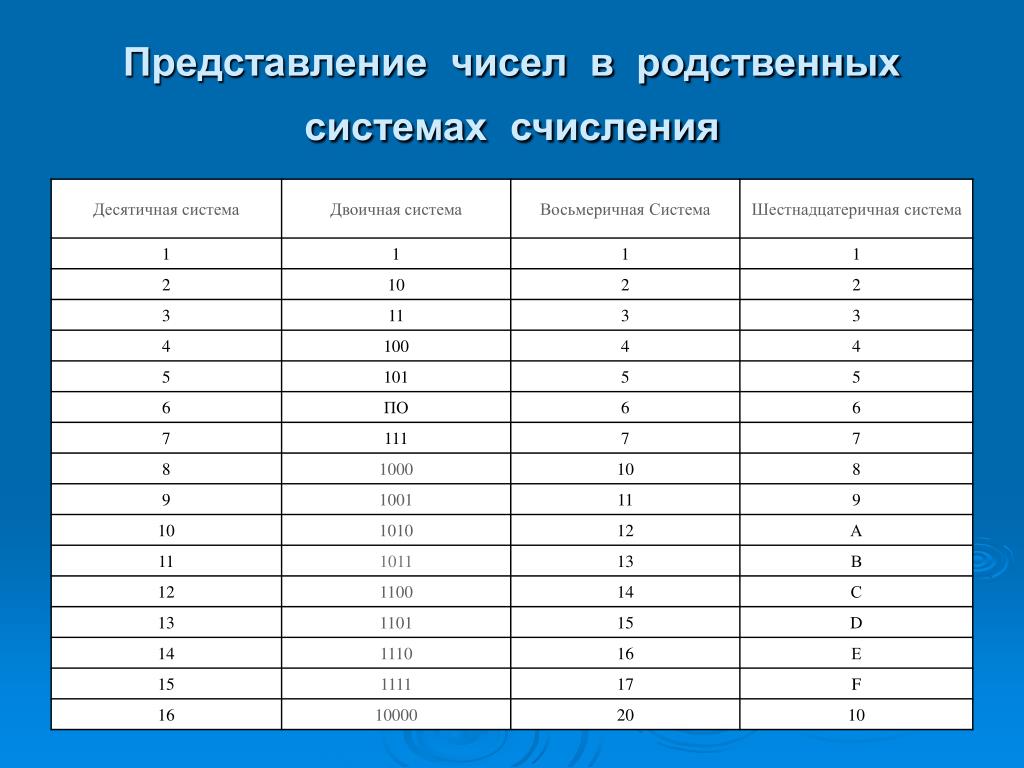
В любой системе счисления цифры служат для обозначения чисел, называемых узловыми; остальные числа (алгоритмические) получаются в результате каких-либо операций из узловых чисел.
Пример 1. У вавилонян узловыми являлись числа 1, 10, 60; в римской системе счисления узловые числа — это 1, 5, 10, 50, 100, 500 и 1000, обозначаемые соответственно I, V, X, L, С, D, М.
Рис. 1.1. Знаки, используемые для записи чисел в различных системах счисления
Системы счисления различаются выбором узловых чисел и способами образования алгоритмических чисел. Можно выделить следующие виды систем счисления:
- 1) унарная система;
- 2) непозиционные системы;
- 3) позиционные системы.
Простейшая и самая древняя система — так называемая унарная система счисления. В ней для записи любых чисел используется всего один символ — палочка, узелок, зарубка, камушек. Длина записи числа при таком кодировании прямо связана с его величиной, что роднит этот способ с геометрическим представлением чисел в виде отрезков. Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Именно унарная система лежит в фундаменте арифметики, и именно она до сих пор вводит первоклассников в мир счёта. Унарную систему ещё называют системой бирок.
Система счисления называется непозиционной, если количественный эквивалент (количественное значение) цифры в числе не зависит от её положения в записи числа.
Пример 2. В древнеегипетской системе счисления числа 1, 2, 3, 4, 10, 13, 40 обозначались соответственно следующим образом:
Те же числа в римской системе счисления обозначаются так: I, II, III, IV, X, XIII, XL. Здесь алгоритмические числа получаются путём сложения и вычитания узловых чисел с учётом следующего правила: каждый меньший знак, поставленный справа от большего, прибавляется к его значению, а каждый меньший знак, поставленный слева от большего, вычитается из него.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа.Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Десятичная система
Десятичная система записи чисел, которой мы привыкли пользоваться в повседневной жизни, с которой мы знакомы с детства, в которой производим все наши вычисления, — пример позиционной системы счисления. Алфавит десятичной системы составляют цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Алгоритмические числа образуются в ней следующим образом: значения цифр умножаются на «веса» соответствующих разрядов, и все полученные значения складываются. Это отчётливо прослеживается в числительных русского языка, например: «три-ста пять-десят семь».
Основанием позиционной системы счисления может служить любое натуральное число q > 1. Алфавитом произвольной позиционной системы счисления с основанием q служат числа 0, 1, …, q—1, каждое из которых может быть записано с помощью одного уникального символа; младшей цифрой всегда является 0.
Основные достоинства любой позиционной системы счисления — простота выполнения арифметических операций и ограниченное количество символов, необходимых для записи любых чисел.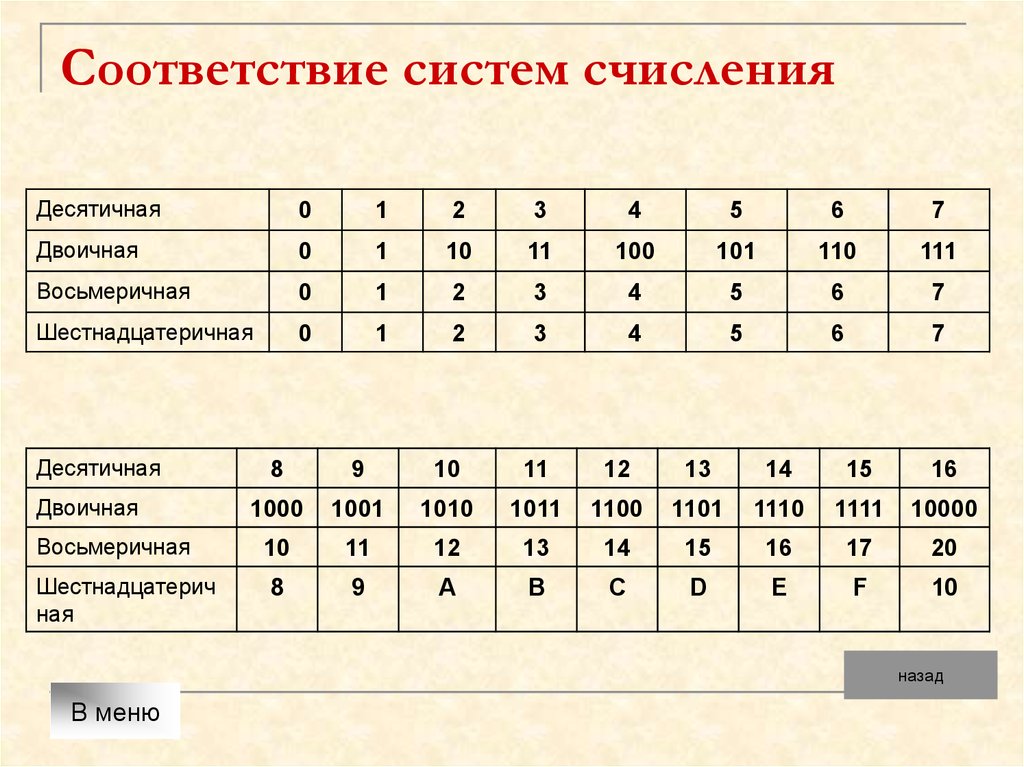
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Запись числа по формуле (1) называется развёрнутой формой записиСвёрнутной формой записи числа называется его представление в виде1 ± an-1an-2…a1a0,a-1…a-m.1 Далее будут рассматриваться только положительные целые числа.
Пример 3. Рассмотрим десятичное число 14351,1. Его свёрнутая форма записи настолько привычна, что мы не замечаем, как в уме переходим к развёрнутой записи, умножая цифры числа на «веса» разрядов и складывая полученные произведения:
- 1 • 104 + 4 • 103 + 3 • 102 + 5 • 101 + 1 • 100 + 1 • 10-1.
1.1.2. Двоичная система счисления
Двоичной системой счисления называется позиционная система счисления с основанием 2. Для записи чисел в двоичной системе счисления используются только две цифры: 0 и 1.
На основании формулы (1) для целых двоичных чисел можно записать:
- аn-1аn-2…а1а0 = an-1 • 2n-1 + аn-2 • 2n-2 +…+ а0 • 20. (1′)
Например:
- 100112 = 1 • 24 + 0 • 23 + 0 • 22 + 1 • 21 + 1 • 20 = 24 + 21 + 20 = 1910.

Такая форма записи «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: необходимо вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Получим правило перевода целых десятичных чисел в двоичную систему счисления из формулы (1′).
Разделим аn-1 • 2n-1 + аn-2 • 2n-2 + … + а0 • 20 на 2. Частное будет равно аn-1 • 2n-2 + … + а1, а остаток будет равен а0.
Полученное частное опять разделим на 2, остаток от деления будет равен а1.
Если продолжить этот процесс деления, то на n-м шаге получим набор цифр:
- а0, а1, а2, … аn-1,.
которые входят в двоичное представление исходного числа и совпадают с остатками при его последовательном делении на 2.
Таким образом, для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на 2 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 4. Переведём десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:
Выписывая остатки от деления в направлении, указанном стрелкой, получим: 1110 = 10112.
Пример 5. Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:
- 36310 = 1011010112
1.1.3. Восьмеричная система счисления
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1,2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
- аn-1аn-2…а1а0 = аn-1 • 8n-1 + аn-2 • 8n-2 + … + а0 • 80.
 (1″)
(1″)
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
10310 = 1478
1.1.4. Шестнадцатеричная система счисления
Основание: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.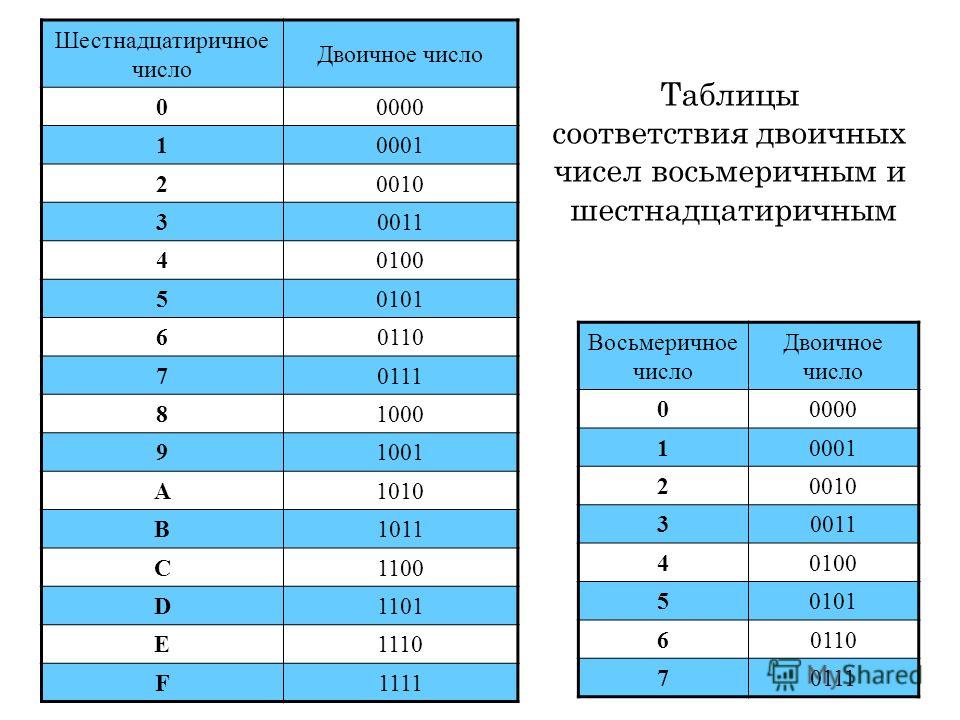
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
- 3AF16 = 3 • 162 + 10 • 161 + 15 • 160 = 768 + 160 + 15 = 94310.
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
15410 = 9А16
1.1.5. Правило перевода целых десятичных чисел в систему счисления с основанием q
Для перевода целого десятичного числа в систему счисления с основанием q следует:
- 1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
- 2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
- 3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.

Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 2010.
В Единой коллекции цифровых образовательных ресурсов (http://sc.edu.ru/) размещена интерактивная анимация «Преобразование десятичного числа в другую систему счисления» (135050). С её помощью можно понаблюдать за переводом произвольного целого числа от 0 до 512 в позиционную систему счисления, основание которой не превышает 16.
В размещённой там же виртуальной лаборатории «Цифровые весы» (135009) вы сможете освоить ещё один способ перевода целых десятичных чисел в другие системы счисления — метод разностей.
1.1.6. Двоичная арифметика
Арифметика двоичной системы счисления основывается на использовании следующих таблиц сложения и умножения:
Пример 8. Таблица двоичного сложения предельно проста. Так как 1 + 1 = 10, то 0 остаётся в младшем разряде, а 1 переносится в старший разряд.
Пример 9. Операция умножения двоичных чисел выполняется по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Операция умножения двоичных чисел выполняется по обычной схеме, применяемой в десятичной системе счисления, с последовательным умножением множимого на очередную цифру множителя.
Таким образом, в двоичной системе счисления умножение сводится к сдвигам множимого и сложениям.
1.1.7. «Компьютерные» системы счисления
В компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ по сравнению с другими системами счисления:
- двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
- представление информации посредством только двух состояний надёжно и помехоустойчиво;
- двоичная арифметика наиболее проста;
- существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно.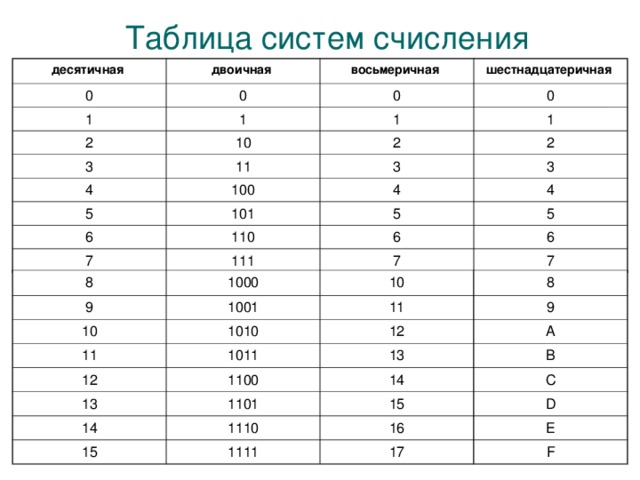 Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
С помощью ресурса «Интерактивный задачник, раздел “Системы счисления»» (128659), размещённого в Единой коллекции цифровых образовательных ресурсов, можно проверить, насколько прочно вы усвоили изученный в этом параграфе материал.
Самое главное о системе счисления
Система счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
- Аq = ± (аn-1 • qn-1 + аn-2 • qn-2 + … + а0 • q0 + а-1 • q-1 + … + а-m • q-m). (1)
Здесь:
- А — число;
- q — основание системы счисления;
- аi — цифры, принадлежащие алфавиту данной системы счисления;
- n — количество целых разрядов числа;
- m — количество дробных разрядов числа;
- qi — «вес» i-го разряда.
Вопросы и задания
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
3. Цифры каких систем счисления приведены на рис. 1.1?
4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
5. Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
6. Запишите в развёрнутой форме числа
7. Вычислите десятичные эквиваленты следующих чисел 172? 2EA??
8. Укажите какое из чисел 1100112, 1114, 358 и 1В16 является
9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
10. Верны ли следующие равенства? а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если: а) 14х = 910;
б) 2002х = 13010.
12. Переведите целые числа из десятичной системы счисления в двоичную: а) 89; б) 600; в) 2010
13. Переведите целые числа из десятичной системы счисления в восьмеричную: а) 513; б) 600; в) 2010.
14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную: а) 513; б) 600; в) 2010.
15. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
16. Выполните операцию сложения над двоичными числами: а) 101010 + 1101; б) 1010 + 1010; в) 10101 + 111.
17. Выполните операцию умножения над двоичными числами: а) 1010 · 11; б) 111 · 101; в) 1010 · 111.
18. Расставьте знаки арифметических операций так, чтобы были верны следующие равенства в двоичной системе: а) 1100 ? 11 ? 100 = 100000; б) 1100 ? 10 ? 10 = 100; в) 1100 ? 11 ? 100 = 0.
19. Вычислите выражения: а) (11111012 + AF16) : 368; б) 1258 + 1012 ? 2A16 ? 1418. Ответ дайте в десятичной системе счисления.
Ответ дайте в десятичной системе счисления.
20. Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?
21. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.
22. Постройте граф, отражающий разновидности систем счисления.
23. Подготовьте небольшое сообщение об одной из систем счисления (когда и где применялась, какие символы использовались и т. д.).
Оглавление
§ 1.1. Системы счисления
§ 1.2. Представление чисел в компьютере
Шестнадцатеричная система счисления
Математика Шестнадцатеричная система счисления
просмотров — 386
Восьмеричная система счисления
Двоичная система счисления
Для записи числа в двоичной системе счисления используются две цифры: 0 и 1.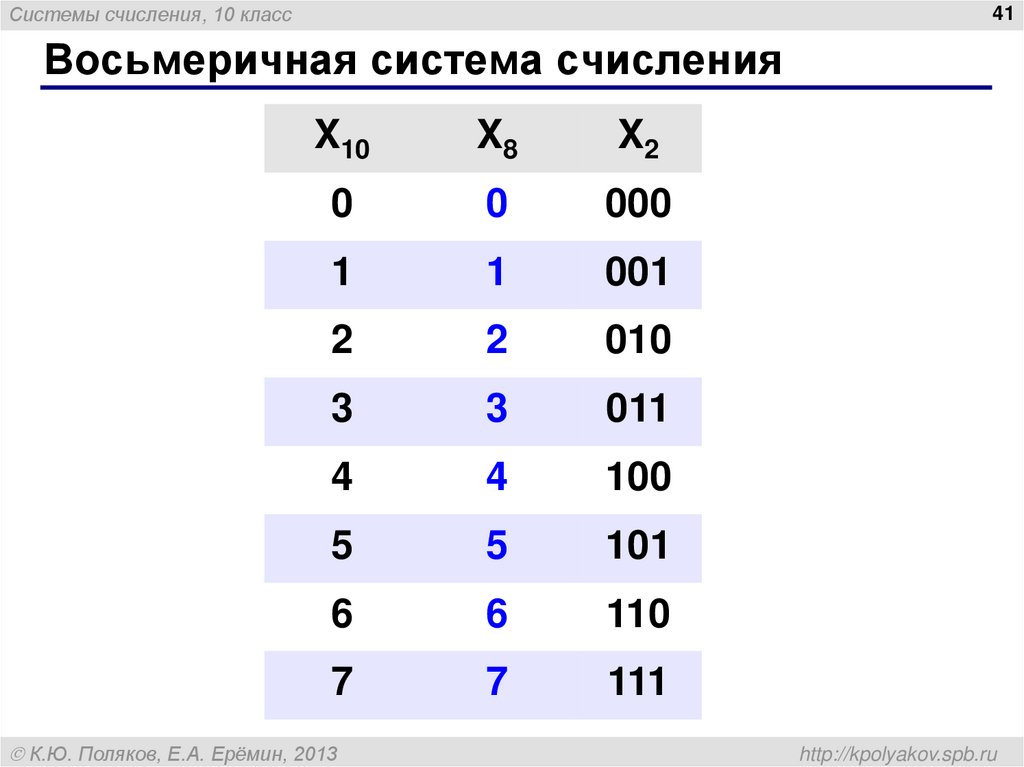 Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью высоких и низких потенциалов или группой запоминающих элементов, способных запоминать одно из двух (0,1) значений. Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной системе счисления.
Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью высоких и низких потенциалов или группой запоминающих элементов, способных запоминать одно из двух (0,1) значений. Арифметические операции в двоичной системе счисления выполняются по тем же правилам, что и в десятичной системе счисления.
| Сложение | Вычитание | Умножение | ||||
| 0+0= 0 | 0-0=0 | 0 · 0=0 | ||||
| 0+1= 1 | 1-0=1 | 0 · 1=0 | ||||
| 1+0= 1 | 1-1=0 | 1 · 0=0 | ||||
| 1+1=10 | 10-1=1 | 1 · 1=1 |
Рассмотрим несколько примеров, демонстрирующих выполнение арифметических операций:
|
В восьмеричной системе счисления используется восемь цифр: 0,1,2 … 7, а основание записывается как 10(8) (810=1·81+0·80). Рассмотрим выполнение операций в восьмеричной системе счисления. При их выполнении используются правила, представленные в таблицах сложения и умножения восьмеричных цифр.
Рассмотрим выполнение операций в восьмеричной системе счисления. При их выполнении используются правила, представленные в таблицах сложения и умножения восьмеричных цифр.
| Сложение | Умножение | |||||||||||||||||
|
В шестнадцатеричной системе счисления используются шестнадцать символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Основание записывается как 10(16) (1610=1*161+0*160).
Основание записывается как 10(16) (1610=1*161+0*160).
| Сложение | Умножение | |||||||||||||||||||||||||||||||
| a | b | c | d | e | f | a | b | c | d | e | f | |||||||||||||||||||||
| а | b | c | d | e | f | a | b | c | d | e | f | |||||||||||||||||||||
| a | b | c | d | e | f | a | c | e | 1a | 1c | 1e | |||||||||||||||||||||
| a | b | c | d | e | f | c | f | 1b | 1e | 2a | 2d | |||||||||||||||||||||
| a | b | c | d | e | f | c | 1c | 2c | 3c | |||||||||||||||||||||||
| a | b | c | d | e | f | a | f | 1e | 2d | 3c | 4b | |||||||||||||||||||||
| a | b | c | d | e | f | c | 1e | 2a | 3c | 4e | 5a | |||||||||||||||||||||
| a | b | c | d | e | f | e | 1c | 2a | 3f | 4d | 5b | |||||||||||||||||||||
| a | b | c | d | e | f | |||||||||||||||||||||||||||
| a | b | c | d | e | f | 1b | 2d | 3f | 5a | 6c | 7e | |||||||||||||||||||||
| a | b | c | d | e | f | a | a | 1e | 3c | 5a | 6e | 8c | ||||||||||||||||||||
| b | c | d | e | f | 1a | b | b | 2c | 4d | 6e | 8f | 9a | a5 | |||||||||||||||||||
| c | d | e | f | 1a | 1b | c | c | 3c | 6c | 9c | a8 | |||||||||||||||||||||
| d | e | f | 1a | 1b | 1c | d | d | 1a | 4e | 5b | 8f | 9c | a9 | b6 | c3 | |||||||||||||||||
| e | f | 1a | 1b | 1c | 1d | e | e | 1c | 2a | 7e | 8c | 9a | a8 | b6 | c4 | d2 | ||||||||||||||||
| f | 1a | 1b | 1c | 1d | 1e | f | f | 1e | 2d | 3c | 4b | 5a | a5 | b4 | c3 | d2 | e1 |
|
Двоичная система счисления
Десятичная система счисления
В числе 2468 каждая цифра имеет свой вес.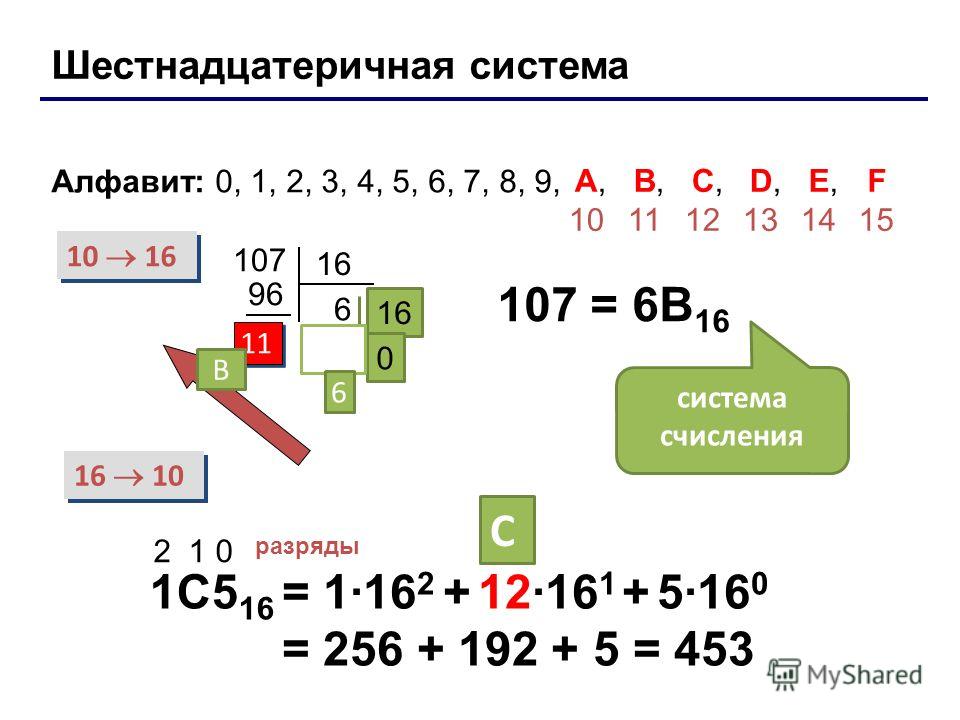 Умножив значение цифры на ее вес, мы получим значение числа:
2*1000 + 4*100 + 6*10 + 8*1 = 246810
Или используя степени числа 10:
2*103 + 4*102 + 6*101 + 8*100 = 246810
Число десять является… [читать подробенее]
Умножив значение цифры на ее вес, мы получим значение числа:
2*1000 + 4*100 + 6*10 + 8*1 = 246810
Или используя степени числа 10:
2*103 + 4*102 + 6*101 + 8*100 = 246810
Число десять является… [читать подробенее]
Чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы. Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в… [читать подробенее]
Перевод целых чисел из десятичной системы счисления в систему счисления с другим основанием Рис. 16. Перевод числа из десятичной СС в двоичную. Для осуществления такого перевода необходимо делить число с остатком на основание системы счисления до тех пор,… [читать подробенее]

№3. №2. Арифметические операции в двоичной системе счисления. №1. Тема: Арифметические операции в позиционных системах счисления.. №2. №1. Ответы на… [читать подробенее]
№3. №2. Арифметические операции в двоичной системе счисления. №1. Тема: Арифметические операции в позиционных системах счисления.. №2. №1. Ответы на… [читать подробенее]
Восьмеричная система счисления
Двоичная система счисления
Для записи числа в двоичной системе счисления используются две цифры: 0 и 1. Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью… [читать подробенее]
Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью… [читать подробенее]
Восьмеричная система счисления Двоичная система счисления Для записи числа в двоичной системе счисления используются две цифры: 0 и 1. Основание системы записывается как 10(2) (210=1·21+0·20). Используя данную систему, любое число можно выразить последовательностью… [читать подробенее]
Пример. 1) 15568=001 101 101 1102=11011011102. 2) 356,7758=011 101 110, 111 111 1012=11101110,1111111012. Восьмеричная арифметика. Ниже приведены таблицы сложения и умножения в восьмеричной системе счисления. Используется восемь цифр: 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Шестнадцатеричная система… [читать подробенее]
Пример. 1) 15568=001 101 101 1102=11011011102.
2) 356,7758=011 101 110, 111 111 1012=11101110,1111111012.
Восьмеричная арифметика. Ниже приведены таблицы сложения и умножения в восьмеричной системе счисления.
Используется восемь цифр: 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система… [читать подробенее]
1) 15568=001 101 101 1102=11011011102.
2) 356,7758=011 101 110, 111 111 1012=11101110,1111111012.
Восьмеричная арифметика. Ниже приведены таблицы сложения и умножения в восьмеричной системе счисления.
Используется восемь цифр: 0, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Шестнадцатеричная система… [читать подробенее]
№3. №2. Восьмеричная система счисления. Основание: q=8. Алфавит: 0, 1, 2, 3, 4, 5, 6 и 7. Записав восьмеричное число А8=7764,1 в развернутом виде и произведя вычисления, получим это число, выраженное в десятичной системе счисления: А8=7*83+7*82+6*81+4*80+1*8-1 = 3584 + 448 + 48 + 4 + 0,125 =… [читать подробенее]
4.16 — Системы счисления (десятичная, двоичная, шестнадцатеричная и восьмеричная) — Learn C++
Alex
Примечание автора
Этот урок не является обязательным.
Будущие уроки ссылаются на шестнадцатеричные числа, так что вы должны хотя бы поверхностно ознакомиться с концепцией, прежде чем продолжить.
В повседневной жизни мы считаем десятичными числами, где каждая числовая цифра может быть 0, 1, 2, 3, 4, 5, 6, 7, 8 или 9.. Десятичное число также называют «основанием 10», потому что существует 10 возможных цифр (от 0 до 9). В этой системе мы считаем так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, … По умолчанию числа в программах на C++ считаются десятичными.
интервал x {12}; // Предполагается, что 12 является десятичным числом В двоичном коде всего 2 цифры: 0 и 1, поэтому он называется «основанием 2». В двоичном формате мы считаем так: 0, 1, 10, 11, 100, 101, 110, 111, …
Десятичная и двоичная — два примера систем счисления, которые представляют собой причудливое название для набора символов (например, цифр). ) используется для представления чисел. В C++ доступны 4 основные системы счисления. В порядке популярности это: десятичная (основание 10), двоичная (основание 2), шестнадцатеричная (основание 16) и восьмеричная (основание 8).
) используется для представления чисел. В C++ доступны 4 основные системы счисления. В порядке популярности это: десятичная (основание 10), двоичная (основание 2), шестнадцатеричная (основание 16) и восьмеричная (основание 8).
Восьмеричные и шестнадцатеричные литералы
Восьмеричное число — это основание 8, то есть доступны только следующие цифры: 0, 1, 2, 3, 4, 5, 6 и 7. В восьмеричном исчислении мы считаем так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, … (примечание: нет 8 и 9, поэтому мы пропускаем от 7 до 10).
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 |
To use an octal literal, prefix ваш литерал с 0 (нулем):
#includeосновной () { интервал х{012}; // 0 перед числом означает, что это восьмеричное число std::cout << x << '\n'; вернуть 0; }
Эта программа печатает:
10
Почему 10 вместо 12? Поскольку по умолчанию числа выводятся в десятичном формате, а 12 восьмеричных = 10 десятичных.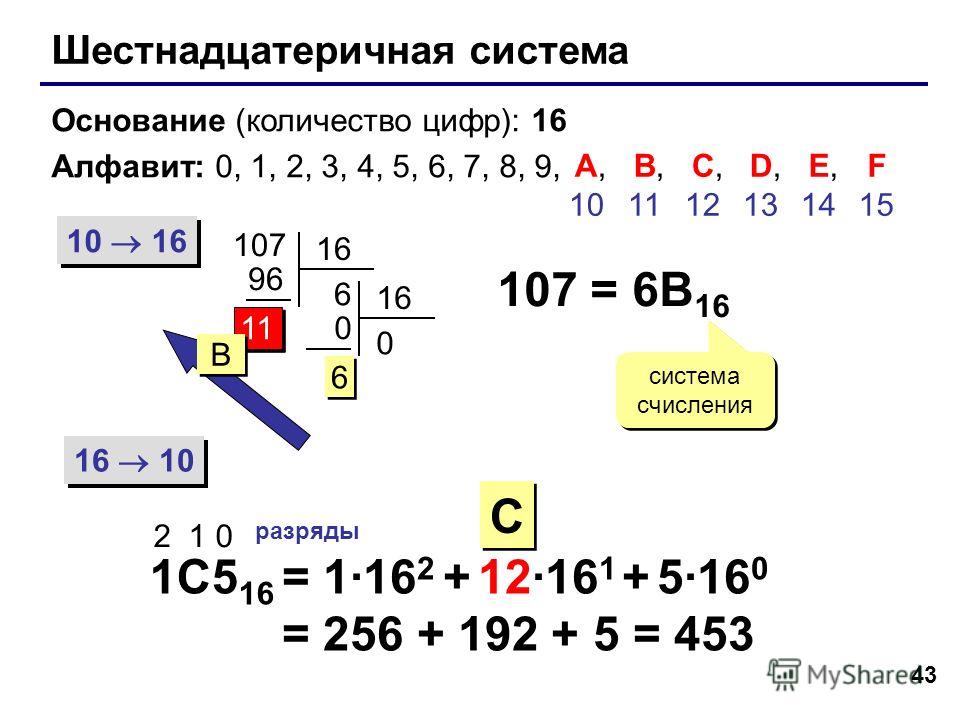
Octal редко используется, и мы рекомендуем вам избегать его.
Шестнадцатеричный код — это основание 16. В шестнадцатеричном формате мы считаем так: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11. , 12, …
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| Hexadecimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | 10 | 11 |
To use a hexadecimal literal, prefix your literal с 0х.
#includeосновной () { интервал х{0xF}; // 0x перед числом означает, что оно шестнадцатеричное std::cout << x << '\n'; вернуть 0; }
Эта программа печатает:
15
Поскольку существует 16 различных значений шестнадцатеричной цифры, мы можем сказать, что одна шестнадцатеричная цифра охватывает 4 бита. Следовательно, пара шестнадцатеричных цифр может использоваться для точного представления полного байта.
Следовательно, пара шестнадцатеричных цифр может использоваться для точного представления полного байта.
Рассмотрим 32-битное целое число со значением 0011 1010 0111 1111 1001 1000 0010 0110. Из-за длины и повторения цифр его нелегко прочитать. В шестнадцатеричном формате это же значение будет: 3A7F 9826, что намного короче. По этой причине шестнадцатеричные значения часто используются для представления адресов памяти или необработанных данных в памяти (тип которых неизвестен).
Двоичные литералы и разделители цифр
До C++14 поддержка двоичных литералов отсутствует. Однако шестнадцатеричные литералы предоставляют нам полезный обходной путь (который вы все еще можете встретить в существующих базах кода):
#includeосновной () { целая корзина {}; // предположим, что это 16-битные целые числа бин = 0x0001; // присваиваем переменной двоичный код 0000 0000 0000 0001 бин = 0x0002; // присваиваем переменной двоичный код 0000 0000 0000 0010 бин = 0x0004; // присваиваем переменной двоичный код 0000 0000 0000 0100 бин = 0x0008; // присваиваем переменной двоичный код 0000 0000 0000 1000 бин = 0x0010; // присваиваем переменной двоичный код 0000 0000 0001 0000 бин = 0x0020; // присваиваем переменной двоичный код 0000 0000 0010 0000 бин = 0x0040; // присваиваем переменной двоичный код 0000 0000 0100 0000 бин = 0x0080; // присваиваем переменной двоичный код 0000 0000 1000 0000 бин = 0x00FF; // присваиваем переменной двоичный код 0000 0000 1111 1111 бин = 0x00B3; // присваиваем переменной двоичный код 0000 0000 1011 0011 бин = 0xF770; // присваиваем переменной двоичный код 1111 0111 0111 0000 вернуть 0; }
В C++14 мы можем использовать бинарные литералы, используя префикс 0b:
#includeосновной () { целая корзина {}; // предположим, что это 16-битные целые числа бин = 0b1; // присваиваем переменной двоичный код 0000 0000 0000 0001 бин = 0b11; // присваиваем переменной двоичный код 0000 0000 0000 0011 бин = 0b1010; // присваиваем переменной двоичный код 0000 0000 0000 1010 бин = 0b11110000; // присваиваем переменной двоичный код 0000 0000 1111 0000 вернуть 0; }
Поскольку длинные литералы трудно читать, в C++14 также добавлена возможность использовать кавычки (‘) в качестве разделителя цифр.
#includeосновной () { интервал бен {0b1011'0010}; // присваиваем переменной двоичный код 1011 0010 длинное значение {2'132'673'462}; // намного легче читать, чем 2132673462 вернуть 0; }
Также обратите внимание, что разделитель не может стоять перед первой цифрой значения:
int bin { 0b'1011'0010 }; // ошибка: ' используется перед первой цифрой значения Вывод значений в десятичном, восьмеричном или шестнадцатеричном формате
По умолчанию C++ выводит значения в десятичном формате. Однако вы можете изменить выходной формат с помощью std::dec , std::oct и std::hex Манипуляторы ввода-вывода:
#includeосновной () { интервал х {12}; std::cout << x << '\n'; // десятичный (по умолчанию) std::cout << std::hex << x << '\n'; // шестнадцатеричный std::cout << x << '\n'; // теперь шестнадцатеричный std::cout << std::oct << x << '\n'; // восьмеричный std::cout << std::dec << x << '\n'; // возвращаемся к десятичной системе std::cout << x << '\n'; // десятичный вернуть 0; }
Это печатает:
12 с с 14 12 12
Обратите внимание, что однажды примененный манипулятор ввода-вывода остается установленным для будущего вывода до тех пор, пока он не будет изменен снова.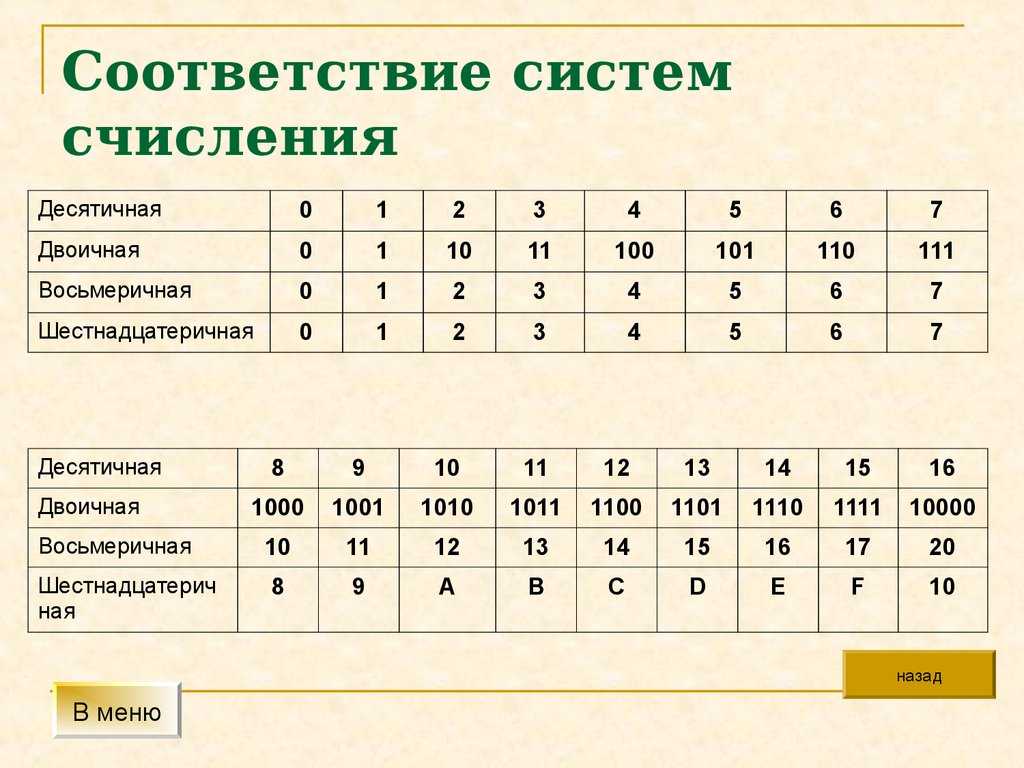
Вывод значений в двоичном формате
Вывод значений в двоичном формате немного сложнее, так как std::cout не имеет такой встроенной возможности. К счастью, стандартная библиотека C++ включает тип std::bitset , который сделает это за нас (в заголовке std::bitset , мы можем определить переменную std::bitset и сообщить std::bitset , сколько бит мы хотим сохранить. Количество битов должно быть константой времени компиляции. std::bitset может быть инициализирован целочисленным значением без знака (в любом формате, включая десятичный, восьмеричный, шестнадцатеричный или двоичный).
#include// для std::bitset #include <иопоток> основной () { // std::bitset<8> означает, что мы хотим хранить 8 бит std::bitset<8> bin1{0b1100'0101}; // бинарный литерал для бинарника 1100 0101 std::bitset<8> bin2{0xC5}; // шестнадцатеричный литерал для двоичного кода 1100 0101 std::cout << bin1 << '\n' << bin2 << '\n'; std::cout << std::bitset<4>{ 0b1010 } << '\n'; // создаем временный набор std::bitset и печатаем его вернуть 0; }
Это печатает:
11000101 11000101 1010
В приведенном выше коде эта строка:
std::cout << std::bitset<4>{ 0b1010 } << '\n'; // создаем временный std::bitset и печатаем его создает временный (безымянный) объект std::bitset с 4 битами, инициализирует его двоичным литералом 0b1010 , печатает значение в двоичном виде, а затем отбрасывает временный объект.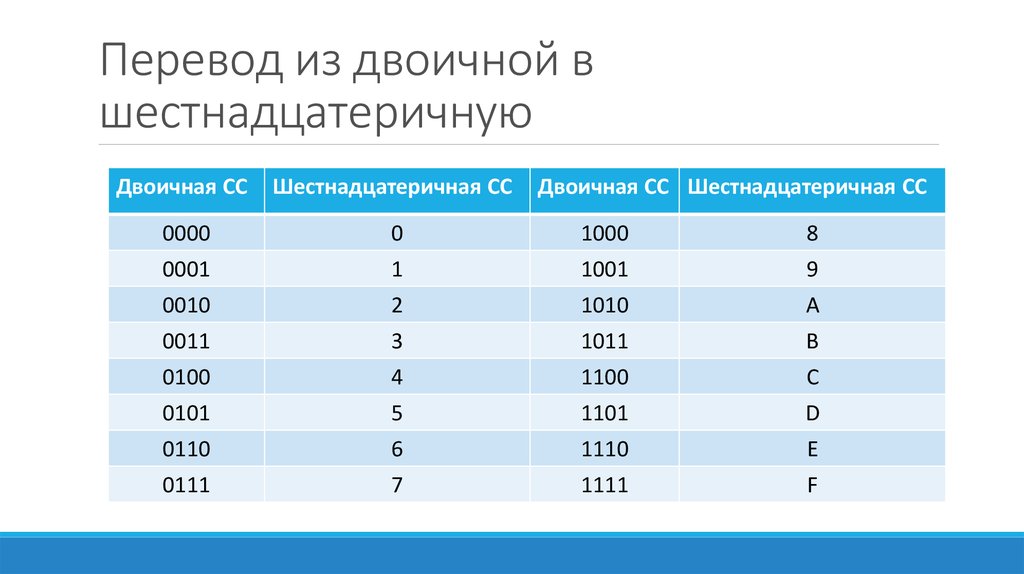
Системы счисления (двоичная, восьмеричная, десятичная, шестнадцатеричная)
Прежде чем мы сможем объяснить некоторые конкретные системы счисления, нам нужно узнать, что такое система счисления. Проще говоря, система счисления — это способ представления чисел.
Мы можем классифицировать системы счисления по типу записи в зависимости от того, используют ли они позиционную запись (также известную как запись разрядного значения), а также проводить дальнейшую категоризацию по системе счисления или основанию.
1. Непозиционная система счисления
Чтобы объяснить непозиционную систему счисления, в качестве примера возьмем римские цифры. В таблице ниже вы можете найти десятичные значения основных символов в римской системе счисления.
Вы можете спросить, есть ли какой-то шаблон для формирования всех остальных символов? Ответ положительный.
- Когда символ с меньшим значением помещается после символа, имеющего равное или большее значение, значения складываются.
 Примеры приведены в таблице ниже.
Примеры приведены в таблице ниже.
- Когда символ с меньшим значением помещается перед символом с большим значением, меньшее значение вычитается из большего. Примеры приведены в таблице ниже.
2. Позиционная система счисления
Позиционная система счисления позволяет расширить исходный набор символов, чтобы их можно было использовать для представления любого произвольно большого (или малого) значения. Число может быть представлено по-разному в разных системах.
Например, два числа $(2A)_{16}$ и $(52)_{8}$ относятся к одному и тому же количеству, $(42)_{10}$.
Система счисления, которую мы используем каждый день, называется десятичной системой счисления или системой счисления с основанием десять. Как видно из названия системы счисления, основание определяет всю систему.
Десятичная система счисления имеет основание 10, потому что мы работаем с 10 цифрами (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), и любое другое большее число может быть составлено из этих 10 цифр.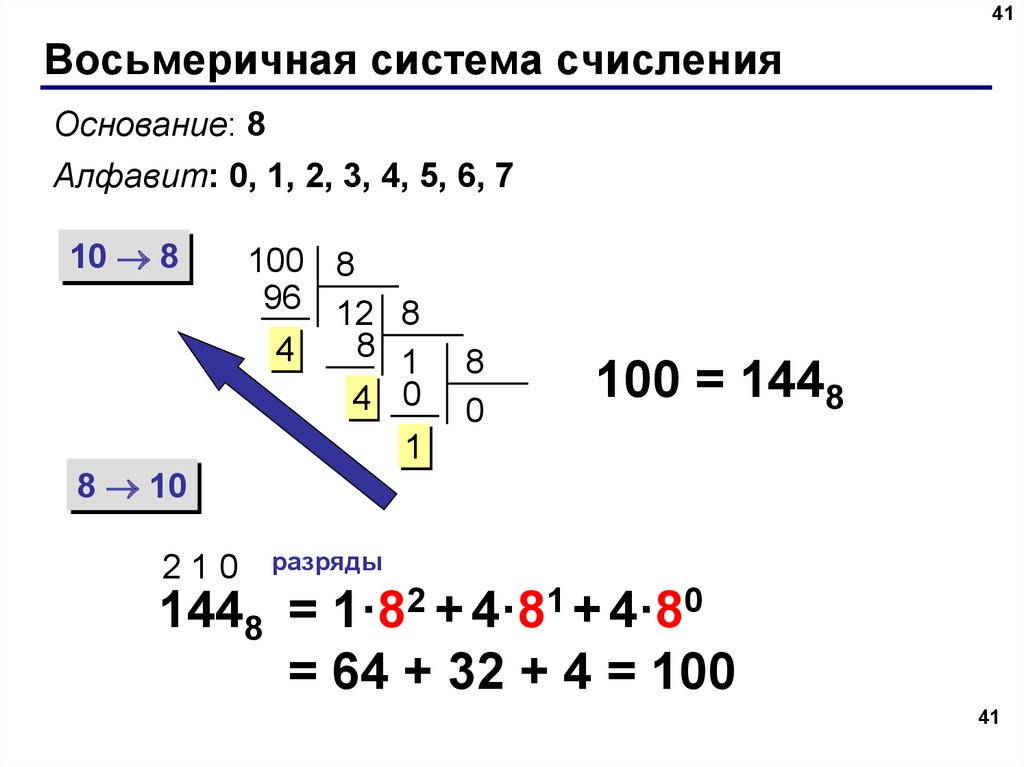 Другими словами, мы используем тот же набор символов, но присваиваем символу другое значение в зависимости от его положения в числе.
Другими словами, мы используем тот же набор символов, но присваиваем символу другое значение в зависимости от его положения в числе.
Положение символа по отношению к другим символам в номере позволяет отдельному символу представлять большее (или меньшее) значение. Это также означает, что каждая цифра умножается на соответствующую степень числа 10 в зависимости от ее положения в числе. 9{0} $
$= 3 \cdot 100+4 \cdot 10+2 \cdot 1$
$=300 + 40 + 2$
В этом уроке мы не будем подробно объяснять десятичную систему, так как она много уроков на странице, посвященной этому.
Помимо десятичной системы счисления существует множество других систем счисления. Мы упомянем только три из них, поскольку они являются наиболее часто используемыми системами счисления после десятичной. Это: двоичная система счисления, восьмеричная система счисления и шестнадцатеричная система счисления. Мы дадим краткое объяснение каждому из них и научимся преобразовывать числа из одной системы в другую.
2.1. Двоичная система счисления
Двоичная система счисления содержит две уникальные цифры (0 и 1). Таким образом, эта система является системой счисления с основанием 2. Относительные величины символов равны 0 < 1. Символы в этой системе часто называют двоичными цифрами или просто битами. Двоичная система счисления является позиционной системой счисления. Позже мы увидим, что, например, $1010_{2}\neq 1100_{2}$.
2.2. Восьмеричная система счисления
Восьмеричная система счисления содержит 8 уникальных цифр (0, 1, 2, 3, 4, 5, 6, 7). Таким образом, эта система является системой счисления с основанием 8. Относительные величины символов равны 0 < 1 < 2 < 3 < 4 < 5 < 6 < 7. Восьмеричная система счисления — еще один пример позиционной системы счисления.
2.3. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления содержит 16 уникальных цифр. Поскольку в десятичной системе всего 10 арабских цифр, нам нужно использовать другие символы для представления оставшихся 6 цифр.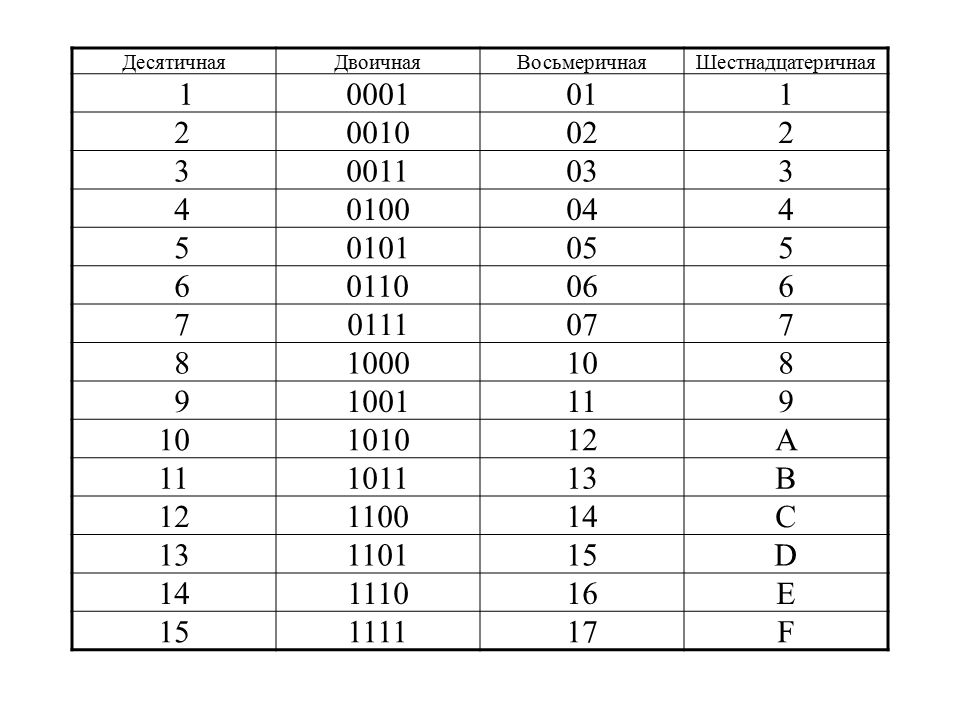 Мы используем алфавитные
Мы используем алфавитные
символа от A до F, чтобы расширить систему до 16 цифр. 16 цифр в шестнадцатеричной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E и F. Относительные величины символов равны
0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < 8 < 9< A < B < C < D < E < F.
Шестнадцатеричная система счисления также является позиционной системой счисления.
3. Преобразование основания
Каждая позиция цифры в числе с основанием b представляет степень числа $b$. Таким образом, когда мы записываем число с основанием b, каждая цифра с основанием b умножается на соответствующую степень $b$ в зависимости от позиции в числе.
3.1. Преобразование в десятичное число
Преобразование числа из любой системы счисления в десятичное число довольно просто. Мы знаем, что значение каждой цифры в числе основано на значении отдельной цифры и позиции цифры. Мы узнали это, изучая десятичные числа. Используя это правило, мы можем преобразовать число из любой системы счисления в десятичное число.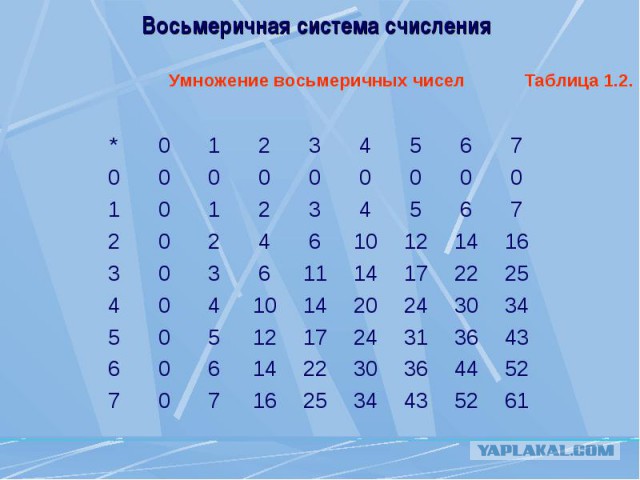 9{-2}=3\cdot 8+4\cdot 1+1\cdot \displaystyle{\frac{1}{8}}+5\cdot \displaystyle{\frac{1}{64}}=28,203125$
9{-2}=3\cdot 8+4\cdot 1+1\cdot \displaystyle{\frac{1}{8}}+5\cdot \displaystyle{\frac{1}{64}}=28,203125$
3.2. Преобразование десятичного числа в любое другое основание
Мы можем преобразовать десятичное число в любое другое основание, выполнив всего несколько простых шагов:
- Разделите десятичное число, которое необходимо преобразовать, на значение нового основания.
- Запишите остаток в сторону
- Разделите частное предыдущего деления на новое основание.
- Запишите остаток в сторону
- Повторяйте шаги 3 и 4, пока частное не станет равным нулю на шаге 3.
Требуемое число состоит из остатков, записанных снизу вверх и слева направо.
Пример 2. Преобразование 25 в двоичное число.
Следуя правилу преобразования десятичных чисел в любую другую систему счисления, необходимое число равно $11001_{2}$.
Пример 3. Преобразование 2489 в шестнадцатеричное число.
Помните, что эквивалентом числа 11 в шестнадцатеричной системе счисления является буква B.
Следуя правилу преобразования десятичных чисел в любую другую систему счисления, необходимое число равно $9B9_{16}$.
3.3. Эквивалентность между различными системами счисления
4. Сочетания клавиш для переключения между основанием 2 и основанием 8 и между основанием 2 и основанием 16
Мы узнали, что можем преобразовать число из любого основания в число с любым основанием с помощью сначала преобразовать его в десятичное. Например, если мы хотим преобразовать число с основанием 3 в число с основанием 7, первым шагом будет преобразование числа с основанием 3 в десятичное, а затем преобразование этого десятичного числа в число с основанием 7.
Мы можем использовать ту же процедуру для преобразования двоичного числа в восьмеричное или шестнадцатеричное число, но есть несколько полезных сокращений, которые упростят этот процесс. Давайте рассмотрим следующий пример:
Давайте рассмотрим следующий пример:
Пример 4. Преобразование $100100010101111_{2}$ в шестнадцатеричное число.
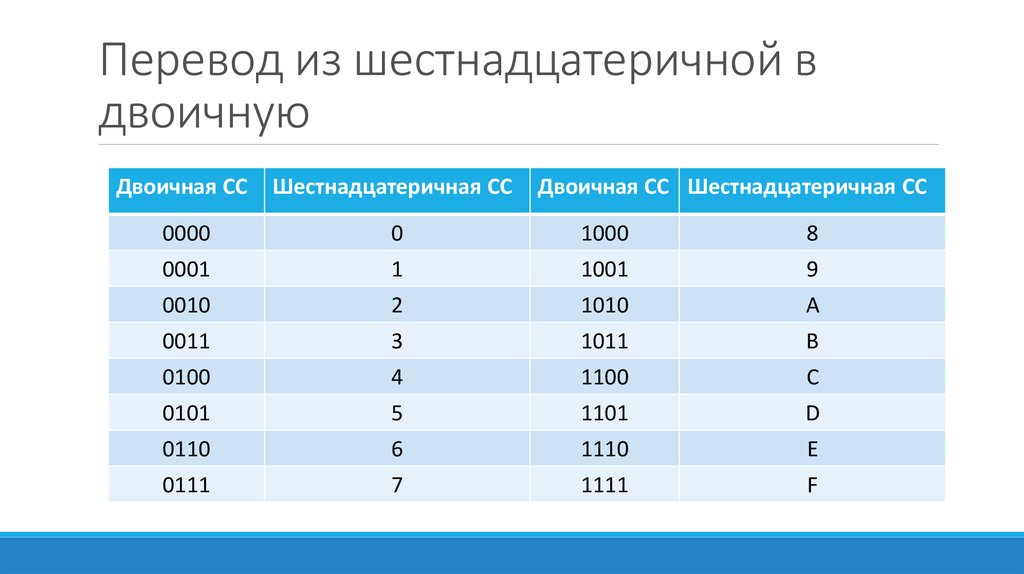
Чтобы преобразовать двоичное число в шестнадцатеричное, мы могли бы просто разбить двоичное число на группы из 4 цифр (начиная справа и добавив начальные нули, если цифры заканчиваются), а затем интерпретировать эти группы из 4 как шестнадцатеричные значения. перечислены в таблице выше. При этом имеем:
$ 1001 000101 к этому, чтобы преобразовать двоичное число в восьмеричное число, мы могли бы просто разбить двоичное число на группы из 3 цифр, а остальная часть процедуры такая же, как преобразование двоичного числа в шестнадцатеричное число. Преобразуем то же двоичное число в восьмеричное:
$100100010101111_{2}=100 100 010 101 111$
$100=4$
$010=2$
$101=5$
$111=7$
$100100010101111_{2}=44257_{8}$
Обратный процесс еще проще. Предположим, мы хотим преобразовать $FC7_{16}$ в двоичную форму. Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
Из таблицы мы можем прочитать двоичные значения для каждой цифры шестнадцатеричного числа:
$F_{16} = 1111_{2}$ $C_{16} = 1100_{2}$ $7_{16} = 0111_{2} $
$FC7_{16}=111111000111_{2}$
Процесс преобразования восьмеричного числа в двоичную форму точно такой же.
Двоичный, восьмеричный и шестнадцатеричный | Введение в математику колледжа |
В современной вычислительной технике и цифровой электронике наиболее часто используются десятичные (по основанию 10), двоичные (по основанию 2), восьмеричные (по основанию 8) и шестнадцатеричные (по основанию 16). Если мы конвертируем между двумя основаниями, отличными от десятичных, нам обычно нужно преобразовать число в основание 10, а затем преобразовать это число во второе основание. Однако мы можем легко преобразовать напрямую из двоичного в восьмеричное и наоборот, а также из двоичного в шестнадцатеричное и наоборот.
В этом видео дается базовое введение в эти преобразования:
youtube.com/embed/5sS7w-CMHkU?feature=oembed" allowfullscreen="">Другое описание больше похоже на лекцию по математике:
три цифры по основанию два. В базе восемь эти числа представлены одной цифрой.
| Базовый 2 (двоичный) номер | Основание 10 (десятичное), эквивалент | Основание 8 (восьмеричное) число |
|---|---|---|
| 000 | 0 | 0 |
| 001 | 1 | 1 |
| 010 | 2 | 2 |
| 011 | 3 | 3 |
| 100 | 4 | 4 |
| 101 | 5 | 5 |
| 110 | 6 | 6 |
| 111 | 7 | 7 |
Теперь, когда мы добираемся до числа 8, нам нужны четыре цифры по основанию 2 и две цифры по основанию 8. На самом деле, числа от 8 до 63 могут быть представлены двумя цифрами по основанию 8. Нам нужны четыре, пять или шесть цифр. по основанию 2 для представления этих же чисел:
На самом деле, числа от 8 до 63 могут быть представлены двумя цифрами по основанию 8. Нам нужны четыре, пять или шесть цифр. по основанию 2 для представления этих же чисел:
| Число по основанию 2 | .Эквивалент | с основанием 10Основание 8 номер |
|---|---|---|
| 1000 | 8 | 10 = 1 × 8 + 0 × 1 |
| 1001 | 9 | 11 = 1 × 8 + 1 × 1 |
| 1010 | 10 | 12 = 1 × 8 + 2 × 1 |
| … | … | … |
| 111100 | 60 | 74 = 7 × 8 + 4 × 1 |
| 111101 | 61 | 75 = 7 × 8 + 5 × 1 |
| 111110 | 62 | 76 = 7 × 8 + 6 × 1 |
| 111111 | 63 | 77 = 7 × 8 + 7 × 1 |
Число 64 в системе счисления 8 представлено как 100 8 = 1 × 8 2 + 0 × 8 1 + 0 × 8 0 = 1 × 64 + 0 × 8 + 0 × 1. В базе 2 , это будет 1000000 2 . Вы видите здесь закономерность? Для одной цифры в базе 8 нам нужно до трех цифр в базе 2. Для двух цифр в базе 8 нам нужно 4, 5 или 6 цифр в базе 2. Для трех цифр в базе 8 нам нужно 7, 8 , или 9цифры в базе 2. Для каждой дополнительной цифры в базе 8 нам нужно до трех пробелов, чтобы представить ее в базе 2. Вот способ запомнить это: 2 3 = 8, поэтому нам нужно три пробела.
В базе 2 , это будет 1000000 2 . Вы видите здесь закономерность? Для одной цифры в базе 8 нам нужно до трех цифр в базе 2. Для двух цифр в базе 8 нам нужно 4, 5 или 6 цифр в базе 2. Для трех цифр в базе 8 нам нужно 7, 8 , или 9цифры в базе 2. Для каждой дополнительной цифры в базе 8 нам нужно до трех пробелов, чтобы представить ее в базе 2. Вот способ запомнить это: 2 3 = 8, поэтому нам нужно три пробела.
Здесь поможет пара примеров.
- Преобразуйте число 6157 8 в основание 2. Мы разделим каждую цифру по основанию 8 на три цифры по основанию 2, используя трехзначный эквивалент по основанию 2, поэтому 6 8 = 110 2 , 1 8 = 001 2 и т. д.
- Преобразуйте число 10111011001010 2 в основание 8. Разбейте это число на наборы по три, , начиная с крайней правой цифры , а затем преобразуйте каждый набор из трех в его эквивалент в основании 8.

Для шестнадцатеричного (основание 16) нам нужно до четырех двоичных цифр для представления каждой отдельной цифры. Запомните это, вспомнив, что 2 4 = 16, поэтому нам нужно четыре цифры.
Вы можете распечатать копии этих листов, чтобы помочь вам с преобразованиями между двоичным и восьмеричным или шестнадцатеричным:
- Преобразование из двоичного в восьмеричный
- Преобразование двоичного формата в шестнадцатеричный
Если вы хотите проверить себя в преобразовании чисел от 0 до 255 в двоичные, восьмеричные и шестнадцатеричные (и между этими основаниями), вот ссылка на представления этих чисел: Двоичные, восьмеричные и шестнадцатеричные числа.
Лицензии и ссылки
Лицензионный контент CC, оригинал
- Математика для гуманитарных наук I. Предоставлено : Институт расширенного обучения муниципального колледжа Северной Вирджинии. Расположен по адресу : https://online.
 nvcc.edu/. Лицензия : CC BY: Атрибуция
nvcc.edu/. Лицензия : CC BY: Атрибуция
Все права защищены.
Автор : MyWhyU. Лицензия : Все права защищены . Условия лицензии : Стандартная лицензия YouTubeДвоичная система счисления, десятичная система счисления, восьмеричная система счисления, шестнадцатеричная система счисления : Pharmaguideline
В двоичной системе число определяется с помощью двоичной системы счисления. Двоичная система использует только две цифры, 0 и 1, для представления числа.
Двоичная система счисления
В двоичной системе число определяется с помощью двоичной системы счисления. Двоичная система использует только две цифры, 0 и 1, для представления числа. Многие компьютерные языки используют двоичные системы счисления, включая Java и C++. Компьютер может понимать только двоичный язык (0 или 1), то есть 0 и 1, поэтому все входные данные перед дальнейшей обработкой преобразуются в последовательность 0 и 1. Чтобы понять смысл информации в этом уроке, я преобразовал десятичное число в двоичное число, а затем вернул двоичное число в десятичное число.
Двоичная система использует только две цифры, 0 и 1, для представления числа. Многие компьютерные языки используют двоичные системы счисления, включая Java и C++. Компьютер может понимать только двоичный язык (0 или 1), то есть 0 и 1, поэтому все входные данные перед дальнейшей обработкой преобразуются в последовательность 0 и 1. Чтобы понять смысл информации в этом уроке, я преобразовал десятичное число в двоичное число, а затем вернул двоичное число в десятичное число.
Двоичный символ "Би" означает "два". Таким образом, линия возвращается к 0 и 1 как к единственным способам представления числа. Двоичные числа могут быть легко выражены в виде десятичных чисел. Различия между двоичной и десятичной системами счисления. Двоичные числа представлены по основанию двойки, а десятичные числа представлены по основанию 10.
Ниже показано, как числа от 1 до 10 выражаются в двоичной системе счисления:
Десятичная система счисления
Числа представлены своими основаниями в системе счисления. Существует четыре основы для чисел: двоичная, восьмеричная, десятичная и шестнадцатеричная. Если основание равно 2, оно двоичное, если 8 — восьмеричное, если 10 — десятичное, а если 16 — шестнадцатеричное. Взять десятичные числа и преобразовать их в другую систему счисления несложно. Однако преобразование десятичных чисел из других систем счисления требует практики.
Существует четыре основы для чисел: двоичная, восьмеричная, десятичная и шестнадцатеричная. Если основание равно 2, оно двоичное, если 8 — восьмеричное, если 10 — десятичное, а если 16 — шестнадцатеричное. Взять десятичные числа и преобразовать их в другую систему счисления несложно. Однако преобразование десятичных чисел из других систем счисления требует практики.
В этой статье мы более подробно рассмотрим десятичные числа и то, как их можно преобразовать в другие системы. Основа 10 представляет десятичные числа в десятичной системе счисления. Также известная как десятичная запись, это способ представления десятичных чисел с основанием 10. Многие компьютерные программы используют этот числовой формат. База-10 — это система счисления, состоящая из 10 цифр, например, 0,1,2,3,4,5,6,7,8,9. Десятичные числа имеют четкую позицию для каждой цифры, и каждая цифра в 10 раз значительнее, чем любая предыдущая цифра. Два в десять раз больше, чем пять, если 25 — десятичное число. Число в десятичной системе представляет собой число от 0 до 9 с использованием цифр от 0 до 9.
В системе счисления с основанием 10 число записывается с нулем или первыми девятью положительными целыми числами, представляющими каждое значение. В конце каждого значения ставится степень 10. Десятикратный размер цифры в разряде десятков означает, что он в десять раз больше десятого в разряде единиц. Подсчет в порядке убывания мощности каждой цифры, которая следует за десятичным нулем (.) в десятичном числе.
Восьмеричная система счисления
В восьмеричной системе счисления числа от 0 до 7 представляют собой восьмизначные числа. Всякий раз, когда восьмеричные числа сгруппированы по три, в качестве представления используются двоичные числа. Системы счисления с основанием «восемь» называются восьмеричными числами. Эта система работает с числами от нуля до семи. По основанию 2 двоичное число является десятичным, по основанию 10 и по основанию 16 — шестнадцатеричным числом. Основание 2 такое же, как основание 8, когда дело доходит до описания восьмеричного числа.
Группируя последовательные двоичные числа в группы по три (для целых чисел, начиная справа), восьмеричные числа легко преобразуются из двоичных представлений (аналогично четверичным числам). Двоичное представление десятичного числа 74, например, 1001010. Добавляя два нуля слева: (00)1 001 010, что соответствует восьмеричным числам 1 1 2, можно получить восьмеричное число 112.
Число с основанием 8, такое как 248, 1098 или 558, является восьмеричным. количество. В восьмеричной системе счисления используются только семь цифр. Больше 7, например 8 или 9, восьмеричные цифры не используются. Единица, деленная на 10, называется восьмеричным числом. Число 19 не представляет собой восьмеричное число.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления существует значение основания 16 для метода представления чисел. Единственными возможными значениями являются 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Например, A представляет собой однобитовое представление десятичных значений 10. , 11, 12, 13, 14 и 15, тогда как B представляет собой двухбитное представление десятичных значений 14 и 15. Значение любой цифры может быть представлено только 4 битами. Префиксы 0x и суффиксы h используются в качестве шестнадцатеричной записи. Вес каждой цифры в степени 16,
Например, A представляет собой однобитовое представление десятичных значений 10. , 11, 12, 13, 14 и 15, тогда как B представляет собой двухбитное представление десятичных значений 14 и 15. Значение любой цифры может быть представлено только 4 битами. Префиксы 0x и суффиксы h используются в качестве шестнадцатеричной записи. Вес каждой цифры в степени 16,
Шестнадцатеричные числа имеют в 16 раз большее значение, чем предшествующие позиции, поэтому для вычисления значения шестнадцатеричного числа умножьте каждую цифру на значение позиции, в которой она стоит, а затем сложите произведения. Помимо взвешенной системы счисления, у нас также есть позиционная система счисления. Для шестнадцатеричных чисел используется только четыре бита, причем каждая группа битов имеет разные значения от 0000 (для 0) до 1111 (для F = 15 = 8+4+2+1). Ниже приведена таблица в двоичной форме эквивалентов шестнадцатеричных чисел.
Как и восьмеричные числа, шестнадцатеричные числа также являются системой чисел.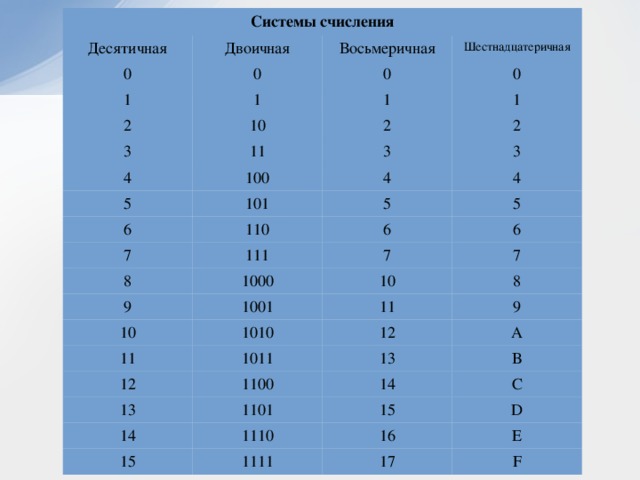 Используя шестнадцатеричные числа, можно преобразовать большие двоичные числа в более мелкие и компактные группы.
Используя шестнадцатеричные числа, можно преобразовать большие двоичные числа в более мелкие и компактные группы.
Получить тематические документы в формате pdf. Посмотреть здесь они полезны. Кратко пройдемся по десятичное , двоичное , восьмеричное и шестнадцатеричное числовое представление.
Десятичный (с основанием 10)
Наиболее распространенной системой представления чисел является десятичный . Все используют его. Это настолько распространено, что большинство людей должно полагать, что это единственное. Он используется в финансах, технике и биологии почти везде, где мы видим и используем числа.
Если кто-то попросит вас думать о числе, вы наверняка будете думать о десятичном числе. Если вы думаете в двоичном или шестнадцатеричном формате, вы должны быть очень увлечены арифметикой или программным обеспечением/программированием.
Как следует из названия, в десятичной системе счисления используется 10 символов/символов.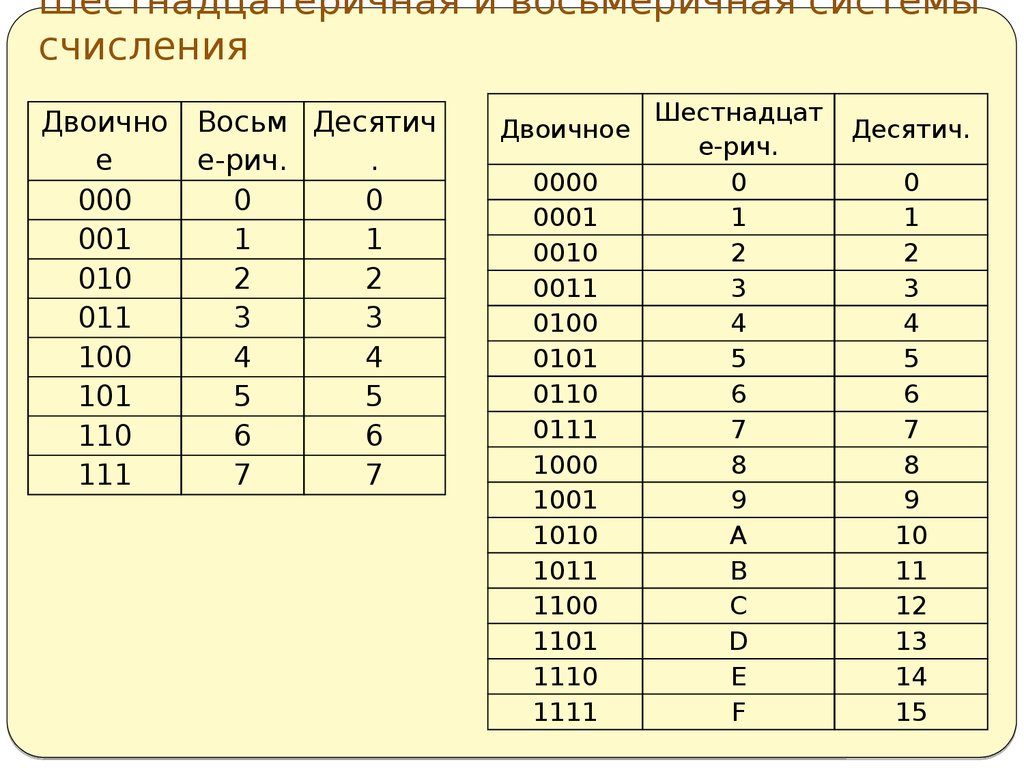 В латинском языке 10 — это «decem», поэтому десятичная дробь может быть связана с латинским словом.
В латинском языке 10 — это «decem», поэтому десятичная дробь может быть связана с латинским словом.
| Decimal Symbols | |||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
As you can see there are 10 символов от 0 до 9 . С помощью этих символов мы можем построить все числа в десятичной системе.
Все числа в десятичной системе можно составить, используя вышеупомянутые символы ( 0 … 9 ), умноженные на степень 10. Степень десятки дает нам единицы, десятки, сотни, тысячи и так далее.
| 10 k | … | 10 5 | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| N | … | 100000 | 10000 | 1000 | 100 | 10 | 1 |
The example below breaks умножьте десятичное число 67049 на степени 10, умноженные на числа от 0 до 9 .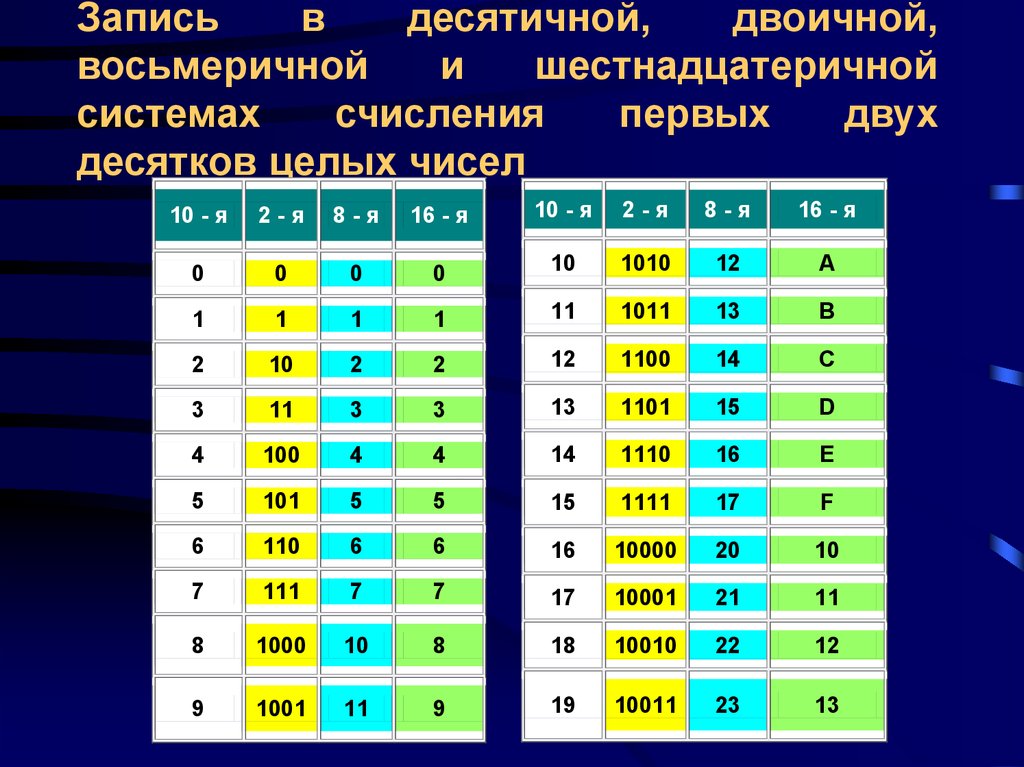 Это просто для того, чтобы показать, что любое число в десятичной системе можно разложить на сумму слагаемых, составленных из произведения степени 10 и символов 9.0221 0 … 9 .
Это просто для того, чтобы показать, что любое число в десятичной системе можно разложить на сумму слагаемых, составленных из произведения степени 10 и символов 9.0221 0 … 9 .
| 67049 | |||||||
| 10 7 | 10 6 | 10 5 | 10 4 | 10 3 | 10 2 | 10 1 | 10 0 |
| 0 | 0 | 0 | 6 | 7 | 0 | 4 | 9 |
| 67049= 6 ⋅ 10 4 + 7 ⋅ 10 3 + 0 ⋅ 10 2 + 4 ⋅ 10 1 + 9 ⋅ 10 0 = 60000 + 7000 + 0 + 40 + 9 | |||||||
Эта же методика будет применяться к двоичной, восьмеричной и шестнадцатеричной системам счисления, являясь по сути методом преобразования числа из десятичной системы в другой формат (базу).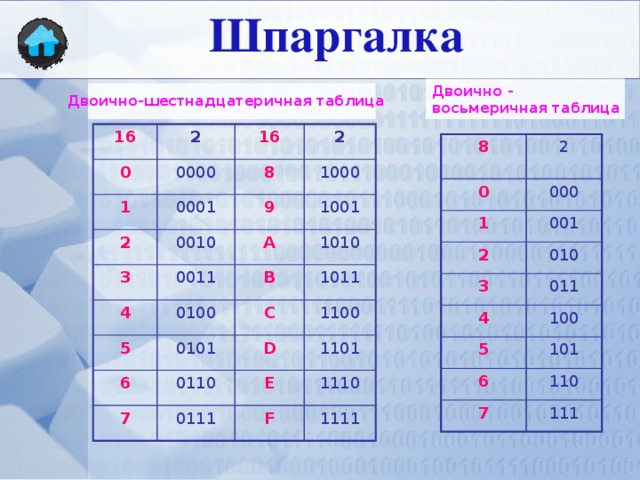
Мы можем помнить следующие характеристики десятичной системы счисления:
- используется 10 символов
- можно разложить на множители, содержащие степени 10
- это наиболее распространенная система представления чисел
Двоичная (по основанию 2)
Теперь давайте перейдем к гиковской стороне.
Другой системой представления чисел является двоичная . Как следует из названия и по аналогии с десятичной системой, мы можем сказать, что двоичная система использует только 2 символа/символа:
| Двоичные символы | |
| 0 | 1 |
В двоичном представлении мы используем только 0 (нули) и 1 (единицы) для представления чисел.
Двоичная система используется везде, где требуется хранить информацию в электронном формате. Все известные вам компьютеры, интеллектуальные устройства, все, что связано с электроникой и микроконтроллерами, используют двоичную систему.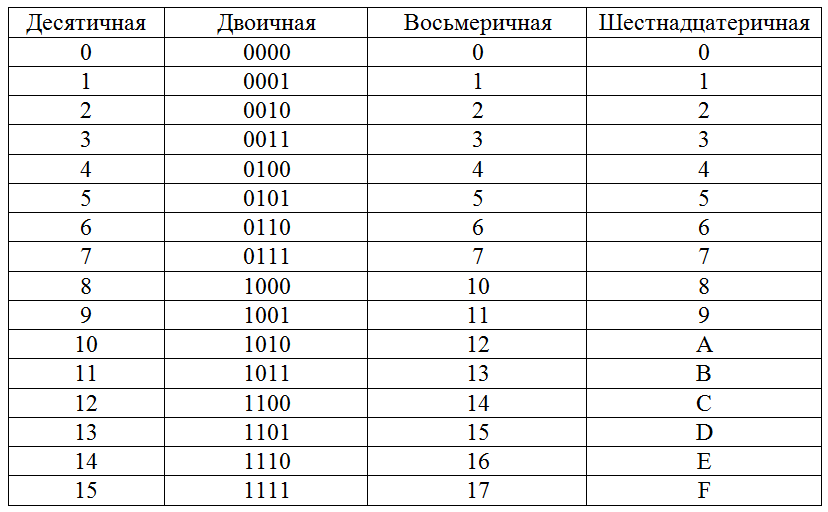
В электронике (цифровой) все операции выполняются с использованием двух уровней напряжения: высокого и низкого. Каждому уровню напряжения присваивается значение/символ: HIGH для 1 и LOW для 0. Для микроконтроллера, на который подается напряжение +5 В, 1 (высокий) будет представлен +5 В, а 0 (низкий) 0 В.
Грубо говоря, мы можем сказать, что используется двоичная система, потому что ее можно перевести в электронный сигнал.
Все десятичные числа, которые мы можем представить, могут быть представлены в виде двоичных символов. Мы делаем это, используя сумму между членами степени 2, умноженной на 0 или 1.0034
В качестве примера.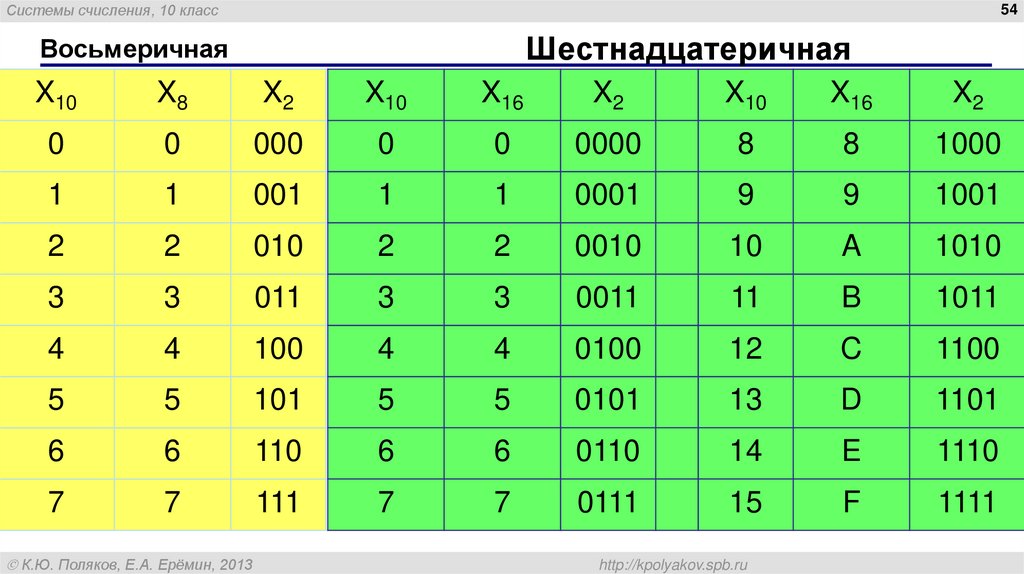 Мы могли бы использовать любое число, но если оно окажется слишком большим, оно превратится в длинную строку нулей и единиц.
Мы могли бы использовать любое число, но если оно окажется слишком большим, оно превратится в длинную строку нулей и единиц.
| 149 | |||||||
| 2 7 | 2 6 | 2 5 | 2 4 | 2 3 | 2 2 | 2 1 | 2 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 149 = 1 ⋅ 2 7 + 0 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 0 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 1283 = 1283 = 1283 = 0 + 16 + 0 + 4 + 0 + 1 | |||||||
Как видите, десятичное число 149 представлено в двоичной системе последовательностью нулей и единиц ( 10010101 ). Обычно, чтобы различать десятичное или двоичное число, мы должны указать основание, на которое мы ссылаемся. Основание описывается как нижний индекс после последнего символа числа 9.0011
Обычно, чтобы различать десятичное или двоичное число, мы должны указать основание, на которое мы ссылаемся. Основание описывается как нижний индекс после последнего символа числа 9.0011
Пример:
| Десятичный (базовая 10) | Двоичный (базу 2) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 149 10 | 10010101 2 | 10010101 2 | 10010101 2 . вероятность путаницы, потому что одно и то же представление (например, 11) может означать разные вещи для разных оснований.
Другой способ избежать путаницы — использовать специальную запись (префикс) для двоичных чисел. Это потому что Кратко характеристики двоичной системы:
восьмеричная (основание 8) Все числа в восьмеричной системе представлены с использованием 8 символов/символов, от У человека 4 промежутка между пальцами одной руки; всего у нас будет 8 пробелов, для обеих рук. В этом случае имеет смысл использовать восьмеричную систему представления чисел вместо десятичной. Недостатком является то, что для более высоких чисел потребуется больше символов по сравнению с десятичным числом.
, представляющие десятичный номер на график, мы распались на десятилевые.
Представление десятичного числа Вкратце характеристики системы представления шестнадцатеричных чисел:
вышеупомянутые системы представления чисел.
Как восьмеричная, так и шестнадцатеричная системы представления чисел связаны с компьютерной системой, в основном с процессорами и микроконтроллерами. Например, если микропроцессор использует 8-битные данные, то для интерфейса данных подходит восьмеричная система. Преобразование шестнадцатеричных чисел в восьмеричныеЧто такое шестнадцатеричные числа?Числа, базовое значение которых равно 16, называются шестнадцатеричными числами. Одно число обычно представлено 16 другими числами. Он обозначается как n16, где n — любое случайное шестнадцатеричное число. 16-значный номер может быть комбинацией цифр и букв. Числа, используемые для представления, находятся в диапазоне от 0 до 9, а алфавиты — в диапазоне от A до F. Что такое восьмеричные числа? Числа, базовое значение которых равно 8, называются шестнадцатеричными числами. Одно число обычно представлено 8 другими числами. Он обозначается как n8, где n — любое случайное восьмеричное число. 8-значный номер может быть комбинацией цифр. Числа, используемые для представления, находятся в диапазоне от 0 до 7. Восьмеричные числа не могут быть представлены 8 и 9. Преобразование шестнадцатеричных чисел в восьмеричныеСуществует два метода преобразования шестнадцатеричных чисел в восьмеричные. Это: Метод 1 : Нельзя напрямую преобразовать шестнадцатеричное число в восьмеричное десятичное число. Сначала вам нужно будет преобразовать шестнадцатеричное число в его десятичный эквивалент, а затем преобразовать десятичный эквивалент в восьмеричное десятичное число. Чтобы лучше понять, выполните шаги, указанные ниже.
Метод 2 Это был метод 1. Если вы сочтете это трудным, вы также можете использовать другой метод, чтобы найти восьмеричное десятичное значение шестнадцатеричного числа. Мы знаем, что шестнадцатеричное число состоит из двоичных цифр. В этом методе вы можете объединить эти двоичные цифры в пары по три и связать их с восьмеричными числами. Шаги, связанные с этим методом, приведены ниже.
Ниже приведены примеры преобразования шестнадцатеричных чисел в восьмеричные Вопрос 1. Преобразуйте следующее шестнадцатеричное число в восьмеричное число 2CD16. Ответ: Дано, 2CD16 — шестнадцатеричное число. 2 → 0010, C → 1100, D → 1101, Теперь вы будете группировать их справа налево, по 3 цифры в каждой. 001, 011, 001, 101 001→1, 011 →3, 001→1, 101→5 Следовательно, 2CD16 = 13158 Вопрос 2. Преобразуйте следующее шестнадцатеричное число 3EC в восьмеричное. Ответ: Дано, 3EC16 – это шестнадцатеричное число. 3 → 0010, E → 1110, C → 1100, Теперь вы будете группировать их справа налево, по 3 цифры в каждой. 001, 011, 101, 100 001→1, 011→3, 101→5, 100→4 Следовательно, 3EC16 = 13548 приведенная ниже таблица для облегчения преобразования.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||



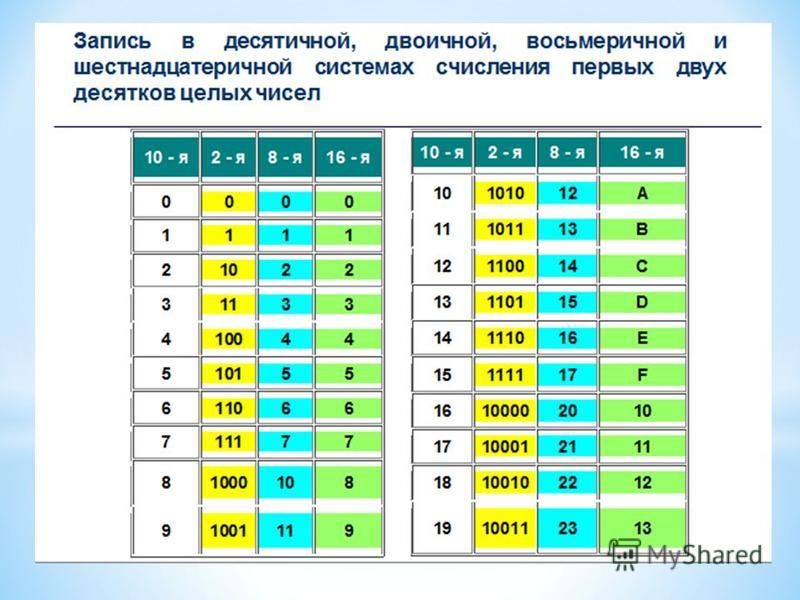 (1″)
(1″)
 Примеры приведены в таблице ниже.
Примеры приведены в таблице ниже.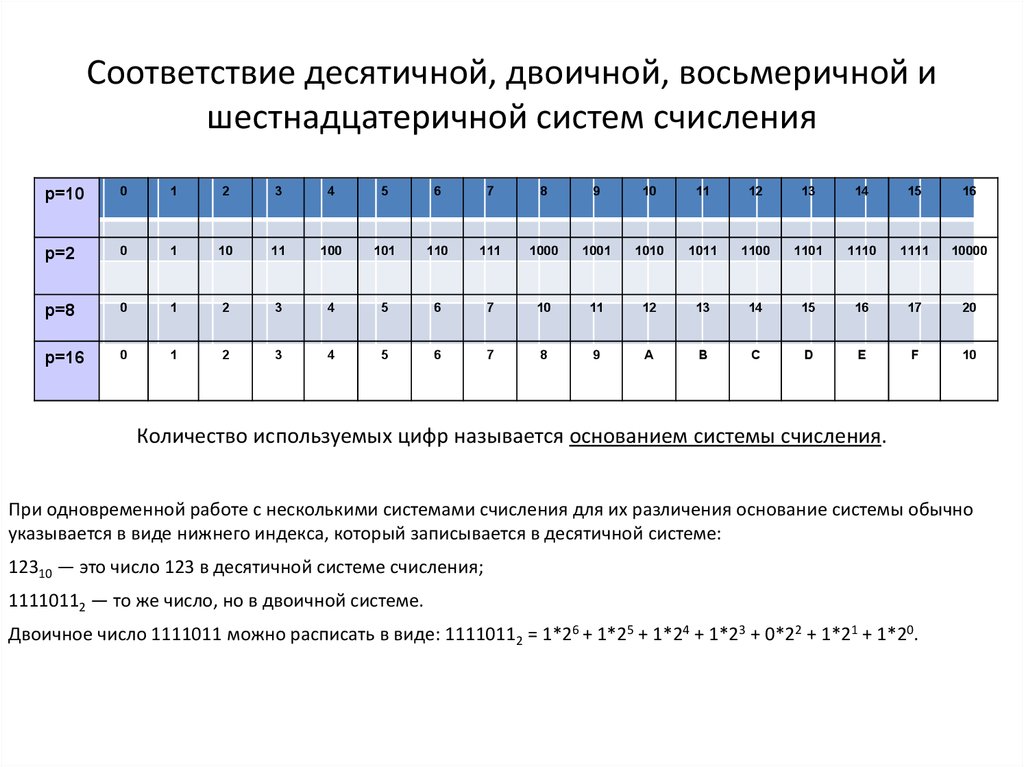
 nvcc.edu/. Лицензия : CC BY: Атрибуция
nvcc.edu/. Лицензия : CC BY: Атрибуция 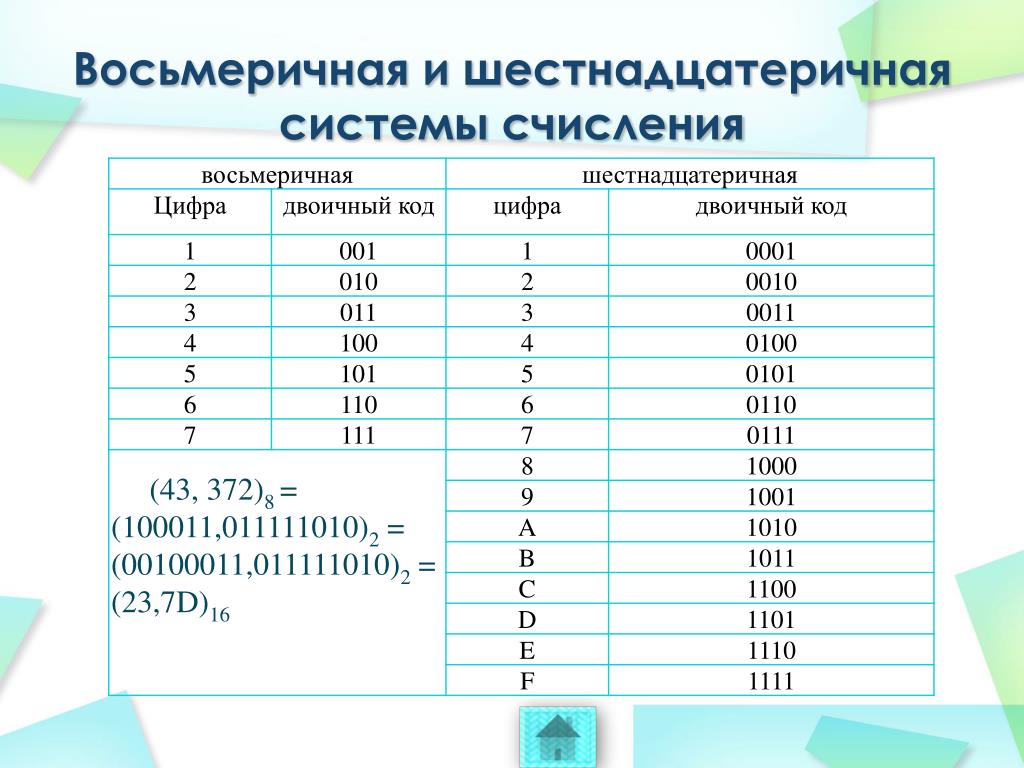 Пример:
Пример:  it into terms containing the power of 8:
it into terms containing the power of 8: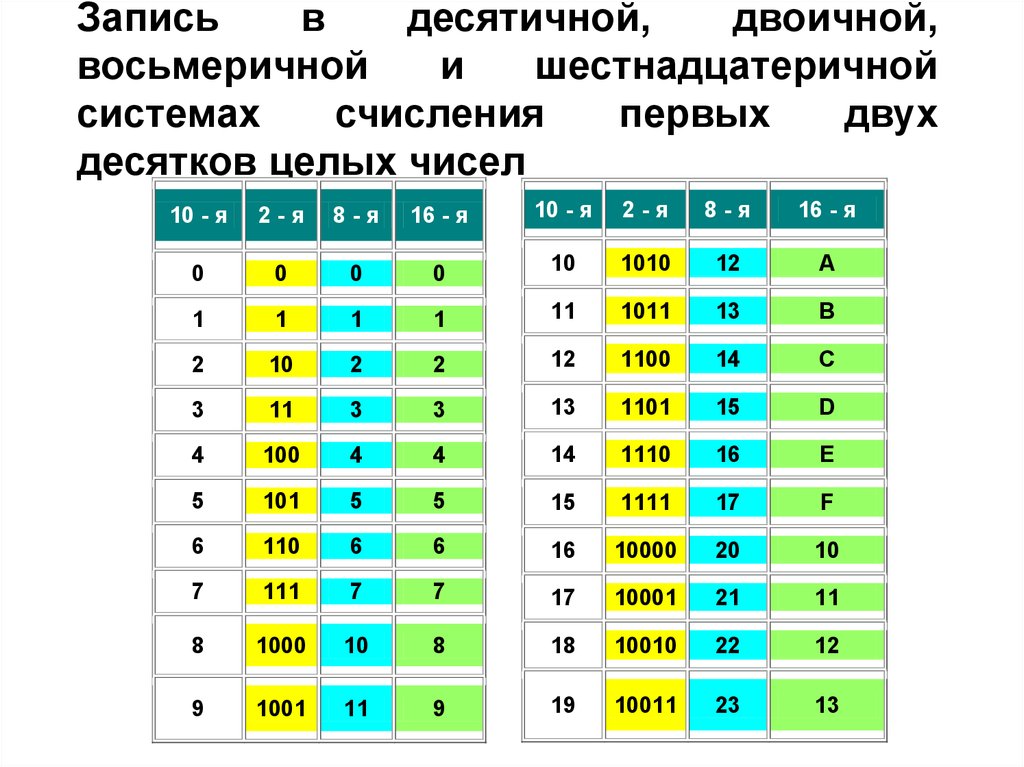
 Each term is a product between a hexadecimal symbol and a power of 16.
Each term is a product between a hexadecimal symbol and a power of 16.
 Если микропроцессор использует 16 бит, то для представления данных подходит шестнадцатеричная система.
Если микропроцессор использует 16 бит, то для представления данных подходит шестнадцатеричная система.