Индуктивность соленоида
Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока внутри катушки является фактически постоянной и (приближенно) равна
где − магнитная постоянная, − число витков, − ток и − длина катушки. Пренебрегая краевыми эффектами на концах соленоида, получим[16], что потокосцепление через катушку равно плотности потока , умноженному на площадь поперечного сечения и число витков :
Отсюда следует формула для индуктивности соленоида (без сердечника):
Если
катушка внутри полностью заполнена
магнитным материалом (сердечником), то
индуктивность отличается на
множитель — относительную
магнитную проницаемость
В
случае, когда ,
можно (следует) под S понимать
площадь сечения сердечника и пользоваться
данной формулой даже при толстой намотке,
если только полная площадь сечения
катушки не превосходит площади сечения
сердечника во много раз.
Более точные формулы для соленоида конечного размера
Для однослойного (с очень тонкой намоткой) соленоида конечных размеров (не бесконечно длинного) существуют более точные, хотя и более сложные формулы[18]:
где
— количество витков,
— радиус цилиндра,
— длина его образующей,
,
— Эллиптические интегралы.
Это дает
для
для
Трансформатор. Энергия магнитного поля. Основы теории Максвелла. Уравнения Максвелла в интегральной форме.
Электрический колебательный контур.
 Затухающие
электромагнитные колебания. Вынужденные
электромагнитные колебания. Явление
резонанса
Затухающие
электромагнитные колебания. Вынужденные
электромагнитные колебания. Явление
резонанса
Колебательный контур — осциллятор, представляющий собой электрическую цепь, содержащую соединённые катушку индуктивности и конденсатор. В такой цепи могут возбуждаться колебания тока (и напряжения).
Колебательный контур — простейшая система, в которой могут происходить свободные электромагнитные колебания
Резонансная частота контура определяется так называемой формулой Томсона:
Принцип действия
Пусть конденсатор ёмкостью C заряжен до напряжения . Энергия, запасённая в конденсаторе составляет
При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток ,
что вызовет в катушке электродвижущую
силу (ЭДС) самоиндукции,
направленную на уменьшение тока в цепи.
Ток, вызванный этой ЭДС (при отсутствии
потерь в индуктивности) в начальный
момент будет равен току разряда
конденсатора, то есть результирующий
ток будет равен нулю.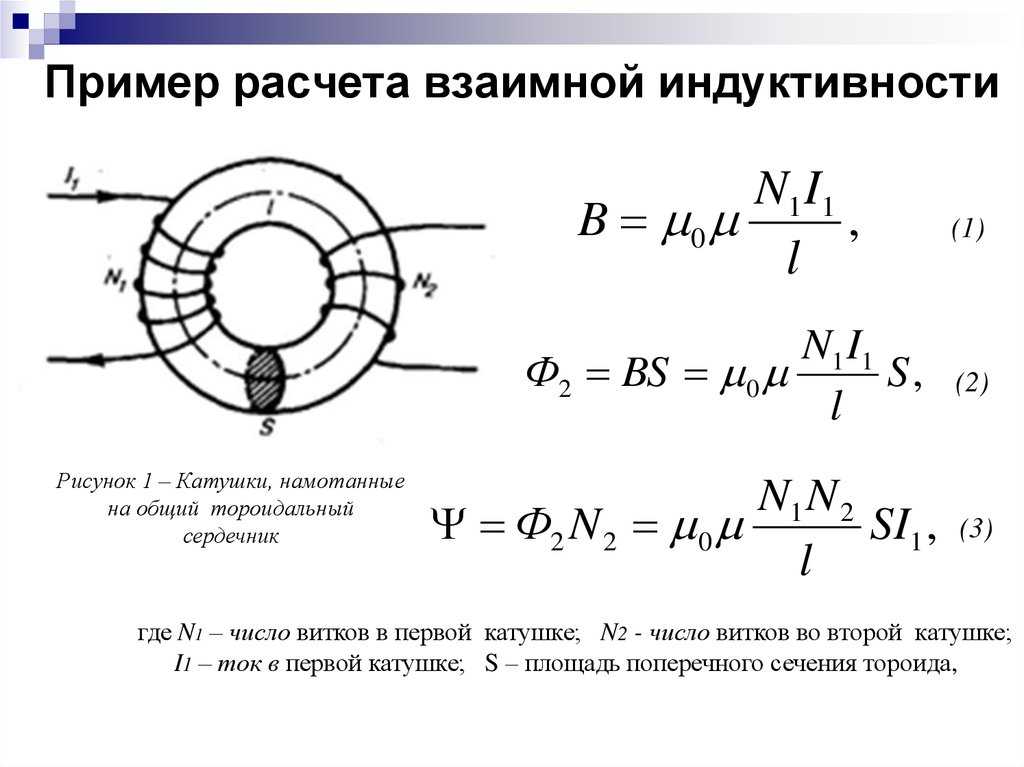 Магнитная энергия
катушки в этот (начальный) момент равна
нулю.
Магнитная энергия
катушки в этот (начальный) момент равна
нулю.
Затем результирующий ток в цепи будет возрастать, а энергия из конденсатора будет переходить в катушку до полного разряда конденсатора. В этот момент электрическая энергия конденсатора . Магнитная же энергия, сосредоточенная в катушке, напротив, максимальна и равна
, где — индуктивность катушки, — максимальное значение тока.
После этого начнётся перезарядка конденсатора, то есть заряд конденсатора напряжением другой полярности. Перезарядка будет проходить до тех пор, пока магнитная энергия катушки не перейдёт в электрическую энергию конденсатора. Конденсатор, в этом случае, снова будет заряжен до напряжения .
В результате в цепи возникают колебания, длительность которых будет обратно пропорциональна потерям энергии в контуре.
В
общем, описанные выше процессы в
параллельном колебательном контуре
называются резонанс
токов,
что означает, что
через индуктивность и ёмкость протекают
токи, больше тока проходящего через
весь контур, причем эти токи больше в
определённое число раз, которое
называется добротностью.
Стоит заметить, что помимо простого колебательного контура, есть ещё колебательные контуры первого, второго и третьего рода, что учитывают потери и имеют другие особенности.
Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.
Принцип
действия генератора переменного тока
легко показать при рассмотрении
вращающейся рамки провода в магнитном
поле.
В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).
Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.
Магнитный поток в момент времени t0 = 0 будет равен Ф = В*8.
При равномерном вращении рамки вокруг оси OO1 с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:
Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную
где Е0= ВSw — амплитуда ЭДС.
Если
с помощью контактных колец и скользящих
по ним щеток соединить концы рамки с
электрической цепью, то под действием
ЭДС индукции, изменяющейся со временем
по гармоническому закону, в электрической
цепи возникнут вынужденные гармонические
колебания силы тока — переменный
ток.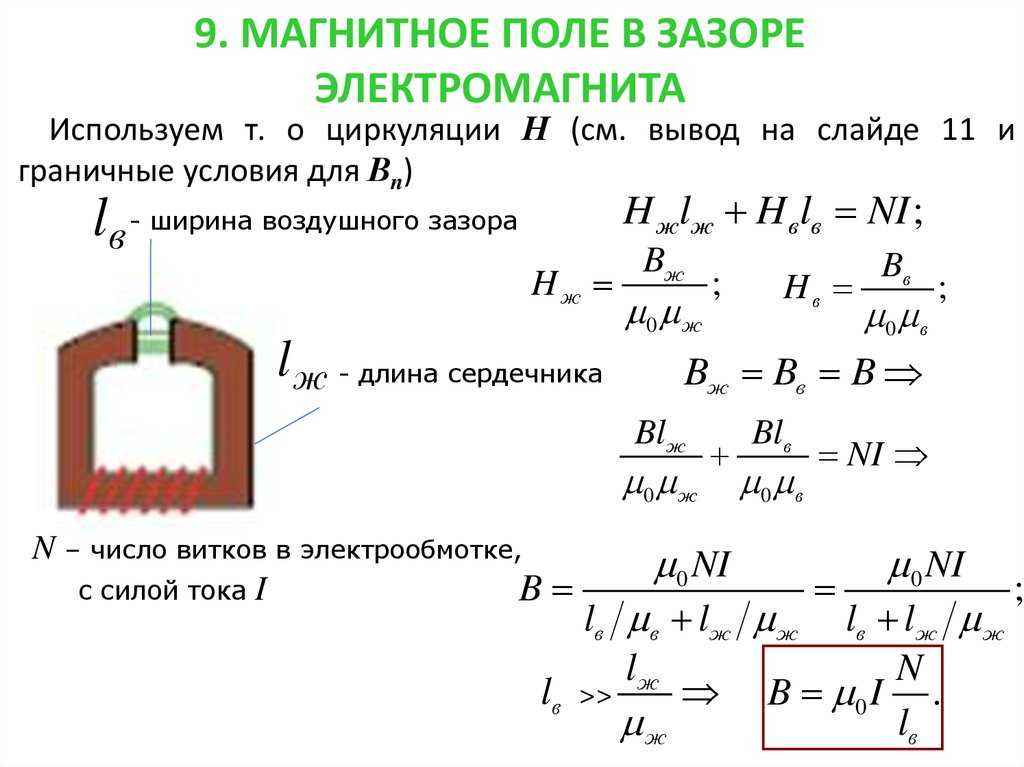
На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец.
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее
условие резонанса для любого двухполюсника можно
сформулировать в виде Im[Z]=0
или Im[Y]=0,
где Z и Y комплексное сопротивление и проводимость
двухполюсника. Следовательно, режим
резонанса полностью определяется
параметрами электрической цепи и не
зависит от внешнего воздействия на нее
со стороны источников электрической
энергии.
Акопов Вачакан Ваграмович /AkopovVachakanVagramovich – учитель физики МОУ СОШ №6, Ставропольский край Курский район,село Полтавское Аннотация: в статье представлен вывод формул индукции поля соленоида, созданного переменным током. Эту формулу можно использовать для углубленного изучения учащимися темы «Магнитное поле» и при решении задач.  101]: L = , где (1)где 101]: L = , где (1)где Приравняв выражения (3) и (4), получим В = . (5)Таким образом, индукция поля соленоида, созданного переменным током, прямо пропорциональна индуцированному в соленоиде напряжению. Как известно, магнитную индукцию поля, созданного постоянным током, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси определяют по формуле [2, с.232]: В = (в вакууме), (6)гдеn=NI – число ампер-витков соленоида,l – длина соленоида,µо –магнитная постоянная.Единица магнитной индукции (тесла) может быть установлена по формуле (6): [В] = ×=, (7)С другой стороны единица магнитной индукции (тесла) может быть установлена по формуле (5): [В] = , (8)Перемножив выражения (7) и (8), получим:[В]2 = ×= = , (9)Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:В2 = ,отсюда В = , (10)где V — объём соленоида,Р – мощность переменного тока. Приравняв выражения (3) и (4), получим В = . (5)Таким образом, индукция поля соленоида, созданного переменным током, прямо пропорциональна индуцированному в соленоиде напряжению. Как известно, магнитную индукцию поля, созданного постоянным током, текущим по виткам бесконечно длинного соленоида, внутри этого соленоида на его оси определяют по формуле [2, с.232]: В = (в вакууме), (6)гдеn=NI – число ампер-витков соленоида,l – длина соленоида,µо –магнитная постоянная.Единица магнитной индукции (тесла) может быть установлена по формуле (6): [В] = ×=, (7)С другой стороны единица магнитной индукции (тесла) может быть установлена по формуле (5): [В] = , (8)Перемножив выражения (7) и (8), получим:[В]2 = ×= = , (9)Тогда заменив единицы измерения в выражении (9) физическими величинами, получим формулу для индукции поля соленоида, созданного переменным током:В2 = ,отсюда В = , (10)где V — объём соленоида,Р – мощность переменного тока. Таким образом, индукция магнитного поля соленоида увеличивается при увеличении мощности переменного тока и уменьшается при увеличении объёма соленоида.Задача 1. Магнитная индукция поля внутри соленоида, состоящего из 2000 витков диаметра 2,8см, подключённого к источнику переменного тока с частотой 50Гц, равна 0,72мТл. Каково индуцированное в соленоиде напряжение? Таким образом, индукция магнитного поля соленоида увеличивается при увеличении мощности переменного тока и уменьшается при увеличении объёма соленоида.Задача 1. Магнитная индукция поля внутри соленоида, состоящего из 2000 витков диаметра 2,8см, подключённого к источнику переменного тока с частотой 50Гц, равна 0,72мТл. Каково индуцированное в соленоиде напряжение?
Теги: созданного переменным током соленоида формул |
||||||||||||||||||||||||||||||||||||||||||
Курс физики (Геворкян Р. Г.)
Курс физики (Геворкян Р. Г.)
ОглавлениеПРЕДИСЛОВИЕЧасть I. МЕХАНИКА § 1. СИСТЕМЫ ОТСЧЕТА; ЛИНЕЙНЫЕ И УГЛОВЫЕ СКОРОСТИ И УСКОРЕНИЯ ДВИЖЕНИЕ ПО КРИВОЛИНЕЙНОЙ ТРАЕКТОРИИ § 2.  ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА. СИСТЕМЫ ЕДИНИЦСИЛА. ДЕФОРМАЦИЯ. МАССА ОСНОВНЫЕ ЗАКОНЫ МЕХАНИКИ ИМПУЛЬС. РАБОТА. МОЩНОСТЬ ЕДИНИЦЫ ФИЗИЧЕСКИХ ВЕЛИЧИН § 3. ДВИЖЕНИЕ ТЕЛА В ПОЛЕ ТЯГОТЕНИЯ ЗЕМЛИ ГРАВИТАЦИОННОЕ ПОЛЕ. ВЕС ТЕЛА ДВИЖЕНИЕ КОСМИЧЕСКИХ ОБЪЕКТОВ § 4. ДВИЖЕНИЕ ТЕЛ С ПЕРЕМЕННОЙ МАССОЙ § 5. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ В МЕХАНИКЕ ПРЕОБРАЗОВАНИЯ КООРДИНАТ, СКОРОСТЕЙ И УСКОРЕНИЙ Глава 2. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ВРАЩАЮЩЕГОСЯ ТЕЛА; МОМЕНТ ИНЕРЦИИ ТЕЛ § 7. ЗАКОНЫ МЕХАНИКИ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ § 8. СВОБОДНЫЕ ОСИ. БАЛАНСИРОВКА РОТОРОВ. ГИРОСКОПЫ Глава 3. ЗАКОНЫ СОХРАНЕНИЯ В СИСТЕМЕ ВЗАИМОДЕЙСТВУЮЩИХ ТЕЛ § 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА (КОЛИЧЕСТВА ДВИЖЕНИЯ) § 10. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА (МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ) § 11. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 12. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ НЕКОТОРЫХ СИСТЕМ § 13. СТОЛКНОВЕНИЕ ШАРОВ § 14. О ЦЕНТРЕ МАСС СИСТЕМЫ Глава 4. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ § 15.  ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ ПЕРИОДИЧЕСКОЕ ДВИЖЕНИЕ; ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ§ 16. СКОРОСТЬ И УСКОРЕНИЕ КОЛЕБЛЮЩЕГОСЯ ТЕЛА. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ § 17. СИЛА И ЭНЕРГИЯ ПРИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЯХ. ПРОСТЕЙШИЕ МЕХАНИЧЕСКИЕ КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ § 18. СОБСТВЕННЫЕ, СВОБОДНЫЕ И ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ. ПАРАМЕТРИЧЕСКОЕ ВОЗБУЖДЕНИЕ КОЛЕБАНИЙ § 19. ПОНЯТИЕ О НЕЛИНЕЙНЫХ КОЛЕБАНИЯХ § 20. СЛОЖЕНИЕ И РАЗЛОЖЕНИЕ КОЛЕБАНИЙ § 21. АВТОКОЛЕБАНИЯ Глава 5. ВОЛНОВЫЕ ПРОЦЕССЫ; ОСНОВЫ АКУСТИКИ § 22. ОБРАЗОВАНИЕ И РАСПРОСТРАНЕНИЕ ВОЛН В УПРУГОЙ СРЕДЕ § 23. ФОРМУЛА ГАРМОНИЧЕСКОЙ ВОЛНЫ ВОЛНА В УПРУГОЙ СРЕДЕ § 24. ПОТОК ЭНЕРГИИ В ВОЛНОВЫХ ПРОЦЕССАХ § 25. ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ ВОЛН. РАСПРОСТРАНЕНИЕ ВОЛН В СРЕДАХ С ДИСПЕРСИЕЙ § 26. СТОЯЧИЕ ВОЛНЫ § 27. ЗВУКОВЫЕ КОЛЕБАНИЯ И ВОЛНЫ ЭФФЕКТ ДОПЛЕРА ХАРАКТЕРИСТИКИ ЗВУКОВОГО ОЩУЩЕНИЯ § 28. УЛЬТРАЗВУКИ И ИХ ПРИМЕНЕНИЯ Глава 6. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ § 29. ГИДРОСТАТИЧЕСКОЕ ДАВЛЕНИЕ. БАРОМЕТРИЧЕСКАЯ ФОРМУЛА § 30.  ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИ ЛАМИНАРНОЕ И ТУРБУЛЕНТНОЕ ТЕЧЕНИЯ. ФОРМУЛА БЕРНУЛЛИСЖИМАЕМОСТЬ И ВЯЗКОСТЬ В ПОТОКЕ РАСПРЕДЕЛЕНИЕ СКОРОСТЕЙ В ЛАМИНАРНОМ ПОТОКЕ Часть II. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА § 1. ТЕПЛОВОЕ ДВИЖЕНИЕ § 2. ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ; ЭНЕРГИЯ СВЯЗИ МОЛЕКУЛ § 3. АГРЕГАТНЫЕ СОСТОЯНИЯ И ФАЗОВЫЕ ПЕРЕХОДЫ. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ СОСТОЯНИЯ И ПРОЦЕССЫ СВОЙСТВА ТЕРМОДИНАМИЧЕСКИХ СИСТЕМ ВИДЫ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ § 4. ВНУТРЕННЯЯ ЭНЕРГИЯ ТЕРМОДИНАМИЧЕСКОЙ СИСТЕМЫ. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ § 5. ВНЕШНЯЯ РАБОТА СИСТЕМЫ И ТЕПЛООБМЕН С ОКРУЖАЮЩЕЙ СРЕДОЙ. ТЕПЛОЕМКОСТЬ ТЕЛ § 6. ИЗОПРОЦЕССЫ; АДИАБАТИЧЕСКИЙ ПРОЦЕСС. ЭНТРОПИЯ СИСТЕМЫ. ЗАМКНУТЫЕ (КРУГОВЫЕ) ПРОЦЕССЫ ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ ИЗОПРОЦЕССОВ КРУГОВЫЕ ПРОЦЕССЫ § 7. ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЗАКОН ВОЗРАСТАНИЯ ЭНТРОПИИ ТЕПЛОВЫЕ И ХОЛОДИЛЬНЫЕ МАШИНЫ ЭНТРОПИЯ И ВЕРОЯТНОСТЬ Глава 2. ИДЕАЛЬНЫЙ ГАЗ § 8. ОСНОВНОЕ УРАВНЕНИЕ КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ. СРЕДНИЕ СКОРОСТИ МОЛЕКУЛ § 9.  УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА§ 10. ИЗОПРОЦЕССЫ В ИДЕАЛЬНОМ ГАЗЕ; ТЕПЛОЕМКОСТИ ГАЗОВ § 11. КРУГОВЫЕ ПРОЦЕССЫ, СОВЕРШАЕМЫЕ ИДЕАЛЬНЫМ ГАЗОМ; ЦИКЛ КАРНО. ЭНТРОПИЯ ИДЕАЛЬНОГО ГАЗА ЦИКЛ КАРНО ПРОЦЕССЫ, ВЫЗЫВАЮЩИЕ ИЗМЕНЕНИЕ ЭНТРОПИИ ПАРАДОКС ГИББСА § 12. ДИФФУЗИЯ, ТЕПЛОПРОВОДНОСТЬ И ВНУТРЕННЕЕ ТРЕНИЕ В ГАЗАХ; ЧИСЛО СТОЛКНОВЕНИЙ И ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ Глава 3. РЕАЛЬНЫЕ ГАЗЫ, ЖИДКОСТИ И ТВЕРДЫЕ ТЕЛА § 13. ОТСТУПЛЕНИЯ ОТ ЗАКОНОВ ИДЕАЛЬНЫХ ГАЗОВ. НАСЫЩЕННЫЕ ПАРЫ. КРИТИЧЕСКОЕ СОСТОЯНИЕ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГАЗОВ ПАР ПЕРЕХОДЫ в СИСТЕМЕ ЖИДКОСТЬ — ПАР — ГАЗ § 14. УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА. ВНУТРЕННЯЯ ЭНЕРГИЯ РЕАЛЬНОГО ГАЗА ПАРАМЕТРЫ КРИТИЧЕСКОГО СОСТОЯНИЯ ПРИМЕНЕНИЯ УРАВНЕНИЯ ВАН-ДЕР-ВААЛЬСА § 15. ЖИДКОСТИ; ИХ ОСНОВНЫЕ СВОЙСТВА. МОЛЕКУЛЯРНОЕ ДАВЛЕНИЕ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ СВОЙСТВА ЖИДКОСТЕЙ МОЛЕКУЛЯРНЫЕ СИЛЫ В ПОВЕРХНОСТНОМ СЛОЕ § 16. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ § 17. ИСПАРЕНИЕ И КИПЕНИЕ ЖИДКОСТЕЙ; КОНДЕНСАЦИЯ ПАРОВ ИСПАРЕНИЕ И КОНДЕНСАЦИЯ КИПЕНИЕ УДЕЛЬНАЯ ТЕПЛОТА ПАРООБРАЗОВАНИЯ § 18.  КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛ КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА. КРИСТАЛЛИЗАЦИЯ, ПЛАВЛЕНИЕ И ИСПАРЕНИЕ ТВЕРДЫХ ТЕЛКРИСТАЛЛИЗАЦИЯ ТЕМПЕРАТУРА ПЛАВЛЕНИЯ ТРОЙНАЯ ТОЧКА § 19. ТИПЫ КРИСТАЛЛИЧЕСКИХ РЕШЕТОК. ТЕПЛОВЫЕ И УПРУГИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ ТЕПЛОЕМКОСТЬ КРИСТАЛЛА ТЕПЛОВОЕ РАСШИРЕНИЕ КРИСТАЛЛОВ УПРУГОСТЬ И ПЛАСТИЧНОСТЬ ЖИДКИЕ КРИСТАЛЛЫ Часть III. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ § 1. ЭЛЕКТРИЧЕСКИЕ ЗАРЯДЫ. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ § 2. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ; ИНДУКЦИЯ И НАПРЯЖЕННОСТЬ ПОЛЯ. ЗАКОН КУЛОНА § 3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ СИСТЕМЫ ЗАРЯДОВ; ТЕОРЕМА ОСТРОГРАДСКОГО—ГАУССА ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО—ГАУССА ФОРМУЛЫ ДЛЯ НАПРЯЖЕННОСТИ ПОЛЯ § 4. РАБОТА ПЕРЕМЕЩЕНИЯ ЗАРЯДА В ЭЛЕКТРИЧЕСКОМ ПОЛЕ; РАЗНОСТЬ ПОТЕНЦИАЛОВ. ЭНЕРГИЯ ВЗАИМОДЕЙСТВИЯ ЗАРЯДОВ § 5. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ § 6. ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ ЭЛЕКТРОСТРИКЦИЯ ПЬЕЗОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ СЕГНЕТОЭЛЕКТРИКИ ЭЛЕКТРЕТЫ § 7. ЭЛЕКТРОЕМКОСТЬ. ЭНЕРГИЯ ЗАРЯЖЕННОГО ПРОВОДНИКА.  ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯ ПЛОТНОСТЬ ЭНЕРГИИ ПОЛЯГлава 2. ЭЛЕКТРИЧЕСКИЙ ТОК § 8. ЭЛЕКТРИЧЕСКИЙ ТОК ПРОВОДИМОСТИ; ПЛОТНОСТЬ ТОКА § 9. ЭЛЕКТРОННАЯ ТЕОРИЯ ПРОВОДИМОСТИ МЕТАЛЛОВ. ЗАКОНЫ ОМА И ДЖОУЛЯ—ЛЕНЦА В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ. СВЯЗЬ МЕЖДУ ЭЛЕКТРОПРОВОДНОСТЬЮ И ТЕПЛОПРОВОДНОСТЬЮ § 10. РАБОТА ЭЛЕКТРИЧЕСКОГО ТОКА. СОПРОТИВЛЕНИЕ ПРОВОДНИКОВ. СВЕРХПРОВОДИМОСТЬ § 11. ЭЛЕКТРОДВИЖУЩАЯ СИЛА; ЗАКОН ОМА И ПРАВИЛА КИРХГОФА ЗАКОН ОМА ДЛЯ ЗАМКНУТОГО КОНТУРА ПРАВИЛА КИРХГОФА ЭЛЕКТРОСТАТИЧЕСКИЙ ГЕНЕРАТОР ТОКА § 12. РАБОТА ВЫХОДА ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА. КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ. ТЕРМОЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ ЭМИССИЯ ЭЛЕКТРОНОВ ИЗ МЕТАЛЛА КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ ЗАКОН ВОЛЬТА. ТЕРМОЭЛЕМЕНТЫ ЭФФЕКТ ПЕЛЬТЬЕ § 13. ТЕРМОЭЛЕКТРОННАЯ ЭМИССИЯ. ЭЛЕКТРИЧЕСКИИ ТОК В ВАКУУМЕ. ЭЛЕКТРОННАЯ ЛАМПА § 14. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ. ПОНЯТИЕ О ПЛАЗМЕ ДВИЖЕНИЕ ИОНОВ В ГАЗЕ ВИДЫ РАЗРЯДОВ В ГАЗАХ ПЛАЗМА § 15. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ. ЗАКОНЫ ФАРАДЕЯ § 16. ПОЛУПРОВОДНИКИ И ИХ ПРИМЕНЕНИЯ ЭЛЕКТРОПРОВОДНОСТЬ ПОЛУПРОВОДНИКОВ ЯВЛЕНИЯ НА ГРАНИЦЕ ДВУХ ПОЛУПРОВОДНИКОВ ПРИМЕНЕНИЯ ПОЛУПРОВОДНИКОВ Глава 3.  ЭЛЕКТРОМАГНЕТИЗМ ЭЛЕКТРОМАГНЕТИЗМ§ 17. МАГНИТНОЕ ПОЛЕ § 18. НАПРЯЖЕННОСТЬ МАГНИТНОГО ПОЛЯ ВОКРУГ ДВИЖУЩЕГОСЯ ЗАРЯДА И ПРОВОДНИКОВ С ТОКАМИ § 19. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ЗАРЯДЫ И ПРОВОДНИКИ С ТОКОМ; СИЛА ЛОРЕНЦА И ЗАКОН АМПЕРА. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ § 20. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА КОНТУР С ТОКОМ. ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ МАГНИТНЫЙ МОМЕНТ ЭЛЕКТРОНА ДВИЖЕНИЕ ЗАРЯДА В МАГНИТНОМ ПОЛЕ ЭФФЕКТ ХОЛЛА § 21. РАБОТА ПЕРЕМЕЩЕНИЯ ПРОВОДНИКА С ТОКОМ В МАГНИТНОМ ПОЛЕ § 22. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ; ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА. ВРАЩАЮЩИИСЯ ВИТОК В МАГНИТНОМ ПОЛЕ РАМКА В МАГНИТНОМ ПОЛЕ ЗАКОНЫ ФАРАДЕЯ И ЛЕНЦА § 23. ЯВЛЕНИЯ САМОИНДУКЦИИ И ВЗАИМОИНДУКЦИИ. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ. ВИХРЕВЫЕ ТОКИ ИНДУКТИВНОСТЬ СОЛЕНОИДА РАСЧЕТ ИНДУКЦИОННЫХ ТОКОВ ВЗАИМНАЯ ИНДУКЦИЯ ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКИ ФУКО § 24. ТОК СМЕЩЕНИЯ И ЕГО МАГНИТНОЕ ПОЛЕ; ТЕОРИЯ МАКСВЕЛЛА § 25. МАГНИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ. ДИАМАГНЕТИЗМ; ПАРАМАГНИТНЫЕ И ФЕРРОМАГНИТНЫЕ ВЕЩЕСТВА НАМАГНИЧЕННОСТЬ МАГНИТНЫЕ СВОЙСТВА АТОМОВ И МОЛЕКУЛ ДИАМАГНЕТИЗМ И ПАРАМАГНЕТИЗМ ФЕРРОМАГНЕТИКИ ПАРАМАГНИТНЫЙ РЕЗОНАНС § 26.  МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕ МАГНИТНОЕ ПОЛЕ В ФЕРРОМАГНИТНЫХ ТЕЛАХ РАЗЛИЧНОЙ ФОРМЫ; МАГНИТОДВИЖУЩАЯ СИЛА И МАГНИТНОЕ СОПРОТИВЛЕНИЕГлава 4. ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ И ВОЛНЫ § 27. КОЛЕБАТЕЛЬНЫЙ КОНТУР. НЕЗАТУХАЮЩИЕ И ЗАТУХАЮЩИЕ КОЛЕБАНИЯ § 28. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ; ЭЛЕКТРИЧЕСКИЙ РЕЗОНАНС § 29. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ УРАВНЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ ИЗЛУЧЕНИЕ ВОЛНЫ ЭЛЕКТРОНОМ ЧЕРЕНКОВСКОЕ ИЗЛУЧЕНИЕ Часть IV. ОПТИКА И ФИЗИКА АТОМА § 1. ВОЛНОВАЯ (ЭЛЕКТРОМАГНИТНАЯ) И КОРПУСКУЛЯРНАЯ (ФОТОННАЯ) ТЕОРИИ СВЕТА СПЕКТРАЛЬНЫЙ СОСТАВ ИЗЛУЧЕНИЯ ХАРАКТЕРИСТИКИ ИЗЛУЧЕНИЯ ИДЕАЛИЗАЦИЯ СВЕТОВОЙ ВОЛНЫ § 2. ФОТОМЕТРИЧЕСКИЕ ПОНЯТИЯ И ВЕЛИЧИНЫ. ДАВЛЕНИЕ СВЕТА § 3. РАСПРОСТРАНЕНИЕ, ОТРАЖЕНИЕ, ПРЕЛОМЛЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА. ДИСПЕРСИЯ. РАССЕЯНИЕ СВЕТА СБЕТ НА ГРАНИЦЕ ДВУХ СРЕД СВЕТ И ЦВЕТ ДИСПЕРСИЯ СВЕТА РАССЕЯНИЕ СВЕТА § 4. ИНТЕРФЕРЕНЦИЯ СВЕТА; КОГЕРЕНТНОСТЬ СВЕТОВЫХ ЛУЧЕЙ. ИНТЕРФЕРОМЕТРЫ § 5. ДИФРАКЦИЯ СВЕТА; ДИФРАКЦИОННЫЙ СПЕКТР ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ ПРЯМОЛИНЕЙНОЙ ТОНКОЙ ЩЕЛИ ДИФРАКЦИЯ ПЛОСКОЙ ВОЛНЫ ОТ НЕСКОЛЬКИХ ЩЕЛЕЙ ДИФРАКЦИОННАЯ РЕШЕТКА § 6.  РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТА РАСПРОСТРАНЕНИЕ СВЕТА В АНИЗОТРОПНОЙ СРЕДЕ, ПОЛУЧЕНИЕ И ПРИМЕНЕНИЕ ПОЛЯРИЗОВАННОГО СВЕТАПОЛЯРИЗОВАННЫЙ СВЕТ СПОСОБЫ ПОЛУЧЕНИЯ ПОЛЯРИЗОВАННОГО СВЕТА ИНТЕРФЕРЕНЦИЯ ПОЛЯРИЗОВАННОГО СВЕТА ОПТИЧЕСКАЯ АНИЗОТРОПИЯ § 7. ЛИНЗЫ; ИХ ОПТИЧЕСКАЯ СИЛА. АБЕРРАЦИИ. ДИАФРАГМЫ В ОПТИЧЕСКИХ ПРИБОРАХ ТОЛСТЫЕ ЛИНЗЫ. АБЕРРАЦИИ § 8. ПОНЯТИЕ О ГОЛОГРАФИИ Глава 2. ФИЗИКА АТОМОВ И МОЛЕКУЛ. ОСНОВЫ КВАНТОВОЙ ТЕОРИИ § 9. СТРОЕНИЕ АТОМА. ОПЫТЫ РЕЗЕРФОРДА, ФРАНКА И ГЕРЦА. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ АТОМА ВОДОРОДА ОПЫТ ФРАНКА И ГЕРЦА СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ ТЕОРИЯ АТОМА ВОДОРОДА § 10. КОРПУСКУЛЯРНО-ВОЛНОВЫЕ СВОЙСТВА ЧАСТИЦ. ФОТОЭЛЕКТРИЧЕСКИЙ ЭФФЕКТ. ФОРМУЛА ДЕ БРОЙЛЯ. ДИФРАКЦИЯ ЭЛЕКТРОНОВ ЭФФЕКТ КОМПТОНА ФОТОН И ЭЛЕКТРОМАГНИТНАЯ ВОЛНА ФОРМУЛА ДЕ БРОЙЛЯ ДИФРАКЦИЯ ЭЛЕКТРОНОВ § 11. ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ ТЕОРИИ. УРАВНЕНИЕ ШРЕДИНГЕРА. СООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ ГЕЙЗЕНБЕРГА УРАВНЕНИЕ ШРЕДИНГЕРА РЕШЕНИЯ УРАВНЕНИЯ ШРЕДИНГЕРА СВОБОДНЫЙ ЭЛЕКТРОН ПОТЕНЦИАЛЬНЫЙ БАРЬЕР ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ АТОМ ВОДОРОДА.  КВАНТОВЫЕ ЧИСЛА КВАНТОВЫЕ ЧИСЛАСООТНОШЕНИЕ НЕОПРЕДЕЛЕННОСТЕЙ § 12. ЧАСТИЦЫ И ФИЗИЧЕСКИЕ СИСТЕМЫ. СТАТИСТИЧЕСКИЕ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО СОСТОЯНИЯМ. ПОНЯТИЕ ТЕМПЕРАТУРЫ РОЛЬ ТЕПЛОВОГО ДВИЖЕНИЯ ЧАСТИЦ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ПО СОСТОЯНИЯМ ТЕМПЕРАТУРА ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИСТЕМЫ РАСПРЕДЕЛЕНИЕ МОЛЕКУЛ ПО СКОРОСТЯМ § 13. ВЗАИМОДЕЙСТВИЕ АТОМОВ И МОЛЕКУЛ. ЭНЕРГИЯ СВЯЗИ АТОМОВ ВЗАИМОДЕЙСТВИЕ МОЛЕКУЛ ИОННАЯ СВЯЗЬ РОЛЬ ЭЛЕКТРОННОГО ГАЗА В МЕТАЛЛАХ Глава 3. ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ ЭНЕРГИИ АТОМАМИ И МОЛЕКУЛАМИ § 14. АТОМНЫЕ И МОЛЕКУЛЯРНЫЕ СПЕКТРЫ ИЗЛУЧЕНИЯ; СПОСОБЫ ВОЗБУЖДЕНИЯ СТРУКТУРА ЭЛЕКТРОННОЙ ОБОЛОЧКИ СПЕКТРЫ ИЗЛУЧЕНИЯ АТОМОВ СПЕКТРЫ ИЗЛУЧЕНИЯ МОЛЕКУЛ КОМБИНАЦИОННОЕ РАССЕЯНИЕ СВЕТА § 15. ТЕПЛОВОЕ ИЗЛУЧЕНИЕ ФОРМУЛА ПЛАНКА ЗАКОНЫ ИЗЛУЧЕНИЯ ЧЕРНОГО ТЕЛА ПРИМЕНЕНИЕ ЗАКОНОВ ТЕПЛОВОГО ИЗЛУЧЕНИЯ § 16. РЕНТГЕНОВСКИЕ ЛУЧИ. ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ЭЛЕМЕНТОВ ХАРАКТЕРИСТИЧЕСКИЙ РЕНТГЕНОВСКИЙ СПЕКТР ДИФРАКЦИЯ И ИНТЕРФЕРЕНЦИЯ РЕНТГЕНОВСКИХ ЛУЧЕЙ ДОЗИМЕТРИЯ § 17.  ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕ ЛЮМИНЕСЦЕНТНОЕ ИЗЛУЧЕНИЕПРИРОДА ЛЮМИНЕСЦЕНЦИИ ХАРАКТЕРИСТИКИ ЛЮМИНЕСЦИРУЮЩИХ ВЕЩЕСТВ ГАШЕНИЕ ЛЮМИНЕСЦЕНЦИИ ПРИМЕНЕНИЯ ЛЮМИНЕСЦЕНЦИИ § 18. ИНДУЦИРОВАННОЕ ИЗЛУЧЕНИЕ. ЛАЗЕРЫ ЛАЗЕРЫ ПРЕИМУЩЕСТВА ЛАЗЕРОВ ПРИМЕНЕНИЕ ЛАЗЕРОВ Глава 4. АТОМНЫЕ ЯДРА И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ § 19. ОСНОВНЫЕ СВОЙСТВА АТОМНЫХ ЯДЕР РАДИОАКТИВНОСТЬ ВНУТРИЯДЕРНЫЕ СИЛЫ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ЯДЕР МЕХАНИЧЕСКИЙ МОМЕНТ ЯДРА МАГНИТНЫЕ МОМЕНТЫ ЯДЕР ЭЛЕКТРИЧЕСКИЕ МОМЕНТЫ ЯДЕР СПЕКТР ВОЗБУЖДЕННЫХ СОСТОЯНИЙ § 20. МОДЕЛЬНЫЕ ПРЕДСТАВЛЕНИЯ О СТРУКТУРЕ ЯДЕР КАПЕЛЬНАЯ МОДЕЛЬ ЯДРА ОБОЛОЧЕЧНАЯ МОДЕЛЬ ОБОБЩЕННАЯ МОДЕЛЬ ОПТИЧЕСКАЯ МОДЕЛЬ УСЛОВИЕ СТАБИЛЬНОСТИ § 21. РАДИОАКТИВНЫЕ ЯДРА И ИХ ИЗЛУЧЕНИЯ СЕМЕЙСТВА РАДИОАКТИВНЫХ ЭЛЕМЕНТОВ ВЗАИМОДЕЙСТВИЯ ЯДЕРНЫХ ИЗЛУЧЕНИЙ С ВЕЩЕСТВОМ БЕТА-РАСПАД ЯДЕР ЭНЕРГИЯ СВЯЗИ ЯДЕР ИЗОМЕРЫ § 22. ЯДЕРНЫЕ РЕАКЦИИ ДЕЛЕНИЯ И СИНТЕЗА. ТЕРМОЯДЕРНЫЕ РЕАКЦИИ БОМБАРДИРОВКА ЯДЕР ЧАСТИЦАМИ ЭФФЕКТИВНЫЕ СЕЧЕНИЯ РЕАКЦИЙ ЯДЕРНЫЕ РЕАКТОРЫ ЯДЕРНЫЙ СИНТЕЗ § 23.  ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫРАСПАДЫ ЧАСТИЦ ВИДЫ ВЗАИМОДЕЙСТВИЯ ЗАКЛЮЧЕНИЕ § 1. ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. СВЯЗЬ МЕЖДУ СПОСОБАМИ ИЗМЕРЕНИЯ ФИЗИЧЕСКИХ ВЕЛИЧИН И ФОРМУЛИРОВКАМИ ЗАКОНОВ ФИЗИКИ § 2. О ТЕОРИИ ОТНОСИТЕЛЬНОСТИ ЭЙНШТЕЙНА § 3. ЗАКОНЫ СОХРАНЕНИЯ, ПРЕВРАЩЕНИЯ И ПЕРЕРАСПРЕДЕЛЕНИЯ ЭНЕРГИИ В ФИЗИЧЕСКИХ СИСТЕМАХ § 4. О ВАРИАЦИОННЫХ ПРИНЦИПАХ ФИЗИКИ § 5. СТАТИСТИЧЕСКИЕ ЗАКОНЫ И ФЛУКТУАЦИИ § 6. О ДУАЛИЗМЕ В ФИЗИКЕ |
Определение индуктивности соленоида, страница 2
Особенно просто, зная активное сопротивление цепи , определить её индуктивность, измерив, время релаксации:
(8)
3. Вынужденные электромагнитные колебания в контуре, их применение для измерения индуктивности.
Рассмотрим
контур, состоящий из последовательно соединенных конденсатора емкостью , активного сопротивления и соленоида индуктивностью .
Для получения незатухающих электромагнитных колебаний необходимо включить в
контур источник тока с периодически изменяющейся ЭДС (Рис.2).
В этом случае колебания в контуре являются вынужденными.
Пусть, внешняя ЭДС изменяется по гармоническому закону
.
Тогда, используя закон Ома, можно получить следующее дифференциальное уравнение вынужденных электромагнитных колебаний
и, решив это уравнение, получить для установившихся вынужденных колебаний следующую связь амплитудных значений силы тока и внешней ЭДС:
(9)
где величина называется полным сопротивлением электрической цепи переменного тока.
В нее входят активное сопротивление контура, емкостное сопротивление и индуктивное сопротивление .
Если электрическая емкость контура стремится к бесконечности , то есть емкостное сопротивление к нулю, то формула (9) упрощается:
(10)
Используя это
выражение, получим рабочую формулу для экспериментального определения
индуктивности соленоида. При этом учтем, что амплитуда падения напряжения на
активном сопротивлении R связана с амплитудой силы тока в цепи формулой
При этом учтем, что амплитуда падения напряжения на
активном сопротивлении R связана с амплитудой силы тока в цепи формулой
(11)
Из выражений (10) и (11) получим
(12)
Схемы измерений
Вариант 1. Оценка индуктивности соленоида
Задание к работе
1. Подключите последовательно соединенные резистор и катушку индуктивности без ферромагнитного сердечника к генератору прямоугольных импульсов (Рис. 3).
2. Подключите
«Y»-вход осциллографа к концам резистора . На
генераторе установите частоту 1200Гц. Получите на экране устойчивую картину
изменения напряжения на этом сопротивлении со временем, подобную изображенной
на Рис. 1. Рекомендуется переключатель скорости развертки «ВРЕМЯ/ДЕЛ.»
установить в положение «´0,2» (см.
приложение).
1. Рекомендуется переключатель скорости развертки «ВРЕМЯ/ДЕЛ.»
установить в положение «´0,2» (см.
приложение).
3. Зная время развертки осциллографа, определите время релаксации , а затем, по формуле (8), вычислите величину индуктивности . При этом общее сопротивление цепи R можно с некоторой точностью заменить значением , пренебрегая внутренним сопротивлением генератора и активным сопротивлением катушки. Поэтому полученное численное значение индуктивности следует рассматривать как оценочное.
4. Повторите измерения , подключая другие резисторы. Проверьте, зависят ли получаемые значения индуктивности от сопротивления.
5. Приступите
к измерению индуктивности вторым способом. Для этого подключите последовательно
соединенные резистор и катушку индуктивности к звуковому генератору (Рис. 4), установив
на нем некоторое значение частоты в диапазоне 5¸15кГц
и некоторое значение амплитуды сигнала. (При таких частотах ток в цепи
определяется в основном индуктивным сопротивлением катушки, что повышает
точность измерения индуктивности).
6. С помощью осциллографа измерьте амплитудное значение падения напряжения на резисторе .
7. Отключите осциллограф от концов резистора, а звуковой генератор от RL -контура и, не изменяя величину его сигнала, измерьте с помощью осциллографа амплитудное значение ЭДС генератора (см. схему рис.5 лаб. раб. №12).
8. Вычислите индуктивность по формуле (12).
9. Определите индуктивность, установив другие значения величин . Проверьте, влияют ли эти параметры на результаты измерения.
10. Сравните результаты измерения индуктивности L1 двумя способами. Объясните различие этих результатов.
Вариант 2. Измерение индуктивности соленоида
Методика измерений
Рассмотрим более подробно первый способ определения индуктивности, основанный на измерении времени релаксации.
Учтем, что общее активное сопротивление контура R равно сумме известного сопротивления R1, к концам которого подключается Y-вход осциллографа, и неизвестного заранее сопротивления R*, обусловленного внутренним сопротивлением генератора, сопротивлением соединительных проводов, сопротивлением провода, из которого сделана катушка соленоида:
.
Учтя это, перепишем формулу (7) в виде
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| JohnyBoro |
| ||
25/09/18 |
| ||
| |||
| rascas |
| ||
30/01/18 |
| ||
| |||
| JohnyBoro |
| ||
25/09/18 |
| ||
| |||
| Александрович |
| ||
21/01/09 |
| ||
| |||
| Andrey_Kireew |
| ||
07/10/15 |
| ||
| |||
| JohnyBoro |
| ||
25/09/18 |
| ||
| |||
| realeugene |
| ||
27/08/16 |
| ||
| |||
| Andrey_Kireew |
| ||
07/10/15 |
| ||
| |||
| asbest |
| ||
04/07/14 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 9 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Что такое самоиндукция и энергия магнитного поля
Оглавление
Время чтения: 4 минуты
417
Опредение
Самоиндукция — это один из случаев электромагнитной индукции, при котором электромагнитный поток создается при протекании через контур тока, при этом он изменяется и вызывает ЭДС индукции.
Понятие об ЭДС самоиндукции
При явлении самоиндукции, если ток конкретного контура изменен, то меняется магнитное поле данного тока, а значит и всего магнитного потока, который проходит через конкретный контур. При этом в контуре создается ЭДС самоиндукции, которая создает препятствие на пути изменения электрического тока в контуре. Если цепь, которая имеет постоянный источник тока, замыкают, то сила тока появляется не мгновенно, при размыкании цепи электрический ток не пропадает сразу, а через некоторое время самоиндукция исчезает.
Формула самоиндукции
Магнитный поток Φ, проходящий через катушку с током или контур постоянных форм и размеров, является пропорциональным силе тока I.
Формулы 1 — 3
Самоиндукция определяется по формуле:
\[\boldsymbol{\Phi}=\boldsymbol{L} \boldsymbol{I}\]
Коэффициент пропорциональности L в формуле Ф = L I, это и будет коэффициент самоиндукции.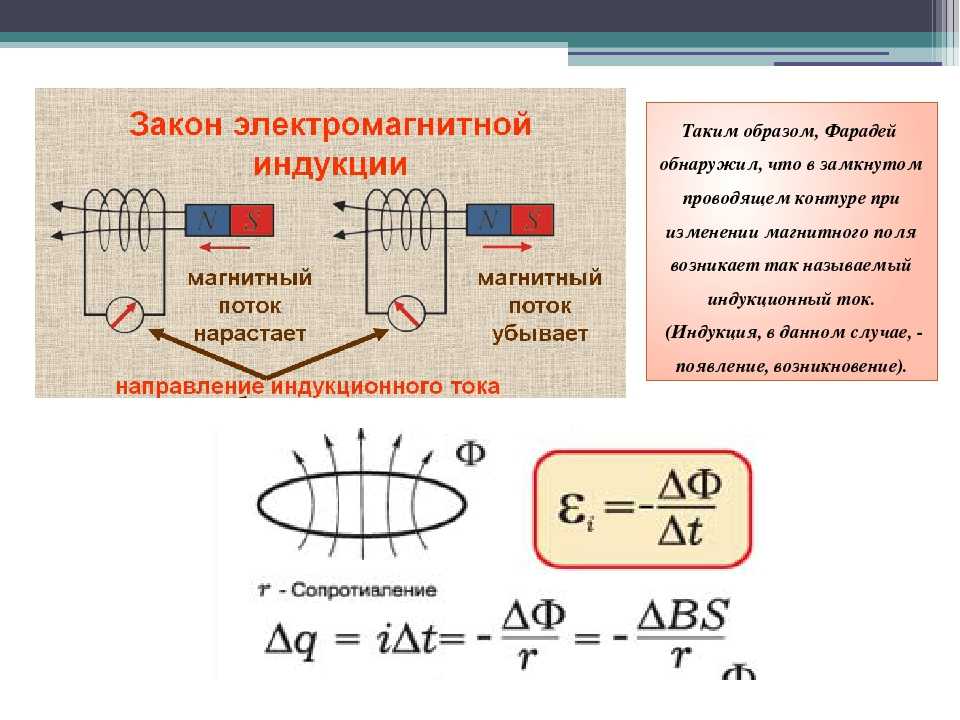 Она тесно связана с формой, размерами контура, магнитными показателями и свойствами вещества, в котором расположен контур.
Она тесно связана с формой, размерами контура, магнитными показателями и свойствами вещества, в котором расположен контур.
Закон, которому подчиняется ЭДС самоиндукции:
\[\varepsilon=-L \frac{d I}{d t}\]
Если контур имеет постоянные размеры и форму, то ЭДС самоиндукции энергии магнитного поля прямо пропорциональна скорости изменения силы тока в конкретном контуре.
Единица индуктивности в СИ имеет общепринятое название Генри, обозначается — Гн.
Индуктивность катушки или контура равна 1 Гн, в случае силы тока в 1 А, поток составляет 1 Вб:
\[1 \Gamma н=\frac{1 B б}{1 A}\]
Сила самоиндукции зависит от скорости увеличения/уменьшения магнитного поля. При этом может меняться магнитное поле, а также контур может менять положение в магнитном поле.
Как рассчитать индуктивность
Для расчета индуктивности рассмотрим длинный соленоид — это цилиндрическая катушка индуктивности, длина которой значительно больше диаметра. {2} \cdot V \]
{2} \cdot V \]
ЭДС самоиндукции в цепи
Формула 4
В соответствии с законом Фарадея, ЭДС самоиндукции записывается по формуле:
\[\delta_{инд}=\delta_{L}=\frac{-\Delta \Phi}{\Delta t}=-L \frac{\Delta I}{\Delta t}\]
ЭДС самоиндукции равна значению, которое прямо пропорционально индуктивности катушки и скорости изменения силы тока, проходящего через нее.
Носителем энергии будет магнитное поле. Катушка, по виткам которой проходит ток, обладает запасом энергии, по аналогии с заряженным конденсатором.
Если параллельно катушке с большим показателем индуктивности включить в цепь постоянного тока электрическую лампу, то при размыкании цепи ЭДС самоиндукции цепи вызовет ток, будет наблюдаться которая вспышка лампы.
Рис. 1. ЭДС самоиндукции, рисунок магнитной энергии катушкиНа рисунке изображена цепь, в момент размыкания ключа К, происходим короткая вспышка электрической лампы. {2}}{2 \mu_{0} \cdot \mu} V\]
{2}}{2 \mu_{0} \cdot \mu} V\]
Максвелл продемонстрировал, что данная формула подходит для любых магнитных полей.
Оценить статью (46 оценок):
Поделиться
Собственная индуктивность соленоида Важные понятия и советы для JEE
Собственная индуктивность — это форма электромагнитной индуктивности. Его можно определить как свойство катушки с током, которая сопротивляется или препятствует изменению тока, протекающего через нее. Его также можно определить как индукцию напряжения в любом проводе с током, если ток в проводе изменяется. Происходит это за счет магнитного поля, создаваемого изменяющимся током. Он индуцирует напряжение в той же цепи, поэтому можно сказать, что напряжение самоиндуцируется.
Напряжение самоиндукции или ЭДС всегда сопротивляется изменению тока. Следовательно, если ток увеличивается, он будет сопротивляться росту тока, и точно так же, когда ток уменьшается, он будет сопротивляться падению тока. Это означает, что направление ЭДС индукции противоположно приложенному напряжению, если ток увеличивается. Точно так же направление ЭДС индукции будет таким же, как и направление приложенного напряжения, если ток падает.
Точно так же направление ЭДС индукции будет таким же, как и направление приложенного напряжения, если ток падает.
Следует отметить, что это свойство катушки существует только для переменных токов, т.е. переменного тока или переменного тока. Это свойство не существует для постоянного или установившегося тока. Собственная индуктивность измеряется в единицах Генри, которые являются единицами СИ и имеют размеры ML 9.0007 2 Т -2 I -2 .
Что такое катушка индуктивности?
Катушка индуктивности — это термин, используемый для описания цепи, обладающей свойством индуктивности. Катушка провода является одним из наиболее распространенных индукторов, поэтому на принципиальных схемах катушка провода используется как символ индуктивного компонента.
Переменный ток, проходящий через любую катушку, создает магнитное поле внутри и вокруг катушки. Это потому, что ток увеличивается или уменьшается. Магнитное поле, создаваемое переменным током, образует концентрические петли вокруг провода, которые затем соединяются вместе, образуя более крупные петли. Когда ток увеличивается в одной петле, окружающее магнитное поле расширяется и пересекает некоторые или все соседние петли проводов. Это индуцирует напряжение в петлях. Таким образом, при изменении тока в катушке индуцируется напряжение.
Когда ток увеличивается в одной петле, окружающее магнитное поле расширяется и пересекает некоторые или все соседние петли проводов. Это индуцирует напряжение в петлях. Таким образом, при изменении тока в катушке индуцируется напряжение.
Ниже приведена диаграмма, изображающая поля в катушке индуктивности. Это принцип классического эксперимента с самоиндукцией катушки.
Катушка индуктивности
Вывод собственной индуктивности
Из диаграммы видно, что количество витков в катушке влияет на величину индуцируемого напряжения. Таким образом, скорость изменения магнитного потока также будет влиять на ЭДС индукции. Это точно отражено в законе Фарадея. Закон Фарадея гласит, что ЭДС индукции прямо пропорциональна скорости изменения магнитного потока.
Более того, закон Ленца гласит, что индуктированный ток имеет такое направление, что его магнитное поле противодействует изменению магнитного поля, которое ранее индуцировало ток.
Это означает, что ЭДС индукции будет иметь вид
Здесь VL — индуцированное напряжение, N — число витков в катушке, а $\dfrac{\mathrm{d} \varphi}{\mathrm{d} t}$ – скорость изменения магнитного потока. Знак минус обусловлен законом Ленца.
Поскольку магнитное поле в проводе с током прямо пропорционально току, поток, создаваемый этим конкретным полем, также будет пропорционален току. Итак,
$\varphi\propto I$
Здесь I — ток, а $\phi$ — магнитный поток. Вышеприведенное выражение можно также записать как
$\varphi=LI$
L — константа пропорциональности, известная как «собственная индуктивность». Для катушки с N витками поток можно записать как
$N\varphi=LI$
Подстановка этого выражения для потока в выражение закона Фарадея даст альтернативное выражение для ЭДС индукции:
$V_L=-L\dfrac{dI}{dt}$
Для расчета величины собственной индуктивности отрицательный знак можно не учитывать. Следовательно, формула самоиндукции будет следующей:
Следовательно, формула самоиндукции будет следующей:
$L=\dfrac{|\varphi|}{\left|\dfrac{dI}{dt}\right|}$
формула коэффициента самоиндукции’. Если кто-то попросит сформулировать выражение для собственной индуктивности катушки, это выражение.
Самоиндукция соленоида
Возьмем соленоид, имеющий N витков длиной l и площадью поперечного сечения A, и пусть через него протекает ток I. В любой заданной точке соленоида будет магнитное поле, поэтому обозначим его через B. Тогда магнитный поток на виток будет равен произведению B на площадь каждого витка.
Мы знаем, что для соленоида
$B=\dfrac{\mu_{0} N I}{l}$
$\mu_{0}$ есть проницаемость свободного пространства. 9{2} A}{l}$
Это собственная индуктивность соленоида.
Заключение
Самоиндукция является разновидностью электромагнитной индукции и свойством, благодаря которому проводник с током сопротивляется любому изменению тока, протекающего через него. Это свойство приводит к возникновению ЭДС индукции, которая противодействует изменению тока в проводнике. Катушка провода обычно используется в качестве индуктора, поэтому символом индуктивных компонентов на принципиальной схеме является катушка провода. Используя закон Фарадея и закон Ленца, собственная индуктивность катушки рассчитывается следующим образом: $L=\dfrac{|\varphi|}{\left|\dfrac{\mathrm{d} I }{\mathrm{d } т}\право|}$. 9{2} A}{l}$.
Это свойство приводит к возникновению ЭДС индукции, которая противодействует изменению тока в проводнике. Катушка провода обычно используется в качестве индуктора, поэтому символом индуктивных компонентов на принципиальной схеме является катушка провода. Используя закон Фарадея и закон Ленца, собственная индуктивность катушки рассчитывается следующим образом: $L=\dfrac{|\varphi|}{\left|\dfrac{\mathrm{d} I }{\mathrm{d } т}\право|}$. 9{2} A}{l}$.
Индуктивность | Физика II |
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор обсуждалось множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы таким образом, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшой потерей энергии в другие формы. Существует ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ положительный, и эта физическая величина называется 9. 0094 индуктивность . Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.
0094 индуктивность . Взаимная индуктивность — это действие закона индукции Фарадея для одного устройства на другое, например, первичная катушка при передаче энергии вторичной обмотке в трансформаторе. См. рис. 1, где простые катушки наводят друг в друге ЭДС.
Рисунок 1. Эти катушки могут индуцировать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность М указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 индуцирует ЭДС в катушке 2. (Заметим, что « E 2 индуктивность» представляет ЭДС индукции в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, поток изменяется за счет изменения тока. Поэтому мы сосредоточимся на скорости изменения тока, ∆ I / ∆ t , как на причине индукции. Изменение тока I 1 в одном устройстве, катушка 1 на рисунке, индуцирует ЭДС 2 в другом. Мы выражаем это в виде уравнения как −MΔtΔI1
Мы выражаем это в виде уравнения как −MΔtΔI1
, где M определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность M , тем эффективнее связь. Например, катушки на Рисунке 1 имеют маленькое значение M по сравнению с катушками трансформатора на Рисунке 3 от компании Transformers. Единицами для M являются (В ⋅ с) / A = Ω ⋅ с, который назван Генри (H) в честь Джозефа Генри. То есть 1 Гн = 1 Ом⋅с. Природа здесь симметрична. Если мы изменим текущий I 2 в катушке 2, мы индуцируем ЭДС 1 в катушке 1, которая определяется как
э.д.с. {I}_{2}}{\Delta t}\\emf1=−MΔtΔI2
,
где M — то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с той же эффективностью или взаимной индуктивностью M . Большая взаимная индуктивность M может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)
Большая взаимная индуктивность M может быть или не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может индуцировать на своем корпусе опасную ЭДС, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность M предназначен для противодействия катушкам, чтобы нейтрализовать создаваемое магнитное поле. (См. рис. 2.)
Рис. 2. Нагревательные спирали электрической сушилки для белья можно намотать встречно, так что их магнитные поля компенсируют друг друга, что значительно снижает взаимную индуктивность с корпусом сушилки.
Самоиндукция , также существует действие закона Фарадея об индукции устройства на себя. Когда, например, ток через катушку увеличивается, магнитное поле и поток также увеличиваются, индуцируя противо-ЭДС, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока Δ I через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Она определяется как
И наоборот, если ток уменьшается, индуцируется ЭДС, препятствующая уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение потока полностью связано с изменением тока Δ I через устройство. ЭДС индукции связана с физической геометрией устройства и скоростью изменения тока. Она определяется как
ЭДС=-LΔIΔt\text{ЭДС}=-L\frac{\Delta I}{\Delta t}ЭДС=-LΔtΔI
, где L — собственная индуктивность прибора. Устройство, обладающее значительной собственной индуктивностью, называется катушкой индуктивности и обозначается символом на рисунке 3.
Рисунок 3.
Знак минус является выражением закона Ленца, указывающим, что ЭДС противодействует изменению тока. Единицами самоиндукции являются генри (Гн), как и для взаимной индуктивности. Чем больше собственная индуктивность L устройства, тем больше его сопротивление любому изменению тока через него.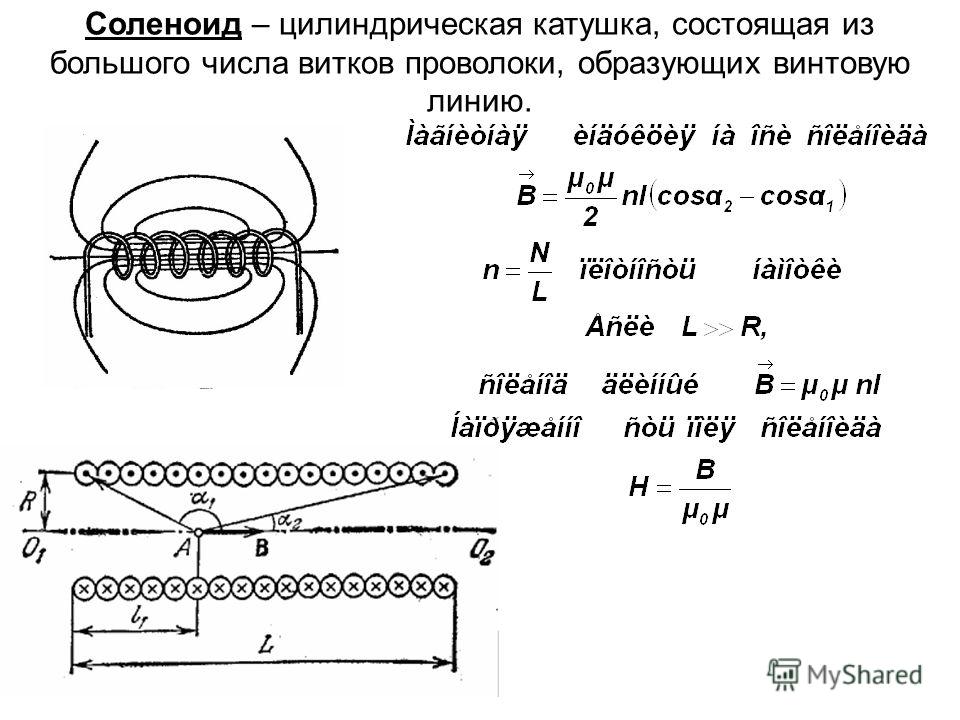 Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшую катушку L , например, путем встречной обмотки катушек, как показано на рис. 2. Катушка индуктивности 1 Гн является большой катушкой индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с л = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, определяемая как ЭДС = − L (Δ I /Δ t ), будет противиться изменению. Таким образом, будет индуцироваться ЭДС, определяемая как ЭДС = — л (Δ I / Δ t ) = (1,0 Гн) [(10 А) / (1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.
Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо получить небольшую катушку L , например, путем встречной обмотки катушек, как показано на рис. 2. Катушка индуктивности 1 Гн является большой катушкой индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с л = 1,0 Гн, через которое протекает ток 10 А. Что произойдет, если мы попытаемся отключить ток быстро, возможно, всего за 1,0 мс? ЭДС, определяемая как ЭДС = − L (Δ I /Δ t ), будет противиться изменению. Таким образом, будет индуцироваться ЭДС, определяемая как ЭДС = — л (Δ I / Δ t ) = (1,0 Гн) [(10 А) / (1,0 мс)] = 10 000 В. Положительный знак означает, что это большое напряжение идет в том же направлении, что и ток, противодействуя его уменьшению. Такие большие ЭДС могут вызывать искрение, повреждая коммутационное оборудование, поэтому может потребоваться более медленное изменение тока.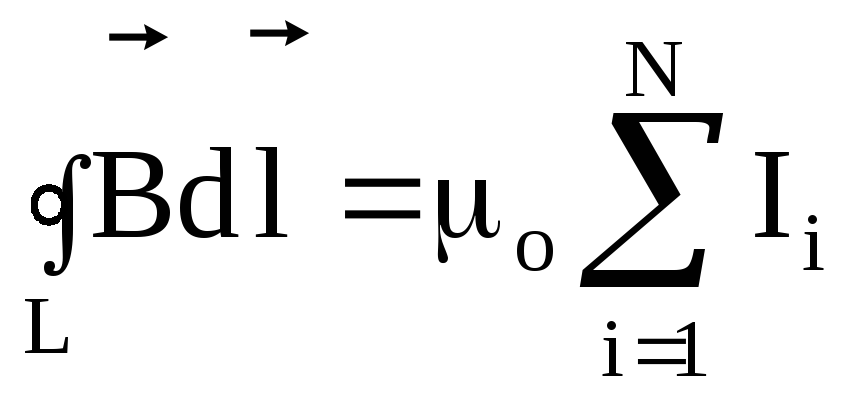 Есть применение такому большому наведенному напряжению. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)
Есть применение такому большому наведенному напряжению. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или осциллятор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи увеличится до более чем одной тысячи вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки. (См. рис. 4.)
Рис. 4. Благодаря быстрому переключению катушки индуктивности батареи напряжением 1,5 В можно использовать для наведения ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, во вспышке фотоаппарата.
Можно рассчитать L для индуктора, зная его геометрию (размер и форму) и зная создаваемое им магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность L обычно заданное количество. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется по закону индукции Фарадея как ЭДС = — Н (Δ Φ / t ) и, по определению самоиндукции, как ЭДС = — л (Δ I / Δ t ). Приравнивание этих выходов
В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность L обычно заданное количество. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности. Начнем с того, что заметим, что ЭДС индукции определяется по закону индукции Фарадея как ЭДС = — Н (Δ Φ / t ) и, по определению самоиндукции, как ЭДС = — л (Δ I / Δ t ). Приравнивание этих выходов
ЭДС = -NΔΦΔt = -LΔIΔt \ текст {ЭДС} = -N \ гидроразрыва {\ Delta \ Phi {\ Delta t} = -L \ гидроразрыва {\ Delta I} {\ Delta t} \\ ЭДС = -NΔtΔΦ =−LΔtΔI
Решение для L дает
L=NΔΦΔIL=N\frac{\Delta \Phi }{\Delta I}\\L=NΔIΔΦ
Это уравнение для собственной индуктивности L устройства всегда верно . Это означает, что собственная индуктивность L зависит от того, насколько эффективен ток в создании потока; тем эффективнее, чем больше Δ Φ / Δ I . Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Так как район A соленоида зафиксирован, изменение потока Δ Φ = Δ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется формулой NI}{\ell}\\B=µ0nI=µ0ℓNI
Воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Так как район A соленоида зафиксирован, изменение потока Δ Φ = Δ( B A ) = A Δ B . Чтобы найти Δ B , заметим, что магнитное поле соленоида определяется формулой NI}{\ell}\\B=µ0nI=µ0ℓNI
. (Здесь n = N / ℓ , где N — количество витков, а ℓ — длина соленоида.) Изменяется только ток, так что 9{2}A}{\ell}\text{(соленоид)}\\L=ℓμ0N2A(соленоид)
. Это собственная индуктивность соленоида с площадью поперечного сечения A и длиной ℓ . Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, соответствующих его определению.
Пример 1. Расчет собственной индуктивности соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см с 200 витками. {2}\right)}{0,100 \text{ m}}\\ & =& 0,632 \text{ mH}\end{array} \\L==0,100 м (4π × 10–7 T⋅ м/А) (200)2 (1,26 × 10–3 м2)0,632 мГн
{2}\right)}{0,100 \text{ m}}\\ & =& 0,632 \text{ mH}\end{array} \\L==0,100 м (4π × 10–7 T⋅ м/А) (200)2 (1,26 × 10–3 м2)0,632 мГн
.
ОбсуждениеЭтот соленоид имеет средние размеры. Его индуктивность около миллигенри также считается умеренной.
Одно распространенное применение индуктивности используется в светофорах, которые могут определить, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещена на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал в катушке передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.
На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать примерное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, что была обнаружена на «подрывнике в нижнем белье».) См. рис. 5.
Рисунок 5. Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (кредит: Alexbuirds, Wikimedia Commons)
Концептуальные вопросы
- Как бы вы поместили две одинаковые плоские катушки в контакт, чтобы они имели наибольшую взаимную индуктивность? В мере?
- Как бы вы придали проводу заданной длины такую форму, чтобы обеспечить наибольшую самоиндукцию? В мере?
- Проверить, как было сделано без доказательства в Примере 1 (выше), что единицы T ⋅ m 2 / А = Ом ⋅ с = Г.
Задачи и упражнения
1. Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?
Две катушки расположены близко друг к другу в физической лаборатории, чтобы продемонстрировать закон индукции Фарадея. Ток 5,00 А в одном отключается за 1,00 мс, индуцируя ЭДС 9,00 В в другом. Чему равна их взаимная индуктивность?
2. Если две катушки, расположенные рядом друг с другом, имеют взаимную индуктивность 5,00 мГн, какое напряжение индуцируется в одной, когда ток силой 2,00 А в другой отключается через 30,0 мс?
3. Ток 4,00 А через катушку индуктивности 7,50 мГн отключается за 8,33 мс. Какая ЭДС индуцирует противодействие этому?
4. Устройство включено, и через него через 0,100 мс проходит ток 3,00 А. Чему равна собственная индуктивность прибора, если ей противодействует ЭДС наведенного напряжения 150 В?
5. Начиная с
emf2=-MΔI1Δt{\text{emf}}_{2}=-M\frac{\Delta {I}_{1}}{\Delta t}\\emf2=-MΔtΔI1
, покажите, что единицами измерения индуктивности являются (В ⋅ с)/A = Ом ⋅ с.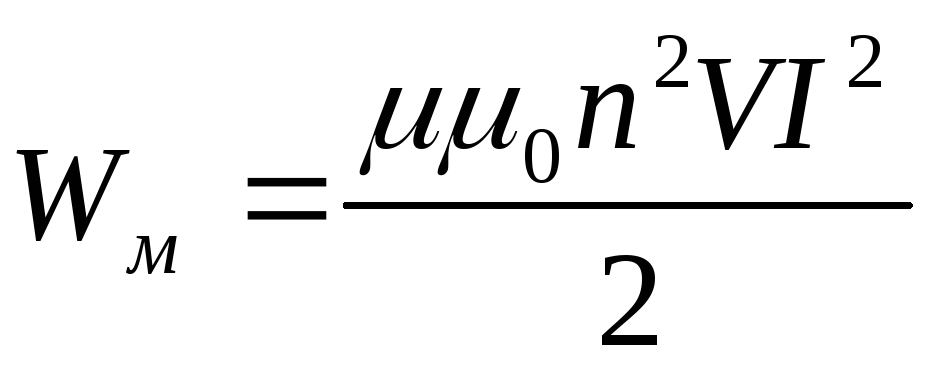
6. Вспышки камеры заряжают конденсатор до высокого напряжения, быстро включая и выключая ток через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через катушку индуктивности 2,00 мГн, чтобы индуцировать ЭДС 500 В?
7. Большой исследовательский соленоид имеет собственную индуктивность 25,0 Гн. а) Какая ЭДС наведения препятствует его отключению, если протекающий через него ток 100 А отключается за 80,0 мс? б) Сколько энергии запасается в катушке индуктивности при полном токе? в) С какой скоростью в ваттах должна рассеиваться энергия, чтобы ток выключился за 80,0 мс? (d) Принимая во внимание ответ на последнюю часть, удивительно ли, что так быстро закрыть его сложно?
8. (a) Рассчитайте собственную индуктивность соленоида длиной 50,0 см и диаметром 10,0 см, имеющего 1000 витков. б) Сколько энергии запасается в этом индукторе при протекании через него тока силой 20,0 А? в) Как быстро его можно выключить, если ЭДС индукции не может превышать 3,00 В?
9. Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?
Прецизионный лабораторный резистор изготовлен из витка проволоки диаметром 1,50 см и длиной 4,00 см и имеет 500 витков. а) Чему равна его собственная индуктивность? б) Какая средняя ЭДС индуцируется, если ток 12,0 А через него включается за 5,00 мс (одна четвертая периода для переменного тока частотой 50 Гц)? в) Какова его индуктивность, если его укоротить наполовину и намотать встречно (два слоя по 250 витков в противоположных направлениях)?
10. Нагревательные спирали в фене имеют диаметр 0,800 см, общую длину 1,00 м и 400 витков. а) Какова их полная собственная индуктивность, если предположить, что они действуют как одиночный соленоид? б) Сколько энергии запасается в них при токе 6,00 А? (c) Какая средняя ЭДС препятствует их отключению, если это делается за 5,00 мс (одна четвертая часть цикла для переменного тока с частотой 50 Гц)?
11. Когда ток 20,0 А через индуктор отключается за 1,50 мс, индуцируется ЭДС 800 В, противодействующая изменению.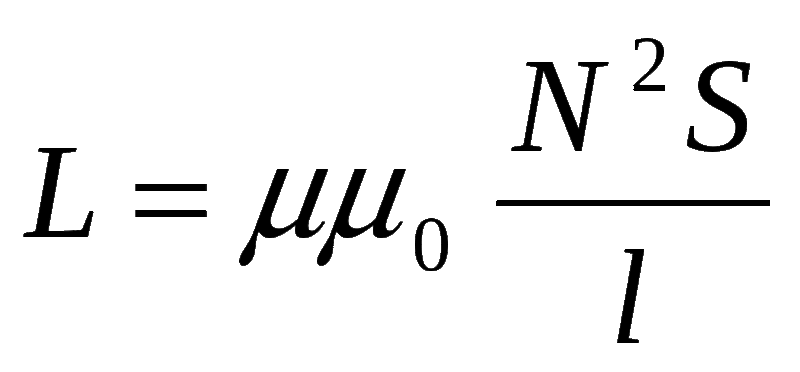 Каково значение собственной индуктивности?
Каково значение собственной индуктивности?
12. Как быстро может быть отключен ток 150 А через дроссель 0,250 Гн, если ЭДС индукции не может превышать 75,0 В?
13. Integrated Concepts Очень большой сверхпроводящий соленоид, такой как тот, который используется в МРТ-сканировании, сохраняет 1,00 МДж энергии в своем магнитном поле при токе 100 А. а) Найдите его индуктивность. (б) Если катушки «идут нормально», они приобретают сопротивление и начинают рассеивать тепловую энергию. Какой прирост температуры произойдёт, если вся накопленная энергия пойдет на нагрев магнита массой 1000 кг при средней удельной теплоемкости 200 Дж/кг · ºC?
14. Необоснованные результаты В катушке индуктивности 25,0 Гн ток 100 А отключается за 1,00 мс. а) Какое напряжение индуцируется, чтобы противостоять этому? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка являются ответственными?
14.
 2 Самоиндукция и катушки индуктивности – University Physics Volume 2
2 Самоиндукция и катушки индуктивности – University Physics Volume 2Глава 14. Индуктивность
Цели обучения
К концу этого раздела вы сможете:
- Соотнесите скорость изменения тока с ЭДС индукции, создаваемой этим током в той же цепи
- Расчет собственной индуктивности цилиндрического соленоида
- Расчет собственной индуктивности прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи. Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ — да, и это явление называется самоиндукция .
Катушки индуктивности
На рис. 14.5 показаны некоторые силовые линии магнитного поля, обусловленные током в круглой проволочной петле. Если ток постоянен, магнитный поток через контур также постоянен. Однако, если бы ток I изменялся со временем, скажем, сразу после замыкания ключа S, то магнитный поток [латекс]{\текст{Ф}}_{\текст{м}}[/латекс] был бы соответственно изменить. Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС [латекс]\эпсилон[/латекс], где
Тогда закон Фарадея говорит нам, что в цепи будет индуцироваться ЭДС [латекс]\эпсилон[/латекс], где
[латекс]\epsilon =-\frac{d{\text{Φ}}_{\text{m}}}{dt}.[/latex]
Так как магнитное поле из-за проводника с током прямо пропорциональна току, поток, обусловленный этим полем, также пропорционален току; то есть
[латекс]{\текст{Ф}}_{\текст{м}}\пропто I.[/латекс]
Рис. 14.5 Магнитное поле создается током I в контуре. Если бы я менялся со временем, магнитный поток через петлю также менялся бы, и в петле индуцировалась бы ЭДС.Это также может быть записано как
[латекс]{\text{Φ}}_{\text{m}}=LI[/латекс]
, где константа пропорциональности L известна как само- индуктивность проволочной петли. Если в петле N витков, это уравнение принимает вид нормаль к контуру связана с током по правилу правой руки, поэтому на рис. 14.5 нормаль направлена вниз. При таком соглашении [латекс]{\текст{Ф}}_{\текст{м}}[/латекс] положителен в уравнении 14. 9., поэтому L всегда имеет положительное значение .
9., поэтому L всегда имеет положительное значение .
Для петли с N витков [латекс]\epsilon =\text{−}Nd{\text{Φ}}_{\text{m}}\text{/}dt,[/latex] поэтому ЭДС индукции может быть записана через самоиндукцию как
[латекс]\эпсилон =\текст{−}L\фрак{дI}{дт}.[/латекс]
При использовании этого уравнения для определения L , проще всего игнорировать знаки [латекс]\эпсилон\фантом{\правило{0.2em}{0ex}}\текст{и}\фантом{\правило{0.2em}{0ex}}dI\text {/}dt,[/latex] и вычислить L как
[латекс]L=\frac{|\epsilon |}{|dI\text{/}dt|}.[/latex]
Поскольку самоиндукция связана с магнитным полем, создаваемым тока любая конфигурация проводников обладает самоиндукцией. Например, помимо проволочной петли длинный прямой провод обладает собственной индуктивностью, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно обнаружить при подключении к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.
Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и собственной индуктивностью, что может иметь нежелательные последствия.
Элемент схемы, используемый для обеспечения собственной индуктивности, известен как катушка индуктивности . Он представлен символом, показанным на рис. 14.6, который напоминает катушку проволоки, основную форму катушки индуктивности. На рис. 14.7 показано несколько типов катушек индуктивности, обычно используемых в цепях.
Рисунок 14.6 Символ, используемый для обозначения катушки индуктивности в цепи. Рисунок 14.7 Различные катушки индуктивности. Независимо от того, заключены ли они в капсулу, как показаны три верхние, или намотаны на катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку провода. (кредит: Уинделл Оскей) В соответствии с законом Ленца отрицательный знак в уравнении 14.10 указывает на то, что ЭДС индукции на катушке индуктивности всегда имеет полярность, которая противостоит изменению тока. Например, если бы ток, протекающий от А к В на рис. 14.8(а), увеличивался, ЭДС индукции (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8 (б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.
Например, если бы ток, протекающий от А к В на рис. 14.8(а), увеличивался, ЭДС индукции (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от А до В уменьшался, то ЭДС индукции имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (рис. 14.8 (б)). Наконец, если бы ток через индуктор был постоянным, в катушке не индуцировалась бы ЭДС.
Одним из распространенных применений индуктивности является определение сигналов светофора, когда транспортные средства ожидают на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом, где остановится ожидающий автомобиль. Кузов автомобиля увеличивает индуктивность, и цепь меняется, посылая сигнал светофору изменить цвет. Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рис. 14.9).). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.
Точно так же металлоискатели, используемые для обеспечения безопасности в аэропортах, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и приемник. Импульсный сигнал от катушки передатчика индуцирует сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рис. 14.9).). Металлодетекторы можно настроить на чувствительность, а также они могут обнаруживать наличие металла на человеке.
Во вспышках фотокамер обнаружены большие индуцированные напряжения. Вспышки камеры используют батарею, две катушки индуктивности, которые функционируют как трансформатор, и систему переключения или генератор для создания больших напряжений. Напомним из книги «Колебания о колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.
Также вспомните (из электромагнитной индукции об электромагнитной индукции), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы индуцировать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой трансформатора во время зарядки конденсатора.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.
Пример
Собственная индуктивность катушки
ЭДС индукции 2,0 В измеряется в катушке из 50 тесно намотанных витков, при этом ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Чему равна собственная индуктивность катушки? б) Чему равен поток через каждый виток катушки при силе тока 5,0 А?
Стратегия
Обе части этой задачи дают всю информацию, необходимую для решения собственной индуктивности в части (a) или потока через каждый виток катушки в части (b). Необходимые уравнения: уравнение 14.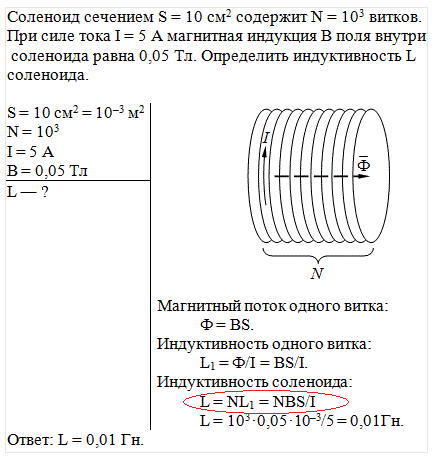 10 для части (а) и уравнение 14.9.{-3}\phantom{\rule{0.2em}{0ex}}\text{Wb}.[/latex]
10 для части (а) и уравнение 14.9.{-3}\phantom{\rule{0.2em}{0ex}}\text{Wb}.[/latex]
Значение
Собственная индуктивность и поток, рассчитанные в частях (a) и (b), являются типичными значениями для катушек, используемых в современных устройствах. Если ток не меняется во времени, поток не меняется во времени, поэтому ЭДС не индуцируется.
Проверьте свое понимание
Ток течет через катушку индуктивности на рис. 14.8 от B к A вместо A к B , как показано на рисунке. Ток увеличивается или уменьшается, чтобы создать ЭДС, указанную на диаграмме (а)? На схеме (б)?
Показать раствор а. уменьшение; б. увеличение; Так как ток течет в противоположном направлении диаграммы, то для получения положительной ЭДС в левой части диаграммы (а) нужно уменьшить ток влево, что создает усиленную ЭДС там, где положительный конец находится с левой стороны. Чтобы получить положительную ЭДС в правой части диаграммы (b), нам нужно увеличить ток влево, что создает усиленную ЭДС, где положительный конец находится на правой стороне.
Проверьте свои знания
Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?
Show Solution40 A/s
Хороший подход к расчету собственной индуктивности катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем: собственная индуктивность
- Предположим, что ток I протекает через катушку индуктивности.
- Определите магнитное поле [латекс]\stackrel{\to }{\textbf{B}}[/латекс], создаваемое током. Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получите магнитный поток, [латекс] {\ текст {Φ}} _ {\ текст {м}}. [/латекс]
- При известном потоке собственная индуктивность может быть найдена из уравнения 14.9, [латекс]L=N{\text{Φ}}_{\text{m}}\text{/}I[/latex].
Чтобы продемонстрировать эту процедуру, мы теперь рассчитаем собственные индуктивности двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A и N витков провода. Мы предполагаем, что длина соленоида настолько больше его диаметра, что мы можем принять магнитное поле равным [латекс] B = {\ mu }_{0} nI [/латекс] во всей внутренней части соленоида, что то есть мы игнорируем концевые эффекты в соленоиде. С током 9{2}\left(V\right),[/latex]
, где [latex]V=Al[/latex] — объем соленоида. Обратите внимание, что собственная индуктивность длинного соленоида зависит только от его физических свойств (таких как число витков провода на единицу длины и объем), а не от магнитного поля или тока. Это справедливо для катушек индуктивности в целом.
Прямоугольный тороид
Тороид прямоугольного сечения показан на рис. 14.10. Внутренний и внешний радиусы тороида равны [латекс]{R}_{1}\phantom{\rule{0.2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}} {R}_{2},\phantom{\rule{0. 2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}h[/latex] — высота тороида . Применяя закон Ампера так же, как мы делали это в примере 13.8 для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также определяется выражением 9{2}[/латекс]
2em}{0ex}}\text{and}\phantom{\rule{0.2em}{0ex}}h[/latex] — высота тороида . Применяя закон Ампера так же, как мы делали это в примере 13.8 для тороида с круглым поперечным сечением, мы находим, что магнитное поле внутри прямоугольного тороида также определяется выражением 9{2}[/латекс]
Резюме
- Текущие изменения в устройстве индуцируют ЭДС в самом устройстве, называемую собственной индуктивностью,
[латекс]\epsilon =\text{−}L\frac{dI}{dt},[/latex]
, где L – собственная индуктивность катушки индуктивности, а [latex]dI\text{/}dt[/latex] – скорость изменения тока через нее. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. Единицей самоиндукции и индуктивности является генри (Гн), где 0ex}}\text{Ω}·\text{s}[/latex]. 9{-7}\phantom{\rule{0.2em}{0ex}}\text{T}·\text{m/A}[/latex] — проницаемость свободного пространства.
Концептуальные вопросы
Зависит ли собственная индуктивность от величины магнитного потока? Зависит ли это от силы тока в проводе? Соотнесите свои ответы с уравнением к текущему. Однако, поскольку магнитный поток зависит от тока I , эти эффекты компенсируются. Это означает, что собственная индуктивность не зависит от тока. Если ЭДС индуцируется в элементе, она зависит от того, как ток изменяется со временем.
Однако, поскольку магнитный поток зависит от тока I , эти эффекты компенсируются. Это означает, что собственная индуктивность не зависит от тока. Если ЭДС индуцируется в элементе, она зависит от того, как ток изменяется со временем.
Будет ли собственная индуктивность туго намотанного соленоида длиной 1,0 м отличаться от собственной индуктивности на метр бесконечного, но в остальном идентичного соленоида?
Обсудите, как можно определить собственную индуктивность на единицу длины длинного прямого провода.
Показать решениеСчитайте концы провода частью цепи RL и определите самоиндукцию по этой цепи.
Собственная индуктивность катушки равна нулю, если через обмотки не проходит ток. Правда или ложь?
Как соотносится собственная индуктивность на единицу длины вблизи центра соленоида (вдали от концов) с ее значением вблизи конца соленоида?
Показать решение Магнитное поле будет расширяться в конце соленоида, поэтому поток через последний виток меньше, чем через середину соленоида.
Задачи
ЭДС 0,40 В индуцируется в катушке, когда ток через нее изменяется равномерно от 0,10 до 0,60 А за 0,30 с. Чему равна собственная индуктивность катушки?
Показать решение0,24 H
Ток, показанный в части (a) ниже, увеличивается, а ток, показанный в части (b), уменьшается. В каждом случае определите, какой конец индуктора находится под более высоким потенциалом.
С какой скоростью изменяется ток через катушку 0,30 Гн, если на катушке индуцируется ЭДС 0,12 В?
Показать решение0,4 A/s
Когда камера использует вспышку, полностью заряженный конденсатор разряжается через катушку индуктивности. За какое время необходимо включить или выключить ток 0,100 А через дроссель 2,00 мГн, чтобы навести ЭДС 500 В?
По катушке с собственной индуктивностью 2,0 Гн протекает ток, изменяющийся со временем по закону [латекс]I\left(t\right)=\left(2.0\phantom{\rule{0.2em}{0ex}} \text{A}\right)\text{sin}\phantom{\rule{0. 2em}{0ex}}120\pi t.[/latex] Найдите выражение для ЭДС, индуцируемой в катушке. 9{2}[/latex] Какова собственная индуктивность соленоида?
2em}{0ex}}120\pi t.[/latex] Найдите выражение для ЭДС, индуцируемой в катушке. 9{2}[/latex] Какова собственная индуктивность соленоида?
По катушке с собственной индуктивностью 3,0 Гн течет ток, уменьшающийся с постоянной скоростью [latex]dI\text{/}dt=-0,050\phantom{\rule{0.2em}{0ex}}\text{ А/с}[/латекс]. Чему равна ЭДС индукции в катушке? Опишите полярность ЭДС индукции.
Показать решение0,15 В. Это та же полярность, что и ЭДС, управляющая током.
Ток I(t) через катушку индуктивности 5,0 мГн изменяется со временем, как показано ниже. Сопротивление индуктора равно [латекс]5,0\фантом{\правило{0,2em}{0ex}}\текст{Ом}.[/латекс] Рассчитайте напряжение на индукторе при [латекс]t=2,0\фантом{\ правило {0.2em} {0ex}} \ text {мс}, t = 4.0 \ фантом {\ правило {0.2em} {0ex}} \ текст {мс}, \ фантом {\ правило {0.2em} {0ex}} \text{and}\phantom{\rule{0.2em}{0ex}}t=8.0\phantom{\rule{0.2em}{0ex}}\text{ms}[/latex].
Длинный цилиндрический соленоид с числом оборотов 100 на сантиметр имеет радиус 1,5 см. (a) Пренебрегая концевыми эффектами, какова собственная индуктивность на единицу длины соленоида? б) Если ток через соленоид изменяется со скоростью 5,0 А/с, какая ЭДС индуцируется на единицу длины?
(a) Пренебрегая концевыми эффектами, какова собственная индуктивность на единицу длины соленоида? б) Если ток через соленоид изменяется со скоростью 5,0 А/с, какая ЭДС индуцируется на единицу длины?
а. 0,089 Гн/м; б. 0,44 В/м
Предположим, что прямоугольный тор имеет 2000 витков и собственную индуктивность 0,040 Гн. отношение его внешнего радиуса к внутреннему радиусу? 9{-7}\phantom{\rule{0.2em}{0ex}}\text{H/m}[/latex]
Глоссарий
- Катушка индуктивности
- часть электрической цепи для обеспечения собственной индуктивности, которая обозначена катушкой провода
- самоиндукция
- действие устройства, индуцирующего ЭДС само по себе
Самоиндукция и катушки индуктивности. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/university-physics-volume-2/pages/14-2-self-inductance-and-inductors. 2 }{l}\cdot I \tag{1}$$
Ясно, что в этом случае, если мы удвоим количество витков (при неизменной длине и токе), мы увеличим общий поток в 4 раза. Это связано с тем, что индуктивность соленоида квадратично зависит от $N$.
Теперь я только что узнал о концепции сопротивление (обозначается $R$) и магнитодвижущая сила (обозначается $m.m.f$), где $m.m.f$ определяется как $m.m.f \equiv N\cdot I$. Эти две величины связаны друг с другом полным потоком по формуле
$$m.m.f = R\cdot \Phi \tag{2}$$
Теперь, применяя приведенную выше формулу (уравнение 2) к случаю соленоидального индуктора, если мы сохраняем постоянный ток, но удваиваем количество витков (N) индуктора, $m.m.f$ только удваивается (поскольку $m.m.f \equiv N\ cdot I$). Но согласно уравнению (1) суммарный поток 92$. Таким образом, для того чтобы уравнение (2) оставалось в силе, сопротивление обязательно должно быть вдвое меньше . То есть для того, чтобы уравнения 1 и 2 были справедливы одновременно, сопротивление должно быть обратно пропорционально количеству витков, так что $R\propto \frac{1}{N}$.
2 }{l}\cdot I \tag{1}$$
Ясно, что в этом случае, если мы удвоим количество витков (при неизменной длине и токе), мы увеличим общий поток в 4 раза. Это связано с тем, что индуктивность соленоида квадратично зависит от $N$.
Теперь я только что узнал о концепции сопротивление (обозначается $R$) и магнитодвижущая сила (обозначается $m.m.f$), где $m.m.f$ определяется как $m.m.f \equiv N\cdot I$. Эти две величины связаны друг с другом полным потоком по формуле
$$m.m.f = R\cdot \Phi \tag{2}$$
Теперь, применяя приведенную выше формулу (уравнение 2) к случаю соленоидального индуктора, если мы сохраняем постоянный ток, но удваиваем количество витков (N) индуктора, $m.m.f$ только удваивается (поскольку $m.m.f \equiv N\ cdot I$). Но согласно уравнению (1) суммарный поток 92$. Таким образом, для того чтобы уравнение (2) оставалось в силе, сопротивление обязательно должно быть вдвое меньше . То есть для того, чтобы уравнения 1 и 2 были справедливы одновременно, сопротивление должно быть обратно пропорционально количеству витков, так что $R\propto \frac{1}{N}$. Однако, куда бы я ни посмотрел, я нахожу, что сопротивление всегда задается уравнениями, которые на независимы от $N$. Например, в Википедии указано, что $R=\frac{l}{\mu A}$. Как это может быть? Как уравнения 1 и 2 могут быть одновременно истинными, если сопротивление не зависит от $N$? Любая помощь по этому вопросу будет принята с благодарностью!
Однако, куда бы я ни посмотрел, я нахожу, что сопротивление всегда задается уравнениями, которые на независимы от $N$. Например, в Википедии указано, что $R=\frac{l}{\mu A}$. Как это может быть? Как уравнения 1 и 2 могут быть одновременно истинными, если сопротивление не зависит от $N$? Любая помощь по этому вопросу будет принята с благодарностью!
- электромагнетизм
- магнитные поля
- электрические цепи
- электрический ток
- электромагнитная индукция
$\endgroup$
$\begingroup$
Сопротивление не зависит от количества витков. Ваше замешательство возникает из-за того, что люди используют слово «поток» для обозначения двух тесно связанных, но разных величин. Напомним, что магнитный поток — это интеграл от $\vec B$ через поверхность. Чтобы говорить о потоке, мы должны сначала определить, что представляет собой эта поверхность. 2B=N\Phi_1.$ Индуктивность рассчитывается как $L =\Phi_2/I$. 92$, как и ожидалось.
2B=N\Phi_1.$ Индуктивность рассчитывается как $L =\Phi_2/I$. 92$, как и ожидалось.
$\endgroup$
$\begingroup$
Источник вашей путаницы в том, что вы не рассматриваете магнитный поток, связанный с цепью соленоида, а вам нужно учитывать магнитный поток, связанный с материалом сердечника соленоида.
Соленоид создает магнитное поле $B=\mu N I /L$, которое создает магнитный поток через материал его сердечника $\Phi = BA = \mu N I A /L$, где $A$ — поперечное сечение площадь ядра.
Таким образом, уравнение $\text{mmf}= R_{\rm m} \Phi$ относится к магнитной цепи, содержащей сердечник, тогда как уравнение $\Phi = LI$ относится к электрической цепи, в которой соленоид является частью.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Преобразователь случайных чисел |
Калькулятор индуктивности однослойной катушкиРасчет индуктивности по заданному количеству витков, диаметру каркаса катушки и длине намотки Однослойный индуктор: D — диаметр каркаса катушки, l — длина витка, p — шаг витка, d — диаметр провода без изоляции, d i — диаметр провода с изоляцией. Калькулятор определяет индуктивность однослойной катушки. Пример: Рассчитайте индуктивность однослойной катушки из 10 витков с воздушным сердечником, намотанной на цилиндрический каркас диаметром 2 см; длина катушки 1 см. Input Coil former diameter D millimeter (mm)centimeter (cm)inch (in) Number of turns N Length of the coil л миллиметр (мм) сантиметр (см) дюйм (дюйм) Доля Выход Индуктивность катушки L мГн Введите диаметр каркаса катушки, количество витков и длину катушки, выберите единицы измерения и нажмите кнопку 90 2 50 904. Рассчитайте количество витков и длину намотки, исходя из данных индуктивности, диаметра каркаса катушки и диаметра провода Пример: Рассчитайте количество витков и длину намотки катушки 10 мкГн с диаметром каркаса 2 см, намотанной на 22 Магнитный провод AWG (0,65 мм без изоляции и 0,7 мм с изоляцией). Вход Требуется индуктивность L Генри (H) Миллихенри (MH) Microhenry (мкл). мм)сантиметр (см)метр (м)дюйм (дюйм) Диаметр провода без изоляции d миллиметр (мм)сантиметр (см)метр (м)дюйм (дюйм)Американский калибр провода Диаметр из изолированного провода D I миллиметра (мм) сантиметр (см) Метр (м) дюйм (дюйм) Совместный L На рисунке выше показан однослойный индуктор: D c диаметр катушки, D диаметр катушки, l длина катушки0900 p — шаг витка, d — диаметр провода без изоляции и d i — диаметр провода с изоляцией. Для расчета индуктивности используется следующая формула из статьи Р. Уивера «Численные методы расчета индуктивности» длина рулона в см, Н — число витков, а L — индуктивность в мкГн. Эта формула действительна только для соленоидального токового слоя. где L S — индуктивность токового слоя, описанная выше, и , где k с — безразмерный поправочный коэффициент для разности и одновиткового токового листа; к м – безразмерный поправочный коэффициент на разницу суммарной взаимной индуктивности набора круглых витков по сравнению с набором токовых витков; D c — диаметр витка в см, измеренный между центрами проволоки; а Н – число витков. Величина Розы к м определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта: 10.4 в статье Дэвида Найта: , где p — шаг проволоки (расстояние между витками, измеренное между центрами проволоки) и d — диаметр проволоки. Обратите внимание, что отношение p/d всегда больше единицы из-за толщины изоляции проводов, а минимально возможное расстояние между двумя круглыми проводами, лежащими рядом, для очень тонкой изоляции составляет диаметр провода d . Факторы, влияющие на индуктивность катушкиНа индуктивность катушки влияет несколько факторов.
Упрощенная схема замещения реальной катушки индуктивности: R w — сопротивление обмоточного провода и его концов; L — индуктивность идеального индуктора; R l – сопротивление за счет потерь в магнитопроводе; и C w — паразитная собственная емкость катушки индуктивности и ее выводов. Паразитная емкость возникает из-за того, что отдельные витки катушки находятся в непосредственной близости друг от друга. Любые два витка провода можно рассматривать как небольшой конденсатор. Витки разделены изолятором, например воздухом, лаком, изоляционной лентой или другой изоляцией проводов. Диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта константа, тем выше емкость. Для уменьшения паразитной емкости катушки с высоким коэффициентом добротности в радиопередатчиках часто изготавливают с разнесенными витками. Тем не менее, оно мало по сравнению с реактивным сопротивлением большой индуктивности на высоких частотах. Однако на низких частотах или при постоянном токе необходимо учитывать сопротивление, поскольку в этих условиях могут быть задействованы значительные токи. Катушки индуктивности и катушки Эта статья написана Анатолием Золотковым Вам могут быть интересны другие калькуляторы из группы Калькуляторы электрических, радиочастотных и электронных устройств:Калькулятор резисторно-конденсаторных (RC) цепей Калькулятор параллельного сопротивления 3 3 Калькулятор параллельной индуктивности Калькулятор конденсаторов серииКалькулятор полного сопротивления конденсатора Калькулятор полного сопротивления катушки индуктивности Калькулятор взаимной индуктивности Калькулятор взаимной индуктивности — Параллельные индукции Калькулятор взаимной индуктивности — индуктивность в серии Параллельный калькулятор схемы схемы RC .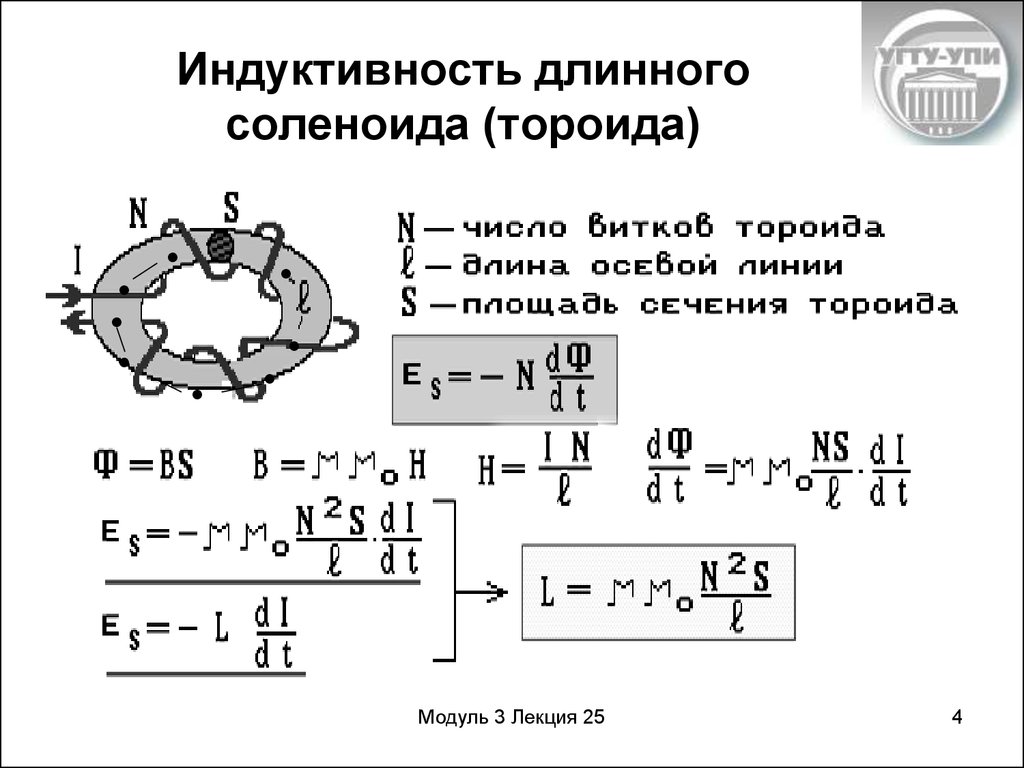 Расплакационный схема 9002. Калькулятор импеданса Калькулятор импеданса цепи LC серии Калькулятор импеданса цепи RL серии Расплакационный схема 9002. Калькулятор импеданса Калькулятор импеданса цепи LC серии Калькулятор импеданса цепи RL серииКалькулятор импеданса цепи RLC Калькулятор энергии и времени работы батареи Калькулятор батареи LiPo для дрона Калькулятор индуктивности плоской спиральной катушки NFC/RFID Калькулятор коаксиального кабеля Калькулятор светодиодов. Расчет токоограничивающих резисторов для одиночного светодиода и светодиодных матриц Калькулятор цветового кода резистора Калькулятор максимальной дальности радара Калькулятор максимальной однозначной дальности радара и частоты повторения импульсов Radar Horizon and Target Visibility Calculator Radio Line of Sight Distance Calculator Effective Antenna Aperture Calculator Dipole Antenna Calculator Aliasing Frequency Calculator DC Power Calculator AC Power Calculator VA to Watts Calculator Калькулятор трехфазной мощности переменного тока (сбалансированная нагрузка) Преобразование вектора: прямоугольно-полярное Калькулятор полного гармонического искажения (THD) Калькулятор закона Ома Калькулятор времени передачи данных Калькулятор внутреннего сопротивления батареи Калькуляторы Электрические, радиочастотные и электронные калькуляторы |
Самоиндукция
СамоиндукцияСледующий: Взаимная индуктивность Вверх: Магнитная индукция Предыдущий: Индуктивность Рассмотрим длинный соленоид длины и радиуса , число витков на единицу длины, и несет ток. Продольный ( т.е. , направленный по оси соленоида) магнитное поле внутри соленоида приблизительно однородно, и дается
| (907) |
Этот результат легко получить, интегрируя закон Ампера по прямоугольному петля, длинные стороны которой идут параллельно оси соленоида, одна внутри соленоида, а другой снаружи, короткие стороны которого проходят перпендикулярно ось.
 Магнитный поток через каждый виток петли равен
. Общий поток через
провод соленоида, который имеет витки,
Магнитный поток через каждый виток петли равен
. Общий поток через
провод соленоида, который имеет витки, | (908) |
Таким образом, собственная индуктивность соленоида равна
| (909) |
Обратите внимание, что самоиндукция зависит только от геометрических величин, таких как число витков на единицу длины соленоида и площади поперечного сечения витков.
Предположим, что ток, протекающий через соленоид, изменяется. Мы должны
предположим, что изменение происходит достаточно медленно, чтобы можно было пренебречь смещением
эффекты тока и запаздывания в наших расчетах. Это означает, что типичный
временной масштаб изменения должен быть намного больше, чем время прохождения световым лучом
схема. Если это так, то приведенные выше формулы остаются в силе.
Если это так, то приведенные выше формулы остаются в силе.
Изменение тока влечет за собой изменение магнитного потока, связывающего соленоид
провод, так как
. По Фарадею
Закон, это изменение
генерирует э.д.с. в проводе. По закону Ленца Э.Д.С. это так
а для противодействия изменению тока — т. е. , это противо-э.д.с. Мы можем написать
| (910) |
где – генерируемая Э.Д.С.
 Падение напряжения
между катушкой индуктивности и резистором равна э.д.с. батареи,
. Падение напряжения на резисторе просто , тогда как
падение напряжения на катушке индуктивности ( т. е. , противоэдс) равно
. Здесь — ток, протекающий через соленоид.
Следует, что
Падение напряжения
между катушкой индуктивности и резистором равна э.д.с. батареи,
. Падение напряжения на резисторе просто , тогда как
падение напряжения на катушке индуктивности ( т. е. , противоэдс) равно
. Здесь — ток, протекающий через соленоид.
Следует, что | (911) |
Это дифференциальное уравнение для тока. Мы можем переставить его на давать
| (912) |
Общее решение
| (913) |
Константа фиксируется граничными условиями. Предположим, что аккумулятор подключен во время , если . Отсюда следует, что что
| (914) |
Эта кривая представлена на рис.
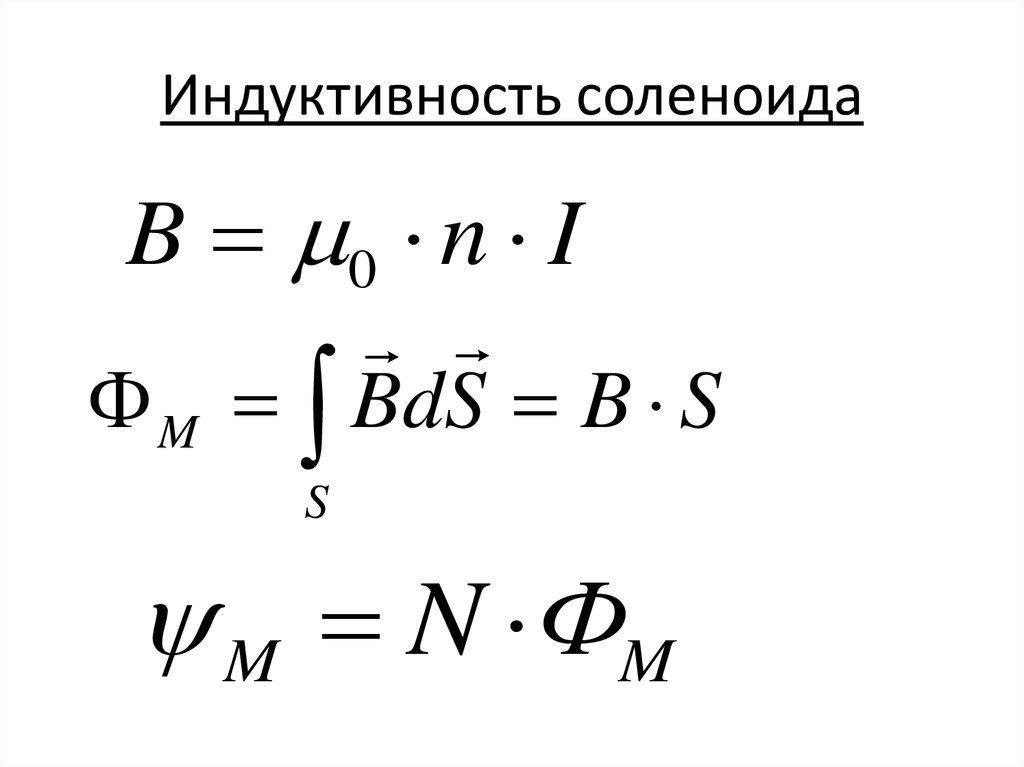 52. Видно, что после подключения батареи ток
нарастает и достигает установившегося значения (которое исходит из уравнения Ома).
закон), на характерном временном масштабе
52. Видно, что после подключения батареи ток
нарастает и достигает установившегося значения (которое исходит из уравнения Ома).
закон), на характерном временном масштабе | (915) |
Эта временная шкала иногда называется постоянной времени схемы или, несколько невообразимо, L за время R цепи.
Теперь мы можем оценить значение самоиндукции. Задняя э.д.с.
генерируемый в катушке индуктивности, поскольку ток пытается измениться, эффективно предотвращает
ток от роста (или падения) намного быстрее, чем время. Этот эффект
иногда выгодно, но часто это большая неприятность.
Все элементы схемы обладают некоторой собственной индуктивностью, а также некоторым сопротивлением и, следовательно, имеют конечное время. Это означает, что когда мы включаем цепь, ток
мгновенно не достигает стационарного значения. Вместо этого
подъем распределяется по времени L/R цепи. Это хорошая вещь.
Если бы ток возрастал мгновенно, то чрезвычайно большие электрические
поля будут генерироваться внезапным скачком индуцированного магнитного поля, ведущим,
неизбежно к пробою и возникновению электрической дуги. Так что, если бы не было такого
как самоиндукция, то каждый раз, когда вы включали или выключали электрическую цепь
будет синяя вспышка из-за искрения между проводниками. Самоиндукция
тоже может быть плохо. Предположим, что у нас есть навороченный источник питания, и мы хотим
использовать его для отправки электрического сигнала по проводу (или линии передачи).
Конечно, провод или линия передачи будут обладать как сопротивлением, так и индуктивностью.
и поэтому будет иметь некоторое характерное время. Предположим, что мы
попробуйте послать прямоугольный сигнал по проводу. Так как ток в проводе
не может расти или опускаться быстрее, чем время, передний и задний фронты
сигнал со временем сглаживается.
Это означает, что когда мы включаем цепь, ток
мгновенно не достигает стационарного значения. Вместо этого
подъем распределяется по времени L/R цепи. Это хорошая вещь.
Если бы ток возрастал мгновенно, то чрезвычайно большие электрические
поля будут генерироваться внезапным скачком индуцированного магнитного поля, ведущим,
неизбежно к пробою и возникновению электрической дуги. Так что, если бы не было такого
как самоиндукция, то каждый раз, когда вы включали или выключали электрическую цепь
будет синяя вспышка из-за искрения между проводниками. Самоиндукция
тоже может быть плохо. Предположим, что у нас есть навороченный источник питания, и мы хотим
использовать его для отправки электрического сигнала по проводу (или линии передачи).
Конечно, провод или линия передачи будут обладать как сопротивлением, так и индуктивностью.
и поэтому будет иметь некоторое характерное время. Предположим, что мы
попробуйте послать прямоугольный сигнал по проводу. Так как ток в проводе
не может расти или опускаться быстрее, чем время, передний и задний фронты
сигнал со временем сглаживается.


 Затухающие
электромагнитные колебания. Вынужденные
электромагнитные колебания. Явление
резонанса
Затухающие
электромагнитные колебания. Вынужденные
электромагнитные колебания. Явление
резонанса (3)
(3) (3)
(3) Подставляя исходные данные, получим:
Подставляя исходные данные, получим: 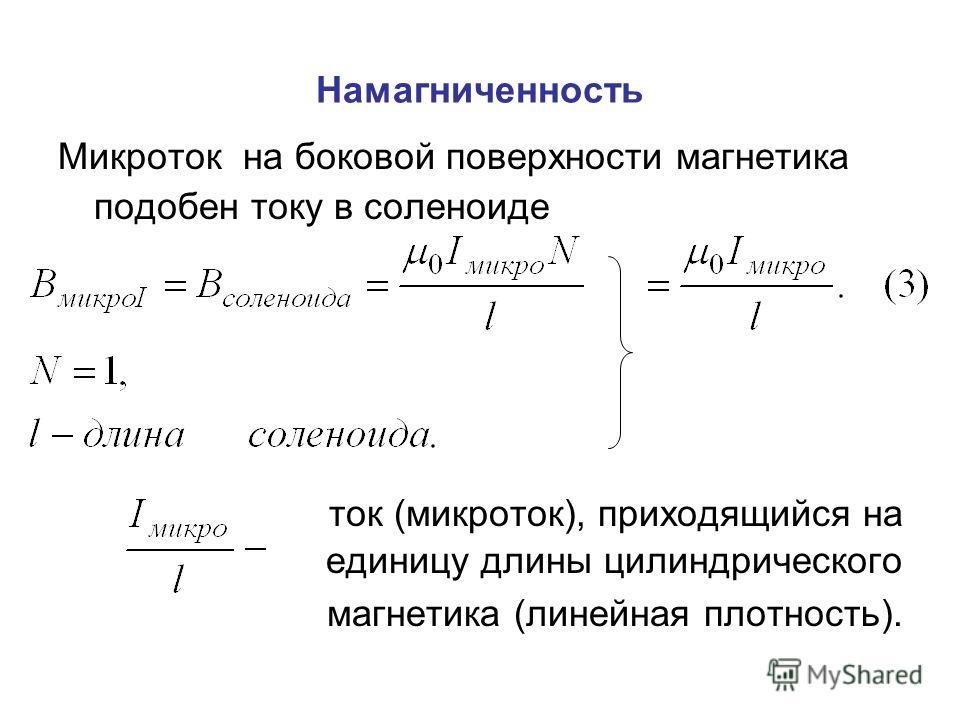
 Помогите пожалуйста, так как я чайник и скорее всего не понимаю элементарных вещей в физике ) Гугл мне не помог, так как я не понял ничего из предложенного им. Вопрос следующий: Правильно ли я понимаю, что чем выше индуктивность намотки соленоида, тем выше его механическая сила втягивания? Я понимаю, что чем больше слоёв намотки, тем выше индуктивность и соответственно сила втягивания больше. Верно ли я понял? Подскажите пожалуйста!)
Помогите пожалуйста, так как я чайник и скорее всего не понимаю элементарных вещей в физике ) Гугл мне не помог, так как я не понял ничего из предложенного им. Вопрос следующий: Правильно ли я понимаю, что чем выше индуктивность намотки соленоида, тем выше его механическая сила втягивания? Я понимаю, что чем больше слоёв намотки, тем выше индуктивность и соответственно сила втягивания больше. Верно ли я понял? Подскажите пожалуйста!) Индуктивность в работе соленоида не принимает участия.
Индуктивность в работе соленоида не принимает участия.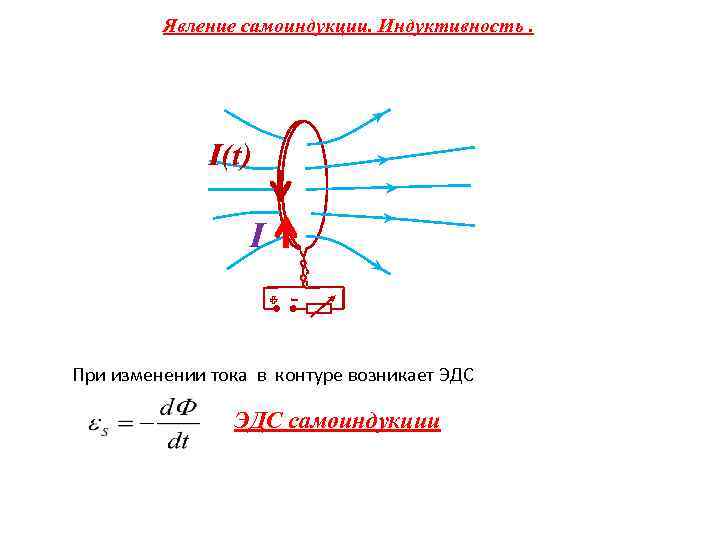 09.2018, 01:57
09.2018, 01:57 

 Напряжённость его равна , — число ампер-витков, — длина соленоида.
Напряжённость его равна , — число ампер-витков, — длина соленоида. У длинного — сила меньше, но он может втянуть сердечник на большее расстояние. Работа, которая совершается при втягивании от длины не зависит.
У длинного — сила меньше, но он может втянуть сердечник на большее расстояние. Работа, которая совершается при втягивании от длины не зависит. Напряжённость его равна , — число ампер-витков, — длина соленоида.
Напряжённость его равна , — число ампер-витков, — длина соленоида.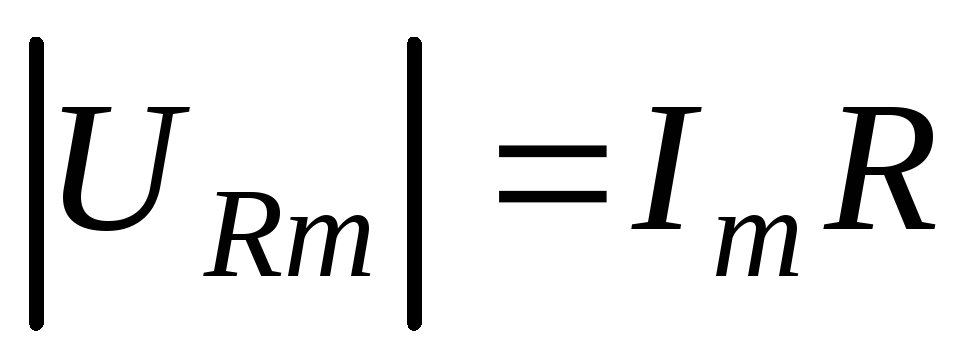 Напряжённость его равна , — число ампер-витков, — длина соленоида.
Напряжённость его равна , — число ампер-витков, — длина соленоида. Диаметр намотки повлияет на силу, только, если вместе с ним увеличится и диаметр втягиваемого сердечника. Это не всегда удобно, т.к. вес сердечника будет большой.
Диаметр намотки повлияет на силу, только, если вместе с ним увеличится и диаметр втягиваемого сердечника. Это не всегда удобно, т.к. вес сердечника будет большой. Правда, если есть постоянные магниты, то понятие индуктивности неприменимо и формула не работает, а в техническом смысле как раз с ними-то и выгодней.
Правда, если есть постоянные магниты, то понятие индуктивности неприменимо и формула не работает, а в техническом смысле как раз с ними-то и выгодней.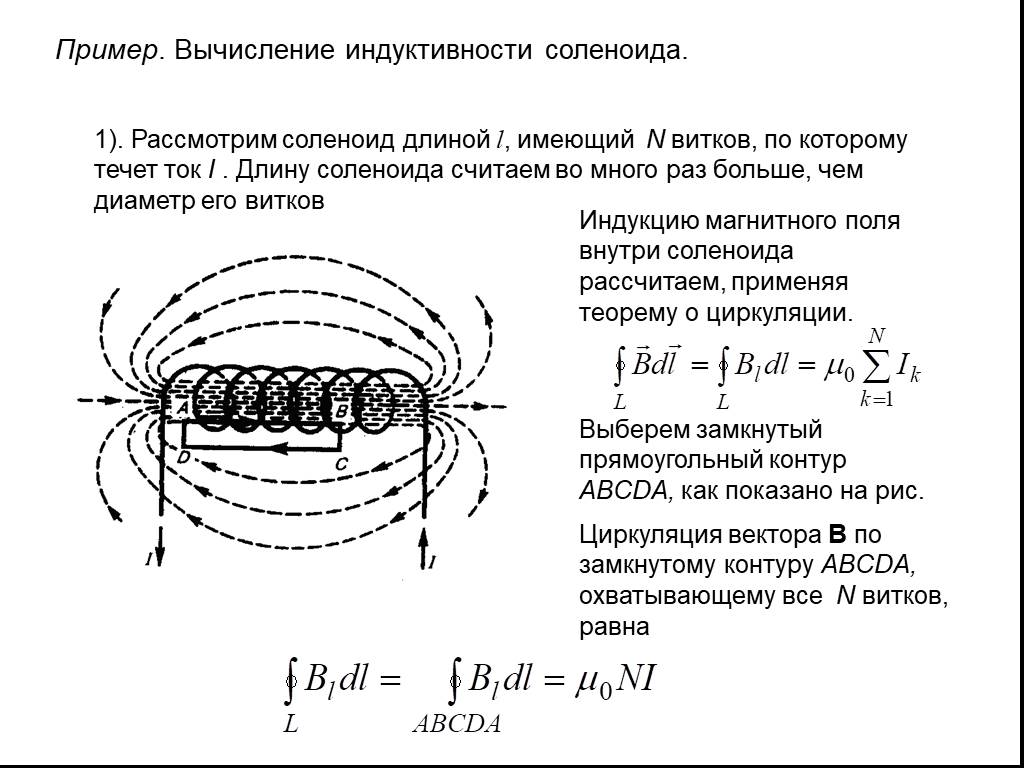
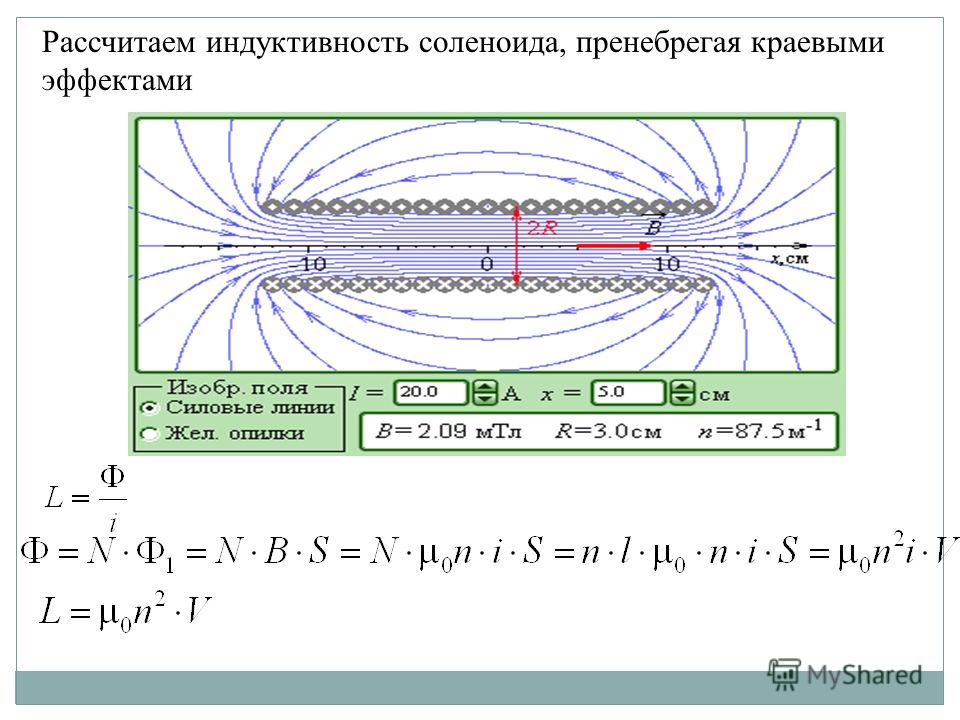
 Токовый лист здесь означает, что катушка намотана очень тонким ленточным проводом без зазоров между соседними витками. Это очень хорошее приближение для катушек круглого провода с большим количеством близко расположенных витков. Американский физик Эдвард Беннет Роза (1873–1921) из Американского национального бюро стандартов (NBS, ныне Национальное бюро стандартов и технологий, NIST) разработал так называемые поправки на круглую проволоку для приведенной выше формулы в виде (формула 10.1 в Статья Дэвида В. Найта):
Токовый лист здесь означает, что катушка намотана очень тонким ленточным проводом без зазоров между соседними витками. Это очень хорошее приближение для катушек круглого провода с большим количеством близко расположенных витков. Американский физик Эдвард Беннет Роза (1873–1921) из Американского национального бюро стандартов (NBS, ныне Национальное бюро стандартов и технологий, NIST) разработал так называемые поправки на круглую проволоку для приведенной выше формулы в виде (формула 10.1 в Статья Дэвида В. Найта):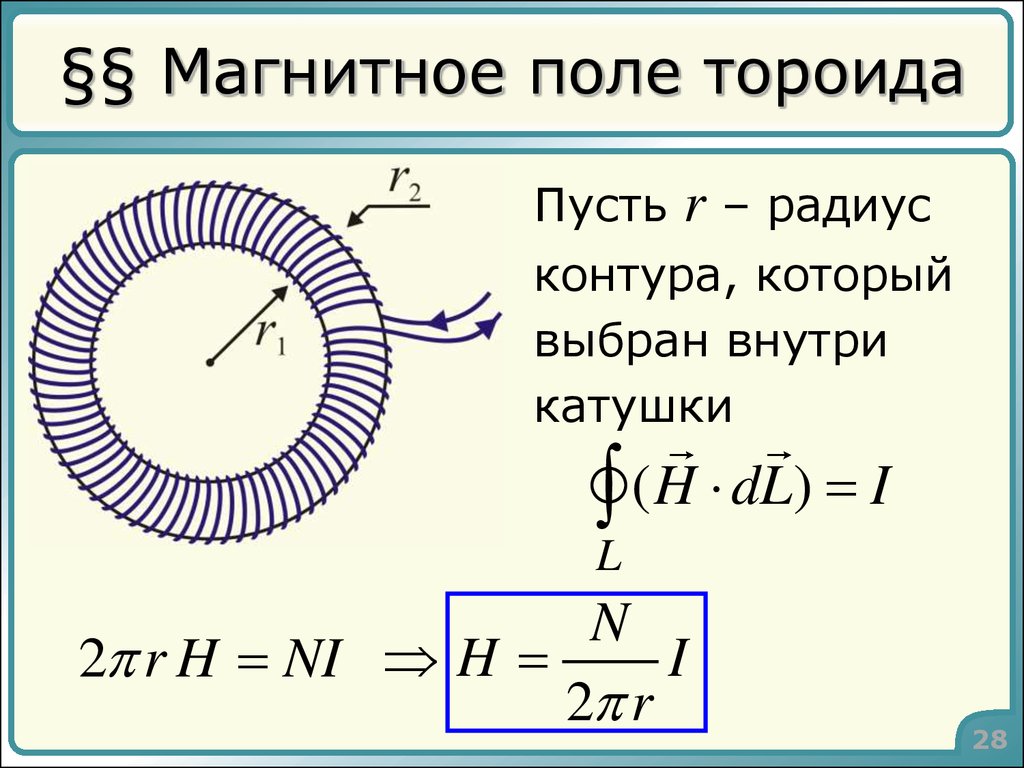
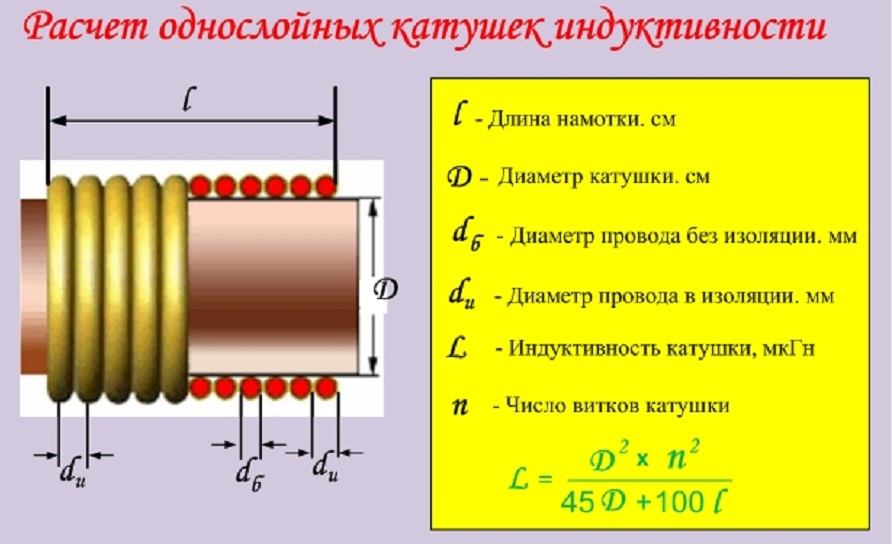 Магнитное поле не может хорошо концентрироваться в натянутой катушке.
Магнитное поле не может хорошо концентрироваться в натянутой катушке. В то же время идеальных компонентов в реальном мире не бывает. Катушки индуктивности обычно имеют наименьшие возможные размеры, чтобы вписаться в небольшие конструкции. Любую реальную катушку индуктивности можно рассматривать как идеальную катушку индуктивности, имеющую резистор и конденсатор, включенные параллельно, и еще один резистор, включенный последовательно. Параллельное сопротивление добавляется из-за потерь в магнитопроводе на вихревые токи, гистерезисных потерь. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и уровня потока сердечника.
В то же время идеальных компонентов в реальном мире не бывает. Катушки индуктивности обычно имеют наименьшие возможные размеры, чтобы вписаться в небольшие конструкции. Любую реальную катушку индуктивности можно рассматривать как идеальную катушку индуктивности, имеющую резистор и конденсатор, включенные параллельно, и еще один резистор, включенный последовательно. Параллельное сопротивление добавляется из-за потерь в магнитопроводе на вихревые токи, гистерезисных потерь. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и уровня потока сердечника. В некоторых случаях между катушкой индуктивности и плоскостью земли может появиться дополнительная емкость, если катушка индуктивности расположена над плоскостью земли. На высоких частотах реактивное сопротивление паразитной емкости может быть довольно большим, и им нельзя пренебречь. Для его уменьшения применяют различные приемы намотки.
В некоторых случаях между катушкой индуктивности и плоскостью земли может появиться дополнительная емкость, если катушка индуктивности расположена над плоскостью земли. На высоких частотах реактивное сопротивление паразитной емкости может быть довольно большим, и им нельзя пренебречь. Для его уменьшения применяют различные приемы намотки. компоненты (резисторы, катушки индуктивности и конденсаторы) и соединения между ними.
компоненты (резисторы, катушки индуктивности и конденсаторы) и соединения между ними.  com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.
com, были правильными. Однако мы не гарантируем, что наши конвертеры и калькуляторы не содержат ошибок. Весь контент предоставляется «как есть», без каких-либо гарантий. Условия и положения.