|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 2 из 2 Таблица 5.8
При правильном выполнении задания — = 27 Таблица 5.8а
5.12. Методы расчёта цепей переменного синусоидального тока Таблица 5.9
При правильном выполнении задания — = 56 Таблица 5.9а
Продолжение задачи (условие смотрите в табл. 5.9) Таблица 5.10
При правильном выполнении задания — = 31 Таблица 5.10а
Лабораторная работа № 5.1 «Исследование катушки в цепи переменного синусоидального тока символическим (комплексным) методом» ⇐ Предыдущая12 Читайте также: Психологические особенности спортивного соревнования Приготовление дезинфицирующих растворов различной концентрации Занятость населения и рынок труда Социальный статус семьи и её типология |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 267; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
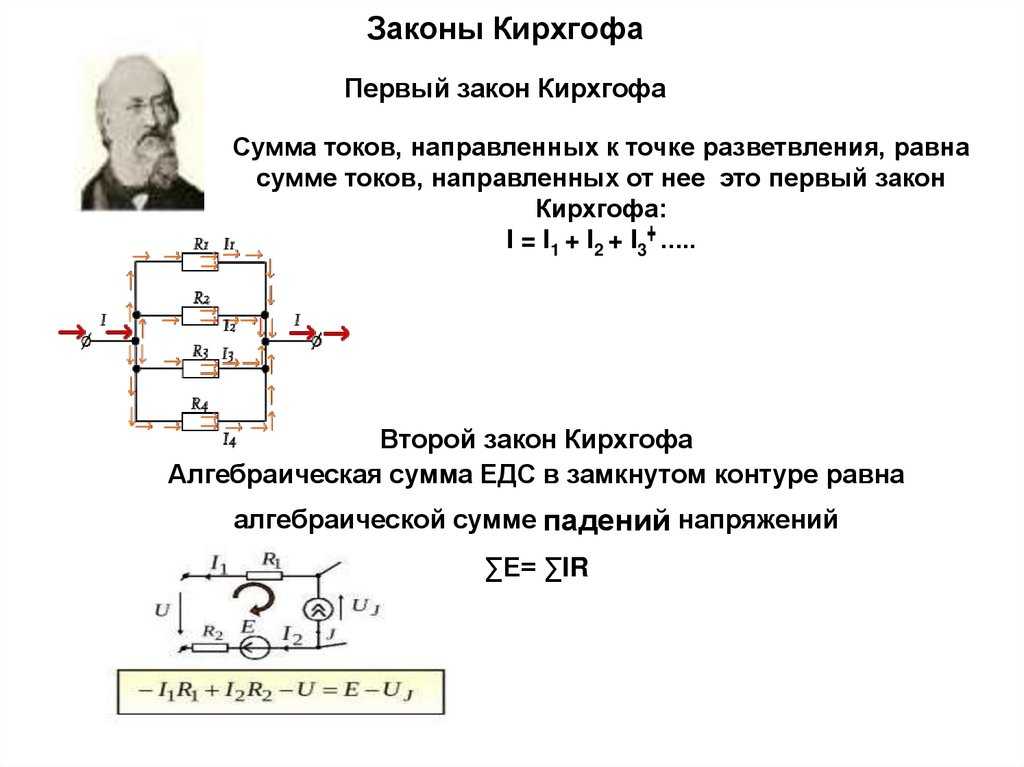
Ознакомление с законами Кирхгофа для разветвлённых электрических цепей
Лабораторная работа № 24
Ознакомление с законами Кирхгофа для разветвлённых электрических цепей
Цель работы: освоение законов Кирхгофа, их экспериментальная проверка и практическое применение
Приборы и принадлежности: разветвлённая электрическая цепь с амперметром, вольтметром и сопротивлениями; магазин сопротивлений; два источника постоянного тока (8÷10 В и 1,5÷3 В), калькулятор.
Теоретическое введение
На практике часто приходится рассчитывать сложные (разветвлённые)
цепи постоянного тока, например, по заданным сопротивлениям участков цепи и
приложенным к ним э.д.с. находить силы токов во всех участках. Эта задача
просто решается с помощью двух законов Кирхгофа. Один из них выражает закон
сохранения заряда, другой является следствием закона Ома.
Один из них выражает закон
сохранения заряда, другой является следствием закона Ома.
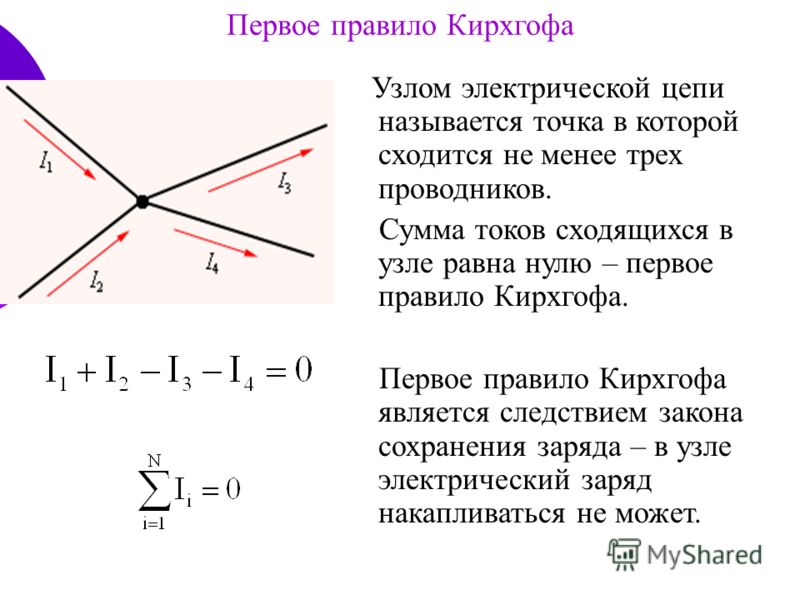
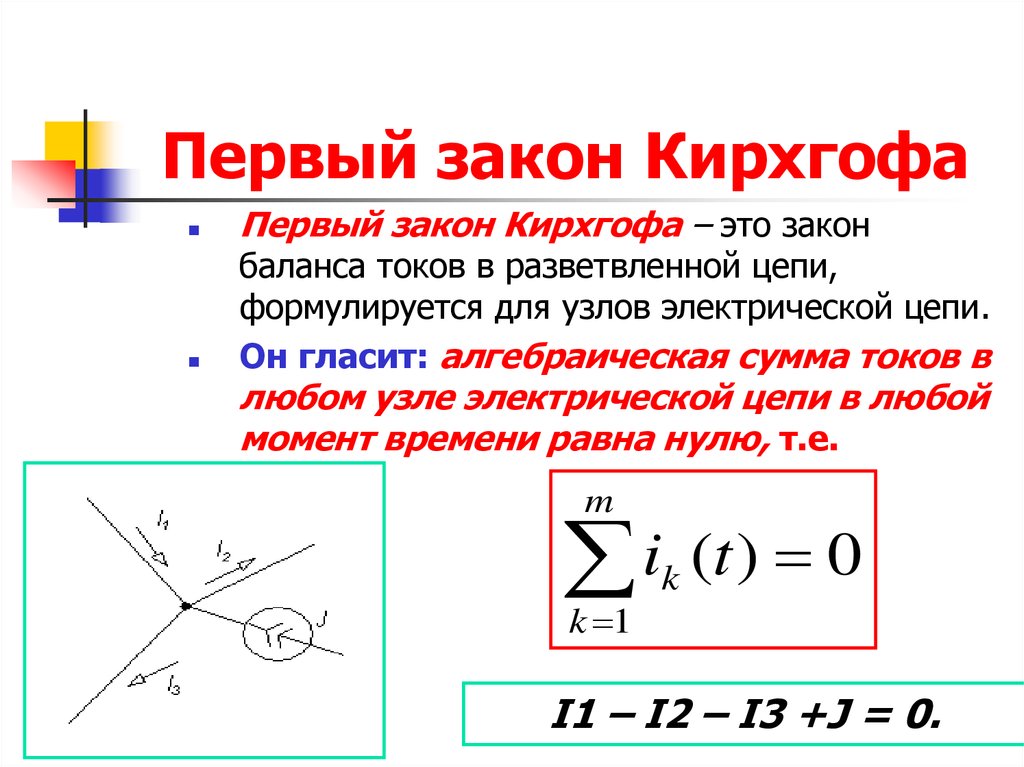
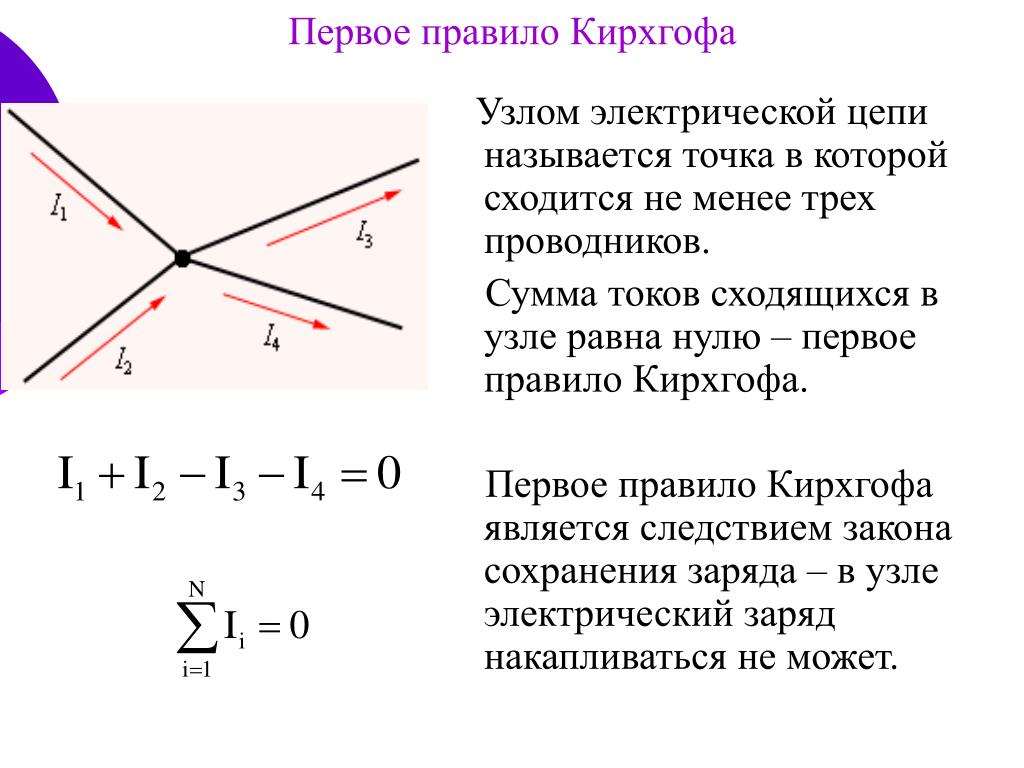
Первый закон Кирхгофа. В каждом узле (точке разветвления проводов) алгебраическая сома сил токов равна нулю:
, (1)
где n – число токов Ii сходящихся в узле.
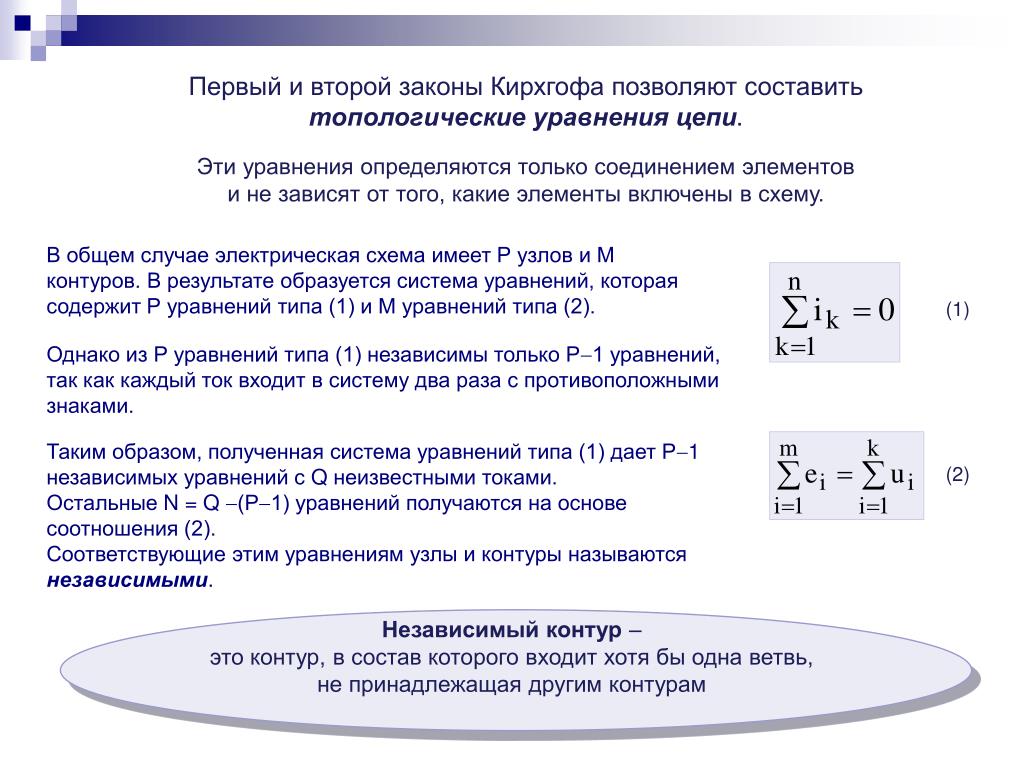
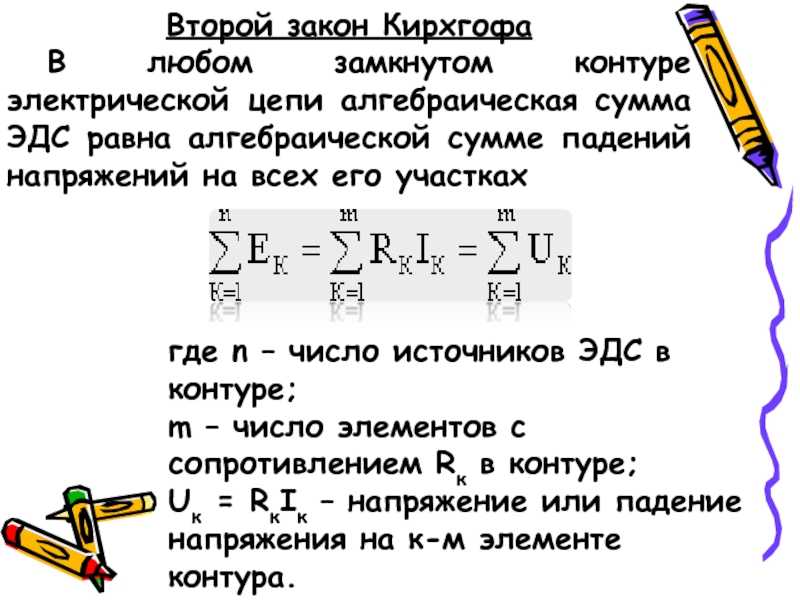
Второй закон Кирхгофа. В любом замкнутом контуре разветвлённой электрической цепи алгебраическая сумма произведений сил токов в отдельных участках этого контура на их сопротивления равна алгебраической сумме электродвижущих сил, действующих в этом контуре:
, (2)
где n – число участков, на которые разбивается узлами данный контур; m – число источников тока, входящих в контур.
Правило знаков при записи законов Кирхгофа.
1. Токам, входящим в узел, приписывать положительный знак, выходящим – отрицательный.
Например, для узла 1 на рис. 1 первый закон Кирхгофа запишется в виде:
.
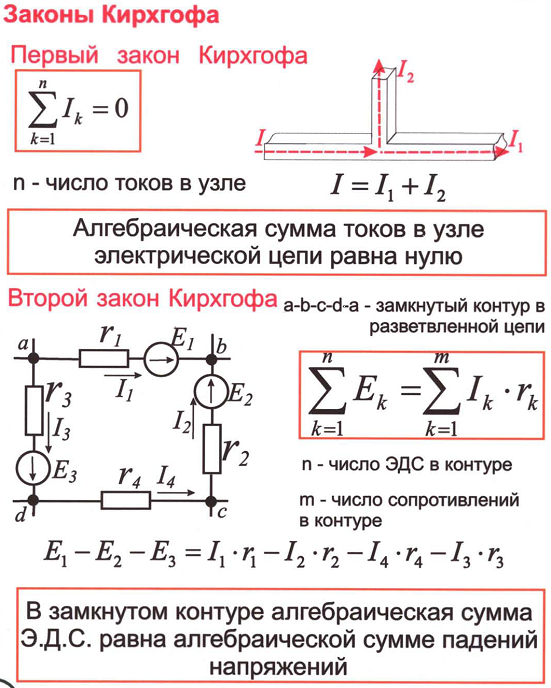
2. При записи второго закона выбирают произвольное направление обхода контура (по или против часовой стрелки). Если направление тока Iкв участке контура совпадает с направлением обхода, то произведение IкRк берётся со знаком плюс, если оно противоположно – со знаком минус. Если по обходу контура источник тока повышает потенциал, то его электродвижущую силу считают положительной, в противном случае её надо считать отрицательной. Например, для контура А14DА на рис. 1 второй закон Кирхгофа запишется следующим образом (обход по часовой стрелке):
.
Здесь сопротивление участка 4DА1 равно сумме сопротивлений R1 и внутреннего сопротивления r1 источника тока ε1.
3.
Если направление токов в
разветвлённой цепи неизвестно, то их расставляют произвольным образом. При
решении уравнений, составленных по указанным выше правилам, ток получается
положительным, если его направление указано правильно, и отрицательным, если
неправильным.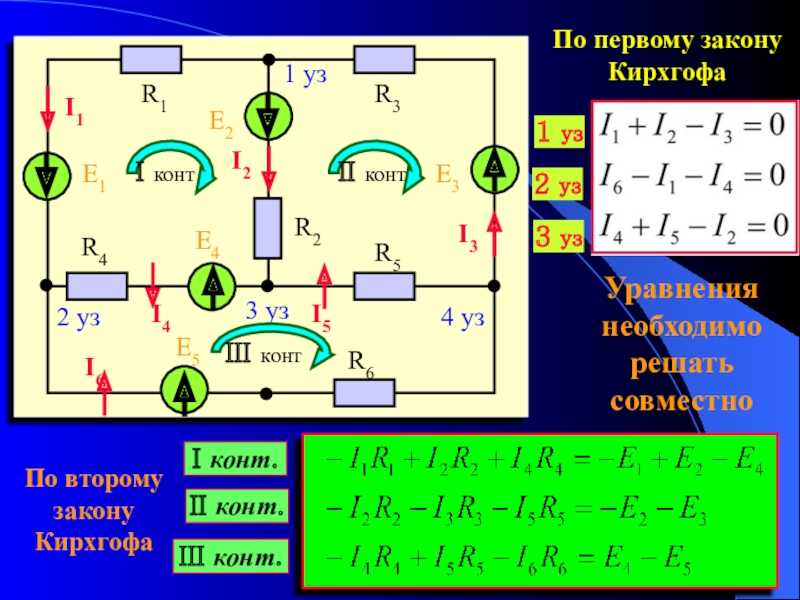
Описание установки
Установка для экспериментальной проверки законов Кирхгофа представляет собой стенд (рис. 2) на вертикальной панели которого смонтирована разветвлённая электрическая цепь. Контакты резисторов, которые выполняют функцию участков электрической цепи, и контакты источников тока выполнены в виде металлических цилиндров, которые находятся на лицевой стороне стенда. Возле схемы располагаются тумблеры включения тока. Отдельно от стенда имеется электронный вольтметр который может выполнять функцию омметра.
Порядок выполнения работы
1. Поставить все тумблеры в положение «выкл».
2. Переключить вольтметр в режим измерения сопротивления, нажав на кнопку «кΩ». Результат измерения на табло будет выводится в килоомах.
3.
Измерить сопротивления всех участков
цепи (R1÷R10), присоединяя
контакты вольтметра последовательно к каждому участку цепи так, как показано на
рис. 3. Показания занести в таблицу.
3. Показания занести в таблицу.
4. Переключить вольтметр в режим измерения постоянного напряжения.
5. Измерить падения напряжения на всех участках цепи (U1÷U10), присоединяя контакты вольтметра последовательно к каждому участку цепи так, как показано на рис. 4. Если на экране вольтметра возникает знак «–», то щупы нужно поменять местами. Показания занести в таблицу. На схеме отметить полярность «+» и «–».
6. Оставив вольтметр в положении измерения постоянного напряжения, перевести все ключи в положение «вкл».
7. Измерить значения э.д.с. на всех источниках тока (ε1÷ε5), присоединяя контакты вольтметра последовательно к каждому источнику тока так, как показано на рис. 5. Если на экране вольтметра возникает знак «–», то щупы нужно поменять местами. Показания занести в таблицу. На схеме отметить полярность «+» и «–».
8.
Рассчитать значения сил токов в
каждом участке цепи.
9. Для заданных преподавателем узлов и контуров проверить 1–й и 2–й законы Кирхгофа.
Контрольные вопросы
1. Сформулируйте законы Кирхгофа и правила знаков для них.
2. Какой вывод нужно сделать, если в результате решения системы уравнений ток получается отрицательным?
3. Сколько независимых уравнений можно записать по 1–му и 2–му законам Кирхгофа в общем случае и конкретно для схемы стенда?
4. Из каких законов вытекают законы Кирхгофа?
5. В чём состоит условие равновесия мостика Уинстона?
|
⇐ ПредыдущаяСтр 3 из 16Следующая ⇒ Закон Ома для участка цепи между зажимами a и b (рисунок 1.8) позволяет найти ток участка по разности потенциалов и сопротивлению этого участка: . (1.6) Рисунок 1.8 – Участок цепи Закон Ома для участка цепи между зажимами b и a (рисунок 1.9) позволяет найти ток участка по разности потенциалов и сопротивлению этого участка: . Рисунок 1.9 – Участок цепи Закон Ома для участка цепи содержащего ЭДС между зажимами a и b (рисунок 1.10 и рисунок 1.11). Рисунок 1.10 – Участок цепи, Рисунок 1.11 – Участок цепи содержащий ЭДС содержащий ЭДС Для схем на рисунках 1.10 и 1.11 закон Ома позволяет найти ток участка по разности потенциалов , а также находящимся на этом участке ЭДС и сопротивлению . Закон Ома для участка цепи, содержащего ЭДС (рисунок 1.10): . (1.8) В случае если на участке цепи между зажимами a и b направление ЭДС будет противоположно току (рисунок 1.11): . (1.9) Законы Кирхгофа. Первый закон Кирхгофа: алгебраическая сумма токов в узле электрической цепи равна нулю. . (1.10) Второй закон Кирхгофа: алгебраическая сумма падений напряжений на элементах контура (под контуром здесь понимается замкнутая последовательность ветвей, не содержащих источников тока) равна алгебраической сумме ЭДС, действующих в этом же контуре: или . Алгоритм решения задач с использованием законов Кирхгофа. 1. Определить количество узлов y и ветвей b электрической цепи. 2. Выбрать произвольно положительные направления искомых токов ветвей и обозначить их на схеме. 3. Определить количество уравнений по первому закону Кирхгофа, которое равно количеству узлов без единицы (y – 1). Записать для произвольно выбранных узлов требуемое количество уравнения по законам Кирхгофа. В алгебраической сумме следует учесть и токи источников тока. 4. Определить количество уравнений по второму закону Кирхгофа. Их число равно количеству ветвей без источников тока (b – bит) за вычетом уравнений, составленных по первому закону Кирхгофа, т.е. (b – bит) – (у – 1), где bит – число ветвей с источниками тока. Записать уравнения по 2-му закону Кирхгофа для независимых контуров. Независимые контуры образуются замкнутыми последовательностями ветвей, не содержащих источников тока, так, чтобы в новом контуре была хоть одна ветвь, не входящая в предыдущие. 5. Объединить уравнения, составленные по первому и второму законам Кирхгофа, в систему уравнений. 6. Решить систему уравнений. Пример использования алгоритма решения задач с использованием законов Кирхгофа для электрической цепи, представленной на рисунке 1.12. Рисунок 1.12 – Схема электрической цепи Решение. 1. Определим количество узлов y и ветвей b электрической цепи. Так, в рассматриваемой цепи имеется три узла, обозначенных цифрами 1, 2 и 3 всего y = 3. Ветви находятся между узлами и в представленной цепи их пять b = 5. 2. Выберем произвольно положительные направления искомых токов , , , ветвей и обозначим их на схеме. 3. Определим количество уравнений по первому закону Кирхгофа, равное количеству узлов без единицы: 3 – 1 = 2. Запишем для произвольно выбранных узлов требуемое количество уравнений по первому закону Кирхгофа. 1 узел: 2 узел: 4. Определим количество уравнений по второму закону Кирхгофа, равное числу ветвей без источников тока (5 – 1) минус два уравнения, составленные по первому закону Кирхгофа, т.е. (5 – 1) – 2 = 2. Запишем уравнения по 2-му закону Кирхгофа для независимых контуров. Независимые контуры образуются замкнутыми последовательностями ветвей, не содержащих источников тока. Уравнения по второму закону Кирхгофа для рассматриваемой электрической цепи. I контур: , II контур: . 5. Объединим уравнения, составленные по первому и второму законам Кирхгофа в систему уравнений. (1.12) 6. Решить полученную систему уравнений можно, если в ней четыре неизвестные. Чаще всего в задачах требуется определить токи (т.е. для данной схемы , , , ), тогда все остальные элементы должны быть известными. Возможны и другие варианты. После решения системы (1.12) необходимо проверить баланс мощностей электрической цепи. Баланс мощностей в электрической цепи. Общая мощность источников электрической энергии для электрической цепи (рисунок 1.12) определяется следующим образом: . (1.13) Знак «минус» в выражении (1.13) у мощности источника ЭДС , ставится потому, что направление тока противоположно направлению ЭДС . Если направление источника ЭДС и тока через него не совпадает, то данный источник ЭДС потребляет электрическую энергию, а не производит ее. Мощность источника тока , т.к. у источника тока потенциал больше, чем . Как определять потенциалы электрической цепи (напряжение на участке цепи), будет рассмотрено ниже в примере построения потенциальной диаграммы. Общая мощность потребителей электрической энергии для электрической цепи (рисунок 1.12) определяется следующим образом: . (1.14) В результате расчетов общая мощность источников электрической энергии должна оказаться равна общей мощности потребителей электрической энергии для рассматриваемой электрической цепи . Пример. Построение потенциальной диаграммы для внешнего контура электрической цепи, представленной на рисунке 1.12. Внешний контур состоит из элементов , , , , , . Перечень элементов производился от наибольшего по номеру узла, в данном случае это узел 3, по часовой стрелке. Из рисунка видно, что при выборе контура в его состав не включены ветви с источником тока, т.к. его сопротивление равно бесконечности, и определить падение напряжения на нем по закону Ома не удастся. Обозначим на электрической схеме точки при переходе от одного элемента к другому. Так, между элементами и получим точку а, между и – точку b, между и обозначим точку с. Используя закон Ома, определим потенциалы всех указанных во внешнем контуре точек. Для этого условно заземлим потенциал точки 3, тогда станет равен нулю. При этом токораспределение в цепи не изменится, т.к. никаких новых ветвей, по которым могли бы протекать токи, не образуется. Тогда потенциалы обозначенных в схеме точек при известных токах определятся следующим образом: Знак «плюс» в формуле ставится потому, что ЭДС повышает потенциал при переходе от потенциала к . Знак «минус» в формуле ставится потому, что ток течет от большего потенциала к меньшему . Чтобы определить меньший потенциал необходимо от большего вычесть падение напряжения на резисторе . Знак «минус» в формуле ставится потому, что ЭДС понижает потенциал при переходе от потенциала к . Знак «плюс» в формуле ставится потому, что ток течет от большего потенциала к меньшему . Чтобы отыскать больший потенциал необходимо к нему прибавить падение напряжения на резисторе . Аналогичным образом ставятся знаки в других уравнениях потенциалов электрической цепи. Представленные формулы для определения потенциалов электрической цепи вытекают из закона Ома. На основании полученных значений потенциалов точек строится потенциальная диаграмма (рисунок 1. Рисунок 1.13 – Потенциальная диаграмма Выводы по лекции К основным элементам топологии электрической цепи относят: ветвь, узел, контур, источник тока, источник ЭДС, электрическое сопротивление. Для определения тока на участке цепи применяют закон Ома. Для расчета токов в ветвях электрической схемы применяют 1 и 2 законы Кирхгофа. Для проверки правильности решения составляют баланс мощностей и строят потенциальную диаграмму. Вопросы для самопроверки 1. Сформулируйте понятия «электрическая цепь», «электрическая схема», «узел», «ветвь», «источник ЭДС» и «источник тока». 2. Что понимают под ВАХ? Нарисуйте ВАХ реального источника, источника ЭДС, источника тока, линейного резистора. 3. Как выбирают положительные направления для токов ветвей и как связаны с ними положительные направления напряжений на сопротивлениях? 4. 6. Сформулируйте закон Ома для участка цепи с ЭДС, первый и второй законы Кирхгофа. Запишите в буквенном виде, сколько уравнений следует составлять по первому и по второму закону Кирхгофа. 7. Чем следует руководствоваться при выборе контуров, для которых следует составлять уравнения по второму закону Кирхгофа. Почему ни в один из этих контуров не должен входить источник тока? 8. Поясните этапы построения потенциальной диаграммы. ⇐ Предыдущая12345678910Следующая ⇒ |
правил Кирхгофа | Физика |
Цели обучения
К концу этого раздела вы сможете:
- Анализировать сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных членов.

Многие сложные схемы, такие как схема на рис. 1, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в книге «Последовательно и параллельно соединенные резисторы и электродвижущая сила: напряжение на клеммах». Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Правила известны как Правила Кирхгофа , в честь их изобретателя Густава Кирхгофа (1824–1887).
Рис. 1. Эту схему нельзя свести к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, эдс.)
Правила Кирхгофа- Первое правило Кирхгофа — правило пересечения.
 Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения. - Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, в котором они используются.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения ) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 2. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы I 1 = I 2 + I 3 (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.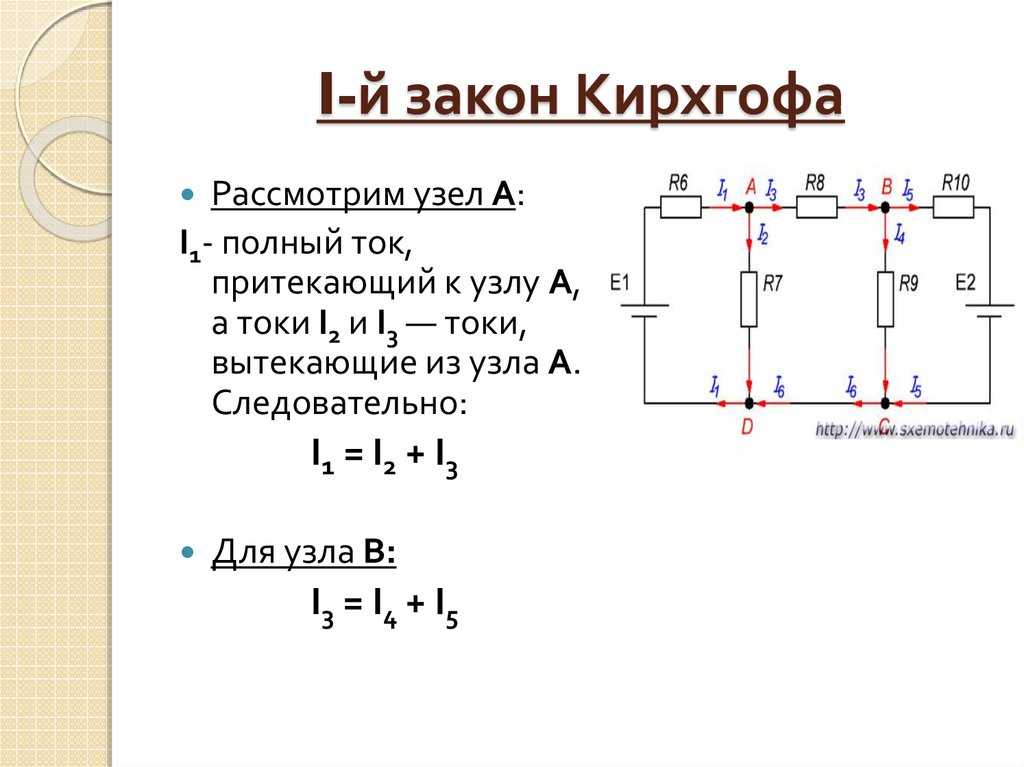
Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.
Рисунок 22. Правило соединения. На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I 1 = I 2 + I 3 . Здесь I 1 должно быть 11 А, так как I 2 равно 7 А, а I 3 равно 4 А.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило цикла ) является применением закона сохранения энергии.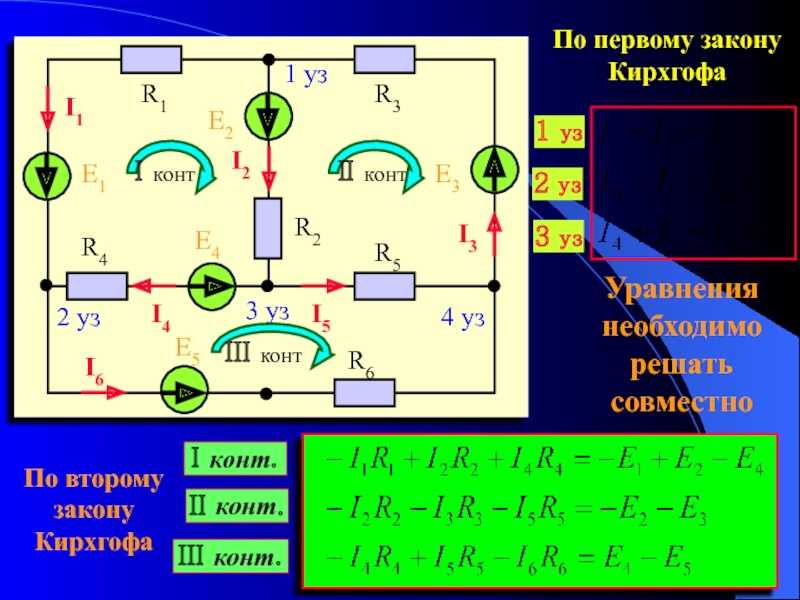 Правило петли сформулировано с точки зрения потенциала, В , а не потенциальной энергии, но они связаны, поскольку PE elec = qV . Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке 3 показаны изменения потенциала в простой последовательной цепи. Второе правило Кирхгофа требует ЭДС − IR — IR 1 — IR 2 = 0. перестроенный, это EMF = IR + IR 1 + IR 2 = 0, что означает EMF EMF MANGE EMF EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MAGIN равно сумме IR (напряжения) падений в контуре.
Правило петли сформулировано с точки зрения потенциала, В , а не потенциальной энергии, но они связаны, поскольку PE elec = qV . Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рисунке 3 показаны изменения потенциала в простой последовательной цепи. Второе правило Кирхгофа требует ЭДС − IR — IR 1 — IR 2 = 0. перестроенный, это EMF = IR + IR 1 + IR 2 = 0, что означает EMF EMF MANGE EMF EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MANGE EMF MAGIN равно сумме IR (напряжения) падений в контуре.
Рис. 3. Правило цикла. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
(a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
- Применяя первое правило Кирхгофа, правило соединения, вы должны пометить ток в каждой ветви и решить, в каком направлении он течет.
 Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I 1 , I 2 , I 3 и I , а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I 1 , I 2 , I 3 и I , а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным. - Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рисунке 3 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; Обход цепи в противоположном направлении меняет знак каждого члена в уравнении, что похоже на умножение обеих частей уравнения на -1.
Рисунок 4 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 4.)
При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 4.)
Рисунок 4. Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)
- Когда резистор перемещается в том же направлении, что и ток, изменение потенциала составляет −IR . (См. рис. 4.)
- Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет + IR . (См. рис. 4.)
- Когда ЭДС перемещается от – к + (в том же направлении, что и положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 4.)
- Когда ЭДС перемещается от + к — (противоположно направлению, в котором движется положительный заряд), изменение потенциала равно — ЭДС. (См. рис. 4.)
Пример 1. Расчет тока: использование правил Кирхгофа
Найдите токи, протекающие в цепи на рисунке 5.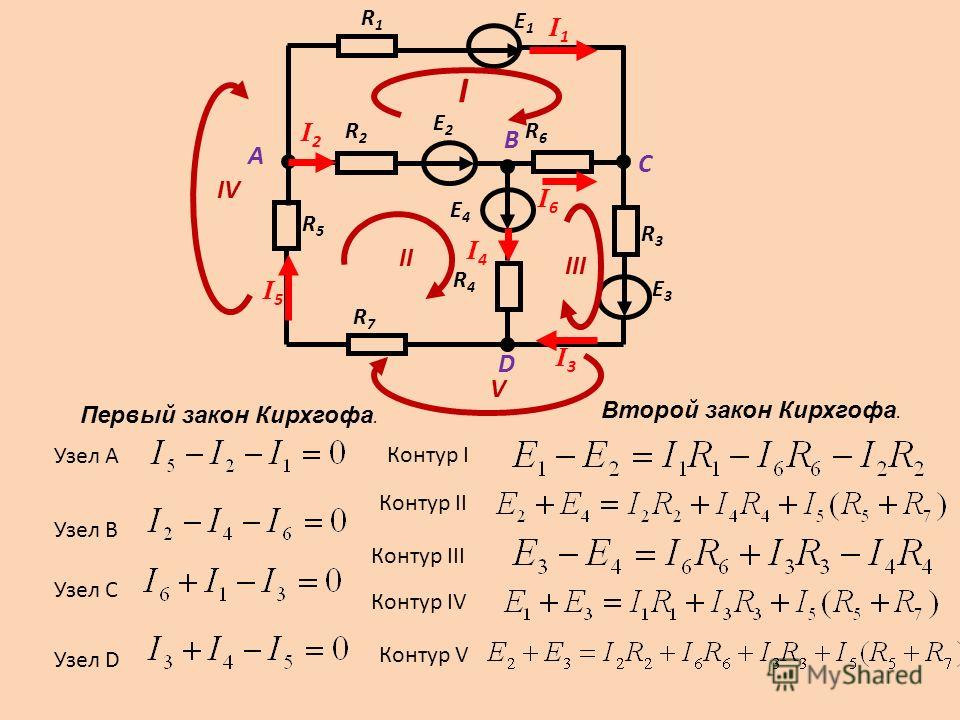
Рисунок 5. Эта цепь аналогична схеме на рисунке 1, но заданы сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.
СтратегияЭта схема достаточно сложна, чтобы токи не могли быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. Токи были обозначены на рисунке I 1 , I 2 и I 3 , и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
Это дает
I 1 = I 2 + I 3 ,
так как I 1 впадает в соединение, а I 2 и I 3 вытекают. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла. Теперь рассмотрим петлю abcdea. Переходя от a к b, мы проходим R 2 в том же (предполагаемом) направлении тока I 2 , поэтому изменение потенциала равно − I 2 R 2 . Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала равно +ЭДС 1 . Пересечение внутреннего сопротивления r 1 от c к d дает − I 2 r 1 . Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала на — I 1 R 1 . Правило цикла гласит, что сумма изменений потенциала равна нулю. Thus,
Завершение цикла путем перехода от d к a снова пересекает резистор в том же направлении, что и его ток, что дает изменение потенциала на — I 1 R 1 . Правило цикла гласит, что сумма изменений потенциала равна нулю. Thus,
− I 2 R 2 + emf 1 − I 2 r 1 − I 1 R 1 = − I 2 ( R 2 + r 1 ) + ЭДС 1 − I 1 0011 Ч 1 = 0,
Подстановка сопротивлений и ЭДС значениями из принципиальной схемы и исключение единиц измерения ампер дает
−3 I 2 + 18 − 6 I 1 = 0,
Теперь применяя правило петли к AEFGHA (мы могли бы выбрать Abcdefgha) аналогично дает
+ I 1 R 1 + I 3 R 3 + 3 R 3 + + 11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111 3 3 . 0012 3 r 2 − emf 2 = + I 1 R 1 + I 3 ( R 3 + r 2 ) − ЭДС 2 = 0,
0012 3 r 2 − emf 2 = + I 1 R 1 + I 3 ( R 3 + r 2 ) − ЭДС 2 = 0,
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы проходятся в противоположном направлении. С введенными значениями это становится
+6 I 1 + 2 I 3 – 45 = 0,
Этих трех уравнений достаточно, чтобы решить для трех неизвестных токов. Сначала решим второе уравнение для I 2 :
I 2 = 6 − 2 I 1 .
Теперь решите третье уравнение для I 3 :
I 3 = 22,5 − 3 I 1 .
Подстановка этих двух новых уравнений в первое позволяет найти значение для I 1 :
I 1 = I 2 + I 3 = (6–2 I 1 ) (2 2 I 1 ) + (2 2 112 1 ) + (2111112 1 ) + (2 I 1 ). 1 ) = 28,5 − 5 I 1 .
1 ) = 28,5 − 5 I 1 .
Объединение членов дает
6 I 1 = 28,5 и
I 1 = 4,75 А.
Подстановка этого значения для I 1 обратно в четвертое уравнение дает 9А Знак минус означает, что I 2 течет в направлении, противоположном принятому на рис. 5. Наконец, подстановка значения I 1 в пятое уравнение дает 3 I 1 = 22,5 − 14 . 25
I 3 = 8,25 А.
ОбсуждениеПросто для проверки отметим, что действительно I 1 = I 2 + I 3 . Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Стратегии решения задач по правилам Кирхгофа- Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи.
 Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет. - Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
- Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 4.9.0008
- Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.

- Проверить разумность и последовательность ответов. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Материал в этом разделе верен в теории. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Проверьте свое понимание
Можно ли применять правила Кирхгофа к простым последовательным и параллельным схемам, или они ограничены для использования в более сложных схемах, не являющихся комбинацией последовательных и параллельных?
Решение Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Резюме раздела
- Правила Кирхгофа можно использовать для анализа любой схемы, простой или сложной.
- Первое правило Кирхгофа — правило соединения: сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли: алгебраическая сумма изменений потенциала вокруг любого замкнутого контура (петли) должна быть равна нулю.
- Два правила основаны соответственно на законах сохранения заряда и энергии.

- При расчете потенциала и тока по правилам Кирхгофа необходимо соблюдать ряд правил для определения правильных знаков различных членов.
- Простые ряды и параллельные правила являются частными случаями правил Кирхгофа.
Концептуальные вопросы
1. Могут ли все токи, входящие в соединение на рисунке 6, быть положительными? Объяснять.
Рисунок 6.
2. Примените правило соединения к соединению b на рис. 7. Получится ли какая-либо новая информация при применении правила соединения в точке e? (На рисунке каждая ЭДС представлена буквой Е.)
Рисунок 7.
3. (a) Какова разность потенциалов при переходе из точки a в точку b на рис. 7? б) Чему равна разность потенциалов при переходе от c к b? в) От е до g? (г) От е до d?
4. Примените правило цикла к циклу afedcba на рис. 7.
7.
5. Примените правило цикла к циклам abgefa и cbgedc на рисунке 7.
Задачи и упражнения
1. Примените правило цикла к циклу abcdefgha, показанному на рис. 5 (снова показано ниже).
Рис. 5. Эта схема аналогична схеме на рис. 1, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.
2. Примените петлевое правило к петле aedcba на рисунке 5.
3. Проверьте второе уравнение в Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), путем подстановки найденных значений токов I 1 и I 2 .
4. Проверьте третье уравнение в Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), подставив найденные значения токов I 1 и I 3 .
5. Примените правило соединения в точке a на рисунке 8.
Рисунок 8.
6. Примените правило цикла к кольцу abcdefghija на рисунке 8.
7. Примените правило цикла к кольцу akledcba на рисунке 8.
8. Найдите токи, протекающие в цепи на рисунке 8. В явном виде покажите, как вы выполняете шаги, описанные в Стратегии решения проблем для последовательных и параллельных резисторов выше.
9. Решите Пример 1 Расчет тока: с использованием правил Кирхгофа (в тексте выше), но используйте цикл abcdefgha вместо цикла akledcba. Явно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов .
10. Найдите токи, протекающие в цепи на рисунке 7 (показанном ниже).
Рисунок 7.
11. Необоснованные результаты Рассмотрим схему на рисунке 9 и предположим, что ЭДС неизвестны, а токи заданы равными I 1 = 5,00 А, I 2 = 3,0 А и I 3 = –2,00 А. а) Не могли бы вы найти ЭДС? б) Что неверно в предположениях?
а) Не могли бы вы найти ЭДС? б) Что неверно в предположениях?
Рисунок 9.
Глоссарий
- Правила Кирхгофа:
- набор из двух правил, основанных на сохранении заряда и энергии, управляющих током и изменениями потенциала в электрической цепи сохранение заряда в переходе; ток — это поток заряда; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу; можно сформулировать правило
I1=I2+I3{I}_{1}={I}_{2}+{I}_{3}I1=I2+I3
- правило цикла:
- Второе правило Кирхгофа , в котором говорится, что в замкнутом контуре любая энергия, поставляемая ЭДС, должна быть передана в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. Таким образом, ЭДС равна сумме
IR\text{IR}IR
(напряжения) падений в контуре и может быть сформулирована следующим образом:ЭДС=Ir+IR1+IR2\text{ЭДС}=\text{Ir}+ {\text{IR}}_{1}+{\text{IR}}_{2}\\emf=Ir+IR1+IR2
- законы сохранения:
- требуют сохранения энергии и заряда в системе
Избранные решения задач и упражнения
1.
−I2R2+emf1−I2r1+I3R3+I3r2−emf2=0-{I}_{2}{R}_{2}+{\text{emf}}_{1}-{\text{ I}}_{2}{r}_{1}+{\text{I}}_{3}{R}_{3}+{\text{I}}_{3}{r}_{ 2}-{\text{emf}}_{2}=\text{0}\\−I2R2+emf1−I2r1+I3R3+I3r2−emf2=0
5. I 3 = I 1 + I 2 7.
emf2-I2r2-I2R2+I1R5+I1r1-emf1+I1R1=0{\text{emf}}_{2} -{\text{I}}_{2}{r}_{2}-{\ текст {I}} _ {2} {R} _ {2} + {\ text {I}} _ {1} {R} _ {5} + {I} _ {1} {r} _ {1} -{\text{emf}}_{1}+{\text{I}}_{1}{R}_{1}=0\\emf2−I2r2−I2R2+I1 R5+I1r1−ЭДС1+I1R1=0
9.(a) I 1 = 4,75 A (b) I 2 = −3,5 A (c) I 3 = 8,25 A
11. (a) Нет, вам придется решать противоречивые уравнения. (б) I 1 ≠ I 2 + I 3 . Предполагаемые токи нарушают правило соединения.
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics.
 Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии
Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии
21.3 Правила Кирхгофа — Колледж Физика 2e
Цели обучения
К концу этого раздела вы сможете:
- Проанализируйте сложную схему, используя правила Кирхгофа, используя соглашения для определения правильных знаков различных термов.
Многие сложные цепи, такие как показанная на рис. 21.21, не могут быть проанализированы с помощью последовательно-параллельных методов, разработанных в разделе Резисторы, включенные последовательно и параллельно, и Электродвижущая сила: напряжение на клеммах. Однако есть два правила анализа цепей, которые можно использовать для анализа любой схемы, простой или сложной. Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Эти правила являются частными случаями законов сохранения заряда и сохранения энергии. Эти правила известны как правила Кирхгофа в честь их изобретателя Густава Кирхгофа (1824–1887).
Рисунок 21.21 Эта схема не может быть сведена к комбинации последовательного и параллельного соединений. Для его анализа можно использовать правила Кирхгофа, специальные приложения законов сохранения заряда и энергии. (Примечание: буква E на рисунке обозначает электродвижущую силу, ЭДС.)
Правила Кирхгофа
- Первое правило Кирхгофа — правило соединения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
- Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Теперь будут даны объяснения двух правил, за которыми следуют советы по решению проблем для применения правил Кирхгофа и рабочий пример, который их использует.
Первое правило Кирхгофа
Первое правило Кирхгофа (правило соединения) представляет собой применение закона сохранения заряда к соединению; это показано на рис. 21.22. Ток — это поток заряда, а заряд сохраняется; таким образом, любой заряд, втекающий в соединение, должен вытекать наружу. Первое правило Кирхгофа требует, чтобы I1=I2+I3I1=I2+I3 (см. рисунок). Подобные уравнения могут и будут использоваться для анализа схем и решения схемных задач.
Установление связей: законы сохранения
Правила Кирхгофа для анализа цепей представляют собой применение законов сохранения к цепям. Первое правило — применение закона сохранения заряда, а второе правило — применение закона сохранения энергии. Законы сохранения, даже используемые в конкретных приложениях, таких как анализ цепей, настолько просты, что составляют основу этого приложения.
Рисунок
21.22
Правило соединения. На диаграмме показан пример первого правила Кирхгофа, где сумма токов, поступающих в соединение, равна сумме токов, выходящих из соединения. В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I1=I2+I3I1=I2+I3. Здесь I1I1 должен быть 11 А, так как I2I2 равен 7 А, а I3I3 равен 4 А.
В этом случае ток, входящий в переход, разделяется и выходит в виде двух токов, так что I1=I2+I3I1=I2+I3. Здесь I1I1 должен быть 11 А, так как I2I2 равен 7 А, а I3I3 равен 4 А.
Второе правило Кирхгофа
Второе правило Кирхгофа (правило цикла) является приложением закона сохранения энергии. Правило цикла сформулировано в терминах потенциала VV, а не потенциальной энергии, но они связаны, поскольку PEelec=qVPEelec=qV. Напомним, что ЭДС — это разность потенциалов источника при отсутствии тока. В замкнутом контуре любая энергия, поставляемая ЭДС, должна быть переведена в другие формы устройствами в контуре, поскольку нет других способов передачи энергии в контур или из него. На рис. 21.23 показаны изменения потенциала в простой последовательной цепи.
Второе правило Кирхгофа требует, чтобы ЭДС-Ir-IR1-IR2=0ЭДС-Ir-IR1-IR2=0. Если переставить, это будет ЭДС=Ir+IR1+IR2ЭДС=Ir+IR1+IR2, что означает, что ЭДС равна сумме падений IRIR (напряжения) в контуре.
Рисунок 21.23 Правило петли. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю. (a) На этой стандартной схеме простой последовательной цепи ЭДС подает напряжение 18 В, которое сводится к нулю сопротивлениями, с 1 В на внутреннем сопротивлении и 12 В и 5 В на двух сопротивлениях нагрузки, для всего 18 В. (b) Этот вид в перспективе представляет потенциал как что-то вроде американских горок, где потенциал повышается за счет ЭДС и снижается за счет сопротивления. (Обратите внимание, что буква E означает ЭДС.)
Применение правил Кирхгофа
Применяя правила Кирхгофа, мы получаем уравнения, позволяющие находить неизвестные в цепях. Неизвестными могут быть токи, ЭДС или сопротивления. Каждый раз, когда применяется правило, создается уравнение. Если независимых уравнений столько же, сколько неизвестных, то задача решаема. При применении правил Кирхгофа вы должны принять два решения. Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
Эти решения определяют знаки различных величин в уравнениях, которые вы получаете, применяя правила.
- Применяя первое правило Кирхгофа, правило соединения, вы должны обозначить ток в каждой ветви и решить, в каком направлении он течет. Например, на рис. 21.21, рис. 21.22 и рис. 21.23 токи обозначены I1I1, I2I2, I3I3 и II, а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
- Применяя второе правило Кирхгофа, правило петли, вы должны определить замкнутую петлю и решить, в каком направлении ее обойти, по часовой или против часовой стрелки. Например, на рис. 21.23 петля была пройдена в том же направлении, что и ток (по часовой стрелке). Опять же, нет никакого риска; обход цепи в противоположном направлении меняет знак каждого члена уравнения на противоположное, что похоже на умножение обеих частей уравнения на –1,–1.
Рисунок 21. 24 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 21.5.)
24 и следующие пункты помогут вам правильно расставить знаки плюс или минус при применении правила цикла. Обратите внимание, что резисторы и ЭДС пересекаются при переходе от a к b. Во многих схемах будет необходимо построить более одного контура. При обходе каждой петли необходимо следить за знаком изменения потенциала. (См. пример 21.5.)
Рисунок 21.24 Каждый из этих резисторов и источников напряжения проходит от a до b. Возможные изменения показаны под каждым элементом и пояснены в тексте. (Обратите внимание, что буква E означает ЭДС.)
- Когда резистор перемещается в том же направлении, что и ток, изменение потенциала равно −IR−IR. (См. рис. 21.24.)
- Когда резистор перемещается в направлении, противоположном току, изменение потенциала составляет +IR+IR. (См. рис. 21.24.)
- Когда ЭДС перемещается от –– к + (в том же направлении, в котором движется положительный заряд), изменение потенциала составляет +ЭДС. (См. рис. 21.24.
 )
) - Когда ЭДС перемещается от + к –– (противоположно направлению движения положительного заряда), изменение потенциала составляет −−ЭДС. (См. рис. 21.24.)
Пример 21,5
Расчет тока: использование правил Кирхгофа
Найдите токи, протекающие в цепи на рис. 21.25.
Рисунок 21.25 Эта схема аналогична схеме на рис. 21.21, но указаны сопротивления и ЭДС. (Каждая ЭДС обозначена буквой E.) Токи в каждой ветви помечены и предполагается, что они движутся в показанных направлениях. В этом примере для нахождения токов используются правила Кирхгофа.
Стратегия
Эта цепь настолько сложна, что токи не могут быть найдены с помощью закона Ома и последовательно-параллельных методов — необходимо использовать правила Кирхгофа. На рисунке токи обозначены I1I1, I2I2 и I3I3, и были сделаны предположения об их направлениях. Места на схеме обозначены буквами от a до h. В решении мы будем применять правила соединения и петли, ища три независимых уравнения, которые позволят нам найти три неизвестных тока.
Решение
Начнем с применения первого правила Кирхгофа или правила соединения в точке а. Это дает
I1=I2+I3,I1=I2+I3,
21,54
, так как I1I1 впадает в соединение, а I2I2 и I3I3 вытекают. Применение правила соединения в точке e дает точно такое же уравнение, так что никакой новой информации не получается. Это одно уравнение с тремя неизвестными — нужны три независимых уравнения, поэтому необходимо применить правило цикла.
Теперь рассмотрим цикл abcdea. Переходя от a к b, мы пересекаем R2R2 в том же (предполагаемом) направлении, что и ток I2I2, поэтому изменение потенциала равно −I2R2−I2R2. Затем, переходя от b к c, мы переходим от – к +, так что изменение потенциала равно +ЭДС1+ЭДС1. Перемещение внутреннего сопротивления r1r1 от c к d дает −I2r1−I2r1. Завершение цикла путем перехода от d к a снова проходит через резистор в том же направлении, что и его ток, что дает изменение потенциала -I1R1-I1R1.
Правило цикла гласит, что сумма изменений потенциала равна нулю. Таким образом,
-I2R2+emf1-I2r1-I1R1=-I2(R2+r1)+emf1-I1R1=0.-I2R2+emf1-I2r1-I1R1=-I2(R2+r1)+emf1-I1R1=0.
21,55
Подстановка значений сопротивления и ЭДС из принципиальной схемы и отмена единицы ампер дает
−3I2+18−6I1=0,−3I2+18−6I1=0.
21,56
Теперь применение правила цикла к aefgha (мы могли бы выбрать и abcdefgha) аналогичным образом дает
+I1R1+I3R3+I3r2-ЭДС2= +I1R1+I3R3+r2-ЭДС2=0.+I1R1+I3R3+I3r2-ЭДС2= +I1R1+I3R3+r2-ЭДС2=0.
21,57
Обратите внимание, что знаки меняются местами по сравнению с другим циклом, потому что элементы перемещаются в противоположном направлении. С введенными значениями это становится
+6I1+2I3-45=0.+6I1+2I3-45=0.
21,58
Этих трех уравнений достаточно для решения трех неизвестных токов. Сначала решим второе уравнение для I2I2:
Сначала решим второе уравнение для I2I2:
I2=6−2I1.I2=6−2I1.
21,59
Теперь решите третье уравнение для I3I3:
I3=22,5−3I1.I3=22,5−3I1.
21,60
Подстановка этих двух новых уравнений в первое позволяет найти значение для I1I1:
I1=I2+I3=(6−2I1)+(22,5−3I1)=28,5−5I1.I1=I2 +I3=(6−2I1)+(22,5−3I1)=28,5−5I1.
21,61
Комбинируемые термины приведены
6i1 = 28,5, и 6i1 = 28,5 и
21,62
I1 = 4,75 A.I1 = 4,75 A.
21,63
I2=6-2I1=6-9,50I2=6-2I1=6-9,50
21,64
I2=-3,50 A.I2=-3,50 A.
21,65
направлении, противоположном предполагаемому на рис. 21.25.
Наконец, подстановка значения I1I1 в пятое уравнение дает
21.67
Обсуждение
Просто для проверки отметим, что действительно I1=I2+I3I1=I2+I3. Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Результаты также можно проверить, введя все значения в уравнение для цикла abcdefgha.
Стратегии решения проблем для правил Кирхгофа
- Убедитесь, что имеется четкая принципиальная схема, на которой вы можете отметить все известные и неизвестные сопротивления, ЭДС и токи. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
- Примените правило соединения к любому соединению в цепи. Каждый раз, когда применяется правило соединения, вы должны получать уравнение с током, которого не было в предыдущем приложении — если нет, то уравнение избыточно.
- Примените правило цикла к такому количеству циклов, которое необходимо для поиска неизвестных в задаче. (Независимых уравнений должно быть столько же, сколько и неизвестных.
 ) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 21.24.
) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 21.24. - Решите уравнения для неизвестных. Это может включать в себя множество алгебраических шагов, требующих тщательной проверки и перепроверки.
- Проверить разумность и последовательность ответов. Числа должны быть правильного порядка, ни чрезмерно большими, ни исчезающе малыми. Признаки должны быть разумными — например, отсутствие сопротивления не должно быть отрицательным. Убедитесь, что полученные значения удовлетворяют различным уравнениям, полученным в результате применения правил. Например, токи должны удовлетворять правилу соединения.
Теоретически материал в этом разделе верен. Мы должны быть в состоянии проверить это, произведя измерения тока и напряжения. На самом деле, некоторые из устройств, используемых для проведения таких измерений, представляют собой прямое применение принципов, рассмотренных до сих пор, и рассматриваются в следующих модулях. Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Как мы увидим, отсюда вытекает очень простой, даже глубокий факт: проведение измерения изменяет измеряемую величину.
Проверьте свое понимание
Можно ли применять правила Кирхгофа к простым последовательным и параллельным цепям, или они ограничены для использования в более сложных цепях, которые не являются комбинацией последовательных и параллельных?
Решение
Правила Кирхгофа можно применить к любой схеме, поскольку они являются приложениями к схемам двух законов сохранения. Законы сохранения являются наиболее широко применимыми принципами в физике. Обычно математически проще использовать правила для последовательной и параллельной схемы в более простых схемах, поэтому мы подчеркиваем правила Кирхгофа для использования в более сложных ситуациях. Но правила последовательностей и параллелей можно вывести из правил Кирхгофа. Кроме того, правила Кирхгофа могут быть распространены на устройства, отличные от резисторов и ЭДС, такие как конденсаторы, и являются одним из основных устройств анализа в анализе цепей.
Что такое 2-й закон Кирхгофа? – Книга Vea
от jai
Содержание
Что такое 2-й закон Кирхгофа?
Закон напряжения Кирхгофа (2-й закон) гласит, что в любой замкнутой петле внутри цепи сумма всех напряжений на компонентах, поставляющих электроэнергию (таких как ячейки или генераторы), должна равняться сумме всех напряжений на других компонентах в цепи. такая же петля.
Что такое формула второго закона Кирхгофа?
Второе правило Кирхгофа требует ЭДС u2212 Ir u2212 IR1 u2212 IR2 0. Если переставить, это будет ЭДС Ir + IR 1 + IR2 0, что означает, что ЭДС равна сумме падений IR (напряжения) в контуре. Пример второго правила Кирхгофа, согласно которому сумма изменений потенциала вокруг замкнутого контура должна быть равна нулю.
Что такое Кирхгоф 2-й класс закона 12?
Петлевой закон также известен как второй закон Кирхгофа. В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
Как по-другому называется второй закон Кирхгофа?
Состояние Второй закон Кирхгофа Второй закон Кирхгофа также известен как закон напряжения Кирхгофа (KVL). Согласно КВЛ, сумма разностей потенциалов на замкнутом контуре должна быть равна нулю.
Что такое второй закон Кирхгофа?
Второй закон Кирхгофа, также известный как закон напряжения Кирхгофа (KVL) , гласит, что сумма всех напряжений вокруг замкнутого контура в любой цепи должна быть равна нулю. Это снова является следствием сохранения заряда, а также сохранения энергии.
Что такое 3-й закон Кирхгофа?
Петлевой закон также известен как второй закон Кирхгофа. В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
Что такое уравнение закона Кирхгофа?
Петлевой закон также известен как второй закон Кирхгофа. В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
Что такое 12 класс второго закона Кирхгофа?
Петлевой закон также известен как второй закон Кирхгофа. В нем говорится, что в замкнутом контуре алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
Что такое 2-й закон Кирхгофа?
Закон напряжения Кирхгофа (2-й закон) гласит, что в любой замкнутой петле внутри цепи сумма всех напряжений на компонентах, поставляющих электроэнергию (таких как ячейки или генераторы), должна равняться сумме всех напряжений на других компонентах в цепи. такая же петля.
Что такое 12-й класс закона Кирхгофа?
Класс 12 Физика Ток Электричество. Кирхгоф Первый закон. Первый закон Кирхгофа: Закон пересечения. Закон соединения также известен как первый закон Кирхгофа. В нем указано, что на стыке сумма токов, входящих в стык, равна сумме токов, выходящих из стыка.
В нем указано, что на стыке сумма токов, входящих в стык, равна сумме токов, выходящих из стыка.
Что такое краткий закон Кирхгофа?
Определение закона Кирхгофа 1 : утверждение в физике: в электрической сети алгебраическая сумма токов во всех ветвях, которые встречаются в любой точке это ноль.
Как иначе называется закон Кирхгофа?
Текущий закон Кирхгофа имеет несколько названий: Первый закон Кирхгофа и Правило соединения Кирхгофа. Согласно правилу соединения, в цепи сумма токов в соединении равна сумме токов вне соединения.
Что такое 2-я Кирхгофа?
Второй закон Кирхгофа применяет к падению напряжения на компонентах цепи. В нем говорится, что вокруг любого замкнутого контура в цепи направленная сумма разностей потенциалов между компонентами равна нулю.
Что такое первый и второй закон Кирхгофа?
первое правило Кирхгофа правило пересечения. Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения. Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Второе правило Кирхгофа — правило петли. Алгебраическая сумма изменений потенциала вокруг любой замкнутой цепи (петли) должна быть равна нулю.
Как иначе называются KCL и KVL?
Законы Кирхгофа обычно называют KCL (закон тока Кирхгофа) и KVL (закон напряжения Кирхгофа). KVL утверждает, что алгебраическая сумма напряжений в узле замкнутой цепи равна нулю.
В чем разница между первым и вторым законами Кирхгофа?
Петлевой закон также известен как второй закон Кирхгофа. В нем говорится, что в замкнутом контуре, алгебраическая сумма ЭДС равна алгебраической сумме произведений сопротивлений и соответствующих токов, протекающих через них
Что утверждает закон Кирхгофа?
Первый закон Кирхгофа для электрической цепи основан на сохранении заряда, а второй закон Кирхгофа для электрической цепи основан на по сохранению энергии.
Что такое 2-й закон Кирхгофа?
Закон напряжения Кирхгофа (2-й закон) гласит, что в любой замкнутой петле внутри цепи сумма всех напряжений на компонентах, поставляющих электроэнергию (таких как ячейки или генераторы), должна равняться сумме всех напряжений на других компонентах в цепи. такая же петля.
такая же петля.
Сколько существует законов Кирхгофа?
два закона
Что вы подразумеваете под законом Кирхгофа?
Определение закона Кирхгофа 1 : утверждение в физике: в электрической сети алгебраическая сумма токов во всех ветвях, которые встречаются в любой точке, равна нулю.
Что такое формула закона Кирхгофа?
Математическое представление закона Кирхгофа: u2211nk1Ik0 u2211 k 1 n I k 0 где Ik — ток k, а n — общее количество проводов, впадающих и выходящих из рассматриваемого соединения. Закон перехода Кирхгофа ограничен в применении к областям, в которых плотность заряда может быть непостоянной.
Что такое закон Кирхгофа в физике?
Закон Кирхгофа о напряжении (2-й закон) гласит , что в любой замкнутой петле внутри цепи сумма всех напряжений на компонентах, поставляющих электроэнергию (таких как ячейки или генераторы), должна равняться сумме всех напряжений на других компонентах в цепи. такая же петля.


 Все правила по сольфеджио
Все правила по сольфеджио








 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)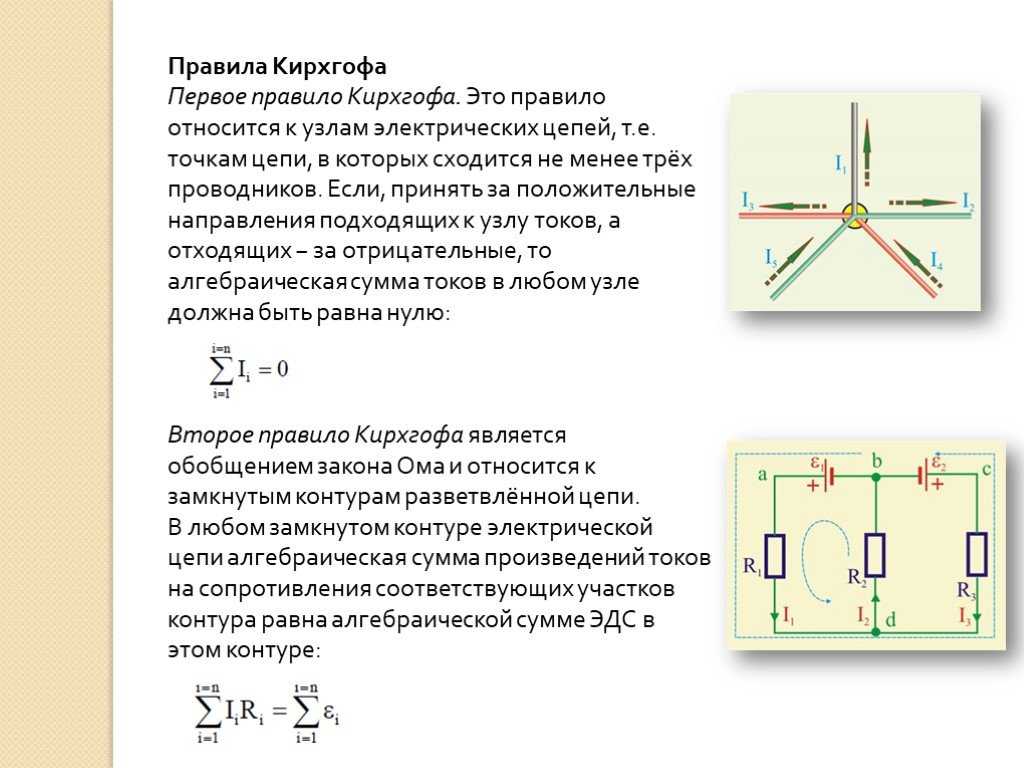 (1.7)
(1.7)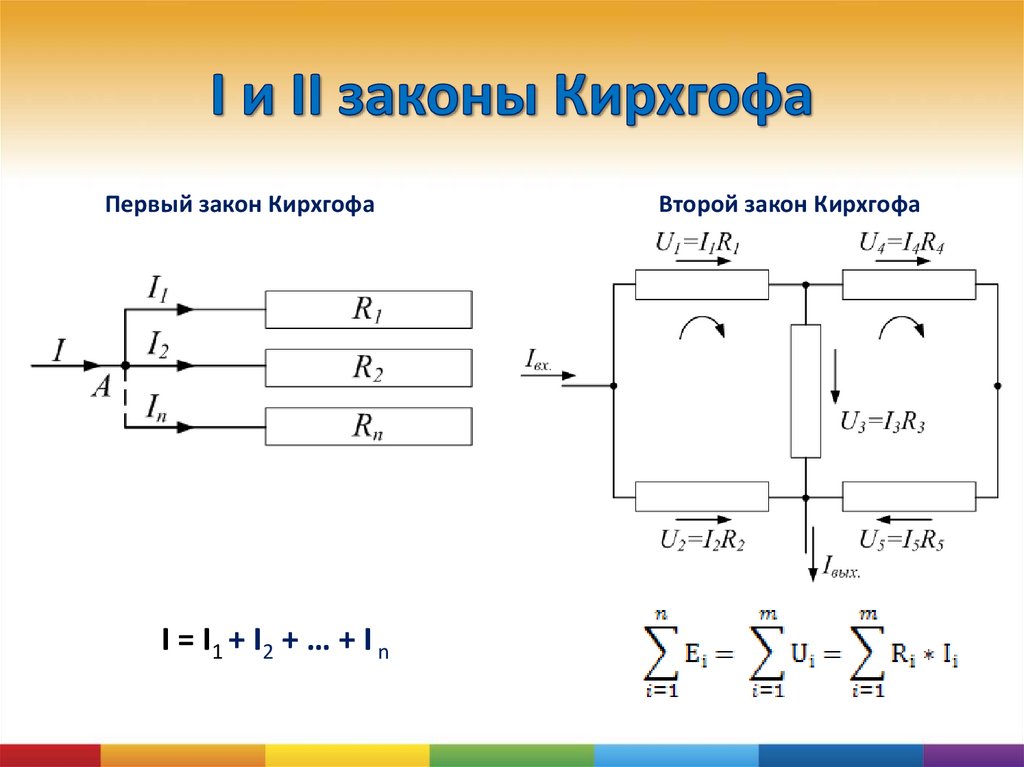 (1.11)
(1.11) (Иногда в некоторых цепях необходимо составлять уравнения, в которые входят уже содержащиеся ветви.)
(Иногда в некоторых цепях необходимо составлять уравнения, в которые входят уже содержащиеся ветви.)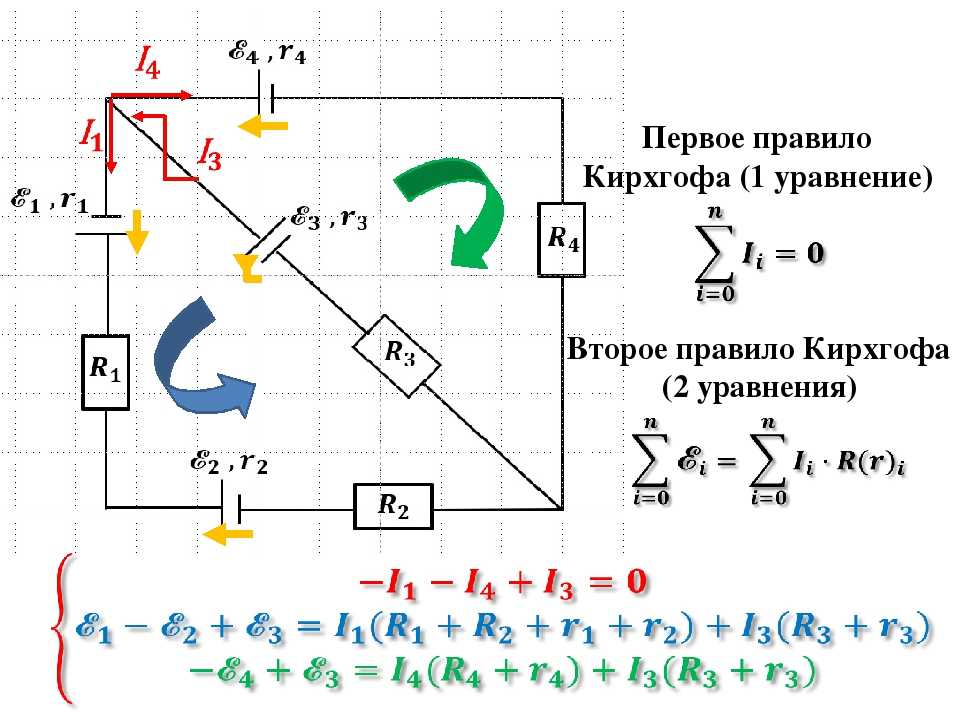 В алгебраической сумме следует учесть и токи источников тока.
В алгебраической сумме следует учесть и токи источников тока.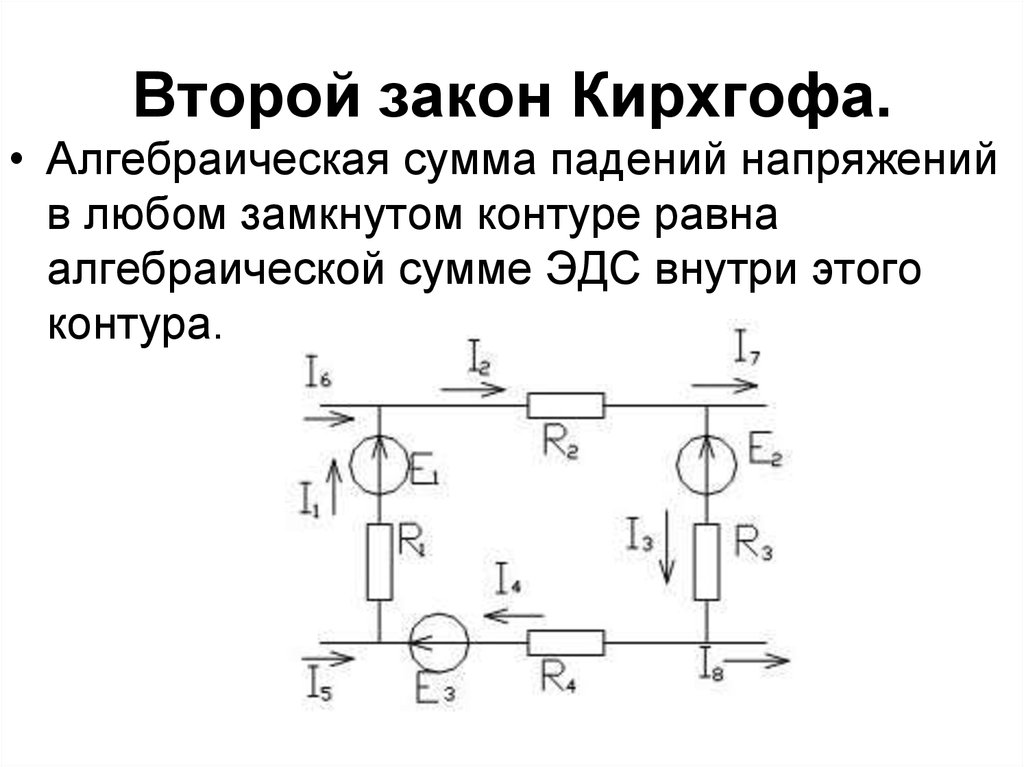
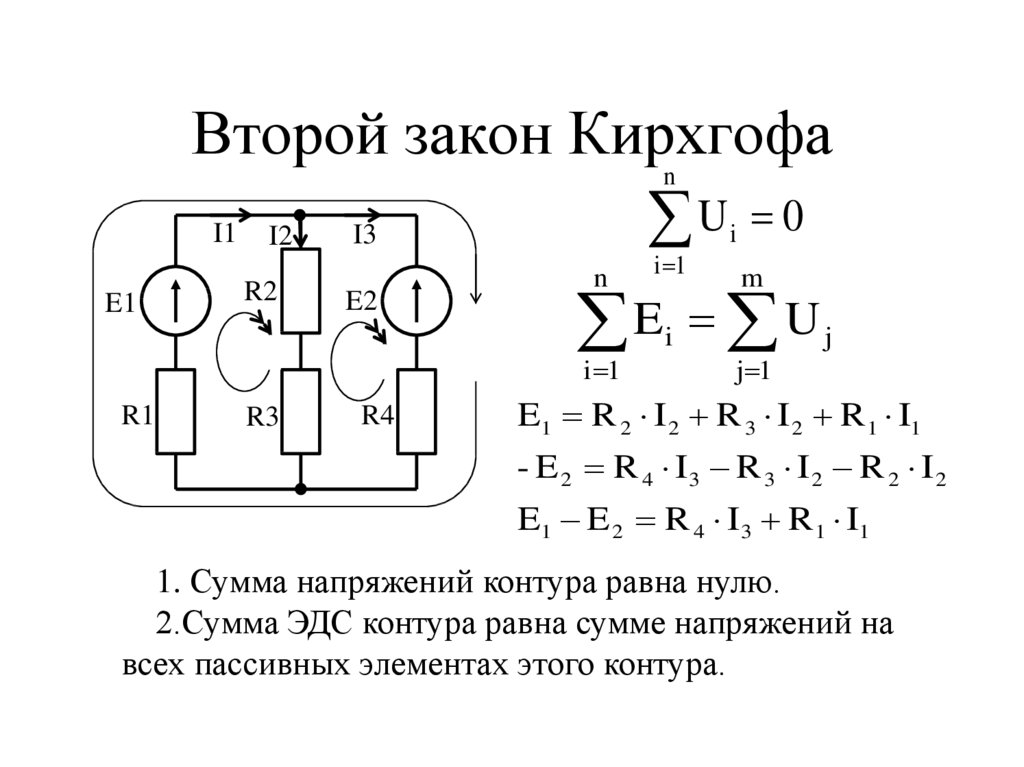 Если равенство не саблюдается, значит, имеются ошибки в расчетах, которые требуется устранить.
Если равенство не саблюдается, значит, имеются ошибки в расчетах, которые требуется устранить.
 13).
13). Как определяется общее сопротивление при последовательном и параллельном соединении сопротивлений?
Как определяется общее сопротивление при последовательном и параллельном соединении сопротивлений?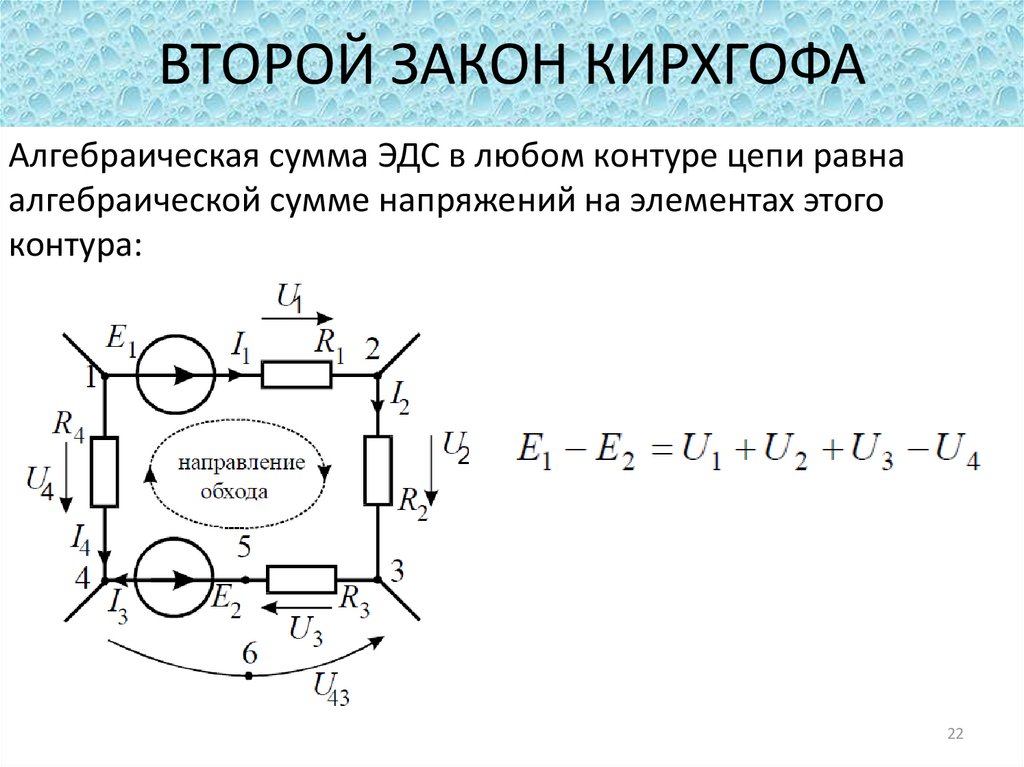
 Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.
Сумма всех токов, входящих в соединение, должна равняться сумме всех токов, выходящих из соединения.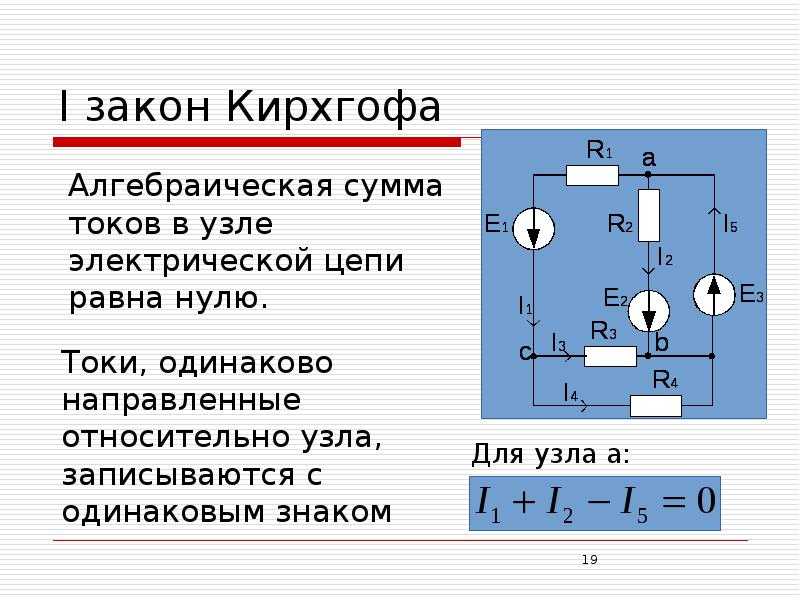 Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I 1 , I 2 , I 3 и I , а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным.
Например, на рис. 1, рис. 2 и рис. 3 токи обозначены I 1 , I 2 , I 3 и I , а стрелки указывают их направления. Здесь нет никакого риска, потому что, если вы выберете неправильное направление, ток будет правильной величины, но отрицательным. Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
Если ток неизвестен, вы должны присвоить ему направление. Это необходимо для определения признаков потенциальных изменений. Если вы зададите направление неправильно, то обнаружится, что ток имеет отрицательное значение — никакого вреда не будет.
 Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии
Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Находится в Лицензии )
) ) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 21.24.
) Чтобы применить правило цикла, вы должны выбрать направление обхода цикла. Затем тщательно и последовательно определите знаки потенциальных изменений для каждого элемента, используя четыре маркированных пункта, рассмотренных выше в сочетании с рис. 21.24.