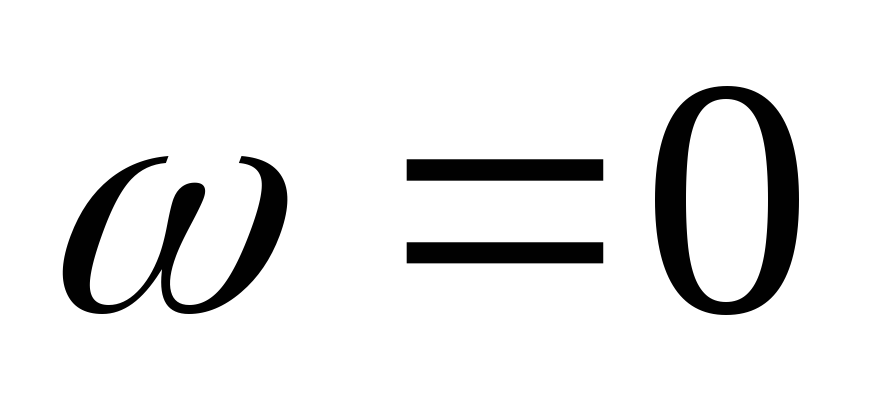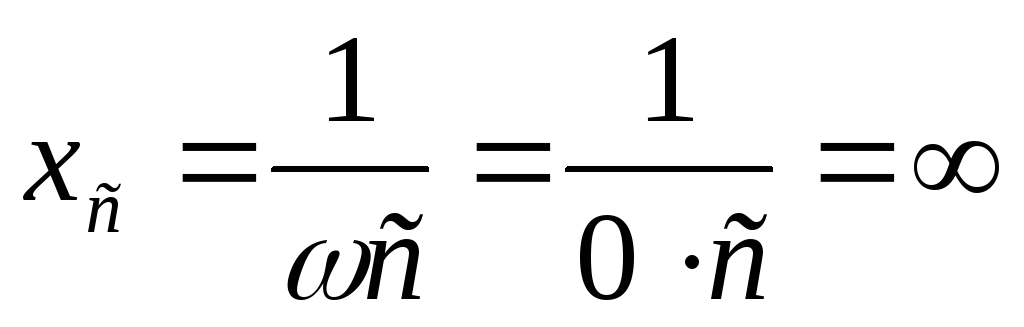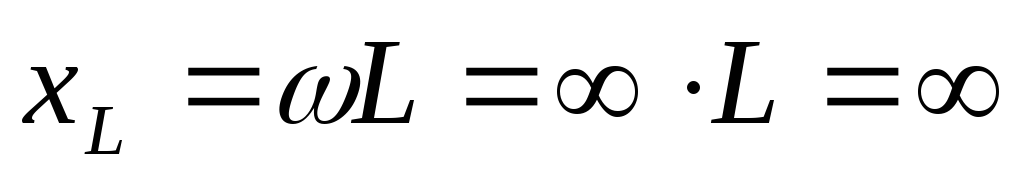Последовательная RL-цепь
Рассмотрим цепь, состоящую из последовательно соединенных резистора R и катушки L, в электротехнике такая цепь часто называется последовательной RL-цепью.
Напряжение, приложенное к цепи равно
По второму Кирхгофа, для рассматриваемой цепи можно записать выражение
Напряжение на резисторе и катушке равно
Тогда напряжение, приложенное к цепи
Ток в цепи равен
Подставив ток в выражение для напряжения, получим
или
Из выше приведенной формулы первое слагаемое это напряжение на резисторе, то есть
Из этого можно сделать вывод, что ток и напряжение в резисторе совпадают по фазе.
Напряжение на катушке
Напряжение на катушке опережает ток на угол π/2.
Реактивное сопротивление катушки равно
Сопротивление катушки зависит от частоты. При постоянном токе, частота равна нулю, а значит и сопротивление тоже.
Сдвиг фаз RL-цепи можно определить по формуле
Полное сопротивление RL-цепи
Амплитудное значение тока
Рассмотрим пример
К цепи, состоящей из последовательно соединенных катушки и резистора приложено синусоидальное напряжение. Ток в цепи равен 1,2 А. Сопротивление резистора 10 Ом, индуктивность катушки 26 мГн. Найдите напряжение U,
Найдем напряжение на каждом из элементов, зная ток в цепи и их сопротивление
Найдем сдвиг фаз между током и напряжением в цепи. В нашем случае реактивное сопротивление x состоит только из индуктивного сопротивления xL
Построим векторную диаграмму напряжений для нашей цепи. Подробнее об этом в статье Построение векторных диаграмм.
Напряжение в цепи найдем из треугольника напряжений
Читайте также — Последовательная RC-цепь
Пассивные RC и RL дифференцирующие и интегрирующие цепи
Святая простота! Что может быть проще?
А проще могут быть чётко сформулированные определения дифференцирующей и интегрирующей цепей, не обременённые ни лингвистическими
излишествами, ни всякого рода необязательными формулами.
Итак, полностью оправдывая свои названия:
— дифференцирующая цепь — это цепь, в которой мгновенное значение напряжения на выходе прямо
пропорционально
дифференциалу входного напряжения,
— интегрирующая цепь — цепь, у которой мгновенное значение выходного напряжения не менее прямо
пропорционально интегралу
входного напряжения.
Эти цепи решают две основные задачи преобразования сигналов:
1. Формирование импульсов малой длительности (укорочение входных импульсов), которые далее используются для запуска
триггеров, одновибраторов и других устройств,
2. Выполнение математической операции дифференцирования (получение производной по времени) для устройств вычислительной
техники, аппаратуры авторегулирования и т.д.
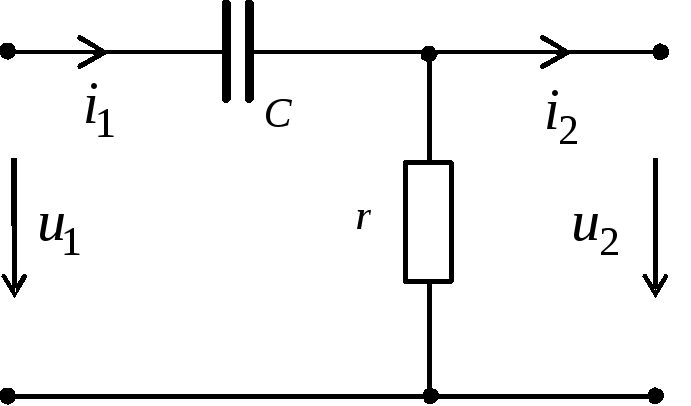
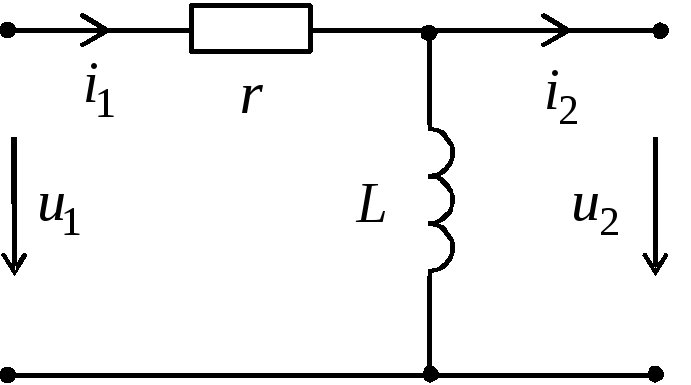
Рис.1.
Основной характеристикой данных цепей является постоянная времени цепи
τ = rC, либо τ = L/r.
U2 = τ×d(U1-U2)/dt.
Однако на практике, выбирая τ и, где Tи — длительность входного импульса, наши схемы приобретают чёткие дифференцирующие свойства, а выходное напряжение U2 становится равным:
U2 = τ×dU1/dt.
Приведём несколько поясняющих картинок.
 На Рис.2 приведены осциллограммы напряжений на выходах дифференцирующих цепей, в зависимости от различных соотношений постоянной времени цепи
τ и длительности входного импульса tи.
На Рис.2 приведены осциллограммы напряжений на выходах дифференцирующих цепей, в зависимости от различных соотношений постоянной времени цепи
τ и длительности входного импульса tи.
В начальный момент подачи входного импульса, напряжение на выходе Uвых практически моментально достигает амплитудного
значения входного Uвх, а затем идёт относительно плавный спад до:
Uвх/√e ≈ 0,61Uвх за время, равное τ/2,
Uвх/e ≈ 0,37Uвх за время, равное τ,
Uвх/e2 ≈ 0,135Uвх за время, равное 2τ,
Uвх/e3 ≈ 0,05Uвх за время, равное 3τ,
где e — это основание натурального логарифма ≈ 2,72.
Переходим к интегрирующим RC и RL цепям.
Интегрирующая цепь предназначена для формирования импульсов большой длительности, т.е. для удлинения или расширения импульсов, преобразования импульсов по интегральному закону, получения линейно изменяющегося напряжения. Отсюда и другое название интегрирующей цепи — удлиняющая цепь.
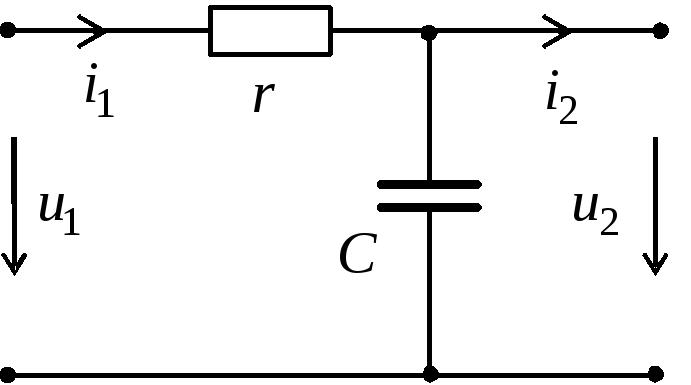

Рис.3.
Значение величины постоянной времени интегрирующей цепи ничем не отличается от дифференцирующих собратьев: τ = rC, либо τ = L/r.
Для корректного выполнения цепью интегрирующих функций должно выполняться условие:
τ >> T
U2 = 1/τ×∫U1dt.
Продолжим уроки рисования.
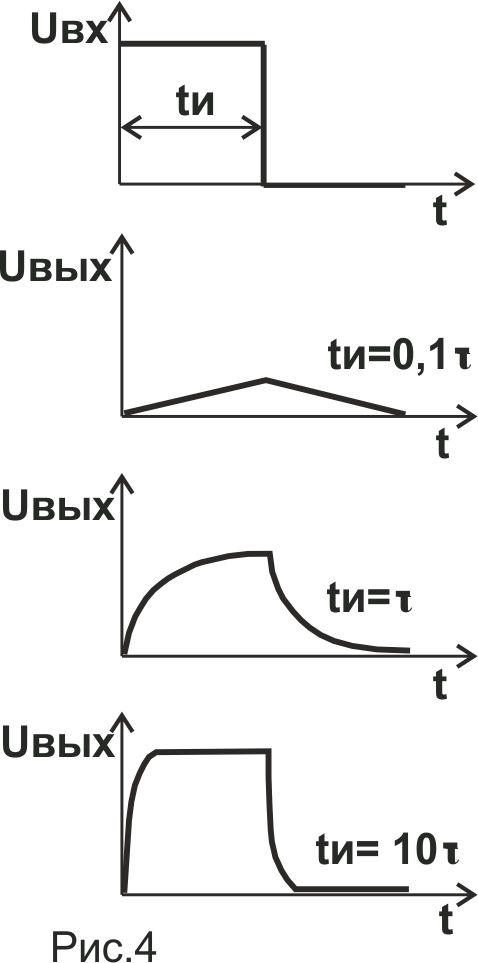 На Рис.4 приведены осциллограммы напряжений на выходах интегрирующих цепей, в зависимости от различных соотношений постоянной времени цепи
τ и длительности входного импульса tи.
На Рис.4 приведены осциллограммы напряжений на выходах интегрирующих цепей, в зависимости от различных соотношений постоянной времени цепи
τ и длительности входного импульса tи.
В начальный момент подачи входного импульса, напряжение на выходе Uвых равно 0, после чего начинает расти со скоростью,
обратно пропорциональной значению τ и достигает следующих значений:
Uвх×(1-1/e) ≈ 0,63Uвх за время, равное τ,
Uвх×(1-1/e2) ≈ 0,86Uвх за время, равное 2τ,
Uвх×(1-1/e3) ≈ 0,95Uвх за время, равное 3τ,
где e — это по-прежнему основание всё того же пресловутого натурального логарифма ≈ 2,72.
Ну и под занавес приведём таблицу для расчёта значения величины постоянной времени дифференцирующих и интегрирующих цепей
τ.
Как уже говорилось — это величина одинакова для обоих типов цепей и равна
τ = rC, либо τ = L/r.
На самом деле, подобные RC/RL Г-образные цепи, помимо дифференцирующих и интегрирующих функций, вполне достойно справляются и c ролью простейших НЧ и ВЧ фильтров 1-го порядка (о них мы поговорили на странице ссылка на страницу), а также сносно проглядываются в качестве пассивных фазосдвигающих цепей, которые мы также уже обсудили на ещё одна ссылка на страницу.
Последовательная RLC-цепь
Рассмотрим цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки индуктивности.
Напряжение на зажимах цепи
или
где
Выполнив подстановку, получим
Подставим в последнее выражение ток в цепи, зная, что он равен
В итоге получим выражение
Из этого выражения можно увидеть сдвиг фаз каждого элемента. У резистора он отсутствует, то есть напряжение и ток совпадают по фазе, у катушки индуктивности напряжение опережает ток на угол π/2, а у конденсатора, напротив, отстает.
Сдвиг фаз RLС-цепи можно определить по формуле
Полное сопротивление RLС-цепи
Амплитудное значение тока
При построении векторной диаграммы RLC-цепи возможны три случая:
1 – Цепь носит активный характер, сдвиг фаз равен нулю, индуктивное и емкостное сопротивления равны. При этом в такой цепи наблюдается резонанс напряжений.
2 – Цепь носит индуктивный характер, в этом случае индуктивное сопротивление больше чем емкостное.
На векторной диаграмме, как правило, сначала откладывают вектор напряжения на катушке индуктивности, а затем из него вычетают напряжение на конденсаторе. После этого проводят вектор общего напряжения и определяют сдвиг фаз φ.
3 – Цепи носит емкостной характер, при этом емкостное сопротивление больше чем индуктивное.
Построение векторной диаграммы выполняется аналогично цепи индуктивного характера, за тем исключением, что здесь сдвиг фаз отрицателен и вычитается индуктивное напряжение из напряжения на емкости.
Пример задачи
Цепь состоит из последовательно включенных резистора сопротивлением 25 Ом, конденсатора емкостью 200 мкФ и катушки индуктивности 30 мГн. Ток, протекающий в цепи, равен 0,75 А. Определите U,UR,UL,UC,φ. Постройте векторную диаграмму и определите характер цепи.
Найдем напряжение на каждом из элементов
И общее в цепи
Сдвиг фаз равен
Векторная диаграмма
Из векторной диаграммы можно сделать вывод, что цепь носит емкостной характер.
Открытая Физика. Квазистационарные процессы. RC- и RL-цепи
В цепях постоянного тока распределение электрических зарядов на проводниках и токов на участках цепи стационарно, то есть неизменно во времени. Электромагнитное поле в таких цепях состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Эти поля существуют независимо друг от друга.
Если на каком-то участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через некоторое время, которое по порядку величины равно времени τ распространения электромагнитного возмущения от одной точки цепи к другой. Так как электромагнитные возмущения распространяются с конечной скоростью, равной скорости света c , то τ≈lc, где l – расстояние между наиболее удаленными точками цепи. Если это время τ много меньше длительности процессов, происходящих в цепи, то можно считать, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях а также сами цепи, называются квазистационарными.
Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.
Из-за огромного значения скорости света время установления в цепи электрического равновесия оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.
Простыми примерами квазистационарных процессов могут служить процессы, происходящие в RC- и RL-цепях при подключении и отключении источника постоянного тока.
На рис. 2.1.1 изображена электрическая цепь, состоящая из конденсатора с емкостью C, резистора с сопротивлением R и источника тока с ЭДС, равной ℰ.
Если замкнуть ключ K в положение 1, то начинается процесс зарядки конденсатора через резистор. Для квазистационарной цепи по закону Ома можно записать: RJ + U = ℰ, где J – мгновенное значение силы тока в цепи, U – мгновенное значение напряжения на конденсаторе. Сила тока J в цепи равна изменению заряда q конденсатора в единицу времени: J=dqdt. Напряжение U на конденсаторе в любой момент времени равно q / C. Из этих соотношений следует CR dUdt+U=ℰ.
Мы получили дифференциальное уравнение, описывающее процесс зарядки конденсатора. Если конденсатор вначале не был заряжен, то решение этого уравнения имеет вид U (t)=ℰ [1 -exp(-tτ)], где τ = RC – так называемая постоянная времени цепи, состоящей из резистора и конденсатора. Величина τ является характеристикой скорости процесса. При t → ∞, U (t) → ℰ. Процесс зарядки конденсатора через резистор изображен на рис. 2.1.2 (I).
Если после того, как конденсатор полностью зарядился до напряжения ℰ, ключ K перебросить в положение 2, то начнется процесс разрядки. Внешний источник тока в цепи разрядки отсутствует (ℰ = 0). Процесс разрядки описывается выражением U (t) = ℰ exp (–t / τ).
Зависимость U (t) в процессе разрядки изображена на рис. 2.1.2 (II). При t = τ напряжение на конденсаторе уменьшается в e ≈ 2,7 раз.
Аналогично протекают процессы в цепи, содержащей катушку с индуктивностью L и резистор с сопротивлением R (рис. 2.1.3).
Если в цепи, изображенной на рис. 2.1.3, ключ K сначала был замкнут, а затем внезапно разомкнут, то начнется процесс установления тока. Следует обратить внимание на то, что в схему последовательно с источником тока включен резистор r с малым сопротивлением, чтобы при замкнутом ключе K батарея не оказалась закороченной. Поскольку r << R, при написании уравнения для процесса установления тока этим сопротивлением можно принебречь. Этот процесс описывается уравнением RJ=ℰ-LdJdt.
Это уравнение по виду совпадает с уравнением, описывающим зарядку конденсатора, только теперь переменной величиной является сила тока J. Решение этого уравнения имеет вид J (t)=ℰR [1 -exp(-tτ)], где постоянная времени τ = L / R. Аналогичным образом можно получить закон убывания тока в RL-цепи после замыкания ключа K: J (t)=ℰRexp(-tτ).
Следует отметить, что процессы в RC- и RL-цепях аналогичны механическим процессам при движении тела в вязкой жидкости.
Квазистационарные процессы. RC- и RL-цепи
Колебательные и волновые процессы, которые изучаются в разных разделах физики, имеют много общих закономерностей. Движения груза на пружине, процессы в электрическом колебательном контуре, распространение света – все эти явления протекают аналогичным образом. Есть смысл говорить об их различной физической природе.
Для решения задачи о колебательных движениях груза на пружине необходимо знать и разбираться в законах Ньютона. Глубокие знания в электродинамике не требуются. Но математические уравнения, которые описывают эти состояния, одинаковые. Также обстоят дела и с волновыми процессами.
Квазистационарные процессы. Заряд и разряд конденсатора
Определение 1Общность колебательных процессов и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.
Цепи постоянного тока распределяют электрический заряд на проводниках и токи на участках цепи стационарно, то есть независимо от времени. Электромагнитное поле таких цепей состоит из электростатического поля неподвижных зарядов и магнитного поля постоянных токов. Существование этих полей производится независимо друг от друга.
Если происходят изменения силы тока или напряжения на определенном участке цепи, то другие могут ощутить их на себе не сразу. Необходимо количество времени, равное времени τ распространения магнитного возмущения от одной точки к другой. Все электромагнитные возмущения обладают конечной скоростью, с которой и происходит их распространение. Она приравнивается к значению скорости света с , тогда τ≈lc, где l является расстоянием между наиболее удаленными точками цепи.
Определение 2При наличии меньшего значения времени τ длительности процессов, происходящих в цепи, считается, что сила тока неизменна в любой момент времени на всех последовательно соединенных участках цепи. Такие процессы получили название квазистационарных.
Их исследуют при помощи законов постоянного тока, применяя к мгновенным значениям сил токов и напряжений на участках цепи.
Так как скорость света имеет достаточно большое значение, то установление электрического равнове
Входные характеристики цепи rl

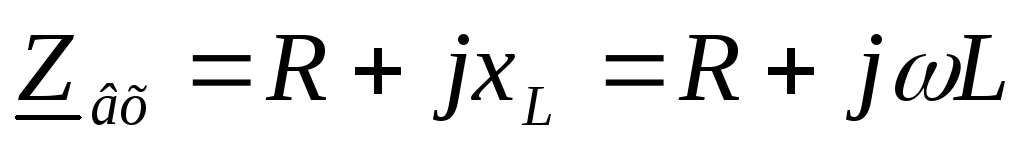
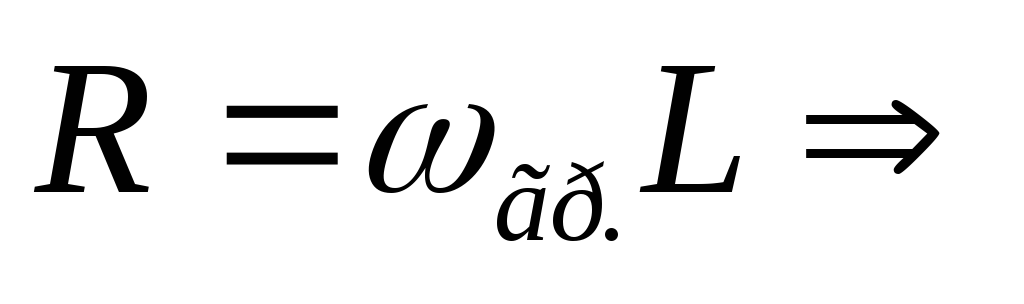
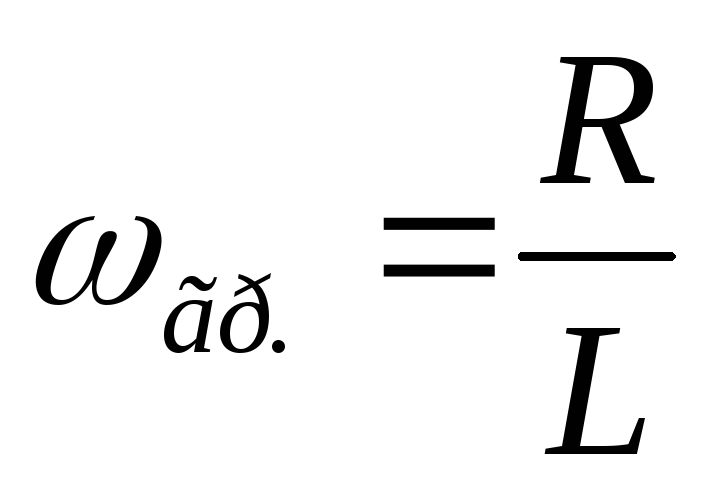 — формула граничной частоты цепиRL
— формула граничной частоты цепиRL
Порядок построения характеристик:
записываем комплексное входное сопротивление:

записываем модуль комплексного входного сопротивления:
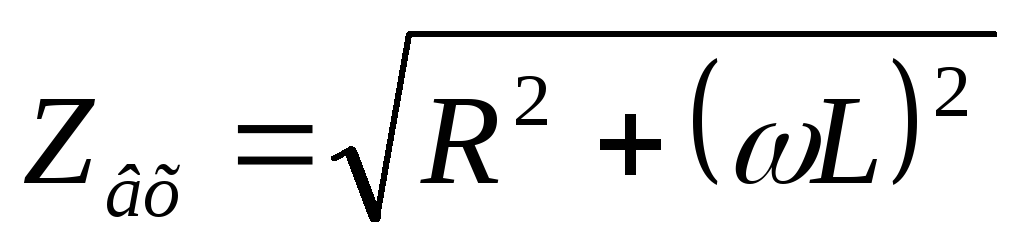
в
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
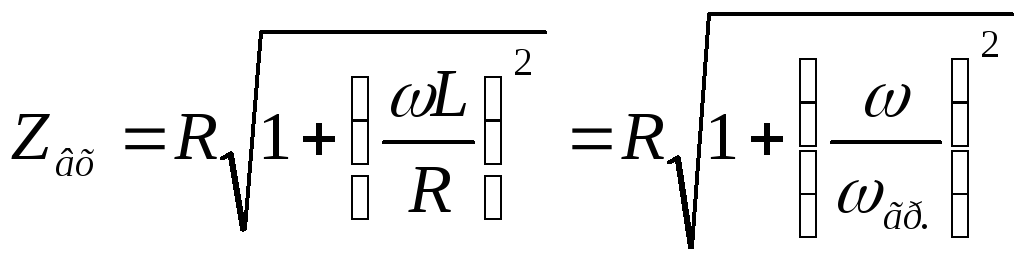
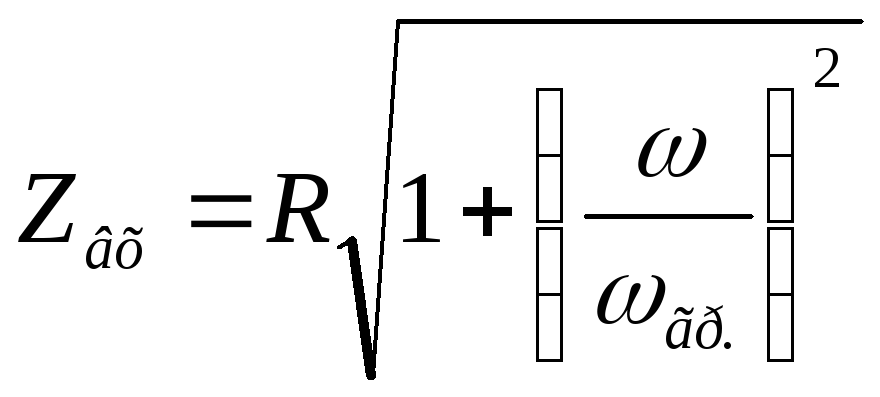 — формула входной АЧХ цепиRL
— формула входной АЧХ цепиRL
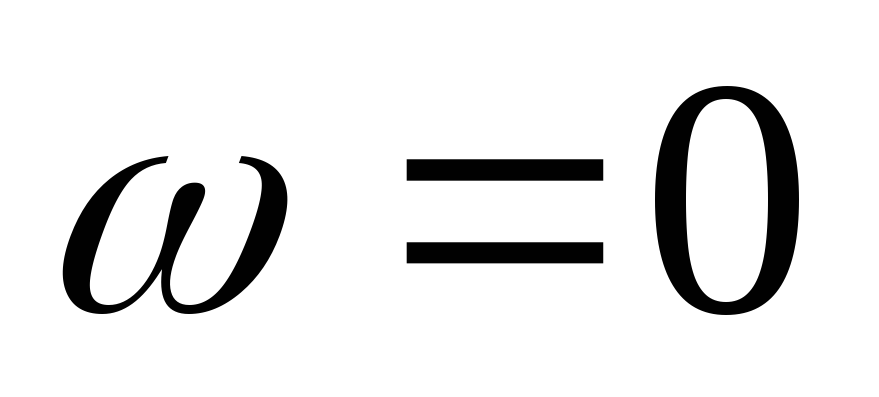


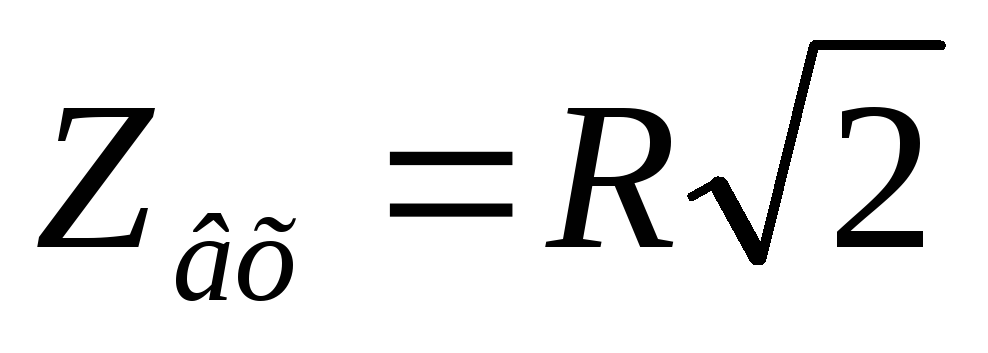
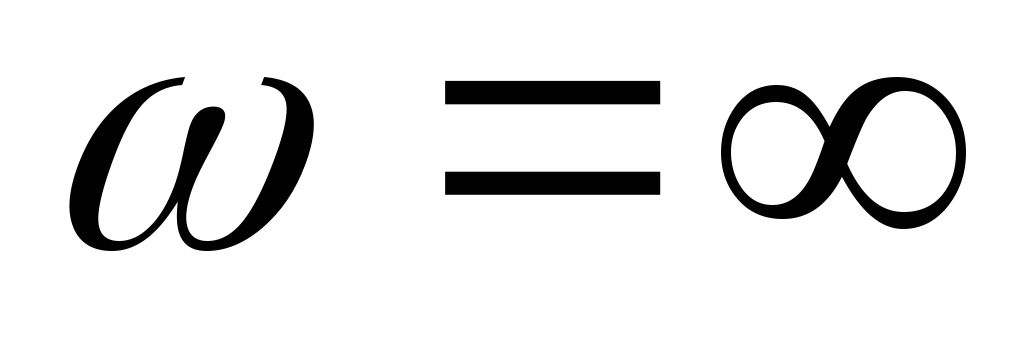
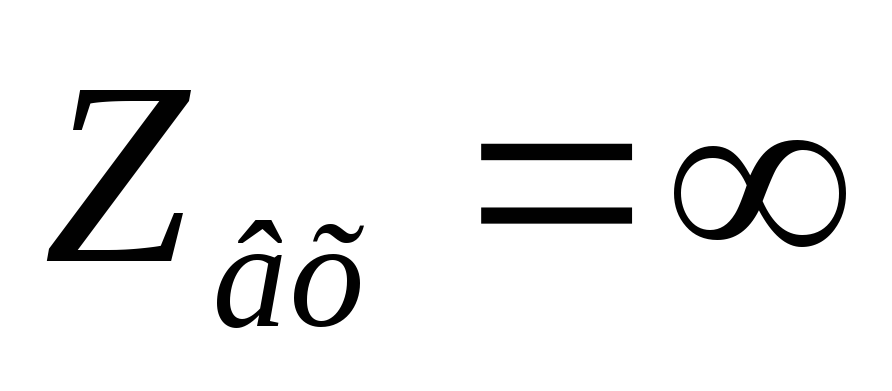
з
 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ:

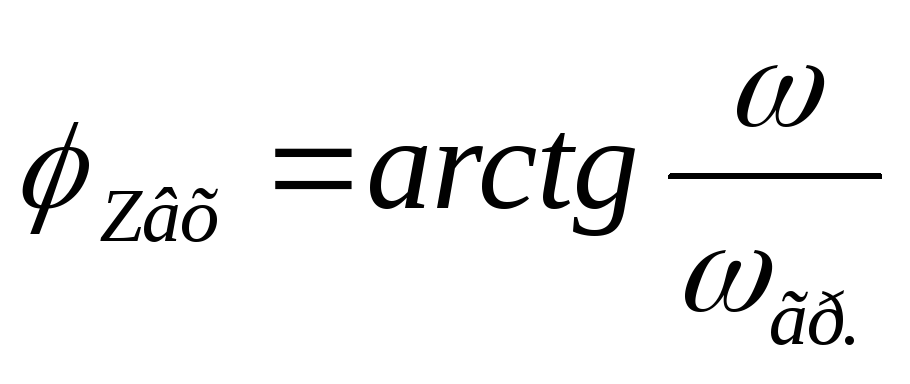 — формула входной ФЧХ цепиRL
— формула входной ФЧХ цепиRL
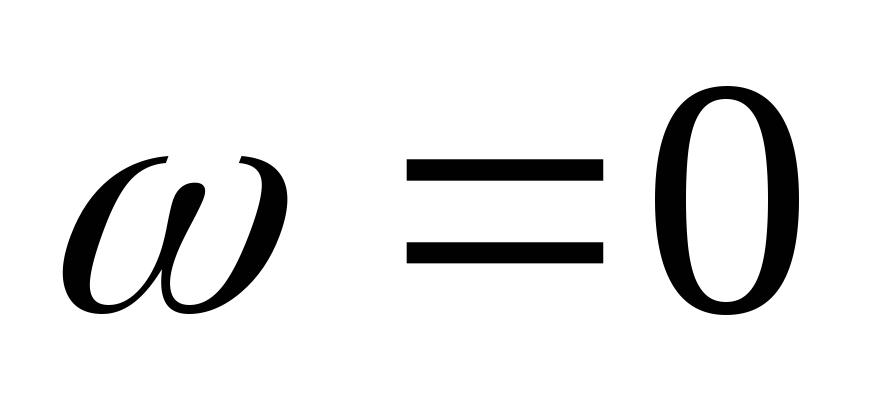

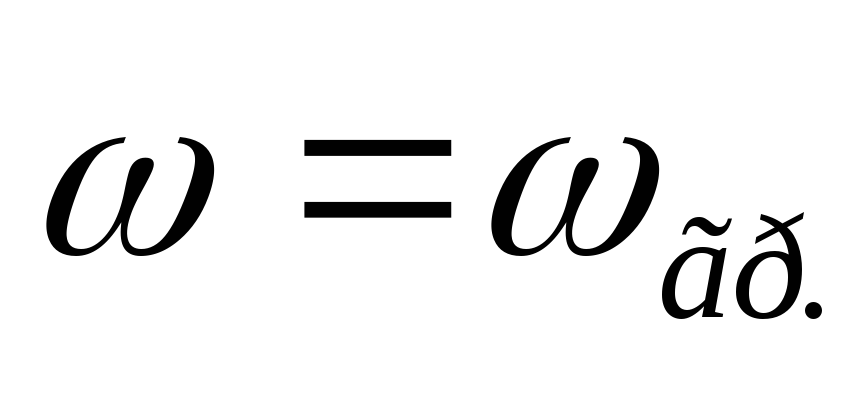
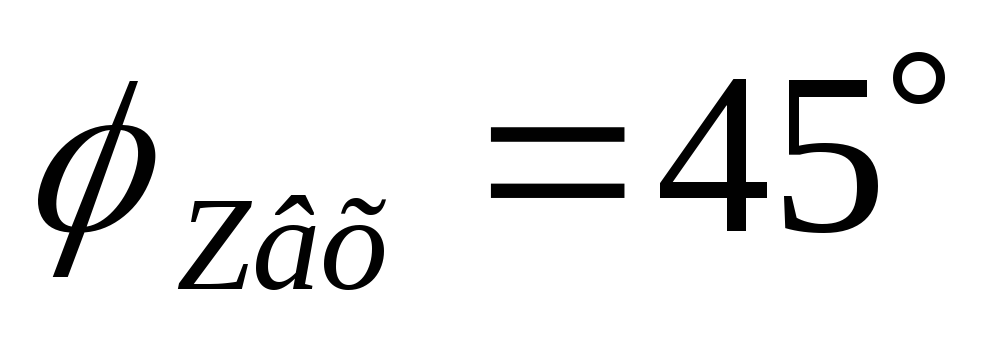
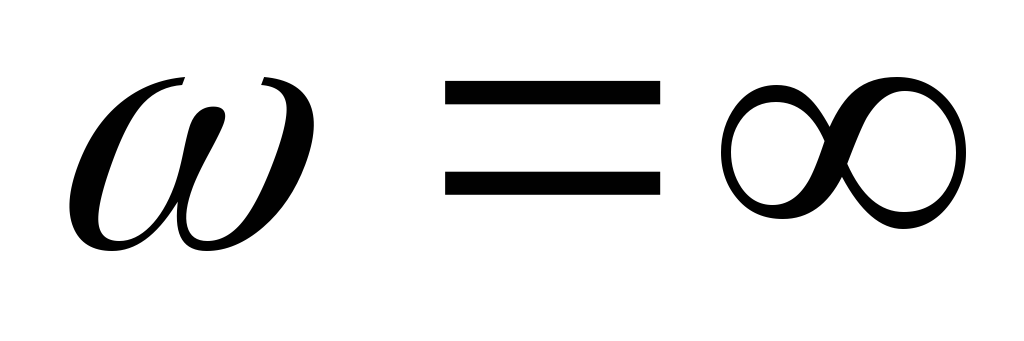
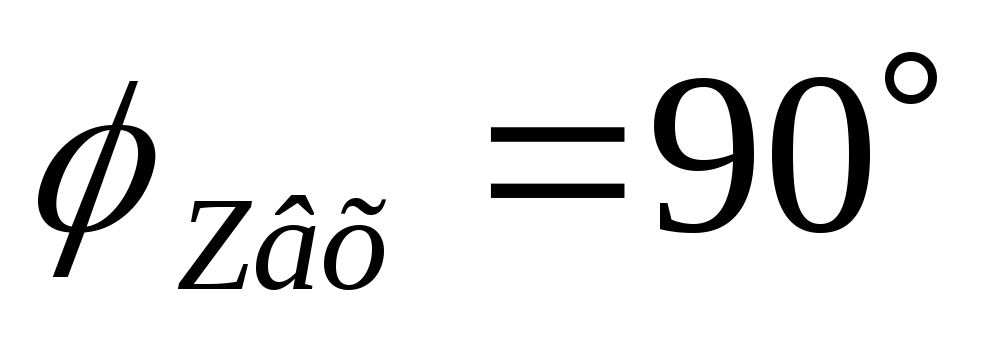
Выводы:
В цепи RLс ростом частоты входное сопротивление растёт.
Входная ФЧХ имеет линейный участок на частотах от
 до
до .
.
Построение входных характеристик качественно
Для сложных электрических цепей
характеристики можно строить только
с помощью вычислительной техники. Можно
построить характеристики качественно,
рассмотрев цепь на двух частотах: 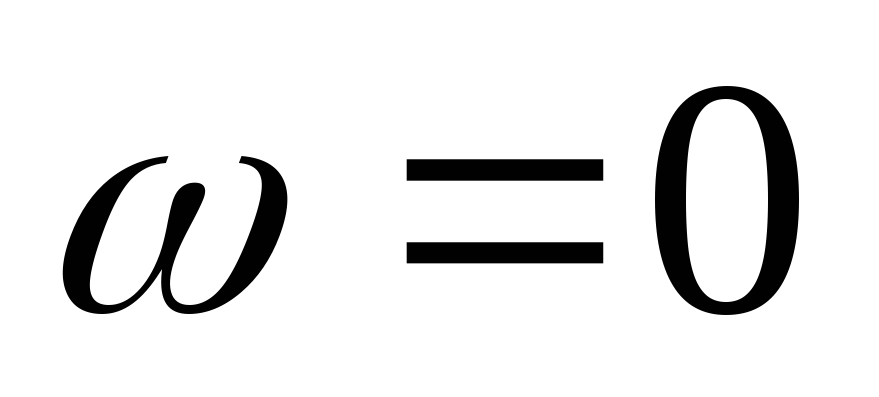 и
и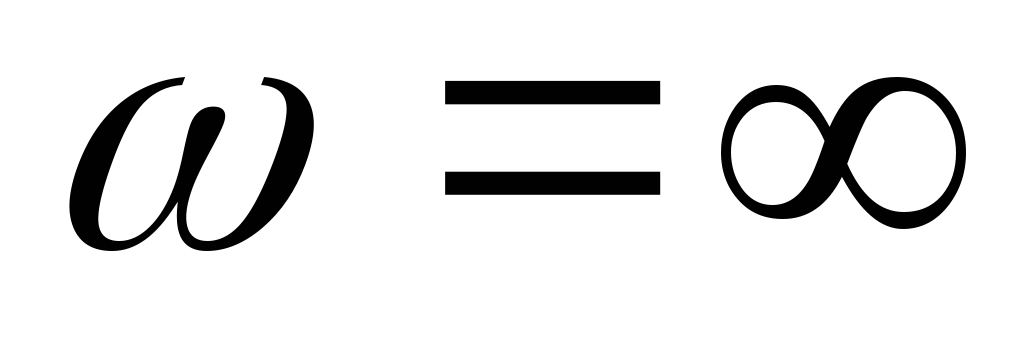 .
.
Надо помнить:
АЧХ и ФЧХ всегда нелинейные
Если в цепи есть индуктивность, то АЧХ возрастает, если ёмкость — АЧХ убывает.
Построим качественно АЧХдля цепи:

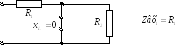
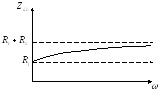
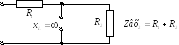
Построим качественно ФЧХдля той же цепи:
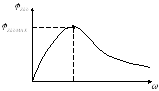
Т. к. цепь RL, то угол — положителен, и если при
— положителен, и если при 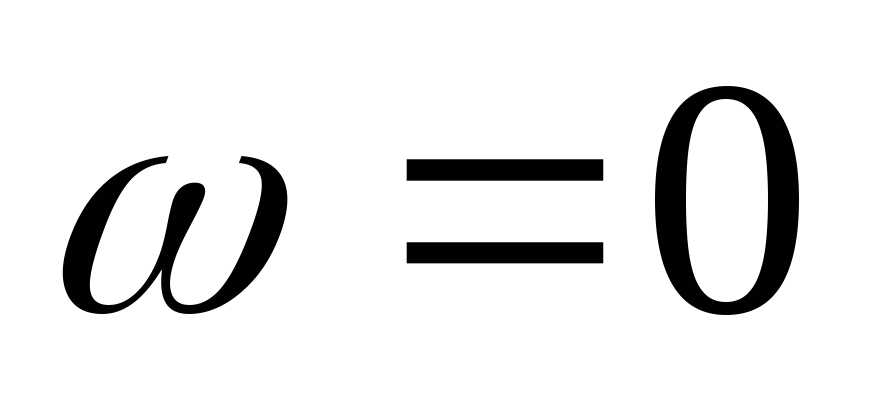 и
и 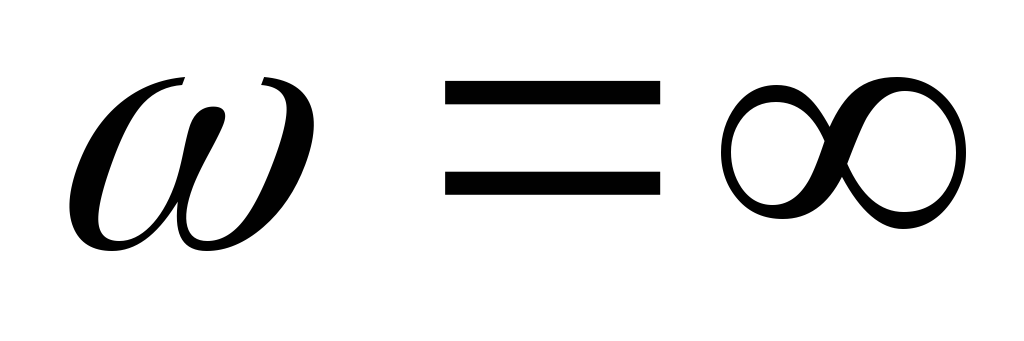
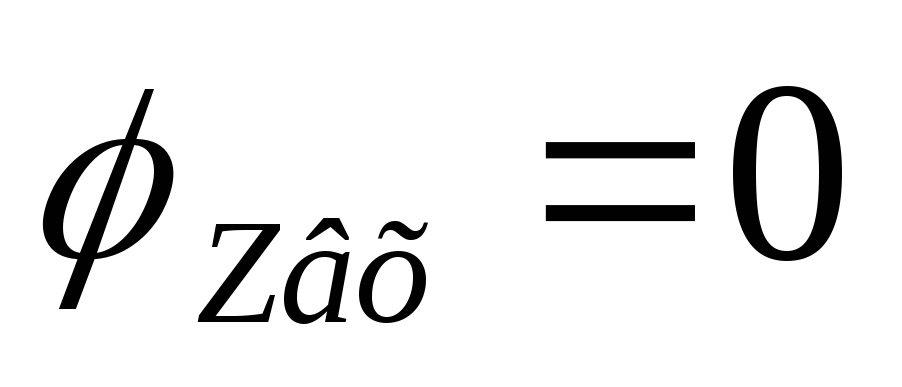 ,
то где-то есть максимум
,
то где-то есть максимум  :
:
Вопрос 41. Входные ачх и фчх rc неразветвлённых и разветвлённых цепей. Определение и понятие граничной частоты. Построение входных характеристик.
Понятие входных АЧХ и ФЧХ, граничной частоты, а также порядок построения характеристик рассмотрены в предыдущем вопросе (см. вопрос 40).
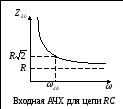
Входные характеристики цепи rc
И спользуем
порядок построения характеристик:
спользуем
порядок построения характеристик:
записываем комплексное входное сопротивление:
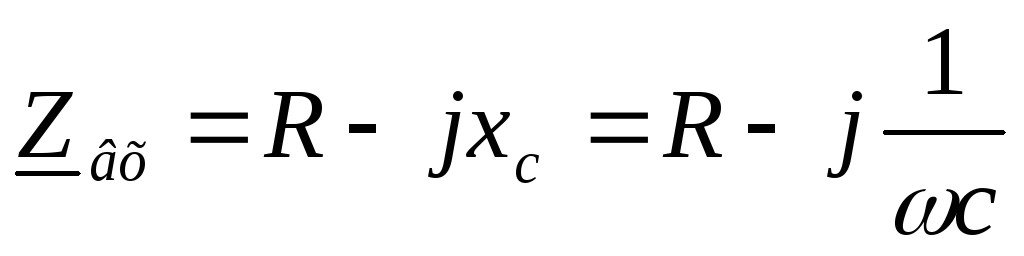
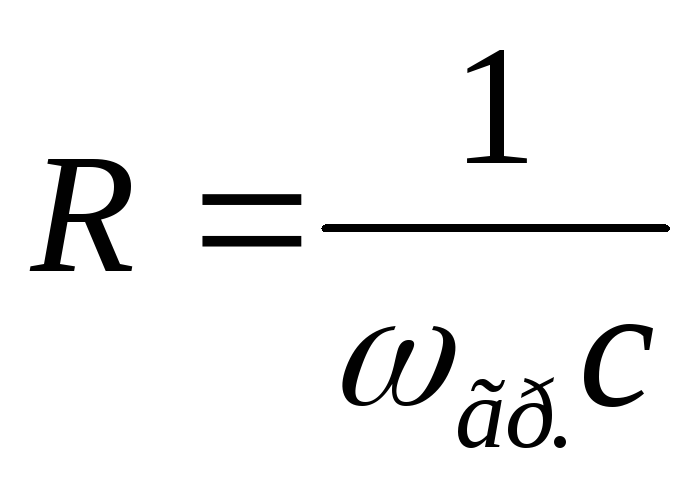
 — формула граничной частоты цепиRC
— формула граничной частоты цепиRC
записываем модуль комплексного входного сопротивления:
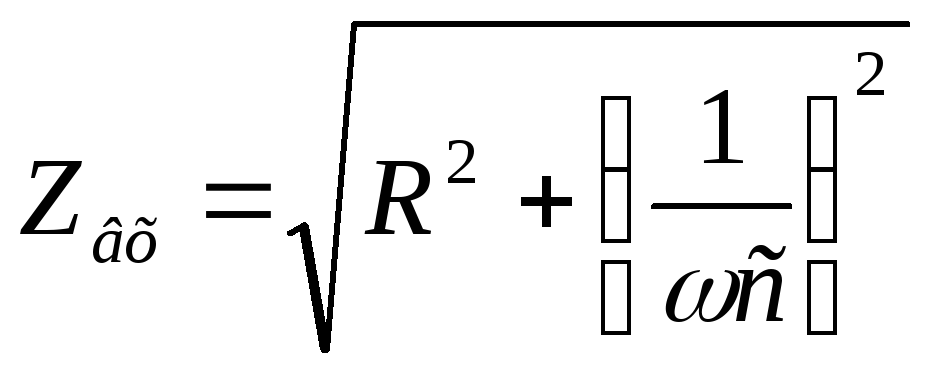
в
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
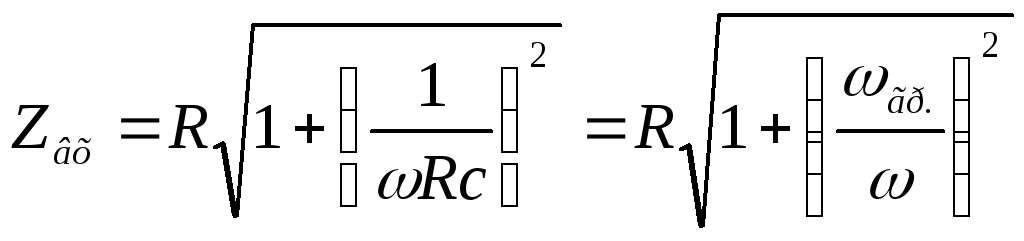
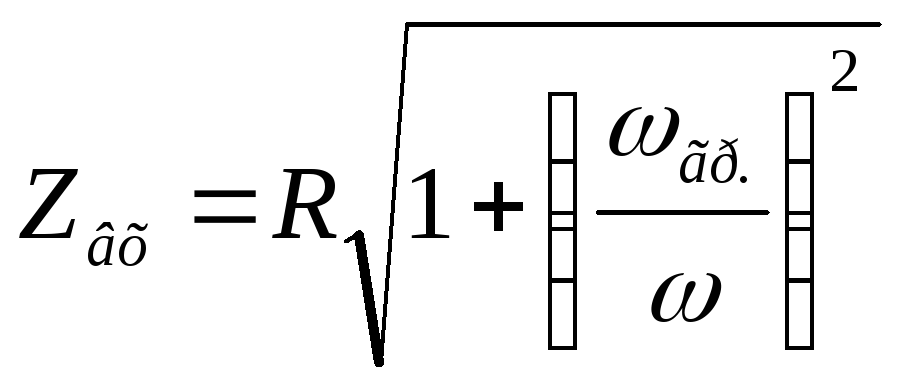 — формула входной АЧХ цепиRС
— формула входной АЧХ цепиRС
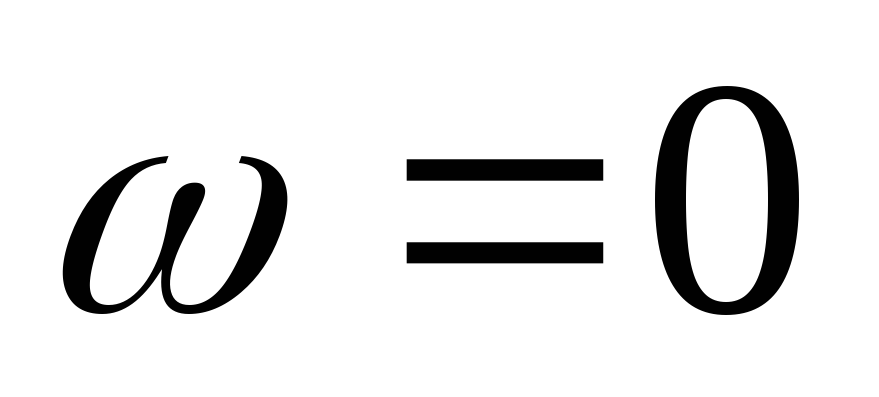
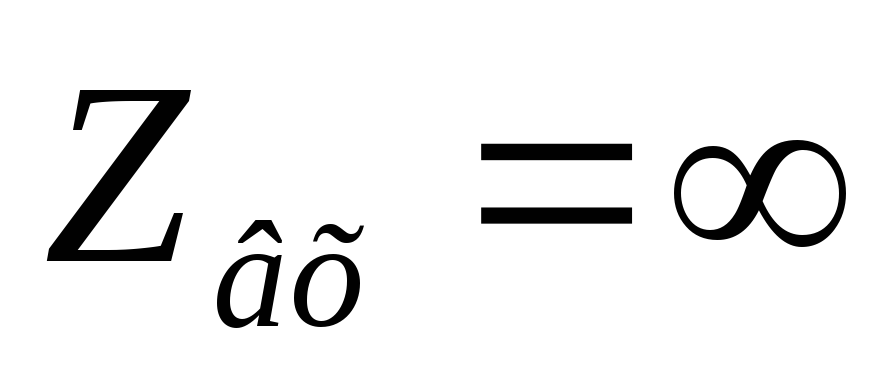
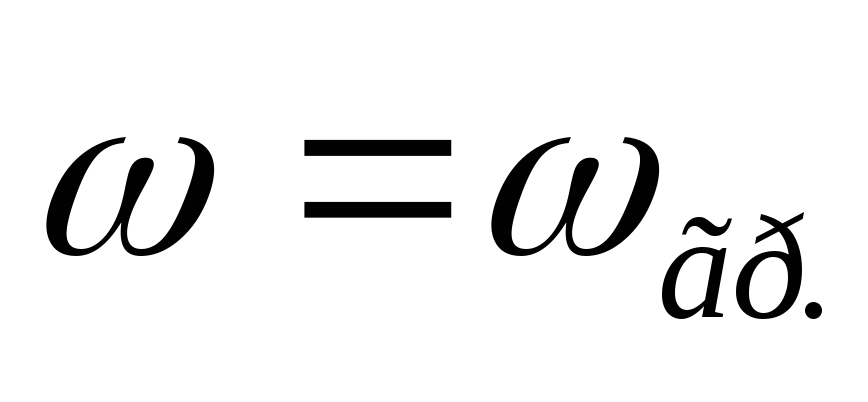
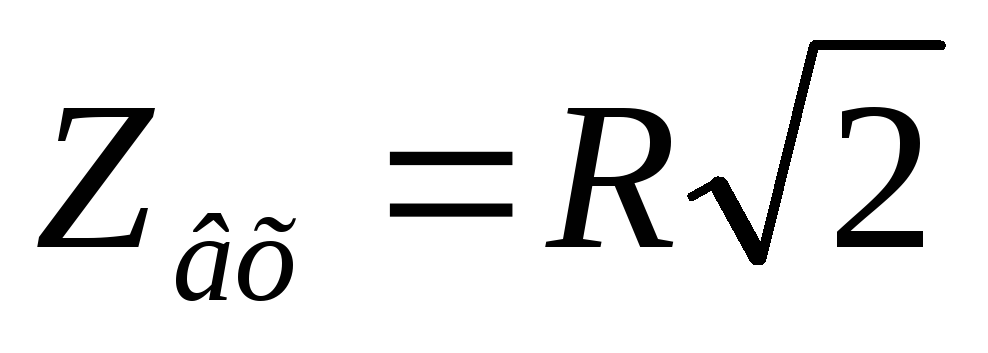
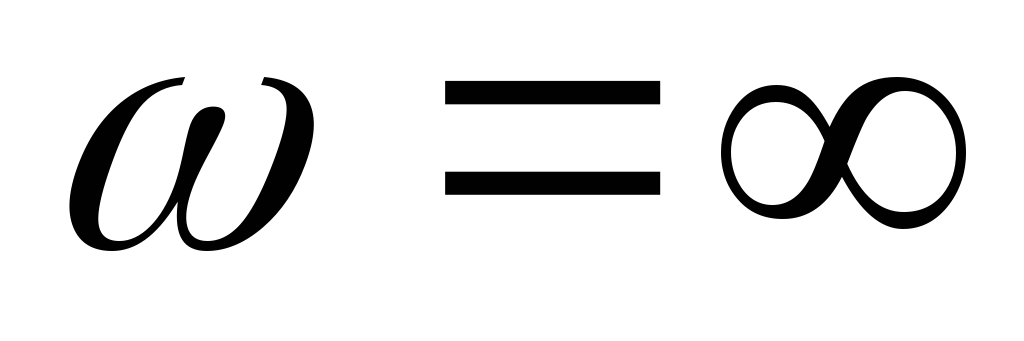

Вывод:
С ростом частоты входное сопротивление цепи RCуменьшается.
з
 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ:
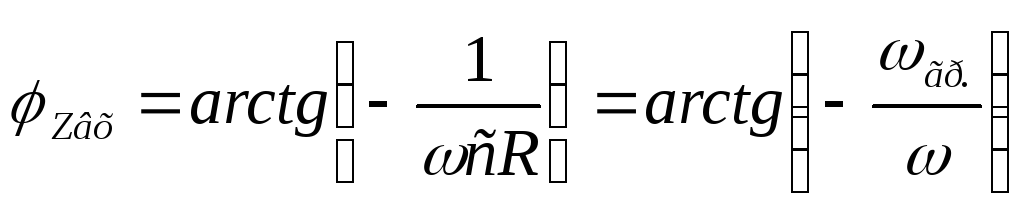
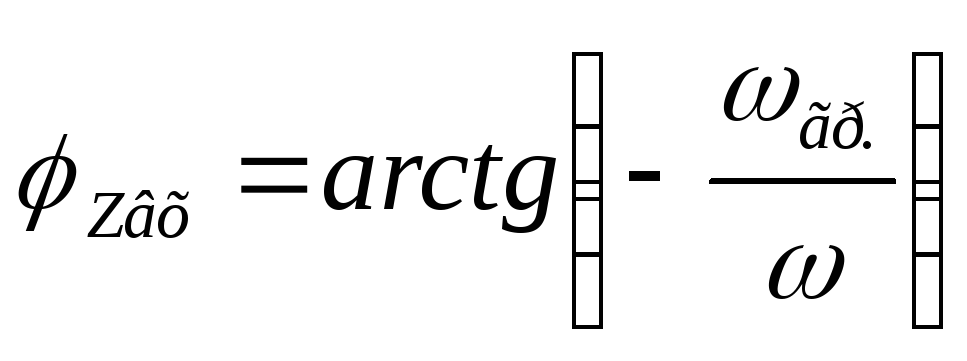 — формула входной ФЧХ цепиRС
— формула входной ФЧХ цепиRС
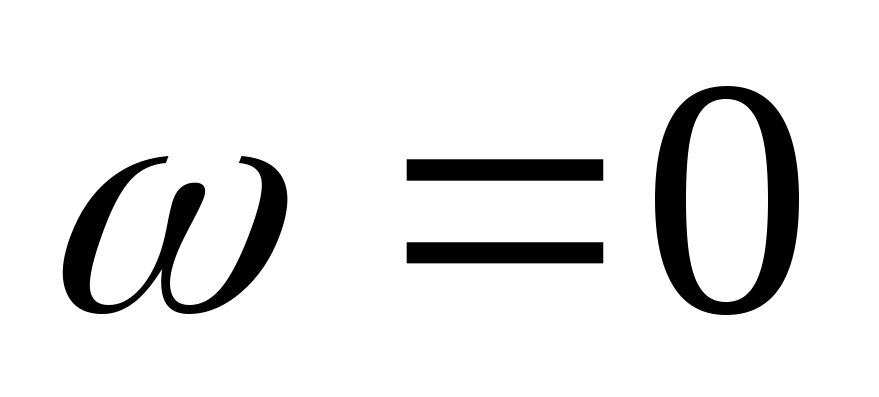
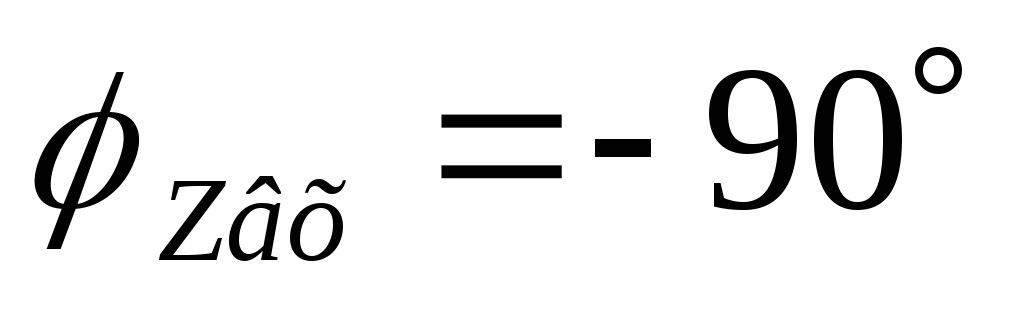
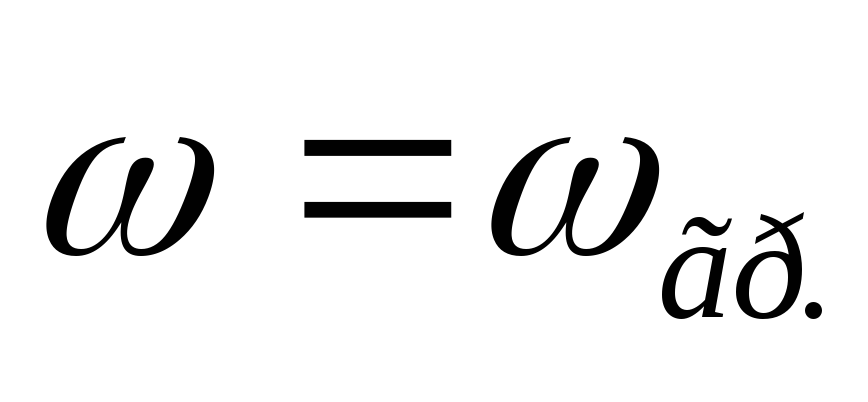
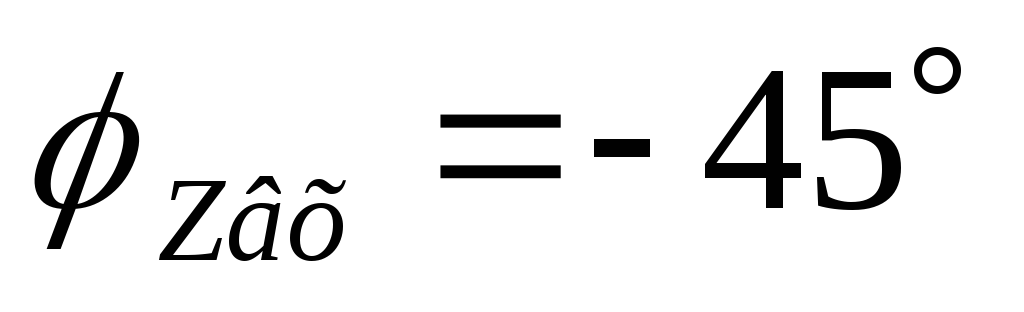
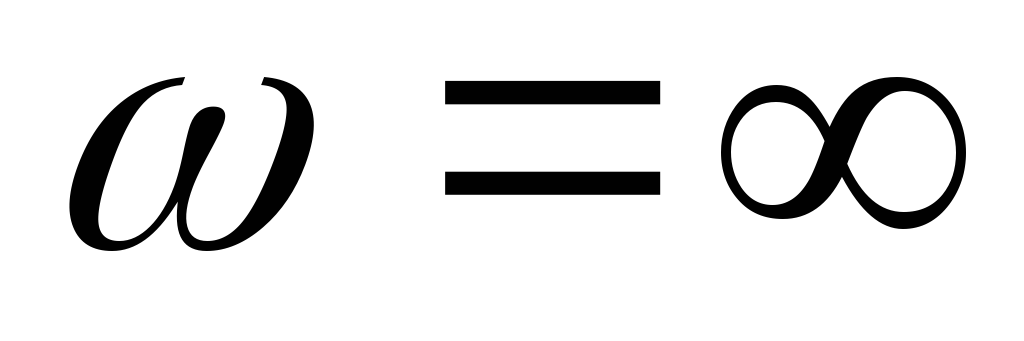
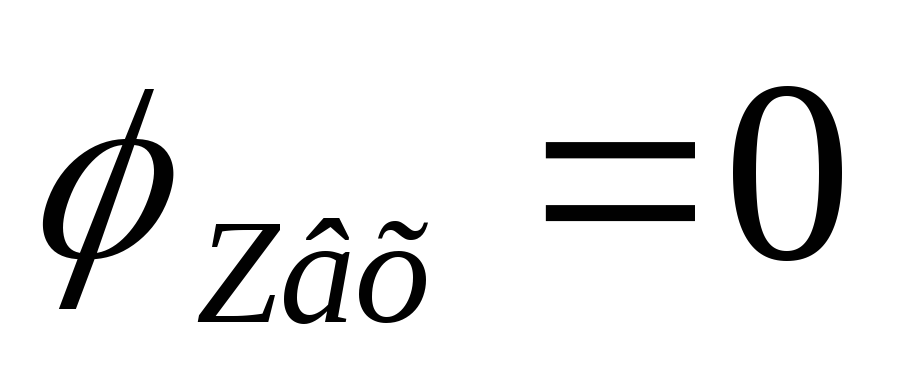
Вывод:
В цепи RCвходная ФЧХ имеет линейный
участок на частотах от до
до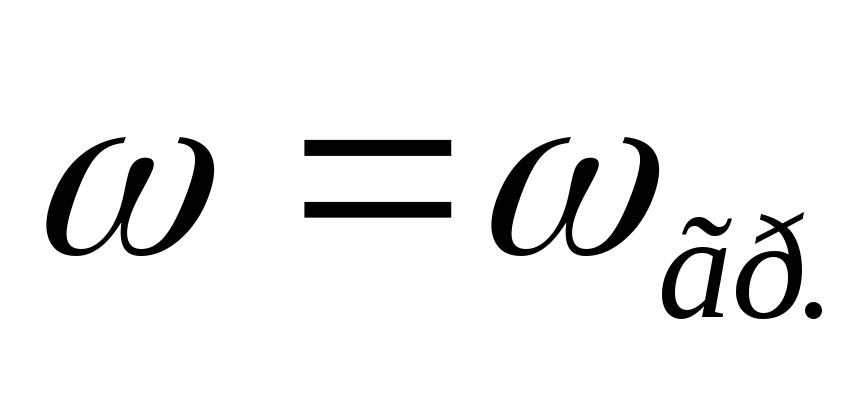 .
.
Вывод (к вопросам 40 – 41): на
граничной частоте в цепях первого
порядка 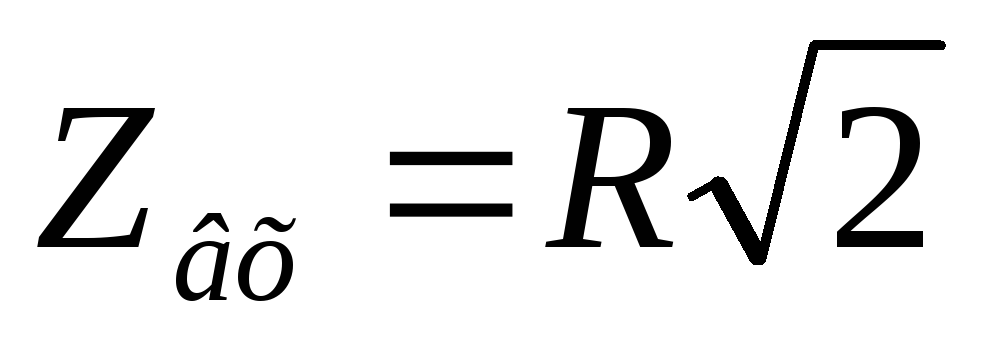 ,
, 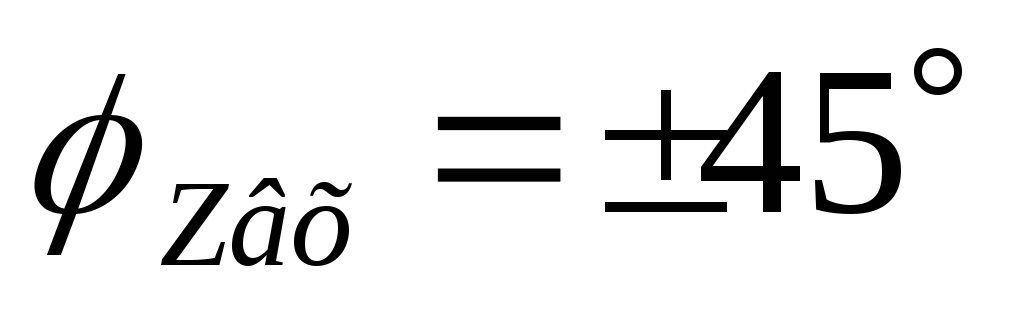 .
.
Построим качественно входные характеристики для цепи:


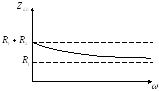
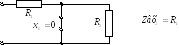
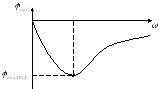
Т. к. цепь RС, то угол — отрицателен, и если при
— отрицателен, и если при 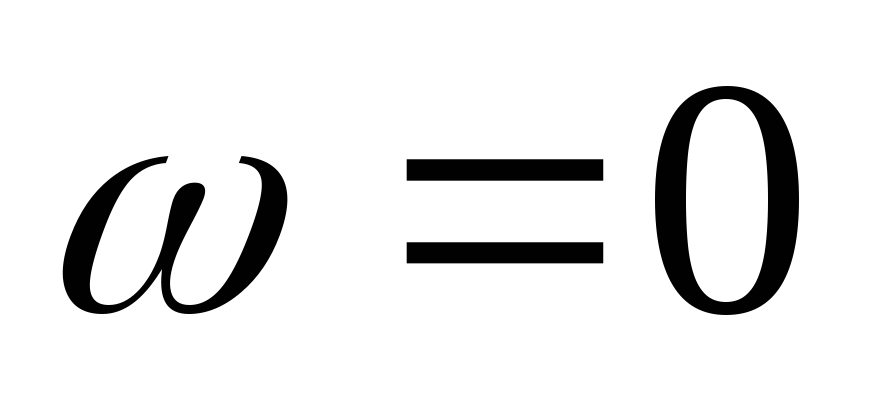 и
и 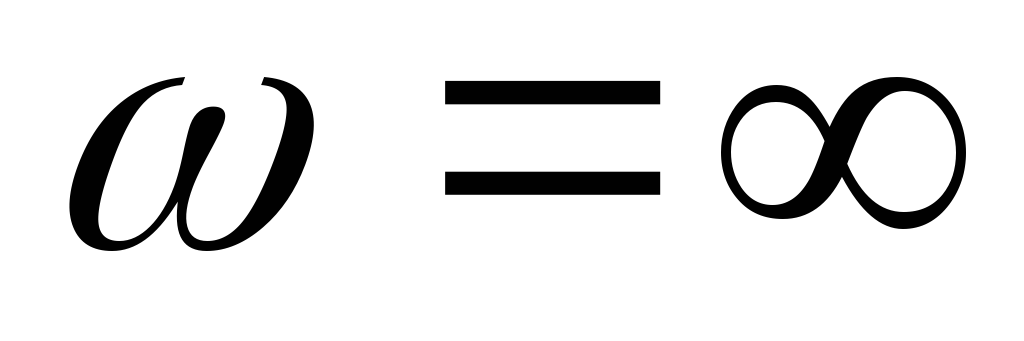
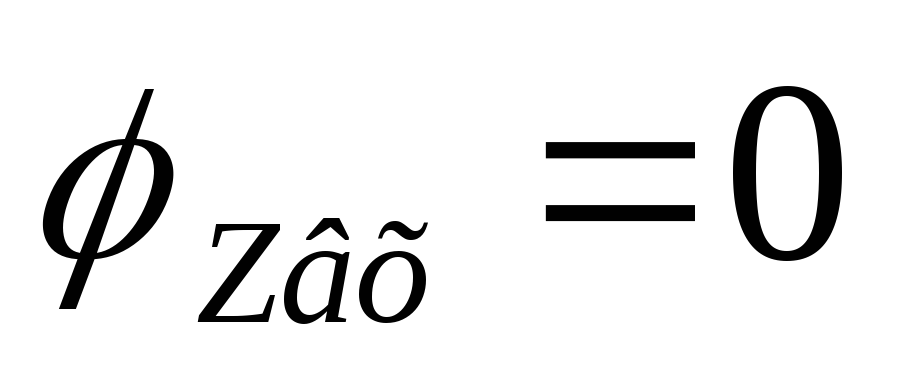 ,
то где-то есть максимум
,
то где-то есть максимум 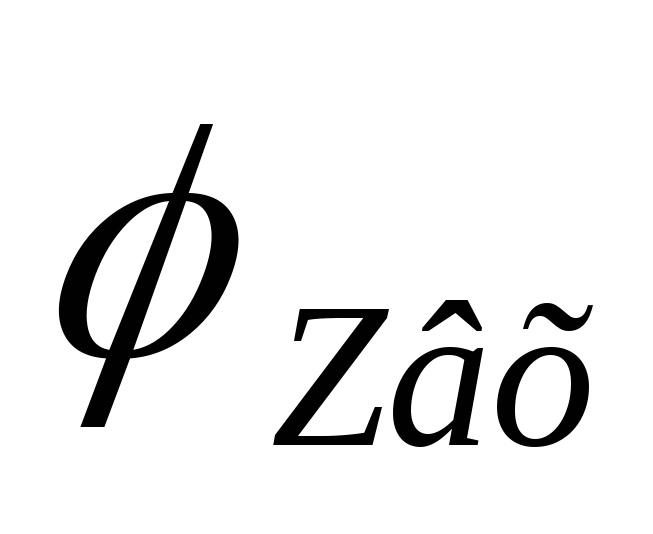 :
:
Вопрос 42. Передаточные ачх и фчх rl неразветвлённых и разветвлённых цепей. Определение. Построение передаточных характеристик.
Передаточные АЧХ и ФЧХ
Отношение комплексного напряжения на выходе к комплексному напряжению на входе называется комплексным коэффициентом передачи:

Зависимость модуля комплексного коэффициента передачи от частоты — передаточная АЧХ:
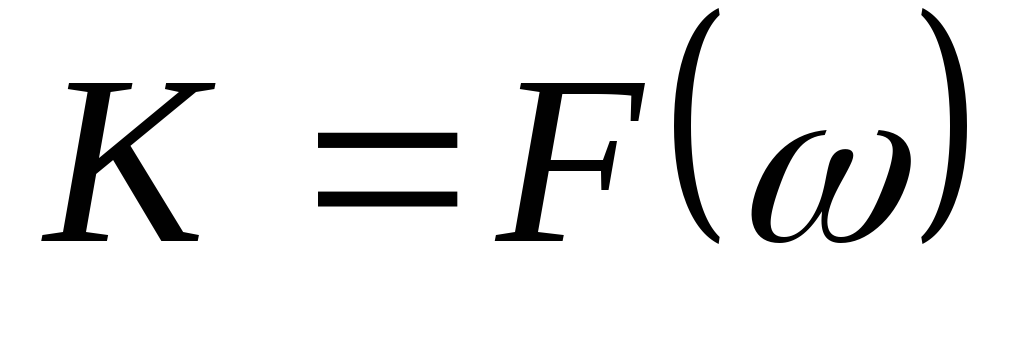 — передаточная АЧХ
— передаточная АЧХ
Зависимость аргумента комплексного коэффициента передачи от частоты — передаточная ФЧХ:

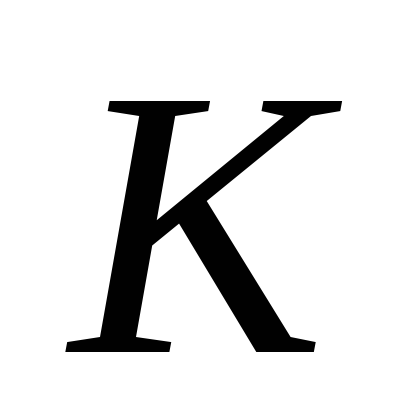 изменяется от 0 до 1.
изменяется от 0 до 1.
Передаточные характеристики зависят от того, какой элемент стоит на выходе.
Передаточные характеристики цепи RL

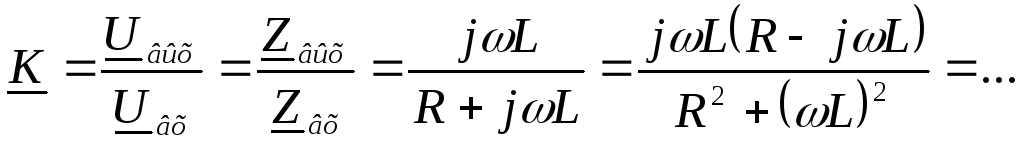
(чтобы выделить действительную и мнимую часть, умножили числитель и знаменатель на комплексно сопряжённое знаменателю число)
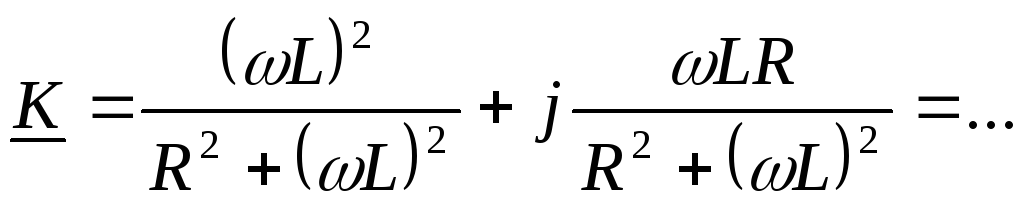
(разделим на 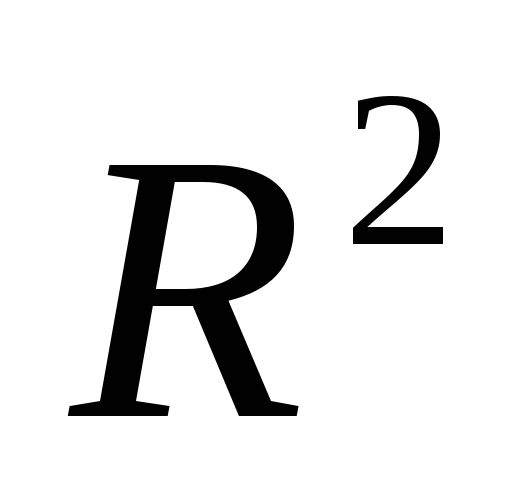 )
)
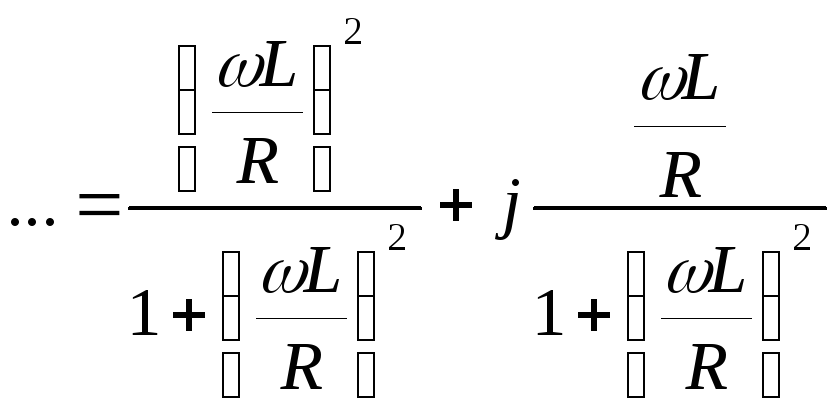
Граничная частотацепиRL: 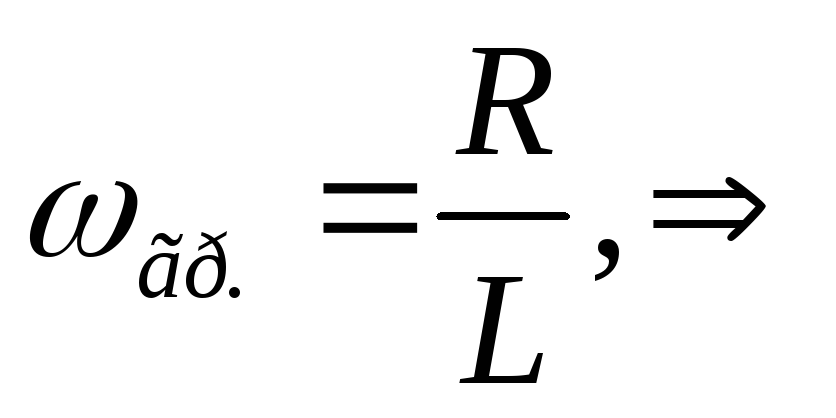
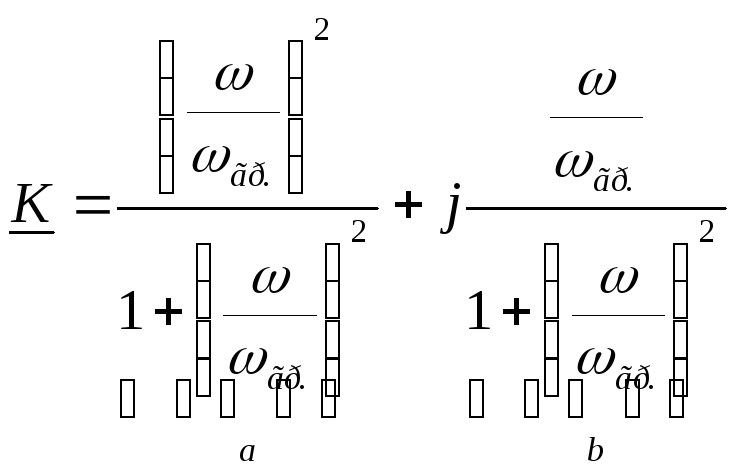
Воспользовавшись формулой 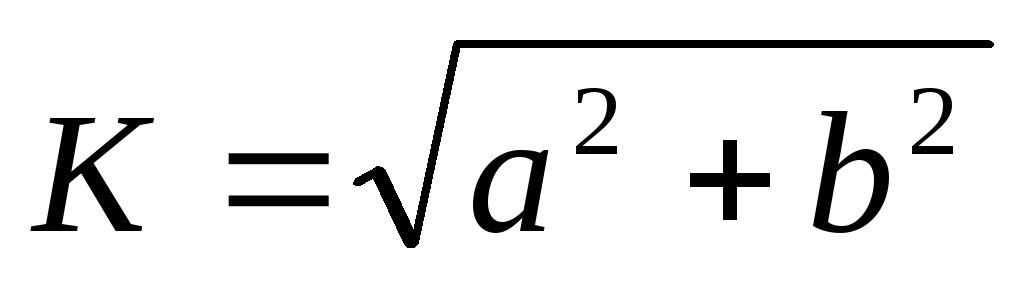 ,
получим передаточную АЧХ цепиRL:
,
получим передаточную АЧХ цепиRL:
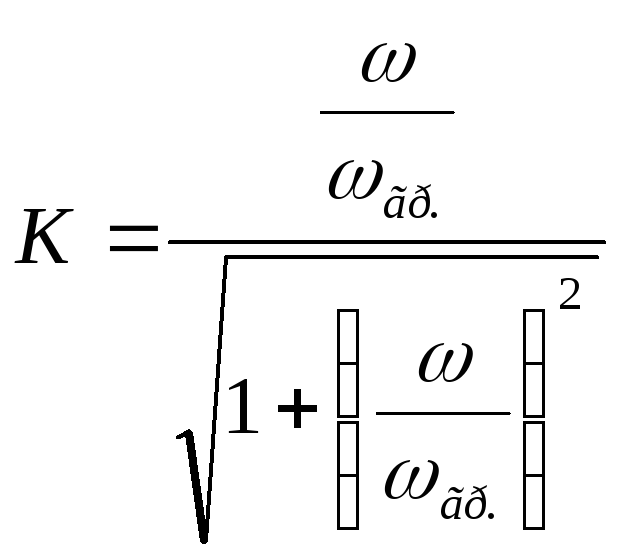 — формула передаточной АЧХ цепиRLсLна выходе
— формула передаточной АЧХ цепиRLсLна выходе

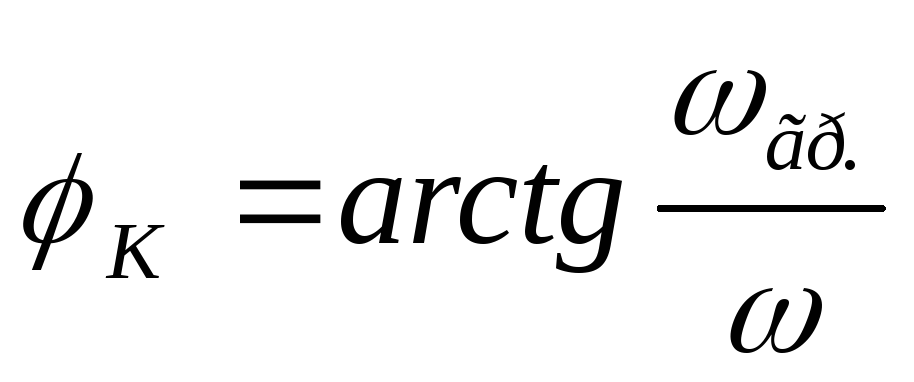 — формула передаточной ФЧХ цепиRLсLна выходе
— формула передаточной ФЧХ цепиRLсLна выходе
Зададимся:
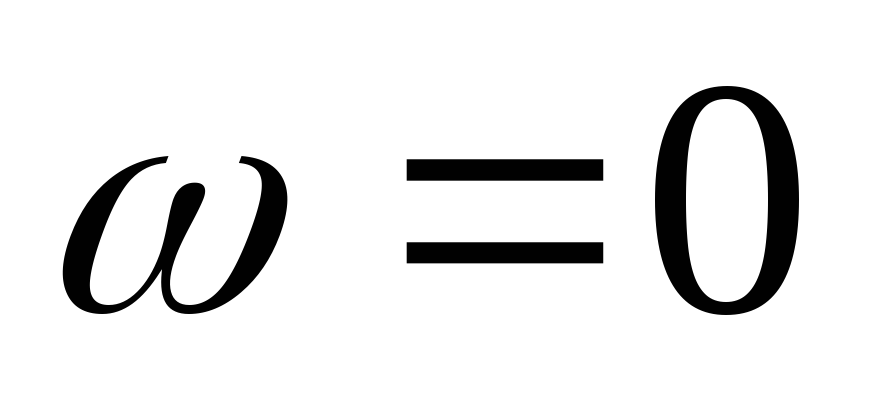
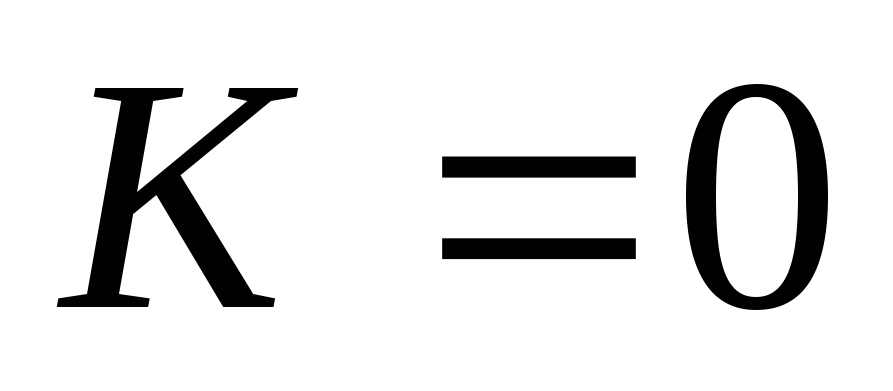
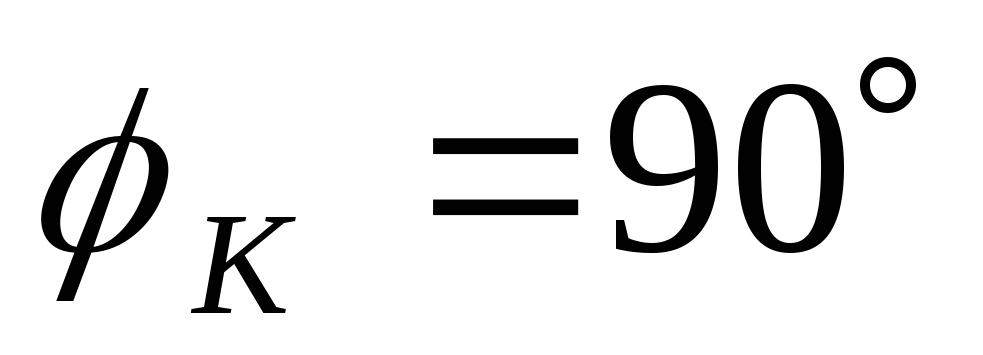
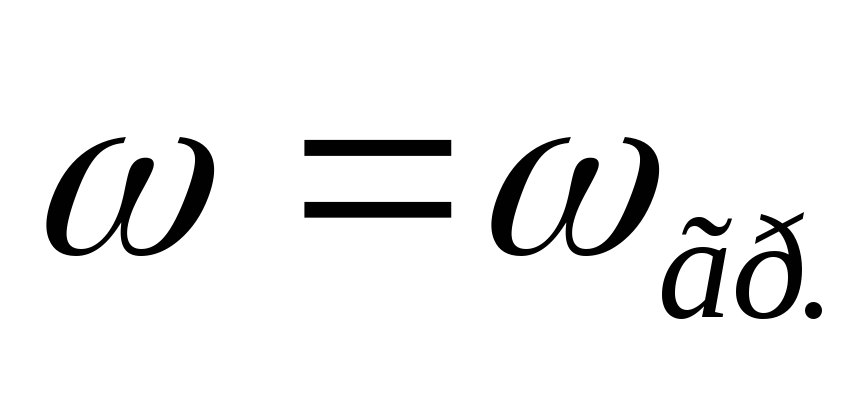
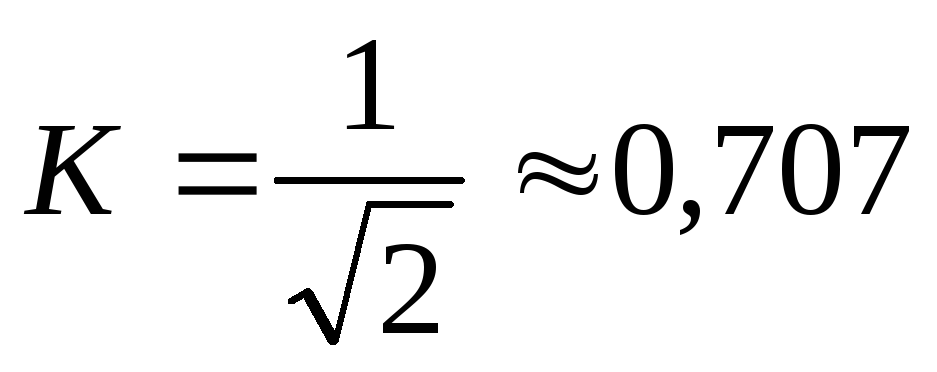
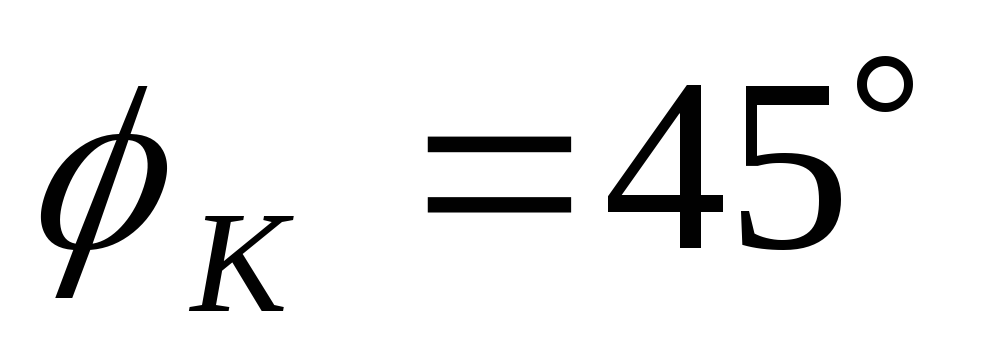
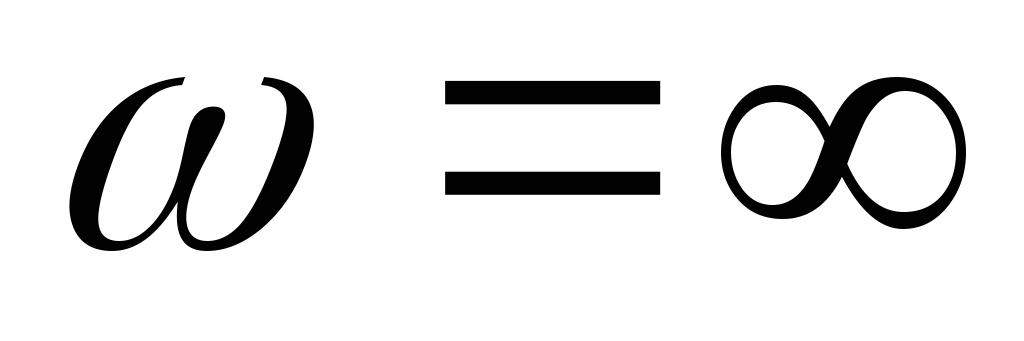

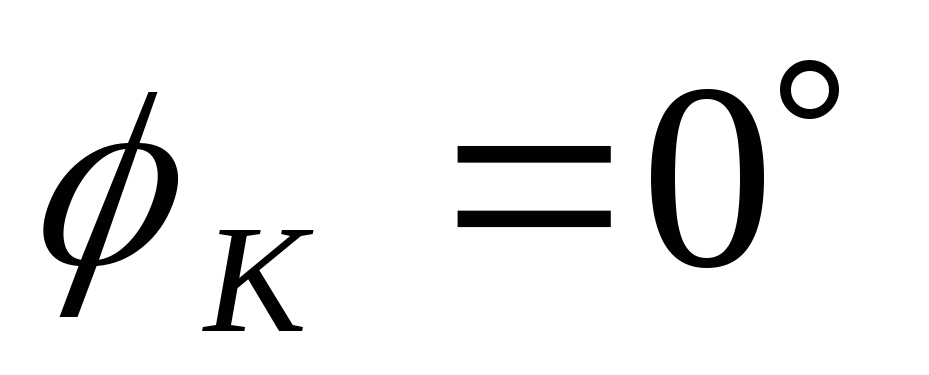


Построим качественно передаточную АЧХ для RL цепи c R на выходе:
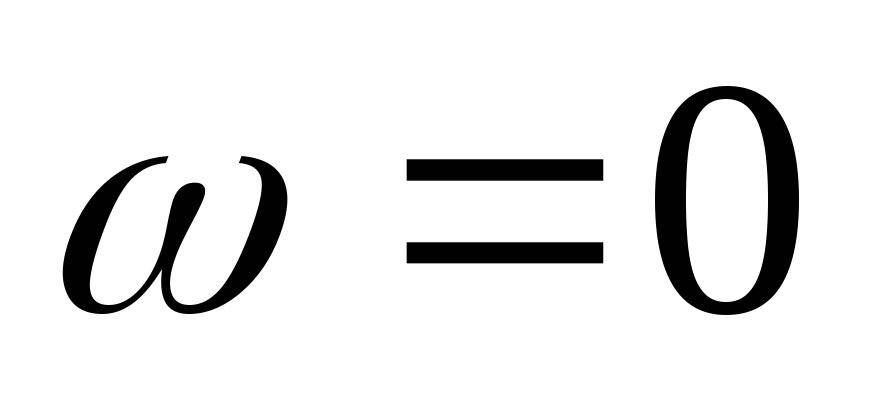
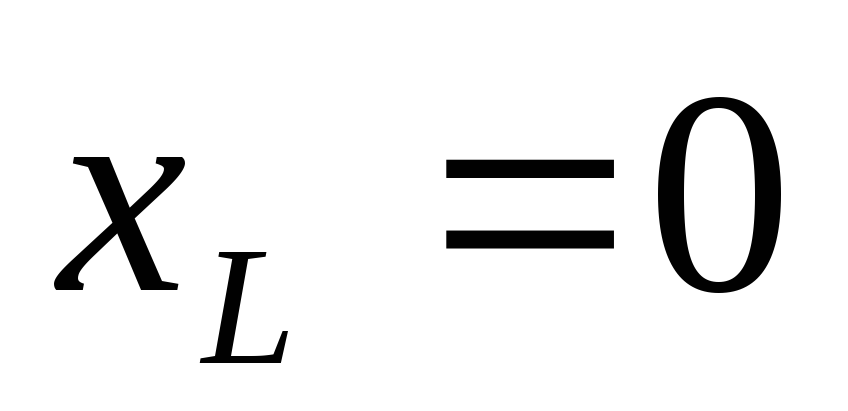
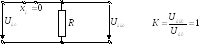

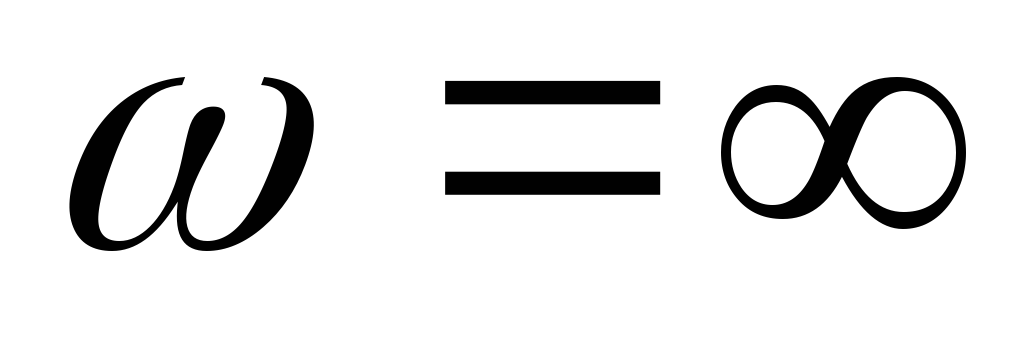

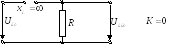
Вопрос 43. Передаточные АЧХ и ФЧХ RC неразветвлённых и разветвлённых цепей. Определение. Построение передаточных характеристик.
Понятие передаточных АЧХ и ФЧХ рассмотрено в предыдущем вопросе (см. вопрос 42).
Передаточные характеристики цепи RC


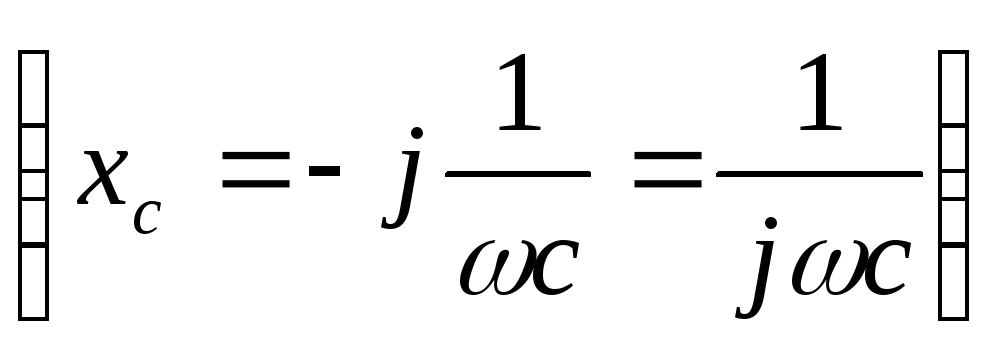
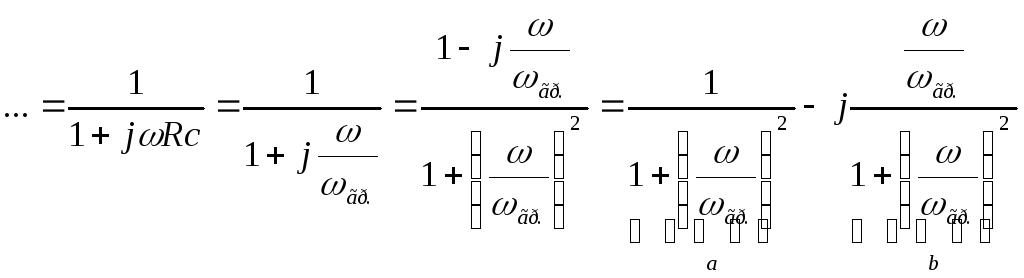
Воспользовавшись формулой 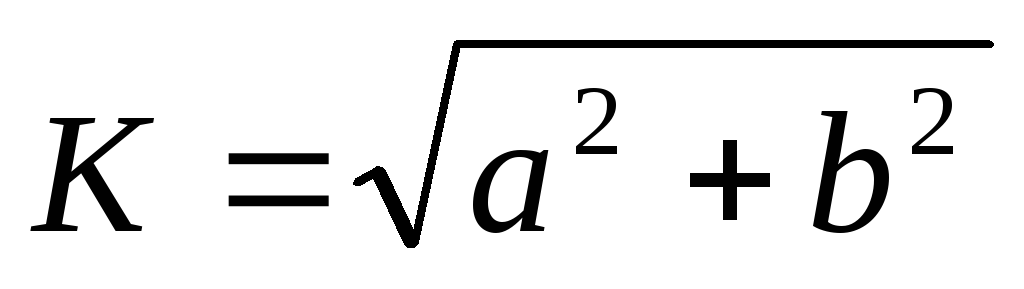 ,
получаем передаточную АЧХ цепиRCс конденсатором на выходе:
,
получаем передаточную АЧХ цепиRCс конденсатором на выходе:
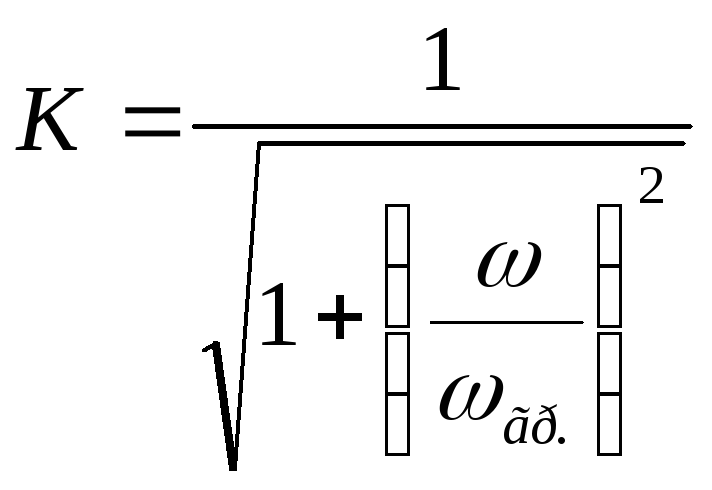 — формула передаточной АЧХ цепиRCсCна выходе
— формула передаточной АЧХ цепиRCсCна выходе
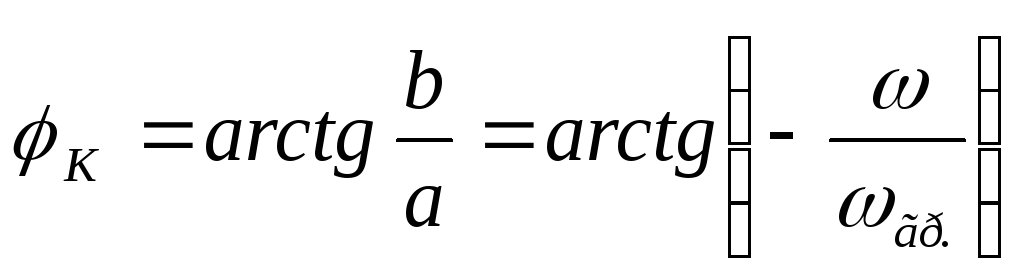
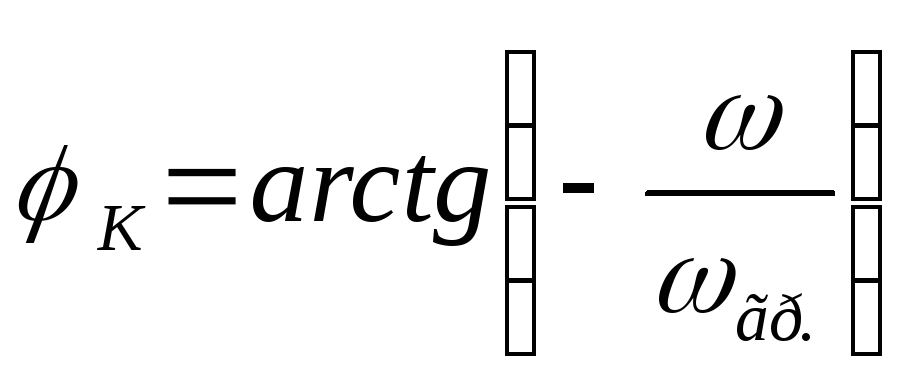 — формула передаточной ФЧХ цепиRCсCна выходе
— формула передаточной ФЧХ цепиRCсCна выходе
Зададимся:

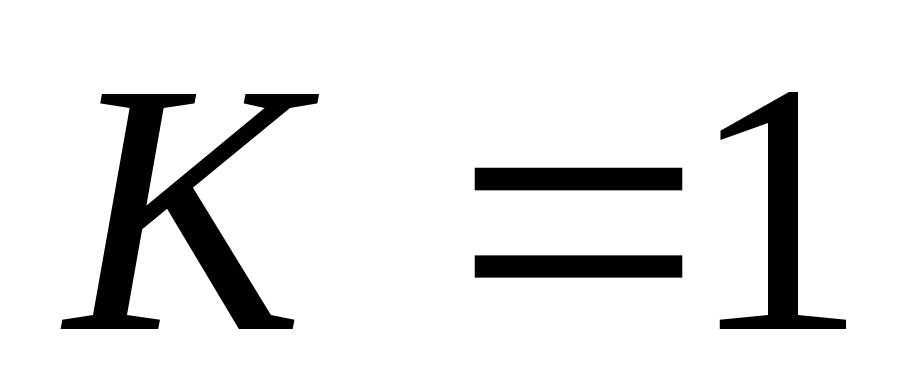
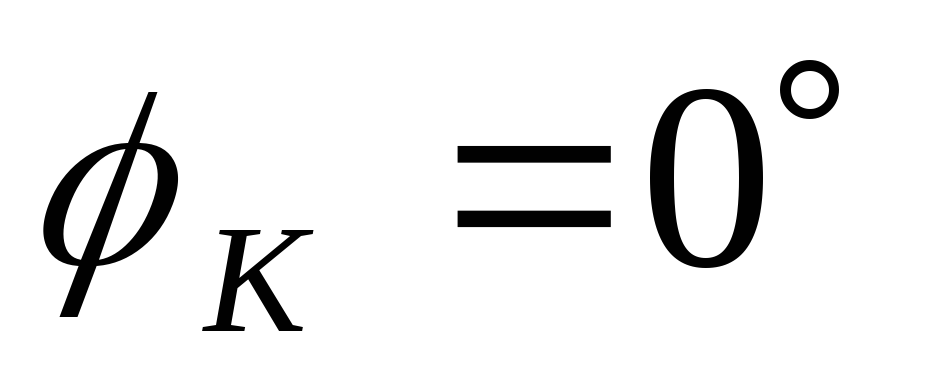
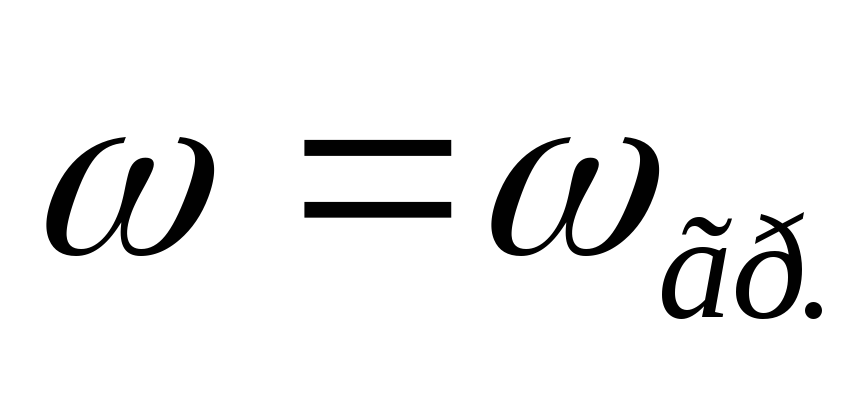
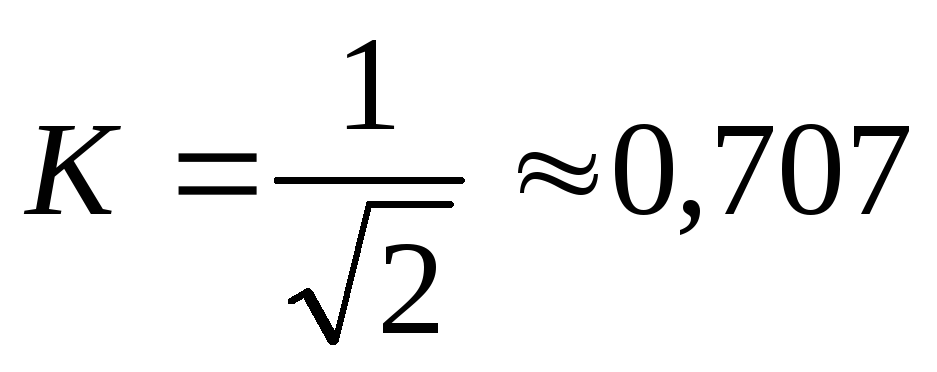
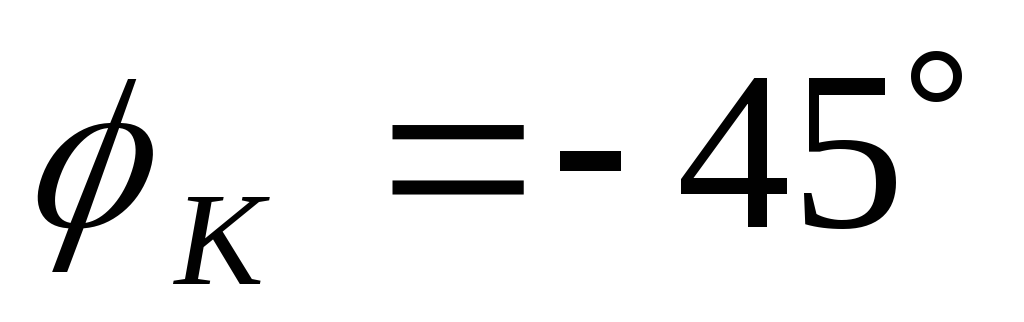
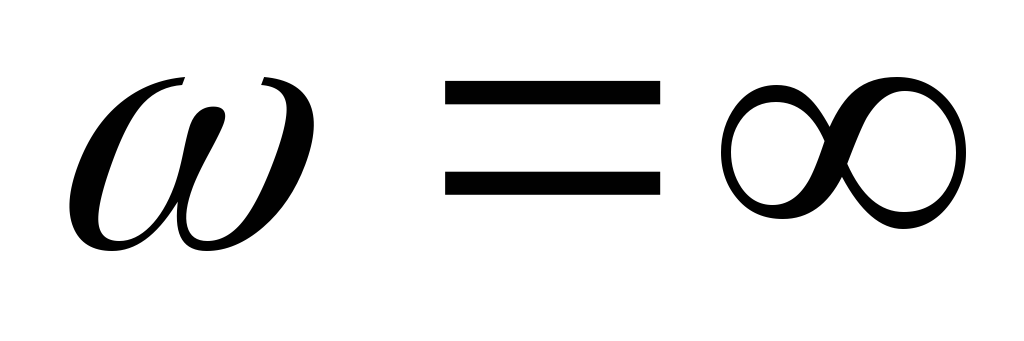
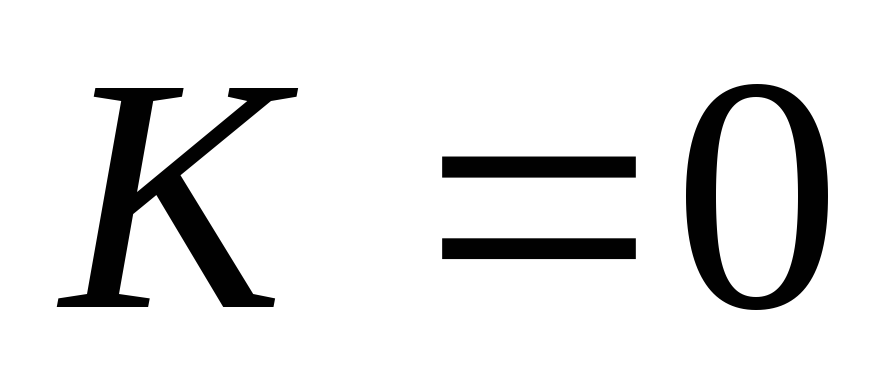
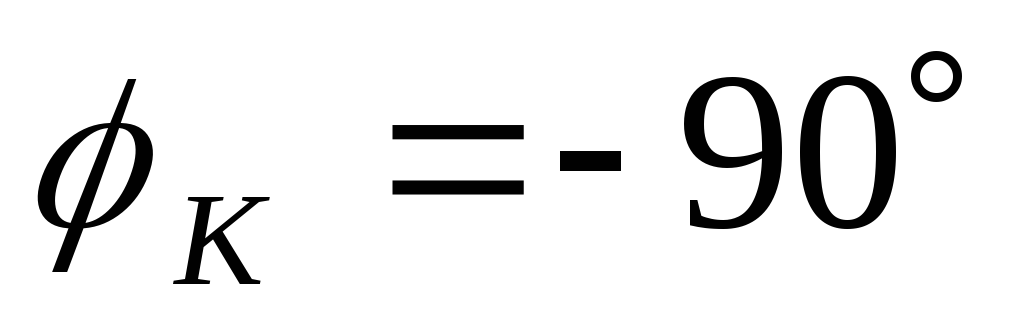


Вывод:передаточная ФЧХ цепиRCимеет линейный участок на частотах от 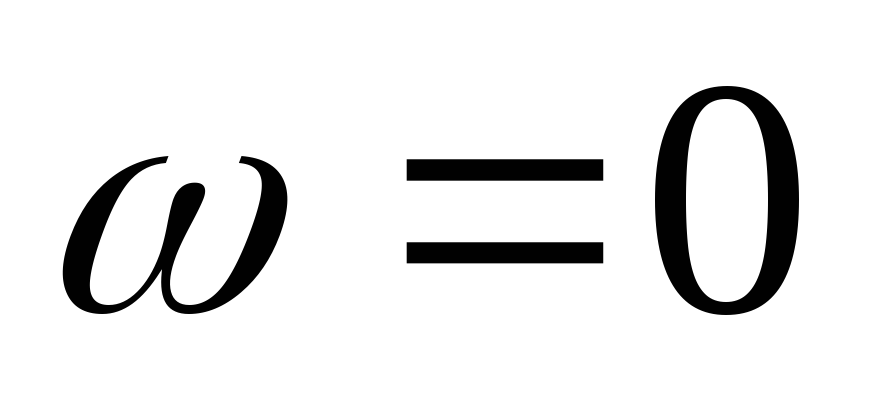 до
до 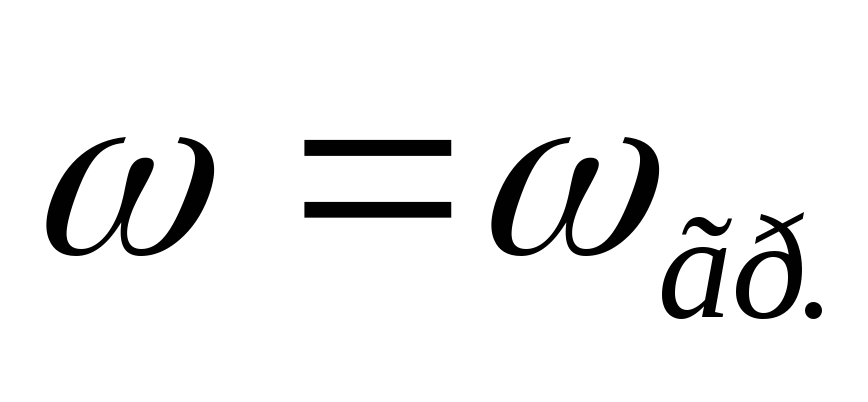 .
.
Вывод (к вопросам 42 – 43): на
граничной частоте в цепях первого
порядка 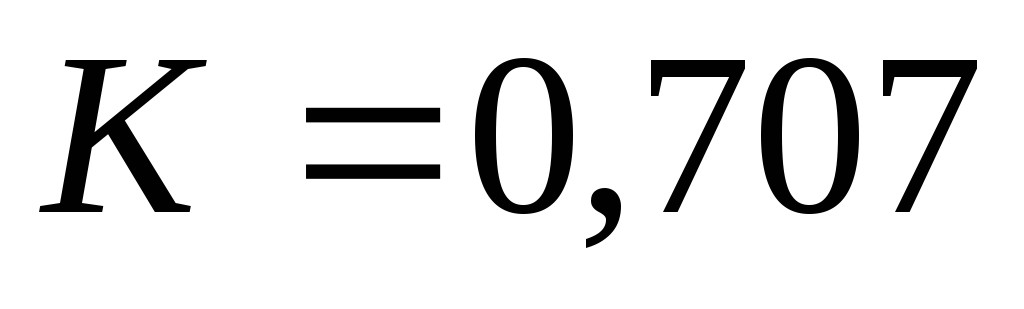 ,
, 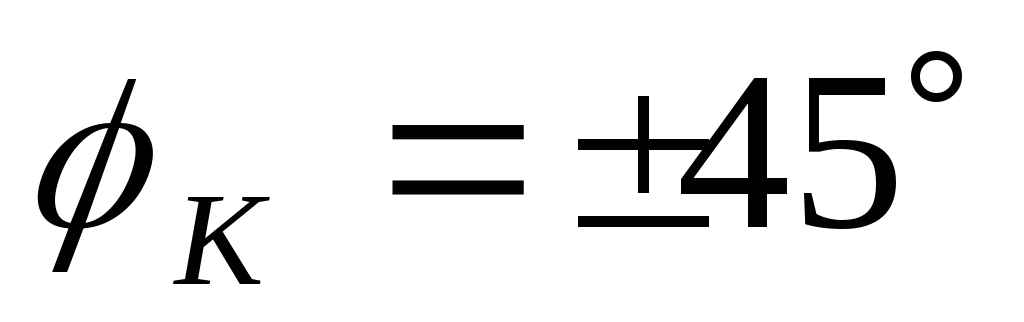 .
.
Вопрос 44.Поверхностный эффект. Явление взаимной индукции. Физический смысл ЭДС взаимной индукции, взаимная индуктивность.
Возьмём две катушки и расположим их близко одна около другой. По первой катушке пропустим переменный ток:

Часть магнитного потока ( )
пронизывает витки второй. Это поток
взаимоиндукции. Этот поток наводит на
концах второй катушки ЭДС, которая
называется ЭДС взаимной индукции. От
этой ЭДС потечёт ток взаимной индукции.
)
пронизывает витки второй. Это поток
взаимоиндукции. Этот поток наводит на
концах второй катушки ЭДС, которая
называется ЭДС взаимной индукции. От
этой ЭДС потечёт ток взаимной индукции.
Явление возникновения ЭДС во второй катушке при изменении тока в первой называется явлением взаимной индукции. Обозначим:
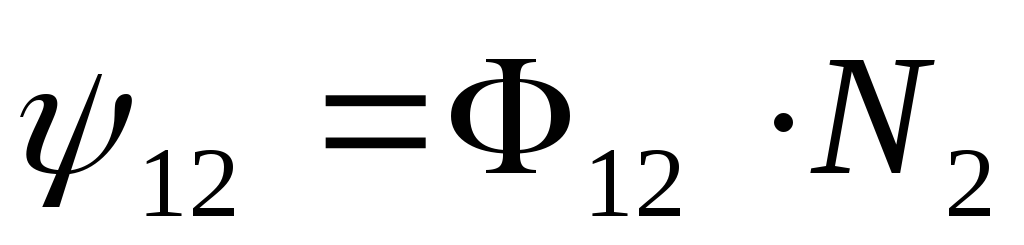 — потокосцепление взаимной индукции;
— потокосцепление взаимной индукции;
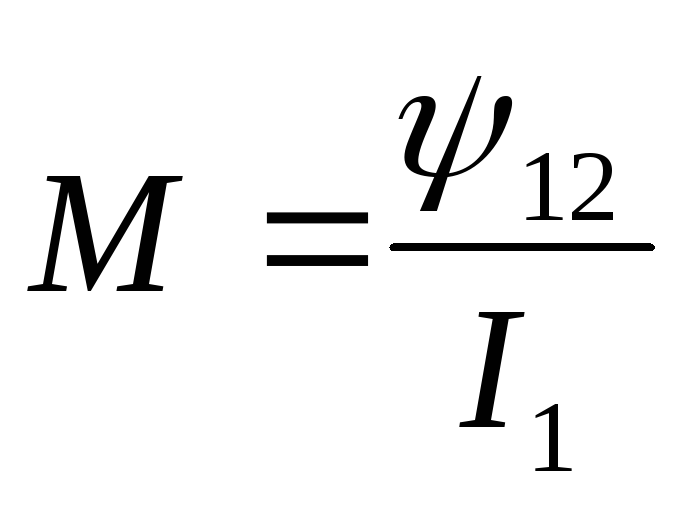 — коэффициент взаимной индукции.
— коэффициент взаимной индукции.

 — основной закон ЭМИ
— основной закон ЭМИ

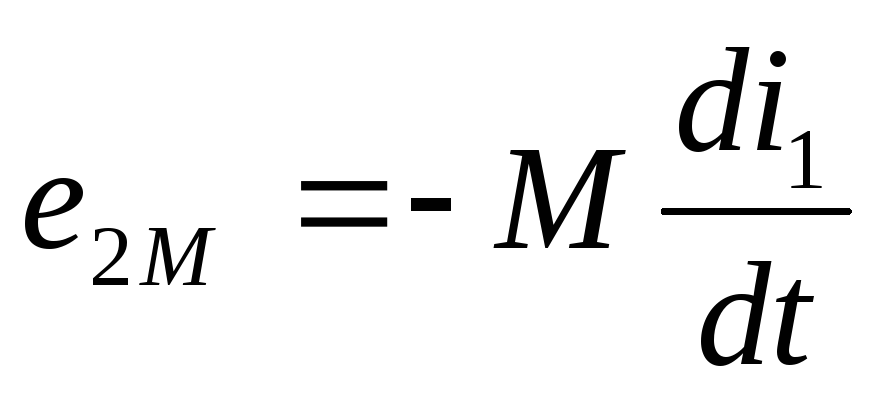
ЭДС взаимоиндукции во второй катушке пропорциональна скорости изменения тока в первой.
ПРОСТЫЕ RLC-ЦЕПИ — ПРОСТАЯ RL-ЦЕПЬ
Страница 4 из 4
ПРОСТАЯ RL-ЦЕПЬ
Простая RL-схема представлена на рис. 2.20, а. В последовательно соединенную RL-цепь подключен источник переменного напряжения с выходным напряжением v.
В последовательной цепи ток на всех компонентах одинаковый. Векторная диаграмма для такой цепи на рис. 2.20, 5, соответствует закону Кирхгоффа:
Сумма напряжений равна сумме векторов. Так как напряжение на резисторе всегда совпадает по фазе с током, а на катушке индуктивности запаздывает от тока
Рис. 2.20. Простая RL-цепь: а — схема; б — векторная диаграмма; в — частотная характеристика.
на 90°, то возникает сдвиг по фазе между током и напряжением источника питания ?. Поэтому величина напряжений:
Если предположить, что амплитуда генерируемого источником напряжения одинакова для всех частот, то траектория треугольника напряжений — это дуга с радиусом v.
На низких частотах (f = 0) XL = ?L = 0 (катушка индуктивности представляет из себя короткое замыкание), следовательно, vL = iXL = 0 и v = vR = iR или і = v/R.
На очень высоких частотах (f = ?) XL = ?L = 2 ?fC = ? (катушка индуктивности представляет из себя разрыв цепи), и тогда i = 0, vL = iR = 0 и v = vL. Графики зависимости токов и напряжений от частоты представлены на рис. 2.20, в.
Если выходное напряжение снимать с резистора (рис. 2.21, а), то оно на низких частотах будет такое же, как входное напряжение. Таким образом, можно сделать вывод, что такую RL-схему можно использовать как фильтр низких частот.
Если напряжение снимать с катушки индуктивности (рис. 2.21, б), то на высоких частотах оно будет такое же, как входное напряжение. В таком виде RL-схему можно использовать как фильтр высоких частот.
Используя комплексную алгебру, из уравнения (2.40) получаем:
Отсюда получаем:
Определим отношение выходного и входного напряжений, коэффициент схемы:
Рис. 2.21. Схемы RL-фильтры: а — низкочастотный; б — высокочастотный.
и
А отношение выходного и входного напряжений, коэффициент схемы:
Мы рассмотрели функционирование RL-схемы на частотах ? = 0 и ? = °°.
Теперь посмотрим, как схема работает при R/?L = 1 или ?= ?0 = R/L. При частоте f Q величина сопротивления резистора равна величине реактивного сопротивления катушки индуктивности. Поэтому:
Из векторной диаграммы 2.20, б, и уравнений (2.44) и (2.46) получаем следующие результаты.
Табл. 2.5. Коэффициент RL-фильтров на основных частотах
Задание 2.5
Катушка индуктивности 10 мОм и резистор 10 кОм соединены последовательно.
Рассчитайте частоту приложенного напряжения 10 В к этой цепи, если известно, что фазовый сдвиг между током и напряжением составляет 30°. Определите амплитуду напряжения на катушке индуктивности на этой частоте.


 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту: апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ: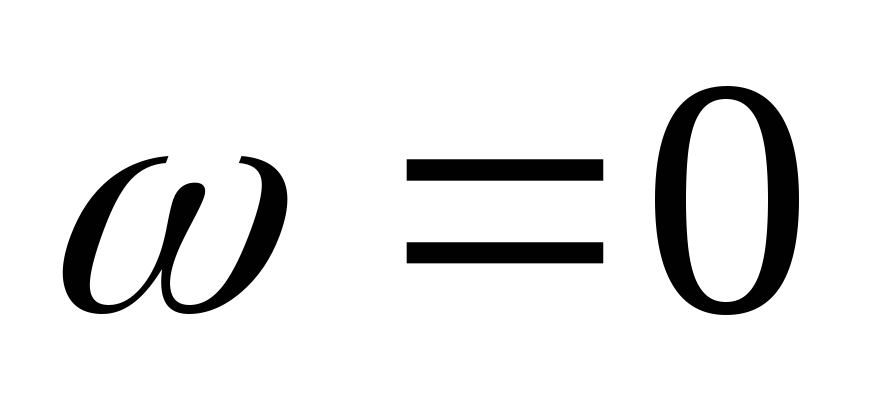 до
до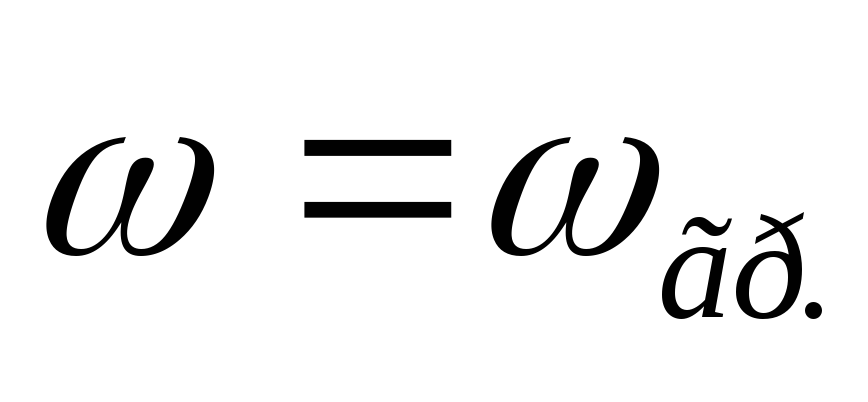 .
.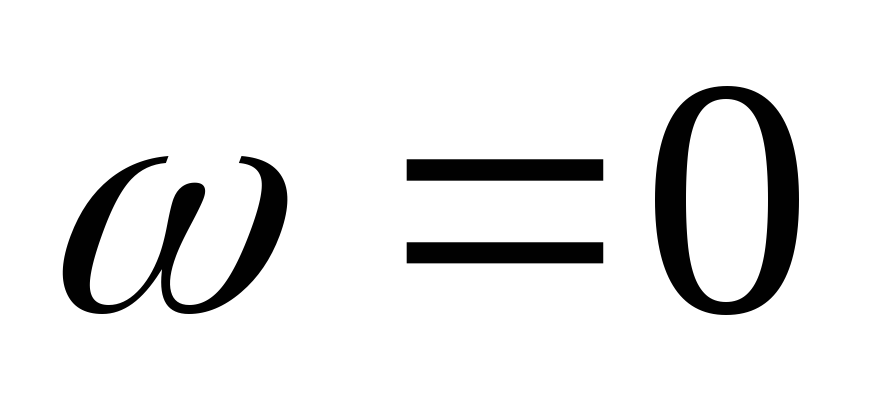
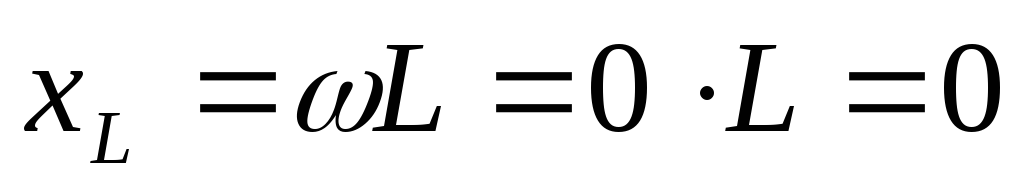

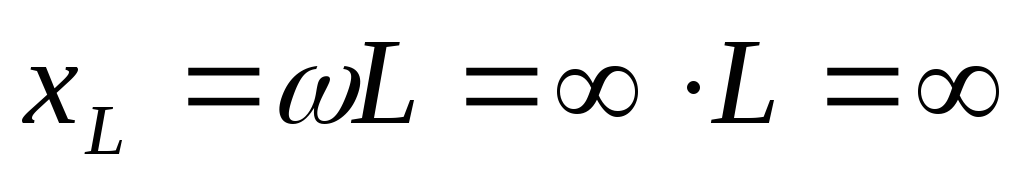
 ыражаем
модуль комплексного входного
сопротивления через граничную частоту:
ыражаем
модуль комплексного входного
сопротивления через граничную частоту: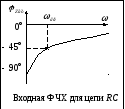 апишем
формулу входной ФЧХ:
апишем
формулу входной ФЧХ: