Методика преподавания темы «Закон всемирного тяготения» в школьном курсе физики

ВВЕДЕНИЕ Ни для кого не секрет, что ничем не удерживаемые тела падают на землю. Это происходит потому, что существует земное тяготение – притяжение тел Землёй. Разные тела притягиваются к ней по-разному. Взгляните на рисунок: одинаковые по размерам гирьки из алюминия и чугуна подвешены к одинаковым пружинам. Однако растяжение пружин различно, поэтому говорят, что вес и масса правой гирьки больше, чем левой. ГЛАВА 1. Явление тяготения и масса тела Ни для кого не секрет, что ничем не удерживаемые тела падают на землю. Это происходит потому, что существует земное тяготение – притяжение тел Землёй. Разные тела притягиваются к ней по-разному. Взгляните на рисунок: одинаковые по размерам гирьки из алюминия и чугуна подвешены к одинаковым пружинам. Однако растяжение пружин различно, поэтому говорят, что вес и масса правой гирьки больше, чем левой. Изучению физической величины «вес» мы уделим особое внимание в теме 3, а пока запомним, что когда речь идёт о притяжении тела к Земле, правильнее употреблять термин «масса».

Оказывается, что тела притягиваются не только к Земле, но и друг к другу! Это можно обнаружить опытами. Упрощённая схема одного из них изображена на рисунке. На очень длинной нити подвешен шарик. Сначала нить висела вертикально. Но, когда слева подкатили большой и очень тяжёлый шар, нить отклонилась. Это произошло из-за притяжения большим шаром маленького шарика. Чтобы этот опыт удался, нить должна быть длиной несколько десятков метров, а масса большого шара – несколько тонн. Взаимное притяжение всех тел в мире имеет собственное название: явление гравитации или явление всемирного тяготения. Гравитационное притяжение любого тела проявляется тем заметнее, чем больше его масса. Поэтому притяжение Земли, масса которой огромна, мы замечаем постоянно, а притяжение других тел можно обнаружить лишь специальным опытом. Гравитационное притяжение Земли (или другой планеты) позволяет нам измерять массу тел с помощью измерительного прибора – весов. Существуют весы различных конструкций, например, пружинные и рычажные, торговые и лабораторные.

Рассмотрим рычажные весы, которые изображены на рисунке. Цифрами

Государственный аппарат и его структура

Государство, его основные признаки и формы правления

Государственный долг РФ

Комментарий к Кодексу об административных правонарушениях РБ

Алиментные обязательства

Закон всемирного тяготения — презентация онлайн

Похожие презентации:

Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов

Газовая хроматография

Геофизические исследования скважин

Искусственные алмазы

Трансформаторы тока и напряжения

Транзисторы

Воздушные и кабельные линии электропередач

Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса

Магнитные аномалии

Нанотехнологии

1.

Презентация по физикена тему
«Закон
всемирного
тяготения
»
Как Исаак Ньютон открыл закон?
На склоне своих дней Исаак Ньютон рассказал, как это произошло: он
гулял по яблоневому саду в поместье своих родителей и вдруг
увидел луну в дневном небе. И тут же на
его глазах с ветки
оторвалось и упало на землю яблоко. Поскольку Ньютон в это самое
время работал над законами движения, он уже знал, что яблоко упало
под воздействием гравитационного поля Земли. Знал он и о том, что
Луна не просто висит в небе, а вращается по орбите вокруг Земли, и,
следовательно, на нее воздействует какая-то сила, которая удерживает
ее от того, чтобы сорваться с орбиты и улететь по прямой прочь, в
открытый космос. Тут ему и пришло в голову, что, возможно, это одна
и та же сила заставляет и яблоко падать на землю, и Луну оставаться на
околоземной орбите. Это был примерно 1665 год, тогда он только
высказал предположение.
В последующие годы Ньютон пытался найти
физическое объяснение законам движения планет
открытых астрономом И. Кеплером в начале XVII
века, и дать количественное выражение для
гравитационных сил. Зная как движутся планеты,
Ньютон хотел определить, какие силы на них
действуют. Такой путь носит название обратной
задачи механики. Если основной задачей механики
является определение координат тела известной
массы и его скорости в любой момент времени по
известным силам, действующим на тело, и заданным
начальным условиям (прямая задача механики), то
при решении обратной задачи необходимо
определить действующие на тело силы, если известно,
как оно движется. Решение этой задачи и привело
Ньютона к открытию закона всемирного тяготения.
Это был примерно 1682 год.

4. Закон

Тела притягиваются друг к другу
силой, модуль которой пропорционален
поизведению их масс и обратно
пропорционален квадрату расстояния
между ними
G(же) – гравитационная постоянная
Независимо друг от друга А.Клеро и
Ж.Даламбер, занимающиеся исследованием в
области ньютоновской механики и теории
тяготения, пришли к одинаковому выводу о
том, что теория Ньютона не способна
объяснить движение перигея Луны и требует
внесения поправок. Такой путь, как небольшая
поправка А.Клеро, подсказал еще сам Ньютон:

7. Самые известные и важные законы в физике, без которых не обойтись в нашем современнном мире, были сформулированы и объяснены

Ньютоном.

8. Факты:

1.
2.
3.
4.
Паление тел на землю
Приливы и отливы
Движение Земли вокруг Солнца
Движение Луны вокруг Земли

9. Применение закона:

1.
2.
Закономерности движения
планет и их спутников
Космонавтика. Расчет движения
спутников.

10. Пределы применимости:

Для материальных точек
Шары
Для шара большого радиуса и тела

11. Гравитационное поле:

присуще всем телам, имеющим
массу
зависит от масс
взаимодействующих сил
зависит от расстояния между
центрами масс тел
переносится гипотетической
частицей — гравитоном

12. Интересно…

Сила тяготения обладает очень интересными,
необычными свойствами. Для нее не существует
никаких преград. Она действует между телами,
разделенными безвоздушным пространством и
находящимися как угодно далеко друг от друга.
Тяготение не поглощается межзвездной средой, не
ослабевает, когда на его пути встречаются какие-либо
тела. Например, в моменты лунных затмений между
Солнцем и Луной находится Земля, которая могла бы
преградить путь силе тяготения между Солнцем и
Луной так же, как лучам света. Это повлияло бы на
движение Луны. Однако такое влияние не
обнаруживается.
Притяжение двух масс
Мы видали много раз
Как привязанные где-то,
К Солнцу тянутся планеты
Опыт Кавендиша доказывает закон. Кавендиш положил
на один конец аптечных весов тело небольших
размеров, а на другой гирьку такой же массы как и
тело, уравняв весы. К телу он поднес свинцовый шар
массой 6000 кг. Тело начало притягиваться к шару,
при этом нарушилось равновесие весов
Существуют много других опытов, доказывающих закон
Луна каждые 24 часа 50 минут вызывает приливы не только в океанах, но
и в коре Земли, и в атмосфере. Под воздействием приливных сил
литосфера вытягивается примерно на полметра. Тяготение Луны
вызывает также прецессию земной оси. Из-за океанских приливов и
отливов возникает сила трения между литосферой и гидросферой,
замедляющая скорость вращения Земли вокруг своей оси. Каждое
столетие продолжительность суток увеличивается приблизительно
на 0,002 с. Два миллиарда лет назад продолжительность земных суток
составляла всего 10 часов, а в отдаленном будущем они будут равны
одному месяцу. Уже теперь благодаря приливным силам Луна постоянно
обращена к Земле одной и той же стороной. Кроме того, притяжение
приливных выступов Земли увлекает Луну по орбите вперед, в
результате чего она удаляется от Земли со скоростью около 3 см в год.
Именно приливные силы, возникшие в гравитационном поле Юпитера,
разорвали ядро кометы Шумейкеров – Леви на множество частей, после
чего несколько лет назад она упала на Юпитер. Закон всемирного
тяготения справедлив только в рамках классической механики. Он, повидимому, нарушается на малых расстояниях (порядка планковской
длины). В 1916 году Альберт Эйнштейн в теории относительности
показал, что свойства пространства и времени изменяются вблизи
больших масс.

16. По гипотезе Ньютона между всеми телами Вселенной действуют силы притяжения (гравитационные силы), направленные по линии,

соединяющей центры масс. У тела в виде однородного шара центр
масс совпадает с центром шара.
При удалении от поверхности Земли сила земного
тяготения и ускорение свободного падения изменяются
обратно пропорционально квадрату расстояния r до
центра Земли. Рисунок иллюстрирует изменение силы
тяготения, действующей на космонавта в космическом
корабле при его удалении от Земли. Сила, с которой
космонавт притягивается к Земле вблизи ее
поверхности, принята равной 700 Н.
В настоящее время ученые занимаются
разработкой нового эксперимента, который,
по их расчетам, позволит более точно
установить предел справедливости закона
всемирного тяготения.
Но все-таки основа, формулировка и самое
главное – идея принадлежит Исааку
Ньютону

English     Русский Правила

Закон всемирного тяготения Ньютона – University Physics Volume 1

Гравитация

Цели обучения

К концу этого раздела вы сможете:

• Перечислить важные вехи в истории гравитации
• Вычислите гравитационную силу между двумя точечными массами
• Оценить гравитационную силу между наборами масс

Сначала мы рассмотрим историю изучения гравитации, уделив особое внимание тем явлениям, которые на протяжении тысячелетий вдохновляли философов и ученых на поиск объяснения. Затем мы исследуем простейшую форму закона всемирного тяготения Ньютона и то, как его применять.

История гравитации

Древние философы задавались вопросом, почему объекты естественным образом имеют тенденцию падать на землю. Аристотель (384–322 гг. до н. э.) считал, что природа камней — искать Землю, а природа огня — искать Небеса.

Брахмагупта (598–665 гг. н. э.) постулировал, что Земля представляет собой сферу и что объекты обладают естественным сродством к ней, падая к центру, где бы они ни находились.

Движение Солнца, нашей Луны и планет также изучалось на протяжении тысячелетий. Эти движения были описаны с поразительной точностью Птолемеем (90–168 г. н.э.), чей метод эпициклов описывал пути планет как круги внутри кругов. Однако мало свидетельств того, что кто-либо связывал движение астрономических тел с движением объектов, падающих на Землю, — до семнадцатого века.

Николай Коперник (1473–1543) обычно считается первым, кто бросил вызов геоцентрической (землецентричной) системе Птолемея и предложил гелиоцентрическую систему, в которой Солнце находится в центре Солнечной системы. Эта идея была поддержана невероятно точными измерениями движения планет невооруженным глазом Тихо Браге и их анализом Иоганном Кеплером и Галилео Галилеем. Кеплер показал, что движение каждой планеты является эллипсом (первый из трех его законов, обсуждаемых в Кеплеровских законах движения планет), а Роберт Гук (тот самый Гук, который сформулировал закон Гука для пружин) интуитивно предположил, что эти движения происходят из-за планеты притягиваются к Солнцу.

Однако именно Исаак Ньютон связал ускорение объектов у поверхности Земли с центростремительным ускорением Луны на ее орбите вокруг Земли.

Наконец, в «Теории гравитации Эйнштейна» мы рассматриваем общую теорию относительности, предложенную Альбертом Эйнштейном в 1916 году. Его теория исходит из совершенно иной точки зрения, в которой гравитация является проявлением массового искривления пространства и времени. Последствия его теории породили множество замечательных предсказаний, практически все из которых были подтверждены в течение многих десятилетий после публикации теории (включая измерение гравитационных волн от слияния двух черных дыр в 2015 году). 9{2}[/latex] раз меньше, чем г . Он мог бы объяснить это, постулируя, что между любыми двумя объектами существует сила, величина которой определяется произведением двух масс, деленным на квадрат расстояния между ними. Теперь мы знаем, что этот закон обратных квадратов вездесущ в природе и является функцией геометрии для точечных источников.

{2}[/латексу]. В последующих главах мы видим эту же форму в электромагнитной силе. 9}{r}}_{12}[/latex] — это единичный вектор, который указывает от объекта 1 к объекту 2.

Как показано на (рис.), [latex]{\stackrel{\to }{F}} _{12}[/latex] вектор указывает от объекта 1 к объекту 2 и, следовательно, представляет силу притяжения между объектами. Равная, но противоположная сила [латекс]{\stackrel{\to}}{F}}_{21}[/латекс] — это сила, действующая на объект 2 со стороны объекта 1.

Гравитационная сила действует вдоль линии, соединяющей центры масса двух предметов.

Эти равные, но противоположные силы отражают третий закон Ньютона, который мы обсуждали ранее. Обратите внимание, что, строго говоря, (Рисунок) относится к точечным массам — вся масса находится в одной точке. Но это в равной степени относится к любым сферически-симметричным объектам, где r — расстояние между центрами масс этих объектов. Во многих случаях он работает достаточно хорошо для несимметричных объектов, если расстояние между ними велико по сравнению с их размером, и мы принимаем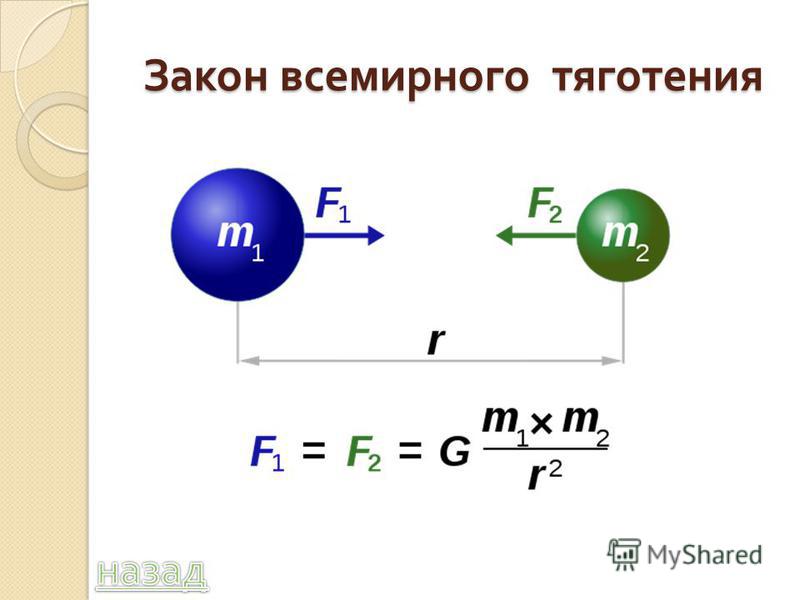

r как расстояние между центрами масс каждого тела.

Эксперимент Кавендиша

Спустя столетие после того, как Ньютон опубликовал свой закон всемирного тяготения, Генри Кавендиш определил константу пропорциональности G , проведя кропотливый эксперимент. Он сконструировал устройство, подобное изображенному на (рис.), в котором на проволоке подвешены небольшие грузы. Находясь в равновесии, два фиксированных больших тела помещаются симметрично рядом с меньшими. Гравитационное притяжение создает кручение (скручивание) несущей проволоки, которое можно измерить. 9{2}[/латекс]. Слово «универсальный» указывает на то, что ученые считают, что эта константа применима к массам любого состава и что она одинакова во всей Вселенной. Значение G — невероятно маленькое число, показывающее, что сила гравитации очень слаба. Притяжение между массами размером с наше тело или даже объектами размером с небоскреб невероятно мало. Например, два груза массой 1,0 кг, расположенные на расстоянии 1,0 м друг от друга, создают силу [латекс]6,7\phantom{\rule{0,2em}{0ex}}×\phantom{\rule{0,2em}{0ex}}{10} ^{-11}\phantom{\rule{0. 2em}{0ex}}\text{N}[/latex] друг на друга. Это вес типичного пыльцевого зерна.

Кавендиш использовал подобный аппарат для измерения гравитационного притяжения между двумя сферами ( м ), подвешенными на проволоке, и двумя неподвижными сферами ( м ). Это обычный эксперимент, проводимый в студенческих лабораториях, но он довольно сложный. Проезжающие мимо лаборатории грузовики могут создавать вибрации, подавляющие гравитационные силы.

Хотя гравитация является самой слабой из четырех фундаментальных сил природы, ее притягательная природа — это то, что удерживает нас на Земле, заставляет планеты вращаться вокруг Солнца, а Солнце — вокруг нашей галактики и связывает галактики в скопления, начиная от нескольких до миллионов. Гравитация — это сила, формирующая Вселенную.

Стратегия решения задач: Закон всемирного тяготения Ньютона

Чтобы определить движение, вызванное силой гравитации, выполните следующие действия:

1. Определите две массы, одну или обе, для которых вы хотите найти силу гравитации.
2. Нарисуйте диаграмму свободного тела, изобразив силу, действующую на каждую массу, и указав расстояние между их центрами масс.
3. Примените второй закон Ньютона к каждой массе, чтобы определить, как она будет двигаться.

Столкновение на орбите
Рассмотрим два почти сферических корабля «Союз «, находящихся на орбите вокруг Земли, каждый массой 9000 кг и диаметром 4,0 м. Первоначально они покоятся друг относительно друга на расстоянии 10,0 м от центра к центру. (Как мы увидим в законах движения планет Кеплера, обе планеты вращаются вокруг Земли с одинаковой скоростью и взаимодействуют почти так же, как если бы они были изолированы в глубоком космосе.) Определите гравитационную силу между ними и их начальное ускорение. Оцените, сколько времени им потребуется, чтобы дрейфовать вместе, и насколько быстро они двигаются при столкновении.

Стратегия
Мы используем закон тяготения Ньютона, чтобы определить силу между ними, а затем используем второй закон Ньютона, чтобы найти ускорение каждого из них. {2}\frac{\left(9){4}\phantom{\rule{0.2em}{0ex}}\text{s}[/latex] или около 4,6 часов.

Значение
Эти расчеты, включая начальную силу, являются только приблизительными, поскольку транспортные средства, вероятно, не являются сферически симметричными. Но вы можете видеть, что сила невероятно мала. Астронавты должны привязывать себя при выполнении работы даже за пределами массивной Международной космической станции (МКС), как на (Рисунок), потому что гравитационное притяжение не может спасти их даже от малейшего отталкивания от станции.

На этой фотографии изображен Эд Уайт, привязанный к космическому шаттлу во время выхода в открытый космос. (кредит: НАСА)

Проверьте свое понимание Что происходит с силой и ускорением, когда транспортные средства падают вместе? Какой будет наша оценка скорости при столкновении выше или ниже реальной скорости? И, наконец, что произошло бы, если бы массы не были одинаковыми? Будет ли сила на каждом из них одинаковой или разной? Как у них с ускорением?

Сила тяжести, действующая на каждый объект, увеличивается пропорционально квадрату обратно пропорционального расстояния, когда они падают вместе, и, следовательно, увеличивается ускорение. Например, если расстояние уменьшить вдвое, сила и ускорение увеличатся в четыре раза. Наше среднее является точным только для линейно возрастающего ускорения, тогда как на самом деле ускорение увеличивается с большей скоростью. Так что наша расчетная скорость слишком мала. Согласно третьему закону Ньютона (силы действия-противодействия) сила притяжения между любыми двумя объектами должна быть одинаковой. Но ускорений не будет, если они будут иметь разные массы.

Эффект гравитации между двумя объектами с массами порядка этих космических аппаратов действительно мал. Тем не менее, влияние гравитации с Земли на вас настолько велико, что падение на Землю всего на несколько футов может быть опасным. Мы исследуем силу гравитации у поверхности Земли в следующем разделе.

Притяжение между галактиками
Найдите ускорение нашей галактики, Млечного Пути, из-за ближайшей галактики сопоставимого размера, галактики Андромеды ((Рисунок)). Приблизительная масса каждой галактики составляет 800 миллиардов солнечных масс (солнечная масса — это масса нашего Солнца), а расстояние между ними составляет 2,5 миллиона световых лет. {30}\ phantom{\rule{0.2em}{0ex}}\text{kg}[/latex], а световой год — это расстояние, которое свет проходит за один год, [latex]9{13}\phantom{\rule{0.2em}{0ex}}\text{m}[/latex] ближе. Это на девять порядков меньше начального расстояния между ними. В действительности такие движения редко бывают простыми. Эти две галактики вместе с примерно 50 другими более мелкими галактиками гравитационно связаны с нашим местным скоплением. Наше локальное скопление гравитационно связано с другими скоплениями в так называемом сверхскоплении. Все это является частью великого космического танца, являющегося результатом гравитации, как показано на (Рисунок).

Основываясь на результатах этого примера, а также на том, что астрономы наблюдали в других местах Вселенной, наша галактика столкнется с галактикой Андромеды примерно через 4 миллиарда лет. (кредит: НАСА)

Резюме

• Все массы притягиваются друг к другу с гравитационной силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.
• Сферически симметричные массы можно рассматривать так, как если бы вся их масса находилась в центре.
• С несимметричными объектами можно обращаться так, как если бы их масса была сосредоточена в их центре масс, при условии, что расстояние до них от других масс велико по сравнению с их размером.

Концептуальные вопросы

Действие на расстоянии, такое как гравитация, когда-то считалось нелогичным и, следовательно, неверным. Что является конечным определителем истины в науке и почему это действие на расстоянии было в конечном счете принято?

Истина в последней инстанции — экспериментальная проверка. Теория поля была разработана, чтобы помочь объяснить, как действует сила без контакта объектов как с гравитационными, так и с электромагнитными силами, действующими со скоростью света. Только с двадцатого века мы смогли измерить, что сила не передается немедленно.

В законе всемирного тяготения Ньютон предположил, что сила пропорциональна произведению двух масс ([латекс]~{м}_{1}{м}_{2}[/латекс]). Хотя все научные предположения должны быть проверены экспериментально, можете ли вы привести аргументы, почему это должно быть так? (Возможно, вы захотите рассмотреть простые примеры, в которых любая другая форма приведет к противоречивым результатам.)

Задачи

Оцените величину гравитационной силы между двумя сферическими стальными шарами массой 5 ​​кг, расстояние между центрами которых составляет 15 см. 9{-8}\phantom{\rule{0.2em}{0ex}}\text{N}[/latex]

Оцените силу притяжения между двумя борцами сумо массами 220 и 240 кг, когда они обнимаются и их центры находятся на расстоянии 1,2 м друг от друга.

В астрологии большое внимание уделяется положению планет в момент рождения. Единственная известная сила, с которой планета действует на Землю, — гравитационная. (a) Вычислите гравитационную силу, действующую на ребенка весом 4,20 кг со стороны отца весом 100 кг, находящегося на расстоянии 0,200 м при рождении (он оказывает помощь, поэтому он находится близко к ребенку). (b) Рассчитайте силу Юпитера, действующую на ребенка, если он находится на самом близком расстоянии от Земли, несколько [латекс] 6.29{-6}\phantom{\rule{0.2em}{0ex}}\text{N}\hfill \\ \frac{{F}_{\text{f}}}{{F}_{\text{ J}}}=0,521\hfill \end{array}[/latex]

Гора в 10,0 км от человека действует на него с силой гравитации, равной 2,00% его веса. а) Вычислите массу горы. б) Сравните массу горы с массой Земли. в) Что неразумного в этих результатах? (d) Какие посылки являются неразумными или непоследовательными? (Обратите внимание, что точные гравитационные измерения могут легко обнаружить влияние близлежащих гор и изменения в местной геологии.) 9{2}[/латекс]

Глоссарий

Закон всемирного тяготения Ньютона

каждая масса притягивает любую другую массу с силой, пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними, и с направлением вдоль линии, соединяющей центр масс каждого

универсальная гравитационная постоянная

постоянная, представляющая силу гравитационной силы, которая считается одинаковой во всей Вселенной

Видео-урок: Закон всемирного тяготения Ньютона

Стенограмма видео

В этом видео мы будем учиться о законе всемирного тяготения Ньютона. Посмотрим, что говорит этот закон, как он был разработан, и как мы можем применить его на практике. Для начала представьте, что вы жили во времена Исаака Ньютона в 1600-х гг. В это время ученые перед сложной задачей. С одной стороны, благодаря астрономических наблюдений, у них были четкие доказательства того, что планеты, небесные тела они звали их, двигались друг вокруг друга по правильным орбитам.

Исходя из этого, казалось очевидным, что между этими движущимися массами существовало какое-то притяжение. Но с другой стороны, на планете Земля с обычными повседневными массами, не было никакого смысла, чтобы эти массы притягиваются друг к другу, даже если их держать очень близко. Пока что тогда казалось как если бы физические законы управляли массивными телами, небесными телами размером планеты, могут иметь другую форму или просто принципиально отличаться от законы, управляющие повседневными размерами более материальных объектов.

Чтобы увидеть, какими были эти два мира вместе взятых, будет полезно узнать о законе вселенского равенства Ньютона. гравитация. Как гласит история, однажды Исаак Ньютон отдыхал под яблоней, размышляя над всеми этими тайнами. Затем, как он сказал, яблоко падает с дерево, бьет его по голове, и у него появляется грандиозная идея. Есть хороший шанс, что история не точная. Но тем не менее он показывает, как Закон Ньютона связывает обычные предметы, с которыми мы знакомы, с гораздо более крупными объектами. в масштабе размеров нашей планеты или других планет.

Одна из причин, по которой этот закон такой значимым является то, что он действительно универсален. Это относится к любым массам независимо от насколько велики они или малы, и неважно, где они расположены во вселенной. Учитывая масштаб этого развития, замечательно, что в одном простом утверждении можно подвести итог гравитационная сила притяжения между любыми двумя массами. Но это как раз то, что Ньютон с помощью современников сделал. Этот универсальный закон гласит, что гравитационная сила между двумя телами, массой один и массой два, равна их произведение, деленное на квадрат расстояния между ними.

Это основа Ньютона. закон с физической точки зрения. И это значение затем умножается постоянной величиной, называемой большой 𝐺. Это значение, называемое универсальным гравитационная постоянная, была разработана для того, чтобы единицы в целом выражение работать. Там есть своя интересная история разработка. Но прежде чем рассказать эту историю, давайте рассмотрим остальную часть этого универсального закона тяготения. Иногда этот закон, являющийся одним из более узнаваемые уравнения в физике, могут стать для нас настолько знакомыми, что мы упустить из виду то, что делает его особенным. На момент своего развития, хотя этот закон вовсе не был очевиден.

Например, рассмотрим в знаменателе, где мы видим 𝑟 квадрат члена. Это означает, что универсальный закон гравитации есть закон обратных квадратов. Хотя мы видим эти законы через физика, это все еще поразительный результат. Почему один больше 𝑟 в квадрате? Почему не один над 𝑟 в кубе или один выше 𝑟 до 1,99? Или даже почему сила сила тяжести уменьшается с увеличением расстояния? Все альтернативы, которые мы можем подумай о том, что отношения один над 𝑟 в квадрате напоминают нам о том, насколько это особенное закон и как он помогает установить структуру нашей вселенной.

Теперь перейдем к рассмотрению значения массы 𝑚 один и 𝑚 два. Этот закон говорит нам, что если мы имеем два объекта любой формы, если они имеют массу, существует гравитационная сила притяжения между ними. Наши массы могут быть сферами или блоки или крокодилы или атомы. Любые объекты, имеющие массу, соответствуют стандарт и, следовательно, имеют гравитационную силу между ними. Независимо от формы наши два массы, когда мы говорим о расстоянии между ними, мы говорим о расстояние между их центрами масс, где бы эти центры ни находились в сама общая масса.

Теперь, допустим, мы попробуем эксперимент. Что, если мы получим две массы и мы пусть их массы равны ровно одному килограмму, и мы разделяем эти массы на ровно метр? Итак, мы можем видеть, когда мы смотрим на это закон гравитации, что у нас будет уравнение, которое читает гравитационную силу притяжение между этими двумя однокилограммовыми массами равно одному килограмму, умноженному на один килограмм, то есть один килограмм в квадрате, умноженный на один метр в квадрате 𝐺, это гравитационная постоянная.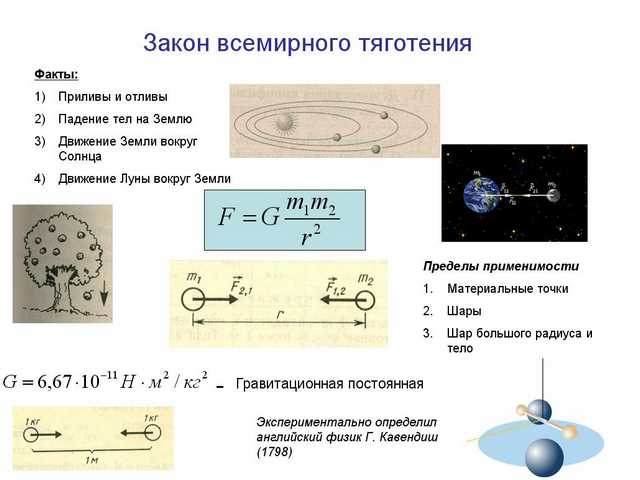

Чтобы показать, почему это нужна гравитационная постоянная, представим на секунду, что ее нет там. Другими словами, пусть он равен один и посмотрим, что мы получим в результате этого расчета. Если бы большой 𝐺 имел это значение без единиц, это означало бы, что гравитационная сила притяжения между этими двумя масса равна одному килограмму на квадратный метр. Но подождите секунду, мы знаем, что сила измеряется в ньютонах и что ньютон имеет базовые единицы килограмм метр на секунду в квадрате. Это означает, что две стороны нашего уравнение не складывается, если мы приравняем большой 𝐺 к единице.

Теперь мы переходим к целому Причина существования гравитационной постоянной в первую очередь. Мы видим, что если его там нет — то есть если он просто равен единице — то все наше выражение для гравитационная сила притяжения не имеет смысла.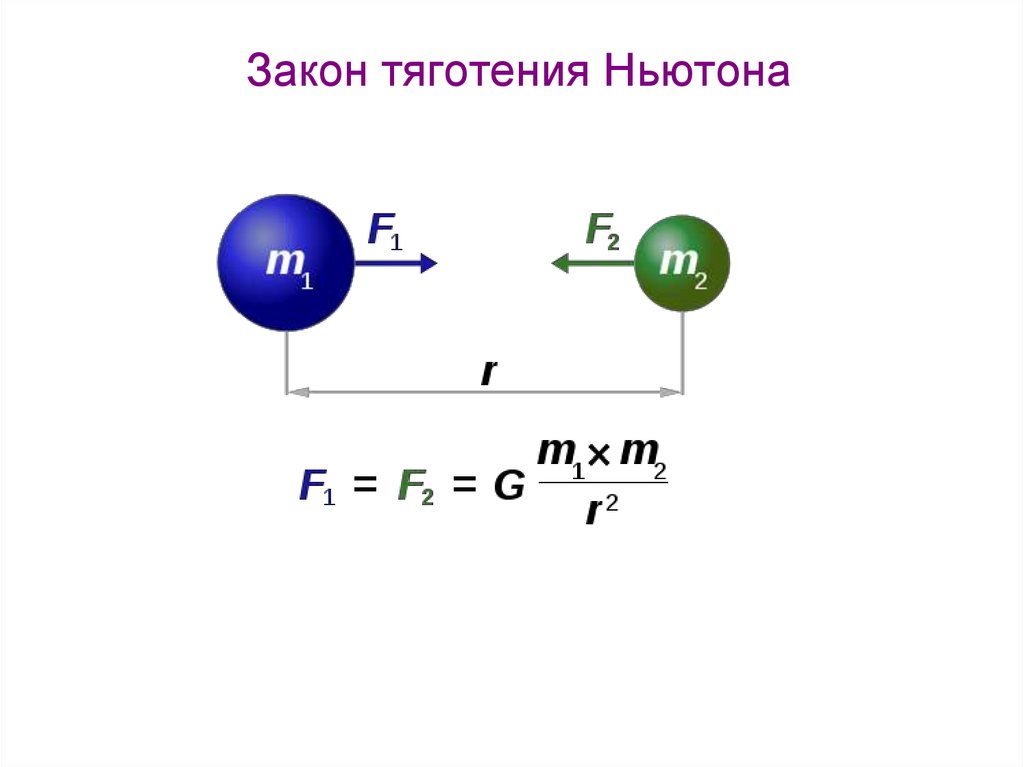 Исаак Ньютон постулировал это постоянна, чтобы придать гравитационным силам правильную величину, а также правильные единицы. Гравитация как самая слабая из четырех фундаментальные силы создают силу притяжения между двумя массами в один килограмм разделенные одним метром намного меньше одного ньютона. Так что 𝐺 выполняет двойную функцию. Это дает нам правильные единицы для нашего выражение, а также величину, которая согласуется с экспериментом.

Мы уже говорили, что гравитация — слабая сила по сравнению с другими четырьмя фундаментальными силами электромагнетизма и сильное и слабое ядерное взаимодействие. Одним из способов увидеть эту слабость в Действие состоит в том, чтобы взять любые два предмета домашнего обихода, скажем, карандаш и стакан воды. Если мы держим эти два объекта вместе, мы не можем почувствовать гравитационную силу притяжения между ними. Это слишком слабо. С другой стороны, если бы у нас было два магниты, по одному в каждой руке, мы определенно могли почувствовать силу притяжения или отвращение между ними, когда они приблизились.

Все это говорит о том, что универсальная гравитационная постоянная большая 𝐺 — очень маленькое значение. Это не одно. На самом деле, это намного меньше, чем один. Он настолько мал на самом деле, что очень трудно измерить большой 𝐺. Один из самых точных и остроумные измерения этой гравитационной постоянной находились под наблюдением джентльмен по имени Генри Кавендиш. В своем эксперименте Кавендиш подвешен на очень тонкой металлической проволоке к прочной раме. С конца этого провода он висел небольшой кусок металла, на котором были массы тщательно измеренных значений на конец. Как только эта система стабилизировалась и в любом случае не двигался и не крутился, Кавендиш принес два относительно больших тяжелых массы близко к противоположным сторонам меньших подвешенных масс.

В ответ на гравитационное притяжения, меньшие подвешенные массы чуть-чуть двигались к большему вызывающие скручивание провода. Кавендиш смог измерить это крутить с высокой точностью. И так как он знал все массы вовлеченных, а также разделяющих их расстояний, у него были значения для 𝑚 один, 𝑚 два, 𝑟, а также сила 𝐹, скручивающая сила, действующая на проволоку. Другими словами, у него были все ингредиенты, необходимые для получения значения для 𝐺. Значение для 𝐺, которое Кавендиш найдено очень близко к значению, которое мы будем часто использовать сегодня, а именно к тому, что 𝐺 примерно равно 6,67 умножить на 10 с минус 11 кубических метров на килограмм вторая в квадрате.

Глядя на это значение, две вещи возможно, выделяются: во-первых, 𝐺 действительно маленький, намного меньше, чем один, а во-вторых, у него есть к нему прилагается странный набор юнитов. Но помните, единицы 𝐺 предназначен для того, чтобы остальные законы всемирного тяготения были согласованными единицы. Измерения для все более точные значения 𝐺 сохраняются и сегодня. Однако для наших целей мы будем хорошо использовать это значение для 𝐺, очень близкое к тому, что Кавендиш найден экспериментально. Давайте попрактикуемся в работе с законом всемирного тяготения Ньютона на примере.

Масса астероида в 4,7 раза больше от 10 до 13 килограммов. Астероид пролетает рядом с Землей, и при его максимальном сближении произошло разделение центров масс астероида и Земля в четыре раза больше среднего радиуса орбиты Луны. Какую силу оказывает астероид на Земле, когда она находится на минимальном расстоянии от Земли? Используйте значение 384400 километров. для среднего радиуса орбиты Луны.

Мы назовем эту силу, мы хотим решите заглавную 𝐹 и начните с наброска ситуации. В этой ситуации наш астероид с пометкой 𝑎 проходит мимо Земли с пометкой 𝐸 на минимальном расстоянии, в четыре раза превышающем радиус орбиты Луны вокруг Земли. Учитывая массу астероида 𝑚 sub 𝑎 и радиус орбиты Луны вокруг Земли 𝑂𝑅 sub 𝑚, мы хотим Решите гравитационную силу притяжения между астероидом и Землей, когда они самые близкие. Чтобы найти эту силу, напомним что гравитационная сила притяжения между любыми двумя массами, 𝑚 единицей и 𝑚 два, равно их произведению, деленному на квадрат расстояния между их все центры масс, умноженные на вселенский гравитационный постоянный капитал 𝐺.

Пусть эта константа 𝐺 будет ровно 6,67 умножить на 10 до минус 11 кубических метров на килограмм в секунду в квадрате. Когда мы применяем математический отношение гравитационной силы к нашему сценарию, мы можем сказать, что 𝐹, сила мы хотим найти, равно 𝐺, умноженной на массу Земли, умноженной на массу количество астероидов, в четыре раза превышающее орбитальный радиус Луны в квадрате. Мы знаем цену в данный нам знаменатель. А еще мы знаем массу астероид, а также постоянная 𝐺. Осталось только решить масса Земли. И мы можем сделать это, посмотрев вверх это значение.

Общепринятое значение для масса Земли составляет 5,95 умножить на 10 в 24-х килограммах. Зная это, мы готовы подключить в и решить для 𝐹. Когда мы подставляем эти значения, мы стараемся преобразовать орбитальный радиус Луны в единицы метров, чтобы это согласуется с единицами в остальной части нашего выражения. Говоря о единицах, давайте возьмем во-вторых, рассмотреть, какими будут конечные единицы этого расчета. Глядя в числитель этого общее выражение, мы видим, что коэффициент килограммов аннулируется. Глядя затем на единицы метров которые появляются в нашем выражении, мы видим, что метр в квадрате в знаменателе будет уберите из нашего числителя два метра, так что в целом мы просто будем иметь метров до первого.

Единицы секунды в квадрате будут остаются в нашем общем знаменателе. Таким образом, мы ожидаем получить конечные единицы килограмм-метров в секунду в квадрате, что согласуется с единицами, которые мы ожидаем для сила, то есть единицы ньютонов. Когда мы вычисляем этот результат, мы найдите с точностью до двух значащих цифр, что это 7,9 умножить на 10 с точностью до девятой ньютона. Это гравитационная сила притяжение между астероидом и Землей.

Подведем итог тому, что мы узнали пока что о законе всемирного тяготения Ньютона.

В этом видео мы видели, что Закон всемирного тяготения Ньютона определяет силу притяжения между любыми двумя массы, разделенные расстоянием. В виде уравнения это говорит о том, что гравитационная сила равна произведению масс на квадрат расстояние между их центрами масс, умноженное на это универсальное гравитационная постоянная называется большой 𝐺.