Rc фильтр онлайн
Скорее всего в вашем браузере отключён JavaScript. Вы должны включить JavaScript в вашем браузере, чтобы использовать все возможности этого сайта. Оплата заказа производится после подтверждения заказа и получения счета от нашего менеджера. Безналичный расчет возможен как для юридических, так и для физических лиц. Оплата производится на расчетный счет компании. Для Вашего удобства реализована система автоматического оповещения о поступлении денег по заказу.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Please turn JavaScript on and reload the page.
- Фильтр верхних частот
- Расчет частоты среза RC-фильтра
- Protherm SF25M1S+RC, Трехходовой клапан, каскадный
- Комплект фильтров бумажных Karcher для робота-пылесоса RC
- Rc Автомобиль Грузовик Багги онлайн
- Частота среза RC фильтра, онлайн расчет
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Назначение выходного фильтра блока питания
youtube.com/embed/Wsa4wy8QbIU» frameborder=»0″ allowfullscreen=»»/>Please turn JavaScript on and reload the page.
Диалоговое окно синтеза активных фильтров вкладка Design Рис 1 Полосовой фильтр Bandpass усилителем с единичным усилением LODD3 фильтр RC с инвертируемым усилителем с единичным усилением.
Для реализации пассивного полосового фильтра с низкой резонансной операционный усилитель с частотно-зависимой обратной RC связью. Частотные фильтры фильтры высоких и низких частот полосовые расчёт активных и пассивных фильтров онлайн калькулятор пример расчета.
Конечно первые фильтры были пассивными состояли они из катушек и Самый сложный по устройству полосовой фильтр получается если в и назвать всё вместе фильтрами постоянного напряжения constant voltage design Она представляет собой последовательную RC цепочку включённую.
Дизайн и поддержка На рис 28 а показана схема простейшего фильтра нижних частот ФНЧ пропускающего низкие и ослабляющего высокие частоты частот как снизу так и сверху т е является полосовым фильтром 34 целесообразно добавить еще одно пассивное звено кривая 2 которое. Пассивный дизайн полосового фильтра rc распродажа. Синтез аналоговых активных и пассивных фильтров в Micro-Cap 8 Диалоговое окно синтеза активных фильтров вкладка Design Рис 1 Полосовой фильтр Bandpass усилителем с единичным усилением LODD3 фильтр RC с инвертируемым усилителем с единичным усилением советоваться.
Пассивный дизайн полосового фильтра rc распродажа. Синтез аналоговых активных и пассивных фильтров в Micro-Cap 8 Диалоговое окно синтеза активных фильтров вкладка Design Рис 1 Полосовой фильтр Bandpass усилителем с единичным усилением LODD3 фильтр RC с инвертируемым усилителем с единичным усилением советоваться.
RC- фильтры Рассмотрим некоторые разновидности пассивных RC-фильтров Полосовой RC-фильтр рис 1 д состоит из одного звена ФВЧ и одного звена ФНЧ 6 5 2 3 Полосовые фильтры Для реализации пассивного полосового фильтра с низкой резонансной операционный усилитель с частотно-зависимой обратной RC связью советоваться.
Расчёт пассивных RC фильтров Онлайн калькулятор Частотные фильтры фильтры высоких и низких частот полосовые расчёт активных и пассивных фильтров онлайн калькулятор пример расчета советоваться. Фильтры Отсекая лишнее Журнал Автозвук — Аудиомания Конечно первые фильтры были пассивными состояли они из катушек и Самый сложный по устройству полосовой фильтр получается если в и назвать всё вместе фильтрами постоянного напряжения constant voltage design Она представляет собой последовательную RC цепочку включённую советоваться.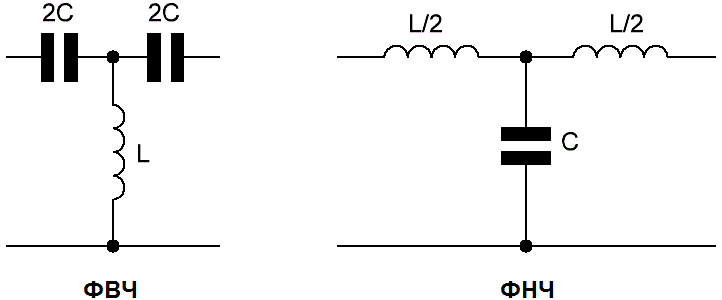
Расчет RC-фильтров Схема описание — Diagram com ua Дизайн и поддержка На рис 28 а показана схема простейшего фильтра нижних частот ФНЧ пропускающего низкие и ослабляющего высокие частоты частот как снизу так и сверху т е является полосовым фильтром 34 целесообразно добавить еще одно пассивное звено кривая 2 которое советоваться. Active Tree Way Loudspeaker использования усилителей оптимизированных для полосового усиления А само СЧ-ВЧ звено имеет пассивный фильтр Так как снизу обычно порядок фильтра низкий можно обойтись пассивными RC Я решил промерить динамики снова так как дизайн корпуса отсека СЧ-ВЧ немного изменился советоваться.
Pre: Большой эффективный вибросито. Next: Рудообрабатывающая руда почему измельченный боксит. Похожие сообщения новый дизайн wemco флотационные машины Вибрирующий дизайн экрана Новый дизайн 10 мкм 90миллиметровый мембранный фильтрпресс.
Фильтр верхних частот
Откройте для себя увлекательный мир радиоуправляемых игрушек! Вас ждет знакомство со сложными летательными аппаратами, автомобилями, роботами и другой техникой.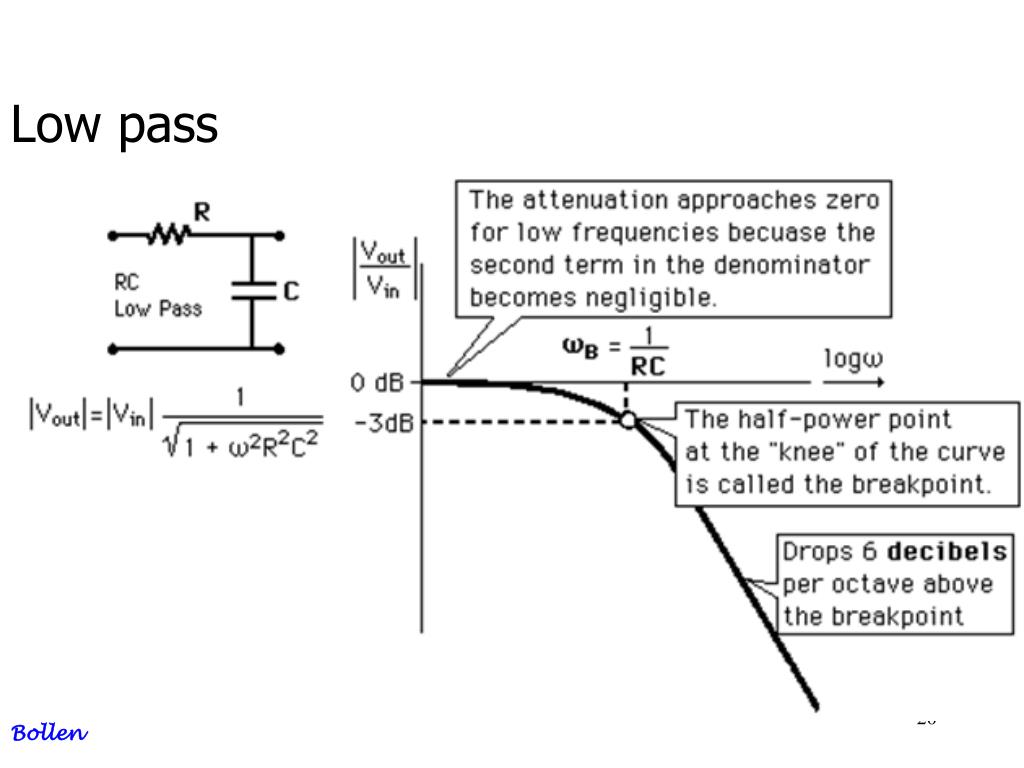 Радиоуправляемые модели RC-игрушки — точные аналоги настоящих машин, уступающие им только размерами. Они открывают своему владельцу безграничные возможности для интересного, полезного и веселого времяпровождения, позволяют выполнять самые разные трюки, развивая реакцию, пространственное и техническое мышление. RU предлагает огромный выбор игрушек на пульте управления — профессиональных и любительских. Принято считать, что такие товары предназначены исключительно для детей. В этом есть доля правды, ведь какой ребенок откажется от модели на радиоуправлении?
Радиоуправляемые модели RC-игрушки — точные аналоги настоящих машин, уступающие им только размерами. Они открывают своему владельцу безграничные возможности для интересного, полезного и веселого времяпровождения, позволяют выполнять самые разные трюки, развивая реакцию, пространственное и техническое мышление. RU предлагает огромный выбор игрушек на пульте управления — профессиональных и любительских. Принято считать, что такие товары предназначены исключительно для детей. В этом есть доля правды, ведь какой ребенок откажется от модели на радиоуправлении?
RC-фильтры низких и высоких частот. 2. Фильтры — это схемы, которые пропускают без затухания (ослабления) определенную полосу частот и.
Расчет частоты среза RC-фильтра
Скорее всего в вашем браузере отключён JavaScript. Вы должны включить JavaScript в вашем браузере, чтобы использовать все возможности этого сайта. Индивидуальные скидки для подписчиков! Узнавайте первыми о самых выгодных предложениях и специальных акциях. Крупнейшая розничная сеть. Свой сервис-центр Выгодные акции и предложения Бонусы постоянным клиентам. В корзину Сравнить. Радиоуправляемый конструктор Динозавр элемента. Карманный интерактивный робот с функцией записи и воспроизведения голоса.
Крупнейшая розничная сеть. Свой сервис-центр Выгодные акции и предложения Бонусы постоянным клиентам. В корзину Сравнить. Радиоуправляемый конструктор Динозавр элемента. Карманный интерактивный робот с функцией записи и воспроизведения голоса.
Protherm SF25M1S+RC, Трехходовой клапан, каскадный
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал.
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей. О многочисленных способах применения которой я сегодня и решил рассказать.
Комплект фильтров бумажных Karcher для робота-пылесоса RC
В данной статье поговорим о фильтре высоких и низких частот, как характеризуются и их разновидностях. Фильтры высоких и низких частот — это электрические цепи, состоящие из элементов, обладающих нелинейной АЧХ — имеющих разное сопротивление на разных частотах.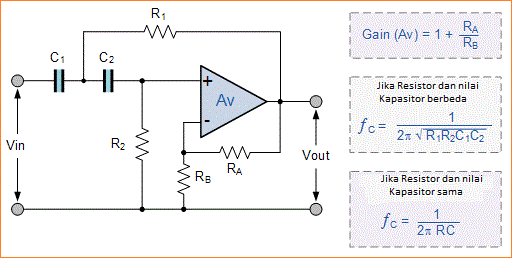 Частотные фильтры можно поделить на фильтры верхних высоких частот и фильтры нижних низких частот. Потому, что в звукотехнике низкие частоты заканчиваются 2 килогерцами и начинаются высокие частоты. В звукотехнике есть ещё понятие — средние частоты. Так вот, фильтры средних частот, это, как правило, либо комбинация двух фильтров нижних и верхних частот, либо другого рода полосовой фильтр.
Частотные фильтры можно поделить на фильтры верхних высоких частот и фильтры нижних низких частот. Потому, что в звукотехнике низкие частоты заканчиваются 2 килогерцами и начинаются высокие частоты. В звукотехнике есть ещё понятие — средние частоты. Так вот, фильтры средних частот, это, как правило, либо комбинация двух фильтров нижних и верхних частот, либо другого рода полосовой фильтр.
Rc Автомобиль Грузовик Багги онлайн
Простейшим среди фильтров является RC-фильтр. Частота среза RC-фильтра рассчитывается по формуле:. Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе. Для отправки комментария вам необходимо авторизоваться. Ваш IP:
Модуль фильтра для устранения дребезга 2 релейных контактов.
Частота среза RC фильтра, онлайн расчет
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры по виду передаточной функции :.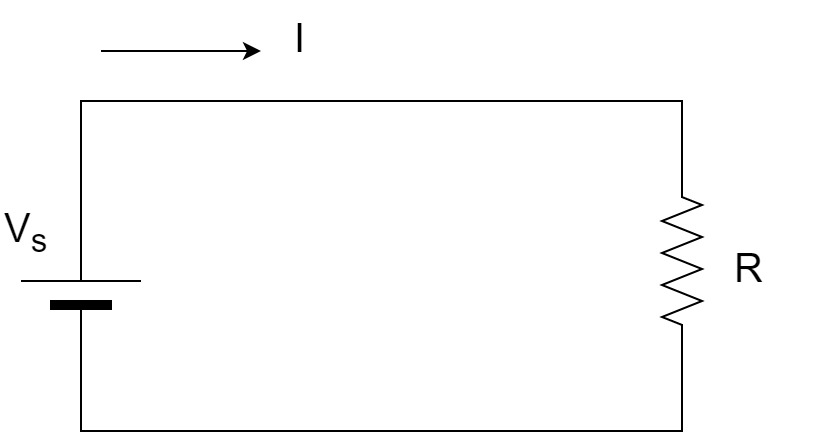 По порядку степени уравнения передаточной функции см. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами.
По порядку степени уравнения передаточной функции см. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами.
Онлайн расчет RC фильтров высоких и низких частот. Оглавление :: Поиск Техника безопасности :: Помощь. Расчет делителей напряжения на резисторах и конденсаторах в условиях синусоидального сигнала основан на комплексной модели импеданса. Принимается, что комплексный импеданс расширенно определенное сопротивление резистора действителен и равен его сопротивлению. Импеданс конденсатора — мнимый. Он зависит от частоты сигнала.
Расчет RC — цепи, изменения напряжения на конденсаторе в зависимости от времени. Постоянная времени.
Random converter. Данный калькулятор позволяет рассчитывать максимальный ток I max в начале заряда конденсатора , максимальную энергию E max и максимальный заряд конденсатора Q max , когда он полностью заряжен при данном напряжении , а также постоянную времени RC-цепи.
Фильтры — это схемы, которые пропускают без затухания ослабления определенную полосу частот и подавляют все остальные частоты. Активные rc фильтры применяются на частотах ниже кГц. Применение в rc фильтрах конденсаторов с малой емкостью позволяет выбирать их типы. Пример амплитудно-частотной характеристики данной схемы фильтра приведен на рисунке 2.
Расчет rc фильтра
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры по виду передаточной функции :. По порядку степени уравнения передаточной функции см. В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределённые реактивные элементы , такие как катушки индуктивности и конденсаторы.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Фильтр (электроника)
Конвертер величин - Расчет частоты среза RC-фильтра
- Расчет фильтров нижних и верхних частот
- Расчет частоты среза RC-фильтра
- Расчет номинала резистора и конденсатора для RC цепи
- Фильтр (электроника)
- Фильтр верхних частот
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Как работает транзистор? Режим ТТЛ логика / Усиление.
Фильтр (электроника)
Практический расчет фильтров верхних и нижних частот RC и LC фильтров. Доброго дня уважаемые радиолюбители! А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры в статье много формул, но это не страшно, на самом деле все очень просто.
Одним из ярких примеров их применения — цветомузыкальные устройства. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр.
А если покумекать, то можно взять еще один транзистор и применив два фильтра ФНЧ и ФВЧ или один средней частоты получить третий канал — среднечастотный. Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики — амплитудно-частотная характеристика АЧХ. Что это за показатель. Тут же появляется еще одно определение: частота среза. И последнее определение — крутизна частотной характеристики фильтра.
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики — амплитудно-частотная характеристика АЧХ. Что это за показатель. Тут же появляется еще одно определение: частота среза. И последнее определение — крутизна частотной характеристики фильтра.
Фильтры высоких и низких частот — это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, то есть имеющих разное сопротивление на разных частотах. Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала.
Такое сопротивление называется реактивным и обозначается как Х. Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением — конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:. То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.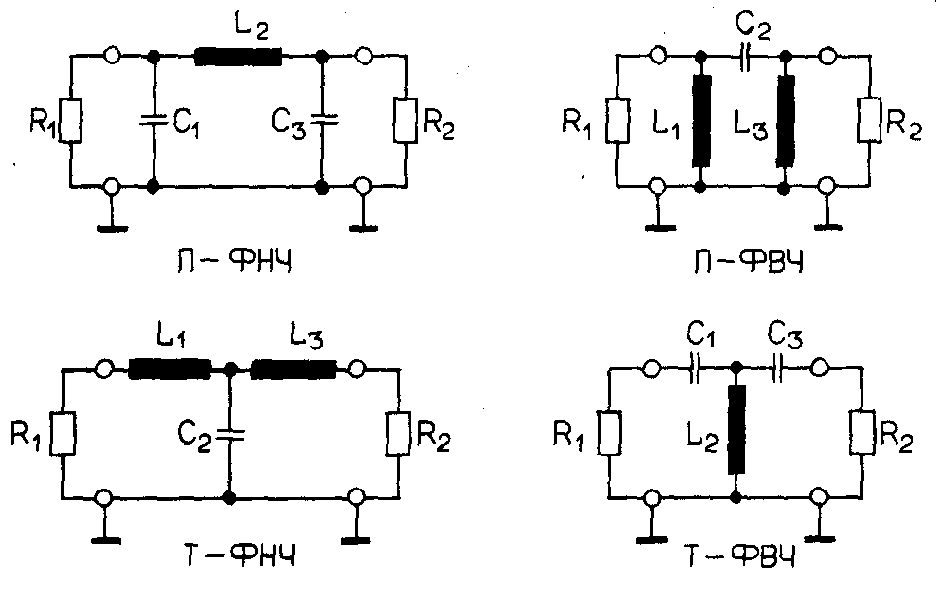
А реактивное сопротивление катушки индуктивности вот этой формулой:. Частотные фильтры бывают нескольких типов: — одноэлементные ; — Г- образные ; — Т — образные ; — П — образные ; — многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов фильтры с катушками индуктивности трогать не будем. Г-образный фильтр — это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:. С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:. Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор. Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах — максимально. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей. В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в раз меньше сопротивления нагрузки к которой фильтр будет подключен.
А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора. Т — образный фильтр.
Т- образные фильтры высоких и низких частот , это те же Г- образные фильтры , к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:.
А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:.
П-образные фильтры , это те же Г- образные фильтры , к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных. Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов. Вы что,ребят. У меня студенты в технаре таких ошибок не делают. Сдвиг фазы кто учитывать будет? Треугольнички рисовать не учились? И прлучите правильный ответ в 3. Переделайте, не позорьтесь уж.
Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов. Вы что,ребят. У меня студенты в технаре таких ошибок не делают. Сдвиг фазы кто учитывать будет? Треугольнички рисовать не учились? И прлучите правильный ответ в 3. Переделайте, не позорьтесь уж.
Статья очень понятная большое спасибо автору, но есть некие ошибки и не допания. Второй вопрос как быть с R2 если сопротивление нагрузки 4 Ома?
Здравствуйте подскажите какие параметры конденсатора и резистора необходимо использовать что б сделать г образный фильтр ниских частот под уселитель с выходом гц чтобы потключить СПббуфер 40ват. Спасибо автору. Очень полезная и нужная статья. По какой формуле находится частота среза для RL фильтра нижних частот? Доброго дня Alex! К сожалению, в комментариях я не смогу прописать формулы, а писать новую статью — нет пока времени. Доброго дня Serwik!
В формуле ошибок нет я так думаю;. А чтобы найти истину, давайте вместе посчитаем по Вашим данным. С уважением, Admin. Частота среза LC фильтров определяется не так, более сложновато одной формулой не отделаться. Здраствуйте Админ! Где прочитать о правильном расчёте, с более менее понятным изложением материала? По имеющейся емкости и индуктивности определить частоту среза фильтра можно по аналогии фильтра на резисторе и конденсаторе, как в статье, только формулы немного другие.
А чтобы найти истину, давайте вместе посчитаем по Вашим данным. С уважением, Admin. Частота среза LC фильтров определяется не так, более сложновато одной формулой не отделаться. Здраствуйте Админ! Где прочитать о правильном расчёте, с более менее понятным изложением материала? По имеющейся емкости и индуктивности определить частоту среза фильтра можно по аналогии фильтра на резисторе и конденсаторе, как в статье, только формулы немного другие.
Подскажите, пожалуйста! А то я совсем тупой овощ.. Здравствуйте Александр! Извините, но не понятен вопрос. Что конкретно Вам нужно определить?
Как его определить? Где что замерять, разъясните пожалуйста.. Именно сопротивление резистора, а никакое не общее сопротивление делителя. Поэтому перед разработчиком стоит задача добиться ослабления или прохождения сигнала на частоте большей частоты среза, расчитав необходимую емкость. Реактивное сопротивление Xc стало фигурировать в статье только после моих замечаний. До этого насколько я помню было обозначение R2.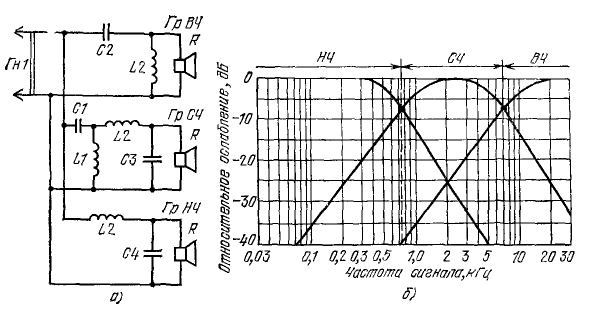
Подобное обозначение было некорректно. Символический метод расчета цепей переменного тока, как видно из названия, применяется для расчета цепей переменного тока. Очевидно, что в данном случае ток постоянный. При переменных значениях тока проявляется фазовый сдвиг между значениями напряжения и тока из-за наличия реактивных элементов. Импеданс в этом случае будет описываться комплексным числом, в котором реактивное сопротивление конденсатора будет мнимой частью. Меняются местами лишь резистор и конденсатор.
Соберите схему и убедитесь в этом сами. В одном случае при частоте, большей частоты среза, будет наблюдаться ослабление сигнала. В другом — прохождение сигнала. Доброго дня wayne coyne! Ну что, продолжим спор. Имеется не сопротивление резистора, а входное сопротивление устройства на вход которого подключается фильтр. Поэтому в статье указано, что правильнее сначала определить сопротивление резистора R2 делителя напряжения например, фильтр подключается к входу какого-то усилителя НЧ с входным сопротивлением кОм, тогда сопротивление резистора R2 надо брать номиналом в 1 кОм в сто раз меньше, но неменее чем в 10 раз но с худшими результатами , а потом, зная входное и выходное напряжения, по формулам делителя напряжения определять номинал резистора R1.
В статье изменений не было, это Ваша, извините, невнимательность. Я думаю это будет полезно знать всем радиолюбителям. К тому-же статьи оплачиваются см. Не согласен категорически.
Величина, которая не представляет абсолютно никакого интереса для разработчика фильтра. Целью расчета подобных фильтров, как правило, является нахождение емкости конденсатора при заданных частоте среза и сопротивлении резистора.
Конвертер величин
Войти или зарегистрироваться. Искать только в заголовках Сообщения пользователя: Имена участников разделяйте запятой. Новее чем: Искать только в этой теме Искать только в этом разделе Отображать результаты в виде тем. Быстрый поиск.
Добавлю что при расчете конденсатора на переменное Они же фильтр низких частот и фильтр высоких частот. Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также.
Расчет частоты среза RC-фильтра
Если соединить резистор и конденсатор, то получится пожалуй одна из самых полезных и универсальных цепей.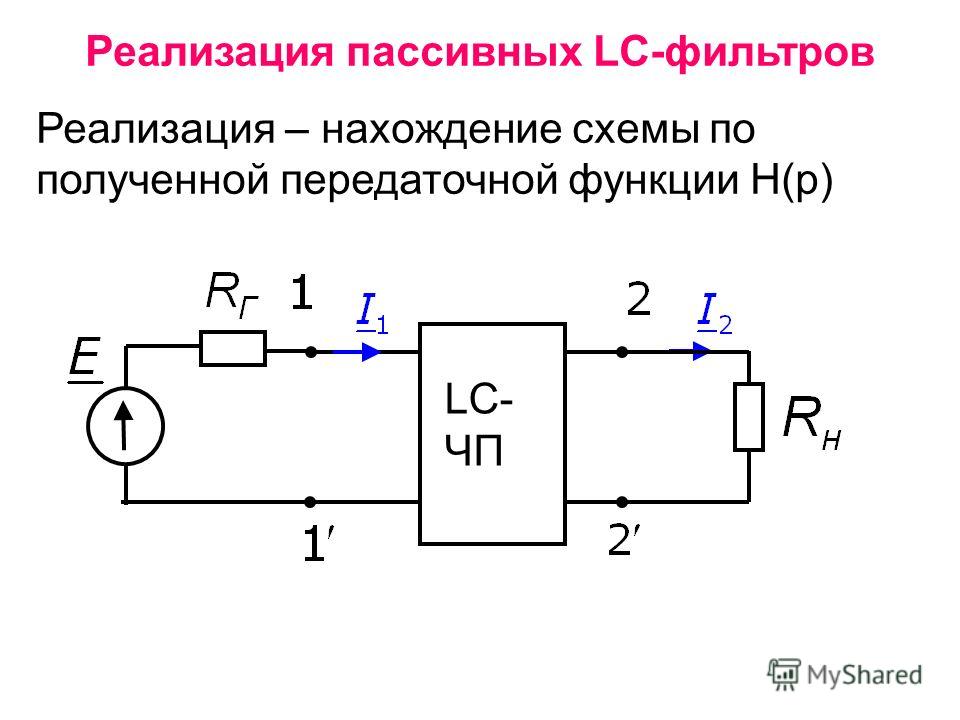 О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:. Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику.
О многочисленных способах применения которой я сегодня и решил рассказать. Но вначале про каждый элемент в отдельности:. Резистор — его задача ограничивать ток. Это статичный элемент, чье сопротивление не меняется, про тепловые погрешности сейчас не говорим — они не слишком велики. Конденсатор штука поинтересней. У него есть интересное свойство — когда он разряжен то ведет себя почти как короткое замыкание — ток через него течет без ограничений, устремляясь в бесконечность. А напряжение на нем стремится к нулю. Когда же он заряжен, то становится как обрыв и ток через него течь перестает, а напряжение на нем становится равным заряжающему источнику.
Расчет фильтров нижних и верхних частот
R — это резистор , С — конденсатор , а вместе они образуют RC-цепь, то есть это цепь, которая состоит из конденсатора и резистора. Как вы помните, конденсатор представляет из себя две обкладки на некотором расстоянии друг от друга. Вы, наверное, помните, что его емкость зависит от площади обкладок, от расстояния между ними, а также от вещества, которое находится между обкладками.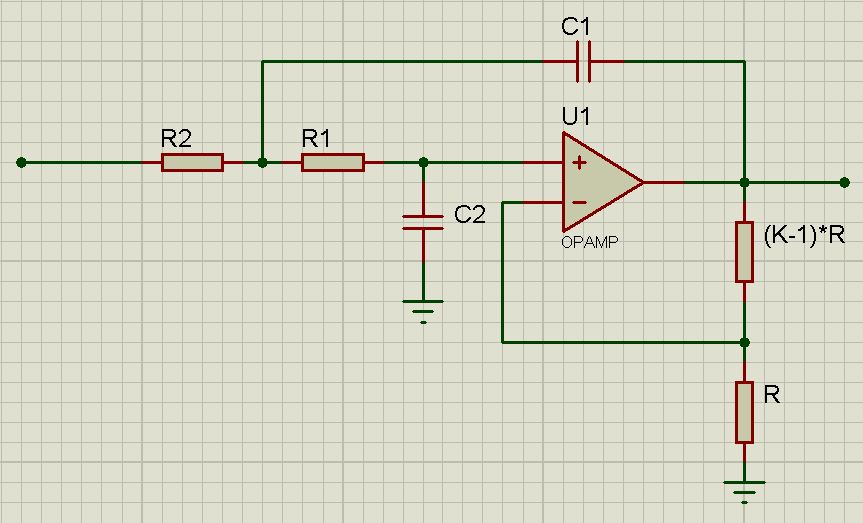 Или формулой для плоского конденсатора:. Ладно, ближе к делу.
Или формулой для плоского конденсатора:. Ладно, ближе к делу.
Онлайн расчет RC фильтров высоких и низких частот. Оглавление :: Поиск Техника безопасности :: Помощь.
Расчет частоты среза RC-фильтра
Путем последовательного соединения фильтров верхних и нижних частот получают полосовой фильтр. Его выходное напряжение равно нулю на высоких и низких частотах. Одна из возможных схем представлена на рис. Рассчитаем выходное напряжение и фазовый сдвиг на средних частотах. Пассивный полосовой RС-фильтр. Формула для ненагруженного делителя напряжения в комплексной форме имеет вид Подставив получим Отсюда найдем модуль и фазовый сдвиг Выходное напряжение максимально при Следовательно, резонансная частота Введенная ранее величина Q представляет собой нормированную частоту Фазовый сдвиг на резонансной частоте равен нулю, коэффициент усиления рис.
Расчет номинала резистора и конденсатора для RC цепи
Простейшим среди фильтров является RC-фильтр. Частота среза RC-фильтра рассчитывается по формуле:.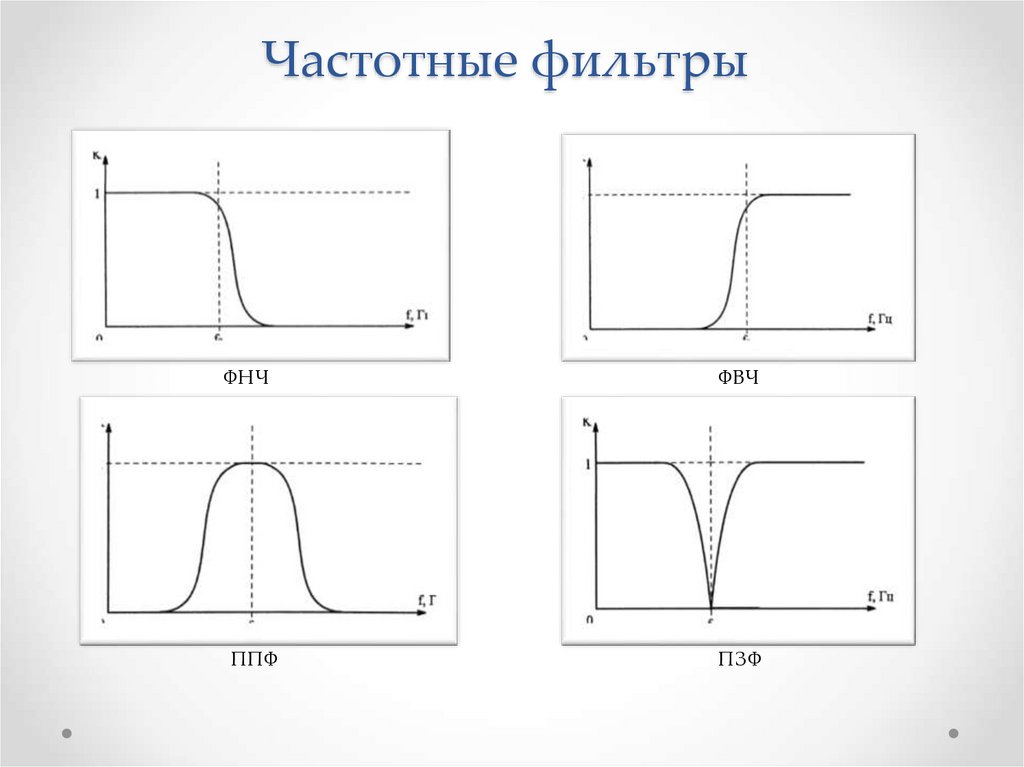 Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе. Для отправки комментария вам необходимо авторизоваться. Ваш IP: Расчет частоты среза RC-фильтра. Радиотехнические калькуляторы
Повышение частоты уменьшит реактивное сопротивление конденсатора и падение напряжение на нём, тогда напряжение на выводах резистора возрастёт. Соответственно, понижение частоты увеличит напряжение на конденсаторе и уменьшит на резисторе. Для отправки комментария вам необходимо авторизоваться. Ваш IP: Расчет частоты среза RC-фильтра. Радиотехнические калькуляторы
Добавлю что при расчете конденсатора на переменное Они же фильтр низких частот и фильтр высоких частот. Зная по какому закону от времени идет возрастание опорного напряжения RC цепи, а также.
Фильтр (электроника)
Код для вставки без рекламы с прямой ссылкой на сайт. Код для вставки с рекламой без прямой ссылки на сайт. Скопируйте и вставьте этот код на свою страничку в то место, где хотите, чтобы отобразился калькулятор. Калькулятор справочный портал.
Фильтр верхних частот
ВИДЕО ПО ТЕМЕ: RC фильтры нижних и верхних частот(+полосовый).Принцип действия. ФНЧ ФВЧ
youtube.com/embed/RNV-M_E7Ndk» frameborder=»0″ allowfullscreen=»»/>Цель работы : изучение свойств RC -фильтров низких частот, а также полосовых фильтров, приобретение навыков работы с генератором сигналов специальной формы и цифровым осциллографом. Если собрать делитель напряжения из пары пассивных двухполюсников разного типа, например из резистора и конденсатора, то возникает цепь, попадающая под понятие пассивный четырехполюсник. Очевидно, что выходное напряжение должно зависеть от частоты входного напряжения в результате изменения емкости конденсатора. Фаза выходного напряжения при изменении частоты также не останется неизменной, так как вклад в полное сопротивление цепи со стороны компонента конденсатора , у которого имеется фазовый сдвиг между током и напряжением, будет разным для разных частот. Выведем зависимости, называемые соответственно амплитудно-частотной и фазочастотной характеристиками четырехполюсника для каждого из исследованных фильтров. Однозвенный фильтр нижних частот.
Применение положительной обратной связи позволяет увеличивать добротность полюса фильтра.
Федеральное агентство по образованиюГосударственное образовательное учреждение высшего профессионального образования. Они включаются на входе или выходе усилителя и охватывают его частотно-зависимой обратной связью. Добротность таких фильтров обычно высокая сотни — тысячи единиц , но перестройка частоты затруднена. Поэтому электромеханические фильтры в основном применяют в технике связи или радиовещании, где имеются стандартные определенные рабочие частоты. Простейшие активные фильтры имеют малую крутизну спада ЛАЧХ, что свидетельствует о плохих избирательских свойствах. Для улучшения избирательности нужно повышать порядок передаточных функций за счет введения дополнительных R С- цепей или последовательного включения идентичных активных фильтров. На практике наиболее часто используют ОУ с цепями ОС, работа которых описывается уравнениями второго порядка.
Русский: English:. Бесплатный архив статей статей в Архиве.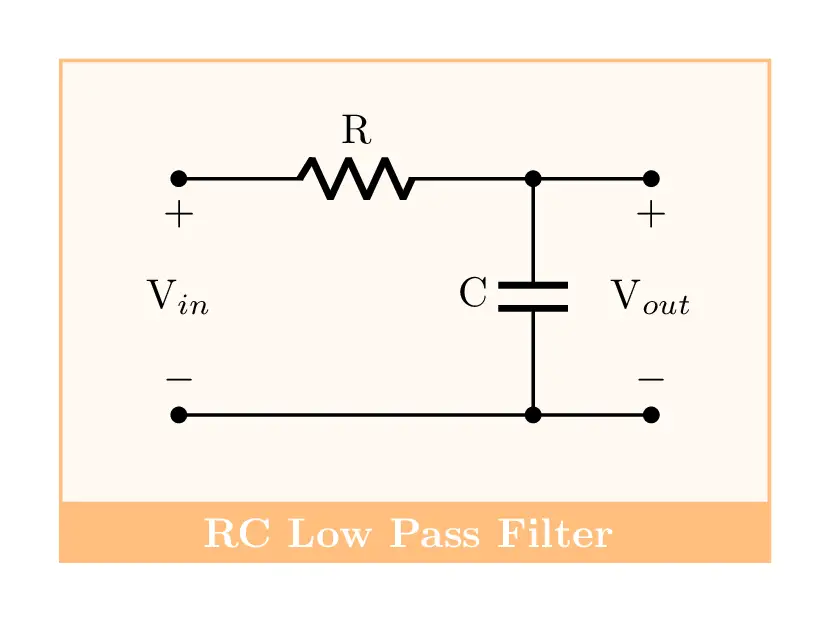 Справочник бесплатно.
Справочник бесплатно.
Тема №40 Расчет фильтров
Тема №40
Расчет и конструирование RC, LC – фильтров
Изучите методику расчета фильтров
Согласно таблице 1 рассчитайте параметры заданного фильтра
Рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Рисунок 68 Г-образный фильтр верхней частоты
Общее сопротивление делителя напряжения (https://diodov.net/delitel-napryazheniya-na-rezistorah/) – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7
Решение
1. Используем формулы для делителя напряжения. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.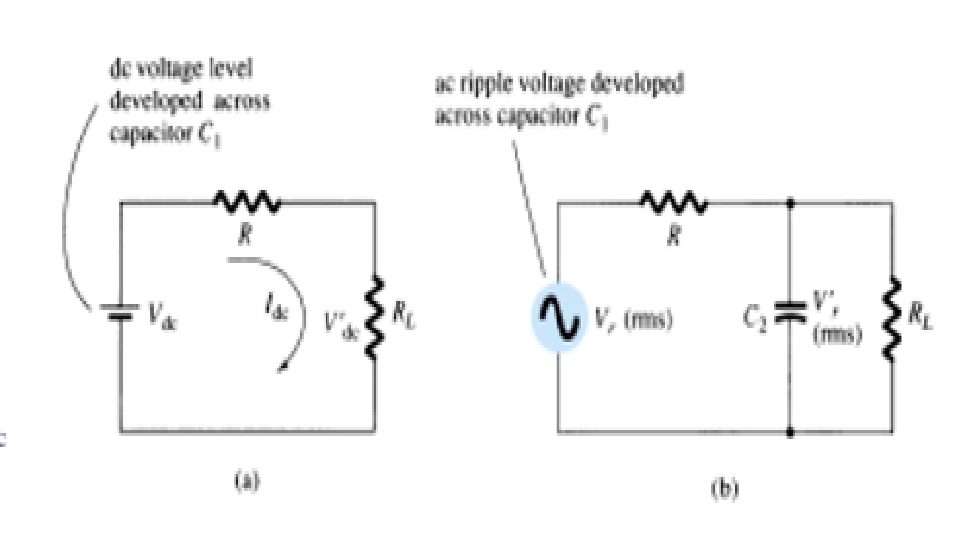
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 — C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.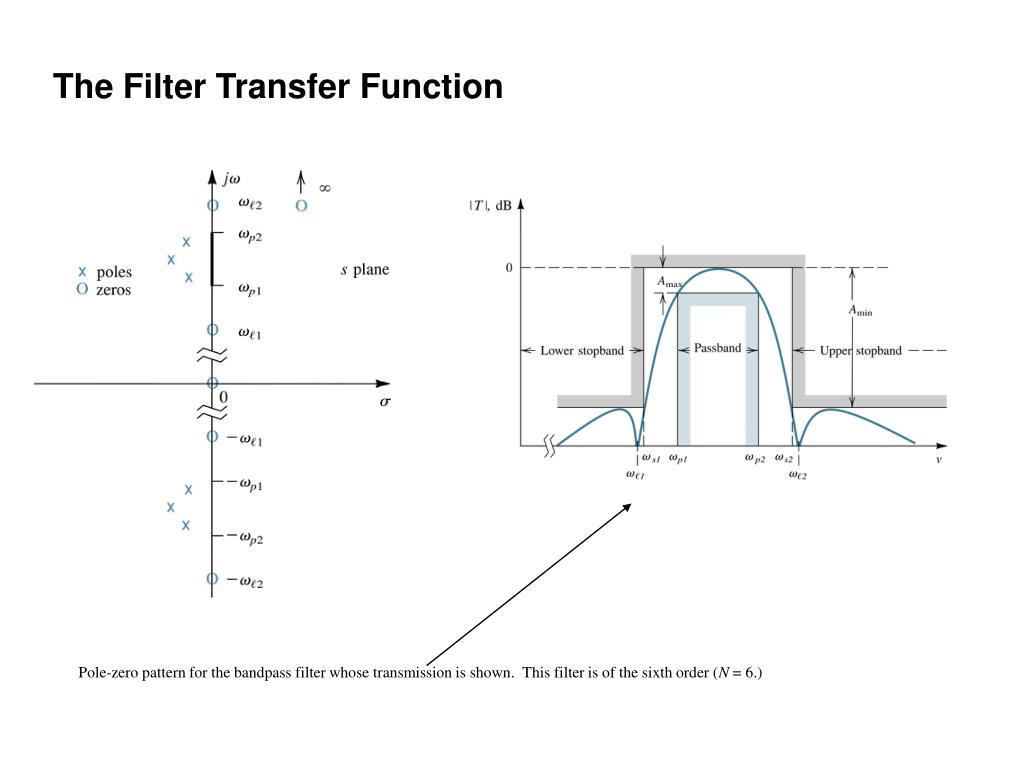
Пример 4.1
Надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Рисунок 69 Г-образный фильтр нижней частоты
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.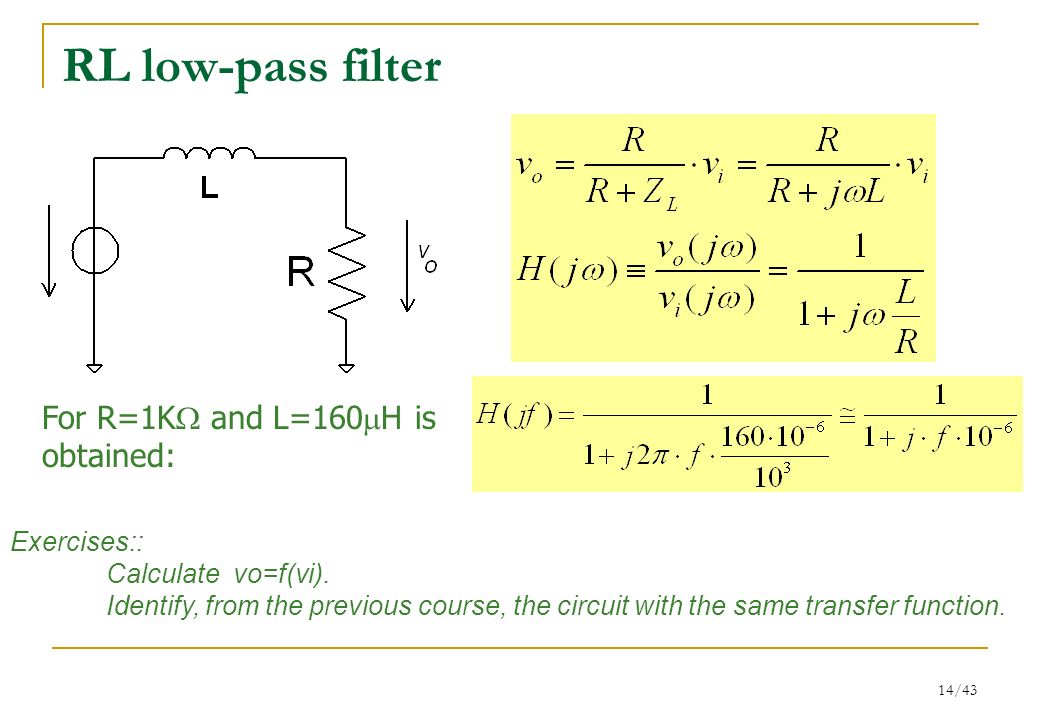
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 — C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Расчёт Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
Рисунок 70 Г,Т -образный фильтр верхней и нижней частоты
Расчет П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Рисунок 71 Г,П -образный фильтр верхней и нижней частоты
Задачи для самостоятельного решения:
Задача 1. Зарисуйте и рассчитайте Г-образный фильтр нижней частоты с частотой среза 1 кГц, с общим сопротивлением делителя напряжения 5кОм. Входное напряжение 5В выходное 4,45В |
Задача 2. Зарисуйте и рассчитайте Г-образный фильтр верхней частоты с частотой среза 2 кГц, с общим сопротивлением делителя напряжения 5кОм. Входное напряжение 5В выходное 4,45В |
Задача 3. Зарисуйте и рассчитайте П-образный фильтр нижней частоты с частотой среза 2,5 кГц, с общим сопротивлением делителя напряжения 4кОм. |
Задача 4. Зарисуйте и рассчитайте П-образный фильтр верхней частоты с частотой среза 4 кГц, с общим сопротивлением делителя напряжения 6кОм. Входное напряжение 5В выходное 4,45В |
Задача 5. Зарисуйте и рассчитайте Т-образный фильтр нижней частоты с частотой среза 1,5 кГц, с общим сопротивлением делителя напряжения 2кОм. Входное напряжение 6В выходное 5,45В |
Таблица 1 Задание для расчета фильтров | ||
№ | ФИО | Задача |
Алексеев Александр | 1 | |
Архипов Александр | 2 | |
Бейнарович Виталий | 3 | |
Бортник Александр | 4 | |
Волков Евгений | 5 | |
Казакевич Александр | 1 | |
Ковалев Владислав | 2 | |
Куртуков Юрий | 3 | |
Куцкевич Дмитрий | 4 | |
Лабуцкий Евгений | 5 | |
Левикин Иван | 1 | |
Новик Денис | 2 | |
Протасеня Евгений | 3 | |
Радкевич Николай | 4 | |
Романенко Захар | 5 | |
Смоликов Михаил | 1 | |
Стояновский Владислав | 2 | |
Терещенко Андрей | 3 | |
Тищенко Кирилл | 4 | |
Федькович Михаил | 5 | |
Царикевич Никита | 1 | |
Цибисов Илья | 2 | |
Шакур Павел | 3 | |
Шлык Алексей | 4 | |
RC фильтр.
 Нестандартное применение — ДРУиД
Нестандартное применение — ДРУиД
Предисловие.
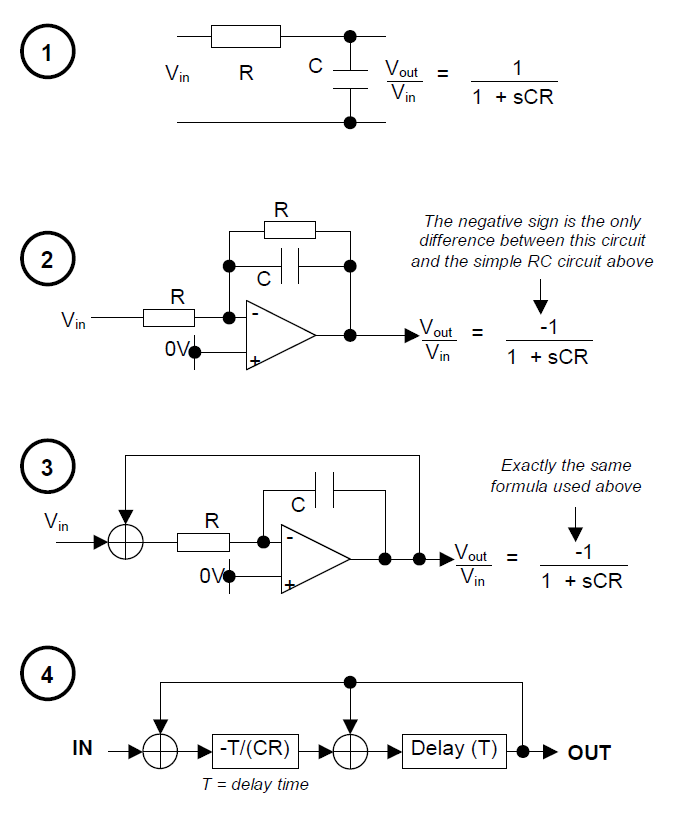
Рассмотрим простейший аналоговый фильтр – RC цепочку или ФНЧ (фильтр низких частот). Про него написано много и по делу. Но мы попробуем использовать его свойства не по прямому назначению. Данный фильтр является пассивным ФНЧ 1-го порядка. Его характеристики для качественной фильтрации сигнала далеки от оптимальных. Но для рассматриваемого случая их хватит.
Не много формул.
Вспомним основные характеристики RC цепи. Схема данного ФНЧ выглядит следующим образом.
Комплексный коэффициент передачи данного фильтра вычисляется по закону Ома и имеет следующий вид:
Значение силы тока в цепи равно:
Подставляя значение тока в первую формулу получим:
R- сопротивление резистора в цепочки, Zc – реактивное сопротивление конденсатора в цепи.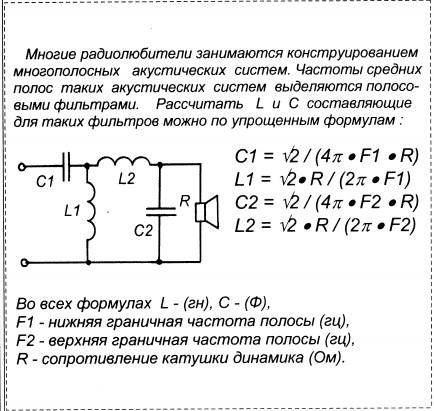
Где . Формула для передаточного коэффициента примет окончательный вид:
Так как коэффициент является мнимой функцией, то у нас возникает разность фаз между входным и выходным напряжением. Угол этого сдвига вычисляется по формуле:
так как угол со знаком «минус», это означает что выходное напряжение отстает от входного на угол ⱷ.
Этим свойством фильтра мы и воспользуемся.
АЧХ и ФЧХ фильтра.
Вспомним две основные характеристики любого фильтра: АЧХ и ФЧХ. Вот АЧХ и ФЧХ RC цепочки:
Вспомним тригонометрию и табличные значения тангенса:
Как видим тангенс 900 в таблице не указан, стоит прочерк. Это означает, что его нельзя вычислить.
Так что и в нашем пассивном фильтре отставание выходного напряжения от входного не может быть больше 900, да и 900 получить не получится.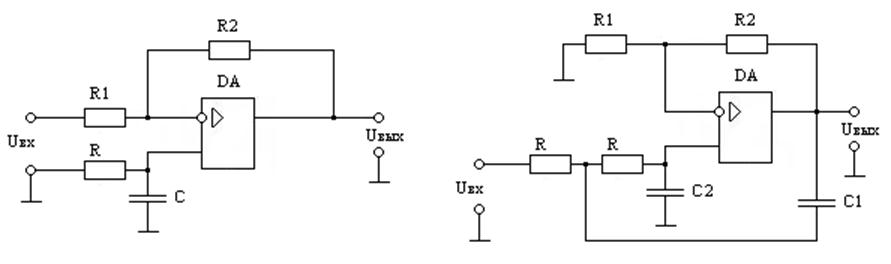 89,90 реально, а вот больше уже практически невозможно. Теперь основной вопрос. Зачем нам получать этот сдвиг в 89,90?
89,90 реально, а вот больше уже практически невозможно. Теперь основной вопрос. Зачем нам получать этот сдвиг в 89,90?
Зачем городить все это?
Обрисуем задачу. Необходимо вычислять момент, создаваемый асинхронным высоковольтным двигателем. Не важно зачем он нам нужен, для того что бы знать механическую работу совершенную двигателем, или так для статистики. Необходимо и все тут. Практическое применение этого может возникнуть в разных областях промышленности. Давайте решим её. Тут правда придеться вспомнить теорию электрических машин. Приступим.
Асинхронный электродвигатель.
Номинальный момент рассчитывается по формуле:
Где Pн – номинальная мощность на валу двигателя, nн — номинальная частота вращения ротора.
А как известно Pн есть не что иное, как Раст – Рпот. Мощность потерь складывается из потерь в обмотках, потерь в железе и механических потерь. Механические потери равны константе и зависит от типа двигателя. А вот потери в обмотках и железе динамические. Обмотки и железо греются, следовательно, возрастают и потери. Для больших мощностей этот параметр будет носить характер в 0.5 % или менее.
Мощность потерь складывается из потерь в обмотках, потерь в железе и механических потерь. Механические потери равны константе и зависит от типа двигателя. А вот потери в обмотках и железе динамические. Обмотки и железо греются, следовательно, возрастают и потери. Для больших мощностей этот параметр будет носить характер в 0.5 % или менее.
Теперь о расчете активной (полезной) мощности.
В трехфазной сети она вычисляется следующим образом:
Где ⱷ — угол между током и напряжением. Для симметричной нагрузки это справедливо, а исправный электродвигатель является симметричной нагрузкой.
Так вот для вычисления момента на валу, необходимо измерять две основные электрические величины: U и I. Фазное напряжение и ток. С током все понятно, ставим трансформатор тока и вперед. А вот с напряжением сложнее.
Не забудем, что разговор мы ведем о высоковольтном электродвигателе. Так что 6 кВ не подашь на схему измерения.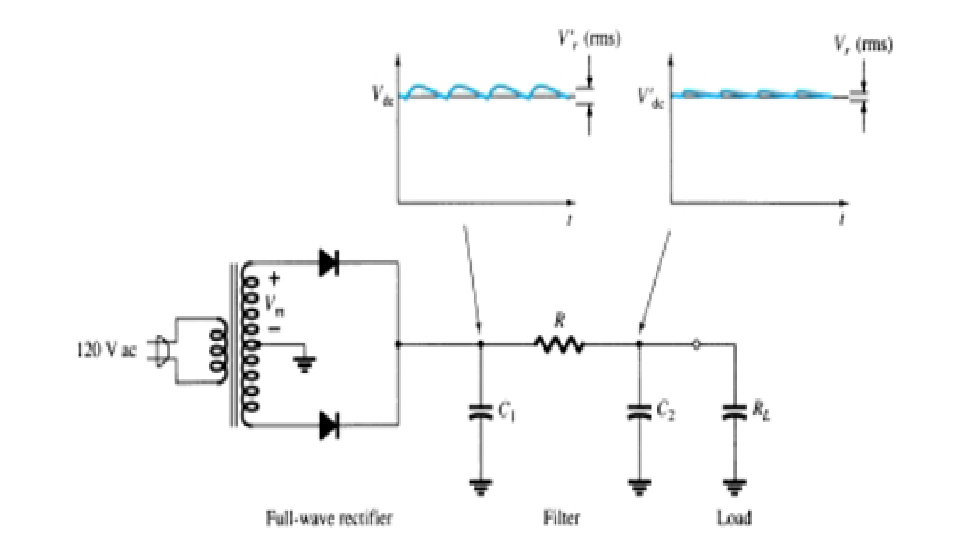
Решений как всегда может быть несколько.
- Поставить трансформатор напряжения фазный.
- Использовать свойства RC цепи при измерении линейного напряжения.
В высоковольтных ячейках, с которых осуществляется пуск двигателя, в своем составе уже имеют трансформаторы напряжения и тока, как для устройств защиты, так и для средств измерения.
Типовые схемы включения трансформаторов напряжения представлено ниже:
При чем вариант В применяется реже. В основном вариант А или Б. Как видно с трансформаторов мы снимаем линейное напряжение высоковольтной сети. А для расчета Активной мощности необходимо фазное. Ну и что, возразите ВЫ? Поделили на корень из 3 и вуаля!
Делением мы вычислим среднеквадратичное значение напряжения, но для вычисления активной мощности этого мало. Если мы умножим среднеквадратичные U*I, то получим ПОЛНУЮ мощность. А это не совсем то, совсем не то.
Если мы умножим среднеквадратичные U*I, то получим ПОЛНУЮ мощность. А это не совсем то, совсем не то.
Применение свойств RC цепи.
Добрались до самой сути статьи.
Если обрабатывать сигналы тока и напряжения МК, что в современных реалиях считается обязательным. То мы придем к следующим формулам. Для среднеквадратичного напряжения:
Где К – коэффициент трансформации, N – количество замеров за период напряжения, u – мгновенные значения напряжения. Для тока все будет тоже самое. Для вычисления полной мощности остается умножить U*I*3 для трехфазной симметричной нагрузки. А как же быть с активной мощностью? Активная мощность может быть вычислена следующим образом:
Осталось только взять замеры тока и напряжения в одни и те же отрезки времени на протяжении периода, просуммировать их произведение.
Рассмотрим типовую схему включения трансформатора напряжения в ВВ ячеки.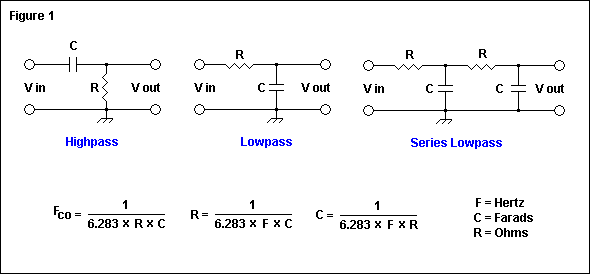 Это вариант А.
Это вариант А.
Трансформатор тока включен в фазу B. Посмотрим диаграмму напряжений в трехфазной сети.
Фазное напряжение Ub и линейное напряжение Uac располагаются под углом в 900. При чем напряжение Uac отстает от фазного напряжения Ub. Ничего не напоминает.
Правда, амплитуда линейного напряжения больше фазного в корень из 3 раз. Но на МК уменьшить коэффициент на эту величину не составляет труда.
Значит у нас два критерия для нашего фильтра. Сдвиг фазы выходного напряжения относительно входного должно составлять ≈900. Коэффициент передачи на данной частоте, должно быть такой, чтобы обеспечить выходное напряжение после фильтра в пределах 1-1.5 вольта.
Приступим к вычислениям.
Расчет фильтра.
С трансформатора напряжения приходит 100 вольт напряжения (стандарт). Это действующее напряжение, следовательно, чтобы нам определить амплитудное значение умножим на корень из 2.
Это действующее напряжение, следовательно, чтобы нам определить амплитудное значение умножим на корень из 2.
ИТОГО: Umax=U*1.41=141В.
Это синусоида, и она имеет как положительную полуволну, так и отрицательную. Значит, нам для МК необходимо эту синусоиду поднять в положительное напряжение.
Напряжение питание МК возьмем 3 в. Значит, средняя точка для синусоиды будет 1.5 вольта. Итого размах полуволны напряжения нам остается 1.5вольта. Отсюда коэффициент передачи RC цепи будет:
Теперь вычислим значение τ=RC, исходя из коэффициента К. Частота сигнала известна 50 Гц.
После математических преобразований получаем: τ=RC = 0,318
Отсюда
Угол нас устраивает. Вычислим погрешность измерений, при ошибки фазы в 0,570, следовательно ошибка равна: (0,570/900)*100%=0,63%, это за четверть периода, следовательно за 3600 и того меньше.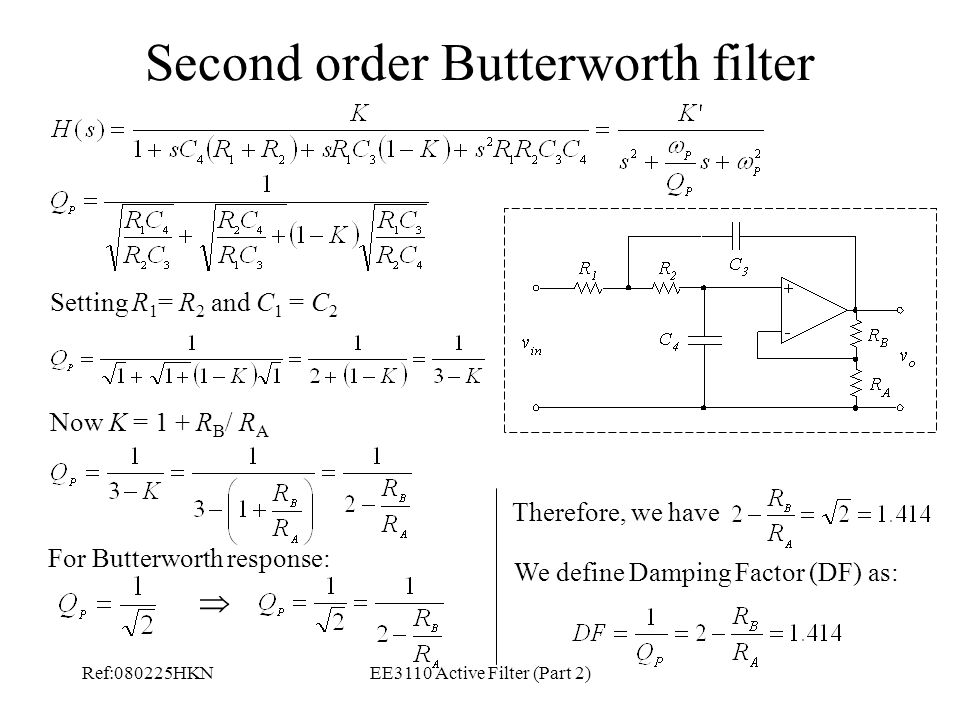 Врядли трансформаторы тока и напряжения будут классом точности выше чем 0,5%. Так что, искажениями, вносимыми нашем фильтром можно пренебречь.
Врядли трансформаторы тока и напряжения будут классом точности выше чем 0,5%. Так что, искажениями, вносимыми нашем фильтром можно пренебречь.
Осталось рассчитать сами значения R и C. Отталкиваться лучше от конденсатора. Возьмем С=4,7 мкФ, отсюда R= τ/С=0,318/4,7*10-6=318*10-3/4,7*10-6=67,66*103 Ом или 67,66 кОм.
Теперь подтвердим наши расчеты симулятором Proteus и посмотрим, отличается ли его математика от нашей.
Проект протеуса прикладываю к статье. Можете убедиться, что расчеты верны.
Вот таким нехитрым способом можно заставить работать RC цепочку не по назначению.
ВИДЕО демонтсрирующее возможности RC фильтра.
Применение на практике данного способа использования RC цепи можно прочитать здесь.
З.Ы. коментарии, вопросы и предложения складываем тут
UDP:
Если затронуть вопрос о реальных сетях, с присутствующими искажениями основной частоты 50 Гц гармониками, то необходимо проверить работу фльтра в таких условиях и просимулировать в протеусе данную ситуацию. Схема протеуса конечно, не реальная картина на производстве, но показывает, что если сигнал основной частоты искажен гармониками небольшой амплитуды, то RC фильтр хорошо выделяет основную частоту и нормализует синус.
Видео, демонстрирующее работу фильтра с сигналом, искаженным гармониками предсатвлен ниже.
Что такое фильтр баттерворта, расчет и схема. Фильтры баттерворта Формула амплитудно частотной характеристики фильтра баттерворта
1 Определим порядок фильтра.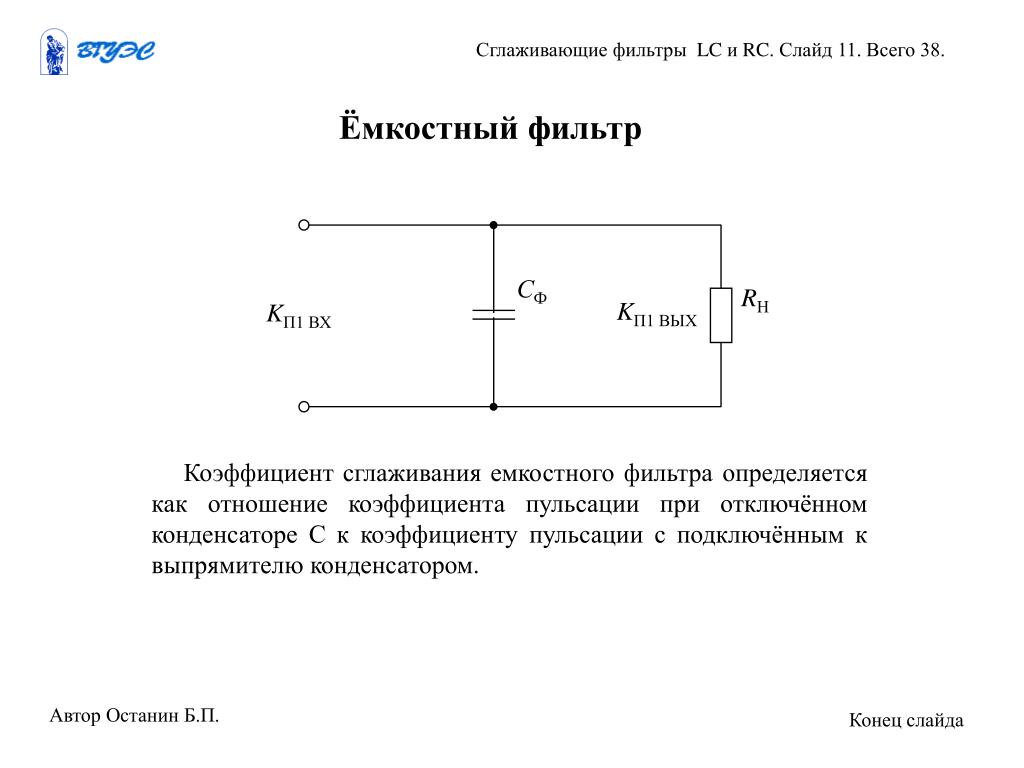 Порядок
фильтра это число реактивных элементов
в ФНЧ и ФВЧ.
Порядок
фильтра это число реактивных элементов
в ФНЧ и ФВЧ.
где
—
функция Баттерворта, соответствующая
допустимой частоте.
— допустимое затухание.
2 Чертим схему фильтра полученного порядка. При практической реализации предпочтительны схемы с меньшим количеством индуктивностей.
3 Рассчитываем постоянные преобразования фильтра.
, мГн
, нФ
4 Для идеального фильтра с сопротивлением
генератора 1 Ом, сопротивление нагрузки
1 Ом,
составлена
таблица нормированных коэффициентов
фильтра Баттерворта. В каждой строке
таблицы коэффициенты симметричны, к
середине увеличиваются, а затем
уменьшаются.
5 Чтобы найти элементы схемы, необходимо постоянные преобразования умножить на коэффициент из таблицы.
Порядок фильтра | Порядковые номера фильтра m | |||||||||
Рассчитать параметры фильтра низких
частот Баттерворта, если ПП=0,15 кГц,
=25
кГц,=30
дБ,
=75
Ом. Найти
Найти
для трех точек.
29.3 Фвч Баттерворта.
Фильтры ФВЧ – это четырехполюсники, у
кторых в диапазоне (
)
затухание мало, а в диапазоне (
)
– велико, то есть фильтр должен пропускать
в нагрузку токи верхних частот.
Так как ФВЧ должен пропускать токи высоких частот, то на пути тока, идущего в нагрузку, должен стоять частотно зависимый элемент, который хорошо пропускает токи высоких частот и плохо токи низких частот. Таким элементом является конденсатор.
Ф
ВЧ
Т-образный
ФВЧ П-образный
Конденсатор ставят последовательно с
нагрузкой, так как
и с ростом частоты
уменьшается, следовательно токи высоких
частот легко проходят в нагрузку через
конденсатор. Катушку индуктивности
ставят параллельно нагрузке, так как
и с увеличением частоты увеличивается
,
поэтому токи низких частот замыкаются
через индуктивности и не попадут в
нагрузку.
Расчет ФВЧ Баттерворта аналогичен расчету ФНЧ Баттерворта, проводится по тем же формулам, только
.
Рассчитать фильтр верхних частот ФВЧ
Баттерворта, если
Ом,
кГц,
дБ,
кГц.
Найти:
.
Тема занятия 30: Полосовые и режекторные фильтры Баттерворта.
Передаточная функция фильтра нижних частот Баттерворта n -го порядка характеризуется выражением:
Амплитудно-частотная характеристика фильтра Баттерворта обладает следующими свойствами:
1) При любом порядке n значение АЧХ
2) на частоте среза щ=щ с
АЧХ ФНЧ монотонно убывает с ростом частоты. По этой причине фильтры Баттерворта называют фильтрами с максимально плоскими характеристиками. На рисунке 3 показаны графики амплитудно-частотных характеристик ФНЧ Баттерворта 1-5 порядков. Очевидно, что чем больше порядок фильтра, тем точнее аппроксимируется АЧХ идеального фильтра нижних частот.
Рисунок 3 — АЧХ для фильтра Баттерворта нижних частот порядка от 1 до 5
На рисунке 4 представлена схемная реализация ФВЧ Баттерворта.
Рисунок 4 — ФВЧ-II Баттерворта
Достоинством фильтра Баттерворта является максимально гладкая АЧХ на частотах полосы пропускания и ее снижение практически до нуля на частотах полосы подавления. Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.
Однако в сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления.
Квадрат модуля передаточной функции фильтра Чебышева определяется выражением:
где — полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где обращается в нуль.
Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.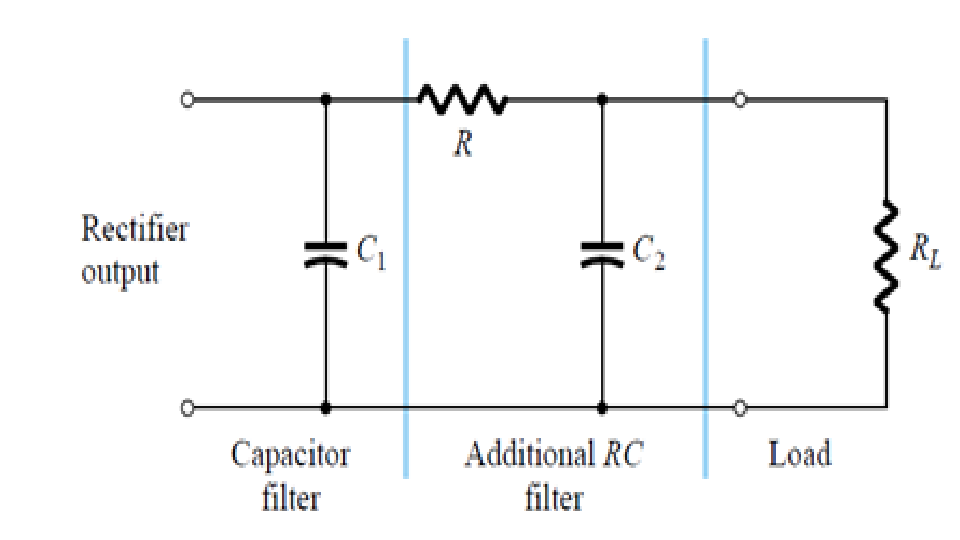
Различают фильтры Чебышева I и II родов.
Фильтр Чебышева I рода. Это более часто встречающаяся модификация фильтров Чебышева. В полосе пропускания такого фильтра видны пульсации, амплитуда которых определяется показателем пульсации е. В случае аналогового электронного фильтра Чебышева его порядок равен числу реактивных компонентов, использованных при его реализации. Более крутой спад характеристики может быть получен если допустить пульсации не только в полосе пропускания, но и в полосе подавления, добавив в передаточную функцию фильтра нулей на мнимой оси jщ в комплексной плоскости. Это, однако, приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.
АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка представлена на рисунке 5.
Рисунок 5 — АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка
Фильтр Чебышева II рода (инверсный фильтр Чебышева) используется реже, чем фильтр Чебышева I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления.
У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления.
АЧХ для фильтра Чебышева нижних частот II рода четвёртого порядка представлена на рисунке 6.
Рисунок 6 — АЧХ для фильтра Чебышева нижних частот II рода
На рисунке 7 представлены схемные реализации ФВЧ Чебышева I и II порядка.
Рисунок 7 — ФВЧ Чебышева: а) I порядка; б) II порядка
Свойства частотных характеристик фильтров Чебышева:
1) В полосе пропускания АЧХ имеет равноволновой характер. На интервале (-1?щ?1) имеется n точек, в которых функция достигает максимального значения, равного 1, или минимального значения, равного. Если n нечетно, если n четно;
2) значение АЧХ фильтра Чебышева на частоте среза равно
3) При функция монотонно убывает и стремится к нулю.
4) Параметр е определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания:
Сравнение АЧХ фильтров Баттерворта и Чебышева показывает, что фильтр Чебышева обеспечивает большее ослабление в полосе пропускания, чем фильтр Баттерворта такого же порядка.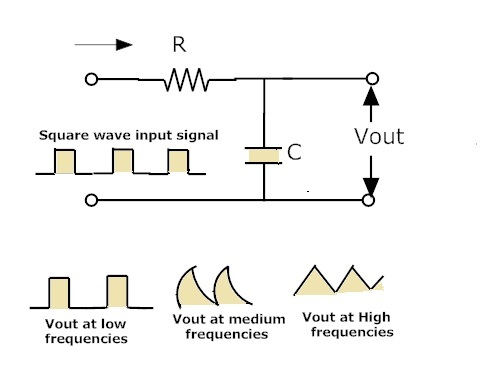 Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.
Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.
Для фильтров Баттерворта и Чебышева имеются подробные таблицы, в которых приведены координаты полюсов и коэффициенты передаточных функций различных порядков.
Значительная часть теории расчета цифровых БИХ-фильтров (т.е. фильтров с бесконечной импульсной характеристикой) требует понимания методов расчета фильтров непрерывного времени. Поэтому в данном разделе будут приведены расчетные формулы для нескольких стандартных типов аналоговых фильтров, включая фильтры Баттерворта, Бесселя и Чебышева типа I и II. Подробный анализ достоинств и недостатков способов аппроксимации заданных характеристик, соответствующих этим фильтрам, можно найти в ряде работ, посвященных методам расчета аналоговых фильтров, поэтому ниже будут лишь кратко перечислены основные свойства фильтров каждого типа и приведены расчетные соотношения, необходимые для получения коэффициентов аналоговых фильтров.
Пусть нужно рассчитать нормированный фильтр нижних частот с частотой среза, равной Ω = 1 рад/с. В качестве аппроксимируемой функции будет, как правило, использоваться квадрат амплитудной характеристики (исключением является фильтр Бесселя). Будем считать, что передаточная функция аналогового фильтра является рациональной функцией переменной S следующего вида:
Фильтры Баттерворта нижних частот характеризуются тем, что имеют максимально гладкую амплитудную характеристику в начале координат в s-плоскости. Это означает, что все существующие производные от амплитудной характеристики в начало координат равны нулю. Квадрат амплитудной характеристики нормированного (т. е. имеющего частоту среза 1 рад/с) фильтра Баттерворта равен:
где n — порядок фильтра. Аналитически продолжая функцию (14.2) на всю S-плоскость, получим
Все полюсы (14.3) находятся на единичной окружности на одинаковом расстоянии друг от друга в S-плоскости . Выразим передаточную функцию Н (s) через полюсы, располагающиеся в левой полуплоскости S :
Где (14. 4)
4)
Где k =1,2…..n (14.5)
а k 0 — константа нормирования. Используя формулы (14.2) и (14.5), можно сформулировать несколько свойств фильтров Баттерворта нижних частот.
Свойства фильтров Баттерворта нижних частот:
1. Фильтры Баттерворта имеют только полюсы (все нули передаточных функций этих фильтров расположены на бесконечности).
2. На частоте Ω=1 рад/с коэффициент передачи фильтров Баттерворта равен (т. е. на частоте среза их амплитудная характеристика спадает на 3 дБ).
3. Порядок фильтра n полностью определяет весь фильтр. На практике порядок фильтра Баттерворта обычно рассчитывают из условия обеспечения определенного ослабления па некоторой заданной частоте Ω t > 1. Порядок фильтра, обеспечивающий на частоте Ω= Ω t
Рис. 14.1. Расположение полюсов аналогового фильтра Баттерворта нижних частот.
Рис. 14.2- Амплитудная и фазовая характеристики, а также характерис- тика групповой задержки аналогового фильтра Баттерворта нижних частот.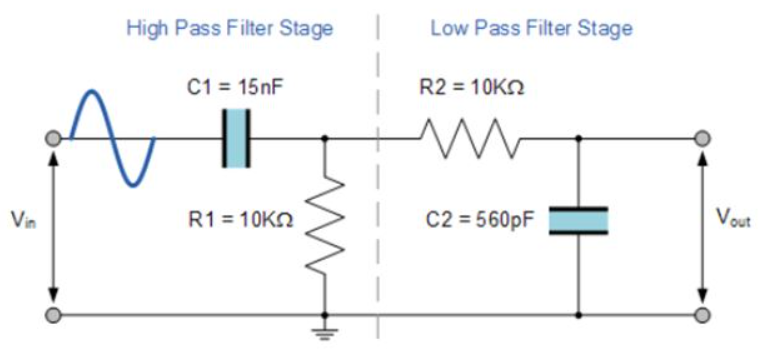
Пусть, например , требуется на частоте Ω t = 2 рад/с обеспечить ослабление, равное А = 100. Тогда
Округлив n в большую сторону до целого числа, найдем, что заданное ослабление обеспечит фильтр Баттерворта 7-го порядка.
Решение . Используя в качестве расчетных характеристик 1/A == 0,0005 (что соответствует ослаблению на 66 дБ) и Ω t = 2 , получим n == 10,97. Округление дает n = 11 . На рис. 14.1 показано расположение полюсов рассчитанного фильтра Баттерворта в s-плоскости . Амплитудная (в логарифмическом масштабе) и фазовая характеристики, а также характеристика групповой задержки этого фильтра представлены на рис. 14.2.
Страница 1 из 2
Определим порядок фильтра исходя из требуемых условий по графику для затухания в полосе задерживания в книге Г.Лэм «Аналоговые и цифровые фильтры» гл.8.1 стр.215.
Понятно, что для необходимого затухания достаточно фильтра 4 порядка. График приведён для случая, когда w с =1 рад/с, а соответственно частота, на которой нужно необходимое затухание – 2 рад/с (соответственно 4 и 8 кГц).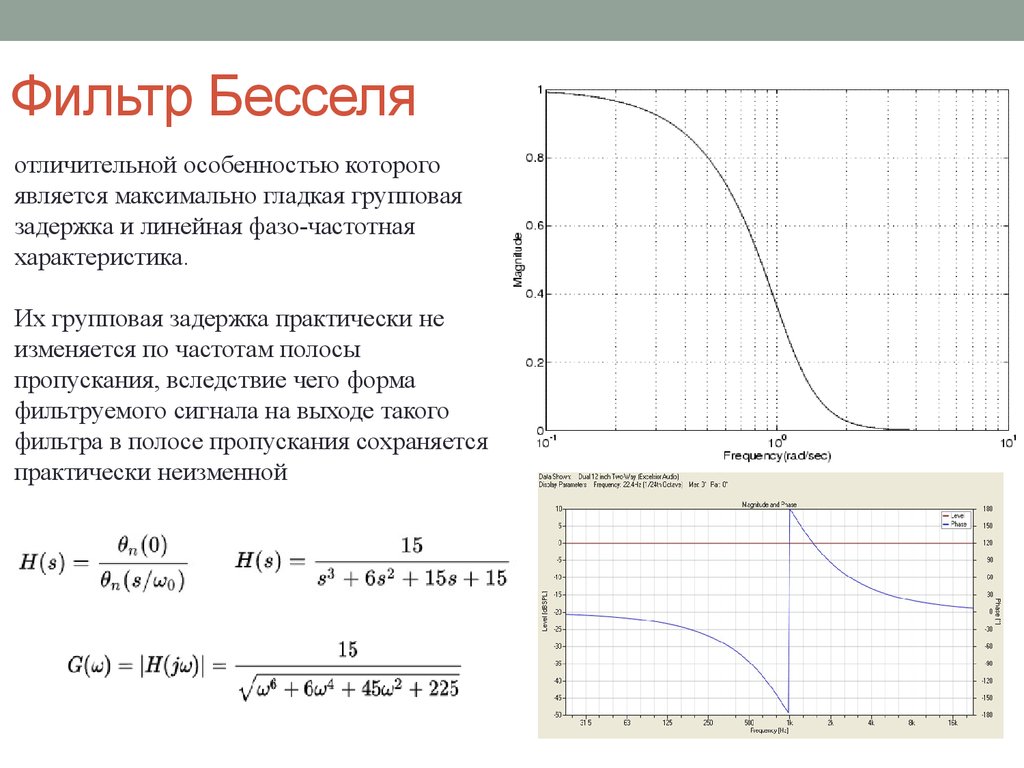 Общий график для передаточной функции фильтра Баттерворта:
Общий график для передаточной функции фильтра Баттерворта:
Определяем схемную реализацию фильтра:
активный фильтр нижних частот четвёртого порядка со сложной отрицательной обратной связью:
Чтобы желаемая схема имела желаемую амплитудно-частотную характеристику, входящие в неё элементы могут быть подобраны с не очень высокой точностью, что является плюсом данной схемы.
активный фильтр нижних частот четвёртого порядка с положительной обратной связью:
В данной схеме коэффициент усиления операционного усилителя должен иметь строго определённое значение, а коэффициент передачи данной схемы будет не больше 3. Поэтому данную схему можно отбросить.
активный фильтр нижних частот четвёртого порядка с омической отрицательной обратной связью
Данный фильтр построен на четырех операционниках, что увеличивает помехи и сложность расчёта данной схемы, поэтому её мы также отбрасываем.
Из рассмотренных схем мы выбираем фильтр со сложной отрицательной обратной связью.
Расчёт фильтра
Определение передаточной функции
Записываем табличные значения коэффициентов для фильтра Баттерворта четвёртого порядка:
a 1 =1.8478 b 1 =1
a 2 =0.7654 b 2 =1
(см. У.Титце, К.Шенк «Полупроводниковая схемотехника» табл.13.6 стр. 195)
Общее выражение передаточной функции для ФНЧ четвёртого порядка:
(см. У.Титце, К.Шенк «Полупроводниковая схемотехника» табл.13.2 стр. 190 и форм. 13.4 стр. 186).
Передаточная функция первого звена имеет вид:
Передаточная функция второго звена имеет вид:
где w с – круговая частота среза фильтра, w с =2pf c .
Расчёт номиналов деталей
Приравняв коэффициенты выражений (2) и (3) коэффициентам выражения (1) получим:
Коэффициенты передачи постоянного сигнала для каскадов, их произведение А 0 должно быть равно 10 по заданию. Они отрицательные, так как данные каскады являются инвертирующими, однако их произведение даёт положительный коэффициент передачи.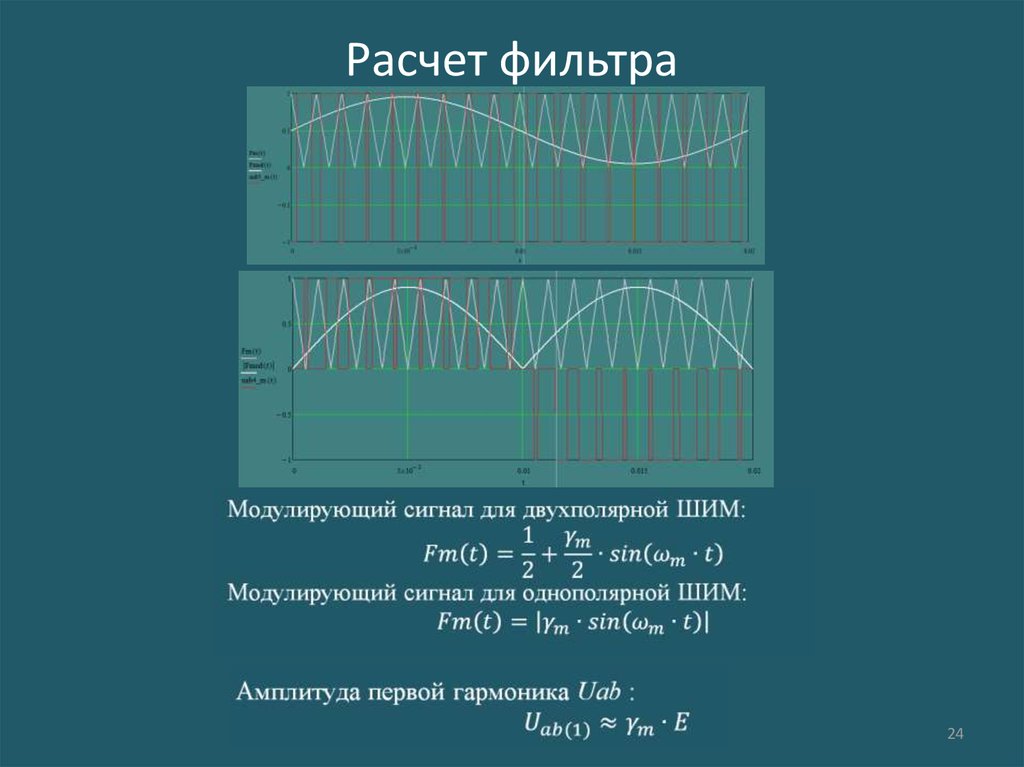
Для расчёта схемы лучше задаться емкостями конденсаторов, при этом для того, чтобы значение R 2 было действительным, должно выполняться условие
и соответственно
Исходя из этих условий выбирается С 1 =С 3 =1 нФ, С 2 =10 нФ, С 4 =33 нФ.
Рассчитываем значения сопротивлений для первого каскада:
Значения сопротивлений второго каскада:
Выбор ОУ
При выборе ОУ необходимо учитывать диапазон частот фильтра: частота единичного усиления ОУ (на которой коэффициент усиления равен единице) должна быть больше произведения частоты среза и коэффициента усиления фильтра K у.
Поскольку максимальный коэффициент усиления равен 3.33, а частота среза 4 кГц, то этому условию удовлетворяют почти все существующие ОУ.
Другим важным параметром ОУ является его входное сопротивление. Оно должно быть больше десятикратного максимального сопротивления резистора схемы.
Максимальное сопротивление в схеме равно 99.6 кОм, следовательно входное сопротивление ОУ должно быть не менее 996 кОм.
Так же необходимо учитывать нагрузочную способность ОУ. Для современных ОУ минимальное сопротивление нагрузки составляет 2 кОм. Учитывая, что сопротивление R1 и R4 равны соответственно 33.2 и 3.09 кОм, выходной ток операционного усилителя будет заведомо меньше максимально допустимого.
В соответствии с вышеприведёнными требованиями выбираем ОУ К140УД601 со следующими паспортными данными (характеристиками):
K у. min = 50 000
R вх = 1 МОм
Харьковский национальный университет радиоэлектроники
Кафедра РЭУ
КУРСОВАЯ РАБОТА
РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ФИЛЬТР ВЕРХНИХ ЧАСТОТ БАТТЕРВОРТА
Харьков 2008 г.
Техническое задание
Спроектировать фильтр верхних частот (ФВЧ) с аппроксимацией амплитудно-частотной характеристики (АЧХ) полиномом Баттерворта, определить необходимый порядок фильтра, если заданы параметры АЧХ (рис.1): К 0 =26дБ
U m Вх =250мВ
где — максимальный коэффициент передачи фильтра;
Минимальный коэффициент передачи в полосе пропускания;
Максимальный коэффициент передачи фильтра в полосе задержки;
Частота среза;
Частота, начиная с которой коэффициент передачи фильтра меньше .
Рисунок 1 – Шаблон ФВЧ Баттерворта.
Обеспечить небольшую чувствительность к отклонениям номиналов элементов.
РЕФЕРАТ
Расчётно-пояснительная записка: 26 с., 11 рис., 6 табл.
Цель работы: синтез схемы активного RC-фильтра верхних частот и расчёт её компонентов.
Метод исследования: аппроксимация АЧХ фильтра полиномом Баттерворта.
Аппроксимированная передаточная функция реализована с помощью активного фильтра. Фильтр построен каскадным соединением независимых звеньев. В активных фильтрах использованы неинвертирующие усилители с конечным усилением, которые реализованы с помощью операционных усилителей.
Результаты работы могут использоваться для синтеза фильтров радиотехнической и бытовой аппаратуры.
Вступление
1. Обзор аналогичных схем
3.1 Осуществление нормировки ФВЧ
3.2 Определение необходимого порядка фильтра
3.3 Определение полинома Баттерворта
3.4 Обратный переход от нормированного к проектируемому ФВЧ
3. 5Переход от передаточной функции к схеме
5Переход от передаточной функции к схеме
3.6Переход от передаточной функции к схеме
4. Расчёт элементов схемы
5. Методика настройки регулировки разработанного фильтра
Вступление
До недавнего времени результаты сопоставления цифровых и аналоговых устройств в радиоаппаратуре и технических средствах электросвязи не могли не вызывать чувства неудовлетворённости. Цифровые узлы, реализуемые с широким использованием интегральных микросхем (ИМС), выгодно отличались своей конструктивно-технологической завершённостью. Иначе обстояло дело с узлами аналоговой обработки сигналов, которые, например, в телекоммуникациях составляли от 40 до 60% объёма и массы аппаратуры связи. Громоздкие, содержащие большое число ненадёжных и трудоёмких намоточных элементов, они выглядели на фоне больших интегральных схем столь удручающе, что породили у ряда специалистов мнение о необходимости “тотальной цифризации” радиоэлектронной аппаратуры.
Последнее, однако, как любая другая крайность, не привело (да и не могло привести) к результатам, адекватным ожидаемым. Истина, как и во всех других случаях, оказалась где-то посередине. В ряде случаев более эффективной оказывается аппаратура, построенная на функциональных аналоговых узлах, элементный базис которых адекватен возможностям и ограничениям микроэлектроники.
Истина, как и во всех других случаях, оказалась где-то посередине. В ряде случаев более эффективной оказывается аппаратура, построенная на функциональных аналоговых узлах, элементный базис которых адекватен возможностям и ограничениям микроэлектроники.
Адекватность в данном случае может быть обеспечена переходом к активным RC-цепям, в элементный базис которых не входят катушки индуктивностей и трансформаторы, принципиально не реализуемые средствами микроэлектроники.
Обоснованность такого перехода определяется в настоящее время, с одной стороны, достижениями теории активных RC-цепей, а с другой – успехами микроэлектроники, предоставившей в распоряжение разработчиков высококачественные линейные интегральные схемы, в том числе и интегральные операционные усилители (ОУ). Эти ОУ, обладая большими функциональными возможностями, существенно обогатили аналоговую схемотехнику. Особенно ярко это проявилось в схемотехнику активных фильтров.
До 60-х годов для реализации фильтров применялись, в основном пассивные элементы, т. е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и ОУ (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приёмниках, традиционные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и ОУ (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приёмниках, традиционные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах – активных RC-фильтрах.
С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах – активных RC-фильтрах.
1. Обзор аналогичных схем
Фильтры – это частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определённых полосах частот.
Фильтры можно классифицировать по их частотным характеристикам:
1. Фильтры нижних частот (ФНЧ) – пропускают все колебания с частотами не выше некоторой частоты среза и постоянную составляющую.
2. Фильтры верхних частот (ФНЧ) – пропускают все колебания не ниже некоторой частоты среза.
3. Полосовые фильтры (ПФ) – пропускают колебания в определённой полосе частот, которая определяется по некоторому уровню частотной характеристики.
4. Полосно-подавляющие фильтры (ППФ) — задерживают колебания в определённой полосе частот, которая определяется по некоторому уровню частотной характеристики.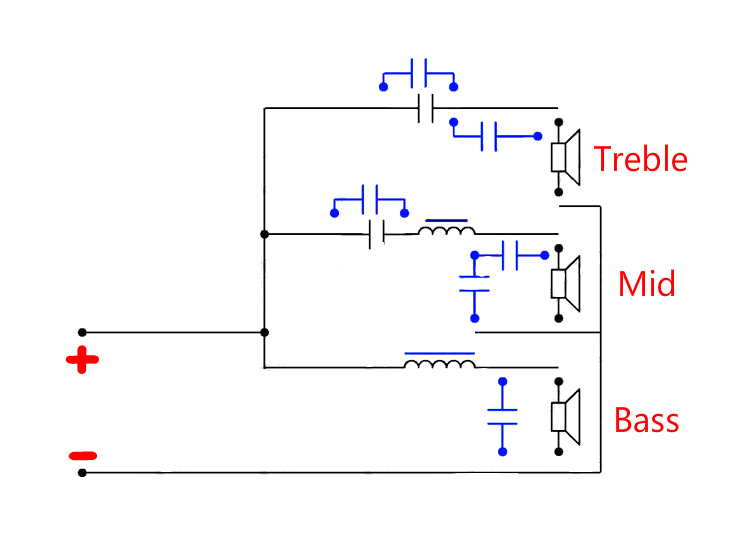
5. Режекторные фильтры (РФ) – вид ППФ, имеющий узкую полосу задержки и называемый ещё фильтром-пробкой.
6. Фазовые фильтры (ФФ) – имеют постоянный в идеальном случае коэффициент передачи на всех частотах и предназначен для изменения фазы входных сигналов (в частности для временной задержки сигналов).
Рисунок 1.1 – Основные типы фильтров
С помощью активных RC-фильтров нельзя получить идеальные формы частотных характеристик в виде показанных на рис.1.1 прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью её реализации. Это называется “проблемой аппроксимации“. Во многих случаях требования к качеству фильтрации позволяют обойтись простейшими фильтрами первого и второго порядков. Некоторые схемы таких фильтров представлены ниже. Проектирование фильтра в этом случае сводиться к выбору схемы с наиболее подходящей конфигурацией и последующему расчёту значений номиналов элементов для конкретных частот.
Некоторые схемы таких фильтров представлены ниже. Проектирование фильтра в этом случае сводиться к выбору схемы с наиболее подходящей конфигурацией и последующему расчёту значений номиналов элементов для конкретных частот.
Однако бывают ситуации, когда требования к фильтрации могут оказаться гораздо более жёсткими, и могут потребоваться схемы более высоких порядков, чем первый и второй. Проектирование фильтров высоких порядков является более сложной задачей, чему посвящена данная курсовая работа.
Ниже приведены некоторые основные схемы первого второго порядков с описанием достоинств и недостатков каждой из них.
1. ФНЧ-I и ФВЧ-Iна основе не инвертирующего усилителя.
Рисунок 1.2 – Фильтры на основе неинвертирующего усилителя:
а) ФНЧ-I, б) ФВЧ-I.
К достоинствам схем фильтров можно отнести главным образом простоту реализации и настройки, недостатки – малая крутизна частотных характеристик, малоустойчивы к самовозбуждению.
2. ФНЧ-IIи ФВЧ-IIс много петлевой обратной связью.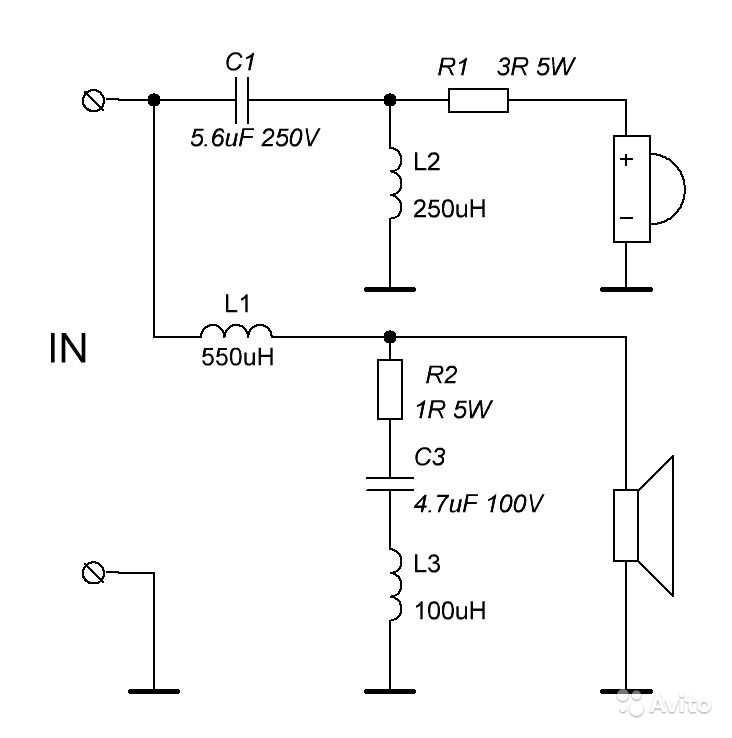
Рисунок 1.3 – Фильтры с многопетлевой обратной связью:
а) ФНЧ-II, б) ФВЧ-II.
Таблица 2.1 – Достоинства и недостатки ФНЧ-II с много петлевой обратной связью
Таблица 2.2 – Достоинства и недостатки ФВЧ-II с много петлевой обратной связью
2. ФНЧ-IIи ФВЧ-IIСаллена-Кея.
Рисунок 1.4 – Фильтры Саллена-Кея:
а) ФНЧ-II, б) ФВЧ-II
Таблица 2.3 – Достоинства и недостатки ФНЧ-II Саллена-Кея.
Таблица 2.4 – Достоинства и недостатки ФВЧ-II Саллена-Кея.
3. ФНЧ-IIи ФВЧ-IIна основе конверторов полного сопротивления.
Рисунок 1.5 – Схема ФНЧ IIна основе конверторов полного сопротивления:
а) ФНЧ-II, б) ФВЧ-II.
Таблица 2.3 – Достоинства и недостатки ФНЧ-II и ФВЧ-II на основе конверторов полного сопротивления.
2. Выбор и обоснование схемы фильтра
Методы проектирования фильтров отличаются по конструктивным особенностям. Проектирования пассивных RC-фильтров большей частью определяется структурной схемой
Активные фильтры АФ математически описывают передаточною функцией. Типам АЧХ предоставлен названия полиномов передаточных функций. Каждый тип АЧХ реализуют определенным количеством полюсов (RC-цепей) в соответствии с заданной крутизной спада АЧХ. Известнейшими, есть аппроксимации Баттерворта, Бесселя, Чебышева.
Типам АЧХ предоставлен названия полиномов передаточных функций. Каждый тип АЧХ реализуют определенным количеством полюсов (RC-цепей) в соответствии с заданной крутизной спада АЧХ. Известнейшими, есть аппроксимации Баттерворта, Бесселя, Чебышева.
Фильтр Баттерворта имеет максимально плоскую АЧХ, в полосе подавления наклон переходного участка равняется 6 дБ/окт на полюс, но он имеет нелинейную ФЧХ, входное импульсное напряжение служит причиной осцилляции на выходе, потому фильтр используется для непрерывных сигналов.
Фильтр Бесселя имеет линейную ФЧХ, небольшую крутизну переходного участка АЧХ. Сигналы всех частот в полосе пропускания имеют одинаковые временные задержки, поэтому он пригодный для фильтрации прямоугольных импульсов, которые надо посылать без искажений.
Фильтр Чебышева — фильтр равных волн в СП, масс плоскую форму за ее пределами, пригодный для непрерывных сигналов в случаях, капы надо иметь крутой склон АЧХ за частотой среза.
Простые схемы фильтров первого и второго порядков применяются лишь, когда нет жестких требований к качеству фильтрации.
Каскадное соединение звеньев фильтра осуществляют, если нужен порядок фильтра выше второго, то есть когда надо сформировать передаточную характеристику с очень большим послаблением сигналов в полосе подавленный и большой крутизной затухания АЧХ Результирующую передаточную функцию получают, перемножая частичные коэффициенты передачи
Цепи строят по одинаковой схеме, но номиналы элементов
R, С разные, и зависят от частот среза фильтра и его ланок: f зр.ф /f зр.л
Однако следует помнить, что каскадное соединение, например, двух фильтров Баттерворта второго порядка не дает фильтр Баттерворта четвертого порядка, так как результирующий фильтр будет иметь другую частоту среза и другую АЧХ. Поэтому необходимо выбирать коэффициенты одиночных звеньев таким образом, чтобы следующее произведение передаточных функций отвечал выбранному типу аппроксимации. Поэтому проектирования АФ вызовет затруднения со стороны получения идеальной характеристики и сложности ее реализации.
Благодаря очень большим входным и маленьким выходным сопротивлениям каждого звена обеспечивается отсутствие искажений заданной передаточной функции и возможность независимого регулирования каждого звена. Независимость звеньев дает возможность широко регулировать свойства каждого звена изменением его параметров.
Независимость звеньев дает возможность широко регулировать свойства каждого звена изменением его параметров.
Принципиально не имеет значения, в котором порядке размещенные частичные фильтры, так как результирующая передаточная функция всегда будет одинаковой. Тем не менее, существуют разнообразные практические рекомендации относительно порядка соединения частичных фильтров. Например, для защиты от самовозбуждения следует организовать последовательность звеньев в порядке возрастания частичной предельной частоты. Другой порядок может привести к самовозбуждению второго звена в области выброса его АЧХ, поскольку фильтры с высшими предельными частотами обычно имеют большую добротность в области граничной частоты.
Другой критерий, связан с требованиями минимизации, уровня шумов на входе. В этом случае последовательность звеньев обратная, так как фильтр с минимальной предельной частотой ослабляет уровень шума, который возникает от предыдущих звеньев каскада.
3. Топологическая модель фильтра и передаточная функция по напряжению
3. 1 В данном пункте будет выбран порядок ФВЧ Баттерворта и определён вид его передаточной функции согласно заданным в ТЗ параметрам:
1 В данном пункте будет выбран порядок ФВЧ Баттерворта и определён вид его передаточной функции согласно заданным в ТЗ параметрам:
Рисунок 2.1 – Шаблон ФВЧ согласно техническому заданию.
Топологическая модель фильтра.
3.2 Осуществление нормировки ФВЧ
За коэффициентом передачи:
К max =K 0 -K п =26-23=3дБ
К min =К 0 -К з =26-(-5)=31дБ
По частоте:
3.3 Определение необходимого порядка фильтра
Округляем nдо ближайшего целого значения: n = 3.
Таким образом, для удовлетворения требований, заданных шаблоном, необходим фильтр третьего порядка.
3.4 Определение полинома Баттерворта
Согласно таблице нормированных передаточных функций фильтров Баттерворта находим полином Баттерворта третьего порядка:
3.5 Обратный переход от нормированного к проектируемому ФВЧ
Проведём обратный переход от нормированного ФВЧ к проектируемому ФВЧ.
· масштабирование по коэффициенту передачи:
· масштабирование по частоте:
Производим замену
В результате масштабирования получаем передаточную функцию W(p) в виде:
Рисунок 2. 2 – АЧХ проектируемого ФВЧ Баттерворта.
2 – АЧХ проектируемого ФВЧ Баттерворта.
3.6 Переход от передаточной функции к схеме
Представим передаточную функцию проектируемого ФВЧ третьего порядка в виде произведения передаточных функций двух активных ФВЧ первого и второго порядка, т.е. в виде
и ,
где – коэффициент передачи на бесконечно высокой частоте;
– частота полюса;
– добротность фильтра (отношение коэффициента усиления на частоте к коэффициенту усиления в полосе пропускания).
Этот переход справедлив, так как общий порядок последовательно соединенных активных фильтров будет равен сумме порядков отдельно взятых фильтров (1 + 2 = 3).
Общий коэффициент передачи фильтра (K0 = 19.952) будет определяться произведением коэффициентов передачи отдельных фильтров (K1, K2).
Разложив передаточную функцию на квадратичные сомножители, получим:
В этом выражении
. (2.5.1)
Нетрудно заметить, что частоты полюсов и добротности передаточных функций отличаются.
Для первой передаточной функции:
частота полюса ;
добротность ФВЧ-Iпостоянна и равна .
Для второй передаточной функции:
частота полюса ;
добротность .
Для того чтобы к операционным усилителям в каждом каскаде предъявлялись примерно равные требования по частотным свойствам, целесообразно общий коэффициент передачи всего фильтра распределить между каждым из каскадов обратно пропорционально добротности соответствующих каскадов, а характерную частоту (частоту единичного усиления ОУ) выбрать максимальную среди всех каскадов.
Так как в данном случае ФВЧ состоит из двух каскадов, то указанное выше условие можно записать в виде:
. (2.5.2)
Подставляя выражение (2.5.2) в (2.5.1), получаем:
;
Проверим правильность расчёта коэффициентов передачи. Общий коэффициент передачи фильтра в разах будет определяться произведением коэффициентов отдельных фильтров. Переведём коэффициент издБ в разы:
Т.е. расчёты верны.
Запишем передаточную характеристику с учётом расcчитанных выше величин ():
.
3.7 Выбор схемы активного ФВЧ третьего порядка
Так как согласно заданию необходимо обеспечить небольшую чувствительность к отклонениям элементов, то выберем в качестве первого каскада ФВЧ-Iна основе не инвертирующего усилителя (рис. 1.2,б), а второго – ФВЧ-IIна основе конверторов полного сопротивления (КПС), схема которого приведена на рис.1.5,б.
1.2,б), а второго – ФВЧ-IIна основе конверторов полного сопротивления (КПС), схема которого приведена на рис.1.5,б.
Для ФВЧ-I на основе не инвертирующего усилителя зависимость параметров фильтра от номиналов элементов схемы таково:
Для ФВЧ-IIна основе КПС параметры фильтра зависят от номиналов элементов следующим образом:
; (3.4)
;
4. Расчёт элементов схемы
· Расчёт первого каскада (ФВЧ I) с параметрами
Выберем R1 исходя из требований к величине входного сопротивления (): R1 = 200 кОм. Тогда из (3.2) следует, что
.
Выберем R2 = 10 кОм, тогда из (3.1) следует, что
· Расчёт второго каскада (ФВЧ II) с параметрами
. .
Тогда (коэффициент в числителе подобран так, чтобы получить номинал ёмкости из стандартного ряда Е24). Итак С2 = 4.3 нФ.
Из (3.3) следует, что
Из (3.1) следует, что
Пусть . Итак С1 = 36 нФ.
Таблица 4.1– Номиналы элементов фильтра
Из данных таблицы 4.1мы можем приступить к моделированию схемы фильтра.
Это мы делаем при помощи специальной программы Workbench5.0.
Схема и результаты моделирования приведены на рис.4.1. и рис.4.2,а-б.
Рисунок 4.1 – Схема ФВЧ Баттерворта третьего порядка.
Рисунок 4.2– Результирующие АЧХ (а) и ФЧХ (б) фильтра.
5. Методика настройки и регулирования разработанного фильтра
Это очень просто сделать для резисторов, если их брать с допуском не более 1%, и тяжелее для емкостей конденсаторов, потому что допуски у них в районе 5-20%. Из-за этого сначала рассчитывается емкость, а потом рассчитывается сопротивление резисторов.
5.1 Выбор типа конденсаторов
· Выберем низкочастотный тип конденсаторов в силу их меньшей стоимости.
· Необходимы небольшие габариты и масса конденсаторов
· Выбирать конденсаторы нужно с как можно меньшими потерями (с маленьким тангенсом угла диэлектрических потерь).
Некоторые параметры группы К10-17 (взяты из ):
Размеры, мм.
Масса, г0,5…2
Допускаемое отклонение ёмкости, %
Тангенс угла потерь0,0015
Сопротивление изоляции, МОм1000
Диапазон рабочих температур, – 60…+125
5. 2 Выбор типа резисторов
2 Выбор типа резисторов
· Для схемы проектируемого фильтра, чтобы обеспечить низкую температурную зависимость, необходимо выбирать резисторы с минимальным ТКС.
· Выбираемые резисторы должны обладать минимальными собственными ёмкостью и индуктивностью, поэтому выберем непроволочный тип резисторов.
· Однако у непроволочных резисторов более высокий уровень токовых шумов, поэтому необходимо учесть и параметр уровня собственных шумов резисторов.
Прецизионные резисторы типа С2-29В удовлетворяют заданным требованиям (параметры взяты из ):
Номинальная мощность, Вт 0.125;
Диапазон номинальных сопротивлений, Ом ;
ТКС (в интервале температур ),
ТКС (в интервале температур ),
Уровень собственных шумов, мкВ/В1…5
Предельное рабочее напряжение постоянного
и переменного тока, В200
5.3 Выбор типа операционных усилителей
· Главный критерий при выборе ОУ – это его частотные свойства, так как реальные ОУ имеют конечную полосу пропускания. Для того чтобы частотные свойства ОУ не влияли на характеристику проектируемого фильтра, необходимо чтоб для частоты единичного усиления ОУ в i-том каскаде выполнялось соотношение:
Для того чтобы частотные свойства ОУ не влияли на характеристику проектируемого фильтра, необходимо чтоб для частоты единичного усиления ОУ в i-том каскаде выполнялось соотношение:
Для первого каскада: .
Для второго каскада: .
Выбирая большее значение, получаем, что частота единичного усиления ОУ не должна быть менее 100 Кгц.
· Коэффициент усиления ОУ должен быть достаточно большим.
· Напряжение питания ОУ должно соответствовать напряжению источников питания, если таковое известно. В противном случае, желательно выбрать ОУ с широким диапазоном напряжений питания.
· При выборе ОУ для многокаскадного ФВЧ лучше выбрать ОУ с возможно меньшим напряжения смещения.
Согласно справочнику выберем ОУ типа 140УД6А, конструктивно оформленный в корпусе типа 301.8-2. ОУ этого типа являются ОУ общего назначения с внутренней частотной коррекцией и защитой выхода при коротких замыканиях нагрузки и имеют следующие параметры:
Напряжение питания , В
Напряжение питания , В
Ток потребления , мА
Напряжение смещения, мВ
Коэффициент усиления ОУ по напряжению
Частота единичного усиления , МГц1
5. 4 Методика настройки и регулировки разработанного фильтра
4 Методика настройки и регулировки разработанного фильтра
Настройка данного фильтра не представляет большой сложности. Параметры частотной характеристики “подгоняются” с помощью резисторов, как первого, так и второго каскадов независимо друг от друга, при чём настройка одного параметра фильтра не влияет на значения других параметров.
Настройка проводится следующим образом:
1. Коэффициент усиления устанавливается резисторами R2 первого и R5 второго каскада.
2. Частота полюса первого каскада настраивается резистором R1, частота полюса второго каскада – резистором R4.
3. Добротность второго каскада регулируется резистором R8, а добротность первого каскада не регулируется (постоянна при любых номиналах элементов).
Итогом данной курсовой работы является получение и расчёт схемы заданного фильтра. ФВЧ с аппроксимацией частотных характеристик полиномом Баттерворта с параметрами, приведенными в техническом задании, имеет третий порядок и представляет собой двокаскадно — соединённых ФВЧ первого порядка (на основе не инвертирующего усилителя) и второго порядка (на основе конвертеров полного сопротивления). Схема содержит три операционных усилителя, восемь резисторов и три ёмкости. В данной схеме используется два источника питания по 15 В каждый.
Схема содержит три операционных усилителя, восемь резисторов и три ёмкости. В данной схеме используется два источника питания по 15 В каждый.
Выбор схемы для каждого каскада общего фильтра проводился на основании технического задания (обеспечить малую чувствительность к отклонениям номиналов элементов) с учётом достоинств и недостатков каждого типа схем фильтров, используемых в качестве каскадов общего фильтра.
Номиналы элементов схемы подбирались и рассчитывались таким образом, чтобы максимально приблизить их к стандартному номинальному ряду Е24, а также, чтобы получить при этом как можно большее входное сопротивление каждого каскада фильтра.
После моделирования схемы фильтра с помощью пакета ElectronicsWorkbench5.0 (рис.5.1) были получены частотные характеристики (рис.5.2), имеющие требуемые параметры, приведённые в техническом задании (рис.2.2).
К достоинствам данной схемы можно отнести простоту настройки всех параметров фильтра, независимую настройку каждого каскада отдельно, малую чувствительность к отклонениям от номиналов элементов.
Недостатками является использование в схеме фильтра трёх операционных усилителей и соответственно его повышенная стоимость, а также относительно невысокое входное сопротивление (порядка 50 кОм).
Список использованной литературы
1. Зеленин А.Н., Костромицкий А.И., Бондарь Д.В. – Активные фильтры на операционных усилителях. – Х.: Телетех, 2001. изд. второе, исправ. и доп. – 150 с.: ил.
2. Резисторы, конденсаторы, трансформаторы, дроссели, коммутационные устройства РЭА: Справ./Н.Н. Акимов, Е.П. Ващуков, В.А. Прохоренко, Ю.П. Ходоренок. – Мн.: Беларусь, 2004. – 591 с.:ил.
Аналоговые интегральные схемы: Справ./А.Л. Булычёв, В.И. Галкин, 382 с.: В.А. Прохоренко. – 2-е изд., перераб. и доп. – Мн.: Беларусь, 1993. – черт.
Расчет фильтра нижних частот – Telegraph
➡➡➡ ДЛЯ ПЕРЕХОДА НАЖМИТЕ ЗДЕСЬ!
Название: Расчет фильтра нижних частот Раздел: Рефераты по коммуникации и связи Тип: курсовая работа Добавлен 06:23:05 07 мая 2011 Похожие работы Просмотров: 3001 Комментариев: 12 2 Пример расчета фильтра нижних частот на заданные параметры.
Реактивная проводимость = равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот…
Задание на курсовой проект «Фильтр нижних частот». фильтр печатный схемотехнический. В ходе выполнения работы был использован БСР для фильтров нижних частот, который Пример расчета фильтра нижних частот (ФНЧ) на заданные параметры.
Методические указания предназначены для использования при выполнении курсовой работы «Расчёт активных фильтров на операционных усилителях» по курсу «Микросхемотехника» и по другим Передаточная функция фильтра нижних частот (ФНЧ) в общем виде может.
tors.psuti.ru/metod_web/otc_filtr_posob.pdf
3. В курсовой работе необходимо рассчитать фильтр нижних частот Баттерворта аналитически и полосовой фильтр Баттерворта — таблич-ным методом. 6. Пример аналитического расчёта фильтра нижних частот с пло-ской характеристикой. ..
..
library.miit.ru/methodics/1884.pdf
…рены примеры расчёта фильтра нижних частот, фильтра верхних частот, поло сового фильтра и транспорте», выполняющий курсо вой проект, но могут быть полезными также при работе над 2. Содержание. 3. Введение. 4. Расчёт фильтра нижних частот (верхних частот…
Таблица расчёта элементов lc- фильтров верхних и нижних частот. Данные ФВЧ и ФНЧ называются Г-образными. Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное…
Картинки по запросу «Курсовая работа: Расчет фильтра нижних частот»
При защите курсовой работы одновременно проводится опрос по всему разделу курса ТЭЦ «Электрические фильтры». 3. Расчет активного RC-фильтра нижних частот (ФНЧ) Баттерворта или Чебышева аналитическим методом.
radio-stv.ru/praktikum-radiolyubitelya/raschet-filtrov-nizkih-i-vyisokih-chastot
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и Порядок расчета Г-образного фильтра нижней частоты. Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Название: Расчет фильтра нижних частот Раздел: Рефераты по коммуникации и связи Тип: курсовая работа Добавлен 06:23:05 07 мая 2011 Похожие работы Просмотров: 3001 Комментариев: 12 2 Пример расчета фильтра нижних частот на заданные параметры.
Реактивная проводимость = равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот…
Задание на курсовой проект «Фильтр нижних частот». фильтр печатный схемотехнический. В ходе выполнения работы был использован БСР для фильтров нижних частот, который Пример расчета фильтра нижних частот (ФНЧ) на заданные параметры.
Методические указания предназначены для использования при выполнении курсовой работы «Расчёт активных фильтров на операционных усилителях» по курсу «Микросхемотехника» и по другим Передаточная функция фильтра нижних частот (ФНЧ) в общем виде может.
tors.psuti.ru/metod_web/otc_filtr_posob.pdf
3. В курсовой работе необходимо рассчитать фильтр нижних частот Баттерворта аналитически и полосовой фильтр Баттерворта — таблич-ным методом. 6. Пример аналитического расчёта фильтра нижних частот с пло-ской характеристикой…
library.miit.ru/methodics/1884.pdf
…рены примеры расчёта фильтра нижних частот, фильтра верхних частот, поло сового фильтра и транспорте», выполняющий курсо вой проект, но могут быть полезными также при работе над 2. Содержание. 3. Введение. 4. Расчёт фильтра нижних частот (верхних частот…
Таблица расчёта элементов lc- фильтров верхних и нижних частот. Данные ФВЧ и ФНЧ называются Г-образными. Для получения более крутых скатов АЧХ используют два или более Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное…
Картинки по запросу «Курсовая работа: Расчет фильтра нижних частот»
При защите курсовой работы одновременно проводится опрос по всему разделу курса ТЭЦ «Электрические фильтры». 3. Расчет активного RC-фильтра нижних частот (ФНЧ) Баттерворта или Чебышева аналитическим методом.
3. Расчет активного RC-фильтра нижних частот (ФНЧ) Баттерворта или Чебышева аналитическим методом.
radio-stv.ru/praktikum-radiolyubitelya/raschet-filtrov-nizkih-i-vyisokih-chastot
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и Порядок расчета Г-образного фильтра нижней частоты. Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Реферат: Понятие логистического сервиса
Реферат: Лекарственные растения 6
Реферат: Информационное обеспечение логистики 2
Дипломная работа: Разработка информационной системы Кадровое агентство выпускников
Дипломная работа: Совершенствование сбытовой деятельности организации
Схемы пассивных фильтров нижних частот первого порядка и второго порядка
В этом руководстве мы узнаем о пассивных RC-фильтрах нижних частот. Как следует из названия, это фильтр нижних частот, разработанный с использованием пассивных компонентов. В следующих разделах вы можете узнать об основной схеме пассивных RC-фильтров нижних частот, их частотной характеристике, выходном напряжении, приложениях и многом другом.
В следующих разделах вы можете узнать об основной схеме пассивных RC-фильтров нижних частот, их частотной характеристике, выходном напряжении, приложениях и многом другом.
Чтобы получить информацию о пассивных RC-фильтрах верхних частот, прочитайте руководство « Пассивные RC-фильтры верхних частот» «.
Краткое описание
Введение
Фильтр представляет собой схему, которая используется для фильтрации сигналов, т. е. она пропускает только необходимые сигналы и избегает нежелательных сигналов. Как правило, фильтры состоят либо из пассивных, либо из активных компонентов.
- К пассивным компонентам относятся резисторы, катушки индуктивности и конденсаторы.
- Активными компонентами являются транзисторы, полевые транзисторы и операционные усилители.
Фильтр нижних частот — это фильтр, пропускающий только низкочастотные сигналы и ослабляющий или останавливающий высокочастотные сигналы. Это позволяет сигналам только от 0 Гц срезать частоту «fc». Это значение частоты среза будет зависеть от стоимости компонентов, используемых в цепи.
Это значение частоты среза будет зависеть от стоимости компонентов, используемых в цепи.
Как правило, эти фильтры предпочтительнее использовать на частотах ниже 100 кГц. Частота среза также называется частотой прерывания или частотой переключения.
[adsense1]
Пассивный фильтр нижних частот
Схема фильтра нижних частот, состоящая из пассивных компонентов, называется пассивным фильтром нижних частот.
На следующем рисунке показана простая схема RC-фильтра нижних частот.
Простое последовательное соединение резистора «R» с конденсатором «C» дает RC-фильтр нижних частот. Его можно просто назвать фильтром нижних частот (ФНЧ). Резистор не зависит от изменений применяемых частот в цепи, но конденсатор является чувствительным компонентом, что означает, что он реагирует на изменения в цепи.
Так как она имеет только один реактивный компонент, эту схему также можно назвать «однополюсным фильтром» или «фильтром первого порядка». Входное напряжение «Vin» прикладывается последовательно к резистору, а выходное напряжение снимается только через конденсатор.
Входное напряжение «Vin» прикладывается последовательно к резистору, а выходное напряжение снимается только через конденсатор.
Поскольку конденсатор является чувствительным компонентом, основная концентрация, которую следует наблюдать, касается «емкостного реактивного сопротивления». Емкостное реактивное сопротивление — это противодействие, создаваемое конденсатором в цепи.
Чтобы сохранить емкость конденсатора, конденсатор будет противодействовать небольшому току, протекающему в цепи. Это противодействие протеканию тока в цепи называется импедансом. Таким образом, емкостное сопротивление уменьшается с увеличением встречного тока.
Таким образом, мы можем сказать, что емкостное сопротивление обратно пропорционально частоте, приложенной к цепи. Значение сопротивления резистора стабильно, тогда как значение емкостного сопротивления изменяется. Падение напряжения на конденсаторе очень меньше по сравнению с потенциалом напряжения конденсатора.
[adsense2]
Это означает, что на низких частотах падение напряжения невелико, а потенциал напряжения велик, но на высоких частотах падение напряжения очень велико, а потенциал напряжения меньше. По этому явлению мы можем сказать, что приведенная выше схема может действовать как схема «частотно-регулируемого делителя напряжения».
По этому явлению мы можем сказать, что приведенная выше схема может действовать как схема «частотно-регулируемого делителя напряжения».
Емкостное сопротивление можно сформулировать следующим образом:
Расчет выходного напряжения
Чтобы получить уравнение делителя потенциала, мы должны учитывать импеданс, емкостное сопротивление, входное напряжение и выходное напряжение. Используя эти термины, мы можем сформулировать уравнение для делителя потенциала RC следующим образом:
Используя это уравнение, мы можем рассчитать значение выходного сигнала на любой применяемой частоте.
Фильтр нижних частот Пример
Давайте рассмотрим эти значения выходного напряжения и значения емкостного реактивного сопротивления, рассмотрев значения резистора и конденсатора. Пусть номинал резистора R равен 4,7 кОм, а конденсатор номиналом 47 нФ. Входное напряжение переменного тока составляет 10 В. Значения частоты, для которых мы собираемся рассчитать, составляют 1 кГц и 10 кГц.
Таким образом, мы можем ясно сказать, что при увеличении частоты емкостное сопротивление уменьшается. Уменьшается не только емкостное сопротивление, но и выходное напряжение.
Из вышеприведенного примера видно, что емкостное сопротивление уменьшилось с 3386,27 Ом до 338,62 Ом, тогда как выходное напряжение уменьшилось с 5,84 В до 0,718 В при увеличении частоты с 1 кГц до 10 кГц.
Частотная характеристика фильтра нижних частот
Из введения в фильтры мы уже видели, что величина |H(jω)| фильтра принимается за коэффициент усиления схемы. Это усиление измеряется как 20 log (V из / V в ), и для любой RC-цепи угол наклона «спада» составляет -20 дБ/декада.
Полоса частот ниже области среза называется «полосой пропускания», а полоса частот после частоты среза называется «полосой заграждения». Из графика видно, что полоса пропускания — это ширина полосы пропускания фильтра.
Из этого графика видно, что до частоты среза коэффициент усиления остается постоянным, поскольку выходное напряжение пропорционально значению частоты на низких частотах. Это связано с емкостным реактивным сопротивлением, которое действует как разомкнутая цепь на низких частотах и пропускает максимальный ток через цепь на высоких частотах. Значение емкостного сопротивления очень велико на низких частотах, поэтому оно имеет большую способность блокировать ток, протекающий по цепи.
Это связано с емкостным реактивным сопротивлением, которое действует как разомкнутая цепь на низких частотах и пропускает максимальный ток через цепь на высоких частотах. Значение емкостного сопротивления очень велико на низких частотах, поэтому оно имеет большую способность блокировать ток, протекающий по цепи.
При достижении значения частоты среза выходное напряжение постепенно снижается и достигает нуля. Коэффициент усиления также уменьшается вместе с выходным напряжением. После частоты среза характеристика наклона схемы достигает точки спада, которая возникает при -20 дБ/декада.
В основном это происходит из-за увеличения частоты, когда частота увеличивается, значение емкостного реактивного сопротивления уменьшается и, таким образом, снижается способность блокировать ток через конденсатор. Когда ток в цепи увеличивается и из-за ограниченной емкости конденсатора цепь действует как короткое замыкание. Таким образом, выходное напряжение фильтра равно нулю на высоких частотах.
Единственный способ избежать этой проблемы — выбрать диапазоны частот, до которых эти резистор и конденсатор могут выдержать. Значения конденсатора и резистора играют основную роль, потому что от этих значений будет зависеть только частота среза «fc». Если диапазоны частот находятся в пределах диапазона частот среза, мы можем решить проблему короткого замыкания.
Эта точка отсечки возникает, когда значение сопротивления и значение емкостного реактивного сопротивления совпадают, что означает, что векторная сумма сопротивления и реактивной емкости равна. То есть, когда R = X c , и в этой ситуации входной сигнал ослабляется на -3 дБ/декаду.
Это затухание составляет примерно 70,7 % входного сигнала. Время, необходимое для зарядки и разрядки пластин конденсатора, зависит от синусоидальной волны. Из-за этого фазовый угол (ø) выходного сигнала отстает от входного сигнала после частоты среза. На частоте среза выходной сигнал сдвинут по фазе на -45°.
Если входная частота фильтра увеличивается, угол запаздывания выходного сигнала схемы увеличивается. Просто для большего значения частоты схема больше не совпадает по фазе.
Просто для большего значения частоты схема больше не совпадает по фазе.
У конденсатора больше времени для зарядки и разрядки пластин на низких частотах, потому что время переключения синусоиды больше. Но с увеличением частоты время переключения на следующий импульс постепенно уменьшается. За счет этого возникают временные вариации, приводящие к фазовому сдвигу выходной волны.
Частота среза пассивного фильтра нижних частот в основном зависит от значений резистора и конденсатора, используемых в цепи фильтра. Эта частота среза обратно пропорциональна значениям резистора и конденсатора. Частота среза пассивного фильтра нижних частот равна
f C = 1/(2πRC)
Фазовый сдвиг пассивного фильтра нижних частот задается как
Как мы уже видели, время, необходимое конденсатору для зарядки и разрядки пластин по отношению к входной синусоидальной волне, приводит к разности фаз. Резистор и конденсатор в последовательном соединении будут производить этот эффект зарядки и разрядки.
Постоянная времени последовательной RC-цепи определяется как время, необходимое конденсатору для зарядки до 63,2 % от конечного установившегося значения, а также как время, необходимое конденсатору для разряда до 36,8 % от установившегося значения. государственное значение. Эта постоянная времени представлена символом «τ».
Связь между постоянной времени и частотой среза следующая:
Постоянная времени τ = RC = 1/ 2πfc и ω c = 1/τ = 1/RC частота как
Таким образом, мы можем сказать, что выход фильтра зависит от частоты, подаваемой на вход, и от постоянной времени.
Пассивный фильтр нижних частот Пример 2
Рассчитаем частоту среза фильтра нижних частот с сопротивлением 4,7 кОм и емкостью 47 нФ.
Мы знаем, что уравнение для частоты среза: Теперь мы изучили фильтр нижних частот первого порядка, который состоит из последовательного соединения резистора и конденсатора. Однако иногда одного каскада может быть недостаточно для удаления всех нежелательных частот, тогда используется фильтр второго порядка, как показано ниже.
RC-фильтр нижних частот второго порядка можно получить, просто добавив еще один каскад к фильтру нижних частот первого порядка. Этот фильтр дает наклон -40 дБ/декаду или -12 дБ/октаву, а фильтр четвертого порядка дает наклон -80 дБ/октаву и так далее.
Пассивный фильтр нижних частот Усиление на частоте среза определяется как
A = (1/√2) n
Где n — порядок или количество ступеней
Частота среза низких частот второго порядка фильтр нижних частот задается как
fc = 1/ (2π√(R1C1R2C2))
Фильтр нижних частот второго порядка -3дБ частота задается как
f (-3дБ) = fc √ (2 (1/n ) – 1)
Где fc частота среза, n количество ступеней и ƒ -3dB — частота полосы пропускания -3dB.
Краткое описание фильтра нижних частот
Фильтр нижних частот состоит из резистора и конденсатора. Не только конденсатор, но и любой реактивный компонент с резистором дает фильтр нижних частот. Это фильтр, который пропускает только низкие частоты и ослабляет высокие частоты.
Это фильтр, который пропускает только низкие частоты и ослабляет высокие частоты.
Частоты ниже частоты среза называются частотами полосы пропускания, а частоты выше частоты среза называются частотами полосы заграждения. Полоса пропускания — это ширина полосы пропускания фильтра.
Частота среза фильтра будет зависеть от номиналов компонентов, выбранных для схемы. Частоту среза можно рассчитать по приведенной ниже формуле.
f C = 1/(2πRC)
Усиление фильтра принимается за величину фильтра, и усиление может быть рассчитано по формуле 20 log (V из / V из ). Выход фильтра остается постоянным до тех пор, пока уровни частоты не достигнут частоты среза.
На частоте среза выходной сигнал составляет 70,7% от входного сигнала, а после частоты среза выходной сигнал постепенно уменьшается до нуля. Фазовый угол выходного сигнала отстает от входного сигнала после частоты среза.
На частоте среза фазовый сдвиг выходного сигнала составляет 45°.
Если поменять местами резистор и конденсатор в цепи фильтра нижних частот, то схема будет вести себя как фильтр верхних частот.
Для синусоидальных входных волн схема ведет себя как фильтр нижних частот первого порядка. Работу фильтра первого порядка мы уже изучили, но при изменении типа входного сигнала необходимо наблюдать за тем, что происходит с выходом фильтра.
Когда мы меняем тип входного сигнала либо на режим переключения (ВКЛ/ВЫКЛ), либо на прямоугольную волну, схема ведет себя как интегратор, который рассматривается следующим образом.
Фильтр нижних частот как схема формирования волны
На приведенном выше рисунке показаны характеристики фильтра для квадратного входного сигнала. Когда вход фильтра нижних частот представляет собой прямоугольную волну, полученный выходной сигнал фильтра будет иметь треугольную форму.
Это связано с тем, что конденсатор не может работать как выключатель ON или OFF. На низких частотах, когда вход фильтра прямоугольный, выход также будет только прямоугольным.
При увеличении частоты выходной сигнал фильтра выглядит как треугольная волна. Тем не менее, если мы увеличим частоту, то амплитуда выходного сигнала уменьшится.
Треугольная волна генерируется из-за действия конденсаторов или просто схема зарядки и разрядки конденсатора приводит к треугольной волне.
Применение фильтра нижних частот
- Цепи фильтра нижних частот в основном используются для предотвращения пульсаций переменного тока на выходе выпрямителя.
Фильтр нижних частот используется в схемах аудиоусилителя. - Используя этот пассивный фильтр нижних частот, мы можем напрямую уменьшить высокочастотный шум до уровня небольших помех в стереосистемах. Фильтр нижних частот
- в качестве интегратора может использоваться в качестве формирователя волны и цепей генерации волны благодаря простоте преобразования одного типа электрического сигнала в другую форму.
- Они также используются в схемах демодулятора для извлечения необходимых параметров из модулированных сигналов.

ltspice — Пассивный RC-фильтр второго порядка с параллельными резисторами — Как рассчитать частоту среза?
Символьный анализ с помощью KCL
Добавлю свой лакомый кусочек.
Использование бесплатного инструмента SymPy:
var('r1 r2 r3 c1 c2 vin vout vx s')
eq1 = Eq( vx/r1 + vx/(1/s/c1) + vx/r2, vin/r1 + vout/r2 )
eq2 = Eq(vout/r2 + vout/r3 + vout/(1/s/c2), vx/r2)
tf2(решить([eq1,eq2],[vx,vout])[vout]/vin)
{омега: sqrt(r1 + r2 + r3)/(sqrt(c1)*sqrt(c2)*sqrt(r1)*sqrt(r2)*sqrt(r3)),
дзета: (c1*r1*r2/2 + c1*r1*r3/2 + c2*r1*r3/2 + c2*r2*r3/2)/(sqrt(c1)*sqrt(c2)*sqrt(r1 )*sqrt(r2)*sqrt(r3)*sqrt(r1 + r2 + r3)),
P: [{A: r3/(r1 + r2 + r3), N: 0}]}
Или,
$$\begin{align*}A&=\frac{R_3}{R_1+R_2+R_3}=\frac{10}{111}\примерно 0,0901\\\\\omega_{_0}& =\ sqrt {\ frac {R_1 + R_2 + R_3} {R_1 R_2 R_3 C_1 C_2}} = 1000 \ sqrt {1110} \ приблизительно 33316,6625 \\\\\ alpha = \ zeta \ omega_ {_0} & = \ frac12 \ влево(\frac1{R_1 C_1}+\frac1{R_2 C_1}+\frac1{R_2 C_2}+\frac1{R_3 C_2}\right)=56000\\\\\zeta&=\frac{R_1 R_2 C_1+R_1 R_3 C_1 + R_1 R_3 C_2 + R_2 R_3 C_2} {2 \ sqrt {\ left (R_1 + R_2 + R_3 \ right) R_1 R_2 R_3 C_1 C_2}} = \ frac {56} {\ sqrt {1110}} \ приблизительно 1,681 \ \\\\frac{V_{_\text{OUT}}}{V_{_\text{IN}}} &= A\frac{\omega_{_0}^2}{s^2+2\zeta\ omega_{_0}s+\omega_{_0}^2}\end{align*}$$ 9\circ\$, ожидайте, что усиление напряжения будет \$20\log_{10}\left(\frac{A}{2\,\zeta}\right)\приблизительно -31,44\:\text{дБ}\$. 2}
\end{выравнивание*}$$
2}
\end{выравнивание*}$$
Я начал, как показано выше, с \$A\$ в числителе. Это потому, что мы ищем \$-3\:\text{dB}\$ вниз на от усиления по постоянному току \$A\$. Не абсолютное число, а относительно начальной точки постоянного тока.
Прежде чем продолжить, необходимо принять во внимание два важных упрощения.
Один из них состоит в том, чтобы нормализовать \$\omega\$, создав новую безразмерную переменную (всегда хорошая идея) путем деления ее на \$\omega_{_0}\$ так, чтобы \$\stackrel{.}{\ omega}=\frac{\omega}{\omega_{_0}}\следовательно, \omega = \omega_{_0} \stackrel{.}{\omega}\$. Это позволит нам избавиться от надоедливой константы \$\omega_{_0}\$, как вы увидите ниже. 92+2\дзета с+1\$.
Единственная разница между фильтром, где \$\omega_{_0}=1\$ и где \$\omega_{_0}\$ — какое-то другое значение, заключается в частотной шкале. Форма полностью определяется \$\zeta\$ и только \$\zeta\$. И только форма имеет значение при определении этих точек пересечения. Не сдвиг частоты.
Не сдвиг частоты.
Итак, это решение уравнения имеет только одну переменную, \$\zeta\$. Результат, которого мы должны были ожидать, поскольку форма зависит исключительно от \$\zeta\$. Какой еще выбор возможен?
При вашем значении \$\zeta\$ вы обнаружите, что \$\stackrel{..}{\omega}\,\приблизительно 0,1063\$. Это означает, что \$\stackrel{.}{\omega}\,=\sqrt{\stackrel{..}{\omega}}\,\приблизительно 0,3260\$ и, следовательно, \$\omega_{{-3\ :\text{дБ}}}=\omega_{_0}\stackrel{.}{\omega}\,\примерно 10862,5\$ или около \$f_{{-3\:\text{дБ}}}=1728,83 \:\текст{Гц}\$.
Проверка Spice, -3 дБ
Давайте проверим с помощью LTspice:
Это также выглядит примерно так, как \$-23,91\:\text{dB}\$ равно \$-3\:\text{dB }\$ по сравнению с \$-20,92+1}} \end{align*}$$
\$b\$ обращается в ноль, когда \$\zeta=\frac1{\sqrt{2}}\$. Это как раз в точке максимальной плоской амплитуды! ( b не может быть меньше -1.)
Построенный против \$\zeta\$ на оси x коэффициент квадратного корня имеет следующую форму:
Сверху легко см. , что как \$\zeta\to \infty\$ (очень сильно затухание), \$\omega_{{-3\:\text{dB}}}\$ стремится к DC, чего и следовало ожидать. А когда \$\zeta\to 0\$ (высокая добротность, отсутствие потерь энергии), фактор достигает своего наивысшего значения \$1,553774\$ или чуть более 55% за пределами \$\omega_{_0}\$.
, что как \$\zeta\to \infty\$ (очень сильно затухание), \$\omega_{{-3\:\text{dB}}}\$ стремится к DC, чего и следовало ожидать. А когда \$\zeta\to 0\$ (высокая добротность, отсутствие потерь энергии), фактор достигает своего наивысшего значения \$1,553774\$ или чуть более 55% за пределами \$\omega_{_0}\$.
Инверсия увеличенного прямоугольника выше выглядит следующим образом:
Следующая диаграмма применима только при недостаточном демпфировании пиков. Таким образом, он охватывает только случаи, когда \$0\le\zeta\le \frac1{\sqrt{2}}\$ или где \$-1\le b\le 0\$:
зеленый ось x кривой равна \$\stackrel{.}{\omega}\$. (Значение 1 означает, что \$\omega=\omega_{_0}\$.) Вы можете ввести слева, выбрав пик в дБ , а затем перейти, чтобы найти, где это значение попадает в зеленый кривая. Значение оси x ниже представляет собой % от \$\omega_{_0}\$, где возникает пик.
Ось x кривой красного цвета представляет собой % диапазона \$0\le\zeta\le \frac1{\sqrt{2}}\$, где происходит то же самое пиковое значение.
Таким образом, вы можете быстро получить обе части информации.
Например, предположим, что вам нужно пиковое значение \$3\:\text{дБ}\$, и вы хотите, чтобы пик возникал точно на частоте \$f_{_\text{PK}}=1\:\text{кГц}\ $. Вы должны войти с левой стороны в \$3\:\text{dB}\$ и найти по зеленой кривой, что это происходит примерно на 84%. Таким образом, это означает, что в вашем проекте должно быть указано \$f_{_0}=\frac1{84\%}\ приблизительно 1,19.0\:\текст{кГц}\$. Кроме того, из красной кривой видно, что это происходит при 54,2%. Это означает, что коэффициент демпфирования будет \$\zeta=\frac{54,2%}{\sqrt{2}}\приблизительно 0,383\$.
Проверка Spice, еще раз
Давайте запустим проверку того, что мы только что вычислили:
Ага. Выглядит как гвоздь (я добавил несколько дополнительных цифр, используя более полные формулы, чтобы помочь Spice в математике). добраться сюда. 92 + 2 \,b \stackrel{..}{\omega} + 1\справа)
\\\\&\следовательно\\\\
0&=2\,\stackrel{. 2 + 2\,b \stackrel{..}{\omega} + 1}
\end{выравнивание*}$$ 92}-1}}
\end{align*}$$
2 + 2\,b \stackrel{..}{\omega} + 1}
\end{выравнивание*}$$ 92}-1}}
\end{align*}$$
Это работает как для пиковых, так и для непиковых случаев. Но давайте посмотрим на наш пиковый случай…
Учитывая более ранний запуск Spice с \$\omega_{_0}=1,1899\:\text{кГц}\$ и \$\zeta=0,383252\$, мы бы вычислили из приведенного выше \$b=-0,70623581\$. Предположим, мы хотим найти точки \$1\:\text{dB}\$, которые окружают пик \$3\:\text{dB}\$ примерно на 84,04% от \$\omega_{_0}\$ (или вправо). при \$1\:\text{кГц}\$.)
Приведенная выше формула предлагает два значения при \$\stackrel{..}{\omega}\,\приблизительно 0,164851239\$ (\$\stackrel{.}{\omega}\,\приблизительно 0,406018767\$ и \$\omega\приблизительно 483,122\:\text{Гц}\$) и \$\stackrel{..}{\ omega}\,\приблизительно 1,24762038\$ (\$\stackrel{.}{\omega}\,\приблизительно 1,11696928\$ и \$\omega\приблизительно 1,3291\:\text{кГц}\$).
Давайте еще раз проверим Spice:
Похоже, мы снова попали в точку. Цифры работают нормально.
Заключительные замечания
Помните, что нормализованная угловая частота очень полезна для избавления от таких неприятностей, как \$\omega_{_0}\$. Для большинства анализов вы хотите избавиться как можно больше от умственный шум , как вы можете, так что вы можете лучше сосредоточиться на мясе вопроса под рукой. Это почти всегда полезно делать во время анализа. Вы всегда можете конвертировать обратно, когда закончите, чтобы позже получить точные цифры.
Также обратите внимание, что очень многое можно сделать с помощью небольшого количества алгебры. Большинство вещей, которые вы, возможно, захотите узнать, станут доступны, если вы просто присядете на минутку и поработаете над деталями.
Личное примечание: Возможно, одной из лучших книг для чтения, если вы новичок во всем этом, является книга Дона Ланкастера 1975 года, «Поваренная книга активного фильтра» . Вот где я порезал себе глаза на эту тему. И, оглядываясь назад, я все еще считаю это отличным переходом для любого новичка в этих вещах. Он использует устаревшую терминологию — например, \$d\$ (у которой есть единицы измерения) вместо гораздо более современной \$\zeta\$ (у которой нет единиц измерения). Но здесь есть все основы… и даже больше. Лично мой опыт показывает, что он может показаться угрюмым в прямом разговоре. Но его письмо (в сочетании с художественными работами, когда он беспокоится) не имеет себе равных. Он всегда будет одним из моих кумиров. То, что он дал мне, больше, чем я когда-либо смогу отплатить.
Он использует устаревшую терминологию — например, \$d\$ (у которой есть единицы измерения) вместо гораздо более современной \$\zeta\$ (у которой нет единиц измерения). Но здесь есть все основы… и даже больше. Лично мой опыт показывает, что он может показаться угрюмым в прямом разговоре. Но его письмо (в сочетании с художественными работами, когда он беспокоится) не имеет себе равных. Он всегда будет одним из моих кумиров. То, что он дал мне, больше, чем я когда-либо смогу отплатить.
RC Пассивный фильтр нижних частот — фильтры
Фильтры
Фильтр нижних частот пропускает частоты ниже определенной частоты среза. и ослабляет те, что выше этой частоты.
RC Фильтр нижних частот.
Первая схема, которую мы будем анализировать, представляет собой RC-фильтр нижних частот, как показано на рисунке.
на рисунке выше. Прежде чем приступить к математическому анализу, мы можем
сделать вывод о некоторых электрических свойствах путем визуального осмотра цепи.
Если приложенное напряжение имеет очень низкую частоту, реактивное сопротивление С будет очень высоким по сравнению с R и C можно считать открытая цепь. Поэтому на низких частотах входное напряжение В в будут появляться на выходе практически без затухания. Отсюда и название фильтра нижних частот. По мере увеличения входной частоты реактивное сопротивление X C становится меньше, в результате чего вход быть все более ослабленным. На бесконечно высокой частоте Х С = 0 и, следовательно, выходное напряжение В вых = 0.
Для математического анализа схемы мы будем использовать делитель напряжения отношения и написать
Мы, однако, решим отношение В из к V в , так как мы обычно хотим выразить
усиления или потери фильтра. Это отношение называется передаточной функцией . Тогда в качестве передаточной функции имеем
Тогда в качестве передаточной функции имеем
где ω C = 1/ RC — характеристическая частота .
Передаточная функция может быть выражена в полярной форме
Частотная характеристика
Наиболее полезное средство отображения частотных характеристик фильтра. заключается в построении величины передаточной функции (амплитудной характеристики) от частоты на одну кривую и фазовую характеристику на отдельную кривой, но с той же осью частот. Амплитудная характеристика, которая может изменяться в широких пределах, удобно изображать в децибелах. Кривые с этим типом отображения известны как Графики Боде и находят широкое применение при анализе цепей переменного тока.
Амплитудная характеристика
Сначала рассмотрим амплитудную характеристику (спектр), соответствующую уравнение выше. Это абсолютное значение (величина) передаточной функции или
В децибелах это становится
Давайте рассмотрим приведенное выше уравнение для очень низких и для очень высоких частот. Для низких частот имеем
Для низких частот имеем
Таким образом, низкочастотное поведение практически не зависит от частоты и может быть представлен горизонтальной прямой линией на уровне 0 дБ, как показано на рисунке ниже. Реальная амплитудная характеристика, заданная передаточной функцией, имеет вид асимптотик этой прямой при малых ω .
Ломаная аппроксимация и фактическая характеристика амплитудного спектра фильтра RC.
Для другой крайности имеем
Это форма Г дБ = -20 х , где x = log 10 ( ω / ω C ). Определенная таким образом прямая линия является высокочастотной асимптотой фактического характеристика. Наклон асимптоты равен dG дБ / dx = -20; то есть когда x увеличивается на одну единицу, G дБ уменьшается на 20 дБ. Но
и так ω / ω С должно увеличиться в множитель
10 или одну декаду , чтобы увеличить x на одну единицу. Следовательно,
наклон высокочастотной асимптоты составляет -20 дБ за декаду.
Некоторые люди предпочитают использовать октаву (отношение частот 2:1).
соответствующий наклон составляет -6 дБ на октаву. Две прямолинейные асимптоты
пересекаются в точке ω / ω C = 1, тогда
амплитудная характеристика имеет нулевое значение. показаны две асимптоты
пунктиром на рисунке выше. Их точка пересечения, ω = ω C , в дополнение к тому, что называется
характерная частота цепи, также называемая точкой разрыва ,
или частота среза . Вместе две асимптоты образуют ломаную линию.
приближение к реальной характеристике. В зависимости от желаемой точности
ни одна из линий не может быть достаточно хорошим приближением к фактическому
характеристика в окрестности ω = ω C .
Можно показать, что максимальная ошибка возникает при ω / ω C = 1 и составляет примерно 3 дБ.
Более того, в октаве от этой точки
(при ω / ω С = 0,5 и ω / ω С = 2)
ошибка составляет примерно 1 дБ.
Следовательно,
наклон высокочастотной асимптоты составляет -20 дБ за декаду.
Некоторые люди предпочитают использовать октаву (отношение частот 2:1).
соответствующий наклон составляет -6 дБ на октаву. Две прямолинейные асимптоты
пересекаются в точке ω / ω C = 1, тогда
амплитудная характеристика имеет нулевое значение. показаны две асимптоты
пунктиром на рисунке выше. Их точка пересечения, ω = ω C , в дополнение к тому, что называется
характерная частота цепи, также называемая точкой разрыва ,
или частота среза . Вместе две асимптоты образуют ломаную линию.
приближение к реальной характеристике. В зависимости от желаемой точности
ни одна из линий не может быть достаточно хорошим приближением к фактическому
характеристика в окрестности ω = ω C .
Можно показать, что максимальная ошибка возникает при ω / ω C = 1 и составляет примерно 3 дБ.
Более того, в октаве от этой точки
(при ω / ω С = 0,5 и ω / ω С = 2)
ошибка составляет примерно 1 дБ. Отсюда легко сделать набросок фактического
амплитудная характеристика с приемлемой точностью. Фактическая характеристика
показано сплошной линией на рисунке выше. Низкочастотный
характеристика цепи хорошо видна на этом рисунке.
Отсюда легко сделать набросок фактического
амплитудная характеристика с приемлемой точностью. Фактическая характеристика
показано сплошной линией на рисунке выше. Низкочастотный
характеристика цепи хорошо видна на этом рисунке.
Фазовая характеристика
Рассмотрим теперь угол передаточной функции фильтра (иногда его называют фазовым спектром), который
Фазовый угол начинается с нуля для ω = 0 и приближается к -π/2.
радианы в целом ω . Фазовая характеристика может быть аппроксимирована
достаточно хорошо тремя прямолинейными отрезками, как показано на рисунке
внизу: низкочастотная аппроксимация при 0 радианах, высокочастотная
приближение при -π/2 радианах и приближение промежуточной частоты
которая касается кривой на уровне -π/4 радиан. Можно показать, что
средний сегмент пересекает низкочастотное приближение при ω / ω C = 1/4,81 и пересекает
высокочастотное приближение при ω / ω C = 4,81. Фактическая характеристика показана сплошной линией на рисунке.
Фактическая характеристика показана сплошной линией на рисунке.
Ломаная аппроксимация и фактическая характеристика фазового спектра фильтра RC.
Калькулятор полюсов частоты RC-фильтра
В Интернете есть множество калькуляторов полюсов RC-фильтра, и я с удовольствием использовал их для быстрых расчетов, когда занимался своими руками. Проблема в том, что эти онлайн-калькуляторы вычисляют полюс частоты, где усиление уменьшается на 3 дБ , что хорошо, но что, если вам нужно знать частоту какого-то ( первого порядка ) фильтра, имея только характеристики отклонения усиления на определенной частоте?
Пример
Раньше я занимался множеством аудиопроектов, таких как предусилители, компрессоры, микрофоны и т. д. Допустим, нам нужна стандартная частотная характеристика HiFi ( 20 Гц — 20 кГц ) нашего предусилителя, и мы хотим, чтобы она была « плоский », что означает, что усиление не должно отклоняться более чем на 0,5 дБ по всему диапазону частот, пока не будет достигнута низкая или высокая частота.
Полоса пропускания (полосовой фильтр): 20 Гц – 20 кГц
Отклонение усиления: -0,5 дБ
Посмотрите, как это сделать, или пропустите этот раздел и используйте файл Python внизу страницы.
Шаг за шагом:
- Преобразование усиления из децибел в относительное усиление.
Например, если фильтр макс. усиление равно 0 дБ, это усиление равно 1.
В нашем случае: -0,5 дБ преобразуется в относительное усиление 0,9441 (в опорное значение 1)
9001 14 Получите передаточную функцию of фильтр.
Например, наш фильтр является пассивным RC-фильтром первого порядка, что означает, что его передаточная функция:
Gf = G0 / sqrt(1+ (f/fc) 2 )
для фильтров нижних частот (когда f растет, общее усиление уменьшается) 9для фильтры верхних частот (когда f понижается, общее усиление уменьшается)
Где:
f — частота нашего фронта (20 или 20 кГц),
fc — частота среза RC, где усиление уменьшается на 3 дБ
G0 — наше эталонное усиление (в нашем случае: 1),
Gf — желаемая девиация на выбранной частоте f
- Найдите fc из приведенного выше уравнения.

fc = f / sqrt( (G0/Gf) 2 -1 )
где f — полюс нижних частот, в нашем случае 20 кГц
и
3 . ( (G0/Gf) 2 -1 )
, где f – полюс верхних частот, в нашем случае 20 Гц
Полюса частоты RC-фильтра, которые мы ищем, находятся по адресу:
- 6,99 Гц для фильтра верхних частот (-0,5 дБ при 20 Гц)
- 57255,50 Гц для фильтра нижних частот (-0,5 дБ при 20 кГц)
- Рассчитать номиналы резисторов или конденсаторов.
fc = 1 / (2 * pi * R * C)
Теперь иногда вам нужна небольшая емкость или вам нужен определенный резистор для удовлетворения требований к усилению схемы фильтра, поэтому вы фиксируете один параметр, а затем вычисляете другой :
R = 1 / (fc * 2 * pi * C) OR C = 1 / (fc * 2 * pi * R)
В любом случае, требуется время , если вы моделируете и меняете требования (или если вы делаете это часто в свободное время 😀 ), чтобы вычислять его снова и снова каждый раз. Вот где скрипт Python удобен, и вы можете скачать его здесь.
Вот где скрипт Python удобен, и вы можете скачать его здесь.
Это сценарий для быстрой проверки частоты полюсов и, при необходимости, расчета значений RC для этой частоты.
Вот настройки:
########### ФИЛЬТР ВЧ - дифференциатор LOW_FREQ = 20 # [Гц] более низкая частота (ФИЛЬТР ВЧ) LOW_FREQ_DEV = 0,5 # [дБ] отклонение отклика на НИЗКОЙ частоте # установить либо XP_RESISTOR_CALCULATE_CAPACITOR, либо XP_CAPACITOR_CALCULATE_RESISTOR, либо ни один из них HP_RESISTOR_CALCULATE_CAPACITOR = Истина RESISTOR_HP = 10e3 #[Ом] HP_CAPACITOR_CALCULATE_RESISTOR = Ложь CAPACITOR_HP = 1e-6 #[F] ########### ФИЛЬТР НЧ - интегратор HIGH_FREQ = 20e3 # [Гц] верхняя частота (ФИЛЬТР НЧ) HIGH_FREQ_DEV = 0,5 # [дБ] отклонение отклика на ВЫСОКОЙ частоте # установить либо XP_RESISTOR_CALCULATE_CAPACITOR, либо XP_CAPACITOR_CALCULATE_RESISTOR, либо ни один из них LP_RESISTOR_CALCULATE_CAPACITOR = Истина RESISTOR_LP = 10e3 # [Ом] LP_CAPACITOR_CALCULATE_RESISTOR = Ложь КОНДЕНСАТОР_LP = 2,2e-6 #[F] ПОДРОБНО = Ложь
Вы можете указать, какой компонент вы хотите рассчитать, а какой установить заранее. Или не используйте эту функцию и просто рассчитайте желаемую частоту.
Или не используйте эту функцию и просто рассчитайте желаемую частоту.
Выходные значения распечатываются следующим образом:
Полюс частоты верхних частот находится на уровне 6,99 Гц для отклонения -0,50 дБ на частоте 20 Гц.
Значения RC:
R: 1,00e+04 Ом
C: 2,28e-06F (рассчитано)
Полюс частоты нижних частот находится на уровне 57255,50 Гц для отклонения -0,50 дБ на частоте 20000 Гц.
Значения RC:
R: 1,00e+04 Ом
C: 2,78e-10 F (рассчитано)
Или так, если DETAIL = True :
Подробно: отклонение отклика -0,50 дБ = относительное усиление 0,9441 относительно эталона 1,00
Подробно: частота полюса составляет 6,99 Гц с девиацией -0,50 дБ при 20 Гц)
Полюс частоты верхних частот находится на уровне 6,99 Гц для отклонения -0,50 дБ на частоте 20 Гц.
Значения RC:
R: 1,00e+04 Ом
C: 2,28e-06F (рассчитано)
Подробно: отклонение отклика -0,50 дБ = относительное усиление 0,9441 относительно эталона 1,00
Подробно: частота полюса 57255,50 Гц с девиацией -0,50 дБ при 20000 Гц)
Полюс частоты нижних частот находится на уровне 57255,50 Гц для отклонения -0,50 дБ на частоте 20000 Гц. Значения RC:
R: 1,00e+04 Ом
C: 2,78e-10 F (рассчитано)
Значения RC:
R: 1,00e+04 Ом
C: 2,78e-10 F (рассчитано)
Код закомментирован, и вы можете легко использовать его как модуль и использовать только такие функции, как (пример для фильтра верхних частот):
freq = get_pole_freq (LOW_FREQ, LOW_FREQ_DEV, HIGH_PASS) res_lp = get_res_cap_value (частота, CAPACITOR_HP)
Загрузите его здесь (.zip с одним файлом Python — 2 КБ).
Схемы, типы, калькуляторы и их применение
В электронных устройствах фильтры представляют собой схемы, которые пропускают нужные частотные компоненты и блокируют все другие частотные компоненты сигнала. Например, в радио или телевидении схема фильтра настройки отбрасывает нежелательные частоты, пропуская только нужный канал. Схемы фильтров делятся на четыре типа в зависимости от диапазона частот, который может разрешить схема, блокируя все остальные частоты. Это фильтры нижних частот, фильтры верхних частот, полосовые фильтры и режекторные фильтры. Эти типы схем фильтров относятся к категории пассивных фильтров, потому что в схеме используются пассивные элементы, резистор, конденсатор и катушки индуктивности. В этой статье описывается фильтр нижних частот с использованием операционного усилителя (активный элемент), который также называется активным ФНЧ.
Эти типы схем фильтров относятся к категории пассивных фильтров, потому что в схеме используются пассивные элементы, резистор, конденсатор и катушки индуктивности. В этой статье описывается фильтр нижних частот с использованием операционного усилителя (активный элемент), который также называется активным ФНЧ.
Определение: Схема фильтра, которая пропускает только низкочастотные компоненты и блокирует все другие высокочастотные компоненты, называется фильтром нижних частот. Само название LPF указывает на частоту низкого диапазона.
Этот тип схемы фильтра пропускает частотные составляющие сигнала меньше, чем срез частотного диапазона сигнала. Коэффициент усиления фильтра нижних частот обратно пропорционален частоте. Если частота входного сигнала увеличивается, коэффициент усиления схемы уменьшается и также становится равным нулю в конце переходной полосы. Таким образом, пропускная способность также ограничена. Но на практике ФНЧ допускает низкочастотные компоненты сигнала, даже если они достигают частоты среза.
Цепь фильтра нижних частот
Схема цепи фильтра нижних частот показана ниже. Он содержит пассивные элементы, резистор и конденсатор, соединенные последовательно с приложенным входным напряжением через резистор, а его выходное напряжение получается через конденсатор.
Цепь фильтра нижних частот
LPF первого порядка
Фильтр нижних частот первого порядка бывает двух типов. Это
Индуктивный тип LPF
Этот тип представляет собой простую RL-цепь, как показано ниже. Когда частота сигнала увеличивается, сопротивление катушки индуктивности увеличивается. Это приводит к блокировке высокочастотных сигналов и пропусканию через цепь только низких частот сигнала.
LPF индуктивного типа
LPF емкостного типа
Этот тип представляет собой простую RC-цепь LPF, как показано на рисунке выше. Его также называют простой схемой фильтра нижних частот. Когда частота сигнала увеличивается, полное сопротивление конденсатора уменьшается, что приводит к блокировке высоких частот сигнала и пропусканию через цепь только низких частот сигнала.
ФНЧ второго порядка
Схема фильтра нижних частот второго порядка представляет собой схему RLC, как показано на схеме ниже. Выходное напряжение получается на конденсаторе. Этот тип ФНЧ работает более эффективно, чем ФНЧ первого порядка, поскольку для блокирования высоких частот входного сигнала используются два пассивных элемента: катушка индуктивности и конденсатор.
Фильтр нижних частот второго порядка
Фильтр нижних частот с использованием операционного усилителя
ФНЧ с использованием операционного усилителя называется активным фильтром нижних частот. Очень легко спроектировать схему фильтра нижних частот с использованием операционного усилителя без использования электрических компонентов, таких как катушка индуктивности, которую очень сложно спроектировать, а также она дорогая. Операционные усилители (операционные усилители) используются в схемах фильтров для усиления сигнала, а также для управления усилением. Операционные усилители изменяют частотную характеристику и обеспечивают лучший коэффициент усиления по напряжению в рамках обратной связи. Он также имеет более высокий входной импеданс, более низкий выходной импеданс, низкий уровень шума и высокий уровень производительности.
Он также имеет более высокий входной импеданс, более низкий выходной импеданс, низкий уровень шума и высокий уровень производительности.
Фильтр нижних частот с использованием операционного усилителя
Работа базовой схемы LPF (пассивного фильтра) и фильтра нижних частот с использованием операционного усилителя (активного фильтра) одинакова, за исключением того, что операционный усилитель подключен к цепи RC-фильтра. . Это может быть инвертирующий или неинвертирующий операционный усилитель. Принципиальная схема фильтра нижних частот с использованием операционного усилителя показана ниже.
Активная схема LPF первого порядка с операционным усилителем
Активная LPC-схема первого порядка состоит из конденсатора, резистора и операционного усилителя, как показано ниже. Инвертирующий или неинвертирующий операционный усилитель подключается к RC-цепи, чтобы получить активную схему ФНЧ. Амплитуда выходного сигнала, полученного от RC-цепи фильтра нижних частот, меньше, чем амплитуда входного сигнала. Этот низкочастотный сигнал цепи RC LPF подается на операционный усилитель в качестве входа для достижения усиления, высокого коэффициента усиления по мощности и стабильности фильтра. Здесь операционный усилитель действует как буферная схема, как повторитель напряжения с коэффициентом усиления по постоянному току = 1,9.0003
Этот низкочастотный сигнал цепи RC LPF подается на операционный усилитель в качестве входа для достижения усиления, высокого коэффициента усиления по мощности и стабильности фильтра. Здесь операционный усилитель действует как буферная схема, как повторитель напряжения с коэффициентом усиления по постоянному току = 1,9.0003
Активный ФНЧ первого порядка
По мере увеличения частоты входного сигнала он проходит через конденсатор для увеличения амплитуды выходного сигнала для усиления, связанного с коэффициентом усиления в полосе пропускания. На низких частотах выходной сигнал RC-цепи проходит непосредственно через операционный усилитель для усиления.
Коэффициент усиления по напряжению определяется как DC = 1+R2/R1
Схема активного LPF второго порядка с использованием операционного усилителя операционный усилитель. Здесь операционный усилитель действует как усилитель-источник, управляемый напряжением. Частотная характеристика такая же, как у активного LPF первого порядка, за исключением того, что усиление в полосе задерживания в два раза больше, чем у активного LPF первого порядка, т.
 е. 40 дБ/декаду. Каскадирование цепей фильтров образует фильтры более высокого порядка, усиление которых является произведением каждой RC-цепи ФНЧ.
е. 40 дБ/декаду. Каскадирование цепей фильтров образует фильтры более высокого порядка, усиление которых является произведением каждой RC-цепи ФНЧ.Активный фильтр нижних частот второго порядка
Мы знаем, что усиление активного фильтра нижних частот первого порядка составляет -3 дБ на частоте среза. Так, усиление активного ФНЧ второго порядка составляет -6 дБ на частоте среза, т.е. усиление увеличилось вдвое.
Коэффициент усиления рассчитывается как
Av = Av1 x Av2
Общий коэффициент усиления в дБ
Av = Av1 + Av2
Принципиальная схема активного LPF второго порядка показана ниже.
Калькулятор LPF
Калькулятор фильтра нижних частот . — расчет частоты среза, коэффициента усиления по напряжению и фазового сдвига схемы ФНЧ.
См. эту ссылку для получения информации о фильтрах нижних частот MCQ
Из схемы LPF (резистивно-емкостная цепь) видно, что «Vi» — это приложенное входное напряжение
«Vo» — это выходное напряжение
При передаче функции цепи, мы получаем
H(s) = V₀(s)/Vᵢ(s) = (1/sC)/(R+(1/sC))
Поскольку 92]
Величина передаточной функции рассчитывается с помощью ‘ω’, т. е. угловой частоты
е. угловой частоты
Если ω = 0, то величина передаточной функции = 0
Если ω = 1/ CR, то величина передаточной функции = 0,707
Если ω = бесконечность, то величина передаточной функции = 0
Чтобы рассчитать коэффициент усиления и сдвиг фазы ФНЧ,
Рассмотрим ω = 1/RC и ω = ωc для приведенного выше уравнения
Тогда приведенное выше уравнение принимает вид 92]
Поскольку общий коэффициент усиления по напряжению равен
Av = 20log10 (Vout /Vin) в дБ
Рассмотрим f = рабочую частоту и fc = частоту среза
Фазовый сдвиг схемы LPF равен
Φ = tan⁻¹ (ω/ωc)
Частота среза контура ФНЧ равна Φ ⁼ tan⁻¹(2πfRC)
Уравнение емкостного сопротивления в омах цепи ФНЧ имеет вид
Xc = 1/2πfC
Где C = емкость в фарадах
f= рабочая частота в Гц
Частотная характеристика представлена между усилением (дБ) и частотой (Гц).
Частотная характеристика
На низких частотах усиление ФНЧ выше усиления фильтра в полосе пропускания
На высоких частотах усиление ФНЧ меньше усиления его полосы пропускания и падает до -20 дБ
По мере увеличения частоты выходное напряжение падает на 70,71% ниже входного напряжения.
Приложения
К приложениям фильтра нижних частот относятся следующие.
- Используется для удаления шума высокочастотных сигналов
- Используется в аудиоприложениях
- Используется в биомедицинских целях
- Используется в электронных устройствах, таких как громкоговорители, сабвуферы и т. д.
- Используется в цифро-аналоговых преобразователях
- Используется в качестве антианализирующих фильтров
- Используется в волновых анализаторах, аудиоусилителях и эквалайзерах.
Перейдите по этой ссылке, чтобы узнать больше о полосовых фильтрах MCQ, КИХ-фильтрах MCQ и фильтрах высоких частот MCQ
Таким образом, это обзор схемы фильтра нижних частот с использованием операционного усилителя, базовой схемы LPF. , активный LPF первого порядка, активный LPF второго порядка, калькулятор фильтра нижних частот и приложения. Назначение фильтра LPF состоит в том, чтобы разрешать только низкочастотные сигналы и блокировать высокочастотные сигналы. Вот несколько вопросов для вас: Каковы преимущества LPF с использованием операционного усилителя? Что такое полосовой фильтр?
, активный LPF первого порядка, активный LPF второго порядка, калькулятор фильтра нижних частот и приложения. Назначение фильтра LPF состоит в том, чтобы разрешать только низкочастотные сигналы и блокировать высокочастотные сигналы. Вот несколько вопросов для вас: Каковы преимущества LPF с использованием операционного усилителя? Что такое полосовой фильтр?
Онлайн калькулятор .:. Фильтр нижних частот Sallen Key
Категории
- Проекты (антиквариат)
- ENVICO : Система мониторинга параметров окружающей среды
- Основной блок ENVICO: «мозг»
- Температурный адаптер ENVICO
- Адаптер барометра ENVICO
- Адаптер влажности ENVICO
- Адаптер освещенности ENVICO
- Адаптер излучения ENVICO γ
- Расчет базы облаков/точки росы
- Похититель программных данных ENVICO
- Дисплей ENVICO @ Thingspeak.com
- Волновой проигрыватель Eprom
- Частотомер • Аксессуары
- Частотомер CETH-60
- DIY Mini VHF Частотный дисплей
- Предусилитель
- Предварительный делитель: 1000/1,5 ГГц
- Предварительный делитель: 1000/12 ГГц
- Предварительный делитель: 1000/17 ГГц
- Предварительный делитель: счетчик 1000/24 ГГц (Arduino)
- Рубидиевый эталон частоты Efratom LPR101
- ОСХО 10 МГц
- Daramod — Усилитель-распределитель 10 МГц
Генератор функций - (с XR2206)
- УКВ-синтезатор с AD9859 :: RF-2859
- Приемник радиодиапазона VHF с Si570 и AD8361
- Измеритель кривых (простой)
- Измеритель кривых (расширенный)
- Генератор сигналов DCF-77 (устаревший)
- Синтезатор DCF-77.
 С Ардуино. Он же «ТаймДуино»
С Ардуино. Он же «ТаймДуино» - Логарифмический усилитель с AD8307
- Усиление — Фаза — Адаптер с использованием AD 8302
- RFID
- Считыватель RFID 125 кГц (устарело)
- Считыватель RFID 125 кГц: CoffeeDuino
- Устройство считывания/записи RFID, 13,56 МГц
- ENVICO : Система мониторинга параметров окружающей среды
- Микропроекты • Инструменты
- Светодиодный панельный измеритель Atmega8 (U,I,°C,°F)
- Счетчик клиентов Corona для магазина/места
- ЖК-адаптер • Интерфейс
- Микрофонный предусилитель
- ПОВОРОТНЫЙ ЭНКОДЕР (STEC11B03)
- SDRSharp и флешка DVB-T: анализатор спектра за 20 евро?
- Датчик магнитного поля до 3 ГГц
- UART-мост RS232 (ST232CDR)
- UART — USB-мост (MCP2200)
- Мост UART — ETHERNET (LANTRONIX XPORT)
- USB — инфракрасный приемопередатчик
- USB-PLL/DDS-интерфейс
- Проекты Arduino • Экраны
- Анализатор спектра • Измерительный приемник
- А DC-19Анализатор спектра 9 МГц VISIONARY с Si4432
- Анализатор спектра 15–2700 МГц с RF Explorer 3G+
- Levelmod — Измеритель мощности микроволн от постоянного тока до дневного света
- Интеллектуальный микродатчик мощности — с AD8319, TMP101
- Polarmod — IQ-процессор с AD9958
- Wacharamod — FM-стереоприемник с TEA5767
- Wanmod, частотно-селективный измеритель уровня, 29,999 МГц
- Частотомер • Эталон частоты
- Countermod — счетчик частоты 1 ГГц
- Daramod — GPS-приемник 10 МГц с NEO-7N
- Daramod — Усилитель-распределитель 10 МГц
- Standardmod — A 10,000000 МГц OCXO
- Генераторы низкой частоты (AF)
- Kilomod — Генератор TTL PWM 15 мГц .
 .. 5 кГц
.. 5 кГц - Mannmod — Генератор PRBS (скоро)
- Генератор сигналов Micro USB — с AD9833
- Kilomod — Генератор TTL PWM 15 мГц .
- Высокочастотный (РЧ) синтезатор
- Kumod — Синтезатор 1 МГц … 200 МГц с AD9958
- Micromod — Синтезатор 220 МГц с Si570
- Macromod — синтезатор 850 МГц с LMK61E2
- Ningmod — ВЧ-синтезатор с AD9953 + коллеги
- Supermod — синтезатор 23,5–6000 МГц с MAX2871
- Teramod — синтезатор от 2 до 15 ГГц
- Ultramod — Синтезатор 9,9–3200 МГц с Si564
- Блоки питания • Стандарты напряжения
- Самроимод — Блок питания 32 В / 1 А
- Sungmod — Блок питания 270 В / 1 мА
- Supplymod — источник питания 20 В / 2 А
- Thormod, источник питания для фотодиодов
- Измерительные устройства • U • I • P
- Nuumod — микровольтметр с LTC2400
- Pingumod — монитор мощности с INA260
- Радиопереключатели • Аттенюаторы
- Switchmod (RF), двойной переключатель SPDT RF с PE4250
- Что это за «.
 .. мод» вообще?
.. мод» вообще? - Дополнительные компоненты для всех модов
- Прочие шилды для Arduino
- Экран BHUMI : Эталон напряжения, программируемый
- CALC-DUINO, простая защита для карманного калькулятора (MAX7219)
- ЧАСЫ-DUINO, часы, чтобы показать моим учителям 🙂
- Щит FLO : Регистратор данных окружающей среды, он же ENVICO light
- Экран FLO : Отображение результатов измерения
- Shield LEO : SMS при отключении питания
- Экран NRVD : Двойной измеритель мощности УВЧ
- Shield MARCELLA : Управляйте своими лабораторными устройствами
- Экран RENÉ : Источник опорного напряжения, он же REFDUINO
- Щит ТАНАЧАЙ : Анализатор характеристик транзистора
- Shield TOBI : скалярный сетевой анализатор 60 МГц, 80 дБ
- Надстройка BRUNO : Универсальный тестер аккумуляторов (зарядка/разрядка)
- Анализатор спектра • Измерительный приемник
- Заключительные проекты Arduino: IPA
- Ipamod 2022: высокоточный цифровой измеритель емкости
- База знаний Arduino
- Фрагменты кода Arduino
- Обзор I 2 C Адреса
- Bluepill • Проекты Blackpill
- Millimod — синтезатор звуковой частоты с AD9102
- Подростковые проекты
- Suthimod — анализатор радиочастотных антенн
- лабораторных экспериментов Python 🐍
- Основы, например, «Привет, Ардуино» и т.
 д.
д. - Долгосрочная регистрация данных в файл (Wanmod)
- Испытательный стенд VCO (Supplymod, Levelmod, Countermod)
- Амплитудная характеристика Полоса пропускания 10,7 МГц (Ningmod, Wanmod)
- Частотный спектр ВЧ-диапазонов (Wanmod)
- Печенье • Панировочные сухари
- Развертка частоты с Ningmod
Источники питания - Основы, например, «Привет, Ардуино» и т.
- • Расчеты
- Искусственный грунт
- Характеристика источника питания
- Конструктор источников питания: исправление
- Конструктор источников питания: Линейный регулятор
- Галерея источников питания (база данных опыта)
- Измерения пульсаций и шума источника питания
- Еще один калькулятор LM317
- Поиск делителя напряжения обратной связи (LM2576 и т. д.)
- Высоковольтный источник питания (MC34063, повышающий)
- Низковольтный источник питания (MC34063, понижающий)
- VB 408 Замена
- Leomod, блок питания ±15 В, 1 А
- Powermod, блок питания с LM317/LM337
- Самроимод — Блок питания 32 В / 1 А
- Sungmod — Блок питания 270 В / 1 мА
- Supplymod — Блок питания 20 В / 2 А
- Thormod, источник питания для фотодиодов
- Источник питания PETH-6 • ± 15 В, 100 мА
- Блок питания PETH-6 • +7,5 В, для Arduino / Genuino
- Источник питания PETH-20 • ± 15 В, 600 мА
- Источник питания PETH-30
- PETH-40 B3 Блок питания ±15 В, 1200 мА
- Источник питания PETH-40-HAM • ± 15 В, 1,5 А
- Источник питания PETH-49 • 1 .
 .. 19 В, 2 А
.. 19 В, 2 А - PETH-200V — Высоковольтный источник питания
- Источник питания PETH-581 • Понижающий преобразователь. с линейным дожигателем
- Источник питания PETH-1074 • Понижающий с помощью LT1074
- PETH-8093 Источник питания • Понижающее и линейное регулирование
- PETH-9910 Источник питания • 8 … 16 В, 10 А
- Конструкция усилителя • Усилители
- MAR, ERA, GALI Калькулятор смещения усилителя
- Конструктор буферного усилителя BJT (смещение обратной связи коллектора)
- Конструктор буферных усилителей BJT (базовая сеть смещения)
- Конструктор буферных усилителей BJT (смещение обратной связи по напряжению)
- Конструктор буферного усилителя BJT (смещение обратной связи эмиттера)
- Широкополосный ОВЧ-усилитель мощности, 3–540 МГц, 1,5 Вт
- Широкополосный предусилитель УВЧ, > 3 ГГц, 20 дБ, NF 2,4 дБ
- Широкополосный измерительный усилитель
- Широкополосный усилитель мощности, 1 Вт, от 2 до 2500 МГц
- Sojamod, ВЧ-усилитель с уровнем усиления 20 дБ и частотой более 1,5 ГГц
- Схемы операционных усилителей • Знания
- Каскадные операционные усилители для увеличения пропускной способности
- Максимальная пропускная способность для каскадных операционных усилителей
- Вопросы скорости нарастания
- Максимальное выходное напряжение в зависимости от частоты
- Выбор подходящего операционного усилителя для управления АЦП (SAR ADC)
- Драйвер АЦП с биполярного напряжения на униполярное напряжение
- Цепь ЦАП с однополярным напряжением на биполярное напряжение
- Дифференциальный усилитель
- Инвертирующий усилитель
- Инвертирующий компаратор с гистерезисом • Триггер Шмитта
- Неинвертирующий усилитель
- Неинвертирующий компаратор с гистерезисом • Триггер Шмитта
- Суммирующий усилитель
- Вспоминая Роберта А.
 Писа, также известного как «RAP»
Писа, также известного как «RAP»
- Конструктор антенн 📡
- Руководство по выбору антенны
- Антенный конструктор Вивальди Antipodal
- Bi-Quad Антенный конструктор
- Галстук-бабочка • Крыло летучей мыши • Дипольный калькулятор бабочки
- Калькулятор антенны
- Конструктор дискоконусных антенн
- Дипольный калькулятор — сложенный
- Дипольный калькулятор — прямой
- Антенный калькулятор HB9CV
- Калькулятор антенны Helix
- Антенна Helix с калькулятором соответствия
- J-образная антенна
- Конструктор наземных самолетов Lambda/4
- Калькулятор логарифмической периодической дипольной антенны
- Калькулятор микрополосковой патч-антенны
- Дизайн Вокатенна
- Конструктор антенн Yagi Uda (техническое примечание NBS 688)
- Конструктор антенн Yagi Uda (Rothammel/DL6WU)
- Конструктор фильтров (аудио, AF)
- Фильтры нижних частот
- Фильтр нижних частот Бесселя 24 дБ/октава
- Фильтр нижних частот Баттерворта 24 дБ/октава
- Фильтр нижних частот Linkwitz 24 дБ/октава
- Саллен-Ки Lowpass
- Полосовые фильтры
- Руководство по проектированию полосового фильтра
- Полосовой фильтр Бесселя 4-го порядка
- Полосовой фильтр Баттерворта 4-го порядка
- Полосовой фильтр Чебышева 4-го порядка
- Полосовой фильтр Делияниса
- Узкополосный фильтр
- Ленточный фильтр Sallen-Key
- Простой полосовой фильтр
- Фильтры верхних частот
- Фильтр высоких частот Бесселя 24 дБ/октава
- Фильтр высоких частот Баттерворта 24 дБ/октава
- Фильтр высоких частот Linkwitz 24 дБ/октава
- Саллен-Ки Highpass
- Полосовые режекторные фильтры • Режекторные фильтры
- Калькулятор узкополосного фильтра Bainter
- Режекторный фильтр Fliege
- Двойной Т-образный режекторный фильтр
- Фильтры нижних частот
- Конструктор фильтров (радио, радио)
- Фильтры нижних частот
- Фильтр нижних частот Баттерворта
- Фильтр нижних частот Чебышева
- Фильтр нижних частот с константой K
- Конструктор коаксиальных фильтров нижних частот со ступенчатым импедансом
- Полосовые фильтры
- Полосовой фильтр Баттерворта
- Керамические полосовые фильтры
- Полосовой фильтр Чебышева
- Конструкция полосового фильтра Combline
- Коаксиальный бак V.
 H.F. (Полосовой) Конструктор фильтров
H.F. (Полосовой) Конструктор фильтров - Полосовой фильтр с константой K
- Crystal Filter Design #0: купите много кристаллов 🙂
- Конструкция кристаллического фильтра № 1: измерение данных замены
- Схема кристаллического фильтра № 2: расчет лестничного фильтра
- Схема кристаллического фильтра №3: проверка результатов
- Конструктор полосовых фильтров резонатора с прямой связью
- Конструктор спиральных полосовых фильтров
- Межштыревой полосовой фильтр
- Фильтры высоких частот
- Фильтр верхних частот Баттерворта
- Фильтр верхних частот Чебышева
- Фильтр верхних частот с константой K
- Полосовые режекторные фильтры • Режекторные фильтры
- Фильтр Butterworth Bandstop (Notch)
- Режекторный режекторный фильтр Чебышева
- Дизайнер коаксиальных узкополосных режекторных фильтров
- Фильтры нижних частот
- PLL, VCO, DDS, генераторы
- Модуль АПД 4350
- Источник опорной частоты 100 МГц, привязанный к 10 МГц
- Дополнительный модуль опорной частоты 100 МГц, форм-фактор DIL-28
- Универсальная плата VCO — MC100EL1648DG и PGA-103+
- Универсальная плата XCO/PLL — NB3N501/502/511
- Осциллятор блокировки впрыска с PLL (и NB3N502)
- МЭМС-генераторы — SiT8008/SiT8208/SiT8209
- Синтезатор DDS — с AD9851, ≈70 МГц
- Дочерняя плата DDS с низким уровнем шума — с AD9859, ≈ 160 МГц
- ВЧ эталонный источник — для калибровки измерителя мощности
- 4046 Калькулятор ГУН
- Мини-синтезатор с 74HCT9046A
- Конструктор контурных фильтров PLL, 2-й и 3-й порядок
- Калькулятор делителя PLL
- Генератор NE 555
- NE 555 Монофлоп
- RC HCT Инверторный генератор
- Генератор венского моста
- Коллекция схем: генераторы
- Микшер • Частот.
 Преобразователи
Преобразователи- Как измерить характеристики смесителя
- A Mixer Tinker Board с почтенным NE/SA 612
- Универсальный преобразователь частоты с Si564
- Широкополосный фазовращатель для приложений микширования IQ (ECL)
- Радиочастотный фазовращатель для приложений IQ-микширования (LVC)
- Шумные вещи
- Шум • Введение
- Расчет каскадного коэффициента шума
- Самодельный источник шума с BFR92
- Самодельный источник шума с 2 разъемами BGA2869 (60 дБ) и сопротивлением 50 Ом
- Что это вообще за ENR?
- Как измерить коэффициент шума с помощью метода Y-фактора
- Как измерить коэффициент шума с помощью метода усиления
- Как измерить уровень шума вашего анализатора спектра
- RF Toolbox, версия 3599
- Бустер (Усилитель) для Red Pitaya e.a.
- Связанный резонатор L-C Bandpass
- Блок постоянного тока
- Эквалайзер • Наклон — компенсатор
- Первопроходец
- Фильтр нижних частот, 9-полюсный, L-C
- Предварительный делитель :2 :4 :8 :10 :20 :40 :80 MC12093 MC12095 MC12080
- Арифметический блок квантового компьютера: сумматор
- Арифметический блок квантового компьютера: вычитатель
- Арифметический блок квантового компьютера: инвертор
- Арифметическая единица квантового компьютера: множитель
- Арифметический блок квантового компьютера: Делитель
- Разделение резистивной мощности, постоянный ток — 3000 МГц, 9,5 дБ, 3 канала
- Ограничитель напряжения (скоро)
- Компоненты • Сети
- Резисторы, NTC
- Цветовой код резистора (декодер:-) :: 4 КОЛЬЦА
- Цветовой код резистора (декодер:-) :: 5 КОЛЬЦЕВ
- Цветовой код резистора (декодер:-) :: 6 КОЛЬЦЕВ
- Основы NTC
- Найти параллельную комбинацию резисторов
- Найти серийный номер Комбинация резисторов
- Калькулятор делителя напряжения 1 (фиксированный)
- Калькулятор делителя напряжения 2 (регулируемый)
- Конденсаторы
- Калькулятор дисковых воздушных конденсаторов
- Калькулятор импеданса: XL, XC
- Катушки индуктивности, трансформаторы
- Широкополосное согласование импеданса с трансформатором
- Тороидальная ферритовая катушка (Amidon)
- Калькулятор спиральной катушки
- Калькулятор импеданса: XL, XC
- Тороидальная катушка из железного порошка (амидон)
- Конструкция силового трансформатора :: EI • M Core
- Калькулятор индуктивности проводов
- Направленные ответвители
- Самодельный двунаправленный ответвитель, 5–1500 МГц, 10/20 дБ
- A Самодельный двухнаправленный ответвитель, 5–2850 МГц, 17 ±1 дБ
- Понимание директивности
- Как измерить направленность направленных ответвителей
- микрополосковая
- Микрополосковый калькулятор импеданса
- Калькулятор микрополоскового угла 90°
- Сети (в основном РФ)
- Коаксиальный разъем питания
- Диплексер Bandpass
- Диплексер нижних частот
- Калькулятор балуна с сосредоточенными элементами
- Соответствующая сеть
- Калькулятор согласованного аттенюатора
- Калькулятор нижних частот ШИМ в постоянный ток
- Резистивная согласующая сеть, L-Pad
- Резистивный делитель равной мощности
- Резистивный неравный делитель мощности
- Уилкинсон Power Split
- Коаксиальный кабель Калькулятор
- Диэлектрический коаксиальный резонатор
- Калькулятор радиатора
- Резисторы, NTC
- конверсий
- Добавление нескольких операторов связи
- AWG • Преобразование в метрические единицы
- Коэффициент шума • Темп.

- Преобразователь коэффициента отражения в импеданс
- Конвертер КСВ в обратные потери (дБ)
- Конвертер величин возвратных потерь (дБ) в КСВ
- Преобразование мощности: дБмВт — вольты — ватты
- Преобразователь фазового шума в фазовый джиттер
- Преобразователь фазового джиттера в фазовый шум Конвертер
- ppm в Гц
- разное Расчеты
- Патлосс / RSSI
- Потеря несоответствия
- Калькулятор IP3/SFDR
- IP3, IP2, 1 дБ комп. Визуализатор SFDR
- Ящик диаграммы SOA (визуализатор зоны безопасной работы)
- Оборудование • Программное обеспечение 💾
- Самодельная подставка для жал SMD
- Обязательное избранное (Windows)
- Инструменты CodeVisionAVR • Фрагменты
- Генератор кодов пользовательских символов с ЖК-дисплеем
- Спецификации • Руководства
- Техническое описание Коллекция наших проектов
- Руководства по обслуживанию FLUKE
- Руководства по обслуживанию HP
- Документы Чанпуака
- Коллекции инженерных формул / Полезности
- Учебники • DHE
- Выберите правильный предохранитель (не путайте 🙂
- Сделайте свою переднюю панель с помощью Gedakop®
- Клиррфактор
- Среднее время наработки на отказ • Вопросы надежности
- Семинар по ФАПЧ
- Семинар №1 по PLL — Теория
- Семинар №2 по PLL — расчеты контурных фильтров
- PLL Семинар №3 — Моделирование с помощью LTSpice
- Коллекции инженерных формул / Полезности
- Доктор Хэт Электроникс
- Устранение неполадок • Ремонт 🔧
- DS1307 (I2C RTC) отображает 165.

- DS1307 (I2C RTC) отображает 165.


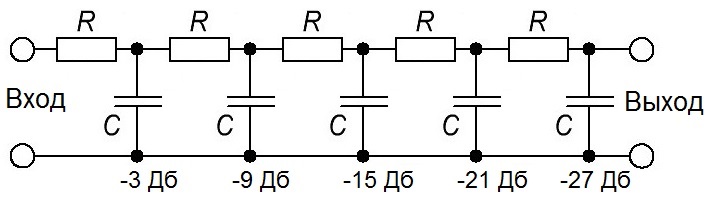 Входное напряжение 6В выходное 5,45В
Входное напряжение 6В выходное 5,45В