Дифференцирующая RC цепь – для новичков в радиоделе
Теперь, как и в случае с диодом поменяем местами конденсатор и резистор Такая RC цепь называется дифференцирующей
Рис 184 Схема опыта с дифференцирующей RC цепью Настройки я сохранил те же, что и в первом опыте
Рис 185 Опыт с дифференцирующей RC цепью
Чем интересны эти два опыта
Обратите внимание на маркеры на осциллограммах На первой маркер установлен тогда, когда импульс переходит из состояния нулевого напряжения в состояние максимального напряжения Напряжение на конденсаторе устанавливается не сразу, а спустя некоторое время Тогда как ток (второй опыт) устанавливается сразу максимальным, и за то же время спадает до нуля Это пример того, что ток через конденсатор опережает напряжение по фазе (по состоянию) Напомню, что в первом опыте мы наблюдали напряжение на конденсаторе, а во втором напряжение на резисторе, сформированное током через конденсатор
Интегрирующая RC цепь оказалась полезна для уменьшения пульсаций на выходе выпрямителя блока питания А где находит применение дифференцирующая RC цепь Например, там, где нам нужен короткий импульс, как в случае записи данных в D-триггер
Когда мы говорили об амплитудно-частотной характеристике каскада усиления, я утверждал, что она похожа на характеристику интегрирующей RC цепи Я утверждал, но, давайте проверим
Мой прибор имеет такую функцию, как работа в режиме плоттера Боде (прибора, снимающего амплитудно-частотную характеристику) Воспользуемся этой возможностью
Рис 186 Амплитудно-частотная характеристика интегрирующей RC цепи
Чтобы получить АЧХ, подключаем генератор к входу цепи, а канал 1 осциллографа к выходу Проверяем на экране осциллографа, что с сигналом всё в порядке (или, настраиваем генератор, чтобы всё было в порядке) Нажимаем кнопку
Как видно на полученной диаграмме, спад АЧХ за верхней граничной частотой – 20 дБ/декада Когда мы будем проводить эксперимент с каскадом усиления, мы снимем его амплитудно- частотную характеристику и сравним с полученной в этом опыте
Интегрирующая RC цепь – это и фильтр низких частот Если воспользоваться маркерами, то можно найти верхнюю граничную частоту или частоту среза
Рис 187 Определение частоты среза
Наличие второго канала у осциллографа позволяет получить и фазочастотную характеристику электрической цепи Настройки такие же, как и при снятии амплитудно-частотной характеристики, второй канал осциллографа подключается к входу RC цепи, а в основном меню в пункте View выбирается добавление фазочастотной характеристики
Рис 188 Фазочастотная характеристика RC цепи
На частоте среза, на рисунке выше это отмечено, фаза меняется на 45 градусов
Наблюдая за тем, как прибор снимает частотные характеристики, можно сказать, что так же характеристики были бы получены, если бы их снимали вручную: начиная с заданной частоты, прибор последовательно, с заданным шагом, меняет частоту и проводит измерение выходного сигнала Результаты этих измерений отображаются в окне отсчётов (в правом нижнем углу) Напряжение выводится в эффективных значениях, а результаты в децибелах получаются расчётным путём
Такой последовательный отсчёт выходных значений можно организовать с помощью микроконтроллера Когда мы вернёмся к этой теме, возможно, рассмотрим, как это сделать
Сдвиг фаз между входным и выходным сигналом при наличии двух каналов можно наблюдать и на экране осциллографа
Рис 189 Сдвиг фаз между входным и выходным напряжением RC цепи
Напомню, что канал 1 (выход) рисуется синим цветом, а канал 2 (вход) красным Об этом напоминают цифры рядом с меткой триггера
Аналогично тому, как мы получили амплитудно-частотную характеристику интегрирующей RC цепи, мы можем получить её и для дифференцирующей RC цепи – достаточно поменять резистор и конденсатор местами
Рис 1810 Амплитудно-частотная характеристика дифференцирующей RC цепи
Для удобства использования графиков есть возможность изменить цвета полученных кривых и маркеров Для этого достаточно зайти в основном меню окна плоттера в раздел Options, где выбрать пункт
Такая частотная характеристика подходит для фильтра высоких частот, каковым RC цепь и является
Используя разные варианты включения резисторов и конденсаторов, можно получить фильтры режекторные, не пропускающие заданные частоты, полосовые, пропускающие заданные частоты Но, рассматривая фильтры низких и высоких частот, мы можем сказать, что они одновременно являются делителями переменного напряжения То есть, уменьшают входное напряжение Чтобы избежать этого, применяют активные фильтры, добавляя транзисторный усилитель, или строят активный фильтр с использованием операционных усилителей
Прежде, чем перейти к опытам с транзистором, рассмотрим ещё один из аспектов полезного применения фильтров Мой прибор позволяет увидеть спектральный состав сигнала Вот, например, спектр прямоугольных импульсов с частотой 140 Гц
Рис 1811 Спектр меандра с частотой 140 Гц
Для получения спектра нужно проверить, не выходит ли сигнал генератора за переделы экрана, соединив вход канала и выход генератора, а затем нажать кнопку Spectrum Analyzer
На рисунке отмечена амплитуда основного тона и третьей гармоники Используем фильтр низких частот предыдущих опытов, подав сигнал на вход фильтра
Рис 1812 Спектр того же сигнала, прошедшего простейший фильтр низких частот
Спектр заметно «похудел» Применяя более сложные фильтры, можно выделить нужные гармонические составляющие, чем мы позже постараемся заняться, чтобы обогатить нашу простейшую домашнюю лабораторию
При создании звуковых усилителей мощности, на которые приходится основная нагрузка, вопрос нелинейных искажений становится одним из важнейших Обычно параметр, определяющий их, называется коэффициент нелинейных искажений Зная спектральные составляющие сигнала, можно вычислить этот коэффициент Следует только иметь в виду, что повторяя «заветную схему», где указаны нелинейные искажения, неплохо узнать, по какой методике они измерялись Иногда применяют измерение этого параметра с взвешивающим фильтром Последний даёт более точное представление о заметности искажений в силу того, что человеческое ухо по- разному воспринимает искажения на разных частотах Но числовое значение при этом может оказаться иным, чем без взвешивающего фильтра
О том, как практически в домашних условиях можно оценить нелинейные искажения, мы тоже поговорим позже (для тех, у кого нет анализатора спектра) А сейчас проведём несколько опытов с транзисторами
Источник: Гололобов ВН,- Самоучитель игры на паяльнике (Об электронике для школьников и не только), – Москва 2012
Дифференцирующие цепи.
Дифференцирующей называется цепь, сигнал на выходе которой пропорционален производной от входного сигнала.
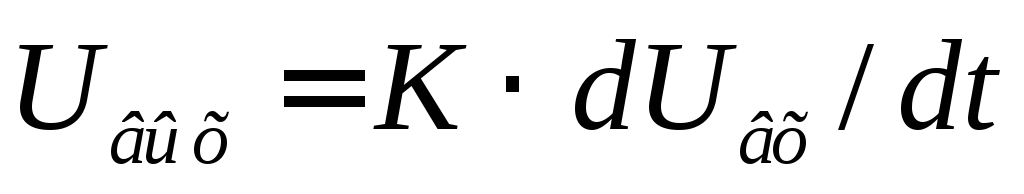 (13.28)
(13.28)
Сигналом называют физическую величину, несущую информацию. Нижу будем рассматривать импульсивные сигналы напряжения – импульсы напряжения.
Схема реальных дифференцирующих цепей показана на рис 13-33 а и 13-33 б.
Коэффициент пропорциональности М
представляет собой постоянную времени
цепи  .
.
Для
цепи RC
 =L/R.
=L/R.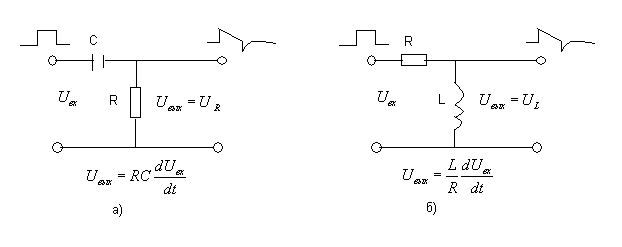
Рис 13-33. Схема дифференцирующих цепей.
Дифференцирующая RC-цепь. (фильтр нижних частот)
Эта
цепь является также четырехполюсником.
В дифференцирующей RC-цепи
сигнал снимается с резистораR,
то есть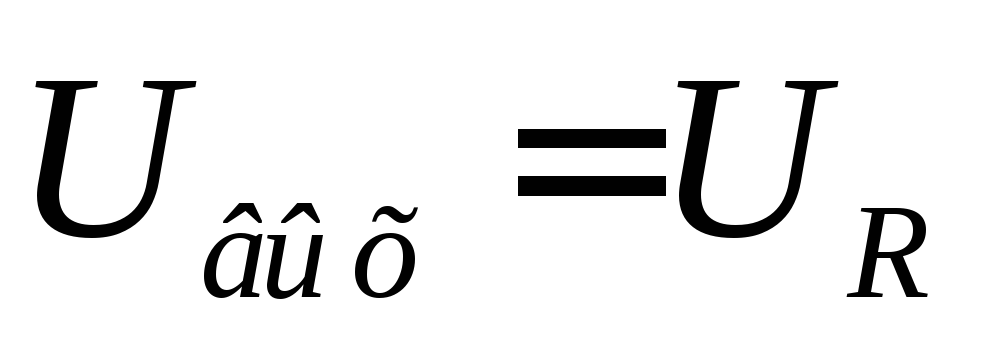 (см
рис 13-33 а). Дифференцирующий (входной)
сигнал имеет прямоугольную форму(см
ниже рис 13-33 а).
(см
рис 13-33 а). Дифференцирующий (входной)
сигнал имеет прямоугольную форму(см
ниже рис 13-33 а).
Рассмотрим действие такого сигнала (импульса напряжения) на дифференцирующую RC-цепь.

Рис
13-34. Дифференцируемый сигнал (а) и сигнал
на выходе дифференцирующей RC-цепи
(б),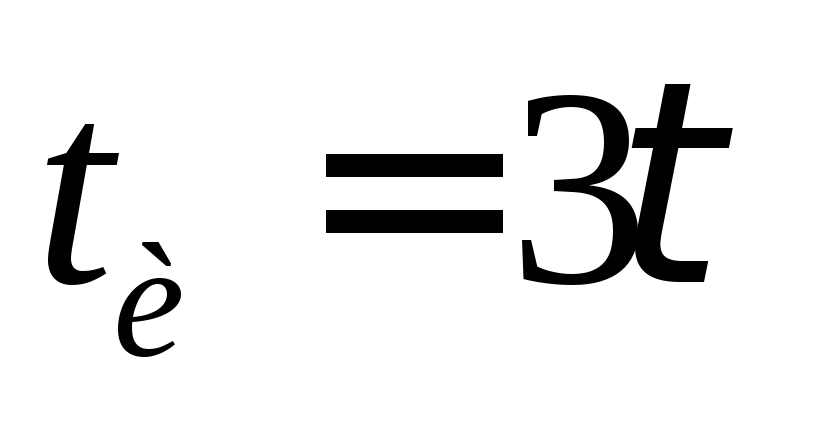
В момент  (включение цепи) напряжение на выходе
(включение цепи) напряжение на выходе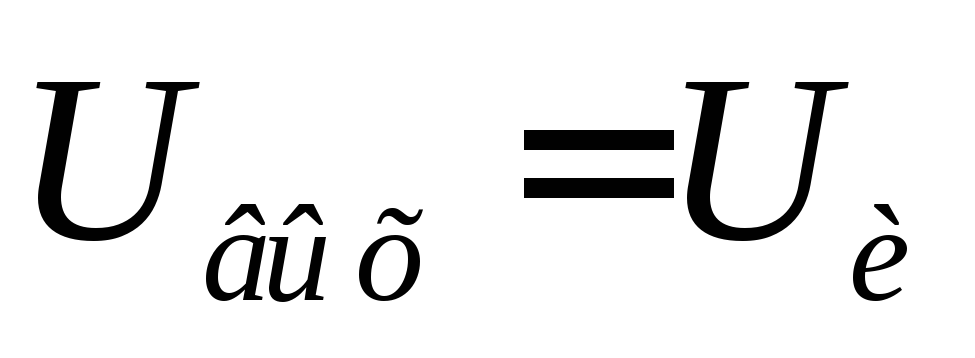 .
Это следует из того, что в момент включения
в цепи по второму закону коммутации
напряжение на конденсаторе сохраняет
свое значение, которое было до коммутации,
то есть равно 0, следовательно, все
напряжение будет приложено к резисторуR(
.
Это следует из того, что в момент включения
в цепи по второму закону коммутации
напряжение на конденсаторе сохраняет
свое значение, которое было до коммутации,
то есть равно 0, следовательно, все
напряжение будет приложено к резисторуR(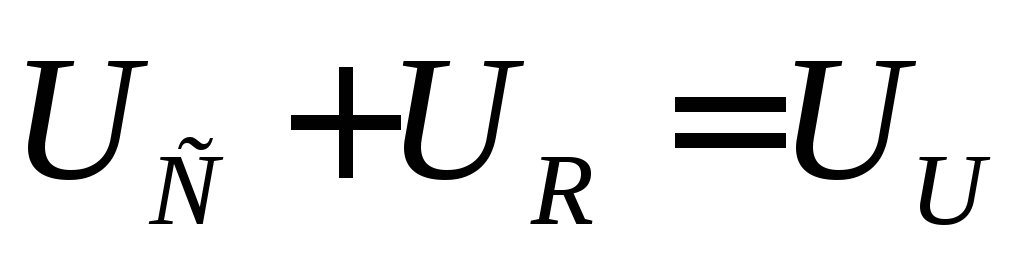
Затем 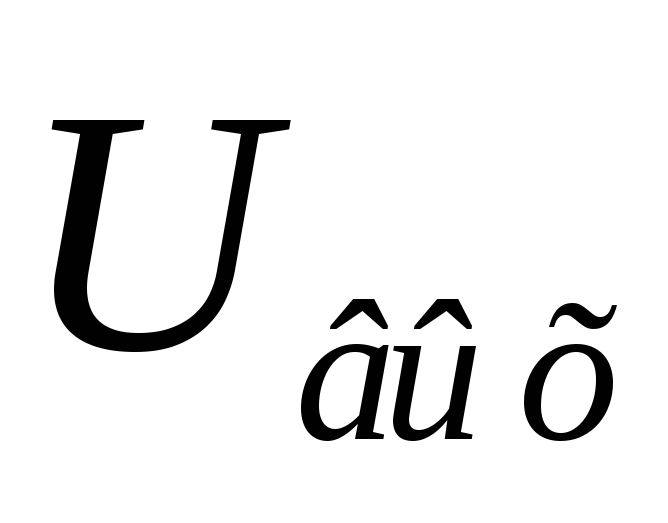 будет
уменьшаться по экспоненциальному закону
будет
уменьшаться по экспоненциальному закону
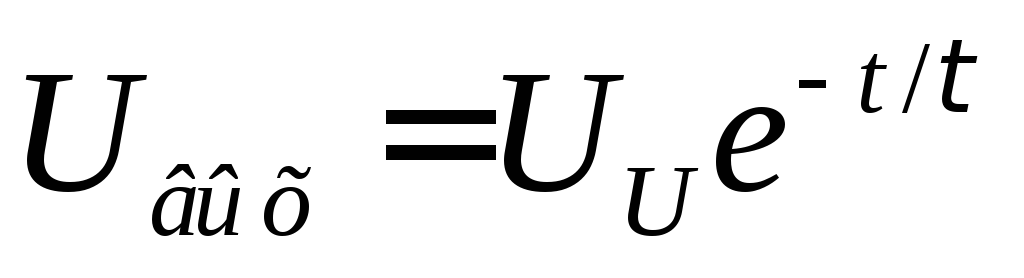 (13.29)
(13.29)
Если 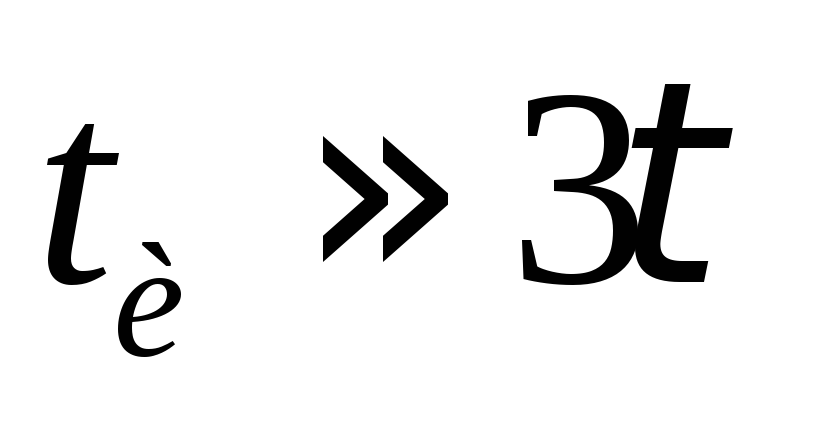 ,за
время действия входного импульса
()конденсатор
почти полностью зарядится и в момент
,за
время действия входного импульса
()конденсатор
почти полностью зарядится и в момент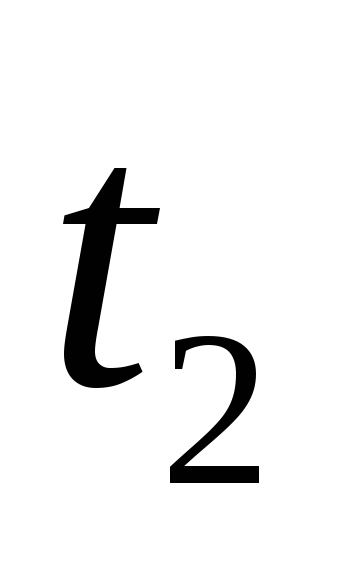 ,
когда действие импульса закончится
,
когда действие импульса закончится 0,
напряжение на конденсаторе
0,
напряжение на конденсаторе станет равно
станет равно (на
рис 13-34 б
(на
рис 13-34 б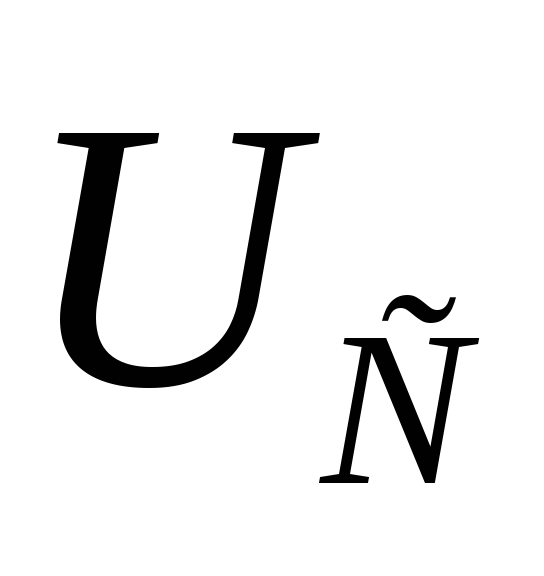 показано пунктиром), а в напряжение на
резистореR
показано пунктиром), а в напряжение на
резистореR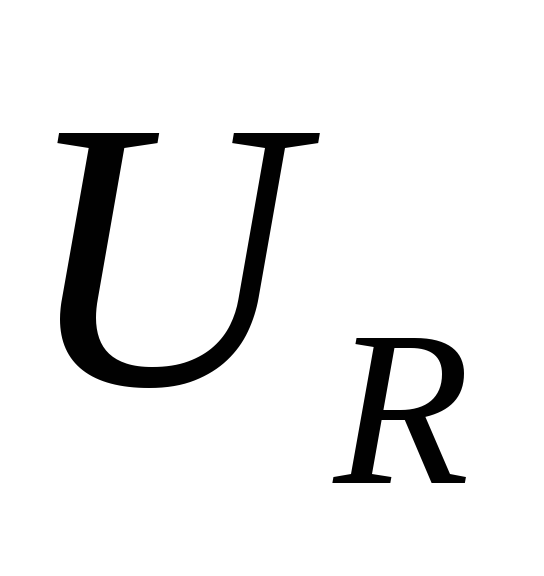 упадет до 0. Так как теперь цепь отключена
от входного напряжения (
упадет до 0. Так как теперь цепь отключена
от входного напряжения ( =0,
=0, ),
конденсатор начнет разряжаться и через
время
),
конденсатор начнет разряжаться и через
время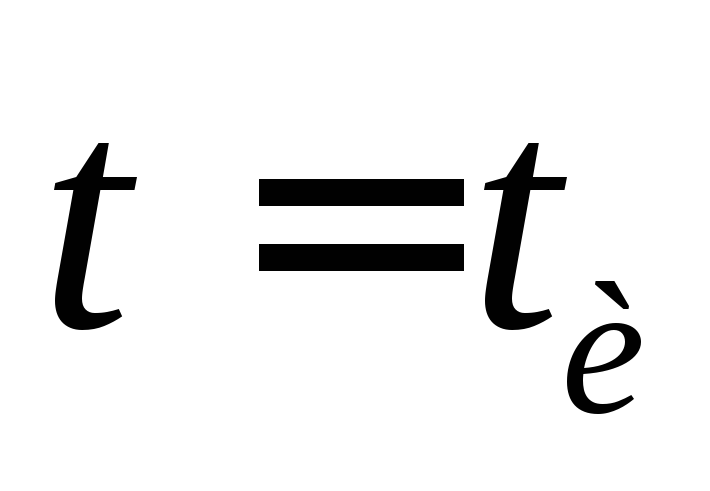 напряжение на нем станет равно 0. Ток в
цепи с момента
напряжение на нем станет равно 0. Ток в
цепи с момента изменит направление, а напряжение на
резистореRв момент
изменит направление, а напряжение на
резистореRв момент скачком станет равно
скачком станет равно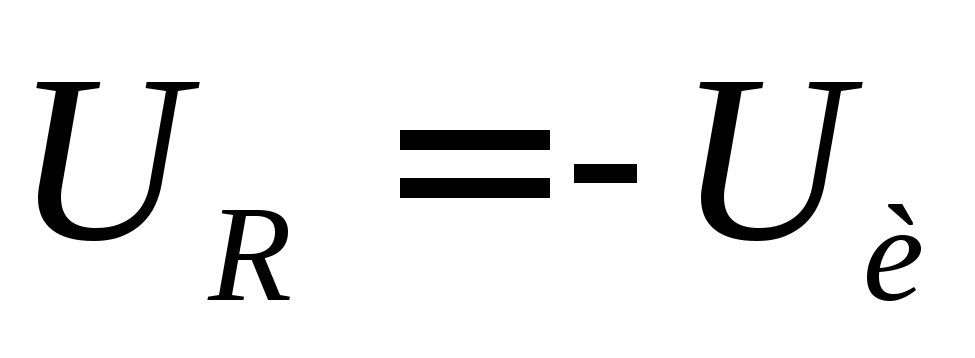 и начнет спадать по экспоненте
и начнет спадать по экспоненте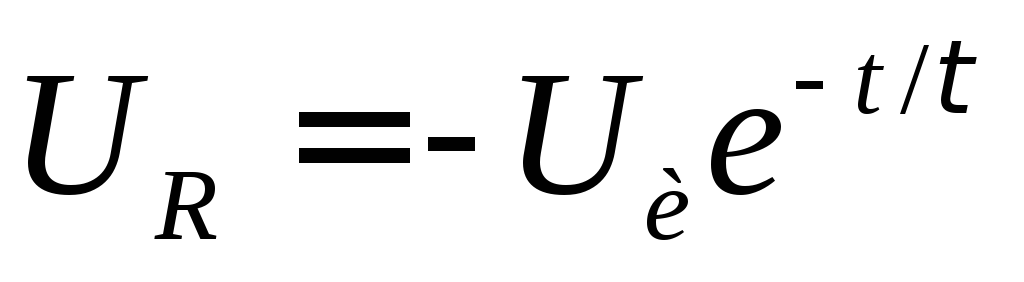 ,
а через время
,
а через время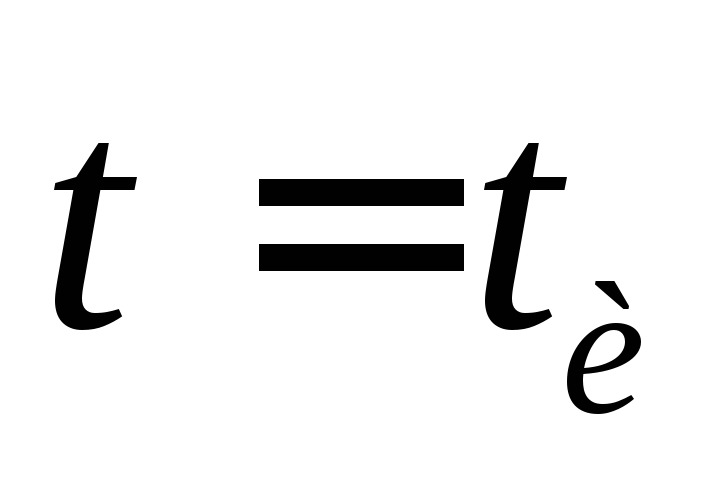 станет равно 0.
станет равно 0.
Таким
образом, на выходе цепи образуется два
остроконечных импульса положительной
и отрицательной полярностей, площади
которых равны, а амплитуда равна 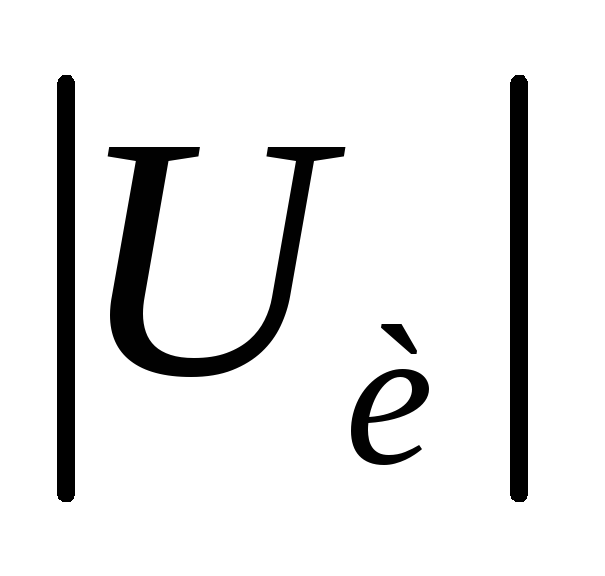 .
.
Если 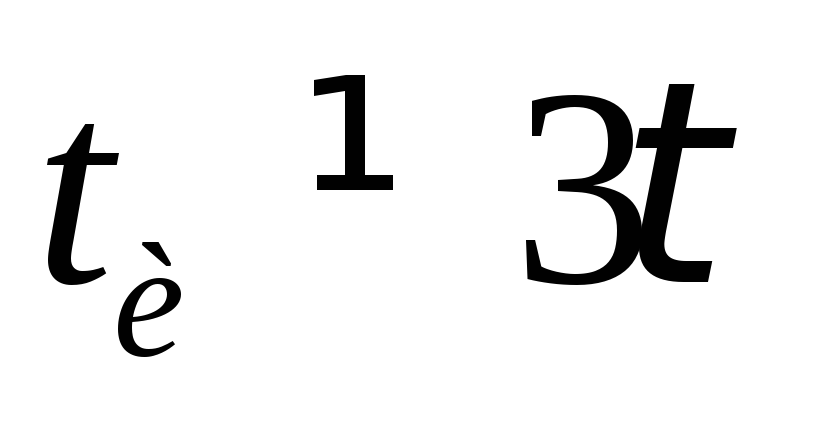 форма выходного импульса
форма выходного импульса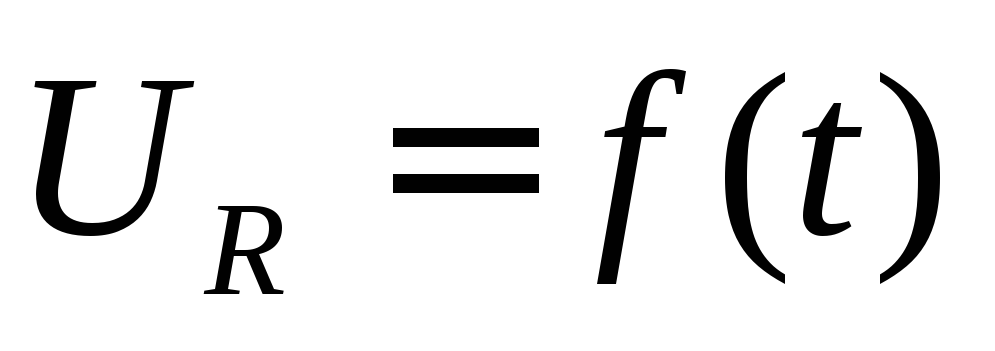 будет иметь другой вид, чем на рис
будет иметь другой вид, чем на рис
13-34 б.
Рассмотрим
два крайних случая: 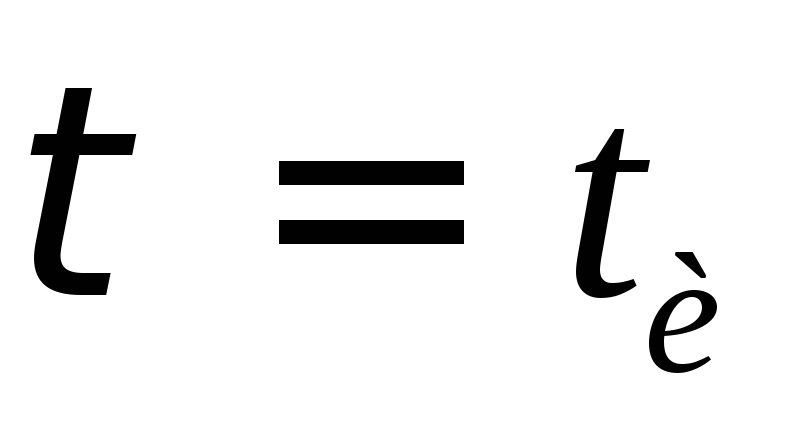 и
и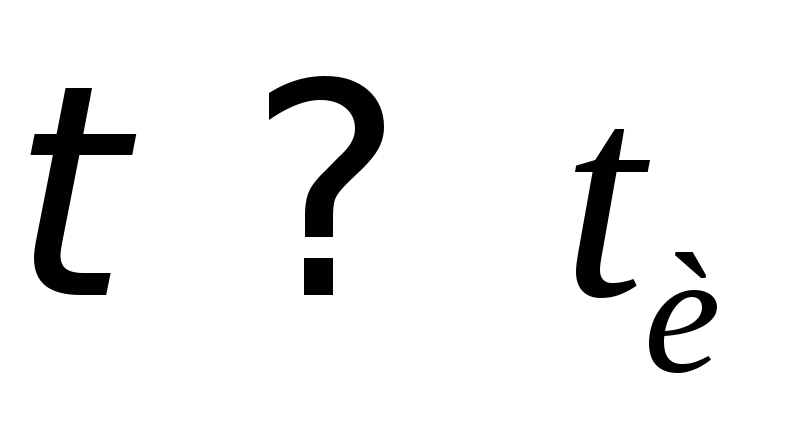 (смотри рис 13-35 б и 13-35 в)
(смотри рис 13-35 б и 13-35 в)
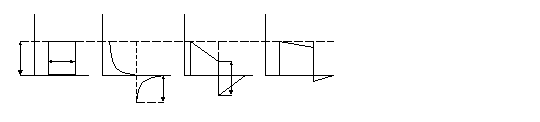
Рис
13-35. Изменение формы импульса на выходе
дифференцирующей цепи в зависимости
от соотношения между  и
и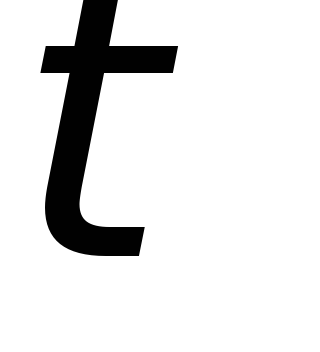 .
.
А. 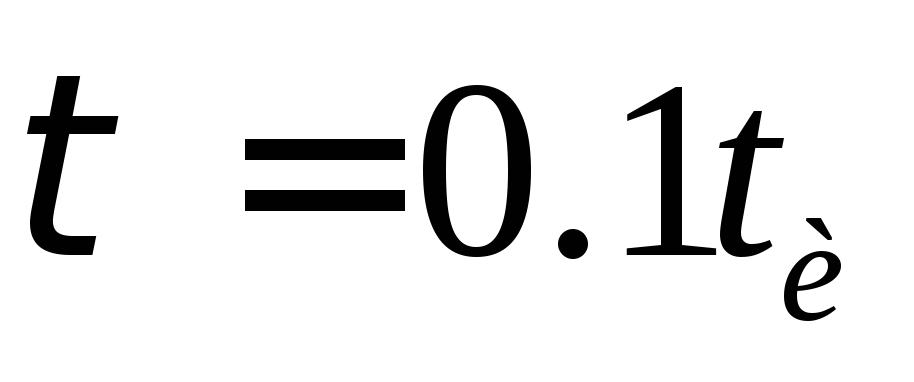 (см
рис 13-35 б)
(см
рис 13-35 б)
В этом случае за время длительности
импульса конденсатор успевает полностью
зарядиться еще до того, как окончится
действие импульса. На резисторе в момент
включения получается скачок напряжения
положительной полярности, равный
амплитуде прямоугольного импульса 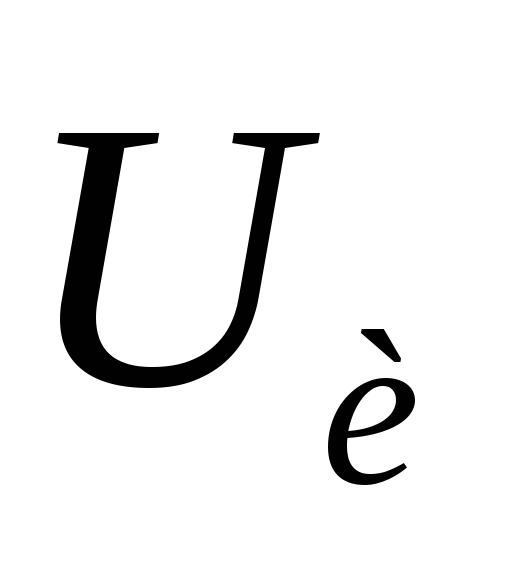 ,
а затем напряжение убывает по крутой
экспоненте и по мере зарядки конденсатора
спадает до нуля до окончания действия
импульса. По окончании действия импульса
(в момент
,
а затем напряжение убывает по крутой
экспоненте и по мере зарядки конденсатора
спадает до нуля до окончания действия
импульса. По окончании действия импульса
(в момент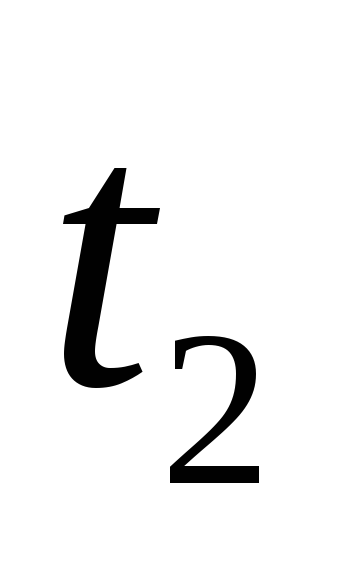 )
конденсатор начнет разряжаться, а за
счет прохождения тока через резисторRна входе образуется
импульс отрицательной полярности
амплитудной —
)
конденсатор начнет разряжаться, а за
счет прохождения тока через резисторRна входе образуется
импульс отрицательной полярности
амплитудной —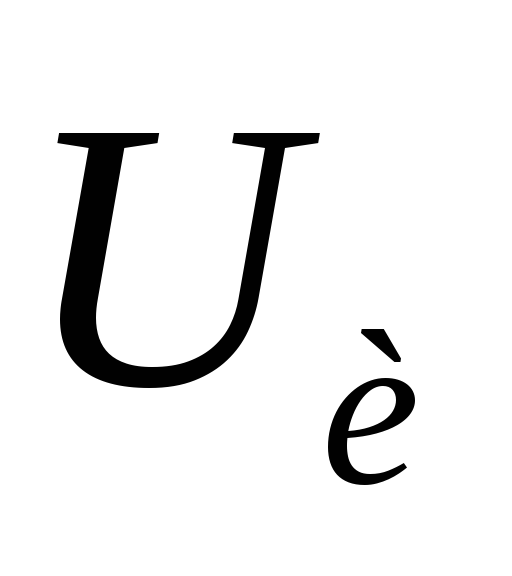 .
Площадь этого импульса будет равна
площади положительного импульса. Такие
цепи называются дифференцирующими
укорачивающими.
.
Площадь этого импульса будет равна
площади положительного импульса. Такие
цепи называются дифференцирующими
укорачивающими.
Б. 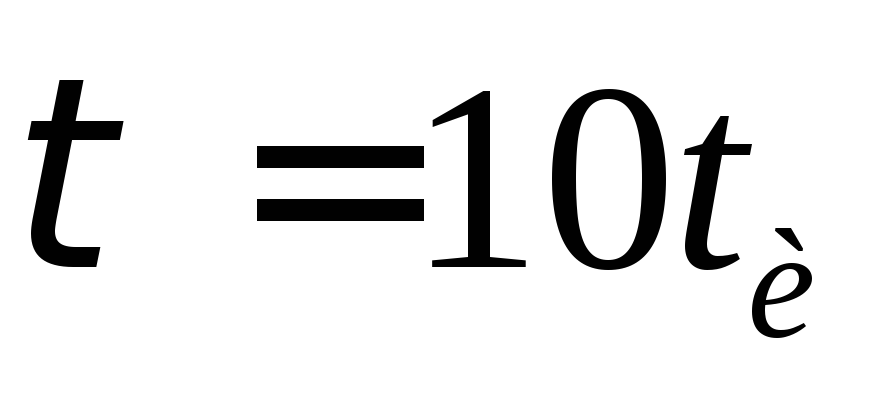 (см
рис 13-35).
(см
рис 13-35).
Так как время зарядки конденсатора
примерно равно  ,
конденсатор успеет зарядиться не ранее,
чем через
,
конденсатор успеет зарядиться не ранее,
чем через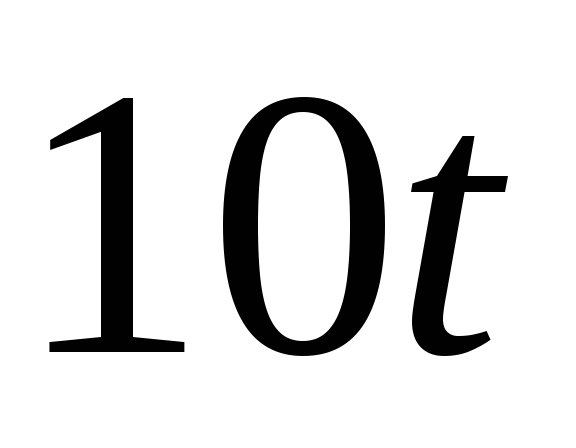 .
Следовательно, и напряжение на резисторе
.
Следовательно, и напряжение на резисторе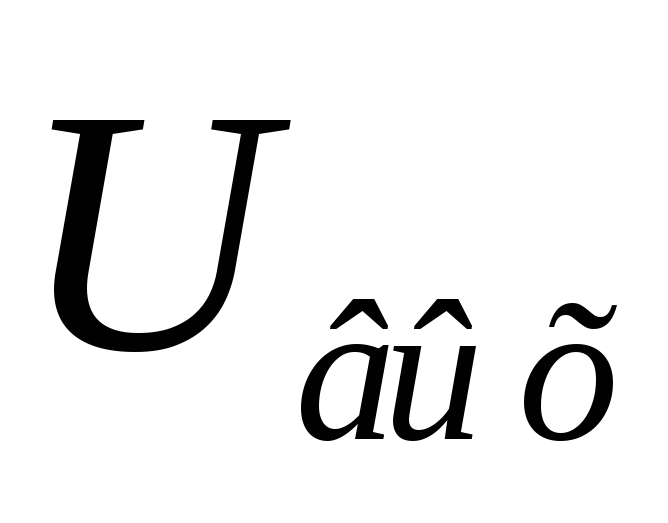 ,
равное в момент
,
равное в момент
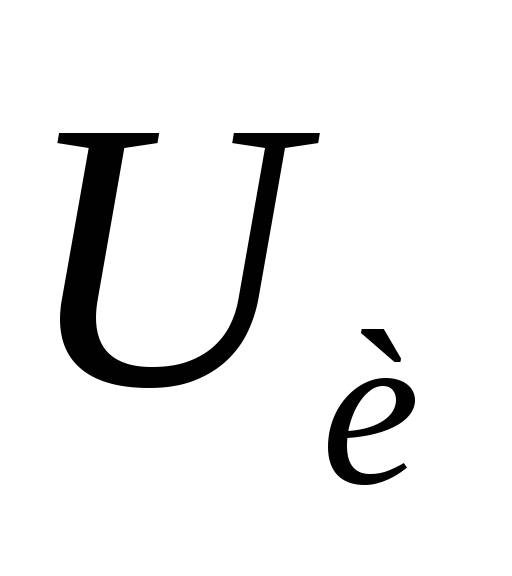 ,
уменьшится по экспоненте, станет равно
нулю через
,
уменьшится по экспоненте, станет равно
нулю через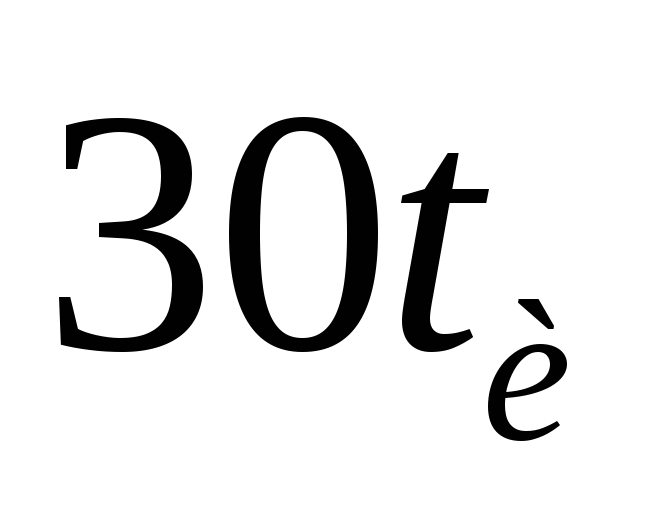 .
Поэтому за время
.
Поэтому за время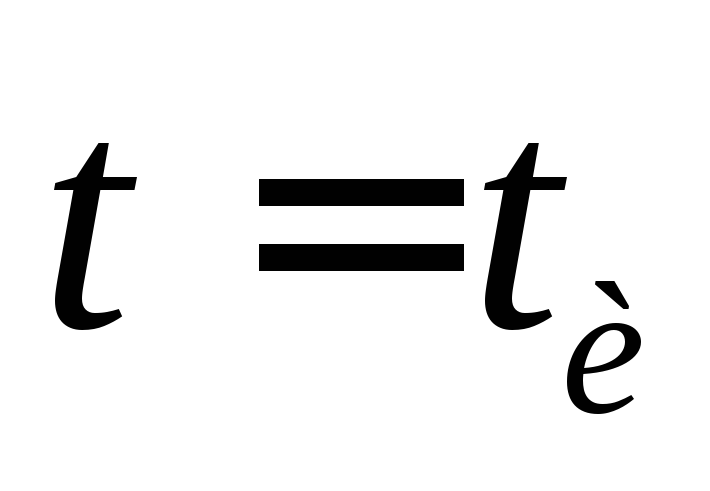 импульс
импульс на сопротивлениеRпрактически не искажается и повторяет
по форме импульс на входе.
на сопротивлениеRпрактически не искажается и повторяет
по форме импульс на входе.
Такая цепь используется как переходная между усилительными каскадами и предназначается для исключения влияния действия постоянной составляющей напряжение с коллектора транзистора предшествующего каскада на последующий.
Из формул и рис 13-34 и 13-35 можно заключить,
что амплитуда выходных импульсов при
различных соотношениях между  и
и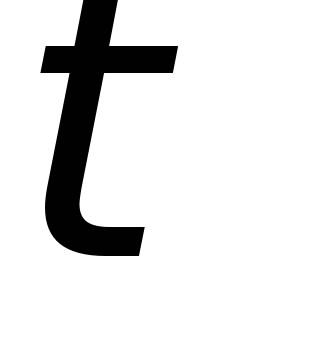 остается неизменной и равной
остается неизменной и равной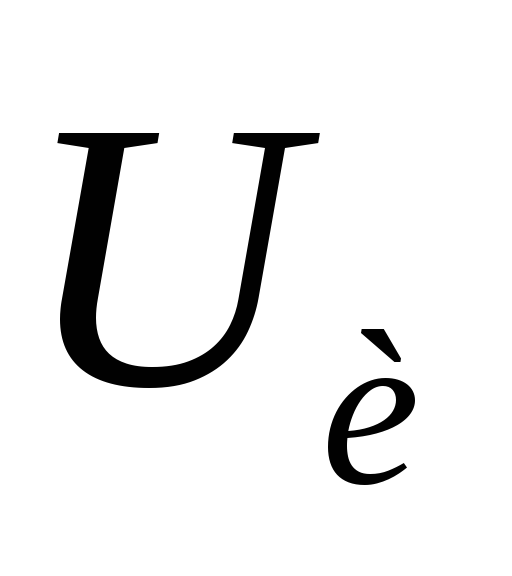 ,
а длительность их с уменьшением
,
а длительность их с уменьшением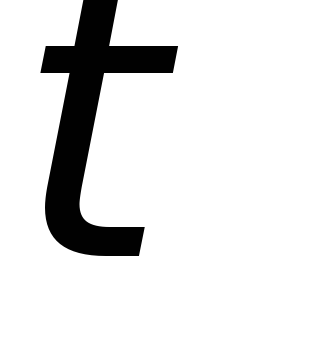 уменьшается. Точность дифференцирования
будет тем выше, чем меньше
уменьшается. Точность дифференцирования
будет тем выше, чем меньше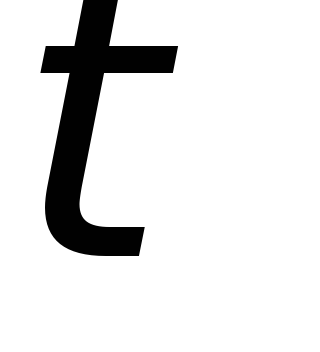 по сравнению с
по сравнению с .
.
Наиболее точное дифференцирование можно получиться с помощью операционных усилителей.
Рассмотрим АЧХ дифференцирующей RC-цепи, изображённой на рис. 13-35а.
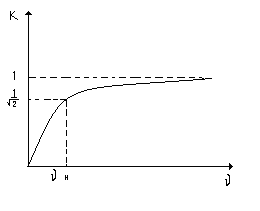
Рис. 13-35 а. АЧХ дифференцирующей цепи RC-цепи.
Частотный коэффициент передачи дифференцирующей RC-цепи равен:
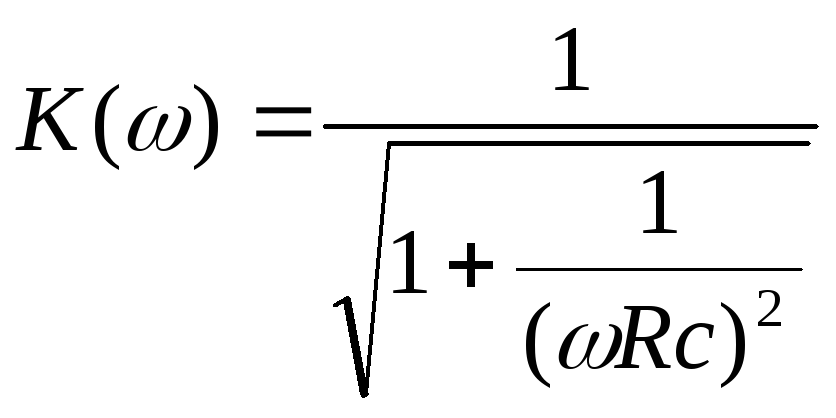
Если приравнять  к 1/
к 1/ ,
то получают нижнюю границу полосы
пропускания дефференцирующейRC-цепи
,
то получают нижнюю границу полосы
пропускания дефференцирующейRC-цепи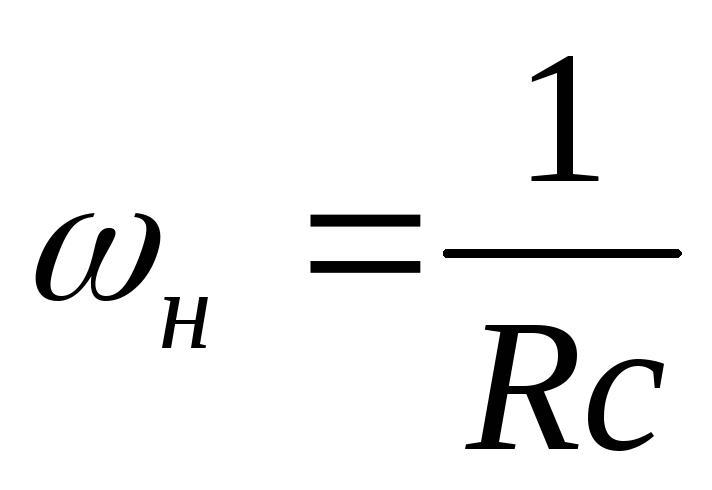 .
.
Из графика 2-35а видно, что полоса пропускания дифференцирующей RC-цепи ограничена только со стороны нижних частот.
Дифференцирующая RC-цепь и ее характеристики
Главная → Теория электрических цепей → Дифференцирующая RC-цепь и ее характеристикиДифференцирующая RC-цепь и ее характеристики
Цепь, схема которой приведена на рис. 6, а, приближенно (при uвыхuвх) реализует операцию дифференцирования, то есть uвых ≈ RC·u’вх (t) = τ·u’вх (t), причем чем меньше постоянная времени цепи τ, тем ярче эффект дифференцирования.Передаточная функция (ПФ) цепи
H (s)=ss+1τ,
частотная характеристика (ЧХ)
H (jω)=jωjω+1τ,
амплитудно-частотная характеристика (АЧХ)
A (ω)=|H (jω)|=ωω2+ (1τ)2 при (ω>0),
фазочастотная характеристика (ФЧХ)
Φ (ω)=90°−arctgτω.
Амплитудно-частотную характеристику приближенно разбивают на частотные интервалы (ЧИ). Низкочастотная зона (ω < 1/τ) – полоса дифференцирования (ПД) с A (ω) ≈ τω, высокочастотная зона (ω > 1/τ) – полоса пропускания (ПП) с A (ω) ≈ const = 1.
а) схема дифференцирующей RC-цепи; б) АЧХ дифференцирующей RC-цепи по частотным интервалам
На рис. 6, б АЧХ, построенная приближенно по частотным интервалам, показана тонкой линией, а уточненная – жирной, причем частота среза ωср = 1/τ соответствует частоте стыка частотных интервалов.
Сравнивая ЧХ цепи со спектром сигнала на входе, можно сделать следующие выводы:
1) A (0) = 0, следовательно, суммарная площадь реакции будет равна нулю;
2) A (∞) = 1, поэтому скачки воздействия без искажения пройдут на выход;
3) если спектр воздействия в основном располагается в полосе дифференцирования, то uвых ≈ τ·u’вх, то есть на выходе будет ярко выражен эффект дифференцирования; если же он располагается в полосе пропускания, то изменения формы реакции будут невелики.Дифференцирующая RC-цепь
26.10.2015, 6096 просмотров.
2.4 Дифференцирующие — цепи
Простейшая
дифференцирующая 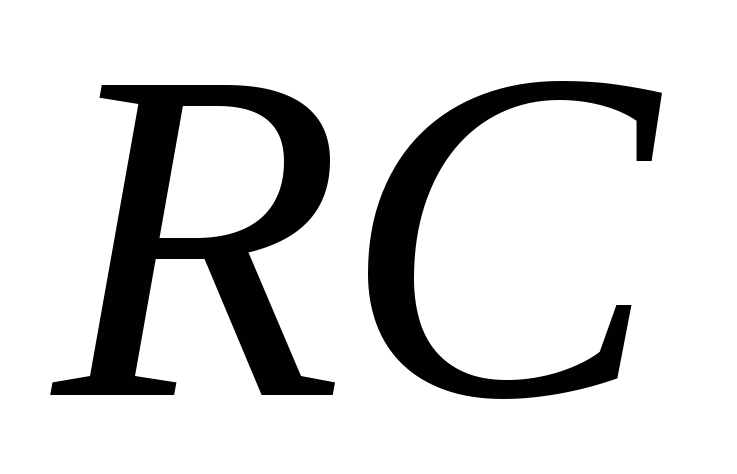 -цепь
образуется из интегрирующей заменой
конденсатора на резистор (рис. 1.28).
-цепь
образуется из интегрирующей заменой
конденсатора на резистор (рис. 1.28).
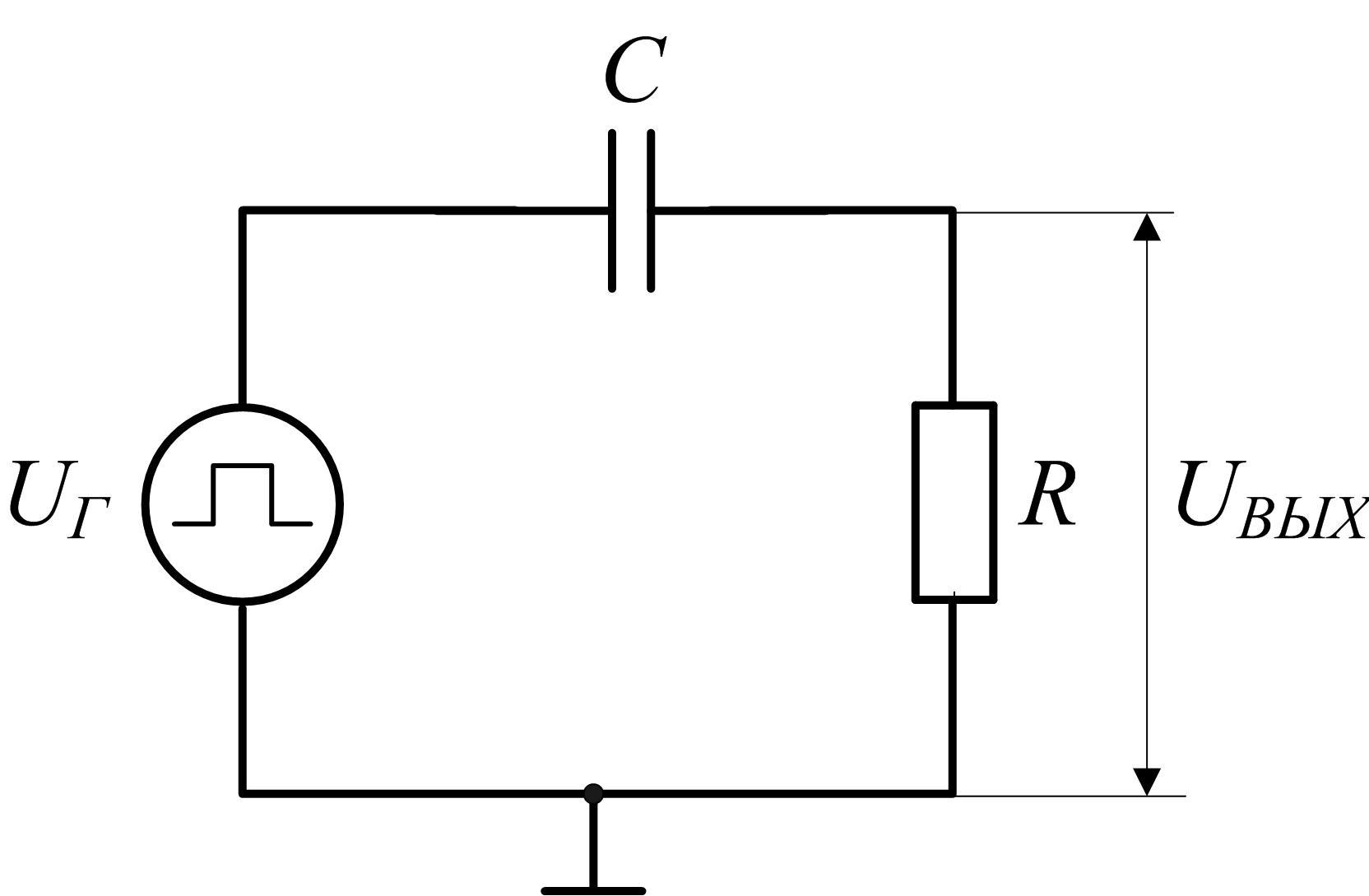
Рис. 1.28 Простейшая
дифференцирующая 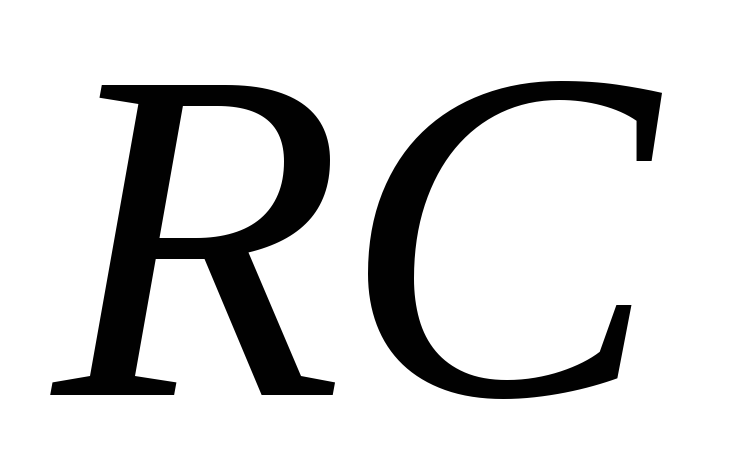 -цепь
-цепь
Напряжение на
выходе цепи будет определяться падением
напряжения на резисторе  :
: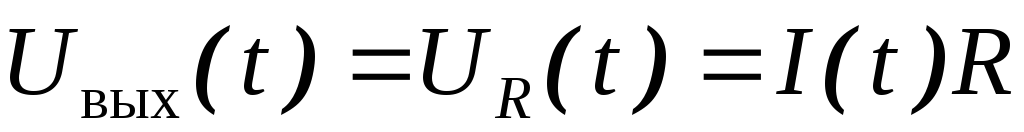 .
Зависимость
.
Зависимость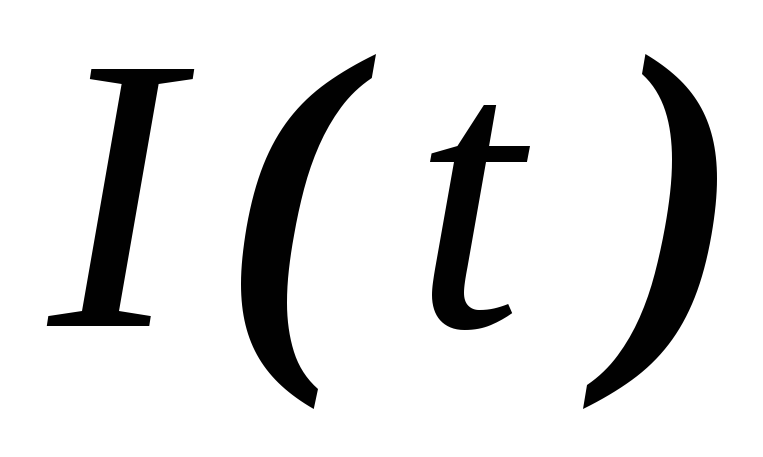 была приведена на рис. 1.17. Следовательно,
напряжение на выходе будет иметь вид,
представленный на рис. 1.29 (окончание
импульса входного напряжения означает
отрицательный скачок напряжения). Цепь
называется дифференцирующей, поскольку
ток через конденсатор можно определить
как производную от приложенного
напряжения.
была приведена на рис. 1.17. Следовательно,
напряжение на выходе будет иметь вид,
представленный на рис. 1.29 (окончание
импульса входного напряжения означает
отрицательный скачок напряжения). Цепь
называется дифференцирующей, поскольку
ток через конденсатор можно определить
как производную от приложенного
напряжения.
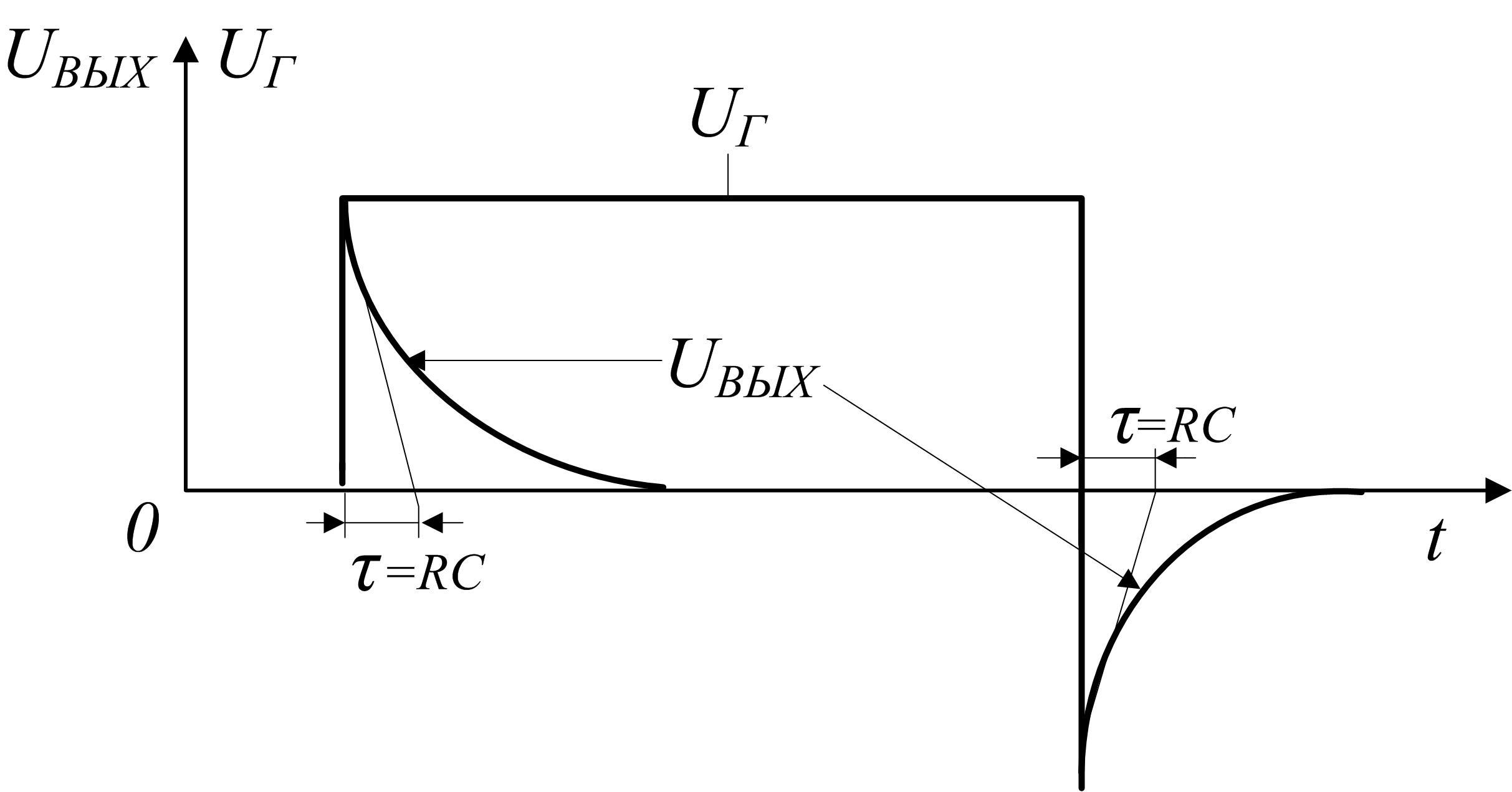
Рис.
1.29 Сигналы на входе и выходе дифференцирующей 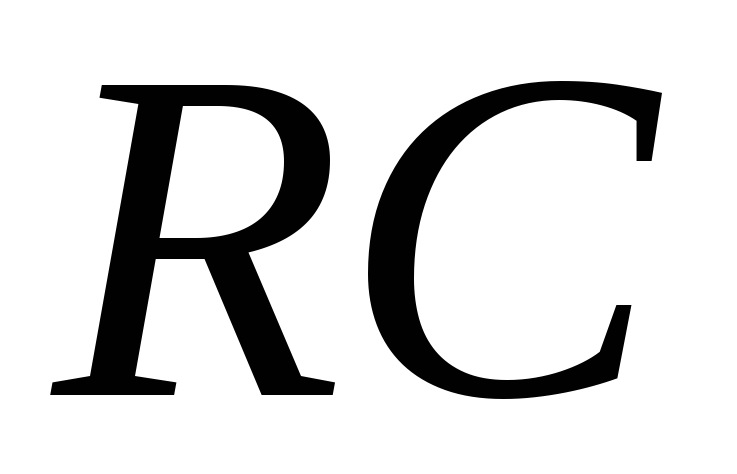 -цепи
-цепи
Действительно,
как было показано, 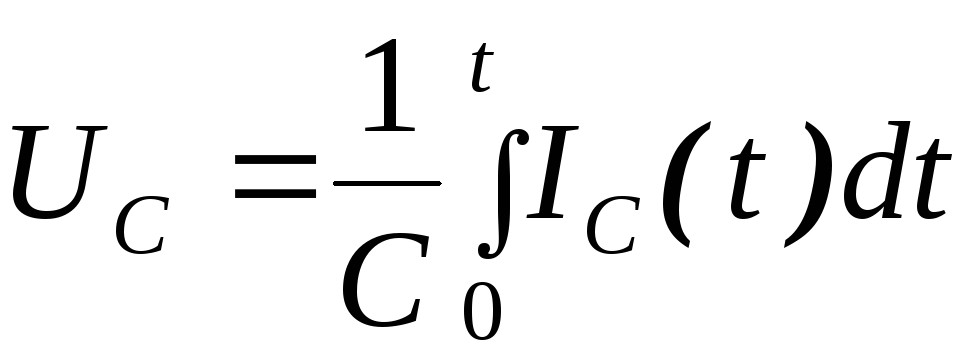 ,
отсюда
,
отсюда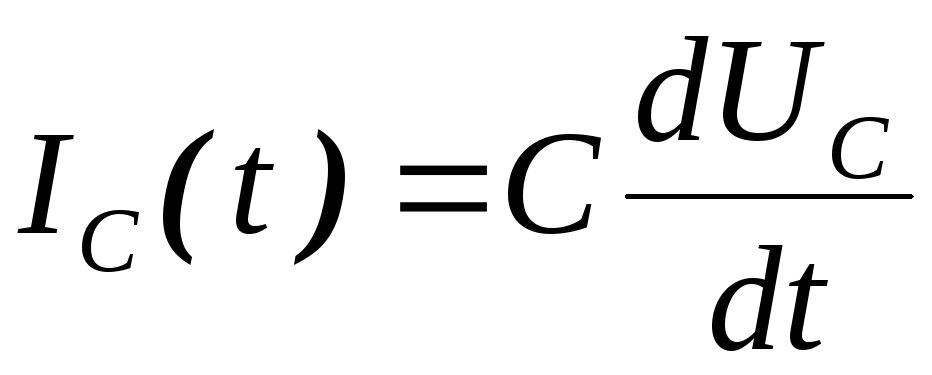 .
Поскольку:
.
Поскольку:
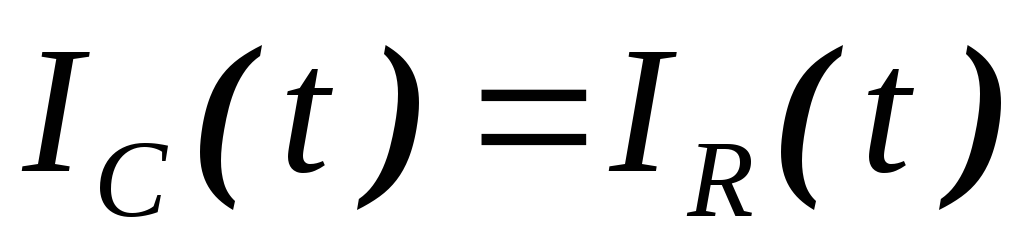 ,
то
,
то 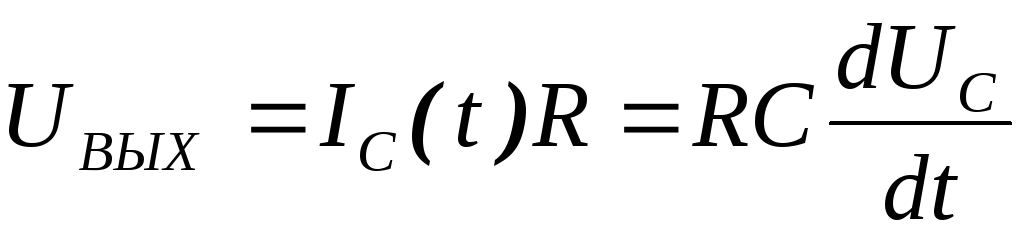 .
.
Как и в случае с интегрирующей цепочкой, можно считать, что дифференцирование входного напряжения происходит лишь в первый момент входного импульса.
Изменение напряжения
на выходе дифференцирующей  -цепочки
можно определить, зная изменение
напряжения на выходе интегрирующей
-цепочки
можно определить, зная изменение
напряжения на выходе интегрирующей -цепи,
т.к.
-цепи,
т.к.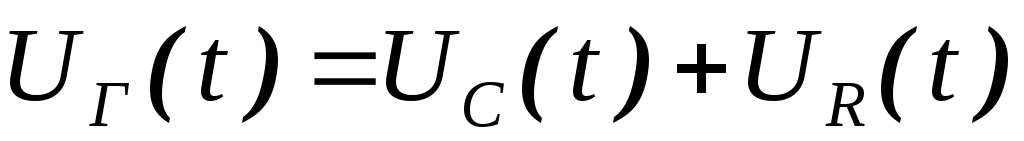 и
и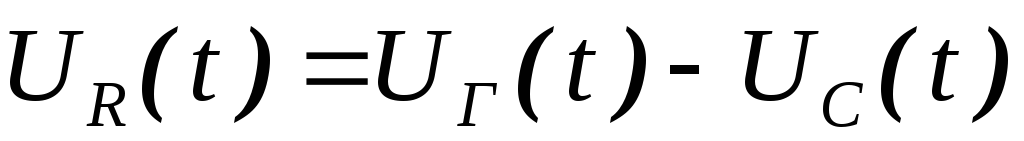 .
Действительно, вычитая из
.
Действительно, вычитая из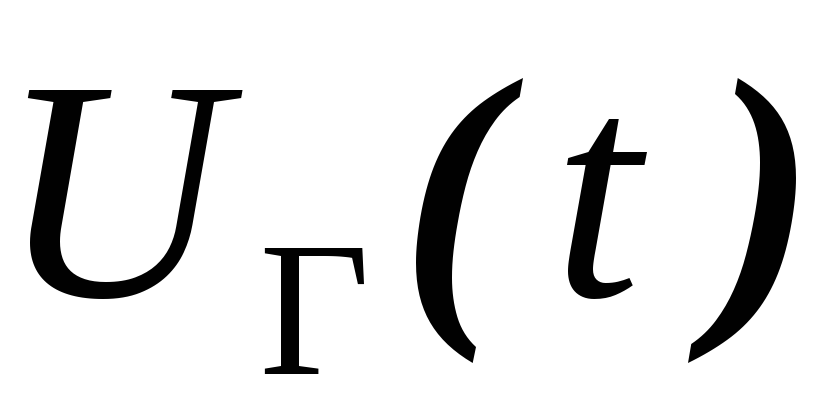 (рис.1.19а) напряжение
(рис.1.19а) напряжение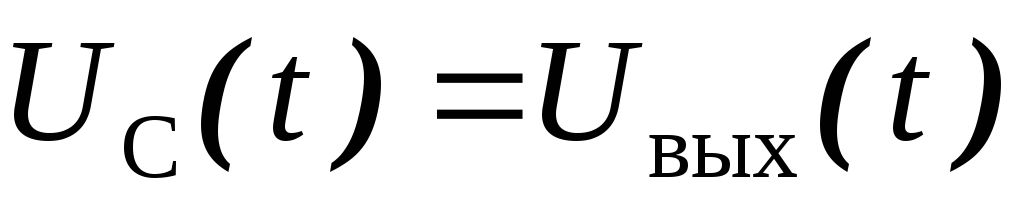 (рис.1.19в), получаем
(рис.1.19в), получаем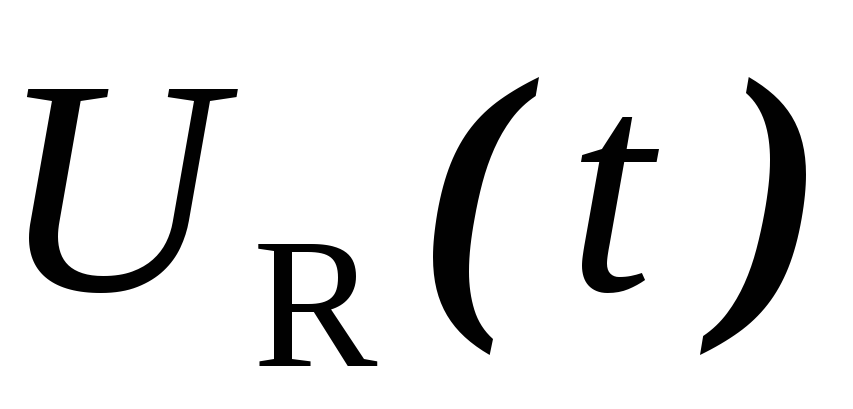 .
Таким же образом можно поступить, если
нужно рассчитать более сложные
дифференцирующие цепи.
.
Таким же образом можно поступить, если
нужно рассчитать более сложные
дифференцирующие цепи.
3. Вопросы для подготовки
1) Что такое э.д.с. источника электрической энергии?
2) Какие бывают источники э.д.с.?
3) Что такое резистор?
4) Сформулируйте закон Ома?
5) Чем определяется сопротивление электрических проводов?
6) Чему равно сопротивление двух последовательно включённых резисторов?
7) Чему равно сопротивление двух параллельно включённых резисторов?
8) Сформулируйте первый и второй закон Кирхгофа.
9) В чём состоит различие между источниками напряжения и тока?
10) Как преобразовать источник напряжения в источник тока и обратно?
11) Что такое линейная электрическая цепь?
12) В чём состоит принцип наложений (суперпозиций)?
13) Как можно использовать принцип наложений для расчёта электрических цепей?
14) Какой компонент электрической цепи называется конденсатором?
15) Что такое ёмкость конденсатора?
16) Чем определяется заряд, накапливаемый в конденсаторе?
17) Что такое катушка индуктивности?
18) Что такое RC-цепь?
19) В каком случае конденсатор, включённый в цепь с источником постоянного напряжения, препятствует электрическому току, а в каком нет?
20) Как определить изменение во времени напряжения на конденсаторе, если известен закон изменения во времени тока, заряжающего или разряжающего конденсатор?
21) Запишите закон изменения тока во времени для простейшей RC-цепи при замыкании ключа.
22) По какому закону происходит заряд конденсатора, осуществляемый от источника постоянного напряжения через резистор?
23) Может ли напряжение на конденсаторе измениться мгновенно? Почему?
24) Как рассчитываются переходные процессы в RC — цепях при воздействии прямоугольного импульса?
25) Как зарядятся два последовательно соединенных конденсатора, присоединенных к источнику постоянного напряжения?
26) Может ли какое-либо напряжение в цепи, содержащей конденсатор, изменится мгновенно?
4. Задания
1) Нарисуйте зависимость напряжения UВЫХ после замыкания и размыкания ключей в следующих схемах (считать, что ключи в исходном состоянии были бесконечно долго):
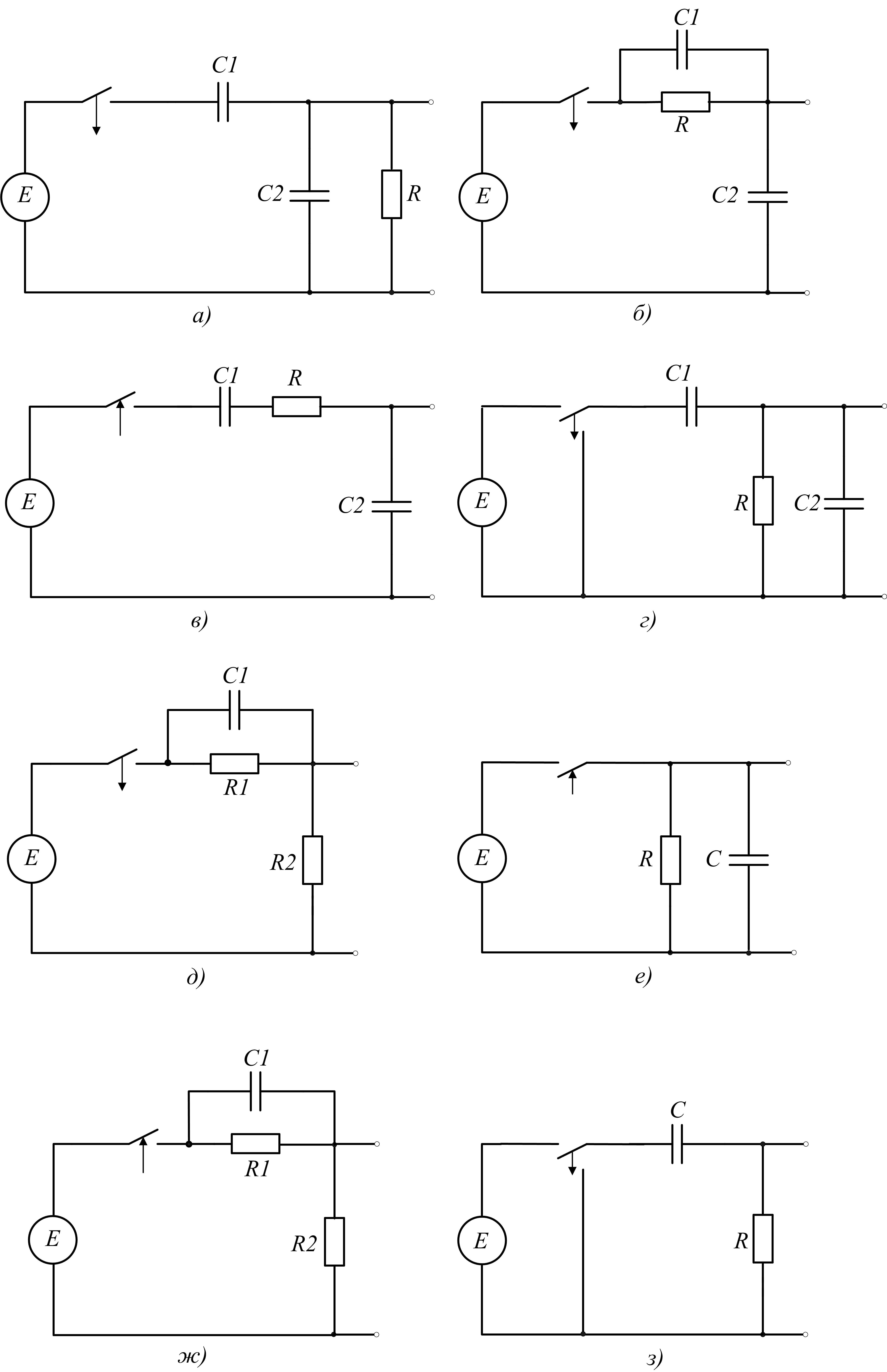
2) Нарисуйте выходные импульсы, которые получатся при подаче прямоугольных импульсов на вход следующих RC– цепочек:
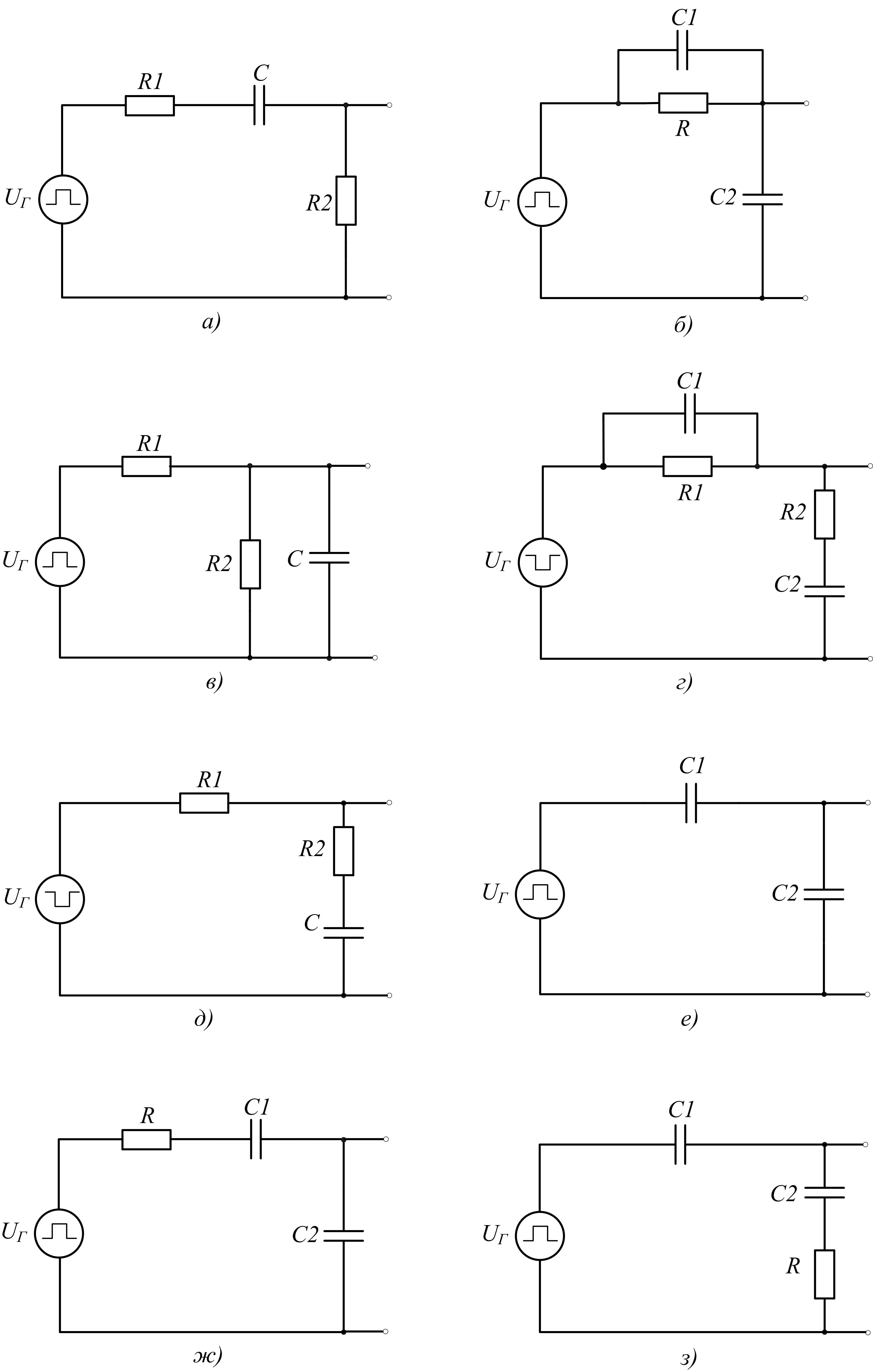
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №2
СИНУСОИДАЛЬНЫЕ СИГНАЛЫ
RC-ЦЕПИ ПЕРЕМЕННОГО ТОКА
1. Цель занятия
Целью занятия является изучение схем переменного тока с применением только пассивных элементов.
2. Краткие теоретические сведения
2.1 RC-цепи при синусоидальном сигнале
Рассмотрим характер процессов, происходящих в металлических проводниках, при приложении к ним синусоидального источника э.д.с. Отметим, прежде всего, что при отсутствии э.д.с. электроны, находящиеся на внешней оболочке и слабо связанные с атомами, при комнатной температуре хаотически и с большими скоростями двигаются в различных направлениях, периодически сталкиваясь с ионизированными атомами. Усреднённый по времени суммарный вектор скоростей движения электронов равен 0. При приложении э.д.с. появляется усреднённый по времени суммарный вектор скоростей электронов, направленный от – к + источника э.д.с., т.е. возникнет дрейф электронов в одном направлении. При постоянной э.д.с. этот усреднённый по времени вектор не изменяет амплитуду и направление.
При приложении к проводникам синусоидального э.д.с. усреднённый вектор скоростей будет изменяться по синусоидальному закону. Если в рассматриваемом металлическом проводнике возникнет разрыв, то электроны не смогут двигаться в направлении действия э.д.с. и ток прекратиться. Но если в место разрыва мы включим конденсатор, то ток в цепи не прекратиться, т.к. конденсатор способен на одной пластине накапливать электроны, а затем освобождаться от них, отдавая их во внешнюю цепь.
Рассмотрим действие конденсатора, если к его клеммам подключён идеальный источник синусоидального тока (рис. 2.1). Поскольку направление тока в источнике периодически изменяется на противоположное, конденсатор относительно общей шины будет заряжаться то до положительного напряжения, то до отрицательного. Очевидно, что при положительной полуволне синусоидального тока конденсатор от некоего отрицательного напряжения будет перезаряжаться до положительного. Рост положительного напряжения закончится, когда ток уменьшится до нуля. Этот момент будет соответствовать максимуму положительного напряжения, т.е. при синусоидальном токе напряжение будет отставать от тока на 90о. После этого начнётся период убывания напряжения.
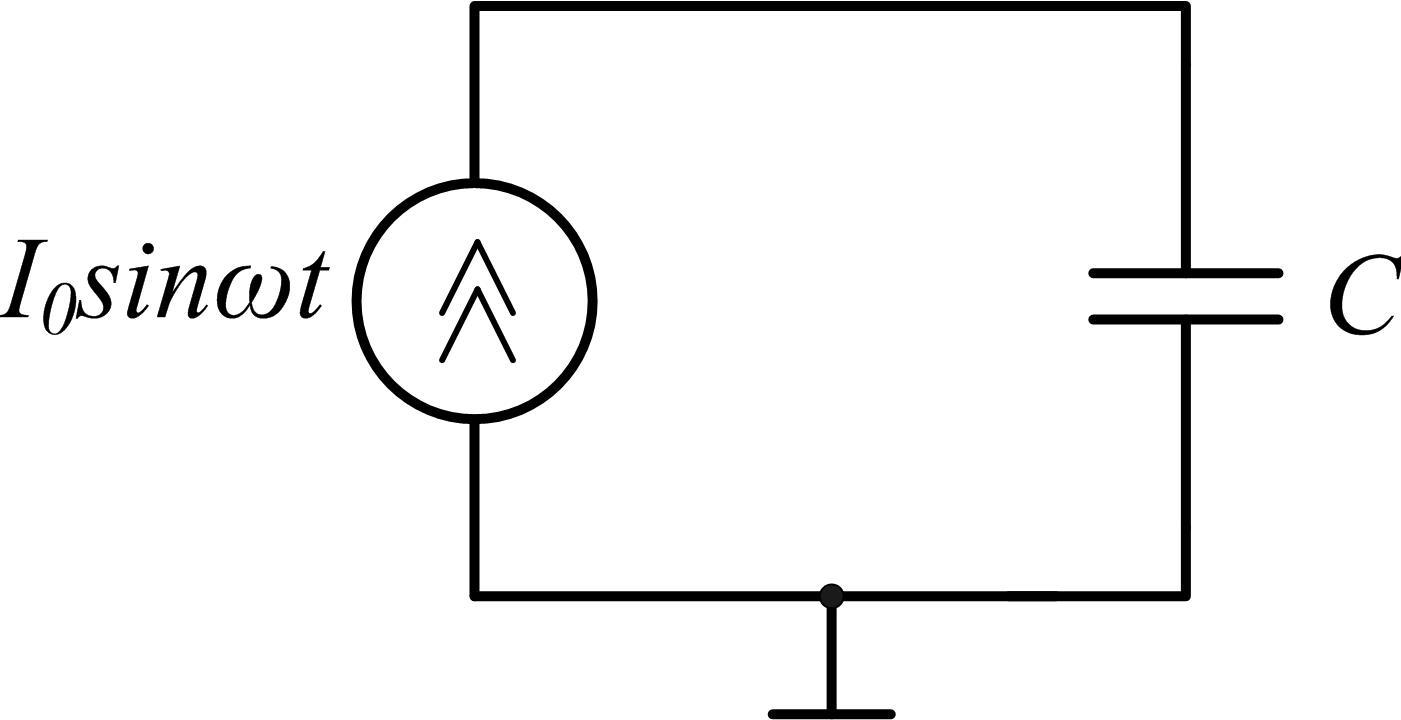
Рис. 2.1 Конденсатор, заряжаемый и разряжаемый источником
синусоидального тока
Нетрудно доказать
высказанные соображения. Действительно,
поскольку 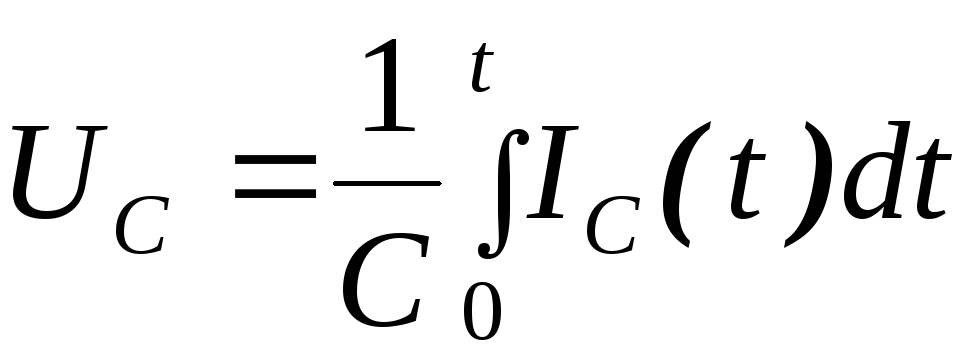 ,
а
,
а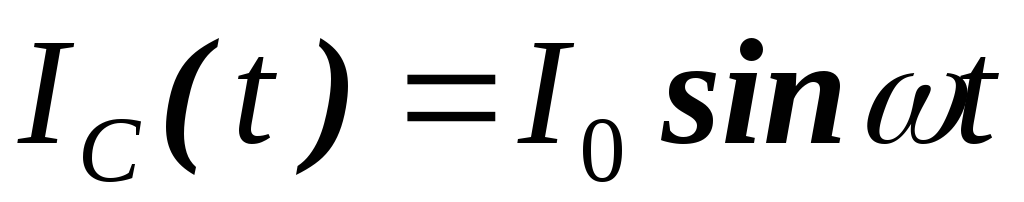 ,
получаем:
,
получаем:
| (2.1) |
Из полученного выражения можно сделать вывод: синусоидальный ток, протекающий через конденсатор, вызывает на нём синусоидальное напряжение, отстающее от тока на 90о (рис. 2.2).
Р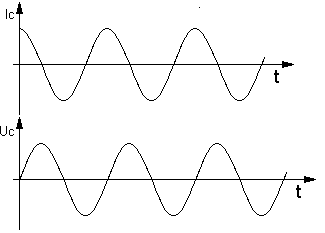 ис.
2.2 Синусоидальные токи и напряжения в
конденсаторе
ис.
2.2 Синусоидальные токи и напряжения в
конденсаторе
В теории электрических цепей используют символический метод, при котором вводят комплексный ток İ следующим образом:
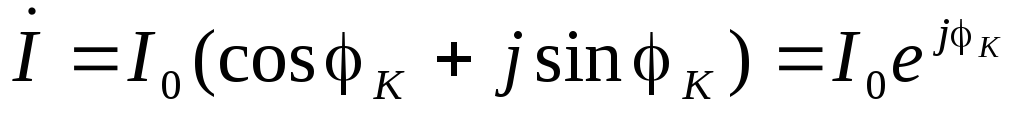 .
Отсюда с учётом (2.1) получаем напряжение
на конденсаторе:
.
Отсюда с учётом (2.1) получаем напряжение
на конденсаторе:
|
Поскольку  получаем окончательно:
получаем окончательно:
| (2.2) |
Введём понятие комплексного сопротивления конденсатора ZС. Используя закон Ома для схемы, приведённой на рис. 2.1,а, применив его к синусоидальным токам и напряжениям, запишем:
| (2.3) |
Сравнивая приведённое
выражение с (2.2), можно установить, что 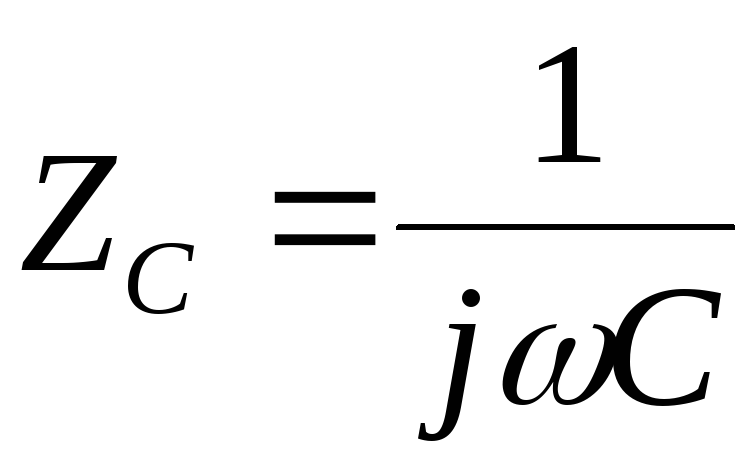 .
Эта формула является ключевой при
анализе цепей, содержащих источники
э.д.с. и тока синусоидальной формы.
.
Эта формула является ключевой при
анализе цепей, содержащих источники
э.д.с. и тока синусоидальной формы.
В случае, если
входной генератор 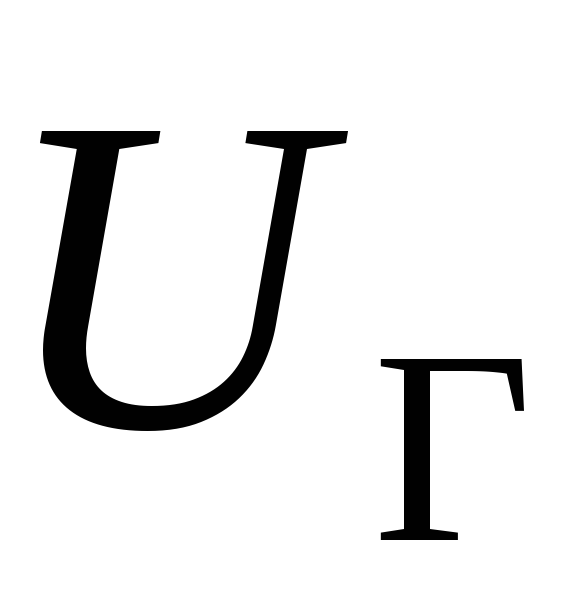 – источник синусоидального напряжения,
схема простейшей интегрирующей
– источник синусоидального напряжения,
схема простейшей интегрирующей -цепи
будет выглядеть так, как показано на
рис. 2.3. Для нахождения частотных
характеристик цепи воспользуемся
символическим методом и определим
коэффициент передачи цепи
-цепи
будет выглядеть так, как показано на
рис. 2.3. Для нахождения частотных
характеристик цепи воспользуемся
символическим методом и определим
коэффициент передачи цепи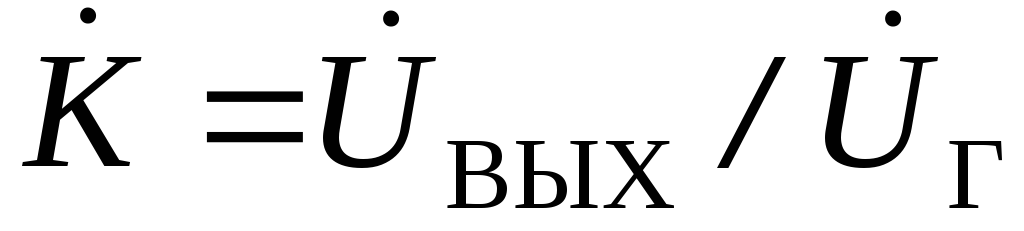 .
.
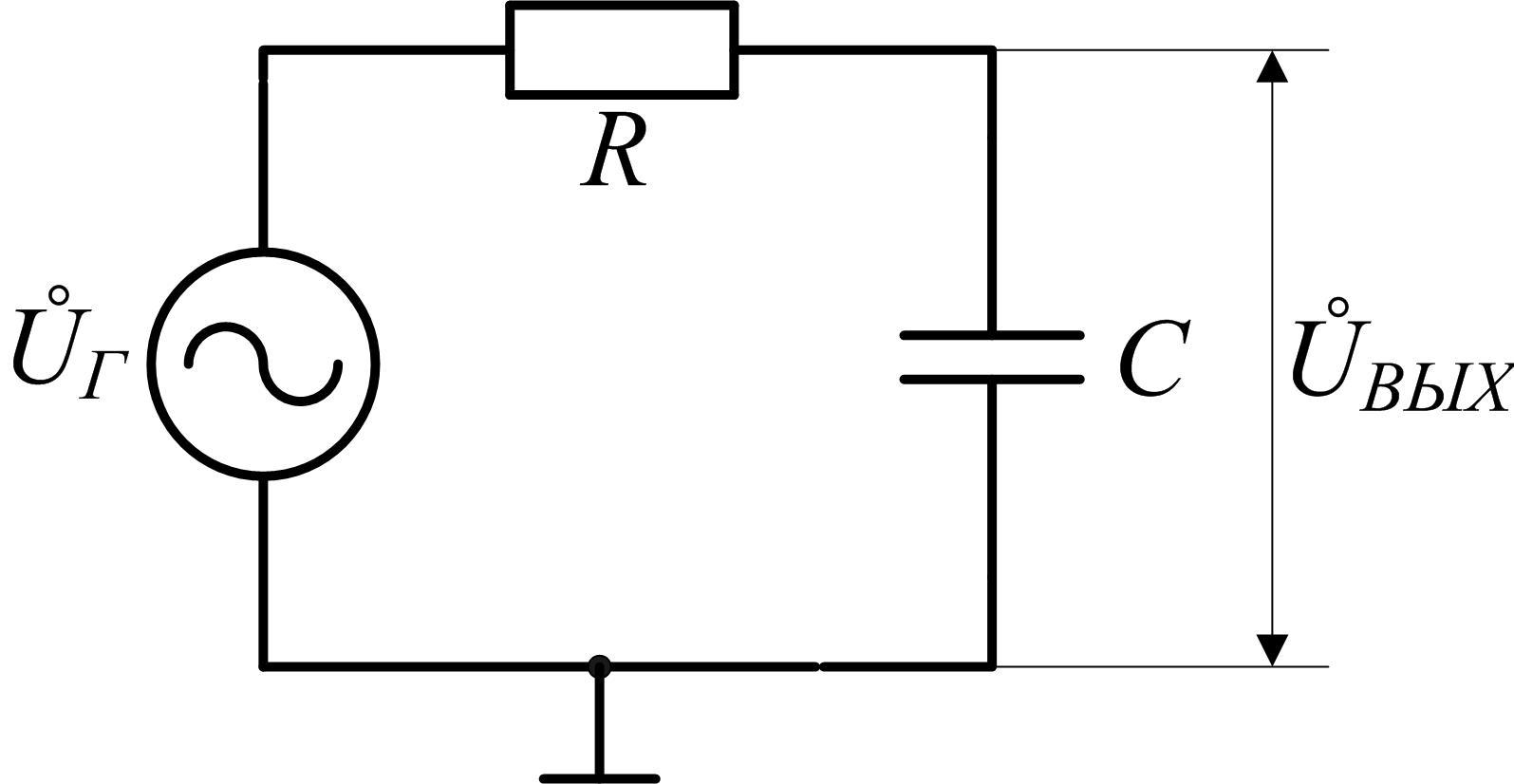
Рис.
2.3 Схема простейшей интегрирующей  -цепи
-цепи
с синусоидальным источником э.д.с.
По второму закону Кирхгофа сумма э.д.с. в замкнутом контуре равна сумме падений напряжений на участках цепи. Отсюда:
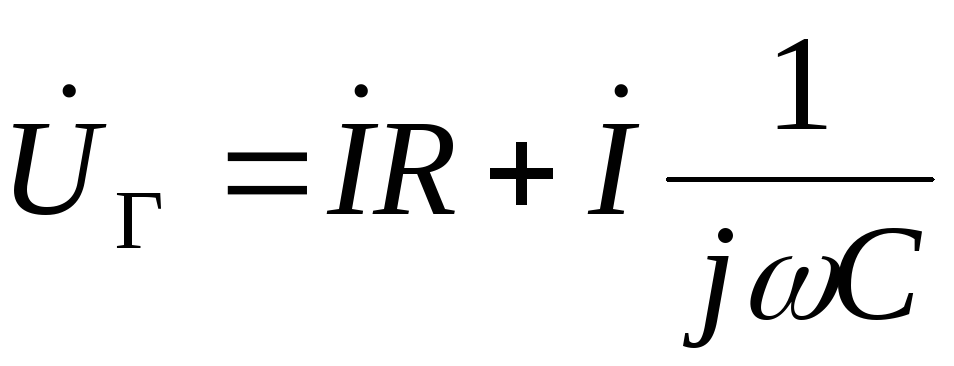 ,
, 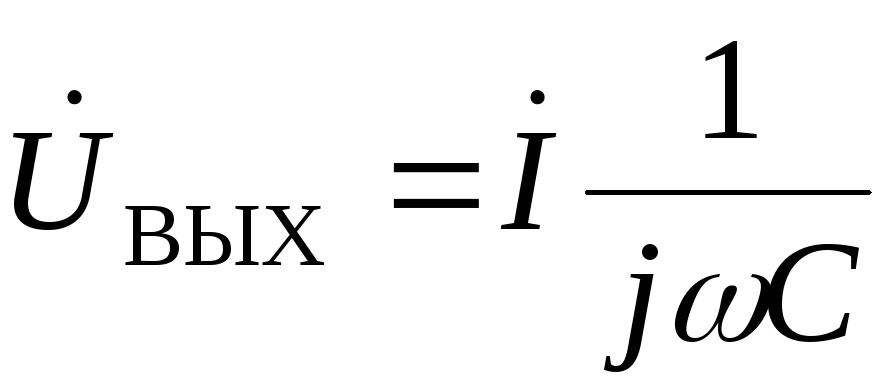 ,
,
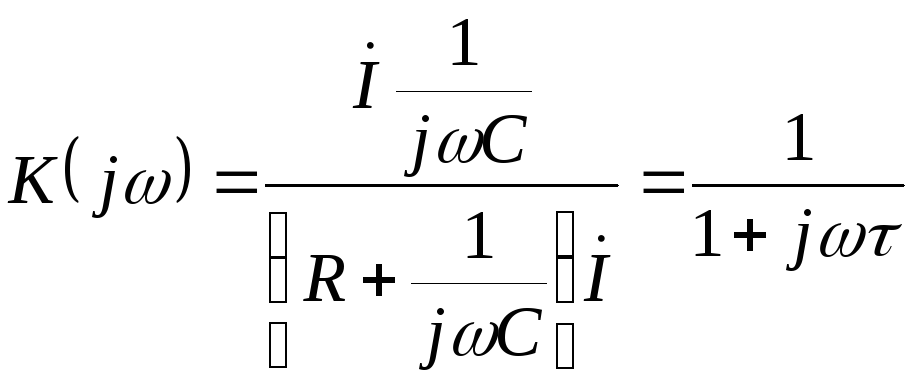 ,
(2.4)
,
(2.4)
где 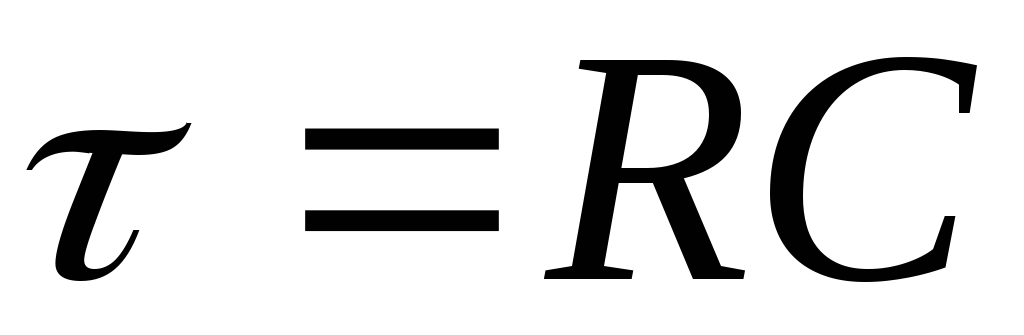 – постоянная времени
– постоянная времени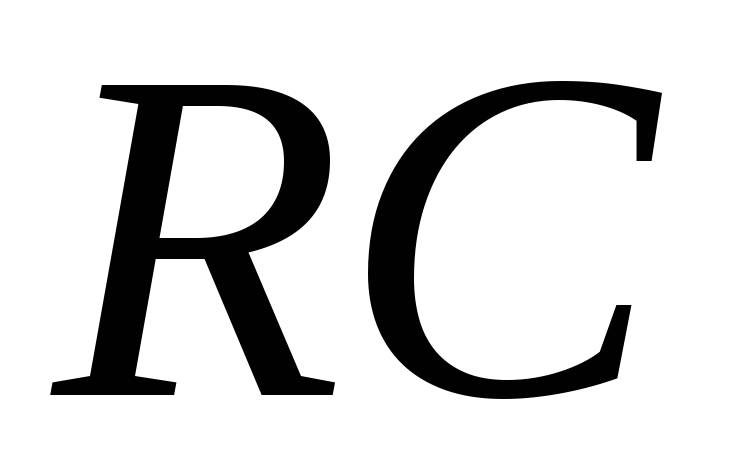 —
цепи.
—
цепи.
Из полученного выражения (4) можно получить формулы для расчета амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик.
Для построения
АЧХ необходимо найти модуль 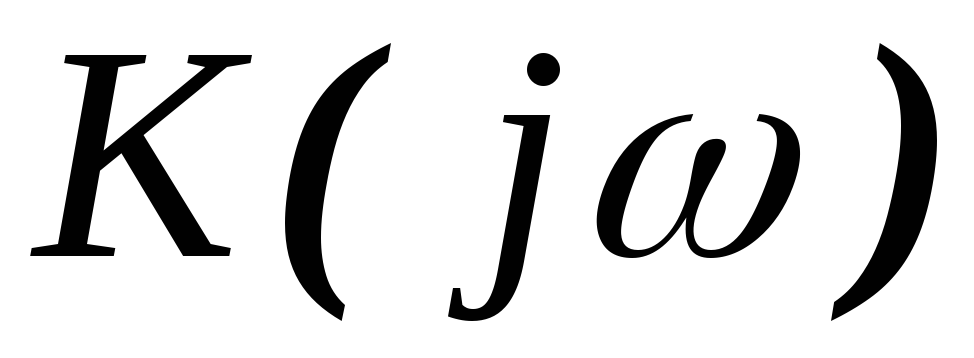 .
Из (2.4) получаем:
.
Из (2.4) получаем:
| (2.5) |
Из
условия 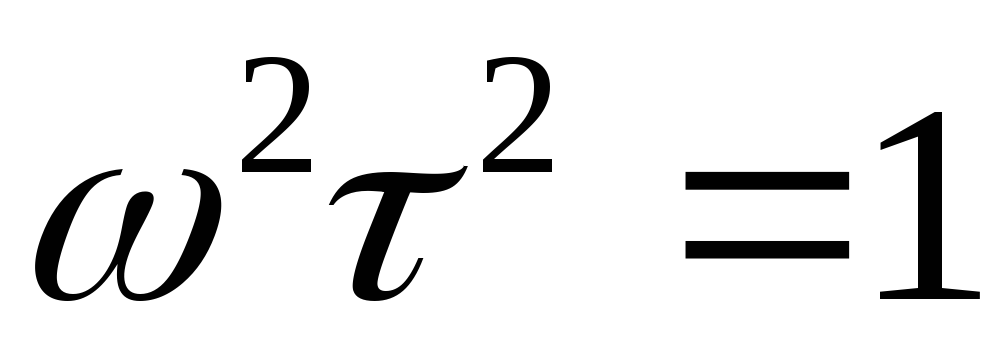 определяем
значение верхней граничной частоты
определяем
значение верхней граничной частоты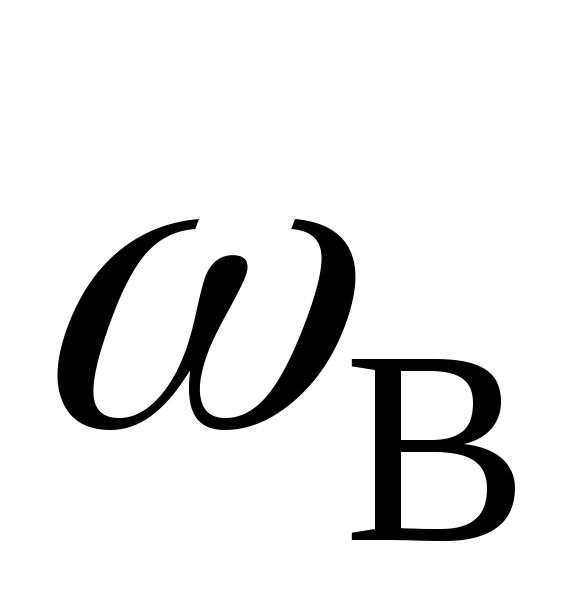 ,
при котором модуль коэффициента усиления
уменьшается по сравнению с коэффициентом
передачи при
,
при котором модуль коэффициента усиления
уменьшается по сравнению с коэффициентом
передачи при в
в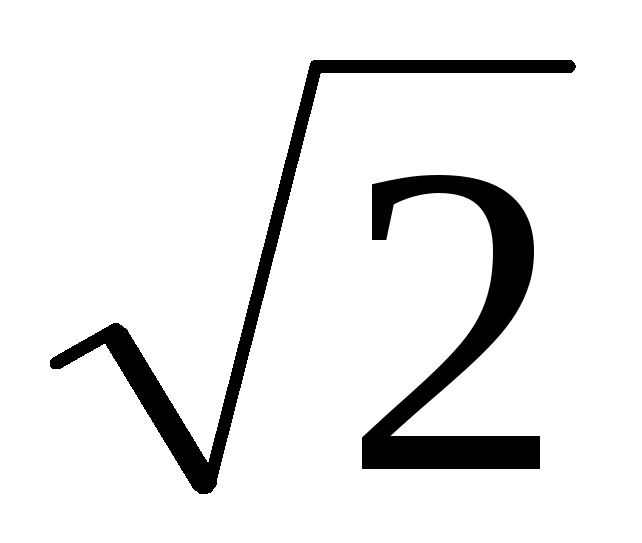 раз:
раз:
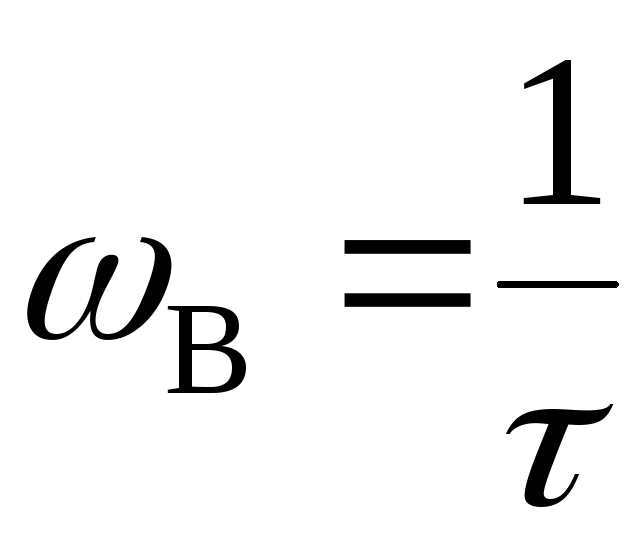 и
и 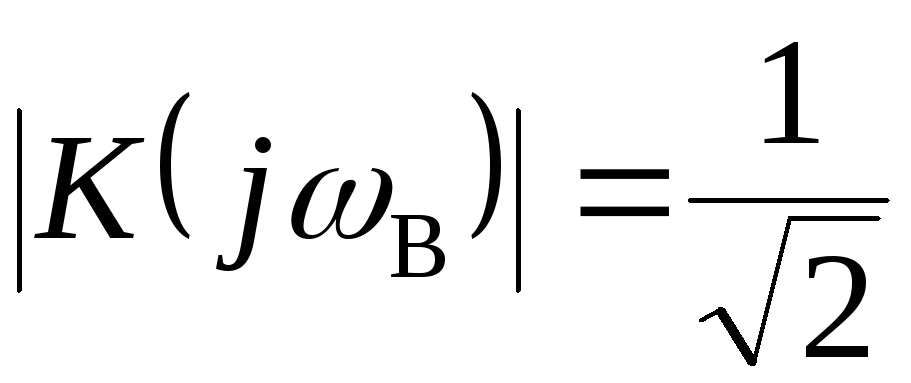 .
.
На
рис. 2.4 приведен вид АЧХ интегрирующей RC-цепочки.
При построении учитывалось, что  , т.е.
, т.е.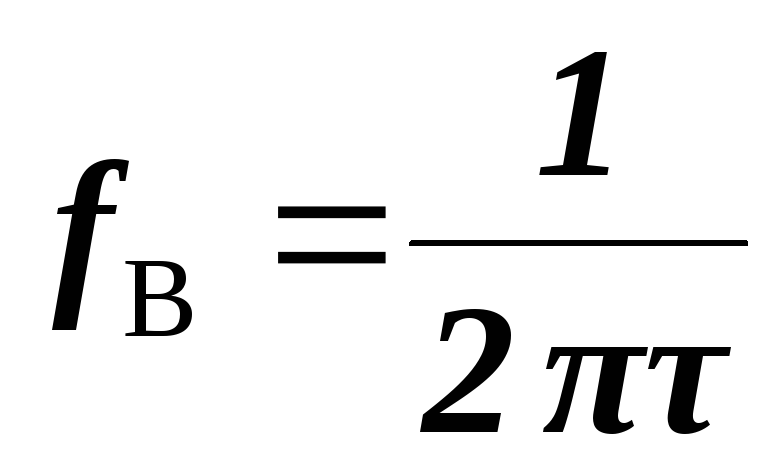 .
.
Для построения ФЧХ умножим числитель и знаменатель передаточной функции (2.4) на комплексно-сопряженную величину. Получим:
| (2.6) |
Из (2.6) следует: 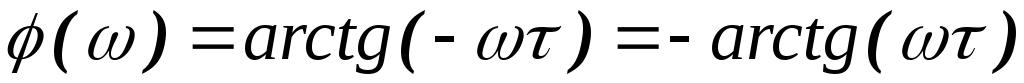 .
Вид ФЧХ приведён на рис. 2.4,б.
.
Вид ФЧХ приведён на рис. 2.4,б.
Необходимо
отметить, что на верхней граничной
частоте 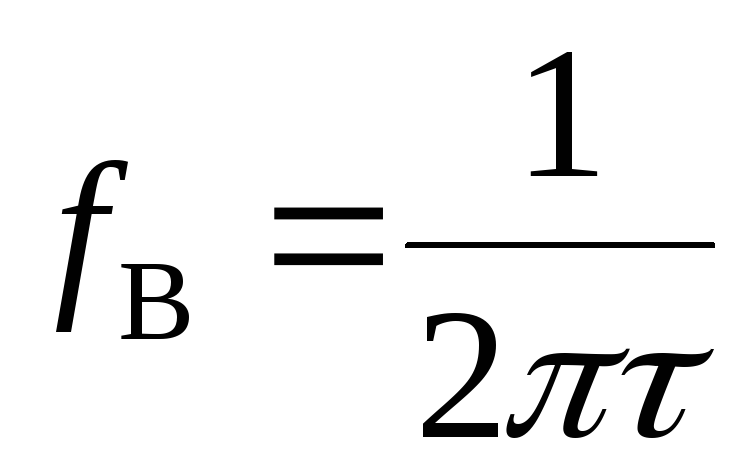 сдвиг по фазе между выходным сигналом
и сигналом генератора составляет 45.
сдвиг по фазе между выходным сигналом
и сигналом генератора составляет 45.
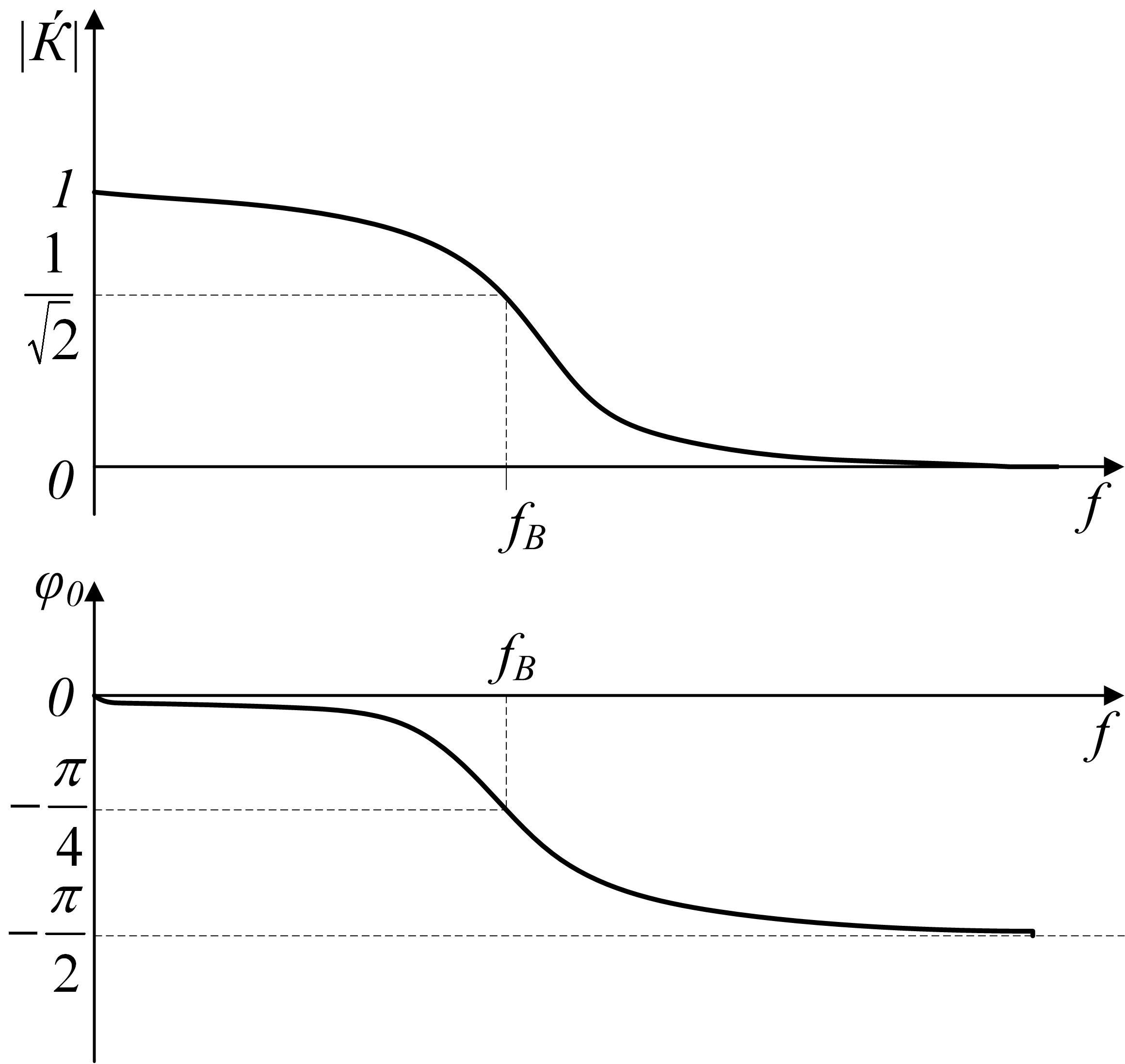
Рис. 2.4 АЧХ (а) и ФЧХ (б) интегрирующей -цепи (рис. 2.3)
Как
уже подчёркивалось, дифференцирующая  -цепь
(рис.2.5) отличается от интегрирующей
тем, что выходной сигнал снимается с
резистора. Амплитудно-частотная и
фазочастотная характеристики получаются
из выражения для коэффициента передачи;
который можно получить аналогично
коэффициенту передачи для интегрирующей
цепи:
-цепь
(рис.2.5) отличается от интегрирующей
тем, что выходной сигнал снимается с
резистора. Амплитудно-частотная и
фазочастотная характеристики получаются
из выражения для коэффициента передачи;
который можно получить аналогично
коэффициенту передачи для интегрирующей
цепи:
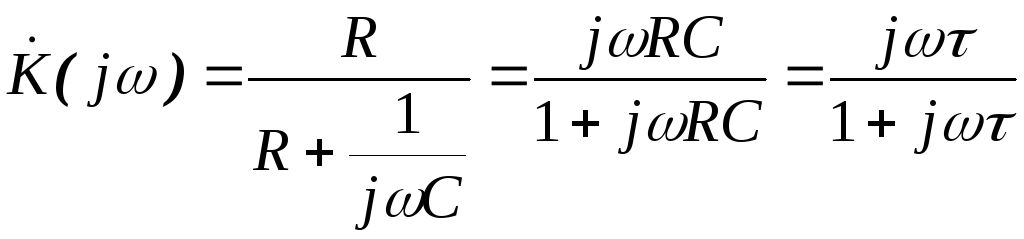 ,
,
где 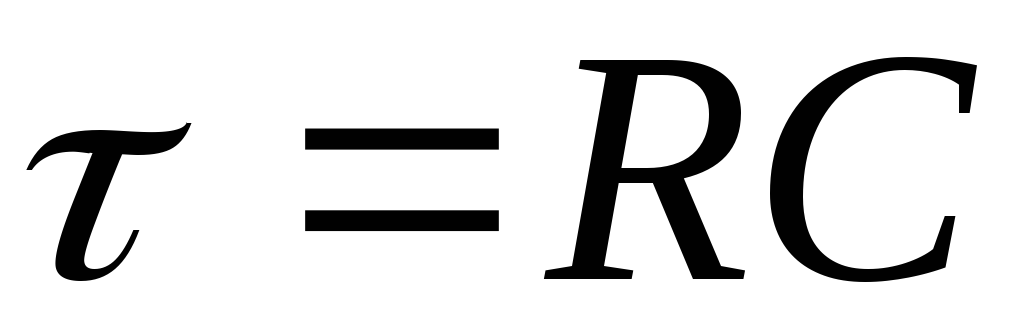 – постоянная времени дифференцирующей
цепи.
– постоянная времени дифференцирующей
цепи.
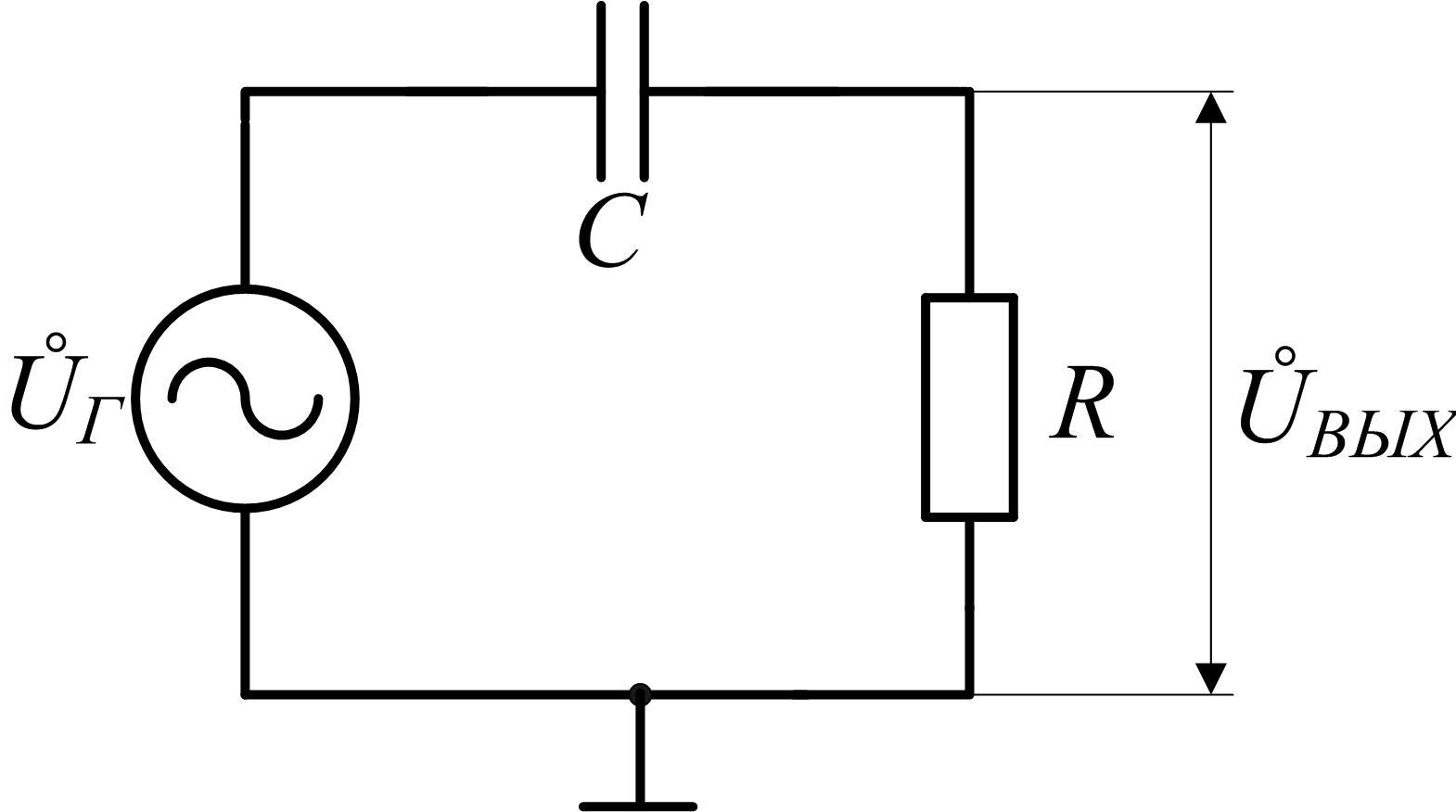
Рис.
2.5 Простейшая дифференцирующая 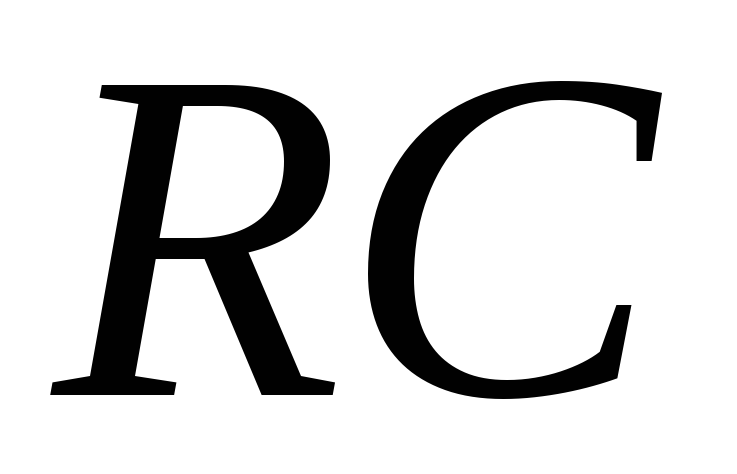 -цепь
-цепь
с синусоидальным источником сигнала
Тогда
АЧХ (рис. 2.6,а)
определяется из выражения 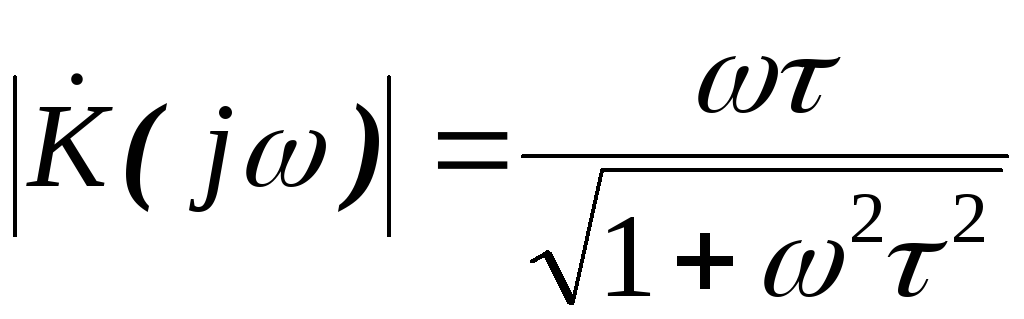 ,
а ФЧХ (рис. 2.6,б):
,
а ФЧХ (рис. 2.6,б): 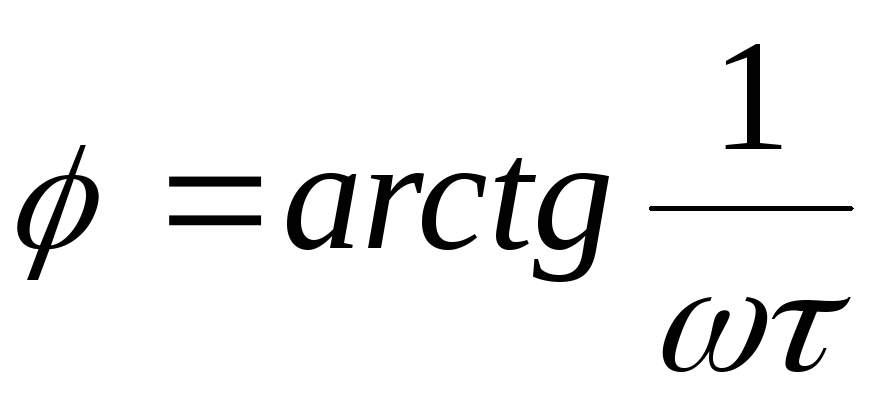 .
При этом формула для нижней граничной
частоты пропускания аналогична формуле
для верхней граничной частоты интегрирующей
.
При этом формула для нижней граничной
частоты пропускания аналогична формуле
для верхней граничной частоты интегрирующей —
цепи:
—
цепи:

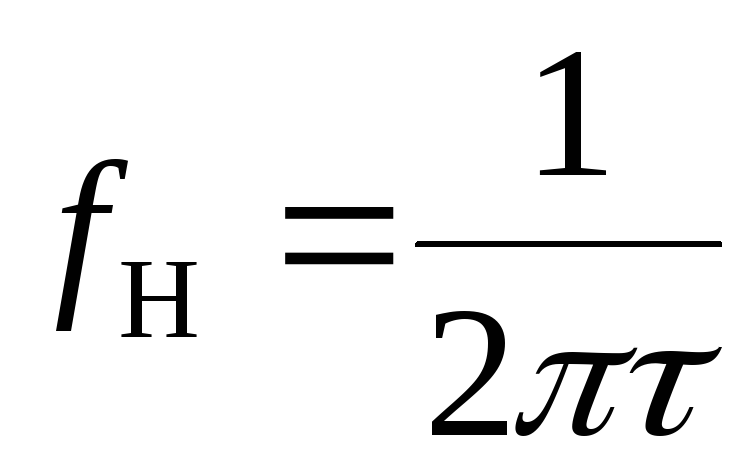 .
.
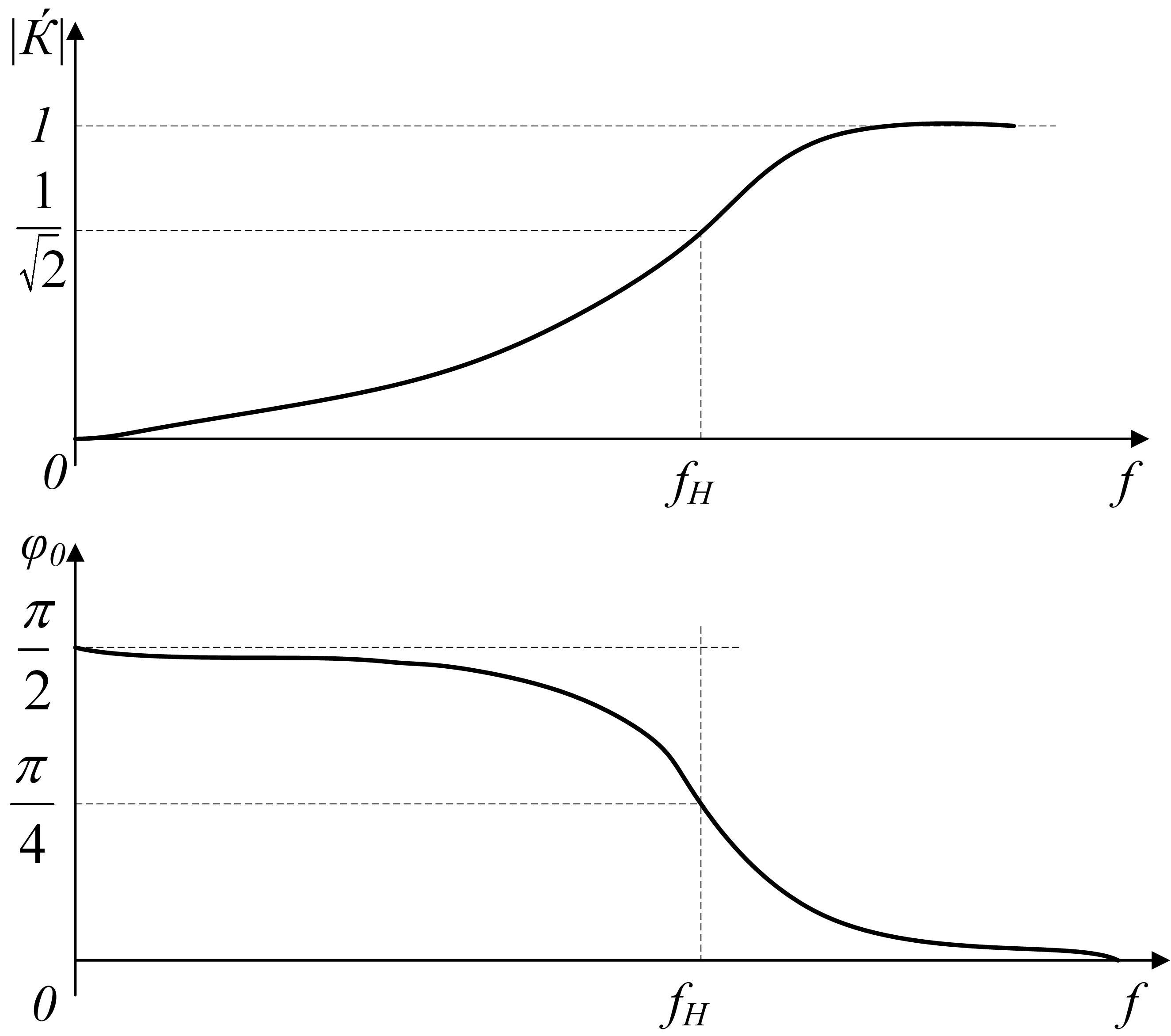
Рис.
2.6 АЧХ (а) и ФЧХ (б) дифференцирующей 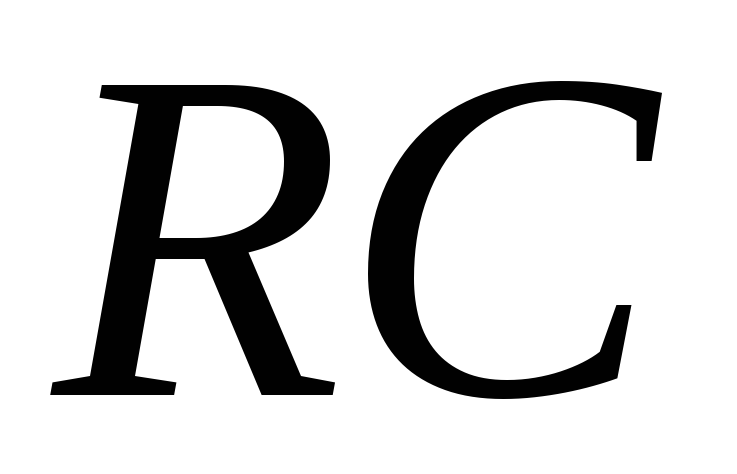 -цепи
(рис. 2.5)
-цепи
(рис. 2.5)
Опыт расчёта
простейших интегрирующих и дифференцирующих 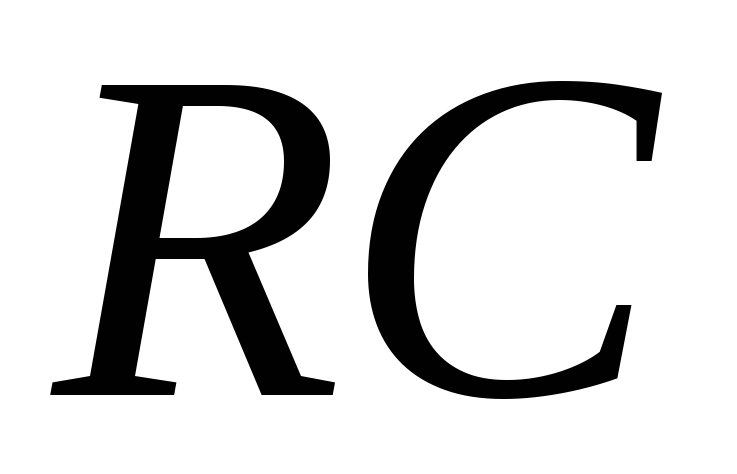 -цепей
может быть использован и для расчёта
более сложных цепочек. Для примера
рассчитаем интегрирующую
-цепей
может быть использован и для расчёта
более сложных цепочек. Для примера
рассчитаем интегрирующую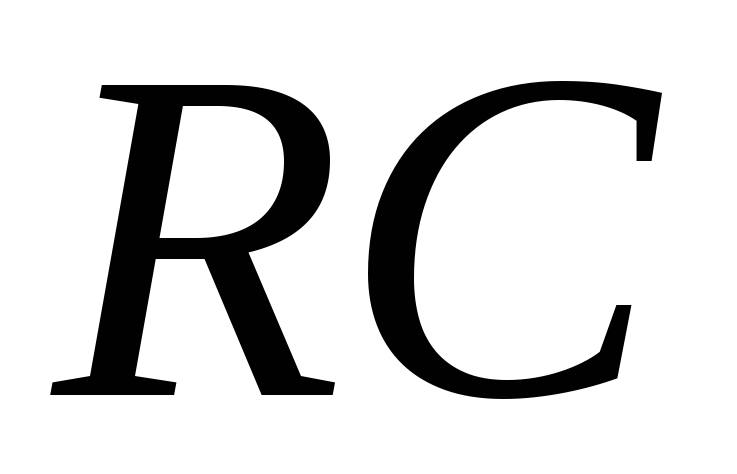 -цепочку,
схема которой приведена на рис. 2.7,а.
-цепочку,
схема которой приведена на рис. 2.7,а.
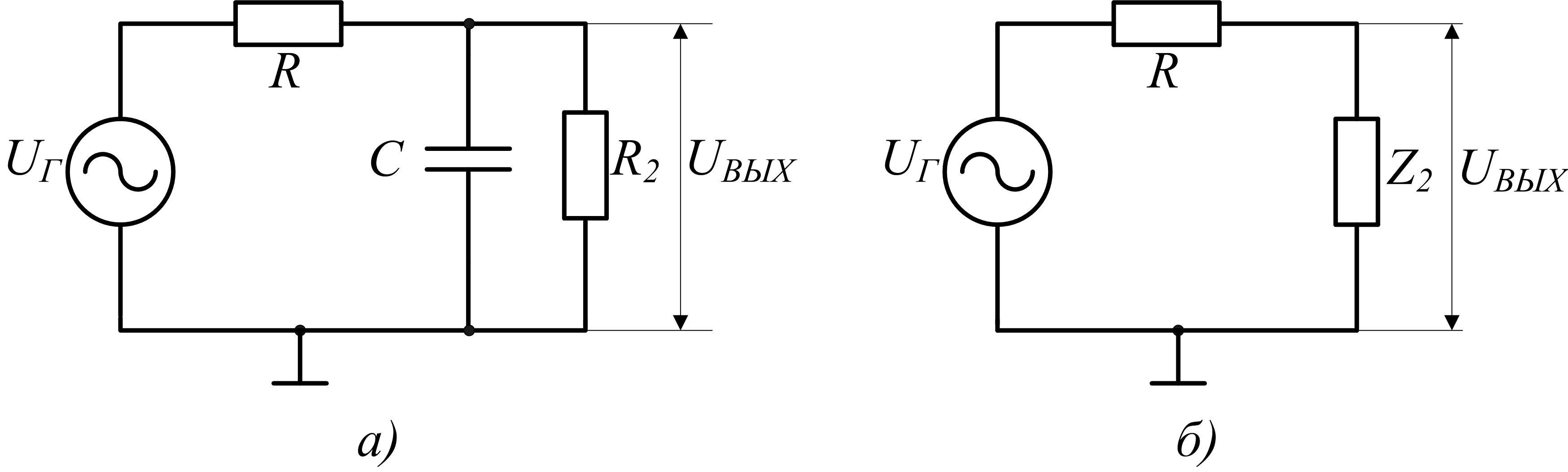
Рис.
2.7 Схема интегрирующей 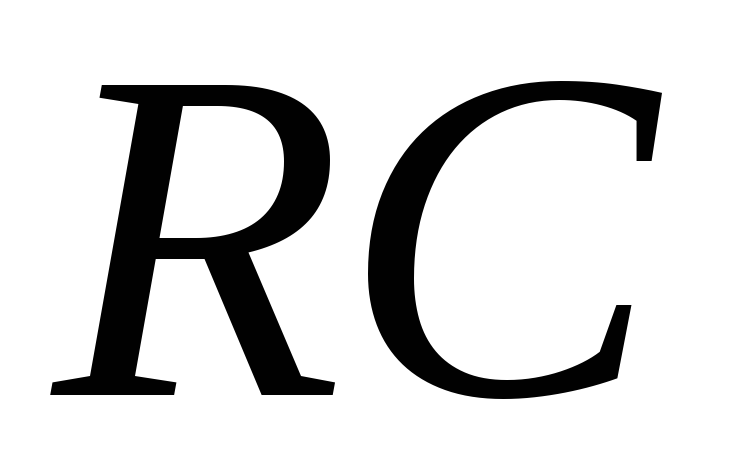 -цепочки
–а;
-цепочки
–а;
её эквивалентная схема – б.
На рис. 2.7,б приведена эквивалентная схема цепи, в
которой параллельное сопротивление
резистора 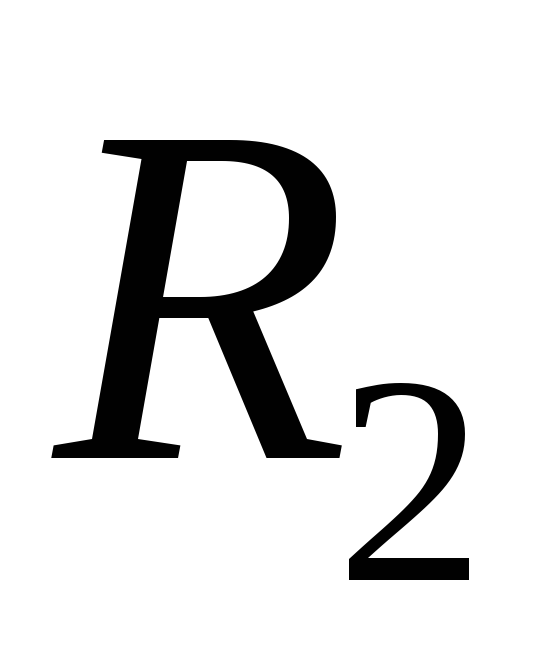 и конденсатора
и конденсатора заменено на эквивалентное комплексное
сопротивление
заменено на эквивалентное комплексное
сопротивление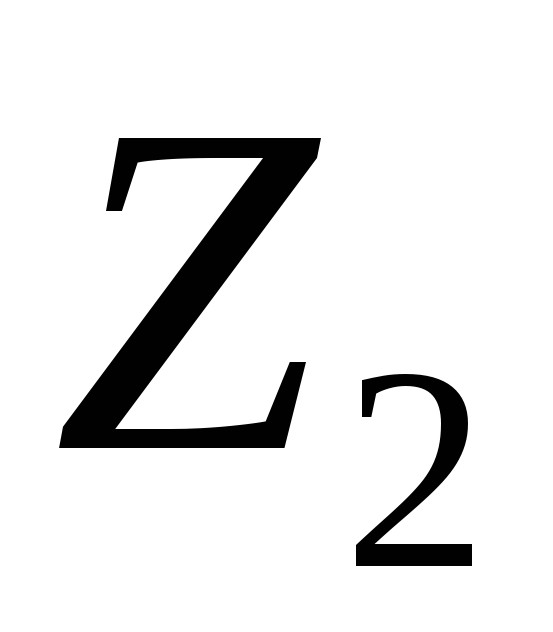 .
Как было показано ранее сопротивление
двух параллельно включённых резисторов
.
Как было показано ранее сопротивление
двух параллельно включённых резисторов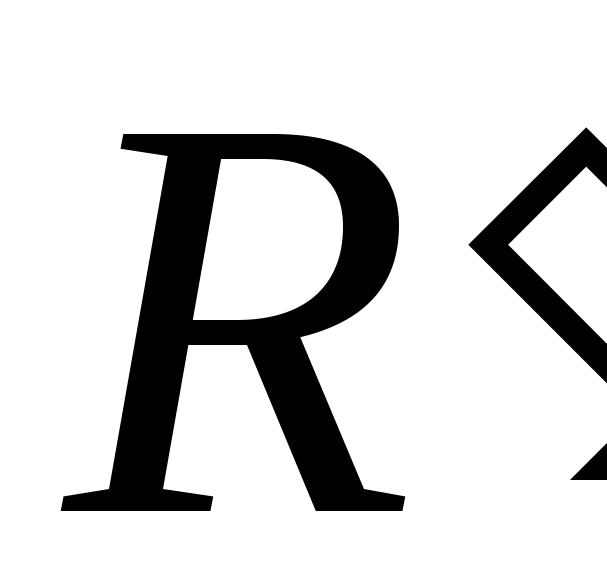 и
и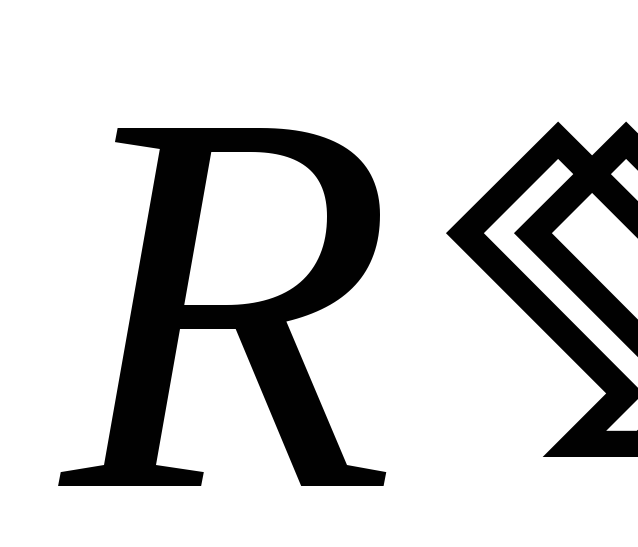 равно:
равно: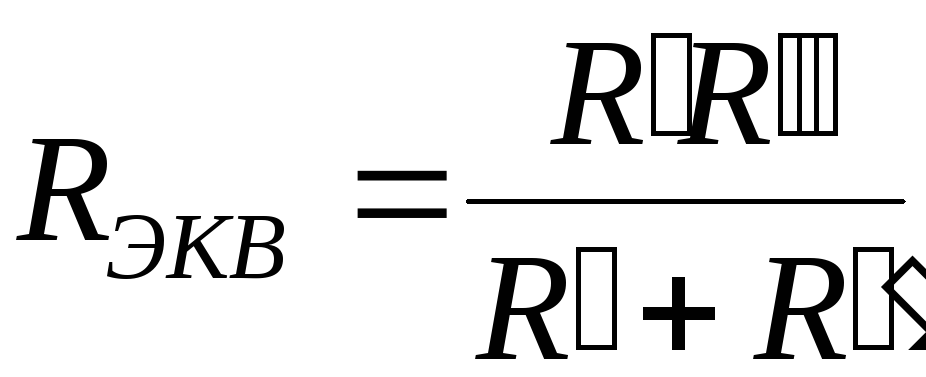 .
Отсюда для получения
.
Отсюда для получения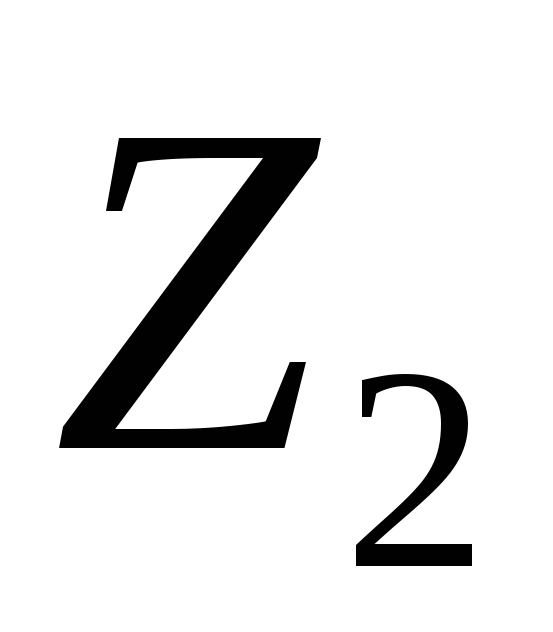 необходимо заменить
необходимо заменить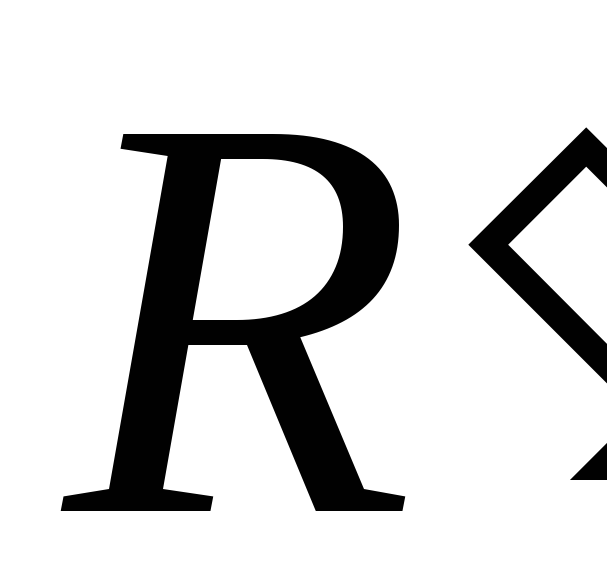 на
на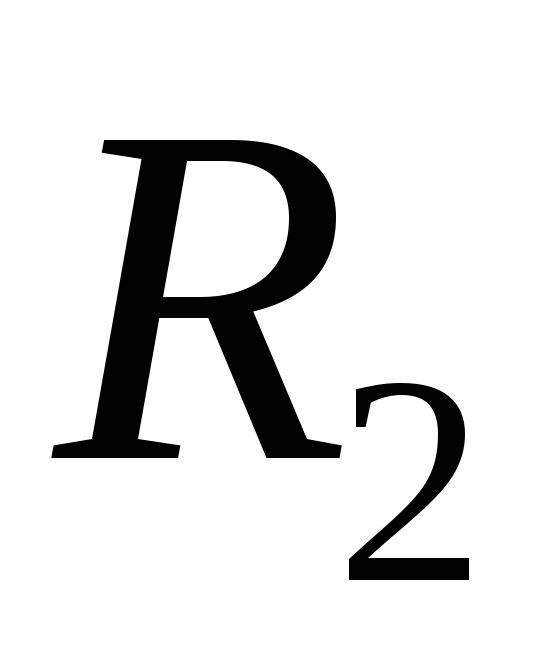 ,
а
,
а на
на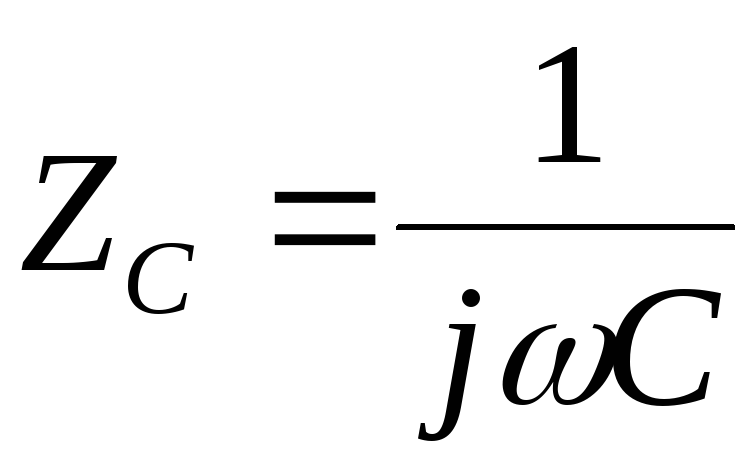 .
В результате замены получим
.
В результате замены получим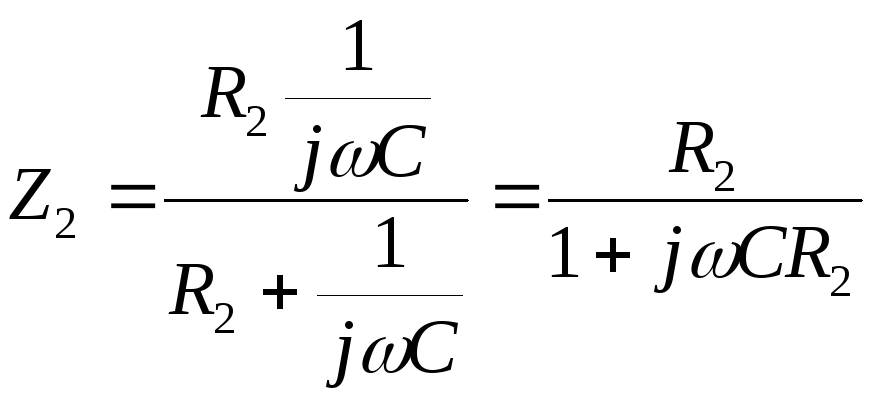 .
Коэффициент передачи напряжения
делителя, состоящего из двух сопротивленийR1 и R2,
равен
.
Коэффициент передачи напряжения
делителя, состоящего из двух сопротивленийR1 и R2,
равен 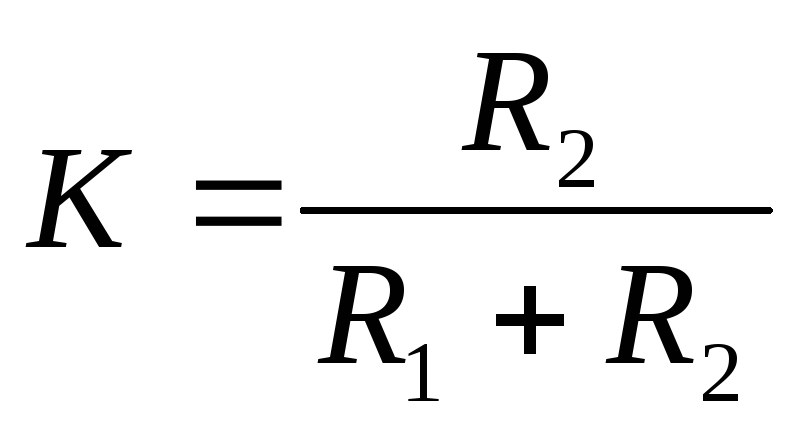 .
ЗаменяяR2 на Z2,
получим:
.
ЗаменяяR2 на Z2,
получим:
| (2.7) |
где 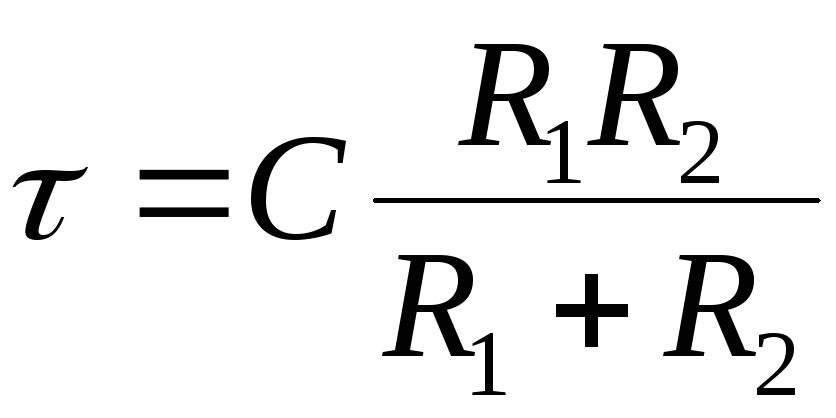 .
.
Сравнивая выражение коэффициента передачи для простейшей интегрирующей цепи (4) и полученное (7), заметим, что они отличаются лишь коэффициентом передачи на нулевой частоте и постоянной времени. АЧХ и ФЧХ цепи приведены на рис. 2.8.
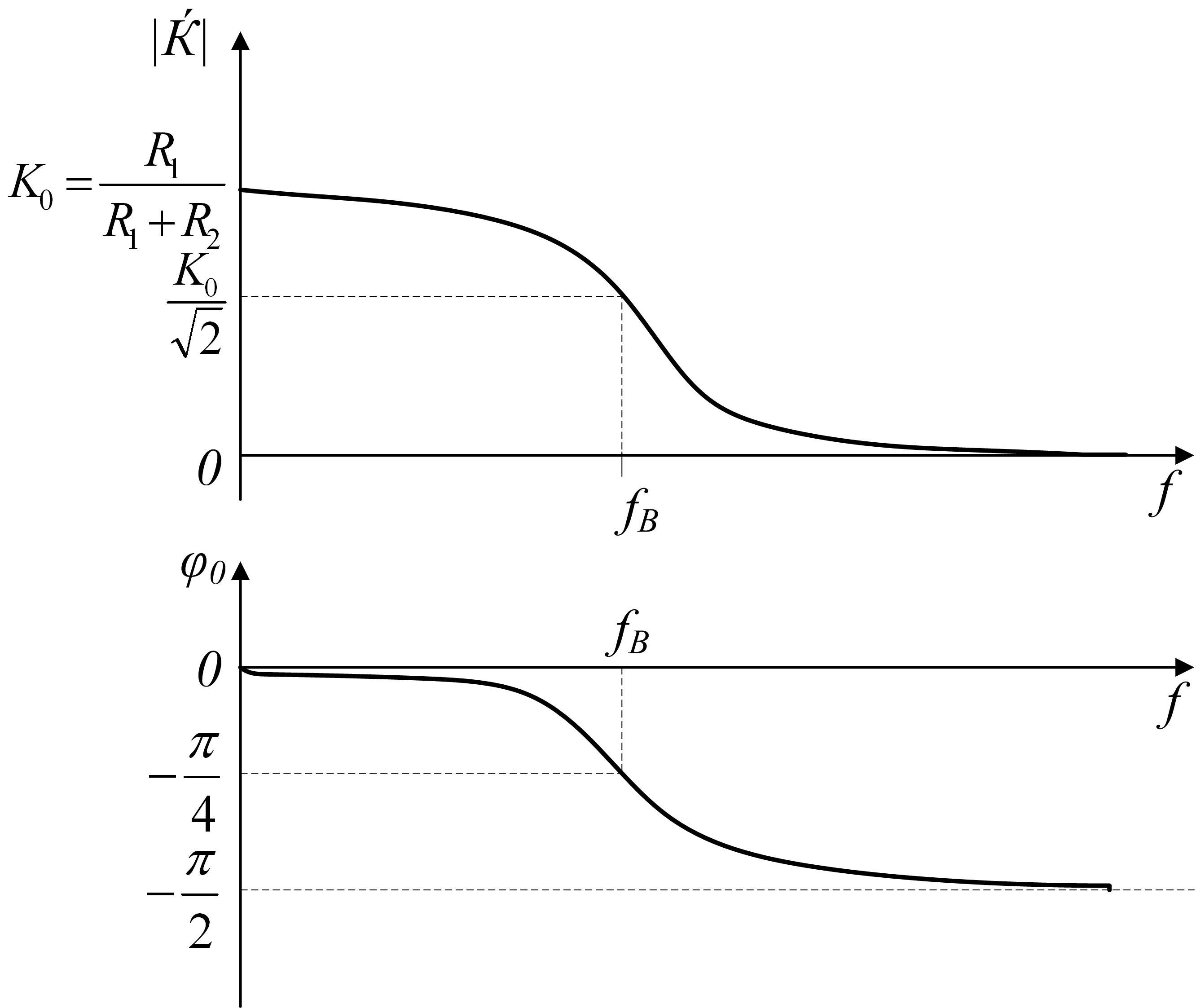
Рис. 2.8 АЧХ и ФЧХ цепи, приведённой на рис. 2.7
Аналогично можно
получить и комплексный коэффициент
передачи интегрирующей  -цепи,
приведённой на рис. 2.9.
-цепи,
приведённой на рис. 2.9.
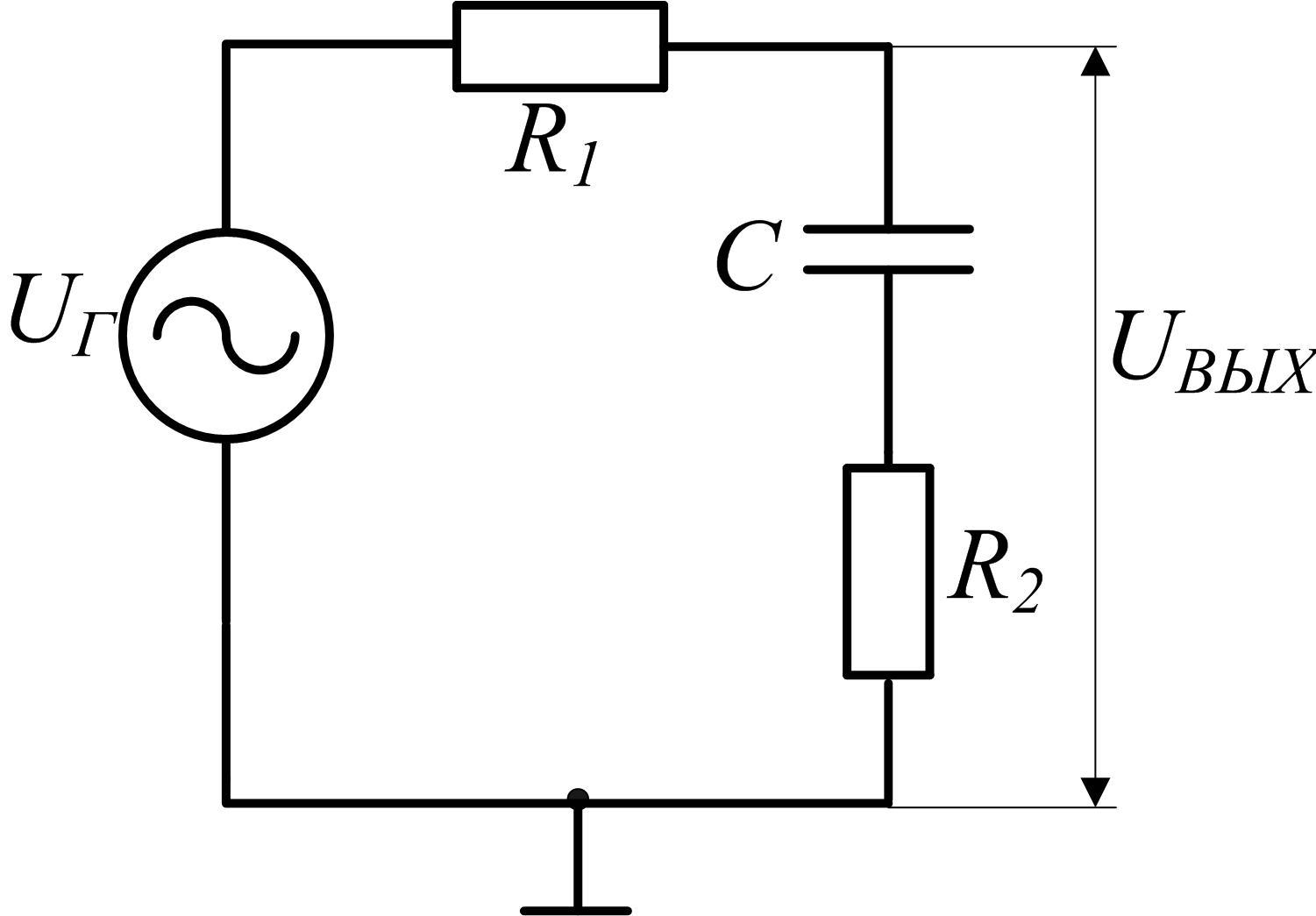
Рис.
2.9 Схема интегрирующей 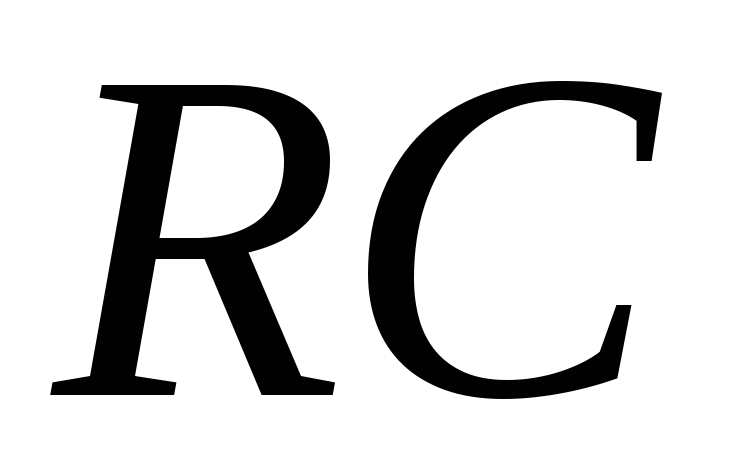 -цепочки
с резистором,
-цепочки
с резистором,
включённым последовательно с конденсатором
В этом случае 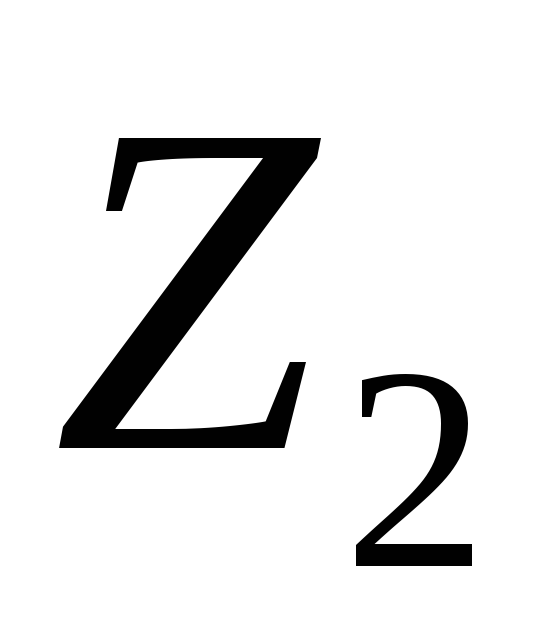 определяется последовательным включением
резистора
определяется последовательным включением
резистора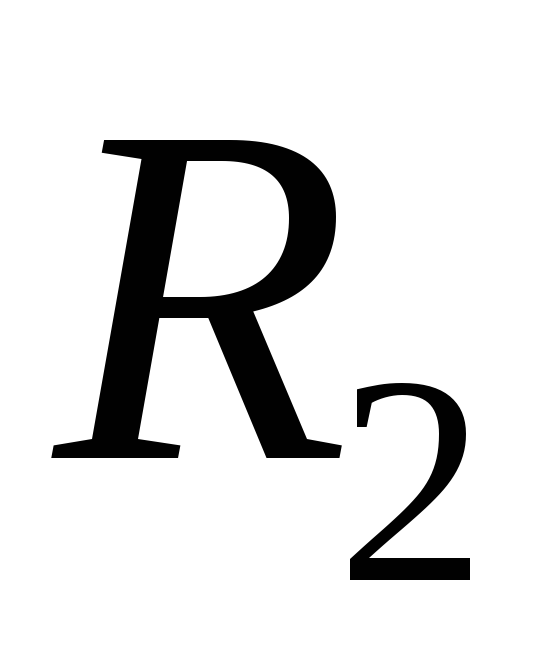 и конденсатора С.
и конденсатора С.
Подставляя в
коэффициент передачи резистивного
делителя 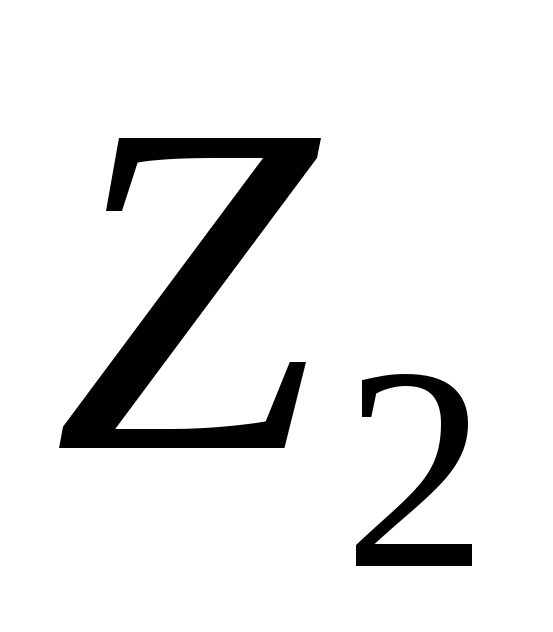 вместо
вместо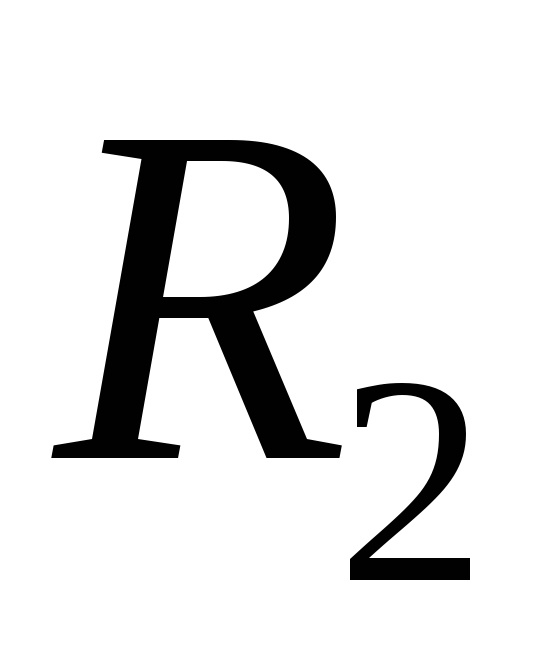 ,
получаем:
,
получаем:
| (2.8) |
АЧХ и ФЧХ такой
интегрирующей  -цепочки
будут отличаться от АЧХ и ФЧХ простейшей
интегрирующей
-цепочки
будут отличаться от АЧХ и ФЧХ простейшей
интегрирующей -цепи.
Для построения АЧХ найдём модуль
-цепи.
Для построения АЧХ найдём модуль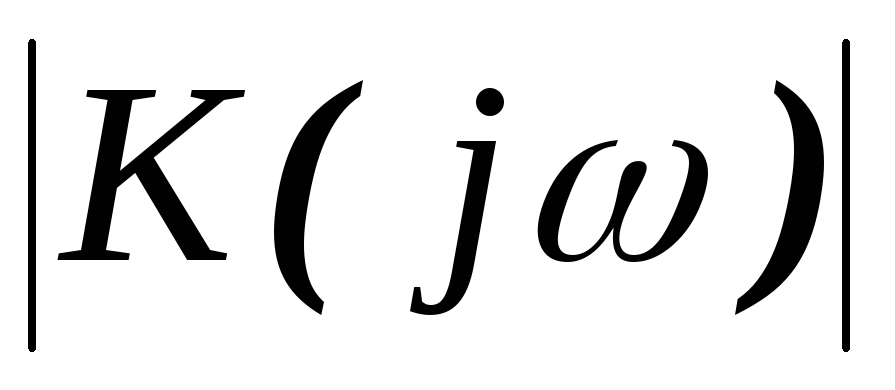 .
Чтобы упростить сейчас и при дальнейших
расчётах процедуру нахождения модуля
комплексного выражения, имеющего вид
.
Чтобы упростить сейчас и при дальнейших
расчётах процедуру нахождения модуля
комплексного выражения, имеющего вид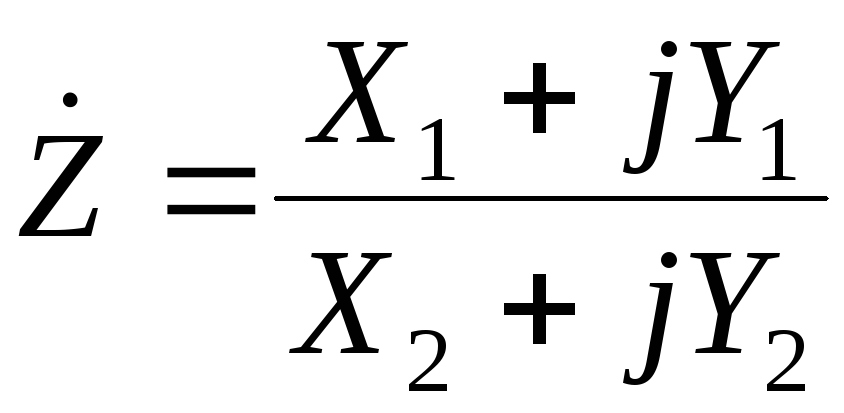 ,
убедимся, что
,
убедимся, что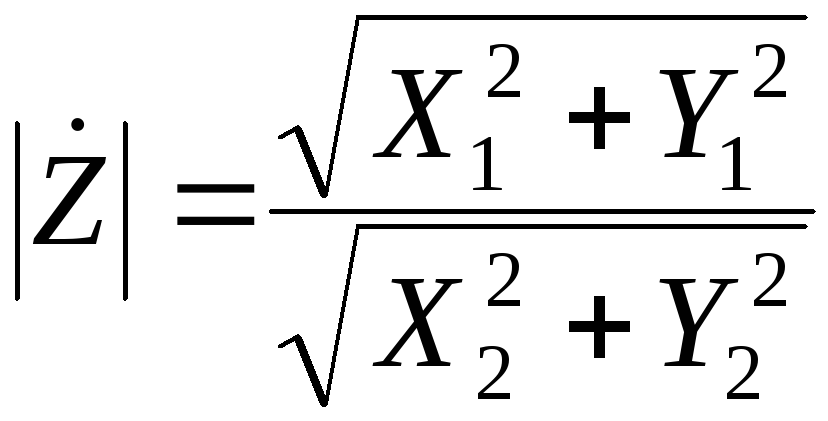 .
Действительно, умножая знаменатель и
числитель выражения для
.
Действительно, умножая знаменатель и
числитель выражения для  на комплексно-сопряжённую величину
знаменателя, получаем:
на комплексно-сопряжённую величину
знаменателя, получаем:
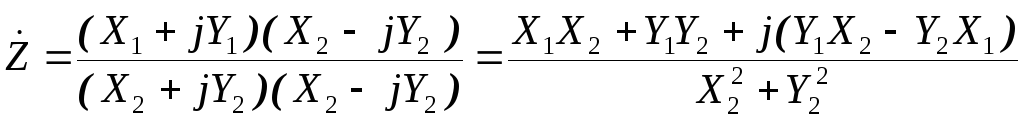 .
.
Отсюда:
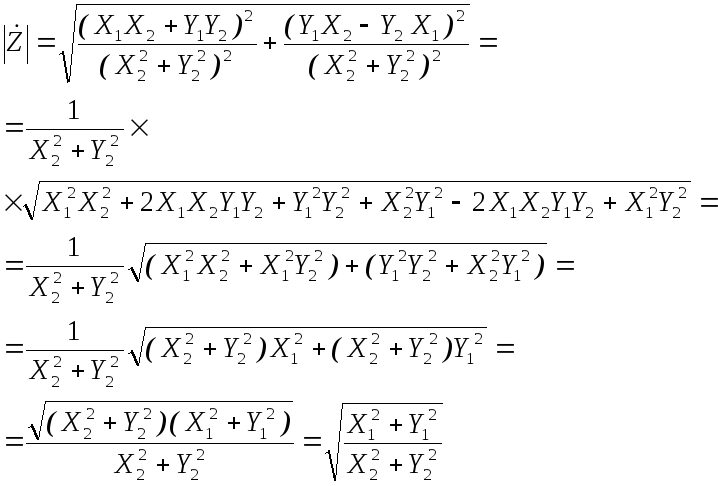 ,
,
что и требовалось доказать.
Учитывая результаты приведённого доказательства, получаем:
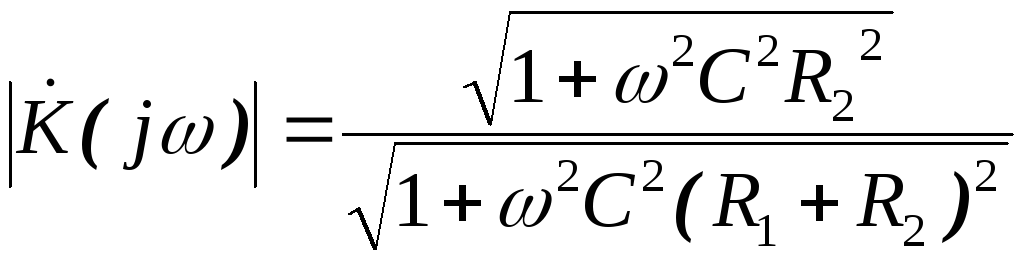 .
.
Полученное выражение
позволяет достаточно просто построить
АЧХ цепи. Для этого положим, что в первом
случае  ,
а во втором
,
а во втором .
Отсюда
.
Отсюда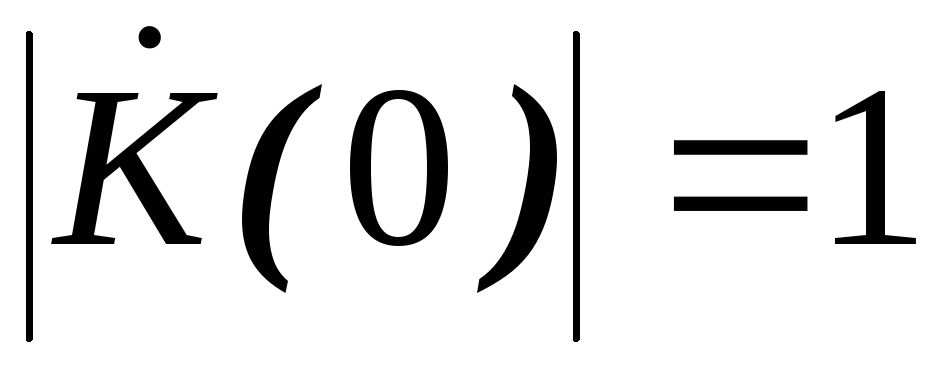 ,
,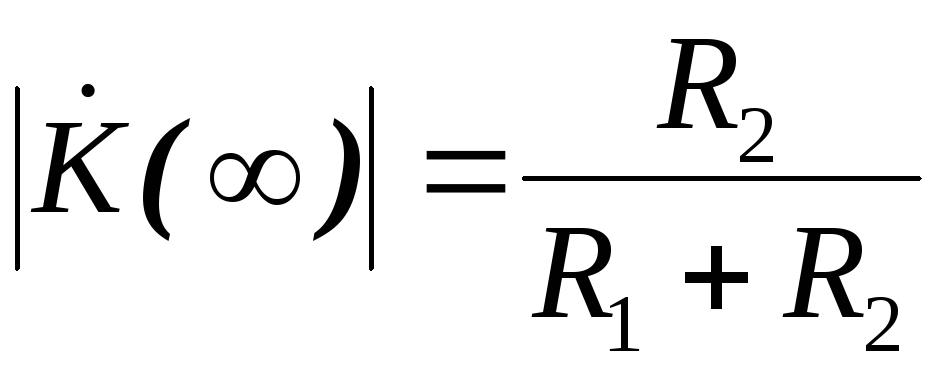 .
Верхнюю граничную частоту схемы можно
определить из условия
.
Верхнюю граничную частоту схемы можно
определить из условия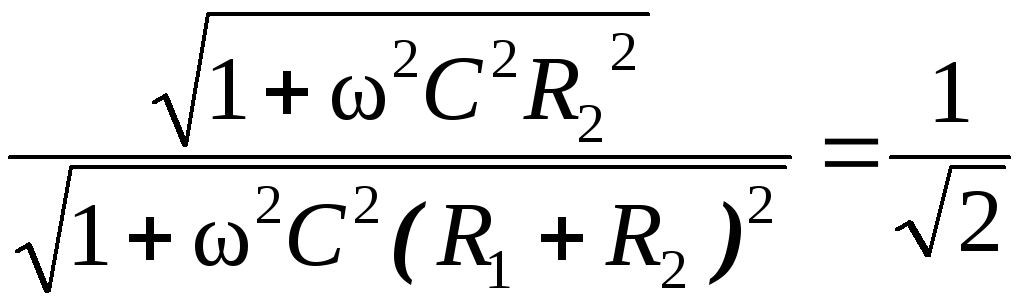 .
Отсюда
.
Отсюда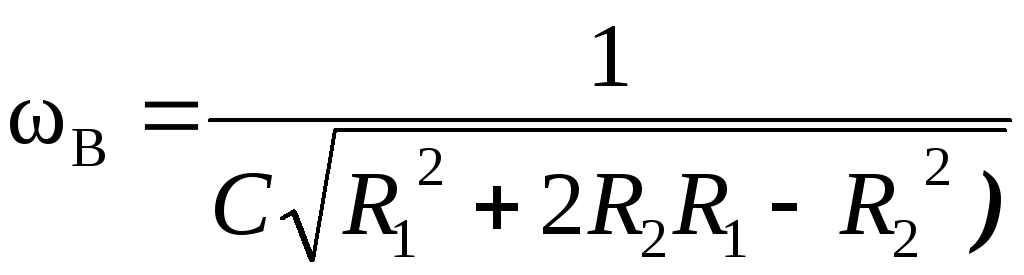 .
При
.
При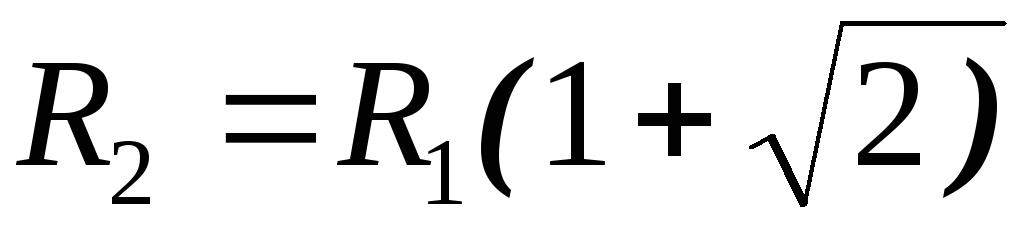 верхняя граничная частота становится
равной
верхняя граничная частота становится
равной ,
т.к. коэффициент передачи при=
становится равным
,
т.к. коэффициент передачи при=
становится равным 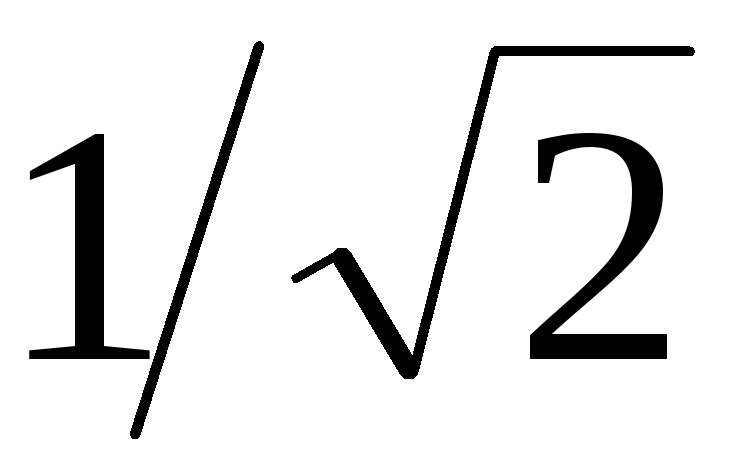 .
При
.
При верхняя граничная частота в схеме будет
отсутствовать, т.к. коэффициент передачи
будет всегда больше
верхняя граничная частота в схеме будет
отсутствовать, т.к. коэффициент передачи
будет всегда больше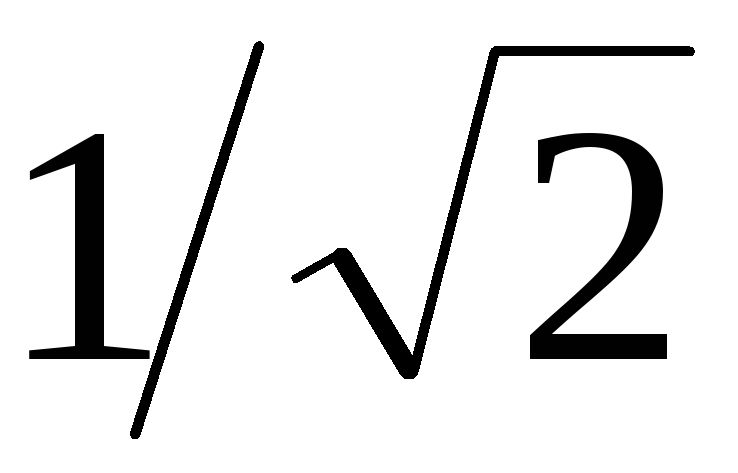 .
.
АЧХ цепи для случая  приведена на рис. 2.10,а.
приведена на рис. 2.10,а.
Для нахождения ФЧХ цепи домножим числитель и знаменатель выражения (2.8) на комплексно-сопряжённую величину знаменателя. Получим:
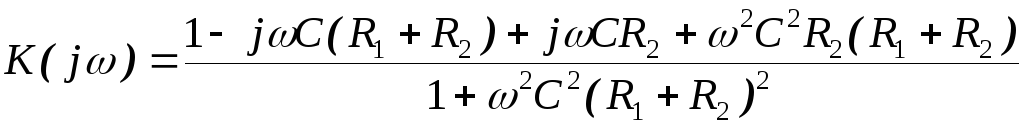 .
.
Отсюда:
| (2.9) |
Заметим, что при  ,
, и при
и при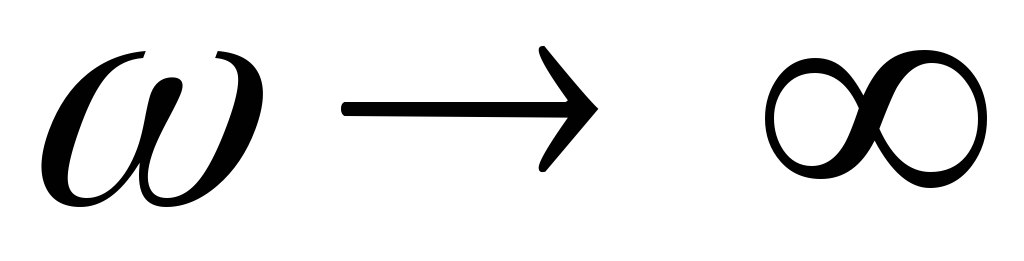 ,
, .
Нетрудно доказать, что
.
Нетрудно доказать, что имеет минимум при
имеет минимум при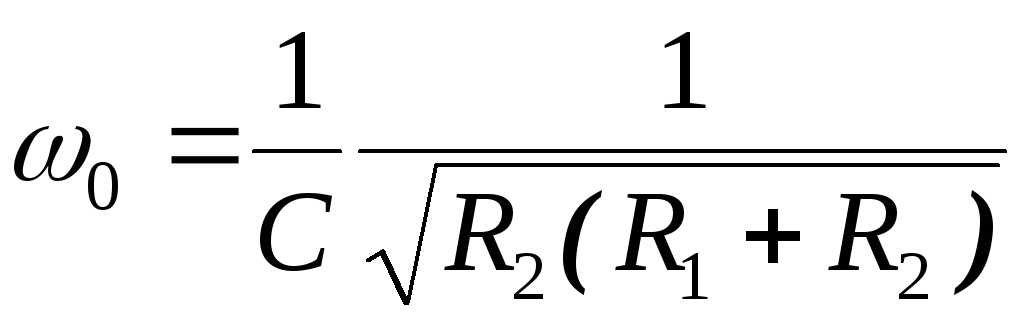 ,
,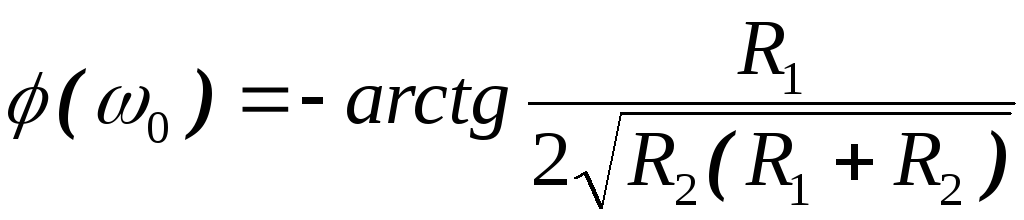 ,
причём при
,
причём при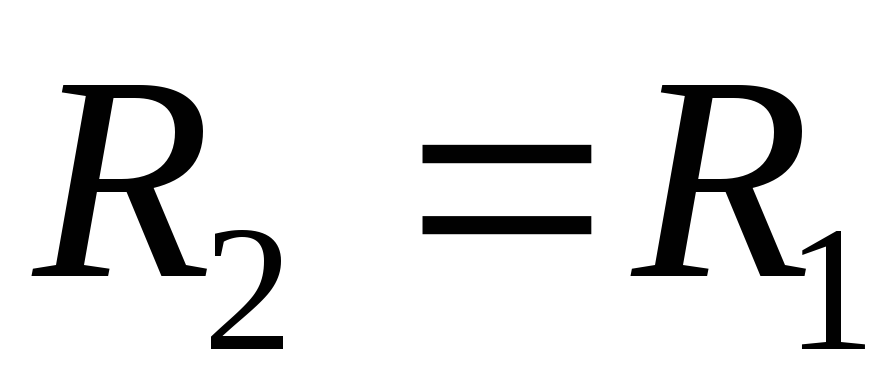 будет
будет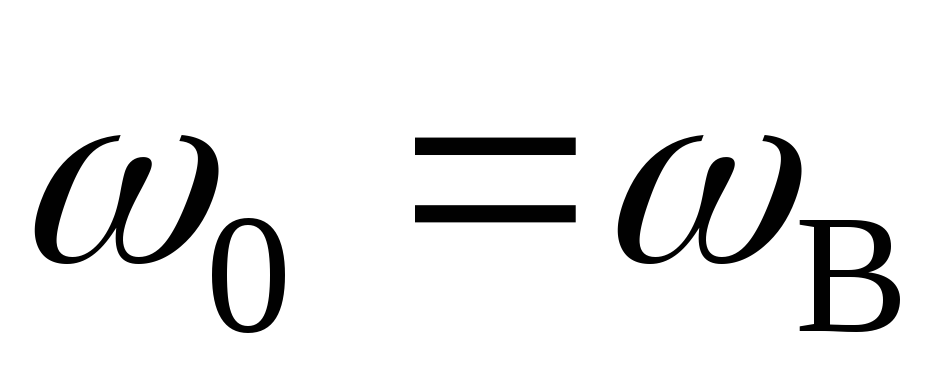 ,
а при
,
а при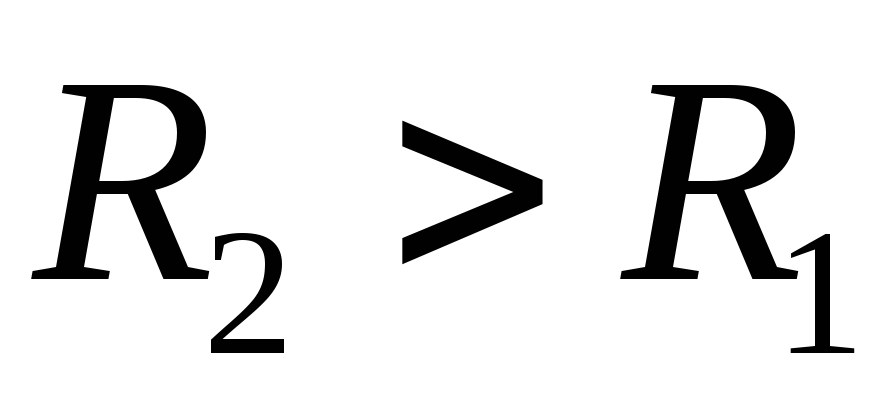 будет
будет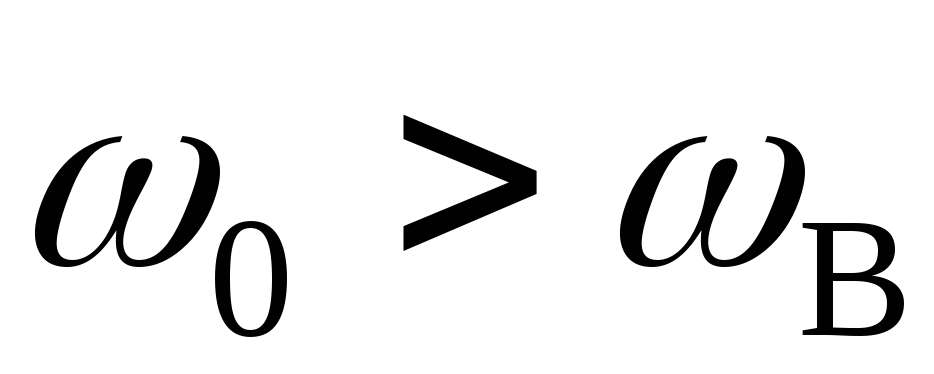 .
.
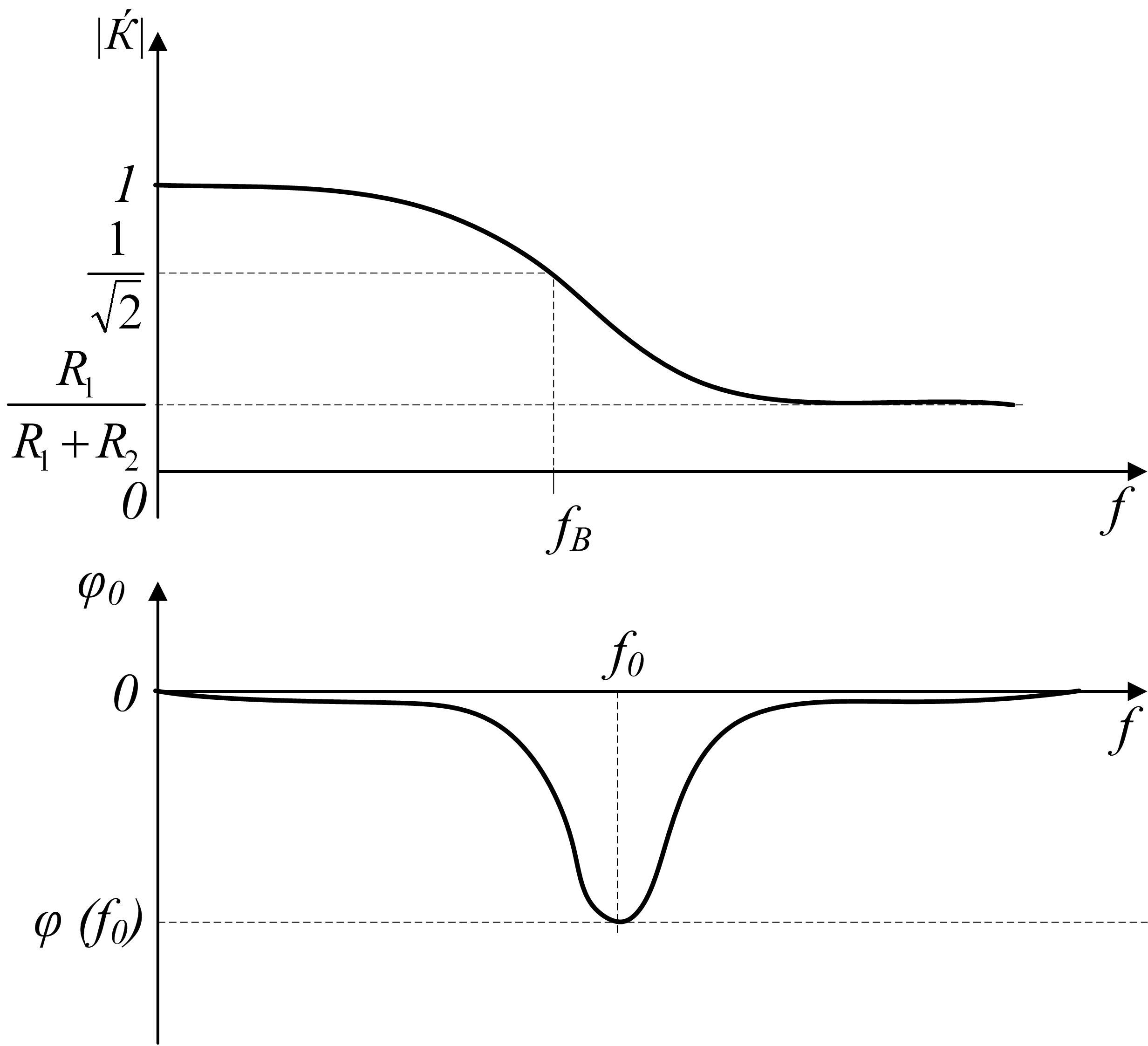
Рис. 2.10 АЧХ (а) и ФЧХ (б) схемы, приведённой на рис. 2.9
В зависимости от
соотношения 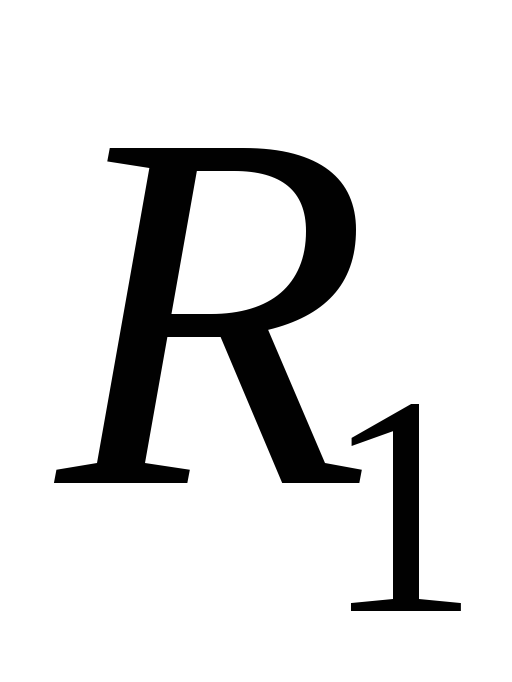 и
и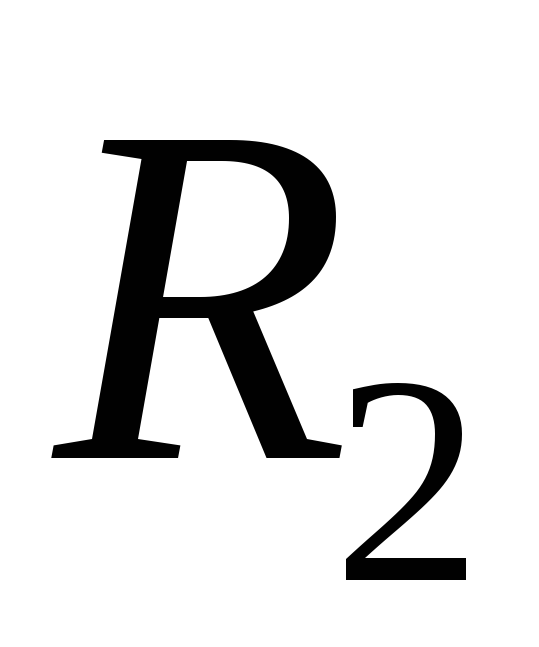 минимум
минимум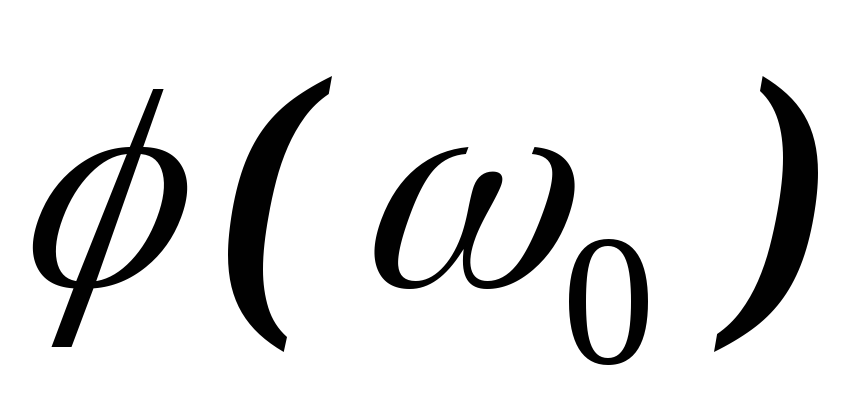 получается разной величины. Например,
при
получается разной величины. Например,
при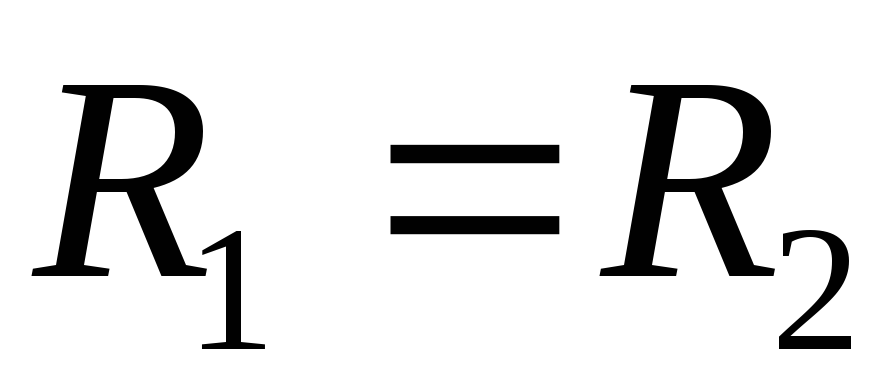 :
: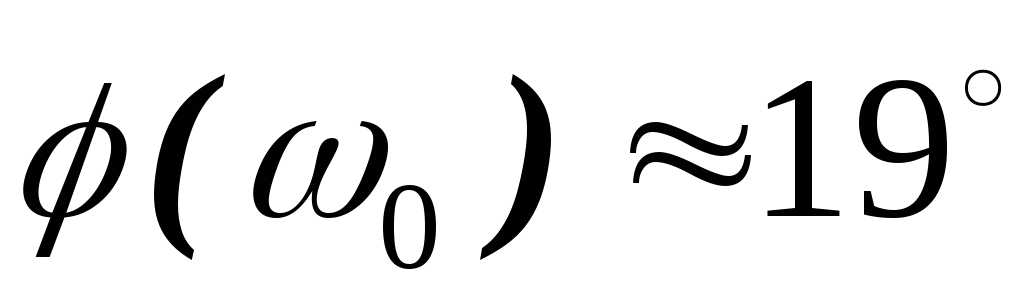 ,
при
,
при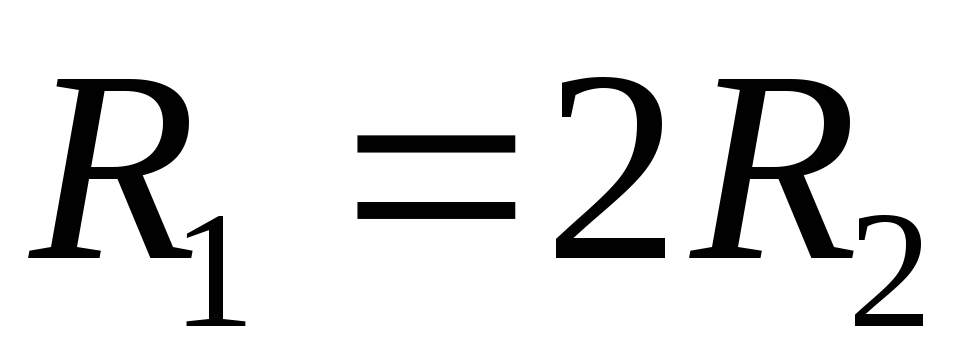 :
: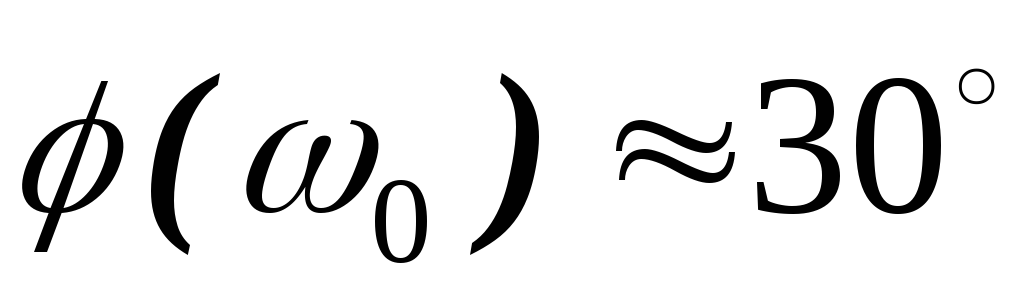 ,
при
,
при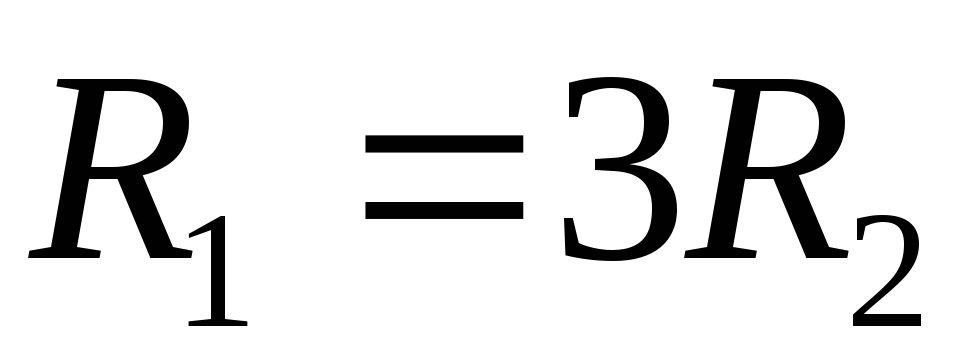 :
: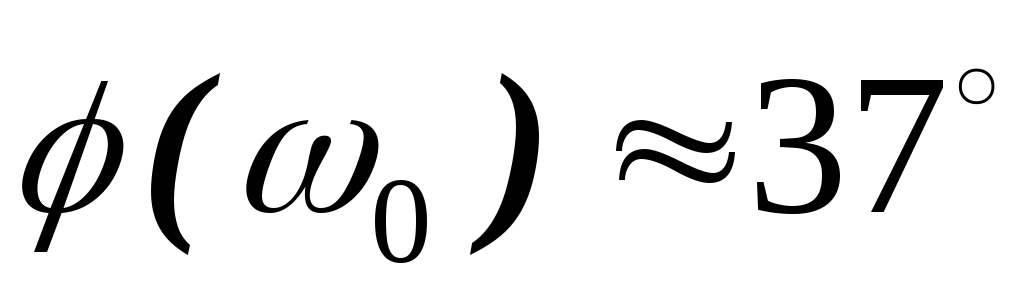 ,
при
,
при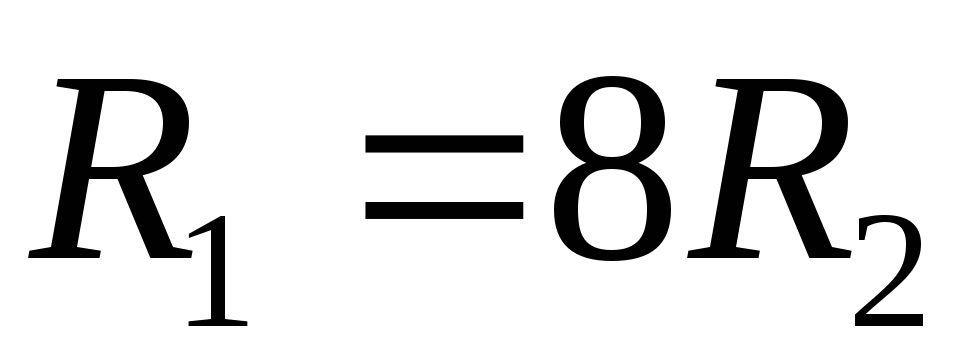 :
: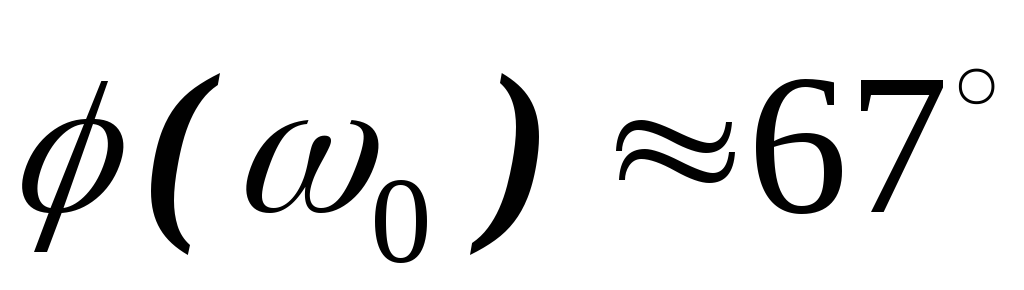 .
Примерный вид ФЧХ приведён на
.
Примерный вид ФЧХ приведён на
рис. 2.10,б.
Аналогично можно рассчитывать АЧХ и ФЧХ дифференцирующих цепей. Например, для схемы, приведённой на рис. 2.11, получаем коэффициент передачи:
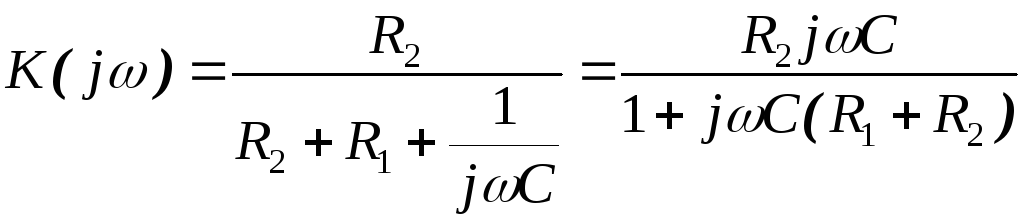 .
.
Модуль коэффициента передачи:
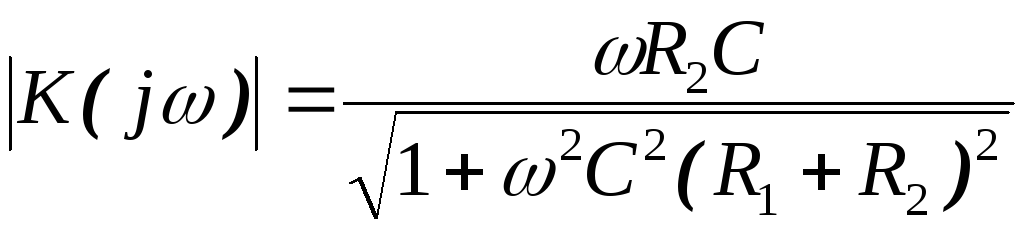 .
.
Умножив числитель и знаменатель на множитель (R1+R2), получим:
| (2.10) |
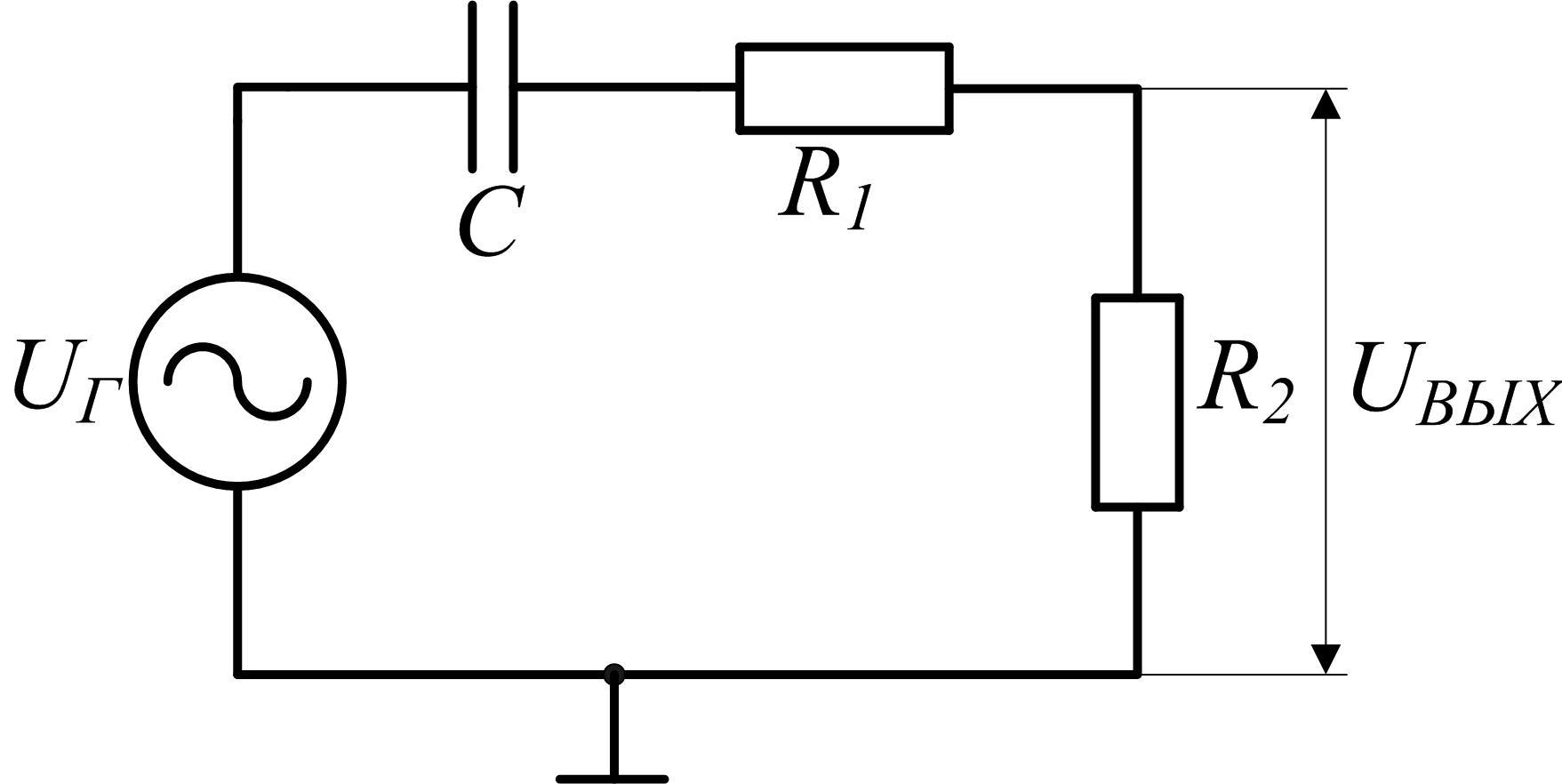
Рис.
2.11 Схема дифференцирующей  -цепи
с дополнительным
-цепи
с дополнительным
резистором, включённым последовательно с конденсатором
Сравнивая (2.8) и (2.10), заметим, что коэффициент передачи простейшей дифференцирующей цепи и схемы, приведённой на
рис.
2.11, отличаются лишь наличием множителя 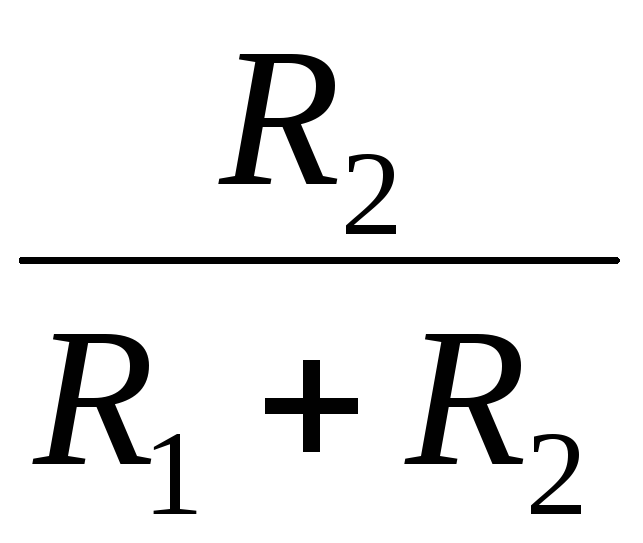 и величиной постоянной времени, которая
в данном случае равна
и величиной постоянной времени, которая
в данном случае равна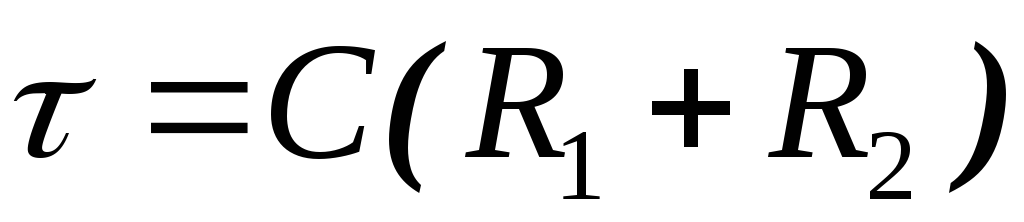 .
.
Для схемы, приведённой на рис. 2.12, получаем следующий коэффициент передачи:
|
где 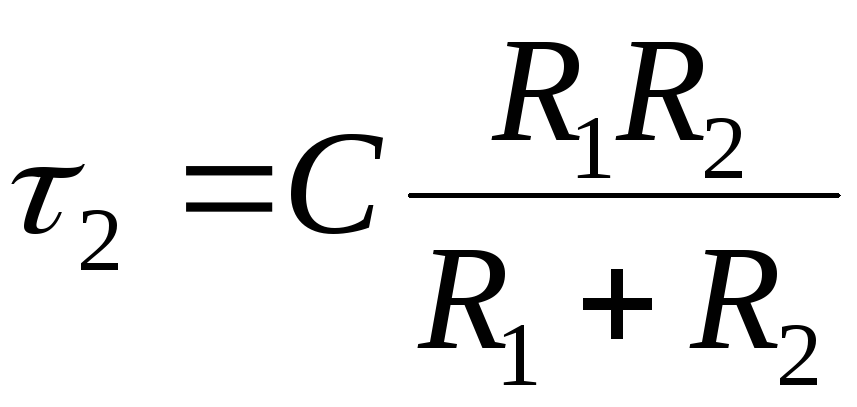 ,
,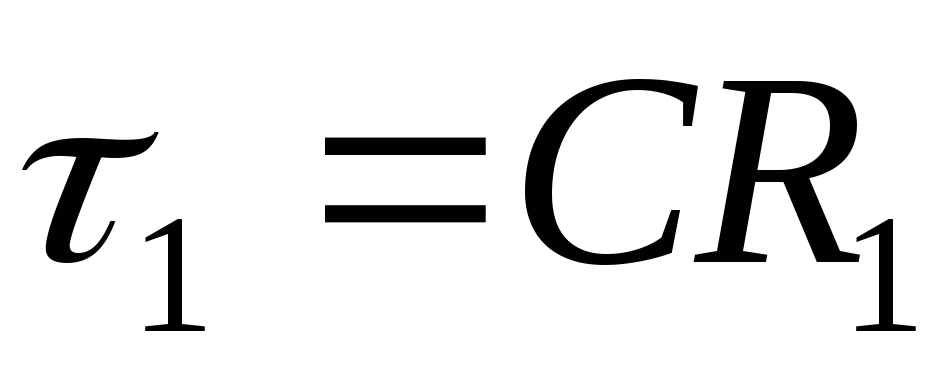 .
.
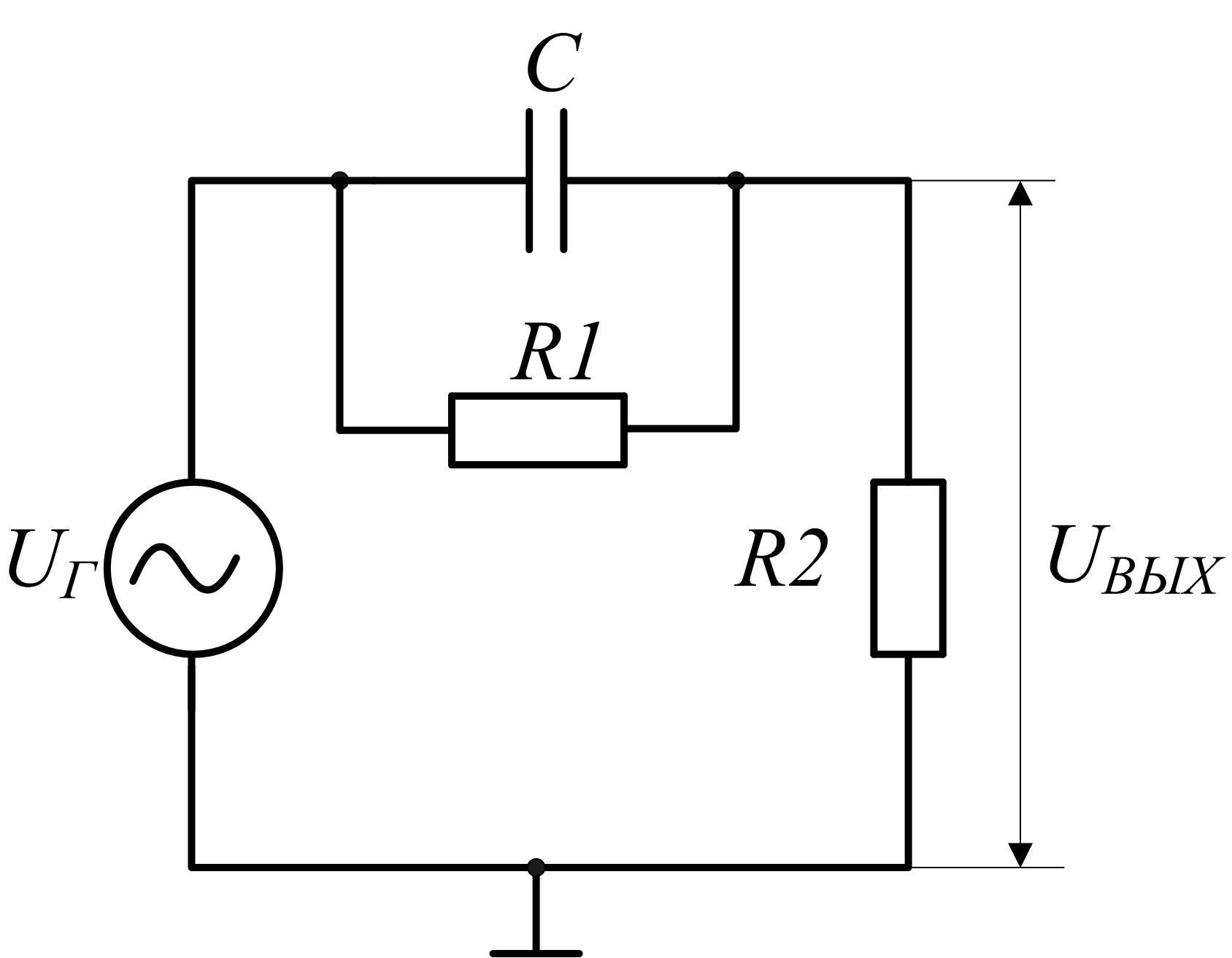
Рис.
2.12 Схема дифференцирующей 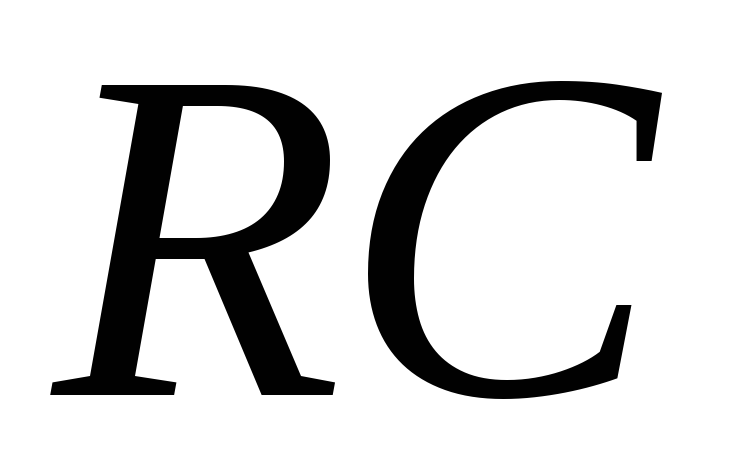 -цепочки
с резистором,
-цепочки
с резистором,
включённым параллельно с конденсатором
Модуль коэффициента передачи:
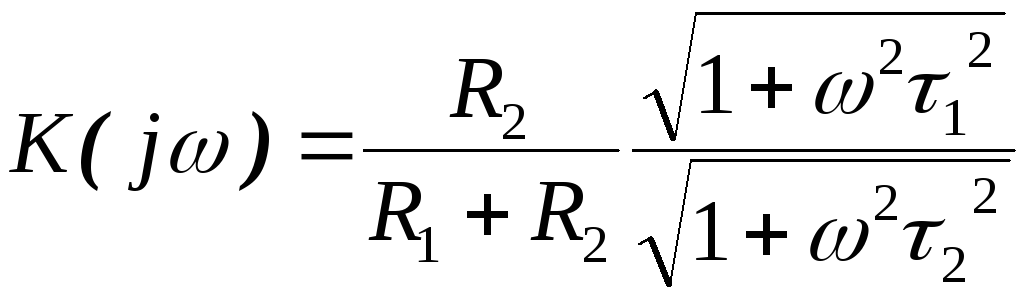 .
.
Для построения
АЧХ учтём, что при 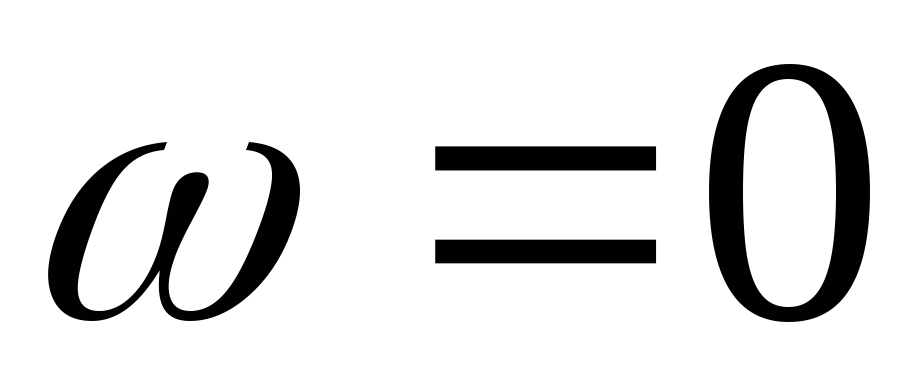
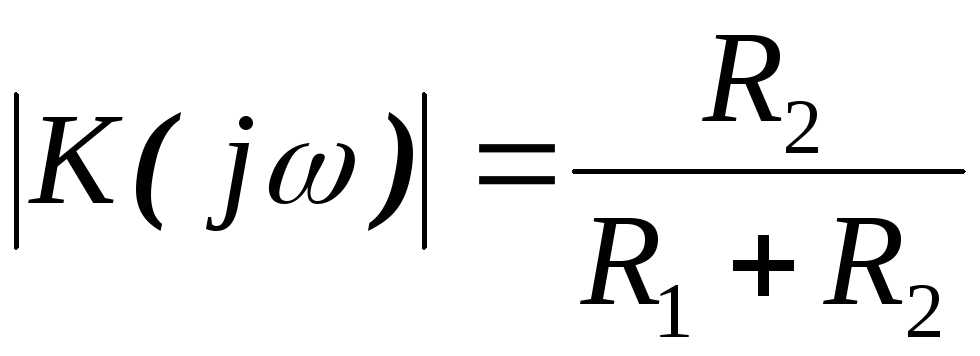 ,
а при
,
а при ,
,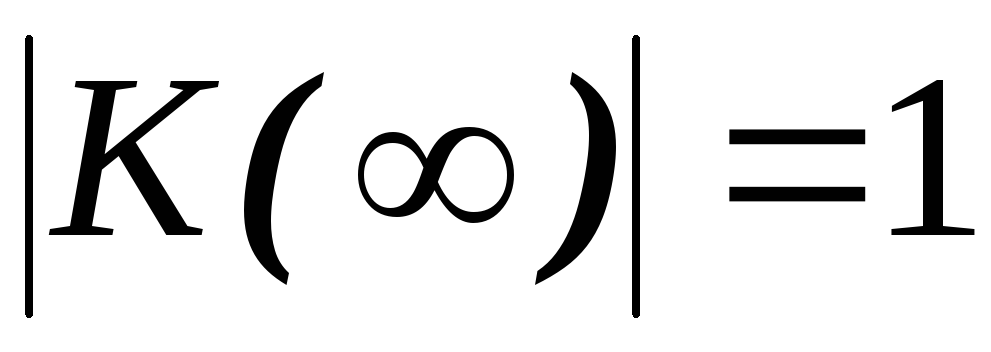 .
АЧХ цепи приведена на рис. 2.13.
.
АЧХ цепи приведена на рис. 2.13.
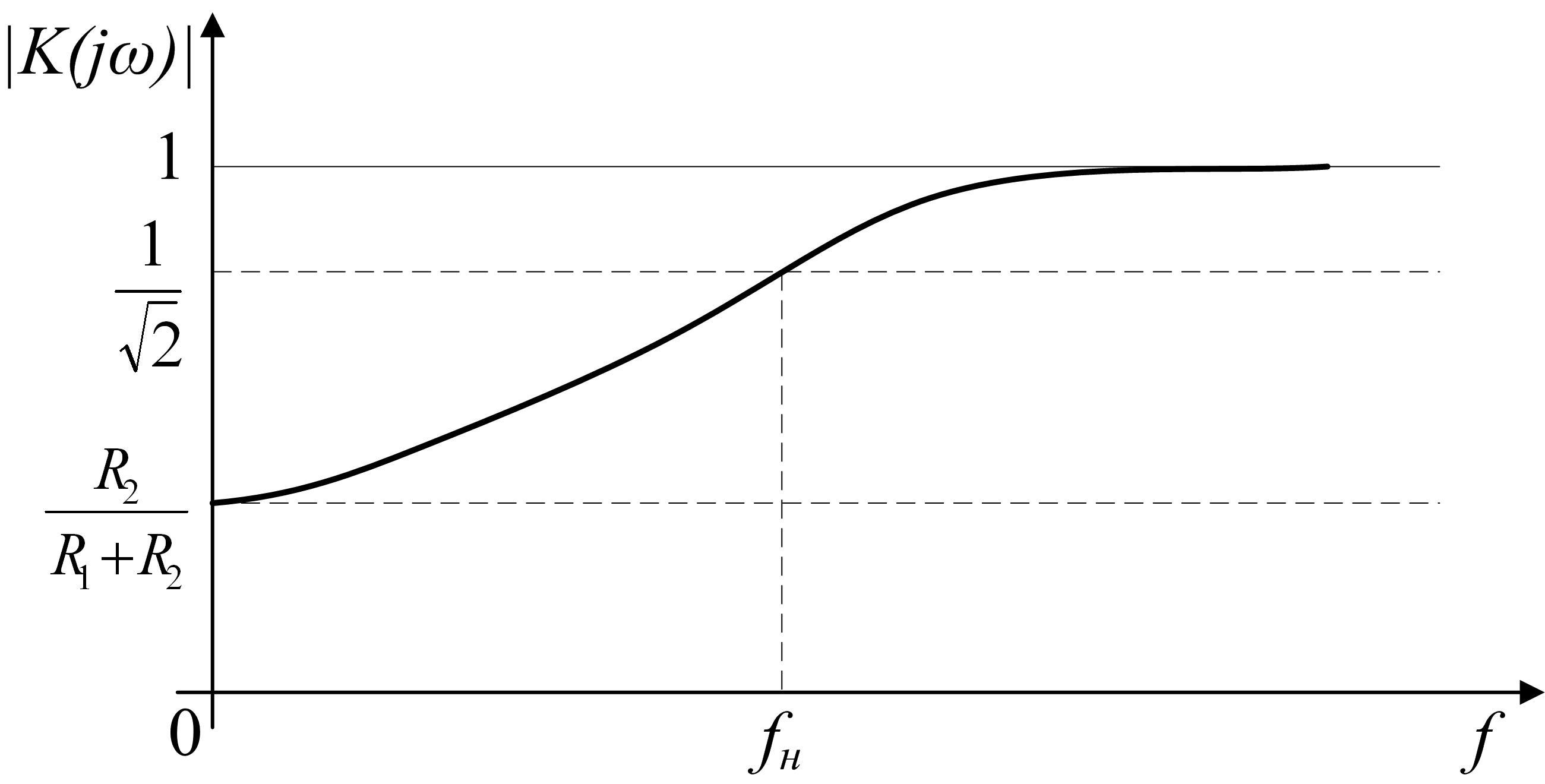
Рис. 2.13 АЧХ схемы, приведённой на рис. 2.12
ФЧХ получается
аналогично схеме, приведённой на рис.
2.8, 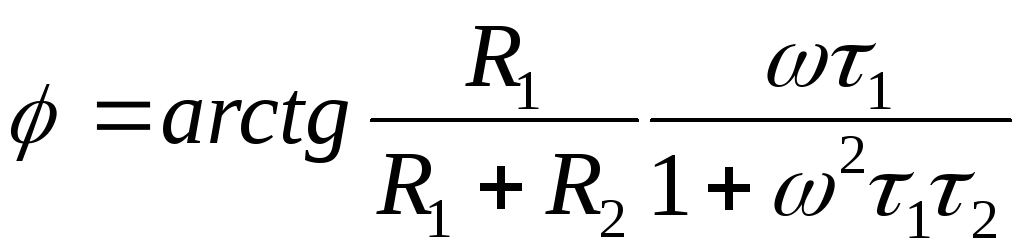 .
Заметим, что при
.
Заметим, что при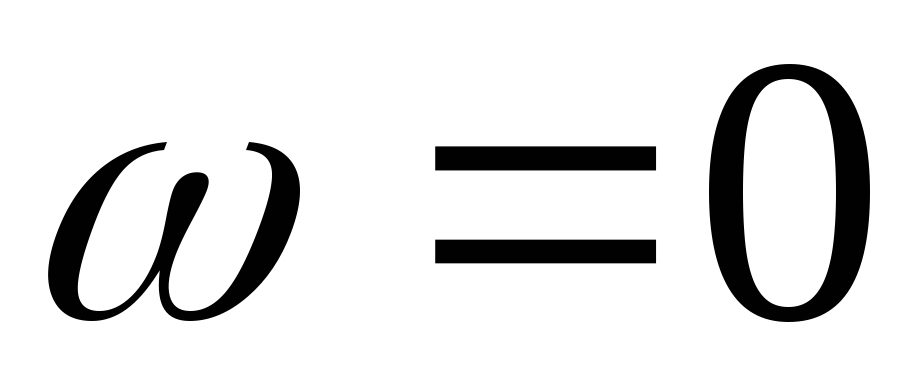 ,
,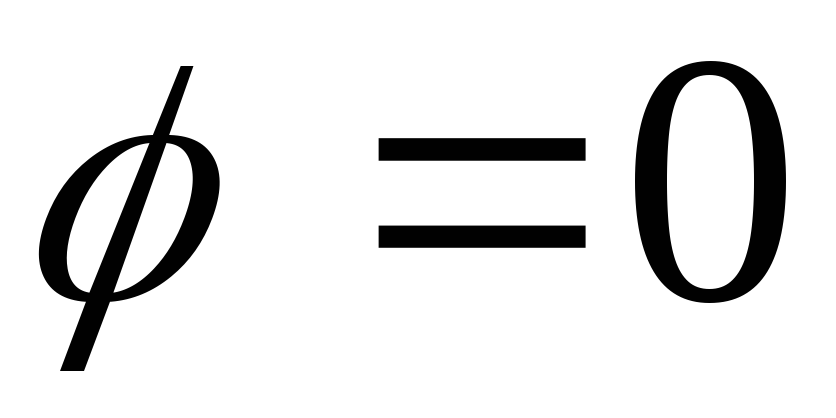 ,
а при
,
а при ,
также
,
также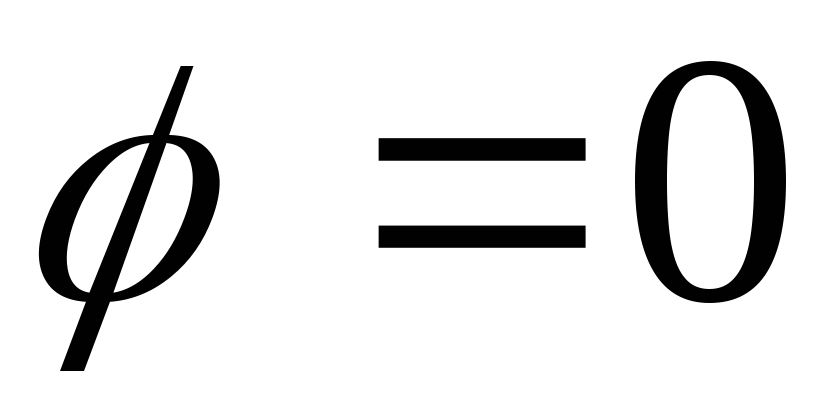 .
ФЧХ имеет максимум при
.
ФЧХ имеет максимум при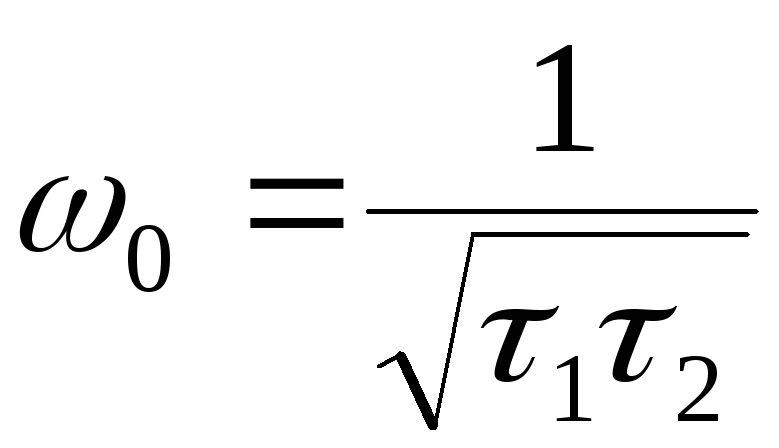 :
:
| (2.11) |
Нетрудно видеть,
что выражения (2.9) и (2.11) идентичны. ФЧХ
для 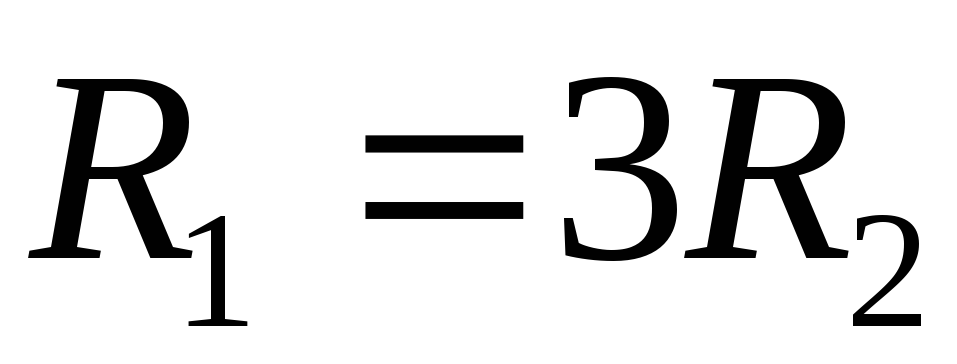 приведена на рис. 2.14.
приведена на рис. 2.14.
Используя приведённую методику, нетрудно вывести формулы коэффициентов передачи более сложных цепей.
Умение получать
выражения для коэффициентов передачи  -цепей
в комплексной форме можно использовать
для нахождения переходных характеристик.
Для этого в выражении для сопротивления
ёмкости синусоидальному току
-цепей
в комплексной форме можно использовать
для нахождения переходных характеристик.
Для этого в выражении для сопротивления
ёмкости синусоидальному току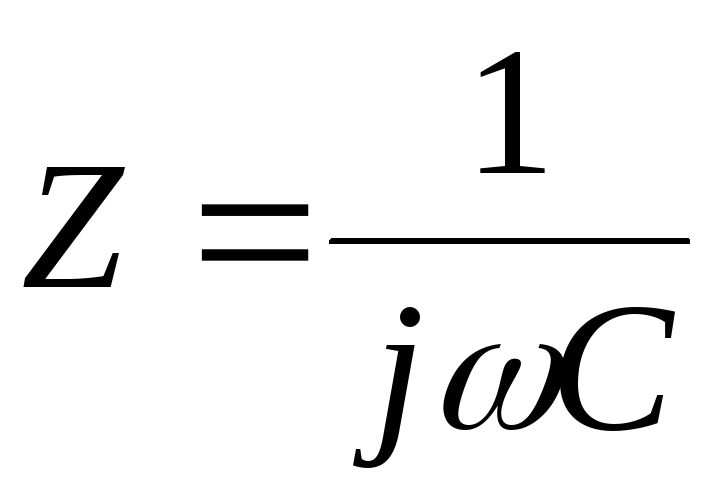 необходимо заменитьjω
на оператор
необходимо заменитьjω
на оператор 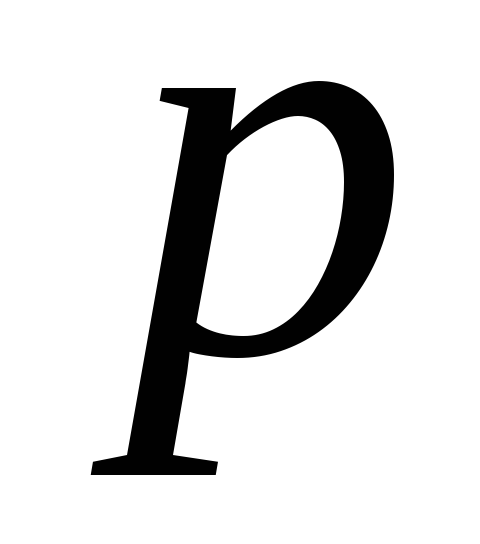 .
При этом получаем операторное выражение
для сопротивления ёмкости
.
При этом получаем операторное выражение
для сопротивления ёмкости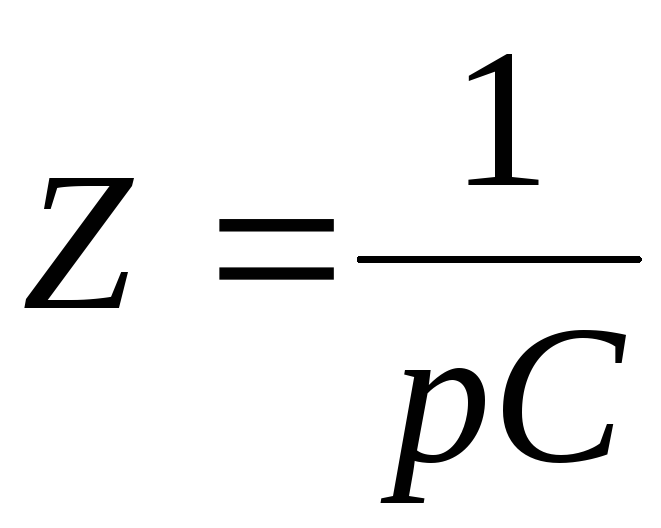 .
.
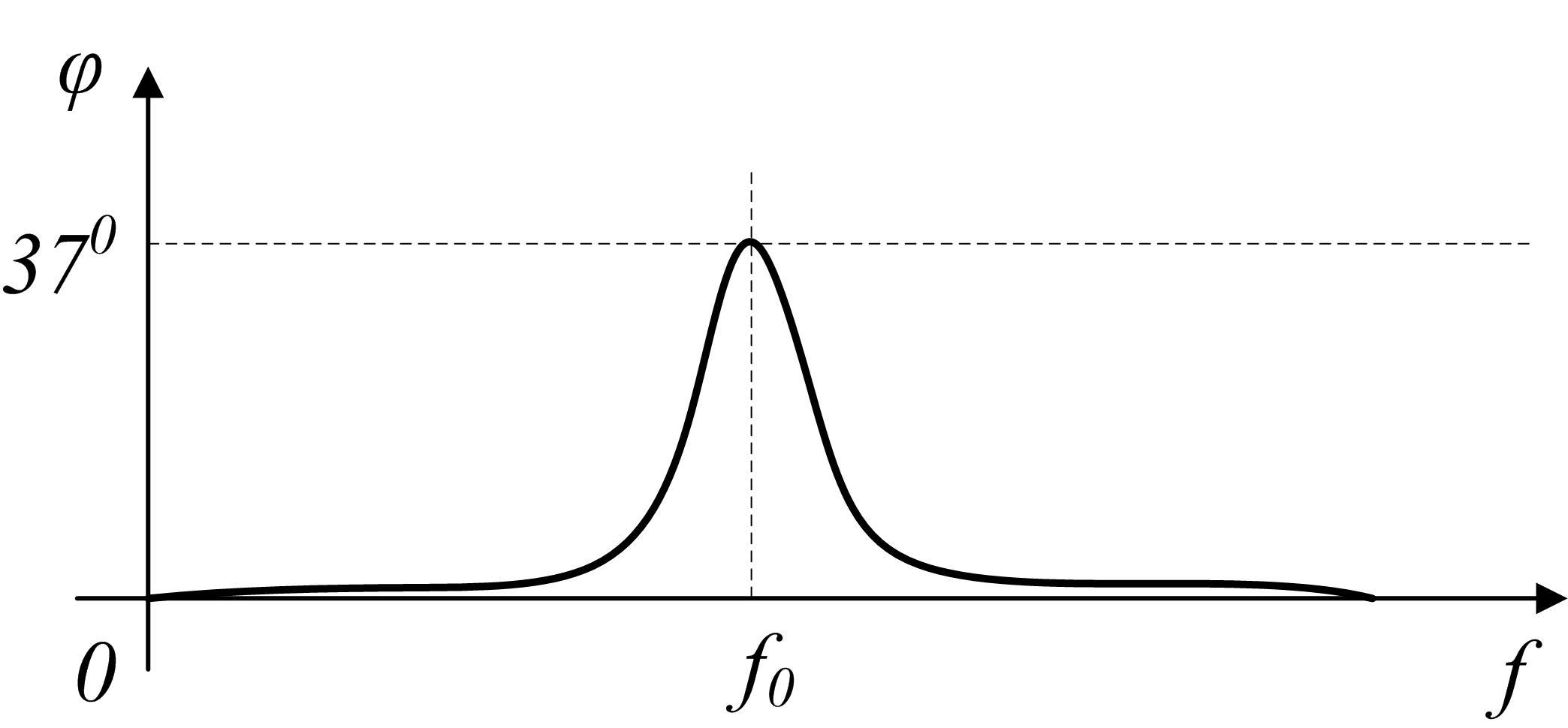
Рис. 2.14 ФЧХ схемы,
приведённой на рис. 2.11, при 
Законы Ома и
Кирхгофа можно также выразить в
операторной форме, заменяя  на
на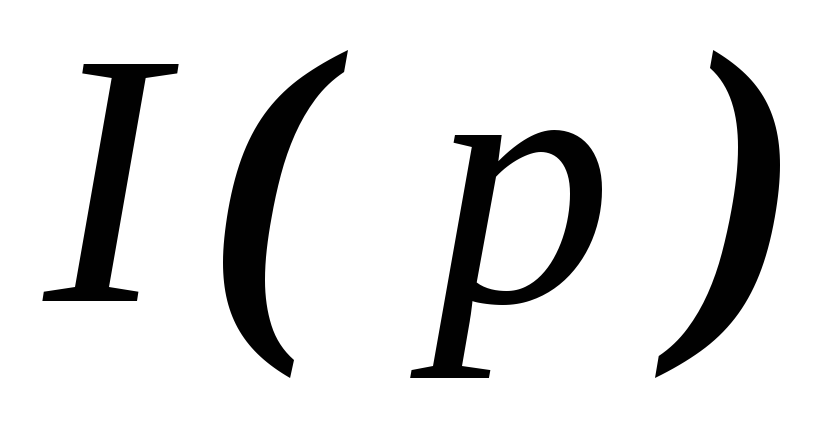 и
и на
на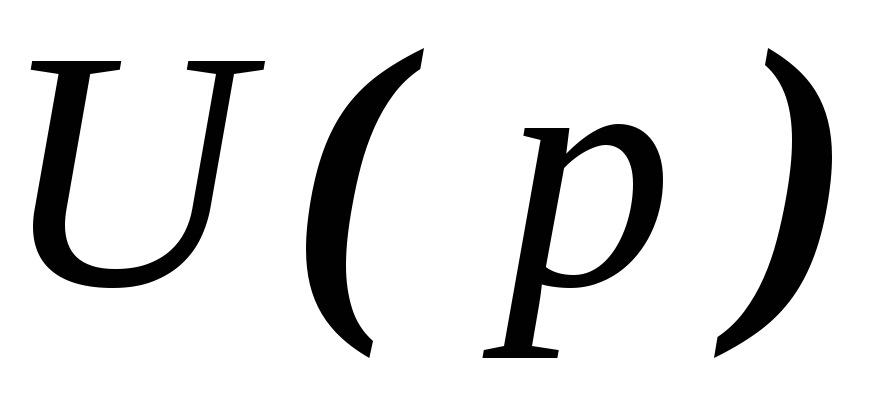 .
Используя эти замены, можно найти
коэффициент передачи
.
Используя эти замены, можно найти
коэффициент передачи -цепи
также в операторной форме. Сделаем это
для простейшей интегрирующей
-цепи
также в операторной форме. Сделаем это
для простейшей интегрирующей -цепочки
(рис.2.3). Запишем уравнения:
-цепочки
(рис.2.3). Запишем уравнения: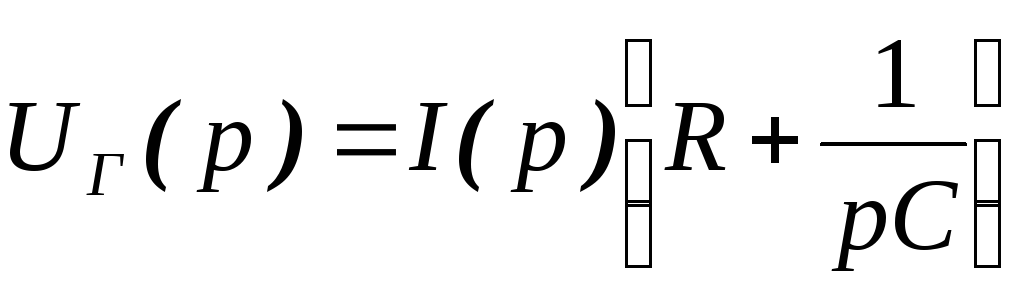 ,
,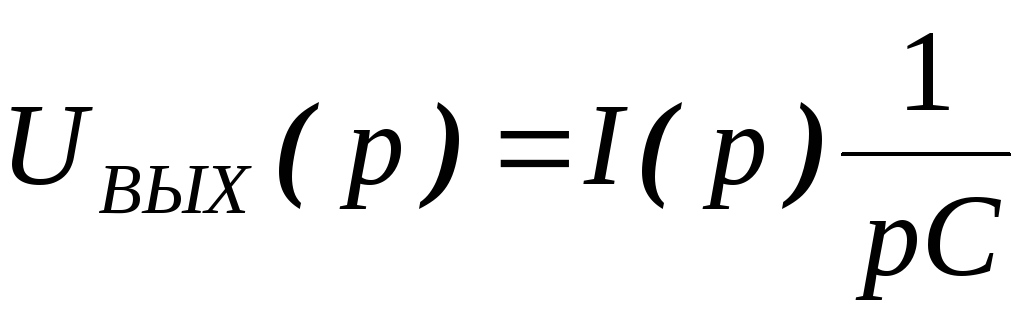 .
Отсюда
.
Отсюда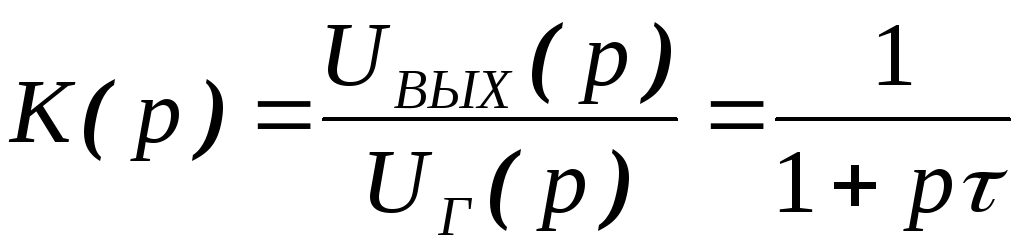 ,
где
,
где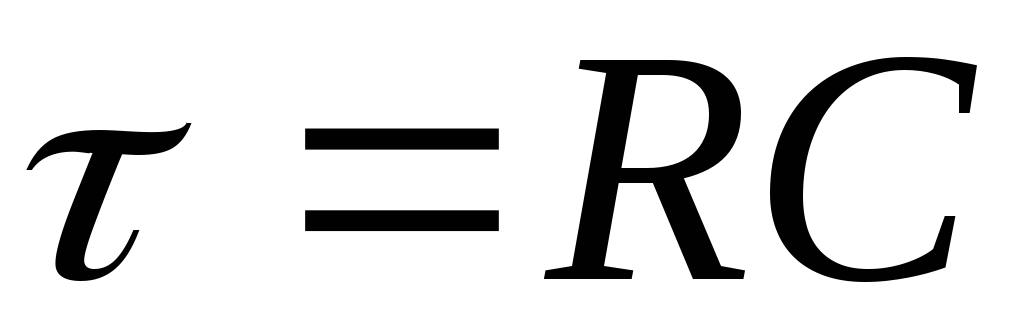 .
.
Для простейшей
дифференцирующей  -цепочки
получим:
-цепочки
получим: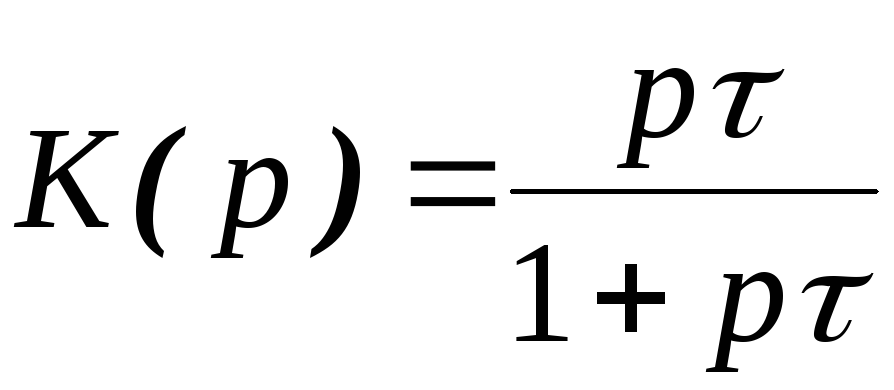 ,
где
,
где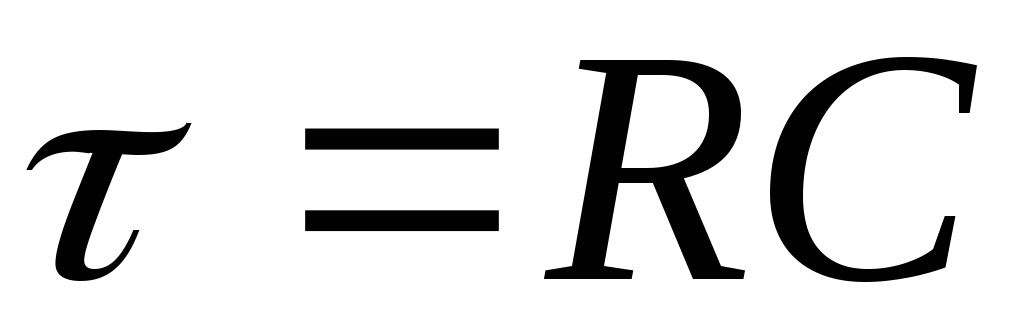 .
.
Для нахождения
переходных характеристик теперь
достаточно от операторной формы 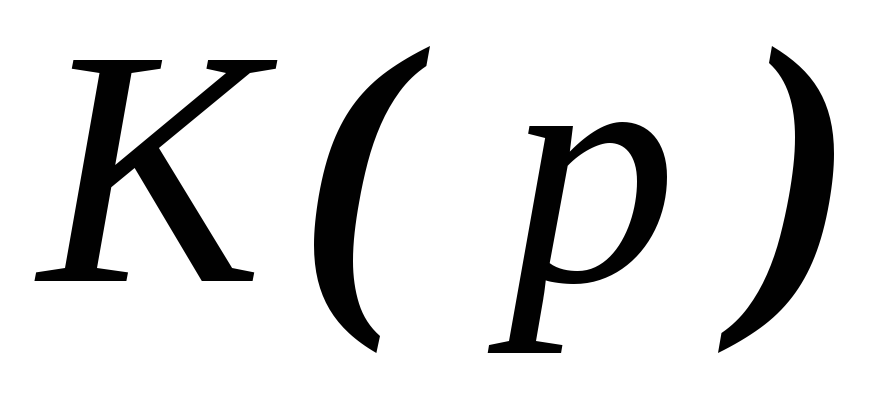 перейти к оригиналу
перейти к оригиналу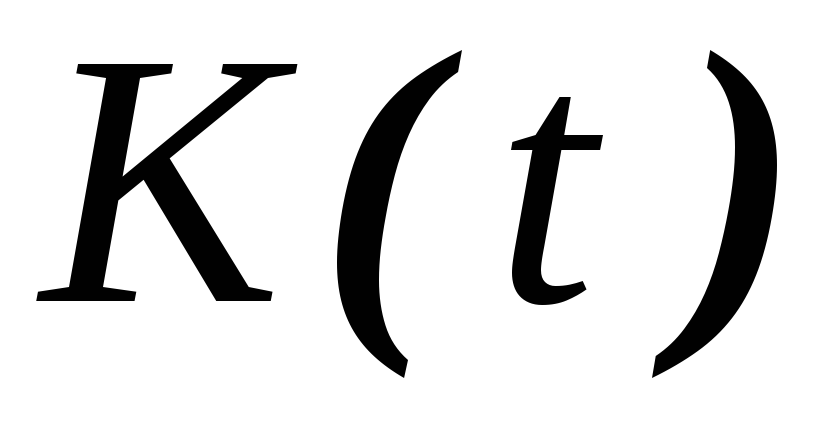 .
Таким образом, если возникают трудности
в построении переходных характеристик
.
Таким образом, если возникают трудности
в построении переходных характеристик -цепей,
то можно используя операторный метод
и таблицы перехода от операторной формы
к оригиналам, получить выражения
переходных характеристик
-цепей,
то можно используя операторный метод
и таблицы перехода от операторной формы
к оригиналам, получить выражения
переходных характеристик -цепей.
-цепей.
ДИФФЕРЕНЦИРУЮЩАЯ ЦЕПЬ • Большая российская энциклопедия
-

-

-

В книжной версии
Том 9. Москва, 2007, стр. 107-108
-

Скопировать библиографическую ссылку:
Авторы: А. П. Сухоруков

Дифференцирующая цепь: а – принципиальная схема; б – форма импульса на входе; в – форма импульса на выходе цепи.
ДИФФЕРЕНЦИ́РУЮЩАЯ ЦЕПЬ, устройство, предназначенное для дифференцирования по времени электрич. сигналов. В Д. ц. выходное напряжение приближённо пропорционально производной по времени от входного напряжения. Различают пассивные и активные Д. ц. Простейшая пассивная Д. ц. состоит из ёмкости $C$ и сопротивления $R$ (рис., а). Входное $U_{вх}$ и выходное $U_{вых}$ напряжения в Д. ц. связаны уравнением $dU_{вх}/dt=U_{вых}(t)+dU_{вых}/dt,$ где $τ_0=RC$ – постоянная времени релаксации. Если за это время амплитуда и фаза входного сигнала не успевают сильно измениться (т. е. даже на самой высокой частоте $ω_в$ спектра сигнала $τ_0ω_в≪1$), то выходной сигнал пропорционален производной входного напряжения: $U_{вых}(t)≈τ_0dU_{вх}/dt$. В спектральном представлении $RC$-цепь характеризуется комплексной передаточной функцией напряжения $K=U_{вых}/U{вх}=iτ_0ω/(1+iτ_0ω).$ Процесс дифференцирования происходит тем точнее, чем меньше $τ_0$, но при этом сильно уменьшается величина выходного напряжения. Этот недостаток устраняется в активных Д. ц. при присоединении $RC$-цепи к операционному усилителю с отрицат. обратной связью. Дифференцирующие $LC$-цепи ($L$ – индуктивность) на практике используются значительно реже из-за наличия активного сопротивления катушки, которое ухудшает характеристики схемы.
Пассивные Д. ц. применяют в импульсных и цифровых устройствах для укорачивания импульсов. На рисунке видно, что прямоугольные импульсы (рис., б) при прохождении через $RC$-цепь преобразуются в короткие запускающие импульсы с крутым фронтом (рис., в). Активные Д. ц. используют как дифференциаторы в аналоговых вычислит. устройствах.
1.2 Прохождение импульсов через rc-цепи.
1.2.1 Напряжение и ток в rc-цепях под воздействием единичного скачка.
На вход RC-цепи (см. рис.1.6) поступает единичный скачок напряжения, изображённый на рис.1.7.
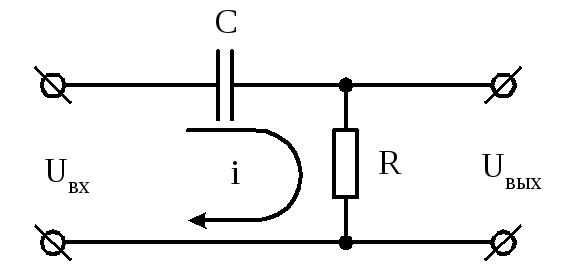
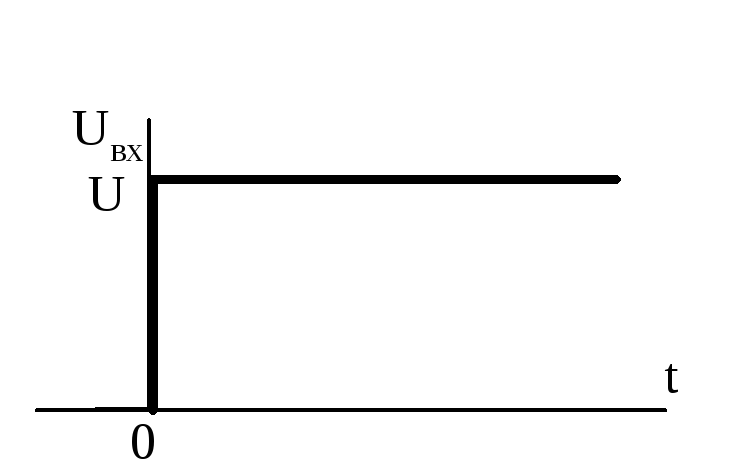
Рис. 1.6 -Принципиальная схема RC-цепи. Рис. 1.7 -График единичного скачка.
Определим реакцию цепи на единичный скачок, т.е. установим зависимости:
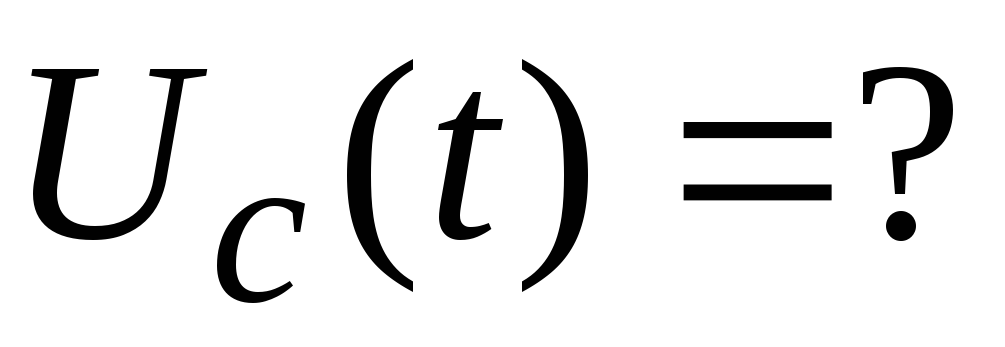 ;
;  ;
;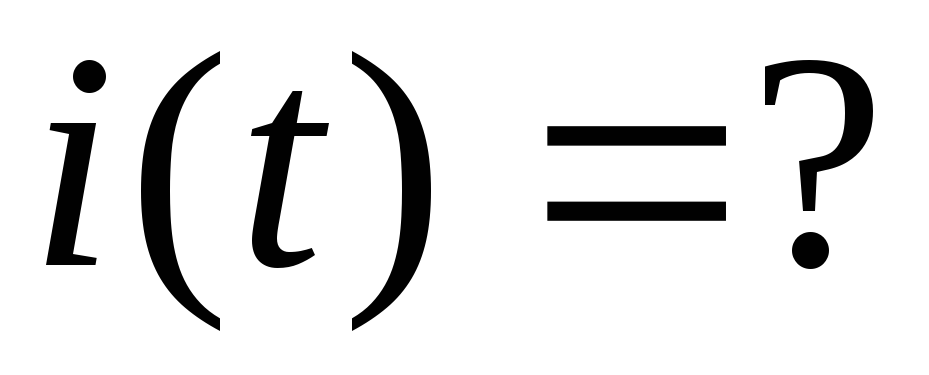 ;
;
У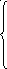 равнение
скачка, т.е. напряжение на входе цепи
описывается в виде:
равнение
скачка, т.е. напряжение на входе цепи
описывается в виде:
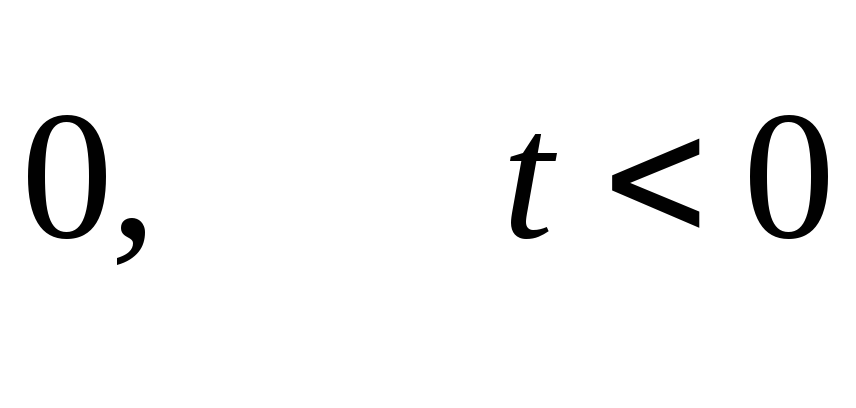 ;
;
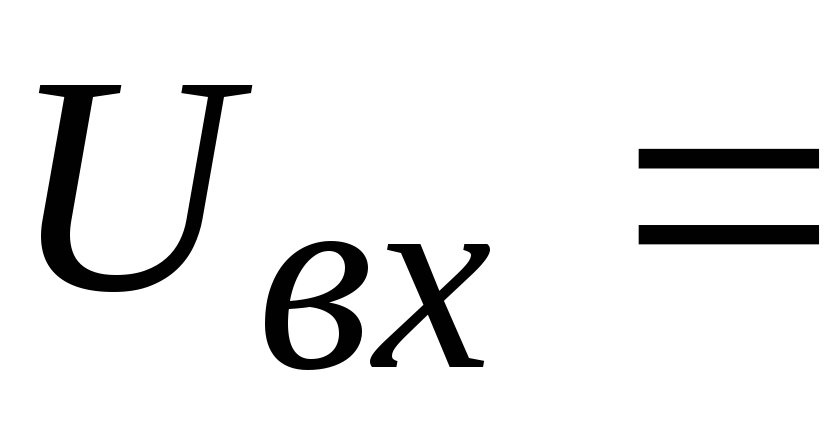
 ;
;
Начальные условия:  ,
,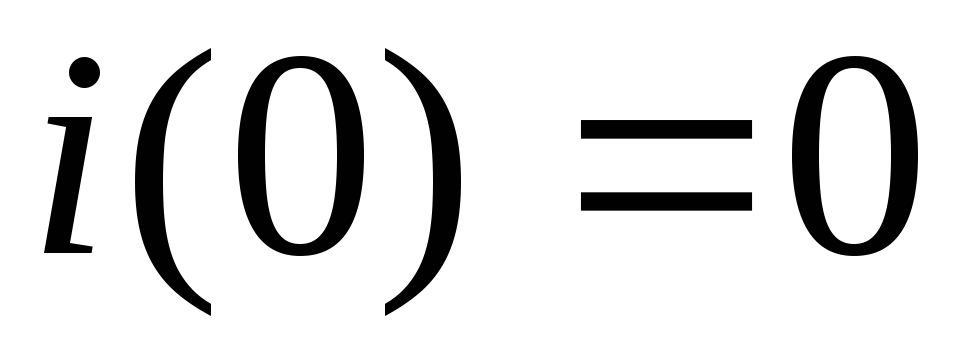 ,
,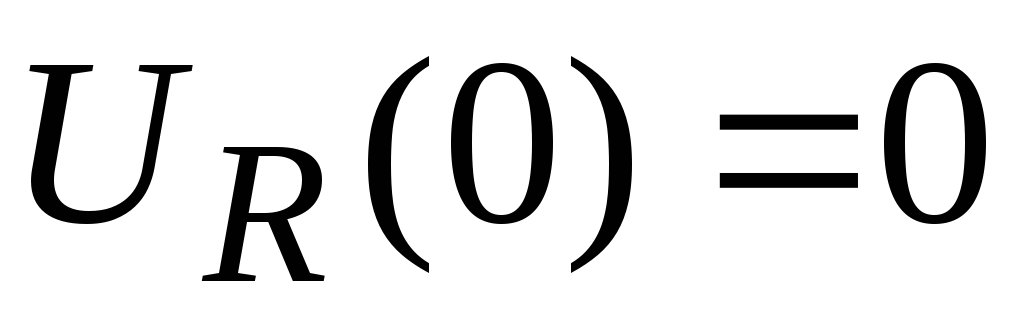 .
.
Уравнение второго закона Кирхгофа для цепи имеет вид:
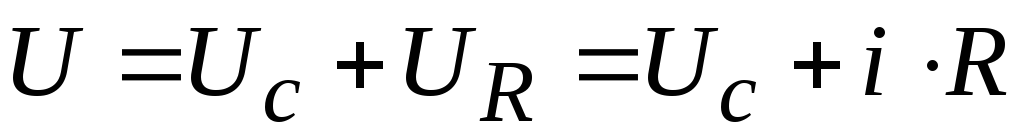 .
.
С учётом 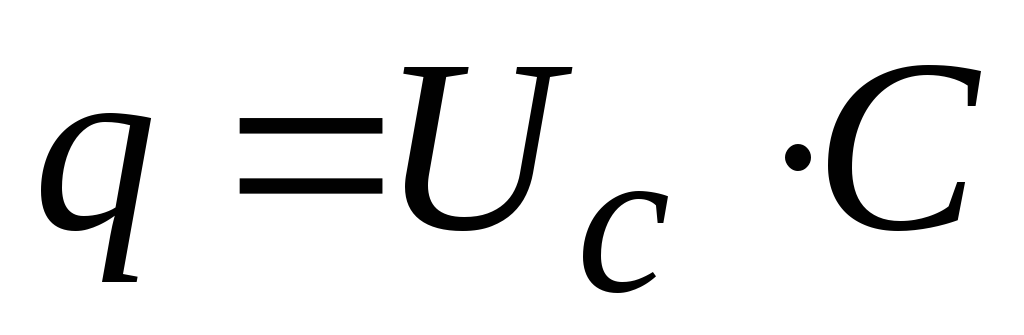 ,
,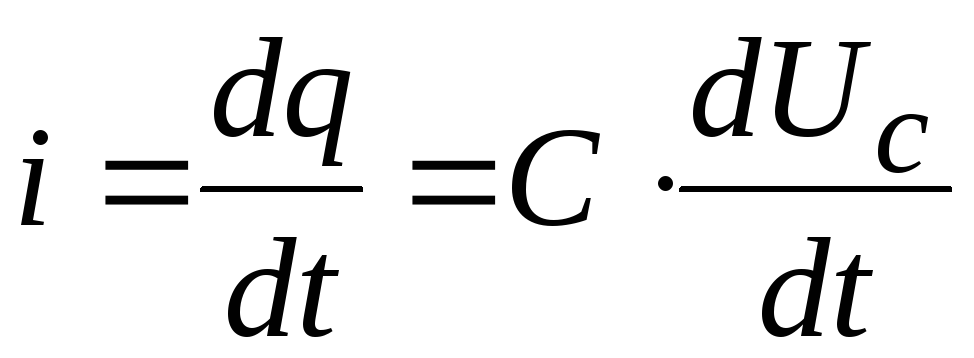 ,
получим
,
получим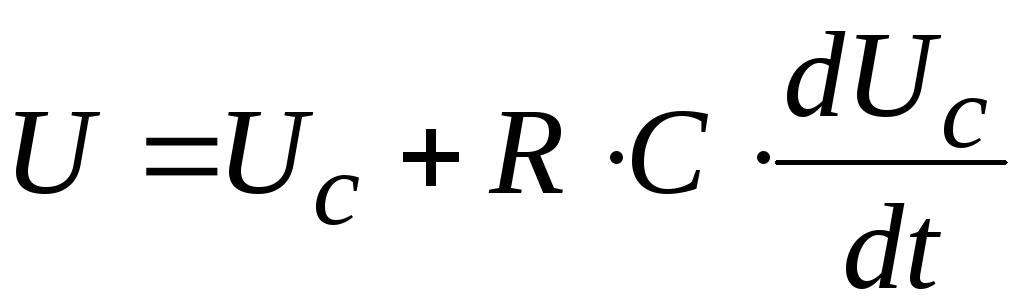 ;
;
Запишем дифференциальное уравнение описывающее RC-цепь в стандартном виде:
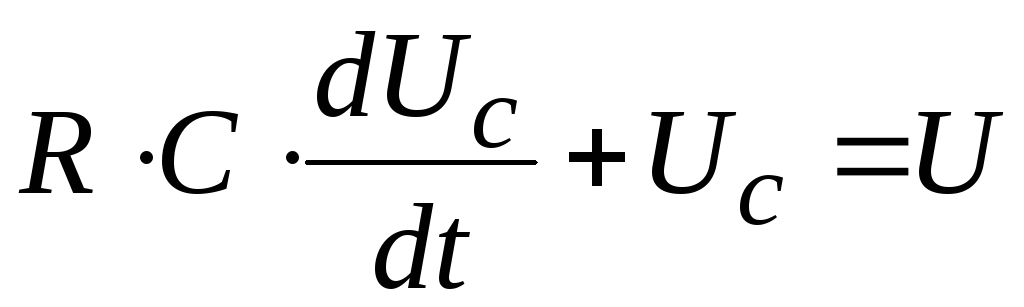 ,
,
с начальными
условиями 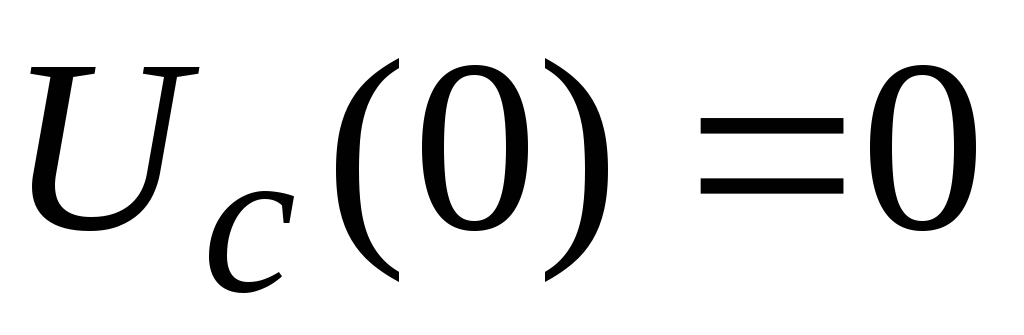 ,
,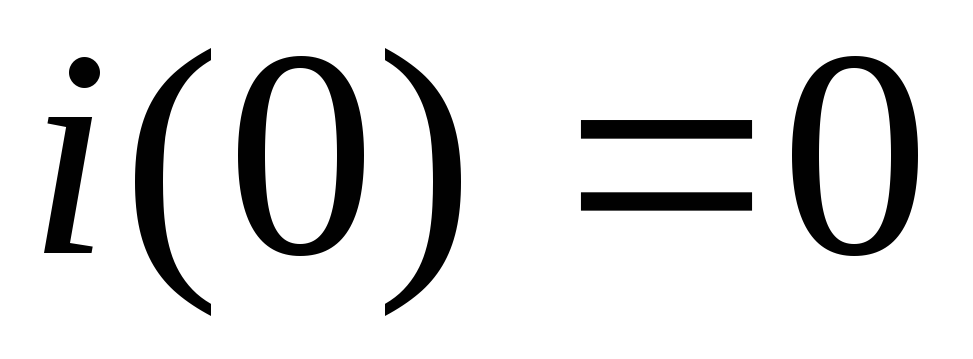 ,
,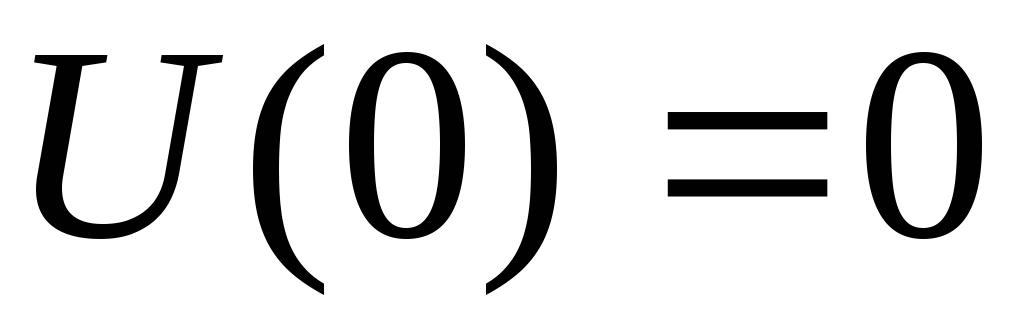 . (1.1)
. (1.1)
Решение такого дифференциального уравнения ищется в виде суммы свободной и вынужденной составляющих:
 .
.
Свободная
составляющая записывается в виде: 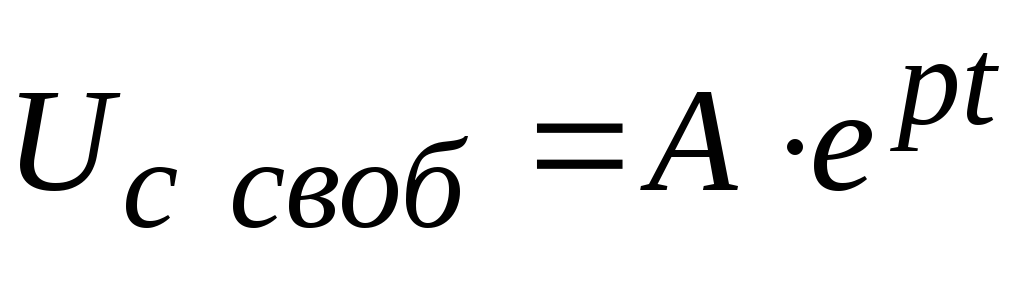 ,
и описывает собственный переходной
процесс в цепи при отсутствии возмущающего
воздействия (т.е. при нулевой правой
части уравнения), следовательно,
,
и описывает собственный переходной
процесс в цепи при отсутствии возмущающего
воздействия (т.е. при нулевой правой
части уравнения), следовательно,
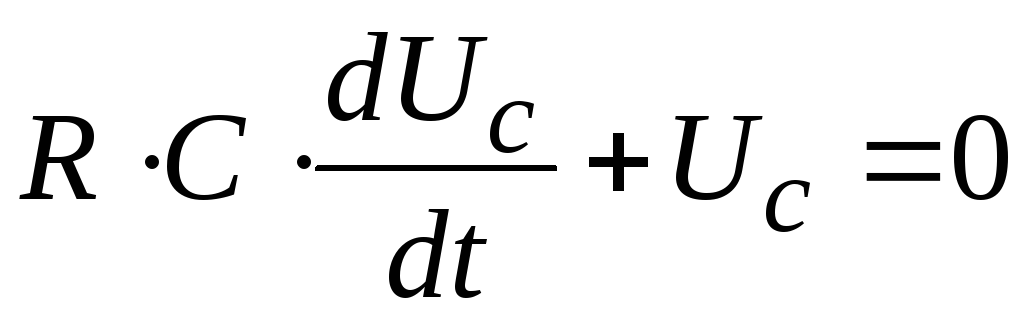 ;
;
обозначив 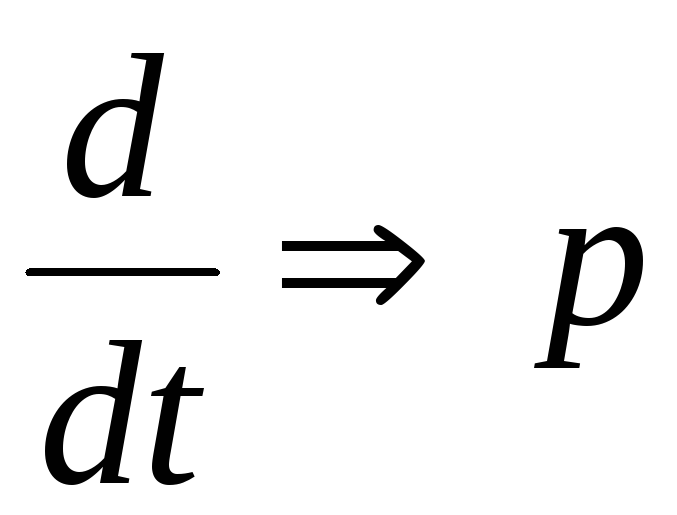 ,
запишем это уравнение в операторной
форме:
,
запишем это уравнение в операторной
форме:
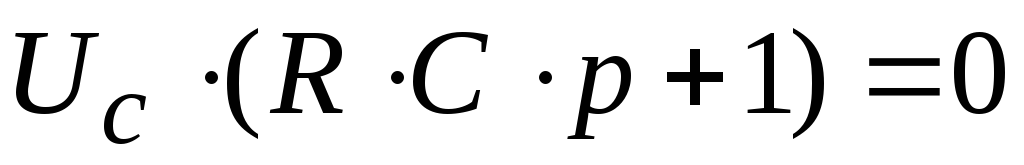 .
.
Поскольку  изменяется во времени переходного
процесса по экспоненциальному закону,
т.е.
изменяется во времени переходного
процесса по экспоненциальному закону,
т.е. ,
то
,
то
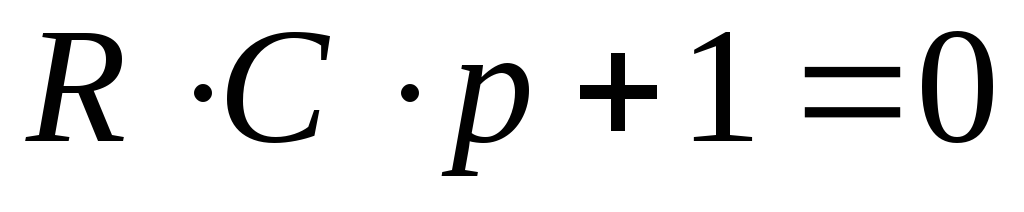 ,
отсюда находим корень характеристического
уравнения
,
отсюда находим корень характеристического
уравнения
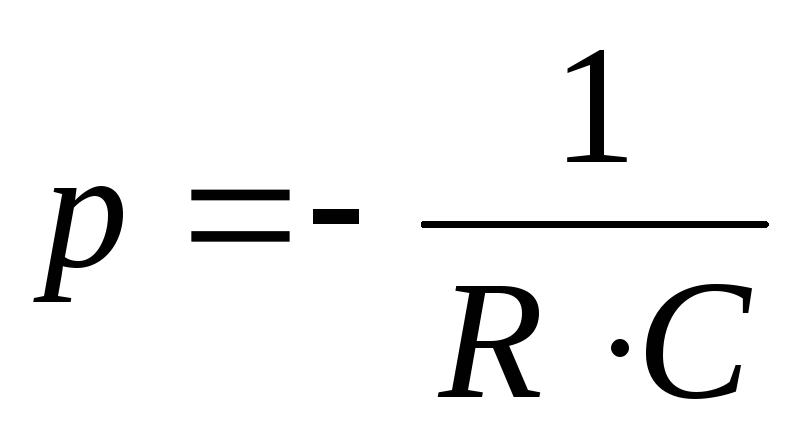 .
.
Подставив его значение в уравнение свободной составляющей, получим:
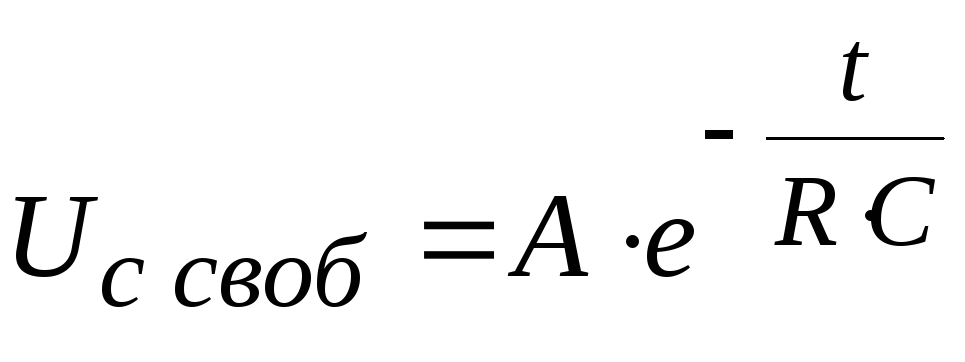 ,
где
,
где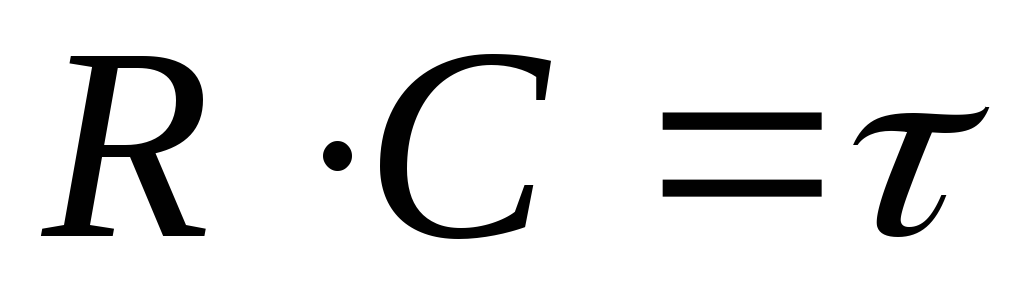 ,
постоянная времениRC-цепи,
,
постоянная времениRC-цепи,
тогда
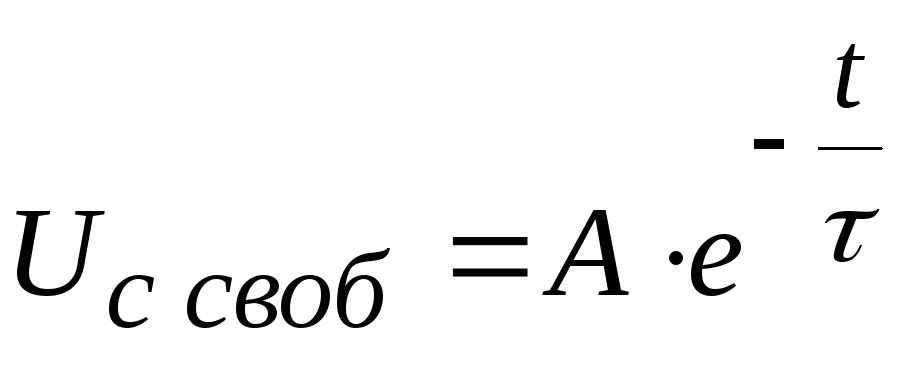 .
.
При 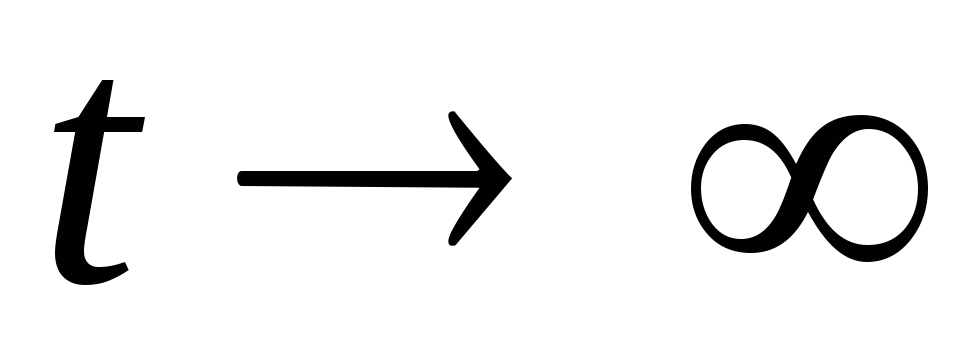 ,
,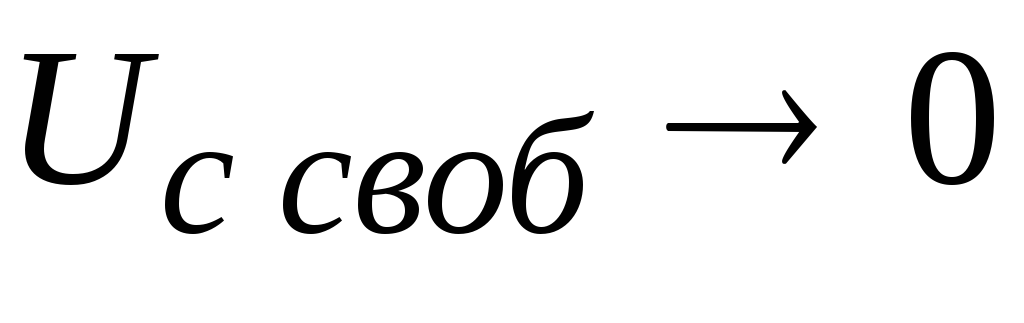 ;
;
Вынужденная
составляющая, обусловленная правой
частью уравнения, имеет место после
окончания переходных процессов
(теоретически при 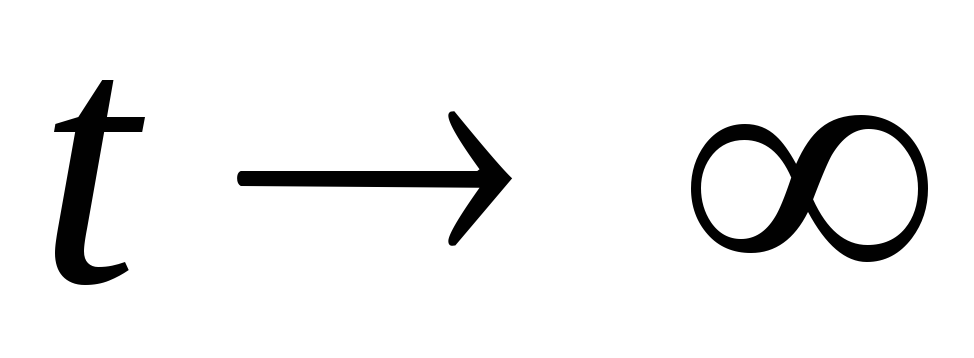 ,
практически при
,
практически при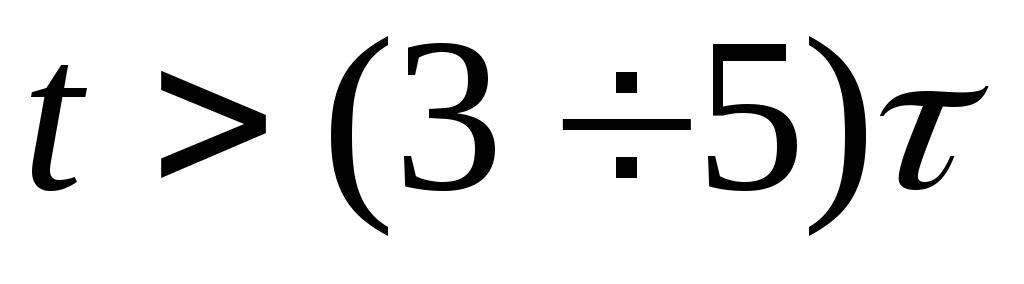 ) определяется в виде:
) определяется в виде:
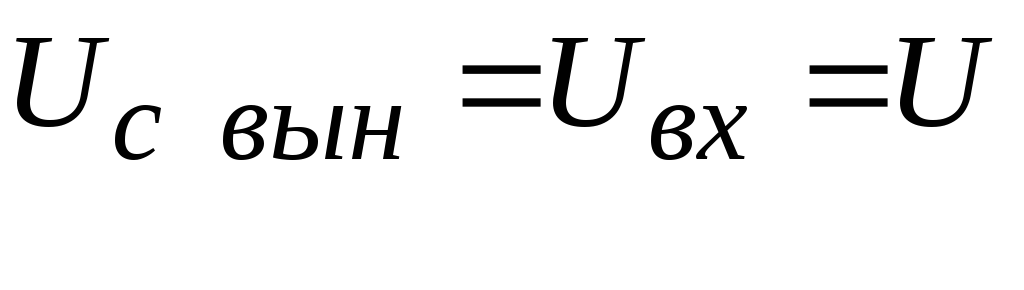 .
.
Теперь запишем полное решение дифференциального уравнения:
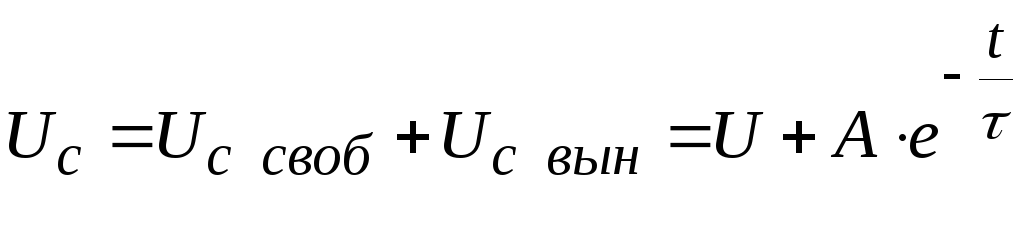 .
.
В этом выражении неизвестной величиной является амплитуда A.ОпределимАиз начальных условий:
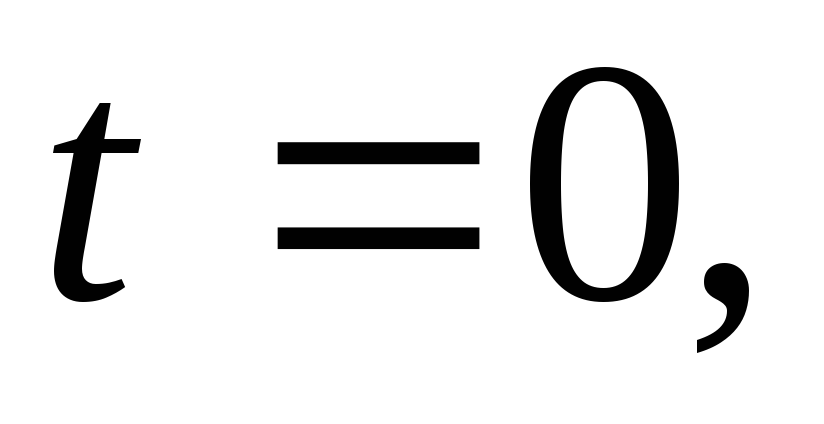
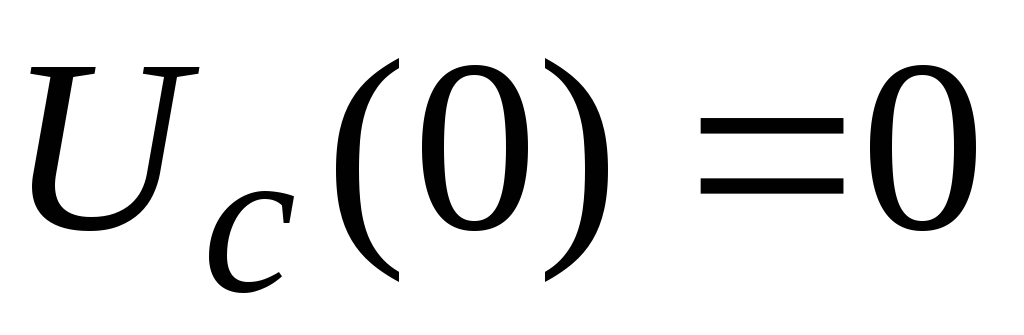 ;
;
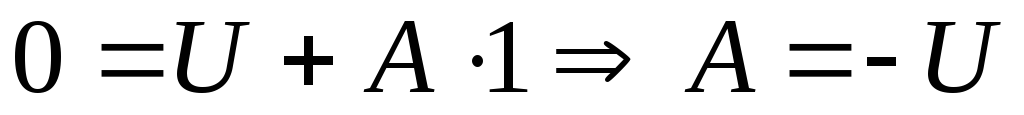 .
.
Окончательное решение дифференциального уравнения имеет вид:
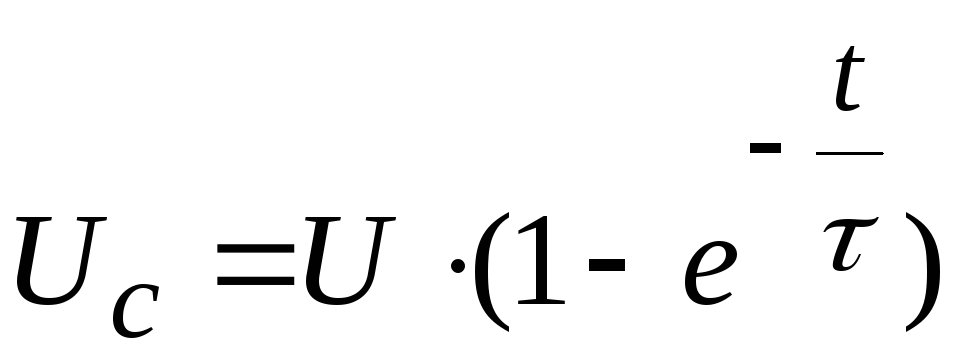 ; (1.2)
; (1.2)
Зависимость  при разных постоянных времениRC-цепи
приведены на рис.1.8
при разных постоянных времениRC-цепи
приведены на рис.1.8
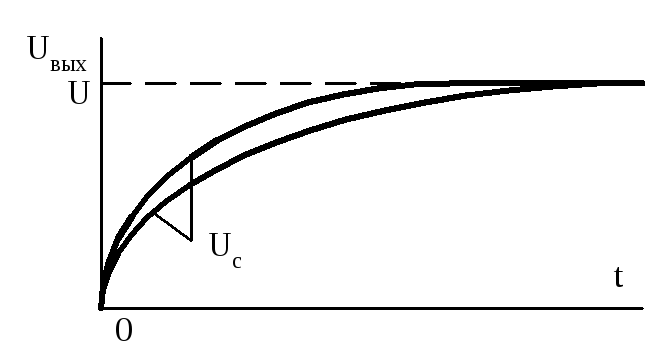

Рис. 1.8
Напряжение на выходе RC-цепи имеет вид:
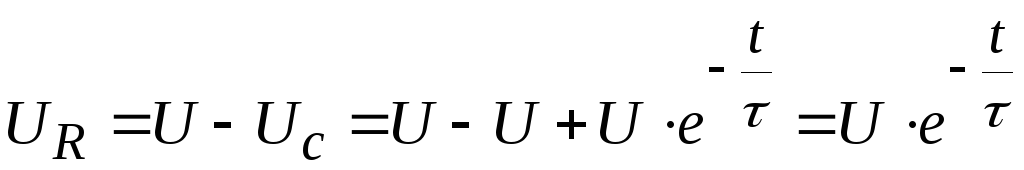 .
.
Зависимости 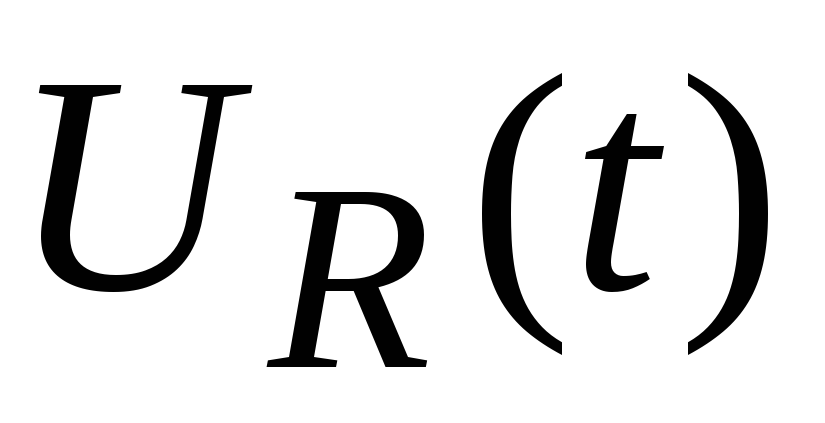 при различных значениях
при различных значениях приведены на рис.1.9.
приведены на рис.1.9.
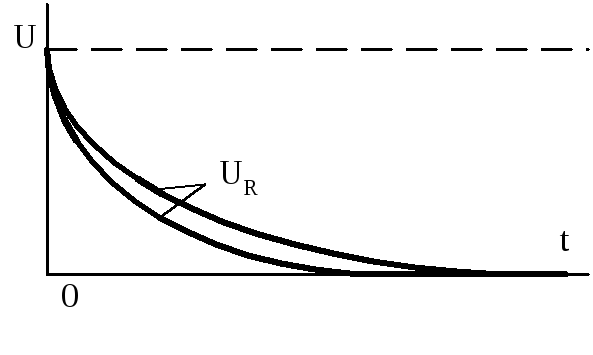
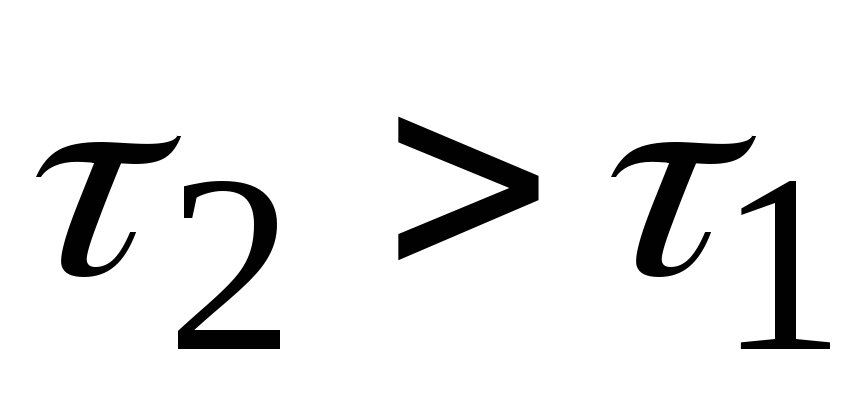

Рис. 1.9
Поскольку 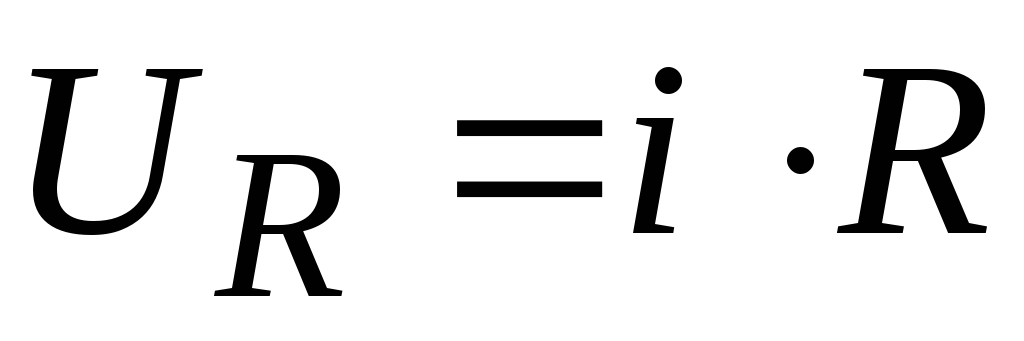 ,
то
,
то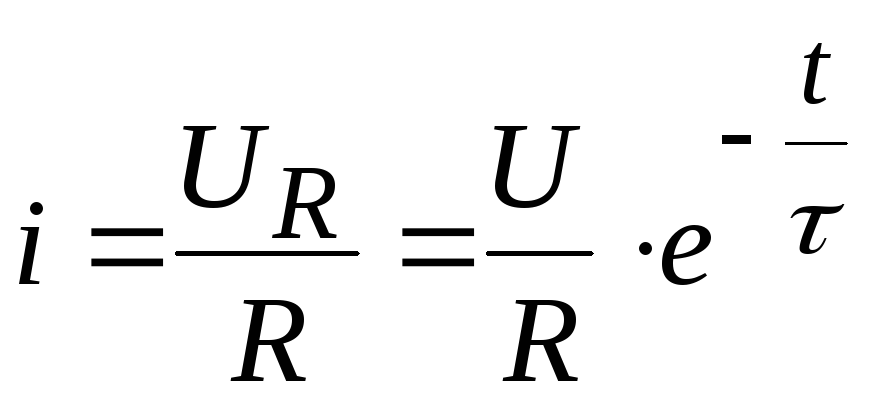 (1.4)
(1.4)
Зависимость 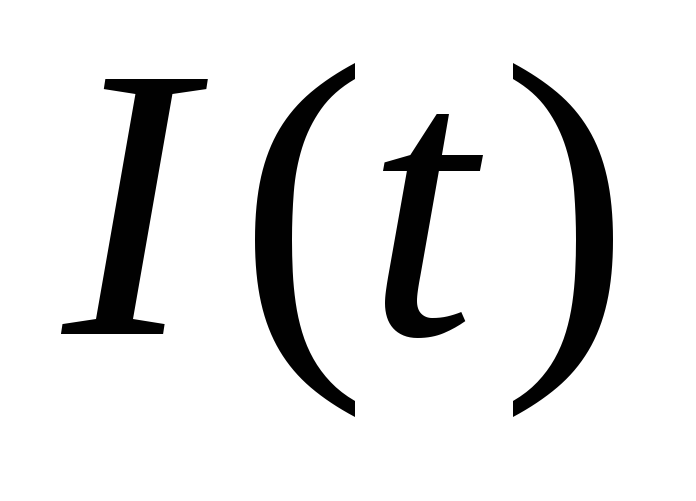 приведена на рис.1.10.
приведена на рис.1.10.
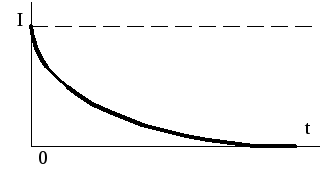
Рис. 1.10
1.2.2 Дифференцирующая (укорачивающая) и разделительная rc-цепи.
Дифференцирующей
цепью называют такую цепь, сигнал на
выходе которой имеет значения,
пропорциональные в каждый момент
производной от входного сигнала.
Следовательно,  .
КоэффициентКдолжен выражаться в
секундах, в противном случае размерность
левой и правой частей равенства не будет
одинакова. Идеальным дифференцирующим
устройством можно считать конденсаторСили катушкуL.
Например, при использовании конденсатораСможно считать входным сигналом
напряжение на нём
.
КоэффициентКдолжен выражаться в
секундах, в противном случае размерность
левой и правой частей равенства не будет
одинакова. Идеальным дифференцирующим
устройством можно считать конденсаторСили катушкуL.
Например, при использовании конденсатораСможно считать входным сигналом
напряжение на нём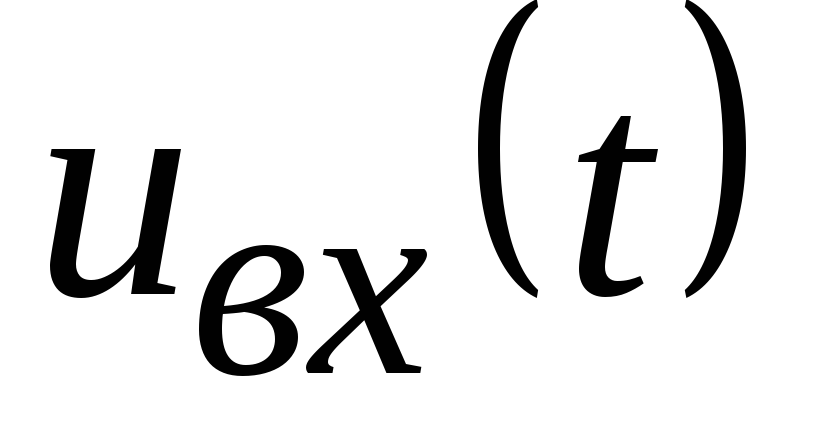 ,
а выходным – ток
,
а выходным – ток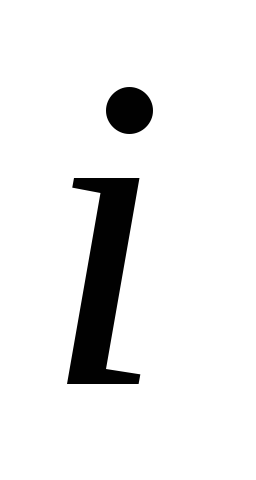 в цепи. Эти переменные связаны известным
соотношением
в цепи. Эти переменные связаны известным
соотношением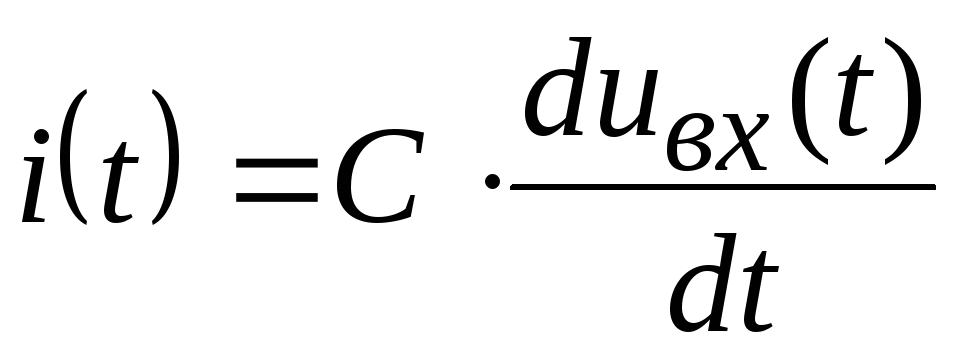 ,
т.е. ток в цепи пропорционален производной
от входного напряжения. Однако использовать
эту схему для практических целей нельзя,
так как она не содержит элемента, который
обеспечивал бы какую-либо регистрацию
значений тока, измерение его значений.
,
т.е. ток в цепи пропорционален производной
от входного напряжения. Однако использовать
эту схему для практических целей нельзя,
так как она не содержит элемента, который
обеспечивал бы какую-либо регистрацию
значений тока, измерение его значений.
Для того чтобы
получить выходной сигнал в форме, удобной
для наблюдения или регистрации, в цепь
последовательно включают токочувствительный
прибор с внутренним сопротивлением R.
В простейшем случаи это может быть
резисторR. Напряжение
на котором пропорционально току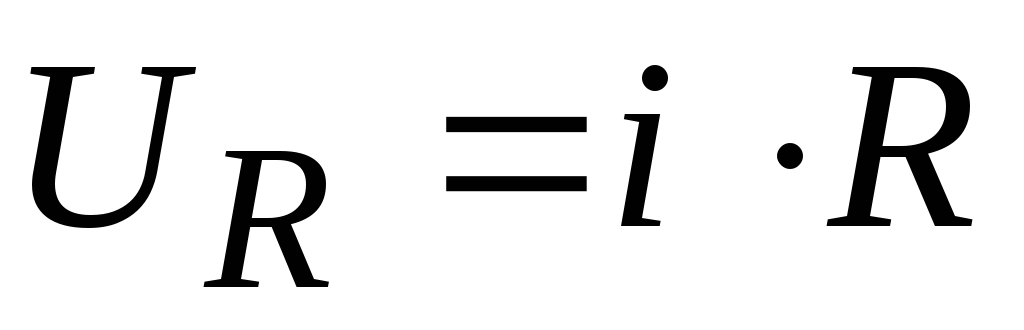 .
.
Рассмотренная RC-цепочка может
выполнять функции как дифференцирующей
(укорачивающей) при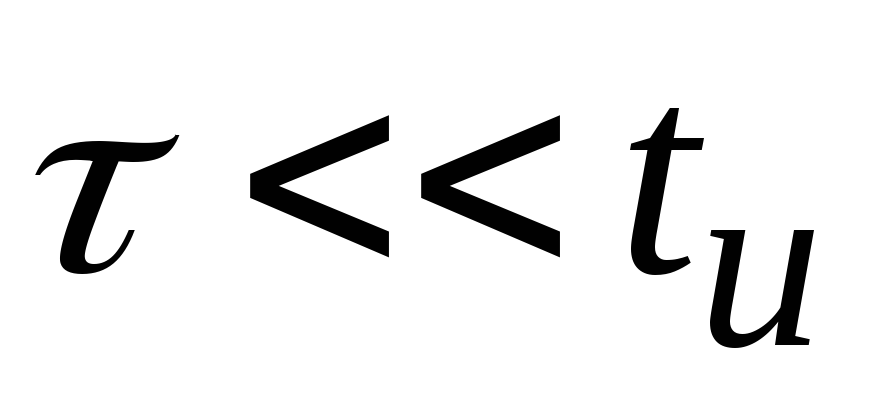 ,
так и разделительной цепи, если
,
так и разделительной цепи, если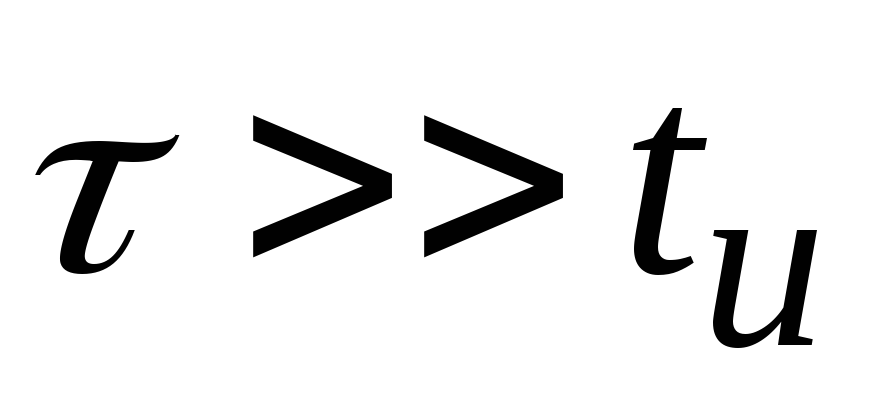 .
.
На рис.1.11 показаны
графики напряжений 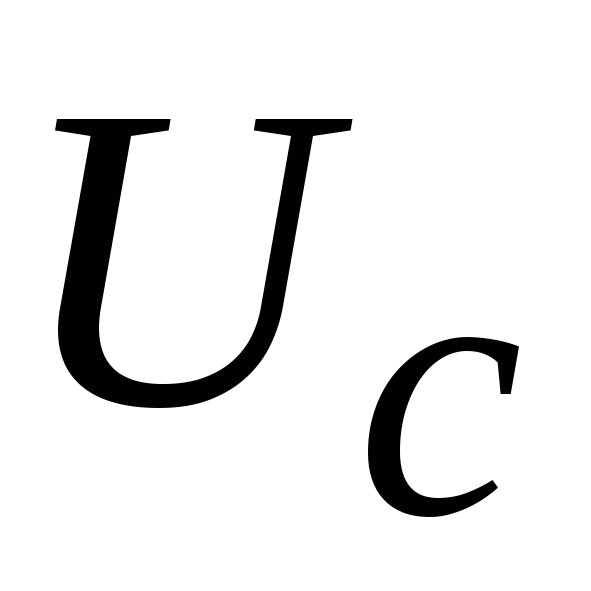 и
и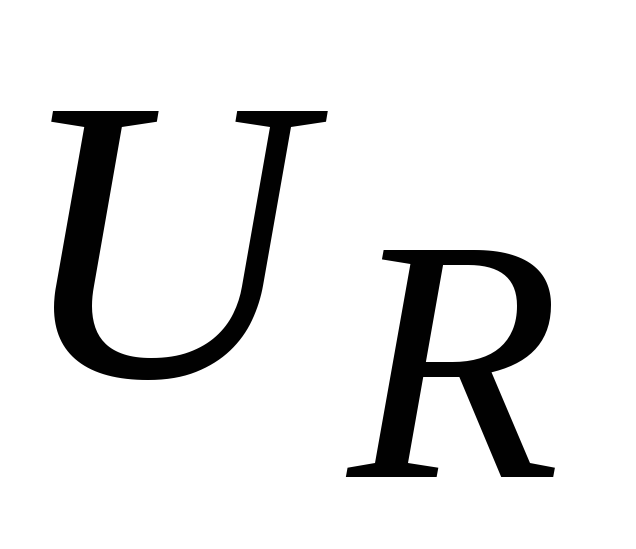 такой
цепочки.
такой
цепочки.
Рассмотрим два режима:
Дифференцирующая цепь –
 ,
при этом возможны два варианта: а)
,
при этом возможны два варианта: а) ;
б)
;
б) ;
;Разделительная цепь –
 ,
при этом также: а)
,
при этом также: а) ;
б)
;
б) ;
;
а) б)
Рис.
1.11 — а) режим 1 – 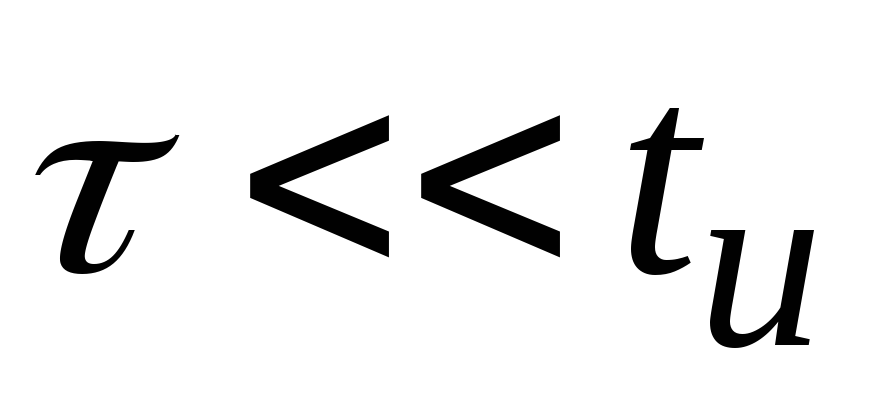 ,
б) режим 2 –
,
б) режим 2 –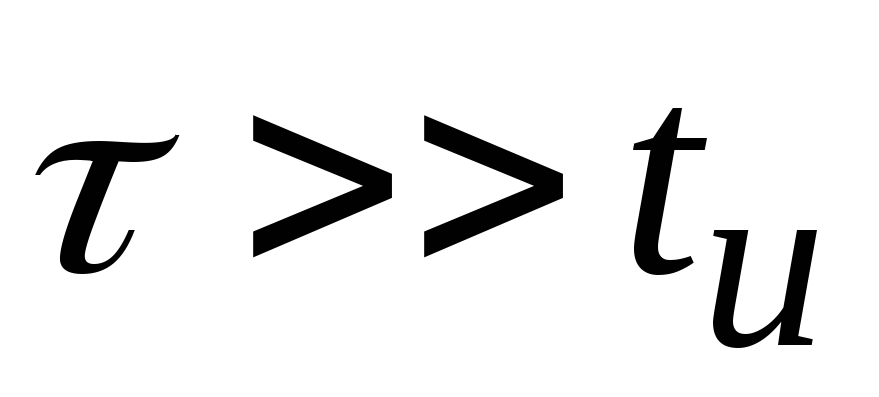 .
.
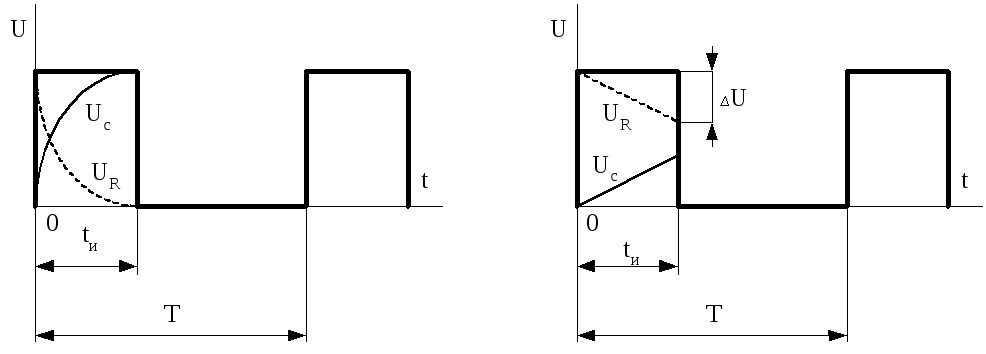
Рассмотрим дифференцирующею цепочку под воздействием импульсной последовательности (рис.1.12).
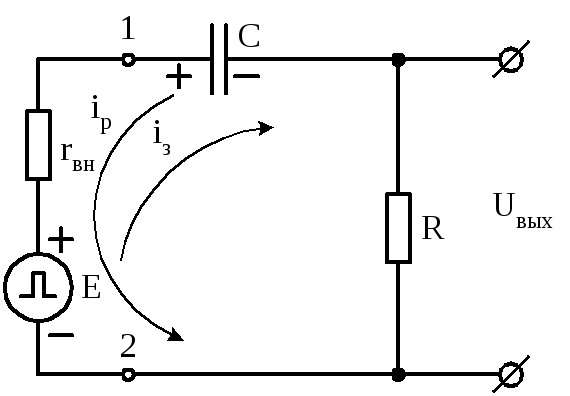
Рис. 1.12 -Принципиальная схема укорачивающей RC-цепочки
При импульсе
конденсатор Сзаряжается под
воздействием зарядного тока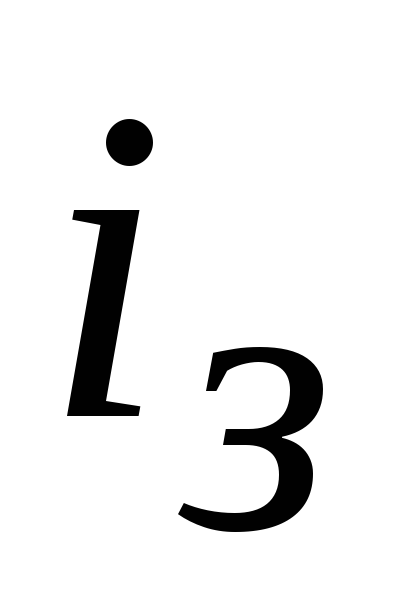 ,
при паузе – разряжается, обуславливая
разрядный ток
,
при паузе – разряжается, обуславливая
разрядный ток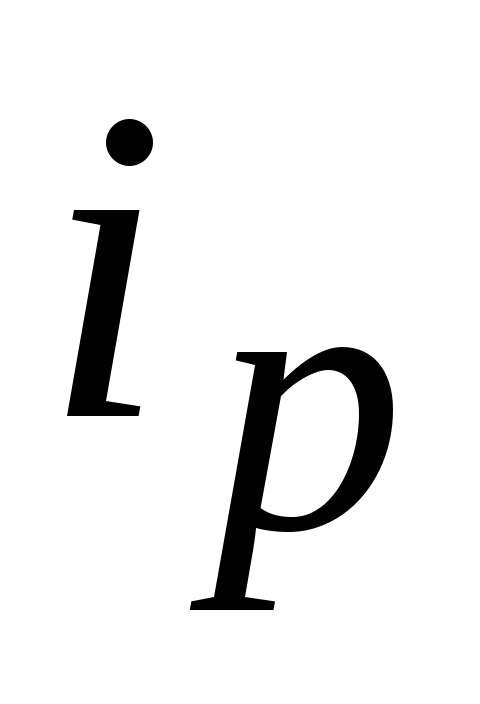 .
При этом
.
При этом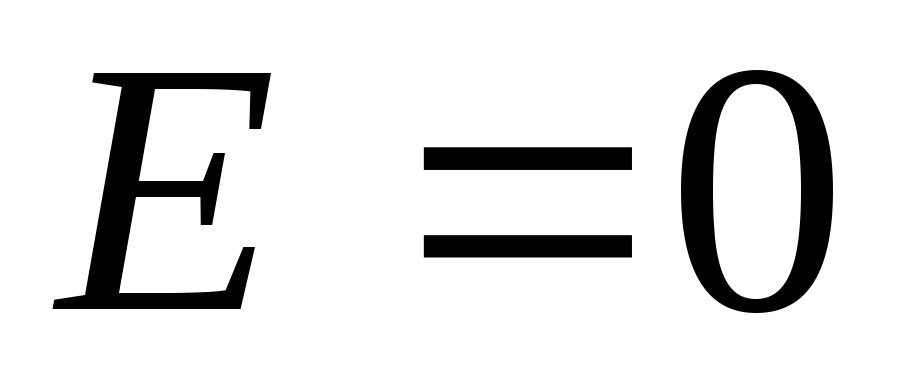 .
.
Допустим
,тогда
им можно пренебречь (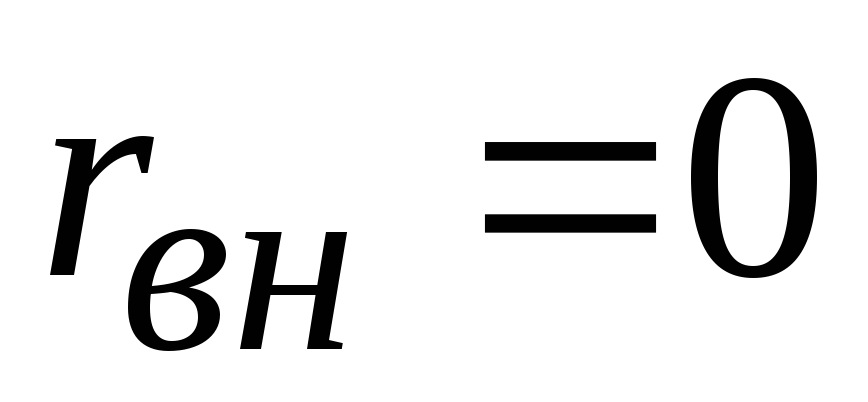 ).
).
Рассмотрим режим
I, вариант а):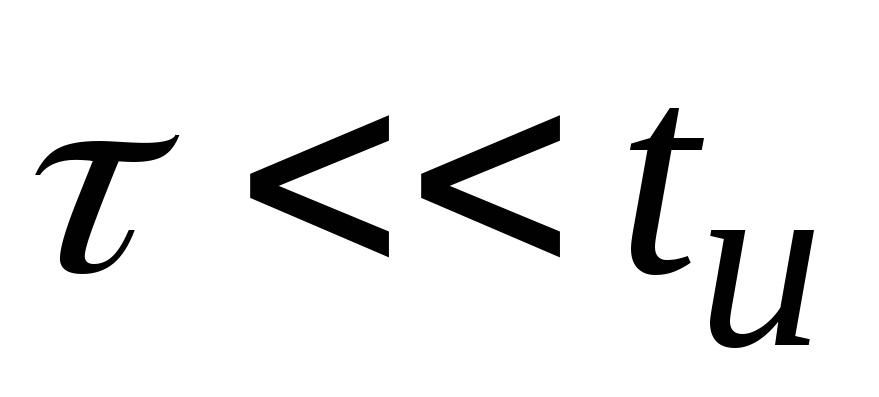 ,
,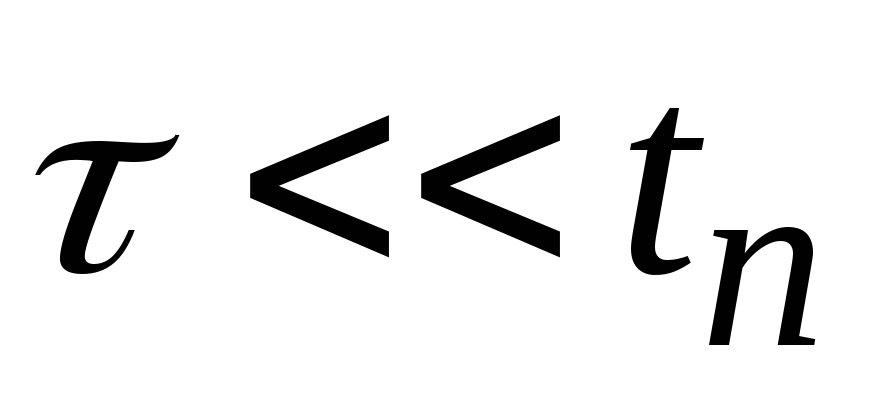 .
.
После окончания
импульса (момент времени  )
) .
.
В период паузы (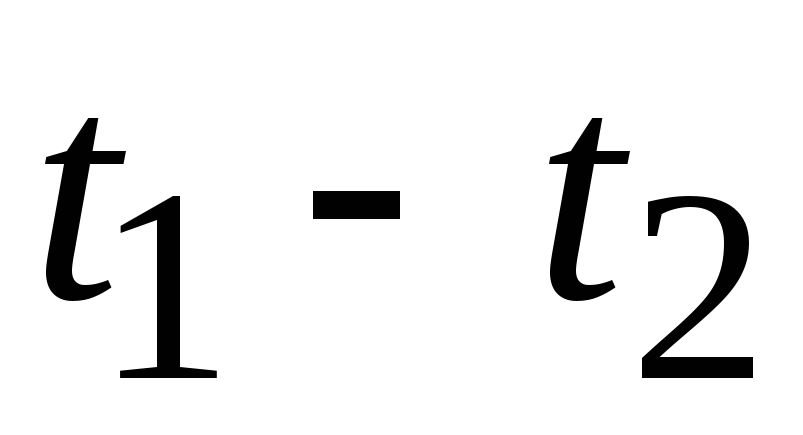 )
разряд конденсатораСполучается
полный, т.к.
)
разряд конденсатораСполучается
полный, т.к.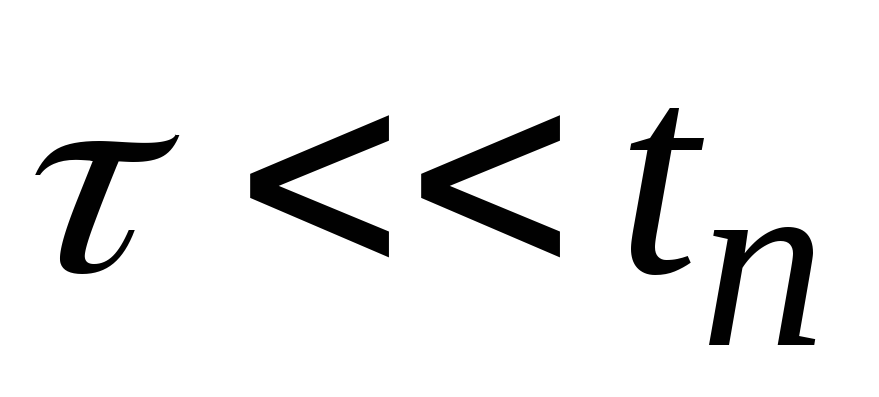 ;
;
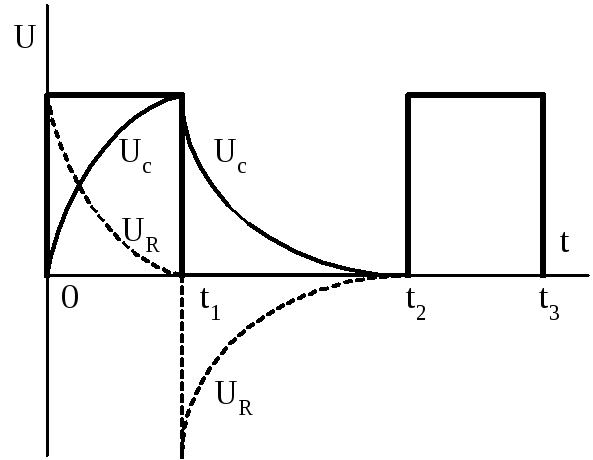
Рис. 1.13
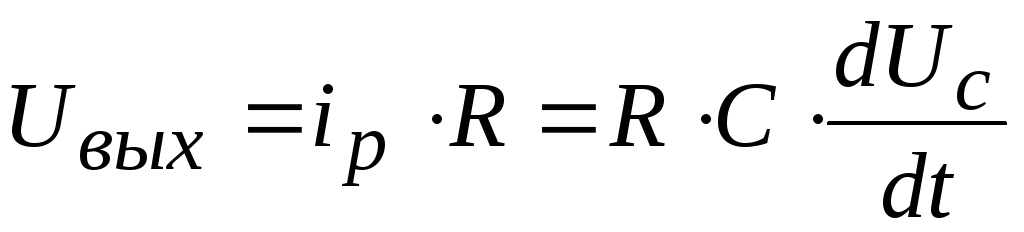 ;
;
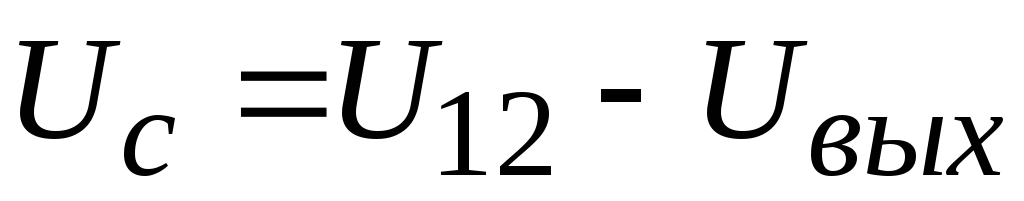 .
.
Тогда
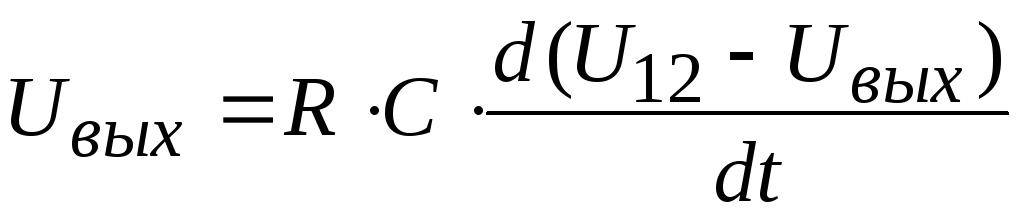 ;
;
При 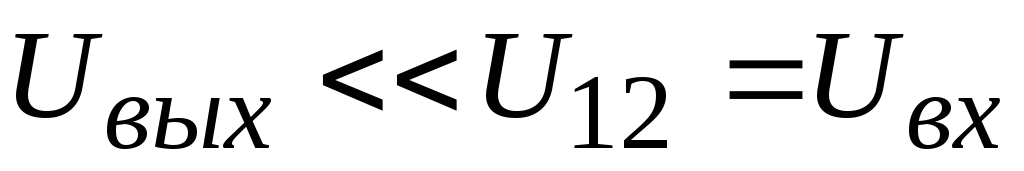 получим:
получим:
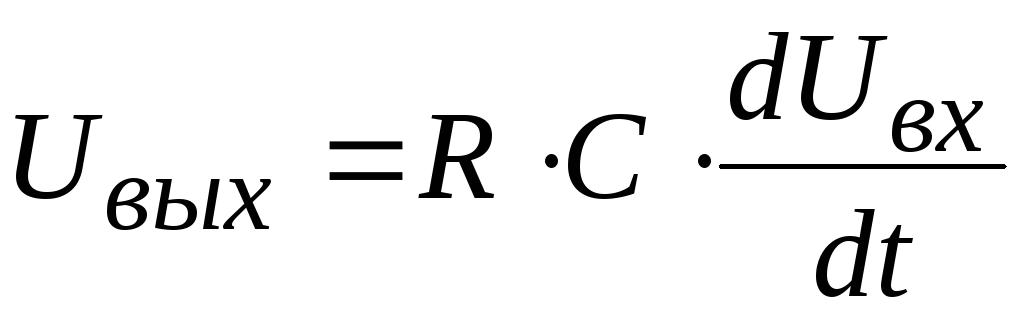 .
.
Значит получена идеальная дифференцирующая цепь. Следовательно для того чтобы цепь была дифференцирующей необходимо выполнение трёх условий:
 ;
; ;
; ;
;
При этом график
напряжения 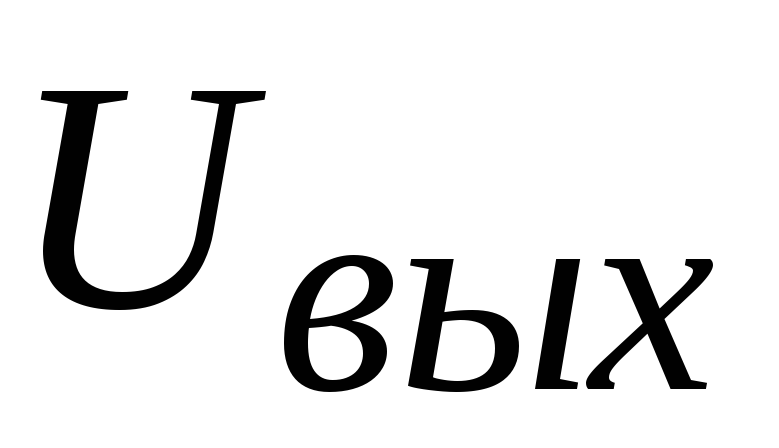 при наличии импульсной последовательности
на входе будет иметь следующий вид
(рис.1.14):
при наличии импульсной последовательности
на входе будет иметь следующий вид
(рис.1.14):
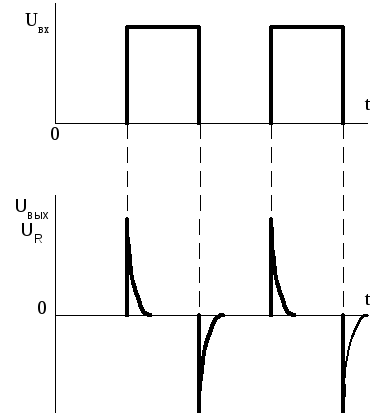
Рис.
1.14 — График напряжения 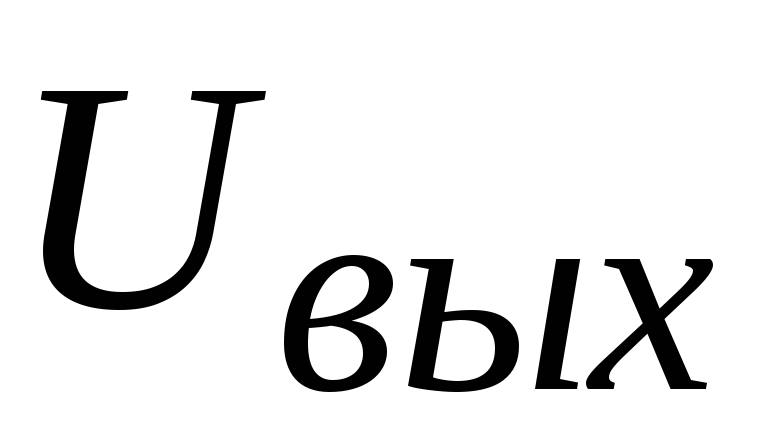 дифференцирующей цепи при наличии
импульсной последовательности на входе.
дифференцирующей цепи при наличии
импульсной последовательности на входе.
Режим I,
вариант б):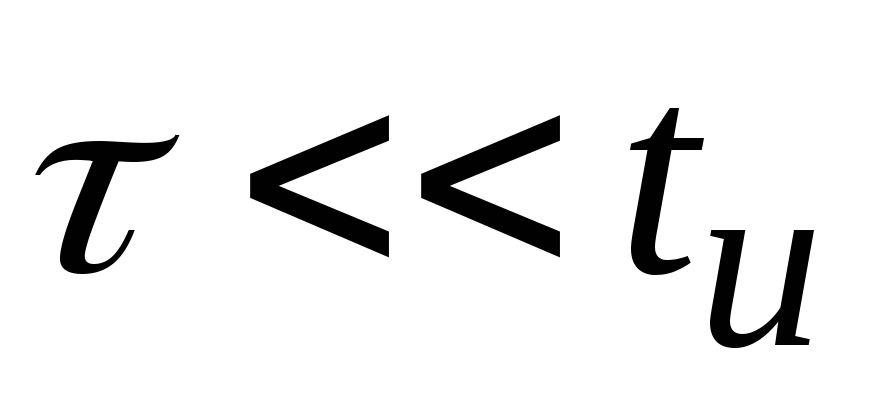 ,
,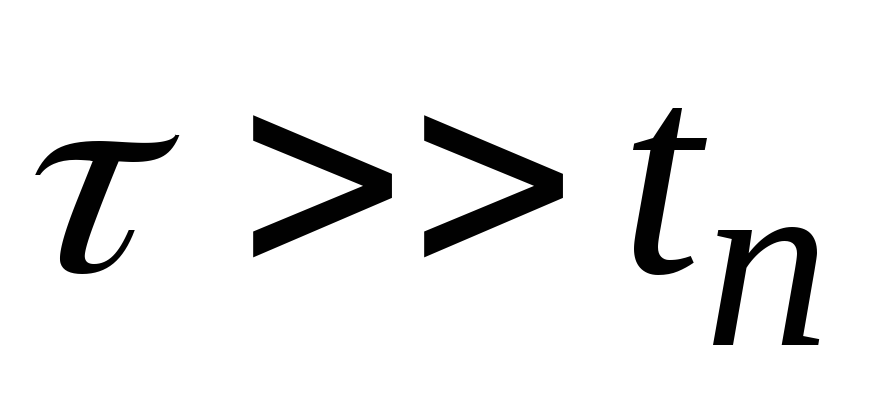 :
:
Графики напряжений 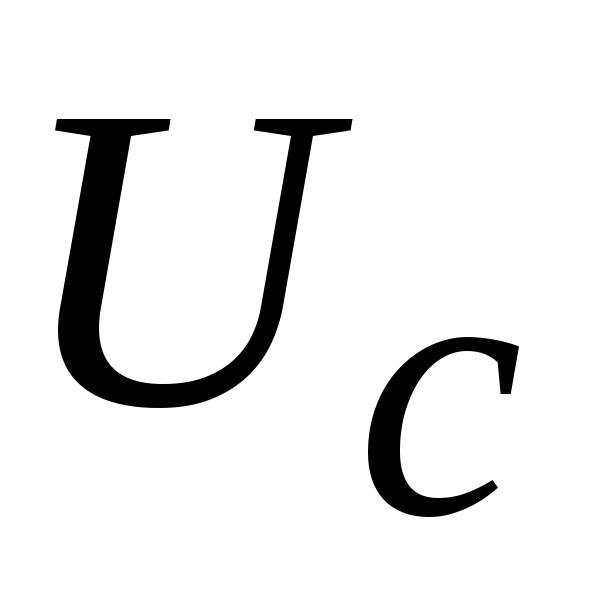 иприведены на рис.1.15. В этом режиме с
момента времени
иприведены на рис.1.15. В этом режиме с
момента времени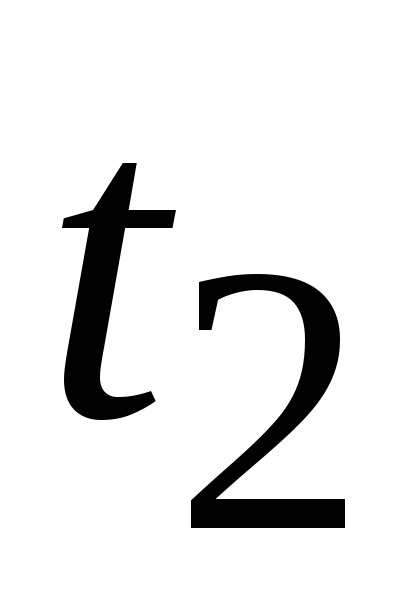 имеют место, в отличие от варианта а),
новые начальные условия
имеют место, в отличие от варианта а),
новые начальные условия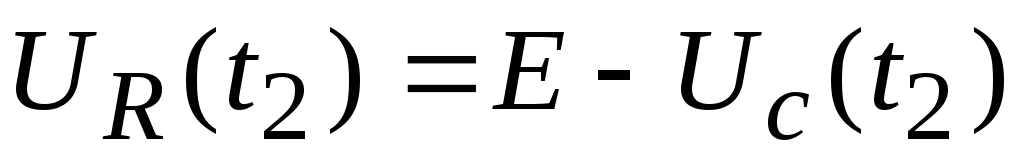 .
Такой режим называют режимом
негармонических возмущений.
.
Такой режим называют режимом
негармонических возмущений.
В период импульса
переходные процессы аналогичны
рассмотренным в варианте а), а в период
паузы конденсатор Сне успевает
разрядиться до нуля за время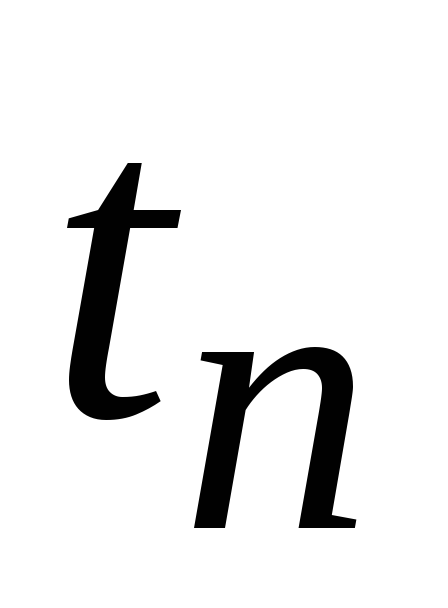 ,
поэтому нулевые начальные условия не
выполняются и для дифференцирующей
цепочки такой вариант неприемлем.
,
поэтому нулевые начальные условия не
выполняются и для дифференцирующей
цепочки такой вариант неприемлем.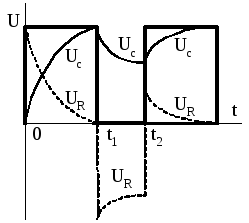
Рис. 1.15
Режим IIпри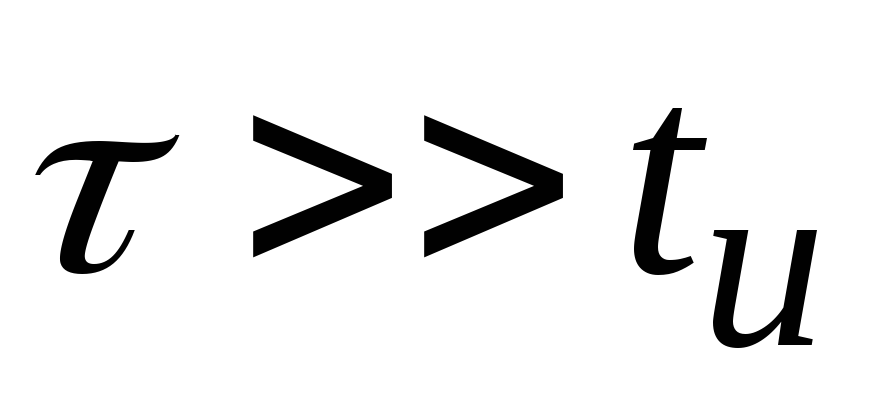 ,
,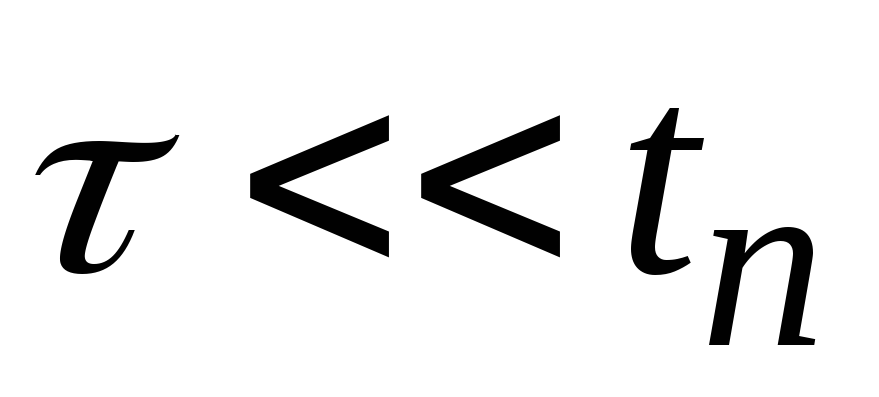 обеспечивает вариант разделительной
цепочки.
обеспечивает вариант разделительной
цепочки.
В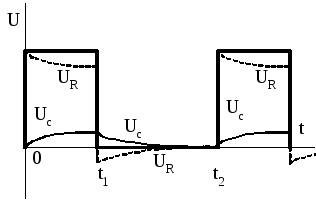 момент времени
момент времени ,
после действия импульса, (см. рис.1.16)
,
после действия импульса, (см. рис.1.16) ,
а в момент времени
,
а в момент времени имеют место нулевые начальные условия.
Сигнал на выходе повторяет сигнал на
входе. Следовательно, такая цепочка
является разделительной
имеют место нулевые начальные условия.
Сигнал на выходе повторяет сигнал на
входе. Следовательно, такая цепочка
является разделительной
Рис. 1.16
Р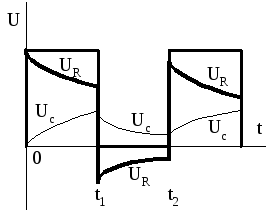 ежимII, при
ежимII, при ,
, ,
аналогичен варианту б) режимаI,
поскольку в момент времени
,
аналогичен варианту б) режимаI,
поскольку в момент времени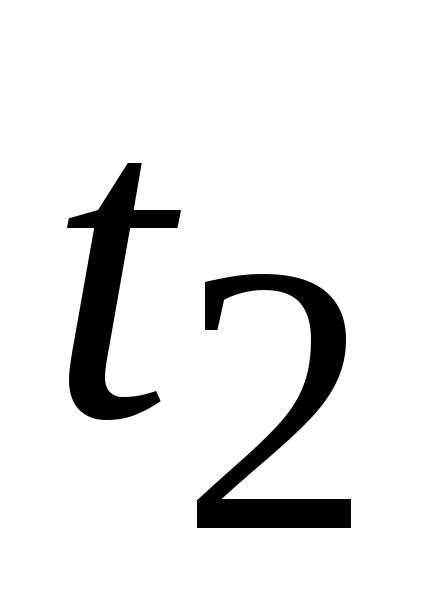 также имеют место новые, ненулевые
начальные условия (рис.1.17) (режим
негармонических возмущений). Для
разделительной цепи такой вариант
неприемлем.
также имеют место новые, ненулевые
начальные условия (рис.1.17) (режим
негармонических возмущений). Для
разделительной цепи такой вариант
неприемлем.
(б)
Рис. 1.17
2.2. Дифференцирующая rc-цепь
Эта цепь, изображенная на рис. 2.5, представляет также последовательное соединение конденсатора и резистора. Только здесь выходное напряжение снимается с резистора, а не с конденсатора, как в предыдущем случае; т. е. оно пропорционально току, который связан с напряжением на конденсаторе соотношением:
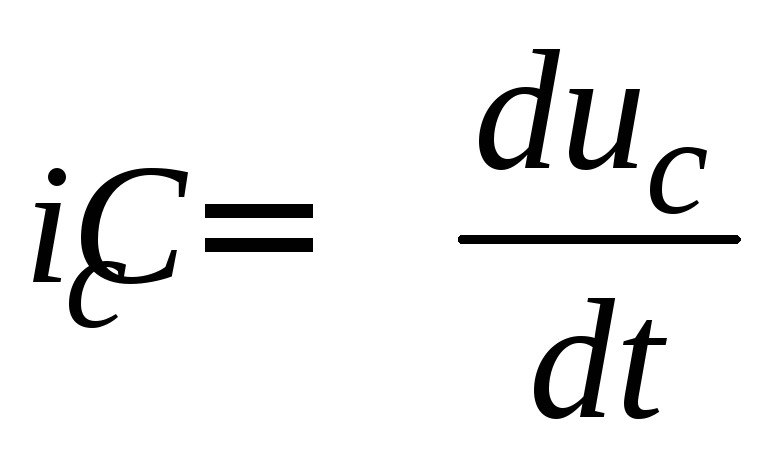
 .
(2.26)
.
(2.26)

Рис. 2.5 Рис. 2.6
Если выбрать величины элементов схемы таким образом, что Uвх >>UC, то общий ток цепи сделается приблизительно равным
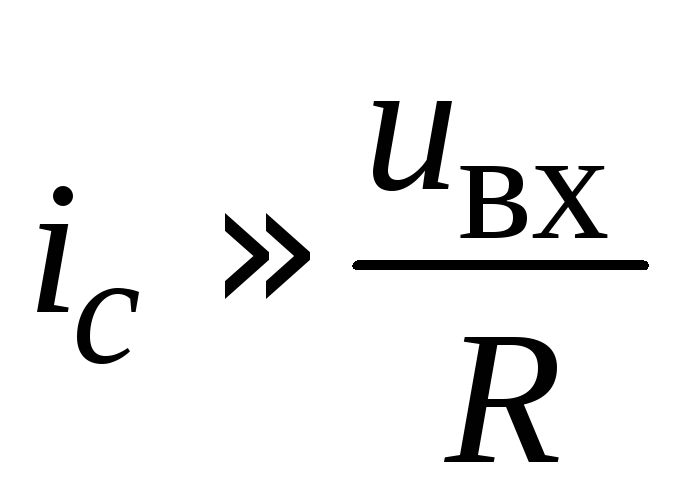 .
(2.27)
.
(2.27)
А это, в свою очередь, означает, что выходное напряжение оказывается пропорциональным производной входного сигнала, что и определяет название цепи. Применительно к гармоническому входному сигналу условие дифференцирования означает обеспечение неравенства
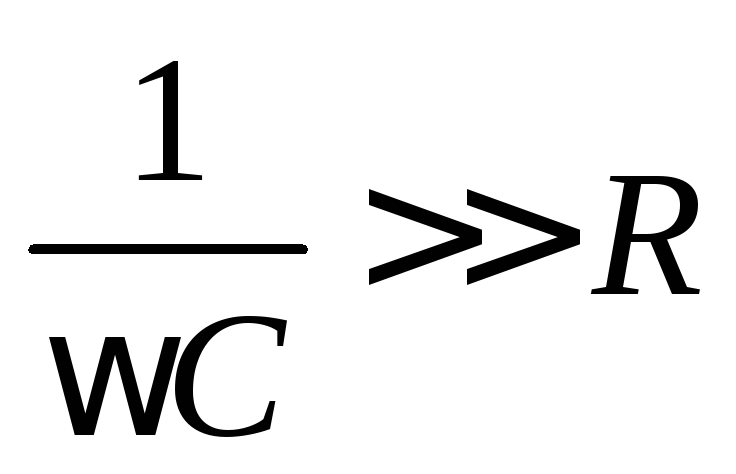 ,
или RC << 1. (2.28)
,
или RC << 1. (2.28)
Если же входной сигнал представляет более сложную функцию, то для операции дифференцирования необходимо выполнить условие дифференцирования для гармоники самой низкой частоты, входящей в состав спектра входного сигнала.
Обратимся теперь непосредственно к анализу переходного процесса в рассматриваемой цепи для ряда входных сигналов.
а) Входной сигнал – скачок напряжения А(t), где (t) – функция включения
Передаточная функция цепи определяется отношением сопротивления Rк входному сопротивлению и имеет следующий вид:
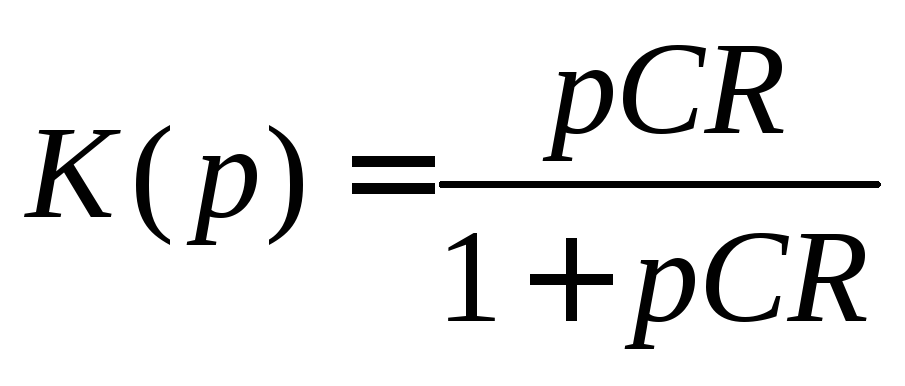 .
(2.29)
.
(2.29)
При подаче импульсного перепада с амплитудой Авыходной сигнал в соответствии с табл. 1 (позиция 2) будет изменяться по закону затухающей экспоненты:
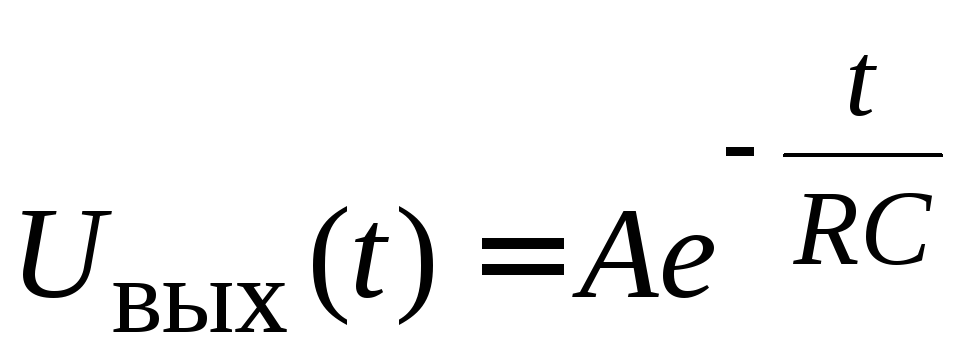 ,
(2.30)
,
(2.30)
принимая максимальное значение при t = 0, как это показано на рис. 2.7. Для определения переходной характеристикиh(t) цепиcледует в уравнении (2.30) положить значениеА = 1.
В некоторый произвольный момент времени tивыходное напряжение уменьшится на величинуUвых, равную:
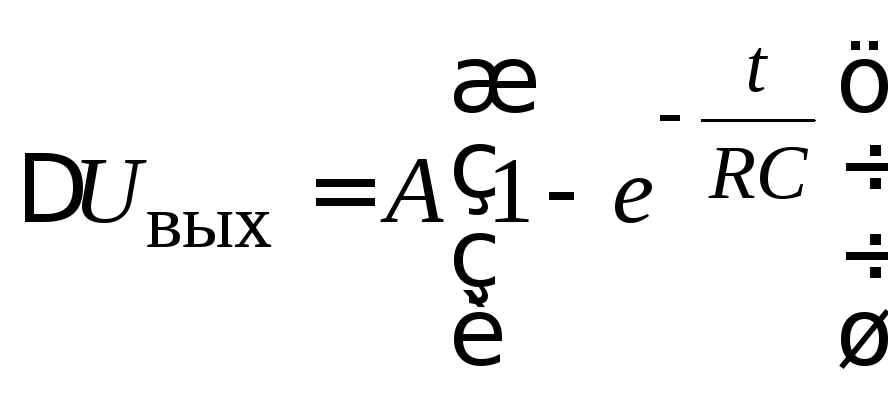 .
(2.31)
.
(2.31)
Отношением 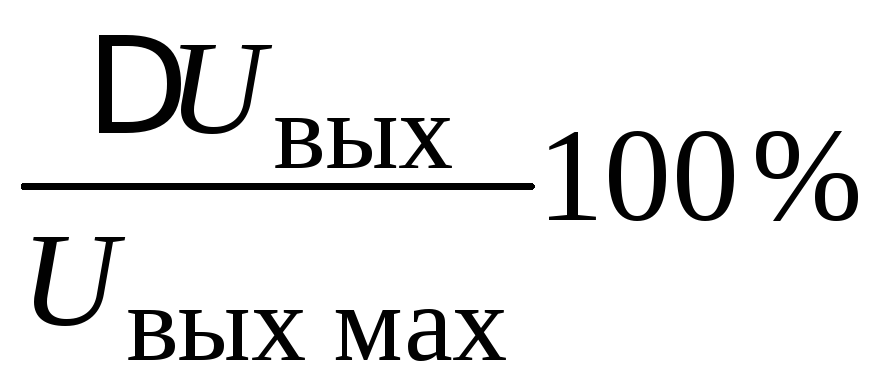 принято характеризовать степень
искажения переходной характеристики
рассматриваемой цепи, что приRC >>tидает
следующий результат:
принято характеризовать степень
искажения переходной характеристики
рассматриваемой цепи, что приRC >>tидает
следующий результат:
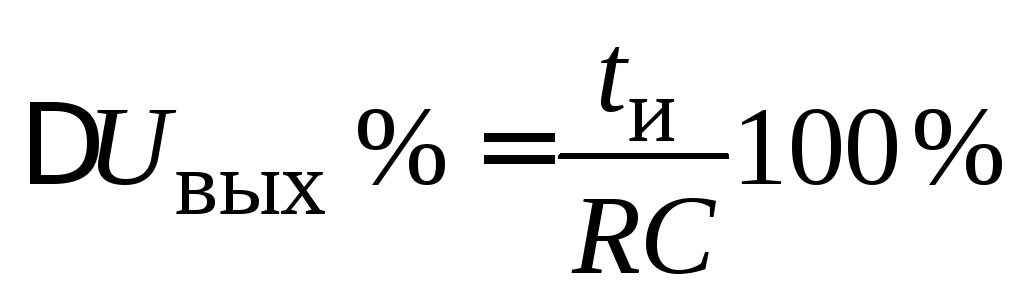 .
(2.32)
.
(2.32)
Полезно вспомнить,
что для этого вида RC-цепи
существует параметр – низшая граничная
частотан =
1/RC, на которой модуль
комплексного коэффициента уменьшается
в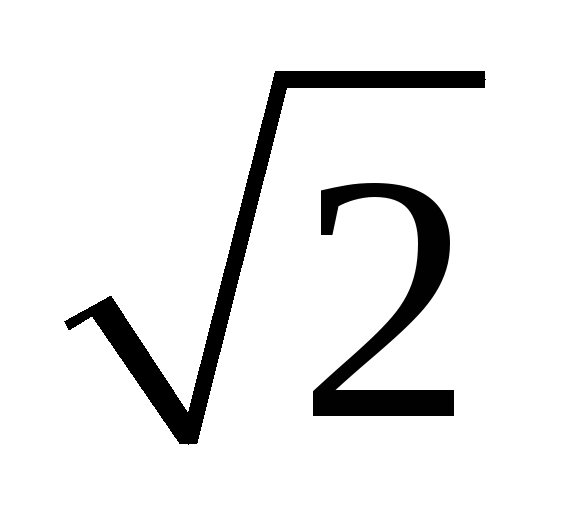 раз
по сравнению с его максимальным значением
на частоте= 0. Легко
убедиться в справедливости равенства:
раз
по сравнению с его максимальным значением
на частоте= 0. Легко
убедиться в справедливости равенства:
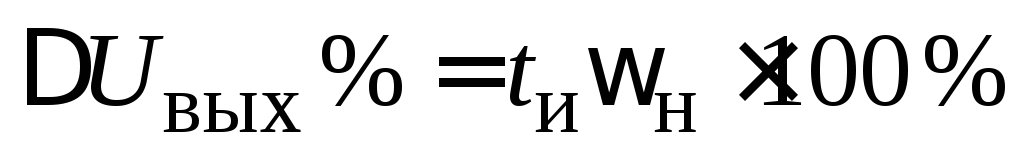 ,
(2.33)
,
(2.33)
что еще раз подчеркивает взаимную связь частотных и временных параметров.
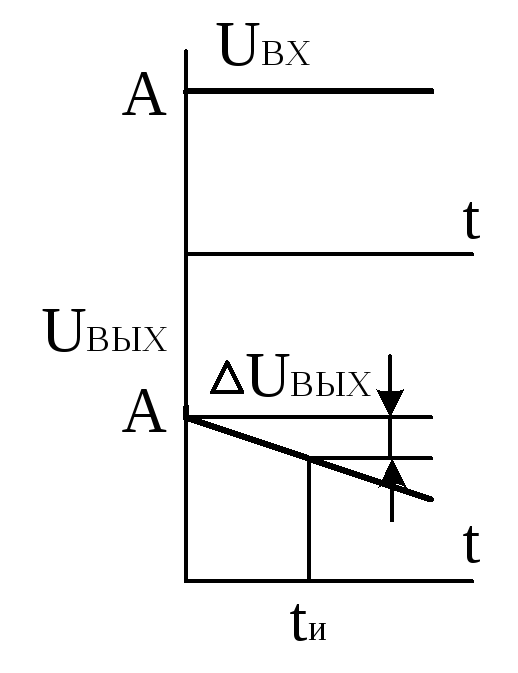
С уменьшением значения постоянной времени цепи =RCcкорость спада выходного напряжения увеличивается и оно приобретает форму затухающего импульсного скачка конечной длительности. Рассмотрим этот процесс при подаче на вход цепи последовательности прямоугольных импульсов.
б) Входной сигнал – последовательность прямоугольных импульсов конечной длительности
По мере поступления входных импульсов происходит постепенное изменение начальных условий заряда и разряда конденсатора, следствием чего является режим, при котором на выходе цепи будет отсутствовать постоянная составляющая входного напряжения, а уровни выходного напряжения в начале и конце периода принимают одинаковое значение. Графики выходного напряжения для этого режима при различных соотношениях между длительностью импульса и постоянной времени приведены на рис. 2.7.
Здесь видно, что при больших значениях RCформа выходных импульсов незначительно отличается от формы входных, и это дает право считать условиеRC >>tиусловием неискаженной передачи импульса через разделительнуюRC-цепь (эта цепь часто используется для того, чтобы постоянная составляющая источника входного сигнала не проходила в нагрузку). УсловиеRC <<tиобеспечивает существенное укорочение длительности выходного импульса, принимает значениеt0 3RC.
Подобное преобразование (или формирование) как раз и отражает важное свойство цепи – способность при определенных условиях реализовать операцию дифференцирования подаваемого на ее вход сигнала.
Р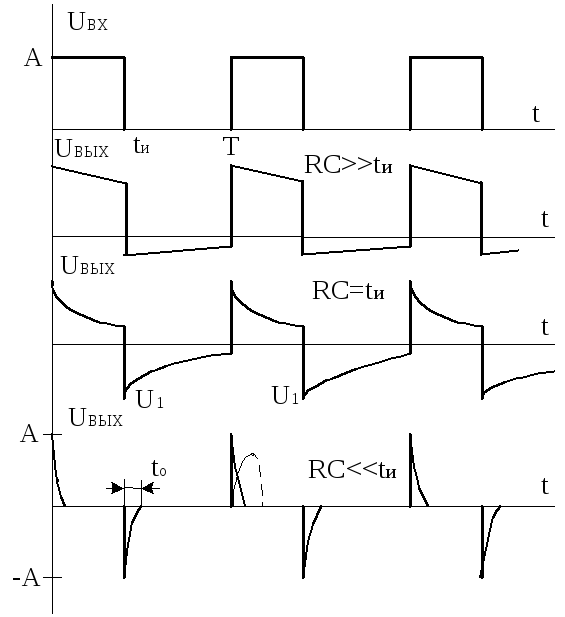 ис.
2.7
ис.
2.7
С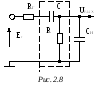 ледует
остановиться на двух основных факторах,
влияющих на свойства рассматриваемой
укорачивающей цепи. В реальной цепи
(рис. 2.8) всегда присутствуют внутреннее
сопротивление источника входного
сигналаRги
емкость нагрузкиСн. Если
имеется только внутреннее сопротивлениеRг, то это приведет
к уменьшению амплитуды импульсного
перепада на выходе и увеличению его
длительности, поскольку возрастает
постоянная времени цепи. Наличие же еще
емкости нагрузки помимо влияния на
амплитуду выходного импульса и его
длительность затягивает фронт нарастания
импульса. В результате форма импульса
делается колоколообразной, как это
показано на рис. 2.7 пунктиром.
ледует
остановиться на двух основных факторах,
влияющих на свойства рассматриваемой
укорачивающей цепи. В реальной цепи
(рис. 2.8) всегда присутствуют внутреннее
сопротивление источника входного
сигналаRги
емкость нагрузкиСн. Если
имеется только внутреннее сопротивлениеRг, то это приведет
к уменьшению амплитуды импульсного
перепада на выходе и увеличению его
длительности, поскольку возрастает
постоянная времени цепи. Наличие же еще
емкости нагрузки помимо влияния на
амплитуду выходного импульса и его
длительность затягивает фронт нарастания
импульса. В результате форма импульса
делается колоколообразной, как это
показано на рис. 2.7 пунктиром.


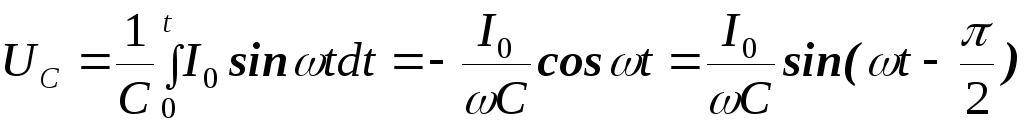 .
.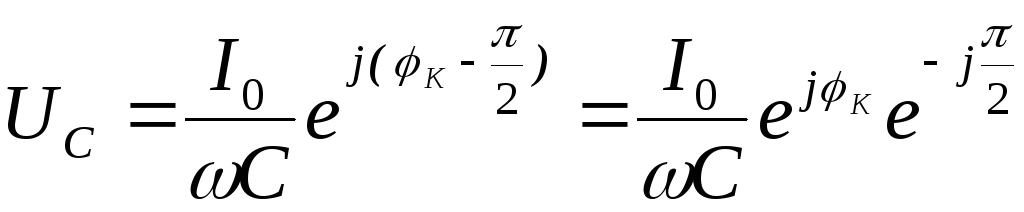 .
.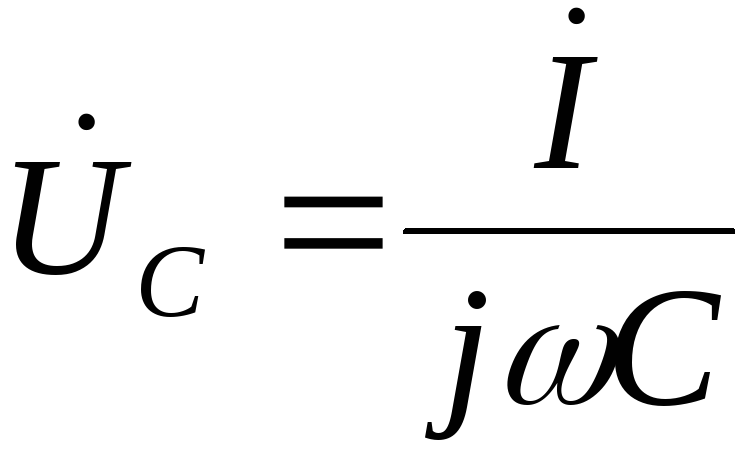 .
.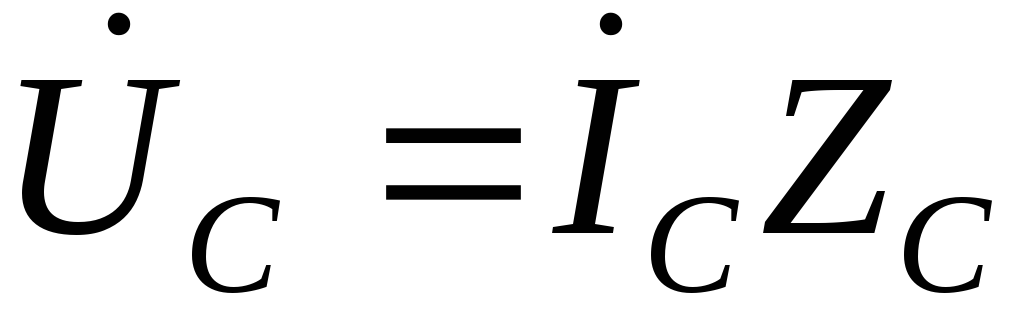 .
.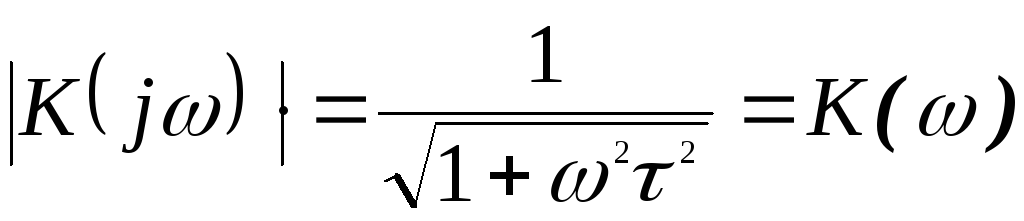 .
.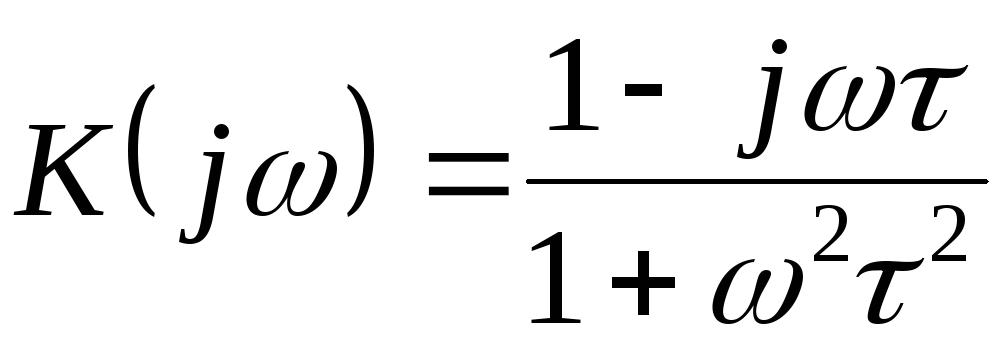 .
.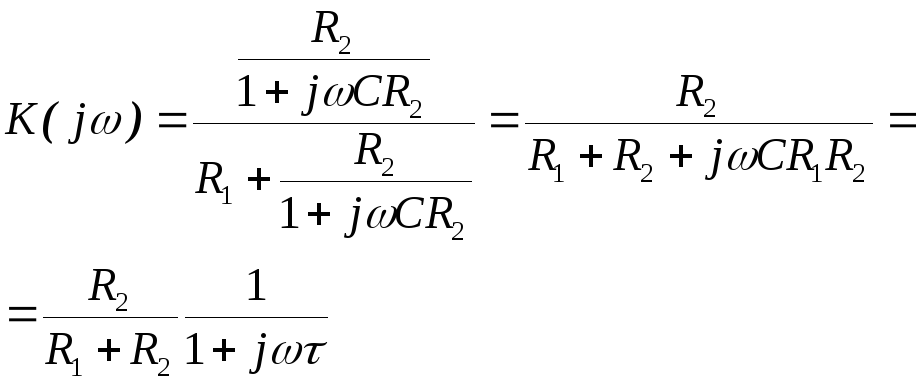 ,
,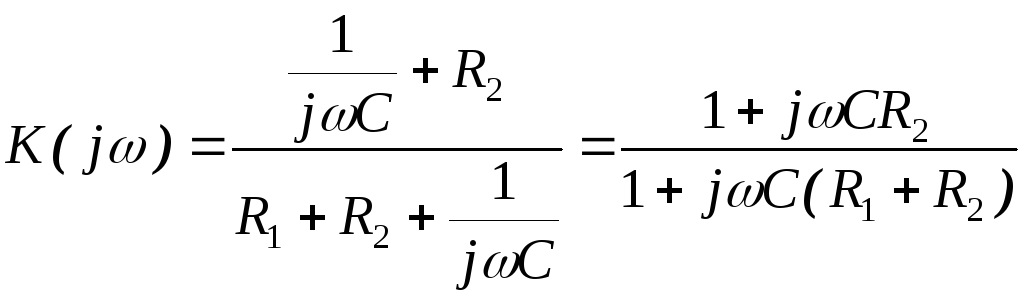 .
.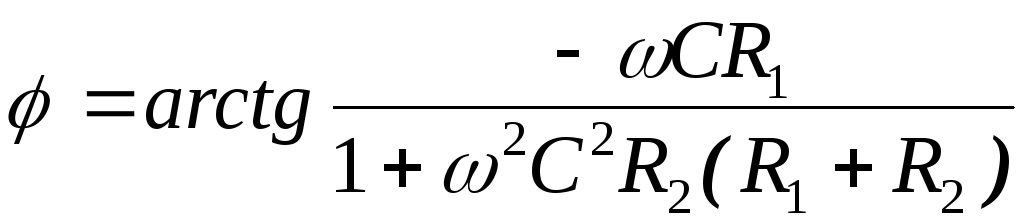 .
.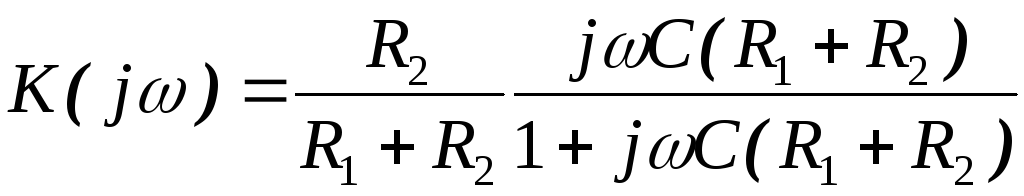 .
.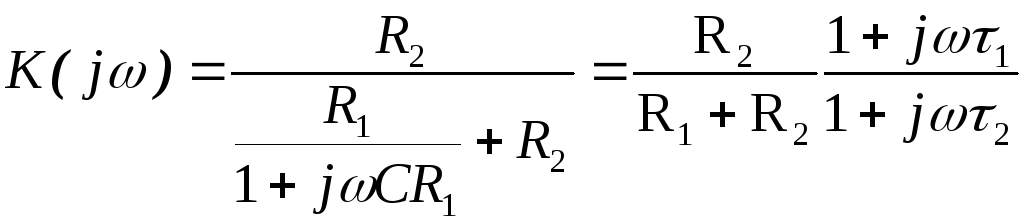 ,
,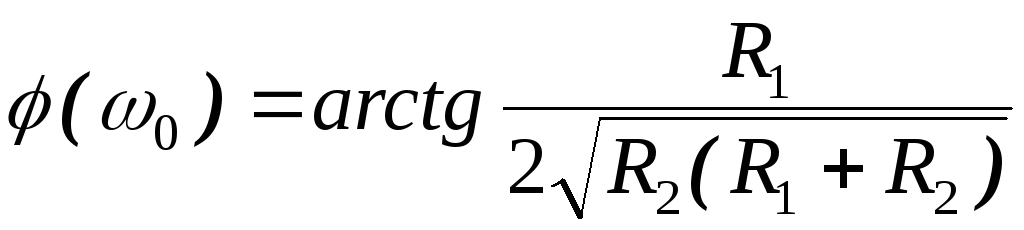 .
.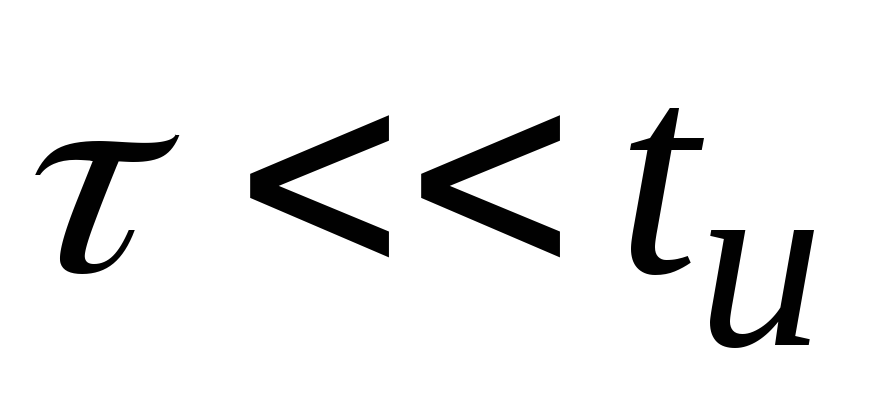 ,
при этом возможны два варианта: а)
,
при этом возможны два варианта: а)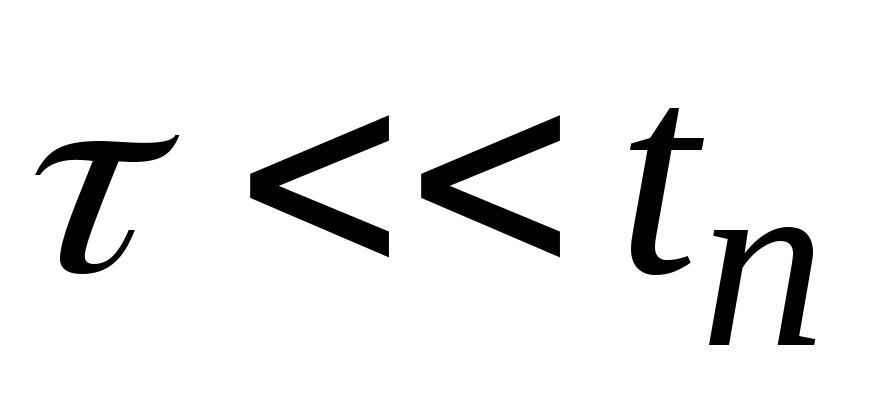 ;
б)
;
б)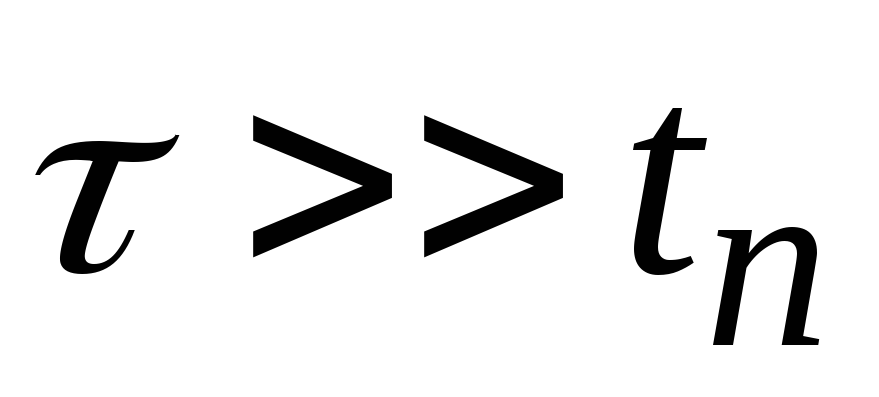 ;
;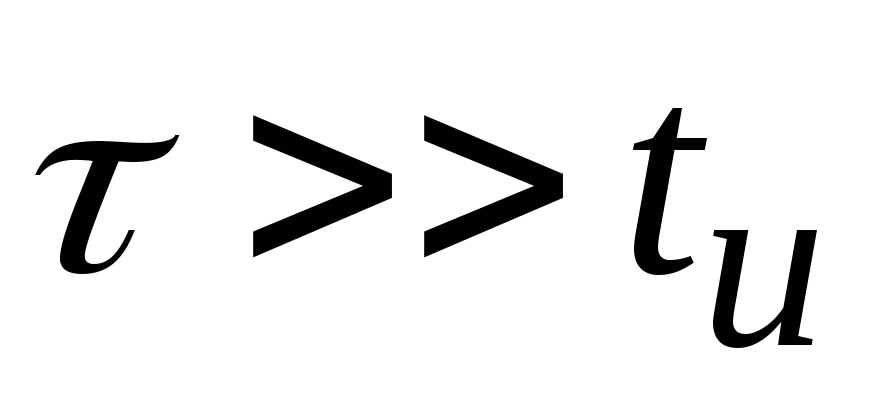 ,
при этом также: а)
,
при этом также: а)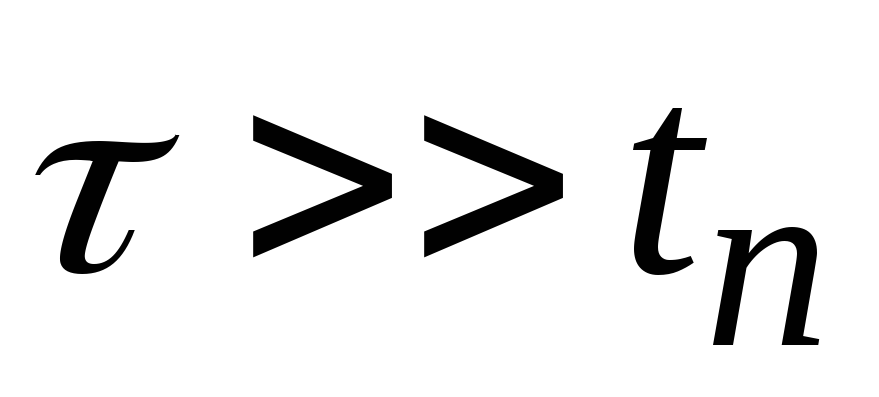 ;
б)
;
б)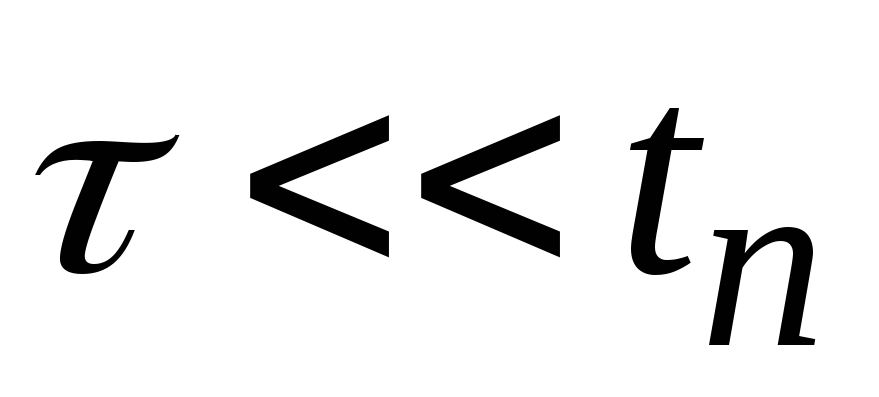 ;
;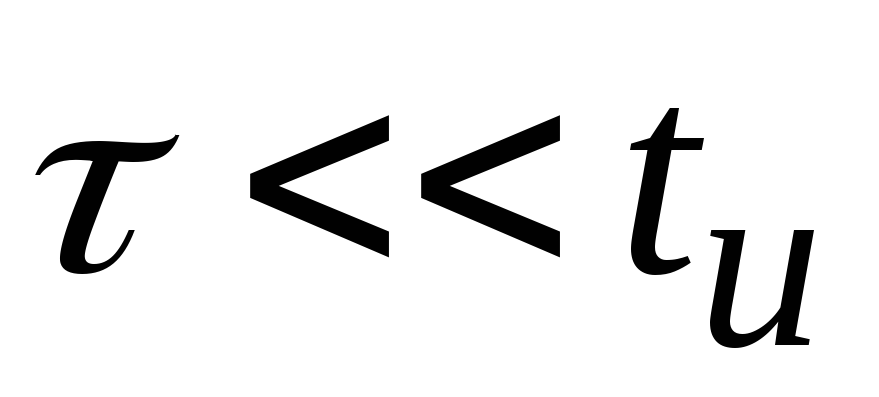 ;
;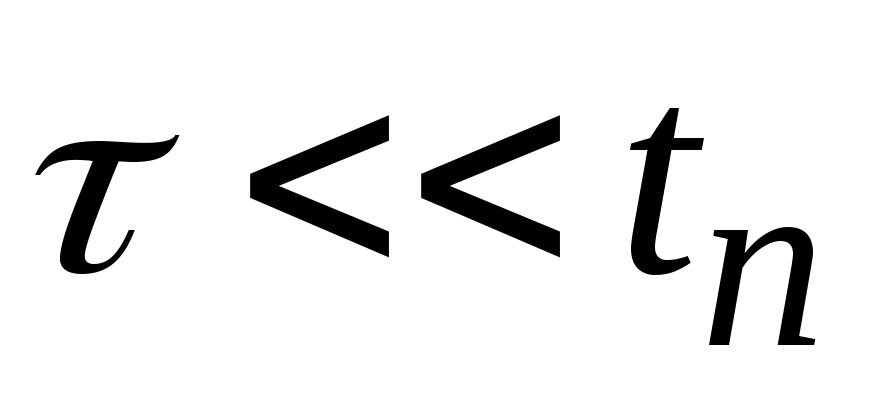 ;
;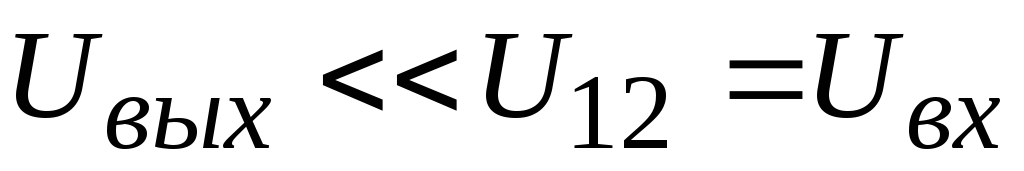 ;
;