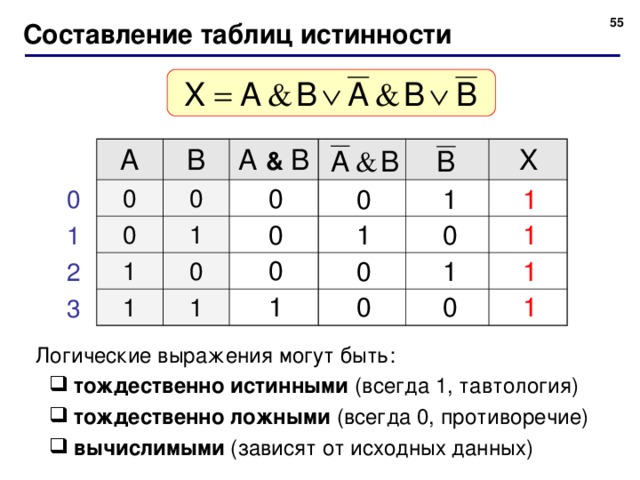
Пусть f функция истинности: Тема 1 Функции алгебры логики — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Тема 1 Функции алгебры логики

1.1 Логические операции

1.2 Булевы функции

Основным объектом дискретной математики являются булевы функции. Предпосылкой их введения служат высказывания, которые составляют основную базу для построения теории булевых функций.

1.1 Логические операции. Алгебра логики – самый простой раздел математической логики. Язык алгебры логики является одним из простейших языков математики. Основными объектами данного раздела являются высказывания. Понятие «высказывание» является первичным, оно не определяется, а поясняется. Под высказыванием понимают предложение, о котором можно сказать одно из двух: истинно оно или ложно. Например, высказывание «2+3=5» – истинное, высказывание «существует действительное число Х такое, что

Х2 = –1» ложное. Очевидно, не каждое предложение является высказыванием. Например, предложения: «Когда ты был дома?», «Пойдем со мной!» не являются высказываниями. Высказывания будем обозначать малыми латинскими буквами

X, y, z,…, а их значения, т.

е. истину и ложь, соответственно 1 и 0. Из двух данных высказываний с помощью связок «не», «и», «или», «если … то», «тогда и только тогда, когда …» можно образовать новые высказывания. Например, из высказываний «число 2 простое», «число 2 четное» с помощью указанных выше связок получаем высказывания «число два простое и четное», «число 2 непростое», «число 2 простое или четное». Высказывание «если π иррационально, то π2 тоже иррационально» получается связыванием двух высказываний связкой «если … то». Эти операции соответствуют упомянутым выше связками, употребляемым в обычной речи.

Рассмотрим примеры логических операций.

1. Логическая операция, соответствующая связке «и», называется

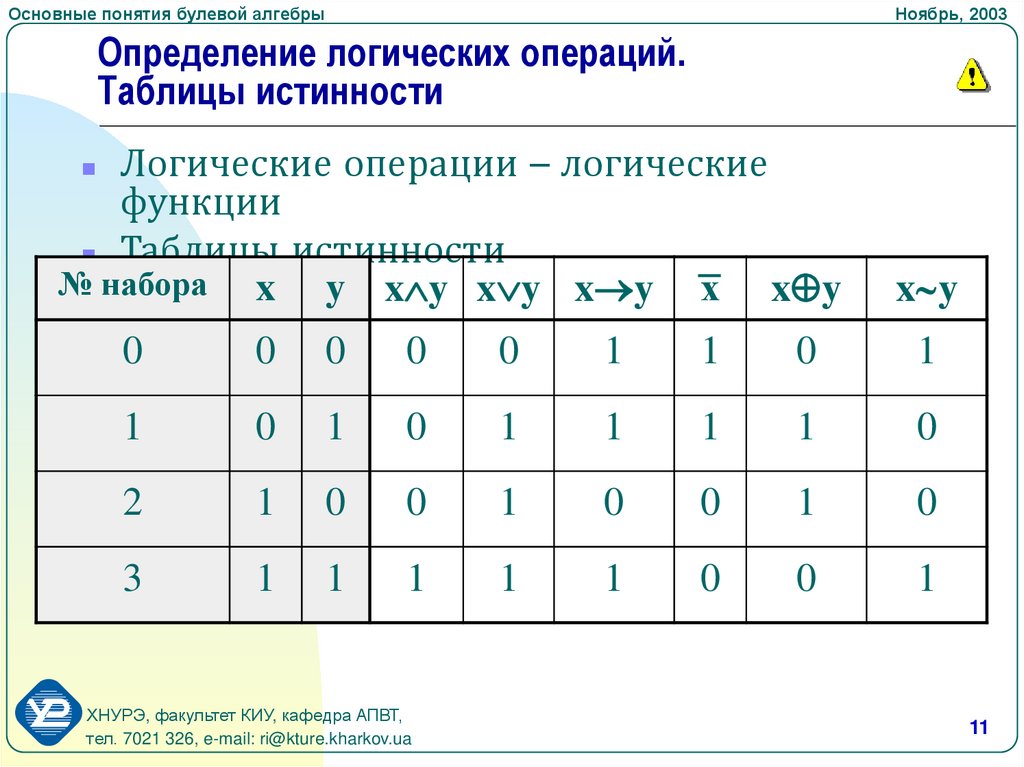
Конъюнкцией и обозначается &. В некоторых книгах эту операцию обозначают символом . Пусть X и y – высказывания. Высказывание X×y назовем конъюнкцией X И Y. Данное высказывание истинно тогда и только тогда, когда истинны оба высказывания X и Y.

Соответствующее определение запишем в виде таблицы истинности

X	Y	Xy
0	0	0
0	1	0
1	0	0
1	1	1

Определение конъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний.

Конъюнкция X1x2…xn, которую мы кратко обозначим через , истинна тогда и только тогда, когда истинны все высказывания.

2. Логическая операция, соответствующая связке «или», называется

Дизъюнкцией и обозначается .

Пусть X и Y – высказывания. Высказывание XÚY назовем дизъюнкцией X и Y. Данное высказывание истинно тогда и только тогда, когда хотя бы одно из высказываний X и Y истинно.

Данное определение запишем в таблицы истинности.

X	Y	XY
0	0	0
0	1	1
1	0	1
1	1	1

Определение дизъюнкции двух высказываний естественным образом распространяется на любое конечное число высказываний. Дизъюнкция X1Ú X2 Ú … Ú XN, которую мы кратко обозначим через , истинна тогда и только тогда, когда хотя бы одно из высказываний X1, X2, …, XN истинно.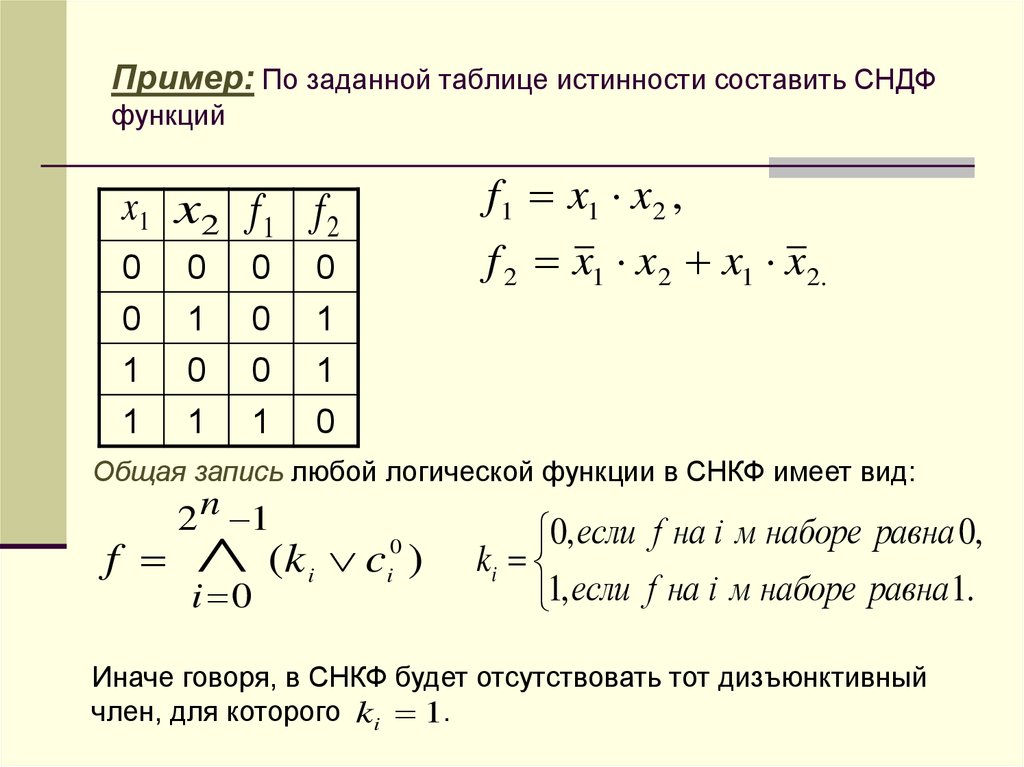

3. Логическая операция, соответствующая связке «не», называется Отрицанием.

Отрицание высказывания X записывается так: и определяется следующей таблицей истинности:

X
0	1
1	0

4. Логическая операция, соответствующая связке «если … то», называется Импликацией. Эту операцию будем обозначать символом _. При этом высказывание «если X, то Y» записывается в виде x_Y. Высказывание

X называется посылкой импликации, Y – ее заключением. Импликация двух высказываний X и Y задается следующей таблицей истинности:

X	Y	X_Y
0	0	1
0	1	1
1	0	0
1	1	1

Из определения импликации вытекает, что:

· импликация с ложной посылкой всегда истинна;

· импликация с истинным заключением всегда истинна;

· импликация ложна тогда и только тогда, когда посылка истинна, а заключение ложно.

5. Логическая операция, соответствующая связке «тогда и только тогда, когда …» называется Эквивалентностью и обозначается символом n.

Пусть X и Y – высказывания. Высказывание XNY назовем эквивалентностью X и Y. Данное высказывание истинно тогда и только тогда, когда оба высказывания

X и Y или истинны или ложны.

Данное определение запишем в виде таблицы истинности:

X	Y	XNY
0	0	1
0	1	0
1	0	0
1	1	1

1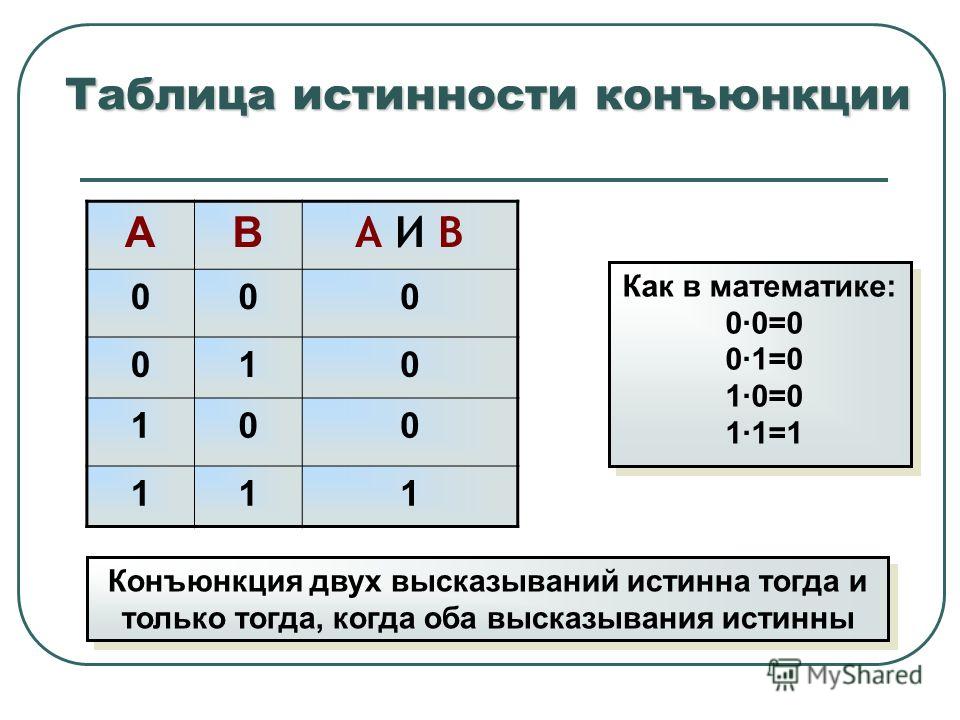. 2 Булевы функции. Пусть исходный алфавит переменных.

Функцией алгебры логики От переменных называется функция, принимающая значения 1, 0 и аргументы которой также принимают значения 1, 0.

Обычно функции алгебры логики называют булевыми функциями. Название «булевы функции» возникло в связи с использованием функций рассматриваемого типа в алгебре логики, начало которой было положено трудами ирландского ученого 19 века Дж. Буля. Областью определения булевой функции от n переменных служат совокупность всевозможных n-мерных упорядоченных наборов , где .

Следует отметить, что любой такой набор можно рассматривать как представление некоторого целого неотрицательного числа в двоичной системе счисления. Например, набору (0,1,0,1) соответствует число , а набору (1,1,1) – число .

Все наборы размерности n нумеруются целыми числами от 0,2n-1. Отсюда нетрудно заметить, что число таких наборов равно 2n.

Всякая булева функция от n переменных может быть задана с помощью таблицы истинности:

Таблица 1

X1	X2	…	XN-1	XN	F(X1,X2,…,XN-1,XN)
0	0	…	0	0	F (0,0,…,0,0)
0	0	…	0	1	F (0,0,…,0,1)
0	0	…	1	0	F (0,0,…,1,0)
…	…	…	…	…	…
1	1	…	1	1	F (1,1,…,1,1)

Данная таблица состоит из 2n строк, причем в ней все наборы расположены в порядке возрастания их номеров.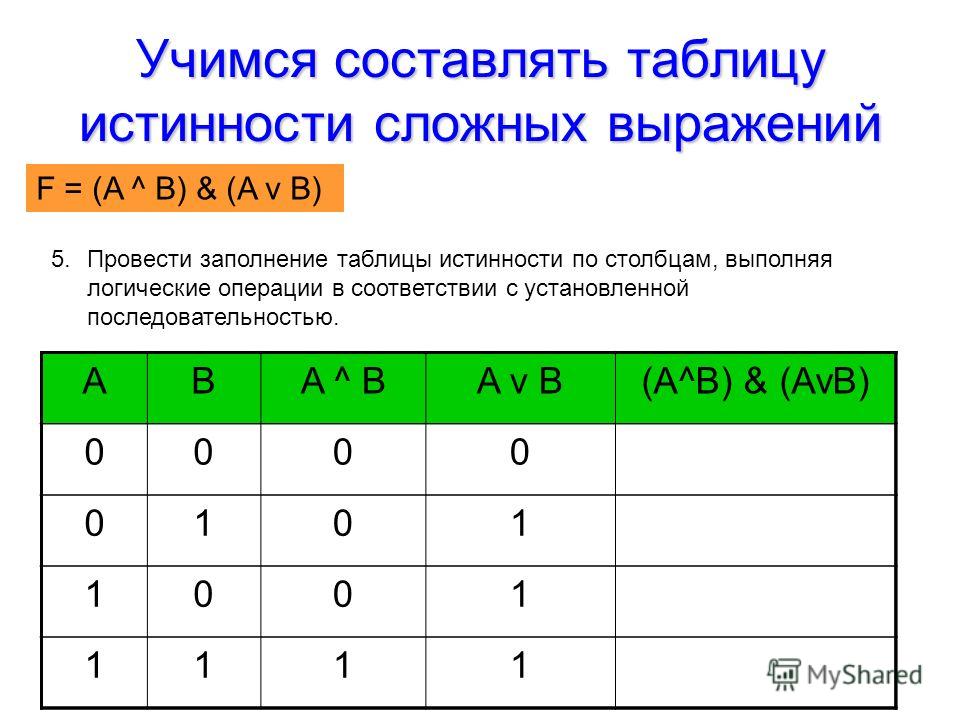

Очевидно, что булевы функции от n переменных однозначно определяются своими последними столбцами из таблицы 1, т. е. наборами из 2n нулей и единиц. Следовательно, различных булевых функций от n переменных будет столько, сколько имеется различных наборов длины 2n, а их число равно . Итак, мы доказали следующую теорему:

Теорема 1. Имеется точно Булевых функций от Переменных.

В алгебре логики особое значение имеют следующие булевы функции, которые называют элементарными булевыми функциями.

— константа 0;

— константа 1;

— тождественная функция;

— отрицание х;

— конъюнкция X и y;

— дизъюнкция х и у;

— импликация х и у;

— эквивалентность х и у;

— сложение х и у по mod2;

— функция Шеффера;

— стрелка Пирса.

Последние три функции задаются следующими таблицами истинности:


0	0	0	1	1
0	1	1	1	0
1	0	1	1	0
1	1	0	0	0

Введенное понятие булевой функции несовершенно тем, что оно не позволяет рассматривать функцию от меньшего числа аргументов как функцию от большего числа аргументов.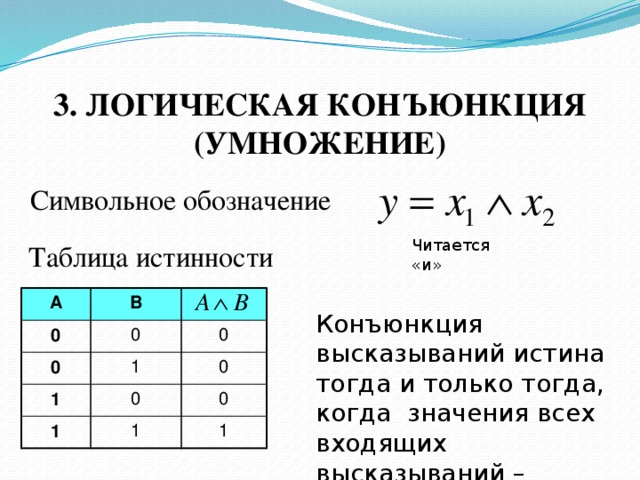 Для устранения этого недостатка введем понятие фиктивной переменной.

Переменная XI в функции называется Фиктивной, если = при любых значениях остальных переменных. В этом случае функция , по существу, зависит от (n-1) – переменной, т. е. представляет собой функцию от (n-1) переменной. Говорят, что функция g получается из функции f удалением фиктивной переменной, а функция f получается из g введение фиктивной переменной, причем эти функции являются равными.

Благодаря введению фиктивных переменных любую булеву функцию от Переменных можно считать функцией от любого большего числа переменных. Поэтому любую конечную совокупность булевых функций можно считать зависящими от одного и того же числа переменных.

< Предыдущая		Следующая >

Страница не найдена | АКВТ

Запрошенную информацию найти не удалось. Возможно, будет полезен поиск по сайту или приведённые ниже ссылки.

Не нашли то, что искали?

Страницы

QR код для оказания благотворительной помощи колледжу
Безопасный Интернет
Виртуальный тур
- Фотогалерея
  - «Мы — Добровольцы!»
  - АКВТ на Дне Победы!
  - АКВТ на митинг-концерте, посвященном Крымской весне
  - Вручение дипломов 2016
  - Встречаем Олимпийский огонь
  - День народного единства 2015
  - День народного единства 2017
  - День Открытых дверей 2015
  - День Открытых Дверей 2016
  - День открытых дверей в АКВТ 2017
  - КРЫМ! Мы с тобой!
  - Мы — добровольцы 2016!
  - Награждение победителей фестиваля «Мисс Зимнее Очарование»
  - Новогодний концерт «АКВТ в Джунглях»
  - Празднование Масленицы 2016
  - Прогноз безопасности в АКВТ!
  - Студенты АКВТ и члены военно-патриотического клуба «Покров» на масленичных забавах
  - Торжественное открытие мемориала «Журавли»
  - Торжественный митинг (Хулхута)
  - Фестиваль «Мисс Зимнее Очарование»
  - Фестиваль студенческой науки 2016
  - Шарик Радости
  - Ярмарка вакансий 2016
Все новости
Дистанционное обучение
Информационная безопасность
Курс «Основы web-дизайна»
Курс «Основы компьютерной грамотности. Комплексная программа»
Курс «Основы разработки web-сайта»
Министерство образования и науки Российской Федерации
Обратная связь
Обращения граждан
Партнеры
- Служба содействия трудоустройству выпускников
Политика в отношении обработки персональных данных
Поступающим
- Приемная кампания 2022
  - Подача документов онлайн
  - Подача документов через операторов почтовой связи
- Обращение директора
- Реализуемые специальности
- Правила приёма
- Контрольные цифры приема на 2022 год
- Количество поданных заявлений
- Информирование поступающих
- Заявление
- Информация о результатах приема по каждой профессии, специальности среднего профессионального образования
- Приказы о зачислении
- Информация о дополнительном наборе
- Платное обучение
- Общежитие
- Подготовительные курсы
  - Заявка на поступление на подготовительные курсы
- Схема проезда
- Горячая линия по вопросам приема, в том числе для лиц с ОВЗ и инвалидов
- Горячая линия Минобрнауки
- Information for Foreign Citizens (Training of foreign citizens)
- Обучение иностранных граждан
Предупреждение распространения коронавирусной инфекции
- Профилактика новой коронавирусной инфекции COVID-19
Преподавателям
- График учебного процесса
- Расписание занятий
  - График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
  - Расписание занятий для студентов заочного отделения
- Оформление документации
  - Преподавателю
  - Заведующему кабинетом/лабораторией
  - Куратору
  - Руководителю курсового/дипломного проектирования
- Аттестация преподавателей
- Нормативные документы, регламентирующие деятельность преподавателей
- Конкурсы
  - Всероссийский конкурс социально рекламы в области формирования культуры здорового и безопасного образа жизни «СТИЛЬ ЖИЗНИ — ЗДОРОВЬЕ! 2020»
- Полезные вкладки
Родителям
- Методические материалы для родителей и классных руководителей по здоровому образу жизни
- О чем молчит подросток
- Отцовство — твой главный жизненный проект
Сведения об образовательной организации
- Герои Великой Победы в миниатюре
  - Диорама 1 «Полундра!»
  - Диорама 2 «Полигон»
  - Диорама 3 «Операция «Уран»
  - Диорама 4 «Тигры перед боем»
  - Диорама 5 «Герои Белостока»
  - Диорама 6 «Школьник Свердловска»
- Международное сотрудничество
- Наставничество
- Основные сведения
- Студенческий спортивный клуб СПО
- Федеральный проект «Молодые профессионалы»
  - Аттестаты о присвоении статуса центра проведения демонстрационного экзамена
  - Банк фотоматериалов
  - Графики работы мастерских
  - Дизайн-проект мастерских
  - Дополнительное профессиональное образование
  - Дополнительные образовательные программы
  - Локальные акты по проекту
  - Программы повышения квалификации
  - Программы профессиональной переподготовки
  - Профессиональное обучение
  - Ссылки на репортажи, публикации в СМИ
- Часто задаваемые вопросы
- Структура и органы управления колледжем
- Документы
  - Антимонопольный комплаенс
  - Нормативные акты Министерства образования и науки Астраханской области
  - Устав колледжа
  - Лицензия на осуществление образовательной деятельности
  - Cвидетельство о государственной аккредитации
  - Локальные нормативные акты
    - Документы, регламентирующие деятельность колледжа в целом
    - Документы, регламентирующие образовательную и воспитательную деятельность
    - Проекты документов
    - Единый план работы колледжа
  - Отчет о результатах самообследования
  - Документ о порядке оказания платных образовательных услуг
  - Предписания органов, осуществляющих государственный контроль в сфере образования
  - Установление размера платы, взимаемой с родителей за присмотр и уход за детьми
- Руководство. Педагогический (научно-педагогический) состав
- Образование
  - Информация о реализуемых образовательных программах
  - Основные профессиональные образовательные программы
  - Календарный учебный график
  - Численность обучающихся по реализуемым образовательным программам
  - Язык, на котором осуществляется образование
  - Информация о результатах приема, перевода, восстановления и отчисления студентов
  - Направления и результаты научно-исследовательской деятельности
- Образовательные стандарты
- Материально-техническое обеспечение и оснащенность образовательного процесса
- Стипендии и меры поддержки обучающихся
- Платные образовательные услуги
- Финансово-хозяйственная деятельность
- Вакантные места для приема (перевода) обучающихся
- Противодействие коррупции
- Доступная среда. Организация получения образования студентами с ОВЗ
- Информация по защите прав обучающихся
Студентам
- Кружки, секции и студии АКВТ
- Студенческое самоуправление
  - Волонтерское движение АКВТ
  - Студенческая газета «Студ&ты»
- График учебного процесса
- Расписание занятий
  - График консультаций для студентов заочного отделения 2 семестр 2018-2019 учебного года
  - Расписание занятий для студентов заочного отделения
- Учебно-методические материалы
  - Компьютерные системы и комплексы
  - Программирование в компьютерных системах
  - Сетевое и системное администрирование
  - Информационные системы и программирование
  - Информационная безопасность автоматизированных систем
  - Обеспечение информационной безопасности автоматизированных систем
  - Техническая эксплуатация и обслуживание электрического и электромеханического оборудования
  - Автоматизация технологических процессов и производств
  - Оснащение средствами автоматизации технологических процессов и производств
  - Специальности НПО
  - Заочное
- Государственная Итоговая Аттестация
- Трудоустройство
- Сдать ЕГЭ
- Библиотека
  - Библиотека сегодня
  - Информационные ресурсы свободного доступа
  - Электронно-библиотечная система
  - Доска объявлений библиотеки
- Полезные вкладки
  - 8 мифов о наркотиках
  - «Народная дружина города Астрахани»
  - Ловушки для пешеходов
  - Противодействие терроризму

Записи

Анонс
- АНОНС. Международная акция «Тест по истории Великой Отечественной войны»
- АНОНС. О проведении VI Международной просветительской акции «Большой этнографический диктант-2021»
- Профессионально-техническому образованию посвящается…
- Объявление по собраниям для студентов нового набора
Новости
- Пушкинская карта
- Кибербезопасность
- Учебно-поисковая экспедиция, посвященная 80-годовщине третьего формирования на территории Астрахани 28-Армии
- Региональная научно-практическая конференция «МЕДИАЦИЯ КАК АЛЬТЕРНАТИВА КОНФРОНТАЦИИ»
- Конкурс чтецов
- Поздравления Президенту РФ
- Праздничный концерт, посвящённый Дню учителя и Дню среднего профессионального образования
- 30-ые Всероссийские соревнования по судомодельному спорту в классах гоночных управляемых яхт «Нижневолжская регата»
- Внимание, опрос!
- Всероссийский день ходьбы
- Презентация проектов РСМ
- Профилактика ПАВ
- Преподаватель Астраханского колледжа вычислительной техники представит Астраханскую область на всероссийском конкурсе «Мастер года — 2022»
- Профилактика преступлений в сфере незаконного оборота наркотиков
- День среднего профессионального образования
- Подготовительный этап VIII Национального чемпионата профессионального мастерства «Абилимпикс»
- Профилактика употребления ПАВ
- Легкоатлетическая эстафета посвященная «Дню города»
- Торжественное мероприятие, в поддержку референдумов о присоединении Донбасса к России
- Всероссийская Неделя безопасности дорожного движения
- 2 октября в России отмечают День профессионально-технического образования
- Митинг-возложение памяти героям 28 Армии
- Полуфинал Всероссийского конкурса «Большая перемена»
- Соревнования по легкой атлетике «Кросс наций»
- Студент АКВТ принял участие в федеральном Просветительском марафоне «Знание»
- Разговоры о важном
- ГБПОУ АО «АКВТ» проводит дополнительный набор
- Каспийский молодёжный образовательный форум «СЕЛИАС»
- «Поделись своим знанием»
- Мастер года 2022
- Всероссийская акция «Поделись своим знанием»
- День знаний 2022!
- Лекция-беседа на тему «Профилактика терроризма и экстремизма в молодёжной среде»
- Праздничные мероприятия 1 сентября 2022 года
- Федеральный марафон «Знание»
- Объявление по собраниям для студентов нового набора
- День Государственного флага Российской Федерации
- Запущена регистрация на Всероссийскую медиашколу «Без срока давности 3. 0» для студентов педагогических вузов и педагогических работников сферы гражданско-патриотического воспитания
- Курсы для школьников «Погружение в специальность»
- Вручение дипломов выпускникам 2022 года!
- Демонстрационный экзамен в соответствии со стандартами Worldskills Russia
- Великий государь великого государства: 350-летие со дня рождения Петра I
- Вместе — ЗА здоровье нации!
- Линейка памяти и скорби
- Открытие мемориальной доски генерал-полковнику Тутаринову Ивану Васильевичу
- XV Международный конкурс ВКР с использованием программных продуктов 1С
- Студент 1 курса АКВТ в составе археологической экспедиции принял участие в «Вахте памяти»
- День России!
- Студенты АКВТ на областной конференции «IT-технологии XXI века: вызовы, становление, развитие»
- Студенты АКВТ на финале Всероссийских просветительских игр
- «Цени своё здоровье»
- Стань Студентом года — 2022!
- Памятка «Безопасность детства»
- V Региональный чемпионат профессионального мастерства «Абилимпикс»
- Итоги областной олимпиады по информатике!
- Городская легкоатлетическая эстафета посвящённая Дню победы
- Военная академия воздушно-космической обороны
- День Победы!
- Праздничный концерт «День Победы»
- ГОРЯЧАЯ ЛИНИЯ В СИСТЕМЕ СПО НА БАЗЕ МИНИСТЕРСТВА ОБРАЗОВАНИЯ И НАУКИ АСТРАХАНСКОЙ ОБЛАСТИ
- Как провести майские праздники вместе с Пушкинской картой
- Праздник Весны и Труда
- Субботник в АКВТ
- Финал по подтягиваниям «Я-Чемпион»
- Спартакиада ПОО среди учащихся по стритболу
- Областная практическая конференция по дисциплинам ОБЖ, БЖ «Астраханская область территория безопасности»
- Акция «Чистые игры»
- Полуфинальный этап соревнований по подтягиваниям «Я-Чемпион»
- Товарищеская игра по мини-футболу
- Интерактивная лекция «Здоровый образ жизни»
- Марафон «Новые горизонты»
- День открытых дверей!
- Турнир по мини-футболу на кубок «Дружбы народов»
- День открытых дверей в АКВТ
- День здоровья в стенах АКВТ!
- Патриотическая акция, посвященная восьмилетию со дня провозглашения Донецкой Народной Республики
- Родительские собрания в группах 1-3 курсов
- Итоги отборочного тура олимпиады по информатике!
- Первенство студенческой лиги по пулевой стрельбе из пневматического оружия
- Агрегатор профориентационных возможностей
- «Всероссийский урок добровольчества»
- Встреча с ветеранами боевых действий
- День открытых дверей
- Профориентационный проект «Загляни за горизонт»
- Акция «Сообщи, где торгуют смертью»
- Областной профориентационный форум «Топ профессий на селе»
- Без срока давности
- Профилактика заболевания туберкулезом
- День открытых дверей в АКВТ 2022
- Методическое объединение преподавателей ССУзов Астраханской области
- Праздничный концерт под девизом «Zа Мир! Zа Россию! Zа Президента!»
- Встреча с представителем Областного центра крови
- Начни свой путь из кандидата в бойцы студенческих отрядов!
- Встреча студентов с медицинским психологом
- Реализация программы «Пушкинская карта»
- С праздником прекрасная половина Астраханского колледжа вычислительной техники!
- С Международным женским днем!
- #МЫВМЕСТЕ
- Соревнования по стрельбе из пневматической винтовки
- «В Питере — учиться»
- Осторожно мошенники!!!
- Спартакиада учащихся ПОО по настольному теннису
- Школа бизнеса «Точка роста»
- Поздравляем с 23 февраля! С Днем защитника Отечества!
- Студент АКВТ награжден дипломом победителя Кубка России по судомодельному спорту
- Презентация РСМ
- С Днем защитника Отечества!
- Турнир по DOTA2
- Международной конкурс-премии уличной культуры и спорта «КАРДО»
- Набор студентов в Корпус общественных наблюдателей
- День снятия блокады Ленинграда
- С Днём студента!
- Региональный этап Всероссийских соревнований по мини-футболу
- Совещание органов студенческого самоуправления
- VI Открытый Региональный Чемпионат «Молодые профессионалы России»: финальный день
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 4
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 2
- VI Открытый Региональный Чемпионат профессионального мастерства «Молодые профессионалы» (WorldSkills Russia) день 1
- Поздравляем победителей международных конкурсов
- Курсы для школьников
- Конкурс на лучшее видео – поздравление «С Новым годом!»
- Конкурс на лучшее видео – поздравление «С Новым годом!»
- Студенты АКВТ приняли участие в открытии памятника легендарному командарму
- Поздравления от Деда Мороза и Снегурочки
- Поздравляем с началом сессии!
- Проведение независимой оценки качества условий осуществления образовательной деятельности ГБПОУ АО «Астраханский колледж вычислительной техники»
- В АКВТ прошла акция Всероссийский тест на знание Конституции РФ
- I заседание МК СПО АО преподавателей информатики 10 декабря 2021 г.
- Конкурс на лучшее видео-поздравление с Новым годом
- Телеканал «Астрахань 24» о выставке студентов АКВТ — участников проекта «Герои Великой Победы в миниатюре» в Музее боевой славы
- Анонс! Массовая просветительская акция Всероссийский тест на знание Конституции РФ
- Интерактивная игра «Я, мои права и обязанности»
- Всероссийский конкурс «Флагманы образования. Студенты»
- Команда АКВТ на фестивале студенческой лиги КВН
- Выставка студентов АКВТ в Музее боевой славы
- Студенты и преподаватели АКВТ прошли исторический тест в День Неизвестного солдата
- В Музее боевой славы пройдёт 2-ая выставка работ студентов АКВТ
- Астраханский колледж вычислительной техники стал площадкой федерального проекта «Билет в будущее»
- С днём матери!
- Акция «Призывник»
- Проведение родительских собраний
- АКВТ посетили участники клуба моделистов «Сталинградский фронт»
- Студент Астраханского колледжа вычислительной техники – победитель Всероссийского конкурса «Большая перемена»
- В АКВТ состоялась встреча, посвящённая сохранению исторической памяти и защите Отечества
- Об организации межведомственного штаба по организации волонтерской деятельности
- О программе «Пушкинская карта»
- Семинар, посвященный всероссийскому конкурсу «Soft Skills Russia»
- VI Международная просветительская акция «Большой этнографический диктант-2021»
- Студенты Астраханского колледжа вычислительной техники – финалисты Всероссийского конкурса «Большая перемена»
- Студенты АКВТ в финале Международной олимпиады в сфере информационных технологий «IT-Планета 2020/21»
- Пушкинская карта
- Анкетирование в рамках проекта «Без срока давности»
- Акция «Сообщи, где торгуют смертью»
- День учителя в стенах АКВТ
- С днем учителя!
- Расписание спортивных секций
- Выставка посвящённая Дню профтехобразования
- «Полетели поздравительные телеграммы…»
- Марафон танцевальных поздравлений
- Студенты АКВТ провели выставку военных диорам на Кубке Прикаспийских государств по рукопашному бою
- В АКВТ прошли первые занятия в рамках проекта «Герои Великой Победы в миниатюре»
- Посвящение в студенты в стенах АКВТ
- АКВТ в полуфинале Всероссийского конкурса «Большая перемена»
- Совещание органов студенческого самоуправления
- Студент нашего колледжа рассказывает о своём незабываемом опыте работы вожатым в детском лагере
- Студенты АКВТ приняли участие в акции по сбору подписей для получения Астрахани звания «Город трудовой доблести»
- АКВТ во Всероссийском историческом квесте «Наша победа»
- Студенты АКВТ приняли участие в областном уроке мужества «Славы героев достойны»
- День знаний в стенах АКВТ!
- Группы 1 курса
- Объявление по собраниям для студентов нового набора
- АКВТ примет участие во Всероссийском конкурсе на лучшую выставку
- Итоги заседания комиссии по переводу с коммерческого обучения на бюджет
- Выпускники АКВТ — 2021
- V Открытый Региональный Чемпионат «Молодые профессионалы России»: 1 день
- Наши студенты на субботнике
- «Молодежный кадровый резерв»
- Информация для участников ЕГЭ 2014 года
- «Проблема сиротства» — проблема нашего будущего»
- Центр гражданского воспитания «Прометей»
- Подготовка студентов по программе прикладного бакалавриата по специальности Компьютерные системы и комплексы

Версия для слабовидящих

X Выбор шрифта:

Функции алгебры логики

Значение формулы алгебры логики полностью зависит от значений входящих в нее высказываний.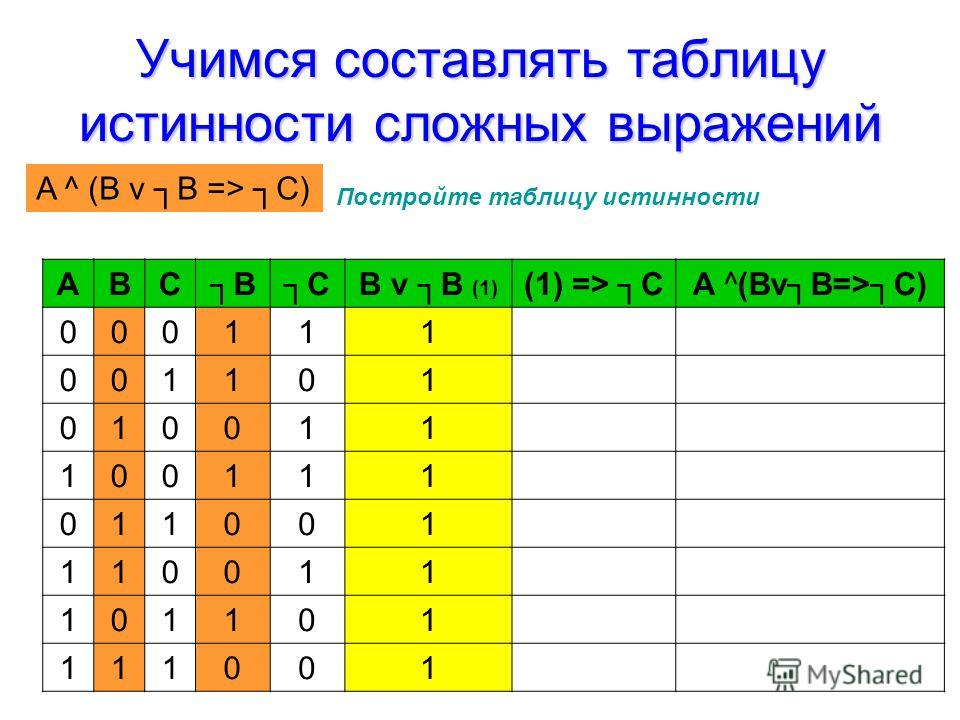 Поэтому такая формула может считаться функцией входящих в нее элементарных высказываний. Например, (xy)zявляется функциейf(x,y,z). Естественно, значения этой функции и входящих в нее элементов могут принимать значения истина или ложь. Тождественно истинные или тождественно ложные функции представляют собой константы.

Каждую функцию алгебры логики можно записать в виде формулы или представить таблицей истинности. Как уже было отмечено выше, таблица истинности для nпеременных содержит 2ⁿстрок. Следовательно, каждая функция алгебры логики принимает 2ⁿзначений, состоящих из 0 или 1. Общее же число наборов значений, состоящих из 0 и 1, длины 2ⁿравно 2²ⁿ. В частности, число различных функций от одной переменной равно четырем.

х	f₁(x)	f₂(x)	f₃(x)	F₄(x)
0	1	1	0	0
1	1	0	1	0

Из этой таблицы следует, что две функции являются константами f₁(x) = 1 иf₂(x) = 0, а остальные –f₃(x) =xиf₄(x) = x.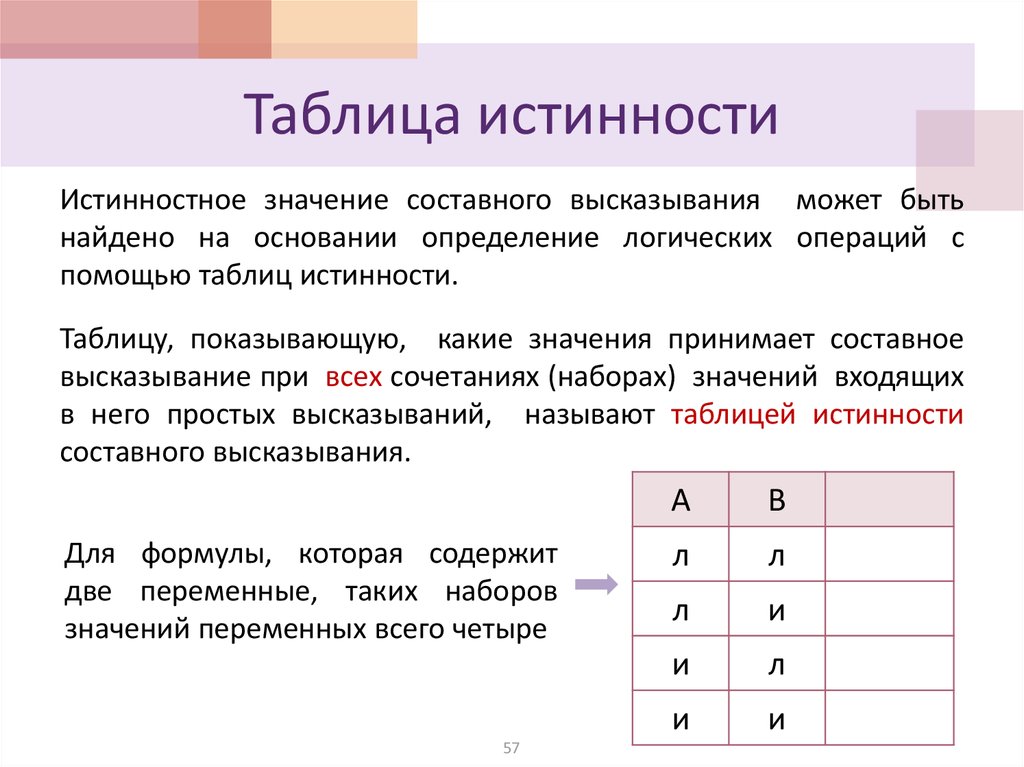

Пусть с помощью таблицы истинности задана произвольная функция алгебры логики nпеременныхF(x₁,x₂, …,x_n). Рассмотрим формулу:

F(1, 1, …, 1)x₁x₂…x_n

 F(1, 1, …, 1, 0)x₁x₂…x_n_-1x_n(1)

 F(1, 1, …, 0, 1)x₁x₂…x_n_-1x_n

 F(0, 0, …, 0)x₁x₂…x_n

которая составлена следующим образом: каждое слагаемое этой логической суммы представляет собой конъюнкцию, в которой первый член является значением функции F при некоторых определенных значениях ее переменных, остальные же члены конъюнкции представляют собой сами переменные или их отрицания.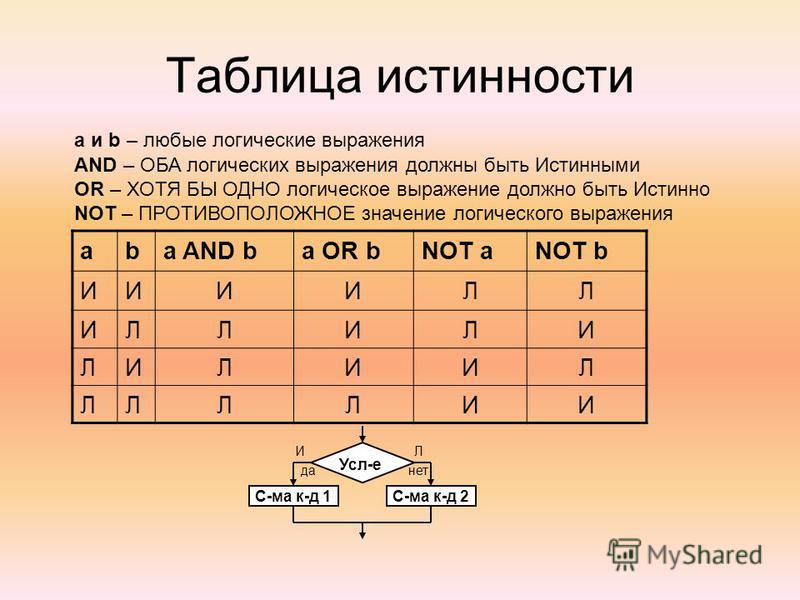 При этом под знаком отрицания находятся те и только те переменные, которые в первом члене конъюнкции имеют значение 0.

Ясно, что формула (1) полностью определяет функцию F. Иначе говоря, значения функции F и формулы (1) совпадают на всех наборах значений переменных x_i. Например, если x₁ принимает значение 0, а остальные переменные принимают значение 1, то функция F принимает значение F(0, 1, 1, …, 1). При этом логическое слагаемое F(0, 1, …, 1)x₁x₂…x_n=F(0, 1, …, 1)01…1, входящее в формулу (1), принимает также значение F(0, l,…, l), а все остальные логические слагаемые формулы (1) имеют значение 0. Действительно, в них знаки отрицания передпеременными распределяются иначе, чем в рассмотренном слагаемом. Таким образом, при подстановке вместо переменных тех же значений в конъюнкцию войдет символ 0 без знака отрицания, а символ 1 под знаком отрицания.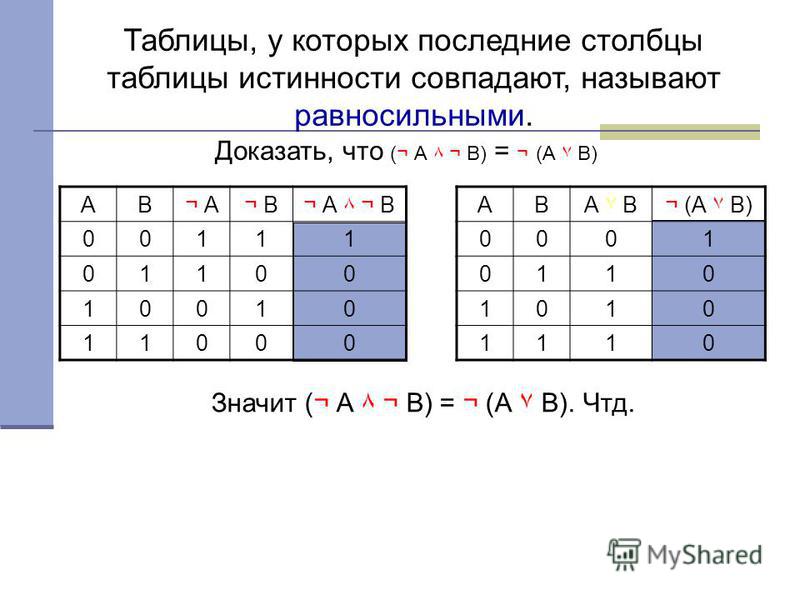 В таком случае один из членов конъюнкции будет иметь значение 0, и поэтому вся конъюнкция также будет иметь значение 0. В связи с этим на основании закона x  0 = x значением формулы (1) является F(0, l,…, l).

Ясно, что вид формулы (1) может быть значительно упрощен, если в ней отбросить те логические слагаемые, в которых первый член конъюнкции имеет значение 0 (и, следовательно, вся конъюнкция имеет значение 0). Если же в логическом слагаемом первый член конъюнкции (то есть определенное значение функции F) имеет значение 1, то, пользуясь законом 1  х = x, этот член конъюнкции можно не выписывать.

Таким образом, в результате получается формула (1), которая содержит только элементарные переменные высказывания и обладает следующими свойствами:

каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x₁,x₂, …,x_n),
все логические слагаемые формулы различны,
ни одно логическое слагаемое формулы не содержит одновременно переменную и ее отрицание,
ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды,

Перечисленные свойства будем называть свойствами совершенства или, коротко, свойствами. Из приведенных рассуждений видно, что каждой не тождественно ложной функции соответствует единственная формула указанного вида.

Если функция F(x₁,x₂, …,x_n) задана таблицей истинности, то соответствующая ей формула алгебры логики может быть получена просто. Действительно, для каждого набора значений переменных, на котором функция F(x₁,x₂, …,x_n) принимает значение 1, записывается конъюнкция элементарных переменных высказываний, взяв за член конъюнкции х_k, если значение x_k на указанном наборе значений переменных функции F есть 1 и  х, если значение x_k есть 0. Дизъюнкция всех записанных конъюнкций и будет искомой формулой.

Пусть, например, функция F(x₁,x₂,x₃) имеет следующую таблицу истинности:

x₁	X₂	x₃	F(x₁,x₂,x₃)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

Для наборов значений переменных (1, 1, 0), (1,0,1), (0,1,0), (0, 0, 0), на которых функция принимает значение 1, запишем конъюнкции x₁x₂x₃, x₁x₂x₃, x₁x₂x₃, x₁x₂x₃.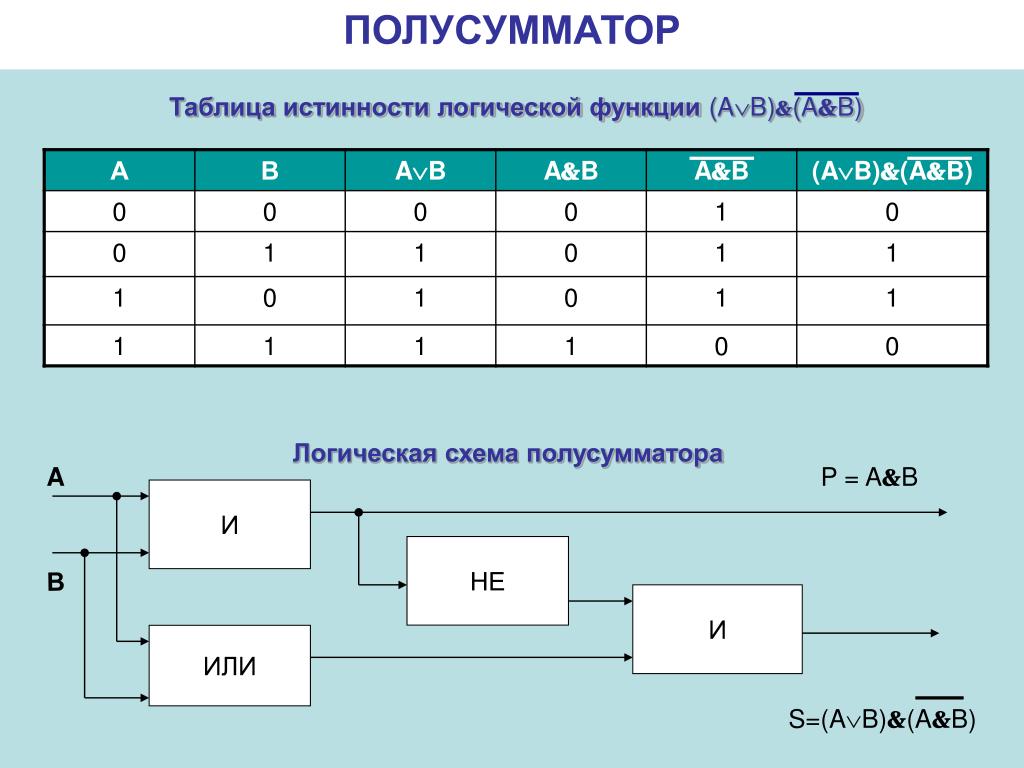 а искомая формула, обладающая свойствами совершенства, будет иметь вид:

x₁x₂x₃  x₁x₂x₃  x₁x₂x₃  x₁x₂x₃.

логика — Поиск функции истинности

Задавать вопрос

Спросил 7 лет, 4 месяца назад

Изменено 6 лет, 8 месяцев назад

Просмотрено 105 раз

$\begingroup$

Я хотел найти функцию истинности $f$, если она существует, которая делает приведенную ниже формулу истинной:

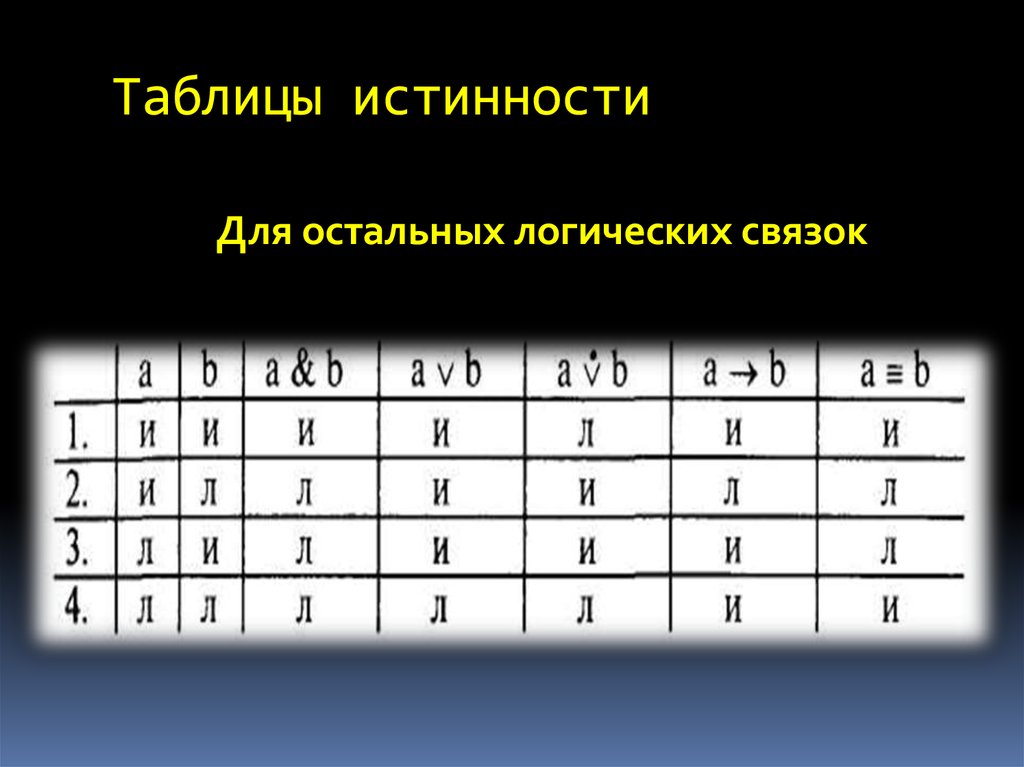
$((p\to \lnot(q \oplus \lnot p)) \to (\lnot r \oplus ( д\п)))$

Где оператор $\oplus$ определяется как:

$(A \oplus B) \equiv ((A \land \lnot B) \lor (B \land \lnot A))$

Насколько я понимаю, чтобы найти функцию истинности, которая делает эту формулу истинной, мне нужно было построить таблицу истинности и записать все строки, в которых LHS $\to $ RHS, например, $f(1,0,1) = 1$ Однако с $\oplus Определение оператора $ таблица истинности будет довольно длинной, поэтому я попытался упростить ее с помощью логических законов, чтобы сделать формулы короче для левой стороны. Я упростил ее до $p \to \lnot q $, но для правой стороны у меня было немного больше проблем. с логическими законами и сумел свести его только к:

$((\lnot r \land (q \land \lnot p)) \lor (r \land (\lnot q \lor p))$

Я на правильном пути с тем, как я пытался это сделать вопрос? Нужно ли упрощать RHS еще больше, прежде чем помещать его в таблицу истинности? $\endgroup$

$\begingroup$

Не думаю, что нужно было бы все упрощать, в нынешнем виде можно вывести таблицу истинности $\small\tt P$ без особого труда, $$\begin{массив}{|с|с|с|с|с|с|с|с|}\hline \small\color{green}{p} &\small \color{green}{q} &\small \color{green}{r} &\small \lnot p &\small (q\oplus\lnot p) & \small \lnot(q\oplus\lnot p) &\small ((p\to \lnot(q \oplus \lnot p)) &\small \lnot r &\small (q\to p)&\small ( \lnot r \oplus (q \to p))) & \small\tt P \\\hline \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{ royalblue}{1} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{royalblue}{ 1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} \\ \hline \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color {royalblue}{1} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{ 1} & \small\color{#C00}{0} & \small\color{royalblue}{1} \\ \hline \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color {#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{ 1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} \\ \hline \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\ color{#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{ 1} & \small\color{#C00}{0} & \small\color{#C00}{0} \\ \hline \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{ #C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{#C00}{ 0} & \small\color{#C00}{0} & \small\color{#C00}{0} \\ \hline \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color {#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{#C00}{ 0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} \\ \hline \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color {royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{ 1} & \small\color{royalblue}{1} & \small\color{royalblue}{1} \\ \hline \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\ color{royalblue}{1} & \small\color{#C00}{0} & \small\color{royalblue}{1} & \small\color{royalblue}{1} & \small\color{royalblue}{ 1} & \small\color{#C00}{0} & \small\color{#C00}{0} \\ \hline \end{массив}$$

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Истинно-функциональная полнота

PL имеет пять операторов: тильда, клин, амперсанд, подкова и тройная черта. Мы знаем, что эти операторы являются функциями истинности. Они принимают значения истинности в качестве входных данных и возвращают значение истинности как выход. Наш вопрос в этом разделе следующий: можем ли мы описать все возможные функции истинности с использованием наших пяти операторов? То есть можем ли мы построить любой функция истинности от входа к выходу с использованием наших операторов? Если ответ да, тогда наша система логики равна правда-функционально полный. Это вопрос в том, что мы называем Металогика , логика логики. Спрашивая об этом вопрос мы задаем вопрос о нашей системе логики, и в отвечая на него, мы доказываем что-то о нашей системе логики. Другой металогические вопросы появятся позже в тексте.

Упрощенная версия вопроса, который мы задаем, такова: Можем ли мы построить все возможные таблицы истинности, используя наши пять операторов? Поскольку таблица истинности представляет собой табличное выражение функции от входа к выходу, если мы может построить все возможные таблицы истинности, то наша система функционально полный.

Конечно, существует бесконечное количество таблиц истинности. Итак, как мы можем показать, что можем выразить их все на PL? Мы показываем что у нас есть рецепт построения любой возможной таблицы истинности.

Таблицы истинности бывают разных размеров. Мы помним, что число строк таблицы истинности равно 2 ⁿ , где n — количество отдельные буквы предложений в wff. Начнем с таблицы истинности для п=1. Это имеет две строки:

А	?
Т	?
Ф	?

Здесь «A» может быть T или F.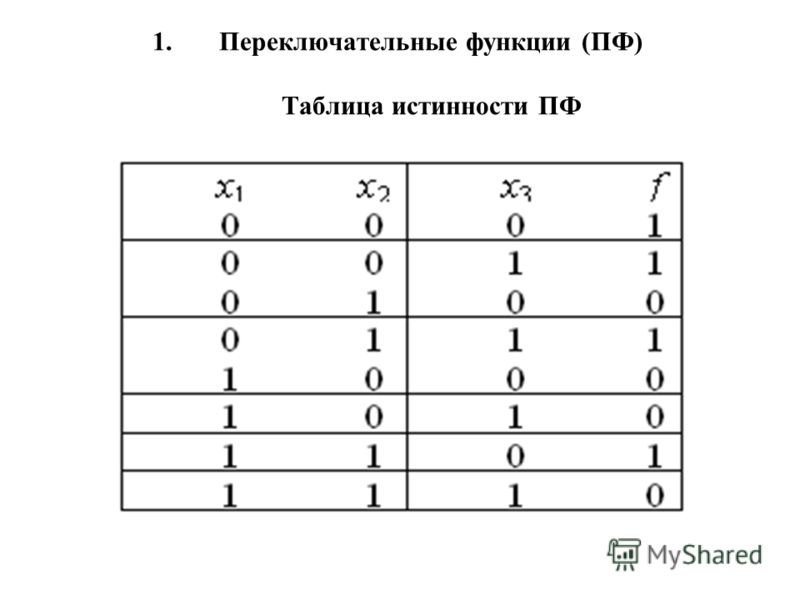 Каковы возможные выходы?

А	?
Т	Т
Ф	Т

Мы могли бы получить все «T» для вывода. Тогда WFF мы потребность — это тавтология. Таким образом, мы можем использовать «(A v ~A)», чтобы получить этот вывод.

А	(А в ~А)
Т	Т
Ф	Т

Теперь рассмотрим возможный результат, при котором мы всегда получаем «Ф»:

А	?
Т	Ф
Ф	Ф

Тогда нужная нам wff является противоречием. Таким образом, мы можем использовать «(A & ~A)», чтобы дать нам этот вывод.

А	(А и ~А)
Т	Ф
Ф	Ф

Далее рассмотрим возможный выход, где выходом является то же, что и ввод:

А	?
Т	Т
Ф	Ф

Для этого мы просто используем саму букву «А».

А	А
Т	Т
Ф	Ф

Наконец, рассмотрим, что происходит, когда мы переходим от входа «Т» на выход «F» или на вход «F» на выход «T»:

А	?
Т	Ф
Ф	Т

Это наша старая добрая тильда!

А	~А
Т	Ф
Ф	Т

Мы только что показали, что можем построить все возможные функция от входных значений истинности к выходным значениям истинности для таблиц истинности с одно предложение, отдельная буква. Теперь нам нужно показать, что мы можем сделать это для таблицы истинности с двумя или более различными буквами предложений. Для любого такого таблицы истинности, будет три разновидности: (1) таблицы истинности, которые все «T» в последнем столбце, (2) таблицы истинности, в которых все «F» в последнем столбце столбец и таблицы истинности, в которых есть хотя бы одна буква «Т» и хотя бы одна буква «F». За в первых двух случаях нам просто нужно построить тавтологии и противоречия. Таким образом, если буква предложения «А» является одной из наших отдельных букв предложения, для таблицы истинности со всеми «Т», мы убеждаемся, что мы отделить «(A v ~A) с другие буквы предложения, и мы получим все буквы «Т» для последнего столбца. Для таблицы истинности со всеми «F», мы соединяем «(A&~A) с буквами предложения и мы получим все «F».

Теперь поговорим о таблицах истинности, где вывод (последний столбец) содержит несколько F и несколько T. Мы формируем wff следующим образом: Начните с первая строка, где все wff оказывается верным: построить соединение следующим образом: для каждого предложения буква, если буква предложения назначена «T», тогда сделайте букву предложения a соединение Если ему присвоено «F», сделайте отрицание буквы предложения a соединение Мы будем называть каждое из этих соединений «ассоциированными соединениями» для тот ряд.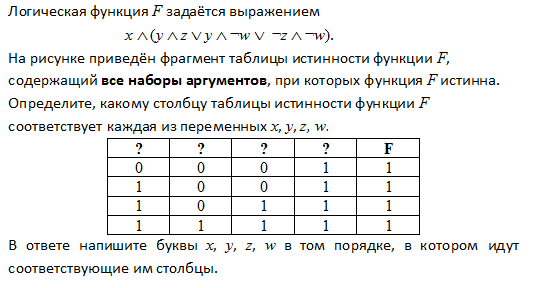 Делайте это для в каждой строке, где wff оказывается верным. Теперь возьмите эти союзы и сформируйте дизъюнкция всех этих союзов, не забудьте использовать только союзы для строки, которые верны в последнем столбце. Результирующий wff является wff с рассматриваемая таблица истинности.

Например, давайте посмотрим на таблицу истинности:

А	Б	?
Т	Т	Ф
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

Следуя нашему рецепту, мы строим связанный союзы (A &~B), для второй строки, и (~A & B) для третьего ряда. Теперь мы разделяем ассоциированные конъюнкции: (A &~B) v (~A & B). (Не беспокойтесь о группировке здесь.) Эта дизъюнкция имеет рассматриваемую таблицу истинности:

А	Б	(А и~В) v (~А и В)
Т	Т	Ф
Т	Ф	Т
Ф	Т	Т
Ф	Ф	Ф

И этот рецепт совершенно общий и будет работать для таблицы истинности любого размера. Итак, мы доказали, что с помощью наших операторов (на самом деле, просто используя отрицание, конъюнкцию и дизъюнкцию — нам не нужно было использовать подкова или тройник) мы можем выразить любой функция истины.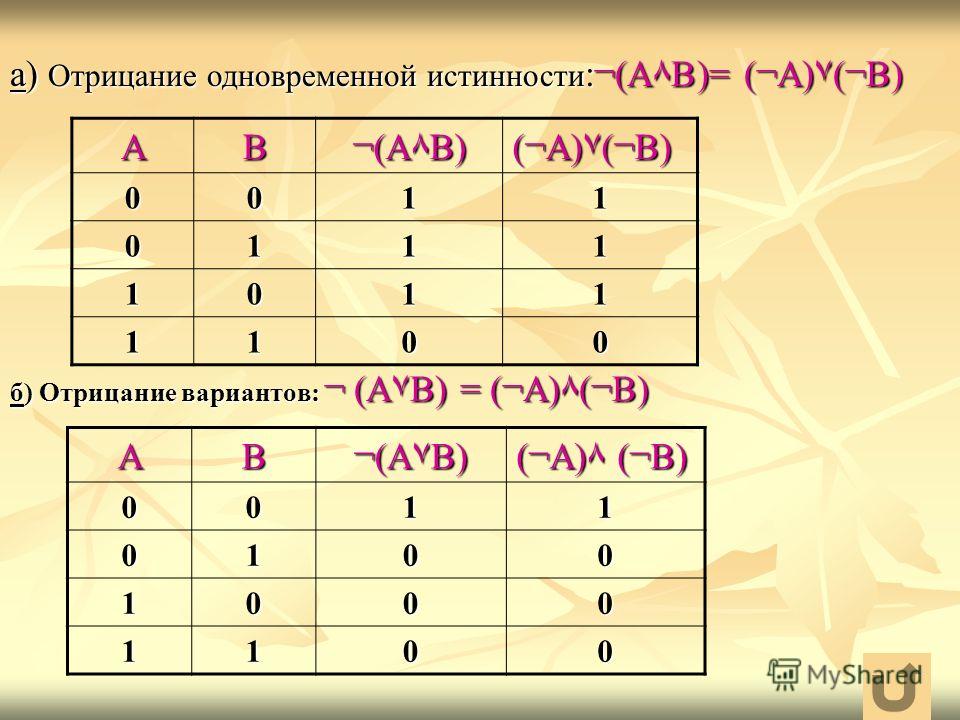 Следовательно, ЯП функционально завершен.

Вот еще. Для чего связан wff:

А	Б	?
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Ф

Сначала мы перечисляем связанные союзы. Для первой строки это (A&B), а для третьего (~A & B). Поскольку wff оказывается верным в первой и третьей строках, мы разделяем соединения из этих строк и получить (A & B) v (~A & B).

А	Б	(А и В) v (~А и В)
Т	Т	Т
Т	Ф	Ф
Ф	Т	Т
Ф	Ф	Ф

В качестве упражнения постройте произвольную таблицу истинности и затем создайте wff, который имеет эту таблицу истинности, используя приведенный выше рецепт. Как еще упражнение, объясните, как наше доказательство в этом разделе также является доказательством ненужность подковы и тройки как операторов в PL.

таблица содержание

Список упражнений

Функции истинности | Заметки Витгенштейна о логике

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Термин поиска мобильного микросайта

Закрыть

Фильтр поиска панели навигации Oxford AcademicЗаметки Витгенштейна о логикеФилософия ХХ векаФилософия математики и логикиКнигиЖурналы Термин поиска на микросайте

Расширенный поиск

Иконка Цитировать Цитировать
Разрешения
Делиться
- Твиттер
- Подробнее

Процитируйте

Поттер, Майкл,

‘Functions’

Заметки Витгенштейна по логике

(

Оксфорд,

2008;

онлайн Edn,

Oxford Academic

, 1 январь 2009 г.

), https: /// // // /// // // // // // // // // // // // // // // // // // // // // // // // // // // // // // // // ////////////////c doi.org/10.1093/acprof:oso/9780199215836.003.0017,

, по состоянию на 16 октября 2022 г.

Выберите формат Выберите format.ris (Mendeley, Papers, Zotero).enw (EndNote).bibtex (BibTex).txt (Medlars, RefWorks)

Закрыть

Advanced Search

Abstract

Функция истинности — это любая функция, принимающая конечный список значений истинности в качестве аргументов и производящая значение истинности в качестве своего результата.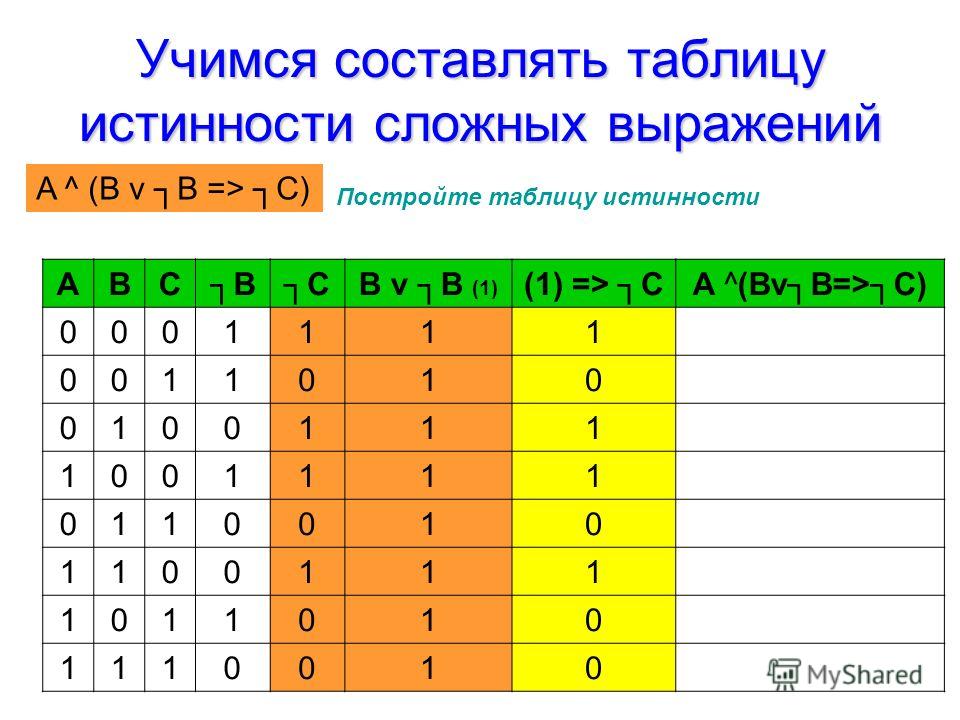 В Notes Витгенштейн назвал их «аб-функциями». В этой главе описываются обозначения, которые Витгенштейн использовал в разное время для описания функции истинности. Поскольку конечная цель будет заключаться в обсуждении отношения между логической связкой и соответствующей функцией истинности, будет разумно провести нотацию между ними.

Ключевые слова: Витгенштейн, аб-функции, таблицы истинности, диаграммы истинности

Предмет

Философия математики и логики Философия ХХ века

В настоящее время у вас нет доступа к этой главе.

Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок. Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:

Доступ на основе IP

Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.

Войдите через свое учреждение

Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.

Щелкните Войти через свое учреждение.
Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
Находясь на сайте учреждения, используйте учетные данные, предоставленные вашим учреждением. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.

Войти с помощью читательского билета

Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.

Члены общества

Доступ члена общества к журналу достигается одним из следующих способов:

Войти через сайт сообщества

Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:

Щелкните Войти через сайт сообщества.
При посещении сайта общества используйте учетные данные, предоставленные этим обществом. Не используйте личную учетную запись Oxford Academic.
После успешного входа вы вернетесь в Oxford Academic.

Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.

Вход через личный кабинет

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.

Личный кабинет

Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.

Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.

Просмотр учетных записей, вошедших в систему

Щелкните значок учетной записи в правом верхнем углу, чтобы:

Просмотр вашей личной учетной записи и доступ к функциям управления учетной записью.

Тема 1 Функции алгебры логики

Страница не найдена | АКВТ

Не нашли то, что искали?

Страницы

Записи

Функции алгебры логики

логика — Поиск функции истинности

Зарегистрируйтесь или войдите в систему

Опубликовать как гость

Опубликовать как гость

Истинно-функциональная полнота

Истинно-функциональная полнота

Функции истинности | Заметки Витгенштейна о логике

Процитируйте

Abstract

Войти

Получить помощь с доступом

Доступ для учреждений

Доступ на основе IP

Войдите через свое учреждение

Войти с помощью читательского билета

Члены общества

Войти через сайт сообщества

Вход через личный кабинет

Личный кабинет

Просмотр учетных записей, вошедших в систему

alexxlab

Добавить комментарий Отменить ответ

Рубрики