Системы счисления – примеры, таблица, обозначение (9 класс, информатика)
4
Средняя оценка: 4
Всего получено оценок: 255.
4
Средняя оценка: 4
Всего получено оценок: 255.
Числа при письме заменяются специальными знаками. Метод представления числовых эквивалентов с помощью специальной знаковой системы называется системой счисления. Системы счисления, как один из важных разделов теоретической информатики, подробно рассматриваются в курсе информатики 9 класса.
Что такое системы счисления
Системой счисления называется система записи чисел с помощью знаков по определенным правилам.
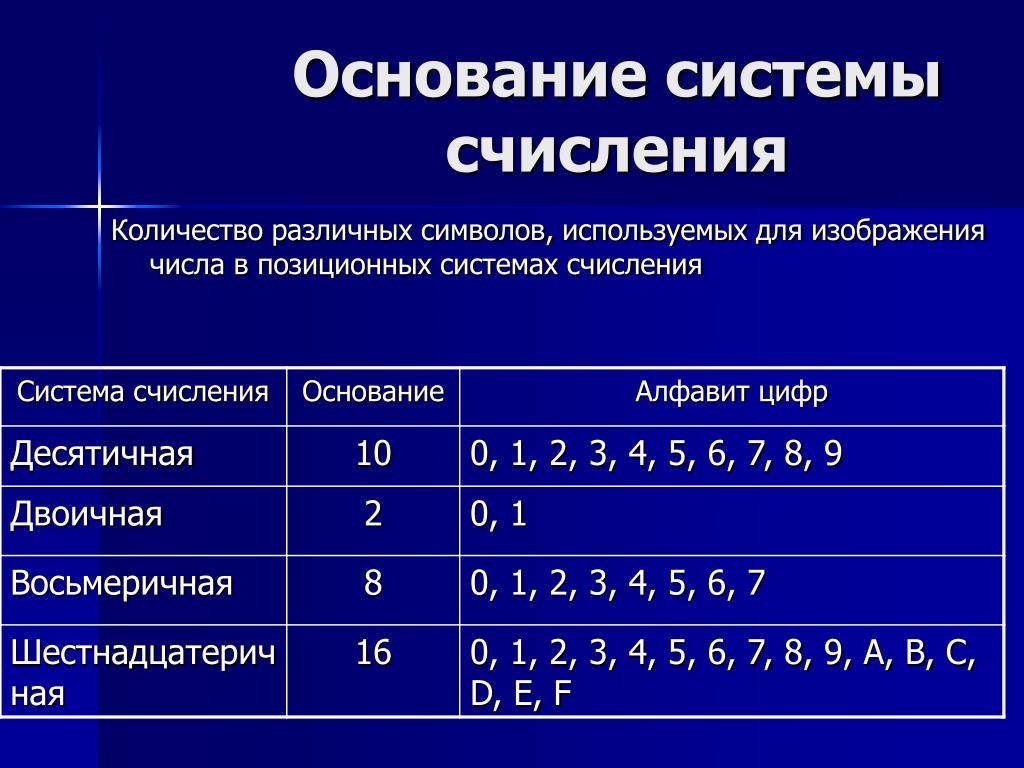
Символы, с помощью которых записываются числовые значения, обычно называют цифрами, а все вместе знаки системы счисления образуют алфавит. Количество знаков, используемых для обозначения чисел, называется основанием системы счисления.
Приведем примеры чисел систем счисления с различным основанием.
Основная десятичная система, привычная и общеупотребимая, имеет десять символов для обозначения всех чисел, то есть ее основание равно 10.
Десятичная система использует арабские цифры. Предположительно арабская система записи чисел возникла в Индии. Индийскую систему записи чисел описал Аль Хорезми в своем трактате «Об индийском счете».
Рис. 1. Портрет Аль Хорезми.Системы счисления в информатике не ограничиваются применением десятичных цифр, самыми распространенными системами являются двоичная, восьмеричная и шестнадцатеричная системы счисления.
В двоичной системе счисления все просто. Основание равно 2. Обозначение чисел выполняется только двумя символами 0 и 1.
Восьмеричная система использует 8 знаков для обозначения чисел: 0, 1, 2, 3, 4, 5, 6, 7. И числовой ряд восьмеричных чисел выглядит так: 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12 … Следует обратить внимание, что после 7 идет двузначное число 10, так как знаков всего восемь и происходит сдвиг разрядной сетки.
Шестнадцатеричная система имеет основание 16. Она применяет в качестве символов арабские цифры от 0 до 9 и затем буквы латинского алфавита A, B, C, D, E, F. В числовом ряду шестнадцатеричных чисел после 9 идет А, а после F идет 10.
Тогда возникает вопрос, как определить, в какой системе счисления, например число 107. Цифры 0, 1, 7 используются как в восьмеричной, так и в десятичной и шестнадцатеричной системе счисления. Для того чтобы различать системы, существует специальное обозначение систем счисления. Числа помечаются индексом с основанием системы. Так, 1078 – это восьмеричное число, 10710 – десятичное число, 10716 – шестнадцатеричное число.
в истории существуют примеры использования и других систем счисления. Так, некоторые коренные культуры Африки и Австралии используют двоичные и троичные системы. Индейцы Юки пользуются четверичной системой счисления, пятеричная система счисления распространена больше (по количеству пальцев на руке), ее элементы встречаются у древних персов и ацтеков, у индейцев племени Таманакос.
Позиционные системы счисления
Рассмотренные системы счисления относятся к классу позиционных систем. В них числовое значение каждой цифры зависит от положения в числе. Например, в десятичном числе 126 единица означает сотню, а в числе 216 единица уже на другом месте и обозначает десять.
Каждое число позиционной системы счисления можно представить как в свернутом виде, например, 126, так и в развернутом: 1*102 + 2*101 + 6*100 , то есть 100 + 20 +6 =126.
Аналогично, двоичное число 111001 = 1*25 + 1*24 + 1*23 + 0*22 + 0*21 + 1*20
Восьмеричное число: 247 = 2*82 + 4*81 + 7*80
Шестнадцатеричное число: 2A5F = 2*163 + A*162 + 5*161 + F*160
Используя развернутую форму, можно переводить числа из любой системы счисления в десятичную систему.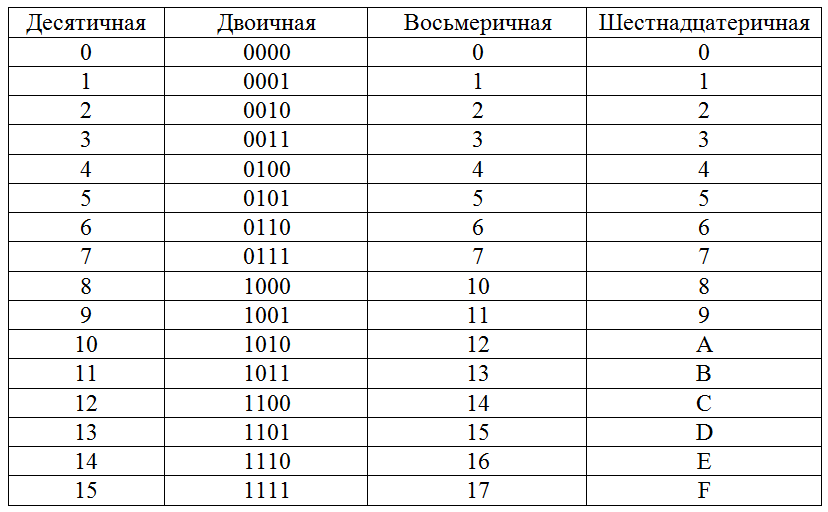
Непозиционные системы счисления
Кроме позиционных систем, существуют также непозиционные системы, в которых расположение цифры в числе не влияет на его числовое значение. Например, римская система цифр строится на основе символов I, V, X, L, C, D, M, которые означают соответственно 1, 5, 10, 50, 100, 500, 1000. Так, римское XVII означает 17. Получено путем суммирования 10 + 5 + 1 + 1.
Еще один пример: число 14 римскими цифрами записывается как XIV. Здесь использованы символы X, I, и V, которые обозначают 10, 1 и 5. Существует правило, согласно которому, меньшее число стоящее слева от большего следует вычитать из него. То есть I (1) меньше V (5), поэтому 5 – 1 = 4. И тогда число XIV получается как 10 + (5 – 1) = 14
Например, 1985 год в римской системе выглядит так MCMLXXXV: 1000 + (1000 – 100) + 50 + 10 + 10 + 10 + 5 = 1985
Рис. 2. Таблица римских цифр и их значений.Самой первой системой счисления в истории человечества была унарная система, в которой использовался только один знак, или точнее один камень, палочка или засечка.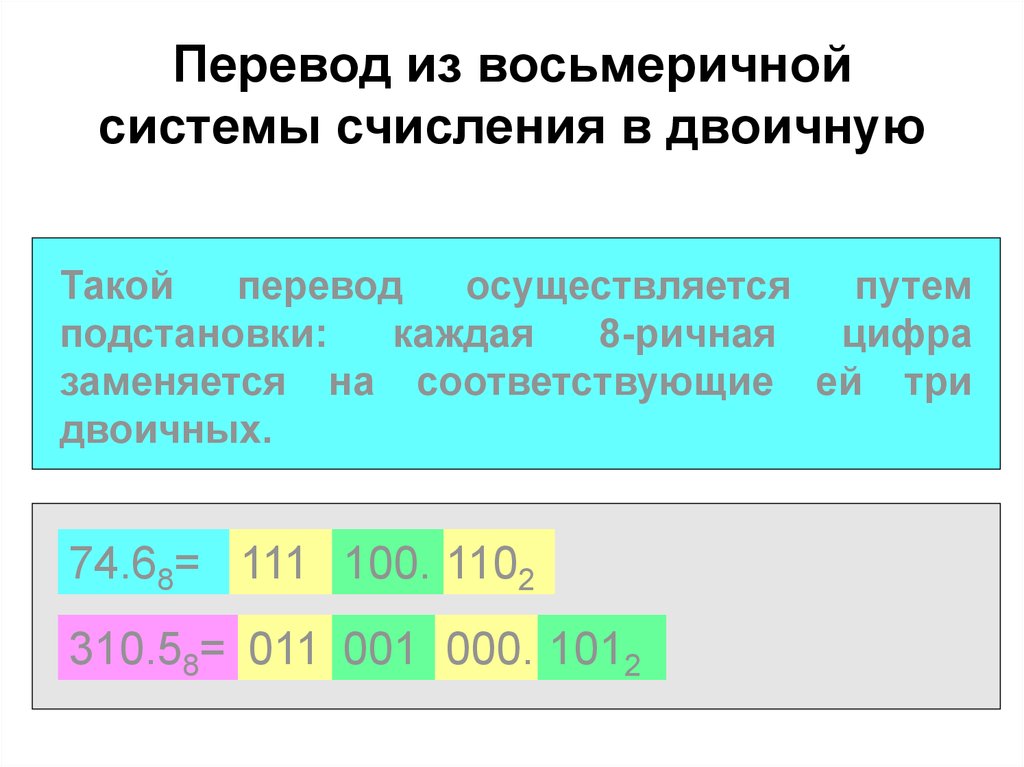 Конечно, с помощью такой системы записать большие числа практически невозможно. Поэтому древние люди стали заменять группы палочек другим символом.
Конечно, с помощью такой системы записать большие числа практически невозможно. Поэтому древние люди стали заменять группы палочек другим символом.
Что мы узнали?
Числа для удобства записи представляются с помощью системы символов, которая называется системой счисления. Существуют позиционные и непозиционные системы счисления. В позиционных системах количество используемых знаков называется основанием. В информатике используются двоичная, восьмеричная, десятичная и шестнадцатеричная системы счисления.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 255.
А какая ваша оценка?
Конспект урока: » Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Перевод целых чисел из одной системы счисления в другую «.

Урок 2
Учитель: Асылбекова Л. С. Класс: 8 Дата: ______________
Тема урока: » Системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Перевод целых чисел из одной системы счисления в другую «.
Цель урока: дать первичное представление о структуре компьютерной памяти, системах счисления.
Задачи:
актуализация изученных ранее в курсе математики подходы к представлению числовой информации;
развитие эмоционально-эстетической отзывчивости учащихся средствами комплексного воздействия информационных технологий;
воспитание интерес к историческим сведениям.
Ход урока:
Изучение нового материала
Общие сведения о системах счисления
Под системой счисления принято понимать совокупность приемов записи чисел. Условные знаки, которые при этом применяются, называют цифрами. В некоторых системах счисления кроме цифр могут использоваться специальные символы. Таким образом, в системах счислениях числа записываются как последовательность цифр или специальных символов. Системы счисления подразделяются на позиционные и непозиционные.
Условные знаки, которые при этом применяются, называют цифрами. В некоторых системах счисления кроме цифр могут использоваться специальные символы. Таким образом, в системах счислениях числа записываются как последовательность цифр или специальных символов. Системы счисления подразделяются на позиционные и непозиционные.
В непозиционной системе счисления значение цифры не зависит от ее положения в записи числа. К непозиционной системе счисления относится, так называемая, Римская система счисления. Например, возьмем число ХХХ из Римской системы счисления. В данном числе цифра Х в любом месте означает число десять.
В позиционных системах счисления значение каждой цифры зависит от ее положения (позиции) в ряду цифр, изображающих это число. Например, в числе 999 (десятичная система счисления) первая справа цифра 9 означает количество единиц, содержащихся в числе, вторая – количество десятков, третья – количество сотен. Принимая за основание системы различные числа можно получить соответствующие системы счисления. Число Р единиц одного разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления, а сама система называется Р-ичной. Поэтому для записи произвольного числа в какой-либо позиционной системе счисления достаточно иметь Р различных цифр. Таким образом, любая позиционная система с любым целым основанием Р (при Р1) использует Р различных цифр а, которые обозначают последовательный ряд чисел от 0 и кончая числом Р-1. Эти цифры называются базисными.
Число Р единиц одного разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления, а сама система называется Р-ичной. Поэтому для записи произвольного числа в какой-либо позиционной системе счисления достаточно иметь Р различных цифр. Таким образом, любая позиционная система с любым целым основанием Р (при Р1) использует Р различных цифр а, которые обозначают последовательный ряд чисел от 0 и кончая числом Р-1. Эти цифры называются базисными.
Число записывается в виде последовательности Р-ичных цифр, которая разделена точкой на целую и дробную части. Если каждый из символов означает некоторую Р-ичную цифру, то запись числа имеет вид . Каждой цифре из этой последовательности принято определенное значение. Цифра, стоящая в некотором разряде, имеет значение в Р раз больше того, которое она имела бы в разряде с номером, меньшим на 1. И наоборот, в Р раз меньшее того, которое она имела бы в разряде с номером, большим на 1.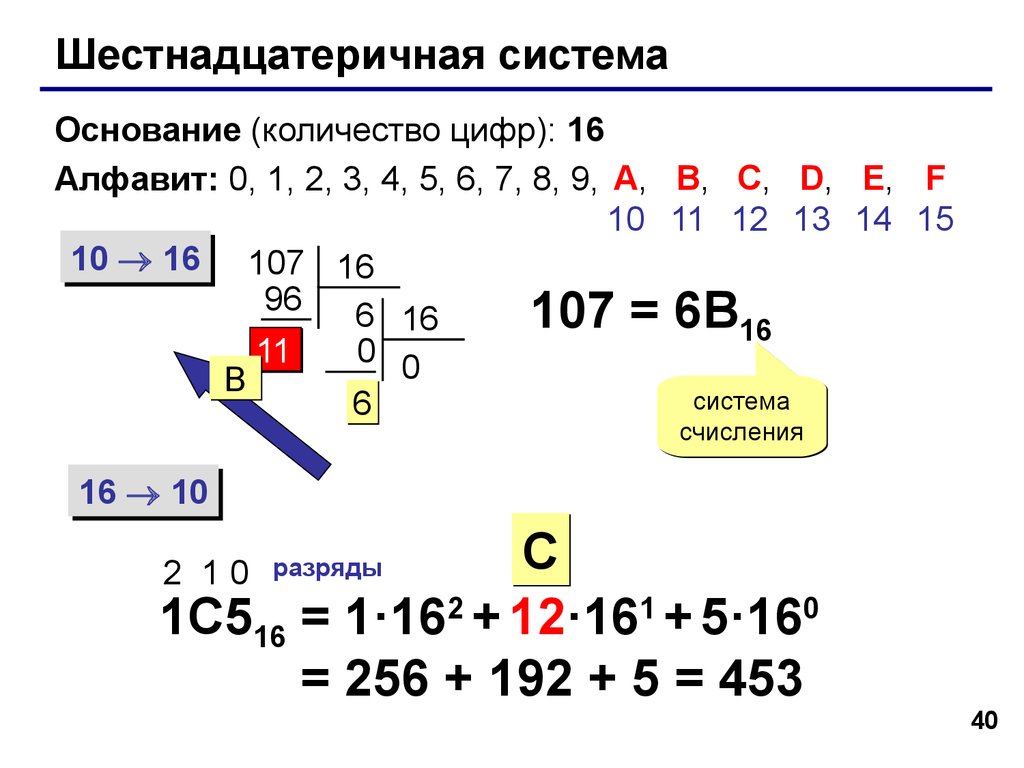
2. Позиционные системы счисления
Как было сказано, количество различных цифр, применяемых в позиционной системе счисления, называют ее основанием. Принимая за основание системы различные числа можно получить соответствующие системы счисления. К позиционным системам счисления, получившим наибольшее распространение, относятся десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления. Для того, чтобы отличать в какой системе представлено то или иное число, в дальнейшем будем записывать число с указанием используемой системы счисления. Например, — число 375 в десятичной системе счисления, а число — число 375 в восьмеричной системе счисления.
2.1. Десятичная система счисления
Это наиболее широко распространенная система счисления, которая использует 10 различных базисных цифр для представления любой величины. При записи чисел в десятичной системе счисления используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Несмотря на простоту и привычность десятичной системы счисления использование ее при передачи информации в вычислительных машинах представляется неудобной и технически не экономичной.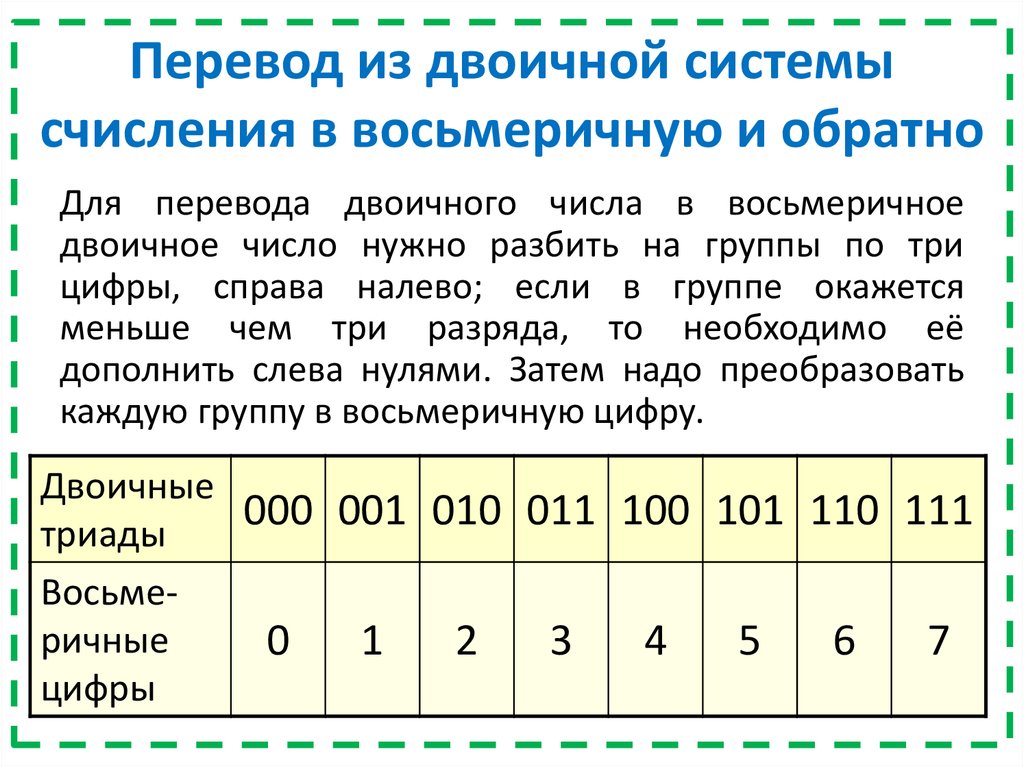 Поэтому при организации вычислительных процессов в ЭВМ используются системы счисления с другими основаниями.
Поэтому при организации вычислительных процессов в ЭВМ используются системы счисления с другими основаниями.
2.2. Двоичная система счисления
Большинство элементов, из которых строится ЭВМ, по своей физической природе могут находиться лишь в одном из двух состояний. Такие элементы называются двухпозиционными. Одно из устойчивых состояний элемента принимается за изображение цифры 0, а другое за изображение цифры 1. С помощью двухпозиционных элементов легко изображаются разряды двоичного числа. Поэтому двоичная система счисления имеет преимущества, и она оказывается очень удобной для применения в ЭВМ. Двоичная система счисления имеет только две цифры: 0 и 1. Это минимальное количество цифр, которое может быть принято в системе счисления.
Как и в десятичной системе счисления, в двоичной системе для отделения дробной части от целой используется точка, а перед отрицательным числом ставится минус (-):
2.3 Восьмеричная система счисления
В цифровых схемах и в электронных системах получила распространение восьмеричная система счисления.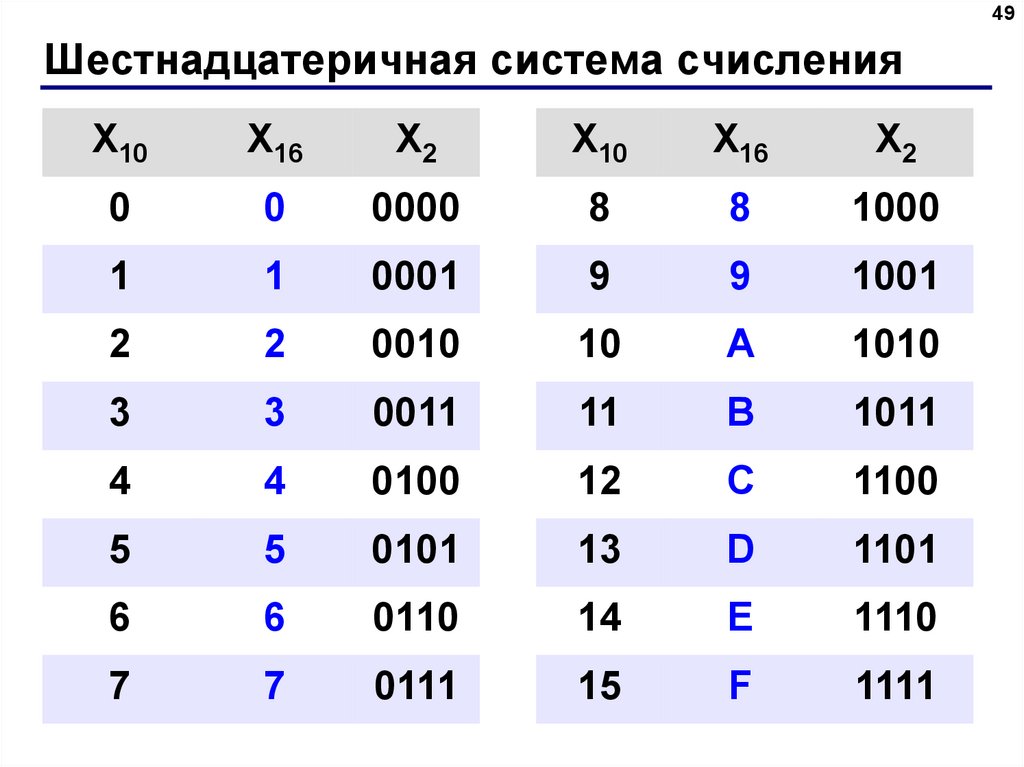 Данная система удобна тем, что восьмеричная запись какого-либо числа в три раза короче его двоичной записи. В данной системе счисления коэффициенты а принимают восемь различных значений — 0, 1, 2, 3, 4, 5, 6, 7.
Данная система удобна тем, что восьмеричная запись какого-либо числа в три раза короче его двоичной записи. В данной системе счисления коэффициенты а принимают восемь различных значений — 0, 1, 2, 3, 4, 5, 6, 7.
Поскольку , то каждый восьмеричный символ может быть представлен трехбитовым числом. Этих чисел восемь, как и символов в восьмеричной системе счисления. Как и в рассмотренных системах счисления, в восьмеричной системе используются дробные и отрицательные числа:
2.4. Шестнадцатеричная система счисления
Для систем счисления с основанием больше “10”, арабских цифр для представления чисел не хватит. Поэтому в этих случаях дополнительно вводят специальные символы. К таким системам счисления относится шестнадцатеричная система счисления.
В шестнадцатеричной системе счисления используются 16 базисных символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, E, F. Выбор шестнадцатеричной системы счисления обуславливается тем, что , т.е. эту систему можно использовать как средство сокращенной записи четырехразрядного двоичного числа.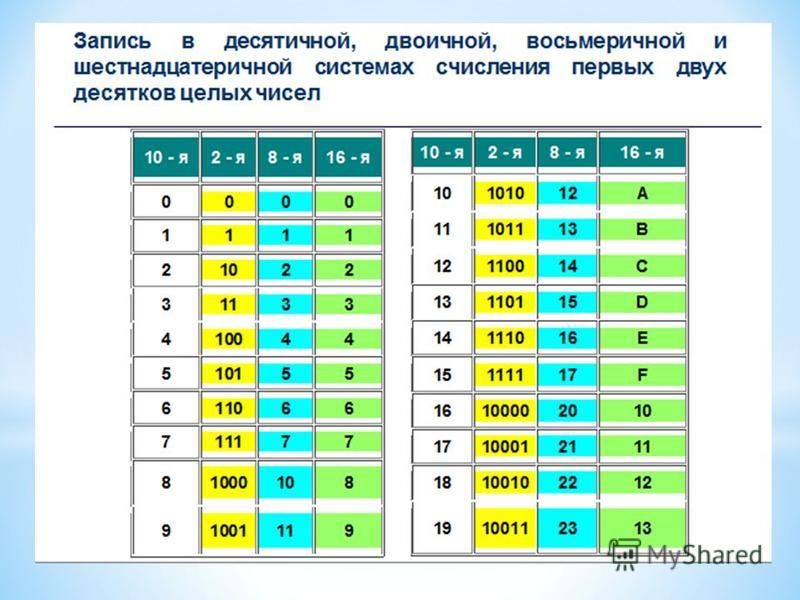
Следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления двоичных чисел.
Для представления дробных и отрицательных шестнадцатеричных чисел используется, соответственно, точка и знак минуса (-):
3. Перевод чисел в позиционных системах счисления
3.1. Перевод из десятичной системы счисления
Для перевода целого десятичного числа в другую систему счисления, необходимо разделить исходное число на основание системы счисления в которое оно переводится. При этом надо определять остатки деления. Остаток первого деления является значением младшего разряда. Затем полученное частное делится на выбранное основание. Процедуру деления продолжают до тех пор пока не станет меньше делителя, т.е. основания системы счисления, в которую осуществляется перевод. Значение последнего частного будет наибольшим разрядом, т.е. запись нового числа производится в обратном порядке: от частного к первому остатку, используя все промежуточные остатки.
При переводе в шестнадцатеричную систему счисления остатки, значения которых больше 9, необходимо заменить соответствующим буквенным эквивалентом: 10-А, 11-В, 12-С, 13-D, 14-E, 15-F.
Пример перевода целого десятичного числа 95:
а) в двоичную систему счисления
95 2
94 47 2
1 46 23 2
1 22 11 2
1 10 5 2
1 4 2 2
1 2 1
0 Место для формулы.
б) в восьмеричную систему счисления
95 8
88 11 8
7 8 1
3
в) в шестнадцатеричную систему счисления
95 16
80 5
15
При переводе правильных десятичных дробей, необходимо умножить значение этой дроби на основание системы счисления, в которую осуществляется перевод. Значение целой части результата первого умножения присваивается старшему разряду дробной части. Затем целая часть не рассматривается и производится следующее умножение дробной части. Процедуру умножения повторяют до тех пор, пока результат умножения не будет равен целому числу и этот результат будет младшим разрядом, либо не будет достигнута требуемая точность.
Примеры перевода правильной десятичной дроби 0.36:
а) в двоичную
*0.36
2
*0.72
2
*1.44
2
*0.88
2
1.76
0.3610 = 0.01012
б) в восьмеричную
*0.36
8
*2.88
8
*7.04
8
*0.32
8
2.56
0.3610 = 0.27028
в) в шестнадцатеричную
*0.36
16
*5.76
16
*12.16
16
*2.56
16
8.96
0.3610 = 0.5C281
Для перевода неправильной десятичной дроби, необходимо перевести отдельно дробную и целую часть, а полученные результаты сложить.
Например, перевести в двоичную систему счисления неправильную десятичную дробь 14.375.
1410 = 11102 0.37510 = 0.0112 14. 37510 = 1110.0112
37510 = 1110.0112
Перевод в десятичную систему счисления
Для перевода из любой позиционной системы счисления в десятичную систему счисления необходимо записать это число в виде суммы:
где Р – основание системы из которой осуществляется перевод; a – число, соответствующее базисной цифре Р-ичной системы счисления; n – число цифр в целой части; m – число цифр в дробной части.
Например, перевести число 110.101 из двоичной системы счисления в десятичную:
110.1012 = 1*22 + 1*21 + 0*20 + 1*2-1 + 0*2-2 + 1*2-3 = 6.62510
Для удобства расчета в табл. 1 приведены значения степеней позиционных систем счисления.
Таблица 1.
Значения степеней позиционных систем счисления
Степень Основание | 4 | 3 | 2 | 1 | -1 | -2 | -3 |
2 | 16 | 8 | 4 | 2 | 0. | 0.25 | 0.125 |
8 | 4096 | 512 | 64 | 8 | 0.125 | 0.0156 | 0.002 |
16 | 65536 | 4096 | 256 | 16 | 0.0625 | 0.004 | 0.0002 |
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную
Основания восьмеричной и шестнадцатеричной систем счисления (q) являются степенью основания двоичной системы (p) : q = pk , где k – целое число, равное 3 для восьмеричной системы счисления и 4 для шестнадцатеричной. Поэтому перевод из двоичной системы осуществляется разбиением двоичного числа на группы по три цифры в каждой для восьмеричной и по четыре для шестнадцатеричной. Отчет ведется от точки разделяющей целую часть от дробной в обе стороны. Затем каждая группа заменяется соответствующей цифрой из соответствующих систем счисления (см. табл. 2 и 3). Недостающие биты двоичного числа дополняются нулями: впереди – для целой части и в конце – для дробной части. Например, необходимо перевести двоичное число 1010001110.00111 в восьмеричное и шестнадцатеричное число:
Затем каждая группа заменяется соответствующей цифрой из соответствующих систем счисления (см. табл. 2 и 3). Недостающие биты двоичного числа дополняются нулями: впереди – для целой части и в конце – для дробной части. Например, необходимо перевести двоичное число 1010001110.00111 в восьмеричное и шестнадцатеричное число:
а) в восьмеричное
1010001100.001112 = 001 010 001 100.001 1102 = 1214.168
б) в шестнадцатеричное
1010001100.001112 = 0010 1000 1100.0011 10002 = 28С.3816
Таблица 2. Таблица 3.
Двоичные – восьмеричные Двоичные – шестнадцатеричные
0100 – 4 0101 – 5 0110 – 6 0111 – 7 1000 – 8 1001 – 9 1010 – А 1011 – В 1100 – С 1101 – D 1110 – E 1111 — F |
Перевод в двоичную систему счисления
из восьмеричной и шестнадцатеричной
Для перевода в двоичную систему из восьмеричной или шестнадцатеричной систем счисления необходимо каждое число заменить двоичным эквивалентом (см. табл.2 и 3). Например: 34.58 = 011 100.1012 ; A3.E16 = 1010 0011.11102.
табл.2 и 3). Например: 34.58 = 011 100.1012 ; A3.E16 = 1010 0011.11102.
Перевод из восьмеричной системы в шестнадцатеричную
Для перевода из восьмеричной системы счисления в шестнадцатеричную систему счисления необходимо представить это число в виде двоичного числа. Затем объединить в группы по 4 бита и заменить соответствующим числом из шестнадцатеричной системы счисления (см. табл.2 и 3). Например: 3458 = 011 100 1012 = 0111001012 = Е516
Перевод из шестнадцатеричной системы в восьмеричную
Для перевода шестнадцатеричной системы счисления в восьмеричную необходимо представить это число в виде двоичного числа. Затем объединить в группы по 3 бита и заменить соответствующим числом из восьмеричной системы счисления (см. табл.2 и 3). Например: В516 = 1011 01012 = 010 110 1012 = 2658
Вопросы учащихся.
Подведение итогов. Выставление оценок.
Домашнее задание п.2-3 стр 7-13 ПЗ в учебнике
5
Презентация для урока на тему Системы счисления (9 класс) доклад, проект
Системы счисления
Системы счисления.
Перевод чисел из одной системы счисления в другую
1.Перевод из десятичной системы
а) целое число
б) правильная десятичная дробь
в) вещественное число.
2. Перевод в десятичную систему
3. Перевод из двоичной в восьмеричную и шестнадцатеричную
системы.
4. Перевод из восьмеричной и шестнадцатеричной системы в
двоичную
5. Перевод из восьмеричной в шестнадцатеричную систему и обратно.
Арифметические операции в позиционных системах счисления
1. сложение
2. вычитание
3. умножение
4. деление
Представление чисел в компьютере
1.
Выход
Системы счисления
Система счисления – совокупность правил наименования и изображения чисел с помощью набора символов, называемых цифрами.
Количественное значение каждой цифры числа зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
0,7 7 70
Количественное значение цифры числа не зависит от того, в каком месте (позиции или разряде) записана та или иная цифра.
XIX
Позиционные
Непозиционные
Системы
счисления
Позиционные системы счисления
Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр!
В XIX веке довольно широкое распространение получила двенадцатеричная система счисления.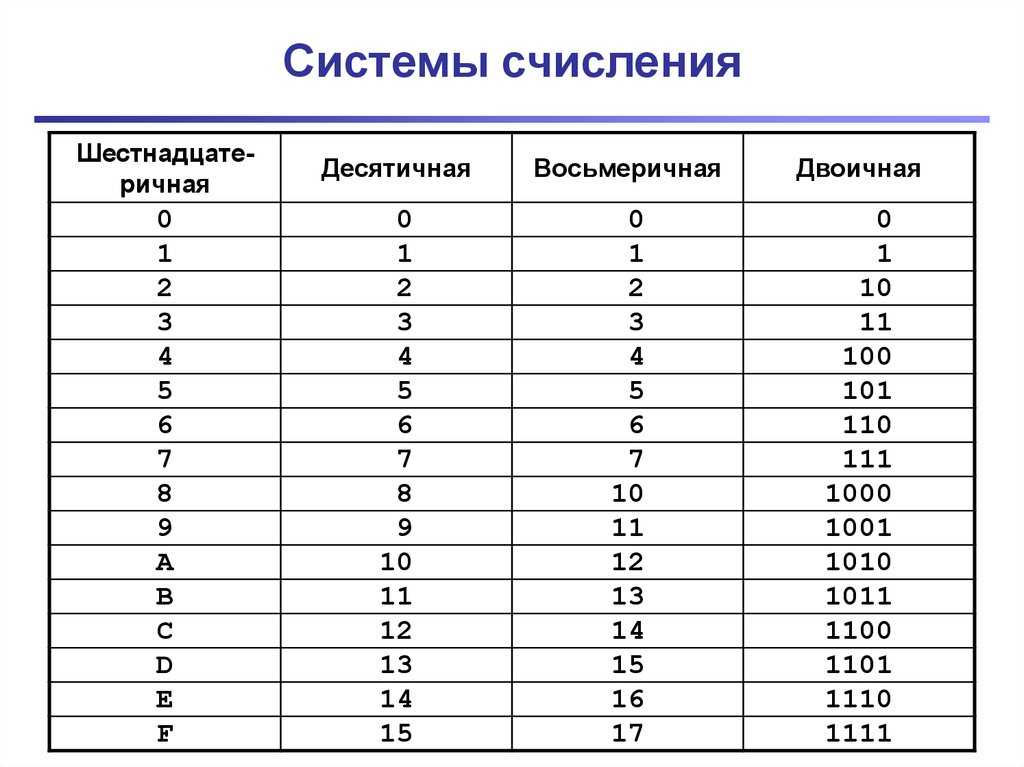
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
«Мысль – выражать все числа немногими знаками, придавая им значение по форме, ещё значение по месту, настолько проста, что именно из-за этой простоты трудно оценить, насколько она удивительна»
Пьер Симон Лапласс
Основание системы счисления
Количество различных символов, используемых для изображения числа в позиционных системах счисления, называется основанием системы счисления.
Позиции цифр называются разрядами.
Основание системы счисления показывает во сколько раз изменяется количественное значение цифры при перемещении её на соседнюю позицию
За основание системы можно принять любое натуральное число не менее 2.
Основание системы счисления
Компьютеры используют двоичную систему так как
для её реализации нужны технические устройства с двумя устойчивыми состояниями,
представление информации с помощью только двух состояний надежно и помехоустойчиво,
возможно применение аппарата булевой алгебры для выполнения логических преобразований,
двоичная арифметика намного проще десятичной
Двоичная система, удобная для компьютера, для человека неудобна из-за её громоздкости и непривычной записи. Для того, чтобы понимать слово компьютера, разработаны восьмеричная и шестнадцатеричная системы счисления. Числа в этих системах требуют в 3/4 раза меньше разрядов, чем в двоичной системе.
Для того, чтобы понимать слово компьютера, разработаны восьмеричная и шестнадцатеричная системы счисления. Числа в этих системах требуют в 3/4 раза меньше разрядов, чем в двоичной системе.
Основание системы счисления
Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
an-1qn-1 + an-2qn-2 + … + a1q1 + a0q0 + a-1q-1 + … + a-mq-m ,
где ai – цифры системы счисления, n и m –число целых и дробных разрядов соответственно
Перевод целых чисел из
десятичной системы счисления
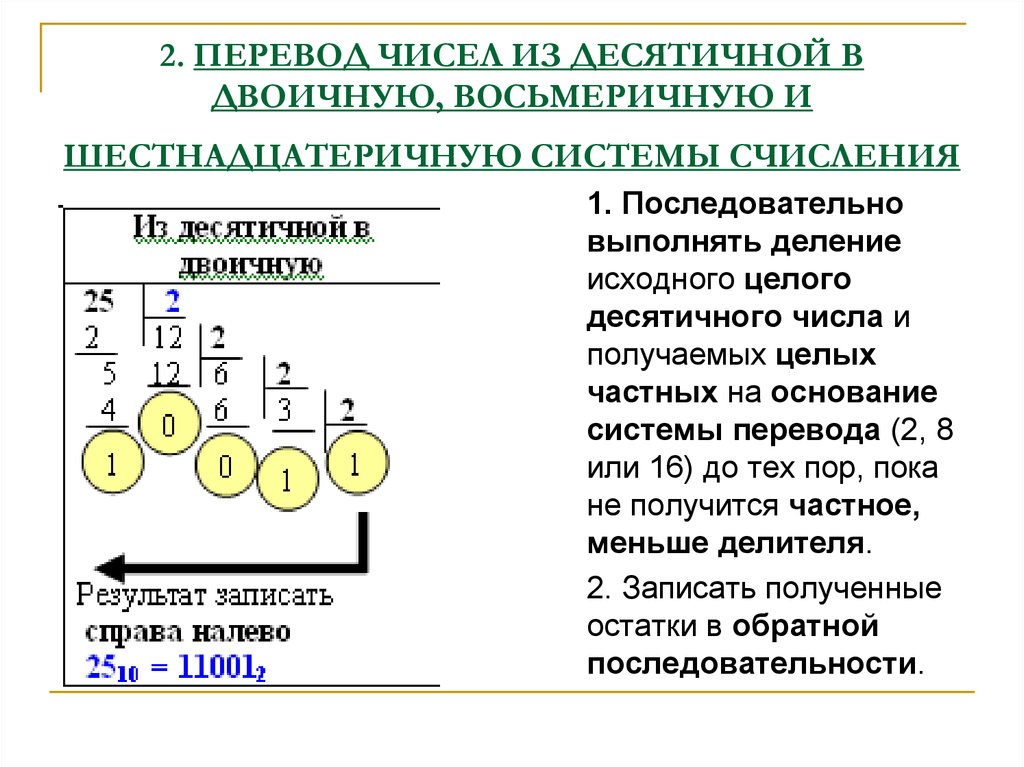
Алгоритм перевода:
Последовательно делить с остатком данное число и получаемые целые частные на основание новой системы счисления до тех пор, пока частное не станет равно нулю.
Полученные остатки выразить цифрами алфавита новой системы счисления
Записать число в новой системе счисления из полученных остатков, начиная с последнего.
Перевод целых чисел из
десятичной системы счисления
Пример. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
75
2
74
1
37
2
36
1
18
2
18
0
9
2
8
1
4
2
4
0
2
2
2
0
2
1
0
0
1
7510 = 10010112
Перевод целых чисел из
десятичной системы счисления
Пример 1. Перевести число 75 из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную.
75
8
72
3
9
8
8
1
1
8
0
1
0
7510 = 1138
75
16
64
11
4
16
0
4
0
7510 = 4B16
В меню
Перевод правильной десятичной дроби из десятичной системы счисления
Алгоритм перевода:
Последовательно умножать десятичную дробь и получаемые дробные части произведений на основание новой системы счисления до тех пор, пока дробная часть не станет равна нулю или не будет достигнута необходимая точность перевода.
Полученные целые части произведений выразить цифрами алфавита новой системы счисления.
Записать дробную часть числа в новой системе счисления начиная с целой части первого произведения.
Перевод правильной десятичной дроби из десятичной системы счисления
Пример. Перевести число 0,35 из десятичной системы в счисления в двоичную, восьмеричную и шестнадцатеричную.
0,35
2
0,70
2
1,40
2
0,80
2
1,60
2
1,20
0,3510 = 0,010112
0,35
8
2,80
8
6,40
8
3,20
0,3510 = 0,2638
0,35
16
5,60
16
9,60
0,3510 = 0,5916
В меню
Перевод чисел в десятичную систему счисления
Пример. Перевести число 1011,1 из двоичной системы счисления в десятичную.
Перевести число 1011,1 из двоичной системы счисления в десятичную.
1 0 1 1, 12
-1
0
1
2
3
= 1∙23 + 0∙22 + 1∙21 + 1∙20 + 1∙2-1 = 11,510
разряды
число
Пример. Перевести число 276,8 из восьмеричной системы счисления в десятичную.
2 7 6, 58
-1
0
1
2
= 2∙82 + 7∙81 + 6∙80 + 5∙8-1 = 190,62510
разряды
число
Пример. Перевести число 1F3 из шестнадцатеричной системы счисления в десятичную.
1 F 316
0
1
2
= 1∙162 + 15∙161 + 3∙160 = 49910
разряды
число
В меню
Перевод из восьмеричной и шестнадцатеричной системы счисления в двоичную
Заменить каждую цифру восьмеричного/шестнадцатеричного числа соответствующим трехразрядным/четырехразрядным двоичным кодом.
Пример. Перевести число 527,18 в двоичную систему счисления.
527,18 =
101
010
111,
001
5
2
7
1
2
Пример. Перевести число 1A3,F16 в двоичную систему счисления.
1A3,F16 =
0001
1010
0011,
1111
1
A
3
F
2
Таблица соответствия
В меню
Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную
Для перехода от двоичной к восьмеричной/шестнадцатеричной системе счисления поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по 3/4 разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из 3/4 разрядов заменяют соответствующей восьмеричной/шестнадцатеричной цифрой.
Пример
1 0 1 0 1 0 0 1,1 0 1 1 1 2
1
5
0
6
0
2
5
= 251,658
1 0 1 0 1 0 0 1,1 0 1 1 1 2
9
B
A
000
8
= A9,B816
Таблица соответствия
В меню
Перевод из восьмеричной системы счисления в шестнадцатеричную и обратно
При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно вначале производится перевод чисел из исходной системы счисления в двоичную, а затем – в конечную систему .
Пример. Перевести число 527,18 в шестнадцатеричную систему счисления.
527,18 =
Пример. Перевести число 1A3,F16 в восьмеричную систему счисления.
1A3,F16 =
101010111,011 2
7
6
0
5
=157,616
000
1
110100011,1111 2
3
7
4
00
6
4
=643,748
Таблица соответствия
В меню
самостоятельные задания
Арифметические операции в позиционных системах счисления
Правила выполнения основных арифметических операций в любой позиционной системе счисления подчиняются тем же законам, что и в десятичной системе.
При сложении цифры суммируются по разрядам, и если при этом возникает переполнение разряда, то производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания системы счисления.
При вычитании из меньшей цифры большей в старшем разряде занимается единица, которая при переходе в младший разряд будет равна основанию системы счисления
Арифметические операции в позиционных системах счисления
Если при умножении однозначных чисел возникает переполнение разряда, то в старший разряд переносится число кратное основанию системы счисления. При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления.
Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе, то есть сводится к операциям умножения и вычитания.
Сложение в позиционных системах счисления
Цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево
1 0 1 0 1
+
1 1 0 1
двоичная
система
0
1+1=2=2+0
1
1
1+0+0=1
0
1+1=2=2+0
1
0
1+1+0=2=2+0
1
0
1+1=2=2+0
1
Ответ: 1000102
2 1 5 4
+
7 3 6
2
4+6=10=8+2
1
1
5+3+1=9=8+1
1
1+7+1=9=8+1
1
3
1+2=3
восьмеричная
система
1
Ответ: 31128
шестнадцатеричная
система
8 D 8
+
3 B C
4
8+12=20=16+4
1
9
13+11+1=25=16+9
8+3+1=12=C16
C
1
Ответ: C9416
В меню
Вычитание в позиционных системах счисления
При вычитании чисел, если цифра уменьшаемого меньше цифры вычитаемого, то из старшего разряда занимается единица основания
двоичная
система
Ответ: 10102
восьмеричная
система
Ответ: 364448
шестнадцатеричная
система
Ответ: 84816
1 0 1 0 1
—
1 0 1 1
0
1-1=0
1
1
2-1=1
0
0-0=0
1
2-1=1
1
0
4 3 5 0 6
—
5 0 4 2
4
6-2=4
1
4
8-4=4
4
4-0=4
6
8+3-5=11-5=6
1
3
С 9 4
—
3 В С
8
16+4-12=20-12=8
1
4
16+8-11=24-11=13=D16
8
11-3=8
1
В меню
3∙3=9=8+1
Умножение в позиционных системах счисления
При умножении многозначных чисел в различных позиционных системах применяется алгоритм перемножения чисел в столбик, но при этом результаты умножения и сложения записываются с учетом основания системы счисления
двоичная
система
Ответ: 1010111112
восьмеричная
система
Ответ: 133518
1 1 0 1 1
х
1 1 0 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 0 1 0 1 1 1 1 1
1+1+1=3=2+1
1
1+1+1=3=2+1
1
1+1=2=2+0
1
1
1 6 3
х
6 3
5 3 1
1
6∙3+1=19=16+3=2∙8+3
2
1∙3+2=5
1 2 6 2
6∙3=18=16+2=8∙2+2
6∙6+2=38=32+6=4∙8+6
2
4
6∙1+4=10=8+2
1 3 3 5 1
6+5=11=8+3
1
В меню
самостоятельные задания
Деление в позиционных системах счисления
Деление в любой позиционной системе производится по тем же правилам, как и деление углом в десятичной системе. При этом необходимо учитывать основание системы счисления.
При этом необходимо учитывать основание системы счисления.
двоичная
система
Ответ: 10,12
восьмеричная
система
Ответ: 638
1 0 0 0 1 1
1 1 1 0
1
1 1 1 0
1 1 1 0
1 1
1
,
0
0
1
0
1 3 3 5 1
1 6 3
6
1 2 6 2
5 3
1
3
5 3 1
0
В меню
самостоятельные задания
Представление чисел в компьютере
Числа в компьютере могут храниться в формате с фиксированной запятой – целые числа и в формате с плавающей запятой – вещественные числа.
Целые числа без знака занимают в памяти один или два байта.
Целые числа со знаком занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа
Применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код.
Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой. Этот формат базируется на экспоненциальной форме записи, в которой может быть представлено любое число
Представление целых чисел в компьютере
Целые числа в компьютере могут представляться со знаком или без знака.
Целые числа без знака занимают в памяти один или два байта.
Пример. Число 7210 = 10010002 в однобайтовом формате
Представление целых чисел в компьютере
Целые числа со знаком занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак «плюс» кодируется нулем, а «минус» — единицей
Представление целых чисел в компьютере
Пример. Число 6210 = 1111102 в однобайтовом формате
В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код и дополнительный код.
Положительные числа в прямом, обратном и дополнительных кодах изображаются одинаково – двоичными кодами с цифрой 0 в знаковом разряде.
Знак числа
Представление целых чисел в компьютере
Пример. Число -5710 = -1110012 в однобайтовом формате
Отрицательные числа в прямом, обратном и дополнительных кодах имеют разное изображение..
Знак числа
Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа – двоичный код его абсолютной величины.
прямой код
Представление целых чисел в компьютере
Пример. Число -5710 = -1110012 в однобайтовом формате
Знак числа
Обратный код. Для образования обратного кода отрицательного двоичного числа необходимо в знаковом разряде поставить 1, а в цифровых разрядах единицы заменить нулями, а нули — единицами.
обратный код
Представление целых чисел в компьютере
Пример. Число -5710 = -1110012 в однобайтовом формате
Знак числа
Дополнительный код отрицательного числа получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду
дополнительный код
Представление целых чисел в компьютере
Отрицательные десятичные числа при вводе в компьютер автоматически преобразуются в обратный или дополнительный код и в таком виде хранятся, перемещаются и участвуют в операциях.
При выводе таких чисел из компьютера происходит обратное преобразование в отрицательные десятичные числа
В меню
Скачать презентацию
Типы системы счисления в компьютере: двоичная, десятичная, восьмеричная и шестнадцатеричная
Компьютеры понимают машинный язык, т. е. каждая буква, символ и т. д., которые пользователь пишет в инструкциях, предоставляемых компьютеру, преобразуется в машинный язык. Этот машинный язык состоит из чисел. Чтобы понять язык, используемый компьютерами и другими цифровыми системами, необходимо лучше знать систему счисления.
е. каждая буква, символ и т. д., которые пользователь пишет в инструкциях, предоставляемых компьютеру, преобразуется в машинный язык. Этот машинный язык состоит из чисел. Чтобы понять язык, используемый компьютерами и другими цифровыми системами, необходимо лучше знать систему счисления.
Система счисления дает уникальное представление чисел. Он также позволяет пользователям выполнять арифметические операции, такие как вычитание, сложение и деление, которые играют важную роль в компьютерных приложениях и цифровых областях.
Системы счисления можно разделить на подтипы на основе этой системы. Основание системы счисления играет жизненно важную роль в понимании системы счисления и преобразовании ее из одного подтипа в другой подтип. Основание иногда также называют основанием; оба эти термина имеют одинаковое значение.
В этой статье о типах систем счисления вы узнаете о восьмеричной, шестнадцатеричной, двоичной и десятичной системах счисления, а также об их представлении, примерах и преобразованиях.
Также читайте больше о бинарных операциях здесь.
Десятичная система счисленияДесятичная система счисления также распознается как система счисления с основанием 10, поскольку в ней используются десять цифр от 0 до 9. В этом типе системы счисления прогрессивная позиция находится слева от десятичной точки. нарисовано единицами, десятками, сотнями, тысячами и так далее.
- База системы равна 10, т. е. «b» равно 10. \((N)_{10}\ for\ например\ (301)_{10}\).
- Диапазон (0–90.1\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =300+1=301\)
\(Здесь\ 3\ называется\ самой\ старшей\ значащей\ цифрой\ и\ 1\ известна\ как\ наименее\ значащая\ цифра\)
Двоичная система счисленияДвоичная система счисления также известна как система с основанием 2, состоящая только из двух цифр 0 и 1. Это делает ее менее сложной, чем другую систему счисления, поскольку она состоит только из двух цифр. Двоичные цифры полезны для оценки результатов устройств, которые имеют два состояния ВКЛ и ВЫКЛ.

- Здесь основание т.е. ‘b’ равно 2 \((N)_2\ т.е. \ (1011)_2\)
- Диапазон (0 – 1) т.е. N может содержать только (0, 1) 1 в двоичной системе называется битами.
- Группа из 4 бит = 1 полубайт
Группа из 8 бит = 1 байт
Также читайте больше о законах булевой алгебры здесь.
Восьмеричная система счисленияЭто очень полезный тип системы, поскольку, применяя восьмеричную систему счисления, пользователь может упростить задачу ввода или чтения компьютерных инструкций.
База для восьмеричной системы счисления, т.е. ‘b’ равна 8. \((N)_{_8}\ т.е.\ (367)_8\)
Диапазон (0 – 7), т.е. N может содержать цифры между (0 ,12,3,4,5,6 и 7).
Шестнадцатеричная система счисленияОснованием для шестнадцатеричной системы счисления является 16. Это означает, что в шестнадцатеричной системе 16 шестнадцатеричных чисел. Он работает по методу группировки четырех битов.
Шестнадцатеричная система счисления содержит цифры (1, 2, 3, 4, 5, 6, 7, 8 и 9) и буквы алфавита (A, B, C, D, E и F), поэтому эта система счисления также называется буквенно-цифровой системой счисления.
 90,5\)
90,5\)\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ =16,14+5\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =224+5 =\left(229\right)_{10}\)
Также читайте больше о двоичных кодах здесь.
Десятичное число в любой системе счисленияЦелая часть — Разделите целую часть на «основание» {2, 16, 8} и запишите остаток, пока полученное частное не станет равным нулю.
Дробная часть — Умножьте дробную часть на «основание» {2, 16, 8} и запишите целую часть, пока мы не получим дробь, равную нулю, или мы получим повторяющийся шаблон.
Для лучшего понимания рассмотрим следующий пример.
Десятичное число в двоичное\(\left(43\right)_{10}\rightarrow\ \left(?\right)_2\)
Преобразование целых десятичных чисел выглядит следующим образом:
Remainder 43 ÷ 2 21 ÷ 2
10 ÷ 2
5 ÷ 2
2 ÷ 2
1 ÷ 2
→ →
→
→
→
→
1 1
0
1
0
1
(LSB) ↑
(MSB)
(MSB)
9(MSB)
99999999999969969969969969 (MSB). 101011)_2
101011)_2The fraction decimal number conversion is as follows:
‘Integer’ 0. - × 2 = 1.8125
0.8125 × 2 = 1.625
0.625 × 2 = 1.25
0.25 × 2 = 0,5
0.5 × 2 = 1.0
0.0 × 2 = 0.0
→ →
→
→
→
→
1 1
1
0
1
0
↓ Теперь дробь становится 0 к десятичной системе счисления. Узнайте больше о представлении чисел со знаком здесь.
Некоторые другие преобразования Шестнадцатеричное число в двоичноеЗамените шестнадцатеричное число его 4-битным двоичным эквивалентом. Рассмотрим пример ниже.
\((4AF)_{16}\ →(0100\ 1010\ 1111)_2\)
Восьмеричное число в двоичноеЗаменить восьмеричное число его 3-битным двоичным эквивалентом.
 Рассмотрим пример ниже.
Рассмотрим пример ниже.\((376)_8→(011\ \ 111\ \ 110)_2\)
Двоичный в восьмеричныйСгруппируйте двоичный битовый поток в пары «3», начиная с LSB.
\(\влево(101101011\вправо)_2\вправо\влево(?\вправо)_8\)
\(\влево(101\\ 101\\011\вправо)_2\вправо\влево(553\вправо )_8\)
Двоичный код в шестнадцатеричныйСгруппируйте двоичный битовый поток в пары «4», начав его с младшего разряда.
\(\влево(000101101011\вправо)_2\вправо\влево(?\вправо)_{16}\)
\(\влево(0001\ 0110\ 1011\вправо)_2\вправо\влево(16B\ справа)_{16}\)
Восьмеричное в шестнадцатеричноеАналогично, для преобразования восьмеричного в шестнадцатеричное сначала преобразуйте его в двоичный эквивалент, а затем выполните преобразование из двоичного в шестнадцатеричное.
\(\влево(553\вправо)_8\стрелка вправо\влево(101\ \ 101\ \ 011\вправо)_2\)
\(\влево(0001\ 0110\ 1011\вправо)_2\стрелка вправо\влево (16B\right)_{16}\)
Шестнадцатеричная система в восьмеричнуюСначала преобразуйте шестнадцатеричную систему в двоичную, а затем выполните преобразование из двоичной в восьмеричную.

\(\влево(16B\вправо)_{16}\вправо\влево(000101101011\вправо)_2\)
\(\влево(000\ 101\ \ 101\ \ 011\вправо)_2\вправо\ влево(0553\вправо)\стрелка вправо\влево(553\вправо)_8\)
Кроме того, ознакомьтесь с другими темами цифровой электроники здесь.
Мы надеемся, что приведенная выше статья о типах систем счисления поможет вам понять и подготовиться к экзамену. Оставайтесь с нами в приложении Testbook, чтобы получать больше обновлений по связанным темам, связанным с цифровой электроникой, и различным подобным предметам. Кроме того, обратитесь к серии тестов, доступных для проверки ваших знаний по нескольким экзаменам.
Часто задаваемые вопросы о типах систем счисленияВ.1 Каковы четыре типа систем счисления?
Ответ 1 Четыре самых популярных типа системы счисления: двоичная система счисления, десятичная система счисления, восьмеричная система счисления, шестнадцатеричная система счисления.

В.2 Почему шестнадцатеричная система счисления называется буквенно-цифровой?
Ответ 2 Шестнадцатеричная система счисления содержит как цифры, так и буквы, поэтому она называется буквенно-цифровой системой счисления.
В.3. Как проще всего преобразовать шестнадцатеричное число в его восьмеричный эквивалент?
Ответ 3 Самый простой процесс преобразования шестнадцатеричного числа в его восьмеричный эквивалент — сначала преобразовать шестнадцатеричное число в двоичное, а затем выполнить преобразование из двоичного в восьмеричное.
Q.4 Какая система счисления используется в цифровой системе и почему?
Ответ 4 В цифровой системе используется двоичная система счисления, поскольку для описания выражения существует только два допустимых логических значения, т. е. либо логическая «1», либо логический «0».
В.5 Какое значение имеют системы счисления?
Ответ 5 Системы счисления необходимы для понимания обработки цифровой системы.
Скачать публикацию в формате PDF Цифровая система использует двоичные, восьмеричные и шестнадцатеричные числа в качестве входных данных, обрабатывает их и генерирует выходные данные. Таким образом, в области информационных технологий или встроенных систем везде требуется хорошо знать систему счисления, чтобы понять ее выполнение.
Цифровая система использует двоичные, восьмеричные и шестнадцатеричные числа в качестве входных данных, обрабатывает их и генерирует выходные данные. Таким образом, в области информационных технологий или встроенных систем везде требуется хорошо знать систему счисления, чтобы понять ее выполнение.Еще на сайте testbook.com
Представление булевых функций: форма SOP, форма POS, таблица истинности, диаграмма Венна и K-карты Законы булевой алгебры: смысл, законы и теоремы Элементы группы 16: Периодические, физические и химические свойства Элементы группы 15: Периодические, физические и химические свойства Элементы группы 14: Периодические, физические и химические свойства Преобразование двоичных, восьмеричных, десятичных и шестнадцатеричных чисел в Python
В Python вы можете обрабатывать числа и строки как двоичные (bin), восьмеричные (oct) и шестнадцатеричные (hex), а также десятичные.
 Они также могут быть преобразованы друг в друга.
Они также могут быть преобразованы друг в друга.В этой статье описывается следующее содержимое.
- Запись целых чисел в двоичной, восьмеричной и шестнадцатеричной системе счисления
- Преобразование чисел в двоичную, восьмеричную и шестнадцатеричную строку
-
bin(),окт(),шестнадцатеричный() -
format(),str.format(), f-строки - Преобразование отрицательного целого числа в строку в представлении с дополнением до двух
-
- Преобразование двоичной, восьмеричной и шестнадцатеричной строки в число
-
int()
-
- Примеры использования
- Арифметика двоичных строк
- Преобразование между двоичными, восьмеричными и шестнадцатеричными числами
Основы преобразования между строкой (
str) и числом (int,float) см. в следующей статье.
- Преобразование строки в число (int, float) в Python
Запись целых чисел в двоичном, восьмеричном и шестнадцатеричном представлении
Добавляя префиксы
0b,0oи0x, целочисленные числа типаintмогут быть записаны в двоичном, восьмеричном и шестнадцатеричном виде соответственно. Выходprint()будет в десятичном представлении.номер_бина = 0b10 число_октября = 0o10 шестнадцатеричное_число = 0x10 печать (bin_num) печать (номер_октября) печать (шестнадцатеричный_номер) № 2 № 8 № 16
источник: numeric_types.py
Вы также можете использовать прописные буквы
0B,0Oи0X.Bin_num = 0B10 Oct_num = 0O10 Шестнадцатеричный_номер = 0X10 печать (Bin_num) печать (номер_октября) печать (Hex_num) № 2 № 8 № 16
источник: numeric_types.py
Даже с префиксом тип является целым числом
в.
печать (тип (bin_num)) печать (тип (oct_num)) печать (тип (hex_num)) # <класс 'целое'> # <класс 'целое'> # <класс 'целое'> печать (тип (Bin_num)) печать (тип (номер_октября)) печать (тип (Hex_num)) # <класс 'целое'> # <класс 'целое'> # <класс 'целое'>
источник: numeric_types.py
Поскольку это
int, с ними можно работать как обычно.результат = 0b10 * 0o10 + 0x10 печать (результат) № 32
источник: numeric_types.py
В Python 3.6 и более поздних версиях вы можете вставлять символы подчеркивания
_в числа. Повторение символов подчеркивания_вызывает ошибку, но вы можете вставлять столько, сколько хотите, если они не повторяются.Знак подчеркивания
_можно использовать в качестве разделителя при наличии большого количества цифр. Например, будет легче читать, если вы будете вводить_через каждые четыре цифры.печать (0b111111111111 == 0b1_1_1_1_1_1_1_1_1_1_1_1) # Истинный bin_num = 0b1111_1111_1111 печать (bin_num) № 4095
источник: numeric_types.
 py
pyПреобразование числа в двоичную, восьмеричную и шестнадцатеричную строку
Для преобразования числа в двоичную, восьмеричную или шестнадцатеричную строку можно использовать следующие функции.
- Встроенная функция
bin(),oct(),hex() - Встроенная функция
format(), строковый методstr.format(), f-строки
Здесь также описывается, как получить строку в виде дополнения до двух для отрицательного значения.
bin(), oct(), hex()
Встроенные функции
bin(),oct()иhex()могут использоваться для преобразования числа в двоичное, восьмеричное и шестнадцатеричная строка. Эти функции возвращают строку с префиксами0b,0oи0xсоответственно.- Встроенные функции — bin() — Документация по Python 3.9.1
- Встроенные функции — oct() — Документация по Python 3.
 9.1
9.1 - Встроенные функции — hex() — Python 3.9.1 документация
я = 255 печать (бен (я)) печать (октябрь (я)) печать (шестнадцатеричный (я)) # 0b11111111 # 0o377 # 0xff печать (тип (бен (я))) печать (тип (октябрь (i))) печать (тип (шестнадцатеричный (i))) # <класс 'ул'> # <класс 'ул'> # <класс 'ул'>
источник: numeric_types.py
Если вам не нужен префикс, используйте срез
[2:]для извлечения завершающих строк или используйтеformat(), как описано ниже.- Как разрезать список, строку, кортеж в Python
печать (бин (я) [2:]) печать (окт (я) [2:]) печать (шестнадцатеричный (я) [2:]) № 11111111 № 377 # фф
источник: numeric_types.py
Если вы хотите преобразовать в десятичную строку, используйте
str().- Встроенные функции — str() — Документация по Python 3.9.1
печать (стр (я)) № 255 печать (тип (стр (я))) # <класс 'ул'>
источник: numeric_types.
 py
pyformat(), str.format(), f-strings
Встроенная функция
format(), строковый методstr.format()и f-строки также можно использовать для преобразования числа в двоичную, восьмеричную и шестнадцатеричную строку.- Встроенные функции — format() — Документация по Python 3.9.1
Указав
b,oиxв строке спецификации формата второго аргументаformat(), число может быть преобразовано в двоичную, восьмеричную и шестнадцатеричную строку соответственно.- string — Мини-язык спецификации формата — Документация Python 3.9.1
печать (формат (i, 'b')) печать (формат (я, 'о')) печать (формат (я, 'х')) № 11111111 № 377 # фф печать (тип (формат (i, 'b'))) печать (тип (формат (я, 'о'))) печать (тип (формат (я, 'х'))) # <класс 'ул'> # <класс 'ул'> # <класс 'ул'>
источник: numeric_types.py
Если вы хотите получить строку символов с префиксом
0b,0o,0x, добавьте#в строку спецификации формата.
печать (формат (i, '# b')) печать (формат (я, '# о')) печать (формат (я, '# х')) # 0b11111111 # 0o377 # 0xff
источник: numeric_types.py
Также можно заполнить ноль (
0) любым количеством цифр. Обратите внимание, что количество символов для префикса (два символа) также необходимо учитывать при заполнении нуля с префиксом.печать (формат (i, '08b')) печать (формат (i, '08o')) печать (формат (я, '08x')) № 11111111 # 00000377 # 000000ff печать (формат (я, '# 010b')) печать (формат (i, '# 010o')) печать (формат (я, '# 010x')) # 0b11111111 # 0o00000377 # 0x000000ff
источник: numeric_types.py
Строковый метод
str.format()можно использовать для того же преобразования.- Встроенные типы str.format() — Документация по Python 3.9.1
печать('{:08b}'.format(i)) печать('{:08o}'.формат(я)) печать ('{: 08x}'. формат (я)) № 11111111 # 00000377 # 000000ffисточник: numeric_types.
 py
pyВ Python3.6 или более поздних версиях вы также можете использовать f-строки (
f'xxx').- 2. Лексический анализ — Форматированные строковые литералы — Python 3.9.1 документация
печать (f'{i:08b}') печать (f'{i:08o}') печать (f'{i:08x}') № 11111111 # 00000377 # 000000ffисточник: numeric_types.py
Преобразование отрицательного целого числа в строку в представлении с дополнением до двух
При использовании
bin()илиformat()отрицательные целые числа преобразуются в абсолютные значения со знаком минус.х = -9 печать (х) печать (бин (х)) # -9 # -0b1001
источник: and_or_bit.py
В Python побитовые операции над отрицательными целыми числами выполняются в представлении с дополнением до двух, поэтому, если вы хотите получить строку, выраженную в представлении с дополнением до двух, используйте побитовое и
имаксимального количества требуемых цифр, например,0b1111(=0xf) для 4-битного,0xffдля 8-битного и0xffffдля 16-битного.
- Дополнение до двух — Википедия
печать (бин (x и 0xff)) печать (формат (x & 0xffff, 'x')) # 0b11110111 # ффф7
источник: and_or_bit.py
Преобразование двоичной, восьмеричной и шестнадцатеричной строки в число
int()
Использование встроенной функции
int()для преобразования двоичной, восьмеричной и шестнадцатеричной строки в число.- Встроенные функции — int() — Документация по Python 3.9.1
Вы можете преобразовать двоичную, восьмеричную и шестнадцатеричную строку в целое число на основе системы счисления с помощью
int(string, radix). Еслиоснованиеопущено, предполагается, что это десятичное число.печать (целое число ('10')) печать (целое ('10', 2)) печать (целое ('10', 8)) печать (целое ('10', 16)) № 10 № 2 № 8 № 16 печать (тип (int ('10'))) печать (тип (int ('10', 2))) печать (тип (int ('10', 8))) печать (тип (int ('10', 16))) # <класс 'целое'> # <класс 'целое'> # <класс 'целое'> # <класс 'целое'>source: numeric_types.
 py
pyIf you set
radixto0, it will be converted according to the prefix (0b,0o,0xor0B,0O,0X).печать (целое число ('0b10', 0)) печать (целое ('0o10', 0)) печать (целое ('0x10', 0)) № 2 № 8 № 16 печать (целое ('0B10', 0)) печать (целое ('0O10', 0)) печать (целое ('0X10', 0)) № 2 № 8 № 16источник: numeric_types.py
Когда система счисления
0, строка без префикса преобразуется в десятичное число. В этом случае обратите внимание, что произойдет ошибка, если начало (слева) будет дополнено0.печать (целое число ('10', 0)) № 10 # печать(целое('010', 0)) # ValueError: недействительный литерал для int() с основанием 0: '010'источник: numeric_types.py
В других случаях строку, дополненную
0, можно преобразовать.печать (целое число ('010')) № 10 печать (целое ('00ff', 16)) печать (целое ('0x00ff', 0)) № 255 № 255источник: numeric_types.
 py
pyВозникает ошибка, если строку невозможно преобразовать на основе указанной системы счисления или префикса.
# print(int('ff', 2)) # ValueError: недействительный литерал для int() с основанием 2: 'ff' # напечатать(целое('0a10', 0)) # ValueError: недействительный литерал для int() с основанием 0: '0a10' # print(int('0bff', 0)) # ValueError: недействительный литерал для int() с основанием 0: '0bff'источник: numeric_types.py
Примеры использования
Арифметика двоичных строк
Например, если вы хотите оперировать двоичной строкой с префиксом
0b, вы можете легко преобразовать ее в целое числоint, выполнить что-то, а затем преобразовать ее обратно в строкуstr.а = '0b1001' б = '0b0011' с = интервал (а, 0) + интервал (б, 0) печать (с) печать (бен (с)) № 12 # 0b1100
источник: numeric_types.py
Преобразование между двоичными, восьмеричными и шестнадцатеричными числами
Также легко преобразовывать двоичные, восьмеричные и шестнадцатеричные строки друг в друга.
 После преобразования в число
После преобразования в число int, его можно преобразовать в строку любого формата.Дополнением нулями и префиксами можно управлять с помощью строки спецификации форматирования.
a_0b = '0b1110001010011' печать (формат (int (a, 0), '# 010x')) # 0x00000009 печать (формат (int (a, 0), '# 010o')) # 0o00000011
источник: numeric_types.py
EIN4611C Глава 6
EIN4611C Глава 6ГЛАВА 6
МАШИННОЕ ПРЕДСТАВЛЕНИЕ ДАННЫХ
НА ДРУГОЙ БАЗЕ SНаиболее часто используемые системы счисления: двоичная, восьмеричная, десятичная и шестнадцатеричная. В двоичной системе счисления используются числа {0,1}, восьмеричная система счисления {0-7}, десятичная система счисления {0-9} и шестнадцатеричная (HEX) система счисления {0-9, A, B, C ,D,E,F}. Говорят, что эти системы счисления представляют собой по основанию чисел. В таблице А.1 указано такое представление. Ниже приведены процедуры преобразования для представления чисел в различных основаниях .

A.1 ТАБЛИЦА ЦИФРОВ
Десятичный Восьмеричный Шестнадцатеричный Двоичный 0 0 0 0000 1 1 1 0001 2 2 2 0010 3 3 3 0011 4 4 4 0100 5 5 5 0101 6 6 6 0110 7 7 7 0111 8 10 8 1000 9 11 9 1001 10 12 А 1010 11 13 Б 1011 12 14 С 1100 13 15 Д 1101 14 16 Е 1110 15 17 F 1111 
Десятичный Восьмеричный Шестнадцатеричный Двоичный 0 0 0 0000 1 1 1 0001 2 2 2 0010 3 3 3 0011 4 4 4 0100 5 5 5 0101 6 6 6 0110 7 7 7 0111 8 10 8 1000 9 11 9 1001 10 12 А 1010 11 13 Б 1011 12 14 С 1100 13 15 Д 1101 14 16 Е 1110 15 17 F 1111 A.
 2 ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ИЗ ОСНОВА 10 В ДРУГУЮ ОСНОВА
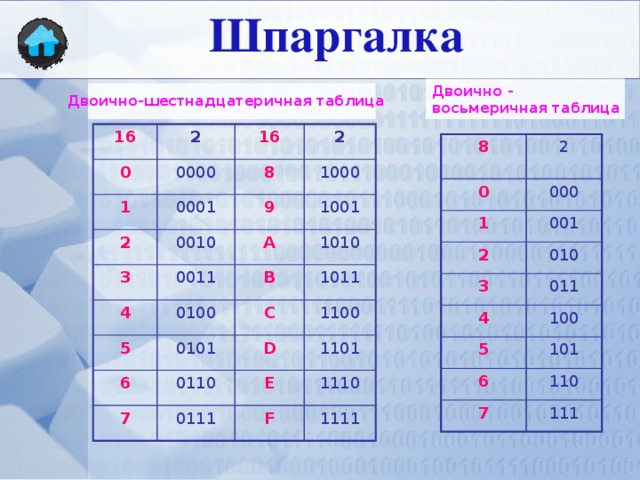
2 ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ИЗ ОСНОВА 10 В ДРУГУЮ ОСНОВА Метод преобразования целого числа из с основанием 10 в другое база это:
Разделить число с основанием 10 на новое число с основанием , т. е. разделить на 2 при преобразовании в с основанием 2, разделить на 8 при преобразовании в с основанием 8, и т. д.
Остаток от деления на шаге 1 представляет собой цифру числа в новой базе . Эта цифра расположена слева от десятичной точки в новом номере по базе .
Если результат деления больше или равен новому по основанию , повторите шаг 1. В противном случае результирующее число располагается слева от предыдущей цифры, т. е. как старшая значащая цифра.
Пример
а) Преобразовать число 105 из по основанию 10 в соответствующее число по основанию 8
105(10) до ? (8)
остаток
8 105 1 105 / 8 : результат = 13, остаток = 1
8 13 5 13 / 8 : результат = 1, остаток = 5
1 1 результат 8, стоп.

Ответ: от 105(10) до 151(8)
б) преобразовать тот же номер из базы 10 до база 2 .
105(10) до ? (2)
остаток 2 105 1 2 52 0 2 26 0 2 13 1 2 6 0 2 3 1 1 1 Ответ: от 105(10) до 1101001(2)
c) Аналогичным образом преобразование в с основанием 16 можно выполнить следующим образом:
105(10) до ? (2)
U>А
остаток 16 105 9 6 6 ответ: от 105(10) до 69(16)
Чтобы представить действительное число, данное в по основанию 10 в другом база , предыдущая процедура для целой части должна применяться к числу слева от десятичной точки.
 Для дробной части применяется следующая процедура.
Для дробной части применяется следующая процедура.Получите дробную часть и умножьте ее на новое число по основанию .
Целая часть произведения, полученного на шаге 1, представляет собой цифру дробной части числа в новой базе . Он расположен справа от десятичной точки и предыдущих цифр, если они есть.
Если дробная часть произведения на шаге 1 равна нулю, остановитесь. В противном случае дробная часть умножения используется для повторения шага 1, пока не будет достигнута желаемая точность.
Пример
а) Преобразовать 0,15(10) в с основанием 16 .
0,15(10) = ? (16)
U>А
целое число 0 .15 х 16 2 .40 х 16 6 .40 х 16 6 .  40 х 16
40 х 16 6 .40 nswer: 0.15(10) = 0,266(16)
б) Преобразовать 0,120(10) в с основанием 8 .
0,120(10) = ? (8)
целое число .120 х 8 0 .960 х 8 7 .680 х 8 5 .440 х 8 3 .520 х 8 4 .160 х 8 1 .280 х 8 2 .240 Answer: 0.
 120(10) = 0.0753412(8)
120(10) = 0.0753412(8) A.3 ОБЩЕЕ ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В РАЗНЫХ ОСНОВАХ S
Процедура получения десятичного представления любого числа в другом основании подчиняется следующему выражению:
Десятичное значение =
, где b — базовый номер , bi — позиционный вес, а di — позиционное значение. Левая цифра после запятой имеет позицию i = 0, значение i увеличивается до ле ft цифр, и уменьшается до правых цифр.
Пример
1101101(2) =
= 64 + 32 + 8 + 4 + 1 = 109(10)
110.11(2) =
= 4 + 2 + 0,5 + 0,25 = 6,75(10)
151(8) = = 54 + 40 + 1 = 105(10)
Таблица 3.2 Счет от 0 до 15 в десятичном и двоичном формате
Десятичный Двоичный Десятичный Двоичный 00 0000 08 1000 01 0001 09 1001 02 0010 10 1010 03 0011 11 1011 04 0100 12 1100 05 0101 13 1101 06 0110 14 1110 07 0111 15 1111 Как отмечалось ранее, компьютеры могут выполнять арифметические и логические операции с соответствующим образом закодированными данными.
 Основываясь на нашем обсуждении логических устройств, мы получили некоторое представление о том, какие типы логических операций могут выполняться и как можно управлять цифровыми устройствами.
предназначен для выполнения таких операций. Пример 3.5 также показал нам, как логические устройства могут выполнять арифметические операции. Поскольку компьютеры основаны на бистабильных устройствах, используемая натуральная система счисления — 9.0814 двоичный ( по основанию 2 )
а не обычное десятичное число ( по основанию 10 ). Сначала мы обсудим двоичную систему счисления и двоичную арифметику, затем кратко представим другие системы счисления (шестнадцатеричную и восьмеричную), которые также полезны при работе с компьютерными системами.
Основываясь на нашем обсуждении логических устройств, мы получили некоторое представление о том, какие типы логических операций могут выполняться и как можно управлять цифровыми устройствами.
предназначен для выполнения таких операций. Пример 3.5 также показал нам, как логические устройства могут выполнять арифметические операции. Поскольку компьютеры основаны на бистабильных устройствах, используемая натуральная система счисления — 9.0814 двоичный ( по основанию 2 )
а не обычное десятичное число ( по основанию 10 ). Сначала мы обсудим двоичную систему счисления и двоичную арифметику, затем кратко представим другие системы счисления (шестнадцатеричную и восьмеричную), которые также полезны при работе с компьютерными системами.Давайте кратко рассмотрим, как работает десятичная система, или по основанию 10 . Последовательность десятичных чисел имеет очень конкретное значение, например,
204 =
412,05 =
Обратите внимание, что у нас есть позиций , представляющих степени числа 10 и несущих весов позиции цифр (например, 100, 101) и цифр 0,1,2 .
 . . 9. Умножаем символ в конкретной позиции на его цифру p
позиция веса и суммы, чтобы получить десятичное число. При счете или сложении мы используем 10 цифр (0 . . . 9), а когда мы превышаем девять, мы переносим единицу на следующую позицию.
. . 9. Умножаем символ в конкретной позиции на его цифру p
позиция веса и суммы, чтобы получить десятичное число. При счете или сложении мы используем 10 цифр (0 . . . 9), а когда мы превышаем девять, мы переносим единицу на следующую позицию.В двоичной системе счисления есть две цифры, 0 и 1, соответствующие двум возможным состояниям цифровых сигналов (например, HI и LO). Таким образом, двоичное число представляет собой последовательность единиц и нулей. Двоичные числа также могут быть представлены множителями. определяя цифру в каждой позиции по их весам позиций цифр (в данном случае степеням двойки), например,
01001101(2) =
, где «(2)» используется для обозначения того, что это двоичное число. Поскольку 0 и 1 — это цифры, используемые в двоичной системе, их часто называют бит , аббревиатурой от b inary dig its. Крайняя левая единица в двоичном числе называется старшим значащим битом (MSB), крайняя правая цифра называется младшим значащим битом (LSB).

Преобразование из двоичных чисел в десятичные числа легко выполняется путем умножения каждого символа на вес позиции его цифры и суммирования, например,
01001101(2) =
= 77(10)
Для преобразования числа из десятичного в двоичное число можно использовать два метода:
Разделите десятичное число на 2 (двоичное основание) и запишите остаток как младший бит двоичного эквивалента. Затем разделите частное от первое деление на два и повторять до тех пор, пока частное не станет равным нулю. Например, чтобы найти двоичный эквивалент числа 29(10):
Таким образом, 29(10) = 111 01(2)Частное Остаток 29/2 = 14 1 (младший бит) 14/2 = 7 0 7/2 = 3 1 3/2 = 0 1 1/2 = 0 1 (MSB) Вычтите максимально возможную степень двойки (двоичное основание) из десятичного числа и поместите 1 в соответствующую позицию веса, повторяйте, пока десятичное число не уменьшится до нуля.
 Если после первого вычитания следующая меньшая степень
из 2 не может быть вычтено, затем поставьте 0 в соответствующую позицию взвешивания. Снова найдем двоичный эквивалент 29(10):
Если после первого вычитания следующая меньшая степень
из 2 не может быть вычтено, затем поставьте 0 в соответствующую позицию взвешивания. Снова найдем двоичный эквивалент 29(10):
Это подтверждает наш предыдущий результат: 29(10) = 11101(2).29- 24 = 29 — 16 = 13 1 (старший бит) 13 — 23 = 13 — 8 = 5 1 5 — 22 = 5 — 4 = 1 1 1 — 21 = (невозможно) 0 1 — 20 = 1 — 1 = 0 1 (младший бит) Двоичное сложение очень похоже на десятичное сложение. Мы добавляем два двоичных символа и, если превышен самый большой символ, мы переносим единицу на следующую позицию или место, например,
и,
До сих пор мы избегали отрицательных чисел и вычитания.
 Есть два распространенных способа их обработки в двоичной арифметике:
Есть два распространенных способа их обработки в двоичной арифметике:Прямое двоичное вычитание похоже на обычное десятичное вычитание, за исключением того, что когда нам нужно заимствовать, мы используем 2 (t бинарная база), например,
Мы должны всегда вычитать меньшее число из большего числа, а затем корректировать знак, например,
Это трудно реализовать на компьютере, поэтому предпочтительнее второй подход.
Арифметика с дополнением до двух используется на компьютерах для отрицательных чисел и вычитания. Дополнением до двух двоичного числа называется такое число, которое при добавлении к исходному числу дает в сумме ноль, например:
Двоичный номер: 110110110110(2)
Дополнение до двух: 001001001010(2)
Бит переноса и сумма: 1 000000000000(2)
Обратите внимание, что бит переноса (1) в результирующей сумме игнорируется. Таким образом, мы работаем с фиксированным количеством битов (в данном примере 12).
 Это похоже на одометр автомобиля. Например, если одометр имеет пять цифр и показывает 99995(10) м.
iles, еще через 5 миль показание становится равным нулю. Чтобы получить дополнение до двух двоичного числа, мы сначала вычисляем дополнение до единицы путем установки каждого бита в противоположное значение, затем и единицы в дополнение до единицы, например,
Это похоже на одометр автомобиля. Например, если одометр имеет пять цифр и показывает 99995(10) м.
iles, еще через 5 миль показание становится равным нулю. Чтобы получить дополнение до двух двоичного числа, мы сначала вычисляем дополнение до единицы путем установки каждого бита в противоположное значение, затем и единицы в дополнение до единицы, например,Двоичный номер: 110(2)
Дополнение до единицы: 001(2)
Дополнение до двух: 010(2)
Таким образом, при фиксированном количестве двоичных разрядов используется запись с дополнением до двух, где два представляют отрицательные числа. Например, с 8-битным двоичным числом мы можем представить 28 = 256 возможных значений (от 00000000(2) до 11111111(2)). Использование двух комплементов В нотации nt мы можем представлять числа в диапазоне от +127(10) до -128(10) (см. рис. 3.10). Крайний левый бит служит битом знака, где ноль означает положительное число, а 1 означает отрицательное число. Обратите внимание, что 0(10) = 000000000(2) считается поз.
 итивное число.
итивное число.Двоичные числа естественны для компьютеров, но очень неудобны для людей. Слишком легко сделать ошибку, а длинные последовательности двоичных цифр трудно интерпретировать. Другие системы счисления, особенно шестнадцатеричная ( по основанию 16 ) и восьмеричная . ( base 8 ), обычно используются программистами. Их иногда называют сгруппированными битовыми системами счисления , поскольку группы из четырех битов легко преобразуются в две шестнадцатеричные, а группы из трех битов легко преобразуются в восьмеричные. Большинство микропроцессоров сегодня используют 8 или 16 бит, что делает группировку по 4 бита более удобной. Таким образом, шестнадцатеричная система, как правило, предпочтительнее и будет подчеркнута здесь.
Восьмеричные числа используют символы 0,1,2 . . . 7 и веса позиций цифр, которые являются степенями числа 8. Точно так же шестнадцатеричные числа используют символы 0,1,2 . . . 9 и A, B, C, D, E и F, а также веса позиций цифр, которые являются степенями 16.
 Числа до 23 (10)
а их шестнадцатеричные, восьмеричные и двоичные эквиваленты показаны в таблице 3.3.
Числа до 23 (10)
а их шестнадцатеричные, восьмеричные и двоичные эквиваленты показаны в таблице 3.3.Таблица 3.3 Десятичные числа до 23 и их шестнадцатеричные, восьмеричные и двоичные эквиваленты
по этой таблице мы можем легко преобразовать двоичные числа в 3-битных группах в их восьмеричный эквивалент, например,Десятичный Гекса- десятичный Окталь Двоичный Десятичный Шестнадцатеричный десятичный Окталь Бинарный С 14 1100151 1 1 1 1 13 D 15 110151 110151 2 2 2 10 14 Е 16 1110 3 3 3 11 15 F 17 111151 4 4 4 100 16 10 20 10000 5 5 5 101 17 11 21 1001516 6 6 110 18 12 22 101517 7 7 111 19 13 23 101518 8 10 1000 20 14 24 10100 9 9 11 1001 21 15 25 10101 10 А 12 1010 22 16 26 101151818 11 Б 13 1011 23 17 27 1011511 1011518Двоичный номер: 011 010 111 101
Восьмеричный эквивалент: 3 2 7 5
Таким образом, 011010111101(2) = 3275(8).
 Точно так же, используя 4-битные группировки, мы можем преобразовать в шестнадцатеричный,
Точно так же, используя 4-битные группировки, мы можем преобразовать в шестнадцатеричный,Двоичный номер: 0110 1011 1101
Шестнадцатеричный эквивалент: 6 B D
Таким образом, 011010111101(2) = 6BD(16). Основные методы и концепции, описанные для двоичных чисел в отношении преобразования, отрицательных чисел и арифметики, также применимы к восьмеричным и шестнадцатеричным числам. Они проиллюстрированы для шестнадцатеричных чисел на экзамене. ples, которые следуют.
Пример 3.6 Преобразование десятичных и шестнадцатеричных чисел
Сначала мы оцениваем десятичный эквивалент 19AF(16).
19AF(16) =
=
= 6575(10)
Теперь преобразуем десятичное число 29(10) в шестнадцатеричное методом деления.
таким образом, 29(10) = 1D(16).Частное Остаток 29/16 = 1 13(10) = D(16) (LSD) 1/16 = 0 1(10) = 1(16) (МСД)  Подтвердите этот результат, вычитая степени основания.
Подтвердите этот результат, вычитая степени основания.Пример 3.7 Шестнадцатеричное сложение
Здесь приведены два примера.
и,
Пример 3.8 Шестнадцатеричное вычитание
Мы можем обрабатывать отрицательные числа и вычитание, используя дополнение до 16 шестнадцатеричного числа. Например, чтобы вычесть 86B(16) из A94(16), мы добавляем дополнение 16 к 86B( 16) до A94(16). Дополнение до 16 для 86B(16) получается путем получения дополнения до 15 для 86B(16) с последующим добавлением единицы. Дополнение до 15 получается вычитанием каждой цифры из 15, например,
15-е дополнение к 86B(16) = 794(16)
Дополнение 16 к 86B(16) = 795(16)
А94(16) 86В(16) = А94(16) + 795(16) = 1229(16)
Пренебрегая переносом, получаем результат 229(16). Проверьте этот результат прямым шестнадцатеричным вычитанием.
3.4 ОБЗОР
В этой главе рассмотрены некоторые справочные материалы, которые будут полезны для понимания работы и программирования микрокомпьютерных систем.



 5
5
 90,5\)
90,5\) 101011)_2
101011)_2 Рассмотрим пример ниже.
Рассмотрим пример ниже.

 Цифровая система использует двоичные, восьмеричные и шестнадцатеричные числа в качестве входных данных, обрабатывает их и генерирует выходные данные. Таким образом, в области информационных технологий или встроенных систем везде требуется хорошо знать систему счисления, чтобы понять ее выполнение.
Цифровая система использует двоичные, восьмеричные и шестнадцатеричные числа в качестве входных данных, обрабатывает их и генерирует выходные данные. Таким образом, в области информационных технологий или встроенных систем везде требуется хорошо знать систему счисления, чтобы понять ее выполнение. Они также могут быть преобразованы друг в друга.
Они также могут быть преобразованы друг в друга.

 py
py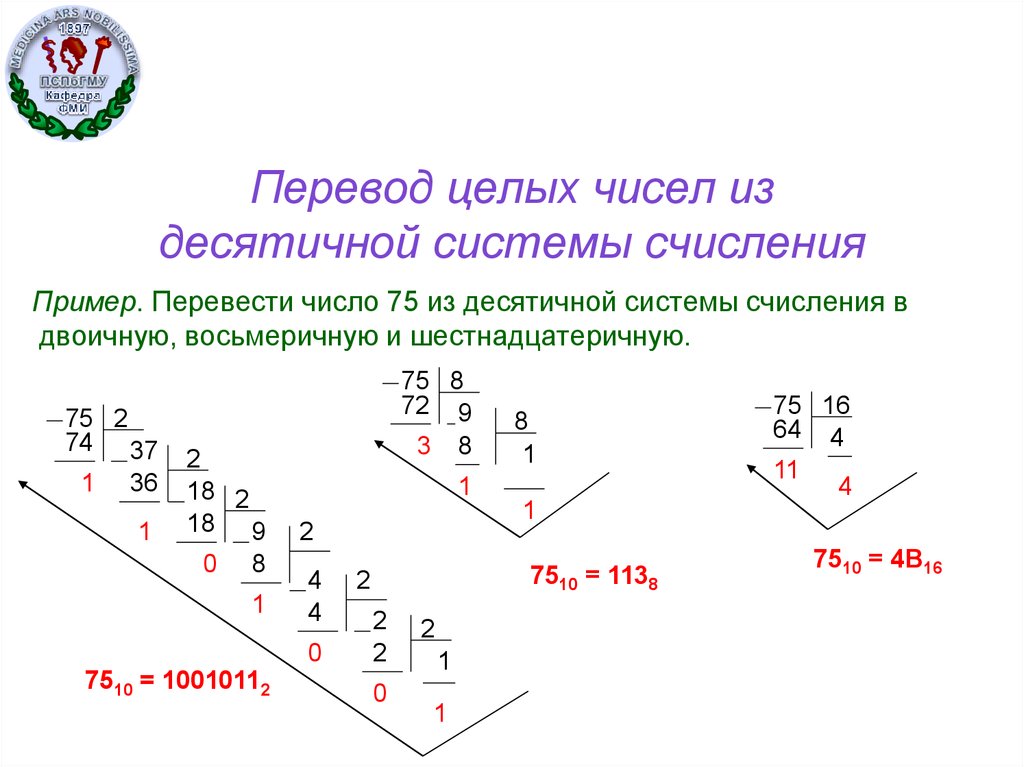 9.1
9.1 py
py
 py
py
 py
py py
py После преобразования в число
После преобразования в число 

 2 ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ИЗ ОСНОВА 10 В ДРУГУЮ ОСНОВА
2 ПРЕДСТАВЛЕНИЕ ЧИСЕЛ ИЗ ОСНОВА 10 В ДРУГУЮ ОСНОВА 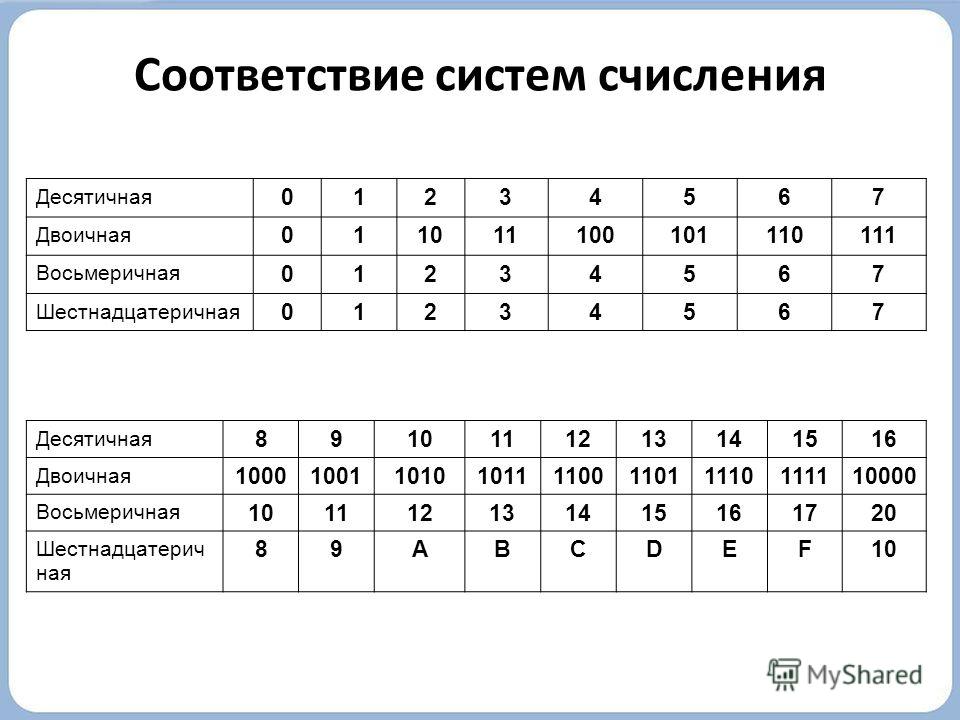
 Для дробной части применяется следующая процедура.
Для дробной части применяется следующая процедура. 40 х 16
40 х 16  120(10) = 0.0753412(8)
120(10) = 0.0753412(8) 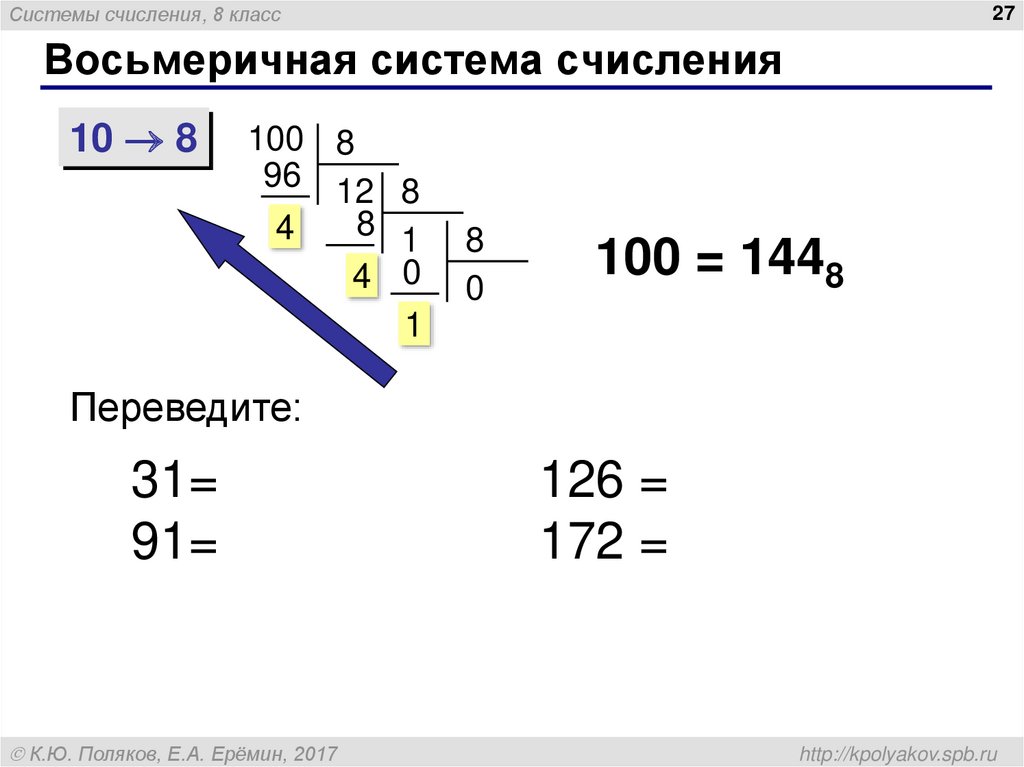 Основываясь на нашем обсуждении логических устройств, мы получили некоторое представление о том, какие типы логических операций могут выполняться и как можно управлять цифровыми устройствами.
предназначен для выполнения таких операций. Пример 3.5 также показал нам, как логические устройства могут выполнять арифметические операции. Поскольку компьютеры основаны на бистабильных устройствах, используемая натуральная система счисления — 9.0814 двоичный ( по основанию 2 )
а не обычное десятичное число ( по основанию 10 ). Сначала мы обсудим двоичную систему счисления и двоичную арифметику, затем кратко представим другие системы счисления (шестнадцатеричную и восьмеричную), которые также полезны при работе с компьютерными системами.
Основываясь на нашем обсуждении логических устройств, мы получили некоторое представление о том, какие типы логических операций могут выполняться и как можно управлять цифровыми устройствами.
предназначен для выполнения таких операций. Пример 3.5 также показал нам, как логические устройства могут выполнять арифметические операции. Поскольку компьютеры основаны на бистабильных устройствах, используемая натуральная система счисления — 9.0814 двоичный ( по основанию 2 )
а не обычное десятичное число ( по основанию 10 ). Сначала мы обсудим двоичную систему счисления и двоичную арифметику, затем кратко представим другие системы счисления (шестнадцатеричную и восьмеричную), которые также полезны при работе с компьютерными системами. . . 9. Умножаем символ в конкретной позиции на его цифру p
позиция веса и суммы, чтобы получить десятичное число. При счете или сложении мы используем 10 цифр (0 . . . 9), а когда мы превышаем девять, мы переносим единицу на следующую позицию.
. . 9. Умножаем символ в конкретной позиции на его цифру p
позиция веса и суммы, чтобы получить десятичное число. При счете или сложении мы используем 10 цифр (0 . . . 9), а когда мы превышаем девять, мы переносим единицу на следующую позицию.
 Если после первого вычитания следующая меньшая степень
из 2 не может быть вычтено, затем поставьте 0 в соответствующую позицию взвешивания. Снова найдем двоичный эквивалент 29(10):
Если после первого вычитания следующая меньшая степень
из 2 не может быть вычтено, затем поставьте 0 в соответствующую позицию взвешивания. Снова найдем двоичный эквивалент 29(10): Есть два распространенных способа их обработки в двоичной арифметике:
Есть два распространенных способа их обработки в двоичной арифметике: Это похоже на одометр автомобиля. Например, если одометр имеет пять цифр и показывает 99995(10) м.
iles, еще через 5 миль показание становится равным нулю. Чтобы получить дополнение до двух двоичного числа, мы сначала вычисляем дополнение до единицы путем установки каждого бита в противоположное значение, затем и единицы в дополнение до единицы, например,
Это похоже на одометр автомобиля. Например, если одометр имеет пять цифр и показывает 99995(10) м.
iles, еще через 5 миль показание становится равным нулю. Чтобы получить дополнение до двух двоичного числа, мы сначала вычисляем дополнение до единицы путем установки каждого бита в противоположное значение, затем и единицы в дополнение до единицы, например,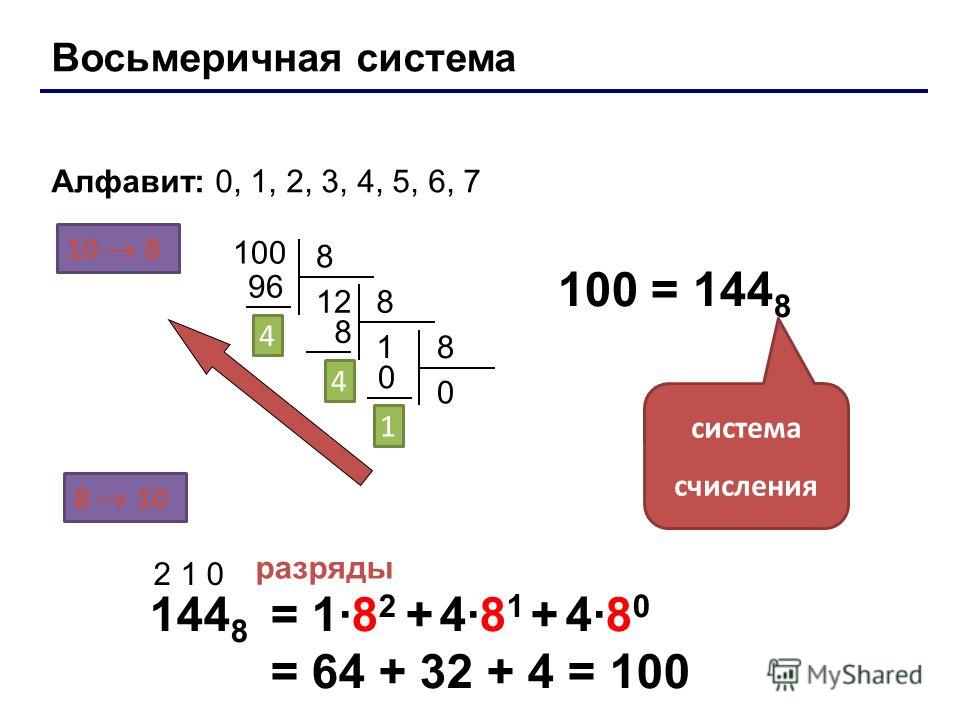 итивное число.
итивное число.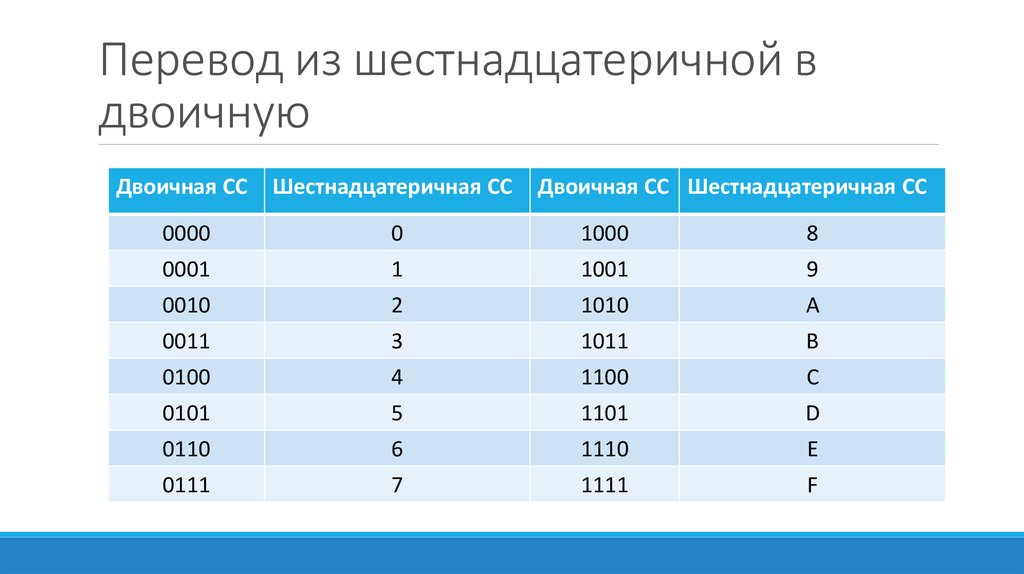 Числа до 23 (10)
а их шестнадцатеричные, восьмеричные и двоичные эквиваленты показаны в таблице 3.3.
Числа до 23 (10)
а их шестнадцатеричные, восьмеричные и двоичные эквиваленты показаны в таблице 3.3.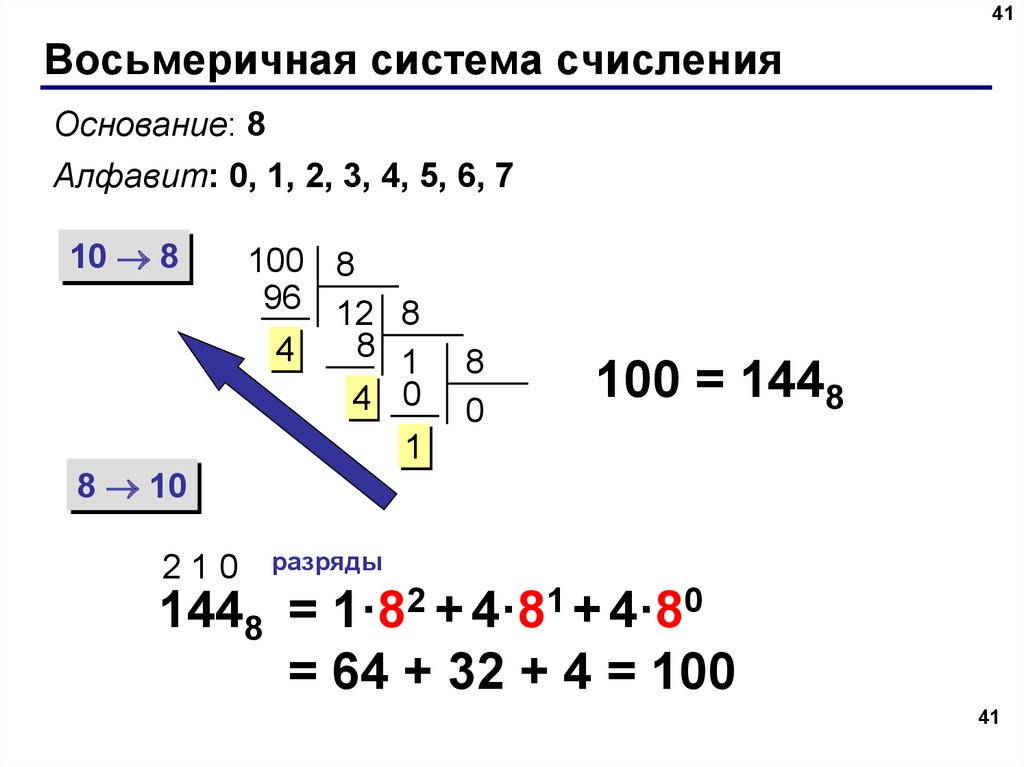 Точно так же, используя 4-битные группировки, мы можем преобразовать в шестнадцатеричный,
Точно так же, используя 4-битные группировки, мы можем преобразовать в шестнадцатеричный, Подтвердите этот результат, вычитая степени основания.
Подтвердите этот результат, вычитая степени основания.