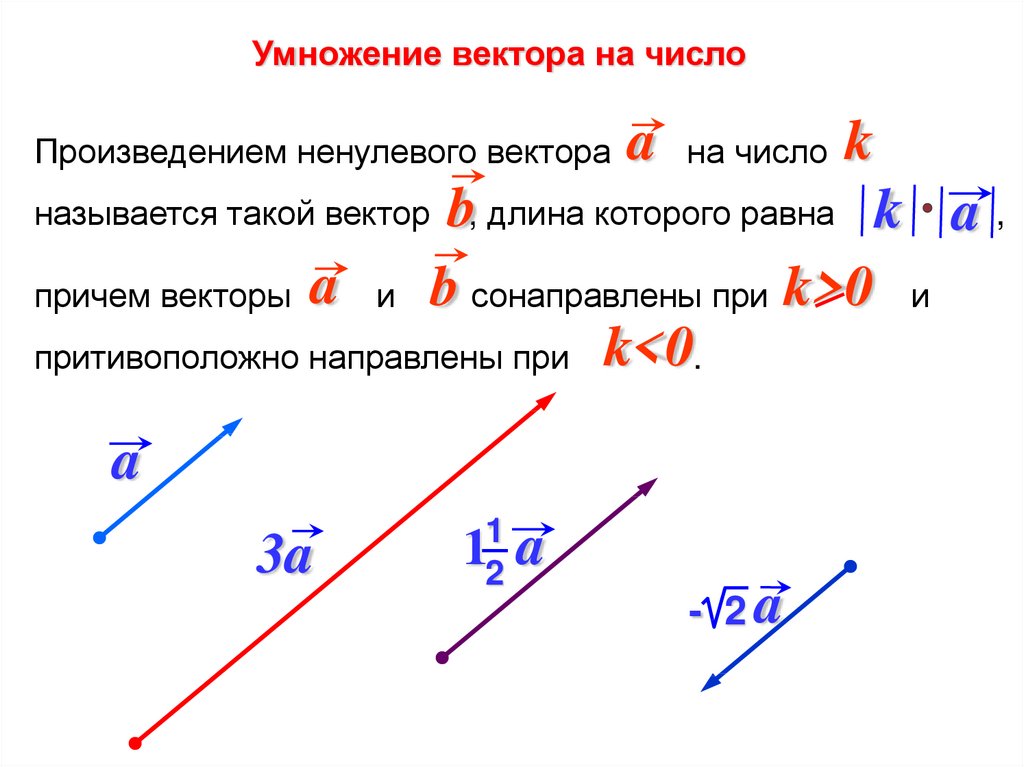
Геометрия Умножение вектора на число
Материалы к уроку
Конспект урока
5. Умножение вектора на число
|
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна модуль |k| умноженный на модуль|а|, причем векторы а и b сонаправлены, если k положительно и противоположно направлены, если k отрицательно. Произведение вектора а на число k обозначается так: ka.
|
Текст Умножение вектора на число
Рисунок векторов
|
|
Для любого числа k и любого вектора а векторы а и ka коллинеарны. Произведением нулевого вектора на любое число считается нулевой вектор. Произведение любого вектора на число нуль есть нулевой вектор.
|
Текст Умножение вектора на число
|
|
Рассмотрим основные свойства умножения вектора на число. Для любых векторов а,b и любых чисел k и l справедливы равенства: Первое. Произведение k и l, умноженное на вектор а, равно произведению k на вектор lа. Это свойство известно как сочетательный закон. На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
Рисунок векторов
Текст
|
|
Второе свойство, первый распределительный закон. На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
|
|
Третье свойство, второй распределительный закон. Произведение суммы чисел k и l на вектор равно сумме произведений чисел k и l на вектор а. На рисунке, на примере показано это свойство.
|
Текст Свойства умножения вектора на число
|
|
Стоит отметить, что произведение числа -1 на любой вектор дает вектор противоположный данному. Согласно определению произведения вектора на число, их длины равны, а направления противоположны. При условии, что вектор а ненулевой.
|
Текст
|
|
Для векторов в пространстве, как и в планиметрии, выполняется следующее условие: Если векторы a и b коллинеарны (то есть лежат на одной прямой или на параллельных прямых) и вектор а ненулевой, то существует число k такое что вектор b равен произведению числа k на вектор а. |
|
|
Решим задачу №347 (а) Необходимо упростить выражение. |
|
|
Решение. Первый распределительный закон позволяет нам раскрыть скобки. А переместительное свойство сложения векторов – привести подобные.
|
.
|
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций. § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой.  § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2.  Окружность. Окружность.§ 3. Эллипс. § 4. Гипербола и ее асимптоты. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных.  § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 8. Некоторые приложения определителей к аналитической геометрии. Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6.  § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ § 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду.  § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей. Общие уравнения прямой. § 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI.  ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА§ 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка. Конструкции В. Г. Шухова. Упражнения Ответы |
Скалярное произведение векторов
Скалярное произведение векторов Скалярное произведение и векторное произведение — два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Скалярное произведение двух векторов можно построить, взяв компонент одного вектора в направлении другого и умножив его на величину другого вектора. Если векторы выражены через единичные векторы i, j и k вдоль направлений x, y и z, скалярное произведение также может быть выражено в виде: Скалярное произведение также называется «внутренним произведением» или «точечным произведением» в некоторых текстах по математике.
| Индекс Векторные понятия | ||
| Назад |
Вы можете ввести значения в любое из полей ниже. Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy. Примечание. Приведенные выше числа не будут принудительно согласованы до тех пор, пока вы не щелкнете либо по скалярному произведению, либо по углу в активной формуле выше. | Индекс Векторные концепции | ||
| Назад |
С геометрической точки зрения скалярное произведение полезно для нахождения направления между произвольными векторами в пространстве. Так как два выражения для произведения: включают компоненты двух векторов, и поскольку величины A и B могут быть рассчитаны из компонентов, используя: , то можно вычислить косинус угла и определить угол. Одним из важных физических применений скалярного произведения является вычисление работы: Скалярное произведение используется для выражения магнитной потенциальной энергии и потенциала электрического диполя. | Индекс Векторные концепции | ||
| Назад |
Иногда удобно представлять векторы в виде матриц-строк или столбцов, а не в виде единичных векторов, как это было сделано выше при рассмотрении скалярного произведения. Если рассматривать обычные пространственные векторы как матрицы-столбцы их компонентов x, y и z, то транспонирование этих векторов будет матрицей-строкой. Тогда мы могли бы написать для векторов A и B: Тогда матричное произведение этих двух матриц даст только одно число, являющееся суммой произведений соответствующих пространственных компонентов двух векторов. Затем это число является скалярным произведением двух векторов. Представленное таким образом скалярное произведение двух векторов иллюстрирует процесс, который используется при умножении матриц, где сумма произведений элементов строки и столбца дает одно число. | Индекс Векторные концепции | ||
| Вернуться |
2.3 Точка, упс, ВНУТРЕННЕЕ произведение
2.3 Точка, упс, ВНУТРЕННЕЕ произведение
|
Далее: 2. 4 Операторы 4 Операторы |
2.3 Точка, упс, ВНУТРЕННИЙ продукт
Скалярное произведение векторов является важным инструментом. Это делает возможным чтобы найти длину вектора, умножив вектор сам на себя и извлечение квадратного корня. Он также используется для проверки того, что два вектора ортогональны: если их скалярный продукт равен нулю, они ортогональны. В этом подраздел, скалярное произведение определено для комплексных векторов и функции.
Обычное скалярное произведение двух векторов и может быть
находится путем умножения компонентов с одинаковым индексом вместе и
подводя итог, что:
(Выразительное равенство обычно используется для обозначения «является по определению равно» или
всегда равно.) Рисунок 2.6 показаны умноженные компоненты одинаковыми цветами.
Обратите внимание на использование числовых индексов, , и
а не , и ; это значит
тоже самое. Числовые индексы позволяют приведенной выше сумме трех членов
записать более компактно как:
Это называется символом суммирования
.
Длина вектора , обозначенного или
просто , обычно вычисляется как
Однако это не работает правильно для сложных векторов. трудность заключается в том, что термины формы уже не обязательно положительные числа. Например, 1.
Поэтому необходимо использовать обобщенное «скалярное произведение» для комплексных векторов, которое ставит комплексное
сопряжение по первому вектору:
| (2.7) |
Если вектор действителен, комплексное сопряжение ничего не делает, и внутренний продукт такой же, как точка продукт .
 В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму.
В противном случае во внутреннем произведении
и больше не взаимозаменяемы; в
сопряженные только по первому фактору, .
Замена и изменение внутреннего
стоимость продукта в его комплексно-сопряженную форму. Длина ненулевого вектора теперь всегда является положительным числом:
| (2.8) |
Физики принимают скалярное произведение за скобкой
устно.
кроме как
и относятся к векторам как бюстгальтеры и кеты.
Внутренний продукт функций определяется точно так же, как и для
вектора, путем умножения значений в одной и той же позиции вместе
и подведение итогов. Но так как значений бесконечно много, то сумма
становится интегралом:
| (2.9) |
На рис.
 2.7 показаны умноженные значения функции с использованием
одинаковые цвета:
2.7 показаны умноженные значения функции с использованием
одинаковые цвета: Эквивалент длины вектора в случае функции
назвал его «нормой»:
| (2.10) |
Двойные черты используются, чтобы избежать путаницы с абсолютным значением функция.
Вектор или функция называются «нормализованными», если их длина или норма равна единице:
| (2.11) |
(«iff» действительно следует читать как
тогда и только тогда, когда)
Два вектора или две функции и по определению ортогональны, если их внутренний продукт равен нулю:
(2.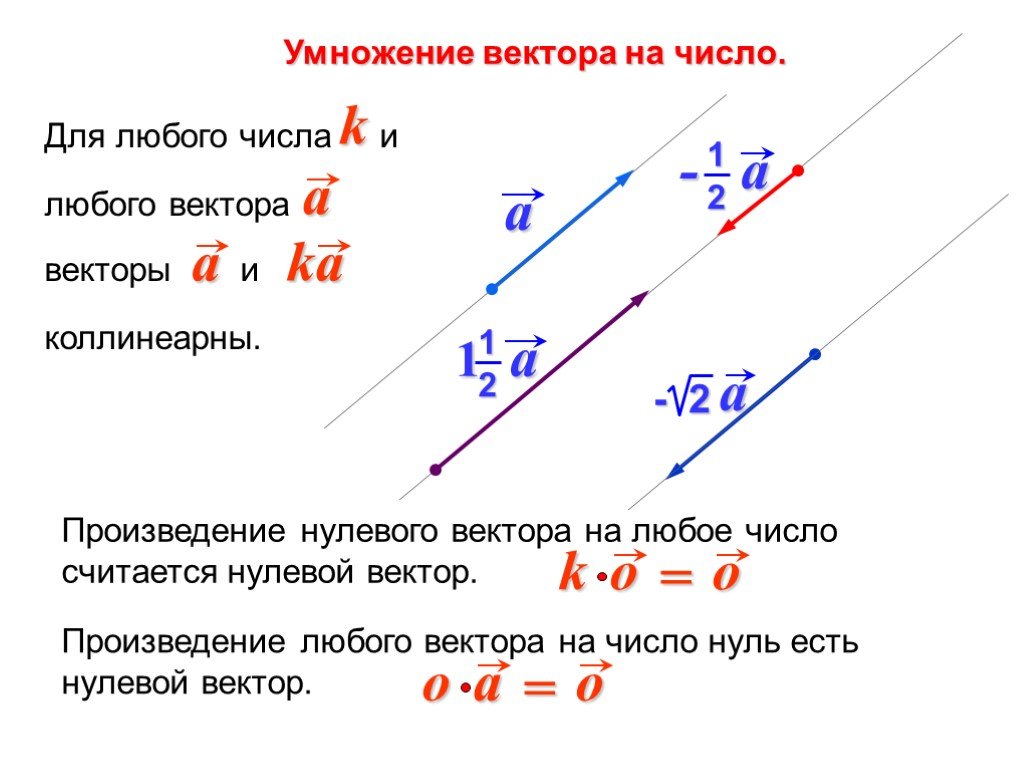 12) 12) |
Наборы векторов или функций, которые все
- взаимно ортогональные, и
- нормализовано
часто используется ортогональный. Этот документ будет правильно называть их ортонормированными.
Итак, набор функций или векторов ортонормирован, если
и
Ключевые моменты
- Для комплексных векторов и функций нормальное скалярное произведение становится внутренним продуктом.
- Чтобы получить скалярное произведение векторов,
- взять комплексные сопряжения компонентов первого вектора;
- перемножить соответствующие компоненты двух векторов вместе;
- сумма этих продуктов.
- Чтобы взять скалярное произведение функций,
- возьмем комплексно-сопряженную первую функцию;
- умножить две функции;
- интегрировать функцию продукта.
- Чтобы найти длину вектора, возьмем внутреннее произведение вектора с самим собой, а затем квадратный корень.
- Чтобы найти норму функции, возьмите внутренний продукт функции с самим собой, а затем квадратный корень.
- Пара векторов или пара функций ортогональны, если их внутренний продукт равен нулю.
- Набор векторов образует ортонормированный набор, если каждый ортогонален всем остальным, и каждый имеет единичную длину.
- Набор функций образует ортонормированный набор, если каждая из них ортогонален всем остальным, и каждый имеет единичную норму.
2. 3 Контрольные вопросы
3 Контрольные вопросы
- 1.
Найдите следующее внутреннее произведение двух векторов:
Раствор точка-а
- 2.
Найдите длину вектора
Раствор точка-б
- 3.
Найдите скалярное произведение функций и на интервале 0 1.
Раствор точка-с
- 4.
Покажите, что функции и ортогональны на интервале 0 .
Раствор точка-d
- 5.
Убедитесь, что это не нормализованная функция на интервале 0 , и нормализуйте ее, разделив на ее норму.
Раствор dot-e
- 6.
Убедитесь, что наиболее общее кратное этому, нормализованному на интервале 0, равно , где любое произвольное действительное число.




 Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.
Произведение числа k на сумму векторов а и b равно сумме произведений этого числа на векторы а и b.

 Много решенных примеров и задач.
Много решенных примеров и задач.
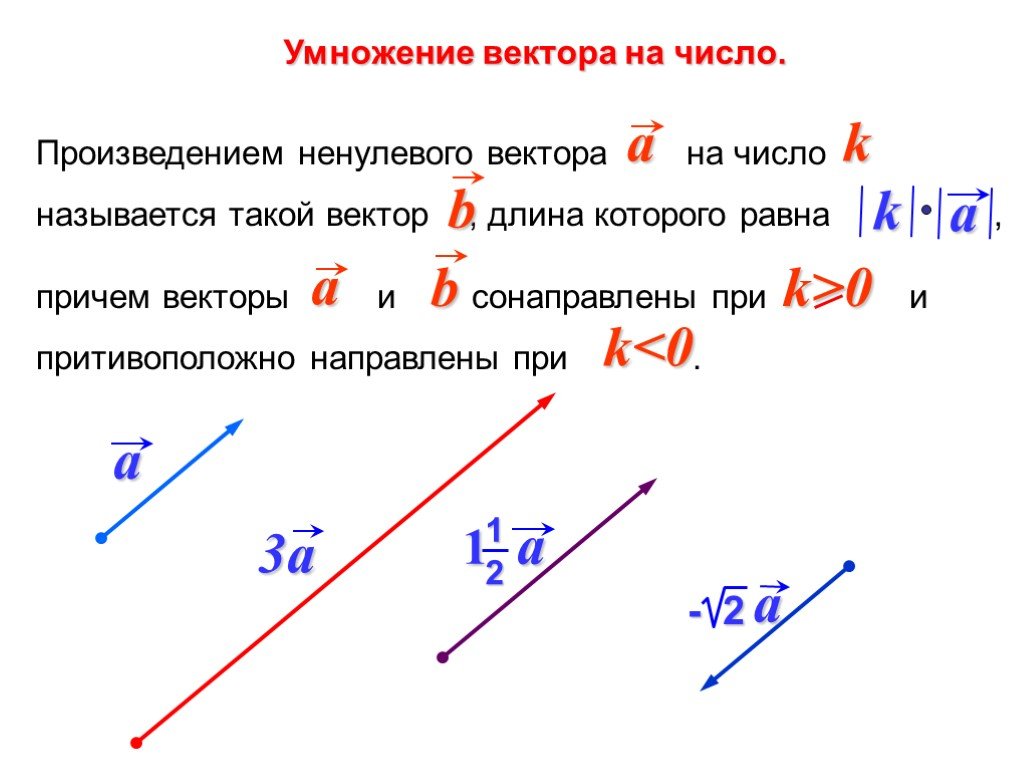 Это можно выразить в виде:
Это можно выразить в виде:


 6: Формирование скалярного произведения двух векторов.
6: Формирование скалярного произведения двух векторов.