Координаты векторного произведения векторов, заданных своими координатами
Рассмотрим два пространственных вектора и. Представим их как линейные комбинации базисных векторов,,:
Запишем векторное произведение , и, используя свойства векторного произведения, раскроем скобки:
Итак, мы получили формулу: .
Смешанное произведение трех пространственных (трехмерных) векторов
Рассмотрим тройку пространственных векторов ,,. Смешанное произведение- эточисло, определяемое формулой:
Геометрический смысл смешанного произведения.
Условие компланарности трех векторов.
Рассмотрим правую тройку некомпланарных векторов ,,. Приведем их в общее начало и построим параллелепипед, в котором векторы,,будут ребрами, выходящими из одной вершины.
Обозначим
буквой
высоту
параллелепипеда, буквойплощадь
его основания (площадь параллелограмма,
построенного на векторах,),
а буквойобъем
параллелепипеда.
Далее: .
В случае левой тройки некомпланарных векторов ,,угол между вектороми векторомбудет тупым, и. Поэтому
Если векторы ,,компланарны, то либо, либо. В обоих случаях. (Можно также повторить предыдущее геометрическое рассмотрение, считая параллелепипед вырожденным, имеющим нулевую высоту или площадь основания).
Итак, мы установили, что смешанное произведение векторов ,,равно объему параллелепипеда построенного на этих векторах в случае, когда тройка правая, или объему, взятому со знаком минус в случае левой тройки.
Кроме того, мы получили условие компланарности трех пространственных векторов: векторы ,,компланарны тогда и только тогда, когда их смешанное произведениеравно нулю.
Используя это условие компланарности, мы получим,
Объем параллелепипеда.
Для
объема параллелепипеда построенного
на тройке векторов ,,имеем
формулу: .
Объем тетраэдра (треугольной пирамиды).
Рассмотрим треугольную пирамиду :
Построим параллелепипед на тройке векторов . Заметим, что площадь основания пирамиды в два раза меньше площади основания параллелепипеда, а высоты у них равны. Получаем:
.
Теперь мы можем доказать остававшееся недоказанным свойство векторного произведения: .
Доказательство.
Докажем, что координаты векторов в правой и левой части равенства совпадают.
Первая координата – это проекция на ось абсцисс, она же проекция на вектор .
Мы использовали свойства скалярногопроизведения и проекций.
Аналогично
доказывается равенство вторых и третьих
координат. Следовательно, векторы в
правой и левой части равенства равны
между собой.
Формула для вычисления смешанного произведения векторов, заданных своими координатами
Рассмотрим три пространственных вектора ,и.
Вектор имеет координаты:.
Используя правило разложения определителя (по третьей строке), получаем:
Итак: .
Свойства смешанного произведения
Следующие свойства вытекают из свойств определителей:
1) ,
2)
3) .
Площадь параллелограмма, построенного на заданных векторах
(через скалярное произведение
и через векторное произведение)
Рассмотрим два вектора , обозначим буквой угол между ними.
Построим параллелограмм, у которого векторы ,приведенные в общее начало, будут смежными сторонами:
Площадь этого параллелограмма будет равна
Площадь
треугольника будет в два раза меньше. Итак:
Итак:
Полученные формулы применимы как для векторов плоскости, так и для векторов в пространстве. Напомним, что для векторов в пространстве, мы можем для нахождения площадей параллелограмма и треугольника использовать векторное произведение:
Для двумерных векторов (на плоскости) нельзя использовать векторное произведение, но можно скалярное.
Координаты вектора в пространстве. Скалярное и векторное произведения векторов
Похожие презентации:
Векторная алгебра. Скалярное произведение векторов. Векторное произведение векторов. Смешанное произведение векторов
Скалярное и векторное произведения векторов
Вектора. Пространства. Скалярное, векторное и смешанное произведение векторов
Векторы. Линейные операции над векторами. Скалярное, векторное, смешанное произведения векторов. Прямая на плоскости
Скалярное произведение векторов
Основы векторной алгебры. Векторы на плоскости и в пространстве
Векторная алгебра.
Векторное произведение векторов
Векторная алгебра
Векторная алгебра
Координаты вектора в пространстве.
Скалярное и векторное произведения
векторов.
8. Пусть в пространстве Oxyz задан вектор
Проекция
,
,
вектора на оси
координат называются координатами вектора
Def: Длина (модуль) вектора равна корню квадратному из суммы
квадратов его координат.
Def: Расстояние между двумя точками пространства равно корню
квадратному из суммы квадратов разностей одноименных
координат этих точек.
9. Введем единичные векторы (орты) i, j, k , направленные по осям
координат. Они не равны, так как являются единичными векторами
Это разложение единственно!
Рассмотренные выше линейные операции над векторами можно
теперь записать в следующем виде:
1)
П- скаляр
При умножении вектора на скаляр координаты вектора
умножаются на этот скаляр.

2)
При сложении (вычитании) векторов их одноименные координаты
складываются (или вычитаются).
Векторы коллинеарные тогда и только тогда, когда их
одноименные координаты пропорциональны.
5. Этой формуле можно придать другой вид.Так как то получаем:
10. Скалярное произведение векторов.Def: Под скалярным произведением двух векторов
и
понимается число, равное произведению длин этих векторов на
косину угла между ними, т.е
Этой формуле можно придать другой вид.Так как
a cos прb a,
b cos прab
то получаем:
ab a прab b прb a
Свойства:
1)
2)
3)
4) Скалярный множитель можно выносить за знак скалярного
произведения, т.е
5) Скалярное произведение линейной комбинации векторов на
произвольный вектор равно такой же линейной комбинации данных
векторов на этот вектор, т.е
6)
Скалярное произведение в координатной
форме.
Перемножим
и
как многочлен и учитывая, что
будем иметь
Скалярное произведение векторов равно сумме парных
произведений их одноименных координат
Проекция вектора на заданное
направление
Нахождение проекции вектора a на направление,
заданное вектором b ,может осуществляться по
формуле
axbx ayby azbz
a b
a b
прb a прa b ), т.
 е.прb a
е.прb a 2
2
2
b
a
bx by bx
Векторное произведение векторов
Def: Под векторным произведением двух векторов
и
понимается вектор
, для которого:
1) Модуль равен площади параллелограмма, построенного на двух
векторах, т.е
, где
2) Этот вектор перпендикулярен
перемножаемым векторам
(перпендикулярен плоскости
параллелограмма), т.е
и
Свойства векторного произведения
1) При изменении порядка сомножителей векторное произведение
меняет свой знак на обратный, сохраняя модуль, т.е
2) Векторный квадрат равен нуль вектору, т.е
3) Скалярный множитель можно выносить за знак векторного
произведения, т.е если п- скаляр, то
4) Для трех векторов
справедливо равенство
Необходимое и достаточное условие коллинеарности двух векторов
и
Векторное произведение в координатной форме
Пусть
Перемножая векторно эти равенства и используя сумму девяти
слагаемых
Для ортов
справедлива следующая «таблица умножения»:
Поэтому получаем:
15.
 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Определение смешанного произведения, его геометрический смыслРассмотрим произведение векторов , и , составленное
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ Определение смешанного произведения, его геометрический смыслРассмотрим произведение векторов , и , составленноеследующим образом: . a b c Здесь первые два вектора
перемножаются векторно, а их результат скалярно на
третий вектор. Такое произведение называется
векторно-скалярным, или смешанным, произведением
трех векторов. Смешанное произведение представляет
собой некоторое число.
Выясним геометрический смысл выражения
и вектор
Построим параллелепипед, ребрами которого
являются векторы a ,b и c
и вектор d a b
Имеем:
a b c d c d
ПР
d
c, d a b S
где — площадь параллелограмма, построенного на
векторах a и b , ПРd c H , для правой тройки
векторов и ПРd c H для левой, где — высота
параллелепипеда.
a b c S H
Получаем:
т.е.
a b c V
где — объем параллелепипеда, образованного
векторами a, b и c
Таким образом, смешанное произведение трех
векторов
равно
объему
параллелепипеда,
построенного на этих векторах, взятому со знаком
«плюс», если эти векторы образуют правую тройку, и
со знаком «минус», если они образуют левую тройку.

Три некомпланарных вектора a , b и c взятые в
указанном порядке, образуют правую тройку,
если с конца третьего вектора c кратчайший
поворот от первого вектора a ко второму вектору b
виден совершающимся против часовой стрелки, и
левую, если по часовой
19. Свойства смешанного произведения
1. Смешанное произведение не меняется прициклической перестановке его сомножителей, т.е.
a b c b c a c a b
2. Смешанное произведение не меняется при
перемене местами знаков векторного и
скалярного умножения, т.е.
a b c a b c
3. Смешанное произведение меняет свой знак при
перемене мест любых двух векторов-сомножителей, т.е.
abc acb, abc bac, abc cba
Смешанное произведение ненулевых векторов
a, b и c равно нулю тогда и только тогда, когда они
компланарны.
4.
Если abc 0 — компланарны
Выражение смешанного произведения через
координаты
ax
ay
az
abc b x
by
bz
cx
cy
cz
21.
 Определение объемов параллелепипеда и треугольной пирамиды Нетрудно показать, что объем параллелепипеда,
Определение объемов параллелепипеда и треугольной пирамиды Нетрудно показать, что объем параллелепипеда,V abc
а объем треугольной пирамиды, построенной на
этих же векторах, равен
1
V
abc
6
Пример. Вершинами пирамиды служат точки
A 1;2;3 , B 0; 1;1 , C 2;5;2 , D 3; 0; 2
Найти объем пирамиды
Решение: Находим векторы
a,
a AB 1; 3; 2 , b AC 1; 3; 1
c AD 2; 2, 5
Находим
2
c
abc
1 3 2
abc 1
b,
3
1 1 17 3 3 2 8 17 9 16 24
2 5
Следовательно,
1
V 24 4
6
English Русский Правила
17.2: Векторное произведение (перекрестное произведение)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 24530
- Питер Дурмашкин
- Массачусетский технологический институт через MIT OpenCourseWare
Пусть \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) — два вектора. Поскольку любые два непараллельных вектора образуют плоскость, мы обозначаем угол θ как угол между векторами \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) как показано на рисунке 17.2. Величина
Поскольку любые два непараллельных вектора образуют плоскость, мы обозначаем угол θ как угол между векторами \(\overrightarrow{\mathbf{A}}\) и \(\overrightarrow{\mathbf{B}}\) как показано на рисунке 17.2. Величина
\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{B}}| \sin (\theta) \номер \]
Угол θ между векторами ограничен значениями \(0 \leq \theta \leq \pi\), гарантирующими, что \(\sin (\theta) \geq 0\).
Рис. 17.2. Геометрия векторного произведения. Рассмотрим направление, перпендикулярное этой плоскости. Есть две возможности: мы выберем одну из этих двух (показанную на рис. 17.2) в качестве направления векторного произведения \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\ ), используя соглашение, которое обычно называют «правилом правой руки».
Рассмотрим направление, перпендикулярное этой плоскости. Есть две возможности: мы выберем одну из этих двух (показанную на рис. 17.2) в качестве направления векторного произведения \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\ ), используя соглашение, которое обычно называют «правилом правой руки».Правило правой руки для направления векторного произведения
Первым шагом является перерисовка векторов \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\) так, чтобы хвосты соприкасаются. Затем нарисуйте дугу, начиная с вектора \(\overrightarrow{\mathbf{A}}\) и заканчивая вектором \(\overrightarrow{\mathbf{B}}\). Согните правые пальцы так же, как дуга. Большой палец правой руки указывает направление векторного произведения \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\) (рис. 17.3).
Рис. 17.3 Правило правой руки. Вы должны помнить, что направление векторного произведения \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\) перпендикулярно плоскости, образованной \(\overrightarrow{\mathbf{ A}} \text { и } \overrightarrow{\mathbf{B}}\). Мы можем дать геометрическую интерпретацию величины векторного произведения, записав величину как
Мы можем дать геометрическую интерпретацию величины векторного произведения, записав величину как
\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\ mathbf{A}}|(|\overrightarrow{\mathbf{B}}| \sin \theta) \nonumber \]
Векторы \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\) образуют параллелограмм. Площадь параллелограмма равна произведению высоты на основание, что является величиной векторного произведения. На рис. 17.4 показаны два разных изображения высоты и основания параллелограмма. Как показано на рис. 17.4а, член \(|\overrightarrow{\mathbf{B}}| \sin \theta\) является проекцией вектора \(\overrightarrow{\mathbf{B}}\) в направлении перпендикулярно вектору \(\overrightarrow{\mathbf{B}}\) Мы могли бы также записать величину векторного произведения как
\[|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=(|\overrightarrow{\mathbf{A}}| \sin\theta)|\overrightarrow{\mathbf {Б}}| \nonumber \]
Член \(|\overrightarrow{\mathbf{A}}| \sin \theta\) является проекцией вектора \(\overrightarrow{\mathbf{A}}\) в направлении, перпендикулярном вектору \(\overrightarrow{\mathbf{B}}\), как показано на рис. 17.4(b). Векторное произведение двух векторов, параллельных (или антипараллельных) друг другу, равно нулю, поскольку угол между векторами равен 0 (или \(\pi\)) и \(\sin (0)=0\) ( или \(\sin (\pi)=0\)). Геометрически два параллельных вектора не имеют уникальной компоненты, перпендикулярной их общему направлению.
17.4(b). Векторное произведение двух векторов, параллельных (или антипараллельных) друг другу, равно нулю, поскольку угол между векторами равен 0 (или \(\pi\)) и \(\sin (0)=0\) ( или \(\sin (\pi)=0\)). Геометрически два параллельных вектора не имеют уникальной компоненты, перпендикулярной их общему направлению.
Свойства векторного произведения
(1) Векторное произведение является антикоммутативным, поскольку изменение порядка векторов меняет направление вектора произведение по правилу правой руки:
\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{ А}} \номер\]
(2) Векторное произведение между вектором \(c \overrightarrow{\mathbf{A}}\), где \(c\) — скаляр, и вектором \(\overrightarrow{\mathbf{B}}\) равно
\[c \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}) \nonumber \]
Аналогично,
\[\overrightarrow{\mathbf{A}} \times c \overrightarrow{\mathbf{B}}=c(\overrightarrow{\mathbf{A}} \times \overrightarrow{ \mathbf{B}}) \номер\]
(3) Векторное произведение суммы двух векторов \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\) на вектор \(\overrightarrow{\ mathbf{C}}\) равно
\[(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}) \times \overrightarrow{\mathbf{C}}=\overrightarrow{\mathbf {A}} \times \overrightarrow{\mathbf{C}}+\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}} \nonumber \]
Аналогично,
\[\overrightarrow {\mathbf{A}} \times(\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B} }+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}} \nonumber \]
Векторное разложение и векторное произведение: декартовы координаты
Сначала вычислим, что величина векторного произведения единичных векторов \(\hat{\mathbf{i}}\) и \(\hat{\mathbf{j} }\):
\[|\hat{\mathbf{i}} \times \hat{\mathbf{j}}|=|\hat{\mathbf{i}} \| \ шляпа {\ mathbf {j}} | \sin (\pi / 2)=1 \nonumber \]
, потому что единичные векторы имеют величину \(|\hat{\mathbf{i}}|=|\hat{\mathbf{j}}|=1\ ) и \(\sin (\pi / 2)=1\). По правилу правой руки направление \(\hat{\mathbf{i}} \times \hat{\mathbf{j}}\) находится в \(+\hat{\mathbf{k}}\) как показано на рисунке 17.5. Таким образом, \(\ hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}\).
По правилу правой руки направление \(\hat{\mathbf{i}} \times \hat{\mathbf{j}}\) находится в \(+\hat{\mathbf{k}}\) как показано на рисунке 17.5. Таким образом, \(\ hat{\mathbf{i}} \times \hat{\mathbf{j}}=\hat{\mathbf{k}}\).
Заметим, что то же правило применяется к единичным векторам в направлениях y и z,
\[\hat{\mathbf{j}} \times \hat{\mathbf{k}}=\hat{\mathbf{i}}, \quad \hat{\mathbf{k}} \times \hat{ \mathbf{i}}=\hat{\mathbf{j}} \nonumber \]
По антикоммутативному свойству (1) векторного произведения
\[\hat{\mathbf{j}} \ раз \ шляпа {\ mathbf {i}} = — \ шляпа {\ mathbf {k}}, \ четырехъядерная \ шляпа {\ mathbf {i}} \ раз \ шляпа {\ mathbf {k}} = — \ шляпа {\ mathbf{j}} \номер \]
Векторное произведение единичного вектора \(\hat{\mathbf{i}}\) на самого себя равно нулю, поскольку два единичных вектора параллельны друг другу, \((\sin (0)=0)\) ,
\[|\hat{\mathbf{i}} \times \hat{\mathbf{i}}|=|\hat{\mathbf{i}}||\hat{\mathbf{i}}| \sin (0)=0 \nonumber \]
Векторное произведение единичного вектора \(\hat{\mathbf{j}}\) на себя и единичный вектор \(\hat{\mathbf{k}} \) с самим собой также равны нулю по той же причине,
\[|\hat{\mathbf{j}} \times \hat{\mathbf{j}}|=0, \quad|\hat{\mathbf{ k}} \times \hat{\mathbf{k}}|=0 \nonumber \]
Имея в виду эти свойства, мы можем теперь построить алгебраическое выражение для векторного произведения через компоненты. Выберем декартову систему координат с вектором \(\overrightarrow{\mathbf{B}}\), указывающим вдоль положительной оси x с положительной x-компонентой \(B_{x}\). Тогда векторы \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\) можно записать как
Выберем декартову систему координат с вектором \(\overrightarrow{\mathbf{B}}\), указывающим вдоль положительной оси x с положительной x-компонентой \(B_{x}\). Тогда векторы \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\) можно записать как
\[\overrightarrow{\mathbf{A}}=A_{ x} \hat{\mathbf{i}}+A_{y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}} \nonumber \]
\[\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}} \nonumber \]
соответственно. Векторное произведение в векторных компонентах равно
\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{x} \hat{\mathbf{i}}+A_ {y} \hat{\mathbf{j}}+A_{z} \hat{\mathbf{k}}\right) \times B_{x} \hat{\mathbf{i}} \nonumber \]
Это становится
\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{x} \hat{\mathbf{i} } \times B_{x} \hat{\mathbf{i}}\right)+\left(A_{y} \hat{\mathbf{j}} \times B_{x} \hat{\mathbf{i} }\right)+\left(A_{z} \hat{\mathbf{k}} \times B_{x} \hat{\mathbf{i}}\right) \\
&=A_{x} B_{x}(\hat{\mathbf{i}} \times \hat{\mathbf{i}})+A_{y} B_{x}(\hat{\mathbf{j }} \times \hat{\mathbf{i}})+A_{z} B_{x}(\hat{\mathbf{k}} \times \hat{\mathbf{i}}) \\
&= -A_{y} B_{x} \hat{\mathbf{k}}+A_{z} B_{x} \hat{\mathbf{j}}
\end{aligned} \nonumber \]
Вектор компонентное выражение для векторного произведения легко обобщается для произвольных векторов }}+A_{z} \hat{\mathbf{k}} \nonumber \]
\[\overrightarrow{\mathbf{B}}=B_{x} \hat{\mathbf{i}}+B_{y} \hat{\mathbf{j}}+B_{z} \hat{\ mathbf{k}} \nonumber \]
, чтобы получить
\[\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=\left(A_{y} B_{z}- A_{z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{ j}}+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \nonumber \]
Векторное разложение и векторное произведение: цилиндрическое Координаты
Вспомним цилиндрическую систему координат, показанную на рис.
. Единичные векторы расположены под прямым углом друг к другу, поэтому по правилу правой руки векторное произведение единичных векторов определяется соотношениями
\[\hat{\mathbf{r}} \ times \hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \nonumber \]
\[\hat{\boldsymbol{\theta}} \times \hat{\mathbf{k}} =\hat{\mathbf{r}} \nonumber \]
\[\hat{\mathbf{k}} \times \hat{\mathbf{r}}=\hat{\boldsymbol{\theta}} \ nonumber \]
Поскольку векторное произведение удовлетворяет условию \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf {A}}\) у нас также есть
\[\hat{\boldsymbol{\theta}} \times \hat{\mathbf{r}}=-\hat{\mathbf{k}} \nonumber \]
\[\hat{\mathbf{ k}} \times \hat{\boldsymbol{\theta}}=-\hat{\mathbf{r}} \nonumber \]
\[\hat{\mathbf{r}} \times \hat{\mathbf {k}}=-\шляпа{\boldsymbol{\theta}} \nonumber \]
Наконец
\[\шляпа{\mathbf{r}} \times \шляпа{\mathbf{r}}=\шляпа {\boldsymbol{\theta}} \times\hat{\boldsymbol{\theta}}=\hat{\mathbf{k}} \times\hat{\mathbf{k}}=\overrightarrow{\mathbf{0} } \номер \]
Пример 17. 1 Произведения векторов
1 Произведения векторов
Для двух векторов \(\overrightarrow{\mathbf{A}}=2 \hat{\mathbf{i}}+-3 \hat{\mathbf{j}}+7 \ шляпа {\ mathbf {k}} \) и \ (\ overrightarrow {\ mathbf {B}} = 5 \ шляпа {\ mathbf {i}} + \ шляпа {\ mathbf {j}} + 2 \ шляпа {\ mathbf{k}}\), найдите \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\).
Решение:
\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{ z} B_{y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j} }+\left(A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\
&=((-3)(2)-(7)(1)) \hat{\mathbf{i}}+((7)(5)-(2)(2)) \hat{\mathbf{ j}}+((2)(1)-(-3)(5)) \шляпа{\mathbf{k}} \\
&=-13 \шляпа{\mathbf{i}}+31 \шляпа{ \mathbf{j}}+17 \hat{\mathbf{k}}
\end{aligned} \nonumber \]
Пример 17.2. Закон синусов
Для треугольника, показанного на рис. 17.7а, докажите закон синусов, \(|\overrightarrow{\mathbf{A}}| / \sin \alpha=|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin\gamma\), используя векторное произведение.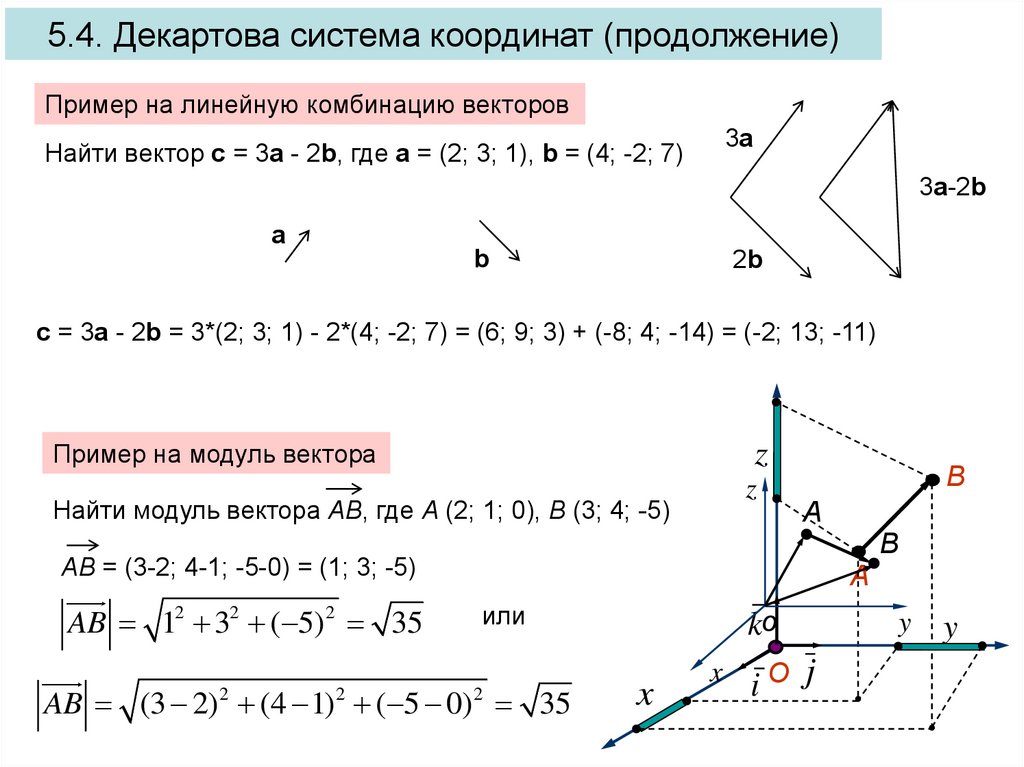
Решение. Рассмотрим площадь треугольника, образованного тремя векторами \(\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf{B}}\) и \(\overrightarrow {\mathbf{C}}\), где \(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0\) (рис. 17.7б). ). Поскольку \(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}}=0\), мы имеем это \(0=\overrightarrow{\mathbf{ A}} \times(\overrightarrow{\mathbf{A}}+\overrightarrow{\mathbf{B}}+\overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \times \overrightarrow {\mathbf{B}}+\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}\). Таким образом, \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}=-\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}\) или \( |\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|\). Из рис. 17.7b видно, что \(|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow{\mathbf{ B}}| \sin \gamma\) и \(|\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{C}}|=|\overrightarrow{\mathbf{A}}||\overrightarrow {\mathbf{C}}|\sin\бета\).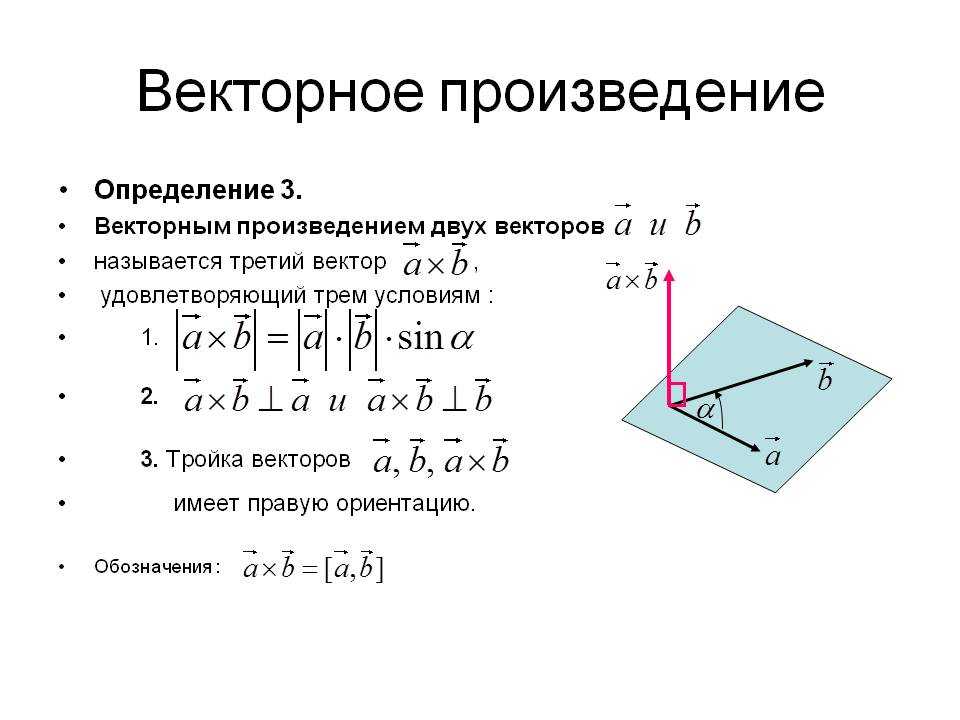 Следовательно, }| \sin \beta\), и, следовательно, \(|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin \gamma\). Аналогичный аргумент показывает, что \(|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{A}}| / \sin \alpha\) доказывает закон синусов.
Следовательно, }| \sin \beta\), и, следовательно, \(|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{C}}| / \sin \gamma\). Аналогичный аргумент показывает, что \(|\overrightarrow{\mathbf{B}}| / \sin \beta=|\overrightarrow{\mathbf{A}}| / \sin \alpha\) доказывает закон синусов.
Пример 17.3. Единичная нормаль
Найдите единичный вектор, перпендикулярный \(\overrightarrow{\mathbf{A}}=\hat{\mathbf{i}}+\hat{\mathbf{j}}-\hat {\mathbf{k}}\) и \(\overrightarrow{\mathbf{B}}=-2 \шляпа{\mathbf{i}}-\шляпа{\mathbf{j}}+3 \шляпа{\mathbf {к}}\).
Решение: векторное произведение \(\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}}\) перпендикулярно обоим \(\overrightarrow{\mathbf{A}} \text { и } \overrightarrow{\mathbf{B}}\). Следовательно, единичные векторы \(\hat{\mathbf{n}}=\pm \overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} /|\overrightarrow{\mathbf{A}} \ времена \overrightarrow{\mathbf{B}}|\) перпендикулярны обоим \(\overrightarrow{\mathbf{A}} \text {и} \overrightarrow{\mathbf{B}}\). Сначала вычисляем
Сначала вычисляем
\[\begin{align}
\overrightarrow{\mathbf{A}} \times \overrightarrow{\mathbf{B}} &=\left(A_{y} B_{z}-A_{z} B_{ y}\right) \hat{\mathbf{i}}+\left(A_{z} B_{x}-A_{x} B_{z}\right) \hat{\mathbf{j}}+\left (A_{x} B_{y}-A_{y} B_{x}\right) \hat{\mathbf{k}} \\
&=((1)(3)-(-1)(-1 )) \ шляпа {\ mathbf {i}} + ((-1) (2) — (1) (3)) \ шляпа {\ mathbf {j}} + ((1) (- 1) — (1) (2)) \шляпа{\mathbf{k}} \\
&=2 \шляпа{\mathbf{i}}-5 \шляпа{\mathbf{j}}-3 \шляпа{\mathbf{k}}
\end{aligned} \nonumber \]
Теперь вычисляем магнитуду 9{1 / 2} \nonumber \]
Пример 17.4 Объем параллелепипеда
Покажите, что объем параллелепипеда с ребрами, образованными векторами \(\overrightarrow{\mathbf{A}}, \overrightarrow{\mathbf {B}}, \text { и }\) \(\overrightarrow{\mathbf{C}}\) задается как \(\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B} } \times \overrightarrow{\mathbf{C}})\).
Решение: Объем параллелепипеда равен площади основания, умноженной на высоту. Если основание образовано векторами \(\overrightarrow{\mathbf{B}} \text { и } \overrightarrow{\mathbf{C}}\), то площадь основания определяется величиной \( \overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}\). Вектор \(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}=|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}| \hat{ \mathbf{n}}\), где \(\hat{\mathbf{n}}\) — единичный вектор, перпендикулярный основанию (рис. 17.8).
Если основание образовано векторами \(\overrightarrow{\mathbf{B}} \text { и } \overrightarrow{\mathbf{C}}\), то площадь основания определяется величиной \( \overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}\). Вектор \(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}=|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}| \hat{ \mathbf{n}}\), где \(\hat{\mathbf{n}}\) — единичный вектор, перпендикулярный основанию (рис. 17.8).
Проекция вектора \(\overrightarrow{\mathbf{A}}\) вдоль направления \(\hat{\mathbf{n}}\) дает высоту параллелепипеда. Эта проекция задается скалярным произведением \(\overrightarrow{\mathbf{A}}\) на единичный вектор и равна \(\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{ п}}=\текст {высота}\). Следовательно,
\[\overrightarrow{\mathbf{A}} \cdot(\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}})=\overrightarrow{\mathbf{A}} \cdot (|\overrightarrow{\mathbf{B}} \times \overrightarrow{\mathbf{C}}|) \hat{\mathbf{n}}=(|\overrightarrow{\mathbf{B}} \times \overrightarrow{ \mathbf{C}}|) \overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{n}}=(\text {площадь})(\text {высота})=(\text {объем} ) \номер\]
Пример 17.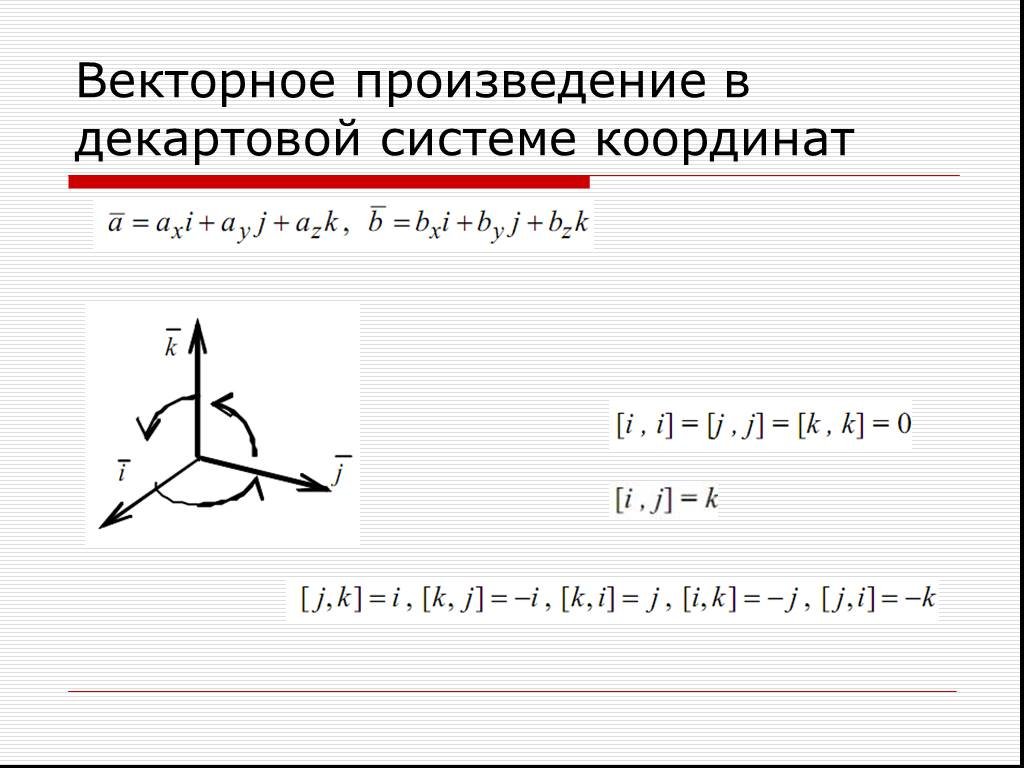 5. Разложение вектора
5. Разложение вектора
Пусть \(\overrightarrow{\mathbf{A}}\) — произвольный вектор, а \(\hat{\mathbf{n}}\) — единичный вектор в некотором фиксированном направление. Покажите, что \mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{n}}\)
Решение: пусть \(\overrightarrow{\mathbf{A}}=A_{ \|} \hat{\mathbf{n}}+A_{\perp} \hat{\mathbf{e}}\), где \(A_{\|}\) — компонент \(\overrightarrow{\mathbf{ A}}\) в направлении \(\hat{\mathbf{n}}, \hat{\mathbf{e}}\) — это направление проекции \(\overrightarrow{\mathbf{A}} \) в плоскости, перпендикулярной \(\hat{\mathbf{n}}\), а \(A_{\perp}\) является компонентой \(\overrightarrow{\mathbf{A}}\) в направление \ (\ шляпа {\ mathbf {e}} \). Поскольку \(\hat{\mathbf{e}} \cdot \hat{\mathbf{n}}=0\), мы имеем, что \(\overrightarrow{\mathbf{A}} \cdot \hat{\mathbf{ n}}=A_{\|}\). Обратите внимание, что
\[\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}=\hat{\mathbf{n}} \times\left(A \hat{\mathbf{n}}+ A_{\perp} \hat{\mathbf{e}}\right)=\hat{\mathbf{n}} \times A_{\perp} \hat{\mathbf{e}}=A_{\perp}( \hat{\mathbf{n}} \times \hat{\mathbf{e}}) \nonumber \]
Единичный вектор \(\hat{\mathbf{n}} \times \hat{\mathbf{e }}\) лежит в плоскости, перпендикулярной \(\hat{\mathbf{n}}\), а также перпендикулярно \(\hat{\mathbf{e}}\). Поэтому \((\hat{\mathbf{n}} \times \hat{\mathbf{e}}) \times \hat{\mathbf{n}}\) также является единичным вектором, параллельным \(\ hat{\mathbf{e}}\) (по правилу правой руки. Итак, \((\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{ n}}=A_{\perp}\hat{\mathbf{e}}\), таким образом,
Поэтому \((\hat{\mathbf{n}} \times \hat{\mathbf{e}}) \times \hat{\mathbf{n}}\) также является единичным вектором, параллельным \(\ hat{\mathbf{e}}\) (по правилу правой руки. Итак, \((\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \hat{\mathbf{ n}}=A_{\perp}\hat{\mathbf{e}}\), таким образом,
\[\overrightarrow{\mathbf{A}}=A_{\|} \hat{\mathbf{n}}+A _{\perp} \hat{\mathbf{e}}=(\overrightarrow{\mathbf {A}} \cdot \hat{\mathbf{n}}) \hat{\mathbf{n}}+(\hat{\mathbf{n}} \times \overrightarrow{\mathbf{A}}) \times \ шляпа {\ mathbf {n}} \ не число \]
Эта страница под названием 17.2: Vector Product (Cross Product) распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Петром Дурмашкиным (MIT OpenCourseWare) посредством исходного содержимого, которое было отредактировано для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Петр Доурмашкин
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- MIT OpenCourseWare
- Показать оглавление
- нет
- Теги
- перекрестное произведение
- источник@https://ocw.
 mit.edu/courses/8-01sc-classical-mechanics-fall-2016/
mit.edu/courses/8-01sc-classical-mechanics-fall-2016/ - векторный продукт
векторных полей — Что такое векторное произведение в сферических координатах?
спросил
Изменено 5 месяцев назад
Просмотрено 82к раз
$\begingroup$ 9{2}\sin{\theta}}\left| \begin{массив}{ccc} \ шляпа {г} и г \ шляпа {\ тета} и г \ грех {\ тета} \ шляпа {\ фи} \\ \dfrac{\partial}{\partial r} & \dfrac{\partial}{\partial \theta} & \dfrac{\partial}{\ partial \phi} \\ A_ {r} и rA _ {\ theta} и r \ sin {\ theta} A _ {\ phi} \конец{массив} \право| \\ & = \ frac {\ hat {r}} {r \ sin {\ theta}} \ bigg [ \ frac {\ partial} {\ partial \ theta} (A _ {\ phi} \ sin {\ theta}) — \ frac {\ partial A _ {\ theta}} {\ partial \ phi} \ bigg] + \ frac {\ hat {\ theta}} {r \ sin {\ theta}} \ bigg [\ frac {\ partial A_ {r }}{\partial\phi}-\sin{\theta}\frac{\partial}{\partial r}(rA_{\phi}) \bigg]+\frac{\hat{\phi}}{r} \bigg[\frac{\partial}{\partial r}(rA_{\theta})-\frac{\partial A_{r}}{\partial\theta} \bigg] \end{выравнивание*} 9{*}) \\ \end{align*}
- системы координат
- векторные поля
$\endgroup$
2
$\begingroup$
Перекрестное произведение в сферических координатах определяется по правилу
$$ \hat{\phi} \times \hat{r} = \hat{\theta},$$ } \times \hat{\phi} = \hat{r},$$
$$ \hat{r} \times \hat{\theta} = \hat{\phi},$$
это приведет к определителю,
$$ \vec{A} \times \vec{B} = \left| \begin{массив}{ccc} \ \ шляпа {r} & \ шляпа {\ theta} & \ шляпа {\ phi} \\ A_r & A_\theta & A_\phi \\ B_r & B_\theta & B_\phi \\ \end{array}\right|$$
Это правило можно проверить, записав эти единичные векторы в декартовых координатах.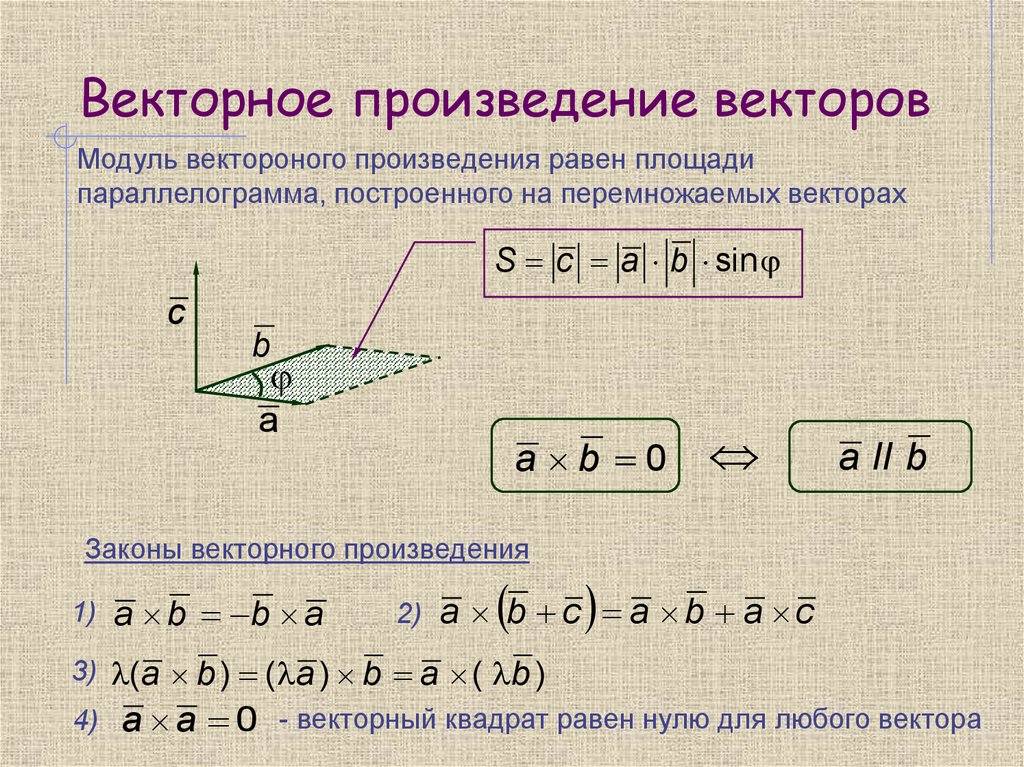


 mit.edu/courses/8-01sc-classical-mechanics-fall-2016/
mit.edu/courses/8-01sc-classical-mechanics-fall-2016/