Векторы в пространстве презентация, доклад
Векторы в пространстве
Понятие вектора
Отрезок, для которого указано, какой из его концов считается началом, а какой – концом, называется вектором.
Направление вектора на рисунках отмечается стрелкой.
А
В
С
D
Нулевой вектор
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым.
Начало и конец нулевого вектора совпадают и он не имеет какого – либо определённого направления.
Т
ТТ – нулевой вектор
Длина вектора
Длиной ненулевого вектора называется длина отрезка АВ.
Длина вектора обозначается так: .
Длина нулевого вектора считается равной нулю.
А
В
А
В
Коллинеарные векторы
Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Сонаправленные векторы
Если два ненулевых вектора АВ и CD коллинеарны и если при этом лучи АВ и CD сонаправлены, то векторы АВ и CD называются сонаправленными.
А
В
С
D
АВ
CD
Противоположно направленные векторы
Если два ненулевых вектора АВ и CD коллинеарны и если при этом лучи АВ и CD не являются сонаправленными, то векторы АВ и CD называются противоположно направленными.
А
В
С
D
АВ
СD
Сонаправленность нулевого вектора
Нулевой вектор условимся считать сонаправленным с любым вектором.
Т
Векторы в параллелепипеде
Векторы AD и AM не являются ни сонаправленными, ни противоположно направленными, так как они не коллинеарны.
С
А
В
D
М
Е
N
К
АМ
KD
AD
ЕК
F
EF
DC
Равные векторы
Векторы называются равными, если они сонаправлены и их длины равны.
Равенство векторов
Если точка А — начало вектора а, то говорят, что вектор а отложен от точки А.
От любой точки можно отложить вектор, равный данному, и притом только один.
А
а
М
N
Правило треугольника
Пусть а и b – два вектора. Отметим произвольную точку А и отложим от этой точки вектор АВ, равный а. Затем от точки В отложим вектор ВС, равный b. Вектор АС называется суммой векторов а и b.
Отметим произвольную точку А и отложим от этой точки вектор АВ, равный а. Затем от точки В отложим вектор ВС, равный b. Вектор АС называется суммой векторов а и b.
а
b
А
В
С
Правило параллелограмма
Чтобы сложить неколлинеарные векторы а и b, нужно отложить от какой-нибудь точки А векторы АВ=а и АD=b и построить параллелограмм АВСD. Тогда вектор АС равен a + b.
а
b
А
В
D
С
Вычитание векторов
Разностью векторов а и b называется такой вектор, сумма которого с вектором b равна вектору а.
b
а
О
А
В
а
b
Вычитание векторов
Теорема:
Для любых векторов а и b справедливо равенство а – b = а + (-b).
а
b
О
А
В
а
-b
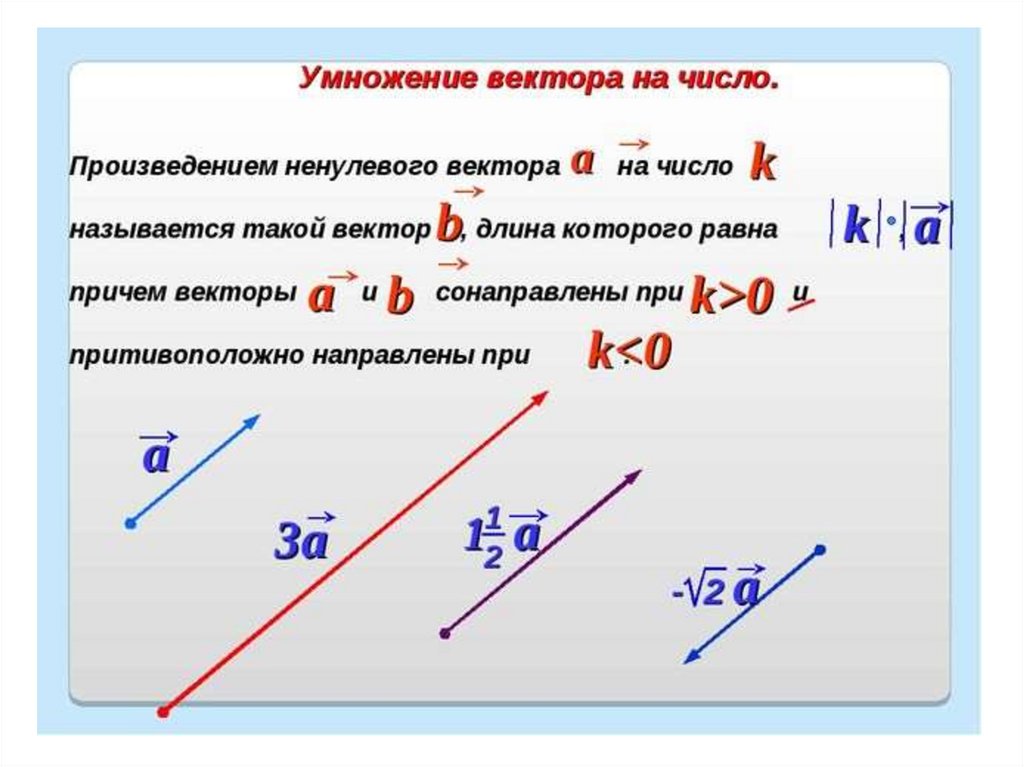
Умножение вектора на число
Произведением ненулевого вектора а на число k называется такой вектор b, длина которого равна |k|*|a|, причём векторы а и b сонаправлены при k 0 и противоположно направлены при kПроизведением нулевого вектора на любое число считается нулевой вектор.
а
k=3
b
k = -2
-2b
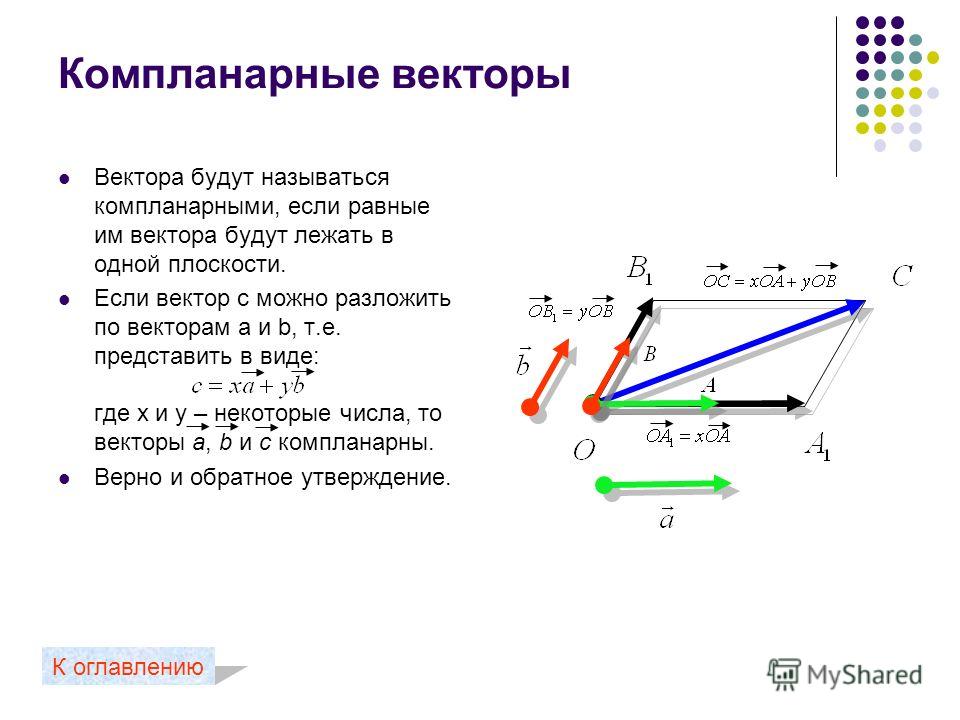
Компланарные векторы
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости
Компланарные векторы
Любые два вектора компланарны.
Три вектора, среди которых имеются два коллинеарных, также компланарны.
Три произвольных вектора могут быть как компланарными, так и не компланарными.
ВВ1, ОD и ОЕ – компланарны
ОА, ОВ, ОС – не компланарны
Признак компланарности трёх векторов
Если вектор с можно разложить по векторам а и b, т.е. представить в виде:
с = xa + yb ,
Где x и y – некоторые числа, то векторы а, b и с компланарны.
О
С
А1
В1
А
В
а
b
с
Обратное утверждение
Если векторы а, b и с компланарны, а векторы а и b не коллинеарны, то вектор с можно разложить по векторам а и b, причём коэффициенты разложения определяются единственным образом.
Правило параллелепипеда
Пусть а, b и с – некомпланарные векторы. Отложим от произвольной точки О пространства векторы ОА = а, ОВ = b, ОС = с и построим параллелепипед так, чтобы отрезки ОА, ОВ и ОС были его рёбрами. Тогда диагональ ОD этого параллелепипеда изображает сумму векторов а, b и с: ОD = а + b + с.
Тогда диагональ ОD этого параллелепипеда изображает сумму векторов а, b и с: ОD = а + b + с.
Е
О
В
А
В1
С
D
А1
Разложение вектора по двум некомпланарным векторам
Если вектор р представлен в виде:
р = xa + yb + zc ,
где x, y и z – некоторые числа, то говорят, что вектор р разложен по векторам а, b и с. Числа x, y и z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трём данным некомпланарным векторам, причём коэффициенты разложения определяются единственным образом.
Координаты вектора на плоскости
Координаты вектора на плоскости
Координаты вектора на плоскости
Координаты вектора на плоскости
Даны точки
Найти длину отрезка
Действия с векторами на плоскости
Координаты вектора в пространстве
Скалярное произведение векторов
Векторное произведение коллинеарных векторов
Смешанное произведение векторов
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа… Оснащения врачебно-сестринской бригады. Устройство и оснащение процедурного кабинета: Решающая роль в обеспечении правильного лечения пациентов отводится процедурной медсестре… Интересное: Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Уполаживание и террасирование склонов: Если глубина оврага более 5 м необходимо устройство берм. Варианты использования оврагов для градостроительных целей… Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒ Отрезок, для которого указано какой из его концов считается началом, а какой концом называется вектором. Длиной ненулевого вектора называется длина самого отрезка АВ. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если два ненулевых вектора коллинеарны и если при этом их лучи сонаправлены, то такие векторы являются сонаправленными, а если эти лучи имеют противоположное направление, то они противоположно направленные. Ненулевой вектор сонаправлен с любым вектором. Векторы называют равными, если они сонаправлены и их длины равны. От любой точки можно отложить вектор, равный данному вектору и притом только один. Отложит от какой-нибудь точки А вектор , из точки В вектор . Вектор будет являться суммой векторов . Это правило сложения называется правилом треугольника. Для любых векторов справедливо следующее: Разностью векторов называется такой вектор, сумма которого с вектором равна . Произведение ненулевого вектора на число ng w:val=»EN-US»/></w:rPr><m:t>k</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR=»00000000″><w:pgSz w:w=»12240″ w:h=»15840″/><w:pgMar w:top=»1134″ w:right=»850″ w:bottom=»1134″ w:left=»1701″ w:header=»720″ w:footer=»720″ w:gutter=»0″/><w:cols w:space=»720″/></w:sectPr></wx:sect></w:body></w:wordDocument>»> называется такой вектор , длина которого |k|· | |, причем векторы и сонаправлены при k ≥ 0 и противоположно направлены при k < 0. Произведением нулевого вектора на любое число считается нулевой вектор. Для любого числа k и любого вектора а векторы а и ka коллинеарны. 3.Найти производную третьего порядка для функции .
Билет № 14  Говорят, что функция y=f(x) имеет максимум и минимум в точке х = а, если у этой точки существует окрестность, в которой f(x)<f(a) (f(x)>f(a)) для х ≠ а. Точки максимума и минимума объединяют общим термином точки экстремума. Если функция y=f(x) имеет экстремум в точке х = а, то либо f’(a)>0, либо f’(a) не существует. Это необходимое условие экстремума. Точки, в которых f’(a)>0 называют стационарными, в точки в которых f’(a) не существует и которые принадлежат области определения функции называют критическими. Экстремумы функций могут достигаться только в стационарных или критических точках. Пусть х = а стационарная или критическая точка функции y=f(x) и пусть существует интервал (b;c) соединяющий точку а внутри себя и такой, что на каждом из интервалов (b;a) и (a;c) производная f’(x) существует и сохраняет постоянный знак. Следует, что Если на (b;a) производная y’ > 0, а на (а;с) производная y’< 0, то х = а точка максимума функции y = f(x) Если на (b;a) производная y’ < 0, а на (а;с) производная y’> 0, то х = а точка минимума функции y = f(x) Если на (b;a) и (а;с) производная y’ > 0 или y’< 0, то х = а не является точкой экстремума функции y = f(x). Чтобы найти экстремумы функции необходимо: Найти производную функции Приравнять производную к нулю и найти корни Подставить полученные корни в функцию и просчитать Выбрать точки максимума и минимума. ⇐ Предыдущая1234567Следующая ⇒ Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни… |
Стр 1 из 2Следующая ⇒ Векторная алгебра Определение 1. Вектором (геометрическим вектором) называется направленный отрезок, то есть отрезок, имеющий определенную длину и направление. Векторы рассматриваются на плоскости (двумерные) и в пространстве (трехмерные). И в том, и в другом случае вектор определяется упорядоченной парой точек, первая из которых – начало вектора, другая – конец вектора. Для обозначения векторов используются символы , , , . Если и соответственно точки начала и конца вектора, то этот вектор обозначается (Рис. 1). Вектор с началом в точке и концом в точке называет противоположным вектору . Длиной или модулем вектора называется число, равное длине отрезка , изображающего вектор. Векторы и имеют один и тот же модуль. Нулевым вектором называется вектор, начало и конец которого совпадают. Нуль-вектор обозначается символом . Модуль нулевого вектора равен нулю. Единичным вектором называет вектор, длина которого равна единице. Единичный вектор, направление которого совпадает с направлением вектора , называется ортом вектора и обозначается . Два ненулевых вектора называются равными, если один из них путем параллельного переноса можно совместить с другим так, что совпадут их начала и концы (рис 2). Обозначают . С точки зрения векторной алгебры вектор не меняется при его параллельном переносе с сохранением его длины и его направления, то есть точку приложения вектора можно помещать в любую точку пространства. Линейными операциями над векторами называются операции сложения, вычитания и умножения вектора на число. Сложение двух векторов и можно выполнить с помощью правила параллелограмма Для построения суммарного вектора не обязательно строить весь параллелограмм , достаточно построить треугольник . Сформулированное правило определения суммы можно заменить более удобным. Суммой двух векторов и называется вектор, соединяющий начало первого слагаемого вектора с концом второго при условии, что начало второго слагаемого совмещено с концом первого (рис. 4). При этом ясно, что результат сложения не зависит от того, в какой точке пространства начало первого слагаемого: при её изменении весь треугольник параллельно переносится. Сложение многих векторов , , , , совершается последовательно: сначала складывается первый вектор со вторым , затем к их сумме прибавляется третий вектор , затем к полученной сумме прибавляется вектор и т.д. (рис. 5). Непосредственно видно, что получается следующее правило для сложения векторов. Правило многоугольника. Суммой нескольких векторов является вектор, соединяющий начало первого слагаемого вектора с концом последнего при условии, что начало каждого последующего вектора совмещено с концом предыдущего (рис. 6). Законы сложения векторов: 1. , 2. , 3. . Разностью двух векторов и называется вектор , который при сложении с вектором даёт вектор (рис. 7). Заметим, что если на векторах и , отложенных от общего начала, можно построить параллелограмм, то одна направленная диагональ является суммой векторов, а другая разностью. Произведением ненулевого вектора на число называется вектор (или ), длина которого равна , а направление совпадает с направлением вектора , при и противоположно ему при . Например, если дан вектор , то векторы и имеют вид и . Законы умножения вектора на число: 1. , 2. , 3. , 4. . Из определения произведения вектора на число следует, что всякий вектор может быть представлен в виде произведения модуля вектора на орт этого вектора. (1) Если над векторами , , , выполнять действия сложения, вычитания и умножения на число, то в результате любого числа таких действий получится вектор вида , представляющий собой линейную комбинацию исходных векторов. Векторы , , , называются линейно зависимыми (связанными линейной зависимостью), если между ними выполняется соотношение следующего вида: , (2) где скалярные коэффициенты не все равны нулю. Если все коэффициенты равны нулю, то соотношение (2) будет выполняться, но оно не будет устанавливать зависимости между векторами. Про векторы , , , говорят, что они линейно независимые. Понятие линейной независимости между векторами используется для алгебраической характеристики взаимного расположения векторов в пространстве. Определение 2 Два ненулевых вектора и называются коллинеарными (обозначают ), если они лежат на одной прямой или на параллельных прямых. Коллинеарные векторы могут быть одинаково направленными (как векторы и ) или противоположно направленными (векторы и (рис 8)). Теорема 1Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны. Следствие. Если между двумя неколлинеарными векторами выполняется равенство , то оба коэффициента должны равняться нулю . Определение 3 Ненулевые векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Любые два вектора всегда компланарны, а три вектора могут и не быть компланарными. Теорема 2 Три вектора линейно зависимы тогда и только тогда, когда они компланарны. — компланарны (3) Представление вектора в виде линейной комбинации векторов и по (3) называется разложением на плоскости по двум неколлинеарным векторам. Рассмотрим произвольный вектор и тройку некомпланарных векторов . Теорема 3Каждый вектор единственным образом разлагается по трем некомпланарным векторам , т.е. представляется в виде (4) Из (4) следует, что любые четыре вектора в пространстве линейно зависимы. Упорядоченная тройка некомпланарных (линейно независимых) векторов называется базисом во множестве геометрических векторов пространства. Скалярные коэффициенты однозначно определяются и называются координатами вектора относительно базиса . Аналогично: упорядоченная пара неколлинеарных (линейно независимых) векторов образует базис геометрических векторов на плоскости. Коэффициенты в разложении (4) есть координаты вектора относительно базиса .
12Следующая ⇒ ©2015 arhivinfo.ru Все права принадлежат авторам размещенных материалов. |
Линейная независимость
Цели
- Понять концепцию линейной независимости.
- Изучите два критерия линейной независимости.
- Понимание взаимосвязи между линейной независимостью и сводными столбцами/свободными переменными.
- Рецепт: проверить, является ли набор векторов линейно независимым / найти уравнение линейной зависимости.
- Изображение: является ли набор векторов в R2 или R3 линейно независимым или нет.
- Словарь: отношение линейной зависимости / уравнение линейной зависимости .

- Основные словарные слова: линейно независимые , линейно зависимые .
Иногда диапазон набора векторов «меньше», чем вы ожидаете от количества векторов, как на рисунке ниже. Это означает, что (по крайней мере) один из векторов является избыточным: его можно удалить, не затрагивая диапазон. В настоящем разделе мы формализуем эту идею в понятии линейная независимость .
Span{v,w}vwSpan{u,v,w}vwuFigure1Изображения наборов линейно зависимых векторов. Обратите внимание, что в каждом случае один вектор находится в диапазоне других, поэтому диапазон не увеличивается.Определение
Набор векторов {v1,v2,…,vk} является линейно независимым , если векторное уравнение
x1v1+x2v2+···+xkvk=0
имеет только тривиальное решение x1=x2=···=xk=0. Множество {v1,v2,…,vk} линейно зависимо иначе.
Другими словами, {v1,v2,…,vk} линейно зависит, если существуют числа x1,x2,. ..,xk, не все равные нулю, такие, что
..,xk, не все равные нулю, такие, что
x1v1+x2v2+···+xkvk=0.
Это называется отношением линейной зависимости или уравнением линейной зависимости .
Обратите внимание, что понятия линейной зависимости и линейной независимости относятся к набору векторов . Нет смысла говорить что-то вроде «этот вектор линейно зависит от этих других векторов» или «эта матрица линейно независима».
Пример(Проверка линейной зависимости)
Пример (Проверка линейной независимости)
Пример (Векторная параметрическая форма)
Приведенные выше примеры приводят к следующему рецепту.
Рецепт: Проверка линейной независимости
Набор векторов {v1,v2,…,vk} линейно независим тогда и только тогда, когда векторное уравнение
x1v1+x2v2+···+xkvk=0
имеет только тривиальное решение тогда и только тогда, когда матричное уравнение Ax=0 имеет только тривиальное решение, где A — матрица со столбцами v1,v2,. ..,vk:
..,vk:
А=Е|||v1v2···vk|||F.
Это верно тогда и только тогда, когда A имеет точку поворота в каждом столбце.
Решение матричного уравнения Ax=0 либо проверяет, что столбцы v1,v2,…,vk линейно независимы, либо создает отношение линейной зависимости, заменяя любые ненулевые значения для свободных переменных.
(Напомним, что Ax=0 имеет нетривиальное решение тогда и только тогда, когда A имеет столбец без опорной точки: см. это наблюдение в разделе 2.4.)
Предположим, что A имеет больше столбцов, чем строк. Тогда A не может иметь опорную точку в каждом столбце (она имеет не более одной опорной точки на строку), поэтому ее столбцы автоматически линейно зависимы.
Широкая матрица (матрица с большим количеством столбцов, чем строк) имеет линейно зависимые столбцы.
Например, четыре вектора в R3 автоматически линейно зависимы. Обратите внимание, что длинная матрица может иметь или не иметь линейно независимых столбцов.
Факты о линейной независимости
- Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны, т.
 е. один из них скалярно кратен другому.
е. один из них скалярно кратен другому. - Любой набор, содержащий нулевой вектор, линейно зависим.
- Если подмножество {v1,v2,…,vk} линейно зависимо, то {v1,v2,…,vk} также линейно зависимо.
Что касается первого факта, обратите внимание, что нулевой вектор кратен любому вектору, поэтому он коллинеарен любому другому вектору. Следовательно, факты 1 и 2 согласуются друг с другом.
В этом подразделе мы даем два критерия линейной независимости набора векторов. Имейте в виду, однако, что фактическое определение приведено выше.
Теорема
Набор векторов {v1,v2,…,vk} линейно зависим тогда и только тогда, когда один из векторов находится в промежутке других.
Любой такой вектор можно удалить, не затрагивая диапазон.
Доказательство
Предположим, например, что v3 находится в Span{v1,v2,v4}, поэтому у нас есть уравнение вида
v3=2v1−12v2+6v4.Мы можем вычесть v3 из обеих частей уравнения, чтобы получить
0=2v1−12v2−v3+6v4.
Это отношение линейной зависимости.
В этом случае любая линейная комбинация v1,v2,v3,v4 уже является линейной комбинацией v1,v2,v4:
x1v1+x2v2+x3v3+x4v4=x1v1+x2v2+x3G2v1-12v2+6v4H+x4v4=(x1+2×3)v1+Gx2-12x3Hv2+(x4+6)v4.Следовательно, Span{v1,v2,v3,v4} содержится в Span{v1,v2,v4}. Любая линейная комбинация v1,v2,v4 также является линейной комбинацией v1,v2,v3,v4 (с коэффициентом v3, равным нулю), поэтому Span{v1,v2,v4} также содержится в Span{v1, v2,v3,v4}, а значит, они равны.
В другом направлении, если у нас отношение линейной зависимости типа
0=2v1−12v2+v3−6v4,, то мы можем переместить любой ненулевой член в левую часть уравнения и разделить на его коэффициент:
v1=12G12v2−v3+6v4H.Это показывает, что v1 находится в Span{v2,v3,v4}.
Мы предоставляем читателю возможность обобщить это доказательство для любого набора векторов.
Предупреждение
В линейно зависимом множестве {v1,v2,…,vk} вообще неверно, что любой вектор vj находится в промежутке других, а только то, что хотя бы один из из них.
Например, множество CA10B,A20B,A01BD линейно зависимо, но A01B не находится в промежутке двух других векторов. Также см. этот рисунок ниже.
Предыдущая теорема уточняет, в каком смысле множество линейно зависимых векторов является избыточным.
Теорема (критерий увеличения диапазона)
Набор векторов {v1,v2,…,vk} линейно независим тогда и только тогда, когда для любого j вектор vj не лежит в Span{v1,v2,…,vj−1}.
Доказательство
Это эквивалентно тому, чтобы показать, что {v1,v2,…,vk} линейно зависимы тогда и только тогда, когда vj находится в Span{v1,v2,…,vj−1} для некоторого j. Импликация «если» является непосредственным следствием предыдущей теоремы. Предположим тогда, что {v1,v2,…,vk} линейно зависимы. Это означает, что некоторые vj находятся в промежутке других. Выберите наибольшее такое j. Мы утверждаем, что этот vj находится в Span{v1,v2,…,vj−1}. Если нет, то
vj=x1v1+x2v2+···+xj−1vj−1+xj+1vj+1+···+xkvk
, где не все xj+1,. ..,xk равны нулю. Предположим для простоты, что xkA=0. Затем мы можем переставить:
..,xk равны нулю. Предположим для простоты, что xkA=0. Затем мы можем переставить:
Это говорит о том, что vk находится в промежутке {v1,v2,…,vp−1}, что противоречит нашему предположению, что vj является последним вектором в промежутке других.
Мы можем перефразировать это следующим образом:
Если вы создаете набор векторов, добавляя по одному вектору за раз, и если диапазон увеличивается каждый раз, когда вы добавляете вектор, то ваш набор является линейно независимым.
Набор, содержащий один вектор {v}, линейно независим, когда vA=0, поскольку xv=0 подразумевает x=0.
Span{v}vНабор из двух неколлинеарных векторов {v,w} линейно независим:
- Ни один из них не находится в промежутке другого, поэтому мы можем применить первый критерий.
- Диапазон стал больше, когда мы добавили w, поэтому мы можем применить критерий увеличения диапазона.
Набор из трех векторов {v,w,u} ниже линейно зависим:
- u находится в Span{v,w}, поэтому мы можем применить первый критерий.

- Диапазон не увеличился, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
На рисунке ниже обратите внимание, что v находится в Span{u,w}, а w находится в Span{u,v}, поэтому мы можем удалить любой из трех векторов, не уменьшая диапазон.
Span{v}Span{w}Span{v,w}vwuДва коллинеарных вектора всегда линейно зависимы:
- w находится в Span{v}, поэтому мы можем применить первый критерий.
- Диапазон не увеличился, когда мы добавили w, поэтому мы можем применить критерий увеличения диапазона.
Эти три вектора {v,w,u} линейно зависимы: действительно, {v,w} уже линейно зависимы, поэтому мы можем использовать третий факт.
Span{v}vwuInteractive: Линейная независимость двух векторов в R2
Interactive: Линейная зависимость трех векторов в R2
Два приведенных ниже вектора {v,w} линейно независимы, поскольку не лежат на одной прямой.
vwSpan{v}Span{w} Три приведенных ниже вектора {v,w,u} линейно независимы: диапазон стал больше, когда мы добавили w, затем еще раз, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
Три компланарных вектора {v,w,u} ниже линейно зависимы:
- u находится в Span{v,w}, поэтому мы можем применить первый критерий.
- Диапазон не увеличился, когда мы добавили u, поэтому мы можем применить критерий увеличения диапазона.
Обратите внимание, что три вектора линейно зависимы тогда и только тогда, когда они компланарны . В самом деле, {v,w,u} линейно зависимы тогда и только тогда, когда один вектор находится в промежутке двух других, который является плоскостью (или линией) (или {0}).
Четыре приведенных ниже вектора {v,w,u,x} линейно зависимы: они являются столбцами широкой матрицы. Обратите внимание, однако, что u не содержится в Span{v,w,x}. См. это предупреждение.
vwuxSpan{v}Span{w}Span{v,w}Рисунок 20. Векторы {v,w,u,x} линейно зависимы, но u не содержится в Span{v,w,x}.Interactive: Линейная независимость двух векторов в R3
Interactive: Линейная независимость трех векторов в R3
В свете этого важного замечания и этого критерия естественно задаться вопросом, какие столбцы матрицы являются избыточными, т. е. какие столбцы мы можем удалить, не затрагивая диапазон столбцов.
е. какие столбцы мы можем удалить, не затрагивая диапазон столбцов.
Теорема
Пусть v1,v2,…,vk — векторы в Rn, и рассмотрим матрицу
А=Е|||v1v2···vk|||F.
Затем мы можем удалить столбцы A без поворотов (столбцы, соответствующие свободным переменным), без изменения Span{v1,v2,…,vk}.
Сводные столбцы линейно независимы, поэтому мы не можем удалить другие столбцы без изменения диапазона.
Доказательство
Если матрица представлена в виде сокращенного эшелона строк:
А=Е102001300001Ф
, то столбец без опоры виден в промежутке между опорными столбцами:
Э230Ф=2Э100Ф+3Э010Ф+0Э001Ф,
, а опорные столбцы линейно независимы:
E000F=x1E100F+x2E010F+x4E001F=Ex1x2x4F=⇒x1=x2=x4=0.
Если матрица не представлена в виде эшелона сокращенных строк, то мы уменьшаем строки:
A=E1723324160-1-2-84FRREF—→E102001300001F.
Следующие два векторных уравнения имеют один и тот же набор решений, поскольку они получены из матриц, эквивалентных строкам:
x1E12-1F+x2E74-2F+x3E2316-8F+x4E304F=0x1E100F+x2E010F+x3E230F+x4E001F=0.
Мы заключаем, что
E2316-8F=2E12-1F+3E74-2F+0E304F
и что
x1E12-1F+x2E74-2F+x4E304F=0
имеет только тривиальное решение.
Обратите внимание, что необходимо уменьшить строку A, чтобы определить, какие столбцы являются его основными. Однако диапазон столбцов сокращенной матрицы строк обычно равен , а не , что равно диапазону столбцов A: необходимо использовать сводные столбцы исходной матрицы из . См. теорему в Разделе 2.7 для переформулировки вышеуказанной теоремы.
Пример
Сводные столбцы и измерение
Пусть d будет количеством опорных столбцов в матрице
А=Е|||v1v2···vk|||F.
- Если d=1, то Span{v1,v2,…,vk} является линией.
- Если d=2, то Span{v1,v2,…,vk} является плоскостью.
- Если d=3, то Span{v1,v2,…,vk} является 3-мерным пространством.
- и так далее.
Число d называется размерностью. Мы обсуждали это понятие в этом важном примечании в разделе 2. 4 и в этом важном примечании в разделе 2.4. Мы строго определим это понятие в разделе 2.7.
4 и в этом важном примечании в разделе 2.4. Мы строго определим это понятие в разделе 2.7.
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
1.3: n-мерное векторное пространство V(n)
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 40992
- Ласло Тиса
- Массачусетский технологический институт через MIT OpenCourseWare
Манипулирование направленными величинами, такими как скорости, ускорения, силы и т.п., имеет большое значение в классической механике и электродинамике. Необходимость упростить довольно сложные операции привела к развитию абстракции: концепции вектора .
Точное значение этого понятия подразумевается в правилах, регулирующих его манипуляции. Эти правила делятся на три основные категории: они относятся к
- добавление векторов,
- умножение векторов на числа (скаляры),
- умножение векторов на векторы (скалярное произведение и векторное произведение.
В то время как тонкие проблемы, связанные с 3, будут рассмотрены в следующей главе, мы продолжим здесь, чтобы показать, что правила, подпадающие под 1 и 2, находят свое точное выражение в абстрактной теории конечномерных векторных пространств.
Правила, относящиеся к сложению векторов, можно кратко выразить следующим образом: векторы — это элементы множества \(V\), которое образует абелеву группу при операции сложения, кратко — аддитивную группу.
Обратным к вектору является его отрицательное значение, нулевой вектор играет роль единицы.
Числа или «скаляры», упомянутые в пункте (ii), обычно считаются действительными или комплексными числами. Для многих соображений, связанных с векторными пространствами, нет необходимости указывать, какая из этих альтернатив выбрана. На самом деле все, что нам нужно, это чтобы скаляры образовывали поле. Точнее говоря, это элементы множества, замкнутого относительно двух бинарных операций: сложения и умножения, которые удовлетворяют общим коммутативным, ассоциативным и дистрибутивным законам; все операции обратимы, если они не включают деление на ноль.
Для многих соображений, связанных с векторными пространствами, нет необходимости указывать, какая из этих альтернатив выбрана. На самом деле все, что нам нужно, это чтобы скаляры образовывали поле. Точнее говоря, это элементы множества, замкнутого относительно двух бинарных операций: сложения и умножения, которые удовлетворяют общим коммутативным, ассоциативным и дистрибутивным законам; все операции обратимы, если они не включают деление на ноль.
Векторное пространство \(V(F)\) над полем F формально определяется как множество элементов, образующих аддитивную группу, которая может быть умножена на элементы поля F .
В частности, мы будем рассматривать вещественные и комплексные векторные поля \(V(R)\) и \(V(C)\) соответственно.
Попутно замечу, что использование понятия поля открывает путь для гораздо большего разнообразия интерпретаций, но в данном контексте это не представляет интереса. Напротив, тот факт, что мы рассматривали «вектор» как неопределенное понятие, позволит нам предложить в дальнейшем интерпретации, выходящие за рамки классической интерпретации как направленных величин. Таким образом, приведенное выше определение согласуется с интерпретацией вектора как пары чисел, указывающих количество двух химических соединений, присутствующих в смеси, или, альтернативно, как точки в фазовом пространстве, охватываемой координатами и импульсами системы массовых точек. .
Таким образом, приведенное выше определение согласуется с интерпретацией вектора как пары чисел, указывающих количество двух химических соединений, присутствующих в смеси, или, альтернативно, как точки в фазовом пространстве, охватываемой координатами и импульсами системы массовых точек. .
Подытожим теперь ряд стандартных результатов теории векторных пространств.
Предположим, у нас есть набор ненулевых векторов \(\{\vec{x}_{1}, \vec{x}_{2}, \cdots , \vec{x}_{n}\}\ ) в V, которые удовлетворяют соотношению
\[\begin{array}{c} {\sum_{k} a_{k}\vec{x}_{k} = 0} \end{array} \label{EQ1.3.1}\]
, где скаляры \(a_{k} \in F\), и не все из них равны нулю. В этом случае говорят, что векторы линейно зависимы. Если, напротив, соотношение \ref{EQ1.3.1} подразумевает, что все \(a_{k} = 0\), то мы говорим, что векторы линейно независимы. 9{m-1} b_{k}\vec{x}_{k}} \end{массив}\]
(линейный) базис в векторном пространстве V представляет собой множество \(E = \{\vec{e}_{1}, \vec{e}_{2}, \cdots , \vec{e}_{ n}\}\) линейно независимых векторов, таких что каждый вектор в V является линейной комбинацией \(\vec{e}_{n}\). Говорят, что базис охватывает или порождает пространство.
Говорят, что базис охватывает или порождает пространство.
Векторное пространство конечномерно, если оно имеет конечный базис. Это фундаментальная теорема линейной алгебры о том, что количество элементов в любом базисе в конечномерном пространстве такое же, как и в любом другом базисе. Это число n является базисно-независимой размерностью V; мы включаем его в обозначение векторного пространства: \(V(n, F)\). 9{k}\vec{e}_{k} (k = l, 2, \cdots, n)\) называются компонентами \(\vec{x}\). Использование надстрочных индексов должно предложить контраст между свойствами преобразования координат и базиса, который будет получен в ближайшее время.
Использование базисов, называемых также системами координат, или фреймами удобно для работы с векторами — таким образом, сложение выполняется путем сложения координат. Однако выбор того или иного базиса вносит в формализм элемент произвольности, что требует контрмер. 9{i}}’} \end{массив} \label{EQ1.3.8}\]
Обратите внимание на характерное «переворачивание» индексов при переходе от уравнения \ref{EQ1. {n}} \end{pmatrix}}&{X = \begin{pmatrix} {\vec{e}_{1}}\\ {\vdots}\\ {\vec{e}_{k}} \end{pmatrix}} \end{массив}\] 9{-1T}X} \end{массив}\]
{n}} \end{pmatrix}}&{X = \begin{pmatrix} {\vec{e}_{1}}\\ {\vdots}\\ {\vec{e}_{k}} \end{pmatrix}} \end{массив}\] 9{-1T}X} \end{массив}\]
Таким образом, мы ясно приходим к результатам, содержащимся в уравнениях \ref{EQ1.3.4} и \ref{EQ1.3.8}. Мы видим, что «объективные» или «инвариантные» представления векторов основаны на процедуре преобразования оснований и координат так называемым контрагредиентным способом.
Сам вектор \(\vec{x}\) иногда называют контравариантным вектором, чтобы отличать его свойства преобразования от ковариантных векторов, которые будут введены позже. 9k\) — элементы поля F, произведения которых все еще находятся в F, это просто числа. Неудивительно, что умножение векторов на другие векторы представляет собой тонкую проблему. Векторные пространства, в которых предусмотрена такая операция, называются алгебрами ; они заслуживают тщательного изучения.
В заключение следует указать, что есть интересные случаи, когда векторы имеют безразмерный характер. Они могут быть составлены из элементов поля F, которые располагаются в виде n-кортежей или в виде матриц \(m \times n\).
Они могут быть составлены из элементов поля F, которые располагаются в виде n-кортежей или в виде матриц \(m \times n\).
Случай \(n \times n\) особенно интересен, потому что умножение матриц превращает эти векторные пространства в алгебры в только что определенном смысле.
Эта страница под названием 1.3: n-мерное векторное пространство V(n) распространяется по лицензии CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Ласло Тисой (MIT OpenCourseWare) через исходный контент, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Ласло Тиса
- Лицензия
- СС BY-NC-SA
- Версия лицензии
- 4,0
- Программа OER или Publisher
- MIT OpenCourseWare
- Показать страницу TOC
- нет
- Теги
- основа
- источник@https://ocw.
 mit.edu/resources/res-8-001-applied-geometric-алгебра-весна-2009
mit.edu/resources/res-8-001-applied-geometric-алгебра-весна-2009 - векторное пространство
Скалярное произведение векторов — GeeksforGeeks
Можно перемножить два вектора или вектор и скаляр. В физике в основном есть два вида произведений векторов: скалярное умножение векторов и векторное произведение (перекрестное произведение) двух векторов. Результатом скалярного произведения двух векторов является число (скаляр). Обычно скалярное произведение используется для определения отношений работы и энергии, таких как нахождение работы, выполняемой над объектом силой (вектором), вызывающей смещение объекта, эта работа может быть определена как скалярное произведение вектора силы с вектором смещения.
Скалярные и векторные величины определяются как:
- Скаляры: это такие величины, которые могут быть полностью описаны только величиной (или числовым значением).
 например. длина объекта, вес объекта, скорость тела и т. д.
например. длина объекта, вес объекта, скорость тела и т. д. - Векторы: это такие величины, которые могут быть полностью описаны как по величине, так и по направлению. например скорость тела, так как она имеет как величину, так и направление.
Скалярное произведение
Скалярное произведение или скалярное произведение двух векторов — это алгебраическая операция, которая берет две последовательности чисел одинаковой длины и возвращает одно число в качестве результата. С геометрической точки зрения, скалярные произведения можно найти, взяв компонент одного вектора в направлении другого вектора и умножив его на величину другого вектора.
Скалярное произведение двух векторов A и B определяется формулой
A.B = |A| × |В| cos ∅
где
- |А| величина вектора A,
- |B| — величина вектора B, а
- ∅ — угол между векторами A и B.
Поскольку скалярное произведение обозначается точкой (. ), его также называют точечным произведением .
), его также называют точечным произведением .
- Скалярное произведение в представлении единичного вектора
В представлении векторов единичным вектором, где i, j, k расположены вдоль оси x, оси y и оси z соответственно. Скалярное произведение можно рассчитать как:
A.B = A x × B x + A Y × B Y + A Z × B Z 99669646464 × B Z 9996646464 × B Z 99966646464 × B Z 99966646464 × B Z × z . i +A y j +A z k
B = B x i +B y j + B z k
- Geometrical interpretation of Scalar Product of Vectors
Произведение двух ненулевых векторов можно представить как произведение величины любого из векторов на величину проекции на него другого вектора.
Случай 1: Когда угол между двумя векторами больше 0 градусов и меньше 90 градусов, результат скалярного произведения равен положительному .
0 < ∅ < 90
Случай 2: Когда угол между двумя векторами больше 90 градусов и меньше 180 градусов, результат скалярного произведения отрицательный .
90 < ∅ < 180
Случай 3: Когда угол между двумя векторами равен 90 градусов, то результат скалярного произведения равен 0 .
∅ = 90
Особые случаи скалярного произведенияМатричное представление скалярного произведения векторов(1) Скалярное произведение двух параллельных векторов: Скалярное произведение двух параллельных векторов — это просто произведение величин двух векторов. Поскольку угол между векторами, когда они параллельны, равен 0 градусов, а cos 0 = 1.
Следовательно,
a.b = |a| × |б| cos 0
= |a| × |б|
(2) Скалярное произведение двух антипараллельных векторов: Скалярное произведение двух антипараллельных векторов отрицательно от произведения модулей двух векторов.
аб, потому что 180 = -|а| × |б| (С тех пор, COS 180 = -1)
(3) Скалярное произведение двух ортогональных векторов: Скалярное произведение двух ортогональных векторов составляет 0.
A.B COS 90 = 0 (с тех пор, COS 90 = 0)
В матричной форме векторы могут быть представлены в виде матриц-строк или матриц-столбцов. Если рассматривать векторы как матрицы-строки их компонентов x, y и z, то транспонирование этих векторов будет матрицей-столбцом, содержащим компоненты x, y и z.
Таким образом, векторы A и B можно рассматривать следующим образом:
A =
| A x | A y | A z |
B =
| B x |
| B y |
| B z |
So,
A. B = A x B x +A y B y + A z B z
B = A x B x +A y B y + A z B z
1. Коммутативные свойства скалярного умножения:
, если A и B — два вектора. б| cos θ , и
b.a = |b||a| cos θ
So a.b = b.a
0429 тогда вектор,
а. (B + C) = A.B + A.C
3. Ассоциативное свойство:
, если A — векторы, а C, D — Scalar. D A ) = (CD) A
4. Свойство идентификации:
IF A — вектор,
1 % A is Vector,
1G a is
1t a is x as x as as as as as as as as x .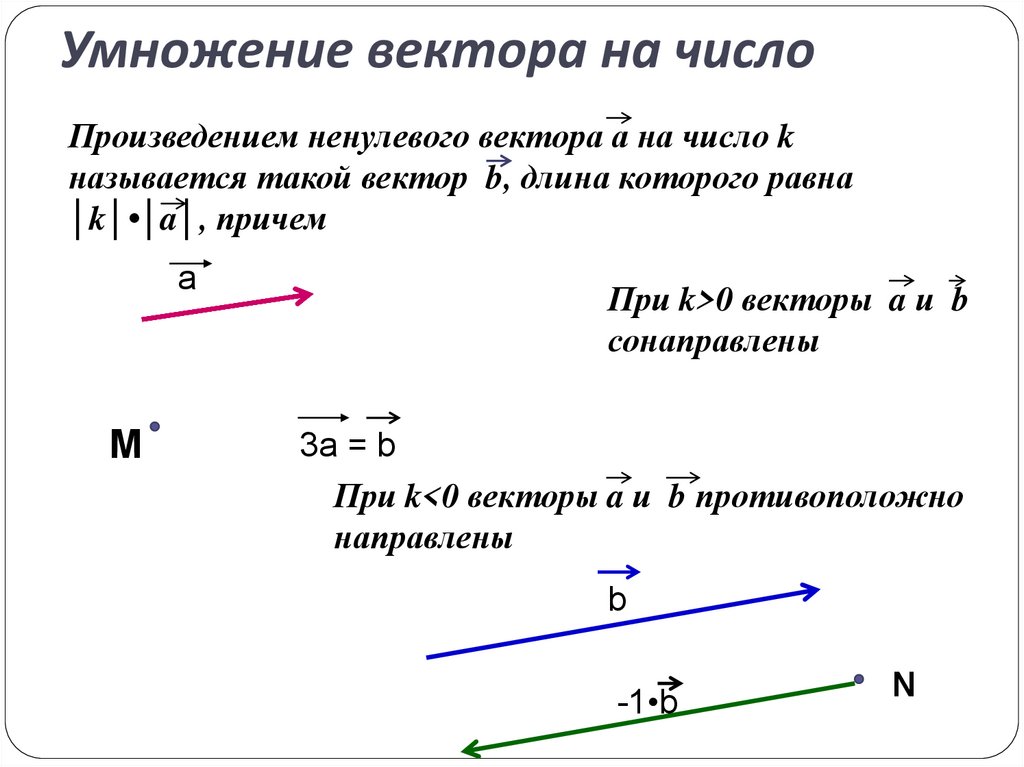 Мультипликативное свойство 0:
Мультипликативное свойство 0:
IF A — вектор,
0 ( A ) = 0
Проблемы с образцамиПроблема 1: Найти Scale Product
. вектор B= 3i + j +2k.
Решение:
9936 889. 2: Частица перемещается из положения 2i + j + 2k в положение 3i + 2j + 5k под действием равномерной силы (7i + 5j +2k) Н. Если перемещение выражено в метрах, вычислите проделанную работу.A. B = (2 * 3) + (5 * 1) + (3 * 2)
= 6 + 5 + 6
= 17
Решение:
Дано,
Окончательная позиция P2 = 3 I + 2 J +5 K
8 J +5 K
9
9928 +5 K
9928 +5 K
9928 +5 K
9928 .
+2 K
Force F = (7 I + 5 J + 2 K ) N
SO
. Дисвязание D
SO
. Д = (3 -2) I + (2 -1) j + (5 -2) K
= I + J + 3 K
работа = F For Work = k
работа = k
669 2 k
j + 3 K
работа j + 3 K
j + 3 K
. . D
= (7 i + 5 j + 2 k ). ( i + j + 3 k )
= ( 7 * 1 ) + ( 5 * 1 ) + ( 2 * 3 )
= 7 + 5 + 6
= 18 3 9J 9004 Задача 3. Найдите такое значение m, что векторы A = 2 i + 3j + k и B = 3 i + 2 j + mk могут быть перпендикулярны.

Решение:
Дано,
A и B перпендикулярны
, поэтому A . B = 0
(2 i + 3 j + k ). ( 3 i + 2 j + m k ) = 0
( 2 * 3 ) + ( 3 * 2 ) + ( 1 * m ) = 0
6 + 6 + m = 0
12 + m = 0
m = -12
Задача 4. Докажите, что векторы U = 2i + 3j + k и V = 4i – 2j + 2k перпендикулярны друг другу.
Решение:
, дано,
U = 2 I + 3 J + K
9 992999299 294298 8 8 89299 2 9 2 9 2 9 2 9. 9. . . . . . . .


 — КиберПедия
— КиберПедия


 Разложение векторов
Разложение векторов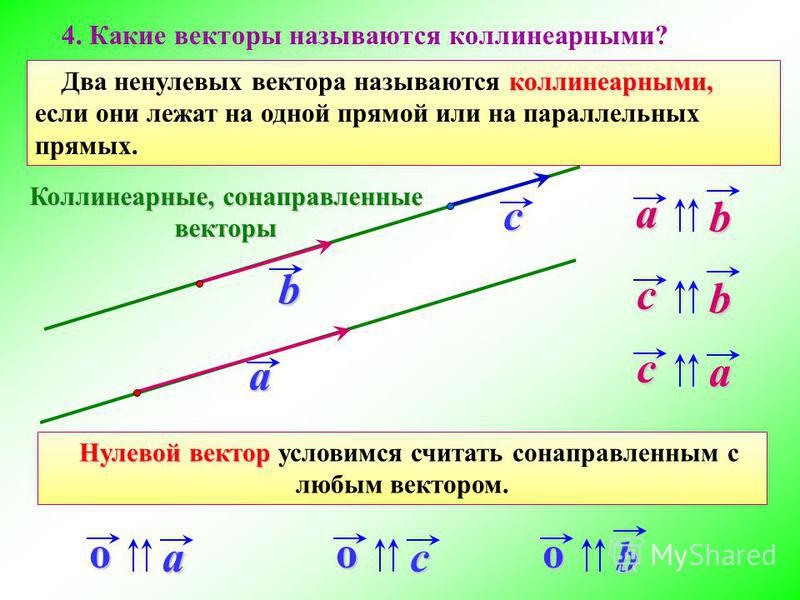
 Такие векторы называются свободными.
Такие векторы называются свободными. Это правило сложения векторов называется правилом треугольника.
Это правило сложения векторов называется правилом треугольника.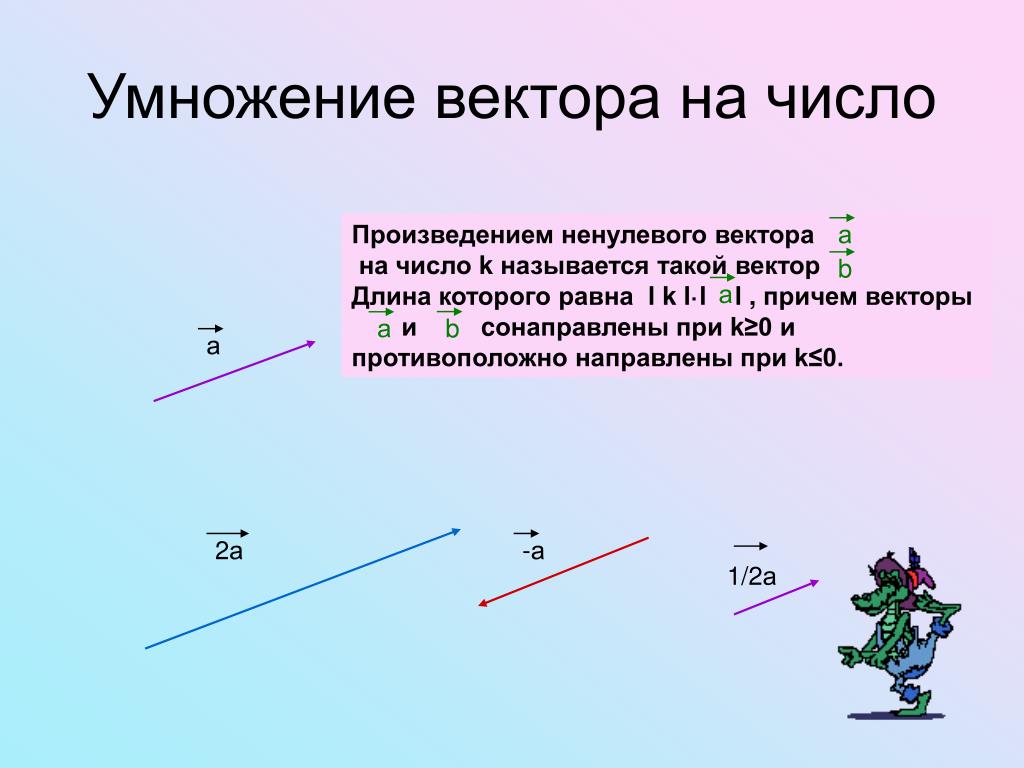




 е. один из них скалярно кратен другому.
е. один из них скалярно кратен другому.
 mit.edu/resources/res-8-001-applied-geometric-алгебра-весна-2009
mit.edu/resources/res-8-001-applied-geometric-алгебра-весна-2009 например. длина объекта, вес объекта, скорость тела и т. д.
например. длина объекта, вес объекта, скорость тела и т. д.
 +2 K
+2 K 
