механика — Стр 2
Варианты ответов:
1)максимален в точке С;
2)во всех точках одинаков;●
3)максимален в точках B и D;
4)максимален в точках А и Е
Задание 15
Вес тела массой m в лифте, поднимающемся вверх с ускорением a > 0 равен…
Варианты ответов:
1)P=ma; 2)P=mg; 3)●P=m(g+a); 4)P=m(g — a)
Задание 16
Человек входит в лифт, который затем начинает двигаться равномерно вверх, при этом…
Варианты ответов:
1)вес человека будет зависеть от скорости движения лифта;
2)вес человека не изменится;●
3)вес человека уменьшится;
4)вес увеличится
Задание 17
Лифт движется вниз с ускорением a>g, при этом …
Варианты ответов:
1)тело будет находиться в невесомости;
2)с телом ничего не произойдет;
3)тело прижмется к полу лифта;
4)тело прижмется к потолку лифта●
Задание 18
Скорость грузового лифта изменяется в соответствии с графиком, представленном на рисунке.
Сила давления груза на пол совпадает по направлению с силой тяжести в промежутке времени…
Варианты ответов:
1)от t2 до t3;
2)от 0 до t1;
3)от t1 до t2;
4)от 0 до t3●
Задание 19
Материальная точка начинает двигаться под действием силы Fx, график временной зависимости которой представлен на рисунке.
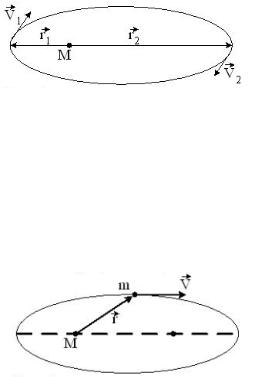
5)
Правильно отражает зависимость величины проекции импульса материальной точки p x от времени график…
Варианты ответов:
Динамика вращательного движения
Задание 1
При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкого кольца перенести из центра масс на край (рис.), то момент инерции относительно новой оси увеличится в …
Варианты ответов: |
|
| |
1) 4 раза; | 2) 1,5 раза; | 3) ●2 раза; | 4) 3 раза |
Задание 2
Момент инерции тонкого стержня длиной l относительно перпендикулярной оси, проходящей через центр, равен I = 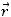
перенести параллельно на один из его концов?
Варианты ответов:
1)увеличится в 2 раза;
2)увеличится в 3 раза;
3)увеличится в 12 раз;
4)увеличится в 4 раза;●
5)увеличится в 6 раз
Задание 3
Момент инерции тонкого обруча массой m, радиусом R относительно оси, проходящей через центр обруча перпендикулярно плоскости, в которой лежит обруч, равен I = mR2. Если ось вращения перенести параллельно в точку на обруче, то момент инерции обруча…
Варианты ответов:
1)увеличится в 1,5 раза;
2)не изменится;
3)уменьшится в 2 раза;
4)уменьшится в 1,5 раза;
5)увеличится в 2 раза●
Задание 4
Четыре маленьких шарика одинаковой массы, жестко закрепленные невесомыми стержнями, образуют квадрат. Отношение моментов инерции системы J1/J2, если ось вращения совпадает со стороной квадрата J1 или с его диагональю J2, равно…
Варианты ответов: |
| |
1) | 2;● | 3) ¼; |
2) | ½; | 4) 4 |
Задание 5
Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние
и расставили симметрично относительно оси OO’.
Для моментов инерции относительно оси OO’ справедливо соотношение…
Варианты ответов
1) | I1 | I2 | I3 ; | |
2) | I1 | I2 | I3 | ; |
3) | I1 | I2 | I3 | ; |
4) | I1 | I2 | I3 | ● |
Задание 6
Из жести вырезали 3 одинаковые детали в виде эллипса. Две детали разрезали на 4 одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО (см рис.). Для моментов инерции относительно
(см рис.). Для моментов инерции относительно
оси ОО´ справедливо соотношение …
Варианты ответов:
1)I1 < I2 = I3;
2)I1 < I2 < I3;●
3)I1 = I2 = I3;
4)I1 > I2 > I3

Задание 7
Тонкостенная трубка и кольцо имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение…
Варианты ответов: |
|
|
| |
1)● | ; | 2) | ; | 3) |
Задание 8
При расчете моментов инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкостенной трубки перенести из центра масс на образующую (рис.), то момент инерции относительно новой оси увеличится в…
Варианты ответов:
1)2 раза;●
2)1,5 раза;
3)3 раза;
4)4 раза
Задание 9
Абсолютно твердое тело вращается с угловым ускорением, изменяющимся по закону β=β0–αt, где α – некоторая положительная константа. Момент инерции тела остается постоянным в течение всего времени вращения. Зависимость от времени момента сил, действующих на тело, определяется графиком …
Варианты ответов:
1)● 2)3) 4) 5)
Задание 10
Если момент инерции тела увеличить в 2 раза и скорость его вращения увеличить в 2 раза, то момент импульса тела…
Варианты ответов:
1)увеличится в 2 раз;
2)не изменится;
3)увеличится в 8 раз;
4)увеличится в 4 раза●
Задание 11
Три маленьких шарика расположены в вершинах правильного треугольника. Момент инерции этой системы относительно оси О1, перпендикулярной плоскости треугольника и проходящей через его центр — I1. Момент инерции этой же системы относительно оси О2, перпендикулярной плоскости треугольника и проходящей через один из шариков – I2. Справедливо утверждение…

at 2 .
Варианты ответов:
1)I1 = I2 ;
2)I1 > I2 ;
3)I1 < I2●
Задание 12
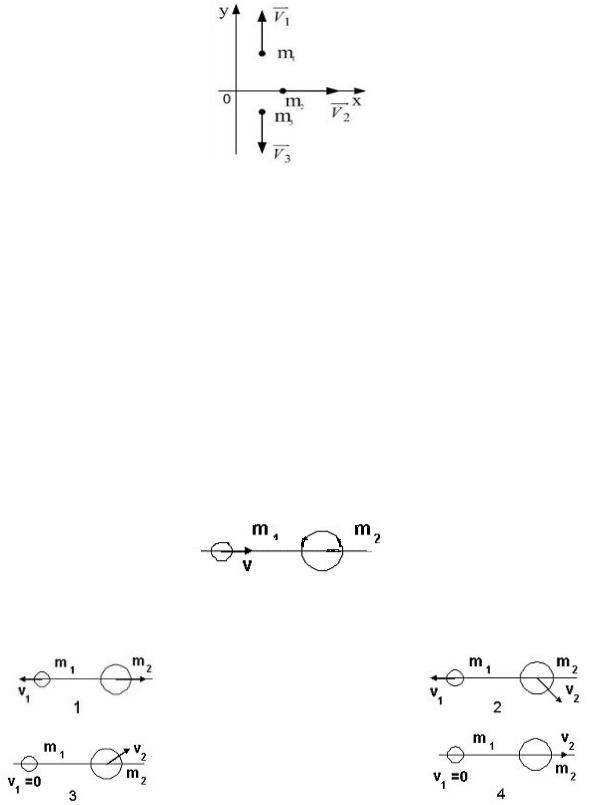
Направления векторов момента импульса и момента сил для равноускоренного вращения твердого тела правильно показаны на рисунке…
Варианты ответов:
1) | 2; |
2) | 4; |
3) | 5; |
4) | 1;● |
5) | 3 |
Задание 13
Момент импульса тела изменяется со временем по закону L(t) = t2 — 6t + 8. Момент действующих на тело сил станет равен нулю через …
Варианты ответов:
1)2 с;
2)1 с;
3)3 с;●
4)4 с
Задание 14
Момент импульса тела относительно неподвижной оси изменяется по закону L Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.
М М М М
| t |
| t | t | t |
| 1 |
| 2 | 3 | 4 |
Варианты ответов: |
|
|
|
| |
1)● 1; | 2) 2; | 3) 3; | 4) 4 |
|
|
Задание 15
Момент импульса вращающегося тела изменяется по закону L = λt – αt2, где α и λ – некоторые положительные константы. Зависимость от времени момента сил, действующих на тело, определяется графиком …
Варианты ответов:
4) | 5) |
|
|
|
|
|
|
|
|
|
| Задание | 16 |
|
|
|
|
|
|
| |
| Момент импульса относительно неподвижной оси изменяется по закону | L(t) | — | 1 | t | 3 | 4t | , | ||
|
|
|
|
|
|
| ||||
3
при этом зависимость момента сил от времени описывается графиком…
Варианты ответов:
1)● | ; 2) | ; 3) | ; 4) | ; 5) |
Задание 17
Диск начинает вращаться под действием момента сил, график временной зависимости которого представлен на рисунке.
Укажите график, правильно отражающий зависимость момента импульса диска от времени.
Варианты ответов:

Задание 18
Физический маятник совершает колебания вокруг оси, проходящей через точку О перпендикулярно плоскости рисунка. Для данного положения маятника момент силы тяжести направлен…
Варианты ответов:
1)вверх в плоскости рисунка;
2)вниз в плоскости рисунка;
3)к нам перпендикулярно плоскости рисунка;
4)от нас перпендикулярно плоскости рисунка●
Работа и энергия
Задание 1
Изменение силы тяги на различных участках пути представлено на графике. Работа максимальна на участке…
Варианты ответов:
1)3-4;
2)1-2;
3)4-5;
4)0-1;●
5)2-3
Задание 2
Зависимость перемещения тела массой 4 кг от времени представлена на рисунке. Кинетическая энергия тела в момент времени t = 3с равна…
Варианты ответов:
1)50Дж;●
2)20Дж;
3)40Дж;
4)25Дж;
5)15Дж
Задание 3
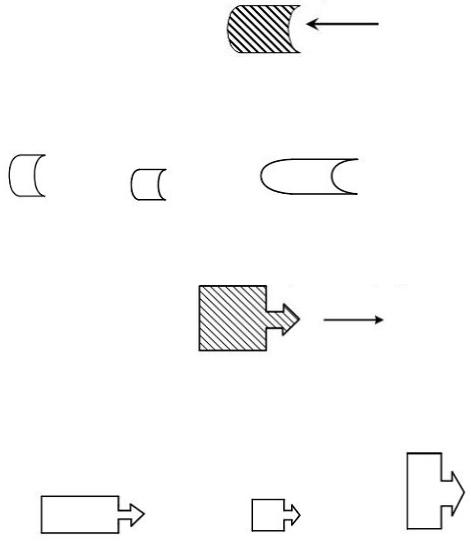
Соотношение работ силы тяжести при движении тела из точки B в точку C по разным траекториям имеет вид…
Варианты ответов:
1)A1 = A2 = A3 = 0;
2)A1 < A2 < A3;
3)A1 = A3 > A2;
4)A1 > A2 > A3;
5)A1 = A2 = A3 ≠ 0●
Задание 4
Небольшая шайба начала движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты x изображена на графике U(x).
На участке AF сила тяжести совершила работу…
Варианты ответов:
1)в 1,4 раза больше, чем на участке AD;
2)в 1,6 раза больше, чем на участке AC;
3)в 5 раз больше, чем на участке AC;●
4)в 1,2 раза больше, чем на участке AE
Задание 5
Шарик, прикрепленный к пружине и насаженный на горизонтальную направляющую, совершает гармонические колебания. На графике представлена зависимость проекции силы упругости пружины на положительное направление оси X от координаты шарика. Работа силы упругости на этапе О – А – В равна…
Варианты ответов:
1)8 · 10-2 Дж;
2)-4 · 10-2 Дж;●
3)0 Дж;
4)4 · 10-2 Дж
Задание 6
Два тела двигались к стенке с одинаковыми скоростями и при ударе остановились. Первое тело катилось, второе скользило. Если при ударе выделилось одинаковое количество тепла, то больше масса тела…
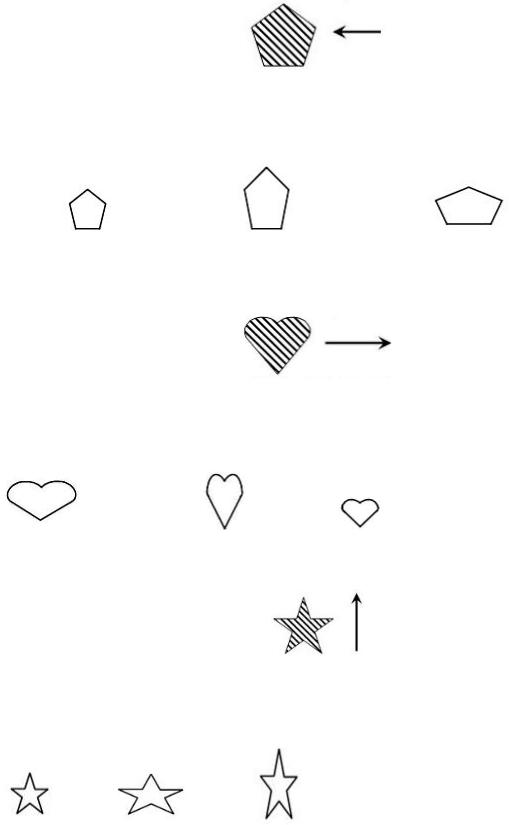
Варианты ответов:
1)первого;
2)одинаковы;
3)второго●
Задание 7
Постоянная сила 2 Н, приложенная по касательной к твердому шару радиусом 2 см, заставила шар совершить один полный оборот вокруг своей оси. Работа этой силы равна …
Варианты ответов:
1)14,4 Дж; 2)40 мДж; 3)7,2 Дж; 4)●0,25 Дж; 5)100 Дж
Задание 8
Два маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r1 друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости ω, при этом была совершена работа A1. Шарики раздвинули симметрично на расстояние r2 = 3r1 и раскрутили до той же угловой скорости.
При этом была совершена работа…
Варианты ответов:
1) |
| ; 2) |
| ; 3)● | ; 4) |
|
|
Задание 9
Два маленьких массивных шарика закреплены на концах невесомого стержня длины d. Стержень может вращаться в горизонтальной плоскости вокруг вертикальной оси, проходящей через середину стержня. Стержень раскрутили до угловой скорости ω1. Под действием трения стержень остановился, при это выделилось тепло Q1. Если стержень раскручен до угловой скорости ω2 = 3ω1, то при остановке стержня выделится тепло…
Варианты ответов:
1)Q2 = Q1;
2)Q2 = Q1;
3)Q2 = Q1;●
4)Q2 = Q1
Задание 10
Для того, чтобы раскрутить диск радиуса R1 вокруг своей оси до угловой скорости ω, необходимо совершить работу А1. Под прессом диск становится тоньше, но радиус его возрастает до R2 = 2R1. Для того, что бы раскрутить его до той же угловой скорости необходимо совершить работу…

Варианты ответов:
1)А2 =А1;
2)А2 = А1;
3)А2 = 4А1;●
4)А2 = А1
Задание 11
Обруч массой m=0,3кг и радиусом R=0,5м привели во вращение, сообщив ему энергию вращательного движения 1200Дж, и опустили на пол так, что его ось вращения оказалась параллельной плоскости пола. Если обруч начал двигаться без проскальзывания, имея кинетическую энергию поступательного движения 200Дж, то сила трения совершила работу, равную…
Варианты ответов:
1)600 Дж;
2)1000 Дж;
3)800 Дж;●
4)1400 Дж
Задание 12
Тело массой m начинает двигаться под действием силы . Если зависимость
скорости тела от времени имеет вид , то мощность, развиваемая силой в момент
времени , равна…
Варианты ответов:
1) ;
2) ;
3) ;
4) ●
Задание 13
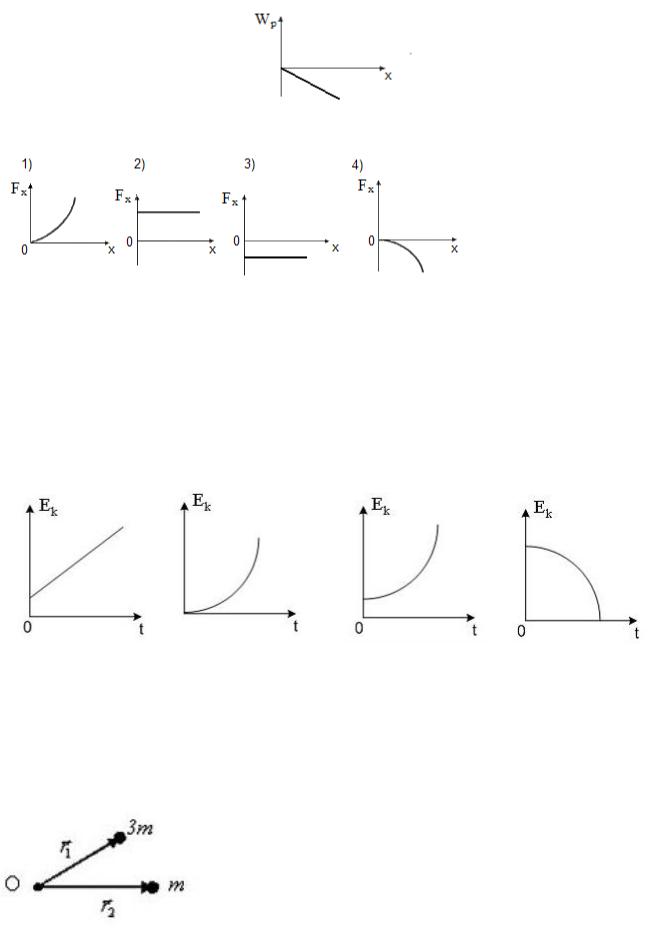
В потенциальном поле сила F пропорциональна градиенту потенциальной энергии W p . Если график зависимости потенциальной энергии W p от координаты х имеет вид:
Варианты ответов:
1) 50 Н; 2) 0,5 н; 3) 30 н; 4) 5 н.
Решение.
С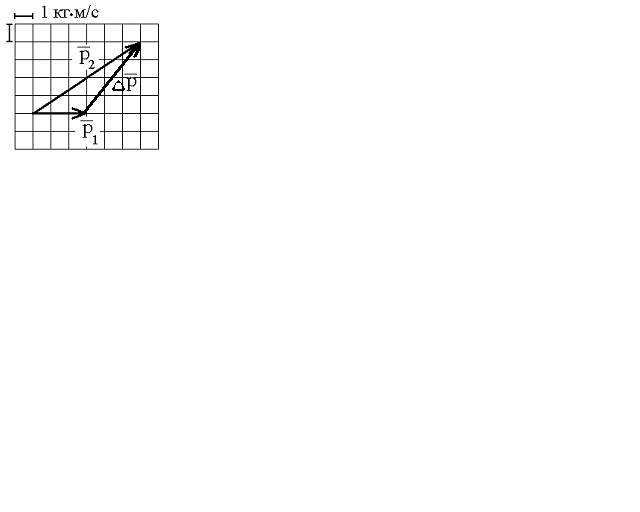 реднюю
силу удара можно определить из второго
закона Ньютона, записанного в общей
форме
реднюю
силу удара можно определить из второго
закона Ньютона, записанного в общей
форме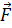 =
=  , где ∆
, где ∆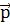 =
=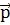 2 —
2 —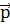 1 — изменение
импульса тела, Δt
– промежуток времени, за который это
изменение произошло. Изменение импульса ∆
1 — изменение
импульса тела, Δt
– промежуток времени, за который это
изменение произошло. Изменение импульса ∆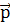 – это вектор, соединяющий конец вектора
– это вектор, соединяющий конец вектора 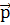 1 с концом вектора
1 с концом вектора 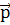 2 (см. рис. в решении).
2 (см. рис. в решении).
Согласно
этому рисунку, горизонтальная компонента
изменения импульса равна: ∆рx=3
кг∙м/с, а вертикальная компонента
изменения импульса равна: ∆рy=4
кг∙м/с. Модуль изменения импульса
вычисляется по теореме Пифагора: ∆р = 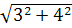 =5 кг∙м/с .Тогда средняя сила удара по
модулю равна: F =
=5 кг∙м/с .Тогда средняя сила удара по
модулю равна: F = 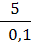 = 50 Н. Ответ:
вариант 1.
= 50 Н. Ответ:
вариант 1.
Тест 1 – 14
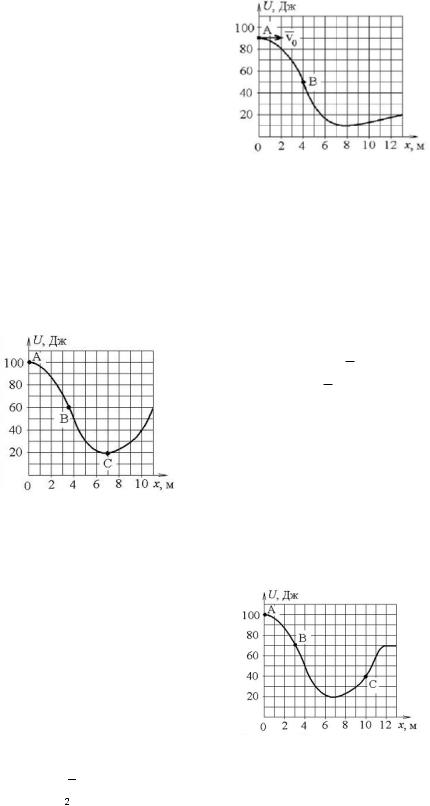
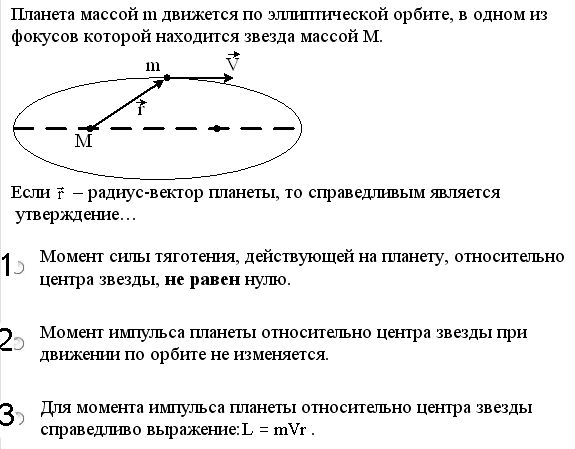 Планета
массой m
движется по эллиптической орбите, в
одном из фокусов которой находится
звезда массой М. Если
Планета
массой m
движется по эллиптической орбите, в
одном из фокусов которой находится
звезда массой М. Если 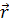 —
радиус-вектор планеты, то
справедливым является утверждение…
—
радиус-вектор планеты, то
справедливым является утверждение…
Варианты ответов:
1) Момент силы тяготения, действующей на планету, относительно центра звезды, не равен нулю.
2)Момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
3)Для момента импульса планеты относительно центра звезды справедливо выражение: L = mvr.
Решение
Проанализируем правильность утверждений.
Модуль момента силы равен :M = F ·r·sin(α), где α – угол между силой
 и радиусом – вектором
и радиусом – вектором  .
Сила тяготения
.
Сила тяготения  направлена
в сторону, противоположную радиусу –
вектору
направлена
в сторону, противоположную радиусу –
вектору  ,
т.е. α = 180˚ , sin (180˚) = 0 и M = 0. Поэтому первое утверждение
является неверным.
,
т.е. α = 180˚ , sin (180˚) = 0 и M = 0. Поэтому первое утверждение
является неверным.Второе утверждение является правильным, т.к. оно соответствует закону сохранения момента импульса: момент импульса замкнутой системы сохраняется. Поэтому момент импульса планеты относительно центра звезды при движении по орбите не изменяется.
3.
Третье утверждение является неправильным,
т.к. модуль момента импульса равен L = mv r· sin α, где α – угол между вектором импульса m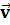 и
радиусом – вектором планеты
и
радиусом – вектором планеты 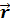 .
Очевидно, что этот угол, а также v в процессе движения изменяются, но mv r· sin α = const.
.
Очевидно, что этот угол, а также v в процессе движения изменяются, но mv r· sin α = const.
Ответ: вариант 2. .
Тест 1 – 15
 Диск
радиуса R
вращается вокруг вертикальной оси
равноускоренно по часовой стрелке.
Укажите направление вектора углового
ускорения.
Диск
радиуса R
вращается вокруг вертикальной оси
равноускоренно по часовой стрелке.
Укажите направление вектора углового
ускорения.
Варианты ответов:
1) Направление 1; 2) Направление 2;
3) Направление 3; 4) Направление 4.
Решение.
При
вращении тела поворот 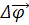 можно
изобразить в виде вектора, направленного
вдоль оси вращения в соответствии с
правилом правого винта. Это значит, что
если головка винта движется по окружности
в направлении вращения, то поступательное
движение винта укажет направление
вектора поворота. В нашем случае при
вращении тела по часовой стрелке винт
(буравчик) будет закручиваться, и вектор
угла поворота будет иметь направление
4. При ускоренном вращении направление
вектора углового ускорения
можно
изобразить в виде вектора, направленного
вдоль оси вращения в соответствии с
правилом правого винта. Это значит, что
если головка винта движется по окружности
в направлении вращения, то поступательное
движение винта укажет направление
вектора поворота. В нашем случае при
вращении тела по часовой стрелке винт
(буравчик) будет закручиваться, и вектор
угла поворота будет иметь направление
4. При ускоренном вращении направление
вектора углового ускорения 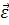 совпадает с направлением вектора
поворота. Следовательно, вектор углового
ускорения надо изобразить в направлении
4.
совпадает с направлением вектора
поворота. Следовательно, вектор углового
ускорения надо изобразить в направлении
4.
Ответ: вариант 4.
Тест 1 – 16
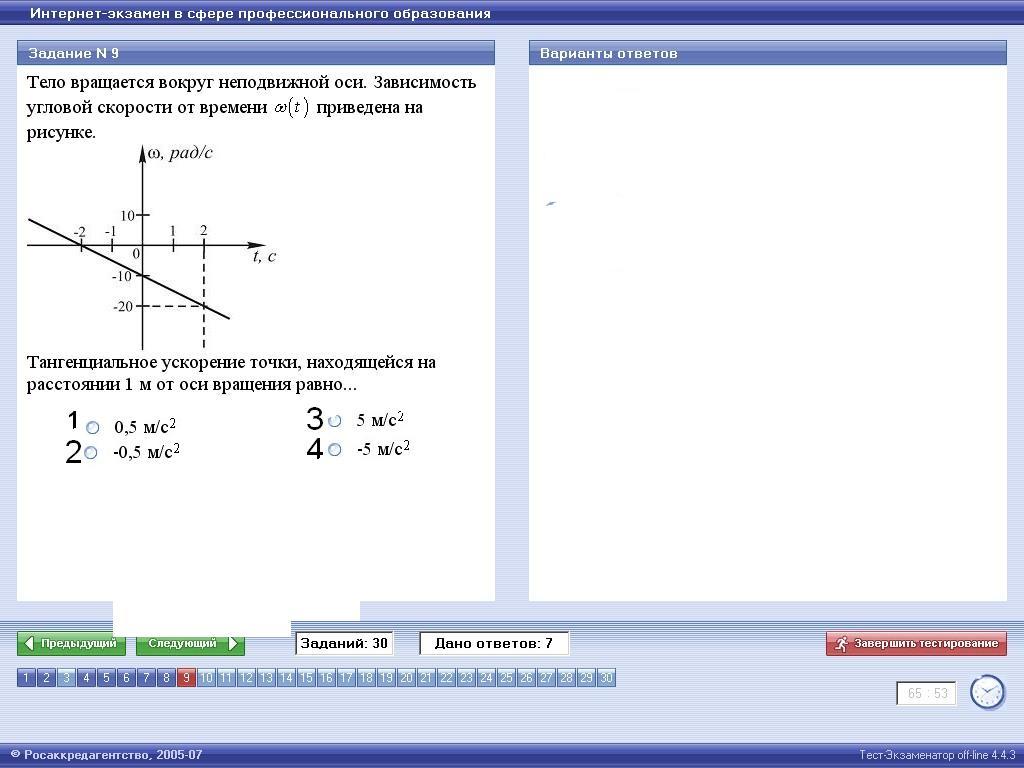 Тело
вращается вокруг неподвижной оси.
Зависимость угловой скорости от времени
Тело
вращается вокруг неподвижной оси.
Зависимость угловой скорости от времени 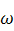 (t)
приведена на рисунке. Тангенциальное
ускорение точки, находящейся на расстоянии
1 м от оси вращения равно…
(t)
приведена на рисунке. Тангенциальное
ускорение точки, находящейся на расстоянии
1 м от оси вращения равно…
Варианты ответов:
1) 0,5 м/с; 2) -0,5 м/с2; 3) 5 м/с2; 4) -5 м/с2.
Решение.
Тангенциальное ускорение по модулю равно произведению углового ускорения на радиус: a τ = ε∙R. По условию задачи радиус R = 1 м. Угловое ускорение при равномерном вращении равно отношению изменения угловой скорости к промежутку времени, за которое это изменение произошло: ε = Δω/ Δt, где Δω = ω2 – ω1, Δt = t2 – t1. Взяв две точки на графике, найдём Δω и Δt. Пусть t1 = 0, ω1 = — 10 рад/с и t2 = 2 с, ω2 = — 20рад/с. Тогда Δω -20–(-10) = — 10 рад/с, Δt =2 – 0 =2с, ε = ( — 10 ) / 2 = -5рад/с2. Следовательно, тангенциальное ускорение точки равно: a τ = (- 5)∙1 = -5 м/с2. Ответ: вариант 4.
Тест 1 — 17
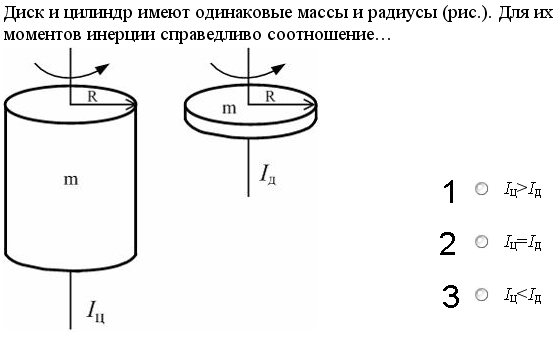 Диск
и цилиндр имеют одинаковые массы и
радиусы (рис.). Для их моментов инерции
справедливо соотношение…
Диск
и цилиндр имеют одинаковые массы и
радиусы (рис.). Для их моментов инерции
справедливо соотношение…
Варианты ответов: 1) IЦ > IД ; 2) IЦ = IД ; 3) IЦ < IД .
Решение.
Моменты инерции сплошного цилиндра и диска вычисляются по одинаковой формуле: I = mR 2/2 . Эта формула показывает, что момент инерции не зависит от длины цилиндра. Следовательно, IЦ = IД .
Ответ: вариант 2.
Тест 1 – 18
Если момент инерции тела увеличить в 2 раза, а скорость его вращения уменьшить в 2 раза, то момент импульса тела…
Варианты ответов: 1) увеличится в 4 раза; 2) уменьшится в 4 раза;
3) уменьшится в 2 раза; 4) не изменится.
Решение.
Момент импульса тела численно равен произведению момента инерции тела на его угловую скорость: L= I·ω. Поэтому, если один сомножитель увеличить в 2 раза, а другой уменьшить в 2 раза, то результат не изменится.
Ответ: вариант 4.
Тест 1 –19
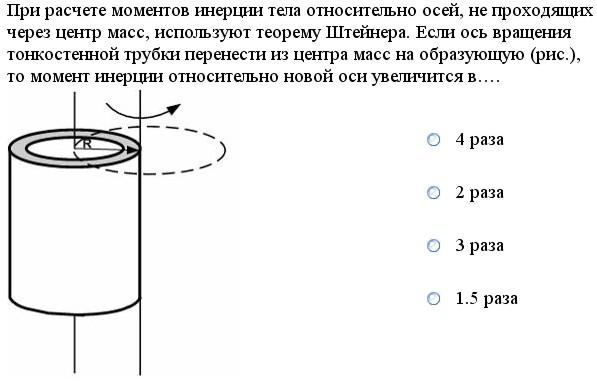 При
расчете моментов инерции тела относительно
осей, не проходящих через центр масс,
используют теорему Штейнера. Если ось
вращения тонкостенной трубки перенести
из центра масс на образующую (рис.), то
момент инерции относительно новой оси
увеличится в….
При
расчете моментов инерции тела относительно
осей, не проходящих через центр масс,
используют теорему Штейнера. Если ось
вращения тонкостенной трубки перенести
из центра масс на образующую (рис.), то
момент инерции относительно новой оси
увеличится в….
Варианты ответов: 1) 4 раза; 2) 2 раза;
3) 3 раза; 4) 1.5 раза.
Решение.
По теореме Штейнера момент инерции тела относительно произвольной оси I равен моменту инерции этого тела относительно оси, параллельной данной и проходящей через центр масс I0, плюс произведение массы тела на квадрат расстояния d между осями: I = I0 + m·d2. Момент инерции тонкостенной трубки относительно оси симметрии вычисляется так же, как момент инерции обруча: I0 = mR2, расстояние между осями, как следует из рисунка, равно d = R. Тогда по теореме Штейнера:
I = mR2 + mR2 = 2mR2 = 2I0. Отсюда следует, что момент инерции увеличится в 2 раза: I/I0=2.
Ответ: вариант 2.
Тест 1 –20
И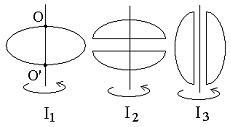 з
жести вырезали три одинаковые детали
в виде эллипса. Две детали разрезали
пополам вдоль оси симметрии. Затем все
части отодвинули друг от друга на
одинаковое расстояние и расставили
симметрично относительно оси OO’.
Для
моментов инерции относительно оси OO’
справедливо соотношение …
з
жести вырезали три одинаковые детали
в виде эллипса. Две детали разрезали
пополам вдоль оси симметрии. Затем все
части отодвинули друг от друга на
одинаковое расстояние и расставили
симметрично относительно оси OO’.
Для
моментов инерции относительно оси OO’
справедливо соотношение …
Варианты ответов:
1) I 1 = I 2 > I 3; 2) I 1 < I 2 = I 3; 3) I 1 = I 2 <I 3; 4) не хватает данных.
Решение.
Моментом инерции твёрдого тела называется сумма призведений масс материальных точек на квадраты их расстояний до оси вращения. Исходя из этого определения, сравним моменты инерции неразрезанной и разрезанных деталей.
Если тело разрезать поперек оси вращения и отодвинуть части друг относительно друга на некоторое расстояние, то при таком расположении частей тела расстояния материальных до оси вращения не изменяются. Поэтому момент инерции тела останется прежним, т. е. I1 = I2.
Если расположить разделенные части тела симметрично относительно оси ОО′ на такое же расстояние, как при поперечном разрезе, показанном на рисунке, то расстояния материальных точек относительно оси вращения для третьей детали уменьшится по сравнению со второй. Поэтому момент инерции I 3< I 2 . Следовательно, справедливо соотношение I 1 = I 2 > I 3 .
Ответ: вариант 1.
Тест 1 –21
В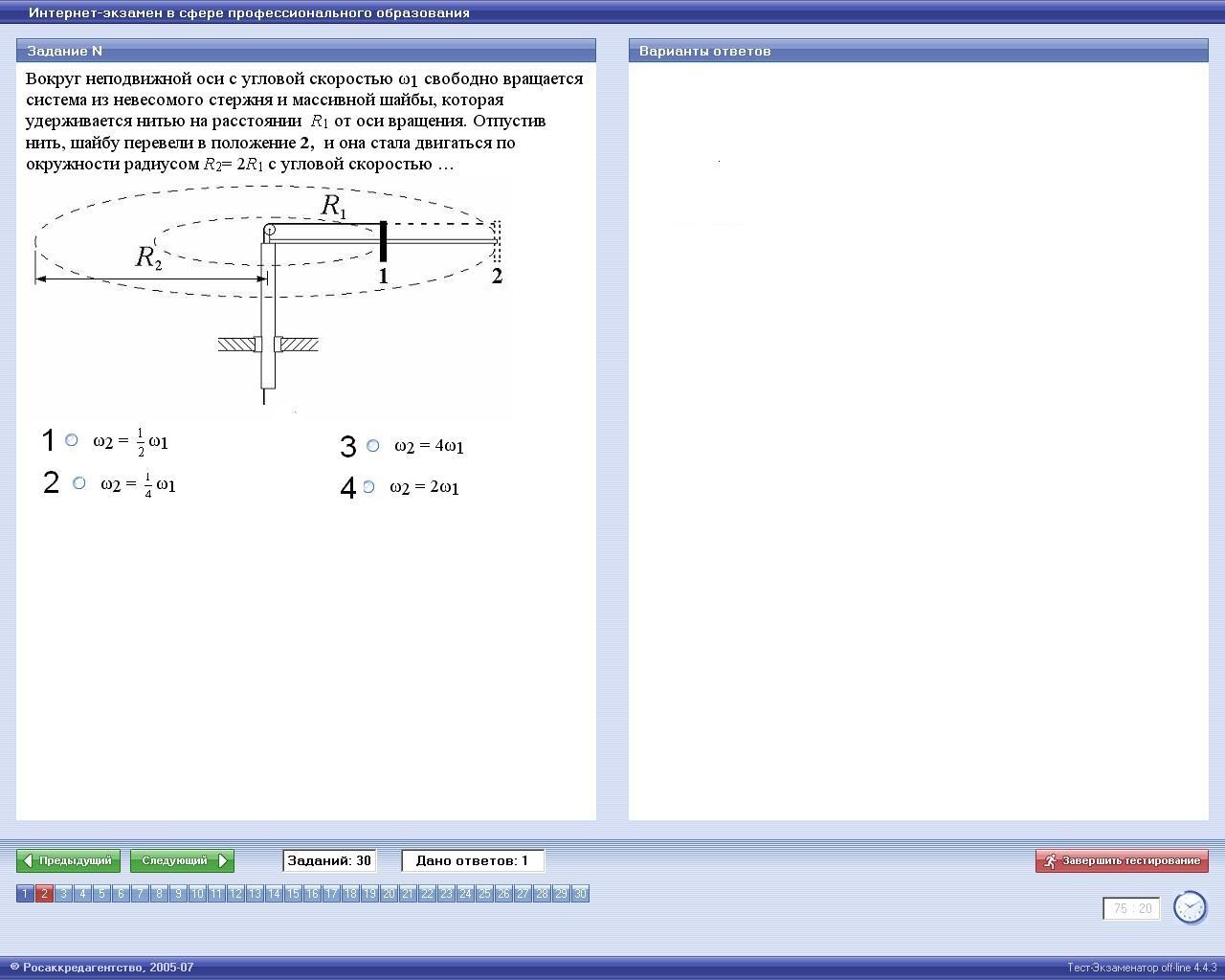 округ
неподвижной оси с угловой скоростью
ω1 свободно вращается система из невесомого
стержня и массивной шайбы, которая
удерживается нитью на расстоянии R 1 от
оси вращения. Отпустив нить, шайбу
перевели в положение 2, и она стала
двигаться по окружности радиусом R2= 2R1 с
угловой скоростью …
округ
неподвижной оси с угловой скоростью
ω1 свободно вращается система из невесомого
стержня и массивной шайбы, которая
удерживается нитью на расстоянии R 1 от
оси вращения. Отпустив нить, шайбу
перевели в положение 2, и она стала
двигаться по окружности радиусом R2= 2R1 с
угловой скоростью …
Варианты ответов:
ω2 = ω1/2; 2) ω2 = ω1/4; 3) ω2 = 4ω1; 4) ω2 = 2ω1.
Решение.
Задача решается по закону сохранения момента импульса: момент импульса замкнутой системы сохраняется. Данную систему можно рассматривать как замкнутую, так как момент силы, перемещающей шайбу вдоль стержня, относительно оси вращения равен нулю. Поэтому момент импульса шайбы до перемещения равен моменту импульса шайбы после перемещения: L1 = L2. Момент импульса твердого тела равен произведению момента инерции тела на угловую скорость: L = I ω, поэтому по закону сохранения момента импульса получим: I1 ω1= I2 ω2 . Шайбу можно рассматривать как материальную точку, момент инерции которой равен произведению массы на квадрат её расстояния до оси вращения: I = m∙R2. Тогда получим:
mR12ω1 = mR22ω2. Отсюда: ω2=R12ω1/R22= ω1·(R1/ R2)2 . Так как по условию задачи R2 = 2R1 , то ω2 = ω1 /4.
Ответ: вариант 2.
 Тест
1 — 22
Тест
1 — 22
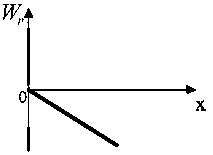
В
потенциальном поле сила 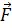 пропорциональна
градиенту потенциальной энергии WP.
Если график зависимости потенциальной
энергии WP от
координаты х имеет вид, представленный
на рисунке, то зависимость проекции
силы Fx на
ось x будет…
пропорциональна
градиенту потенциальной энергии WP.
Если график зависимости потенциальной
энергии WP от
координаты х имеет вид, представленный
на рисунке, то зависимость проекции
силы Fx на
ось x будет…
Варианты ответов:
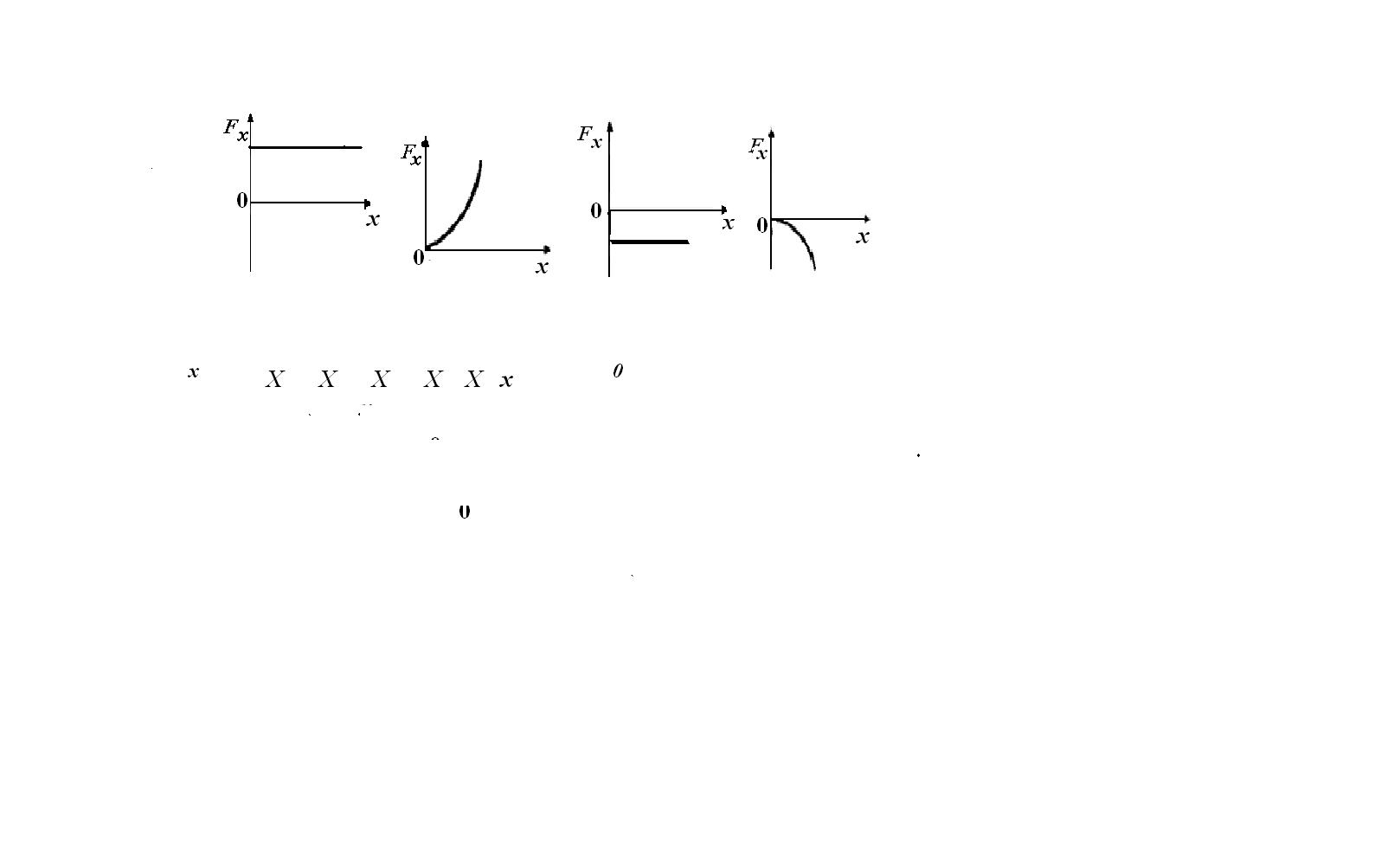
Момент инерции тела относительно нецентральной оси Теорема Штейнера
Пусть тело вращается вокруг неподвижной нецентральной оси. Это тело обладает кинетической энергией
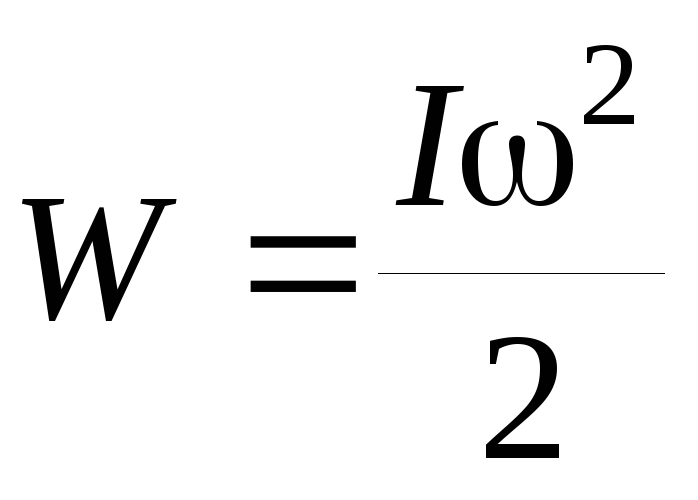 ,
(1)
,
(1)
где I — момент
инерции тела относительно данной
нецентральной оси .
Проведём
через центр масс С о
.
Проведём
через центр масс С о
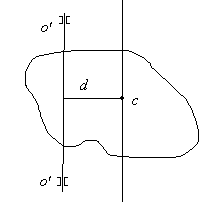
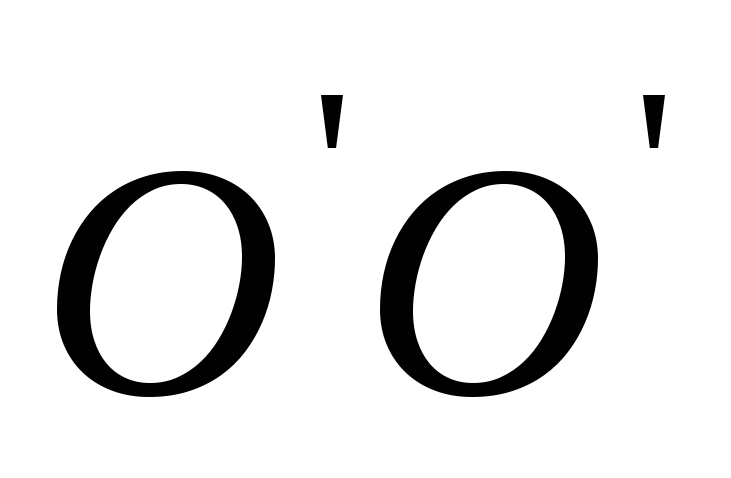 .
Тогда вращение твёрдого
тела можно представить как результат
вращения центра масс С вокруг оси
.
Тогда вращение твёрдого
тела можно представить как результат
вращения центра масс С вокруг оси 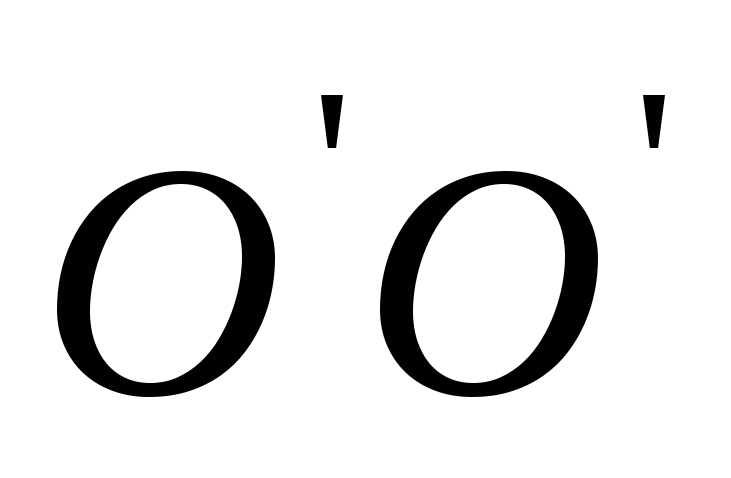 и вращение твёрдого тела вокруг
центральной оси ОО тоже с угловой скоростью .
Кинетическую энергию
тоже можно представить как сумму двух
слагаемых :
и вращение твёрдого тела вокруг
центральной оси ОО тоже с угловой скоростью .
Кинетическую энергию
тоже можно представить как сумму двух
слагаемых : 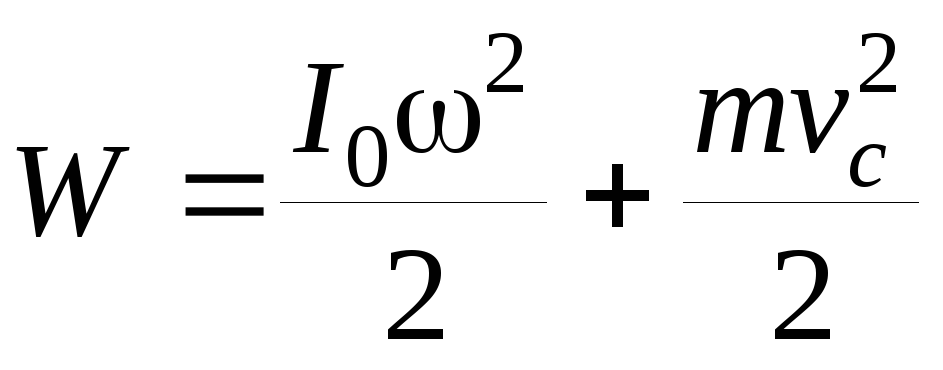 ,
(2)
,
(2)
где 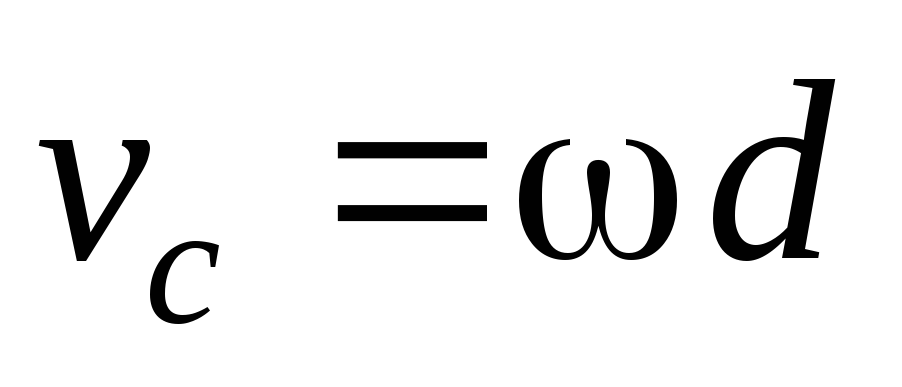 —
линейная скорость центра масс.
C учётом
(1) и (2) получаем
—
линейная скорость центра масс.
C учётом
(1) и (2) получаем
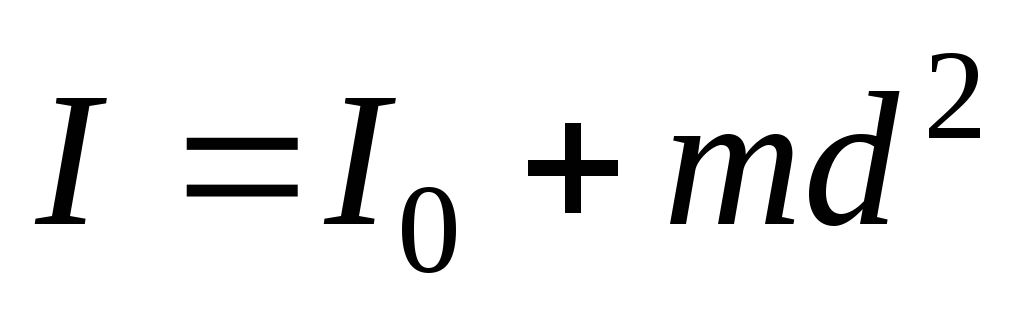 — теорема
Штейнера.
— теорема
Штейнера.
Теорема Штейнера: Момент инерции I относительно произвольной оси равен сумме момента инерции I0 относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями :
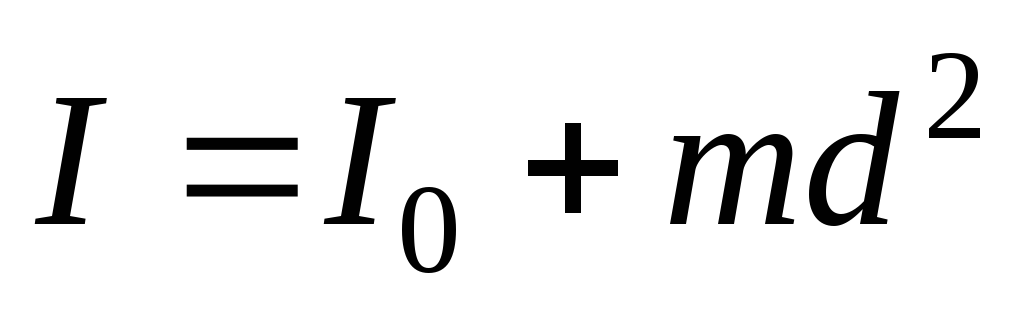
Таким образом, теорема Штейнера, по существу, сводит вычисление момента инерции относительно произвольной оси к вычислению момента инерции относительно оси, проходящей через центр масс тела.
Момент импульса твёрдого тела относительно закреплённой оси. Главные оси и главные моменты инерции
Р
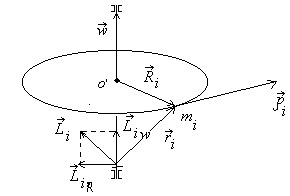
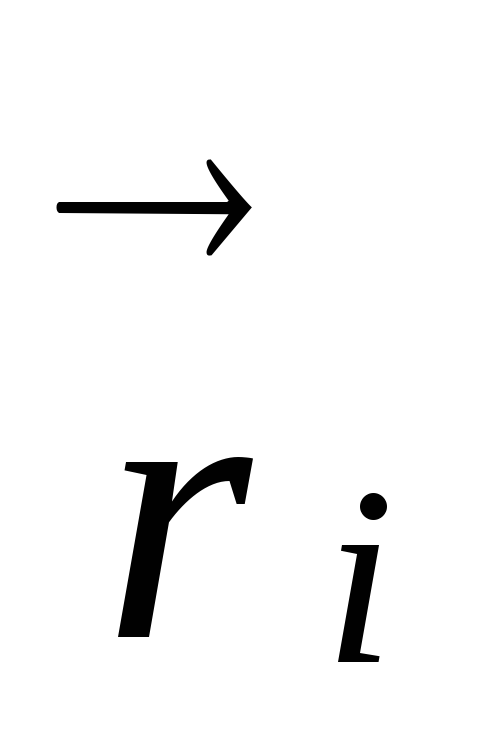 ,
проведённых из этой точки. На рисунке
показанаi-я
материальная точка с массой
,
проведённых из этой точки. На рисунке
показанаi-я
материальная точка с массой 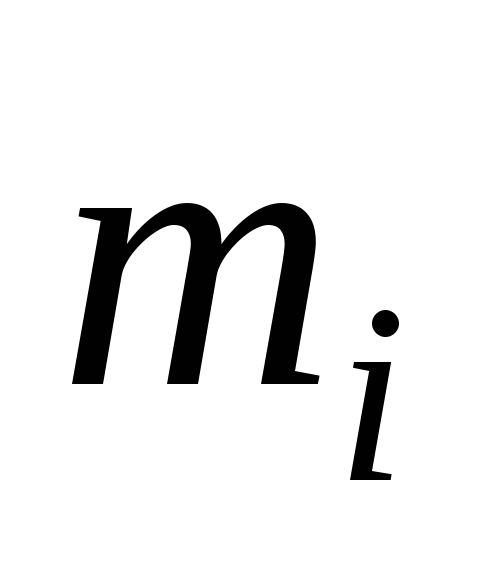 .
Согласно определению
момент импульса i-ой
материальной точки относительно точки О равен
.
Согласно определению
момент импульса i-ой
материальной точки относительно точки О равен 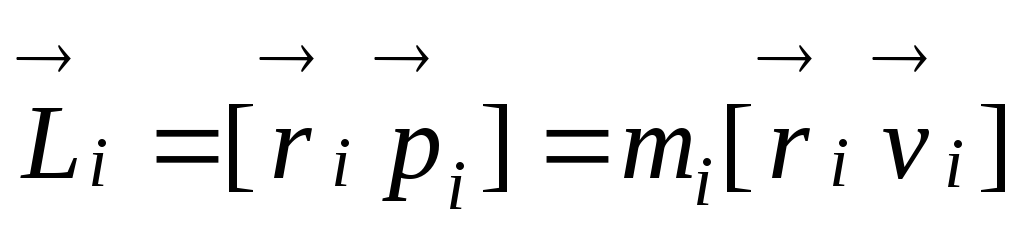 ,
,или,
используя связь 
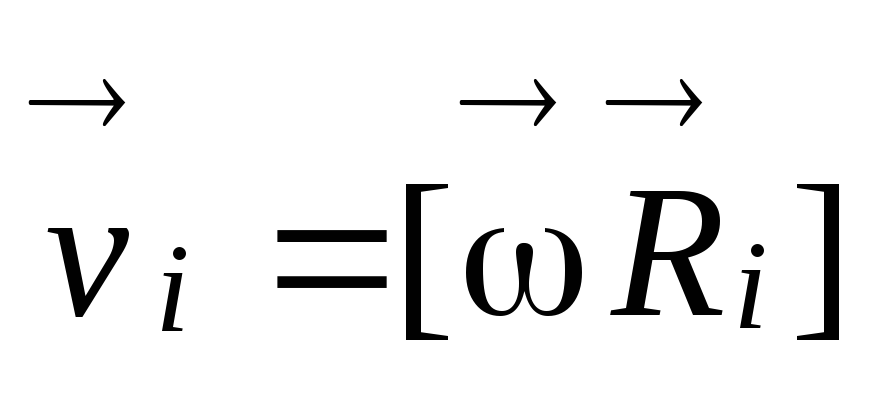 ,
,
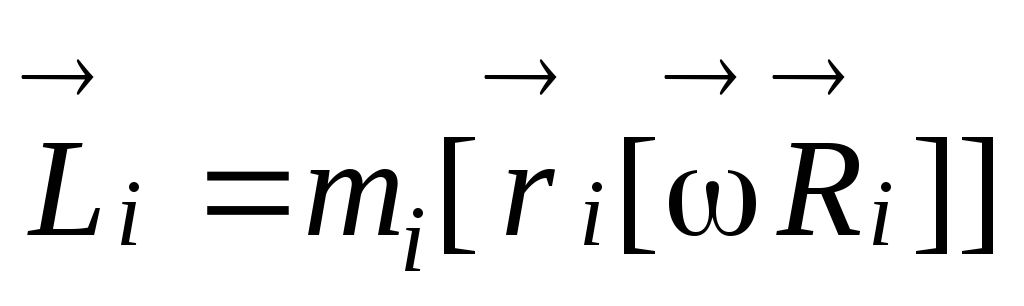 .
.
Для раскрытия двойного векторного произведения воспользуемся формулой
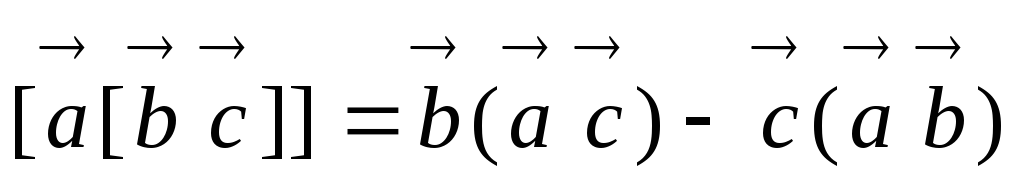
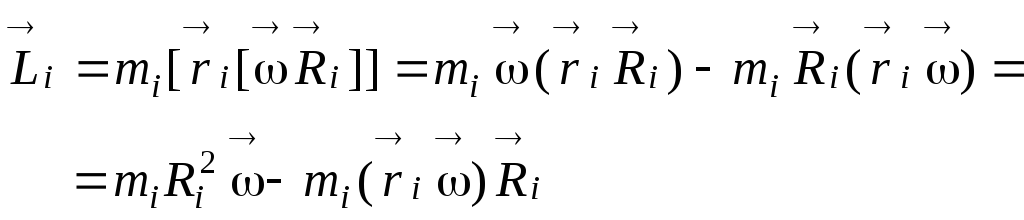 .
.
Мы
видим что, момент импульса i-ой
материальной точки 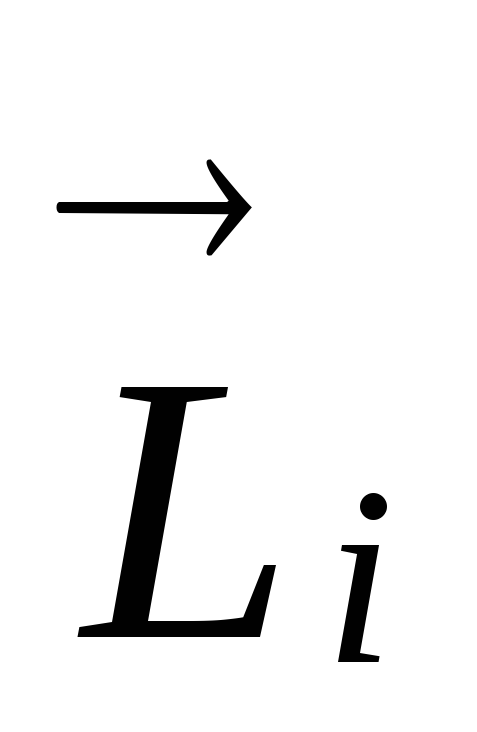 не совладает по направлению с угловой
скоростью
не совладает по направлению с угловой
скоростью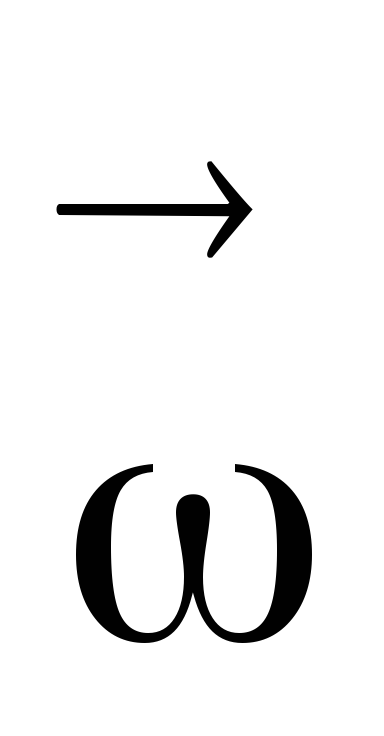 ,
и его можно представить как сумму двух
составляющих:
осевой
,
и его можно представить как сумму двух
составляющих:
осевой 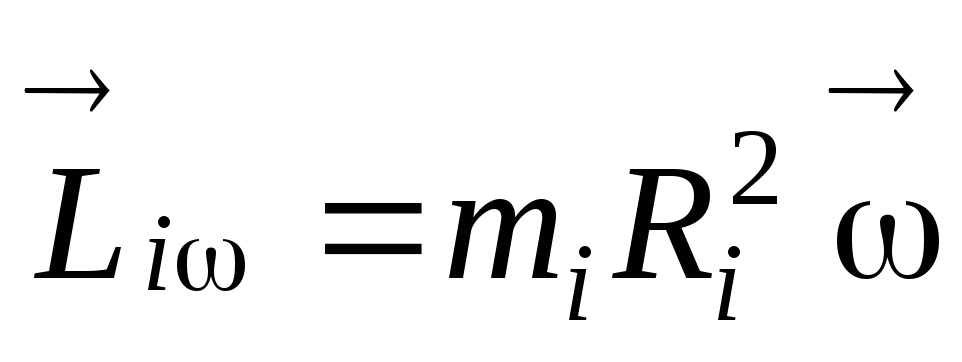 и радиальной
и радиальной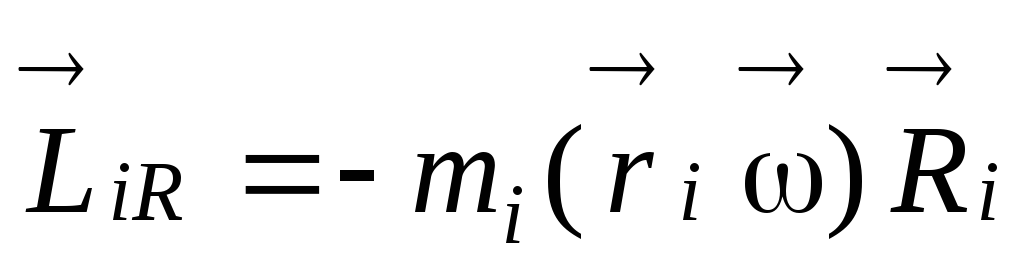
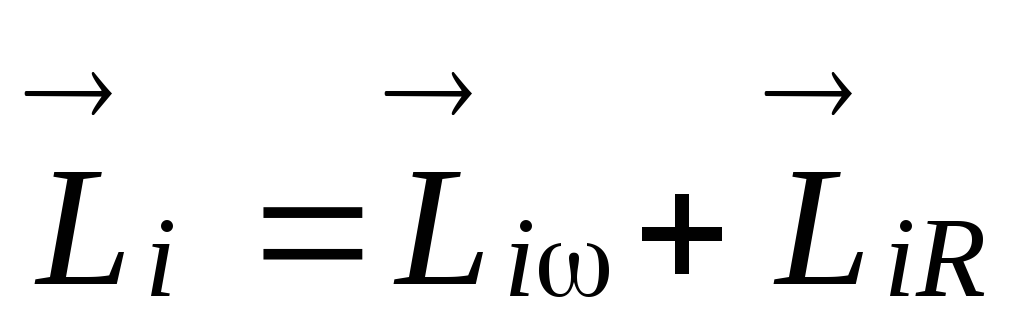 .
.
Момент импульса всего твёрдого тела равен
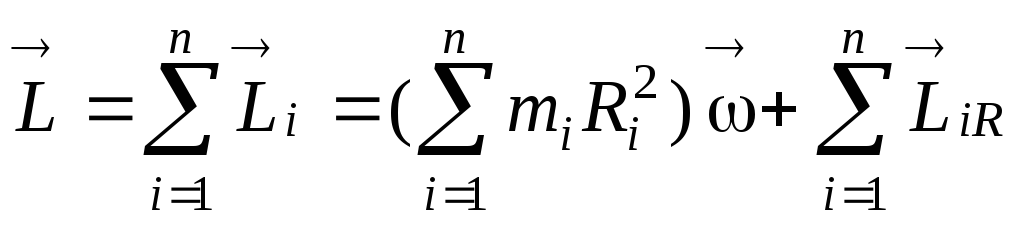 или
или 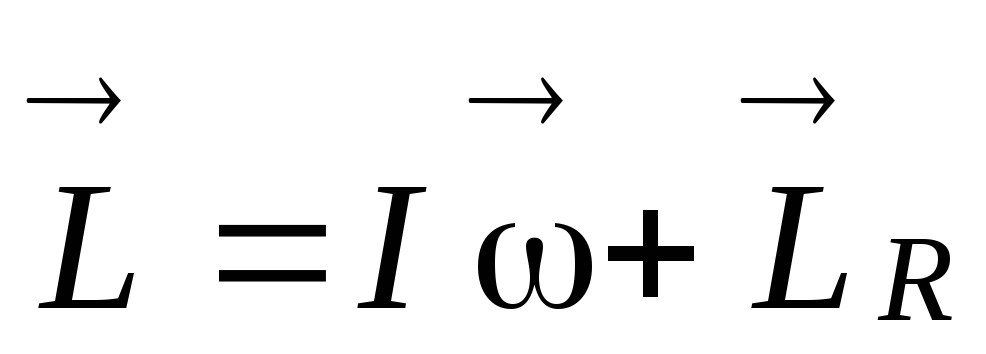
где I — момент
инерции твёрдого тела относительно оси
вращения, 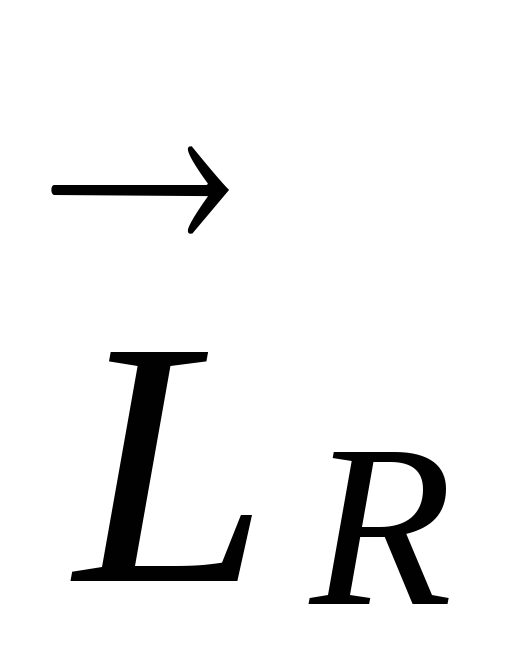 — составляющая момента импульса тела,
перпендикулярная оси вращения. .
— составляющая момента импульса тела,
перпендикулярная оси вращения. .
Нетрудно
сообразить, что для однородного тела
симметричного относительно оси вращения
(для однородного тела вращения ) суммарный
момент импульса направлен вдоль оси
вращения в ту же сторону что и  ,
и равен
,
и равен
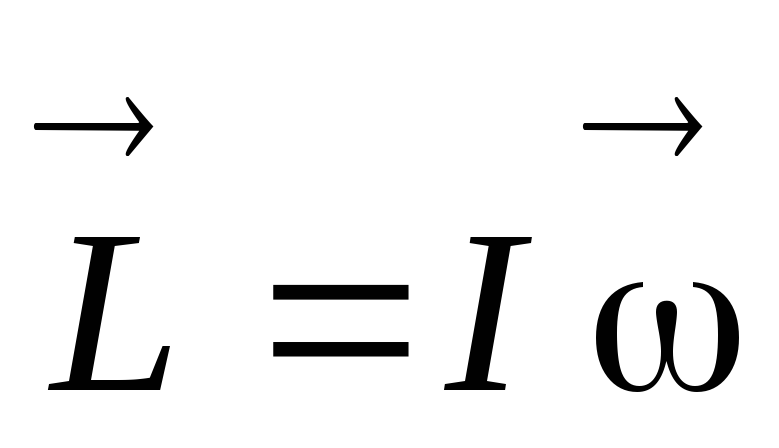 .
.
Действительно
в этом случаи тело можно разбить на
пары равных по массе, расположенных
симметрично материальных точек. Сумма
моментов каждой пары направлена вдоль
вектора 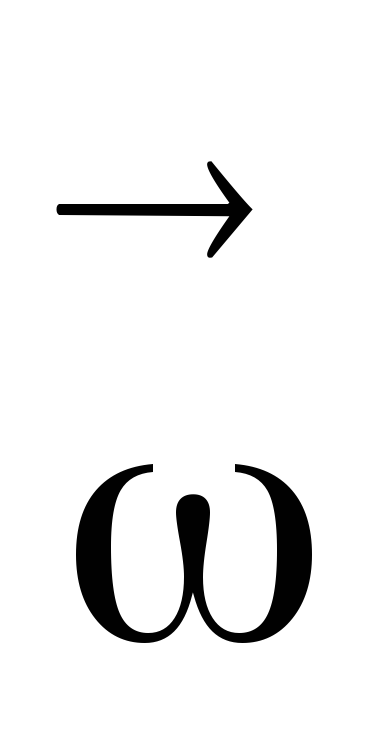 ,
следовательно, и суммарный момент
импульса
,
следовательно, и суммарный момент
импульса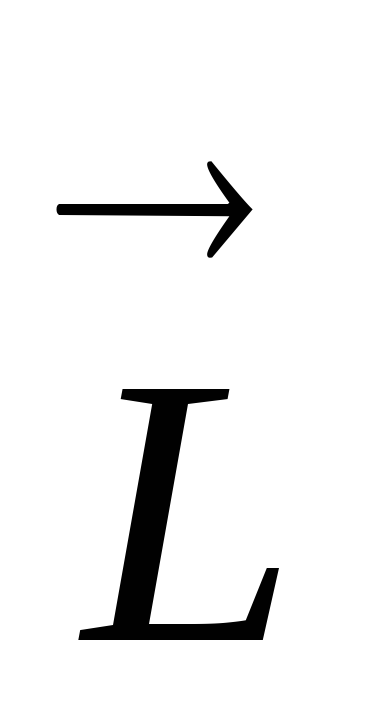 будет совпадать по направлению с
будет совпадать по направлению с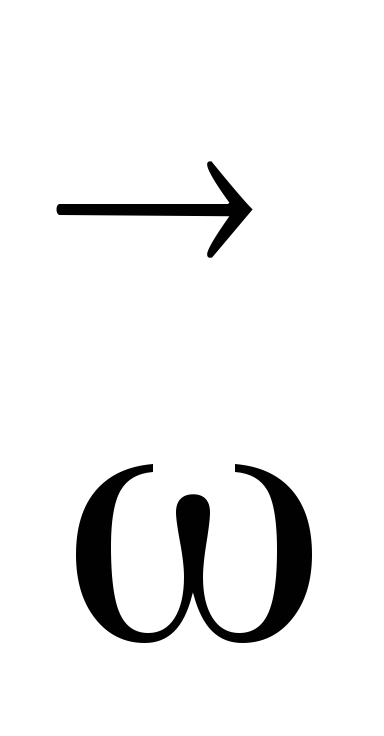 и равен
и равен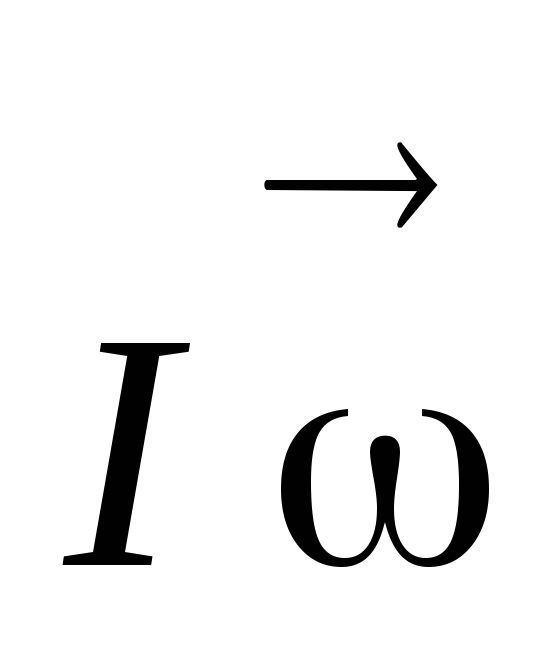 .
.
Для несимметричного
(или неоднородного) тела момент импульса 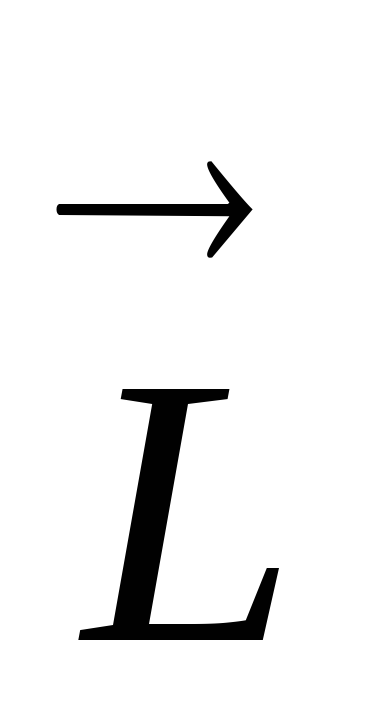 ,
вообще говоря, не совпадает по направлению
с вектором
,
вообще говоря, не совпадает по направлению
с вектором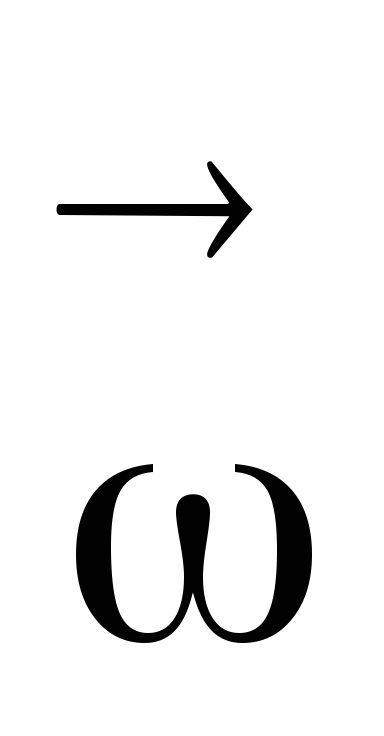 .
При вращении тела вектор
.
При вращении тела вектор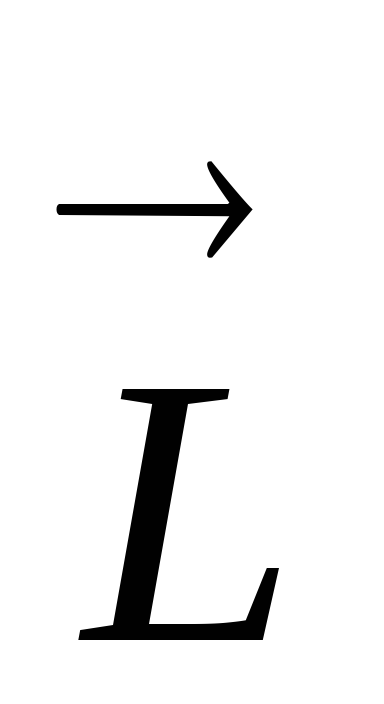 поворачивается вместе с ним, описывая
конус .
поворачивается вместе с ним, описывая
конус .
Заметим, что в случае вращения однородного симметричного тела, силы бокового давления подшипников на ось не возникают. В отсутствие силы тяжести подшипники можно было бы убрать, – ось и без них сохраняла бы своё положение в пространстве. Ось, положение которой в пространстве остаётся неизменным при вращении вокруг неё тела в отсутствии внешних сил, называется свободной осьютела
Можно доказать, что для тела любой формы и с произвольным распределением масс существуют три взаимно перпендикулярные, проходящие через центр масс оси, которые могут служить свободными осями: эти оси называются главными осями инерции тела. Моменты инерции относительно главных осей называютсяглавными моментами инерции тела.
В общем случае эти
моменты различны: 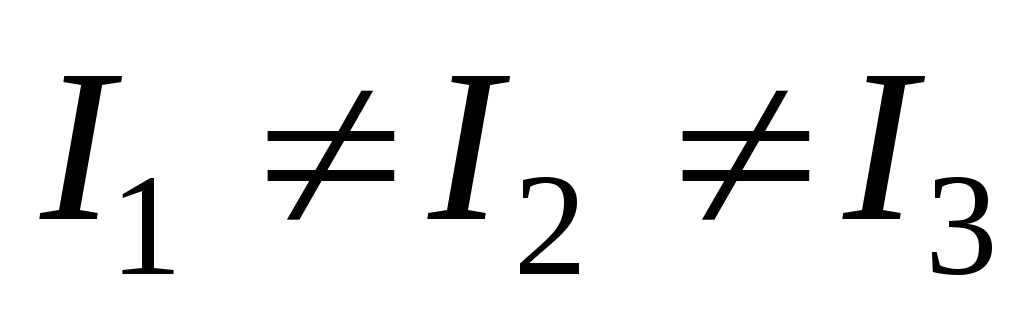 .
.
Для тела с осевой
симметрией два главных момента инерции
имеют одинаковую величину, третий же,
вообще говоря, отличен от них: 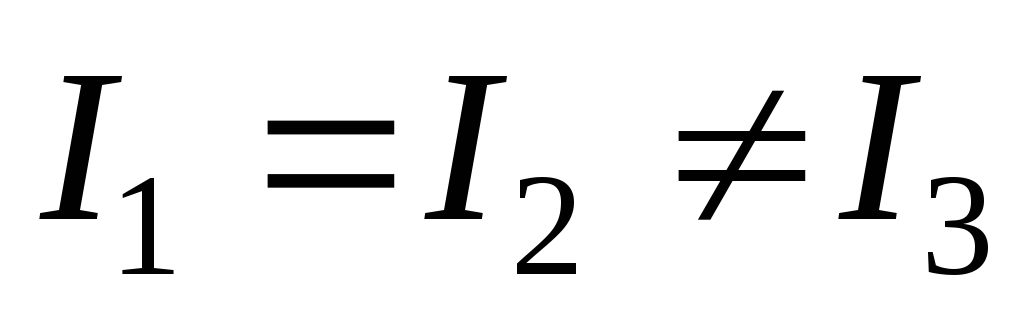 .
.
И, наконец, в случае
тела с центрально симметрией, все три
главных момента одинаковы: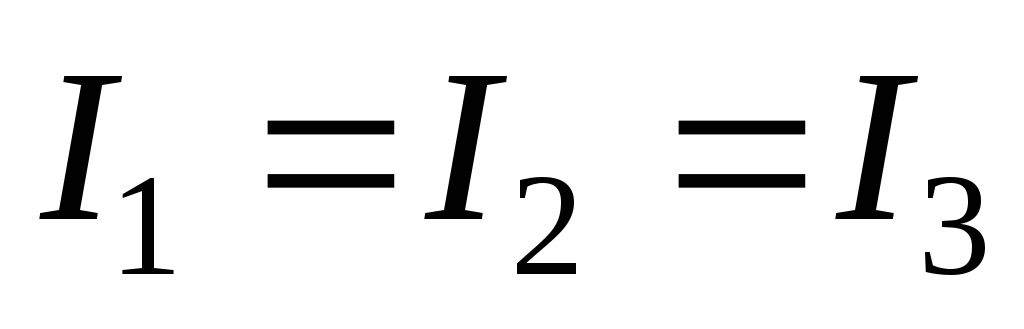 .
.
Методические указания к практическим занятиям дисциплины «Физика», страница 5
Рассчитаем an, сократив массу
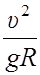 = tg a, отсюда υ =
= tg a, отсюда υ = 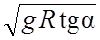 =41,5 м/с.
=41,5 м/с.
3. МЕХАНИКА ТВЕРДОГО ТЕЛА
Основные формулы
Мерой инертности твердого тела при вращательном движении является момент инерции:
I= Σmi∙ri2, где mi – элементарная масса i – го кусочка тела, ri – расстояние этого кусочка от оси вращения.
Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:
Полый цилиндр I = m ( R12 + R22).
Тонкий обруч I = mR2.
Сплошной цилиндр I = 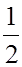 mR2.
mR2.
Шар I = 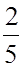 mR2.
mR2.
Тонкий
стержень I = 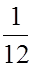 ml2.
ml2.
Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:
I = I0 + ma2, где I – момент инерции тела относительно данной оси, I0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, m – масса тела, а – расстояние между осями.
Основное уравнение динамики вращательного движения твердого тела: I e = M, где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Момент силы F равен: M = Fl, где l – расстояние от линии, вдоль которой действует сила, до оси вращения.
Момент импульса твердого тела относительно неподвижной оси: L = Iω, где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.
Момент импульса материальной точки относительно неподвижной оси: L = mυr, где m – масса частицы, υ – ее скорость, r – расстояние от линии, вдоль которой движется частица, до данной оси.
В замкнутой системе частиц полный момент импульса не меняется: ΣLi = const.
Кинетическая энергия вращающегося тела:
Ek = 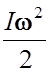 , где I – момент инерции тела, ω – его угловая скорость.
, где I – момент инерции тела, ω – его угловая скорость.
Кинетическая энергия катящегося тела:
Ek = 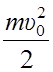 +
+ 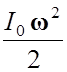 , где m – масса тела, υ0 – скорость
поступательного движения центра масс, I0 – момент инерции тела
относительно оси, проходящей через центр масс, ω – угловая
скорость вращения тела.
, где m – масса тела, υ0 – скорость
поступательного движения центра масс, I0 – момент инерции тела
относительно оси, проходящей через центр масс, ω – угловая
скорость вращения тела.
Примеры решения задач
Задача 13
Прямой круглый однородный конус имеет массу m и радиус основания R. Найти момент инерции конуса относительно его оси.
Решение
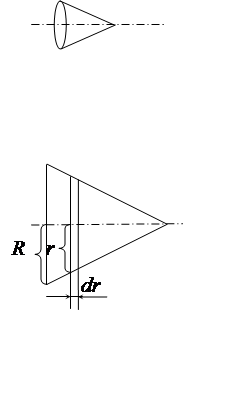 Разобьём конус
на цилиндрические слои ось толщиной dr. Масса такого
слоя
Разобьём конус
на цилиндрические слои ось толщиной dr. Масса такого
слоя
dm = rpr2dr, где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя
dI = dm.r2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I = 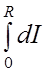 =
= 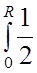 ρπ r4dr =
ρπ r4dr = 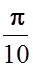 ρR5.
ρR5.
Остаётся выразить его через массу всего цилиндра:
m = 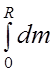 =
=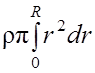 =
=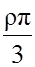 R3, отсюда
ρ =
R3, отсюда
ρ = 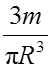 ,
,
I = 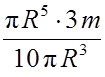 =
= 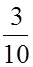 mR2.
mR2.
Задача 14
Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Решение
При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.
ω 0 = 2 π ν0, ω = 0,
0 = 2 π ν0 — ε t, отсюда
ε
= 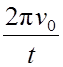 .
.
Это ускорение обусловлено действием момента сил трения
Mтр = I ε = 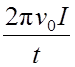 .
.
Полный угол поворота при равнозамедленном движении находится из соотношения:
φ =ω0t— 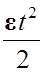 ,
,
φ =2π N, ω 0
= 2
π ν0, ε = 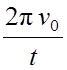 .
.
Перепишем соотношения для угла в виде:
2π N = 2 π ν0t — 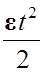 = 2 π ν0 t —
= 2 π ν0 t — 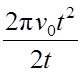 =
= 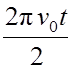 .
.
11. Наибольший момент инерции относительно оси
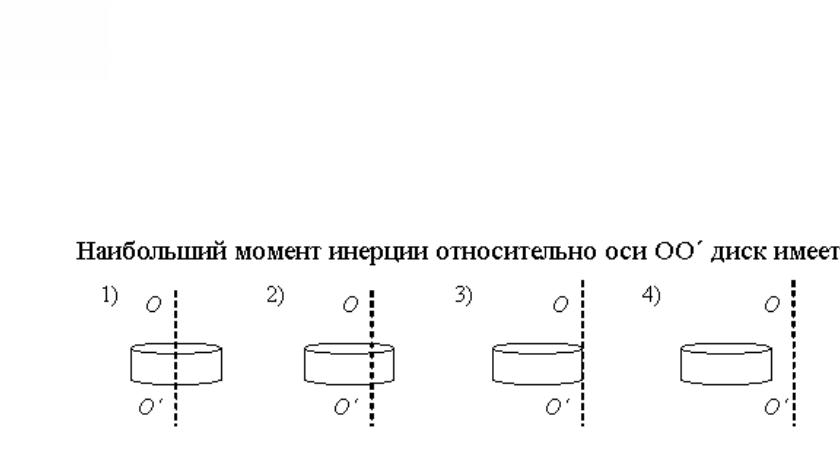
ОО’ диск имеет в случае …
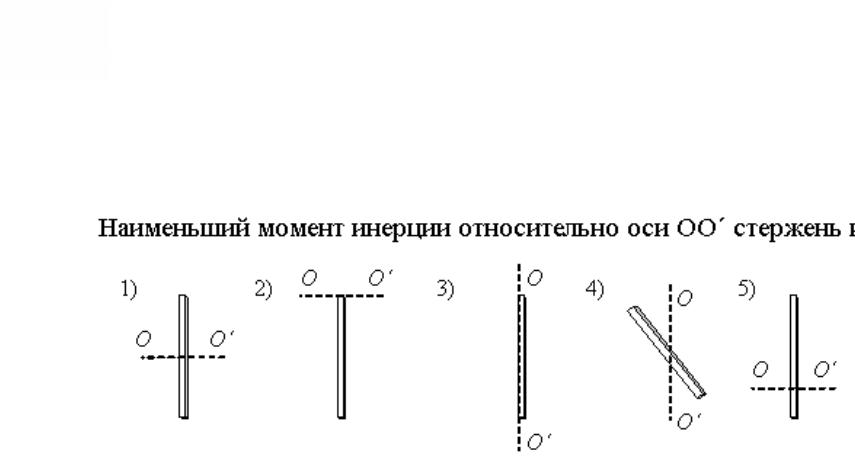
12. Наименьший момент инерции относительно оси
ОО’ стержень имеет в случае …

13.Тонкостенная трубка и кольцо имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение…
1)IT > IK
2)IT < IK
3)IT = IK

14. Алюминиевый и стальной цилиндры имеют одинаковую высоту и равные массы. Относительно моментов инерции этих цилиндров справедливо следующее суждение…
1)моменты инерции цилиндров равны
2)момент инерции алюминиевого цилиндра больше момента инерции стального цилиндра
3)момент инерции стального цилиндра больше момента инерции алюминиевого цилиндра
4)понятие момента инерции неприменимо к цилиндрам
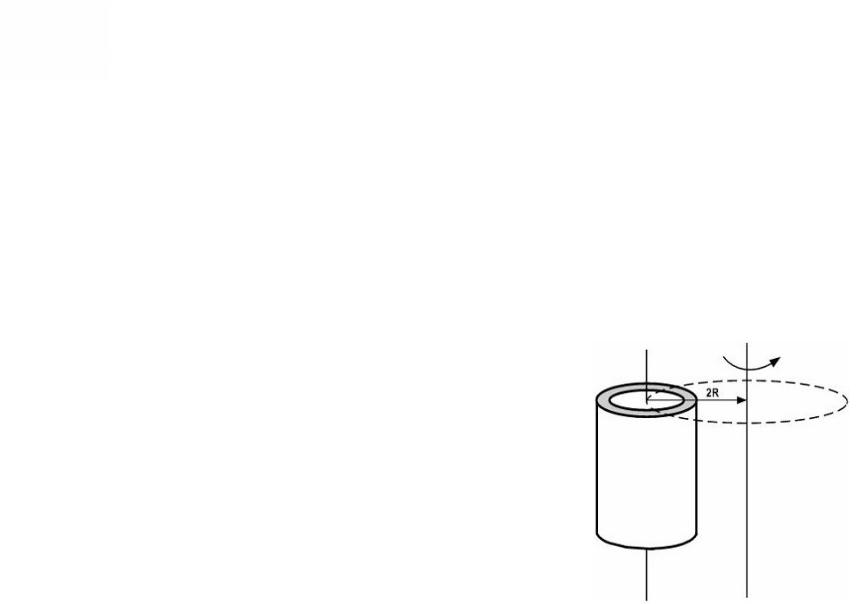
15. При расчете момента инерции тела относительно осей, не проходящих через центр масс, используют теорему Штейнера. Если ось вращения тонкостенной трубки перенести из центра масс на расстояние 2R (рис.), то момент инерции относительно новой оси увеличится в …
1)5 раз
2)2 раза
3)3 раза
4)4 раза
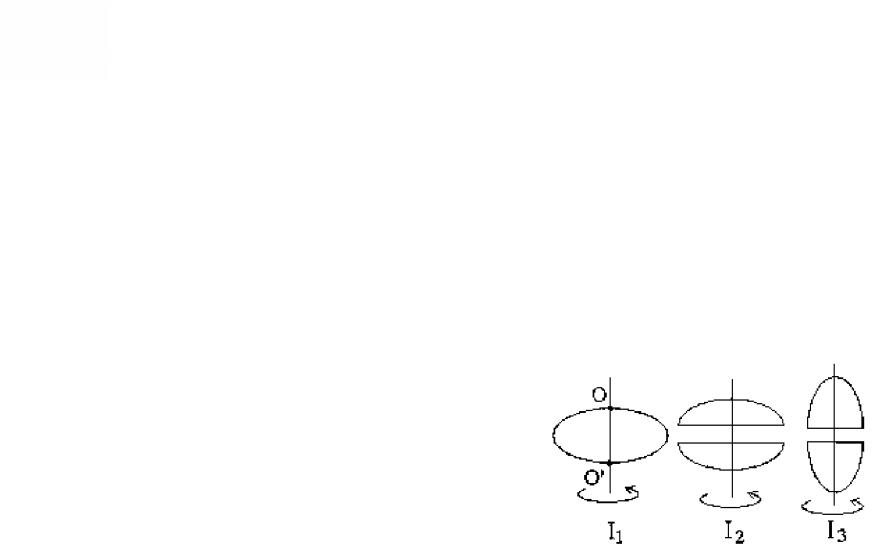
16. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на одинаковое расстояние н расставили симметрично относительно оси ОО’. Для моментов инерции относительно оси ОО’ справедливо соотношение …
I1 I2 I3
I1 I2 I3
I1 I2 I3
I1 I2 I3
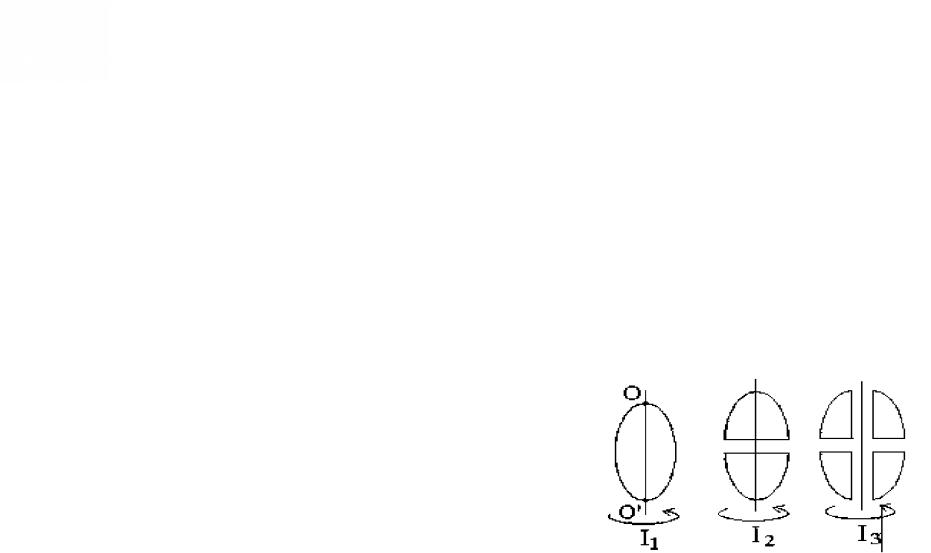
17. Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну -пополам вдоль оси симметрии, а вторую — на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси ОО’. Для моментов инерции относительно оси ОО’ справедливо соотношение …
I1 I2 I3
I1 I2 I3
I1 I2 I3
I1 I2 I3

18. Четыре шарика расположены вдоль прямой а. Расстояния между соседними шариками одинаковы. Массы шариков слева направо: 1 г, 2 г, 3 г, 4 г. Если поменять местами шарики 1 и 3, то момент инерции этой системы относительно оси О, перпендикулярной прямой а и проходящей через середину системы …
1)увеличится
2)уменьшится
3)не изменится
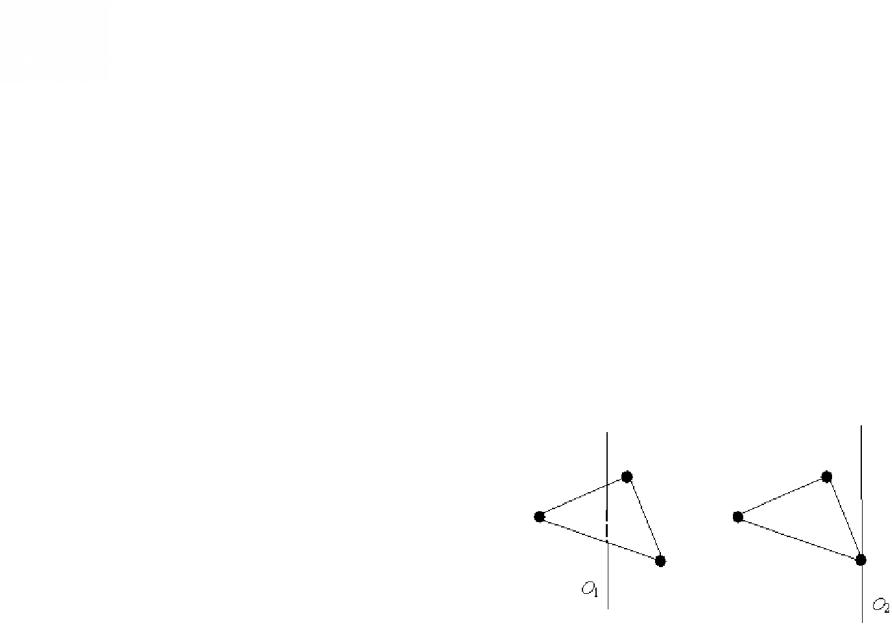
19. Три маленьких шарика расположены в вершинах правильного треугольника. Момент инерции этой системы относительно оси O1, перпендикулярной плоскости
треугольника и проходящей через его центр – I1. Момент инерции этой же системы относительно оси О2,
перпендикулярной плоскости треугольника и проходящей через один из шариков – I2. Справедливо утверждение …
1)I1 > I2
2)I1 < I2
3)I1 = I2

20. Кинетическая энергия вращающегося шара (угловая скорость 4 рад/с, момент инерции шара относительно данной оси 6 кг·м2), равна … (Дж)
48 Дж
Моменты инерции относительно смещенных осей
Рассмотрим плоское сечение произвольной формы площадью A.
Выделим в нем элементарную площадку dA с координатами x и y относительно системы координат проходящей через центр тяжести сечения O:
Покажем новую систему координат, y1O1x1, отстоящую от осей x и y первой системы на a и b соответственно
Новое положение элементарной площадки после смещения осей:
Осевые моменты инерции относительно смещенных осей x1 и y1.
Здесь Ix и Iy — осевые моменты инерции сечения.
Радиус инерции сечения >
Примеры решения задач >
Вы находитесь здесь:
Техническая механика > Сопротивление материалов > Лекции по сопромату > Моменты инерции относительно смещенных осей1. Момент инерции твердого тела относительно плоскости, относительно оси, относительно полюса.
Лекция №12
План
1)Момент инерции твердого тела относительно плоскости, относительно оси, относительно полюса.
2)Момент инерции относительно декартовых координат.
3)Моменты инерции относительно параллельных осей. Момент инерции однородного тонкого стержня относительно оси. Момент инерции однородной круглой пластины. Момент инерции однородного круглого цилиндра.
4)Количество движения точки и системы. Элементарный и полный импульс силы.
5) Теорема об изменении количества движения механической системы. Момент количества движения материальной точки и системы.
6) Теорема об изменении момента количества движения материальной точки. Теорема об изменении кинетического момента механической системы.
Движение тел существенным образом зависит от характера распределения масс. Положение центра масс не характеризует распределения массы. Поэтому при изучении динамики механических систем точек и при изучении динамики твердого тела, вводится еще одна характеристика –момент инерции системы материальных точек и момент инерции твердого тела.
Моментом инерции системы материальных точек массой mk относительно точки О, состоящий из N точек ,называется сумма произведений масс этих точек на квадраты их расстояний аk до точки О.
J0 = 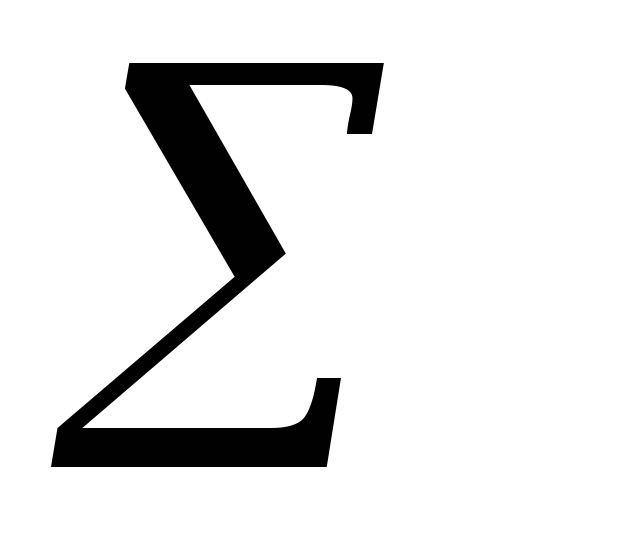 mka
mka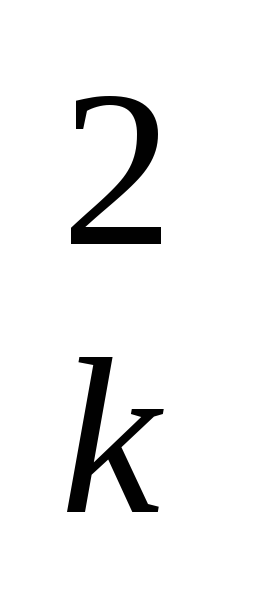
k =1,2,3…N
=1,2,3…N
М

hk
dmk
омент инерции относительно т
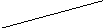 очки
называется полярным
очки
называется полярным
моментом инерции
L

Момент инерции твердого тела относительно точки О будет определяться :
J0= 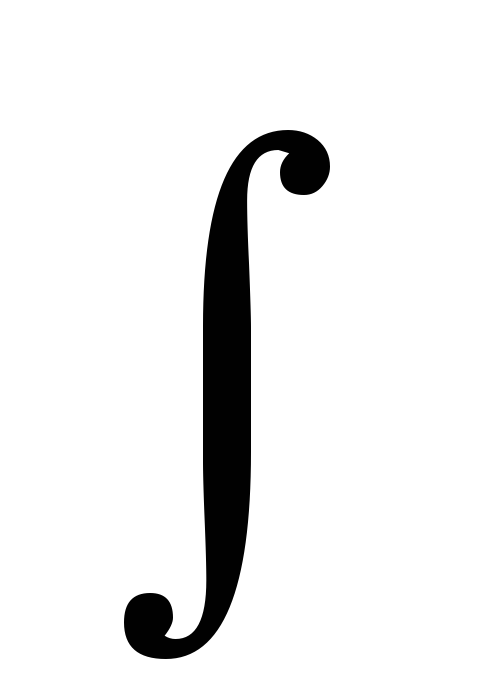 a
a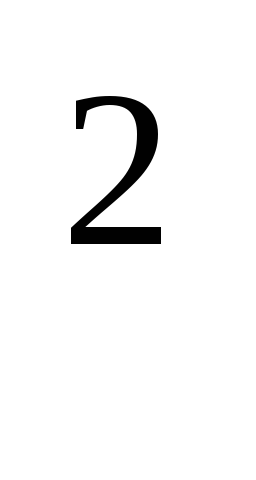 dm
dm
где dm-масса элементарной части тела ,принимаемой в пределе за точку.
а- расстояние частиц тела до точки О.
Интегрирование ведется по всему объему.
Моментом инерции Jkсистемы материальных точек относительно оси L называется сумма произведений масс этих точек на квадраты их расстояний hk до оси L.
JL= 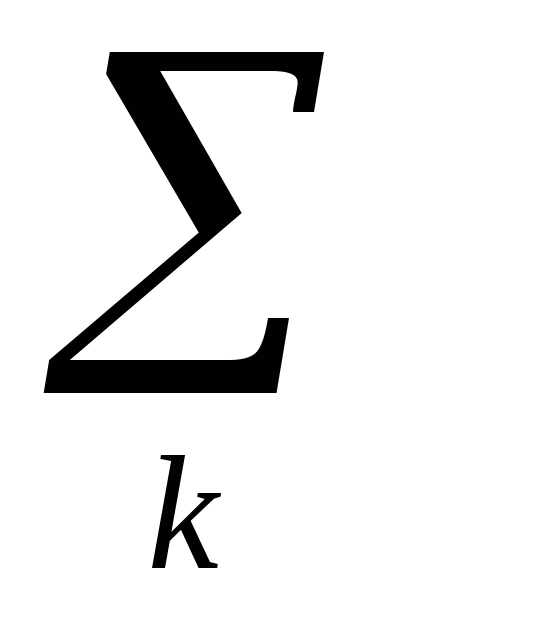 mkh
mkh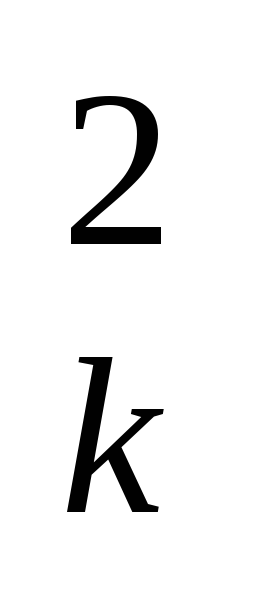
k=1,2,3…N
В случае твердого тела сумму следует заменить интегралом
JL = 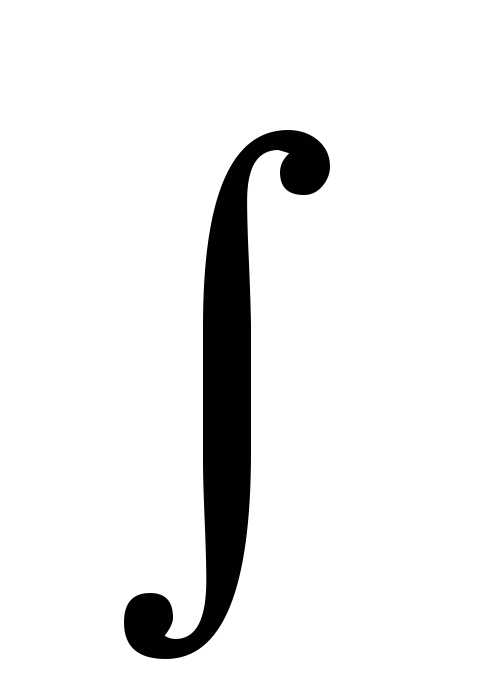 h
h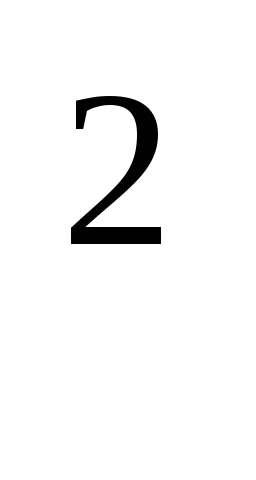 dm
dm
dm= dV,
-плотность
тела,V-объем
тела.
dV,
-плотность
тела,V-объем
тела.
Моменты инерции одинаковых по форме тел ,изготовленных из различных материалов ,отличаются друг от друга характеристикой ,не зависящей от массы тела является радиус инерции.
Радиус инерции 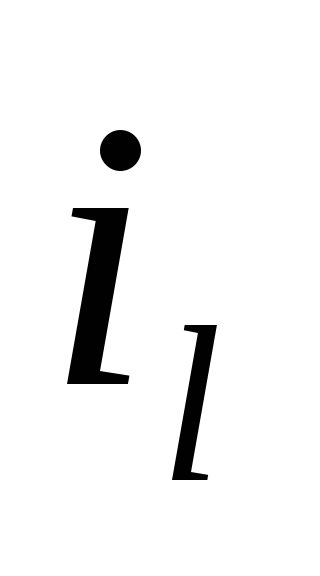 относительно осиL
определяется равенством :
относительно осиL
определяется равенством :
i=iL=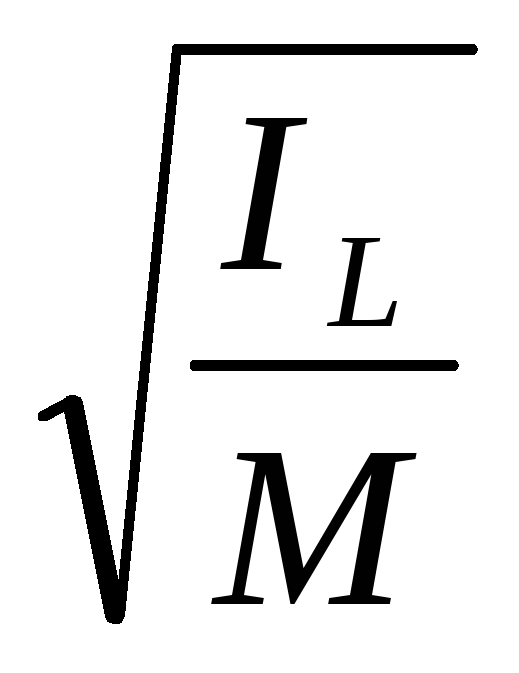
Тогда момент инерции относительно оси можно определить по формуле
JL =Mi2
2. Момент инерции относительно декартовых координат.
Выразим момент инерции системы материальных точек относительно оси JL для декартовых осей координат. Расстояние k-ой частицы до оси Х определяется из геометрии.
h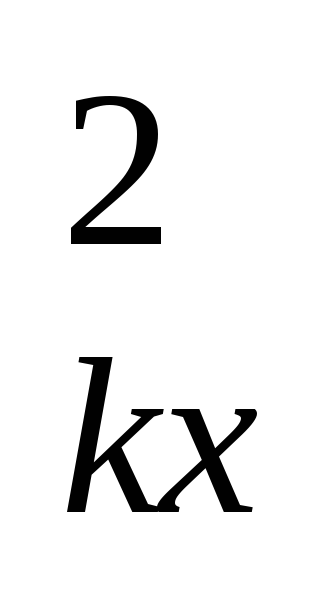 =Z
=Z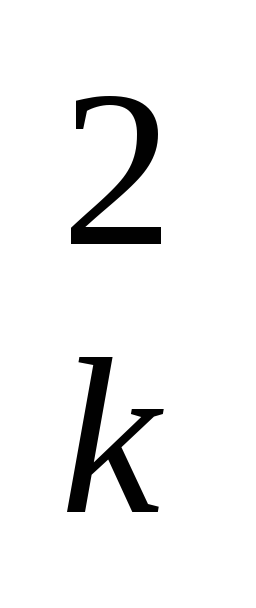 +Y
+Y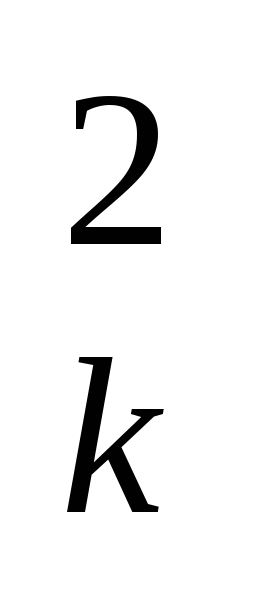
h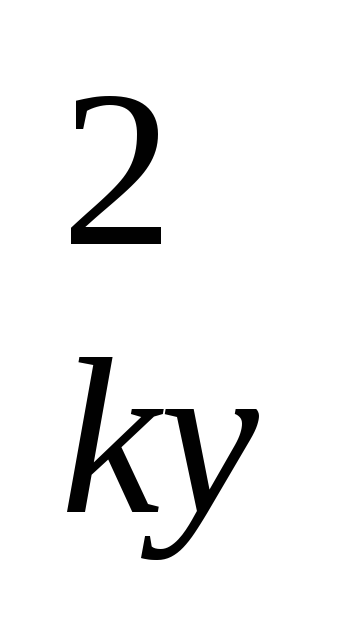 =X
=X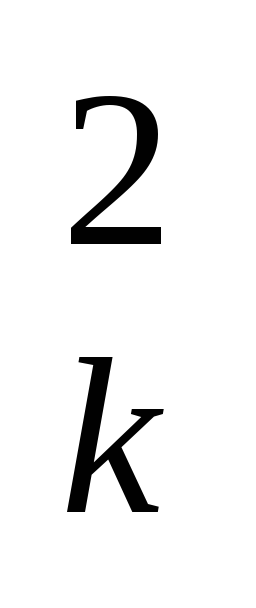 +Z
+Z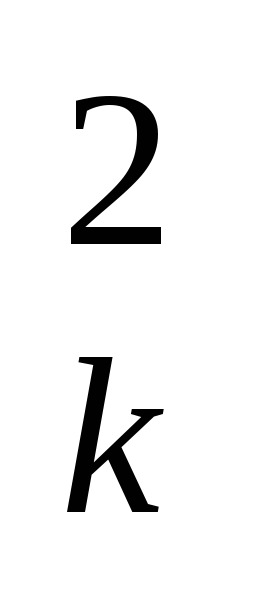
h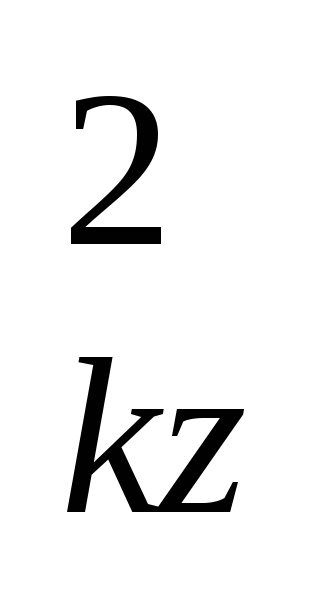 =X
=X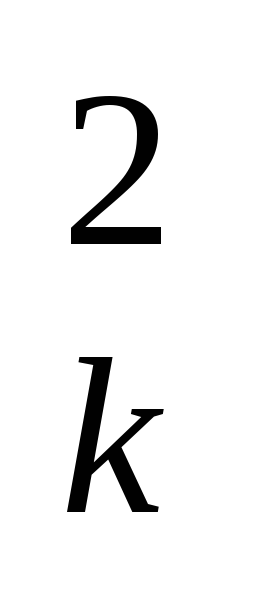 +Y
+Y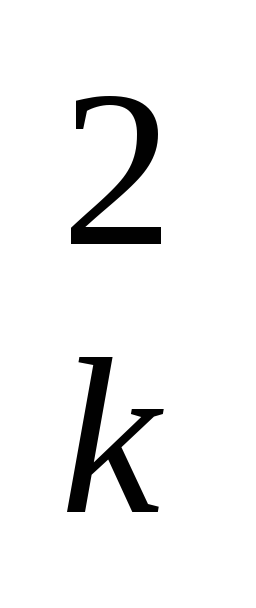
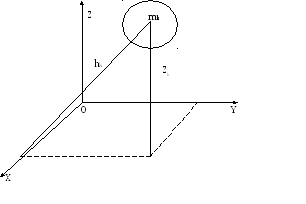
Подставим в формулу
JL = 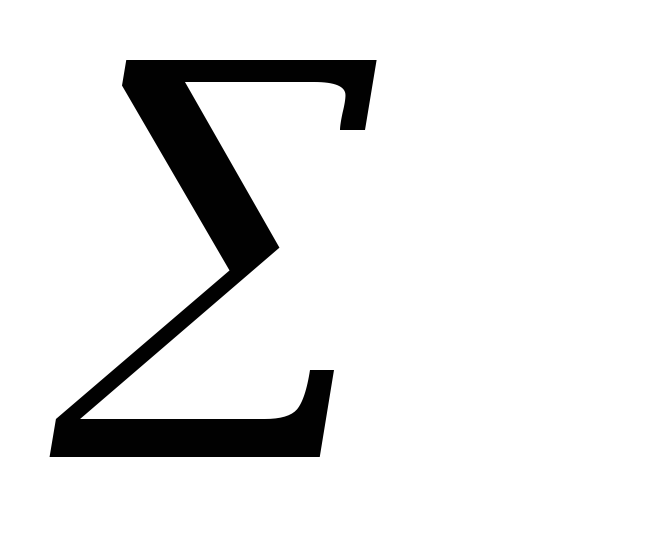 mkh
mkh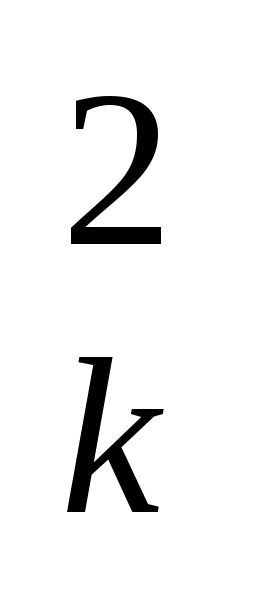 получим
моменты инерции относительно осей
координат:
получим
моменты инерции относительно осей
координат:
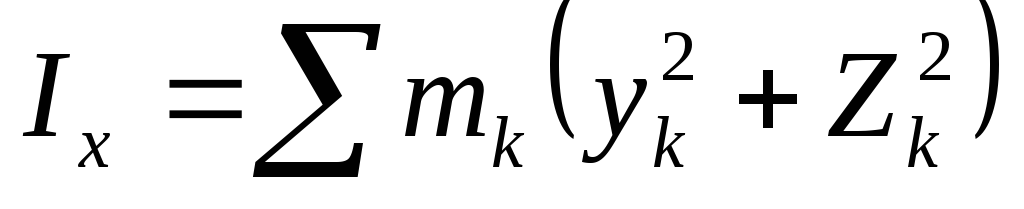
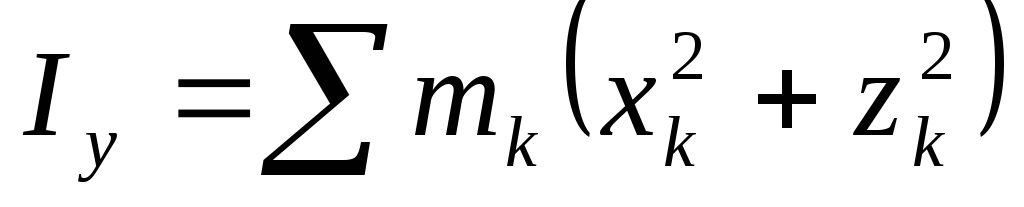
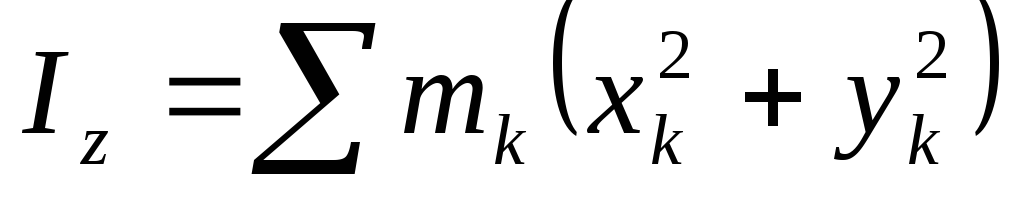
Расстояние k-ой
частицы до центра О определяется 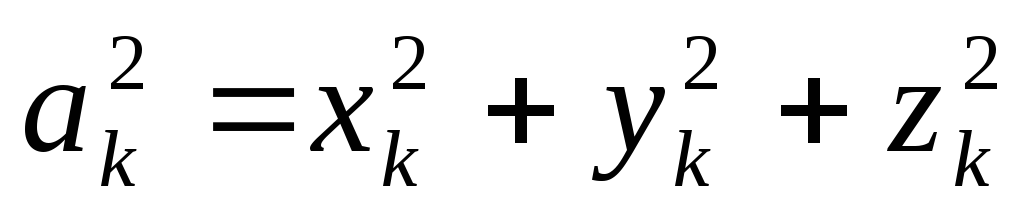
Момент инерции относительно этого центра
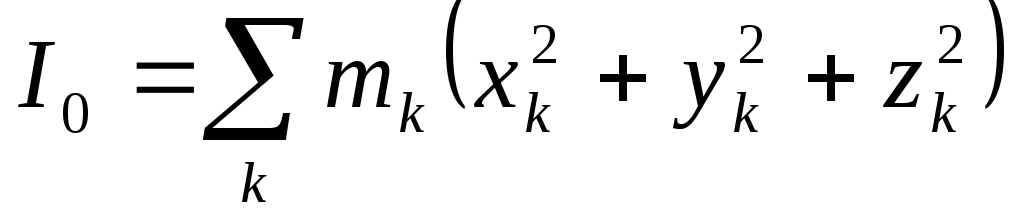
Для сплошных твердых тел
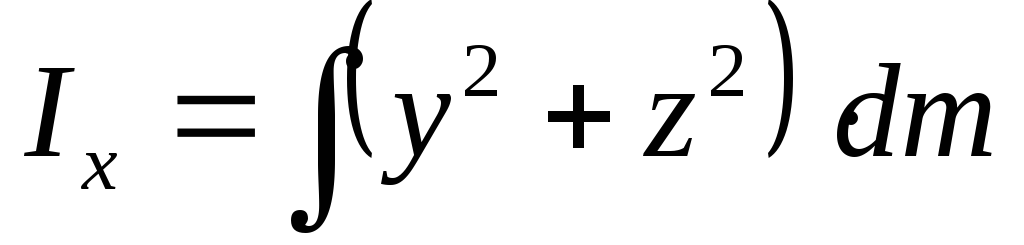
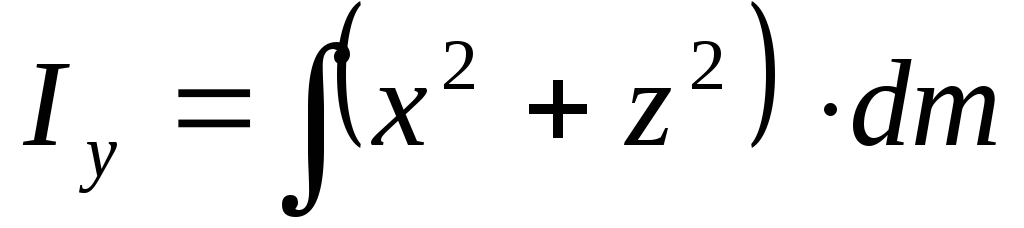
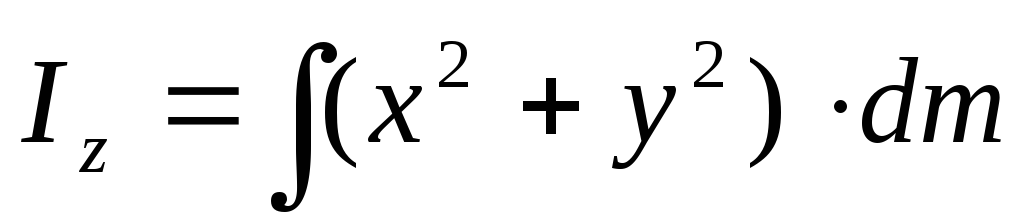
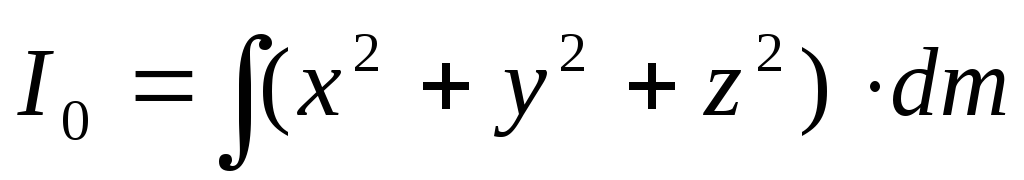
2I0=Ix+Iy+Iz
Центробежные моменты инерции
В механике в
качестве характеристик, учитывающих
несимметричность в распределении масс,
вводят еще так называемые центробежные
моменты инерции. Если через любую точку
О провести координатные оси OXYZ
,то по отношению к этим осям центробежными
моментами инерции называют величины
I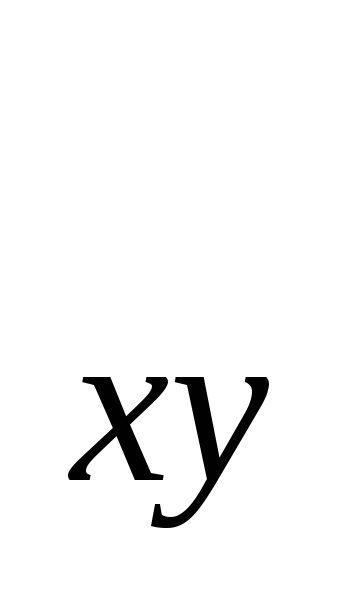 ,I
,I ,I
,I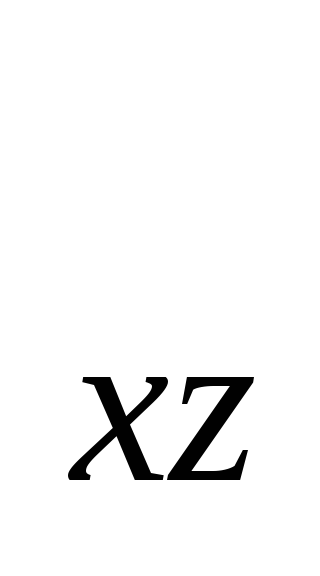
I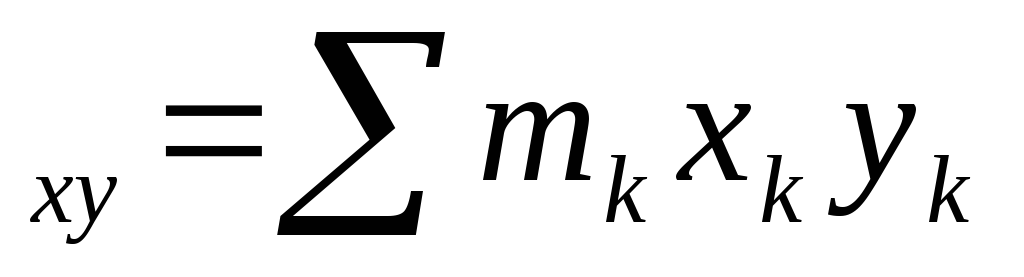
I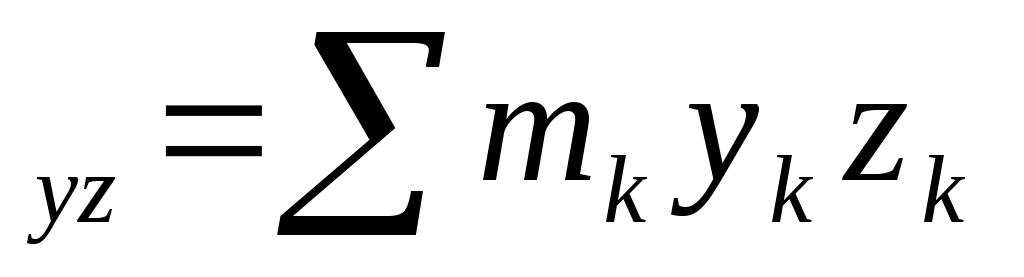
I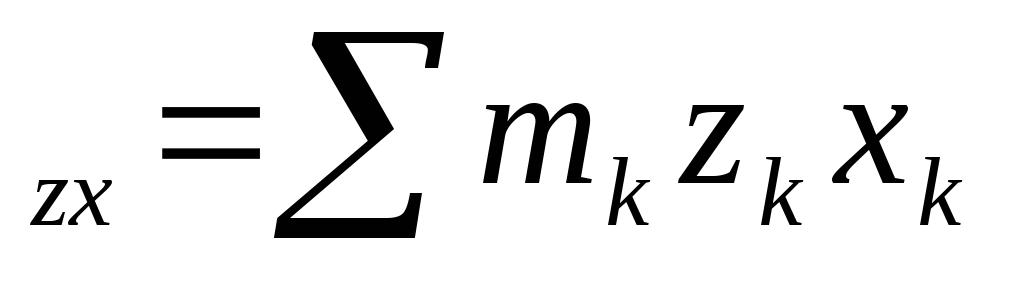
где m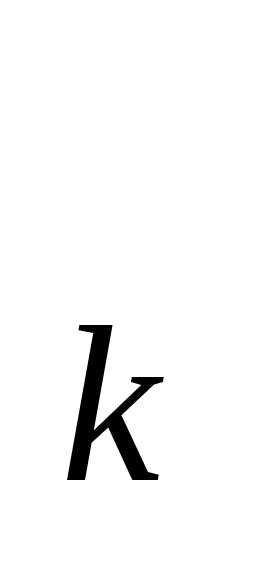 –массы
точек ,
–массы
точек ,
x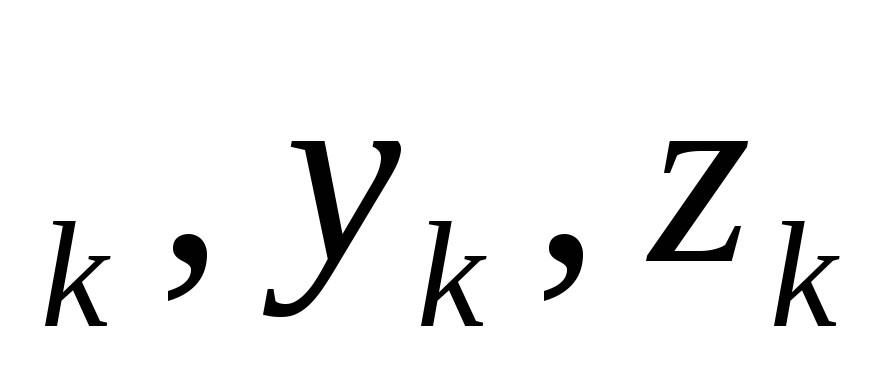 -координаты
точек .
-координаты
точек .
Очевидно, что I и т.д.
Для твердых тел формулы примут вид:
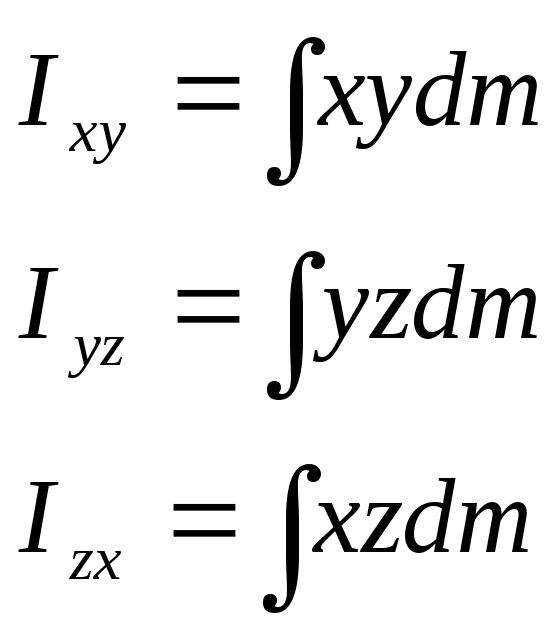
В отличие от осевых моменты инерции могут быть как положительными, так и отрицательными.
Момент инерции относительно параллельных осей .
Существует простая связь между моментом инерции тела относительно параллельных осей .Одна из которых проходит через центр масс.
Теорема
Момент инерции тела Iz, относительно некоторой оси Z1 равен сумме момента инерции Izc тела относительно оси Zc проходящий через центр масс параллельно данной и произведения массы тела на квадрат расстояний между осями:
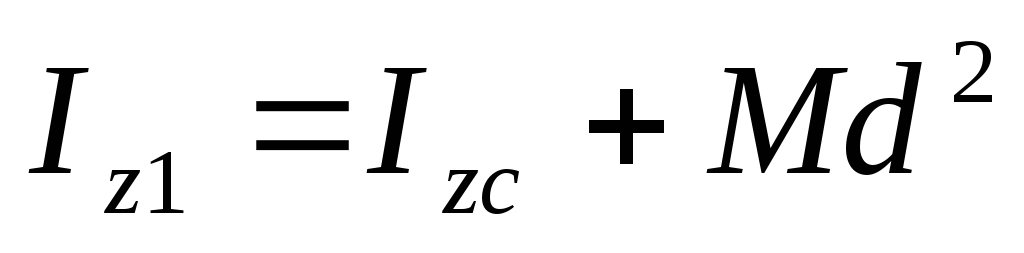
М-масса тела
d- расстояние между двумя параллельными осями


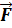 и радиусом – вектором
и радиусом – вектором 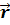 .
Сила тяготения
.
Сила тяготения 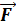 направлена
в сторону, противоположную радиусу –
вектору
направлена
в сторону, противоположную радиусу –
вектору 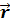 ,
т.е. α = 180˚ , sin (180˚) = 0 и M = 0. Поэтому первое утверждение
является неверным.
,
т.е. α = 180˚ , sin (180˚) = 0 и M = 0. Поэтому первое утверждение
является неверным.