Электричество и магнетизм
Теорема установлена М.В. Остроградским (рис. 1.33) в виде общей математической теоремы для любого векторного поля и К. Гауссом — применительно к электростатическому полю.
Рис. 1.33. М. Острогра́дский (1801–1861) — российский математик и механик
Закон Кулона и принцип суперпозиции позволяют вычислить потенциал поля любого распределения заряда
.
Используя связь или непосредственно с помощью закона Кулона и принципа суперпозиции, можно вычислить и напряженность поля
Однако, практическое вычисление написанных выше сумм и интегралов далеко не всегда так просто, как просто выглядят сами суммы и интегралы. Они вычисляются достаточно непринужденно, когда зарядов два, три, может быть, десяток. Если же речь идет о макроскопических заряженных телах, когда число точечных зарядов (протонов, электронов и т. п.) макроскопически велико, прямое вычисление подобных выражений становится очень сложной задачей.
Мы хотим подчеркнуть, что при решении макроскопических задач, в подавляющем большинстве случаев, можно считать, что заряд распределён непрерывно, соответственно, вычислять надо не суммы, а интегралы. Поэтому встает задача: на базе закона Кулона и принципа суперпозиции, написать интегральные и/или дифференциальные уравнения, которым удовлетворяет напряженность поля произвольного распределения зарядов. Эту задачу в ряде случаев успешно решает обсуждаемая в этом параграфе теорема Гаусса для вектора .
Рассмотрим некоторую поверхность и на ней бесконечно малый участок (бесконечно малую площадку) площадью (рис. 1.34).
Рис. 1.34. Бесконечно малый участок поверхности
Показанный на рисунке «вектор площадки» имеет следующий смысл: 1) он направлен по нормали к поверхности в той её точке, в окрестности которой находится площадка; 2) его модуль равен площади площадки . Вектор , а вместе с ним и вектор всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен.
Вектор , а вместе с ним и вектор всегда направлены по перпендикуляру к поверхности в данном её месте, а вот в какую сторону: налево вверх, как на рисунке выше, или в противоположную сторону (направо вниз, «под» поверхность), — в общем случае это дело произвольного выбора. Однако в ряде случаев, по умолчанию, действуют определенные правила. Например, если поверхность замкнутая, то есть представляет собой некоторую замкнутую «оболочку», то по умолчанию берется «внешняя» нормаль, направленная наружу. Выбор «внутренней» нормали ничему не противоречит, но должен быть специально оговорен. Если поверхность не замкнутая и опирается на некоторый контур, а, кроме того, задано направление обхода этого контура, то направление нормали общепринято связывать с направлением обхода правилом правого винта. С той же оговоркой, что и выше: направление обхода контура и направление нормали к поверхности, которая на него опирается, можно связать, используя левый, а не правый винт, такой выбор ничему не противоречит, но должен быть специально оговорен.
Введём в рассмотрение поток произвольного вектора через выбранную площадку. По определению:
|
Поток вектора через бесконечно малую площадку есть скалярное произведение вектора на вектор площадки
|
Формально рассматривается бесконечно малая площадка, фактически (например, при численном суммировании) она должна быть настолько мала, чтобы в её пределах вектор можно было считать неизменным (однородным), а саму площадку плоской, тогда не возникает проблемы, в какой точке внутри площадки проводить нормаль к ней.
Для общности определения (в физике рассматриваются потоки и других векторов) выше был рассмотрен произвольный вектор , применительно к вектору напряженности электрического поля , с учетом замечания о размерах площадки, определение потока иллюстрирует рис.
Рис. 1.35. Поток вектора напряженности электрического поля через бесконечно малую площадку
Согласно определению, поток вектора напряженности через площадку равен (здесь и в дальнейшем, для краткости, когда это будет удобным, будем писать: «площадка» и указывать при этом вектор этой площадки, которым полностью определены и её площадь и ориентация):
|
|
(1.43) |
где α — угол между векторами и , — нормальная к поверхности составляющая вектора . Подчеркнем, что изменение направления нормали как и изменение направления вектора напряженности на обратное меняет знак потока на противоположный, таким образом, поток вектора — величина алгебраическая.
Поток вектора через произвольную поверхность S равен сумме потоков через все площадки, на которые разбита поверхность S, то есть интегралу по этой поверхности вида:
|
|
(1. |
Если векторное поле однородно, то есть , а поверхность плоская, то
Здесь S — площадь этой поверхности. Для обозначения интеграла по замкнутой поверхности используется специальный значок интеграла, а именно: с кружком в середине (S — замкнутая поверхность) (рис. 1.36):
Рис. 1.36. Поток вектора напряженности электрического поля через замкнутую поверхность
Для уяснения смысла такой величины как поток вектора весьма полезно, в силу наглядности, рассмотрение потока жидкости, например, в реке или в трубе.
Пусть, для простоты несжимаемая жидкость, с плотностью течет со скоростью . Указание зависимости вектора скорости от координат точки и времени означает задание векторного поля, в данном случае: поля вектора скорости . Как и всякое векторное поле, поле скоростей удобно изобразить с помощью линий поля, которые в данном случае принято называть «линиями тока».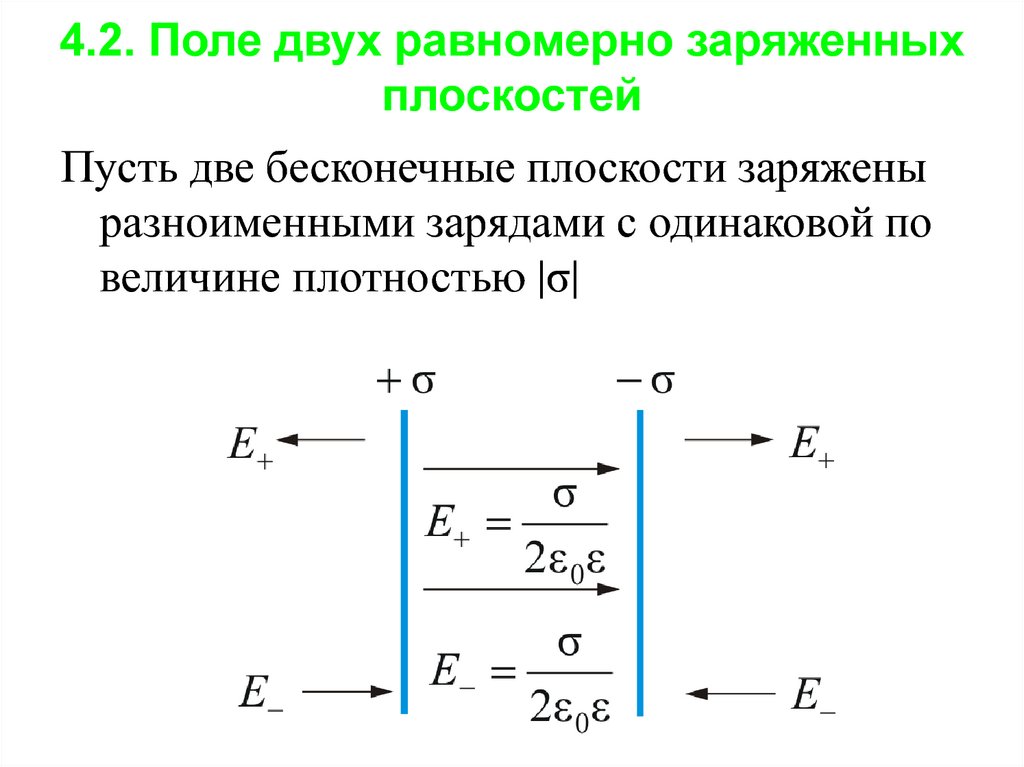 По определению, в любой точке вектор скорости жидкости направлен по касательной к линии тока. Выделим внутри жидкости площадку (см. рис. 1.37) настолько малую, что скорость во всех точках этой площадки можно считать одной и той же. Возьмем временной интервал настолько малый, что скорость за это время сколько-нибудь заметно измениться не успевает и поставим такой вопрос: «Какая масса жидкости протекает сквозь площадку
По определению, в любой точке вектор скорости жидкости направлен по касательной к линии тока. Выделим внутри жидкости площадку (см. рис. 1.37) настолько малую, что скорость во всех точках этой площадки можно считать одной и той же. Возьмем временной интервал настолько малый, что скорость за это время сколько-нибудь заметно измениться не успевает и поставим такой вопрос: «Какая масса жидкости протекает сквозь площадку
Рис. 1.37. К выводу соотношения для потока вектора
На рисунке выше жидкость, которая успеет за время пересечь площадку , занимает заштрихованный объём
, где
В написанной выше формуле вектор есть характеристика именно потока жидкости, определяемая её плотностью и скоростью течения. Величины и являются параметрами «постановки эксперимента». При том же потоке жидкости можно рассмотреть другую площадку и выбрать другое время регистрации массы. Вектор называется вектором плотности потока массы. Единица его измерения наглядно демонстрирует его физический смысл: величина вектора показывает, сколько килограмм жидкости протекает за секунду через квадратный метр площадки перпендикулярной потоку. Такой же смысл имеют его проекции на оси, с тем отличием, что численно равно массе жидкости протекающей за секунду сквозь квадратный метр площадки перпендикулярной оси
Величины и являются параметрами «постановки эксперимента». При том же потоке жидкости можно рассмотреть другую площадку и выбрать другое время регистрации массы. Вектор называется вектором плотности потока массы. Единица его измерения наглядно демонстрирует его физический смысл: величина вектора показывает, сколько килограмм жидкости протекает за секунду через квадратный метр площадки перпендикулярной потоку. Такой же смысл имеют его проекции на оси, с тем отличием, что численно равно массе жидкости протекающей за секунду сквозь квадратный метр площадки перпендикулярной оси
Если разделить на плотность получится — вектор плотности потока объёма, измеряемый в . Модуль этого вектора численно равен числу кубометров жидкости проходящих за секунду сквозь квадратный метр площадки перпендикулярной потоку жидкости. Знание этого вектора требуется, например, при расчете пропускной способности газо- или нефтепровода, как впрочем, и водопровода.
Доказанная ниже теорема Гаусса для вектора (см. соотношение ) показывает, что источниками электростатического поля являются электрические заряды.
Рассмотрим для начала частный, но очень простой, пример прямого вычисления потока вектора через поверхность.
Пример 6. Полусфера радиусом R с плоским основанием помещена в постоянное однородное электрическое поле E, перпендикулярное основанию полусферы (рис. 1.38). Найти поток вектора напряженности через основание полусферы, саму полусферу и через всю замкнутую поверхность этого тела.
Рис. 1.38. Пример расчета потока вектора напряженности электрического поля
Решение. Проще всего рассчитать поток через основание полусферы. Направим ось z вдоль поля. Направление вектора внешней нормали к основанию обратно направлению вектора E. При этом вектор E одинаков во всех точках основания. Поток через основание получается равным взятому с обратным знаком произведению E на площадь основания
При этом вектор E одинаков во всех точках основания. Поток через основание получается равным взятому с обратным знаком произведению E на площадь основания
Найдем теперь поток напряженности через поверхность полусферы. Используя сферические координаты — углы и — для определения положения точки на полусфере, мы видим, что
и
Поэтому поток через элементарную площадку на полусфере равен
Учитывая, что
а
записываем поток в виде
откуда находим полный поток через поверхность полусферы
Мы получили, что поток через поверхность полусферы равен по абсолютной величине потоку через ее основание, так что с учетом знаков полный поток через замкнутую поверхность равен нулю
.
Теорема Гаусса для вектора позволяет связать поток вектора напряженности через некоторую замкнутую поверхность с величиной зарядов, находящихся внутри этой поверхности. Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд.
Рассмотрим для начала частный случай, а именно: определим поток вектора напряженности через произвольную воображаемую сферическую поверхность, в центре которой расположен точечный заряд.
Линии напряжённости векторного поля точечного заряда представляют собой радиальные прямые, направленные от заряда, если он положителен, и к заряду, если он отрицателен (см. рис. 1.12). Поток вектора напряженности поля точечного заряда через сферическую поверхность радиусом r, центр которой совпадает с положением заряда и началом координат, равен
|
|
(1.33) |
Здесь , где — элемент телесного угла, мы воспользовались значением полного телесного угла
Можно показать, что поток вектора напряженности через любую замкнутую поверхность, охватывающую заряд q, не зависит от формы поверхности и равен так же, как и для сферы. Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
Физический смысл этого утверждения опять-таки заключается в том, что силовые линии начинаются и кончаются на зарядах. Поэтому непрерывная (без разрывов) деформация поверхности (показана на рис. 1.39-1 пунктиром) не изменит полного числа линий напряженности, выходящих наружу. Как следствие, поток через произвольную поверхность, охватывающую заряд, будет таким же, как и для сферы (см. рис. 1.39-1).
Рис. 1.39. Поток вектора Е через замкнутую поверхность:
1 — заряд находится внутри поверхности; 2 — заряд находится вне поверхности
Если же заряд находится вне ограниченного замкнутой поверхностью пространства, то линии напряжённости пронизывают поверхность чётное число раз (снаружи внутрь и изнутри наружу), в результате полный поток через поверхность, не охватывающую заряд, равен нулю (рис. 1.39-2).
Вывод теоремы Гаусса для точечного заряда, расположенного в произвольной точке, приведен в Дополнении 5.
Пусть теперь внутри и вне данной замкнутой поверхности имеется произвольное число точечных зарядов любого знака. В силу принципа суперпозиции суммарная напряженность поля будет представлять собой векторную сумму напряженностей полей каждого из зарядов
Полный поток напряженности поля через эту поверхность есть
Используя , получаем соотношение, известное как теорема Гаусса для вектора :
|
Поток вектора напряженности электрического поля через замкнутую поверхность равен полному заряду внутри этой поверхности делённому на
|
Подчеркнем еще раз тривиальное, но важное обстоятельство: если внутри поверхности нет зарядов, то поток вектора через эту поверхность равен нулю (рис. 1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна . Присутствие в последней формуле электрической постоянной есть результат выбора системы единиц (СИ) и физического смысла не имеет.
1.40). Источниками электростатического поля являются электрические заряды и суммарная мощность источников электростатического поля внутри поверхности равна . Присутствие в последней формуле электрической постоянной есть результат выбора системы единиц (СИ) и физического смысла не имеет.
Рис. 1.40. Если внутри поверхности нет зарядов, то поток вектора через эту поверхность равен нулю
При непрерывном распределении заряда по объёму теорему Гаусса естественно записать в следующем виде
|
|
(1.35) |
В правой части этого соотношения интеграл берется по объёму ограниченному поверхностью , поток через которую вычисляется в левой его части. При непрерывном распределении заряда по некоторой поверхности справа будет стоять интеграл вида только по той части несущей заряд поверхности, которая оказалась внутри поверхности , стоящей слева.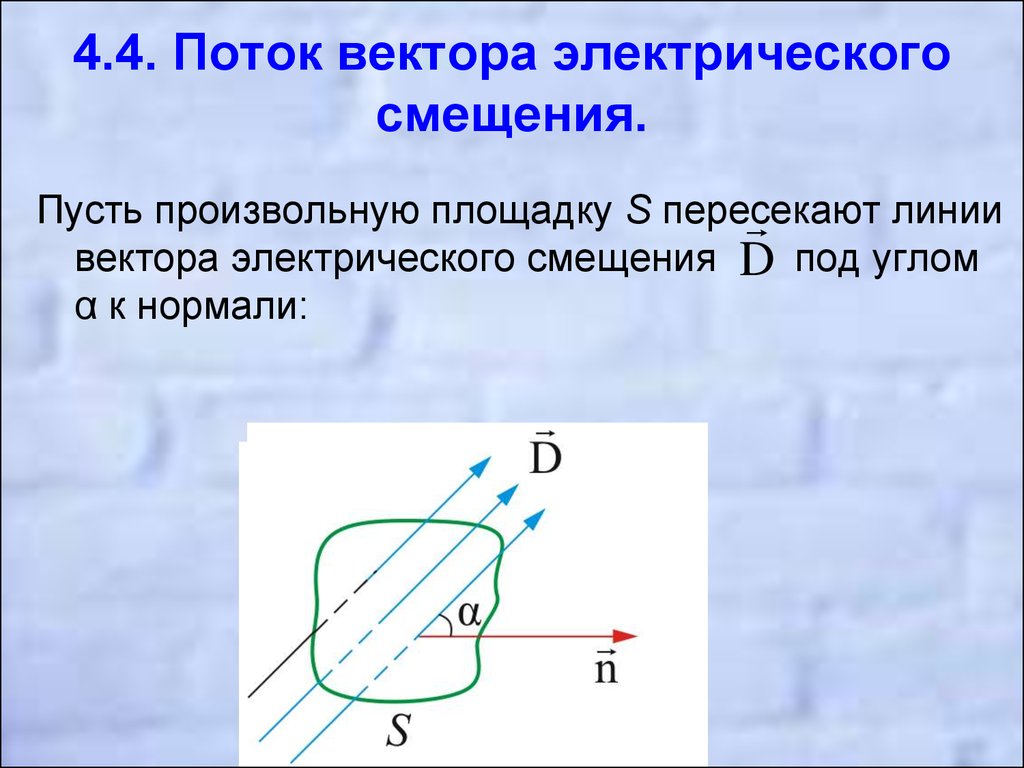 При непрерывном распределении заряда вдоль некоторой линии справа будет стоять интеграл вида также только по той части несущей заряд линии, которая оказалась внутри поверхности . Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля.
При непрерывном распределении заряда вдоль некоторой линии справа будет стоять интеграл вида также только по той части несущей заряд линии, которая оказалась внутри поверхности . Короче, необходимо любым приемлемым способом вычислить заряд внутри той замкнутой поверхности, по которой вычисляется поток вектора напряженности электрического поля.
Примеры расчёта полей, в которых главным инструментом является теорема Гаусса, даны в следующем разделе 1.5.
5/7
Поток вектора напряженности электрического поля
Содержание статьи
1. Элементарный поток вектора напряженности
2. Направление нормали
Определение
Потоком вектора $\overrightarrow{a}\ $через поверхность $S$ называют алгебраическую величину${\ Ф}_a$, которая определяется следующим образом:
\[Ф_a=\int\limits_S{\overrightarrow{a}d\overrightarrow{S}}\ \left(1\right).\]
При этом знак потока зависит от выбора направления нормали к элементарной площадке $dS$.
Элементарный поток вектора напряженности
Обратимся к электрическому полю. Модуль напряженности равен количеству силовых линий, которые пересекают поверхность площадь, которой равна единице, причем поверхность должна быть перпендикулярна линиям поля в данном месте. Количество линий поля, которые пересекают вышеназванную поверхность, называются потоком вектора напряженности. Если выделить элементарную площадку поверхности (dS), построить нормаль к этой площадке $\overrightarrow{n}$, при этом угол между направлением вектора нормали и направлением вектора напряженности составит $\alpha $, то элементарный поток вектора напряженности ($dФ_E$) можно записать как:
\[dФ_E=EdScos\alpha =\overrightarrow{E}\cdot d\overrightarrow{S}\ \left(2\right),\]
где
\[d\overrightarrow{S}=\overrightarrow{n}dS\ \left(3\right).\]
В уравнении (3) $\overrightarrow{n}$ единичная нормаль к площадке $dS$.
Если рассматривать какую — либо произвольную поверхность $S$, то в соответствии с определением потока вектора (1) можно записать, что поток вектора напряженности ($Ф_E$):
\[Ф_E=\int\limits_S{\overrightarrow{E}\cdot d\overrightarrow{S}}\ \ \left(4\right). \]
\]
Направление нормали
Как и в общем случае, поток вектора напряженности алгебраическая величина. Знак потока зависит от конфигурации поля и направления вектора — нормали $\overrightarrow{n}$. Направление нормали условно. Можно сказать, что интеграл в уравнении (4) характеризует суммарную мощность источников вектора $\overrightarrow{E}$, коими являются заряды, внутри объема, который ограничивает поверхность $S$.
Принято считать, что если имеют дело с замкнутой поверхностью, то нормаль имеет положительное направление наружу. Поток вектора напряженности в случае замкнутой поверхности записывают через криволинейный интеграл по замкнутой поверхности:
\[Ф_E=\oint\limits_S{\overrightarrow{E}\cdot d\overrightarrow{S}}\ \ \left(5\right).\]
Пример 1
Задание: Напряженность электростатического поля задана формулой в декартовых координатах:
\[\overrightarrow{E}=\frac{x\overrightarrow{i}+y\overrightarrow{j}}{x^2+y^2},\]
где $\overrightarrow{i},\ \overrightarrow{j}$ — единичные орты осей OX и OY.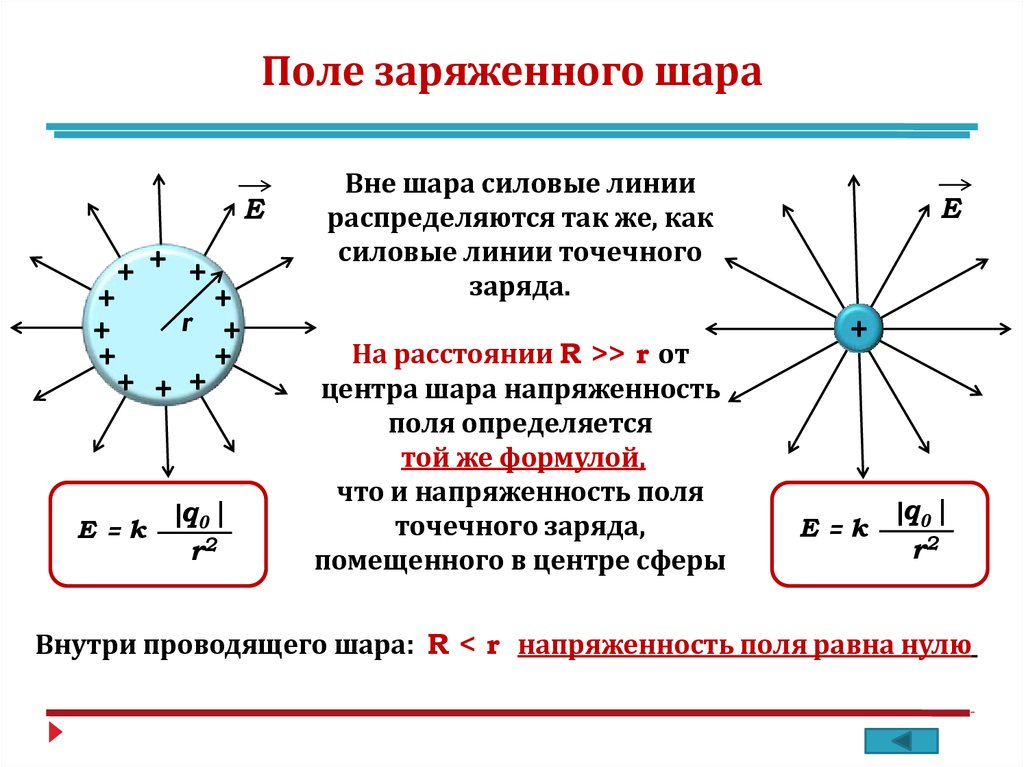 2}{R}}=4\pi R.\]
2}{R}}=4\pi R.\]
Ответ: $Ф_E=4\pi R.$
Пример 2
Задание: Определите поток вектора напряженности через поверхность сферы, если внутри нее находится два точечных заряда $+q_1$ и ${-q}_2$.
Решение:
В качестве основы для решения можно взять формулу для потока вектора напряженности в виде:
\[Ф_E=\overrightarrow{E}\cdot S\overrightarrow{n}=EScos\alpha \ \left(2.1\right),\]
где $\alpha $ — угол между нормалью к поверхности, через который ищем поток и вектором напряженности. Поле точечного заряда имеет сферическую симметрию (рис.1). Следовательно, вектор напряженности поля и вектор — нормаль будут сонаправлены ($cos\alpha ={cos 0\ }=1$). На рис. 1 изображено поле положительного заряда.
Рис. 1
Результирующая напряженность поля может быть найдена в соответствии с принципом суперпозиции полей двух зарядов, с учетом знаков.
Запишем выражение для модуля напряженности поля, которое создает первый заряд:
\[E_1=k\frac{q_1}{r^2}\left(2. 2=\frac{q_1-q_2}{\varepsilon_0}.\]
2=\frac{q_1-q_2}{\varepsilon_0}.\]
Ответ: $Ф_E=\frac{q_1-q_2}{{\varepsilon }_0}.$
Сообщество экспертов Автор24
Автор этой статьи Дата последнего обновления статьи: 03.12.2021
| 2. Теорема Гаусса. Использование теоремы Гаусса для расчета полей (примеры решения задач) Поток электрического поляПример 2.1. Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найдите поток вектора напряженности через круг радиуса R, плоскость которого перпендикулярна отрезку прямой, соединяющей заряды, и проходит через его середину. Решение. Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга радиуса и ширины (см.рис) . В записи потока учтено, что вектор перпендикулярен поверхности круга. Выразим напряженность электрического поля через, используя подобие треугольников показанных на рисунке:, . Вычисление потока сводится к взятию интеграла:
Электрическое поле заряженной сферыПример 2.2. По поверхности сферы радиуса однородно распределен заряд . Определите напряженность электрического поля в произвольной точке пространства вне сферы и внутри нее. Полученный результат представьте на графике , где проекция вектора напряженности на ось r, проведенную из центра сферы. Решение. Электрическое поле, порождаемое сферически-симметричным распределением заряда сферы, в любой точке пространства направлено вдоль луча от центра сферы и в равноудаленных точках имеет одинаковую величину, т.е. . При таком свойстве симметрии поля в качестве замкнутой гауссовой поверхности возьмем концентрическую сферу радиуса . Поток сквозь выбранную поверхность равен . Согласно теореме Гаусса, он определяется зарядом внутри гауссовой поверхности. При заряд внутри поверхности равен заряду сферы, а при равен нулю. Знак заряда определяет знак проекции , а следовательно и направление самого вектора . Он направлен от центра заряженной сферы () или к центру (). Внутри однородно заряженной сферической поверхности электрическое поле отсутствует. График зависимости проекции вектора напряженности на ось , проведенную из центра сферы, показан на Рис. 1 в предположении .
Электрическое поле заряженного шараПример 2.3. По объему шара однородно распределен заряд . Пренебрегая влиянием вещества шара, определите напряженность электрического поля в произвольной точке пространства вне шара и внутри него. Полученный результат представьте на графике , где проекция вектора напряженности на ось r, проведенную из центра шара. Решение. Поле такой системы зарядов центрально-симметричное, поэтому в качестве гауссовой замкнутой поверхности следует взять концентрическую сферу радиуса . 1) Найдем напряженность электрического поля внутри шара . Векторы напряженности направлены по радиусам выбранной сферы, а модули векторов зависят только от расстояния до центра сферы, то есть, одинаковы по поверхности сферы. Поэтому поток поля вектора через выбранную сферу можно записать(Рис.2а). Заряд, охватываемый сферой , равен , где — объемная плотность заряда. Согласно теореме Гаусса . В результате напряженность поля внутри однородно заряженного шара равна: , т.е. поле внутри шара возрастает по линейному закону от нуля в центре до значенияна его поверхности. 2) Найдем напряженность электрического поля вне шара . Свойство симметрии поля остается неизменным. Поэтому гауссову поверхность представим концентрической сферой радиуса (Рис.2а). Согласно теореме Гаусса имеем: , где заряд шара. Для величины напряженности поля получим: . Поле вне однородно заряженного шара убывает обратно пропорционально . Объединяя полученные зависимости, запишем: . График зависимости проекции вектора напряженности на ось , проведенную из центра шара, представлен на Рис. 2б.
Пример 2.4. Шар заряжен однородно с объемной плотностью . В шаре сделана сферическая полость, положение центра которой характеризуется радиусом-вектором (этот вектор проведен из центра шара в центр полости). Найти поле в полости. Решение. Представим, что имеем два шара с центрами в точках и , заряженные однородно с объемной плотностью первый и второй. Выберем произвольную точку , которая принадлежит обоим шарам. Воспользовавшись решением примера 2.3., для первого шара в точке поле равно: (). Для второго шара в точке поле равно: .
Чтобы определить напряженность поля в полости наложим распределение зарядов двух шаров, как показано на Рис.3. Тогда по принципу суперпозиции найдем поле в полости: . Заметим, что поле внутри полости однородно заряженного шара оказывается однородным, а его величина и направление определяется вектором смещения . Пример 2.5. Шар радиуса имеет положительный заряд, объемная плотность которого зависит от расстояния r до его центра как , где — положительная постоянная. Пренебрегая влиянием вещества шара, найдите модуль вектора напряженности электрического поля внутри и вне шара как функцию r. Решение. Поле этой системы зарядов центрально-симметричное, поэтому в качестве замкнутой гауссовой поверхности выберем сферу, концентрическую с шаром. 1) Для нахождения поля вне шара радиус сферы , согласно теореме Гаусса: , где полный заряд шара. Чтобы найти , мысленно представим шар в виде набора бесконечно тонких шаровых слоев радиуса ширины (Рис. Подставив полученное выражение для в правую часть соотношения для потока, получим напряженность поля вне шара: . 2) Найдем напряженность электрического поля внутри шара. В качестве замкнутой гауссовой поверхности снова выберем сферу, концентрическую с шаром, радиус которой (рис.4б). Согласно теореме Гаусса , где заряд внутри выбранной сферы. Величину найдем также как и в пункте 1), подставив соответствующие пределы интегрирования: . Подставив величину заряда в соотношение для потока, найдем: . График зависимости проекции вектора на ось , проведенную из центра шара, показан на Рис.4в, из которого видно, что напряженность достигает максимума на расстоянии от центра шара.
Электрическое поле заряженной плоскостиПример 2.6. Используя формулировку электростатической теоремы Гаусса, покажите, что в любой точке поля, созданного бесконечной плоскостью, заряженной с постоянной поверхностной плотностью , величина напряженности электрического поля вычисляется по формуле . Введите ось Х перпендикулярно заряженной плоскости с началом отсчета на плоскости. Изобразите график Ex(x). Решение. В силу симметрии распределения заряда вектор напряженности электрического поля в произвольной точке вблизи заряженной поверхности направлен перпендикулярно самой поверхности, а его величина в равноудаленных от поверхности точках одинакова. Поэтому линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны (Рис.2.5а). Учитывая это, в качестве замкнутой гауссовой поверхности выберем поверхность цилиндра, основания которого параллельны и симметричны заряженной плоскости, а ось перпендикулярна ей. . Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания: . Так как образующие цилиндра параллельны линиям напряженности , то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю: , поэтому полный поток сквозь поверхность цилиндра равен сумме потоков сквозь его основания: . Заряд q, заключенный внутри построенной цилиндрической поверхности, равен . Согласно теореме Гаусса , откуда . Из полученной формулы видно, что напряженность электрического поля во всех точках пространства одинакова по модулю, то есть поле равномерно заряженной плоскости однородно в каждом полупространстве (Рис.2.5б).
Пример 2.7. Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда и . Площадь каждой пластины S, расстояние между пластинами d значительно меньше их продольных размеров. Определите: а) напряженность электрического поля, созданного этими пластинами, б) силу, с которой одна пластина действует на другую. Решение. а) Согласно принципу суперпозиции, поля, создаваемые каждой заряженной пластиной в отдельности, накладываются друг на друга, причем каждая заряженная пластина создает электрическое поле независимо от присутствия другой заряженной пластины (Рис.6а). На рисунке верхние стрелки соответствуют векторам напряженности поля от положительно заряженной пластины, нижние – от отрицательно заряженной пластины. Напряженности однородных электрических полей, создаваемых положительно и отрицательно заряженными пластинами, соответственно равны: , . Слева и справа от пластин векторы напряженности поля пластин направлены противоположно друг другу. Поэтому величина напряженности результирующего поля равна разности напряженностей полей пластин: . В области между пластинами векторы напряженности направлены в одну сторону, поэтому результирующая напряженность равна . Направления векторов результирующего поля показаны жирными стрелками на Рис.6а. б) Заряд отрицательно заряженной пластины находится в поле, созданном зарядом положительно заряженной пластины. Следовательно, на отрицательный заряд действует сила (Рис.6б) , где — напряженность поля, создаваемого зарядом положительно заряженной пластины. Аналогично можно определить силу, которая действует на положительно заряженную пластину, находящуюся в поле отрицательно заряженной пластины , где — напряженность поля, создаваемого зарядом отрицательно заряженной пластины. Силы, с которыми пластины действуют друг на друга, равны по величине .
Пример 2.8. Определите, какая сила будет действовать на отрицательно заряженную тонкую пластину с поверхностной плотностью заряда со стороны помещенных параллельно ей справа и слева от нее на одинаковых расстояниях d тонких пластин с поверхностными плотностями заряда и . Решение. Воспользуемся результатом предыдущей задачи. Сила, с которой положительно заряженная с поверхностной плотностью пластина действует на отрицательно заряженную пластину, равна: , направление силы показано на Рис.7. Аналогично, сила, с которой отрицательно заряженная с поверхностной плотностью пластина действует на отрицательно заряженную пластину, равна: . Направление силы показано на Рис.7. Силы, действующие на среднюю пластину со стороны крайних, и равны по величине и противоположны по направлению. Поэтому, согласно принципу суперпозиции результирующая сила F,действующая на среднюю пластину со стороны крайних равна .
При условии, что площадь каждой пластины S значительно больше расстояний между пластинами d, сила, действующая со стороны крайних пластин на среднюю, не зависит от положения пластин. Электрическое поле заряженной пластины Пример 2.9. Область пространства, ограниченная двумя параллельными друг другу бесконечными плоскостями, расположенными на расстоянии 2а друг от друга, заряжена однородно по объему с плотностью . Используя формулировку электростатической теоремы Гаусса, покажите, что Ось Х перпендикулярна упомянутым бесконечным плоскостям, а точка х = 0 выбрана в центре слоя. Решение. В силу симметрии распределения заряда, линии напряженности перпендикулярны рассматриваемому слою и направлены от центральной плоскости слоя в обе стороны. Поэтому в качестве замкнутой гауссовой поверхности построим цилиндр, основания которого параллельны и симметричны плоскости, соответствующей положению x=0 заряженного слоя, а ось перпендикулярна ему. Согласно теореме Гаусса: . Так как образующие цилиндра параллельны линиям напряженности , то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю. А полный поток через гауссову поверхность равен сумме потоков через его основания, то есть равен . Используя теорему Гаусса, найдем напряженность электрического поля вне и внутри заряженного слоя. При заряд, заключенный внутри цилиндрической поверхности, равен , поэтому напряженность электрического поля внутри слоя равна . При заряд, заключенный внутри цилиндрической поверхности, равен , поэтому напряженность электрического поля снаружи слоя равна . График напряженности проекции показан на Рис.8.
Электрическое поле заряженной нити Пример 2.10. Вычислить напряженность электрического поля бесконечно тонкой и бесконечно длинной прямолинейной нити, однородно заряженной электричеством с линейной плотностью l. Решение. Найдем напряженность электрического поляс помощью теоремы Гаусса. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор направлен радиально к линии заряда или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина Е может зависеть только от расстояния до заряженной нити Е =Е( r ). Для определения этой зависимости выберем гауссову поверхность следующим образом. Построим цилиндр с боковой поверхностью удаленной от нити на расстояние r и основаниями, перпендикулярными к нити (Рис.9а). Поток вектора через оба основания цилиндра равен нулю, т.к. . Поток через боковую поверхность равен Е× S , т.к. , S — площадь боковой поверхности. Поэтому полный поток через выбранную Гауссову поверхность равен . Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l: Применяя теорему Гаусса, получим соотношение: , откуда найдем . График зависимости представлен на Рис.9б.
Электрическое поле заряженного цилиндраПример 2.11. Поверхность бесконечного длинного кругового цилиндра заряжена однородно с линейной плотностью λ. Определите напряженность электрического поля внутри и вне цилиндра. Полученный результат представьте на графике , где- проекция вектора напряженности на ось r, перпендикулярную поверхности цилиндра, с началом отсчета на его оси симметрии. Решение. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор направлен радиально — к линии оси цилиндра или от нее, в зависимости от знака заряда. Ввиду той же симметрии величина напряженности может зависеть только от расстояния до оси цилиндра: Е = Е ( r ). Для определения этой зависимости выберем гауссову поверхность следующим образом. Построим цилиндр с боковой поверхностью удаленной от оси на расстояние и основаниями, перпендикулярными к оси цилиндра. Поток вектора через оба основания цилиндра равен нулю, т.к. . Поток через боковую поверхность равен Е× S , т. Для величины проекции получим: , если rR, , если> R. График этой зависимости, представленный на Рис.10, характеризуется скачком величины напряженности при , что отражает идеализацию распределения заряда на геометрической поверхности.
Пример 2.12. Область внутри бесконечного длинного кругового прямого цилиндра радиуса R заряжена однородно с объемной плотностью ρ. Определите напряженность электрического поля внутри и вне цилиндра. Полученный результат представьте на графике, где — проекция вектора напряженности на ось r, перпендикулярную поверхности цилиндра, с началом отсчета на его оси симметрии. Решение. Наличие осевой симметрии в распределении заряда, позволяет сделать вывод о том, что вектор направлен радиально — к линии оси распределения заряда или от нее, в зависимости от знака заряда. Е = Е ( r ) Для определения этой зависимости выберем гауссову поверхность следующим образом . Построим цилиндр с боковой поверхностью удаленной от нити на расстояние r и основаниями, перпендикулярными к нити. Высота цилиндра . Поток вектора через оба основания цилиндра равен нулю, т.к. . Поток через боковую поверхность равен Е× S , т.к. , S- площадь боковой поверхности. Из теоремы Гаусса следует: Для величины проекции получим: при при . График, представленный на Рис.11 характеризуется отсутствием скачка величины напряженности поля при r=R в отличие от случая распределения заряда на поверхности цилиндра.
Пример 2.14 Вычислите дивергенцию напряженности электрического поля точечного заряда в произвольной точке пространства в декартовой системе координат. Решение. Локальная форма теоремы Гаусса позволяет выразить дивергенцию напряженности электрического поля через локальную плотность распределения заряда по соотношению . Плотность объемного распределения точечного заряда равна нулю в любой точке вне заряда. Следовательно, , при . Конечно же, этот результат можно получить и прямым расчетом: так как =,=,= жүктеу/скачать 1. Достарыңызбен бөлісу: |
Электричество и магнетизм
Электричество и магнетизм
1. Электрическое поле в вакууме 1.5. Применение теоремы Гаусса для расчетов напряженности электрического поля
Теорема Гаусса для вектора
может быть успешно использована как эффективный инструмент расчета напряженности и потенциала электрического поля некоторого распределения заряда, когда стоящий слева интеграл может быть превращен в произведение площади поверхности, по которой производится интегрирование, на величину нормальной к поверхности составляющей вектора , то есть когда
.
Вполне очевидно, что для расчета вектора этого будет достаточно, во-первых, когда вектор перпендикулярен поверхности. Следовательно, поверхность интегрирования должна быть эквипотенциальной поверхностью рассчитываемого поля. Её форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
Её форму надо знать заранее. Наконец, во-вторых, во всех точках этой — эквипотенциальной — поверхности нормальная к ней составляющая должна иметь одну и ту же величину, в противном случае, её нельзя будет вынести из-под знака интеграла и будет возможно найти лишь среднее на эквипотенциальной поверхности значение . Подчеркнем, что из факта эквипотенциальности поверхности, а именно, из того, что
вовсе не вытекает, что и
в точках этой поверхности. Забегая вперед, укажем, что, например, поверхность заряженного проводника при условии равновесного распределения заряда на нем всегда эквипотенциальна, но, если это не шар, а тело сложной формы, то в окрестности выступов (острий) напряженность поля может быть на порядки больше, чем в окрестности впадин на поверхности. Требование постоянства — отдельное требование.
Из сказанного выше вытекает, что теорема Гаусса в состоянии быстро и просто привести к результату (вектору ) лишь в том случае, когда создающее поле распределение заряда обладает высокой степенью симметрии, соответственно, заранее известна форма эквипотенциальных поверхностей поля и есть уверенность в том, что на этих поверхностях. Если всё это имеет место, то решение выглядит следующим простым образом:
Если всё это имеет место, то решение выглядит следующим простым образом:
|
|
(1.36) |
Остается выбрать поверхность согласно симметрии распределения заряда и вычислить заряд внутри .
Сферическая симметрия
При сферически симметричном распределении заряда поле, создаваемое им, также сферически симметрично. Векторные (и скалярные) поля с такой симметрией принято также называть центральными полями. Центрально симметричное поле в общем случае можно записать в виде
.
Здесь — радиус-вектор, начинающийся в центре симметрии поля r — его модуль, — радиальная составляющая напряженности поля, зависящая только от расстояния до его центра симметрии. Потенциал такого поля зависит только от и
Потенциал такого поля зависит только от и
|
|
(1.37) |
И, кроме того, как следует из , при произвольной нормировке потенциал поля имеет вид
|
|
(1.38) |
Таким образом, условия применимости выполнены и мы можем воспользоваться этим соотношением.
Возьмем в качестве эквипотенциальную сферическую поверхность некоторого текущего радиуса r, её площадь . Виду предполагаемой непрерывности распределения заряда, для используем выражение:
.
где — объёмная плотность заряда. Опять-таки, учитывая сферическую симметрию распределения заряда — зависит только от , в качестве элемента объёма естественно взять бесконечно тонкий сферический слой с внутренним радиусом и внешним радиусом .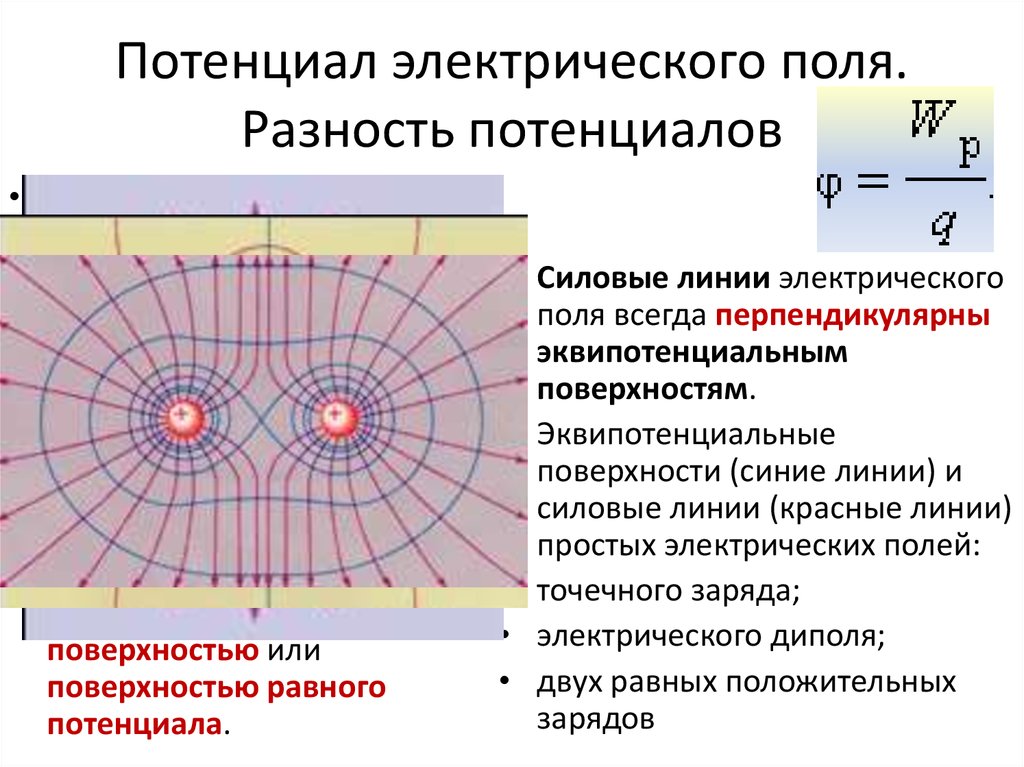 Объём такого слоя , в результате получаем
Объём такого слоя , в результате получаем
.
Окончательно, для любого сферически симметричного распределения заряда, когда , получаем
|
|
(1.39) |
Продолжение вычислений требует конкретизации вида зависимости плотности заряда от модуля радиус-вектора .
Поле однородно по объёму заряженного шара
Равномерное по объёму шара радиуса распределение заряда (рис. 1.41) означает, что его плотность заряда имеет вид
Рис. 1.41. Силовые линии электрического поля однородно заряженного шара
Не следует забывать, что по условию вне шара зарядов нет.
Поскольку в точке плотность заряда меняется скачком: предел «слева» отличен от нуля , а предел «справа» равен нулю , вычисление придется проводить в два этапа: сначала для сферической поверхности радиуса (она лежит внутри шара), а потом для сферической поверхности радиуса (она охватывает шар). В первом случае
В первом случае
.
Соответственно, поле
|
|
(1.40) |
растет линейно с ростом расстояния до центра шара, что объясняется просто: площадь поверхности , а заряд внутри неё
Во втором случае интеграл «обрезается сверху» при :
и поле
.
В последнем выражении учтено, что , где — полный заряд шара. Таким образом, вне шара его поле есть поле точечного заряда равного полному заряду шара и помещенного в центр этого шара:
.
Оба выражения можно объединить в одну формулу. Если использовать полный заряд шара , получим:
|
|
(1.41) |
Если вместо полного заряда шара использовать в качестве параметр плотность заряда , эти формулы приобретут следующий вид (рис. 1.42):
1.42):
|
|
(1.42) |
Рис. 1.42. Распределение напряженности электрического поля однородно заряженного шара
Формулы и выражают одну и ту же зависимость, их удобство определяется тем, какие параметры заданы: или . Из этих формул наглядно видно, что на поверхности шара напряженность поля непрерывна, то есть не имеет разрыва. Это обусловлено тем, что в данном случае разрыв плотности заряда на поверхности шара первого рода — конечной величины: с на нуль. Поэтому, как в , так и в в верхней и в нижней формулах поставлены знаки нестрогих неравенств. В каких случаях напряженность поля может терпеть разрыв, будет ясно из следующего примера.
Потенциал поля легко найти, подставив, например, из в и выполнив интегрирование. Получаем:
|
(1. |
где и — постоянные интегрирования, которые находятся из следующих соображений. Константа определяется из условия нормировки, например, на нуль на бесконечности
Откуда . Константа определяется из условия непрерывности потенциала на поверхности шара, то есть при :
|
|
(1.44) |
или
откуда
Отметим, что требование непрерывности потенциала нередко называют «сшивкой» двух решений на границе раздела. В данном случае это граница раздела двух областей: областью, где есть заряд (внутри шара), и областью, где его нет (вне шара). Уже сейчас можно отметить, что потенциал непрерывен во всех случаях, кроме одного: так называемого «двойного слоя». Представьте поверхность, по одной стороне которой с плотностью распределен положительный заряд, а по другой стороне которой с плотностью распределен отрицательный заряд. Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.
Такая поверхность и называется двойным слоем, на этой поверхности потенциал терпит разрыв. Такую (плоскую) поверхность можно получить, неограниченно сближая две обкладки плоского конденсатора. То же самое можно проделать для конденсатора любой формы, например, сферического или цилиндрического. Во всех остальных случаях потенциал непрерывен.
Подставляя полученные значения констант интегрирования в , запишем окончательный результат в виде
|
|
(1.45) |
При такой нормировке потенциал в центре шара отличен от нуля и равен
.
Полученные результаты иллюстрирует приведенный ниже рисунок 1.43.
Рис. 1.43. Напряженность (1) и потенциал (2) электрического поля равномерно заряженного шара радиусом R в единицах напряженности и потенциала на его поверхности (r = R)
Поле равномерно заряженной сферической поверхности
В данном случае равномерного распределения заряда по сферической поверхности, как и в предыдущем, имеет место сферическая симметрия, поэтому общие формулы, полученные выше, применимы и здесь. Однако относиться к ним необходимо с известной осторожностью по следующей причине. Входящая в правую часть объемная плотность заряда ведет себя в данном случае следующим интересным образом:
Однако относиться к ним необходимо с известной осторожностью по следующей причине. Входящая в правую часть объемная плотность заряда ведет себя в данном случае следующим интересным образом:
Рис. 1.44. Напряженность электрического поля равномерно заряженной сферы
Действительно, заряд имеется только на поверхности, то есть при , всюду внутри, то есть при и всюду снаружи, то есть при зарядов нет. То, что объемная плотность заряда в точках поверхности обращается в бесконечность (+∞ в случае положительного заряда и –∞ в случае отрицательного) можно показать следующим образом. На рисунке рядом изображен участок некоторой поверхности, по которой с поверхностной плотностью распределен заряд. Для определения величины объёмной плотности заряда в некоторой точке поверхности рассмотрим цилиндр (рис. 1.45), верхнее основание которого находится над поверхностью, а нижнее — под поверхностью. Площадь оснований цилиндра равна , высота — , объём . Заряд внутри цилиндра , объёмная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объёма «физически бесконечно малого»). Получаем
Площадь оснований цилиндра равна , высота — , объём . Заряд внутри цилиндра , объёмная плотность заряда по определению равна пределу отношения заряда, находящегося внутри некоторого объема, к величине этого объема при стремлении последнего к нулю (со всеми оговорками относительно объёма «физически бесконечно малого»). Получаем
Рис. 1.45. Плотность заряда на поверхности
Важно, что плотность на поверхности равна бесконечности. Функции такого рода (везде, кроме одной точки — нуль, а в этой единственной точке — бесконечность) относятся к классу так называемых обобщенных функций, называются функциями Дирака в честь физика Дирака, впервые введшего в обиход физики такую функцию для удовлетворения нужд квантовой механики. Мы не будем здесь подробно исследовать и использовать в расчетах такого рода функции. Наша цель показать, что рассмотрение формально бесконечно тонких заряженных поверхностей приводит к появлению у объёмной плотности заряда разрывов (бесконечных), что, в свою очередь, порождает бесконечные разрывы на такой заряженной поверхности у напряженности электрического поля. Подчеркнем, что потенциал поля при этом остается непрерывным.
Подчеркнем, что потенциал поля при этом остается непрерывным.
Выход из положения прост. При всех используем первую из формул с , получаем, что всюду внутри однородно заряженной сферической оболочки поле отсутствует: . При всех справедлива вторая формула из . Как и в случае однородно по объёму заряженного шара, вне однородно заряженной сферической оболочки, её поле есть поле точечного заряда, помещенного в центр этой оболочки и равного её полному заряду. В данном случае, разумеется .
Окончательный результат такой:
|
|
(1.46) |
На самой сферической поверхности напряженность поля в этом случае терпит разрыв. Зависимость радиальной компоненты поля от расстояния до центра сферической поверхности показана на рис. 1.46.
Рис. 1.46. Зависимость поля от расстояния до центра сферической оболочки
Зависимость потенциала от расстояния до центра сферической оболочки можно получить, интегрируя . При нормировке на нуль на бесконечности результат выглядит следующим образом:
При нормировке на нуль на бесконечности результат выглядит следующим образом:
|
|
(1.47) |
Зависимость показана на рис. 1.47.
Рис. 1.47. Потенциал равномерно заряженной сферы
Однородное (равномерное) распределение заряда по бесконечно длинной цилиндрической поверхности (рис. 1.48) обладает цилиндрической, трансляционной и зеркальной симметрией. Это означает следующее. При повороте такого распределения заряда вокруг оси цилиндрической поверхности на любой угол оно совпадает само с собой. При сдвиге (переносе, трансляции) такого распределения заряда на любое расстояние вдоль оси симметрии оно также совпадает само с собой. И, наконец, если через любую точку на оси симметрии провести плоскость перпендикулярную к оси, и отразить в этой плоскости как в зеркале «верхнюю» часть распределения заряда, то отражение «верхней» части совпадет с «нижней» и наоборот, отражение «нижней» совпадет с «верхней». Другими словами, это распределение заряда инвариантно относительно указанных преобразований. Следовательно, и создаваемое этим распределением заряда электрическое поле должно быть инвариантно (совпадать само с собой) при указанных преобразованиях.
Другими словами, это распределение заряда инвариантно относительно указанных преобразований. Следовательно, и создаваемое этим распределением заряда электрическое поле должно быть инвариантно (совпадать само с собой) при указанных преобразованиях.
Рис. 1.48. Бесконечно длинная цилиндрическая поверхность
Введем цилиндрическую систему координат: ось направим по оси симметрии, — расстояние до оси симметрии, — азимутальный угол, угол поворота вокруг оси симметрии, — по-прежнему потенциал поля.
Из свойств симметрии вытекает, что потенциал поля не может зависеть ни от координаты — нарушится трансляционная симметрия, ни от координаты — нарушится осевая (цилиндрическая) симметрия. Остается только зависимость от — расстояния до оси цилиндра. Таким образом:
|
|
(1.48) |
Соответственно
|
|
(1. |
вектор напряженности электрического поля направлен по радиальным прямым, перпендикулярным оси симметрии (рис. 1.49), и его величина зависит только от расстояния до оси. Потенциальные поверхности представляют собой цилиндры соосные с заряженной цилиндрической поверхностью.
Рис. 1.49. Вектор напряженности электрического поля направлен по радиальным прямым
Используя эти обстоятельства, будем интегрировать в левой части теоремы Гаусса по замкнутой поверхности цилиндра с радиусом основания и высотой , соосного с рассматриваемой, заряженной цилиндрической поверхностью радиуса . Поток через основания цилиндра равен нулю ввиду того, что на основаниях , а поток через его боковую поверхность равен произведению на её площадь: . Соответственно, суммарный (через всю замкнутую поверхность рассматриваемого цилиндра) поток вектора равен
|
|
(1. |
При , находящийся внутри цилиндра заряд, равен
где — линейная плотность заряда численно равная заряду, приходящемуся на единицу длины цилиндрической поверхности. Согласно теореме Гаусса
откуда для получаем
.
При внутри цилиндра, через поверхность которого вычисляется поток вектора , зарядов нет, и потому поле равно нулю. Объединяя эти два результата, получаем окончательно (рис. 1.50):
|
|
(1.51) |
Ввиду поверхностного характера распределения заряда (см. подробнее предыдущий расчёт) на самой заряженной поверхности, то есть при радиальная компонента поля терпит разрыв.
Рис. 1.50. Напряженность электрического поля равномерно заряженной цилиндрической поверхности
Интегрирование (1. 51) (см. также (1.49)), требование непрерывности потенциала при , и нормировка , приводят к следующей зависимости потенциала от расстояния до оси цилиндрической поверхности:
51) (см. также (1.49)), требование непрерывности потенциала при , и нормировка , приводят к следующей зависимости потенциала от расстояния до оси цилиндрической поверхности:
|
(1.52) |
В данном случае, когда бесконечно большой по модулю заряд распределен по бесконечно длинному цилиндру, относится к тем случаям, когда нормировка на нуль на бесконечности лишена смысла. Как видно из (1.52), зависимость потенциала от расстояния до оси логарифмическая, нормировка на нуль на бесконечности, на языке формул (1.52), означает, что , но, тогда потенциал будет бесконечно большим по модулю на любом конечном расстоянии от оси заряженной поверхности, что лишено смысла. Выбор того конечного расстояния от оси симметрии, на котором удобно потенциал считать равным нулю трудностей не вызывает и обусловлен спецификой задачи. Например, ничто не мешает положить , тогда потенциал всюду внутри и на самой заряженной поверхности будет равен нулю.
Например, ничто не мешает положить , тогда потенциал всюду внутри и на самой заряженной поверхности будет равен нулю.
Поле бесконечной равномерно заряженной плоскости
Пусть поверхностная плотность заряда равна . Такое распределение заряда по бесконечной плоскости характеризуется тем, что его вид не зависит от: а) поворота на любой угол вокруг любой оси перпендикулярной плоскости, б) сдвига на любое расстояние вдоль прямой лежащей в плоскости и любого направления. Наконец, в) отражение данного распределения заряда в зеркале, совпадающем с самой плоскостью, оставит его неизменным.
Из анализа симметрии достаточно очевидно, что потенциал в любой точке вне плоскости может зависеть только от расстояния от этой точки до плоскости. Направим ось декартовой системы координат перпендикулярно плоскости, а оси и пусть принадлежат самой плоскости, тогда
|
(1. |
Причем, в силу зеркальной симметрии, поле «перед» плоскостью отличается от поля «за» плоскостью только направлением вектора . Это означает, что зависимость от должна быть нечетной, а зависимость потенциала от должна быть четной.
В силу этих соображений возьмём замкнутую поверхность — ту, для которой будем писать теорему Гаусса, — следующего вида (рис 1.51).
Рис. 1.51. Электрическое поле заряженной плоскости
Это цилиндр с боковой поверхностью перпендикулярной плоскости и с основаниями параллельными плоскости. Высота цилиндра , площадь оснований . Учитывая нечетность зависимости , основания цилиндра удобно расположить на одинаковом расстоянии от плоскости, тогда вклад оснований в поток будет одинаков. Напряженность поля на основаниях, во-первых, им перпендикулярна, во-вторых, сонаправлена с внешней нормалью, в-третьих, она одинакова во всех их точках по абсолютной величине
Вклад в поток вектора от боковой поверхности равен нулю, так как на боковой поверхности .
Поэтому полный поток через всю замкнутую цилиндрическую поверхность равен
|
|
(1.54) |
Внутри рассматриваемой цилиндрической поверхности находится заряд
где — плотность заряда на плоскости. По теореме Гаусса
,
следовательно, модуль напряженности поля заряженной плоскости равен
Подчеркнём, что результат очевидным образом не зависит от того, на каком расстоянии от плоскости расположены основания рассмотренного цилиндра. Отсюда следует, что с каждой стороны от плоскости создаваемое ею электрическое поле однородно.
Используя введенную ранее ось перпендикулярную заряженной плоскости, поле с обеих сторон от плоскости можно описать одной формулой, пригодной при любом знаке заряда на плоскости
|
|
(1. |
Здесь — орт оси .
Интегрируя с учетом
,
для зависимости от потенциала поля плоскости нетрудно получить:
|
|
(1.56) |
Потенциал в нормирован условием . Здесь, как и в примере с бесконечно длинной заряженной цилиндрической поверхностью, потенциал растет при удалении на бесконечность, поэтому нормировка на нуль на бесконечности лишена смысла.
Силовые линии поля заряженной плоскости показаны на рис. 1.52 и 1.53.
Рис. 1.52. Поле положительно заряженной плоскости
Рис. 1.53. Поле отрицательно заряженной плоскости
Поле плоского конденсатора
Определим напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными однородно и разноименно. Плотности заряда на плоскостях по модулю одинаковы и равны, соответственно: и (идеальный плоский конденсатор). С помощью рис. 1.54 нетрудно сообразить, что в зазоре между плоскостями, создаваемые ими поля направлены в одну сторону, поэтому внутри суммарное поле в два раза больше поля от каждой из плоскостей. Снаружи от плоскостей создаваемые ими поля направлены в противоположные стороны, соответственно, суммарное поле от обеих плоскостей равно нулю (рис. 1.55).
Плотности заряда на плоскостях по модулю одинаковы и равны, соответственно: и (идеальный плоский конденсатор). С помощью рис. 1.54 нетрудно сообразить, что в зазоре между плоскостями, создаваемые ими поля направлены в одну сторону, поэтому внутри суммарное поле в два раза больше поля от каждой из плоскостей. Снаружи от плоскостей создаваемые ими поля направлены в противоположные стороны, соответственно, суммарное поле от обеих плоскостей равно нулю (рис. 1.55).
|
|
(1.57) |
Рис. 1.54. Электрическое поле плоского конденсатора
Рис. 1.55. Электрическое поле разноименно заряженных плоскостей
|
(1. |
Рис. 1.56. Напряженность электрического поля разноименно заряженных плоскостей
В Дополнении 6 разобран пример с движением заряженной частицы в постоянном электрическом поле.
Потенциал поля заряженного диска
Как уже не раз отмечалось, зная потенциал поля точечного заряда и используя принцип суперпозиции, в принципе всегда, можно вычислить потенциал поля, создаваемого любым распределением зарядов.
Найдем для примера потенциал электрического поля, создаваемого на оси тонкого диска радиуса R, равномерно заряженного с поверхностной плотностью заряда (рис. 1.57). В силу осевой симметрии в точках на оси две перпендикулярных к оси составляющих напряженности поля равны нулю: , остается найти — составляющую поля, направленную вдоль оси.
Рис. 1.57. Вычисление потенциала на оси заряженного диска
Выделим на диске кольцо радиусом s и шириной ds (заштриховано на рис. 1.57). Площадь кольца равна и потому на нем сосредоточен заряд
1.57). Площадь кольца равна и потому на нем сосредоточен заряд
Поскольку все элементы кольца находятся на одинаковом расстоянии
от точки наблюдения А, то потенциал , создаваемый кольцом в точке А, дается все той же формулой с заменой в ней на :
Полный же потенциал поля, создаваемый всем диском в точке A, равен сумме потенциалов от всех возможных колец с радиусами s, где 0 < s < R
|
|
(1.59) |
При больших расстояниях от центра диска квадратный корень можно разложить в ряд, ограничившись первыми двумя членами разложения
тогда формула упрощается и, как и должно быть, превращается в формулу для потенциала точечного заряда
где — полный заряд диска
Используя связь напряженности поля с потенциалом , можно найти напряженность поля на оси диска
|
|
(1. |
Закон Кулона и размерность пространства
Пространство, в котором мы живем, имеет три измерения. Иными словами, нужны три координаты (например, в декартовой или в сферической системах) для задания положения точки А (рис. 1.58). Оказывается, число 3 тесно связано с формой закона Кулона. Мы видели, что теорема Остроградского — Гаусса следует из закона Кулона. Верно и обратное, закон Кулона можно вывести из теоремы Остроградского — Гаусса. Но эта теорема носит более общий характер, чем закон Кулона. В частности, она применима к пространствам с размерностью , где не обязательно должно быть равно трем.
Рис. 1.58. Декартовая и сферическая системы координат
В самом деле, теорема в сущности утверждает, что силовые линии начинаются и заканчиваются на зарядах или уходят в бесконечность. Размерность пространства не играет здесь роли. Поэтому давайте предположим, что мы живем в пространстве с какой-то размерностью и посмотрим, какой будет физика в этом странном мире. Возьмем точечный заряд и мысленно окружим его сферой радиусом Прежде чем продолжать знакомство с мерной физикой, условимся о терминологии.
Возьмем точечный заряд и мысленно окружим его сферой радиусом Прежде чем продолжать знакомство с мерной физикой, условимся о терминологии.
Объем сферы будет измеряться в единицах подобно тому, как в нашем мире мы измеряем объем в . Так, в двумерном пространстве роль объема играет наша площадь. Действительно, сфера — это геометрическое место точек пространства, равноудаленных от центра. Согласно этому определению, двумерная сфера — это окружность радиусом двумерные существа считали бы ее объемом то, что мы воспринимаем как площадь круга В этом параграфе мы будем называть объемом сферы в мерном пространстве ту величину, которая пропорциональна Аналогично, площадь поверхности мерной сферы пропорциональна В двумерном пространстве это — длина окружности и именно ее двумерные существа воспринимали бы как площадь поверхности. С другой стороны, площадь поверхности в четырехмерном мире — это наши трехмерные объемы.
Итак, площадь сферы в мерном мире пропорциональна (коэффициент пропорциональности сейчас нам не важен). Поток вектора напряженности электрического поля в таком мире пропорционален и должен быть пропорционален также величине электрического заряда внутри сферы (теорема Остроградского — Гаусса). Отсюда получаем, что
Поток вектора напряженности электрического поля в таком мире пропорционален и должен быть пропорционален также величине электрического заряда внутри сферы (теорема Остроградского — Гаусса). Отсюда получаем, что
|
|
(10.49) |
где — некий коэффициент пропорциональности. Аналогичное выражение справедливо для гравитационного поля в мерном мире.
При получаем отсюда закон обратных квадратов (закон Кулона). При находим На самом деле мы уже знакомы с таким поведением электрического поля. Именно такой закон (10.17) мы вывели для поля бесконечного заряженного цилиндра. Если как следует подумать и вспомнить расположение силовых линий цилиндра, то станет ясно, что ничего не зависит от координаты вдоль оси цилиндра. Таким образом, эта система имитирует электрическое поле в двумерном мире. Теперь легче понять, что заряженная плоскость имитирует точечный заряд в одномерном мире: все зависит только от одной координаты — расстояния до плоскости. Но мы нашли выше, что электрическое поле от этого расстояния не зависит. И из формулы (10.49) при также следует, что напряженность то есть постоянна. В четырехмерном же мире закон Кулона принял бы форму Таким образом, закон обратных квадратов является прямым следствием трехмерности нашего мира.
Теперь легче понять, что заряженная плоскость имитирует точечный заряд в одномерном мире: все зависит только от одной координаты — расстояния до плоскости. Но мы нашли выше, что электрическое поле от этого расстояния не зависит. И из формулы (10.49) при также следует, что напряженность то есть постоянна. В четырехмерном же мире закон Кулона принял бы форму Таким образом, закон обратных квадратов является прямым следствием трехмерности нашего мира.
Из выражения (10.49) следует поведение потенциала в мерном мире:
|
|
(10.50) |
Эти формулы являются следствием того, что дифференцирование потенциала (операция grad) должно дать выражение для напряженности электрического поля.
Отсюда следуют любопытные выводы. Поскольку в одно- и двумерном мирах потенциалы растут на бесконечности, нужна бесконечно большая работа, чтобы развести два притягивающихся заряда.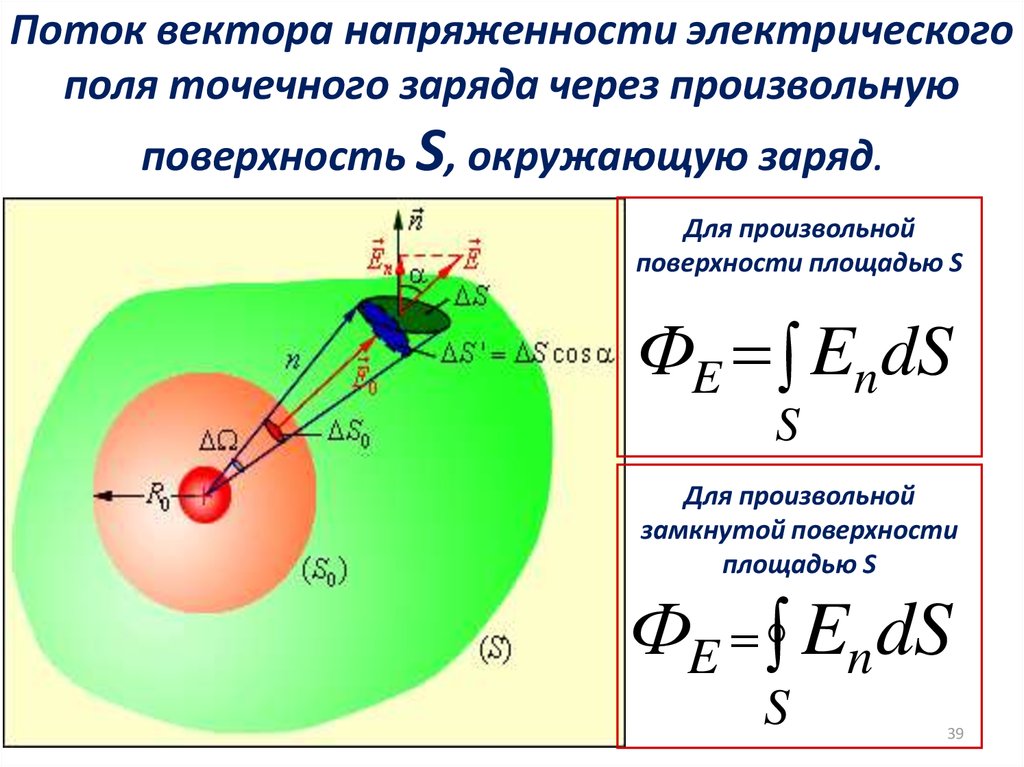 Это означает, что в мирах малой размерности возможно лишь финитное движение двух притягивающихся тел (зарядов, масс). Напомним, что финитным называется движение в ограниченной области пространства. Поэтому в мирах с нельзя ионизировать атом, нельзя запустить спутник за пределы Солнечной системы и т. п. В таком мире не было бы химических реакций, не могли бы эволюционировать галактики и звезды. Словом, жизнь там была бы застойно скучна.
Это означает, что в мирах малой размерности возможно лишь финитное движение двух притягивающихся тел (зарядов, масс). Напомним, что финитным называется движение в ограниченной области пространства. Поэтому в мирах с нельзя ионизировать атом, нельзя запустить спутник за пределы Солнечной системы и т. п. В таком мире не было бы химических реакций, не могли бы эволюционировать галактики и звезды. Словом, жизнь там была бы застойно скучна.
Можно было бы ожидать более приятного времяпрепровождения в многомерных мирах. Увы, и это оказывается иллюзией. Исследование уравнения движения
приводит к выводу, что при в сущности отсутствует финитное движение: оно реализуется только для круговых орбит, да и то является неустойчивым — малейшее возмущение приводит к падению электрона (планеты) на притягивающий центр или его (ее) убеганию на бесконечно большое расстояние. Выходит, в таком мире атомы, планетные системы и все остальное вообще не могло бы образоваться.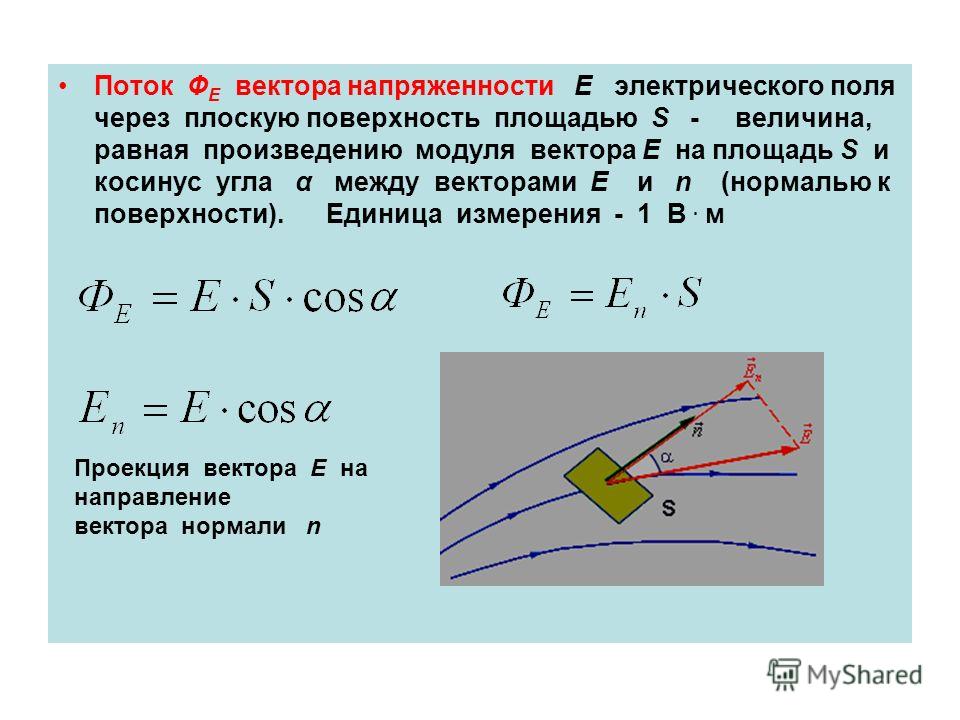 Никакой стабильности в мирах высшей размерности — вот альтернатива «застойным» маломерным мирам. Только при возможно как устойчивое финитное, так и инфинитное движения. Получается, что трехмерное пространство — единственно удобная форма существования и движения материи, по крайней мере, известных нам ее видов, которые мы изучаем в физике.
Никакой стабильности в мирах высшей размерности — вот альтернатива «застойным» маломерным мирам. Только при возможно как устойчивое финитное, так и инфинитное движения. Получается, что трехмерное пространство — единственно удобная форма существования и движения материи, по крайней мере, известных нам ее видов, которые мы изучаем в физике.
Дополнительная информация
http://hea.iki.rssi.ru/~nik/astro/spher.htm — сферическая система координат;
http://edu.ioffe.ru/register/?doc=physica/lect3.ch3.tex — финитное движение, задача Кеплера.
6/7
Теорема Гаусса
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка ΔS.
Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка ΔS.
Элементарный поток вектора напряженности (через площадку S) – это физическая величина, равная произведению модуля вектора E→, площади ΔS и косинуса угла α между вектором и нормалью к площадке:
ΔΦ=EΔScos α=EnΔS.
В данной формуле En является модулем нормальной составляющей поля E→.
Рисунок 1.3.1. Иллюстрация элементарного потока ΔΦ.
Пример 1Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S. Разобьем заданную поверхность на площадки небольшого размера ΔSi, рассчитаем элементарные потоки ΔΦi поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
Φ=∑∆Φi=∑Em∆Si
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
Рисунок 1. 3.2. Расчет потока Ф через произвольную замкнутую поверхность S.
3.2. Расчет потока Ф через произвольную замкнутую поверхность S.
Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Теорема 1Поток вектора напряженности электростатического поля E→ через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Уравнение Гаусса имеет вид:
Φ=1ε0∑qвнутр
Доказательство 1Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S. В центре заданной поверхности расположен точечный заряд q. Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
E=En=14πε0·qR2,
где R является радиусом сферы.
Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4πR2. Тогда: Φ=1ε0q.
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R0(рис.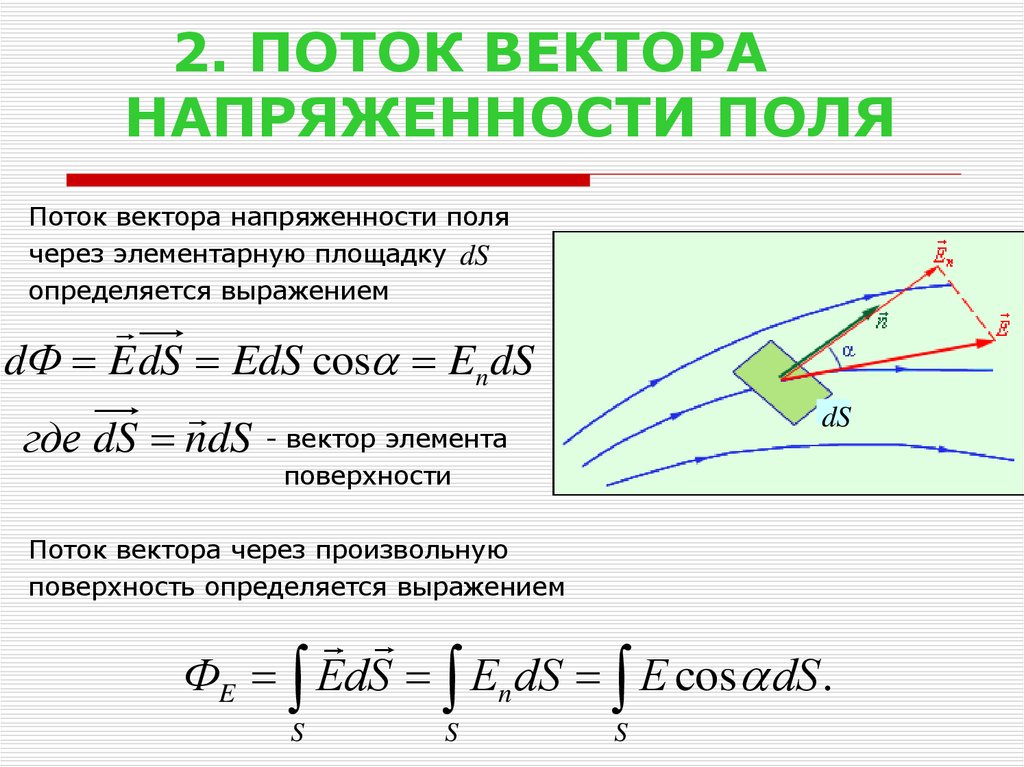 1.3.3).
1.3.3).
Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом ΔΩ при вершине. Рассматриваемый конус задаст на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки являются одинаковыми. В самом деле:
ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS’,
где выражением ΔS’=ΔS cos α определяется площадка, которая задастся конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Поскольку ∆S0∆S’=R02r2, то ∆Φ0=∆Φ. Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Φ=Φ0=qε0.
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φi электрических полей отдельных зарядов. Когда заряд qiрасположен внутри поверхности S, он дает вклад в поток, равный qiε0. В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Замечание 1Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Применение теоремы Гаусса
Пример 2В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R. Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
Рисунок 1.3.4. Иллюстрация поля однородно заряженного цилиндра. OO’ – ось симметрии.
Если r≥R, то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим:
Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим:
Φ=E2πrl=τlε0.
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
E=τ2πε0r.
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r<R. В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ=E2πrl. Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Пример 4Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1.3.5).
Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2E∆S=σ∆Sε0 или E=σ2ε0.
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Автор: Роман Адамчук
Преподаватель физики
Поток вектора электрической индукции. Вектор индукции электрического поля
Теорема Гаусса для электрической индукции (электрического смещения)[
Для
поля в диэлектрической
среде электростатическая
теорема Гаусса может быть записана еще
и иначе (альтернативным образом) —
через поток вектора электрического
смещения(электрической
индукции). При этом формулировка теоремы
выглядит следующим образом: поток
вектора электрического
смещения через
замкнутую поверхность пропорционален
заключённому внутри этой поверхности
свободному электрическому заряду:
При этом формулировка теоремы
выглядит следующим образом: поток
вектора электрического
смещения через
замкнутую поверхность пропорционален
заключённому внутри этой поверхности
свободному электрическому заряду:
В дифференциальной форме:
Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
или в дифференциальной форме
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле . Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым .
Теорема Гаусса для ньютоновской гравитации
Для напряжённости поля ньютоновской гравитации (ускорения свободного падения) теорема Гаусса практически совпадает с таковой в электростатике, за исключением только констант (впрочем, всё равно зависящих от произвольного выбора системы единиц) и, главное, знака :
где g —
напряжённость гравитационного поля, M —
гравитационный заряд (то есть масса)
внутри поверхности S , ρ —
плотность массы, G — ньютоновская
константа.
Проводниками
называют тела, через которые электрические
заряды могут переходить от заряженного
тела к незаряженному. Способность
проводников пропускать через себя
электрические заряды объясняется
наличием в них свободных носителей
заряда. Проводники — металлические тела
в твердом и жидком состоянии, жидкие
растворы электролитов.
Свободные
заряды проводника, внесенного в
электрическое поле, под его действием
приходят в движение. Перераспределение
зарядов вызывает изменение электрического
поля. Когда напряженность электрического
поля в проводнике становится равной
нулю, электроны прекращают движение.
Явление
разделения разноименных зарядов в
проводнике, помещенным в электрическое
поле называется электростатической
индукцией.
Внутри проводника
электрического поля нет. Это используют
для электростатической защиты — защиты
с помощью металлических проводников
от электрического поля.
Поверхность
проводящего тела любой формы в
электрическом поле является
эквипотенциальной поверхностью.
Конденсаторы
Для получения устройств, которые при небольшом относительно среды потенциале накапливали бы на себе (конденсировали) заметные по величине заряды используют тот факт, что электроемкость проводника возрастает при приближении к нему других тел. Действительно, под действием поля, создаваемого заряженными проводниками, на поднесенном к нему теле возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды (рис.15.5). Заряды, противоположные по знаку заряду проводника q располагаются ближе к проводнику, чем одноименные с q, и, следовательно, оказывают большое влияние на его потенциал.
Поэтому при поднесении к заряженному проводнику какого либо тела напряженность поля уменьшается, а, следовательно, уменьшается потенциал проводника. Согласно уравнение это означает увеличение емкости проводника.
Конденсатор
состоит из двух проводников (обкладок)
(рис.15.6), разделенных прослойкой
диэлектрика. При приложении к проводнику
некоторой разности потенциалов его
обкладки заряжаются равными по величине
зарядами противоположного знака. Под
электроемкостью конденсатора понимается
физическая величина, пропорциональная
заряду q и обратно пропорциональна
разности потенциалов между обкладками
Под
электроемкостью конденсатора понимается
физическая величина, пропорциональная
заряду q и обратно пропорциональна
разности потенциалов между обкладками
Определим емкость плоского конденсатора.
Если площадь обкладки S , а заряд на ней q, то напряженность поля между обкладками
С другой стороны разность потенциалов между обкладками откуда
Энергия системы точечных зарядов, заряженного проводника и конденсатора.
Всякая система зарядов обладает некоторой потенциальной энергией взаимодействия, которая равна работе, затраченной на создание этой системы. Энергия системы точечных зарядов q 1 , q 2 , q 3 ,… q N определяется следующим образом:
где φ 1 –
потенциал электрического поля,
создаваемого всеми зарядами кроме q 1 в
той точке, где находится зарядq 1 и
т.д. Если изменяется конфигурация системы
зарядов, то изменяется и энергия системы.
Для изменения конфигурации системы
необходимо совершение работы.
Потенциальную энергию системы точечных зарядов можно рассчитать другим способом. Потенциальная энергия двух точечных зарядов q 1 , q 2 на расстоянии друг от друга равна. Если зарядов несколько, то потенциальную энергию этой системы зарядов можно определить как сумму потенциальных энергий всех пар зарядов, которые можно составить для этой системы. Так, для системы трех положительных зарядов энергия системы равна
Электрическое поле точечного заряда q 0 на расстоянии от него в среде с диэлектрической проницаемостьюε (см. рисунок 3.1.3). Рисунок 3.1.3 | ; Потенциал – скаляр, его знак зависит от знака заряда, создающего поле. |
Рисунок 3.1.4. Электрическое
поле равномерно заряженной сферы
радиуса в
точке С на расстоянииот
её поверхности (рисунок 3.1.4). Электрическое
поле сферы аналогично полю точечного
заряда, равного заряду сферыq сф
и сосредоточенного в её центре. | Вне сферы: ; Потенциал внутри сферы постоянен и равен , а напряженность внутри сферы равна нулю |
Электрическое поле равномерно заряженной бесконечной плоскости с поверхностной плотностью σ (см. рисунок 3.1.5). Рисунок 3.1.5. | Поле, напряженность которого во всех точках одинакова, называется однородным . Поверхностная плотность σ – заряд единицы поверхности (, где– соответственно заряд и площадь плоскости). Размерность поверхностной плотности заряда. |
Электрическое поле плоского конденсатора с одинаковыми по величине, но противоположными по знаку зарядами на пластинах (см. рисунок 3.1.6). Рисунок 3.1.6 | Напряженность между обкладками плоского конденсатора , вне конденсатораЕ =0. Разность
потенциалов u между
пластинами (обкладками) конденсатора: ,
гдеd –
расстояние между обкладками, –
диэлектрическая проницаемость
диэлектрика, помещённого между
пластинами конденсатора. Поверхностная плотность заряда на пластинах конденсатора равна отношению величины заряда на ней к площади пластины:. |
Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен , а емкость — С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная . Но потенциал электростатического поля данного проводника в бесконечности равен нулю . Тогда
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:
Применяя соотношение , можно получить следующие выражения для потенциальной энергии W:
Для заряженного конденсатора разность потенциалов (напряжение) равна поэтому соотношение для полной энергии его электростатического поля имеют вид
Когда
зарядов много, при расчётах полей
возникают некоторые трудности.
Преодолеть их помогает теорема Гаусса. Суть теоремы Гаусса сводится к следующему: если произвольное количество зарядов мысленно окружить замкнутой поверхностью S, то поток напряжённости электрического поля через элементарную площадку dS можно записать как dФ = Есоsα۰dS где α — угол между нормалью к плоскости и вектором напряжённости . (рис.12.7)
Полный же поток через всю поверхность будет равен сумме потоков от всех зарядов, произвольным образом распределённых внутри её и пропорционально величине этого заряда
(12.9)
Определим поток вектора напряжённости сквозь сферическую поверхность радиуса r, в центре которой расположен точечный заряд +q (рис.12.8). Линии напряжённости перпендикулярны поверхности сферы, α =0, следовательно соsα = 1. Тогда
Если поле образовано системой зарядов, то
Теорема
Гаусса: поток вектора напряжённости
электростатического поля в вакууме
сквозь любую замкнутую поверхность
равен алгебраической сумме зарядов,
заключенных внутри этой поверхности,
делённой на электрическую постоянную.
(12.10)
Если внутри сферы зарядов нет, то Ф = 0.
Теорема Гаусса позволяет сравнительно просто рассчитать электрические поля при симметрично распределённых зарядов.
Введём понятие о плотности распределенных зарядов.
Линейная плотность обозначается τ и характеризует заряд q, приходящийся на единицу длины ℓ. В общем виде может быть рассчитана по формуле
(12.11)
При равномерном распределении зарядов линейная плотность равна
Поверхностная плотность обозначается σ и характеризует заряд q, приходящийся на единицу площади S. В общем виде определяется по формуле
(12.12)
При
равномерном распределении зарядов по
поверхности поверхностная плотность
равна
Объёмная плотность обозначается ρ, характеризует заряд q, приходящийся на единицу объёма V. В общем виде определяется по формуле
(12.13)
При
равномерном распределении зарядов она
равна
.
Так как заряд q располагается на сфере равномерно, то
σ
= const. Применим теорему Гаусса. Проведём сферу
радиусом через точку А. Поток вектора
напряжённости рис.12.9 сквозь
сферическую поверхность радиуса равен
соsα
= 1, так как α
= 0. По теореме Гаусса,
Применим теорему Гаусса. Проведём сферу
радиусом через точку А. Поток вектора
напряжённости рис.12.9 сквозь
сферическую поверхность радиуса равен
соsα
= 1, так как α
= 0. По теореме Гаусса,
.
или
(12.14)
Из
выражения (12.14) следует, что напряжённость
поля вне заряженной сферы такая же, как
напряжённость поля точечного заряда,
помещённого в центре сферы. На поверхности
сферы, т.е. r 1
= r 0
, напряжённость
.
Внутри сферы r 1
Цилиндр радиусом r 0 равномерно заряжен с поверхностной плотностью σ (рис.12.10). Определим напряжённость поля в произвольно выбранной точке А. Проведём через точку А воображаемую цилиндрическую поверхность радиусом R и длиной ℓ. Вследствие симметрии поток будет выходить только через боковые поверхности цилиндра, так как заряды на цилиндре радиуса r 0 распределены по его поверхности равномерно, т.е. линии напряжённости будут радиальными прямыми, перпендикулярными боковым поверхностям обоих цилиндров. Так как поток через основание цилиндров равен нулю (cos α = 0), а боковая поверхность цилиндра перпендикулярна силовым линиям (cos α = 1), то
или
(12. 15)
15)
Выразим величину Е через σ — поверхностную плотность. По определению,
следовательно,
Подставим значение q в формулу (12.15)
(12.16)
По
определению линейной плотности,
, откуда
;
подставляем это выражение в формулу
(12.16):
(12.17)
т.е. напряжённость поля, создаваемого бесконечно длинным заряженным цилиндром, пропорциональна линейной плотности заряда и обратно пропорциональна расстоянию.
Определим
напряжённость поля, создаваемого
бесконечной равномерно заряженной
плоскостью в точке А. Пусть поверхностная
плотность заряда плоскости равна σ. В
качестве замкнутой поверхности удобно
выбрать цилиндр, ось которого
перпендикулярна плоскости, а правое
основание содержит точку А. Плоскость
делит цилиндр пополам. Очевидно, что
силовые линии перпендикулярны плоскости
и параллельны боковой поверхности
цилиндра, поэтому весь поток проходит
только через основания цилиндра. На
обоих основаниях напряжённость поля
одинакова, т.к. точки А и В симметричны
относительно плоскости. Тогда поток,
через основания цилиндра равен
Тогда поток,
через основания цилиндра равен
Согласно теореме Гаусса,
Так
как
,
то
,
откуда
(12.18)
Таким образом, напряжённость поля бесконечной заряженной плоскости пропорциональна поверхностной плотности заряда и не зависит от расстояния до плоскости. Следовательно, поле плоскости является однородным.
Результирующее
поле, создаваемое двумя плоскостями,
определяется по принципу суперпозиции
полей:
(рис.12.12). Поле, создаваемое каждой
плоскостью, является однородным,
напряжённости этих полей равны по
модулю, но противоположны по направлению:
.
По принципу суперпозиции напряжённость
суммарного поля вне плоскости равна
нулю:
Между плоскостями напряжённости полей имеют одинаковые направления, поэтому результирующая напряжённость равна
Таким
образом, поле между двумя разноименно
равномерно заряженными плоскостями
однородно и его напряжённость в два
раза больше, чем напряжённость поля,
создаваемого одной плоскостью. Слева
и справа от плоскостей поле отсутствует.
Такой же вид имеет и поле конечных
плоскостей, искажение появляется только
вблизи их границ. С помощью полученной
формулы можно рассчитать поле между
обкладками плоского конденсатора.
Слева
и справа от плоскостей поле отсутствует.
Такой же вид имеет и поле конечных
плоскостей, искажение появляется только
вблизи их границ. С помощью полученной
формулы можно рассчитать поле между
обкладками плоского конденсатора.
Основная
прикладная задача электростатики –
расчет электрических полей, создаваемых
в различных приборах и аппаратах. В
общем виде эта задача решается с помощью
закона Кулона и принципа суперпозиции.
Однако эта задача очень усложняется
при рассмотрении большого числа точечных
или пространственно распределенных
зарядов. Еще большие трудности возникают
при наличии в пространстве диэлектриков
или проводников, когда под действием
внешнего поля Е 0 происходит
перераспределение микроскопических
зарядов, создающих свое дополнительное
поле Е. Поэтому для практического решения
этих задач используют вспомогательные
методы и приемы, использующие сложный
математический аппарат. Мы рассмотрим
самый простой метод, основанный на
применении теоремы Остроградского –
Гаусса. Чтобы сформулировать эту теорему
введем несколько новых понятий:
Чтобы сформулировать эту теорему
введем несколько новых понятий:
А)плотность заряда
Если заряженное тело велико, то нужно знать распределение зарядов внутри тела.
Объемная плотность заряда – измеряется зарядом единицы объема:
Поверхностная плотность заряда – измеряется зарядом единицы поверхности тела (когда заряд распределяется по поверхности):
Линейная плотность заряда (распределение заряда вдоль проводника):
б) вектор электростатической индукции
Вектором электростатической индукции (вектором электрического смещения) называется векторная величина, характеризующая электрическое поле.
Вектор равен произведению векторана абсолютную диэлектрическую проницаемость среды в данной точке:
Проверим размерность D в системе единиц СИ:
,
т.к.
,
то размерности D и Е не совпадают, а также различны и их численные значения.
Из определения следует, что для поля вектораимеет место тот же принцип суперпозиции, как и для поля:
Поле
графически изображается линиями
индукции, точно так же как и поле . Линии индукции проводятся так, что
касательная в каждой точке совпадает
с направлением
,
а число линий равно численному значениюD
в данном месте.
Линии индукции проводятся так, что
касательная в каждой точке совпадает
с направлением
,
а число линий равно численному значениюD
в данном месте.
Чтобы понять смысл введения рассмотрим пример.
ε> 1 | на границе полости с диэлектриком концентрируются связанные отрицательные заряды и поля уменьшается враз и скачком уменьшается густота. | |
Для этого же случая:D = Eεε 0 | , тогда: линииидут непрерывно. Линииначинаются на свободных зарядах (уна любых – связанных или свободных), и на границе диэлектрика их густота остается неизменной. Таким образом – непрерывность линий индукции значительно облегчает вычисление , а, зная связьсможно найти вектор. | |
в) поток вектора электростатической индукции
Рассмотрим в электрическом поле поверхность S и выберем направление нормали
1. Если поле однородно, то число силовых
линий через поверхность S:
Если поле однородно, то число силовых
линий через поверхность S:
2. Если поле неоднородно, то поверхность разбивают на бесконечно малые элементы dS, которые считают плоскими и поле возле них однородным. Поэтому поток через элемент поверхности равен: dN = D n dS,
а полный поток через любую поверхность:
(6)
Поток индукции N – величина скалярная; в зависимости от может быть > 0 или
Закон взаимодействия электрических зарядов — закон Кулона — можно сформулировать иначе, в виде так называемой теоремы Гаусса. Теорема Гаусса получается как следствие закона Кулона и принципа суперпозиции. Доказательство основывается на обратной пропорциональности силы взаимодействия двух точечных зарядов квадрату расстояния между ними. Поэтому теорема Гаусса применима к любому физическому полю, где действует закон обратных квадратов и принцип суперпозиции, например к гравитационному полю.
Рис. 9. Линии напряженности электрического поля точечного заряда, пересекающие замкнутую поверхность X
Для того чтобы сформулировать теорему Гаусса, вернемся к картине силовых линий электрического поля неподвижного точечного заряда. Силовые линии уединенного точечного заряда представляют собой симметрично расположенные радиальные прямые (рис. 7). Можно провести любое число таких линий. Обозначим полное их число через Тогда густота силовых линий на расстоянии от заряда, т. е. число линий, пересекающих единицу поверхности сферы радиуса равна Сравнивая это соотношение с выражением для напряженности поля точечного заряда (4), видим, что густота линий пропорциональна напряженности поля. Мы можем сделать эти величины численно равными, надлежащим образом выбрав полное число силовых линий N:
Силовые линии уединенного точечного заряда представляют собой симметрично расположенные радиальные прямые (рис. 7). Можно провести любое число таких линий. Обозначим полное их число через Тогда густота силовых линий на расстоянии от заряда, т. е. число линий, пересекающих единицу поверхности сферы радиуса равна Сравнивая это соотношение с выражением для напряженности поля точечного заряда (4), видим, что густота линий пропорциональна напряженности поля. Мы можем сделать эти величины численно равными, надлежащим образом выбрав полное число силовых линий N:
Таким образом, поверхность сферы любого радиуса, охватывающей точечный заряд пересекает одно и то же число силовых линий. Это значит, что силовые линии непрерывны: в промежутке между любыми двумя концентрическими сферами разных радиусов ни одна из линий не обрывается и не добавляется ни одной новой. Поскольку силовые линии непрерывны, то такое же число силовых линий пересекает любую замкнутую поверхность (рис. 9), охватывающую заряд
Силовые линии имеют направление. В случае положительного заряда они выходят наружу из окружающей заряд замкнутой поверхности, как показано на рис. 9. В случае отрицательного заряда они входят внутрь поверхности. Если число выходящих линий считать положительным, а входящих — отрицательным, то в формуле (8) можно опустить знак модуля у заряда и записать ее в виде
В случае положительного заряда они выходят наружу из окружающей заряд замкнутой поверхности, как показано на рис. 9. В случае отрицательного заряда они входят внутрь поверхности. Если число выходящих линий считать положительным, а входящих — отрицательным, то в формуле (8) можно опустить знак модуля у заряда и записать ее в виде
Поток напряженности. Введем теперь понятие потока вектора напряженности поля через поверхность. Произвольное поле можно мысленно разбить на малые области, в которых напряженность меняется по модулю и направлению столь мало, что в пределах этой области поле можно считать однородным. В каждой такой области силовые линии представляют собой параллельные прямые и имеют постоянную густоту.
Рис. 10. К определению потока вектора напряженности поля через площадку
Рассмотрим, какое число силовых линий пронизывает малую площадку направление нормали к которой образует угол а с направлением линий напряженности (рис. 10). Пусть — проекция на плоскость, перпендикулярную силовым линиям. Так как число линий, пересекающих одинаково, а густота линий, согласно принятому условию, равна модулю напряженности поля Е, то
Так как число линий, пересекающих одинаково, а густота линий, согласно принятому условию, равна модулю напряженности поля Е, то
Величина а представляет собой проекцию вектора Е на направление нормали к площадке
Поэтому число силовых линий пересекающих площадку равно
Произведение носит название потока напряженности поля через поверхность Формула (10) показывает, что поток вектора Е через поверхность равен числу силовых линий, пересекающих эту поверхность. Отметим, что поток вектора напряженности, как и число проходящих через поверхность силовых линий, есть скаляр.
Рис. 11. Поток вектора напряженности Е через площадку
Зависимость потока от ориентации площадки относительно силовых линий иллюстрируется рис.
Поток напряженности поля через произвольную поверхность представляет собой сумму потоков через элементарные площадки, на которые можно разбить эту поверхность. В силу соотношений (9) и (10) можно утверждать, что поток напряженности поля точечного заряда через любую охватывающую заряд замкнутую поверхность 2 (см. рис. 9), как число выходящих из этой поверхности силовых линий равен При этом вектор нормали к элементарным площадкам замкнутой поверхности следует направлять наружу. Если заряд внутри поверхности отрицателен, то силовые линии входят внутрь этой поверхности и связанный с зарядом поток вектора напряженности поля также отрицателен.
рис. 9), как число выходящих из этой поверхности силовых линий равен При этом вектор нормали к элементарным площадкам замкнутой поверхности следует направлять наружу. Если заряд внутри поверхности отрицателен, то силовые линии входят внутрь этой поверхности и связанный с зарядом поток вектора напряженности поля также отрицателен.
Если внутри замкнутой поверхности находится несколько зарядов, то в соответствии с принципом суперпозиции будут складываться потоки напряженностей их полей. Полный поток будет равен где под следует понимать алгебраическую сумму всех зарядов, находящихся внутри поверхности.
Если внутри замкнутой поверхности электрических зарядов нет или их алгебраическая сумма равна нулю, то полный поток напряженности поля через эту поверхность равен нулю: сколько силовых линий входит в объем, ограниченный поверхностью, столько же и выходит наружу.
Теперь можно окончательно сформулировать теорему Гаусса: поток вектора напряженности электрического поля Е в вакууме через любую замкнутую поверхность пропорционален полному заряду находящемуся внутри этой поверхности. Математически теорема Гаусса выражается той же формулой (9), где под понимается алгебраическая сумма зарядов. В абсолютной электростатической
Математически теорема Гаусса выражается той же формулой (9), где под понимается алгебраическая сумма зарядов. В абсолютной электростатической
системе единиц СГСЭ коэффициент и теорема Гаусса записывается в виде
В СИ и поток напряженности через замкнутую поверхность выражается формулой
Теорема Гаусса широко используется в электростатике. В некоторых случаях с ее помощью легко рассчитываются поля, создаваемые симметрично расположенными зарядами.
Поля симметричных источников. Применим теорему Гаусса для расчета напряженности электрического поля равномерно заряженного по поверхности шара радиуса . Будем для определенности считать его заряд положительным. Распределение зарядов, создающих поле, обладает сферической симметрией. Поэтому такой же симметрией обладает и поле. Силовые линии такого поля направлены по радиусам, а модуль напряженности одинаков во всех точках, равноудаленных от центра шара.
Для того чтобы найти напряженность поля на расстоянии от центра шара, проведем мысленно концентрическую с шаром сферическую поверхность радиуса Поскольку во всех точках этой сферы напряженность поля направлена перпендикулярно ее поверхности и одинакова по модулю, то поток напряженности просто равен произведению напряженности поля на площадь поверхности сферы:
Но эту величину можно выразить и с помощью теоремы Гаусса. Если нас интересует поле вне шара, т. е. при то, например, в СИ и, сравнивая с (13), находим
Если нас интересует поле вне шара, т. е. при то, например, в СИ и, сравнивая с (13), находим
В системе единиц СГСЭ, очевидно,
Таким образом, снаружи шара напряженность поля такая же, как у поля точечного заряда помещенного в центр шара. Если же интересоваться полем внутри шара, т. е. при то так как весь распределенный по поверхности шара заряд находится вне мысленно проведенной нами сферы. Поэтому поле внутри шара отсутствует:
Аналогично с помощью теоремы Гаусса можно рассчитать электростатическое поле, создаваемое бесконечной заряженной
плоскостью с плотностью постоянной во всех точках плоскости. По соображениям симметрии можно считать, что силовые линии перпендикулярны плоскости, направлены от нее в обе стороны и имеют всюду одинаковую густоту. Действительно, если бы густота силовых линий в разных точках была различной, то перемещение заряженной плоскости вдоль самой себя приводило бы к изменению поля в этих точках, что противоречит симметрии системы — такой сдвиг не должен изменять поле. Другими словами, поле бесконечной равномерно заряженной плоскости является однородным.
Другими словами, поле бесконечной равномерно заряженной плоскости является однородным.
В качестве замкнутой поверхности для применения теоремы Гаусса выберем поверхность цилиндра, построенного следующим образом: образующая цилиндра параллельна силовым линиям, а основания имеют площади параллельны заряженной плоскости и лежат по разные стороны от нее (рис. 12). Поток напряженности поля через боковую поверхность равен нулю, поэтому полный поток через замкнутую поверхность равен сумме потоков через основания цилиндра:
Рис. 12. К вычислению напряженности поля равномерно заряженной плоскости
По теореме Гаусса этот же поток определяется зарядом той части плоскости, которая лежит внутри цилиндра, и в СИ равен Сравнивая эти выражения для потока, находим
В системе СГСЭ напряженность поля равномерно заряженной бесконечной плоскости дается формулой
Для равномерно заряженной пластины конечных размеров полученные выражения приближенно справедливы в области, находящейся достаточно далеко от краев пластины и не слишком далеко от ее поверхности. Вблизи краев пластины поле уже не будет однородным и его силовые линии искривляются. На очень больших по сравнению с размерами пластины расстояниях поле убывает с расстоянием так же, как поле точечного заряда.
Вблизи краев пластины поле уже не будет однородным и его силовые линии искривляются. На очень больших по сравнению с размерами пластины расстояниях поле убывает с расстоянием так же, как поле точечного заряда.
В качестве других примеров полей, создаваемых симметрично распределенными источниками, можно привести поле равномерно заряженной по длине бесконечной прямолинейной нити, поле равномерно заряженного бесконечного кругового цилиндра, поле шара,
равномерно заряженного по объему, и т. п. Теорема Гаусса позволяет во всех этих случаях легко рассчитывать напряженность поля.
Теорема Гаусса дает связь между полем и его источниками, в некотором смысле обратную той, что дает закон Кулона, который позволяет определить электрическое поле по заданным зарядам. С помощью теоремы Гаусса можно определить суммарный заряд в любой области пространства, в которой известно распределение электрического поля.
В чем различие концепций дальнодействия и близкодействия при описании взаимодействия электрических зарядов? В какой мере эти концепции можно применить к гравитационному взаимодействию?
Что такое напряженность электрического поля? Что имеют в виду, когда ее называют силовой характеристикой электрического поля?
Каким образом по картине силовых линий можно судить о направлении и модуле напряженности поля в некоторой точке?
Могут ли силовые линии электрического поля пересекаться? Аргументируйте свой ответ.
Нарисуйте качественную картину силовых линий электростатического поля двух зарядов таких, что .
Поток напряженности электрического поля через замкнутую поверхность выражается разными формулами (11) и (12) в системах единиц ГСЭ и в СИ. Как это увязать с геометрическим смыслом потока, определяемого числом силовых линйй, пересекающих поверхность?
Как использовать теорему Гаусса для нахождения напряженности электрического поля при симметричном распределении создающих его зарядов?
Как применить формулы (14) и (15) к вычислению напряженности поля шара с отрицательным зарядом?
Теорема Гаусса и геометрия физического пространства. Посмотрим на доказательство теоремы Гаусса с несколько иной точки зрения. Вернемся к формуле (7), из которой был сделан вывод о том, что через любую окружающую заряд сферическую поверхность проходит одно и то же число силовых линий. Этот вывод связан с тем, что происходит сокращение в знаменателях обеих частей равенства.
В правой части возникло из-за того, что сила взаимодействия зарядов, описываемая законом Кулона, обратно пропорциональна квадрату расстояния между зарядами. В левой части появление связано с геометрией: площадь поверхности сферы пропорциональна квадрату ее радиуса.
В левой части появление связано с геометрией: площадь поверхности сферы пропорциональна квадрату ее радиуса.
Пропорциональность площади поверхности квадрату линейных размеров — это отличительная черта евклидовой геометрии в трехмерном пространстве. Действительно, пропорциональность площадей именно квадратам линейных размеров, а не какой-либо иной целой степени, характерно для пространства
трех измерений. То, что этот показатель степени равен точно двум, а не отличается от двойки пусть даже на ничтожно малую величину, свидетельствует о неискривленности этого трехмерного пространства, т. е. о том, что его геометрия именно евклидова.
Таким образом, теорема Гаусса — это проявление свойств физического пространства в фундаментальном законе взаимодействия электрических зарядов.
Идея о тесной связи фундаментальных законов физики со свойствами пространства высказывалась многими выдающимися умами еще задолго до установления самих этих законов. Так, И. Кант за три десятилетия до открытия закона Кулона писал о свойствах пространства: «Трехмерность происходит, по-видимому, оттого, что субстанции в существующем мире действуют одна на другую таким образом, что сила действия обратно пропорциональна квадрату расстояния».
Закон Кулона и теорема Гаусса фактически представляют один и тот же закон природы, выраженный в различных формах. Закон Кулона отражает концепцию дальнодействия, в то время как теорема Гаусса исходит из представления о силовом поле, заполняющем пространство, т. е. из концепции близкодействия. В электростатике источником силового поля является заряд, и связанная с источником характеристика поля — поток напряженности — не может измениться в пустом пространстве, где нет других зарядов. Поскольку поток можно наглядно представлять себе как совокупность силовых линий поля, то неизменность потока проявляется в непрерывности этих линий.
Теорема Гаусса, основанная на обратной пропорциональности взаимодействия квадрату расстояния и на принципе суперпозиции (аддитивности взаимодействия), применима к любому физическому полю, в котором действует закон обратных квадратов. В частности, она справедлива и для гравитационного поля. Ясно, что это не просто случайное совпадение, а отражение того, что и электрическое, и гравитационное взаимодействия разыгрываются в трехмерном евклидовом физическом пространстве.
На какой особенности закона взаимодействия электрических зарядов основана теорема Гаусса?
Докажите, основываясь на теореме Гаусса, что напряженность электрического поля точечного заряда обратно пропорциональна квадрату расстояния. Какие свойства симметрии пространства используются в этом доказательстве?
Каким образом геометрия физического пространства отражается в законе Кулона и теореме Гаусса? Какая особенность этих законов свидетельствует об евклидовом характере геометрии и трехмерности физического пространства?
Общая формулировка: Поток вектора напряжённости электрического поля через любую, произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.
В системе СГСЭ:
В системе СИ:
— поток вектора напряженности электрического поля через замкнутую поверхность .
— полный заряд, содержащийся в объеме, который ограничивает поверхность .
— электрическая постоянная.
Данное выражение представляет собой теорему Гаусса в интегральной форме.
В дифференциальной форме теорема Гаусса соответствует одному из уравнений Максвелла и выражается следующим образом
в системе СИ:
,
в системе СГСЭ:
Здесь — объёмная плотность заряда (в случае присутствия среды — суммарная плотность свободных и связанных зарядов), а — оператор набла.
Для теоремы Гаусса справедлив принцип суперпозиции, то есть поток вектора напряжённости через поверхность не зависит от распределения заряда внутри поверхности.
Физической основой теоремы Гаусса является закон Кулона или, иначе, теорема Гаусса является интегральной формулировкой закона Кулона.
Теорема Гаусса для электрической индукции (электрическое смещение).
Для поля в веществе электростатическая теорема Гаусса может быть записана иначе — через поток вектора электрического смещения (электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
Если же рассматривать теорему для напряжённости поля в веществе, то в качестве заряда Q необходимо брать сумму свободного заряда, находящегося внутри поверхности и поляризационного (индуцированного, связанного) заряда диэлектрика:
,
где ,
— вектор поляризации диэлектрика.
Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:
.
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является вихревым.
Применение теоремы Гаусса
Для вычисления электромагнитных полей используются следующие величины:
Объёмная плотность заряда (см. выше).
Поверхностная плотность заряда
где dS — бесконечно малый участок поверхности.
Линейная плотность заряда
где dl — длина бесконечно малого отрезка.
Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, расположенным относительно плоскости симметрично. В силу симметрии . Поток вектора напряжённости равен . Применив теорему Гаусса, получим:
В силу симметрии . Поток вектора напряжённости равен . Применив теорему Гаусса, получим:
,
из которого
в системе СГСЭ
Важно отметить, что несмотря на свою универсальность и общность, теорема Гаусса в интегральной форме имеет сравнительно ограниченное применение в силу неудобства вычисления интеграла. Однако в случае симметричной задачи решение её становится гораздо более простым, чем с использованием принципа суперпозиции.
17.1: Поток электрического поля
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19487
- Howard Martin пересмотрено Аланом Нг
- University of Wisconsin-Madison
Закон Гаусса использует понятие «поток». Поток всегда определяется на основе:
Поток всегда определяется на основе:
- Поверхность А.
- Векторное поле (например, электрическое поле).
и может рассматриваться как мера количества силовых линий векторного поля, пересекающих данную поверхность. По этой причине обычно говорят о «потоке электрического поля через поверхность». Это показано на рисунке \(\PageIndex{1}\) для однородного горизонтального электрического поля и плоской поверхности, вектор нормали которой \(\vec A\) показан. Если поверхность перпендикулярна полю (левая панель), и, таким образом, вектор поля параллелен вектору \(\vec A\), то поток через эту поверхность максимален. Если поверхность параллельна полю (правая панель), то никакие силовые линии не пересекают эту поверхность, и поток через эту поверхность равен нулю. Если поверхность вращается относительно электрического поля, как на средней панели, то поток через поверхность находится между нулем и максимальным значением.
Рисунок \(\PageIndex{1}\): Поток электрического поля через поверхность, образующую разные углы по отношению к электрическому полю. На крайнем левом рисунке поверхность ориентирована так, чтобы поток через нее был максимальным. На самой правой панели нет силовых линий, пересекающих поверхность, поэтому поток через поверхность равен нулю.
На крайнем левом рисунке поверхность ориентирована так, чтобы поток через нее был максимальным. На самой правой панели нет силовых линий, пересекающих поверхность, поэтому поток через поверхность равен нулю. Мы определяем вектор \(\vec A\), связанный с поверхностью, так что величина \(\vec A\) равна площади поверхности, а направление \(\vec A\) таков, что он перпендикулярен поверхности, как показано на рисунке \(\PageIndex{1}\). Мы определяем поток \(\Phi_E\) электрического поля \(\vec E\) через поверхность, представленную вектором, \(\vec A\), как: \[\begin{aligned} \ Phi_E=\vec E\cdot \vec A=EA\cos\theta\end{aligned}\], так как это будет иметь те же свойства, которые мы описали выше (например, отсутствие потока, когда \(\vec E\) и \(\ vec A\) перпендикулярны, поток пропорционален числу силовых линий, пересекающих поверхность). Обратите внимание, что поток определяется только до общего знака, поскольку есть два возможных выбора направления вектора \(\vec A\), поскольку требуется, чтобы он был перпендикулярен поверхности. По соглашению мы обычно выбираем \(\vec A\) так, чтобы поток был положительным.
По соглашению мы обычно выбираем \(\vec A\) так, чтобы поток был положительным.
Упражнение \(\PageIndex{1}\)
Каковы единицы измерения электрического потока в системе СИ?
- \(\text{N}\cdot\text{m/C}\)
- \(\текст{V}\cdot\текст{м}\)
- \(\text{В/м}\)
- Единицы потока зависят от размеров заряженного объекта.
- Ответить
Единицы потока зависят от размеров заряженного объекта.
Пример \(\PageIndex{1}\)
Однородное электрическое поле определяется как: \(\vec E=E\cos\theta\hat x+E\sin\theta\hat y\) во всем пространстве. Прямоугольная поверхность определяется четырьмя точками \((0,0,0)\), \((0,0,H)\), \((L,0,0)\), \((L, 0,Н)\). Чему равен поток электрического поля через поверхность?
Решение :
Заданная поверхность соответствует прямоугольнику на плоскости \(xz\) с площадью \(A=LH\). Поскольку прямоугольник лежит в плоскости \(xz\), вектор, перпендикулярный поверхности, будет направлен в направлении \(y\). Мы выбираем положительное направление \(y\), так как это даст положительное число для потока (поскольку электрическое поле имеет положительную составляющую в направлении \(y\)). Вектор \(\vec A\) определяется как: \[\begin{aligned} \vec A =A\hat y=LH\hat y\end{aligned}\] Таким образом, поток через поверхность определяется как: \[\begin{align} \Phi_E&=\vec E\cdot \vec A=(E\cos\theta\hat x+E\sin\theta\hat y)\cdot(LH\hat y)\\ &= ELH\sin\theta\end{aligned}\], где следует отметить, что угол \(\theta\) в данном случае не является углом между \(\vec E\) и \(\vec A\) , а скорее дополнение этого угла.
Поскольку прямоугольник лежит в плоскости \(xz\), вектор, перпендикулярный поверхности, будет направлен в направлении \(y\). Мы выбираем положительное направление \(y\), так как это даст положительное число для потока (поскольку электрическое поле имеет положительную составляющую в направлении \(y\)). Вектор \(\vec A\) определяется как: \[\begin{aligned} \vec A =A\hat y=LH\hat y\end{aligned}\] Таким образом, поток через поверхность определяется как: \[\begin{align} \Phi_E&=\vec E\cdot \vec A=(E\cos\theta\hat x+E\sin\theta\hat y)\cdot(LH\hat y)\\ &= ELH\sin\theta\end{aligned}\], где следует отметить, что угол \(\theta\) в данном случае не является углом между \(\vec E\) и \(\vec A\) , а скорее дополнение этого угла.
Обсуждение:
В этом примере мы рассчитали поток однородного электрического поля через прямоугольник площадью \(A=LH\). Поскольку мы знали компоненты вектора электрического поля \(\vec E\) и поверхностного вектора \(\vec A\), мы использовали их скалярное произведение для определения потока через поверхность. В некоторых случаях проще работать с величиной векторов и углом между ними для определения скалярного произведения (хотя обратите внимание, что в этом примере угол между \(\vec E\) и \(\vec A\ ) равно \(9{\circ}-\тета\)).
В некоторых случаях проще работать с величиной векторов и углом между ними для определения скалярного произведения (хотя обратите внимание, что в этом примере угол между \(\vec E\) и \(\vec A\ ) равно \(9{\circ}-\тета\)).
Неоднородные поля
До сих пор мы рассматривали поток однородного электрического поля \(\vec E\) через поверхность \(S\), описываемую вектором \(\vec A\ ). В этом случае поток \(\Phi_E\) определяется как: \[\begin{aligned} \Phi_E=\vec E\cdot \vec A\end{aligned}\] Однако, если электрическое поле не постоянны по величине и/или по направлению на всей поверхности, то мы разделяем поверхность \(S\) на множество бесконечно малых поверхностей \(dS\) и суммируем (интегрируем) потоки с этих бесконечно малых поверхностей:
\[\Phi_{E}=\int\vec E\cdot d\vec A\]
где \(d\vec A\) — вектор нормали к бесконечно малой поверхности, \(dS\) . Это показано на рисунке \(\PageIndex{2}\), на левой панели которого показана поверхность, для которой электрическое поле изменяет величину вдоль поверхности (поскольку силовые линии ближе в нижней левой части поверхности). ), а на правой панели — сценарий, в котором направление и величина электрического поля меняются вдоль поверхности.
), а на правой панели — сценарий, в котором направление и величина электрического поля меняются вдоль поверхности.
Чтобы вычислить поток через всю поверхность, мы сначала вычисляем поток через бесконечно малую поверхность \(dS\), над которой мы предполагаем, что \(\vec E\) постоянна по величине и направлению, а затем, мы суммируем (интегрируем) потоки со всех бесконечно малых поверхностей вместе. Помните, что поток через поверхность связан с количеством силовых линий, пересекающих эту поверхность; таким образом, имеет смысл подсчитать линии, пересекающие бесконечно малую поверхность, \(dS\), а затем сложить их вместе по всем бесконечно малым поверхностям, чтобы определить поток через всю поверхность, \(S\).
Пример \(\PageIndex{2}\)
Электрическое поле указывает направление \(z\) повсюду в пространстве. Величина электрического поля линейно зависит от положения \(x\) в пространстве, так что вектор электрического поля определяется выражением: \(\vec E=(a-bx)\hat z\), где \( a\) и \(b\) являются константами. Чему равен поток электрического поля через квадрат со стороной \(L\), расположенный в положительной плоскости \(ху\) с одним из углов в начале координат? Нам нужно вычислить поток электрического поля через квадрат со стороной \(L\) в плоскости \(xy\). Электрическое поле всегда направлено \(z\), поэтому угол между \(\vec E\) и \(d\vec A\) (вектор нормали для любого бесконечно малого элемента площади) будет оставаться постоянным.
Решение :
Мы можем вычислить поток через квадрат, разделив квадрат на тонкие полоски длины \(L\) в направлении \(y\) и бесконечно малой ширины \(dx\) в \ (x\), как показано на рисунке \(\PageIndex{3}\). В этом случае, поскольку электрическое поле не изменяется с \(y\), размерность бесконечно малого элемента площади в направлении \(y\) конечна (\(L\)). 2\end{выровнено}\]
2\end{выровнено}\]
Обсуждение:
В этом примере мы показали, как рассчитать поток электрического поля, величина которого меняется в зависимости от положения. Мы смоделировали квадрат со стороной \(L\) состоящим из множества тонких полосок длины \(L\) и ширины \(dx\). Затем мы рассчитали поток через каждую полосу и сложили их вместе, чтобы получить общий поток через квадрат.
Закрытые поверхности
Различают «закрытую» и «открытую» поверхности. Поверхность называется замкнутой, если она полностью определяет объем, который можно было бы, например, заполнить жидкостью. Замкнутая поверхность имеет четкое «внутри» и «снаружи». Например, поверхность сферы, куба или цилиндра — все это примеры замкнутых поверхностей. С другой стороны, плоскость, треугольник и диск являются примерами «открытых поверхностей».
Для замкнутой поверхности можно однозначно определить направление вектора \(\vec A\) (или \(d\vec A\)) как направление, в котором он перпендикулярен поверхности и указывает наружу . Таким образом, знак потока за пределы замкнутой поверхности имеет смысл. Поток будет положительным, если есть чистое количество силовых линий, выходящих из объема, определяемого поверхностью (поскольку \(\vec E\) и \(\vec A\) будут в среднем параллельны), а поток будет отрицательным если в объем входит чистое количество линий поля (поскольку \(\vec E\) и \(\vec A\) в среднем будут антипараллельными). Таким образом, поток через замкнутую поверхность равен нулю, если количество силовых линий, входящих в поверхность, равно количеству силовых линий, выходящих из поверхности.
Таким образом, знак потока за пределы замкнутой поверхности имеет смысл. Поток будет положительным, если есть чистое количество силовых линий, выходящих из объема, определяемого поверхностью (поскольку \(\vec E\) и \(\vec A\) будут в среднем параллельны), а поток будет отрицательным если в объем входит чистое количество линий поля (поскольку \(\vec E\) и \(\vec A\) в среднем будут антипараллельными). Таким образом, поток через замкнутую поверхность равен нулю, если количество силовых линий, входящих в поверхность, равно количеству силовых линий, выходящих из поверхности.
При расчете потока над замкнутой поверхностью мы используем другой символ интегрирования, чтобы показать, что поверхность замкнута: \[\begin{aligned} \Phi_E=\oint \vec E\cdot d\vec A\end{aligned }\], который является тем же символом интегрирования, который мы использовали для обозначения интеграла по путям, когда начальная и конечная точки совпадают (см., например, раздел 8.1).
Упражнение \(\PageIndex{2}\)
Рисунок \(\PageIndex{4}\): Неоднородное электрическое поле, протекающее через замкнутую поверхность неправильной формы.
Неоднородное электрическое поле \(\vec E\) протекает через замкнутую поверхность неправильной формы, как показано на рисунке \(\PageIndex{4}\). Поток через поверхность
- положительный.
- ноль.
- отрицательный.
- Ответить
Пример \(\PageIndex{3}\)
Отрицательный электрический заряд \(-Q\) расположен в начале системы координат. Вычислите поток электрического поля через сферическую поверхность радиуса \(R\) с центром в начале координат. 92}\end{aligned}\] согласно закону Кулона для точечного заряда. Хотя вектор \(\vec E\) меняет направление повсюду вдоль поверхности, он всегда образует один и тот же угол (-180) с соответствующим вектором \(d\vec A\) в любом конкретном месте. Действительно, для точечного заряда электрическое поле указывает в радиальном направлении (внутрь для отрицательного заряда) и, таким образом, перпендикулярно сферической поверхности во всех точках. 2\). Поток через сферическую поверхность отрицательный, потому что заряд отрицательный, а силовые линии направлены в сторону \(-Q\). 92)=-\frac{Q}{\epsilon_0}\end{aligned}\], что, как ни странно, не зависит от радиуса сферической поверхности. Обратите внимание, что мы использовали \(\epsilon_0\) вместо константы Кулона, \(k\), так как результат более чистый без дополнительного множителя \(4\pi\).
2\). Поток через сферическую поверхность отрицательный, потому что заряд отрицательный, а силовые линии направлены в сторону \(-Q\). 92)=-\frac{Q}{\epsilon_0}\end{aligned}\], что, как ни странно, не зависит от радиуса сферической поверхности. Обратите внимание, что мы использовали \(\epsilon_0\) вместо константы Кулона, \(k\), так как результат более чистый без дополнительного множителя \(4\pi\).
Обсуждение:
В этом примере мы вычислили поток электрического поля от отрицательного точечного заряда через сферическую поверхность, концентрическую с зарядом. Мы обнаружили, что поток отрицателен, что имеет смысл, поскольку силовые линии направляются к отрицательному заряду, и, таким образом, на сферическую поверхность попадает определенное количество силовых линий. Возможно, неожиданно мы обнаружили, что полный поток через поверхность не зависит от радиуса поверхности! На самом деле это утверждение в точности соответствует закону Гаусса: суммарный поток от замкнутой поверхности зависит только от количества заряда, содержащегося на этой поверхности (и константы \(\epsilon_0\)). Закон Гаусса, конечно, более общий и применим к поверхностям любой формы, а также к зарядам любой формы (тогда как закон Кулона справедлив только для точечных зарядов).
Закон Гаусса, конечно, более общий и применим к поверхностям любой формы, а также к зарядам любой формы (тогда как закон Кулона справедлив только для точечных зарядов).
Эта страница под названием 17.1: Flux of the Electric Field распространяется в соответствии с лицензией CC BY-SA, автором, ремиксом и/или куратором выступил Ховард Мартин, редакция Алана Нг.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Райан Мартин и др.
- Лицензия
- CC BY-SA
- Показать оглавление
- нет
- Теги
- флюс
Электрический поток и закон Гаусса | безграничная физика |
Электрический поток
Электрический поток — это скорость потока электрического поля через заданную площадь.
Цели обучения
Выразите электрический поток для однородных и неоднородных электрических полей
Основные выводы
Ключевые положения
- Если электрическое поле однородно, электрический поток, проходящий через поверхность векторной площади S, равен
ΦE=E⋅S=EScos θ\Phi_\text{E} = \mathbf{\text{E}} \cdot \mathbf{\text{S}} = \text{ES} \cos \thetaΦE=E⋅S=EScosθ
. - Для неоднородного электрического поля электрический поток равен.
- Электрический поток измеряется в вольтметрах (В·м) в системе СИ.
Ключевые термины
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
Электрический поток — это скорость потока электрического поля через заданную площадь (см. ). Электрический поток пропорционален количеству силовых линий электрического поля, проходящих через виртуальную поверхность.
Электрический поток : Визуальный электрический поток. Кольцо показывает границы поверхности. Красные стрелки для линий электрического поля.
Если электрическое поле однородно, электрический поток, проходящий через поверхность векторной площади S, равен
ΦE=E⋅S=EScosθ\Phi_\text{E} = \mathbf{\text{E}} \cdot \ mathbf{\text{S}} = \text{ES} \cos \thetaΦE=E⋅S=EScosθ
где E — величина электрического поля (в единицах В/м), S — площадь поверхности, а θ — угол между силовыми линиями электрического поля и нормалью (перпендикуляром) к S.
Для неоднородного электрического поля электрический поток dΦE через небольшую площадь поверхности dS определяется выражением
dΦE=E⋅dS\text{d}\Phi_\text{E} = \mathbf{\text{E }} \cdot \text{d}\mathbf{\text{S}}dΦE=E⋅dS
(электрическое поле E, умноженное на компонент площади, перпендикулярный полю).
Закон Гаусса описывает электрический поток на поверхности S как поверхностный интеграл:
ΦE=∬SE⋅dS\Phi_\text{E} = \iint_\text{S} \mathbf{\text{E}} \cdot \text{d}\mathbf{\text{S}}ΦE=∬SE⋅dS
, где E — электрическое поле, а dS — дифференциальная площадь на замкнутой поверхности S с направленной наружу нормалью к поверхности, определяющей ее направление.
Важно отметить, что хотя на электрический поток не влияют заряды, не находящиеся внутри замкнутой поверхности, на результирующее электрическое поле E в уравнении закона Гаусса могут влиять заряды, находящиеся вне замкнутой поверхности . Хотя закон Гаусса справедлив для всех ситуаций, он полезен только для «ручных» расчетов, когда в электрическом поле существуют высокие степени симметрии. Примеры включают сферическую и цилиндрическую симметрию.
Электрический поток измеряется в СИ в вольтметрах (В·м) или, что эквивалентно, в ньютон-метрах в квадрате на кулон (Н·м 2 C −1 ). Таким образом, основные единицы СИ электрического потока составляют кг·м 3 · с −3 ·A −1 .
Таким образом, основные единицы СИ электрического потока составляют кг·м 3 · с −3 ·A −1 .
Закон Гаусса
Закон Гаусса — это закон, связывающий распределение электрического заряда с результирующим электрическим полем.
Цели обучения
Описать связь между законом Гаусса и законом Кулона
Ключевые выводы
Ключевые моменты
- Закон Гаусса — одно из четырех уравнений Максвелла, составляющих основу классической электродинамики.
- Закон Гаусса можно использовать для вывода закона Кулона и наоборот.
- Закон Гаусса гласит, что: Общий направленный наружу нормальный электрический поток через любую замкнутую поверхность пропорционален общему электрическому заряду, заключенному внутри этой замкнутой поверхности.
Ключевые термины
- электрическое поле смещения : Векторное поле, которое появляется в уравнениях Максвелла.

- электрический заряд : Квантовое число, определяющее электромагнитные взаимодействия некоторых субатомных частиц; по соглашению электрон имеет электрический заряд -1, а протон +1, а кварки имеют дробный заряд.
- электрическое поле : область пространства вокруг заряженной частицы или между двумя напряжениями; он воздействует на заряженные объекты поблизости.
Закон Гаусса, также известный как теорема Гаусса о потоках, представляет собой закон, связывающий распределение электрического заряда с результирующим электрическим полем.
Закон был сформулирован Карлом Фридрихом Гауссом (см. ) в 1835 году, но не публиковался до 1867 года. Это одно из четырех уравнений Максвелла, которые составляют основу классической электродинамики, а остальные три — это закон Гаусса для магнетизма, закон Фарадея. индукции и закона Ампера с поправкой Максвелла.
Карл Фридрих Гаусс : Карл Фридрих Гаусс (1777–1855), картина Кристиана Альбрехта Йенсена
Закон Гаусса можно использовать для вывода закона Кулона и наоборот. Обратите внимание, что, поскольку закон Кулона применяется только к неподвижным зарядам, нет оснований ожидать, что закон Гаусса будет выполняться для движущихся зарядов, основываясь только на этом выводе. На самом деле закон Гаусса справедлив для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.
Обратите внимание, что, поскольку закон Кулона применяется только к неподвижным зарядам, нет оснований ожидать, что закон Гаусса будет выполняться для движущихся зарядов, основываясь только на этом выводе. На самом деле закон Гаусса справедлив для движущихся зарядов, и в этом отношении закон Гаусса является более общим, чем закон Кулона.
Проще говоря, закон Гаусса гласит, что: Общий направленный наружу нормальный электрический поток через любую замкнутую поверхность пропорционален общему электрическому заряду, заключенному внутри этой замкнутой поверхности.
Закон может быть выражен математически с использованием векторного исчисления в интегральной и дифференциальной формах, оба эквивалентны, поскольку связаны теоремой о дивергенции, также называемой теоремой Гаусса. Каждая из этих форм, в свою очередь, также может быть выражена двумя способами: через отношение между электрическим полем Е и полным электрическим зарядом или через электрическое поле смещения D и свободный электрический заряд.
Закон Гаусса имеет близкое математическое сходство с рядом законов в других областях физики, таких как закон Гаусса для магнетизма и закон Гаусса для гравитации. На самом деле любой «закон обратных квадратов» можно сформулировать аналогично закону Гаусса: например, сам закон Гаусса по существу эквивалентен закону обратных квадратов Кулона, а закон Гаусса для гравитации по существу эквивалентен закону обратных квадратов. квадратный закон всемирного тяготения Ньютона.
Лицензии и атрибуты
Содержимое по лицензии CC, опубликованное ранее
- Курирование и доработка. Предоставлено : Boundless.com. Лицензия : CC BY-SA: Attribution-ShareAlike
Лицензионный контент CC, конкретное указание авторства
- электрическое поле. Предоставлено : Викисловарь. Расположен по адресу : https://en.wiktionary.org/wiki/electric_field. Лицензия : CC BY-SA: Attribution-ShareAlike
- Электрический поток.
 Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike - Предоставлено : Wikimedia. Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/7/72/Flux_diagram.png. Лицензия : CC BY-SA: Attribution-ShareAlike
- Закон Гаусса. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- электрическое поле смещения. Предоставлено : Википедия. Лицензия : CC BY-SA: Attribution-ShareAlike
- электрический заряд. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- электрическое поле. Предоставлено : Викисловарь. Лицензия : CC BY-SA: Attribution-ShareAlike
- Предоставлено : Wikimedia.
 Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/7/72/Flux_diagram.png. Лицензия : CC BY-SA: Attribution-ShareAlike
Расположен по адресу : https://upload.wikimedia.org/wikipedia/commons/7/72/Flux_diagram.png. Лицензия : CC BY-SA: Attribution-ShareAlike - Предоставлено : Wikimedia. Лицензия : CC BY-SA: Attribution-ShareAlike
Электрический поток и закон Гаусса
В этой лекции мы узнаем об электрическом потоке и законе Гаусса. В электростатике основная цель закона Гаусса состоит в том, чтобы найти электрическое поле для данного распределения заряда, заключенного в замкнутую поверхность.
Вы можете посмотреть следующее видео или прочитать письменный учебник под видео.
Электрический поток
Чтобы понять закон Гаусса, сначала нам нужно понять термин Электрический поток.
Электрический поток — это скорость потока электрического поля через данную поверхность.
Это количество электрического поля, проникающего через поверхность. И эта поверхность может быть открытой или закрытой.
И эта поверхность может быть открытой или закрытой.
Электрический поток через открытые поверхности
Сначала мы рассмотрим пример электрического потока через открытую поверхность.
Красные линии представляют однородное электрическое поле. Мы внесем в это поле прямоугольник, представляющий собой открытую область, и разделим его на очень маленькие элементы, каждый размером dA (дифференциал площади).
Теперь мы сделаем площадь dA вектором с величиной dA. Направление вектора всегда перпендикулярно малому элементу dA.
Электрический поток, проходящий через эту небольшую площадь dφ (также называемый дифференциалом потока), определяется как скалярное произведение величины электрического поля E и величины площади вектора dA, умноженное на угол между этими два вектора θ.
Общий поток будет интегралом от dφ или интегралом по всей площади E·dA.
Это скалярная величина, и конечный результат может быть положительным или отрицательным . Если поток идет изнутри наружу, мы называем это положительным потоком, если он идет снаружи внутрь, это отрицательный поток.
Если поток идет изнутри наружу, мы называем это положительным потоком, если он идет снаружи внутрь, это отрицательный поток.
Единицей электрического потока является ньютон-метр в квадрате на кулон (Нм
2 /C).Чтобы лучше понять, что такое электрический поток, я внесу в это электрическое поле три прямоугольника. Фактически эти прямоугольники представляют собой один прямоугольник с разными ориентациями. Теперь давайте объясним поток через каждую из этих открытых областей.
В первом случае площадка перпендикулярна электрическому полю, а угол между их векторами θ равен 0°. Cos0° равен 1, поэтому электрический поток будет EdA. Здесь у нас , максимальный поток .
Во втором случае угол между E и dA θ равен 60°, а cos60° равен 0,5, поэтому электрический поток будет вдвое меньше EdA.
В третьем случае площадь параллельна электрическому полю, значит, их векторы перпендикулярны друг другу, а угол θ между ними равен 90°. Cos90° равен 0, поэтому электрический поток здесь будет равен 0. Это означает, что ничего не проходит через этот прямоугольник, поэтому у нас есть нулевой поток .
Это означает, что ничего не проходит через этот прямоугольник, поэтому у нас есть нулевой поток .
Связано: Закон Кулона
Электрический поток через замкнутые поверхности
Теперь давайте посмотрим на полностью замкнутую поверхность.
Как определить поток?
Здесь мы поместили нормали dAs в разных направлениях. По соглашению нормаль к замкнутой поверхности всегда направлена изнутри наружу.
Теперь мы можем рассчитать общий поток, проходящий через эту замкнутую поверхность. Полный поток равен интегралу от dφ по всей этой поверхности, который мы запишем как интеграл по этой замкнутой поверхности E·dA.
Суммарный поток может быть положительным, отрицательным или равным нулю. Если одинаковое количество потока входит и выходит из поверхности, у нас есть нулевой общий поток . Если уходит больше потока, чем поступает на поверхность, то мы имеем положительных суммарных потоков . Наоборот, если больше потока входит, чем уходит с поверхности, мы имеем отрицательный общий поток .
Закон Гаусса
Давайте рассмотрим другой пример и посмотрим, как электрический поток связан с законом Гаусса.
У нас есть точечный заряд +Q в центре сферы радиусом R. Теперь возьмем небольшой отрезок dA, вектор которого перпендикулярен поверхности и направлен радиально наружу. Электрическое поле, создаваемое Q в этой точке, также направлено радиально наружу. Это означает, что dA и E в любом месте на поверхности этой сферы параллельны друг другу, угол между ними θ равен 0°, а cos0° равен 1,9.0032
Дифференциал потока через небольшую площадь поверхности dφ равен EdA.
Полный поток Φ будет интегралом от dφ, который представляет собой интеграл по замкнутой поверхности EdA. Величина электрического поля везде одинакова, потому что расстояние от заряда одинаково в каждой точке, так что мы можем вытащить это из интеграла, и у нас останется EA.
Общая площадь сферы A равна 4πR 2 .
Из предыдущих видео мы знаем, что E равно k, умноженному на Q, деленному на r 2 , что равно Q, деленному на 4πE 0 R 2 .
И полный поток через эту замкнутую поверхность просто E умножить на 4πR 2 . Здесь мы можем сократить 4πR 2 и заметить, что общий поток равен Q, деленному на E 0 , где E 0 — диэлектрическая проницаемость свободного пространства.
Поток не зависит от расстояния r. Мы получили бы один и тот же результат независимо от размера замкнутой поверхности вокруг точечного заряда.
Что, если мы поместим больше зарядов внутрь закрытой поверхности?
Уравнение также должно выполняться для любой системы зарядов внутри.
Это приводит нас к закону Гаусса, который гласит, что электрический поток, проходящий через замкнутую поверхность, равен сумме всех зарядов Q внутри этой замкнутой поверхности, деленной на диэлектрическую проницаемость свободного пространства E 0 .
Если этот поток равен нулю, это означает, что внутри формы нет чистого заряда. Внутри формы могут быть положительные и отрицательные заряды, но сеть равна нулю.
Какой бы странной ни была форма, закон Гаусса всегда выполняется, пока существует симметрия в распределении заряда внутри поверхности.
Итак, чтобы рассчитать электрическое поле, вам нужна симметрия. И есть три типа симметрии : сферическая, цилиндрическая и плоская симметрия.
См. также: Что такое электрический заряд и как работает электричество
Сферическая симметрия: электрическое поле, вызванное точечным зарядом
Мы начнем со сферической симметрии.
Это тонкая полая сфера радиусом R, и мы нанесем на тонкую оболочку положительный заряд Q. Заряд распределен равномерно.
Теперь нужно найти электрическое поле внутри сферы, на расстоянии R 1 от центра, и вне сферы, на расстоянии R 2 от центра. Для этого нам нужно определить нашу поверхность Гаусса. В этом случае мы выберем концентрические сферы в качестве поверхностей Гаусса, одну меньшую с радиусом R 1 и другие более крупные с радиусом R 2 .
Теперь нам нужно использовать два аргумента симметрии, которые помогут нам рассчитать электрическое поле:
- Первый аргумент симметрии показывает, что величина электрического поля одинакова в любой точке, так как заряд здесь распределен равномерно.
- Второй аргумент симметрии показывает, что если есть электрическое поле, оно должно быть направлено либо радиально наружу, либо радиально внутрь. В этом примере у нас есть положительный заряд, что означает, что поле направлено наружу.
Из предыдущих уравнений мы знаем, что площадь поверхности сферы, равная 4πr 2 , умноженная на величину электрического поля E, равна заряду внутри сферы Q, деленному на диэлектрическую проницаемость свободного пространства. Е 0 . Но у нас нет заряда внутри меньшей сферы, поэтому электрическое поле равно нулю.
Если замкнутая поверхность не имеет заключенного в ней суммарного заряда, то суммарный поток через нее будет равен нулю.
Теперь давайте посмотрим, что происходит с большей сферой.
Аргументы симметрии справедливы и для этой сферы. Но если мы посмотрим на уравнение, то заметим, что Q не равно нулю, внутри этой сферы есть заряд.
Итак, величина электрического поля будет равна Q заключенному делённому на 4πE 0 R 2 2 .
График для сферической симметрии
На этом графике мы имеем расстояние r по оси x и величину электрического поля E по оси y. До точки R, которая является радиусом нашей исходной сферы, у нас нет электрического поля, но затем оно достигает своего максимального значения и уменьшается по мере увеличения расстояния.
Связанный: Работа и электрическая потенциальная энергия
Цилиндрическая симметрия: электрическое поле, обусловленное линией заряда
Второй тип симметрии — цилиндрическая симметрия.
Допустим, у нас есть бесконечная линия положительного заряда с однородной линейной плотностью заряда λ, и мы хотим выяснить, каково электрическое поле в некоторой точке над линией на расстоянии R. Здесь мы выберем цилиндр как гауссова поверхность с центром вдоль линии заряда. У нас нет электрического поля через торцевые крышки, электрическое поле будет направлено через стенку цилиндра. Кроме того, здесь у нас есть симметрия, которая позволяет нам использовать закон Гаусса для расчета электрического поля.
Здесь мы выберем цилиндр как гауссова поверхность с центром вдоль линии заряда. У нас нет электрического поля через торцевые крышки, электрическое поле будет направлено через стенку цилиндра. Кроме того, здесь у нас есть симметрия, которая позволяет нам использовать закон Гаусса для расчета электрического поля.
Мы можем рассчитать поток, используя то же уравнение, которое мы использовали ранее. Но теперь нам нужно найти площадь поверхности цилиндра, включая стенку, без торцевых крышек. Для этого нам нужно разрезать цилиндр по его длине, и мы обнаружим, что площадь равна 2πrL. Таким образом, 2πRL, умноженное на E, равно заключенному заряду, деленному на E 0 .
Плотность заряда λ представляет собой общий заряд Q на длину L, поэтому Q , заключенный в , равен λL. Итак, 2πRLE равно λL, деленному на E 0 .
Электрическое поле равно λL, деленному на 2πRLE 0 . L компенсируется, поэтому электрическое поле равно λ, деленному на 2πRE 0 .
Плоская симметрия: электрическое поле бесконечной пластины
Последний тип симметрии — плоская симметрия.
В этом примере у нас есть плоская бесконечно большая горизонтальная пластина. Нанесем на эту пластину заряд с равномерной плотностью заряда σ.
σ фактически представляет собой количество заряда на единицу площади, выраженное в кулонах на квадратный метр (Кл/м 2 ).
Теперь мы хотим рассчитать электрическое поле вокруг этой пластины, скажем, на расстоянии d. В этом случае мы снова выберем цилиндр в качестве поверхности Гаусса. Цилиндр пересекает пластину, и в этом пересечении заключен заряд.
Чтобы рассчитать электрическое поле, необходимо выполнить три условия:
- Во-первых, торцевые крышки цилиндра площадью A должны быть параллельны пластине.
- Во-вторых, стенки цилиндра должны быть перпендикулярны пластине.
- В-третьих, расстояние от пластины до торцевых заглушек d должно быть одинаковым над и под пластиной.

Теперь, когда мы выполнили требования симметрии, мы можем рассчитать электрическое поле, используя закон Гаусса. У нас не будет горизонтальной составляющей электрического поля, только вертикальная, выходящая из двух торцевых крышек.
σ равен заряду, деленному на поверхность. Из этого уравнения видно, что заряд Q равен σ, умноженному на площадь A.
Поток от стенки цилиндра равен нулю, поэтому общий поток состоит из двух составляющих: потока через верхнюю крышку плюс поток через нижнюю крышку цилиндра. Это равно Q , заключенному в , деленному на E 0 , или σA, деленному на E 0 . Но также поток через верх и поток через низ можно выразить как EA, поэтому общий поток равен 2EA.
Наконец, электрическое поле равно сигме, деленной на 2E 0 .
Если пластина заряжена положительно, электрическое поле будет направлено наружу. Если бы пластина была заряжена отрицательно, электрическое поле было бы направлено внутрь.
График плоской симметрии
Если мы нарисуем график с расстоянием d по оси x и электрическим полем E по оси y, мы заметим, что электрическое поле имеет постоянное значение σ/2E 0 , и это не зависит от расстояния до самолета.
Связано: электрический потенциал и разность электрических потенциалов (напряжение)
Плоская симметрия: электрическое поле, создаваемое двумя параллельными пластинами
Теперь давайте рассмотрим другую, более сложную ситуацию с двумя бесконечно большими параллельными пластинами.
Первая пластина имеет поверхностную плотность заряда +σ, а нижняя пластина имеет поверхностную плотность заряда -σ. Расстояние между ними d.
Итак, что такое электрическое поле в любом месте космоса?
Положительно заряженная пластина имеет направленное от пластины электрическое поле, равное σ/2E 0 . Она не зависит от расстояния до плиты, поэтому продолжается ниже.
Отрицательно заряженная пластина имеет направленное к пластине электрическое поле, также равное σ/2E 0 .
Чтобы рассчитать полное электрическое поле, мы воспользуемся принципом суперпозиции путем сложения векторов.
Векторы, направленные в противоположные стороны, компенсируются, поэтому электрическое поле здесь равно нулю. Векторы между пластинами имеют одинаковое направление, поэтому электрическое поле равно σ/E 0 .
Линии электрического поля будут направлены от положительно заряженной пластины к отрицательно заряженной пластине, а электрическое поле снаружи будет равно нулю.
Это все, что касается электрического потока и закона Гаусса. Надеюсь, вам понравился этот урок и вы узнали что-то новое. Не стесняйтесь задавать любые вопросы в разделе комментариев ниже.
Электрический заряд и электрическое поле — Электрический поток, закон Кулона, примеры задач
Слово « электричество » происходит от греческого слова «Электрон», что означает « янтарь ». Магнитные и электрические силы, присутствующие в материалах, атомах и молекулах, влияют на их свойства. Термин «электрический заряд» относится всего к двум типам сущностей. Эксперимент выявил две формы электризации: во-первых, одноименные заряды, которые отталкиваются друг от друга, и во-вторых, разноименные заряды, которые притягиваются друг к другу. Полярность заряда является отличительным элементом между этими двумя видами зарядов.
Термин «электрический заряд» относится всего к двум типам сущностей. Эксперимент выявил две формы электризации: во-первых, одноименные заряды, которые отталкиваются друг от друга, и во-вторых, разноименные заряды, которые притягиваются друг к другу. Полярность заряда является отличительным элементом между этими двумя видами зарядов.
Эксперимент с электрическими зарядами, генерируемыми фрикционным электричеством, показал, что проводники способствуют прохождению электрического заряда, а изоляторы — нет. Металлы, земля и человеческие тела являются проводниками, тогда как фарфор, нейлон и дерево являются изоляторами, обеспечивающими существенное сопротивление потоку электричества через них.
Электрическое поле
Электрический заряд создает электрическое поле, представляющее собой область пространства вокруг электрически заряженной частицы или объекта, где заряд ощущается принудительно. Электрическое поле существует повсюду в пространстве и может быть изучено путем введения в него другого заряда.
Если заряды достаточно далеко друг от друга, электрическое поле может быть приблизительно равно нулю для практических целей. Электрические поля представляют собой векторную величину, представленную стрелками, указывающими на заряды или от них. Линии должны указывать радиально наружу, от положительного заряда, или радиально внутрь, к отрицательному заряду.
Величина электрического поля рассчитывается по формуле:
E = F/q
- где E — напряженность электрического поля,
- F — электрическая сила,
- q — пробный заряд.
Свойства линий электрического поля
- Линии электрического поля представляют собой непрерывные кривые.
- Они начинаются с положительно заряженного тела и заканчиваются отрицательно заряженным.
- Направление напряженности электрического поля в любой точке определяется касательной к линии электрического поля.
- Не существует двух пересекающихся линий электрического поля.

- Линии электрического поля всегда параллельны поверхности проводника.
Закон Кулона
Сила, существующая между двумя точечными зарядами, описывается законом Кулона. В физике термин «точечный заряд» относится к тому факту, что линейно заряженные объекты имеют малый размер по сравнению с расстоянием между ними. В результате мы рассматриваем их как точечные заряды, поскольку вычислить силу притяжения/отталкивания между ними несложно.
Графическое представление закона Кулона
Заявление, как правило, включает два заряда: q 1 и q 2 . Сила притяжения/отталкивания между зарядами обозначается буквой «F», а расстояние между ними — буквой «r». Тогда закон Кулона выражается математически как величины контактирующих зарядов, т. е. F ∝ q 1 q 2 .
F обратно пропорциональна квадрату расстояния между двумя контактирующими зарядами, то есть F ∝ 1/ r 2 .
Давайте сложим их вместе следующим образом:
F ∝ q 1 q 2 / r 2
Теперь, если мы введем k, удалим пропорциональность;
F = k q 1 q 2 / r 2
где k — константа пропорциональности, равная 1/40, а 0 — эпсилон not, который обозначает диэлектрическую проницаемость вакуума. k было рассчитано равным 9× 10 9 Н·м 2 / C 2 .
k было рассчитано равным 9× 10 9 Н·м 2 / C 2 .
Согласно Кулону, одноименные заряды отталкиваются, а разноименные притягиваются. Это указывает на то, что заряды одного знака отталкиваются, а заряды противоположных знаков притягиваются.
Электрический поток
Электрический поток — это общее количество линий электрического поля, проходящих через определенную область за заданный промежуток времени. Однако, в отличие от потока жидкости, здесь нет потока физически наблюдаемой величины.
Прежде всего, определение электрического потока через элемент площади S выглядит следующим образом:
Δθ= E.ΔS= E ΔS cosθ
Количество силовых линий, пересекающих элемент площади, определяет это. В данном случае угол — это угол, образованный точками E и S. На замкнутой поверхности, когда предварительно установлено соглашение, это угол, образованный точкой E и внешней нормалью к элементу площади. Чтобы определить общий поток через заданную поверхность, разделите ее на элементы небольшой площади, вычислите поток на каждом элементе, а затем сложите их вместе. В результате полный поток через поверхность S равен E.S. Поскольку электрическое поле E предполагается постоянным на элементе малой площади, используется символ аппроксимации.
Чтобы определить общий поток через заданную поверхность, разделите ее на элементы небольшой площади, вычислите поток на каждом элементе, а затем сложите их вместе. В результате полный поток через поверхность S равен E.S. Поскольку электрическое поле E предполагается постоянным на элементе малой площади, используется символ аппроксимации.
Электрический диполь: Он состоит из пары одинаковых или противоположных зарядов A и -B, разделенных 2x. Вектор дипольного момента имеет величину 2Ax и указывает от -B до A в направлении оси диполя.
Примеры вопросов
Задача 1. Заряд 2 Кл помещен в центр 8-сантиметрового 3 куба. Какова величина электрического потока, проходящего через одну из граней?
Решение:
Поскольку объем данного куба равен 8 см3, длина его стороны равна 2 см.
Электрический поток над замкнутой поверхностью равен заряду, заключенному внутри замкнутой поверхности, деленному на диэлектрическую проницаемость среды в соответствии с теоремой Гаусса.
Если среда внутри куба воздух или вакуум, то полный электрический поток через замкнутую поверхность равен
= Q / Eo
= 2 / ( 8,854 10 -12 )
= 2,259 N 10 9
102978 1 -1 м 2 .Электрический поток, проходящий через одну грань = ( 2,259 × 10 11 ) / 6 = 3,765 × 10 10 N C -1 м 2 .
Задача 2: Почему две линии электрического поля никогда не пересекаются?
Решение:
В точке, где соединяются две линии, будут две касательные и, следовательно, два направления чистого электрического поля, что невозможно. В результате две линии электрического поля не пересекаются.
Задача 3: Сила 8 Н действует, когда два точечных заряда, разделенных расстоянием 1 м, имеют одинаковые заряды. Какую силу они почувствуют, если их обоих одновременно погрузить в воду? (Предположим, что K воды = 80)
Решение:
Сила, действующая между двумя точками
F воздух = Q1Q2/4πeoxr2
F Water = Q1Q2/4πeokxr2
.
вода=80
F вода=8/80
=1/10N
Задача 4: Как уменьшается электрическое поле внутри диэлектрика, когда он помещен во внешнее электрическое поле?
Решение:
Когда на диэлектрик воздействует электрическое поле (вектор E), в нем индуцируется заряд, создавая электрическое поле в направлении, противоположном направлению E. В результате результирующее электрическое поле равно пониженный.
E net = вектор E −Ep
, где Ep обозначает поле, создаваемое диэлектрической поляризацией.
Задача 5. Рассмотрим систему из двух зарядов величиной 3 × 10-7 Кл и 4 × 10-7 Кл, на которые действует сила 0,1 Н. Каково расстояние между двумя зарядами?
Решение:
Учитывая, что
Первый заряд, q 1 равен 3 × 10 -7 C.
Второй заряд, q0524 2 равно 4 × 10 -7 Кл.
Сила, действующая на них, F равна 0,1 Н.
Формула для расчета электростатической силы между зарядами: / r 2
Подставьте указанные значения в приведенное выше выражение как (4 × 10 -7 С) / (r) 2
r = 0,103 м
Следовательно, расстояние между двумя зарядами r равно 0,103 м.
Узнать о выражении для электрического потока
выражение для электрического потока Определение
Электрический поток можно описать как свойство электрического поля, отображающее кластер из двух или более линий электрического поля, пересекающихся друг с другом в определенной области . Эти линии электрического поля также называются электрическими силовыми линиями, и считается, что они возникают или генерируются положительными электрическими зарядами и заканчиваются на отрицательном конце. Теперь линии электрического поля
направленные к компактной или замкнутой поверхности, считаются отрицательными. В то время как линии электрического поля, направленные наружу от замкнутой поверхности, считаются положительными. Таким образом, электрический поток обеспечивает меру скорости потока электрических зарядов через определенную область.
В то время как линии электрического поля, направленные наружу от замкнутой поверхности, считаются положительными. Таким образом, электрический поток обеспечивает меру скорости потока электрических зарядов через определенную область.
Обзор выражения для электрического потока
В соответствии с электромагнетизмом мера электрического поля, проходящего через определенную или заданную замкнутую поверхность, представлена электрическим потоком. Однако электрическое поле не следует понимать как текущее физически или буквально, а как описание напряженности поля, вызванного зарядом из точки. Электрическое поле может оказывать воздействие на любой электрический заряд в любом месте в пространстве или в непосредственной близости, и поле пропорционально градиенту напряжения.
Электрон представляет собой электрический заряд в космосе, вокруг него должно быть электрическое поле, которое его окружает. Заряд излучает силовые линии или потоки. Эти силовые линии также называются линиями Гаусса. Электрический поток прямо пропорционален количеству силовых линий в электрическом поле или силовых линий, проходящих через замкнутое пространство. Как уже было описано, линии электрического поля
движение внутрь к закрытой поверхности считается отрицательным, а удаление считается положительным. Однако, учитывая ситуацию, когда суммарный заряд замкнутой системы равен нулю, силовые линии будут продолжаться внутри поверхности, а затем будут направлены наружу в пространстве. Отрицательный поток равен положительному потоку по величине, таким образом, суммарный чистый поток равен нулю. В отличие от этого, если есть значительное количество отрицательных или положительных
заряженных внутри замкнутой системы, поверхностный поток будет соответственно ему пропорционален.
Эти силовые линии также называются линиями Гаусса. Электрический поток прямо пропорционален количеству силовых линий в электрическом поле или силовых линий, проходящих через замкнутое пространство. Как уже было описано, линии электрического поля
движение внутрь к закрытой поверхности считается отрицательным, а удаление считается положительным. Однако, учитывая ситуацию, когда суммарный заряд замкнутой системы равен нулю, силовые линии будут продолжаться внутри поверхности, а затем будут направлены наружу в пространстве. Отрицательный поток равен положительному потоку по величине, таким образом, суммарный чистый поток равен нулю. В отличие от этого, если есть значительное количество отрицательных или положительных
заряженных внутри замкнутой системы, поверхностный поток будет соответственно ему пропорционален.
Есть вопрос по этой теме?
Что вы узнаете:
- Выражение для определения электрического потока
- Обзор выражения для электрического потока
- Составление электрического потока
- Закон Гаусса и электрический флюкс
- • Интегральная форма в Законе Гусса
Flux
Flux

Рассмотрим сценарий силовых линий электрического поля величиной E, проходящих через поверхность векторной площади S и поле однородное. Угол между силовыми линиями электрического поля и нормалью равен θ. Следуя определению, количество силовых линий, проходящих через электрическое поле в данную единицу времени, называется электрическим потоком. Во-первых, учитывая, что угол перпендикулярен силовым линиям или потоку заряда, таким образом, выражение для электрического потока дается как
∅P=ES\emptyset_{P}=ES∅P=ES
Рис. (2)
Теперь, учитывая, что плоскость наклонена, θ представляет собой угол между плоскостью и параллельной осью к потоку заряда, таким образом, имея некоторую величину. Таким образом, проектируемая площадь для силовых линий задается как Scosθ{\mathop{\rm Scos}\nolimits} \thetaScosθ. Мера электрического потока выражается as,
∅=EScosθ\emptyset= ES\cos \theta∅=EScosθ
Далее важно учитывать наличие неоднородного поля для потока. Малая поверхность dS рассматривается для электрического потока d∅Ed{\emptyset _E}d∅Eи может быть представлена как
Малая поверхность dS рассматривается для электрического потока d∅Ed{\emptyset _E}d∅Eи может быть представлена как
Электрический поток можно описать как произведение электрического поля и составляющей площади, перпендикулярной электрическому полю. Однако в случае, когда площадь не плоская, оценка электрического поля может быть достигнута с помощью интеграла площади, поскольку угол будет подвергаться изменению. Таким образом, электрический поток будет выражен как на рассматриваемую территорию. Направление вектора также перпендикулярно рассматриваемой области.
Закон Гаусса и электрический поток
Закон Гаусса устанавливает связь между распределением электрического заряда и его результатом в электрическом поле. В физике закон Гаусса гласит, что чистое количество электрического заряда, нормального и направленного наружу через замкнутую систему, пропорционально чистому заряду, содержащемуся внутри системы. Этот закон в физике обычно выражается математически с использованием интеграла и дифференциала векторного исчисления, поскольку оба относятся к теореме о дивергенции. Эти две формы далее, возможно, выражаются двумя основными способами. Один представляет собой отношение между электрическим полем и суммарным электрическим зарядом, а другой — электрическое поле смещения со свободным электрическим зарядом.
Эти две формы далее, возможно, выражаются двумя основными способами. Один представляет собой отношение между электрическим полем и суммарным электрическим зарядом, а другой — электрическое поле смещения со свободным электрическим зарядом.
Рис. (3)
В соответствии с законом Гаусса результирующая электрическая сила, выходящая из замкнутого устройства или системы, будет равна заряду, содержащемуся или заключенному внутри системы, деленному на диэлектрическую проницаемость. Это может быть определено как
∅=Q0\emptyset= \frac{Q}{{{_0}}}∅=0Q
Закон Гаусса, однако, является полезным инструментом, который можно использовать для оценки количество заключенного или содержащегося заряда в системе. Это можно было бы сделать с помощью хорошего отображения электрического поля на поверхности вне распределения заряда. Это упрощает оценку и расчет электрического поля. Другим способом было бы визуализировать и рассмотреть площадь A, которая может измерять поток, перпендикулярный этой области. Чистая мера заряда в закрытой системе будет определяться как
Чистая мера заряда в закрытой системе будет определяться как
Δ∅=EΔA\Delta \emptyset= E\Delta AΔ∅=EΔA
• Интегральная форма в законе Гаусса
Интеграл площади по электрическому полю относительно любой замкнутой поверхности будет равен свободной или чистой поверхности заряд, содержащийся в системе или на поверхности, деленный на диэлектрическую проницаемость среды. Этот процесс помогает в оценке электрического поля путем формирования гауссовой поверхности вблизи распределения заряда и, таким образом, расчета потока через систему.
∮E⃗⋅dA→=Q0\oint {\vec E} \cdot \overrightarrow {dA}=\frac{Q}{{{_0}}}∮E⋅dA=0Q
Рис. 4 Электрический поток в системе СИ измеряется в вольт-метрах (В·м).
Продолжайте учиться
Что следует изучить дальше на основе учебной программы колледжа
Электрический токЭлектрический потенциал Проблемы с энергиейТерапия электрическим полемРазница электрических потенциаловЭлектробезопасностьЭлектрометрЭлектростатический воздухоочистительИндукционная катушка
Закон Гаусса для электрических полей.
 Электромагнитная геофизика
Электромагнитная геофизикаРис. 32 Зарядка прилагается
Закон Гаусса для электрического поля описывает статическое электрическое поле генерируются распределением электрических зарядов. В нем указано, что электрический поток через любую замкнутую поверхность пропорционален полному электрическому заряду окруженный этой поверхностью. Условно положительный электрический заряд генерирует положительное электрическое поле. Закон был опубликован посмертно в 1867 г. как часть сборник работ известного немецкого математика Карла Фридриха Гаусс.
Интегральное уравнение
Закон Гаусса в интегральной форме приведен ниже:
(34)\[\int_V \boldsymbol{\nabla} \cdot \mathbf{e} \; ~dv =\oint_{S} \mathbf{e} \cdot \hat{\mathbf{n}} \; ~da = \frac{Q}{\varepsilon_{0} }\;,\]
где:
\(\mathbf{e}\) — электрическое поле
\(Q\) — вложенный электрический заряд
\(\varepsilon_0\) — электрическая проницаемость свободного пространства
\(\hat{\mathbf{n}}\) — нормаль, направленная наружу
Поток — это мера силы поля, проходящего через поверхность. Электрический поток в целом определяется как
Электрический поток в целом определяется как
(35)\[\boldsymbol{\Phi} = \int_S \mathbf{e} \cdot \hat{\mathbf{n}} \, \mathrm{d}a.\]
Мы можем думать об электрическом поле как о плотности потока. Закон Гаусса говорит нам, что чистый электрический поток через любую замкнутую поверхность равен нулю, если только объем не ограничен этой поверхностью содержит чистый заряд.
Дифференциальная форма
Рассматривая пространственно протяженное заряженное тело, мы можем думать о его заряде постоянно распределяется по всему телу с плотностью \(\ро\). Тогда общий заряд определяется интегралом от заряда плотность по объему тела.
(36)\[Q = \int_V \rho \; \mathrm{d}v\;.\]
Используя это определение и применяя теорему о расходимости к левой руке части закона Гаусса (34), мы можем переписать закон как:
(37)\[\int_V \boldsymbol{\nabla} \cdot \mathbf{e} \; \mathrm{d}v = \int_V \frac{\rho}{\varepsilon_0} \; \mathrm{d}v \;.\]
Поскольку это уравнение должно выполняться для любого объема \(V\), мы можем приравнять интегранты, дающие дифференциальную форму закона Гаусса:
(38)\[\boldsymbol{\nabla} \cdot \mathbf{e} = \frac{\rho}{\varepsilon_0}. \]
\]
Можно показать, что закон Гаусса для электрических полей эквивалентен закону Кулона закон (см. Эквивалентность закона Гаусса для электрических полей закону Кулона)
Закон Гаусса в материи
Закон Гаусса для электрических полей легче всего понять, если пренебречь электрическим смещением (\(\mathbf{d}\)). В веществе диэлектрическая проницаемость может не равняться диэлектрической проницаемости свободного пространства (т.е. \(\varepsilon \neq \varepsilon_0\)). В материи плотность электрических зарядов можно разделить на «свободную» плотность заряда (\(\rho_f\)) и «ограниченную» плотность заряда (\(\rho_b\)), так что:
(39)\[\rho = \rho_f + \rho_b\]
Плотность свободного заряда относится к зарядам, которые свободно текут под действием электрического поля; т. е. они производят ток без дивергенции. Плотность ограниченного заряда относится к электрическим зарядам, связанным с электрической поляризацией (\(\mathbf{p}\)). Комбинируя уравнения (38) и (39) с нашим определением электрической поляризации, мы находим, что:
(40)\[\nabla \cdot \mathbf{d} — \nabla \cdot \mathbf{p} = \rho_f + \rho_b\]
Используя определяющее соотношение \(\mathbf{d} = \varepsilon \mathbf{e}\) и разделив предыдущее уравнение на ограниченный и свободный вклады, мы находим, что:
(41)\[-\набла\cdot\mathbf{p} = \rho_b\]
и
(42)\[\набла\cdot\mathbf{d} = \rho_f\]
Приведенное выше уравнение представляет собой дифференциальную форму уравнения Гаусса в материи .



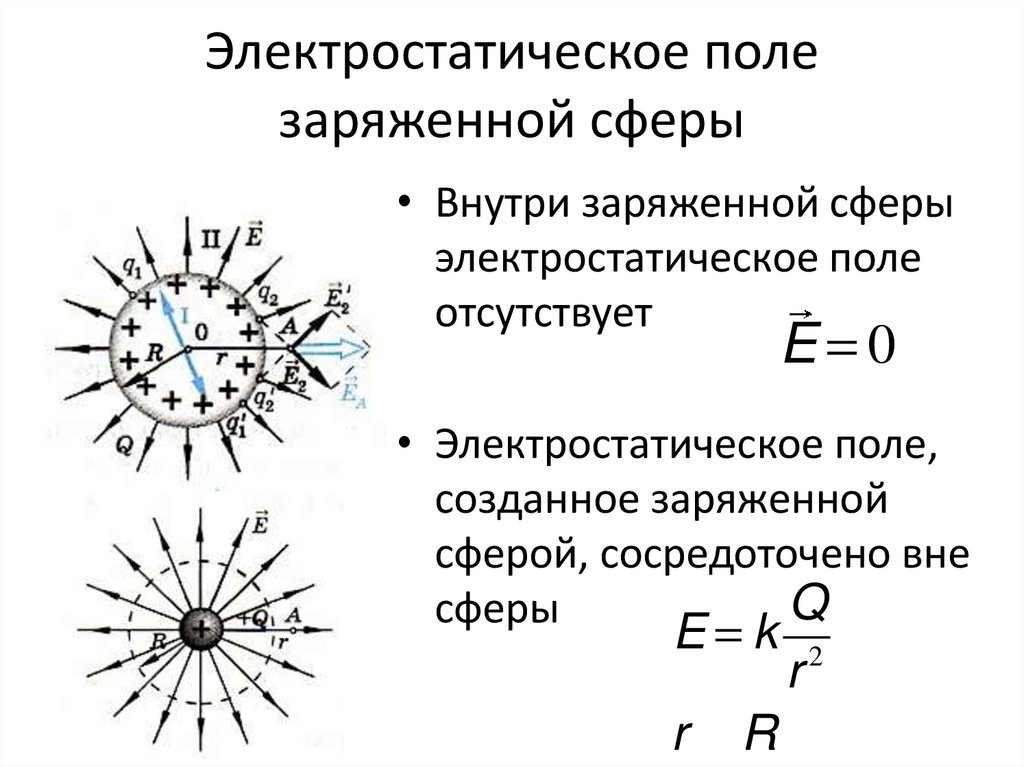
 Поэтому:
Поэтому:

 3
3  4а). Объем шарового слоя , тогда , а .Интегрируя, получим:
4а). Объем шарового слоя , тогда , а .Интегрируя, получим: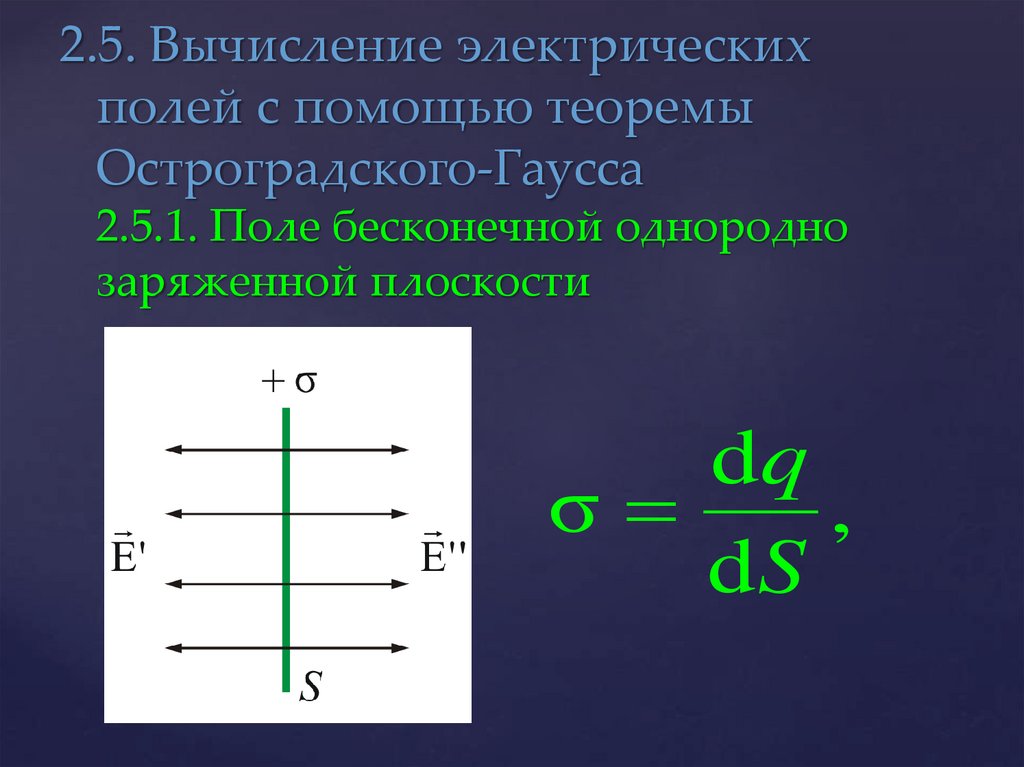 4а
4а  Согласно теореме Гаусса:
Согласно теореме Гаусса: 5б
5б 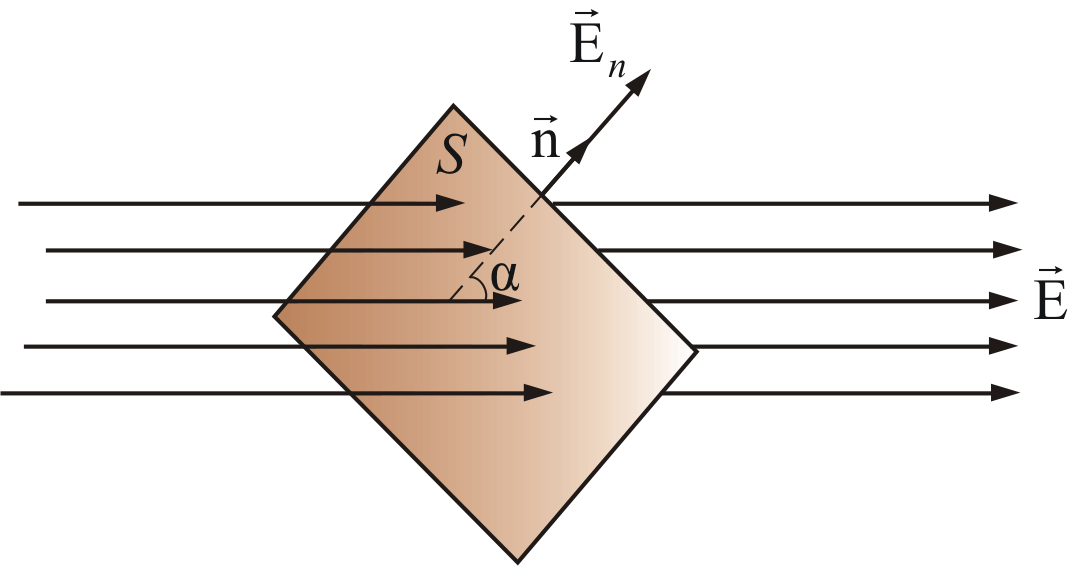

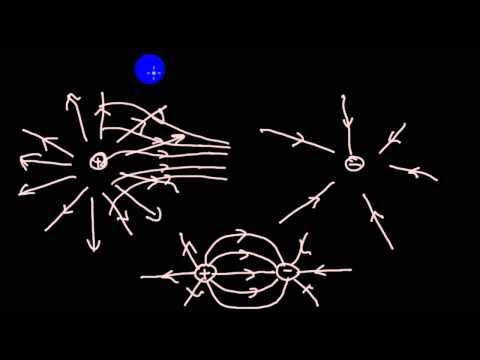
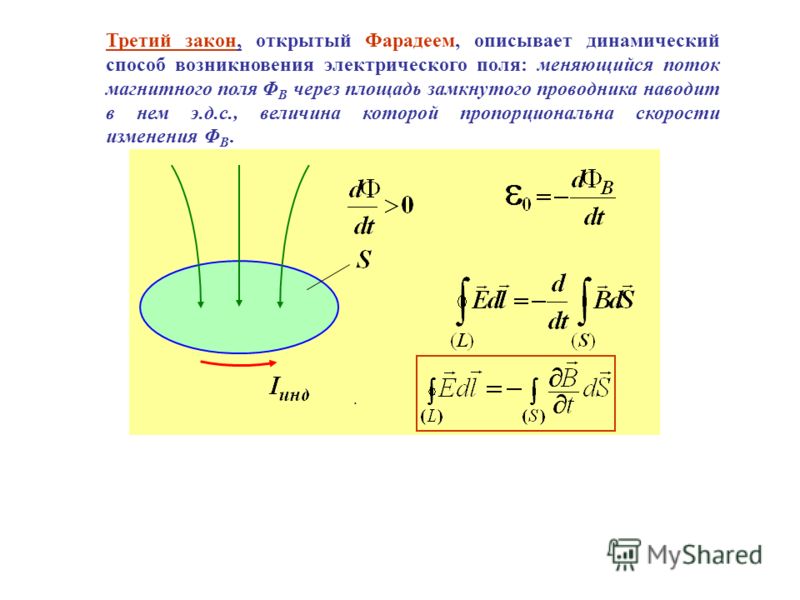 Зависимость Ex(x) представьте графически.
Зависимость Ex(x) представьте графически.


 к. , S- площадь боковой поверхности. Из теоремы Гаусса следует:
к. , S- площадь боковой поверхности. Из теоремы Гаусса следует: Ввиду той же симметрии величина Е может зависеть только от расстояния до оси:
Ввиду той же симметрии величина Е может зависеть только от расстояния до оси: 13
13 41 Mb.
41 Mb. 43)
43) 49)
49) 50)
50)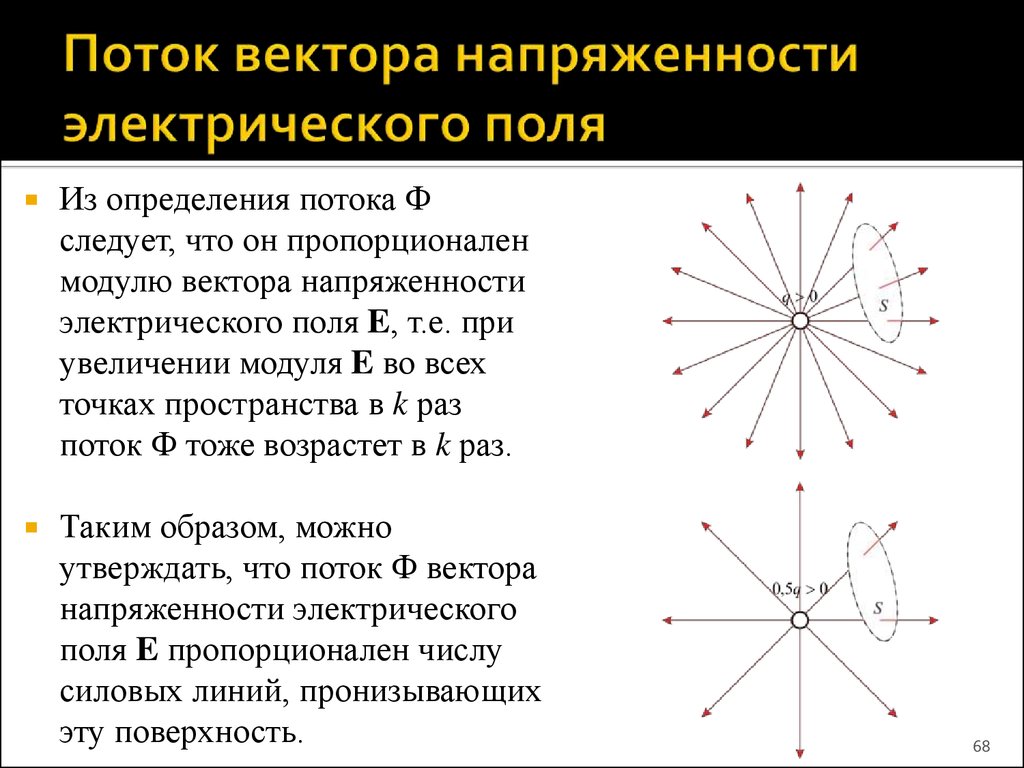 53)
53) 55)
55) 58)
58) 60)
60)