Электродвижущая сила формула
Для поддержания электрического тока в проводнике длительное время, необходимо чтобы от конца проводника, имеющего меньший потенциал учтем, что носители тока предполагаются положительными зарядами постоянно убирались доставляемые током заряды, при этом к концу с большим потенциалом заряды постоянно подводились. То есть следует обеспечить круговорот зарядов. В этом круговороте заряды должны перемещаться по замкнутому пути. Движение носителей тока при этом реализуется при помощи сил неэлектростатического происхождения. Такие силы именуются сторонними.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- III.
Основы электродинамики
Работа сторонних сил в цепи постоянного тока и источники ЭДС - Электродвижущая сила
- ЭДС. Закон Ома для полной цепи
- Электродвижущая сила и напряжение источника тока
- Электродвижущая сила.
- Связь ЭДС и напряжения
- Формула ЭДС
- Электродвижущая сила и конечное напряжение
III. Основы электродинамики
Загрузить всю книгу. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счёт работы сил не электростатического происхождения. Такие устройства называют источниками тока , а силы не электростатического происхождения — называют сторонними. Сторонние силы способны перемещать заряды от точки с меньшим потенциалом к точке с большим потенциалом. Природа сторонних сил может быть различна, эти силы могут быть обусловлены химическими процессами, электрическими полями но не электростатическими , порождаемыми меняющимися во времени магнитными полями.
Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счёт работы сил не электростатического происхождения. Такие устройства называют источниками тока , а силы не электростатического происхождения — называют сторонними. Сторонние силы способны перемещать заряды от точки с меньшим потенциалом к точке с большим потенциалом. Природа сторонних сил может быть различна, эти силы могут быть обусловлены химическими процессами, электрическими полями но не электростатическими , порождаемыми меняющимися во времени магнитными полями.
Характеристикой сторонних сил является ЭДС :. ЭДС — физическая величина равная отношению работы сторонних сил по перемещению положительного единичного заряда к величине этого заряда:. Сторонняя сила , действующая на заряд q , может быть выражена как:. Разделив эту работу на q , получим ЭДС, действующую на данном участке 1—2, то есть ,. В цепи, кроме сторонних сил, действуют ещё и электростатические силы:.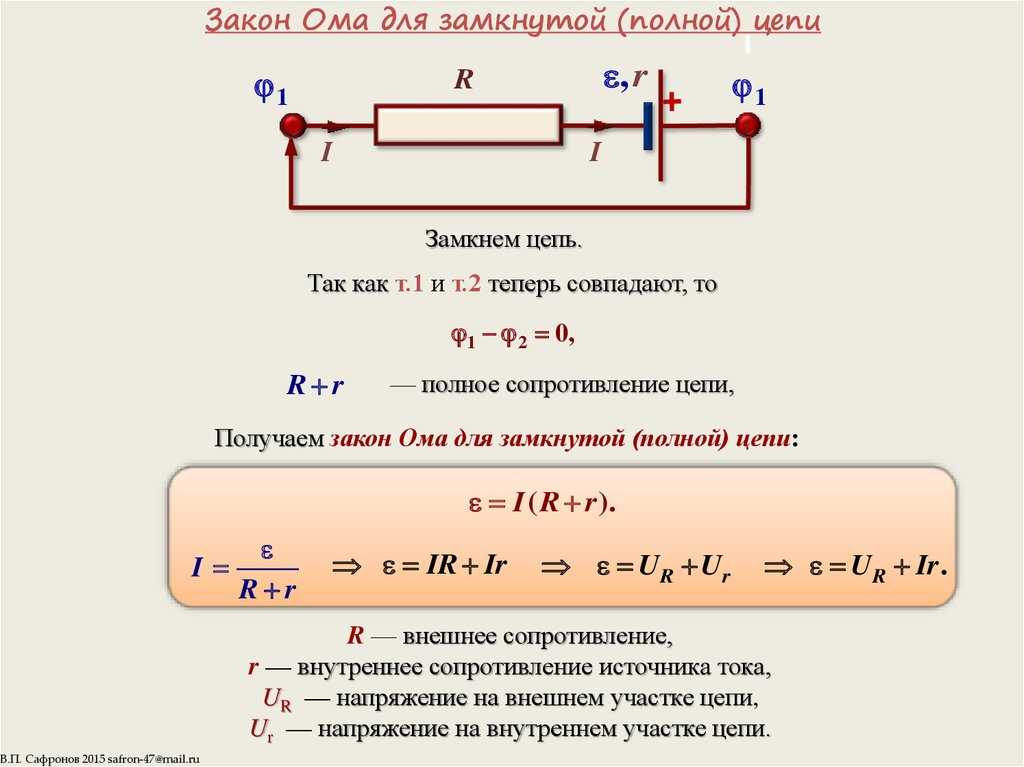
Работа, совершаемая этой силой над зарядом q на участке цепи , определяется выражением:. Величина, численно равная работе, совершаемой электростатическими и сторонними силами при перемещении положительного единичного заряда, называется падением напряжения или просто напряжением — U на данном участке цепи.
Участок цепи, на котором на носители тока действуют сторонние силы, называются неоднородным, для него:. Электронное хранилище учебных материалов Курс лекций, модуль 5.
Работа сторонних сил в цепи постоянного тока и источники ЭДС
В электротехнике источники питания электрических цепей характеризуются электродвижущей силой ЭДС. Во внешней цепи электрического контура электрические заряды двигаются от плюса источника к минусу и создают электрический ток. Для поддержания его непрерывности в цепи источник должен обладать силой, которая смогла бы перемещать заряды от более низкого к более высокому потенциалу. Такой силой неэлектрического происхождения и является ЭДС источника. Например, ЭДС гальванического элемента. ЭДС представляет собой работу, которую совершают сторонние силы для перемещения единичного заряда по электрической цепи.
Такой силой неэлектрического происхождения и является ЭДС источника. Например, ЭДС гальванического элемента. ЭДС представляет собой работу, которую совершают сторонние силы для перемещения единичного заряда по электрической цепи.
Количественной мерой электрического тока служит сила тока I – скалярная физическая . Формула Электродвижущая сила источника тока (ЭДС).
Электродвижущая сила
На нашем сайте собрано более бесплатных онлайн калькуляторов по математике, геометрии и физике. Не можете решить контрольную?! Мы поможем! Более 20 авторов выполнят вашу работу от руб! Здесь — ЭДС, — работа сторонних сил, — величина заряда. ЭДС — скалярная величина. В замкнутом контуре ЭДС равна работе сил по перемещению аналогичного заряда по всему контуру. При этом ток в контуре и внутри источника тока будут течь в противоположных направлениях. Внешняя работа, которая создаёт ЭДС, должна быть не электрического происхождения сила Лоренца, электромагнитная индукция, центробежная сила, сила, возникающая в ходе химических реакций.
ЭДС. Закон Ома для полной цепи
В разгар учебного года многим ученым деятелям требуется эдс формула для разных расчетов. Эксперименты, связанные с гальваническим элементом, так же нуждаются в информации об электродвижущей силе. Но для начинающих не так-то просто понять, что же это такое. ЭДС или электродвижущая сила — это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового положительного заряда вдоль всего контура.
Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения т. Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами.
Электродвижущая сила и напряжение источника тока
В электротехнике источники питания электрических цепей характеризуются электродвижущей силой ЭДС. Во внешней цепи электрического контура электрические заряды двигаются от плюса источника к минусу и создают электрический ток. Для поддержания его непрерывности в цепи источник должен обладать силой, которая смогла бы перемещать заряды от более низкого к более высокому потенциалу. Такой силой неэлектрического происхождения и является ЭДС источника. Например, ЭДС гальванического элемента.
Во внешней цепи электрического контура электрические заряды двигаются от плюса источника к минусу и создают электрический ток. Для поддержания его непрерывности в цепи источник должен обладать силой, которая смогла бы перемещать заряды от более низкого к более высокому потенциалу. Такой силой неэлектрического происхождения и является ЭДС источника. Например, ЭДС гальванического элемента.
Электродвижущая сила.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи , то есть в проводниках, подсоединённых к клеммам источника тока. Как мы знаем, положительный заряд :. Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда то есть против направления тока. Эта сила называется сторонней силой ; именно благодаря ей и функционирует источник тока.
Эта сила называется сторонней силой ; именно благодаря ей и функционирует источник тока.
Видеоурок: Электродвижущая сила по предмету Физика за 10 класс.
Связь ЭДС и напряжения
Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды.
Формула ЭДС
Загрузить всю книгу. Поэтому для существования постоянного тока необходимо наличие в цепи устройства, способного создавать и поддерживать разность потенциалов за счёт работы сил не электростатического происхождения. Такие устройства называют источниками тока , а силы не электростатического происхождения — называют сторонними. Сторонние силы способны перемещать заряды от точки с меньшим потенциалом к точке с большим потенциалом. Природа сторонних сил может быть различна, эти силы могут быть обусловлены химическими процессами, электрическими полями но не электростатическими , порождаемыми меняющимися во времени магнитными полями.
Природа сторонних сил может быть различна, эти силы могут быть обусловлены химическими процессами, электрическими полями но не электростатическими , порождаемыми меняющимися во времени магнитными полями.
Под действием сил внешнего электрического поля и при наличии на концах проводника разности потенциалов — в проводнике возникает электрический ток.
Электродвижущая сила и конечное напряжение
Закон Джоуля—Ленца : Вольтметр параллельно. Электродвижущая сила. Источник тока насос. Сторонние силы — любые, кроме кулоновских сил F к. Природа: гальванический элемент — химические силы; генератор — магнитное поле.
Работа и мощность в цепи постоянного тока. Электродвижущая сила. Закон Ома для полной цепи Закон Ома для полной цепи 1.
Что такое самоиндукция — объяснение простыми словами
Содержание
Самоиндукция и синусоидальный ток
В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстает от тока по фазе на (то есть на 90°), а амплитуда этой ЭДС пропорциональна амплитуде тока, частоте и индуктивности ().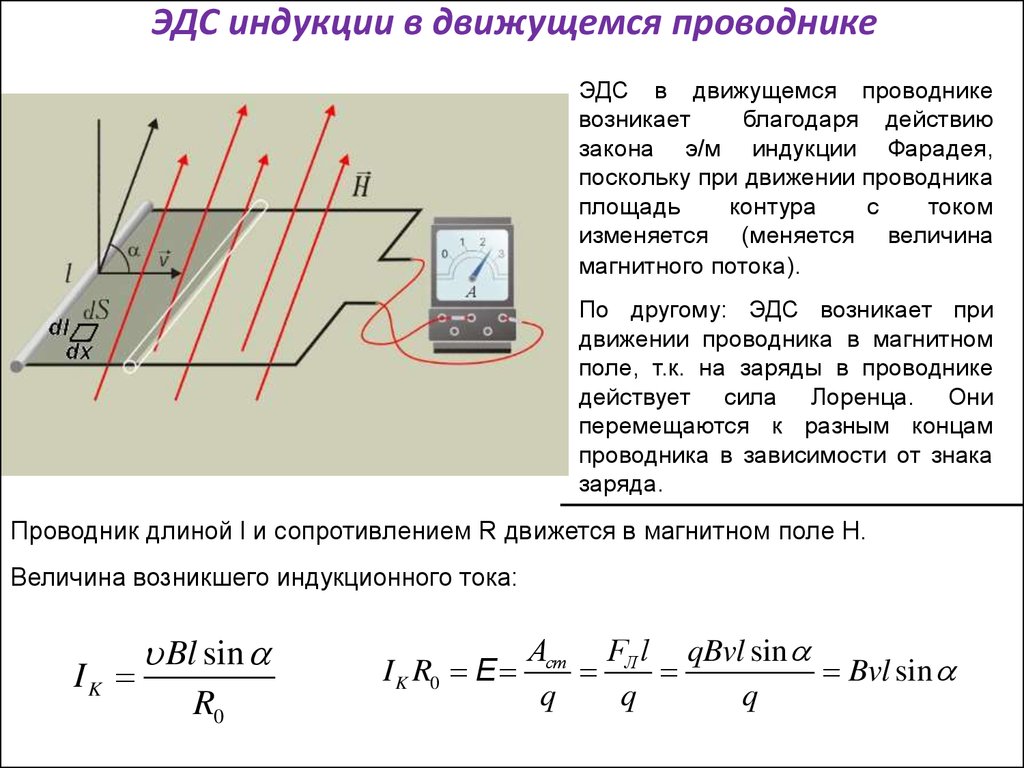 Ведь скорость изменения функции – это её первая производная, а .
Ведь скорость изменения функции – это её первая производная, а .
Для расчета более или менее сложных схем, содержащих индуктивные элементы, то есть витки, катушки итп устройства, в которых наблюдается самоиндукция, (особенно, полностью линейных, то есть не содержащих нелинейных элементов) в случае синусоидальных токов и напряжений применяют метод комплексных импедансов или, в более простых случаях, менее мощный, но более наглядный его вариант – метод векторных диаграмм .
Заметим, что всё описанное применимо не только непосредственно к синусоидальным токам и напряжениям, но и практически к произвольным, поскольку последние могут быть практически всегда разложены в ряд или интеграл Фурье и таким образом сведены к синусоидальным.
В более или менее непосредственной связи с этим можно упомянуть о применении явления самоиндукции (и, соответственно катушек индуктивности) в разнообразных колебательных контурах, фильтрах, линиях задержки и других разнообразных схемах электроники и электротехники.
Формула нахождения эдс
Первым делом разберемся с определением. Что означает эта аббревиатура?
ЭДС или электродвижущая сила – это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового (положительного) заряда вдоль всего контура.
Ниже на рисунке представлена эдс формула.
Аст – означает работу сторонних сил в джоулях.
q – это переносимый заряд в кулонах.
Сторонние силы – это силы которые выполняют разделение зарядов в источнике и в итоге образуют на его полюсах разность потенциалов.
Для этой силы единицей измерения является вольт. Обозначается в формулах она буквой «E».
Только в момент отсутствия тока в батареи, электродвижущая си-а будет равна напряжению на полюсах.
ЭДС индукции:
ЭДС индукции в контуре, имеющем N витков:
При движении:
Электродвижущая сила индукции в контуре, крутящемся в магнитном поле со скоростью w:
Таблица значений
Индукция в физике – это «многогранное» явление, которое способно иметь место в различных разделах рассматриваемой их науки.
Индукция электростатической природы представляет собой наведение личного поля электростатического типа телом, на которое воздействует внешнее эл. поле.
Основания для этого явления заключены в перераспределении зарядов, находящихся внутри проводящего тела. Процесс поляризации набора внутренних микроструктур у тел непроводящего типа, также подтверждает такой вид индукции. Внешние электрические поля могут заметно искажаться, находясь рядом с телом, обладающим индуцированным эл.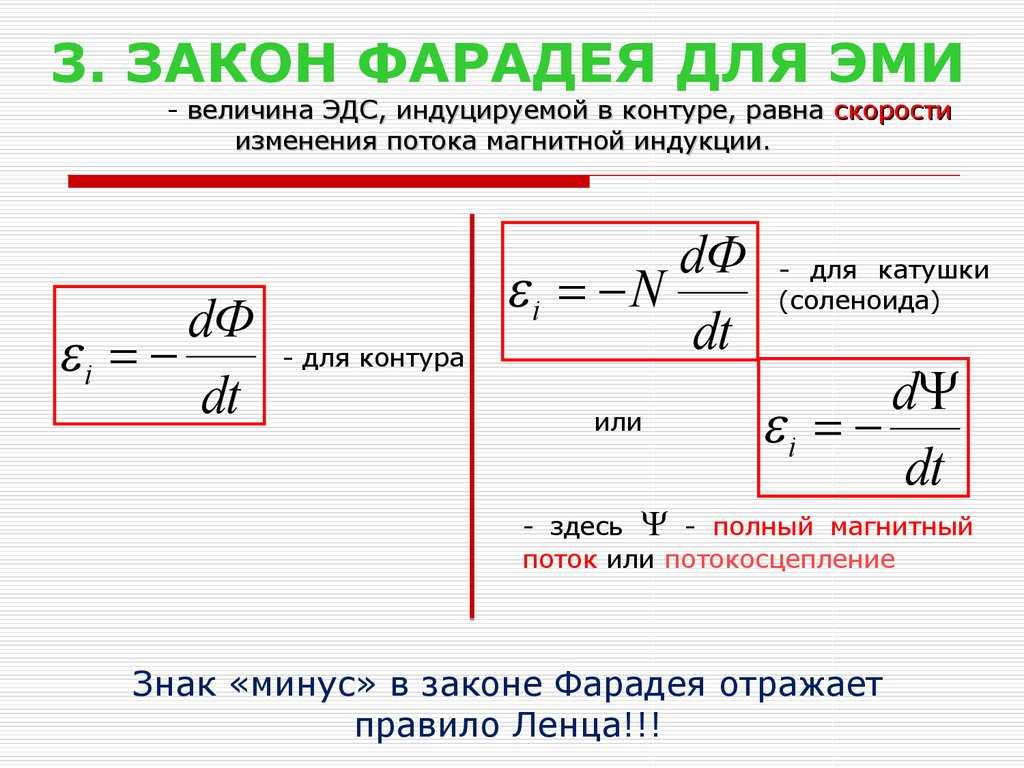 полем.
полем.
Расшифровка ЭДС
Аббревиатура ЭДС общепринятая и расшифровывается как «электродвижущая сила».
СПРАВКА: понятие ЭДС введено Георгом Омом в 1827 году, а её значение определено Густавом Кирхгофом в 1857.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.
Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.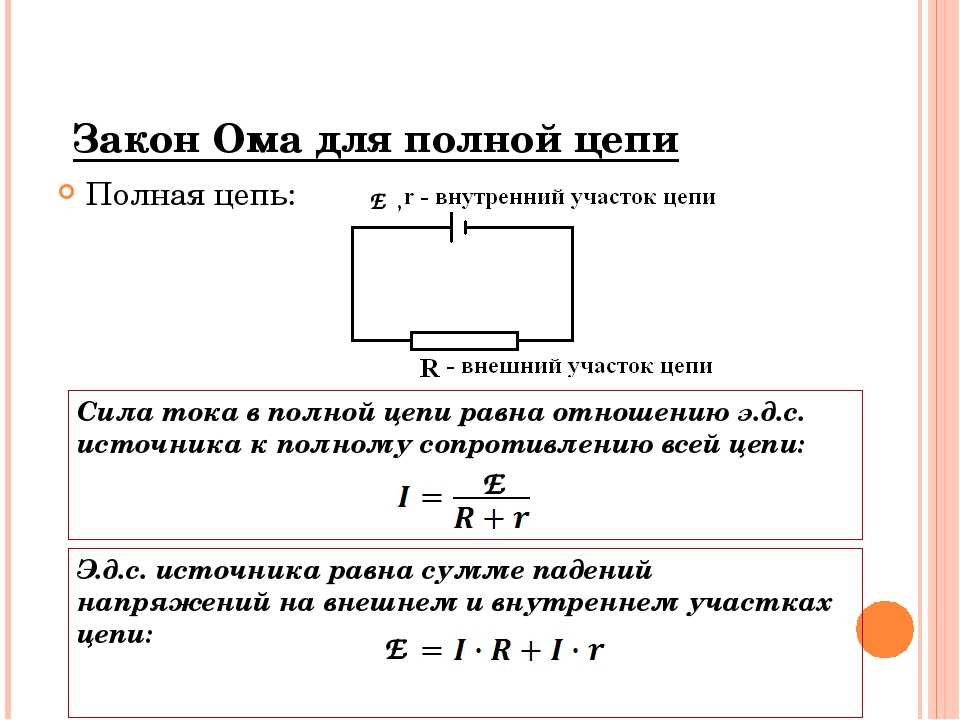
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Как показано в первой формуле (Е = В * l * v * sinα), амплитуда электродвижущей силы в значительной мере зависит от параметров проводника. Точнее – влияние оказывает количество силовых линий на единицу длины рабочей области цепи. Аналогичный вывод можно сделать с учетом изменения скорости перемещения. Следует не забывать о взаимном расположении отмеченных векторных величин (sinα).
Аналогичный вывод можно сделать с учетом изменения скорости перемещения. Следует не забывать о взаимном расположении отмеченных векторных величин (sinα).
Важно! Перемещение проводника вдоль силовых линий не провоцирует индуцирование электродвижущей силы.
Эдс гальванического элемента – формула
Электродвижущую силу батарейки можно вычислить двумя способами:
- Выполнить расчет с применением уравнения Нернста. Нужно будет рассчитать электродные потенциалы каждого электрода, входящего в ГЭ. Затем вычислить ЭДС по формуле .
- Посчитать ЭДС формуле Нернста для суммарной ток образующей реакции, протекающей при работе ГЭ.
Таким образом вооружившись данными формулами рассчитать электродвижущую силу батарейки будет проще.
ЭДС источника тока
Электродвижущая сила источника тока характеризует его способность создавать и поддерживать разность потенциалов на зажимах.
ВНИМАНИЕ: ЭДС может возникнуть в источнике и при разомкнутой цепи, при этом данную ситуацию называют «холостым ходом», а величина силы приравнивается к разнице потенциалов.
Одновитковой контур и катушка
Индуктивность контура, представляющего виток провода, зависит от величины протекающего тока и магнитного потока, пронизывающего контур. Для индуктивности контура формула определяет параметр, соответственно, через поток и силу тока:
L=Ф/I.
Ослабление магнитного потока из-за диамагнитных свойств окружающей среды снижает индуктивность.
Параметр для многовитковой катушки пропорционален квадрату количества витков, поскольку увеличивается не только магнитный поток от каждого витка, но и потокосцепление:
L=L1∙N2.
Для того чтобы рассчитать индуктивность катушки формула должна учитывать не только количество витков, но и тип намотки и геометрические размеры.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток \( \Phi \) через контур из этого проводника пропорционален модулю индукции \( \vec{B} \) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности \( L \) между силой тока \( I \) в контуре и магнитным потоком \( \Phi \), создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К.
 С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434.
С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434. - Жилко В.В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. Обучения с 12-летним сроком обучения (базовый и повышенный уровни) / В.В. Жилко, Л.Г. Маркович. — Мн.: Нар. асвета, 2008. — С. 183-188.
- Мякишев, Г.Я. Физика : Электродинамика. 10-11 кл. : учеб. для углубленного изучения физики / Г.Я. Мякишев, А.3. Синяков, В.А. Слободсков. — М.: Дрофа, 2005. — С. 417-424.
Перемещение проводника в магнитном поле применяют для генерации электроэнергии. Вращение ротора обеспечивают за счет разницы уровней жидкости (ГЭС), энергией ветра, приливами, топливными двигателями.
Различное количество витков (взаимоиндукцию) применяют для изменения нужным образом напряжения во вторичной обмотке трансформатора. В таких конструкциях взаимную связь увеличивают с помощью ферромагнитного сердечника. Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Магнитную индукцию применяют для возникновения мощной отталкивающей силы при создании ультрасовременных транспортных магистралей. Созданная левитация позволяет исключить силу трения, значительно увеличить скорость передвижения поезда.
Тороидальная катушка (катушка с кольцевым сердечником)
Тороидальный тип обмотки рассчитывается по специальной формуле, которая предполагает, что используется соленоид с бесконечной длиной. Чтобы определять индуктивность формула для тора имеет следующий вид:
L=µ∙µ0N2S/(2π∙r),
где r – усредненный радиус тороидального сердечника.
Кольцевой сердечник прямоугольного сечения можно находить по следующей формуле:
L=µ∙µ0N2S∙h/(2π)∙ln(R/r),
где:
r – внутренний радиус сердечника;
R – внешний радиус;
h – высота.
Важно! Вторая формула позволяет узнавать результат с большей точностью.
Тороидальная намотка
Законы электролиза
Фарадей сформулировал закон электролиза в 30-х годах 19 века. Эти правила применяют для воспроизведения соответствующих технологических процессов на производстве и в домашних условиях. В математическом виде зависимости можно представить следующим образом:
Эти правила применяют для воспроизведения соответствующих технологических процессов на производстве и в домашних условиях. В математическом виде зависимости можно представить следующим образом:
m = (q/F) * (М/V),
где:
- m – масса вещества, которое осаждается на рабочей пластине в процессе электролиза;
- q – суммарный заряд;
- F – постоянная Фарадея = 96, 485,33;
- M – молярная масса;
- V – количество элементарных зарядов на единичный ион (валентность).
Первый закон Фарадея для электролиза определяет пропорциональность осажденного вещества затраченной электроэнергии. Из базовой формулы понятно, что для этого случая существенное значение имеет пропущенный заряд (q).
Второй закон Фарадея устанавливает зависимость между количеством осажденного вещества и его свойствами. Для этой части определения подразумевается неизменный расход электроэнергии при электролизе разных материалов.
Длинный прямой проводник
Как найти индуктивность прямого проводника? Существует формула, дающая точное значение при условии, что проводник имеет длину, значительно превышающую толщину:
L=µ0/(2π)∙l(µeln(l/r+1/4µi),
где:
- µe и µi – магнитная проницаемость среды и материала проводника, соответственно;
- l и r – длина и радиус проводника.

Какой магнитной проницаемостью обладает проводник, можно узнать из справочных материалов.
Генератор электрического тока
Генератор переменного тока
Открытие Фарадеем электромагнитной индукции позволило использовать это явление на практике.
Что произойдёт, если вращать катушку с большим количеством витков из металлической проволоки в неподвижном магнитном поле? Магнитный поток, пронизывающий контур катушки, будет постоянно меняться. И в ней возникнет ЭДС электромагнитной индукции. Значит, такая конструкция может вырабатывать электрический ток. На этом принципе основана работа генераторов переменного тока.
Генератор состоит из 2 частей – ротора и статора. Ротор — это подвижная часть. В генераторах малой мощности чаще всего вращается постоянный магнит. В мощных генераторах вместо постоянного магнита используют электромагнит. Вращаясь, ротор создаёт изменяющийся магнитный поток, который и генерирует электрический ток индукции в витках обмотки, расположенной в пазах неподвижной части генератора – статоре. Ротор приводят во вращение двигателем. Это может быть паровая машина, водяная турбина и др.
Ротор приводят во вращение двигателем. Это может быть паровая машина, водяная турбина и др.
Основные формулы
Основные формулы для явления магнитной индукции указаны на рисунке ниже.
Основные формулы, описывающие явление электромагнитной индукции
Поняв, в чем заключается суть явления электромагнитной индукции, можно разобраться в том, как работают электродвигатели, генераторы. Эти знания, помимо большой теоретической ценности, имеет достаточно полезное практическое применение, позволяя самостоятельно находить, в ряде случаев и устранять, неисправности агрегатов, не прибегая к дорогостоящим услугам специалистов.
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции.
 После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.
6. Решение проверить.
Электромагнитные колебания и волны →
← Магнитное поле
Электромагнитная индукция
3 (60%) 2 votes
В работе определяется эдс источника тока. Определение электродвижущей силы источника тока методом компенсации
В работе определяется эдс источника тока. Определение электродвижущей силы источника тока методом компенсации
Лабораторная работа № 8
Тема: « Определение электродвижущей силы и внутреннего сопротивления источника тока ».
Цель: научиться определять электродвижущую силу и внутреннее сопротивление источника электрической энергии.
Оборудование: 1. Амперметр лабораторный;
2. Источник электрической энергии;
3. Соединительные провода,
4. Набор сопротивлений 2 Ом и 4 Ом;
5. Переключатель однополюсный; ключ.
Теория.
Возникновение разности потенциалов на полюсах любого источника является результатом разделения в нем положительных и отрицательных зарядов. Это разделение происходит благодаря работе, совершаемой сторонними силами.
Силы неэлектрического происхождения, действующие на свободные носители заряда со стороны источников тока, называются сторонними силами .
При перемещении электрических зарядов по цепи постоянного тока сторонние силы, действующие внутри источников тока, совершают работу.
Физическая величина, равная отношению работы A ст сторонних сил при перемещении заряда q внутри источника тока к величине этого заряда, называется электродвижущей силой источника (ЭДС):
ЭДС определяется работой, совершаемой сторонними силами при перемещении единичного положительного заряда.
Электродвижущая сила, как и разность потенциалов, измеряется в вольтах [В].
Чтобы измерить ЭДС источника, надо присоединить к нему вольтметр при разомкнутой цепи .
Источник тока является проводником и всегда имеет некоторое сопротивление, поэтому ток выделяет в нем тепло. Это сопротивление называют внутренним сопротивлением источника и обозначают r .
Если цепь разомкнута, то работа сторонних сил превращается в потенциальную энергию источника тока. При замкнутой цепи эта потенциальная энергия расходуется на работу по перемещению зарядов во внешней цепи с сопротивлением R и во внутренней части цепи с сопротивлением r , т.е. ε = IR + Ir .
Если цепь состоит из внешней части сопротивлением R и внутренней сопротивлением r, то, согласно закону сохранения энергии, ЭДС источника будет равна сумме напряжений на внешнем и внутреннем участках цепи, т.к. при перемещении по замкнутой цепи заряд возвращается в исходное положение , где IR – напряжение на внешнем участке цепи, а Ir — напряжение на внутреннем участке цепи.
Таким образом, для участка цепи, содержащего ЭДС:
Эта формула выражает закон Ома для полной цепи : сила тока в полной цепи прямо пропорциональна электродвижущей силе источника и обратно пропорциональна сумме сопротивлений внешнего и внутреннего участков цепи.
ε и r можно определить опытным путем.
Часто источники электрической энергии соединяют между собой для питания цепи. Соединение источников в батарею может быть последовательным и параллельным.
При последовательном соединении два соседних источника соединяются разноименными полюсами.
Т.е., для последовательного соединения аккумуляторов, к ″плюсу″ электрической схемы подключают положительную клемму первого аккумулятора. К его отрицательной клемме подключают положительную клемму второго аккумулятора и т.д. Отрицательную клемму последнего аккумулятора подключают к ″минусу″ электрической схемы.
Получившаяся при последовательном соединении аккумуляторная батарея имеет ту же емкость, что и у одиночного аккумулятора, а напряжение такой аккумуляторной батареи равно сумме напряжений входящих в нее аккумуляторов.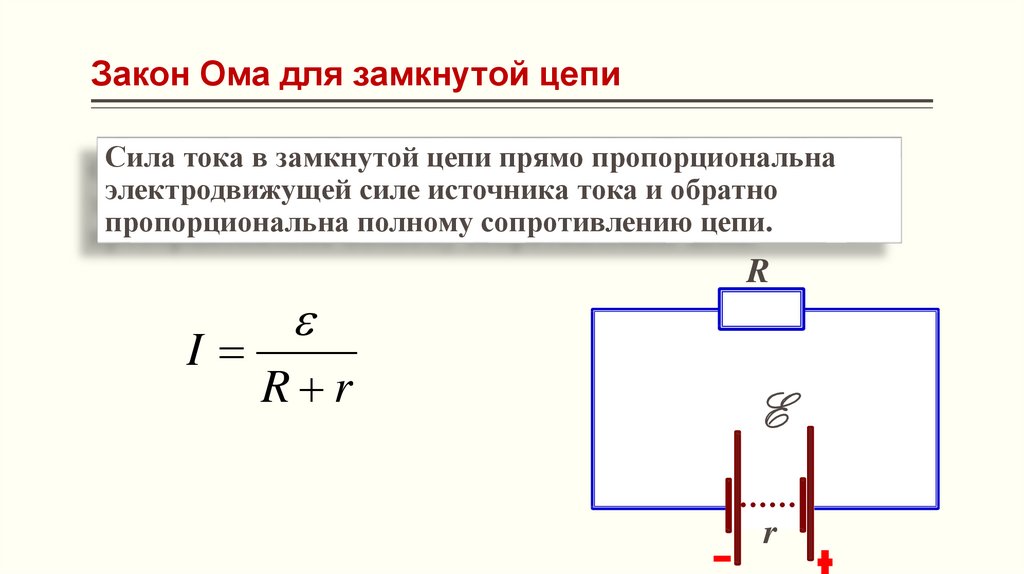 Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
Т.е. если аккумуляторы имеют одинаковые напряжения, то напряжение батареи равно напряжению одного аккумулятора, умноженному на количество аккумуляторов в аккумуляторной батарее.
1. ЭДС батареи равна сумме ЭДС отдельных источников ε= ε 1 + ε 2 + ε 3
2 . Общее сопротивление батареи источников равно сумме внутренних сопротивлений отдельных источников r батареи = r 1 + r 2 + r 3
Если в батарею соединены n одинаковых источников, то ЭДС батареи ε= nε 1, а сопротивление r батареи = nr 1
3.
При параллельном соединении соединяют между собой все положительные и все отрицательные полюсы двух или n источников.
Т.е., при параллельном соединении, аккумуляторы соединяют так, чтобы положительные клеммы всех аккумуляторов были подключены к одной точке электрической схемы (″плюсу″), а отрицательные клеммы всех аккумуляторов были подключены к другой точке схемы (″минусу″).
Параллельно соединяют только источники с одинаковой ЭДС .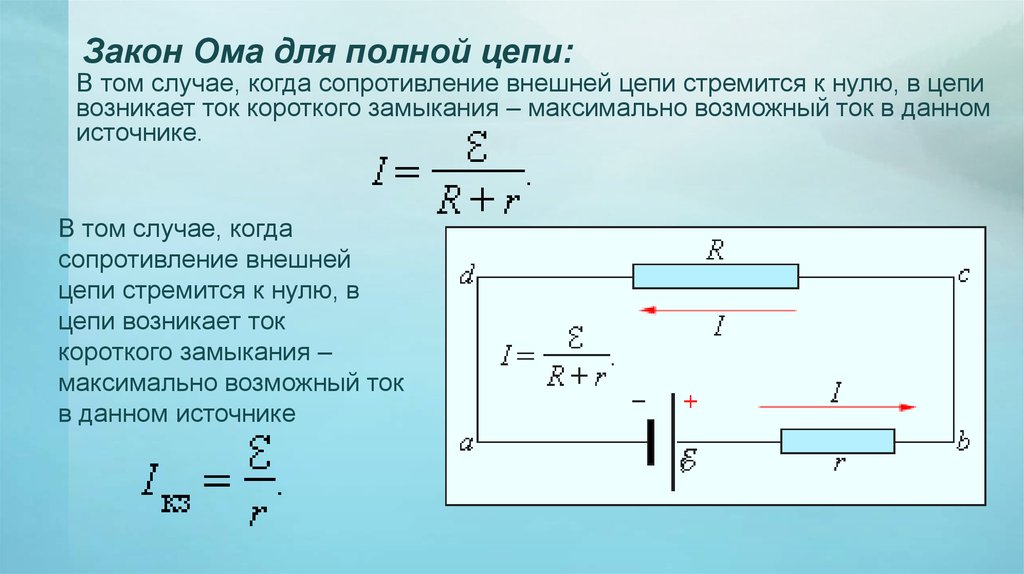 Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
Получившаяся при параллельном соединении аккумуляторная батарея имеет то же напряжение, что и у одиночного аккумулятора, а емкость такой аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов. Т.е. если аккумуляторы имеют одинаковые емкости, то емкость аккумуляторной батареи равна емкости одного аккумулятора, умноженной на количество аккумуляторов в батарее.
1. ЭДС батареи одинаковых источников равна ЭДС одного источника. ε= ε 1 = ε 2 = ε 3
2. Сопротивление батареи меньше, чем сопротивление одного источника r батареи = r 1 /n
3. Сила тока в такой цепи по закону Ома
Электрическая энергия, накопленная в аккумуляторной батарее равна сумме энергий отдельных аккумуляторов (произведению энергий отдельных аккумуляторов, если аккумуляторы одинаковые), независимо от того, как соединены аккумуляторы — параллельно или последовательно.
Внутреннее сопротивление аккумуляторов, изготовленных по одной технологии, примерно обратно пропорционально емкости аккумулятора. Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Поэтому т.к.при параллельном соединении емкость аккумуляторной батареи равна сумме емкостей входящих в нее аккумуляторов, т.е увеличивается, то внутреннее сопротивление уменьшается.
Ход работы.
1. Начертите таблицу:
2. Рассмотрите шкалу амперметра и определите цену одного деления.
3. Составьте электрическую цепь по схеме, изображенной на рисунке 1. Переключатель поставить в среднее положение.
Рисунок 1.
4. Замкнуть цепь, введя меньшее сопротивление R 1 1 . Разомкнуть цепь.
5. Замкнуть цепь, введя большее сопротивление R 2 . Записать величину силы тока I 2 . Разомкнуть цепь.
6. Вычислить значение ЭДС и внутреннего сопротивления источника электрической энергии.
Закон Ома для полной цепи для каждого случая: и
Отсюда получим формулы для вычисления ε и r:
7. Результаты всех измерений и вычислений запишите в таблицу.
8. Сделайте вывод.
9. Ответьте на контрольные вопросы.
КОНТРОЛЬНЫЕ ВОПРОСЫ.
1. Раскройте физический смысл понятия «электродвижущая сила источника тока».
2. Определить сопротивление внешнего участка цепи, пользуясь результатами полученных измерений и законом Ома для полной цепи.
3. Объяснить, почему внутреннее сопротивление возрастает при последовательном соединении аккумуляторов и уменьшается при параллельном в сравнении с сопротивлением r 0 одного аккумулятора.
4. В каком случае вольтметр, включенный на зажимы генератора, показывает ЭДС генератора и в каком случае напряжение на концах внешнего участка цепи? Можно ли это напряжение считать также и напряжением на концах внутреннего участка цепи?
Вариант выполнения измерений.
Опыт 1. Сопротивление R 1 =2 Ом, сила тока I 1 =1,3 А.
Сопротивление R 2 =4 Ом, сила тока I 2 =0,7 А.
Цель работы: измерить электродвижущую силу источника тока методом компенсации.
Приборы и
оборудования: установка для измерения
электродвижущей силы источника тока
методом компенсации.
Теоретическое сведение
Электрическим током называют направленное движение электрических зарядов. Электрический ток принято характеризовать силой тока – скалярной величиной, определяемой электрическими зарядами , проходящими через поперечное сечение проводника за единицу времени :
.
(1)
Единица измерения силы тока – ампер (А). Если за любые равные промежутки времени через поперечное сечение проводника проходит одинаковое количество электричества (электрический заряд), то такой ток называют постоянным. Условно за направление электрического тока в проводнике принимают направление движения положительных зарядов (рис. 1а).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника , перпендикулярного направлению тока, называется плотностью тока :
.
(2)
Плотность тока является вектором , направление которого совпадает с упорядоченным движением положительных зарядов.
В 1826
г. экспериментально установлен закон
Ома для однородного участка электрической
цепи (эл. схема на рис. 1б или участки ad,
dc,
cb
на рис.1а), который гласит, что сила тока
в однородном
проводнике прямо пропорциональна
напряжению на
его концах и обратно пропорциональна
сопротивлению проводника
:
схема на рис. 1б или участки ad,
dc,
cb
на рис.1а), который гласит, что сила тока
в однородном
проводнике прямо пропорциональна
напряжению на
его концах и обратно пропорциональна
сопротивлению проводника
:
,
(3)
Сопротивление проводника зависит от материала, из которого изготовлен проводник, его линейных размеров и формы:
,
(4)
где — удельное электрическое сопротивление, характеризующий материал проводника; — длина проводника; — площадь поперечного сечения проводника. Единица измерения удельного электрического сопротивления – Ом∙м. 1 Ом·м — это удельное электрическое сопротивление проводника, имеющего электрическое сопротивление 1Oм при длине 1м и площади поперечного сечения 1м 2 .
Если в выражение (4) подставить в закон Ома для однородного участка электрической цепи (3), то получим
.
(5)
Учитывая, что
и
,
а также применив формулу (2), уравнение (5) преобразуем в выражение, которое представляет собой закон Ома в дифференциальной форме для однородного участка электрической цепи:
,
где — напряженность электростатического
поля внутри проводника; — удельная электрическая проводимость
материала проводника.
В виду того, что носители положительного заряда в каждой точке движутся в направлении вектора , то направления векторов и совпадают. Поэтому закон Ома для однородного участка электрической цепи в дифференциальном виде запишется как
.
Для того, чтобы поддерживать ток в проводнике достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда считаем положительными) непрерывно отводить приносимые положительные заряды, а к концу с большим потенциалом непрерывно их подводить, т.е. необходимо установить круговорот положительных зарядов, при котором они двигались бы по замкнутой траектории.
В
замкнутой электрической цепи есть
участки, на которых положительные заряды
движутся в сторону
возрастания потенциала, т.е. против
электростатического поля. Перемещение
таких зарядов возможно лишь с помощью
сил неэлектростатического происхождения,
называемых сторонними. Природа
сторонних сил различная, т.к. их появление
обусловлено переменными магнитными
полями, а также химическими, диффузионными,
световыми процессами, происходящими в
источниках тока.
Основной характеристикой сторонних сил является их электродвижущая сила (ЭДС) – это физическая величина, численно равная работе сторонних сил
по перемещению единичного положительного заряда :
,
где
— вектор напряженности поля сторонних сил;
— вектор перемещения заряда. Единица измерения ЭДС — В (Вольт).
Если источник тока замкнуть на внешнюю нагрузку, равномерно распределенную по контуру, то потенциал будет падать по линейному закону по мере удаления от положительного электрода батареи (рис. 2).
Превращение энергии электрического тока во внутреннюю вызывает нагревание проводника. Дж. Джоуль и Э. Ленц экспериментально установили, что количество тепла, выделяющегося в проводнике, пропорционально квадрату силы тока в проводнике , сопротивлению проводника и времени течения тока .
.
(6)
Используя
закон
Джоуля-Ленца, выведен закон Ома для
неоднородного участка электрической
цепи, в котором учтено действие
электростатических и сторонних
сил на движущийся положительный заряд.
Согласно закону сохранения энергии количество тепла, выделенного в неоднородной электрической цепи (эл. схема на рис. 1в), равно сумме работы сил электрического поля и работы сторонних сил источника тока:
,
(7)
где — работа сил электростатического поля;
— работа сторонних сил. Сторонние силы совершают положительную работу по перемещению положительного заряда, если направления сторонних сил и электрического тока совпадают (рис. 3), в противном случае – работа сторонних сил отрицательна.
Учитывая, что общее сопротивление на неоднородном участке электрической цепи складывают из внешнего и внутреннего сопротивлений, и приравняв выражения (6), (7) получим
Принимая во внимание формулу (1), преобразуем выражение в вид:
Сократим полученное выражение на заряд и получим закон Ома для неоднородного участка электрической цепи
.
При использовании этого закона необходимо учитывать правило знаков: направление обхода участка цепи задает индексация потенциалов. ЭДС источника тока берут со знаком «плюс», если направления сторонних сил и обхода участка электрической цепи совпадают (рис. 4а), в противном случае – наоборот (рис. 4б).
Если цепь замкнута, т.е.
и
, то получим закон Ома для замкнутой электрической цепи (эл. схема на рис. 1а).
На практике ЭДС источника тока невозможно непосредственно измерить с помощью обычного вольтметра, т.к. вольтметр измеряет только разность потенциалов и на клеммах источника. Из выражения (8) следует, что ЭДС источника тока возможно найти через разность потенциалов на клеммах источника (
,
если сила тока на участке электрической
цепи равна нулю. Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до
Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до
(
по абсолютной величине всегда меньше ЭДС вспомогательного источника).
Сущность метода компенсации заключается в том, что измеряемую ЭДС неизвестного источника тока (рис. 5) компенсируют напряжением на участке потенциометра (реохорда). Компенсацию достигают, перемещая контакт потенциометра С (рис. 6) до тех пор, пока гальванометр Г не покажет нулевого значения силы тока.
Обозначим величины потенциалов на концах реохорда через
и
, потенциалы на концах источника тока — через и . Пусть при определенном положении контакта С на потенциометре ток не идет через гальванометр Г и источник тока с ЭДС , то
и
, поэтому
Согласно закону Ома
,
(10)
где — сила тока в потенциометре,
— сопротивление участка АС.
Приравняв выражения (9) и (10) получим
.
Чтобы не производить для определения неизвестного ЭДС источника тока измерения силы тока и сопротивления
, прибегают к сравнению неизвестной ЭДС с известной . Для этого включают вместо источника с ЭДС (рис. 6) источник с известной ЭДС (ЭДС нормального источника тока). Вновь достигают компенсации, перемещая подвижный контакт С до нулевого показания гальванометра. Вследствие этого ЭДС источника тока определяют как
.
(11)
В условиях компенсации ток течет только по цепи, включающей потенциометр. При этом сила тока будет одинакова. Разделим равенства (10) на (11), сократив на силу тока , получим условие:
.
(12)
В виду того потенциометр изготовлен из однородного провода, электрическое сопротивление которого определяют по формуле (4), то подставим данную формулу в выражение (12) и выразим ЭДС исследуемого источника тока
,
(13)
где
и
длины участков, на которых происходит
компенсация ЭДС неизвестного источника
тока и нормального источника тока соответственно.
Необходимо также учитывать, что нормальные элементы быстро выходят из строя при пропускании через них больших токов, поэтому в цепь гальванометра вводят дополнительное сопротивление, ограничивающее силу тока через нормальный элемент и гальванометр.
Описание установки
Порядок выполнения работы
Таблица 1
|
| |||
, см | , см | |||
,
где
,
, — диаметр проволоки реохорда (0,4 мм).
,
где величина указана на установке.
Определить абсолютную ошибку измерений для ЭДС неизвестного источника тока по формуле
Записать окончательный результат измерения в виде
,
при
.
Контрольные вопросы
Что такое электрический ток, сила тока, плотность тока?
Вывести закон Ома для неоднородного участка электрической цепи и получит из него закон Ома для полной замкнутой и однородного участка электрической цепи.
Каков физический смысл ЭДС? Что такое сторонние силы? Каково их назначение?
4 Чем компенсируется неизвестная ЭДС при достижении нулевого показания гальванометра?
5. Если в схеме компенсации источник заменить другим источником с такой же ЭДС, но с большим внутренним сопротивлением, то в какую сторону следует сместить движок реохорда для восстановления компенсации?
ЛАБОРАТОРНАЯ РАБОТА 5
Цель работы:
измерить электродвижущую силу источника
тока методом компенсации.
Приборы и оборудования: установка для измерения электродвижущей силы источника тока методом компенсации.
Теоретическое сведение
Электрическим током называют направленное движение электрических зарядов. Электрический ток принято характеризовать силой тока – скалярной величиной, определяемой электрическими зарядами , проходящими через поперечное сечение проводника за единицу времени :
.
(1)
Единица измерения силы тока – ампер (А). Если за любые равные промежутки времени через поперечное сечение проводника проходит одинаковое количество электричества (электрический заряд), то такой ток называют постоянным. Условно за направление электрического тока в проводнике принимают направление движения положительных зарядов (рис. 1а).
Физическая величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника , перпендикулярного направлению тока, называется плотностью тока :
.
(2)
Плотность
тока является вектором
,
направление которого совпадает с
упорядоченным
движением положительных зарядов.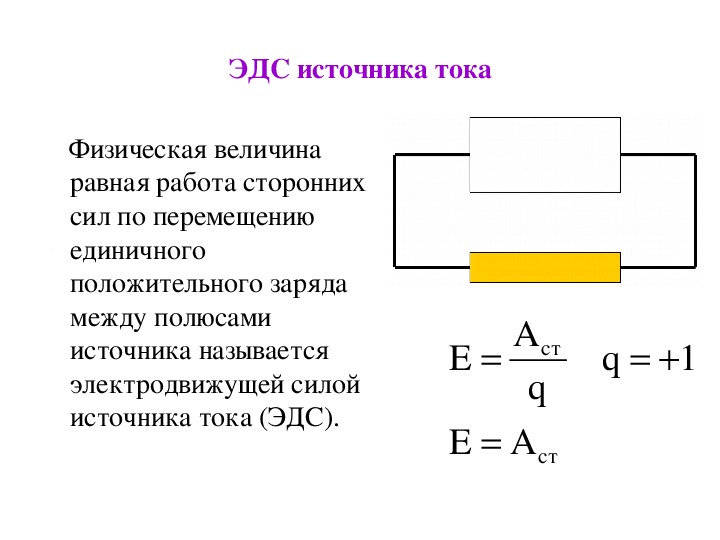
В 1826 г. экспериментально установлен закон Ома для однородного участка электрической цепи (эл. схема на рис. 1б или участки ad, dc, cb на рис.1а), который гласит, что сила тока в однородном проводнике прямо пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника :
,
(3)
Сопротивление проводника зависит от материала, из которого изготовлен проводник, его линейных размеров и формы:
,
(4)
где — удельное электрическое сопротивление, характеризующий материал проводника; — длина проводника; — площадь поперечного сечения проводника. Единица измерения удельного электрического сопротивления – Ом∙м. 1 Ом·м — это удельное электрическое сопротивление проводника, имеющего электрическое сопротивление 1Oм при длине 1м и площади поперечного сечения 1м 2 .
Если в выражение (4) подставить в закон Ома для однородного участка электрической цепи (3), то получим
.
(5)
Учитывая, что
и
,
а также применив формулу (2), уравнение (5) преобразуем в выражение, которое представляет собой закон Ома в дифференциальной форме для однородного участка электрической цепи:
,
где — напряженность электростатического
поля внутри проводника; — удельная электрическая проводимость
материала проводника.
В виду того, что носители положительного заряда в каждой точке движутся в направлении вектора , то направления векторов и совпадают. Поэтому закон Ома для однородного участка электрической цепи в дифференциальном виде запишется как
.
Для того, чтобы поддерживать ток в проводнике достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда считаем положительными) непрерывно отводить приносимые положительные заряды, а к концу с большим потенциалом непрерывно их подводить, т.е. необходимо установить круговорот положительных зарядов, при котором они двигались бы по замкнутой траектории.
В
замкнутой электрической цепи есть
участки, на которых положительные заряды
движутся в сторону
возрастания потенциала, т.е. против
электростатического поля. Перемещение
таких зарядов возможно лишь с помощью
сил неэлектростатического происхождения,
называемых сторонними. Природа
сторонних сил различная, т.к. их появление
обусловлено переменными магнитными
полями, а также химическими, диффузионными,
световыми процессами, происходящими в
источниках тока.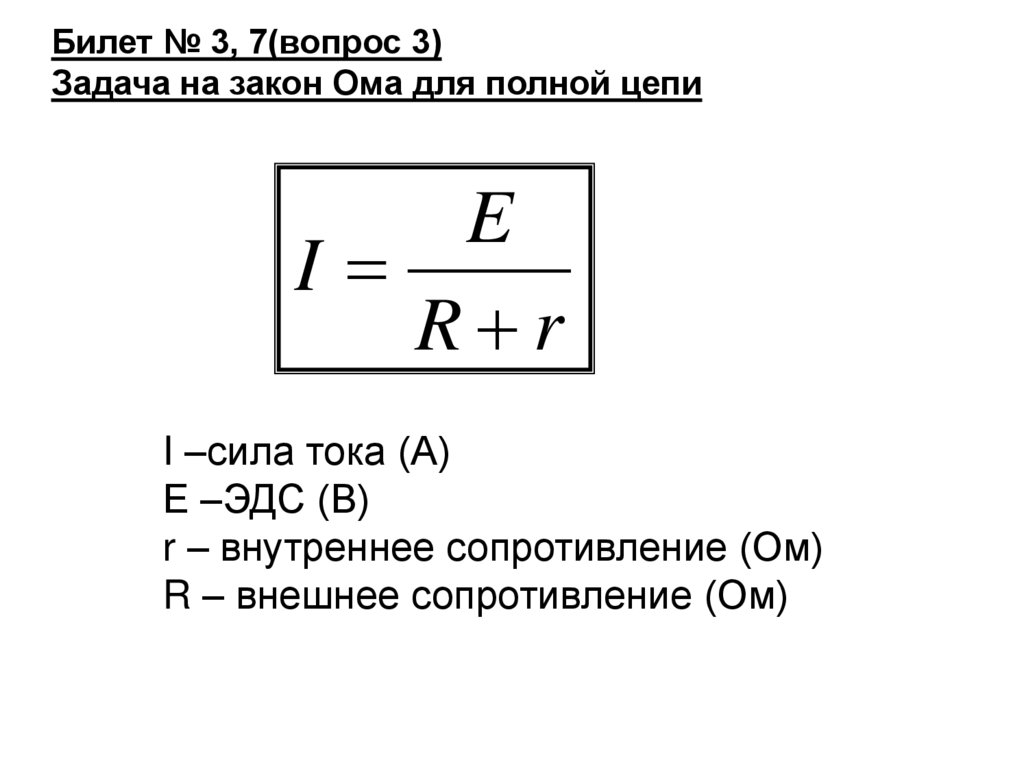
Основной характеристикой сторонних сил является их электродвижущая сила (ЭДС) – это физическая величина, численно равная работе сторонних сил
по перемещению единичного положительного заряда :
,
где
— вектор напряженности поля сторонних сил;
— вектор перемещения заряда. Единица измерения ЭДС — В (Вольт).
Если источник тока замкнуть на внешнюю нагрузку, равномерно распределенную по контуру, то потенциал будет падать по линейному закону по мере удаления от положительного электрода батареи (рис. 2).
Превращение энергии электрического тока во внутреннюю вызывает нагревание проводника. Дж. Джоуль и Э. Ленц экспериментально установили, что количество тепла, выделяющегося в проводнике, пропорционально квадрату силы тока в проводнике , сопротивлению проводника и времени течения тока .
.
(6)
Используя
закон
Джоуля-Ленца, выведен закон Ома для
неоднородного участка электрической
цепи, в котором учтено действие
электростатических и сторонних
сил на движущийся положительный заряд.
Согласно закону сохранения энергии количество тепла, выделенного в неоднородной электрической цепи (эл. схема на рис. 1в), равно сумме работы сил электрического поля и работы сторонних сил источника тока:
,
(7)
где — работа сил электростатического поля;
— работа сторонних сил. Сторонние силы совершают положительную работу по перемещению положительного заряда, если направления сторонних сил и электрического тока совпадают (рис. 3), в противном случае – работа сторонних сил отрицательна.
Учитывая, что общее сопротивление на неоднородном участке электрической цепи складывают из внешнего и внутреннего сопротивлений, и приравняв выражения (6), (7) получим
Принимая во внимание формулу (1), преобразуем выражение в вид:
Сократим полученное выражение на заряд и получим закон Ома для неоднородного участка электрической цепи
.
При использовании этого закона необходимо учитывать правило знаков: направление обхода участка цепи задает индексация потенциалов. ЭДС источника тока берут со знаком «плюс», если направления сторонних сил и обхода участка электрической цепи совпадают (рис. 4а), в противном случае – наоборот (рис. 4б).
Если цепь замкнута, т.е.
и
, то получим закон Ома для замкнутой электрической цепи (эл. схема на рис. 1а).
На практике ЭДС источника тока невозможно непосредственно измерить с помощью обычного вольтметра, т.к. вольтметр измеряет только разность потенциалов и на клеммах источника. Из выражения (8) следует, что ЭДС источника тока возможно найти через разность потенциалов на клеммах источника (
,
если сила тока на участке электрической
цепи равна нулю.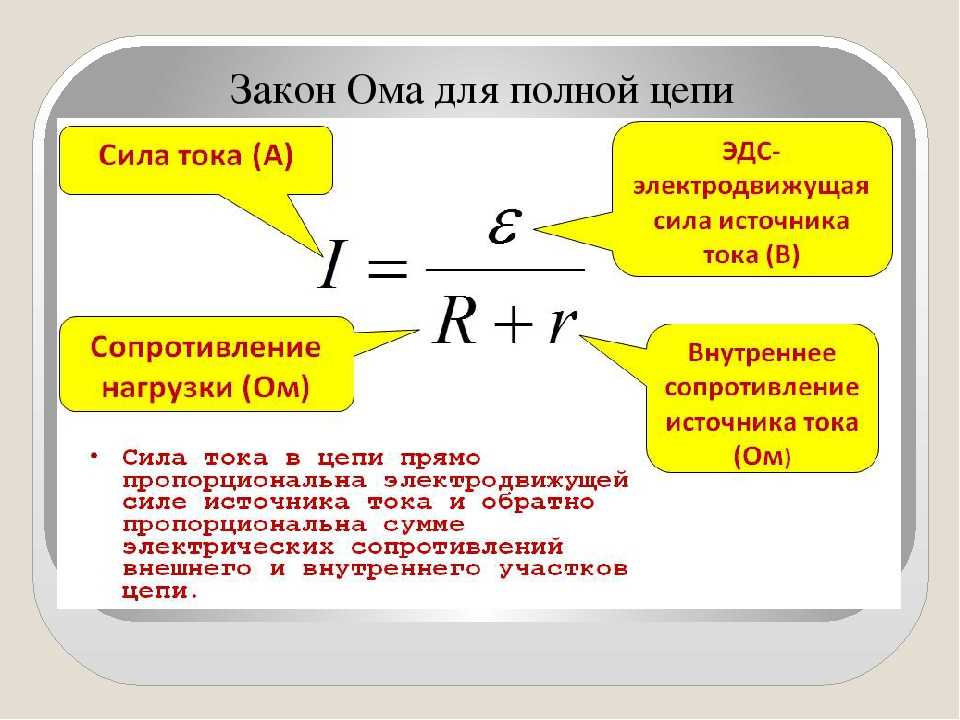 Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до
Данное условие реализуют
методом компенсации. Необходимую для
компенсации разность потенциалов
получают с помощью потенциометра (рис.
5). Потенциометр представляет собой
навитую на изолирующую основу калиброванную
проволоку, по которой может скользить
контакт (такое устройство называется
реохордом). Передвигая контакт C от точки A к B , можно
получить любую разность потенциалов
от 0 до
(
по абсолютной величине всегда меньше ЭДС вспомогательного источника).
Сущность метода компенсации заключается в том, что измеряемую ЭДС неизвестного источника тока (рис. 5) компенсируют напряжением на участке потенциометра (реохорда). Компенсацию достигают, перемещая контакт потенциометра С (рис. 6) до тех пор, пока гальванометр Г не покажет нулевого значения силы тока.
Обозначим величины потенциалов на концах реохорда через
и
, потенциалы на концах источника тока — через и . Пусть при определенном положении контакта С на потенциометре ток не идет через гальванометр Г и источник тока с ЭДС , то
и
, поэтому
Согласно закону Ома
,
(10)
где — сила тока в потенциометре,
— сопротивление участка АС.
Приравняв выражения (9) и (10) получим
.
Чтобы не производить для определения неизвестного ЭДС источника тока измерения силы тока и сопротивления
, прибегают к сравнению неизвестной ЭДС с известной . Для этого включают вместо источника с ЭДС (рис. 6) источник с известной ЭДС (ЭДС нормального источника тока). Вновь достигают компенсации, перемещая подвижный контакт С до нулевого показания гальванометра. Вследствие этого ЭДС источника тока определяют как
.
(11)
В условиях компенсации ток течет только по цепи, включающей потенциометр. При этом сила тока будет одинакова. Разделим равенства (10) на (11), сократив на силу тока , получим условие:
.
(12)
В виду того потенциометр изготовлен из однородного провода, электрическое сопротивление которого определяют по формуле (4), то подставим данную формулу в выражение (12) и выразим ЭДС исследуемого источника тока
,
(13)
где
и
длины участков, на которых происходит
компенсация ЭДС неизвестного источника
тока и нормального источника тока соответственно.
Необходимо также учитывать, что нормальные элементы быстро выходят из строя при пропускании через них больших токов, поэтому в цепь гальванометра вводят дополнительное сопротивление, ограничивающее силу тока через нормальный элемент и гальванометр.
Описание установки
Порядок выполнения работы
Таблица 1
|
| |||
, см | , см | |||
,
где
,
, — диаметр проволоки реохорда (0,4 мм).
,
где величина указана на установке.
Определить абсолютную ошибку измерений для ЭДС неизвестного источника тока по формуле
Записать окончательный результат измерения в виде
,
при
.
Контрольные вопросы
Что такое электрический ток, сила тока, плотность тока?
Вывести закон Ома для неоднородного участка электрической цепи и получит из него закон Ома для полной замкнутой и однородного участка электрической цепи.
Каков физический смысл ЭДС? Что такое сторонние силы? Каково их назначение?
4 Чем компенсируется неизвестная ЭДС при достижении нулевого показания гальванометра?
5. Если в схеме компенсации источник заменить другим источником с такой же ЭДС, но с большим внутренним сопротивлением, то в какую сторону следует сместить движок реохорда для восстановления компенсации?
ЛАБОРАТОРНАЯ РАБОТА 5
Электродвижущая сила — определение, формула, единица измерения, разница, часто задаваемые вопросы
Что такое электродвижущая сила?
При отсутствии электрического тока электродвижущей силой является напряжение на клеммах источника. Фраза «электродвижущая сила» относится к количеству работы, необходимой для разделения носителей заряда в токе источника таким образом, чтобы сила, действующая на заряды на клеммах источника, не была прямым результатом действия поля. Внутреннее сопротивление приводит к развитию ЭДС.
Фраза «электродвижущая сила» относится к количеству работы, необходимой для разделения носителей заряда в токе источника таким образом, чтобы сила, действующая на заряды на клеммах источника, не была прямым результатом действия поля. Внутреннее сопротивление приводит к развитию ЭДС.
Полная форма ЭДС — электродвижущая сила.
Что такое определение электродвижущей силы?
ЭДС Определение: Количество работы, выполненной при преобразовании (или преобразовании) энергии, и количество электричества, которое проходит через источник электроэнергии или генератор, определяется как электродвижущая сила (ЭДС). Символ электродвижущей силы (ЭДС) — ε и измеряется в вольтах (или В). В основном мы будем говорить о том, что такое электродвижущая сила, что такое ЭДС в физике и какова формула электродвижущей силы? и другие связанные темы в этой статье.
Что такое ЭДС в физике?
Теперь мы узнаем, что такое ЭДС в физике и что означает ЭДС в физике: когда из ячейки поступает нулевой ток, электродвижущая сила представляет собой наибольшую разность потенциалов между двумя электродами. Электродвижущая сила представлена буквой E; однако иногда он также обозначается знаком ε.
Электродвижущая сила представлена буквой E; однако иногда он также обозначается знаком ε.
Мы знаем, что заряды движутся в электрической цепи; однако мы должны приложить внешнюю силу для перемещения зарядов в определенной электрической цепи. Определение электродвижущей силы состоит в том, что это сила, прикладываемая батареей или внешним источником электричества, таким как батарея, для ускорения заряда. Это не форма силы, несмотря на свое название, а скорее разность потенциалов.
Читайте также —
- Решения NCERT для 11 класса физики
- Решения NCERT для 12 класса физики
- Решения NCERT для всех предметов
Что является источником ЭДС?
Рассмотрим базовую схему лампочки, подключенной к батарее, чтобы развеять эти сомнения.
Определить ЭДС ячейки.
Аккумулятор (или любой другой гальванический элемент) можно рассматривать как устройство с двумя контактами, один из которых находится под более высоким потенциалом, чем другой. Положительную клемму, которая имеет более высокий электрический потенциал, иногда называют положительной клеммой и обычно обозначают знаком плюс. Отрицательная клемма, помеченная знаком минус, является клеммой с более низким потенциалом. Это называется источником электродвижущей силы или ЭДС.
Положительную клемму, которая имеет более высокий электрический потенциал, иногда называют положительной клеммой и обычно обозначают знаком плюс. Отрицательная клемма, помеченная знаком минус, является клеммой с более низким потенциалом. Это называется источником электродвижущей силы или ЭДС.
Нет потока зарядов внутри источника электродвижущей силы, когда источник отделен от света. Заряды перетекают от одной клеммы к другой, проходя через лампочку после повторного подключения батареи к лампочке. Это заставляет лампочку светиться. Положительные заряды покидают положительную клемму, проходят через лампу и входят в отрицательную клемму источника ЭДС с положительным током, также известным как обычный ток. Вот как вы настраиваете источник ЭДС.
Итак, что такое электродвижущая сила?
Разность потенциалов, создаваемая на обоих концах батареи, является электродвижущей силой элемента.
Что такое единица измерения электродвижущей силы?
Что такое единица СИ для электродвижущей силы? Давайте посмотрим, что такое единица электродвижущей силы. Формула электродвижущей силы выглядит следующим образом:
Формула электродвижущей силы выглядит следующим образом:
V+Ir=ε
Где,
Приложенная разность потенциалов обозначается буквой V.
I- Количество тока, протекающего через цепь.
r- Внутреннее сопротивление цепи.
Таким образом, вольт является единицей электродвижущей силы. Электродвижущая сила (ЭДС) рассчитывается путем деления количества джоулей энергии, подаваемой источником, на каждый кулон, необходимый для переноса одного электрического заряда по цепи. С точки зрения математики это выглядит следующим образом:
ε = Джоуль/Кулон
В результате размеры электродвижущей силы [M 1 L 2 T — 3 I -1 ].
В чем разница между напряжением на клеммах и электродвижущей силой (ЭДС)?
Различия ЭДС и напряжения на клеммах следующие:
Разность потенциалов между клеммами нагрузки, когда цепь включена, называется напряжением на клеммах. ЭДС, с другой стороны, определяется как самая высокая разность потенциалов, создаваемая батареей, когда ток не течет.
ЭДС, с другой стороны, определяется как самая высокая разность потенциалов, создаваемая батареей, когда ток не течет.
Напряжение на клеммах измеряется вольтметром, а ЭДС измеряется потенциометром.
Может ли электродвижущая сила быть отрицательной?
Да, электродвижущая сила может быть отрицательной. Рассмотрим случай катушки индуктивности, которая генерирует ЭДС, противодействующую входящей мощности. Таким образом, результирующая ЭДС интерпретируется как отрицательная, поскольку направление потока противоположно направлению истинной мощности. В результате электродвижущая сила может быть отрицательной.
Читайте также:
- NCERT Solutions для физики класса 12 Глава 3 Текущее электричество
- NCERT Пример Пример. Электродвижущая сила
Разность потенциалов
Работа, совершаемая над единицей заряда, определяется как ЭДС. 
Энергия, рассеиваемая при прохождении единичного заряда через компоненты, определяется как разность потенциалов. ЭДС не меняется. Разность потенциалов непостоянна. ЭДС не зависит от сопротивления цепи. Сопротивление между двумя точками цепи во время измерения определяет разность потенциалов. E или ε — его символ. Символ разности потенциалов V. Связь между электродвижущей силой, напряжением на клеммах и внутренним сопротивлением
Разность потенциалов
Количество работы, выполненной при перемещении единичного положительного заряда из одной точки в другую, определяется как разность потенциалов. между двумя точками электрической цепи.
Выполненная работа делится на количество перенесенного заряда, равного разности потенциалов.
В=Вт/кв
Здесь символом разности потенциалов является V
Пример
Когда мы утверждаем, что разность потенциалов между двумя точками составляет 3 вольта, мы имеем в виду, что для перемещения положительной единицы заряда между ними требуется 3 джоуля энергии.

Напряжение на клеммах
Напряжение на клеммах определяется при подаче тока, напряжение на клеммах представляет собой фактическую разность потенциалов на клеммах питания.
Примечание:
Когда электроны перемещаются от отрицательных клемм к положительным в замкнутой цепи, напряжение на клеммах падает ниже значения ЭДС.
Внутреннее сопротивление
Химические реакции в ячейке не поспевают за скоростью разделения зарядов, чтобы поддерживать максимальное разделение зарядов. Заряды должны протекать между электролитом и клеммами, и этому всегда есть некоторое внутреннее сопротивление (r).
В результате при протекании тока возникает внутреннее падение напряжения, равное Ir, и формула напряжения на клеммах определяется как V T = ε — Ir.
Обратите внимание, что при токе I=0 напряжение на клеммах равно ε.

Вот изображение источника напряжения и внутреннего сопротивления для лучшего понимания.
Также, Check-
- NCERT Imeplar Class 11th Physics Solutions
- NCERT IMEPLAR CLASTER SOLUTION 11-й курс физики
- NCERT Notes Class 12-й курс физики
- NCERT Примечания для всех субъектов
Electromotive SIGCL Электрический потенциалESU электрического потенциалаФемтовольтГигавольтГектовольтКиловольтМегавольтМикровольтМилливольтНановольтПетавольтПиковольтПланковское напряжениеСтавольтТеравольтВольтВатт на АмперYоктовольтЗептовольт
+10%
-10%
✖electric Curich -это скорость потока заряда через область поперечного сечения. Единица ДециамперДекаамперEMU токаESU токаExaampereФемтоамперГигаамперGilbertГектоамперKiloamperMegaampereMicroampereMilliampereNanoamperePetaamperePicoampereStatampereTeraampereYoctoampereYottaampereZeptoampereZettaampere
+10%
-10%
✖Сопротивление – это мера сопротивления протеканию тока в электрической цепи.
 Its S.I unit is ohm.ⓘ Resistance [R]
Its S.I unit is ohm.ⓘ Resistance [R]AbohmEMU of ResistanceESU of ResistanceExaohmGigaohmKilohmMegohmMicrohmMilliohmNanohmOhmPetaohmPlanck ImpedanceQuantized Hall ResistanceReciprocal SiemensStatohmVolt per AmpereYottaohmZettaohm
+10%
-10%
✖Напряжение — это разность электрических потенциалов между двумя точками, которая определяется как работа, необходимая на единицу заряда для перемещения пробного заряда между двумя точками.ⓘ Электродвижущая сила при зарядке батареи [В]
AbvoltAttovoltCentivoltDecivoltDekavoltEMU электрического потенциалаESU электрического потенциалаFemtovoltGigavoltHectovoltKilovoltMegavoltMicrovoltMillivoltNanovoltPetavoltPicovoltPlanck VoltageStatvoltTeravoltVoltWatt per AmpereYoctovoltZeptovolt
⎘ Копировать
👎
Формула
Перезагрузить
👍
Электродвижущая сила при зарядке аккумулятора Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовую единицу
Электродвижущая сила: 1,8 В —> 1,8 В Преобразование не требуется
< 10+ текущих калькуляторов электроэнергии
Электрический ток: 2,1 ампер —> 2,1 ампер. Преобразование не требуется.
Преобразование не требуется.
Сопротивление: 10,1 Ом —> 10,1 Ом. Преобразование не требуется. -> Преобразование не требуетсяЭлектродвижущая сила при зарядке аккумулятора Формула
Напряжение = (электродвижущая сила) + (электрический ток * сопротивление)
V = (ε)+(i*R)Как рассчитывается электродвижущая сила при зарядке аккумулятора?
Когда аккумулятор заряжается, аккумулятор действует как нагрузка. Он рассчитывается по формуле V = ε + ir.
где V — напряжение, также известное как напряжение на клеммах,
ε — электродвижущая сила,
i — электрический ток, r — сопротивлениеКак рассчитать электродвижущую силу при зарядке аккумулятора?
Калькулятор электродвижущей силы при зарядке батареи использует Напряжение = (электродвижущая сила)+(электрический ток*сопротивление) для расчета напряжения.
 потенциальную клемму к клемме с более высоким потенциалом внутри батареи. Напряжение обозначается цифрой В символ.
потенциальную клемму к клемме с более высоким потенциалом внутри батареи. Напряжение обозначается цифрой В символ.Как рассчитать электродвижущую силу при зарядке аккумулятора с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для расчета электродвижущей силы при зарядке аккумулятора, введите электродвижущую силу (ε) , электрический ток (i) и сопротивление (R) и нажмите кнопку расчета. Вот как можно объяснить расчет электродвижущей силы при зарядке аккумулятора с заданными входными значениями -> 23,01 = (1,8) + (2,1 * 10,1) .
Часто задаваемые вопросы
Что такое электродвижущая сила при зарядке аккумулятора?
Электродвижущая сила при зарядке батареи представляет собой работу, совершаемую батареей для прохождения заряда в 1 колонку от клеммы с более низким потенциалом к клемме с более высоким потенциалом внутри батареи, и выражается как В = (ε)+(i*R) или Напряжение = (Электродвижущая сила)+(Электрический ток*Сопротивление) .
 Электродвижущая сила — это способность системы пропускать заряд, электрический ток — это временная скорость протекания заряда через площадь поперечного сечения, а сопротивление — это мера сопротивления протеканию тока в электрической цепи. Его единица S.I — ом.
Электродвижущая сила — это способность системы пропускать заряд, электрический ток — это временная скорость протекания заряда через площадь поперечного сечения, а сопротивление — это мера сопротивления протеканию тока в электрической цепи. Его единица S.I — ом.Как рассчитать электродвижущую силу при зарядке аккумулятора?
Электродвижущая сила при зарядке аккумулятора — это работа, выполняемая аккумулятором для прохождения заряда в 1 колонку от клеммы с более низким потенциалом к клемме с более высоким потенциалом внутри батареи, рассчитывается по формуле Напряжение = (Электродвижущая сила) + (Электрический ток * Сопротивление) . Чтобы рассчитать электродвижущую силу при зарядке аккумулятора, вам нужно электродвижущая сила (ε) , электрический ток (i) и сопротивление (R) . С помощью нашего инструмента вам нужно ввести соответствующие значения для электродвижущей силы, электрического тока и сопротивления и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.

Сколько существует способов расчета напряжения?
В этой формуле напряжение использует электродвижущую силу, электрический ток и сопротивление. Мы можем использовать 2 других способа (способов) для вычисления того же самого, которые заключаются в следующем:
- Напряжение = Электрический ток * Сопротивление
- Напряжение = (Электродвижущая сила) — (Электрический ток * Сопротивление)
Доля
Скопировано!
Электродвижущая сила | Что такое, характеристики, как измеряется, формула, примеры
Электродвижущая сила | Что такое, характеристики, как измеряется, формула, примерыРеклама
Публикация
Физика
Электродвижущая сила (ЭДС), — это энергия, исходящая от любых средств, каналов или устройств, которые обеспечивают электрический ток , представляющий собой всю энергию, способную обеспечить или служить для обеспечения жизнеспособного электрического тока, который может использоваться устройством без использования движущихся частей, таких как батареи или портативные аккумуляторы.

Что такое электродвижущая сила?
Электродвижущая сила, представленная как ЭДС , представляет собой любое отношение, существующее между потребляемой электрической энергией и электрическим зарядом, проходящим через нее , обеспечивающий протекание тока в направлении генерируемой электрической цепи. Это может происходить как в открытом, так и в закрытом контуре. Полезность электродвижущей силы заключается в обеспечении энергией устройства без использования движущихся частей , например, батарей, для правильного функционирования которых требуется ЭДС.
- Характеристики электродвижущей силы
- Как измеряется электродвижущая сила
- Формула
- Источники
- Как возникает электродвижущая сила
- Примеры
Характеристики электродвижущей силы
Для того, чтобы соотношение электродвижущей силы имело место, необходимо существование разности потенциалов между двумя полюсами , где один отрицательный и один положительный, чтобы иметь возможность умилостивлять электрические заряды посредством разомкнутой или замкнутой цепи.

Цепи электродвижущей силы могут быть как разомкнутыми, так и замкнутыми, разомкнутая цепь характеризуется тем, что она генерирует электрический ток, который, будучи прерванным или нет, не передается электрическим проводником, не протекает . Это приводит к тому, что он не может производить надлежащий поток энергии, производя эту энергию, которая не используется электрическим током, и соединение неэффективно, когда оно открыто.
С другой стороны, замкнутая или параллельная электрическая цепь работает правильно благодаря тому, что электрический ток продвигается от источника вырабатывающей энергию , например батареи, токопроводящего провода по направлению к приемникам , например, лампочке, проходит через выключатель и включает генератор там, где он подключен, обеспечивая эффективность работы электрическая цепь.
Как измеряется электродвижущая сила
Электродвижущая сила измеряется или рассчитывается по напряжению , которое называется потенциалом или напряжением .
 Сила с электрическими зарядами движется от отрицательного заряда к положительному полюсу. Это делится на его значение в кулонах (это представлено в джоулях/кулонах). Это резюмируется, говоря о вольтах (V), что эквивалентно джоулям между кулонами (J/C).
Сила с электрическими зарядами движется от отрицательного заряда к положительному полюсу. Это делится на его значение в кулонах (это представлено в джоулях/кулонах). Это резюмируется, говоря о вольтах (V), что эквивалентно джоулям между кулонами (J/C).Формула
Электродвижущая сила в замкнутом контуре эквивалентна изменению индукционного потока магнитного поля . Это выражается следующей формулой, ссылающейся на закон Фарадея:
Эта формула также может иметь знак минус «-».
Источники
Электродвижущая сила может быть получена из различных источников:
- Прямой источник электродвижущей силы : Получает поток электрического заряда от устройств прямого действия, таких как батареи, перезаряжаемые батареи, неперезаряжаемые и солнечные батареи, аккумуляторы. Это приводит к тому, что генерируемый ток имеет постоянное значение и интервал относительно большой продолжительности и пропорционален размеру и силе генерирующего устройства.

- Источник переменной электродвижущей силы : В этом случае получаемый электрический ток изменяется во времени, как в случае с автомобильными генераторами, которые обеспечивают электроэнергию для его надлежащего функционирования.
- Источник переменной электродвижущей силы, непеременной подвержены влиянию окружающей среды, приобретая таким образом фактор малой долговечности.
Как генерируется электродвижущая сила
Она может создаваться посредством статического электричества, когда силы притяжения и отталкивания на другие электрические заряды создаются путем трения, например, при трении пластиковой расчески, и генерируется статический электрический заряд . Точно так же электродвижущая сила может быть получена посредством индукции , когда электрические заряды приобретают движение, когда они находятся в жизнеспособном магнитном поле.
Примеры
- Батареи : Внесены в каталог как источники электродвижущей энергии, поскольку они способны генерировать энергию химическим путем.
 Некоторые из них, как в случае с угольно-цинковыми и щелочными батареями, при потреблении их максимальной емкости не подлежат перезарядке. С другой стороны, батареи, состоящие из никель-кадмиевых (NiCad), никелевых и металлогидридных (Ni-MH) и литий-ионных, могут перезаряжаться.
Некоторые из них, как в случае с угольно-цинковыми и щелочными батареями, при потреблении их максимальной емкости не подлежат перезарядке. С другой стороны, батареи, состоящие из никель-кадмиевых (NiCad), никелевых и металлогидридных (Ni-MH) и литий-ионных, могут перезаряжаться. - Электромагнитные машины : Это машины, которые вырабатывают электрическую энергию на основе магнитных и механических средств, таких как небольшие динамо-машины и генераторы, такие, например, как те, которые часто используются в автомобилях, портативных электрических установках и т. д. . Они способны снабжать электроэнергией крупные сооружения, такие как промышленные предприятия и города.
Автор: Габриэла Брисеньо В.
Рекомендуется для вас
Электродвижущая сила — определение, формула, единица измерения, разница
Тег: Что такое ЭДС в физике
Мы знаем, что генератор или батарея используются для преобразования энергии из одной формы в другую. В этих устройствах один вывод заряжается положительно, а другой — отрицательно. Следовательно, электродвижущая сила – это работа, совершаемая над единицей электрического заряда.
В этих устройствах один вывод заряжается положительно, а другой — отрицательно. Следовательно, электродвижущая сила – это работа, совершаемая над единицей электрического заряда.Содержание
- Что такое электродвижущая сила?
- Символ электродвижущей силы
- Что такое формула электродвижущей силы?
- Какова единица измерения ЭДС?
- Размер электродвижущей силы
- Разница между электродвижущей силой и разностью потенциалов
- Может ли электродвижущая сила быть отрицательной?
- В чем разница между напряжением на клеммах и ЭДС?
- Часто задаваемые вопросы – Часто задаваемые вопросы
Что такое электродвижущая сила?
Электродвижущая сила определяется как электрический потенциал, создаваемый либо электрохимической ячейкой, либо изменением магнитного поля. ЭДС — это обычно используемая аббревиатура для обозначения электродвижущей силы.

Генератор или батарея используются для преобразования энергии из одной формы в другую. В этих устройствах один вывод заряжается положительно, а другой — отрицательно. Следовательно, электродвижущая сила – это работа, совершаемая над единицей электрического заряда.
Электродвижущая сила используется в электромагнитном расходомере, который является применением закона Фарадея .
Символ электродвижущей силы
Символ электродвижущей силы ε.
Что такое формула электродвижущей силы?
Ниже приведена формула для электродвижущей силы:
ε = V + Ir Где,
- В — напряжение ячейки
- I — ток в цепи
- Ом — внутреннее сопротивление элемента
- ε — электродвижущая сила
Какова единица ЭДС?
Единицей измерения электродвижущей силы по стандарту является вольт.
ЭДС численно выражается как количество джоулей энергии, отдаваемой источником, деленное на каждый кулон, чтобы позволить единице электрического заряда двигаться по цепи.

\(\begin{array}{l}Вольты=\frac{Джоули}{Кулоны}\end{массив} \)
Размер электродвижущей силы
ЭДС дается как отношение работы, выполненной на единицу заряда, которая представлена следующим образом:
\(\begin{array}{l}ЭДС=\frac{Джоули}{Кулоны}\end{массив} \)
Следовательно, размерность ЭДС дается как M 1 L 2 T -3 I -1
Разница между электродвижущей силой и разностью потенциалов
Электродвижущая сила Разница потенциалов ЭДС определяется как работа, совершаемая на единицу заряда Разность потенциалов определяется как энергия, которая рассеивается при прохождении единичного заряда через компоненты ЭДС остается постоянной Разность потенциалов непостоянна ЭДС не зависит от сопротивления цепи Разность потенциалов зависит от сопротивления между двумя точками во время измерения За счет ЭДС возникает электрическое, магнитное и гравитационное поля Из-за разности потенциалов индуцируется только электрическое поле Обозначается E Обозначается V Может ли электродвижущая сила быть отрицательной?
Да, электродвижущая сила может быть отрицательной.
 Рассмотрим пример, когда катушка индуктивности генерирует ЭДС, противодействующую поступающей мощности. Тогда создаваемая ЭДС принимается отрицательной, так как направление потока противоположно реальной мощности. Следовательно, электродвижущая сила может быть отрицательной.
Рассмотрим пример, когда катушка индуктивности генерирует ЭДС, противодействующую поступающей мощности. Тогда создаваемая ЭДС принимается отрицательной, так как направление потока противоположно реальной мощности. Следовательно, электродвижущая сила может быть отрицательной.В чем разница между напряжением на клеммах и ЭДС?
Ниже приведены различия между напряжением на клеммах и ЭДС:
- Напряжение на клеммах определяется как разность потенциалов на клеммах нагрузки, когда цепь включена. В то время как ЭДС определяется как максимальная разность потенциалов, которую обеспечивает батарея при отсутствии тока.
- Вольтметр используется для измерения напряжения на клеммах, тогда как потенциометр используется для измерения ЭДС.
Ниже представлено видео, объясняющее, как индуцируется ЭДС из-за движения проводника в магнитном поле:
Часто задаваемые вопросы – Часто задаваемые вопросы
Определение электродвижущей силы.

Электродвижущая сила определяется как электрический потенциал, создаваемый либо электрохимической ячейкой, либо изменением магнитного поля.
Какова размерность электродвижущей силы?
Размер ЭДС указан как M 1 L 2 T -3 I -1
Какова единица ЭДС?
Единицей измерения электродвижущей силы является вольт.
Определение разницы потенциалов.
Разность потенциалов определяется как энергия, которая рассеивается при прохождении единичного заряда через компоненты.
Какое напряжение на клеммах?
Напряжение на клеммах определяется как разность потенциалов на клеммах нагрузки, когда цепь включена.
Как найти электродвижущую силу в магнитном поле?
ЭДС, вызванная движением проводника поперек магнитного поля, представляет собой движущую электродвижущую силу. Уравнение задается как E = -vLB .
 Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.Какое уравнение для движущей электродвижущей силы?
ЭДС, вызванная движением проводника поперек магнитного поля, представляет собой движущую электродвижущую силу. Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны.
Какова формула электродвижущей силы?
Движущая электродвижущая сила ЭДС, вызванная движением проводника поперек магнитного поля, является движущей электродвижущей силой. Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны.
Что такое движущие электродвижущие силы?
Давайте узнаем о них больше. ЭДС, вызванная движением проводника поперек магнитного поля, является движущей электродвижущей силой. Уравнение задается как E = -vLB .
Как найти электродвижущую силу в магнитном поле?
ЭДС, вызванная движением проводника поперек магнитного поля, представляет собой движущую электродвижущую силу.
 Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.Какова формула ЭДС движения?
Ответ: ЭДС, вызванная движением относительно магнитного поля, известна как ЭДС движения. Это представлено уравнением ЭДС = LvB, где L — длина объекта, движущегося со скоростью, обозначенной символом v, относительно силы магнитного поля B.
Что такое электродвижущая сила (ЭДС)?
Электродвижущая сила определяется как электрический потенциал, создаваемый либо электрохимической ячейкой, либо изменением магнитного поля. ЭДС — это обычно используемая аббревиатура для электродвижущей силы.
Что такое электродвижущая сила (Е)?
Электродвижущая сила, сокращение Е или ЭДС, энергия на единицу электрического заряда, передаваемая источником энергии, например, электрическим генератором или батареей. Энергия преобразуется из одной формы в другую в генераторе или аккумуляторе, поскольку устройство работает за счет переноса электрического заряда внутрь себя.

Какова размерность электродвижущей силы (ЭДС)?
Электродвижущая сила (ЭДС) рассчитывается путем деления количества джоулей энергии, отдаваемой источником, на каждый кулон, необходимый для передачи единицы электрического заряда по цепи. Математически это так: В результате размерность электродвижущей силы равна M1L2T-3I-1.
Что означает ЭДС?
Электродвижущая сила, сокращенно ЭДС (обозначается и измеряется в вольтах), представляет собой электрическое воздействие, создаваемое неэлектрическим источником. Устройство, которое преобразует другие формы энергии в электрическую («преобразователь»), такое как батарея (преобразование химической энергии) или генератор (преобразование механической энергии).
Может ли электродвижущая сила ЭДС быть отрицательной?
Рассмотрим пример, когда катушка индуктивности генерирует ЭДС, противодействующую входящей мощности. Тогда создаваемая ЭДС принимается отрицательной, так как направление потока противоположно реальной мощности.
 Следовательно, электродвижущая сила может быть отрицательной. В чем разница между напряжением на клеммах и ЭДС?Электродвижущая сила – определение, формула, U…byjus.
Следовательно, электродвижущая сила может быть отрицательной. В чем разница между напряжением на клеммах и ЭДС?Электродвижущая сила – определение, формула, U…byjus.Как найти электродвижущую силу в магнитном поле?
ЭДС, вызванная движением проводника поперек магнитного поля, представляет собой движущую электродвижущую силу. Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Как найти электродвижущую силу проводника?
ЭДС, вызванная движением проводника поперек магнитного поля, представляет собой движущую электродвижущую силу. Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Какова формула электромагнитной электродвижущей силы?
Движущая электродвижущая сила. ЭДС, вызванная движением проводника поперек магнитного поля, является движущей электродвижущей силой.
 Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.Как понять движущую электродвижущую силу?
Чтобы понять движущую электродвижущую силу, давайте сделаем определенную установку. Возьмем прямоугольную катушку, металлический стержень длиной L, движущийся со скоростью V через магнитное поле B. В каком-то месте есть магнитное поле. Длина, скорость и магнитное поле всегда должны быть под прямым углом друг к другу.
Что такое электродвижущая сила (ЭДС)?
Электродвижущая сила определяется как электрический потенциал, создаваемый либо электрохимической ячейкой, либо изменением магнитного поля. ЭДС — это обычно используемая аббревиатура для электродвижущей силы.
Каким образом ЭДС движения индуцируется движением?
Ответ: ЭДС, индуцированная движением по отношению к магнитному полю B, известна как ЭДС движения и задается формулой ЭДС = B″v, обозначаемой как B†, и v перпендикулярно, где мы можем сказать, что символ â „“ — длина объекта, движущегося со скоростью v относительно поля.
 Q2. Как представлена ЭДС движения? ЭДС движения – объяснение, закон, расчет… www.
Q2. Как представлена ЭДС движения? ЭДС движения – объяснение, закон, расчет… www.Когда механическая энергия постоянна?
ЭДС движения ЭДС движения, ЭДС, ЭДС индукции Все мы знаем, что когда электрический проводник вводится в магнитное поле, за счет его динамического взаимодействия с магнитным полем в нем индуцируется ЭДС. Эта ЭДС известна как ЭДС индукции.
Что такое ЭДС движения?
ЭДС индукции, вызванная движением электрического проводника в присутствии магнитного поля, называется ЭДС движения. Таким образом, ЭДС может индуцироваться двумя основными способами: За счет движения проводника в присутствии магнитного поля. Из-за изменения магнитного потока, охваченного цепью.
Как мы производим ЭДС из магнитного поля?
E = Blv ЭДС индукции Blv – это электродвижущая сила движения. Итак, мы создаем ЭДС, перемещая проводник внутри однородного магнитного поля. Мощность, необходимая для перемещения стержня проводника в магнитном поле, равна,Motional Electromotive Force – Toppr-guideswww.

Что означает ЭДС?
ЭДС движения, ЭДС, ЭДС индукции Все мы знаем, что когда электрический проводник вводится в магнитное поле, за счет его динамического взаимодействия с магнитным полем в нем индуцируется ЭДС. Эта ЭДС известна как ЭДС индукции.
электродвижущая сила – Чтение Фейнмана
В моем предыдущем посте я представил электродвигатели, генераторы и трансформаторы. Все они работают из-за правила Фарадея для потоков : изменение магнитного потока создаст некоторую циркуляцию из электрического поля. Формула для правила потока приведена ниже:
Это действительно замечательная вещь, но ее нелегко понять интуитивно . Это одно из этих уравнений, где я должен процитировать введение Фейнмана в электромагнетизм: «Законы Ньютона было очень просто записать, но они имели много сложных следствий, и нам потребовалось много времени, чтобы изучить их все. Законы электромагнетизма не так просто записать, а это значит, что последствия будут более сложными, и нам потребуется довольно много времени, чтобы понять их все .

Среди законов Максвелла этот, безусловно, самый сложный! Однако это не должно нас останавливать. 🙂 Вспоминая Теорема Стокса помогает понять, что представляет собой интеграл в левой части:
У нас есть линейный интеграл вокруг некоторого замкнутого контура Γ слева, а справа у нас есть поверхностный интеграл по некоторой поверхности S, границей которой является Γ. На иллюстрации ниже показана геометрия ситуации. Вы знаете, что все это значит. Если нет, то, боюсь, мне придется вернуть вас к исходной точке, т.е. к моим постам о векторном анализе. Ага. Извиняюсь. Не могу продолжать копировать материал и делать свои посты все длиннее и длиннее. 🙂
Чтобы понять правило потоков, вы должны представить, что петля Γ представляет собой некоторую петлю электрического провода, а затем вы просто замените C на E , вектор электрического поля. Циркуляция E , вызванная изменением магнитного потока, называется электродвижущей силой (э.
 д.с.) , и это тангенциальная сила ( E ·d ) за единицу заряда в проволоке интегрированной по всей длине вокруг петли , который здесь обозначен буквой Γ и который охватывает поверхность S.
д.с.) , и это тангенциальная сила ( E ·d ) за единицу заряда в проволоке интегрированной по всей длине вокруг петли , который здесь обозначен буквой Γ и который охватывает поверхность S.Теперь вы можете перейти от линейного интеграла к поверхностному интегралу, учитывая закон Максвелла: −∂ B /∂t = ∇ × Е . На самом деле это то же самое правило потока, но в дифференциальной форме. Что касается ( ∇ × E ) n , то есть компонента ∇ × E , который является нормальным к поверхности, вы знаете, что любой вектор, умноженный на единичный вектор нормали, даст его нормальную компоненту. В любом случае, если вы это читаете, значит, вы уже должны быть со всем этим знакомы. Давайте рассмотрим концепцию электродвижущей силы, а затем применим ее к нашей первой электрической цепи.
 🙂
🙂Действительно, настало время для небольшой серии статей о схемах, так что мы начнем прямо здесь и сейчас, но… Ну… обо всем по порядку. 🙂
Электродвижущая сила: понятие и единицы измерения
Термин «сила» в «электродвижущей силе» на самом деле несколько вводит в заблуждение. Конечно, здесь задействована сила, но ЭДС не является силой. ЭДС выражается в вольт . Это согласуется с его определением как обращение E : сила, умноженная на расстояние, составляет работа , или энергия (один джоуль равен одному ньютон-метру), а поскольку E есть сила на единицу заряда , циркуляция E выражается в джоулей 9 9 кулон . , то есть напряжение: 1 вольт = 1 джоуль/кулон. Следовательно, в левой части уравнения Фарадея у нас нет никакого измерения времени: это энергии на единицу заряда , то есть x джоуль на кулон .
 Полная остановка.
Полная остановка.В правой части, однако, у нас есть скорость изменения времени магнитного потока . через поверхность S. Магнитный поток представляет собой поверхностный интеграл, поэтому его величина выражается в [B]·m 2 , где [B] — единица измерения напряженности магнитного поля. Временная скорость изменения потока тогда, конечно, выражается в [Б]·м 2 в секунду , т. е. [Б]·м 2 /с. Какова теперь единица напряженности магнитного поля B, которую мы обозначили как [B]?
Ну… [B] — это особая единица измерения: это , а не , измеряемая как некоторая сила на единицу заряда, то есть в ньютонах на кулон, как напряженность электрического поля E. № [B] измеряется в ( N/C)/(м/с). Почему? Потому что магнитная сила равна не F = q E , а F = q v × B . Следовательно, чтобы единицы измерения были правильными, нам нужно выразить B в (Н·с)/(Кл·м), что является единицей, известной как 90 559 тесла 90 560 (1 T = Н·с/C· м), чтобы почтить сербско-американский гений Никола Тесла.
 [Я знаю, что это немного короткий и глупый ответ, но полный ответ довольно сложен: это связано с относительностью магнитной силы, которую я объяснил в другом посте: оба v в F = q v × B Уравнение , а также единица измерения м/с в [B] должны заставить вас задуматься: , чья скорость ? В какой системе отсчета? Но это то, что я не могу обобщить в двух строках, поэтому просто нажмите на ссылку, если хотите узнать больше. Мне нужно вернуться к уроку.]
[Я знаю, что это немного короткий и глупый ответ, но полный ответ довольно сложен: это связано с относительностью магнитной силы, которую я объяснил в другом посте: оба v в F = q v × B Уравнение , а также единица измерения м/с в [B] должны заставить вас задуматься: , чья скорость ? В какой системе отсчета? Но это то, что я не могу обобщить в двух строках, поэтому просто нажмите на ссылку, если хотите узнать больше. Мне нужно вернуться к уроку.]Теперь, когда мы говорим о единицах, я должен отметить, что единица потока также получила специальное название, вебер , в честь одного из самых известных физиков Германии, Вильгельма Эдуарда Вебера: как и следовало ожидать, 1 Wб = 1 Тл·м 2 . Но не беспокойтесь об этих странных именах. Кроме известных вам единиц, таких как джоулей и ньютонов , я буду использовать только вольт , , которые получили свое название в честь другого физика, Алессандро Вольта, изобретателя электрической батареи.
 Или… Ну… я мог бы упомянуть ватт и в какой-то момент… 🙂
Или… Ну… я мог бы упомянуть ватт и в какой-то момент… 🙂Так как же это работает? С одной стороны, у нас есть что-то, выраженное 90 559 в секунду 90 560 — то есть на единицу 90 559 времени 90 560, — а с другой стороны у нас есть нечто, выраженное 90 559 на кулон 90 560 — то есть на единицу 90 559 заряда 90 560. Связь между ними — это в степени , так что это скорость выполнения работы . Она выражается в джоулей в секунду . Итак… Ну… Да. Вот так: в честь еще одного гения, Джеймса Уатта, единица мощности тоже получила свое особое название: Вт . 🙂 В приведенном ниже аргументе я покажу, что мощность, которая генерируется генератором, и которая потребляется в цепи (через резистивный нагрев , например, или что-то еще, отбирающее энергию схемы) равна ЭДС , умноженной на ток . Однако на данный момент я просто предполагаю, что вы мне верите. 🙂
Теперь нам действительно нужно посмотреть на всю схему, в которой наш маленький генератор (то есть наша петля или катушка провода) является лишь одним из Элементы схемы .
 Единицы измерения получаются правильными: мощность = ЭДС · ток произведение выражается в вольт·кулон/секунду = (джоуль/кулон)·(кулон/секунда) = джоуль/секунда. Так что да, выглядит нормально. Но что происходит на самом деле? Как это работает буквально?
Единицы измерения получаются правильными: мощность = ЭДС · ток произведение выражается в вольт·кулон/секунду = (джоуль/кулон)·(кулон/секунда) = джоуль/секунда. Так что да, выглядит нормально. Но что происходит на самом деле? Как это работает буквально?Небольшое отступление: о законе Ома и электричестве
Итак… Позвольте мне сначала напомнить основные понятия, которые, хотите верьте, хотите нет, но, вероятно, проще всего объяснить, кратко вспомнив Закон Ома , который вы наверняка помните из школьных уроков физики. На самом деле все очень просто: у нас есть какое-то сопротивление в небольшой цепи, так что это то, что сопротивляется прохождению электрического тока, а также у нас есть источник напряжения . Теперь закон Ома говорит нам, что отношение (i) напряжения В на сопротивлении (то есть между двумя точками, отмеченными как + и -) и (ii) текущий буду какой-то константой.
 Это то же самое, что сказать, что V и I обратно пропорциональны друг другу. Константа пропорциональности называется самим сопротивлением , и, хотя ее часто рассматривают как свойство самой схемы, мы можем воплотить ее в самом элементе схемы : резисторе , как показано ниже.
Это то же самое, что сказать, что V и I обратно пропорциональны друг другу. Константа пропорциональности называется самим сопротивлением , и, хотя ее часто рассматривают как свойство самой схемы, мы можем воплотить ее в самом элементе схемы : резисторе , как показано ниже.Итак, мы пишем R = V/I, и краткое изложение выше должно напомнить вам о емкость конденсатора, что было еще одной константой пропорциональности. В самом деле, вместо питания резистора (так что вся энергия рассеивается), мы могли бы заряжать конденсатор от источника напряжения, так что это устройство хранения энергии, и тогда мы находим, что отношение между (i) заряд на конденсаторе и (ii) напряжение на конденсаторе тоже было константой, которую мы определили как емкость конденсатора, поэтому мы написали C = Q/V. Так что да, еще одна константа пропорциональности (в электричестве их много!).

В любом случае, суть в следующем: чтобы увеличить ток в приведенной выше цепи, нужно увеличить напряжение, но увеличение обоих равнозначно увеличению мощности , потребляемой в цепи, потому что мощность — это напряжение время действительно актуально, поэтому P = V·I (или v·i, если я использую строчные буквы, которые используются в двух анимациях ниже). Например, если мы хотим удвоить ток, нам нужно удвоить напряжение, и поэтому мы учетверяем мощность: (2·В)·(2·I) = 2 · 2 ·V·I. Итак, у нас есть закон квадрата-куба для мощности, который мы получаем, подставляя V вместо R·I или подставляя I вместо V/R, так что мы можем записать мощность P как P = V 2 /R = I 2 ·Р. Этот закон квадрата-куба говорит то же самое: если вы хотите удвоить напряжение или ток, вам фактически придется удвоить и то, и другое, и, следовательно, вы увеличите мощность в четыре раза. Теперь давайте посмотрим на анимацию ниже (ссылка на Википедию).

Они показывают, как энергия используется в электрической цепи с точки зрения мощности. [Обратите внимание, что маленькие движущиеся плюс соответствуют соглашению о том, что ток определяется как движение положительных зарядов, поэтому мы пишем I = dQ/dt вместо I = −dQ/dt. Это также объясняет направление силовой линии E, которая была добавлена, чтобы показать, что источник энергии эффективно перемещает заряды против поля и, следовательно, против электрической силы.] Здесь мы имеем то, что на одной стороне цепи какой-то генератор или источник напряжения создадут ЭДС , толкая зарядов, а затем некоторая нагрузка создаст потребляют 90 560 своей энергии, поэтому они 90 559 теряют 90 560 своего толчка. Таким образом, мощность , то есть энергии в единицу времени , поступает, а затем потребляется.
Назад к ЭДС…
Теперь я упомянул, что эдс представляет собой отношение двух членов: числитель выражается в джоулей , а знаменатель выражается в кулонов .
 Таким образом, вы можете подумать, что у нас здесь некоторый компромисс — что-то вроде: если мы 90 559 удвоим 90 560 энергии 90 559 половины 90 560 отдельных зарядов, то мы все равно получим ту же 90 559 ЭДС 90 560 . Или наоборот: мы могли бы, пожалуй, удвоить количество зарядов и зарядить их только половиной энергии. Одно можно сказать наверняка: мы не можем оба.
Таким образом, вы можете подумать, что у нас здесь некоторый компромисс — что-то вроде: если мы 90 559 удвоим 90 560 энергии 90 559 половины 90 560 отдельных зарядов, то мы все равно получим ту же 90 559 ЭДС 90 560 . Или наоборот: мы могли бы, пожалуй, удвоить количество зарядов и зарядить их только половиной энергии. Одно можно сказать наверняка: мы не можем оба.Хм… Ну… Давайте посмотрим на эту линию рассуждений, записав ее более формально.
- Скорость изменения магнитного потока во времени создает некоторую ЭДС , которую мы можем и должны рассматривать как свойство петли или катушки провода, в которой он генерируется. Действительно, магнитный поток через него зависит от его ориентации, размера и формы. Так что это действительно очень похоже на емкость конденсатора или сопротивление проводника. Итак, мы пишем: ЭДС = Δ(поток)/Δt. [На самом деле, ЭДС пытается противодействует изменению потока, поэтому я должен добавить знак минус, но вы поняли.
 ]
] - Для однородного магнитного поля поток равен напряженности поля B, умноженной на площадь поверхности S. [Чтобы быть точным, нам нужно взять нормальную составляющую B , поэтому поток равен B · S = B·S·cosθ.] Таким образом, поток может измениться из-за изменения B или из-за изменения S , или из-за того и другого.
- Формула ЭДС = Δ(поток)/Δt ясно показывает, что очень0559 медленное изменение потока (то есть то же Δ(поток) при гораздо большем Δt) создаст небольшую ЭДС . Напротив, очень быстрое изменение (то есть то же Δ(поток) при гораздо меньшем Δt) создаст большую ЭДС . Таким образом, в этом смысле ЭДС — это , а не , как емкость или сопротивление, потому что она переменная: она зависит от Δ(потока), а также от Δt. Тем не менее, вы все равно должны думать об этом как о свойстве цикла или «генератора», о котором мы здесь говорим.

- Теперь мощность , которая вырабатывается или потребляется в цепи, в которой наш «генератор» является лишь одним из элементов, равна ЭДС, умноженной на тока. Мощность — это скорость изменения энергии во времени, а энергия — это работа , совершаемая в цепи (которую я обозначу ΔU), поэтому мы пишем: ЭДС · ток = ΔU/Δt.
- Теперь ток равен скорости изменения заряда во времени, поэтому I = ΔQ/Δt. Следовательно, ЭДС равна ЭДС = (ΔU/Δt)/I = (ΔU/Δt)/(ΔQ/Δt) = ΔU/ΔQ. Отсюда следует, что: э.д.с. = Δ(поток)/Δt = ΔU/ΔQ, что можно переписать как:
Δ(поток) = ΔU·Δt/ΔQ
Это говорит о следующем. При заданной величине изменения магнитного потока (поэтому мы считаем Δ(поток) постоянным в приведенном выше уравнении), мы могли бы выполнить больше работы с тем же зарядом (ΔQ) — мы могли бы удвоить ΔU, перемещая тот же заряд по разность потенциалов, например, в два раза больше, но тогда Δt нужно сократить вдвое.
 Таким образом, одно и то же изменение магнитного потока может сделать в два раза больше работы если изменение происходит в в половине случаев .
Таким образом, одно и то же изменение магнитного потока может сделать в два раза больше работы если изменение происходит в в половине случаев .Значит ли это, что ток удваивается? Мы говорим об одном и том же ΔQ и половине Δt, так что… Ну? Нет. Δt здесь измеряет время изменения потока, так что это не dt в I = dQ/dt. Чтобы ток изменился, нам нужно было бы переместить тот же заряд быстрее, то есть на большее расстояние за то же время. Мы не сказали, что сделаем это выше: мы только сказали, что будем перемещать заряд через большую разность потенциалов: мы не сказали, что изменим расстояние , на которое они перемещаются.
ОК. Это имеет смысл. Но мы еще не совсем закончили. Давайте сначала попробуем что-нибудь другое, чтобы потом каким-то другим путем вернуться туда, где мы сейчас находимся. 🙂 Можем ли мы изменить ΔQ? Здесь нам нужно взглянуть на физику позади. На самом деле происходит то, что изменение магнитного потока вызывает индуцированный 90 559 ток 90 560, который состоит из свободных электронов в петле Γ.
 Таким образом, у нас есть электроны, движущиеся в нашей петле и из нее, и на самом деле через всю цепь, но свободных электронов не так много на единицу длины в проводе. Однако , если мы эффективно удвоим напряжение, то их скорость эффективно увеличится пропорционально , поэтому у нас будет больше из них , проходящих через в секунду . Теперь этот эффект , безусловно, влияет на ток. Это то, что мы написали выше: при прочих равных условиях, включая сопротивление , мы также удвоим ток , поскольку удвоим напряжение.
Таким образом, у нас есть электроны, движущиеся в нашей петле и из нее, и на самом деле через всю цепь, но свободных электронов не так много на единицу длины в проводе. Однако , если мы эффективно удвоим напряжение, то их скорость эффективно увеличится пропорционально , поэтому у нас будет больше из них , проходящих через в секунду . Теперь этот эффект , безусловно, влияет на ток. Это то, что мы написали выше: при прочих равных условиях, включая сопротивление , мы также удвоим ток , поскольку удвоим напряжение.Так где же , эффект в правиле потока? Ответ: его нет. Циркуляция E по контуру такова: это некоторая энергия на единицу заряда . Не в единицу времени. Таким образом, наше правило потока дает нам напряжение, которое говорит нам о том, что 90 559 подтолкнут 90 560 к зарядам в проводе, но ничего не говорит нам о токе.
 Чтобы узнать ток, мы должны знать скорость движущихся зарядов, которую мы можем вычислить из толчка, если мы также получим некоторую другую информацию (например, задействованное сопротивление), но ее нет в формуле правила потока. Вы будете возражать: справа стоит Δt! Да, это правда. Но это не Δt в уравнении v = Δs/Δt для наших зарядов. Полная остановка.
Чтобы узнать ток, мы должны знать скорость движущихся зарядов, которую мы можем вычислить из толчка, если мы также получим некоторую другую информацию (например, задействованное сопротивление), но ее нет в формуле правила потока. Вы будете возражать: справа стоит Δt! Да, это правда. Но это не Δt в уравнении v = Δs/Δt для наших зарядов. Полная остановка.Хм… Я, наверное, уже потерял тебя. Если нет, пожалуйста, продолжайте читать. Позвольте мне донести мысль, задав еще один вопрос. Подумайте о следующем: мы можем переписать приведенное выше уравнение Δ(поток) = ΔU·Δt/ΔQ как уравнение Δ(поток) = (ΔU/ΔQ)·Δt. Означает ли это, что с 9 0559 такое же изменение в поток , т. е. то же самое Δ(поток), и, что важно, при одном и том же Δt мы могли бы удвоить как ΔU, так и ΔQ? Я имею в виду: (2·ΔU)/(2·ΔQ) = ΔU/ΔQ, поэтому уравнение выполняется, математически , то есть. […] Подумай об этом.
Теперь вам следует покачать головой, и это правильно, потому что, хотя уравнение Δ(поток) = (ΔU/ΔQ)·Δt предполагает, что это возможно, это совершенно нелогично.
 Мы ничего не меняем в реальном мире (что происходит там такое же изменение потока за такое же количество времени), но так мы бы получили в два раза больше энергии и в два раза больше заряда?! Конечно, мы могли бы поставить и 3, или 20 000, или 9.0559 минус миллион. Так кто решает, что мы получим? Вы поняли: возможно , а не . Опять же, что мы можем изменить, так это скорость свободных электронов, но не их количество, и чтобы изменить их скорость, вам нужно будет проделать больше работы, и поэтому реальность такова, что мы всегда смотрим на одно и то же. ΔQ, поэтому, если мы хотим получить большее ΔU, нам потребуется большее изменение потока или более короткое Δt, в течение которого происходит это изменение потока.
Мы ничего не меняем в реальном мире (что происходит там такое же изменение потока за такое же количество времени), но так мы бы получили в два раза больше энергии и в два раза больше заряда?! Конечно, мы могли бы поставить и 3, или 20 000, или 9.0559 минус миллион. Так кто решает, что мы получим? Вы поняли: возможно , а не . Опять же, что мы можем изменить, так это скорость свободных электронов, но не их количество, и чтобы изменить их скорость, вам нужно будет проделать больше работы, и поэтому реальность такова, что мы всегда смотрим на одно и то же. ΔQ, поэтому, если мы хотим получить большее ΔU, нам потребуется большее изменение потока или более короткое Δt, в течение которого происходит это изменение потока.Ну и что можно сделаем? Мы можем изменить физику ситуации. Мы можем сделать это разными способами, например, изменить длину цикла или его форму. Одна особенно интересная вещь, которую можно сделать, это увеличить количество петель , чтобы вместо одной петли у нас могла быть некая катушка , скажем, с N витками, так что это N из этих Γ петель.
 Так что же происходит тогда? На самом деле, вопреки тому, что вы могли бы ожидать, ΔQ по-прежнему не меняется по мере того, как он перемещается в катушку, а затем от петли к петле, чтобы выйти, а затем по цепи: это все тот же ΔQ. Но работа , которая может быть выполнена этим током, становится намного больше. На самом деле, два контура дают нам , удвоенную , ЭДС одного контура, а N контуров дают нам N-кратную ЭДС одного контура. Тогда мы можем заставить свободные электроны двигаться быстрее, чтобы они покрывали на 90 559 больше расстояния за 90 560 90 559 за то же время 90 560 (а вы знаете, что работа равна силе, умноженной на расстояние), или мы можем переместить их через 90 559 большую разность потенциалов на том же расстоянии. (и поэтому мы двигаем их против большей силы, так что это также подразумевает, что мы делаем больше работы ). Первый случай — больший ток, а второй — большее напряжение. Так что же это будет?
Так что же происходит тогда? На самом деле, вопреки тому, что вы могли бы ожидать, ΔQ по-прежнему не меняется по мере того, как он перемещается в катушку, а затем от петли к петле, чтобы выйти, а затем по цепи: это все тот же ΔQ. Но работа , которая может быть выполнена этим током, становится намного больше. На самом деле, два контура дают нам , удвоенную , ЭДС одного контура, а N контуров дают нам N-кратную ЭДС одного контура. Тогда мы можем заставить свободные электроны двигаться быстрее, чтобы они покрывали на 90 559 больше расстояния за 90 560 90 559 за то же время 90 560 (а вы знаете, что работа равна силе, умноженной на расстояние), или мы можем переместить их через 90 559 большую разность потенциалов на том же расстоянии. (и поэтому мы двигаем их против большей силы, так что это также подразумевает, что мы делаем больше работы ). Первый случай — больший ток, а второй — большее напряжение. Так что же это будет?Подумайте еще раз о физике ситуации: чтобы заставить заряды двигаться быстрее, вам понадобится большая сила, поэтому у вас будет большая разность потенциалов, то есть большее напряжение.
 Что касается тока, я объясню ниже. Прежде чем я это сделаю, позвольте мне рассказать еще несколько основ.
Что касается тока, я объясню ниже. Прежде чем я это сделаю, позвольте мне рассказать еще несколько основ.В разоблачении ниже мы снова поговорим о мощности, а также о нагрузке. Что такое нагрузка? Подумайте о том, каково это в реальной жизни: покупая аккумулятор для большой машины, мы хотим большой аккумулятор, поэтому мы не смотрим только на напряжение (они все равно 12-вольтовые). Посмотрим сколько ампер это может поставить, и как долго. Стартер в машине, например, может высосать вроде 200 А, но только на очень короткое время, конечно, так как должен включаться сам автомобильный двигатель. Так вот почему емкость аккумуляторов выражается в ампер-часы .
Теперь, как мы получаем такие большие токи, такие большие нагрузки ? Что ж… Воспользуйтесь законом Ома: чтобы получить 200 А при 12 В, сопротивление стартера должно быть всего 0,06 .Ом . Так что большие токи связаны с очень низким сопротивлением .
 Думайте практично: лампочка на 240 вольт 60 ватт потребляет 0,25 А, и, следовательно, ее внутреннее сопротивление составляет около 960 Ом. Также подумайте о том, что происходит в вашем доме: у нас там много резисторов, параллельно потребляющих мощность. Формула для полного сопротивления: 1/R общее = 1/R 1 + 1/R 2 + 1/R 3 + … Таким образом, чем больше приборов, тем меньше сопротивления, вот что привлекает внимание. больший ток.
Думайте практично: лампочка на 240 вольт 60 ватт потребляет 0,25 А, и, следовательно, ее внутреннее сопротивление составляет около 960 Ом. Также подумайте о том, что происходит в вашем доме: у нас там много резисторов, параллельно потребляющих мощность. Формула для полного сопротивления: 1/R общее = 1/R 1 + 1/R 2 + 1/R 3 + … Таким образом, чем больше приборов, тем меньше сопротивления, вот что привлекает внимание. больший ток.Дело в том, что при рассмотрении цепей э.д.с. — это одно, а энергия и мощность, т. Итак, мы говорим о токах, но наше правило потока 90 559, а не 90 560 говорит, какой ток будет производить наш генератор: это зависит от нагрузки. ХОРОШО. Нам действительно нужно вернуться к уроку сейчас.
Цепь с генератором переменного тока
Ситуация показана ниже. У нас есть катушка провода, скажем, из N витков провода, и мы будем использовать ее для создания переменный ток (AC) в цепи.

Катушка действительно похожа на петлю провода в том примитивном электродвигателе, который я представил в предыдущем посте, но теперь мы используем двигатель в качестве генератора. Для упрощения анализа предположим, что мы будем вращать нашу катушку с проволокой в однородном магнитном поле 90 559 90 560, как показано силовыми линиями B .
Наша катушка, конечно, не петля: два конца катушки выведены на внешние соединения через какие-то скользящие контакты, но это не меняет правила потока: a изменение магнитного потока создаст ЭДС и, следовательно, ток в катушке.
ОК. Это достаточно ясно. Давайте посмотрим, что происходит на самом деле. Когда мы вращаем нашу катушку с проволокой, мы изменяем магнитный поток через нее. Если S — площадь катушки, а θ — угол между магнитным полем и нормалью к плоскости катушки, то поток через катушку будет равен B·S·cosθ. Теперь, если мы вращаем катушку с постоянной угловой скоростью ω, то θ изменяется со временем как θ = ω·t.
 Теперь каждый виток катушки будет иметь ЭДС, равную скорости изменения потока, т. е. d(B·S·cosθ)/dt. У нас есть N витков провода, поэтому общая ЭДС, которую мы будем обозначать через Ɛ (ага, новый символ), будет равна:
Теперь каждый виток катушки будет иметь ЭДС, равную скорости изменения потока, т. е. d(B·S·cosθ)/dt. У нас есть N витков провода, поэтому общая ЭДС, которую мы будем обозначать через Ɛ (ага, новый символ), будет равна:Теперь это просто хорошая синусоидальная функция, которая будет выглядеть как график ниже.
Когда по проводу не поступает ток, это Ɛ фактически будет разностью потенциалов между двумя проводами. На самом деле происходит то, что ЭДС создает ток в катушке, который выталкивает некоторые заряды к проводу, и поэтому они остаются там на некоторое время, и между ними возникает разность потенциалов , которую мы обозначим через V, и эта разность потенциалов будет равна Ɛ. Это имеет , чтобы быть равным Ɛ, потому что, если бы это было иначе, у нас, конечно, был бы уравнительный противоток. [Это хороший момент, так что вы должны подумать об этом.] Итак, мы можем написать:
Итак, что происходит, когда мы делаем подключение проводов к цепи, так что у нас есть эта замкнутая цепь , изображенная выше (и ниже)?
Тогда через цепь будет проходить ток I, и закон Ома говорит нам, что отношение между (i) напряжение на сопротивлении в этой цепи (мы предполагаем, что соединения между генератором и самим резистором являются идеальными проводниками) и (ii) ток будет некоторой постоянной, поэтому мы имеем R = V/I и, следовательно:
[Чтобы быть полностью полным, я должен отметить, что, когда другие элементы схемы, кроме резисторов, задействованы, например, конденсаторы и индукторы , у нас будет разность фаз между функциями напряжения и тока.
 , и поэтому мы должны смотреть на полное сопротивление Ом цепи, а не ее сопротивление. Для получения более подробной информации см. приложение под этим сообщением.]
, и поэтому мы должны смотреть на полное сопротивление Ом цепи, а не ее сопротивление. Для получения более подробной информации см. приложение под этим сообщением.]ОК. Давайте теперь посмотрим на задействованную силу и энергию.
Энергия и мощность в цепи переменного тока
Вероятно, у вас возникнет много вопросов по поводу приведенного выше анализа. Вам следует. Я делаю. Самое замечательное, пожалуй, в том, что этот анализ говорит о том, что напряжение не падает, когда мы подключаем генератор к цепи. Должно. Почему бы и нет? Почему заряды на обоих концах провода просто разряд по цепи? В реальной жизни, безусловно, существует такая тенденция : внезапные большие изменения нагрузки будут эффективно производить временные изменения напряжения. Но тогда это как пишет Фейнман : « ЭДС будет продолжать обеспечивать заряд проводов по мере того, как от них отводится ток, пытается удерживать провода всегда при одной и той же разности потенциалов ».

Так сколько тока они потребляют? Как я объяснял выше, это зависит не на генераторе а на цепи и точнее на нагрузке , так что в данном случае это резистор. Опять же, сопротивление представляет собой (постоянное) отношение напряжения к току: R = V/I. Так что подумайте об увеличении или уменьшении сопротивления. Если напряжение остается прежним, это означает, что ток должен соответственно уменьшаться или увеличиваться, поскольку R = V/I подразумевает, что I = V/R. Таким образом, ток обратно пропорционален R, как я объяснял выше при обсуждении автомобильных аккумуляторов, ламп и нагрузок. 🙂
Теперь мне еще нужно доказать, что мощность , выдаваемая нашим генератором, фактически равна P = Ɛ·I, но если это так, то это означает, что выдаваемая мощность будет обратно пропорциональна R. Действительно, когда Ɛ и/или V остаются прежними, поскольку мы добавляем в цепь большее сопротивление, тогда P = Ɛ·I = Ɛ 2 /R, и, таким образом, подаваемая мощность будет обратно пропорциональна R.
 Для ясности , у нас будет связь между P и R, как показано ниже.
Для ясности , у нас будет связь между P и R, как показано ниже.Это несколько странно. Почему? Ну… Я также должен показать вам, что мощность, которая идет на перемещение нашей катушки в магнитном поле, то есть скорость механической работы, необходимой для вращения катушки против магнитных сил, равна электрической мощности Ɛ· I, то есть скорость, с которой электрическая энергия доставляется ЭДС генератора. Однако я отложу это на некоторое время и поэтому просто еще раз попрошу вас поверить мне на слово. 🙂 Теперь, если это так, то если механическая мощность равна электрической мощности, то это означает, что большее сопротивление будет уменьшить механическую мощность, необходимую для поддержания угловой скорости ω. Подумайте о практическом примере: если мы удвоим сопротивление (т. е. 90 559 уменьшим нагрузку вдвое по сравнению с 90 560), а напряжение останется прежним, то ток уменьшится вдвое, а мощность тоже уменьшится вдвое. И давайте подумаем о предельных ситуациях: когда сопротивление стремится к бесконечности, отдаваемая мощность падает до нуля, а ток падает до нуля, а если сопротивление падает до нуля, то и ток, и мощность падают до нуля.
 бесконечность!
бесконечность!Ну… На самом деле мы знаем это также правда в реальной жизни: настоящие генераторы потребляют больше топлива, когда нагрузка увеличивается , поэтому, когда они вырабатывают больше энергии, а намного меньше топлива, поэтому меньше мощности , когда вообще нет нагрузки. Вы будете знать это, по крайней мере, когда будете жить в развивающейся стране с большим количеством сбросов нагрузки! 🙂 А разница огромна: никакой или совсем небольшой груз будет потреблять всего 10% от необходимого при полной загрузке. Это полностью соответствует тому, что я написал о взаимосвязи между сопротивлением и потребляемым током. Так что да, это имеет смысл:
ЭДС действительно производит больший ток, если сопротивление в цепи низкое (т.
Это очень замечательная вещь. Это означает, что если бы мы поместили большую нагрузку на наш маленький генератор переменного тока, потребовалось бы на больше механической работы , чтобы поддерживать вращение катушки с той же угловой скоростью ω.
 Но… Какие изменения? Изменение потока такое же, Δt такое же, и что на самом деле меняется? Что изменяется, так это ток, проходящий через катушку , и это не изменение указанного выше коэффициента ΔQ, а изменение его скорости v .
Но… Какие изменения? Изменение потока такое же, Δt такое же, и что на самом деле меняется? Что изменяется, так это ток, проходящий через катушку , и это не изменение указанного выше коэффициента ΔQ, а изменение его скорости v . Хм… Все это выглядит довольно сложно, не так ли? Так и есть, так что давайте вернемся к анализу того, что у нас есть, так что мы просто предположим, что у нас есть некое динамическое равновесие, подчиняющееся приведенной выше формуле, и поэтому I и R являются тем, чем они являются, и мы связываем их с Ɛ в соответствии с приведенным выше уравнением, то есть:
Теперь позвольте мне доказать эти формулы на мощности нашего генератора и в цепи. У нас есть все эти заряды в нашей катушке, которые получают некоторую энергию. Теперь скорость , с которой они получают энергию, равна F · v .
А? Да.
 Поясню: работа , совершаемая зарядом по некоторому пути, есть прямой интеграл ∫ F ·d s вдоль этого пути. Но бесконечно малое расстояние d s равно v ·dt, as d s /dt = v (обратите внимание, что мы записываем s и v как векторы, поэтому скалярное произведение с F дает нам компонент F , касательная к траектории). Итак, ∫ F · d s = ∫ ( F · v )dt. Таким образом, 90 559 время 90 560 скорость изменения энергии, которая является мощностью, составляет F · v . Просто возьмите производную интеграла по времени. 🙂
Поясню: работа , совершаемая зарядом по некоторому пути, есть прямой интеграл ∫ F ·d s вдоль этого пути. Но бесконечно малое расстояние d s равно v ·dt, as d s /dt = v (обратите внимание, что мы записываем s и v как векторы, поэтому скалярное произведение с F дает нам компонент F , касательная к траектории). Итак, ∫ F · d s = ∫ ( F · v )dt. Таким образом, 90 559 время 90 560 скорость изменения энергии, которая является мощностью, составляет F · v . Просто возьмите производную интеграла по времени. 🙂Теперь предположим, что у нас есть n движущихся зарядов на единицу длины нашей катушки (так что это соответствует тому, что я написал о ΔQ выше), тогда мощность, подаваемая на любой элемент ds катушки, равна ( F · v )·n·ds, что может быть записано как: ( F ·d s )·n·v.
 [Почему? Потому что v и d s имеют одинаковое направление: направление обоих векторов является тангенциальным к проводу, всегда .] Теперь все, что нам нужно сделать, это выяснить, сколько мощности передается в цепь нашего генератора переменного тока это интегрирование этого выражения по катушке, поэтому нам нужно найти:
[Почему? Потому что v и d s имеют одинаковое направление: направление обоих векторов является тангенциальным к проводу, всегда .] Теперь все, что нам нужно сделать, это выяснить, сколько мощности передается в цепь нашего генератора переменного тока это интегрирование этого выражения по катушке, поэтому нам нужно найти:Однако ЭДС (Ɛ) определяется как линейный интеграл ∫ E ·d с линия, взятая вокруг всей катушки, и E = F /q, а ток I равен I = q·n·v. Итак, мощность нашего маленького генератора переменного тока действительно равна:
Итак, готово. Теперь мне нужно выполнить другое мое обещание, а именно показать, что произведение Ɛ·I равно механическая мощность, необходимая для вращения катушки в магнитном поле. Итак, как мы это делаем?
Мы знаем, что будет крутящий момент из-за тока в катушке.
 Его формула имеет вид τ = μ × B . Какое магнитное поле? Что ж… Позвольте мне отослать вас к моему посту о магнитном диполе и его крутящем моменте: это не магнитное поле , вызванное током, а внешнее магнитное поле, так что это B, о котором мы говорили здесь все это время. Итак… Ну… я не пытаюсь вас одурачить. 🙂 Однако магнитный момент μ было , а не , определяемым этим внешним полем, а током в катушке и ее площадью. Действительно, величина μ была произведением тока на площадь, так что в данном случае это N·I·S. Конечно, нам нужно быть начеку, потому что μ само по себе является вектором, и поэтому нам нужен угол между μ и B , чтобы вычислить это векторное произведение τ = μ × B . Однако, если вы проверите, как мы определили направление µ , вы увидите, что она нормальна к плоскости катушки и, следовательно, угол между µ и B и есть тот самый θ = ω·t, с которого мы начали наш анализ.
Его формула имеет вид τ = μ × B . Какое магнитное поле? Что ж… Позвольте мне отослать вас к моему посту о магнитном диполе и его крутящем моменте: это не магнитное поле , вызванное током, а внешнее магнитное поле, так что это B, о котором мы говорили здесь все это время. Итак… Ну… я не пытаюсь вас одурачить. 🙂 Однако магнитный момент μ было , а не , определяемым этим внешним полем, а током в катушке и ее площадью. Действительно, величина μ была произведением тока на площадь, так что в данном случае это N·I·S. Конечно, нам нужно быть начеку, потому что μ само по себе является вектором, и поэтому нам нужен угол между μ и B , чтобы вычислить это векторное произведение τ = μ × B . Однако, если вы проверите, как мы определили направление µ , вы увидите, что она нормальна к плоскости катушки и, следовательно, угол между µ и B и есть тот самый θ = ω·t, с которого мы начали наш анализ. Короче говоря, величина крутящего момента τ равна:
Короче говоря, величина крутящего момента τ равна:τ = (N·I·S)·B·sinθ
Теперь мы знаем, что крутящий момент также равен работа, выполненная 90 559 на единицу пройденного расстояния 90 560 (то есть вокруг оси вращения), поэтому τ = dW/dθ. Теперь dθ = d(ω·t) = ω·dt. Итак, теперь мы можем найти работу, выполненную в единицу времени, так что это мощность еще раз:
dW/dt = ω·τ = ω·(N·I·S)·B·sinθ
Но мы нашли, что Ɛ = N·S·B·ω·sinθ, так что… Итак… Мы находим, что:
dW/dt = Ɛ·I
Теперь это уравнение не решает наш вопрос о том, сколько мощности на самом деле входит в цепь и выходит из нее, когда мы помещаем некоторые нагрузите ее , но это то, что мы обещали сделать: я показал, что механическая работа, которую мы совершаем на катушке, равна электрической энергии , которая передается в цепь. 🙂
Все это довольно загадочно, не так ли? Это. И мы не включили другие важные здесь вещи, такие как явление самоиндукции: переменный ток в катушке фактически будет создавать свое собственное магнитное поле, и, следовательно, на практике мы получим некоторую «противоэдс».
 в цепи. Эта «противоэдс» равна 90 559 против 90 560 тока, когда 90 559 увеличивается 90 560, и 90 559 в направлении 90 560 тока, когда он 90 559 уменьшается. Короче говоря, эффект самоиндукции заставляет ток иметь «инерцию»: индуктивные эффекты пытаются поддерживать постоянный поток, так же как механическая инерция пытается поддерживать постоянной скорость объекта. Но… Ну… я пропустил это. Я возьму в следующий раз, потому что…
в цепи. Эта «противоэдс» равна 90 559 против 90 560 тока, когда 90 559 увеличивается 90 560, и 90 559 в направлении 90 560 тока, когда он 90 559 уменьшается. Короче говоря, эффект самоиндукции заставляет ток иметь «инерцию»: индуктивные эффекты пытаются поддерживать постоянный поток, так же как механическая инерция пытается поддерживать постоянной скорость объекта. Но… Ну… я пропустил это. Я возьму в следующий раз, потому что…[…] Ну… Уже вечереет, и поэтому я должен предположить, что это своего рода «достаточно хорошо» для введения в то, чем мы будем заниматься на следующей неделе. Будьте осторожны, и я поговорю с вами снова в ближайшее время. 🙂
Возможно, одно небольшое замечание по поводу вопроса, который мог возникнуть, когда вы читали все вышеизложенное: так как же настоящие генераторы поддерживают высокое напряжение? Что ж… Большинство генераторов переменного тока на самом деле представляют собой так называемые устройства 90 559 с постоянной скоростью 90 560.
 Вы можете загрузить некоторые руководства из Интернета, и вы найдете такие вещи: не работайте на скоростях выше 4% от номинальной скорости или более чем на 1% ниже номинальной скорости. К счастью, так называемая регулятор двигателя возьмет на себя эту машину. 🙂
Вы можете загрузить некоторые руководства из Интернета, и вы найдете такие вещи: не работайте на скоростях выше 4% от номинальной скорости или более чем на 1% ниже номинальной скорости. К счастью, так называемая регулятор двигателя возьмет на себя эту машину. 🙂Приложение : Понятие импеданса
В одном из моих постов об осцилляторах я объясняю понятие импеданса , которое эквивалентно сопротивлению , но для цепей переменного тока. Как и сопротивление, импеданс также измеряет «сопротивление», которое цепь оказывает току при приложении напряжения, но это комплексное отношение , в отличие от R = V/I. Это буквально сложное отношение, потому что импеданс имеет величину 9.0559 и направление, или фаза , как ее обычно называют. Следовательно, импеданс (обозначаемый как Z ) часто записывают по формуле Эйлера:
Z = | З | e i θ
Иллюстрация ниже (снова ссылка на Википедию) объясняет, что происходит.
 Это довольно общий вид той же цепи переменного тока. Правда в том, что если мы применим переменный ток, то и ток, и напряжение будут увеличиваться и уменьшаться, но 9Сигнал тока 0559 обычно отстает от сигнала напряжения , и фазовый коэффициент θ говорит нам, насколько. Следовательно, используя систему комплексных чисел, мы пишем:
Это довольно общий вид той же цепи переменного тока. Правда в том, что если мы применим переменный ток, то и ток, и напряжение будут увеличиваться и уменьшаться, но 9Сигнал тока 0559 обычно отстает от сигнала напряжения , и фазовый коэффициент θ говорит нам, насколько. Следовательно, используя систему комплексных чисел, мы пишем:V = I ∗ Z = I ∗| З | e i θ
Теперь, хотя это напоминает формулу V = R·I, обратите внимание на жирный шрифт для V и I , а также на символ *, который я использую. здесь для умножения. Сначала символ *: чтобы было ясно, что мы не говорим о векторном векторном произведении A × B здесь, но произведение двух комплексных чисел. Жирным шрифтом для V и I подразумевается, что они подобны векторам или комплексным числам: так что они тоже имеют фазу и, следовательно, мы можем записать их как:
- V = | В | e i (ωt + θ В )
- I = | я | e i (ωt + θ я )
Чтобы быть полностью завершенным — вы можете пропустить все это, если хотите, но это не так сложно и не очень долго — все работает следующим образом.
 Пишем:
Пишем:В = I ∗ Z = | я | e i (ωt + θ I ) ∗| З | e i θ = | я || З | и и (ωt + θ I + θ) = | В | e i (ωt + θ V )
Теперь это уравнение должно выполняться для всех t, поэтому мы можем приравнять величины и фазы и, следовательно, мы получаем: | В | = | я || З | и так мы получаем нужную нам формулу, т.е. фаз разность между нашей функцией для напряжения и нашей функцией для тока.
θ В = θ I + θ
Вы, конечно, скажете: напряжение и ток — нечто реальное, не так ли? Так что там с комплексными числами? Ты прав.
 Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций.
Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций.Ох… И еще обратите внимание, что, как было сказано выше, у нас нет такой задержки или разности фаз, когда задействованы только резисторы. Поэтому нам не нужна концепция импеданса в приведенном выше анализе. С этим дополнением я просто хотел быть как можно более полным. 🙂
Некоторый контент на этой странице был отключен 16 июня 2020 г. в результате уведомления Калифорнийского технологического института об удалении в соответствии с Законом США «Об авторском праве в цифровую эпоху». Вы можете узнать больше о DMCA здесь:
https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторый контент на этой странице был отключен 16 июня 2020 г. в результате уведомления об удалении DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.
 com/copyright-and-the-dmca/
com/copyright-and-the-dmca/
Некоторый контент на этой странице был отключен 16 июня 2020 г. в результате уведомления Калифорнийского технологического института об удалении в соответствии с Законом США «Об авторском праве в цифровую эпоху». Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторый контент на этой странице был отключен 16 июня 2020 г. в результате уведомления об удалении DMCA от Калифорнийского технологического института. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторый контент на этой странице был отключен 17 июня 2020 г. в результате уведомления Майкла А. Готлиба, Рудольфа Пфайффера и Калифорнийского технологического института об удалении DMCA. Вы можете узнать больше о DMCA здесь:https://en.support.wordpress.com/copyright-and-the-dmca/
Некоторый контент на этой странице был отключен 20 июня 2020 г. в результате уведомления об удалении DMCA от Майкла А.


 С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434.
С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 351-355, 432-434.
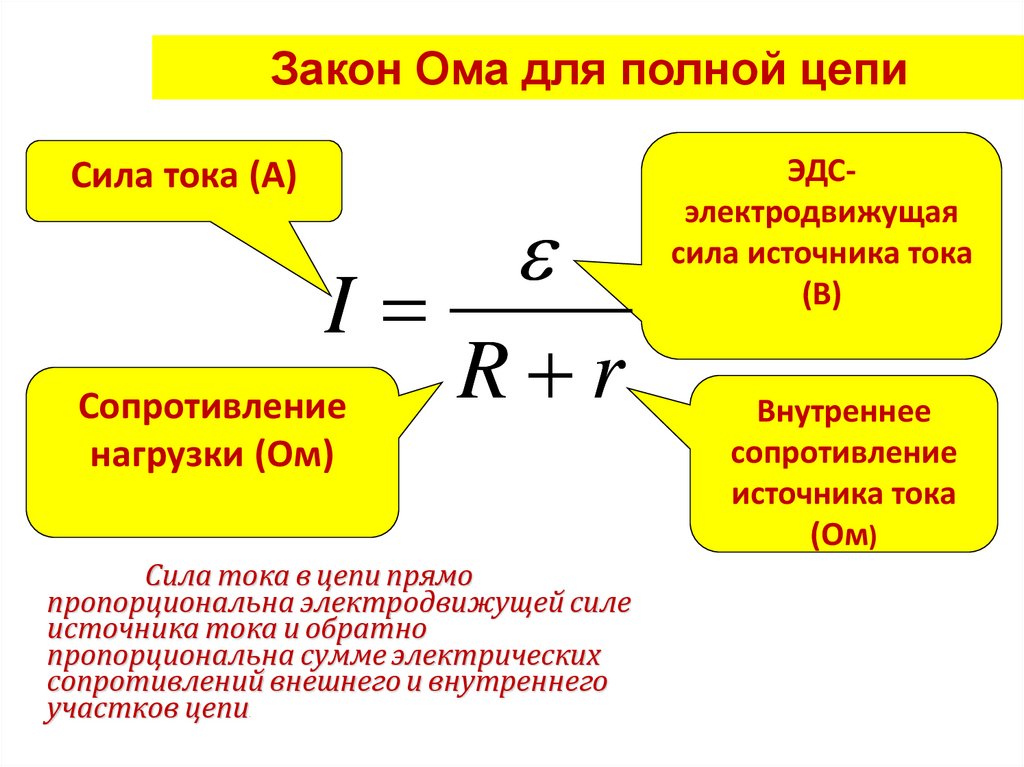 После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.


 Its S.I unit is ohm.ⓘ Resistance [R]
Its S.I unit is ohm.ⓘ Resistance [R] Преобразование не требуется.
Преобразование не требуется. 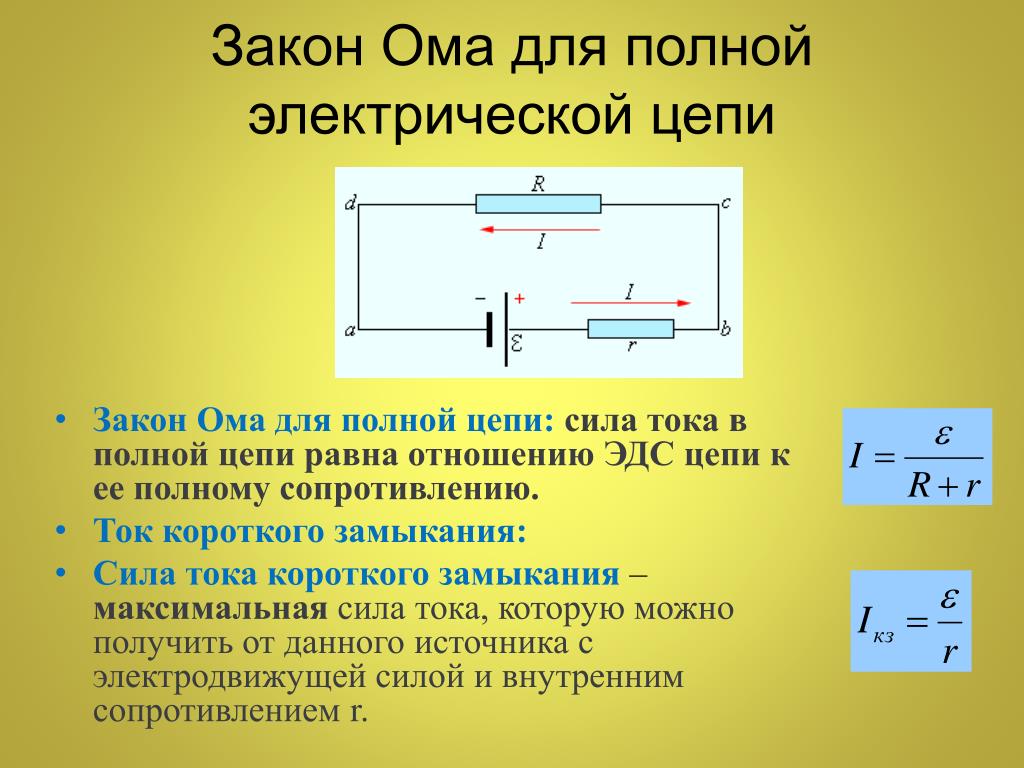 потенциальную клемму к клемме с более высоким потенциалом внутри батареи. Напряжение обозначается цифрой В символ.
потенциальную клемму к клемме с более высоким потенциалом внутри батареи. Напряжение обозначается цифрой В символ.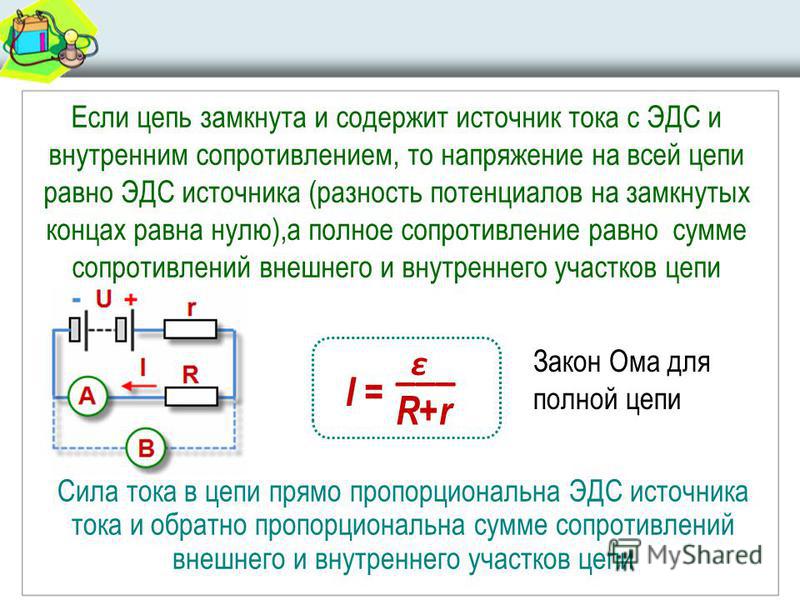 Электродвижущая сила — это способность системы пропускать заряд, электрический ток — это временная скорость протекания заряда через площадь поперечного сечения, а сопротивление — это мера сопротивления протеканию тока в электрической цепи. Его единица S.I — ом.
Электродвижущая сила — это способность системы пропускать заряд, электрический ток — это временная скорость протекания заряда через площадь поперечного сечения, а сопротивление — это мера сопротивления протеканию тока в электрической цепи. Его единица S.I — ом.


 Сила с электрическими зарядами движется от отрицательного заряда к положительному полюсу. Это делится на его значение в кулонах (это представлено в джоулях/кулонах). Это резюмируется, говоря о вольтах (V), что эквивалентно джоулям между кулонами (J/C).
Сила с электрическими зарядами движется от отрицательного заряда к положительному полюсу. Это делится на его значение в кулонах (это представлено в джоулях/кулонах). Это резюмируется, говоря о вольтах (V), что эквивалентно джоулям между кулонами (J/C).
 Некоторые из них, как в случае с угольно-цинковыми и щелочными батареями, при потреблении их максимальной емкости не подлежат перезарядке. С другой стороны, батареи, состоящие из никель-кадмиевых (NiCad), никелевых и металлогидридных (Ni-MH) и литий-ионных, могут перезаряжаться.
Некоторые из них, как в случае с угольно-цинковыми и щелочными батареями, при потреблении их максимальной емкости не подлежат перезарядке. С другой стороны, батареи, состоящие из никель-кадмиевых (NiCad), никелевых и металлогидридных (Ni-MH) и литий-ионных, могут перезаряжаться.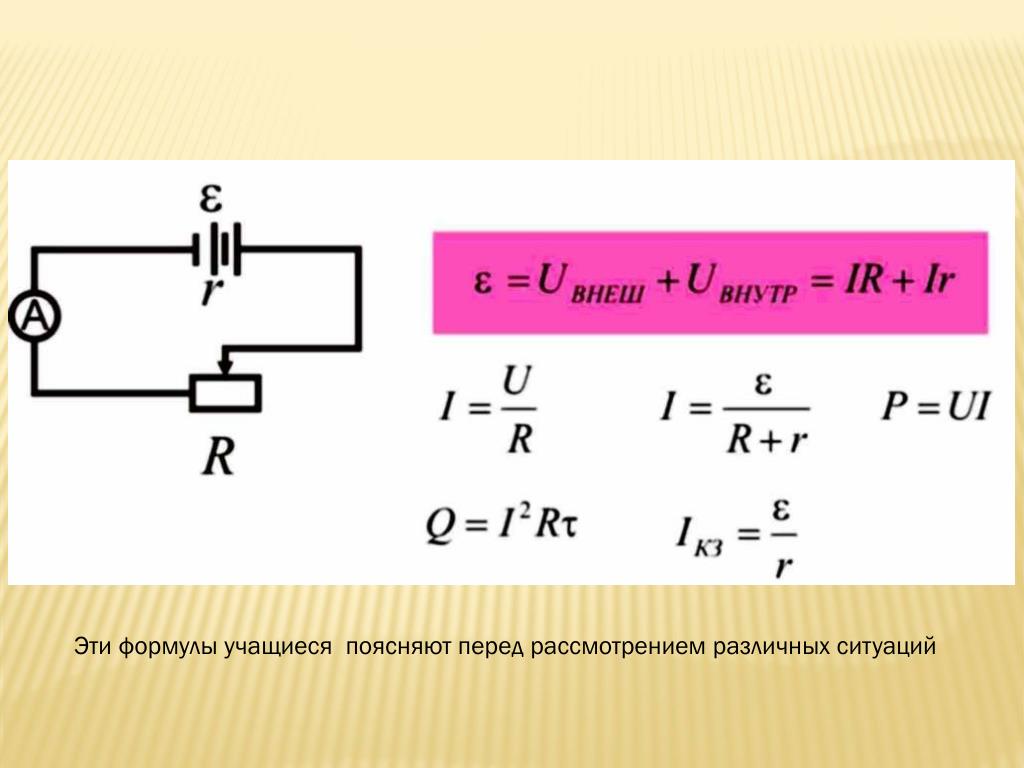 В этих устройствах один вывод заряжается положительно, а другой — отрицательно. Следовательно, электродвижущая сила – это работа, совершаемая над единицей электрического заряда.
В этих устройствах один вывод заряжается положительно, а другой — отрицательно. Следовательно, электродвижущая сила – это работа, совершаемая над единицей электрического заряда.

 Рассмотрим пример, когда катушка индуктивности генерирует ЭДС, противодействующую поступающей мощности. Тогда создаваемая ЭДС принимается отрицательной, так как направление потока противоположно реальной мощности. Следовательно, электродвижущая сила может быть отрицательной.
Рассмотрим пример, когда катушка индуктивности генерирует ЭДС, противодействующую поступающей мощности. Тогда создаваемая ЭДС принимается отрицательной, так как направление потока противоположно реальной мощности. Следовательно, электродвижущая сила может быть отрицательной.
 Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца. Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Уравнение задается как E = -vLB . Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.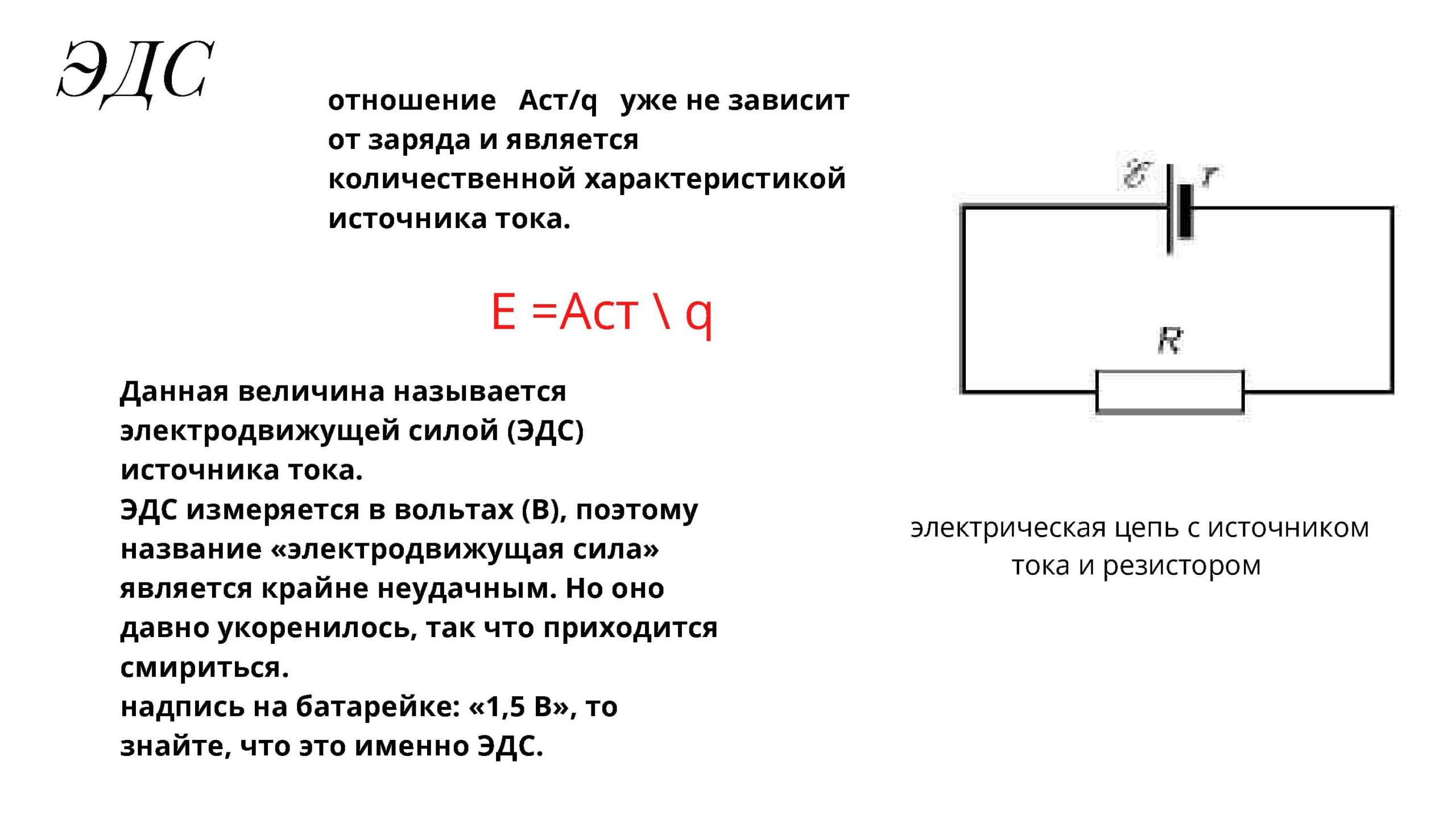
 Следовательно, электродвижущая сила может быть отрицательной. В чем разница между напряжением на клеммах и ЭДС?Электродвижущая сила – определение, формула, U…byjus.
Следовательно, электродвижущая сила может быть отрицательной. В чем разница между напряжением на клеммах и ЭДС?Электродвижущая сила – определение, формула, U…byjus.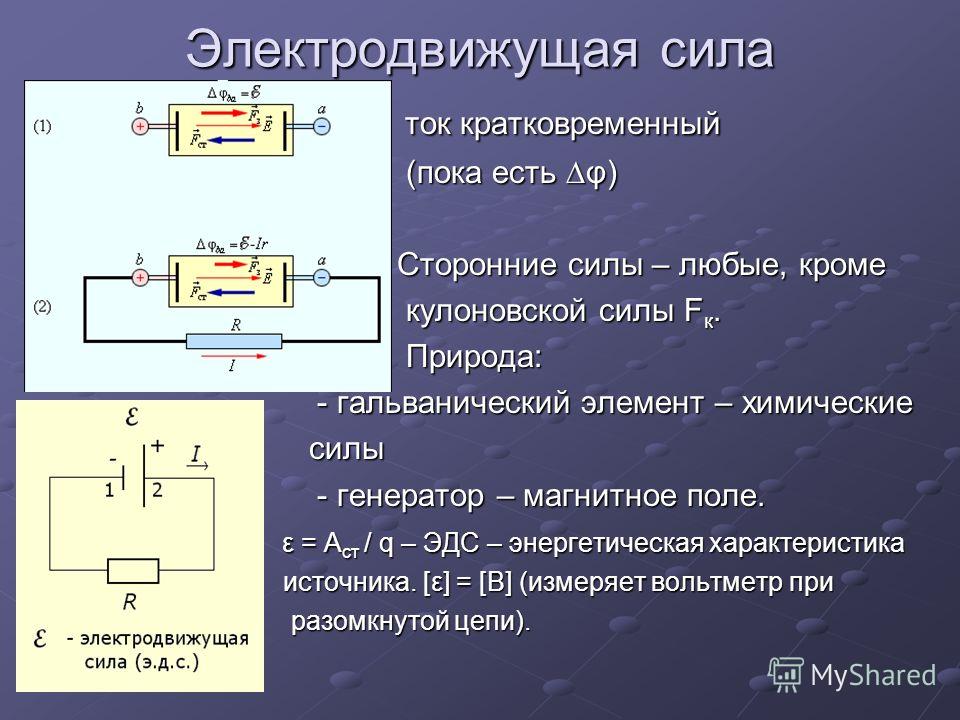 Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца.
Уравнение задается как E = -vLB. Это уравнение верно, пока скорость, поле и длина взаимно перпендикулярны. Знак минус связан с законом Ленца. Q2. Как представлена ЭДС движения? ЭДС движения – объяснение, закон, расчет… www.
Q2. Как представлена ЭДС движения? ЭДС движения – объяснение, закон, расчет… www.

 д.с.) , и это тангенциальная сила ( E ·d ) за единицу заряда в проволоке интегрированной по всей длине вокруг петли , который здесь обозначен буквой Γ и который охватывает поверхность S.
д.с.) , и это тангенциальная сила ( E ·d ) за единицу заряда в проволоке интегрированной по всей длине вокруг петли , который здесь обозначен буквой Γ и который охватывает поверхность S. 🙂
🙂 Полная остановка.
Полная остановка. [Я знаю, что это немного короткий и глупый ответ, но полный ответ довольно сложен: это связано с относительностью магнитной силы, которую я объяснил в другом посте: оба v в F = q v × B Уравнение , а также единица измерения м/с в [B] должны заставить вас задуматься: , чья скорость ? В какой системе отсчета? Но это то, что я не могу обобщить в двух строках, поэтому просто нажмите на ссылку, если хотите узнать больше. Мне нужно вернуться к уроку.]
[Я знаю, что это немного короткий и глупый ответ, но полный ответ довольно сложен: это связано с относительностью магнитной силы, которую я объяснил в другом посте: оба v в F = q v × B Уравнение , а также единица измерения м/с в [B] должны заставить вас задуматься: , чья скорость ? В какой системе отсчета? Но это то, что я не могу обобщить в двух строках, поэтому просто нажмите на ссылку, если хотите узнать больше. Мне нужно вернуться к уроку.] Или… Ну… я мог бы упомянуть ватт и в какой-то момент… 🙂
Или… Ну… я мог бы упомянуть ватт и в какой-то момент… 🙂 Единицы измерения получаются правильными: мощность = ЭДС · ток произведение выражается в вольт·кулон/секунду = (джоуль/кулон)·(кулон/секунда) = джоуль/секунда. Так что да, выглядит нормально. Но что происходит на самом деле? Как это работает буквально?
Единицы измерения получаются правильными: мощность = ЭДС · ток произведение выражается в вольт·кулон/секунду = (джоуль/кулон)·(кулон/секунда) = джоуль/секунда. Так что да, выглядит нормально. Но что происходит на самом деле? Как это работает буквально? Это то же самое, что сказать, что V и I обратно пропорциональны друг другу. Константа пропорциональности называется самим сопротивлением , и, хотя ее часто рассматривают как свойство самой схемы, мы можем воплотить ее в самом элементе схемы : резисторе , как показано ниже.
Это то же самое, что сказать, что V и I обратно пропорциональны друг другу. Константа пропорциональности называется самим сопротивлением , и, хотя ее часто рассматривают как свойство самой схемы, мы можем воплотить ее в самом элементе схемы : резисторе , как показано ниже.

 Таким образом, вы можете подумать, что у нас здесь некоторый компромисс — что-то вроде: если мы 90 559 удвоим 90 560 энергии 90 559 половины 90 560 отдельных зарядов, то мы все равно получим ту же 90 559 ЭДС 90 560 . Или наоборот: мы могли бы, пожалуй, удвоить количество зарядов и зарядить их только половиной энергии. Одно можно сказать наверняка: мы не можем оба.
Таким образом, вы можете подумать, что у нас здесь некоторый компромисс — что-то вроде: если мы 90 559 удвоим 90 560 энергии 90 559 половины 90 560 отдельных зарядов, то мы все равно получим ту же 90 559 ЭДС 90 560 . Или наоборот: мы могли бы, пожалуй, удвоить количество зарядов и зарядить их только половиной энергии. Одно можно сказать наверняка: мы не можем оба.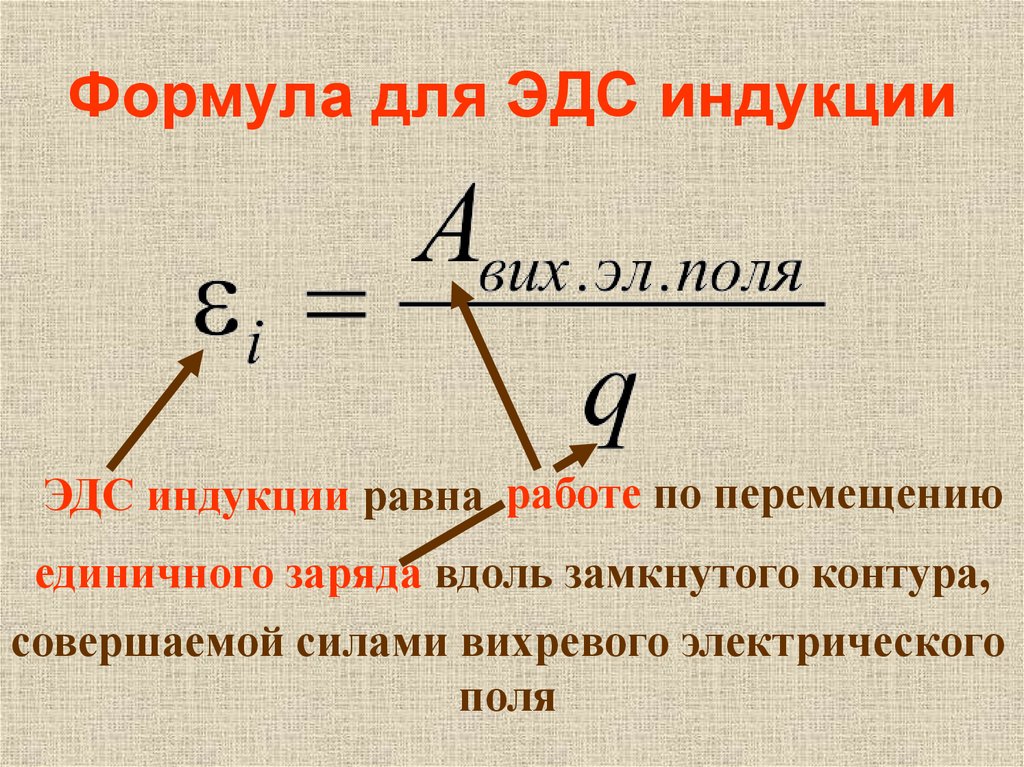 ]
]
 Таким образом, одно и то же изменение магнитного потока может сделать в два раза больше работы если изменение происходит в в половине случаев .
Таким образом, одно и то же изменение магнитного потока может сделать в два раза больше работы если изменение происходит в в половине случаев . Таким образом, у нас есть электроны, движущиеся в нашей петле и из нее, и на самом деле через всю цепь, но свободных электронов не так много на единицу длины в проводе. Однако , если мы эффективно удвоим напряжение, то их скорость эффективно увеличится пропорционально , поэтому у нас будет больше из них , проходящих через в секунду . Теперь этот эффект , безусловно, влияет на ток. Это то, что мы написали выше: при прочих равных условиях, включая сопротивление , мы также удвоим ток , поскольку удвоим напряжение.
Таким образом, у нас есть электроны, движущиеся в нашей петле и из нее, и на самом деле через всю цепь, но свободных электронов не так много на единицу длины в проводе. Однако , если мы эффективно удвоим напряжение, то их скорость эффективно увеличится пропорционально , поэтому у нас будет больше из них , проходящих через в секунду . Теперь этот эффект , безусловно, влияет на ток. Это то, что мы написали выше: при прочих равных условиях, включая сопротивление , мы также удвоим ток , поскольку удвоим напряжение. Чтобы узнать ток, мы должны знать скорость движущихся зарядов, которую мы можем вычислить из толчка, если мы также получим некоторую другую информацию (например, задействованное сопротивление), но ее нет в формуле правила потока. Вы будете возражать: справа стоит Δt! Да, это правда. Но это не Δt в уравнении v = Δs/Δt для наших зарядов. Полная остановка.
Чтобы узнать ток, мы должны знать скорость движущихся зарядов, которую мы можем вычислить из толчка, если мы также получим некоторую другую информацию (например, задействованное сопротивление), но ее нет в формуле правила потока. Вы будете возражать: справа стоит Δt! Да, это правда. Но это не Δt в уравнении v = Δs/Δt для наших зарядов. Полная остановка.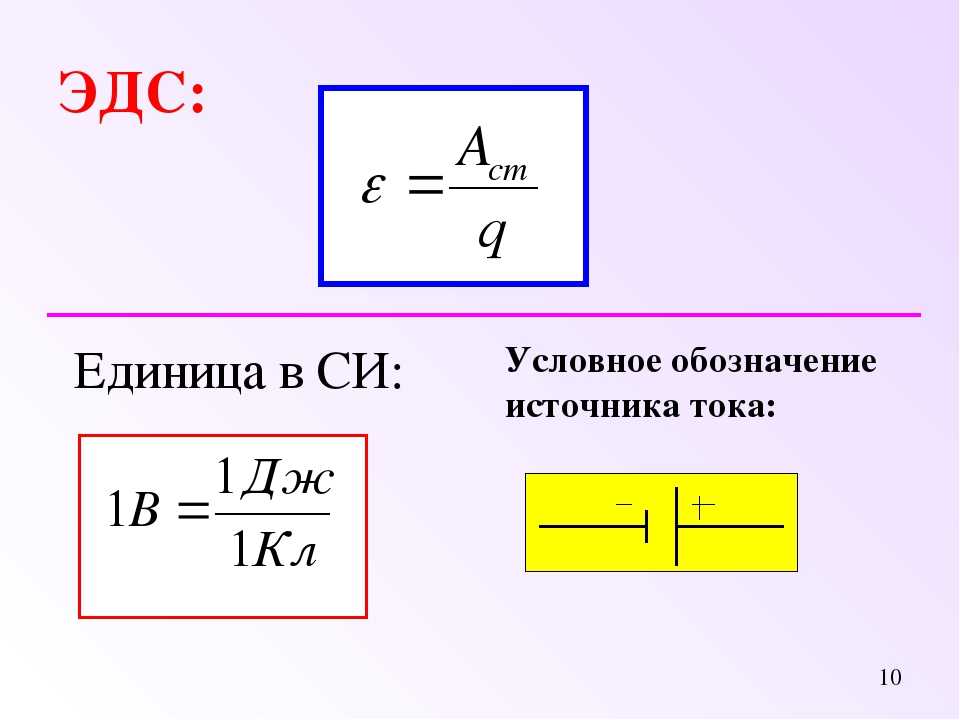 Мы ничего не меняем в реальном мире (что происходит там такое же изменение потока за такое же количество времени), но так мы бы получили в два раза больше энергии и в два раза больше заряда?! Конечно, мы могли бы поставить и 3, или 20 000, или 9.0559 минус миллион. Так кто решает, что мы получим? Вы поняли: возможно , а не . Опять же, что мы можем изменить, так это скорость свободных электронов, но не их количество, и чтобы изменить их скорость, вам нужно будет проделать больше работы, и поэтому реальность такова, что мы всегда смотрим на одно и то же. ΔQ, поэтому, если мы хотим получить большее ΔU, нам потребуется большее изменение потока или более короткое Δt, в течение которого происходит это изменение потока.
Мы ничего не меняем в реальном мире (что происходит там такое же изменение потока за такое же количество времени), но так мы бы получили в два раза больше энергии и в два раза больше заряда?! Конечно, мы могли бы поставить и 3, или 20 000, или 9.0559 минус миллион. Так кто решает, что мы получим? Вы поняли: возможно , а не . Опять же, что мы можем изменить, так это скорость свободных электронов, но не их количество, и чтобы изменить их скорость, вам нужно будет проделать больше работы, и поэтому реальность такова, что мы всегда смотрим на одно и то же. ΔQ, поэтому, если мы хотим получить большее ΔU, нам потребуется большее изменение потока или более короткое Δt, в течение которого происходит это изменение потока. Так что же происходит тогда? На самом деле, вопреки тому, что вы могли бы ожидать, ΔQ по-прежнему не меняется по мере того, как он перемещается в катушку, а затем от петли к петле, чтобы выйти, а затем по цепи: это все тот же ΔQ. Но работа , которая может быть выполнена этим током, становится намного больше. На самом деле, два контура дают нам , удвоенную , ЭДС одного контура, а N контуров дают нам N-кратную ЭДС одного контура. Тогда мы можем заставить свободные электроны двигаться быстрее, чтобы они покрывали на 90 559 больше расстояния за 90 560 90 559 за то же время 90 560 (а вы знаете, что работа равна силе, умноженной на расстояние), или мы можем переместить их через 90 559 большую разность потенциалов на том же расстоянии. (и поэтому мы двигаем их против большей силы, так что это также подразумевает, что мы делаем больше работы ). Первый случай — больший ток, а второй — большее напряжение. Так что же это будет?
Так что же происходит тогда? На самом деле, вопреки тому, что вы могли бы ожидать, ΔQ по-прежнему не меняется по мере того, как он перемещается в катушку, а затем от петли к петле, чтобы выйти, а затем по цепи: это все тот же ΔQ. Но работа , которая может быть выполнена этим током, становится намного больше. На самом деле, два контура дают нам , удвоенную , ЭДС одного контура, а N контуров дают нам N-кратную ЭДС одного контура. Тогда мы можем заставить свободные электроны двигаться быстрее, чтобы они покрывали на 90 559 больше расстояния за 90 560 90 559 за то же время 90 560 (а вы знаете, что работа равна силе, умноженной на расстояние), или мы можем переместить их через 90 559 большую разность потенциалов на том же расстоянии. (и поэтому мы двигаем их против большей силы, так что это также подразумевает, что мы делаем больше работы ). Первый случай — больший ток, а второй — большее напряжение. Так что же это будет?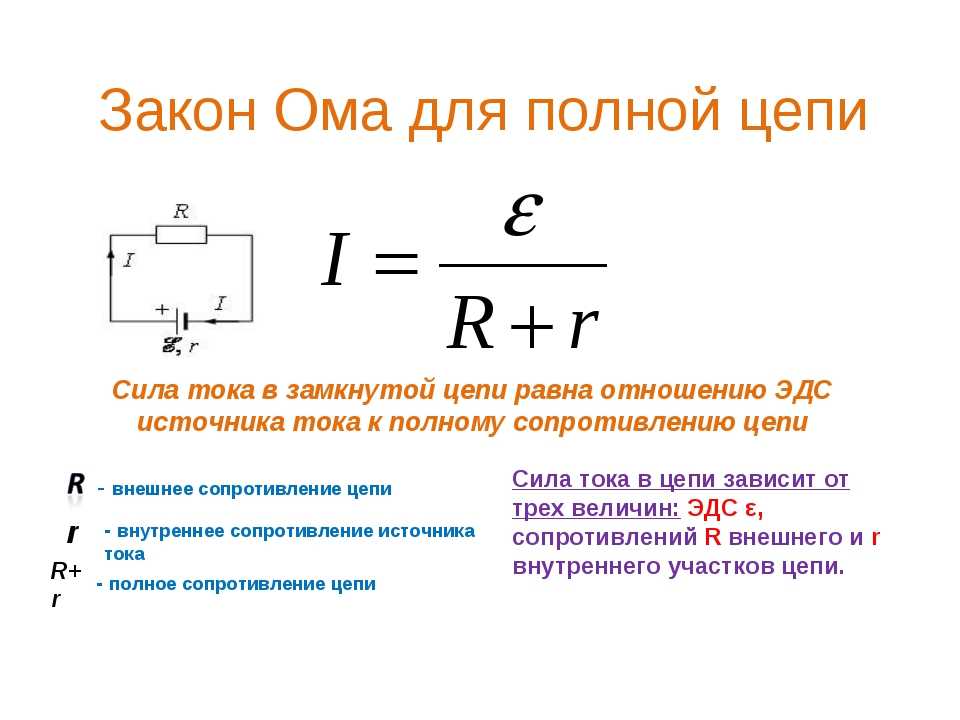 Что касается тока, я объясню ниже. Прежде чем я это сделаю, позвольте мне рассказать еще несколько основ.
Что касается тока, я объясню ниже. Прежде чем я это сделаю, позвольте мне рассказать еще несколько основ. Думайте практично: лампочка на 240 вольт 60 ватт потребляет 0,25 А, и, следовательно, ее внутреннее сопротивление составляет около 960 Ом. Также подумайте о том, что происходит в вашем доме: у нас там много резисторов, параллельно потребляющих мощность. Формула для полного сопротивления: 1/R общее = 1/R 1 + 1/R 2 + 1/R 3 + … Таким образом, чем больше приборов, тем меньше сопротивления, вот что привлекает внимание. больший ток.
Думайте практично: лампочка на 240 вольт 60 ватт потребляет 0,25 А, и, следовательно, ее внутреннее сопротивление составляет около 960 Ом. Также подумайте о том, что происходит в вашем доме: у нас там много резисторов, параллельно потребляющих мощность. Формула для полного сопротивления: 1/R общее = 1/R 1 + 1/R 2 + 1/R 3 + … Таким образом, чем больше приборов, тем меньше сопротивления, вот что привлекает внимание. больший ток.
 Теперь каждый виток катушки будет иметь ЭДС, равную скорости изменения потока, т. е. d(B·S·cosθ)/dt. У нас есть N витков провода, поэтому общая ЭДС, которую мы будем обозначать через Ɛ (ага, новый символ), будет равна:
Теперь каждый виток катушки будет иметь ЭДС, равную скорости изменения потока, т. е. d(B·S·cosθ)/dt. У нас есть N витков провода, поэтому общая ЭДС, которую мы будем обозначать через Ɛ (ага, новый символ), будет равна: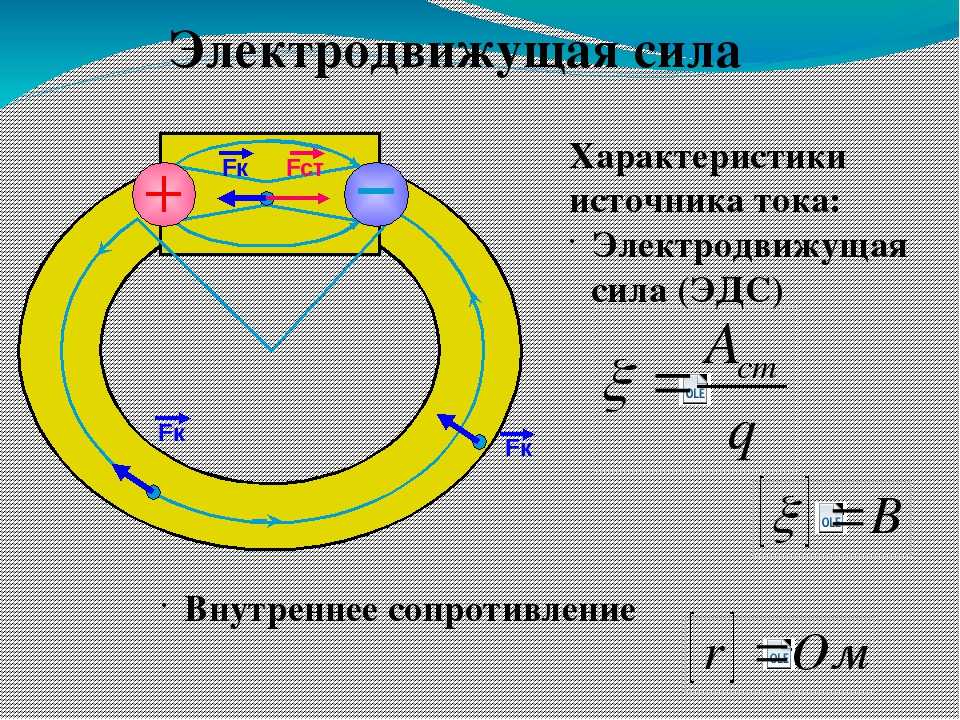 , и поэтому мы должны смотреть на полное сопротивление Ом цепи, а не ее сопротивление. Для получения более подробной информации см. приложение под этим сообщением.]
, и поэтому мы должны смотреть на полное сопротивление Ом цепи, а не ее сопротивление. Для получения более подробной информации см. приложение под этим сообщением.]
 Для ясности , у нас будет связь между P и R, как показано ниже.
Для ясности , у нас будет связь между P и R, как показано ниже. бесконечность!
бесконечность! Но… Какие изменения? Изменение потока такое же, Δt такое же, и что на самом деле меняется? Что изменяется, так это ток, проходящий через катушку , и это не изменение указанного выше коэффициента ΔQ, а изменение его скорости v .
Но… Какие изменения? Изменение потока такое же, Δt такое же, и что на самом деле меняется? Что изменяется, так это ток, проходящий через катушку , и это не изменение указанного выше коэффициента ΔQ, а изменение его скорости v .  Поясню: работа , совершаемая зарядом по некоторому пути, есть прямой интеграл ∫ F ·d s вдоль этого пути. Но бесконечно малое расстояние d s равно v ·dt, as d s /dt = v (обратите внимание, что мы записываем s и v как векторы, поэтому скалярное произведение с F дает нам компонент F , касательная к траектории). Итак, ∫ F · d s = ∫ ( F · v )dt. Таким образом, 90 559 время 90 560 скорость изменения энергии, которая является мощностью, составляет F · v . Просто возьмите производную интеграла по времени. 🙂
Поясню: работа , совершаемая зарядом по некоторому пути, есть прямой интеграл ∫ F ·d s вдоль этого пути. Но бесконечно малое расстояние d s равно v ·dt, as d s /dt = v (обратите внимание, что мы записываем s и v как векторы, поэтому скалярное произведение с F дает нам компонент F , касательная к траектории). Итак, ∫ F · d s = ∫ ( F · v )dt. Таким образом, 90 559 время 90 560 скорость изменения энергии, которая является мощностью, составляет F · v . Просто возьмите производную интеграла по времени. 🙂 [Почему? Потому что v и d s имеют одинаковое направление: направление обоих векторов является тангенциальным к проводу, всегда .] Теперь все, что нам нужно сделать, это выяснить, сколько мощности передается в цепь нашего генератора переменного тока это интегрирование этого выражения по катушке, поэтому нам нужно найти:
[Почему? Потому что v и d s имеют одинаковое направление: направление обоих векторов является тангенциальным к проводу, всегда .] Теперь все, что нам нужно сделать, это выяснить, сколько мощности передается в цепь нашего генератора переменного тока это интегрирование этого выражения по катушке, поэтому нам нужно найти: Его формула имеет вид τ = μ × B . Какое магнитное поле? Что ж… Позвольте мне отослать вас к моему посту о магнитном диполе и его крутящем моменте: это не магнитное поле , вызванное током, а внешнее магнитное поле, так что это B, о котором мы говорили здесь все это время. Итак… Ну… я не пытаюсь вас одурачить. 🙂 Однако магнитный момент μ было , а не , определяемым этим внешним полем, а током в катушке и ее площадью. Действительно, величина μ была произведением тока на площадь, так что в данном случае это N·I·S. Конечно, нам нужно быть начеку, потому что μ само по себе является вектором, и поэтому нам нужен угол между μ и B , чтобы вычислить это векторное произведение τ = μ × B . Однако, если вы проверите, как мы определили направление µ , вы увидите, что она нормальна к плоскости катушки и, следовательно, угол между µ и B и есть тот самый θ = ω·t, с которого мы начали наш анализ.
Его формула имеет вид τ = μ × B . Какое магнитное поле? Что ж… Позвольте мне отослать вас к моему посту о магнитном диполе и его крутящем моменте: это не магнитное поле , вызванное током, а внешнее магнитное поле, так что это B, о котором мы говорили здесь все это время. Итак… Ну… я не пытаюсь вас одурачить. 🙂 Однако магнитный момент μ было , а не , определяемым этим внешним полем, а током в катушке и ее площадью. Действительно, величина μ была произведением тока на площадь, так что в данном случае это N·I·S. Конечно, нам нужно быть начеку, потому что μ само по себе является вектором, и поэтому нам нужен угол между μ и B , чтобы вычислить это векторное произведение τ = μ × B . Однако, если вы проверите, как мы определили направление µ , вы увидите, что она нормальна к плоскости катушки и, следовательно, угол между µ и B и есть тот самый θ = ω·t, с которого мы начали наш анализ. Короче говоря, величина крутящего момента τ равна:
Короче говоря, величина крутящего момента τ равна: в цепи. Эта «противоэдс» равна 90 559 против 90 560 тока, когда 90 559 увеличивается 90 560, и 90 559 в направлении 90 560 тока, когда он 90 559 уменьшается. Короче говоря, эффект самоиндукции заставляет ток иметь «инерцию»: индуктивные эффекты пытаются поддерживать постоянный поток, так же как механическая инерция пытается поддерживать постоянной скорость объекта. Но… Ну… я пропустил это. Я возьму в следующий раз, потому что…
в цепи. Эта «противоэдс» равна 90 559 против 90 560 тока, когда 90 559 увеличивается 90 560, и 90 559 в направлении 90 560 тока, когда он 90 559 уменьшается. Короче говоря, эффект самоиндукции заставляет ток иметь «инерцию»: индуктивные эффекты пытаются поддерживать постоянный поток, так же как механическая инерция пытается поддерживать постоянной скорость объекта. Но… Ну… я пропустил это. Я возьму в следующий раз, потому что… Вы можете загрузить некоторые руководства из Интернета, и вы найдете такие вещи: не работайте на скоростях выше 4% от номинальной скорости или более чем на 1% ниже номинальной скорости. К счастью, так называемая регулятор двигателя возьмет на себя эту машину. 🙂
Вы можете загрузить некоторые руководства из Интернета, и вы найдете такие вещи: не работайте на скоростях выше 4% от номинальной скорости или более чем на 1% ниже номинальной скорости. К счастью, так называемая регулятор двигателя возьмет на себя эту машину. 🙂 Это довольно общий вид той же цепи переменного тока. Правда в том, что если мы применим переменный ток, то и ток, и напряжение будут увеличиваться и уменьшаться, но 9Сигнал тока 0559 обычно отстает от сигнала напряжения , и фазовый коэффициент θ говорит нам, насколько. Следовательно, используя систему комплексных чисел, мы пишем:
Это довольно общий вид той же цепи переменного тока. Правда в том, что если мы применим переменный ток, то и ток, и напряжение будут увеличиваться и уменьшаться, но 9Сигнал тока 0559 обычно отстает от сигнала напряжения , и фазовый коэффициент θ говорит нам, насколько. Следовательно, используя систему комплексных чисел, мы пишем: Пишем:
Пишем: Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций.
Я использовал комплексную нотацию только для упрощения исчисления, поэтому учитывается только действительная часть тех комплекснозначных функций. com/copyright-and-the-dmca/
com/copyright-and-the-dmca/ 