§6. Потенциальность электрического поля | Политех в Сети

Работа в электрическом поле.

Так как сила, действующая в электрическом поле на точечный заряд Q Равна

(6.1)

То при перемещении заряда Q на расстояние

Эта сила совершает работу:

(6.2)

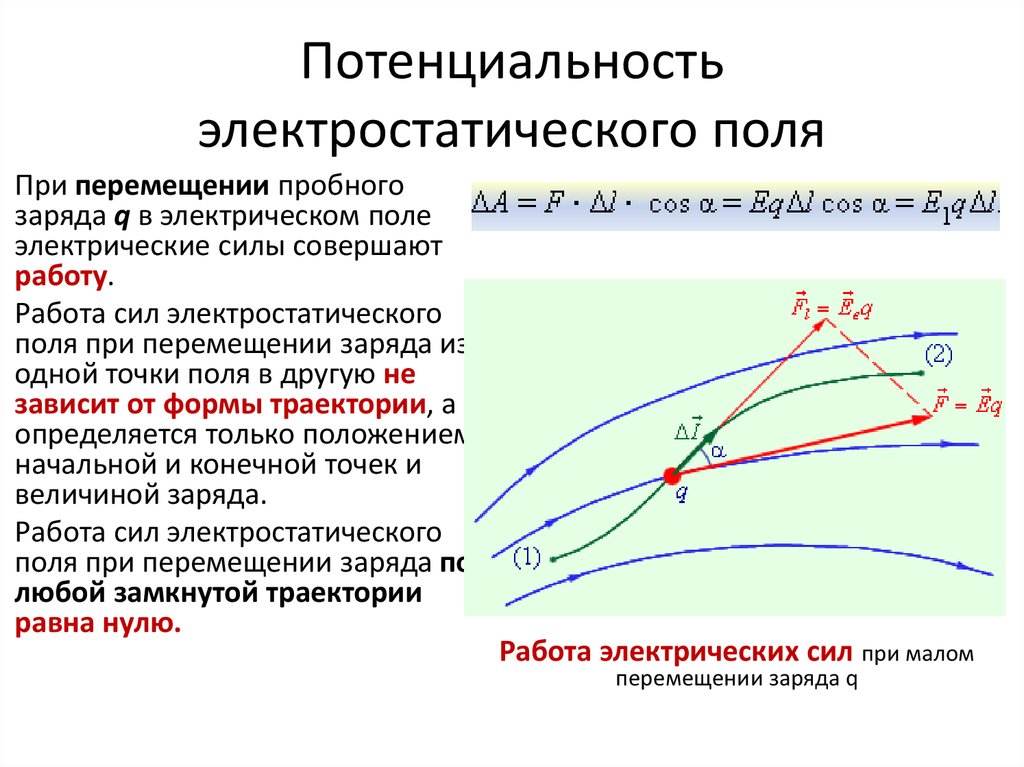
При перемещении заряда из точки 1 в точку 2 по траектории

работа равна:

(6.3)

Потенциальность кулоновского поля.

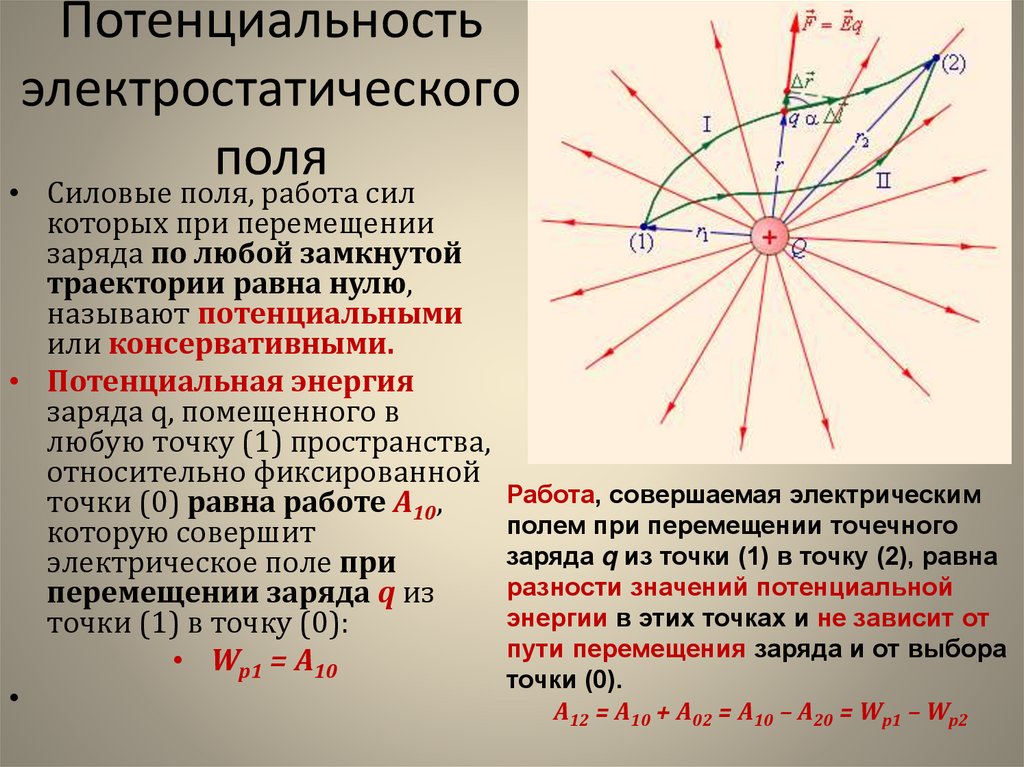
Поле, созданное кулоновскими зарядами, потенциально. Поле сил называется потенциальным, если при перемещении в этом поле работа зависит лишь от начального и конечного положения точек (тела) пути и не зависит от формы пути — траектории. Вторым эквивалентным определением потенциальности поля является условие равенства нулю работы при перемещении в нем по любому замкнутому контуру.

Вся математическая часть учения о потенциале была разработана в рамках теории тяготения, а понятие о потенциале возникло в работах Ж. Л. Лагранжа (1736-1813) в 1777г. Выражение “потенциал” было введено в науку в 1828 г. Дж. Грином и независимо К. Ф. Гауссом (1775-1855). Большой вклад в теорию потенциала был внесен П. С. Лапласом (1749-1827) и С. Д. Пуассоном (1781-1840).

На основании принципа суперпозиции из потенциальности поля точечного заряда следует потенциальность произвольного электростатического поля.

Из сказанного следует, что

, тогда условие потенциальности электрического поля

(6.4)

(6.4) – интегральная формулировка потенциальности электрического поля.

Дифференциальная формулировка потенциальности поля.

Если воспользоваться формулой Стокса

, то из (6.4) следует дифференциальная формулировка потенциальности поля:

(6. 5)

Непосредственной проверкой можно убедиться, что

. (6.6)

Тогда сопоставляя (6.6) и (6.5) можно записать:

, (6.7)

где

— некоторая скалярная функция, которая называется потенциалом. Знак «-» выбран для того, чтобы вектор напряженности Е был направлен в сторону убывания . Скалярная функция называется скалярным потенциалом электрического поля.

Если напряженность поля можно измерить экспериментально, то потенциал

не имеет определенного числового значения и бессмысленно говорить об экспериментальном определении его значения. Потенциал определен с точностью до некоторого постоянного значения.

Для того, чтобы не было неоднозначности, используют процедуру нормировки потенциала. При решении пространственных задач за ноль принимают потенциал бесконечно удаленной точки. А при решении задач, связанных с изучением электрических полей вблизи поверхности Земли, за ноль принимают потенциал Земли.

Выражение работы через потенциал.

Если заряд перемещается между точками (1) и (2), то

(6.8)

Если сопоставить (6.8) и (6.3), то

, откуда следует

(6.9)

Таким образом, с помощью (6.9) можно вычислить разность потенциалов между двумя точками поля.

Потенциал поля точечного заряда.

Будем нормировать потенциал на нуль в бесконечности. Считая, что в формуле (6.9) точка (2) находится в бесконечности, полагаем

и получаем выражение для потенциала в точке (1):

. (6.10)

Воспользовавшись выражением для напряженности поля точечного заряда получим:

. (6.11)

Соотношение (6.11) определяет потенциал поля, создаваемого точечным зарядом.

Потенциал поля системы точечных зарядов.

Если имеется система из точечных зарядов, то потенциал поля в некоторой точке А равен

. (6.12)

В случае, когда заряд распределен непрерывно с объемной плотностью

=, потенциал в некоторой точке (x, y, z) поля:

(6.13) — расстояние от точечного заряда находящегося в точке до точки где вычисляется потенциал.

Если заряд распределен по поверхности, то потенциал определяется формулой

, (6.14)

где R –расстояние между элементом площадки DS и точкой, где

Вычисляется потенциал.

Бесконечность потенциала поля точечного заряда.

Из (6.14) следует, что при

потенциал . Это связано с тем, что точечный заряд формально имеет бесконечную объемную плотность, поскольку его объем равен нулю. Именно бесконечная объемная плотность заряда и обуславливает обращение в бесконечность потенциала.

При непрерывном распределении заряда с конечной плотностью потенциал нигде не обращается в бесконечность, т. е. потенциал функция конечная.

Конечность потенциала при непрерывном распределении заряда с конечной плотностью.

При непрерывном распределении заряда с конечной плотностью потенциал нигде не обращается в бесконечность. В этом можно убедиться при вычислении потенциала по формуле (6.13). Причем точку (X,Y,Z) за начало координат (X=Y=Z=0) и будем вести расчет в сферической системе координат. Элемент объема в ней выражается формулой

, где . Тогда [см. (6.13)]

.

Следовательно, Если

Конечно, то и потенциал конечен, Что и требовалось доказать.

Непрерывность потенциала.

Производная от потенциала по декартовой координате дает соответствующую компоненту напряженности электрического поля. Ясно, что напряженность не может быть бесконечной, значит, производные по координатам от потенциала должны быть конечными. А это означает, что потенциал является непрерывной функцией. Таким образом, потенциал

является непрерывной и конечной функцией с конечными производными по координатам. Эти условия важны при решении дифференциальных уравнений для .

Теорема Ирншоу.

Эта теорема утверждает, что не существует такой конфигурации неподвижных зарядов, которая была бы устойчивой, если нет других сил, кроме сил кулоновского взаимодействия между зарядами системы. Устойчивые конфигурации неподвижных зарядов могут существовать лишь тогда, когда кроме сил электрического взаимодействия между ними имеются некоторые посторонние силы, удерживающие заряды в положении равновесия.

Доказательство теоремы Ирншоу следует из теоремы Гаусса. Допустим, что равновесие устойчиво. Тогда при смещении любого из зарядов системы из его положения равновесия в любом направлении на него должна действовать сила, стремящаяся возвратить заряд в прежнее положение. А это означает, что напряженность поля, создаваемого вблизи каждого из покоящихся зарядов всеми другими зарядами, направлена вдоль радиусов, исходящих из точки нахождения этого заряда. Поток напряженности этого поля сквозь замкнутую поверхность вокруг заряда отличен от нуля, поскольку напряженность направлена вдоль радиусов в одном направлении (вблизи положительного заряда – к заряду, вблизи отрицательного – от заряда). По теореме Гаусса поток сквозь замкнутую поверхность создается зарядом, находящимся в ограничиваемом ею объеме. Это противоречит исходному предположению о том, что он создается зарядами, находящимися вне объема. Тем самым отвергается допущение об устойчивости конфигурации неподвижных зарядов, и теорема Ирншоу доказана.

Устойчивые конфигурации неподвижных зарядов могут существовать лишь тогда, когда кроме сил взаимодействия между ними имеются какие-то посторонние силы, удерживающие заряды в положениях равновесия. Устойчивые состояния движущихся зарядов возможны, как, например, движение двух разноименных зарядов по эллипсам вокруг центра масс (если, конечно, пренебречь излучением).

Потенциал электростатического поля точечного заряда – формула, кратко о разности потенциалов (10 класс)

4. 9

Средняя оценка: 4.9

Всего получено оценок: 93.

Обновлено 26 Ноября, 2020

4.9

Средняя оценка: 4.9

Всего получено оценок: 93.

Обновлено 26 Ноября, 2020

Проявление электрического поля заключается в силовом взаимодействии между зарядами. Электрическое поле имеет ряд характеристик, одной из которых является потенциал. Рассмотрим это понятие, выведем формулу потенциала электростатического поля точечного заряда.

Понятие потенциала

Из курса электродинамики в 10 классе известно, что для определения взаимного влияния электрических зарядов используется понятие напряженности.

Рис. 1. Напряженность электрического поля.

Однако для электротехники такая характеристика поля неудобна. В самом деле, напряженность — это векторная величина, предполагающая движение зарядов в пространстве. Но в электротехнических схемах заряды могут двигаться только по проводникам, направление которых однозначно определено. И имеет значение только движение вдоль проводников.

Здесь было бы удобнее рассматривать не векторную, а скалярную характеристику поля.

Для введения такой скалярной характеристики вспомним, что основной задачей электротехники является получение и преобразование энергии. А электрическое поле — потенциально, и работа в нем не зависит от пути, по которому двигался заряд. Важна лишь разница потенциальных энергий в конечных точках траектории.

Все это позволяет ввести специальную энергетическую характеристику электростатического поля — потенциал.

Потенциальная энергия взаимодействия двух зарядов равна:

$$W_{потенц}=k{q_1q_2\over r}$$

Из этой формулы следует, что потенциальная энергия электрического поля пропорциональна заряду, и отношение потенциальной энергии к этому заряду постоянно. Это отношение и есть потенциал $\varphi$:

$$\varphi={W_{потенц}\over q}$$

Как и в случае с потенциальной энергией, конкретная величина потенциала не несет большой информации. Практически всегда используется разность потенциалов между двумя точками. Зная ее, можно рассчитать работу, которую совершает заряд при движении от одной точки к другой.

Потенциал поля точечного заряда

Из двух приведенных выше формул легко получить формулу потенциала точечного заряда. Подставив первую во вторую, получим:

$$\varphi=k{q\over r}$$

Коэффициент $k$ здесь, как и в законе Кулона, зависит от выбранной системы единиц. Для системы СИ ($\varepsilon_0$ — электрическая постоянная):

$$k={1\over 4\pi\varepsilon_0}$$

Таким образом, потенциал электростатического поля точечного заряда пропорционален величине заряда и обратно пропорционален расстоянию от него. Если $r=∞$, то $\varphi=0$. По сути, потенциал поля точечного заряда равен энергии, которая необходима для удаления единичного пробного заряда в бесконечность.

Рис. 2. Силовые линии точечного заряда.

Потенциал системы точечных зарядов

Поскольку электрическое поле потенциально, и в нём действует принцип суперпозиции, это позволяет легко находить потенциал системы зарядов. Он равен алгебраической сумме элементарных зарядов:

$$\varphi_{общ} =\varphi_1+\varphi_2+…+\varphi_n$$

Эта же формула используется в том случае, если заряд распределен по телу неравномерно. Тело разбивается на множество элементарных областей, в каждой из которых заряд можно считать точечным. После этого потенциал всех областей суммируется.

Рис. 3. Потенциал системы зарядов.

Что мы узнали

Электростатический потенциал — это скалярная энергетическая характеристика электростатического поля. Она равна работе, которую надо совершить для того, чтобы удалить пробный единичный заряд из поля в бесконечность. Поскольку электрическое поле потенциально, и в нём работает принцип суперпозиции, потенциал системы точечных зарядов равен сумме потенциалов каждого заряда.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.

9

Средняя оценка: 4.9

Всего получено оценок: 93.

---

А какая ваша оценка?

электростатика — Как определяется точка отсчета потенциальной энергии в электрических полях?

спросил 2 года, 2 месяца назад

Изменено 2 года, 2 месяца назад

Просмотрено 230 раз

$\begingroup$

Рассмотрим приведенную ниже диаграмму положительного заряда и трех точек, отмеченных в поле X, Y и Z.

Я понимаю, что для гравитационного поля мы определяем потенциальную энергию как всегда отрицательную и приближающуюся к нулю по мере удаления от ее источника. Мои вопросы, почему это? и как это отличается для потенциала в электрическом поле, подобном показанному выше? Является ли потенциал выше или ниже в точке Y, и зависит ли этот ответ от того, исследуете ли вы положительно заряженную или отрицательно заряженную частицу в точке Y? Кроме того, становится ли нулевая точка источником поля для другого типа заряда (+ или -), вызывающего поле?

• электростатика
• электрические поля
• потенциал
• потенциал-энергия
• условности

$\endgroup$

1

$\begingroup$

Видите ли, для гравитационных или электростатических полей Потенциал принимается равным нулю на бесконечности. Потенциал всегда определяется относительно положительного заряда $q_0$. Следовательно, высокий потенциал в точке означает, что положительный заряд $q_0$ в этой точке будет нестабилен. (Думайте с точки зрения: больше энергии $\имеет$ меньшую стабильность). Таким образом, для положительного заряда точка рядом с ним имеет более высокий потенциал, чем удаленная точка (потенциал равен нулю на бесконечности и положителен в противном случае для положительного заряда). Поскольку $q_0$ отталкивает положительный заряд и хочет быть как можно дальше от него, чтобы быть устойчивым. Для отрицательного заряда потенциал равен нулю на бесконечности и отрицателен в противном случае. Отсюда ближе точка к отрицательному заряду, меньший потенциал, большая стабильность, так как $q_0$ хочет быть как можно ближе к отрицательному заряду.

Для гравитации дело обстоит так же, как с двумя разными зарядами, отсюда и такое же понятие отрицательного заряда.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 2}$$, где $R$ – радиус сферы, и каждая точка на поверхности имеет такой же потенциал. Я ошибаюсь ?

• электростатика
• электрические поля
• потенциал

$\endgroup$

6

$\begingroup$

Как указано в комментариях, слово область используется для обозначения набора точек с ненулевым 3D-объемом. Напротив, ваш контрпример представляет собой двумерную поверхность, которая не является областью в том смысле, в каком ее имел в виду ваш инструктор.

Если я воспользуюсь математическим определением и попытаюсь получить поле путем дифференцирования постоянного потенциала, то ответ будет равен нулю. Но я пытаюсь смотреть на это через призму интуиции, а не математики.

Интуиция и математическая точность не исключают друг друга. Интуиция строится на опыте, а математическая точность — это инструмент, который вы должны использовать для ее усовершенствования.

Действительно, с определенной точки зрения, это вы указываете на математическую технику. Вы утверждаете, что если мы рассмотрим поверхность или кривую, потенциал вдоль поверхности или кривой может быть постоянным даже в присутствии ненулевого электрического поля, что, безусловно, верно. Однако, если речь идет о регионе 93$ — это означает, что каждая точка в области окружена маленьким трехмерным шаром, который также находится в области — тогда постоянный потенциал означает, что электрическое поле должно быть тождественно равным нулю везде в пределах области.

Таким образом, разрешение кажущегося противоречия заключается в простом более четком определении ваших терминов, то есть с большей математической точностью.

$\endgroup$

1

$\begingroup$

В электростатике составляющая электрического поля относительно направления пропорциональна скорости изменения потенциала на единицу длины вдоль этого направления , что мы называем градиентом .