5.2. Моменты инерции плоских сечений

Полярным моментом инерции сечения называется сумма произведений элементарных площадок(dA) на квадраты их расстояний () до какого-либо полюса, лежащего в плоскости сечения, распространённая на всю площадь сечения (рис. 5.2):

. (5.7)

Рис. 5.2

Осевым моментом инерции площади сечения относительно какой-либо оси, лежащей в её плоскости, называется сумма произведений элементарных площадок на квадраты расстояний их до этой оси:

(5.8)

Из рис. 5.2 видно, что Подставим это выражение в (5.7) и получим

(5.9)

Следовательно, сумма осевых моментов инерции плоского сечения относительно двух перпендикулярных осей равна полярному моменту инерции относительно полюса, представляющего точку пересечения этих осей.

Осевые и полярные моменты инерции измеряются в метрах в четвертой степени (м⁴). Они всегда положительны и не могут быть равны нулю.

5.3. Моменты инерции простых плоских сечений

Определим моменты инерции наиболее распространенных плоских сечений.

1. Прямоугольник (рис. 5.3). Вычислим момент инерции сечения относительно оси х, проходящей через центр тяжести параллельно основанию. Выделим на расстоянии у от оси х бесконечно узкую площадку высотой dy, тогда dA=b dy. В соответствии с (5.8):

. (5.10)

Рис. 5.3

Аналогично находим осевой момент инерции относительно оси у:

(5.11)

Для квадратного сечения со стороной а:

(5.12)

2. Круг радиуса r (рис. 5.4). Определим вначале полярный момент инерции относительно центра круга. За dA примем площадь бесконечно тонкого кольца толщиной и радиусом, тогдаПодставим это значение в (5.7):

(5.13)

Определим теперь осевые моменты инерции. Согласно формуле (5.9) для круглого сечения

Следовательно,

(5.14)

Рис. 5.4

3. Кольцо (рис. 5.5). Воспользуемся формулой (5.13), приняв пределы интегрирования от R до r.

Рис. 5.5

Обозначим отношение . Тогда

(5.15)

Аналогично сплошному сечению (5.14) определим осевой момент инерции кольца:

(5.16)

5.4. Центробежный момент инерции

Центробежным моментом инерции называется сумма произведений элементарных площадок на их координаты, распространённая на всю площадь сечения (рис. 5.6)

. (5. 17)

Рис. 5.6

Центробежный момент инерции имеет размерность – метр в четвертой степени (м⁴) и может быть величиной положительной, отрицательной и равной нулю.

Если взаимно перпендикулярные оси х и у или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю.

5.5. Изменение моментов инерции при повороте осей

Найдём зависимость между моментами инерции относительно осей

х и у и моментами инерции относительно осей ,, повёрнутых на угол

(рис. 5.7). Пусть J_x > J_y и положительный угол отсчитывается от осих против хода часовой стрелки.

Найдём зависимость между координатами площадки в исходных и повёрнутых осях.

,

.

Теперь определим моменты инерции относительно осей и:

Или

. (5.18)

.

После преобразований

. (5.19)

Рис. 5.7

Центробежный момент инерции

. (5.20)

Сложим (5.18) и (5.19):

(5.21)

Вычтем (5.19) из (5.18):

Анализ формулы (5.21): сумма моментов инерции относительно любых взаимно-перпендикулярных осей не меняется при их повороте.

Формула (5.22) может быть использована для определения центробежного момента инерции по известным осевым моментам инерции относительно осей

х, у и

Момент инерции — Студопедия

Поделись  

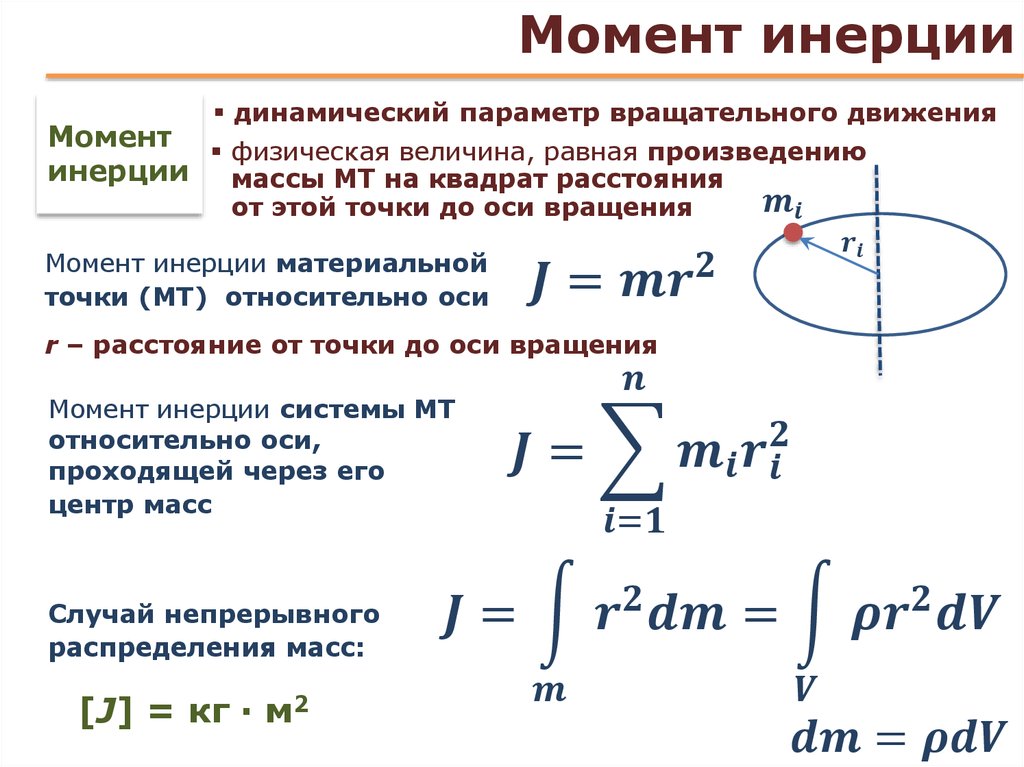
Рассмотрим материальную точку массой m, которая находится на расстоянии r, от неподвижной оси (рис. 26). Моментом инерции J материальной точки относительно оси называется скалярная физическая величина, равная произведению массы m на квадрат расстояния r до этой оси:

J = mr²(75)

Момент инерции системы N материальных точек будет равен сумме моментов инерции отдельных точек:

(76)

Рис. 26.

К определению момента инерции точки.

Если масса распределена в пространстве непрерывно, то суммирование заменяется интегрированием. Тело разбивается на элементарные объемы dv, каждый из которых обладает массой dm.

В результате получается следующее выражение:

(77)

Для однородного по объему тела плотность ρ постоянна, и записав элементарную массу в виде:

dm = ρdv, преобразуем формулу (70) следующим образом:

(78)

Размерность момента инерции – кг*м².

Момент инерции тела является мерой инертности тела во вращательном движении, подобно тому, как масса тела является мерой его инертности при поступательном движении.

Момент инерции — это мера инертных свойств твердого тела при вращательном движении, зависящая от распределения массы относительно оси вращения. Иными словами, момент инерции зависит от массы, формы, размеров тела и положения оси вращения.

Всякое тело, независимо от того, вращается оно или покоится, обладает моментом инерции относительно любой оси, подобно тому, как тело обладает массой независимо от того, движется оно или находиться в покое. Аналогично массе момент инерции является величиной аддитивной.

В некоторых случаях теоретический расчёт момента инерции достаточно прост. Ниже приведены моменты инерции некоторых сплошных тел правильной геометрической формы относительно оси, проходящей через центр тяжести.

Момент инерции бесконечно плоского диска радиуса R относительно оси, перпендикулярной плоскости диска:

Момент инерции шара радиуса R:

Момент инерции стержня длиной L относительно оси, проходящей через середину стержня перпендикулярно ему:

Момент инерции бесконечно тонкого обруча радиуса R относительно оси, перпендикулярной его плоскости:

Момент инерции тела относительно произвольной оси рассчитывается с помощью теоремы Штейнера:

Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр масс параллельно данной, и произведения массы тела на квадрат расстояния между осями.

Рассчитаем при помощи теоремы Штейнера момент инерции стержня длиной L относительно оси, проходящей через конец перпендикулярно ему (рис. 27).

Рис. 27.

К расчету момента инерции стержня

Согласно теореме Штейнера, момент инерции стержня относительно оси O′O′ равен моменту инерции относительно оси OO плюс md²

. Отсюда получаем:

Очевидно: момент инерции неодинаков относительно разных осей, и поэтому, решая задачи на динамику вращательного движения, момент инерции тела относительно интересующей нас оси каждый раз приходится искать отдельно. Так, например, при конструировании технических устройств, содержащих вращающиеся детали (на железнодорожном транспорте, в самолетостроении, электротехнике и т. д.), требуется знание величин моментов инерции этих деталей. При сложной форме тела теоретический расчет его момента инерции может оказаться трудно выполнимым. В этих случаях предпочитают измерить момент инерции нестандартной детали опытным путем.

Рис. 28.

Момент силы F относительно точки O



Размеры момента инерции

Момент инерции тела – это его способность сопротивляться угловому ускорению. Он вычисляет величину крутящего момента, необходимого телу для достижения желаемого углового ускорения на вращающейся оси. Момент инерции тела определяется суммой моментов инерции каждой частицы, а момент инерции каждой частицы определяется произведением массы и квадрата расстояния частицы от оси вращения.

Сопротивление тела изменению скорости вращения вдоль оси под действием крутящего момента измеряется в MOI. Ось может быть внутренней или внешней, и она может быть фиксированной или нефиксированной. Ось может быть внутренней или внешней, и она может быть фиксированной или нет. Момент инерции сравним с массой при прямолинейном движении при расчете углового момента твердого тела. Составной единицей измерения является единица момента инерции. В Соединенных Штатах m измеряется в слаговых единицах (1 слаг = 32,2 фунта), а r измеряется в футах, где I представлено в единицах площади слаг-футов.

Важность момента инерции:

Момент инерции является важным предметом, который рассматривается в большинстве физических задач, связанных с массой во вращательном движении. MOI обычно используется для вычисления углового момента. В следующих параграфах мы узнаем больше об этом предмете.

Момент инерции определяется как величина, на которую тело сопротивляется угловому ускорению, которое представляет собой сумму произведения массы каждой частицы на квадрат ее расстояния от оси вращения. Проще говоря, это число, определяющее величину крутящего момента, необходимого для определенного углового ускорения вращающейся оси. Угловая масса или инерция вращения — это другие названия момента инерции.

Момент инерции часто выражается по отношению к определенной оси вращения. MOI изменяется в зависимости от используемой оси.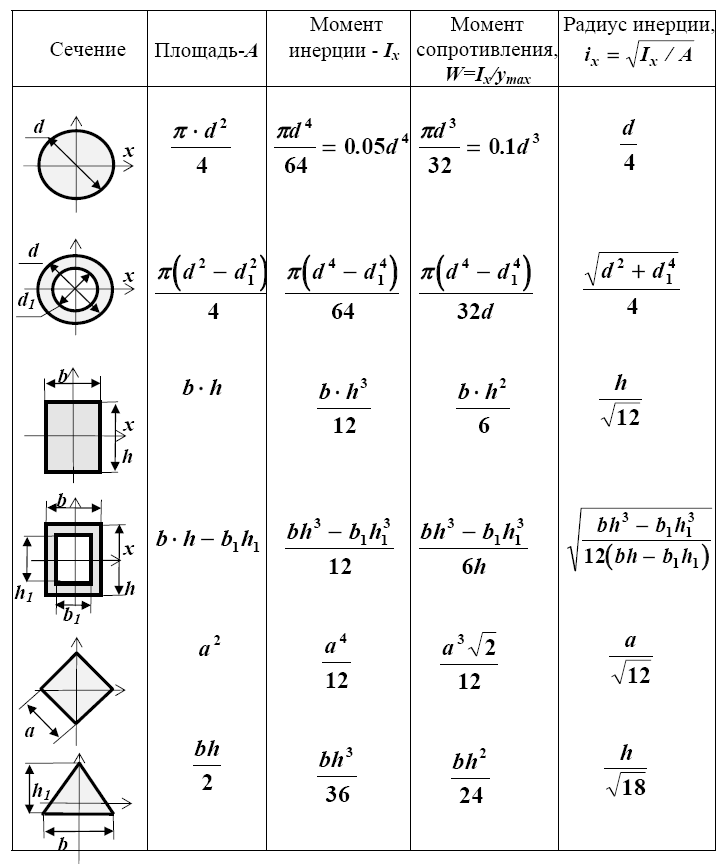

Обычно момент инерции записывается как  I = m × r²

, где

m = сумма произведений масс.

r = Расстояние от оси вращения.

, а также интегральная форма: I = ∫dI = ∫0M r² dm

M¹ L² T⁰ – размерная формула момента инерции.

При прямолинейном движении момент инерции играет ту же роль, что и масса. Это измерение сопротивления тела изменению вращательного движения. Он постоянен для заданной жесткой рамы и оси вращения.

MOI, I = I = ∑mi ri². . . . . . . (1)

КЭ, К = К = ½ I ω² . . . . . . . . . (2)

На момент инерции влияют следующие факторы:

Плотность материала

Форма и размер тела

Ось вращения

Системы вращающихся тел далее классифицируются следующим образом: )

Согласованное (Твердое тело)

Интегральный подход используется для расчета момента инерции непрерывного распределения массы. Если система разбита на бесконечно малый элемент массы «dm», а «x» — это расстояние между элементом массы и осью вращения, момент инерции равен:

я знак равно ∫ r2 дм . . . . . . (3)

Как видно из таблицы выше, на момент инерции влияет ось вращения. Что бы мы ни определили до сих пор, это момент инерции этих объектов, когда ось проходит через их центр масс. После выбора двух разных осей вы увидите, что элемент по-разному сопротивляется изменению вращения.

Следующие теоремы могут быть использованы для расчета момента инерции вдоль любой заданной оси:

Теорема о параллельной оси

Теорема о перпендикулярной оси

Момент инерции вокруг параллельной оси, проходящей через центр масс, определяется выражением

I = Icm + Md²

Если момент инерции (I) тела массой m вокруг оси выражается как:

I = Mk²

В этом случае k называется радиусом вращения тела вокруг указанной оси. Это радиальное расстояние от указанной оси вращения, на котором можно считать, что полная масса тела сосредоточена, чтобы его инерция вращения оставалась постоянной. 9{2}}{5}\] , или k = \[\sqrt{\frac{2}{5}}\] \[\times\] R.

Размеры момента инерции

Момент инерции характеризуется как количество, сообщаемое телом, противодействующее точному увеличению скорости, которое является результатом произведения массы каждой молекулы на квадрат ее расстояния от оси вращения. Или, с другой стороны, в более прямом смысле, его обычно изображают как величину, которая определяет, какая сила требуется для определенного точного увеличения скорости вращения. Снимок Инерции иначе называется точной массой или вращательной бездеятельностью. Единица СИ моментального снимка задержки — кг м ² .

Присоединяйтесь к программе регулярных занятий Infinity Learn!

Загрузите БЕСПЛАТНО PDF-файлы, решенные вопросы, работы за предыдущий год, викторины и головоломки!

+91

Проверить OTP-код (обязательно)

Класс
—Класс 6Класс 7Класс 8Класс 9Класс 10Класс 11Класс 12

Шри Чайтанья Студент?
НетДа

Я согласен с условиями и политикой конфиденциальности.

Снимок состояния покоя обычно определяется как выбранный стержень вращения. Он в основном основан на циркуляции массы вокруг центра вращения. MOI колеблется в зависимости от выбранного концентратора.

Момент инерции Формула

В общей структуре момент инерции передается как I = m × r ²

где,

m = сумма результата массы.

r = Расстояние от оси вращения.

кроме того, Интегральная структура: I = ∫dI = ∫ ₀ ^M r ² dm

⇒ Многоуровневое уравнение, существующее помимо всего остального, для задержки определяется как, M 7 7 T 20077 8 9007 ⁰ .

Работа, существующая отдельно от всего остального праздности, эквивалентна работе массового непрямого движения. Это оценка противодействия тела приспособлению его вращательного движения. Он соответствует конкретному жесткому корпусу и конкретной ступице поворота.

Снимок простоя, I = ∑m _i r _i ² . . . . . . (1)

Активная энергия, K = ½ I ω ² . . . . . . . . . (2)

От каких факторов зависит момент инерции?

Момент инерции зависит от сопутствующих элементов,

• Толщина материала
• Форма и размер корпуса
• Ступица поворота (присвоение массы относительно ступицы)

Дополнительно можно заказать каркасы поворотных тел:

1. Дискретные (Система частиц)
2. Постоянный (жесткий корпус)

Размерная формула момента инерции

Многослойное уравнение моментального снимка задержки определяется выражением, M ¹ L ² T ⁰

Где,

• M = Масса
• Д = длина
• Т = Время

Вычет

Снимок инерции (MOI) = Масса × [Радиус вращения] ² . . . . (1)

Так как, многослойное уравнение масс = M ¹ L ⁰ T ⁰ . . . . . . (2)

Более того, компоненты размаха вращения = M ⁰ L ¹ Т ⁰ . . . . . (3)

При подсоединении условий (2) и (3) к условию (1) получаем,

Моментальный снимок инерции = масса × [радиус вращения] ²

Или еще раз, MOI = [M ¹ L ⁰ T ⁰ ] × [M ⁰ L ¹ T ⁰ ] ² = M ¹ L ² T ⁰ .

Таким образом, моментальный снимок задержки соответственно адресуется как M ¹ л ² т ⁰ .

Читайте также: Размеры Newton

Часто задаваемые вопросы

Что такое моментальный снимок бездействия в общих чертах?

Пропорция препятствия тела к точному увеличению скорости вокруг заданного поворота, которая эквивалентна сумме результатов каждого компонента массы в теле и квадрату отделения компонента от ступицы.