PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.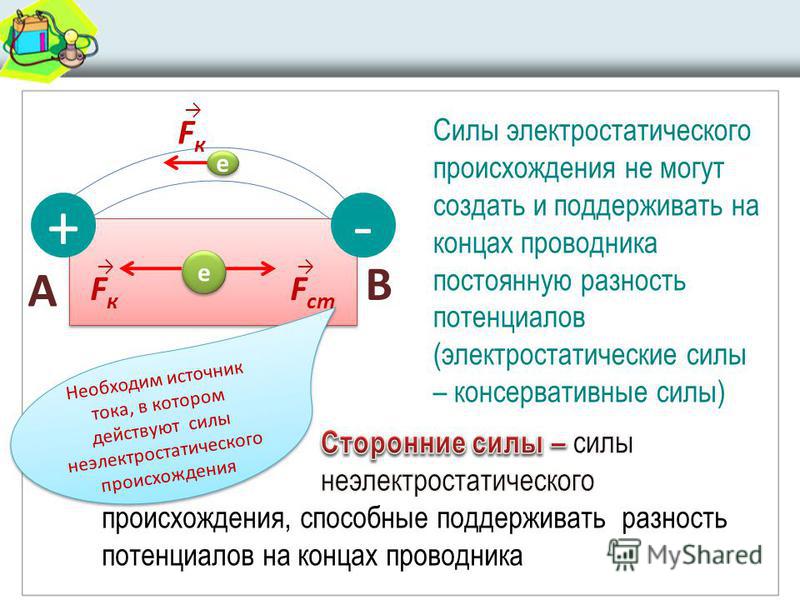

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

электростатика

 на главную   

 

Официальный сайт АНО ДО Центра «Логос», г.Глазов

http://logos-glz. ucoz.net/

 

ГОТОВИМСЯ К УРОКУ

Кинематика

Динамика

МКТ

Термодинамика 

Электростатика

Электрический ток

Электрический ток в средах

Магнитное поле Электромагнитная индукция

Оптика

Методы познания

электростатика                                                       немного о физике:   

Электродинамика – раздел физики, изучающий законы взаимодействия электрических зарядов и действия на них электромагнитных полей. 

Электростатика — раздел электродинамики, изучающий взаимодействие покоящихся электрических зарядов и действия на них электромагнитных полей.

 

 

 

В процессе познания природы человек обнаружил, что не все явления можно объяснить с помощью законов механики и молекулярно-кинетической теории.

Было замечено, что некоторые тела (янтарь, стекло, смола и др.), испытавшие трение, начинают притягивать к себе более мелкие тела. Изучение этого явления показало, что оно вызвано появлением на телах электрического заряда.

Тело, обладающее свойством притягивать к себе легкие тела, благодаря наличию на нем электрического заряда, называют наэлектризованным. Явление возникновения зарядов на телах называют

электризацией.

Опыты по взаимодействию наэлектризованных тел показали, что в природе проявляются только два вида взаимодействия: притяжение и отталкивание.

 Поэтому можно сделать вывод, что в природе существует только два рода зарядов, которые условно названы положительный и отрицательный. Принято, что стеклянная палочка, потертая о шелк, приобретает положительный заряд, а эбонитовая палочка, потертая о шерсть – отрицательный заряд.

 

Получить заряды на телах можно следующими способами:

1.

В состав всех тел входят атомы, которые состоят из ядра и вращающихся вокруг него электронов. Электроны в атомах одних веществ удерживаются сильнее, в атомах  других — слабее. При соприкосновении  тел электроны, удерживаемые слабо,  переходят на поверхность другого тела, перенося с собой свой отрицательный заряд  – 1,6 ×10^-19 Кл. Поэтому тело с избытком электронов стает отрицательно заряженным, а тело с недостатком электронов – положительно заряженным.

 Натирание тел позволяет увеличить площадь соприкосновения, что способствует переходу большего количества электронов, а, следовательно, получению больших по модулю зарядов тел.

2.

При соприкосновении незаряженного тела с заряженным происходит перераспределение заряда. При этом оба тела будут иметь одинаковые по знаку заряды.

Так,  при соприкосновении нейтрального тела с отрицательно заряженным телом происходит переход определенной доли избыточных электронов с отрицательно заряженного тела на первоначально нейтральное тело.  Поэтому при таком соприкосновении оба тела будут иметь отрицательные заряды.

Если происходит соприкосновение нейтрального тела с положительно заряженным телом, то электроны с нейтрального тела переходят на положительно заряженное тело, частично компенсируя его заряд. При этом на первоначально нейтральном теле появляется недостаток электронов, что определяет получение им положительного заряда.

 

3.

Под воздействием световых лучей электроны могут покидать атомы, унося с собой отрицательный заряд.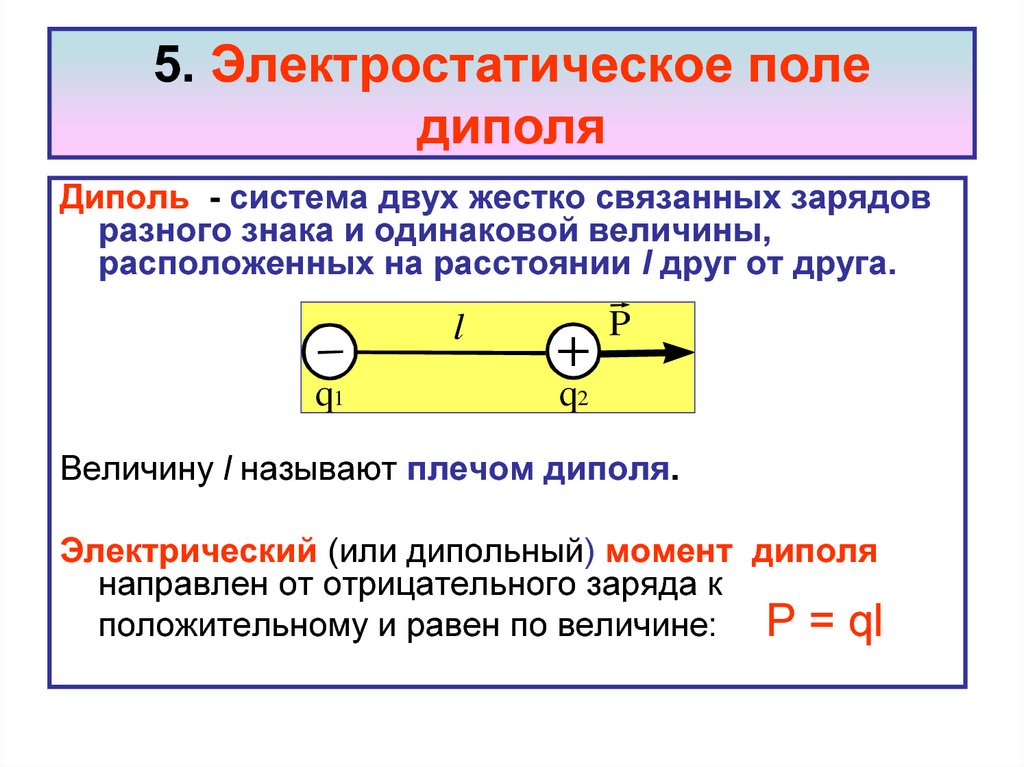

Следовательно, в составе тел появляется не скомпенсированный положительный заряд, и  тела  стают положительно заряжены.

 

Что называют электрическим зарядом?

Электрический заряд – физическая величина, определяющая интенсивность электромагнитных взаимодействий.

Принято электрический заряд  обозначать Q  или q.

Модуль заряда тела определяется по формуле:

 Q= n ∙ e

 где е = 1,6 × 10^-19Кл — элементарный заряд, n-количество избыточных (недостающих) электронов.

 

 

 

Закон сохранения электрического заряда.

 

Т.к. электризация  обусловлена только переходом электронов, а, следовательно, переходом  соответствующего отрицательного заряда с одного тела на  другое, то можно утверждать:

внутри изолированной системы при любых взаимодействиях алгебраическая сумма электрических зарядов остается постоянной.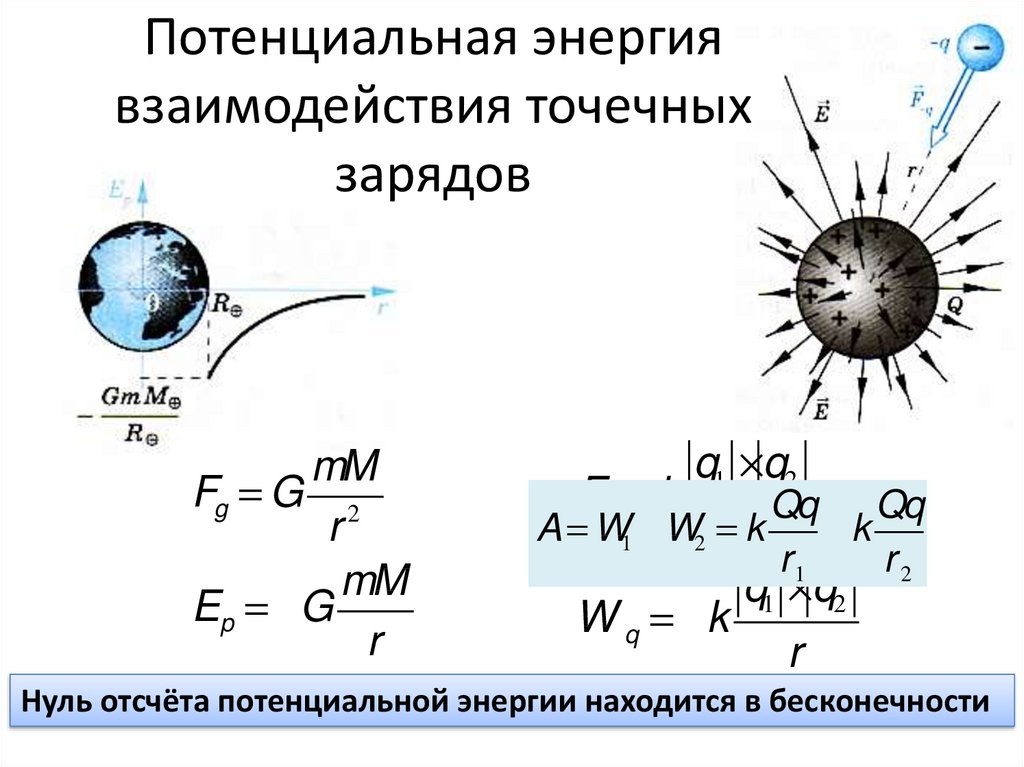

q₁ + q₂^{+ q₃ + q}_n = const

 

Систему называют изолированной или замкнутой, если в нее не вводятся или из нее не выводятся электрические заряды.

 

 

Как взаимодействуют заряженные тела?

 

Мы можем наблюдать, что заряженные тела взаимодействуют  (притягиваются или отталкиваются), находясь на некотором расстоянии друг от друга.

Взаимодействие неподвижных зарядов, находящихся на некотором расстоянии друг от друга, осуществляется посредством электрического поля, порожденного зарядами. Это взаимодействие происходит не мгновенно, а распространяется в вакууме со скоростью с

Закон Кулона:

Сила  взаимодействия двух точечных неподвижных зарядов в вакууме прямо пропорциональна произведению модулей этих зарядов и обратно пропорциональна квадрату расстояния между зарядами.

 

где  ε₀ = 8,854 ∙ 10 ^-12 Кл² /(Н м²) — электрическая постоянная,  k = 9 ∙ 10⁹ Нм²/ Кл² .

 

 

Электростатическое поле и его характеристики.

 

Электрический заряд, помещенный в некоторую точку пространства, изменяет свойства данного пространства. То есть заряд порождает вокруг себя электрическое поле.

Электростатическое  поле — вид материи, существующий вокруг неподвижный заряженных тел.

Электростатическое поле не изменяется во времени.

Оно действует на заряд, помещенный в какую-либо его точку.

 

Силовой характеристикой электрического поля является напряженность.

Напряженностью электрического поля в данной точке  называется векторная физическая величина, численно равная  силе, действующей на единичный положительный заряд, помещенный в данную точку поля.

где — напряженность электрического поля,

 — сила, действующая со стороны электрического поля на пробный заряд .

 

За единицу измерения напряженности электрического поля в системе СИ  принимают

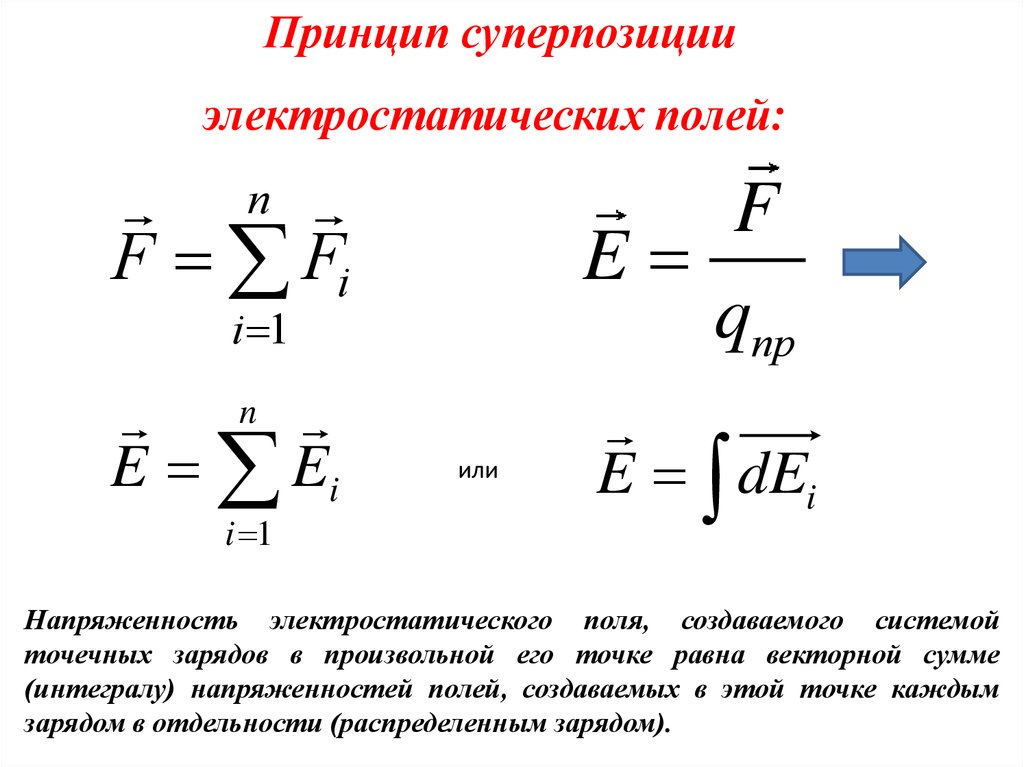
Если на пробный заряд, действуют силы со стороны нескольких  зарядов, то эти силы по принципу суперпозиции сил независимы, и результирующая этих сил равна векторной сумме сил. Поэтому можно сформулировать принцип суперпозиции (наложения) электрических полей.

 

Напряженность электрического поля системы зарядов в данной точке пространства  равна векторной сумме напряженностей электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:

.

 

Электрическое поле удобно представлять графически  с помощью силовых линий.

Силовыми линиями (линиями напряженности электрического поля) называют такие линии, касательные к которым в каждой точке поля совпадают с направлением вектора напряженности в данной точке.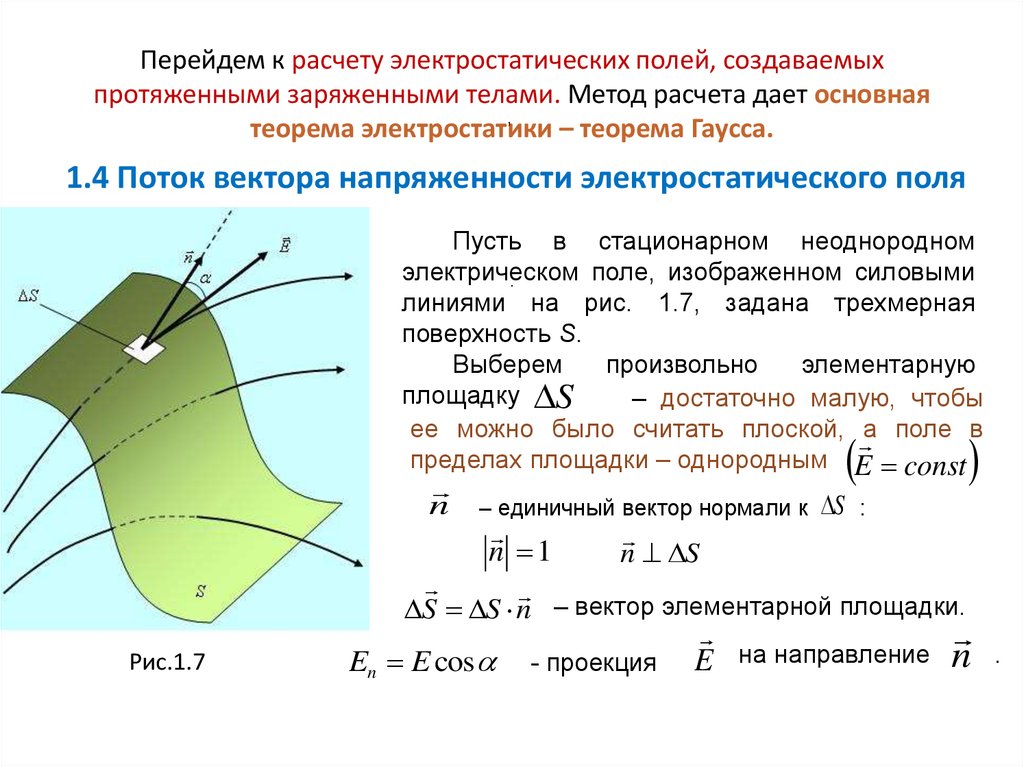

Силовые линии начинаются на положительном заряде и заканчиваются на отрицательном.

Густота линий напряженности характеризует напряженность поля (чем плотнее располагаются линии, тем поле сильнее).

Силовые линии электростатических полей точечных зарядов.

Электростатическое поле точечного заряда неоднородно ( ближе к заряду поле  сильнее).

 

 

 

Силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.

Электростатическое поле бесконечных равномерно заряженных плоскостей однородно .

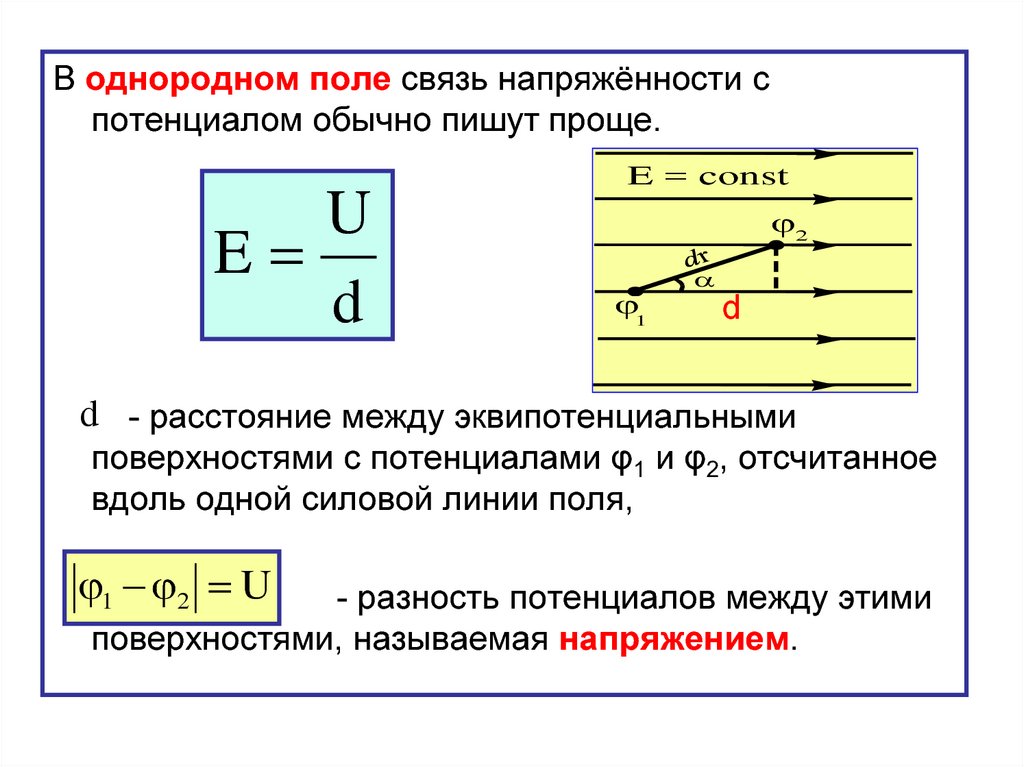
Электрическое поле, напряженность во всех точках которого одинакова, называется однородным.

 

 

 

 

 

Силовые линии электростатических полей двух точечных зарядов.

 

 

 

 

Число силовых линий, пронизывающих некоторую площадку, площадью S, и перпендикулярных ей, определяет поток вектора напряженности электрического поля.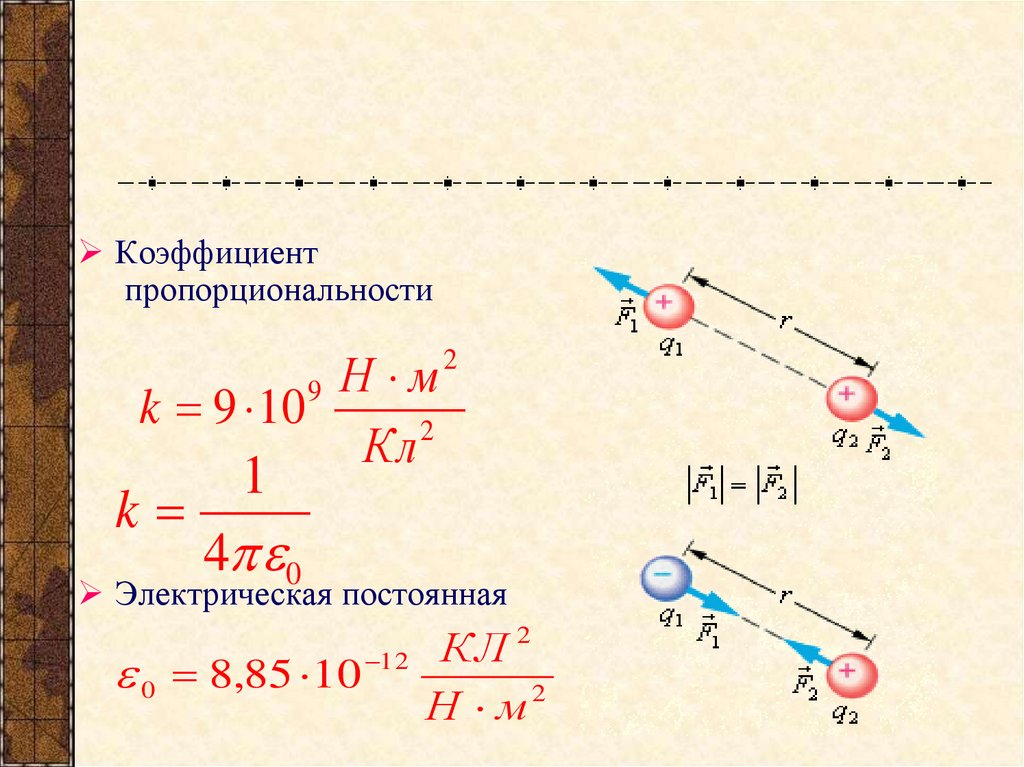

Поток вектора напряженности сквозь площадку площадью S равен:

где Е_n — проекция вектора напряженности на нормаль к площадке.

Теорема Остроградского-Гаусса: поток вектора напряженности электрического поля в вакууме сквозь любую замкнутую поверхность равен отношению алгебраической суммы зарядов, заключенных внутри этой поверхности, к значению электрической постоянной

 

 

 

Потенциал — энергетическая характеристика электрического поля.

Потенциал — скалярная физическая величина,  равная отношению потенциальной энергии, которой облает электрический заряд в данной точке электрического поля, к величине этого заряда.

Потенциал показывает какой потенциальной энергией будет обладать  единичный положительный заряд, помещенный в данную точку электрического поля.

где — потенциал в данной точке поля,  — потенциальная энергия заряда в данной точке поля.

За единицу измерения потенциала в системе СИ принимают 

(1В = 1Дж/Кл )

За единицу потенциала принимают потенциал в такой точке, для перемещения в которую из бесконечности  электрического заряда 1 Кл, требуется совершить работу, равную 1 Дж.

 

Рассматривая электрическое поле, созданное системой зарядов, следует для определения потенциала поля использовать принцип суперпозиции:

Потенциал электрического поля системы зарядов в данной точке пространства  равен алгебраической сумме потенциалов электрических полей, создаваемых в данной точке пространства, каждым зарядом системы в отдельности:

Воображаемая поверхность, во всех точках которой потенциал принимает одинаковые значения, называется эквипотенциальной поверхностью. При перемещении электрического заряда  от точки к точке вдоль эквипотенциальной поверхности энергия его не меняется.

Эквипотенциальных поверхностей для заданного электростатического поля  может быть построено бесконечное множество.

Вектор напряженности в каждой точке поля всегда перпендикулярен к эквипотенциальной поверхности, проведенной через данную точку поля.

Вектор напряженности в данной точке поля всегда направлен в область уменьшения потенциала.

 

 

Примеры электрических полей.

1. Электрическое поле точечного заряда.

Напряженность  и потенциал поля точечного заряда в данной точке электрического поля равны:

                              

где q — значение заряда, ε — диэлектричеcкая постоянная, r — расстояние от заряда до точки поля, в которой определяются напряженность и потенциал.

Эквипотенциальные поверхности и силовые линии электростатических полей точечных зарядов.

 

2. Электрическое поле бесконечной равномерно  заряженной плоскости.

Напряженность электрического поля равна:

     

где σ — поверхностная плотность заряда

 q — значение заряда, s — площадь поверхности плоскости, ε — диэлектрическая постоянная.

 

Эквипотенциальные поверхности и силовые линии электростатических полей бесконечных равномерно заряженных плоскостей.

 

 

3. Электрическое поле бесконечно длинной заряженной нити.

Напряженность электрического поля равна:

где τ — линейная плотность заряда,

 q — значение заряда, l -длина нити, ε — диэлектрическая постоянная, r — расстояние от нити до точки , в которой определяется напряженность

 

 

Электричество — Закон Кулона — Физика 299

Электричество — Закон Кулона — Физика 299

«Когда человек захотел сделать машину, которая ходить он создал колесо, которое не похоже на ногу»
Гийом Аполлинер

• Величина силы притяжения (или отталкивания), Ф ₁₂ между двумя точечными зарядами q ₁ и q ₂  составляет дается законом Кулона.





где R ₁₂   — расстояние между обвинения. k — константа пропорциональности, известная как кулоновская постоянная, имеющая значение 9 x 10 ⁹  Н.м ² / C ²  в вакуум.

Обратите внимание, что постоянная Кулона k равна часто заменяется на (1/4π ε ₀ ), где ε ₀ — диэлектрическая проницаемость вакуума (подробнее позже).


• Направление этой силы вдоль линии, соединяющей два обвинения со смыслом, определяемым относительными знаками зарядов
• Обратите внимание, что сила, действующая на каждый заряд, имеет одинаковую величину (как требуется третьим законом Ньютона).


• Для двух зарядов по 1 Кулону, разнесенных на 1 метр, величина силы определяется,
  F = (9 x 10 ⁹   x 1 x 1 )/ 1  =  9 x 10 ⁹ Ньютонов

  Это чрезвычайно большая сила (достаточная переместиться на гору Эверест с ускорением 1 см/с ² ). Кулон очень большая единица. Типичные макроскопические заряды измеряются в микрокулонах (10 ^-6 C).

• Чтобы справиться с ситуациями с более чем одним зарядом, заряды должны рассматривать попарно, так что общая сила на один заряд будет векторная сумма силы из-за каждого из других обвинений. Например сила на q ₁ в связи со всеми другими расходами q ₂ , q ₃ , q ₄ … бы быть данный по,

Ф ₁ = Ф ₂₁ + F ₃₁ + F ₄₁ + …

• Уведомление в сходство из Закон Кулона к закону всемирного тяготения Ньютона

оба являются законами обратных квадратов. Заменить заряд на массу и «k» вместо «G», и у вас есть закон Кулона.
Относительные величины Кулона постоянная k = 9 x 10 ⁹ и гравитационная постоянная G = 6,67 x 10 ^-11 , является показателем относительной силы две силы. Электрическая сила притяжения очень, очень сильнее гравитационной силы притяжения.

» беспроводной телеграф является нет трудный к понимать. Обычный телеграф похож на очень длинную кошку. Вы тянете хвост в Нью-Йорке, и это мяукает в Лос-Анджелес. Беспроводная связь то же самое, только без кота.»
Альберт Эйнштейн




Dr. C.L. Davis
Факультет физики
Университет Луисвилля
электронная почта : [email protected]
 

Единицы в законе Кулона и константа Кулона

Ричард Фейнман сказал, что почти все действительно интересно, если вникнуть в него достаточно глубоко. В этом духе я собираюсь углубиться в единицы постоянной Кулона. Это оказывается интересной кроличьей тропой.

Закон Кулона гласит, что сила между двумя заряженными частицами пропорциональна произведению их зарядов и обратно пропорциональна расстоянию между ними.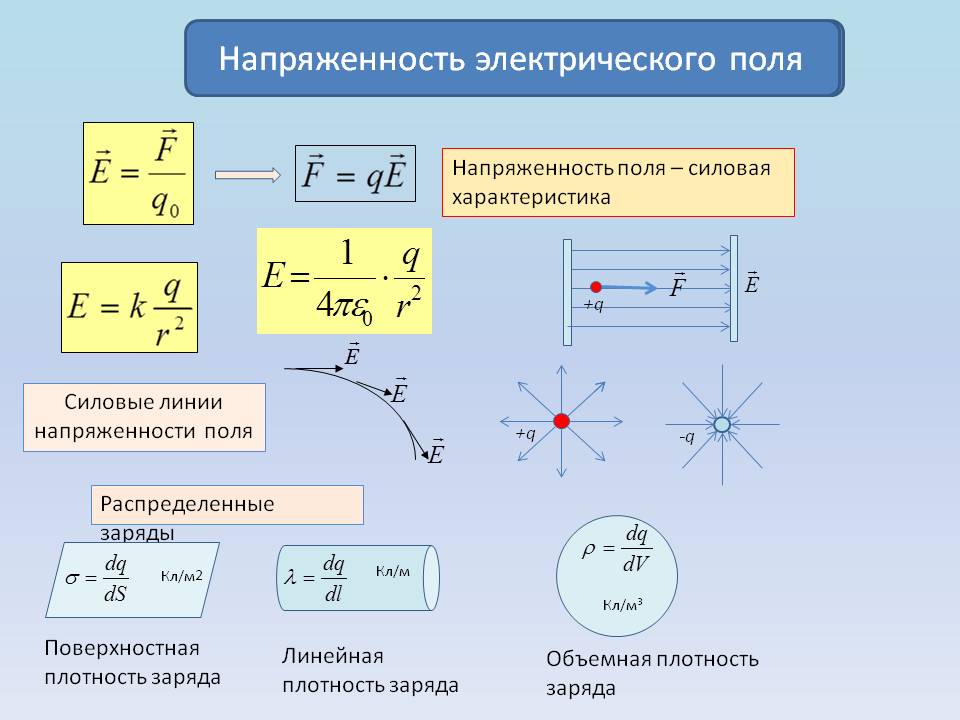 В символах,

Константа пропорциональности, член k _e , известна как постоянная Кулона .

Единицы

В каких единицах выражается постоянная Кулона? Ну, они такие, какими должны быть. Левая часть представляет собой силу, поэтому она измеряется в ньютонов , Н . Заряды измеряются в кулонов , а расстояния в метра , поэтому правая часть, кроме постоянной Кулона, имеет единицы измерения кулоны в квадрате на квадратный метр, C² / m². Так k _e должны иметь единицы Н м² / C².

Хорошо, но что такое кулон ? Вот где все становится интересно.

Неофициальное определение, которое вы можете встретить в учебнике, состоит в том, что кулона — это количество заряда на определенном количестве электронов, а ампера — это ток такого количества электронов, протекающих в секунду.

Формальное определение до двух лет назад состояло в том, что кулона определяли количество заряда, переносимого током в одну девятку.0154 ампер в секунду [1], а ампер был определен как

тот постоянный ток, который, если его поддерживать в двух прямолинейных параллельных проводниках бесконечной длины с ничтожно малым круглым поперечным сечением, расположенных на расстоянии одного метра друг от друга в вакууме, будет создают между этими проводниками силу, равную 2×10 ⁻⁷ ньютонов на метр длины.

Великое переопределение

В определениях единиц СИ было несколько вещей, которые были менее чем удовлетворительными. Например, бесконечно длинные проводники в определении ампера в дефиците.

Определения основных единиц со временем менялись по мере изменения технологии измерения. Например, килограмм был определен как масса конкретного физического объекта, прототипный международный килограмм. Очевидно, это неудобно, но до недавнего времени технически невозможно было сделать что-то лучше.

Основные единицы СИ были изменены с 20 мая 2019 г.0148 e = 1,602176634×10 ⁻¹⁹ кулона.

Это уравнение раньше было эмпирическим утверждением, измеренным значением элементарного заряда в кулонах. Теперь уравнение считается точным по определению , определяющему кулон.

Теперь, когда мы знаем, что такое кулон, вернемся к константе Кулона. Мы сказали, что k _e должны иметь единицы N m²/C². Мы сказали, что такое кулоны, но как насчет ньютонов и метров? Ньютон определяется в терминах килограмма, метра и секунды, и определения всех этих единиц также изменились.

Скорость света теперь равна

c = 299792458 м⋅с ⁻¹

по определению . Секунда определяется так, что частота перехода атома цезия-133 составляет 9 192 631 770 циклов в секунду, а метр определяется через скорость света и секунду.

Постоянная Планка теперь точно равна

ч = 6,62607015×10 ⁻³⁴ кг м²/с

по определению, которое определяет килограмм с точки зрения метра, секунды и 9.0148 ч . Теперь кто-то на далекой планете, не имеющий доступа к стандартному килограмму, может определить, сколько весит килограмм, измерив скорость света, частоту атома цезия-133 и постоянную Планка.

Постоянная Кулона

Постоянная Кулона равна

где ε ₀ равно диэлектрической проницаемости вакуума .

Теперь

, где c — скорость света, а μ ₀ — проницаемость вакуума.

Раньше считалось, что

μ ₀ = 4π × 10 ⁻⁷ N/A ²

по определению, но теперь, когда скорость света определена как точная по определению, μ _{0 9001 является измеряемой величиной. Тем не менее, измеренное значение очень близко к предыдущему определению с точностью до девяти значащих цифр.}