Первый закон Кирхгофа

Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.

Последовательное соединение проводников

Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).

Рисунок 1. Схема последовательного соединения проводников

Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:

r = r₁ + r₂ + r₃ + … + r_n.

Ток на отдельных участках последовательной цепи везде одинаков:

I₁ = I₂ = I₃ = I.

Видео 1. Последовательное соединение проводников

Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 5 Ом. Требуется определить показания вольтметров V₁, V₂, V₃ и V₄, если ток в цепи равен 4 А.

Сопротивление всей цепи

r = r₁ + r₂ + r₃ = 2 + 3 + 5 =10 Ом.

По закону Ома напряжение на зажимах цепи равно току цепи, умноженному на ее сопротивление:

U = I × r = 4 × 10 = 40 В.

Следовательно, вольтметр V, присоединенный к зажимам источника напряжения, покажет напряжение 40 В.

Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи

В сопротивлении r₁ при протекании тока будет падение напряжения:

U₁ = I × r₁ = 4 × 2 = 8 В.

Вольтметр V₁, включенный между точками а и б, покажет 8 В.

В сопротивлении r₂ также происходит падение напряжения:

U₂ = I × r₂ = 4 × 3 = 12 В.

Вольтметр V₂, включенный между точками в и г, покажет 12 В.

Падение напряжения в сопротивлении r₃:

U₃ = I × r₃ = 4 × 5 = 20 В.

Вольтметр V₃, включенный между точками д и е, покажет 20 В.

Если вольтметр присоединить одним концом к точке а, другим концом к точке г, то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r₁ и r₂ (8 + 12 = 20 В).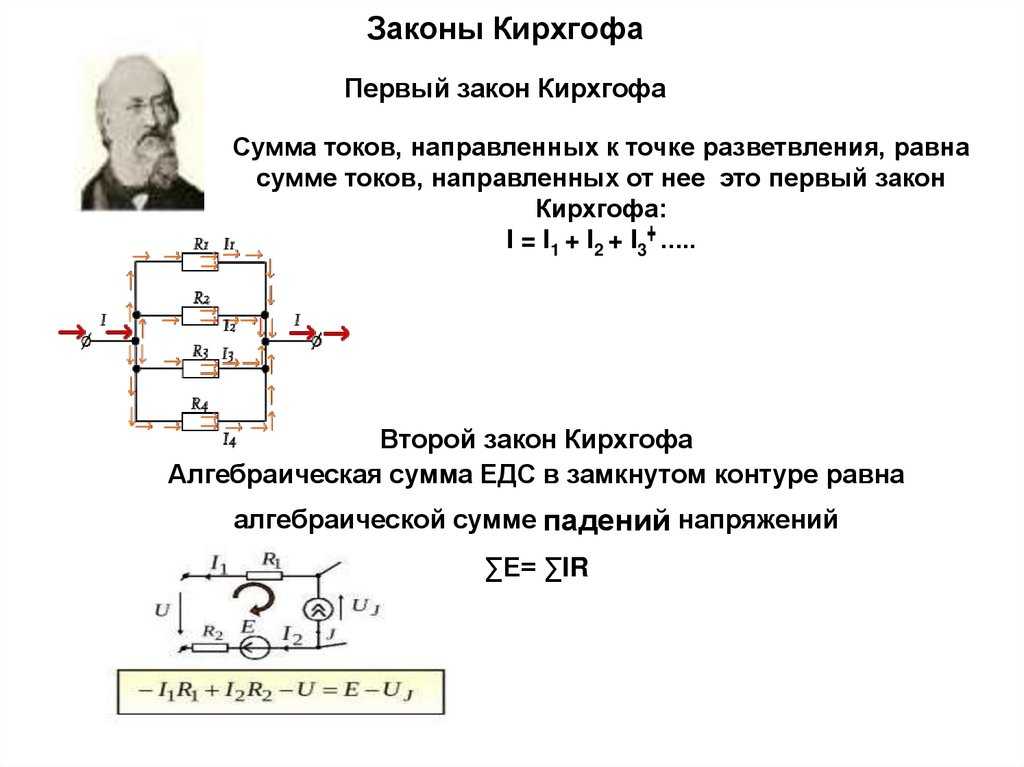

Таким образом, вольтметр V, измеряющий напряжение на зажимах цепи и включенный между точками а и е, покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r₁, r₂ и r₃.

Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.

Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.

Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.

U₁ = I × r₁ = 5 ×10 = 50 В,
U₂ = I × r₂ = 5 ×15 = 75 В,
U₃ = I × r₃ = 5 ×20 = 100 В.

Рисунок 3. К примеру 2

Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:

U = U₁ + U₂ + U₃ = 50 + 75 + 100 = 225 В.

Параллельное соединение проводников

Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.

Рисунок 4. Схема параллельного соединения проводников

Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А, растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:

I = I₁ + I₂ + I₃.

Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:

то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа. Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.

Видео 2. Первый закон Кирхгофа

Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.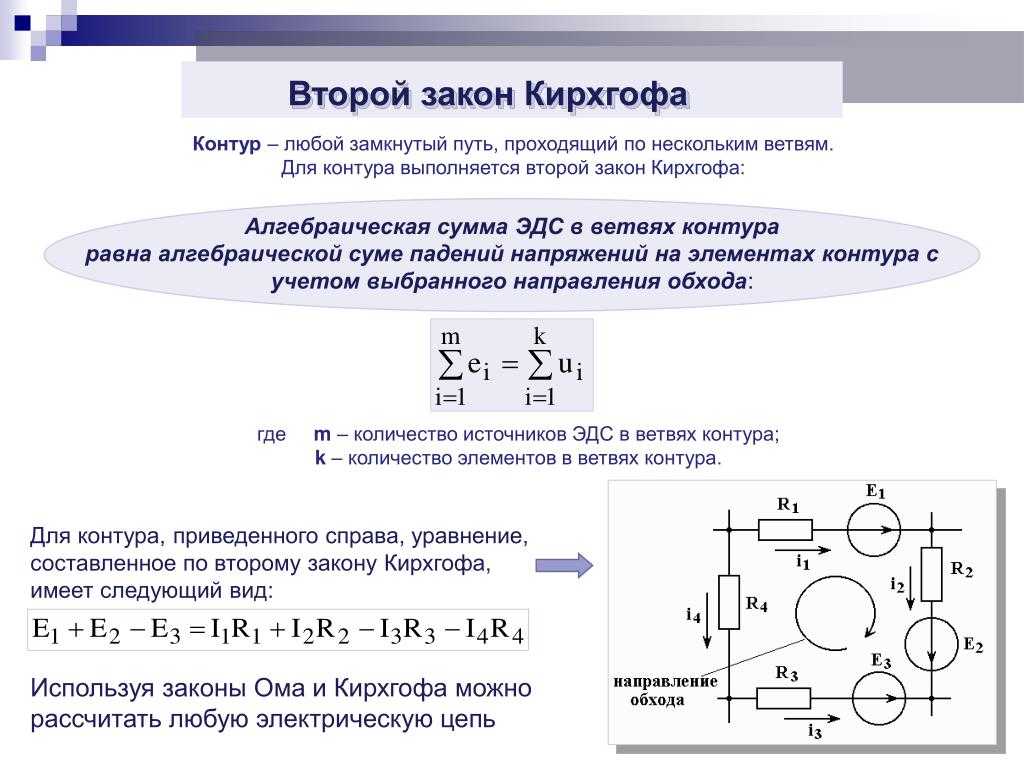

Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.

Общий ток, приходящий к точке А, равен:

Токи в каждой из ветвей имеют значения:

      

По формуле первого закона Кирхгофа

I = I₁ + I₂ + I₃

или

Вынося U в правой части равенства за скобки, получим:

Сокращая обе части равенства на U, получим формулу подсчета общей проводимости:

или

g = g₁ + g₂ + g₃.

Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость.

Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 4 Ом.

откуда

Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:

откуда

Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.

Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r₁, деленному на число ветвей n:

Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:

Для проверки попробуем найти сопротивление разветвления по формуле:

откуда

Как видим, ответ получается тот же.

Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а.

Рисунок 5. К примеру 6

Найдем общее сопротивление цепи:

откуда

Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б).

Падение напряжения на участке между точками А и Б будет:

U = I × r = 22 × 1,09 = 24 В.

Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б.

Рассматривая первую ветвь разветвления с сопротивлением r₁, мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:

Ток второй ветви

Ток третьей ветви

Проверим по первому закону Кирхгофа

I = I₁ + I₂ + I₃ = 12 + 6 + 4 = 22 А.

Следовательно, задача решена верно.

Обратим внимание на то, как распределяются токи в ветвях нашего параллельного соединения.

Первая ветвь: r₁ = 2 Ом, I₁ = 12 А.
Вторая ветвь: r₂ = 4 Ом, I₂ = 6 А.
Третья ветвь: r₃ = 6 Ом, I₃ = 4 А.

Как видим, сопротивление первой ветви в два раза меньше сопротивление второй ветви, а ток первой ветви в два раза больше тока второй ветви. Сопротивление третьей ветви в три раза больше сопротивления первой ветви, а ток третьей ветви в три раза меньше тока первой ветви. Отсюда можно сделать вывод, что токи в ветвях при параллельном соединении распределяются обратно пропорционально сопротивлениям этих ветвей. Таким образом, по ветви с большим сопротивлением потечет ток меньший, чем по ветви с малым сопротивлением.

Для двух параллельных ветвей можно также, конечно, пользоваться данной выше формулой.

Однако общее сопротивление проводника при параллельном соединении в этом случае легче подсчитать по формуле:

или окончательно:

Смешанное соединение проводников

Смешанным соединением проводников называется такое соединение, где имеются и последовательное и параллельное соединения отдельных проводников. Примером может служить соединение, изображенное на рисунке 6.

Рисунок 6. Схема смешанного соединения проводников

Видео 3. Смешанное соединение проводников

Пример 7. Определить общее сопротивление смешанного соединения, представленного на рисунке 6, если

r₁ = 2 Ом, r₂ = 3 Ом, r₃ = 5 Ом, r₄ = 4 Ом, r₅ = 8 Ом и r₆ = 6 Ом.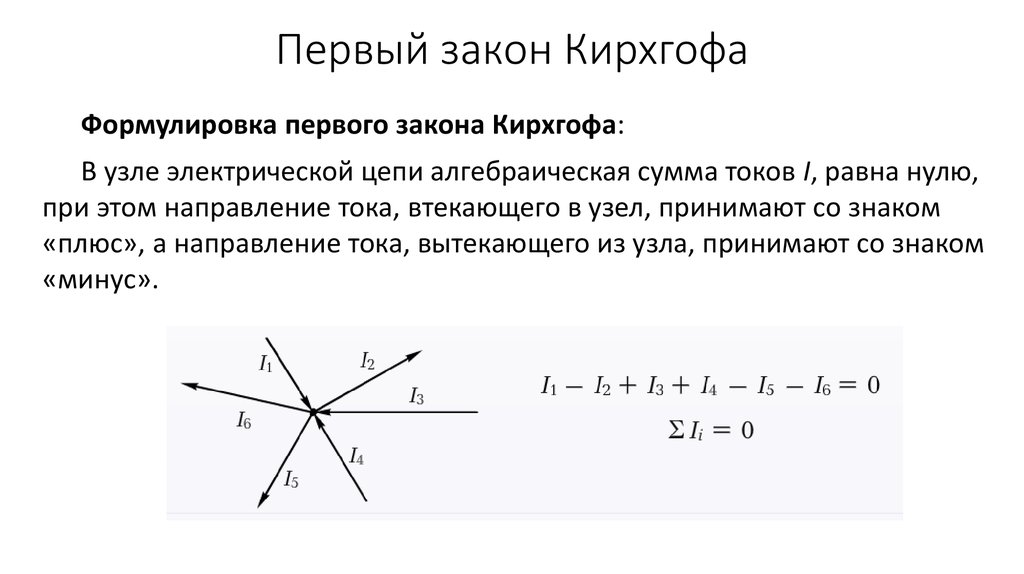

Находим общее сопротивление первого разветвления:

откуда

Общее сопротивление второго разветвления:

откуда

Общее сопротивление цепи:

r = r_1,2 + r₃ + r_4,5,6 = 1,2 + 5 + 1,85 = 8,05 Ом.

Источник: Кузнецов М. И., «Основы электротехники» – 9-е издание, исправленное – Москва: Высшая школа, 1964 – 560с.

Правила (законы) Кирхгофа простыми словами: формулировки и расчеты

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

Ток I1 входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I1 = I2 + I3.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i1, i2, i3, i4 то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i1 + i2 + i3 + i4 = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Рис. 2. Абстрактный узел

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Первый закон

Первый закон Кирхгофа устанавливает зависимость между то­ками для узлов электрической цепи, к которым подходит несколько ветвей. Согласно этому закону алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

?I = 0 (16)

При этом токи, направленные к узлу, берут с одним знаком (например, положительным), а токи, направленные от узла,— с противоположным знаком (отрицательным). Например, для узла А

I1 + I2 + I3 – I4 – I5 = 0 (17)

Это интересно! Все о полупроводниковых диодах.

Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла:

I1 + I2 + I3 = I4 + I5 (17′)

В данном случае имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах.

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа.

Второй закон Кирхгофа устанавливает зависимость между э. д. с. и напряжением в замкнутой электрической цепи. Согласно этому закону во всяком замкнутом контуре алгебраическая сумма э. д. с. равна алгебраической сумме падений напряжения на сопротивлениях, входящих в этот контур:

?E = ?IR (18)

При составлении формул, характеризующих второй закон Кирхгофа, значения э. д. с. E и падений напряжений IR считают положительными, если направления э. д. с. и токов на соответствующих участках контура совпадают с произвольно выбранным направлением обхода контура. Если же направления э. д. с. и токов на соответствующих участках контура противоположны выбранному направлению обхода, то такие э. д. с. и падения напряжения считают отрицательными.

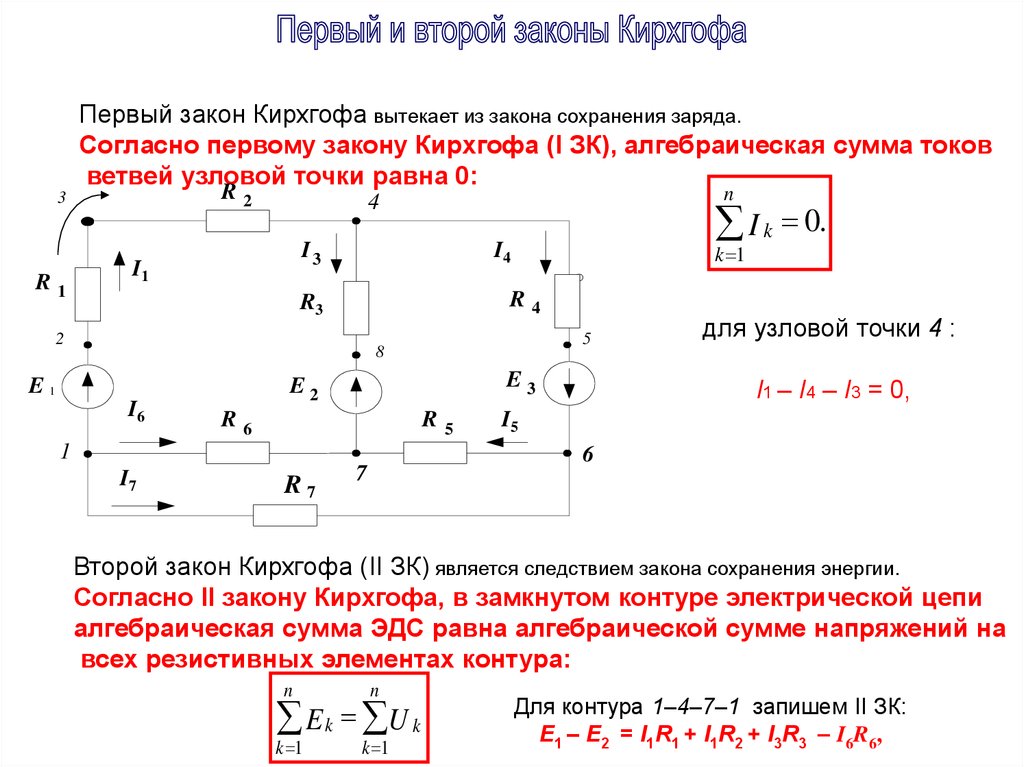
Рассмотрим в качестве примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2, внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для «этой цепи и выбирая направление ее обхода по часовой стрелке,

Будет интересно➡ Что такое анод и катод, в чем их практическое применение

получим:

E1 – E2 = IR01 + IR02 + IR1 + IR.

При этом э. д. с. E1 и ток I совпадают с выбранным направлением обхода контура и считаются положительными, а э. д. с. Е2, противоположная этому направлению, считается отрицательной. Если в электрической цепи э. д. с. источников электрической энергии при обходе соответствующего контура направлены навстречу друг другу (см. рис. 24, а), то такое включение называют встречным. В этом случае на основании второго закона Кирхгофа ток I = (E1-E2)/(R1+R2+R01+R02).

Встречное направление э. д. с. имеет место, например, на э. п. с.при включении электродвигателей постоянного тока (их можно рассматривать как некоторые источники э. д. с.) в две параллельные группы, а также при параллельном включении аккумуляторов в батарее.

Если же э. д. с. источников электрической энергии имеют по контуру одинаковое направление (рис. 24, б), то такое включение называют согласным и ток I = (E1-E2)/(R1+R2+R01+R02). В некоторых случаях такое включение недопустимо, так как ток в цепи резко возрастает.

Если в электрической цепи имеются ответвления (рис. 24, в), то по отдельным ее участкам проходят различные токи I1 и I2. Согласно второму закону Кирхгофа E1-E2=I1R01+I1R1-I2R2-I2R02-I2R3+I1R4.

При составлении этого уравнения э. д. с. Е1 и ток I1 считаются положительными, так как совпадают с принятым направлением обхода контура, э. д. с. Е2 и ток I2 — отрицательными.

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где Lk и Ck – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Метод непосредственного применения законов Кирхгофа

Обоснование последовательности расчета

На рисунке 3.38. представлена электрическая цепь с заданными величинами сопротивлений резисторов

и величинами .

В задачах анализа электрических цепей необходимо выполнить расчет величин токов в ветвях электрической цепи.

На первом этапе целесообразно произвольно выбрать направления токов в ветвях, упростить цепь, применив замену источников тока на источники ЭДС, где

может служить внутренним сопротивлением модели реального источника энергии, состоящего из источника тока и резистора .

Резистор

на рисунке 3.39 отсутствует, т.к. он подключен последовательно с бесконечным сопротивлением источника тока . Последовательно с резистором в схеме (рисунок 3.39) появляется ЭДС .

Так как метод непосредственного применения законов Кирхгофа состоит в составлении необходимого и достаточного количества уравнений по первому и второму законам Кирхгофа и дальнейшему их решению, на втором этапе необходимо подсчитать количество ветвей, и следовательно, неизвестных токов

и количество узлов , пронумеровав их. Для рисунка 3.39 и .

Если составить уравнения по первому закону Кирхгофа для всех узлов схемы, то в полученную систему уравнений каждый из токов войдет дважды, но с различными знаками. Если сложить уравнения, то полученная сумма будет равна нулю, что указывает на взаимную зависимость полученной системы уравнений.

Для цепи, изображенной на рисунке 3.39, например, система уравнений, составленных по первому закону Кирхгофа, для всех узлов при положительном выборе знака токов, отходящих от узла, имеет вид:

Сумма всех уравнений в системе (3.25) равна нулю, а сумма только трех любых уравнений приводит к уравнению исключенного узла.

Поэтому, количество независимых уравнений, составленных по первому закону Кирхгофа, на единицу меньше количества узлов к. Для данной цепи

-1=4-1=3.

На третьем этапе необходимо составить по второму закону Кирхгофа недостающее количество уравнений для независимых контуров:

Независимые контуры должны отличаться друг от друга хотя бы одной новой ветвью.

Для выбора независимого контура можно использовать любое дерево графа цепи, дополняя его последовательно ветвями соединения (пунктирные линии). На рисунке 3.40 представлен граф заданной электрической цепи, изображенной на рисунке 3.39.

Независимые контуры показаны на рисунке 3.40. Направление обхода контуров выбрано совпадающим с направлением тока периферийной ветви, входящей только в один контур.

Для выбранных контуров и направлений обхода элементов система уравнений по второму закону Кирхгофа будет иметь вид:

В четвертом этапе решаем общую систему уравнений (3.25), (3.27) подстановкой, без уравнения для четвертого узла, можно найти все токи данной цепи, а величина тока

(рисунок 3.38) может быть найдена по уравнению .

Пятый этап посвящен проверке величин вычисленных токов как по выполнению исходных уравнений (1), (2), так и по уравнению баланса мощностей. Уравнение баланса мощностей для примера цепи на рисунке 3.39 имеет вид:

В левой части уравнения (3.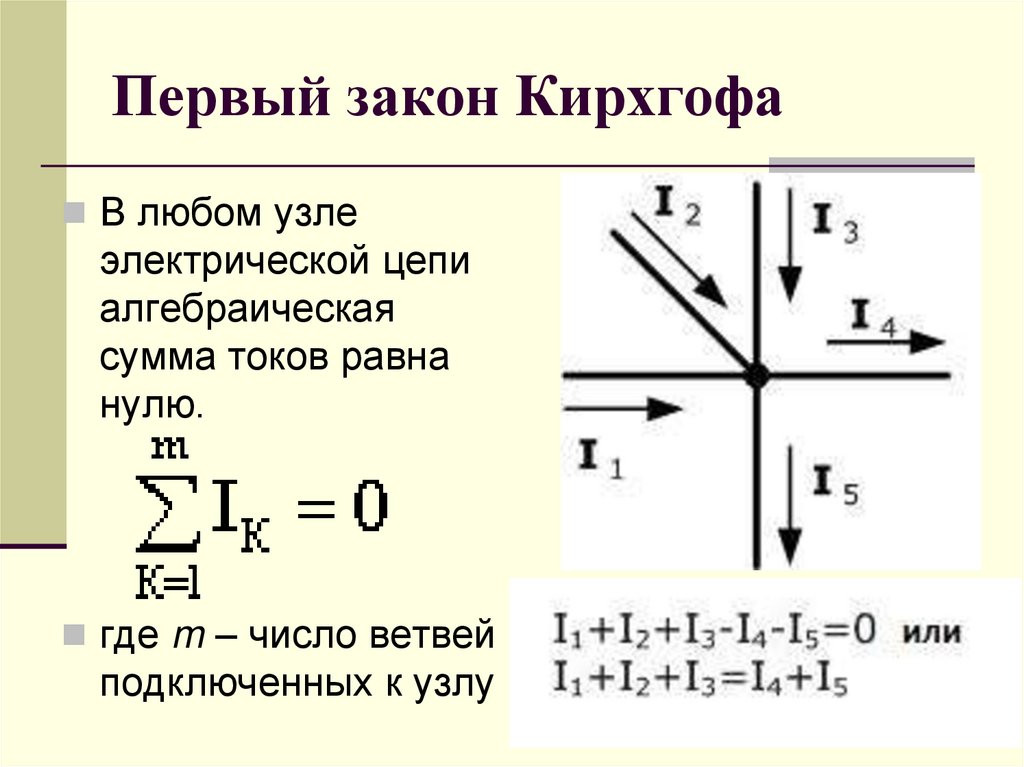 28) мощности могут быть как положительными (в режиме генератора), так и отрицательными (в режиме приемника).

Эта страница взята со страницы задач по электротехнике:

Электротехника — решения задач и примеры выполнения заданий

Возможно эти страницы вам будут полезны:

Эквивалентные преобразования резисторов, включенных в виде «треугольника» или трехлучевой «звезды»

Эквивалентные преобразования участков цепи с источниками энергии

Матричная форма уравнений по методу непосредственного применения законов Кирхгофа (МНЗ)

Метод контурных токов (MKT)

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

Рис. 4. Магнитные контуры цепей

В частности: ∑Ф=0.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Первый закон Кирхгофа: определение, формула, вывод, преимущество

Дом »Физика

Дивья Каре | Обновлено: 7 ноября 2022 г. 13:36 IST

0

Сохранить

Скачать публикацию в формате PDF

Законы Кирхгофа помогают в разработке сложных схем с различными электрическими компонентами, которые используются в повседневной жизни. Это также помогает в исследовании любых электрических цепей, например, сколько тока протекает в различных участках электрической цепи.

Законы Кирхгофа были названы в честь Густава Роберта Кирхгофа, немецкого физика. Он также помог продвинуть наше понимание излучения черного тела и спектроскопии. В 1845 году он впервые нашел закон. Это основа сетевого анализа и обычно используется во временной и частотной областях цепей. Закон Кирхгофа представляет собой комбинацию закона тока Кирхгофа и закона напряжения Кирхгофа. Закон Кирхгофа — это другое название первого закона Кирхгофа.

В этой статье по физике мы более подробно обсудим первый закон Кирхгофа.

Первый закон Кирхгофа

Первый закон Кирхгофа гласит, что в любом узле (узле) цепи сумма токов, проходящих в этот узел, эквивалентна сумме токов, вытекающих из этого узла. Это означает, что если мы думаем об узле как о резервуаре для воды, скорость потока воды, заполняющего резервуар, равна скорости его опорожнения.

В случае электричества сумма токов, входящих в узел, равна сумме токов, выходящих из узла.

Формула

Токи, втекающие в точку (A) = Токи, вытекающие из точки (A)

\( \sum l_{\text {(in)}}=\sum l_{\text {( out) }}\)

Ток, втекающий в точку, а также вытекающий из нее, имеет положительный знак (+) в месте соединения (узла).

\( I_1+I_2+I_3=I_4+I_5+I_6\)

В замкнутой цепи алгебраическая сумма токов в переходе равна нулю.

\( \sum l=0\)

Ток, втекающий в точку, имеет положительный знак (+) в узле, тогда как ток, вытекающий из точки, имеет отрицательный знак (-).

\( I_1+I_2+I_3-I_4-I_5-I_6=0\)

Первый закон Кирхгофа и сохранение заряда

Первый закон Кирхгофа для электрических цепей основан на сохранении заряда, а второй закон Кирхгофа для электрических цепей — на основе энергосбережения. Концепция Кирхгофа известна как закон сохранения заряда, потому что ток сохраняется вокруг перехода без потери тока.

Поскольку сила электрического тока в (Амперах) соответствует количеству электрических зарядов в (Кулонах), пересекающих площадь поперечного сечения за одну секунду, первый закон Кирхгофа является применением принципа сохранения заряда (количество заряда втекающий в узел эквивалентен количеству заряда, вытекающему из этого узла).

Преимущества и недостатки Законы Кирхгофа

Преимущества

Законы Кирхгофа применяются для определения:

• Значения тока, напряжения и внутреннего сопротивления в цепях постоянного тока.
• Мы также можем использовать этот закон, чтобы найти неизвестное сопротивление в цепи.
• Законы Кирхгофа широко используются при строительстве моста Уитстона. Это полезно для анализа сетки и узлов.

Недостатки

• Законы Кирхгофа неприменимы к высокочастотным цепям переменного тока. Закон тока применяется только тогда, когда электрический заряд в цепи постоянен.
• КВЛ используется в предположении, что магнитные поля в замкнутом контуре не изменяются. В результате мы не можем использовать КВЛ при флуктуациях магнитного поля внутри цепи.

Решенные примеры для первого закона Кирхгофа

Пример 1. Найдите текущий \(i_3\) в узле, показанном ниже.

Решение 1. В узел втекают токи \(i_1\) и \(i_2\), а из него вытекают токи \(i_3\) и \(i_4\). Примените текущий закон Кирхгофа к указанному узлу.

\(i_1+i_2 = i_3+i_4\)

Подставить известные значения

\(2+9=i_3+4\)

\(i_3=7 A\)

Сразу установить приложение Testbook воспользоваться их всеобъемлющими и надежными учебными материалами, а также помощью экспертов Testbook, чтобы успешно сдать желаемый конкурсный экзамен. Воспользуйтесь невероятной экономией прямо сейчас, установив бесплатное приложение Testbook.

Часто задаваемые вопросы о первом законе Кирхгофа

В. 1 Что такое первый закон Кирхгофа?

Ответ 1 Первый закон Кирхгофа или правило соединения Кирхгофа утверждает, что сумма токов, втекающих в любой узел (соединение) электрической цепи, равна сумме токов, вытекающих из этого узла.

Q.2 Применим ли первый закон Кирхгофа к цепям переменного тока?

Ответ 2 Да, закон Кирхгофа применим к цепям переменного тока.

Q.3 Какова формула действующего закона Кирхгофа?

Ответ 3 \(\sum l _{\text {(in)}}=\sum l_{\text {(out)}}\)

Q.4 Каково значение Первый закон Кирхгофа?

Ответ 4 Первый закон Кирхгофа выражает сохранение зарядов.

В.5 Что такое закон Кирхгофа для тока и закон напряжения?

Ответ 5 Анализ цепей с сосредоточенными параметрами основан на законе тока Кирхгофа и законе напряжения Кирхгофа. Эти правила в сочетании с вольтамперными характеристиками частей схемы системы позволяют проводить систематический анализ любой электрической сети.

Скачать публикацию в формате PDF

Читать Подробнее посты

Изучите двойной эксперимент Янга
Закон Хаббла: Заявление, Формула, Деривация, Применение и ограничения. Приложения
Центростремительная и центробежная сила: определение, формула, различия, примеры и приложения
Фазовые изменения: узнайте значение, примеры и характеристики

Первый закон Кирхгофа | Закон тока Кирхгофа (KCL)

Последнее обновление: 12 декабря 2021 г., 09:40

Густав Кирхгоф, выдающийся немецкий физик, является автором первого закона Кирхгофа, касающегося электрического тока. Этот закон также известен как Текущий закон Кирхгофа или KCL. KCL утверждает, что для любой точки или узла электрической цепи сумма токов в этой точке равна сумме токов из этой точки.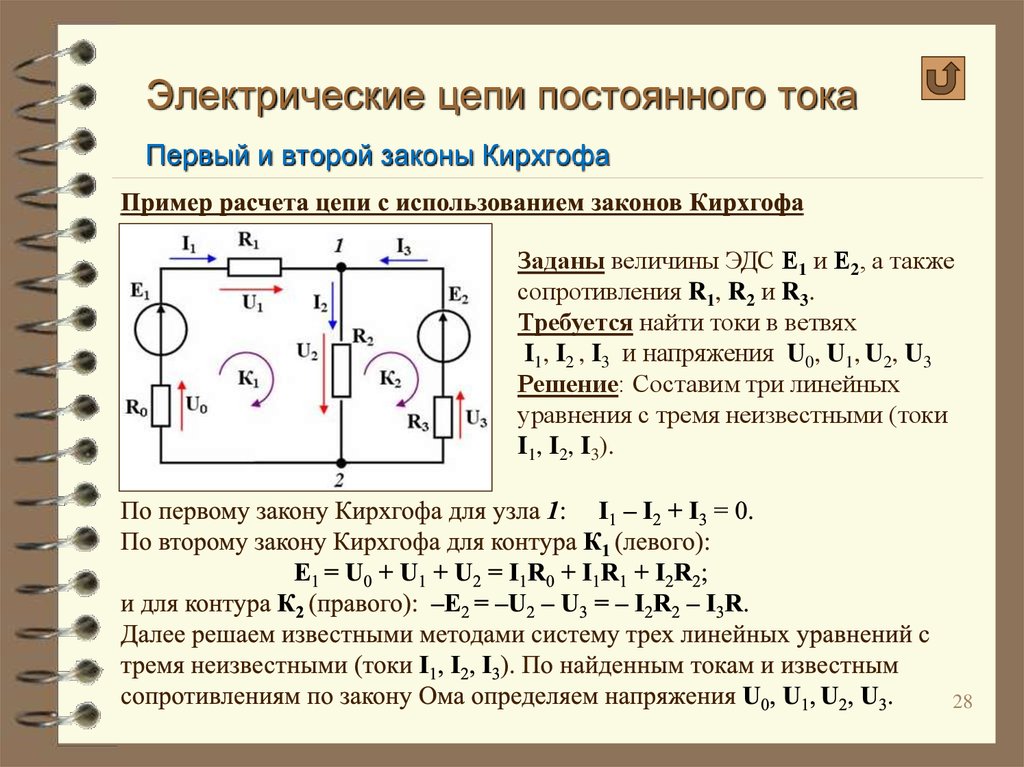

[ Знать о Второй закон Кирхгофа (KVL)]

Содержание

1. Укажите первый закон Кирхгофа или KCL | Объясните первый закон Кирхгофа с помощью диаграммы
2. Что такое закон сохранения заряда?
3. Получение первого закона Кирхгофа из закона сохранения заряда
4. Параллельная схема и применение KCL

Укажите первый закон Кирхгофа или KCL | Объясните первый закон Кирхгофа с помощью диаграммы

Первый закон Кирхгофа или закон тока (KCL) гласит, что для любой точки электрической цепи сумма токов в этой точке равна сумме токов из этой точки.

Первый закон Кирхгофа – пояснение к диаграмме [диаграмма 1 (A,B и C)]

Приведенная выше диаграмма поможет понять первый закон Кирхгофа. Закон можно записать как Σi _в = ΣI _из , где Σ обозначает «сумма».
Σi _в это сумма тока в точку и ΣI _из — это сумма тока из этой точки.

На диаграмме (1-a) в узел втекает ток 9 ампер, а затем снова (5+4) ампер, т. е. 9 ампер выходит из того же узла.

На диаграмме (1-b) суммарный (6+4) Ампер = 10 Ампер ток входит в узел и снова 10 Ампер ток выходит из узла.

Наконец, на диаграмме (1-c) общий ток, поступающий в показанный узел, равен (5 +2) Ампер = 7 Ампер.

И общий выходной ток также (4+3) Ампер = 7 Ампер. Все эти примеры помогают понять первый закон Кирхгофа (KCL).

Что такое

Закон о сохранении заряда ?

Закон сохранения заряда утверждает, что электрический заряд не может быть ни создан, ни уничтожен. Общее количество электрического заряда во Вселенной постоянно.

Получение первого закона Кирхгофа из закона сохранения заряда

Первый закон Кирхгофа можно вывести из закона сохранения заряда. Заряд является фундаментальным физическим свойством и одним из свойств, которые должны сохраняться.

Первый закон Кирхгофа основан на законе сохранения заряда, где заряд (в кулонах) есть произведение тока (в амперах) на время (в секундах).