Как найти вектор по двум точкам?



Если даны две точки плоскости  и , то вектор  имеет следующие координаты:

Если даны две точки пространства  и , то вектор  имеет следующие координаты:

То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора. Таким образом, для противоположно направленного вектора формулы запишутся так:

Задача 1

Даны две точки плоскости  и . Найти координаты вектора

Решение: по соответствующей формуле:

Как вариант, можно использовать следующую запись:

Эстеты решат и так:

Лично я привык к первой версии записи.

Ответ:

По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения важного момента, не поленюсь:

И момент здесь таков:
в чём различие между координатами точек и координатами векторов?

Координаты точек – это обычные координаты в прямоугольной системе координат (единичные векторы тут вообще ни при чём). Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.

Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при желании мы легко можем переобозначить его через  и отложить от какой-нибудь другой точки плоскости. Следует отметить, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости .

Записи координат точек  и координат вектора  формально одинаковы, но смысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.

Дамы и господа, набиваем руку:

Задача 2

а) Даны точки  и .

Найти векторы  и .
б) Даны точки  и . Найти векторы  и .
в) Даны точки  и . Найти векторы  и .
г) Даны точки . Найти векторы .

Пожалуй, достаточно…. Не пропускаем! Решаем письменно и «от руки»! Чертежи делать не нужно (коль скоро, не требовалось). Решения и ответы в конце книги.

Для проверки вычислений удобно использовать Геометрический калькулятор, приложенные к данному курсу. Дабы избежать нелепых ошибок а-ля «2 + 2 = 5». А подобные «затмения» бывают. Даже у профессоров. Отвлёкся – и студентка сбежала 🙂

1.5.2. Как найти длину отрезка?

1.4. Координаты вектора на плоскости и в пространстве

| Оглавление |



Автор: Aлeксaндр Eмeлин

Элементы векторного исчисления

Лаптев Г. Ф. Элементы векторного исчисления. М., 1975 г. — 336 с. Книга представляет собой учебное руководство для студентов втузов. В пен содержится предусмотренный учебными программами материал но векторной алгебре, дифференциальной геометрии и теории поля. Изложение построено с учетом потребностей технических дисциплин, в которых используется векторное исчисление. Книга написана просто и ясно; это делает ее доступной пониманию студентов первого курса, впервые приступающих к изучению высшей математики. Книга окажется полезной и в условиях заочного обучения. Оглавление ВВЕДЕНИЕ ЧАСТЬ ПЕРВАЯ. ВЕКТОРНАЯ АЛГЕБРА Глава I. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ 2. Скаляры и векторы. 3. Равенство векторов. 4. Скользящие и приложенные векторные величины. 5. Модуль вектора. 6. Орт вектора. 7. Угол между двумя векторами. § 2. Сложение векторов 1. Сложение двух векторов. 2. Сложение более чем двух векторов. 3. Модуль суммы. 4. Законы сложения. § 3. Вычитание векторов § 4. Умножение и деление вектора на скаляр 2. Законы умножения вектора на скаляр. 3. Деление вектора на скаляр. 4. Выражение вектора через его модуль и орт. § 5. Линейные зависимости между векторами 2. Коллинеарные векторы. 3. Компланарные векторы. 4. Разложение вектора по трем некомпланарным векторам. 5. Метод координат. Глава II. ТЕОРИЯ ПРОЕКЦИЙ. ПРЯМОУГОЛЬНЫЕ КООРДИНАТЫ § 1. Проекции векторов на ось § 2. Основные теоремы о скалярных проекциях § 3. Прямоугольная система координат в пространстве 1. Правая и левая прямоугольные системы координат. 2. Разложение вектора по ортам осей 3. Линейные операции над векторами в координатной форме. 4. Радиус-вектор и координаты точки. 5. Определение вектора по его началу и концу. 6. Деление отрезка в данном отношении. Глава III. ПРОИЗВЕДЕНИЯ ДВУХ ВЕКТОРОВ § 1. Скалярное произведение двух векторов 2. Работа силы. 3. Определение. 4. Равенство скалярного произведения нулю. 5. Законы скалярного умножения. 7. Скалярные произведения координатных ортов. 8. Скалярное произведение в координатной форме. 9. Неопределенность действия, обратного скалярному умножению. § 2. Векторное произведение двух векторов 3. Условия равенства нулю векторного произведения. 4. Законы векторного умножения. 5. Векторные произведения координатных ортов. 6. Определители. 7. Векторное произведение в координатной форме. 8. Неопределенность действия, обратного векторному умножению. Глава IV. ПРОИЗВЕДЕНИЯ ТРЕХ ВЕКТОРОВ § 1. Простейшее произведение трех векторов § 2. Векторно-векторное произведение трех векторов 3. Правило разложения векторно-векторного произведения. § 3. Векторно-скалярное произведение трех векторов 2. Законы векторно-скалярного умножения 3. Обращение в нуль векторно-скалярного произведения трех векторов. 4. Векторно-скалярное произведение в координатной форме. § 4. Выражение векторно-скалярного произведения через скалярные произведения Глава V. ФУНКЦИИ ВЕКТОРОВ § 1. Произведения четырех векторов 2. Выражение скалярного произведения двух векторных произведений (а x b), (р x q) через скалярные произведения. 3. Разложение вектора (а, b, с) R по трем векторам a, b, c. 4. Разложение вектора (a, b, c) по векторным произведениям b x с, c x a, а x b § 2. Произведения пяти и шести векторов 2. Разложение вектора (a, b, c) (m x n) по векторам a, b, c. 3. Выражение произведения двух смешанных произведений (a, b, c) (l, m, n) через скалярные произведения. § 3. Основные теоремы о функциях векторов 1. Рациональные функции векторов. 2. Элементарные функции векторов. 3. Произвольные скалярные функции от векторов. 4. Произвольные векторные функции векторов. Глава VI. ОСНОВНЫЕ ЗАДАЧИ § 2. Основные задачи, связанные со скалярным умножением векторов § 3. Основные задачи, связанные с векторным умножением векторов § 4. 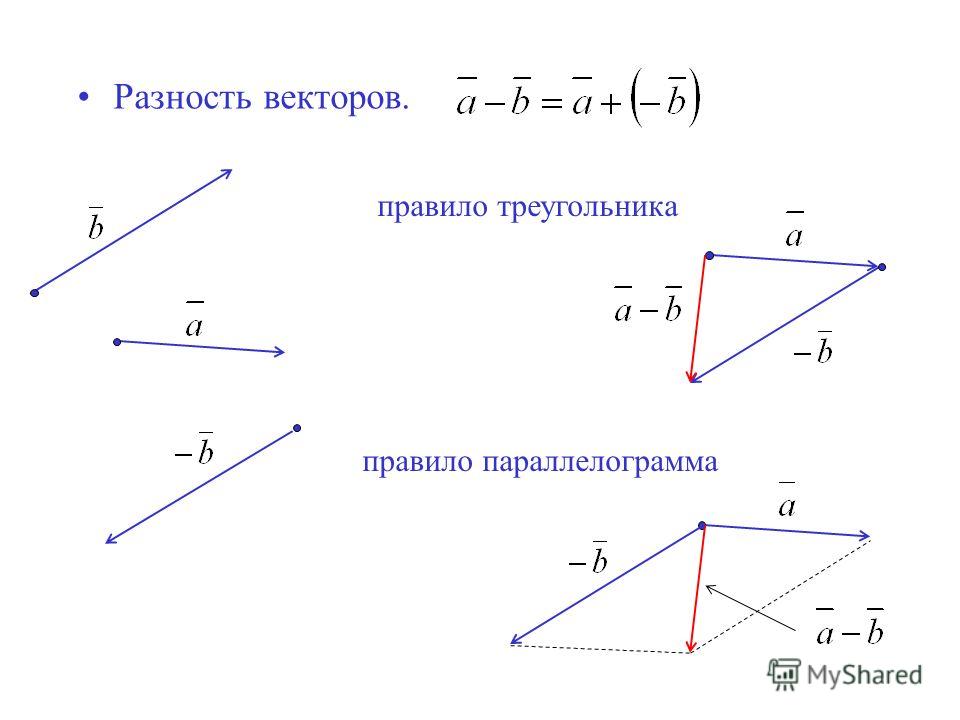Основные задачи, связанные с произведениями трех и более векторов § 5. Простейшие векторные уравнения § 6. Геометрические инварианты фигур 2. Треугольник. 3. Полные системы инвариантов треугольника. 4. Тетраэдр. 5. Полные системы инвариантов тетраэдра. 6. Гексаэдр с треугольными гранями. ЧАСТЬ ВТОРАЯ. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ § 1. Векторы, зависящие от скаляра 2. Вектор-функция в координатной форме. 3. Годограф вектора. 4. Предел вектора. § 2. Дифференцирование вектора по скаляру 2. Геометрический смысл производной вектора по скаляру. 3. Механический смысл производной. 5. Дифференциал вектора. 6. Инвариантность дифференциала. 7. Связь дифференциала вектора с его приращением. § 3. Формула Тейлора Глава VIII. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ЛИНИИ В ПРОСТРАНСТВЕ § 1. Основные дифференциально-геометрические понятия, связанные с линией 2. Касательная. 3. Соприкасающаяся плоскость. 4. Главная нормаль и бинормаль. 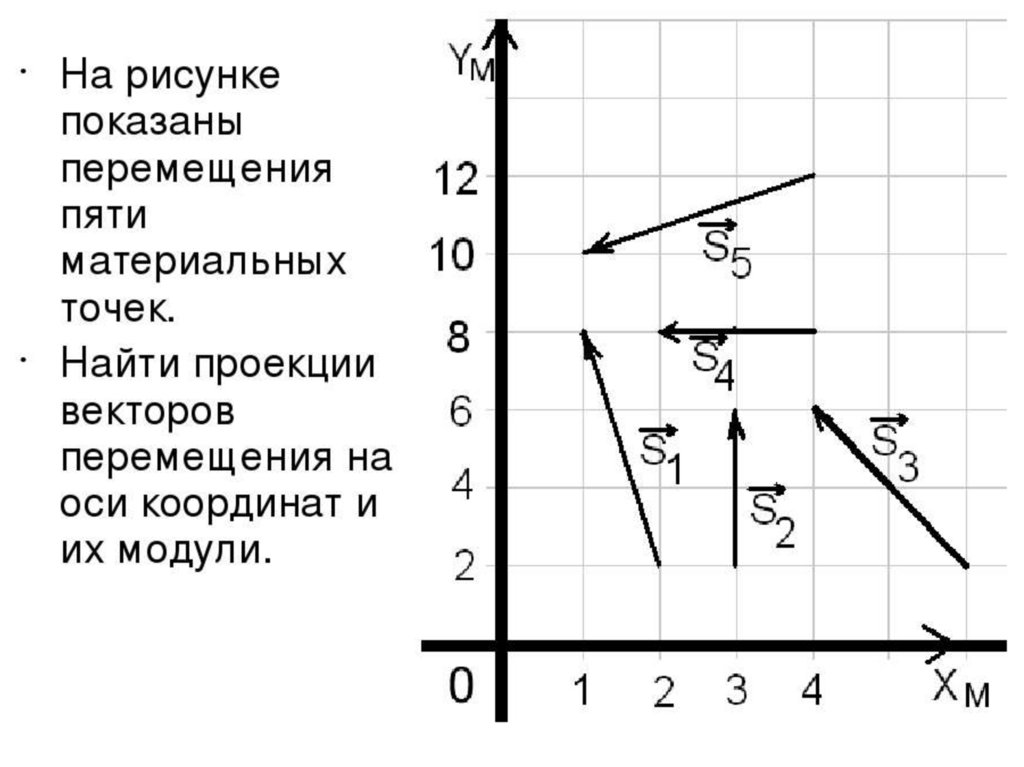5. Кривизна. 6. Кручение. 7. Длина дуги. § 2. Основные формулы дифференциальной геометрии линий в пространстве 1. Дуга как параметр. Дифференциал дуги. 2. Орт касательной. Первая основная формула. 3. Инвариантность геометрических понятий. 4. Главная нормаль и кривизна. Вторая основная формула. 5. Бинормаль и кручение. Третья основная формула. 6. Винтовая линия. § 3. Сопровождающий трехгранник 2. Система дифференциальных уравнений движения сопровождающего трехгранника. 3. Расположение линии относительно сопровождающего трехгранника. 4. Линии без кривизны. 5. Линии без кручения. § 4. Инвариантные формулы Глава IX. ПЛОСКИЕ ЛИНИИ § 1. Дифференциальные уравнения плоской линии § 2. Кривизна плоской линии § 3. Круг кривизны § 4. Эволюта § 5. Эвольвента Глава X. ПРИЛОЖЕНИЯ К МЕХАНИКЕ § 1. Скорость и ускорение точки § 2. Движение твердого тела вокруг неподвижной точки 2. Формула Эйлера. 3. Угловая скорость. 4. Доказательстве существования угловой скорости твердого тела. § 3. Относительная производная вектора 2. Абсолютная и относительная производные вектора. 3. Общий случай движения твердого тела. Глава XI. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ ПОВЕРХНОСТИ § 1. Векторные функции нескольких скалярных аргументов § 2. Параметризованная поверхность 2. Поверхность в декартовых координатах. 3. Параметрическая сеть. 4. Линия на параметризованной поверхности. § 3. Касательная плоскость и нормаль 3. Нормальный вектор. 4. Преобразование параметров. § 4. Площадь области на поверхности 2. Площадь области на поверхности. 3. Формула для вычисления площади поверхности, заданной уравнением z=z(x,y). 4. Элемент площади поверхности. 5. Векторный элемент площади поверхности. § 5. Первая квадратичная форма поверхности 2. Внутренняя геометрия поверхности. 3. Длина дуги линии на поверхности. 4. Угол между линиями на поверхности. 5. Площадь области на поверхности. § 6. Вторая квадратичная форма поверхности 2. Нормальная кривизна линии на поверхности. 3. Теорема Менье. § 7. Главные направления и главные кривизны поверхности 2. Главные направления на поверхности. 3. Перпендикулярность главных направлений. 4. Формула Эйлера. 5. Полная и средняя кривизны поверхности. ЧАСТЬ ТРЕТЬЯ. ТЕОРИЯ ПОЛЯ § 1. Функция поля. Поверхности уровня § 2. Градиент поля 2. Первая теорема о градиенте. § 3. Производная по направлению 2. Выражение производной по направлению через градиент. 3. Вторая теорема о градиенте. § 4. Направляющие косинусы нормали поверхности Глава XIII. КРИВОЛИНЕЙНЫЙ И ПОВЕРХНОСТНЫЙ ИНТЕГРАЛЫ § 1. Криволинейный интеграл как определенный интеграл от сложной функции 2. Криволинейный интеграл от линейной формы по произвольной кривой. 3. Основные свойства криволинейного интеграла. 4. Обобщенный криволинейный интеграл. 5. Примеры. § 2. Криволинейный интеграл как предел криволипейной интегральной суммы § 3. Поверхностный интеграл как двойной интеграл от сложной функции 2. Определение простейшего поверхностного интеграла. 3. Поверхностный интеграл от билинейной формы по произвольной поверхности. § 4. Поверхностный интеграл как предел поверхностной интегральной суммы § 5. Поверхностный интеграл в параметрической форме 2. Параметрический поверхностный интеграл. 3. Поверхностный интеграл как предел суммы. § 6. Кратный интеграл как предел обобщенной интегральной суммы 2. Обобщение основной теоремы о кратном интеграле. Глава XIV. ВЕКТОРНОЕ ПОЛЕ И ЕГО ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ § 1. Векторное поле § 2. Векторные линии § 3. Циркуляция поля вдоль линии § 4. Поток поля через поверхность Глава XV. ТЕОРЕМА ОСТРОГРАДСКОГО. ДИВЕРГЕНЦИЯ ПОЛЯ § 1. Формула Остроградского § 2. Дивергенция поля 2. Дивергенция как предел отношения. 3. Гидромеханический смысл дивергенции. 4. Теорема Остроградского. Глава XVI. ТЕОРЕМА СТОКСА. РОТАЦИЯ ПОЛЯ § 1. Формула Стокса § 2. Ротация поля § 3. Оператор Гамильтона Глава XVII. СПЕЦИАЛЬНЫЕ ВЕКТОРНЫЕ ПОЛЯ § 1. Потенциальное поле 3. Циркуляция потенциального поля по замкнутому контуру. 4. Циркуляция потенциального поля между двумя точками. 5. Потенциал. 6. Элемент циркуляции. 7. Характеристические признаки потенциального поля. 8. Вычисление потенциала. 9. Центральное поле. 10. Вихревые шнуры. § 2. Соленоидальное поле 3. Поток соленоидального поля через замкнутую поверхность. 4. Трубчатое строение соленоидального поля. 5. Векторный потенциал. 6. Характеристические признаки соленоидального поля. 7. Источники и стоки. § 3. Потенциальное несжимаемое поле Глава XVIII. ПРОСТЕЙШИЕ ЭЛЕКТРОМАГНИТНЫЕ ПОЛЯ § 1. Электростатическое поле точечного заряда 2. Дивергенция поля точечного заряда. 3. Поток поля точечного заряда через замкнутую поверхность. 4. Ротация поля точечного заряда. 5. Потенциал поля точечного заряда. § 2. Электростатическое поле системы точечных зарядов 2. Дивергенция и ротация поля системы точечных зарядов. 3. Поток поля системы точечных зарядов через замкнутую поверхность. 4. Потенциал поля системы точечных зарядов. 5. Непрерывно распределенный заряд. § 3. Магнитное поле тока 2. Напряженность магнитного поля тока, текущего по бесконечному прямолинейному проводу. 3. Векторные линии поля H. 4. Потенциал поля Н. 5. Провод как вихревой шнур. Глава XIX. ВЕКТОРНОЕ ПОЛЕ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ § 1. Криволинейные координаты 3. Координатные поверхности и линии. 4. Линейный элемент. 5. Элемент объема. 6. Подвижной репер. 7. Векторное поле в криволиненных координатах. § 2. Дифференциальные операции в криволинейных координатах 2. Дивергенция в криволинейных координатах. 3. Ротация в криволинейных координатах. § 3. Ортогональные координаты § 4. Цилиндрические координаты 2. Линейный элемент и элемент объема в цилиндрических координатах. 3. Дифференциальные операции в цилиндрических координатах. § 5. Сферические координаты

Установить вектор из исходников | Документация по вектору

На этой странице рассматривается установка Vector из исходного кода с использованием собственного набора инструментов для хоста.

Вектор также можно скомпилировать в статический двоичный файл для Linux для архитектур x86_64, ARM64 и ARMv7. Подробнее см. в разделе компиляция с использованием Docker.

Мы рекомендуем устанавливать Vector через поддерживаемую платформу, диспетчер пакетов или предварительно созданный архив, если это возможно. Они управляют разрешениями, созданием каталога и другими тонкостями, описанными в разделе «Следующие шаги».

Установка

Линукс

Установить Rust:

 curl --proto '=https' --tlsv1. 2 -sSf https://sh.rustup.rs | sh -s -- -y --default-toolchain стабильный
 

Установите зависимости компиляции, в частности, компиляторы C и C++ (GCC или Clang) и GNU make , если они не предустановлены в вашей системе.

Скачать Источник вектора:

 # Latest (0.27.1)
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://api.github.com/repos/vectordotdev/vector/tarball/v0.27.1 | \
  tar xzf - -C вектор --strip-components=1
# Владелец
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://github.com/vectordotdev/vector/archive/master.tar.gz | \
  tar xzf - -C вектор --strip-components=1
 

Перейдите в каталог векторов:

 cd vector
 

Вектор компиляции:

 [FEATURES=",,..."] make build
 

Переменная среды FEATURES не является обязательной. Вы можете переопределить функции по умолчанию, используя эту переменную. См. флаги функций для получения дополнительной информации.

По завершении двоичный файл Vector помещается в target//release/vector . Например, если вы создаете Vector на своем Mac, целевая тройка — 9.0017 x86_64-apple-darwin , а двоичный файл Vector будет расположен по адресу target/x86_64-apple-darwin/release/vector .

Наконец, вы можете запустить Vector:

 target//release/vector --config config/vector.toml
 

Окна

Установите Rust с помощью rustup . Если у вас нет инструментов сборки VC++, программа установки предложит вам установить их.

Установите и добавьте CMake в PATH .

Установить и добавить Protoc к ПУТЬ .

Установите Perl для Windows.

Добавьте Perl в ваш PATH . В среде Rust/MSVC (например, используя x64 Native Tools Command Prompt ) добавьте двоичный каталог Perl, установленный на предыдущем шаге, в PATH . Например, для установки Strawberry Perl по умолчанию это

 set PATH=%PATH%;C:\Strawberry\perl\bin
 

Получить исходный код Vector с помощью Git:

 # Последний
клон git https://github.com/vectordotdev/vector
git проверка v0.27.1
компакт-диск вектор
# Владелец
клон git https://github.com/vectordotdev/vector
компакт-диск вектор
 

Вектор сборки в режиме выпуска:

 установить RUSTFLAGS=-Ctarget-feature=+crt-static
сборка грузов --no-default-features --features default-msvc --release
 

Начальный вектор. После этих шагов будет создан двоичный файл vector.exe в target\release . Его можно запустить, выполнив:

 .\target\release\vector --config config\vector.toml
 

Докер

Вы можете создавать статически скомпонованные двоичные файлы Vector для Linux, используя перекрестие в Docker. Если вы это сделаете, зависимости, перечисленные в предыдущем разделе, не нужны, так как все они будут автоматически загружены Docker.

Сначала загрузите Источник вектора:

 # Последняя версия (0.27.1)
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://api.github.com/repos/vectordotdev/vector/tarball/v0.27.1 | \
  tar xzf - -C вектор --strip-components=1
# Владелец
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://github.com/vectordotdev/vector/archive/master.tar.gz | \
  tar xzf - -C вектор --strip-components=1
 

Во-вторых, установить крестовину.

А затем построить вектор, используя крест:

 # Linux (x86_64)
сделать пакет-x86_64-неизвестный-linux-musl-все
# Линукс (ARM64)
сделать пакет-aarch64-неизвестный-linux-musl-все
# Линукс (ARMv7)
сделать пакет-armv7-неизвестный-linux-muslueabihf-все
 

Приведенная выше команда создает образ Docker с набором инструментов Rust для цели Linux для соответствующей архитектуры, используя musl в качестве библиотеки C, затем запускает контейнер из этого образа, а затем выполняет сборку внутри контейнера. Целевой двоичный файл находится по адресу target//release/vector 9.0018 как и в предыдущем случае.

Следующие шаги

Настройка

Файл конфигурации Vector находится по адресу:

 config/vector.toml
 

Примеры конфигураций находятся в config/vector/examples/* . Вы можете узнать больше о настройке Vector в документации по конфигурации.

Каталог данных

Мы рекомендуем создать каталог данных, который может использовать Vector:

 mkdir /var/lib/vector
 

Убедитесь, что этот каталог доступен для записи вектор процесс.

Vector предлагает глобальную опцию data_dir , которую вы можете использовать для указания пути к вашему каталогу:

 data_dir = "/var/lib/vector" # по умолчанию
 

Менеджеры по обслуживанию

Векторные архивы поставляются со служебными файлами на случай, если они вам понадобятся:

Init.

d

Чтобы установить Vector в Init.d, запустите:

 cp -av etc/init.d/vector /etc/init.d
 

Системд

Чтобы установить Vector в Systemd, выполните:

 cp -av и т. д./systemd/vector.service /etc/systemd/система
 

Обновление

Чтобы обновить Vector, следуйте приведенным выше инструкциям по установке.

Как это работает

Флаги функций

Vector поддерживает множество флагов функций, позволяющих указать, какие функции включаются в сборку. По умолчанию, все источники, преобразования и приемники включены. Чтобы просмотреть полный список функций, они перечислены в разделе «[функции]» здесь.

Установить вектор из исходников | Векторная документация

На этой странице рассматривается установка Vector из исходного кода с использованием собственного набора инструментов для хоста.

Вектор также можно скомпилировать в статический двоичный файл для Linux для архитектур x86_64, ARM64 и ARMv7. Подробнее см. в разделе компиляция с использованием Docker.

Мы рекомендуем устанавливать Vector через поддерживаемую платформу, диспетчер пакетов или предварительно созданный архив, если это возможно. Они управляют разрешениями, созданием каталога и другими тонкостями, описанными в разделе «Следующие шаги».

Установка

Линукс

Установить Rust:

 curl --proto '=https' --tlsv1.2 -sSf https://sh.rustup.rs | sh -s -- -y --default-toolchain стабильный
 

Установите зависимости компиляции, в частности, компиляторы C и C++ (GCC или Clang) и GNU make , если они не предустановлены в вашей системе.

Скачать Источник вектора:

 # Latest (0.27.1)
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://api.github.com/repos/vectordotdev/vector/tarball/v0.27.1 | \
  tar xzf - -C вектор --strip-components=1
# Владелец
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://github.com/vectordotdev/vector/archive/master.tar.gz | \
  tar xzf - -C вектор --strip-components=1
 

Перейдите в каталог векторов:

 cd vector
 

Вектор компиляции:

 [FEATURES=",,..."] make build
 

Переменная среды FEATURES не является обязательной. Вы можете переопределить функции по умолчанию, используя эту переменную. См. флаги функций для получения дополнительной информации.

По завершении двоичный файл Vector помещается в target//release/vector . Например, если вы создаете Vector на своем Mac, целевая тройка — 9. 0017 x86_64-apple-darwin , а двоичный файл Vector будет расположен по адресу target/x86_64-apple-darwin/release/vector .

Наконец, вы можете запустить Vector:

 target//release/vector --config config/vector.toml
 

Окна

Установите Rust с помощью rustup . Если у вас нет инструментов сборки VC++, программа установки предложит вам установить их.

Установите и добавьте CMake в PATH .

Установить и добавить Protoc к ПУТЬ .

Установите Perl для Windows.

Добавьте Perl в ваш PATH . В среде Rust/MSVC (например, используя x64 Native Tools Command Prompt ) добавьте двоичный каталог Perl, установленный на предыдущем шаге, в PATH . Например, для установки Strawberry Perl по умолчанию это

 set PATH=%PATH%;C:\Strawberry\perl\bin
 

Получить исходный код Vector с помощью Git:

 # Последний
клон git https://github. com/vectordotdev/vector
git проверка v0.27.1
компакт-диск вектор
# Владелец
клон git https://github.com/vectordotdev/vector
компакт-диск вектор
 

Вектор сборки в режиме выпуска:

 установить RUSTFLAGS=-Ctarget-feature=+crt-static
сборка грузов --no-default-features --features default-msvc --release
 

Начальный вектор. После этих шагов будет создан двоичный файл vector.exe в target\release . Его можно запустить, выполнив:

 .\target\release\vector --config config\vector.toml
 

Докер

Вы можете создавать статически скомпонованные двоичные файлы Vector для Linux, используя перекрестие в Docker. Если вы это сделаете, зависимости, перечисленные в предыдущем разделе, не нужны, так как все они будут автоматически загружены Docker.

Сначала загрузите Источник вектора:

 # Последняя версия (0. 27.1)
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://api.github.com/repos/vectordotdev/vector/tarball/v0.27.1 | \
  tar xzf - -C вектор --strip-components=1
# Владелец
mkdir -p вектор && \
  curl -sSfL --proto '=https' --tlsv1.2 https://github.com/vectordotdev/vector/archive/master.tar.gz | \
  tar xzf - -C вектор --strip-components=1
 

Во-вторых, установить крестовину.

А затем построить вектор, используя крест:

 # Linux (x86_64)
сделать пакет-x86_64-неизвестный-linux-musl-все
# Линукс (ARM64)
сделать пакет-aarch64-неизвестный-linux-musl-все
# Линукс (ARMv7)
сделать пакет-armv7-неизвестный-linux-muslueabihf-все
 

Приведенная выше команда создает образ Docker с набором инструментов Rust для цели Linux для соответствующей архитектуры, используя musl в качестве библиотеки C, затем запускает контейнер из этого образа, а затем выполняет сборку внутри контейнера. Целевой двоичный файл находится по адресу target//release/vector 9. 0018 как и в предыдущем случае.

Следующие шаги

Настройка

Файл конфигурации Vector находится по адресу:

 config/vector.toml
 

Примеры конфигураций находятся в config/vector/examples/* . Вы можете узнать больше о настройке Vector в документации по конфигурации.

Каталог данных

Мы рекомендуем создать каталог данных, который может использовать Vector:

 mkdir /var/lib/vector
 

Убедитесь, что этот каталог доступен для записи вектор процесс.

Vector предлагает глобальную опцию data_dir , которую вы можете использовать для указания пути к вашему каталогу:

 data_dir = "/var/lib/vector" # по умолчанию
 

Менеджеры по обслуживанию

Векторные архивы поставляются со служебными файлами на случай, если они вам понадобятся:

Init.