Секунда — Википедия

Секу́нда (русское обозначение: с; международное: s) — единица измерения времени, одна из основных единиц Международной системы единиц (СИ) и системы СГС. Кроме того, является единицей времени и относится к числу основных единиц в системах МКС, МКСА , МКСК, МКСГ, МКСЛ, МСК, МСС, МКГСС и МТС^[1].

Представляет собой интервал времени, равный 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, находящегося в покое при 0 К. Точный текст действовавшего определения секунды, утверждённого XIII Генеральной конференцией по мерам и весам (ГКМВ) в 1967 году, таков^[2][3]:

Секунда — время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.

В 1997 году Международный комитет мер и весов (МКМВ) уточнил, что данное определение относится к атому цезия, находящемуся в покое при температуре 0 К^[2].

Термин заимствован в XVIII веке из латыни, где secunda — сокращение выражения pars minuta secunda — «часть мелкая вторая» (часа), в отличие от pars minuta prima — «часть мелкая первая» (часа).

С единицей измерения «секунда», как правило, используются только дольные приставки СИ (кроме деци- и санти-). Для измерения больших интервалов времени используются единицы минута, час, сутки, и т. д.

Кратные				Дольные
величина	название	обозначение		величина	название	обозначение
101 с	декасекунда	дас	das	10−1 с	децисекунда	дс	ds
102 с	гектосекунда	гс	hs	10−2 с	сантисекунда	сс	cs
103 с	килосекунда	кс	ks	10−3 с	миллисекунда	мс	ms
106 с	мегасекунда	Мс	Ms	10 −6 с	микросекунда	мкс	µs
109 с	гигасекунда	Гс	Gs	10−9 с	наносекунда	нс	ns
1012 с	терасекунда	Тс	Ts	10−12 с	пикосекунда	пс	ps
1015 с	петасекунда	Пс	Ps	10−15 с	фемтосекунда	фс	fs
1018 с	эксасекунда	Эс	Es	10−18 с	аттосекунда	ас	as
1021 с	зеттасекунда	Зс	Zs	10−21 с	зептосекунда	зс	zs
1024 с	иоттасекунда	Ис	Ys	10−24 с	иоктосекунда	ис	ys
применять не рекомендуется      не применяются или редко применяются на практике

Эквивалентность другим единицам измерения времени[править | править код]

1 секунда равна:

Слово секунда происходит от латинского словосочетания secunda divisio^[4]. Это означает второе деление часа (в шестидесятиричной системе счисления).

Перед появлением механических часов[править | править код]

Жители Древнего Египта делили дневную и ночную половины суток каждую на 12 часов уже, по крайней мере, с 2000 года до н. э. В силу разных длительностей ночного и дневного периодов в разное время года продолжительность египетского часа была величиной переменной. Греческие астрономы периода эллинистической Греции Гиппарх и Птолемей делили день на основе шестидесятеричной системы счисления и также использовали усреднённый час (¹⁄₂₄ суток), простые доли часа (¹⁄₄, ²⁄₃ и т. п.) и время-градусы (¹⁄₃₆₀ суток, или 4 современные минуты), но не современные минуты или секунды^[5].

В Вавилонии после 300 года до н. э. день делился шестидесятирично, то есть на 60, полученный отрезок — ещё на 60, потом — ещё раз на 60 и т. д. до, по крайней мере, шести разрядов после шестидесятиричного разделителя (что давало точность больше двух современных микросекунд). Например, для длительности их года использовалась 6-разрядное дробное число от длительности одного дня, хотя они были не в состоянии измерить столь малый промежуток физически. Ещё одним примером может служить определённая ими длительность синодического месяца, которая составила 29;31,50,8,20 дня (четыре дробных шестидесятиричных разряда), что было повторено Гиппархом и Птолемеем и что является ныне продолжительностью среднего синодического месяца в еврейском календаре, хотя и исчисляемого как 29 дней 12 часов и 793 хелека (где 1080 хелеков составляют 1 час)

[6]. Вавилоняне не использовали единицу времени «час», вместо этого использовался двойной час длительностью 120 современных минут, а также время-градус длительностью 4 минуты и «третья часть» длительностью 3¹⁄₃ современных секунды (хелек в современном еврейском календаре)^[7], но эти меньшие единицы они уже не делили. Ни одна из шестидесятиричных частей дня никогда не использовалась как независимая единица времени.

В 1000 году персидский учёный Аль-Бируни определил времена полнолуний для конкретных недель через количество дней, часов, минут, секунд, третей и четвертей, отсчитывая от полудня воскресенья

[8]. В 1267 году английский философ и естествоиспытатель Роджер Бэкон установил временные промежутки между полнолуниями через количество часов, минут, секунд, третей и четвертей (horae, minuta, secunda, tertia, quarta) после полудня определённых дней^[9]. Терция — «треть», в значении «третье деление часа», — существует для обозначения ¹⁄₆₀ секунды и сейчас в некоторых языках, например польск. tercja и тур. salise, однако эта единица является малоиспользуемой и мелкие периоды времени выражаются десятичными долями секунды (тысячными, миллионными и т. д.).

Секунды во времена механических часов[править | править код]

Первым известным экземпляром пружинных часов с секундной стрелкой являются часы неизвестного мастера с изображением Орфея из коллекции Фремерсдорфа, датируемые между 1560 и 1570 годами

[10]^{:417–418[11]}. В 3-й четверти XVI века османский энциклопедист Такиюддин аш-Шами создал часы с отметками каждую 1/5 минуты^[12]. В 1579 году швейцарский часовщик и приборостроитель Йост Бюрги сконструировал часы для ландграфа Вильгельма IV, которые показывали секунды^[10]:105. В 1581 году датский учёный Тихо Браге переконструировал часы в своей обсерватории, которые показывали минуты, так, что они стали показывать и секунды. Однако механизм ещё не был достаточно проработан, чтобы отмерять секунды с приемлемой точностью. В 1587 году Тихо Браге выказывал досаду, что показания его четырёх часов разнятся друг от друга на ±4 секунды ^[10]:104. Отмерять секунды с достаточной точностью стало возможно с изобретением механических часов, позволяющих поддерживать «среднее время» (в противоположность «относительному времени», показываемому солнечными часами). В 1644 году французский математик Марен Мерсенн рассчитал, что маятник с длиной 39,1 дюйма (0,994 м) будет иметь период колебаний при стандартной гравитации точно 2 секунды — 1 секунду на движение вперёд и 1 секунду на движение обратно, — позволяя отсчитывать таким образом точные секунды.

В 1670 году лондонский часовщик Уильям Клемент добавил такой секундный маятник к исходным маятниковым часам Христиана Гюйгенса

[13]. С 1670 по 1680 год Клемент несколько раз усовершенствовал свой механизм, после чего представил сделанный им часовой шкаф общественности. В этих часах был применён механизм анкерного спуска с секундным маятником, показывающим секунды на небольшом вспомогательном циферблате. Этот механизм благодаря меньшему трению требовал меньших затрат энергии, чем ранее применявшаяся конструкция штыревого спускового механизма, и был достаточно точен, чтобы отмерять секунды как ¹⁄₆₀ минуты. В течение нескольких лет производство подобных часов было освоено английскими часовщиками, а затем распространилось и в другие страны. Таким образом, с этих пор появилась возможность с надлежащей точностью отмерять секунды.

Как единица времени, секунда (в том значении, что час делится на 60 два раза, первый раз получаются минуты, во второй раз (second) — секунды) вошла в английский язык в конце XVII века, примерно за сто лет перед тем, как она была с достаточной точностью измерена. Учёные и исследователи, писавшие на латыни, такие, например, как Роджер Бэкон, Тихо Браге и Иоганн Кеплер, использовали латинский термин secunda с тем же самым значением, начиная ещё с 1200-х годов.

В 1832 году немецкий математик Карл Фридрих Гаусс предложил использовать секунду в качестве базовой единицы времени в своей системе единиц, использующей наряду с секундой миллиметр и миллиграмм. Британская Научная Ассоциация (англ. British Science Association) в 1862 году постановила, что «Все учёные согласились употреблять секунду среднего солнечного времени как единицу времени» (англ. All men of science are agreed to use the second of mean solar time as the unit of time

[14]). Ассоциация разработала систему единиц измерения СГС (сантиметр-грамм-секунда) в 1874 году, которая в течение дальнейших семидесяти лет была постепенно заменена системой МКС (метр-килограмм-секунда). Обе этих системы использовали одну и ту же секунду в качестве базовой единицы. Система МКС получила международное применение в 1940-х годах, и определяла секунду как 1/86400 средних солнечных суток.

В 1956 году определение секунды было скорректировано и привязано к понятию «года» (период обращения Земли вокруг Солнца), взятого для определённой эпохи, поскольку к тому времени стало известно, что вращение Земли вокруг своей оси не может быть использовано в качестве достаточно надёжного основания, ввиду того, что это вращение замедляется, а также подвержено нерегулярным скачкам. Движение Земли было описано в таблицах Ньюкомба (англ. Newcomb’s Tables of the Sun) (1895), которые предлагали формулу для оценки движения Солнца на 1900-е годы, основываясь на астрономических наблюдениях, сделанных между 1750 и 1892 годами^[15].

Таким образом, секунда получила следующее определение:

«1/31 556 925,9747 доля тропического года для 0 января 1900 в 12 часов эфемеридного времени» (англ. the fraction 1/31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time.)[15]

Это определение было принято XI ГКМВ в 1960 году^[16], на этой же конференции была утверждена Международная система единиц (СИ) в целом.

«Тропический год» в определении 1960 года не был измерен, а был рассчитан по формуле, описывающей средний тропический год, который увеличивается линейно с течением времени. Это соответствовало шкале эфемеридного времени, принятой Международным астрономическим союзом в 1952 году^[17]. Это определение приводило в соответствие наблюдаемое расположение небесных тел с теорией Ньютона об их движении. На практике на протяжении почти всего двадцатого века использовались таблицы Ньюкомба (с 1900 по 1983 годы) и таблицы Эрнеста Уильяма Брауна (с 1923 по 1983 годы)^[15].

Таким образом, в 1960 году определение, данное в системе СИ, отменило всякую явную связь между секундой в научном понимании и продолжительностью дня, как его понимает большинство людей. С изобретением атомных часов в начале 1960-х, было решено использовать международное атомное время как основу для определения секунды взамен обращения Земли вокруг Солнца. Основной принцип квантовой механики — это неразличимость частиц. Таким образом, пока мы не учитываем внешних воздействий, строение всех атомов данного изотопа полностью идентично. Поэтому они представляют собой идеальные механизмы, которые воспроизводятся по желанию исследователя с точностью, ограниченной лишь степенью влияния внешних воздействий. Поэтому развитие часов — хранителей времени, привело к тому, что точность шкалы времени, реализуемой атомными часами, превысила точность астрономического определения, которое к тому же страдало от невозможности точной воспроизводимости эталона секунды. Поэтому было решено перейти к реализации секунды на основе атомных часов, взяв за основу какой-то переход в атомах, слабо подверженных внешнему воздействию. После обсуждения было решено взять атомы цезия, обладающие дополнительно тем достоинством, что цезий имеет только один стабильный изотоп, а новое определение секунды составить таким образом, чтобы она наиболее точно соответствовала применяемой эфемеридной секунде.

После нескольких лет работ, Льюис Эссен из Национальной физической лаборатории Великобритании (Теддингтон (англ. Teddington), Англия) и Уильям Марковиц (англ. William Markowitz) из Военно-морской обсерватории США определили связь перехода между двумя сверхтонкими уровнями основного состояния атома цезия-133 с эфемеридной секундой^[15][18]. Используя метод, основанный на получении сигналов от радиостанции WWV (англ. WWV (radio station))^[19], они определили орбитальное движение Луны вокруг Земли, из которого могло быть определено движение Солнца в понятиях времени, измеряемого атомными часами. Они нашли, что секунда эфемеридного времени имеет длительность в 9 192 631 770 ± 20 периодов излучения цезия^[18]. Как результат, в 1967 году XIII ГКМВ определила секунду атомного времени как:

FOCS 1, атомные часы в Швейцарии с погрешностью 10⁻¹⁵ , то есть не более секунды за 30 миллионов лет

Секунда есть время, равное 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133.[15]

Эта секунда, ссылающаяся на атомное время, была позднее проверена на соответствие с секундой эфемеридного времени, определяемой лунными наблюдениями и совпала с ней в пределах 1 к 10^10[20]. Несмотря на это, данная секунда уже была чуть короче чем прежняя секунда, определявшаяся по среднему солнечному времени^[21][22].

В течение 1970-х годов было обнаружено, что гравитационное замедление времени влияет на секунды, отсчитываемые атомными часами, в зависимости от их возвышения над поверхностью Земли. Универсальная секунда была получена путём корректировки значений каждых атомных часов приведением их к среднему уровню моря, удлиняя таким образом секунду примерно на 1⋅10⁻¹⁰. Эта корректировка была проведена в 1977 году и узаконена в 1980 году. В терминах теории относительности секунда Международного атомного времени определена как собственное время на вращающемся геоиде^[23].

Позднее, в 1997 году, на совещании Международного комитета мер и весов определение секунды было уточнено с добавлением следующего определения^[2]:

Это определение относится к атому цезия, не возмущённому внешними полями при температуре 0 К. (англ. This definition refers to a caesium atom at rest at a temperature of 0 K.)

Пересмотренное утверждение подразумевает, что идеальные атомные часы содержат один атом цезия в покое, испускающий волну постоянной частоты. На практике, однако, это определение означает, что высокоточные измерения секунды должны уточняться с учётом внешней температуры (излучение абсолютно чёрного тела) в которой работают атомные часы, и экстраполироваться к значению секунды при абсолютном нуле.

Изменения определений основных единиц СИ 2018—2019 годов не затронуло секунду с содержательной точки зрения, однако из стилистических соображений было принято формально новое определение^[24]:

Секунда, обозначение с, является единицей времени в СИ; её величина устанавливается фиксацией численного значения частоты сверхтонкого расщепления основного состояния атома цезия-133 ΔνCs{\displaystyle \Delta \nu _{\text{Cs}}} равным в точности 9 192 631 770, когда она выражена единицей СИ Гц, что эквивалентно с⁻¹.

1. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 103. — 240 с. — ISBN 5-7050-0118-5.
2. ↑ ^{1 2 3} Unit of time (second) (англ.). SI Brochure: The International System of Units (SI). BIPM. Дата обращения 9 октября 2015.
3. ↑ Положение о единицах величин, допускаемых к применению в Российской Федерации (неопр.) (недоступная ссылка). Федеральный информационный фонд по обеспечению единства измерений. Росстандарт. Дата обращения 28 февраля 2018. Архивировано 18 сентября 2017 года.
4. ↑ Секунда // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. — С. 484. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
5. ↑ Toomer, G. J. (англ.)русск.. Ptolemy’s Almagest (неопр.). — Princeton, New Jersey: Princeton University Press, 1998. — С. 6—7, 23, 211—216. — ISBN 978-0-691-00260-6.
6. ↑ O Neugebauer. A history of ancient mathematical astronomy (англ.). — Springer-Verlag, 1975. — ISBN 0-387-06995-X.
7. ↑ O Neugebauer. The astronomy of Maimonides and its sources (англ.) // Hebrew Union College Annual (англ.)русск. : journal. — 1949. — Vol. 22. — P. 325.
8. ↑ al-Biruni (англ.)русск.. The chronology of ancient nations: an English version of the Arabic text of the Athar-ul-Bakiya of Albiruni, or «Vestiges of the Past» (англ.). — 1879. — P. 147—149.
9. ↑ R Bacon. The Opus Majus of Roger Bacon (неопр.). — University of Pennsylvania Press (англ.)русск., 2000. — С. table facing page 231. — ISBN 978-1-85506-856-8.
10. ↑ ^{1 2 3} Landes, David S. Revolution in Time (неопр.). — Cambridge, Massachusetts: Harvard University Press, 1983. — ISBN 0-674-76802-7.
11. ↑ Willsberger, Johann. Clocks & watches (неопр.). — New York: Dial Press (англ.)русск., 1975. — ISBN 0-8037-4475-7. full page color photo: 4th caption page, 3rd photo thereafter (neither pages nor photos are numbered).
12. ↑ Taqi al-Din
13. ↑ Jessica Chappell. The Long Case Clock: The Science and Engineering that Goes Into a Grandfather Clock (англ.) // Illumin : journal. — 2001. — 1 October (vol. 1, no. 0). — P. 1.
14. ↑ Reports of the committee on electrical standards (неопр.). British Association for the Advancement of Science (1873).
15. ↑ ^{1 2 3 4 5} Leap Seconds (неопр.). Time Service Department, United States Naval Observatory. Дата обращения 31 декабря 2006. Архивировано 27 мая 2012 года.
16. ↑ Резолюция 9 XI Генеральной конференции по мерам и весам (1960)  (англ.)
17. ↑ Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac (prepared jointly by the Nautical Almanac Offices of the United Kingdom and the United States of America, HMSO, London, 1961), at Sect. 1C, p.9), stating that at a conference «in March 1950 to discuss the fundamental constants of astronomy … the recommendations with the most far-reaching consequences were those that defined ephemeris time and brought the lunar ephemeris into accordance with the solar ephemeris in terms of ephemeris time. These recommendations were addressed to the International Astronomical Union and were formally adopted by Commission 4 and the General Assembly of the Union in Rome in September 1952.»
18. ↑ ^{1 2} W Markowitz, RG Hall, L Essen, JVL Parry. Frequency of cesium in terms of ephemeris time (неопр.) // Physical Review Letters. — 1958. — Т. 1, № 3. — С. 105—107. — DOI:10.1103/PhysRevLett.1.105. — Bibcode: 1958PhRvL…1..105M.
19. ↑ S Leschiutta. The definition of the ‘atomic’ second (неопр.) // Metrologia^[en]. — 2005. — Т. 42, № 3. — С. S10—S19. — DOI:10.1088/0026-1394/42/3/S03. — Bibcode: 2005Metro..42S..10L.
20. ↑ W Markowitz (1988). «{{{title}}}» in IAU Sumposia #128. The Earth’s Rotation and Reference Frames for Geodesy and Geophysics: 413–418. 
21. ↑ DD McCarthy, C Hackman, R Nelson. The Physical Basis of the Leap Second (англ.) // The Astronomical Journal. — IOP Publishing, 2008. — Vol. 136, no. 5. — P. 1906—1908. — DOI:10.1088/0004-6256/136/5/1906. — Bibcode: 2008AJ….136.1906M.
22. ↑ In the late 1950s, the caesium standard was used to measure both the current mean length of the second of mean solar time (UT2) (9 192 631 830 cycles) and also the second of ephemeris time (ET) (9 192 631 770 ± 20 cycles), see L Essen. Time Scales (неопр.) // Metrologia^[en]. — 1968. — Т. 4, № 4. — С. 161—165. — DOI:10.1088/0026-1394/4/4/003. — Bibcode: 1968Metro…4..161E.. As noted in page 162, the 9 192 631 770 figure was chosen for the SI second. L Essen in the same 1968 article stated that this value «seemed reasonable in view of the variations in UT2».
23. ↑ See page 515 in RA Nelson; McCarthy, D D; Malys, S; Levine, J; Guinot, B; Fliegel, H F; Beard, R L; Bartholomew, T R. et al. The leap second: its history and possible future (неопр.) // Metrologia^[en]. — 2000. — Т. 38, № 6. — С. 509—529. — DOI:10.1088/0026-1394/38/6/6. — Bibcode: 2001Metro..38..509N.
24. ↑ SI base units (неопр.) (недоступная ссылка). BIPM. Дата обращения 22 июня 2019. Архивировано 23 декабря 2018 года.

• Время и частота (сборник статей), под редакцией Д. Джесперсена и других, перевод с английского, М., 1973.

запишите единицы измерения всех величин,входящих в формулу для определения периода колебаний математического маятника

а теперь на русском

<img src=»//otvet.imgsmail.ru/download/554726ba72e3cd45107ca402d826cc4d_i-173.jpg» > T — период (секунда) пи — математическая константа l — длина маятника (метр) g — ускорение свободного падения (м/с&#178;).

Т = секунды, пи = ничего, эль = метры (длина) джи = метры/секунду в квадрате (ускорение свободного падения)

ллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииилллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллллиииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииияяяяяяяяяяяяяяяяяяяяяяяяяяяя: ты

Единицы измерения периода и частоты

    Настоящие Правила распространяются на диапазон частот 100 кГц — 300 000 МГц. Единицей измерения частоты является герц (Гц)—частота переменного тока, меняющего направление со скоростью одного периода в секунду. В соответствии с международным регламентом радиосвязи действует следующая классификация радиочастот (табл. 1). [c.559]

    Единицей измерения частоты в системе СИ является герц (Гц). Его размер 1/с. Период Г измеряется в секундах (с). Длина [c.6]

    Модуль G (oj) определяется как отношение составляюще напряжения, находящейся в фазе с синусоидально изменяющейся деформацией, к величине этой деформации. При сравнении различных систем при одинаковых амплитудах деформации он является мерой энергии, запасаемой и освобождаемой за период колебаний в единице объема данного материала. Зависимость упругого модуля от угловой частоты в логарифмических координатах представлена на фиг. 14. Поскольку как G(i), так и G (o>) определяют запасенную упругую энергию, а динамические нз.мерения при частоте (О качественно эквивалентны измерениям неравновесных свойств при t = 1/о), 10 приведенные зависимости являются в первом приближении зеркальным отображением относительно оси. модуля соответствующих зависимостей, описывающих релаксацию напряжения. В частности, когда G(t) изменяется очень медленно, G(t) G (l//), так что значения Gg и Ge, характеризующие поведение материала при высоких и низких частотах, те же самые, что и значения, характеризующие поведение материала при малых и больших временах наблюдения соответственно. [c.46]

    В качестве основной единицы времени применяется продолжительность периода при частоте генератора. Выбор этой частоты ориентируется по скорости звука и по требуемой точности измерения времени прохождения или толщины стенки. [c.272]

    Максимальная быстрота записи спектра достигается при развертке какого-либо участка спектра на экране катодного осциллоскопа [105]. Для получения максимальной чувствительности напряжение развертки (варьируемое пилообразно при помощи реостата, приводимого мотором) должно изменяться сравнительно медленно [106]. Наилучшие результаты для очень слабых ионных токов получены при периоде развертки от 1 до 30 сек. Для изображения спектра масс в диапазоне до 200 массовых единиц быJ i использован осциллоскоп с большим периодом послесвечения при желании любая часть спектра могла быть получена в большем масштабе. Сири [1071 описал компактный 180-градусный масс-работающий на переменном токе, в котором. т1ине11но растущее напряжение развертки от О до 200 в при частоте 200 гц накладывалось на постоянное ускоряющее напряжение, что позволяло одновременно выбирать как область спектра, так и масштаб развертки. Выходное напряжение из специальных усилителем подавалось на осциллоскоп. Разрешающая спла была достаточна до массового числа 65. Достигнута чувствительность в 2-10″ а на 1 см отклонения. Нри измерениях высоты пиков (с использованием делителя напряжения для приведения больших пиков к стандартной высоте), по словам автора, достигалась точность от 2 до 5%. Такие приборы, не будучи в такой же степени точными, как дрз гие регистрирующие установки д.ля слабых токов, тем не менее имеют важное применение при изучении быстро проходящих эффектов (например, когда появление и исчезновение интересую-нюго исследователя компонента происходит очень быстро). Этим методом исследованы респираторные газы с целью наблюдения за быстро исчезающпми компонентами. [c.91]

---

Период колебаний — это… Что такое Период колебаний?

Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание (то есть возвращается в то же состояние^[1], в котором он находился в первоначальный момент, выбранный произвольно).

В принципе совпадает с математическим понятием периода функции, но имея ввиду под функцией зависимость физической величины, совершающей колебания, от времени.

Это понятие в таком виде применимо как к гармоническим, так и к ангармоническим строго периодическими колебаниям (а приближенно — с тем или иным успехом — и непериодическим колебаниям, по крайней мере к близким к периодичности).

В случае, когда речь идет о колебаниях гармонического осциллятора с затуханием, под периодом понимается период его осциллирующей составляющей (игнорируя затухание), который совпадает с удвоенным временным промежутком между ближайшими прохождениями колеблющейся величины через ноль. В принципе, это определение может быть с большей или меньшей точностью и пользой распространено в некотором обобщении и на затухающие колебания с другими свойствами.

Обозначения: обычное стандартное обозначение периода колебаний: (хотя могут применяться и другие, наиболее часто это , иногда и т. д.).

Единицы измерения: секунда

Период колебаний связан соотношением взаимной обратности с частотой:

Для волновых процессов период связан кроме того очевидным образом с длиной волны

где — скорость распространения волны (точнее^[2] — фазовая скорость).

В квантовой физике период колебаний прямо связан с энергией (поскольку в квантовой физике энергия объекта — например, частицы — есть частота^[3] колебаний его волновой функции).

Теоретическое нахождение периода колебаний той или иной физической системы сводится, как правило, к нахождению решения динамических уравнений (уравнения), описывающего эту систему. Для категории линейных систем (а приближенно — и для линеаризуемых систем в линейном приближении, которое зачастую является очень хорошим) существуют стандартные сравнительно простые математические методы, позволяющие это сделать (если известны сами физические уравнения, описывающие систему).

Для экспериментального определения периода используются часы, секундомеры, частотомеры, стробоскопы, строботахометры, осциллографы. Также применяются биения, метод гетеродинирования в разных видах, используется принцип резонанса. Для волн можно померить период косвенно — через длину волны, для чего применяются интерферометры, дифракционные решетки итп. Иногда требуются и изощренные методы, специально разработанные для конкретного трудного случая (трудность могут представлять как само измерение времени, особенно если речь идет о предельно малых или наоборот очень больших временах, так и трудности наблюдения колеблющейся величины).

Периоды колебаний в природе

Представление о периодах колебаний различных физических процессов дает статья Частотные интервалы (учитывая то, что период в секундах есть обратная величина частоты в герцах).

Некоторое представление о величинах периодов различных физических процессов также может дать шкала частот элетромагнитных колебаний (см. Электромагнитный спектр) .

Периоды колебаний слышимого человеком звука находятся в диапазоне

от 5·10^-5с до 0,2с

(четкие границы его несколько условны).

Периоды электромагнитных колебаний, соответствующих разным цветам видимого света — в диапазоне

от 1,1·10^-15с до 2,3·10^-15с.

Поскольку при экстремально больших и экстремально маленьких периодах колебаний методы измерения имеют тенденцию становятся всё более косвенными (вплоть до плавного перетекая в теоретические экстраполяции), трудно назвать четкую верхнюю и нижнюю границы для периода колебаний, измеренного непосредственно. Какую-то оценку для верхней границы может дать время существования современной науки (сотни лет), а для нижней — период колебаний волновой функции самой тяжелой из известных сейчас частиц ().

В любом случае границей снизу может служить планковское время, которое столь мало, что по современным представлениям не только вряд ли может быть вообще как-то физически измерено^[4], но и вряд ли в более-менее обозримом будущем представляется возможность приблизиться к измерению величин даже на много порядков меньших. а границей сверху — время существования Вселенной — более десяти миллиардов лет.

Периоды колебаний простейших физических систем

Пружинный маятник

Период колебаний пружинного маятника может быть вычислен по следующей формуле:

,

где  — масса груза,  — жёсткость пружины.

Математический маятник

Период колебаний математического маятника:

где  — длина подвеса (к примеру нити),  — ускорение свободного падения.

Период колебаний (на Земле) математического маятника длиной 1 метр с хорошей точностью^[5] равен 2 секундам.

Физический маятник

Период колебаний физического маятника:

где — момент инерции маятника относительно оси вращения, — масса маятника, — расстояние от оси вращения до центра масс.

Крутильный маятник

Период колебаний крутильного маятника:

где  — момент инерции тела, а  — вращательный коэффициент жёсткости маятника.

Электрический колебательный (LC) контур

Период колебаний электрического колебательного контура:

,

где — индуктивность катушки, — ёмкость конденсатора.

Эту формулу вывел в 1853 году английский физик У. Томсон.

Примечания

1. ↑ Состояние механической системы характеризуется положениями и скоростями всех ее материальных точек (строже говоря — координатами и скоростями, соответствующими всем степеням свободы данной системы), для немеханической — их формальными аналогами (которые также можно назвать координатами и скоростями в смысле абстрактного описания динамической системы — в количестве, также равном количеству ее степеней свободы).
2. ↑ Для монохроматических волн это уточнение самоочевидно, для близких к монохроматическим — интуитивно очевидно по аналогии со строго монохроматическими, для существенно немонохроматических — наиболее ясный случай сводится к тому, что фазовые скорости всех монохроматических компонент совпадают друг с другом, поэтому комментируемое утверждение ьакже верно.
3. ↑ С точностью до единиц измерения: в традиционных (обычных) системах физических единиц частота и энергия измеряются в разных единицах (поскольку до появления квантовой теории совпадение энергии и частоты было неизвестно, и, естественно, для каждой из величин была выбрана своя независимая единица измерения), поэтому при измерении их в обычных (разных) единицах, например, джоулях и герцах требуется переводной коэффициент (так называемая константа Планка). Однако можно выбрать систему единиц измерения так, чтобы в ней константа Планка стала равной 1 и пропала из формул; в такой системе единиц энергия любой частицы просто равна частоте колебания ее волновой функции (а значит обрата периоду этого колебания).
4. ↑ Имеется в виду, конечно же, невозможность экспериментального измерения времен конкретных процессов или периодов колебаний такого порядка, а не просто вычисление некоторого числа.
5. ↑ Лучше, чем 0,5%, если взять метрологическое или принятое техническое значение ускорения свободного падения; И с разбросом ~0.53% для максимального и минимального значений ускорения свободного падения, наблюдаемых на земле.

Ссылки

1.5.1 Гармонические колебания. Амплитуда и фаза колебаний

Видеоурок: Гармонические колебания — Физика в опытах и экспериментах

Лекция: Гармонические колебания. Амплитуда и фаза колебаний

Гармонические колебания

Во время колебаний все состояния системы повторяются с некоторой периодичностью. 

Если данную периодичность можно описать законами синуса или косинуса, то такие колебания называются гармоническими.

Уравнения гармонических колебаний имеют следующий вид:

Данная зависимость позволит определить положение тела или состояние системы относительно начального состояния в любой момент времени.

Характеристика гармонических колебаний

1. Амплитуда — максимальное отклонение от начального положения. Обозначается [Хмак] = 1м.

2. Период — ФВ, характеризующая время одного полного колебания. Основная единица измерений — секунда (с).

 

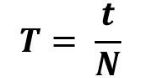
t — все время движения

N — количество колебаний

В СИ период колебаний выражается в секундах [T]=c

3.  Частота — ФВ, определяющая количество колебаний, совершенных в единицу времени. Основной единицей измерения являются Герцы (Гц).

v — частота — число колебаний за 1 сек.

t — все время движения

N — количество колебаний
[v] = [Гц]

Частота и период связаны друг с другом обратной зависимостью.

4. Фаза — ФВ, определяющая временные рамки, на протяжении которых рассматриваются колебания системы. В уравнении колебаний фаза — аргумент функции. Измеряется в радианах (рад). Начальная фаза — это положение переменных величин в начальный момент времени.

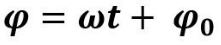
ф — фаза колебаний
w — циклическая частота

 

5. Циклическая частота — это количество колебаний тела за 2п секунд. Измеряется в рад/с. В уравнении колебаний находится в аргументе функции перед временем.

Находится по формуле:

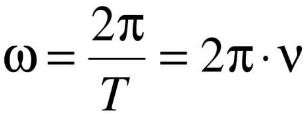
6. Скорость и ускорение колебаний. Так как скорость — первая производная от координаты, а ускорение — вторая производная, то, чтобы определить скорость и ускорение в любой момент времени следует воспользоваться следующей функцией:

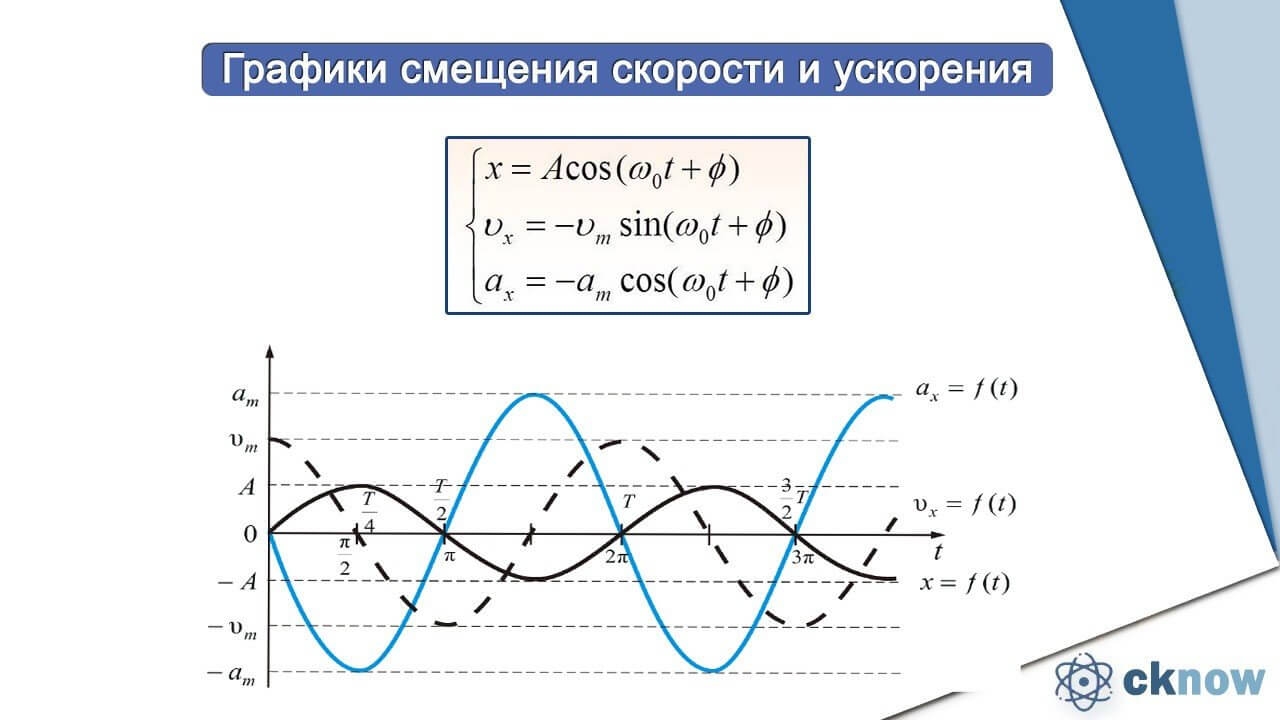
 7. Сила, приводящая к гармоническим колебаниям:

Превращение энергии гармонических колебаний

Во время совершения гармонических колебаний справедлив закон сохранения энергии.

Вся механическая энергия, сумма потенциальной и кинетической энергии, во время гармонических колебаний остается неизменной.

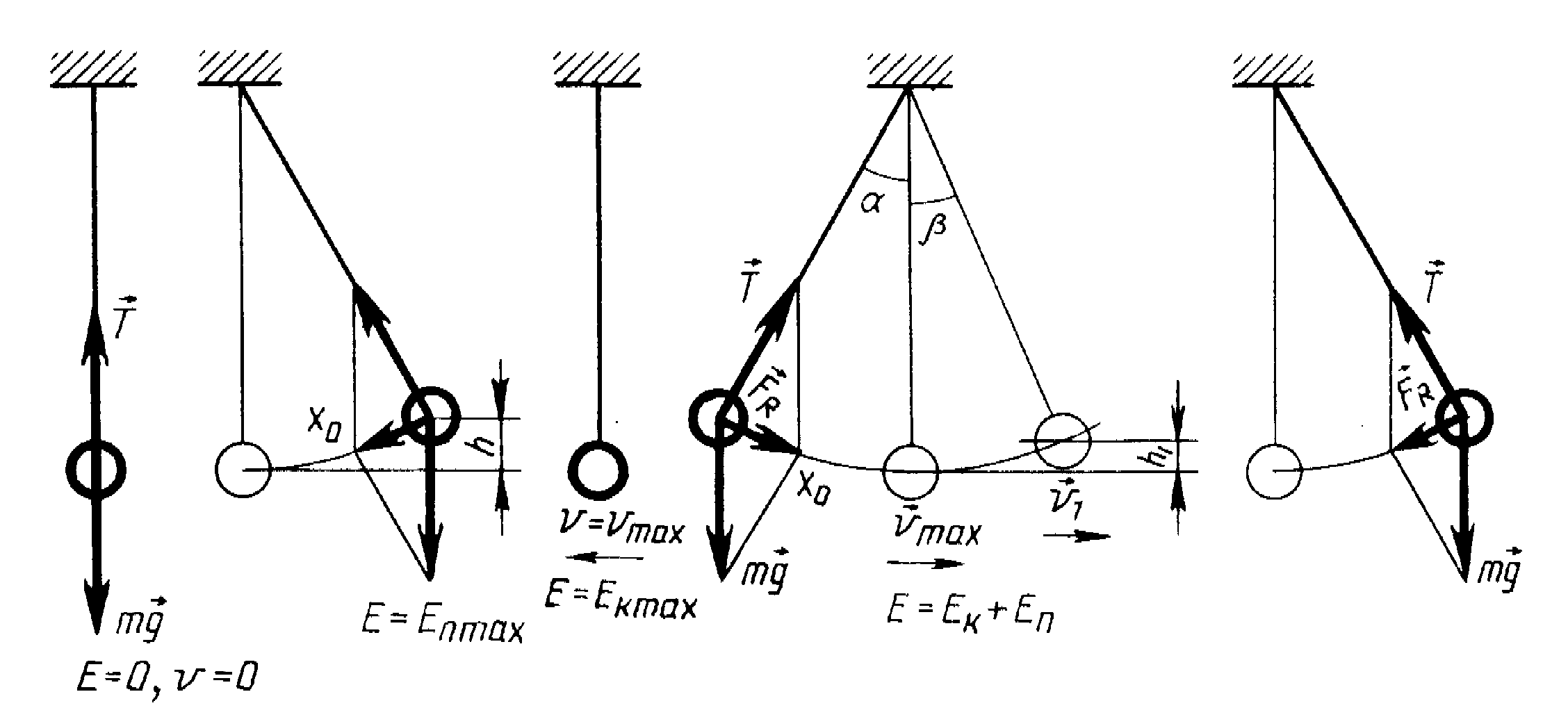
В самой нижней точке, в начальном положении математического маятника, кинетическая энергия достигает своего максимума, так как в этой точке значение скорости максимальное.

В точке, где маятник достигает максимальной амплитуды, тело достигает максимальное значение потенциальной энергии.

В промежуточных значениях механическая энергия состоит из суммы кинетической и потенциальной энергии.

Е = Ек + Еп = Ек.мах = Еп.мах.

Эти же правила справедливы и для пружинного маятника.

Древние единицы измерения — Википедия

Материал из Википедии — свободной энциклопедии

Сравнительная таблица единиц измерения массы Ближнего Востока[править | править код]

Меры длины[править | править код]

Название-перевод	Древняя Греция Древний Рим	Линейное значение в системе СИ (часто приблизительное)	Другие варианты линейных значений
«палец»
«1/12 целого»[2]		2,46 см = 4/3 дигита = 1/12 римского фута
«ладонь»	пальм большой (лат. palmus major)	1 палайста = 4 дактилям = ок. 7 см 7,39 см 22,18 см = 3 пальма
«ступня»	пес монеталис (лат. pes monetalis) пес натуралис (лат. pes naturalis) пес друзианус (лат. pes drusianus)	29,62 см пес = 1 римский фут = 12 унций 29,62 см 25,00 см 33,27 см	29,57 см; 29,6352 см
«локоть»	пигон (др.-греч. πῠγών) самосский локоть	38,53 см = 20 дактилей 51,80 см = 28 дактилей 44,4 см = 6 пальмов
		0,74 м = 10 пальмов
«двойной шаг»		1,48 м 1,48 м = 5 пес (римских футов)
			1,776 м; 1,851 м; 2,34 м
		2,963 м = 10 пес (римских футов)
	аттический олимпийский эллинистический	177,6 м 192,27 м 185 м
«день пути»	итер педестр (лат. iter pedestre)
«тысяча шагов»	милле пасс (лат. mille passus)

Меры площади[править | править код]

Меры объёма[править | править код]

• Котила — античная единица измерения ёмкости, равная 0,275 литра.
• Арбата — античная единица измерения объёма, равная 55,08 л.
• Метрет — античная единица измерения ёмкости, равная 38,88 литра.
• Хеник — античная единица измерения ёмкости, равная 1,08 литра.
• Хус — античная единица измерения ёмкости, равная 3,24 литра.

Меры объёма сыпучих тел[править | править код]

Меры объёма жидких тел[править | править код]

Меры объёма жидких и сыпучих тел[править | править код]

Меры массы[править | править код]

Греция, архаический период[править | править код]

Греция и Рим, классический период[править | править код]

Меры длины[править | править код]

Египетская система (с 5 по 1 вв. включительно до н. э.):

• Атур обычный = 3 милям = 5,235 км.
• Атур царский = 1 1/2 парасангам = 10,47 км.
• Парасанг = 1 1/9 шема = 6,98 км.
• Шем = 1 1/5 атура обычного = 6,282 км.
• Миля = 10 стадиям = 1,745 км.
• Стадий = 3 1/3 хета = 174,5 м. (употребляется также стадий = 209,4 м.)
• Хет (сенус) = 25 оргиям = 52,35 м.
• Канна = 5 шагам = 11 2/3 зерецам = 4,07 м.
• Оргия = 1 1/3 ксилона = 2,094 м.
• Ксилон = 3 локтям царским = 1,57 м.
• Шаг = 2 1/3 зерецам = 81,44 см.
• Локоть царский = 1 1/6 локтя малого = 1 1/5 пигона = 52,35 см.
• Локоть малый = 44,83 см.
• Пигон = 1 1/4 зерца = 43,625 см.
• Зерец (фут) = 1 1/3 спитама = 2 дихасам = 34,9 см.
• Спитам = 1 1/2 дихаса = 26,175 см.
• Дихас = 2 шеспам = 17,45 см.
• Шесп = 4 тебам = 8,725 см.
• Теб (палец) = 2,18 см.

Меры веса[править | править код]

• 1 кантар = 139,78 кг.
• 1 киккар = 42,5 кг.
• 1 ойпе = 4 гекатам = 8,56 кг.
• 1 кедет = ⅓ унции = 9,096 г.

Меры объёма[править | править код]

• 1 лог = ¹/₄ кава = 0,54 л
• 1 бат = 72 лога = 38,9 л
• 1 кав = 4 лога = ¹/₆ сеа = 2,16 л
• 1 сеа = 6 кав = 12,6 л
• 1 кор = 180 кав = 389 л
• 1 эйфа = 24 883 см³
• 1 омер = ¹/₁₀ эйфы

Меры длины[править | править код]

• 1 эцба (палец) = 2 см
• 1 тефах (ладонь) = 4 эцба = ¹/₆ локтя = 8 см
• 1 ама (локоть) = 6 тефах = 48 см
• 1 зерет = ¹/₂ ама = 24 см

Меры объёма[править | править код]

Ка — древняя вавилонская единица измерения объёма жидкостей, равная объёму куба, длина ребра которого составляет ширину ладони. Вес воды объёмом 1 ка составляет 1 большую мину.

5 ка = 1 шиклу

100 ка = 1 имеру

300 ка = 1 гур

Меры площади[править | править код]

Меры длины[править | править код]

• Gyllenbok J. Encyclopaedia of Historical Metrology, Weights, and Measures. Springer International Publishing, 2018. T. 1 ISBN 3319575988, 9783319575988
• Hultsch F. Griechische und Römische Metrologie. Berlin: Weidmannsche Buchhandlung, 1882 [1]
• Mensura // Реальный словарь классических древностей / авт.-сост. Ф. Любкер ; Под редакцией членов Общества классической филологии и педагогики Ф. Гельбке, Л. Георгиевского, Ф. Зелинского, В. Канского, М. Куторги и П. Никитина. — СПб., 1885. — С. 858—859.
• Меры и вес // Еврейская энциклопедия Брокгауза и Ефрона. — СПб., 1908—1913.
• Меры // Словарь античности = Lexikon Der Antike (неопр.). — М.: СП «Внешсигма», 1992. — С. 346. — ISBN 5-86290-008-X.
• М. И. Грамм. Занимательная энциклопедия мер, единиц и денег. — Челябинск: «Урал Л.Т.Д.», 2000. — ISBN 5-8029-0098-9.
• Белобров В. А. Метрология Древней Месопотамии.
• Белобров В. А. Византийская система мер длины.
• Белобров В. А. Метрология Страны ариев.
• Белобров В. А. Была ли Земля плоской?