Передаточная функция фильтра: Понятие передаточных функций фильтров нижних частот — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Понятие передаточных функций фильтров нижних частот

Добавлено 21 декабря 2019 в 07:01

Данная статья дает некоторое представление о взаимосвязи между передаточной функцией в s-области и поведением фильтра нижних частот первого порядка.

В последнее время я довольно много пишу на тему фильтров, и хотя я сосредоточился на практических соображениях, я чувствую необходимость объяснить некоторые важные теоретические концепции в пользу тех, кто хотел бы более подробно понять и проанализировать поведение аналоговых фильтров. В настоящее время каждый имеет доступ к программным инструментам, которые делают сложное проектирование фильтров относительно безболезненным, но я не думаю, что было бы разумно полностью игнорировать математические основы просто потому, что они не являются строго необходимыми для выполнения многих реальных задач проектирования.

s-область

Отклик фильтра может быть выражен передаточной функцией в s-области; переменная s появляется из преобразования Лапласа и представляет комплексную частоту. Например:

\[T(s) = \frac{K}{1+ \left( \frac{s}{\omega_0} \right) }\]

Эта передаточная функция является математическим описанием поведения фильтра нижних частот первого порядка в частотной области. Выражение в s-области эффективно передает общие характеристики, и если мы хотим вычислить конкретную информацию об амплитуде и фазе, всё, что нам нужно сделать, это заменить s на jω, а затем вычислить выражение при заданной угловой частоте.

Вам может быть интересно, откуда берутся K и ω₀ – вы, вероятно, никогда не видели принципиальной схемы, в которой значения компонентов были выражены в значениях K и ω₀. Идея в том, что K и ω₀ подобны частям шаблона, и в следующем разделе мы рассмотрим взаимосвязь между этим шаблоном и принципиальной схемой.

Анализ схем в s-области

RC фильтр нижних частот является частотно-зависимым делителем напряжения. При анализе в s-области импеданс резистора равен R, а импеданс конденсатора равен \(\frac{1}{sC}\).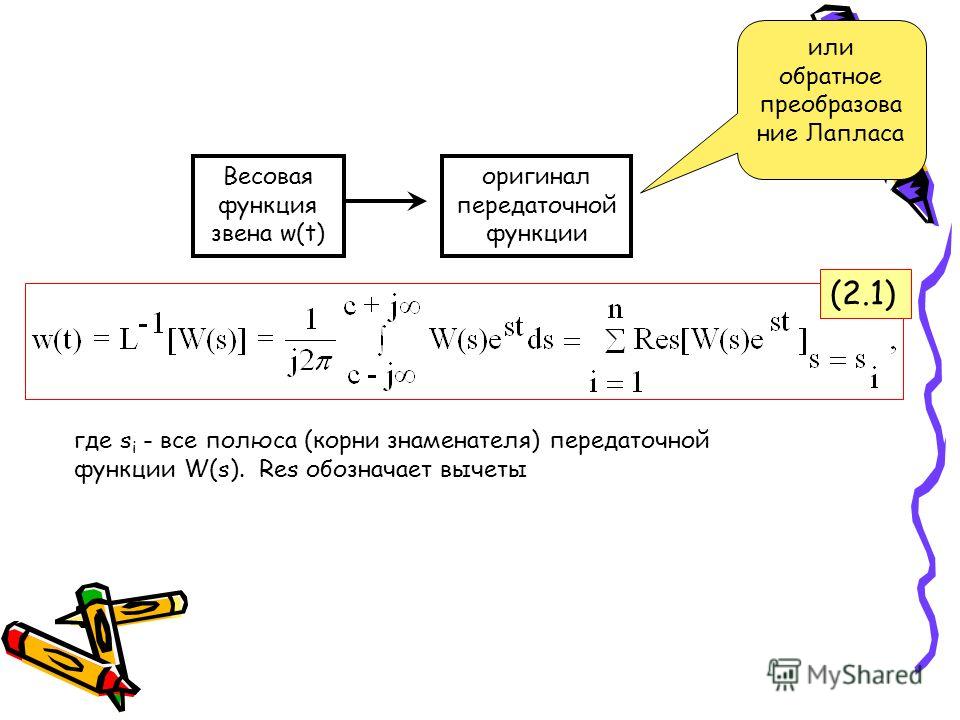

Рисунок 1 – RC фильтр нижних частот является частотно-зависимым делителем напряжения

\[\frac{V_{вых}}{V_{вх}} = {\frac{1}{sC} \over \frac{1}{sC} + R} = \frac{1}{1+sRC}\]

Если мы сравним это выражение с нормированной передаточной функцией, то увидим, что K = 1 и \(\omega_0 = \frac{1}{RC}\). Удобство использования нормированной формы становится понятным, как только вы узнаете, что представляют собой K и ω₀: K – это коэффициент усиления схемы при постоянном напряжении, а ω₀ – это частота среза. Таким образом, сравнивая передаточную функцию схемы с нормированной передаточной функцией, вы можете сразу же сформулировать выражения для двух определяющих характеристик фильтра нижних частот первого порядка, а именно для коэффициента усиления при постоянном напряжении и частоты среза.

Другой нормированной формой передаточной функции фильтра нижних частот первого порядка является следующее:

\[T(s)=\frac{a_0}{s+\omega_0}\]

Мы можем встроить передаточную функцию схемы в этот шаблон, если разделим числитель и знаменатель на RC:

\[T(s)= \frac{1}{1+sRC} \rightarrow { \frac{1}{RC} \over s + \frac{1}{RC} } \]

Таким образом, \(a_0=\frac{1}{RC}\), и \(\omega_0 = \frac{1}{RC}\). Эта форма напрямую не дает нам коэффициент усиления по постоянному напряжению, но если мы вычислим нормированное выражение для s = 0, то получим

\[T(s=0) = \frac{a_0}{\omega_0}\]

Это означает, что коэффициент усиления по постоянному напряжению нашего RC-фильтра равен

\[\left( \frac{1}{RC} \right) / \left( \frac{1}{RC} \right) = 1\]

А коэффициент усиления по постоянному напряжению, равный единице, – это именно то, что мы ожидаем от пассивного фильтра нижних частот.

Понятие частоты среза

Мы видели, что ω₀ в стандартной передаточной функции представляет частоту среза, но каково математическое основание этого факта?

Во-первых, давайте, преобразуем стандартную передаточную функцию в s-области в эквивалентную передаточную функцию jω.

\[T(s) = \frac{K}{1 + \frac{s}{\omega_0}} \rightarrow T(j\omega) = \frac{K}{1 + j\frac{\omega}{\omega_0}}\]

Теперь давайте вычислим выражение при частоте среза.

\[T(j\omega = j\omega_0) = \frac{K}{1 + j\frac{\omega_0}{\omega_0}}= \frac{K}{1+j}\]

Знаменатель является комплексным числом, поэтому модуль будет равен

\[|T(j\omega = j\omega_0)|= \frac{K}{\sqrt{1^2+1^2}} = \frac{K}{\sqrt{2}}\]

Поскольку K – это коэффициент усиления по постоянному напряжению, очень низкочастотный входной сигнал с амплитудой в один вольт приведет к выходному сигналу с амплитудой в K вольт. Если входная частота увеличивается до ω₀ радиан в секунду, выходная амплитуда будет равна \(\frac{K}{\sqrt{2}}\). Коэффициент \(\frac{1}{\sqrt{2}}\) соответствует –3 дБ, и, как вы, вероятно, знаете, другое название частоты среза – это частота –3 дБ.

Рисунок 2 – Амплитудно-частотная характеристика пассивного фильтра нижних частот первого порядка (амплитуда откладывается в дБ в зависимости от частоты в логарифмическом масштабе)

Этот простой анализ передаточной функции ясно продемонстрировал, что частота среза – это просто частота, на которой амплитудно-частотная характеристика фильтра снижается на 3 дБ относительно выходного уровня на очень низкой частоте.

Частота среза и сдвиг фазы

Частота среза фильтра нижних частот имеет особое значение также в отношении фазо-частотной характеристики схемы. Если мы напишем комплексное число в форме x + jy, мы рассчитаем фазу следующим образом:

\[\theta=\text{arctg}\left( \frac{y}{x} \right)\]

Таким образом, общая фазо-частотная характеристика нашего RC фильтра низких частот следующей:

\[\theta(\omega)= -\text{arctg}\left( \frac{\frac{\omega}{\omega_0}}{1} \right)= -\text{arctg}\left( \frac{\omega}{\omega_0} \right)\]

Если мы вычислим это выражение при ω = ω₀, сдвиг фазы будет равен

\[-\text{arctg}\left( \frac{\omega_0}{\omega_0} \right) = -\text{arctg}\left( 1 \right) = -45^\circ\]

Рисунок 3 – Фазо-частотная характеристика пассивного фильтра нижних частот первого порядка (фаза откладывается в зависимости от частоты в логарифмическом масштабе)

Максимальный сдвиг фазы, создаваемый фильтром нижних частот первого порядка, составляет 90°, поэтому этот анализ говорит нам, что частота среза является «центром» фазо-частотной характеристики схемы – другими словами, это частота, на которой фильтр создает половину своего максимального сдвига фазы.

Заключение

Я надеюсь, что вам понравилось это краткое введение в концепции s-области и анализ передаточных функций. Поначалу математические основы схем аналоговых фильтров могут быть немного пугающими, но я думаю, что стоит потратить некоторое время на то, чтобы получить некоторое представление об этих темах. Я продолжу исследовать эту тему в будущих статьях.

Оригинал статьи:

Robert Keim. Understanding Low-Pass Filter Transfer Functions

s-областьАЧХ (амплитудно-частотная характеристика)Комплексные числаПередаточная функцияПреобразование ЛапласаСдвиг фазыФНЧ (фильтр нижних частот)ФЧХ (фазо-частотная характеристика)Частота среза

Передаточные функции аналоговых фильтров.

Оглавление

1. Назначение, классификация и принцип работы пассивных фильтров. Передаточные функции аналоговых фильтров. Описание RC-фильтров. Сравнение пассивных фильтров с другими видами фильтров. 3

2. Назначение, классификация и принцип работы пассивных фильтров. Передаточные функции аналоговых фильтров. Описание LC-фильтров. Сравнение пассивных фильтров с другими видами фильтров. 12

3. Описание и классификация активных фильтров. Фильтр нижних частот. 22

4. Описание и классификация активных фильтров. Фильтр верхних частот. 27

5. Описание и классификация активных фильтров. Полосовые фильтры. 31

6. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Генератор на основе моста Вина. 35

7. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Генератор на основе сдвига фаз с одним ОУ. 48

8. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Буферированный генератор на основе сдвига фаз. 58

9. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Генератор Буббы. 68

10. Генераторы гармонических сигналов. Теоретические сведения. Принцип работы. Квадратурный генератор. 78

6 – 10 вопросы. Заключение по всем генераторам. 88

11. Модуляция и разновидности модулированных сигналов. Общие сведения о модуляции. Широтно-импульсная модуляция. 89

12. Инверторы. Общие сведения, принцип работы, схемотехника. Автономный однофазный инвертор. Полумостовая и мостовая топологии. 94

13. Инверторы. Общие сведения, принцип работы, схемотехника. Автономный трехфазный инвертор. Способы управления. 102

14. Принципы автоматического управления. Общие сведения о структурах систем управления. Регуляторы. 111

15. Электрический ток в вакууме. Вакуумный диод. Вакуумный триод. 119

16. Ламповый генератор с независимым возбуждением. 126

17. Ламповый генератор с самовозбуждением. 140

Назначение, классификация и принцип работы пассивных фильтров. Передаточные функции аналоговых фильтров.
Описание RC-фильтров. Сравнение пассивных фильтров с другими видами фильтров.
Назначение, классификация и принцип работы пассивных фильтров.

Электронный фильтр – это частотно-избирательное устройство, которое служит для передачи (пропускания) сигналов в заданном диапазоне частот (полосе пропускания) и подавления сигналов в других диапазонах частот (полоса задерживания). Фильтры широко используются в системах связи, в схемах защиты электронных систем от помех. Основное назначение фильтра состоит в том, чтобы исключить прохождение сигналов определенного диапазона частот и в то же время обеспечить передачу сигналов другого диапазона частот.

Функциональная схема трехфазного тиристорного выпрямителя показана ниже, одним из составляющих данной схемы является фильтр.

Различают аналоговые фильтры, в которых обрабатываемый сигнал имеет аналоговую форму, и цифровые фильтры, предназначенные для обработки цифровых сигналов. Рассмотрим аналоговые фильтры.

Фильтры делятся на активные и пассивные. Активные фильтры представляют собой частотно-избирательный усилительный каскад. К пассивным фильтрам относятся

RC- и LC-фильтры. Фильтры также можно классифицировать исходя из диапазона частот, которые они пропускают или подавляют.

Существуют четыре типа фильтров:

Фильтр нижних частот, который пропускает все сигналы с частотой ниже некоторого заданного значения и подавляет сигналы более высоких частот.
Фильтр верхних частот, который пропускает все сигналы с частотой выше некоторого заданного значения и подавляет сигналы более низких частот.
Полосно-заграждающий фильтр (режекторный), который используется для подавления сигналов определенного диапазона частот, тогда как сигналы с частотами выше и ниже этого диапазона проходят беспрепятственно.
Полосно-пропускающий фильтр (полосовой), который пропускает сигналы заданной полосы частот и препятствует прохождению сигналов любых других частот.

Амплитудно-частотные характеристики данных четырех типов фильтров представлены выше, где:

а) фильтр нижних частот;

б) фильтр верхних частот;

в) полосно-пропускающий фильтр;

г) полосно-заграждающий фильтр.

Частотой среза фильтра называют частоту, при которой амплитуда выходного сигнала составляет 1/√2 (≈0,71) от амплитуды входного сигнала или -3 дБ (по логарифмической шкале).

Аналоговый фильтр представляет линейную частотно-селективную цепь, поведение которой определяется операторной передаточной функцией H(p). Операторная передаточная функция – отношение изображений по Лапласу выходного и входного сигналов (см. выражение (1)), где U₁(p) и U₂(p) – изображения напряжений на входе и выходе фильтра, р – комплексная частотная переменная.

Известно, что передаточная функция линейной цепи является дробно-рациональной, т. е. представляет отношение двух полиномов от комплексной переменной

р (см. выражение (2)).

Полагая в (2) p = jω, получаем комплексную передаточную функцию, определяющую реакцию фильтра на гармоническое воздействие (см. выражение (3)).

Представим передаточную функцию в показательной форме (см. выражение (4)).

Модуль комплексной передаточной функции – амплитудно-частотная характеристика, а ее аргумент – фазочастотная характеристика.

Операторная передаточная функция H(p). Числитель и знаменатель H(p) можно записать в виде произведения сомножителей первого порядка в соответствии с выражением (5).

Корни полинома числителя называют нулями, а корни полинома знаменателя – полюсами передаточной функции. Расположение полюсов и нулей

H(p) на комплексной плоскости определяет поведение цепи как в частотной, так и во временной областях. В частности, от расположения полюсов и нулей зависит форма частотных характеристик фильтра.

Как правило, нули передачи частотно-селективных фильтров расположены на мнимой оси, включая начало координат и бесконечность.

В простейших случаях нули передачи расположены в начале координат (ФВЧ) или в бесконечности (ФНЧ). Такие фильтры имеют меньшую селективность, чем фильтры с нулями передачи на мнимой оси. Однако уменьшение селективности окупается значительным упрощением структуры цепи, реализующей передаточную функцию с нулями в начале координат или бесконечности.

В общем случае для получения передаточной функции, обеспечивающей заданную форму частотных характеристик, используют методы оптимизации. На практике часто используют типовые передаточные функции, имеющие аналитическое решение. Перечислим наиболее распространенные передаточные функции, аппроксимирующие АЧХ фильтра нижних частот:

Фильтр Баттерворта с максимально плоской амплитудно-частотной характеристикой.
Фильтр Чебышева с равноволновой характеристикой в полосе пропускания.
Инверсный фильтр Чебышева с равноволновой характеристикой в полосе задерживания.
Эллиптический фильтр, имеющий равноволновые характеристики в полосе пропускания и полосе задерживания.
Фильтр Бесселя с фазочастотной характеристикой, близкой к линейной.

Порядок передаточной функции n выбирают из условия обеспечения требуемого затухания в полосе задерживания на частоте ω > ω_с:

Схема фильтра верхних частот, реализованная на основе сопротивления R и емкости C, и его амплитудно-частотная характеристика показаны ниже.

В этой схеме входное напряжение прикладывается и к резистору, и к конденсатору. Выходное же напряжение снимается с сопротивления. При уменьшении частоты сигнала возрастает реактивное сопротивление конденсатора, а, следовательно, и полное сопротивление цепи. Поскольку входное напряжение остается постоянным, то ток, протекающий через цепь, уменьшается.

Таким образом, снижается и ток через активное сопротивление, что приводит к уменьшению падения напряжения на нем.

Фильтр характеризуется затуханием, выраженным в децибелах, которое он обеспечивает на заданной частоте. RC-фильтры рассчитываются таким образом, чтобы на выбранной частоте среза коэффициент передачи снижался приблизительно на 3 дБ (т.е. составлял 0,707 входного значения сигнала). Частота среза фильтра по уровню -3 дБ определяется по формуле (6).

Фильтр нижних частот имеет аналогичную структуру, только емкость и сопротивление меняются местами (см. ниже).

В этой цепи входное напряжение также прикладывается и к резистору, и к конденсатору, но выходное напряжение снимается с конденсатора. При увеличении частоты сигнала реактивное сопротивление конденсатора, а, следовательно, и полное сопротивление уменьшаются. Однако, поскольку это полное сопротивление состоит из реактивного и фиксированного активного сопротивлений, его значение уменьшается не так быстро, как реактивное сопротивление.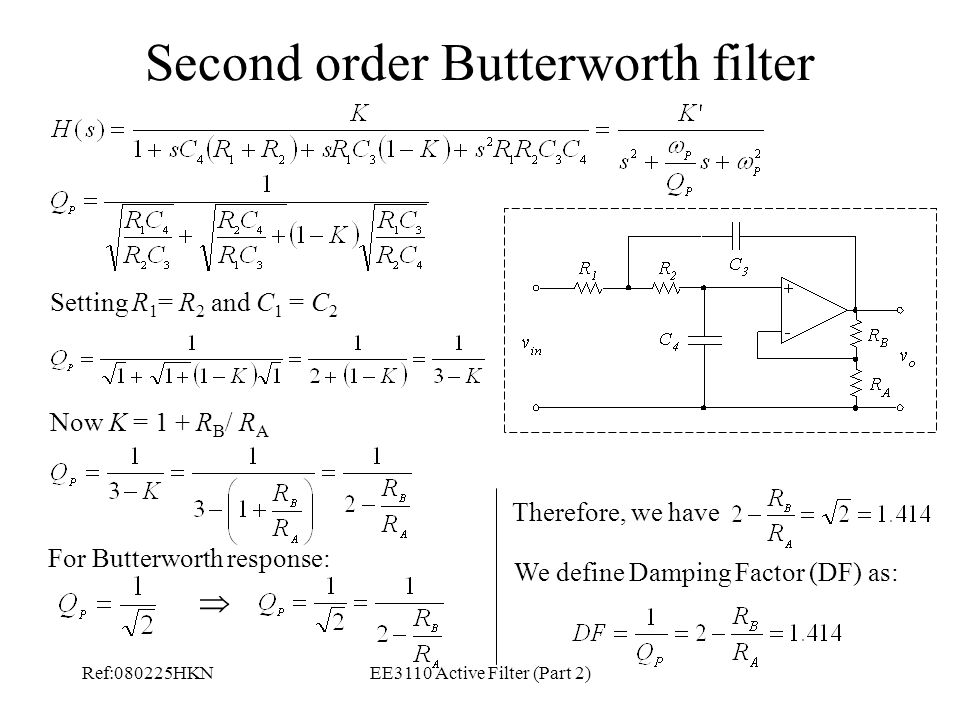 Следовательно, при увеличении частоты снижение реактивного сопротивления (относительно полного сопротивления) приводит к уменьшению выходного напряжения. Частота среза этого фильтра по уровню -3 дБ также определяется по формуле (6).

Рассмотренные выше фильтры представляют собой RC-цепи, которые характеризуются тремя параметрами, а именно: активным, реактивным и полным сопротивлениями. Обеспечиваемая этими RC-фильтрами величина затухания зависит от отношения активного или реактивного сопротивления к полному сопротивлению.

П ри расчете любого RC-фильтра можно задать номинал либо резистора, либо конденсатора и вычислить значение другого элемента фильтра на заданной частоте среза. При практических расчетах обычно задают номинал сопротивления, поскольку он выбирается на основании других требований. Например, сопротивление фильтра является его выходным или входным полным сопротивлением.

Соединяя фильтры верхних и нижних частот, можно создать полосовой RC-фильтр. Схема и амплитудно-частотная характеристика приведены выше.

На схеме R₁ – полное входное сопротивление; R₂ – полное выходное сопротивление, а частоты низкочастотного и высокочастотного срезов определяются по формулам (7) и (8).

Следует отметить, что значение верхней частоты среза (f_с2) должно быть, по крайней мере, в 10 раз больше нижней частоты среза (f_с1), поскольку только в этом случае полосно-пропускающий фильтр будет работать достаточно эффективно.

Заграждающий RC-фильтр состоит из одного звена ФНЧ и одного звена ФВЧ, включенных параллельно.

Одиночный RC-фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области довольно часто используют многозвенные фильтры (см. ниже).

Частота среза многозвенного фильтра определяется по формуле ВЧ, НЧ RC-фильтра. Добавление каждого звена приводит к увеличению затухания на заданной частоте среза примерно на 6 дБ.

На рисунке а) – многозвенный ФВЧ, б) – многозвенный ФНЧ.

Что такое фильтр баттерворта, расчет и схема. Расчёт фильтра с характеристикой Баттерворта Передаточная функция фильтра баттерворта

Передаточная функция фильтра нижних частот Баттерворта n -го порядка характеризуется выражением:

Амплитудно-частотная характеристика фильтра Баттерворта обладает следующими свойствами:

1) При любом порядке n значение АЧХ

2) на частоте среза щ=щ с

АЧХ ФНЧ монотонно убывает с ростом частоты. По этой причине фильтры Баттерворта называют фильтрами с максимально плоскими характеристиками. На рисунке 3 показаны графики амплитудно-частотных характеристик ФНЧ Баттерворта 1-5 порядков. Очевидно, что чем больше порядок фильтра, тем точнее аппроксимируется АЧХ идеального фильтра нижних частот.

Рисунок 3 — АЧХ для фильтра Баттерворта нижних частот порядка от 1 до 5

На рисунке 4 представлена схемная реализация ФВЧ Баттерворта.

Рисунок 4 — ФВЧ-II Баттерворта

Достоинством фильтра Баттерворта является максимально гладкая АЧХ на частотах полосы пропускания и ее снижение практически до нуля на частотах полосы подавления. Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.

Однако в сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления.

Квадрат модуля передаточной функции фильтра Чебышева определяется выражением:

где — полином Чебышева. Модуль передаточной функции фильтра Чебышева равен единице на тех частотах, где обращается в нуль.

Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.

Различают фильтры Чебышева I и II родов.

Фильтр Чебышева I рода. Это более часто встречающаяся модификация фильтров Чебышева. В полосе пропускания такого фильтра видны пульсации, амплитуда которых определяется показателем пульсации е. В случае аналогового электронного фильтра Чебышева его порядок равен числу реактивных компонентов, использованных при его реализации. Более крутой спад характеристики может быть получен если допустить пульсации не только в полосе пропускания, но и в полосе подавления, добавив в передаточную функцию фильтра нулей на мнимой оси jщ в комплексной плоскости. Это, однако, приведёт к меньшему эффективному подавлению в полосе подавления. Полученный фильтр является эллиптическим фильтром, также известным как фильтр Кауэра.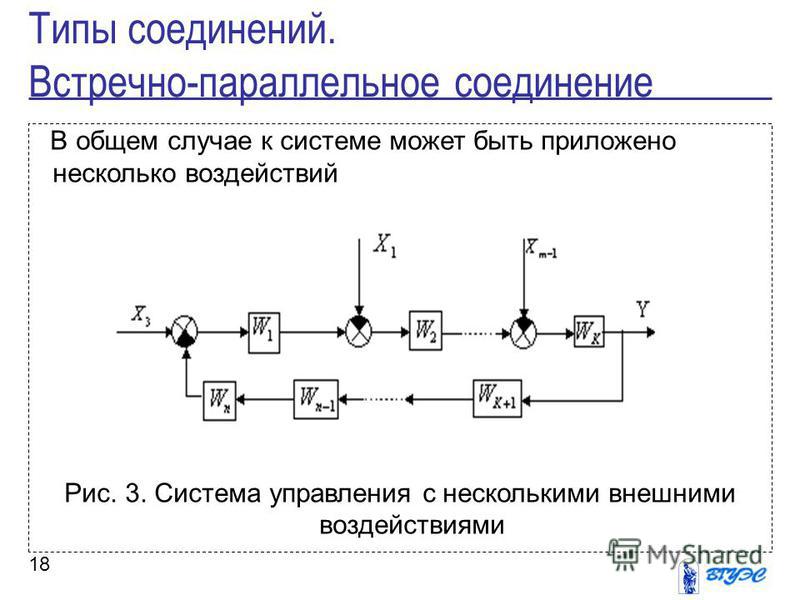

АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка представлена на рисунке 5.

Рисунок 5 — АЧХ для фильтра Чебышева нижних частот I рода четвёртого порядка

Фильтр Чебышева II рода (инверсный фильтр Чебышева) используется реже, чем фильтр Чебышева I рода ввиду менее крутого спада амплитудной характеристики, что приводит к увеличению числа компонентов. У него отсутствуют пульсации в полосе пропускания, однако присутствуют в полосе подавления.

АЧХ для фильтра Чебышева нижних частот II рода четвёртого порядка представлена на рисунке 6.

Рисунок 6 — АЧХ для фильтра Чебышева нижних частот II рода

На рисунке 7 представлены схемные реализации ФВЧ Чебышева I и II порядка.

Рисунок 7 — ФВЧ Чебышева: а) I порядка; б) II порядка

Свойства частотных характеристик фильтров Чебышева:

1) В полосе пропускания АЧХ имеет равноволновой характер. На интервале (-1?щ?1) имеется n точек, в которых функция достигает максимального значения, равного 1, или минимального значения, равного. Если n нечетно, если n четно;

2) значение АЧХ фильтра Чебышева на частоте среза равно

3) При функция монотонно убывает и стремится к нулю.

4) Параметр е определяет неравномерность АЧХ фильтра Чебышева в полосе пропускания:

Сравнение АЧХ фильтров Баттерворта и Чебышева показывает, что фильтр Чебышева обеспечивает большее ослабление в полосе пропускания, чем фильтр Баттерворта такого же порядка. Недостаток фильтров Чебышева заключается в том, что их фазочастотные характеристики в полосе пропускания значительно отличаются от линейных.

Для фильтров Баттерворта и Чебышева имеются подробные таблицы, в которых приведены координаты полюсов и коэффициенты передаточных функций различных порядков.

Харьковский национальный университет радиоэлектроники

Кафедра РЭУ

КУРСОВАЯ РАБОТА

РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

ФИЛЬТР ВЕРХНИХ ЧАСТОТ БАТТЕРВОРТА

Харьков 2008 г.

Техническое задание

Спроектировать фильтр верхних частот (ФВЧ) с аппроксимацией амплитудно-частотной характеристики (АЧХ) полиномом Баттерворта, определить необходимый порядок фильтра, если заданы параметры АЧХ (рис. 1): К 0 =26дБ

U m Вх =250мВ

где — максимальный коэффициент передачи фильтра;

Минимальный коэффициент передачи в полосе пропускания;

Максимальный коэффициент передачи фильтра в полосе задержки;

Частота среза;

Частота, начиная с которой коэффициент передачи фильтра меньше .

Рисунок 1 – Шаблон ФВЧ Баттерворта.

Обеспечить небольшую чувствительность к отклонениям номиналов элементов.

РЕФЕРАТ

Расчётно-пояснительная записка: 26 с., 11 рис., 6 табл.

Цель работы: синтез схемы активного RC-фильтра верхних частот и расчёт её компонентов.

Метод исследования: аппроксимация АЧХ фильтра полиномом Баттерворта.

Аппроксимированная передаточная функция реализована с помощью активного фильтра. Фильтр построен каскадным соединением независимых звеньев. В активных фильтрах использованы неинвертирующие усилители с конечным усилением, которые реализованы с помощью операционных усилителей.

Результаты работы могут использоваться для синтеза фильтров радиотехнической и бытовой аппаратуры.

Вступление

1. Обзор аналогичных схем

3.1 Осуществление нормировки ФВЧ

3.2 Определение необходимого порядка фильтра

3.3 Определение полинома Баттерворта

3.4 Обратный переход от нормированного к проектируемому ФВЧ

3.5Переход от передаточной функции к схеме

3.6Переход от передаточной функции к схеме

4. Расчёт элементов схемы

5. Методика настройки регулировки разработанного фильтра

Вступление

До недавнего времени результаты сопоставления цифровых и аналоговых устройств в радиоаппаратуре и технических средствах электросвязи не могли не вызывать чувства неудовлетворённости. Цифровые узлы, реализуемые с широким использованием интегральных микросхем (ИМС), выгодно отличались своей конструктивно-технологической завершённостью. Иначе обстояло дело с узлами аналоговой обработки сигналов, которые, например, в телекоммуникациях составляли от 40 до 60% объёма и массы аппаратуры связи. Громоздкие, содержащие большое число ненадёжных и трудоёмких намоточных элементов, они выглядели на фоне больших интегральных схем столь удручающе, что породили у ряда специалистов мнение о необходимости “тотальной цифризации” радиоэлектронной аппаратуры.

Последнее, однако, как любая другая крайность, не привело (да и не могло привести) к результатам, адекватным ожидаемым. Истина, как и во всех других случаях, оказалась где-то посередине. В ряде случаев более эффективной оказывается аппаратура, построенная на функциональных аналоговых узлах, элементный базис которых адекватен возможностям и ограничениям микроэлектроники.

Адекватность в данном случае может быть обеспечена переходом к активным RC-цепям, в элементный базис которых не входят катушки индуктивностей и трансформаторы, принципиально не реализуемые средствами микроэлектроники.

Обоснованность такого перехода определяется в настоящее время, с одной стороны, достижениями теории активных RC-цепей, а с другой – успехами микроэлектроники, предоставившей в распоряжение разработчиков высококачественные линейные интегральные схемы, в том числе и интегральные операционные усилители (ОУ). Эти ОУ, обладая большими функциональными возможностями, существенно обогатили аналоговую схемотехнику. Особенно ярко это проявилось в схемотехнику активных фильтров.

До 60-х годов для реализации фильтров применялись, в основном пассивные элементы, т.е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и ОУ (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приёмниках, традиционные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.

Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах – активных RC-фильтрах.

1. Обзор аналогичных схем

Фильтры – это частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определённых полосах частот.

Фильтры можно классифицировать по их частотным характеристикам:

1. Фильтры нижних частот (ФНЧ) – пропускают все колебания с частотами не выше некоторой частоты среза и постоянную составляющую.

2. Фильтры верхних частот (ФНЧ) – пропускают все колебания не ниже некоторой частоты среза.

3. Полосовые фильтры (ПФ) – пропускают колебания в определённой полосе частот, которая определяется по некоторому уровню частотной характеристики.

4. Полосно-подавляющие фильтры (ППФ) — задерживают колебания в определённой полосе частот, которая определяется по некоторому уровню частотной характеристики.

5. Режекторные фильтры (РФ) – вид ППФ, имеющий узкую полосу задержки и называемый ещё фильтром-пробкой.

6. Фазовые фильтры (ФФ) – имеют постоянный в идеальном случае коэффициент передачи на всех частотах и предназначен для изменения фазы входных сигналов (в частности для временной задержки сигналов).

Рисунок 1.1 – Основные типы фильтров

С помощью активных RC-фильтров нельзя получить идеальные формы частотных характеристик в виде показанных на рис.1.1 прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью её реализации. Это называется “проблемой аппроксимации“. Во многих случаях требования к качеству фильтрации позволяют обойтись простейшими фильтрами первого и второго порядков. Некоторые схемы таких фильтров представлены ниже. Проектирование фильтра в этом случае сводиться к выбору схемы с наиболее подходящей конфигурацией и последующему расчёту значений номиналов элементов для конкретных частот.

Однако бывают ситуации, когда требования к фильтрации могут оказаться гораздо более жёсткими, и могут потребоваться схемы более высоких порядков, чем первый и второй. Проектирование фильтров высоких порядков является более сложной задачей, чему посвящена данная курсовая работа.

Ниже приведены некоторые основные схемы первого второго порядков с описанием достоинств и недостатков каждой из них.

1. ФНЧ-I и ФВЧ-Iна основе не инвертирующего усилителя.

Рисунок 1. 2 – Фильтры на основе неинвертирующего усилителя:

а) ФНЧ-I, б) ФВЧ-I.

К достоинствам схем фильтров можно отнести главным образом простоту реализации и настройки, недостатки – малая крутизна частотных характеристик, малоустойчивы к самовозбуждению.

2. ФНЧ-IIи ФВЧ-IIс много петлевой обратной связью.

Рисунок 1.3 – Фильтры с многопетлевой обратной связью:

а) ФНЧ-II, б) ФВЧ-II.

Таблица 2.1 – Достоинства и недостатки ФНЧ-II с много петлевой обратной связью

Таблица 2.2 – Достоинства и недостатки ФВЧ-II с много петлевой обратной связью

2. ФНЧ-IIи ФВЧ-IIСаллена-Кея.

Рисунок 1.4 – Фильтры Саллена-Кея:

а) ФНЧ-II, б) ФВЧ-II

Таблица 2.3 – Достоинства и недостатки ФНЧ-II Саллена-Кея.

Таблица 2.4 – Достоинства и недостатки ФВЧ-II Саллена-Кея.

3. ФНЧ-IIи ФВЧ-IIна основе конверторов полного сопротивления.

Рисунок 1.5 – Схема ФНЧ IIна основе конверторов полного сопротивления:

а) ФНЧ-II, б) ФВЧ-II.

Таблица 2.3 – Достоинства и недостатки ФНЧ-II и ФВЧ-II на основе конверторов полного сопротивления.

2. Выбор и обоснование схемы фильтра

Методы проектирования фильтров отличаются по конструктивным особенностям. Проектирования пассивных RC-фильтров большей частью определяется структурной схемой

Активные фильтры АФ математически описывают передаточною функцией. Типам АЧХ предоставлен названия полиномов передаточных функций. Каждый тип АЧХ реализуют определенным количеством полюсов (RC-цепей) в соответствии с заданной крутизной спада АЧХ. Известнейшими, есть аппроксимации Баттерворта, Бесселя, Чебышева.

Фильтр Баттерворта имеет максимально плоскую АЧХ, в полосе подавления наклон переходного участка равняется 6 дБ/окт на полюс, но он имеет нелинейную ФЧХ, входное импульсное напряжение служит причиной осцилляции на выходе, потому фильтр используется для непрерывных сигналов.

Фильтр Бесселя имеет линейную ФЧХ, небольшую крутизну переходного участка АЧХ. Сигналы всех частот в полосе пропускания имеют одинаковые временные задержки, поэтому он пригодный для фильтрации прямоугольных импульсов, которые надо посылать без искажений.

Фильтр Чебышева — фильтр равных волн в СП, масс плоскую форму за ее пределами, пригодный для непрерывных сигналов в случаях, капы надо иметь крутой склон АЧХ за частотой среза.

Простые схемы фильтров первого и второго порядков применяются лишь, когда нет жестких требований к качеству фильтрации.

Каскадное соединение звеньев фильтра осуществляют, если нужен порядок фильтра выше второго, то есть когда надо сформировать передаточную характеристику с очень большим послаблением сигналов в полосе подавленный и большой крутизной затухания АЧХ Результирующую передаточную функцию получают, перемножая частичные коэффициенты передачи

Цепи строят по одинаковой схеме, но номиналы элементов

R, С разные, и зависят от частот среза фильтра и его ланок: f зр.ф /f зр.л

Однако следует помнить, что каскадное соединение, например, двух фильтров Баттерворта второго порядка не дает фильтр Баттерворта четвертого порядка, так как результирующий фильтр будет иметь другую частоту среза и другую АЧХ. Поэтому необходимо выбирать коэффициенты одиночных звеньев таким образом, чтобы следующее произведение передаточных функций отвечал выбранному типу аппроксимации. Поэтому проектирования АФ вызовет затруднения со стороны получения идеальной характеристики и сложности ее реализации.

Благодаря очень большим входным и маленьким выходным сопротивлениям каждого звена обеспечивается отсутствие искажений заданной передаточной функции и возможность независимого регулирования каждого звена. Независимость звеньев дает возможность широко регулировать свойства каждого звена изменением его параметров.

Принципиально не имеет значения, в котором порядке размещенные частичные фильтры, так как результирующая передаточная функция всегда будет одинаковой. Тем не менее, существуют разнообразные практические рекомендации относительно порядка соединения частичных фильтров. Например, для защиты от самовозбуждения следует организовать последовательность звеньев в порядке возрастания частичной предельной частоты. Другой порядок может привести к самовозбуждению второго звена в области выброса его АЧХ, поскольку фильтры с высшими предельными частотами обычно имеют большую добротность в области граничной частоты.

Другой критерий, связан с требованиями минимизации, уровня шумов на входе. В этом случае последовательность звеньев обратная, так как фильтр с минимальной предельной частотой ослабляет уровень шума, который возникает от предыдущих звеньев каскада.

3. Топологическая модель фильтра и передаточная функция по напряжению

3.1 В данном пункте будет выбран порядок ФВЧ Баттерворта и определён вид его передаточной функции согласно заданным в ТЗ параметрам:

Рисунок 2.1 – Шаблон ФВЧ согласно техническому заданию.

Топологическая модель фильтра.

3.2 Осуществление нормировки ФВЧ

За коэффициентом передачи:

К max =K 0 -K п =26-23=3дБ

К min =К 0 -К з =26-(-5)=31дБ

По частоте:

3.3 Определение необходимого порядка фильтра

Округляем nдо ближайшего целого значения: n = 3.

Таким образом, для удовлетворения требований, заданных шаблоном, необходим фильтр третьего порядка.

3.4 Определение полинома Баттерворта

Согласно таблице нормированных передаточных функций фильтров Баттерворта находим полином Баттерворта третьего порядка:

3.5 Обратный переход от нормированного к проектируемому ФВЧ

Проведём обратный переход от нормированного ФВЧ к проектируемому ФВЧ.

· масштабирование по коэффициенту передачи:

· масштабирование по частоте:

Производим замену

В результате масштабирования получаем передаточную функцию W(p) в виде:

Рисунок 2.2 – АЧХ проектируемого ФВЧ Баттерворта.

3.6 Переход от передаточной функции к схеме

Представим передаточную функцию проектируемого ФВЧ третьего порядка в виде произведения передаточных функций двух активных ФВЧ первого и второго порядка, т.е. в виде

и ,

где – коэффициент передачи на бесконечно высокой частоте;

– частота полюса;

– добротность фильтра (отношение коэффициента усиления на частоте к коэффициенту усиления в полосе пропускания).

Этот переход справедлив, так как общий порядок последовательно соединенных активных фильтров будет равен сумме порядков отдельно взятых фильтров (1 + 2 = 3).

Общий коэффициент передачи фильтра (K0 = 19.952) будет определяться произведением коэффициентов передачи отдельных фильтров (K1, K2).

Разложив передаточную функцию на квадратичные сомножители, получим:

В этом выражении

. (2.5.1)

Нетрудно заметить, что частоты полюсов и добротности передаточных функций отличаются.

Для первой передаточной функции:

частота полюса ;

добротность ФВЧ-Iпостоянна и равна .

Для второй передаточной функции:

частота полюса ;

добротность .

Для того чтобы к операционным усилителям в каждом каскаде предъявлялись примерно равные требования по частотным свойствам, целесообразно общий коэффициент передачи всего фильтра распределить между каждым из каскадов обратно пропорционально добротности соответствующих каскадов, а характерную частоту (частоту единичного усиления ОУ) выбрать максимальную среди всех каскадов.

Так как в данном случае ФВЧ состоит из двух каскадов, то указанное выше условие можно записать в виде:

. (2.5.2)

Подставляя выражение (2.5.2) в (2.5.1), получаем:

;

Проверим правильность расчёта коэффициентов передачи. Общий коэффициент передачи фильтра в разах будет определяться произведением коэффициентов отдельных фильтров. Переведём коэффициент издБ в разы:

Т.е. расчёты верны.

Запишем передаточную характеристику с учётом расcчитанных выше величин ():

3.7 Выбор схемы активного ФВЧ третьего порядка

Так как согласно заданию необходимо обеспечить небольшую чувствительность к отклонениям элементов, то выберем в качестве первого каскада ФВЧ-Iна основе не инвертирующего усилителя (рис.1.2,б), а второго – ФВЧ-IIна основе конверторов полного сопротивления (КПС), схема которого приведена на рис.1.5,б.

Для ФВЧ-I на основе не инвертирующего усилителя зависимость параметров фильтра от номиналов элементов схемы таково:

Для ФВЧ-IIна основе КПС параметры фильтра зависят от номиналов элементов следующим образом:

; (3. 4)

;

4. Расчёт элементов схемы

· Расчёт первого каскада (ФВЧ I) с параметрами

Выберем R1 исходя из требований к величине входного сопротивления (): R1 = 200 кОм. Тогда из (3.2) следует, что

Выберем R2 = 10 кОм, тогда из (3.1) следует, что

· Расчёт второго каскада (ФВЧ II) с параметрами

. .

Тогда (коэффициент в числителе подобран так, чтобы получить номинал ёмкости из стандартного ряда Е24). Итак С2 = 4.3 нФ.

Из (3.3) следует, что

Из (3.1) следует, что

Пусть . Итак С1 = 36 нФ.

Таблица 4.1– Номиналы элементов фильтра

Из данных таблицы 4.1мы можем приступить к моделированию схемы фильтра.

Это мы делаем при помощи специальной программы Workbench5.0.

Схема и результаты моделирования приведены на рис.4.1. и рис.4.2,а-б.

Рисунок 4.1 – Схема ФВЧ Баттерворта третьего порядка.

Рисунок 4.2– Результирующие АЧХ (а) и ФЧХ (б) фильтра.

5. Методика настройки и регулирования разработанного фильтра

Это очень просто сделать для резисторов, если их брать с допуском не более 1%, и тяжелее для емкостей конденсаторов, потому что допуски у них в районе 5-20%. Из-за этого сначала рассчитывается емкость, а потом рассчитывается сопротивление резисторов.

5.1 Выбор типа конденсаторов

· Выберем низкочастотный тип конденсаторов в силу их меньшей стоимости.

· Необходимы небольшие габариты и масса конденсаторов

· Выбирать конденсаторы нужно с как можно меньшими потерями (с маленьким тангенсом угла диэлектрических потерь).

Некоторые параметры группы К10-17 (взяты из ):

Размеры, мм.

Масса, г0,5…2

Допускаемое отклонение ёмкости, %

Тангенс угла потерь0,0015

Сопротивление изоляции, МОм1000

Диапазон рабочих температур, – 60…+125

5.2 Выбор типа резисторов

· Для схемы проектируемого фильтра, чтобы обеспечить низкую температурную зависимость, необходимо выбирать резисторы с минимальным ТКС.

· Выбираемые резисторы должны обладать минимальными собственными ёмкостью и индуктивностью, поэтому выберем непроволочный тип резисторов.

· Однако у непроволочных резисторов более высокий уровень токовых шумов, поэтому необходимо учесть и параметр уровня собственных шумов резисторов.

Прецизионные резисторы типа С2-29В удовлетворяют заданным требованиям (параметры взяты из ):

Номинальная мощность, Вт 0.125;

Диапазон номинальных сопротивлений, Ом ;

ТКС (в интервале температур ),

Уровень собственных шумов, мкВ/В1…5

Предельное рабочее напряжение постоянного

и переменного тока, В200

5.3 Выбор типа операционных усилителей

· Главный критерий при выборе ОУ – это его частотные свойства, так как реальные ОУ имеют конечную полосу пропускания. Для того чтобы частотные свойства ОУ не влияли на характеристику проектируемого фильтра, необходимо чтоб для частоты единичного усиления ОУ в i-том каскаде выполнялось соотношение:

Для первого каскада: .

Для второго каскада: .

Выбирая большее значение, получаем, что частота единичного усиления ОУ не должна быть менее 100 Кгц.

· Коэффициент усиления ОУ должен быть достаточно большим.

· Напряжение питания ОУ должно соответствовать напряжению источников питания, если таковое известно. В противном случае, желательно выбрать ОУ с широким диапазоном напряжений питания.

· При выборе ОУ для многокаскадного ФВЧ лучше выбрать ОУ с возможно меньшим напряжения смещения.

Согласно справочнику выберем ОУ типа 140УД6А, конструктивно оформленный в корпусе типа 301.8-2. ОУ этого типа являются ОУ общего назначения с внутренней частотной коррекцией и защитой выхода при коротких замыканиях нагрузки и имеют следующие параметры:

Напряжение питания , В

Ток потребления , мА

Напряжение смещения, мВ

Коэффициент усиления ОУ по напряжению

Частота единичного усиления , МГц1

5.4 Методика настройки и регулировки разработанного фильтра

Настройка данного фильтра не представляет большой сложности. Параметры частотной характеристики “подгоняются” с помощью резисторов, как первого, так и второго каскадов независимо друг от друга, при чём настройка одного параметра фильтра не влияет на значения других параметров.

Настройка проводится следующим образом:

1. Коэффициент усиления устанавливается резисторами R2 первого и R5 второго каскада.

2. Частота полюса первого каскада настраивается резистором R1, частота полюса второго каскада – резистором R4.

3. Добротность второго каскада регулируется резистором R8, а добротность первого каскада не регулируется (постоянна при любых номиналах элементов).

Итогом данной курсовой работы является получение и расчёт схемы заданного фильтра. ФВЧ с аппроксимацией частотных характеристик полиномом Баттерворта с параметрами, приведенными в техническом задании, имеет третий порядок и представляет собой двокаскадно — соединённых ФВЧ первого порядка (на основе не инвертирующего усилителя) и второго порядка (на основе конвертеров полного сопротивления). Схема содержит три операционных усилителя, восемь резисторов и три ёмкости. В данной схеме используется два источника питания по 15 В каждый.

Выбор схемы для каждого каскада общего фильтра проводился на основании технического задания (обеспечить малую чувствительность к отклонениям номиналов элементов) с учётом достоинств и недостатков каждого типа схем фильтров, используемых в качестве каскадов общего фильтра.

Номиналы элементов схемы подбирались и рассчитывались таким образом, чтобы максимально приблизить их к стандартному номинальному ряду Е24, а также, чтобы получить при этом как можно большее входное сопротивление каждого каскада фильтра.

После моделирования схемы фильтра с помощью пакета ElectronicsWorkbench5.0 (рис.5.1) были получены частотные характеристики (рис.5.2), имеющие требуемые параметры, приведённые в техническом задании (рис.2.2).

К достоинствам данной схемы можно отнести простоту настройки всех параметров фильтра, независимую настройку каждого каскада отдельно, малую чувствительность к отклонениям от номиналов элементов.

Недостатками является использование в схеме фильтра трёх операционных усилителей и соответственно его повышенная стоимость, а также относительно невысокое входное сопротивление (порядка 50 кОм).

Список использованной литературы

1. Зеленин А.Н., Костромицкий А.И., Бондарь Д.В. – Активные фильтры на операционных усилителях. – Х.: Телетех, 2001. изд. второе, исправ. и доп. – 150 с.: ил.

2. Резисторы, конденсаторы, трансформаторы, дроссели, коммутационные устройства РЭА: Справ./Н.Н. Акимов, Е.П. Ващуков, В.А. Прохоренко, Ю.П. Ходоренок. – Мн.: Беларусь, 2004. – 591 с.:ил.

Аналоговые интегральные схемы: Справ./А.Л. Булычёв, В.И. Галкин, 382 с.: В.А. Прохоренко. – 2-е изд., перераб. и доп. – Мн.: Беларусь, 1993. – черт.

АЧХ фильтра Баттерворта описывается уравнением

Особенности фильтра Баттерворта: нелинейная ФЧХ; частота среза не зависящая от числа полюсов; колебательный характер переходной характеристики при ступенчатом входном сигнале. С увеличением порядка фильтра колебательный характер усиливается.

Фильтр Чебышева

АЧХ фильтра Чебышева описывается уравнением

где T n 2 (ω/ω н ) – полином Чебышева n –го порядка.

Полином Чебышева вычисляется по рекуррентной формуле

Особенности фильтра Чебышева: повышенная неравномерность ФЧХ; волнообразная характеристика в полосе пропускания.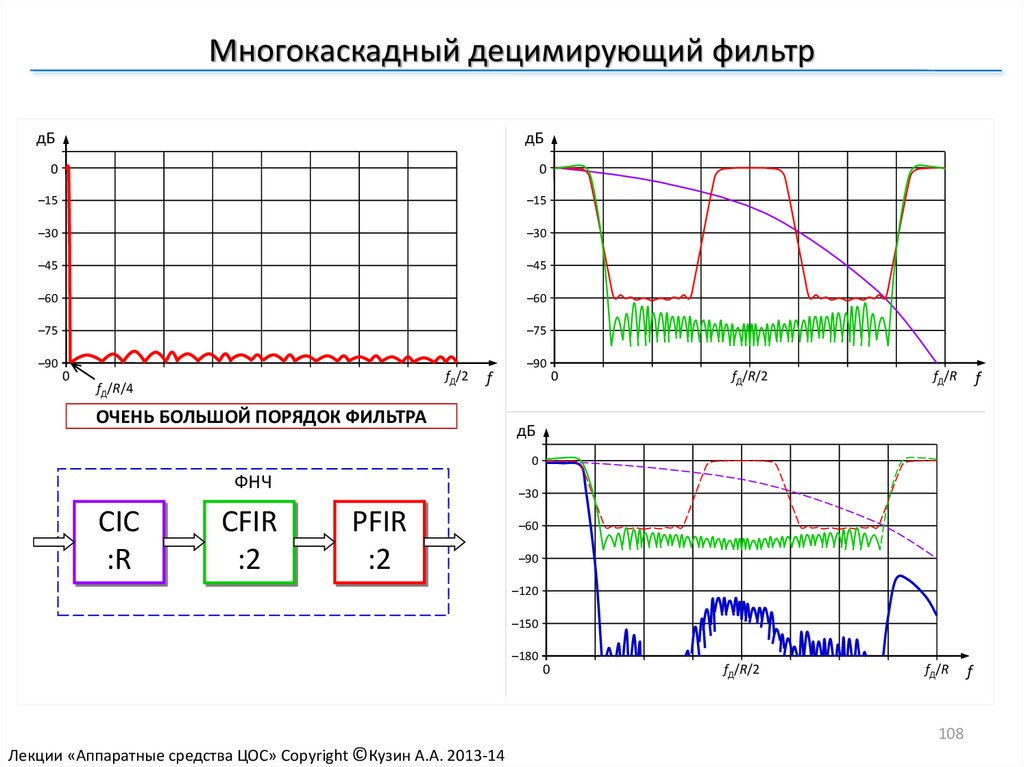 Чем выше коэффициент неравномерности АЧХ фильтра в полосе пропускания, тем более резкий спад в переходной области при одном и том же порядке. Колебания переходного процесса при ступенчатом входном сигнале сильнее, чем у фильтра Баттерворта. Добротность полюсов фильтра Чебышева выше, чем у фильтра Баттерворта.

Фильтр Бесселя

АЧХ фильтра Бесселя описывается уравнением

где
;B n 2 (ω/ω cp з ) – полином Бесселя n -го порядка.

Полином Бесселя вычисляется по рекуррентной формуле

Особенности фильтра Бесселя: достаточно равномерные АЧХ и ФЧХ, аппроксимируемые функцией Гаусса; фазовый сдвиг фильтра пропорционален частоте, т.е. фильтр обладает частотно-независимым групповым временем задержки. Частота среза изменяется при изменении количества полюсов фильтра. Спад АЧХ фильтра обычно более пологий, чем у Баттерворта и Чебышева. Особенно хорошо этот фильтр подходит для импульсных цепей и фазочувствительной обработки сигнала.

Фильтр Кауэра (эллиптический фильтр)

Общий вид передаточной функции фильтра Кауэра

Особенности фильтра Кауэра: неравномерная АЧХ в полосе пропускания и в полосе задерживания; самый резкий спад АЧХ из всех приведенных фильтров; реализует требуемые передаточные функции при меньшем порядке фильтра, чем при использовании фильтров других типов.

Определение порядка фильтра

Требуемый порядок фильтра определяется по приведенным ниже формулам и округляется в сторону ближайшего целого значения. Порядк фильтра Баттерворта

Порядка фильтра Чебышева

Для фильтра Бесселя не существует формулы расчета порядка, вместо этого приводятся таблицы соответствия порядка фильтра минимально необходимым на заданной частоте отклонению времени задержки от единичной величины и уровню потерь в дБ).

При расчете порядка фильтра Бесселя задаются следующие параметры:

Допустимое процентное отклонение группового времени задержки на заданной частоте ω ω cp з ;

Может быть задан уровень ослабления коэффициента передачи фильтра в дБ на частоте ω , нормированной относительно ω cp з .

На основании этих данных определяется требуемый порядок фильтра Бесселя.

Схемы каскадов фнч 1–го и 2–го порядка

На рис. 12.4, 12.5 приведены типовые схемы каскадов ФНЧ.

а ) б )

Рис. 12.4. Каскады ФНЧ Баттерворта, Чебышева и Бесселя: а – 1–го порядка; б – 2–го порядка

а ) б )

Рис. 12.5. Каскады ФНЧ Кауэра: а – 1–го порядка; б – 2–го порядка

Общий вид передаточных функций ФНЧ Баттерворта, Чебышева и Бесселя 1–го и 2–го порядка

,
.

Общий вид передаточных функций ФНЧ Кауэра 1–го и 2–го порядка

,
.

Ключевым отличием фильтра Кауэра 2–го порядка от заграждающего фильтра является то, что в передаточной функции фильтра Кауэра отношение частот Ω s ≠ 1.

Методика расчета ФНЧ Баттерворта, Чебышева и Бесселя

Данная методика построена на основе коэффициентов, приведенных в таблицах и справедлива для фильтров Баттерворта, Чебышева и Бесселя. Методика расчета фильтров Кауэра приводится отдельно. Расчет ФНЧ Баттерворта, Чебышева и Бесселя начинается с определения их порядка. Для всех фильтров задаются параметры минимального и максимального ослабления и частота среза. Для фильтров Чебышева дополнительно определяется коэффициент неравномерности АЧХ в полосе пропускания, а для фильтров Бесселя – групповое время задержки. Далее определяется передаточная функция фильтра, которая может быть взята из таблиц, и рассчитываются его каскады 1–го и 2–го порядка, соблюдается следующий порядок расчета:

В зависимости от порядка и типа фильтра выбираются схемы его каскадов, при этом фильтр четного порядка состоит из n /2 каскадов 2–го порядка, а фильтр нечетного порядка – из одного каскада 1–го порядка и (n – 1)/2 каскадов 2–го порядка;

Для расчета каскада 1–го порядка:

По выбранному типу и порядку фильтра определяется значение b 1 каскада 1–го порядка;

Уменьшая занимаемую площадь, выбирается номинал емкости C и рассчитывается R по формуле (можно выбрать и R , но рекомендуется выбирать C , из соображения точности)

;

Вычисляется коэффициента усиления К у U 1 каскада 1–го порядка, который определяется из соотношения

где К у U – коэффициент усиления фильтра в целом; К у U 2 , …, К у Un – коэффициенты усиления каскадов 2–го порядка;

Для реализации усиления К у U 1 необходимо задать резисторы, исходя из следующего соотношения

R B = R A ּ(К у U1 –1) .

Для расчета каскада 2–го порядка:

Уменьшая занимаемую площадь выбраются номиналы емкостей C 1 = C 2 = C ;

Выбраются по таблицам коэффициенты b 1 i и Q pi для каскадов 2–го порядка;

По заданному номиналу конденсаторов C рассчитываются резисторы R по формуле

;

Для выбранного типа фильтра необходимо задать соответствующий коэффициент усиления К у Ui = 3 – (1/Q pi ) каждого каскада 2-го порядка, посредством задания резисторов, исходя из следующего соотношения

R B = R A ּ(К у Ui –1) ;

Для фильтров Бесселя необходимо умножить номиналы всех емкостей на требуемое групповое время задержки.

План:

1 Обзор
- 1.1 Нормированные полиномы Баттерворта
- 1.2 Максимальная гладкость
- 1. 3 Спад характеристики на высоких частотах
2 Проектирование фильтра
- 2.1 Топология Кауэра
- 2.2 Топология Саллена-Кея
3 Сравнение с другими линейными фильтрами
4 Пример

Введение

Фильтр Баттерво́рта — один из типов электронных фильтров. Фильтры этого класса отличаются от других методом проектирования. Фильтр Баттерворта проектируется так, чтобы его амплитудно-частотная характеристика была максимально гладкой на частотах полосы пропускания.

Подобные фильтры были впервые описаны британским инженером Стефаном Баттервортом в статье «О теории фильтрующих усилителей» (англ. On the Theory of Filter Amplifiers ), в журнале Wireless Engineer в 1930 году.

1. Обзор

АЧХ фильтра Баттерворта максимально гладкая на частотах полосы пропускания и снижается практически до нуля на частотах полосы подавления. При отображении частотного отклика фильтра Баттерворта на логарифмической АФЧХ, амплитуда снижается к минус бесконечности на частотах полосы подавления.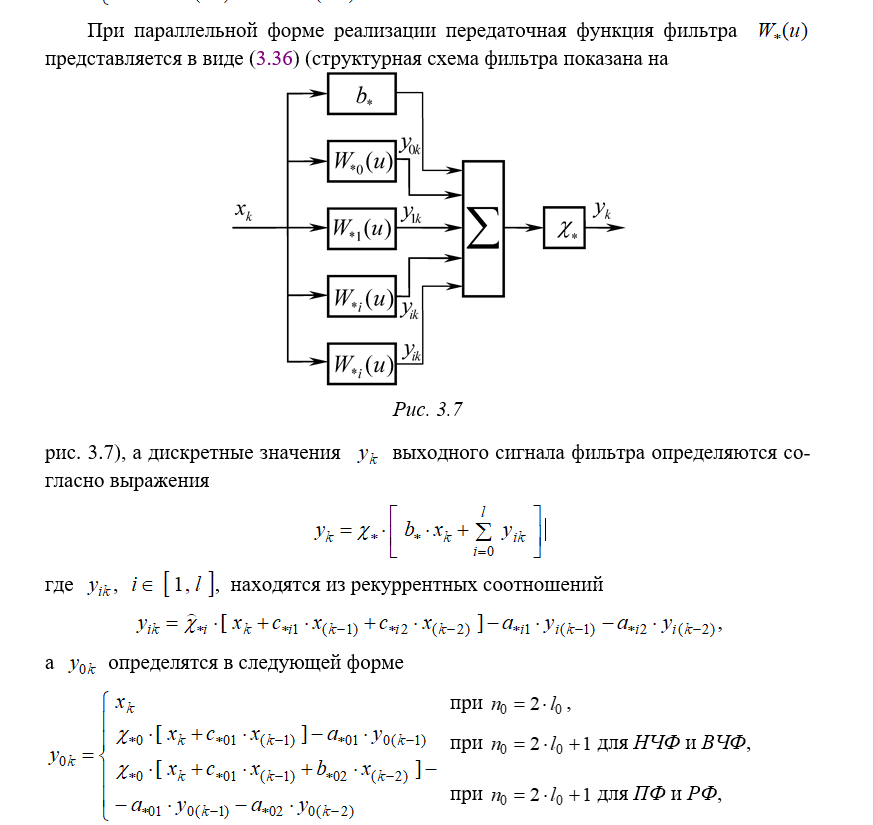 В случае фильтра первого порядка АЧХ затухает со скоростью −6 децибел на октаву (-20 децибел на декаду) (на самом деле все фильтры первого порядка независимо от типа идентичны и имеют одинаковый частотный отклик). Для фильтра Баттерворта второго порядка АЧХ затухает на −12 дБ на октаву, для фильтра третьего порядка — на −18 дБ и так далее. АЧХ фильтра Баттерворта — монотонно убывающая функция частоты. Фильтр Баттерворта — единственный из фильтров, сохраняющий форму АЧХ для более высоких порядков (за исключением более крутого спада характеристики на полосе подавления) тогда как многие другие разновидности фильтров (фильтр Бесселя, фильтр Чебышева, эллиптический фильтр) имеют различные формы АЧХ при различных порядках.

В сравнении с фильтрами Чебышева I и II типов или эллиптическим фильтром, фильтр Баттерворта имеет более пологий спад характеристики и поэтому должен иметь больший порядок (что более трудно в реализации) для того, чтобы обеспечить нужные характеристики на частотах полосы подавления. Однако фильтр Баттерворта имеет более линейную фазо-частотную характеристику на частотах полосы пропускания.

АЧХ для фильтров Баттерворта нижних частот порядка от 1 до 5. Наклон характерстики — 20n дБ/декаду, где n — порядок фильтра.

Как и для всех фильтров при рассмотрении частотных характеристик используют фильтр нижних частот, из которого легко можно получить фильтр высоких частот, а, включив несколько таких фильтров последовательно, — полосовой фильтр или режекторный фильтр.

Амплитудно-частотная характеристика фильтра Баттерворта -го порядка может быть получена из передаточной функции :

Легко заметить, что для бесконечных значений АЧХ становится прямоугольной функцией, и частоты ниже частоты среза будут пропускаться с коэффициентом усиления , а частоты выше частоты среза будут полностью подавляться. Для конечных значений спад характеристики будет пологим.

С помощью формальной замены представим выражение в виде :

Полюсы передаточной функции расположены на круге радиуса равноудалённо друг от друга в левой полуплоскости. То есть передаточную функцию фильтра Баттерворта можно определить лишь определением полюсов его передаточной функции в левой полуплоскости s-плоскости. -й полюс определяется из следующего выражения:

Передаточную функцию можно записать в виде:

Аналогичные рассуждения применимы и к цифровым фильтрам Баттерворта, с той лишь разницей, что соотношения записываются не для s -плоскости, а для z -плоскости.

Знаменатель этой передаточной функции называется полиномом Баттерворта.

1.1. Нормированные полиномы Баттерворта

Полиномы Баттерворта могут записываться в комплексной форме, как показано выше, однако обычно они записываются в виде соотношений с вещественными коэффициентами (комплексно-сопряжённые пары объединяются с помощью умножения). Нормируются полиномы по частоте среза: . Нормированные полиномы Баттерворта, таким образом, имеют следующую каноническую форму:

, — чётно , — нечётно

Ниже представлены коэффициенты полиномов Баттерворта для первых восьми порядков:

	Коэффициенты полиномов
1
2
3
4
5
6
7
8

1.

2. Максимальная гладкость

Приняв и , производная амплитудной характеристики по частоте будет выглядеть следующим образом:

Она монотонно убывает для всех так как коэффициент усиления всегда положителен. Таким образом, АЧХ фильтра Баттерворта не имеет пульсаций. При разложении амплитудной характеристи в ряд, получим:

Другими словами, все производные амплитудно-частотной характерситики по частоте до 2n -й равны нулю, из чего следует «максимальная гладкость».

1.3. Спад характеристики на высоких частотах

Приняв , найдём наклон логарифма АЧХ на высоких частотах:

В децибелах высокочастотная асимптота имеет наклон −20n дБ/декаду.

2. Проектирование фильтра

Существует ряд различных топологий фильтра, с помощью которых реализуются линейные аналоговые фильтры. Эти схемы отличаются только значениями элементов, структура же остаётся неизменной.

2.1. Топология Кауэра

Топология Кауэра использует пассивные элементы (ёмкости и индуктивности) . Фильтр Баттеворта с заданной передаточной функцией может быть построен в форме Кауэра 1 типа. k-й элемент фильтра задаётся соотношением:

; k нечётно ; k чётно

2.2. Топология Саллена-Кея

Топология Саллена-Кея использует помимо пассивных также и активные элементы (операционные усилители и ёмкости). Каждый каскад схемы Саллена-Кея представляет собой часть фильтра, математически описываемую парой комплексно-сопряжённых полюсов. Весь фильтр получается последовательным соединением всех каскадов. В случае, если попадается действительный полюс, он должен быть реализован отдельно, обычно в виде RC-цепочки, и включён в общую схему.

Передаточная функция каждого каскада в схеме Саллена-Кея имеет вид:

Нужно, чтобы знаменатель представлял собой один из множителей полинома Баттерворта. Приняв , получим:

Последнее соотношение даёт две неизвестных, которые могут быть выбраны произвольно.

3. Сравнение с другими линейными фильтрами

Рисунок ниже показывает АЧХ фильтра Баттерворта в сравнении с другими популярными линейными фильтрами одинакового (пятого) порядка:

Из рисунка видно, что спад АЧХ фильтра Баттерворта самый медленный из четырёх, однако он имеет и самую гладкую АЧХ на частотах полосы пропускания.

4. Пример

Аналоговый фильтр Баттерворта нижних частот (топология Кауэра) с частотой среза со следующими номиналами элементов: фарад, ом, и генри.

Логарифмический график плотности передаточной функции H(s) на плоскости комплексного аргумента для фильтра Баттерворта третьего порядка с частотой среза . Три полюса лежат на круге единичного радиуса в левой полуплоскости.

Рассмотрим аналоговый низкочастотный фильтр Баттерворта третьего порядка с фарад, ом, и генри. Обозначив полное сопротивление ёмкостей C как 1/Cs и полное сопротивление индуктивностей L как Ls , где — комплексная переменная, и используя уравнения для расчёта электрических схем, получим следующую передаточную функцию для такого фильтра:

АЧХ задаётся уравнением:

а ФЧХ задаётся уравнением:

Групповая задержка определяется как минус производная фазы по круговой частоте и является мерой искажений сигнала по фазе на различных частотах. Логарифмическая АЧХ такого фильтра не имеет пульсаций ни в полосе пропускания, ни в полосе подавления.

График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.

Заменив каждую индуктивность ёмкостью, а ёмкости — индуктивностями, получим высокочастотный фильтр Баттерворта.

И групповая задержка фильтра Баттерворта третьего порядка с частотой среза

Литература

В.А. Лукас Теория автоматического управления. — M.: Недра, 1990.
Б.Х. Кривицкий Справочник по теоретическим основам радиоэлектроники. — М .: Энергия, 1977.
Miroslav D. Lutovac Filter Design for Signal Processing using MATLAB© and Mathematica©. — New Jersey, USA.: Prentice Hall, 2001. — ISBN 0-201-36130-2
Richard W. Daniels Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1974. — ISBN 0-07-015308-6
Steven W. Smith The Scientist and Engineer’s Guide to Digital Signal Processing. — Second Edition. — San-Diego: California Technical Publishing, 1999. — ISBN 0-9660176-4-1
Britton C. Rorabaugh Approximation Methods for Electronic Filter Design. — New York: McGraw-Hill, 1999. — ISBN 0-07-054004-7
B. Widrow, S.D. Stearns Adaptive Signal Processing. — Paramus, NJ: Prentice-Hall, 1985. — ISBN 0-13-004029-0
S. Haykin Adaptive Filter Theory. — 4rd Edition. — Paramus, NJ: Prentice-Hall, 2001. — ISBN 0-13-090126-1
Michael L. Honig, David G. Messerschmitt Adaptive Filters — Structures, Algorithms, and Applications. — Hingham, MA: Kluwer Academic Publishers, 1984. — ISBN 0-89838-163-0
J.D. Markel, A.H. Gray, Jr. Linear Prediction of Speech. — New York: Springer-Verlag, 1982. — ISBN 0-387-07563-1
L.R. Rabiner, R.W. Schafer Digital Processing of Speech Signals. — Paramus, NJ: Prentice-Hall, 1978. — ISBN 0-13-213603-1
Richard J. Higgins Digital Signal Processing in VLSI. — Paramus, NJ: Prentice-Hall, 1990. — ISBN 0-13-212887-X
A. V. Oppenheim, R. W. Schafer Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1975. — ISBN 0-13-214635-5
L. R. Rabiner, B. Gold Theory and Application of Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1986. — ISBN 0-13-914101-4
John G. Proakis, Dimitris G. Manolakis Introduction to Digital Signal Processing. — Paramus, NJ: Prentice-Hall, 1988. — ISBN 0-02-396815-X

В данной статье мы поговорим про фильтр Баттерворта, рассмотрим порядки фильтров, декады и октавы, подробно разберем фильтр низких частот Баттерворта третьего порядка с расчетом и схемой.

Введение

В устройствах, которые используют фильтры для формирования частотного спектра сигнала, например, в системах связи или управления, форма или ширина спада, также называемая «полосой перехода», для простого фильтра первого порядка может быть слишком длинной или необходимы широкие и активные фильтры, разработанные с более чем одним «заказом». Эти типы фильтров обычно известны как фильтры «высокого порядка» или «n- го порядка».

Порядок фильтров

Сложность или тип фильтра определяется «порядком» фильтров и зависит от количества реактивных компонентов, таких как конденсаторы или катушки индуктивности в его конструкции. Мы также знаем, что скорость спада и, следовательно, ширина полосы перехода зависит от порядкового номера фильтра и что для простого фильтра первого порядка он имеет стандартную скорость спада 20 дБ / декаду или 6 дБ / октава.

Тогда для фильтра, имеющего n- й порядковый номер, он будет иметь последующую скорость спада 20n дБ / декаду или 6n дБ / октаву. Таким образом:

фильтр первого порядка имеет скорость спада 20 дБ / декаду (6 дБ / октава)
фильтр второго порядка имеет скорость спада 40 дБ / декаду (12 дБ / октава)
фильтр четвертого порядка имеет частоту спада 80 дБ / декада (24 дБ / октава) и т. д.

Фильтры высокого порядка, такие как третий, четвертый и пятый, обычно формируются путем каскадного объединения одиночных фильтров первого и второго порядка.

Например, два фильтра нижних частот второго порядка могут быть соединены каскадно для получения фильтра нижних частот четвертого порядка и так далее. Несмотря на то, что порядок фильтра, который может быть сформирован, не ограничен, при увеличении порядка увеличиваются его размер и стоимость, а также снижается его точность.

Декады и октавы

Последний комментарий о Декадах и Октавах . По шкале частот декада — это десятикратное увеличение (умножение на 10) или десятикратное уменьшение (деление на 10). Например, от 2 до 20 Гц представляют одну декаду, тогда как от 50 до 5000 Гц представляют две декады (от 50 до 500 Гц, а затем от 500 до 5000 Гц).

Октава — это удвоение (умножить на 2) или уменьшение в два раза (деление на 2) по шкале частот. Например, от 10 до 20 Гц представляет одну октаву, а от 2 до 16 Гц — это три октавы (от 2 до 4, от 4 до 8 и, наконец, от 8 до 16 Гц), каждый раз удваивая частоту. В любом случае, логарифмические шкалы широко используются в частотной области для обозначения значения частоты при работе с усилителями и фильтрами, поэтому важно понимать их.

Поскольку резисторы, определяющие частоту, все равны, как и конденсаторы, определяющие частоту, отсечка или угловая частота (ƒ C) для первого, второго, третьего или даже для фильтра четвертого порядка также должны быть равны и найдены, используя знакомое уравнение:

Как и в случае фильтров первого и второго порядка, фильтры верхних частот третьего и четвертого порядка формируются простым взаимным обменом положений определяющих частоту компонентов (резисторов и конденсаторов) в эквивалентном фильтре нижних частот. Фильтры высокого порядка можно спроектировать, следуя процедурам, которые мы видели ранее в руководствах по фильтру нижних частот и фильтрам верхних частот. Однако общий коэффициент усиления фильтров высокого порядка является фиксированным, поскольку все компоненты, определяющие частоту, являются одинаковыми.

Аппроксимации фильтра

До сих пор мы рассматривали низкочастотные и высокочастотные схемы фильтра первого порядка, их результирующие частотные и фазовые характеристики. Идеальный фильтр дал бы нам спецификации максимального усиления полосы пропускания и плоскостности, минимального затухания полосы пропускания, а также очень крутой полосы пропускания, чтобы остановить спад полосы (полоса перехода), и поэтому очевидно, что большое количество сетевых откликов будет удовлетворять эти требования.

Неудивительно, что в линейном дизайне аналоговых фильтров есть ряд «аппроксимационных функций», в которых используется математический подход для наилучшего приближения передаточной функции, которая требуется нам для проектирования фильтров.

Такие конструкции известны как Эллиптический , Баттерворт , Чебышев , Бессель , Кауэр и многие другие. Из этих пяти «классических» функций аппроксимации линейного аналогового фильтра только фильтр Баттерворта и особенно конструкция фильтра Баттерворта нижних частот будут рассматриваться здесь как его наиболее часто используемая функция.

Низкочастотный фильтр Баттерворта

Частотная характеристика аппроксимационной функции фильтра Баттерворта также часто называется «максимально плоской» (без пульсаций) характеристикой, поскольку полоса пропускания спроектирована так, чтобы иметь частотную характеристику, которая является настолько плоской, насколько это математически возможно, от 0 Гц (DC) до частоты среза -3 дБ без пульсаций. Более высокие частоты за пределами точки отсечки снижаются до нуля в полосе останова на уровне 20 дБ / декада или 6 дБ / октава. Это потому, что он имеет «фактор качества», «Q» всего 0,707.

Однако одним из основных недостатков фильтра Баттерворта является то, что он достигает этой плоскостности полосы пропускания за счет широкой полосы перехода, когда фильтр изменяется от полосы пропускания к полосе остановки. Он также имеет плохие фазовые характеристики. Идеальная частотная характеристика, называемая фильтром «кирпичной стены», и стандартные аппроксимации Баттерворта для различных порядков фильтра приведены ниже.

Обратите внимание, что чем выше порядок фильтра Баттерворта, тем больше количество каскадных ступеней в конструкции фильтра и тем ближе фильтр подходит к идеальному отклику «кирпичной стены».

Однако на практике идеальная частотная характеристика Баттерворта недостижима, поскольку она вызывает чрезмерную пульсацию в полосе пропускания.

Где обобщенное уравнение, представляющее фильтр Баттерворта «n-го» порядка, частотная характеристика дается как:

Где: n представляет порядок фильтра, ω равно 2πƒ, а ε — максимальное усиление полосы пропускания (A max).

Если A max определено на частоте, равной угловой точке отсечки -3 дБ (ƒc), тогда ε будет равно единице и, следовательно, ε 2 также будет равно единице. Однако, если вы теперь хотите определить A max при другом значении усиления по напряжению, например, 1 дБ или 1.1220 (1 дБ = 20 * logA max), тогда новое значение ε находится по формуле:

Подставляя данные в уравнения, получаем:

Частотная характеристика фильтра может быть определена математически его передаточной функции с стандартом передачи напряжения Функция H (jω) и записывается в виде:

Примечание: (jω) также можно записать как (s) для обозначения S-области. и результирующая передаточная функция для фильтра нижних частот второго порядка задается как:

Нормализованные полиномы фильтра Баттерворта низких частот

Чтобы помочь в разработке своих фильтров нижних частот, Баттерворт создал стандартные таблицы нормализованных полиномов нижних частот второго порядка с учетом значений коэффициента, которые соответствуют частоте отсечки угла 1 радиан / с.

N	Нормализованные полиномы знаменателя в факторизованной форме
1	(1 + S)
2	(1 + 1,414 с + с 2)
3	(1 + с) (1 + с + с 2)
4	(1 + 0,765 с + с 2) (1 + 1,848 с + с 2)
5	(1 + с) (1 + 0,618 с + с 2) (1 + 1,618 с + с 2)
6	(1 + 0,518 с + с 2) (1 + 1,414 с + с 2) (1 + 1,932 с + с 2)
7	(1 + с) (1 + 0,445 с + с 2) (1 + 1,247 с + с 2) (1 + 1,802 с + с 2)
8	(1 + 0,390 с + с 2) (1 + 1,111 с + с 2) (1 + 1,663 с + с 2) (1 + 1,962 с + с 2)
9	(1 + с) (1 + 0,347 с + с 2) (1 + с + с 2) (1 + 1,532 с + с 2) (1 + 1,879 с + с 2)
10	(1 + 0,313 с + с 2) (1 + 0,908 с + с 2) (1 + 1,414 с + с 2) (1 + 1,782 с + с 2) (1 + 1,975 с + с 2)

Расчет и схема фильтра Баттерворта низких частот

Найти порядок активного фильтра Баттерворта нижних частот, чьи характеристики приведены в качестве: A макс = 0,5 дБ на частоте полосы пропускания (ωp) 200 радиан / сек (31. 8 гЦ), и A min = -20 дБ на частоте полосы остановки (ωs) 800 радиан / сек. Также разработайте подходящую схему фильтра Баттерворта, соответствующую этим требованиям.

Во-первых, максимальное усиление полосы пропускания A max = 0,5 дБ, которое равно усилению 1,0593 , помните, что: 0,5 дБ = 20 * log (A) на частоте (ωp) 200 рад / с, поэтому значение эпсилона ε находится по:

Во-вторых, минимальное усиление полосы остановки A min = -20 дБ, которое равно усилению 10 (-20 дБ = 20 * log (A)) на частоте полосы остановки (ωs) 800 рад / с или 127,3 Гц.

Подстановка значений в общее уравнение для частотной характеристики фильтров Баттерворта дает нам следующее:

Так как n всегда должно быть целым числом, то следующим самым высоким значением 2,42 будет n = 3 , поэтому «требуется фильтр третьего порядка», и для создания фильтра Баттерворта третьего порядка, ступени фильтра второго порядка требуется каскадное соединение со ступенью фильтра первого порядка.

Из приведенной выше таблицы нормализованных полиномов Баттерворта низких частот коэффициент для фильтра третьего порядка дается как (1 + s) (1 + s + s 2), и это дает нам усиление 3-A = 1 или A = 2 . В А = 1 + (Rf / R1) , выбирая значение как для резистора обратной связи Rf и резистора R1 дает нам значения 1 кОм и 1 кОм, соответственно, как: (1 кОм / 1 кОм) + 1 = 2 .

Мы знаем, что угловая частота отсечки, точка -3 дБ (ω o) может быть найдена с помощью формулы 1 / CR , но нам нужно найти ω o по частоте полосы пропускания ω p ,

Таким образом, частота отсечки угла задается как 284 рад / с или 45,2 Гц (284 / 2π), и, используя знакомую формулу 1 / RC, мы можем найти значения резисторов и конденсаторов для нашей схемы третьего порядка.

Обратите внимание, что ближайшее предпочтительное значение до 0,352 мкФ будет 0,36 мкФ или 360 нФ.

И, наконец, наша схема низкочастотного фильтра Баттерворта третьего порядка с угловой частотой среза 284 рад / с или 45,2 Гц, максимальным усилением полосы пропускания 0,5 дБ и минимальным усилением полосы остановки 20 дБ строится следующим образом.

Таким образом, для нашего фильтра низких частот Баттерворта 3-го порядка с угловой частотой 45,2 Гц, C = 360 нФ и R = 10 кОм

Цифровые фильтры с конечной импульсной характеристикой

Автор: Торгушин Иван Васильевич

Рубрика: Информационные технологии

Опубликовано в Молодой учёный №19 (361) май 2021 г.

Дата публикации: 10.05.2021 2021-05-10

Статья просмотрена: 70 раз

Скачать электронную версию

Скачать Часть 1 (pdf)

Библиографическое описание:

Торгушин, И. В. Цифровые фильтры с конечной импульсной характеристикой / И. В. Торгушин. — Текст : непосредственный // Молодой ученый. — 2021. — № 19 (361). — С. 28-30. — URL: https://moluch.ru/archive/361/80840/ (дата обращения: 28.09.2022).

Описаны основные характеристики цифровых фильтров, включая фильтры с конечной импульсной характеристикой. Показано, что изменение частоты дискретизации позволяет практически плавно изменять крутизну фазочастотной характеристики фильтра.

Ключевые слова: цифровой фильтр, конечная импульсная характеристика, фазочастотная характеристика.

Проблемой, ограничивающей использование цифровых фильтров (ЦФ) в различных системах передачи данных, является необходимость работы в широком диапазоне частот. При увеличении частот использования ЦФ уменьшается интервал дискретизации, что ограничивает максимально допустимый порядок цифровых фильтров.

Главной характеристикой ЦФ является алгоритм фильтрации. По алгоритму фильтрации осуществляется реализация фильтра.

Импульсной характеристикой ЦФ h ( n ) является реакция фильтра на единичный импульс при нулевых начальных условиях. Импульсная характеристика позволяет определить выходной сигнал фильтра по формуле дискретной свёртки входного сигнала [1].

С импульсной характеристикой фильтра связана передаточная функция H ( z ). Она определяется как отношение Z -преобразований выходного и входного сигналов. Импульсная и передаточная функции связаны парой Z -преобразований. С помощью передаточной функции H ( z ) так же можно найти реакцию фильтра на любое входное воздействие.

Комплексная частотная характеристика фильтра H exp( jT ) определяется как отношение преобразований Фурье выходного и входного сигналов при нулевых начальных условиях. Комплексная частотная характеристика равна значениям передаточной функции на единичной окружности Z -плоскости, и связана с импульсной характеристикой парой преобразований Фурье. Комплексная частотная характеристика является периодической по частоте с периодом, который равен частоте дискретизации [2].

Импульсная характеристика, передаточная функция и комплексная частотная характеристика дают полное описание ЦФ как линейной стационарной системы.

Модуль комплексной частотной характеристики рассматривают как амплитудно-частотную характеристику A ( T ) (АЧХ), а аргумент — как фазочастотную характеристику  ( T ) (ФЧХ). Они также являются периодическими функциями с периодом, который равен частоте дискретизации.

По алгоритму работы ЦФ делятся на рекурсивные и нерекурсивные.

В рекурсивных алгоритмах фильтрации процесс вычисления выходного сигнала в заданный момент времени осуществляется с использованием предыдущих отсчётов входного и выходного сигналов. В рекурсивных фильтрах имеет место обратная связь. Количество используемых отсчётов выходного сигнала характеризует глубину рекурсии [3].

В нерекурсивных алгоритмах фильтрации процесс вычисления выходного сигнала в заданный момент времени осуществляется только с использованием предыдущих отсчётов входного сигналов. Обратная связь отсутствует. Нерекурсивные алгоритмы являются частными случаями рекурсивных алгоритмов при глубине рекурсии равной нулю.

В зависимости от расположения нулей передаточной функции на Z -плоскости различают фильтры минимально-фазового и неминимально-фазового типа. У минимально-фазовых фильтров A ( T ) и  ( T ) связаны между собой парой дискретных преобразований Гильберта.

У неминимально-фазовых фильтров A ( T ) и  ( T ) являются независимыми. То есть, при неизменной A ( T ) можно получить необходимую характеристику  ( T ). Кроме этого, в классе неминимально-фазовых фильтров существуют фильтры с идеальными линейными  ( T ).

Последнее свойство ЦФ является наиболее важным, так как позволяет выполнить условие линейности характеристик разработанных генераторных преобразователей, обладающих повышенной чувствительностью.

Рассмотрим условия реализации ЦФ с линейными ФЧХ [4]. Их реализация возможна в классе одномерных скалярных вещественных стационарных нерекурсивных линейных неминимально-фазовых цифровых фильтров.

Известны 4 вида фильтров с линейными ФЧХ.

Фильтры вида 1 имеют импульсную характеристику симметричную относительно центра, а значение отсчётов импульсной характеристики М является чётным: . Такие фильтры могут быть фильтрами нижних частот, верхних частот, полосными и режекторными.

В фильтрах 2-го вида импульсная характеристика симметрична относительно центра, а значение отсчётов импульсной характеристики М является нечётным: . Такие фильтры могут быть фильтрами нижних частот или полосными.

У фильтров вида 3 импульсная характеристика асимметрична относительно центра, а значение отсчётов импульсной характеристики М является чётным: . Такие фильтры могут быть только полосными.

У фильтров вида 4 импульсная характеристика антисимметрична относительно центра, а значение отсчётов импульсной характеристики М является нечётным: . Такие фильтры могут быть фильтрами верхних частот или полосными.

Сравнительный анализ фильтров указанных видов показывает, что предпочтение следует отдать фильтрам вида 1. Используя метод «окон» получим фильтры с конечной импульсной характеристикой или КИХ-фильтры.

ЦФ с конечной импульсной характеристикой (КИХ) имеют один неоспоримый плюс: линейные фазочастотные характеристики.

ФЧХ КИХ-фильтров ступенчатые и всегда проходят через начало координат, либо смещены на 90 градусов. Для получения большей точности необходимо увеличивать частоту дискретизации системы. Однако быстродействие процессора не всегда позволяет получить необходимую частоту дискретизации, а, соответственно, и точность.

Кратко остановимся на двух характеристиках КИХ-фильтров.

Как уже отмечалось выше, ФЧХ КИХ-фильтров является ступенчатой прямой, проходящей через начало координат или с постоянным смещением относительно начала координат. Чтобы фазовый сдвиг изменился скачком на одну ступеньку, надо чтобы период входного сигнала фильтра получил приращение, равное периоду дискретизации. Крутизна ФЧХ S __{зависит от порядка фильтра R и частоты дискретизации F _d :}

Порядок фильтра определяется количеством отсчётов КИХ, длина которой равна RT . Порядок фильтра в основном определяет форму АЧХ. Изменение порядка фильтра приводит к скачкообразному изменению крутизны ФЧХ, поэтому этот способ настройки ФЧХ не подходит.

Изменение частоты дискретизации позволяет практически плавно изменять крутизну ФЧХ. Этот способ настройки ФЧХ наиболее удобен.

Литература:

1. Антонью, А. Цифровые фильтры: анализ и проектирование [Текст] / А. Антонью; Пер. с англ. — М.: Радио и связь, 1983. — 320 с.

Гадзиковский, В. И. Теоретические основы цифровой обработки сигналов [Текст] / В. И. Гадзиковский. — М.: Радио и связь, 2004. — 378 с.
Голденберг, Л. М. Цифровая обработка сигналов: Справочник [Текст] / Л. М. Голденберг, Б. Д. Матюшкин, М. Н. Поляк и др. — М.: Радио и связь, 1985–312 с.
Сергиенко, А. Б. Цифровая обработка сигналов [Текст] / А. Б. Сергиенко. — СПб.: Питер, 2004. — 608 с.

Основные термины (генерируются автоматически): импульсная характеристика, фильтр, передаточная функция, комплексная частотная характеристика, входной сигнал, конечная импульсная характеристика, выходной сигнал, порядок фильтра, частота дискретизации, обратная связь.

Ключевые слова

цифровой фильтр, конечная импульсная характеристика, фазочастотная характеристика

Передаточная функция FIR

Фильтр передаточной функции использует передаточную функцию и Теорема свертки изготовить фильтр. В этой статье обсуждается пример такого фильтра, использующего конечную импульсную характеристику, и показано применение фильтра в реальных данных.

Содержание

1 FIR (Finite Impulse Response) Линейные фильтры
2 Математическая модель
3 Односторонний линейный фильтр
- 3.1 Функция ввода
- 3.2 Односторонний фильтр
4 Двусторонний фильтр
5 КИХ Передаточная функция Линейный фильтр Применение
6 Рекомендации

FIR (Finite Impulse Response) Линейные фильтры

В цифровой обработке КИХ-фильтр — это непрерывный во времени фильтр, инвариантный со временем. Это означает, что фильтр не зависит от конкретного момента времени, а скорее зависит от продолжительности времени. В спецификации этого фильтра используется функция передачи который имеет частотную характеристику, которая будет передавать только желаемые частоты входного сигнала. Этот тип фильтра является нерекурсивным, что означает, что выходные данные могут быть полностью получены из комбинации входных данных без каких-либо рекурсивных значений выходных данных. {T} х (т- тау) , ч ( тау) , д тау}

час(τ{ Displaystyle тау}) — передаточная функция импульсного отклика на вход. В свертка позволяет активировать фильтр только тогда, когда на входе записан сигнал с тем же значением времени. Этот фильтр возвращает входные значения (x (t)), если k попадает в область поддержки функции h. По этой причине этот фильтр называется конечным откликом. Если k находится за пределами области поддержки, импульсная характеристика равна нулю, что делает выход равным нулю. Центральная идея этого h (τ{ Displaystyle тау}) можно рассматривать как частное двух функций.^[2]

По словам Хуана (1981)^[3] Используя эту математическую модель, существует четыре метода проектирования нерекурсивных линейных фильтров с различными параллельные конструкции фильтров:

Метод оформления окон
Метод частотной выборки
Обычное линейное программирование
Итеративное линейное программирование

Односторонний линейный фильтр

Функция ввода

Определите входной сигнал:

у(т)=грех⁡(т)+рапd([1200]){ Displaystyle у (т) = грех (т) + рандом ({ begin {bmatrix} 1 & 200 end {bmatrix}})}

рапd([1200]){ displaystyle rand ({ begin {bmatrix} 1 & 200 end {bmatrix}})} добавляет случайное число от 1 до 200 к синусоидальной функции, которая служит для искажения данных. {- t}, & forall & 0 & leq & t & leq + infty end {case}}}

Изучите этот фильтр в его частотной области, мы увидим, что характеристика амплитуды соответствует той же тенденции, что и односторонний фильтр. Однако пропускаемые частоты меньше, чем у одностороннего фильтра. Это привело к более плавному выходу. Существенным из этого следствия является то, что типы двусторонних фильтров линейных фильтров лучше являются фильтрами.

КИХ Передаточная функция Линейный фильтр Применение

Линейный фильтр работает лучше, если это двусторонний фильтр. Это требует, чтобы данные были известны заранее, что затрудняет правильное функционирование этих фильтров в ситуациях, когда сигналы не могут быть известны заранее, например, при обработке радиосигналов. Однако это означает, что линейные фильтры чрезвычайно полезны при фильтрации предварительно загруженных данных. Кроме того, из-за своей нерекурсивной природы, которая сохраняет фазовые углы входа, линейные фильтры обычно используются в обработка изображений, обработка видео, обработка данных или обнаружение закономерностей. Хуанг, Т. С. (1981). Темы прикладной физики: двумерная цифровая обработка сигналов I (3-е изд., Том 42, разделы прикладной физики). Берлин: Springer.

:::Режекторный фильтр с регулируемой величиной добротности для подавления помехи от силовой сети (50 Гц) :::

Режекторный фильтр с регулируемой величиной добротности для подавления помехи от силовой сети (50 Гц)

Регулируемый активный режекторный фильтр

Заявляемое устройство относится к приборостроению, а именно к частотноизбирательным средствам, и предназначено для использования в устройствах фильтрации сигналов от помех на фиксированных частотах, в частности сетевой частоты 50 или 60 Гц, а также в акустических системах для устранения акустической “завязки”
Известно, что режекторные фильтры (РФ) широко применяются в системах связи, в различных измерительных приборах для соответствующей обработки сигналов
В литературе описано множество вариантов таких фильтров, построенных на основе RC-звеньев [Harris, 1968[3]; Steber & Kraeger, 1969[6]; Inigo, 1969[4]; Chakraborty & Choudhary, 1969[2]; Bhattacharyya & Swamy, 1970[1]]
Для режекторных фильтров требуется, чтобы на частоте среза коэффициент передачи фильтра равнялся нулю. Но на практике это условие бывает трудновыполнимым. Для точной регулировки таких фильтров желательно иметь возможность подстройки величины коэффициента добротности независимо от величины коэффициента передачи
Коэффициент передачи или передаточная функция фильтра являются основными характеристиками, отражающими способность фильтра к частотной селективности
Для исходного фильтра, который является неинвертирующим симметричным режекторным фильтром второго порядка,   передаточная функция имеет вид
(1)
где р = j×ω – оператор Лапласа, ω = 2×π×f – круговая частота режекции,
Qисх – коэффициент добротности исходного фильтра,
Nрф(р) – числитель передаточной функции, Dрф(р) – её знаменатель.
При этом не учитывается, с помощью каких конкретно RC или LC звеньев обеспечивается селективность фильтра.
Величина добротности Qисх = ω_{0 / (}ω_{2 –}ω_{1 )} характеризует селективные свойства режекторного фильтра, во многих случаях бывает недостаточна и требуется увеличение добротности режекторного фильтра.
Каскадное включение двух режекторных фильтров с одинаковой добротностью    не позволяет увеличить добротность , поскольку дает режекторный фильтр с более низкой добротностью, чем исходный.
Из уровня техники известен    РФ 2-го порядка с включением на вход исходного РФ дополнительного корректирующего фильтра, являющегося амплитудным корректором и имеющим частоту подьема усиления, совпадающего с частотой режекции.
Каскадное (последовательного) включение   звеньев фильтров [5],   позволяет получить повышение добротности имеющегося исходного режекторного фильтра (РФ) за счет последовательного включения с ним корректирующего звена   [1] , имеющего подьем коэффициента усиления на частоте режекции РФ.
При последовательном включении амплитудного корректора с передаточной функцией (2) и исходного РФ (1) происходит компенсация низкодобротных полюсов знаменателя передаточной функции исходного РФ нулями числителя амплитудного корректора. При этом полиномом знаменателя РФ становится полином знаменателя амплитудного корректора, имеющего большую добротность, что и обеспечивает повышение добротности результирующего режекторного фильтра (3)
(2)
(3)
Однако недостатком такого решения является необходимость использования дополнительных усилительных и реактивных элементов в частотно- избирательных цепях активного корректирующего фильтра, что усложняет и удорожает режекторный фильтр. Кроме того, усложняется настройка величины добротности из-за необходимости регулировки большого числа элементов.
Практически невозможно оперативно регулировать добротность нового режекторного фильтра.
Известны устройства РФ с повышением величины   добротности за счет введение в исходный режекторный фильтр частотнонезависимой положительной обратной связи (ПОС) [ 3-5 ] в селективную цепь на основе Т или 2Т мостов.
РФ с 2Т–мостом и частотно независимым резистивным делителем [4] позволяет регулировать добротность РФ, но компоненты 2Т–моста требуют тщательного подбора и поддержания точного значений номиналов резисторов и конденсаторов 2Т–моста, что также усложняет и удорожает производство РФ
Такое повышение добротности за счет введения ПОС в частотноселективную цепь Т–моста не позволяет регулировать добротность РФ в процессе эксплуатации. Кроме того, использование положительной обратной связи повышает уровень шумов фильтра.
Наиболее близким аналогом по совокупности существенных признаков к предлагаемому режекторному фильтру является режекторный фильтр по патенту США   № 4 242 642 (МПК Н03F1/34, 1980)
Схема этого режекторного фильтра содержит дифференциальный операционный усилитель, инвертирующий вход которого соединен с первым резистором, а также с первыми выводами второго и третьего резисторов, который образует резистивный делитель. Выход дифференциального операционного усилителя соединен со входом исходного режекторного фильтра и с вторым выводом третьего резистора, неинвертирующий вход дифференциального операционного усилителя и один вывод исходного режекторного фильтра подсоединены к общему проводу (заземлению) Выход исходного режекторного фильтра соединен со вторым выводом второго резистора.
Схема прототипа приведена на фиг. 1.
Достоинством этого режекторного фильтра являются:
—    исключение дополнительных реактивных элементов, усложняющих настройку фильтра,
—  использование только отрицательной обратной связи для подстройки величины добротности,
Недостатком прототипа являются трудности оперативной регулировки величины добротности.

Фиг.1. Схема режекторного фильтра-прототипа

Фиг.2. Граф схемы режекторного фильтра-прототипа

Определим передаточную функцию схемы режекторного фильтра-прототипа по графу фиг. 2:
(4)
Из рассмотрения полученной передаточной функции РФ (4) имеем
(5)
(6)
Из формул (5), (6) следует что регулирование величины добротности Qнов, можно обеспечить путём изменения величины резистора R3 при фиксированном R2. Однако варьирование резистора R3 вызывает изменение величин пеедачи фильтра на постоянном токе Ko, что нежелательно и является недостатком схемы фильтра.На фиг.2 приведены АЧХ фильтра в различных точках схемы

Фиг.2 Амплитудно-частотные характеристики схемы РФ- прототипа в различных точках схемы: кривая 1- АЧХ исходного режекторногофильтра с низкой добротностью. кривая 3 – АЧХ корректирующего фильтра на выходе первого ОУ кривая 2 — АЧХ режекторного фильтра с повышенной добротностью

Технический результат, на достижение которого направлено предлагаемое техническое решение, заключается в повышении добротности исходного режекторного фильтра (неинвертирующего симметричного второго порядка) с обеспечением его оперативной подстройки путем регулировки одного элемента, а также в исключении влияния изменения величины добротности на коэффициент передачи фильтра на постоянном токе и в уменьшении общего количества используемых в схеме элементов, что удешевляет устройство.
Для достижения этого технического результата предлагаемый активный режекторный фильтр, так же как и известный, содержит дифференциальный операционный усилитель, инвертирующий вход которого соединен с первыми выводами первого и второго резисторов, а выход соединен со входом исходного режекторного фильтра и со вторым выводом второго резистора, при этом вывод исходного режекторного фильтра соединен со вторым выводом первого резистора и один вывод исходного режекторного фильтра подсоединен к общему проводу заземления, но в отличие от известного неинвертирующий вход дифференциального операционного усилителя является входом активного режекторного фильтра.

На фиг.3 приведена схема предлагаемого активного режекторного фильтра с регулированием добротности

Фиг . 4 Схема предлагаемого регулируемого активного режекторного фильтра

Схема содержит дифференциальный операционный усилитель, неинвертирующий режекторный фильтр второго порядка, резистивный делитель, включённый между выходом и входом неинвертирующего режекторного фильтра второго порядка, причём отвод резистивного делителя подключен к инвертирующему входу дифференциального операционного усилителя блок фильтрации 4, зажим 1 являющийся его входом, который соединён с резистором 2 (R1), другой конец резистора 2 соединён с инвертирующим входом 5 дифференциального операционного усилителя 8, а также с резисторами 3 (R2) и 7 (R3). Выход 9 дифференциального операционного усилителя 8 соединён со входом 10 исходного РФ 11 и с резистором 7. Выход 13 исходного РФ 11 соединяется с резистором 3 и зажимом 14, являющимся выходом блока фильтрации 4. Неинвертирующий вход 6 дифференциального операционного усилителя 8 и РФ 8 подсоединены к общему проводу заземления 12
Получим передаточную функцию предлагаемого режекторного фильтра.

где B = R3 / (R2 + R3)

тогда имеем

Из рассмотрения последнего уравнения   (7) можно сделать следующие выводы
— добротность фильтра зависит только от коэффициента B
— коэффициент передачи на постоянном токе равен единице и не зависит от B, что выгодно отличает предлагемую схему от прототипа
Регулируемый активный режекторный фильтр работает следующим образом.
При положении движка на левом краю потенциометра, т.е. при соединении выхода операционного усилителя с его инвертирующим входом, имеем коэффициент передачи операционного усилителя, равный единице, ( ОУ работает в режиме повторителя напряжения ) следовательно весь фильтр с учетом работы повторителя напряжения становится режекторным фильтром с исходной (начальной) величиной добротности   Q исх. )
При перемещении движка к положению на середине потенциометра, т.е. когда сопротивления левой и правой части потенциометра равны, тогда на частоте режекции, где передача исходного режекторным фильтра равна нулю, передача сигнала с неинвертирующего входа на выход операционного усилителя будет равна двум, т.е. на входе исходного режекторным фильтр будет действовать удвоеное входное напряжение
Увеличение частотнозависимого напряжения на входе исходного режекторного фильтра компенсирует снижение усиления исходного режекторного фильтра за счет его малого значения исходной величины добротности Q исх, что приводит к увеличению добротности всего режекторного фильтра
При указанном положении движка потенциометра и расстройке от частоты режекции Fo режекторного фильтра в сторону снижения частоты на выходе всего фильтра будет появляться напряжение с фазовым сдвигом, причем в сторону отставания или   в сторону опережения при отклонении частоты в сторону повышения.
При большом отклонение частоты от значения Fo в сторону понижения или повышения частоты фаза выходного напряжения относительно входного напряжения становится равной нулю. Можно считать что выходное напряжение всего фильтра будет в тойже фазе, что и входное.
На правом выводе потенциометра будет появляться напряжение в той же фазе , что и на левом выводе, причем равное по амплитуде,Формула изобретения поэтому из-за равенства напряжения на выводах потенциометра ток через потенциометр протекать не будет.
В результате на всех трех выводах потенциометра при больших расстройках частоты входного напряжения будет действовать одинаковое входное напряжение, вследствие “виртуального нуля” напряжения между входами дифференциального операционного усилителя. Из этого следует, что коэффициент передачи со входа на выход будет равен единице
Можно также сделать вывод , что перемещение движка потенциометра на частотах, достаточно удаленных от частоты режекции, не влияет на величину коэффициента передачи режекторного фильтра.
Формула   изобретения
Регулируемый активный режекторный фильтр с плавной регулировкой     добротности, содержащий дифференциальный операционный усилитель, неинвертирующий режекторный фильтр второго порядка, резистивный делитель, включённый между выходом и входом неинвертирующего режекторного фильтра второго порядка, причём отвод резистивного делителя подключен к инвертирующему входу дифференциального операционного усилителя,   отличающийся тем, что   резистивный делитель выполнен в виде   потенциометра, включенного крайними выводами ко входу и выходу неинвертирующего режекторного фильтра второго порядка, движок потенциометра подключён к инвертирующему входу дифференциального операционного усилителя, при этом входом фильтра является неинвертирующий вход дифференциального операционного усилителя, а выходом схемы является выход неинвертирующего режекторного фильтра второго порядка

Анализ передаточной функции | Введение в цифровые фильтры

В этой главе обсуждаются передаточные функции фильтра и связанные с ними анализ. Передаточная функция обеспечивает алгебраическое представление линейного стационарного (LTI) фильтра в частотной области:

Передаточную функцию также называют системной функцией . [60].

Обозначим импульсную характеристику фильтра. получается получается (как мы покажем), что передаточная функция равна z преобразование импульсной характеристики :

Поскольку умножение входного преобразования на передаточную функцию дает выходное преобразование, мы видим, что воплощает в себе передают характеристики фильтра—отсюда и название.

Остается определить « z преобразование» и доказать, что z преобразование импульсная характеристика всегда дает передаточную функцию, что мы и сделаем доказав теорему свертки для z преобразований.

Преобразование

Двустороннее z преобразование сигнала дискретного времени определяется как

(7.

где комплексная переменная. Поскольку сигналы обычно определяются начинаться (становиться ненулевым) в момент времени , и поскольку фильтры часто считается причинным, ^7.1 нижний предел суммирования, указанный выше, может быть записан как 0, а не как дать односторонний z преобразование :
(7.2)

Чаще всего используется одностороннее преобразование z . Для инвертирования преобразований z см. §6.8.
Напомним (§4.1), что математическое представление сигнал дискретного времени отображает каждое целое число к комплексу количество ( ) или действительное число ( ). z преобразование of , с другой стороны, отображает каждое комплексное число на новый комплексный номер . На более высоком уровне, преобразование z , рассматриваемое как линейный оператор , отображает весь сигнал к его преобразованию z . Мы думаем об этом как о «функции для сопоставление функций. Мы можем сказать, что это преобразование z , написав
или, используя операторную запись,
который можно сократить как
Можно также увидеть удобное, но, возможно, вводящее в заблуждение обозначение
, в котором и следует понимать как обозначающий все домены
и
, как в отличие от обозначения конкретных фиксированных значений.
Преобразование сигнала z можно рассматривать как полином в , с коэффициентами, заданными образцами сигнала. Например, сигнал
имеет z преобразование
.
Существование
Z Трансформировать
Преобразование z конечно-амплитудного сигнал всегда будет существовать при условии, что (1) сигнал начинается в конечное время и (2) он асимптотически экспоненциально ограничено , т. е. , существует конечные целые и конечные действительные числа и , такой, что для всех . ограничивающая экспонента может даже расти вместе с (). Это не самые общие условия существования z трансформируются, но они достаточно для большинства практических целей.
Для сигнала, растущего как , для одного естественно ожидать, что преобразование z будет определено только в область, край сложной плоскости. Это ожидается потому что бесконечный ряд
требуется
для обеспечения сходимости. С
для разлагающегося экспоненциальной, мы видим, что область сходимости преобразование затухающей экспоненты всегда включает единичный круг самолет .
В более общем случае оказывается, что во всех случаях, представляющих практический интерес, домен может быть расширен для включения вся комплексная плоскость , за исключением изолированной «сингулярной» точек ^7.2 в каких подходах бесконечность (например, в когда ). Математическая техника для этого называется аналитическим методом. продолжение и описано в §D.1 применительно к Преобразование Лапласа (непрерывный аналог преобразования z ). Однако следует отметить, что в области расширения (все точки такой, что в приведенном выше примере) сигнал компонента, соответствующая каждой особенности внутри расширения область «перевернута» во временной области. То есть «причинно-следственный». экспоненты становятся «антикаузальными» экспонентами, как обсуждалось в §8.7.
Преобразование z более подробно обсуждается в другом месте. [52,60], и ниже мы выведем только что нам понадобится.
В этом разделе мы докажем очень полезную теорему о сдвиге и теорема свертки для односторонних z преобразований. Мы рассматриваем пространство г. бесконечно длинные, причинно-следственные, сложные последовательности , , с за .
Теорема о сдвиге
Теорема сдвига говорит, что задержки отсчетов во временной области соответствует умножению на в частотной области:
S HIFT
или, используя более распространенные обозначения,
Таким образом,
, то есть сигнал, задержанный на образцы, имеет преобразование z
.

Доказательство:

где мы использовали предположение причинности для .
Теорема свертки

9Теорема свертки 0003 для z преобразует утверждает, что для любого (действительного или) сложные причинно-следственные сигналы и , свертка во временной области есть умножение в домен , т. е. ,

или, используя операторную запись,

где

. (Видеть [84] для развития теоремы свертки для дискретных преобразования Фурье.)

Доказательство:

Теорема свертки является краеугольным камнем линейных систем. теория. Это подразумевает, например, что любой стабильный причинно-следственный фильтр LTI (рекурсивный или нерекурсивный) может быть реализован путем свертки входных данных сигнал с импульсной характеристикой фильтра, как показано в следующем раздел.

Из уравнения (5.5) получаем, что выход линейного задан стационарный фильтр с входной и импульсной характеристикой к свертка а , т.е. ,

(7.

где «’ означает свертку, как и раньше. Используя преобразование z обе части уравнения (6.3) и применяя теорему свертки из предыдущий раздел дает

(7.4)

где H(z) — преобразование z импульсной характеристики фильтра. Мы можем разделить уравнение (6.4) на, чтобы получить

Это показывает, что, как прямой результат теоремы свертки, z преобразование импульсной характеристики равно передаче функция

фильтра при условии, что фильтр линейный и неизменен во времени.

Начиная с z преобразование представления свертки для цифровых фильтров было так плодотворно, давайте применим его теперь к общему разностному уравнению, Уравнение (5. 1). Для этого требуются два свойства z преобразование, линейность (легко показать) и теорема о сдвиге (получено в §6.3 выше). Используя эти два свойства, мы может записать преобразование z любого разностного уравнения путем проверки, как сейчас покажем. В В §6.8.2 мы также покажем, как инвертировать путем проверки.

Повторяя общее разностное уравнение для фильтров LTI, имеем (из уравнения (5.1))

Возьмем z преобразование обеих сторон, обозначающее преобразование . Потому что является линейным оператором, его можно распределить через члены в правой части как следует: ^7,3 где мы использовали суперпозиционные и скейлинговые свойства линейности указано на странице , после чего используется сдвиг теорема именно в таком порядке. Термины в могут быть сгруппированы вместе с левой стороны, чтобы получить

Факторизация общих терминов и дает

Определение многочленов

преобразование z разностного уравнения дает

Наконец, решение для , которое по определению передаточная функция дает

(7.

Таким образом, преобразование общего разностного уравнения z привело к новому формула для передаточной функции в терминах разностного уравнения коэффициенты. (Теперь знаки минус для коэффициентов обратной связи в объясняются разностные уравнения (5.1).)

Факторная форма

По основной теореме алгебры каждый многочлен th порядка может быть разложено на в произведении полиномов первого порядка. Следовательно, уравнение (6.5) выше может быть записано в виде с учетом формы как

(7.6)

Корни числителя

называются нулями передаточной функции, а корни знаменателя

называются полюсами фильтра. Полюса и нули обсуждается далее в главе 8.

Передаточная функция удобно фиксирует алгебраическая структура операции фильтрации по отношению к серия или параллельная комбинация . В частности, у нас есть следующие случаи:

Передаточные функции последовательно соединенных фильтров перемножаются.
Передаточные функции фильтров, включенных параллельно, суммируются.

Случай серии

На рис. 6.1 показано последовательное соединение двух фильтры а также . Выход фильтра 1 используется как вход для фильтра 2. Таким образом, общая передаточная функция

Таким образом, если выходные данные фильтра заданы как входные данные для фильтр (последовательная комбинация), как показано на рис.6.1, общая передаточная функция равна

—передача функции фильтров, соединенных последовательно умножьте вместе.

Параллельный случай

Рисунок 6.2 иллюстрирует параллельную комбинацию двух фильтры. Фильтры и приводятся в действие тот же входной сигнал и соответствующие им выходы и суммируются . Передаточная функция параллельного комбинация поэтому

где нам нужна была только линейность z преобразовать, чтобы получить это

Комбинация серий коммутативна

Так как умножение комплексных чисел коммутативно, то

что означает, что любое последовательное расположение фильтров приводит к одинаковая общая передаточная функция. Обратите внимание, однако, что численное обычно влияет на производительность общего фильтра заказом ступеней фильтрации в последовательной комбинации [103]. Глава 9дополнительно рассматривает числовую производительность структур реализации фильтра.

По теореме свертки для z преобразований, из коммутативности произведения передаточных функций следует, что свертка коммутативна :

Расширение частичной дроби

Важный инструмент для инвертирования преобразования z и преобразования между цифровыми структуры реализации фильтра — это неполная дробь расширение (PFE). Термин «расширение частичной дроби» относится к разложение рациональной передаточной функции в сумму первых и/или термины второго порядка. Случай членов первого порядка является наиболее простым и самое основное:

(7.7)

куда

а также . (Случай рассматривается в следующем разделе.) Коэффициенты знаменателя называются полюса шт. передаточная функция, а каждый числитель называется остаток столба . Уравнение (6.7) является общим, только если полюса являются различными . (Повторяющиеся полюса рассматриваются в §6.8.5 ниже.) И полюса, и их остатки могут быть сложный. Полюса можно найти, разложив полином на множители в члены первого порядка, ^7.4 напр. , используя функцию root в Matlab. Вычет, соответствующий полюсу, может быть найден аналитически как

(7.8)

когда полюса различны. Функция Matlab

остаткиz

^7.5 найдет столбы и остатки вычислительно, учитывая разностное уравнение (передаточная функция) коэффициенты.

Обратите внимание, что в уравнении (6.8) всегда присутствует нулевая компенсация полюса в точке . То есть термин всегда отменяется тождественный член в знаменателе , который должен существовать, потому что имеет полюс в . Остаток — это просто коэффициент однополюсного члена частично дробное расширение at . Передаточная функция это , в пределе, как .

Пример

Рассмотрим двухполюсный фильтр

Полюса и . Тогда соответствующие остатки

Таким образом, мы заключаем, что

В качестве проверки мы можем добавить два однополюсных члена выше, чтобы получить

как и ожидалось.

Сложный пример

Чтобы проиллюстрировать пример со сложными полюсами, рассмотрим фильтр

где может быть любое действительное или комплексное значение. (Когда реально, фильтр в целом тоже реален.) Полюсы то и (или наоборот), а факторизованная форма может быть записана как

Используя уравнение (6.8), остатки равны

Таким образом,

Более сложный пример разложения частичной дроби на комплексную. однополюсные секции приведены в §3.12.1.

PFE в Real, разделы второго порядка

Когда все коэффициенты и действительны (имеется в виду, что является передаточной функцией настоящий фильтр ), он будет всегда случается, что сложные однополюсные фильтры встречаются в комплексно-сопряженные пары . Обозначим любой однополюсный сечение в ПФЭ уравнения (6.7). Тогда если сложно и описывает реальный фильтр, мы также найдем где-то среди членов однополюсного разложения. Эти два термина можно объединить в сформировать реальный раздел второго порядка выглядит следующим образом:

Выражая полюс в полярной форме как , а остаток как , последнее выражение выше можно переписать как

Использование коэффициентов полярной формы обсуждается далее в разделе на двухполюсных фильтрах (§B.1.3).

Разложение передаточной функции в сумму членов второго порядка с реальные коэффициенты дают нам коэффициенты фильтра для параллельного банка реальных секций фильтра второго порядка. (Конечно, каждый реальный полюс может реализовать в своей реальной однополюсной секции параллельно другие разделы.) Ввиду вышеизложенного, мы можем заключить, что каждый реальный фильтр с может быть реализован как параллельный банк из биквадраты . ^7.6 Однако полная общность биквадрата сечение (два полюса и два нуля) не нужно, т.к. требуется только один нуль на член второго порядка.

Чтобы понять, почему мы должны оговаривать в уравнении (6.7), рассмотрим сумму двух членов первого порядка прямым вычислением:

(7.9)

Обратите внимание, что порядок числителя, рассматриваемый как многочлен от , равен на один меньше порядка знаменателя. Таким же образом легко математической индукцией показано, что сумма однополюсных членов

может дать числитель порядка не более (в то время как порядок знаменателя, если нет полюс-ноль Аннулирование). Следуя терминологии, используемой для аналоговых фильтров, мы назвать дело строго правильным переводом функция . ^7.7 Таким образом, каждый строго может быть реализована правильная передаточная функция (с разными полюсами) с использованием параллельного набора двухполюсных секций фильтра с одним нулем.

Инвертирование Z-преобразования

Разложение на частичные дроби (PFE) обеспечивает простое средство для обращение преобразования z рациональных передаточных функций. ОФЭ дает сумму членов первого порядка вида

Легко проверить, что таким членом является преобразование z

Таким образом, обратное преобразование z просто

Таким образом, импульсная характеристика каждого строго правильного фильтра LTI (с отчетливыми полюсов) можно интерпретировать как линейная комбинация выборки комплексные экспоненты . Напомним, что равномерная экспонента — это то же самое, что и геометрическая . последовательность . Таким образом, является линейной комбинацией геометрических последовательности. Отношение членов th геометрической последовательности равно полюса, , а коэффициент го последовательность — остаток, .

В случае неправильных , обсуждаемом в следующем разделе, мы дополнительно получить КИХ-часть в преобразовании z для инвертирования:

КИХ-часть (многочлен конечного порядка по ) также легко перевернут осмотром.

Случай повторяющихся полюсов рассматривается в §6.8.5 ниже.

FIR Часть PFE

Когда в уравнении (6.7) мы можем выполнить шаг деления в длину для производства FIR часть параллельно с строго правильная часть IIR:

(7.

10)

куда

Когда , мы определяем . Этот тип разложения вычисляется функцией остатка (функция Matlab для вычисление полного разложения частичной дроби, как показано на §6.8.8 ниже).

Альтернативная КИХ-часть получается путем выполнения длинного деления на инвертировали коэффициента полинома, чтобы получить

(7.11)

где

снова порядок FIR-части. Этот тип разложения вычисляется (как часть PFE) на

остаток

, описанный в §J.6 и проиллюстрированный численно в §6.8.8 ниже.

Мы можем сравнить эти две альтернативы PFE следующим образом: Обозначим , , а также . ( То есть , мы используем нижний индекс для обозначения полиномиального порядка, а `’ опущен для простоты обозначений. ) Тогда для имеем два случая:

В первой форме, коэффициенты «левые» оправдано» в реконструированном числителе, а во второй форме они «право оправданы». Вторая форма, как правило, более эффективен для целей моделирования , поскольку числитель IIR часть ( ) может использоваться для сопоставления дополнительных термины в импульсной характеристике после того, как часть КИХ имеет «вымерли».

Таким образом, передаточная функция произвольного цифрового фильтра с различные полюса всегда могут быть выражены как параллельная комбинация из комплексные однополюсные фильтры вместе с параллельной КИХ-частью когда . Когда есть часть FIR, строго правильный IIR часть может быть задержана таким образом, что ее импульсная характеристика начинается там, где части FIR уходит.

В приложениях с искусственной реверберацией КИХ-часть может соответствовать к ранним отражениям , в то время как часть IIR обеспечивает поздняя реверберация , обычно плотная, гладкая и экспоненциально затухает [86]. predelay («предварительная задержка») контроль в некоторых коммерческих ревербераторах количество чистой задержки в начале ревербератора импульсивный ответ. Таким образом, пренебрегая ранними отражениями, порядок часть FIR можно рассматривать как величину предварительной задержки для части IIR.

Пример: General Biquad PFE

Общий случай второго порядка с (т.н. biquad section) можно записать когда как

Чтобы выполнить разложение частичной дроби, нам нужно извлечь порядок 0 (длина 1) FIR-часть через длинное деление. Пусть и переписать как отношение полиномов от :

Тогда длинное деление дает
уступающий

или же

Задержанная форма разложения частичной дроби получается с помощью оставляя коэффициенты в их первоначальном порядке. Это соответствует записать как отношение полиномов от :

Длинное деление теперь выглядит как
давать

Численные примеры разложения неполных дробей приведены в §6. 8.8. ниже. Другой рабочий пример, в котором фильтр преобразуется в набор параллельных, второго порядка разделы приведены в §3.12. См. также §9.2 относительно преобразование в разделы второго порядка в целом и §G.9.1 (особенно Уравнение (G.22)) относительно подход в пространстве состояний к разложению частичной дроби.

Альтернативные методы PFE

Другой метод нахождения полюсных вычетов состоит в том, чтобы записать общее форма ФФЭ, получить общий знаменатель, расширить числитель условия для получения одного многочлена, и приравнять подобные степени . Это дает линейную систему уравнений с неизвестными, .

Еще один метод нахождения остатков — с помощью рядов Тейлора. разложения числителя и знаменателя по каждому полюс, используя l’Hôpital’s правило..

Наконец, в качестве альтернативы можно построить пространство состояний . реализация строго правильной передаточной функции (с использованием, например, , tf2ss в матлабе), а затем диагонали через преобразование подобия . (См. Приложение G для введение в модели в пространстве состояний и их диагонализация с помощью преобразования подобия.) Передаточная функция диагонализированной модели в пространстве состояний имеет вид тривиально получается как сумма однополюсных членов — т.е. , PFE. В других словами, неявно диагонализируя реализацию фильтра в пространстве состояний выполняет частичное расширение передачи фильтра функция. Когда полюса различны, модель в пространстве состояний может быть диагональный; когда есть повторяющиеся полюса, это может быть вместо этого блочно-диагональные, как обсуждается далее в §G.10.

Повторяющиеся поляки

Когда полюса повторяются, возникает новое интересное явление. К посмотрим, что происходит, давайте рассмотрим два одинаковых полюса, расположенных в параллельно и последовательно. В параллельном случае имеем

В случае серии получаем

Таким образом, два однополюсных фильтра параллельно эквивалентны новому однополюсный фильтр ^7,8 (при совпадении полюсов), а те же два фильтры серии дают двухполюсный фильтр с повторным столб. Чтобы учесть обе возможности, общая частичная дробь расширение должно включать термины

для полюса, имеющего кратность 2.

Аналитическая работа с повторяющимися полюсами

Полюс кратности имеет остатки, связанные с ним. Например,


			(7.12)

и три остатка, связанные с полюсом, это 1, 2 и 4.

Обозначим th остаток, связанный с полюсом , . Последовательно дифференцируя раз с относительно и установка изолирует остаток:

или же

Пример

Для примера уравнения (6. 12) получаем

Импульсная характеристика повторяющихся полюсов

Во временной области повторяющиеся полюса дают полином огибающие амплитуды на затухающих экспонентах, соответствующих (устойчивые) столбы. Например, в случае повторения одного полюса дважды, у нас есть

Доказательство: Сначала обратите внимание, что

Следовательно,






			(7. 13)

Обратите внимание, что это полином первого порядка по . Аналогично, столб повторенный три раза соответствует компоненту импульсного отклика, который представляет собой экспоненциальное затухание, умноженное на квадратичный полином в , и так далее. Пока импульсная характеристика будет в конечном итоге затухает до нуля, потому что экспоненциальный затухание всегда настигает полиномиальный рост в пределе при стремлении к бесконечности.

Итак, что случилось с повторяющимися полюсами?

В предыдущем разделе мы обнаружили, что повторяющиеся полюса порождают полиномиальные амплитудные огибающие, умножающие экспоненциальный спад из-за к полюсу. С другой стороны, два различных полюса могут только дают свертку (или сумму) двух разных экспоненциальных распадов с полиномиальная оболочка не допускается. Это правда, независимо от того, насколько близко полюса сходятся; полиномиальная оболочка может иметь место только тогда, когда полюса точно сливаются. Это может нарушить интуитивную ожидание непрерывного изменения при переходе от двух близких разнесенные полюса к повторяющемуся полюсу.

Для дальнейшего изучения этого явления рассмотрим свертку двух однополюсные импульсные характеристики а также :

(7.14)

Конечные пределы суммирования возникают из-за того, что оба и являются причинными. Напомним сумму усеченного геометрический ряд:

Применяя это к уравнению (6.14), получаем

Заметим, что результат симметричен относительно и . Если

, то становится пропорциональным для больших, а если

, становится вместо пропорционально .

Возвращаясь к уравнению (6. 14), имеем

(7.15)

Настройка урожайности

(7.16)

что является случаем полиномиальной амплитуды-огибающей первого порядка для повторный полюс. Мы видим, что переход от «двух свернутых экспоненты» в «одну экспоненту с полиномиальной амплитудой конверт» совершенно непрерывен, как и следовало ожидать.

Мы также видим, что полиномиальная амплитуда огибает фундаментально возникают из повторных сверток . Это соответствует повторные полюса расположены в серии , а не в параллельно. Простейший случай, когда повторяющийся полюс находится в точке , в в этом случае его импульсная характеристика является постоянной:

Свертка константы с самой собой представляет собой рампу:

Свертка константы и рампы является квадратичной, поэтому на: ^7,9

Альтернативный Критерий стабильности

В §5. 6 (стр.) фильтр был определен для быть стабильным , если его импульсная характеристика затухает до 0 в величина с течением времени стремится к бесконечности. В §6.8.5 мы видели, что импульсная характеристика каждого фильтра LTI конечного порядка может быть выражена как возможная КИХ-часть (которая всегда стабильна) плюс линейная сочетание терминов формы , где какой полином конечного порядка по , и является th полюсом фильтр. В таком виде видно, что импульсная характеристика всегда затухает до нуля, когда каждый полюс находится строго внутри единичной окружности самолет, т.е. , когда . Таким образом, имея все полюса строго внутри единичного круга находится достаточный критерий для фильтрации стабильность. Если фильтр наблюдаемых (имеется в виду, что есть в передаточной функции от входа к выход), то это тоже необходимый критерий.

Говорят, что передаточная функция без нулевого сокращения полюса неприводимый . Например, является неприводимый, в то время как приводим, так как есть общий фактор в числителе и знаменатель. Используя эту терминологию, мы можем констатировать следующее. Критерий стабильности:

Эта характеристика устойчивости будет продолжена в §8.4. и еще один тест на стабильность (наиболее часто используемый на практике) дано в §8.4.1.

Резюме разложения частичной дроби

Таким образом, разложение частичной дроби можно использовать для расширения любое рациональное преобразование z

в виде суммы членов первого порядка

(7.17)

для и

(7.

18)

для , где термин

является необязательным, но часто предпочтительно. Для реальных фильтров комплексные однополюсные члены могут быть объединены в пары. до получения членов второго порядка с действительными коэффициентами. Процедура PFE выполняется в два или три этапа:

При , выполните шаг длинного деления, чтобы получить часть FIR и строго правильная часть IIR .
Найди полюса, (корни из ).
Если полюса различны, найти остатки , из
Если есть повторяющиеся полюса, найти дополнительные остатки через метод §6.8.5, а общая форма PFE такова:
(7.19)

где обозначает количество различных полюсов, а обозначает кратность -го полюса.

На шаге 2 полюса обычно находятся с помощью факторизации полином знаменателя. Это опасный шаг численно который может выйти из строя, когда есть много полюсов, особенно когда много полюсов сгруппированы близко друг к другу в плоскости.

Следующий код Matlab иллюстрирует факторинг к получить три корня, , :

А = [1 0 0 -1]; % Полином знаменателя фильтра
полюса = корни (A) % полюсов фильтра

Дополнительные сведения о цифровых фильтрах см. в главе 9. реализованы как параллельные разделы (особенно §9.2.2).

Программное обеспечение для разложения неполных дробей

Рисунок 6.3 иллюстрирует использование вычетаz (§J.5). для выполнения разложения частичной дроби на передаточную функцию

Комплексно-сопряженные члены можно комбинировать, чтобы получить два действительных секции второго порядка, что в сумме дает одну реальную секцию первого порядка параллельно с двумя реальными секциями второго порядка, как обсуждалось и изображено в §3. 12. 95]; [r,p,f] = остатокz(B,A) % г = % 0,16571 % 0,22774 — 0,02016i % 0,22774 + 0,02016i % 0,18940 + 0,03262i % 0,18940 — 0,03262i % % р = % -0,

% -0,27812 — 0,85595i % -0,27812 + 0,85595i % 0,72812 — 0,52901i % 0,72812 + 0,52901i % %f = [](0x0)

Пример 2

Для фильтра

			(7.20)
			(7.21)

мы получаем вывод

остатков

(§J.6), показанный в Рис.6.4. В отличие от остатка

, остатка

задерживает часть IIR до окончания части FIR. В отличие от этого результата,

остатокz

возвращает

r=[-24;16]

f=[10;2]

, соответствующий ПФЭ

(7.22)

в котором части FIR и IIR имеют перекрывающиеся импульсные характеристики.

См. Разделы J.5 и J.6, начиная со стр. списки остатковz, остатков и родственных обсуждение.

**Рисунок 6.4:** Использование остатка для выполнения частичное разложение передаточной функции БИХ-фильтра .
В=[2 6 6 2]; А=[1 -2 1]; [r,p,f,m] = остаток(B,A) % г = % 8 % 16 % % р = % 1 % 1 % % ф = % 2 10 % % м = % 1 % 2

Полиномиальное умножение в Matlab

Функция Matlab conv ( свертка ) может использоваться для выполнить полиномиальное умножение . Например:

В1 = [1 1]; % 1-я строка треугольника Паскаля
В2 = [1 2 1]; % 2-я строка треугольника Паскаля
B3 = конв(B1,B2)% 3-я строка
% В3 = 1 3 3 1
B4 = конв(B1,B3)% 4-я строка
% В4 = 1 4 6 4 1
% ...

Matlab

conv(B1,B2)

идентичен

filter(B1,1,B2)

, за исключением того, что

conv

возвращает полную свертку двух своих входные векторы, а фильтр

усекает результат до длина «входного сигнала»

В2

. ^7.10 Таким образом, если

дополненный нулями

length(B1)-1

нулей, будет возвращена полная свертка:

В1 = [1 2 3];
В2 = [4 5 6 7];
конв(B1,B2)
% и = 4 13 28 34 32 21
фильтр(B1,1,B2)
% исп = 4 13 28 34
фильтр(B1,1,[B2,нули(1,длина(B1)-1)])
% и = 4 13 28 34 32 21

Полиномиальное деление в Matlab

Функция Matlab deconv ( 92 [первая часть, остаток] = deconv(B,A) % часть = % 2 10 % остаток = % 0 0 24 -8

Таким образом, этот пример находит то, что написано в уравнении (6. 21). Этот результат можно проверить, найдя общий знаменатель, чтобы чтобы пересчитать числитель прямой формы:

Bh = остаток + конв (первая часть, A)
% = 2 6 6 2

Операция deconv(B,A) может быть реализована с использованием фильтровать способом, аналогичным полиномиальному случай умножения (см. §6.8.8 выше):

firpart = filter(B,A,[1,zeros(1,length(B)-length(A))])
% = 2 · 10
остаток = B - conv(Firstpart,A)
% = 0 0 24 -8

В том, что это должно работать, можно убедиться, взглянув на уравнение (6.21) и отметив, что импульсная характеристика остатка (строго часть) не начинается до времени , так что первые два образца импульсного отклика исходят только из FIR-части.

Таким образом, мы можем удобно использовать свертки и деконволюции для выполнять полиномиальное умножение и деление соответственно, например при преобразовании передаточных функций в различные альтернативные формы.

При выполнении разложения частичной дроби на передаточную функцию порядок числителя которого равен или превышает знаменатель порядок, необходимым предварительным шагом является выполнение длинного деления на получить КИХ-фильтр параллельно со строго правильным переносом функция. В этом разделе описывается, как КИХ-часть любой длины может быть извлекаются из БИХ-фильтра, и это можно использовать как для PFE, так и для для более сложных приложений [].

См. http://ccrma.stanford.edu/~jos/filtersp/Transfer_Function_Analysis_Problems.html.

Следующий раздел:
Анализ частотной характеристики
Предыдущий раздел:
Представления цифрового фильтра во временной области

Работа с передаточными функциями фильтра нижних частот в моделировании | Блог Advanced PCB Design

Мой папа недавно взял в аренду новый автомобиль, который заменит его проверенный 20-летний грузовик. Как только он получает новую игрушку, ему всегда нравится нажимать на все кнопки и смотреть, какие странные вещи он может делать. В последнее время он играет с изменением выхода динамика для любой музыки или звука и возится со своими пассажирами. Это напоминает мне игру с эквалайзером на старой аналоговой стереосистеме. Эти ручки тогда были подключены к схеме фильтра.

Из различных типов фильтров фильтры нижних частот очень важны для получения чистых сигналов в ряде систем. Итак, как проще всего посмотреть, как работает конкретный фильтр нижних частот? Это функция передачи фильтра нижних частот пригодится.

Фильтры нижних частот и их передаточные функции

Как следует из названия, фильтр нижних частот представляет собой электронное устройство, позволяющее низкочастотным сигналам переменного тока пропускать ток через схему фильтра. Выходной сигнал схемы фильтра будет ослаблен в зависимости от частоты входного сигнала. Для построения схем фильтров с различными характеристиками можно использовать ряд различных активных и пассивных компонентов. Некоторые фильтры включают фильтры нижних частот, верхних частот, полосовые, всепроходные эллиптические фильтры, фильтры Чебышева и Баттерворта.

Самый простой способ описать поведение фильтра — определить передаточную функцию. Передаточная функция сообщает вам, как выходной сигнал связан с входным сигналом на различных частотах. Если вы проектируете схему фильтра, вы можете легко определить передаточную функцию по графику выходного сигнала на различных частотах. Вы также можете рассчитать передаточную функцию, используя законы Кирхгофа, чтобы получить дифференциальное уравнение, управляющее цепью.

Определение передаточной функции, ее величины и фазы для синусоидального сигнала

Когда сигнал проходит через фильтр, фильтр применяет некоторый фазовый сдвиг к выходному сигналу по отношению к входному сигналу. Это означает, что передаточная функция фильтра является сложной функцией частоты, а передаточная функция содержит всю информацию, необходимую для определения величины выходного сигнала и его фазы. Общее определение передаточной функции, ее величина и фаза показаны на изображении выше. Зная передаточную функцию фильтра, вы можете преобразовать ее в график Боде, чтобы получить представление о передаточной функции в дБ.

Если эта идея передаточной функции, определяющей поведение фильтра, вам незнакома, удобно рассматривать передаточную функцию в терминах импеданса. Подобно тому, как импеданс представляет собой комплексное число, определяющее частотно-зависимое сопротивление, передаточная функция определяет частотно-зависимое затухание или усиление. Вместо того, чтобы связывать выходной ток и входное напряжение, как в случае с законом Ома, вы просто меняете значение входного напряжения на какое-то другое значение. Передаточные функции фильтра нижних частот существенно увеличивают затухание по мере увеличения частоты.

Передаточные функции фильтра нижних частот высшего порядка

В некоторых приложениях вы можете обнаружить, что спад в передаточной функции фильтра нижних частот недостаточно крутой. Это означает, что в выходном сигнале все еще присутствует некоторый высокочастотный контент, который пропускается через фильтр. Если вам нужна более качественная фильтрация этих более высоких частот, вы можете создать фильтр более высокого порядка, соединив несколько фильтров последовательно. В общем, простой фильтр, построенный из RLC или аналогичной схемы, называется фильтром первого порядка. Два фильтра первого порядка, соединенные последовательно, называются фильтром второго порядка, и так далее…

Фильтр более высокого порядка похож на стопку кофейных фильтров

более высокие частоты. Это очень полезно для подавления высокочастотного шума. Один пример включает в себя сбор сигнала от массива датчиков, которые могут быть чувствительны к радиочастотам. Если вы пропускаете сигнал через фильтр нижних частот, вы можете значительно подавить радиочастотные сигналы на более высоких частотах. Средние и высокие частоты будут подавлены в большей степени при использовании фильтра более высокого порядка.

Более общие передаточные функции

Обратите внимание, что передаточная функция часто определяется в терминах преобразования Лапласа для дифференциального уравнения, описывающего цепь. Однако вы можете записать передаточную функцию через частоту синусоидального источника, используя приведенное выше уравнение. Это делается путем подстановки s=iω в типичную передаточную функцию. Это дает вам удобное представление передаточной функции для отдельных частот.

В случае цепи с гармоническим возбуждением, которая не выходит из равновесия, передаточная функция может быть легко определена простым преобразованием Фурье дифференциального уравнения, описывающего цепь. Использование преобразования Лапласа для получения передаточной функции обычно предпочтительнее в системах с обратной связью, поэтому вам нужно будет определить, является ли система стабильной. Если вы не проектируете фильтр нижних частот с активной обратной связью (например, фильтр Баттерворта), при синусоидальном возбуждении не следует учитывать элемент стабильности, поэтому подход Фурье подходит для большинства приложений.

Если вы используете развертку частоты переменного тока с пакетом SPICE и измеряете выходное напряжение фильтра нижних частот, вы можете определить амплитуду и фазу на каждой частоте возбуждения и построить график передаточной функции в частотной области. Для определения переходной характеристики цепи необходимо использовать поиск во временной области при импульсном управлении или управлении ступенчатой функцией.

Операционные усилители присутствуют в ряде схем фильтров

Наконец, при работе с активными компонентами вы можете использовать анализ во временной области для схемы на разных частотах, если хотите проверить стабильность. Это требует некоторого времени, поскольку вы изучаете влияние двух параметров. Если вы выполняете развертку по частоте, вы можете увидеть пик передаточной функции вблизи собственной частоты схемы, соответствующий усилению в системе вблизи отсечки.

Определение передаточной функции и построение диаграммы Боде для любой схемы и любого типа источника значительно упрощается при использовании мощного пакета SPICE, упрощающего анализ сложных схем в частотной области. Пакет OrCAD PSpice Simulator от Cadence позволяет выполнять развертку по частоте, анализ переходных процессов и многие другие задачи, важные для проектирования и анализа аналоговых схем для любого приложения.

Этот уникальный пакет адаптирован для сложных конструкций печатных плат, напрямую взаимодействует с вашими проектными данными и помогает создавать передаточные функции для ваших схем фильтров.

Если вы хотите узнать больше о решениях, которые Cadence предлагает вам, обратитесь к нам и нашей команде экспертов.

Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.

Подпишитесь на LinkedIn Посетить сайт Больше контента от Cadence PCB Solutions

Веб-сайт RF Wireless World является домом для поставщиков и ресурсов RF и Wireless. На сайте представлены статьи, учебные пособия, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тесты и измерения, калькуляторы, новости, книги, загрузки и многое другое.

Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, оптоволокно, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. д. Эти ресурсы основаны на стандартах IEEE и 3GPP. Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и дисциплинам MBA.

Система обнаружения падений для пожилых людей на основе IoT : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей. В нем упоминаются преимущества или преимущества системы обнаружения падения IoT. Подробнее➤
См. также другие статьи о системах на основе IoT:
• Система очистки туалетов AirCraft. • Система измерения удара при столкновении • Система отслеживания скоропортящихся продуктов и овощей • Система помощи водителю • Система умной розничной торговли • Система мониторинга качества воды • Система интеллектуальной сети • Умная система освещения на основе Zigbee • Умная система парковки на базе Zigbee • Умная система парковки на базе LoRaWAN.

Этот раздел статей охватывает статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE/3GPP и т. д. , стандарты. Он также охватывает статьи, связанные с испытаниями и измерениями, посвященные испытаниям на соответствие, используемым для испытаний устройств на соответствие RF/PHY. СМ. УКАЗАТЕЛЬ СТАТЕЙ >>.

В этом разделе рассматриваются функции 5G NR (новое радио), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. д. 5G NR Краткий справочный указатель >>
• Мини-слот 5G NR • Часть полосы пропускания 5G NR • БАЗОВЫЙ НАБОР 5G NR • Форматы 5G NR DCI • 5G NR UCI • Форматы слотов 5G NR • IE 5G NR RRC • 5G NR SSB, SS, PBCH • 5G NR PRACH • 5G NR PDCCH • 5G NR PUCCH • Опорные сигналы 5G NR • 5G NR m-Sequence • Золотая последовательность 5G NR • 5G NR Zadoff Chu Sequence • Физический уровень 5G NR • MAC-уровень 5G NR • Уровень 5G NR RLC • Уровень PDCP 5G NR

В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводным сетям. Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, беспроводная сеть, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. д. См. ИНДЕКС УЧЕБНЫХ ПОСОБИЙ >>

Учебное пособие по 5G — В этом учебном пособии по 5G также рассматриваются следующие подтемы, посвященные технологии 5G:
Учебник по основам 5G Диапазоны частот учебник по миллиметровым волнам Рамка волны 5G мм Зондирование канала миллиметровых волн 5G 4G против 5G Испытательное оборудование 5G Архитектура сети 5G Сетевые интерфейсы 5G NR звучание канала Типы каналов 5G FDD против TDD Нарезка сети 5G NR Что такое 5G NR Режимы развертывания 5G NR Что такое 5G ТФ

В этом учебнике GSM рассматриваются основы GSM, сетевая архитектура, сетевые элементы, системные спецификации, приложения, Типы пакетов GSM, структура кадров GSM или иерархия кадров, логические каналы, физические каналы, Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM или настройка вызова или процедура включения питания, Вызов MO, вызов MT, модуляция VAMOS, AMR, MSK, GMSK, физический уровень, стек протоколов, основы мобильного телефона, Планирование RF, нисходящая линия связи PS и восходящая линия связи PS.
➤Подробнее.

LTE Tutorial , описывающий архитектуру системы LTE, включая основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он предоставляет ссылку на обзор системы LTE, радиоинтерфейс LTE, терминологию LTE, категории LTE UE, структуру кадра LTE, физический уровень LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, Voice Over LTE, расширенный LTE, Поставщики LTE и LTE vs LTE advanced.➤Подробнее.

На этой странице мира беспроводных радиочастот описывается пошаговое проектирование преобразователя частоты на примере повышающего преобразователя частоты 70 МГц в диапазон C. для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO, амортизирующие прокладки. ➤Читать дальше.
➤ Проектирование и разработка РЧ приемопередатчика ➤Дизайн радиочастотного фильтра ➤Система VSAT ➤Типы и основы микрополосковых ➤Основы волновода

В этом разделе рассматриваются ресурсы по контролю и измерению, контрольно-измерительное оборудование для тестирования тестируемых устройств на основе Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE. ИНДЕКС испытаний и измерений >>
➤Система PXI для контрольно-измерительных приборов. ➤ Генерация и анализ сигналов ➤ Измерения физического уровня ➤ Тестирование устройства WiMAX на соответствие ➤ Тест на соответствие Zigbee ➤ Тест на соответствие LTE UE ➤ Тест на соответствие TD-SCDMA

Волоконно-оптический компонент основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель, фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д. Эти компоненты используются в оптоволоконной связи. ИНДЕКС оптических компонентов >>
➤Руководство по оптоволоконной связи ➤APS в SDH ➤Основы SONET ➤ Структура кадра SDH ➤ SONET против SDH

Поставщики ВЧ-компонентов, включая ВЧ-изолятор, ВЧ-циркулятор, ВЧ-смеситель, ВЧ-усилитель, ВЧ-адаптер, ВЧ-разъем, ВЧ-модулятор, ВЧ-трансивер, PLL, VCO, синтезатор, антенну, осциллятор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексер, дуплексер, чип-резистор, чип-конденсатор, чип-индуктор, ответвитель, ЭМС, программное обеспечение RF Design, диэлектрический материал, диод и т. д. Поставщики радиочастотных компонентов >>
➤Базовая станция LTE ➤ РЧ-циркулятор ➤РЧ-изолятор ➤Кристаллический осциллятор

Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW. Эти коды полезны для новичков в этих языках. СМОТРИТЕ ИНДЕКС ИСТОЧНИКОВ >>
➤ 3–8 код VHDL декодера ➤Скремблер-дескремблер Код MATLAB ➤32-битный код ALU Verilog ➤ T, D, JK, SR триггер коды labview

*Общая медицинская информация*
Сделайте эти пять простых вещей, чтобы помочь остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: Мойте их чаще
2. ЛОКОТЬ: кашляйте в него
3. ЛИЦО: не прикасайтесь к нему
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВУЙТЕ: заболели? Оставайтесь дома
Используйте технологию отслеживания контактов >> , следуйте рекомендациям по социальному дистанцированию >> и установить систему наблюдения за данными >> спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таких стран, как США и Китай, чтобы остановить распространение COVID-19так как это заразное заболевание.
Радиочастотные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц измерения. Они охватывают беспроводные технологии, такие как GSM, UMTS, LTE, 5G NR и т. д. СМ. КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR ➤ 5G NR ARFCN и преобразование частоты ➤ Калькулятор скорости передачи данных LoRa ➤ LTE EARFCN для преобразования частоты ➤ Калькулятор антенны Yagi ➤ Калькулятор времени выборки 5G NR
IoT-Интернет вещей Беспроводные технологии
В разделе, посвященном IoT, рассматриваются беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet, 6LoWPAN, RF4CE, Bluetooth, Bluetooth с низким энергопотреблением (BLE), NFC, RFID, INSTEON, X10, KNX, ANT+, Wavenis, Dash7, HomePlug и другие. Он также охватывает датчики IoT, компоненты IoT и компании IoT.
См. главную страницу IoT>> и следующие ссылки.
➤РЕЗЬБА ➤EnOcean ➤ Учебник LoRa ➤ Учебник по SIGFOX ➤ WHDI ➤6LoWPAN ➤Зигби RF4CE ➤NFC ➤Лонворкс ➤CEBus ➤УПБ

СВЯЗАННЫЕ ПОСТЫ

Учебники по беспроводным радиочастотам
GSM ТД-СКДМА ваймакс LTE UMTS GPRS CDMA SCADA беспроводная сеть 802.11ac 802.11ad GPS Зигби z-волна Bluetooth СШП Интернет вещей Т&М спутник Антенна РАДАР RFID

Различные типы датчиков
Датчик приближения Датчик присутствия против датчика движения Датчик LVDT и RVDT Датчик положения, смещения и уровня датчик силы и датчик деформации Датчик температуры датчик давления Датчик влажности датчик МЭМС Сенсорный датчик Тактильный датчик Беспроводной датчик Датчик движения Датчик LoRaWAN Световой датчик Ультразвуковой датчик Датчик массового расхода воздуха Инфразвуковой датчик Датчик скорости Датчик дыма Инфракрасный датчик Датчик ЭДС Датчик уровня Активный датчик движения против пассивного датчика движения

Поделиться этой страницей

Перевести эту страницу
СТАТЬИ Раздел T&M ТЕРМИНОЛОГИИ Учебники Работа и карьера ПОСТАВЩИКИ Интернет вещей Онлайн калькуляторы исходные коды ПРИЛОЖЕНИЕ. ЗАМЕТКИ Всемирный веб-сайт T&M
Обработка сигналов (scipy.signal) — SciPy v1.9.1 Manual
свертка
свертка (in1, in2[ режим, метод])
Свернуть два N-мерных массива.
корреляция (in1, in2[ режим, метод])
Взаимная корреляция двух N-мерных массивов.
fftconvolve (in1, in2[ режим, оси])
Свертка двух N-мерных массивов с помощью БПФ.
oaconvolve (in1, in2[ режим, оси])
Свертка двух N-мерных массивов с использованием метода сложения-наложения.
convolve2d (in1, in2[ режим, граница, значение заполнения])
Свернуть два двумерных массива.
корреляция2d (вх1, вх2[ мода, граница, . ..])
Взаимная корреляция двух двумерных массивов.
sepfir2d (ввод, hrow, hcol)
Convolve с двухмерным отделяемым КИХ-фильтром.
Choose_conv_method (in1, in2[ режим, мера])
Найдите самый быстрый метод свертки/корреляции.
корреляция_лаги (in1_len, in2_len[ mode])
Вычисляет массив индексов запаздывания/смещения для одномерной кросс-корреляции.
B-шлицы
сплайн (х, п)
Базисная функция B-сплайна порядка n.
куб. (х)
Кубический B-сплайн.
квадратичный (x)
Квадратичный B-сплайн.
gauss_spline (x, n)
Гауссова аппроксимация базисной функции B-сплайна порядка n.
cspline1d (сигнал [ ягненок])
Вычислить коэффициенты кубического сплайна для массива ранга 1.
qspline1d (сигнал [ баранина])
Вычислить коэффициенты квадратичного сплайна для массива ранга 1.
cspline2d (ввод [ лямбда, точность])
Коэффициенты для двумерного кубического (3-го порядка) B-сплайна.
qspline2d (ввод[ лямбда, точность])
Коэффициенты для двумерного квадратичного (2-го порядка) B-сплайна:
cspline1d_eval (cj, newx[ dx, x0])
Оценить кубический сплайн в новом наборе точек.
qspline1d_eval (cj, newx[ dx, x0])
Оцените квадратичный сплайн в новом наборе точек.
spline_filter (Iin[ lmbda])
Сглаживающая сплайновая (кубическая) фильтрация массива ранга 2.
Фильтрация
order_filter (a, домен, ранг)
Выполнить фильтр порядка на массиве N-D.
медфильтр (объем[ размер_ядра])
Выполнение медианного фильтра для N-мерного массива.
medfilt2d (вход[ kernel_size])
Медианный фильтр двумерного массива.
сосиска (im[ mysize, шум])
Фильтр Винера для N-мерного массива.
symiirorder1 (ввод, c0, z1[ точность])
Реализуйте сглаживающий БИХ-фильтр с зеркально-симметричными граничными условиями, используя каскад секций первого порядка. Во втором разделе используется обратная последовательность. Это реализует систему со следующей передаточной функцией и зеркально-симметричными граничными условиями::.
symiirorder2 (ввод, r, омега[ точность])
Реализовать сглаживающий БИХ-фильтр с зеркально-симметричными граничными условиями, используя каскад секций второго порядка. Во втором разделе используется обратная последовательность. Это реализует следующую передаточную функцию::.
lфильтр (b, a, x[ ось, zi])
Фильтрация данных по одному измерению с помощью БИХ- или КИХ-фильтра.
фильтр (б, а, у[ х])
Построить начальные условия для lfilter заданных входных и выходных векторов.
lfilter_zi (б, а)
Создание начальных условий для lfilter для установившегося режима отклика на скачок.
фильтрфильтр (b, a, x[ ось, padtype, padlen, …])
Применение цифрового фильтра к сигналу вперед и назад.
savgol_filter (x, window_length, polyorder[ …])
Применение фильтра Савицкого-Голея к массиву.
деконволюция (сигнал, делитель)
Деконволюция делителя из сигнала с помощью обратной фильтрации.
сосфилт (сос, х[ ось, зи])
Фильтрация данных по одному измерению с использованием каскадных секций второго порядка.
sosfilt_zi (сос)
Построение начальных условий для sosfilt для установившегося режима переходной характеристики.
sosfiltfilt (sos, x[ ось, padtype, padlen])
Цифровой фильтр прямого и обратного действия, использующий каскадные секции второго порядка.
гильберт (x[ N, ось])
Вычислите аналитический сигнал, используя преобразование Гильберта.
гильберт2 (x[ N])
Вычисление ‘2-D’ аналитического сигнала x
прореживание (x, q[ n, ftype, ось, zero_phase])
Понижает дискретизацию сигнала после применения сглаживающего фильтра.
удаление тренда (данные [ ось, тип, бит, перезапись_данных])
Удалить линейный тренд вдоль оси из данных.
повторная выборка (x, число[ t, ось, окно, домен])
Передискретизируйте x до num выборок, используя метод Фурье вдоль заданной оси.
resample_poly (x, вверх, вниз [ ось, окно, …])
Передискретизировать x вдоль заданной оси с использованием многофазной фильтрации.
вверх (h, x[ вверх, вниз, ось, режим, cval])
Повышение частоты дискретизации, КИХ-фильтр и понижение частоты дискретизации.
Конструкция фильтра
билинейная (б, а[ фс])
Возврат цифрового БИХ-фильтра из аналогового с помощью билинейного преобразования.
bilinear_zpk (z, p, k, fs)
Возврат цифрового БИХ-фильтра из аналогового с помощью билинейного преобразования.
findfreqs (num, den, N[ kind])
Найдите массив частот для вычисления отклика аналогового фильтра.
Fils (нумерация, полосы, желаемый [ вес, nyq, fs])
Конструкция КИХ-фильтра с использованием минимизации ошибки методом наименьших квадратов.
firwin (нумерация, отсечка [ ширина, окно, …])
Расчет КИХ-фильтра оконным методом.
firwin2 (numtaps, freq, gain[ nfreqs, . ..])
КИХ-фильтр с использованием оконного метода.
частоты (б, а[ работа, сюжет])
Вычисление частотной характеристики аналогового фильтра.
freqs_zpk (z, p, k[ work])
Вычисление частотной характеристики аналогового фильтра.
частота (б[ а, работа, целое, сюжет, фс, …])
Расчет частотной характеристики цифрового фильтра.
freqz_zpk (z, p, k[ work, integer, fs])
Расчет частотной характеристики цифрового фильтра в форме ZPK.
sosfreqz (sos[ работа, целое, fs])
Расчет частотной характеристики цифрового фильтра в формате SOS.
гамматон (частота, ftype[ порядок, numtaps, fs])
Гамматоновый фильтр.
group_delay (система[ w, целое, fs])
Вычислить групповую задержку цифрового фильтра.
iirdesign (wp, ws, gpass, gstop[ аналог, …])
Полная конструкция цифровых и аналоговых фильтров IIR.
iirfilter (N, Wn[ rp, rs, btype, аналог, …])
Конструкция цифровых и аналоговых фильтров IIR с заданным порядком и критическими точками.
kaiser_atten (нумерация, ширина)
Вычислите затухание КИХ-фильтра Кайзера.
kaiser_beta (а)
Вычислить параметр Кайзера бета , учитывая затухание и .
kaiserord (волна, ширина)
Определите параметры окна фильтра для метода окна Кайзера.
минимальная_фаза (h[ метод, n_fft])
Преобразование КИХ-фильтра с линейной фазой в режим минимальной фазы
savgol_coeffs (window_length, polyorder[ . ..])
Вычислите коэффициенты для одномерного КИХ-фильтра Савицкого-Голея.
ремез (нумерация, диапазоны, желаемый [ вес, Гц, …])
Рассчитайте минимаксный оптимальный фильтр, используя алгоритм обмена Ремеза.
unique_roots (p[ tol, rtype])
Определите уникальные корни и их кратности из списка корней.
остаток (б, а[ тол, ртип])
Вычисление частичной дроби b(s) / a(s).
остатокz (б, а[ тол, тип])
Вычисление частичной дроби b(z) / a(z).
инверсия (r, p, k[ tol, rtype])
Вычислить b(s) и a(s) из разложения неполных дробей.
инврез (р, п, к[ тол, ртип])
Вычислить b(z) и a(z) из разложения неполных дробей.
Плохие коэффициенты
Предупреждение о плохо подготовленных коэффициентах фильтра
Конструктивные функции фильтра нижнего уровня:
abcd_normalize ([A, B, C, D])
Проверить матрицы пространства состояний и убедиться, что они двумерные.
band_stop_obj (wp, ind, passb, stopb, gpass, …)
Целевая функция Band Stop Функция минимизации ордеров.
бесселап (N[ норма])
Возврат (z,p,k) для аналогового прототипа фильтра Бесселя N-го порядка.
(N)
Возврат (z,p,k) для аналогового прототипа фильтра Баттерворта N-го порядка.
чеб1ап (Н, рп)
Возврат (z,p,k) для аналогового фильтра нижних частот типа I Чебышева N-го порядка.
чеб2ап (Н, рс)
Возврат (z,p,k) для аналогового фильтра нижних частот Чебышева N-го порядка типа I.
cmplx_sort (p)
Сортировка корней по величине.
эллипап (N, rp, rs)
Возврат (z,p,k) эллиптического аналогового фильтра нижних частот N-го порядка.
lp2bp (б, а[ во, чб])
Преобразование прототипа фильтра нижних частот в полосовой фильтр.
lp2bp_zpk (z, p, k[ wo, bw])
Преобразование прототипа фильтра нижних частот в полосовой фильтр.
lp2bs (б, а[ во, чб])
Преобразование прототипа фильтра нижних частот в полосовой режекторный фильтр.
lp2bs_zpk (z, p, k[ wo, bw])
Преобразование прототипа фильтра нижних частот в полосовой режекторный фильтр.
lp2hp (b, a[ wo])
Преобразование прототипа фильтра нижних частот в фильтр верхних частот.
lp2hp_zpk (z, p, k[ wo])
Преобразование прототипа фильтра нижних частот в фильтр верхних частот.
lp2lp (б, а[ во])
Преобразование прототипа фильтра нижних частот на другую частоту.
lp2lp_zpk (z, p, k[ wo])
Преобразование прототипа фильтра нижних частот на другую частоту.
нормализовать (б, а)
Нормировать числитель/знаменатель непрерывной передаточной функции.
БИХ-фильтр в стиле Matlab
масло сливочное (N, Wn[ btype, аналог, output, fs])
Конструкция цифровых и аналоговых фильтров Баттерворта.
buttord (wp, ws, gpass, gstop[ аналог, fs])
Выбор порядка фильтра Баттерворта.
cheby1 (N, rp, Wn[ btype, аналог, выход, fs])
Конструкция цифровых и аналоговых фильтров Чебышева типа I.
cheb1ord (wp, ws, gpass, gstop[ аналог, fs])
Выбор порядка фильтра Чебышева I типа.
cheby2 (N, rs, Wn[ btype, аналог, выход, fs])
Конструкция цифрового и аналогового фильтра Чебышева II типа.
cheb2ord (wp, ws, gpass, gstop[ аналог, fs])
Выбор порядка фильтра Чебышева II типа.
эллипс (N, rp, rs, Wn[ btype, аналог, выход, fs])
Эллиптический (Кауэр) цифровой и аналоговый фильтр.
ellipord (wp, ws, gpass, gstop[ аналог, fs])
Выбор порядка эллиптического (Кауэра) фильтра.
бессель (N, Wn[ btype, аналог, выход, норма, fs])
Конструкция цифровых и аналоговых фильтров Bessel/Thomson.
iirnotch (w0, Q[ fs])
Разработка цифрового режекторного БИХ-фильтра второго порядка.
iirpeak (w0, Q[ fs])
Разработка пикового (резонансного) БИХ-фильтра второго порядка.
iircomb (w0, Q[ ftype, fs, pass_zero])
БИХ-режимный или обостряющий цифровой гребенчатый фильтр.
Линейные системы с непрерывным временем
лти (*система)
Базовый класс линейной стационарной инвариантной системы с непрерывным временем.
StateSpace (*система, **kwargs)
Линейная инвариантная во времени система в форме пространства состояний.
TransferFunction (*система, **kwargs)
Класс линейной инвариантной во времени системы в форме передаточной функции.
ZerosPolesGain (*system, **kwargs)
Класс системы Linear Time Invariant в виде нулей, полюсов, коэффициента усиления.
lsim (система, U, T[ X0, Interp])
Моделирование выходных данных линейной системы с непрерывным временем.
lsim2 (система [ U, T, X0])
Моделирование выходных данных линейной системы с непрерывным временем с помощью решателя ОДУ scipy.integrate.odeint .
импульс (система[ X0, T, N])
Импульсная характеристика системы непрерывного действия.
импульс2 (система[ X0, T, N])
Импульсная характеристика линейной системы непрерывного действия с одним входом.
шаг (система[ X0, T, N])
Переходная характеристика системы непрерывного времени.
шаг 2 (система[ X0, T, N])
Переходная характеристика системы непрерывного времени.
частота соотв. (система[ w, n])
Рассчитайте частотную характеристику системы с непрерывным временем.
код (система [ w, n])
Расчет амплитуды Боде и фазовых данных системы с непрерывным временем.
Линейные системы с дискретным временем
dlti (*system, **kwargs)
Базовый класс дискретной линейной стационарной системы.
StateSpace (*система, **kwargs)
Линейная инвариантная во времени система в форме пространства состояний.
TransferFunction (*system, **kwargs)
Класс линейной инвариантной во времени системы в форме передаточной функции.
ZerosPolesGain (*system, **kwargs)
Класс системы Linear Time Invariant в виде нулей, полюсов, коэффициента усиления.
dlsim (система, u[ t, x0])
Моделирование выходных данных линейной системы с дискретным временем.
импульсный (система [ x0, t, n])
Импульсная характеристика системы с дискретным временем.
dstep (система[ x0, t, n])
Переходная характеристика системы с дискретным временем.
dfreqresp (система [ w, n, целое])
Рассчитайте частотную характеристику системы с дискретным временем.
dbode (система [ w, n])
Расчет модуля Боде и фазовых данных системы с дискретным временем.
Представления LTI
tf2zpk (б, а)
Возвращает ноль, полюс, представление усиления (z, p, k) из числителя, представление знаменателя линейного фильтра.
tf2sos (б, а[ сопряжение, аналог])
Возврат секций второго порядка из представления передаточной функции
tf2ss (номер, ден)
Передать функцию в представление в пространстве состояний.
зпк2тф (з, п, к)
Возврат представления полиномиальной передаточной функции из нулей и полюсов
zpk2sos (z, p, k[ сопряжение, аналог])
Возврат секций второго порядка из нулей, полюсов и усиления системы
зпк2сс (з, п, к)
Представление с нулевым коэффициентом усиления в представление в пространстве состояний
ss2tf (A, B, C, D[ ввод])
Пространство состояний для передаточной функции.
ss2zpk (A, B, C, D[ ввод])
Представление в пространстве состояний в представление с нулевым коэффициентом усиления.
сос2зпк (сос)
Обратные нули, полюса и усиление ряда секций второго порядка
sos2tf (sos)
Возврат одной передаточной функции из серии секций второго порядка
cont2discrete (система, dt[ метод, альфа])
Преобразование непрерывной в дискретную систему в пространстве состояний.
place_poles (A, B, полюса [ метод, rtol, maxiter])
Вычислить K так, чтобы собственные значения (A — точка(B, K))=полюса.
Сигналы
чирп (t, f0, t1, f1[ method, phi, vertex_zero])
Генератор косинусов с изменяемой частотой.
gausspulse (t[ fc, bw, bwr, tpr, retquad, …])
Возврат модулированной по Гауссу синусоиды:
max_len_seq (nbits[ state, length, taps])
Генератор последовательности максимальной длины (MLS).
зубчатый (t[ ширина])
Возвращает периодический пилообразный или треугольный сигнал.
квадратный (т[ долг])
Возврат периодического прямоугольного сигнала.
wipe_poly (т, поли[ фи])
Генератор косинусов с изменяемой частотой и частотой, зависящей от времени.
unit_impulse (форма [ idx, dtype])
Единичный импульсный сигнал (дискретная дельта-функция) или единичный базисный вектор.
Оконные функции
Для оконных функций см. пространство имен scipy.signal.windows .
В пространстве имен scipy.signal есть удобная функция для получить эти окна по имени:
get_window (окно, Nx[ fftbins])
Возврат окна заданной длины и типа.
Вейвлеты
каскад (hk[ J])
Возврат (x, phi, psi) в двоичных точках K/2**J из коэффициентов фильтра.
мазня (р)
Коэффициенты КИХ-фильтра нижних частот, создающего вейвлеты Добеши.
морле (M[ w, s, полный])
Сложный вейвлет Морле.
qmf (hk)
Обратный фильтр верхних частот qmf из фильтра нижних частот
рикер (точки, а)
Возвращает вейвлет Рикера, также известный как «мексиканский вейвлет шляпы».
морле2 (М, с[ ш])
Сложный вейвлет Морле, предназначенный для работы с cwt .
cwt (данные, вейвлет, ширина [ dtype])
Непрерывное вейвлет-преобразование.
Определение пика
аргрелмин (данные [ ось, порядок, режим])
Вычислить относительные минимумы данных .
argrelmax (данные [ ось, порядок, режим])
Рассчитать относительные максимумы данные .
argrelextrema (данные, компаратор[ ось, …])
Вычислить относительные экстремумы данных .
find_peaks (x[ высота, порог, расстояние, …])
Поиск пиков внутри сигнала на основе свойств пиков.
find_peaks_cwt (вектор, ширина [ вейвлет, …])
Поиск пиков в одномерном массиве с помощью вейвлет-преобразования.
пиковые_выступы (x, пики [ wlen])
Вычислите заметность каждого пика в сигнале.
ширина пика (x, пики[ отн._высота, …])
Рассчитать ширину каждого пика сигнала.
Спектральный анализ
периодограмма (x[ fs, window, nfft, detrend, …])
Оценка спектральной плотности мощности с помощью периодограммы.
welch (x[ fs, window, nperseg, nooverlap, …])
Оценка спектральной плотности мощности по методу Уэлча.
csd (x, y[ fs, window, nperseg, nooverlap, . ..])
Оцените перекрестную спектральную плотность мощности, Pxy, используя метод Уэлча.
когерентность (x, y[ fs, window, nperseg, …])
Оцените оценку квадрата амплитуды когерентности, Cxy, сигналов X и Y с дискретным временем, используя метод Уэлча.
спектрограмма (x[ fs, window, nperseg, …])
Вычислите спектрограмму с помощью последовательных преобразований Фурье.
lombscargle (x, y, частоты)
Вычисляет периодограмму Ломба-Скаргла.
vectorstrength (события, период)
Определить силу вектора событий, соответствующих заданному периоду.
stft (x[ fs, window, nperseg, nooverlap, …])
Вычисление краткосрочного преобразования Фурье (STFT).
istft (Zxx[ fs, window, nperseg, noverlap, . ..])
Выполните обратное кратковременное преобразование Фурье (iSTFT).
check_COLA (окно, nperseg, nooverlap[ tol])
Проверьте, соблюдается ли ограничение Constant OverLap Add (COLA).
check_NOLA (окно, nperseg, nooverlap[ tol])
Проверьте, соблюдается ли ограничение добавления ненулевого перекрытия (NOLA).
Чирп Z-преобразование и масштабирование БПФ
чт (х[ м, ш, а, ось])
Вычислите АЧХ вокруг спирали в плоскости Z.
zoom_fft (x, fn[ m, fs, конечная точка, ось])
Вычислить ДПФ x только для частот в диапазоне fn .
9 крон1381 (н[ м, ш, а])
Создайте вызываемую функцию z-преобразования щебета.
ZoomFFT (n, fn[ m, fs, конечная точка])
Создайте вызываемую функцию преобразования БПФ масштабирования.
czt_points (м[ ш, а])
Возвращает точки, в которых вычисляется z-преобразование ЛЧМ.
Функции проще в использовании, чем классы, но менее эффективны, когда используя одно и то же преобразование для многих массивов одинаковой длины, поскольку они повторно генерировать один и тот же сигнал щебета с каждым вызовом. В этих случаях, вместо этого используйте классы для создания повторно используемой функции.
Allpass Filter: все, что вам нужно знать
Что такое allpass фильтр? Для чего это используется?

Всечастотный фильтр представляет собой фильтр с единичным коэффициентом усиления на всех частотах . Это означает, что никакая частота, проходящая через этот фильтр, не будет усиливаться или ослабляться. Однако он вводит частотно-зависимую задержку .
Таким образом, несмотря на то, что звук на выходе фильтра allpass ничем не отличается от звука на входе, эта простая структура, используемая в сочетании с другими элементами, обладает невероятной силой, которая присутствует практически во всех музыкальных программах.
Цифровой всепропускающий фильтр может быть реализован как фильтр с конечной импульсной характеристикой (КИХ) или фильтр с бесконечной импульсной характеристикой (БИХ), обычно первого или второго порядка. Его применение разнообразно: он используется для реализации
искусственной реверберации,
фильтры (например, фильтр верхних частот, фильтр нижних частот, режекторный),
звуковых эффекта (например, фазер),
выравнивание фазы
и многое другое.
В этой статье мы подробно обсудим цифровой всепропускающий фильтр, представим его различные формы, приведем их характеристики, схемы и реализацию и, наконец, обсудим, как вы можете использовать всепропускающий фильтр в своем музыкальном программном обеспечении, таком как VST или AAX. плагины.
Коротко
Фильтр всех частот
Фильтр всех частот имеет усиление, равное 1 на всех частотах.
Задерживает все частотные компоненты входа, каждый на свой фазовый сдвиг.
Выпускается в различных формах, но наиболее популярными являются формы IIR первого и второго порядка.
Это строительный блок огромного количества алгоритмов обработки звука, таких как реверберация или фильтры.
Содержание
Определение фильтра Allpass
Типы систем Allpass
Система FIR Allpass
IIR Allpass первого порядка
Реализация
Величина отклика
Фазовый отклик
Добыть самому?
Свойства фильтра Allpass первого порядка
Каскадные фильтры Allpass
IIR Allpass второго порядка
Фазовая характеристика
Реализация
Свойства фильтра Allpass второго порядка
БИХ-фильтр Allpass высшего порядка
Применение фильтров Allpass
Реверберация
Параметрический эквалайзер
Фазер
Выравнивание фаз
Пример плагина Allpass VST
Резюме
Библиография
Определение фильтра Allpass
Всепропускающий фильтр — это фильтр, который не изменяет амплитуду любой частотной составляющей, проходящей через него [2].
Формально, если обозначить передаточную функцию всепроходного фильтра через HAP(jω)H_\text{AP}(j\omega)HAP(jω), можно написать ∣HAP(jω)∣=1|H_\ текст{AP}(j\omega)| = 1∣HAP(jω)∣=1. Здесь ω=2πf/fs\omega = 2 \pi f / f_sω=2πf/fs, где fff — частота в Гц, а fsf_sfs — частота дискретизации в Гц.
Но подождите, раз величина не меняется, зачем нам всепроходные фильтры? Они нам нужны, потому что они вносят частотно-зависимую фазовую задержку . Другими словами, мы можем манипулировать фазой частотных составляющих без изменения их величины.
Примечание. Передаточная функция цифрового фильтра представляет собой преобразование Фурье или zzz-преобразование его импульсной характеристики. Обозначим их через H(jω)H(j\omega)H(jω) и H(z)H(z)H(z) соответственно. 9{-1}HAP(z)=z−1 также является фильтром allpass. Фаза может быть неизменной или инвертированной (умножение на 1 или -1 соответственно), потому что мы работаем в реальном домене. {-1}}, \quad (2)HAP1(z)=1+ a1z−1a1+z−1, (2)
где a∈Ra \in \mathbb{R}a∈R, потому что мы рассматриваем только фильтры с действительными значениями. Приведенное выше уравнение соответствует следующему разностному уравнению
y[n]=a1x[n]+x[n−1]−a1y[n−1]⏟d[n−1],(3)y[n] = a_1 x[n] + \underbrace{x[n - 1] - a_1 y[n-1]}_{d[n-1]}, \quad (3)y[n]=a1x[n] +d[n−1]x[n−1]−a1y[n−1], (3)
, где x[n]x[n]x[n] — входной сигнал, y[ n]y[n]y[n] — выходной сигнал, а d[n−1]d[n-1]d[n−1] можно сохранить в буфере как промежуточное значение (небольшой совет по реализации для ты 😉).
Реализация
Разностное уравнение 3 эквивалентно следующей DSP-диаграмме.
Рис. 2. Блок-схема универсального фильтра первого порядка.
Как увидеть эквивалентность? Во-первых, обратите внимание, что здесь мы имеем комбинацию двух гребенчатых фильтров: гребенчатого фильтра с обратной связью и гребенчатого фильтра с прямой связью [4].
Разностное уравнение гребенчатого фильтра обратной связи:
v[n]=x[n]−a1v[n−1]. (4)v[n] = x[n] - a_1 v[n-1]. \quad (4)v[n]=x[n]−a1v[n−1].(4) 9{-j\omega} \Bigr\rvert = 1∣∣∣∣e−jω∣∣∣∣=1 и ∣z‾z∣=1 \Bigl\lvert \frac{\overline{z}}{z } \Bigr\rvert = 1∣∣∣∣zz∣∣∣∣=1.
Фазовая характеристика
Какова роль коэффициента a1a_1a1 ( allpass )? Он управляет частотой прерывания фильтра allpass. Какая частота перерывов? Это частота, при которой фазовый сдвиг всепропускающего фильтра первого порядка точно равен −π2-\frac{\pi}{2}−2π рад. Чтобы понять частоту излома, нам нужно взглянуть на фазово-частотную характеристику фильтра allpass.
Рис. 3. Фазовая характеристика всепропускающего фильтра первого порядка для разных частот излома fbf_\text{b}fb.
Здесь имеется в виду цифровая частота, т. е. отношение частоты fff в Гц к частоте дискретизации fsf_sfs в Гц.
Синими пунктирными линиями на рисунке отмечены частоты изломов отдельных кривых. Красной линией отмечен фазовый сдвиг на −π2-\frac{\pi}{2}−2π рад. Если мы хотим установить желаемую частоту излома fbf_\text{b}fb в радианах, мы можем использовать следующую формулу для вычисления коэффициента a1a_1a1 [3,4,5]
a1 = tan⁡(πfb/fs)−1tan⁡(πfb/fs)+1.(9)a_1 = \frac{\tan(\pi f_\text{b} / f_s) - 1}{\tan (\pi f_\text{b} / f_s) + 1}. \quad (9)a1=tan(πfb/fs)+1tan(πfb/fs)−1.(9)
Как получены уравнения 2 и 9? Они являются результатом преобразования аналогового универсального фильтра в цифровую область посредством билинейного преобразования . Объяснение этого процесса выходит за рамки этой статьи; если вам интересно, ознакомьтесь с отличным объяснением в [4]. После производных мы точно приходим к передаточной функции из уравнения 2 с коэффициентом a1a_1a1, заданным уравнением 9.
Как генерируются графики на приведенном выше рисунке? Они получены из аргумента (в смысле комплексных чисел) всепроходной передаточной функции HAP1 (jω) H _ {\ text {AP} _1} (j \ omega) HAP1 (jω). Это можно сделать в программном обеспечении, используя функцию freqz Matlab или scipy. signal . В качестве альтернативы вы можете использовать следующую готовую формулу [5]
Сдвиг фазы (f) = −2πf/fs+2arctan⁡(a1sin⁡(2πf/fs)1+a1cos⁡(2πf/fs) ).(10)\text{Фазовый сдвиг}(f) = - 2 \pi f / f_s + 2 \arctan \left( \frac{a_1 \sin (2 \pi f / f_s)}{1 + a_1 \cos (2 \pi f / f_s)} \right). \quad (10)Фазовый сдвиг(f)=−2πf/fs+2arctan(1+a1cos(2πf/fs)a1sin(2πf/fs)).(10)
Получить самому?
Почему я говорю, что формула в уравнении 10 нестандартна? Я не смог вывести его сам. Однако после ручных вычислений мне удалось получить формулу, эквивалентную с точки зрения графиков. Сравнение с freqz также дало идентичный результат.
Вы знаете, как вывести уравнение 10? Если это так, пожалуйста, дайте мне знать в комментариях!
Свойства всепроходного фильтра первого порядка
Когда вы посмотрите на рисунок с фазовой характеристикой всепропускающего фильтра первого порядка, вы увидите интересные свойства.
Фазовый сдвиг при постоянном токе (f=0f = 0f=0) равен 0.
Фазовый сдвиг на частоте Найквиста (f/fs=0,5f / f_s = 0,5f/fs=0,5) составляет −π-\pi−π рад и всегда равен максимальной фазовой задержке.
Фазовый сдвиг на частоте излома fbf_\text{b}fb составляет −π2-\frac{\pi}{2}−2π рад.
Каскадные фильтры Allpass
Последовательное расположение фильтров Allpass дает суммирование фазовых задержек . Таким образом, мы можем получить фазовую задержку −Nπ-N \pi−Nπ при f/fs=0,5f / f_s = 0,5f/fs=0,5, каскадно используя фильтры NNN первого порядка. Этот принцип лежит в основе алгоритма фазовращателя. 9{-2}}, \quad (11)HAP2(z)=1+d(1−c)z−1−cz−2−c+d(1−c)z−1+z−2 ,(11)
где параметр ddd управляет частотой излома (центральной, среза) фильтра fbf_\text{b}fb (на которой фазовый сдвиг равен −π-\pi−π), а параметр ccc равен вычисляется из параметра BWBWBW, который определяет ширину полосы (крутизна наклона фазового перехода вокруг частоты излома). Соотношения между этими параметрами задаются уравнениями 1}{\tan(\pi BW / f_s) + 1}, \quad (12)c=tan(πBW/fs)+1tan(πBW/fs)−1, (12)
d=-cos⁡(2πfb/fs),(13)d = - \cos(2\pi f_\text{b} / f_s), \quad (13)d=-cos(2πfb/fs ),(13)
, где fsf_sfs — частота дискретизации. Параметры BWBWBW, fbf_\text{b}fb и fsf_sfs задаются в Гц.
Обратите внимание, что BWBWBW связан с ccc, но не с ddd, а fbf_\text{b}fb связан с ddd, но не с ccc. Это позволяет нам плавно управлять свойствами нашего фильтра.
Фазовая характеристика
Фазовая характеристика универсального фильтра второго порядка с различными частотами излома fbf_\text{b}fb выглядит следующим образом:
Рис. 4. Фазовая характеристика всепропускающего фильтра второго порядка для разных частот излома fbf_\text{b}fb и полосы пропускания BW/fs=0,022BW / f_s = 0,022BW/fs=0,022.
Как видно выше, частота излома определяет точку фазового сдвига на −π-\pi−π. Однако все склоны имеют одинаковую кривизну.
Если вместо этого оставить частоту излома постоянной и изменить параметр полосы пропускания, мы получим следующие фазовые характеристики:
Рис. 5. Фазовая характеристика всепропускающего фильтра второго порядка для различных полос пропускания BWBWBW и частоты излома fb/fs=1/8f_\text{b} / f_s = 1/8fb/fs=1/8.
Кривизна склона становится мягче с увеличением параметра BWBWBW, но точка сдвига −π-\pi−π остается на той же частоте.
Что на самом деле показывают эти графики? Они показывают, что всепропускающий фильтр второго порядка является невероятно гибким инструментом . Мы можем независимо изменять значимые параметры, такие как частота разрыва или полоса пропускания, обеспечивая при этом стабильность фильтра. Это свойство имеет решающее значение для реализации параметрических фильтров (параметрический эквалайзер, эквалайзер), потому что мы хотим иметь возможность изменять свойства фильтра интуитивно понятным и безопасным способом.
Реализация
Разностное уравнение второго порядка allpass [3]
v[n]=x[n]−d(1−c)v[n−1]+cv[n−2], (14)v[n] = x[n] - d(1 - c)v[n-1] + c v[n-2], \quad (14)v[n]=x[n]−d( 1−c)v[n−1]+cv[n−2], (14) y[n]=−cv[n]+d(1−c)v[n−1]+v[n−2].(15)y[n] = -c v[n] + d (1-c ) v[n-1] + v[n-2]. \quad (15)y[n]=−cv[n]+d(1−c)v[n−1]+v[n−2]. (15)
Если это кажется сложным, диаграмма должна сделать понятно 🙂
Рисунок 6. Блок-схема всепроходного фильтра второго порядка.
Свойства всепроходного фильтра второго порядка
Пропускной фильтр второго порядка имеет следующие свойства:
Фазовый сдвиг на постоянном токе (f=0f = 0f=0) равен 0.
Фазовый сдвиг на частоте Найквиста (f/fs=0,5f / f_s = 0,5f/fs=0,5) составляет −2π-2 \pi−2π рад и всегда равен максимальной фазовой задержке.
Фазовый сдвиг на частоте излома fbf_\text{b}fb составляет −π-\pi−π рад.
Мы можем управлять частотой прерывания fbf_\text{b}fb и пропускной способностью BWBWBW независимо друг от друга. Это невозможно при allpass первого порядка: там, чем выше частота изломов, тем менее крутой наклон. 9{-1})A~(z)=z−NA(z−1). Другими словами, A~(z)\tilde{A}(z)A~(z) получается путем обращения полиномиальных коэффициентов A(z)A(z)A(z).
Обратите внимание, что здесь мы добавили возможную инверсию фазы и дополнительную задержку. Таким образом, эта формулировка является на 100% общей и может быть применена к каждому вещественному случаю.
Однако всепропускающие фильтры высших порядков редко используются в практике звукового программирования, так как их использование требует сложного анализа и в большинстве случаев достаточно БИХ-проходных фильтров первого и второго порядка.
Применение фильтров Allpass
Хотя для одноканального аудио мы не можем услышать эффект фазовой задержки, фильтры Allpass невероятно полезны в музыкальных приложениях. Почему?
Они стабильны.
Они имеют значимое сопоставление параметров с коэффициентами (например, частота прерывания с коэффициентом ddd в полном проходе второго порядка).
Они эффективны в вычислительном отношении.
Их свойства хорошо изучены.
Как мы можем использовать их в обработке звука? Например, что произойдет, если мы добавим два синуса на одной частоте: один с задержкой на −π-\pi−π по отношению к другому? Они компенсируются ( деструктивная интерференция ), и выход равен нулю.
Где мы можем использовать свойства всепроходных фильтров? Ниже приведены некоторые отобранных приложений.
Реверберация
Фильтры Allpass активно используются в искусственной реверберации: эффекте, создающем впечатление прослушивания музыки в некотором пространстве (например, в комнате, концертном зале) [4]. Фильтры Allpass присутствуют в некоторых известных подходах к моделированию реверберации.
Ревербератор Шредера состоит из ряда всепроходных фильтров, параллельного банка гребенчатых фильтров обратной связи и матрицы смешения [4]. Это было предложено еще в 1962 году!
Алгоритм Freeverb использует параллельный банк гребенчатых фильтров обратной связи и серию всепроходных фильтров [4].
Примечание. Если вам интересно, как реализовать Freeverb с помощью Rust, посмотрите это видео с Яном Хобсоном (ex-Ableton).
Параметрический эквалайзер
Задумывались ли вы когда-нибудь, как фильтры верхних и нижних частот, полочные, режекторные или полосовые фильтры реализованы в плагинах цифровых аудио рабочих станций (DAW)? Ну, держу пари, что большинство из них используют Поваренную книгу RBJ в качестве основы. Поваренная книга RBJ представляет собой набор рецептов для стабильных, управляемых и эффективных фильтров любого типа. Оказывается, во всех этих рецептах используются всепроходные фильтры первого или второго порядка! Более подробную информацию о том, как вывести эти формулы, можно найти в [3]… но я надеюсь, что вы скоро сможете прочитать о них и на WolfSound 🙂.
Phaser
Знаете ли вы, какой эффект применяется к гитарам в Eruption Van Halen? Это фейзер : эффект, который прокручивает метки в спектре входного сигнала. Одним из способов реализации цифрового фейзера является использование цепочки всепроходных фильтров, выходной сигнал которых суммируется с нефильтрованным входным сигналом [3,4,5].
Фазовая коррекция
Различные микрофоны могут создавать различные задержки в зависимости от частоты. Смешивание их сигналов путем суммирования может привести к компенсации фазы независимо от того, инвертируем ли мы фазу одного из сигналов или нет. Предотвратить это можно, только выборочно регулируя фазовую задержку частотных составляющих одного из этих сигналов. Какая система может изменить фазовую задержку без изменения амплитуды частотной составляющей? Надеюсь, вы уже знаете ответ 🙂.
Пример плагина Allpass VST
В плагине ReaEQ VST для Reaper доступен фильтр allpass.
Рисунок 7. Фильтр Allpass в плагине ReaEQ VST для Reaper.
Как соблюсти частотно-зависимую фазовую компенсацию при параллельном проходе? Вот краткое руководство:
Рис. 8. Применение параллельного всепроходного фильтра с ReaEQ для создания режекции.
Шаги для воспроизведения:
Загрузите звуковую дорожку в Reaper и продублируйте ее.
Добавьте плагин ReaEQ VST от Reaper к одному из треков.
Откройте плагин и удалите все полосы частот, кроме 1.
Измените тип оставшейся полосы частот на «All Pass».
Во время прослушивания мастер-трека измените параметр «Частота [Гц]» в режиме allpass. Вы слышите провал в частотном спектре?
Вы также можете загрузить ReaEQ на мастер-трек и наблюдать там вырез.
Веселись! 🎧
Резюме
В этой статье мы обсудили фильтр allpass. Теперь вы понимаете
что такое allpass фильтр,
какие типы музыкально полезных фильтров allpass существуют,
как их реализовать,
как они применяются в различных эффектах,
как использовать allpass фильтр в DAW.
Спасибо за прочтение! Если вам понравилась статья и вы хотите узнать еще больше, подпишитесь на мою рассылку! Вы станете экспертом в области цифровых звуковых эффектов без необходимости читать толстые книги по DSP.
Если у вас есть какие-либо вопросы, не стесняйтесь задавать их ниже!
Библиография
[1] Алан В. Оппенгейм, Алан С. Уиллски, с С. Хамидом Сигналы и системы , 2-е издание, Пирсон, 1997.
[2] Алан В. Оппенгейм, Рональд В. Шафер, Дискретный -Time Signal Processing , 3-е издание, Pearson 2010.
[3] Zölzer, U., DAFX: Digital Audio Effects , 2-е изд. Университет Гельмута Шмидта – Университет федеральных вооруженных сил, Гамбург, Германия: John Wiley & Sons Ltd, 2011.
[4] JO Smith, Physical Audio Signal Processing , онлайн-книга, издание 2010 г. Проверено 19 октября 2021 г.
[5] Р. Кииски, Ф. Эскеда и В. Валимяки, Моделирование серого ящика во времени педали Phaser , в материалах 19-й Международной конференции по цифровым аудиоэффектам ( DAFx-16), Брно, Чехия, 5–9 сентября, стр. 121–128, 2016 г.
Ссылки выше могут быть партнерскими. Это означает, что я могу заработать комиссию, если вы решите совершить покупку. Это не влечет за собой никаких затрат для вас. Спасибо.
ФНЧ 3-го порядка с 1 операционным усилителем / Habr
Обычный подход к построению ФНЧ 3-го порядка заключается в использовании двух каскадов схемы и двух операционных усилителей. Сделать хороший дизайн одного операционного усилителя не всегда легко, но возможно.

Основные уравнения для фильтров нижних частот третьего порядка
Передаточная функция ФНЧ 3-го порядка:
А Н(с) = —————————————————————————————— (1 + с/ω₁)(1 + с/(Q ω₂) + с²/ω₂²)
где:
А – коэффициент усиления по постоянному току;
ω₁ – радиальная частота первой ступени, К1×ω;
ω₂ – радиальная частота второй ступени, К2×ω;
Q – добротность второй ступени;
ω – радиальная частота полосы пропускания фильтра;
s – комплексная частота.
Откройте скобки, чтобы получить другую форму передаточной функции:
А А А Н(с) = ———————————————————————— = ——————————————————— знак равно (1 + a s)(1 + b s + c s²) 1 + (a + b) s + (a b + c) s² + a c s³ 1 + ps1 s + ps2 s² + ps3 s³ ps1 = 1 / ω₁ + 1 / (Q ω₂) ps2 = 1 / (ω₁ Q ω₂) + 1/ω₂² ps3 = 1 / (ω₁ ω₂²)
Зная частоту -3 дБ и тип фильтра, мы можем получить K1 и K2 из таблиц в книгах [1] или вычислить их, чтобы получить ω1 и ω2.
Также, зная ps1, ps2, ps3, можно решить уравнения для нахождения радиальных частот фильтра и добротности. Решение очень длинное, поэтому опущено. Вы можете найти его с помощью математического программного обеспечения.
Способы построения фильтра нижних частот третьего порядка
Стандартный подход к построению многоступенчатых фильтров состоит в том, чтобы расположить стадии от низкой до высокой добротности. Для фильтров 3-го порядка это означает, что ступень однополюсного фильтра является первой.
[2] говорит, что имеет смысл переместить ступень первого порядка в конец схемы, чтобы уменьшить шум фильтра. Эта конфигурация также позволяет избежать пиков из-за секций с высокой добротностью.
Таким образом, самый простой способ построить фильтр нижних частот 3-го порядка только с одним операционным усилителем — это добавить RC-цепь на выходе фильтра второго порядка. К сожалению, если фильтр должен иметь низкое выходное сопротивление, этот метод использовать нельзя.
Если мы удалим операционный усилитель из каскада первого порядка и подключим RC-цепь напрямую к каскаду второго порядка, входное сопротивление каскада повлияет на параметры RC-цепи. Когда оно достаточно велико по сравнению со значением R, это можно сделать. Обычно это не так, поэтому необходимо учитывать входное сопротивление. Поскольку это зависит от частоты, не так просто вычислить значения компонентов фильтра.
На картинке выше показаны 4 варианта ФНЧ Чебышева 3-го порядка с топологией Саллена-Ки. Сверху вниз:
Первая схема показывает стандартный способ проектирования фильтра нижних частот третьего порядка, зеленая линия на графике.
Вторая схема показывает, что если RC-цепь находится в конце, частотная характеристика такая же, голубая линия на графике. Минимальное значение резистора определяется минимальной нагрузкой используемого операционного усилителя.
Третья схема показывает, что если значение R RC-цепи низкое по сравнению с входным сопротивлением цепи, частотная характеристика почти такая же, желтая линия. Значение резистора должно быть низким, поэтому предыдущая ступень будет иметь довольно большую нагрузку.
Четвертая схема показывает, что если первый операционный усилитель убрать из стандартной схемы, а значения RC останутся прежними, АЧХ резко изменится, фиолетовая линия.
Внутриконтурный фильтр нижних частот с одним операционным усилителем третьего порядка

Расчетные уравнения
Этот фильтр имеет активное входное сопротивление, которое определяется его входным сопротивлением, виртуально связанным с землей, и его передаточную функцию несложно записать в классической форме для идеального операционного усилителя:
− R3 / (R1 + R2) H(s) = ——————————————————————————————————————————— ————————————— (1 + s C1 [R1 || R2])(1 + s C2 [R3 + R4] + C2 C3 R3 R4 s²)
Таким образом, мы можем написать, что радиальные частоты среза составляют:
1 ω1 = ————————————— С1 (Р1 || Р2) 1 ω2 = —————————————— √{С2 С3 Р3 Р4}
добротность:
√{С2 С3 Р3 Р4} Q = —————————————————————————— С2 (R3 + R4 + R3 R4 / РЛ)
усиление по постоянному току:
А = - R3 / (R1 + R2)

Пример
Давайте вычислим фильтр Баттерворта третьего порядка с полосой пропускания 150 кГц и единичным коэффициентом усиления.
Для фильтра Баттерворта 3-го порядка K1 = K2 = 1, поэтому ω1 и ω2 равны его радиальной частоте полосы пропускания, а Q = 1,
Выберите значение R3 обратной связи, например, 1 кОм, и значение R4, например, 100 Ом.
Теперь мы можем вычислить значения других компонентов, предполагая, что RL достаточно высок и им можно пренебречь.
1 1 C2 = ———————————————— = —————————————————————————————— —————————— ≈ 1 нФ (E24) (R3 + R4) Q K2 ω (1 Ом + 100 Ом) × 1 × 1 × 2 π × 150 кГц (R3 + R4) Q (1 кОм + 100 Ом) × 1 C2 = ——————————— = —————————————————————————————————— ≈ 12 нФ (E24) R3 R4 K2 ω 1 кОм × 100 Ом × 1 × 2 π × 150 кГц R3 1 кОм R1 + R2 = —— = —————— = 1 кОм (E96) А 1
Установите
R1 = R2
, поэтому
R1 = R2 = 500 Ом ≈ 499 Ом (E96)
.
R1 + R2 499 Ом + 499 Ом C1 = —————————— = ——————————————————————————————————— —— ≈ 4,3 нФ (Е24) R1 R2 K1 ω (499 Ом × 499 Ом) × 1 × 2 π × 150 кГц
Используйте симулятор, чтобы проверить наше решение.
Величина входного импеданса изменяется от (R1+R2) на низких частотах до значения R1 на высоких частотах.
Давайте удостоверимся, что схема стабильна, и посмотрим на переходную характеристику схемы, используя параметры из таблицы данных OPA2134.
Переходная характеристика почти равна идеальной переходной характеристике фильтра, которую можно найти в книгах.
Полностью дифференциальный усилитель также можно использовать, но значения C1 и C3 необходимо разделить на 2.0020 Передаточная функция:
А Н(с) = —————————————————————————— 1 + ps1 с + ps2 с² + ps3 с³
Предполагая идеальный операционный усилитель, коэффициенты:
C1 R1 R2 + C3 [R3 R4 + (R1 + R2)(R3 + R4)] ps1 = ———————————————————————————————————————— Р1 + Р2 C3 [C1 R1 (R3 R4 + R2 R3 + R2 R4) + C2 R3 R4 (R1 + R2)] ps2 = ————————————————————————————————————————————— ——————— Р1 + Р2 С1 С2 С3 Р1 Р2 Р3 Р4 ps3 = ———————————————————— Р1 + Р2
усиление по постоянному току:
А = - R3 / (R1 + R2)
Аналитическое решение для получения параметров фильтра, если оно вообще существует, огромно, поэтому единственный способ найти решение — решить уравнения численно.
Пример
Давайте вычислим тот же фильтр Баттерворта 3-го порядка с полосой пропускания 150 кГц и единичным коэффициентом усиления.
Установите R1 = R2 = 1 кОм (E96).
R3 = −A (R1 + R2) = −(−1) × (1 кОм + 1 кОм) = 2 кОм (E96) 1 1 1 1 ps1 = ———— + —————— = ———————————————— + —————————————————— ——— ≈ 2,122e−6 K1 ω Q K2 ω 1 × 2 π × 150 кГц 1 × 1 × 2 π × 150 кГц 1 1 1 1 ps2 = ——————————— + ——————— = ——————————————————————————— ——————————— + ——————————————————— ≈ 2,2516e−12 K1 ω Q K2 ω (K2 ω)² 1 × 2 π × 150 кГц × 1 × 1 × 2 π × 150 кГц (1 × 2 π × 150 кГц)² 1 1 ps3 = ———————————— = ————————————————————————————————— ————— ≈ 1,195e−18 K1 ω (K2 ω)² 1 × 2 π × 150 кГц × (1 × 2 π × 150 кГц)²
Есть 3 уравнения и 4 неизвестных: C1, C2, C3, R4.
Анализ показывает, что уравнения имеют решения для C1, C2, C3 при любых значениях R4. C2 не может быть слишком низким, C3 не может быть слишком большим, а C1 также определяет R1, R2, R3. Это также показывает, что не существует решения с C1 = C2 = C3.
Таким образом, единственный подходящий способ найти решение — установить значение R4 и решить уравнения, чтобы найти C1, C2, C3.
Установим R4 = 100 Ом (E96).
Решение: C1 ≈ 2,22 нФ ≈ 2,2 нФ (E24), C2 ≈ 11,7 нФ ≈ 12 нФ (E24), C3 ≈ 460 пФ ≈ 470 пФ (E24).
Моделирование подтверждает правильность нашего решения.
Величина входного импеданса изменяется от (R1+R2) на низких частотах до значения R1 на высоких частотах.
Давайте удостоверимся, что схема стабильна, и посмотрим на переходную характеристику схемы, используя параметры из таблицы данных OPA2134.
Также можно использовать полностью дифференциальный усилитель, но значения C1 и C2 необходимо разделить на 2. Передаточная функция:
А Н(с) = —————————————————————————— 1 + ps1 с + ps2 с² + ps3 с³
Предполагая идеальный операционный усилитель, коэффициенты:
ps1 = C1 R1 + C2 (R1 + R2 + R3) − C3 (R1 + R2) R5 / R4 ps2 = C1 R1 (C2 (R2 + R3) − C3 R2 R5 / R4) + C2 C3 R3 (R1 + R2) ps3 = C1 C2 C3 R1 R2 R3
усиление по постоянному току:
А = 1 + R5 / R4

Пример
Давайте вычислим тот же фильтр Баттерворта 3-го порядка с полосой пропускания 150 кГц и единичным коэффициентом усиления.
Для единичного усиления: R5 = 0, R4 не установлен.
Значения факторов уже известны:
ps1 ≈ 2,122e−6 ps2 ≈ 2,2516e−12 ps3 ≈ 1,195e−18
Есть 3 уравнения и 6 неизвестных: C1, C2, C3, R1, R2, R3.
Обычно инженеры хотят оптимизировать спецификацию материалов, поэтому наиболее интересны решения с C1=C2=C3 и R1=R2=R3.
Решения с C1=C2=C3 могут быть найдены, когда коэффициент усиления примерно больше 2.
Положим R1 = R2 = R3 = 1 кОм и с помощью математических программ найдем, что C1 ≈ 1,48 нФ ≈ 1,5 нФ (E24), C2 ≈ 215 пФ ≈ 220 пФ (Е24), С3 ≈ 3,76 нФ ≈ 3,9 нФ (Е24).
Моделирование подтверждает правильность нашего решения.
Величина входного импеданса изменяется от очень высокого значения на низких частотах до значения R1 на высоких частотах.
Давайте удостоверимся, что схема стабильна, и посмотрим на переходную характеристику схемы, используя параметры из таблицы данных OPA2134.
Переходная характеристика аналогична переходной характеристике идеального фильтра. Осцилляции нет, поэтому схему можно использовать.
Заключение
Есть несколько способов построить фильтр нижних частот 3-го порядка, используя только один операционный усилитель:
Добавьте RC-цепь в конце каскада второго порядка. Преимущество заключается в уменьшении шума и пиков. Недостатком является увеличение выходного сопротивления.
Добавьте RC-цепь перед каскадом второго порядка без учета входного импеданса. Он работает только в том случае, если значение R намного меньше, чем входное сопротивление второго каскада, или если импеданс постоянен во всем диапазоне частот и может быть учтен, как в фильтре нижних частот In-The-Loop.
Добавьте RC-цепь перед каскадом второго порядка и решите уравнения, чтобы найти соответствующие значения компонентов.
Зная решение для некоторого случая, можно масштабировать значения компонентов, чтобы найти другие решения, чтобы избежать решения уравнений с нуля. Этот способ используется в некоторых онлайн-инструментах. Но если вы хотите оптимизировать свою спецификацию материалов и минимизировать допуски, вам нужно решить уравнения, варьируя начальные значения, чтобы найти наилучшие значения компонентов.
Ссылки

Analog Devices. «Справочник по проектированию линейных цепей». Глава 8, «Аналоговые фильтры».
Бонни Бейкер, «Безболезненное уменьшение шума аналогового фильтра».
Л.К. Вадхва, «Один операционный усилитель имитирует системы третьего порядка с двойным выводом».
Кристофер Пол, «Разработайте фильтры Саллена-Ки второго и третьего порядка с одним операционным усилителем».
Кристофер Пол, «Создание фильтров нижних частот третьего порядка с оптимальной чувствительностью на одном операционном усилителе».
Кристофер Пол, «Набор инструментов для проектирования фильтров нижних частот Sallen-Key».
OKAWA Electronic Design, «Инструмент проектирования фильтра нижних частот Саллена-Ки 3-го порядка».

`свертка` (in1, in2[ режим, метод])	Свернуть два N-мерных массива.
`корреляция` (in1, in2[ режим, метод])	Взаимная корреляция двух N-мерных массивов.
`fftconvolve` (in1, in2[ режим, оси])	Свертка двух N-мерных массивов с помощью БПФ.
`oaconvolve` (in1, in2[ режим, оси])	Свертка двух N-мерных массивов с использованием метода сложения-наложения.
`convolve2d` (in1, in2[ режим, граница, значение заполнения])	Свернуть два двумерных массива.
`корреляция2d` (вх1, вх2[ мода, граница, . ..])	Взаимная корреляция двух двумерных массивов.
`sepfir2d` (ввод, hrow, hcol)	Convolve с двухмерным отделяемым КИХ-фильтром.
`Choose_conv_method` (in1, in2[ режим, мера])	Найдите самый быстрый метод свертки/корреляции.
`корреляция_лаги` (in1_len, in2_len[ mode])	Вычисляет массив индексов запаздывания/смещения для одномерной кросс-корреляции.

`сплайн` (х, п)	Базисная функция B-сплайна порядка n.
`куб.` (х)	Кубический B-сплайн.
`квадратичный` (x)	Квадратичный B-сплайн.
`gauss_spline` (x, n)	Гауссова аппроксимация базисной функции B-сплайна порядка n.
`cspline1d` (сигнал [ ягненок])	Вычислить коэффициенты кубического сплайна для массива ранга 1.
`qspline1d` (сигнал [ баранина])	Вычислить коэффициенты квадратичного сплайна для массива ранга 1.
`cspline2d` (ввод [ лямбда, точность])	Коэффициенты для двумерного кубического (3-го порядка) B-сплайна.
`qspline2d` (ввод[ лямбда, точность])	Коэффициенты для двумерного квадратичного (2-го порядка) B-сплайна:
`cspline1d_eval` (cj, newx[ dx, x0])	Оценить кубический сплайн в новом наборе точек.
`qspline1d_eval` (cj, newx[ dx, x0])	Оцените квадратичный сплайн в новом наборе точек.
`spline_filter` (Iin[ lmbda])	Сглаживающая сплайновая (кубическая) фильтрация массива ранга 2.

`order_filter` (a, домен, ранг)	Выполнить фильтр порядка на массиве N-D.
`медфильтр` (объем[ размер_ядра])	Выполнение медианного фильтра для N-мерного массива.
`medfilt2d` (вход[ kernel_size])	Медианный фильтр двумерного массива.
`сосиска` (im[ mysize, шум])	Фильтр Винера для N-мерного массива.
`symiirorder1` (ввод, c0, z1[ точность])	Реализуйте сглаживающий БИХ-фильтр с зеркально-симметричными граничными условиями, используя каскад секций первого порядка. Во втором разделе используется обратная последовательность. Это реализует систему со следующей передаточной функцией и зеркально-симметричными граничными условиями::.
`symiirorder2` (ввод, r, омега[ точность])	Реализовать сглаживающий БИХ-фильтр с зеркально-симметричными граничными условиями, используя каскад секций второго порядка. Во втором разделе используется обратная последовательность. Это реализует следующую передаточную функцию::.
`lфильтр` (b, a, x[ ось, zi])	Фильтрация данных по одному измерению с помощью БИХ- или КИХ-фильтра.
`фильтр` (б, а, у[ х])	Построить начальные условия для lfilter заданных входных и выходных векторов.
`lfilter_zi` (б, а)	Создание начальных условий для lfilter для установившегося режима отклика на скачок.
`фильтрфильтр` (b, a, x[ ось, padtype, padlen, …])	Применение цифрового фильтра к сигналу вперед и назад.
`savgol_filter` (x, window_length, polyorder[ …])	Применение фильтра Савицкого-Голея к массиву.
`деконволюция` (сигнал, делитель)	Деконволюция делителя из сигнала с помощью обратной фильтрации.
`сосфилт` (сос, х[ ось, зи])	Фильтрация данных по одному измерению с использованием каскадных секций второго порядка.
`sosfilt_zi` (сос)	Построение начальных условий для sosfilt для установившегося режима переходной характеристики.
`sosfiltfilt` (sos, x[ ось, padtype, padlen])	Цифровой фильтр прямого и обратного действия, использующий каскадные секции второго порядка.
`гильберт` (x[ N, ось])	Вычислите аналитический сигнал, используя преобразование Гильберта.
`гильберт2` (x[ N])	Вычисление ‘2-D’ аналитического сигнала x
`прореживание` (x, q[ n, ftype, ось, zero_phase])	Понижает дискретизацию сигнала после применения сглаживающего фильтра.
`удаление тренда` (данные [ ось, тип, бит, перезапись_данных])	Удалить линейный тренд вдоль оси из данных.
`повторная выборка` (x, число[ t, ось, окно, домен])	Передискретизируйте x до num выборок, используя метод Фурье вдоль заданной оси.
`resample_poly` (x, вверх, вниз [ ось, окно, …])	Передискретизировать x вдоль заданной оси с использованием многофазной фильтрации.
`вверх` (h, x[ вверх, вниз, ось, режим, cval])	Повышение частоты дискретизации, КИХ-фильтр и понижение частоты дискретизации.

`билинейная` (б, а[ фс])	Возврат цифрового БИХ-фильтра из аналогового с помощью билинейного преобразования.
`bilinear_zpk` (z, p, k, fs)	Возврат цифрового БИХ-фильтра из аналогового с помощью билинейного преобразования.
`findfreqs` (num, den, N[ kind])	Найдите массив частот для вычисления отклика аналогового фильтра.
`Fils` (нумерация, полосы, желаемый [ вес, nyq, fs])	Конструкция КИХ-фильтра с использованием минимизации ошибки методом наименьших квадратов.
`firwin` (нумерация, отсечка [ ширина, окно, …])	Расчет КИХ-фильтра оконным методом.
`firwin2` (numtaps, freq, gain[ nfreqs, . ..])	КИХ-фильтр с использованием оконного метода.
`частоты` (б, а[ работа, сюжет])	Вычисление частотной характеристики аналогового фильтра.
`freqs_zpk` (z, p, k[ work])	Вычисление частотной характеристики аналогового фильтра.
`частота` (б[ а, работа, целое, сюжет, фс, …])	Расчет частотной характеристики цифрового фильтра.
`freqz_zpk` (z, p, k[ work, integer, fs])	Расчет частотной характеристики цифрового фильтра в форме ZPK.
`sosfreqz` (sos[ работа, целое, fs])	Расчет частотной характеристики цифрового фильтра в формате SOS.
`гамматон` (частота, ftype[ порядок, numtaps, fs])	Гамматоновый фильтр.
`group_delay` (система[ w, целое, fs])	Вычислить групповую задержку цифрового фильтра.
`iirdesign` (wp, ws, gpass, gstop[ аналог, …])	Полная конструкция цифровых и аналоговых фильтров IIR.
`iirfilter` (N, Wn[ rp, rs, btype, аналог, …])	Конструкция цифровых и аналоговых фильтров IIR с заданным порядком и критическими точками.
`kaiser_atten` (нумерация, ширина)	Вычислите затухание КИХ-фильтра Кайзера.
`kaiser_beta` (а)	Вычислить параметр Кайзера бета , учитывая затухание и .
`kaiserord` (волна, ширина)	Определите параметры окна фильтра для метода окна Кайзера.
`минимальная_фаза` (h[ метод, n_fft])	Преобразование КИХ-фильтра с линейной фазой в режим минимальной фазы
`savgol_coeffs` (window_length, polyorder[ . ..])	Вычислите коэффициенты для одномерного КИХ-фильтра Савицкого-Голея.
`ремез` (нумерация, диапазоны, желаемый [ вес, Гц, …])	Рассчитайте минимаксный оптимальный фильтр, используя алгоритм обмена Ремеза.
`unique_roots` (p[ tol, rtype])	Определите уникальные корни и их кратности из списка корней.
`остаток` (б, а[ тол, ртип])	Вычисление частичной дроби b(s) / a(s).
`остатокz` (б, а[ тол, тип])	Вычисление частичной дроби b(z) / a(z).
`инверсия` (r, p, k[ tol, rtype])	Вычислить b(s) и a(s) из разложения неполных дробей.
`инврез` (р, п, к[ тол, ртип])	Вычислить b(z) и a(z) из разложения неполных дробей.
`Плохие коэффициенты`	Предупреждение о плохо подготовленных коэффициентах фильтра

`abcd_normalize` ([A, B, C, D])	Проверить матрицы пространства состояний и убедиться, что они двумерные.
`band_stop_obj` (wp, ind, passb, stopb, gpass, …)	Целевая функция Band Stop Функция минимизации ордеров.
`бесселап` (N[ норма])	Возврат (z,p,k) для аналогового прототипа фильтра Бесселя N-го порядка.
(N)	Возврат (z,p,k) для аналогового прототипа фильтра Баттерворта N-го порядка.
`чеб1ап` (Н, рп)	Возврат (z,p,k) для аналогового фильтра нижних частот типа I Чебышева N-го порядка.
`чеб2ап` (Н, рс)	Возврат (z,p,k) для аналогового фильтра нижних частот Чебышева N-го порядка типа I.
`cmplx_sort` (p)	Сортировка корней по величине.
`эллипап` (N, rp, rs)	Возврат (z,p,k) эллиптического аналогового фильтра нижних частот N-го порядка.
`lp2bp` (б, а[ во, чб])	Преобразование прототипа фильтра нижних частот в полосовой фильтр.
`lp2bp_zpk` (z, p, k[ wo, bw])	Преобразование прототипа фильтра нижних частот в полосовой фильтр.
`lp2bs` (б, а[ во, чб])	Преобразование прототипа фильтра нижних частот в полосовой режекторный фильтр.
`lp2bs_zpk` (z, p, k[ wo, bw])	Преобразование прототипа фильтра нижних частот в полосовой режекторный фильтр.
`lp2hp` (b, a[ wo])	Преобразование прототипа фильтра нижних частот в фильтр верхних частот.
`lp2hp_zpk` (z, p, k[ wo])	Преобразование прототипа фильтра нижних частот в фильтр верхних частот.
`lp2lp` (б, а[ во])	Преобразование прототипа фильтра нижних частот на другую частоту.
`lp2lp_zpk` (z, p, k[ wo])	Преобразование прототипа фильтра нижних частот на другую частоту.
`нормализовать` (б, а)	Нормировать числитель/знаменатель непрерывной передаточной функции.

`масло сливочное` (N, Wn[ btype, аналог, output, fs])	Конструкция цифровых и аналоговых фильтров Баттерворта.
`buttord` (wp, ws, gpass, gstop[ аналог, fs])	Выбор порядка фильтра Баттерворта.
`cheby1` (N, rp, Wn[ btype, аналог, выход, fs])	Конструкция цифровых и аналоговых фильтров Чебышева типа I.
`cheb1ord` (wp, ws, gpass, gstop[ аналог, fs])	Выбор порядка фильтра Чебышева I типа.
`cheby2` (N, rs, Wn[ btype, аналог, выход, fs])	Конструкция цифрового и аналогового фильтра Чебышева II типа.
`cheb2ord` (wp, ws, gpass, gstop[ аналог, fs])	Выбор порядка фильтра Чебышева II типа.
`эллипс` (N, rp, rs, Wn[ btype, аналог, выход, fs])	Эллиптический (Кауэр) цифровой и аналоговый фильтр.
`ellipord` (wp, ws, gpass, gstop[ аналог, fs])	Выбор порядка эллиптического (Кауэра) фильтра.
`бессель` (N, Wn[ btype, аналог, выход, норма, fs])	Конструкция цифровых и аналоговых фильтров Bessel/Thomson.
`iirnotch` (w0, Q[ fs])	Разработка цифрового режекторного БИХ-фильтра второго порядка.
`iirpeak` (w0, Q[ fs])	Разработка пикового (резонансного) БИХ-фильтра второго порядка.
`iircomb` (w0, Q[ ftype, fs, pass_zero])	БИХ-режимный или обостряющий цифровой гребенчатый фильтр.

`лти` (*система)	Базовый класс линейной стационарной инвариантной системы с непрерывным временем.
`StateSpace` (система, *kwargs)	Линейная инвариантная во времени система в форме пространства состояний.
`TransferFunction` (система, *kwargs)	Класс линейной инвариантной во времени системы в форме передаточной функции.
`ZerosPolesGain` (system, *kwargs)	Класс системы Linear Time Invariant в виде нулей, полюсов, коэффициента усиления.
`lsim` (система, U, T[ X0, Interp])	Моделирование выходных данных линейной системы с непрерывным временем.
`lsim2` (система [ U, T, X0])	Моделирование выходных данных линейной системы с непрерывным временем с помощью решателя ОДУ `scipy.integrate.odeint` .
`импульс` (система[ X0, T, N])	Импульсная характеристика системы непрерывного действия.
`импульс2` (система[ X0, T, N])	Импульсная характеристика линейной системы непрерывного действия с одним входом.
`шаг` (система[ X0, T, N])	Переходная характеристика системы непрерывного времени.
`шаг 2` (система[ X0, T, N])	Переходная характеристика системы непрерывного времени.
`частота соотв.` (система[ w, n])	Рассчитайте частотную характеристику системы с непрерывным временем.
`код` (система [ w, n])	Расчет амплитуды Боде и фазовых данных системы с непрерывным временем.

`dlti` (system, *kwargs)	Базовый класс дискретной линейной стационарной системы.
`StateSpace` (система, *kwargs)	Линейная инвариантная во времени система в форме пространства состояний.
`TransferFunction` (system, *kwargs)	Класс линейной инвариантной во времени системы в форме передаточной функции.
`ZerosPolesGain` (system, *kwargs)	Класс системы Linear Time Invariant в виде нулей, полюсов, коэффициента усиления.
`dlsim` (система, u[ t, x0])	Моделирование выходных данных линейной системы с дискретным временем.
`импульсный` (система [ x0, t, n])	Импульсная характеристика системы с дискретным временем.
`dstep` (система[ x0, t, n])	Переходная характеристика системы с дискретным временем.
`dfreqresp` (система [ w, n, целое])	Рассчитайте частотную характеристику системы с дискретным временем.
`dbode` (система [ w, n])	Расчет модуля Боде и фазовых данных системы с дискретным временем.

`tf2zpk` (б, а)	Возвращает ноль, полюс, представление усиления (z, p, k) из числителя, представление знаменателя линейного фильтра.
`tf2sos` (б, а[ сопряжение, аналог])	Возврат секций второго порядка из представления передаточной функции
`tf2ss` (номер, ден)	Передать функцию в представление в пространстве состояний.
`зпк2тф` (з, п, к)	Возврат представления полиномиальной передаточной функции из нулей и полюсов
`zpk2sos` (z, p, k[ сопряжение, аналог])	Возврат секций второго порядка из нулей, полюсов и усиления системы
`зпк2сс` (з, п, к)	Представление с нулевым коэффициентом усиления в представление в пространстве состояний
`ss2tf` (A, B, C, D[ ввод])	Пространство состояний для передаточной функции.
`ss2zpk` (A, B, C, D[ ввод])	Представление в пространстве состояний в представление с нулевым коэффициентом усиления.
`сос2зпк` (сос)	Обратные нули, полюса и усиление ряда секций второго порядка
`sos2tf` (sos)	Возврат одной передаточной функции из серии секций второго порядка
`cont2discrete` (система, dt[ метод, альфа])	Преобразование непрерывной в дискретную систему в пространстве состояний.
`place_poles` (A, B, полюса [ метод, rtol, maxiter])	Вычислить K так, чтобы собственные значения (A — точка(B, K))=полюса.

`чирп` (t, f0, t1, f1[ method, phi, vertex_zero])	Генератор косинусов с изменяемой частотой.
`gausspulse` (t[ fc, bw, bwr, tpr, retquad, …])	Возврат модулированной по Гауссу синусоиды:
`max_len_seq` (nbits[ state, length, taps])	Генератор последовательности максимальной длины (MLS).
`зубчатый` (t[ ширина])	Возвращает периодический пилообразный или треугольный сигнал.
`квадратный` (т[ долг])	Возврат периодического прямоугольного сигнала.
`wipe_poly` (т, поли[ фи])	Генератор косинусов с изменяемой частотой и частотой, зависящей от времени.
`unit_impulse` (форма [ idx, dtype])	Единичный импульсный сигнал (дискретная дельта-функция) или единичный базисный вектор.

`каскад` (hk[ J])	Возврат (x, phi, psi) в двоичных точках `K/2**J` из коэффициентов фильтра.
`мазня` (р)	Коэффициенты КИХ-фильтра нижних частот, создающего вейвлеты Добеши.
`морле` (M[ w, s, полный])	Сложный вейвлет Морле.
`qmf` (hk)	Обратный фильтр верхних частот qmf из фильтра нижних частот
`рикер` (точки, а)	Возвращает вейвлет Рикера, также известный как «мексиканский вейвлет шляпы».
`морле2` (М, с[ ш])	Сложный вейвлет Морле, предназначенный для работы с `cwt` .
`cwt` (данные, вейвлет, ширина [ dtype])	Непрерывное вейвлет-преобразование.

`аргрелмин` (данные [ ось, порядок, режим])	Вычислить относительные минимумы данных .
`argrelmax` (данные [ ось, порядок, режим])	Рассчитать относительные максимумы данные .
`argrelextrema` (данные, компаратор[ ось, …])	Вычислить относительные экстремумы данных .
`find_peaks` (x[ высота, порог, расстояние, …])	Поиск пиков внутри сигнала на основе свойств пиков.
`find_peaks_cwt` (вектор, ширина [ вейвлет, …])	Поиск пиков в одномерном массиве с помощью вейвлет-преобразования.
`пиковые_выступы` (x, пики [ wlen])	Вычислите заметность каждого пика в сигнале.
`ширина пика` (x, пики[ отн._высота, …])	Рассчитать ширину каждого пика сигнала.

`периодограмма` (x[ fs, window, nfft, detrend, …])	Оценка спектральной плотности мощности с помощью периодограммы.
`welch` (x[ fs, window, nperseg, nooverlap, …])	Оценка спектральной плотности мощности по методу Уэлча.
`csd` (x, y[ fs, window, nperseg, nooverlap, . ..])	Оцените перекрестную спектральную плотность мощности, Pxy, используя метод Уэлча.
`когерентность` (x, y[ fs, window, nperseg, …])	Оцените оценку квадрата амплитуды когерентности, Cxy, сигналов X и Y с дискретным временем, используя метод Уэлча.
`спектрограмма` (x[ fs, window, nperseg, …])	Вычислите спектрограмму с помощью последовательных преобразований Фурье.
`lombscargle` (x, y, частоты)	Вычисляет периодограмму Ломба-Скаргла.
`vectorstrength` (события, период)	Определить силу вектора событий, соответствующих заданному периоду.
`stft` (x[ fs, window, nperseg, nooverlap, …])	Вычисление краткосрочного преобразования Фурье (STFT).
`istft` (Zxx[ fs, window, nperseg, noverlap, . ..])	Выполните обратное кратковременное преобразование Фурье (iSTFT).
`check_COLA` (окно, nperseg, nooverlap[ tol])	Проверьте, соблюдается ли ограничение Constant OverLap Add (COLA).
`check_NOLA` (окно, nperseg, nooverlap[ tol])	Проверьте, соблюдается ли ограничение добавления ненулевого перекрытия (NOLA).

`чт` (х[ м, ш, а, ось])	Вычислите АЧХ вокруг спирали в плоскости Z.
`zoom_fft` (x, fn[ m, fs, конечная точка, ось])	Вычислить ДПФ x только для частот в диапазоне fn .
`9 крон1381 (н[ м, ш, а])`	Создайте вызываемую функцию z-преобразования щебета.
`ZoomFFT` (n, fn[ m, fs, конечная точка])	Создайте вызываемую функцию преобразования БПФ масштабирования.
`czt_points` (м[ ш, а])	Возвращает точки, в которых вычисляется z-преобразование ЛЧМ.

Понятие передаточных функций фильтров нижних частот

s-область

Анализ схем в s-области

Понятие частоты среза

Частота среза и сдвиг фазы

Заключение

Теги

Передаточные функции аналоговых фильтров.

Что такое фильтр баттерворта, расчет и схема. Расчёт фильтра с характеристикой Баттерворта Передаточная функция фильтра баттерворта

Харьковский национальный университет радиоэлектроники

Кафедра РЭУ

КУРСОВАЯ РАБОТА

РАСЧЁТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

ФИЛЬТР ВЕРХНИХ ЧАСТОТ БАТТЕРВОРТА

РЕФЕРАТ

Топологическая модель фильтра.

Фильтр Чебышева

Фильтр Бесселя

Фильтр Кауэра (эллиптический фильтр)

Определение порядка фильтра

Схемы каскадов фнч 1–го и 2–го порядка

План:

Введение

1. Обзор

1.1. Нормированные полиномы Баттерворта

1.

1.3. Спад характеристики на высоких частотах

2. Проектирование фильтра

2.1. Топология Кауэра

2.2. Топология Саллена-Кея

3. Сравнение с другими линейными фильтрами

4. Пример

Литература

Введение

Порядок фильтров

Декады и октавы

Аппроксимации фильтра

Низкочастотный фильтр Баттерворта

Нормализованные полиномы фильтра Баттерворта низких частот

Расчет и схема фильтра Баттерворта низких частот

Цифровые фильтры с конечной импульсной характеристикой

Ключевые слова

Похожие статьи

Активные и пассивные электрические

ПИД-регулятор понижающего преобразователя напряжения

Методы z-преобразования для расчета

Аналого-цифровое преобразование | Статья в журнале…

Принципы проектирования систем автоматизации повышенной…

Разработка КИХ-

Реакция рекурсивной ЛДС с

Исследование процесса цифровой обработки

Алгоритмы преобразования Фурье и их применение при анализе…

Похожие статьи

Активные и пассивные электрические

ПИД-регулятор понижающего преобразователя напряжения

Методы z-преобразования для расчета

Аналого-цифровое преобразование | Статья в журнале…

Принципы проектирования систем автоматизации повышенной…

Разработка КИХ-

Реакция рекурсивной ЛДС с

Исследование процесса цифровой обработки

Алгоритмы преобразования Фурье и их применение при анализе…

Передаточная функция FIR

Содержание

FIR (Finite Impulse Response) Линейные фильтры

Односторонний линейный фильтр

Функция ввода

КИХ Передаточная функция Линейный фильтр Применение

:::Режекторный фильтр с регулируемой величиной добротности для подавления помехи от силовой сети (50 Гц) :::

Анализ передаточной функции | Введение в цифровые фильтры

Преобразование

Существование

Теорема о сдвиге

Теорема свертки

Факторная форма

Случай серии

Параллельный случай

Комбинация серий коммутативна

Расширение частичной дроби

Пример