PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.
 1 Электростатика
1 Электростатика - 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 4.
- 5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.
 6 СТО
6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Документ без названия
Документ без названияРабота сил электростатического поляСила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Направление силы, действующей в любой точке пространства на заряд, проходит через центр заряда, создающего поле, а значение силы зависит только от расстояния до этого заряда до точки наблюдения. (Например, поле силы тяжести является полем центральных сил).
Направление силы, действующей в любой точке пространства на заряд, проходит через центр заряда, создающего поле, а значение силы зависит только от расстояния до этого заряда до точки наблюдения. (Например, поле силы тяжести является полем центральных сил).
Рис. 3,1
Если тело поставлено в такие условия, что в каждой точке пространства оно подвержено воздействию других тел с силой, закономерно изменяющейся от точки к точке, то говорят, что это тело находится в поле сил. Центральное поле сил потенциально. Убедимся, что электрическое поле потенциально. Вычислим работу, которая совершается силами поля неподвижного точечного заряда q над перемещающимся в этом поле точечным зарядом (рис. 3.1). Работа на элементарном пути равна: или
,
так как . Отсюда на пути 1–2
(1)
Видно, что работа не зависит от пути, по которому перемещался в электрическом поле заряд  Следовательно, силы, действующие на заряд q’ в поле неподвижного заряда q, являются консервативными, а поле этих сил потенциальным. Этот вывод легко распространяется на поле любой системы неподвижных зарядов, так как сила , действующая на точечный заряд q‘ в таком поле, может по принципу суперпозиции быть представлена в виде , где – сила, обусловленная i-м зарядом создающей поле системы. Работа в этом случае равна алгебраической сумме работ, совершаемых отдельными силами: . Каждое из слагаемых в правой части этого выражения не зависит от пути. Поэтому не зависит от пути и работа
Следовательно, силы, действующие на заряд q’ в поле неподвижного заряда q, являются консервативными, а поле этих сил потенциальным. Этот вывод легко распространяется на поле любой системы неподвижных зарядов, так как сила , действующая на точечный заряд q‘ в таком поле, может по принципу суперпозиции быть представлена в виде , где – сила, обусловленная i-м зарядом создающей поле системы. Работа в этом случае равна алгебраической сумме работ, совершаемых отдельными силами: . Каждое из слагаемых в правой части этого выражения не зависит от пути. Поэтому не зависит от пути и работа
Из механики известно, что работа потенциальных сил на замкнутом пути равна нулю. Работа, совершаемая силами поля над зарядом q’ при обходе по замкнутому контуру, может быть представлена как , где –проекция вектора на направление элементарного перемещения , то, следовательно:
(2)
Это соотношение должно выполняться для любого замкнутого контура.
Выражение вида называется циркуляцией вектора по данному контуру. Таким образом, характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.
Теорема о циркуляции вектора напряженности электростатического поля
Итак, мы утверждаем, что циркуляция вектора в любом электростатическом поле равна нулю, т.е. . Это утверждение называют теоремой о циркуляции вектора .
 Так как работа в заданном поле не зависит от формы пути, то работа по перемещению заряда по пути 1а2 равна работе по перемещению заряда по пути 1б2 или
Так как работа в заданном поле не зависит от формы пути, то работа по перемещению заряда по пути 1а2 равна работе по перемещению заряда по пути 1б2 или
Рисунок 3.2
Из сказанного выше следует, что
(Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути:
(3)
или (4)
Поле, обладающее такими свойствами, называется потенциальным. Любое электростатическое поле является потенциальным.Потенциальная энергия и потенциал электростатического поля
Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа может быть представлена как разность значений потенциальных энергий, которыми обладает заряд q’ в точках 1 и 2 поля заряда q
Можно показать также, что, так как ,

Отсюда для потенциальной энергии заряда в поле заряда q получаем:
(6)
Значение const в (6) обычно выбирают таким образом, чтобы при удалении заряда q’ на бесконечность () потенциальная энергия обращалась в нуль. При этом условии получается, что
(7)
Будем считать q’ пробным зарядом. Тогда потенциальная энергия, которой обладает пробный заряд, зависит не только от его значения , но и от значения q и r, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
(8)
называется потенциалом поля в данной точке и используется наряду с напряженностью поля , для описания электрических полей.

Как следует из (8) потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Таким образом, для потенциального поля точечного заряда получаем следующее выражение:
(9)
Если поле создано системой точечных зарядов q1, q2, …, qn, находящихся на расстояниях соответственно r1, r2,…, rn до точки поля, в которой находится заряд , то работа, совершаемая силами этого поля над зарядом , будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
.
Но каждая из работ равна:
где расстояние от заряда до начального положения заряда , расстояние от заряда до конечного положения заряда .
Следовательно:
.
Сопоставляя это выражение с соотношением , получаем для потенциальной энергии заряда в поле системы зарядов выражение:
, (10)
откуда
.
 (11).
(11).Следовательно, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Из соотношения вытекает, что заряд , находящийся в точке поля с потенциалом , обладает потенциальной энергией . Следовательно, работа сил поля над зарядом может быть выражена через разность потенциалов:
(12)
Таким образом, работа, совершаемая над зарядом силами поля, равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд из точки с потенциалом удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
или ,
т. е, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля в бесконечность, или работе, которую надо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля.

За единицу потенциала следует принять потенциал в такой точке поля, для перемещения заряда в которую из бесконечности необходимо совершить работу, равную
1 Джоулю (система единиц “Си”)Связь между напряженностью электростатического поля и потенциалом
Напряженность электрического поля – величина, численно равная силе, действующей на заряд. Потенциал – величина, численно равная потенциальной энергии заряда. Таким образом, между этими величинами должна существовать связь, аналогичная связи между потенциальной энергией и силой (т.е. ). Работа сил поля над зарядом на отрезке пути может быть представлена как , а убыль потенциальной энергии заряда, которая при этом будет возникать: . Откуда из равенства находим:
или , (21)
где через обозначено произвольно выбранное направление.
Тогда,
, , , (22)
Откуда
, (23)
где орты координатных осей, т. е., единичные вектора. Вектор с компонентами , где скалярная функция координат называется градиентом функции и обозначается символом (или , где – оператор набла). Таким образом, градиент потенциала:
е., единичные вектора. Вектор с компонентами , где скалярная функция координат называется градиентом функции и обозначается символом (или , где – оператор набла). Таким образом, градиент потенциала:
(24)
и из (23) и (24) следует , что
(25)
Так как градиент – это вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой, то градиентом потенциала (где r–радиус-вектор) называется вектор, направленный в сторону наиболее быстрого возрастания потенциала, численно равный быстроте его изменения на единицу длины в этом направлении.
Поскольку – векторная величина, то его модуль выражается как:
, (26)
подобно тому, как модуль вектора :
(27)
Знак “–” (25) указывает на то, что напряженность направлена в сторону убывания потенциала. Формула (25) позволяет по известным значениям найти напряженность поля в каждой точке или решить обратную задачу, т.е., по заданным значения в каждой точке найти разность потенциалов между двумя произвольными точками поля.
Формула (25) позволяет по известным значениям найти напряженность поля в каждой точке или решить обратную задачу, т.е., по заданным значения в каждой точке найти разность потенциалов между двумя произвольными точками поля.
Потенциал электростатического поля представляет собой функцию, меняющуюся от точки к точке. Однако, во всяком реальном случае можно выделить совокупность точек, потенциалы которых одинаковы.
Геометрическое место точек постоянного потенциала называется поверхностью равного потенциала или эквипотенциальной поверхностью.
Возьмем равномерно заряженную бесконечную плоскость (рис. 3.6). Поле, создаваемое такой плоскостью однородно, а линии напряженности нормальны к плоскости. Отсюда следует, что работа перемещения заряда из некоторой точки В1 в любую другую точку В2, находящуюся на таком же расстоянии от заряженной поверхности, что и точка В1 равна нулю. Действительно, при перемещении некоторого заряда q по прямой В1В2 сила, действующая на заряд со стороны поля, будет все время перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но эта работа может быть представлена, с другой стороны, в виде:
Действительно, при перемещении некоторого заряда q по прямой В1В2 сила, действующая на заряд со стороны поля, будет все время перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но эта работа может быть представлена, с другой стороны, в виде:
, (28)
где и – соответственно потенциалы точек В1 и В2. Отсюда, так как А = 0, то =, т.е., потенциалы точек, равноудаленных от заряженной плоскости, одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные поверхности) являются плоскостями, параллельными заряженной плоскости. Если плоскость заряжена положительно, то значение потенциала убывает по мере удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала расположены симметрично по обе стороны от заряженной плоскости.
Эквипотенциальные поверхности поля точечного заряда это сферы с радиусом r , центр которых находится в центре точечного заряда, т. е. (рис. 3.7). На рис. 3.6 и рис. 3.7 вектор напряженности перпендикулярен эквипотенциальным поверхностям.
е. (рис. 3.7). На рис. 3.6 и рис. 3.7 вектор напряженности перпендикулярен эквипотенциальным поверхностям.
Покажем, что вектор напряженности перпендикулярен эквипотенциальной поверхности. Рассмотрим работу по перемещению заряда по поверхности равного потенциала на малом участке пути ?S (рис. 3.7). При этом, работа электрической силы на данном пути будет:
, (29)
где α – угол между направлением силы f и перемещением ?S. С другой стороны, эта работа может быть выражена как произведение величины перемещающегося заряда на разность потенциалов в начальном и конечном положениях заряда, т.е. .
Так как перемещение идет по эквипотенциальной поверхности, то разность потенциалов и , или cosα = 0, значит α = 900 т.е. угол между направлением силы и перемещением ?S равен 900. Но , т.е. направления и совпадают, поэтому угол между и ?S, α=900 т.е. направление вектора напряженности электростатического поля всегда перпендикулярно к эквипотенциальной поверхности.
Эквипотенциальных поверхностей вокруг заряженного тела можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине , однако при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине.
Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям в каждой точке поля найти разность потенциаловмежду двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:
С другой стороны работу можно представить в виде:
, тогда
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, т.к. работа сил поля не зависит от пути.
При обходе по замкнутому контуру получим:
т. е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных зарядах заканчиваются (стоки) или уходят в бесконечность.
Обобщим теорему Гаусса и теорему о циркуляции вектора напряженности электростатического поля в вакууме. Так как , а , то . Поскольку (- оператор Лапласа), то для потенциала φ получим выражение или , которое называется уравнением Пуассона.
Это уравнение позволяет по известному распределению заряда и заданным граничным условием для потенциала φ определить значения во всех точках поля, а затем по формуле найти напряженность поля, т. е. решить прямую задачу электростатики.
е. решить прямую задачу электростатики.
Потенциал поля точечного заряда: .
потенциал Диполя
Найдем потенциал, создаваемый в точке P(r) двумя равными по величине зарядами противоположных знаков, расположенными на небольшом расстоянии друг от друга вблизи начала координат.
Рис. 3.1 |
|
(3.1) |
где обозначено ql=p или
(3.2) |
где вектор p определен как p=ql и называется электрическим моментом диполя или дипольным моментом.
Найдем в полярной системе координат компоненты Er и Eq вектора напряженности поля, создаваемого диполем. Для этого воспользуемся известной связью между напряженностью поля и потенциалом:
Выразим оператор набла в полярной системе координат
|
|
Тогда квадрат модуля вектора напряженности равен
а модуль
(3.5) |
Выразим вектор E через радиус вектор r и вектор дипольного момента p. Для этого применим соотношение (3.3) к потенциалу диполя в виде (3.2). Ввиду громоздкости выкладок, найдем векторE покомпонентно
Для этого применим соотношение (3.3) к потенциалу диполя в виде (3.2). Ввиду громоздкости выкладок, найдем векторE покомпонентно
По аналогии можно получить
Тогда окончательно будем иметь
(3.6) |
Полученное выражение не зависит от системы координат и выражает вектор напряженности поля через известные вектора p и r.
Потенциал системы зарядов
| Пусть вблизи начала координат находится некоторое количество точечных зарядов. Определим потенциал поля, создаваемого этими зарядами в точке P, расположенной на большом удалении (по сравнению с расстояниями между зарядами) от начала координат.
|
Для определения расстояния от i-того заряда до точки P воспользуемся теоремой косинусов (см. рис. 3.3):
Учитывая, что ri/ro << 1, выражение в скобках можно представить как (1+Δx), где Δx — малая величина, по степеням которой можно сделать разложение в ряд. Ограничиваясь линейными по ri/roчленами, получим следующее выражение:
Тогда для потенциала (3.7) будем иметь
Величинаназывается электрическим дипольным моментом системы зарядов.
Окончательно для потенциала системы зарядов, расположенной вблизи начала координат, в удаленной от нее точке, характеризуемой радиус-вектором r, имеем
(3.8) |
Как следует из полученного выражения, при не равном нулю суммарном заряде потенциал определяется в основном первым членом, стоящим в скобках в (3. 8), потому что он ~1/r, тогда как второй член ~1/r2. Однако во многих важных случаях суммарный заряд системы равен нулю, как это имеет место, например, для молекулы. Расположение же зарядов может быть таково, что дипольный момент системы отличен от нуля. Тогда потенциал определяется вторым членом. Заметим, что и при равном нулю дипольном моменте потенциал системы, вообще говоря, не равен нулю, а определяется членами высших порядков в разложении по степеням ri/ro. Напомним, что речь все время идет о потенциале в точках, расположенных на большом удалении от системы.
8), потому что он ~1/r, тогда как второй член ~1/r2. Однако во многих важных случаях суммарный заряд системы равен нулю, как это имеет место, например, для молекулы. Расположение же зарядов может быть таково, что дипольный момент системы отличен от нуля. Тогда потенциал определяется вторым членом. Заметим, что и при равном нулю дипольном моменте потенциал системы, вообще говоря, не равен нулю, а определяется членами высших порядков в разложении по степеням ri/ro. Напомним, что речь все время идет о потенциале в точках, расположенных на большом удалении от системы.
Проводники в электростатическом поле. Школьный курс физики
Главная | Физика 10 класс | Проводники в электростатическом поле
Свободные заряды.
Что происходит с телами, если их зарядить или поместить в электрическое поле? Проще всего ответить на этот вопрос, если рассмотреть случай проводника. В проводниках, к которым в первую очередь относятся металлы, имеются заряженные частицы, которые способны перемещаться внутри проводника под действием внешнего электрического поля. По этой причине заряды этих частиц называют свободными. В металлах носителями свободных зарядов являются электроны. Свободные электроны участвуют в тепловом (хаотическом) движении, подобно молекулам газа, и могут перемещаться по всему объёму металла в любом направлении.
В проводниках, к которым в первую очередь относятся металлы, имеются заряженные частицы, которые способны перемещаться внутри проводника под действием внешнего электрического поля. По этой причине заряды этих частиц называют свободными. В металлах носителями свободных зарядов являются электроны. Свободные электроны участвуют в тепловом (хаотическом) движении, подобно молекулам газа, и могут перемещаться по всему объёму металла в любом направлении.
Электростатическое поле внутри проводника.
Обобщим основные свойства электростатического поля внутри проводника.
1. Пpu равновесии зарядов на проводнике поле внутри проводника отсутствует. Это связано с тем, что свободные электроны в металлическом проводнике, помещённом в электростатическое поле, под действием сил поля будут перемещаться в направлении, противоположном его напряжённости. На рисунке 9.45 изображён проводник ABCD, находящийся в однородном электростатическом поле, напряжённость которого направлена слева направо. На поверхности проводника AC появляется избыточный отрицательный заряд, а на другой, BD, — избыточный положительный заряд.
На поверхности проводника AC появляется избыточный отрицательный заряд, а на другой, BD, — избыточный положительный заряд.
Таким образом, проводник, помещённый в однородное электростатическое поле, электризуется. При этом заряды, появляющиеся на поверхности проводника, создадут внутри проводника своё электростатическое поле напряжённостью . Силовые линии данного поля показаны пунктиром на рисунке 9.45.
Рис. 9.45
Они направлены противоположно силовым линиям внешнего электростатического поля. Перемещение зарядов будет происходит до тех пор, пока напряжённость результирующего электростатического поля внутри проводника не станет равной нулю 1.
1 Утверждение об отсутствии поля внутри проводника справедливо как для незаряженного проводника, помещённого во внешнее электростатическое поле, так и для проводника, которому сообщён некоторый избыточный заряд.
В этом состоит явление электростатической индукции. Появившиеся на поверхности проводника заряды (их называют индуцированными) создают своё поле, которое накладывается на внешнее электростатическое поле и его компенсирует.
Появившиеся на поверхности проводника заряды (их называют индуцированными) создают своё поле, которое накладывается на внешнее электростатическое поле и его компенсирует.
Для доказательства того факта, что внутри заряженного проводника или полости в проводнике электрическое поле отсутствует, Фарадей предложил прибор, называемый клеткой Фарадея (рис. 9.46).
Рис. 9.46
Он состоит из двух цилиндров, выполненных из проволочной сетки и расположенных внутри друг друга на основании из формованного пластика. Внешний цилиндр является экраном. Он позволяет наблюдать за тем, что происходит внутри внутреннего цилиндра (собственно клетки). Клетка закреплена на изолированных стержнях (изоляторах). Разность потенциалов такой конструкции с Землёй была настолько сильной, что при приближении к ней тел, соединённых с земной поверхностью, с внешней поверхности клетки вылетали искры.
В одном из опытов Фарадей сам располагался внутри клетки с очень чувствительным электроскопом. При этом электроскоп внутри клетки не показывал никакого отклонения. Другими словами, внутри клетки не действуют никакие электрические силы, хотя на наружной поверхности накапливался значительный заряд. Так было убедительно доказано, что электростатического поля внутри проводника нет.
При этом электроскоп внутри клетки не показывал никакого отклонения. Другими словами, внутри клетки не действуют никакие электрические силы, хотя на наружной поверхности накапливался значительный заряд. Так было убедительно доказано, что электростатического поля внутри проводника нет.
На этом свойстве основана так называемая электростатическая защита. Для того чтобы защитить чувствительные к электрическому полю приборы, их заключают в металлические ящики.
2. Рассмотрим более подробно ещё один вид электризации тел — электризацию через влияние. Для этого проведём опыт.
Исследования физических явлений опытным путём
При приближении наэлектризованного тела к лёгкому проводнику, например к лёгкому бузиновому цилиндру, подвешенному па нити, на нём появятся индуцированные заряды обоих знаков (рис. 9.47).
Рис. 9.47
Заряд противоположного знака будет притягиваться к телу, а одноимённый — отталкиваться. Так как последний находится на стороне цилиндра, более удалённой от тела, то равнодействующей этих сил будет сила притяжения. Под действием этой силы цилиндр притянется к телу. При их соприкосновении индуцированный заряд противоположного знака нейтрализуется частью заряда тела, равного ему по величине. На цилиндре останется заряд того же знака, что и на теле. Так как цилиндр теперь имеет заряд одного знака с телом, то он оттолкнётся от тела, что и наблюдается на опыте.
Так как последний находится на стороне цилиндра, более удалённой от тела, то равнодействующей этих сил будет сила притяжения. Под действием этой силы цилиндр притянется к телу. При их соприкосновении индуцированный заряд противоположного знака нейтрализуется частью заряда тела, равного ему по величине. На цилиндре останется заряд того же знака, что и на теле. Так как цилиндр теперь имеет заряд одного знака с телом, то он оттолкнётся от тела, что и наблюдается на опыте.
3. Внутри проводника при равновесии зарядов не только напряжённость поля равна нулю, равен нулю и заряд. Весь статический заряд проводника сосредоточен на его поверхности.
Объяснить скапливание заряда на поверхности проводника одним отталкиванием одноимённых зарядов нельзя. Кавендиш экспериментально доказал, что заряд проводника целиком распределяется на его поверхности. Для этого он поместил заряженный проводящий шар на изолирующей подставке внутрь сферы, образованной двумя металлическими полусферами, плотно соединёнными друге другом.
В одной из полусфер было сделано маленькое отверстие, через которое можно было соединить заряженный шар и полусферы металлической проволокой (рис. 9.48).
Рис. 9.48
После соединения шара и полусфер проволокой полусферы раздвигались и измерялся заряд шара. Он оказался равным нулю.
4. Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряжённости поля вдоль поверхности проводника. Она вызывала бы перемещение зарядов вдоль поверхности. Но это противоречит необходимому равновесному распределению зарядов на поверхности заряженного проводника.
5. Поверхность любого проводника в электростатическом поле яв ляется эквипотенциальной. Это связано с тем, что силовые линии электрического поля перпендикулярны поверхности проводника. Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость ноля внутри проводника равна нулю, поэтому равна нулю и разность потенциалов между любыми точками проводника.
Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал. Напряжённость ноля внутри проводника равна нулю, поэтому равна нулю и разность потенциалов между любыми точками проводника.
6. Многочисленные эксперименты свидетельствуют о том, что напряжённость электростатического поля зависит от кривизны поверхности. Чем сильнее искривлена поверхность, тем больше поверхностная плотность заряда (см. § 61 «Напряжённость поля различной конфигурации зарядов») в этом месте. На острие заряженного проводника поверхностная плотность заряда может стать настолько большой, что заряды начинают с него «стекать».
Причина этого явления состоит в большой напряжённости и значительной неоднородности электростатического поля вблизи острия. В сильном поле нейтральные молекулы воздуха поляризуются, коснувшись острия, молекулы приобретают одинаковый с ним заряд и отталкиваются от него. Заряженные молекулы удаляются от острия с большими скоростями, чем они приближались к нему, и увлекают за собой другие молекулы воздуха. Возникает так называемый «электрический ветер», которым можно даже погасить зажжённую свечу. В демонстрационном приборе — колесе Франклина — «электрический ветер», образующийся при стекании зарядов с остриёв, приводит во вращение изогнутые спицы с остриями на концах (рис. 9.49).
Возникает так называемый «электрический ветер», которым можно даже погасить зажжённую свечу. В демонстрационном приборе — колесе Франклина — «электрический ветер», образующийся при стекании зарядов с остриёв, приводит во вращение изогнутые спицы с остриями на концах (рис. 9.49).
Рис. 9.49
Вопросы:
1. Почему заряды в проводниках называют свободными?
2. Объясните, почему при равновесии зарядов на проводнике электростатическое поле внутри проводника отсутствует.
3. В чём состоит явление электростатической индукции?
4. Какой вывод можно сделать на основе опытов с клеткой Фарадея?
5. Какой способ электризации тел называют электризацией через влияние?
6. Почему поверхность проводника является эквипотенциальной?
Вопросы для обсуждения:
1. Если коснуться стержня заряженного электроскопа пальцем, то электроскоп разрядится. Произойдёт ли то же самое, если вблизи электроскопа находится заряженное тело?
2. Металлический заряженный цилиндр соединён с электроскопом. Наличие каких зарядов покажет электроскоп в тех случаях, когда:
Металлический заряженный цилиндр соединён с электроскопом. Наличие каких зарядов покажет электроскоп в тех случаях, когда:
а) в цилиндр вносится положительно заряженный шарик, не соприкасающийся с ним;
б) заряженным шариком касаются внутренней поверхности цилиндра?
Пример решения задачи
Положительный точечный заряд, модуль которого равен 3 ∙ 10 -7 Кл, находится на расстоянии 5 см от поверхности незаряженного проводящего шара радиусом 3 см. Определите потенциал поверхности шара. Найдите модуль заряда, который появится на шаре при его заземлении.
Рис. 9.50
В созданном зарядом q электрическом поле незаряженный шар электризуется. В результате на его поверхности появляются индуцированные заряды —qинд и ÷qинд. Используя формулу для потенциала поля точечного заряда, запишем:
Подставляя числовые данные, получим:
Определим модуль заряда, который появится на шаре при его заземлении (рис. 9.51).
9.51).
Рис. 9.51
Шар заземлён, поэтому φ0 = 0, так же, как и потенциал любой точки шара (положительный заряд уйдёт в землю). C учётом этого запишем:
Подставляя числовые данные, получим:
Ответ: φ0 ≈ 3,4 • 10 4 В, Q ≈ 1,1 • 10 -7 Кл.
Упражнения:
1. К заряженному электрометру подносят с большого расстояния отрицательно заряженный предмет. По мере приближения предмета показания электрометра сначала уменьшаются, а с некоторого момента вновь увеличиваются. Заряд какого знака был на электрометре?
2. Допустим, в вашем распоряжении имеются два изолированных металлических шара одинакового диаметра. Каким образом можно на них получить равные по модулю заряды:
а) разноимённые;
б) одноимённые?
3. Две металлические концентрические сферы радиусами 15 и 30 см расположены в воздухе. На внутренней сфере расположен заряд, равный -20 нКл. При этом потенциал внешней сферы равен 450 В. Вычислите напряжённость и потенциал электростатического поля в точках, удалённых от центра сфер:
При этом потенциал внешней сферы равен 450 В. Вычислите напряжённость и потенциал электростатического поля в точках, удалённых от центра сфер:
а) на 10 см;
б) 20 см;
в) 36 см.
4. Металлический шар радиусом 3,2 см, заряженный до потенциала 100 В, находится далеко от других заряженных тел и Земли. Чему будет равен модуль заряда на шаре, если его соединить длинным проводником с незаряженным металлическим шаром радиусом 32 см?
Предыдущая страницаСледующая страница
Связь между зарядом и потенциалом проводника — справочник студента
Формулы электричества и магнетизма. Изучение основ электродинамики традиционно начинается с электрического поля в вакууме.
Для вычисления силы взаимодействия между двумя точными зарядами и вычисления напряженности электрического поля, созданного точечным зарядом, нужно уметь применять закон Кулона.
Для вычисления напряженностей полей, созданных протяженными зарядами (заряженной нитью, плоскостью и т. д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
д.), применяется теорема Гаусса. Для системы электрических зарядов необходимо применять принцип
При изучении темы «Постоянный ток» необходимо рассмотреть во всех формах законы Ома и Джоуля-Ленца При изучении «Магнетизма» необходимо иметь в виду, что магнитное поле порождается движущимися зарядами и действует на движущиеся заряды. Здесь следует обратить внимание на закон Био-Савара-Лапласа. Особое внимание следует обратить на силу Лоренца и рассмотреть движение заряженной частицы в магнитном поле.
Электрические и магнитные явления связаны особой формой существования материи — электромагнитным полем. Основой теории электромагнитного поля является теория Максвелла.
Смотрите также основные формулы оптики
Таблица основных формул электричества и магнетизма
| Физические законы, формулы, переменные | Формулы электричество и магнетизм | ||||||||
Закон Кулона: где q1 и q2 — величины точечных зарядов, ԑ1 — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1),r — расстояние между зарядами. | |||||||||
| Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля. | |||||||||
|
| ||||||||
| Потенциал электрического поля: где W — потенциальная энергия заряда q0 . | |||||||||
| Потенциал поля точечного заряда на расстоянии r от заряда: | |||||||||
| По принципу суперпозиции полей, напряженность: | |||||||||
| Потенциал: где Ēi и ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.  | |||||||||
| Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 : | |||||||||
|
| ||||||||
| Электроемкость уединенного проводника: | |||||||||
| Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение. | |||||||||
| |||||||||
| Энергия заряженного конденсатора: | |||||||||
| Сила тока: | |||||||||
| Плотность тока: где S — площадь поперечного сечения проводника. | |||||||||
| |||||||||
|
| ||||||||
| Закон Джоуля-Ленца 1) для однородного участка цепи постоянного тока: где Q — количество тепла, выделяющееся в проводнике с током, t — время прохождения тока; 2) для участка цепи с изменяющимся со временем током: |
| ||||||||
| Мощность тока: | |||||||||
| Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1),µ0 — магнитная постоянная,H — напряженность магнитного поля.  | |||||||||
| Магнитная индукция (индукция магнитного поля): 1) в центре кругового тока где R — радиус кругового тока, 2) поля бесконечно длинного прямого тока где r — кратчайшее расстояние до оси проводника; 3) поля, созданного отрезком проводника с током где ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля; 4) поля бесконечно длинного соленоида где n — число витков на единицу длины соленоида. |
| ||||||||
| Сила Лоренца: по модулю где F — сила, действующая на заряд, движущийся в магнитном поле,v — скорость заряда q,α — угол между векторами v и B. | |||||||||
| Поток вектора магнитной индукции (магнитный поток через площадку S): 1) для однородного магнитного поля , где α — угол между вектором B и нормалью к площадке, 2) для неоднородного поля | |||||||||
Потокосцепление (полный поток): где N — число витков катушки. | |||||||||
| Закон Фарадея-Ленца: гдеԑi — ЭДС индукции. | |||||||||
| ЭДС самоиндукции: где L — индуктивность контура. | |||||||||
| Индуктивность соленоида: где n — число витков на единицу длины соленоида, V — объем соленоида. | |||||||||
| Энергия магнитного поля: | |||||||||
| Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура. | |||||||||
| Работа по перемещению замкнутого контура с током I в магнитном поле: |
Источник: https://infotables.ru/fizika/95-osnovnye-formuly-po-fizike-elektrichestvo-i-magnetizm
Потенциал. Связь между напряженностью электрического поля и потенциалом
Потенциалом называется скалярная величина, равная отношению потенциальной энергии, которой обладает пробный заряд, помещенный в данную точку поля, к величине этого заряда
Потенциал поля точечного заряда q выражается формулой
Работу сил поля над зарядом q0 можно выразить через разность потенциалов
Разность потенциалов (φ1 — φ2) равна напряжению U
Тогда работа по перемещению заряда в электрическом поле равна
За единицу потенциала принят вольт (В),
Существует связь между двумя характеристиками электрического поля: потенциалом и напряженностью. Для того, чтобы эту связь установить, надо вычислить работу по перемещению заряда q на расстояние d.
Для того, чтобы эту связь установить, надо вычислить работу по перемещению заряда q на расстояние d.
Получим ее для однородного электрического поля, т. е. при . По формуле (2.3) .
По формулам механики (1.25)
По формулам работы в электричестве (2.17)
- Приравнивая работы, получим
- Здесь d — расстояние вдоль линии напряженности между двумя точками с потенциалами φ1 и φ2.
- Согласно формуле (2.19), напряженность электрического поля выражается в вольтах на метр, причем
- Задания и вопросы для самоконтроля
1. Сформулируйте законы квантования, сохранения и инвариантности электрических зарядов.
2. Сформулируйте закон Кулона.
3. Что называется напряженностью электрического поля? Приведите примеры выражений для напряженности полей.
4. В чем заключается принцип суперпозиции?
5. Что называется потоком вектора напряженности электрического поля? Сформулируйте теорему Гаусса.
6. Что называется потенциалом?
7. Как вычисляется работа по перемещению заряда в электростатическом поле?
8. Получите связь между напряженностью и разностью потенциалов для однородного электрического поля (формулу (2.19)).
- Постоянный ток
- В этом разделе изучается направленное движение электрических зарядов.
- Понятие об электрическом токе
- Электрическим током называется упорядоченное движение электрических зарядов. Условиями существования электрического тока являются:
- 1) наличие свободных зарядов в проводнике;
- 2) наличие электрического поля внутри проводника.
- Проводниками являются металлы, растворы, расплавы электролитов, газы.
В металлах носителями зарядов являются свободные электроны. В растворах и расплавах электролитов ток обусловлен движением ионов обоих знаков. В газах носителями зарядов являются ионы и электроны.
Под действием электрического поля положительные заряды перемещаются по полю (вдоль вектора ), отрицательные — против поля (против вектора ). Полный ток определяется как сумма токов, образованных носителями каждого знака. Независимо от знака носителей зарядов, за направление тока условно принято направление движения положительных зарядов.
- Сила и плотность тока
- Основной характеристикой тока является сила тока.
- Силой тока называется скалярная величина, равная отношению величины заряда, протекающего через поперечное сечение проводника за некоторый интервал времени, к величине этого интервала.
Для постоянного тока, т. е. тока, не изменяющегося со временем, справедлива следующая формула
- В общем случае, если ток переменный, то сила тока вычисляется как производная от заряда по времени:
- Плотностью тока называется вектор, величина которого равна отношению силы тока, протекающего через элементарную площадку, перпендикулярную направлению движения зарядов, к площади этой площадки:
Единица плотности тока — . Вектор плотности тока направлен в сторону движения положительных электрических зарядов.
Вектор плотности тока направлен в сторону движения положительных электрических зарядов.
- Плотность тока может быть выражена через концентрацию носителей заряда n и среднюю скорость их упорядоченного движения
- где e — заряд одного носителя.
Источник: https://cyberpedia.su/9xdbd9.html
Потенциалы и заряженные проводники
Физика > Потенциалы и заряженные проводники
Узнайте, чему равен потенциал заряженного проводника. Изучите формулу электрического потенциала, состояние электрического поля, потенциал на концах проводника.
В заряженном проводнике электрический потенциал приравнивается к нулю. Но за его пределами может рассчитываться по ненулевому значению.
Задача обучения
- Выявить электрический потенциал внутри и снаружи заряженного проводника.
Основные пункты
- Формула для электрического потенциала:
- Электрическое поле постоянно = 0 для любого участка в заряженном проводнике, поэтому нельзя, чтобы разность потенциалов обладала отличным от 0 значением.

- Если точки расположены вне проводника, то потенциал отличается от нуля.
Термины
- Электрический потенциал – потенциальная энергия на единицу заряда в точке статического электрического поля.
- Работа – мера энергии, которую тратят на смещение объекта.
- Электрическое поле – участок пространства вокруг заряженной частички или между двумя напряжениями.
В момент подзарядки проводника, заряд распределяется по поверхности, пока не сформируется электростатическое равновесие.
То есть, поверхность становится эквипотенциальной.
Все точки внутри заряженного проводника оказываются в электрическом поле, приравниваемом к нулю. Дело в том, что полевые линии зарядов на поверхности оказываются противоположными друг другу. Но, даже при нулевом значении электрического поля, энергетический потенциал способен отличаться. И это можно доказать, если объединить электрическое поле и потенциал.
Отталкивающие силы в более изогнутой поверхности справа стараются вырваться наружу, а не вдоль поверхности
Работа отображает разницу конечной и стартовой потенциальной энергии.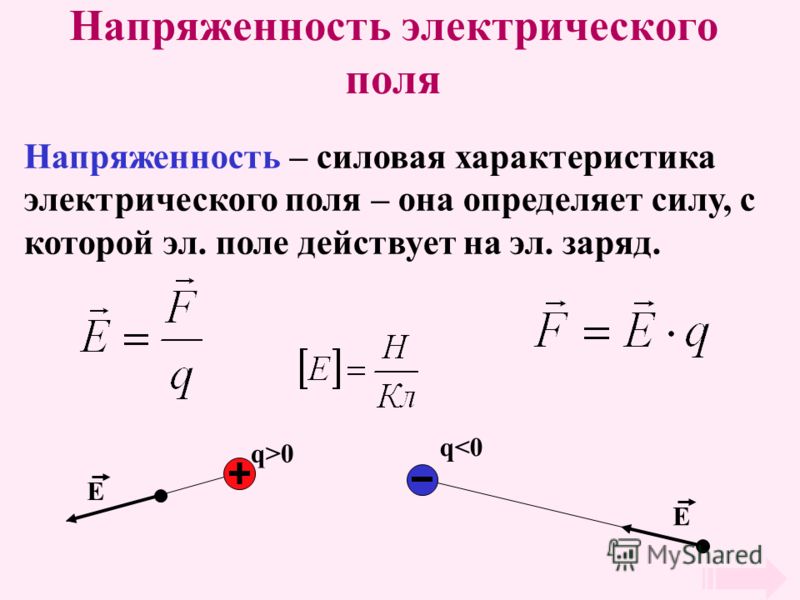 Эту разницу можно объединить с точечным произведением силы на каждой бесконечно малой дистанции:
Эту разницу можно объединить с точечным произведением силы на каждой бесконечно малой дистанции:
Это формула для работы, где вместо W поставили ΔU. Далее можно утверждать, что:
Делим обе части на составляющую q и упрощаем:
В итоге, выходим на:
Становится понятным, что при электрическом поле = 0 для любого места в заряженном проводнике, разность потенциалов достигает того же значения.
Но точки вне проводника отличаются по потенциалу электрического поля от 0 и их можно вычислить по тому же уравнению.
Читайте нас на Яндекс.Дзен
Источник: https://v-kosmose.com/fizika/potentsialyi-i-zaryazhennyie-provodniki/
Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
Напомним, что на прошлых уроках мы изучили две характеристики электрического поля: напряженность и разность потенциалов. Напряженность — это векторная величина, которая является силовой характеристикой поля:
Потенциал — это скалярная величина, которая является энергетической характеристикой поля:
Мы получили две формулы, описывающие работу поля при перемещении заряда: в одном случае работа выражена через напряженность, а во втором случае — через разность потенциалов, то есть, через электрическое напряжение:
Исходя из этих двух формул, мы можем вывести связь между напряжением и напряженностью:
Итак, в данной формуле, Е — это напряженность поля, U— это разность потенциалов между некоторыми точками 1 и 2, а d — это вектор перемещения, соединяющий эти точки. Из формулы видно, что чем меньше меняется потенциал на расстоянии дэ, тем меньше напряженность поля.
Из формулы видно, что чем меньше меняется потенциал на расстоянии дэ, тем меньше напряженность поля.
Если мы рассмотрим перемещение положительного заряда из точки 1 в точку 2, то убедимся, что поле совершает положительную работу. Это говорит о том, что потенциал в точке 1 больше, чем потенциал в точке 2.
Поэтому, вектор напряженности электрического поля направлен в сторону убывания потенциала.
Необходимо отметить, что формула, связывающая разность потенциалов и напряженность справедлива только в том случае, если мы рассматриваем однородное поле.
Заметим, тем не менее, что мы можем считать однородным любое электростатическое поле, при рассмотрении достаточно малой области пространства.
Таким образом, наша формула также будет справедлива в том случае, если расстояние d настолько мало, что изменением напряженности на этом расстоянии можно пренебречь.
Рассмотрим еще один интересный случай: перемещение заряда в направлении, перпендикулярном линиям напряженности однородного поля.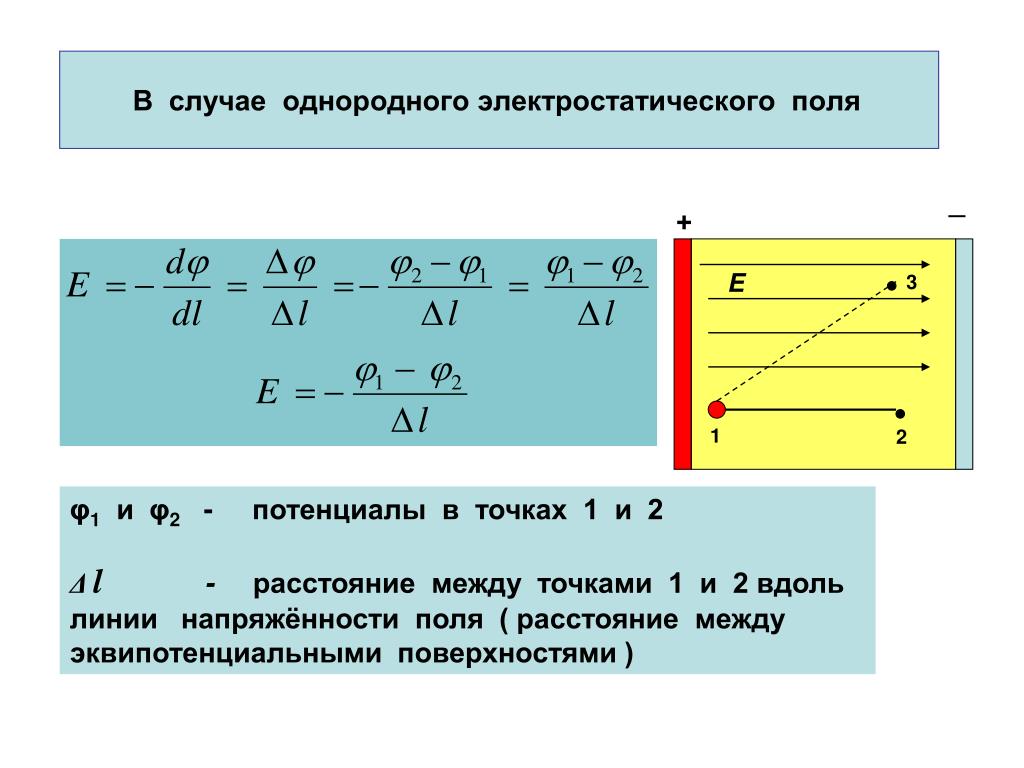
Как вы понимаете, при этом перемещении, электрическое поле не совершает работу, поскольку вектор силы и вектор перемещения перпендикулярны. Из этого можно заключить, что все точки поверхности, перпендикулярной линиям напряженности обладают одинаковым потенциалом.
Такие поверхности называют эквипотенциальными. Как видно из чертежа, эквипотенциальные поверхности однородного поля являются параллельными плоскостями.
Что касается поля точечного заряда, то его эквипотенциальные поверхности представляют собой концентрические сферы.
Действительно, в каждой точке поверхности этих сфер, вектор напряженности перпендикулярен этим поверхностям. Следовательно, поверхность любой сферы, центром которой является точечный заряд, является эквипотенциальной.
Напомним, что когда мы рассматривали проводники в электростатическом поле, мы убедились, что все линии напряженности поля перпендикулярны поверхности проводника.
Это означает, что поверхность любого проводника в электростатическом поле является эквипотенциальной. Также мы выяснили, что внутри проводника напряженность поля равна нулю.
Также мы выяснили, что внутри проводника напряженность поля равна нулю.
Следовательно, все точки внутри проводника обладают одинаковым потенциалом.
Пример решения задачи.
Задача. На рисунке показано перемещение положительного точечного заряда в однородном поле другого точечного заряда. Длина отрезка AB равна 2 см.
Предполагая, что во всей рассматриваемой области напряженность поля остается постоянной и равной 300 Н/Кл, определите разность потенциалов между точками E и F, указанными на рисунке.
Также, опишите, как менялась потенциальная энергия системы, какая работа была совершена на каких участках.
Источник: https://videouroki.net/video/66-sviaz-miezhdu-napriazhiennost-iu-eliektrostatichieskogho-polia-i-raznost-iu-potientsialov-ekvipotientsial-nyie-povierkhnosti.html
Потенциал электростатического поля и разность потенциалов — Класс!ная физика
«Физика — 10 класс»
Обладает ли электрическое поле энергией? В чём это выражается? Как рассчитать энергию поля?
В механике взаимное действие тел друг на друга характеризуют силой и потенциальной энергией. Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.
Электростатическое поле, осуществляющее взаимодействие между зарядами, также характеризуют двумя величинами. Напряжённость поля — это силовая характеристика. Теперь введём энергетическую характеристику — потенциал.
- Потенциал поля.
- Работа любого электростатического поля при перемещении в нём заряженного тела из одной точки в другую также не зависит от формы траектории, как и работа однородного поля.
- На замкнутой траектории работа электростатического поля всегда равна нулю.
- Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным.
- Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.
Работу потенциального поля можно выразить через изменение потенциальной энергии. Формула А = — (Wп2 — Wп1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой (14. 14).
14).
Потенциальная энергия заряда в электростатическом поле пропорциональна заряду. Это справедливо как для однородного поля (см. формулу (14.14)), так и для неоднородного. Следовательно, отношение потенциальной энергии к заряду не зависит от помещённого в поле заряда.
Это позволяет ввести новую количественную характеристику поля — потенциал, не зависящую от заряда, помещённого в поле.
Для определения значения потенциальной энергии, как мы знаем, необходимо выбрать нулевой уровень её отсчёта. При определении потенциала поля, созданного системой зарядов, как правило, предполагается, что потенциал в бесконечно удалённой точке поля равен нулю.
Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.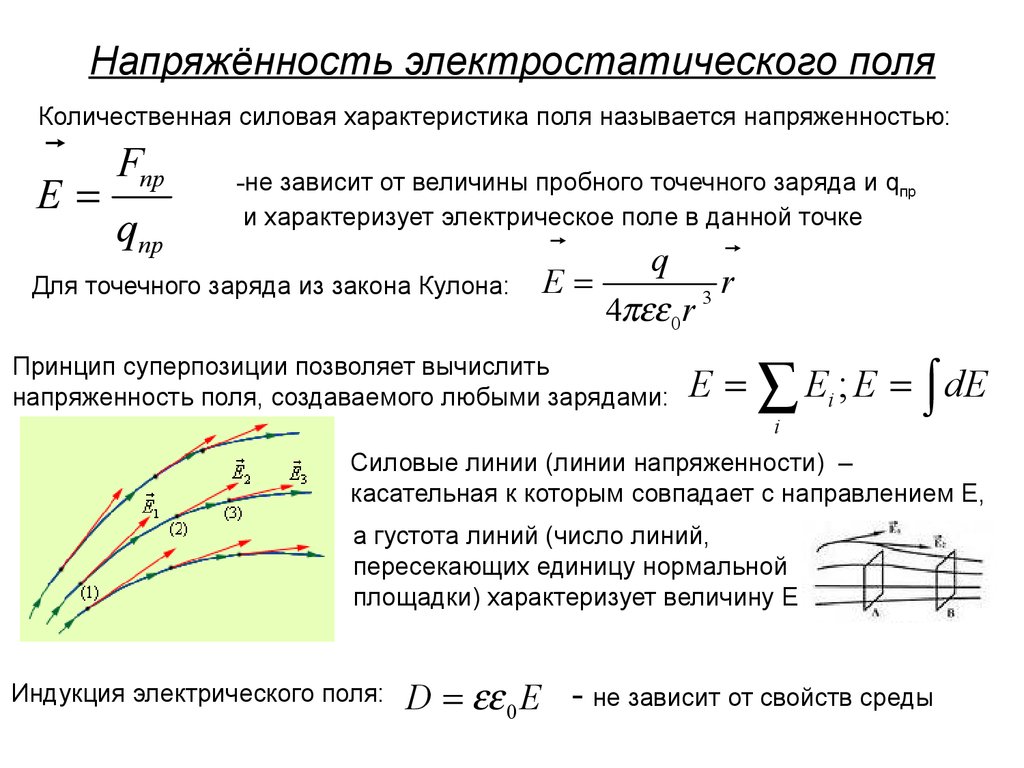
Согласно данному определению потенциал равен:
Из этой формулы следует, что потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
Напряжённость поля — векторная величина. Она представляет собой силовую характеристику поля, которая определяет силу, действующую на заряд q в данной точке поля. А потенциал φ — скаляр, это энергетическая характеристика поля; он определяет потенциальную энергию заряда q в данной точке поля.
Если в примере с двумя заряженными пластинами в качестве точки с нулевым потенциалом выбрать точку на отрицательно заряженной пластине (см. рис. 14.31), то согласно формулам (14.14) и (14.15) потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
Разность потенциалов.
Подобно потенциальной энергии, значение потенциала в данной точке зависит от выбора нулевого уровня для отсчёта потенциала, т. е. от выбора точки, потенциал которой принимается равным нулю.
Изменение потенциала не зависит от выбора нулевого уровня отсчёта потенциала.
Так как потенциальная энергия Wn = дчр, то работа сил поля равна:
А = — (Wп2 — Wп1) = -q(φ2 — φ1) = q(φ1 — φ2) = qU. (14.17)
Здесь
U = φ1 — φ2 — (14.18)
разность потенциалов, т. е. разность значений потенциала в начальной и конечной точках траектории.
Разность потенциалов называют также напряжением.
Согласно формулам (14.17) и (14.18) разность потенциалов между двумя точками оказывается равной:
Если за нулевой уровень отсчёта потенциала принять потенциал бесконечно удалённой точки поля, то потенциал в данной точке равен отношению работы электростатических сил по перемещению положительного заряда из данной точки в бесконечность к этому заряду.
Единица разности потенциалов.
Единицу разности потенциалов устанавливают с помощью формулы (14.19). В Международной системе единиц работу выражают в джоулях, а заряд — в кулонах.
Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.
Выразим единицу разности потенциалов через основные единицы СИ. Так как
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Назад в раздел «Физика — 10 класс, учебник Мякишев, Буховцев, Сотский»
Электростатика — Физика, учебник для 10 класса — Класс!ная физика
Что такое электродинамика — Электрический заряд и элементарные частицы. Закон сохранения заряд — Закон Кулона. Единица электрического заряда — Примеры решения задач по теме «Закон Кулона» — Близкодействие и действие на расстоянии — Электрическое поле — Напряжённость электрического поля. Силовые линии — Поле точечного заряда и заряженного шара.
Принцип суперпозиции полей — Примеры решения задач по теме «Напряжённость электрического поля.
Принцип суперпозиции полей» — Проводники в электростатическом поле — Диэлектрики в электростатическом поле — Потенциальная энергия заряженного тела в однородном электростатическом поле — Потенциал электростатического поля и разность потенциалов — Связь между напряжённостью электростатического поля и разностью потенциалов.
Эквипотенциальные поверхности — Примеры решения задач по теме «Потенциальная энергия электростатического поля. Разность потенциалов» — Электроёмкость. Единицы электроёмкости. Конденсатор — Энергия заряженного конденсатора. Применение конденсаторов — Примеры решения задач по теме «Электроёмкость. Энергия заряженного конденсатора»
Источник: http://class-fizika.ru/10_a177.html
Связь между потенциалом и напряженностью электрического поля
- Найдем связь потенциала с напряженностью электрического поля.
- Пусть заряд перемещается из точки 1 в точку 2, которые располагаются на оси OX. Тогда электрическое поле совершит работу:
- или .

Для бесконечно малого перемещения: . В случае смещения по трем координатам: Тогда связь между напряженностью и потенциалом электрического поля определяется соотношением: , где – оператор Набла, grad – векторный оператор, называемый «градиент».
Для выяснения геометрического смысла вводится понятие эквипотенциальных поверхностей или поверхностей равного потенциала. Эквипотенциальная поверхность есть такая поверхность, на которой потенциал остается постоянным. Потенциал может меняться только при переходе от одной эквипотенциальной поверхности к другой.
Возьмем на эквипотенциальной поверхности произвольную точку О и введем систему координат, начало которой совместим с точкой О.
Ось ΟΖ направим по нормали к эквипотенциальной поверхности в сторону возрастания потенциала . То же направление примем за положительное направление .
Координатная плоскость YX совместится с касательной плоскостью к эквипотенциальной поверхности. Тогда в точке Ο . Кроме того: , , тогда: .
Тогда в точке Ο . Кроме того: , , тогда: .
Функция возрастает наиболее быстро в направлении нормали . Поэтому: градиент функции есть вектор, направленный в сторону максимального возрастания этой функции, а его длина равна производной функции в том же направлении.
При движении вдоль эквипотенциальной поверхности потенциал поля не изменяется, поэтому элементарная работа при этом: . Вместе с тем, элементарная работа определяется соотношением при движении вдоль эквипотенциальной поверхности.
Отсюда следует, – напряженность электростатического поля направлена перпендикулярно к эквипотенциальной поверхности. Следовательно, и силовые линии электростатического поля направлены перпендикулярно эквипотенциальным поверхностям.
Вектор направлен противоположно вектору градиента потенциала . Электрические силовые линии являются, таким образом, линиями, вдоль которых потенциал изменяется наиболее быстро. Они направлены по нормали к эквипотенциальным поверхностям. Обычно их чертят так, что при переходе от одной эквипотенциальной поверхности к соседней потенциал получает одно и то же приращение .
Обычно их чертят так, что при переходе от одной эквипотенциальной поверхности к соседней потенциал получает одно и то же приращение .
Внутри проводника , а поэтому потенциал должен иметь одно и то же значение во всех точках проводника. Здесь эквипотенциальная поверхность вырождена в эквипотенциальный объем.
Электроемкость уединенного проводника
Различные по величине заряды распределяются на уединенном проводнике так, что отношение плотностей заряда в двух произвольных точках поверхности проводника при любой величине заряда будет одним и тем же.
Увеличение в n раз заряда повлечет изменение напряженности электрического поля в n раз; работа, по перемещению единичного заряда из бесконечности увеличится в n раз. Следовательно . Или: , где C – коэффициент пропорциональности, называемый электроемкостью.
– электроемкость численно равна заряду, сообщение которого проводнику повышает его потенциал на единицу. За единицу емкости принимают 1Ф (1 фарада) – емкость такого проводника, потенциал которого изменяется на 1В при сообщение ему заряда в 1Кл.
За единицу емкости принимают 1Ф (1 фарада) – емкость такого проводника, потенциал которого изменяется на 1В при сообщение ему заряда в 1Кл.
Поскольку для уединенного шара радиуса R потенциал равен , то, следовательно, электроемкость уединенного шара . Электроемкость в 1Ф соответствует уединенному шару с R= 9·109 м =1,5·103 RЗемли. Для измерения электроемкости используются дольные единицы:
- 1мФ (миллифарада) = 10-3 Ф; 1мкФ (микрофарада) =10-6 Ф;
- 1нФ (нанофарада) = 10-9 Ф; 1пФ (пикофарада) = 10-12 Ф.
- Конденсаторы
На практике существует потребность в устройствах, которые при небольшом относительно окружающих тел потенциале накапливали бы на себе («конденсировали») заметные по величине заряды. Такие устройства называют конденсаторами. Конденсаторы делают в виде двух проводников, помещенных близко друг к другу. Образующий конденсатор проводники называют их обкладками.
Чтобы внешние тела не оказывали влияния на емкость конденсатора, обкладками придают такую форму и так располагают друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было сосредоточено внутри конденсатора.
Этому удовлетворяют две пластинки, или два цилиндра, или две сферические поверхности, расположенные близко друг к другу (соответственно плоские, цилиндрические, сферические конденсаторы).
Ранее, используя терему Остроградского-Гаусса, были получены выражения, которые можно использовать для определения модуля напряженности электрического поля для вакуумного пространства между обкладками соответствующих конденсаторов: ; ; . За обкладками напряженность равна нулю.
Основной характеристикой конденсатора является его емкость, под которой понимают величину, пропорциональную заряду q и обратно пропорциональную напряжению между обкладками: ; , где .
Зарядом конденсатора q называется величина заряда одной из обкладок конденсатора. При этом под зарядом обкладок конденсатора нужно понимать только заряды, расположенные на внутренних, обращенных друг к другу поверхностях этих обкладок. Емкость конденсаторов измеряется, как и емкость уединенных проводников, в фарадах.
При этом под зарядом обкладок конденсатора нужно понимать только заряды, расположенные на внутренних, обращенных друг к другу поверхностях этих обкладок. Емкость конденсаторов измеряется, как и емкость уединенных проводников, в фарадах.
Величина емкости определяется геометрией конденсатора, а также свойствами среды, заполняющей пространство между конденсаторами. Найдем формулу для емкости плоского конденсатора, между обкладками которого находится вакуум. Напряженность между обкладками конденсатора: . Напряжение на обкладках конденсатора: .
Отсюда следует: ; . Если q U C > 0. Электроемкость плоского конденсатора растет при сближении пластин и увеличении их площади. Результат получен при условии d .Суммарный заряд: (здесь N – число конденсаторов в батарее). Поэтому емкость батареи : .
2) При последовательном соединении к источнику присоединяют по одной обкладке конденсаторов, остальные обкладки соединяют попарно.
Все конденсаторы получают одинаковый заряд, но неодинаковые напряжения: ; (здесь N – число конденсаторов в батарее). Поэтому величина, обратная емкости батареи : .
Поэтому величина, обратная емкости батареи : .
Рекомендуемые страницы:
Источник: https://lektsia.com/2x3c07.html
Потенциальная энергия заряженного тела. Потенциал. Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности. презентация к уроку по физике (10 класс)
Слайд 1
Потенциальная энергия заряженного тела. Потенциал. Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
Слайд 2
Заряженные тела притягивают или отталкивают друг друга. При перемещении заряженных тел действующие на них силы совершают работу. Из механики известно, что система, способная совершить работу благодаря взаимодействию тел друг с другом, обладает потенциальной энергией. Значит , система заряженных тел обладает потенциальной энергией, называемой электростатической или электрической – +
Слайд 3
С точки зрения теории близкодействия на заряд непосредственно действует электрическое поле, созданное другим зарядом. При перемещении заряда действующая на него со стороны поля сила совершает работу.
При перемещении заряда действующая на него со стороны поля сила совершает работу.
- Слайд 4
- Работа при перемещении заряда в однородном электростатическом поле Однородное поле создают большие металлические пластины, имеющие заряды противоположного знака.
- Слайд 5
- Это поле действует на заряд q с постоянной силой подобно тому, как Земля действует с постоянной силой на камень вблизи её поверхности.
- Слайд 6
- Потенциальная энергия Поскольку работа электростатической силы не зависит от формы траектории точки её приложения, сила является консервативной, и её работа равна изменению потенциальной энергии, взятому с противоположным знаком:
- Слайд 7
Важно! Потенциальная энергия заряда в однородном электростатическом поле равна: W п = qEd , где d — расстояние от точки 2 до любой точки, находящейся с точкой 2 на одной силовой линии. Потенциальная энергия
Слайд 8
Важно! На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю: A= — ΔW п = -(W п1 — W п1 ) = 0.
- Слайд 9
- На замкнутой траектории, когда заряд возвращается в начальную точку, работа поля равна нулю .
- Слайд 10
Потенциал поля Важно! На замкнутой траектории работа электростатического поля всегда равна нулю . Запомни! Поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю, называют потенциальным .
Слайд 11
Запомни! Потенциалом точки электростатического поля называют отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.
- Слайд 12
- Потенциал поля неподвижного точечного заряда q в данной точке поля, находящейся на расстоянии r от заряда, равен:
- Слайд 13
- Потенциал φ — скаляр, это энергетическая характеристика поля ; он определяет потенциальную энергию заряда q в данной точке поля. Потенциал однородного поля в точке, отстоящей на расстоянии d от неё, равен:
- Слайд 14
Разность потенциалов Важно! Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении положительного заряда из начальной точки в конечную к этому заряду. Запомни! Разность потенциалов называют также напряжением .
Запомни! Разность потенциалов называют также напряжением .
Слайд 15
Единица разности потенциалов Важно! Разность потенциалов между двумя точками численно равна единице, если при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу в 1 Дж. Эту единицу называют вольтом (В): 1 В = 1 Дж/1 Кл.
- Слайд 16
- Модуль вектора напряжённости поля равен: В этой формуле U — разность потенциалов между точками 1 и 2, лежащими на одной силовой линии поля
- Слайд 17
Формула показывает : чем меньше меняется потенциал на расстоянии Δd , тем меньше напряжённость электростатического поля . Если потенциал не меняется совсем, то напряжённость поля равна нулю. Важно! Напряжённость электрического поля направлена в сторону убывания потенциала.
Слайд 18
Единица напряжённости электрического поля Важно! Напряжённость электрического поля численно равна единице, если разность потенциалов между двумя точками, лежащими на одной силовой линии, на расстоянии 1 м в однородном поле равна 1 В. Единица напряжённости — вольт на метр (В/м)
Единица напряжённости — вольт на метр (В/м)
Слайд 19
Эквипотенциальные поверхности Запомни! Поверхности равного потенциала называют эквипотенциальными . Важно! Эквипотенциальной является поверхность любого проводника в электростатическом поле.
Ведь силовые линии перпендикулярны поверхности проводника. Причём не только поверхность, но и все точки внутри проводника имеют один и тот же потенциал.
Напряжённость поля внутри проводника равна нулю, значит, равна нулю и разность потенциалов между любыми точками проводника.
- Слайд 20
- Эквипотенциальные поверхности однородного поля представляют собой плоскости Эквипотенциальные поверхности поля точечного заряда представляют собой концентрические сферы
- Слайд 21
п. 93,94,95 задание стр. 320 № А1, А2 Домашнее задание
Источник: https://nsportal.ru/shkola/fizika/library/2019/03/25/potentsialnaya-energiya-zaryazhennogo-tela-potentsial-svyaz-mezhdu
Силовые и эквипотенциальные линии поля.
 §9 Силовые линии и эквипотенциали
§9 Силовые линии и эквипотенциалиЭквипотенциальные поверхности это такие поверхности каждая из точек, которых обладают одинаковым потенциалом. То есть на эквипотенциальной поверхности электрический потенциал имеет неизменное значение. Такой поверхностью является поверхности проводников, так как их потенциал одинаков.
Представим себе такую поверхность, для двух точек которой разность потенциалов будет равна нулю. Это и будет эквипотенциальная поверхность. Поскольку потенциал на ней одинаков. Если рассматривать эквипотенциальную поверхность в двухмерном пространстве, допустим на чертеже, то она будет иметь форму лини. Работа сил электрического поля по перемещению электрического заряда вдоль этой лини будет равна нулю.
Одним из свойств эквипотенциальных поверхностей является то, что они всегда перпендикулярны силовым линиям поля. Это свойство можно сформулировать и наоборот. Любая поверхность, которая перпендикулярна во всех точках к линиям электрического поля и называется эквипотенциальной.
Также такие поверхности никогда не пересекаются между собой. Так как это означало бы различие потенциала в пределах одной поверхности, что противоречит определению. Еще они всегда замкнуты. Поверхности равного потенциала не могут начаться и уйти в бесконечность, не имея при этом четких границ.
Как правило, на чертежах нет необходимости изображать поверхности целиком. Чаще изображают перпендикулярное сечение к эквипотенциальным поверхностям. Таким образом, они вырождаются в линии. Этого оказывается вполне достаточно для оценки распределения данного поля. При изображении графически поверхности располагают с одинаковым интервалом. То есть между двумя соседними поверхностям соблюдается одинаковый, шаг скажем в один вольт. Тогда по густоте линий образованных сечением эквипотенциальных поверхностей можно судить о напряжённости электрического поля.
Для примера рассмотрим поле, создаваемое точечным электрическим зарядом. Силовые линии такого поля радиальные. То есть они начинаются в центре заряда и направлены на бесконечность, если заряд положительный.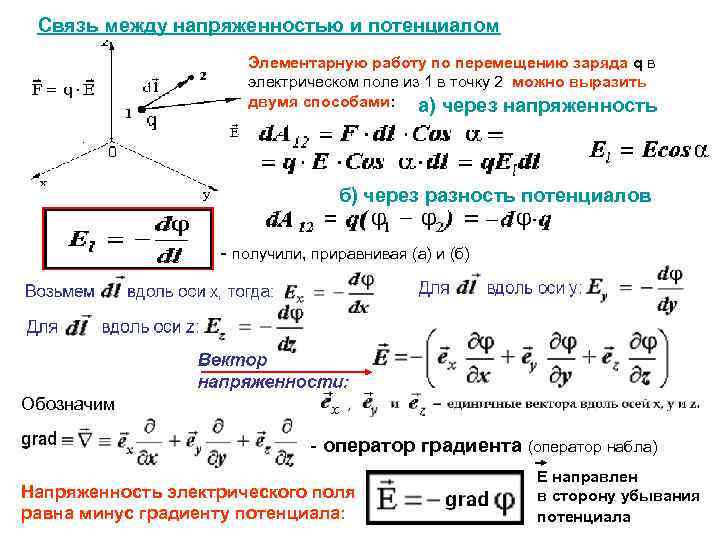 Или направлены к заряду, если он отрицательный. Эквипотенциальные поверхности такого поля будут иметь форму сфер с центром в заряде и расходящихся от него. Если же изобразить двухмерное сечение, то тогда эквипотенциальные лини будут в виде концентрических окружностей, центр которых также расположен в заряде.
Или направлены к заряду, если он отрицательный. Эквипотенциальные поверхности такого поля будут иметь форму сфер с центром в заряде и расходящихся от него. Если же изобразить двухмерное сечение, то тогда эквипотенциальные лини будут в виде концентрических окружностей, центр которых также расположен в заряде.
Рисунок 1 — эквипотенциальные лини точечного заряда
Для однородного поля такого как, например поле между обкладками электрического конденсатора поверхности равного потенциала будут иметь форму плоскостей. Эти плоскости расположены параллельно друг другу на одинаковом расстоянии. Правда на краях обкладок картина поля исказится вследствие краевого эффекта. Но мы представим себе, что обкладки бесконечно длинные.
Рисунок 2 — эквипотенциальные линии однородного поля
Чтобы изобразить эквипотенциальные лини для поля, создаваемого двумя равными по величине и противоположными по знаку зарядами не достаточно применить принцип суперпозиции. Так как в этом случае при наложении двух изображений точечных зарядов будут точки пересечения линий поля. А этого быть не может, так как поле не может быть направлено сразу в две разные стороны. В этом случае задачу необходимо решить аналитически.
Так как в этом случае при наложении двух изображений точечных зарядов будут точки пересечения линий поля. А этого быть не может, так как поле не может быть направлено сразу в две разные стороны. В этом случае задачу необходимо решить аналитически.
Рисунок 3 — Картина поля двух электрических зарядов
> Эквипотенциальные линии
Характеристика и свойства линий эквипотенциальной поверхности : состояние электрического потенциала поля, статическое равновесие, формула точечного заряда.
Эквипотенциальные линии поля – одномерные области, где электрический потенциал остается неизменным.
Задача обучения
- Охарактеризовать форму эквипотенциальных линий для нескольких конфигураций заряда.
Основные пункты
- Для конкретного изолированного точечного заряда потенциал основывается на радиальной дистанции. Поэтому эквипотенциальные линии выступают круглыми.
- Если контактирует несколько дискретных зарядов, то их поля пересекаются и демонстрируют потенциал.
 В итоге, эквипотенциальные линии перекашиваются.
В итоге, эквипотенциальные линии перекашиваются. - Когда заряды распределяются по двум проводящим пластинам в статическом балансе, эквипотенциальные линии практически прямые.
Термины
- Эквипотенциальный – участок, где каждая точка обладает единым потенциалом.
- Статическое равновесие – физическое состояние, где все компоненты пребывают в покое, а чистая сила приравнивается к нулю.
Эквипотенциальные линии отображают одномерные участки, где электрический потенциал остается неизменным. То есть, для такого заряда (где бы он ни находился на эквипотенциальной линии) не нужно осуществлять работу, чтобы сдвинуться с одной точки на другую в пределах конкретной линии.
Линии эквипотенциальной поверхности бывают прямыми, изогнутыми или неправильными. Все это основывается на распределении зарядов. Они располагаются радиально вокруг заряженного тела, поэтому остаются перпендикулярными к линиям электрического поля.
Одиночный точечный заряд
Для одиночного точечного заряда формула потенциала:
Здесь наблюдается радиальная зависимость, то есть, независимо от дистанции к точечному заряду потенциал остается неизменным. Поэтому эквипотенциальные линии принимают круглую форму с точечным зарядом в центре.
Поэтому эквипотенциальные линии принимают круглую форму с точечным зарядом в центре.
Изолированный точечный заряд с линиями электрического поля (синий) и эквипотенциальными (зеленый)
Множественные заряды
Если контактирует несколько дискретных зарядов, то мы видим, как перекрываются их поля. Это перекрытие заставляет потенциал объединяться, а эквипотенциальные линии перекашиваться.
Если присутствует несколько зарядов, то эквипотенциальные линии формируются нерегулярно. В точке между зарядами контрольный способен ощущать эффекты от обоих зарядов
Непрерывный заряд
Если заряды расположены на двух проводящих пластинах в условиях статического баланса, где заряды не прерываются и находятся на прямой, то и эквипотенциальные линии выпрямляются. Дело в том, что непрерывность зарядов вызывает непрерывные действия в любой точке.
Если заряды вытягиваются в линию и лишены прерывания, то эквипотенциальные линии идут прямо перед ними. В качестве исключения можно вспомнить только изгиб возле краев проводящих пластин
В качестве исключения можно вспомнить только изгиб возле краев проводящих пластин
Непрерывность нарушается ближе к концам пластин, из-за чего на этих участках создается кривизна – краевой эффект.
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РАБОТЫ.
Между напряженностью электрического доля и электрическим потенциалом существует интегральная и дифференциальная связь:
j 1 — j 2 = ∫ Е dl (1)
E = -grad j (2)
Электрическое поле может быть представлено графически двумя способами, дополняющими друг друга: с помощью эквипотенциальных поверхностей и линий напряженности (силовых линий).
Поверхность, все точки которой имеют одинаковый
потенциал, называется эквипотенциальной поверхностью. Линия пересечения ее с
плоскостью чертежа называется эквипотенциалью. Силовые линии — линии,
касательные к которым в каждой точке совпадают с направлением вектора Е . На рисунке 1 пунктирными линиями показаны эквипотенциали, сплошными — силовые
линии электрического поля.
На рисунке 1 пунктирными линиями показаны эквипотенциали, сплошными — силовые
линии электрического поля.
Рис.1
Разность потенциалов между точками 1 и 2 равна 0, так как они находятся на одной эквипотенциали. В этом случае из (1):
∫Е dl = 0 или ∫Е dlcos ( Edl ) = 0 (3)
Поскольку Е и dl в выражении (3) не равны 0, то cos ( Edl ) = 0 . Следовательно, угол между эквипотенциалью и силовой линией составляет p/2.
Из дифференциальной связи (2) следует, что силовые линии всегда направлены в сторону убывания потенциала.
Величина напряженности электрического поля
определяется «густотой» силовых линий. Чем гуще силовые линии, тем меньше
расстояние между эквипотенциалями, так что силовые линии и эквипотенциали
образуют «криволинейные квадраты». Исходя из этих принципов, можно
построить картину силовых линий, располагая картиной эквипотенциалей, и
наоборот.
Исходя из этих принципов, можно
построить картину силовых линий, располагая картиной эквипотенциалей, и
наоборот.
Достаточно полная картина эквипотенциалей поля позволяет рассчитать в разных точках значение проекции вектора напряженности Е на выбранное направление х , усредненное по некоторому интервалу координаты ∆х :
Е ср. ∆х = — ∆ j /∆х,
где ∆х — приращение координаты при переходе с одной эквипотенциали на другую,
∆ j — соответствующее ему приращение потенциала,
Е ср. ∆х — среднее значение Е х между двумя потенциалами.
ОПИСАНИЕ УСТАНОВКИ И МЕТОДИКА ИЗМЕРЕНИЙ.
Для моделирования электрического поля удобно
использовать аналогию, существующую между электрическим полем, созданным
заряженными телами и электрическим полем постоянного тока, текущего по
проводящей пленке с однородной проводимостью. При этом расположение силовых
линий электрического поля оказывается аналогично расположению линий
электрических токов.
При этом расположение силовых
линий электрического поля оказывается аналогично расположению линий
электрических токов.
То же утверждение справедливо для потенциалов. Распределение потенциалов поля в проводящей пленке такое же, как в электрическом поле в вакууме.
В качестве проводящей пленки в работе используется электропроводная бумага с одинаковой во всех направлениях проводимостью.
На бумаге устанавливаются электроды так, чтобы обеспечивался хороший контакт между каждым электродом и проводящей бумагой.
Рабочая схема установки приведена на рисунке 2.
Установка состоит из модуля II, выносного элемента I, индикатора III,
источника питания IV. Модуль служит для подключения всех используемых
приборов. Выносной элемент представляет собой диэлектрическую панель 1, на
которую помещают лист белой бумаги 2, поверх нее — лист копировальной бумаги
3, затем — лист электропроводящей бумаги 4, на котором крепятся электроды 5.
Напряжение на электроды подается от модуля II с помощью
соединительных проводов. Индикатор III и зонд 6 используются для
определения потенциалов точек на поверхности электропроводящей бумаги.
Индикатор III и зонд 6 используются для
определения потенциалов точек на поверхности электропроводящей бумаги.
В качестве зонда применяется провод со штекером на конце. Потенциал j зонда равен потенциалу той точки поверхности электропроводящей бумаги, которой он касается. Совокупность точек поля с одинаковым потенциалом и есть изображение эквипотенциали поля. В качестве источника питания IV используется блок питания ТЕС – 42, который подключается к модулю с помощью штепсельного разъема на задней стенке модуля. В качестве индикатора Ш используется вольтметр В7 – 38.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.
1. Установить на панели 1 лист белой бумаги 2. На него положить копировальную бумагу 3 и лист электропроводящей бумаги 4 (рис.2).
2. Установить на электропроводящей бумаге электроды 5 и закрепить гайками.
3. Подключить к модулю блок питания IV
(ТЕС – 42) с помощью штепсельного разъема на задней стенке модуля.
4. С помощью двух проводников подключить индикатор III (вольтметр В7 – 38) к гнездам «PV» на лицевой панели модуля. Нажать соответствующую кнопку на вольтметре для измерения постоянного напряжения (рис.2).
5. С помощью двух проводников подключить электроды 5 к модулю П.
6. Подключить зонд (провод с двумя штекерами) к гнезду на лицевой панели модуля.
7. Подключить стенд к сети 220 В. Включить общее питание стенда.
Связь между напряженностью и потенциалом.
Для потенциального поля, между потенциальной (консервативной) силой и потенциальной энергией существует связь
где («набла») — оператор Гамильтона.
Поскольку то
Знак минус показывает, что вектор Е направлен в сторону убывания потенциала.
Для графического изображения распределения потенциала используются эквипотенциальные поверхности — поверхности во всех точках которых потенциал имеет одно и то же значение.
Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше. На рисунке пунктиром изображены силовые линии, сплошными линиями — сечения эквипотенциальных поверхностей для: положительного точечного заряда (а), диполя (б), двух одноименных зарядов (в), заряженного металлического проводника сложной конфигурации (г).
Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше. На рисунке пунктиром изображены силовые линии, сплошными линиями — сечения эквипотенциальных поверхностей для: положительного точечного заряда (а), диполя (б), двух одноименных зарядов (в), заряженного металлического проводника сложной конфигурации (г).
Для точечного заряда потенциал поэтому эквипотенциальные поверхности — концентрические сферы. С другой стороны, линии напряженности — радиальные прямые. Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям.
Можно показать, что во всех случаях вектор Е перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала.
Примеры расчета наиболее важных симметричных электростатических полей в вакууме.
1. Электростатическое поле электрического диполя в вакууме.
Электрическим диполем (или двойным электрическим полюсом) называется система двух равных по модулю разноименных точечных зарядов (+q,-q), расстояние l между которыми значительно меньше расстояния до рассматриваемых точек поля (l
Плечо диполя l — вектор, направленный по оси диполя от отрицательного заряда к положительному и равный расстоянию между ними.
Электрический момент диполя ре — вектор, совпадающий по направлению с плечом диполя и равный произведению модуля заряда |q| на плечо I:
Пусть r — расстояние до точки А от середины оси диполя. Тогда, учитывая что
2)Напряженность поля в точке В на перпендикуляре, восстановленном к оси диполя из его середины при
Точка В равноудалена от зарядов +q и -q диполя, поэтому потенциал поля в точке В равен нулю. Вектор Ёв направлен противоположно вектору l .
3)Во внешнем электрическом поле на концы диполя действует пара сил, которая стремится повернуть диполь таким образом, чтобы электрический момент ре диполя развернулся вдоль направления поля Ё (рис.(а)).
Во внешнем однородном поле момент пары сил равен M = qElsin а или Во внешнем неоднородном поле (рис.(в)) силы, действующие на концы диполя, неодинаковы и их результирующая стремится передвинуть диполь в область поля с большей напряженностью — диполь втягивается в область более сильного поля.
2. Поле равномерно заряженной бесконечной плоскости.
Бесконечная плоскость заряжена с постоянной поверхностной плотностью Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны.
В качестве Гауссовой поверхности примем поверхность цилиндра, образующие которого перпендикулярны заряженной плоскости, а основания параллельны заряженной плоскости и лежат по разные стороны от нее на одинаковых расстояниях.
Так как образующие цилиндра параллельны линиям напряженности, то поток вектора напряженности через боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания 2ES. Заряд, заключенный внутри цилиндра, равен . По теореме Гаусса откуда:
Е не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю. Такое поле называется однородным.
Разность потенциалов между точками, лежащими на расстояниях х1 и х2 от плоскости, равна
3. Поле двух бесконечных параллельных разноименно заряженных плоскостей с равными по абсолютному значению поверхностными плотностями зарядов σ>0 и — σ.
Поле двух бесконечных параллельных разноименно заряженных плоскостей с равными по абсолютному значению поверхностными плотностями зарядов σ>0 и — σ.
Из предыдущего примера следует, что векторы напряженности Е 1 и E 2 первой и второй плоскостей равны по модулю и всюду направлены перпендикулярно плоскостям. Поэтому в пространстве вне плоскостей они компенсируют друг друга, а в пространстве между плоскостями суммарная напряженность . Поэтому между плоскостями
(в диэлектрике. ).
Поле между плоскостями однородное. Разность потенциалов между плоскостями.
(в диэлектрике ).
4.Поле равномерно заряженной сферической поверхности.
Сферическая поверхность радиуса R с общим зарядом q заряжена равномерно с поверхностной плотностью
Поскольку система зарядов и, следовательно, само поле центрально-симметрично относительно центра сферы, то линии напряженности направлены радиально.
В качестве Гауссовой поверхности выберем сферу радиуса r, имеющую общий центр с заряженной сферой. Если r>R, то внутрь поверхности попадает весь заряд q. По теореме Гаусса , откуда
Если r>R, то внутрь поверхности попадает весь заряд q. По теореме Гаусса , откуда
При r
Разность потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 от центра сферы
(r1 >R,r2 >R), равна
Вне заряженной сферы поле такое же, как поле точечного заряда q, находящегося в центре сферы. Внутри заряженной сферы поля нет, поэтому потенциал всюду одинаков и такой же, как на поверхности
Найдем взаимосвязь между напряженностью электростатического поля, являющейся его силовой характеристикой, и потенциалом — энергетической характеристикой поля. Работа по перемещению единичного точечного положительного заряда из одной точки поля в другую вдоль оси х при условии, что точки расположены бесконечно близко друг к другу и x 1 – x 2 = dx, равна E x dx. Та же работа равна j 1 -j 2 = dj. Приравняв оба выражения, можем записать
где символ частной производной подчеркивает, что дифференцирование производится только по х. Повторив аналогичные рассуждения для осей y и z, можем найти вектор Е:
Повторив аналогичные рассуждения для осей y и z, можем найти вектор Е:
где i, j, k — единичные векторы координатных осей х, у, z.
Из определения градиента (12.4) и (12.6). следует, что
т. е. напряженность Е поля равна градиенту потенциала со знаком минус. Знак минус определяется тем, что вектор напряженности Е поля направлен в сторону убывания потенциала.
Для графического изображения распределения потенциала электростатического поля, как и в случае поля тяготения (см. § 25), пользуются эквипотенциальными поверхностями — поверхностями, во всех точках которых потенциал jимеет одно и то же значение.
Если поле создается точечным зарядом, то его потенциал, согласно (84.5),
Таким образом, эквипотенциальные поверхности в данном случае — концентрические сферы. С другой стороны, линии напряженности в случае точечного заряда — радиальные прямые. Следовательно, линии напряженности в случае точечного заряда перпендикулярны эквипотенциальным поверхностям.
Линии напряженности всегда нормальны к эквипотенциальным поверхностям. Действительно, все точки эквипотенциальной поверхности имеют одинаковый потенциал, поэтому работа по перемещению заряда вдоль этой поверхности равна нулю, т. е. электростатические силы, действующие на заряд, всегда направлены по нормалям к эквипотенциальным поверхностям. Следовательно, вектор Е всегда нормален к эквипотенциальным поверхностям, а поэтому линии вектора Е ортогональны этим поверхностям.
Эквипотенциальных поверхностей вокруг каждого заряда и каждой системы зарядов можно провести бесчисленное множество. Однако их обычно проводят так, чтобы разности потенциалов между любыми двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности рас положены гуще, напряженность поля больше.
Итак, зная расположение линий напряженности электростатического поля, можно построить эквипотенциальные поверхности и, наоборот, по известному расположению эквипотенциальных поверхностей можно определить в каждой точке поля модуль и направление напряженности поля. На рис. 133 для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б).
На рис. 133 для примера показан вид линий напряженности (штриховые линии) и эквипотенциальных поверхностей (сплошные линии) полей положительного точечного заряда (а) и заряженного металлического цилиндра, имеющего на одном конце выступ, а на другом — впадину (б).
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 22Следующая ⇒ Градиент потенциала представляет собой вектор, направление которого совпадает с направлением наибыстрейшего возрастания потенциала. Знак «минус» указывает на то, что вектор напряженности электрического поля направлен в сторону убывания потенциала.
Эквипотенциальные поверхности. При перемещении заряда в направлении, перпендикулярном вектору напряженности электрического поля работа не совершается . Это значит, что траектория заряда принадлежит поверхности, точки которой имеют один и тот же потенциал. Такие поверхности называют эквипотенциальными поверхностями. Эквипотенциальные поверхности совместно с силовыми линиями используют для графического изображения электрических полей. Примеры графического изображения электрических полей представлены ниже:
Элементы теории поля. 1. Поток вектора
Циркуляция вектора. Циркуляцией некоторого вектора , вдоль замкнутого контура ,называют криволинейный интеграл по контуру от скалярного произведения вектора дифференциал длины дуги контура .
-Т. Остроградского -Т. Стокса
2)
2)
3) 4)
5)
6) 7)
Оператор Набла
Оператор Лапласа
div a = : :
ДИВЕРГЕНЦИЕЙ — ( расхождение ) вектора ( а ) называют предел отношения потока вектора ( а ) через замкнутую поверхность к величине объема, ограниченного этой поверхностью при условии, что объем стремится к нулю
“ ДИВЕРГЕНЦИЯ “ — это родник в лесу , а поток это количество воды прошедшее через поперечное течение русла реки
— оператор Набла
теорема Остаградского-Гауса или уравнение Максвелла
Этот закон можно представить в виде: .
Приведенное соотношение часто называют теоремой Остроградского-Гаусса. Понятие потока вектора является одним из фундаментальных понятий электродинамики. Рассмотрим его более подробно. Выделим в электрическом поле небольшую плоскую площадку площадью . Поток вектора через выделенную площадку будет равен скалярному произведению векторов и . Площадку представляют вектором , величина которого равна площади площадки, а направление совпадает с направлением единичного вектора нормали к этой площадке. Другими словами Поэтому поток вектора через площадку будет равен . Поток вектора через произвольную замкнутую поверхность будет равен сумме или интегралу элементарных потоков . Покажем справедливость теоремы Остроградского-Гаусса на примере электрического поля, созданного точечным зарядом. В силу сферической симметрии электрического поля вектор в любой точке сферы будет перпендикулярен поверхности сферы и иметь одну и ту же величину.
. Из полученного соотношение следует, что величина напряженности электрического поля точечного заряда на расстоянии от него, будет равна Точно такое же значение для напряженности поля точечного заряда было получено ранее с помощью закона Кулона.
Чтобы сформулировать другой фундаментальный закон электродинамики введем в рассмотрение новое математическое понятие — понятие о циркуляции вектора. Циркуляцией некоторого вектора вдоль элементарного участка произвольной кривой называют интеграл от скалярного произведения вектора на элементарное перемещение или . . Используя понятие циркуляции вектора, независимость работы консервативных сил от вида траектории можно представить в виде утверждения о том, что циркуляция вектора консервативной силы на замкнутой траектории равна нулю. В силу того, что напряженность электрического поля равна консервативной силе, действующей на единичный положительный заряд, для циркуляции вектора электрической напряженности будет справедливо соотношение . Из приведенного соотношения следует, что циркуляция вектора электрической напряженности для любого замкнутого контура равна нулю. Данное утверждение будет справедливо тогда, когда отсутствуют магнитные поля. В присутствие магнитных полей циркуляция вектора на замкнутом контуре не равна нулю. Она определяется скоростью изменения магнитного потока, пронизывающего данный контур. Это утверждение представляет собой содержание одного из фундаментальных законов электродинамики. Его записывают в виде . (II) Приведенное соотношение представляет собой известный закон Фарадея об электромагнитной индукции, в соответствие с которым ЭДС, наведенная в замкнутом контуре, равна скорости изменения магнитного потока, пронизывающего этот контур. Два других закона электродинамики касаются свойств магнитного поля и его связи с электрическим полем. Один из них утверждает, что поток вектора магнитной индукции через любую замкнутую поверхность равен нулю: .
Приведенное соотношение указывает на то, что в природе не существуют магнитные заряды. В отличие от силовых линий электрического поля, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах, силовые линии магнитного поля являются замкнутыми линиями, Они нигде не начинаются и нигде не заканчиваются. Поэтому говорят, что магнитное поле в отличие потенциального электрического поля является соленоидальным полем.
Примеры расчета электрических полей простейших систем электрических зарядов. ПРИМЕНЕНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО-ГАУССА ДЛЯ РАСЧЕТА ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
1. Равномерно заряженная плоскость 2.
Ф = 2 Ф (1) + 4 Ф (2) = 2 E S + 4 Eфсos90 ` = 2ES
2. Две равномерно заряженные плоскости.
3. Равномерно заряженный бесконечный цилиндр.
Ф = Ф бок + 2 Ф осн = E Sбок cos 0` + 2 E (1) S осн cos90`= E 2 ПrL +0
E
r R
4. Равномерно заряженный шар
Если сфера радиусом центрально симметрично окружает шар, то Или
По поводу термина электростатического смещения:
Электрическое смещение — физическая величина численно равная величине заряда “сместившегося “ изнутри проводника к поверхности на единицу поверхности .
Проведем оценку структуры электрического поля бесконечно протяженной, однородно заряженной плоскости. Поток вектора через цилиндрическую поверхность можно представить двумя слагаемыми . Очевидно, что поток вектора через боковую поверхность равен нулю, а поток вектора через основания цилиндра будет равен , где напряженность поля, например, в точке , принадлежащей основанию цилиндра. Теперь из теоремы Остроградского-Гаусса для напряженности получим . Принимая во внимание, что величина характеризует поверхностную плотность заряда, для напряженности электрического поля равномерно заряженной бесконечно протяженной плоскости получим следующую формулу Из полученной формулы следует, что электрическое поле, бесконечно протяженной равномерно заряженной плоскости является однородным. Чтобы найти потенциал в каждой точки поля, воспользуемся соотношением, связывающим его с напряженностью поля Если ось направить вдоль вектора напряженности поля , то можно получить . Интегрируя последнее выражение, для разности потенциалов между точками электрического поля бесконечно протяженной равномерно заряженной плоскости получим . Из приведенной формулы следует, что эквипотенциальные поверхности параллельны заряженной плоскости, и что разность потенциалов между эквипотенциальными поверхностями растет линейно с расстоянием между ними. Представим графически структуру электрического поля бесконечно протяженной равномерно заряженной плоскости, несущей положительный и отрицательный за ряды Аналогичную структуру имеет гравитационное поле Земли вблизи ее поверхности. . Используя теорему Остроградского – Гаусса, легко показать, что электрическое поле равномерно заряженной сферы за пределами сферы будет иметь вид Если заряд сферы распределен равномерно по ее поверхности, то напряженность электрического поля внутри сферы будет равна нулю, а потенциал точек внутри сферы будет одинаковым, равным потенциалу ее поверхности. Если радиус сферы равен , то ее потенциал определится формулой Величина напряженности электрического поля вблизи поверхности сферы может быть представлена соотношением , где — поверхностная плотность заряда, распределенного по поверхности сферы. Используя теорему Остроградского-Гаусса, подсчитаем напряженность и потенциал электрического поля, созданного бесконечно протяженной равномерно заряженной нитью. Принимая во внимание, что величина характеризует линейную плотность заряда, для напряженности электрического поля бесконечно протяженной равномерно заряженной нити получим следующую формулу . Для получения формулы для разности потенциалов в электрическом поле нити, заметим, что . Интегрируя приведенное выражение, для разности потенциалов получим . Разность потенциалов называют напряжением. В Международной системе единиц — СИ потенциал и разность потенциалов (напряжение) измеряют в вольтах: . С учетом этого ранее приведенные формулы для разности потенциалов между двумя эквипотенциальными поверхностями можно представить в виде: 1. В однородном электрическом поле напряжение и напряженность связаны между собой соотношениями: . Поэтому напряженность электрического поля измеряют также в . 2. В сферически симметричном поле: . 3. В поле с цилиндрической симметрией (бесконечно протяженной заряженной нити): , . Принимая во внимание формулу для работы электрических сил , введем новую единицу для работы и энергии. Это электрон-вольт – 1эВ=1,6 10-19Дж. 1эВ равен работе поля по перемещению электрического заряда, равного заряду электрона, между точками поля с разностью потенциалов 1 В.
2.1.2. Лекция 2. Электростатика. Электрическое поле в вакууме. План: 2.1. Электризация тел. Законы сохранения электрического заряда и Кулона. 2.2. Основные характеристики электрического поля: напряженность и потенциал. 2.3. Принцип суперпозиции электрических полей. 2.4. Напряженность электрического поля как градиент его потенциала. 2.5. Работа электрического поля по перемещению электрического заряда.
2.1. Электризация тел. Законы сохранения электрического заряда и Кулона.
Электрический заряд — физическая величина, характеризующая свойство тел или частиц вступать в электромагнитные взаимодействия и определяющая значения сил и энергий при таких взаимодействиях. Электрические заряды делятся на положительные и отрицательные. Закон сохранения электрического заряда — физический закон, в соответствии с которым в замкнутой системе взаимодействующих тел алгебраическая сумма электрических зарядов (полный электрический заряд) остается неизменной при всех взаимодействиях. Закон сохранения заряда гласит, что алгебраическая сумма зарядов электрически замкнутой системы, сохраняется. q1+q2+q3+…qn = const Требование релятивистской инвариантности приводит к тому, что закон сохранения заряда имеет локальный характер: изменение заряда в любом наперёд заданном объёме равно потоку заряда через его границу. Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность можно записать в математической форме: Здесь Ω — некоторая произвольная область в трёхмерном пространстве, — граница этой области, ρ — плотность заряда, — плотность тока (плотность потока электрического заряда) через границу. Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме Закон Кулона — основной закон электростатики, выражающий зависимость силы взаимодействия двух неподвижных точечных зарядов от расстояния между ними. Два неподвижных точечных заряда взаимодействуют с силой прямо пропорциональной произведению величин этих зарядов и обратно пропорциональной квадрату расстояния между ними и диэлектрической проницаемости среды, в которой находятся заряды. Важно отметить, что для того, чтобы закон был верен необходимы: 3. точечность зарядов — то есть расстояние между заряженными телами много больше их размеров. 4. их неподвижность. Иначе уже надо учитывать возникающее магнитное поле движущегося заряда. В векторном виде закон записывается следующим образом:
где e0 = 8,85×10-12 Ф/м – электрическая постоянная; q1, q2 – величины взаимодействующих зарядов; r1,2 – расстояние между зарядами; r0 – единичный вектор, показывающий направление силы.
2.2. Основные характеристики электрического поля: напряженность и потенциал. Для количественной характеристики электрического поля вводится в рассмотрение физическая величина, называемая напряженностью электрического поля. Напряженность электрического поля – векторная физическая величина. Она численно равна силе, действующей на положительный единичный заряд, помещенный в данную точку поля. Если электрическое поле создается точечным зарядом q, то согласно определению напряженность такого поля . (1.3) Напряженность электрического поля является его силовой характеристикой. Направление вектора E совпадает с направлением силы, действующей на заряд, помещенный в данную точку поля. Он направлен по радиальной прямой, проходящей через заряд и рассматриваемую точку поля от заряда, если он положительный, и к заряду, если он отрицательный (рис. 1.2). За единицу напряженности электрического поля принимается напряженность в такой точке, в которой на заряд, равный единице, действует сила, равная единице. В системе СИ напряженность электрического поля измеряется в Кл/м или В/м. Электростатический потенциал — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Напряжённость электростатического поля Е и потенциал φ связаны соотношением: В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль.
2.3. Принцип суперпозиции электрических полей. Если электрическое поле создано системой точечных зарядов: q1, q2, q3,………, то в произвольной точке пространства «А» каждый из них порождает свое собственное поле с соответствующей напряженностью: E1, E2, E3,. Величину и направление результирующего вектора напряженности E можно определить правилами геометрического сложения. Таким образом, для электрических полей оказывается справедливым принцип суперпозиции.
2.4. Напряженность электрического поля как градиент его потенциала. Градиент — вектор равный сумме произведений частных производных некоторой скалярной функции U=j( )по переменным на их единичные векторы.в направлении быстрейшего изменения х,у,z некоторого скаляра, характеризующий быстроту этого изменения. Напряженность электростатического поля равна градиенту его потенциала: E= — gradφ.
В однородном электрическом поле: — единица измерения напряженности электрического поля.
2.5. Работа электрического поля по перемещению электрического заряда. Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд qo, то сила, приложенная к заряду, совершает работу. где dr = dl×cosa. Работа при перемещении заряда q из точки 1 в точку 2 где k – коэффициент пропорциональности, зависящий от выбора системы единиц измерения физических величин. В системе СИ k = 1/4pe0; q1 – заряд, создающий электрическое поле; q2 – заряд, перемещаемый в электрическом поле; r1, r2 – начальное и конечное расстояния между зарядами. Из формулы видно, что работа сил электрического поля по перемещению электрического заряда не зависит от траектории перемещения, а определяется только начальным и конечным положением зарядов. Следовательно, электростатическое поле электрических зарядов является потенциальным, а электростатические силы – консервативными силами.
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА.
Плотность заряда : линейная
поверхностная : обьемная
Z
X
Y
d Ф (AA`BB` ) = E ( x,y,z ) dxdy cos 180 = — E ( x,y,z ) dxdy d Ф ( DD`CC` ) = E ( x+dx,y,z)dxdy cos0 = E ( x+dx,y,z ) dxdy E ( x+dx,y,z ) = E ( x,y,z) + d Ф ( 1-2 ) = E ( x,y,z + ) dxdy — E ( x,y,z ) dxdy = dxdydz d Ф ( 3-4 ) = dxdydz d Ф ( 5-6 ) = dxdydz dФ = ( + + ) dxdydz div a = : :
ДИВЕРГЕНЦИЕЙ — ( расхождение ) вектора ( а ) называют предел отношения потока вектора ( а ) через замкнутую поверхность к величине объема ограниченного зтой поверхностью при условии , что объем стремится к нулю
“ ДИВЕРГЕНЦИЯ “ — это родник в лесу , а поток это количество воды прошедшее через поперечное течение русла реки
— оператор Набла
теорема Остаградского-Гауса или уравнение Максвелла
Часть III Электрическое поле в среде. Диполь. Различают полярные и неполярные диэлектрики. Дипольный момент определяется соотношением
в котором — величина одного из зарядов, — расстояние между ними. Вектор направлен от отрицательного к положительному заряду. Примеры: H2O, NH3, SO2, CO. В неполярных молекулах в отсутствие электрического поля центры положительных и отрицательных зарядов совпадают. N2, H2, O2, CO2, CH4, но при внесении неполярной молекулы в однородное электрическое поле центры зарядов смещаются. Молекула поляризуется и в результате приобретает дипольный момент. Этот момент пропорционален величине напряженности этого поля.
. Силы создают вращающий момент: или , ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Техника нижней прямой подачи мяча Комплекс физических упражнений для развития мышц плечевого пояса Стандарт Порядок надевания противочумного костюма Общеразвивающие упражнения без предметов |
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 355; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Проводники и электрические поля в статическом равновесии
Цели обучения
К концу этого раздела вы сможете:
- Перечислить три свойства проводника в электростатическом равновесии.
- Объясните влияние электрического поля на свободные заряды в проводнике.
- Объясните, почему внутри проводника не может быть электрического поля.
- Опишите электрическое поле, окружающее Землю.
- Объясните, что происходит с электрическим полем, приложенным к проводнику неправильной формы.
- Опишите, как работает громоотвод.
- Объясните, как металлический автомобиль может защитить находящихся внутри пассажиров от опасных электрических полей, вызванных касанием обрыва кабеля к автомобилю.
Проводники содержат бесплатных заряда , которые легко перемещаются. Когда на проводник помещается избыточный заряд или проводник помещается в статическое электрическое поле, заряды в проводнике быстро реагируют, чтобы достичь устойчивого состояния, называемого электростатическим равновесием .
Когда на проводник помещается избыточный заряд или проводник помещается в статическое электрическое поле, заряды в проводнике быстро реагируют, чтобы достичь устойчивого состояния, называемого электростатическим равновесием .
На рисунке 1 показано влияние электрического поля на свободные заряды в проводнике. Свободные заряды движутся до тех пор, пока поле не станет перпендикулярным поверхности проводника. В электростатическом равновесии не может быть компоненты поля, параллельной поверхности, поскольку, если бы она была, она вызывала бы дальнейшее движение заряда. Показан положительный свободный заряд, но свободные заряды могут быть как положительными, так и отрицательными, а в металлах они фактически отрицательны. Движение положительного заряда эквивалентно движению отрицательного заряда в противоположном направлении.
Рис. 1. Когда к проводнику приложено электрическое поле E, свободные заряды внутри проводника перемещаются до тех пор, пока поле не станет перпендикулярным поверхности. (а) Электрическое поле является векторной величиной, имеющей как параллельные, так и перпендикулярные компоненты. Параллельная составляющая (E∥) воздействует на свободный заряд q с силой (F∥), которая перемещает заряд до тех пор, пока F∥=0. (b) Результирующее поле перпендикулярно поверхности. Свободный заряд переносится на поверхность проводника, оставляя электростатические силы в равновесии.
(а) Электрическое поле является векторной величиной, имеющей как параллельные, так и перпендикулярные компоненты. Параллельная составляющая (E∥) воздействует на свободный заряд q с силой (F∥), которая перемещает заряд до тех пор, пока F∥=0. (b) Результирующее поле перпендикулярно поверхности. Свободный заряд переносится на поверхность проводника, оставляя электростатические силы в равновесии.
Проводник, помещенный в электрическое поле , будет поляризован . На рисунке 2 показан результат помещения нейтрального проводника в изначально однородное электрическое поле. Поле усиливается вблизи проводника, но полностью исчезает внутри него.
Рис. 2. На этом рисунке показан сферический проводник в статическом равновесии с первоначально однородным электрическим полем. Свободные заряды движутся внутри проводника, поляризуя его, пока линии электрического поля не станут перпендикулярны поверхности. Силовые линии заканчиваются на избыточном отрицательном заряде на одном участке поверхности и снова начинаются на избыточном положительном заряде на противоположной стороне. Внутри проводника не существует электрического поля, поскольку свободные заряды в проводнике будут продолжать двигаться в ответ на любое поле, пока оно не будет нейтрализовано.
Внутри проводника не существует электрического поля, поскольку свободные заряды в проводнике будут продолжать двигаться в ответ на любое поле, пока оно не будет нейтрализовано.
Предупреждение о неправильном представлении: электрическое поле внутри проводника
Избыточные заряды, размещенные на сферическом проводнике, отталкиваются и перемещаются до тех пор, пока не распределятся равномерно, как показано на рис. 3. Избыточный заряд выталкивается на поверхность до тех пор, пока поле внутри проводника не станет равным нулю. Вне проводника поле точно такое же, как если бы проводник был заменен точечным зарядом в его центре, равным избыточному заряду.
Рис. 3. Взаимное отталкивание избыточных положительных зарядов на сферическом проводнике равномерно распределяет их по его поверхности. Результирующее электрическое поле перпендикулярно поверхности и равно нулю внутри. Вне проводника поле идентично точечному заряду в центре, равному избыточному заряду.
Свойства проводника в электростатическом равновесии
- Электрическое поле внутри проводника равно нулю.

- Сразу за пределами проводника силовые линии электрического поля перпендикулярны его поверхности и заканчиваются или начинаются на зарядах на поверхности.
- Любой избыточный заряд находится полностью на поверхности или поверхностях проводника.
Свойства проводника согласуются с уже рассмотренными ситуациями и могут использоваться для анализа любого проводника в электростатическом равновесии. Это может привести к новым интересным выводам, как описано ниже.
Как создать очень однородное электрическое поле? Рассмотрим систему из двух металлических пластин с противоположными зарядами на них, как показано на рис. 4. Свойства проводников, находящихся в электростатическом равновесии, указывают на то, что электрическое поле между пластинами будет однородным по напряженности и направлению. За исключением краев, избыточные заряды распределяются равномерно, создавая силовые линии, которые расположены на одинаковом расстоянии друг от друга (следовательно, одинаковы по силе) и перпендикулярны поверхностям (следовательно, однородны по направлению, поскольку пластины плоские). Краевые эффекты менее важны, когда пластины расположены близко друг к другу.
Краевые эффекты менее важны, когда пластины расположены близко друг к другу.
Рис. 4. Две металлические пластины с равными, но противоположными избыточными зарядами. Поле между ними однородно по силе и направлению, кроме краев. Одним из применений такого поля является создание равномерного ускорения зарядов между пластинами, например, в электронной пушке телевизионной трубки.
Электрическое поле Земли
Рис. 5. Электрическое поле Земли. (a) Поле хорошей погоды. Земля и ионосфера (слой заряженных частиц) являются проводниками. Они создают однородное электрическое поле около 150 Н/Кл. (кредит: DH Parks) (b) Штормовые поля. При наличии грозовых облаков локальные электрические поля могут быть больше. При очень высоких полях изолирующие свойства воздуха нарушаются, и может возникнуть молния. (кредит: Ян-Йост Верхуф)
Почти однородное электрическое поле напряженностью около 150 Н/Кл, направленное вниз, окружает Землю, величина которого немного увеличивается по мере приближения к поверхности. Что вызывает электрическое поле? Примерно в 100 км над поверхностью Земли находится слой заряженных частиц, называемый ионосферой . Ионосфера отвечает за ряд явлений, включая электрическое поле, окружающее Землю. В хорошую погоду ионосфера положительна, а Земля в значительной степени отрицательна, поддерживая электрическое поле (рис. 5а).
Что вызывает электрическое поле? Примерно в 100 км над поверхностью Земли находится слой заряженных частиц, называемый ионосферой . Ионосфера отвечает за ряд явлений, включая электрическое поле, окружающее Землю. В хорошую погоду ионосфера положительна, а Земля в значительной степени отрицательна, поддерживая электрическое поле (рис. 5а).
В условиях шторма образуются облака, а локализованные электрические поля могут быть сильнее и иметь противоположное направление (рис. 5b). Точное распределение заряда зависит от местных условий, и возможны вариации рисунка 5b.
Если электрическое поле достаточно велико, изолирующие свойства окружающего материала нарушаются, и он становится проводящим. Для воздуха это происходит примерно при 3 × 10 6 N/C. Воздух ионизирует ионы, а электроны рекомбинируют, и мы получаем разряд в виде искр молний и коронного разряда.
Электрические поля на неровных поверхностях
До сих пор мы рассматривали избыточные заряды на гладкой симметричной поверхности проводника. Что произойдет, если проводник имеет острые углы или заострен? Избыточные заряды на неоднородном проводнике концентрируются в наиболее острых точках. Кроме того, избыточный заряд может перемещаться по проводнику или от него в самых острых точках.
Что произойдет, если проводник имеет острые углы или заострен? Избыточные заряды на неоднородном проводнике концентрируются в наиболее острых точках. Кроме того, избыточный заряд может перемещаться по проводнику или от него в самых острых точках.
Чтобы понять, как и почему это происходит, рассмотрим заряженный проводник на рис. 6. Электростатическое отталкивание одинаковых зарядов наиболее эффективно раздвигает их на самой плоской поверхности, поэтому там они меньше всего концентрируются. Это связано с тем, что силы между одинаковыми парами зарядов на обоих концах проводника одинаковы, но компоненты сил, параллельных поверхностям, различны. Составляющая, параллельная поверхности, наибольшая на самой плоской поверхности и, следовательно, более эффективна в перемещении заряда.
Такой же эффект на проводник оказывает внешнее электрическое поле, как показано на рис. 6с. Поскольку силовые линии должны быть перпендикулярны поверхности, больше их сосредоточено на наиболее искривленных участках.
Рис. 6. Избыточный заряд на неоднородном проводнике больше всего концентрируется в месте наибольшей кривизны. а) Силы между одинаковыми парами зарядов на обоих концах проводника одинаковы, но компоненты сил, параллельных поверхности, различны. это F ∥ , который раздвигает заряды, когда они достигают поверхности. (b) F ∥ наименьший на более остром конце, заряды оставлены ближе друг к другу, создавая показанное электрическое поле. (c) Незаряженный проводник в первоначально однородном электрическом поле поляризуется так, что наиболее концентрированный заряд находится на его самом остром конце.
Применение проводников
Рис. 7. Проводник с очень острым концом имеет большую концентрацию заряда в конце. Электрическое поле в этой точке очень сильное и может создавать силу, достаточную для переноса заряда на проводник или с него. Молниеотводы используются для предотвращения накопления больших избыточных зарядов на конструкциях и, таким образом, имеют остроконечную форму.
На очень сильно искривленной поверхности, такой как показанная на рисунке 7, заряды настолько сконцентрированы в точке, что результирующее электрическое поле может быть достаточно сильным, чтобы убрать их с поверхности. Это может быть полезно.
Молниеотводы работают лучше всего, когда они наиболее остроконечные. Большие заряды, образующиеся в грозовых облаках, вызывают противоположный заряд на здании, что может привести к удару молнии в здание. Индуцированный заряд постоянно отводится громоотводом, предотвращая более драматический удар молнии.
Конечно, иногда мы хотим предотвратить передачу заряда, а не облегчить ее. В этом случае проводник должен быть очень гладким и иметь как можно больший радиус кривизны. (См. рис. 8.) Гладкие поверхности используются, например, на высоковольтных линиях электропередачи, чтобы избежать утечки заряда в воздух.
Другим устройством, в котором используются некоторые из этих принципов, является клетка Фарадея . Это металлический щит, ограждающий объем. Все электрические заряды будут находиться на внешней поверхности этого экрана, и внутри не будет электрического поля. Клетка Фарадея используется, чтобы не допустить, чтобы блуждающие электрические поля в окружающей среде мешали чувствительным измерениям, таким как электрические сигналы внутри нервной клетки.
Это металлический щит, ограждающий объем. Все электрические заряды будут находиться на внешней поверхности этого экрана, и внутри не будет электрического поля. Клетка Фарадея используется, чтобы не допустить, чтобы блуждающие электрические поля в окружающей среде мешали чувствительным измерениям, таким как электрические сигналы внутри нервной клетки.
Во время грозы, если вы управляете автомобилем, лучше оставаться внутри автомобиля, так как его металлический корпус действует как клетка Фарадея с нулевым электрическим полем внутри. Если в непосредственной близости от удара молнии, его воздействие ощущается снаружи автомобиля, а внутри не затрагивается, при условии, что вы полностью остаетесь внутри. Это актуально и в том случае, если действующий («горячий») электрический провод оборвался (в грозу или аварию) и упал на ваш автомобиль.
Рис. 8. (a) Молниеотвод направлен для облегчения передачи заряда. (Фото: Romaine, Wikimedia Commons) (b) Этот генератор Ван де Граафа имеет гладкую поверхность с большим радиусом кривизны, что предотвращает перенос заряда и позволяет генерировать большое напряжение. Взаимное отталкивание одноименных зарядов проявляется в волосах человека при прикосновении к металлическому шару. (кредит: Джон «ShakataGaNai» Дэвис/Wikimedia Commons).
Взаимное отталкивание одноименных зарядов проявляется в волосах человека при прикосновении к металлическому шару. (кредит: Джон «ShakataGaNai» Дэвис/Wikimedia Commons).
Резюме раздела
- Проводник позволяет свободным зарядам перемещаться внутри него.
- Электрические силы вокруг проводника заставят свободные заряды перемещаться внутри проводника, пока не будет достигнуто статическое равновесие.
- Любой избыточный заряд будет накапливаться на поверхности проводника.
- Проводники с острыми углами или точками будут накапливать больше заряда в этих точках.
- Громоотвод — это проводник с заостренными концами, который собирает избыточный заряд на здании, вызванный грозой, и позволяет ему рассеяться обратно в воздух.
- Электрические бури возникают, когда электрическое поле поверхности Земли в определенных местах становится более сильно заряженным из-за изменения изолирующего эффекта воздуха.
- Клетка Фарадея действует как щит вокруг объекта, предотвращая проникновение электрического заряда внутрь.

Концептуальные вопросы
- Является ли объект на рисунке 9 проводником или изолятором? Обосновать ответ.
Рисунок 9.
- Линии внешнего поля, входящие в объект с одного конца и выходящие с другого, показаны линиями.
Если бы линии электрического поля на рисунке выше были перпендикулярны объекту, обязательно ли он был бы проводником? Объяснять. - Обсуждение электрического поля между двумя параллельными проводящими пластинами в этом модуле утверждает, что краевые эффекты менее важны, если пластины расположены близко друг к другу. Что значит близко? То есть имеет ли решающее значение фактическое расстояние между пластинами или отношение расстояния между пластинами к площади пластины?
- Будет ли электрическое поле, созданное самим собой на конце заостренного проводника, такого как громоотвод, удалять положительный или отрицательный заряд с проводника? Будет ли снят тот же знаковый заряд с нейтрального заостренного проводника приложением такого же электрического поля, созданного извне? (Ответы на оба вопроса имеют значение для передачи заряда с использованием баллов.
 )
) - Почему игрок в гольф с металлической клюшкой на плече уязвим для молнии на открытом фервее? Будет ли ей безопаснее под деревом?
- Может ли ремень ускорителя Ван де Граафа быть проводником? Объяснять.
- Вы в относительной безопасности от молнии внутри автомобиля? Назовите две причины.
- Обсудите плюсы и минусы заземления громоотвода по сравнению с простым прикреплением к зданию.
- Используя симметрию расположения, покажите, что суммарная кулоновская сила, действующая на заряд [латекс]q[/латекс] в центре квадрата ниже (рис. 10), равна нулю, если заряды в четырех углах точно равны.
Рисунок 10. Четыре точка сбоя Q A , Q B , Q C и Q D лжи на углах квадрата и Q . центр.
- (a) Используя симметрию расположения, покажите, что электрическое поле в центре квадрата на рисунке 10 равно нулю, если заряды в четырех углах точно равны.
 (b) Покажите, что это также верно для любой комбинации зарядов, в которой q a = q b и q b = q c
(b) Покажите, что это также верно для любой комбинации зарядов, в которой q a = q b и q b = q c - (a) Каково направление полной кулоновской силы на q на рисунке 10, если q отрицательно, q a = q c и оба отрицательны, = q c и оба положительны? б) Каково направление электрического поля в центре квадрата в этой ситуации?
- Рассматривая рисунок 10, предположим, что q a = q d и q b = q c . Сначала покажите, что q находится в статическом равновесии. (Вы можете пренебречь силой гравитации.) Затем обсудите, является ли равновесие устойчивым или неустойчивым, отметив, что это может зависеть от знаков зарядов и направления смещения q от центра квадрата.

- Если q a = 0 на рисунке 10, при каких условиях не будет чистой кулоновской силы на q ?
- В регионах с низкой влажностью возникает особая «хватка» при открытии дверей автомобиля или прикосновении к металлическим дверным ручкам. Это предполагает размещение на устройстве как можно большей части руки, а не только кончиков пальцев. Обсудите индуцированный заряд и объясните, почему это сделано.
- Пункты взимания платы за проезд на дорогах и мостах обычно имеют кусок проволоки, воткнутый в тротуар перед ними, который будет касаться приближающегося автомобиля. Почему это делается?
- Предположим, женщина несет избыточную плату. Чтобы поддерживать свой заряженный статус, может ли она стоять на земле в любой паре обуви? Как бы вы ее выписали? Каковы последствия, если она просто уйдет?
Задачи и упражнения
- Нарисуйте линии электрического поля вблизи проводника на рисунке 11, учитывая, что изначально поле было однородным и параллельным длинной оси объекта.
 Является ли результирующее поле малым вблизи длинной стороны объекта?
Является ли результирующее поле малым вблизи длинной стороны объекта?Рисунок 11
- Нарисуйте линии электрического поля вблизи проводника на рисунке 12, учитывая, что изначально поле было однородным и параллельным длинной оси объекта. Является ли результирующее поле малым вблизи длинной стороны объекта?
Рисунок 12.
- Нарисуйте электрическое поле между двумя проводящими пластинами, показанными на рисунке 13, при условии, что верхняя пластина имеет положительный заряд, а нижняя пластина имеет такое же количество отрицательного заряда. Обязательно укажите распределение заряда на пластинах.
Рисунок 13.
- Нарисуйте линии электрического поля вблизи заряженного изолятора на рисунке 14 , отметив его неоднородное распределение заряда.
Рис. 14. Заряженный изолирующий стержень, который можно использовать для демонстрации в классе.
- Какая сила действует на заряд, расположенный на расстоянии x = 8,00 см на рис.
 15а, при условии, что q = 1,00 мкКл?
15а, при условии, что q = 1,00 мкКл?Рис. 15. (а) Точечные заряды, расположенные на расстоянии 3,00, 8,00 и 11,0 см по оси x. (b) Точечные заряды, расположенные на расстоянии 1,00, 5,00, 8,00 и 14,0 см по оси x.
- (a) Найдите полное электрическое поле при x = 1,00 см на рисунке 15b, учитывая, что q = 5,00 нКл. (b) Найдите полное электрическое поле при x = 11,00 см на рисунке 15b. (в) Если позволить зарядам двигаться и в конечном итоге останавливаться за счет трения, какова будет окончательная конфигурация заряда? (То есть будет ли одинарная плата, двойная плата и т. д., и каковы будут ее значения?)
- (a) Найдите электрическое поле при x = 5,00 см на рис. 15а, учитывая, что q = 1,00 мкКл. (b) В каком положении между 3,00 и 8,00 см общее электрическое поле такое же, как и для -2 q один? в) Может ли электрическое поле быть равным нулю где-то между 0,00 и 8,00 см? (d) При очень больших положительных или отрицательных значениях x электрическое поле приближается к нулю как в (a), так и (b).
 В каком случае он быстрее всего стремится к нулю и почему? (e) В каком положении справа от 11,0 см полное электрическое поле равно нулю, кроме как на бесконечности? (Подсказка: графический калькулятор может помочь в решении этой проблемы.)
В каком случае он быстрее всего стремится к нулю и почему? (e) В каком положении справа от 11,0 см полное электрическое поле равно нулю, кроме как на бесконечности? (Подсказка: графический калькулятор может помочь в решении этой проблемы.) - (a) Найдите полную кулоновскую силу на заряде 2,00 нКл, расположенном на расстоянии x = 4,00 см на рисунке 15b, учитывая, что q = 1,00 мкКл. (b) Найдите положение x , в котором электрическое поле равно нулю на рисунке 15b.
- Используя симметрию расположения, определите направление силы на q на рисунке ниже, учитывая, что q a = q b = +7,50 мкКл и q c = q d = -7,50 мкКл. б) Рассчитайте величину силы, действующей на заряд q , учитывая, что сторона квадрата равна 10,0 см, а q = 2,00 мкКл.
Рисунок 16.
- (a) Используя симметрию расположения, определите направление электрического поля в центре квадрата на рисунке, учитывая, что q a = q b = -1,00 мкКл и q c = q d = +1,00 мкКл.
 (b) Рассчитайте величину электрического поля в точке q, учитывая, что сторона квадрата равна 5,00 см.
(b) Рассчитайте величину электрического поля в точке q, учитывая, что сторона квадрата равна 5,00 см. - Найдите электрическое поле на месте Q A на рисунке 16, учитывая, что Q B = Q C = Q D = +2,00 NC, Q D = +2,00 NC Q = = = = = = = = = = +2,00 NC, Q D 1,00 нКл, а сторона квадрата 20,0 см.
- Найти полную кулоновскую силу на заряде q на рис. 16, учитывая, что q = 1,00 μ Кл, q a = 2,00 μ 0 9 0 9
Кл, 4 Кл0
= −3,00 µ C, q c = −4,00 µ C, а q d = +1,00 µ C на стороне а. - (a) Найдите электрическое поле на месте Q A на рисунке 17, учитывая, что Q B = +10,00 μ C и Q C = –5.00 Q C.
 (b) Какова сила, действующая на q и , если q а = +1,50 нКл?
(b) Какова сила, действующая на q и , если q а = +1,50 нКл?Рис. 17. Точечные заряды, расположенные в углах равностороннего треугольника со стороной 25,0 см.
- (a) Найдите электрическое поле в центре треугольной конфигурации зарядов на рис. 17, учитывая, что q a = +2,50 нКл, q b = −8,00 нКл и q c = +1,50 нКл. (b) Существует ли какая-либо комбинация сборов, кроме q a = q b = q c , что создаст электрическое поле нулевой напряженности в центре треугольной конфигурации?
Глоссарий
проводник: объект, свойства которого позволяют зарядам свободно перемещаться внутри него
свободный заряд: электрический заряд (положительный или отрицательный), который может двигаться отдельно от своей основной молекулы
электростатическое равновесие: 90 088 электростатически сбалансированное состояние, в котором все свободные электрические заряды перестали двигаться примерно через
поляризованный: состояние, при котором положительные и отрицательные заряды внутри объекта собираются в разных местах
ионосфера: слой заряженных частиц, расположенный примерно в 100 км над поверхностью Земли, который отвечает за диапазон явлений, включая электрическое поле, окружающее Землю
Клетка Фарадея: металлический экран, предотвращающий проникновение электрического заряда на его поверхность
Избранные решения задач и упражнений
6. (а) E x = 1,00 см = −∞; (б) 2,12 × 10 5 Н/З; (в) один заряд + q
(а) E x = 1,00 см = −∞; (б) 2,12 × 10 5 Н/З; (в) один заряд + q
8. (а) 0,252 Н влево; (b) x = 6,07 см
10. (a) Электрическое поле в центре квадрата будет направлено вверх, так как q a и q b положительны, а
3 q
положительны c и q d отрицательны и имеют одинаковую величину; (б) 2,04 × 10 9{\circ}\\[/latex] , ниже горизонтали; (b) №Экзамен по физике 1 MC Flashcards
CardsQuiz
Matching
ОБНОВЛЕНО
BingoРаспечатать
РаспечататьУстановить детали Поделиться
1
Диэлектрический материал, например бумага, помещается между пластин конденсатора, так как конденсатор удерживает фиксированный заряд на своих тарелки. Что происходит с электрическим полем между пластинами при вставлен диэлектрик?
Поле становится сильнее.
Поле становится слабее.
Поле уменьшается до нуля.
В поле нет изменений.
Нет ответа: Сильнее поле
Ответ: Я думаю, что слабее ответ?
Почему:
2
На рисунке показаны силовые линии электрического поля, возникающие из двух небольших
заряженных частиц P и Q. Рассмотрим следующие два
заявления:
(i) Заряд P меньше
чем заряд на Q.
(ii) Электростатический
сила, действующая на P, меньше, чем сила, действующая на Q.
Какие из приведенных выше утверждений верны?
И (i), и (ii) верны.
Только (i) верно.
Ни (i), ни (ii) неверны.
Только (ii) верно.
Ответ: Я считаю, что «только (i) верно» является ответом?
Почему:
3
Двухточечные заряды, Q 1 и Q 2 , разделены расстоянием R . Если величины обоих зарядов удваиваются, а их разделение также вдвое, что происходит с электрической силой, которую каждый заряд воздействует на другого?
Остается прежним.
Уменьшается в 2 раза
Увеличивается в 4 раза. Увеличивается в 2 раза.
Увеличивается в 2 раза
Оба раза правильно ответили 🙂 : F остается прежним 92
4) F (4/4) = (4/4)
5) F(1) = (1)
6) F остается прежним 🙂
4
Когда электрон движется в направлении силовых линий электрического поля …..
движется от низкого потенциала к высокому потенциалу и набирает обороты электрическая потенциальная энергия.
он движется от высокого потенциала к низкому потенциалу и теряет электрическая потенциальная энергия.
он движется от высокого потенциала к низкому потенциалу и набирает обороты электрическая потенциальная энергия.
он движется от низкого потенциала к высокому потенциалу и теряет электрическая потенциальная энергия.
его электрический потенциал и электрическая потенциальная энергия остаются постоянными.
Вы оба раза правильно поняли 🙂
Ответ: он движется от высокого потенциала к низкому потенциалу и
приобретая электрическую потенциальную энергию.
Почему: Посмотреть изображение 🙂
5
Что из следующего увеличит емкость плоский конденсатор?
увеличение площади пластин и уменьшение расстояния между пластинами
увеличение заряда на пластинах
увеличение разности потенциалов между пластинами
уменьшение площади пластин и увеличение отрыв пластин
уменьшение разности потенциалов между пластинами
Вы оба раза правильно поняли 🙂
Ответ: увеличение площади пластин и уменьшение расстояния между пластинами
Почему: C относительный A/d
Просмотреть изображение
6
При введении диэлектрического материала между пластинами конденсатор с плоскими пластинами и полностью заполняет пространство, емкость увеличивается в 4 раза. Что такое диэлектрическая постоянная введенного материала?
4
Ни один из других вариантов не является правильным.
2
1/4
0.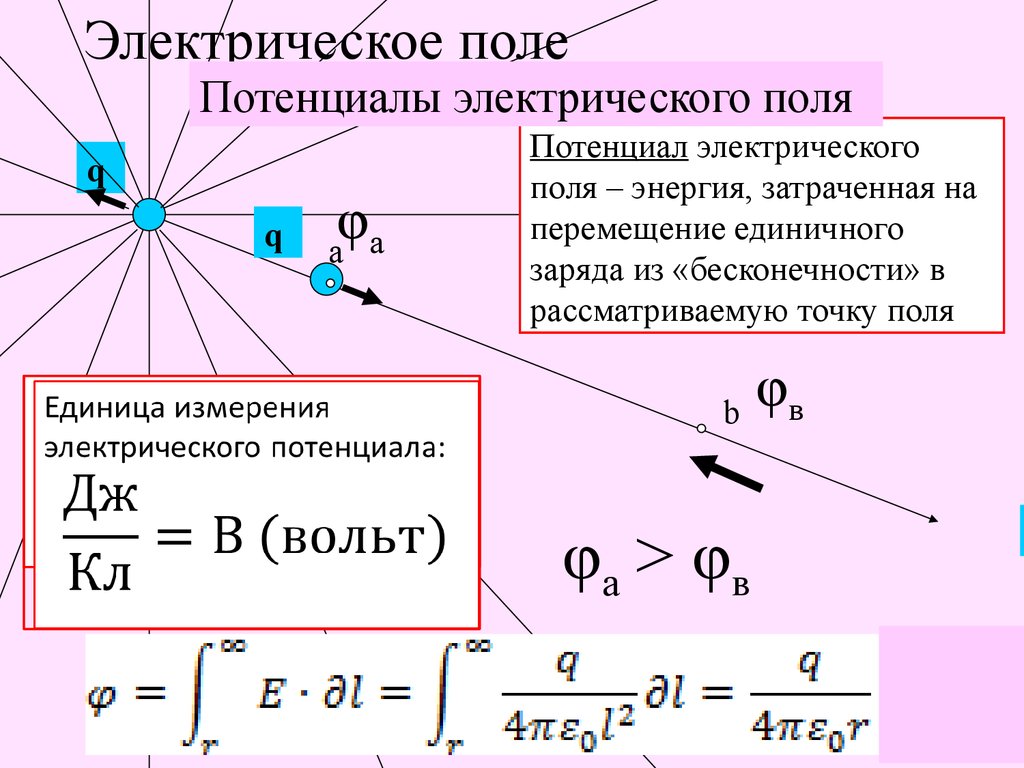 4
4
У вас ушла минута, но вы снова справились 🙂
Ответ: 4
Почему: Посмотрите на картинку
7
Пластиковый стержень заряжается, протирая шерстяную ткань, и доведены до изначально нейтрального металлического шара, изолированного с земли. Разрешается коснуться шара на несколько секунд, а затем отделяется от сферы на небольшом расстоянии. После стержень отделяется, стержень
притягивается к сфере.
отталкивается сферой.
не чувствует силы из-за сферы.
Ответ: Я считаю, что это «не чувствует силы из-за сферы».
Почему:
8
Идеальный конденсатор с плоскими пластинами имеет емкость С . Если площадь пластин увеличить вдвое, а расстояние между пластинами вдвое, какова новая емкость?
C/4
C/2
2C
4C
Нет ответа: 2C
Ответ:
Почему:
9 Какая из стрелок, показанных на рисунке, лучше всего представляет направление электрического поля между двумя равномерно заряженные металлические пластины?
A
C
B
D
Ни один из этих
Вы оба раза правильно ответили 🙂 ничего не заполнять)
10
X и Y — две изначально незаряженные металлические сферы на
изолирующие стойки, и они соприкасаются друг с другом. А
положительно заряженный стержень R приближается к X, как показано на рис.
часть (а) рисунка. Сфера Y теперь отодвинута от X, как показано
в части (б). Каковы конечные зарядовые состояния X и Y?
А
положительно заряженный стержень R приближается к X, как показано на рис.
часть (а) рисунка. Сфера Y теперь отодвинута от X, как показано
в части (б). Каковы конечные зарядовые состояния X и Y?
И X, и Y отрицательны.
X — нейтральный, Y — положительный.
X отрицательный, а Y положительный.
И X, и Y нейтральны.
X положительный, Y нейтральный.
Нет ответа: И X, и Y нейроны
Ответ:
Почему:
11
Электрон изначально движется вправо, когда входит в однородное электрическое поле направлено вверх, как показано на рисунке. По какой траектории (X, Y, Z или W) пойдет электрон в поле?
траектория Z
траектория X
траектория W
траектория Y
Ответ: Я думаю, что это «траектория Z»
Почему:
5 12 Две крошечные бусины на расстоянии 25 см друг от друга без других зарядов или полей
подарок. Бусинка A несет заряд 10 мкКл, а бусина В — 1 мкКл.
Какое из следующих утверждений верно относительно величин
электрических сил на эти шарики?
Бусинка A несет заряд 10 мкКл, а бусина В — 1 мкКл.
Какое из следующих утверждений верно относительно величин
электрических сил на эти шарики?
Сила, действующая на B, в 100 раз больше силы, действующей на A.
Сила, действующая на B, в 10 раз больше силы, действующей на A.
Сила, действующая на A, в точности равна силе, действующей на B.
Сила, действующая на A, в 100 раз превышает силу, действующая на B. в 10 раз больше силы, действующей на B.
Ответ: Я считаю, что «сила на A в точности равна силу на Б.»
Почему:
13
Двухточечные заряды, Q 1 и Q 2 , разделены расстоянием Р . Если величины обоих зарядов уменьшаются вдвое, и их разделение также вдвое, что происходит с электрической силой, которую оказывает каждый заряд на другой?
Увеличится в 16 раз.
Увеличится в 8 раз.
Увеличится в 4 раза.
Увеличится в 2 раза.
Не изменится.
Оба раза все правильно 🙂
Ответ: Сила остается прежней.
Почему: Просмотр изображения
14
Электрическое поле в точке P из-за точечного заряда Q на расстоянии R от P имеет величину Е . Для удвоения величины поля в P , вы могли бы….. (Примечание: это был бессмысленный вопрос, который она удалила)
уменьшить расстояние
удвоить заряд
уменьшить расстояние
удвоить заряд и в то же время уменьшить расстояние
удвоить расстояние
Ответ: Я думаю, уменьшить расстояние на 1/2 или удвоить заряд
Почему:
15
Электрон-вольт является единицей….
электрического поля.
энергия.
оплата.
электрическая сила.
электрический потенциал.
Ответ: энергия
Почему: Потому что это ответ 🙂
16
Электрический потенциал на расстоянии 4 м от определенного
точечный заряд 200 В относительно бесконечности. Каков потенциал
(относительно бесконечности) на расстоянии 2 м от того же заряда?
Каков потенциал
(относительно бесконечности) на расстоянии 2 м от того же заряда?
400 В
600 В
200 В
100 В
50 В
Область пространства содержит однородное электрическое поле, направленное вправо, как показано на рисунке. Какое утверждение об этом ситуация правильная?
Потенциалы в точках А и В равны, а потенциал в точка C выше, чем потенциал в точке A.
Потенциал во всех трех точках одинаков.
Потенциалы в точках А и В равны, а потенциал в точка C ниже, чем потенциал в точке A.
Потенциал в точке A самый высокий, потенциал в точке B является вторым по величине, а потенциал в точке C является самым низким.
Оба раза правильно ответили 🙂
Ответ: Потенциалы в точках А и В равны, а потенциал в точке C ниже, чем потенциал в точке A.
Почему: View image
18
Когда протон движется в направлении, перпендикулярном электрическому
линии поля. …
…
он движется от низкого потенциала к высокому потенциалу и набирает обороты электрическая потенциальная энергия.
он движется от низкого потенциала к высокому потенциалу и теряет электрическая потенциальная энергия.
он движется от высокого потенциала к низкому потенциалу и набирает обороты электрическая потенциальная энергия.
его электрический потенциал и электрическая потенциальная энергия остаются постоянными.
он движется от высокого потенциала к низкому потенциалу и теряет электрическая потенциальная энергия.
Ответ: Помощь
Почему:
19
Отрицательно заряженный пластиковый стержень подносится близко (но не не касаться) нейтральный металлический шар, соединенный с землей. После подождав несколько секунд, заземление удаляется (без касаясь сферы), и после этого стержень также удаляется. сфера теперь…
нейтральная.
отрицательно заряжен.
положительно заряжен.
Ответ: Думаю, «положительно заряжен».
Почему:
20
Конденсатор состоит из двух больших параллельных пластин площадью A разделены очень небольшим расстоянием d . Этот конденсатор подключен к аккумулятору и заряжается до тех пор, пока его пластины нести заряды + Q и — Q , а потом отключить от батареи. Если расстояние между пластинами теперь удвоенная, разность потенциалов между пластинами будет…..
разрезать пополам.
двойной.
четырехместный.
будет сокращен в четвертом.
без изменений.
Ответ: удвоенный
Почему:
Электрический потенциал
Электрический (или электростатический) потенциал можно определить как работу, проделанную по доведению единичного положительного заряда из этой точки в бесконечности она также определяется как потенциальная энергия на единицу заряда, связанная со статическим (стационарным) электрическим полем
Измеряется в вольт (В) .
Это скалярная величина .
Разность электрических потенциалов между двумя точками известна как разность потенциалов или напряжение .
Вы привыкли жить в материальном измерении, в котором объекты «тяготеют» к точке или от нее из-за градиента ландшафта вокруг них. Неподвижный мяч всегда будет катиться вниз по склону, если его положить на наклонную поверхность, и останется неподвижным на ровной поверхности.
Подумайте об «электрическом измерении». Тот, где заряды создают пейзаж, на который реагируют все заряженные объекты.
Посмотрите на приведенное выше определение электрического потенциала и подумайте о нем с точки зрения гравитационного потенциала. Мы могли бы сказать, что гравитационное потенциальное (положение в гравитационном поле) — это потенциальная энергия на единицу веса, связанная с гравитационным полем — эти два параметра сопоставимы
Размерность материи | Электрический размер |
Высота над уровнем моря (м) | Электрический потенциал (В) |
Гравитационная потенциальная энергия (Нм = Дж) = mgh = вес x рост | Электрическая потенциальная энергия (CV = J) = заряд x электрический потенциал |
Вес (Н) | Заряд (С) |
Если вы думаете об электрическом поле как о «ландшафте для заряда» — холмах и долинах, которые заставят свободно «катящийся» заряд ускоряться и/или замедляться, когда он проходит через него, то вы можно думать об электрическом потенциале как о «высоте» различных точек на этом «ландшафте» 9. |
Вы можете нанести точки эквипотенциала вокруг заряда, чтобы получить «контурную карту» этого электрического ландшафта. Говорят, что точка в пространстве, находящаяся на бесконечном расстоянии от любого заряда, находится при нулевом напряжении. На трехмерной диаграмме выше вы видите это как «плоскость» — плоскую область в ландшафте электрического измерения, уходящую в бесконечность. Посмотрите, как на трехмерной диаграмме показан более крутой градиент поля между зарядами, что соответствует более близким контурным линиям. Градиент поля называется напряженностью электрического поля или напряженностью электрического поля . |
Электрический потенциал является скалярной величиной. Это доставляет людям проблемы, потому что имеет знак (положительный или отрицательный). Вы должны думать о знаке как об указании того, находится ли эта точка в пространстве выше или ниже нулевой плоскости.
Это доставляет людям проблемы, потому что имеет знак (положительный или отрицательный). Вы должны думать о знаке как об указании того, находится ли эта точка в пространстве выше или ниже нулевой плоскости.
Чтобы рассчитать потенциал точки, на которую воздействуют поля нескольких зарядов , вам нужно выяснить, какое влияние оказывает каждый заряд на высоту «рельефа» в этой точке. Положительный заряд поднимет его выше нуля, а отрицательный заряд поднимет ниже нуля. Вы просто суммируете «корректировку электрической высоты» вместе, чтобы получить окончательное значение.
Пример вопроса:
Каков электростатический потенциал в точке X?
по уравнению:
определите потенциал в точке X от каждого из зарядов.
Результат положительного заряда равен 1,12 x 10 4 вольт (точка X поднимается из-за наличия этого заряда), а результат отрицательного заряда равен -1,12 x 10 4 вольт (точка X опускается из-за наличия этого заряда). наличие этого заряда). Их сумма представляет собой нулевой потенциал (X имеет нулевой потенциал — тот же уровень, который был бы, если бы вообще не было зарядов!).
наличие этого заряда). Их сумма представляет собой нулевой потенциал (X имеет нулевой потенциал — тот же уровень, который был бы, если бы вообще не было зарядов!).
Пару лет назад вопрос с несколькими вариантами ответов вызвал много беспокойства. Это был тип истинного/ложного, и утверждение, которое многие считали верным, было следующим:
«Электрический потенциал равен нулю, когда напряженность электрического поля равна нулю»
Это ЛОЖНОЕ утверждение, но многие студенты не могли понять, что оно было ложным.
Напряженность или напряженность электрического поля является вектором, поэтому, если равные притяжения или толчки воздействуют на «пробную частицу» в точке пространства, на которую вы смотрите, они компенсируют друг друга. НО потенциал в этой точке пространства будет подвержен изменению потенциала из-за влияния всех зарядов в данной местности. Посмотрите на схему.
Положительные заряды толкают положительный тестовый заряд с одинаковой силой, компенсируя эффект ускорения. Таким образом, напряженность электрического поля в этой точке равна нулю, НО оба заряда влияют на электрический потенциал точки X. Наличие одного из них затрудняет перенос единичного положительного заряда из бесконечности, а наличие второго удваивает как тяжело!. Эта точка в «электрическом пространстве» как бы поднимается в два раза выше благодаря наличию вторых зарядов.
Таким образом, напряженность электрического поля в этой точке равна нулю, НО оба заряда влияют на электрический потенциал точки X. Наличие одного из них затрудняет перенос единичного положительного заряда из бесконечности, а наличие второго удваивает как тяжело!. Эта точка в «электрическом пространстве» как бы поднимается в два раза выше благодаря наличию вторых зарядов.
Электрический потенциал можно представить как «давление». в следующей аналогии: если два человека толкают воздушный шар, по одному с каждой стороны, с одинаковой силой, общая сила будет равна нулю — чистой силы нет, но давление в воздушном шаре выше, чем при приложении истинной нулевой силы.
Потенциальная электрическая энергия — физические ресурсы MCAT
Все физические ресурсы MCAT
8 диагностических тестов 303 практических теста Вопрос дня Карточки Учитесь по концепции
Физическая помощь MCAT » Физика » Электричество и магнетизм » Электростатика и электрические поля » Electric Potential Energy
Если электрическая потенциальная энергия между двумя одинаковыми зарядами увеличивается в четыре раза, опишите изменение расстояния между частицами.
Возможные ответы:
Расстояние уменьшилось вдвое
Расстояние увеличилось вдвое
Расстояние увеличилось в четыре раза
Расстояние не изменилось
Расстояние было разделено на четыре части
Правильный ответ:
Расстояние было разделено на четыре части
Пояснение:
Электрическая потенциальная энергия определяется уравнением .
Электрическая потенциальная энергия обратно пропорциональна расстоянию между двумя зарядами. Если энергия увеличилась в четыре раза, то (расстояние между двумя одинаковыми зарядами) должно было уменьшиться пропорционально.
Чтобы энергия увеличилась в четыре раза, радиус нужно разделить на четыре.
Сообщить об ошибке
Для следующего:
Если заряд +4e удерживается на месте в 3 морских милях от заряда -5e, который также удерживается на месте. Чему равна потенциальная энергия системы?
Чему равна потенциальная энергия системы?
Возможные ответы:
Правильный ответ:
Объяснение:
Учитывая уравнение и подставляя значения e и k, мы получаем, что
Важно помнить, что заряд дается в вопросе и должен быть включен в формулу путем умножения каждого заряда на это значение.
Сообщить об ошибке
Что из следующего неверно относительно электрического потенциала?
Возможные ответы:
Когда положительный заряд перемещается из области с низким потенциалом в область с высоким потенциалом, электрическое поле совершает над зарядом положительную работу
Все эти утверждения верны
Электрический потенциал может быть выражен в Вольтах или Джоулях на Кулон
Положительная клемма батареи имеет более высокий электрический потенциал, чем отрицательная клемма
Отрицательный заряд перемещается от низкого потенциала к высокому потенциал ускорит
Правильный ответ:
Когда положительный заряд перемещается из области с низким потенциалом в область с высоким потенциалом, электрическое поле совершает положительную работу над зарядом
Объяснение:
Положительный тестовый заряд естественным образом перейдет от высокого потенциала к низкому. Если его перемещать в противоположном направлении, то электрическое поле будет совершать работу против его движения (отрицательная работа). Это видно из уравнения для работы электрического поля:
Если его перемещать в противоположном направлении, то электрическое поле будет совершать работу против его движения (отрицательная работа). Это видно из уравнения для работы электрического поля:
— работа, совершаемая электрическим полем, — заряд, — разность потенциалов. Если положительно (конечный потенциал выше начального потенциала) и также положительно, то работа, совершаемая полем, отрицательна.
Сообщить об ошибке
Какую работу необходимо совершить, чтобы свести три заданных заряда из бесконечности в углы равностороннего треугольника со стороной 1 см?
Возможные ответы:
Правильный ответ:
Объяснение:
Соответствующие уравнения:
Шаг 1: Поскольку работа по сборке зарядов равна их потенциальной энергии в этом расположении, найдите потенциальную энергию между каждой парой зарядов. Работа равна изменению потенциальной энергии; поскольку заряды начинаются на бесконечном расстоянии, изначально потенциальная энергия равна нулю.
Работа равна изменению потенциальной энергии; поскольку заряды начинаются на бесконечном расстоянии, изначально потенциальная энергия равна нулю.
Стоимость 1 и 2
Стоимость 1 и 3
Зарядки 2 и 3
Шаг 2: Соберите все эти потенциальные энергии, чтобы найти общую энергию.
Сообщить об ошибке
Стандартная розетка переменного тока может подавать ток. Какое максимально возможное напряжение выдает розетка.
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку заданное напряжение представляет собой среднеквадратичное напряжение, мы должны умножить напряжение на , чтобы найти максимальное напряжение.
Определяем, что максимальное напряжение, выдаваемое розеткой, равно .
Сообщить об ошибке
Уведомление об авторских правах
Все физические ресурсы MCAT
8 Диагностические тесты 303 практических теста Вопрос дня Карточки Учитесь по концепции
Применение электрических полей в биологии и медицине
- Вход в панель авторов
Что такое открытый доступ?
Открытый доступ — это инициатива, направленная на то, чтобы сделать научные исследования бесплатными для всех. На сегодняшний день наше сообщество сделало более 100 миллионов загрузок. Он основан на принципах сотрудничества, беспрепятственного открытия и, самое главное, научного прогресса. Будучи аспирантами, нам было трудно получить доступ к нужным нам исследованиям, поэтому мы решили создать новое издательство с открытым доступом, которое уравняет правила игры для ученых со всего мира. Как? Упрощая доступ к исследованиям и ставя академические потребности исследователей выше деловых интересов издателей.
На сегодняшний день наше сообщество сделало более 100 миллионов загрузок. Он основан на принципах сотрудничества, беспрепятственного открытия и, самое главное, научного прогресса. Будучи аспирантами, нам было трудно получить доступ к нужным нам исследованиям, поэтому мы решили создать новое издательство с открытым доступом, которое уравняет правила игры для ученых со всего мира. Как? Упрощая доступ к исследованиям и ставя академические потребности исследователей выше деловых интересов издателей.
Наши авторы и редакторы
Мы являемся сообществом из более чем 103 000 авторов и редакторов из 3 291 учреждения в 160 странах, в том числе лауреатов Нобелевской премии и некоторых самых цитируемых исследователей мира. Публикация на IntechOpen позволяет авторам получать цитирование и находить новых соавторов, а это означает, что больше людей увидят вашу работу не только из вашей собственной области исследования, но и из других смежных областей.
Оповещения о содержимом
Краткое введение в этот раздел, описывающий открытый доступ, особенно с точки зрения IntechOpen
Как это работаетУправление предпочтениями
Контакты
Хотите связаться? Свяжитесь с нашим головным офисом в Лондоне или командой по работе со СМИ здесь:
Карьера:
Наша команда постоянно растет, поэтому мы всегда ищем умных людей, которые хотят помочь нам изменить мир научных публикаций.
Рецензируемая глава в открытом доступе
Автор:
Фрэнсис X. Харт и Джон Р. Палисано
Представлено: 12 июня 2017 г. Рецензировано: 13 октября 2017 г. Опубликовано: 20 декабря 2017 г.
DOI: 10.5772/intechopen.71683
СКАЧАТЬ БЕСПЛАТНОИз отредактированного тома
Под редакцией Мохсена Шейхолеслами Канделуси
Сведения о книге Заказ в печати
Обзор показателей главы
6
5 2 871 загрузка глав
Посмотреть полные показатели
СКАЧАТЬ БЕСПЛАТНОРекламное объявление
Abstract
Мы обсуждаем широкий спектр приложений электрических полей в биологии и медицине. Например, поля физиологической силы (<500 В/м) используются для улучшения заживления ран, стимуляции нейронов, а также позиционирования и активации клеток на каркасах в целях тканевой инженерии. Короткие сильные импульсы, используемые при электропорации, используются для улучшения введения лекарств в опухоли и ДНК в ядра клеток. Ссылки направляют читателей к подробным обзорам этих приложений. Механизм, с помощью которого клетки обнаруживают поля физиологической силы, не совсем понятен. Мы также описываем механизм полевой трансдукции, который имеет общие черты с обнаружением сдвига жидкости клетками. Затем мы предоставляем некоторые экспериментальные данные, подтверждающие нашу модель.
Например, поля физиологической силы (<500 В/м) используются для улучшения заживления ран, стимуляции нейронов, а также позиционирования и активации клеток на каркасах в целях тканевой инженерии. Короткие сильные импульсы, используемые при электропорации, используются для улучшения введения лекарств в опухоли и ДНК в ядра клеток. Ссылки направляют читателей к подробным обзорам этих приложений. Механизм, с помощью которого клетки обнаруживают поля физиологической силы, не совсем понятен. Мы также описываем механизм полевой трансдукции, который имеет общие черты с обнаружением сдвига жидкости клетками. Затем мы предоставляем некоторые экспериментальные данные, подтверждающие нашу модель.
Ключевые слова
- электрическое поле
- заживление ран
- электропорация
- гальванотаксис
- гликокаликс
Физиологическая сила (~100 В/м) электрических полей постоянного тока важна для развития, поддержания и контроля клеток и тканей.
 Их роль в заживлении ран, эмбриональном развитии и регенерации тканей подробно описана в обзорах Pullar [1], McCaig et al. [2] и Робинсон и Мессерли [3]. Эндогенные электрические поля постоянного тока также важны для формирования эмбрионального паттерна [4]. В тканевой инженерии пролиферацию клеток на матриксах можно контролировать с помощью таких полей [5]. На тканевом уровне электрические поля используются для измерения состава тела [6] и ускорения заживления ран [7]. Важным новым достижением стало использование сильных электрических полей для доставки лекарств. Очень сильные импульсные поля могут способствовать прохождению лекарств через мембраны [8] или внедрению ДНК в ядро для целей генной инженерии [9].].
Их роль в заживлении ран, эмбриональном развитии и регенерации тканей подробно описана в обзорах Pullar [1], McCaig et al. [2] и Робинсон и Мессерли [3]. Эндогенные электрические поля постоянного тока также важны для формирования эмбрионального паттерна [4]. В тканевой инженерии пролиферацию клеток на матриксах можно контролировать с помощью таких полей [5]. На тканевом уровне электрические поля используются для измерения состава тела [6] и ускорения заживления ран [7]. Важным новым достижением стало использование сильных электрических полей для доставки лекарств. Очень сильные импульсные поля могут способствовать прохождению лекарств через мембраны [8] или внедрению ДНК в ядро для целей генной инженерии [9].]. До сих пор не решены вопросы о механизмах, с помощью которых поля достигают своего эффекта. Для полей физиологической силы было изучено большое разнообразие биохимических путей внутри клетки после первоначального обнаружения поля [10], но первоначальный механизм трансдукции изучен недостаточно. Для высоковольтных импульсных полей детали порообразования мембраны остаются неясными.
Для высоковольтных импульсных полей детали порообразования мембраны остаются неясными.
Многие статьи были опубликованы в этой очень широкой области в течение многих лет. Невозможно охватить многие приложения электрических полей в биологии. Сначала мы опишем некоторые репрезентативные применения электрических полей в биологии и медицине. Далее мы обсудим механизмы, ответственные за эти эффекты, и исследуем оставшиеся пробелы в нашем понимании этих процессов. Приведены ссылки на обзоры, чтобы читатели, желающие более подробно обсудить эти приложения, могли их найти. Для эффектов слабого поля мы также описываем экспериментальные процедуры, используемые для точного измерения гальванотаксиса, процесса, связанного с несколькими описанными здесь приложениями, и представляем некоторые типичные результаты.
Объявление
2. Воздействие физиологических силовых полей постоянного и переменного тока низкой частоты на клетки и ткани
2.
 1. Заживление ран
1. Заживление ран При повреждении ткани в месте раны создается электрическое поле. На рис. 1 показано, как возникают такие поля при повреждении эпителиальной ткани, такой как кожа. Три верхних слоя кожи – это роговой слой, эпидермис и дерма. На рисунке показаны три типичные клетки, расположенные подряд в эпидермисе. На верхней или апикальной мембране клетки ионы натрия проникают в клетку через натрий-специфические каналы. На нижней или базолатеральной мембране ионы калия покидают клетку. Эти ионные переносы связаны с биохимической реакцией внутри клетки с участием АТФ, которая представляет собой молекулу со связями для передачи высокой энергии в клетке. На рисунке 1а показан этот процесс переноса до развития раны для трех клеток. Ячейки соединены плотными контактами (TJ), которые обычно не пропускают заряд. Поток заряда через клетку, произведенный этим биохимическим процессом, связан с током I. Слой над апикальной мембраной отдал положительный заряд натриевым каналам и, таким образом, имеет относительный отрицательный заряд. Слой ниже базолатеральной мембраны приобрел относительный положительный заряд. Этот дисбаланс заряда компенсируется его обратным потоком по парацеллюлярному пути, то есть через более отдаленные соединения, которые не так тесно связаны. Поскольку с этим путем связано электрическое сопротивление R, по всему эпителиальному слою создается разность потенциалов ΔV = IR. В зависимости от конкретной ткани и деталей пути ΔV колеблется от 15 до 60 мВ [11].
Слой ниже базолатеральной мембраны приобрел относительный положительный заряд. Этот дисбаланс заряда компенсируется его обратным потоком по парацеллюлярному пути, то есть через более отдаленные соединения, которые не так тесно связаны. Поскольку с этим путем связано электрическое сопротивление R, по всему эпителиальному слою создается разность потенциалов ΔV = IR. В зависимости от конкретной ткани и деталей пути ΔV колеблется от 15 до 60 мВ [11].
Рис. 1.
Схематическая диаграмма электрического поля, создаваемого в месте кожной раны.
На рис. 1б показана ситуация, когда средняя ячейка повреждена. Теперь есть свободный проход для обратного потока к апикальному слою. Положительный заряд с обоих направлений будет течь вдоль слоя базолатеральной мембраны к ране. Таким образом, имеется связанное электрическое поле Е, направленное к ране с обеих сторон. Напряженность этого эндогенного поля в месте раны составляет около 100–200 В/м. Более подробное объяснение биохимического происхождения поля см. в обзоре Нуччителли [11]. Примеры того, насколько широко распространены раневые поля в биологических системах (например, растениях), см. в обзоре Робинсона и Мессерли [3].
Напряженность этого эндогенного поля в месте раны составляет около 100–200 В/м. Более подробное объяснение биохимического происхождения поля см. в обзоре Нуччителли [11]. Примеры того, насколько широко распространены раневые поля в биологических системах (например, растениях), см. в обзоре Робинсона и Мессерли [3].
Точно так же, как клетки мигрируют в ответ на химический градиент (хемотаксис), большинство типов клеток также мигрируют в ответ на электрическое поле (гальванотаксис или электротаксис). В ответ на близлежащую рану типы клеток, такие как кератиноциты, фибробласты, макрофаги и лимфоциты, мигрируют к ране под контролем поля [12, 13]. Большинство клеток мигрируют в направлении поля к отрицательному полюсу. Однако ситуация сложная. Макрофаги движутся к положительному полюсу, хотя их предшественники, моноциты, мигрируют к отрицательному полюсу [14]. Более того, когда в месте раны не создается эндогенное поле, рана не заживает должным образом. Применение внешнего электрического поля может затем улучшить заживление ран, которые не зажили сами по себе, направляя миграцию клеток к месту раны, а также побуждая эти клетки производить биохимические вещества, способствующие заживлению [13]. Например, отрицательный электрод можно поместить на рану, а один или несколько электродов, соединенных с положительным полюсом, разместить рядом. Kloth [12] провел обзор ряда клинических исследований, в которых изучалось, улучшает ли применение таких полей лечение ран по сравнению со стандартным уходом за ранами. Применяемые поля в таких исследованиях представляют собой либо постоянный постоянный ток (DC), либо импульсный постоянный ток. Анализируя широкий спектр устройств, Клот [12] обнаружил, что в наиболее эффективных методах лечения используется ток в диапазоне от 250 до 500 мкА. Некоторые из этих устройств были одобрены регулирующими органами для заживления ран в ЕС и для антибактериального действия на раны в США.
Например, отрицательный электрод можно поместить на рану, а один или несколько электродов, соединенных с положительным полюсом, разместить рядом. Kloth [12] провел обзор ряда клинических исследований, в которых изучалось, улучшает ли применение таких полей лечение ран по сравнению со стандартным уходом за ранами. Применяемые поля в таких исследованиях представляют собой либо постоянный постоянный ток (DC), либо импульсный постоянный ток. Анализируя широкий спектр устройств, Клот [12] обнаружил, что в наиболее эффективных методах лечения используется ток в диапазоне от 250 до 500 мкА. Некоторые из этих устройств были одобрены регулирующими органами для заживления ран в ЕС и для антибактериального действия на раны в США.
2.2. Электрическая стимуляция нервной системы
Импульсные и низкочастотные поля переменного тока (AC), применяемые с имплантированными или поверхностными электродами, используются либо для стимуляции, либо для подавления нервной активности. При глубокой стимуляции мозга (DBS) [15] электроды могут быть хирургически имплантированы в определенные области мозга для подачи импульсных сигналов, которые подавляют эндогенные сигналы, вызывающие тремор при болезни Паркинсона или эпилептические припадки. Нейростимулятор, подключенный к электродам, обычно имплантируют под ключицу. DBS обычно применяется в качестве дополнения к обычным лекарствам и только после того, как лекарства больше не облегчают симптомы. Со временем электроды могут покрыться налетом и, возможно, потребуется их замена.
Нейростимулятор, подключенный к электродам, обычно имплантируют под ключицу. DBS обычно применяется в качестве дополнения к обычным лекарствам и только после того, как лекарства больше не облегчают симптомы. Со временем электроды могут покрыться налетом и, возможно, потребуется их замена.
Электростимуляция (ЭС) [16] успешно применялась для восстановления мышечной функции у пациентов, перенесших обширную травму спинного мозга (ТСМ). Хотя спинной мозг был поврежден, мышечная система, которую он обычно стимулирует, может оставаться неповрежденной. Если электрические сигналы могут быть переданы этим мышцам, они могут реагировать как обычно. ЭС можно воздействовать на периферическую нервную систему или непосредственно на спинной мозг. Для периферической стимуляции электроды предпочтительно вживляют в ткани вблизи нервов. В противном случае используются поверхностные электроды. Биполярные импульсы используются для предотвращения электрохимического повреждения тканей вблизи электродов. Сложные движения, такие как хватание руками, требуют стимуляции множества нервов в определенном временном паттерне. По этой причине источник питания должен генерировать заранее запрограммированные отдельные сигналы для отдельных нейронов. Подробное описание систем ЭС и их применения для восстановления функции стояния, контроля мочевого пузыря, профилактики пролежней и других состояний см. в обзоре Ho et al. [16].
Сложные движения, такие как хватание руками, требуют стимуляции множества нервов в определенном временном паттерне. По этой причине источник питания должен генерировать заранее запрограммированные отдельные сигналы для отдельных нейронов. Подробное описание систем ЭС и их применения для восстановления функции стояния, контроля мочевого пузыря, профилактики пролежней и других состояний см. в обзоре Ho et al. [16].
Спинной мозг может генерировать свои собственные сложные модели нервной стимуляции, если он получает соответствующую электрическую стимуляцию. SCI может повредить спинной мозг над областью, где он обычно генерирует сигналы для стояния и ходьбы, так что эти действия не могут быть выполнены. Рейц и соавт. [17] сообщают, что применение импульсов от массива электродов, вставленных в эпидуральные пространства спинного мозга, позволило нескольким параличам нижних конечностей встать с минимальной помощью. Схемы пульса должны подбираться индивидуально. Солопова и соавт. [18] использовали накожные электроды для подачи двухфазных прямоугольных импульсов на нижние отделы позвоночника детей, страдающих церебральным параличом. Это лечение в сочетании с тренировкой на беговой дорожке улучшило двигательную функцию по сравнению с тренировкой только на локомотор.
Это лечение в сочетании с тренировкой на беговой дорожке улучшило двигательную функцию по сравнению с тренировкой только на локомотор.
Чрескожная электрическая стимуляция нервов (ЧЭНС) — это метод лечения, при котором низкочастотные импульсы применяются кожными электродами для уменьшения боли. Хотя электроды обычно размещают в месте возникновения боли (например, в нижней части спины), первичный эффект, по-видимому, связан со стимуляцией центральной нервной системы. Импульсы более низкой частоты (<10 Гц) применяются с относительно высокой интенсивностью для создания безболезненных двигательных сокращений, тогда как импульсы высокой частоты (>50 Гц) применяются с относительно низкой интенсивностью и не вызывают сокращений. Оба типа стимулов активируют опиоидные рецепторы в спинном и головном мозге, которые уменьшают боль, но тип продуцируемых опиоидов различается для двух стимулов. Подробнее см. в обзоре DeSantana et al. [19].
2.3. Индуцированные электрические поля и заживление костей и стимуляция мозга
2.
 3.1. Изменение магнитных полей создает электрические поля
3.1. Изменение магнитных полей создает электрические поляТолько что описанные электрические поля создаются разностью электрических потенциалов, создаваемой батареями или источниками питания. Линии электрического поля текут от положительных зарядов к отрицательным. Такие источники хорошо подходят для поверхностных применений, таких как заживление ран, восстановление роговицы или даже стимуляция головного и спинного мозга с близко расположенными вставленными электродами. Однако они не подходят для широкого применения электрических полей к более глубоким тканям из-за электрического импеданса ткани. Другой метод создания электрических полей использует закон Фарадея, который описывает, как изменяющееся во времени магнитное поле создает индуцированное электрическое поле с силовыми линиями, которые представляют собой замкнутые контуры. Магнитные поля беспрепятственно проникают в ткани, так что значительные индуцированные поля могут создаваться значительно ниже поверхности тела.
Рассмотрим пространственно однородное магнитное поле B, которое меняется со временем t. Предположим, что поле приложено перпендикулярно поверхности круглого металлического диска. Электрическое поле E, индуцируемое на расстоянии r от центра диска, представляет собой круговую петлю радиуса r с величиной
Предположим, что поле приложено перпендикулярно поверхности круглого металлического диска. Электрическое поле E, индуцируемое на расстоянии r от центра диска, представляет собой круговую петлю радиуса r с величиной
Er=r2dBdt. E1
Следует отметить, что такое же поле будет создаваться и в отсутствие металлического диска. Само поле не зависит от материала. Однако индуцированный электрический ток зависит от материала благодаря его проводимости. Для систем более сложных, чем круговой диск, расчет индуцированного поля сложен и требует численных методов. Простой пример квадратной чашки с изолирующими включениями (например, клетками) см. в Hart et al. [20].
2.3.2. Два примера иллюстрируют клиническое использование изменяющихся во времени магнитных полей
В течение многих лет электрические поля использовались для ускорения заживления переломов костей, которые не реагировали на обычное лечение. Поскольку переломы расположены глубоко в тканях, имплантированные электроды обычно не используются. Однако есть еще два способа, с помощью которых внешние системы доставки могут создавать требуемые внутренние поля. Возьмем, к примеру, перелом большеберцовой кости. Подушечки электродов можно размещать с любой стороны голени пациента. Высокочастотный сигнал, подаваемый на эти электроды, будет емкостно связан с внутренними тканями, включая место перелома, для создания там электрического поля. В качестве альтернативы, система катушек может быть обернута вокруг теленка. Изменяющийся во времени ток в катушках создает изменяющееся во времени магнитное поле в голени, которое, в свою очередь, генерирует импульсное электромагнитное поле (ИЭМП) в месте перелома. PEMF стимулирует остеобласты, чтобы кость росла и пролиферировала для заживления перелома. Два метаанализа [21, 22] клинических исследований электростимулированного заживления костей показывают некоторые улучшения у пациентов, но необходимы более четкие исследования.
Однако есть еще два способа, с помощью которых внешние системы доставки могут создавать требуемые внутренние поля. Возьмем, к примеру, перелом большеберцовой кости. Подушечки электродов можно размещать с любой стороны голени пациента. Высокочастотный сигнал, подаваемый на эти электроды, будет емкостно связан с внутренними тканями, включая место перелома, для создания там электрического поля. В качестве альтернативы, система катушек может быть обернута вокруг теленка. Изменяющийся во времени ток в катушках создает изменяющееся во времени магнитное поле в голени, которое, в свою очередь, генерирует импульсное электромагнитное поле (ИЭМП) в месте перелома. PEMF стимулирует остеобласты, чтобы кость росла и пролиферировала для заживления перелома. Два метаанализа [21, 22] клинических исследований электростимулированного заживления костей показывают некоторые улучшения у пациентов, но необходимы более четкие исследования.
При транскраниальной магнитной стимуляции (ТМС) вокруг головы пациента размещают катушки различной конструкции. Как и при лечении переломов костей, катушки создают изменяющееся во времени магнитное поле, которое индуктивно генерирует электрическое поле в нужном месте мозга. Конструкция системы катушек выбрана для создания локализованного электрического поля в нужном месте мозга. Этот метод используется, например, для лечения депрессии или для оценки того, правильно ли конкретная двигательная область мозга стимулирует связанную с ней мышечную систему. Подробнее и примеры биомагнитной стимуляции см. в обзоре Уэно и Секино [23]).
Как и при лечении переломов костей, катушки создают изменяющееся во времени магнитное поле, которое индуктивно генерирует электрическое поле в нужном месте мозга. Конструкция системы катушек выбрана для создания локализованного электрического поля в нужном месте мозга. Этот метод используется, например, для лечения депрессии или для оценки того, правильно ли конкретная двигательная область мозга стимулирует связанную с ней мышечную систему. Подробнее и примеры биомагнитной стимуляции см. в обзоре Уэно и Секино [23]).
2.4. Электрические поля для диагностических целей
В предыдущих разделах было описано, как приложение электрических полей к клеткам и тканям может оказывать положительное воздействие на эти мишени. Однако электрические поля также можно применять для мониторинга физиологического состояния тканей в диагностических целях. Все материалы, включая ткань, имеют соответствующее сопротивление R и емкость C [24]. Если к ткани приложить переменное напряжение, через ткань будет протекать ток, зависящий как от R, так и от C. Емкости ограничивают протекание тока низкой частоты, но пропускают токи высокой частоты. Величина C определяет диапазон частот перехода для прохождения и блокировки переменного тока. Для тканей эта частота составляет около 100 кГц–1 МГц.
Емкости ограничивают протекание тока низкой частоты, но пропускают токи высокой частоты. Величина C определяет диапазон частот перехода для прохождения и блокировки переменного тока. Для тканей эта частота составляет около 100 кГц–1 МГц.
На рис. 2 представлена модель схемы Фрике, обычно используемая для исследования тканей. Re и Ri представляют, соответственно, сопротивление внеклеточного и внутриклеточного сопротивления. Оба сопротивления определяются в первую очередь содержанием воды. C представляет емкость клеточной мембраны. Низкочастотные токи блокируются C изнутри клетки и, таким образом, служат мерой внеклеточной воды. C позволяет высокочастотным токам проникать внутрь ячейки и, таким образом, измерять комбинацию Re и Ri. Использование двух частот позволяет разделить Re и Ri и, таким образом, определить содержание внутриклеточной и внеклеточной воды.
Рис. 2.
w3.org/2001/XMLSchema-instance»> Модель схемы Фрике.Эти принципы можно использовать для измерения состава тела [6]. У здоровых людей существует четко определенная зависимость между общей безжировой массой тела и общей массой воды в организме. Знание общей безжировой массы тела и общей массы тела позволяет определить жировую массу тела и, следовательно, процентное содержание жира в организме. В зависимости от положения электродов этот метод можно использовать для измерений на всем теле или на отдельных конечностях. Определение изменения отношения Re к Ri может дать информацию о возможности затекания жидкости (отека) в конечность.
Другое применение модели Фрике полезно при мониторинге дыхания. Воздух в легких не пропускает ток и может быть смоделирован как изменяющийся во времени C. Измерение тока во времени дает частоту дыхания и, таким образом, служит монитором апноэ во сне. То, как R и C изменяются в широком диапазоне частот, можно использовать для дифференциации здоровой ткани от больной. Чувствительность устройств, выявляющих опухоли молочной железы, еще недостаточна для получения одобрения правительства. Подробный обзор различных диагностических применений электрических полей см. в обзоре Харта [6].
Чувствительность устройств, выявляющих опухоли молочной железы, еще недостаточна для получения одобрения правительства. Подробный обзор различных диагностических применений электрических полей см. в обзоре Харта [6].
2.5. Тканевая инженерия
Применение электрических полей к клеточным системам может вызывать широкий спектр физических эффектов в клетках в дополнение к гальванотаксису. Подобные эффекты подробно описаны в обзорной монографии CRC под редакцией Пуллара [1]. Эта комбинация эффектов электрического поля оказывается полезной в тканевой инженерии, при которой клетки помещаются на подложку (скаффолд) и стимулируются к росту в более сложные ткани. Например, применение импульсных полей постоянного тока к кардиомиоцитам, культивируемым на каркасе из коллагеновой губки, стимулировало их выравнивание, сопряжение и синхронные сокращения [25]. Такая сборка служила бы сердечной заплатой для жертв сердечного приступа. Импульсные поля способствовали росту и ориентации нейритов на полипиррол/коллагеновом каркасе [26]. Целью таких исследований является разработка способности заменять поврежденные нервы. Поле постоянного тока, воздействующее на остеобласты, костеобразующие клетки, нанесенные на титановую подложку, увеличивало их адгезию к подложке и их пролиферацию [27]. Природа и структура субстрата важны, поскольку они могут обеспечивать механическую стимуляцию, которая также влияет на поведение клеток на каркасе. Оптимизация как контактного наведения, так и приложенного электрического поля дает результаты, которые лучше, чем те, которые были получены для любого из методов отдельно для фибробластов и кардиомиоцитов [28], а также для эпителиальных клеток роговицы и хрусталика [29].].
Целью таких исследований является разработка способности заменять поврежденные нервы. Поле постоянного тока, воздействующее на остеобласты, костеобразующие клетки, нанесенные на титановую подложку, увеличивало их адгезию к подложке и их пролиферацию [27]. Природа и структура субстрата важны, поскольку они могут обеспечивать механическую стимуляцию, которая также влияет на поведение клеток на каркасе. Оптимизация как контактного наведения, так и приложенного электрического поля дает результаты, которые лучше, чем те, которые были получены для любого из методов отдельно для фибробластов и кардиомиоцитов [28], а также для эпителиальных клеток роговицы и хрусталика [29].].
Тканевая инженерия обычно использует электрические поля, которые прикладывают снаружи к каркасу. Недавно Аринзе и соавт. [30] сообщили, что сам каркас может обеспечивать электрическое поле, используемое для контроля и стимуляции клеток. Они разработали леса, которые были частично керамическими и частично пластиковыми. Один из пластиковых материалов, которые они использовали, был пьезоэлектрическим; то есть он генерировал электрическое поле при механическом воздействии. При правильном механическом текстурировании пьезоэлектрических каркасов они смогли усилить регенерацию аксонов в нейритах с целью содействия восстановлению спинного мозга. Более того, используя подходящие пьезоэлектрические материалы и текстуры каркаса, они смогли заставить стволовые клетки формировать кость или хрящ. Для более подробного обсуждения использования электрических полей в тканевой инженерии см. обзор Hronik-Tupaj и Kaplan [31].
Один из пластиковых материалов, которые они использовали, был пьезоэлектрическим; то есть он генерировал электрическое поле при механическом воздействии. При правильном механическом текстурировании пьезоэлектрических каркасов они смогли усилить регенерацию аксонов в нейритах с целью содействия восстановлению спинного мозга. Более того, используя подходящие пьезоэлектрические материалы и текстуры каркаса, они смогли заставить стволовые клетки формировать кость или хрящ. Для более подробного обсуждения использования электрических полей в тканевой инженерии см. обзор Hronik-Tupaj и Kaplan [31].
Реклама
3. Клеточная дозиметрия
Чтобы понять, как клетки производят наблюдаемые эффекты, сначала необходимо понять, как приложенное поле распределяется внутри клетки в зависимости от времени. Предположим, что сферическая клетка радиуса R помещена в культуральную среду вдали от параллельных пластинчатых электродов. В момент времени t = 0 между пластинами приложено электрическое поле E. Модель Фрике, показанную на рисунке 2, можно использовать для понимания результирующего заряда клеточной мембраны и индуцированного трансмембранного напряжения TMVi. Ячейка ведет себя как последовательная RC-цепь. Когда поле приложено, заряд течет через резистор, чтобы зарядить конденсатор. Как только конденсатор полностью заряжен для установления TMVi, поток заряда через резистор R прекращается. Постоянная времени процесса равна τ. Для времен, значительно меньших τ, существует значительный поток заряда и связанное с ним электрическое поле внутри клетки (цитоплазма). Напряжение на конденсаторе TMVi постепенно увеличивается. В течение времени, значительно превышающего τ, поток заряда прекращается, и связанное с ним электрическое поле внутри цитоплазмы незначительно. TMVi достиг своего максимального значения. Без приложенного поля существует естественное трансмембранное напряжение TMVo, которое создается системой ионных насосов и каналов в мембране. TMVo составляет порядка 70 мВ для большинства типов клеток, при этом внутренняя часть клетки более отрицательна, чем внешняя.
Модель Фрике, показанную на рисунке 2, можно использовать для понимания результирующего заряда клеточной мембраны и индуцированного трансмембранного напряжения TMVi. Ячейка ведет себя как последовательная RC-цепь. Когда поле приложено, заряд течет через резистор, чтобы зарядить конденсатор. Как только конденсатор полностью заряжен для установления TMVi, поток заряда через резистор R прекращается. Постоянная времени процесса равна τ. Для времен, значительно меньших τ, существует значительный поток заряда и связанное с ним электрическое поле внутри клетки (цитоплазма). Напряжение на конденсаторе TMVi постепенно увеличивается. В течение времени, значительно превышающего τ, поток заряда прекращается, и связанное с ним электрическое поле внутри цитоплазмы незначительно. TMVi достиг своего максимального значения. Без приложенного поля существует естественное трансмембранное напряжение TMVo, которое создается системой ионных насосов и каналов в мембране. TMVo составляет порядка 70 мВ для большинства типов клеток, при этом внутренняя часть клетки более отрицательна, чем внешняя. Таким образом, общее трансмембранное напряжение, TMVt, представляет собой сумму TMVo и TMVi. Трансмембранный вольтаж меняется со временем [32] в соответствии с:
Таким образом, общее трансмембранное напряжение, TMVt, представляет собой сумму TMVo и TMVi. Трансмембранный вольтаж меняется со временем [32] в соответствии с:
TMVt=1,5ERcosΘ1-exp-t/t+TMVo E2
, где Θ — угол между электрическим полем и нормалью к поверхности клетки. Фактор 1,5 связан со сферической формой клетки и имеет более высокие значения для клеток более асимметричной формы. Для ячеек неправильной формы требуется численное моделирование, как обсуждалось в разделе 6.
На рис. 3 представлена стилизованная диаграмма, иллюстрирующая ячейку, помещенную в изначально однородное электрическое поле Eo. Когда поле приложено впервые (t <  Диаметр небольшой ячейки составляет порядка 10 мкм, так что разность потенциалов на ячейке составляет порядка 1 мВ. В состоянии равновесия внутри клетки существует незначительная разность потенциалов. 1 мВ разделяется мембраной на ее концах, что дает расчетное значение TMVi, равное 0,5 мВ. Сферичность ячейки добавляет дополнительный коэффициент 1,5, чтобы получить фактическое TMVi 0,75 мВ. Обратите внимание, что это значение намного меньше, чем TMVO. Для ячейки диаметром 50 мм TMVi будет составлять 3,75 мВ, что все еще мало по сравнению с TMVo. Для приложенного поля 10 кВ/м TMVi будет составлять 75 мВ для ячейки диаметром 10 мкм и 375 мВ для ячейки диаметром 50 мкм. В этих случаях TMVi сравним или превышает Vo соответственно.
Диаметр небольшой ячейки составляет порядка 10 мкм, так что разность потенциалов на ячейке составляет порядка 1 мВ. В состоянии равновесия внутри клетки существует незначительная разность потенциалов. 1 мВ разделяется мембраной на ее концах, что дает расчетное значение TMVi, равное 0,5 мВ. Сферичность ячейки добавляет дополнительный коэффициент 1,5, чтобы получить фактическое TMVi 0,75 мВ. Обратите внимание, что это значение намного меньше, чем TMVO. Для ячейки диаметром 50 мм TMVi будет составлять 3,75 мВ, что все еще мало по сравнению с TMVo. Для приложенного поля 10 кВ/м TMVi будет составлять 75 мВ для ячейки диаметром 10 мкм и 375 мВ для ячейки диаметром 50 мкм. В этих случаях TMVi сравним или превышает Vo соответственно.
Рис. 3.
Зависимость трансмембранного напряжения от приложенного поля.
Реклама
4.
 Электропорация
Электропорация4.1. Основные принципы
Приложения, описанные до этого момента, предназначены для прикладных полей физиологической силы; то есть менее примерно 300 В/м. Частоты этих полей также меньше 1 МГц с соответствующими временными масштабами более 1 микросекунды. Как отмечалось выше, для таких масштабов времени результирующее цитоплазматическое электрическое поле пренебрежимо мало, поэтому любое прямое взаимодействие должно происходить на поверхности клетки. В этом разделе мы обсуждаем приложения, создаваемые полями порядка 10 кВ/м или выше с частотами компонентов, часто превышающими 1 МГц. Такие поля достаточно сильны, чтобы проницать клеточную мембрану; то есть разрешить прохождение атомов и молекул внутрь клетки. Принципиальная модель, используемая для описания этого процесса, предполагает открытие небольших (радиусом в несколько нанометров) отверстий или пор. По этой причине процесс называют электропорацией, хотя иногда используется термин электропермеабилизация. Таким образом, ранее введенные лекарства, которые обычно не могут пройти через мембрану, могут проникнуть внутрь клетки (электрохимиотерапия, ЭСТ) или ДНК/РНК могут быть вставлены в ядро клетки (электрогенетическая терапия, ЭГТ).
Таким образом, ранее введенные лекарства, которые обычно не могут пройти через мембрану, могут проникнуть внутрь клетки (электрохимиотерапия, ЭСТ) или ДНК/РНК могут быть вставлены в ядро клетки (электрогенетическая терапия, ЭГТ).
Приложенное поле принимает форму прямоугольных импульсов с амплитудой электрического поля, E, числом, N, длительностью импульса, T, и частотой повторения импульсов, F. Как правило, по мере увеличения любого из этих параметров вероятность введения лекарства или ДНК увеличивается, но и вероятность повреждения клеток. Таким образом, существует компромисс между успехом внедрения и выживаемостью клеток. Обычно E составляет от 10 кВ/м до 100 кВ/м, а T составляет от миллисекунд до микросекунд. В настоящее время наносекундные импульсы с Е порядка 1 МВ/м изучаются для потенциальных клинических применений. Ниже определенного порога, который зависит от свойств клеток (например, типа, радиуса, расположения в ткани и т. д.), электропорация не происходит. Для импульсов от миллисекунд до микросекунд обратимая электропорация начинается выше примерно 10 кВ/м. В этих условиях происходит транспорт внутрь клетки, и клетка выживает в этом процессе. При более высоких полях происходит слишком много повреждений, и клетки не выживают. Есть две категории этой необратимой электропорации. Клетки могут погибнуть, потому что мембрана настолько сильно повреждена, что не может адекватно закрыться. При такой нетермической необратимой электропорации (NTIRE) клетки-мишени могут быть уничтожены без повреждения окружающих вен и внеклеточного матрикса [8]. При более высоких полях клетки и часть их окружения разрушаются при нагревании.
В этих условиях происходит транспорт внутрь клетки, и клетка выживает в этом процессе. При более высоких полях происходит слишком много повреждений, и клетки не выживают. Есть две категории этой необратимой электропорации. Клетки могут погибнуть, потому что мембрана настолько сильно повреждена, что не может адекватно закрыться. При такой нетермической необратимой электропорации (NTIRE) клетки-мишени могут быть уничтожены без повреждения окружающих вен и внеклеточного матрикса [8]. При более высоких полях клетки и часть их окружения разрушаются при нагревании.
Электропорация основана на изменении разности потенциалов на мембране. Как отмечалось выше, прикладываемые поля порядка от 10 до 100 кВ/м могут создавать TMVi, сравнимый с TMVo или превышающий его. Поскольку внешняя поверхность ячейки положительна по отношению к внутренней, ВТМt будет наибольшей на конце ячейки, обращенном к положительному электроду (аноду). На противоположном конце, обращенном к отрицательному электроду (катоду), TMVo существенно вычитается из TMVi, так что TMVt велико, но несколько меньше, чем на положительном конце. уравнение (2) выше полезно для понимания параметров, влияющих на обычную электропорацию. Для импульсов в диапазоне от микросекунды до миллисекунды t> > τ, так что член в скобках сокращается просто до 1. На средней линии, где cos Θ = 0, TMVt = TMVo. Поскольку самые большие TMVts находятся на двух концах, это места, где обычно ожидается максимальное введение. Минимальная вставка ожидается по средней линии. По мере увеличения E вставки будут происходить все дальше и дальше от полюсов. Для достижения определенного TMVi требуются большие поля для меньших ячеек. Как только пора открывается, молекулы окружающей жидкости проходят через нее внутрь клетки. Более крупные молекулы требуют более длительных импульсов для расширения пор и поддержания электрической движущей силы в течение более длительного периода времени. Площадь проницаемой поверхности клетки зависит от Е, тогда как уровень проницаемости поверхности зависит от количества и длительности импульсов.
уравнение (2) выше полезно для понимания параметров, влияющих на обычную электропорацию. Для импульсов в диапазоне от микросекунды до миллисекунды t> > τ, так что член в скобках сокращается просто до 1. На средней линии, где cos Θ = 0, TMVt = TMVo. Поскольку самые большие TMVts находятся на двух концах, это места, где обычно ожидается максимальное введение. Минимальная вставка ожидается по средней линии. По мере увеличения E вставки будут происходить все дальше и дальше от полюсов. Для достижения определенного TMVi требуются большие поля для меньших ячеек. Как только пора открывается, молекулы окружающей жидкости проходят через нее внутрь клетки. Более крупные молекулы требуют более длительных импульсов для расширения пор и поддержания электрической движущей силы в течение более длительного периода времени. Площадь проницаемой поверхности клетки зависит от Е, тогда как уровень проницаемости поверхности зависит от количества и длительности импульсов.
В настоящее время нерешенной проблемой теории электропорации является то, что клеточная мембрана не полностью запечатывается после снятия поля. Электропорированные простые липидные мембраны повторно запечатываются в течение микросекунд, тогда как клеточные мембраны остаются частично проницаемыми в течение временных масштабов порядка минут. Были предложены две модели задержки полной повторной герметизации [32]. Оба связаны с липидами, одним из основных компонентов клеточной мембраны. Один включает изменение конформации липидов, что приводит к образованию метастабильной мембранной структуры, для распада которой требуется значительное время. Другой — окисление липидов, которое изменяет ряд свойств мембраны.
Электропорированные простые липидные мембраны повторно запечатываются в течение микросекунд, тогда как клеточные мембраны остаются частично проницаемыми в течение временных масштабов порядка минут. Были предложены две модели задержки полной повторной герметизации [32]. Оба связаны с липидами, одним из основных компонентов клеточной мембраны. Один включает изменение конформации липидов, что приводит к образованию метастабильной мембранной структуры, для распада которой требуется значительное время. Другой — окисление липидов, которое изменяет ряд свойств мембраны.
4.2. Клиническое применение электропорации
Важные противораковые препараты, такие как цисплатин и блеомицин, не могут легко проникать через клеточную мембрану. Применение импульсов электропорации открывает поры в мембране, через которые могут пройти лекарства. Поскольку введение лекарства в клетку теперь стало более эффективным, доза, вводимая пациенту, может быть значительно снижена и иметь меньше побочных эффектов. ЭСТ используется во многих центрах Европы для лечения широкого спектра опухолей [8]. При глубоко расположенных опухолях NTIRE используется для уничтожения раковых клеток при сохранении окружающих тканей. Глубокие опухоли требуют сложных процедур. Обычно МРТ используется для детального картирования типов тканей, окружающих опухоль. Знание диэлектрических свойств различных типов тканей позволяет рассчитать поле, которое будет приложено к месту опухоли при различных возможных положениях электродов. Как только будет принято решение об оптимальном размещении электродов, МРТ может быть использована для руководства хирургом по размещению электродов [33].
ЭСТ используется во многих центрах Европы для лечения широкого спектра опухолей [8]. При глубоко расположенных опухолях NTIRE используется для уничтожения раковых клеток при сохранении окружающих тканей. Глубокие опухоли требуют сложных процедур. Обычно МРТ используется для детального картирования типов тканей, окружающих опухоль. Знание диэлектрических свойств различных типов тканей позволяет рассчитать поле, которое будет приложено к месту опухоли при различных возможных положениях электродов. Как только будет принято решение об оптимальном размещении электродов, МРТ может быть использована для руководства хирургом по размещению электродов [33].
Введение лекарств через кожные пластыри (трансдермальная доставка лекарств) требует, чтобы лекарства успешно проходили через кожу в нижележащие ткани. Такой проход обычно блокируется роговым слоем, который является самым наружным слоем кожи. Роговой слой представляет собой сухой слой мертвых клеток толщиной примерно 15 мкм. Подобно тому, как этот слой защищает тело, ограничивая потерю жидкости из тела в окружающую среду, он также предотвращает прохождение жидкости с поверхности внутрь. В традиционных системах доставки лекарств с помощью электричества (ионофорез) электроды размещают на поверхности и прикладывают поле. В вспомогательном транспорте лекарств участвуют два фактора [34]. Во-первых, электрическое поле протолкнет положительно заряженные лекарства от анода через кожу к катоду. Отрицательно заряженные лекарства выталкиваются с катода. Во-вторых, заряженные ионы тянут за собой часть жидкости (электроосмос) и таким образом усиливают перенос. Этим методом можно транспортировать нейтральные молекулы лекарств.
В традиционных системах доставки лекарств с помощью электричества (ионофорез) электроды размещают на поверхности и прикладывают поле. В вспомогательном транспорте лекарств участвуют два фактора [34]. Во-первых, электрическое поле протолкнет положительно заряженные лекарства от анода через кожу к катоду. Отрицательно заряженные лекарства выталкиваются с катода. Во-вторых, заряженные ионы тянут за собой часть жидкости (электроосмос) и таким образом усиливают перенос. Этим методом можно транспортировать нейтральные молекулы лекарств.
Электропорация может предложить улучшенный метод трансдермальной доставки лекарств [8]. Поскольку роговой слой имеет гораздо большее электрическое сопротивление, чем нижние слои кожи, в нем концентрируется электрическое поле прикладываемых импульсов. Импульсы увеличивают его проницаемость для лекарств, открывая пути через него. Кроме того, поле может прикладывать сильную электрофоретическую силу к заряженным молекулам лекарства, чтобы протолкнуть их через роговой слой.
Поскольку ДНК значительно больше, чем противораковые препараты, ее труднее внедрить в клетку. ДНК встраивается в виде плазмид, которые представляют собой небольшие, часто круглые сегменты, содержащие генетическую информацию. Более того, ДНК заряжена отрицательно, как и внешняя поверхность клетки, так что происходит естественное отталкивание ДНК от мембраны. По этим причинам для введения ДНК (или РНК) в клетку используются два импульса. На первом этапе применяется типичный короткий импульс высокого напряжения, чтобы открыть поры. На втором этапе импульс более низкого напряжения применяется в течение более длительного времени, чтобы ввести отрицательно заряженную плазмиду ДНК в клеточную мембрану. Этот электрофоретический толчок будет эффективен только на той стороне клетки, которая обращена к отрицательному электроду. Использование биполярных импульсов позволяет проникать ДНК в обе стороны клетки. В конце импульсов часть процесса, связанная с электрическим полем, завершается, а ДНК все еще находится в мембране. В этот момент происходит процесс, называемый эндоцитозом, при котором клетка образует везикулу вокруг плазмиды, а затем втягивает ее внутрь клетки. Затем плазмида не диффундирует пассивно в ядро клетки, а активно транспортируется внутриклеточными механизмами. Процессы эндоцитоза и активного транспорта требуют часов после окончания импульса, чтобы плазмида проникла в ядро и экспрессировалась. Детали этих процессов изучены недостаточно [9].].
В этот момент происходит процесс, называемый эндоцитозом, при котором клетка образует везикулу вокруг плазмиды, а затем втягивает ее внутрь клетки. Затем плазмида не диффундирует пассивно в ядро клетки, а активно транспортируется внутриклеточными механизмами. Процессы эндоцитоза и активного транспорта требуют часов после окончания импульса, чтобы плазмида проникла в ядро и экспрессировалась. Детали этих процессов изучены недостаточно [9].].
EGT используется клинически для вакцинации или лечения рака [9]. При типичной вакцинации молекула (антиген) вводится в мышцу, чтобы вызвать специфический иммунный ответ организма. При вакцинации EGT вводят плазмиду, кодирующую антиген. Ядра клеток включают плазмиду, а затем продуцируют антигены, вызывающие иммунный ответ. Клинические испытания были успешно проведены для таких состояний, как ВИЧ и вирусы гепатита В и С. Для лечения рака плазмиды вводят в опухоли. Для получения продуктов, способствующих, например, стимуляции самоубийства клеток, активации иммунного ответа или подавлению роста кровеносных сосудов, можно использовать несколько стратегий экспрессии генов. ЭГТ можно комбинировать с ЭСТ, чтобы обеспечить двухэтапную атаку на опухоли.
ЭГТ можно комбинировать с ЭСТ, чтобы обеспечить двухэтапную атаку на опухоли.
4.3. Нанопорация
Напомним из раздела 3, что за времена, много меньшие постоянной времени мембраны τ, электрическое поле проникает внутрь клетки. Затем можно порировать клеточное ядро и другие субклеточные структуры. Поскольку размер этих структур намного меньше самой клетки, согласно уравнению. (2) для этого должны быть приложены соответственно более сильные электрические поля. В нанопорах электрические поля порядка 1–10 МВ/м прикладывают в течение времени порядка наносекунд (нс). Фактическая длительность импульса важна для определения того, где наноимпульсы имеют наибольший эффект. Согласно уравнению (2) при τ ~ 1 мкс длительность импульса 10 нс или меньше приведет к незначительным изменениям TMVi. Таким образом, электрическое поле внутри клетки велико и может разрушать внутренние структуры. И наоборот, длительность импульса более 100 нс приводит к большой поляризации мембраны и уменьшению внутреннего поля. Применение очень коротких импульсов и их анализ сложны, поэтому воспроизводимые результаты с использованием таких импульсов трудно получить. Импульсы длительностью в диапазоне от 11 до 100 нс наиболее эффективны для получения воспроизводимых результатов внутри клетки, таких как апоптоз (самоубийство клеток) и высвобождение кальция из внутриклеточных запасов [35].
Применение очень коротких импульсов и их анализ сложны, поэтому воспроизводимые результаты с использованием таких импульсов трудно получить. Импульсы длительностью в диапазоне от 11 до 100 нс наиболее эффективны для получения воспроизводимых результатов внутри клетки, таких как апоптоз (самоубийство клеток) и высвобождение кальция из внутриклеточных запасов [35].
Реклама
5. Механизмы и эксперименты
Мы приводим здесь краткое описание проведенных нами исследований [36, 37] по определению механизма, с помощью которого клетки первоначально обнаруживают электрические поля физиологической силы. Выявление и понимание этого механизма важно для дальнейшей разработки различных приложений, описанных выше. Мы также представляем сокращенное описание некоторых экспериментов, подтверждающих эту идентификацию.
5.1. Как клетки обнаруживают электрические поля
Как описано выше, электрические поля постоянного тока и низкочастотные электрические поля вызывают широкий спектр биологических эффектов на клеточном и тканевом уровнях. Хотя акцент здесь делается на миграции клеток, заживлении ран и стимуляции нервной системы, электрические поля оказывают широкий спектр других воздействий на клетки, как описано в обзоре CRC [1]. Как только клетка впервые обнаруживает поле, информация передается по всей клетке, вызывая широкий спектр биохимических эффектов. Главный вопрос заключается в том, каков первоначальный механизм трансдукции, с помощью которого клетка обнаруживает поле?
Хотя акцент здесь делается на миграции клеток, заживлении ран и стимуляции нервной системы, электрические поля оказывают широкий спектр других воздействий на клетки, как описано в обзоре CRC [1]. Как только клетка впервые обнаруживает поле, информация передается по всей клетке, вызывая широкий спектр биохимических эффектов. Главный вопрос заключается в том, каков первоначальный механизм трансдукции, с помощью которого клетка обнаруживает поле?
Как отмечалось выше, для полей постоянного тока и частот переменного тока ниже примерно 1 МГц приложенные электрические поля не могут проникнуть через плазматическую мембрану, поскольку имеется достаточно времени для перераспределения заряда в цитоплазме, чтобы по существу нейтрализовать приложенное поле. Таким образом, для полей постоянного тока начальная трансдукция должна происходить на плазматической мембране или сразу за ней. Процесс трансдукции также должен передавать эту информацию внутрь клетки. Было предложено три механизма этого начального процесса трансдукции: (1) электродиффузия/осмос [38, 39], (2) открытие потенциалзависимых каналов [40] и (3) электромеханический крутящий момент, воздействующий на гликокаликс [41]. Модель электродиффузии/осмоса требует полей, более сильных, чем типичные поля физиологической силы, применяемых в течение относительно длительных интервалов времени, и изменения трансмембранного потенциала, вызываемые такими полями, недостаточны для открытия потенциалзависимых каналов [37].
Модель электродиффузии/осмоса требует полей, более сильных, чем типичные поля физиологической силы, применяемых в течение относительно длительных интервалов времени, и изменения трансмембранного потенциала, вызываемые такими полями, недостаточны для открытия потенциалзависимых каналов [37].
Фундаментальный принцип электромеханической модели заключается в том, что электрические поля и силы сдвига жидкости имеют общий механизм преобразования — создание крутящих моментов на трансмембранных гликопротеинах. В модели гидродинамических сил [42] сдвиги жидкости в ядре гликокаликса передаются цитоскелету в виде сил, которые затем передаются в виде механических сигналов по всей внутренней части клетки для активации биохимических сигнальных путей. Гликокаликс представляет собой богатую углеводами зону на поверхности клетки [43]. Он покрывает поверхность всех эукариотических клеток, включая раковые и стволовые клетки [44]. Многие гликопротеины, входящие в состав гликокаликса, заряжены отрицательно, особенно содержащие сиаловую кислоту [45]. Более того, будучи помещенным в электрическое поле, приложенное параллельно поверхности клетки, отрицательно заряженный гликокаликс испытывает электрическую силу, касательную к поверхности, аналогичную силе, приложенной сдвигом жидкости. Мы применили эту концепцию к структурной модели Weinbaum et al. [42], в которых силы, воздействующие на щеточную структуру гликокаликса, передаются на цитоскелет и, таким образом, по всей клетке. В частности, эти силы создают электромеханический крутящий момент вокруг точки соединения цитоскелета и, таким образом, силу на сам цитоскелет [41, 46]. Величина этой цитоскелетной силы сравнима с механическими силами, вызывающими физиологические эффекты [41]. Более полное описание этой модели представлено ниже.
Более того, будучи помещенным в электрическое поле, приложенное параллельно поверхности клетки, отрицательно заряженный гликокаликс испытывает электрическую силу, касательную к поверхности, аналогичную силе, приложенной сдвигом жидкости. Мы применили эту концепцию к структурной модели Weinbaum et al. [42], в которых силы, воздействующие на щеточную структуру гликокаликса, передаются на цитоскелет и, таким образом, по всей клетке. В частности, эти силы создают электромеханический крутящий момент вокруг точки соединения цитоскелета и, таким образом, силу на сам цитоскелет [41, 46]. Величина этой цитоскелетной силы сравнима с механическими силами, вызывающими физиологические эффекты [41]. Более полное описание этой модели представлено ниже.
Предсказания электромеханической модели согласуются с гальванотаксисом кератиноцитов [36] и амеб [37]. Гальванотаксис служит удобным эффектом для сравнения трех предложенных механизмов, поскольку это процесс, который легко воспроизводится и легко измеряется в реальном времени. Можно фиксировать действие поля по мере его возникновения, а не ждать результатов биохимического анализа. Такой же начальный процесс преобразования должен присутствовать и для множества других полевых эффектов. Модель успешно предсказала, что наложение синусоидального сигнала 40 В/м, 1,6 Гц на поле постоянного тока 100 В/м уменьшит направленность, тогда как наложение поля 40 В/м, 160 Гц не уменьшит направленность по сравнению с чистым полем. поле 100 В/м постоянного тока. Дальнейшее подтверждение электромеханической модели, которая идентифицирует гликокаликс как место трансдукции, было предоставлено Finkelstein et al. [47], которые показали, что удаление основных отрицательно заряженных молекул в гликокаликсе в клетках 3 T3 и HeLa устраняет гальванотаксис. Более того, влияние наложенных полей на подвижность клеток (скорость) также объясняется моделью [37]. Увеличение подвижности клеток часто, но не всегда, сопровождает увеличение направленности к полю. Приложенное поле создает изгибающий момент на отрицательно заряженном гликокаликсе между клеткой и субстратом.
Можно фиксировать действие поля по мере его возникновения, а не ждать результатов биохимического анализа. Такой же начальный процесс преобразования должен присутствовать и для множества других полевых эффектов. Модель успешно предсказала, что наложение синусоидального сигнала 40 В/м, 1,6 Гц на поле постоянного тока 100 В/м уменьшит направленность, тогда как наложение поля 40 В/м, 160 Гц не уменьшит направленность по сравнению с чистым полем. поле 100 В/м постоянного тока. Дальнейшее подтверждение электромеханической модели, которая идентифицирует гликокаликс как место трансдукции, было предоставлено Finkelstein et al. [47], которые показали, что удаление основных отрицательно заряженных молекул в гликокаликсе в клетках 3 T3 и HeLa устраняет гальванотаксис. Более того, влияние наложенных полей на подвижность клеток (скорость) также объясняется моделью [37]. Увеличение подвижности клеток часто, но не всегда, сопровождает увеличение направленности к полю. Приложенное поле создает изгибающий момент на отрицательно заряженном гликокаликсе между клеткой и субстратом. Гликокаликс отгибается от субстрата, увеличивая разделение гликокаликса и субстрата и увеличивая адгезию клеток. В результате подвижность клеток может увеличиться. Однако, если клеточная адгезия уже оптимальна, поле не вызывает значительного дополнительного увеличения подвижности. Добавление положительно заряженных ионов кальция, которые связываются с отрицательно заряженным гликокаликсом, уменьшало увеличение направленности и подвижности, вызванное полем на амебе, что обеспечивает дальнейшее подтверждение электромеханической модели [37]. Подробности представлены ниже.
Гликокаликс отгибается от субстрата, увеличивая разделение гликокаликса и субстрата и увеличивая адгезию клеток. В результате подвижность клеток может увеличиться. Однако, если клеточная адгезия уже оптимальна, поле не вызывает значительного дополнительного увеличения подвижности. Добавление положительно заряженных ионов кальция, которые связываются с отрицательно заряженным гликокаликсом, уменьшало увеличение направленности и подвижности, вызванное полем на амебе, что обеспечивает дальнейшее подтверждение электромеханической модели [37]. Подробности представлены ниже.
Поскольку столь разные типы клеток демонстрируют сходное поведение, мы предполагаем, что этот механизм обнаружения поля должен был присутствовать в ранних клетках. Мы предполагаем [37], что этот механизм изгиба гликокаликса изначально использовался для обнаружения изменений потока жидкости. Поскольку эта система обнаружения оказалась отрицательно заряженной, она также могла обнаруживать электрические поля. С эволюцией многоклеточных организмов эта способность могла стать полезной для управления некоторыми процессами развития [4]. Затем последовали другие процессы зондирования поля.
Затем последовали другие процессы зондирования поля.
5.2. Детали механической модели
5.2.1. Увеличение направленности
Первый механизм, с помощью которого электрическое поле обнаруживается клеткой, включает создание полем электромеханического крутящего момента на гликокаликсе, аналогичного крутящему моменту, создаваемому сдвигом жидкости. Хотя гликокаликс покрывает поверхность всех эукариотических клеток [44], детальное моделирование его функциональности было проведено прежде всего для эндотелиальных клеток. По этой причине параметры, используемые при моделировании, основаны на параметрах гликокаликса эндотелиальных клеток и их компонентов. В своем обзоре структуры эндотелиального гликокаликса Карри и Адамсон [48] описывают внутренний слой толщиной 100–150 нм, обладающий квазипериодической структурой. За этим слоем находится область до 400 нм, необходимая для обнаружения сдвига жидкости. Напряжение сдвига жидкости, приложенное к верхней части этой области, передается более жесткому внутреннему слою, а затем передается мембране в виде твердой механической силы [44].
Рисунок 4 иллюстрирует базовую электромеханическую модель [36]. На нем показаны силы, действующие на заряженный цилиндрический гликопротеин, который своим основанием соединен с цитоскелетом. F elec = QE(t) представляет собой электрическую силу, действующую на эффективный заряд Q гликопротеина приложенным электрическим полем E(t) в момент времени t. Поскольку гликокаликс заряжен отрицательно, сила F, действующая на него со стороны поля E, противоположна направлению E. окружающей внеклеточной жидкости. Угловое смещение стержня θ (t) определяется балансом крутящего момента [46], а c — коэффициент сопротивления трения. Для стержня c = 2πL’ 2 /(ln[L’/r] − 0,447), где L’ — длина стержня, r — его радиус [41]. F memb = -khθ (t) – гармоническая восстанавливающая сила, действующая на колеблющийся стержень со стороны клеточной мембраны, где k – силовая постоянная, h – расстояние от центра мембраны до точки соединения основания с цитоскелетом [ 41]. F основание — сила, действующая цитоскелетом на стержень в месте соединения. Согласно третьему закону Ньютона сила, с которой палочка действует на цитоскелет, равна –F база . Второй закон Ньютона гласит, что результирующая сила, F net , действующая на стержень, равна
F основание — сила, действующая цитоскелетом на стержень в месте соединения. Согласно третьему закону Ньютона сила, с которой палочка действует на цитоскелет, равна –F база . Второй закон Ньютона гласит, что результирующая сила, F net , действующая на стержень, равна
Fnet=Ma=Felec+Fdrag+Fmemb+Fbase E3
, где M — масса стержня, а — ускорение его центра масс. Здесь a = (L’/2)d 2 θ/dt 2 . Решая, имеем
Fbase=ML/2d2θt/dt2–QEt+cdθt/dt+khθt E4
Рис. 4.
Схема сил, действующих на стержень гликокаликса под действием электрического поля.
Комбинации пружины и амортизатора, соединенные с основанием на рис. 4, указывают на передачу результирующих продольных механических сигналов вдоль цитоскелета к остальной части клетки. Угловое смещение иллюстрирует ситуацию, в которой приложенное поле имеет как постоянную, так и переменную составляющие. Для чисто постоянного поля θ AC и E AC равны нулю.
Для чисто постоянного поля θ AC и E AC равны нулю.
Применение вышеуказанной модели к массиву из 27 стержней гликокаликса в модели гликокаликса Вейнбаума [42] дает силу, приложенную к цитоскелету, порядка 0,5 пН для приложенного электрического поля 100 В/м. Такая сила сравнима с некоторыми внутриклеточными механическими силами [41]. Следовательно, вполне вероятно, что силы, предсказанные электромеханической моделью, будут иметь физиологические эффекты.
Сила вязкого сопротивления, действующая на стержень со стороны окружающей внеклеточной жидкости, увеличивается линейно с частотой приложенного поля. Важность этой частотной зависимости становится очевидной, когда поле переменного тока накладывается на чистое поле постоянного тока. Сопротивление, оказываемое на стержни для поля 1,6 Гц, очень мало, поэтому общая сила (AC + DC) на цитоскелет сильно модулируется. Сила сопротивления для поля 160 Гц в 100 раз больше, так что результирующая модуляция незначительна, а общая сила практически идентична силе, создаваемой чистым полем постоянного тока [41]. Мы предполагаем, что сильная модуляция на частоте 1,6 Гц вносит значительный механический сигнальный шум в цитоскелет, который снижает общую трансдукцию по сравнению с чистым полем постоянного тока. Наложенное поле частотой 160 Гц не могло бы вызвать такого снижения. Таким образом, электромеханическая модель согласуется с результатами, представленными для кератиноцитов [36] и для амеб [37].
Мы предполагаем, что сильная модуляция на частоте 1,6 Гц вносит значительный механический сигнальный шум в цитоскелет, который снижает общую трансдукцию по сравнению с чистым полем постоянного тока. Наложенное поле частотой 160 Гц не могло бы вызвать такого снижения. Таким образом, электромеханическая модель согласуется с результатами, представленными для кератиноцитов [36] и для амеб [37].
5.2.2. Увеличение подвижности
Описанный выше механизм не может объяснить увеличение скорости, вызванное приложенными полями постоянного и/или переменного тока. Подвижность клеток частично определяется адгезией клетки к субстрату [49]. Клетки, которые либо слишком плотно, либо слишком слабо связаны, будут иметь более низкую подвижность, чем клетки с промежуточной адгезией. Адгезия снижается отрицательно заряженным гликокаликсом [50, 51]. Увеличение расстояния между гликокаликсом и субстратом должно увеличить адгезию и увеличить подвижность.
Описанная выше модель направленности предполагает взаимодействие поля с относительно жестким внутренним гликокаликсом. Описанная здесь модель увеличения подвижности включает взаимодействие с относительно гибким внешним гликокаликсом. Недавние измерения показали, что весь гликокаликс эндотелиальных клеток может простираться до 11 000 нм с рыхлой фибриллярной сетью удлиненных элементов [52].
Описанная здесь модель увеличения подвижности включает взаимодействие с относительно гибким внешним гликокаликсом. Недавние измерения показали, что весь гликокаликс эндотелиальных клеток может простираться до 11 000 нм с рыхлой фибриллярной сетью удлиненных элементов [52].
Амебы имеют отрицательно заряженный гликокаликс [53], полный объем которого неизвестен. Электронные микрофотографии, сделанные Топфом и Стокемом [54], показали, что гликокаликс состоит из компактного базового слоя толщиной примерно 70 нм с внешним нитевидным слоем толщиной примерно 400 нм. Как отмечалось выше, недавние достижения в области микроскопии указывают на то, что типичная толщина гликокаликса составляет порядка нескольких тысяч нанометров или более. Гребецкий и соавт. [55] показали, что Amoeba proteus прикрепляется к субстрату с помощью дискретно расположенных «миниподий» толщиной около 500 нм и длиной до 8000 нм. Следовательно, внешний гликокаликс между телом клетки амебы и субстратом не сжат, а должен быть относительно свободен для переориентации в приложенном поле.
Круз-Чу и др. [56] использовали молекулярно-динамическое моделирование для исследования влияния сдвига жидкости на модельный гликокаликс. Они обнаружили, что приложенный сдвиг в 0,47 МПа приводит к резкому изгибу гликокаликса (см. их рисунок 5b). Напряжения около 3 МПа и выше значительно разрушали гликокаликс. Хотя их модель была применена в первую очередь к внутреннему гликокаликсу, подобный изгиб должен происходить и в менее жестком внешнем гликокаликсе, взаимодействующем с субстратом.
Рисунок 5.
Схема системы, используемой для воздействия на амебу приложенным электрическим полем.
Мы можем оценить тангенциальный сдвиг, создаваемый электрическим полем физиологической напряженности. Для простоты мы моделируем гликокаликс амебы как однородный, отрицательно заряженный прямоугольный твердый гель, который заполняет пространство между телом амебы и субстратом. Будем считать, что амеба уже вытянута в направлении поля. Длина L и ширина W прямоугольного тела такие же, как у амебы, которые мы принимаем равными L = 0,2 мм и W = 0,05 мм. За толщину гликокаликса принимаем длину мининожек амебы, T = 8 мкм [55]. Типичная оценка плотности заряда гликокаликса: ρ = 25 мэкв/л или 2,5 × 10 6 С/м 3 [57]. Тогда электрическая сила на этой модели гликокаликса равна F = ρLWTE. Напряжение сдвига, σ, представляет собой силу, деленную на поперечное сечение, к которому она приложена, или
Будем считать, что амеба уже вытянута в направлении поля. Длина L и ширина W прямоугольного тела такие же, как у амебы, которые мы принимаем равными L = 0,2 мм и W = 0,05 мм. За толщину гликокаликса принимаем длину мининожек амебы, T = 8 мкм [55]. Типичная оценка плотности заряда гликокаликса: ρ = 25 мэкв/л или 2,5 × 10 6 С/м 3 [57]. Тогда электрическая сила на этой модели гликокаликса равна F = ρLWTE. Напряжение сдвига, σ, представляет собой силу, деленную на поперечное сечение, к которому она приложена, или
σ=ρLWTE/WT=ρLE E5
Для электрического поля 200 В/м σ составляет 0,1 МПа. Наше расчетное напряжение сдвига, создаваемое полем, должно быть достаточным, чтобы согнуть гликокаликс. Изгиб гликокаликса увеличивает его отделение от субстрата. Увеличение расстояния увеличивает адгезию клетки и, следовательно, ее подвижность.
Реакция на напряжение сдвига зависит от механических свойств гликокаликса. Модуль напряжения сдвига и модуль потери сдвига гликокаликса увеличиваются с частотой приложенного напряжения [58]. Следовательно, изгиб, создаваемый электрическим полем с частотой 160 Гц, должен быть меньше, чем изгиб, создаваемый полем с частотой 1,6 Гц. В результате увеличение подвижности должно быть меньше для поля 160 Гц, чем для поля 1,6 Гц, как сообщается в Ref. [37].
Следовательно, изгиб, создаваемый электрическим полем с частотой 160 Гц, должен быть меньше, чем изгиб, создаваемый полем с частотой 1,6 Гц. В результате увеличение подвижности должно быть меньше для поля 160 Гц, чем для поля 1,6 Гц, как сообщается в Ref. [37].
5.3. Эксперименты с гальванотаксисом для проверки модели
5.3.1. Экспериментальная установка
Амебы были приобретены у компании Carolina Biological Company (Берлингтон, Северная Каролина, США) и культивированы в контейнере, в котором они были доставлены, в течение не менее 3 дней, прежде чем их использовали в экспериментах. Детали дизайна и конструкции аппарата (рис. 5), использованного для всех экспериментов, можно найти у Харта и Палисано [37]. Вкратце, клетки амебы изолировали от лунок, содержащих источник тока из платиновой проволоки, и помещали в желоб, который мы соединяли с лунками, в которые подавался электрический ток с помощью солевых мостиков.
Из-за сложной геометрии было необходимо численно смоделировать поле внутри желоба для заданного напряжения, приложенного к скважинам, с помощью COMSOL Multiphysics (COSMOL Inc. , Берлингтон, Массачусетс, США). COSMOL Multiphysics также использовался для моделирования повышения температуры электрических полей в течение 40-минутного временного интервала экспериментов и показал, что полученное повышение температуры составило более 1°C. Расчеты поля и температуры были подтверждены измерениями с помощью вольтметра и термопары соответственно.
, Берлингтон, Массачусетс, США). COSMOL Multiphysics также использовался для моделирования повышения температуры электрических полей в течение 40-минутного временного интервала экспериментов и показал, что полученное повышение температуры составило более 1°C. Расчеты поля и температуры были подтверждены измерениями с помощью вольтметра и термопары соответственно.
Во всех экспериментах каждая амеба служила своим контролем. В течение первых 20 минут записи движение клеток амебы происходило в отсутствие электрического поля. В последние 40 минут прикладывалось электрическое поле. Движения клеток записывались в течение всего 60-минутного эксперимента, а кадры из фильма делались с интервалом в 1 минуту и преобразовывались в замедленную съемку. Положения каждой амебы на каждом 1-минутном интервале были оцифрованы из фильма с использованием программного обеспечения LoggerPro (Venier Software & Technology, Beaverton, OR, USA).
5.3.2. Результаты гальванотаксиса
Мы применяли электрические поля постоянного тока в диапазоне от 15 В/м до 800 В/м. Количество клеток, отслеживаемых в эксперименте, обычно колеблется от 25 до 35. Положение каждой амебы отслеживается с интервалом в 1 минуту в течение 20-минутного контрольного периода, в течение которого поле не применяется, и в последующий 40-минутный интервал, в течение которого применяется поле. За каждую 1 мин амеба проходит расстояние d. Сумма всех этих расстояний за определенный интервал времени представляет собой общее пройденное расстояние D за этот интервал. Средняя скорость или подвижность отдельной амебы в каждом интервале равна D/T, где T — продолжительность интервала, здесь 10 минут. Мы рассматриваем отношение D/T для последних 10 минут контроля как контрольную подвижность, а это отношение для последних 10 минут поля как конечную подвижность. Поле направлено вдоль оси x. За любой 10-минутный интервал расстояние, пройденное амебой в направлении поля, равно Δx. Ориентация движения амебы относительно поля параметризуется углом Φ, где cos Φ = Δx/D. Мы называем cos Φ «направленностью» амебы.
Количество клеток, отслеживаемых в эксперименте, обычно колеблется от 25 до 35. Положение каждой амебы отслеживается с интервалом в 1 минуту в течение 20-минутного контрольного периода, в течение которого поле не применяется, и в последующий 40-минутный интервал, в течение которого применяется поле. За каждую 1 мин амеба проходит расстояние d. Сумма всех этих расстояний за определенный интервал времени представляет собой общее пройденное расстояние D за этот интервал. Средняя скорость или подвижность отдельной амебы в каждом интервале равна D/T, где T — продолжительность интервала, здесь 10 минут. Мы рассматриваем отношение D/T для последних 10 минут контроля как контрольную подвижность, а это отношение для последних 10 минут поля как конечную подвижность. Поле направлено вдоль оси x. За любой 10-минутный интервал расстояние, пройденное амебой в направлении поля, равно Δx. Ориентация движения амебы относительно поля параметризуется углом Φ, где cos Φ = Δx/D. Мы называем cos Φ «направленностью» амебы. Значение cos Φ = +1 указывает на миграцию параллельно полю, тогда как -1 представляет миграцию прямо напротив поля. Мы рассматриваем косинус для последних 10 минут управления как направленность управления, а косинус для последних 10 минут поля как направленность поля.
Значение cos Φ = +1 указывает на миграцию параллельно полю, тогда как -1 представляет миграцию прямо напротив поля. Мы рассматриваем косинус для последних 10 минут управления как направленность управления, а косинус для последних 10 минут поля как направленность поля.
На рис. 6 сравнивается разность направленности поля и управления отдельной ячейки, усредненная по всем ячейкам, в зависимости от приложенного поля. Следовательно, каждая ячейка служит своим собственным контролем. Как свидетельствует увеличение направленности, клетки начинают обнаруживать поля более чем примерно 30 В/м. Увеличение направленности улучшается по мере увеличения поля и становится относительно устойчивым для полей выше примерно 200 В/м. Есть заметные различия в увеличении для низких полей, но общая тенденция очевидна. Для более слабых полей требуется почти 40 минут, чтобы обнаружить увеличение направленности. Таким образом, сравнения увеличения направленности для различных прикладных полей производятся для последних 10 минут полевого применения.
Рис. 6.
Увеличение направленности в поле постоянного тока: Косинус за последние 10 минут в поле минус косинус за последние 10 минут контроля для каждой отдельной ячейки, усредненный по всем ячейкам. Столбики погрешностей представляют собой стандартную ошибку среднего.
Измерение клеточной подвижности показало, что клетки с низкой контрольной подвижностью увеличивали свою скорость гораздо более резко, чем клетки с высокой исходной подвижностью [37]. Явное увеличение подвижности примерно на 50% началось выше примерно 60 В/м и улучшилось примерно до 200 В/м, за пределами которого наблюдалась значительная вариабельность. Увеличение подвижности становилось меньшим с большей контрольной подвижностью. Не было четкой соответствующей вариации увеличения направленности с контрольной подвижностью.
Одной из целей данного исследования является изучение того, насколько широко применима электромеханическая модель. Харт и др. [36] продемонстрировали, что он хорошо описывает потерю направленности кератиноцитов при наложении более слабого низкочастотного переменного поля на более сильное постоянное поле. Рисунок 7 показывает, что аналогичная реакция наблюдалась у Amoeba proteus , свободноживущей клетки. Направленность и подвижность амебы сравнивались при воздействии только поля постоянного тока 65 В/м, поля переменного тока 32 В/м, 1,6 Гц, наложенного на поле постоянного тока 65 В/м, или поля переменного тока 32 В/м, 160 Гц. накладывается на поле постоянного тока 65 В/м. В каждом случае среднее электрическое поле составляло 65 В/м постоянного тока. Все три набора клеток поступили из одной партии и, таким образом, перед экспериментами находились в одинаковых условиях.
Харт и др. [36] продемонстрировали, что он хорошо описывает потерю направленности кератиноцитов при наложении более слабого низкочастотного переменного поля на более сильное постоянное поле. Рисунок 7 показывает, что аналогичная реакция наблюдалась у Amoeba proteus , свободноживущей клетки. Направленность и подвижность амебы сравнивались при воздействии только поля постоянного тока 65 В/м, поля переменного тока 32 В/м, 1,6 Гц, наложенного на поле постоянного тока 65 В/м, или поля переменного тока 32 В/м, 160 Гц. накладывается на поле постоянного тока 65 В/м. В каждом случае среднее электрическое поле составляло 65 В/м постоянного тока. Все три набора клеток поступили из одной партии и, таким образом, перед экспериментами находились в одинаковых условиях.
Рисунок 7.
Влияние на направленность и подвижность наложения меньшего поля переменного тока на поле постоянного тока. В каждом случае поле постоянного тока составляло около 65 В/м, а поле переменного тока составляло около 32 В/м. Светлая заливка указывает на значения, полученные в течение первых 10 минут воздействия поля; темная штриховка, последние 10 минут. Столбики погрешностей представляют собой стандартную ошибку среднего. (A) иллюстрирует различия в направленности; (B) различия в скорости.
В каждом случае поле постоянного тока составляло около 65 В/м, а поле переменного тока составляло около 32 В/м. Светлая заливка указывает на значения, полученные в течение первых 10 минут воздействия поля; темная штриховка, последние 10 минут. Столбики погрешностей представляют собой стандартную ошибку среднего. (A) иллюстрирует различия в направленности; (B) различия в скорости.
На рис. 7A показано, что направленность устраняется для добавленного поля 1,6 Гц в течение первых 10 минут, но сопоставима и значительна для чистого постоянного тока и добавленных полей 160 Гц. Направленность улучшена для всех трех случаев в течение последних 10 минут. Несмотря на значительное улучшение, направленность для добавленного случая 1,6 Гц все же меньше, чем в двух других случаях. Эти результаты аналогичны полученным для кератиноцитов [36]. На рисунке 7B показано, что подвижность в течение первых 10 минут для случая с добавленной частотой 1,6 Гц намного ниже, чем для других примененных полей. Как и в случае с направленностью, подвижность для случая с добавленной частотой 1,6 Гц улучшилась за последние 10 минут, но все еще меньше, чем подвижность для двух других случаев. Эти результаты согласуются с описанной выше моделью подвижности.
Как и в случае с направленностью, подвижность для случая с добавленной частотой 1,6 Гц улучшилась за последние 10 минут, но все еще меньше, чем подвижность для двух других случаев. Эти результаты согласуются с описанной выше моделью подвижности.
Объявление
6. Численное моделирование
Применимость описанных выше методов требует знания детального распределения электрического поля в месте его применения. Поскольку распределение поля зависит от электрических свойств и физической формы различных вовлеченных клеток и тканей, для расчета необходимо использовать численные методы [59]. Эти методы претерпели значительные изменения с годами. Например, ячейки электронной таблицы можно использовать для представления небольших объемных элементов конечности. Величина ячейки представляет собой электрический потенциал элемента Vo. Это значение связано с потенциалом шести окружающих клеток в трехмерной модели. Установка тока, входящего в ячейку, равным выходному току, связывает Vo с потенциалами окружающих ячеек через межэлементные сопротивления. Таким образом можно ввести электрическую анизотропию ткани. Фундаментальные уравнения могут быть введены во многие подобные ячейки одновременно и решены методом последовательной сверхрелаксации в электронной таблице Excel. Этот подход был использован для определения того, как развивалось электрическое поле в месте перелома большеберцовой кости по мере заживления травмы во время электролечения переломов [60]. Метод может быть даже расширен для расчета распределения электрического поля, индуцированного сложным распределением клеток в культуральной чашке [61].
Таким образом можно ввести электрическую анизотропию ткани. Фундаментальные уравнения могут быть введены во многие подобные ячейки одновременно и решены методом последовательной сверхрелаксации в электронной таблице Excel. Этот подход был использован для определения того, как развивалось электрическое поле в месте перелома большеберцовой кости по мере заживления травмы во время электролечения переломов [60]. Метод может быть даже расширен для расчета распределения электрического поля, индуцированного сложным распределением клеток в культуральной чашке [61].
В последнее время коммерческие программы используются для более точного и быстрого определения распределения поля в сложных ситуациях. Как отмечалось выше в разделе 5.3.1, программа COMSOL Multiphysics (COSMOL Inc., Берлингтон, Массачусетс, США) использовалась для определения распределения как электрического поля, так и температуры в нашей экспериментальной установке. Размещение электродов для введения импульсов электропорации требует детального численного анализа результирующих полей на участке опухоли и вокруг него [8]. Теперь доступны виртуальные модели всего тела животных и человека для очень подробных расчетов электрического поля [62]. Модели содержат информацию об электрических, тепловых и реологических свойствах различных тканей. Таким образом, можно провести всесторонний анализ распределения поля и связанных с ним физических эффектов для различных мест размещения электродов.
Теперь доступны виртуальные модели всего тела животных и человека для очень подробных расчетов электрического поля [62]. Модели содержат информацию об электрических, тепловых и реологических свойствах различных тканей. Таким образом, можно провести всесторонний анализ распределения поля и связанных с ним физических эффектов для различных мест размещения электродов.
Объявление
7. Выводы
Электрические поля имеют самые разнообразные применения в биологии и медицине. Поля физиологической силы используются для улучшения заживления ран, стимуляции нейронов, а также позиционирования и активации клеток на каркасах в целях тканевой инженерии. Короткие сильные импульсы, используемые при электропорации, используются для улучшения введения лекарств в опухоли и ДНК в ядра клеток. Необходимо использовать численное моделирование для выбора надлежащей напряженности поля, которая будет применяться в клинических условиях. Некоторые фундаментальные вопросы все еще решаются; в частности, как клетки на самом деле обнаруживают поля? Описанная здесь электромеханическая модель согласуется с экспериментальными данными, тогда как другие модели — нет.
Каталожные номера
- 1. Pullar CE, редактор. Физиология биоэлектричества в развитии, регенерации тканей и раке. Бока-Ратон, Флорида: CRC Press; 2011. 342 p
- 2. McCaig CD, Rajnicek AM, Song B, Zhao M. Электрическое управление поведением клеток: текущие взгляды и будущий потенциал. Физиологические обзоры. 2005;85:943-978. DOI: 10.1152/physrev.00020.2004
- 3. Робинсон К.Р., Мессерли М.А. Влево/вправо, вверх/вниз: роль эндогенных электрических полей как направленных сигналов в развитии, восстановлении и вторжении. Биоэссе. 2003;25:759-766. DOI: 10.1002/bies.10307
- 4. Левин М. Молекулярное биоэлектричество: как эндогенные потенциалы напряжения контролируют поведение клеток и определяют регуляцию паттернов in vivo. Молекулярная биология клетки. 2014; 25:3835-3850. DOI: 10.1091/mbc.E13-12-0708
- 5. Meng S, Rouabhia M, Zhang Z.
 Электрическая стимуляция модулирует пролиферацию остеобластов и выработку костного белка посредством биоактивируемых гепарином проводящих каркасов. Биоэлектромагнетизм. 2013;34:189-199. DOI: 10.1002/bem.21766
Электрическая стимуляция модулирует пролиферацию остеобластов и выработку костного белка посредством биоактивируемых гепарином проводящих каркасов. Биоэлектромагнетизм. 2013;34:189-199. DOI: 10.1002/bem.21766 - 6. Харт FX. Биоимпеданс в клинике. Здравственний вестник. 2009;78:782-790
- 7. Пуллар К.Э., Иссерофф Р.Р. Циклический AMP обеспечивает направленную миграцию кератиноцитов в электрическом поле. Журнал клеточной науки. 2005;118:2023-2034. DOI: 10.1242/jcs.02330
- 8. Ярмуш М.Л., Голберг А., Серса Г., Котник Т., Миклавич Д. Технологии на основе электропорации для медицины: принципы, приложения и проблемы. Ежегодный обзор биомедицинской инженерии. 2014;16:295-320. DOI: 10.1146/annurev-bioeng-071813-104622
- 9. Розацца С., Меглик С.Х., Цумбуш А., Ролс М.П., Миклавчич Д. Электроперенос генов: механистическая перспектива. Современная генная терапия. 2016;16:98-129
- 10.
 Pullar CE, Isseroff RR, Nuccitelli R. Циклическая АМФ-зависимая протеинкиназа играет роль в направленной миграции кератиноцитов человека в постоянном электрическом поле. Подвижность клеток и цитоскелет. 2001;50:207-217
Pullar CE, Isseroff RR, Nuccitelli R. Циклическая АМФ-зависимая протеинкиназа играет роль в направленной миграции кератиноцитов человека в постоянном электрическом поле. Подвижность клеток и цитоскелет. 2001;50:207-217 - 11. Нуччителли Р. Роль эндогенных электрических полей в заживлении ран. Актуальные темы биологии развития. 2003;58:1-26
- 12. Ткань LC. Технологии электростимуляции для заживления ран. Достижения в области заживления ран. 2014;3:81-90. DOI: 10.1089/рана.2013.0459
- 13. Pullar CE. Биологическая основа электростимуляции как терапии хронических ран. Журнал раневых технологий. 2009;N6:20-24
- 14. Хоар Дж.Дж., Райничек А.М., Маккейг К.Д., Баркер Р.Н., Уилсон Х.М. Электрические поля являются новыми детерминантами функций макрофагов человека. Журнал биологии лейкоцитов. 2016;99:1141-1151. DOI: 10.1189/jlb.3A0815-390R
- 15. Фонд Паркинсона.
 Глубокая стимуляция мозга http://www.parkinson.org/under-standing-parkinsons/treatment/surgery-treatment-options/Deep-Brain-Stimulation
Глубокая стимуляция мозга http://www.parkinson.org/under-standing-parkinsons/treatment/surgery-treatment-options/Deep-Brain-Stimulation - 16. Ho CH et al. Функциональная электростимуляция и повреждение спинного мозга. Клиники физической медицины и реабилитации Северной Америки. 2014;25:631-ix. DOI: 10.10.1016/j.pmr.2014.05.001
- 17. Rejc A, Angeli C, Harkema S. Эффекты эпидуральной стимуляции пояснично-крестцового отдела спинного мозга при стоянии после хронического полного паралича у людей. ПЛОС ОДИН; 10(7): e0133998. https://doi.org/10.1371/journal.pone.0133998
- 18. Солопова И.А., Сухотина И.А., Жванский Д.С., Икоэба Г.А., Виссарионов С.В., Баиндурашвили А.Г., Эджертон В.Р., Герасименко Ю.П., Мошонкина Т.Р. Влияние стимуляции спинного мозга на двигательные функции у детей с детским церебральным параличом. Неврологические письма. 2017;639:192-198. DOI: 10.1016/j.neulet.2017.01.003
- 19.
 DeSantana JM, Walsh DM, Vance C, Rakel BA, Sluka KA. Эффективность чрескожной электронейростимуляции для лечения гипералгезии и боли. Текущие отчеты по ревматологии. 2008;10:492-499
DeSantana JM, Walsh DM, Vance C, Rakel BA, Sluka KA. Эффективность чрескожной электронейростимуляции для лечения гипералгезии и боли. Текущие отчеты по ревматологии. 2008;10:492-499 - 20. Hart FX, Evely K, Finch C. Использование программы электронных таблиц для расчета распределения электрического поля/тока, вызванного низкочастотными магнитными полями в неоднородных биологических структурах неправильной формы. Биоэлектромагнетизм. 1993;14:161-172
- 21. Гриффин М., Баят А. Электрическая стимуляция при заживлении костей: критический анализ путем оценки уровней доказательности. Эпластика. 2011;11:303-353
- 22. Алим И.С., Алим И., Эваниев Н., Буссе Дж.В., Яшемский М., Агарвал А., Эйнхорн Т., Бхандари М. Эффективность электростимуляторов для заживления костей: метаанализ рандомизированной имитации -контролируемые испытания. Научные отчеты. 2016;6:31724. DOI: 10.1038/srep31724
- 23.
 Уэно С., Секино М. Биомагнетизм: принципы и применение биомагнитной стимуляции и визуализации. Бока-Ратон, Флорида: CRC Press; 2017. 342 стр.
Уэно С., Секино М. Биомагнетизм: принципы и применение биомагнитной стимуляции и визуализации. Бока-Ратон, Флорида: CRC Press; 2017. 342 стр. - 24. Миклавчич Д., Павлель Н., Харт Ф.Х. Электрические свойства тканей. В: Акай М, редактор. Энциклопедия биомедицинской инженерии Wiley. Том. 6. Нью-Йорк: Уайли. 2006. с. 3578-3589
- 25. Radisic M, Park H, Shing H, Consi T, Schoen FJ, Langer R, Freed LE, Vunjak-Novakovic G. Функциональная сборка сконструированного миокарда путем электрической стимуляции сердечных миоцитов, культивируемых на каркасах. ПНАС. 2004;101:18129-18134. www.pnas.org/cgi. DOI: 10.1073/pnas.0407817101
- 26. Венг Б., Лю С., Шеперд Р., Уоллес Г.Г. Полипиррол/коллагеновый каркас, напечатанный с помощью струйной печати: сочетание пространственного контроля и электрической стимуляции клеток PC12. Синтетические металлы. 2012;162:1375-1380. DOI: 10.1016/j.synnthmet.2012.05.022
- 27.
 Bodhak S, Bose S, Kinsel WC, Bandyopadhyay A. Исследование адгезии и пролиферации костных клеток in vitro на Ti с использованием стимуляции постоянным током. Материаловедение и инженерия. 2012; С32: 2163-2168. DOI: 10.1016/j.msec.2012.05.032
Bodhak S, Bose S, Kinsel WC, Bandyopadhyay A. Исследование адгезии и пролиферации костных клеток in vitro на Ti с использованием стимуляции постоянным током. Материаловедение и инженерия. 2012; С32: 2163-2168. DOI: 10.1016/j.msec.2012.05.032 - 28. Hoi Ting HA, Cheng I, Chowdhury MF, Radisic M. Интерактивные эффекты топографии поверхности и стимуляции пульсирующим электрическим полем на ориентацию и удлинение фибробластов и кардиомиоцитов. Биоматериалы. 2007; 28:4277-4293. DOI: 10.1016/j.biomaterials.2007.06.001
- 29. Rajnicek AM, Foubister LE, McCaig CD. Выравнивание эпителиальных клеток роговицы и хрусталика за счет совместного воздействия топографии субстрата и электрических полей постоянного тока. Биоматериалы. 2008;29:2082-2095. DOI: 10.1016/j.biomaterials.2008.01.015
- 30. Аринзе Т.Л., Мэй Дж., Хуанг Г.П. Структурная поддержка для восстановления поврежденных тканей. Американский ученый. 2017;105:298-305
- 31.
 Хроник-Тупай М., Каплан Д.Л. Обзор реакции двух- и трехмерных искусственных тканей на электрические поля. Тканевая инженерия: Часть B. 2012; 18:167-180. DOI: 10.1089/ten.teb.2011.0244
Хроник-Тупай М., Каплан Д.Л. Обзор реакции двух- и трехмерных искусственных тканей на электрические поля. Тканевая инженерия: Часть B. 2012; 18:167-180. DOI: 10.1089/ten.teb.2011.0244 - 32. Ремс Л., Миклавчич Д. Учебное пособие: Электропорация клеток в сложных материалах и тканях. Журнал прикладной физики. 2016;119:201101-1-21. DOI: 10.1063/1.4949264
- 33. Миклавчич Д., Давалос Р.В. Электрохимиотерапия (ЭСТ) и необратимая электропорация (НЭП) – передовые методы лечения глубоко расположенных опухолей, основанные на электропорации. Биомедицинская инженерия онлайн. 2015;14(Suppl 3):I1
- 34. Roustit M, Blaise S, Cracowski J-L. Испытания и невзгоды ионофореза кожи в терапии. Британский журнал клинической фармакологии. 2013;77:63-71. DOI: 10.1111/bcp.12128
- 35. Напотник Т.Б., Реберсек М., Вернье П.Т., Мали Б., Миклавчич Д. Влияние наносекундных электрических импульсов высокого напряжения на эукариотические клетки (in vitro): систематический обзор.
 Биоэлектрохимия. 2016;110:1-12. DOI: 10.1016/j.bioelectrochem.2016.02.011
Биоэлектрохимия. 2016;110:1-12. DOI: 10.1016/j.bioelectrochem.2016.02.011 - 36. Hart FX, Laird M, Riding A, Pullar CE. Гальванотаксис кератиноцитов в комбинированных электрических полях постоянного и переменного тока поддерживает механизм электромеханического восприятия трансдукции. Биоэлектромагнетизм. 2013;34:85-94. DOI: 10.1002/bem.21748
- 37. Hart FX, Palisano JR. Изгиб гликокаликса электрическим полем увеличивает подвижность клеток. Биоэлектромагнетизм. 2017;38:482-493. DOI: 10.1002/bem.22060
- 38. Джаффе Л.Ф., Нуччителли Р. Электрические средства управления развитием. Ежегодный обзор биофизики и биоинженерии. 1977;6:445-476
- 39. Маклафлин С., Пу М-М. Роль электроосмоса в индуцированном электрическим полем движении заряженных макромолекул на поверхности клеток. Биофизический журнал. 1981;34:85-93
- 40. Джамгоз М.Б., Мицельска М., Мадея З., Фрейзер С.
 П., Корохода В. Направленное движение клеток рака предстательной железы крыс в электрическом поле постоянного тока: участие потенциалзависимой активности Na+-канала. Журнал клеточной науки. 2001;114:2697-2705
П., Корохода В. Направленное движение клеток рака предстательной железы крыс в электрическом поле постоянного тока: участие потенциалзависимой активности Na+-канала. Журнал клеточной науки. 2001;114:2697-2705 - 41. Hart FX. Цитоскелетные силы, создаваемые электрическими полями чрезвычайно низкой частоты, воздействующими на внеклеточные гликопротеины. Биоэлектромагнетизм. 2010;31:77-84. DOI: 10.1002/bem.20525
- 42. Вейнбаум С., Чжан С., Хан Ю., Винк Х., Коуин С.К. Механотрансдукция и поток через эндотелиальный гликокаликс. Труды Национальной академии наук. 2003;100:7988-7995 www.pnas.org/cgi/doi/10.1073/pnas.1332808100
- 43. Альбертс Б., Джонсон А., Льюис Дж., Рафф М., Робертс К., Уолтер П. Молекулярная биология клетки. 6-е изд. Нью-Йорк: Гарленд Пресс; 2015. с. 582
- 44. Тарбелл Дж.М., Ши З-Д. Влияние слоя гликокаликса на передачу внутритканевого напряжения сдвига потока встроенным клеткам.
 Биомеханика и моделирование в механобиологии. 2013;12:111-121. DOI: 10.1007/s10237-012-0385-8
Биомеханика и моделирование в механобиологии. 2013;12:111-121. DOI: 10.1007/s10237-012-0385-8 - 45. Баркер А.Л., Конопацкая О., Нил К.Р., Макферсон Дж.В., Уотмор Дж.Л., Уинлов С.П., Анвин П.Р., Шор А.С. Наблюдение и характеристика гликокаликса жизнеспособных эндотелиальных клеток человека с помощью конфокальной лазерной сканирующей микроскопии. Физическая химия Химическая физика. 2004;6:1006-1011. DOI: 10.1039/b312189e
- 46. Hart FX. Механическая трансдукция электрических полей физиологической силы. Биоэлектромагнетизм. 2008; 29:447-455. DOI: 10.1002/bem.20411
- 47. Финкельштейн Э.И., Чао П.Г., Хун К.Т., Булински Дж.К. Индуцированная электрическим полем поляризация заряженных белков клеточной поверхности не определяет направление гальванотаксиса. Подвижность клеток и цитоскелет. 2007;64:833-846. DOI: 10.1002/см.20227
- 48. Карри Ф.Е., Адамсон Р.Х. Эндотелиальный гликокаликс: барьер проницаемости и механосенсор.
 Анналы биомедицинской инженерии. 2012;40:828-839. DOI: 10.1007/s10439-011-0429-8
Анналы биомедицинской инженерии. 2012;40:828-839. DOI: 10.1007/s10439-011-0429-8 - 49. Барнхарт Э.Л., Ли К.С., Керен К., Моглинер А., Териот Дж.А. Зависимое от адгезии переключение между механизмами, определяющими форму подвижных клеток. Биология PLoS. 2011;9:e1001059. DOI: 10.1371/journal.pbio.1001059
- 50. Колодзейчик Дж., Клопоцка В.К., Лопатовска А., Гребецка Л., Гребецки А. Возобновление движения Amoeba proteus, прикрепляющегося к разным субстратам. Протоплазма. 1995;189:180-186
- 51. Sabri S, Soler M, Foa C, Pierres A, Benoliel AM, Bongrand P. Модуляция гликокаликса является физиологическим средством регуляции клеточной адгезии. Журнал клеточной науки. 2000;11:1589-1600
- 52. Ebong EE, Macaluso FP, Spray DC, Tarbell JM. Визуализация эндотелиального гликокаликса in vitro с помощью просвечивающей электронной микроскопии с быстрым замораживанием/замораживанием. Артериосклероз, тромбоз и сосудистая биология.
 2011;31:1908-1915. DOI: 10.1161/ATVBAHA.111.225268
2011;31:1908-1915. DOI: 10.1161/ATVBAHA.111.225268 - 53. Брюэр Дж. Э., Белл Л. Г. Э. Дальние электростатические взаимодействия амеб с анионообменными частицами. Экспериментальные исследования клеток. 1970;61:397-402
- 54. Topf PM, Stockem W. Белковый и липидный состав комплекса клеточной поверхности Amoeba proteus (Rhizopoda: Amoebida). Европейский журнал протистологии. 1996;32:156-170
- 55. Grebecki A, Grebecka L, Wasik A. Миниподии, адгезивные структуры, активные при локомоции и эндоцитозе амеб. Acta Protozoologica. 2001;40:235-247
- 56. Круз-Чу Э.Р., Малафеев А., Паярскас Т., Пивкин И.В., Кумуцакос П. Структура и реакция на течение слоя гликокаликса. Биофизический журнал. 2014;106:232-243. DOI: 10.1016/j.bpj.2013.09.060
- 57. Чен Б., Фу Б.М. Электродиффузионно-фильтрационная модель влияния поверхностного гликокаликса эндотелия на проницаемость микрососудов для макромолекул.
 Журнал биомеханической инженерии. 2004; 126:614-624. DOI: 10.1115/1.1800571
Журнал биомеханической инженерии. 2004; 126:614-624. DOI: 10.1115/1.1800571 - 58. Nijenhuis N, Mizuno D, Spaan JAE, Schmidt CF. Вязкоупругий ответ модельного эндотелиального гликокаликса. Физическая биология. 2009 г.;6:1-8. DOI: 10.1088/1478-3975/6/2/025014
- 59. Hart FX. Исследовательские системы для изучения биологических эффектов слабых физиологических электрических полей. В: Пуллар С, редактор. Физиология биоэлектричества в развитии, регенерации тканей и раке. Бока-Ратон, Флорида: CRC Press; 2011. стр. 17–38
- 60. Hart FX. Изменения распределения электрического поля в месте повреждения при заживлении под действием электростимуляции. Журнал биоэлектричества. 1991;10:33-51
- 61. Харт Ф.С. Дозиметрия клеточных культур для низкочастотных магнитных полей. Биоэлектромагнетизм. 1996;17:48-57
- 62. IT IS Фонд. ЭМ Исследования. Виртуальное население.
 https://www.itis.ethz.ch/virtual-population/
https://www.itis.ethz.ch/virtual-population/
Разделы
Информация об авторе
- 1.Введение
- 2.Применение полей физиологической силы постоянного тока и низкочастотного переменного тока к клеткам и тканям
- 3. Клеточная дозиметрия
- 4. Электропорация
- 5. Механизмы и эксперименты
- 6. Численное моделирование
- 7. Выводы
Ссылки
Реклама
Написано
Фрэнсис X. Харт и Джон Р. Палисано
Отправлено: 12 июня 2017 г. Обзор: 13 октября 2017 г. Авторы). Лицензиат IntechOpen. Эта глава распространяется в соответствии с условиями лицензии Creative Commons Attribution 3.0, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.
Авторы). Лицензиат IntechOpen. Эта глава распространяется в соответствии с условиями лицензии Creative Commons Attribution 3.0, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии правильного цитирования оригинальной работы.
Введение в теорию электростатики
Электромагнетизм Электростатика
Электростатика в свободном пространстве
Электростатика — это раздел электромагнетизма, описывающий электрическое поле, создаваемое статическими (неподвижными) зарядами. Начиная со свободного пространства, при плотности объемного заряда связь с электрическим полем , равна:
(1)
где – универсальная постоянная природы, называемая диэлектрической проницаемостью свободного пространства.
Это соотношение означает, что в электростатике плотность пространственного заряда действует как объемный источник. Соотношения заряд-поле недостаточно, но уравнения Максвелла подразумевают дополнительное требование, чтобы электрическое поле было безвихревым (без завитков):
Соотношения заряд-поле недостаточно, но уравнения Максвелла подразумевают дополнительное требование, чтобы электрическое поле было безвихревым (без завитков):
(2)
, что является статической версией закона Фарадея.
Статическое электрическое поле, окружающее две пластины конденсатора, является примером безвихревого векторного поля. Статическое электрическое поле, окружающее две пластины конденсатора, является примером безвихревого векторного поля.
Для безвихревого поля существует скалярный потенциал, что приводит к определению электрического потенциала:
(3)
любое достаточно гладкое скалярное поле для и обеспечивает безвихревость поля. Отрицательный знак для электрического потенциала — это старая условность.
Поле электрического потенциала, окружающее две пластины конденсатора. Поле электрического потенциала, окружающее две пластины конденсатора. 
Объединив вышеизложенное, информацию, содержащуюся в уравнениях электростатики Максвелла, можно закодировать всего одним уравнением: материалы. Чтобы решить эту проблему, теория дополнена эффектами индуцированной поляризации.
Электростатика в диэлектрических материалах
Идеализированный диэлектрический материал характеризуется тем, что он не имеет свободных зарядов, а вместо этого имеет связанные заряды. На микроскопическом уровне эти связанные заряды могут быть смещены внешним электрическим полем и привести к индуцированным электрическим диполям. Эти индуцированные электрические диполи представляют собой пары положительных и отрицательных зарядов, которые каким-то образом выравниваются с электрическим полем. Это приводит к возникновению электрического поля внутри диэлектрического материала, отличного от поля в свободном пространстве. Для макроскопического описания этого явления удобно ввести векторное поле поляризации
Для макроскопического описания этого явления удобно ввести векторное поле поляризации
, а плотность поляризационного заряда . Они связаны соотношением:
(6)
Эффекты поляризации локально изменяют электрическое поле внутри материала в соответствии с:
(7)
или эквивалентно:
5 (8)
На основании этого можно ввести новую фундаментальную величину. Поле электрического смещения определяется как:
(9)
Используя это определение, уравнение электростатики, также известное как закон Гаусса, принимает вид:
(10)
Для полного описания явления электростатики необходимо выполнение условия безвихревости электрического поля (закон Фарадея). Поскольку это условие закодировано в электрическом потенциале, уравнения электростатики можно объединить в одно уравнение:
(11)
Поле вокруг объекта с более высокой диэлектрической проницаемостью, чем его окружение. На изображениях показан диэлектрический объект, окруженный воздухом, между двумя пластинами конденсатора (не показаны). Верхний и нижний электроды имеют положительный и отрицательный электрический потенциал соответственно. Изображение слева показывает величину электрического поля цветом и его направление стрелками. На изображении справа показана величина электрического поля смещения, , цветом и его направление стрелками. Красный и синий представляют высокое и низкое значение магнитуды соответственно.
На изображениях показан диэлектрический объект, окруженный воздухом, между двумя пластинами конденсатора (не показаны). Верхний и нижний электроды имеют положительный и отрицательный электрический потенциал соответственно. Изображение слева показывает величину электрического поля цветом и его направление стрелками. На изображении справа показана величина электрического поля смещения, , цветом и его направление стрелками. Красный и синий представляют высокое и низкое значение магнитуды соответственно.
Поле вокруг объекта с более низкой диэлектрической проницаемостью, чем его окружение. На изображениях показана воздушная полость, окруженная диэлектрическим материалом, между двумя пластинами конденсатора. Верхний и нижний электроды имеют положительный и отрицательный электрический потенциал соответственно. Изображение слева показывает величину электрического поля цветом и его направление стрелками. На изображении справа показана величина электрического поля смещения, , цветом и его направление стрелками. Красный и синий представляют высокое и низкое значение магнитуды соответственно.
На изображении справа показана величина электрического поля смещения, , цветом и его направление стрелками. Красный и синий представляют высокое и низкое значение магнитуды соответственно.
Линейные диэлектрические материалы
В электростатике часто можно предположить, что материал является линейным. Это означает, что поле вектора поляризации пропорционально электрическому полю:
(12)
где константа пропорциональности , есть электрическая восприимчивость.
В случае анизотропного материала восприимчивость может быть тензором три на три:
(13)
Объедините это с соотношением между и :
(14)
и могут быть введены две новые полезные величины: относительная диэлектрическая проницаемость , и абсолютная диэлектрическая проницаемость .
Возможно, наиболее важным определяющим соотношением для линейных диэлектрических материалов является:
(15)
и поля могут быть не идеально выровнены.
Используя электростатический потенциал, основное уравнение электростатики в линейных материалах имеет вид:
(17)
Уравнения электростатики и граничные условия на границах раздела материалов
Закон Гаусса и закон Фарадея можно рассматривать как определяющие условия для дивергенция и вихрь электрического поля соответственно. Согласно теореме Гельмгольца, это определяет электрическое поле с точностью до константы. В качестве примечания: эта неизвестная константа в конечном итоге делает необходимым определение уровня земли для электрического потенциала. На границах раздела материалов условие дивергенции подразумевает условие на нормальную составляющую поля, а условие закручивания подразумевает условие на тангенциальную составляющую поля. Материальные интерфейсы представляют собой разрывы, и чтобы легче понять, какие условия наложить на границы, обычно используются соответствующие интегральные формы. Затем формулировки границ выводятся путем принятия предела сжимающейся замкнутой поверхности (закон Гаусса) и предела сжимающегося замкнутого контура (закон Фарадея) соответственно, которые охватывают часть границы раздела материалов.
Это обобщено в следующей таблице:
| Название уравнения | Дифференциальная форма | Интегральная форма | Граничное условие |
|---|---|---|---|
| Закон Гаусса | |||
| Закон Фарадея (электростатика) | , | , |
где объемный заряд и поверхностный заряд на границе раздела материалов.
Моделирование слева показывает индуцированную поверхностную плотность заряда на идеально проводящих металлических объектах, а моделирование справа показывает электрические потенциалы. На правом изображении красный и синий представляют собой положительный и отрицательный потенциал соответственно. Верхняя и нижняя пластины удерживаются при фиксированных, но разных электрических потенциалах. Средняя замкнутая поверхность имеет наведенный постоянный плавающий потенциал, который в силу симметрии является средним из потенциалов пластин. Плотность поверхностного заряда распределяется так, что каждая металлическая поверхность представляет собой эквипотенциальную поверхность, что следует из закона Гаусса.
Средняя замкнутая поверхность имеет наведенный постоянный плавающий потенциал, который в силу симметрии является средним из потенциалов пластин. Плотность поверхностного заряда распределяется так, что каждая металлическая поверхность представляет собой эквипотенциальную поверхность, что следует из закона Гаусса.
Может быть полезно обобщить значение этих уравнений словами:
| Название уравнения | Дифференциальная форма | Интегральная форма | Граничное условие |
|---|---|---|---|
| Закон Гаусса | Все линии полей начинаются и заканчиваются зарядами. | Полный поток через замкнутую поверхность равен ее замкнутому заряду. | Поверхностный заряд на границе раздела материалов равен скачку нормальной составляющей поля смещения. |
| Закон Фарадея (электростатика) | Электрическое поле безвихревое. | Электрическое поле консервативно. | На границе раздела материалов тангенциальная составляющая электрического поля непрерывна. |
Следует отметить, что для случая переменного во времени электрическое поле не является безвихревым, и в законе Фарадея появляется дополнительный член, соответствующий электромагнитной индукции.
Два заряда противоположных знаков заключены в зеленую и синюю сферы. Электрическое поле визуализируется голубыми линиями потока. Красная сфера не имеет замкнутого заряда. Закон Гаусса гласит, что поток электрического поля смещения через зеленую сферу равен заключенному заряду, и то же самое для синей сферы. Красная сфера без заряда имеет столько же входящих силовых линий, сколько и выходящих, что соответствует чистому нулевому потоку. Два заряда противоположных знаков заключены в зеленую и синюю сферы. Электрическое поле визуализируется голубыми линиями потока.


 6 СТО
6 СТО 7)
7)


 В итоге, эквипотенциальные линии перекашиваются.
В итоге, эквипотенциальные линии перекашиваются.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления

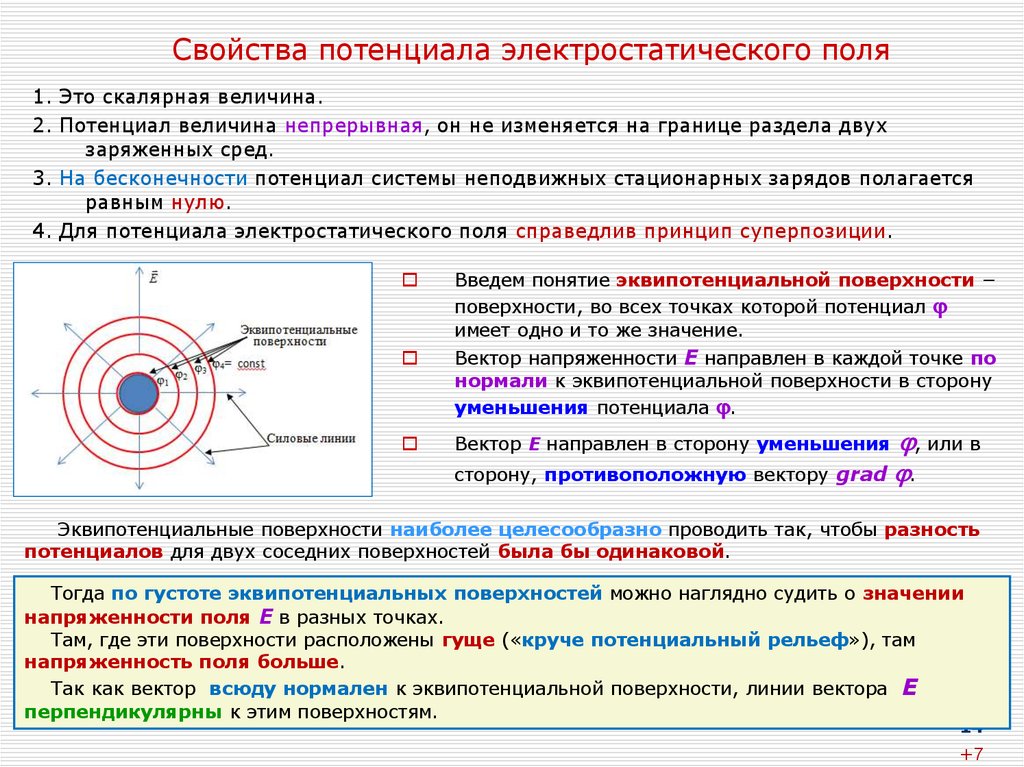 (I)
(I) Поэтому поток через выделенную сферическую поверхность, в центре которой находится заряд, будет равен
Поэтому поток через выделенную сферическую поверхность, в центре которой находится заряд, будет равен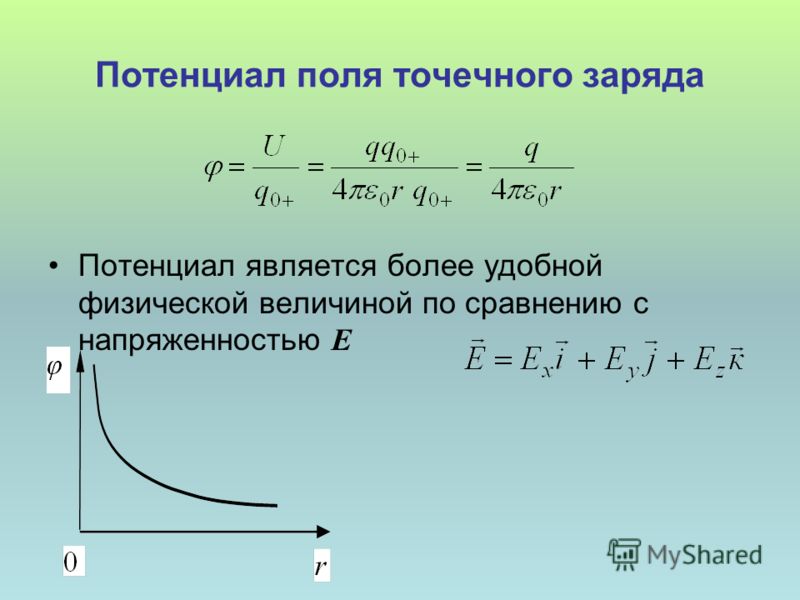
 Источником магнитного поля являются движущиеся электрические заряды – электрический ток.
Источником магнитного поля являются движущиеся электрические заряды – электрический ток.
 Для расчета напряженности электрического поля заметим, что силовые линии электрического поля от бесконечно протяженной плоскости будут перпендикулярны этой плоскости. Чтобы воспользоваться теоремой Остроградского-Гаусса (I-м законом электродинамики) выделим на плоскости площадку DS и построим на ней замкнутую цилиндрическую поверхность, образующие которой параллельны линиям вектора . Поток вектора через замкнутую поверхность равен заряду, находящемуся внутри этой поверхности
Для расчета напряженности электрического поля заметим, что силовые линии электрического поля от бесконечно протяженной плоскости будут перпендикулярны этой плоскости. Чтобы воспользоваться теоремой Остроградского-Гаусса (I-м законом электродинамики) выделим на плоскости площадку DS и построим на ней замкнутую цилиндрическую поверхность, образующие которой параллельны линиям вектора . Поток вектора через замкнутую поверхность равен заряду, находящемуся внутри этой поверхности На любом расстоянии от плоскости вектор напряженности имеет одну и ту же величину и направление, перпендикулярное плоскости.
На любом расстоянии от плоскости вектор напряженности имеет одну и ту же величину и направление, перпендикулярное плоскости. Вектором напряженности гравитационного поля являетсяускорение свободного падения , как сила, действующая на единичную массу. Потенциалом гравитационного поля является величина, определяемая потенциальной энергией единичной массы
Вектором напряженности гравитационного поля являетсяускорение свободного падения , как сила, действующая на единичную массу. Потенциалом гравитационного поля является величина, определяемая потенциальной энергией единичной массы Очевидно, что силовые линии электрического поля перпендикулярны нити. Поэтому в качестве поверхности удобно выбрать цилиндрическую поверхность сосную с нитью. Поток вектора через выбранную поверхность будет определяться потоком только через боковую поверхность. Поток через основания цилиндра равен нулю. Учитывая это, получим
Очевидно, что силовые линии электрического поля перпендикулярны нити. Поэтому в качестве поверхности удобно выбрать цилиндрическую поверхность сосную с нитью. Поток вектора через выбранную поверхность будет определяться потоком только через боковую поверхность. Поток через основания цилиндра равен нулю. Учитывая это, получим

 В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
В изначальной формулировке был бы возможен следующий процесс: заряд исчезает в одной точке пространства и мгновенно возникает в другой. Однако, такой процесс был бы релятивистски неинвариантен: из-за относительности одновременности в некоторых системах отсчёта заряд появился бы в новом месте до того, как исчез в предыдущем, а в некоторых — заряд появился бы в новом месте спустя некоторое время после исчезновения в предыдущем. То есть был бы отрезок времени, в течение которого заряд не сохраняется. Требование локальности позволяет записать закон сохранения заряда в дифференциальной и интегральной форме.
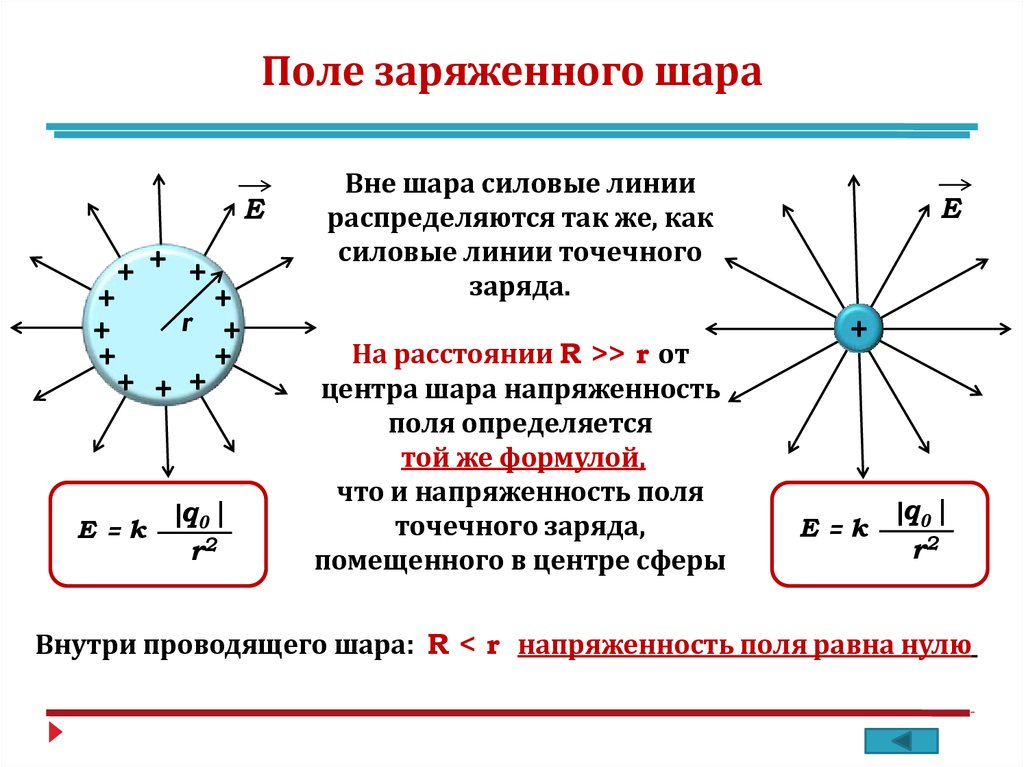

 …….. . Результирующее поле в этом случае будет характеризоваться результирующим вектором напряженности электрического поля:
…….. . Результирующее поле в этом случае будет характеризоваться результирующим вектором напряженности электрического поля: Работа силы F на элементарном перемещении dl равна
Работа силы F на элементарном перемещении dl равна
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.117 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.117 с.)

 )
) (b) Покажите, что это также верно для любой комбинации зарядов, в которой q a = q b и q b = q c
(b) Покажите, что это также верно для любой комбинации зарядов, в которой q a = q b и q b = q c 
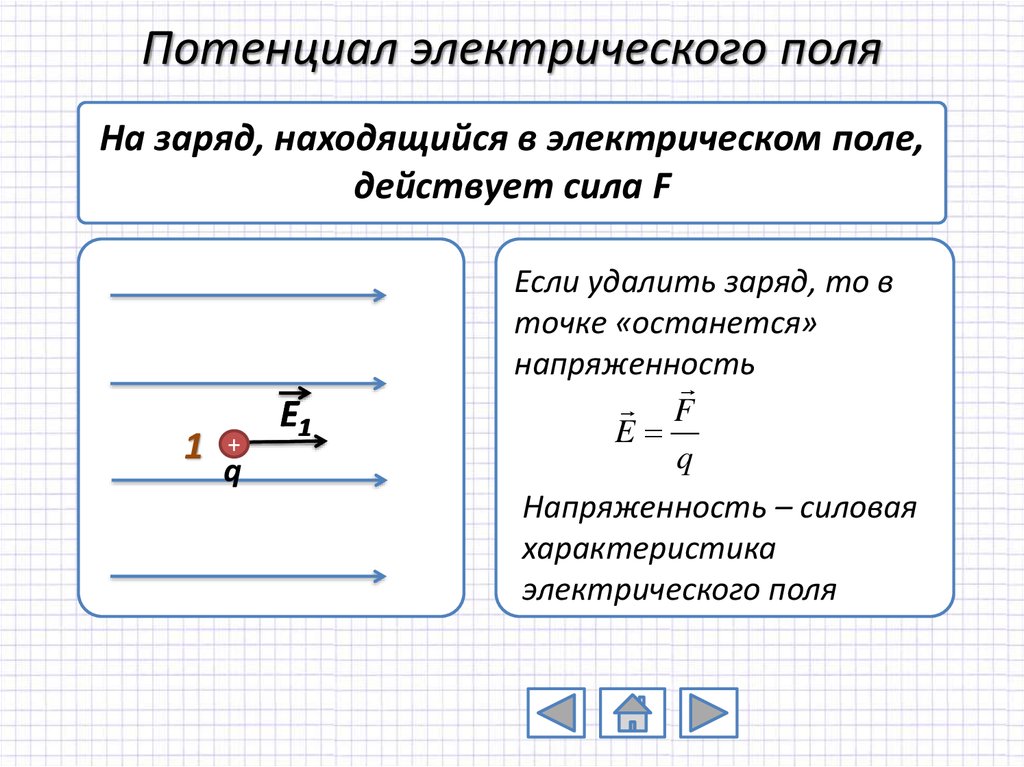 Является ли результирующее поле малым вблизи длинной стороны объекта?
Является ли результирующее поле малым вблизи длинной стороны объекта? 15а, при условии, что q = 1,00 мкКл?
15а, при условии, что q = 1,00 мкКл?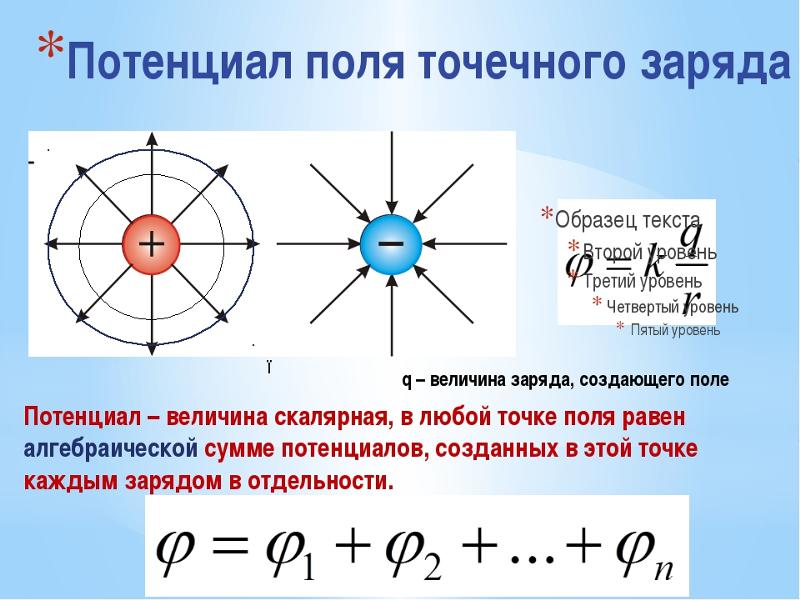 В каком случае он быстрее всего стремится к нулю и почему? (e) В каком положении справа от 11,0 см полное электрическое поле равно нулю, кроме как на бесконечности? (Подсказка: графический калькулятор может помочь в решении этой проблемы.)
В каком случае он быстрее всего стремится к нулю и почему? (e) В каком положении справа от 11,0 см полное электрическое поле равно нулю, кроме как на бесконечности? (Подсказка: графический калькулятор может помочь в решении этой проблемы.) (b) Рассчитайте величину электрического поля в точке q, учитывая, что сторона квадрата равна 5,00 см.
(b) Рассчитайте величину электрического поля в точке q, учитывая, что сторона квадрата равна 5,00 см. (b) Какова сила, действующая на q и , если q а = +1,50 нКл?
(b) Какова сила, действующая на q и , если q а = +1,50 нКл?