1. Пассивные RC – цепи
В задачах рассматриваются вопросы расчета амплитудно-частотных, фазочастотных и переходных характеристик в пассивных RC — цепях.
Для расчета названных характеристик необходимо знать и уметь использовать законы Ома и Кирхгофа. Для расчета частотных характеристик пассивных RC — цепей необходимо использовать символический метод и помнить, что сопротивление синусоидальному
току конденсатора с ёмкостью С определяется формулой: Z c = jω1 C ,
где ω — круговая частота, j — мнимая единица. Для расчета переходной характеристики необходимо использовать закон коммутации: напряжение на емкости скачком измениться не может, а также операторный метод учитывая, что сопротивление емкости в операторной форме имеет вид:
Z c (p)= pC1 .
Задача. 1.1 Рассчитать и нарисовать амплитудно-частотную и фазочастотную характеристики интегрирующей RC — цепочки,
приведенной на рис. 1.1.
Рис. 1.1 Схема интегрирующей RC – цепочки.
Решение. 1.
K (jω)= U&вых& . Uг
Для этого воспользуемся вторым законом Кирхгофа: сумма ЭДС в замкнутом контуре равна сумме падений напряжений на участках цепи; и законом Ома. Отсюда:
& | & & | 1 |
| & | & | 1 |
|
U | г = IR + I | jωC | , | U вых | = I | jωC | , |
|
|
|
|
|
| ||
|
|
|
| 4 |
|
|
|
|
|
| & | 1 |
|
|
|
|
|
|
|
| |
|
|
| I |
|
|
|
|
|
|
| 1 |
|
|
K (j ω )= |
|
|
| j ω C |
|
|
| = |
| , | (1. | ||
|
|
| 1 |
|
| & | 1 + | j ωτ | |||||
|
| R | + |
|
|
|
| I |
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
| j ω C |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
| |
где I& -ток в цепи, а τ=RC — постоянная времени RC — цепи.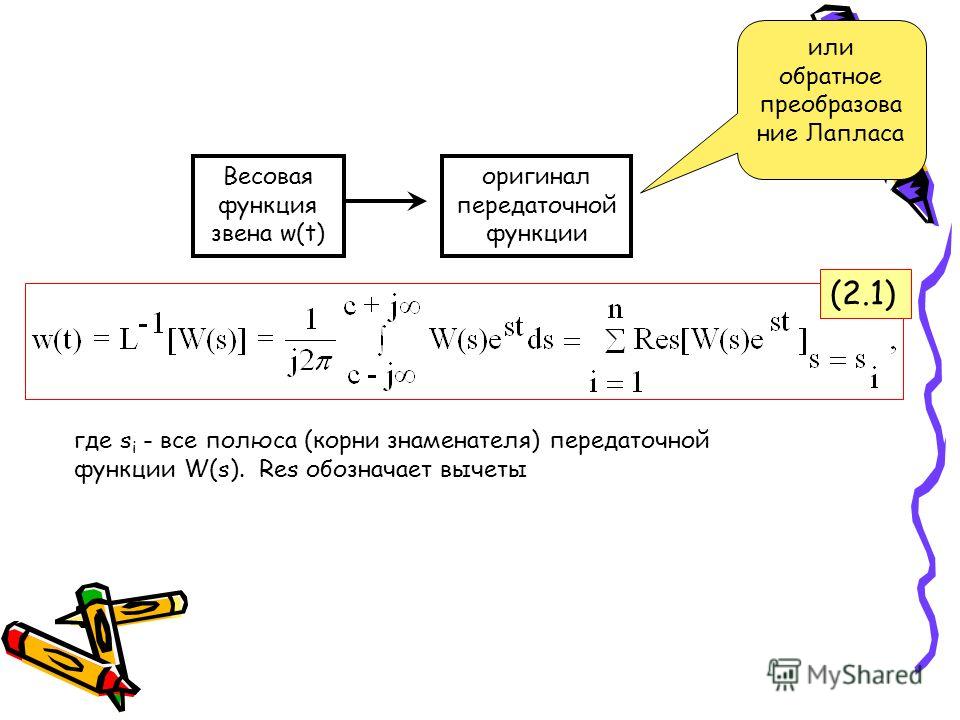
2. Из полученного выражения (1.1) можно получить формулы для расчета амплитудно-частотной (АЧХ) и фазочастотной (ФЧХ) характеристик.
Для построения АЧХ необходимо найти модуль К(jω). Из (1.1) получаем:
K (jω) = | 1 | . | (1.2) | |
1 +ω2 τ2 | ||||
|
|
Из условияω2τ2 =1 определяем значение верхней граничной частоты, при котором модуль коэффициента усиления уменьшается по сравнению
с коэффициентом передачи при ω=0 в | 2 раз: |
|
|
| |||||
ω = | 1 | и K | (jω | в | ) = 1 . |
| |||
в | τ |
|
|
|
| 2 |
| ||
На рис. 1.2 приведен вид АЧХ интегрирующей RC — цепочки. При | |||||||||
построении учитывалось, что f | = | ω | ; | .ет. | f в = |
| 1 | . | |
| |||||||||
|
| 2 π |
|
|
|
| 2 πτ | ||
Рис. 1.2. АЧХ интегрирующей RC – цепочки.
Для построения ФЧХ умножим числитель и знаменатель передаточной функции (1.1) на комплексно — сопряженную величину (1- jωτ).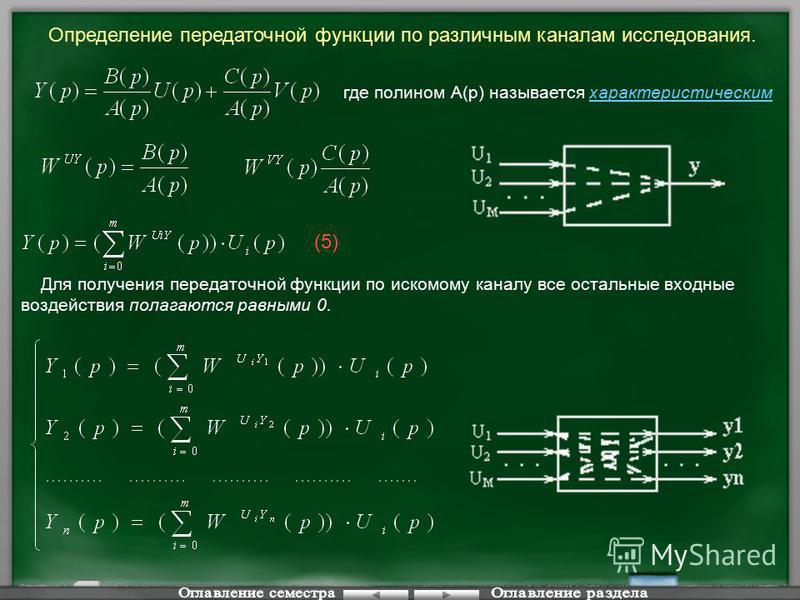 Получим
Получим
K (jω)= | 1 − jωτ | . | (1.3) |
| |||
| 1 + ω2τ2 |
| |
| 5 |
| |
Из (1.3) следует: ϕ(ω)=arctg(-ωτ)=-arctg(ωτ), т.е. напряжение на выходе цепи отстаёт от напряжения на входе.
Отметим, что на верхней граничной частоте fв = 21πτ сдвиг по фазе
между выходным сигналом и сигналом генератора составляет 45°.
На рис. 1.3 приведена фазочастотная характеристика интегрирующей RC — цепи.
Рис. 1.3 Фазочастотная характеристика интегрирующей RC – цепи.
Задача 1.2. Найти такие значения емкости и сопротивления интегрирующей RC — цепочки, при которых изменения сопротивления генератора RГ и паразитной емкости нагрузки СП приводили бы к наименьшему изменению верхней граничной частоты.
fВ = 16 кГц, RГ ≤ 100 Ом, СП ≤ 10 пФ.
Решение. 1. С учетом RГ и СП схему на рис. 1.1 можно заменить схемой на рис. 1.4 ,а и преобразовать к виду, изображенному на рис. 1.4,б,
где RЭКВ=RГ+R, а CЭКВ=С+СП.
Рис. 1.4 Схема интегрирующей RC — цепочки с учетом сопротивления генератора и емкости нагрузки (а) и ее эквивалентная схема (б).
Схема на рис. 1.4,б аналогична схеме на рис. 1.1, поэтому
6
fв = 1 , τЭКВ=RЭКВСЭКВ .
2πτэкв
Полагая fВ=16 кГц, получаем
τэкв = | 1 |
| = 0.995 10−5 | ≈10−5 с . | (1.4) | |
2π 16 | 103 | |||||
|
|
|
|
Очевидно, что обеспечить необходимое значение τэкв можно при разных RЭКВ и СЭКВ. Например, при RЭКВ=1 кОм и СЭКВ=10 нФ или
Например, при RЭКВ=1 кОм и СЭКВ=10 нФ или
RЭКВ=100 кОм и СЭКВ= 100 пФ: τЭКВ=10-5 с.
При RЭКВ=1 кОм изменение RГ может привести к сравнительно большому изменению τЭКВ, а при СЭКВ=100 пФ изменение СП может привести к большому изменению τЭКВ.
2. Найдем оптимальное значение R и С. Для этого найдем
производную | dτэкв | . |
| Выразим τЭКВ через R и С : |
| ||||||||||||||
|
|
| |||||||||||||||||
|
|
|
|
| dR |
|
|
|
|
|
|
|
|
|
|
| |||
|
|
|
|
|
| τЭКВ=R(1+δR)C(1+δC)=τ(1+δR+δC+δRδC) , | (1. | ||||||||||||
где δR = | Rг | , δС = | Cп | ,τ=RC. |
|
|
|
| |||||||||||
|
|
|
|
|
| ||||||||||||||
|
| R |
|
| C |
|
|
| Rг |
|
|
|
|
|
|
| |||
Отсюда τ | экв | = τ+ R С | п | + τ | + RC | п | . |
|
| ||||||||||
|
| ||||||||||||||||||
|
|
|
|
| г |
|
| R |
|
|
| ||||||||
Пусть τ=const, тогда |
|
|
|
|
|
|
| ||||||||||||
|
| dτэкв |
|
| τRг |
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
| = − | +Cп =0. |
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
| 2 |
| |||||
|
|
|
|
|
|
|
|
|
|
|
| dR |
| R |
| ||||
Приравниваем производную нулю, получаем |
| ||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| − | τRг | +Сп = 0 . |
| ||||
|
|
|
|
|
|
|
|
|
|
|
| 2 |
| ||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
| R |
|
|
|
| |
|
|
|
|
|
|
|
| RCП=RГС или δR=δC=δ . | (1.6) | ||||||||||
|
|
|
|
|
|
|
|
|
| ||||||||||
3.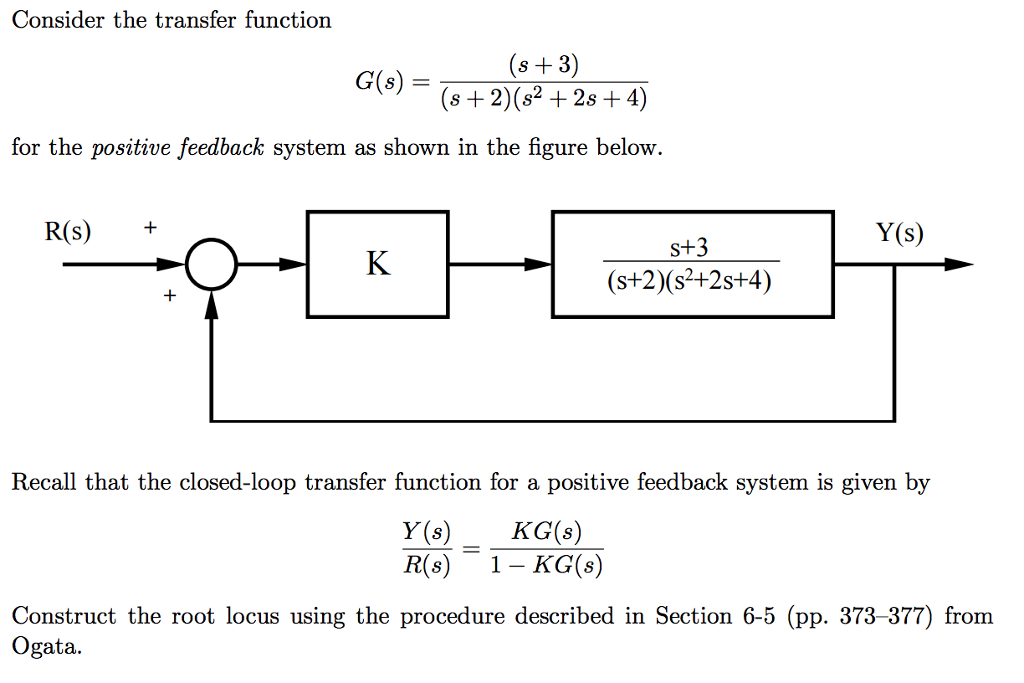 Найдем R и С из условия, что величины сопротивлений генератора
Найдем R и С из условия, что величины сопротивлений генератора
иемкости нагрузки максимальны. Положим, что δ<<1. Отсюда τЭКВ≈RC и
R = | 10−5 | . Из (1.6) получаем C 2 = | Cп 10−5 | Ф2 или С=1 нФ, а R=10 кОм. |
| C |
| R |
|
|
|
| г |
|
В этом случае максимальные значения δR и δC будут равны 1%, а изменение верхней граничной частоты по сравнению со случаем, когда RГ=0 и СП=0, будет минимальным и составит 2%.
7
Задача 1.3. Рассчитать и нарисовать амплитудно-частотную и фазочастотную характеристики дифференцирующей RC — цепи, приведенной на рис. 1.5.
Рис. 1.5. Схема дифференцирующей RC – цепи.
Решение. Задача решается аналогично задаче 1.1. Результаты решения приведены ниже.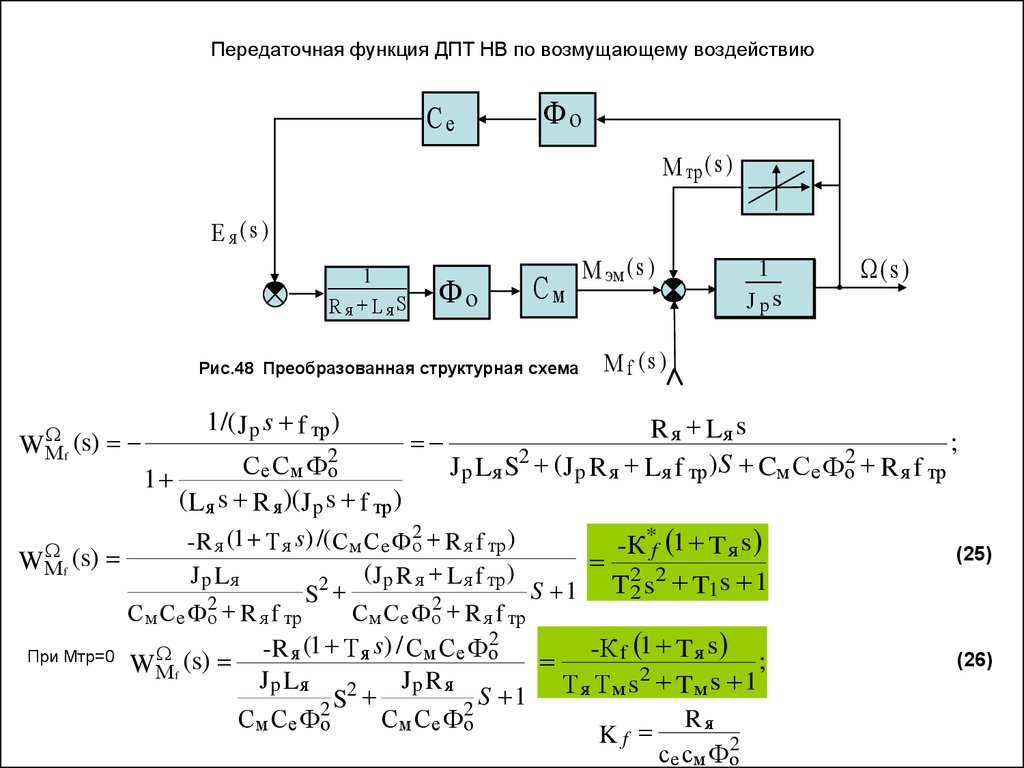 Передаточная функция цепи:
Передаточная функция цепи:
K (jω)= | U&вых | = |
|
|
| jωτ | , где τ=RC; | |||
& | 1 | + jωτ | ||||||||
| Uг | ωτ |
|
|
| |||||
K (jω) = |
|
|
| , ϕ = arctg | 1 | . | ||||
|
|
|
|
|
| |||||
| 1 + ω2τ2 |
|
| ωτ | ||||||
Амплитудно-частотная и фазочастотная характеристики цепи приведены на рис. 1.6,а и 1.6,б. При этом fH — нижняя граничная частота цепи.
1.6,а и 1.6,б. При этом fH — нижняя граничная частота цепи.
Рис. 1.6. Амплитудно-частотная (а) и фазочастотная (б) характеристики дифференцирующей RC – цепи.
8
Задача 1.4. Рассчитать передаточную функцию дифференцирующей RC — цепи, учитывая влияние сопротивления генератора RГ и паразитной емкости нагрузки СП. Нарисовать АЧХ схемы.
Решение. 1. Передаточную функцию дифференцирующей RC — цепи с учетом RГ и СГ можно рассчитать из схемы, представленной на рис. 1.7.
Учитывая, что параллельное сопротивление резистора R и емкости СП
R
равно 1 + jωRCп , получаем:
|
|
|
| R |
| ||
K(jω)= |
| 1+ jωRCп |
| ||||
|
| R | |||||
| R + | 1 | + |
| |||
jωC | 1+ jωRC | ||||||
| г |
| |||||
|
|
|
|
|
| п | |
= |
| jωRC |
| (1. | |||
| Rг |
| Cп | 2 | |||
|
|
| |||||
| 1+ jωRC 1+ |
| + |
|
| −ω RCR C | |
|
| R |
| C | г п | ||
|
|
|
| ||||
Рис. 1.7. Схема дифференцирующей RC — цепи с учетом сопротивления
генератора RГ и паразитной емкости нагрузки СП.
2. Анализ (1.7) показывает, что K (jω) имеет максимум при выполнении условия
| ω02RCRГCП=1. |
|
|
|
|
| (1. | |||||
Отсюда | 1 |
|
|
|
|
|
|
|
| |||
| ω0 = |
|
|
| . |
|
| (1.9) | ||||
|
| RCRгCп |
|
| ||||||||
|
|
|
|
|
|
|
| |||||
При ω=ω0 получаем |
|
|
| 1 |
|
|
|
|
|
| ||
| K (jω0 ) |
| = |
|
|
|
|
| . | (1.10) | ||
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
| ||||||
|
|
| 1 + | Rг |
| + |
| Cп |
|
|
| |
|
|
| R | C |
| |||||||
|
|
|
|
|
|
|
| |||||
Вид АЧХ представлен на рис.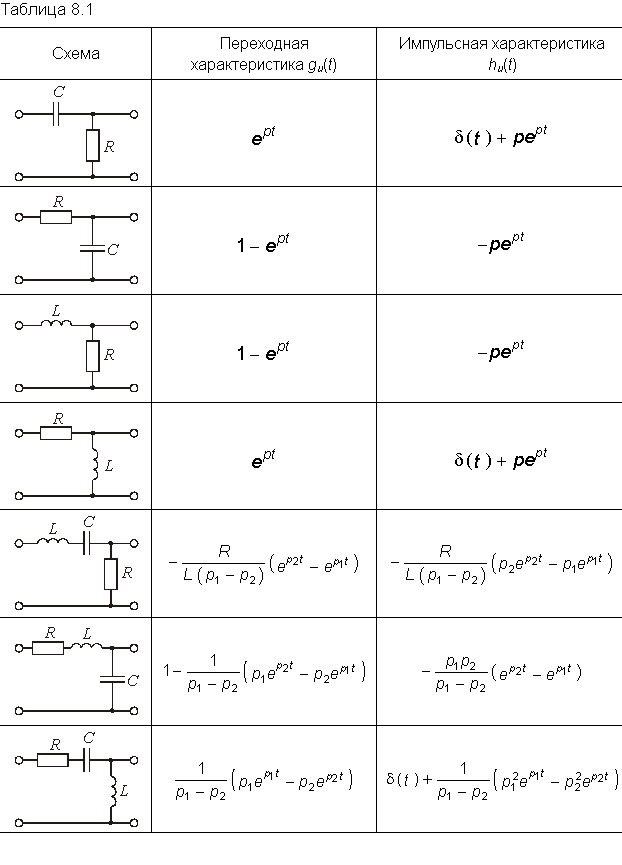 1.8.
1.8.
9
Рис. 1.8. АЧХ дифференцирующей цепочки с учетом RГ и СП.
Задача 1.5. Определить верхнюю и нижнюю граничные частоты в схеме, приведенной на рис. 1.7, при условии, что R=100 кОм, С=0.1 мкФ,
RГ=50 Ом, СП=50 пФ.
Решение. 1. Из (1.10) определим модуль коэффициента передачи цепи на частоте ω0:
| K (jω0 ) |
| = |
|
| 1 |
| = 0.999 ≈1 . |
|
|
|
|
| ||||
|
| 1 | + 0.0005 | + 0.0005 | ||||
|
|
|
|
| ||||
С учетом полученного результата представим передаточную функцию (1. 7) в следующем виде:
7) в следующем виде:
K (jω)≈ |
| jωRC |
|
| = |
|
| jωRC | × |
| 1 |
| . | (1.11) | |
(1 | + jωRC)(1 | + jωR C |
| ) | 1 | + jωRC | 1 + jωR C |
| |||||||
| п |
|
| п |
| ||||||||||
|
|
| г |
|
|
|
|
|
|
| г |
| |||
2. Из (1.11) можно сделать вывод, что передаточная функция цепи на низких частотах определяется передаточной функцией дифференцирующей RC – цепи с постоянной времени RС, а на высоких частотах — передаточной функцией интегрирующей RC — цепи с постоянной времени RГСП.
Из (1.11) можно сделать вывод, что передаточная функция цепи на низких частотах определяется передаточной функцией дифференцирующей RC – цепи с постоянной времени RС, а на высоких частотах — передаточной функцией интегрирующей RC — цепи с постоянной времени RГСП.
Отсюда получаем: | fн = | 1 | ≈16 Гц, а | fв = | 1 |
| ≈ 63 МГц. |
2πRC | 2πR C |
| |||||
|
|
|
|
| г | п | |
Задача 1.6. При замыкании ключа рассчитать переходной процесс в интегрирующей RC — цепи, схема которой приведена на рис. 1.9, и нарисовать график изменения выходного напряжения.
10
Рис. 1.9. Схема интегрирующей RC – цепи с источником постоянного напряжения и ключом.
Схема интегрирующей RC – цепи с источником постоянного напряжения и ключом.
Решение. 1. Заменяя jω на оператор р в формуле (1.1) получаем передаточную функцию цепи в операторной форме:
K (p)= |
|
| 1 | . | (1.12) | |
1 | + pCR | |||||
|
|
| ||||
Оригиналом данной передаточной функции является выражение
K(t)=1 −e− | t |
|
τ , где τ=RC . | (1.13) |
График зависимости K=f(t) приведен на рис 1.10.
Рис. 1.10. Переходная характеристика интегрирующей RC – цепи.
2. Зная, что зависимость K(t) представляет собой экспоненту, можно построить переходную характеристику без нахождения передаточной функции. Для этого нужно определить напряжение на выходе интегрирующей RC — цепи при t=0 и при t=∞.
Для этого нужно определить напряжение на выходе интегрирующей RC — цепи при t=0 и при t=∞.
2.1. Полагая, что напряжение на конденсаторе не может измениться скачком, получаем:
UС(0)=UВЫХ(0)=0, а I (0)= ER , где I(0) ток в цепи при t=0.
2.2. При t=∞ ток через резистор R протекать не должен I(∞)=0, следовательно UВЫХ(∞)=UС(∞)=E-I(∞)R=E.
11
Задача 1.7. Нарисовать график изменения выходного напряжения при замыкании ключа в цепочке дифференцирующего типа, приведенной на рис 1.11.
Решение. 1. Полагая, что напряжение на емкости в первый момент должно равняться нулю, получаем E=I(0)(RГ+R), UВЫХ(0)=I(0)R.
Отсюда Uвых(0)= E RгR+ R .
Рис. 1.11. Схема RC — цепи дифференцирующего типа с источником постоянного напряжения и ключом.
2. При t=∞ ток в цепи будет равен нулю, поэтому UВЫХ(∞)=I(∞)R=0. Постоянная времени заряда конденсатора равна τ=C(RГ+R) . Следовательно, график зависимости UВЫХ(t) будет иметь вид,
представленный на рис 1.12.
Рис.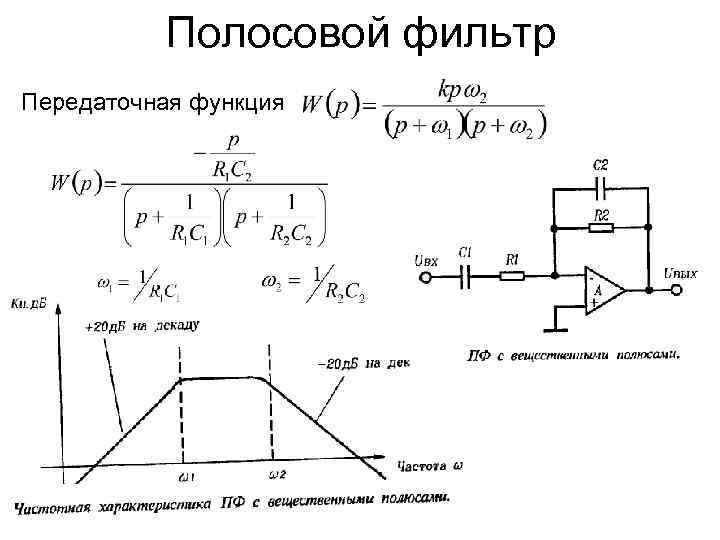 1.12. Переходная характеристика цепи, приведённой на рис.1.11.
1.12. Переходная характеристика цепи, приведённой на рис.1.11.
Задача 1.8. Нарисовать импульс напряжения на выходе RC — цепи при подаче на вход схемы, приведенной на рис. 1.13, прямоугольного
импульса длительности ТИ.
12
ВЫХ2
Рис. 1.13. Схема RC — цепи дифференцирующего типа с источником импульсного напряжения.
Решение. 1. Прямоугольный импульс напряжения можно рассматривать как две ступеньки напряжения, смещенные во времени на время ТИ (рис. 1.14).
Рис. 1.14. Представление прямоугольного импульса как суммы двух ступенек напряжения.
Таким образом, задача сводится к нахождению реакции RC — цепи на каждую ступеньку напряжения.
2. Аналогично предыдущим задачам получаем:
UВЫХ1(0)=Е, | Uвых1 (∞) | = E |
| R2 | , UВЫХ2(ТИ)=-Е, Uвых2 | (∞)= −E |
| R2 | , | ||||
R1 | + R2 | R1 | + R2 | ||||||||||
|
|
|
|
|
|
|
|
| |||||
τ = E | R1R2 |
| , | где UВЫХ1 | — выходное напряжение от воздействия первой | ||||||||
R + R | 2 | ||||||||||||
|
|
|
|
|
|
|
|
|
|
| |||
| 1 |
|
|
|
|
|
|
|
|
|
| ||
ступеньки напряжения, а U — выходное напряжение от воздействия второй ступеньки.
3. Используя метод наложений принцип (суперпозиций), находим результирующее напряжение: UВЫХ(0)=Е, UВЫХ(ТИ)=-Е, UВЫХ(∞)=0.
График выходного напряжения представлен на рис. 1.15.
13
«Частотные характеристики rc-цепей»
Цель:изучить частотные характеристикиRC-цепей, сравнить и проанализировать их для двух предложенных схем.
Краткие теоретические сведения
1) Схема простейшейRC-цепипредставлена на рис. 4.
. U1 . U2 |
Рис. 4 – Схема RC-цепи
Полное комплексное входное сопротивление RC-цепи:
Zвх = Rвх + jXвх = R + 1/(jωC)
= R[1 – j/(ωCR)]. | (3) |
Активная часть входного сопротивления Rвх = Rне зависит от частоты, реактивнаяХвх = -1/(ωС) – зависит. Величинаτ =RC имеет размерность времени и называется постоянной времениRC—цепи (это есть время, за которое свободный процесс затухает в е = 2,72 раз).
Комплексный коэффициент передачи напряжения цепи равен
Ku (jω) = Ů2/Ů1=[1/(jωC)]/Zвх = 1/(1+jωC). | (4) |
Ампллитудно-частотная и фазо-частотная характеристики имеют вид
Ku (ω) = 1/√ 1+ω2τ2 ; φ(ω)
= arctg (Im K(jω)/Re K(jω))
= — arctg ωτ . | (5) |
Графики амплитудно-частотной и фазо-частотной характеристик представлены на рис. 5.
ωср ωср |
Рис. 5 – Амплитудно-частотная и фазо-частотная характеристики
Как видно из графиков (рис. 5), RC-цепочка пропускает только низкочастотные колебания и не пропускает высокочастотные. Сдвиг фаз между входным и выходным сигналами с ростом частоты достигает 90о.
Полоса пропусканияцепи определяется как полоса, в которой
Ku (ω) ≥ 1/√ 2 . | (6) |
Частота, начиная
с которой выполняется условие (6)
называется частотой срезаωср. На частоте среза (пунктирная линия на
рис. 5):
На частоте среза (пунктирная линия на
рис. 5):
Ku (ωср) = 1/√ 1+(ωср) 2τ2 = 1/√2. | (7) |
Отсюда частота среза ωср = 1/τ.
На комплексной
плоскости можно изобразить годограф RC– цепи (рис. 6). Длина
изображающего вектора годографа на
каждой частоте равна соответствующему
значению амплитудно-частотной
характеристики на данной частоте, а
фазовый угол – значению частотной
характеристики. Приω =0точкаKu (jω)находится на реальной оси. При увеличении
вектор поворачивается по часовой
стрелке, а длина уменьшается.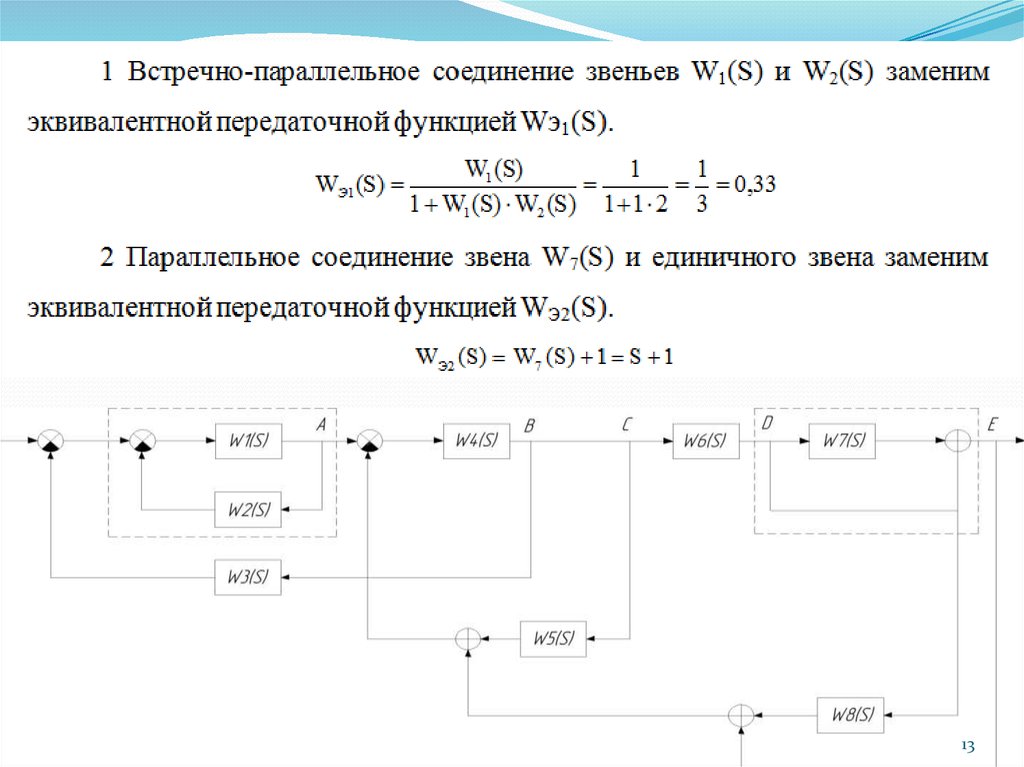
Рис. 6 – Годограф комплексной передаточной функции RC-цепи
Задание. Собрать схему, представленную на рис. 7. Изменяя значения R и C, снять амплитудно-частотные и фазо-частотные характеристики цепи. Результаты измерений занести в таблицу.
Порядок выполнения (1 способ).
1) Подготовка схемы
измерения. Выставить значения
сопротивления и емкости, указанные на
рис. 7. В меню Analysis выбрать режим AC Frecuensy – режим
анализа амплитудно-частотных и
фазо-частотных характеристик. В
появившемся окне установить указанные
параметры моделирования (рис. 8). В данном
примере частота входного сигнала будет
меняться от 1 Гц до 1000 кГц. Амплитуда
сигналов в точках 1 и 2 схемы (Nodes for analysis) в пределах 0 В – 1 В и фазы сигнала в
пределах 0о – 90о будут откладываться по вертикальной
оси в линейном масштабе (Linear),
частота по горизонтали – по декадам
(10Гц, 100Гц, 1кГц и т.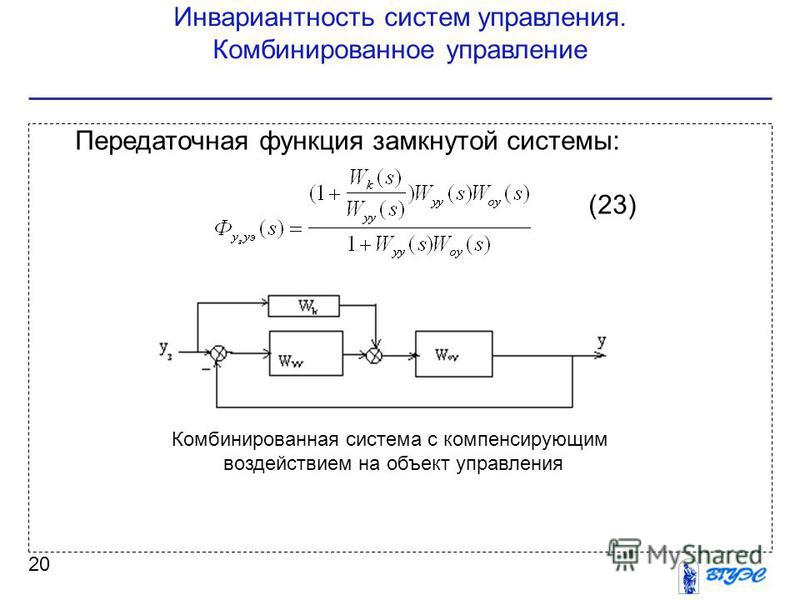 д.).
д.).
2) Измерения. Нажать кнопку Simulate (рис. 8). На экране появится окно, в котором будут представлены амплитудно-частотная (верхняя) и фазо-частотная (нижняя) характеристики для заданных параметров RC-цепи (рис. 9).
Рис. 7 – Схема исследования RC– цепи
Рис. 8 – Настройка параметров измерений
Рис. 9 – Результаты измерений
Для получения численных значений необходимо подвести курсор к интересующей кривой, щелкнуть левой клавишей мыши, затем нажать на кнопку
. | |
Рис. 10 – Численные результаты измерений
На графиках появятся визирные линии и окна с численными значениями (рис. 10). Визирную линию можно передвигать, поставив на нее курсор и удерживая левую клавишу мыши. При этом в соседнем окне отражаются численные значения, в частности Х1, Y1– частота и амплитуда точки пересечения первой визирной линии и характеристики (1000 Гц и 846,733 мВ), X2, Y2 – частота и амплитуда точки пересечения второй визирной линии и характеристики (10 кГц и 157,1767 мВ).
Используя визирные линии, снять амплитудно-частотную и фазо-частотную характеристики, занести результаты в таблицы 3 и 4.
Изменяя параметры цепи и, используя описанную методику измерений, снять характеристики для различных значений R и C. Результаты занести в таблицы 3 и 4.
По результатам
измерений построить амплитудно-частотные
и фазо-частотные характеристики, а также
годографы комплексной передаточной
функции RC-цепи.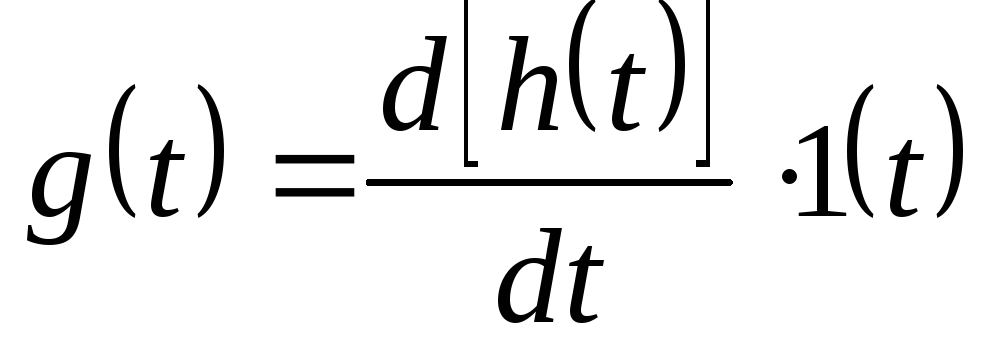 Проанализировать полученные графики.
Проанализировать полученные графики.
Табл.3
R(Ом) | C(мкФ) | К1 (мВ) | f1 (Гц) | … | … | Кn (мВ) | fn (Гц) |
1 | 1 | ||||||
10 | |||||||
100 | |||||||
10 | 1 | ||||||
10 | |||||||
100 | |||||||
100 | 1 | ||||||
10 | |||||||
100 |
Табл. 4.
4.
R(Ом) | C(мкФ) | φ1 (рад) | f1 (Гц) | … | … | φn (рад) | fn (Гц) |
1 | 1 | ||||||
10 | |||||||
100 | |||||||
10 | 1 | ||||||
10 | |||||||
100 | |||||||
100 | 1 | ||||||
10 | |||||||
100 |
Порядок
выполнения (2 способ). Для исследования использовать схему,
представленную на рис. 7.
Для исследования использовать схему,
представленную на рис. 7.
1) Подготовка схемы измерения. Выставить значения параметров генератора, сопротивления и емкости, указанные на рис. 7. В меню Analysis выбрать режим Transient – режим анализа переходных характеристик. В появившемся окне (рис. 11) установить указанные параметры моделирования. В данном примере частота входного сигнала 50 Гц, амплитуда 1 В. Длительность времени анализа End time (TSTOP) = 0,04 с. (Длительность интервала выбирать таким образом, чтобы на осциллограмме укладывалось 2–5 периода исследуемых колебаний).
2) Измерения. Нажать
кнопку Simulate (рис.
11). На экране появится окно, в котором
будут представлены входной и выходной
сигнал (на рис. 12 для частоты 50 Гц). Как
видно из рисунка, для данных параметровRC-цепи сдвиг фаз между
входным и выходным сигналами равен 0,
амплитуды сигналов практически равны. Изменяя частоту генератора, снять
амплитудно-частотную и фазо-частотную
характеристики. Для изменения частоты
генератора подвести курсор к его
изображению и щелкнуть правой клавишей
мыши. Изображение генератора изменит
цвет на красный, на экране появится
меню. Выбрать опциюComponent Propertiesи в появившемся
меню (закладкаValue)
выставить новое значение частоты
генератора. На рис. 13 представлены
результаты анализа для частоты 10 кГц
(TSTOP=0,0002).
Изменяя частоту генератора, снять
амплитудно-частотную и фазо-частотную
характеристики. Для изменения частоты
генератора подвести курсор к его
изображению и щелкнуть правой клавишей
мыши. Изображение генератора изменит
цвет на красный, на экране появится
меню. Выбрать опциюComponent Propertiesи в появившемся
меню (закладкаValue)
выставить новое значение частоты
генератора. На рис. 13 представлены
результаты анализа для частоты 10 кГц
(TSTOP=0,0002).
Рис. 11 – Настройка параметров измерения режима Transient
Для получения численных значений необходимо подвести курсор к интересующей кривой, щелкнуть левой клавишей мыши, затем нажать на кнопку
. |
На графиках появятся
визирные линии и окна с численными
значениями (рис. 13). Визирную линию можно
передвигать, поставив на нее курсор и
удерживая левую клавишу мыши. При этом
в соседнем окне отражаются численные
значения (в частности Х1, Y1–
время и амплитуда точки пересечения
первой визирной линии и характеристики.
Х2,Y2– время и амплитуда
точки пересечения второй визирной линии
и характеристики).
13). Визирную линию можно
передвигать, поставив на нее курсор и
удерживая левую клавишу мыши. При этом
в соседнем окне отражаются численные
значения (в частности Х1, Y1–
время и амплитуда точки пересечения
первой визирной линии и характеристики.
Х2,Y2– время и амплитуда
точки пересечения второй визирной линии
и характеристики).
Для каждой частоты измерить амплитуды выходного (Авых) и входного (Авх) сигналов, а также величину Δt(сдвиг по времени входного и выходного сигналов), по которой можно вычислить сдвиг фаз:
φ = ωΔt = 2πfΔt(радиан). | (8) |
Поскольку за
несколько периодов переходные процессы
не успевают закончиться (изменяется
постоянная составляющая сигнала, рис.
13), в качестве амплитудных значений
нужно брать полный размах колебаний.
Рис. 12 – Результаты измерений на частоте 50 Гц
Рис. 13 – Результаты измерений на частоте 10 кГц
Результаты измерений занести в таблицу 5.
Табл.5.
50 Гц | … | … | 100 кГц | |
Авых/Авх | ||||
φ,град |
По результатам
измерений построить амплитудно-частотную
и фазо-частотную характеристики, а также
годограф комплексной передаточной
функции RC-цепи. Проанализировать полученные графики.
Проанализировать полученные графики.
Порядок выполнения (3 способ). Для исследования использовать схему, представленную на рис. 7.
1) Подготовка схемы измерения. Подключить к схеме осциллограф (рис. 14). Линии подключения ко входам осциллографа сделать разного цвета (такого же цвета будут осциллограммы соответствующих сигналов на экране). Выставить значения параметров генератора, сопротивления и емкости, указанные на рис. 14.
Рис. 14 – Схема исследования RC– цепи с помощью осциллографа
2) Измерения. Развернуть переднюю панель осциллографа, дважды щелкнув левой клавишей мыши по его изображению. Нажать кнопку
на
передней панели осциллографа. Появится
увеличенное изображение передней панели
осциллографа. Запустить режим моделирования
кнопкой
Появится
увеличенное изображение передней панели
осциллографа. Запустить режим моделирования
кнопкой
. |
Выбрать длительность
развертки (Time Base)
и масштаб по вертикальной оси (Channel А) таким
образом, чтобы на экране помещались
несколько периодов колебаний. С помощью
визирных линий измерить амплитуду
входного Авх и выходного Авых сигнала
RC–цепи
(рис. 15). Значение коэффициента передачи
цепи на данной частоте равно Авых/Авх. Измерить
временной сдвиг между входным и выходным
сигналом и вычислить сдвиг фаз по формуле
(8). На рис. 15 для частоты 50 кГц с помощью
левой визирной линией измеряется
амплитуда входного сигнала Авх (VA1
= 1.3864 В), с помощью правой визирной линии
– амплитуда выходного сигнала Авых (VB2
= 43.8695 мВ), в третьем окне – временной
сдвиг между сигналами (Т2–Т1 = 4.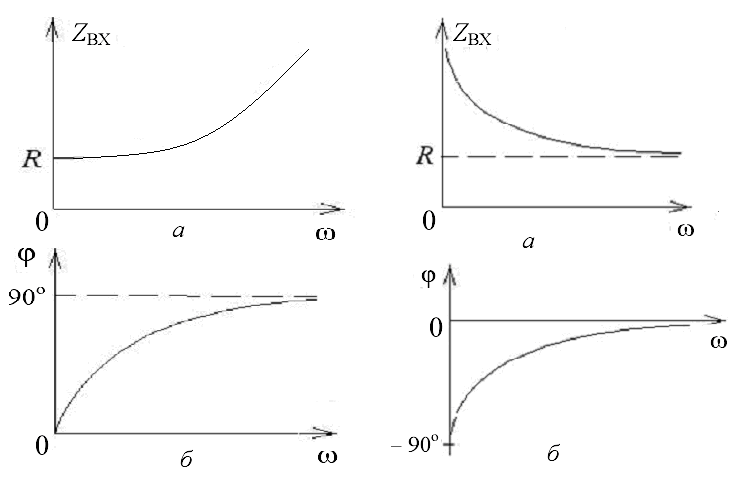 7600 мкс).
7600 мкс).
Изменяя частоту генератора, снять амплитудно-частотную и фазо-частотную характеристики, результаты занести в таблицу 6.
Рис. 15 – Измерение параметров сигнала
Табл.6.
50 Гц | … | … | 100 кГц | |
Авых/Авх | ||||
φ,град |
По результатам
измерений построить амплитудно-частотную
и фазо-частотную характеристики, а также
годограф комплексной передаточной
функции RC-цепи.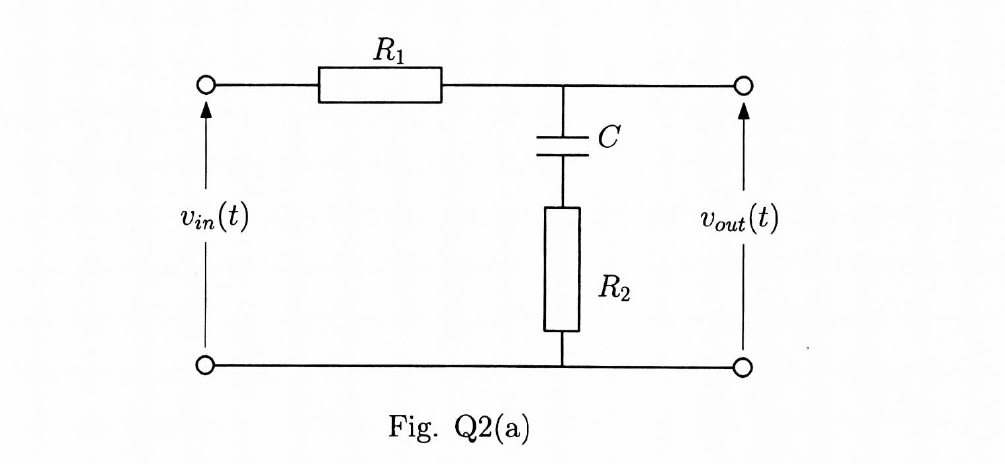 Проанализировать полученные графики.
Проанализировать полученные графики.
2) Принципиальная схемаCR-цепипредставлена на рис. 16.
Рис. 16 – Схема CR-цепи
Входное сопротивление цепи определяется формулой (3). Комплексная передаточная функция по напряжению имеет вид
Ku (jω) = Ů2/Ů1= R/Zвх = 1/[1+ 1/(jωC)]. | (9) |
Амплитудно-частотная и фазо-частотная характеристики
Ku (ω) = 1/√ 1+ (1/ωτ)2 ; φ(ω) = arctg (1/ ωτ) | (10) |
показаны на рис. 17 (здесь также τ =RC).
17 (здесь также τ =RC).
CR-цепь пропускает колебания с частотами выше частоты срезаωср = 1/τ. Сверху полоса пропускания не ограничена. Сдвиг фаз между входным и выходным сигналами на низких частотах составляет 90о, на высоких – стремится к нулю.
Задание. Собрать схему, представленную на рис. 16. Изменяя значения R и C, снять амплитудно-частотные и фазо-частотные характеристики цепи. Результаты измерений занести в таблицы 7,8. Порядок выполнения изложен выше.
Рис. 17 – Амплитудно-частотная и фазо-частотная характеристики CR– цепи
Табл.7
R(Ом) | C(мкФ) | К1 (мВ) | f1 (Гц) | … | … | Кn (мВ) | fn (Гц) |
1 | 1 | ||||||
10 | |||||||
100 | |||||||
10 | 1 | ||||||
10 | |||||||
100 | |||||||
100 | 1 | ||||||
10 | |||||||
100 |
Табл.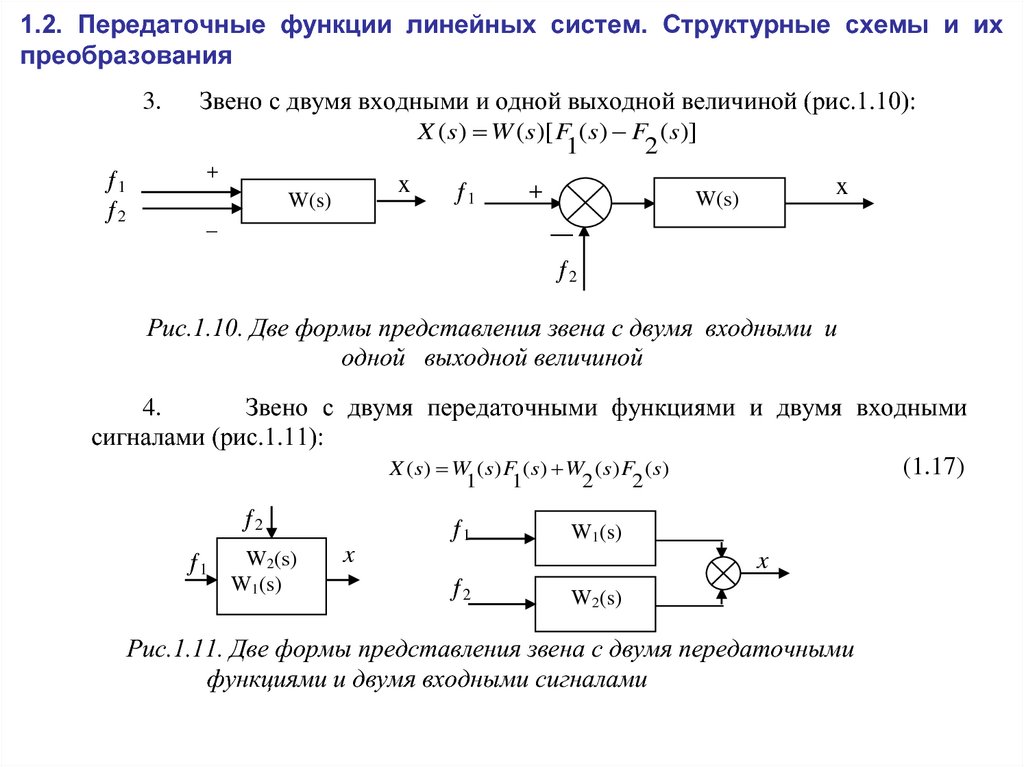 8.
8.
R(Ом) | C(мкФ) | φ1 (рад) | f1 (Гц) | … | … | φn (рад) | fn (Гц) |
1 | 1 | ||||||
10 | |||||||
100 | |||||||
10 | 1 | ||||||
10 | |||||||
100 | |||||||
100 | 1 | ||||||
10 | |||||||
100 |
По результатам
измерений построить амплитудно-частотную
и фазо-частотную характеристики, а также
годограф комплексной передаточной
функции СR-цепи.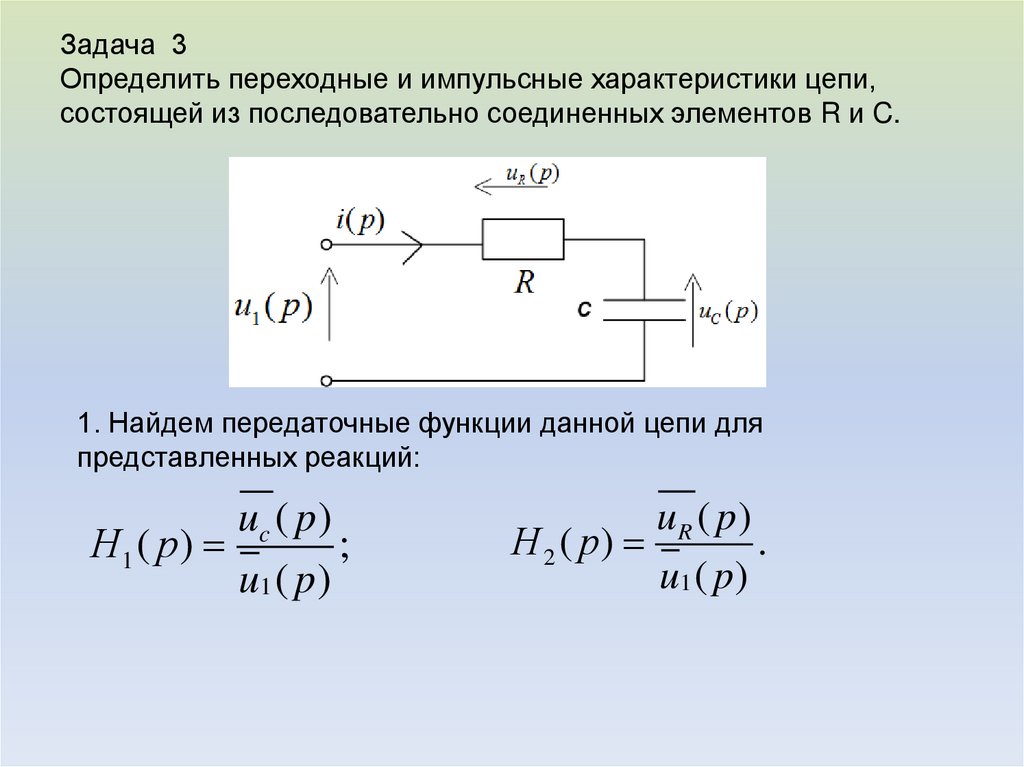 Провести
сравнительный анализ полученных для
двух схем АЧХ и ФЧХ.
Провести
сравнительный анализ полученных для
двух схем АЧХ и ФЧХ.
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 5
Понимание коэффициента усиления передаточной функции RC-цепи
\$\начало группы\$
Я изучаю передаточные функции 1-го порядка и пытаюсь понять это на практических примерах систем, потому что мне все еще кажется странным, как одна и та же функция может описывать различные физические системы. В настоящее время я смотрю на передаточную функцию простой RC-цепи.
Обозначается как
Взглянув на стандартную функцию, мы можем сказать, что у нас есть усиление 1 в этой функции, как объяснено в этом посте
Меня устраивает тот факт, что постоянная времени tau равна RC в этом конкретном примере из реальной жизни, так как сопротивление, умноженное на емкость, можно упростить до единиц времени, что немного похоже на скорость, умноженную на расстояние. .
впрочем, я не уверен, как на это смотреть и, отделив всю математику, интуитивно понять, почему прирост должен быть 1, а не что-то еще. Мне нужна помощь, чтобы понять, в чем заключается концепция усиления, потому что я полностью потерян.
Мне нужна помощь, чтобы понять, в чем заключается концепция усиления, потому что я полностью потерян.
Большое спасибо!
- анализ цепей
- передаточная функция
\$\конечная группа\$
10
\$\начало группы\$
Коэффициент усиления передаточной функции показывает, какой коэффициент усиления вы получите через бесконечное время после стабилизации входного сигнала. И это действительно 1, потому что по прошествии достаточного количества времени Vout всегда равняется Vin.
Чтобы понять, что происходит с реальным (изменяющимся) входом, необходимо изучить частотную характеристику системы, то есть использовать преобразование Фурье вместо преобразования Лапласа. Для вашей передаточной функции вы можете просто заменить \$s\$ на \$j\omega \$. 92} $$
Как видите, усиление равно 1, когда частота равна нулю, и меньше единицы в противном случае.
\$\конечная группа\$
\$\начало группы\$
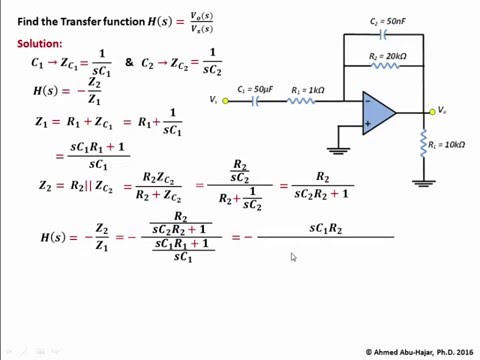
Показанный обычный простой RC-фильтр нижних частот имеет указанную передаточную функцию Vout/Vin = K/(1+sT) . Фактор K равен 1, потому что при 0 Гц (т.е. при s=0) передаточная функция должна получить значение =1. Фактор T равен =RC. Все это легко вычисляется с помощью элементарного анализа цепей s-домена.
Вставив усилитель перед фильтром, можно получить вариант с K>1.
Или вставив пассивный аттенюатор, можно получить вариант с K<1. Следующая версия имеет передаточную функцию Vout/Vin = 0,5/(1 + sRC). Сопротивления выбираются таким образом, чтобы множитель s был равен RC: Форма заказа Vout/Vin = K/(1+sT)
K по-прежнему =1, но T = L/R. Если вы установите R = 1 Ом и L = 1 Генри, вы получите T = 1 секунду. Эффект фильтрации такой же, как и с простым RC-фильтром, который имеет R = 1 Ом и C = 1 Фарад.
Передаточная функция не определяет структуру схемы, одна и та же передаточная функция возможна с бесконечным множеством различных цепей.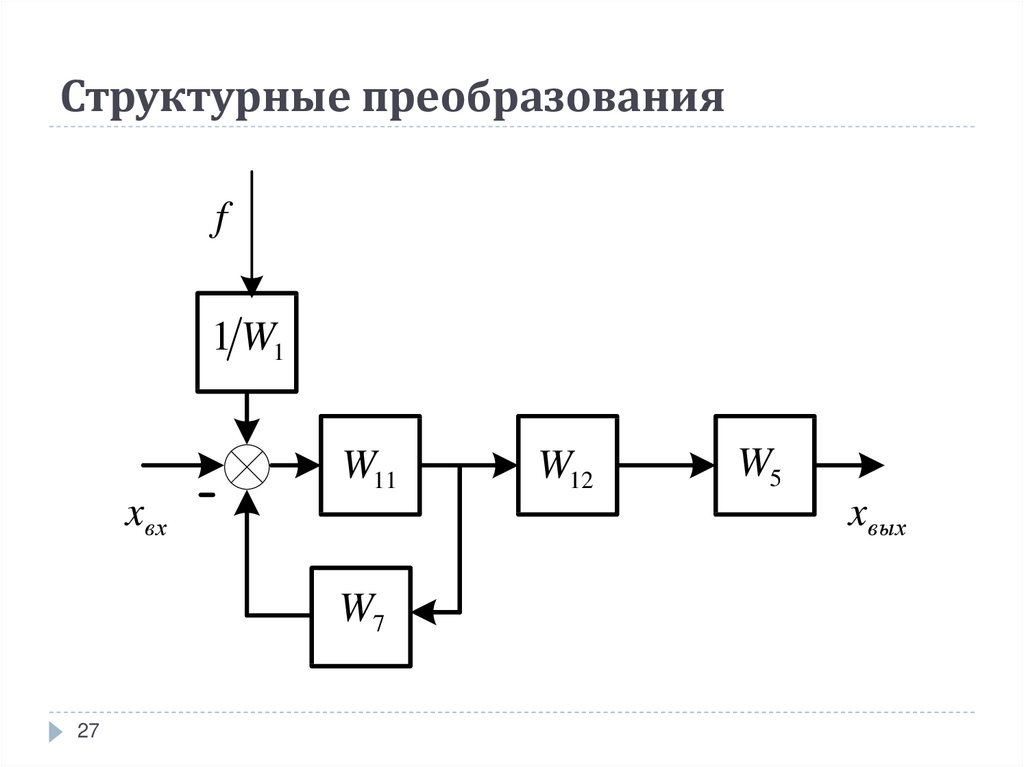 Но если вы видите, что в цепи LRC есть N катушек индуктивности и M конденсаторов, порядок передаточной функции должен быть M+N или меньше. Может быть и меньше, потому что часть конденсаторов или катушек индуктивности может быть избыточной, т.к. ex 2 последовательно включенных конденсатора влияют только как один.
Но если вы видите, что в цепи LRC есть N катушек индуктивности и M конденсаторов, порядок передаточной функции должен быть M+N или меньше. Может быть и меньше, потому что часть конденсаторов или катушек индуктивности может быть избыточной, т.к. ex 2 последовательно включенных конденсатора влияют только как один.
Если вы хотите узнать, как передаточные функции получаются из цепей, я предлагаю изучить анализ цепей. Для краткого описания расчетов скажу, что все показанные схемы являются делителями напряжения, которые подчиняются обычному правилу делителя напряжения. Верхняя и нижняя половины делителей напряжения представляют собой импедансы в s-области.
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Передаточная функция базовой RC-цепи
спросил
Изменено 7 лет, 8 месяцев назад
Просмотрено 7к раз
\$\начало группы\$
Я никак не могу найти передаточную функцию.
У меня есть схема, которая выглядит так: 9{-1}}$$, где s = jω. Как они это получили?
Будем очень признательны за помощь.
- передаточная функция
\$\конечная группа\$
\$\начало группы\$
Рискуя сделать за вас домашнюю работу,
Начните с правила делителя напряжения
$$\frac{V_o}{V_i}=\frac{Z_C}{R+Z_C+Z_C}$$
где \$Z_C\$ — импеданс конденсатора со значением C .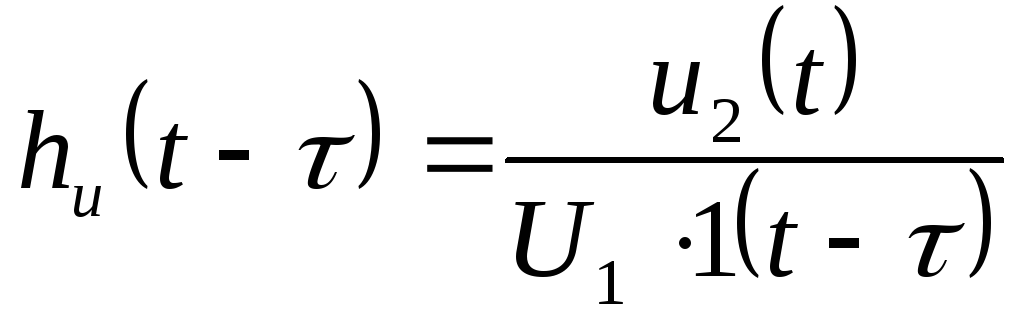


 1)
1)
 5)
5)

 7)
7) 8)
8)


