общие сведения, формулы расчета • Мир электрики

Содержание

1. Видео: Последовательное и параллельное соединение проводников
2. Параллельное соединение: общая информация
3. Расчет сопротивления
4. Видео: Пример расчёта сопротивления
5. Пример расчёта
6. Важные нюансы
7. Видео: Правильное подключение светодиодов

В каждой электрической схеме присутствует резистор, имеющий сопротивление электрическому току. Резисторы бывают двух типов: постоянные и переменные. Во время разработки любой электрической схемы и ремонта электронных изделий часто приходится применять резистор, обладающий необходимым номиналом.

Несмотря на то что для резисторов предусмотрены различные номиналы, может случиться так, что не будет возможности найти необходимый или же вообще ни один элемент не сможет обеспечить требуемый показатель.

Решением этой проблемы может стать применение последовательного и параллельного соединения. Ознакомившись с этой статьей, вы узнаете об особенностях выполнения расчета и подбора различных номиналов сопротивлений.

Видео: Последовательное и параллельное соединение проводников

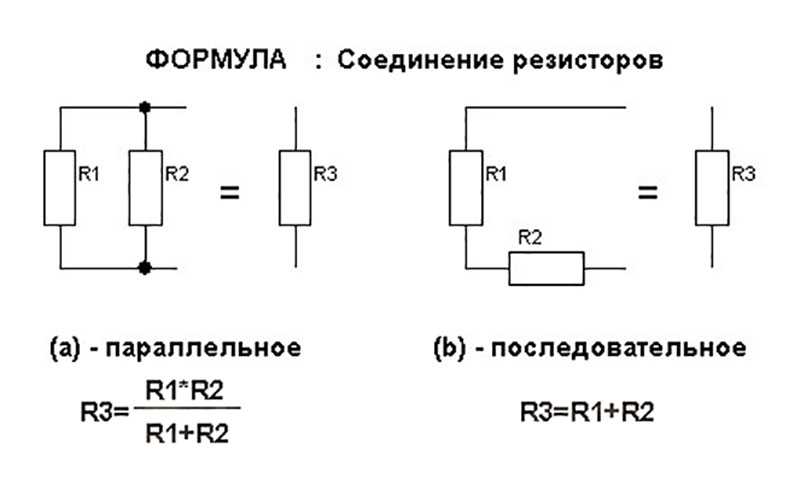
Часто при изготовлении какого-либо устройства используют резисторы, которые соединяются в соответствии с последовательной схемой. Эффект от применения такого варианта сборки сводится к увеличению общего сопротивления цепи. Для данного варианта соединения элементов создаваемое ими сопротивление рассчитывается как сумма номиналов. Если же сборка деталей выполняется по параллельной схеме, то здесь потребуется рассчитать сопротивление, используя нижеописанные формулы.

К схеме параллельного соединения прибегают в ситуации, когда стоит задача по снижению суммарного сопротивления, а, помимо этого, увеличения мощности для группы элементов, подключенных по параллельной схеме, которое должно быть больше, чем при их отдельном подключении.

Расчет сопротивления

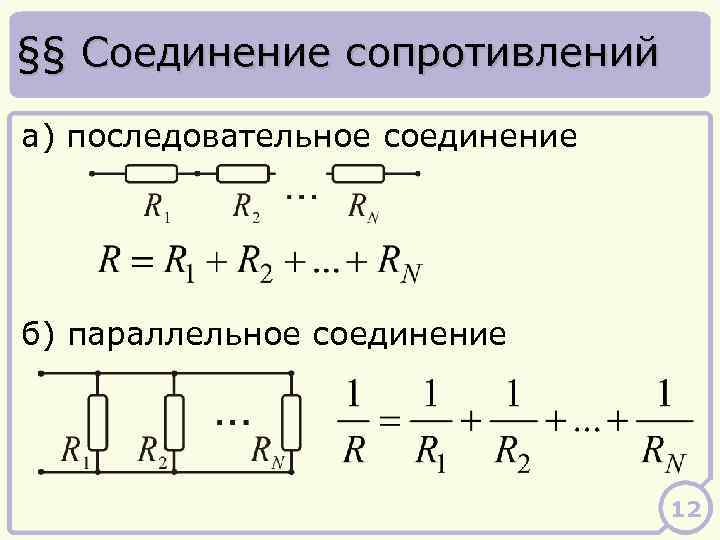
В случае подключения деталей друг с другом, с применением параллельной схемы для расчета суммарного сопротивления, будет использоваться следующая формула:

R(общ)=1/(1/R1+1/R2+1/R3+1/Rn).

причем :

• R(общ) – суммарное значение сопротивления;
• R1- R3 и Rn – резисторы, подсоединенные по параллельной схеме.

Причем, если цепь создается на основе только двух элементов, то для определения суммарного номинального сопротивления следует использовать такую формулу:

R(общ)=R1*R2/R1+R2.

причем:

• R(общ) – суммарное сопротивление;
• R1 и R2 – резисторы, подсоединенные по параллельной схеме.

Видео: Пример расчёта сопротивления

Применительно к радиотехнике следует уделить внимание одному важному правилу: если подключаемые друг к другу элементы по параллельной схеме

имеют одинаковый показатель, то для расчета суммарного номинала необходимо общее значение разделить на число подключенных узлов:

R(общ)=R1n.

причем :

• R(общ) – суммарное значение сопротивления;
• R – номинал резистора, подсоединенного по параллельной схеме;
• n – число подключенных узлов.

Особое внимание следует обратить на то, что конечный показатель сопротивления в случае использования параллельной схемы подключения обязательно будет меньше

по сравнению с номиналом любого элемента, подключаемого в цепь.

Пример расчёта

Для большей наглядности можно рассмотреть следующий пример: допустим, у нас есть три резистора, чьи номиналы соответственно равны 100, 150 и 30 Ом. Если воспользоваться первой формулой для определения общего номинала, то получим следующее:

R(общ)=1/(1/100+1/150+1/30)=

1/(0,01+0,007+0,03)=1/0,047=21,28Ом.

Если выполнить несложные расчеты, то можно получить следующее: для цепи, включающей в себя три детали, где наименьший показатель сопротивления составляет 30 Ом, результирующее значение номинала будет равно 21,28 Ом. Этот показатель будет меньше минимального значения номинала в цепи практически на 30%.

Важные нюансы

Обычно для резисторов параллельное соединение применяется тогда, когда стоит задача по созданию сопротивления большей мощности.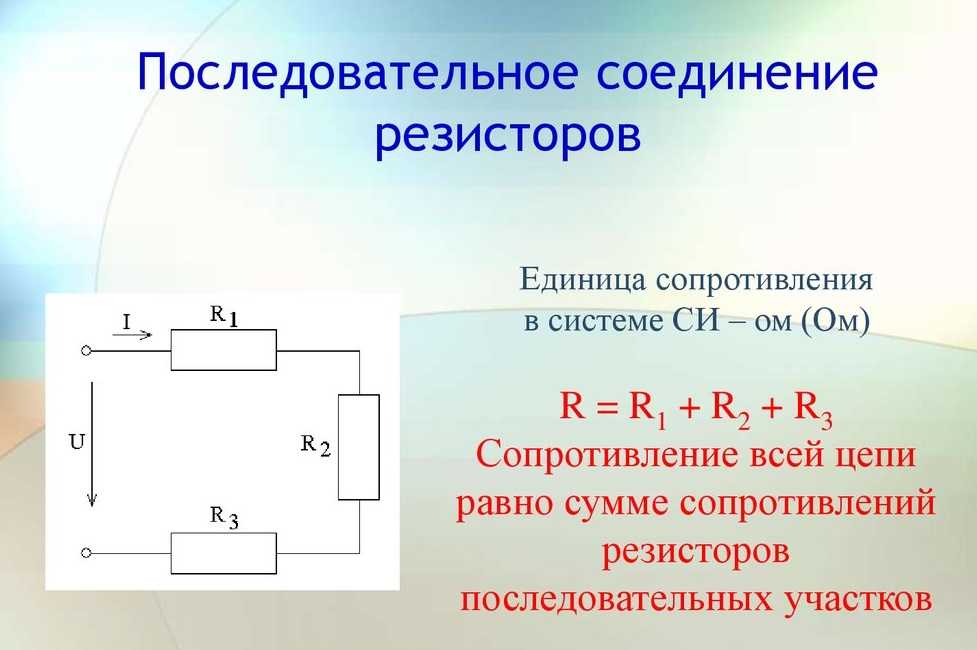 Для ее решения потребуются резисторы, которые должны иметь равные показатели сопротивления и мощности. При таком варианте определить общую мощность можно следующим образом: мощность одного элемента необходимо перемножить с суммарным числом всех резисторов, из которых состоит цепь, подсоединенных друг с другом в соответствии с параллельной схемой.

Скажем, если нами будут использоваться пять резисторов, чей номинал составляет 100 Ом, а мощность каждого равна 1 Вт, которые присоединены друг к другу в соответствии с параллельной схемой, то суммарный показатель сопротивления будет равен 20 Ом, а мощность составит 5 Вт.

Если взять те же резисторы, но подсоединить их в соответствии с последовательной схемой, то конечная мощность составит 5 Вт, а суммарный номинал будет равен 500 Ом.

Видео: Правильное подключение светодиодов

Параллельная схема подключения резисторов очень востребована по той причине, что часто возникает задача по созданию такого номинала, которого невозможно добиться при помощи простого параллельного соединения.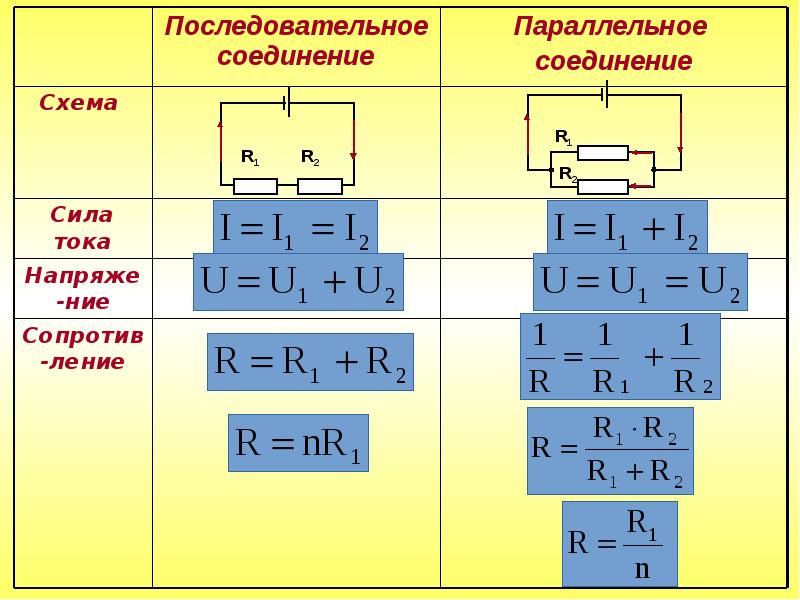 При этом процедура расчета этого параметра отличается достаточной сложностью, где необходимо учитывать разные параметры.

Здесь важная роль отводится не только количеству подключаемых элементов, но и рабочим параметрам резисторов — прежде всего, сопротивлению и мощности. Если один из подключаемых элементов будет иметь неподходящий показатель, то это не позволит эффективно решить задачу по созданию требуемого номинала в цепи.

7. Резисторы. Виды резисторов. Параллельные и последовательные соединения резисторов.

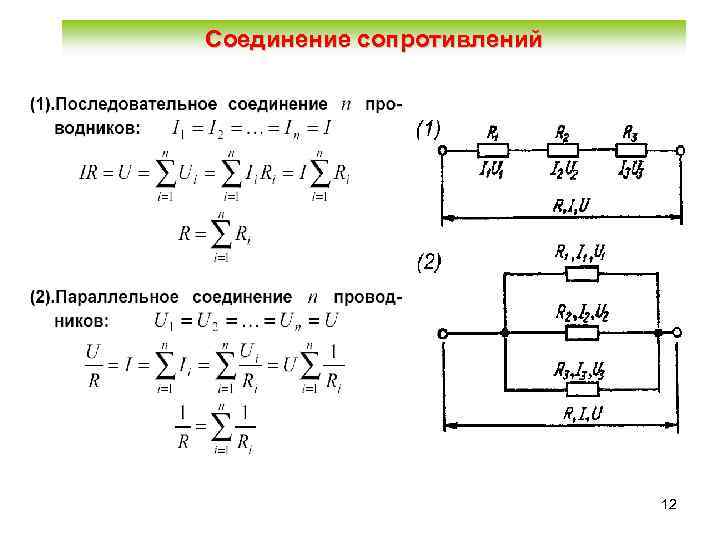
В электрических схемах необходимые сопротивления участков цепей создается с помощью специальных радиоэлементов, называемых резисторами. Они могут быть постоянными (рис1 а), подстроечными (рис1 б) или переменными (рис1 в) и имеют различные номиналы.

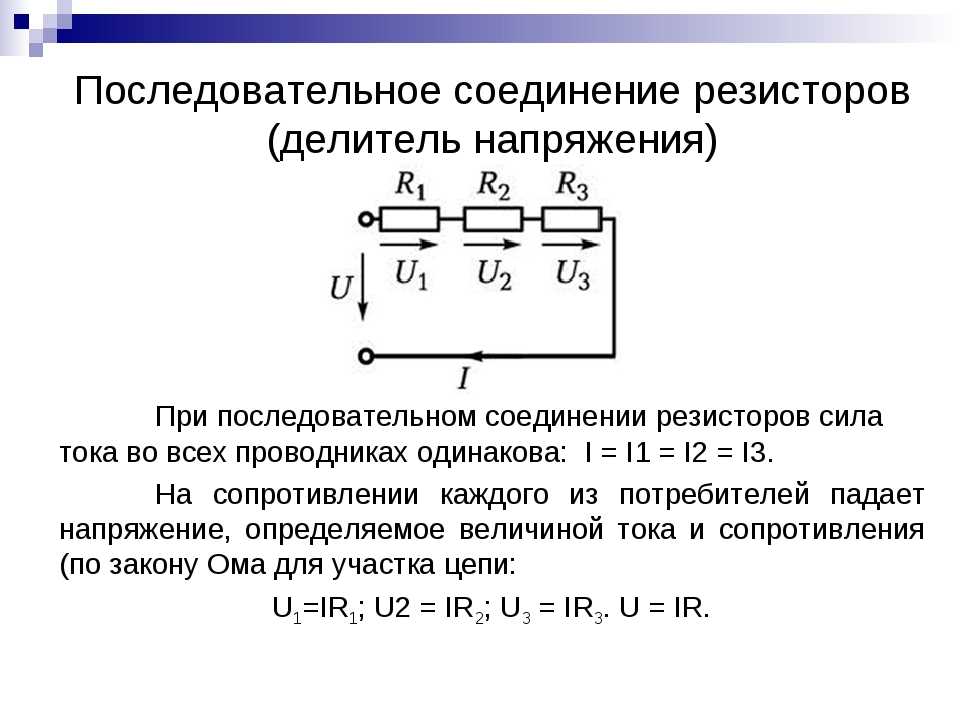
При последовательном соединении резисторов сопротивление увеличивается :

R_посл=R₁+R₂+R₃ (рис 1 д),

А при параллельном соединении общее сопротивление R_пар будет меньше наименьшего сопротивления и может быть определено по формуле:

1/R_пар=1/R₁

+1/R₂+1/R₃ (рис 1 г)

При параллельном соединении двух резисторов R₁ и R₂ получим :

R_пар= R₁* R₂/( R₁+ R₂) (1. 6)

Рис. 1

8. Закон Ома для участка и полной электрической цепи.

Как было отмечено в п. 1.5.1. сила тока в цепи при неизменном значении э.д.с. источника питания зависит от сопротивления этой цепи. Эта зависимость была установлена немецким ученым Георгом Омом в 1827г. И математически записывается в виде:

I=U/R (1.7)

Зависимость (1.7) называется «законом Ома для участка цепи»

Из формулы (1.7) следует другое определение единицы сопротивления. За единицу сопротивления 1 Ом принимают сопротивление такого проводника, по которому проходит ток 1А при напряжении на его концах 1 В.

Для цепи с последовательным соединением резисторов (рис 1 а) значение протекающего в ней тока равно:

I=U₁/R₁= U₂/R₂= U₃/R₃=U/(R₁+R₂+R₃)

В цепи с параллельным включением резисторов токи, протекающие через эти резисторы, зависят от сопротивлений этих резисторов и на основании закона Ома определяются по формулам:

I₁=U/R

1; I₂= U/R₂; I₃= U/R₃

Общий ток I_общ=I₁+I₂+I₃

В отличие от э.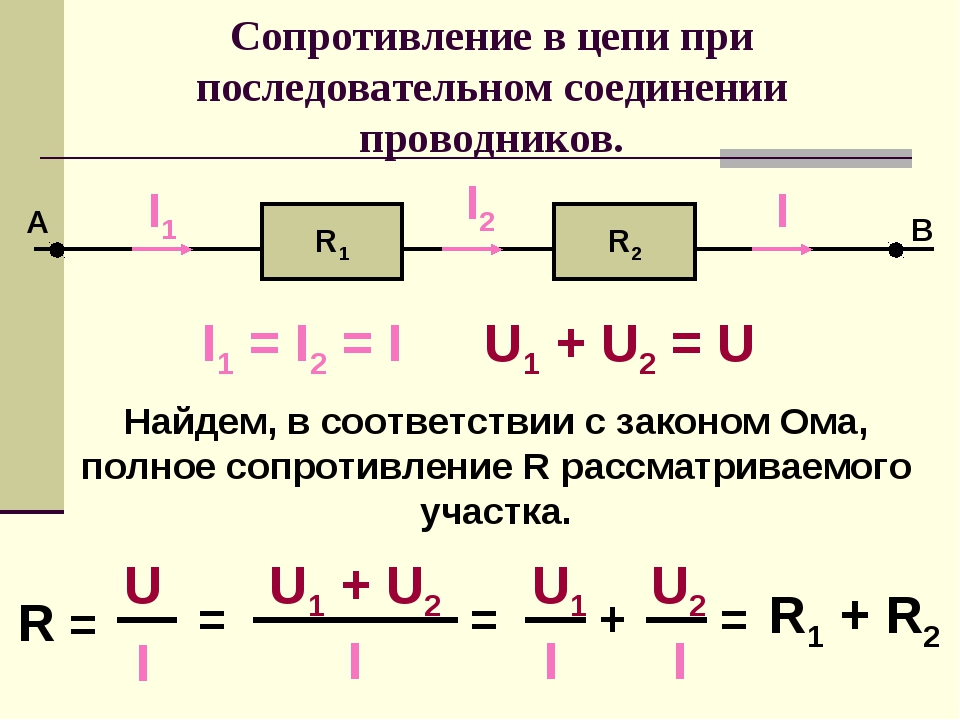 д.с. или напряжения источника тока напряжение на сопротивлении участка цепи (резисторе) называют падением напряжения, подчеркивая этим, что сопротивления не создают напряжения, а на них лишь происходит распределение (падение) напряжения источника тока.

Любой источник питания характеризуется не только э.д.с., но и внутренним сопротивлением R_i. Поэтому если к такому источнику подключить нагрузку с сопротивлением R_h, то возникший в цепи ток будет протекать как через нагрузку , так и внутреннее сопротивление (

рис 1). Следовательно закон Ома для неполной цепи имеет вид:

I=E/(R_i+R_h) (1.8)

E=I*R_i+I*R_h (1.9)

Формула (1.9) показывает, что э.д.с. источника равна сумме падений напряжении на внутреннем сопротивлении источника и на нагрузке. Чем больше R_i , тем больше напряжение на нем падает, а напряжение на нагрузке U_h уменьшается.

Рис. 1

Рис. 2

9.

Законы Кирхгофа.

Первый закон Кирхгофа гласит, что сумма всех токов, протекающих через узел, равна нулю. Согласно этому закону применительно к узлу А (рис 1 а) можно записать:

I

1+I₂-I₃=0 (1.10)

В этом уравнении токи I₁ и I₂, втекающие в узел, приняты положительными, а ток I₃, вытекающий из узла, — отрицательным.

Первый закон Кирхгофа можно сформулировать иначе: сумма токов, втекающих в узел, равна сумме токов вытекающих из узла.

Согласно второму закону Кирхгофа сумма всех напряжений замкнутой цепи равна нулю.

Пусть дана электрическая цепь (рис 1 б), содержащая два источника U₁ и U₂ и резистор R₁ и R₂. Выберем произвольно направление общего тока I. Напряжения, направления которых совпадает с направлением тока I будем считать положительными, неудовлетворяющие этим требованиям — отрицательными. Тогда можно записать:

U₃+U₂-U₄-U₁=0

Рис.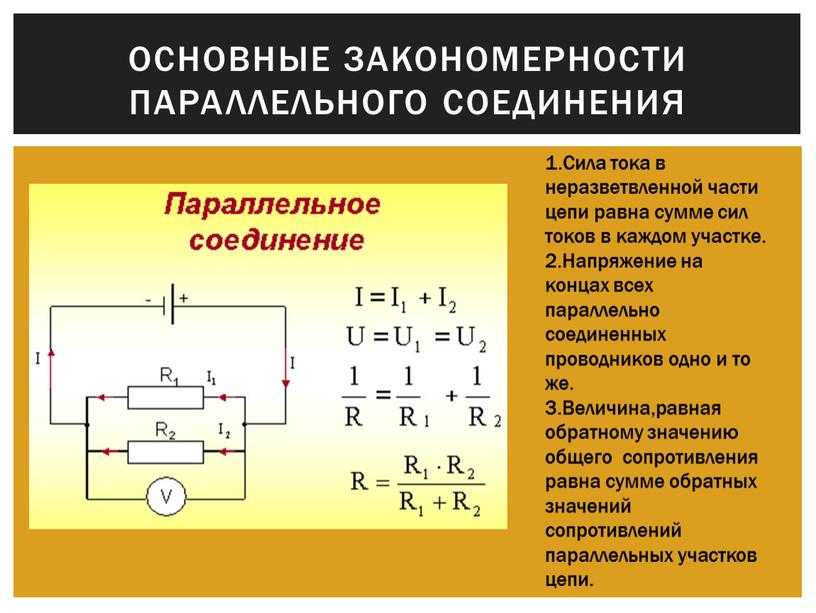 1

Рис. 2

Анализ цепи

— Доказательство формулы для параллельных резисторов

спросил 2 года, 7 месяцев назад

Изменено 2 года, 7 месяцев назад

Просмотрено 2к раз

\$\начало группы\$

В настоящее время я изучаю Искусство электроники , третье издание, Горовиц и Хилл. В упражнении 1.3 предлагается доказать формулы для последовательных и параллельных резисторов. Я получил следующую соответствующую информацию ранее в этой главе:

1. Сумма токов в точке цепи равна сумме выходных токов (сохранение заряда). Иногда его называют текущим законом Кирхгофа (KCL). Инженеры любят называть такую ​​точку узлом . Отсюда следует, что для последовательной цепи (куча двухполюсников, соединенных встык) ток везде одинаков.
   
2. Вещи, соединенные параллельно (рис. 1.1), имеют одинаковое напряжение на них. Другими словами, сумма «падений напряжения» от A до B по одному пути в цепи равна сумме по любому другому пути и представляет собой просто напряжение между A и B . Другими словами, сумма падений напряжения на любой замкнутой цепи равна нулю. Это закон напряжения Кирхгофа (KVL).

Я пытаюсь использовать эту информацию (и закон Ома \$V = IR\$, конечно) для доказательства параллельного случая \$R = \dfrac{R_1 R_2}{R_1 + R_2} \$. Однако я не понимаю, как предоставленной информации достаточно, чтобы сделать такой вывод.

Мне сказали, что это хороший учебник, так что, возможно, я просто новичок в электронике и поэтому чего-то не понимаю. Или, возможно, дело в том, что авторы не смогли предоставить достаточно информации для решения этой проблемы без внешних знаний. Я был бы очень признателен, если бы люди нашли время, чтобы объяснить, как это можно сделать с помощью данной информации.

• анализ цепей
• резисторы
• сопротивление
• закон Ома

\$\конечная группа\$

4

\$\начало группы\$

AoE — это не особо теоретическая книга, это скорее практическое руководство с минимальным количеством математики, которое требуется для проведения анализа. «Хорошо» это или нет, зависит от ваших целей в изучении электроники.

В любом случае, если мы хотим заменить два резистора одним эквивалентным, мы можем рассчитать эквивалентный резистор по протекающему току. Принято считать, что напряжение на каждом резисторе одинаково.

Для R1 ток равен I1 = V/R1, для R2 ток I2 = V/R2, поэтому общий ток равен:

I1 + I2 = V(1/R1+1/R2) и наш «эквивалентный» резистор Rp = 1/(1/R1+1/R2) = R1R2/(R1+R2).

Добавление токов в узел: Ip — I1 — I2 = 0 (KCL), поэтому Ip = I1 + I2

\$\конечная группа\$

4

\$\начало группы\$

Возможно, будет легче понять, как это работает, если использовать обратное сопротивление — проводимость.

В параллельной цепи каждый компонент имеет одинаковое напряжение, поэтому ток, протекающий через него, не зависит от других. Общий ток — это сумма отдельных токов, поэтому общая проводимость — это просто сумма отдельных проводимостей.

Возьмем приведенный ниже пример:

^{смоделируйте эту схему — схема создана с помощью CircuitLab}

R1 имеет проводимость 1/1 Ом = 1 А/В, R2 составляет 1/2 Ом = 0,5 А/В. , а R3 составляет 1/4 Ом = 0,25 А/В. Сложите их все вместе, чтобы получить общую проводимость 1,75 А/В, затем инвертируйте результат, чтобы получить общее сопротивление 1/1,75 = 0,571 Ом.

Это дает общую формулу для параллельных сопротивлений:-

\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1}{R2} + …\frac{1 }{Rn}\$

В частном случае только двух резисторов, подключенных параллельно, вы можете изменить формулу из

\$\frac{1}{Rt} = \frac{1}{R1} + \frac{1 }{R2}\$

до

\$Rt = \frac{R_1 R_2}{R_1 + R_2}\$

\$\конечная группа\$

3

\$\начало группы\$

^{смоделируйте эту цепь — схема создана с помощью CircuitLab}

Полный ток в цепи будет It = V/Rt

Согласно KCL It = I1+I2, где I1 — ток, протекающий через резистор R1 и I2 — ток, протекающий через резистор R2.

Если подставить (закон Ома):

V/Rt = V1/R1+V2/R2. Но поскольку резисторы включены параллельно V1 = V2.

Но так как между источником напряжения и резисторами нет резистора V = V1 = V2.

V/Rt = V1/R1+V2/R2 -> V/Rt = V/R1+V/R2 и если мы разделим на V, мы получим 1/Rt = 1/R1 + 1/R2.

\$\конечная группа\$

3

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Действие: последовательные и параллельные резисторы

Эта версия (03 марта 2022 г. , 17:10) была одобрена Дугом Мерсером. Доступна ранее утвержденная версия (26 января 2021 г., 15:25).

Содержание

• Деятельность: Последовательные и параллельные резисторы — ADALM1000

  • Цель:

  • Последовательные и параллельные цепи

    • Цепи серии

      Определены

    • Определение параллельных цепей

  • Эксперименты

    • Материалы:

    • Резисторы в серии:

    • Параллельные резисторы:

    • Комбинированные цепи

Цель:

Целью этой лабораторной работы является исследование резисторов, соединенных последовательно и параллельно.

Последовательные и параллельные цепи

Простые схемы, состоящие всего из нескольких компонентов, обычно просты для понимания новичками. Но все становится сложнее, когда в смесь входит большее количество компонентов. Куда течет ток? Что делают напряжения узлов? Можно ли упростить схему и сделать ее более понятной? Следующая информация должна помочь.

В этой лабораторной работе мы сначала обсудим разницу между последовательными и параллельными цепями, используя схемы, содержащие самые основные компоненты, резисторы и батареи (или источники напряжения), чтобы показать разницу между двумя конфигурациями.

Прежде чем мы углубимся в объяснение, нам нужно определить, что такое узел схемы. Узел в цепи — это не что иное, как электрическое соединение между двумя или более компонентами. Когда цепь изображена на схеме, такой как рисунок 1, узлы представлены проводами (линиями) между компонентами.

Рис. 1. Схема примера узла

На схеме показана цепь с 4 резисторами и источником напряжения. Есть также четыре уникальных узла. Цветные узлы (линии) Красный соединяет (+) конец источника напряжения с резистором R ₁ , Оранжевый соединяет R ₁ и R ₂ вместе, Синий соединяет R ₂ с R ₃ и R ₄ , а зеленый соединяет (–) конец источника напряжения с R _{5 и R 3 Р 4 . Обратите внимание, что мы обычно определяем один узел как общий узел, на который ссылаются все остальные узлы, в данном случае зеленый наземный узел.}

Нам также необходимо понять, как ток течет по цепи. Условный ток течет от более высокого или более положительного напряжения к более низкому или менее положительному напряжению в цепи. Некоторое количество тока будет протекать по каждому пути, который может пройти, чтобы добраться до точки с самым низким напряжением, обычно называемой землей (0 вольт). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы источника напряжения к отрицательной клемме.

Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂ ) ток на входе такой же, как и на выходе. В других узлах (в частности, в трехстороннем соединении между R ₂ , R ₃ и R ₄ ) основной (красный) ток разделяется на два разных: фиолетовый ток, текущий в R ₃ , и оранжевый ток течет в R ₄ . Также обратите внимание, что токи I _R3 и I _R4 рекомбинируют в зеленый ток. Это подчеркивает ключевое различие между последовательным и параллельным соединениями.

Цепи серии

Определены

Когда резисторы соединены последовательно (как показано на рисунке 2), вывод одного резистора соединяется непосредственно с выводом следующего резистора, без каких-либо других возможных путей, так что весь ток в одном резисторе должен течь в следующий и скоро.

Когда резисторы соединены последовательно, их можно комбинировать или объединять вместе как эквивалентный одиночный резистор с сопротивлением, равным сумме последовательных сопротивлений, , т. е. ,

Рисунок 2: Последовательные резисторы, R _СЕРИЯ = R ₁ + R ₂ + R ₃ +…

Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.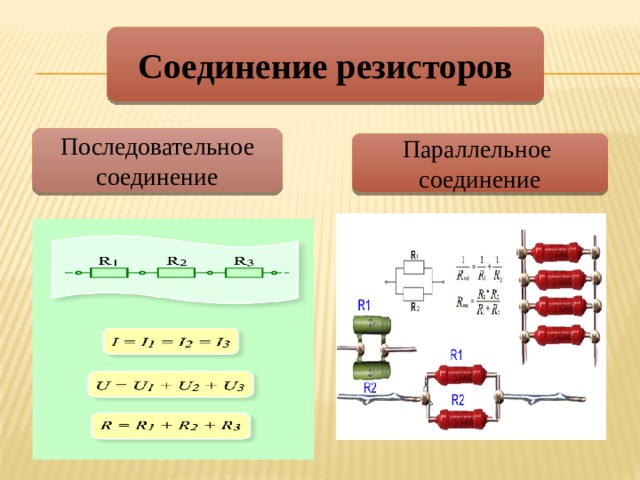 Итак, для приведенной выше последовательной схемы:

Мы знаем, что все резисторы имеют одинаковый ток I _S .

Аналогично для остальных трех резисторов:

Или выделим I _S :

Таким образом, общее эквивалентное сопротивление — это просто сумма их значений.

Определение параллельных цепей

Когда резисторы соединены параллельно (как показано на рисунке 3), все их первые выводы соединены вместе, а все их вторые выводы соединены вместе.

Когда резисторы подключены параллельно, их можно комбинировать или объединять вместе как эквивалентный одиночный резистор, значение которого определяется следующим уравнением:

Для двух резисторов, включенных параллельно, это упрощается до:

Рисунок 3: Параллельные резисторы

Почему это правда? Закон Ома говорит нам, что напряжение на резисторе равно току через резистор, умноженному на сопротивление.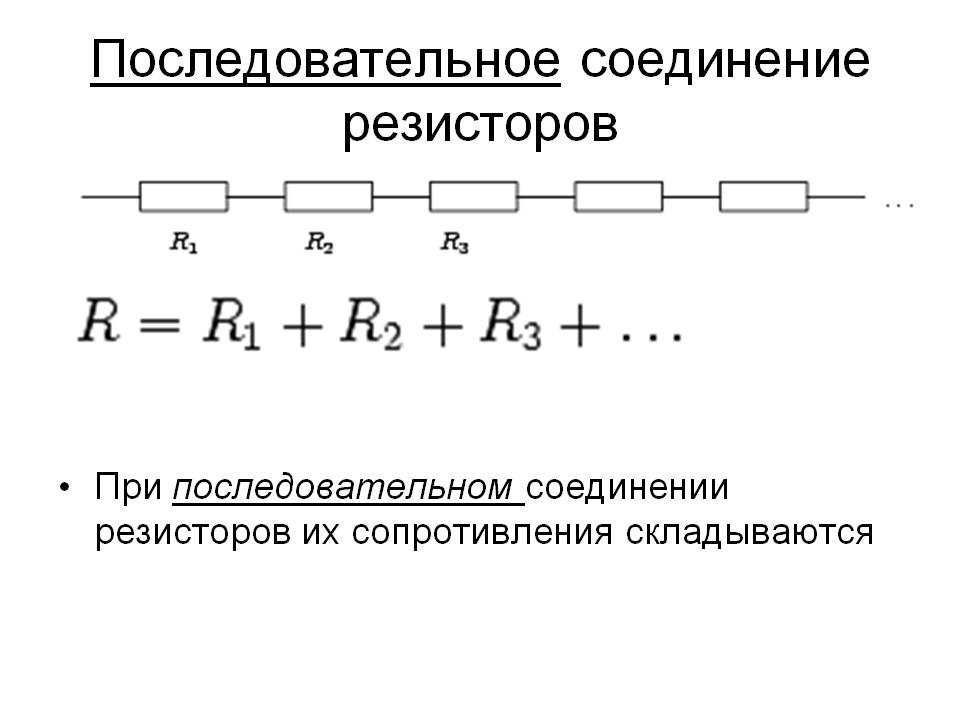 Итак, для приведенной выше параллельной схемы:

Мы знаем, что все резисторы имеют одинаковое напряжение В _S .

Ток, подаваемый источником напряжения В _S — сумма токов в резисторах.

Подставляя четыре резистора, получаем:

Или выделим V _S :

Переставляя сопротивления, получаем общее эквивалентное сопротивление:

Эксперименты

Материалы:

Аппаратный модуль ADALM1000
Макетная плата без пайки и перемычки
3 – резисторы 100 Ом
3 – резисторы 470 Ом

Резисторы в серии:

Поместите последовательно три 100-омных резистора на макетную плату, как показано на рис. 4. Соедините с помощью перемычек вход CH A с левой стороны первого резистора, а вход CH B с правой стороны того же резистора.

Рис. 4. Резисторы, соединенные последовательно.

Запустите инструмент ALICE M1K Ohm Meter. Экран показан здесь. Программное обеспечение использует известный резистор для проверки неизвестного резистора. ADALM1000 имеет встроенный резистор 50 Ом, который можно использовать для этого. Убедитесь, что выбрана опция Int. Уровень напряжения, который используется для измерения резистора, может быть установлен. Тестирование при максимальном напряжении 5,0 В дает наилучшие результаты для большинства номиналов резисторов. Нажмите «Выполнить», и вы должны увидеть что-то подобное с одним резистором 100 Ом.

Переместите перемычку CH B на правый конец второго резистора, как показано ниже.

Рисунок 5, два резистора последовательно

Теперь омметр должен показывать значение для двух последовательно соединенных резисторов или около 200 Ом. Теперь переместите перемычку CH B на правый конец третьего резистора, как показано ниже.

Рисунок 6, три последовательно соединенных резистора

Теперь омметр должен показывать значение для трех последовательных резисторов или около 300 Ом.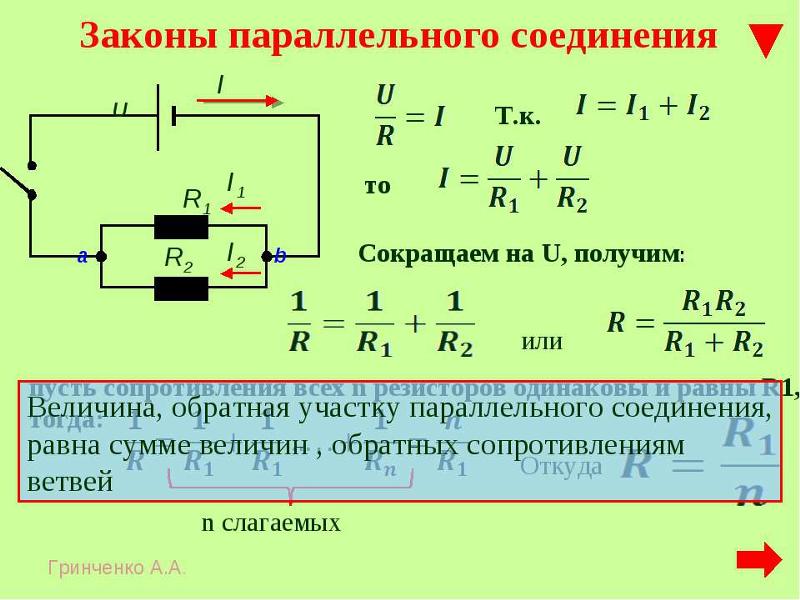

Параллельные резисторы:

Теперь замените резисторы 100 Ом на резисторы 470 Ом, как показано на рисунке 7.

Измерение одного резистора 470 Ом

Теперь омметр должен показывать значение для одного резистора или около 470 Ом. Переместите средний резистор 470 Ом так, чтобы он был параллелен резистору справа, как показано ниже.

Измерение двух резисторов 470 Ом параллельно

Теперь омметр должен считать значение для двух резисторов по 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?

Переместите третий резистор 470 Ом так, чтобы он был параллелен двум другим резисторам справа, как показано ниже.

Измерение трех резисторов по 470 Ом параллельно

Теперь омметр должен считать значение трех резисторов по 470 Ом, включенных параллельно. Соответствует ли измеренное значение формуле для параллельных резисторов?

Поэкспериментируйте с другими комбинациями резисторов и номиналов, чтобы убедиться, что формулы верны для любого номинала резистора.

Комбинированные цепи

Более сложные соединения резисторов обычно представляют собой просто комбинации последовательного и параллельного соединений. Это часто встречается, особенно когда учитывается сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Комбинированная цепь может быть разбита на аналогичные части, которые могут быть либо последовательными, либо параллельными, как показано на рисунке 7. На рисунке общее сопротивление можно рассчитать, соединив три резистора друг с другом как последовательно или параллельно.

Комбинированные последовательные и параллельные резисторы

R ₂ и R ₃ соединены параллельно друг другу, поэтому мы знаем, что для этих двух резисторов эквивалентное сопротивление будет:

Суммарное сопротивление R ₂ и R ₃ включено последовательно с R1, поэтому общее эквивалентное сопротивление будет:

Для более сложных комбинационных цепей различные части могут быть идентифицированы как последовательные или параллельные, приведенные к их эквивалентам, а затем уменьшены до тех пор, пока не останется одно сопротивление.