Статика. Момент силы

На данном уроке, тема которого: «Момент силы», мы поговорим о силе, с которой нужно подействовать на тело, чтобы изменить его скорость, а также о точке приложения этой силы. Рассмотрим примеры поворота разных тел, например качели: в какую точку нужно подействовать силой, чтобы качели начали движение или остались в равновесии.

Представьте, что вы футболист и перед вами футбольный мяч. Чтобы он полетел, его нужно ударить. Всё просто: чем сильнее ударите, тем быстрее и дальше полетит, и бить будете, скорее всего, в центр мяча (см. рис. 1).

А чтобы мяч в полете вращался и летел по искривленной траектории, вы ударите не в центр мяча, а сбоку, что и делают футболисты, чтобы обмануть соперника (см. рис. 2).

Рис. 2. Кривая траектория полета мяча

Здесь уже важно, в какую точку бить.

Еще один простой вопрос: в каком месте нужно взять палку, чтобы она при подъеме не перевернулась? Если палка равномерная по толщине и плотности, то возьмем мы её посередине. А если она с одного края массивнее? Тогда мы возьмем её ближе к массивному краю, иначе он перевесит (см. рис. 3).

Рис. 3. Точка подъема

Представьте: папа сел на качели-балансир (см. рис. 4).

Рис. 4. Качели-балансир

Чтобы его перевесить, вы сядете на качели поближе к противоположному концу.

Во всех приведённых примерах нам важно было не просто подействовать на тело с некоторой силой, но и важно, в каком месте, на какую именно точку тела действовать. Эту точку мы выбирали наугад, пользуясь жизненным опытом. А если на палке будет три разных груза? А если поднимать ее вдвоем? А если речь идёт о подъемном кране или вантовом мосте (см. рис. 5)?

Рис. 5. Примеры из жизни

Для решения таких задач интуиции и опыта недостаточно. Без четкой теории их решить уже нельзя. О решении таких задач сегодня и пойдёт речь.

Обычно в задачах у нас есть тело, к которому приложены силы, и мы их решаем, как всегда до этого, не задумываясь над точкой приложения силы.

Достаточно знать, что сила приложена просто к телу. Такие задачи встречаются часто, мы умеем их решать, но бывает, что недостаточно приложить силу просто к телу, — становится важно, в какую точку.

Пример задачи, в которой размеры тела не важны

Например, на столе лежит маленький железный шарик, на который действует сила тяжести 1 Н. Какую силу нужно приложить, чтобы его поднять? Шарик притягивается Землей, мы будем действовать на него вверх, прикладывая некоторую силу.

Силы, действующие на шарик, направлены в противоположные стороны, и, чтобы поднять шарик, нужно подействовать на него с силой, большей по модулю, чем сила тяжести (см. рис. 6).

Рис. 6. Силы, действующие на шарик

Сила тяжести равна , значит, на шарик нужно подействовать вверх с силой:

Мы не задумывались, как именно мы берем шарик, мы его просто берем и поднимаем. Когда мы показываем, как мы поднимали шарик, мы вполне можем нарисовать точку и показать: мы воздействовали на шарик (см. рис. 7).

Рис. 7. Действие на шарик

Когда мы можем так поступить с телом, показать его на рисунке при объяснении в виде точки и не обращать внимания на его размеры и форму, мы считаем его материальной точкой. Это модель. Реально же шарик имеет форму и размеры, но мы на них в этой задаче не обращали внимания. Если тот же шарик нужно заставить вращаться, то просто сказать, что мы воздействуем на шарик, уже нельзя. Здесь важно, что мы толкали шарик с краю, а не в центр, заставляя его вращаться. В этой задаче тот же шарик уже нельзя считать точкой.

Мы уже знаем примеры задач, в которых нужно учитывать точку приложения силы: задача с футбольным мячом, с неоднородной палкой, с качелями.

Точка приложения силы важна также в случае с рычагом. Пользуясь лопатой, мы действуем на конец черенка. Тогда достаточно приложить небольшую силу (см. рис. 8).

Рис. 8. Действие малой силы на черенок лопаты

Что общего между рассмотренными примерами, где нам важно учитывать размеры тела? И мяч, и палка, и качели, и лопата — во всех этих случаях речь шла о вращении этих тел вокруг некоторой оси. Мяч вращался вокруг своей оси, качели поворачивались вокруг крепления, палка — вокруг места, в котором мы ее держали, лопата — вокруг точки опоры (см. рис. 9).

Рис. 9. Примеры вращающихся тел

Рассмотрим поворот тел вокруг неподвижной оси и увидим, что заставляет тело поворачиваться. Будем рассматривать вращение в одной плоскости, тогда можно считать, что тело поворачивается вокруг одной точки О (см. рис. 10).

Рис. 10. Точка вращения

Если мы захотим уравновесить качели, у которых балка будет стеклянной и тонкой, то она может просто сломаться, а если балка из мягкого металла и тоже тонкая — то согнуться (см. рис. 11).

Такие случаи мы рассматривать не будем; будем рассматривать поворот прочных жестких тел.

Неправильно будет сказать, что вращательное движение определяется только силой. Ведь на качелях одна и та же сила может вызвать их вращение, а может и не вызвать, смотря где мы сядем. Дело не только в силе, но и в расположении точки, на которую воздействуем.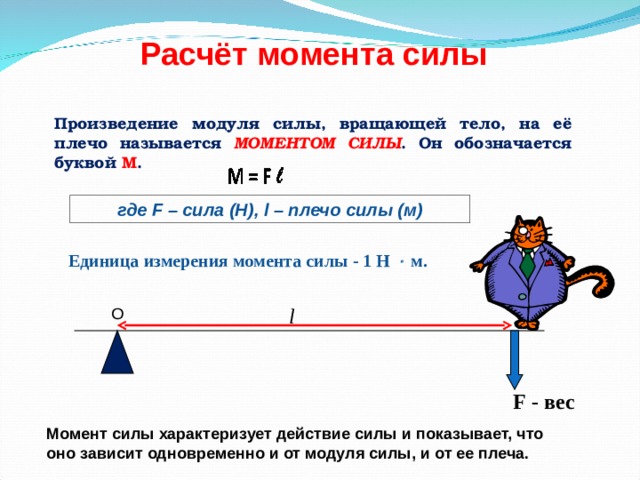 Все знают, насколько трудно поднять и удержать груз на вытянутой руке. Чтобы определять точку приложения силы, вводится понятие плеча силы (по аналогии с плечом руки, которой поднимают груз).

Плечо силы — это минимальное расстояние от заданной точки до прямой, вдоль которой действует сила.

Из геометрии вы наверняка уже знаете, что это перпендикуляр, опущенный из точки О на прямую, вдоль которой действует сила (см. рис. 12).

Рис. 12. Графическое изображение плеча силы

Почему плечо силы — минимальное расстояние от точки О до прямой, вдоль которой действует сила

Может показаться странным, что плечо силы измеряется от точки О не до точки приложения силы, а до прямой, вдоль которой эта сила действует.

Проделаем такой опыт: привяжем к рычагу нить. Подействуем на рычаг с некоторой силой в точке, где привязана нить (см. рис. 13).

Рис. 13. Нить привязана к рычагу

Если создастся момент силы, достаточный для поворота рычага, он повернется.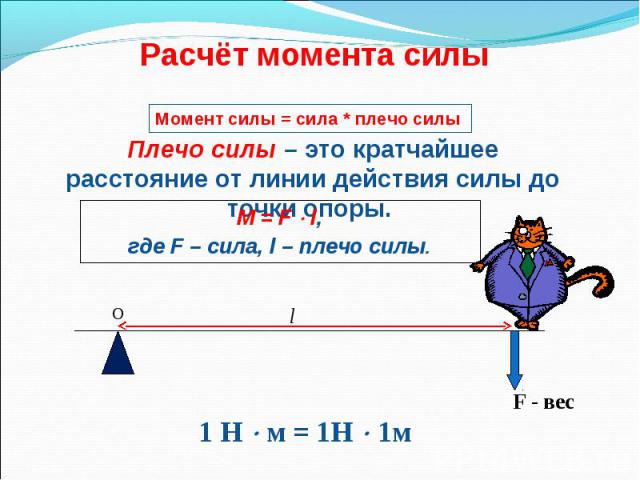 Нить покажет прямую, вдоль которой направлена сила (см. рис. 14).

Попробуем потащить рычаг с той же силой, но теперь взявшись за нить. В воздействии на рычаг ничего не изменится, хотя точка приложения силы поменяется. Но сила будет действовать вдоль той же прямой, ее расстояние до оси вращения, то есть плечо силы, останется тем же. Попробуем подействовать на рычаг под углом (см. рис. 15).

Рис. 15. Действие на рычаг под углом

Теперь сила приложена к той же точке, но действует вдоль другой прямой. Ее расстояние до оси вращения стало малό, момент силы уменьшился, и рычаг может уже не повернуться.

На тело оказывается воздействие, направленное на вращение, на поворот тела. Это воздействие зависит от силы и от её плеча. Величина, характеризующая вращательное воздействие силы на тело, называется момент силы , иногда его называют еще вращающим или крутящим моментом.

Значение слова «момент»

Нам привычно употреблять слово «момент» в значении очень короткого промежутка времени, как синоним слова «мгновение» или «миг».

Тогда не совсем понятно, какое отношение имеет момент к силе. Обратимся к происхождению слова «момент».

Слово происходит от латинского momentum, что означает «движущая сила, толчок». Латинский глагол movēre означает «двигать» (как и английское слово move, а movement означает «движение»). Теперь нам ясно, что вращающий момент — это то, что заставляет тело вращаться.

Момент силы — это произведение силы на ее плечо.

Единица измерения — ньютон, умноженный на метр: .

Если увеличивать плечо силы, можно уменьшить силу и момент силы останется прежним. Мы очень часто используем это в повседневной жизни: когда открываем дверь, когда пользуемся плоскогубцами или гаечным ключом.

Остался последний пункт нашей модели — надо разобраться, что делать, если на тело действует несколько сил. Мы можем вычислить момент каждой силы. Понятно, что если силы будут вращать тело в одном направлении, то их действие сложится (см. рис. 16).

Рис. 16. Действие сил складывается

Если в разных направлениях — моменты сил будут уравновешивать друг друга и логично, что их нужно будет вычесть. Поэтому моменты сил, которые вращают тело в разных направлениях, будем записывать с разными знаками. Например, запишем, если сила предположительно вращает тело вокруг оси по часовой стрелке, и — если против (см. рис. 17).

Рис. 17. Определение знаков

Тогда мы можем записать одну важную вещь: чтобы тело пребывало в равновесии, сумма моментов действующих на него сил должна быть равна нулю .

Формула для рычага

Мы уже знаем принцип действия рычага: на рычаг действуют две силы, и во сколько раз больше плечо рычага, во столько раз меньше сила:

Рассмотрим моменты сил, которые действуют на рычаг.

Выберем положительное направление вращения рычага, например против часовой стрелки (см. рис. 18).

Рис. 18. Выбор направления вращения

Тогда момент силы будет со знаком плюс, а момент силы — со знаком минус. Чтобы рычаг был в равновесии, сумма моментов сил должна быть равна нулю. Запишем:

Математически это равенство и соотношение, записанное выше для рычага, — одно и то же, и то, что мы получили экспериментально, подтвердилось.

Например, определим, будет ли пребывать в равновесии рычаг, изображенный на рисунке. На него действуют три силы (см. рис. 19). , и . Плечи сил равны , и .

Рис. 19. Рисунок к условию задачи 1

Чтобы рычаг пребывал в равновесии, сумма моментов сил, которые на него действуют, должен быть равен нулю.

На рычаг по условию действуют три силы: , и . Их плечи соответственно равны , и .

Направление вращения рычага по часовой стрелке будем считать положительным. В этом направлении рычаг вращает сила , ее момент равен:

Силы и вращают рычаг против часовой стрелки, их моменты запишем со знаком минус:

Осталось вычислить сумму моментов сил:

Суммарный момент не равен нулю, значит, тело не будет пребывать в равновесии. Суммарный момент положительный, значит, рычаг будет поворачиваться по часовой стрелке (в нашей задаче это положительное направление).

Мы решили задачу и получили результат: суммарный момент сил, действующих на рычаг, равен . Рычаг начнет поворачиваться. И при его повороте, если силы не изменят направление, будут изменяться плечи сил. Они будут уменьшаться, пока не станут равны нулю, когда рычаг повернется вертикально (см. рис. 20).

Рис. 20. Плечи сил равны нулю

А при дальнейшем повороте силы станут направлены так, чтобы вращать его в противоположном направлении. Поэтому, решив задачу, мы определили, в какую сторону начнет вращаться рычаг, не говоря о том, что будет происходить потом.

Теперь вы научились определять не только силу, с которой нужно действовать на тело, чтобы изменить его скорость, но и точку приложения этой силы, чтобы оно не поворачивалось (или поворачивалось, как нам нужно).

Как толкать шкаф, чтобы он не перевернулся?

Мы знаем, что, когда мы толкаем шкаф с силой в верхней его части, он переворачивается, а чтобы этого не произошло, мы толкаем его ниже. Теперь мы можем объяснить это явление. Ось его вращения находится на том его ребре, на котором он стоит, при этом плечи всех сил, кроме силы , либо малы, либо равняются нулю, поэтому под действием силы шкаф падает (см. рис. 21).

Рис. 21. Действие на верхнюю часть шкафа

Прикладывая силу ниже, мы уменьшаем ее плечо , а значит, и момент этой силы, и опрокидывания не происходит (см. рис. 22).

Рис. 22. Сила приложена ниже

Шкаф как тело, размеры которого мы учитываем, подчиняется тому же закону, что и гаечный ключ, дверная ручка, мосты на опорах и т. п.

На этом наш урок окончен. Спасибо за внимание!

Список литературы

1. Соколович Ю.А., Богданова Г.С Физика: Справочник с примерами решения задач. — 2-е издание передел. — X.: Веста: Издательство «Ранок», 2005. — 464 с.
2. Перышкин А.В. Физика. 7 кл.: учеб. для общеобразоват. учреждений — 10-е изд., доп. — М.: Дрофа, 2006. — 192 с.: ил.

1. Abitura.com ().
2. Solverbook.com ().

Домашнее задание

В физике рассмотрение задач с вращающимися телами или системами, которые находятся в равновесии, осуществляется с использованием концепции «момент силы». В этой статье будет рассмотрена формула момента силы, а также ее использование для решения указанного типа задач.

в физике

Как было отмечено во введении, в данной статье пойдет речь о системах, которые могут вращаться либо вокруг оси, либо вокруг точки. Рассмотрим пример такой модели, изображенной на рисунке ниже.

Мы видим, что рычаг серого цвета закреплен на оси вращения. На конце рычага имеется черный кубик некоторой массы, на который действует сила (красная стрелка). Интуитивно понятно, что результатом воздействия этой силы будет вращение рычага вокруг оси против часовой стрелки.

Моментом силы называется величина в физике, которая равна векторному произведению радиуса, соединяющего ось вращения и точку приложения силы (зеленый вектор на рисунке), и самой внешней силе. То есть силы относительно оси записывается следующим образом:

Результатом этого произведения будет вектор M¯. Направление его определяют, исходя из знания векторов-множителей, то есть r¯ и F¯. Согласно определению векторного произведения, M¯ должен быть перпендикулярен плоскости, образованной векторами r¯ и F¯, и направлен в соответствии с правилом правой руки (если четыре пальца правой руки расположить вдоль первого умножаемого вектора в направлении к концу второго, то отставленный вверх большой палец укажет, куда направлен искомый вектор). На рисунке можно видеть, куда направлен вектор M¯ (синяя стрелка).

Скалярная форма записи M¯

На рисунке в предыдущем пункте сила (красная стрелка) действует на рычаг под углом 90 o . В общем же случае она может быть приложена под совершенно любым углом. Рассмотрим изображение ниже.

Здесь мы видим, что на рычаг L сила F уже действует под некоторым углом Φ. Для этой системы формула момента силы относительно точки (показана стрелкой) в скалярном виде примет форму:

M = L * F * sin(Φ)

Из выражения следует, что момент силы M будет тем больше, чем ближе направление действия силы F к углу 90 o по отношению к L.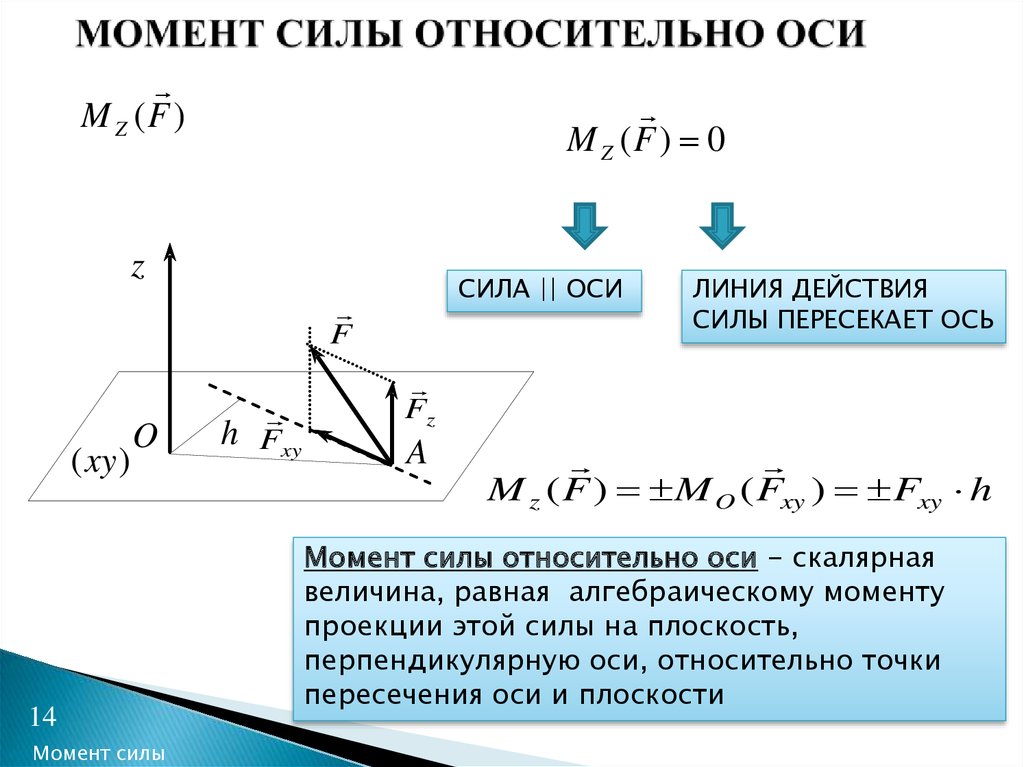 Наоборот, если F действует вдоль L, то sin(0) = 0, и сила не создает никакого момента (M = 0).

При рассмотрении момента силы в скалярной форме часто пользуются понятием «рычага силы». Эта величина представляет собой расстояние между осью (точкой вращения) и вектором F. Применяя это определение к рисунку выше, можно сказать, что d = L * sin(Φ) — это рычаг силы (равенство следует из определения тригонометрической функции «синус»). Через рычаг силы формулу для момента M можно переписать так:

Физический смысл величины M

Рассматриваемая физическая величина определяет способность внешней силы F оказывать вращательное воздействие на систему. Чтобы привести тело во вращательное движение, ему необходимо сообщить некоторый момент M.

Ярким примером этого процесса является открывание или закрывание двери в комнату. Взявшись за ручку, человек прикладывает усилие и поворачивает дверь на петлях. Каждый сможет это сделать. Если же попытаться открыть дверь, воздействуя на нее вблизи петель, то потребуется приложить большие усилия, чтобы сдвинуть ее с места.

Другим примером является откручивание гайки ключом. Чем короче будет этот ключ, тем труднее выполнить поставленную задачу.

Указанные особенности демонстрирует формула момента силы через плечо, которая была приведена в предыдущем пункте. Если M считать постоянной величиной, то чем меньше d, тем большую F следует приложить для создания заданного момента силы.

Несколько действующих сил в системе

Выше были рассмотрены случаи, когда на систему, способную к вращению, действует всего одна сила F, но как быть, когда таких сил несколько? Действительно, эта ситуация является более частой, поскольку на систему могут действовать силы различной природы (гравитационная, электрическая, трение, механическая и другие). Во всех этих случаях результирующий момент силы M¯ может быть получен с помощью векторной суммы всех моментов M i ¯, то есть:

M¯ = ∑ i (M i ¯), где i — номер силы F i

Из свойства аддитивности моментов следует важный вывод, который получил название теоремы Вариньона, названной так по фамилии математика конца XVII — начала XVIII века — француза Пьера Вариньона. Она гласит: «Сумма моментов всех сил, оказывающих воздействие на рассматриваемую систему, может быть представлена в виде момента одной силы, которая равна сумме всех остальных и приложена к некоторой точке». Математически теорему можно записать так:

∑ i (M i ¯) = M¯ = d * ∑ i (F i ¯)

Эта важная теорема часто используется на практике для решения задач на вращение и равновесие тел.

Совершает ли работу момент силы?

Анализируя приведенные формулы в скалярном или векторном виде, можно прийти к выводу, что величина M — это некоторая работа. Действительно, ее размерность равна Н*м, что в СИ соответствует джоулю (Дж). На самом деле момент силы — это не работа, а лишь величина, которая способна ее совершить. Чтобы это произошло, необходимо наличие кругового движения в системе и продолжительного во времени действия M. Поэтому формула работы момента силы записывается в следующем виде:

В этом выражении θ — это угол, на который было произведено вращение моментом силы M. В итоге единицу работы можно записать как Н*м*рад или же Дж*рад. Например, значение 60 Дж*рад говорит о том, что при повороте на 1 радиан (приблизительно 1/3 окружности) создающая момент M сила F совершила работу в 60 джоулей. Эту формулу часто используют при решении задач в системах, где действуют силы трения, что будет показано ниже.

Момент силы и момент импульса

Как было показано, воздействие на систему момента M приводит к появлению в ней вращательного движения. Последнее характеризуется величиной, которая получила название «момент импульса». Его можно вычислить, применяя формулу:

Здесь I — это момент инерции (величина, которая играет такую же роль при вращении, что и масса при линейном движении тела), ω — угловая скорость, она связана с линейной скоростью формулой ω = v/r.

Оба момента (импульса и силы) связаны друг с другом следующим выражением:

M = I * α, где α = dω / dt — угловое ускорение.

Приведем еще одну формулу, которая важна для решения задач на работу моментов сил.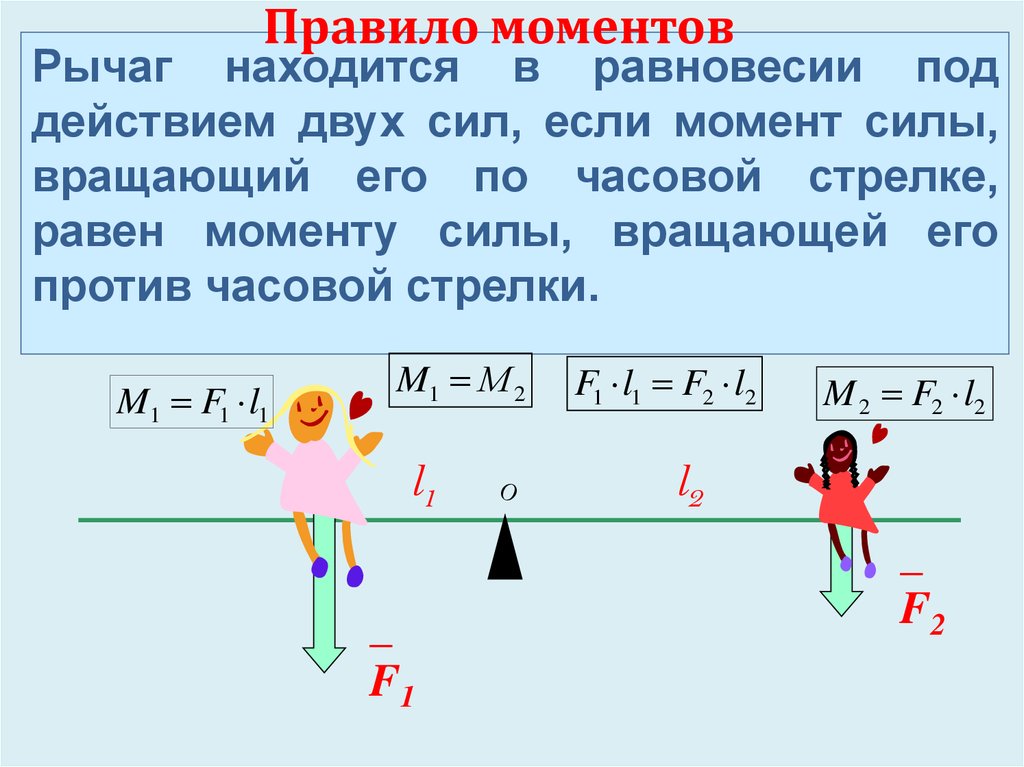 С помощью этой формулы можно вычислить кинетическую энергию вращающегося тела. Она выглядит так:

Равновесие нескольких тел

Первая задача связана с равновесием системы, в которой действуют несколько сил. На рисунке ниже приведена система, на которую действуют три силы. Необходимо рассчитать, какой массы предмет необходимо подвесить к этому рычагу и в какой точке это следует сделать, чтобы данная система находилась в равновесии.

Из условия задачи можно понять, что для ее решения следует воспользоваться теоремой Вариньона. На первую часть задачи можно ответить сразу, поскольку вес предмета, которые следует подвесить к рычагу, будет равен:

P = F 1 — F 2 + F 3 = 20 — 10 + 25 = 35 Н

Знаки здесь выбраны с учетом того, что сила, вращающая рычаг против часовой стрелки, создает отрицательный момент.

Положение точки d, куда следует подвесить этот вес, вычисляется по формуле:

M 1 — M 2 + M 3 = d * P = 7 * 20 — 5 * 10 + 3 * 25 = d * 35 => d = 165/35 = 4,714 м

Отметим, что с помощью формулы момента силы тяжести мы вычислили эквивалентную величину M той, которую создают три силы.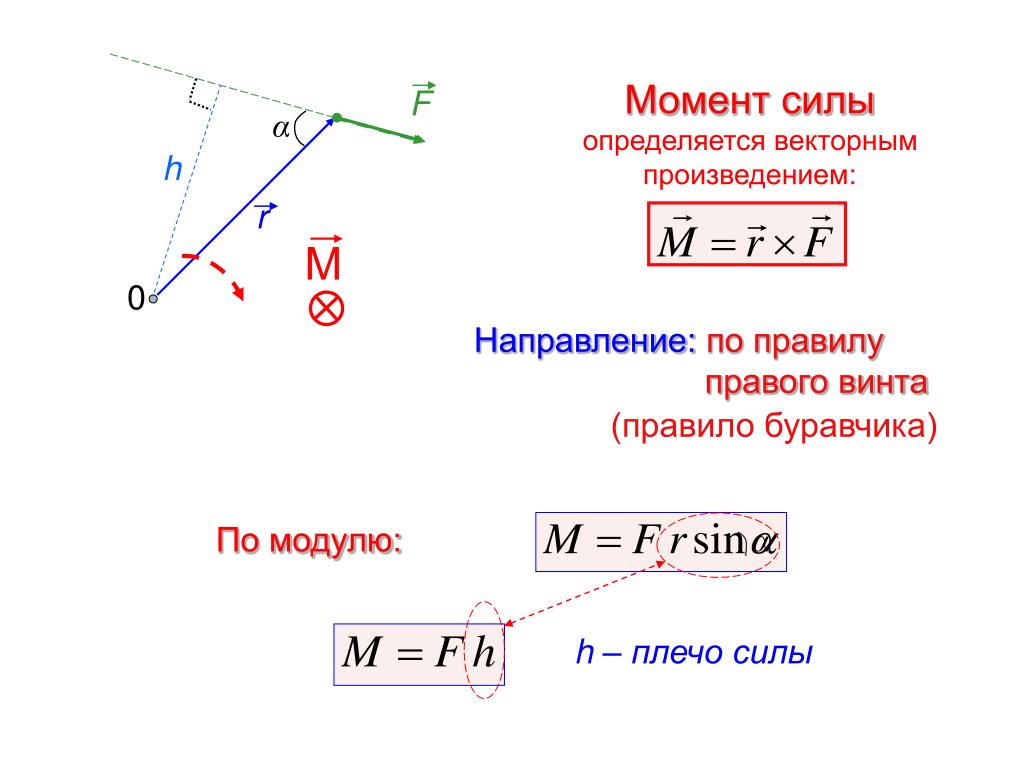 Чтобы система находилась в равновесии, необходимо подвесить тело весом 35 Н в точке 4,714 м от оси с другой стороны рычага.

Задача с движущимся диском

Решение следующей задачи основано на использовании формулы момента силы трения и кинетической энергии тела вращения. Задача: дан диск радиуса r = 0,3 метра, который вращается со скоростью ω = 1 рад/с. Необходимо рассчитать, какое расстояние способен он пройти по поверхности, если коэффициент трения качения равен μ = 0,001.

Эту задачу легче всего решить, если воспользоваться законом сохранения энергии. Мы располагаем начальной кинетической энергией диска. Когда он начнет катиться, то вся эта энергия расходуется на нагрев поверхности за счет действия силы трения. Приравнивая обе величины, получим выражение:

I * ω 2 /2 = μ * N/r * r * θ

Первая часть формулы — это кинетическая энергия диска. Вторая часть — это работа момента силы трения F = μ * N/r, приложенной к краю диска (M=F * r).

Учитывая, что N = m * g и I = 1/2m * r 2 , вычисляем θ:

θ = m * r 2 * ω 2 /(4 * μ * m * g) = r 2 * ω 2 /(4 * μ *g) = 0,3 2 * 1 2 /(4 * 0,001 * 9,81) = 2,29358 рад

Поскольку 2pi радиан соответствуют длине 2pi * r, тогда получаем, что искомое расстояние, которое пройдет диск, равно:

s = θ * r = 2,29358 * 0,3 = 0,688 м или около 69 см

Отметим, что на данный результат масса диска никак не влияет.

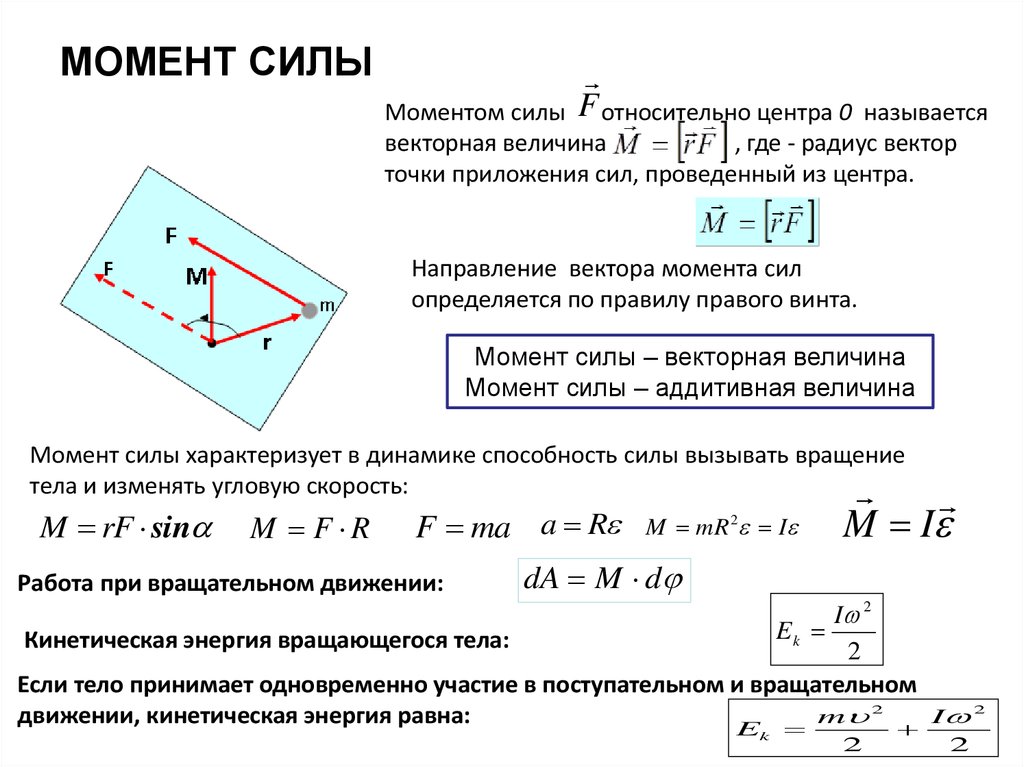
Моментом силы относительно оси вращения называется физическая величина, равная про­изведению силы на ее плечо.

Момент силы определяют по формуле:

М — FI , где F — сила, I — плечо силы.

Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела.

На рис. 1.33, а изображено твердое тело, способное вращаться вокруг оси. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой О. Пле­чом силы F здесь является расстояние 1Хот оси вращения до линии действия силы. Находят его следующим образом. Сначала проводят линию действия силы. Затем из точки О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, чтобы получить желаемый результат, т. е. один и тот же момент силы (см. (1.33)). Именно поэтому открыть дверь, толкая ее возле петель, гораздо труднее, чем берясь за ручку, а гайку отвернуть гораздо проще длинным, чем коротким гаечным ключом.

За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н м).

Правило моментов

Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки:

М1 = -М2 или F 1 ll = — F 2 l 2 .

Правило моментов является следствием одной из теорем механики, сформулированной фран­цузским ученым П. Вариньоном в 1687 г.

Если на тело действуют две равные и противоположно направленные силы, не лежащие на одной прямой, то такое тело не находится в равновесии, поскольку результирующий момент этих сил относительно любой оси не равен нулю, т. к. обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил.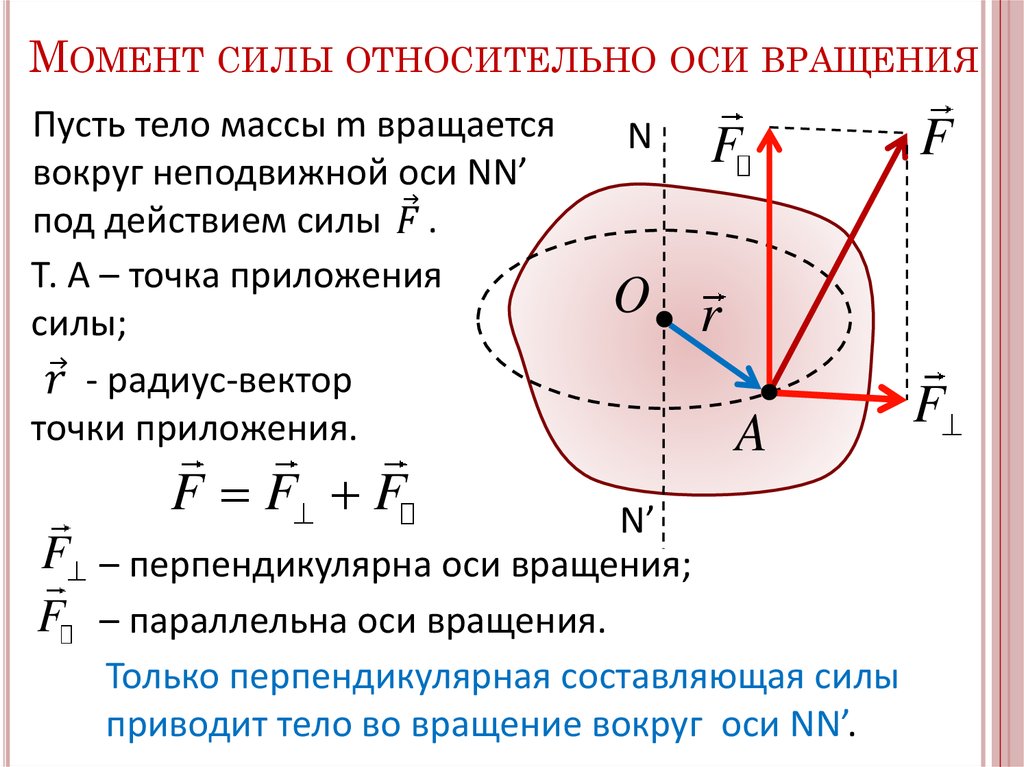 Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена ксвободному телу, то оно будет вращаться вокруг оси, проходящей через центр тяжести тела, рис. 1.33, б.

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары,независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары:

M = Fll + Fl2=F(l1 + l2) = Fl.

Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи­тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме­нить действием одной пары сил с тем же моментом.

Когда решают задачи на перемещение объектов, то в ряде случаев пренебрегают их пространственными размерами, вводя понятие материальной точки. Для другого типа задач, в которых рассматриваются покоящиеся или вращающиеся тела, важно знать их параметры и точки приложения внешних сил. В этом случае речь идет о моменте сил относительно оси вращения. Рассмотрим этот вопрос в статье.

Понятие о моменте силы

Перед тем как приводить относительно оси вращения неподвижной, необходимо пояснить, о каком явлении пойдет речь. Ниже дан рисунок, на котором изображен гаечный ключ длиной d, к концу его приложена сила F. Нетрудно представить, что результатом ее воздействия будет вращение ключа против часовой стрелки и откручивание гайки.

Согласно определению, момент силы относительно оси вращения представляет собой произведение плеча (d в данном случае) на силу (F), то есть можно записать следующее выражение: M = d*F. Сразу же следует оговориться, что приведенная формула записана в скалярном виде, то есть она позволяет рассчитать абсолютное значение момента M. Как видно из формулы, единицей измерения рассматриваемой величины являются ньютоны на метр (Н*м).

— векторная величина

Как выше было оговорено, момент M в действительности представляет собой вектор. Для пояснения этого утверждения рассмотрим другой рисунок.

Здесь мы видим рычаг длиной L, который закреплен на оси (показано стрелкой). К его концу приложена сила F под углом Φ. Нетрудно себе представить, что эта сила будет вызывать подъем рычага. Формула для момента в векторной форме в этом случае запишется так: M¯ = L¯*F¯, здесь черта над символом означает, что рассматриваемая величина — это вектор. Следует пояснить, что L¯ направлен от к точке приложения силы F¯.

Приведенное выражение является векторным произведением. Его результирующий вектор (M¯) будет направлен перпендикулярно плоскости, образованной L¯ и F¯. Для определения направления момента M¯ существуют несколько правил (правой руки, буравчика). Чтобы не заучивать их и не путаться в порядке умножения векторов L¯ и F¯ (от него зависит направление M¯), следует запомнить одну простую вещь: момент силы будет направлен таким образом, что если смотреть с конца его вектора, то воздействующая сила F¯ будет вращать рычаг против часовой стрелки. Это направление момента условно принято за положительное. Если же система совершает вращение по часовой стрелки, значит, результирующий момент сил имеет отрицательное значение.

Таким образом, в рассматриваемом случае с рычагом L величина M¯ направлена вверх (от рисунка к читателю).

В скалярной форме формула для момента запишется в виде: M = L*F*sin(180-Φ) или M = L*F*sin(Φ) (sin(180-Φ) = sin(Φ)). Согласно определению синуса, можно записать равенство: M = d*F, где d = L*sin(Φ) (см. рисунок и соответствующий прямоугольный треугольник). Последняя формула является аналогичной той, которая была приведена в предыдущем пункте.

Проведенные выше вычисления демонстрируют, как работать с векторными и скалярными величинами моментов сил, чтобы не допустить ошибок.

Физический смысл величины M¯

Поскольку два рассмотренных в предыдущих пунктах случая связаны с вращательным движением, то можно догадаться, какой смысл несет момент силы. Если сила, действующая на материальную точку, является мерой увеличения скорости линейного перемещения последней, то момент силы — это мера ее вращательной способности применительно к рассматриваемой системе.

Приведем наглядный пример. Любой человек открывает дверь, взявшись за ее ручку. Также это можно сделать, если толкнуть дверь в зоне ручки. Почему никто не открывает ее, толкая в области петель? Очень просто: чем ближе к петлям приложена сила, тем труднее открыть дверь, и наоборот. Вывод предыдущего предложения следует из формулы для момента (M = d*F), откуда видно, что при M = const величины d и F находятся в обратной зависимости.

Момент силы — аддитивная величина

Во всех рассмотренных выше случаях имела место лишь одна действующая сила. При решении же реальных задач дело обстоит гораздо сложнее. Обычно на системы, которые вращаются или находятся в равновесии, действуют несколько сил кручения, каждая из которых создает свой момент. В этом случае решение задач сводится к нахождению суммарного момента сил относительно оси вращения.

Суммарный момент находится путем обычной суммы отдельных моментов для каждой силы, однако, следует не забывать использовать правильный знак для каждого из них.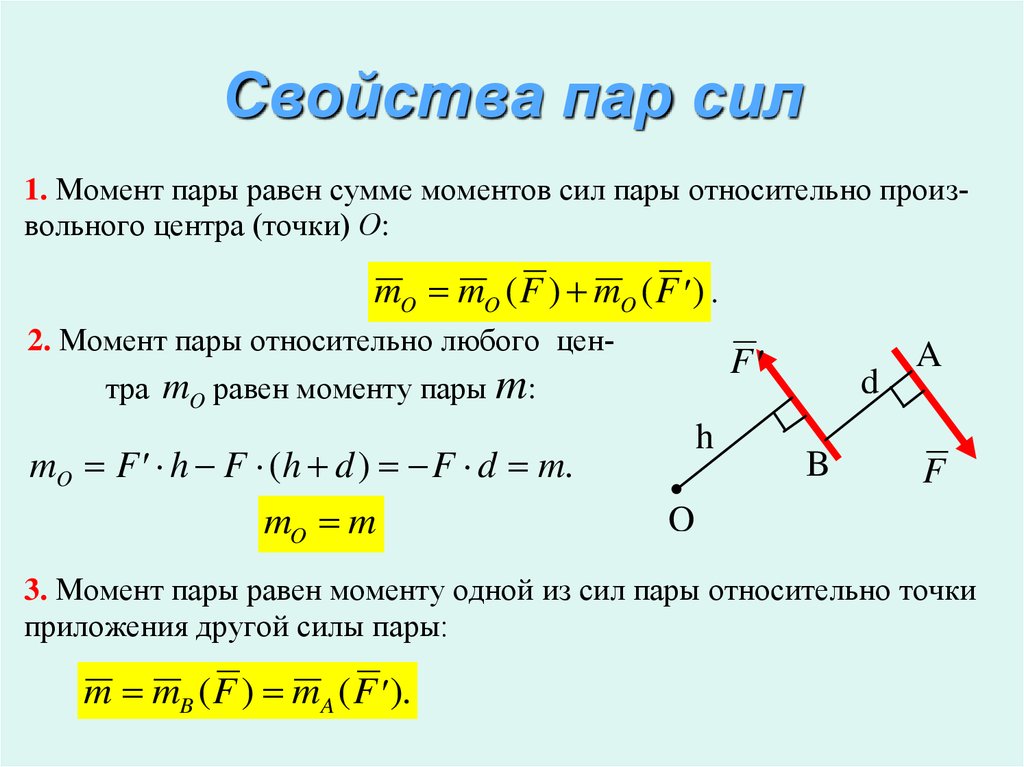

Пример решения задачи

Для закрепления полученных знаний предлагается решить следующую задачу: необходимо вычислить суммарный момент силы для системы, изображенной на рисунке ниже.

Мы видим, что на рычаг длиной 7 м действуют три силы (F1, F2, F3), причем они имеют разные точки приложения относительно оси вращения. Поскольку направление сил перпендикулярно рычагу, то нет необходимости применять векторное выражение для момента кручения. Можно рассчитать суммарный момент M, используя скалярную формулу и не забывая о постановке нужного знака. Поскольку силы F1 и F3 стремятся повернуть рычаг против часовой стрелки, а F2 — по часовой стрелке, то момент вращения для первых будет положительным, а для второй — отрицательным. Имеем: M = F1*7-F2*5+F3*3 = 140-50+75 = 165 Н*м. То есть суммарный момент является положительным и направлен вверх (на читателя).

Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.

Кинетические характеристики:

Вращение твердого тела, как целого характеризуется углом , измеряющегося в угловых градусах или радианах, угловой скоростью (измеряется в рад/с)и угловым ускорением(единица измерения — рад/с²).

При равномерном вращении (T оборотов в секунду):

Частота вращения — число оборотов тела в единицу времени.-

Период вращения — время одного полного оборота. Период вращения T и его частота связаны соотношением.

Линейная скорость точки, находящейся на расстоянии R от оси вращения

Угловая скорость вращения тела

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение. Момент импульса замкнутой системы сохраняется

Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

16.Уравнение динамики вращательного движения. Момент инерции.

Основное уравнение динамики вращательного движения материальной точки — угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции.

М = E*J или E = M/J

Сравнивая полученное выражение со вторым законом Ньютона с поступательным законом, видим, что момент инерции J является мерой инертности тела во вращательном движении. Как и масса величина аддитивная.

Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).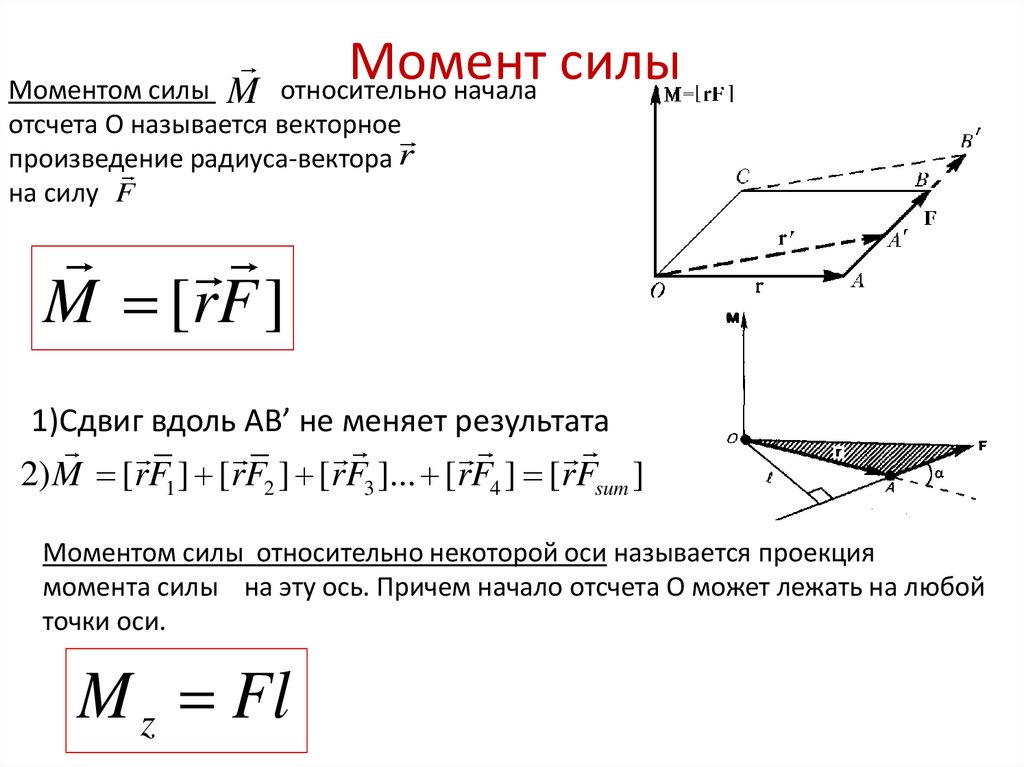

Единица измерения СИ: кг·м².Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.

Свойства момента инерции:

1.Момент инерции системы равен сумме момента инерции её частей.

2.Момент инерции тела является величиной, иманентно присущей этому телу.

Момент инерции твердого тела — это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.

Формула момента инерции:

Теорема Штейнера:

Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R — расстояние между осями.

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

Центральный момент инерции (или момент инерции относительно точки O) — это величина

.

Момент сил. Применение рычагов.

Курсы для учителей от 600 ₽ (36 часов). Документы об окончании по почте БЕСПЛАТНО, комфортное обучение из дома

 

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Тест по физике для 7 класса на тему «Момент сил. Применение рычагов.»

Вопрос 1

Моментом силы называют:

Варианты ответов

• произведение модуля силы, действующей на тело, на пройденное ее точкой приложения расстояние.
• произведение модуля силы, поворачивающей тело, на ее плечо.
• произведение модуля силы, вращающей тело, на время ее действия.
• произведение веса силы, под действием которого поворачивается рычаг, на его плечо.

Вопрос 2

Момент силы равен

Варианты ответов

• Fs
• Pl
• Ft
• Fl

Вопрос 3

Каковы моменты сил, действующих на рычаг № 1? На рычаг № 2?

Варианты ответов

• 1
• 2
• 3
• 4

Вопрос 4

От каких величин зависит момент силы?

Варианты ответов

• Только от модуля силы: чем он больше, тем больше момент силы.
• От модуля силы и ее плеча, чем они больше, тем больше момент силы.
• Только от плеча силы, чем оно длиннее, тем больше момент силы.

Вопрос 5

В каких единицах измеряют момент силы?

Варианты ответов

• Н*м
• Дж
• Вт
• Дж/с

Вопрос 6

Какие формулы моментов сил соответствуют условию равновесия рычага?

Варианты ответов

• 1
• 2
• 3
• 4

Вопрос 7

Рычаг под действием сил F₁ = 3Н и F₂ =9Н находится в равновесии. Сравните моменты этих сил.

Варианты ответов

• Момент второй силы больше момента первой
• Моменты этих сил равны
• Момент второй силы меньше момента первой
• Сравнить моменты этих сил нельзя, т.к. неизвестны их плечи

Вопрос 8

Вычислите моменты сил F₁ = 35Н и F₂ = 70Н, если плечо первой силы l₁ = 1м. Рычаг под действием этих сил находится в равновесии.

Варианты ответов

• 1
• 2
• 3
• 4

Вопрос 9

Силы, модули которых F₁ = 8Н и F₂ = 40Н, уравновешены на рычаге.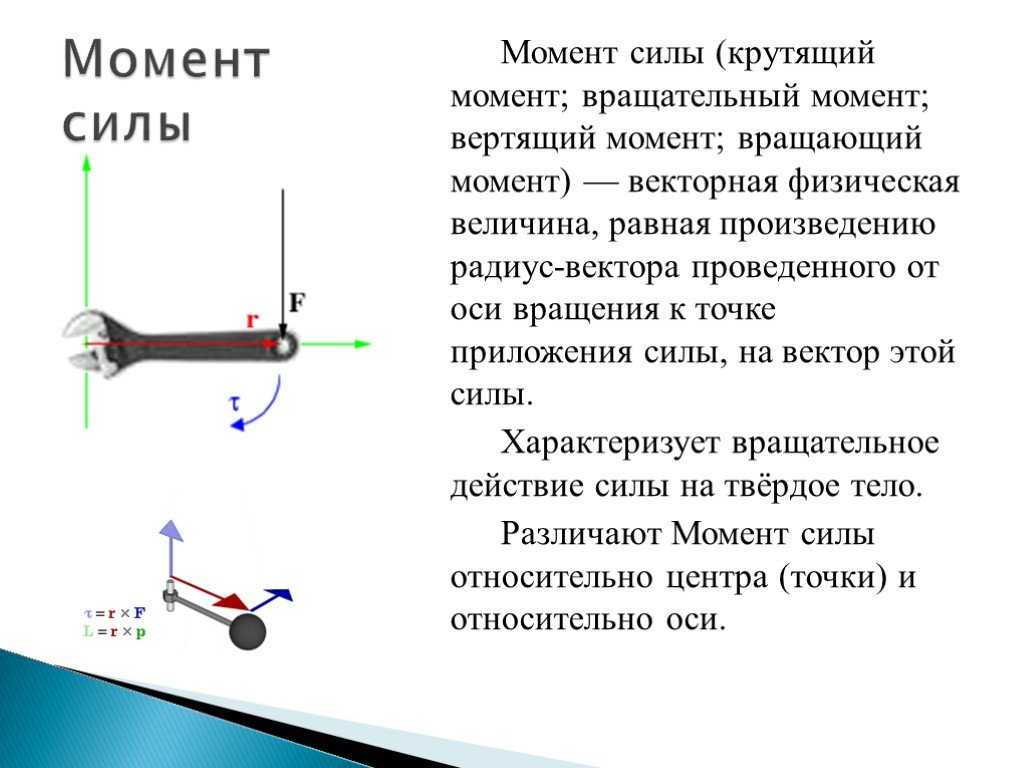 При этом их моментыравны 20 Нм. Каковы плечи этих сил?

Варианты ответов

• 1
• 2
• 3
• 4

Вопрос 10

В каких случаях применяют рычаги? Как часто это делают?

Варианты ответов

• Когда надо получить выигрыш в силе; очень часто.
• В случае необходимости выиграть в расстоянии; очень часто.
• Когда хотят получить выигрыш и в силе, и в расстоянии; это невозможно.
• Все ответы верные.

Вопрос 11

На каком из рисунков изображены устройства, действие которых основано на применении рычагов?

Варианты ответов

• 1
• 2
• 3
• 4

Пройти тест

Сохранить у себя:

© 2021, Царёва Светлана Геннадьевна  297

Момент силы буква.

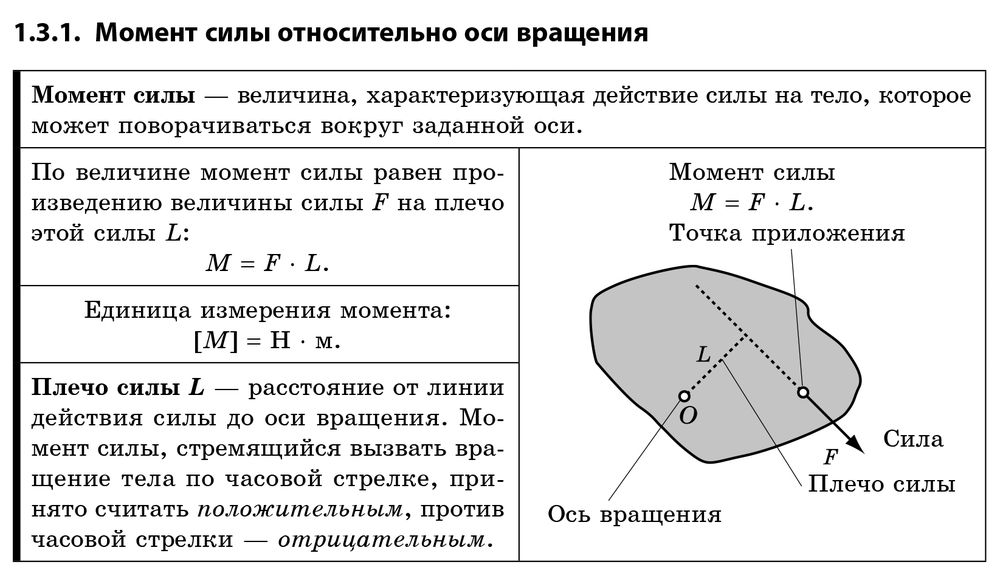Момент силы. Использование силы и плеча момента

Моментом силы относительно оси вращения называется физическая величина, равная про­изведению силы на ее плечо.

Момент силы определяют по формуле:

М — FI , где F — сила, I — плечо силы.

Плечом силы называется кратчайшее расстояние от линии действия силы до оси вращения тела.

На рис. 1.33, а изображено твердое тело, способное вращаться вокруг оси. Ось вращения этого тела перпендикулярна плоскости рисунка и проходит через точку, обозначенную буквой О. Пле­чом силы F здесь является расстояние 1Хот оси вращения до линии действия силы. Находят его следующим образом. Сначала проводят линию действия силы. Затем из точки О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра является плечом данной силы.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу надо приложить, чтобы получить желаемый результат, т.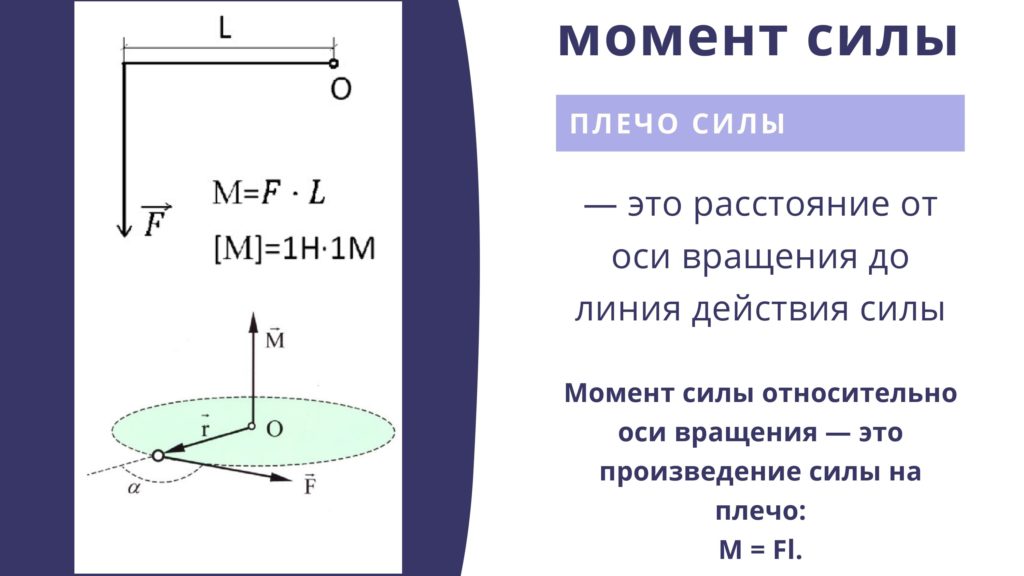 е. один и тот же момент силы (см. (1.33)). Именно поэтому открыть дверь, толкая ее возле петель, гораздо труднее, чем берясь за ручку, а гайку отвернуть гораздо проще длинным, чем коротким гаечным ключом.

За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н м).

Правило моментов

Твердое тело, способное вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М, вращающей его по часовой стрелке, равен моменту силы М2, вращающей его против часовой стрелки:

М1 = -М2 или F 1 ll = — F 2 l 2 .

Правило моментов является следствием одной из теорем механики, сформулированной фран­цузским ученым П. Вариньоном в 1687 г.

Если на тело действуют две равные и противоположно направленные силы, не лежащие на одной прямой, то такое тело не находится в равновесии, поскольку результирующий момент этих сил относительно любой оси не равен нулю, т. к. обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил.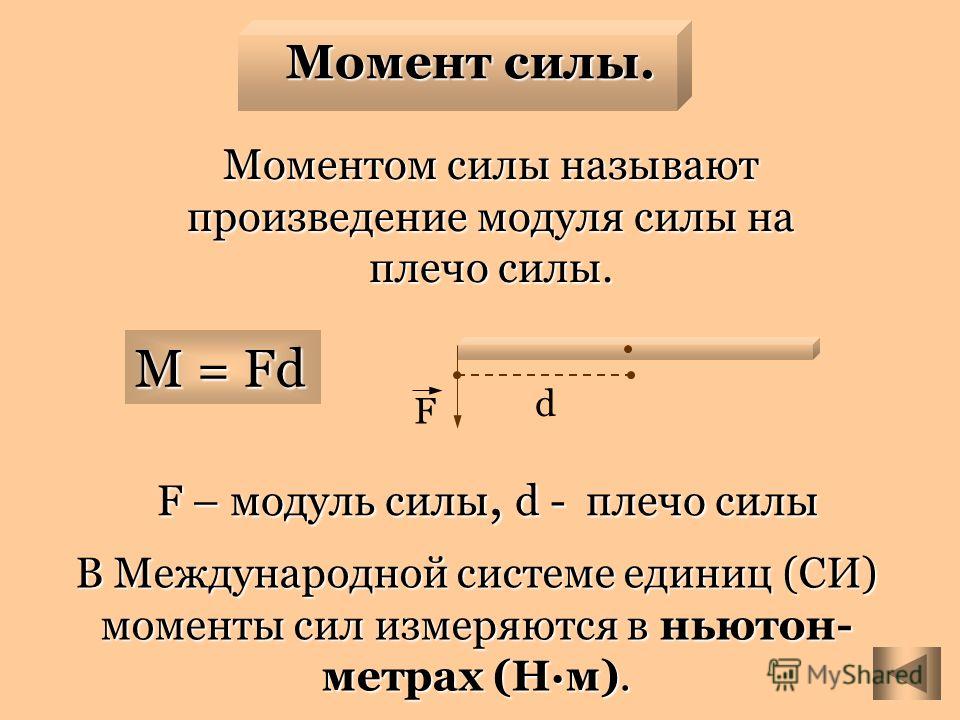 Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена ксвободному телу, то оно будет вращаться вокруг оси, проходящей через центр тяжести тела, рис. 1.33, б.

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние I между силами, которое называется плечом пары,независимо от того, на какие отрезки и /2 разделяет положение оси плечо пары:

M = Fll + Fl2=F(l1 + l2) = Fl.

Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи­тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме­нить действием одной пары сил с тем же моментом.

Момент силы относительно оси или просто момент силы называется проекция силы на прямую, которая перпендикулярна радиусу и проведена в точке приложения силы умноженная на расстояние от этой точки до оси. Либо произведение силы на плечо ее приложения. Плечо в данном случае это расстояние от оси до точки приложения силы. Момент силы характеризует вращательное действие силы на тело. Ось в данном случае это место крепления тела, относительно которого оно может совершать вращение. Если тело не закреплено, то осью вращения можно считать центр масс.

Формула 1 — Момент силы.

F — Сила действующая на тело.

r — Плечо силы.

Рисунок 1 — Момент силы.

Как видно из рисунка, плечо силы это расстояние от оси до точки приложения силы. Но это в случае если угол между ними равен 90 градусов. Если это не так, то необходимо вдоль действия силы провести линию и из оси опустить на нее перпендикуляр. Длинна этого перпендикуляра и будет равна плечу силы. А перемещение точки приложения силы вдоль направления силы не меняет ее момента.

Принято считать положительным такой момент силы, который вызывает поворот тела по часовой стрелки относительно точки наблюдения. А отрицательным соответственно вызывающий вращение против нее. Измеряется момент силы в Ньютонах на метр. Один Ньютонометр это сила в 1 Ньютон действующая на плечо в 1 метр.

Если сила, действующая на тело, проходит вдоль лини идущей через ось вращения тела, или центр масс, если тело не имеет оси вращения. То момент силы в этом случае будет равен нулю. Так как эта сила не будет вызывать вращения тела, а попросту будет перемещать его поступательно вдоль лини приложения.

Рисунок 2 — Момент силы равен нулю.

В случае если на тело действует несколько сил, то момент силы будет определять их равнодействующая. К примеру, на тело могут действовать две силы равные по модулю и направленные противоположно. При этом суммарный момент силы будет равен нулю. Так как эти силы будут компенсировать друг друга. Если по простому, то представьте себе детскую карусель. Если один мальчик ее толкает по часовой стрелке, а другой с той же силой против, то карусель останется неподвижной.

Определение 1

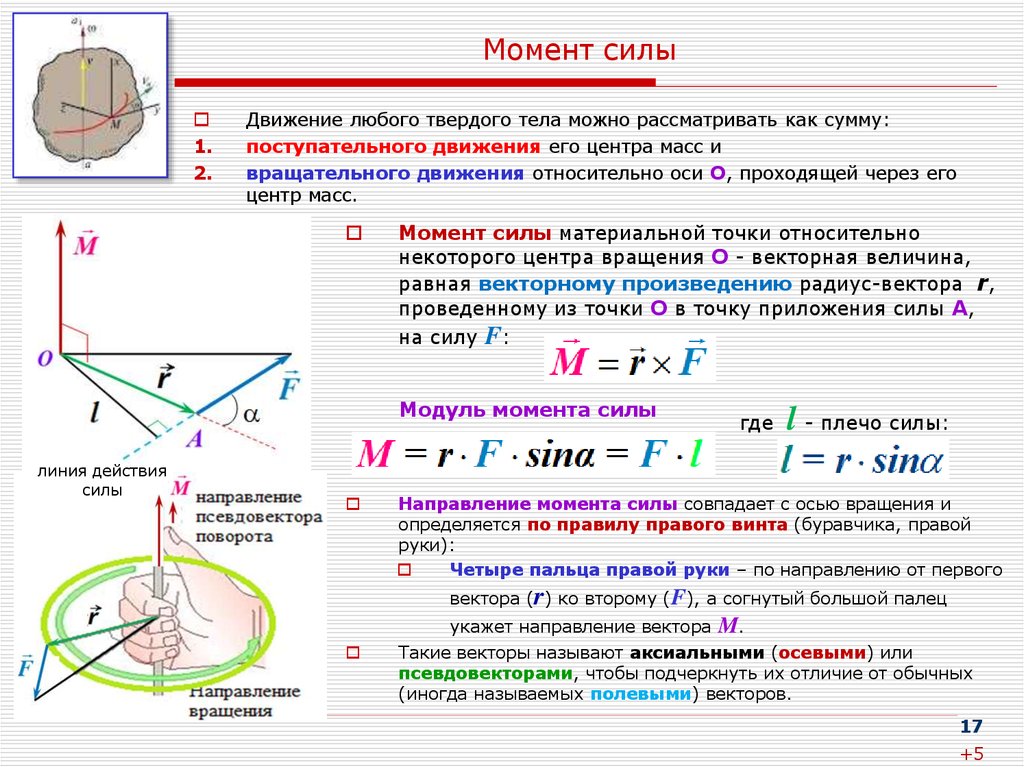
Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.

Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.

Момент силы выступает характеристикой вращательного воздействия силы на твердое тело. Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.

В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).

Понятие момента силы

Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.

Замечание 1

В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.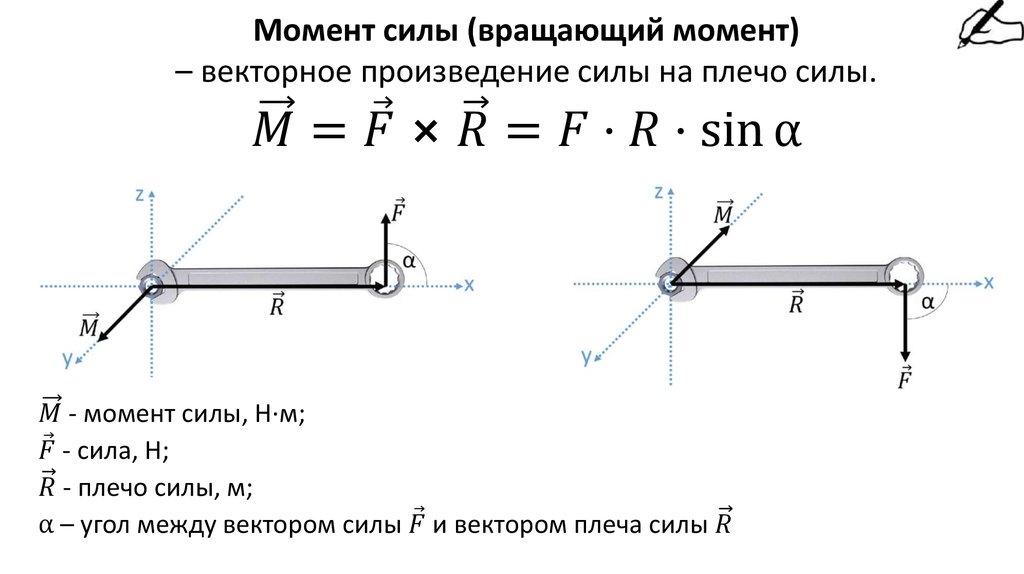

К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:

$\vec {M}=\vec{r}\vec{F}$, где:

• $\vec {F}$ представляет силу, воздействующая на частицу,
• $\vec {r}$ является радиусом вектора частицы.

В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:

$E = M\theta $, где:

• $E$ представляет энергию;
• $M$ считается вращающимся моментом;
• $\theta $ будет углом в радианах.

Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.

Формулы расчета момента силы

Интересным в физике является вычисление момента силы в поле, производимого по формуле:

$\vec{M} = \vec{M_1}\vec{F}$, где:

• $\vec{M_1}$ считается моментом рычага;
• $\vec{F}$ представляет величину действующей силы.

Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину. При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:

$\vec{T}=\vec{r}\vec{F}$

При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.

$P = \vec {M}\omega $

В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы- в ньютон-метрах.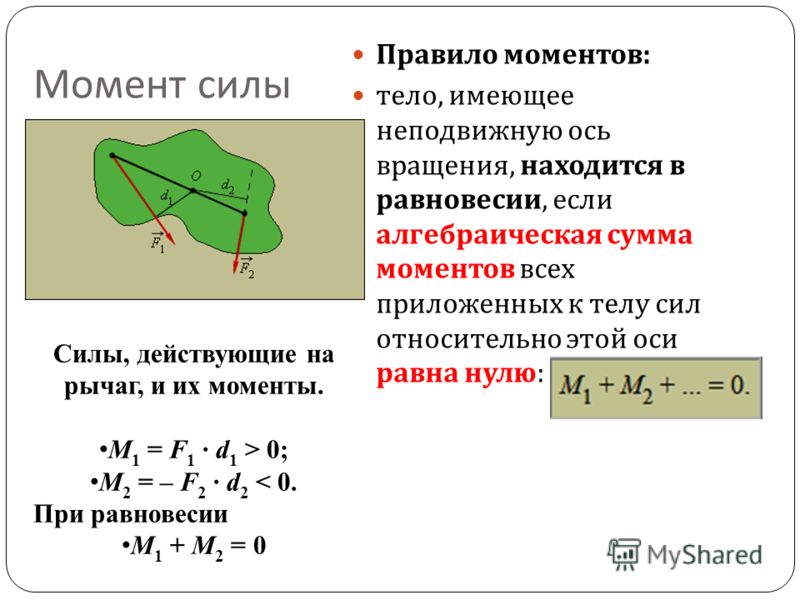 При этом угловая скорость определяется в радианах в секунду.

Момент нескольких сил

Замечание 2

При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия. Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).

В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.

Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.

$M={FL_1+FL-2} = F{L_1+L_2}=FL$

В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.

Часто мы слышим выражения: «он инертный», «двигаться по инерции», «момент инерции». В переносном значении слово «инерция» может трактоваться как отсутствие инициативы и действий. Нас же интересует прямое значение.

Что такое инерция

Согласно определению инерция в физике – это способность тел сохранять состояние покоя или движения в отсутствие действия внешних сил.

Если с самим понятием инерции все понятно на интуитивном уровне, то момент инерции – отдельный вопрос. Согласитесь, сложно представить в уме, что это такое. В этой статье Вы научитесь решать базовые задачи на тему «Момент инерции» .

Определение момента инерции

Из школьного курса известно, что масса – мера инертности тела .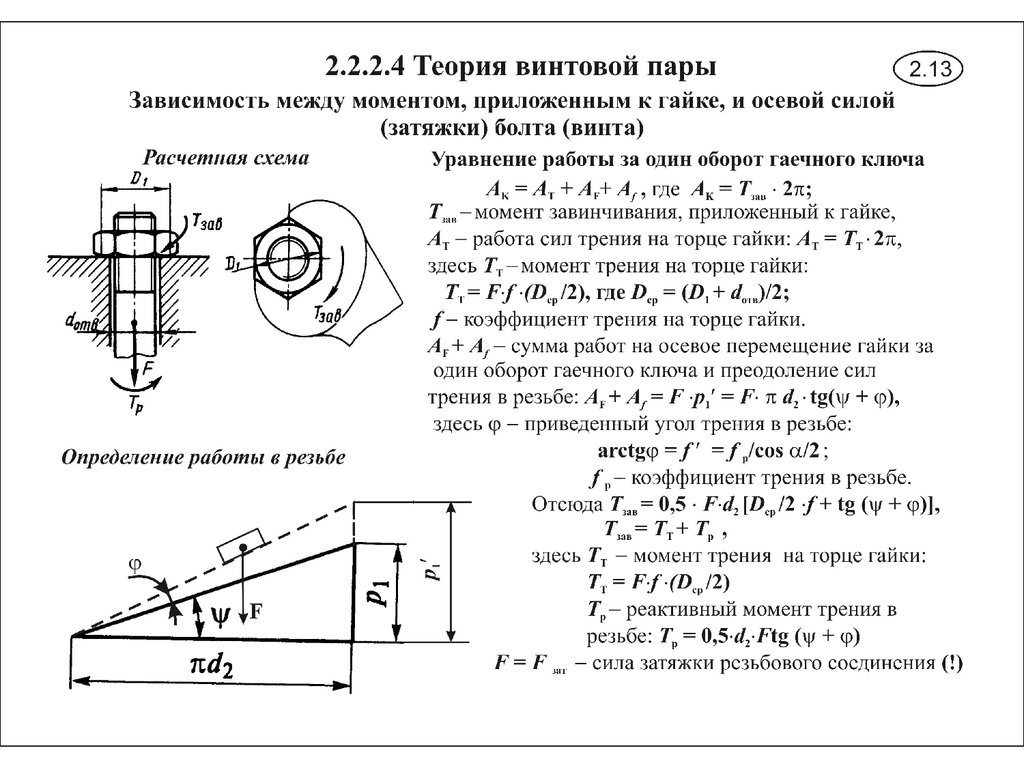 Если мы толкнем две тележки разной массы, то остановить сложнее будет ту, которая тяжелее. То есть чем больше масса, тем большее внешнее воздействие необходимо, чтобы изменить движение тела. Рассмотренное относится к поступательному движению, когда тележка из примера движется по прямой.

По аналогии с массой и поступательным движением момент инерции – это мера инертности тела при вращательном движении вокруг оси.

Момент инерции – скалярная физическая величина, мера инертности тела при вращении вокруг оси. Обозначается буквой J и в системе СИ измеряется в килограммах, умноженных на квадратный метр.

Как посчитать момент инерции? Есть общая формула, по которой в физике вычисляется момент инерции любого тела. Если тело разбить на бесконечно малые кусочки массой dm , то момент инерции будет равен сумме произведений этих элементарных масс на квадрат расстояния до оси вращения.

Это общая формула для момента инерции в физике. Для материальной точки массы m , вращающейся вокруг оси на расстоянии r от нее, данная формула принимает вид:

Теорема Штейнера

От чего зависит момент инерции? От массы, положения оси вращения, формы и размеров тела.

Теорема Гюйгенса-Штейнера – очень важная теорема, которую часто используют при решении задач.

Кстати! Для наших читателей сейчас действует скидка 10% на

Теорема Гюйгенса-Штейнера гласит:

Момент инерции тела относительно произвольной оси равняется сумме момента инерции тела относительно оси, проходящей через центр масс параллельно произвольной оси и произведения массы тела на квадрат расстояния между осями.

Для тех, кто не хочет постоянно интегрировать при решении задач на нахождение момента инерции, приведем рисунок с указанием моментов инерции некоторых однородных тел, которые часто встречаются в задачах:

Пример решения задачи на нахождение момента инерции

Рассмотрим два примера. Первая задача – на нахождение момента инерции. Вторая задача – на использование теоремы Гюйгенса-Штейнера.

Задача 1. Найти момент инерции однородного диска массы m и радиуса R. Ось вращения проходит через центр диска.

Решение:

Разобьем диск на бесконечно тонкие кольца, радиус которых меняется от 0 до R и рассмотрим одно такое кольцо. Пусть его радиус – r , а масса – dm . Тогда момент инерции кольца:

Массу кольца можно представить в виде:

Здесь dz – высота кольца. Подставим массу в формулу для момента инерции и проинтегрируем:

В итоге получилась формула для момента инерции абсолютного тонкого диска или цилиндра.

Задача 2. Пусть опять есть диск массы m и радиуса R. Теперь нужно найти момент инерции диска относительно оси, проходящей через середину одного из его радиусов.

Решение:

Момент инерции диска относительно оси, проходящей через центр масс, известен из предыдущей задачи.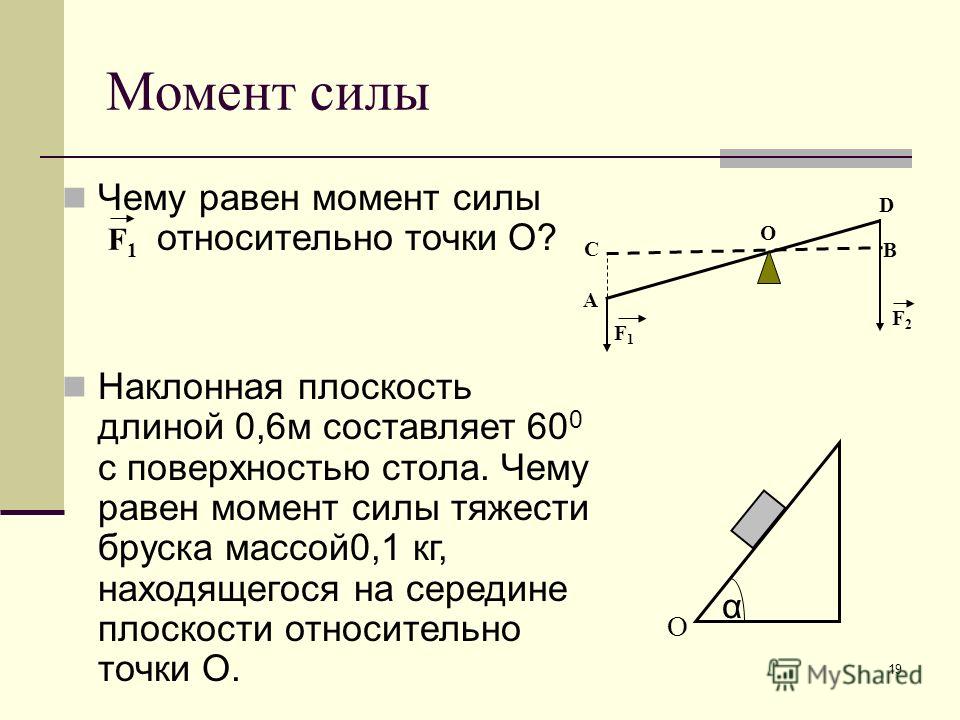 Применим теорему Штейнера и найдем:

Кстати, в нашем блоге Вы можете найти и другие полезные материалы по физике и .

Надеемся, что Вы найдете в статье что-то полезное для себя. Если в процессе расчета тензора инерции возникают трудности, не забывайте о студенческом сервисе . Наши специалисты проконсультируют по любому вопросу и помогут решить задачу в считанные минуты.

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью

Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.

Момент силы относительно оси равен 0 в двух случаях:

Если сила параллельна оси

Если сила пересекает ось

Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.

27. Связь между моментом силы относительно оси и векторным моментом силы относительно точки.

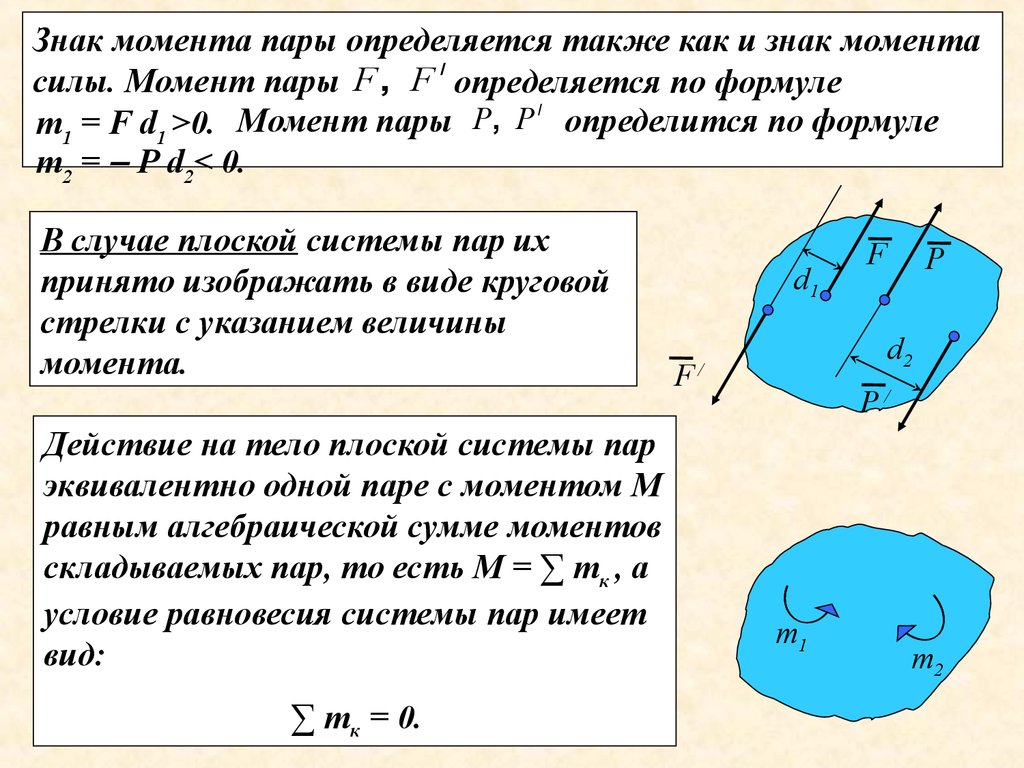
Mz(F)=Mo(F)*cosαМомент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.

28. Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил.

Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

Главным вектором системы сил называется вектор R , равный векторной сумме этих сил:

R = F 1 + F 2 + … + F n = F i .

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L O , равный сумме векторных моментов этих сил относительно точки О:

L O = M O (F 1) + M O (F 2) + . .. + M O (F n) = M O (F i).

Вектор R не зависит от выбора центра О, а вектор L O при изменении положения центра О может в общем случае изменяться.

Теорема Пуансо: Произвольную пространственную систему сил можно заменить одной силой главным вектором системы сил и парой сил с главным моментом не нарушая состояния твердого тела. Главный вектор представляет собой геометрическую сумму всех сил действующих на твердое тело и расположен в плоскости действия сил. Главный вектор рассматривается через его проекции на оси координат.

Чтобы привести силы к заданному центру приложенному в некоторой точке твердого тела необходимо: 1) перенести параллельно силу самой себе к заданному центру не изменяя модуля силы; 2) в заданном центре приложить пару сил, векторный момент которой равен векторному моменту перенесенной силы относительного нового центра, эту пару называют присоединенной парой.

Зависимость главного момента от выбора центра приведения. Главный момент относительно нового центра приведения равен геометрической сумме главного момента относительно старого центра приведения и векторного произведения радиуса-вектора, соединяющего новый центр приведения со старым, на главный вектор.

29 Частные случаи приведения пространственной системы сил

	Значения главного вектора и главного момента	Результат приведения
		Система сил приводится к паре сил, момент которой равен главному моменту (главный момент системы сил не зависит от выбора центра приведения О).
		Система сил приводится к равнодействующей, равной , проходящей через центр О.
		Система сил приводится к равнодействующей , равной главному векторуи параллельной ему и отстоит от него на расстоянии. Положение линии действия равнодействующей должно быть таким, чтобы направление ее момента относительно центра приведения О совпадало с направлениемотносительно центра О.
	, причем векторы ине перпендикулярны	Система сил приводится к динаме (силовому винту) – совокупности силы и пары сил, лежащей в плоскости, перпендикулярной к этой силе.
		Система сил, приложенных к твердому телу, является уравновешивающейся.

30. Приведение к динаме. Динамой в механике называют такую совокупность силыи пары сил () действующих на твердое тело, у которой сила перпендикулярна плоскости действия пары сил. Используя векторный моментпары сил, можно также определить динаму как совокупность силы и пары, у которы сила параллельна векторному моменту пары сил.

Уравнение центральной винтовой оси Предположим, что в центре приведения, принятом за начало координат, получены главный вектор с проекциями на оси координат и главный момент с проекциями При приведении системы сил к центру приведения О 1 (рис. 30) получается динама с главным вектором и главным моментом , Векторы и как образующие линаму. параллельны и поэтому могут отличаться только скалярным множителем k 0. Имеем, так как .Главные моменты и , удовлетворяют соотношению

Q7 Укажите два фактора, влияющих на момент силы…

Перейти к

• Объективные вопросы
• Вопросы с короткими/длинными ответами
• Числа

• Иметь значение
• Физические величины и измерения
• Сила и давление
• Энергия
• Световая энергия
• Теплопередача
• Звук
• Электричество

Главная > Селина Солюшнс Класс 8 Физика > Глава 3 — Сила и давление > Упражнение: Вопросы с короткими/длинными ответами > Вопрос 7

Вопрос 7 Вопросы с короткими/длинными ответами

Q7) Укажите два фактора, влияющих на момент силы.

Ответ:

Решение:

Факторы, от которых зависит момент силы:

(i) Величина приложенной силы.

(ii) Расстояние линии действия силы от оси вращения.

Стенограмма видео

здравствуйте, добро пожаловать в комнату, меня зовут нирасана, сегодня мы собираемся проверить, образуют ли следующие величины пропорцию или нет, поэтому здесь у нас есть уравнения Пи, поэтому нужно ли нам проверить, что это собираемся составить пропорцию или нет, первый вопрос 3x7x 24 и 56, поэтому, когда вы проверите это здесь, просто 3x 3x в 56 равно 7x в 24, да, тогда 168x равно 168x, поэтому правая сторона — это левая равна правая сторона будет сформируйте пропорцию теперь ладно эта пропорциональная форма проверьте для второй это первая проверьте вторую таким же образом ноль целых восемь целых девять равно двум целых четыре четверти это также образует семь целых две десятых равно семи целых десятых давайте просто уравняем хранение это также проверка пропорции формулы с третьим так же, как третий дается ну да, так что один на два в 93 на 4 равно 3 1 на 4 в 4 1 на 2. Теперь, если вы проверите это, получится пропорция 1 1 на 1 1 7 на восемь равно 1 1 7 по выходу, это также из пропорции, которую вы теперь можно также проверить четвертый и пятый позвольте мне сделать вы можете сделать здесь да проверить четвертый один здесь таким же образом 0,4 в 3,5 равно ноль целых пять десятых в две целых девять десятых будет одна целых четыре десятых ноль будет равна одной целых четыре десятых нулевая пропорция образуется для четвертого также если вы проверяете для пятого 5 на 2 в 6.0 равно 11 на 2 в 3.0 равно 30 на 2 равно 30 на 2 это тоже формирует операцию пятый тоже так Я надеюсь, вы поняли это видео, нам нужно проверить, что левая сторона равна правой во всех случаях, тогда она сформирует пропорцию, спасибо за просмотр этого видео, если у вас есть какие-либо вопросы, вы можете задать их в разделе комментариев

Связанные вопросы

Q1) Дайте определение силы. Укажите его единицу СИ.

Q2) Назовите два действия силы, приложенной к телу.

В3) Чем отличается действие силы, когда она приложена к (а) твердому телу (б) нетвердому телу?

Q4) Укажите действие силы F на следующей диаграмме.

Q5) Дайте определение термину «момент силы».

Q6) Укажите единицу измерения момента силы в системе СИ.

Фейсбук WhatsApp

Копировать ссылку

Было ли это полезно?

Exercises

Objective Questions

Short/Long Answer Questions

Numericals

Chapters

Matter

Physical Quantities and Measurement

Force and Pressure

Energy

Light Energy

Heat Transfer

Sound

Электричество

Курсы

Быстрые ссылки

Условия и политика

Условия и политика

2022 © Quality Tutorials Pvt Ltd.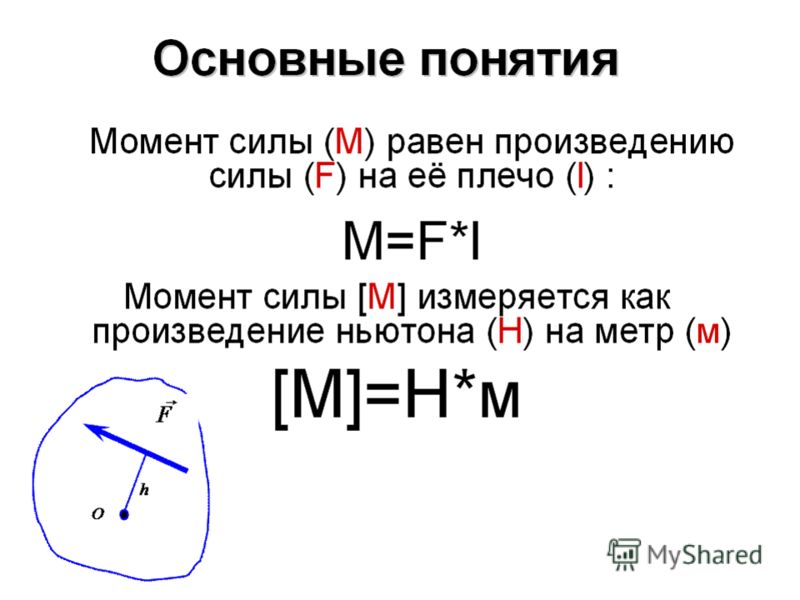 Все права защищены.

Ньютоновская механика. Почему момент зависит от расстояния от точки вращения до силы?

$\begingroup$

Формула для момента:

$$M = Fd$$

Где F — сила, приложенная к объекту, а d — расстояние по перпендикуляру от точки вращения до линии действия силы.

Почему? Интуитивно понятно, что момент зависит от силы, поскольку сила «увеличивает интенсивность». Но почему расстояние? Почему расстояние от линии действия силы до точки напряженности влияет на момент?

Я НЕ ищу вывод приведенной выше формулы из формулы перекрестного произведения, я ищу интуицию. Я понимаю, как, когда я поворачиваю ключ, если ключ короче, его труднее поворачивать, но я не понимаю, ПОЧЕМУ.

Спасибо.

• ньютоновская механика
• классическая механика
• крутящий момент
• статика

$\endgroup$

$\begingroup$

Почему?

Поскольку момент — это проявление силы на расстоянии, точно так же скорость — это проявление вращения на расстоянии.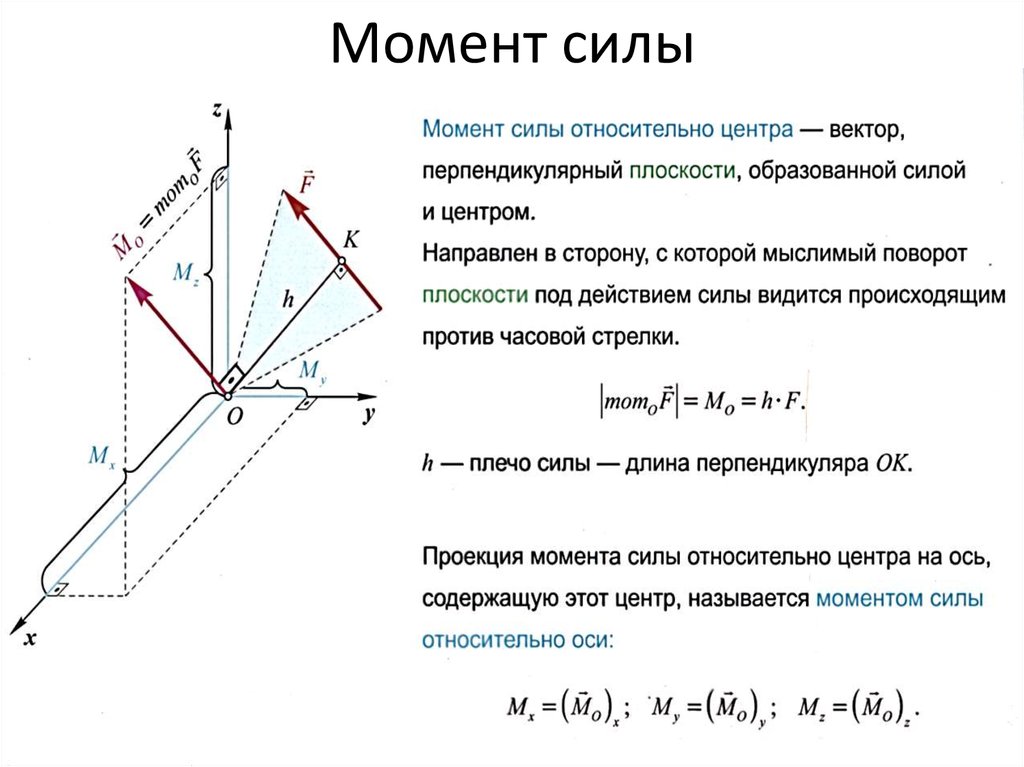 Учитывая два очка A и B вы это знаете $$ \vec{M}_A = \vec{r}_{AB} \times \vec{F}_B \\ \vec{v}_A = \vec{r}_{AB} \times \vec{\omega}_B $$

Сила в B вызывает крутящий момент в A , аналогично тому, как вращение в B вызывает скорость в A .

Так почему же?

И силы/моменты, и скорости/вращения являются трехмерными винтами, обладающими следующими свойствами. а) линия направления, б) амплитуда, в) шаг. Забудьте пока о b) и c) и сосредоточьтесь на линии.

Как описать линию в 3D. Линия имеет 4 степени свободы и обычно представляется с помощью 6 компонентов с так называемыми координатами Плюкера. Здесь участвуют два вектора, каждый из которых имеет 3 компонента. Первый вектор, который я называю $\vec{F}$, задает направление прямой линии, но его величина не важна. Таким образом, от вектора используются две степени свободы. Второй вектор, который я называю $\vec{M}$, дает момент линии относительно начала координат и используется для описания ближайшей точки линии к началу координат. Он тоже использует две степени свободы, потому что точка по линии неважно. Он представляет собой либо а) момент силы вдоль линии, либо б) скорость тела, вращающегося вокруг линии. Расположение линии определяется как

$$ \vec{r} = \frac{\vec{F} \times \vec{M}}{\vec{F} \cdot \vec{F}} = — \frac{\vec{M} \times \vec{F}}{\vec{F} \cdot \vec{F}} $$ в зависимости от того, что вам больше нравится.

Аналогично для движений

$$ \vec{r} = \frac{\vec{\omega} \times \vec{v}}{\vec{\omega} \cdot \vec{\omega}} = — \frac{\vec{v} \times \vec{\omega}}{\vec{\omega} \cdot \vec{\omega}} $$.

Итак, момент есть проявление линии на расстоянии.

$\endgroup$

2

$\begingroup$

Я понимаю, как когда я поворачиваю ключ, если ключ короче, его труднее поворачивать, но я не понимаю, ПОЧЕМУ.

Предположим, что болт можно открутить за один оборот, и на этот процесс расходуется $E$ джоулей. Тогда, поскольку $w=F d$, имеем $$E=2\pi rF.$$ Таким образом $$F=\frac{E}{2\pi r}.$$ Вот почему открутить болт с помощью короткого ключа сложнее. Вам нужно нажимать сильнее. Отвечает ли это на ваш вопрос?

$\endgroup$

$\begingroup$

Причина, по которой крутящий момент (сила вращения) зависит от расстояния $d$ от точки вращения (т. е. почему крутящий момент является моментом), заключается в следующем:

Крутящий момент определяется как изменение углового момента; если масса постоянна, это означает изменение угловой скорости.

Чтобы добиться изменения угловой скорости с помощью тангенциальной силы $F$, нам нужно пройти большее расстояние, когда мы находимся дальше от центра. Или другими словами, сила $F$ изменяет только линейную скорость; для достижения изменения угловой скорости требуется тем больше, чем дальше мы находимся.

$\endgroup$

1

$\begingroup$

Лучшим определением крутящего момента (или момента) является работа на единицу угла поворота (в джоулях на радиан), которую может совершить сила, действующая таким образом, что стремится вызвать вращение. Это означает, что вам нужна составляющая силы, действующей вдоль дуги, умноженная на длину дуги, деленная на угол (в радианах). Но длина дуги s = rθ, а s/θ = r. Таким образом, вы в конечном итоге умножаете составляющую силы на радиус.

$\endgroup$

$\begingroup$

Интуитивно понятно, что крутящий момент — это количество «крутящего момента», которое вы можете придать чему-либо. Принцип, который вы упомянули, основан на том, как работает гаечный ключ: он увеличивает $r$ от вашей руки и всего, что вы пытаетесь свернуть, например. болт — и таким образом увеличивает крутящий момент.

Или, наоборот, если бы нам дали набор гаечных ключей и сказали попробовать с их помощью открутить различные болты, мы бы заметили, что длинные гаечные ключи крутят болт легче, чем короткие, а если взять длинный гаечный ключ и использовать его с вашей рукой близко к болту, это было бы не так просто. Таким образом, если бы нам затем поручили разработать меру силы поворота болта, которую можно проявить при использовании данного гаечного ключа, необходимо принять во внимание как прямую приложенную силу, так и и также длина ключа.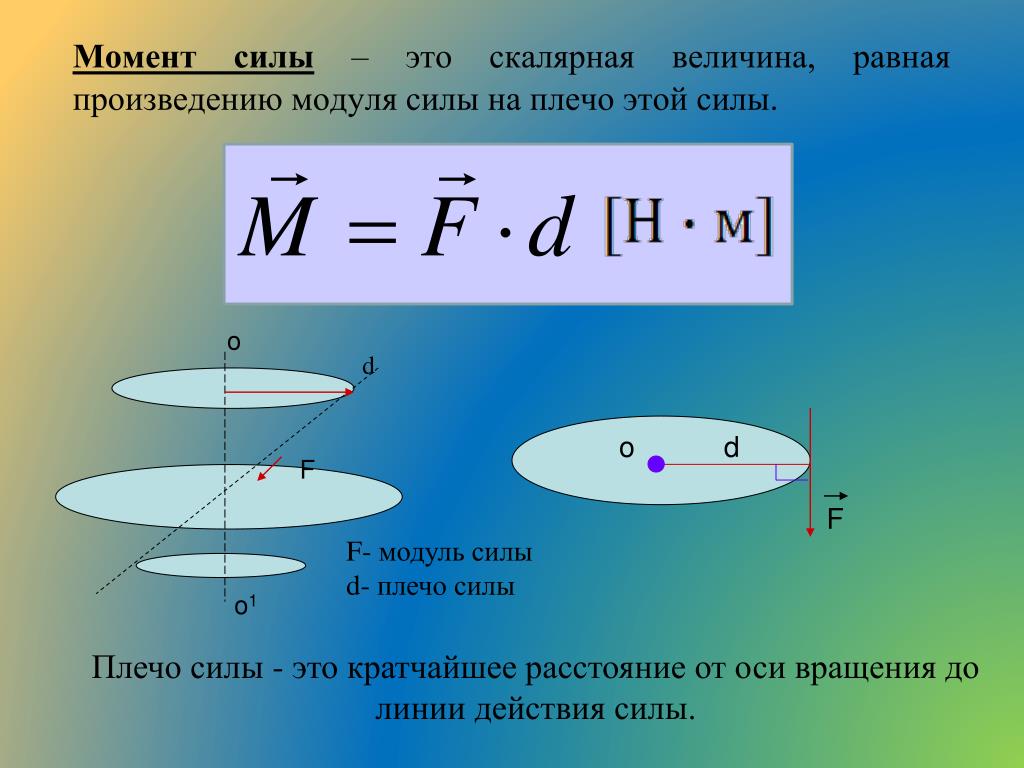

Таким образом, математическое выражение просто уточняет это, описывая точную форму зависимости. (Кроме того, синусоидальная часть, опущенная в выражении, приведенном в OP, фактически просто отражает, что это 90 143 перпендикулярная 90 144 часть силы, которая вызывает крутящий момент. Это должно иметь смысл, поскольку скорость вращения всегда перпендикулярна радиальной Следовательно, чтобы изменить скорость вращения, вам нужна сила в этом направлении.)

$\endgroup$

$\begingroup$

Поймите, что есть компромисс. Вы можете применить меньшее усилие с помощью большего ключа, но вам придется перемещать его на большее расстояние (длина дуги), чтобы выполнить тот же объем работы (сила x расстояние).

$\endgroup$

$\begingroup$

Интуиция, я думаю, может быть, это потому, что, когда вы прикладываете силу на дальнем расстоянии, больше этого объекта следует за движением, которое дает сила. Когда я встряхиваю свой карандаш, зажимая его конец, он движется намного больше, чем когда я держу его ближе к кончику карандаша, потому что больше карандаша повторяет движение, которое я придал карандашу, когда я встряхиваю его, когда он длиннее. . Представьте себе угол в 30 градусов, хоть он и узкий, если линии образующие угол длинные, то он довольно широкий, я думаю поэтому расстояние влияет на момент

Еще одна вещь, хотя и небольшая, может заключаться в том, что если вы сожмете карандаш ближе к кончику, это означает, что часть карандаша окажется за вашими пальцами, и вес этой части карандаша может уменьшить движение, потому что ваши пальцы должны приложите достаточную силу, чтобы сдвинуть весь карандаш, чтобы он качался и двигался, кончик карандаша не сгибался, чтобы он качался.

$\endgroup$

$\begingroup$

кажется вы задали любопытный вопрос мне 14 лет и я решаю такие вопросы своим воображением без вывода сложных математических формул и прочего. так что просто представьте себе отрезок линии и сделайте две точки (поворот) в начале), а на самой внешней стороне теперь подумайте о перемещении этой линии вокруг этого стержня {так вы увидите, что сила в углу перемещает отрезок линии по кругу } теперь возьмите еще один отрезок линии, сделайте две точки (поворот) в начале), а на самой внешней стороне и 3-ю в центре примените силу к самой внешней точке на линии с центром в центре, и теперь вы можете видеть, что линия движется в круговое направление. теперь приложите силу немного между точкой, в которой вы видите меньше движения, и в центре, где вы не видите никакого движения. теперь просто снова перейдите к первому шагу и переместите его от самого внешнего конца, вы увидите, что внешняя сторона сегмента линии имеет большую силу, чем внутренняя, и если у нее больше силы, чем она попытается толкнуть опорное слово назад и, следовательно, приведет двигаться вперед. и если сила приложена рядом с шарниром, то внутренняя часть имеет большую силу и будет пытаться толкнуть себя и шарнир дальше, следовательно, в то же время она будет толкать его назад. ТЕПЕРЬ ВЫ СКАЖЕТЕ, ЧТО СИЛЫ УБАЛАНСИРОВАНЫ, НО КОГДА СИЛА ПРИЛОЖЕНА НИЖЕ ОПРЕДЕЛЕННОЙ ТОЧКИ, ОНА УХОДИТ В МИНУС. МОЙ СОВЕТ БУДЕТ ПОНИМАТЬ КРУТЯЩИЙ МОМЕНТ ПОЛНЫЙ И ЗАТЕМ ПРИМЕНИТЬ ЕГО К ЭТОМУ. И БУДЬТЕ ЛЮБОПЫТНЫМИ 🙂

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

момент

Главная > Фундамент > Момент силы

Момент силы (крутящий момент)

Момент силы ( крутящий момент ) или просто момент является причиной углового движения (вращения). Момент силы создается силой, которая не проходит через центр вращения (COR). На рис. 1 показана система гаечных ключей, которая используется для вращения круглого объекта (назовем его гайкой). Поскольку задача здесь состоит в том, чтобы вращать круглую гайку, COR расположен в центре гайки. Сила ( F ), который прикладывается рукой для вращения гайки, а ключ воздействует на точку действия (POA) на рукоятке вдоль линии действия (LOA; пунктирная линия). В этом примере плоскостью действия является экран монитора, перпендикулярный линии обзора. Если усилие достаточно велико, ключ и гайка будут вращаться по часовой стрелке в плоскости действия или плоскости вращения .

Рис. 1. Плечо момента, образованное силой руки, действующей на гаечный ключ

На самом деле вращение гайки на Рисунке 1 вызывает момент, создаваемый силой руки. Величина момента, создаваемого силой руки, зависит от двух параметров: величины силы и длины плеча момента . Плечо момента (на рисунке 1) — это кратчайшее (то есть перпендикулярное) расстояние от COR до LOA. Плечо момента определяется в плоскости действия/вращения. Момент, создаваемый силой руки ( F ) на рисунке 1 выглядит следующим образом:

Где M = величина момента. Момент пропорционален приложенной силе и плечу момента, образованному силой по отношению к COR (уравнение 1).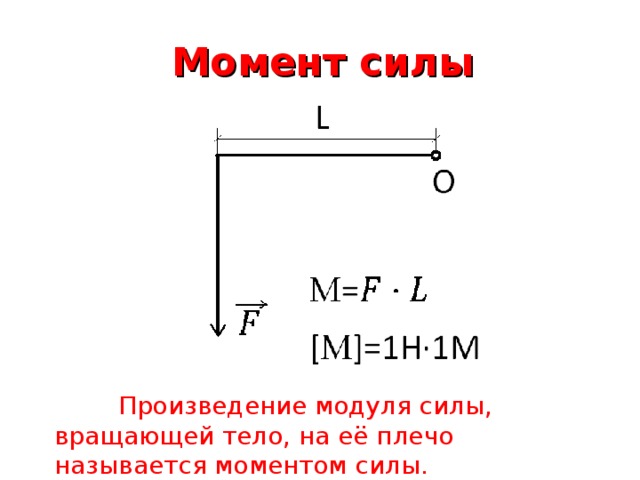

Момент — это вектор, поэтому он должен иметь свое направление. Направление момента, создаваемого силой, всегда перпендикулярно плоскости действия. Плоскость действия — это плоскость, образованная плечом момента и вектором силы. Правило правого винта используется для определения направления момента; когда четыре пальца правой руки выровнены по направлению вращения, большой палец показывает направление момента (рис. 2). Правый винт движется вперед, когда он вращается по часовой стрелке.

Рис. 2. Направление вращения в зависимости от направления момента, вызывающего вращение (источник изображения: http://www.wikipedia.com)

В отличие от простого плоского движения, при котором плоскость действия перпендикулярна прямой видимости (рис. 1), определение плеча момента и направления результирующего момента, действующего на свободно вращающееся тело в трехмерном пространстве, является более сложным. Например, на рис. 3 показана GRF ( F ), действующая на ведущую ногу, и момент ( M ), создаваемый этой силой относительно ЦМ тела. Поскольку вращение тела не стеснено и в этом случае нет фиксированного КОР, то ЦДТ тела может служить КОР с точки зрения углового воздействия ГРФ ведущей стопы на тело.

Рис. 3. Момент силы, создаваемый ФГР ведущей стопы относительно тела COM вблизи EDA

Здесь следует отметить, что ФГР ведущей стопы не обязательно находится во фронтальной плоскости: т. е. ее составляющая вперед/назад не равна нулю. Самый простой способ визуализировать плоскость действия в трехмерном пространстве — нарисовать стрелку ( r ) от COM (COR) к POA. Это вектор относительного положения POA к COR. Плоскость, определяемая r и F , является плоскостью действия. Плечо момента можно определить на плоскости действия. Плечо момента образует прямой угол с линией действия ФГР (рис.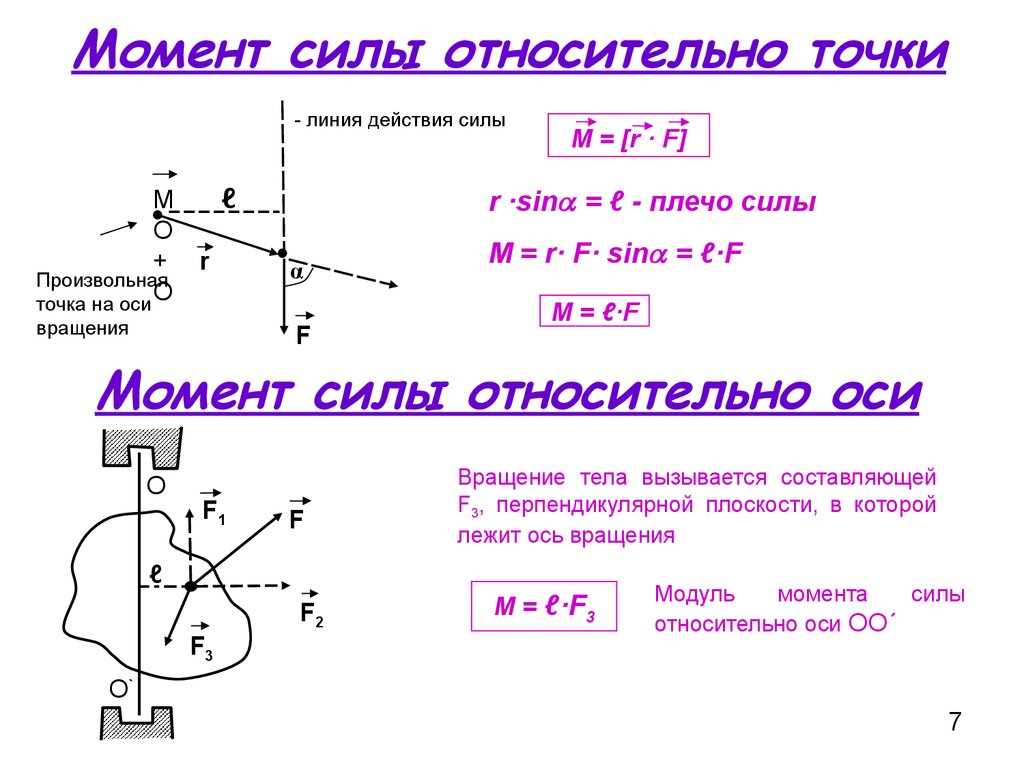 3).

Математически момент ( M ) может быть выражен как векторное произведение вектора положения ( r ) и вектора силы ( Ф ):

Произведение векторов — это особый способ умножения двух векторов. Из-за используемого символа креста (‘x’) эта математическая операция также называется перекрестным произведением . Когда относительное положение и сила даны в компонентах, момент также может быть выражен в компонентах:

Результирующий вектор момента ( M ), заданный в компонентах уравнения 3, удовлетворяет двум требованиям: (1) его величина равна длине плеча момента, умноженному на величину силы; (2) его направление перпендикулярно плоскости действия в соответствии с правилом правого винта.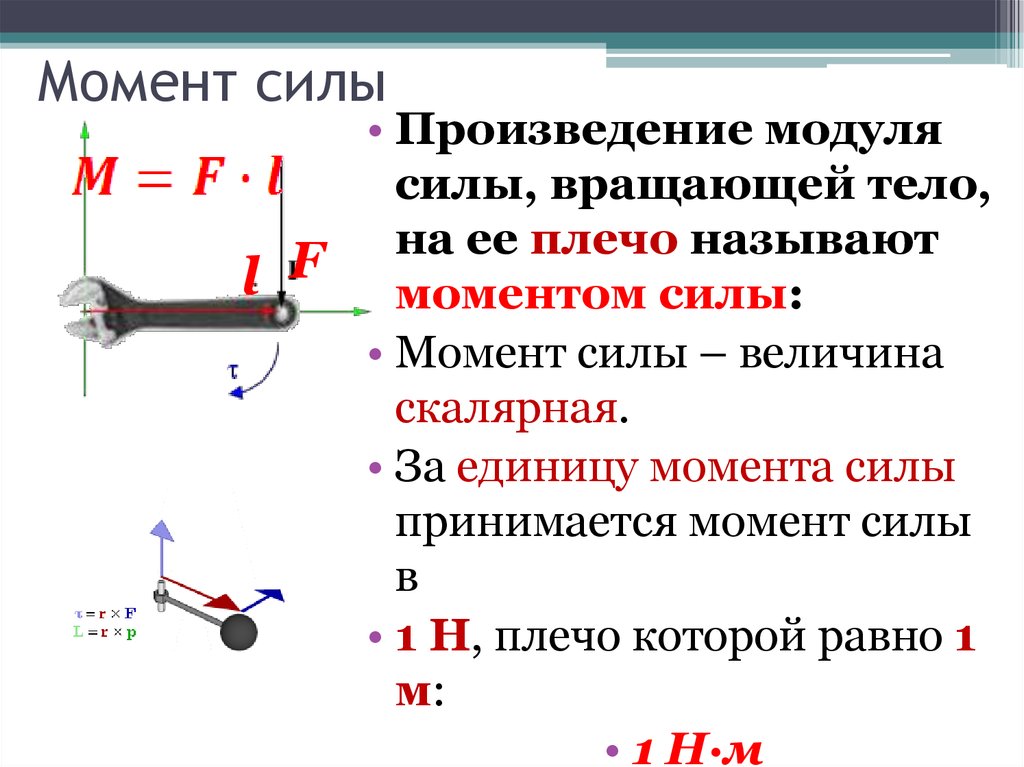 Вектор момента также имеет три перпендикулярные составляющие:

На рис. 4 показаны три позы элитного гольфиста-мужчины, наблюдаемые в трех различных проекциях: спереди (A) вблизи EDA, сбоку (B) вблизи BI и горизонтально (C) вблизи EDA. X -, Y — и Z — оси системы отсчета выровнены по направлениям вперед/назад (F/B), вперед/назад (T/A) и вверх/вниз (U/D ; вертикальные) оси соответственно. На рисунке 4A представлена ​​проекция GRF ведущей опоры на плоскость YZ , перпендикулярную оси F/B (ось X ). — плечо момента, образованное этой силой с реакцией на ЦМ на YZ -плоскость. На рисунке 4B вектор GRF был спроецирован на XZ 9.0144 -плоскость () и от этой силы определялось плечо момента () на этой же плоскости. Точно так же оба и на рисунке 4C определены в горизонтальной плоскости. Таким образом, величины компонентов момента:

Знаки (+/-) компонентов должны быть определены на основе направлений компонентов момента. Если составляющая момента направлена ​​против часовой стрелки (рис. 4А и 4С), знак должен быть положительным. Момент по часовой стрелке (рис. 4B) отрицательный.

Рис. 4. Компоненты момента, наблюдаемые в трех проекциях: анфас (А), сбоку (В) и горизонтально (С).

Каждая составляющая момента может быть далее разбита на два отдельных члена, генерируемых отдельными составляющими силы. Например, на рис. 5 (вид спереди) показаны моменты, создаваемые и . В этом случае Y — и Z — компоненты вектора относительного положения POA к COR ( y и z ) служат моментными плечами компонентов силы. Обе составляющие силы на рисунке 5 создают моменты в направлении против часовой стрелки (положительные). С Y -компонент r ( y ) и Z -компонент F оба положительны, поэтому y * F z также должны быть положительными.