Site Loader
Posted on 15.01.2023

13, 15 Момент инерции твердого тела.13.Теорема штейнера

Найдем сначала выражение для момента импульса твердого тела относительно оси вращения 001,

где и – масса и расстояние от оси вращения частицы твердого тела;

– ее угловая скорость.Обозначив величину, стоящую в круглых скобках через I получим:

где I – так называемый момент инерции твердого тела относительно оси 001:

Момент инерции твердого тела зависит от распределения масс относительно интересующей нас оси и является величиной аддитивной.

Вычисление момента инерции тела проводится по формуле:

где dm и dv – масса и объем элемента тела, находящегося на расстоянии R от интересующей нас оси z, – плотность тела в данной точке В некоторых случаях нахождения момента инерции значительно упрощается, если воспользоваться

теоремой Штейнера: Момент инерции I относительно произвольной оси равен моменту инерции относительно оси z, параллельной и проходящей через центр инерции С тела, плюс произведение массы тела m на квадрат расстояния a между осями . Таким образом, если известен момент инерции Iс, например для стержня, то I относительно оси, перпендикулярной стержню и проходящей через его конец, равен

.

Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр инерции тела, приводятся в специальных таблицах. Расчетом их займетесь на занятиях по решению задач. Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:

где mi— масса i-й частицы тела, ri — ее расстояние от заданного центра или оси. Для описания вращательного движения тела существенно значение его момента инерции. По определению момент инерции твердого тела равен сумме моментов инерции отдельных его частиц:

где mi— масса i-й частицы тела, ri — ее расстояние от заданного центра или оси.

Предположим, что масса выделенной частицы тела mi, расстояние от нее до начала координат (т. о) ri, а координаты, соответственно, xi,yi,zi (рис. 58).

Момент инерции относительно т. О по определению равен

(рис. 58)

а относительно координатных осей:

Сравнивая, получим связь момен­та инерции тела относительно начала координат с моментами инерции относительно координатных осей:

Если одним из размеров тела можно пренебречь по сравнению с двумя другими (плоское тело), эта связь запишется в виде

Теорема Штейнера гласит, что момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящий через центр масс тела и произведения массы тела на квадрат расстояния между осями.

Момент инерции. Из определения следует что, момент инерции – величина аддитивная. Момент инерции существует без относительного вращения тела. Поэтому любое покоящееся тело обладает определенным моементом инерции относительно выбранной оси, подобно как покоящееся тело обладает массой. Распределение массы в пределах вещества, можно охарактеризовать с помощью плотности вещества.

При описании распределения масс с помощью плотности вещества, момент инерции будет: . Вычисление момента инерции с помощью записанной ф-лы существенно упрощается, когда рассматриваемая ось является осью симметрии. В ином случае используют Т. Штейна. Т: Момент инерции I относительно проивзольной оси равен моменту инерции , относительно оси параллельной данной и проходящей через центр масс тела суммированного с проивзедением массы тела на квадрат расстояния между этими осями.

Определение момента инерции твердого тела на основе законов равноускоренного движения

приобрести
Определение момента инерции твердого тела на основе законов равноускоренного движения
скачать (157. 5 kb.)
Доступные файлы (1):

n1.doc158kb.18.09.2012 19:35скачать
    Смотрите также:
  • Изучение законов вращательного движения твёрдого тела (Лабораторная работа)
  • Измерение момента инерции твердого тела методом крутильных колебаний (Документ)
  • Методички к лабораторным работам. Механика и молекулярная физика (Документ)
  • Лабораторные работы по курсу общей физики (Документ)
  • Лабораторная работа — Изучение законов поступательного движения твердого тела (Лабораторная работа)
  • Определение момента инерции твердых тел с помощью машины Атвуда (Документ)
  • Шпаргалки на экзамен по физике (Документ)
  • Зачет по физике (Документ)
  • Измерение момента инерции тела (Документ)
  • Григорьян А.Т., Фрадлин Б.Н. История механики твердого тела (Документ)
  • Определение изменения энтропии твердого тела (Шпаргалка)
  • Лысак О.Н. (сост.) Кинематика точки и простейшие движения твёрдого тела (Документ)

n1.

doc

Санкт-Петербургский Государственный

Университет Точной Механики и Оптики

Лабораторная работа №4а

Определение момента инерции твердого тела на основе законов равноускоренного движения

г. Санкт-Петербург

2008г.

Цель работы: экспериментальное исследование законов динамики вращательного движения.

1.Теория работы

Основной закон динамики вращательного движения:

? — угловое ускорение.

I – величина, характеризующая инерционность тела при вращении, называется моментом инерции.

Для проверки законов вращательного движения в данной работе используется установка изображённая на рисунке. Исследуемым телом является закреплённое на неподвижной оси колесо 1. Момент инерции передвигая в радиальном направлении четыре симметрично расположенных груза 2. Колесо приводится во вращение гирей 3, которая подвешивается на нити, намотанной на шкив радиуса r0.
Вращение колеса происходит под действием момента М силы натяжения нити и противоположно направленного момента сил сопротивления Мс. Следовательно:

или . Из формулы видно, что сила сопротивления не зависит от скорости и зависимость величины М от ? является линейной. Таким образом, момент инерции колеса I можно найти, проведя экспериментальное исследование взаимосвязи между моментом силы натяжения нити и угловым ускорением.

Движение гири происходит согласно уравнению:

, где а – ускорение движения гири, которое можно найти, зная время t ее опускания и пройденный путь h:

Получаем:

Зная соотношение находим:

Формулы позволяют найти момент силы натяжения силы М и угловое ускорение ?. Проведя опыт с гирями различной массы, можно исследовать зависимость М от ? и построить график. Поэтому определение момента инерции колеса сводится к определению углового коэффициента найденной функции М(?).

График прилагается.

Записав уравнение М(?) для разных двух точек на построенной прямой, имеем:

Из этой системы получаем:

Величины М(?’) и М(?’’) находятся из графика, то есть являются результатом усреднения ряда экпериментальных данных, то погрешность определения I в данном случае будет меньше, чем при подстановке в последнее равенство полученных непосредственно из опыта значений (?).

2.Результаты измерений

Были сделаны измерения для трёх положений грузов 2 и трёх различных масс гири 3. Приборная погрешность .
Ниже приведены таблицы измерений.


h (м)
r (м)
m1(кг)
t1(с)
m2(кг)
t2(с)
m3(кг)
t3(с)
m4(кг)
t4(c)

1
0,4
0,2
0,053
6,240
0,095
4,241
0,137
3,552
0. 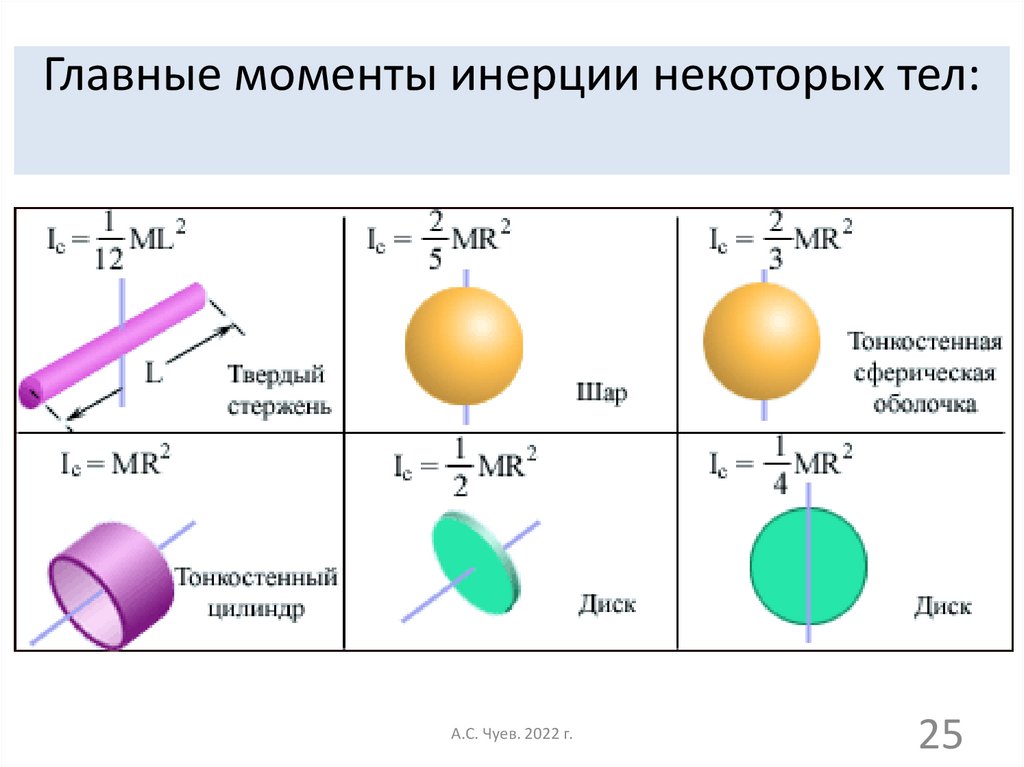179
2.475

2
0,4
0,2
0,053
6,552
0,095
4,464
0,137
3,720
0.179
2.482

3
0,4
0,2
0,053
6,510
0,095
4,419
0,137
3,589
0.179
2.711

4
0,4
0,2
0,053
6,315
0,095
4,589
0,137
3,665
0.179
2.702

5
0,4
0,2
0,053
6,470
0,095
4,427
0,137
3,603
0. 179
2.483

Ср.
0,4
0,2
0,053
6,417
0,095
4,428
0,137
3,626
0.179
2.571

h (м)
r (м)
m1(кг)
t1(с)
m2(кг)
t2(с)
m3(кг)
t3(с)
m4(кг)
t4(c)

1
0,4
0,15
0,053
5,329
0,095
3,669
0,137
2,775
0. 179
1.980

2
0,4
0,15
0,053
5,723
0,095
3,515
0,137
2,825
0.179
1.993

3
0,4
0,15
0,053
5,607
0,095
3,647
0,137
2,833
0.179
1.952

4
0,4
0,15
0,053
5,630
0,095
3,620
0,137
2,891
0.179
1.976

5
0,4
0,15
0,053
5,377
0,095
3,609
0,137
2,876
0. 179
1.966

Ср.
0,4
0,15
0,053
5,533
0,095
3,612
0,137
2,840
0.179
1.973

h (м)
r (м)
m1(кг)
t1(с)
m2(кг)
t2(с)
m3(кг)
t3(с)
m4(кг)
t4(c)

1
0,4
0,1
0,053
3,867
0,095
2,851
0,137
2,155
0. 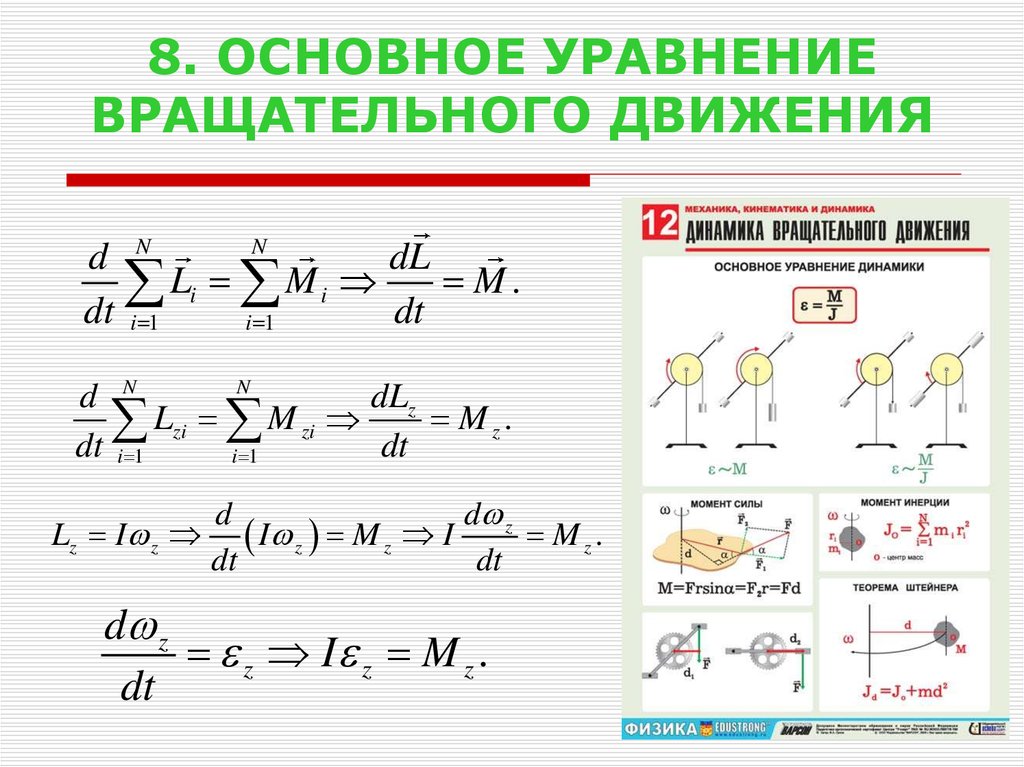179
1.576

2
0,4
0,1
0,053
4,002
0,095
2,703
0,137
2,174
0.179
1.644

3
0,4
0,1
0,053
4,016
0,095
2,723
0,137
2,120
0.179
1.638

4
0,4
0,1
0,053
4,010
0,095
2,608
0,137
2,137
0.179
1.658

5
0,4
0,1
0,053
3,897
0,095
2,713
0,137
2,123
0. 179
1.663

Ср.
0,4
0,1
0,053
3,958
0,095
2,720
0,137
2,142
0.179
1.634

Для выбранного значения r расчитаем по формулам и
величины M и ? при различных m. Построим график функции M(?), аппроксимируя экспериментальные результаты линейной зависимостью.Он приведён в приложении 1.
Расчёты момента силы и углового ускорения

Таблица резултата расчётов момента силы и углового ускорения

r=0.2 м


№ опыта
М
?

1
0.021
0.48

2
0. 037
1.02

3
0.053
1.52

4
0.069
3.03

r=0.15 м


№ опыта
M
?

1
0.021
0.65

2
0.037
1.54

3
0.053
2.5

4
0.069
5.3

r=0.1 м


№ опыта
M
?

1
0.021
1.3

2
0. 037
2.5

3
0.053
4.4

4
0.069
7.3

Значения M и ɛ при r=0.2 м:

ɛ при r=0.15 м:


ɛ
при r=0.10 м:

Используя формулу подсчитываем моменты инерции колеса для разных r


При r=0.2м

При r=0.15м

При r=0.1м

Используя полученные результаты, строим график зависимости I(r2). Он приведён в приложении 2.

Расчет погрешности

Погрешность вычисляется по формуле:

где N – число точек, — экспериментальное значение, М(?i) – значение по графику, Sn-1 – коэффициент Стьюдента.

Погрешность ?I можно найти по формуле:

Но лучше рассчитать по вытекающей из первых двух формуле:


Результат
В результате момент инерции колеса при разных r изображен в следующей таблице:


r (м)
0,10
0,15
0,20

I (кг м2)
(0,008 ± 0,007)
(0,010 ± 0,007)
(0,018 ± 0,007)

По графику I(r2) , изображённому на приложении 2, видно, что в пределах погрешности измерений, если размерами грузов можно пренебречь, экспериментальные точки находятся на одной прямой. Это подтверждает справедливость соотношения I = mr2

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ И МОМЕНТЫ ИНЕРЦИИ

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ И МОМЕНТЫ ИНЕРЦИИ

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ И МОМЕНТЫ ИНЕРЦИИ

 

Нажмите здесь, чтобы посмотреть видео эксперимента

ОБОСНОВАНИЕ:

Не все движения происходят по прямой или даже по криволинейной траектории. Некоторыми очень распространенными движениями являются вращения, при которых твердый объект вращается вокруг фиксированной или движущейся оси. Хотя концептуально возможно анализировать движение такого объекта, применяя уравнения и методы линейного движения к каждой точке объекта, подавляющая сложность такого подхода делает его непрактичным для обычного использования. Таким образом, вращательное движение рассматривается с использованием тех же принципов физики, но применяется с другой системой координат, что значительно упрощает результаты. Оказывается, у каждого принципа или закона линейной физики есть аналогичное уравнение в области физики вращения. Таким образом, если кто-то хорошо понимает принципы линейного движения, он должен понимать и принципы вращательного движения, потому что они одинаковы, а меняются только имена переменных.

В этом эксперименте учащийся исследует, как количество и размещение массы в простой вращающейся системе влияет на ее вращательное движение, и сможет сравнить эти эффекты с аналогичными эффектами в системах с линейным движением.

 

КОНКРЕТНЫЕ ЗАДАЧИ:

Когда вы завершите это экспериментальное задание, вы сможете: (1) определить термины крутящий момент, угловое ускорение и момент инерции; (2) написать и применить второй закон Ньютона для вращательного движения; (3) рассчитать момент инерции для простой системы вращения; 4) уметь экспериментально определять момент инерции системы; (5) понимать взаимосвязь между линейным ускорением и угловым ускорением; и (6) понять различия и сходства силы и крутящего момента.

 

ЭКСПЕРИМЕНТАЛЬНАЯ ДЕЯТЕЛЬНОСТЬ:

Этот опыт позволяет определить момент инерции различных объектов относительно осей вращения, проходящих не только через центр масс, но и через другие точки. Объект заставляют вращаться вокруг вертикальной оси, прикладывая к нему постоянный крутящий момент. Этот крутящий момент G вызывает постоянное угловое ускорение, значение которого равно крутящему моменту, деленному на момент инерции I, как показано в уравнении (1):

          (1)

Схема аппарата показана на рисунке. Объект, момент инерции которого необходимо измерить, представляет собой длинный тонкий стержень, закрепленный на шпинделе радиусом r, свободно вращающемся вокруг вертикальной оси. Легкая струна, поддерживающая груз, проходит по шкиву и затем наматывается на шпиндель. Натяжение струны обеспечивает крутящий момент, который производит вращение системы. Стержень должен быть зажат так, чтобы он вращался вокруг своего центра масс. Грузы могут быть закреплены в различных положениях вдоль стержня, после чего можно определить момент инерции всей системы.

 

Угловое ускорение измеряется косвенно. Груз падает с линейным ускорением a, а значение a определяется путем измерения времени, необходимого для падения груза на измеримое расстояние s. Для объекта, находящегося в состоянии покоя, расстояние, которое он проходит за время t, определяется как:

          (2)

, что позволяет вычислить a как:

          (3)

Угловое ускорение можно рассчитать, так как:

          (4)

где r — радиус вращающегося шпинделя.

 Момент инерции стержня и шпинделя

Первая процедура заключается в определении момента инерции шпинделя и стержня без каких-либо дополнительных масс на стержне. Выберите какую-нибудь удобную точку отсчета для падающего груза, чтобы вы могли каждый раз начинать его с одной и той же точки, и измеряйте расстояние, на которое он упадет, как можно точнее с помощью измерительной линейки. Используйте падающий груз весом от 50 до 100 граммов (включая подвеску для груза) и замерьте время его падения на измеренном расстоянии. Повторите три раза и используйте среднее значение времени в своих расчетах. Запишите все испытания в свою таблицу данных. Используйте микрометр для измерения диаметра шпинделя и запишите диаметр и радиус шпинделя в таблицу данных. При измерении шпинделя измерьте от 7 до 10 раз, записывая каждое измерение, а затем используйте среднее значение в своих расчетах. Поскольку очень распространенной ошибкой является использование в расчетах диаметра, а не радиуса, не забудьте вычислить и использовать радиус там, где это требуется.

Теперь вычислите линейное ускорение падающей массы с помощью уравнения (3) и используйте это значение в уравнении (4) для вычисления углового ускорения. Следующим шагом является вычисление крутящего момента, который затем можно использовать в уравнении (1) для определения момента инерции.

Крутящий момент представляет собой векторную величину, величина которой определяется произведением приложенной силы и перпендикулярного расстояния между осью вращения и линией действия силы. В этом эксперименте крутящий момент, заставляющий шпиндель вращаться, создается натяжением нити, которая действует вдоль линии, касательной к поверхности шпинделя. Поскольку перпендикулярное расстояние от оси до струны равно радиусу шпинделя, то крутящий момент имеет величину:

          (5)

Теперь натяжение нити определяется как:

          (6)

, поскольку падающая масса ускоряется. Поскольку вы знаете и массу, и ее ускорение a, можно легко вычислить натяжение T, а затем найти крутящий момент из уравнения (5). Найдите и запишите эти значения, затем определите момент инерции, используя уравнение (1).

Момент инерции симметричных масс

Теперь утяжелите стержень, поместив 100-граммовые грузы рядом с двумя концами стержня. Расположите их так, чтобы они находились на одинаковом расстоянии от оси вращения, и тщательно измерьте это расстояние. Повторите наблюдения и расчеты предыдущей части, чтобы определить момент инерции системы в ее новой конфигурации. Следуйте той же систематической процедуре, что и раньше. Запишите полученное значение как экспериментальное.

Значение, используемое для сравнения, получено путем рассмотрения теории момента инерции. В вашем учебнике показано, что момент инерции I системы дискретных частиц определяется формулой:

          (7)

, где m — масса объекта, а x — смещение этого объекта от центра шпинделя.

Таким образом, момент инерции тела зависит не только от его полной массы, но и от того, как масса распределена относительно оси.

Выбор другой оси вращения приведет к другому моменту инерции, потому что массы не будут находиться на таком же расстоянии от новой оси, как и от старой.

 

Момент инерции вашей экспериментальной системы можно математически описать как сумму трех членов, по одному для стержня и шпинделя и по одному для двух добавленных вами масс. Таким образом, мы имеем:

          (8)

где I o — момент инерции стержня и шпинделя, определенный ранее. Рассчитайте момент инерции вашей системы, используя уравнение (8), и сравните его с экспериментальным значением, используя разницу в процентах. Что является наиболее вероятным источником ошибки? В итоговой сводке укажите среднее значение.

Момент инерции для несимметричных масс

Меняйте массы на стержне до тех пор, пока расположение не станет несимметричным. Не заходите слишком далеко в своем расположении, так как это вызовет сильное колебание прибора, что повлияет на точность ваших результатов. Повторите наблюдения и измерения таким же образом, как и для симметричного расположения, включая расчеты как экспериментальных, так и теоретических значений момента инерции системы. Снова сравните соответствующие значения с разницей в процентах. В итоговой сводке укажите среднее значение.

ОКОНЧАТЕЛЬНЫЙ РЕЗЮМЕ:

Запишите значения инерции для каждой детали. Сравните эти значения. Какие выводы вы можете сделать из этих сравнений? Объясните аддитивный характер инерции.

ВОПРОСЫ:

  1. Как соотносятся линейные ускорения для трех частей?
  2. Как соотносятся угловые ускорения трех частей?
  3. Как соотносятся напряжения в трех частях?
  4. Как соотносятся крутящие моменты для трех частей?
  5. Какие выводы можно сделать из всех сравнений?

 

Вернуться к оглавлению

Момент инерции: определение, формула, теоремы, применение

  • Автор Вишнус_C
  • Последнее изменение 14-11-2022

Момент инерции: Задумывались ли когда-нибудь учащиеся о том, почему дверные ручки прикреплены далеко от шарнирной точки? Вы когда-нибудь сталкивались с тем, что легче двигать ключ, если держать его в самом дальнем положении? Какова роль момента инерции в этом явлении? Почему легче вращать молоток, если мы вращаем его вокруг головы, чем если мы вращаем его вокруг хвоста? Это то же самое, что масса? Формула момента инерции важна для студентов.

Момент инерции определяется как величина, отражаемая телом, сопротивляющимся угловому ускорению, которая представляет собой сумму произведения массы каждой частицы на квадрат ее расстояния от оси вращения. Проще говоря, это число, определяющее величину крутящего момента, необходимого для определенного углового ускорения вращающейся оси. Угловая масса или инерция вращения — это другие названия момента инерции. Продолжайте читать статью, чтобы узнать больше деталей, таких как формула момента инерции и многое другое.

Изучение инерции и ее видов здесь

Момент инерции означает момент массы относительно оси. В практических сценариях мы имеем дело как с поступательным, так и с вращательным движением. Роль момента инерции во вращательном движении аналогична роли массы в поступательном движении.

Момент инерции зависит от распределения массы и оси, относительно которой мы вычисляем момент инерции; тело с большей массой может иметь меньший момент инерции, чем тело с меньшей массой.

Жесткое тело

В практических сценариях большую часть времени мы не имеем дело с частицами. Вместо этого мы имеем дело с непрерывными телами, которые имеют некоторый объем и занимают пространство. Твердое тело можно рассматривать как совокупность бесконечного числа частиц. Твердые тела недеформируемы; таким образом, расстояние между любыми двумя составляющими частицами всегда остается одним и тем же; то есть, если мы отметим любые две точки на твердом теле, то независимо от ориентации твердого тела расстояние между двумя точками не изменится. 92})\)

Следует отметить, что момент инерции зависит от распределения масс вокруг осей; таким образом, фигура с подобным распределением имеет аналогичное выражение для момента инерции.

Теорема о параллельной оси

Теорема о параллельной оси помогает нам легко определить момент инерции относительно оси, проходящей через точку, отличную от центра масс.

Согласно этой теореме,

Момент инерции относительно оси, которая находится на расстоянии \(‘{\rm{d}}’\) от центра масс, определяется выражением, 92}\)

Где

\({{\rm{I}}_{\rm{O}}}\) — момент инерции относительно оси на расстоянии \(‘{\rm{ г}}’\) от центра масс.
\({{\rm{I}}_{{\rm{см}}}}\) — момент инерции относительно центра масс тела.

\({\rm{M}}\) — масса твердого тела.

\(d\) — расстояние от оси до центра масс.

Важно отметить, что оси должны быть параллельны друг другу. Если оси не параллельны друг другу, то теорема о параллельных осях неприменима. Отсюда и название теоремы о параллельных осях.

Из теоремы о параллельных осях можно сказать, что момент инерции минимален относительно оси, проходящей через центр масс.

Теорема о перпендикулярной оси

Теорема о перпендикулярной оси упрощает определение момента инерции плоского объекта. Эта теорема справедлива только для плоских объектов.

Согласно этой теореме момент инерции относительно оси, перпендикулярной плоскости тела, равен сумме моментов инерции относительно любых двух осей, перпендикулярных друг другу в плоскости тела.

\({{\rm{I}}_{\rm{z}}} = {{\rm{I}}_{\rm{x}}} + {{\rm{I}}_{ \rm{y}}}\)

Где,

\({{\rm{I}}_{\rm{z}}}\) — момент инерции относительно оси, перпендикулярной плоскости тело.

\({{\rm{I}}_{\rm{x}}}\;{\rm{and}}\;{{\rm{I}}_{\rm{y}}}\ ) — две оси, перпендикулярные друг другу в плоскости тела.

Радиус инерции

Радиус инерции тела вокруг любой оси определяется как эффективное расстояние от этой оси, на котором предполагается, что вся масса тела сосредоточена так, что момент инерции равен начальному . 92}\)

Где

\({\rm{M}}\) – это масса тела, а \({\rm{k}}\) – радиус вращения.

Таким образом, радиус вращения будет зависеть от распределения массы и оси вращения.

Применение момента инерции

Момент инерции в динамике вращения и статике аналогичен массе в линейной статике и динамике.

Момент инерции используется для записи уравнений крутящего момента при анализе динамики твердого тела.

\({\rm{\tau}}\, = {\rm{I\alpha}}\)

Где,

\({\rm{\tau}}\,\) — чистый крутящий момент в теле.

\({\rm{\alpha }}\) — угловое ускорение тела.

\({\rm{I}}\) — момент инерции тела.

Дробилка сахарного тростника использует колеса с большим моментом инерции, чтобы увеличить угловой момент и легко раздавить сахарный тростник.

Решенные примеры момента инерции

Q.1. Тонкая проволока длиной \({\rm{l}}\) и массой \({\rm{m}}\) изогнута в виде полукруга. Его момент инерции относительно оси, соединяющей его свободные концы, будет равен :

. Для полукруга мы знаем, что
\({\rm{\pi r}}\, = \,{\rm{l}}\ )
Где
\({\rm{r}}\) — радиус полукруга.
\(\следовательно {\rm{r}} = \frac{1}{{\rm{\pi }}}\)
Используя теорему об перпендикулярной оси, мы имеем,
\({{\rm{I}} _{{\rm{CM}}}}\, = \,{\rm{2}}{{\rm{I}}_{\rm{d}}}\) 9{”}} = \frac{5}{2}{\rm{I}}\)

Итог

Роль массы в поступательном движении аналогична роли момента инерции во вращательном движении. Момент инерции зависит от распределения массы и оси, относительно которой мы вычисляем момент инерции. Тело с большей массой может иметь меньше моментов инерции, чем тело с меньшей массой. Момент инерции относительно оси, которая находится на расстоянии «d» от центра масс, определяется выражением 92}\)

Согласно теореме о перпендикулярной оси момент инерции относительно оси, перпендикулярной плоскости тела, равен сумме моментов инерции относительно любых двух осей, перпендикулярных друг другу в плоскости тела .

\({{\rm{I}}_{\rm{z}}} = {{\rm{I}}_{\rm{x}}}\, + \,{{\rm{I }}_{\rm{y}}}\)

Часто задаваемые вопросы о моменте инерции

Q.1: Что подразумевается под моментом величины?
Ответ: Момент физической величины можно определить как эффективность конкретной величины по отношению к точке или оси. Например, действие силы на точку или ось известно как момент силы или крутящий момент. Эффект или эффективность массы или инерции относительно точки или оси известен как момент инерции.

Q. 2: Может ли тело с меньшей массой иметь больший момент инерции, чем тело с большей массой?
Ответ: Момент инерции зависит от распределения массы и оси, относительно которой мы вычисляем момент инерции; следовательно, можно иметь большую массу, которая может иметь меньший момент инерции, чем тело с меньшей массой.

Q.3: Почему выражение для момента инерции для точечной массы и кругового кольца относительно оси, проходящей через центр перпендикулярно кольцу, одинаково?
Ответ: Момент инерции зависит от распределения массы и оси, относительно которой мы вычисляем момент инерции, а круговое кольцо и частица имеют одинаковое распределение массы, то есть масса сосредоточена на некотором расстоянии; таким образом, они имеют одинаковое выражение для момента инерции.

Q.4: Что такое радиус вращения?
Ответ: Радиус вращения тела вокруг любой оси определяется как эффективное расстояние от этой оси, на котором можно предположить, что вся масса тела сосредоточена так, что момент инерции равен исходный.

Q.5: Может ли тело с массой и некоторым объемом иметь нулевые моменты инерции?
Ans : Нет, тело имеет минимальный момент инерции, если ось проходит через центр масс, таким образом, для твердых тел момент инерции не может быть равен нулю, но для частиц, если ось проходит через нее, то момент инерции относительно этой оси будет равен нулю.

Изучение первого закона движения Ньютона

Мы надеемся, что эта подробная статья о моменте инерции поможет вам в подготовке. Если вы застряли, сообщите нам об этом в разделе комментариев ниже, и мы свяжемся с вами в ближайшее время.

Последние обновления

Даты 7-го экзамена CBSE

Центральный совет среднего образования (CBSE) определяет учебную программу для учащихся 7-го класса, обучающихся в школах, связанных с CBSE. Но ежегодные экзамены для учащихся 7-го класса проводятся внутри соответствующих школ в. ..

Подробнее