Формула Гаусса — Остроградского — Википедия
Материал из Википедии — свободной энциклопедии
Фо́рмула Гаусса — Остроградского — математическая формула, которая выражает поток непрерывно-дифференцируемого векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:
- ∭ V d i v F d V = ∬ S ⊂ ⊃ F ⋅ n d S , {\displaystyle \iiint \limits _{V}\mathrm {div} \,\mathbf {F} \,dV=\iint \limits _{S}\!\!\!\!\!\!\!\!\!\!\!\;\!\!\;\subset \!\!\supset \mathbf {F} \cdot \mathbf {n} \,dS,}
то есть интеграл от дивергенции векторного поля F {\displaystyle \mathbf {F} } , распространённый по некоторому объёму V {\displaystyle V} , равен потоку вектора через поверхность S {\displaystyle S} , ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.
В работе Остроградского формула записана в следующем виде:
- ∫ ( d P d x + d Q d y + d R d z ) ω = ∫ ( P cos α + Q cos β + R cos γ ) s , {\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)\omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )s,}
где
ω
{\displaystyle \omega }
и
s
{\displaystyle s}
— дифференциалы объёма и поверхности соответственно.
P
=
P
(
x
,
y
,
z
)
,
Q
=
Q
(
x
,
y
,
z
)
,
R
=
R
(
x
,
y
,
z
)
{\displaystyle P=P(x,\;y,\;z),\;Q=Q(x,\;y,\;z),\;R=R(x,\;y,\;z)}
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью
Современная запись формулы:
- ∫ ( d P d x + d Q d y + d R d z ) d Ω = ∫ ( P cos α + Q cos β + R cos γ ) d S , {\displaystyle \int \left({\frac {dP}{dx}}+{\frac {dQ}{dy}}+{\frac {dR}{dz}}\right)d\Omega =\int (P\cos \alpha +Q\cos \beta +R\cos \gamma )dS,}
где
cos
α
d
S
=
d
y
d
z
{\displaystyle \cos \alpha \,{dS}={dy}{dz}}
,
cos
β
d
S
=
d
x
d
z
{\displaystyle \cos \beta \,{dS}={dx}{dz}}
и
cos
γ
d
S
=
d
x
d
y
{\displaystyle \cos \gamma \,{dS}={dx}{dy}}
. В современной записи
ω
=
d
Ω
{\displaystyle \omega =d\Omega }
— элемент объёма,
s
=
d
S
{\displaystyle s=dS}
— элемент поверхности
Обобщением формулы Остроградского является формула Стокса для многообразий с краем.
История
Впервые теорема была установлена Лагранжем в 1762[2]
Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830 гг.) на примере задач электродинамики[3].
В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году[3]. С помощью данной формулы Остроградский нашёл выражение производной по параметру от n {\displaystyle n} -кратного интеграла с переменными пределами и получил формулу для вариации n {\displaystyle n} -кратного интеграла.
За рубежом формула как правило называется «теоремой о дивергенции» (англ. divergence theorem), иногда — формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».
См. также
Литература
- Остроградский М. В. Note sur les integrales definies. // Mem. l’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
- Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. l’Acad., 1, стр. 35—58, 24/1 1834 (1838).
Примечания
- ↑ 1 2 Ильин В. А. и др. Математический анализ. Продолжение курса / В. А. Ильин, В. А. Садовничий, Бл. X. Сендов. Под ред. А. Н. Тихонова. — М.: Изд-во МГУ, 1987.— 358 с.
- ↑ В работе по теории звука в 1762 г. Лагранж рассматривает частный случай теоремы: Lagrange (1762) «Nouvelles recherches sur la nature et la propagation du son» (Новые исследования о природе и распространении звука), Miscellanea Taurinensia (Mélanges de Turin), 2: 11 — 172. Репринтное издание: «Nouvelles recherches sur la nature et la propagation du son» в кн.: J.A. Serret, ed., Oeuvres de Lagrange, (Paris, France: Gauthier-Villars, 1867), vol. 1, pages 151—316; на страницах 263—265 Лагранж преобразовывает тройные интегралы в двойные с помощью интегрирования по частям.
- ↑ 1 2 Александрова Н. В.
Формула Гаусса—Остроградского — это… Что такое Формула Гаусса—Остроградского?
Фо́рмула Острогра́дского — математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью:
то есть интеграл от дивергенции векторного поля , распространённый по некоторому объёму , равен потоку вектора через поверхность , ограничивающую данный объём.
Формула применяется для преобразования объёмного интеграла в интеграл по замкнутой поверхности.
В работе Остроградского формула записана в следующем виде:
где и — дифференциалы объёма и поверхности соответственно. В современной записи — элемент объёма, — элемент поверхности. — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
Обобщением формулы Остроградского является формула Стокса для многообразий с краем.
История
Общий метод преобразования тройного интеграла к поверхностному впервые показал Карл Фридрих Гаусс (1813, 1830 гг.) на примере задач электродинамики[1].
В 1826 году М. В. Остроградский вывел формулу в общем виде, представив её в виде теоремы (опубликовано в 1831 году). Многомерное обобщение формулы М. В. Остроградский опубликовал в 1834 году
За рубежом формула называется формулой Гаусса или «формулой (теоремой) Гаусса—Остроградского».
См. также
Литература
- Остроградский М. В. Note sur les integrales definies. // Mem. 1’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
- Остроградский М. В. Memoire sur le calcul des variations des integrales multiples. // Mem. 1’Acad., 1, стр. 35—58, 24/1 1834 (1838).
Примечания
- ↑ 1 2 Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, стр. 150-151.
Формула Гаусса-Остроградского — это… Что такое Формула Гаусса-Остроградского?
- Формула Гаусса-Остроградского
Теорема Остроградского — Гаусса — утверждение интегрального исчисления функций многих переменных, устанавливающее связь между n-кратным интегралом по области и (n − 1)-кратным интегралом по её границе. Пусть V = (v1,v2,…,vn) есть векторное поле на
 , такое что функции vi вместе со своими частными производными
, такое что функции vi вместе со своими частными производными  интегрируемы по Лебегу в ограниченной области Ω, граница
интегрируемы по Лебегу в ограниченной области Ω, граница  которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.
которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.Тогда формула Остроградского имеет вид
где
есть дивергенция поля V.
Формула Остроградского — Гаусса в векторной форме имеет вид
 ,
,то есть интеграл от дивергенции векторного поля
 , распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.
, распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.Формула применяется для преобразования объёмного интеграла в интеграл по поверхности, ограничивающей данный объём, то есть замкнутых, таких как поверхность воздушного шарика, и не применима к поверхностям, таким как воздушный шар с подогревом.
В работе Остроградского формула записана в следующем виде,
 ,
,где ω и s дифференциалы объёма и поверхности. В современной записи ω = dΩ — элемент объема, s = dS — элемент поверхности.
 — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.История
Для гладких функций эта формула была впервые получена в трёхмерном случае Остроградским в 1828 (опубликована в 1831). На n-мерный случай была обобщена им же в 1834 (опубликовано в 1838). С помощью этой формулы Остроградский нашёл выражение производной по параметру от n-кратного интеграла с переменными пределами и получил формулу для вариации n-кратного интеграла. При n = 3 для одного частного случая формула Остроградского была получена Гауссом в 1813, поэтому иногда она называется также формулой Остроградского — Гаусса. Что интересно, в западной литературе порядок фамилий изменён — она именуется как «теорема Гаусса — Остроградского». Обобщением формулы Остроградского является формула Стокса для многообразий с краем.
Литература
- Остроградский М. В., Note sur les integrales definies. Mem. 1’Acad. (VI), 1, стр. 117—122, 29/Х 1828 (1831).
- Остроградский М. В., Memoire sur le calcul des variations des integrales multiples. Mem. 1’Acad., 1, стр. 35—58, 24/1 1834 (1838)
Wikimedia Foundation. 2010.
- Формула Бине
- Формула Гаусса—Бонне
Смотреть что такое «Формула Гаусса-Остроградского» в других словарях:
Формула Гаусса—Остроградского — Формула Остроградского математическая формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью: то есть интеграл от дивергенции векторного… … Википедия
ГАУССА-ОСТРОГРАДСКОГО ФОРМУЛА — одна из основных интегральных теорем векторного анализа, связывающая объемный интеграл с поверхностным: Здесь замкнутая поверхность, ограничивающая 3 мерную область V, а п проекция вектора на внеш. нормаль к поверхности. Получена Дж. Грином (G.… … Физическая энциклопедия
Остроградского формула — Теорема Остроградского Гаусса утверждение интегрального исчисления функций многих переменных, устанавливающее связь между n кратным интегралом по области и (n − 1) кратным интегралом по её границе. Пусть V = (v1,v2,…,vn) есть векторное поле… … Википедия
Формула Остроградского — Формула Остроградского формула, которая выражает поток векторного поля через замкнутую поверхность интегралом от дивергенции этого поля по объёму, ограниченному этой поверхностью: то есть интеграл от дивергенции векторного поля ,… … Википедия
ОСТРОГРАДСКОГО ФОРМУЛА — формула интегрального исчисления функций многих переменных, устанавливающая связь между n кратным интегралом по области и ( п 1) кратным интегралом но ее границе. Пусть функции Xi=Xi(x1,x2,…, х п).вместе со своими частными производными , i=1, 2 … Математическая энциклопедия
Теорема Гаусса — Классическая электродинамика … Википедия
Теорема Гаусса (значения) — Существует несколько утверждений, называемых теоремой Гаусса: Теорема Гаусса (закон Гаусса) в электростатике и электродинамике и общая формулировка ее формальной части Теорема Гаусса Остроградского в векторном анализе. Теорема Гаусса Ванцеля о… … Википедия
Магнитный закон Гаусса — Классическая электродинамика Магнитное поле соленоида Электричество · Магнетизм Электростатика Закон Кулона … Википедия
Остроградский, Михаил Васильевич — профессор математики, ординарный академик Императорской Академии Наук. М. В. Остроградский родился 12 сентября 1801 года в принадлежавшей его отцу деревне Пашенной, Кобелякского уезда, Полтавской губернии, где и провел свои детские годы.… … Большая биографическая энциклопедия
СТОКСА ТЕОРЕМА — обобщение Стокса формулы, утверждениео равенстве интеграла от внеш. дифференциала dw дифференциальной формы поориентированному компактному многообразию М интегралу от самой формыпо ориентированному (согласованно с ориентацией многообразия М )краю … Физическая энциклопедия
Теорема Гаусса Остроградского и Теорема Стокса формулы
В статье расскажем про теорему Гаусса-Остроградского (теорема дивергенции) и теорему Стокса (теорема вращения).
Замечательные и компактные уравнения Максвелла, полученные в предыдущих лекциях, имеют такой же фундаментальный и глубокий смысл в электродинамике, как и уравнение в механике. Эти уравнения представлены в интегральной форме, и теперь мы найдем их дифференциальную форму, необходимую для локального описания электрических и магнитных полей.
Уравнения Максвелла в дифференциальной форме получаются в результате только математических преобразований уравнений в интегральной форме. Это означает, что уравнения Максвелла в интегральных и дифференциальных уравнениях полностью эквивалентны друг другу.
Мы будем использовать две математические теоремы для преобразования уравнений Максвелла из одной формы в другую:
- Теорема Гаусса-Остроградского
- Теорема Стокса
Теорема Гаусса — Остроградского
Теорема Гаусса-Остроградского (теорема дивергенции) связывает поверхностный интеграл любой вектор-функции K на замкнутой поверхности A с объемным интегралом по объему V, ограниченному поверхностью A, и решает, что поток вектора K через замкнутую поверхность A равен интегралу объема от дивергенции векторного поля K, объем V ограниченной площади.


В основном, эта теорема утверждает, что чем больше поток поля К,


через замкнутую поверхность А чем больше производительность (дивергенция) источников поля K,


содержащихся в объеме V, ограниченном поверхностью закрытой A. Если внутри поверхности, А будет столько же точек положительной дивергенции (источников), что и в дивергенции отрицательной, то поток поля K через поверхность будет равен нулю.


Теорема Стокса
Теорема Стокса (теорема вращения) связывает линейный интеграл от вектор-функции K после замкнутого контура L с поверхностным интегралом на плоскости A, ограниченным контуром L, и решает, что циркуляция вектора K на контуре L равна вращению вектора через плоскость A




Чтобы увидеть это, мы покрываем поверхность профиля А сеткой сколь угодно малых контуров, например сеткой прямоугольников, и вычисляем циркуляцию векторного поля К вдоль каждого из этих контуров. Чем тоньше мы выберем сетку, тем циркуляция вектора K по краям сетки будет более точно приближать значение вращения векторного поля K. Интегрирование в двух противоположных направлениях вдоль соседних сторон приводит к нулю. Ненулевые остаются только те значения, которые являются результатом интегрирования по фрагментам контура, ограничивающего поверхностью А. После завершения такого интегрирования по всей поверхности профиля А мы получаем только вектор К, циркулирующий вдоль контура, ограничивающего этот участок. Это содержание теоремы Стокса.
Описанная процедура изображена на анимации ниже.


Мы уже встречали уравнение Максвелла в интегральной форме. В следующей лекции мы будем использовать теорему Гаусса-Остроградского и теорему Стокса для получения уравнений Максвелла в дифференциальной форме.
Формула Гаусса-Остроградского — Студопедия
Теорема (Остроградский). Пусть 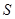 – замкнутая гладкая ориентируемая поверхность, являющаяся границей тела
– замкнутая гладкая ориентируемая поверхность, являющаяся границей тела 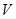 и n
и n 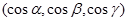 – единичная внешняя нормаль к
– единичная внешняя нормаль к 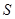 . Пусть векторное поле F
. Пусть векторное поле F 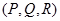 – непрерывно дифференцируемо на
– непрерывно дифференцируемо на 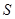 и в V. Тогда
и в V. Тогда
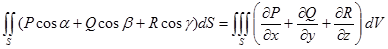 . .
| (3) |
Выражение, стоящее под знаком интеграла в правой части равенства (3), представляет собой дивергенцию векторного поля F, интеграл, стоящий слева, представляет собой поток векторного поля F через поверхность 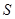 в направлении внешней нормали. Поэтому формула (3) может быть переписана в виде:
в направлении внешней нормали. Поэтому формула (3) может быть переписана в виде:
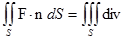 F
F 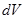 .
.
Формулу Гаусса-Остроградского часто применяют для вычисления потока векторного поля через замкнутую поверхность 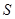 . Однако следует иметь в виду, что для применения этой формулы необходимо, чтобы векторное поле было непрерывно дифференцируемым внутри поверхности
. Однако следует иметь в виду, что для применения этой формулы необходимо, чтобы векторное поле было непрерывно дифференцируемым внутри поверхности 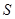 . Это условие всегда будет выполнено, если область
. Это условие всегда будет выполнено, если область 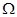 , в которой рассматривается поверхность
, в которой рассматривается поверхность 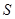 , пространственно односвязная.
, пространственно односвязная.
Область 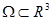 называется пространственно односвязной, если из того, что замкнутая поверхность
называется пространственно односвязной, если из того, что замкнутая поверхность 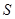 лежит в
лежит в 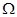 , следует, что тело V, границей которого является поверхность
, следует, что тело V, границей которого является поверхность 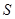 , тоже лежит в
, тоже лежит в 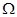 .
.
Пример 1. Вычислить поток векторного поля F 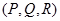 через поверхность
через поверхность 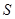 в сторону, определяемую вектором единичной нормали n к поверхности
в сторону, определяемую вектором единичной нормали n к поверхности 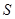 , если:
, если:
а) F 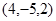 , а
, а 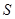 – часть плоскости
– часть плоскости 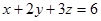 , расположенная в октанте
, расположенная в октанте 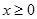 ,
, 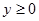 ,
, 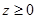 , n образует острый угол с осью
, n образует острый угол с осью 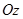 ;
;
б) F 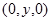 ,
, 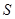 – часть плоскости
– часть плоскости 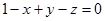 , расположенная в октанте
, расположенная в октанте 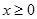 ,
, 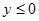 ,
, 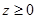 , а n образует острый угол с осью
, а n образует острый угол с осью 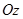 ;
;
в) F 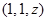 ,
, 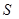 – часть параболоида
– часть параболоида 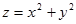 , удовлетворяющая условию
, удовлетворяющая условию 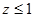 , а n – внешняя нормаль к параболоиду.
, а n – внешняя нормаль к параболоиду.
Решение. а) Нормальным вектором к плоскости является вектор, координаты которого суть коэффициенты при неизвестных в уравнении плоскости. В нашем случае – это вектор m 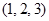 . Поскольку m·F
. Поскольку m·F 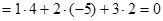 , то нормаль m к плоскости, (а значит, и единичная нормаль n к этой плоскости) перпендикулярна векторному полю. Но тогда
, то нормаль m к плоскости, (а значит, и единичная нормаль n к этой плоскости) перпендикулярна векторному полю. Но тогда
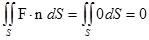 .
.
б) Вычислим поток векторного поля с помощью поверхностного интеграла второго рода (формула(2))
П 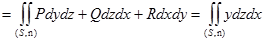
(в нашем случае 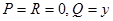 ). Для вычисления последнего интеграла изобразим на чертеже поверхность
). Для вычисления последнего интеграла изобразим на чертеже поверхность 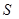 (рис. 39) и ее проекцию
(рис. 39) и ее проекцию 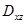 на плоскость
на плоскость 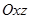 (рис. 40).
(рис. 40).
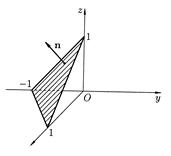 Рис. 39
Рис. 39
| 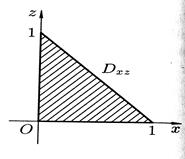 Рис. 40
Рис. 40
|
Нормаль n к плоскости 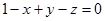 , образующая острый угол с осью
, образующая острый угол с осью 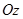 , образует тупой угол с осью
, образует тупой угол с осью 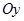 (это видно из чертежа; однако несложно показать, что нужную сторону поверхности
(это видно из чертежа; однако несложно показать, что нужную сторону поверхности 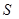 задает единичная нормаль n
задает единичная нормаль n 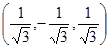 ; здесь
; здесь 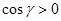 , а
, а 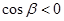 , следовательно, и образует острый угол с осью
, следовательно, и образует острый угол с осью 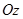 и тупой – с осью
и тупой – с осью 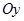 ). Поэтому при сведении поверхностного интеграла к двойному по области
). Поэтому при сведении поверхностного интеграла к двойному по области 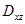 перед двойным интегралом необходимо поставить минус:
перед двойным интегралом необходимо поставить минус:
П 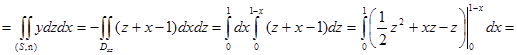
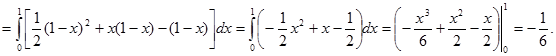
в) Изобразим поверхность 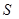 вместе с требуемой в условии задачи нормалью на рис. 41.
вместе с требуемой в условии задачи нормалью на рис. 41.
Из геометрических соображений понятно, что единичная нормаль n (т. к. она – внешняя нормаль) образует тупой угол с осью 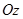 . Также ясно, что она образует острый угол с осью
. Также ясно, что она образует острый угол с осью 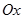 в тех точках, где
в тех точках, где 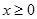 и тупой – в тех, где
и тупой – в тех, где 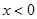 . Аналогично, n образует острый (тупой) угол с осью
. Аналогично, n образует острый (тупой) угол с осью 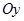 в точках, где выполняется неравенство
в точках, где выполняется неравенство 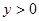 (
( 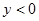 ). Для вычисления потока векторного поля напишем интеграл второго рода:
). Для вычисления потока векторного поля напишем интеграл второго рода:
П 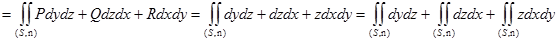 .
.
Вычислим каждый из трех интегралов отдельно. Для вычисления интеграла
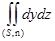
разобьем поверхность 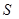 на две части:
на две части: 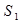 и
и 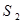 плоскостью
плоскостью 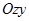 (
( 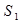 отвечает той части параболоида, где
отвечает той части параболоида, где 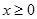 ). Необходимость разбиения заключается, в том что нормаль n на
). Необходимость разбиения заключается, в том что нормаль n на 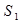 образует острый угол с осью
образует острый угол с осью 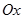 (т.е.
(т.е. 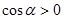 ), а на
), а на 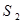 – тупой. Проекцией и
– тупой. Проекцией и 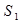 и
и 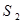 на плоскость
на плоскость 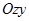 является одна и та же область
является одна и та же область 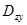 , показанная на рис. 42. Следовательно,
, показанная на рис. 42. Следовательно,
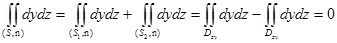 .
.
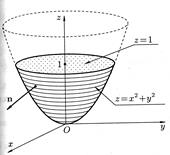 Рис. 41
Рис. 41
| 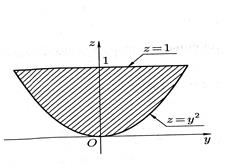 Рис. 42
Рис. 42
|
Знак минус перед вторым интегралом поставлен так как на 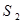 нормаль образует тупой угол с осью
нормаль образует тупой угол с осью 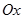 (т.е.
(т.е. 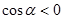 ). Из соображений симметрии понятно, что и
). Из соображений симметрии понятно, что и
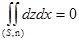 .
.
Осталось вычислить
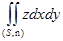 .
.
Как отмечено выше, 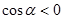 . Поэтому имеем:
. Поэтому имеем:
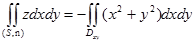 ,
,
где 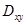 – проекция поверхности
– проекция поверхности 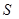 на плоскость
на плоскость 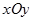 (она изображена на рис. 43). Для вычисления последнего интеграла перейдем к полярным координатам:
(она изображена на рис. 43). Для вычисления последнего интеграла перейдем к полярным координатам:
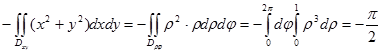 .
.
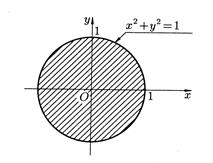
Рис. 43
Таким образом, поток векторного поля равен 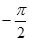 .
.
Контрольные вопросы:
- Дайте определение потока векторного поля F через поверхность
 .
. - Приведите формулу Гаусса-Остроградского.
Теорема Остроградского — Гаусса
Рассмотрим поле точечного заряда $q$, найдем поток вектора напряжённости ($\overrightarrow{E}$) через замкнутую поверхность $S$. Будем считать, что заряд находится внутри поверхности. Поток вектора напряженности через любую поверхность равен количеству линий вектора напряженности, которые выходят наружу (начинаются на заряде, если $q>0$) или количеству линий $\overrightarrow{E}$входящих внутрь, если $q \[Ф_E=\frac{q}{{\varepsilon }_0}\ \left(1\right),\]
где знак потока совпадает со знаком заряда.
Допустим, что внутри поверхности S находится N точечных зарядов, величины $q_1,q_2,\dots q_N.$ Из принципа суперпозиции мы знаем, что результирующая напряженность поля всех N зарядов может быть найдена как сумма напряженностей полей, которые создаются каждым из зарядов, то есть:
Следовательно, для потока системы точечных зарядов можно записать:
Уравнение (4) значит, что поток вектора напряженности электрического поля через замкнутую поверхность равен алгебраической сумме зарядов, которые находятся внутри данной поверхности, деленой на электрическую постоянную. Это теорема Остроградского — Гаусса в интегральной форме. Данная теорема является следствием закона Кулона. Значение данной теоремы заключается в том, что она позволяет довольно просто вычислять электрические поля при различных распределениях зарядов.
Как следствие теоремы Остроградского — Гаусса надо сказать, что поток вектора напряженности ($Ф_E$) через замкнутую поверхность в случае при котором заряды находятся вне данной поверхности, равен нулю.
В том случае, когда можно не учитывать дискретность зарядов используют понятие объемной плотности заряда ($\rho $), если заряд распределен по объему. Она определена как:
\[\rho =\frac{dq}{dV}\left(5\right),\]где $dq$ — заряд, который можно считать точечным, $dV$ — малый объем. (Относительно $dV$ необходимо сделать следующее замечание. Данный объем мал настолько, чтобы плотность заряда в нем можно было считать постоянной, но достаточно велик, чтобы не начала проявляться дискретность заряда). Суммарный заряд, который находится в полости, можно найти как:
\[\sum\limits^N_{i=1}{q_i\ }=\int\limits_V{\rho dV}\left(6\right).\]В таком случае формулу (4) перепишем в виде:
\[\oint\limits_S{\overrightarrow{E}d\overrightarrow{S}}=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV}\left(7\right).\]Теорема Остроградского — Гаусса в дифференциальной форме
Используя формулу Остроградского — Гаусса для любого поля векторной природы, с помощью которой осуществляется переход от интегрирования по замкнутой поверхности к интегрированию по объему:
\[\oint\limits_S{\overrightarrow{a}\overrightarrow{dS}=\int\nolimits_V{div}}\overrightarrow{a}dV\ \left(8\right),\]где $\overrightarrow{a}-$вектор поля (в нашем случае это $\overrightarrow{E}$), $div\overrightarrow{a}=\overrightarrow{\nabla }\overrightarrow{a}=\frac{\partial a_x}{\partial x}+\frac{\partial a_y}{\partial y}+\frac{\partial a_z}{\partial z}$ — дивергенция вектора $\overrightarrow{a}$ в точке с координатами (x,y,z), которая отображает векторное поле на скалярное. $\overrightarrow{\nabla }=\frac{\partial }{\partial x}\overrightarrow{i}+\frac{\partial }{\partial y}\overrightarrow{j}+\frac{\partial }{\partial z}\overrightarrow{k}$ — оператор набла. (В нашем случае будет $div\overrightarrow{E}=\overrightarrow{\nabla }\overrightarrow{E}=\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}$) — дивергенция вектора напряженности. Следуя вышесказанному, формулу (6) перепишем как:
\[\oint\limits_S{\overrightarrow{E}\overrightarrow{dS}=\int\nolimits_V{div}}\overrightarrow{E}dV=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV}\left(9\right).\]Равенства в уравнении (9) выполняются для любого объема, а это осуществимо только, если функции, которые находятся в подынтегральных выражениях, равны в каждой токе пространства, то есть мы можем записать, что:
Выражение (10) — теорема Остроградского — Гаусса в дифференциальной форме. Трактовка ее такова: заряды являются источниками электрического поля. Если $div\overrightarrow{E}>0$, то в этих точках поля (заряды положительные) мы имеем источники поля, если $div\overrightarrow{E}
Пример 1
Задание: Заряд равномерно распределен по объему, в этом объеме выделена кубическая поверхность, со стороной b. Она вписана в сферу. Найдите отношение потоков вектора напряженности сквозь эти поверхности.

Рис. 1
Решение:
Согласно теореме Гаусса поток ($Ф_E$) вектора напряженности $\overrightarrow{E}$ через замкнутую поверхность при равномерном распределении заряда по объему равен:
\[Ф_E=\frac{1}{{\varepsilon }_0}Q=\frac{1}{{\varepsilon }_0}\int\limits_V{\rho dV=\frac{\rho }{{\varepsilon }_0}\int\limits_V{dV}=\frac{\rho V}{{\varepsilon }_0}}\left(1.1\right).\]Следовательно, нам необходимо определить объемы куба и шара, если шар описать вокруг этого куба. Для начала, объем куба ($V_k$) если сторона его b равен:
\[V_k=b^3\left(1.2\right).\]Найдем объем шара ($V_{sh}$) по формуле:
\[V_{sh}=\frac{1}{6}\pi D^3\left(1.3\right),\]где $D$ — диаметр шара и (так как шар описан вокруг куба), главная диагональ куба. Следовательно, нам необходимо выразить диагональ куба через его сторону. Это легко сделать, если использовать теорему Пифагора. Для вычисления диагонали куба, например, (1,5) нам сначала необходимо найти диагональ квадрата (нижнего основания куба) (1,6). Длина диагонали (1,6) равна:
\[d_{16}=\sqrt{b^2+b^2\ \ \ }\left(1.4\right),\]В таком случает длина диагонали (1,5) равна:
\[{D=D}_{15}=\sqrt{b^2+{(\sqrt{b^2+b^2\ \ \ })}^2}=b\sqrt{3}\ \left(1.5\right).\]Подставим в (1.3) найденный диаметр шара, получим:
\[V_{sh}=\frac{1}{6}\pi b^3{\left(3\right)}^{\frac{3}{2}}=\frac{\sqrt{3}}{2}\pi b^3\left(1.6\right).\]Теперь мы можем найти потоки вектора напряженности через поверхность куба, она равна:
\[Ф_{Ek}=\frac{\rho V_k}{{\varepsilon }_0}=\frac{\rho b^3}{{\varepsilon }_0}\left(1.7\right),\]через поверхность шара:
\[Ф_{Esh}=\frac{\rho V_{sh}}{{\varepsilon }_0}=\frac{\rho }{{\varepsilon }_0}\frac{\sqrt{3}}{2}\pi b^3\ \left(1.8\right).\]Найдем отношение $\frac{Ф_{Esh}}{Ф_{Ek}}$:
\[\frac{Ф_{Esh}}{Ф_{Ek}}=\frac{\frac{с}{\varepsilon_0}\frac{\sqrt{3}}{2} \pi b^3}{\frac{сb^3}{\varepsilon_0}}=\frac{\pi}{2}\sqrt{3}\ \approx 2,7\left(1.9\right).\]Ответ: Поток через поверхность шара в 2,7 раза больше.
Теорема и формула Остроградского — Гаусса :: SYL.ru
М.В. Остроградский — российский математик и физик времен Российской империи, академик. Внес огромный вклад в развитие математического анализа, теории вероятностей, механики (раздела физики), теории чисел. В 1826 году вывел формулу, называемую сейчас формулой Остроградского — Гаусса.
История открытия
Впервые формула Остроградского — Гаусса была упомянута Жозефом Лагранжем в 1762 году.
Далее основной способ приведения тройного интеграла к поверхностному был доказан Карлом Гауссом , который использовал в качестве основы для доказательства решение проблем в электродинамике. Произошло это в первой половине XIX века.
Далее формула в общем виде была представлена Михаилом Остроградским. С ее помощью стало возможно выразить значение дифференциала по параметру от N-кратного интеграла.
Смысл формулы Остроградского
Формула Остроградского-Гаусса соотносит тройной интеграл по пространственному объему с интегралом по поверхности на его грани. Она является аналогом формулы Грина, которая соотносит двойной интеграл по плоскости с криволинейным по ее границам.
Вывод формулы
Формула Остроградского — Гаусса: вывод. Допустим, что в области W определена подынтегральная функция R (x, y, z), которая является определенной и непрерывной. Аналогичной является и ее производная во всей области W, включая ее границу. В таком виде известна сейчас теорема Остроградского — Гаусса (формула приведена ниже).
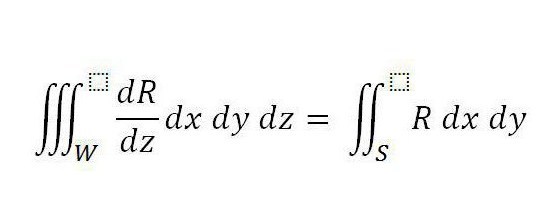
Причем S — поверхность, которая ограничивает тело, а интеграл справа распространен на ее внешнюю сторону.
И абсолютно верно,
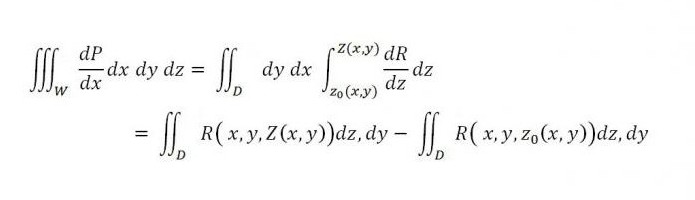
Если аналогично брать во внимание и интегралы по поверхности, то
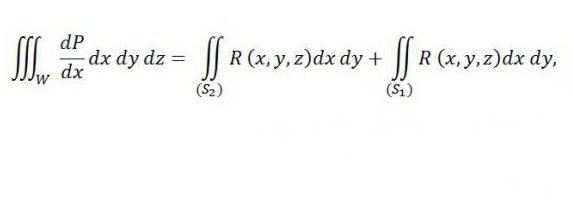
при этом справа находится сумма двух интегралов — первый из них соотносится с верхней частью поверхности (S2), а второй — с нижней частью поверхности (S1). Если приписать к данному равенству справа интеграл, указанный ниже, то его справедливость не будет нарушена:
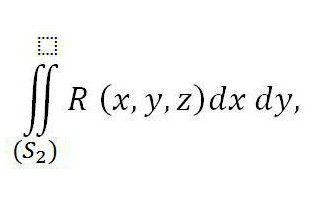
Он соотносится с внешней частью поверхности S3 по причине равенства нулю.
Если объединить все три вышеуказанных интеграла в один, будет получен частный случай формулы Остроградского.
Несложно осознать, что данная формула верна для более широкого класса тел и справедлива так же для фигур, ограниченных абсолютно любыми нелинейными поверхностями.
Аналогично справедливы и следующие формулы:
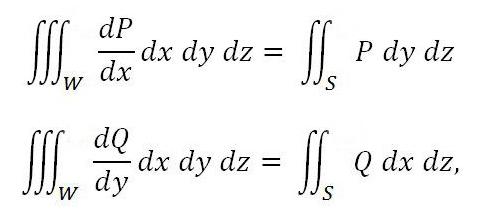
если функции Q и P непрерывны в области вместе со своими производными dP/dx и dQ/dy.
Если сложить оба равенства, будет получено выражение формулы Остроградского. Она отображает интеграл по поверхности, соотнесенный с внешней частью поверхности, через тройной интеграл, который берется по самому телу, границей которого является вышеуказанная поверхность.
Следует понимать, что формулы Грина, Стокса и Остроградского выражают интеграл, связанный с некоторым геометрическим телом, через интеграл, который берется на его границе. Формула Грина используется только в случае двумерности пространства, формула Стокса — к искривленному двумерному пространству.
Формулу Ньютона-Лейбница можно также рассматривать как некоторый аналог этих формул, но для одномерного пространства.
Применение данной формулы
Пусть в какой-либо незамкнутой области пространства заданы непрерывные функции A, B и C. Взяв любую замкнутую поверхность, находящуюся в данной области и ограничивающую некоторое тело, можно рассмотреть следующий интеграл по поверхности:
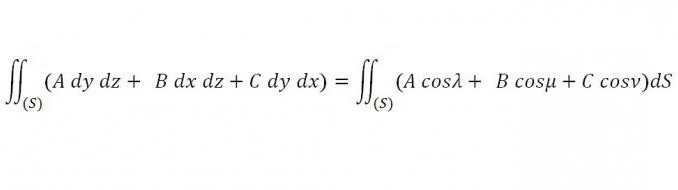
Необходимо найти такие значения A, B и C, чтобы при любых x, y и z данный интеграл оказывался равен нулю.
Для этого необходимо использовать формулу Остроградского-Гаусса. Одним из подразумеваемых условий является определенность и непрерывность функций A, B и C и их производных.
Так же требуется специально ввести наиболее данное для данного случая ограничение: и тело, и ограничивающая его поверхность должны содержаться одновременно в конкретной и указанной области, называемую односвязной. Основная его особенность заключается в отсутствии пустого пространства (в том числе и точечного). Таким образом, границей тела будет являться одна и при том единственная поверхность.
После применения формулы возможно получение следующего условия, которое является достаточным:
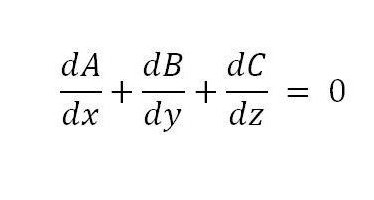
Чтобы доказать, что условие является так же и необходимым, достаточно воспользоваться дифференцированием тройного интеграла.
В заключении необходимо сказать об областях использования.
Как же применяется на практике формула Остроградского-Гаусса? Примеры использования можно обнаружить в самых разных сферах: для вывода некоторых формул в физике (например, уравнение диффузии), преобразования интегралов, вычисления интегралов Гаусса, доказательства некоторых формул и многого иного.
формул Гаусса — Большая химическая энциклопедия
Этот масштаб F1 с единичным аргументом можно суммировать с помощью формулы Гаусса 7. 2) и выражения для найденного S. Отсюда следует, что … [Pg.39]С учетом формулы Гаусса выражение (8.105) можно представить в виде … [Pg.220]
Теперь преобразуем поверхностный интеграл в (13.133) ) в интеграл по объему по формуле Гаусса. Согласно уравнению (13.15) нормальные напряжения P могут быть выражены тензором напряжений следующим образом… [Pg.422]
Подставляя выражение (13.134) в поверхностный интеграл и применяя формулу Гаусса, мы находим … [Pg.422]
Один важный вопрос, касающийся распределения измерений относительно их среднего, — это ожидаемое частота появления ошибки в зависимости от величины ошибки. Наиболее часто используемая функция, которая хорошо описывает относительную частоту появления случайных ошибок в больших наборах измерений, дается формулой Гаусса (см. Также отн.(9) Раздел 5.2) … [Pg.165]
Sk и Si — это векторы, определяющие положение тессер k и I, соответственно, а Rk — радиус сферы, которой принадлежит тессера k. Диагональный член D, который собирает вклад поля реакции, индуцированного зарядом, помещенным на тессеру k, на самого себя, выводится по формуле Гаусса для бесконечной заряженной плоскости с поправочным членом ic, учитывающим кривизну выпуклой тессеры. [Pg.238]
Уравнение (5.69) с использованием формулы Гаусса (5.1), преобразуется в закон сохранения массы для каждой фазы в дифференциальной форме … [Pg.72]
Было предложено множество алгоритмов для выполнения численного интегрирования функций. Мы рассматриваем только две семейства алгоритмов, которые являются основой для разработки и реализации четного числа общих программ численного интегрирования формул Ньютона-Котеса и Гаусса. [Pg.23]
Другие открытые и полуоткрытые формулы Ньютона-Котеса представляют чисто исторический интерес: открытые формулы менее эффективны, чем формулы Гаусса, и как открытая, так и полуоткрытая формулы сложнее, чем их закрытые формулы… [Pg.24]
Формулы Гаусса используют положения Xi как степени свободы для повышения точности за счет сохранения количества точек, в которых вычисляется функция. [Pg.24]
Для использования формул Гаусса необходимо знать нули многочлена Z и веса Wi. Они приведены для многих семейств ортогональных многочленов и для многих комбинаций a, b и r x). [Pg.26]
Порядок формул Гаусса, использующий n внутренних точек, равен p = 2 — n. [Стр.26]
Формулы Гаусса имеют определенные преимущества по сравнению с формулами Ньютона-Котеса. [Стр.35]
Формулы Гаусса открыты. Их можно использовать, даже если функция имеет числовые проблемы на крайних интервалах. [Pg.35]
В то время как формулы Ньютона-Котеса становятся менее эффективными с увеличением порядка и поэтому редко используются помимо формулы Буля, формулы Гаусса становятся все более эффективными почти для каждой задачи. [Pg.36]
Эта проблема возникает из-за того, что ортогональные многочлены (на которых основаны формулы Гаусса) имеют разные нули для разных порядков полиномов.Поскольку точки, в которых должна быть вычислена функция, являются нулями ортогонального многочлена, они различны в каждой формуле из одного и того же семейства (кроме центральной точки). [Стр.36]
Прямым следствием этого факта является сложность оценки ошибки с использованием конкретной формулы Гаусса. [Pg.36]
Если мы хотим управлять формулой Гаусса с помощью формулы более высокого порядка, необходимо вычислить функцию во всех точках двух формул (иногда за исключением центральной точки).[Pg.36]
Как уже упоминалось, полезно использовать вес r (x) оптимальным образом, чтобы максимально использовать формулы Гаусса, а оставшаяся часть функции должна быть хорошо представлена полиномом. [Стр.36]
| Таблица 1.5. Значения x / и w, — для формулы Гаусса с семью точками. |  |
Если кто-то желает оценить дисперсию (или стандартное отклонение) результата, рассчитанного на основе ряда данных fx, y, z …), каждый из которых сам имеет определенные стандартные отклонения, мы можем использовать Gauss формула распространения ошибки … [Pg.232]
Два последних выражения включают массовый расход твердых частиц в головном погоне, а первое — нет. Использование формулы Гаусса с первым выражением (10.A.6a) для 77 дает … [Pg.232]
Однако мы должны ограничить это обсуждение.Если исходная и собранная фракции могут быть определены намного точнее, чем фракция перелива, мы могли бы прийти к другому выводу при использовании формулы Гаусса с новыми оценками ошибок измерения. Это могло бы произойти, например, если бы мы могли точно взвесить сырье и уловленные твердые частицы, будучи при этом вынужденными выполнять отбор пробы фракции перелива в режиме онлайн. [Pg.233]
.
Формула Гаусса — это … Что такое формула Гаусса?
Уравнения Гаусса – Кодацци — В римановой геометрии уравнения Гаусса – Кодацци – Майнарди являются фундаментальными уравнениями теории вложенных гиперповерхностей в евклидовом пространстве и, в более общем смысле, подмногообразий римановых многообразий. У них также есть приложения для встроенных… Wikipedia
Теорема Гаусса – Бонне — Теорема Гаусса – Бонне или формула Гаусса – Бонне в дифференциальной геометрии — важное утверждение о поверхностях, которое связывает их геометрию (в смысле кривизны) с их топологией (в смысле эйлеровой характеристики ).Он называется… Wikipedia
Гаусс, Карл Фридрих — (1777–1855) Немецкий математик Гаусс происходил из крестьянского происхождения в Брауншвейге, Германия, и его необычайный талант к математике проявился в очень раннем возрасте. К трем годам он открыл для себя достаточно арифметических действий, чтобы быть…… Учеными
Квадратурная формула Гаусса – Кронрода — В вычислительной математике квадратурная формула Гаусса – Кронрода представляет собой метод численного интегрирования (вычисление приближенных значений интегралов).Квадратура Гаусса – Кронрода — это вариант квадратур Гаусса, в котором точки оценки…… Wikipedia
Алгоритм Гаусса – Ньютона — Алгоритм Гаусса – Ньютона — это метод, используемый для решения нелинейных задач наименьших квадратов. Это можно рассматривать как модификацию метода Ньютона для поиска минимума функции. В отличие от метода Ньютона, алгоритм Гаусса – Ньютона может использоваться только…… Wikipedia
Лемма Гаусса (теория чисел) — Эта статья посвящена лемме Гаусса в теории чисел.Лемма Гаусса (полином) касается факторизации полиномов. Лемма Гаусса в теории чисел дает условие того, что целое число является квадратичным вычетом. Хотя это бесполезно с вычислительной точки зрения… Wikipedia
Система координат Гаусса-Крюгера — В картографии термин Гаусс Крюгер, названный в честь Карла Фридриха Гаусса и Иоганна Генриха Луи Крюгера, используется тремя немного разными способами. * Часто это просто синоним поперечной проекции карты Меркатора.Другой синоним — Гаусс… Википедия
Константа Гаусса — В математике константа Гаусса, обозначаемая G, определяется как величина, обратная среднему геометрическому арифметическому 1 и квадратному корню из 2 :: G = frac {1} {mathrm {agm} ( 1, sqrt {2})} = 0,8346268 точек Константа названа в честь Карла Фридриха Гаусса,…… Википедия
Gauss Moutinho Cordeiro — Информационное окно Имя человека = Gauss Moutinho Cordeiro размер изображения = подпись = имя при рождении = дата рождения = 17 апреля 1952 г. Место рождения = дата смерти = место смерти = причина смерти = место отдыха = координаты места отдыха = место жительства = национальность = флаг | Бразилия… Википедия
Список тем, названных в честь Карла Фридриха Гаусса — Карл Фридрих Гаусс (1777 ndash; 1855) является эпонимом всех тем, перечисленных ниже.Темы, в том числе Гаусса * Премия Карла Фридриха Гаусса, премия по математике * Размагничивание для размагничивания объекта * Гаусс (единица), единица магнитного поля (B)…… Wikipedia
Линза с двойным гауссом — конструкция с двойным гауссом и оптическими лучами Двойная линза с гауссом — это составная линза, используемая в основном в объективах фотоаппаратов, которая уменьшает оптические аберрации в большой фокальной плоскости. Содержание 1 Дизайн… Википедия
Формула Гаусса — это … Что такое формула Гаусса?
Уравнения Гаусса – Кодацци — В римановой геометрии уравнения Гаусса – Кодацци – Майнарди являются фундаментальными уравнениями теории вложенных гиперповерхностей в евклидовом пространстве и, в более общем смысле, подмногообразий римановых многообразий. У них также есть приложения для встроенных… Wikipedia
Теорема Гаусса – Бонне — Теорема Гаусса – Бонне или формула Гаусса – Бонне в дифференциальной геометрии — важное утверждение о поверхностях, которое связывает их геометрию (в смысле кривизны) с их топологией (в смысле эйлеровой характеристики ).Он называется… Wikipedia
Гаусс, Карл Фридрих — (1777–1855) Немецкий математик Гаусс происходил из крестьянского происхождения в Брауншвейге, Германия, и его необычайный талант к математике проявился в очень раннем возрасте. К трем годам он открыл для себя достаточно арифметических действий, чтобы быть…… Учеными
Квадратурная формула Гаусса – Кронрода — В вычислительной математике квадратурная формула Гаусса – Кронрода представляет собой метод численного интегрирования (вычисление приближенных значений интегралов).Квадратура Гаусса – Кронрода — это вариант квадратур Гаусса, в котором точки оценки…… Wikipedia
Алгоритм Гаусса – Ньютона — Алгоритм Гаусса – Ньютона — это метод, используемый для решения нелинейных задач наименьших квадратов. Это можно рассматривать как модификацию метода Ньютона для поиска минимума функции. В отличие от метода Ньютона, алгоритм Гаусса – Ньютона может использоваться только…… Wikipedia
Лемма Гаусса (теория чисел) — Эта статья посвящена лемме Гаусса в теории чисел.Лемма Гаусса (полином) касается факторизации полиномов. Лемма Гаусса в теории чисел дает условие того, что целое число является квадратичным вычетом. Хотя это бесполезно с вычислительной точки зрения… Wikipedia
Система координат Гаусса-Крюгера — В картографии термин Гаусс Крюгер, названный в честь Карла Фридриха Гаусса и Иоганна Генриха Луи Крюгера, используется тремя немного разными способами. * Часто это просто синоним поперечной проекции карты Меркатора.Другой синоним — Гаусс… Википедия
Константа Гаусса — В математике константа Гаусса, обозначаемая G, определяется как величина, обратная среднему геометрическому арифметическому 1 и квадратному корню из 2 :: G = frac {1} {mathrm {agm} ( 1, sqrt {2})} = 0,8346268 точек Константа названа в честь Карла Фридриха Гаусса,…… Википедия
Gauss Moutinho Cordeiro — Информационное окно Имя человека = Gauss Moutinho Cordeiro размер изображения = подпись = имя при рождении = дата рождения = 17 апреля 1952 г. Место рождения = дата смерти = место смерти = причина смерти = место отдыха = координаты места отдыха = место жительства = национальность = флаг | Бразилия… Википедия
Список тем, названных в честь Карла Фридриха Гаусса — Карл Фридрих Гаусс (1777 ndash; 1855) является эпонимом всех тем, перечисленных ниже.Темы, в том числе Гаусса * Премия Карла Фридриха Гаусса, премия по математике * Размагничивание для размагничивания объекта * Гаусс (единица), единица магнитного поля (B)…… Wikipedia
Линза с двойным гауссом — конструкция с двойным гауссом и оптическими лучами Двойная линза с гауссом — это составная линза, используемая в основном в объективах фотоаппаратов, которая уменьшает оптические аберрации в большой фокальной плоскости. Содержание 1 Дизайн… Википедия
Fórmula del área de gauss
Википедия todavía no tiene una página llamada «Fórmula del área de gauss».
Busca Fórmula del área de gauss en otros proyectos hermanos de Wikipedia:
 | Wikcionario (diccionario) |
 | Wikilibros (обучающие / руководства) |
 | Викицитатник (цитаты) |
 | Wikisource (biblioteca) |
 | Викинотики (нотиции) |
 | Wikiversidad (Contenido académico) |
 | Commons (изображения и мультимедиа) |
 | Wikiviajes (viajes) |
 | Викиданные (данные) |
 | Викивиды (особые виды) |
-
 Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla.
Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla. -
 Busca «Fórmula del área de gauss» en el texto de otras páginas de Wikipedia que ya existen.
Busca «Fórmula del área de gauss» en el texto de otras páginas de Wikipedia que ya existen. -
 Проконсультируйтесь по списку произведений искусства по «Fórmula del área de gauss».
Проконсультируйтесь по списку произведений искусства по «Fórmula del área de gauss». -
 Busca las páginas de Wikipedia que tienen включает «Fórmula del área de gauss».
Busca las páginas de Wikipedia que tienen включает «Fórmula del área de gauss». -
 Si ya habías creado la página con este nombre, limpia la caché de tu navegador.
Si ya habías creado la página con este nombre, limpia la caché de tu navegador. -
 También puede que la página que buscas haya sido borrada.
También puede que la página que buscas haya sido borrada.
Si el artículo incluso así no existe:
-
 Crea el artículo utilizando nuestro asistente o solicita su creación.
Crea el artículo utilizando nuestro asistente o solicita su creación. -
 Puedes traducir este artículo de otras Wikipedias.
Puedes traducir este artículo de otras Wikipedias. -
 En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatibles con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.
En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatibles con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия. -
 Ten en cuenta también que:
Ten en cuenta también que:- Artículos vacíos o con información minima serán borrados —véase «Википедия: Esbozo» -.
- Artículos de publicidad y autopromoción serán borrados —véase «Википедия: Lo que Wikipedia no es» -.


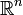 , такое что функции vi вместе со своими частными производными
, такое что функции vi вместе со своими частными производными 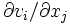 интегрируемы по Лебегу в ограниченной области Ω, граница
интегрируемы по Лебегу в ограниченной области Ω, граница 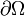 которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.
которой является объединением конечного множества кусочно гладких (n − 1)-мерных гиперповерхностей, ориентированных с помощью внешней единичной нормали ν.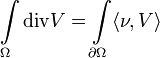

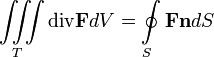 ,
,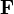 , распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.
, распространённый по некоторому объёму T, равен потоку вектора через поверхность S, ограничивающую данный объём.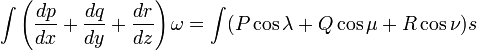 ,
,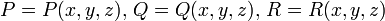 — функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью.
— функции, непрерывные вместе со своими частными производными первого порядка в замкнутой области пространства, ограниченного замкнутой гладкой поверхностью. Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla.
Comprueba si имеет escrito el nombre del artículo de forma correa, y que Wikipedia es el lugar donde debería estar la información que buscas.Si el título es righto, a la derecha figuran otros proyectos Wikimedia donde quizás podrías encontrarla. Busca «Fórmula del área de gauss» en el texto de otras páginas de Wikipedia que ya existen.
Busca «Fórmula del área de gauss» en el texto de otras páginas de Wikipedia que ya existen. Проконсультируйтесь по списку произведений искусства по «Fórmula del área de gauss».
Проконсультируйтесь по списку произведений искусства по «Fórmula del área de gauss». Busca las páginas de Wikipedia que tienen включает «Fórmula del área de gauss».
Busca las páginas de Wikipedia que tienen включает «Fórmula del área de gauss». Si ya habías creado la página con este nombre, limpia la caché de tu navegador.
Si ya habías creado la página con este nombre, limpia la caché de tu navegador. También puede que la página que buscas haya sido borrada.
También puede que la página que buscas haya sido borrada. Crea el artículo utilizando nuestro asistente o solicita su creación.
Crea el artículo utilizando nuestro asistente o solicita su creación. Puedes traducir este artículo de otras Wikipedias.
Puedes traducir este artículo de otras Wikipedias. En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatibles con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.
En Wikipedia únicamente pueden include enciclopédicos y que tengan derechos de autor Compatibles con la Licencia Creative Commons Compartir-Igual 3.0. Никаких текстовых текстов, которые не используются в веб-сайтах, и не предусмотрены специальные условия.  Ten en cuenta también que:
Ten en cuenta también que: