Алгебра свободных и скользящих векторов

Алгебра свободных и скользящих векторов

Меркин Д.Р. Алгебра свободных и скользящих векторов. М: изд-во «Физматгиз», 1962 — 165 с. В книге дается подробное изложение алгебры свободных и скользящих векторов. Содержание первой главы соответствует в основном программе по векторной алгебре курса высшей математики втузов. Во второй главе рассматривается теория преобразования системы скользящих векторов и приведения их к простейшему виду. Эта теория имеет важное значение в различных вопросах физики и техники; она может рассматриваться также, как вводная глава винтового исчисления. В книге большое внимание уделено примерам и разъяснению некоторых деталей и особенностей векторного исчисления, весьма важных в приложениях. Книга может служить учебным пособием для студентов и преподавателей втузов и университетов. Она рассчитана также на инженеров, желающих повысить свою теоретическую подготовку. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ ГЛАВА I. ВЕКТОРНАЯ АЛГЕБРА 2. Определение вектора. 3. Классификация векторов. 4. Равенство векторов. 5. Перенос вектора. 6. Нуль-вектор. 7. Компланарность и коллинеарность векторов. 8. Прямопротивоположные векторы. § 2. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ 2. Сумма векторов. 3. Свойства суммы векторов. 4. Правила параллелограмма и параллелепипеда. 5. Разность двух векторов. 6. Свойства модуля суммы векторов. § 3. УМНОЖЕНИЕ И ДЕЛЕНИЕ ВЕКТОРА НА ЧИСЛО 2. Свойства произведения. 3. Деление вектора на число. 4. Единичные векторы. 5. Орт оси. 6. Коллинеарность двух векторов. § 4. РАЗЛОЖЕНИЕ ВЕКТОРОВ 3. Разложение вектора по трем другим векторам. 4. Разложение вектора по ортам базиса. § 5. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ 2. Условие коллинеарности двух векторов. 3. Условие компланарности трех векторов. 4. Линейная зависимость четырех векторов. § 6. ПРОЕКЦИИ ВЕКТОРА 2. Свойства составляющих вектора. 3. Проекция вектора на ось. 4. Свойства проекций. 5. Угол между векторами. 6. Вычисление проекций вектора. 7. Теорема о проекции сумммы векторов. 8. Псевдоскаляры. § 7. СПОСОБЫ ЗАДАНИЯ ВЕКТОРА 2. Естественный способ задания свободного вектора. 3. Задание свободного вектора с помощью его проекций (координатный метод). 4. Связь между естественным и координатным способами задания вектора. 5. Задание несвободного вектора. 6. Задание скользящего вектора. 7. Некоторые приложения. § 8. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ 2. Свойства скалярного произведения. 3. Выражение скалярного произведения через проекции векторов. 4. Векторные уравнения геометрических мест. 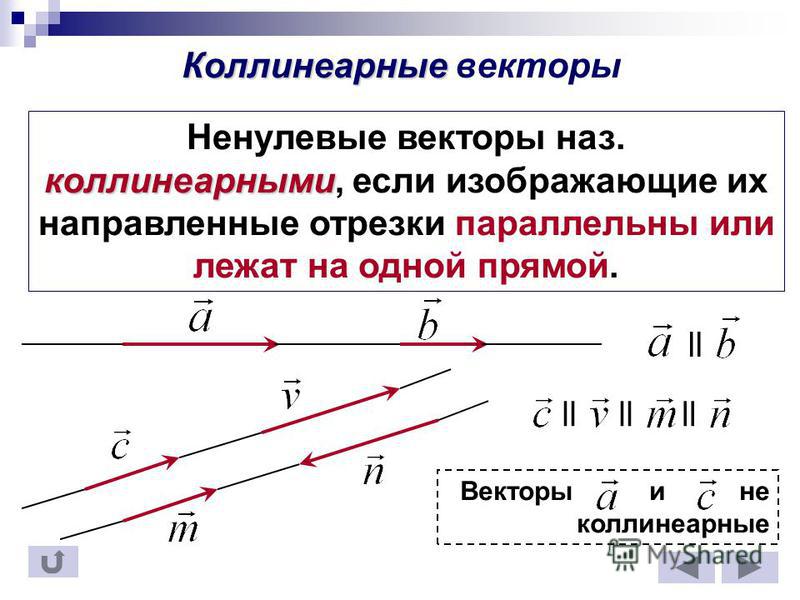5. Уравнение плоскости. 7. Изменение проекций вектора при преобразовании координат. 8. Другое определение вектора. § 9. ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ 2. Примеры из физики. 3. Способ Н. Е. Жуковского построения векторного произведения. 4. Свойства векторного произведения. 5. Разложение вектора-произведения по координатным ортам. 6. Условие коллинеарности двух векторов. 7. Тождество Лагранжа. 8. Полярные и аксиальные векторы. § 10. СЛОЖНЫЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ 2. Двойное векторное произведение. 3. Разложение вектора по трем другим векторам. 4. Скалярное произведение двух векторных произведений. 5. Векторное произведение двух векторных произведений. 6. Произведение двух смешанных произведений. 7. Взаимные реперы. § 11. ВЕКТОРНЫЕ УРАВНЕНИЯ ПРЯМОЙ ЛИНИИ 2. Уравнение прямой, проходящей через две заданные точки. 3. Плюкерово уравнение прямой в пространстве. 4. Прямая как пересечение двух плоскостей. § 12. ИНВАРИАНТЫ ОТНОСИТЕЛЬНО ПРЕОБРАЗОВАНИЯ ОСЕЙ ГЛАВА II. 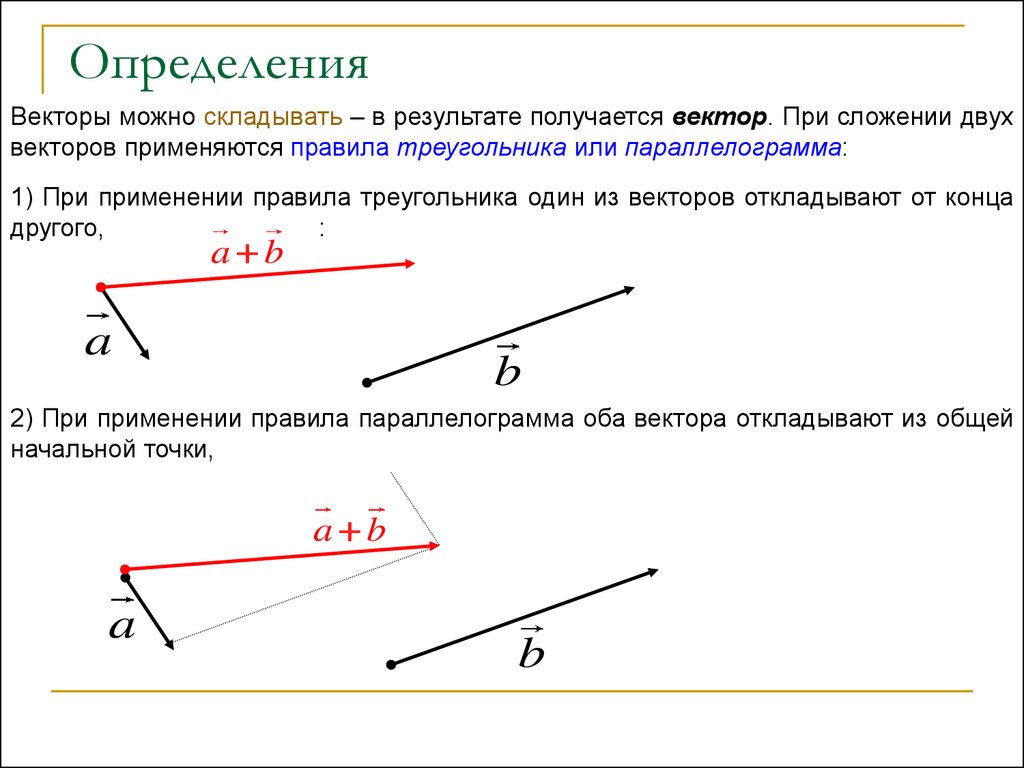АЛГЕБРА СКОЛЬЗЯЩИХ ВЕКТОРОВ § 13. МОМЕНТ ВЕКТОРА ОТНОСИТЕЛЬНО ТОЧКИ И ОСИ. ЗАДАНИЕ СКОЛЬЗЯЩЕГО ВЕКТОРА 2. Момент вектора относительно точки. 3. Проекции момента. 4. Момент вектора относительно оси. 5. Задание скользящего вектора его проекциями и моментами относительно координатных осей. § 14. ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИСТЕМЫ ВЕКТОРОВ 2. Главный вектор системы векторов. 3. Главный момент системы векторов. 4. Система двух равнопротивоположных векторов. 5. Первая теорема Вариньона. 6. Изменение главного момента с изменением полюса. 7. Инварианты системы векторов. 8. Минимальный момент и центральная ось системы. 9. Распределение главных моментов в пространстве. 10. Понятие о винте. 11. Винт системы векторов. § 15. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ ВЕКТОРОВ 2. Основные определения и аксиомы. § 16. ПРИВЕДЕНИЕ СИСТЕМЫ СВОБОДНЫХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ § 17. ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Приведение произвольной системы скользящих векторов к системе двух векторов (геометрическое решение). 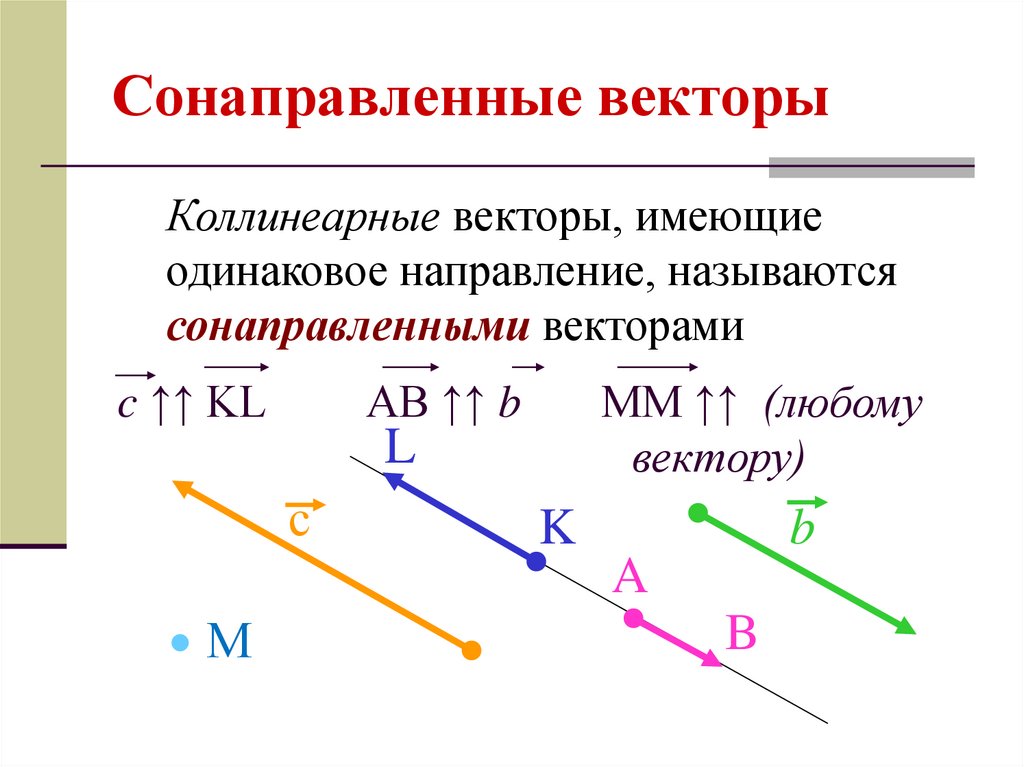§ 18. УСЛОВИЯ ЭКВИВАЛЕНТНОСТИ ДВУХ СИСТЕМ СКОЛЬЗЯЩИХ ВЕКТОРОВ 2. Условия эквивалентности двух систем скользящих векторов. 3. Преобразование эквивалентных систем. § 19. ТЕОРИЯ ПАР 1. Пара векторов и ее момент. 2. Свойства пар. 3. Винт § 20. ПРИВЕДЕНИЕ СИСТЕМЫ СКОЛЬЗЯЩИХ ВЕКТОРОВ К ПРОСТЕЙШЕМУ ВИДУ 2. Приведение системы скользящих векторов к системе двух векторов (аналитическое решение). 3. Приведение системы скользящих векторов к вектору и паре. 4. Пример из кинематики. 5. Приведение системы скользящих векторов к винту. 6. Примеры. 7. Уравнения равновесия векторов. 8. Вторая теорема Вариньона. § 21. ИССЛЕДОВАНИЕ ЧАСТНЫХ СЛУЧАЕВ 2. Плоская система скользящих векторов. 3. Система параллельных скользящих векторов. 4. Центр системы параллельных векторов.

Определение вектора в пространстве — презентация онлайн

1. Векторы в пространстве

вход
5klass. net

2. Содержание

I.
II.
III.
IV.
V.
VI.
Понятие вектора в пространстве
Коллинеарные векторы
Компланарные векторы
Действия с векторами
Разложение вектора
Базисные задачи
Проверь себя
Об авторе
Помощь в управлении презентацией
Выход

3. Понятие вектора в пространстве

Вектор(направленный отрезок) –
отрезок, для которого указано какой из его
концов считается началом, а какой – концом.
В
А
AB
a
M
MM 0
Длина вектора AB – длина отрезка AB.
AB AB
0 0

4. Коллинеарные векторы

Два ненулевых вектора называются
коллинеарными, если они лежат на одной
прямой или параллельных прямых.
Среди коллинеарных различают:
• Сонаправленные векторы
• Противоположно направленные векторы

5. Сонаправленные векторы

Сонаправленные векторы — векторы, лежащие
по одну сторону от прямой, проходящей через их
начала.
a
a b
b
Нулевой вектор считается сонаправленным с
любым вектором.
• Равные векторы

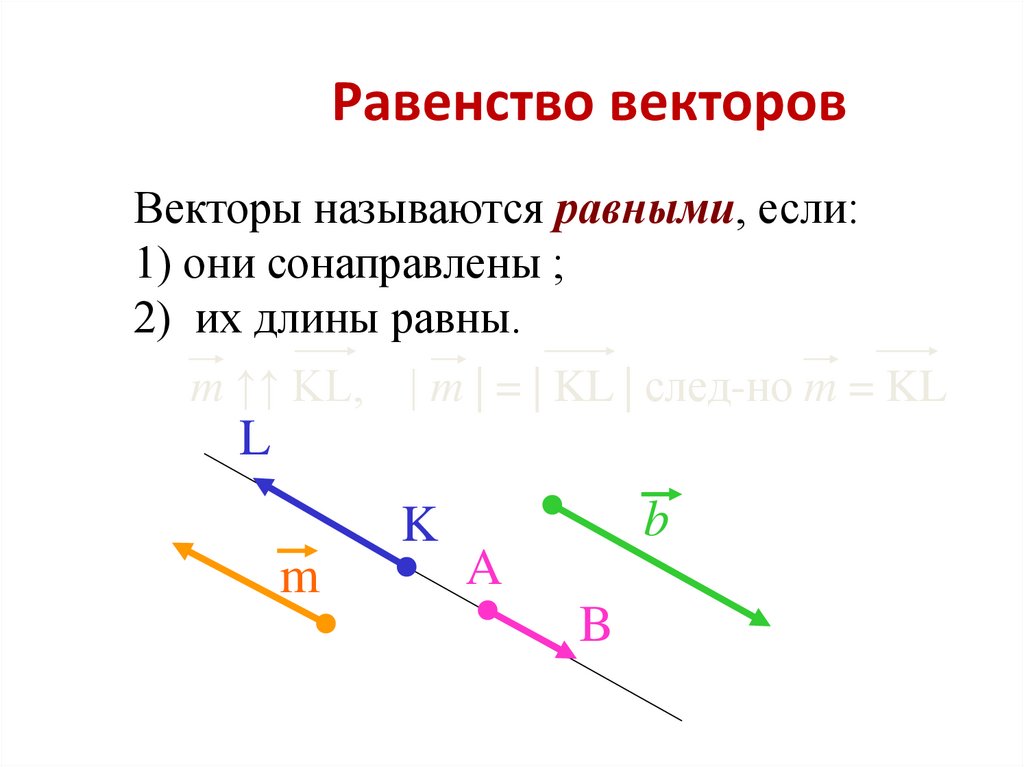
6. Равные векторы

Равные векторы — сонаправленные векторы,
длины которых равны.
a
a b a b, a b
b
От любой точки можно отложить вектор,
равный данному, и притом только один.

7. Противоположно направленные векторы

Противоположно направленные векторы –
векторы, лежащие по разные стороны от прямой,
проходящей через их начала.
a
a b
b
Противоположные векторы

8. Противоположные векторы

Противоположные векторы – противоположно
направленные векторы, длины которых равны.
a
a b a b, a b
b
Вектором, противоположным нулевому,
считается нулевой вектор.

9. Признак коллинеарности

Если существует такое число k при котором
выполняется равенство a k b и при том
вектор b 0, то векторы a и b коллинеарны.
Доказательство

10. Доказательство признака коллинеарности

Два вектора a и b коллинеарны тогда и
только тогда, когда имеет место равенство
a kb
вектор k a b, если k 0
( следует из определения
вектор k a b, если k 0
произведения вект ора на число)
Значит вектор b и k a коллинеарны,
т. 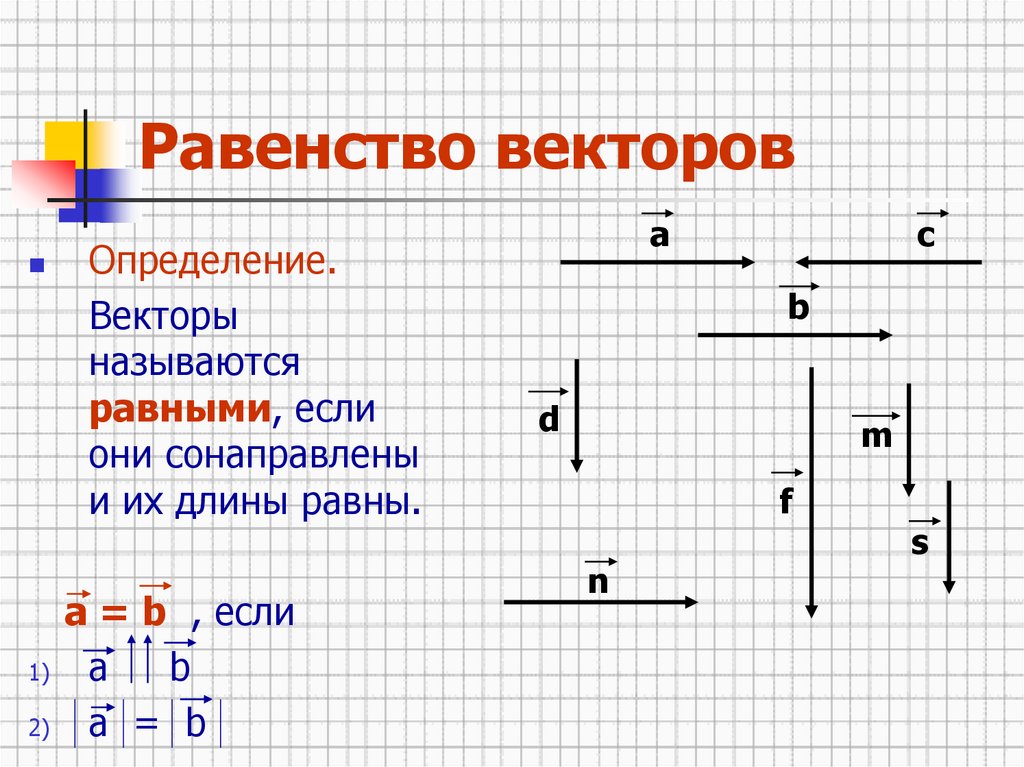к. сонаправленные и противоложно
направленные векторы лежат на одной
или параллельных прямых.
ч.т.д.

11. Определение компланарных векторов

Компланарные векторы – векторы, при
откладывании которых от одной и той же точки
пространства, они будут лежать в одной
плоскости.
Пример:
B1
A1
C1
D1
B
А
C
D
BB1 , AC,AC 1 компланарн ы, т.к.
BB1 AA1 , а векторы AA1 , AC , AC1
лежат в плоскости (AA1C)

12. О компланарных векторах

Любые два вектора всегда компланарны.
α
a
b
a
b
a
b
a и b компланарн ы
Три вектора, среди которых имеются два
коллинеарных, компланарны.
a, b и c
компланарн ы
если
a, b, c
a kb

13. Признак компланарности

Если вектор c можно разложить по векторам
а и b, т.е. представить в виде
с xa yb
где х и у некоторые числа, то векторы a, b
и c компланарн ы.
Доказательство
Задачи

14. Задачи на компланарность

1)
2)
Компланарны ли векторы:
а) a, b, 2a, 3b;
б) a, b, a b, a b ?
Справка
Решение
Известно, что векторы a , b и c компланарны.
Компланарны ли векторы:
а) a, 2b, 3c;
б) a b, a 2c, 2b 3c ?
Справка
Решение

15. Решение

а )векторы a и 2a коллинеарны,
векторы b и 3b коллинеарн ы,
значит векторы a, b, 2a и 3b компланарн ы
б )векторы a, b и a b компланарн ы,
векторы a, b и a b компланарн ы,
значит векторы a, b, a b и a b компланарн ы

16. Решение

a) если векторы a , 2b , 3c компланарн ы,
то существуют такие х и у,что
a xb y c
проверяем существуют ли такие т и п,что
a m 2b n 3c
имеем :
x
2m x m
2
y
3n y n
3
m и п определяют ся единственным образом,
значит векторы компланарн ы

17. Решение

б)если векторы a b , a 2c , 2b 3c
компланарн ы, то существуют такие х и у,что
a b x( a 2c ) y(2b 3c )
a b x a 2xc 2yb 3y c
a(1 x) b(1 2y) c( 2x 3y) 0
1 x 0 x 1
0
2y
1
1
y
3y 2x 0
2
1
a b a 2c (2b 3c )
2
искомые х и у существуют,
значит векторы компланарн ы

18.

Доказательство признака компланарностиB1 OC xOA yOB
С
c
b B
A
A1
O
a
Дано :
с x a yb
x, y некоторые числа
Доказать :
a, b и с компланарны
Доказательство :
Пусть a и b не коллинеарны
О произвольная точка
OA a , OB b
OA ,OB ,OA1 ,OB1 (OAB)
OA1 x OA OB1 y OB
OC c OA1 OB1 x OA y OB
OA a ,OB b ,OC c лежат в одной плоскости
a ,b ,c компланарн ы ч.т.д

19. Свойство компланарных векторов

Если векторы a, b и c компланарн ы, то один из них
можно выразить линейным образом через два других,
т.е. представить в виде :
с xa yb
причем коэффициен ты разложения
определяются единственным образом.

20. Действия с векторами

Сложение
Вычитание
Умножение вектора на число
Скалярное произведение

21. Сложение векторов

Правило треугольника
Правило параллелограмма
Правило многоугольника
Правило параллелепипеда
Свойства сложения

22.

Правило треугольникаДля сложения двух векторов необходимо :
1. отложить от какой нибудь точки А вектор
AB, равный а
2. от точки В отложить вектор BC , равный b
3. вектор AC называется суммой векторов a и b
B
a
a
А
b
a b
b
C

23. Правило треугольника

B
a
А
a b
b
C
Для любых трех точек А, В и С справедливо равенство:
AB BC AC

24. Правило параллелограмма

Для сложения двух векторов необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от точки А отложить вектор AC, равный b
3. достроить фигуру до параллелограмма , проведя
дополнительные линии параллельно данным
векторам
4. диагональ параллелограмма сумма векторов
B
a
a
b
А
с
b
с a b
C

25. Свойства сложения

Для любых векторов a , b и c справедливы
равенства :
a b b a
a b с а b с
переместительный закон
сочетательный закон

26.

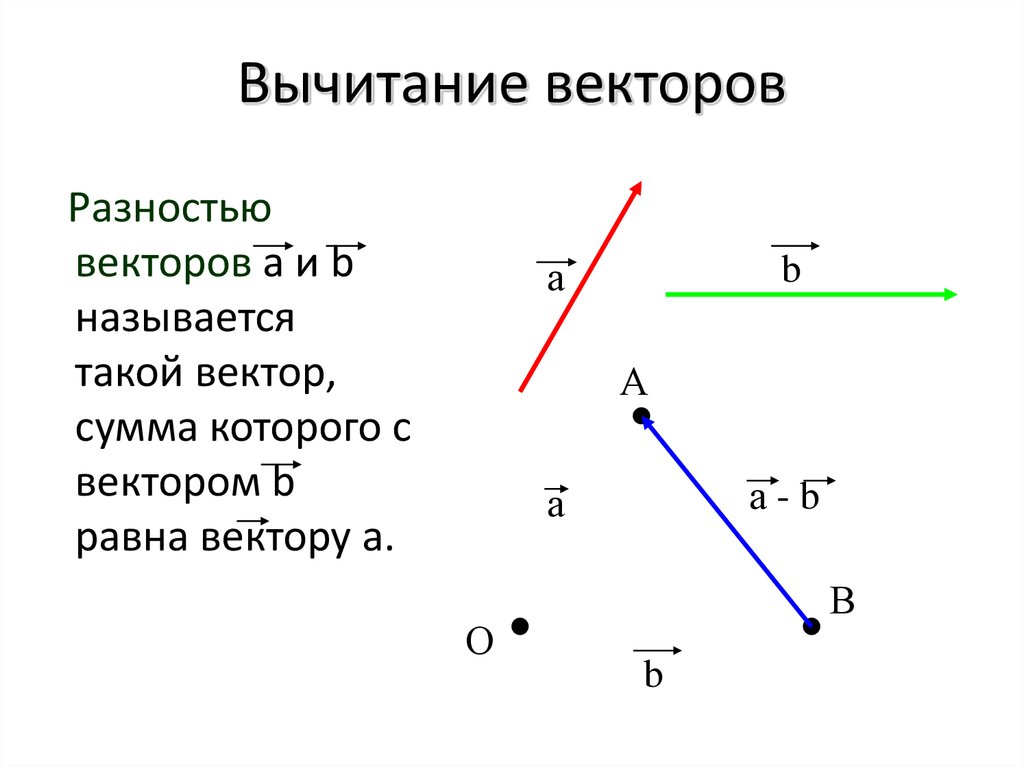Правило многоугольникаСумма векторов равна вектору, проведенному
из начала первого в конец последнего(при
последовательном откладывании).
a
B
b
C
A
a b c d e
e
c
E
d
Пример
D
AB BC CD DE AE

27. Пример

B1
A1
C1
D1
B
A
C
D
AA1 D1C1 A1 D BA CB 0

28. Правило параллелепипеда

Вектор, лежащий на диагонали параллелепипеда,
равен сумме векторов, проведенных из той же
точки и лежащих на трех измерениях
параллелепипеда.
B
A1
C1
1
d
AB b
D1
с bB
C
А
a
AD a
D
AC1 AD AB AA1
AA1 c
AC1 d

29. Свойства

B1
C1
A1
d
D1
с aB
А
C
b
D
d a b c для любого параллелепипеда
d 2 a 2 b 2 c 2 для прямоуголь ного
параллелепипеда

30. Вычитание векторов

• Вычитание
• Сложение с противоположным

31. Вычитание

Разностью векторов a и b называется такой
вектор, сумма которого с вектором b равна
вектору a .

32. Вычитание

Для вычитания одного вектора из другого необходимо :
1. отложить от какой нибудь точки А
вектор AB, равный а
2. от этой же точки А отложить вектор AC,
равный b
3. вектор CB называется разностью векторов a и b
B
a
b
Правило трех точек
a
a b
A
b
C

33. Правило трех точек

Любой вектор можно представить как разность
двух векторов, проведенных из одной точки.
B
BK AK AB
А
BK
K

34. Сложение с противоположным

Разность векторов
как сумму вектора
a
a
и
b можно представить
и вектора,
противоположного вектору
b.
a b a b
a
B
b
a b
b
O
А
a

35. Умножение вектора на число

Произведением ненулевог о вектора a на число k
называется такой вектор b , длина которог о
равна к а , при чем векторы a и b сонаправле ны
при k 0 и противоположно направлены при k 0.
a
2a
b
1
b
3

36.

Свойства• Произведением нулевого вектора на любое число
считается нулевой вектор.
0 n 0
• Произведение любого вектора на число нуль есть
нулевой вектор.
n 0 0

37. Свойства

Для любыхвект оровa и b и любых
чисел k, l справедливы равенст ва:
(kl)a k(la )
сочет ат ельный закон
k( a b ) k a k b
(k l)a k a l a
1 ый распределит ельный
закон
2 ой распределит ельный
закон

38. Скалярное произведение

Скалярным произведением двух векторов
называется произведение их длин на косинус угла
между ними.
ab a b cos( a ; b )
Справедливые утверждения
Вычисление скалярного произведения в координатах
Свойства скалярного произведения

39. Справедливые утверждения

• скалярное произведение ненулевых векторов
равно нулю тогда и только тогда, когда эти
векторы перпендикулярны
a b 0 a 0 b 0 a b
• скалярный квадрат вектора (т.е. скалярное
произведение вектора на себя) равен квадрату
его длины
2
a
а
2
а
2

40.

Вычисление скалярного произведения в координатахСкалярное произведение векторов a x1 ; y1 ; z1
и b x 2 ; y2 ; z 2 выражается формулой
a b x 1 x 2 y1 y 2 z 1 z 2
Доказательство

41. Доказательство формулы скалярного произведения

Доказательство :
I . при a 0 или b 0, равенство
ab x1 x2 y 1 y2 z1 z 2 справедливо, т.к . 0 0;0;0
II . при a 0, b 0
О произвольн ая точка
B
b
OA a, OB b
если a и b неколлинеа рны, то
α a
AB 2 OA 2 OB 2 2 OA OB cosα ( по т еоремOекосинусов)
A
это равенство верно и в том случае когда векторы
a и b коллинеарн ы
O
B
A
2
2
cosα 1, AB (OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcosα
B
b
O
a
A
2
2
cosα 1, AB (OA OB)
2
2
OA OB 2OA OB
2
2
OA OB 2OA OBcosα

42. Доказательство формулы скалярного произведения

Так как AB b a , OA a , OB b , то
2
2
2
1
ab ( a b b a )
2
a x1 ; y1 ; z1 b x2 ; y2 ; z 2 b a x2 x1 ; y2 y1 ; z 2 z1
2
2
a x y z , b x22 y22 z 22 ,
2
1
2
1
2
1
2
b a (x2 x1 )2 (y 2 y1 )2 (z 2 z1 )2
1
ab (x12 y12 z12 x22 y22 z 22 (x2 x1 )2 (y 2 y1 )2
2
1
(z 2 z1 )2 ) (x12 y12 z12 x22 y22 z 22 x22 2×1 x2
2
x12 y22 2y1 y2 y12 z 22 2z1 z 2 z12 ) x1 x2 y1 y2 z1 z 2

43.

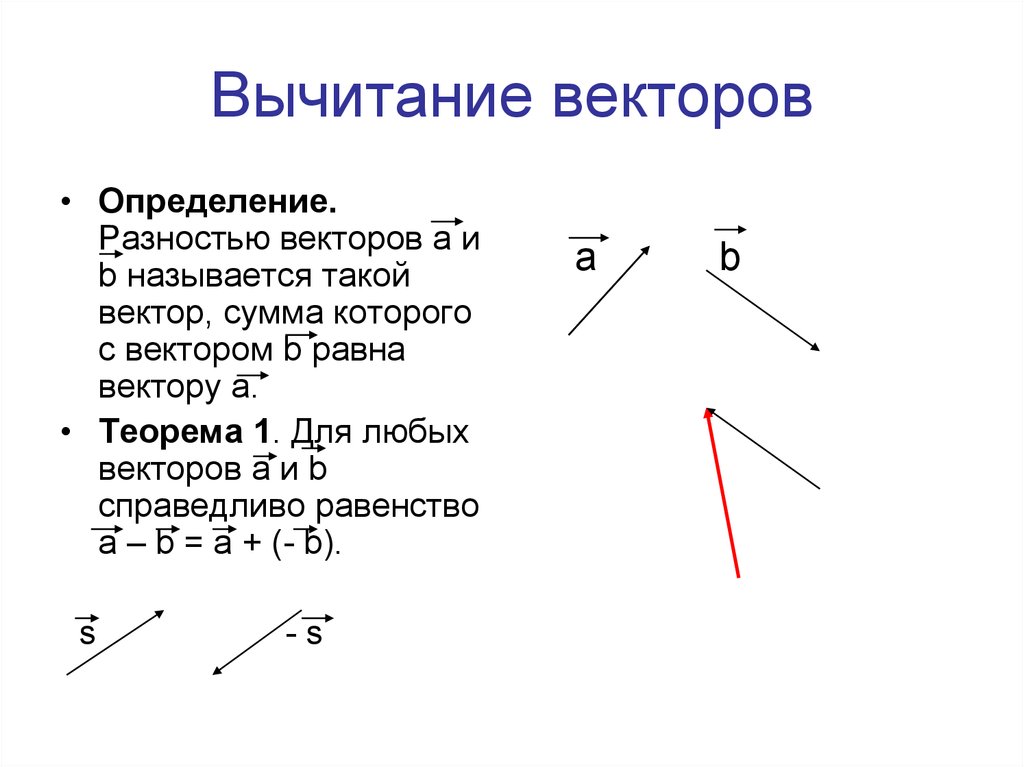Свойства скалярного произведенияДля любых векторов a , b и с и любого
числа k справедливы равенства :
10.
2
a 0 причем a 0 при a 0
20. a b ba (переместительный закон)
(распределительный
0
a
b
c
a
c
b
c
3.
закон)
40. k a b k a b (сочетательный закон)

44. Разложение вектора

• По двум неколлинеарным векторам
• По трем некомпланарным векторам

45. Разложение вектора по двум неколлинеарным векторам

Теорема.
Любой вектор можно разложить по двум
данным неколлинеарным векторам, причем
коэффициенты разложения определяются
единственным образом.
Доказательство

46. Доказательство теоремы

Дано :
b
a, b неколлинеа рные
векторы
Доказать :
p
a
P
B
p
a
A
p коллинеарен b .
p yb , где y –
1)Пусть
Тогда
некоторое число.
Следовательно,
b
O
p x a yb
Доказатель ство :
A1
p 0 a y b
т.е. p разложен по
векторам a и b .

47. Доказательство теоремы

2) p не коллинеарен ни вектору a , ни вектору b .
Отметим О – произвольную точку.
OA a OB b OP p
PA BO PA OA A
1
1
1
p OA1 A1 P(пп правилу треугольника)
но : OA1 и A1 P коллинеарн ы a и b соответственно,
значит OA1 x a , A1 P yb ,
следовательно p x a yb , т.е. p разложен по a и b
ч.т.д.

48. Доказательство теоремы

Докажем, что коэффициенты разложения
определяются единственным образом.
Допустим: p x1 a y1 b
Тогда: p x a y b z c
1
1
—
1
p x a yb z c
0 (x x1 )a (y y1 )b
x x1 0, y y1 0,
если бы x x1 0 то a
y y1
b
x x1
а значит a , и b коллинеарн ы, что
противоречит условию теоремы
значит x x1 0, y y1 0, откуда
x x1 и y y1 .

49. Разложение вектора по трем некомпланарным векторам

Если вектор p представлен в виде
p xa yb z c
где x, y, z – некоторые числа, то говорят, что вектор
p разложен по векторам a , b и c .
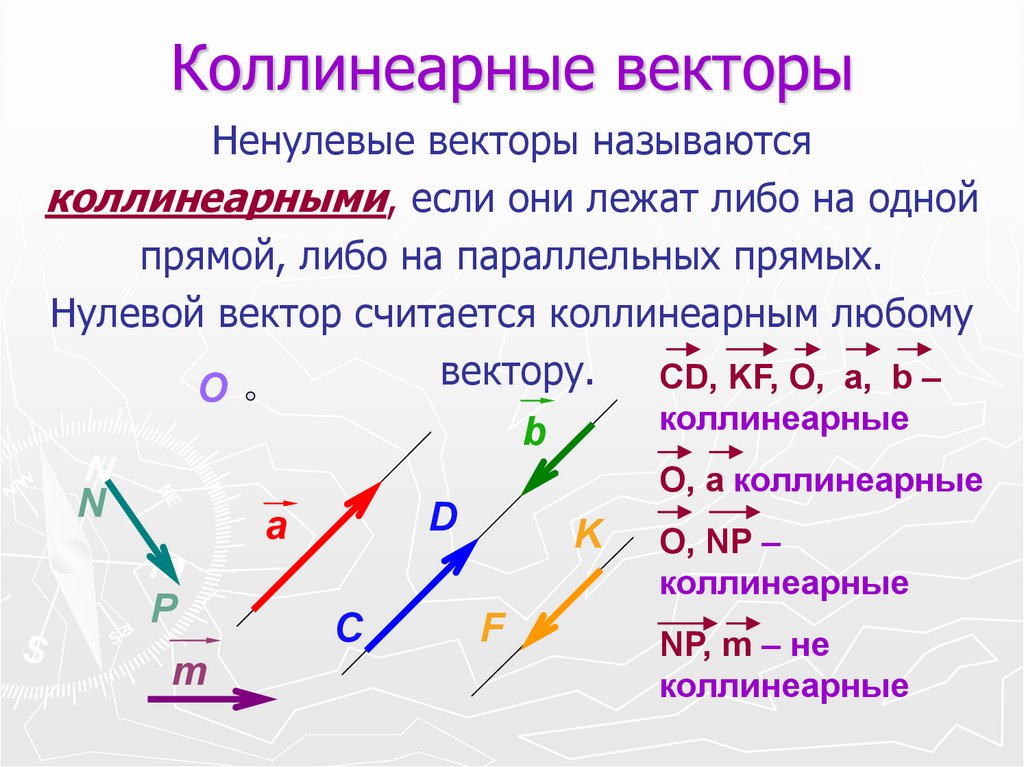
Числа x, y, z называются коэффициентами разложения.
Теорема
Любой вектор можно разложить по трем данным
некомпланарным векторам, причем коэффициенты
разложения определяются единственным образом.
Доказательство

50. Доказательство теоремы

С
с
P
p
b
O
B
P2
P1
aA
Доказательство :
О произвольная точка
Дано :
abc
некомпланрные
векторы
p x a yb z c
OA a OB b OC c OP p
AP OC AP (AOB) P1 P2 P1 OB
OP OP2 P2 P1 P1 P
OP2 , и OA , PP1 и OB , P1 P , OC коллинеарны
OP2 x OA , P2 P1 y OB , P1 P z OC
OP x OA y OB z OC
p x a yb z c ч.т.д.

51. Доказательство теоремы

Докажем, что коэффициенты разложения
определяются единственным образом.
Допустим: p x1 a y1 b z1 c
Тогда: p x a y b z c
1
p x a yb z c
1
—
1
0 (x x1 )a (y y1 )b (z z1 )c
x x1 0, y y1 0, z z1 0
x x1
y y1
если бы z z1 0 то с
a
b
z z1
z z1
а значит a , b , и с компланарн ы, что
противоречит условию теоремы
значит x x1 , y y1 , z z1

52.

Базисные задачиВектор, проведенный в середину отрезка
Вектор, проведенный в точку отрезка
Вектор, соединяющий середины двух отрезков
Вектор, проведенный в центроид треугольника
Вектор, проведенный в точку пересечения
диагоналей параллелограмма
Вектор, лежащий на диагонали параллелепипеда

53. Вектор, проведенный в середину отрезка,

равен полусумме векторов, проведенных из той же
точки в его концы.
С
A
B
O
1
1
1
OC ( OA OB ) OA OB
2
2
2
Доказательство

54. Доказательство

С
A
B
O
Доказательство :
OC OA AC
OC OB BC
Дано :
AB отрезок
AC CB
Доказать :
1
OC ( OA OB )
2
2OC OA AC OB BC OA OB (
AC
BC
)
o
2OC OA OB 2
1
OC ( OA OB ) ч.т.д.
2

55. Вектор, проведенный в точку отрезка

Точка С делит отрезок АВ в отношении т : п.
A
m
Сn
B
O
n
m
OC
OA
OB
m n
m n
Доказательство

56.

ДоказательствоA
m
Сn
O
Доказательство :
B
Дано :
AB отрезок
AC m
CB n
Доказать :
OC
OC OA AC
m
m
AC
AB
(OB OA)
m n
m n
m
m
OC OA
OB
OA
m n
m n
m
m
OA
OA
OB ч.т.д.
m n
m n
n
m
OA
OB
m n
m n

57. Вектор, соединяющий середины двух отрезков,

равен полусумме векторов, соединяющих их концы.
С
N
D
B
С
N
D
B
M
M
A
A
1
1
MN ( AD BC ) ( AC BD )
2
2
Доказательство

58. Доказательство

С
N
D
B
M
A
Доказательство :
MN MA AC CN
MN MB BD DN
2 MN AC BD
1
MN ( AC BD ) ч.т.д.
2
Дано :
AB; CD
BM AM
CN ND
Доказать :
1
MN ( AC BD )
2

59. Вектор, проведенный в центроид треугольника,

равен одной трети суммы векторов, проведенных из
этой точки в вершины треугольника.
Центроид – точка пересечения медиан
треугольника.
O
С
A
M
B
1
OM ( OA OB OC )
3
Доказательство

60. Доказательство

O
С
A
M
K
B
Дано :
ΔABC
M центроид
Доказать :
1
OM ( OA OB OC )
3
Доказательство :
1
2
OM OA OK
3
3
1
2 1
OA ( ( OC OB ))
3
3 2
1
1
1
1
OA OB OC ( OA OB OC ) ч.т.д.
3
3
3
3

61. Вектор, проведенный в точку пересечения диагоналей параллелограмма,

равен одной четверти суммы векторов, проведенных
из этой точки в вершины параллелограмма.
O
C
B
M
A
D
1
OM ( OA OB OC OD )
4
Доказательство

62. Доказательство

O
B
C
M
Дано :
ABCD пар м
BD AC M
Доказать :
1
OM ( OA OB OC OD )
4
A
D
1
OM ( OA OC )
2
1
OM ( OB OD )
2
1
1
1
1
2OM OA OB OC OD
2
2
2
2
1
1
1
1
OM OA OB OC OD
4
4
4
4
1
( OA OB OC OD ) ÷. ò.ä.
4

63. Вектор, лежащий на диагонали параллелепипеда,

равен сумме векторов, лежащих на трех его ребрах,
исходящих из одной вершины.
B1
C1
A1
a
A
d
D1
B
C
b
с
D
d a b c
Доказательство

64. Доказательство

B1
C1
A1
a
A
d
AA1 a
D1
B
C
b
D
с
Доказательство :
AC1 AA1 AB1 BC1
AA1 AB AD
a b c ч.т.д.
Дано :
ABCDA1B1C1D1 пар м
AB b
AD c
AC1 d
Доказать :
d a b c

65. Помощь в управлении презентацией

• управление презентацией осуществляется с
помощью левой клавиши мыши
• переход от одного слайда к другому и на
гиперссылки по одиночному щелчку
• завершение презентации при нажатии кнопки
выход
переход к следующему слайду
возврат к содержанию
возврат к подтеме
возврат с гиперссылок

66. Проверь себя

• Устные вопросы
• Задача 1. Задача на доказательство
• Задача 2. Разложение векторов
• Задача 3. Сложение и вычитание векторов
• Задача 4. Скалярное произведение

67. Устные вопросы

Справедливо ли утверждение:
а) любые два противоположно направленных
вектора коллинеарны?
б) любые два коллинеарных вектора сонаправлены?
в) любые два равных вектора коллинеарны?
г) любые два сонаправленных вектора равны?
д) если a b, b c, то a c ?
е) существуют векторы a , b и c такие, что a
и c не коллинеарны, b и c не коллинеарны, а a
и b коллинеарны?
Ответы

68. Ответы

а) ДА
б) НЕТ (могут быть и противоположно
направленными)
в) ДА
г) НЕТ (могут иметь разную длину)
д) ДА
е) ДА

69. Задача 1. Задача на доказательство

B1
A1
M
B M1 2
А
Решение
C1
D1
C
D
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1

70. Решение

B1
A1
M
B M1 2
C1
D1
C
Дано :
ABCDA1 B1C1 D1 пар д
М 1 , М 2 точки пересечения
медиан ΔА1 ВD и ΔD1CB1
соответственно
Доказать :
AM 1 M 1 M 2 M 2 C1
А
D
Доказательство :
Рассм. тетраэдр AA1 BD
M 1 центроид ΔA1 M 1 B
1
AM 1 ( AA1 AB AD )
3
AC1 AA1 AB AD по правилу пар да
1
AM 1 AC1
3
1
M AC1 AM 1 AC1
3
1
аналогично M 2 AC1 C1 M 2 AC1
3
следовательно AM 1 M 1 M 2 M 2 C1 ч.т.д.

71. Задача 2. Разложение векторов

Разложите вектор по a , b и c :
D
N точка пересечения
медиан ABC
a
A
b
N
c
а) DB
б) CB
в) DC
г) DN
Решение
B
C

72. Решение

а) DB b a
б) CB b c
в) DC c a
г) DN a 1 AN a 1 ( 1 ( b c ))
3
1
1
a b c
6
6
3 2

73. Задача 3. Сложение и вычитание

Упростите выражения:
а)
б)
в)
г)
д)
е)
CM MK
DM MA
SD ST
PL PK
AC BC PM AP BM
AD MP EK EP MD
Решение

74. Решение

а) CM MK CK
б) DM MA DA
в) SD ST TD
г) PL PK KL
д) AC BC PM AP BM
AC CB MP PA BM
AB MA BM AM MA 0
е) AD MP EK EP MD
AD DM MP PE EK
AK

75.

Задача 4. Скалярное произведениеВычислить скалярное произведение векторов:
C1
B1
A1
D1
a
B
A
а) AD B1C1
б) AC C 1 A1
в)D1 B AC
г)BA1 BC 1
Решение
C
D
Дано :
ABCDA1 B1C1 D1 куб
AB a

76. Задача 4. Скалярное произведение

Вычислить скалярное произведение векторов:
B1
C1
O1
A1
D1
a
B
A
д) A1O1 A1 C1
е)DO1 B1O1
ж)BO1 C1 B
Решение
C
D
Дано :
ABCDA1 B1C1 D1 куб
AB a
A1C1 B1 D1 O1

77. Решение

2
а) AD B1C1 AD AD 2 a 2
б)AC диагональ квадрата
AC A1C1 C1 A1
AC C 1 A1 AC ( A1C1 ) AC A1C1 (a 2 )2 2a 2
в)D1 B диагональ куба
D1 B a 2 (a 2 )2 3a(п( т.Пифагора из ΔDD1 B)
2
a3 3
D1 B AC 3a 2 a 2 cos45 a 3 6
2
г)BA1 , BC 1 диагонали квадратов
ΔA1 BC 1 равносторонний, A1 BC 1 60
1 2a 2
a2
BA1 BC 1 a 2 a 2
2
2

78. Решение

д)A1O1 половина диагонали квадрата
A1C1 диагональ квадрата
O1 A1C1 0
a 2
A1O1 A1 C1
a 2 cos0 a 2
2
е)D1O1 , B1O 1 половины диагонали квадрата
a 2 a 2
a2
D1O1 B1O1 D1O1 ( O1 B1 )
2
2
2

79.

Решениеж)I способ решение по определению :
B1
C1
O1
a 2 2 a 6
A1
BO1 a 2 (
)
D1
2
2
C1 B диагональ квадрата
c
B
1
1
C
b a
O1 BC 1 A1 BC 1 60 30
2
2
A
a 6
3 2 D
BO1 C1 B BO1 ( BC 1 )
a 2 cos30 a
2
2
II способ разложение по базису :
1
1
BO1 a b c
2
2
C1 B b a
2
1
1
BO1 C1 B ( a b c ) ( a b ) ( a ab
2
2
2
1
1
1
1 2
1 2
3
ac bc ab b ) ( a a ) a 2
2
2
2
2
2
2

80. Об авторе

Презентация выполнена
ученицей 11 «Б» класса средней
школы №316 Фрунзенского
района с углубленным изучением
английского языка Силичевой
Алисой.
Огромная благодарность
выражается руководителю
проекта Подольской Анастасии
Васильевне.

Определение и значение вектора | Dictionary.com

• Основные определения
• Тест
• Связанный контент
• Примеры
• Британский
• Научный
• Культурный

Уровень сложности этого слова показывается на основе уровня сложности.

[ век-тер ]

/ ˈvɛk tər /

Сохранить это слово!

См. синонимы для: вектор / векторы на Thesaurus.com

Показывает уровень оценки в зависимости от сложности слова.

---

сущ.

Математика.

1. величина, обладающая как величиной, так и направлением, представленная стрелкой, направление которой указывает направление величины, а длина пропорциональна величине. Сравните скаляр (по определению 4).
2. такая величина с дополнительным требованием, чтобы такие величины подчинялись закону сложения параллелограмма.
3. такая величина с дополнительным требованием, чтобы такие величины определенным образом преобразовывались при изменении системы координат.
4. любое обобщение вышеуказанных величин.

направление или курс, по которому следует самолет, ракета и т.п.

Биология.

1. насекомое или другой организм, который переносит патогенный грибок, вирус, бактерию и т. д.
2. любой агент, который действует как носитель или транспортер, как вирус или плазмида, который переносит генно-инженерный сегмент ДНК в клетку-хозяин.

Компьютеры. массив данных, упорядоченный таким образом, что отдельные элементы могут быть расположены с помощью одного индекса или нижнего индекса.

глагол (используется с дополнением)

Аэронавтика. направлять (самолет) в полете, указывая соответствующий курс.

Аэрокосмическая промышленность. изменить направление (тяги реактивного или ракетного двигателя), чтобы управлять кораблем.

ТЕСТ

МОЖЕТЕ ЛИ ВЫ ОТВЕЧАТЬ НА ЭТИ ОБЫЧНЫЕ ГРАММАТИЧЕСКИЕ СПОРЫ?

Есть грамматические дебаты, которые никогда не умирают; и те, которые выделены в вопросах этой викторины, наверняка снова всех разозлят. Знаете ли вы, как отвечать на вопросы, которые вызывают самые ожесточенные споры по грамматике?

Вопрос 1 из 7

Какое предложение верно?

Происхождение вектора

1695–1705; <Латинское: тот, который передает, эквивалентный vec-, вариант основы слова vehere для переноски + -tor-tor

ДРУГИЕ СЛОВА ИЗ вектора

vec·to·ri·al [vek-tawr-ee-uhl, -tohr- ], /vɛkˈtɔr i əl, -ˈtoʊr-/, прилагательноеvec·to·ri·al·ly, наречие

Слова рядом вектор

vealy, веблен, вебленизм, вебленизм, вектор, вектор, сложение векторов, векторный анализ, векторный бозон , векторкардиограмма, векторкардиография

Dictionary. com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc., 2023

Слова, относящиеся к вектору

цель, угол, азимут, курс, направление, линия, точка, маршрут, трек, траектория, путь

Как использовать вектор в предложении

• Он производит вложения в векторное пространство с 12 288 измерениями.

  Добро пожаловать на новый уровень чуши — Выпуск 89: Темная сторона|Рафаэль Мильер|9 сентября 2020 г.|Наутилус

• Оксфорд использовал существующую технологию, вектор вакцины против аденовируса шимпанзе, чтобы сделать свою вакцину.

  Больше, чем просто производство: отечественные вакцины против COVID в Индии могут изменить фармацевтическую промышленность|Наоми Сю Элегант|6 сентября 2020 г.|Fortune

• Они также ввели контрольной модели миРНК без вектора.

  Нейроны, появившиеся из ниоткуда — Выпуск 89: Темная сторона|Наянах Шива|2 сентября 2020 г.|Наутилус

• Остальные из нас, кто может работать удаленно, не должны выступать в качестве вектора распространения среди сообщества.

  Я врач и генеральный директор. Почему я не верну своих сотрудников в офис до Дня труда 2021 года|matthewheimer|26 августа 2020 года|Fortune

• Майкл Джарвис, вирусолог из Плимутского университета, возглавляет группу, которая создала вакцины против Эбола и туберкулез с цитомегаловирусами, которые, по его словам, предлагают большую гибкость в качестве переносчиков.

  Могут ли вакцины для диких животных предотвратить человеческие пандемии?|Родриго Перес Ортега|24 августа 2020 г.|Журнал Quanta

• Похоже, что в какой-то степени «правоохранительный вектор» способствовал радикализации Абу Омара.

  ИГИЛ — проблема Путина, и одна из причин этого — этот чеченец.|Анна Немцова|29 сентября 2014|DAILY BEAST

• Аденовирус, который он получил, был просто переносчиком, доставившим недостающий ген в его клетку.

  Вакцина против лихорадки Эбола мало поможет в нынешнем кризисе|Кент Сепковиц|28 августа 2014 г.|DAILY BEAST

• Для первопроходцев Homestar Runner была такой легкой, в векторной графике с экшн-скриптом.

  Бегущий по Звезде, Трогдор Сжигатель и рождение Интернета|Рич Гольдштейн|22 апреля 2014 г.|DAILY BEAST

• Секс является основным вектором в отношениях, но есть и эмоциональные привязанности.

  Китайская культура наложниц продолжает жить в деревнях госпожи|Брендон Хонг|14 апреля 2014 г.|DAILY BEAST

• Или, как точно выразился Симс, зомби «вслепую движутся по вектору памяти».

  Зомби, зомби повсюду: что делать писателю?|Дж.Т. Цена|21 июня 2013 г.|DAILY BEAST

• Линия, проведенная от солнца к любой точке орбиты (нитка от булавки до точки карандаша), является радиус-вектором.

  Учебник астрономии|Джордж С. Комсток

• Радиус-вектор каждой планеты проходит равные площади за равные промежутки времени.

  Учебник астрономии|Джордж К. Комсток

• Радиус-вектор (или линия, соединяющая солнце и планету) заметает равные площади за равные промежутки времени.

  Пионеры науки|Оливер Лодж

• Суточные неравенства на севере и западе легко поддаются построению так называемых векторных диаграмм.

  Британская энциклопедия, 11-е издание, том 17, часть 3|Разное

• Однако при значительном изменении широты форма векторных диаграмм сильно меняется.

  Encyclopaedia Britannica, 11th Edition, Volume 17, Slice 3|Various

Определения вектора 9 в Британском словаре0076

вектор

/ (ˈvɛktə) /

---

существительное

Также называется: полярная векторная математика переменная величина, такая как сила, которая имеет величину и направление и может быть разложена на компоненты, являющиеся нечетными функциями координат. В печати он представлен жирным курсивным символом: F или ̄FСравнить псевдоскаляр, псевдовектор, скаляр (по умолч. 1), тензор (по умолчанию 2)

математика элемент векторного пространства

Также называется: переносчик патолого организма, esp насекомое, которое переносит болезнетворный микроорганизм от одного хозяина к другому либо внутри, либо на поверхности своего тела

Также называется: клонирование вектора Генетика Агент, такой как бактериофаг или плазмида, с помощью которого фрагмент чужеродной ДНК встраивается в клетку-хозяин для получения клона гена в генной инженерии

курс или направление по компасу самолет

любое поведенческое влияние, сила или побуждение

глагол (tr)

направлять или направлять (пилота, самолета и т. д.) по направлениям, передаваемым по радио

изменять направление (тяги реактивного самолета двигатель) как средство управления самолетом

Производные формы вектора

векторный (vɛkˈtɔːrɪəl), прилагательноевекторно, наречие

Происхождение слова для вектора

C18: от латинского: носитель, от vehere передать

© William Collins Sons & Co. Ltd., 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

Научные определения для вектора

вектор

[ vĕk′tər ]

---

Величина, такая как скорость объекта или сила, действующая на объект, которая имеет как величину, так и направление. Сравните скаляр.

Организм, такой как комар или клещ, который переносит патогены от одного хозяина к другому.

Бактериофаг, плазмида или другой агент, переносящий генетический материал из одной клетки в другую.

Научный словарь American Heritage® Авторские права © 2011. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Культурные определения вектора

вектора

---

В физике и математике любая величина, имеющая как величину, так и направление. Например, скорость — это вектор, потому что она описывает как быстро что-то движется, так и в каком направлении оно движется. Поскольку скорость является вектором, другие величины, в которых скорость является фактором, например, ускорение и импульс, также являются векторами.

Новый словарь культурной грамотности, третье издание Авторское право © 2005 г., издательство Houghton Mifflin Harcourt Publishing Company. Опубликовано издательством Houghton Mifflin Harcourt Publishing Company. Все права защищены.

Что такое вектор?

К

• Пол Кирван

Что такое вектор?

Вектор — это величина или явление, обладающее двумя независимыми свойствами: величиной и направлением.

Термин также обозначает математическое или геометрическое представление такой величины.

Примерами векторов в природе являются скорость, импульс, сила, электромагнитные поля и вес. Величина или явление, которое показывает только величину без определенного направления, называется скаляром. Примеры скаляров включают скорость, массу, электрическое сопротивление и емкость жесткого диска.

Что такое векторные атрибуты?

Векторы обычно представляются стрелкой с началом или хвостом и концом или наконечником, который обычно обозначается стрелкой. Векторы очерчивают движение из точки А в точку В и могут быть определены как объект с обозначением, например вектор .

Рис. 1. Вектор на двумерной декартовой плоскости.

В математике декартова система координат изображает векторы с помощью пары чисел, как показано на рис. 1. В этом примере вектор представляет собой направленный отрезок, определяемый как (0,0), (7,7) с помощью его пронумерованных пар. Векторы и скаляры можно использовать в математических процессах и векторных операциях, таких как сложение векторов, вычитание векторов и умножение векторов.

Векторы в компьютерной графике

Векторы могут быть представлены графически в двух или трех измерениях. Величина вектора показана как длина сегмента линии. Направление вектора показано ориентацией сегмента линии и стрелкой на одном конце.

При создании изображений в векторной графике графический файл представляет собой последовательность операторов вектора, описывающих ряд точек, соединяющихся для формирования изображения. Примеры программного обеспечения для векторной графики включают Adobe Illustrator и CorelDraw.

Преимущества векторной графики

Векторная графика используется для многих типов графических изображений. Эта технология завоевала популярность среди графических иллюстраторов по следующим причинам:

• Гибкость и масштабируемость. Дизайнер может изменить размер изображения практически в любой ориентации и разместить его в любом месте экрана.
• Разработка приложений и веб-сайтов. Разработчики приложений и веб-сайтов любят векторную графику из-за ее масштабируемости и возможности создавать изображения на различных устройствах.
• Анимация. Векторная графика облегчает перемещение изображений с помощью анимации.
• Системы инженерного проектирования. Приложения для автоматизированного проектирования используют векторную графику из-за масштабируемости и возможности легко работать со сложными математическими, научными и инженерными формулами.

Векторная и растровая графика

Растровая графика отображает отдельные биты, каждый из которых имеет свои собственные свойства, например цвет, в изображение с помощью компонентов, называемых пикселями или элементами изображения. Растровые изображения обычно имеют фиксированное количество пикселей и менее масштабируемы, чем векторные изображения. По мере увеличения изображения отдельные пиксели могут стать видимыми, в результате чего изображение будет не таким четким и качественным, как эквивалентное векторное изображение.

При работе с растровыми изображениями компьютеры должны хранить каждый пиксель, а не серию векторных точек. Это часто приводит к тому, что растровые файлы имеют больший размер, чем файлы векторной графики. Adobe Illustrator и Adobe Photoshop являются примерами программного обеспечения, которое используется для преобразования растровых изображений в файлы векторной графики и наоборот.

Рис. 2. Векторные и растровые изображения часто выглядят по-разному, потому что векторная графика имеет отдельную форму для каждого цветового оттенка, в то время как растровые изображения окрашивают каждый пиксель таким образом, что градации цвета и глубина отображаются более четко. При больших размерах растровые изображения пикселизируются; векторных изображений нет.

Векторы в кибербезопасности

В сфере кибербезопасности путь, по которому злоумышленник или хакер доставляет свою полезную нагрузку, например вирус или программу-вымогатель, в систему или сеть, называется вектором атаки. Именно так хакеры используют уязвимости в системе или сети.

Вектор атаки также может быть человеком, в случае социальной инженерии, когда преступник использует хитрые методы коммуникации, чтобы ввести пользователей в заблуждение и заставить их выдать ценную информацию, такую ​​как пароли. Типичные векторы атак включают вредоносное ПО, вложения электронной почты, мгновенные сообщения и всплывающие окна.

Системы обнаружения и смягчения киберугроз включают брандмауэры, системы обнаружения вторжений, системы предотвращения вторжений и антивирусное программное обеспечение. Доступны многочисленные продукты и услуги для предотвращения использования злоумышленниками векторов атак и устранения угроз.

Узнайте об основных векторах атак программ-вымогателей и о том, как их избежать.

Последнее обновление: декабрь 2022 г.

Продолжить чтение О векторе

• Принципы дизайна интерфейса приложений, которые должны знать все разработчики

• Лучшие методы визуализации данных и способы их наилучшего использования

• Полное руководство по программам-вымогателям

• Как мобильные брандмауэры защищают от уникальных векторов угроз

• 11 навыков работы с данными для машинного обучения и искусственного интеллекта

объектно-реляционное сопоставление

Объектно-реляционное сопоставление (ORM) — это способ согласования программного кода со структурами базы данных.

Сеть

• поставщик сетевых услуг (NSP)

  Поставщик сетевых услуг (NSP) — это компания, которая владеет, управляет и продает доступ к магистральной инфраструктуре Интернета и . ..

• неэкранированная витая пара (UTP)

  Неэкранированная витая пара (UTP) — это повсеместно распространенный тип медных кабелей, используемых в телефонной проводке и локальных сетях (LAN).

• Многопротокольная коммутация по меткам (MPLS)

  Многопротокольная коммутация по меткам (MPLS) — это механизм коммутации, используемый в глобальных сетях (WAN).

Безопасность

• данные держателя карты (CD)

  Данные держателя карты (CD) — это любая личная информация (PII), связанная с лицом, у которого есть кредитная или дебетовая карта.

• Уровни продавца PCI DSS

  Стандарт безопасности данных индустрии платежных карт (PCI DSS) ранжирует продавцов по количеству транзакций за …

• CSR (запрос на подпись сертификата)

  Запрос на подпись сертификата (CSR) — это специально отформатированное зашифрованное сообщение, отправленное с цифрового протокола Secure Sockets Layer (SSL) . ..

ИТ-директор

• корпоративная социальная ответственность (КСО)

  Корпоративная социальная ответственность (КСО) — это стратегия компаний, направленная не только на увеличение прибыли, но и на активную …

• системы, основанные на знаниях (KBS)

  Системы, основанные на знаниях (KBS), — это компьютерные программы, которые используют централизованное хранилище данных, известное как база знаний, для …

• Закон Сарбейнса-Оксли

  Закон Сарбейнса-Оксли от 2002 года — это федеральный закон, устанавливающий широкомасштабные аудиторские и финансовые правила для публичных компаний.

HRSoftware

• вовлечения сотрудников

  Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.

• кадровый резерв

  Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.

• разнообразие, равенство и инклюзивность (DEI)

  Разнообразие, равенство и инклюзивность — термин, используемый для описания политики и программ, которые способствуют представительству и …

Отдел обслуживания клиентов

• точка взаимодействия с клиентом

  Точка соприкосновения с покупателем — это любой прямой или косвенный контакт покупателя с брендом.

• устав обслуживания клиентов

  Устав обслуживания клиентов — это документ, в котором описывается, как организация обещает работать со своими клиентами, а также …

• представитель по развитию продаж (SDR)

  Представитель по развитию продаж (SDR) — это лицо, занимающееся поиском, перемещением и квалификацией потенциальных клиентов через .