Скалярное произведение векторов. Профильный уровень 11 класс онлайн-подготовка на Ростелеком Лицей

Длина вектора. Расстояние между точками

 

 Мы продолжаем расширять модель вектора для трехмерного пространства. На прошлом уроке мы рассмотрели определение вектора с использованием двух подходов (геометрического и алгебраического), ввели основные операции (сложение и вычитание векторов, умножение вектора на число), рассмотрели некоторые свойства.

 

Также мы определили длину вектора как длину соответствующего отрезка с использованием теоремы Пифагора: длина вектора равна корню из суммы квадратов его координат (утверждение остается верным, независимо от количества этих самых координат) (см. рис. 1):

Рис. 1. Вектор

Если вектор задан координатами начала и конца, то его собственные координаты находятся как разности координат этих точек (см. рис. 2):

Рис. 2. Вектор

Таким образом, формула длины вектора через его координаты эквивалентна утверждению, что расстояние между двумя точками находится как корень из суммы квадратов попарных разностей их координат:

Для трехмерного пространства ситуация повторяется абсолютно. Т. к. длина вектора – это длина диагонали прямоугольного параллелепипеда с измерениями, равными координатам вектора, то его длина находится как корень квадратный из суммы квадратов его координат (см. рис. 3):

Рис. 3. Вектор

Если две точки заданы своими координатами, то мы можем их рассматривать как начало и конец вектора (см. рис. 4):

Тогда мы можем найти координаты вектора и его длину, т. е. расстояние между точками:

Рис. 4. Вектор

 

Скалярное произведение векторов

 

 

 Вспомним задачу о нахождении работы силы по перемещению объекта.

 

Задача 1. Мальчик тащит санки за веревку по горизонтальной поверхности. Чему равна работа силы натяжения по перемещению санок (см. рис. 5)?

Рис. 5. Иллюстрация к задаче 1

Решение

Если мы умножим силу на расстояние, то ответ будет верным только в том случае, если веревка натянута строго горизонтально, т. е. векторы силы и перемещения сонаправлены (см. рис. 6).

Рис. 6. Иллюстрация к задаче 1

Если же веревка натянута под углом, то за перемещение отвечает не сама сила, а ее проекция на вектор перемещения (грубо говоря, помогает тянуть нам только та часть силы, которая действует вдоль перемещения, она и совершает работу) (см. рис. 7):

Рис. 7. Иллюстрация к задаче 1

Длина проекции равна длине вектора силы, умноженной на косинус угла между силой и перемещением (см. рис. 8):

Рис. 8. Иллюстрация к задаче 1

Тогда:

Ответ: .

 

Рассуждая таким образом, в планиметрии мы ввели понятие скалярного произведения двух векторов. Произведение двух векторов равно произведению модуля одного вектора на проекцию второго вектора на первый (см. рис. 9):

Рис. 9. Векторы  и

Если нам известны длины векторов и угол между ними, то формула для вычисления скалярного произведения имеет вид:

Часто для обозначения модуля вектора  используют просто букву , подчеркивая, что длина вектора и длина соответствующего отрезка – это одно и то же:

Результатом скалярного произведения является число. В примере с санками – это работа силы, величина скалярная. Очевидно, для скалярного произведения справедлив переместительный закон (если поменять местами сомножители, то результат не изменится):

Все вышесказанное нам известно из планиметрии. Если мы возьмем два вектора в пространстве и совместим их начала, то они будут лежать в одной плоскости (см. рис. 10).

Рис 10. Векторы  и  лежат в одной плоскости

Следовательно, для них будет справедливо то же самое определение скалярного произведения:

Физический смысл скалярного произведения остается тем же самым.

Разница появляется только в описании через координаты, т. к. в планиметрии у вектора две координаты, а в пространстве – три:

Произведение вектора  на себя называют скалярным квадратом. Подставим его в формулу скалярного произведения:

Таким образом, скалярный квадрат вектора равен квадрату его длины.

 

Скалярное произведение в координатах

 

 

Если вектор задан координатами, то мы можем найти его скалярный квадрат, так как уже умеем искать его длину:

 

Итак, скалярный квадрат вектора равен сумме квадратов его координат:

Рассмотрим теперь, как выражается скалярное произведение двух произвольных векторов через их координаты. Мы это уже делали в планиметрии, и результат будет аналогичным. Тем не менее повторим эти рассуждения.

Пусть два вектора,  и  не коллинеарны. Совместим их в общее начало. Построим вектор  (см. рис. 11).

Рис. 11. Вектор

По теореме косинусов имеем:

Если векторы коллинеарны, то данное равенство окажется верным и для него. Таким образом, дальнейшие рассуждения верны для любой пары векторов.

Выражение  – это скалярное произведение векторов. Тогда имеем:

Выразим скалярное произведение:

В правой части равенства у нас только скалярные квадраты векторов. Мы умеем находить их через координаты. Сделаем это:

Упростим выражение и получим:

Итак, мы получили формулу, знакомую нам из планиметрии: скалярное произведение векторов равно сумме попарных произведений их соответствующих координат.

Если в формулу скалярного произведения подставить один и тот же вектор , то получим знакомую уже формулу скалярного квадрата.

Итак, повторим:

1.      С геометрической точки зрения скалярное произведение двух векторов равно произведению их длин на косинус угла между ними:

2.      С алгебраической точки зрения скалярное произведение равно сумме попарных произведений их соответствующих координат:

Теперь мы можем сформулировать основные свойства скалярного произведения:

, причем , при . Оно непосредственно следует из того:

Переместительный закон, который следует как из геометрической, так и из алгебраической интерпретации произведения:

Распределительный закон, который следует из координатной формы записи скалярного произведения:

Сочетательный закон, который очень легко доказать, используя как геометрическую, так и координатную формы скалярного произведения (сделайте это самостоятельно):

В самом деле: в формуле для вычисления скалярного произведения фигурирует косинус угла между векторами. Т. к. данный угол может принимать значения только от  до , то единственное значение, при котором косинус равен , это .

 

Угол между векторами

 

 

Если мы знаем длины векторов и угол между ними, то мы можем найти скалярное произведение по формуле:

 

Пример. Найти скалярное произведение двух векторов, длины которых равны  и , а угол равен .

Решение

:

Вспоминаем: если сила и перемещение сонаправлены, то работа силы (которая и равна скалярному произведению векторов силы и перемещения) максимальна и равна произведению их модулей.

:

Как только веревка санок поднимается, проекция силы на перемещение уменьшается, уменьшается и работа силы. В данном случае в два раза.

:

Если сила направлена вертикально вверх, то работа такой силы по перемещению санок равна нулю.

:

Веревка направлена вверх и назад, горизонтальная проекция силы препятствует движению, работа отрицательна.

:

Сила направлена прямо противоположно перемещению. Работа отрицательна и максимальна по модулю (мы мешали движению как могли сильно) (см. рис. 12).

Рис. 12. Иллюстрация к примеру

Ответ: .

 

Задача может быть и обратной. Известны длины векторов и скалярное произведение. Тогда мы можем найти угол между векторами. В самом деле:

Тогда:

Эта формула позволяет найти угол между векторами. Проблема в том, что если длина векторов часто может быть известна из постановки задачи, то скалярное произведение вряд ли. Другое дело, если нам известны координаты векторов. Тогда мы можем найти и их длины, и их скалярное произведение.

 

Задача 2.

Найти угол между ребром куба и диагональю.

Решение

В силу симметрии куба не важно, между каким ребром и диагональю искать угол.

Найдем угол между ребром  и диагональю , а для этого рассмотрим соответствующие векторы. Свяжем с кубом систему координат так, чтобы точка  совместилась с началом координат (см. рис. 13).

Рис. 13. Иллюстрация к задаче 2

Координаты вектора , координаты вектора . Найдем косинус угла между векторами:

Найдем угол:

Ответ: .

Рассмотрим еще одну задачу на применение скалярного произведения, а более подробно сделаем это уже на практическом уроке.

 

Задача 3. Доказать, что четыре точки являются вершинами квадрата (см. рис. 14). Найти его площадь:

Рис. 14. Иллюстрация к задаче 3

Решение

Для начала докажем, что данный четырехугольник  – параллелограмм. Рассмотрим векторы противоположных сторон:

Векторы противоположных сторон равны, следовательно, они имеют равную длину и параллельны. Но это признак параллелограмма.

Осталось показать, что смежные стороны перпендикулярны. Найдем координаты вектора:

Перемножим векторы  и :

Скалярное произведение векторов равно нулю, следовательно, векторы перпендикулярны.

Осталось найти площадь. Перемножим длины смежных сторон:

Ответ: .

 

Список литературы

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
2. Мордкович А.Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
3. Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал yaklass.ru
2. Интернет-портал webmath.ru
3. Интернет-портал math34.ru

 

Домашнее задание

1. Найти длину вектора , если  и .
2. Даны векторы  и . Найти значение , при котором .
3. Доказать, что четырехугольник  с вершинами  есть параллелограмм.

 

Скалярное произведение векторов

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Конструирование Математика

• Главная
/
• Статьи
/
• Математика

2.5 Скалярным произведением двух векторов именуется такое число, которое равно произведению длин векторов на косинус угла между ними.

При обозначении скалярного произведения черезили , (рис. 2.13)

.

Применяя свойство 1⁰ для проекции вектора на ось, получаем

.

 

Рис. 2.13

Свойства скалярного произведения:

1⁰ . Переместительный закон: — получаем из определения.

2⁰ . Сочетательный закон:.

?

3⁰ . Распределительный закон:.

?.

4⁰ . Скалярный квадратвектора равняется квадрату его длины:.

Это свойство есть следствие определения, поскольку .

5⁰ . Равенство скалярного произведения ненулевых векторовиесть необходимое и достаточное условием их перпендикулярности.

Свойство выводится из определения скалярного произведения, поскольку.

Из свойств 1⁰ – 3⁰ следует, что в случае скалярного умножения является возможным такое же раскрытие скобок, как и при умножении многочленов.

Задача. Дано

Найти.

? ?

Запишем скалярное произведениечерез координаты векторови.

Допустим заданы координаты векторов,. Имея в виду, что перемножаем скалярно.

Получаем формулу

Основные возможности применения скалярного умножения:

1) Определение работысилыпри перемещении из т.в т.(рис. 2.14)

Рис. 2.14

2) определение угла между векторами:

3) определения проекций одного вектора на другой:

Задача. Определить работусилыв т., если,.
? Определяем координаты, работаед. работы ?

Нравится

Твитнуть

Теги Математика

Сюжеты Математика

Понятие об автоматах, их задание графами

(38.4.) Сформулируем понятие конечного автомата, обозначим входной алфавит, выходной алфавит, алфавит состояний, функцию переходов, функцию выходов, на рисунке изобразим граф переходов.

4097 0

Некоторые классы графов

(38.3.) Большинство графов, которые используются в приложениях (например, графы сортировок, классификаций) предполагают наличие диаграмм, именуемых деревьями. Связный неориентированный граф без циклов, в частности, предполагающий отсутствие петель и кратных ребер, именуют деревом. Несвязный неориентированный граф без цикла — лес, его связные компоненты являются деревьями.

10093 0

Маршруты, цепи и циклы

(38.2.) В рамках обозначенной темы рассмотрим случай определения связного неориентированного мультиграфа в качестве эйлерова и гамильтонова графа.

13603 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

линейная алгебра — Какая польза от скалярного произведения двух векторов?

спросил 9 лет, 6 месяцев назад

Изменено 3 месяца назад

Просмотрено 59 тысяч раз

$\begingroup$

Предположим, у вас есть два вектора a и b , из которого вы хотите взять скалярное произведение, теперь это делается довольно просто, беря каждую соответствующую координату каждого вектора, перемножая их, а затем складывая результат вместе.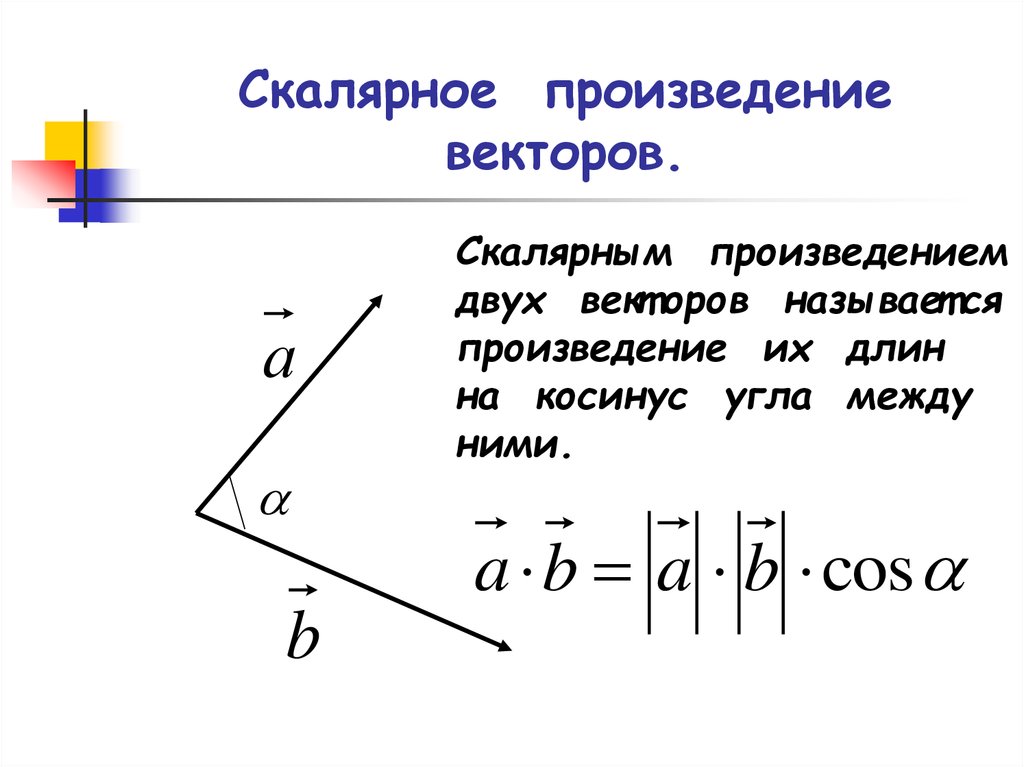 В конце выполнения нашей операции у нас остается постоянное число.

Мой вопрос, поэтому, что мы можем сделать с этим числом, почему мы, так сказать, вычисляем его? Я имею в виду, что это кажется мне почти бесполезным по сравнению с перекрестным произведением двух векторов (где вы получаете фактический вектор).

• линейная алгебра

$\endgroup$

3

$\begingroup$

Re: «[точечный продукт] кажется мне почти бесполезным по сравнению с векторным произведением двух векторов».

См. статью Википедии о скалярном произведении, чтобы узнать больше о значении скалярного произведения и о графических изображениях, которые помогают визуализировать значение скалярного произведения (в частности, геометрическую интерпретацию). Кроме того, вы узнаете больше о том, как он используется. Например, прокрутите вниз до «Физики» (в связанной записи), чтобы прочитать некоторые из ее применений: 9T.\;$

Но скалярное произведение также имеет эквивалентное геометрическое определение :

В евклидовом пространстве евклидов вектор — это геометрический объект, обладающий как величиной, так и направлением. Вектор можно изобразить в виде стрелки. Его величина — это его длина, а его направление — это направление, на которое указывает стрелка. Величина вектора A обозначается $\|\mathbf{A}\|.$ Скалярное произведение двух евклидовых векторов A и B определяется как

$$\mathbf A\cdot\mathbf B = \|\mathbf A\|\,\|\mathbf B\|\cos\theta,\quad\text{где $\theta$ — угол между $A $ и $B.$} \tag{1}$$

С помощью $(1)$, например, мы видим, что можем вычислить (определить) угол между двумя векторами, зная их координаты: $$\cos \theta = \frac{\mathbf A\cdot\mathbf B}{\|\mathbf A\|\,\|\mathbf B\|}$$

$\endgroup$

6

$\begingroup$

Первоначальная мотивация геометрическая: скалярное произведение можно использовать для вычисления угла $\alpha$ между двумя векторами $a$ и $b$:

$a\cdot b=|a|\cdot|b|\cdot \cos(\alpha)$.

Обратите внимание, что знак этого выражения зависит только от косинуса угла, поэтому скалярное произведение равно

• $<0$, если угол тупой ,
• $>0$ если угол острый ,
• $=0$, если $a$ и $b$ ортогональны .

Другой важный частный случай появляется, когда $a=b$: Корень скалярного произведения вектора с самим собой имеет длину 92$.

Есть еще одно интересное применение скалярного произведения в сочетании с перекрестным произведением: если у вас есть три вектора $a$, $b$ и $c$, они определяют параллелепипед, и вы можете вычислить его (со знаком) объем $V$ следующим образом, используя так называемое скалярное тройное произведение:

$V=(a\times b)\cdot c$

(Обратите внимание, что это обобщение $|a\times b|$ площадь параллелограмма, заданного $a$ и $b$.)

$\endgroup$

4

$\begingroup$

Прежде чем ответить на ваш вопрос, я хочу сказать, что это очень хороший вопрос, и вы правы, ожидая, что точечный продукт имеет смысл/значение.

Во-первых, важно думать о векторах отдельно от их координат. Хотя верно то, что мы часто представляем векторы как серию координат вдоль четко определенных осей, это делается исключительно из вычислительных соображений. Вектор как идея «существует» в пространстве без какой-либо предопределенной системы координат. Я говорю это, потому что существует два определения скалярного произведения, одно из которых равно 9.0040 без координат (т.е. $\mathbf a\cdot\mathbf b = \|\mathbf a\|\,\|\mathbf b\|\cos\theta$), а другой основан на координатах (т.е. $\mathbf a\cdot\mathbf b = \sum_i{a_i b_i}$). Из этих двух скалярное произведение лучше всего рассматривать с точки зрения первого, поскольку оно не зависит от системы координат. (Относительно легко показать, что последнее может быть получено из первого, но в этом выводе есть неявное предположение, что система координат, используемая для представления скалярного произведения, равна ортогональный .)

Во-вторых, учитывая бескоординатное определение, фундаментальная идея скалярного произведения состоит в том, что проекция . Тем самым он дает единственное число, которое указывает компонент вектора в направлении другого вектора. Ваше наблюдение о несхожести между точечным и перекрестным произведением является правильным, однако скалярное произведение также используется для создания вектора, оно просто делает это покомпонентно. Предположим, что у нас есть вектор $\mathbf v$, представленный своими компонентами в заданной системе координат. Далее предположим, что у нас есть ортонормированный базис, определенный в той же системе координат, что и набор вектор-столбцов $\{\mathbf u_1, \mathbf u_2, \ldots, \mathbf u_n\}$. Наконец, предположим, что мы хотим представить $\mathbf v$ в этом базисе как $\mathbf w$. Вопрос в том, как мы это делаем? Конечно, мы используем скалярное произведение! Таким образом, первый компонент $\mathbf w$ будет тогда $w_1 = \mathbf u_1\cdot \mathbf v$, а второй компонент будет $w_2 = \mathbf u_2\cdot \mathbf v$ и так далее. (Обратите внимание, что поскольку $\|\mathbf u_i\| = 1$, мы имеем $\mathbf u_1\cdot \mathbf v= \|\mathbf v\|\cos\theta_i$. ) Если затем мы подумаем о векторе $ \mathbf w$ определены как таковые, мы имеем 9T\mathbf v$$

Наконец, мы заключаем, что скалярное произведение играет ключевую роль в преобразовании вектора из одного базиса в другое и что скалярное произведение скрыто в определении умножения матриц в этом одно из представлений о матрично-векторном произведении состоит в том, что каждый элемент произведения представляет собой скалярное произведение между строкой слева и столбцом справа.

Надеюсь, это поможет.

$\endgroup$

1

$\begingroup$

Скалярный продукт является важным ингредиентом матричного продукта. Произведением двух матриц $A$ и $B$ (совместимых размеров, т. е. число столбцов матрицы $A$ равно числу строк матрицы $B$) называется матрица, $(i, j)$ которой является скалярным произведением $i$-й строки таблицы $A$ и $j$-го столбца таблицы $B$. {t}$ имеет в своей позиции $(i, j)$ количество студентов, принимающих как $c_{i}$, так и $c_{j}$.

Эта матрица, конечно, полезна при составлении расписания занятий.

$\endgroup$

$\begingroup$

Геометрическая идея скалярного произведения была затронута, но существует обширное обобщение этого произведения в геометрической алгебре , алгебре не только ориентированных линий (векторов), но плоскостей, объемов и т. д. (называемых лезвиями). ).

В геометрической алгебре у нас есть обобщенное скалярное произведение вектора $a$ и другого лезвия $B$, обозначаемое $a \cdot B$. Это произведение имеет простую геометрическую интерпретацию как часть $B$, ортогональная проекции $a$, с величиной $|a||B|| \cos \theta|$, где $\theta$ угол $a$ образует со своей проекцией в $B$.

(Примечание: на самом деле $a \cdot B$ также ортогонален $a$, не только его проекция в $B$, но размышление об этом приводит к некоторым трудностям, а размышление о том, что перпендикулярно проекции нет. )

Если $B$ является 2-лопастным (также называемым бивектором ), то вы должны быть в состоянии представить это непосредственно: если $a$ полностью лежит в $B$, то $a \ cdot B$ — это просто вектор, перпендикулярный $a$ в $B$. Если $a$ не лежит целиком в $B$, то его можно разложить на касательную и нормальную части. Мы отбрасываем нормальную часть, и к тангенциальной части применяется предыдущая логика.

Если $B$ является трехмерным лезвием (тривектором), то в трехмерном пространстве $a$ должно лежать в $B$ (поскольку не существует трехмерного объема, который не может быть охвачен вектором), и произведение $a \cdot B$ — это «двойственная по Ходжем» плоскость, перпендикулярная $a$.

В этом свете скалярное произведение векторов может оказаться самой неинтуитивной частью этого рассуждения. Когда вы берете скалярное произведение, остается только скаляр — не остается вектора или другого многомерного объекта, который был бы ортогонален $a$. Опять же, именно поэтому я подчеркиваю, что $a \cdot B$ — это часть $B$, ортогональная проекция $a$ на $B$. Когда $B$ является вектором, ясно, что нет другого вектора или чего-то еще, что могло бы быть ортогональным проекции $a$, поскольку $B$ и эта проекция параллельны, поэтому результат обязательно будет просто скаляром.

$\endgroup$

$\begingroup$

При вычислении A.B происходят два измерения: измерение того, насколько мал угол между ними, и какова длина A и Б ар. A.B в основном означает длину проекции A на B , при этом эта длина масштабируется на абсолютную длину B .

Один из способов интерпретации скалярного произведения состоит в том, чтобы подумать, как максимизировать или минимизировать скалярное произведение между двумя векторами. Предположим, мы пытаемся максимизировать скалярное произведение между двумя векторами, которые мы можем изменить:

Скалярное произведение будет увеличиваться по мере уменьшения угла между двумя векторами. Скалярный продукт A.B также будет увеличиваться по мере увеличения абсолютных длин A и B . Это связано с тем, что по мере того, как A становится больше, его проекционная длина будет больше, а по мере увеличения длины B масштабирование проекции A будет увеличиваться, учитывая, что B абсолютная длина будет действовать как скейлер длины проекции A .

Следовательно, в задачах, где желательно максимизировать или минимизировать размер векторов и минимизировать отклонение или угол между ними, может быть полезно количественное определение с помощью скалярного произведения.

$\endgroup$

$\begingroup$

Я не вижу здесь достаточно простых английских ответов, если честно. Один простой пример: в стелс-игре вы можете определить, находится ли объект в пределах 90-градусной прямой видимости чего-либо или нет.

$\endgroup$

Зарегистрируйтесь или войдите

Зарегистрироваться через Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

легкий вопрос — Значение скалярных произведений в отношении линейной алгебры

Позвольте мне попытаться мотивировать скалярное произведение с несколько иной точки зрения.

Я полагаю, вы уже поняли, что измерение длины, $\|v\|,$ важно и полезно. 92 + 2\langle u, v\rangle,$$ здесь я использовал тот факт, что $g$ симметричен. Теперь вы видите, что внутренний продукт $u,v$ измеряет несоответствий этих векторов теореме Пифагора : $\langle u,v\rangle$ равно нулю, когда векторы перпендикулярны, положительны, когда $u$ и $v$ указывают в одном направлении и отрицательные, если векторы указывают в противоположных направлениях. Таким образом, скалярное произведение кодирует угол между векторами $u$ и $v$, и на самом деле угол может быть определен как 9Tgv$, что она билинейна и симметрична по своим аргументам.

---

Рано или поздно в учебе вы столкнетесь с нормами , отличными от евклидовой нормы .