Правило Ленца – закон, формула

4.7

Средняя оценка: 4.7

Всего получено оценок: 329.

4.7

Средняя оценка: 4.7

Всего получено оценок: 329.

Изменение магнитного поля, пронизывающего рамку с током, вызывает появление в ней электродвижущей силы (ЭДС), в рамке возникает ток. Направление этого тока определяется специальным правилом Ленца для закона электромагнитной индукции. Рассмотрим это правило.

Действие индукционного тока

В результате электромагнитной индукции изменение магнитного поля через проводящий контур приводит к появлению в нем ЭДС и электрического тока, который называется индукционным. Индукционный ток, как и любой другой ток, должен привести к появлению нового магнитного поля. Эти два поля (внешнее и появившееся) должны взаимодействовать точно так же, как взаимодействуют обычные постоянные магниты. Так ли это ? Происходит ли взаимодействие ?

Опыт Ленца

Для ответа на заданные вопросы проводится следующий опыт. На концах легко вращающегося коромысла закрепляются два проводящих кольца – одно сплошное, а другое с разрезом.

Рис. 1. Опыт демонстрирующий правило Ленца.

Теперь, если взять постоянный магнит и внести его в кольцо с разрезом – ничего не произойдет. Однако, если попытаться внести постоянный магнит в сплошное кольцо – коромысло начнет вращаться, уводя кольцо от магнита.

Данное явление можно объяснить только возникновением тока в сплошном кольце. Этот ток, в свою очередь, порождает новое магнитное поле, которое и начинает взаимодействовать с полем постоянного магнита. В кольце с разрезом ток не возникает, и взаимодействующего поля нет.

Правило Ленца

Проводя описанный опыт, русский физик Э.Ленц вывел правило, определяющее направление индуцированного тока в проводящем контуре.

Рис. 2. Э. Ленц.

индукционный ток, возникающий в замкнутом контуре направлен так, чтобы противодействовать причине, его вызывающей.

Применение правила Ленца для определения направления индукционного тока предусматривает следующие шаги.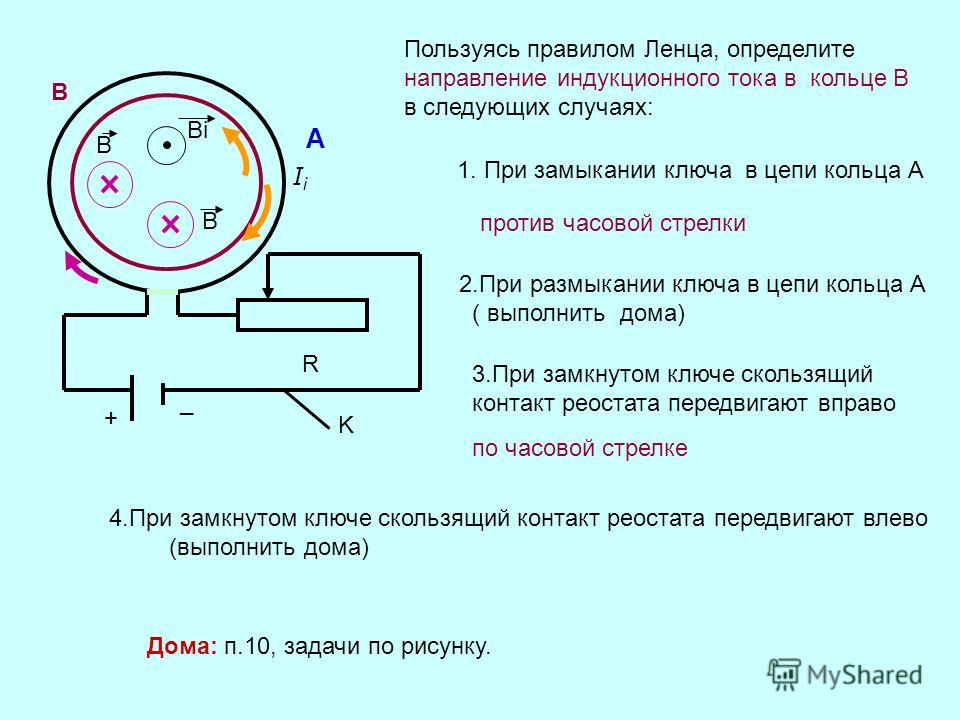

• Используя формулу магнитного потока $Ф=BScos\alpha$, определяется, как изменяется магнитный поток через контур – увеличивается ли он или уменьшается.
• Определяются направление возникающей индукции. Оно, согласно правилу Ленца, должно быть направлено так, чтобы противодействовать причине его вызывающей. То есть, если магнитный поток возрастает, то возникающая индукция должна быть направлена против внешней индукции, если поток уменьшается – то вдоль.
• По правилу буравчика или правилу охвата правой руки определяется направление индукционного тока.

Правило Ленца обуславливается законом сохранения энергии. Поскольку в контуре возникает ток, он совершает работу (вся она уходит на нагрев кольца), а эта работа может возникнуть только за счет сторонних сил. В опыте Ленца такими силами являются механические силы, вводящие магнит в кольцо, совершающие при этом работу.

Если для опыта Ленца взять сверхпроводящую пластину (при очень низких температурах), не имеющую сопротивления, и расположить магнит снизу, то индуцированная ЭДС создаст ток такой силы, что его магнитное поле не даст пластине приблизиться к магниту, пластина сможет парить в воздухе, над магнитом, не опускаясь вниз.

Рис. 3. Левитация пластины сверхпроводника над магнитом.

Что мы узнали?

Индукционный ток, возникающий в контуре при изменении магнитного потока через контур, имеет такое направление, чтобы противодействовать причине, его вызывающей. Это правило называется Правилом Ленца для закона электромагнитной индукции.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.7

Средняя оценка: 4.7

Всего получено оценок: 329.

---

А какая ваша оценка?

Правило Ленца • Джеймс Трефил, энциклопедия «Двести законов мироздания»

200 законов мироздания > Физика

Индукционный электрический ток в проводнике, возникающий при изменении магнитного потока, направлен таким образом, что его магнитное поле противодействует изменению магнитного потока.

В 1831 году английский физик Майкл Фарадей открыл то, что теперь называют законом электромагнитной индукции Фарадея, согласно которому изменение магнитного потока внутри проводящего контура возбуждает в этом контуре электрический ток даже при отсутствии в контуре источника питания.

Оставленный Фарадеем открытым вопрос о направлении индукционного тока вскоре решил российский физик Эмилий Христианович Ленц.

Представьте себе замкнутый круговой токопроводящий контур без подключенной батареи или иного источника питания, в который северным полюсом начинают вводить магнит. Это приведет к увеличению магнитного потока, проходящего через контур, и, согласно закону Фарадея, в контуре возникнет индуцированный ток. Этот ток, в свою очередь, согласно закону Био—Савара будет генерировать магнитное поле, свойства которого ничем не отличаются от свойств поля обычного магнита с северным и южным полюсами. Ленцу как раз и удалось выяснить, что индуцированный ток будет направлен таким образом, что северный полюс генерируемого током магнитного поля будет ориентирован в сторону северного полюса вдвигаемого магнита. Поскольку между двумя северными полюсами магнитов действуют силы взаимного отталкивания, наведенный в контуре индукционный ток потечет именно в таком направлении, что будет противодействовать введению магнита в контур.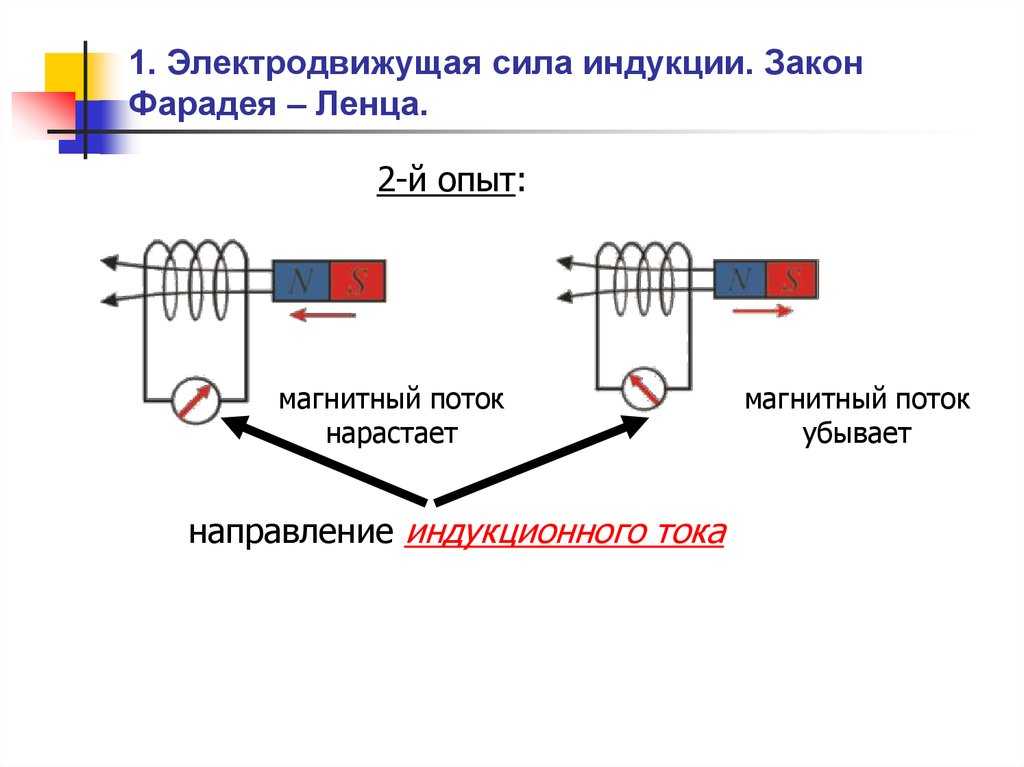

И это лишь частный случай, а в обобщенной формулировке правило Ленца гласит, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его первопричине.

Правило Ленца сегодня пытаются использовать в междугороднем пассажирском транспорте. Уже построены и испытываются опытные образцы поездов на так называемой магнитной подушке. Под днищем вагона такого поезда смонтированы мощные магниты, расположенные в считанных сантиметрах от стального полотна. При движении поезда магнитный поток, проходящий через контур полотна, постоянно меняется, и в нем возникают сильные индукционные токи, создающие мощное магнитное поле, отталкивающее магнитную подвеску поезда (аналогично тому, как возникают силы отталкивания между контуром и магнитом в вышеописанном опыте). Сила эта настолько велика, что, набрав некоторую скорость, поезд буквально отрывается от полотна на 10-15 сантиметров и, фактически, летит по воздуху. Поезда на магнитной подушке способны развивать скорость свыше 500 км/ч, что делает их идеальным средством междугороднего сообщения средней дальности.

См. также:

1879	Эффект Холла

Эмилий Христианович ЛЕНЦ
Heinrich Friedrich Emil Lenz, 1804–65

Российский физик. Родился в Дерпте (ныне Тарту, Эстония), окончил Дерптский университет. Еще будучи студентом, участвовал в кругосветной геологической экспедиции. Преподавал в Петербургском университете, с 1836 года в качестве профессора. Ленц играл видную роль в российских научных кругах своего времени. Все основные научные исследования Ленца были направлены на изучение явлений электропроводности и электромагнетизма.

---

Написать комментарий

---

1785	Закон Кулона
1820	Открытие Эрстеда
1820	Закон Ампера
1820	Закон Био—Савара
1831	Законы электромагнитной индукции Фарадея
1833	Правило Ленца

---

1919

Правило октета

1877

Правило Аллена

Новостная рассылка  

«Элементы» в соцсетях: 

Дифференциальные уравнения.

Определения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 1.1: Определения

Дифференциальное уравнение

Первым определением, которое мы должны рассмотреть, должно быть определение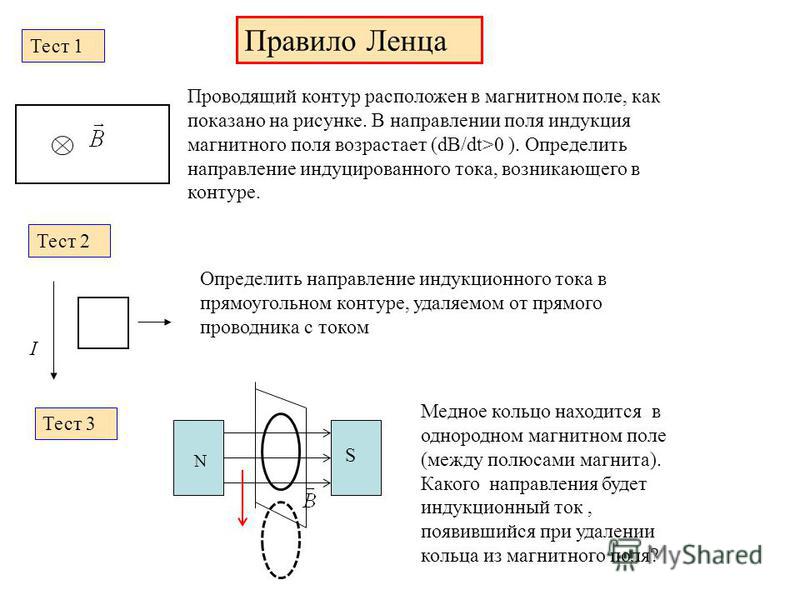

дифференциального уравнения . Дифференциальное уравнение — это любое уравнение, которое содержит производные, либо обычные производные, либо частные производные.

Существует одно дифференциальное уравнение, которое, вероятно, известно каждому, это второй закон движения Ньютона. Если объект массы \(m\) движется с ускорением \(a\) и на него действует сила \(F\), то второй закон Ньютона говорит нам об этом.

\[\begin{уравнение}F = ma \label{eq:eq1} \end{уравнение}\] 92}}} \метка{eq:eq2}\конец{уравнение}\]

Где \(v\) — скорость объекта, а \(u\) — функция положения объекта в любой момент времени \(t\). Мы также должны помнить в этот момент, что сила \(F\) также может быть функцией времени, скорости и/или положения.

Итак, учитывая все это, второй закон Ньютона теперь можно записать в виде дифференциального уравнения относительно скорости \(v\) или положения \(u\) объекта следующим образом. 92\partial t}} = 1 + \frac{{\partial u}}{{\partial y}} \label{eq:eq10}\end{equation}\]

Порядок

порядок дифференциального уравнения является наибольшей производной, присутствующей в дифференциальном уравнении. В перечисленных выше дифференциальных уравнениях \(\eqref{eq:eq3}\) является дифференциальным уравнением первого порядка, \(\eqref{eq:eq4}\), \(\eqref{eq:eq5}\), \( \eqref{eq:eq6}\), \(\eqref{eq:eq8}\) и \(\eqref{eq:eq9}\) — дифференциальные уравнения второго порядка, \(\eqref{eq:eq10}\ ) — дифференциальное уравнение третьего порядка, а \(\eqref{eq:eq7}\) — дифференциальное уравнение четвертого порядка.

Обратите внимание, что порядок не зависит от того, есть ли в дифференциальном уравнении обычные или частные производные.

В этих заметках мы будем рассматривать почти исключительно дифференциальные уравнения первого и второго порядка. Как вы увидите, большинство методов решения дифференциальных уравнений второго порядка можно легко (и естественно) распространить на дифференциальные уравнения более высокого порядка, и мы обсудим эту идею позже.

Обыкновенные уравнения и уравнения с частными производными

Дифференциальное уравнение называется обыкновенным дифференциальным уравнением , сокращенно ода, , если оно содержит обыкновенные производные. Точно так же дифференциальное уравнение называется дифференциальным уравнением в частных производных , сокращенно pde, , если в нем есть частные производные. В приведенных выше дифференциальных уравнениях \(\eqref{eq:eq3}\) — \(\eqref{eq:eq7}\) являются одами, а \(\eqref{eq:eq8}\) — \(\eqref{eq: eq10}\) являются pde.

Подавляющее большинство этих заметок посвящено оде. Единственным исключением из этого правила будет последняя глава, в которой мы кратко рассмотрим распространенную и базовую технику решения задач pde. 9{\left( {n — 1} \right)}}\left( t \right) + \cdots + {a_1}\left( t \right)y’\left( t \right) + {a_0}\left ( t \right)y\left( t \right) = g\left( t \right) \label{eq:eq11}\end{equation}\]

В отношении линейных дифференциальных уравнений важно отметить, что нет произведений функции \(y\left( t \right)\) и ее производных, и ни функция, ни ее производные не входят ни в какую другую степень, кроме первая власть. Также обратите внимание, что ни функция, ни ее производные не находятся «внутри» другой функции, например, \(\sqrt {y’} \) или \({{\bf{e}}^y}\).

Коэффициенты \({a_0}\left( t \right),\,\, \ldots \,\,{a_n}\left( t \right)\) и \(g\left( t \right )\) могут быть нулевыми или ненулевыми функциями, постоянными или непостоянными функциями, линейными или нелинейными функциями. Только функция \(y\left( t \right)\) и ее производные используются для определения того, является ли дифференциальное уравнение линейным.

Если дифференциальное уравнение не может быть записано в виде \(\eqref{eq:eq11}\), то оно называется нелинейным дифференциальным уравнением.

В \(\eqref{eq:eq5}\) — \(\eqref{eq:eq7}\) выше только \(\eqref{eq:eq6}\) является нелинейным, два других являются линейными дифференциальными уравнения. Мы не можем классифицировать \(\eqref{eq:eq3}\) и \(\eqref{eq:eq4}\), так как не знаем, какой вид имеет функция \(F\). Они могут быть как линейными, так и нелинейными в зависимости от \(F\).

Решение

Решение дифференциального уравнения на отрезке \(\alpha < t < \beta \) есть любая функция \(y\left( t \right)\), которая удовлетворяет рассматриваемому дифференциальному уравнению на интервал \(\alpha Важно отметить, что решения часто сопровождаются интервалами, и эти интервалы могут сообщить некоторую важную информацию о решении. Рассмотрим следующий пример. 93}} }}\]

В этой форме ясно, что нам нужно как минимум избежать \(x = 0\), так как это дало бы деление на ноль.

Кроме того, есть общее практическое правило, с которым мы будем работать в этом классе. Это эмпирическое правило: начните с реальных чисел, закончите реальными числами. Другими словами, если наше дифференциальное уравнение содержит только действительные числа, нам не нужны решения, дающие комплексные числа. Итак, чтобы избежать комплексных чисел, нам также нужно будет избегать отрицательных значений \(x\).

Итак, в последнем примере мы видели, что даже если функция может символически удовлетворять дифференциальному уравнению, из-за определенных ограничений, налагаемых решением, мы не можем использовать все значения независимой переменной и, следовательно, должны наложить ограничение на независимую переменную. переменная. Так будет со многими решениями дифференциальных уравнений.

Обратите внимание, что в последнем примере существует гораздо больше возможных решений данного дифференциального уравнения. Например, все следующее также является решением 9{ — \frac{1}{2}}}\end{align*}\]

Мы предоставим вам подробности, чтобы убедиться, что это действительно решения. Учитывая эти примеры, можете ли вы найти какие-либо другие решения дифференциального уравнения? На самом деле существует бесконечное множество решений этого дифференциального уравнения.

Итак, учитывая, что существует бесконечное число решений дифференциального уравнения в последнем примере (при условии, что вы все равно верите нам, когда мы это говорим….), мы можем задать естественный вопрос. Какое решение мы хотим, или имеет значение, какое решение мы используем? Этот вопрос приводит нас к следующему определению в этом разделе. 9{\ влево ( k \ вправо)}} \ влево ( {{t_0}} \ вправо) = {y_k} \]

Другими словами, начальные условия — это значения решения и/или его производной (производных) в определенных точках.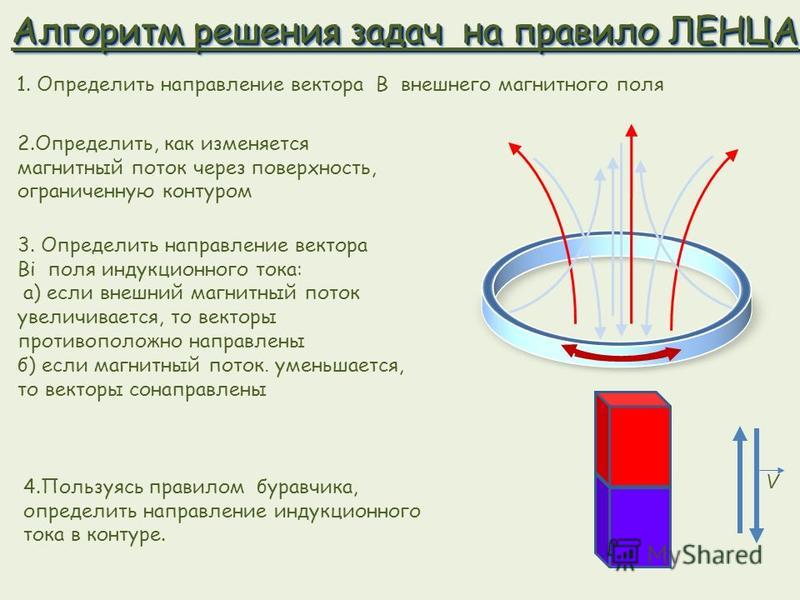 Как мы со временем увидим, решения «достаточно хороших» дифференциальных уравнений уникальны, и, следовательно, только одно решение удовлетворяет заданным начальным условиям.

Количество начальных условий, необходимых для данного дифференциального уравнения, будет зависеть от порядка дифференциального уравнения, как мы увидим. 92}y» + 12xy’ + 3y = 0\hspace{0.25in}y\left( 4 \right) = \frac{1}{8},\,\,\,\,y’\left( 4 \справа) = — \frac{3}{{64}}\]

Пример 4 Вот еще один IVP.

\[2t\,y’ + 4y = 3\hspace{0.25in}\,\,\,\,\,\,y\left( 1 \right) = — 4\]

Как мы отмечали ранее, количество требуемых начальных условий будет зависеть от порядка дифференциального уравнения.

Интервал действия

Интервал действия для IVP с начальным условием(ями) 9{\ влево ( k \ вправо)}} \ влево ( {{t_0}} \ вправо) = {y_k} \]

— это максимально возможный интервал, на котором решение действительно и содержит \({t_0}\). Их легко определить, но бывает трудно найти, поэтому мы собираемся отложить что-либо еще об этом до тех пор, пока мы не приступим к решению дифференциальных уравнений и нам не понадобится интервал достоверности.

Общее решение

Общее решение дифференциального уравнения является наиболее общей формой, которую может принять решение, и не принимает во внимание никаких начальных условий. 92}}}\) является общим решением для \[2т\,у’ + 4у = 3\]

Мы предоставим вам проверить, действительно ли эта функция является решением данного дифференциального уравнения. На самом деле все решения этого дифференциального уравнения будут именно в таком виде. Это одно из первых дифференциальных уравнений, которое вы научитесь решать, и вскоре вы сможете сами в этом убедиться.

Фактическое решение

Фактическое решение дифференциального уравнения — это конкретное решение, которое не только удовлетворяет дифференциальному уравнению, но также удовлетворяет заданным начальным условиям.

Пример 6 Каково фактическое решение следующей IVP? \[2t\,y’ + 4y = 3\hspace{0.25in}\,\,\,\,\,\,y\left( 1 \right) = — 4\]

Показать решение

На самом деле это сделать проще, чем может показаться на первый взгляд. Из предыдущего примера мы уже знаем (ну это при условии, что вы верите в наше решение этого примера…), что все решения дифференциального уравнения имеют форму. 92}}}\]

Из этого последнего примера видно, что если у нас есть общее решение дифференциального уравнения, то поиск фактического решения представляет собой не что иное, как применение начальных условий и поиск констант, которые входят в общее решение.

Неявное/явное решение

В этом случае проще определить явное решение, затем рассказать, чем неявное решение не является, а затем привести пример, показывающий разницу. Итак, это то, что мы будем делать. 2} — 3} \]

В этом случае мы смогли найти явное решение дифференциального уравнения. Следует, однако, отметить, что не всегда удается найти явное решение.

Также обратите внимание, что в этом случае мы смогли получить только явное фактическое решение, потому что у нас было начальное условие, которое помогло нам определить, какая из двух функций будет правильным решением.

Теперь мы разобрались с большинством основных определений и можем перейти к другим темам.

Как перестать прокрастинировать с помощью «Правила двух минут»

Эта статья представляет собой отрывок из книги «Атомные привычки», моего бестселлера по версии New York Times.

В последнее время я следую простому правилу, которое помогает мне перестать откладывать дела на потом и в то же время помогает придерживаться хороших привычек.

Сегодня я хочу поделиться им с вами, чтобы вы могли попробовать и посмотреть, как это работает в вашей жизни.

Лучшая часть? Это простая стратегия, которую очень легко использовать.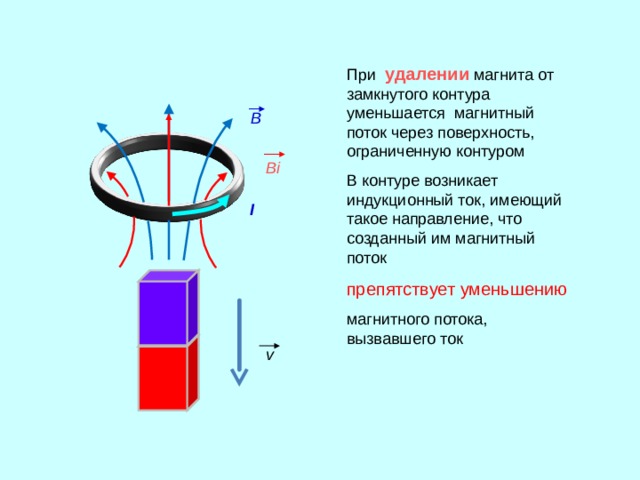

Вот что вам нужно знать…

Как перестать прокрастинировать с помощью «Правила двух минут»

Правило двух минут1 гласит: «Когда вы начинаете новую привычку, это займет не более двух минут».

Вы обнаружите, что почти любую привычку можно сократить до двухминутной версии:

• «Читать перед сном каждый вечер» становится «Читать одну страницу».
• «Позанимайся йогой тридцать минут» становится «Достань мой коврик для йоги».
• «Изучение для класса» становится «Открыть мои заметки».
• «Сложить белье» становится «Сложить одну пару носков».
• «Пробеги три мили» становится «Свяжи мои кроссовки».

Идея состоит в том, чтобы сделать ваши привычки как можно проще. Любой может помедитировать одну минуту, прочитать одну страницу или убрать один предмет одежды. И, как мы только что обсудили, это мощная стратегия, потому что, начав поступать правильно, продолжать делать это гораздо легче. Новая привычка не должна восприниматься как вызов. Последующие действия могут быть сложными, но первые две минуты должно быть легко. То, что вам нужно, — это «привычка входа», которая естественным образом ведет вас по более продуктивному пути.

Обычно вы можете определить основные привычки, которые приведут к желаемому результату, наметив свои цели по шкале от «очень легко» до «очень сложно». Например, пробежать марафон очень сложно. Пробежать 5 км тяжело. Пройти десять тысяч шагов довольно сложно. Пройти десять минут легко. А надеть кроссовки очень просто. Ваша цель может состоять в том, чтобы пробежать марафон, но ваша привычка — надеть кроссовки. Вот как вы следуете Правилу двух минут.

Почему правило двух минут работает

Люди часто думают, что это странно, когда они зацикливаются на том, чтобы прочитать одну страницу, помедитировать в течение одной минуты или сделать один звонок для продажи. Но дело не в том, чтобы делать что-то одно. Суть в том, чтобы выработать привычку показываться. Правда в том, что привычка должна быть установлена, прежде чем ее можно будет улучшить. Если вы не можете освоить базовый навык появления, то у вас мало шансов овладеть более мелкими деталями. Вместо того, чтобы с самого начала пытаться выработать идеальную привычку, делайте более простые вещи более последовательно. Вы должны стандартизировать, прежде чем сможете оптимизировать.

По мере того, как вы овладеваете искусством появления, первые две минуты просто становятся ритуалом в начале более крупной рутины. Это не просто лайфхак, облегчающий привычки, но на самом деле идеальный способ овладеть сложным навыком. Чем больше вы ритуализируете начало процесса, тем больше вероятность того, что вы сможете соскользнуть в состояние глубокого сосредоточения, которое требуется для совершения великих дел. Делая одну и ту же разминку перед каждой тренировкой, вы облегчаете достижение состояния максимальной производительности. Следуя тому же творческому ритуалу, вам будет легче погрузиться в тяжелую работу по творчеству. Вырабатывая постоянную привычку выключать питание, вы облегчаете себе возможность ложиться спать в разумное время каждую ночь. Возможно, вы не сможете автоматизировать весь процесс, но вы можете сделать первое действие бессмысленным. Упростите начало, а остальное приложится.

Некоторым правило двух минут может показаться уловкой. Вы знаете, что настоящая цель — сделать больше, чем две минуты, поэтому может показаться, что вы пытаетесь обмануть себя. На самом деле никто не стремится прочитать одну страницу, сделать одно отжимание или открыть свои заметки. И если вы знаете, что это умственный трюк, зачем вам на него клюнуть?

Если правило двух минут кажется вам навязчивым, попробуйте следующее: выполняйте его в течение двух минут, а затем остановитесь. Идите на пробежку, но вы должны остановиться через две минуты. Начните медитировать, но вы должны остановиться через две минуты. Изучайте арабский язык, но вы должны остановиться через две минуты. Это не стратегия для начала, это все. Ваша привычка может длиться всего сто двадцать секунд.

Один из моих читателей использовал эту стратегию, чтобы сбросить более ста фунтов. Сначала он ходил в спортзал каждый день, но сказал себе, что ему нельзя оставаться там более пяти минут. Он мог пойти в спортзал, потренироваться в течение пяти минут и уйти, как только его время истекло. Через несколько недель он огляделся и подумал: «Ну, я все равно всегда сюда прихожу. Я мог бы также начать оставаться немного дольше. Через несколько лет вес ушел.

Подобные стратегии работают и по другой причине: они усиливают индивидуальность, которую вы хотите создать. Если вы появляетесь в спортзале пять дней подряд — даже если это всего на две минуты — вы голосуете за свою новую личность. Вы не беспокоитесь о том, чтобы привести себя в форму. Вы сосредоточены на том, чтобы стать тем человеком, который не пропускает тренировки. Вы предпринимаете наименьшее действие, которое подтверждает тип человека, которым вы хотите быть.

Мы редко думаем об изменениях таким образом, потому что все поглощены конечной целью. Но одно отжимание лучше, чем отсутствие упражнений. Одна минута занятий на гитаре лучше, чем ничего. Одна минута чтения лучше, чем никогда не брать книгу в руки. Гораздо лучше сделать меньше, чем вы надеялись, чем вообще ничего не делать.

Всякий раз, когда вы боретесь с привычкой, вы можете использовать правило двух минут. Это простой способ сделать ваши привычки легкими.

Эта статья представляет собой отрывок из главы 13 моего бестселлера New York Times «Атомные привычки». Подробнее здесь.

Сноски

1. Совет Дэвиду Аллену, чья версия правила двух минут гласит: « Если это займет меньше двух минут, сделайте это сейчас». Для получения дополнительной информации см. Дэвид Аллен, Getting Things Done (Нью-Йорк: Penguin, 2015).

2. Автор Кэл Ньюпорт использует ритуал отключения, в ходе которого он проверяет последнюю электронную почту, готовит список дел на следующий день и говорит «завершение работы завершено», чтобы завершить работу на день. Дополнительную информацию см. в Cal Newport, Deep Work (Boston: Little, Brown, 2016).