Значение слова МОМЕНТ. Что такое МОМЕНТ?

МОМЕ́НТ, -а, м.

1. Очень короткий промежуток времени; миг, мгновение. Мы с замиранием сердца ждали, что вот еще один момент, и баржа будет перерезана цепью. Чехов, Остров Сахалин. Не желая замочить обувь, я стал выбирать моменты, когда волна откатывалась, и перебегать с одного места на другое. Миклухо-Маклай, Путешествия. || чего. Время, когда осуществляется, наступает какое-л. действие. Наступил момент обеда — и все общество уселось за столик. Тургенев, Вешние воды. Каждое приказание вытекает из другого и никогда не относится к целому ряду событий, а всегда только к одному моменту события. Л. Толстой, Война и мир.

2. Отдельный промежуток времени, определенный период в развитии чего-л. Текущий момент. □ Ни один век не хуже и не лучше другого, потому что он есть необходимый момент в развитии человечества или общества. Белинский, Герой нашего времени. Соч. М. Лермонтова.

С годами подробности больших событий теряются. Память хранит только узловые драматические моменты. Песков, Путешествие с молодым месяцем.

3. Отдельная сторона какого-л. явления или обстоятельство, сопутствующее условие. Положительные моменты. Отрицательный момент. □ Будь то военное, хозяйственное положение или какой-либо другой момент социального уклада, борьба продолжается, и основной закон классовой борьбы подтверждается нашей революцией. Ленин, Речь на III Всероссийском съезде профессиональных союзов 7 апреля 1920 г.

4. Спец. Определенная величина, мера в механике. Момент количества движения. Момент силы. Момент инерции.

5. в знач. нареч.

моме́нтом. Прост. Очень быстро, тотчас. — Я этот Сахалин моментом освою! Он хитро подмигнул. Чаковский, У нас уже утро. [Петя:] Ну, снимай брюки. Да скорее —. Мы сейчас моментом зашьем. Киршон, Чудесный сплав.

◊

В (один) момент — очень быстро, тотчас.

В данный момент — в данное время.

В любой момент — в любое время, всегда.

[Лат. momentum]

МОМЕНТ — это… Что такое МОМЕНТ?

момент — а, м. moment> нем. Moment, пол. moment. <лат. momentum время, период; краткое время, миг. 1. О событии одновременном акту речи. Все министры генерально смотрят на свою прибыль, а разсуждения об интересе государственном никакого не имеют, и… …   Исторический словарь галлицизмов русского языка

МОМЕНТ — Интереснее всего установить принципы и методы включения заимствованного слова в русскую семантическую систему и последующего его смыслового развития. Тут намечаются не только пути интернациональных языковых связей, но и оригинальные приемы… …   История слов

момент — МОМЕНТ, момента, м. [латин. momentum]. 1. Кратчайший отрезок времени, миг, мгновение. В один момент. В благоприятный, подходящий момент. || чего. Миг, мгновение, время, когда осуществляется, наступает какое н. действие. Момент выстрела. В момент… …   Толковый словарь Ушакова

момент — мгновение, миг, секунда, минута; время, пора, час, минута, миг; одну секунду, пункт, отрезок времени, старт, не уходи, фактор, этап, не уходите, штрих, побудьте здесь, побудь на месте, одну минуту, фаза, секундочку, срок, минуточку, постой,… …   Словарь синонимов

МОМЕНТ — (от лат. momentum движущая сила толчок), понятие теории вероятностей; характеристика распределения значений случайной величины Х. В простейшем случае, когда Х может принимать лишь конечное число значений x1, x2,…, xn с вероятностями p1, p2 …   Большой Энциклопедический словарь

МОМЕНТ — (1) (см.) мгновение в физике, играющее ту же роль, какую играет точка для линии, траектории; (2) М. вращающий мера внешнего воздействия, изменяющего угловую скорость вращающегося тела. М. вращающий физ. величина, равная произведению момента (см.) …   Большая политехническая энциклопедия

МОМЕНТ — МОМЕНТ, а, муж. 1. Миг, мгновение, короткое время, в к рое происходит что н. Сделать в один м. (быстро). Упустить нужный м. Благоприятный м. В данный м. (в настоящее время). В тот самый м. как… или когда… (именно тогда). Сейчас самый м.… …   Толковый словарь Ожегова

МОМЕНТ — муж. миг, мгновенье, минт; | пора, срок, короткое срочное время. Момент силы, мех.: произведенье силы на отвес. инерции, косность, сила сопротивленья тела движенью. Моментальный, минутный, миговой, мгновенный. Толковый словарь Даля. В.И. Даль.… …   Толковый словарь Даля

МОМЕНТ — (от лат. momentum – движущая сила, толчок) мгновение, временная точка, определенное мгновение; существенное обстоятельство, составная часть. В философию это понятие было введено Гегелем для обозначения составной части обширного целого, выделенной …   Философская энциклопедия

Момент — осциллятор, который вычисляется как разница между значениями цены за определенный временной интервал. Сигналами служат понижения и повышения моментов относительно нуля, а также пересечения графика момента с нулевым уровнем. По английски: Momentum …   Финансовый словарь

Определение неизвестного момента при кручении

Задача

Вал нагружен скручивающими моментами. Определить величину и направление неизвестного уравновешивающего момента M₂ (рис. 1), если M₁=30кНм, M₃=44кНм, M₄=6кНм

рис. 1

Пример решения

Величина и направление неизвестного скручивающего момента M₂ определяется из условия неподвижности вала.

Конечно на самом деле вал при работе вращается, собственно для этого он и предназназначен — вращаясь передавать крутящий момент.

Но в сопротивлении материалов, при расчетах валов, часть крутящего момента необходимая для вращения вала отбрасывается, и учитываются только моменты деформирующие (скручивающие) вал.

Таким образом будем полагать что рассматриваемый вал не вращается. Для этого должно выполняться следующее условие: сумма крутящих моментов относительно продольной оси вала должна быть равна нулю

Для составления уравнения равновесия зададим произвольным образом направление искомого крутящего момента M₂, например по ходу часовой стрелки (рис. 2)

рис. 2

Запишем уравнение равновесия вала относительно продольной оси z, при этом моменты вращающие вал в одну сторону запишем со знаком «+», а моменты обратного направления соответственно со знаком «-«:

отсюда следует, что

Знак «-» в результате показывает, что реальное направление крутящего момента M₂ противоположно ранее выбранному, т.е. в данном случае момент M₂ направлен против хода часовой стрелки и равен 8кНм.

Проверить себя можно сложив отдельно величины крутящих моментов направленных по ходу часовой стрелки и моментов обратного направления. Эти суммы должны получиться одинаковыми.

Другие примеры решения задач >

определение, формула, физический смысл. Работа момента силы

Вращение вокруг оси или точки различных объектов является одним из важных видов движения в технике и в природе, который изучают в курсе физики. Динамика вращения, в отличие от динамики линейного движения, оперирует понятием момента той или иной физической величины. Данная статья посвящена вопросу, что такое момент сил.

Понятие о моменте силы

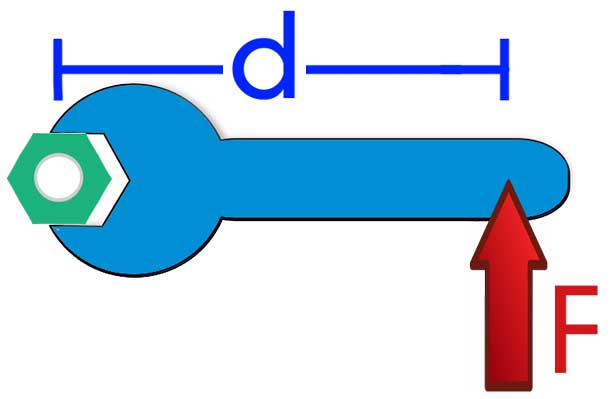
Каждый любитель велосипеда хотя бы один раз в своей жизни раскручивал рукой колесо своего «железного коня». Если описанное действие выполнять, взявшись рукой за покрышку, то раскрутить колесо гораздо легче, чем взявшись за спицы ближе к оси вращения. Это простое действие описывается в физике с помощью момента силы или вращающего момента.

Что такое момент силы? Ответить на этот вопрос можно, если представить себе систему, которая может вращаться вокруг оси O. Если в некоторой точке P к системе приложить вектор силы F¯, тогда момент действующей силы F¯ будет равен:

M¯ = [OP¯*F¯].

То есть момент M¯ представляет собой векторную величину, равную произведению векторной силы F¯ на радиус-вектор OP¯.

Записанная формула позволяет отметить важный факт: если внешняя сила F¯ приложена под любым углом к любой точке оси вращения, то момента она не создает.

Абсолютная величина момента силы

В предыдущем пункте мы рассмотрели определение, что такое момент силы относительно оси. Теперь обратимся к рисунку ниже.

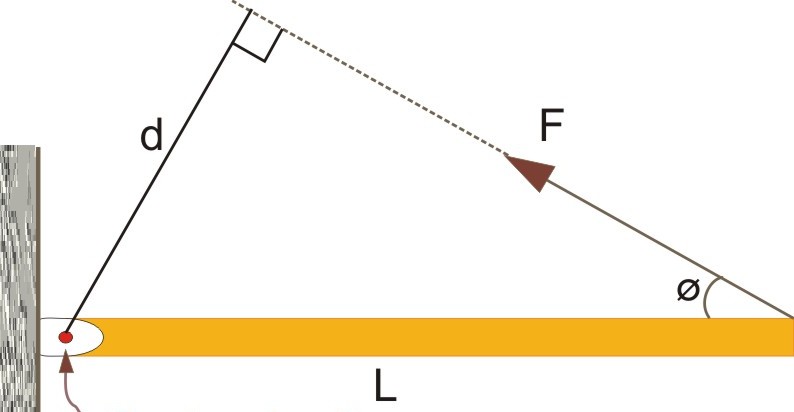
Здесь изображен некоторый стержень, имеющий длину L. С одной стороны он закреплен через шарнирное соединение на вертикальной стене. Другой конец стержня является свободным. На этот конец оказывает действие сила F¯. Также известен угол между стержнем и вектором силы. Он равен φ.

Вращающий момент определяется через векторное произведение. Модуль такого произведения равен произведению абсолютных значений векторов на синус угла между ними. Применяя тригонометрические формулы, приходим к следующему равенству:

M = L*F*sin(φ).

Обращаясь снова к рисунку выше, можно это равенство переписать в следующей форме:

M = d*F, где d = L*sin(φ).

Величина d, которая равна расстоянию от вектора силы до оси вращения, получила название рычага силы. Чем больше значение d, тем больший момент создаст сила F.

Направление момента силы и его знак

Изучение вопроса, что такое момент силы, не может быть полным, если не рассмотреть его векторную природу. Вспоминая свойства векторного произведения, можно с уверенностью сказать, что момент силы будет перпендикулярен плоскости, построенной на векторах-множителях.

Конкретное направление M¯ определяется однозначно, если применить так называемое правило буравчика. Звучит оно просто: вращая буравчик по направлению кругового движения системы, поступательным движением буравчика определяется направление момента силы.

Если смотреть на вращающуюся систему вдоль ее оси, то вектор момента силы, приложенный к точке, может быть направлен как на читателя, так и от него. В связи с этим при количественных расчетах используют понятие о положительном или об отрицательном моменте. В физике принято положительным считать тот момент силы, который приводит к вращению системы против хода часовой стрелки.

В чем смысл величины M¯?

Имеется в виду физический смысл. Действительно, в механике линейного движения известно, что сила — это мера возможности придать линейное ускорение телу. По аналогии, момент силы точки — это мера возможности сообщения углового ускорения системы. Момент силы является причиной появления углового ускорения и ему прямо пропорционален.

Разную возможность совершения вращения или поворота легко понять, если вспомнить, что дверь открывается легче, если ее толкнуть подальше от дверных петель, то есть в области ручки. Еще один пример: любой более-менее тяжелый предмет легче удержать, если прижать руку к телу, чем держать его на вытянутой руке. Наконец, открутить гайку проще, если воспользоваться длинным ключом. В названных примерах момент силы изменяется за счет уменьшения или увеличения рычага силы.

Здесь уместно привести аналогию философского характера, взяв за пример книгу Экхарта Толле «Сила момента Сейчас». Книга относится к психологическому жанру и учит жить без стресса в данный момент своей жизни. Только текущее мгновение имеет смысл, только во время него совершаются все действия. Учитывая названную идею книги «Сила момента Сейчас» можно сказать, что вращающий момент в физике осуществляет ускорение или замедление вращения в текущий момент времени. Поэтому главное уравнение моментов имеет следующий вид:

dL = M*dt.

Где dL — изменение момента импульса за бесконечно малый промежуток времени dt.

Важность понятия о моменте силы для статики

Многие знакомы с задачами на рычаги разного рода. Практически во всех этих задачах статики требуется найти условия равновесия системы. Для нахождения этих условий проще всего воспользоваться концепцией момента силы.

Если система не движется и находится в состоянии равновесия, то сумма всех моментов сил относительно оси, точки или выбранной опоры должна быть равна нулю, то есть:

∑_i=1ⁿM_i¯ = 0.

Где n — число действующих сил.

Напомним, что абсолютные значения моментов M_i в равенство выше нужно подставлять с учетом их знака. Сила реакции опоры, которая рассматривается в качестве оси вращения, вращающего момента не создает. Ниже приводится видео, которое поясняет тему этого пункта статьи.

Момент силы и его работа

Многие читатели обратили внимание, что момент силы рассчитывается в ньютонах на метр. Это означает, что он имеет такую же размерность, что работа или энергия в физике. Тем не менее концепция момента силы — это величина векторная, а не скалярная, поэтому работой момент M¯ считать нельзя. Однако работу он может выполнять, что рассчитывается по такой формуле:

A = M*θ.

Где θ — центральный угол в радианах, на который система повернулась за известное время t.

Правила знаков для сил и моментов в уравнениях равновесия

При составлении уравнений статики для систем находящихся в равновесии (например при определении опорных реакций) правила знаков могут быть упрощены до следующего вида:

Нагрузки направленные в одну сторону принимаются положительными, а соответственно, нагрузки обратного направления записываются со знаком минус.

Знаки проекций сил

То есть, для уравнений сумм проекций сил на оси:
Проекции сил и нагрузок на координатную ось имеющие одинаковое направление принимаются положительными, а проекции усилий противоположного направления – отрицательными.

Например, для такой схемы нагружения:

уравнение суммы сил имеет вид

А так как суммы проекций разнонаправленных сил равны, то данное уравнение можно записать и так:

Здесь F(q) – равнодействующая от распределенной нагрузки, определяемая произведением интенсивности нагрузки на ее длину.

Знаки моментов

Сосредоточенные моменты и моменты сил стремящиеся повернуть систему относительно рассматриваемой точки по ходу часовой стрелки записываются в уравнения с одним знаком, и соответственно моменты, имеющие обратное направление с противоположным знаком.

Например, для суммы моментов относительно точки A

получаем

или, что одно и то же

Здесь m(F) – моменты сил F относительно точки A.
M(q) – моменты распределенных нагрузок q относительно рассматриваемой точки.

Примеры решения задач >

Момент распределенной нагрузки — Лекции и примеры решения задач технической механики

Вопрос: Как определить момент в точке балки, возникающий от распределенной нагрузки?

Ответ: При расчетах балок, в сопромате часто возникает задача определить изгибающий момент в сечениях балки вызванный действием равномерно распределенной нагрузки q.

В этом случае, как правило, удобнее пользоваться понятием равнодействующей силы R_q, которой можно заменить распределенную нагрузку.

Рассмотрим пример нахождения момента в произвольной точке C от равномерно распределенной между точками A и B нагрузки интенсивностью q.

Для определения момента нагрузки необходимо знать ее длину

a и расстояние z от любого ее края до рассматриваемой точки.

Заменим распределенную нагрузку ее равнодействующей R_q, которая для равномерного случая распределения будет располагаться ровно посередине нагрузки, при этом ее величина определяется как произведение интенсивности q нагрузки на ее длину a

R_q=qa

Как известно момент силы определяется произведением силы на плечо

M=Fl

В данном случае силой в вышеуказанном выражении является равнодействующая R_q.

Плечом этой силы является расстояние от точки C до равнодействующей нагрузки

l=a/2+z

Таким образом, момент нагрузки равен произведению интенсивности q нагрузки на ее длину a и на расстояние от ее середины до рассматриваемой точки a/2+z

M_С=R_ql=qa(a/2+z)

Для случая, когда точка лежит в пределах действия нагрузки, аналогично:

M_С= R_ql=qa(a/2-z)

Примечания:

1. В случае действия неравномерно распределенной нагрузки ее интенсивность задается функцией.
2. Для нагрузки, распределенной по площади (объему) при вычислении равнодействующей вместо длины надо подставлять площадь (объем) ее действия.
3. Момент части распределенной нагрузки определяется аналогично.

Примеры решения задач >
Краткая теория >

Правила знаков в сопромате — Лекции и примеры решения задач технической механики

В сопротивлении материалов, а также в технической и прикладной механике при решении задач принимаются следующие правила знаков:

При растяжении-сжатии

Внутренняя продольная сила N, которая стремится растянуть рассматриваемую часть бруса, считается положительной. Сжимающая продольная сила имеет отрицательный знак.

Положительное направление внутренней продольной силы N

Подборка видео по всем правилам знаков:

При кручении

Внутренний скручивающий момент T считается положительным, если он стремится повернуть рассматриваемую часть бруса против хода часовой стрелки, при взгляде на него со стороны внешней нормали.

Положительное направление внутреннего скручивающего момента T

При изгибе

Внутренняя поперечная сила Q считается положительной, в случае, когда она стремится повернуть рассматриваемую часть бруса по ходу часовой стрелки.

Положительное направление внутренней поперечной силы Q

Внутренний изгибающий момент M положителен, когда он стремится сжать верхние волокна бруса.

Положительное направление внутреннего изгибающего момента M

Примечание: Величина и знак внутренних сил и моментов зависит от вызывающих их внешних усилий, поэтому указанные правила знаков в том же виде справедливы и для внешних нагрузок.

Правило знаков при внецентренном нагружении

Положительными принимаются внешние усилия стремящиеся вызвать растяжение первой четверти сечения.

Положительное направление действия внешних нагрузок

Нормальные напряжения σ положительны, если они растягивают выделенный элемент бруса.

Положительные нормальные напряжения

Касательные напряжения τ будут положительными, если они стремятся повернуть рассматриваемый элемент бруса по ходу часовой стрелки.

Положительные касательные напряжения

Правило знаков для деформаций и перемещений

Деформация при растяжении-сжатии Δl считается положительной, если длина стержня при этом увеличивается.

Положительная деформация при продольном нагружении

При плоском поперечном изгибе

Вертикальное перемещение сечения бруса принимается положительным, если оно направлено вверх от начального положения.

Положительные перемещения сечений балки при изгибе

Для проекций сил на оси системы координат

Проекции внешних сил на оси системы координат принимаются положительными, если их направление совпадает с положительным направлением соответствующей оси.

Для моментов

Сосредоточенные моменты и моменты сил в уравнениях статики записываются с положительным знаком, если они стремятся повернуть рассматриваемую систему против хода часовой стрелки.

При составлении уравнений равновесия статичных (неподвижных) систем (например, при определении опорных реакций), последние два правила упрощаются до вида:

Проекции сил и моменты, имеющие одинаковое направление записываются с одинаковыми знаками, соответственно проекции сил и моменты обратного направления – с противоположными.

Метод сечений >
Примеры решения задач >