Векторное произведение векторов калькулятор
Результатом векторного произведения двух векторов будет являться вектор, перпендикулярный обоим исходным векторам, длина которого равна площади параллелограмма, образованного исходными векторами.
Укажите форму представления первого вектора Координаты точек начала и конца первого вектораКоординаты первого вектора
Укажите форму представления второго вектора Координаты точек начала и конца второго вектораКоординаты второго вектора
Задайте координаты первого вектора
a̅ =
{
;
;
}
Задайте координаты второго вектора
b̅ =
{
;
;
}
Векторное произведение векторов
Векторным произведением двух векторов a и b в трехмерном евклидовом пространстве – называется вектор c. Модуль вектора c, численно равен площади параллелограмма OABQ, построенного на векторах

Векторное произведение векторов a и b обозначается как: [a b], [a, b], a × b, a ∧ b
Параллелограмм OABQНаправление получившегося вектора c будет перпендикулярно плоскости параллелограмма OABQ.
В правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (aybz — byaz) — j̅ (axbz — b
Формула для координат векторного произведения вычисляется из определителя третьего порядка, где первая строка – векторы i, j, k (i = (1 0 0), j(0 1 0), k = (0 0 1)), а вторая и третья строки – координаты векторов a и b:
[a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axbax ay bx by
i̅ (aybz — byaz) — j̅ (axbz — bxaz) + k̅ (axby — bxay)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то в правом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] =
i̅
((By — Ay)(Dz — Cz) — (D
Векторное произведение не обладает переместительным свойством, поэтому при перестановке множителей векторное произведение изменит знак: b × a = -(a × b)
Векторное произведение равно нулю, когда векторы
 е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.
е. лежат на параллельных прямых или на одной прямой), а также если один из векторов или оба – нуль вектора.В левом ортонормированном базисе векторное произведение векторов определяется как:
[a × b] = i̅ (azby — bzay) + j̅ (axbz — bxaz) + k̅ (aybx — byax)
Примеры векторного произведения векторов
Пример 1. Найдем векторное произведение векторов. Координаты обоих векторов заданны точками.
Координаты точки А вектора
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
N̅ = [AB × CD] =
= i̅i̅ j̅ k̅ ABx ABy ABz CDx CDy CDz
— j̅ABy ABz CDy CDz
+ k̅ABx ABz CDx CDz
= i̅ AByCDz — i̅ ABzCDy — j̅ ABxCDz + j̅ ABzCDx + k̅ ABxCDy — k̅ AByCDx = ABx ABy CDx CDy
i̅ (AByCDz
Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0. 2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy; D
ABx = -8
ABy = -1/5
ABz = -275/4
CDx = 7
CDy = 6
CDz = 7
N̅ = [AB × CD] = i̅ (-1/5 ⋅ 7 — 6 ⋅ (-275/4)) — j̅ (-8 ⋅ 7 — 7 ⋅ (-275/4)) + k̅ (-8 ⋅ 6 — 7 ⋅ (-1/5)) = i̅ (-7/5 — (-825/2)) — j̅ (-56 — (-1925/4)) + k̅ (-48 — (-7/5)) = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = [AB × CD] = (4111/10)i̅ — (1701/4)j̅ — (233/5)k̅
N̅ = {4111/10 ; -1701/4 ; -233/5}
N̅ = {411.1 ; -425.25 ; -46.6}
Пример 2. Найдем векторное произведение векторов.
Найдем векторное произведение векторов.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)
N̅ = [a × b] =
= i̅i̅ j̅ k̅ ax ay az bx by bz
— j̅ay az by bz
+ k̅ax az bx bz
= i̅ aybz — i̅ azby — j̅ axbz + j̅ azbx + k̅ axby — k̅ aybx = ax ay bx by
i̅ (aybz — by
ax = 5
ay = 1
az = 7
bx = 2
by = 4
bz = 6
N̅ = [a × b] = i̅ (1 ⋅ 6 — 4 ⋅ 7) — j̅ (5 ⋅ 6 — 2 ⋅ 7) + k̅ (5 ⋅ 4 — 2 ⋅ 1) = i̅ (6 — 28) — j̅ (30 — 14) + k̅ (20 — 2) = -22i̅ -16j̅ +18k̅
N̅ = [a × b] = -22i̅ -16j̅ +18k̅
N̅ = {-22 ; -16 ; 18}
Найти скалярное произведение векторов — онлайн калькулятор
Чтобы найти скалярное произведение векторов онлайн, необходимо:
- Указать размерность векторов (векторы на плоскости или в пространстве).

- Определиться с формой задания векторов (они могут быть заданы координатами либо точками).
- Задать значения векторов в соответствующих полях.
- Нажать «рассчитать».
Как найти скалярное произведение двух векторов с помощью онлайн-калькулятора
Рассмотрим простой пример, наглядно демонстрирующий нахождение скалярного произведения двух векторов с помощью онлайн-калькулятора. Никаких формул и вычислений, лишь несколько простых действий:
- Определяем размерность векторов. Онлайн-калькулятор позволяет находить скалярное произведение как для двумерных векторов на плоскости, так и для трехмерных векторов в пространстве.
Выберем размерность 2, что соответствует векторам на плоскости.
- Далее следует выбрать форму представления обоих векторов. Их можно задать координатами, либо точками.
Для вектора a выберем координаты, а для вектора b – точки. - Теперь в поля ниже, в соответствии с выбранной формой представления вектора, нужно вписать соответствующие значения, непосредственно задающие его.
 Для вектора a:
Для вектора a:
Для вектора b:
Заполним поля, задав произвольные векторы, и нажмем «Рассчитать»:
После этого калькулятор предоставит ответ и решение с пояснениями и промежуточными выкладками:
Материалы, которые помогут вам лучше разобраться в теме:
- Векторы на плоскости и в пространстве — основные определения
- Операции над векторами и их свойства: сложение и умножение
- Координаты вектора в декартовой системе координат (ДСК)
- Нахождение координат вектора через координаты точек
- Векторное произведение — определения, свойства, формулы, примеры и решения
- Операции над векторами в прямоугольной системе координат
- Смешанное произведение векторов, его свойства, примеры и решения
- Скалярное произведение векторов: свойства, примеры вычисления, физический смысл
Ответ:
Решение
Ответ:
- list» :key=»`error-${eIdx}`» v-html=»e»/>
Похожие калькуляторы:
- Длина вектора. Модуль вектора
- Векторное произведение векторов
- Умножение вектора на число
- Угол между векторами
- Смешанное произведение векторов
- Сложение и вычитание двух векторов
- Определение вектора по двум точкам
- Разложение вектора по базису
- Проверить являются ли вектора базисом
- Ортогональность векторов
- Компланарность векторов
- Коллинеарность векторов
- Проекция вектора на вектор
- Площадь треугольника, построенного на векторах
- Площадь параллелограмма, построенного на векторах
Скалярное произведение векторов онлайн
Чтобы найти скалярное произведение векторов не обязательно помнить соответствующую формулу и иметь под рукой бумагу и ручку. Даже если вы забыли нужную формулу или не располагаете временем для проведения расчетов, онлайн-калькулятор поможет найти скалярное произведение векторов быстро и без ошибок.
Даже если вы забыли нужную формулу или не располагаете временем для проведения расчетов, онлайн-калькулятор поможет найти скалярное произведение векторов быстро и без ошибок.
Программа выдаст не только ответ, но и подробно пояснит ход решения, а вы сможете освежить свои знания или проверить правильность своих расчетов. Данный сервис будет полезен школьникам и студентам в самостоятельной подготовке, преподавателям и просто любителям математики.
Понравился калькулятор? Поделись с друзьями!
Произведение трех векторов онлайн калькулятор. Векторное произведение векторов. Смешанное произведение векторов
Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение b x c , т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc .
Назначение
. Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word
. Дополнительно создается шаблон решения в Excel
.
Полученное решение сохраняется в файле Word
. Дополнительно создается шаблон решения в Excel
.
b (; ; )
c (; ; )
При вычислении определителя использовать правило треугольников
Признаки компланарности векторов
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.
Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая.
Свойства смешанного произведения
- При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
Вытекает из геометрического смысла.
- (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
Вытекает из определения смешанного произведения. - (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. - Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0 .
Пример №1 . Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc .
Пример №2 . (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca . Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc .
Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k .
Решение . Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде.
Запишем систему в виде.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах.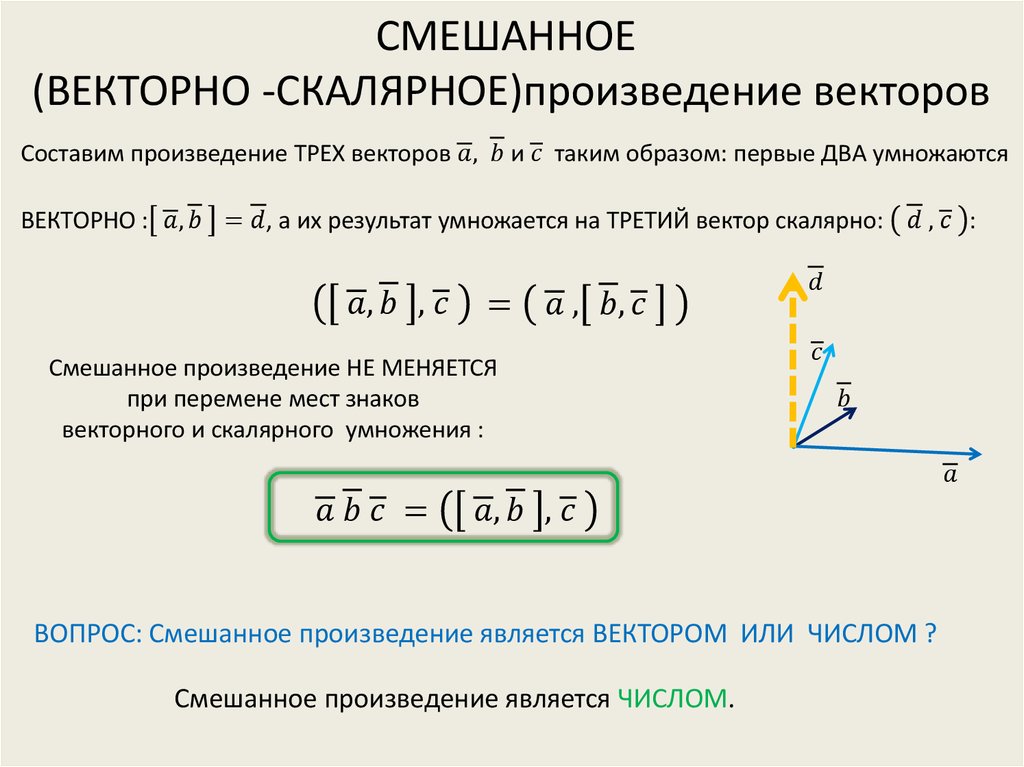 Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения.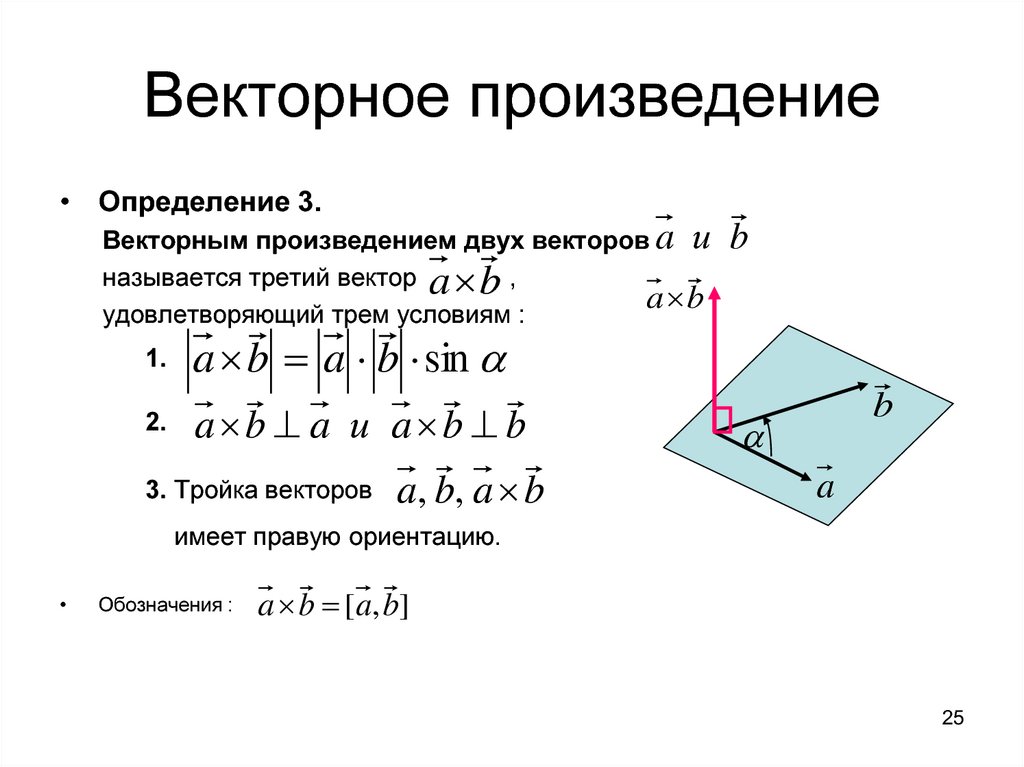 Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Тема напрямую связана с такими терминами, как скалярное и векторное произведение. В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.
Yandex.RTB R-A-339285-1
Термин
Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.
Определение 1
Смешанным произведением a → , b → и d → является та величина, которая равняется скалярному произведению a → × b → и d → , где a → × b → — умножение a → и b → . Операцию умножения a → , b → и d → зачастую обозначают a → · b → · d → . Можно преобразовать формулу так: a → · b → · d → = (a → × b → , d →) .
Умножение в системе координат
Мы можем умножить вектора, если они указаны на координатной плоскости.
Возьмем i → , j → , k →
Произведение векторов в данном конкретном случае будет иметь следующий вид: a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Определение 2
Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.
Из этого следует:
a → × b → = (a y · b z — a z · b y) · i → + (a z · b x + a x · b z) · j → + (a x · b y + a y · b x) · k → = a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k →
Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
a → × b → = (a y a z b y b z · i → — a x a z b x b z · j → + a x a y b x b y · k → , d x · i → + d y · j → + d z · k →) = = a y a z b y b z · d x — a x a z b x b z · d y + a x a y b x b y · d z = a x a y a z b x b y b z d x d y d z
Таким образом, можно сделать вывод, что:
a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z
Определение 3
Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a → · b → · d = a → × b → , d → = a x a y a z b x b y b z d x d y d z .
Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.
Ниже мы приведем основные свойства.
- (λ · a →) · b → · d → = a → · (λ · b →) · d → = a → · b → · (λ · d →) = λ · a → · b → · d → λ ∈ R ;
- a → · b → · d → = d → · a → · b → = b → · d → · a → ; a → · d → · b → = b → · a → · d → = d → · b → · a → ;
- (a (1) → + a (2) →) · b → · d → = a (1) → · b → · d → + a (2) → · b → · d → a → · (b (1) → + b (2) →) · d → = a → · b (1) → · d → + a → · b (2) → · d → a → · b → · (d (1) → + d (2) →) = a → · b → · d (2) → + a → · b → · d (2) →
Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль.
Результатом умножения также будет нуль в том случае, если два или больше множителей равны.
Действительно, если a → = b → , то, следуя определению векторного произведения [ a → × b → ] = a → · b → · sin 0 = 0 , следовательно, смешанное произведение равно нулю, так как ([ a → × b → ] , d →) = (0 → , d →) = 0 .
Если же a → = b → или b → = d → , то угол между векторами [ a → × b → ] и d → равен π 2 . По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
По определению скалярного произведения векторов ([ a → × b → ] , d →) = [ a → × b → ] · d → · cos π 2 = 0 .
Свойства операции умножения чаще всего требуются во время решения задач.
Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.
Пример 1
Докажите равенство ([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) , где λ — некоторое действительное число.
Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →)
Мы разобрали, что (([ a → × b → ] , b →) = 0 . Из этого следует, что
([ a → × b → ] , d → + λ · a → + b →) = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + ([ a → × b → ] , b →) = = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →) + 0 = ([ a → × b → ] , d →) + ([ a → × b → ] , λ · a →)
Согласно первому свойству ([ a ⇀ × b ⇀ ] , λ · a →) = λ · ([ a ⇀ × b ⇀ ] , a →) , а ([ a ⇀ × b ⇀ ] , a →) = 0 . , d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
, d →) ≤ ≤ a → · b → · 1 · d → · 1 = a → · b → · d →
Неравенство доказано.
Разбор типовых задач
Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z .
Пример 3
В прямоугольной системе координат представлены 3 вектора с такими координатами: a → = (1 , — 2 , 3) , b → (- 2 , 2 , 1) , d → = (3 , — 2 , 5) . Необходимо определить, чему равно произведение указанных векторов a → · b → · d → .
Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a → · b → · d → = (a → × b → , d →) = a x a y a z b x b y b z d x d y d z = 1 — 2 3 — 2 2 1 3 — 2 5 = = 1 · 2 · 5 + (- 1) · 1 · 3 + 3 · (- 2) · (- 2) — 3 · 2 · 3 — (- 1) · (- 2) · 5 — 1 · 1 · (- 2) = — 7
Пример 4
Необходимо найти произведение векторов i → + j → , i → + j → — k → , i → + j → + 2 · k → , где i → , j → , k → — орты прямоугольной декартовой системы координат.
Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i → + j → = (1 , 1 , 0) i → + j → — k → = (1 , 1 , — 1) i → + j → + 2 · k → = (1 , 1 , 2)
Используем формулу, которая использовалась выше
i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 1 1 0 1 1 — 1 1 1 2 = 0 i → + j → × (i → + j → — k → , (i → + j → + 2 · k →) = 0
Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.
Пример 5
В прямоугольной системе координат расположены три вектора a → , b → и d → , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4 , 2 и 3 . Необходимо умножить вектора.
Обозначим c → = a → × b → .
Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a → · b → · d → = ([ a → × b → ] , d →) = c → , d → = c → · d → · cos (c → , d → ^) .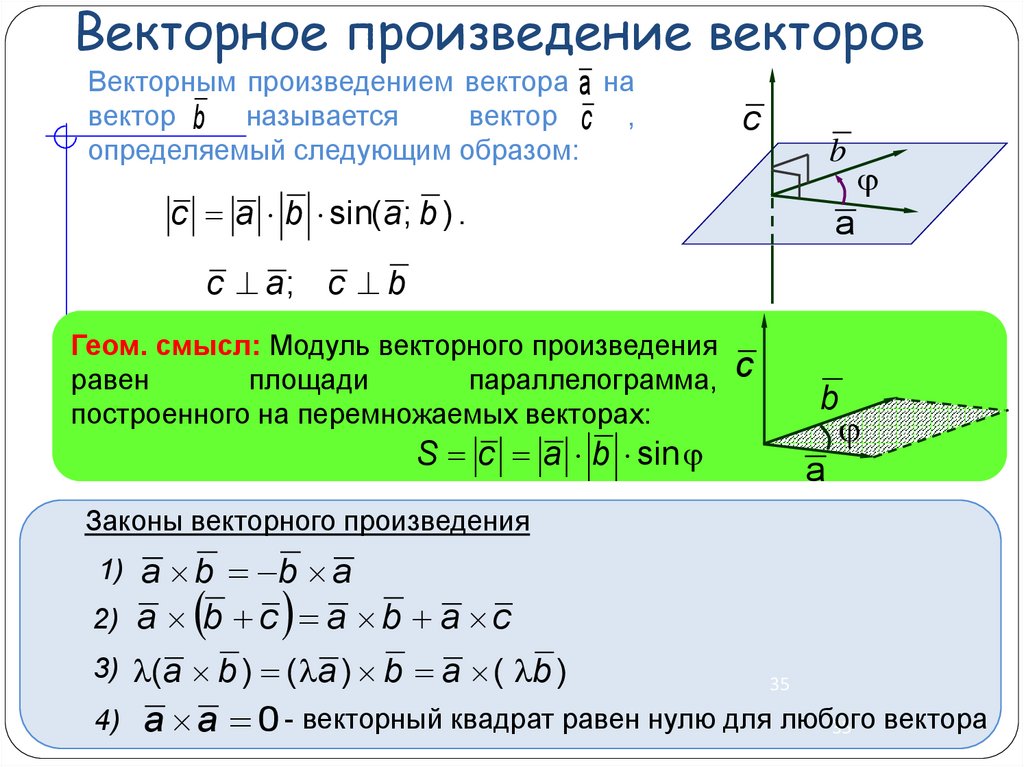 ) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
) = c → · n p c → d → , где n p c → d → — числовая проекция вектора d → на направление вектора c → = [ a → × b → ] .
Абсолютная величина n p c → d → равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a → , b → и d → в качестве сторон. Исходя из этого, следует уточнить, что c → = [ a → × b → ] перпендикулярен a → и вектору и вектору согласно определению умножения векторов. Величина c → = a → x b → равняется площади параллелепипеда, построенного на векторах a → и b → .
Делаем вывод, что модуль произведения a → · b → · d → = c → · n p c → d → равен результату умножения площади основания на высоту фигуры, которая построена на векторах a → , b → и d → .
Определение 4
Абсолютная величина векторного произведения является объемом параллелепипеда : V п а р а л л е л е п и п и д а = a → · b → · d → .
Данная формула и является геометрическим смыслом.
Определение 5
Объем тетраэдра , который построен на a → , b → и d → , равняется 1 / 6 объема параллелепипеда Получаем, V т э т р а э д а = 1 6 · V п а р а л л е л е п и п и д а = 1 6 · a → · b → · d → .
Для того, чтобы закрепить знания, разберем несколько типичных примеров
Пример 6
Необходимо найти объем параллелепипеда, в качестве сторон которого используются A B → = (3 , 6 , 3) , A C → = (1 , 3 , — 2) , A A 1 → = (2 , 2 , 2) , заданные в прямоугольной системе координат. Объем параллелепипеда можно найти, используя формулу об абсолютной величине. Из этого следует: A B → · A C → · A A 1 → = 3 6 3 1 3 — 2 2 2 2 = 3 · 3 · 2 + 6 · (- 2) · 2 + 3 · 1 · 2 — 3 · 3 · 2 — 6 · 1 · 2 — 3 · (- 2) · 2 = — 18
Тогда, V п а р а л л е л е п и п е д а = — 18 = 18 .
V п а р а л л е л е п и п и д а = 18
Пример 7
В системе координат заданы точки A (0 , 1 , 0) , B (3 , — 1 , 5) , C (1 , 0 , 3) , D (- 2 , 3 , 1) . Следует определить объем тетраэдра, который расположен на этих точках.
Воспользуемся формулой V т э т р а э д р а = 1 6 · A B → · A C → · A D → . Мы можем определить координаты векторов по координатам точек: A B → = (3 — 0 , — 1 — 1 , 5 — 0) = (3 , — 2 , 5) A C → = (1 — 0 , 0 — 1 , 3 — 0) = (1 , — 1 , 3) A D → = (- 2 — 0 , 3 — 1 , 1 — 0) = (- 2 , 2 , 1)
Дальше определяем смешанное произведение A B → · A C → · A D → по координатам векторов: A B → · A C → · A D → = 3 — 2 5 1 — 1 3 — 2 2 1 = 3 · (- 1) · 1 + (- 2) · 3 · (- 2) + 5 · 1 · 2 — 5 · (- 1) · (- 2) — (- 2) · 1 · 1 — 3 · 3 · 2 = — 7 Объем V т э т р а э д р а = 1 6 · — 7 = 7 6 .
V т э т р а э д р а = 7 6 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Данный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение
трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c .
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать:
| abc =([ab ],c ) |
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю.
Следствие 1. Имеет место следующее равенство:
Следовательно нам достаточно доказать, что
| ([ab ],c )=([bc ],a ) | (3) |
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Последнее выражение можно записать, используя определители второго порядка:
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
| . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс , где
Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1:
Конечная точка вектора a .
Скалярное произведение векторов определение, основные свойства, формулы и условия вычисления, примеры задач с решениями, онлайн-калькулятор
В старших классах на уроках алгебры, геометрии и физики ученики решают задачи с числами-скалярами. Для нахождения результата используется формула скалярного произведения векторов: (а, а) > 0, для всех а≠0. Полученное значение не зависит от системы координат. Оно характеризует длину сомножителей и угол, образованный между ними. Подобной операции соответствует линейность.
Трактовка понятий
Под скалярным произведением (СП) в пространстве над полем вещественных чисел подразумевается функция (x, y) для соответствующих элементов, принадлежащих указанному координатному пространству. Из определения вытекает линейность СП по первичному аргументу.
Для косинуса и синуса справедливо смешанное сопряжение. СП принимает положительную определённость, если соблюдается условие, что x=0. Для вычислений показателя в алгебре используется следующая форма: а = [a1, a2, …, an] и b = [b1, b2, …, bn].
Пример: нужно найти в трёхмерном пространстве произведение двух скаляров [1, 3, −5] и [4, −2, −1]. Решение: необходимо перемножить градиенты (вектора). [1, 3, −5] х [4, −2, −1] = 1 х 4 + 3 х (-2) + (-5) х (-1) = 3.
Геометрическое определение отличается от физического и алгебраического. Чтобы вычислить СП, используя длину и угол между градиентами, которые введены независимым способом, используется следующее выражение: (а, b) = lal x lbl x cos (a, b). Базисом аксиоматики считается скалярное произведение. После его нахождения определяется длина основного вектора и угла.
В современных теоремах понятие СП находится в основе некоторых производных, включая евклидову норму. Термин «длина» используется по отношению к конечномерным векторам. Если имеет смысл криволинейный путь, тогда применяются векторы ненулевой длины. Чаще они находятся в бесконечномерном пространстве.
youtube.com/embed/TmiuKqikyMc»/>Угол между такими величинами отличен от нуля. Его значением является число, косинус которого — отношение их СП к произведению их длин. Если пространство псевдоевклидовое (конечномерное, для которого характерна невырожденная индефинитная метрика), понятие «угол» применяется относительно скаляров без изотропных прямых.
Сам угол является числом. Чтобы дать ему значение, вычисляется гиперболический косинус: отношение модуля СП к произведению длин векторов. При перпендикулярности либо ортогональности на плоскости СП равняется нулю. Это свойство скалярного произведения векторов характерно для любого промежутка с положительно определённым СП.
При соблюдении такого условия пространство называется вещественным либо комплексным. Конечномерный вещественный промежуток с положительным СП называется евклидовым, а комплексный — унитарным (эрмитовым).
Если скалярное произведение отрицательное либо не считается знакоопределённым, промежуток называется индефинитной метрикой. Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:
Примером такого промежутка является пространство Минковского. СП на таких участках не порождает нормы. Из бесконечномерных выделяются пространства:
- Крейна.
- Понтрягина.
Описание свойств
С помощью специальных математических онлайн сервисов или калькулятора легко находится значение СП через теорему косинусов: a = arccos (a, b)/√(а, а)(b, b). Знак зависит от косинуса угла. В норме значения векторов только положительные. СП больше нуля, если угол острый, и меньше, когда он тупой.
Главные свойства умножения скаляров:

Задача 1: вычислить СП векторов а = {1;2} и b = {4;8}. Решение: а х b = 1 х 4 + 2 х 8 = 20.
Задача 2: найти СП скаляров а и b, если из длины равны 3 и 6, а угол — 60 градусов. Решение: а х b = lal x lbl cos α = 3 х 6 х cos60 = 9. Для лучшего усвоения материала два вектора перемножается с помощью матрицы. Чтобы различать множители, первый оформляется в строку, а второй — в столбец. Если в условиях задачи указываются три величины, тогда последняя оформляется в скобки в форме квадратов. Их скалярное произведение вычисляется путём умножения матриц. Результат — единственное число.
Задача 3: нужно найти СП пар векторов: а = (1; 5; 1), b = (1; -5; 2) и с = (2; 1; 3/2), d = (0; 0; 1). Решение: вычисления проводятся с помощью матричного представления.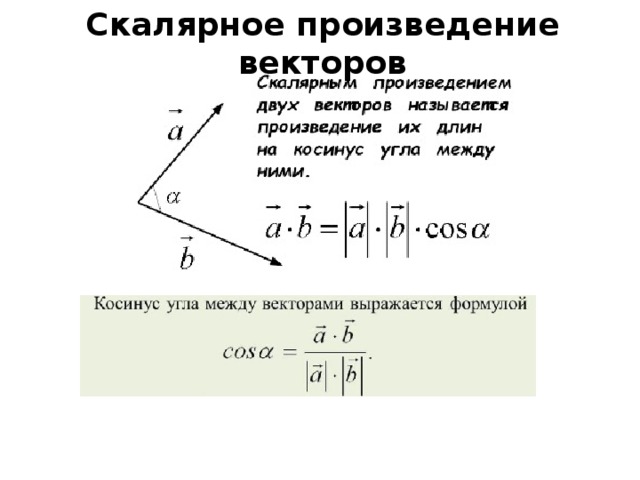 Первый вектор записывается в строку, а второй — в столбец. Чтобы найти скалярное произведение векторов, потребуется умножить матрицу-строку на матрицу-столбец. Если вектор а умножить на вектор b, получится -22. Аналогично находится значение второй пары. Результат равен 3/2. Простым обобщением конечномерного СП в тензорной (линейной) алгебре считается свёртка с повторяющимся индексом.
Первый вектор записывается в строку, а второй — в столбец. Чтобы найти скалярное произведение векторов, потребуется умножить матрицу-строку на матрицу-столбец. Если вектор а умножить на вектор b, получится -22. Аналогично находится значение второй пары. Результат равен 3/2. Простым обобщением конечномерного СП в тензорной (линейной) алгебре считается свёртка с повторяющимся индексом.
Применение в физике
Впервые скалярное произведение ввёл У. Гамильтон в 1846 году. Одновременно учёные начали использовать в своих работах векторное произведение, сумму скаляров. Понятие получило широкое применение и в физике. На его основе сформулированы главные законы электродинамики и механики.
Скаляр является физической величиной. Чтобы его задать, используется одно число. Примеры скаляров в физике:
- масса тела, равная 4 кг;
- температура воздуха на уровне +10 градусов.

В каждом предложенном варианте величина задаётся с помощью одного числа, поэтому масса тела и температура относятся к скалярам. Но это понятие в физике не считается простым числом. Для него характерна размерность.
Если в условиях задачи известно, что масса тела равна 3, необходимо указывать единицу измерения (килограммы, граммы). В математике можно сложить числа 3 и 10, а в физике суммируются только скаляры с одинаковой размерностью: массы с массой, градусы с градусами.
Если рассматривать векторную физическую величину, она характеризуется следующим образом:
Понятие скаляр — модуль вектора либо абсолютная величина. Если предположить, что транспортное средство двигается со скоростью 60 км/ч, такая информация считается неполной. В физике важно знать направление движения. Кроме модуля скорости как абсолютной величины, потребуется знать направление в пространстве, поэтому скорость считается векторной величиной.
Если на земле лежит кирпич массой в 1 кг и на него действует сила в 100 Н (модуль), потребуется найти направление движения объекта. Невозможно выяснить параметр, если нет информации о направлении действия силы. Если она идёт вверх, тогда и кирпич будет двигаться в аналогичном направлении.
Если сила идёт вдоль горизонта, тогда объект поедет горизонтально. При вертикальном воздействии силы вниз кирпич останется на прежнем месте. Он будет вжиматься в землю. Подобные явления указывают на то, что сила является вектором, поэтому для неё характерна размерность, модуль.
Для обозначения вектора в физике используются латинские буквы и стрелка:
- вектор скорости: →v;
- вектор силы: →F.
Стрелка является направленным отрезком. Её начальная точка — начало вектора, а конечная или остриё — конец вектора. В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.
В математике величина с начальной точкой А и концом В обозначается →АВ. Если начало и конец направленного отрезка совпадают, тогда получается нулевой вектор. Он обозначается →0.
Такой отрезок считается точкой. У него нет конкретного направления, а длина равняется нулю. К безразмерным скалярам относятся коэффициенты трения и полезного действия, показатель преломления света.
Площадь параллелограмма на векторах онлайн калькулятор. Векторное произведение векторов. Смешанное произведение векторов
Площадь параллелограмма , построенного на векторах , вычисляется как произведение длин этих векторов на синус угла между ними. Если известны только координаты векторов, то для вычисления нужно применять координатные методы, в том числе и для определения угла между векторами.
Вам понадобится
- — понятие вектора;
- — свойства векторов;
- — декартовы координаты;
- — тригонометрические функции.

Инструкция
- В том случае, если известны длины векторов и угол между ними, то для того, чтобы найти площадь параллелограмма , построенного на векторах , найдите произведение их модулей (длин векторов), на синус угла между ними S=│a│ │ b│ sin(α).
- Если векторы заданы в декартовой системе координат, то для того, чтобы найти площадь параллелограмма , построенного на них, проделайте следующие действия:
- Найдите координаты векторов, если они не даны сразу, отняв от соответствующих координат концов векторов, координаты из начал. Например, если координаты начальной точки вектора (1;-3;2), а конечной (2;-4;-5), то координаты вектора будут (2-1;-4+3;-5-2)=(1;-1;-7). Пусть координаты вектора а(x1;y1;z1), вектора b(x2;y2;z2).
- Найдите длины каждого из векторов. Возведите каждую из координат векторов в квадрат, найдите их сумму x1²+y1²+z1². Из получившегося результата извлеките корень квадратный. Для второго вектора проделайте ту же процедуру.
 Таким образом, получится │a│и│ b│.
Таким образом, получится │a│и│ b│. - Найдите скалярное произведение векторов. Для этого перемножьте их соответствующие координаты и сложите произведения │a b│= x1 x2+ y1 y2+ z1 z2.
- Определите косинус угла между ними для чего скалярное произведение векторов, получившееся в п.3 поделите на произведение длин векторов, которые были рассчитаны в п. 2 (Cos(α)= │a b│/(│a│ │ b│)).
- Синус полученного угла будет равен корню квадратному из разности числа 1, и квадрата косинуса того же угла, рассчитанного в п. 4 (1-Cos²(α)).
- Рассчитайте площадь параллелограмма , построенного на векторах найдя произведение их длин, вычисленное в п. 2, а результат умножьте на число, получившееся после расчетов в п.5.
- В том случае, если координаты векторов заданны на плоскости, при расчетах координата z просто отбрасывается. Данный расчет является числовым выражением векторного произведения двух векторов.
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылка, кому нужно именно оно) . Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов , требуется ещё и ещё. Такая вот векторная наркомания. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение , даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников , чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленные читатели могут знакомиться с информацией выборочно, я постарался собрать максимально полную коллекцию примеров, которые часто встречаются в практических работах
Чем вас сразу порадовать? Когда я был маленьким, то умел жонглировать двумя и даже тремя шариками. Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
Ловко получалось. Сейчас жонглировать не придётся вообще, поскольку мы будем рассматривать только пространственные векторы , а плоские векторы с двумя координатами останутся за бортом. Почему? Такими уж родились данные действия – векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве. Уже проще!
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора . Пусть это будут нетленные буквы .
Само действие обозначается следующим образом: . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос : если в скалярном произведении векторов участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница ? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО:
Результатом векторного произведения векторов является ВЕКТОР : , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву .
Сначала будет определение с картинкой, затем комментарии.
Определение : Векторным произведением неколлинеарных векторов , взятых в данном порядке , называется ВЕКТОР , длина которого численно равна площади параллелограмма , построенного на данных векторах; вектор ортогонален векторам , и направлен так, что базис имеет правую ориентацию:
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы , обозначенные красными стрелками, по определению не коллинеарны . Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы взяты в строго определённом порядке : – «а» умножается на «бэ» , а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
Результатом умножения векторов является ВЕКТОР , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор (малиновый цвет). То есть, справедливо равенство .
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора (а, значит, и малинового вектора ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах . На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание : чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними . Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах (красная штриховка), можно найти по формуле:
4) Не менее важный факт состоит в том, что вектор ортогонален векторам , то есть . Разумеется, противоположно направленный вектор (малиновая стрелка) тоже ортогонален исходным векторам .
5) Вектор направлен так, что базис имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости , и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки . Мысленно совместите указательный палец с вектором и средний палец с вектором . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
В результате большой палец – векторное произведение будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он). Теперь поменяйте векторы (указательный и средний пальцы ) местами, в результате большой палец развернётся, и векторное произведение уже будет смотреть вниз. Это тоже правоориентированный базис. Возможно, у вас возник вопрос: а какой базис имеет левую ориентацию? «Присвойте» тем же пальцам левой руки векторы , и полУчите левый базис и левую ориентацию пространства (в этом случае большой палец расположится по направлению нижнего вектора) . Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение;-)
…как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторовОпределение подробно разобрано, осталось выяснить, что происходит, когда векторы коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если , то . Строго говоря, само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно просто равно нулю.
Частный случай – векторное произведение вектора на самого себя:
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица , чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов , если
б) Найти площадь параллелограмма, построенного на векторах , если
Решение : Нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
Ответ :
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах . Площадь данного параллелограмма численно равна длине векторного произведения:
Ответ :
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры , соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что и – это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах , если
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторовНекоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов и произвольного числа справедливы следующие свойства:
1) В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
Поэтому пусть будет.
2) – свойство тоже разобрано выше, иногда его называют антикоммутативностью . Иными словами, порядок векторов имеет значение.
3) – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти , если
Решение: По условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ :
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах , если
Решение : Площадь треугольника найдём по формуле . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов . Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение через векторное произведение , по сути, выразим вектор через вектор . О длинах пока ни слова!
(1) Подставляем выражения векторов .
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
Данное действие напоминает Пример 3:
3) Найдём площадь искомого треугольника:
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ :
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти , если
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров;-)
Векторное произведение векторов в координатах, заданных в ортонормированном базисе , выражается формулой :
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а)
б)
Решение : Проверка основана на одном из утверждений данного урока: если векторы коллинеарны, то их векторное произведение равно нулю (нулевому вектору): .
а) Найдём векторное произведение:
Таким образом, векторы не коллинеарны.
б) Найдём векторное произведение:
Ответ : а) не коллинеарны, б)
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов :
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка:
Определение : Смешанным произведением некомпланарных векторов , взятых в данном порядке , называется объём параллелепипеда , построенного на данных векторах, снабжённый знаком «+», если базис правый, и знаком «–», если базис левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
Погружаемся в определение:
2) Векторы взяты в определённом порядке , то есть перестановка векторов в произведении , как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ : . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через , а результат вычислений буквой «пэ».
По определению смешанное произведение – это объем параллелепипеда , построенного на векторах (фигура прочерчена красными векторами и линиями чёрного цвета). То есть, число равно объему данного параллелепипеда.
Примечание : чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: .
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах .
Площадь параллелограмма, построенного на векторах, равняется произведению длин этих векторов на угол угла, который лежит между ними.
Хорошо, когда по условиям даны длины этих самых векторов. Однако бывает и так, что применить формулу площади параллелограмма, построенного на векторах можно только после расчетов по координатам.
Если повезло, и по условиям даны длины векторов, то нужно просто применить формулу, которую мы уже подробно разбирали в статье . Площадь будет равняться произведению модулей на синус угла между ними:
Рассмотрим пример расчета площади параллелограмма построенного на векторах.
Задача: параллелограмм построен на векторах и . Найдите площадь, если , а угол между ними 30°.
Выразим вектора через их значения:
Возможно, у вас возник вопрос – откуда взялись нули? Стоит вспомнить, что мы работаем с векторами, а для них . также обратите внимание, что если в результате мы получаем выражение ,то оно будет преобразовано в. Теперь проводим итоговые вычисления:
Вернемся к проблеме, когда длины векторов не указаны в условиях. Если ваш параллелограмм лежит в декартовой системе координат, то потребуется сделать следующее.
Расчет длин сторон фигуры, заданной координатами
Для начала находим координаты векторов и отнимаем от координат конца соответствующие координаты начала. Допустим координаты вектора a
(x1;y1;z1), а вектора b
(x3;y3;z3).
Теперь находим длину каждого вектора. Для этого каждую координату необходимо возвести в квадрат, потом сложить полученные результаты и из конечного числа извлечь корень. По нашим векторам будут следующие расчеты:
Теперь потребуется найти скалярное произведение наших векторов. Для этого их соответствующие координаты множатся и складываются.
Имея длины векторов и их скалярное произведение, мы можем найти косинус угла, лежащего между ними .
Теперь можем найти синус этого же угла:
Теперь у нас есть все необходимые величины, и мы можем запросто найти площадь параллелограмма построенного на векторах по уже известной формуле.
Объем тетраэдра через смешанное произведение. Смешанное произведение векторов, его свойства, примеры и решения.
 Векторное произведение коллинеарных векторов
Векторное произведение коллинеарных векторовДанный онлайн калькулятор вычисляет смешанное произведение векторов. Дается подробное решение. Для вычисления смешанного произведения векторов выберите способ представления векторов (по координатам или по двум точкам) введите данные в ячейки и нажимайте на кнопку «Вычислить.»
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Смешанное произведение векторов (теория)
Смешанное произведение
трех векторов это число, которое получается при скалярном произведении результата векторного произведения первых двух векторов на третьий вектор. Другими словами, если заданы три вектора a, b и c , то для получения смешанного произведения этих векторов, сначала векторно умножаются первые два вектора и полученный вектор [ab ] скалярно умножается на вектор c .
Смешанное произведение трех векторов a, b и c обозначается так: abc или так (a,b,c ). Тогда можно записать:
| abc =([ab ],c ) |
Прежде чем сформулировать теорему, представляющую геометрический смысл смешанного произведения, ознакомьтесь с понятиями правая тройка, левая тройка, правая система координат, левая система координат (определения 2, 2″ и 3 на странице векторное произведение векторов онлайн).
Для определенности, в дальнейшем мы будем рассматривать только правые системы координат.
Теорема 1. Смешанное произведение векторов ([ab ],c ) равно объему параллелипеда, построенного на приведенных к общему началу векторах a, b, c , взятому со знаком плюс, если тройка a, b, c правая, и со знаком минус, если тройка a, b, c левая. Если векторы a, b, c компланарны, то ([ab ],c ) равно нулю.
Следствие 1. Имеет место следующее равенство:
Следовательно нам достаточно доказать, что
| ([ab ],c )=([bc ],a ) | (3) |
Из выражения (3) видно, что левая и правая часть равны объему параллелипеда. Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Но и знаки правой и левой частей совпадают, так как тройки векторов abc и bca имеют одинаковую ориентацию.
Доказанное равенство (1) позволяет записать смешанное произведение трех векторов a, b, c просто в виде abc , не указывая, какие именно два вектора перемножаются векторно первые два или последние два.
Следствие 2. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Доказательство вытекает из теоремы 1. Действительно, если векторы компланарны, то смешанное произведение этих векторов равно нулю. Обратное, если смешанное произведение равно нулю, то из теоремы 1 вытекает компланарность этих векторов (так как объем параллелипеда, построенного на приведенных к общему началу векторах равно нулю).
Следствие 3. Смешанное произведение трех векторов, два из которых совпадают, равно нулю.
Действительно. Если два вектора из трех совпадают, то они компланарны. Следовательно, смешанное произведение этих векторов равно нулю.
Смешанное произведение векторов в декартовых координатах
Теорема 2. Пусть три вектора a, b и c определены своими декартовыми прямоугольными координатами
Доказательство. Смешанное произведение abc равно скалярному произведению векторов [ab ] и c . Векторное произведение векторов [ab ] в декартовых координатах вычисляется формулой ():
Последнее выражение можно записать, используя определители второго порядка:
необходимо и достаточно равенство нулю определителя, строки которой заполнены координатами этих векторов, т.е:
| . | (7) |
Для доказательства следствия достаточно рассмотреть формулу (4) и следствие 2.
Смешанное произведение векторов на примерах
Пример 1. Найти смешанное произведение векторов abс , где
Смешанное произведение векторов a, b, c равен определителю матрицы L . Вычислим определитель матрицы L , разложив определитель по строке 1:
Конечная точка вектора a .
8.1. Определения смешанного произведения, его геометрический смысл
Рассмотрим произведение векторов а , b и с , составленное следующим образом: (а хb ) с . Здесь первые два вектора перемножаются векторно, а их результат скалярно на третий вектор. Такое произведение называется векторноскалярным, или смешанным, произведением трех векторов. Смешанное произведение представляет собой некоторое число.
Выясним геометрический смысл выражения (а хb )*с . Построим параллелепипед, ребрами которого являются векторы а , b , с и вектор d =а хb (см. рис. 22).
Имеем: (а х b ) с = d с = |d | пр d с , |d |=|а х b | =S , где S — площадь параллелограмма, построенного на векторах а и b , пр d с = Н Для правой тройки векторов и пр d с = — Н для левой, где Н- высота параллелепипеда. Получаем: (a xb )*c =S *(±H ), т. е. (a xb )*c =±V , где V — объем параллелепипеда, образованного векторами а , b и с .
Таким образом, смешанное произведение трех векторов равно объему
параллелепипеда, построенного на этих векторах, взятому со знаком «плюс», если
эти векторы образуют правую тройку, и со знаком «минус», если они образуют
левую тройку.
8.2. Свойства смешанного произведения
1. Смешанное произведение не меняется при циклической перестановке его сомножителей, т. е. (а х b ) с =(b х с ) а =(с х а ) b .
Действительно, в этом случае не изменяется ни объем параллелепипеда, ни ориентация его ребер
2. Смешанное произведение не меняется при перемене местами знаков вкторного и скалярного умножения, т. е. (а хb ) с =а *(b x с ).
Действительно, (а хb ) с =±V и а (b хс )=(b хс ) а =±V . Знак в правой части этих равенств берем один и тот же, так как тройки векторов а , b , с и b , с , а — одной ориентации.
Следовательно, (a хb ) с =a (b хс ). Это позволяет записывать смешанное произведение векторов (а х b )с в виде abc без знаков векторного, скалярного умножения.
3. Смешанное произведение меняет свой знак при перемене мест любых вух векторов-сомножителей, т. е. abc =-acb , abc =-bac , abc =-cba .
Действительно, такая перестановка равносильна перестановке сомножителей в
векторном произведении, меняющей у произведения знак.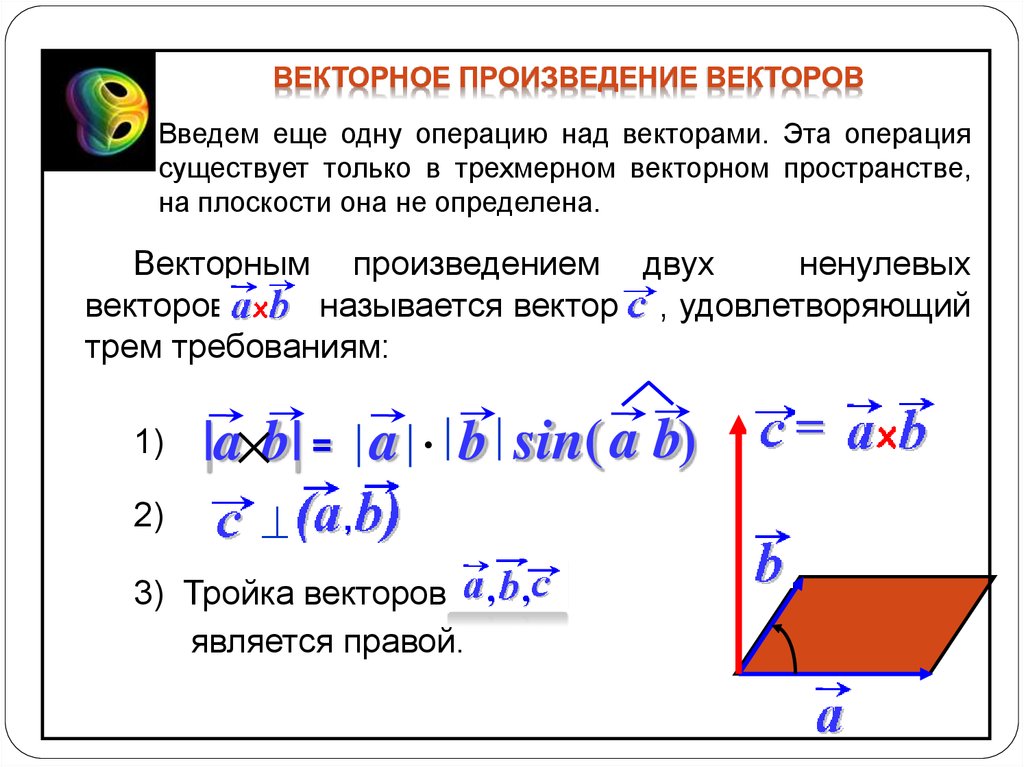 с
. Поэтому
d
с
=0
,
т. е. abc
=0
.
с
. Поэтому
d
с
=0
,
т. е. abc
=0
.
8.3. Выражение смешанного произведения через координаты
Пусть заданы векторы a =а х i +a y j +a z k , b =b x i +b y j +b z k , с =c x i +c y j +c z k . Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
Полученную формулу можно записать короче:
так как правая часть равенства (8.1) представляет собой разложение определителя третьего порядка по элементам третьей строки.
Итак, смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.
8.4. Некоторые приложения смешанного произведения
Определение взаимной ориентации векторов в пространстве
Определение взаимной ориентации векторов а, b и с основано на следующих соображениях. Если abc > 0 , то а , b , с — правая тройка; если abc
Установление компланарности векторов
Векторы а , b и с компланарны тогда и только тогда, когда их смешанное произведение равно нулю
Определение объемов параллелепипеда и треугольной пирамиды
Нетрудно показать, что объем параллелепипеда, построенного на векторах
а
, b
и с
вычисляется как V
=|аbс
|, а объем треугольной пирамиды, построенной
на этих же векторах, равен V
=1/6*|abc
|.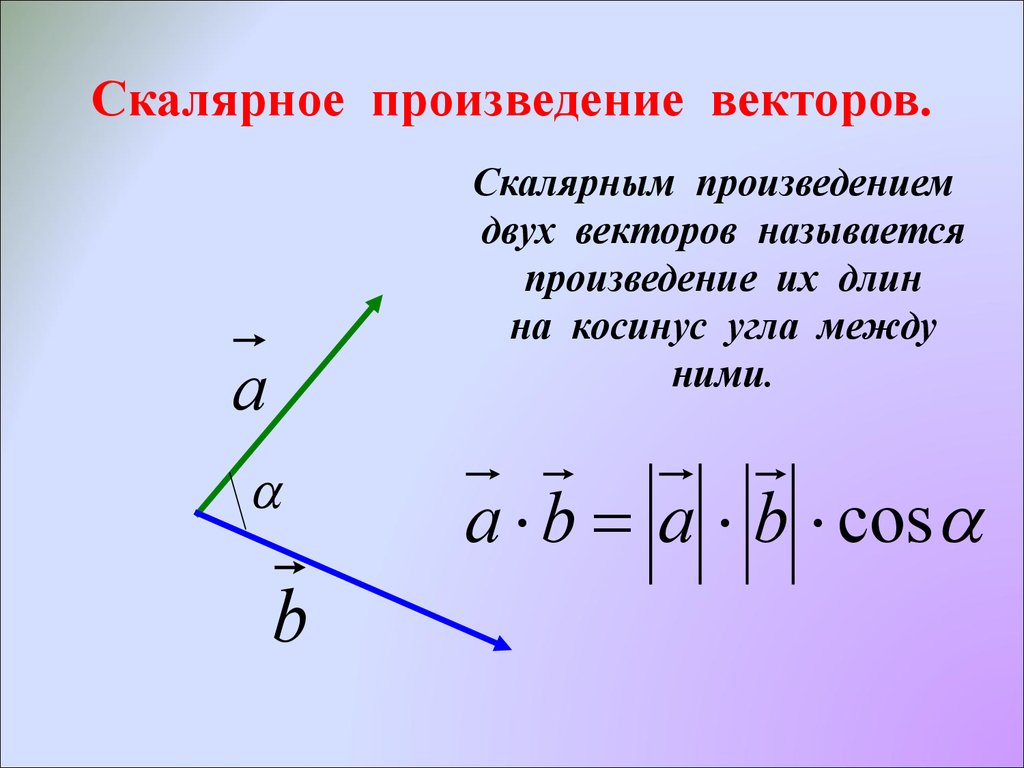
Пример 6.3.
Вершинами пирамиды служат точки А(1; 2; 3), В(0; -1; 1),С(2; 5; 2) и D (3; 0; -2). Найти объем пирамиды.
Решение: Находим векторы а ,b ис :
а=AB =(-1;-3;-2), b =АС=(1;3;-1), с=AD =(2; -2; -5).
Находима , b и с :
=-1 (-17)+3 (-3)-2 (-8)=17-9+16=24.
Следовательно, V =1/6*24=4
Смешанным (или векторно-скалярным) произведением трех векторов a, b, c (взятых в указанном порядке) называется скалярное произведение вектора a на векторное произведение b x c , т. е. число a(b x c), или, что то же, (b x c)a.
Обозначение: abc .
Назначение . Онлайн-калькулятор предназначен для вычисления смешанного произведения векторов. Полученное решение сохраняется в файле Word . Дополнительно создается шаблон решения в Excel .
Признаки компланарности векторов
Три вектора (или большее число) называются компланарными, если они, будучи приведены к общему началу, лежат в одной плоскости.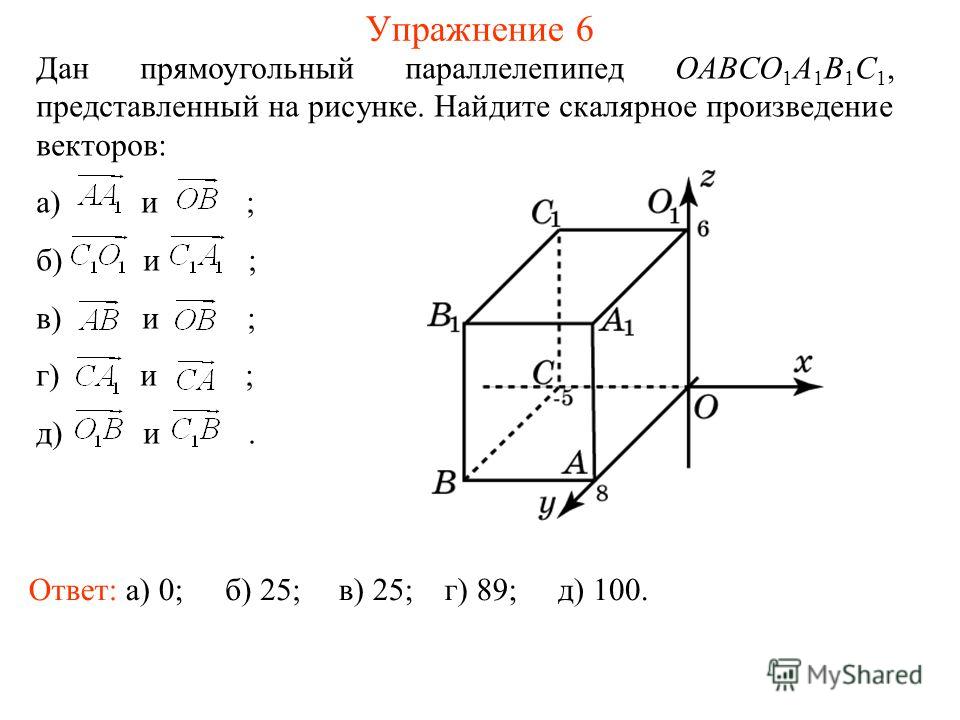
Если хотя бы один из трех векторов – нулевой, то три вектора тоже считаются компланарными.
Признак компланарности . Если система a, b, c – правая, то abc>0 ; если левая, то abcГеометрический смысл смешанного произведения . Смешанное произведение abc трех некомпланарных векторов a, b, c равно объему параллелепипеда, построенного на векторах a, b, c , взятому со знаком плюс, если система a, b, c – правая, и со знаком минус, если эта система левая.
Свойства смешанного произведения
- При круговой перестановке сомножителей смешанное произведение не меняется, при перестановке двух сомножителей – меняет знак на обратный: abc=bca=cab=-(bac)=-(cba)=-(acb)
Вытекает из геометрического смысла. - (a+b)cd=acd+bcd (распределительное свойство). Распространяется на любое число слагаемых.
Вытекает из определения смешанного произведения. - (ma)bc=m(abc) (сочетательное свойство относительно скалярного множителя).
Вытекает из определения смешанного произведения. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения. - Смешанное произведение, имеющее хотя бы два равных сомножителя, равно нулю: aab=0 .
Пример №1 . Найти смешанное произведение. ab(3a+2b-5c)=3aba+2abb-5abc=-5abc .
Пример №2 . (a+b)(b+c)(c+a)= (axb+axc+bxb+bxc)(c+a)= (axb+axc +bxc)(c+a)=abc+acc+aca+aba+bcc+bca . Все члены, кроме двух крайних, равны нулю. Кроме того, bca=abc . Поэтому (a+b)(b+c)(c+a)=2abc .
Пример №3
. Вычислить смешанное произведение трех векторов a=15i+20j+5k, b=2i-4j+14k, c=3i-6j+21k .
Решение . Чтобы вычислить смешанное произведение векторов, необходимо найти определитель системы, составленной из координат векторов. Запишем систему в виде.
Смешанным
произведением векторов называется
число,
равное скалярному произведению
векторана
векторное произведение векторови.
Смешанное произведение обозначается.
1. Модуль смешанного произведения некомпланарных векторов равен объемупараллелепипеда, построенного на этих векторах. Произведениеположительно, если тройка векторов- правая, и отрицательно, если тройка- левая, и наоборот.
2. Смешанное произведение равно нулю тогда и только тогда, когда векторыкомпланарны:
векторы компланарны.
Докажем первое свойство. Найдем по определению смешанное произведение: , где- угол между векторамии. Модуль векторного произведения (по геометрическому свойству 1) равен площадипараллелограмма, построенного на векторахи: . Поэтому. Алгебраическое значениедлины проекции векторана ось, задаваемую вектором, равно по модулю высотепараллелепипеда, построенного на векторах(рис. 1.47). Поэтому модуль смешанного произведения равен объемуэтого параллелепипеда:
Знак
смешанного произведения определяется
знаком косинуса угла .
Если тройкаправая,
тои
смешанное произведениеположительно.
Если же тройкалевая,
тои
смешанное произведениеотрицательно.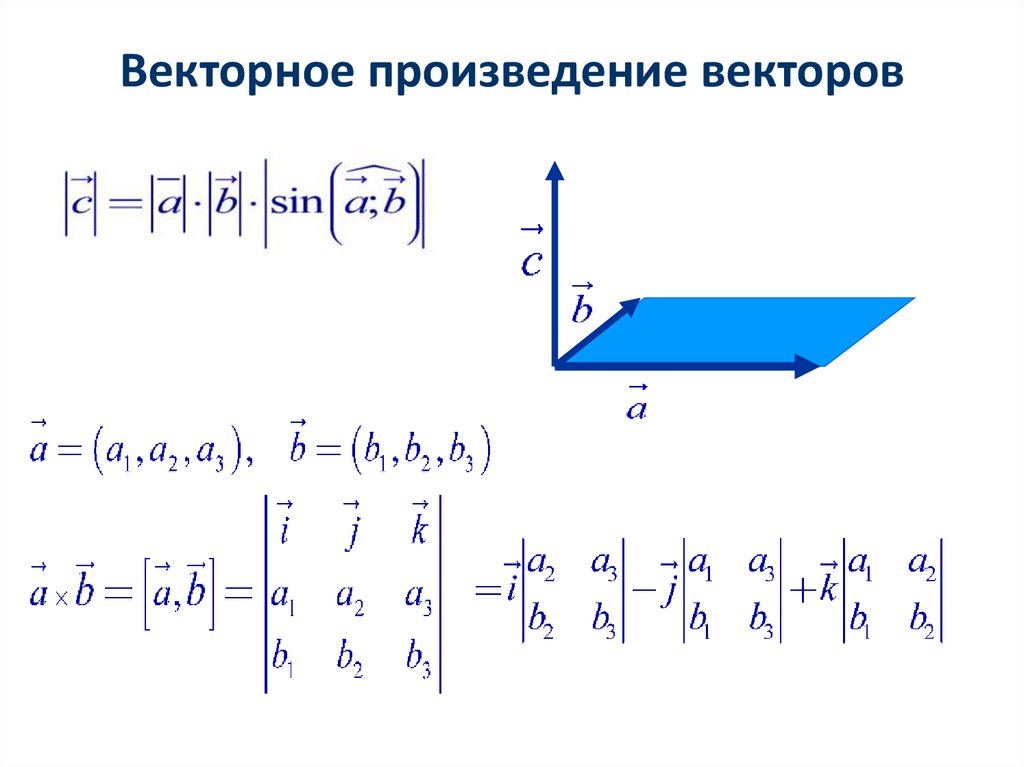
Докажем второе свойство. Равенство возможно в трех случаях:или(т.е.),или(т.е. векторпринадлежит плоскости векторови). В каждом случае векторыкомпланарны (см. разд. 1.1).
Смешанным произведением трех векторов называется число, равное векторному произведению первых двух векторов,, умноженному скалярно на вектор. Векторами это можно представить так
Так как векторы на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатамВ силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный
Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный — если левую.
Геометрические
свойства смешанного произведения 1.
Объем параллелепипеда, построенного
на векторах равен
модулю смешанного произведения этих
векторов. 2.
Объем четырехугольной пирамиды равен
трети модуля смешанного произведения3.
Объем треугольной пирамиды равен одной
шестой модуля смешанного произведения4.
Векторы планарных
тогда и только тогда, когдаВ
координатах условие компланарности
означает равенство нулю определителяДля
практического усвоения рассмотрим
примеры. Пример
1.
2.
Объем четырехугольной пирамиды равен
трети модуля смешанного произведения3.
Объем треугольной пирамиды равен одной
шестой модуля смешанного произведения4.
Векторы планарных
тогда и только тогда, когдаВ
координатах условие компланарности
означает равенство нулю определителяДля
практического усвоения рассмотрим
примеры. Пример
1.
Определить, какой тройкой (правой или левой) являются векторы
Решение.
Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют
Векторы образуют правую тройку Векторы образуют правую тройкуВекторы образуют левую тройкуДанные векторы линейно зависимы.. Смешанным произведением трех векторов. Смешанным произведением трех векторов называется число
Геометрическое свойство смешанного произведения:
Теорема 10.1. Объём параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов
или объём тетраэдра (пирамиды), построенного на векторах равен одной шестой модуля смешанного произведения
Доказательство. Из
элементарной геометрии известно, что
объём параллелепипеда равен произведению
высоты на площадь основания
Из
элементарной геометрии известно, что
объём параллелепипеда равен произведению
высоты на площадь основания
Площадь основания параллелепипеда S равна площади параллелограмма, построенного на векторах (см. рис. 1). Используя
Рис. 1. К доказательству теоремы 1. геометрический смысл векторного произведения векторов , получаем, что
Отсюда
получаемЕсли
тройка векторов левая,
то вектор и
вектор направлены
противоположно, тогдаилиТаким
образом, попутно доказано, что знак
смешанного произведения определяет
ориентацию тройки векторовтройка
правая и ‑
тройка левая). Докажем теперь вторую
часть теоремы. Из рис. 2 очевидно, что
объем треугольной призмы, построенной
на трех векторахравен
половине объема параллелепипеда,
построенного на этих векторах, то
есть
Рис.
2. К доказательству теоремы 1.
Но
призма состоит из трех одинакового
объема пирамид OABC , ABCD и ACDE .
Действительно, объемы пирамид ABCD и ACDE равны,
так как они имеют равные по площади
основания BCD и CDE и
одинаковую высоту, опущенную из вершины A . То же справедливо для высот и оснований
пирамид OABC и ACDE. Отсюда
То же справедливо для высот и оснований
пирамид OABC и ACDE. Отсюда
Калькулятор перекрестного произведения
Форма представления первого вектора:
По координатам По точкам
Форма представления второго вектора:
По координатам По точкам
Первый вектор
Второй вектор
РЕЗУЛЬТАТЫ
Заполните форму калькулятора и нажмите кнопку «Рассчитать», чтобы получить результат здесь
Решение:
—
Получить Индивидуальный калькулятор для вашего веб-сайта
Получить сейчас
ИЛИ
Получить Калькулятор кросс-продуктов Для вашего веб-сайта
Получить сейчас
Содержание:
| 1 | Что представляет собой поперечный продукт | |||
| 2 | Формула поперечного продукта | |||
| 3 | Как сделать поперечный продук | 9 | . | |
| 5 | Как пользоваться Калькулятором кросс-продуктов | |||
| 6 | Метод координат и метод начальных точек | |||
| 7 | скалярное произведение против перекрестного произведения |
Возникли проблемы с вычислением суммы двух траекторий? Не беспокойтесь, вы в правильном месте! Наш бесплатный векторный калькулятор нормалей поможет вам в этом. Просто введите значения в этот инструмент, и все готово!
Что такое Cross-Product
Чтобы понять это, давайте сначала разберемся с вектором: это математический инструмент с четко определенными величиной и направлением. Он используется в физике, математике, технике и информатике.
Кросс-произведение (не путать со скалярным произведением), проще говоря, представляет собой бинарную операцию над двумя траекториями в трехмерном пространстве. Он представлен знаком «х» (читай: крест). Рассмотрим два линейно самоопределяющихся из них, «a» и «b»; перекрестное произведение этих двух векторов будет траекторией, перпендикулярной как a, так и b.
Формула перекрестного произведения
Опять же, давайте рассмотрим «a x b», где «x» является результатом их умножения.
Итак, формула выглядит так:
C=a×b=∣a∣∣b∣sin(θ)n\mathbf{C = a \times b = |a| |б| sin(\theta) n}C=a×b=∣a∣∣b∣sin(θ)n
Где,
C=?C=?C=?
a – первый вектор,
b – вторая траектория,
θ – угол между обоими указанными векторами,
n – третий результирующий путь линия, перпендикулярная к точкам a и b.
Как сделать кросс-продукт
Если вы знаете, как выполнять умножение, то это становится довольно просто. Все, что вам нужно сделать, это использовать вышеуказанную формулу, и все готово. Кроме того, как вы, возможно, уже знаете, результатом двух линий пути является третий маршрут, который находится под прямым углом к обоим предыдущим векторам.
Однако здесь уместно отметить, что когда обе траектории ‘a’ и ‘b’ указывают в одном и том же или противоположном направлении, длина третьей линии пути равна 0. Однако, когда и ‘a’, и ‘b’ ‘b’ расположены под прямым углом друг к другу, длина третьего максимальна.
Однако, когда и ‘a’, и ‘b’ ‘b’ расположены под прямым углом друг к другу, длина третьего максимальна.
Определим «a» и «b» с координатами ax, ay и az и bx, by и bz соответственно. Теперь, естественно, предположим, что результирующий вектор ‘c’ идет с координатами cx, cy и cz.
Рассмотрим значения:
a=(4,5,6)a = (4,5,6)a=(4,5,6)
b=(7,8,9)b = (7 ,8,9)b=(7,8,9)
c=?c =?c=?
Давайте посчитаем и узнаем!
cx=aybz−azby=5×9−6×8=45−48=−3\mathbf{cx = aybz — azby} = 5\times9 — 6\times8 = 45 — 48 = -3cx=aybz-azby =5×9−6×8=45−48=−3
cy=azbx−axbz=6∗7−4∗9=42−36=6\mathbf{cy = azbx — axbz} = 6*7 — 4*9 = 42 — 36 = 6cy=azbx−axbz=6∗7−4∗9=42−36=6
cz=axby−aybx=4∗8−5∗7=32−35=−3\mathbf{cz = axby — aybx} = 4*8 — 5*7 = 32 — 35 = -3cz=axby-aybx=4∗8−5∗7=32−35=−3
ваш ответ = −3,6,−3 -3,6,-3−3,6,−3
Или, если вам не интересно заниматься всей математикой, вы можете просто использовать наш калькулятор перекрестного умножения и автоматически получить ответ за доли секунды.
Перекрестное произведение двух векторов
Два вектора ‘a’ и ‘b’ подчиняются приведенным ниже правилам:
(ya)xb=y(axb)=ax(yb)(ya) x b=y (a x b)=a x (yb)(ya )xb=y(axb)=ax(yb),
ax(b+c)=a×b+a×ca x (b+c)=a×b+a×cax(b+c)=a ×b+a×c
(b+c)×a=b×a+c×a(b+c) × a=b × a+c × a(b+c)×a=b×a+ c×a
Где c — значение суммы, а y — коэффициент масштабирования. Мы можем использовать эти свойства, чтобы придумать формулу для результата умножения по отношению к компонентам.
Как пользоваться Калькулятором кросс-продуктов
Возвращаясь к нашей цифровой штуковине, вы можете определить результаты траектории с помощью нашего калькулятора векторного умножения. Он чрезвычайно прост в использовании. Есть два способа определить ответ. Либо вы можете использовать метод координат или метод начальных точек.
Оба варианта приведены в нашем калькуляторе декартовых произведений. Вы можете выбрать любой из этих двух вариантов для расчета.
Метод координат и метод начальных точек
- В методе координат вы должны ввести координаты (x, y, z) для единичных траекторий, траекторию продукта которых вы хотите определить, и это все.

- С другой стороны, при подходе к начальным точкам вы должны ввести начальные точки, а также конечные точки обеих линий траектории, чтобы получить ответ.
Все, что вам нужно сделать, это просто выполнить шаги, указанные ниже:
- Введите значения (координаты или начальные точки) двух траекторий
- Нажмите «Рассчитать», чтобы найти ответ.
Скалярное произведение против перекрестного произведения
Люди часто задаются вопросом «Скалярное произведение совпадает с перекрестным произведением?» эти двое — полные противоположности. Умножение точек по своей природе является скейлером, а скейлер не определяется конкретным направлением, в то время как вектор, с другой стороны, описывается с конкретным направлением.
Рейтинги пользователей
- Всего отзывов 1
- Общий рейтинг 5/5
- Звезды
Спасибо! Для вашего рассмотрения
Ваш отзыв скоро появится.
Отправить свой отзыв Закрыть
Отзывы
Пожалуйста, заполните 1 строку
Обратная связь
Отправьте нам свой отзыв!
Нужна помощь? Вы можете связаться с нами в любое время.
Калькулятор перекрестного произведения с формулой и шагами
Калькулятор перекрестного произведения вычисляет векторное произведение двух заданных векторов, a и b. Чтобы найти векторное произведение, введите значения x, y и z двух векторов в калькулятор ниже, чтобы вычислить результирующее векторное произведение.
X
=
(0, 0, 0)
Как пользоваться калькулятором перекрестного произведения
Этот векторный калькулятор умножения прост и удобен в использовании. Вместо ручных вычислений он предоставляет вам векторное перекрестное произведение за считанные секунды. Используйте наш онлайн-калькулятор векторных произведений, чтобы найти перекрестные произведения.
- Введите 3 значения для вектора a (x, y, z).
- Введите 3 значения для вектора b (x, y, z).
- После того, как вы введете все значения, вы получите решение, векторные произведения вектора c (x, y, z)
Формула векторного произведения
Формула для вычисления нового вектора векторного произведения двух векторов:
где:
θ – угол между a и b в плоскости, содержащей их (от 0 до 180 градусов) б
п — единичный вектор, перпендикулярный a и b
Координаты вектора
В терминах векторных координат приведенную выше формулу можно упростить следующим образом: b 3 — a 3 b 2 , a 3 b 1 — a 1 b 3 , a 1 b 2 — a 2 b 1 )
Где:
и b — векторы с координатами (a 1 ,a 2 ,a 3 ) и (b 1 ,b 2 ,b 3 ).
Направление результирующего вектора можно определить по правилу правой руки.
Векторы в трех измерениях: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)
Из определения применяются следующие правила:
i × j = k j × i = i k × i = j
j × i = — k k × j = — i i × k = — j
i × i = j × j = k × k = 0
the cross product of both vectors will be:
a × b = (a 1 i + a 2 j + a 3 k ) × (b 1 i + b 2 j + b 3 k )
Example of how to calculate the cross product of two vectors
Во-первых, нам нужны два вектора a и b
Дано:
вектор a имеет координаты (2,1,4) и
вектор b имеет координаты (3,1,2).
Во-вторых, используйте приведенное выше упрощенное уравнение для вычисления результирующих векторных координат перекрестного произведения.
a × b = (a 2 b 3 — a 3 b 2 , a 3 b 1 — a 1 b 3 , a 1 b 2 — a 2 b 1 )
Нам нужно найти координату x. По приведенной выше формуле мы находим, что x равно 1 * 2 — 4 * 1 = 2 — 4 = -2.
Используя то же уравнение, мы находим y и z равными 8 и -1 соответственно.
Наконец, мы находим новый вектор из перекрестного произведения a × b равно (-2, 8, -1)
Важно: не забывайте, что в векторном произведении результат a × b не совпадает с b × и . На самом деле a × b = — b × a .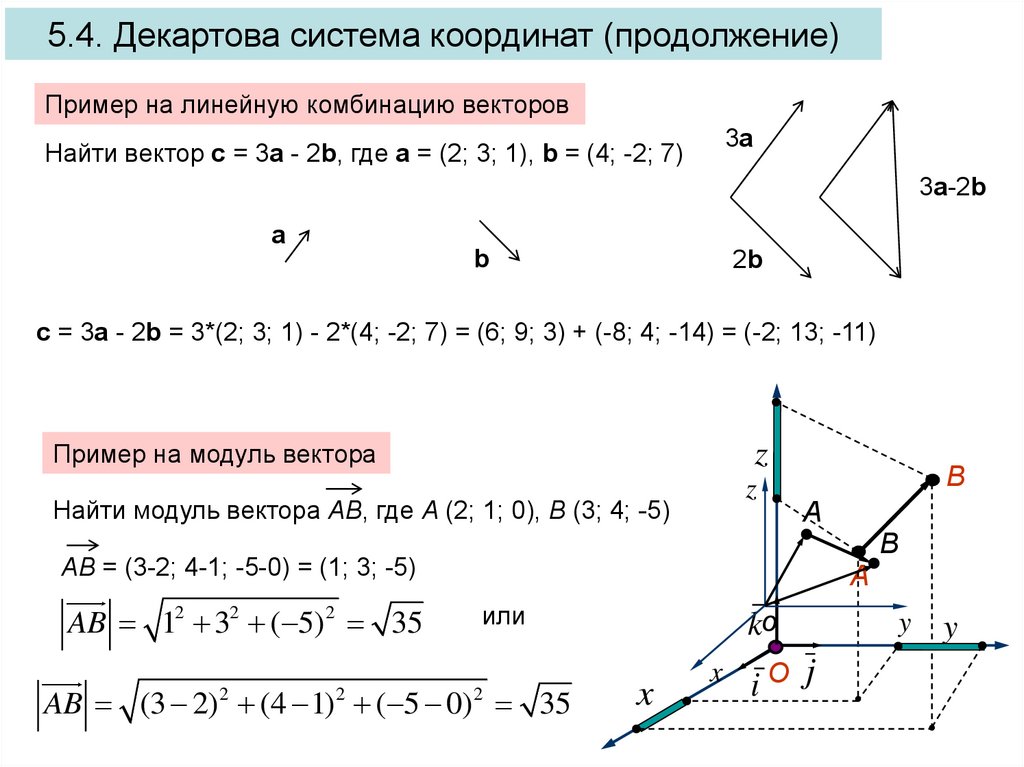
Часто задаваемые вопросы
Что такое векторное произведение?
Перекрестное произведение — это векторное произведение, которое перпендикулярно обоим исходным векторам и имеет одинаковую величину.
Определение перекрестного произведения
Перекрестное произведение (также известное как векторное произведение) — это результат перекрестного произведения двух векторов, т. е. новый вектор, перпендикулярный обоим векторам. Величина нового вектора равна площади параллелограмма со сторонами двух исходных векторов.
Как вычислить векторное произведение
Умножение векторов относится к векторному произведению и может быть выполнено двумя из следующих способов, в зависимости от того, какие входные данные вам известны.
1. Величина векторов А и В
Перекрестное произведение показывает, как различные измерения взаимодействуют друг с другом. Если вы знаете величину вектора a и b , то вы можете вычислить величину, умножив их на синусоидальный угол, образующийся между обоими векторами.
∥ A ∥ = √ (A 1 2 +A 2 2 +A 3 2 )
923 A 9024. × × × × × × 00 2 ). б ‖ sin(θ) н
2. Правило правой руки
Мы также можем найти направление вектора векторного произведения, используя правило правой руки. Расположите указательный, указательный и большой пальцы так, чтобы они образовали систему координат X, Y и Z. Затем переместите руку в точку, где указательный палец указывает на вектор a , а средний палец указывает на вектор b . Ваш большой палец укажет направление вектора векторного произведения.
линейная алгебра — Как рассчитать один из векторов, порождающих заданное перекрестное произведение?
Задавать вопрос
Спросил
Изменено 6 лет, 8 месяцев назад
Просмотрено 3к раз
$\begingroup$
Учитывая вектор: $$\vec b=(-0,361728, 0,116631, 0,924960)$$ и его векторное произведение: $$\vec a \times \vec b=(-0,877913, 0,2
, -0,380054)$$ Как рассчитать $\vec a$?
Я давно не изучал аналитическую геометрию, поэтому моя интерпретация проблемы может быть совершенно неправильной.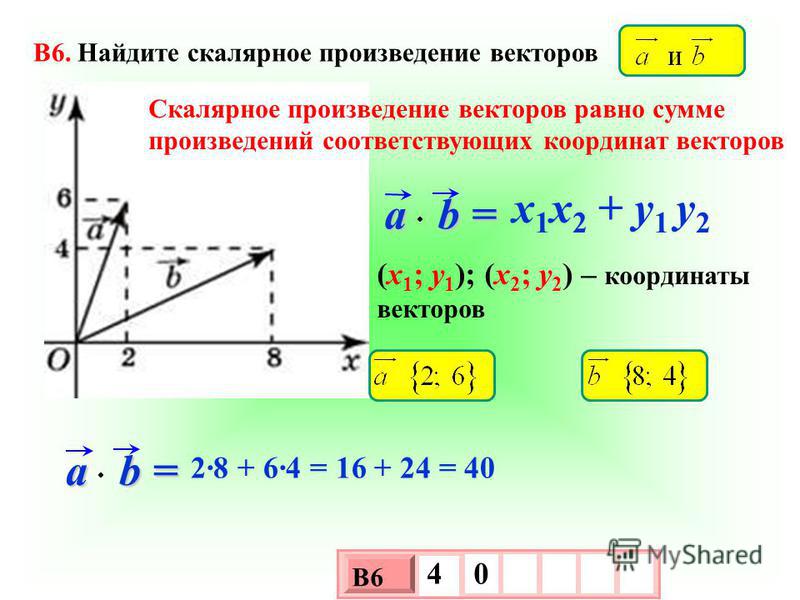
Что я сделал: $$\vec a \times \vec b= \begin{vmatrix} \vec i & \vec j & \vec k \\ а_1 и а_2 и а_3 \\ б_1 & б_2 & б_3 \\ \end{vmatrix}$$ $$\vec a \times \vec b= \begin{vmatrix} \vec i & \vec j & \vec k \\ а_1 и а_2 и а_3 \\ -0,361728 и 0,116631 и 0,924960 \\ \end{vmatrix}$$ $$\begin{vmatrix} \vec i & \vec j & \vec k \\ а_1 и а_2 и а_3 \\ -0,361728 и 0,116631 и 0,924960 \\ \end{vmatrix}=-0,877913\vec i + 0,2
\vec j -0,380054\vec k$$ Использование правила Сарруса: $$(0,924960a_2-0,116631a_3)\vec i+(-0,361728a_3 -0,924960a_1)\vec j+(0,116631a_1 +0,361728a_2)\vec k=-0,877913\vec i + 0,2
\vec j -5\vec j -0,380 k $$
$$
\оставил\{
\начать{массив}{с}
(0,924960a_2-0,116631a_3)\vec i=-0,877913\vec i \\
(-0,361728a_3 -0,924960a_1)\vec j=0,2\vec j \\
(0,116631a_1 +0,361728a_2)\vec k=-0,380054\vec k
\конец{массив}
\Правильно.
$$
Используя матричное решение для решения системы линейных уравнений:
$$
A=\begin{bmatrix}
0 и 0,9{-1}= \not \exists$ и система не имеет решений.

Но…
Я ЗНАЮ у этой системы есть решение, и оно таково:
$$
\vec a=(-0,313722, -0,949510, -0,002962)
$$
Итак, что я делаю неправильно?
- линейная алгебра
- векторы
- аналитическая геометрия
- перекрестное произведение
$\endgroup$
1
$\begingroup$
Неправда, что система не может иметь решения, если $A$ необратима. Например, чтобы выбрать глупый пример,
$$ \begin{bmatrix}1 & 0 \\ 0 & 0 \end{bmatrix} x = \begin{bmatrix}1\\0\end{bmatrix} $$ имеет решения $x=(1,t)$ для каждые $t$. Что нулевой определитель означает только то, что решение, если оно существует, не будет уникальный .
Однако вместо того, чтобы решать все эти общие задачи линейной алгебры, я бы сделал следующее, используя известные свойства векторного произведения:
Сначала проверьте, что ваши значения для $b$ и $a\times b$ ортогональны — — иначе ваши данные не согласуются.
Во-вторых, будет бесконечное количество решений для $a$, отличающихся кратными $b$ (поскольку $(a+tb)\times b = (a\times b)+t(b\times b)= a\times b$. Давайте произвольно выберем, чтобы найти одно из решений, ортогональное к $b$. Это конкретное решение будет кратно $b\times(a\times b)$, поэтому вам нужно найти такое $u$, что
$$ u(b\times (a\times b)) \times b = a\times b $$
Этого должно быть достаточно для одной из трех координат, поэтому просто выберите численно наибольшую составляющую $a\times b$ и разделите ее на соответствующую составляющую $b\times (a\times b)$, получив $u$.
Затем вы можете добавить произвольное число, кратное $b$, по своему усмотрению.
$\endgroup$
1
$\begingroup$
Фундаментальная проблема заключается в том, что существует бесконечное количество решений.
Использование вашего подхода с одновременным уравнением создает обманчивое впечатление, что у нас есть три уравнения с тремя неизвестными. Это не совсем так, поскольку система не полностью определена.
Это не совсем так, поскольку система не полностью определена.
Определение векторного произведения говорит нам, что:
$$\vec{c}=\vec{a}\times\vec{b}=\vec{n}\,|\vec{a}|\ ,|\vec{b}|sin\theta$$
Где $\vec{n}$ — единичная нормаль, перпендикулярная к $\vec{a}$ и $\vec{b}$, построенная по правилу правой руки, а $\theta$ — угол между $\vec{ а}$ и $\vec{b}$.
Все, что мы можем сделать в обратном порядке, это получить:
$$|\vec{a}|sin\theta=\frac{|\vec{c}|}{|\vec{b}|}$$
Но, не зная ни $|\vec{a}|$, ни $sin\theta$, мы не можем найти оба значения только из $\vec{b}$ и перекрестного произведения.
Конечно, известное вам значение $\vec{a}$ является допустимым решением, но таких правильных решений бесконечное множество.
Другой способ представить это — построить вектор $v$ таким образом, что:
$$\vec{v}:=\lambda \vec{a} + \mu \vec{b}$$ некоторые произвольные скаляры $\lambda$ и $\mu$.
Теперь рассмотрим $\vec{v}\times\vec{b}$ :
$$\vec{v}\times\vec{b}=\lambda(\vec{a}\times\vec{b })+\mu(\vec{b}\times\vec{b})$$
Но $\vec{b}\times\vec{b}=0$ поэтому:
$$\vec{v }\times\vec{b}=\lambda(\vec{a}\times\vec{b})$$
Но это означает, что существует бесконечное число возможных векторов $\vec{v}$ с произвольным значения $\mu$, которые дают то же перекрестное произведение с $\vec{b}$. А так как у нас нет информации о $\mu$, мы не можем его определить.
А так как у нас нет информации о $\mu$, мы не можем его определить.
Таким образом, векторное произведение необратимо однозначно.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Калькулятор перекрестного произведения — векторный расчет
Перекрестное произведение, онлайн-исчисление
Резюме:
Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
перекрестное произведение онлайн
Описание :
Калькулятор перекрестного произведения может выполнять вычисления, указав шага вычисления 9vec(v)` образуют прямую ортогональную ссылку. Расчет векторного произведения онлайн
Расчет векторного произведения двух векторов онлайн выполняется очень быстро с помощью калькулятора векторного произведения ,
просто введите координаты двух векторов, а затем нажмите кнопку, позволяющую выполнить расчет векторного произведения. Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Синтаксис:
cross_product(vector;vector)
Примеры:
В этом примере показано, как использовать калькулятор перекрестного произведения:
cross_product(`[1;1;1];[5;5;6]`), возвращает [1;-1;0]
Расчет онлайн с помощью cross_product (калькулятор перекрестного произведения)
См. также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов : vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов : vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Напоминания о курсах, калькуляторы, упражнения и игры: Векторы
Научитесь считать с векторами
Подборка бесплатных математических ресурсов (калькуляторы, упражнения, игры, викторины, напоминания о курсах), обучающих методам векторного исчисления.
Векторы : Напоминание
Координаты вектора из двух точек
Пусть (O, `vec (i)`, `vec (j)`) система, A и B две точки, которые являются соответствующими координатами (`x_a`,`y_(a)`) и (`x_(b)` ,`y_(b)`) в
система (O,`vec(i)`,`vec(j)`) .
Координаты вектора `vec(AB)` равны (`x_(b)`-`x_(a)`,`y_(b)`-`y_(a)`) в системе (O,`vec (i)`,`vec(j)`).
калькулятор векторных координат
позволяет вам сделать этот тип расчета.
Направляющий вектор прямой
Если в системе линия D имеет уравнение `y=m*x+p`, то вектор `vecu(1;m)` является направляющим вектором D.
Координаты середины отрезка
Середина [AB] имеет координаты `((x_(a)+x_(b))/2;(y_(a)+y_(b))/2)` в система (O,`vec(i)`,`vec(j)`).
Расстояние между двумя точками
92)`, расстояние AB также является нормой вектора `vec(AB)`, который можно вычислить с помощью
калькулятор векторной нормы
.
Точечный продукт
В плане в ортонормированной системе `(O,vec(i),vec(j))` ,
`vec(u)` представляет собой вектор координат (x,y), а `vec(v)` представляет собой вектор координат (x’,y’), скалярное произведение определяется формулой
хх’+уу’.
калькулятор скалярного произведения
позволяет этот тип расчета для n-мерных векторов.
9vec(v)` и вектор `vec(w)`.
Его можно рассчитать с помощью
скалярный калькулятор тройного произведения.
Определитель двух векторов (2×2)
В ортонормированной системе координат (O,`vec(i)`,`vec(j)`) вектор `vec(u)` имеет координаты (x,y)
(`vec(i)`,`vec(j)`), вектор `vec(v)` имеет координаты (x’,y’). Определитель для vec(u) и vec(v) задается формулой формула xx’-yy’ .
Этот
Пример показывает вычисление определителя векторов [[3;12];[45;2]], выполненное с помощью калькулятора определителя 2×2.
Примечание. Когда определитель двух векторов равен нулю, эти два вектора коллинеарны.
Определитель трех векторов (3×3)
В ортонормированной системе координат (O,`vec(i)`,`vec(j)`,`vec(k)`) вектор `vec(u)` имеет координаты (х, у, z)
, вектор `vec(v)` имеет координаты (x’,y’,z’), вектор `vec(k)` имеет координаты (x»,y»,z»). Определитель `vec(u)`, `vec(v)`, `vec(k)` задается формулой xy’z»+x’y»z+x»yz’- xy»z’-x’yz»-x»y’z .
Определитель `vec(u)`, `vec(v)`, `vec(k)` задается формулой xy’z»+x’y»z+x»yz’- xy»z’-x’yz»-x»y’z .
Это
пример, сделанный с калькулятором определителя 3×3, подробно описывает вычисление определителя векторов [[3;1;0];[3;2;1];[4;0;7]]
.
Векторы: калькуляторы
- cross_product : калькулятор перекрестного произведения. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- определитель : калькулятор определителя. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- dot_product : Калькулятор скалярного произведения. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.
- product_vector_number : произведение вектора на число.
 Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
Векторный калькулятор позволяет вычислить произведение вектора на число онлайн. - scalar_triple_product : вычисление скалярного тройного произведения. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- vector_calculator : векторный калькулятор. Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
- vector_coordinates : вычисление координат вектора по двум точкам. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек онлайн.
- vector_difference : вычисление разницы двух векторов. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- vector_norm : вычисление нормы вектора.
 Векторный калькулятор позволяет рассчитать норму вектора онлайн.
Векторный калькулятор позволяет рассчитать норму вектора онлайн. - vector_sum : вычисление суммы двух векторов. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Векторы: игры и викторины
- Викторина по векторам (векторам): Эта викторина позволяет попрактиковаться в векторном исчислении: вычисление координат, нормы, середины отрезка, скалярного произведения.
Векторы : упражнения
- Упражнение 1524, ордината вектора направления прямой — векторы — уравнения — уравнения прямых и линейных систем : Цель этого упражнения состоит в том, чтобы определить ординату вектора направления из уравнения прямой.
- Упражнение 3441, координаты вектора по координатам двух точек — векторы : Цель этого исправленного упражнения состоит в том, чтобы вычислить координаты вектора по координатам двух точек.

- Упражнение 3442, вычисление расстояния между двумя точками — векторами. Целью этого исправленного упражнения является вычисление расстояния между двумя точками по их координатам.
- Упражнение 3443, вычисление координат середины отрезка — векторы : Целью этого упражнения с исправленной аналитической геометрией является вычисление координат середины отрезка по координатам.
Алгебраический расчет | Уравнения | Финансы | Реальные функции | Тригонометрические функции | Фракции | Геометрия | Матрицы | Числа | Комплексные числа | Статистика | Числовые последовательности | Время | Векторы
Векторный калькулятор — со всеми шагами
- Калькуляторы
- ::
- Матрицы и векторы
- ::
- Векторный калькулятор
Этот калькулятор выполняет все векторные операции в двух- и трехмерном пространстве. Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов.
Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов.
Для каждой операции калькулятор пишет пошаговое, простое для понимания объяснение того, как была выполнена работа.
Векторы 2D
Векторы 3D
Входные векторы $V_1$ и $V_2$
В 1 =
(
,
)
В 2 =
(
,
)
Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r17 } = \sqrt{17}} ~ \right) $.
Примеры:
Выберите, что вычислить Величина (длина) $ V_1 $ $ v_1 \cdot v_2 $ ( скалярное произведение ) $ v_1 + v_2 $ $ v_1 — v_2 $ Угол между $v_1$ и $v_2$ Проверить, являются ли $v_1$ и $v_2$ линейно зависимыми Найдите проекцию $v_1$ на $v_2$
Настройки: Найдите приближенное решение
не может найти точное решение. «> Скрыть шаги Входные векторы $V_1$, $V_2$ и $V_3$
В 1 =
(
,
,
)
В 2 =
(
,
,
)
В 3 =
(
,
,
)
Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r17 } = \sqrt{17}} ~ \right) $.
Пример:
Выберите, что вычислить
«> Скрыть шаги Входные векторы $V_1$, $V_2$ и $V_3$
В 1 =
(
,
,
)
В 2 =
(
,
,
)
В 3 =
(
,
,
)
Введите r для ввода квадратных корней $ \left( \color{blue}{\text{ r17 } = \sqrt{17}} ~ \right) $.
Пример:
Выберите, что вычислить Величина (длина) $ V_1 $ $ v_1 \cdot v_2 $ ( скалярное произведение ) $ v_1 \times v_2 $ ( перекрестное произведение ) $ v_1 + v_2 $ $ v_1 — v_2 $ Угол между $v_1$ и $v_2$ Проверить, являются ли $v_1$, $v_2$ и $v_3$ линейно зависимыми Найдите проекцию $v_1$ на $v_2$
Настройки: Найдите приближенное решение
не может найти точное решение.»> Скрыть шаги работающий…
Полиномиальные калькуляторы
Факторные полиномы
- Полиномиальные корни
- Синтетический отдел
- Полиномиальные операции
- Графические полиномы
- Расширить и упростить
- Генерировать из корней
Рациональные выражения
Упрощение
- Умножение/деление
- Сложение/вычитание
Подкоренные выражения
Рационализировать знаменатель
- Упрощение
Решение уравнений
Квадратные уравнения (с шагами)
- Полиномиальные уравнения
- Решение уравнений — с шагами
Квадратное уравнение
Решение (с шагами)
- Квадратичный плоттер
- Факторинг трехчленов
Геометрия
Равносторонний треугольник
- Прямоугольный треугольник
- Косой треугольник
- Калькулятор площади
- Калькулятор прямоугольника
- Калькулятор круга
Калькулятор шестиугольника
- Калькулятор ромба
Комплексные номера
Модуль, обратный, полярная форма
- Подразделение
- Упростить выражение
Системы уравнений
Система 2х2
- Система 3х3
- Система 4×4
Матрицы
Векторы (2D и 3D)
- Сложить, вычесть, умножить
- Калькулятор определителя
- Матрица обратная
- Характеристический полином
- собственные значения
- Собственные векторы
- Разложение матрицы
Расчетные калькуляторы
Калькулятор лимита
- Калькулятор производных
- Интегральный калькулятор
Последовательности и серии
Арифметические последовательности
- Геометрические последовательности
- Найти n й Срок
Аналитическая геометрия
Расстояние и середина
- Калькулятор треугольника
- Графические линии
- Пересечение линий
- Двухточечная форма
- Расстояние от линии до точки
- Параллельно/Перпендикулярно
- Уравнение окружности
- Круг из 3 точек
- Пересечение круговой линии
Тригонометрия
Градуса в Радиан
- Триггер Уравнения
Номера
Длинная дивизия
- Вычислить выражения
- Калькулятор дробей
- Наибольший общий делитель НОД
- Наименее распространенное кратное LCM
- Простые множители
- Научная нотация
- Калькулятор процентов
- Dec / Bin / Hex
- Калькулятор вероятности
- Распределения вероятностей
Описательная статистика
- Стандартное отклонение
- Z — Калькулятор очков
- Нормальное распределение
- Калькулятор Т-теста
- Корреляция и регрессия
Финансовые калькуляторы
Простые проценты
- Сложные проценты
- Калькулятор амортизации
- Калькулятор ренты
Прочие калькуляторы
Наборы
Проблемы с работой
ПРИМЕРЫ
пример 1:ex 1:
Учитывая вектор $v_1 = (8, -4)$, вычислить величину.
пример 2:ex 2:
Вычислить разность векторов $v_1 = \left(\dfrac{3}{4}, 2\right)$ и $v_2 = (3, -2)$.
пример 3:ex 3:
Вычислить скалярное произведение векторов $v_1 = \left(-\dfrac{1}{4}, \dfrac{2}{5}\right)$ и $v_2 = \left (-5, -\dfrac{5}{4}\right)$.
пример 4:ex 4:
Найдите угол между векторами $v_1 = (3, 5, −7)$ и $v_2 = (-3, 4, -2)$.
пример 5:ex 5:
Найдите векторное произведение $v_1 = \left(-2, \dfrac{2}{3}, −3 \right)$ и $v_2 = \left(4, 0, -\dfrac{1}{2} \right)$.
пример 6:ex 6:
Определите, является ли линейно независимым набор векторов: $v_1 = (3, -2, 4)$ , $v_2 = (1, -2, 3)$ и $v_3 = (3, 2, -1)$.
ОБУЧЕНИЕ
Векторные операции 92} = \sqrt{20} = 2\sqrt{5} $$
Пример 02: Найдите величину вектора $ \vec{v} = \left(\dfrac{2}{3}, \sqrt{3}, 2\right) $.
Решение
2 : Скалярное произведение
Формула скалярного произведения векторов $ \vec{v} = (v_1, v_2) $ и $ \vec{w} = (w_1, w_2) $ равна
$$ \vec{v} \cdot \vec{w}= v_1 \cdot w_1 + v_2 \cdot w_2 $$
Два вектора ортогональны друг другу, если их скалярное произведение равно нулю.
Пример 03: Вычислить скалярное произведение $ \vec{v} = \left(4, 1 \right) $ и $ \vec{w} = \left(-1, 5 \right) $.
Проверьте, взаимно ортогональны ли векторы.
Чтобы найти скалярный продукт, мы используем формулу компонента:
$$ \begin{выровнено}
\vec{v} \cdot \vec{w} &= \left(4, 1 \right) \cdot \left(-1, 5 \right) = \\[1 em]
&= 4 \cdot (-1) + 1 \cdot 5 = -4 + 5 = 1
\end{выровнено}
$$
Поскольку скалярное произведение не равно нулю, мы можем заключить, что векторы НЕ ортогональны.
Пример 04: Найдите скалярное произведение векторов $ \vec{v_1} = \left(\dfrac{1}{2}, \sqrt{3}, 5 \right) $ и $ \vec{v_2 } = \left( 4, -\sqrt{3}, 10 \right) $.
Решение
3 : Угол между двумя векторами
Чтобы найти угол $ \alpha $ между векторами $ \vec{a} $ и $ \vec{b} $, мы используем следующую формулу:
$$ \cos \alpha = \dfrac{\vec{a} \cdot \vec{b}}{ \|\vec{a}\| \, \|\vec{b}\|} $$
Обратите внимание, что $ \vec{a} \cdot \vec{b} $ — скалярное произведение, а $\|\vec{a}\|$ и $\|\vec{b}\|$ — величины векторов $\vec{a}$ и $\vec{b}$.

 Это не совсем так, поскольку система не полностью определена.
Это не совсем так, поскольку система не полностью определена. А так как у нас нет информации о $\mu$, мы не можем его определить.
А так как у нас нет информации о $\mu$, мы не можем его определить.Расчет векторного произведения онлайн
Расчет векторного произведения двух векторов онлайн выполняется очень быстро с помощью калькулятора векторного произведения ,
просто введите координаты двух векторов, а затем нажмите кнопку, позволяющую выполнить расчет векторного произведения. Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Чтобы вычислить векторное произведение следующих векторов `vec(u)` [1;1;1] и `vec(v)` [5;5;6] ,
введите выражение
cross_product(`[1;1;1];[5;5;6]`) после вычисления возвращаются результаты [1;-1;0].
Синтаксис:
cross_product(vector;vector)
Примеры:
В этом примере показано, как использовать калькулятор перекрестного произведения:
cross_product(`[1;1;1];[5;5;6]`), возвращает [1;-1;0]
Расчет онлайн с помощью cross_product (калькулятор перекрестного произведения)
См. также
Список связанных калькуляторов:
- Векторный калькулятор : vector_calculator.
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты. - Вычисление координат вектора по двум точкам. : вектор_координаты. Векторный калькулятор позволяет вычислить координаты вектора по координатам двух точек в режиме онлайн.
- Калькулятор определителя: определитель. Функция определителя вычисляет онлайн определитель векторов или определитель матрицы.
- Вычисление разности двух векторов : vector_difference. Функция vector_difference используется для вычисления разницы двух векторов в режиме онлайн.
- Вычисление нормы вектора: vector_norm. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
- Исчисление скалярного тройного произведения: scalar_triple_product. Калькулятор скалярного тройного произведения позволяет онлайн рассчитать скалярное тройное произведение.
- Калькулятор скалярного произведения: dot_product. Калькулятор скалярного произведения позволяет вычислить скалярное произведение двух векторов онлайн по их координатам.

- Произведение вектора на число: product_vector_number. Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
- Калькулятор перекрестного произведения: перекрестное_произведение. Векторный калькулятор позволяет вычислить векторное произведение двух векторов онлайн по их координатам.
- Вычисление суммы двух векторов : vector_sum. Векторный калькулятор позволяет вычислить сумму двух векторов онлайн.
Напоминания о курсах, калькуляторы, упражнения и игры: Векторы
Научитесь считать с векторами
Подборка бесплатных математических ресурсов (калькуляторы, упражнения, игры, викторины, напоминания о курсах), обучающих методам векторного исчисления.
Векторы : Напоминание
Координаты вектора из двух точек
Пусть (O, `vec (i)`, `vec (j)`) система, A и B две точки, которые являются соответствующими координатами (`x_a`,`y_(a)`) и (`x_(b)` ,`y_(b)`) в
система (O,`vec(i)`,`vec(j)`) .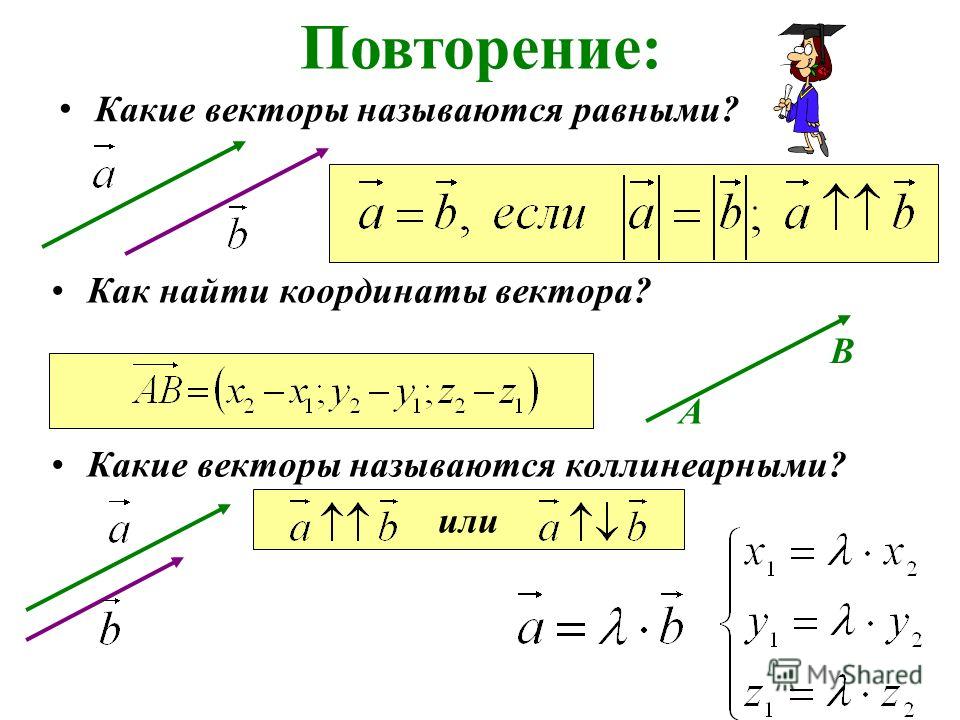
Координаты вектора `vec(AB)` равны (`x_(b)`-`x_(a)`,`y_(b)`-`y_(a)`) в системе (O,`vec (i)`,`vec(j)`).
калькулятор векторных координат
позволяет вам сделать этот тип расчета.
Направляющий вектор прямой
Если в системе линия D имеет уравнение `y=m*x+p`, то вектор `vecu(1;m)` является направляющим вектором D.
Координаты середины отрезка
Середина [AB] имеет координаты `((x_(a)+x_(b))/2;(y_(a)+y_(b))/2)` в система (O,`vec(i)`,`vec(j)`).
Расстояние между двумя точками
92)`, расстояние AB также является нормой вектора `vec(AB)`, который можно вычислить с помощью калькулятор векторной нормы .
калькулятор скалярного произведения позволяет этот тип расчета для n-мерных векторов. 9vec(v)` и вектор `vec(w)`. Его можно рассчитать с помощью скалярный калькулятор тройного произведения.
Примечание. Когда определитель двух векторов равен нулю, эти два вектора коллинеарны.
 Определитель `vec(u)`, `vec(v)`, `vec(k)` задается формулой xy’z»+x’y»z+x»yz’- xy»z’-x’yz»-x»y’z .
Определитель `vec(u)`, `vec(v)`, `vec(k)` задается формулой xy’z»+x’y»z+x»yz’- xy»z’-x’yz»-x»y’z . Векторный калькулятор позволяет вычислить произведение вектора на число онлайн.
Векторный калькулятор позволяет вычислить произведение вектора на число онлайн. Векторный калькулятор позволяет рассчитать норму вектора онлайн.
Векторный калькулятор позволяет рассчитать норму вектора онлайн.
 Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов.
Вы можете складывать, вычитать, находить длину, находить векторные проекции, находить точечные и векторные произведения двух векторов. Для каждой операции калькулятор пишет пошаговое, простое для понимания объяснение того, как была выполнена работа.
Факторные полиномы
Упрощение
Рационализировать знаменатель
Квадратные уравнения (с шагами)
Решение (с шагами)
Равносторонний треугольник
Калькулятор шестиугольника
Модуль, обратный, полярная форма
Система 2х2
Векторы (2D и 3D)
Калькулятор лимита
Арифметические последовательности
Расстояние и середина
Градуса в Радиан
Длинная дивизия
Описательная статистика
Простые проценты
Наборы
Проблемы с работой






 Для вектора a:
Для вектора a:


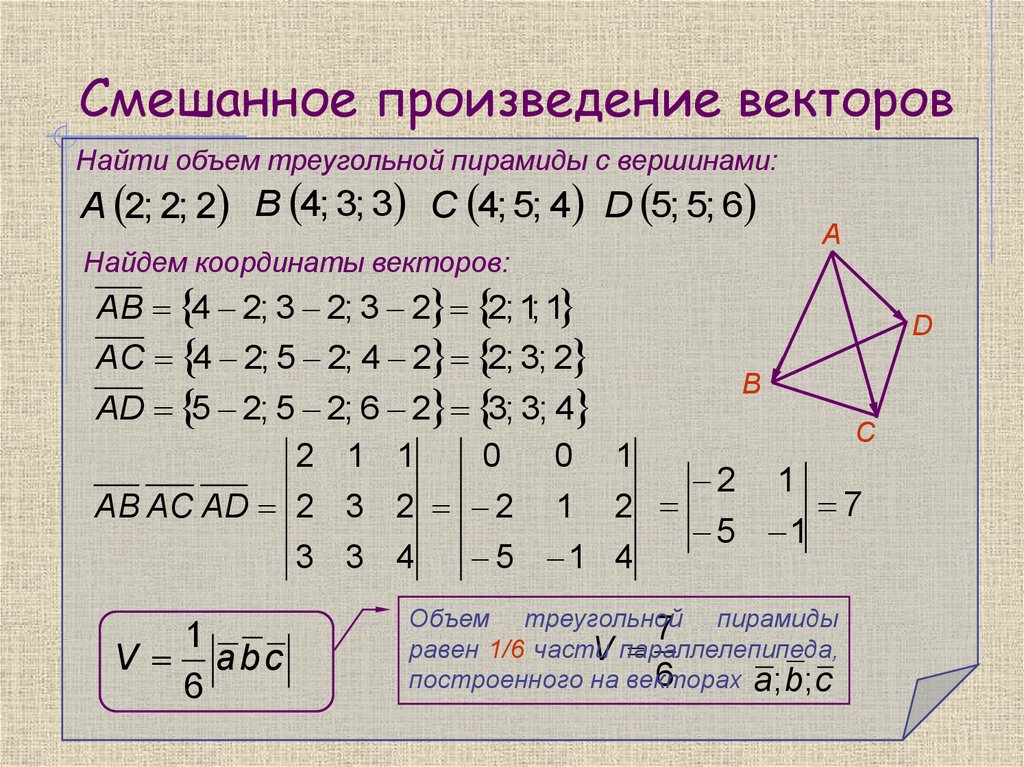 Таким образом, получится │a│и│ b│.
Таким образом, получится │a│и│ b│. Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
Эти свойства позволяют применять к смешанным произведениям преобразования, отличающиеся от обычных алгебраических лишь тем, что менять порядок сомножителей можно только с учетом знака произведения.
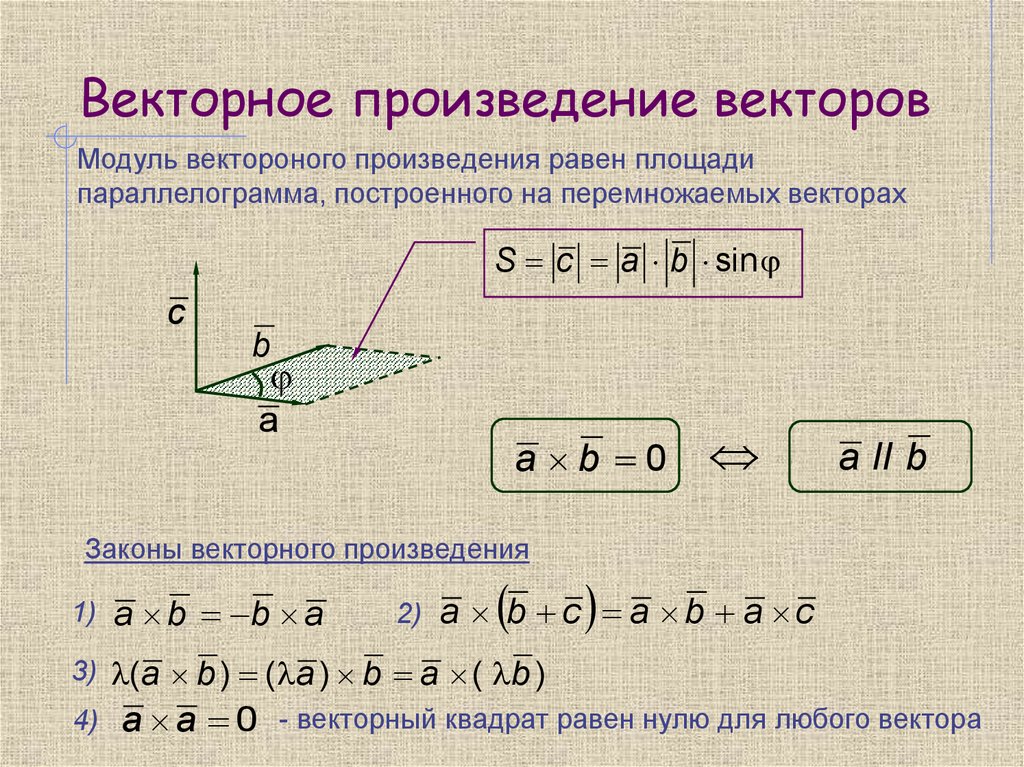
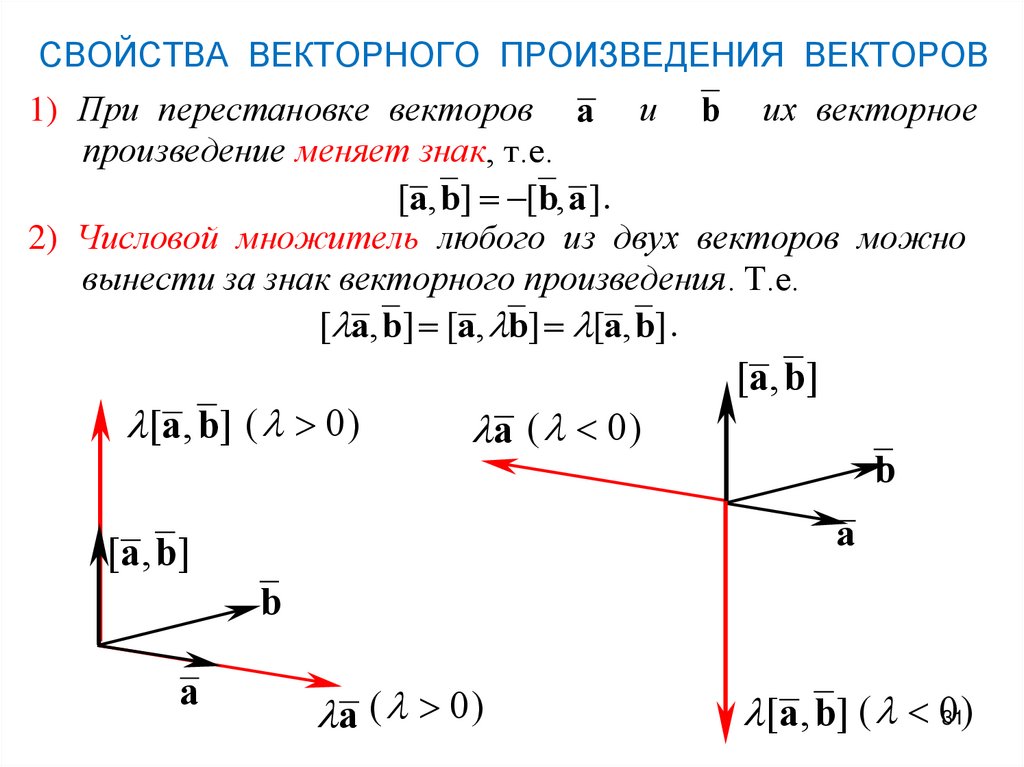
 Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.
Векторный калькулятор позволяет производить вычисления с векторами, используя координаты.