что измеряется в Омах, что такое Ом в физике, обозначение
Таблица кодов SMD резисторов и их значений
| Код smd | Значение | Код smd | Значение | Код smd | Значение | Код smd | Значение |
|---|---|---|---|---|---|---|---|
| R10 | 0.1 Ом | 1R0 | 1 Ом | 100 | 10 Ом | 101 | 100 Ом |
| R11 | 0.11 Ом | 1R1 | 1.1 Ом | 110 | 11 Ом | 111 | 110 Ом |
| R12 | 0.12 Ом | 1R2 | 1.2 Ом | 120 | 12 Ом | 121 | 120 Ом |
| R13 | 0.13 Ом | 1R3 | 1.3 Ом | 130 | 13 Ом | 131 | 130 Ом |
| R15 | 0.15 Ом | 1R5 | 1.5 Ом | 150 | 15 Ом | 151 | 150 Ом |
| R16 | 0.16 Ом | 1R6 | 1.6 Ом | 160 | 16 Ом | 161 | 160 Ом |
| R18 | 0. 18 Ом 18 Ом | 1R8 | 1.8 Ом | 180 | 18 Ом | 181 | 180 Ом |
| R20 | 0.2 Ом | 2R0 | 2 Ом | 200 | 20 Ом | 201 | 200 Ом |
| R22 | 0.22 Ом | 2R2 | 2.2 Ом | 220 | 22 Ом | 221 | 220 Ом |
| R24 | 0.24 Ом | 2R4 | 2.4 Ом | 240 | 24 Ом | 241 | 240 Ом |
| R27 | 0.27 Ом | 2R7 | 2.7 Ом | 270 | 27 Ом | 271 | 270 Ом |
| R30 | 0.3 Ом | 3R0 | 3 Ом | 300 | 30 Ом | 301 | 300 Ом |
| R33 | 0.33 Ом | 3R3 | 3.3 Ом | 330 | 33 Ом | 331 | 330 Ом |
| R36 | 0.36 Ом | 3R6 | 3.6 Ом | 360 | 36 Ом | 361 | 360 Ом |
| R39 | 0.39 Ом | 3R9 | 3.9 Ом | 390 | 39 Ом | 391 | 390 Ом |
| R43 | 0. 43 Ом 43 Ом | 4R3 | 4.3 Ом | 430 | 43 Ом | 431 | 430 Ом |
| R47 | 0.47 Ом | 4R7 | 4.7 Ом | 470 | 47 Ом | 471 | 470 Ом |
| R51 | 0.51 Ом | 5R1 | 5.1 Ом | 510 | 51 Ом | 511 | 510 Ом |
| R56 | 0.56 Ом | 5R6 | 5.6 Ом | 560 | 56 Ом | 561 | 560 Ом |
| R62 | 0.62 Ом | 6R2 | 6.2 Ом | 620 | 62 Ом | 621 | 620 Ом |
| R68 | 0.68 Ом | 6R8 | 6.8 Ом | 680 | 68 Ом | 681 | 680 Ом |
| R75 | 0.75 Ом | 7R5 | 7.5 Ом | 750 | 75 Ом | 751 | 750 Ом |
| R82 | 0.82 Ом | 8R2 | 8.2 Ом | 820 | 82 Ом | 821 | 820 Ом |
| R91 | 0.91 Ом | 9R1 | 9.1 Ом | 910 | 91 Ом | 911 | 910 Ом |
| Код smd | Значение | Код smd | Значение | Код smd | Значение | Код smd | Значение |
|---|---|---|---|---|---|---|---|
| 102 | 1 кОм | 103 | 10 кОм | 104 | 100 кОм | 105 | 1 МОм |
| 112 | 1.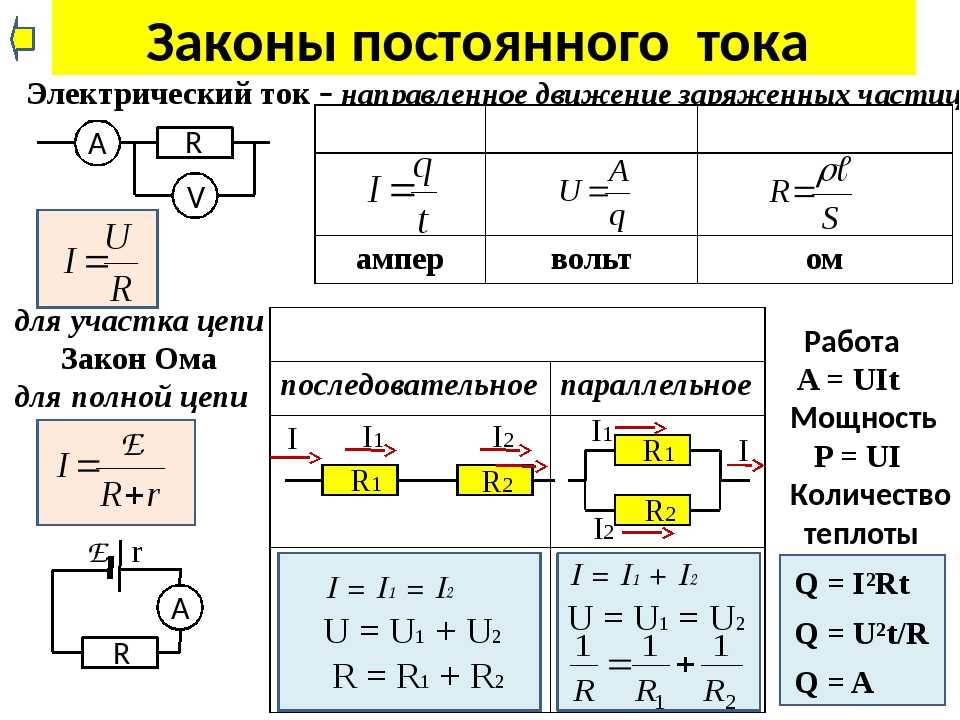 1 кОм 1 кОм | 113 | 11 кОм | 114 | 110 кОм | 115 | 1.1 МОм |
| 122 | 1.2 кОм | 123 | 12 кОм | 124 | 120 кОм | 125 | 1.2 МОм |
| 132 | 1.3 кОм | 133 | 13 кОм | 134 | 130 кОм | 135 | 1.3 МОм |
| 152 | 1.5 кОм | 153 | 15 кОм | 154 | 150 кОм | 155 | 1.5 МОм |
| 162 | 1.6 кОм | 163 | 16 кОм | 164 | 160 кОм | 165 | 1.6 МОм |
| 182 | 1.8 кОм | 183 | 18 кОм | 184 | 180 кОм | 185 | 1.8 МОм |
| 202 | 2 кОм | 203 | 20 кОм | 204 | 200 кОм | 205 | 2 МОм |
| 222 | 2.2 кОм | 223 | 22 кОм | 224 | 220 кОм | 225 | 2.2 МОм |
| 242 | 2.4 кОм | 243 | 24 кОм | 244 | 240 кОм | 245 | 2. 4 МОм 4 МОм |
| 272 | 2.7 кОм | 273 | 27 кОм | 274 | 270 кОм | 275 | 2.7 МОм |
| 302 | 3 кОм | 303 | 30 кОм | 304 | 300 кОм | 305 | 3 МОм |
| 332 | 3.3 кОм | 333 | 33 кОм | 334 | 330 кОм | 335 | 3.3 МОм |
| 362 | 3.6 кОм | 363 | 36 кОм | 364 | 360 кОм | 365 | 3.6 МОм |
| 392 | 3.9 кОм | 393 | 39 кОм | 394 | 390 кОм | 395 | 3.9 МОм |
| 432 | 4.3 кОм | 433 | 43 кОм | 434 | 430 кОм | 435 | 4.3 МОм |
| 472 | 4.7 кОм | 473 | 47 кОм | 474 | 470 кОм | 475 | 4.7 МОм |
| 512 | 5.1 кОм | 513 | 51 кОм | 514 | 510 кОм | 515 | 5.1 МОм |
| 562 | 5.6 кОм | 563 | 56 кОм | 564 | 560 кОм | 565 | 5. 6 МОм 6 МОм |
| 622 | 6.2 кОм | 623 | 62 кОм | 624 | 620 кОм | 625 | 6.2 МОм |
| 682 | 6.8 кОм | 683 | 68 кОм | 684 | 680 кОм | 685 | 6.8 МОм |
| 752 | 7.5 кОм | 753 | 75 кОм | 754 | 750 кОм | 755 | 7.5 МОм |
| 822 | 8.2 кОм | 823 | 82 кОм | 824 | 820 кОм | 815 | 8.2 МОм |
| 912 | 9.1 кОм | 913 | 91 кОм | 914 | 910 кОм | 915 | 9.1 МОм |
Кодовая маркировка резисторов.
Помимо цветовой маркировки используется так называемая кодовая. Для обозначения номинала резистора в данном случае используются буквы и цифры (четыре или пять знаков). Первые знаки (все, кроме последнего) используются для обозначения номинала резистора и включают в себя две или три цифры и букву. Буква определяет положение запятой десятичного знака, а также множитель. Последний же символ определяет допустимое отклонение сопротивления резистора. Возможны следующие значения:
Последний же символ определяет допустимое отклонение сопротивления резистора. Возможны следующие значения:
Для букв, обозначающих множитель возможны такие варианты:
Давайте для наглядности рассмотрим несколько примеров:
С этим типом маркировки мы разобрались, давайте теперь изучим всевозможные способы маркировки SMD резисторов.
Резистор.
Итак, начнем с основного определения резистора. Резистор — это, в первую очередь, пассивный элемент электрической цепи, который имеет определенное значение сопротивления (оно может быть постоянным и переменным). Предназначен этот элемент для линейного преобразования силы тока в напряжение и наоборот. Ведь как мы помним из закона Ома, напряжение и сила тока связаны друг с другом как раз через величину сопротивления:
I = \frac{U}{R}
Резисторы являются одними из самых широко используемых компонентов. Редко можно встретить схему, в которой бы не было ни одного резистора Основным параметром резистора, как уже понятно из определения, является его электрическое сопротивление, измеряемое в Омах (Ом).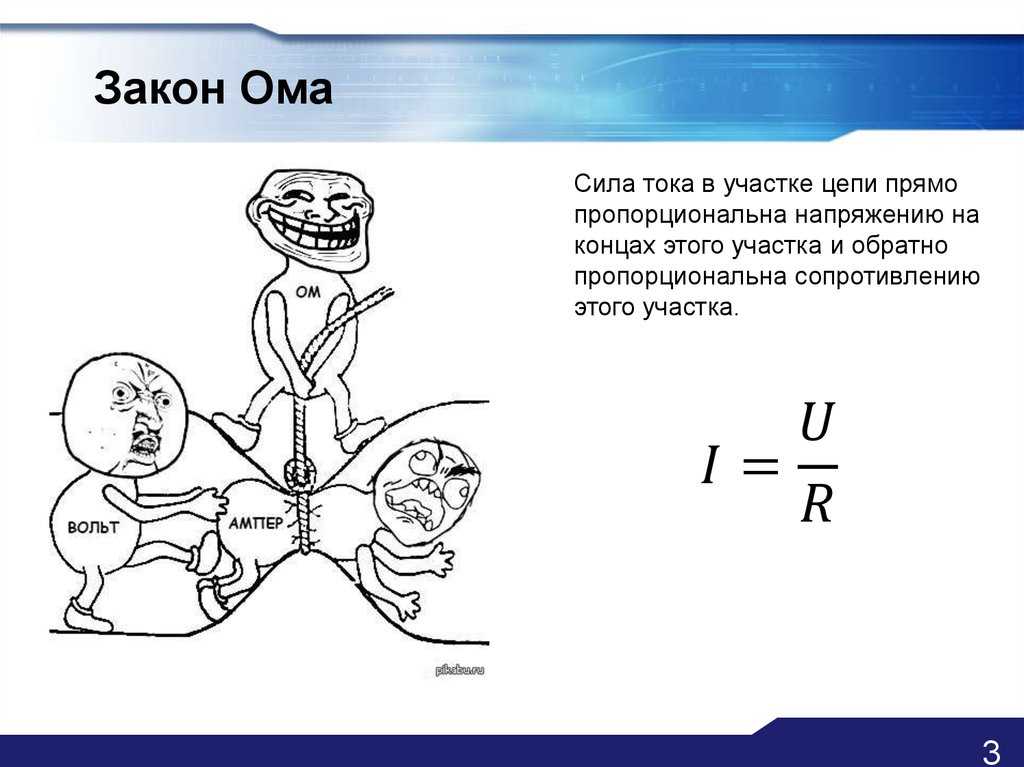
Расчет резисторов
Для подбора и установки элементов в схему необходимо предварительно рассчитать номинал и мощность компонентов.
Формула для расчета сопротивления и мощности
Сопротивление тока: формула
Используют Закон Ома для участка цепи, чтобы вычислить сопротивление резистора, формула имеет вид:
R = U/I,
где:
- U – напряжение на выводах элемента, В;
- I – сила тока на участке цепи, А.
Эта формула применима для токов постоянного направления. В случае расчётов для переменного тока берут в расчёт импеданс цепи Rz.
Важно! Строение схем не ограничивается установкой только одного резистора. Обычно их множество, соединены они между собой параллельно и последовательно
Для нахождения общего показателя применяют отдельные методы и формулы.
Последовательное соединение
При таком соединении «выход» одного элемента соединяется с «входом» другого, они идут последовательно друг за другом. Как рассчитать резистор в этом случае? Можно использовать электронный онлайн-калькулятор, можно применить формулу.
Общее значение будет составлять сумму сопротивлений компонентов, входящих в последовательное соединение:
R123 = R1+R2+R3.
На каждом из них произойдёт одинаковое падение напряжения: U1, U2, U3.
Параллельное соединение
При выполнении данного вида соединения одноимённые выводы соединяются попарно, формула имеет вид:
R = (R1 x R2)/ (R1 + R2).
Обычно полученное значение R бывает меньше меньшего из всех значений соединённых элементов.
Последовательное и параллельное соединения
Информация. На практике параллельное или последовательное присоединение применяют, когда нет детали необходимого номинала. Элементы для таких случаев подбирают одинаковой мощности и одного типа, чтобы не получить слабого звена.
Смешанное соединение
Рассчитывать общее сопротивление смешанных соединений возможно, применяя правило объединения. Сначала выбирают все параллельные и последовательные присоединения и составляют эквивалентные схемы замещения. Их начинают рассчитывать, используя формулы для каждого случая. Из полученной более простой схемы вновь выделяют параллельные и последовательные звенья и опять производят расчёты. Делают это до тех пор, пока не получат самое элементарное соединение или один эквивалентный элемент. Вычисленный результат будет являться искомым.
Их начинают рассчитывать, используя формулы для каждого случая. Из полученной более простой схемы вновь выделяют параллельные и последовательные звенья и опять производят расчёты. Делают это до тех пор, пока не получат самое элементарное соединение или один эквивалентный элемент. Вычисленный результат будет являться искомым.
Метод расчёта при смешанном соединении
Мощность
Одного поиска значения сопротивления недостаточно для того, чтобы применить деталь. Необходимо узнать, на какую мощность должен быть рассчитан элемент. В противном случае он будет перегреваться и выйдет из строя. Мощные детали при поверхностном монтаже лучше устанавливать на радиатор.
Расчет мощности резистора выполняется по формуле:
Р = I² * R = U²/R,
где:
- Р – мощность, Вт;
- I – ток, А;
- U – напряжение, В;
- R – сопротивление, Ом.
После определения мощности резисторов по формуле подбирают комплектующие, исходя из графического обозначения на схемах.
Основные обозначения мощности резисторов
Кривая импеданса для разных видов устройств
Посмотрим, как зависит частота от сопротивления в различных устройствах. Пределы частоты зададим значениями в 20 и 20000 Гц.
Полноразмерная гарнитура динамического типа создает кривую импеданса, формирующую небольшие подъемы при функционировании на низких и высоких частотах. Это означает, что, даже если задано стандартное сопротивление в наушниках на 32 Ом, реальное сопротивление может отклоняться от указанного в два или три раза.
У внутриканальных устройств кривая импеданса является прямой линией, без каких-либо отклонений. Линия лежит в горизонтальной плоскости, параллельно шкале Гц. Это верно, когда мы задаем стандартные значения сопротивления Ом в 16, 24 и 32.
Аппаратура с изодинамическими и ортодинамическими свойствами, тоже имеют импеданс, выраженный горизонтальной линией. Тем не менее, на ультравысоких частотах могут возникать локальные отклонения. Это происходит только с некоторыми моделями и не является обязательным правилом.
Арматурная гарнитура внутриканального вида дает чистый красивый звук на высоких частотах. Причиной этому является то, что график импеданса взлетает на высокой частоте. Такое происходит во многих однодрайверных устройствах. Отсутствие искажений звука позволяет полнее им наслаждаться.
Когда речь идет о многодрайверных наушниках и о гибридным типе гарнитуры, можно отметить, что на значениях свыше 500 Гц кривая импеданса непредсказуемо мечется то вниз, то вверх. Просадка снижается до показателя в 4 Ом. В это же время производители заявляют о том, что просадка составляет 100 Ом на 1кГц
Закон Ома для цепи
Закон Ома для участка цепи, безусловно, можно описать известной из школьного курса физики формулой: I=U/R, но некоторые изменения и уточнения внести, думаю, стоит. Возьмем замкнутую электрическую цепь и рассмотрим ее участок между точками 1-2. Для простоты я взял участок электрической цепи, не содержащий источников ЭДС (Е).
Итак, закон Ома для рассматриваемого участка цепи имеет вид:
φ1-φ2=I*R, где
- I – ток, протекающий по участку цепи.

- R – сопротивление этого участка.
- φ1-φ2 – разность потенциалов между точками 1-2.
Если учесть, что разность потенциалов это напряжение, то приходим к производной формулы закона Ома, которая приведена в начале страницы: U=I*R. Это формула закона Ома для пассивного участка цепи (не содержащего источников электроэнергии).
В неразветвленной электрической цепи (рис.2) сила тока во всех участках одинакова, а напряжение на любом участке определяется его сопротивлением:
- U1=I*R1
- U2=I*R2
- Un=I*Rn
- U=I*(R1+R2+…+Rn
Отсюда можно получить формулы, которые пригодятся при практических вычислениях. Например:
U=U1+U2+…+Un или U1/U2/…/Un=R1/R2/…/Rn
Расчет сложных (разветвленных) цепей осуществляется с помощью законов Кирхгофа.
Закон Ома для участка цепи.
Для ЭДС
Перед тем как рассмотреть закон Ома для полной (замкнутой) цепи приведу правило знаков для ЭДС, которое гласит: Если внутри источника ЭДС ток идет от катода (-) к аноду (+) (направление напряженности поля сторонних сил совпадает с направлением тока в цепи, то ЭДС такого источника считается положительной. В противном случае – ЭДС считается отрицательной.
В противном случае – ЭДС считается отрицательной.
Практическим применением этого правила является возможность приведения нескольких источников ЭДС в цепи к одному с величиной E=E1+E2+…+En, естественно, с учетом знаков, определяемых по вышеприведенному правилу. Например (рис.3.3) E=E1+E2-E3. При отсутствии встречно включенного источника E3 (на практике так почти никогда не бывает) имеем широко распространенное последовательное включение элементов питания, при котором их напряжения суммируются.
Для полной цепи
Закон Ома для полной цепи – его еще можно назвать закон ома для замкнутой цепи, имеет вид I=E/(R+r). Приведенная формула закона Ома содержит обозначение r, которое еще не упоминалось. Это внутреннее сопротивление источника ЭДС. Оно достаточно мало, в большинстве случаев при практических расчетах им можно пренебречь (при условии, что R>>r – сопротивление цепи много больше внутреннего сопротивления источника). Однако, когда они соизмеримы, пренебрегать величиной r нельзя.
Как вариант можно рассмотреть случай, при котором R=0 (короткое замыкание). Тогда приведенная формула закона Ома для полной цепи примет вид: I=E/r, то есть величина внутреннего сопротивления будет определять ток короткого замыкания. Такая ситуация вполне может быть реальной. Закон Ома рассмотрен здесь достаточно бегло, но приведенных формул достаточно для проведения большинства расчетов, примеры которых, по мере размещения других материалов я буду приводить.
Полноценную цепь составляет уже участок (участки), а также источник ЭДС. То есть, фактически к существующему резистивному компоненту участка цепи добавляется внутреннее сопротивление источника ЭДС. Поэтому логичным является некоторое изменение выше рассмотренной формулы:
I = U / (R + r)
Конечно, значение внутреннего сопротивления ЭДС в законе Ома для полной электрической цепи можно считать ничтожно малым, правда во многом это значение сопротивления зависит от структуры источника ЭДС. Тем не менее, при расчетах сложных электронных схем, электрических цепей с множеством проводников, наличие дополнительного сопротивления является важным фактором.
Как для участка цепи, так и для полной схемы следует учитывать естественный момент – использование тока постоянной или переменной величины. Если отмеченные выше моменты, характерные для закона Ома, рассматривались с точки зрения использования постоянного тока, соответственно с переменным током всё выглядит несколько иначе.
Способы определения сопротивления резистора
При отсутствии буквенно-цифровой маркировки можно воспользоваться одним из следующих способов:
- Самым простым методом является определение номинала по документации. Наиболее легко это сделать, если деталь приобретается отдельно и имеет сопроводительный документ. Если резистор является частью электрического аппарата, то на общей электрической схеме указываются его характеристики либо непосредственно рядом с ним (правее или ниже), либо внизу в спецификации.
- Если резистор – отдельная деталь, то его сопротивление можно измерить омметром или мультиметром.
- Произвести точное распознавание детали, находящейся в составе устройства, можно только после ее выпаивания.

Единица измерения сопротивления в системе СГС
В системе СГС (сантиметр, грамм, секунда) единица сопротивления не имеет названия, вернее она называется единица сопротивления СГС, обозначается как $ед.{СГС}_R$. Единица электрического сопротивления в СГС ($1\ ед.{СГС}_R$) равна сопротивлению участка цепи, при котором постоянный ток силой 1 единица СГС тока (1 $ед.\ {СГС}_I$), вызывает падение напряжения 1 СГС напряжения (1$\ ед.\ {СГС}_U$). При этом:
\=\frac{c}{см}.\]
Между омом и единицей сопротивления в СГС следующее соотношения:
\
В расширениях к системе СГС единицы сопротивление называют: статом. Статом — единица измерения сопротивления в системе СГСЭ и системе Гаусса. Это сопротивление проводника у которого при напряжении на концах в один статвольт течет ток один статампер. Обозначают статом как $1stat{\mathbf \Omega }$\textbf{.}\textit{}
\
В другом расширении системы СГС, СГСМ сопротивление измеряют в абомах($ab{\mathbf \Omega }$).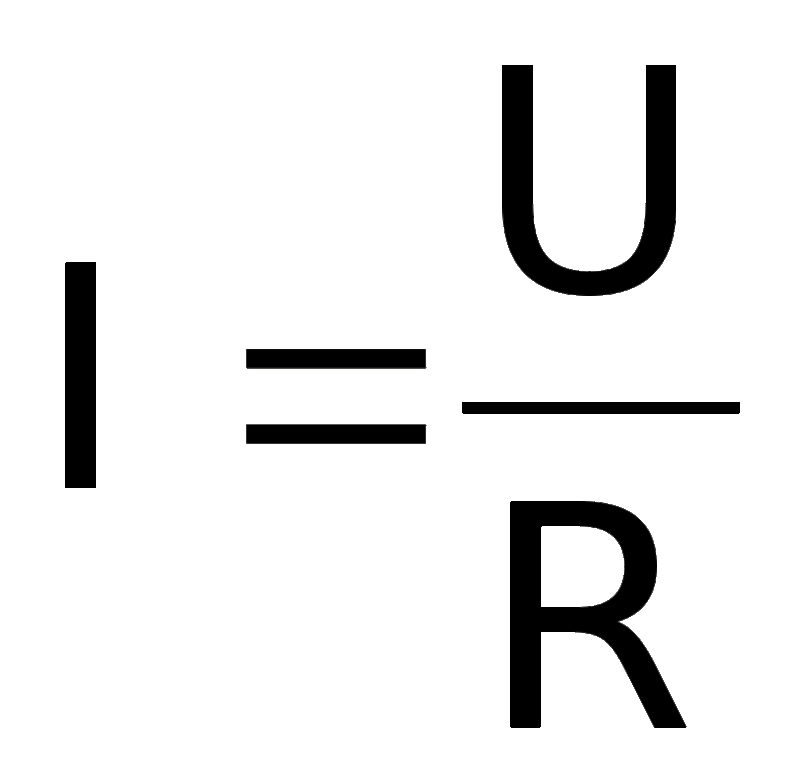 Абом соотносится с омом как:
Абом соотносится с омом как:
\
В системе СГСМ выполняется равенство:
\
где $abV$ — абвольт; $abA$ — абампер.
Мегаом в ом
В измерительных радиоэлектронных устройствах используются резисторы повышенной точности (так называемые прецезионные резисторы).
Мощность резистора
Тепловая энергия, выделяемая в резисторе при протекании тока, рассеивается с его поверхности в окружающее пространство.
Однако если мощность, выделяемая в резисторе, будет велика, то тепло с его поверхности не будет успевать отводиться. Резистор станет чрезмерно нагреваться и даже может сгореть. Поэтому каждый резистор имеет строго определенное максимальное допустимое значение мощности, которую он способен рассеивать.
Мощности резисторов обычно узнают по их размерам (чем больше размер резистора, тем больше его мощность) или по обозначению на корпусах.
На принципиальных схемах обычно указывается мощность используемого резистора. Отсутствие указания мощности резистора означает, что на нем выделяется ничтожно малая мощность и можно применять любой резистор с данным сопротивлением.
Переменные резисторы
Переменный резистор служит для плавного регулирования силы тока и напряжения.
Переменные резисторы делят на регулировочные и подстроенные.
Резисторы, с помощью которых осуществляют различные регулировки изменением их сопротивления, называют переменными резисторами или потенциометрами. Резисторы, сопротивление которых изменяют только в процессе налаживания (настройки) устройства, называют подстроечными.
Переменные резисторы имеют три вывода, один из которых связан с подвижным контактом, скользящим по поверхности проводящего слоя. Движок регулировочного резистора перемещают рукой посредством поворота выступающей ручки, подстроечного — отверткой, вставленной в прорезь.
Сопротивление между любым крайним выводом переменного резистора и подвижным контактом зависит от положения движка.
Цветоваямаркировка резисторов
Тип маркировки, при котором на корпус резистора наносится краска в виде цветных колец или точек, называют цветовым кодом. Каждому цвету соответствует определенное цифровое значение. Цветовая маркировка на резисторах сдвинута к одному из выводов и читается слева направо.
Каждому цвету соответствует определенное цифровое значение. Цветовая маркировка на резисторах сдвинута к одному из выводов и читается слева направо.
Если из-за малого размера резистора цветовую маркировку нельзя разместить у одного из выводов, то первый знак делается полосой шириной в два раза больше, чем остальные.
Цветовая маркировка зарубежных малогабаритных резисторов, распространенных в России, состоит чаще всего из четырех цветовых колец.
Номинал сопротивления определяют первые три кольца (две цифры и множитель). Четвертое кольцо содержит информацию о допустимом отклонении сопротивления от номинального значения в процентах.
Чтобы не путать ноль и букву «О», «Ом» часто пишут буквой «омега»:
Время на расшифровку цветового кода резисторов можно значительно сократить, если воспользоваться специальным онлайн-калькулятором цветовой маркировки резисторов.
Обозначение резисторов на схеме
| Постоянный резистор без указания номинальной мощности рассеивания |
| Постоянный резистор номинальной мощностью рассеивания 0,05 Вт |
| Постоянный резистор номинальной мощностью рассеивания 0,125 Вт |
| Постоянный резистор номинальной мощностью рассеивания 0,25 Вт |
| Постоянный резистор номинальной мощностью рассеивания 0,5 Вт |
| Постоянный резистор номинальной мощностью рассеивания 1 Вт |
| Постоянный резистор номинальной мощностью рассеивания 2 Вт |
| Постоянный резистор номинальной мощностью рассеивания 5 Вт |
Обозначение переменных, подстроечных и нелинейных резисторов на схемах:
Обозначение по ГОСТ 2. 728-74 728-74 | Описание |
| Переменный резистор (реостат). | |
| Переменный резистор, включенный как реостат (ползунок соединён с одним из крайних выводов). | |
| Подстроечный резистор. | |
| Подстроечный резистор, включенный как реостат (ползунок соединён с одним из крайних выводов). | |
| Варистор (сопротивление зависит от приложенного напряжения). | |
| Термистор (сопротивление зависит от температуры). | |
| Фоторезистор (сопротивление зависит от освещённости). |
Условное обозначение резистора на схеме – прямоугольник размерами 4х10 мм. На схемах значение сопротивления постоянного резюка менее кОма проставляется рядом с его условным обозначением числом без единицы измерения. При номинале от одного кОм до 999 кОм рядом с числом ставят букву «К», от одного МОм – букву «М». Характеристики резисторов указывают на их поверхности, для чего применяют буквенно-цифровой код или группу цветных полосок.
Примеры буквенно-цифрового обозначения для сопротивления, выраженного целым числом:
- 25 Ом – 25 R;
- 25 кОм – 25 K;
- 25 МОм – 25 M.
Если для выражения величины сопротивления используется десятичная дробь, то порядок расположения цифр и букв будет иным, например:
- 0,25 Ом – R 25;
- 0,25 кОм – K 25;
- 0,25 МОм – M 25.
Если сопротивление выражается числом, отличным от нуля и с десятичной дробью, то буква в обозначении играет роль запятой, например:
- 2,5 Ом – 2R5;
- 2,5 кОм – 2K5;
- 2,5 МОм – 2M5.
Производители в силу несовершенства производственной технологии не в состоянии на 100% гарантировать соответствие заявленного значения сопротивления фактическому. Допустимая погрешность обозначается в % и проставляется после номинального значения, например ±5%, ±10%, ±20%. Класс точности может определяться буквой, в зависимости от производителя, – русской или латинской.
| Допустимая погрешность, ±% | 20 | 10 | 5 | 2 | 1 | 0,5 | 0,2 | 0,1 |
| Буква | ||||||||
| Русская | В | С | И | Л | Р | Д | У | Ж |
| Латинская | M | K | J | G | F | D | C | B |
Таблица удельных сопротивлений проводников
| Материал проводника | Удельное сопротивление ρ в |
| Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль | 0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5 |
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2.
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2.
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2.
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
температурный коэффициент сопротивления —
это изменение сопротивления проводника при его нагревании,
приходящееся на 1 Ом первоначального сопротивления и на 1° температуры,
обозначается буквой α.
Если при температуре t сопротивление проводника равно r, а при температуре t равно rt, то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Сопротивление проводника
Сопротивление проводника напрямую зависит от его геометрических размеров, а также материала изготовления. Меньшее сопротивление протеканию электрического тока будет оказывать проводник более толстого сечения и меньшей длины. Математически это выглядит следующим образом:
R = p l/S
- R – электрическое сопротивление проводника, Ом.
- p – удельное сопротивление проводника, Ом·мм2/м.
- l – длина проводника, м.
- S – площадь сечения проводника, м2.
Самыми меньшими удельными сопротивлениями обладают:
- серебро – 0,016 Ом·мм2/м;
- медь – 0,0175 Ом·мм2/м;
- золото – 0,023 Ом·мм2/м;
- алюминий – 0,029 Ом·мм2/м.

Наибольшие удельные сопротивления у графита – 13 Ом·мм2/м, фарфора – 1019 Ом·мм2/м, эбонита – 1020 Ом·мм2/м.
Единица измерения сопротивления, теория и онлайн калькуляторы
Единица измерения сопротивления, теория и онлайн калькуляторыВ соответствии с законом Ома для участка цепи сила тока ($I$) на рассматриваемом участке пропорциональна напряжению ($U$) на концах участка:
\[I=\frac{U}{R}\left(1\right),\]
где $R$ — физическая величина, называемая электрическим сопротивлением, характеризует участок цепи. Из закона Ома (1) следует, что:
\[R=\frac{U}{I}\left(2\right).\]
Ом — единица измерения сопротивления в системе СИ
Из формулы (2) следует, что сопротивление численно равно отношению напряжения на концах участка к силе тока, который в нем течет. Единицу измерения сопротивления можно определить как:
\[\left[R\right]=\frac{\left[U\right]}{\left[I\right]}=\frac{В}{А}.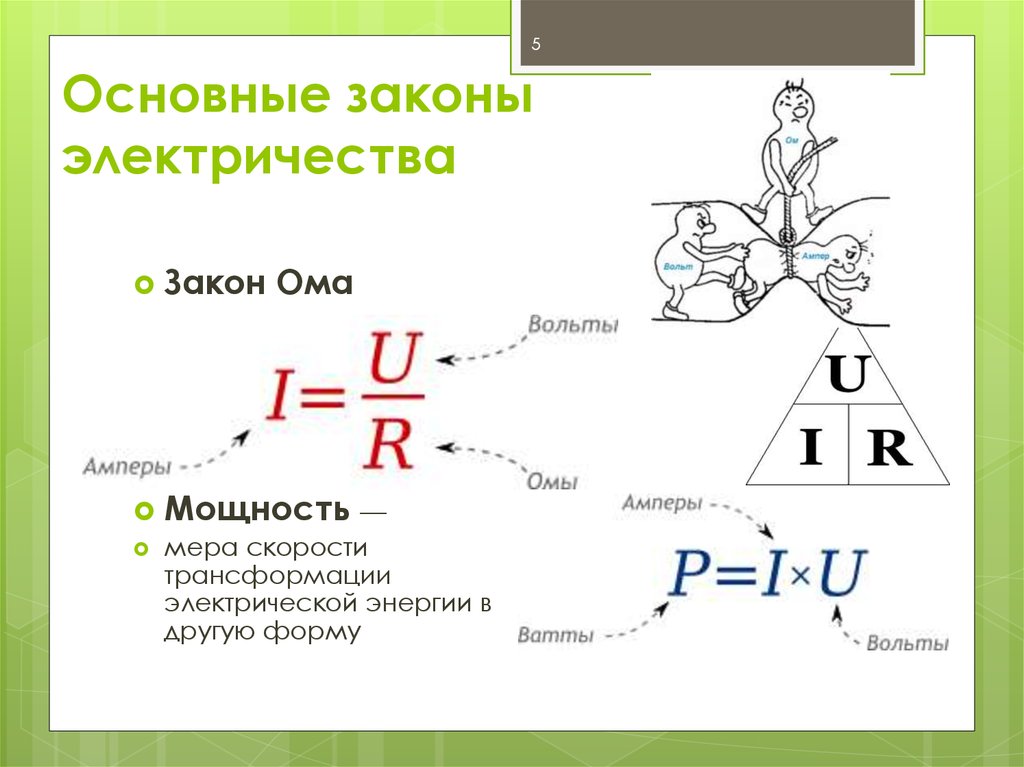 {-9}Ом.\]
{-9}Ом.\]
В системе СГСМ выполняется равенство:
где $abV$ — абвольт; $abA$ — абампер.
Примеры задач с решением
Пример 1
Задание. Чему равно добавочное сопротивление ($R$), которое подключают к вольтметру для того, чтобы предельная величина измеряемого напряжения была увеличена в 4 раза, если внутреннее сопротивление самого вольтметра равно $R_V=5\ кОм$. Ответ запишите в омах.\textit{}
Решение. Схема подключения дополнительного сопротивления к вольтметру с целью увеличения напряжения, которое он может измерять указана на рис.1.
К вольтметру последовательно подключают дополнительное сопротивление. Сила тока на этом участке цепи остается без изменения, обозначим ее $I$, используя закон Ома, мы можем записать, что падение напряжения на вольтметре (рис.1) равно:
\[U_V=IR_{V\ }\left(1. 1\right).\]
1\right).\]
При этом падение напряжения на дополнительном сопротивлении составляет:
\[U=IR\ \left(1.2\right).\]
Падение напряжения на концах соединения AB. составляет:
\[IR_{V\ }+IR=4U_V\ \left(1.3\right),\]
так как по условию падение напряжения после подключения дополнительного сопротивления к вольтметру должно быть рано $4U_V$ (где $U_V=IR_V$ — падение напряжения на вольтметре при отсутствии дополнительного сопротивления).
\[IR_{V\ }+IR=4\left(IR_V\right)\to R=3R_V.\]
Вычислим величину дополнительного сопротивления:
\[R=3\cdot 5=15\ \left(кОм\right).\]
Зная, что:
\[1\ кОм=1000\ Ом,\]
получим:
\[R={\rm 15}{\rm кОм}{\rm =15000\ }{\rm Ом}\]
Ответ. $R=15000$ Ом
Пример 2
Задание.
Ответ. Из какого закона не получали бы мы сопротивление, всегда в системе СИ единицами его измерения должен быть Ом.
Читать дальше: единица измерения ускорения.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
формула, определение простыми словами, задачи с решением
Закон Ома — главный закон электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом. Вместе с экспертом разберем формулировку, формулу и задачи на закон Ома с решением
Борис Михеев
Автор КП
Николай Герасимов
Старший преподаватель физики в
Домашней школе «ИнтернетУрок»
Физика — наука эмпирическая. Ее основные законы вытекают из практического опыта и частенько много лет не имеют теоретических обоснований. Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Именно так обстоит дело с главным законом электротехники, который открыл в 1826 году выдающийся немецкий ученый Георг Симон Ом.
Электрические явления люди наблюдали сотни лет. Но никак не связывали между собой заряженность потертого янтаря и молнию. Только на исходе XVIII столетия электричество стали внимательно исследовать. В 1795 году Алессандро Вольта изобрел «вольтов столб», химическую батарею, и обнаружил появление тока в проводнике, соединяющем ее полюса. Сферы применения электричества стремительно множились, и появилась острая необходимость в расчетных формулах для инженеров. Эту задачу решали многие ученые, но первым сформулировал главную формулу электротехники именно Георг Ом. Он ввел в обиход понятие сопротивления и опытным путем установил зависимость между основными характеристиками электрической цепи.
Определение закона Ома простыми словами
Электрическая цепь состоит из двухполюсного источника напряжения, то есть батареи, аккумулятора или генератора. Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.
Если полюса источника соединить проводами, то по ним потечет электрический ток. Его величина определяется сопротивлением проводников. Наглядное представление этой зависимости — обыкновенный водопровод. Аналогом источника напряжения является насос или водонапорная башня, создающая давление в магистрали, количество воды, прошедшее по трубе, — подобие силы тока, а кран соответствует сопротивлению. Полностью открытый, он не ограничивает поток, по мере закручивания отверстие для воды уменьшается, пока не закроется совсем.
Закон Ома для участка цепи
Опытным путем исследователь установил взаимосвязь характеристик электрической цепи. Классическая формулировка закона Ома звучит так:
«Сила тока на участке цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению».
Формула закона Ома для участка цепи
Где I – сила тока, измеряемая в Амперах (А), U – напряжение, измеренное в Вольтах (В), R – сопротивление, измеряемое в Омах (Ом).
В таком виде закон Ома приведен в школьных учебниках физики. Согласно этой простой формуле, для определения уровня тока в проводнике достаточно величину напряжения на его сторонах разделить на некий условно постоянный коэффициент, то есть на сопротивление. Почему «условно»? Потому что величина сопротивления может меняться в зависимости от температуры. Поэтому, кстати, лампы накаливания чаще всего перегорают при включении. Сопротивление холодной спирали ниже, чем нагретой, скачок тока при подаче напряжения вызывает ее резкое расширение и разрыв. Но если этот момент преодолен и нить накала уцелела, то ее сопротивление растет, и ток ограничивается. А при температуре жидкого гелия, например, сопротивление падает до нуля, наступает сверхпроводимость.
Закон Ома для замкнутой полной цепи
Предыдущая формулировка годится только для участка цепи, где отсутствует сам источник электродвижущей силы. В реальности ток течет по замкнутому контуру, где обязательно есть батарея или генератор, имеющий собственное внутреннее сопротивление. Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Поэтому формула закона Ома для полной цепи выглядит несколько сложнее
Формула закона Ома для замкнутой полной цепи
Где I – сила тока, измеряемая в Амперах (А), Е – электродвижущая сила, измеренная в Вольтах (В), R – сопротивление, измеряемое в Омах (Ом), r — внутреннее сопротивление источника ЭДС.
Применение закона Ома
Георг Ом дал в руки инженеров средство для решения задач, связанных с электрическими цепями. Тепловые и световые приборы, электродвигатели, генераторы, линии электропередач, кабели связи рассчитываются на основе этой простой формулы. Нет такой области электротехники, где она не находит применения. Даже в радиотехнике используется закон Ома, но в дифференциальной форме. «Все гениальное — просто», как считали Еврипид, Леонардо да Винчи, Наполеон Бонапарт и Альберт Эйнштейн, несомненные гении. Закон Ома целиком и полностью подтверждает эту истину.
Задача на закон Ома с решением
Задача для участка электрической цепи
Электрочайник, включенный в сеть с напряжением 220 В, потребляет ток 1,1 А. Каково сопротивление электрочайника.
Каково сопротивление электрочайника.
Дано:
U = 220 В
I = 1,1 А
Решение:
Согласно закону Ома для участка цепи:
R=U/I=220/1,1=200 Ом
Ответ: R = 200 Ом.
Задача для полной замкнутой цепи
Источник постоянного тока с ЭДС E = 24 В и внутренним сопротивлением r = 1,5 Ом замкнут на внешнее сопротивление R = 11 Ом. Определить силу тока в цепи.
Дано:
Е=24 В, r=1,5 Ом, R = 11 Ом
Решение:
По закону Ома для замкнутой цепи: I = E/(R + r) = 24/(11+1,5) = 1,92 А.
Ответ: I=1, 92 А.
Популярные вопросы и ответы
Отвечает Николай Герасимов, старший преподаватель физики в Домашней школе «ИнтернетУрок»
Сколько всего законов Ома в физике?
— Существует два закона Ома: закон Ома для участка цепи и закон Ома для полной (замкнутой) цепи.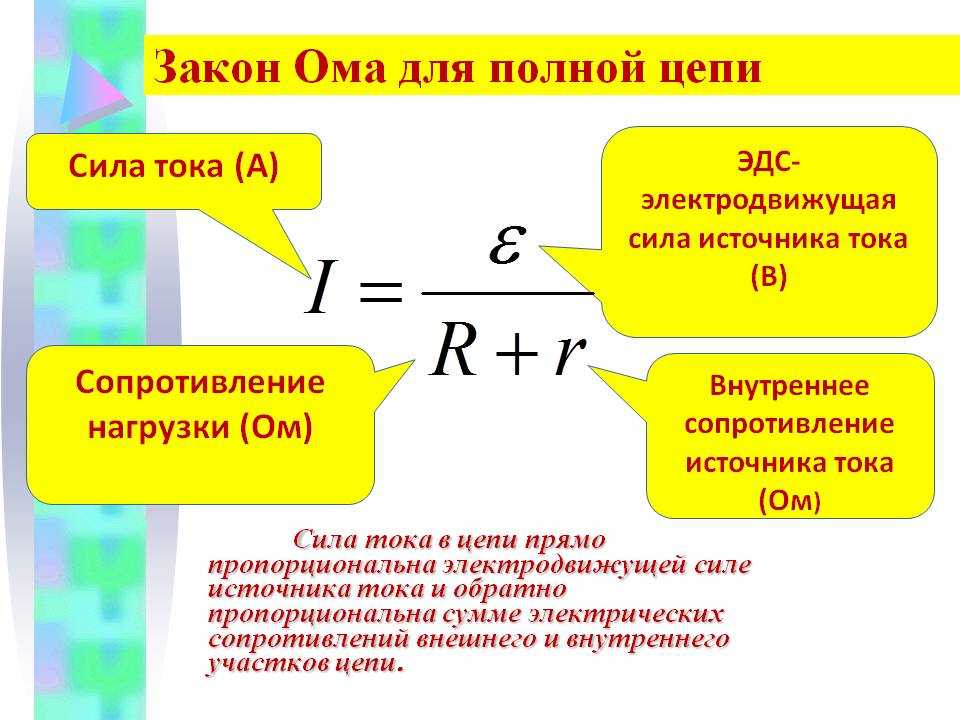 Первый связывает сопротивление участка, силу тока в нём и разность потенциалов (напряжение) на его концах. Кроме того, в нем отражено наличие в цепи источника тока.
Первый связывает сопротивление участка, силу тока в нём и разность потенциалов (напряжение) на его концах. Кроме того, в нем отражено наличие в цепи источника тока.
Второй учитывает и потребителей электрического тока (электрические лампы, обогреватели, телевизоры и так далее), и его источники (генераторы, батарейки, аккумуляторы). Дело в том, что любой источник тока обладает внутренним сопротивление, которое влияет на силу тока. Именно это и учитывается в законе Ома для полной (замкнутой) цепи.
При каких условиях выполняется закон Ома?
Согласно закону Ома, существует линейная зависимость между силой тока в участке цепи и напряжением на его концах. Он отлично выполняется для металлических проводников при любых напряжениях, а вот для тока в вакууме, газе, растворах или расплавах электролитов, полупроводниках линейная зависимость нарушается, и применять закон Ома в том виде, в котором его изучают в школьном курсе, уже нельзя.
Для чего нужен закон Ома?
— Трудно переоценить значимость этого закона. Он позволил производить расчет электрических цепей, без которых практически невозможно представить жизнь современного человека, так как они лежат в основе любого электроприбора, начиная от обычной лампы накаливания и заканчивая самыми современными компьютерами.
Он позволил производить расчет электрических цепей, без которых практически невозможно представить жизнь современного человека, так как они лежат в основе любого электроприбора, начиная от обычной лампы накаливания и заканчивая самыми современными компьютерами.
В каком классе проходят закон Ома?
— В школьном курсе ученики впервые знакомятся с электрическими явлениями и законом Ома для участка цепи в 8 классе. Более подробно о причинах возникновения электрического тока и его источниках ученики знакомятся в курсе старшей школы (10 или 11 класс, в зависимости от программы). Здесь же ученики впервые встречаются и с законом Ома для полной (замкнутой) цепи.
Фото на обложке: pixabay.com
Презентация по физике на тему Закон Ома. Удельное сопротивление доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация по физике на тему Закон Ома. Удельное сопротивление, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 26 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Удельное сопротивление, предмет презентации: Физика. Этот материал в формате pptx (PowerPoint) содержит 26 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Закон Ома.
Расчёт сопротивления проводника.
8 класс
Закон Ома для участка цепи
Опыты показывают, что
сила тока, напряжение и сопротивление – величины, связанные между собой.
Впервые эту связь установил немецкий физик Георг Ом в 1826 г.
( 1787 – 1854 )
Схема опыта
А
V
+
—
Реостат – прибор, используемый для регулирования силы тока в цепи
Устройство реостата
Ползунок
Стержень
Зажим 1
Зажим 2
Керамический цилиндр
Проволока
Правила пользования прибором
Сопротивление реостата изменяется перемещением ползунка по стержню.
Реостат нельзя полностью выводить, так как сопротивление его при этом становится равным нулю, и если в цепи нет других приемников тока, то сила тока может оказаться очень большой и амперметр испортится
Зависимость силы тока от напряжения
Сила тока прямо пропорциональна напряжению
I, А
0,2
0,8
0,6
0,4
0
U, B
1
2
3
4
Линейная зависимость или
прямая пропорциональность
I ~ U
2В
0,4 А
3В
0,6 А
4В
0,8 А
2. Зависимость силы тока от сопротивления
Сила тока обратно пропорциональна сопротивлению
I,А
1
График – ветвь гиперболы
обратная пропорциональность
R
~
I
1
R, Ом
4 Ом
2 Ом
1 Ом
5 В
5 В
5 В
1 А
2 А
4 А
4
2
2
4
1
0
U — const
Электрическое сопротивление
R — электрическое сопротивление – физическая величина, определяющая зависимость силы тока от свойств проводника:
СИ : [R] = = 1 Ом
1 Ом – сопротивление такого проводника, в котором при напряжении на концах 1 В сила тока равна 1 А.
I =
1 . I ~ U – прямая зав — ть
2 . I ~ 1/R – обратная зав — ть
Георг Симон Ом (1789–1854)
Закон Ома для участка цепи
1827 год
Формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.
Формула и формулировка закона Ома
Сила тока на участке цепи прямо пропорциональна электрическому напряжению на концах участка и обратно пропорциональна электрическому сопротивлению данного участка цепи.
Треугольник формул
U
I
X
R
Вольт-амперная характеристика проводника
График, выражающий зависимость силы тока от напряжения, называется
вольт-амперной характеристикой проводника.
Используя формулу расчета сопротивления проводника и опытные данные , определите сопротивление проводников
Чем меньше сопротивление проводника,
тем круче проходит его вольт-амперная характеристика
Расчет сопротивления проводника
В цепь источника тока по очереди включали различные проводники:
никелиновые проволоки одинаковой толщины, но различной длины;
никелиновые проволоки одинаковой длины, но различной толщины;
никелиновую и нихромовую проволоки одинаковой длины и толщины
Опыты показали, что:
1) из двух никелиновых проволок одинаковой толщины более длинная проволока имеет большее сопротивление;
2) из двух никелиновых проволок одинаковой длины большее сопротивление имеет проволока с меньшим поперечным сечением;
3) никелиновая и нихромовая проволоки одинаковых размеров имеют разное сопротивление.
Ом на опытах установил, что:
сопротивление
прямо пропорционально
длине проводника,
обратно пропорционально
площади его поперечного сечения
и зависит
от вещества проводника.
Формула сопротивления проводника
Формула для расчёта
сопротивления проводника:
Удельное сопротивление
Сопротивление проводника из данного вещества длиной 1 м и площадью 1м2 поперечного сечения называется удельным сопротивлением этого вещества.
Формулы
Единицы измерения
СИ: [ ρ ] = = 1 Ом · м
На практике чаще используется:
[ ρ ] =
Удельное сопротивление проводника – сопротивление проводника длиной 1 метр и площадью поперечного сечения 1 мм2.
Единица измерения (Ом·мм2)/м – это табличное значение. Формула: ρ = (R·S)/l.
Длина проводника в метрах
Формула расчета сопротивления проводника (Ом)
Площадь поперечного сечения проводника в мм2.
Если сечение – круг, то S=π·r2
Закон Ома для полной цепи
Сила тока в цепи прямо пропорциональна электродвижущей силе источника тока и обратно пропорциональна сумме электрических сопротивлений внешнего и внутреннего участков цепи.
Сила тока (А)
ЭДС-электродвижущая сила источника тока (В)
Сопротивление
нагрузки (Ом)
Внутреннее сопротивление источника тока (Ом)
Домашнее задание
§ 8-9, ?? к § § — устно,
зад. 9.3 стр43
Зад. 8.1; 8.2 стр38
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
ом (единица измерения)
Конвертер величин, перевод единиц измерений
Поиск по алфавиту
CАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЭЮЯ
ABCČDEFGHIJKLMNOÔÖPQRSTUVWXYZ
ohm
Ом — единица электрического сопротивления в системе СИ. Если проводник соединяет две точки с разными электрическими потенциалами, то через проводник течёт ток. Величина тока зависит от разности потенциалов, а также от сопротивления проводника этому току. Электрическое сопротивление является характеристикой цепи и измеряется в омах. Один ом представляет собой “электрическое сопротивление между двумя точками проводника, когда постоянная разность потенциалов 1 вольт, приложенная к этим точкам, создаёт в проводнике ток 1 ампер, а в проводнике не действует какая-либо электродвижущая сила”. CIPM, резолюция 2, 1946 год.
Это небольшое сопротивление, в применяемых на практике цепях сопротивление часто измеряется в мегаомах, то есть в миллионах ом. Единица «ом» названа в честь немецкого физика Георга Симона Ома (1787–1854). Имя Ома впервые было применено в качестве электрической единицы в 1861 году, когда Чарльз Брайт и Латимер Кларк предложили использовать название «ohma» для единицы электродвижущей силы. В качестве обозначения для ома применяется большая греческая буква омега, поскольку букву «O» можно легко принять за ноль.
Время
Динамическая вязкость
Кинематическая вязкость
Давление, механическое напряжение
Длина и расстояние
Объем данных
Скорость передачи данных
Количество вещества
Концентрация вещества
Массовая концентрация
Молярная концентрация
Крутящий момент
Магнитная индукция
Магнитный поток
Магнитодвижущая сила
Напряженность магнитного поля
Масса
Момент инерции
Мощность
Объем, емкость
Площадь
Мощность поглощенной дозы ионизирующего излучения
Радиация. Поглощённая доза
Радиация. Экспозиционная доза
Радиоактивность. Радиоактивный распад
Расход массовый
Расход молярный
Расход объемный
Свет, фотометрия
Освещенность
Сила света
Яркость
Сила
Линейная скорость
Угловая скорость (скорость вращения)
Ускорение линейное
Ускорение угловое
Твердость
Температура
Коэффициент теплоотдачи
Термическое сопротивление
Удельная теплопроводность
Удельная теплота сгорания (по массе)
Удельная теплота сгорания топлива (по объему)
Удельная теплоёмкость
Энергетическая экспозиция, мощность теплового излучения
Углы
Уровень звука
Частота
Индуктивность
Линейная плотность заряда
Напряжённость электрического поля
Объемная плотность заряда
Поверхностная плотность заряда
Поверхностная плотность тока
Удельная электрическая проводимость
Удельное электрическое сопротивление
Электрическая емкость
Электрическая проводимость
Электрический заряд
Электрический ток
Электрическое сопротивление
Электростатический потенциал и напряжение
Энергия и работа
Разрешение в компьютерной графике
Поглощённая доза
Радиация. Экспозиционная доза
Радиоактивность. Радиоактивный распад
Расход массовый
Расход молярный
Расход объемный
Свет, фотометрия
Освещенность
Сила света
Яркость
Сила
Линейная скорость
Угловая скорость (скорость вращения)
Ускорение линейное
Ускорение угловое
Твердость
Температура
Коэффициент теплоотдачи
Термическое сопротивление
Удельная теплопроводность
Удельная теплота сгорания (по массе)
Удельная теплота сгорания топлива (по объему)
Удельная теплоёмкость
Энергетическая экспозиция, мощность теплового излучения
Углы
Уровень звука
Частота
Индуктивность
Линейная плотность заряда
Напряжённость электрического поля
Объемная плотность заряда
Поверхностная плотность заряда
Поверхностная плотность тока
Удельная электрическая проводимость
Удельное электрическое сопротивление
Электрическая емкость
Электрическая проводимость
Электрический заряд
Электрический ток
Электрическое сопротивление
Электростатический потенциал и напряжение
Энергия и работа
Разрешение в компьютерной графике
Подробнее
Подробнее
«Электрическое сопротивление.
 Закон Ома» 8 класс онлайн-подготовка на Ростелеком Лицей |
Закон Ома» 8 класс онлайн-подготовка на Ростелеком Лицей |Формулы, необходимые для решения задач
На предыдущих уроках мы говорили, что сила тока зависит от напряжения и сопротивления проводника. Также мы выяснили, что сопротивление проводника зависит от его геометрических размеров и материала, из которого он сделан. На этом уроке будут рассмотрены задачи, связанные именно с этими двумя положениями.
Первая формула, которая понадобится для решения задач, – закон Ома для участка цепи:
Сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению. Сила тока измеряется в Амперах (I=[А]), напряжение – в Вольтах (U=[В]), сопротивление – в Омах (R=[Ом]). Тогда из закона Ома можно сказать, что .
Еще одна формула, которая нам понадобится, – формула зависимости сопротивления проводника от его параметров:
Сопротивление проводника равно его удельному сопротивлению, умноженному на дробь, где в числителе – длина проводника, в знаменателе – площадь поперечного сечения проводника. При этом сопротивление измеряется в Омах (R=[Ом]), длина – в метрах (l=[м]). В единицах измерения СИ (система интернациональная) площадь измеряется в метрах квадратных, но поскольку сечение провода невелико, то имеет смысл измерять площадь поперечного сечения в миллиметрах квадратных (S=[м2]=[мм2]). Удельное сопротивление, как правило, определяется по таблицам: зная материал, из которого сделан проводник, можно определить его удельное сопротивление. Единицы измерения удельного сопротивления:
При этом сопротивление измеряется в Омах (R=[Ом]), длина – в метрах (l=[м]). В единицах измерения СИ (система интернациональная) площадь измеряется в метрах квадратных, но поскольку сечение провода невелико, то имеет смысл измерять площадь поперечного сечения в миллиметрах квадратных (S=[м2]=[мм2]). Удельное сопротивление, как правило, определяется по таблицам: зная материал, из которого сделан проводник, можно определить его удельное сопротивление. Единицы измерения удельного сопротивления:
Первая запись единиц измерения используется для удобства (), а в таблицах значение обычно подается в виде второй записи (). Можно увидеть, что записи эквивалентны, т. к. если перевести миллиметры в метры, то метры сократятся.
Задача №1
Рассмотрим следующую задачу: надо определить силу тока в проводнике, длина которого 100 м, а сечение этого проводника – 0,5 мм2.
Этот проводник выполнен из меди и включен в цепь таким образом, что на его концах наблюдается напряжение 6,8 В. Стоит отметить, что в задаче дан материал, из которого сделан проводник. Значит, можно узнать значение удельного сопротивления из таблицы.
Стоит отметить, что в задаче дан материал, из которого сделан проводник. Значит, можно узнать значение удельного сопротивления из таблицы.
Рис. 1. Решение задачи №1
Сначала следует записать краткое условие задачи. На рис. 1. слева от вертикальной черты показано, как это нужно сделать. Значение длины (l=100 м), площади поперечного сечения (S=0,5 мм2) и напряжения (U=6,8 В) дано в условии. Значение удельного сопротивления меди () мы взяли из таблицы. Под горизонтальной чертой на рис. 1 написано, что нужно найти в задаче – силу тока.
Для решения задачи запишем закон Ома для участка цепи: . Также нам потребуется выражение для сопротивления проводника: . Далее постараемся записать решение в общем виде, то есть выражение для сопротивления мы подставим в закон Ома. Поскольку R в законе Ома стоит в знаменателе, то ρ и l окажутся в знаменателе, S перейдет в числитель. Получаем:
Теперь подставим значения данных величин:
Ответ: I=2A.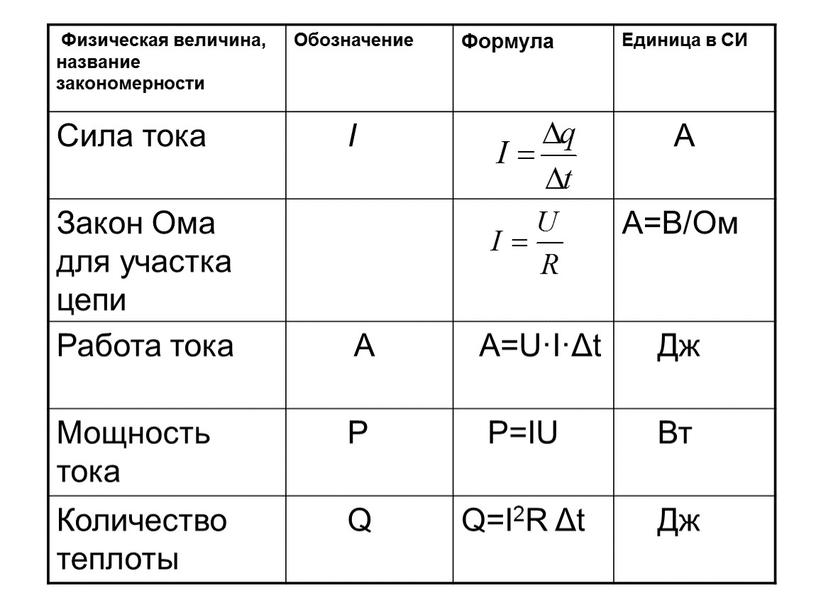
Это можно понять так: если подключить амперметр последовательно к данному проводнику, то он покажет значение 2А. Стоит обратить внимание, что ничего сложного в таких задачах нет. Стоит только разобраться, какие величины куда подставить. Обычно такие задачи в дальнейшем будут использоваться как составная часть более сложных задач.
Задача №2
В предыдущей задаче мы находили значение силы тока. Но эту характеристику можно измерить соответствующим прибором – амперметром. Поэтому, как правило, есть другие задачи, в которых требуется найти характеристики проводника. Если мы хотим сделать какое-то сопротивление, то мы должны знать эти характеристики проводника: длину, площадь сечения, материал. Решая такие задачи, мы сможем их найти, зная силу тока и напряжение.
Рассмотрим пример именно такой задачи. По вольфрамовой проволоке протекает электрический ток. Длина проволоки – 4 м, сила тока составляет 0,05 А. Напряжение, под которым находится данный проводник, составляет 5 В. Необходимо определить величину площади поперечного сечения.
Необходимо определить величину площади поперечного сечения.
Рис. 2. Решение задачи №2
Как и в первом случае, запишем краткое условие задачи (рис. 2, слева от вертикальной черты). Нам даны сила тока I=0,05 А, напряжение U=5 В и длина проволоки l=4 м. Значение удельного сопротивления вольфрама можно найти из таблицы. Под горизонтальной чертой написано то, что требуется найти: S, площадь поперечного сечения проволоки.
Как и в предыдущей задаче запишем две формулы. Первая – это формула для вычисления сопротивления проводника: . Отсюда можно выразить площадь сечения проводника:
Из этого уравнения мы не сможем сразу найти сечение, поскольку нам неизвестно сопротивление. Для его определения потребуется вторая формула – закон Ома для участка цепи: . Из него можно выразить значение сопротивления всей проволоки:
Подставив это выражение в формулу для площади сечения, получим:
Получаем дробь, где в числителе стоит произведение трех величин: удельного сопротивления, длины проводника и силы тока, а в знаменателе стоит только напряжение. Подставим численные значения:
Подставим численные значения:
Получаем ответ: площадь поперечного сечения проволоки . Как видим, сечение проволоки невелико, то есть проволока будет очень тонкой.
Применение задач на практике
Стоит отметить, что для решения конкретных технических задач, подобных решенной ранее, обычно используются данные, которые получают при помощи приборов. Например, имеется катушка с намотанным на нее проводником. Требуется измерить, например, длину этого проводника. Разматывать катушку не имеет смысла, поскольку провод может быть очень длинным. Как же тогда поступить?
Рис. 3. Схема для измерения длины проводника в катушке
По небольшому образцу такого провода измеряют площадь его сечения. По внешнему виду проводника можно определить материал, из которого он сделан, а значит, и узнать его удельное сопротивление. Далее катушку (обозначена желтым цветом на рис. 3) подключают к источнику тока и при помощи амперметра и вольтметра определяют напряжение на этой катушке и силу тока, протекающего по проводнику, который намотан на эту катушку. В результате получаем задачу, похожую на ту, что мы решали ранее, но найти надо длину проводника. Используя формулу для сопротивления и закон Ома, получим:
В результате получаем задачу, похожую на ту, что мы решали ранее, но найти надо длину проводника. Используя формулу для сопротивления и закон Ома, получим:
В заключение стоит сказать, что такие задачи не являются трудными, но достаточно показательны. Из большого количества величин, данных в задаче, можно легко получить значение требуемой величины.
Список литературы
- Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
- Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
- Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети интернет
- Фестиваль педагогических идей «Открытый урок» (Источник)
- ПроШколу.ру (Источник)
- Электрознайка (Источник)
Домашнее задание
- Стр.
 106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010. - Длина и площадь поперечного сечения алюминиевого и железного проводов одинаковые. На них подается одинаковое напряжение. В каком из проводов сила тока будет больше?
- Можно ли вычислить напряжение в проводнике, зная силу тока в нем, его длину и площадь сечения, но не зная, из какого материала он сделан?
- Для уменьшения потерь энергии соединительные провода делают так, чтобы ток в них был как можно меньше. Для этого их должны делать большего или меньшего диаметра?
электрическое сопротивление — Определение Ом в основных единицах СИ прописью
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 42к раз
$\begingroup$
Один из способов, которым Википедия определяет Ом (этому также учат в школе):
$$1\Omega =1{\dfrac {{\mbox{V}}}{{\mbox{A}}}}$$
Это определение они описывают и словами: 9{2}}}$$
Мне действительно трудно понять, что это определение правильное. Понятно, что математические расчеты подтверждают это определение. Но как описать определение SI словами, подобными этому абзацу в Википедии?
Понятно, что математические расчеты подтверждают это определение. Но как описать определение SI словами, подобными этому абзацу в Википедии?
Редактировать: Как бы вы описали ? Хотя это не принято делать таким образом, я думаю, что описание этого таким образом может быть очень интересным.
единицы измерения электрического сопротивления
92$ потому, что это удобно и выражает отношение , которое вы хотите передать при использовании в другом месте (например, $F=-kx$ для пружины).Точно так же удобно «спрятать» основные единицы МКС в один термин, в данном случае потенциал $V$, чтобы формулу было легче запомнить и чтобы было передано отношение, в данном случае отношение между разность потенциалов, ток и сопротивление.
$\endgroup$
92}\cdot \frac1{\text{A}\cdot\text{s}}\cdot \frac1{\text{A}} \\ &= \frac{\text{J}/\text{C}}{\text{A}}\\ &= \frac{\text{V}}{\text{A}} \end{выравнивание} $$
Это всего лишь доказательство эквивалентности между двумя определениями, но не ожидайте получить красивое словесное описание определения СИ.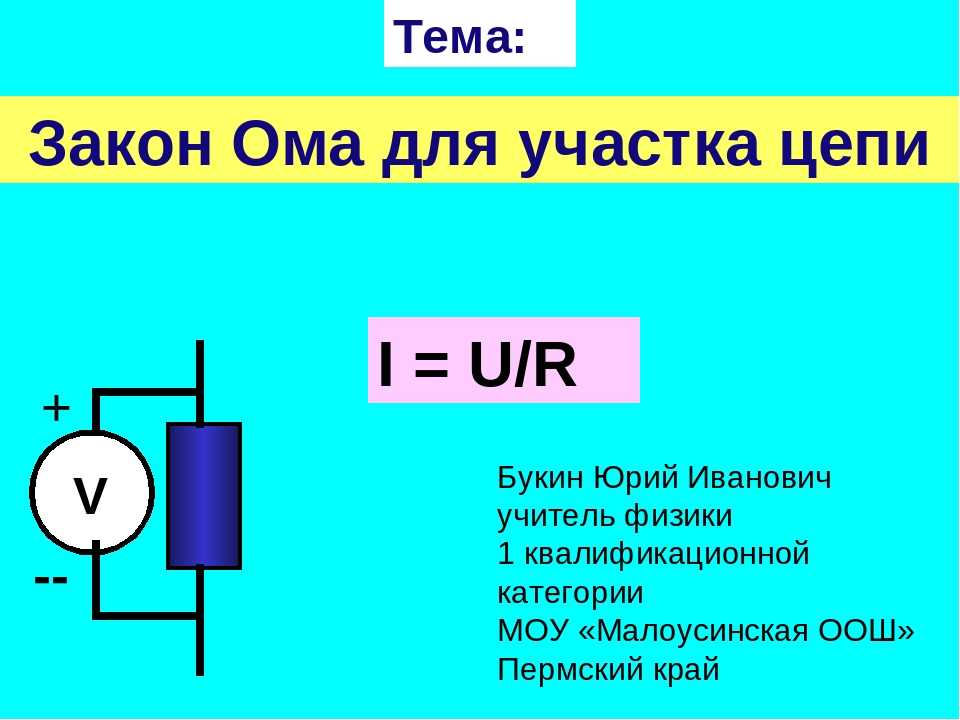 2}}$ 9{-2}}$
2}}$ 9{-2}}$
Итак, я думаю, вы можете сказать, что ом — это сопротивление, когда электрическая сила в один ньютон заставляет носитель заряда смещаться на один метр за одну секунду при токе в один ампер.
Я бы продолжил и сказал, что это сопротивление, когда носитель заряда в один килограмм ускоряется со скоростью один метр в секунду в квадрате, и это ускорение заставляет носитель заряда смещаться на один метр за одну секунду, производя ток в один ампер. Но я не очень уверен в части «носитель заряда в один килограмм».
$\endgroup$
3
$\begingroup$
Я бы описал это как (пример) 120 джоулей на кулон (120 вольт), деленное на 60 кулонов в секунду (60 ампер), равно 2 (Ом) сопротивления, что означает, что у вас есть 1/2 или 2 раза меньше ампер, чем Напряжение». так что, возможно, ом может быть n из VpA (количество вольт [SI] на ампер [SI] или, в этом случае, # N кг на заряд для каждого заряда в секунду). Но это по-прежнему дает формулы.
Но это по-прежнему дает формулы.
$\endgroup$
$\begingroup$
Я знаю, что отвечаю с опозданием на 3 года, но вот что я думаю.
Сопротивление в кабеле означает, насколько сильно электроны каждого кабеля сталкивают друг друга. Если они не сталкивают друг друга, они могут свободно двигаться с максимальной скоростью и не тратят энергию ни на что другое, кроме своего движения. Если они столкнутся друг с другом, половина их энергии превратится в тепло, и они потеряют половину своей скорости.
Теперь предположим, что у вас есть три кабеля из трех разных материалов, а так как материал разный, то сопротивление тоже разное.
Давайте также предположим, что у вас есть 1 миллион электронов, которые вы расположили в линию, один за другим.
Первый имеет небольшое сопротивление, поэтому, когда вы устанавливаете разницу в 1 В между началом и концом кабеля
вы получаете 1 А тока, что является большим числом, а это означает, что электроны движутся очень быстро от начала до конца. В любой точке кабеля проходит 1 c/s, что составляет (случайный выбор числа) около 500 электронов, проходящих один за другим каждую секунду. Кабель дал вам 1A = 1c/s для напряжения 1V, поэтому он имеет сопротивление 1Ω.
В любой точке кабеля проходит 1 c/s, что составляет (случайный выбор числа) около 500 электронов, проходящих один за другим каждую секунду. Кабель дал вам 1A = 1c/s для напряжения 1V, поэтому он имеет сопротивление 1Ω.
Второй кабель является худшим проводником, поэтому при подаче 1 В вы получаете только 0,5 А, проходя через которые 250 электронов один за другим проходят через любую точку кабеля в любую секунду
для 1 В вы получаете 0,5 А, поэтому у вас есть 2 Ом потому что электроны двигались медленнее.
Надеюсь, вы уловили суть. Сопротивление — это то, сколько ампер вы получите, если поместите разницу в 1 В по сторонам кабеля.
$\endgroup$
$\begingroup$
92. Единицы там тоже не описательные. Вместо этого мы просто думаем об этом с точки зрения соотношения потенциал/скорость потока. Другими словами, сопротивление на самом деле лучше всего рассматривать как вольт/ампер, отношение работы или потерь тепла на единицу потока заряда. Продолжая аналогию с водой, если вы поднимете воду только на 1 м в воздух, вам понадобится гораздо более широкая труба, чтобы получить 1 кг/с на конце, чем если бы вода была поднята в воздух на 10 м. Таким образом, для 1 В требуется крошечный резистор на 1 Ом, чтобы обеспечить 1 ампер. Если вы поднимете напряжение до 10 В, вы получите в 10 раз больше тока, проходящего через тот же резистор. Это имеет смысл, и это действительно то, что описывает сопротивление. 92s}$$
Продолжая аналогию с водой, если вы поднимете воду только на 1 м в воздух, вам понадобится гораздо более широкая труба, чтобы получить 1 кг/с на конце, чем если бы вода была поднята в воздух на 10 м. Таким образом, для 1 В требуется крошечный резистор на 1 Ом, чтобы обеспечить 1 ампер. Если вы поднимете напряжение до 10 В, вы получите в 10 раз больше тока, проходящего через тот же резистор. Это имеет смысл, и это действительно то, что описывает сопротивление. 92s}$$$$R = \frac{N-m}{A . С}$$ Поскольку работа на единицу заряда равна вольту (сила x расстояние / заряд = вольт)
$$R = \frac{V}{A}$$
$\endgroup$
1
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
электрических цепей. Может ли кто-нибудь интуитивно объяснить мне закон Ома?
спросил
Изменено 2 года, 3 месяца назад
Просмотрено 7к раз
$\begingroup$
Кто-нибудь может интуитивно объяснить мне закон Ома?
Я понимаю, что такое напряжение и как оно представляет собой электрическую потенциальную энергию, и что оно является интегралом напряженности электрического поля и т. д. Я также понимаю, что ток — это скорость, с которой заряд течет в определенной точке цепи, и я Я понимаю, что удельное сопротивление противоположно проводимости и в некотором роде аналогично трению, но я никак не могу получить полную картину и соединить 3 вместе.
электрические цепи электрический ток электрическое сопротивление напряжение
$\endgroup$
5
$\begingroup$
В дополнение к другим ответам, вот кое-что для интуиции:
$$V=RI$$
Большее «давление» $V$ (вернее: большее «давление» разница с одной стороны к другому) требуется, чтобы поток зарядов $I$ оставался постоянным, когда потоку сопротивляется сопротивление $R$. Тонкая проволока имеет большее сопротивление, чем толстая, $R=\rho L/A$, аналогично «узкому месту» в пробке.
$\endgroup$
14
$\begingroup$
Подумайте о водопроводе для близкой аналогии. Напряжение — это то, насколько сильно вы нажимаете, а ток — это то, сколько течет.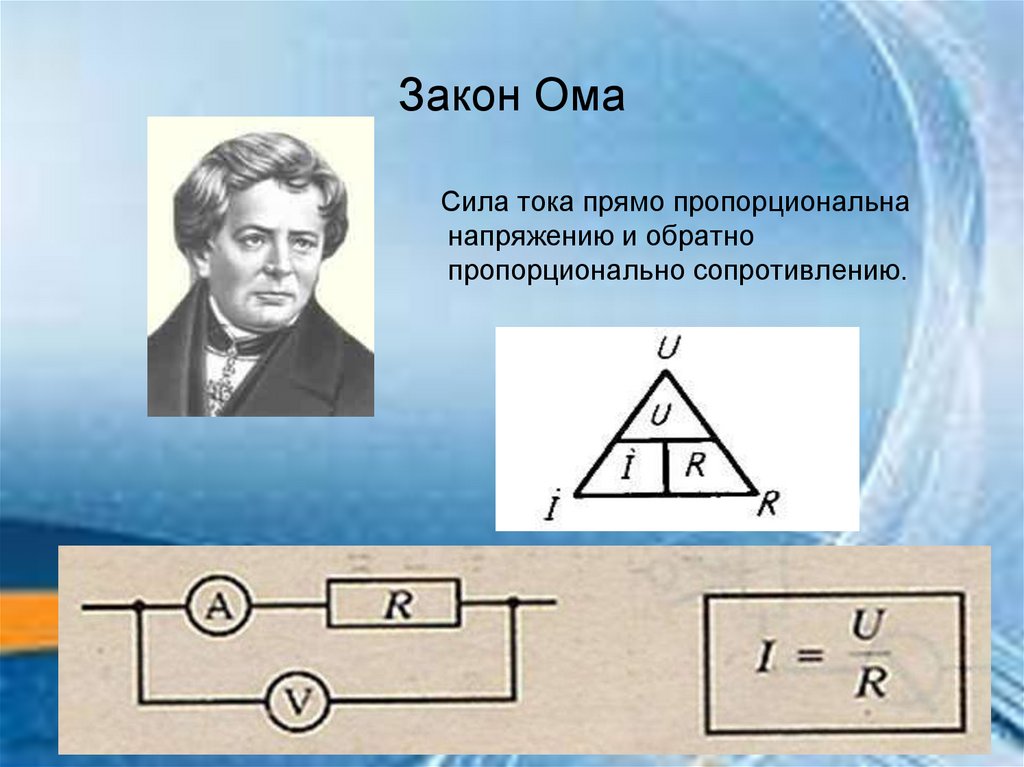 Соотношение пишется само собой: зачем вам получать больше или меньше потока от одного и того же насоса? Мера того, сколько усилий используется для получения потока (это имеет больше смысла, поскольку обратное: сколько потоков на единицу усилия) является интересным свойством, и оно определено так, чтобы точно соответствовать этому соотношению.
Соотношение пишется само собой: зачем вам получать больше или меньше потока от одного и того же насоса? Мера того, сколько усилий используется для получения потока (это имеет больше смысла, поскольку обратное: сколько потоков на единицу усилия) является интересным свойством, и оно определено так, чтобы точно соответствовать этому соотношению.
Проводимость — это сколько тока течет на единицу напряжения. Это определяется этим наблюдением. Закупорка, трение, сужение и тому подобное в трубе уменьшают поток при том же усилии. Например. узкая труба или изогнутый участок гофрированной трубы будут иметь более высокое сопротивление.
$\endgroup$
$\begingroup$
Вы видели модель Друде? Меня учили чему-то подобному еще в школе, и я запомнил это как интуитивный способ понимания.
Мы хотим понять, почему ток (скорость потока заряда) должен быть линейным с разностью потенциалов.
Идея друдов, как вы заметили, связана с трением.
Во-первых, ЭМ поле линейно по разности потенциалов. Это создает силу, действующую на электроны в проводнике.
Затем электроны ускоряются полем. Если бы их путь был беспрепятственным, они бы постоянно ускорялись. Вместо этого они «сталкиваются» с атомами в структуре проводника и «отскакивают» от них. В устойчивом состоянии скорость удельного импульса, передаваемого от отскоков, должна уравновешивать силу электромагнитного поля.
Ключевое наблюдение Друде состоит в том, что скорость электрона в момент столкновения будет прямо пропорциональна силе поля.
Пожалуйста, имейте в виду, что это всего лишь интуитивная модель, хотя и дающая удивительное понимание, несмотря на то, что она довольно грубая.
$\endgroup$
$\begingroup$
Если вы создадите цепь с любым компонентом (не только резисторами), подключенным к источнику напряжения, вы обнаружите, что ток, протекающий через компонент, зависит от напряжения. В большинстве случаев, чем выше напряжение, тем выше ток, который вы получите.
В большинстве случаев, чем выше напряжение, тем выше ток, который вы получите.
И наоборот, вы можете спросить: какое напряжение требуется, чтобы через компонент прошел определенный ток? Опять же, это зависит от тока, который вы хотите пропустить через компонент. Для получения малых токов достаточно малых напряжений. Для больших токов нужны большие напряжения.
Это качественное наблюдение объединяет почти все электрические компоненты. Но количественное изучение ситуации приведет к вопросу такого рода: сколько вольт мне нужно на ампер, чтобы через компонент протекал желаемый ток. Ответ зависит от компонента, а физическая величина называется сопротивлением.
Пример: резистор на два Ом. Два ома означают, что вам нужно два вольта на ампер. Итак, если вы хотите, чтобы через резистор проходило 10 ампер, вам нужно 20 вольт.
$\endgroup$
$\begingroup$
Если идти вглубь удельного сопротивления, то через точку пройти будет легко. Напряжение является причиной движения (потока) электронов, которые производят ток (заряд, деленный на время). Если у вас есть много электронов и атомов на пути (например, барьеры, например, когда вы бежите в толпе!) они уменьшают скорость потока заряда. Теперь ясно, что если барьеров больше (зависит от таких вещей, как геометрия, форма, материал), вы получите меньший ток.
Напряжение является причиной движения (потока) электронов, которые производят ток (заряд, деленный на время). Если у вас есть много электронов и атомов на пути (например, барьеры, например, когда вы бежите в толпе!) они уменьшают скорость потока заряда. Теперь ясно, что если барьеров больше (зависит от таких вещей, как геометрия, форма, материал), вы получите меньший ток.
$\endgroup$
$\begingroup$
Я всегда рассматривал это как аналогию «падению потенциальной энергии». ${M*g*H}$ — потенциальная энергия массы, которая удерживается на расстоянии $H$ над землей. Если он упадет на полпути, то он будет иметь половину потенциальной энергии.
Если ток проходит через резистор, падение напряжения или «падение потенциальной энергии» равно $I*R$. Теперь у вас меньше «движущей силы», чтобы протолкнуть желаемый ток через следующий резистор, если он есть.
Другими словами, батарея может пропускать только определенное количество тока через существующую систему резисторов.
$\endgroup$
1
$\begingroup$
На этом рисунке труба, наполненная водой, изображает провод, по которому течет электричество.
Ампер, также известный как ток, можно рассматривать как объем воды, и он контролируется размером провода (или трубки здесь, представленного в виде Ом, также известного как сопротивление). Вольты будут давлением воды или интенсивностью электричества.
Таким образом, размер провода ограничивает силу тока, так же как размер трубы ограничивает воду.
$\endgroup$
Закон Ома и взаимосвязь V-I-R
В физике есть определенные формулы, настолько мощные и всеобъемлющие, что они достигли уровня общеизвестности. Студент-физик столько раз записывал такие формулы, что запоминал их, даже не пытаясь. Конечно, для профессионалов в этой области такие формулы настолько важны, что они запечатлеваются в их сознании. В области современной физики есть E = m • c 2 . В области ньютоновской механики есть F net = m • a. В области волновой механики есть v = f • λ. А в области тока электричества есть ΔV = I • R.
В области современной физики есть E = m • c 2 . В области ньютоновской механики есть F net = m • a. В области волновой механики есть v = f • λ. А в области тока электричества есть ΔV = I • R.
Преобладающее уравнение, которое пронизывает изучение электрических цепей, это уравнение две точки на цепи ( ΔV ) эквивалентно произведению тока между этими двумя точками ( I ) и общее сопротивление всех электрических устройств между этими двумя точками ( R ). В оставшейся части этого раздела «Класс физики» это уравнение станет наиболее распространенным уравнением, которое мы видим. Это уравнение, часто называемое уравнением закона Ома , является мощным предсказателем взаимосвязи между разностью потенциалов, током и сопротивлением.
Закон Ома как показатель силы тока
Уравнение закона Ома можно преобразовать и выразить как
В качестве уравнения это служит алгебраическим рецептом для расчета тока, если известны разность электрических потенциалов и сопротивление. Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, оно представляет собой гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Сила тока в цепи прямо пропорциональна разности электрических потенциалов на ее концах и обратно пропорциональна общему сопротивлению внешней цепи. Чем больше напряжение батареи (т. е. разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток. Заряд течет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. В самом деле, двукратное увеличение напряжения батареи приведет к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
Тем не менее, хотя это уравнение служит мощным рецептом решения проблем, оно представляет собой гораздо больше. Это уравнение указывает две переменные, которые могут повлиять на величину тока в цепи. Сила тока в цепи прямо пропорциональна разности электрических потенциалов на ее концах и обратно пропорциональна общему сопротивлению внешней цепи. Чем больше напряжение батареи (т. е. разность электрических потенциалов), тем больше ток. И чем больше сопротивление, тем меньше ток. Заряд течет с наибольшей скоростью, когда напряжение батареи увеличивается, а сопротивление уменьшается. В самом деле, двукратное увеличение напряжения батареи приведет к двукратному увеличению тока (если все остальные факторы остаются равными). А увеличение сопротивления нагрузки в два раза приведет к уменьшению тока в два раза до половины его первоначального значения.
В таблице ниже эта взаимосвязь иллюстрируется качественно и количественно для нескольких цепей с различными напряжениями и сопротивлениями аккумуляторов.
Сопротивление | ||||
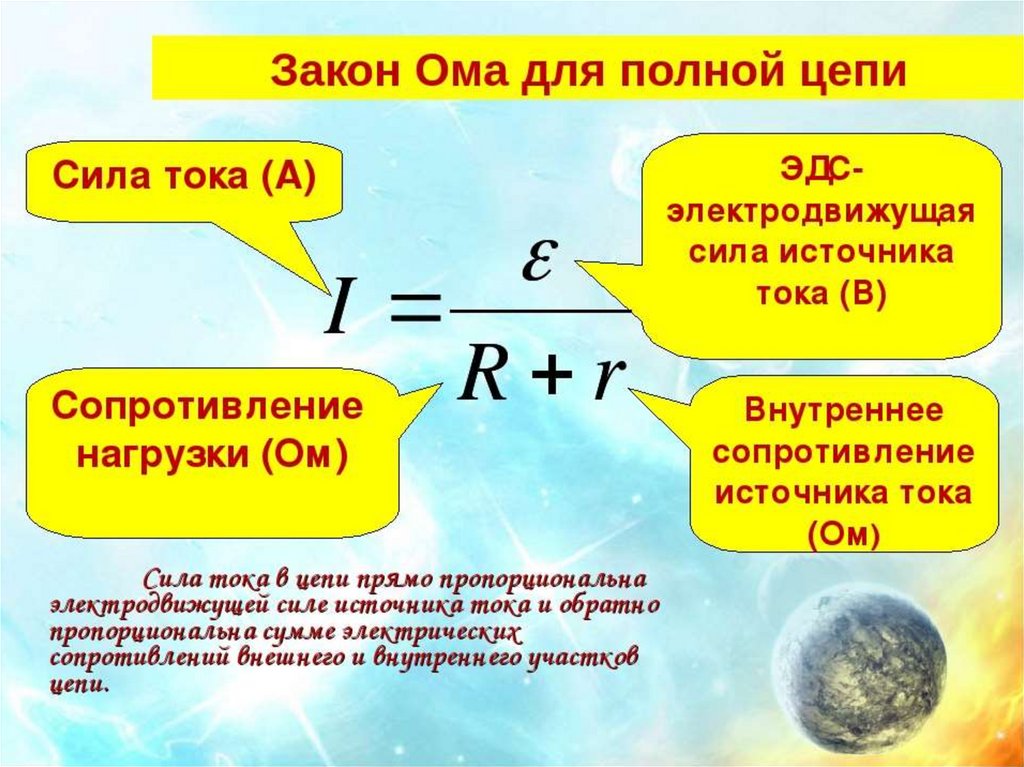 | ||||
Строки 1, 2 и 3 показывают, что удвоение и утроение напряжения батареи приводит к удвоению и утроению тока в цепи. Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления позволяет вдвое уменьшить ток в цепи.
Сравнение строк 1 и 4 или строк 2 и 5 показывает, что удвоение общего сопротивления позволяет вдвое уменьшить ток в цепи.
Поскольку на ток в цепи влияет сопротивление, резисторы часто используются в цепях электроприборов, чтобы влиять на величину тока, присутствующего в его различных компонентах. Увеличивая или уменьшая величину сопротивления в конкретной ветви цепи, производитель может увеличивать или уменьшать величину тока в этой ветви . Кухонные приборы, такие как электрические смесители и регуляторы освещенности, работают, изменяя ток на нагрузке путем увеличения или уменьшения сопротивления цепи. Нажатие различных кнопок на электрическом миксере может изменить режим с смешивания на взбивание, уменьшив сопротивление и позволив большему току в миксере. Точно так же поворот диска на диммерном переключателе может увеличить сопротивление его встроенного резистора и, таким образом, уменьшить ток.
На приведенной ниже схеме изображена пара цепей, содержащих источник напряжения (батарейный блок), резистор (лампочка) и амперметр (для измерения силы тока). В какой цепи лампочка имеет наибольшее сопротивление? Нажмите кнопку «Просмотреть ответ», чтобы убедиться, что вы правы.
В какой цепи лампочка имеет наибольшее сопротивление? Нажмите кнопку «Просмотреть ответ», чтобы убедиться, что вы правы.
Уравнение закона Ома часто изучается в физических лабораториях с использованием резистора, аккумуляторной батареи, амперметра и вольтметра. Амперметр — это прибор, используемый для измерения силы тока в заданном месте. Вольтметр — это устройство, оснащенное щупами, которые можно прикоснуться к двум точкам цепи, чтобы определить разность электрических потенциалов в этих точках. Изменяя количество элементов в аккумуляторной батарее, можно изменять разность электрических потенциалов во внешней цепи. Вольтметр можно использовать для определения этой разности потенциалов, а амперметр можно использовать для определения тока, связанного с этим ΔV. Батарея может быть добавлена к блоку батарей, и процесс может быть повторен несколько раз, чтобы получить набор данных I-ΔV. График зависимости I от ΔV даст линию с наклоном, эквивалентным обратной величине сопротивления резистора. Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.
Это можно сравнить с заявленным производителем значением, чтобы определить точность лабораторных данных и достоверность уравнения закона Ома.
Величины, символы, уравнения и единицы!
Склонность обращать внимание на единицы измерения — неотъемлемая черта любого хорошего студента-физика. Многие трудности, связанные с решением задач, могут быть связаны с неспособностью уделить внимание единицам. По мере того, как все больше и больше электрических величин и соответствующих им метрических единиц вводятся в этом разделе учебника «Класс физики», становится все более важным организовать информацию в вашей голове. В таблице ниже перечислены некоторые количества, которые были введены до сих пор. Символ, уравнение и соответствующие метрические единицы также перечислены для каждой величины. Было бы разумно часто обращаться к этому списку или даже сделать свою собственную копию и дополнять ее по мере продвижения модуля. Некоторые учащиеся считают полезным сделать пятую колонку, в которой указано определение каждой величины.
(он же напряжение) | ΔV = I • R | |||
I = ΔV/R | или В/Ом | |||
(больше будет) | ||||
R = ΔV / I | ||||
ΔPE = P • t | Вт • с |
(Обратите внимание, что символ единицы измерения C представляет единицу измерения Кулоны.)
В следующем разделе Урока 3 мы еще раз рассмотрим количественную мощность. Новое уравнение для мощности будет введено путем объединения двух (или более) уравнений из приведенной выше таблицы.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного конструктора цепей постоянного тока. Вы можете найти его в разделе Physics Interactives на нашем сайте. Конструктор цепей постоянного тока предоставляет учащимся набор для создания виртуальных схем. Легко перетащите источник напряжения, резисторы и провода на рабочую область. Соедините их, и у вас есть схема. Добавьте амперметр для измерения тока и используйте датчики напряжения для определения падения напряжения. Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Это так просто. И не нужно беспокоиться о поражении электрическим током (если, конечно, вы не читаете это в ванной).
Посетите: DC Circuit Builder
1. Что из следующего приведет к уменьшению тока в электрической цепи? Выберите все подходящие.
а. уменьшить напряжение
б. уменьшить сопротивление
в. увеличить напряжение
д. увеличить сопротивление
2. Некоторая электрическая цепь содержит батарею с тремя ячейками, провода и лампочку. Что из нижеперечисленного заставит лампочку светить менее ярко? Выберите все подходящие.
а. увеличить напряжение батареи (добавить еще одну ячейку)
б. уменьшить напряжение батареи (удалить элемент)
в. уменьшить сопротивление цепи
д.
увеличить сопротивление цепи
3. Вас, вероятно, предупредили о необходимости избегать контакта с электроприборами или даже электрическими розетками мокрыми руками. Такой контакт более опасен, когда ваши руки мокрые (а не сухие), потому что мокрые руки вызывают ____.
а. напряжение цепи должно быть выше
б. напряжение цепи должно быть ниже
в. ваше сопротивление должно быть выше
д. ваше сопротивление должно быть ниже
эл. ток через вас будет ниже
4. Если сопротивление цепи увеличить втрое, то ток в цепи будет ____.
а. одна треть
б. в три раза больше
с. без изменений
д. … бред какой то! Не было бы никакой возможности сделать такой прогноз.
5. Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
Если напряжение в цепи увеличить в четыре раза, то ток в цепи будет ____.
а. одна четвертая часть
б. в четыре раза больше
в. без изменений
д. … бред какой то! Не было бы никакой возможности сделать такой прогноз.
6. Цепь соединена с источником питания, резистором и амперметром (для измерения тока). Амперметр показывает ток 24 мА (миллиампер). Определить новый ток, если напряжение источника питания было…
а. … увеличилось в 2 раза, а сопротивление осталось постоянным.
б. … увеличилось в 3 раза, а сопротивление осталось постоянным.
в. … уменьшилось в 2 раза, а сопротивление осталось постоянным.
д. … оставался постоянным, а сопротивление увеличивалось в 2 раза.
эл. … оставался постоянным, а сопротивление увеличивалось в 4 раза.
ф. … оставался постоянным, а сопротивление уменьшалось в 2 раза.
г. … увеличилось в 2 раза, а сопротивление увеличилось в 2 раза.
час. … увеличилось в 3 раза, а сопротивление уменьшилось в 2 раза.
я. … уменьшилось в 2 раза, а сопротивление увеличилось в 2 раза.
7. Используйте уравнение закона Ома, чтобы дать численные ответы на следующие вопросы:
а. Электрическое устройство с сопротивлением 3,0 Ом пропустит через себя ток силой 4,0 А, если на устройство будет воздействовать падение напряжения ________ Вольт.
б. Когда на электрический нагреватель подается напряжение 120 В, через нагреватель потечет ток силой 10,0 ампер, если сопротивление составляет ________ Ом.
в. Фонарик, который питается от 3 Вольт и использует лампочку с сопротивлением 60 Ом, будет иметь силу тока ________ Ампер.
8. Используйте уравнение закона Ома, чтобы определить недостающие значения в следующих цепях.
9. См. вопрос 8 выше. В цепях схем А и Б каким способом регулировали ток в цепях? А в цепях схем С и Г каким методом регулировали ток в цепях?
Следующий раздел:
Перейти к следующему уроку:
Закон Ома: значение, формула и сопротивление
Закон Ома был сформулирован в 1827 году немецким физиком Георгом Симоном Омом на основе экспериментов, которые он проводил с простыми электрическими цепями, содержащими провода различной длины.
Закон Ома является одним из самых фундаментальных и важных принципов электрических цепей.
Закон Ома утверждает, что напряжение в двух точках электрической цепи прямо пропорционально 0211 текущий , проходящий между этими двумя точками. Константа пропорциональности равна сопротивлению .
Константа пропорциональности равна сопротивлению .
Формула закона Ома:
Здесь V — напряжение на проводнике, I — ток, протекающий через проводник, а R — электрическое сопротивление проводника. Сопротивление в законе Ома всегда равно постоянному значению и может быть рассчитано путем проведения серии измерений напряжения и тока в подходящем диапазоне значений перед нанесением данных на прямолинейный график и вычислением его градиента.
Прежде чем продолжить объяснение закона Ома, мы должны рассмотреть некоторые основные понятия, касающиеся электрических цепей.
Закон Ома: электрические цепи
Электрическая цепь представляет собой набор электрических компонентов, соединенных проводниками, по которым может проходить электрический ток. Электрический ток состоит из движущихся электронов, которые обтекают провод под действием приложенного напряжения. Чтобы электрические компоненты могли пропускать электрический заряд, они должны быть изготовлены из электропроводящие материалы . Проводник представляет собой материал или электрический компонент, который способствует прохождению заряда (электрического тока) в одном или нескольких направлениях. Мы говорим, что такие материалы являются хорошими проводниками электричества.
Проводник представляет собой материал или электрический компонент, который способствует прохождению заряда (электрического тока) в одном или нескольких направлениях. Мы говорим, что такие материалы являются хорошими проводниками электричества.
Пример электрической цепи, адаптировано из изображения: MikeRun CC BY-SA 4.0
Металлы являются хорошими проводниками электричества, поэтому мы создаем электрические цепи, такие как те, которые используются в бытовой электронике, из меди. , который обладает высокой проводимостью.
При изучении электрических цепей мы часто проводим различие между омическими проводниками и неомическими проводниками.
Омический проводник — это проводник, который подчиняется закону Ома .
График зависимости напряжения от силы тока омического проводника имеет линейную зависимость, чего нельзя сказать о неомических проводниках.
График зависимости напряжения от тока для омического и неомического материала, Iñaki Caparros-StudySmarter Originals
Неомический проводник не подчиняется закону Ома . Зависимость между напряжением и током для неомического проводника нелинейна.
Зависимость между напряжением и током для неомического проводника нелинейна.
Поведение неомических проводников не обязательно такое же, как показано на рисунке выше. Важной особенностью является то, что существует нелинейная зависимость между током и напряжением, что означает, что график зависимости напряжения от тока не является прямой линией. Некоторыми примерами неомических проводников являются нити накала лампы или некоторые полупроводники, такие как транзисторы или диоды.
Некоторые материалы плохо проводят электричество. Мы называем такие материалы или электрические компоненты, изготовленные из таких материалов, как изоляторы .
Изоляторы могут использоваться для замедления или остановки потока заряда и могут использоваться в различных реальных условиях, например, в качестве пластикового покрытия электрических проводов, которое защищает нас от удара электрическим током.
Закон Ома: напряжение
Напряжение также известно как разность потенциалов.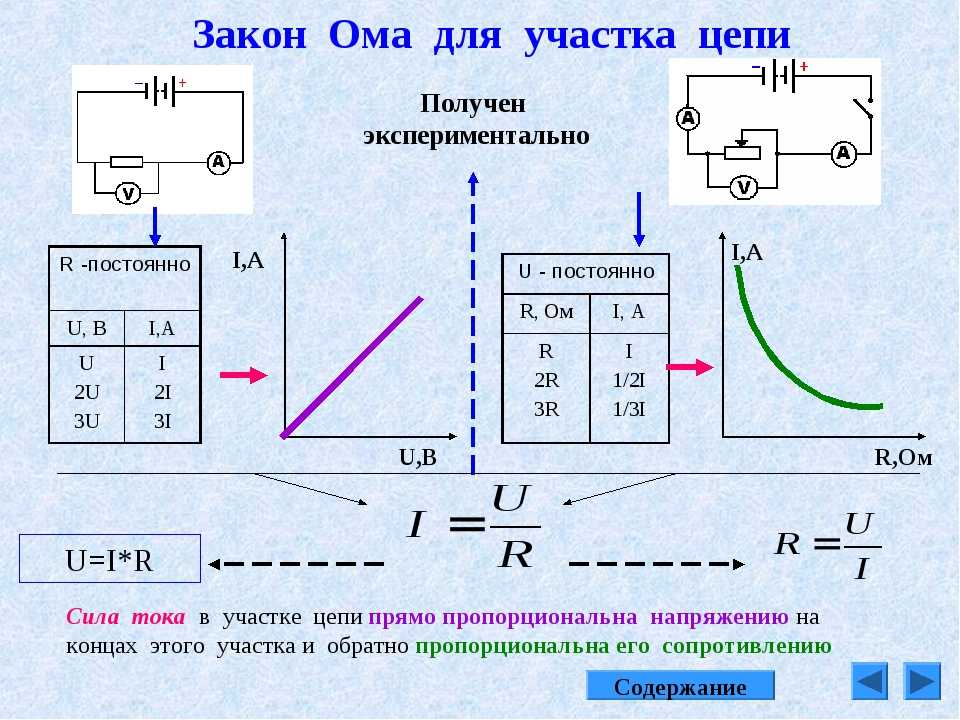 Разность потенциалов между двумя точками проводника равна разности электрических потенциалов между двумя точками. Разность потенциалов в электрической цепи создается элементами или батареями. В стандартных единицах мы выражаем разность потенциалов/напряжение в вольт (В).
Разность потенциалов между двумя точками проводника равна разности электрических потенциалов между двумя точками. Разность потенциалов в электрической цепи создается элементами или батареями. В стандартных единицах мы выражаем разность потенциалов/напряжение в вольт (В).
В электрических цепях напряжение генерируется ячейкой или батареей, у которых есть положительная клемма с более высоким потенциалом и отрицательная клемма с более низким потенциалом.
Закон Ома: Ток
Ток – это скорость протекания электрического заряда. Прибор, который мы используем для измерения силы тока в электрической цепи, называется амперметром . Стандартной единицей электрического тока является А мпер (А).
Закон Ома: сопротивление
Сопротивление — это мера сопротивления проводников потоку электричества. Стандартной единицей сопротивления является O hm (Ом). Сопротивление электрического проводника увеличивается с длиной и уменьшается с толщиной. Сопротивление также зависит от типа материала, из которого он изготовлен.
Сопротивление электрического проводника увеличивается с длиной и уменьшается с толщиной. Сопротивление также зависит от типа материала, из которого он изготовлен.
Алюминиевый провод имеет более высокое сопротивление, чем медный провод той же длины и площади поперечного сечения, что означает, что медь является лучшим проводником электричества, чем алюминий. Но алюминиевый провод имеет меньшее сопротивление, чем медный провод, в четыре раза превышающий его длину.
Чтобы увеличить электрическое сопротивление электрической цепи, мы можем добавить компонент, называемый резистором . Фиксированный резистор подчиняется закону Ома, и разные постоянные резисторы имеют разные постоянные сопротивления для разных целей.
Примеры резисторов с различным сопротивлением в электрических цепях, wikipedia.org
Вывод закона Ома
Точного вывода формулы закона Ома не существует. Как упоминалось ранее, закон был сформулирован в 1827 году Георгом Симоном Омом, но это эмпирический закон, а это означает, что он изначально был основан на наблюдениях, а не выведен из первых принципов.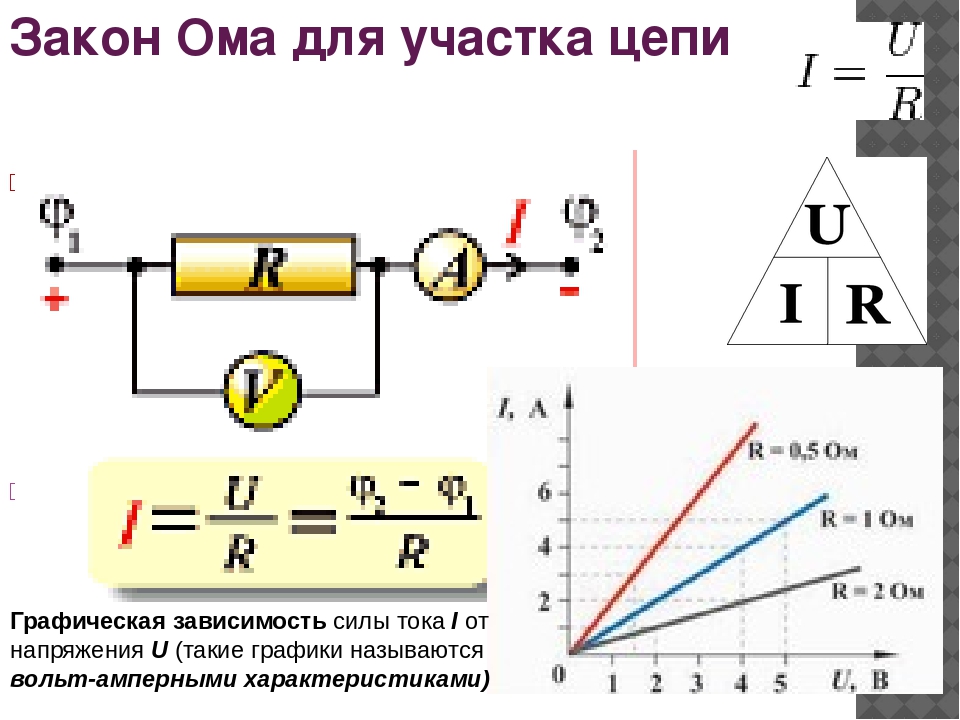 Ом открыл закон, наблюдая за поведением омических проводников при подаче на них тока. Основываясь на полученных данных, Ом констатировал наличие линейной зависимости между током и силой тока, но теоретически закон не вывел.
Ом открыл закон, наблюдая за поведением омических проводников при подаче на них тока. Основываясь на полученных данных, Ом констатировал наличие линейной зависимости между током и силой тока, но теоретически закон не вывел.
Новый взгляд на формулу закона Ома
Теперь, когда мы выяснили, что означает каждый термин в законе Ома, давайте вспомним формулу: уравнение, что существует прямая зависимость между напряжением и силой тока. Мы говорим, что напряжение на проводнике прямо пропорционально протекающему по нему току. Это означает, что если мы увеличим ток, проходящий через проводник, в определенный раз, напряжение увеличится во столько же раз, и наоборот. Например, если мы удвоим разность потенциалов на проводе, ток, проходящий через него, также удвоится.
Мы можем изменить формулу закона Ома, чтобы сделать сопротивление или ток объектом формулы. Если мы знаем значения любых двух переменных в законе Ома, мы можем вычислить значение оставшейся отсутствующей переменной. Например, если мы знаем ток, проходящий через компонент в электрической цепи, и мы также знаем разность потенциалов между двумя сторонами компонента, мы можем рассчитать сопротивление проводника по следующей формуле:
Например, если мы знаем ток, проходящий через компонент в электрической цепи, и мы также знаем разность потенциалов между двумя сторонами компонента, мы можем рассчитать сопротивление проводника по следующей формуле:
Это по-прежнему закон Ома, только измененный, чтобы сделать R предметом формулы. Точно так же, если мы знаем разность потенциалов на компоненте и его сопротивление, мы можем вычислить ток I, проходящий через него: мы знаем значения двух других.
Треугольник закона Ома с напряжением (V), током (I) и сопротивлением (R), Iñáki Caparros-StudySmarter Originals
Этот треугольник называется треугольником закона Ома . Чтобы напомнить себе, как вычислять каждый из V, I и R, мы создали треугольник с V в верхнем сегменте и I и R в нижних сегментах. Чтобы вычислить значение любой из переменных в нижней части треугольника, мы просто делим значение V на значение другой оставшейся переменной в нижней части треугольника. V просто рассчитывается путем умножения значений двух переменных в нижнем сегменте треугольника, а именно I и R.
Если вам сложно переставить уравнения, вы можете предпочесть вычислить V, I и R с помощью треугольника закона Ома. Только не забудьте нарисовать треугольник и разделить его на три части: часть вверху, содержащая V, и две нижние части, содержащие I и R.
Батарея 9 В производит ток силой 3 А в проводе. Каково сопротивление провода?
Для решения этой задачи воспользуемся законом Ома. Используя наши знания о преобразовании уравнений или законе треугольника Ома, мы находим, что формула для вычисления сопротивления:
Чтобы найти любую из двух переменных нижнего уровня треугольника закона Ома, мы делим напряжение на другую переменную нижнего уровня. В этом случае делим V на I, чтобы найти R.
Следовательно, сопротивление провода в данном примере равно:
Определить напряжение электрической цепи с током 0,5 А и сопротивлением 20 Ом .
В этом случае нам нужно использовать первую форму закона Ома. Формулу закона Ома для напряжения находим по треугольнику закона Ома:
Теперь мы можем ввести данные для электрической цепи, представленные в вопросе, подставив 0,5 А для тока и 20 Ом для сопротивления: переключатель замкнут.
Электрическая цепь с напряжением V= 30 В и сопротивлением R= 10 Ом, Iñaki Caparros-StudySmarter Originals
Как видно из рисунка выше, электрическая цепь имеет разность потенциалов 30 В на своих клеммах, и резистор имеет сопротивление 10 Ом. Мы должны изменить первоначальную форму формулы закона Ома. Если мы посмотрим на треугольник закона Ома, мы можем изменить формулу для расчета тока:
Используя значения переменных, представленных на рисунке, мы можем рассчитать ток следующим образом:
Закон Ома – основные выводы в двух точках электрической цепи
пропорционально проходящему через нее току , а константой пропорциональности является сопротивление . Материалы, плохо проводящие электричество, называются изоляторами .
Материалы, плохо проводящие электричество, называются изоляторами . Определения и основные понятия физики
Знаете ли вы, что электрические цепи повсеместно используются в нашей повседневной жизни? От простой проводки на выключателе лампочки до сложных интегральных схем, управляющих устройством, которое вы используете, электрические схемы окружают нас повсюду.
Узнавая больше о том, как работают электрические цепи, мы можем глубже погрузиться в ключевые физические понятия, связанные с темой сопротивления, и связанные с ним понятия, связанные с электричеством, такие как закон Ома. Вот что вам нужно знать, чтобы начать!
Определение и законы сопротивления
Сопротивление – это мера противодействия протеканию тока. Это противостояние возникает из-за повторяющихся столкновений носителей заряда в тестируемом материале друг с другом. Знаете ли вы, что сопротивление материала также зависит от площади поперечного сечения и длины? Чем меньше площадь поперечного сечения и чем длиннее материал, тем выше будет сопротивление!
Закон Ома
Закон Ома гласит, что разность потенциалов (напряжение) на металлическом проводнике прямо пропорциональна току, проходящему через него, при условии, что физические условия не меняются. Это справедливо для омических материалов, сопротивление которых постоянно. Этот закон позволяет нам рассчитать соответствующие значения, когда мы знаем разность потенциалов (V), ток (I) и сопротивление (R) материала.
Этот закон позволяет нам рассчитать соответствующие значения, когда мы знаем разность потенциалов (V), ток (I) и сопротивление (R) материала.
Единицей сопротивления в системе СИ является Ом (Ом). 1 Ом сопротивления позволит 1 Вольту разности потенциалов генерировать 1 Ампер тока. Следующая формула описывает эту связь:
R = V / I
(R – сопротивление (Ом), V – разность потенциалов на компоненте (В), I – ток (А))
Как экспериментально измерить сопротивление материала
Что вам нужно:
1. Вольтметр
2. Источник питания (например, батарейки)
3. Амперметр
Ниже приведены шаги для измерения сопротивления и определения сопротивления металлического проводника:
1. Подключите электрическую схему согласно приведенному выше рисунку, где V — вольтметр, A — амперметр, Ω — неизвестный резистор.
2. Убедитесь, что токоизмерительный амперметр включен последовательно с материалом резистора.
3. Подключите вольтметр к резистору.
Подключите вольтметр к резистору.
4. Измерьте текущие показания амперметра. Это будет значение «I» в формуле.
5. Измерьте разность потенциалов на резисторе с помощью вольтметра. Это будет значение «V» в формуле.
6. Теперь можно рассчитать сопротивление материала по формуле: R =V/I
Измерение эффективного сопротивления резисторов
Существует два основных метода соединения резисторов или других устройств. Резисторы могут быть соединены параллельно или последовательно. Как найти эффективное сопротивление резисторов при последовательном и параллельном соединении?
Резисторы, соединенные последовательно
Для последовательно соединенных резисторов существует только один путь прохождения тока, и ток от одного резистора течет к следующему. Эффективное сопротивление (R) трех резисторов R1, R2 и R3 составляет: 9 Ом.0005
R = R 1 + R 2 + R 3
Если в ряду n резисторов, эффективное сопротивление рассчитывается следующим образом:
R = R 1 + R 4 + … + R n
Совет по исследованию! Важно отметить, что для эффективного сопротивления при последовательном соединении R должно быть больше, чем наибольшее из индивидуальных сопротивлений.
Подавайте заявку!
Каково эффективное сопротивление этой цепи?
R = 6 Ом + 6 Ом = 12 Ом
Резисторы, включенные параллельно
Резисторы в параллельных цепях расположены друг напротив друга, обеспечивая несколько путей прохождения тока. Эффективное сопротивление R в резисторах R1, R2 и R3, включенных параллельно, выглядит следующим образом:
Если имеется n резисторов, включенных параллельно, эффективное сопротивление рассчитывается следующим образом:
Совет для экзамена! Важно отметить, что для параллельных соединений эффективное сопротивление R всегда меньше, чем сопротивление каждого отдельного элемента.
Подавайте заявку!
Каково эффективное сопротивление этой цепи?
R = 1/0,0117 = 85,6 Ом
Бонус: как мы можем измерить сопротивление в цепи с параллельными и последовательными соединениями?
Мы можем найти общее сопротивление, рассчитав эффективное сопротивление резисторов, включенных параллельно, а затем добавив это значение сопротивления к резисторам, включенным последовательно, для получения общего сопротивления.
Сопротивление последовательного резистора: 6 Ом
Сопротивление параллельного резистора:
R = 1/0,0167 = 6 Ом общее сопротивление цепи аналогично тому, как мы сделали бы с обычной последовательной схемой.
Общее сопротивление цепи: 6 Ом + 6 Ом = 12 Ом. провода, А — площадь поперечного сечения провода.
Повышение температуры металлических проводников
График I/V металлического проводника изображается прямой линией, проходящей через оси X и оси Y. Сопротивление не зависит от тока, так как они подчиняются закону Ома. В металле сопротивление известно как уменьшение скорости электронов из-за столкновения, которое происходит с ионами решетки.
Если температура металлического проводника останется постоянной, размер колебаний в ионах решетки останется прежним. Таким образом, сопротивление металлического проводника также останется прежним. Вот пример графика I/V для металлического проводника при постоянной температуре:
Повышение температуры лампы накаливания
На графике I/V при увеличении тока отношение V/I также увеличивается. Таким образом, при повышении температуры лампы накаливания увеличивается и ее сопротивление.
Таким образом, при повышении температуры лампы накаливания увеличивается и ее сопротивление.
Разность потенциалов в лампе накаливания будет увеличиваться вместе с током из-за рассеивания энергии и увеличения тепла, что приводит к повышению температуры. Вот пример графика I/V для лампы накаливания.
График I/V для полупроводникового диода
Диод — это полупроводник, который имеет высокое сопротивление и низкое сопротивление в противоположных направлениях. Если к диоду приложена разность потенциалов в направлении низкого сопротивления, он будет смещен в прямом направлении. Если разность потенциалов приложена в направлении высокого сопротивления, она будет иметь обратное смещение.
Если разность потенциалов обратного смещения слишком велика, диод может выйти из строя, в результате чего ток станет бесконечным и произойдет короткое замыкание. Вот график I/V для полупроводникового диода.
Заключение
О сопротивлении электрических токов можно рассказать так много, и если вы не уверены, это может показаться ошеломляющим. Если вы так считаете, вам следует записаться на уроки физики уже сегодня! Вы сможете прояснить все темы, которые вам неясны, а ваш преподаватель может помочь вам с определениями, примерами и приложениями важных концепций физики.
Если вы так считаете, вам следует записаться на уроки физики уже сегодня! Вы сможете прояснить все темы, которые вам неясны, а ваш преподаватель может помочь вам с определениями, примерами и приложениями важных концепций физики.
Запишитесь на уроки физики сегодня и улучшите свой опыт изучения физики!
История закона Ома
Вы когда-нибудь задумывались, сколько из того, что мы делаем, вы могли бы понять с нуля? Сейчас завязать шнурки может показаться простым делом, но детям трудно овладеть этим навыком, а придумать его в первый раз еще сложнее. То же самое относится и ко многим технологиям, которые мы используем каждый день. Вы бы придумали компьютерную мышь или даже компьютер, если бы их еще не было? Однако, конечно же, одно из самых простых и полезных математических уравнений, лежащих в основе электроники, — закон Ома — было бы легко понять, верно? Часто это первое, что узнаешь об электронике, но понять это в первый раз оказалось довольно сложно.
Парнем, обнаружившим связь, был Георг Ом, учитель математики и физики средней школы из Кёльна. Чего вы, возможно, не знаете, так это того, что в первый раз, когда он опубликовал это, он ошибся. Но, к счастью для нас, он понял свою ошибку и смог ее исправить.
Чего вы, возможно, не знаете, так это того, что в первый раз, когда он опубликовал это, он ошибся. Но, к счастью для нас, он понял свою ошибку и смог ее исправить.
Это не просто хорошая идея…
Закон Ома прост. Для линейного резистора ток через резистор пропорционален приложенному к нему напряжению. Константа пропорциональности обратно пропорциональна значению сопротивления в, что неудивительно, омах. Это просто причудливый математический способ сказать, что I=E/R, где E — напряжение, I — ток, а R — сопротивление. Конечно, алгебра скажет вам, что E=IR и R=E/I.
Дважды отмерь
Куча Вольта из меди и цинка.Хотя сегодня это кажется очевидным, в 1800-х годах это было не так уж и много. Некоторые сведения об электричестве были известны еще в Древней Греции. Однако до 1800 года, когда Вольта создал «гидроэлектрическую» батарею — то есть это был мокрый элемент — не было простого способа создать постоянный ток для научных исследований.
Таким образом, с 1800 по 1820 год наука могла использовать гальваническую батарею для производства электричества. Но было большое ограничение. Не было возможности измерить силу тока в цепи. В 1781 году Генри Кавендиш экспериментировал с лейденскими банками (в основном это был высоковольтный конденсатор) и стеклянными трубками разного диаметра и длины, наполненными физиологическим раствором. Не имея возможности измерить ток, он использовал свое тело и отмечал, насколько сильным был удар. Он отметил, что ток связан с напряжением, но не упомянул об этом другим ученым, и это оставалось в значительной степени неизвестным, пока Максвелл не опубликовал результат в 1879 году..
Но было большое ограничение. Не было возможности измерить силу тока в цепи. В 1781 году Генри Кавендиш экспериментировал с лейденскими банками (в основном это был высоковольтный конденсатор) и стеклянными трубками разного диаметра и длины, наполненными физиологическим раствором. Не имея возможности измерить ток, он использовал свое тело и отмечал, насколько сильным был удар. Он отметил, что ток связан с напряжением, но не упомянул об этом другим ученым, и это оставалось в значительной степени неизвестным, пока Максвелл не опубликовал результат в 1879 году..
Проблема измерения тока была решена в 1820 году, когда Эрстед показал, что ток создает магнитное поле. Это привело Швайггера и Поггендорфа к изобретению гальваноскопа в 1821 году. По сути, это катушка с компасом внутри. Ток в проводе отклонит стрелку компаса, а величина отклонения скажет вам, какой ток был в проводе.
Ом хотел изучить природу протекания электрического тока и построил батарею и гальваноскоп. Его эксперименты были направлены на описание силы тока, протекающего по проводу заданной длины. Он измерял ток, протекающий от батареи, используя только свой гальваноскоп, а затем вставлял отрезок проволоки и отмечал разницу в показаниях.
Он измерял ток, протекающий от батареи, используя только свой гальваноскоп, а затем вставлял отрезок проволоки и отмечал разницу в показаниях.
Ой…
В 1825 году Ом объявил миру свою формулу в статье, озаглавленной «Предварительное уведомление о законе, согласно которому металлы проводят контактное электричество». Не совсем кликбейтный заголовок. Однако возникла проблема: формула у него была неверная.
Имейте в виду, что были не все единицы, к которым мы привыкли сегодня, поэтому формула Ома измеряла V, уменьшение отклонения стрелки, вызванное тестовой проволокой. Ключевыми факторами были длина провода X и приложенное напряжение M, а также удельное сопротивление провода R. Неправильная формула была:
V=M log(1+X/R)
С тем, что мы знаем сегодня, вы можете посмотреть на это и сразу же понять, что это неверно. Однако в 1825 году это было не так очевидно. Статья была принята к публикации, но прежде чем она отправилась в печать, Ом провел новые эксперименты с другим источником питания. Он понял, что его формула неверна, но было слишком поздно.
Он понял, что его формула неверна, но было слишком поздно.
Исправление
Проблема заключалась в аккумуляторе. Хотя сегодня это может показаться очевидным, в 1825 году не было общего представления о том, что напряжение жидкостного элемента будет меняться под нагрузкой. Друг Ома Поггендорф предложил ему использовать термоэлектрическую батарею — то, что мы назвали бы термопарой.
В «Определении закона, по которому металлы проводят контактное электричество, вместе с изложением теории аппарата Вольта и гальваноскопа Швайггера» Ом понял правильно. (Ему нравились длинные заголовки.) Формула не совсем походила на то, что мы думаем о законе Ома, но на самом деле это так, если учесть сопротивление источника питания. В современных обозначениях мы бы написали:
E=I*(Rb+R)
Здесь Rb — сопротивление батареи. В 1827 году Ом также опубликовал «Гальваническую батарею, трактованную математически», показывающую, что, по крайней мере, его способность писать хорошие заголовки улучшилась. Все в порядке?
Все в порядке?
Not So Fast
Казалось бы, все обрадуются закону Ома и сразу же начнут его применять. Этого не произошло. В то время наука была настроена скептически — и вы можете возразить, что это так и сейчас — и правящие круги того времени считали, что закон Ома слишком прост, чтобы ускользать от внимания сообщества в течение тридцати с лишним лет. Было также сильное мнение, что Ом поспешил с формулировкой, и отвращение к его практическим экспериментальным методам. Истеблишмент считал Ома — более или менее — позером.
Министр образования Германии заявил, что «профессор, проповедующий такие ереси, недостоин преподавать науку». Другие говорили, что работа была «паутиной обнаженных фантазий».
В течение шести лет мир по большей части продолжал игнорировать закон Ома. Однако в 1831 году Пуйе опубликовал статью, в которой он, сам того не зная, заново открыл формулу Ома. Вероятно, он был разочарован, когда после публикации закона Пуйе другие указали, что Ом проделал ту же работу несколькими годами ранее.
Errata
Вам может показаться странным, что Ом опубликовал неверную формулу или Пуйе повторил эксперимент, но тогда все было совсем по-другому. На самом деле Барлоу пытался решить ту же проблему в 1825 году и опубликовал открытие, согласно которому сила тока в проводе обратно пропорциональна квадратному корню из длины провода.
Этот результат был неправильным, но соответствовал данным, потому что Барлоу не смог учесть внутреннее сопротивление батареи, как это сделал Ом. Даже Барлоу признал, что не уверен в правильности своего закона. С положительной стороны, Барлоу действительно изобрел колесо Барлоу, которое представляло собой умную форму двигателя, использующего металлическое колесо, магнит и ртуть.
Признание
В конце концов, работа Ома была признана, и он не только получил должное признание, но и его имя до сих пор у нас на устах каждый день.





 106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
106–108: вопросы № 1–4. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.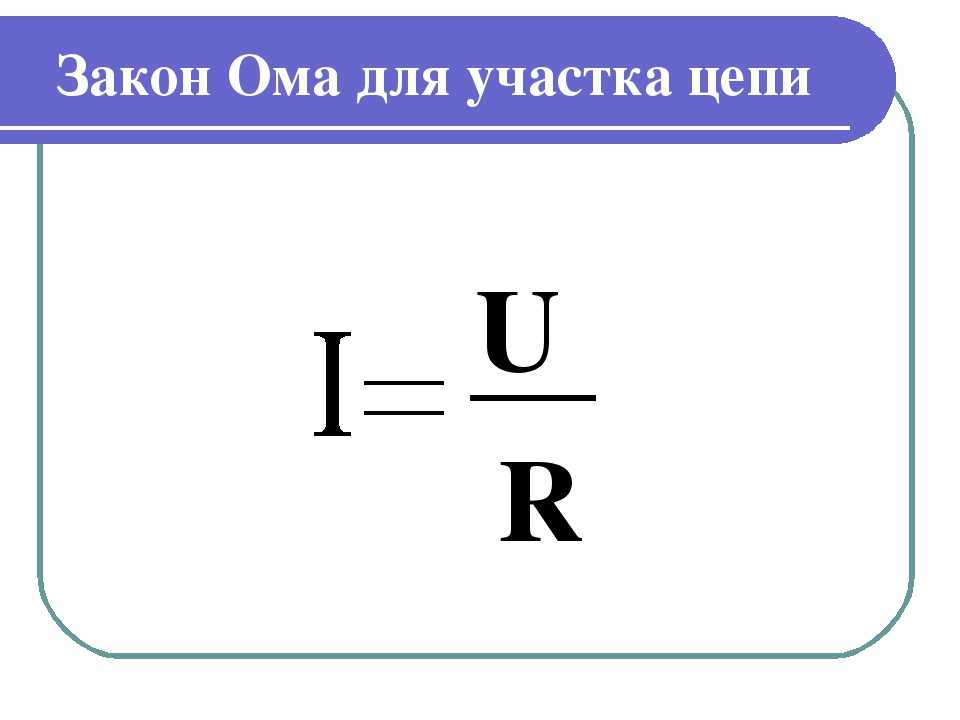 )
) увеличить сопротивление цепи
увеличить сопротивление цепи