Вектор. Определение и основные понятия
- Главная
- Справочник
- Геометрия
- Вектора
- Вектор. Определение и основные понятия
- Обозначение вектора
- Длина вектора
- Нулевой вектор
- Длина вектора на плоскости
- Длина вектора в трехмерном пространстве
- Длина вектора в n-мерном пространстве
- Коллинеарные вектора
- Сонаправленные вектора
- Противоположно направленные вектора
- Компланарные вектора
- Равные вектора
Вектор — это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины.
Обозначение вектора
Вектор началом которого есть точка , а концом — точка , обозначается . Также вектора обозначают одной маленькой буквой, например
Направление вектора (от начала к концу) на рисунках отмечается стрелкой.
Длина вектора
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора .
Нулевой вектор
Нулевой вектор обычно обозначается как .
Длина нулевого вектора равна нулю.
Любая точка пространства также может рассматриваться как вектор. Такой вектор называется нулевым. Начало и конец нулевого вектора совпадают, и он не имеет какого-либо определенного направления.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Длина вектора на плоскости
Длина вектора в трехмерном пространстве
Длина вектора в n-мерном пространстве
Коллинеарные вектора
Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами
Сонаправленные вектора
Два коллинеарных вектора и называются сонаправленными векторами, если их направления совпадают:
Противоположно направленные вектора
Два коллинеарных вектора и называются противоположно направленными векторами, если их направления совпадают:
Компланарные вектора
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.![]()
Равные вектора
Вектора и называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны.
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
, если и .
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Вектора Формулы Геометрия Алгебра Теория Обозначения 31276
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Координаты вектора
Координатами вектора называются проекции вектора на оси координат
Вектора Формулы Геометрия Алгебра Теория Обозначения
Сложение и вычитание векторов
Суммой двух векторов a и b называется третий вектор c, проведенный из начала a к концу b, если начало вектора b совпадает с концом вектора a.
 Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.Вектора Формулы Геометрия Алгебра Теория Обозначения
Декартовы координаты и векторы в пространстве
Декартовы координаты — система координат, состоящая из двух перпендикулярных осей.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Умножение вектора на число
Произведением вектора u≠0 на число λ≠0 называется вектор w, модуль которого равен |λ||u|, направление которого совпадает с вектором u при λ>0 и противоположно ему при λ
Вектора Формулы Геометрия Алгебра Теория Обозначения
Скалярное произведение векторов
Скалярным произведением векторов u и v называется произведение их модулей на косинус угла между ними.
Вектора Формулы Геометрия Алгебра Теория Обозначения
Векторное произведение векторов
Векторным произведением векторов u и v называется третий вектор w, модуль которого равен произведению модулей векторов u и v на синус угла θ между ними и перпендикулярен им.

Вектора Формулы Геометрия Алгебра Теория Обозначения
Смешанное произведение векторов
Смешанным произведением трех векторов u, v и w называется скалярное произведение вектора u на векторное произведение векторов v и w
Вектора Формулы Геометрия Алгебра Теория Обозначения
Русский алфавит
Современный русский алфавит состоит из 33 букв.
Литература 1 класс Литература Алфавит Азбука
Что такое баррель. Чему равен 1 баррель в литрах?
Американский нефтяной баррель равен 42 галлонам в английской системе мер или 158,988 л в метрической системе.
Масса и вес Масса Физика Теория Единицы измерения
Что такое Ватт
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.
Электротехника Формулы Физика Теория Электричество
Четырёхугольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.

Фигуры Математика Формулы Геометрия Теория Фигуры
1 mBTC это сколько BTC ? Чему равен 1 сатоши ? Что такое сатоши ?
Bitcoin, Биткойн, часто Биткоин (от англ. bit — единица информации «бит», англ. coin — «монета») — пиринговая (как торрент или e-mule) электронная платёжная система, использующая одноимённую виртуальную валюту.
Разное Единицы измерения Деньги Справочник
Формула периметра трапеции
Периметр трапеции равен сумме длин всех четырех сторон
Формулы периметра Расчёт Площадь Математика Тригонометрия Формулы Теория
Формула площади треугольника
Площадь треугольника равна произведению половины основания треугольника (a) на его высоту (h)
Формулы площади Площадь Формулы Геометрия
Закон Авогадро
В равных объемах газов (V) при одинаковых условиях (температуре Т и давлении Р) содержится одинаковое число молекул.
Законы термодинамики Формулы Физика Теория 10 класс Закон Термодинамика Динамика
Обозначения Дирака — Azure Quantum
- Статья
- Чтение занимает 10 мин
Нотация Дирака — это язык, который разработан для точного выражения состояния в квантовой механике. Примеры в этой статье можно рассматривать как предложения и использовать их для краткого выражения идей в квантовых вычислениях.
Примеры в этой статье можно рассматривать как предложения и использовать их для краткого выражения идей в квантовых вычислениях.
Ограничения нотации для вектора-столбца
Хотя нотация для векторов-столбцов широко используется в линейной алгебре, она часто может иметь громоздкий вид в квантовых вычислениях, особенно при работе с несколькими кубитами. Например, когда вы определяете $\psi$ как вектор, то не всегда очевидно, является ли $\psi$ вектором-строкой или вектором-столбцом. Таким образом, если $\phi$ и $\psi$ — векторы, то опять-таки непонятно, задан ли $\phi\psi$, поскольку в определенном контексте формы $\phi$ и $\psi$ могут быть не совсем ясны. Помимо неоднозначности в формах векторов, выражение даже простых векторов с использованием линейной алгебраические нотации может иметь громоздкий вид. Например, если вам нужно описать $n$-кубитное состояние, в котором каждый кубит принимает значение $0$, то формально выразите состояние как
$$\begin{bmatrix}1 \\ 0 \end{bmatrix}\otimes\cdots\otimes\begin{bmatrix}1 \\ 0 \end{bmatrix}.
Ниже приведен прием, который используется для описания квантовых состояний, которые кодируют значения 0 и 1 (однокубитные состояния на вычислительной базе):
$$\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\ket{{0},\qquad\begin{bmatrix} 0 \\ 1 \end{bmatrix}=\ket{{1}. $$
Пример. Представление операции Адамара с помощью нотации Дирака
Следующую нотацию часто используют для описания состояний, возникающих в результате применения вентиля Адамара к $\ket{0}$ и $\ket{1}$. Эти состояния соответствуют единичным векторам в направлениях $+x$ и $-x$ в сфере Блоха:
$$\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 \\ 1 \end{bmatrix}=H\ket{0}=\ket{+},\qquad\frac{1}{\sqrt{{2}}\begin{bmatrix} 1 \\ -1 \end{bmatrix}=H\ket{{1}=\ket{{-} . $$
С помощью нотации Дирака эти состояния также можно развернуть в виде сумм $\ket{0}$ и $\ket{1}$:
$$\ket{+}=\frac{{1}{\sqrt{2}}(\ket{0} + \ket{1}),\qquad\ket{{-}=\frac{{1}{\sqrt{{2}}(\ket{{0} — \ket{1}). $$
Векторы вычислительной базы
Эти состояния часто называют вычислительной базой по следующей причине: каждое квантовое состояние всегда можно выразить в виде сумм векторов вычислительной базы, и такие суммы можно легко выразить с помощью нотации Дирака. Обратное утверждение также верно в том смысле, что состояния $\ket{+}$ и $\ket{-}$ также образуют базис для квантовых состояний. Это подтверждается тем фактом, что
Обратное утверждение также верно в том смысле, что состояния $\ket{+}$ и $\ket{-}$ также образуют базис для квантовых состояний. Это подтверждается тем фактом, что
$$\ket{{0}=\frac{1}{\sqrt{2}}(\ket{+} + \ket{-}),\qquad\ket{{1}=\frac{{1}{\sqrt{{2}}(\ket{+} — \ket{-}). $$
В качестве примера нотации Дирака рассмотрим braket $\braket{0 | 1}$, который является внутренним произведением $0$ и $1$. Это можно записать как
$$\braket{0 | 1}=\begin{bmatrix} 1 & 0 \end{bmatrix}\begin{bmatrix}0\\ 1\end{bmatrix}=0. $$
Этот пример говорит о том, что $\ket{{0}$ и $\ket{{1}$ являются ортогональными векторами, т. е. $\braket{0 | 1}=\braket{1 | 0}=0$. Кроме того, по определению $\braket{0 | 0}=\braket{1 | 1}=1$, что означает, что два вектора вычислительной базы также можно назвать ортонормальными.
Эти ортонормальные свойства пригодятся в следующем примере. Если у вас есть состояние $\ket{\psi}={\frac{3}{5}}\ket{{1} + {\frac{{4}{5}}\ket{0}$, то так как $\braket{1 | 0}=0$ вероятность измерения $1$ составляет
$$\big|\braket{1 |\psi}\big|^2=\left|\frac{{3}{5}\braket{1 | 1} +\frac{{4}{5}\braket{1 | 0}\right|^2=\frac{{9}{{25}.![]() $$
$$
Нотация тензорного произведения
Нотация Дирака также включает неявную структуру тензорного произведения. Эта структура важна, поскольку в квантовых вычислениях вектор состояния, описанный двумя некоррелированными квантовыми регистрами, является тензорным произведением двух векторов состояния. Сжатое описание структуры тензорного произведения или его отсутствие имеет критически важное значение, если необходимо разъяснить квантовые вычисления. Структура тензорного произведения подразумевает, что вы можете записать $\psi\otimes\phi$ для любых двух векторов квантового состояния $\phi$ и $\psi$ как $\ket{\psi}\otimes\ket{\phi}$. Но, как правило, запись $\otimes$ между векторами не требуется, и вы можете просто записать $\ket{\psi}\ket{\phi}=\ket{\psi\phi}$. Дополнительные сведения о векторах и тензорных произведениях см. в статье Векторы и матрицы в квантовых вычислениях. Например, состояние с двумя кубитами, инициализированное в нулевом состоянии, задано как
$$\ket{0}\otimes\ket{0}=\ket{{0}\ket{{0}=\ket{{00}=\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}. \dagger$ для векторов квантовых состояний $\psi$ и $\phi$. Самый простой и, вероятно, наиболее распространенный пример этой нотации
\dagger$ для векторов квантовых состояний $\psi$ и $\phi$. Самый простой и, вероятно, наиболее распространенный пример этой нотации
$$\ket{{0}\bra{0}=\begin{bmatrix}1\\ 0 \end{bmatrix}\begin{bmatrix}1&0 \end{bmatrix}=\begin{bmatrix}1 &0\\ 0 &0\end{bmatrix}\qquad\ket{1}\bra{1}=\begin{bmatrix}0\\ 1 \end{bmatrix}\begin{bmatrix}0&1 \end{bmatrix}=\begin{bmatrix}0 &0\\ 0 &1\end{bmatrix}. $$
Ketbra часто называют проекторами, так как они проецируют квантовое состояние на зафиксированное значение. Так как эти операции не являются унитарными (и даже не сохраняют норму вектора), то квантовый компьютер не может детерминированно применить проектор. Однако проекторы выполняют полезную задачу, описывая воздействие, которое оказывает измерение на квантовое состояние. Например, если вы измеряете состояние $\ket{\psi}$ и получаете значение $0$, тогда результирующее преобразование состояния в результате измерения будет
$$\ket{\psi}\rightстрелка \frac{(\ket{{0}\bra{{0})\ket{\psi}}{|\braket{0 |\psi}|}=\ket{{0},$$
что и ожидалось, когда в результате измерения состояния получено значение $\ket{0}$. {\dagger}$ (то есть $\rho$ — это эрмитова матрица).
{\dagger}$ (то есть $\rho$ — это эрмитова матрица).
В совокупности эти условия гарантируют, что матрицу $\rho$ можно рассматривать как ансамбль. Оператор плотности для вектора квантового состояния $\ket{\psi}$ имеет вид $\rho =\sum_i p_i \ket{\psi_i}\bra{\psi_i}$, то есть разложение собственного значения $\rho$. В этом случае $\rho$ описывает ансамбль $\rho ={\ket{\psi_i}\text{ с вероятностью }p_i}$.
Чистые квантовые состояния — это такие состояния, которые характеризуются одним кет-вектором или волновой функцией и не могут быть записаны в виде статистического сочетания (или выпуклой комбинации) других квантовых состояний. Смешанное квантовое состояние — это статистический ансамбль чистых состояний.
Эта концепция представления состояния в виде матрицы, а не вектора зачастую удобна тем, что она позволяет удобный способ представления вычислений вероятности, а также позволяет описать как статистическую неопределенность, так и квантовую неопределенность в рамках одно и той же математической модели.![]() 2$ можно получить так:
2$ можно получить так:
print((rho_pure ** 2).tr())
0.9999999999999996
Для однокубитных систем смешанные состояния могут отображаться на сфере Блоха так же, как векторы состояния. Чистые состояния — это те состояния, которые находятся на поверхности сферы Блоха, а смешанные состояния в общем случае могут находиться «внутри» нее.
import matplotlib.pyplot as plt plt.figure(figsize=(6, 6)) bloch = qt.bloch.Bloch() bloch.add_states([rho_pure], kind='point') print(bloch.show())
plt.figure(figsize=(6, 6)) bloch = qt.bloch.Bloch() bloch.add_states([rho_mixed], kind='point') bloch.show()
Состояние в центре сферы Блоха является максимально смешанным. В отличие от чистых состояний максимально смешанное состояние возвращает результаты 50/50 для любого идеального измерения Паули.
Дополнительные сведения об операторах плотности и чистых и смешанных состояниях можно получить в одной из справочных книг, представленных в разделе Рекомендуемое содержимое.![]() {\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.
{\otimes n}\ket{0}$. Это экспоненциально более короткое описание состояния не только имеет то преимущество, что можно аргументировать его в рамках классической модели, но оно также четко определяет операции, которые необходимо распространить через программный стек для реализации алгоритма. По этой причине Q# предназначен для создания последовательностей ворот, а не квантовых состояний, однако на теоретическом уровне эти две перспективы эквивалентны.
Вектор (математика) | это… Что такое Вектор (математика)?
Вектор
У этого термина существуют и другие значения, см. Вектор.
Ве́ктор — понятие, определяемое в разных разделах математики различно.
Содержание
|
Пусть — некоторое поле с аддитивной операцией +, мультипликативной операцией *, аддитивной единицей 0 и мультипликативной единицей 1. Пусть — некоторая абелева группа с единицей . Если существует операция , такая что для любых и для любых выполняются соотношения:
1. ,
2. ,
3. ,
4. ,
тогда называется векторным пространством над полем , элементы V называются векторами, элементы F — скалярами, а указанная операция — умножением вектора на скаляр.
Понятие вектора в стандартном евклидовом n-мерном пространстве
Вектор в арифметическом n-мерном пространстве
Является частным случаем определения вектора в абстрактной алгебре. Если в качестве взять поле действительных чисел с операциями сложения и умножения. , где — декартова степень множества R; для операцию «+» зададим следующим образом: , нейтральный элемент: =(0,…,0), обратный элемент: ; операцию умножения на скаляр: . Тогда вектор, задаваемый кортежем длиной n, состоящим из действительных чисел является арифметическим вектором векторного пространства над полем действительных чисел .
n-мерное пространство задается как — декартова степень множества действительных чисел, точка — как кортеж длины n из действительных чисел, что соответствует определению пространства как множества точек.
Вектор в планарной евклидовой геометрии (связанный вектор) — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора.
Два вектора равны, если разности по каждой из координат с одинаковыми номерами конечной и начальной точки для этих векторов равны. Эти разности называются пространственными координатами вектора.
Эти разности называются пространственными координатами вектора.
Свободный вектор задается классом всех равных связанных векторов и полагается равным каждому из этих связанных векторов и таким образом может быть определен как вектор в арифметическом пространстве (кортеж чисел длины n (пространственных координат равных ему связанных векторов) с операциями сложения и умножения на скаляр).
Результатом операций со связанными векторами принимается вектор, начальная точка которого совпадает с начальной точкой первого слагаемого при сложении векторов и начальной точке исходного вектора при умножении вектора на скаляр.
Нуль-вектор — вектор, начало и конец которого совпадают.
Также существует более распространенное определение вектора как направленного отрезка, но оно требует определения прямой и отрезка в n-мерном пространстве.
Прямая, на которой лежит ненулевой вектор с началом в точке , заданный свободным вектором с пространственными координатами — множество точек , удовлетворяющее условию:
Отрезок MN — множество всех точек O(удовлетворяющих условию ), все различные точки которого принадлежат одной прямой, точки M и N называются концевыми точками отрезка. Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
Отрезок называется направленным, если его концевые точки упорядочены. Если концы отрезка совпадают, он состоит из 1 точки.
При введение скалярного произведения, угла и длины вектора, задающей расстояние между двумя точками как расстояние между начальной и конечной точками вектора(как показано ниже([1], [2], [3])) векторное пространство становится евклидовым нормированным пространством и при n=3 соответствует модели физического трехмерного пространства; при n=2 — плоскости этого пространства; при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю; при n=0 существует только одна точка(задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор; пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трёхмерно.
Скалярное произведение определяется по формуле: , [1]
(где — пространственные координаты векторов )
Длина вектора: , [2]
(где — пространственные координаты вектора. )
)
Угол между двумя векторами (где — пространственные координаты векторов ) определяется через скалярное произведение:
, [3]
Вектор в линейном пространстве
Линейное пространство — это множество элементов, называемых векторами, над которыми определённым образом определены операции сложения и умножения на число. В любом линейном пространстве можно выделить особую систему векторов, называемых базисом линейного пространства. Количество векторов в базисе равно размерности пространства. Любой вектор из пространства можно представить, как линейную комбинацию базисных векторов. То есть, если у нас есть базис , то , где — это поле, над которым определенно линейное пространство .
Выбор базиса в линейном пространстве неоднозначен, однако коэффициенты векторов при измерении базиса связанны определённым образом. Пусть есть базис и . Причём: . Матрица , полученная из коэффициентов называться матрицей перехода от базиса к базису и связывает координаты вектора в различных базисах следующем образом: . Связь между матрицами перехода между двумя базисами: . Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
Связь между матрицами перехода между двумя базисами: . Векторы могут иметь различную природу: направленные отрезки, матрицы, числа, функции и другие, однако все линейные пространства одной размерности изоморфны между собой.
Операции над векторами
Пусть в линейном пространстве выбран базис и в нём представлены вектора , , тогда суммой векторов будет называется следующий вектор: .
Пусть есть число , тогда произведением вектора на число будет называться следующий вектор:
Два ненулевых вектора и называются коллинеарными, если .
Евклидовы и нормированные пространства
Основная статья: Евклидово пространство
Основная статья: Нормированное пространство
Функция (в другом обозначении ), ставящая любым двум векторам в соответствие число и удовлетворяющая следующим аксиомам:
- Линейность по первому аргументу:
- Эрмитова симметричность: (в случае если векторы определены над полем действительных чисел, то )
- Положительная определённость: тогда и только тогда, когда ,
называется скалярным произведением вектора на вектор . Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
Конечномерное линейное пространство с введённым скалярным произведением называется евклидовым. Для пространств над полем комплексных чисел иногда применяют термин унитарное пространство.
Два ненулевых вектора называются ортогональными, если .
Базис евклидова пространства называется ортогональным, если . Базис называется ортонормированным, если , где — символ Кронекера.
Скалярное произведение является билинейной формой, поэтому его можно записать в следующем виде:
, где — матрица Грамма.
В случае ортонормированного базиса матрица будет единичной, и тогда, если , , то
в случае действительного пространства и в случае комплексного.
Так же в линейном пространстве можно ввести понятие нормы. Это функция, ставящая в соответствие любому вектору линейного пространства неотрицательное вещественное число и удовлетворяющая следующим аксиомам:
- тогда и только тогда, когда .
- .
- .
Угол между векторами определяется, как
.
Геометрическая интерпретация
Вектор в геометрии — упорядоченная пара точек (или направленный отрезок), одна из которых называется началом, вторая — концом вектора. Операция сложения вводится по правилу треугольника: пусть есть векторы и . Оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.
Операция умножения вектора на число вводится следующим образом: пусть есть вектор и число , тогда вектор получается изменением длины вектора в раз. Направление вектора сохраняется, если и меняется, если .
Нулевой вектор — такой, начало которого совпадает с его концом.
Противоположным данному называется вектор, начало которого совпадает с концом данного, а конец с началом данного (то есть такой, сумма которого с данным дает нулевой вектор).
Два геометрических вектора называются ортогональными, если они (как направленные отрезки) перпендикулярны друг другу.
Норма геометрического вектора определяется как длина соответвующего ему отрезка. Чаще всего называется модулем вектора и обозначается как .
Свободные, скользящие и фиксированные векторы
Иногда вместо того, чтобы рассматривать в качестве векторов множество всех равных направленных отрезков, берут только некоторую модификацию этого множества (фактормножество). Так, говорят о «свободных» (когда отождествляются все равные по длине и направлению направленные отрезки, считаясь полностью равными или — одним и тем же вектором), «скользящих» (отождествляются между собой все направленные отрезки, равные в смысле свободных векторов, начала и концы которых расположены на одной прямой) и «фиксированных» векторах (по сути дела, просто о направленных отрезках, когда разное начало означает уже неравенство векторов).
Иными словами, подразумевается, что свободный вектор может быть перенесен (параллельным переносом) как угодно (так, чтобы его начало совпало с любой точкой пространства), однако не перестает от этого быть собой.![]() Скользящий же вектор может так же свободно переноситься только вдоль прямой, на которой он лежит, а фиксированный вообще не может переноситься. То есть его приложение к другой точке не имеет смысла; в частности любые операции, такие как сложение или вычитание, фиксированного вектора с фиксированным вектором, имеющим другое начало («приложенным к другой точке») не определены (не имеют смысла).
Скользящий же вектор может так же свободно переноситься только вдоль прямой, на которой он лежит, а фиксированный вообще не может переноситься. То есть его приложение к другой точке не имеет смысла; в частности любые операции, такие как сложение или вычитание, фиксированного вектора с фиксированным вектором, имеющим другое начало («приложенным к другой точке») не определены (не имеют смысла).
- Важно заметить, что все операции над векторами (сложение, умножение на число, скалярное и векторное произведения, вычисление модуля или длины, угла между векторами итд) в принципе определены одинаково для всех типов векторов (свободных, скользящих или фиксированных), различие в типах сводится в этом отношении только к тому, что для скользящих и фиксированных наложено ограничение на возможность осуществления операций между двумя векторами, имеющими разное начало (так, для двух фиксированных векторов запрещено — или лишено смысла — сложение, если их начала отличаются; однако для всех случаев, когда эта операция разрешена — или имеет смысл — она такова же, как для свободных векторов).
 Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса итп), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Поэтому часто тип вектора вообще явно не указывается, подразумевается, что он очевиден из контекста. Более того, один и тот же вектор в зависимости от контекста задачи может рассматриваться как фиксированный, скользящий или свободный, например, в механике векторы сил, приложенных к телу, могут суммироваться независимо от точки приложения при нахождении равнодействующей (и в статике, и в динамике при исследовании движения центра масс, изменения импульса итп), но не могут складываться друг с другом без учета точек приложения при вычислении вращающего момента (также и в статике и в динамике).
Можно дать такие строгие определения:
Говорят, что свободные векторы и равны, если найдутся точки и такие, что четырёхугольники и — параллелограммы.
- Замечание. «Ухищрение» (введение дополнительных точек) в определении равенства касается, прежде всего, случая, когда точки располагаются на одной прямой. В противном случае определение выглядит проще:
Говорят, что свободные векторы и , не лежащие на одной прямой, равны, если четырёхугольник — параллелограмм.
Говорят, что скользящие векторы и равны, если
- точки располагаются на одной прямой,
- векторы и равны между собой как свободные векторы.
Неформально говоря, скользящему вектору разрешено двигаться вдоль его прямой без изменения величины и направления.
- Замечание. Скользящие векторы особо употребимы в механике. Простейший пример скользящего вектора в механике — сила. Перенос такого начала вектора вдоль прямой, на которой он лежит, не меняет момента силы ни относительно никакой точки; перенос же его на другую прямую, даже если не менять величины и направления вектора, может вызвать изменение его момента (скорее даже почти всегда вызовет): поэтому нельзя рассматривать силу как свободный вектор.
Говорят, что фиксированные векторы и равны, если попарно совпадают точки и , и .
Вектором в одном случае называется направленный отрезок, а в других случаях различные векторы — это разные классы эквивалентности направленных отрезков, определяемые неким конкретным отношением эквивалентности.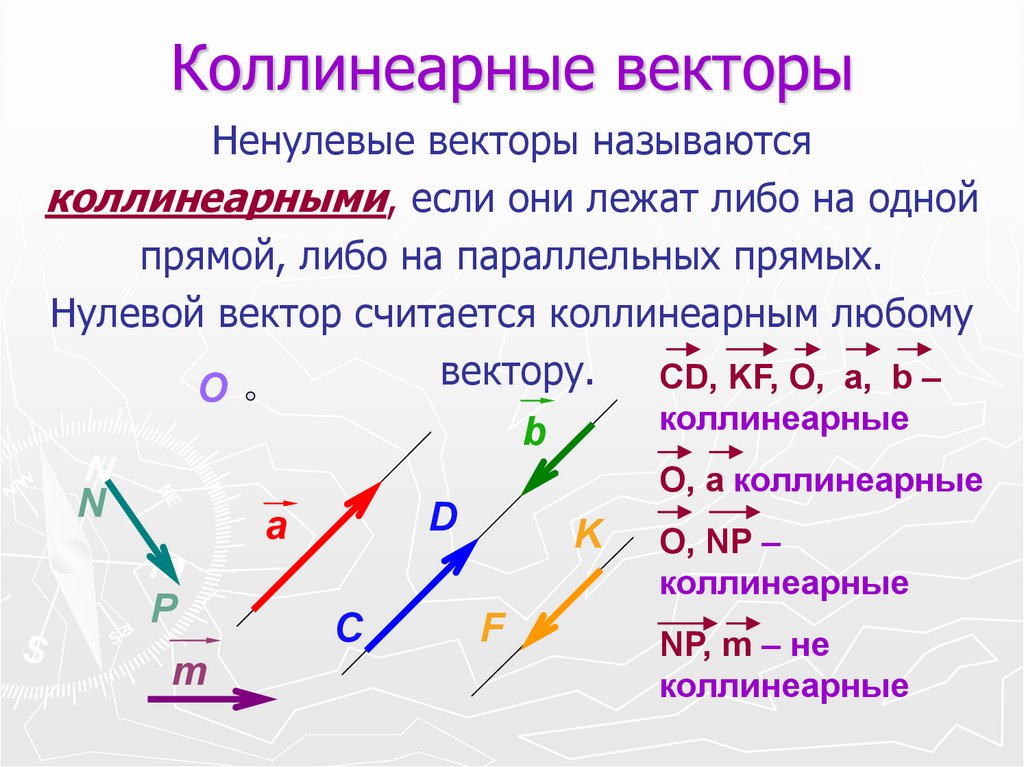 Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Причем отношение эквивалентности может быть разным, определяя тип вектора («свободный», «фиксированный» итд). Проще говоря, внутри класса эквивалентности все входящие в него направленные отрезки рассматриваются как совершенно равные, и каждый может равно представлять весь класс.
Операции над векторами
Сложение
Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый их которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, так как не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, то есть удобно для сложения векторов с началом в одной точке, в добавок имея то преимущество, что в нем более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.
Два вектора u, v и вектор их суммы
Правило треугольника. Для сложения двух векторов и по правилу треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора. Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной: начало второго вектор совмещается с концом первого, начало третьего — с концом второго и т. д., сумма же n векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом n-го (то есть изображается направленным отрезком, замыкающим ломаную).
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:
(Могут быть использованы прямоугольные или косоугольные координаты; правило сложения остаются одинаковыми для обоих этих типов координат).
- Модуль (длину) вектора суммы можно вычислить, например, используя теорему косинусов где — угол между отрезками, изображающими данные векторы, когда начало одного вектора совпадает с концом другого. Или: где — угол между векторами (выходящими из одной точки).
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.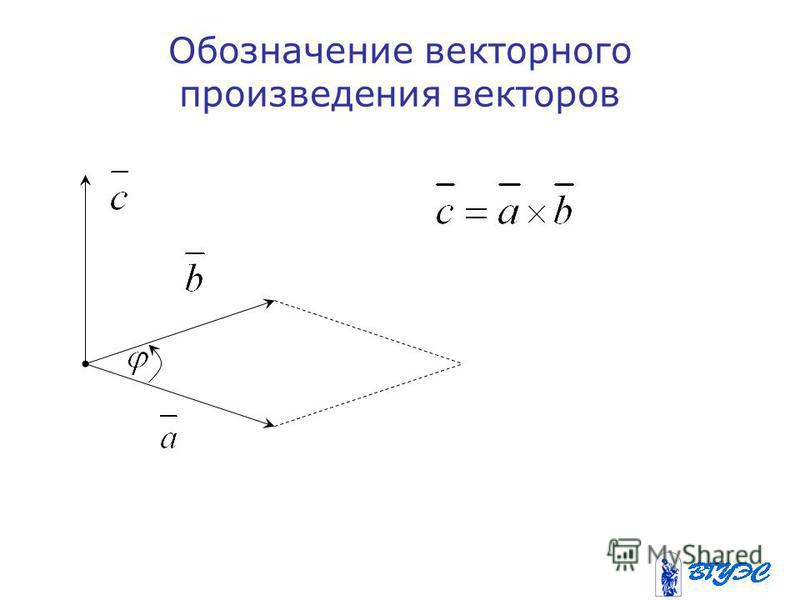
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
- Сложение коллинеарных скользящих векторов
Если скользящие векторы параллельны, то при их сложении главная трудность состоит в определении прямой, на которой будет расположена их сумма. (Величину и направление вектора суммы было бы естественно определить точно так же, как и в случае сложения свободных векторов.) В механике при изучении статики для решения вопроса о сложении параллельных сил, которые, как известно, задаются скользящими векторами, вводится дополнительная гипотеза: к системе векторов можно добавить два вектора, равных по величине, противоположных по направлению и расположенных на одной прямой, пересекающей прямые, на которых расположены данные векторы. Пусть, например, надо сложить скользящие векторы и , расположенные на параллельных прямых. Добавим к ним векторы и , расположенные на одной прямой. Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , и пересекаются. Поэтому определены векторы
Прямые, на которых расположены векторы и , пересекаются всегда, за исключением случая, когда векторы и равны по величине и противоположны по направлению, в котором говорят, что векторы и образуют пару (векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Вычитание
Операция вычитания из вектора вектора сводится к сложению первого вектора и вектора, противоположного второму:
(Само сложение при этом осуществляется так, как описано в параграфе выше, пользуясь, если это удобно, любым из приведенных там альтернативных способов).
Однако легко видеть, что из правила треугольника можно получить и отдельное геометрическое определение разности. Для этого достаточно посмотреть на чертеж, иллюстрирующий сложение по правилу треугольника и осознать, что разность векторов и на этом чертеже есть вектор Отсюда прямо формулируется правило треугольника для вычитания векторов:
разность двух векторов с общим началом (или перенесенных параллельно так, чтобы начала совпали) есть вектор с началом, совпадающим с концом вычитаемого и концом, совпадающим с концом уменьшаемого.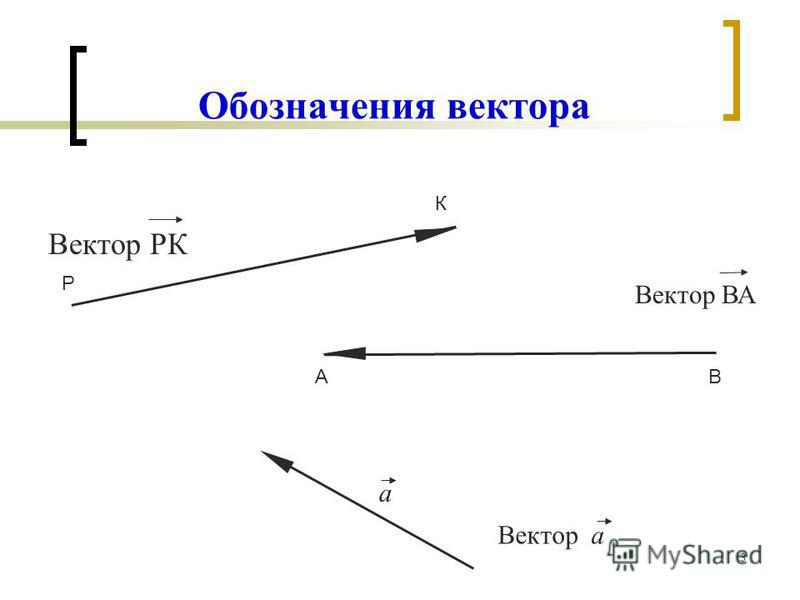
Это правило также может быть удобным.
Скалярное произведение
Основная статья: Скалярное произведение
Скалярное произведение двух векторов
Скалярное произведение на множестве геометрических векторов вводится, как
Скалярное произведение любого вектора и какого-то единичного вектора есть проекция (ортогональная проекция) вектора на направление этого единичного вектора:
Легко видеть, что скалярное произведение может быть записано через операцию (ортогонального) проецирования:
(где — проекция вектора на направление , — проекция вектора на направление ).
- В абстрактном подходе обычно сперва вводят скалярное произведение, а уже через него определяют понятие угла, ортогональность, ортогональную проекцию.
Векторное произведение
Основная статья: Векторное произведение
Векторное произведение двух векторов
Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла φ между ними
- вектор ортогонален каждому из векторов и
- вектор направлен так, что тройка векторов является правой.

Обозначение:
Геометрически векторное произведение есть ориентированная площадь параллелограмма, построенного на векторах , представленная псевдовектором, ортогональным этому параллелограмму.
Свойства векторного произведения:
- При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
- Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
- Векторное произведение обладает распределительным свойством:
Геометрическая интерпретация смешанного произведения.
Смешанное произведение
Основная статья: Смешанное произведение
Сме́шанное произведе́ние векторов — скалярное произведение вектора на векторное произведение векторов и :
(равенство здесь записано для разных обозначений скалярного и векторного произведения, часто встречающихся в литературе).
Иногда смешанное произведение называют тройным скалярным произведением векторов, по всей видимости из-за того, что результатом является скаляр (точнее — псевдоскаляр).
Геометрически смешанное произведение есть (ориентированный) объём параллелепипеда, построенного на векторах .
То есть абсолютная величина его есть просто объем этого параллелепипеда (в общем случае — косоугольного), а знак определяется тем, представляют ли векторы правую тройку (тогда плюс) или левую (тогда минус). Иногда при использовании левого базиса знак может быть определен противоположным образом.
Базис и разложение по базису
Разложение вектора по трём ортогональным векторам трёхмерного евклидова пространства
Векторы (как направленные отрезки), лежащие на прямых, параллельных одной прямой, называются коллинеарными, а векторы, лежащие в плоскостях, параллельных одной плоскости — компланарными. Для свободных векторов коллинеарность и компланарность определяется как такие понятия для изображающих их направленных отрезков (то есть представителей соответствующих свободным векторам классов эквивалентности).
Каждый вектор плоскости можно единственным образом разложить по двум определённым неколлинеарным векторам этой плоскости, а каждый вектор трёхмерного евклидова пространства можно единственным образом разложить по трём определённым некомпланарным векторам. Эти векторы, взятые в определённом порядке называются базисом плоскости (пространства). Сопоставлением каждому вектору данной плоскости (пространства) его коэффициентов в таком его разложении, определяется аффинная система координат на плоскости (в пространстве). Если векторы, по которым производится разложение, ортогональны и единичны, то получаем прямоугольную декартову систему координат на плоскости (в пространстве). Разложение геометрического вектора по базису есть упорядоченная совокупность проекций вектора на базисные вектора.
Обозначения
Вектор, представленный набором элементов (компонент) допустимо обозначить следующим способами:
- .
Для того, чтобы подчеркнуть, что это вектор (а не скаляр), используют черту сверху, стрелочку сверху, жирный или готический шрифт:
Сложение векторов почти всегда обозначается знаком плюс:
- .

Умножение на число — просто написанием рядом, без специального знака, например:
- ,
причём число при этом обычно пишут слева.
Умножение на матрицу также обозначают написанием рядом, без специального знака, но здесь перестановка сомножителей в общем случае влияет на результат. Действие линейного оператора на вектор также обозначается написанием оператора слева, без специального знака.
Вектор как последовательность
Вектор — (последовательность, кортеж) однородных элементов. Это наиболее общее определение в том смысле, что может быть не задано обычных векторных операций вообще, их может быть меньше, или они могут не удовлетворять обычным аксиомам линейного пространства. Именно в таком виде вектор понимается в программировании, где, как правило, обозначается именем-идентификатором с квадратными скобками (например, object[]). Перечень свойств моделирует принятое в теории систем определение класса и состояния объекта. Так типы элементов вектора определяют класс объекта, а значения элементов — его состояние. Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.
Впрочем, вероятно, это употребление термина уже выходит за рамки обычно принятого в алгебре, да и в математике вообще.
С другой стороны, многие математические объекты (например матрицы, тензоры, функции и т. д.), в том числе обладающие структурой более общей, чем конечный (а иногда даже и чем счётный) упорядоченный список, удовлетворяют аксиомам векторного пространства, то есть являются с точки зрения алгебры векторами.
История
Интуитивно вектор понимается как объект, имеющий величину, направление и (необязательно) точку приложения. Зачатки векторного исчисления появились вместе с геометрической моделью комплексных чисел (Гаусс, 1831). Развитые операции с векторами опубликовал Гамильтон как часть своего кватернионного исчисления (вектор образовывали мнимые компоненты кватерниона). Гамильтон предложил сам термин вектор (лат. vector, несущий) и описал некоторые операции векторного анализа. Этот формализм использовал Максвелл в своих трудах по электромагнетизму, тем самым обратив внимание учёных на новое исчисление.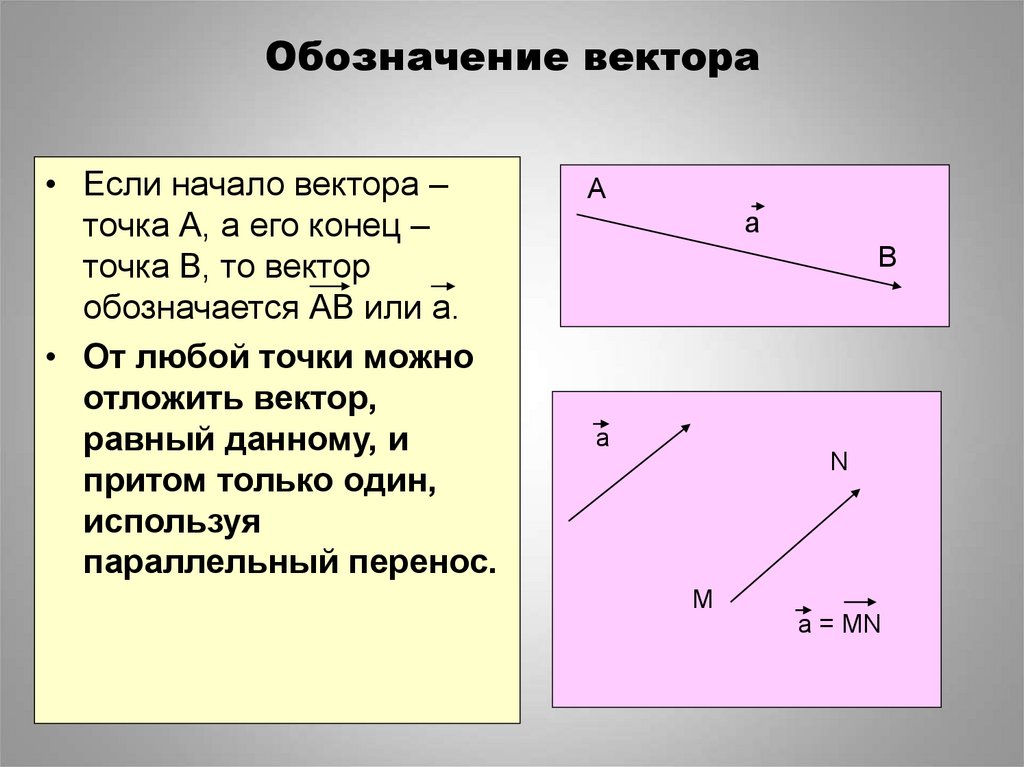 Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
Вскоре вышли «Элементы векторного анализа» Гиббса (1880-е годы), а затем Хевисайд (1903) придал векторному анализу современный вид.
См. также
- Векторная величина
- Векторное поле
- Векторное пространство
- Векторный анализ
- Нулевой вектор
- Псевдовектор
- Радиус-вектор
- Тензор
Литература
- Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
- Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
Ссылки
- На Викискладе есть медиафайлы по теме Вектор (математика)
Физические основы механики
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения за это время к промежутку времени , за которое это перемещение имело место:
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <. ..> , как это сделано выше.
..> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
Действительно
Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения при стремлении промежутка времени t2 – t1 к нулю.![]() Сделаем переобозначения: t1 = t и t2 = t + и перепишем верхнее соотношение в виде:
Сделаем переобозначения: t1 = t и t2 = t + и перепишем верхнее соотношение в виде:
Скорость в момент времени t равна пределу отношения перемещения за время к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
Рис. 2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если и есть конечное перемещение и конечный промежуток времени, то и — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
есть ничто иное как дробь — частное от деления на , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.![]()
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения , , или , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
Учитывая постоянство декартовых единичных векторов , , , продифференцируем это выражение по времени
С другой стороны, разложение по базису вектора скорости имеет вид
опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть
Модуль вектора скорости равен
Получим ещё одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при величина || все меньше и меньше отличается от соответствующего пути (см. рис. 2). Поэтому
и в пределе (>0)
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени , в который мгновенная скорость равна средней путевой скорости за первые секунд движения точки.
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени
будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости точке соответствующей моменту времени t*. Средний модуль скорости за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
Как обозначить вектор? — Ответы на вопросы про технологии и не только
Содержание
- — Как записывается вектор?
- — Как обозначаются вектора?
- — Как обозначаются вектор и его модуль?
- — Какие бывают вектора?
- — Какие координаты имеет нулевой вектор?
- — Как построить векторы в пространстве?
- — Как обозначаются Сонаправленные векторы?
- — Как обозначаются равные векторы?
- — Как понять что векторы сонаправлены?
- — Какая величина называется вектором Что такое модуль вектора как обозначаются вектор и его модуль?
- — Какие параметры характеризуют вектор?
- — Что такое Векторы в пространстве?
- — Какие векторы называют коллинеарны?
- — Чем отличается отрезок от вектора?
- — Какие бывают Векторы на плоскости?
Вектором называется направленный отрезок ; точка — начало, точка — конец вектора (рис. 1). Вектор обозначается либо двумя большими буквами — своим началом и концом: либо одной малой буквой: . Если начало и конец вектора совпадают, то такой вектор называется нулевым.
1). Вектор обозначается либо двумя большими буквами — своим началом и концом: либо одной малой буквой: . Если начало и конец вектора совпадают, то такой вектор называется нулевым.
Как записывается вектор?
1) Векторы можно записать двумя большими латинскими буквами: и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
Как обозначаются вектора?
Вектор – это направленный отрезок, для которого указано, какая из его граничных точек является началом, а какая – концом. Если – начало вектора, – его конец, то вектор обозначается как A B → . Вектор также можно обозначать одной маленькой буквой: .
Как обозначаются вектор и его модуль?
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB. Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Какие бывают вектора?
Вектор — направленный отрезок. Векторы бывают коллинеарными — лежащими на одной или параллельных прямых. И при этом делятся на сонаправленные (стрелки в одну сторону) и противоположно-направленные (в разные стороны).
Векторы бывают коллинеарными — лежащими на одной или параллельных прямых. И при этом делятся на сонаправленные (стрелки в одну сторону) и противоположно-направленные (в разные стороны).
Какие координаты имеет нулевой вектор?
Нулевой вектор определяет тождественное движение пространства, при котором каждая точка пространства переходит в себя. С нулевым вектором не связывают никакого направления в пространстве. Все координаты нулевого вектора в любой аффинной системе координат равны нулю. …
Как построить векторы в пространстве?
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z: … Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости.
Как обозначаются Сонаправленные векторы?
Вектор обозначается либо двумя большими буквами — своим началом и концом: ¯AB либо одной малой буквой: ¯a. Если начало и конец вектора совпадают, то такой вектор называется нулевым. … Два коллинеарных вектора ¯a и ¯b называются сонаправленными, если их направления совпадают: ¯a↑↑¯b (рис. 3, а).
Как обозначаются равные векторы?
Векторы с равными модулями и одинаковыми направлениями называются равными векторами. Равные векторы a → и b → записываются так: a → = b → или b → = a → . Векторы с равными модулями и противоположными направлениями называются противоположными векторами.
Как понять что векторы сонаправлены?
Векторы называются сонаправленными, если они коллинеарны и их направления совпадают (рис. 1). Векторы называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
1). Векторы называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
Какая величина называется вектором Что такое модуль вектора как обозначаются вектор и его модуль?
Вектором называется направленный отрезок, то есть отрезок, у которого указаны начало (наз. также точкой приложения вектора) и конец. Длина направленного отрезка, изображающего вектор, называется длиной, или модулем, вектора.
Какие параметры характеризуют вектор?
Ве́ктор (от лат. vector, «несущий») — в простейшем случае математический объект, характеризующийся величиной и направлением. Например, в геометрии и в естественных науках вектор есть направленный отрезок прямой в евклидовом пространстве (или на плоскости). Примеры: радиус-вектор, скорость, момент силы.
Что такое Векторы в пространстве?
Вектором называется направленный отрезок. Любая точка пространства может рассматриваться как нулевой вектор, начало и конец которого совпадают. Нулевой вектор обозначают O → . Длиной вектора называется длина соответствующего ему отрезка.
Нулевой вектор обозначают O → . Длиной вектора называется длина соответствующего ему отрезка.
Какие векторы называют коллинеарны?
linearis — линейный) — отношение параллельности векторов: два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Чем отличается отрезок от вектора?
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Какие бывают Векторы на плоскости?
Коллинеарные и неколлинеарные векторы на плоскости
Два вектора на плоскости называют коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых (рис. 2). В противном случае векторы называются неколлинеарными. коллинеарен любому другому вектору плоскости.
коллинеарен любому другому вектору плоскости.
Интересные материалы:
Как полностью очистить SD карту?
Как полностью очистить жесткий диск через командную строку?
Как правильно очистить дом при помощи свечей?
Как правильно очистить Озу на Android?
Как правильно очистить планшет?
Как правильно очистить внешний жесткий диск?
Как правильно очистить winsxs?
Как приготовить отвар из овса для очистки печени?
Как приготовить овес для очистки печени?
Как сразу очистить всю историю яндекса?
Математика. Основы геометрии: Координаты и векторы
Прямоугольная декартова система координат
Рассмотрим на плоскости числовую прямую \(x\) с началом отсчета в точке \(O\). Повернем эту прямую вокруг точки \(O\) на угол \(+90°\) и обозначим ее новое положение через \(y\) (мы поставили знак плюс перед значением угла, чтобы подчеркнуть, что поворот осуществляется в положительном направлении, то есть против часовой стрелки). Первоначальное положение числовой прямой мы, однако, не исключаем из нашего рассмотрения и сохраняем за ним прежнее обозначение \(x\).
Первоначальное положение числовой прямой мы, однако, не исключаем из нашего рассмотрения и сохраняем за ним прежнее обозначение \(x\).
Полученная конструкция носит название прямоугольной системы координат. Иногда ее также называют декартовой системой координат (в честь французского математика Рене Декарта). С ее помощью очень удобно задавать положение любой точки на плоскости. Действительно, возьмем произвольную точку \(A\) и опустим из нее перпендикуляр на каждую из прямых \(x\) и \(y\). Обозначим соответствующие точки пересечения через \(A_x\) и \(A_y\). Они называются проекциями точки \(A\) на оси \(x\) и \(y\). Пусть положение точки \(A_x\) вдоль числовой прямой \(x\) характеризуется числом \(x_A\), а положение точки \(A_y\) вдоль прямой \(y\) — числом \(y_A\). Тогда пара чисел \((x_A, y_A)\) называется прямоугольными (или декартовыми) координатами точки \(A\).
Теперь допустим, что нам даны два произвольных действительных числа \(x_B\) и \(y_B\) и известно, что они являются декартовыми координатами некоторой точки \(B\). По этим данным мы теперь легко можем найти саму точку \(B\). Вначале найдем ее проекции: отметим на оси \(x\) точку \(B_x\), положение которой вдоль этой оси задается числом \(x_B\), а на оси \(y\) отметим точку \(B_y\), положение которой задается числом \(y_B\). Затем проведем через проекции \(B_x\) и \(B_y\) прямые, параллельные соответственно осям \(y\) и \(x\):
По этим данным мы теперь легко можем найти саму точку \(B\). Вначале найдем ее проекции: отметим на оси \(x\) точку \(B_x\), положение которой вдоль этой оси задается числом \(x_B\), а на оси \(y\) отметим точку \(B_y\), положение которой задается числом \(y_B\). Затем проведем через проекции \(B_x\) и \(B_y\) прямые, параллельные соответственно осям \(y\) и \(x\):
У нас получился параллелограмм. Его вершина, расположенная напротив вершины \(O\), и есть, очевидно, искомая точка \(B\).
Плоскость, снабженная прямоугольной системой координат, называется координатной плоскостью. Мы только что выяснили, что между точками координатной плоскости и парами действительных чисел существует взаимно-однозначное соответствие: каждой точке \(A\) соответствует строго определенная координатная пара \((x_A, y_A)\), а каждой координатной паре \((x_B, y_B)\) соответствует строго определенная точка \(B\). Тут всё очень похоже на то, как устроена числовая прямая — с той только разницей, что для задания точки на числовой прямой требуется одно действительное число, а для задания точки на координатной плоскости требуется два действительных числа. По этой причине прямую иногда называют одномерным пространством, а плоскость — двухмерным пространством.
По этой причине прямую иногда называют одномерным пространством, а плоскость — двухмерным пространством.
Отметим, что порядок следования чисел в паре координат имеет принципиальное значение: так, координаты \((1, 2)\) задают вовсе не ту же самую точку, что и координаты \((2, 1)\). Первая координата в паре \((x_A, y_A)\) называется абсциссой, а вторая — ординатой. В соответствии с этим, прямую \(x\) часто называют осью абсцисс, а прямую \(y\) осью ординат. Точка пересечения координатных осей, обозначаемая обычно буквой \(O\), называется началом координат. Вместо слов «точка \(A\) с координатами \((x_A, y_A)\)» часто пишут просто «точка \(A(x_A, y_A)\)» или же, еще короче, «точка \((x_A, y_A)\)».
Векторы
Давайте начертим числовую прямую с началом отчета в точке \(O\) и рассмотрим ее хорошенько:
Здесь возле одних и тех же засечек по одну сторону от прямой стоят обозначения точек \(O\), \(A\) и \(B\), а по другую сторону — соответствующие им числа \(0\), \(a\) и \(b\). Чем же числа отличаются от точек? Отличие состоит в том, что число — это не сама точка, а скорее краткая инструкция, как найти ее местоположение. Числовую прямую правильнее было бы рисовать следующим образом:
Чем же числа отличаются от точек? Отличие состоит в том, что число — это не сама точка, а скорее краткая инструкция, как найти ее местоположение. Числовую прямую правильнее было бы рисовать следующим образом:
Обычно так не рисуют лишь по той причине, что чертеж в этом случае получается более громоздким. Число \(a\) описывает смещение, переводящее точку \(O\) в точку \(A\), и тем самым задает положение точки \(A\) на числовой прямой. Это смещение может быть как положительным, так и отрицательным. Принципиальным моментом тут является то, что числа можно складывать между собой, а точки — нельзя.
В случае координатной плоскости дело обстоит очень похожим образом, только вместо чисел здесь фигурируют координатные пары. Координаты \((x_A, y_A)\) можно рассматривать как инструкцию для определения местонахождения соответствующей точки \(A\). Для этого надо встать в начало координат, точку \(O\). Затем сделать \(x_A\) единичных шагов в том направлении, в котором указывает ось \(x\) (если число \(x_A\) отрицательно, то фактически движение осуществляется в противоположном направлении), а после этого сделать \(y_A\) единичных шагов в направлении, в котором указывает ось \(y\). В результате мы оказываемся в точке \(A\).
В результате мы оказываемся в точке \(A\).
Однако же, когда речь идет о координатной плоскости, вместо слова «инструкция» более принято употреблять другое слово, а именно вектор. На чертежах, во избежание излишней громоздкости, векторы изображают не в виде двух отдельных шагов, как это мы сделали выше, а в виде одного прямолинейного отрезка-стрелки:
Векторам часто присваивают буквенное обозначение. Вектор \({\bf a}\), соответствующий точке \(A\), имеет те же координаты \((x_A, y_A)\), что и сама точка. Применительно к векторам координаты также называют компонентами. Между вектором и парой его компонентов можно ставить знак равенства: \({\bf a} = (x_A, y_A)\). Букву, обозначающую вектор, обычно выделяют на печати полужирным шрифтом, чтобы его нельзя было спутать с обычным числом. В рукописных текстах, где применение полужирного шрифта было бы не слишком практичным, над обозначением вектора принято ставить стрелочку: \(\vec a\). Иногда для лучшего зрительного восприятия координаты вектора записывают в столбик:
Иногда для лучшего зрительного восприятия координаты вектора записывают в столбик:
\({\bf a} = \begin{pmatrix} x_A \\ y_A \end{pmatrix}\) или \(\vec{a} = \begin{pmatrix} x_A \\ y_A \end{pmatrix}\).
Заметим, что понятия координат и векторов применимы, в принципе, и в случае, когда мы рассматриваем одномерную числовую прямую: положение точки на прямой часто называют ее одномерной координатой, а смещение вдоль прямой является фактически одномерным вектором. Одномерная координата, как и одномерный вектор — это обычные действительные числа.
Полярная система координат
Представим себя на месте человечка, которому надо добраться из начала координат \(O\) в некоторую точку \(A(x_A, y_A)\). В этой ситуации инструкция, записанная в виде декартовых координат, нас бы, наверное, не очень обрадовала. Ведь если мы вначале будем идти в направлении оси \(x\), а потом в направлении оси \(y\), то мы проделаем не самый близкий путь. Нет уж, — скажем мы, — вы лучше с самого начала укажите нам точное направление на точку \(A\) и сообщите, сколько шагов надо сделать: так-то мы доберемся быстрее.
Что ж, такая возможность тоже имеется.
Направление можно задать, например, с помощью углового смещения \(\varphi_A\), отсчитываемого от положительного направления оси \(x\). Величина \(\varphi_A\) носит название полярного угла или полярной координаты. Число шагов — это не что иное, как расстояние \(r_A\) между началом координат и точкой \(A\). Иначе говоря, \(r_A = |OA|\). Величину \(r_A\) называют иногда радиальной координатой. Новая инструкция записывается в виде пары \((r_A, \varphi_A)\), которая называется полярными координатами точки \(A\).
Мы, однако же, договорились вместо слова «инструкция» говорить «вектор». Таким образом, вектор \({\bf a}\), соответствующий точке \(A\), — это совокупность направления, задаваемого углом \(\varphi_A\), и расстояния \(r_A\), которое надо проделать в этом направлении.
Но мы еще совсем недавно отождествляли вектор \({\bf a}\) с парой декартовых координат \((x_A, y_A)\). Что же такое вектор на самом деле? Тут важно то, что обе инструкции — как «декартова» \((x_A, y_A)\), так и «полярная» \((r_A, \varphi_A)\), — хотя и отличаются в деталях, описывают одно и то же смещение, и в этом смысле они являются разными представлениями одного и того же вектора \({\bf a}\). Впрочем, во избежание путаницы, знак равенства между вектором \({\bf a}\) и его полярными координатами \((r_A, \varphi_A)\) писать не принято.
Что же такое вектор на самом деле? Тут важно то, что обе инструкции — как «декартова» \((x_A, y_A)\), так и «полярная» \((r_A, \varphi_A)\), — хотя и отличаются в деталях, описывают одно и то же смещение, и в этом смысле они являются разными представлениями одного и того же вектора \({\bf a}\). Впрочем, во избежание путаницы, знак равенства между вектором \({\bf a}\) и его полярными координатами \((r_A, \varphi_A)\) писать не принято.
Заметим, что если \(r_A = 0\), то полярному углу \(\varphi_A\) можно приписать любое значение. В остальных случаях, как нетрудно убедиться, между точками на плоскости и их полярными координатами имеется взаимно-однозначное соответствие. А значит, полярные и декартовы координаты также связаны между собой взаимно-однозначным соответствием: по полярным координатам можно единственным образом восстановить декартовы, и наоборот, по декартовым координатам можно единственным образом восстановить полярные.
Сложение и вычитание векторов
Смещение, инструкция о котором записана в векторе, можно, разумеется, применить не только к началу координат \(O\), но и вообще к произвольной точке, лежащей на плоскости. Пусть нам даны два вектора \({\bf a}\) и \({\bf b}\), соответствующие точкам \(A\) и \(B\).
Пусть нам даны два вектора \({\bf a}\) и \({\bf b}\), соответствующие точкам \(A\) и \(B\).
Сместим точку \(A\) в соответствии с инструкцией, заложенной в векторе \({\bf b}\). Но в нашем распоряжении две инструкции — «декартова» \((x_B, y_B)\) и «полярная» \((r_A, \varphi_A)\). Какой лучше воспользоваться? Если мы ищем графическое решение с помощью чертежа, то «полярная» инструкция оказывается удобнее.
Из исходной точки \(A\) проведем луч параллельно лучу \(OB\) и пройдем по нему расстояние, равное длине отрезка \(OB\). Мы попадем в некоторую точку \(C\), которая, собственно, и является результатом проделанного смещения. Однако если мы теперь захотим рассчитать ее полярные координаты, то обнаружится, что это очень непростая задача. Попробуем проделать то же самое смещение, следуя «декартовой» инструкции.
Для этого, исходя из точки \(A\), сделаем \(x_B\) шагов в направлении оси абсцисс и \(y_B\) шагов в направлении оси ординат (опять-таки, если число шагов отрицательно, движение фактически осуществляется в противоположную сторону). Поскольку инструкции по сути эквивалентны, мы окажемся всё в той же точке \(C\). Однако, так как на этот раз мы имеем дело с декартовыми координатами, вычислить их не составляет труда.
Поскольку инструкции по сути эквивалентны, мы окажемся всё в той же точке \(C\). Однако, так как на этот раз мы имеем дело с декартовыми координатами, вычислить их не составляет труда.
Как хорошо видно из рисунка, точке \(C\) соответствует вектор
\({\bf c} = \begin{pmatrix} x_C \\ y_C \end{pmatrix} = \begin{pmatrix} x_A + x_B\\ y_A +y_B \end{pmatrix}\).
В таких случаях говорят, что вектор \({\bf c}\) является суммой векторов \({\bf a}\) и \({\bf b}\):
\({\bf c} = {\bf a} + {\bf b}\).
Вместе с тем, координаты вектора \({\bf b}\) можно представить в виде
\({\bf b} = \begin{pmatrix} x_B \\ y_B \end{pmatrix} = \begin{pmatrix} x_C — x_A\\ y_C — y_A \end{pmatrix}\).
Вектор \({\bf b}\) естественно назвать разностью векторов \({\bf c}\) и \({\bf a}\):
\({\bf b} = {\bf c} — {\bf a}\).
Чтобы хорошенько запомнить определения суммы и разности векторов, выпишем их еще раз, обведя в рамку:
\(\begin{array}{|c|} \hline \begin{align*} \phantom{\Bigg[}\hspace{0mm}{\bf a} + {\bf b} = \begin{pmatrix}x_A\\y_A\end{pmatrix} + \begin{pmatrix}x_B\\y_B\end{pmatrix} = \begin{pmatrix}x_A + x_B\\y_A + y_B\end{pmatrix} = \begin{pmatrix}x_C\\y_C\end{pmatrix} = {\bf c}\hspace{0mm}\phantom{\Bigg]}\\ \phantom{\Bigg[}\hspace{0mm}{\bf c} — {\bf a} = \begin{pmatrix}x_C\\y_C\end{pmatrix} — \begin{pmatrix}x_A\\y_A\end{pmatrix} = \begin{pmatrix}x_C — x_A\\y_C — y_A\end{pmatrix} = \begin{pmatrix}x_B\\y_B\end{pmatrix} = {\bf b}\hspace{0mm}\phantom{\Bigg]} \end{align*} \\ \hline \end{array} \)
Вектор \({\bf c} — {\bf a} = \big(\begin{smallmatrix}x_C — x_A\\y_C — y_A\end{smallmatrix}\big)\), переводящий точку \(A\) в точку \(C\), принято также обозначать как \(\overrightarrow{AC}\). В этих обозначениях определение сложения и вычитания принимает вид:
В этих обозначениях определение сложения и вычитания принимает вид:
\(\begin{align*} \overrightarrow{OC} = \overrightarrow{OA} + \overrightarrow{AC},\\ \overrightarrow{AC} = \overrightarrow{OC} — \overrightarrow{OA}. \end{align*}\)
Здесь под точкой \(O\) подразумевается, как и прежде, начало координат, но данные равенства, разумеется, сохранятся, если ее заменить на любую другую точку \(D\):
\(\begin{align*} \overrightarrow{DC} = \overrightarrow{DA} + \overrightarrow{AC},\\ \overrightarrow{AC} = \overrightarrow{DC} — \overrightarrow{DA}. \end{align*}\)
Задача \({\bf 4.11.1.}\) Пусть на координатной плоскости заданы три точки \(A\), \(B\) и \(C\). Изобразить в виде отрезков-стрелок векторы \( \overrightarrow{AB} + \overrightarrow{AC} \) и \( \overrightarrow{AB} — \overrightarrow{AC} \).
Одно из возможных решений представлено на рисунке.
Для нахождения разности нам не понадобилось делать никаких дополнительных построений: оказалось достаточным просто соединить имеющиеся точки \(C\) и \(B\). Для нахождения же суммы пришлось построить дополнительную точку \(D\), такую чтобы четырехугольник \(ACDB\) представлял собой параллелограмм.
Для нахождения же суммы пришлось построить дополнительную точку \(D\), такую чтобы четырехугольник \(ACDB\) представлял собой параллелограмм.
Очевидно, что сложение векторов обладает свойствами коммутативности и ассоциативности:
\(\bf{a} + \bf{b} = \bf{b} + \bf{a}\),
\(\bf{a} + (\bf{b} + \bf{c}) = (\bf{a} + \bf{b}) + \bf{c}\).
На практике это означает, что суммирование большого числа векторов можно производить в любой последовательности. Также естественно считать, что
\({\bf a} + {\bf a} = 2{\bf a}\),
\({\bf a} + {\bf a} + {\bf a} = 3{\bf a}\).
Вообще, умножение вектора \({\bf a} = (x_a, y_a)\) на произвольное действительное число \(k\) определяется как
\(\boxed{ k{\bf a} = k \begin{pmatrix}x_a\\y_a\end{pmatrix} = \begin{pmatrix}k x_a\\k y_a\end{pmatrix} }\)
В частности, для всякого вектора \({\bf a} = (x_a, y_a)\) определен противоположный ему вектор, равный
\(-{\bf a} = (-1){\bf a} = \begin{pmatrix}-x_a\\-y_a\end{pmatrix}\).
Для векторов, переводящих точку \(A\) в точку \(B\) и обратно, справедливо равенство
\( \overrightarrow{AB} = — \overrightarrow{BA}\).
Как несложно убедиться,
\({\bf a} + (-{\bf b}) = {\bf a} — {\bf b}\),
\({\bf a} — (-{\bf b}) = {\bf a} + {\bf b}\).
На основании этих равенств мы можем предложить еще одно решение рассмотренной ранее задачи \(4.11.1\), в которой требовалось по заданным точкам \(A\), \(B\) и \(C\) построить векторы \( \overrightarrow{AB} + \overrightarrow{AC} \) и \( \overrightarrow{AB} — \overrightarrow{AC} \):
Отметим также, что умножение вектора на число обладает свойством дистрибутивности:
\(k({\bf a} + {\bf b}) = k{\bf a} + k{\bf b}\),
\(k({\bf a} — {\bf b}) = k{\bf a} — k{\bf b}\).
Это легко проверить непосредственно с помощью определений, по которым производятся операции с векторами.
Переход между разными системами прямоугольных координат
Мы рассмотрели случай, когда на плоскости задана одна единственная прямоугольная система координат. Но на самом деле таких систем может быть сколь угодно много.
Но на самом деле таких систем может быть сколь угодно много.
Задача \({\bf 4.11.2.}\) Пусть на плоскости заданы две прямоугольные системы координат. Первая — с началом в точке \(O\) и осями \(x\) и \(y\). Вторая — с началом в точке \(O’\) (читается: «о-штрих») и осями \(x’\) и \(y’\), причем ось \(x’\) сонаправлена с осью \(x\) первой системы. Координаты точки \(A\) в первой системе равны \((x_A, y_A)\). Каковы ее координаты \((x_A’, y_A’)\) во второй системе, если изветно, что \(\overrightarrow{OO’} = (x_0, y_0)\)?
Координаты точки \(A\) в первой системе, очевидно, совпадают с координатами вектора \(\overrightarrow{OA}\), а координаты этой же точки во второй системе совпадают с координатами вектора \(\overrightarrow{O’\!A}\). Эти векторы связаны между собой соотношением
\(\overrightarrow{OA} = \overrightarrow{OO’} + \overrightarrow{O’\!A}\) или же \(\overrightarrow{O’\!A} = \overrightarrow{OA} — \overrightarrow{OO’}\).
Отсюда получаем ответ:
\(\begin{pmatrix}x_A’\\y_A’\end{pmatrix} = \overrightarrow{O’\!A}
= \begin{pmatrix} x_A \\ y_A \end{pmatrix} — \begin{pmatrix} x_0 \\ y_0 \end{pmatrix}
= \begin{pmatrix}x_A — x_0\\y_A — y_0\end{pmatrix} \).
Запомним этот результат хорошенько, потому что нам предстоит часто использовать его в будущем.
Конспект
\(1\). Система прямоугольных координат на плоскости: две числовые оси \(x\) и \(y\), расположенные так, что ось \(y\) повернута относительно оси \(x\) на \(+90°\) и начала отсчета обеих осей совпадают с точкой пересечения \(O\).
\(2\). Если построить проекции произвольной точки \(A\) на числовые прямые \(x\) и \(y\), то их положение на этих прямых будет характеризоваться некоторыми числами \(x_A\) и \(x_B\), соответственно. Пара чисел \((x_A, y_A)\) носит название прямоугольных координат точки \(A\). Первая координата в паре \((x_A, y_A)\) называется абсциссой, а вторая — ординатой.
\(3\). Полярные координаты \((r_A, \varphi_A)\) точки \(A\): если мы находимся в начале координат \(O\), то это — во-первых, расстояние \(r_A = |OA|\) до точки \(A\), а во-вторых, направление на эту точку (иначе говоря, направление луча \(OA\)), которое задается угловым смещением \(\varphi_A\), отсчитываемым от оси \(x\).
\(4\). Вектор \({\bf a} = \overrightarrow{OA}\): инструкция по перемещению начала координат \(O\) в точку \(A\), которая может быть задана как в виде прямоугольных координат \({\bf a} = \big(\begin{smallmatrix}x_A\\y_A\end{smallmatrix}\big)\), так и в виде полярных координат \((r_A, \varphi_A)\). Применима не только к точке \(O\), но и к любой другой точке \(B\). Если при этом точка \(B\) перемещается в точку \(C\), то это записывают как \(\overrightarrow{BC} = \overrightarrow{OA} = {\bf a}\).
\(5\). Пусть координаты векторов \({\bf a} = \big(\begin{smallmatrix}x_a\\y_a\end{smallmatrix}\big)\), \({\bf b} = \big(\begin{smallmatrix}x_b\\y_b\end{smallmatrix}\big)\) и \({\bf c} = \big(\begin{smallmatrix}x_c\\y_c\end{smallmatrix}\big)\) связаны между собой соотношением
\(x_a + x_b = x_c\),
\(y_a + y_b = y_c\).
Тогда вектор \({\bf c}\) называетеся суммой вектров \({\bf a}\) и \({\bf b}\), а вектор \({\bf b}\) — разностью векторов \({\bf c}\) и \({\bf a}\):
\({\bf c} = {\bf a} + {\bf b}\),
\({\bf b} = {\bf c} — {\bf a}\).
\(6\). Для любых трех точек \(A\), \(B\) и \(C\) справедливо:
\(\overrightarrow{AC} = \overrightarrow{AB} + \overrightarrow{BC}\),
\(\overrightarrow{BC} = \overrightarrow{AC} — \overrightarrow{AB}\).
\(7\). Умножение вектора \({\bf a} = \big(\begin{smallmatrix}x_a\\y_a\end{smallmatrix}\big)\) на число \(k\) определяется как \(k{\bf a} = k \big(\begin{smallmatrix}x_a\\y_a\end{smallmatrix}\big) = \big(\begin{smallmatrix}k x_a\\k y_a\end{smallmatrix}\big)\).
\(8\). Свойства сложения и вычитания векторов похожи на свойства сложения и вычитания чисел:
\(\bf{a} + \bf{b} = \bf{b} + \bf{a}\),
\(\bf{a} + (\bf{b} + \bf{c}) = (\bf{a} + \bf{b}) + \bf{c}\),
\({\bf a} + (-{\bf b}) = {\bf a} — {\bf b}\), где \(-{\bf b} = (-1){\bf b}\),
\({\bf a} — (-{\bf b}) = {\bf a} + {\bf b}\),
\(k({\bf a} + {\bf b}) = k{\bf a} + k{\bf b}\),
\(k({\bf a} — {\bf b}) = k{\bf a} — k{\bf b}\).
\(9\). Преобразование прямоугольных координат при переходе в новую систему: если оси обоих систем сонаправлены, а начало новой системы сдвинуто относительно старой на вектор \(\big(\begin{smallmatrix}x_0\\ y_0\end{smallmatrix}\big)\), то новые координаты \(\big(\begin{smallmatrix}x_A’\\ y_A’\end{smallmatrix}\big)\) точки \(A\) выражаются через старые \(\big(\begin{smallmatrix}x_A\\ y_A\end{smallmatrix}\big)\) как \(\big(\begin{smallmatrix}x_A’\\y_A’\end{smallmatrix}\big) = \big(\begin{smallmatrix}x_A — x_0\\y_A — y_0\end{smallmatrix}\big)\).
Символы вектор скачать бесплатно векторов скачать бесплатно графика
Символы вектор скачать бесплатно векторов скачать бесплатно новую коллекцию Расширенный поиск Запросить дизайн
[ Векторы ] символ ислама знак значок плоские классические симметричные формы ( .ai .eps .svg 1.59MB )
All-free-download.com
[ Векторы ] эскиз красочных символов элементов медицинского дизайна ( .ai .eps 5.04MB )
All-free-download.com
[ Векторы ] символ ислама знак логотип черный белый плоский классический эскиз ( .ai .eps .svg 952.27KB )
All-free-download.com
[ Векторы ] шаблон символа буддизма элегантные симметричные кривые лотоса форма рамки ( . ai .eps .svg 1.37MB )
ai .eps .svg 1.37MB )
All-free-download.com
[ Векторы ] Символы прачечной на этикетках одежды (ai, eps 4.28MB)
All-free-download.com
[ Векторы ] буддизм символ лотоса значок черный белый плоский классический симметричный контур ( .ai .eps .svg 1.59MB )
All-free-download.com
[ Векторы ] Абстрактный символ линзы затвора ( ai , eps 3.10MB )
All-free-download.com
[ Векторы ] Символы стирки ( ai , eps 1.29MB )
All-free-download. com
com
[ Векторы ] буддизм символ лотоса значок плоский элегантный классический симметричный контур формы круга ( .ai .eps .svg 3.12MB )
All-free-download.com
[ Векторы ] символ буддизма значок лента лотоса декор симметричный дизайн ( .ai .eps .svg 1.74MB )
All-free-download.com
[ Векторы ] Абстрактный символ ( ai , eps 1.48MB )
All-free-download.com
[Векторы] в мире, где вы можете быть кем угодно, будьте добры цитата шаблон футболки красочная каллиграфия символ аутизма головоломка суставы кусок декор ( .ai .eps 2.57MB )
All-free-download. com
com
[Векторы] жена мама оставшаяся в живых шаблон футболки симметричный текст символы рака контур контрастный дизайн ( .ai .eps 1.56MB )
All-free-download.com
[ Векторы ] христианство узор шаблон черный белый повторяющиеся традиционные религиозные символы элементы декора ( .ai .eps .svg 3.08MB )
All-free-download.com
[Векторы] Черные символы — Трофеи (ai, eps 1.04MB)
All-free-download.com
[ Векторы ] фондовый рынок глобальная торговля фон глобус бизнес символы эскиз ( .ai .eps 13.19МБ)
All-free-download. com
com
[ Векторы ] lanfricaicon логотип африканские символы карты силуэт эскиз ( .ai .eps .svg 2.47MB )
All-free-download.com
[Векторы] мир любовь биткойн футболка шаблон плоский контрастный текст символы эскиз (.ai .eps 1.45MB)
All-free-download.com
[ Векторы ] Green Eco Symbols ( ai , eps 1.01MB )
All-free-download.com
[ Векторы ] значок символа колеса буддизма плоский динамический симметричный контур ( .ai .eps .svg 1.50MB )
All-free-download. com
com
[ Векторы ] христианство узор шаблон ретро символы элементы декор повторяющийся дизайн ( .ai .eps .svg 3.43MB )
All-free-download.com
[Векторы] шаблон флаера для торговли на форексе динамический глобус символы валюты декор ( .ai .eps 2.54MB )
All-free-download.com
[ Векторы ] Крест Религиозный символ Христианская религия ( ai , eps 769.51KB )
All-free-download.com
[Векторы] Элементы дизайна | абстрактные символы (ai, eps 11.82MB)
All-free-download. com
com
[ Векторы ] Зеленый символ ( ai , eps 1.75MB )
All-free-download.com
скачать бесплатно бесплатно скачать символы символы скачать символы бесплатно символы вектор вектор скачать вектор бесплатно мужской женский символ вектор бесплатно мужской и женский символ вектор бесплатно usb символ вектор бесплатно символ сна вектор бесплатно скачать спортивные символы вектор вектор бесплатно
Загрузка дополнительных элементов, пожалуйста, подождите…
Идет загрузка дополнительных элементов, пожалуйста, подождите…
Критерий поиска:
Тип поиска:
Совпадение с любымСовпадение со всеми
Искать в:
ВекторыИконкиФотоШрифтыШаблоны сайтовPSD
Лицензия:
Все лицензииРазрешить коммерческое использование
Результат сортировки:
Сначала лучшее совпадениеСначала новыеСначала много загрузокСначала меньше загрузок
- Дом
- Лицензии
- Срок
- Конфиденциальность
- О
- Связаться с
Symbol Vector Art HD Images
Save PNG EPS
infinity symbol logo icons vector illustration
5000*5000
Save EPS
abstract human or people vector icon and symbol
1200*1200
Save PNG AI
shree ganeshay namah hindi calligraphy logo with lord ganesha symbol vector
5000*5000
PNG EPS
значки прямой трансляции красные символы и кнопки вектора
1200*1200
0249 AI
Shree Ganeshay Namh хинди текст каллиграфия с лордом Ганеша -вектор
5000*5000
Save PNG EPS
PNG EPS . эффект звезды вспышка украшения мерцание светящиеся всплески коллекция
эффект звезды вспышка украшения мерцание светящиеся всплески коллекция6250*6250
PNG AI
3d расположение значок дизайн символ png прозрачный фон вектор
2500*2500
Сохранить PNG EPS
Знак.
христианский религиозный символ крест кисть иллюстрация вектор0003
2500*2500
Save PNG EPS
pentagon lotus symbol vector
1200*1200
Save PNG AI
instagram social media icon user user button stories символ вектор
1200*1200
Сохранить PNG EPS
garuda pancasila логотип индонезийской страны символ дня независимости вектор
3000*3000
Сохранить PNG EPS
Bullish Dicar значок символ дизайн логотип умная идея вектор скачать
8333*8333
Сохранить PNG EPS
перо чернила значок иллюстрация изолированный вектор знак символ
2400*2400
Save PNG AI
shree ganeshay namah hindi calligraphy with lord ganesha symbol vector
5000*5000
Save PNG EPS
bulb icon вектор лампочка идеи символ иллюстрация
6250*6250
сохранить PNG EPS
шаблон логотипа и ресторан шеф-повар творческий символ концепция повар лицо усы и шляпа вектор
5000*5000
Сохранить PNG EPS
Один линейный рисунок музыкальных нот изолированного вектора.
 PNG AI
PNG AIкод сайта символ связаться с нами вектор0003
2000*2000
Save PNG EPS
sai baba hindi calligraphy with symbol vector
1200*1200
Save PNG EPS
tick and cross signs green галочка ок и красный x значки на белом фоне простые знаки графический дизайн символы да и нет кнопка для голосования решение веб векторная иллюстрация0248 PNG EPS
Продажа специального предложения 50 Символ с дисконтированной ценой красной метки для рекламной кампании в розничной розничной векторе
2000*2000
Save 3
Save 373
373
. символ баланса правосудия шкала в векторе логотипа пера пера для судебных служб и фирм правосудия
5000*5000
0002 Продажа 30 Выкл. Вектор символов скидки
1200*1200
Сохранить PNG EPS
Idea Vector Vect
зеленая галочка значок галочка да символ положительный принять одобрить вектор изолированный0003
1200*1200
Save PNG AI
blue minimalistic check symbol vector
8333*8333
Save PNG EPS
black illustration christian religious symbol cross vector
3000*3000
Сохранить PNG AI
простой стиль правильный символ значок материал вектор
8333*8333
Save PNG EPS
sparkling black and white symbol vector a set of original sparkling starter icons
6250*6250
Save PNG EPS
bulb icon vector l bulb идеи символ иллюстрации
6250*6250
сохранить PNG AI
зеленая галочка значок галочка да символ положительный принять одобрить вектор изолированные
2500*2500
Save PNG EPS
nimantran hindi calligraphy local lettering with lord ganesha symbol vector
5000*5000
Save PNG AI
lord ganesha и ом двойная символическая линия искусства вектор0003
5000*5000
Save PNG AI
bengali celebrations indian festival decorative hanging hindu religion symbol vector
5000*5000
Save PNG EPS
website symbol веб значок вектор изолированных
4000*4000
Сохранить PNG EPS
бесплатная доставка и быстрая машина значок символ вектор
2000*2000
Save PNG AI
circle eco friendly logo symbol vector
2500*2500
Save PNG EPS
flash sale sign or symbol for баннер вектор
2000*2000
Сохранить PNG EPS
Wi-Fi символ на прозрачном фоне вектор
2918*2913
3Save PNG EPS
medical snake health symbol medical snakes wings wand as medicine system and концепция здравоохранения медицинский символ значок вектор0003
1200*1200
Сохранить PNG AI
Скажите NO TO DRUGS CLIPART SYMBO вектор плоского дизайна0003
Сохранить PNG EPS
сверкающий черно-белый символ вектор набор оригинальных стартовых иконок блестящий блеск световой эффект звезды вспышка украшения мерцание светящиеся всплески коллекция
3000*0 Symbol90 920103 902 Vector 04 04 Vector 902 Biohazard Иллюстрации и векторные изображения
29.
 934 Графики
934 Графики- Фотографии
- Фотографии
- Графики
- Векторы
- Видео
Beste Qualität
Durchstöbern Sie 29.934
вектор символов биологической опасности lizenzfree Stock- und Vektorgrafiken. Oder starten Sie eine neuesuche, um noch mehr faszinierende Stock-Bilder und Vektorarbeiten zu entdecken. biohazard-vektorsymbol — вектор символа биологической опасности — графика, -клипарт, -мультфильмы и -символ био-гефаренрисико-лого-символ. заражение вирусом эпидемии gefahr zeichen. векторные иллюстрациибилд. isoliert auf weißem Hintergrund. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символФорма предупреждения о вирусе короны MERS. Био-Gefahrenrisiko-Лого-Символ.
коронавирус dünne linie symbol gesetzt, covid-19 symbole legen sammlung oder vektorskizzen. 2019-ncov zeichen für computer-web gesetzt, das lineare piktogramm stil paket isoliert auf weißemhintergrund, eps 10. — вектор биологической опасности — графика, -клипарт, -мультфильмы и -символ
2019-ncov zeichen für computer-web gesetzt, das lineare piktogramm stil paket isoliert auf weißemhintergrund, eps 10. — вектор биологической опасности — графика, -клипарт, -мультфильмы и -символCoronavirus Dünne Line Symbol gesetzt, Covid-19 Symbole легенда…
линия коронавирус covid-19 schutzsymbole — символ биологической опасности вектор сток-график, -клипарт, -мультфильмы и -символЛиния Coronavirus COVID-19 Schutzsymbole
Line Coronavirus covid-19 schutzsymbole — символ биологической опасности вектор сток-график, -клипарт, -мультфильмы и -symbole клипарт, -мультфильмы и -символWarnung und Gefahr
промышленность-концепт. reihe von verschiedenen zeichen: chemische, radioaktive, gefährlich, giftig, giftige, gefährliche substanzen. вектор-иллюстрация. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символИндустри-Концепт. Reihe von verschiedenen Zeichen: chemische,…
medizinische psa-linie symbole. векторные иллюстрации энтальтен символ как gesichtsmaske, handschue, arztkleid, haarschutz, biohazard abfall, umriss пиктограмма der schutzausrüstung 64 x 64 пикселя совершенный editierbarstrich — биологический символ символа вектор сток-графики, -клипарт, -мультфильмы и -symboleMedizinische PSA-Line Symbole.
коронавирус dünne linie symbol gesetzt. набор символов covid-19 или векторных изображений. Coronavirus zeichen für computer-web, линейный стиль пиктограммы, пакет isoliert auf weißem undergrund. векторграфик. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символ Векторные иллюстрации воодушевляют…
Векторные иллюстрации воодушевляют…Coronavirus Dünne Linie Symbol gesetzt. Covid-19-Symbole…
значки и символы биологической опасности — векторные символы биологической опасности Cartoons und -symboleBiologische Gefährdung Symbole
коронавирус-кранхейт covid-19 infektion medizinisch. новое официальное название для коронавируса-krankheit namens covid-19, pandemierisiko auf der Weltkarte Hintergrund — вектор символа биологической опасности — графика, -клипарт, -мультфильмы и -символCoronavirus-Krankheit COVID-19 Infektion medizinisch. Neuer…
набор символов для дезинфекции и восстановления. Bearbeitbarer vektorstrich — векторная графика символов биологической опасности, клипарт, мультфильмы и символыDesinfektions- und Reinigungssymbol-Set.
satz von dreieck gelbe warnung zeichen gefahr hautschuppen aufmerksamkeit symbole chemische brennbaren sicherheit strahlung vorsicht symbol vektor-illustration — biohazard symbol vector stock-grafiken, -clipart, -cartoons und -symbole Bearbeitbarer…
Bearbeitbarer…Satz von Dreieck gelbe Warnung Zeichen Gefahr Hautschuppen…
biogefährdung — векторный символ биологической опасности — графика, -клипарт, -мультфильмы и -символBiogefährdung
in der luft übertragen virus-spread-linie-symbol. человек атем вирус бактерия Skiriss стиль пиктограммы auf Weißem Hintergrund. covid-19 verbreitet in atemzeichenkonzept и веб-дизайн. векторграфикен. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символIn der Luft übertragen Virus-Spread-Line-Symbol. Пункт персоны…
gefahrenzeichen желтый вектор. strahlung schild, biohazard zeichen, toxischen zeichen. — векторный рисунок символа биологической опасности, клипарт, мультфильмы и символЖелтый векторный рисунок.
lineo editierbare schlaganfall — work für wissenschaft und line-symbole — biohazard symbol vector stock-grafiken, -clipart, -cartoons und -symbole Strahlung Schild, Biohazard Zeichen,
Strahlung Schild, Biohazard Zeichen,Lineo editierbare Schlaganfall — Labor für Wissenschaft und line-S
ecology — dünnlinien -вектор-символ-набор. пиксель идеальный. медвежий барер строгий. das set enthält iconen: ökologie, klimawandel, umweltschutz, альтернативная энергия, грубая технология. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символЭКОЛОГИЯ — Dünnlinien-Vektor-Symbol-Set. Идеальный пиксель….
предупреждение. gelbes dreieck warnt symbole, aufmerksamkeit chemische, brennbare und strahlung sendegefahr, unfall ausrufeausrufe vorsicht vektorsymbole — векторный символ биологической опасности — графика, -клипарт, -мультфильмы и -символWarnzeichen. Gelbes Dreieck warnt Symbole, Aufmerksamkeit…
satz von bakterien, probiotika und viruszeilensymbolen. микроб, кейме, целле, икра, петрисхейл, иммунная система и многое другое. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символ
— векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символSatz von Bakterien, Probiotika und Viruszeilensymbolen. Mikrobe,…
dna-kette dünne linie symbol. Генетическая медицина и эволюция символа Umriss Stil Piktogramm Auf Weißem Hintergrund. covid-19 и медицинские услуги для мобильных устройств, концепции и веб-дизайна. векторграфикен. — вектор символа биологической опасности, графика, клипарт, мультфильмы и символыDNA-Kette dünne Line Symbol. Genetische Medizin und Evolution…
warnung und hazard iconen — line serie — biohazard symbol vector stock-grafiken, -clipart, -cartoons und -symboleWarnung und Hazard Ikonen — Серия
Coronavirus-liniensymbol gesetzt. Вирус covid19 zeichen sammlung oder skizzen, веб-символ эпидемии ncov, линейный стиль пиктограммы, изолированный на заднем плане. векторграфикен. — векторная графика символов биологической опасности, клипарт, мультфильмы и символыCoronavirus-Liniensymbol gesetzt. Вирус Covid19 Zeichen Sammlung.
satz von zeichen sicherheit gefahr — вектор символов биологической опасности — графика, -клипарт, -мультфильмы и -символ ..
..Satz von Zeichen Sicherheit Gefahr
Серия предупреждающих и опасных векторных линий — символ биологической опасности векторный фондовый график, -клипарт, -мультфильмы и -символ символ вектор сток-графика, -клипарт, -мультфильмы и -символMedizinische Schutzmaske Symbol
satz von gefahrenwarnzeichen. символ vorsicht gefahr, векторная иллюстрация, набор иконок isolierter. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символSatz von Gefahrenwarnzeichen. Vorsicht Gefahr Symbol,…
Предупреждающий символ — символ биологической опасности, векторный рисунок, клипарт, -мультфильмы и символПредупреждающий символ, символ
, предупреждение вируса — векторный векторный символ. пиксель идеальный. медвежий барер строгий. das set enthält symbole: коронавирус, вирус, карантин, импфунг, символ биологической опасности, ручная работа, социальная угроза, gesichtsmaske. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символ
— векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символПредотвращение вирусов — Dünnlinien-Vektor-Symbol gesetzt. Pixel…
Infektionsprävention und schutz sich vor vor corona virus symbole banner web-symbol, waschen hande, vermeiden berühren, tragen maske, soziale distanz und arbeit von zu aus aus. вектор-инфографик. — вектор символа биологической опасности — графика, -клипарт, -мультфильмы и -символInfektionsprävention und Schutz sich vor Corona Virus Symptome…
профилактика коронавируса. набор иконок — вектор символа биологической опасности, графика, клипарт, мультфильмы и символПрофилактика коронавируса. Icon-Set
medizinische persönliche schutzausrüstung vor virusinfektionen und verschmutzung. vektor-illustration von schutzkleidung — символ биологической опасности вектор сток-графика, -клипарт, -мультфильмы и -символMedizinische personliche Schutzausrüstung vor Virusinfektionen…
48 предупреждений и символов — вектор символа биологической опасности сток-графика, -клипарт, -мультфильмы и — symbole48 Warnzeichen und Symbole
abchirmung — символ биологической опасности вектор сток-графика, -клипарт, -мультфильмы и -символAbschirmung
handwäsche-symbol zur infektionsprävention — вектор символа биологической опасности сток-график, -clipart, -cartoons und -symbole symboleWissenschaft & Physik Symbole
menschen mit schmerzen und krankheiten — векторный символ биологической опасности — графика, -клипарт, -мультфильмы и -символMenschen mit Schmerzen und Krankheiten
mobico icons-gefahr und warnung — вектор символов биологической опасности сток-графика, -клипарт, -мультфильмы и -символMobico icons-Gefahr und Warnung
человек schädel — вектор символов биологической опасности сток-графика, -клипарт, -мультфильмы и -символЧеловек Schädel
krankenschwester injiziert Coronavirus-impfstoff zu kleinem kind. mutter mit baby auf ärztlicher untersuchung. impfung zum schutz der menschen. konzept von gesundheit und medizin. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символ
mutter mit baby auf ärztlicher untersuchung. impfung zum schutz der menschen. konzept von gesundheit und medizin. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символKrankenschwester injiziert Coronavirus-Impfstoff zu kleinem Kind.
zahnpasta Tube Symbol medizinische zahnmedizin gesundheitswesen набор zahnmedizin гигиены gesundheitswesen символ — символ биологической опасности вектор сток-графика, -клипарт, -мультфильмы и -symboleZahnpasta Tube Symbol medizinische Zahnmedizin Gesundheitswesen…
предупреждает и gefahrenliniensymbole. медвежий барер строгий. пиксель идеальный. для мобильных устройств и Интернета. enthält symbole wie warnzeichen, gefahr, warnung, unfall, vorsicht, stopp, kommunikation, computervirus, hacker, identitätsdieb, biohazard, schutz, fehlermeldung. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символПредупреждение и Gefahrenliniensymbole. Беарбайтбарер Стрих. Пиксель…
человек с вирусом и вирусом — векторная графика, клипарт, мультфильмы и символычеловек с вирусом и вирусом
affenpockenviruszellen ausbruch medizinisches banner. — вектор символа биологической опасности — графика, клипарт, мультфильмы и символы
— вектор символа биологической опасности — графика, клипарт, мультфильмы и символыAffenpockenviruszellen Ausbruch medizinisches Banner.
wissenschaft — gliederung-icon-set — вектор символов биологической опасности — графика, -клипарт, -мультфильмы и -символWissenschaft — Gliederung-Icon-set
liniensymbole für medizinische abfallgeräte. vektorillustration enthalten symbol — handchuh, maske, biomedizinische, giftige, chemische, spritzenumriss piktogramm für gefahrenmüll. 64×64 пикс. Идеальный, медвежий контур — вектор символов биологической опасности, графика, клипарт, мультфильмы и символыСимволы для медицинских учреждений. Векторная иллюстрация…
антисептический символ. drei verschiedene pakete mit antiseptika zur desinfektion. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символАнтисептический символ. Drei verschiedene Pakete mit Antiseptika…
флюсовый защитный и gewaschene ручной символ линии. ручная гигиена schutz umriss stil piktogramm auf weißem hintergrund. waschschutzvirus для мобильных концепций и веб-дизайна. векторграфикен. — векторные изображения биологической опасности, -клипарт, -мультфильмы и -символ
waschschutzvirus для мобильных концепций и веб-дизайна. векторграфикен. — векторные изображения биологической опасности, -клипарт, -мультфильмы и -символ. Handwäsche…
affenpockenvirus. баннер де affenpockenvirus auf schwarzem hintergrund. gefährliche krankheit. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символАффенпокенвирус. Banner des Affenpockenvirus auf schwarzem…
предупреждающий и символический символ. медвежий барер строгий. пиксель идеальный. для мобильных устройств и Интернета. enthält symbole wie warnzeichen, gefahr, warnung, unfall, vorsicht, stopp, kommunikation, computervirus, hacker, identitätsdieb, biohazard, schutz, fehlermeldung. — векторный рисунок символа биологической опасности, -клипарт, -мультфильмы и -символПредупреждающий и символический символ. Беарбайтбарер Стрих. Пиксель…
вектор изолированных иконок вируса neuartigen 2019-ncov, дас уханьский коронавирус. — векторный символ биологической опасности — графика, -клипарт, -мультфильмы и -символВектор изолированных изображений нового вируса 2019-нКоВ, из Уханя.
символ медицинской маски. schutz vor viren und krankheiten, die durch tröpfchen in der luft übertragen werden. weiße maske auf einem blauen sechseck in einem einfachen stil. векторная иллюстрация для дизайна и Интернета, изоляция. — вектор символа биологической опасности, графика, клипарт, мультфильмы и символы ..
..Символ медицинской маски. Schutz vor Viren und Krankheiten, умер…
vektorillustration des affensymbols mit viruszellen auf dunklem hintergrund. Новый вирус обезьяньей оспы 2022 — вирус вируса оспы обезьян 2022 года — вирус, вызывающий раздражение, аффект в einfachem flachen stil isoliert — символ биологической опасности, векторный рисунок, -клипарт, -мультфильмы и -символ-serie — векторный рисунок символа биологической опасности, -clipart, -cartoons und -symbole
Warnung und Hazard Ikonen — Acme-Serie
atk-testzeilensymbolsatz. enthalten sind die symbole wie rt pcr, schnelltest, covid-19, speicheltest und mehr. — векторная графика символов биологической опасности, клипарт, мультфильмы и символыATK-Testzeilensymbolsatz.
dna-kettenlinie und volumenkörper-symbol. Генетический и эволюционный символ представляет собой пиктограмму на фоне неба. covid-19 и медицинские услуги для мобильных устройств, концепции и веб-дизайна. векторграфикен. — векторная графика символов биологической опасности, -клипарт, -мультфильмы и -символ Включайте символы с помощью RT PCR,…
Включайте символы с помощью RT PCR,…DNA-Kettenlinie und Volumenkörper-Symbol. Генетика и…
символ для концепта zur reaktion auf krankheitsausbrüche. — вектор символа биологической опасности — графика, клипарт, мультфильмы и символыSymbol für das Konzept zur Reaktion auf Krankheitsausbrüche.
Chemische Industrie-Ikonen — выберите серию — символ биологической опасности векторный фондовый график, -клипарт, -мультфильмы и -symbole остановить коронавирус covid-19 zeichen, инфографика, иллюстрация, векторный дизайн символов. коронавирус (COVID-19концепт дизайна пандемии. — вектор символа биологической опасности — графика, -клипарт, -мультфильмы и -символВектор-иллюстрация Коронавирус COVID-19 Дизайн.
от 100 Стоп…
Стоп…19.991.608 Символ Стоковые векторные иллюстрации и роялти бесплатно Символ Клипарт
Иконки туалета: мужчина, женщина, мужской и женский символ
Символ галочки, вектор
Мужской и женский символ, мужские и женские гендерные иконки.
Значки символов бесконечности
Непрерывная линия, рисующая два обнимающих сердца, черно-белая векторная минималистская иллюстрация концепции любви минимализма, нарисованная одной рукой, эскиз романтической темы.
Значок почтового вектора. значок электронной почты. иллюстрация конверта. сообщение
Зеленая галочка вектор значок для символа маркера флажка
Значок логотипа петли бесконечности. вектор неограниченная бесконечность, бесконечный знак формы линии
Значок рукопожатия сердца
Значки символов бесконечности
Символ бесконечности
Символы музыкальных нот
Набор значков погоды. мультфильм красочные художественные векторные иллюстрации.
 липкие символы прогноза. метеорологические инфографические знаки. векторный дизайн веб-иконок
липкие символы прогноза. метеорологические инфографические знаки. векторный дизайн веб-иконокЗначок женского пола. дамский знак. женский символ. белый женский символ на фоне розового круга. векторная иллюстрация.
Векторная иллюстрация креста с сердцем
Набор монохромных иконок с символами адинкра для вашего дизайна
Символ бесконечности с ярким, зеленым, художественным павлиньим пером на белом фоне. стиль татуировки.
Жест рукой v знак победы или мира, векторная иконка для приложений и веб-сайтов
Инструкции по стирке одежды, набор иконок для стирки, иконки для стирки одежды
Символ пола. вектор шаблона дизайна
Векторная иллюстрация символа инь и ян на белом фоне
Флоренция, Италия — 9 апреля 2018 г.: логотип WhatsApp Messenger. WhatsApp Messenger — это приложение для обмена мгновенными сообщениями для смартфонов, работающее по бизнес-модели подписки.
Символы уборной, туалета, очертания мужских и женских простых силуэтов, вектор
Религиозная графика в векторном качестве.

Универсальный вегетарианский символ – этикетка v с листом, созданная Европейским вегетарианским союзом.
Значок компаса карта ветра северо-западная векторная иллюстрация
Символ бесконечности неонового света
Значок стрелки севера или символ направления n и навигационной точки. векторный логотип для карты GPS-навигатора на белом фоне
Токсичный векторный знак
Мужской и женский значок, набор символов. векторная иллюстрация дизайна веб-сайта на белом фоне.
Веб-сайт со значком электронной почты, свяжитесь с нами, символ eps10, векторная иллюстрация на белом фоне.
Мужчина мужской силуэт изолированный значок векторной иллюстрации дизайн
Электрические и электронные значки, символы электрических схем. элементы схемы. иконы топить, изолированные на белом фоне.
Набор векторных значков телефонных звонков с зеленой кнопкой вызова или ответа и красной кнопкой повесить трубку или отклонить. дизайн для сайта, мобильного приложения.

Вектор контура обещания с красным сердцем
Международные упаковочные символы с названием. (значок хрупкости, значок ручки с осторожностью, значок держать в сухости, значок этой стороной вверх)
Золото, ювелирный символ бесконечности с золотыми звездами на черном фоне. дизайн с золотой звездой.
Большой набор алхимических символов на белом фоне. рисованные и письменные элементы для дизайна вывесок. вдохновение мистической, эзотерической, оккультной тематикой. вектор.
Мемориальная графика в векторном качестве
Символ товарного знака. символ авторского права. зарегистрированный символ. символ патента. векторный набор предупредительных этикеток. товарный знак, авторское право, зарегистрированный, значок патента.
Бесконечность простая черная иконка на белом фоне. элементы для компании, печатной продукции, страницы и веб-декора. векторная иллюстрация.
Наклейка на индуистскую мебель для украшения стены
Мемориальная графика в векторном качестве
Художественно нарисованный символ бесконечности с красивым радужным пером на белом фоне.
 стиль татуировки.
стиль татуировки.Знак градиента Versus с трещиной, изолированной на прозрачном фоне для боя, спорта, соревнований, соревнований, матчевых игр, объявления двух бойцов. против значка. вектор
Иконки школьных линий, набор знаков, вектор. детская школа наброски концепции иллюстрации: школа, образование, книга, ребенок, автобус
Математическая иконка на белом фоне. плоский стиль. значок математики и числа для дизайна вашего веб-сайта, логотипа, приложения, пользовательского интерфейса. символ математических расчетов. знак математических расчетов.
Значок рукопожатия символ сотрудничества и партнерства. соглашение и символ единства, руки пожимают друг другу векторные иллюстрации, изолированные на белом фоне.
Зодиак поет созвездие, символы алхимии астрологии астрономии, изолированные значки. планеты, звезды пиктограммы. большой эзотерический набор в штриховой графике черно-белое цветное геометрическое искусство
Любовное сердце в знаке бесконечности.
 знак на открытке ко дню святого валентина, свадебный отпечаток. векторная каллиграфия и надпись иллюстрации, изолированные на белом фоне.
знак на открытке ко дню святого валентина, свадебный отпечаток. векторная каллиграфия и надпись иллюстрации, изолированные на белом фоне.Символ Рейки. священный знак. чо ку рей.
Древняя векторная эмблема медицины
Символ рыбы, нарисованный вручную чернильной кистью
Правда или ложь набор модных плоских галочек и крестиков. векторные иллюстрации, изолированные на прозрачном фоне. — вектор
Символ вектора медицинского креста. плоская пиктограмма выделена на белом фоне. медицинский крест пиктограмма разработана в простом стиле.
Символ Рейки. священный знак. хон ша зе шо нэн.знак пространства-времени. духовная энергия. нетрадиционная медицина. эзотерический. вектор.
Символ векторной иллюстрации бесконечности каллиграфии. вечная безграничная эмблема. черный силуэт ленты Мебиуса. современный мазок кисти. концепция бесконечной жизни цикла. элемент графического дизайна для татуировки карты и логотипа
Мужчины и женщины подписывают
Иконки с ацтекскими знаками дня календаря
Символ флажка, значок флажка
Зеленые стрелки перерабатывают эко-символ векторные иллюстрации, изолированные на белом фоне.
 переработанный знак. цикл переработанный значок. символ переработанных материалов.
переработанный знак. цикл переработанный значок. символ переработанных материалов.Значок джентльмена. векторный стиль представляет собой плоский знаковый символ с закругленными углами, черный цвет, белый фон.
Большой набор алхимических символов, выделенных на белом фоне
Обращение с набором значков упаковки, включая знаки хрупкости, переработки и предостережения и т. д. значок галочки. значок кнопки контрольного списка
Любовное слово в знаке бесконечности. знак на открытке ко дню святого валентина, тату, печать. векторная каллиграфия и надпись иллюстрации, изолированные на белом фоне.
Глобальные бизнес-услуги, значок и символ
Троицкое воскресенье.
Значки линии любви. подарочная коробка, разбитое сердце и романтическое письмо. обручальные кольца, бокалы с шампанским, иконы любовного сердца. счастливая пара, держащая сердце, романтический громкоговоритель. элемент качественного дизайна. вектор
Контур значок бесконечности векторные иллюстрации, изолированные на белом символе eps 10
Векторная иллюстрация зеленый символ корзины, изолированные на белом фоне.
 знак утилизации в плоском стиле.
знак утилизации в плоском стиле.Иконки литературных строк для Интернета и мобильных устройств. редактируемые штриховые знаки. литература наброски концепции иллюстрации
Хрупкий плоский значок с трещиной и черной рамкой, изолированные на белом фоне. символ хрупкой посылки. векторная иллюстрация этикетки.
Символ закона и справедливости. концепция закона и справедливости. весы правосудия, молоток и книга. векторная иллюстрация. может использоваться в качестве легальности логотипа.
Вектор туалета со смывом
Иллюстрация иконки ветеринарной. векторный силуэт на белом фоне. символ срочности для животного.
Набор из двух карточек с соболезнованиями в виде сердца и крыла, черно-белые
Проверить простой значок. утвержденный знак галочки. подтвердить, сделать или принять символ. качественные элементы дизайна. классический стиль.
Значок доллара. денежный знак символ счета плоский платеж, значок валюты доллар.
Низкополигональный пси-символ, состоящий из точек, линий
Дизайн значков символов дзен и ом
Значок бесконечности из линий и треугольников, точка, соединяющая сеть на синем фоне.
 иллюстрация вектор
иллюстрация векторСимвол здоровья
Значок знака энергии и молнии. шаблон для вашего дизайна
Значок формы сердца. рукопожатие. символ дня дружбы, любви.
Древняя греческая монета из Афин, винтажная иллюстрация. старая гравированная иллюстрация меандра совы и греческого орнамента, изолированная на белом, векторная иллюстрация
Группа детей на иллюстрации значка математики
Держите значок линии сердца. друзья любят знак. символ руки дружбы. элемент качественного дизайна. линейный стиль держите значок сердца. редактируемый штрих. вектор
Одно каллиграфическое черное сердце с двумя закорючками на ленте
Горный силуэт — векторный значок. скалистые вершины. горные хребты. черно-белый значок горы изолированы
Wi-Fi
Значок Интернет. символ веб-сайта. Знак земного шара
Набор ретро-иконок основных ценностей. целостность, лидерство, качество и развитие, креативность, подотчетность, простота, надежность, честность, прозрачность, страсть, воля к победе, последовательность, смелость и значки обслуживания клиентов.

Фигурка человека, стоящего спереди, в разных позах, набор векторных иконок. черно-белые вырезанные люди человеческий силуэт на белом фоне
Значок слабости. простая иллюстрация элемента. дизайн символа слабости концепции. можно использовать для сети
Большой набор алхимических символов на тему старых рукописей с оккультными текстами алфавита и символов. эзотерические письменные знаки, вдохновленные средневековыми писаниями. вектор
Символы бесконечности
Абстрактный неоновый треугольник со светящимися линиями.
Рукопожатие, нарисованное от руки значок каракули. эскиз иллюстрации рукопожатия для печати, Интернета, мобильных устройств и инфографики, изолированные на белом фоне. деловая сделка, команда и концепция сотрудничества.
С++ — ошибка, символ «вектор» не может быть разрешен
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 47 тысяч раз
Я использую eclipse в Linux для разработки приложения на С++, и я получаю эту ошибку аннотации редактора «Символ ‘вектор’ не может быть разрешен» из следующих строк кода
std::vector
buffer; Мне кажется, что какой-то библиотеки не хватает или не заданы пути.
 Я явно загрузил STL, но это бесполезно. Нужно ли мне переустанавливать GCC на моем Linux?
Я явно загрузил STL, но это бесполезно. Нужно ли мне переустанавливать GCC на моем Linux?Затмение линукса С++
3
В Eclipse щелкните правой кнопкой мыши имя проекта… Выберите «Индекс»… «Перестроить».
1
Вам необходимо включить определение вектора STL в вашу программу. Поместите:
#include
вверху вашего файла, и это должно работать.
4
У меня была такая же проблема. Я считаю, что проблема возникает из-за того, как обновляется автозаполнение std::. Eclipse должен получить это из Пути и Символов, но это может быть ошибкой. Мне пришлось очистить все настройки Eclipse после обновления gcc (таким образом, g++), так как вы находитесь в Linux, они находятся в вашей домашней папке ~/.eclipse/.
Итак,
1) Перезапустил Eclipse после очистки ~/.
 eclipse/.
eclipse/.2) проверил, что путь и символы (при щелчке правой кнопкой мыши по проекту> Общие> Путь и символы) включают все обновленные каталоги gcc и c++ include (вектор должен находиться в ./gcc/version/include/c++/version/)
3) Перестроить индекс.
4) Создан файл *.cpp, который включает *.h, в котором отображается ошибка. Это заставит Eclipse отслеживать зависимости для *.h.
5) Перестроить индекс и/или перезапустить несколько раз по мере необходимости, теперь я вижу вектор в конце std:: autocompletion.
(см. рисунок)
Надеюсь, это поможет!
1
См. Также связанный вопрос: Eclipse CDT: символ «cout» не может быть разрешен
для меня проблема заключалась в том, что в
#includeгде-то есть#include, который имеет другой путь включения, чем#includeт. е.:
/usr/include/c++/4. 6/x86_64-linux-gnu
6/x86_64-linux-gnu #include<вектор>
должен быть включен вверху.
0
#include <вектор>
Кроме того, std::vector является типом шаблона, поэтому вы должны использовать его как
std::vector
buffer; Мне кажется, что какой-то библиотеки не хватает или не заданы пути.
Да, это похоже на ошибку компоновщика. Линкеры имеют дело с символами.
Я специально загрузил STL, но это бесполезно.
Надеюсь, вы имеете в виду libstdc++, реализацию GNU стандартной библиотеки C++, и вам, вероятно, не следовало этого делать. Ваш набор инструментов поставляется с правильной реализацией stdlib.
Нужно ли мне переустанавливать GCC на моем Linux?
Вероятно, мудро. И пусть эта установка справляется со стандартной библиотекой.
Кроме того, на случай, если вы играете с командной строкой компиляции, не забудьте вызвать
g++неgcc;g++автоматически связывается со средой выполнения C++ и реализацией stdlib, тогда какgccпредназначен для C.
0
По-видимому, вектор принадлежит стандартной библиотеке шаблонов C++ с точки зрения MinGW. поэтому в дополнение к
#include
Добавить
, используя пространство имен std;
после включения заголовочного файла.
Создан файл
*.cpp, который включает*.h, в котором отображается ошибка. Это заставит Eclipse отслеживать зависимости для*.h.
У меня работает…Скорее всего, в ваших настройках отсутствуют какие-то специфичные для системы каталоги включения, из-за чего индексатор не может правильно анализировать iostream, отсюда и ошибки. Выбрав Индекс
-> Поискдля неразрешенных включений в контекстном меню проекта, вы получите список неразрешенных включений, которые вы можете найти в/usr/includeи добавьте содержащие каталоги в C++. Включить пути и символы в свойствах проекта.
В моей системе мне пришлось добавить
/usr/include/c++/4.6/x86_64-linux-gnuдля разрешениябит/c++config.hи еще несколько каталогов.Не забудьте перестроить индекс (Index -> Rebuild) после добавления включаемых каталогов.
Я знаю, что эта проблема уже решена, но она по-прежнему отображается в топе результатов Google.
Использование Eclipse Neon для Linux Я решил это с помощью
Quick Fix:- щелкните правой кнопкой мыши на «векторе» в редакторе,
- , затем «Быстрое исправление»
добавление #include
Символ вектор бесплатно | AI, SVG и EPS
- 902:30
- Все
- АИ
- CDR
- EPS
- СВГ
- Все
- Белый 902:30
- Красный
- Апельсин
- Желтый
- Зеленый 902:30
- Аква
- Синий
- Пурпурный
- Розовый 902:30
- Черный
- Серый
Stock Symbols Город Мир вектор
Бесплатный векторный набор искусства
набор символов бесплатный вектор
Продовольственные векторные символы
Векторные символы граффити
Набор символов векторной переработки
Набор иконок недвижимости
Значок черепа и скрещенных костей на белом фоне.
 Вектор
ВекторВеб-иконки и RSS-символы
Глянцевые символы гороскопа
Двенадцать различных дорожных знаков
Формы Spin Dot
Торговые иконки
Набор векторных иконок 2
Вектор иконы страховой группы
Вектор коллекции символов солнца
Библиотеки символов Яна
Infinity Design Векторная иконка Иллюстрация Дизайн логотипа
Шесть шагов цикла бесконечного процесса Инфографика
Символы электронных схем
Символы02
Финансы, банковское дело, экономика иконы
бесплатно покер векторов
Красный и зеленый craigSoup Glossy Icons
Набор векторных иконок 3
Глобально согласованная система классификации и маркировки химических веществ вектор на белом фоне иллюстрации
Иконки со стрелками бесплатный вектор
Бесплатный набор векторных иконок 1, содержащий 25 иконок
красочные векторные элементы
бесшовный рисунок с оккультными знаками и магическими рунами
Пробки от бутылок векторная графика
Спортивные символы
Символы солнца или векторный набор иконок
Набор иконок экономики с блестящим стилем
Рождественский бесплатный векторный набор vol.

30002 Save PNG EPS
love heart with the symbol of infinity vector
2500*2500


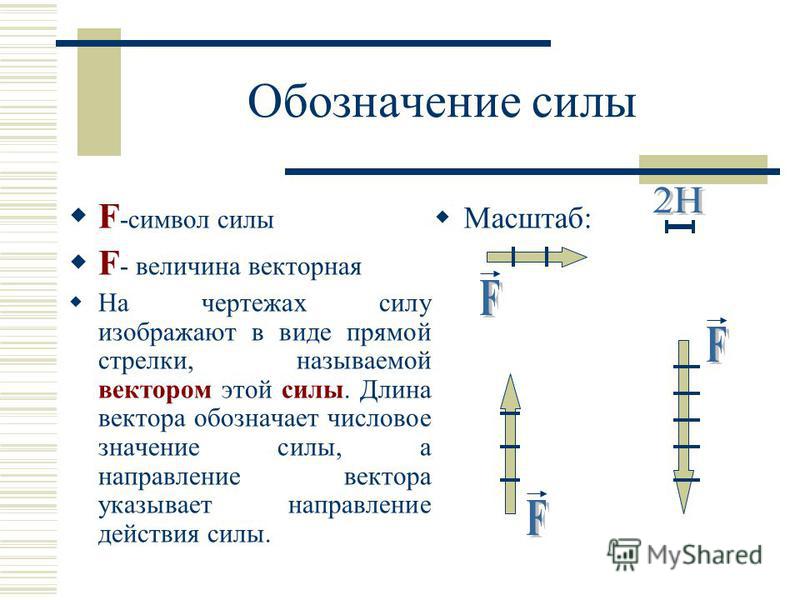 Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.
Разностью двух векторов a и b называется вектор c при условии: c = a − b, если c + b =a.

