| Неоднородное поле | Fiziku5
Неоднородное поле. В этом случае на положительный и отрицательный заряды диполя будут действовать неодинаковые силы (на рис. F2 > F1). Найдем выражение для силы, действующей на диполь для случая, когда напряженность зависит только от одной переменной х. Пусть поле характеризуется градиентом dE/dx. Найдем результирующую силу F = F2 — F1.
изменение напряженности на отрезке l×cosa, a — угол между векторами рэл и Е | ||
результирующая сила [12] и дипольный момент; подставляя, получим: | ||
сила, действующая на диполь в неоднородном электрическом поле |
Таким образом, в неоднородном

Работа по повороту диполя в однородном внешнем электрическом поле.
Если внести диполь в однородное электростатическое поле так, что его дипольный момент будет составлять угол a с вектором напряженности поля Е, силы поля F будут поворачивать диполь (на рис. – по часовой стрелке) до достижения им положения равновесия.
работа при вращательном движении, М — вращающий момент, a — угол поворота | ||
работа по повороту диполя в однородном внешнем электростатическом поле | ||
Если диполь из положения равновесия повернуть так, что между дипольным моментом и вектором напряженности внешнего поля образуется угол a, диполь получит запас потенциальной энергии Wпот. Так как работа равна убыли потенциальной энергии, то в общем случае получим:
Изменение потенциальной энергии диполя во внешнем электростатическом поле | |
Потенциальная энергия диполя во внешнем поле. |
Поляризация диэлектриков.
Все вещества состоят из нейтральных атомов или молекул. И в атоме, и в молекуле поровну отрицательно заряженных частиц (электронов) и положительно заряженных ядер. В тех веществах, которые образуют металлические кристаллы,
от каждого атома (или молекулы) отрываются по 1-2 электрона, атомы становятся ионами, образуя кристаллическую решетку, а электроны свободно перемещаются по всему кристаллу. Эти электроны называют свободными зарядами
 Эти общие электроны как-бы цементируют атомы, и образуется молекула. Все виды молекул, из которых состоят диэлектрики, можно отнести к двум типам:
Эти общие электроны как-бы цементируют атомы, и образуется молекула. Все виды молекул, из которых состоят диэлектрики, можно отнести к двум типам: Если диэлектрик внести во внешнее электрическое поле, на его поверхностях появляются заряды. Это явление называется поляризацией диэлектриков, а сами заряды называются связанными, так как они могут смещаться только в пределах самой молекулы. При снятии внешнего поля поляризация практически мгновенно исчезает. В зависимости от того, из какого типа молекул состоит диэлектрик различают следующие типы поляризации.
1) Деформационная (электронная) поляризация наблюдается для веществ с неполярными молекулами. При внесении такого диэлектрика во внешнее электрическое поле, его молекулы растягиваются и образуют диполь с дипольным моментом рэл.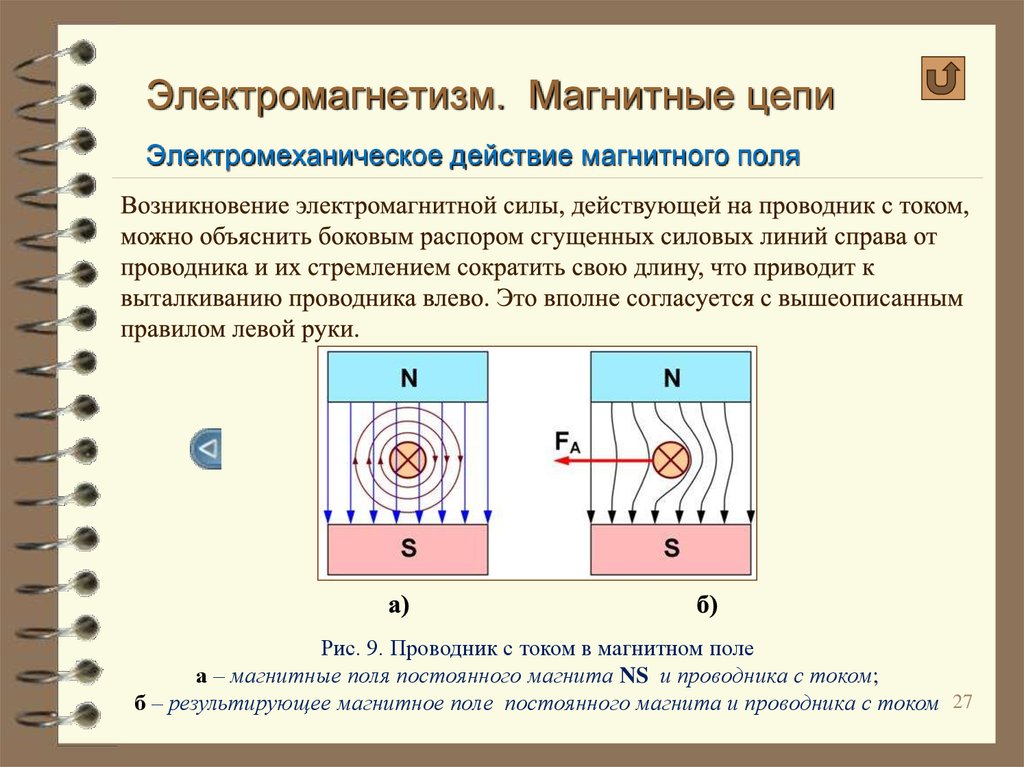 При не очень сильных внешних полях рэл оказывается пропорциональным напряженности поля Е: рэл ~ Е и можно записать:
При не очень сильных внешних полях рэл оказывается пропорциональным напряженности поля Е: рэл ~ Е и можно записать:
индуцированный дипольный момент одной молекулы неполярного диэлектрика | |
a — коэффициент поляризуемости (поляризуемость) молекулы |
Примерами веществ, для которых наблюдается деформационная поляризация, являются: водород Н2, парафин, ССl4 и др.
2) Ориентационная (дипольная) поляризация наблюдается для веществ с полярными молекулами. На рис. полярные молекулы символически показаны в виде диполей. При отсутствии внешнего поля молекулы ориентированы хаотически. Во внешнем поле молекулы-диполи стремятся ориентироваться по полю, но им «мешает» тепловое движение, поэтому строгой ориентации не происходит, но тем не менее на поверхностях диэлектрика появляются связанные заряды с поверхностной плотностью
 Средний дипольный момент молекул áрñ из-за влияния теплового движения оказывается не равным собственному дипольному моменту молекулы р0. Для не очень сильных внешних полей расчеты дают формулу:
Средний дипольный момент молекул áрñ из-за влияния теплового движения оказывается не равным собственному дипольному моменту молекулы р0. Для не очень сильных внешних полей расчеты дают формулу:средний дипольный момент одной полярной молекулы во внешнем электрическом поле р0 –собственный дипольный момент молекулы |
К веществам с полярными молекулами относятся вода, HCl, NH3,
3) Существует еще один тип поляризации диэлектриков – ионная поляризация. Например, кристалл NaCl представляет собой вдвинутые друг в друга решетки из положительных и отрицательных ионов. Под воздействием внешнего электрического поля происходит смещение одной кристаллической решетки относительно другой. Мы не будем подробно рассматривать этот тип поляризации.
Характеристики электрического поля в диэлектриках и их диэлектрических свойств.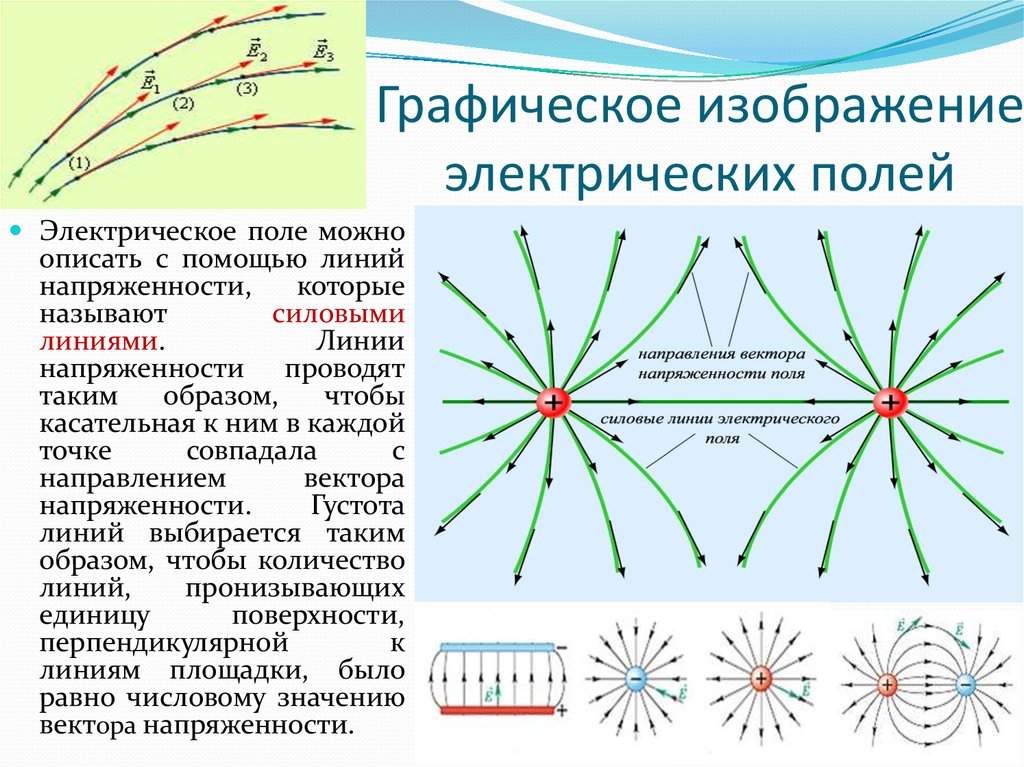
Поляризация диэлектриков характеризуется физической величиной, называемой
(Кл/м2) n | Здесь: pi – дипольный момент молекулы, V – объем диэлектрика. Вектор поляризации по смыслу представляет собой векторную сумму дипольных моментов всех молекул в единице объема диэлектрика. |
Найдем связь величины вектора поляризации Р с поверхностной плотностью связанных зарядов s¢связ. Пусть кусок диэлектрика в форме параллелепипеда с боковой поверхностью S и длиной L помещен во внешнее поле с напряженностью Е. (см. рис.). На его поверхности образуются связанные заряды.
Неоднородное электрическое поле — Большая Энциклопедия Нефти и Газа, статья, страница 1
Cтраница 1
Неоднородное электрическое поле
 [1]
[1]Неоднородное электрическое поле формируется в зазоре между электродами с различной кривизной поверхности, на которые подается напряжение в несколько киловольт. [2]
Простейшее неоднородное электрическое поле может быть получено с помощью системы электродов в виде двух бесконечно длинных концентрических цилиндров с радиусами г, и гг В такой системе при отсутствии пространственного заряда поле в любой точке обратно пропорционально расстоянию от оси. [3]
Градиент неоднородного электрического поля, создаваемого на ядре окружающими зарядами, также представляет собой симметричный тензор, след которого Uxx Uyy Uzz0, а в системе главных осей тензор диагоналей. [4]
В неоднородном электрическом поле поляризация диэлектрика тоже неоднородна: его поляризованность Р зависит от координат. В этом случае кроме поверхностных поляризационных зарядов могут возникать еще и объемные поляризационные заряды. [5]
[5]
| Ширина полосы резонанса Na23 в металлическом натрии, измеренная между пиками поглощения. [6] |
В неоднородном электрическом поле электрический квадру-польный Момент ядер, имеющих J1I2, вызывает уширение линии ядерного резонанса. [7]
В неоднородном электрическом поле поляризация диэлектрика тоже неоднородна: его поляризованность Р зависит от координат. В этом случае кроме поверхностных поляризационных зарядов могут возникать еще и объемные поляризационные заряды. [8]
В неоднородных электрических полях, когда диэлектрические свойства частиц и окружающей среды различны, появляются силы, приводящие кроме ориентации к возникновению движения частиц в определенном направлении. [9]
Зависимость пробивного напряжения лолиэтилена и неоднородном поле от радиуса кривизны иглы при 330 К и расстоянии между электродами 500 мкм. | Зависимость максимальной напряженности при пробое от радиуса кривизны игольчатого электрода ( -. для полиэтилена при 333 К и расстоянии между электродами 50 мкм (.| Зависимость электрической прочности полиэтилена от температуры в однородном ( а и неоднородном ( б поле.
[10] | Зависимость максимальной напряженности при пробое от радиуса кривизны игольчатого электрода ( -. для полиэтилена при 333 К и расстоянии между электродами 50 мкм (.| Зависимость электрической прочности полиэтилена от температуры в однородном ( а и неоднородном ( б поле.
[10] |
В неоднородном электрическом поле наблюдается заметная зависимость пробивного напряжения от полярности электродов. [11]
В неоднородных электрических полях, так же как и в газах, может быть неполный пробой — корона. Околь-либо длительно корона в жидких диэлектриках недопустима, так как она вызывает разложение жидкости. Многократно повторяющиеся искровые разряды в сравнительно небольшом объеме жидкости могут вызывать как падение электрической прочности, так и повышение. Первое возможно в том случае, когда повторные разряды приводят к осушению жидкости, не склонной под влиянием разрядов к большому выделению углеродистых образований — копоти; это наблюдается в нефтяном масле. Второе наблюдается в жидкостях, образующих под влиянием электрических разрядов большое количество копоти, например в соволе.
[12]
Второе наблюдается в жидкостях, образующих под влиянием электрических разрядов большое количество копоти, например в соволе.
[12]
В неоднородных электрических полях, так же как и в газах, может быть неполный пробой — корона. Длительно корона в жидких диэлектриках недопустима, так как она вызывает разложение жидкости. Многократно повторяющиеся искровые разряды в сравнительно небольшом объеме жидкости могут вызывать как падение электрической прочности, так и ее повышение. Повышение возможно в том случае, когда повторные разряды приводят к осушению жидкости, несклонной под влиянием разрядов к большому выделению углеродистых образований — сажи; это наблюдается в нефтяном масле. Понижение наблюдается в жидкостях, образующих под влиянием электрических разрядов большое количество копоти, например в соволе. При достаточной мощности пробой жидкого диэлектрика может быть дуговым. При этом происходит интенсивное разложение жидкости. [13]
В неоднородном электрическом поле получить сплошную корону в виде светящейся оболочки трудно. Коронный разряд в масле представляет собой ряд беспокойных то возникающих, то пропадающих незавершенных искр, длина которых зависит от величины приложенного напряжения. Это явление имеет сходство с незавершенными разрядами в воздухе, возникающими между электродами с относительно большим радиусом закругления. При разряде образующееся небольшое количество газа растворяется в масле, происходит быстрая деионизация и диэлектрические свойства снова восстанавливаются. При этом для повторного пробоя может понадобиться дальнейшее повышение напряжения, но значительно меньшее, чем в однородном пол.
[14]
Коронный разряд в масле представляет собой ряд беспокойных то возникающих, то пропадающих незавершенных искр, длина которых зависит от величины приложенного напряжения. Это явление имеет сходство с незавершенными разрядами в воздухе, возникающими между электродами с относительно большим радиусом закругления. При разряде образующееся небольшое количество газа растворяется в масле, происходит быстрая деионизация и диэлектрические свойства снова восстанавливаются. При этом для повторного пробоя может понадобиться дальнейшее повышение напряжения, но значительно меньшее, чем в однородном пол.
[14]
В неоднородном электрическом поле интенсивность движения микрокапель воды по траекториям линий поля повышается с увеличением градиента его напряженности. Для необходимого градиента требуется довольно высокое напряжение на электродах ( более 3 кВ), которое зависит от расстояния между электродами. Необходимо учитывать, что с уменьшением межэлектродного расстояния градиент напряженности увеличивается, однако возрастает опасность пробоя. [15]
[15]
Страницы: 1 2 3 4
Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. Тема урока:Электрическое поле. Однородное и неоднородное электрическое поле. Напряженность электрического поля. Принцип
суперпозицииэлектростатических
2. Электрическое поле
В пространстве вокруг электрическогозаряда существует электрическое поле.

Электрическое поле можно изобразить
графически с помощью силовых линий
электрического поля, которые имеют
направление.
Электрическое поле
положительного заряда
отрицательного заряда
Напряженностью электрического поля
называется отношение силы, с которой поле
воздействует на точечный заряд, к величине этого
заряда.
Напряженность, как и сила, векторная величина.
Направление вектора напряженности совпадает с
направлением силы, действующей на
положительный заряд.
Так как F~q то F=Eq, где F-вектор; qскаляр, тогда и E-вектор
Электростатическое поле, не меняющееся со временем, создается только
электрическими зарядами.
Если помещать в одну и ту же точку поля разные точечные заряды, то
оказывается, что сила, действующая на эти заряды прямо пропорциональна
величине этих зарядов.
Напряженность является силовой характеристикой поля, так как зависит только
от свойств поля и не зависит от свойств внесенного в это поле заряда
Напряженность, поля точечного
заряда.
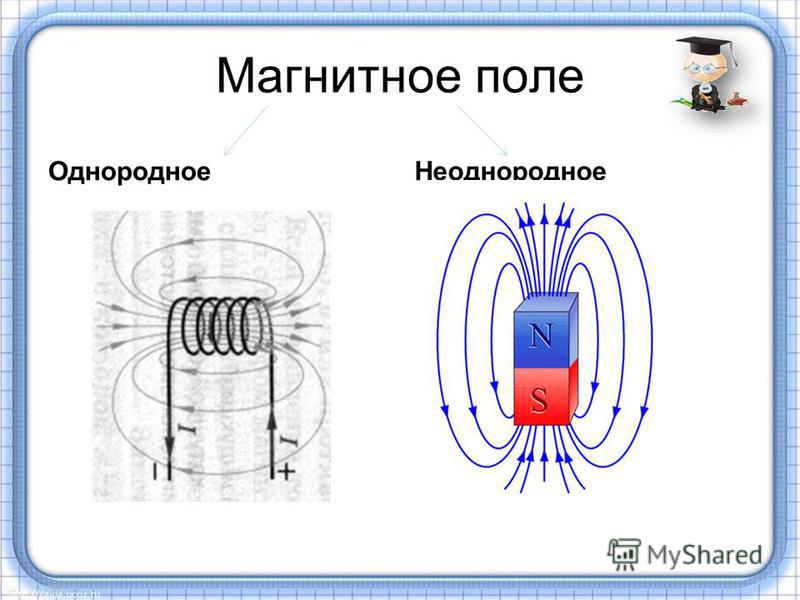
Напряженность поля неподвижного точечного
заряда можно вычислить, используя закон
Кулона.
+
Так как
тогда
+
+
Коэффициент пропорциональности тот же,
что и в законе Кулона.
Вектор напряженности направлен от заряда, если
заряд положительный, и к заряду, если он
отрицательный.
Принцип суперпозиции
электрических полей
Если на тело действует несколько сил, то согласно законам
механики результирующая сила равна геометрической сумме
сил: F = Fl+F2+ F3…
На электрические заряды действуют силы со стороны
электрического поля.
Если в данной точке пространства существуют поля,
создаваемые несколькими зарядами, то,
напряженность в данной точке поля равна векторной
сумме напряженностей полей, создаваемых каждым
из этих зарядов.
В этом состоит принцип суперпозиции
(наложения) полей.
E = El+E2+ E3…
Силовыми линиями
электрического поля или
линиями напряженности
называются непрерывные линии,
касательные к которым в каждой точке,
через которую они проходят, совпадают
с вектором напряженности.
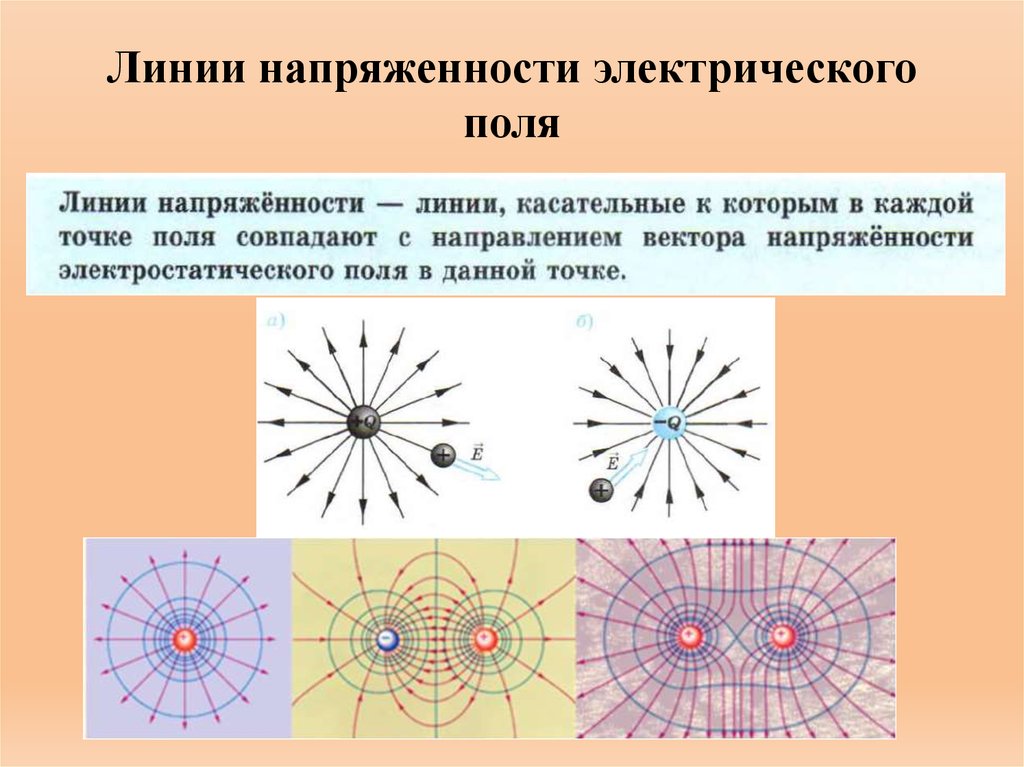
Электрическое поле, напряженность
которого одинакова во всех точках
пространства, называется однородным.
Густота линий больше вблизи
заряженных тел, где напряженность
больше.
Силовые линии одного и того же поля не
пересекаются.
Напряжённость поля заряженного
шара
Силовые линии электрического поля, как
вытекает из соображений симметрии,
направлены вдоль продолжений радиусов шара
(рис. а).
Обратите внимание! Силовые линии вне шара
распределены в пространстве точно так же, как и
силовые линии точечного заряда (рис. б).
Если совпадают картины силовых линий, то
можно ожидать, что совпадают и напряженности
полей. Поэтому на расстоянии r >= R от центра
шара напряженность поля определяется той же
формулой, что и напряженность поля точечного
заряда, помещенного в центре сферы.
Внутри шара Е=0 и q=0
(весь заряд на поверхности шара)
Система заряженных тел обладает
потенциальной энергией,
называемой электростатической
или электрической.
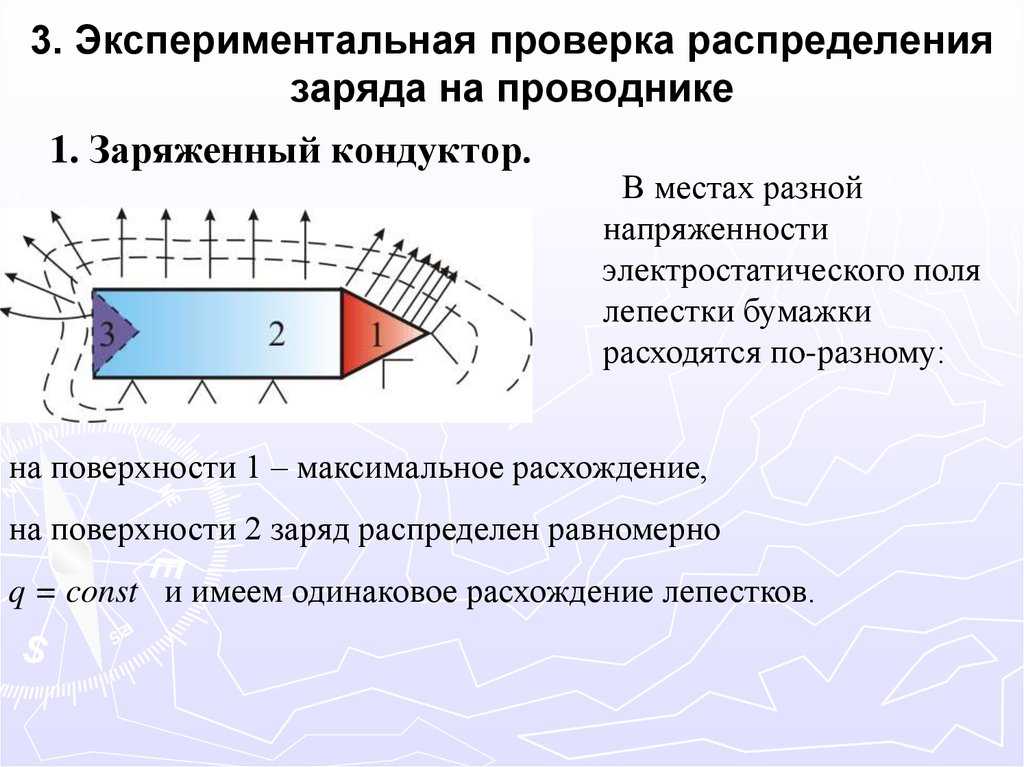
11. потенциальная энергия заряда в однородном электростатическом поле равна:
Если поле совершаетположительную работу, то
потенциальная энергия
заряженного тела в поле
уменьшается:
И наоборот, если работа
отрицательна, то
На замкнутой траектории, когда
заряд возвращается в начальную
точку, работа поля равна нулю:
Это интересно
«ЖИВОЕ» ЭЛЕКТРИЧЕСТВО
Первое упоминание об электрических рыбах датируется более чем 5000
лет назад. На древних египетских надгробьях изображен африканский
электрический сом.
Египтяне полагали, что этот сом является «защитником рыб» — рыбак,
вытаскивающий сеть с рыбой, мог получить приличный электрический
разряд и выпустить сеть из рук, отпустив весь пойманный улов назад в
реку.
«Электрическое» зрение рыб.
Рыбы с помощью электрических органов обнаруживают в воде
посторонние предметы. Некоторые рыбы все время генерируют
электрические импульсы. Вокруг их тела в воде текут электрические токи.

Если в воду поместить посторонний предмет, то электрическое поле
искажается и электрические сигналы, поступающие на чувствительные
электрорецепторы рыб меняются. Мозг сравнивает сигналы от многих
рецепторов и формирует у рыбы представление о размерах, форме и
скорости движения предмета.
Наиболее известные электрические
охотники — это скаты. Скат наплывает на
жертву сверху и парализует ее серией
электрических разрядов. Однако его
«батареи» разряжаются , и на подзарядк
ему требуется некоторое время.
Древние греки и римляне (500 д.н.э.-500
н.э.) знали об электрическом скате. .
Плиний в 113 н.э. описывал, как скат
использует «магическую силу» для того,
чтобы обездвижить свою добычу. Греки
знали, что «магическая сила» может
передаваться через металлические
предметы, например, копья, которыми
они охотились на рыб.
Рыбы-электроищейки.
Некоторые рыбы, пытаясь спастись, зарываются
в песок и замирают там.
 Но и у них нет никаких
Но и у них нет никакихшансов, поскольку пока они живы, их тела
генерируют
электрические
поля, которые
улавливает, например,
своей необычной головой
акула-молот, бросающаяся,
как кажется, прямо на
пустой грунт и
вытаскивающая из него
бьющуюся жертву.
Электрические рыбы
используют
электрические
сигналы для
общения между
собой. Они
оповещают других
особей, что данная
территория занята или,
что ими обнаружена пища.
Есть электрические сигналы:
«вызываю на бой « или
«сдаюсь». Все эти
сигналы хорошо
принимаются
рыбами на
расстоянии
порядка 10 метров
English Русский Правила
Математическое моделирование неоднородного электрического поля в аппаратах для разделения водонефтяных эмульсий
Библиографическое описание: Зайковский, В. В. Математическое моделирование неоднородного электрического поля в аппаратах для разделения водонефтяных эмульсий / В. В. Зайковский. — Текст : непосредственный // Молодой ученый. — 2014. — № 15 (74). — С. 71-74. — URL: https://moluch.ru/archive/74/12611/ (дата обращения: 30.09.2022).
В. Зайковский. — Текст : непосредственный // Молодой ученый. — 2014. — № 15 (74). — С. 71-74. — URL: https://moluch.ru/archive/74/12611/ (дата обращения: 30.09.2022).
Добыча и подготовка нефтяного сырья неразрывно связана с такими процессами как увеличение давления в пластовой зоне с помощью нагнетательных водных скважин, смешение нефти с водой при ее поднятии, обессоливание нефти с помощью промывки водой. На сегодняшний день водонефтяные эмульсии являются естественным продуктом инженерного процесса получения жидких углеводородов. Совершенствование процессов разделения (демульсификации, обезвоживания) водонефтяных эмульсий — одна из актуальных научно-производственных задач нефтяного хозяйства, решение которой способно принести значительный экономический эффект, повысить надежность промыслового и магистрального транспорта нефти, улучшить качество нефтепродуктов [1, c. 157].
В настоящее время в качестве физического принципа разделения водонефтяных эмульсий в промышленных масштабах на объектах нефтедобычи используется эффект электрофореза (движения заряженных частиц вдоль линий напряженности электрического поля) и диэлектрофореза (движения поляризованных веществ в сторону наибольшей напряженности электрического поля).
Наибольшее распространение получила конструкция электродегидратора, при которой водонефтяная эмульсия подвергается воздействию однородного электрического поля плоского конденсатора (Рис. 1).
Рис. 1. Схема типового цилиндрического электродегидратора горизонтального исполнения [2, с. 67].
При этом, в межэлектродном пространстве заряды в каплях воды приходят в движение (электрофорез), концентрируются на противоположных концах капель и вытягивают каплю вдоль линий электрического поля. Заряды, сконцентрированные на концах капель, создают мелкомасштабную неоднородность электрического поля, которая, в свою очередь, создает условия для взаимного притяжения капель под действием сил диэлектрофореза. Основной физический механизм, приводящий к взаимному слиянию капель (диэлектрофорез), при такой конструкции электродегидратора, реализуется лишь при небольших расстояниях между поляризованными каплями [3, c. 67].
Интенсификация электрокоалесценции капель возможна при расширении масштаба действия эффекта диэлектрофореза, а именно, за счет использования изначально неоднородного электрического поля. В неоднородном электрическом поле за счет диэлектрофореза капли воды, даже при значительных расстояниях между другими каплями, будут стремиться двигаться в сторону наибольшего возрастания напряженности электрического поля. Таким образом реализуется дополнительный сближающий механизм, который будет приводить к сокращению расстояния между каплями воды и интенсификации их слияния.
В неоднородном электрическом поле за счет диэлектрофореза капли воды, даже при значительных расстояниях между другими каплями, будут стремиться двигаться в сторону наибольшего возрастания напряженности электрического поля. Таким образом реализуется дополнительный сближающий механизм, который будет приводить к сокращению расстояния между каплями воды и интенсификации их слияния.
Основная цель данной работы состоит в составлении алгоритма к расчету сложной конфигурации неоднородного электрического поля, возникающего в электродегидраторах с несимметричной конфигурацией электродов. Именно наличие неоднородного электрического поля во всем объеме электродегидратора является необходимым условием к появлению сил диэлектрофореза.
Основным рабочим органом современных электродегидраторов является симметричный плоский конденсатор, модуль напряженности поля внутри которого однозначно определяется напряжением на электродами и расстоянием между ними, а направление поля строго перпендикулярно электродам (Рис. 2).
2).
Рис. 2. Схематичное изображение поля симметричного плоского конденсатора. Слева и справа от пластин — изображение «краевого эффекта» — неоднородности электрического поля
В практике расчетов симметричных плоских конденсаторов как правило пренебрегают так называемыми «краевыми» эффектами — неоднородностью поля на краях электродов, в связи с чем обобщенные соотношения к расчету таких конфигураций поля отсутствуют. Таким образом, для расчета случая несимметричной конфигурации электродов, при котором основную роль будет играть именно неоднородное электрическое поле, необходима разработка нового алгоритма к расчету таких полей, а также «краевых» эффектов поля конденсатора любой конфигурации.
Соотношение к расчету напряженности стационарного электрического поля, исходя из определения данной величины, может быть записано для двумерного случая как вектор в виде набора координат [4, с. 2]:
Принимая во внимание, что в расчетной области между пластинами конденсатора отсутствуют свободные заряды, для вычислений потенциала используем уравнение Лапласа, которое для двумерного случая может быть записано в виде [4, с. 8]:
8]:
Данное уравнение дополним краевыми условиями нескольких видов исходя из особенностей расчетной области, которая представлена на рисунке 3.
Рис. 3. Расчетная область плоского несимметричного конденсатора.
Для границ расчетной области, которые должны находиться на достаточном удалении от пластин конденсатора, примем потенциал равным нулю, то есть:
Для верхней и нижней пластин конденсатора потенциал должен быть различен, известен и задан условиями расчета, то есть:
Для численного расчета приведенные выше соотношения аппроксимируются с использованием конечно-разностного метода. Таким образом, для получения результата, необходимо построить численный алгоритм к вычислению потенциала в точках между и вокруг пластин конденсатора, учитывающий постоянные значения потенциала как на границе, так и внутри расчетной области.
Блок-схема разработанного алгоритма представлена на Рисунке 4.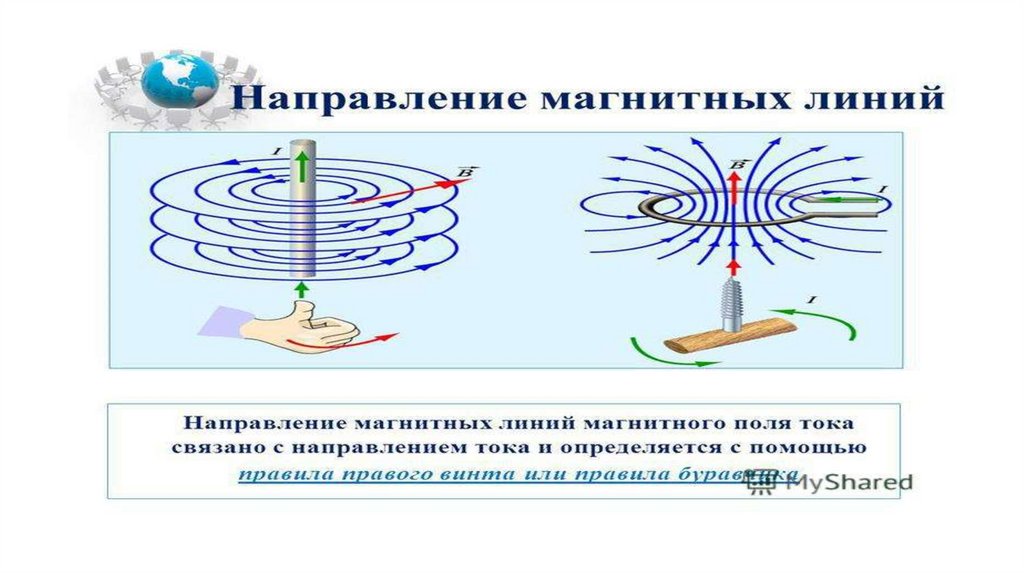 Вследствие того, что рассматривается статическое электрическое поле, можно, без больших потерь в производительности, вместо итерационного способа расчета использовать единовременное построение и решение системы уравнений для всех точек потенциала. Однако, для расчета потенциала в рамках рассматриваемой задачи, с учетом наличия «внутренних» краевых условий, указанный способ нуждается в модификации.
Вследствие того, что рассматривается статическое электрическое поле, можно, без больших потерь в производительности, вместо итерационного способа расчета использовать единовременное построение и решение системы уравнений для всех точек потенциала. Однако, для расчета потенциала в рамках рассматриваемой задачи, с учетом наличия «внутренних» краевых условий, указанный способ нуждается в модификации.
Рис. 4. Блок-схема алгоритма к расчету напряженности поля несимметричного конденсатора
Внутренние краевые условия требуют, чтобы, при использовании способа «единовременного» расчета, из вычислений были исключены те уравнения, которые описывают потенциал точек конденсатора, так как он задается заранее и поддерживается постоянным в течение всего срока эксплуатации установки. Для этой цели предлагается вычислять координаты точек конденсатора на расчетной сетке, а также их порядковые номера, и затем исключать из системы алгебраических уравнений, описывающих потенциал по всей расчетной области, уравнения для расчета уже известных значений потенциала пластин конденсатора.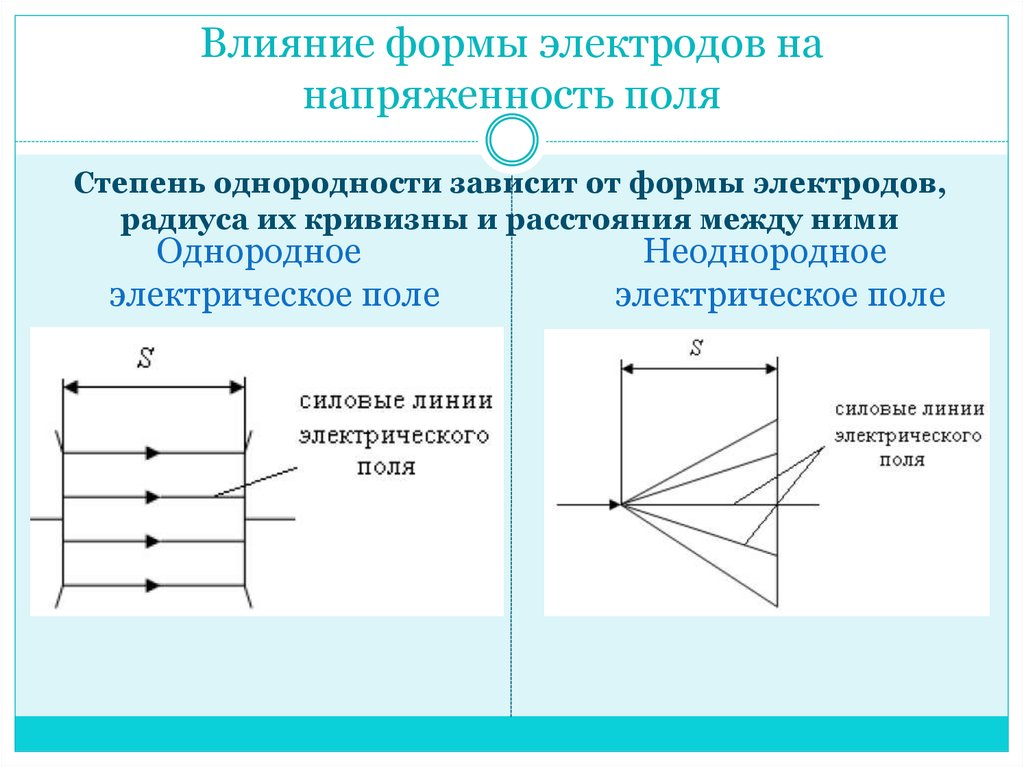 Таким образом исключаются ошибки, связанные с возможностью повторного расчета и замены значений потенциала, повышается точность значений, так как используются максимально достоверные данные из соседних точек расчетной сетки.
Таким образом исключаются ошибки, связанные с возможностью повторного расчета и замены значений потенциала, повышается точность значений, так как используются максимально достоверные данные из соседних точек расчетной сетки.
Приведенный алгоритм расчета был апробирован на двумерном расчете плоского несимметричного конденсатора с параметрами, представленными в Таблице 1.
Таблица 1
Исходные данные для апробации алгоритма.
|
Параметр, единица измерения: |
Значение: |
|
Длина верхней пластины конденсатора, м |
0,5 |
|
Длина нижней пластины конденсатора, м |
0,1 |
|
Напряжение на верхней пластине конденсатора, В |
2000 |
|
Напряжение на нижней пластине конденсатора, В |
0 |
|
Расстояние между пластинами конденсатора, м |
0,2 |
|
Количество точек расчетной сетки в горизонтальном направлении, штук |
100 |
|
Количество точек расчетной сетки в вертикальном направлении, штук |
200 |
Результаты апробации приведены на рисунке 5, где показаны результаты совместного расчета полей потенциала и напряженности электрического поля в исследуемой области.
Рис. 5. Иллюстрация совмещенных скалярного поля потенциала (белое — 1800–2000 В, темное — 0–200 В) и векторного поля напряженности в расчетной области
Видно, что поля не смещены относительно друг друга и физическая природа передана верно — вектора поля напряженности направлены перпендикулярно эквипотенциальным поверхностям. Также наблюдается 4 зоны скопления силовых линий напряженности поля: у левого и правого краев верхней пластины, и у левого и правого краев нижней пластины.
В результате выполнения исследования был составлен и апробирован алгоритм к расчету неоднородного электрического поля плоского несимметричного конденсатора. Указанный алгоритм без существенных изменений может быть расширен для трехмерного случая, а также для конденсаторов и электродов более сложной конфигурации.
Дальнейшим направлением исследования является расчет поля сил диэлектрофореза, а также моделированием движения капли воды в поле сил, совместно с постановкой физического эксперимента по оценке степени достоверности результатов математического моделирования, а также предложение конкретных технических решений по модернизации принципа работы существующих электрообессоливающих установок.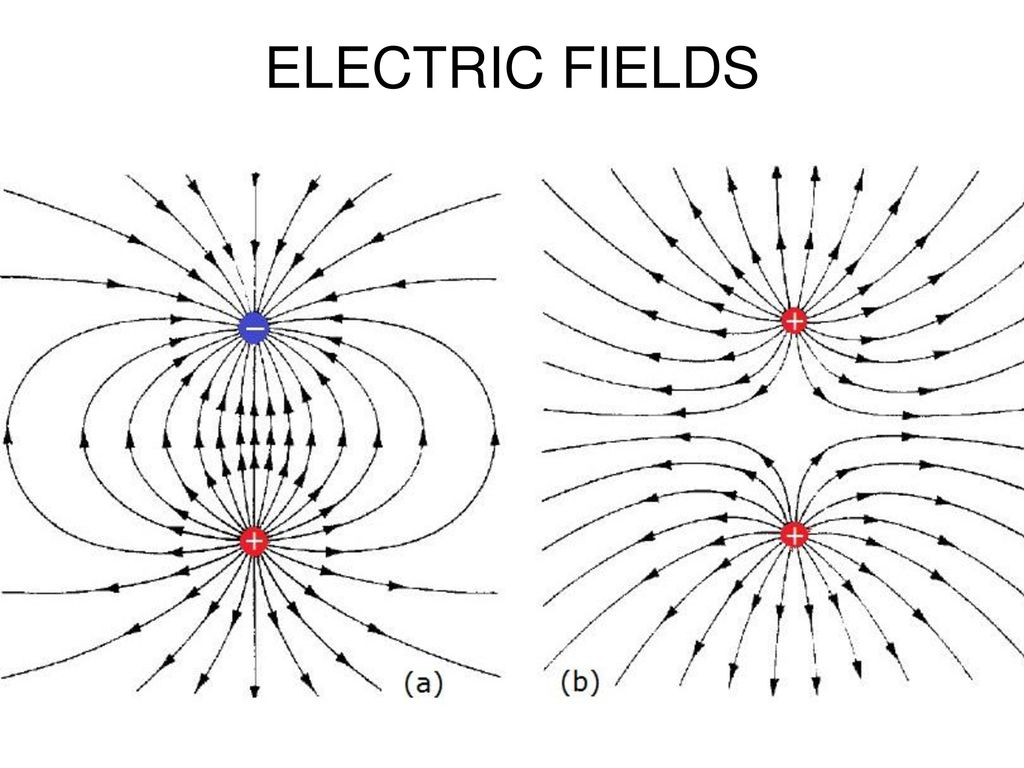
Литература:
1. Байков Н. М., Колесников Б. В., Челпанов П. И. Сбор, транспорт и подготовка нефти. — М., «Недра», 1975. — 317 с.
2. Левченко Д. Н. Эмульсии нефти с водой и методы их разрушения / Д. Н. Левченко, Н. В. Бергштейн, А. Д. Худякова, Н. М. Николаева. — М., Издательство «Химия», 1967. — 200 с.
3. Панченков, Г. М. Поведение эмульсии во внешнем электрическом поле / Г. М. Панченков, Л. К. Цабек. — М.: Химия, 1969. — 190 с.
4. James R. Nagel Solving the Generalized Poisson Equation Using the Finite-Difference Method (FMD). URL: http://www.ieeeaps.org/pdfs/ FA_Numerical_Poisson_Nagel.pdf (дата обращения: 28.08.2014).
Основные термины (генерируются автоматически): расчетная область, электрическое поле, неоднородное электрическое поле, пластина конденсатора, расчетная сетка, капля воды, плоский несимметричный конденсатор, нижняя пластина, правый край, симметричный плоский конденсатор.
Описание лабораторной работы «Исследование кривой Пашена самостоятельного разряда в воздухе», страница 3
Физика \ Электрогидродинамика
В промежутках с неоднородным электрическим полем критическое значение напряженности достигается сначала у электродов с малым радиусом кривизны, и разрядные явления происходят при сравнительно низкой средней напряженности поля в промежутке. В однородном и слабонеоднородном полях разряд происходит при средней напряженности, практически равной критической. Поэтому промежутки с однородным полем всегда имеют разрядные напряжения выше, чем промежутки той же длины с неоднородным полем.
Тип электрического поля
При рассмотрении электрических полей различают
однородные, слабо-неоднородные поля и резко-неоднородные поля. В первых двух
случаях отношение максимальной напряженности поля в промежутке к ее среднему
значению, называемое коэффициентом неоднородности поля kн,
составляет 1 (единица) для однородного поля, или не превышает 1,3÷1,5 — для слабо-неоднородного поля. В однородном поле напряжённость задаётся
выражением E=U/d, где U – разность потенциалов между двумя произвольными
точками пространства, d – расстояние между этими точками. В случае большого
коэффициента неоднородности (kн ≥ 4) поле в
промежутке является резко-неоднородным.
В однородном поле напряжённость задаётся
выражением E=U/d, где U – разность потенциалов между двумя произвольными
точками пространства, d – расстояние между этими точками. В случае большого
коэффициента неоднородности (kн ≥ 4) поле в
промежутке является резко-неоднородным.
В зависимости от напряженности электрического поля и степени его неоднородности в газовом промежутке может установиться разная форма электрического разряда. При этом основные электрофизические процессы, приводящие к развитию разряда, во всех газах примерно одинаковы, меняется только их интенсивность.
Ф. Пик исследовал высоковольтные явления, начиная от миниатюрного коронного разряда, заканчивая гигантскими молниями.
На примере системы концентрических цилиндров Пик показал, что при резко неоднородном электрическом поле напряжение зажигания коронного разряда существенно ниже напряжения искрового пробоя межэлектродного промежутка (рис.3).
Пиком были получены формулы для расчёта напряжённости электрического поля E0 у коронирующего электрода и напряжения на межэлектродном промежутке U0 в момент зажигания коронного разряда в системе коаксиальных цилиндров:
, | (7) |
где r0 – радиус внутреннего цилиндра, δ –
относительная плотность среды в межэлектродном промежутке, δ ~ P, P – давление.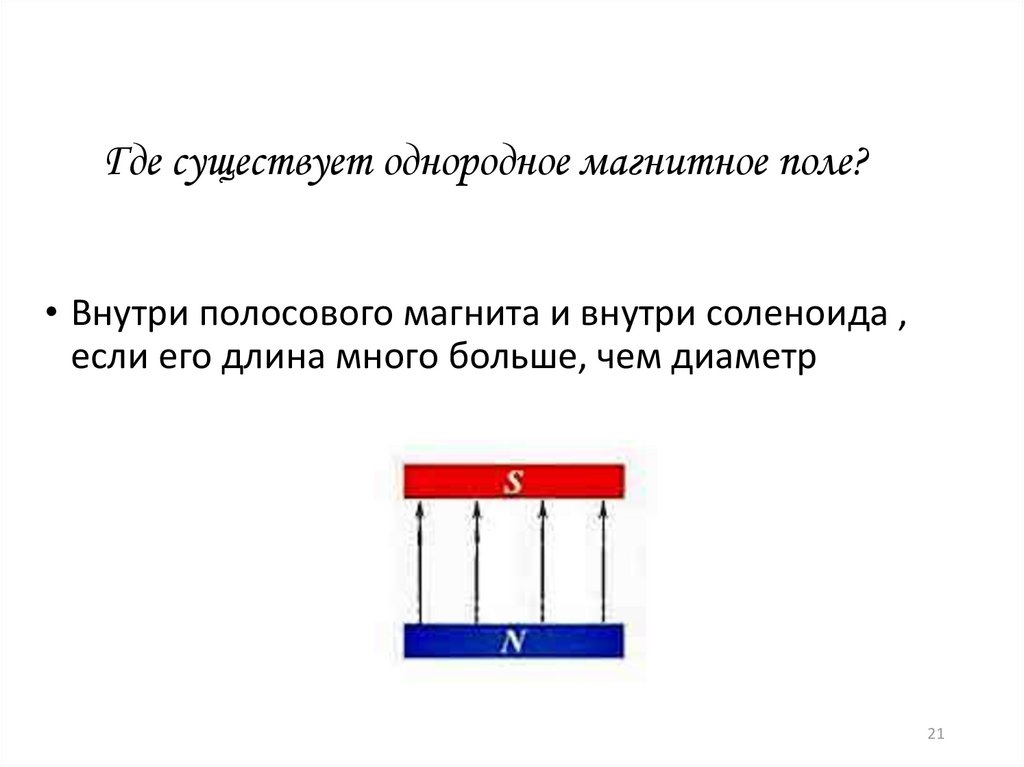 Для атмосферного давления δ = 1;
Для атмосферного давления δ = 1;
,
где R – радиус внешнего цилиндра.
Развитие разряда в резко-неоднородных полях
Резко-неоднородное поле характерно для промежутков, создаваемых электродами типа игла-плоскость, провод-плоскость, а также стержень-плоскость или шар-плоскость при малом радиусе закругления шара и большом расстоянии между электродами. Особенностью резко-неоднородных полей являются высокие напряженности поля у электрода с малым радиусом закругления даже при сравнительно небольшом напряжении на промежутке. Это означает, что в этой области могут идти процессы ударной ионизации, возникать лавины электронов, и выполняться условие самостоятельности разряда, когда зона ионизации охватывает только малую часть промежутка. Соответствующее значение напряжения (U0) носит название начального напряжения зажигания разряда.
При высоких значениях приложенного напряжения разряд
около электрода с малым радиусом кривизны проходит несколько стадий. Сначала
возникают лавины, которые в зависимости от направления поля, т.е. в зависимости
от полярности подаваемого на электрод напряжения, развиваются к электроду или
от него. В результате разделения зарядов в лавинах, около электрода образуется
избыточный объемный заряд одного знака с электродом (рис.3.10, b),
который создает собственное поле (рис.), снижающее поле у электрода (эффект
экранирования) и значительно усиливающий поле в промежутке перед зарядом.
Сначала
возникают лавины, которые в зависимости от направления поля, т.е. в зависимости
от полярности подаваемого на электрод напряжения, развиваются к электроду или
от него. В результате разделения зарядов в лавинах, около электрода образуется
избыточный объемный заряд одного знака с электродом (рис.3.10, b),
который создает собственное поле (рис.), снижающее поле у электрода (эффект
экранирования) и значительно усиливающий поле в промежутке перед зарядом.
Рисунок 4. a — искажения внешнего электрического поля объёмным зарядом лавин при отрицательном напряжении на стержне в системе электродов стержень-плоскость. —— напряжённость неискажённого поля Е1, — суммарная напряжённость электрического поля в зависимости от расстояния от стержня. b — объёмный заряд у стержня.
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
Электричество и магнетизм
Чтобы понять механизм поведения диэлектриков в поле на микроскопическом уровне, нам надо сначала объяснить, как может электрически нейтральная система реагировать на внешнее электрическое поле. Простейший случай — полное отсутствие зарядов — нас не интересует. Мы знаем наверняка, что в диэлектрике имеются электрические заряды — в составе атомов, молекул, ионов кристаллической решетки и т. д. Поэтому мы рассмотрим следующую по простоте конструкции электронейтральную систему — два равных по величине и противоположных по знаку точечных заряда +q и –q, находящихся на расстоянии l друг от друга. Такая система называется электрическим диполем.
Такая система называется электрическим диполем.
|
Электрический диполь — это система, состоящая из двух точечных равных по величине и противоположных по знаку зарядов, находящихся на расстоянии l друг от друга (рис. 3.6). |
Рис. 3.6. Электрический диполь
Линии напряженности электрического поля и эквипотенциальные поверхности электрического диполя выглядят следующим образом (рис. 3.7, 3.8, 3.9)
Рис. 3.7. Линии напряженности электрического поля электрического диполя
Рис. 3.8. Эквипотенциальные поверхности электрического диполя
Рис. 3.9. Линии напряженности электрического поля и эквипотенциальные поверхности
Основной характеристикой диполя является электрический дипольный момент. Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как
Введем вектор l, направленный от отрицательного заряда (–q) к положительному (+q), тогда вектор р, называемый электрическим моментом диполя или просто дипольным моментом, определяется как
|
|
(3.5) |
Рассмотрим поведение «жесткого» диполя — то есть расстояние которого не меняется — во внешнем поле Е (рис. 3.10).
Рис. 3.10. Силы, действующие на электрический диполь, помещенный во внешнее поле
Пусть направление дипольного момента составляет с вектором Е угол . На положительный заряд диполя действует сила, совпадающая по направлению с Е и равная F1 = +qE, а на отрицательный — противоположно направленная и равная F2 = –qE.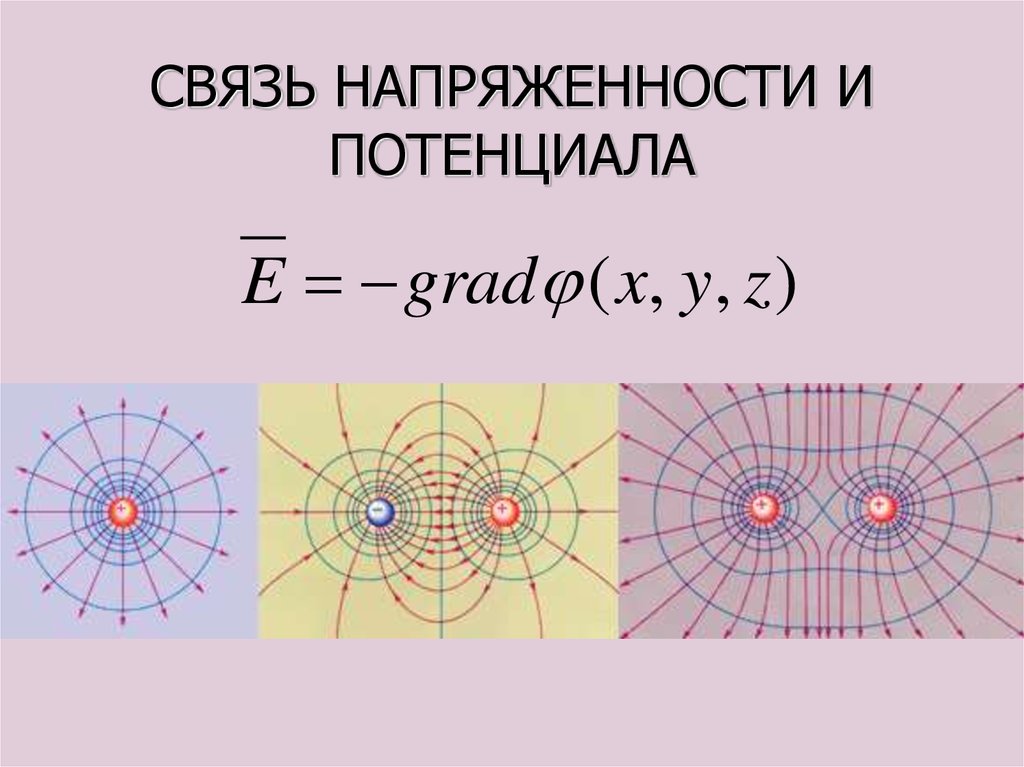 Вращающий момент этой пары сил равен
Вращающий момент этой пары сил равен
|
(3.6) |
Так как ql = р, то М = рЕ sin или в векторных обозначениях
(Напомним, что символ
означает векторное произведение векторов а и b.) Таким образом, при неизменном дипольном моменте молекулы () механический момент, действующий на нее, пропорционален напряженности Е внешнего электрического поля и зависит от угла между векторами р и E.
Под действием момента сил М диполь поворачивается, при этом совершается работа
|
(3. |
которая идет на увеличение его потенциальной энергии. Отсюда получаем потенциальную энергию диполя в электрическом поле
откуда
или
|
|
(3.8) |
если положить const = 0.
Из рисунка видно, что внешнее электрическое поле стремится повернуть диполь таким образом, чтобы вектор его электрического момента р совпал по направлению с вектором Е. В этом случае , а, следовательно, и М = 0. С другой стороны, при потенциальная энергия диполя во внешнем поле принимает минимальное значение , что соответствует положению устойчивого равновесия. При отклонении диполя от этого положения снова возникает механический момент, который возвращает диполь в первоначальное положение.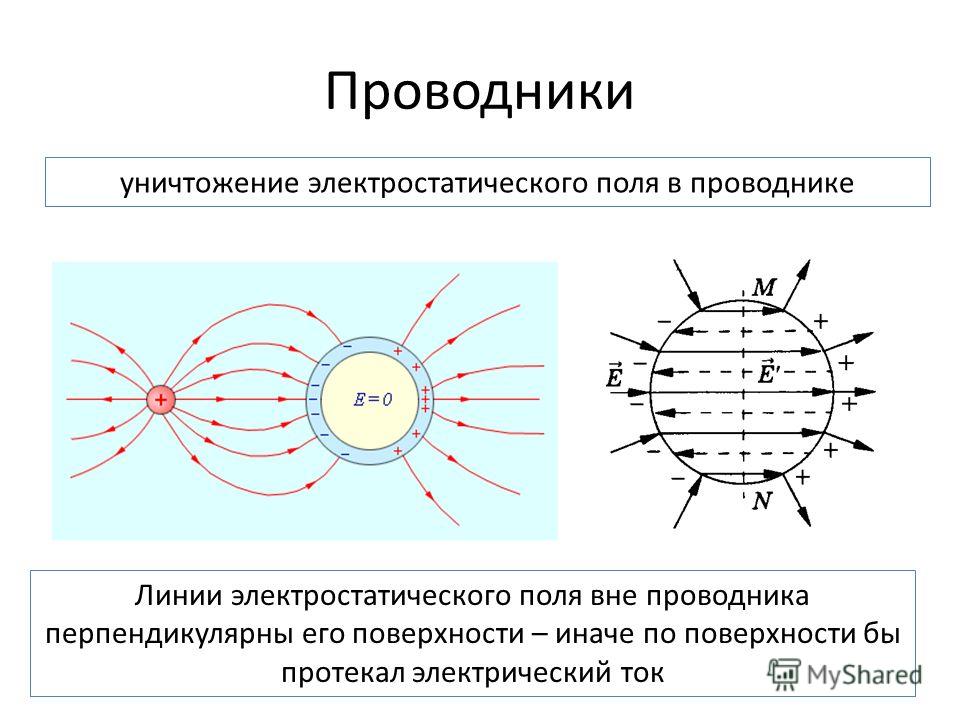 Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.
Другое положение равновесия, когда дипольный момент направлен против поля является неустойчивым. Потенциальная энергия в этом случае принимает максимальное значение и при небольших отклонениях от такого положения возникающие силы не возвращают диполь назад, а еще больше отклоняют его.
На рис. 3.11 показан опыт, иллюстрирующий возникновение момента электрических сил, действующих на диэлектрик в электрическом поле. На удлиненный диэлектрический образец, расположенный под некоторым углом к силовым линиям электростатического поля, действует момент сил, стремящийся развернуть этот образец вдоль поля. Диэлектрическая палочка, подвешенная за середину внутри плоского конденсатора, разворачивается перпендикулярно его пластинам после подачи на них высокого напряжения от электростатической машины. Появление вращающего момента обусловлено взаимодействием поляризовавшейся палочки с электрическим полем конденсатора.
Рис. 3.11.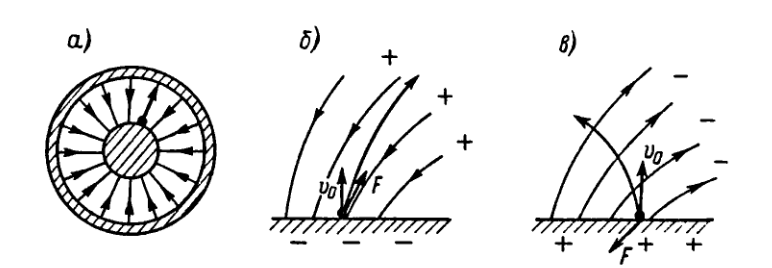 Момент электрических сил, действующих на диэлектрик в электрическом поле
Момент электрических сил, действующих на диэлектрик в электрическом поле
В случае неоднородного поля на рассматриваемый диполь будет действовать еще и равнодействующая сила Fpaвн, стремящаяся его сдвинуть. Мы рассмотрим здесь частный случай. Направим ось х вдоль поля Е. Пусть диполь под действием поля уже повернулся вдоль силовой линии, так что отрицательный заряд находится в точке с координатой x, а положительный заряд расположен в точке с координатой х + l. Представим себе, что величина напряженности поля зависит от координаты х. Тогда равнодействующая сила Fpaвн равна
|
(3.9) |
Такой же результат может быть получен из общего соотношения
где энергия П определена в (3. 8). Если Е увеличивается с ростом x, то
8). Если Е увеличивается с ростом x, то
и проекция равнодействующей силы положительна. Это значит, что она стремиться втянуть диполь в область, где напряженность поля больше. Этим объясняется известный эффект, когда нейтральные кусочки бумаги притягиваются к наэлектризованной расческе. В плоском конденсаторе с однородным полем они остались бы неподвижными.
Рассмотрим несколько опытов, иллюстрирующих возникновение силы, действующей на диэлектрик, помещенный в неоднородное электрическое поле.
На рис. 3.12 показано втягивание диэлектрика в пространство между обкладками плоского конденсатора. В неоднородном электростатическом поле на диэлектрик действуют силы, втягивающие его в область более сильного поля.
Рис. 3.12. Втягивание жидкого диэлектрика в плоский конденсатор
Это демонстрируется при помощи прозрачного сосуда, в который помещен плоский конденсатор, и налито некоторое количество жидкого диэлектрика — керосина (рис.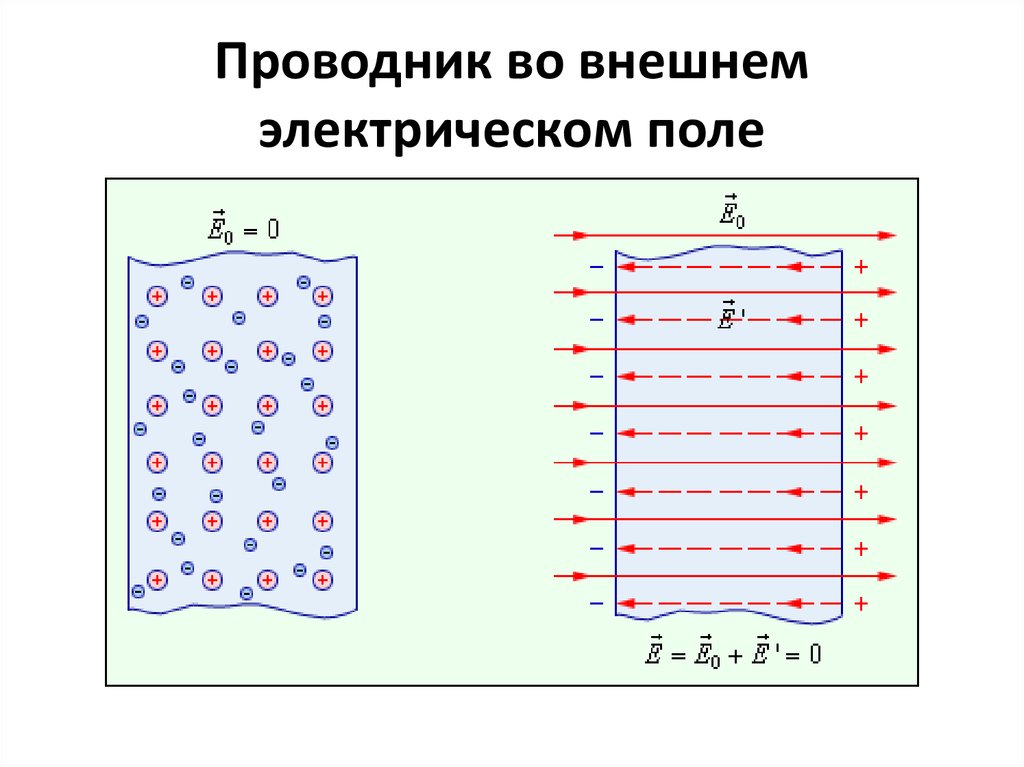 3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.
3.13). Конденсатор присоединен к высоковольтному источнику питания — электростатической машине. При ее работе на нижнем краю конденсатора, в области неоднородного поля, на керосин действует сила, втягивающая его в пространство между пластинами. Поэтому уровень керосина внутри конденсатора устанавливается выше, чем снаружи. После выключения поля уровень керосина между пластинами падает до его уровня в сосуде.
Рис. 3.13. Втягивание керосина в пространство между обкладками плоского конденсатора
Видео 3.1. Эксперимент по втягиванию жидкого диэлектрика в конденсатор.
В реальных веществах нечасто встречаются диполи, образованные только двумя зарядами. Обычно мы имеем дело с более сложными системами. Но понятие электрического дипольного момента применимо и к системам со многими зарядами. В этом случае дипольный момент определяется как
|
(3. |
где , — величина заряда с номером i и радиус-вектор, определяющий его местоположение, соответственно. В случае двух зарядов мы приходим к прежнему выражению
Пусть наша система зарядов электрически нейтральна. В ней есть положительные заряды, величины которых и местоположения мы обозначим индексом «+». Индексом «–» мы снабдим абсолютные величины отрицательных зарядов и их радиус-векторы. Тогда выражение (3.10) может быть записано в виде
|
(3.11) |
В (3.11) в первом слагаемом суммирование ведется по всем положительным зарядам, а во втором — по всем отрицательным зарядам системы.
Электрическая нейтральность системы означает равенство полного положительного заряда и суммы абсолютных величин всех отрицательных зарядов
|
(3. |
Введем теперь понятие «центр зарядов» — положительных R+ и отрицательных R–
|
(3.13) |
Выражения (3.13) аналогичны формулам для центра масс в механике, и потому мы назвали их центрами положительных и отрицательных зарядов, соответственно. С этими обозначениями и с учетом соотношения (3.12) мы записываем электрический дипольный момент (3.11) системы зарядов в виде
|
|
(3.14) |
где l-вектор, проведенный из центра отрицательных зарядов в центр положительных зарядов. Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.
Смысл нашего упражнения заключается в демонстрации, что любую электрически нейтральную систему зарядов можно представить как некий эквивалентный диполь.
Дополнительная информация
http://webmath.exponenta.ru/dnu/lc/age/pyartli1/node9.htm — Векторное произведение.
Измерение электрического поля, индуцированного магнитными катушками в неоднородных объемных проводниках: приложение к нейрогеометрии позвоночника человека
. 1991 г., июнь; 81 (3): 224–37.
doi: 10.1016/0168-5597(91)
-а.
П. Дж. Маккавей 1 , В. Э. Амассиан, Л. П. Эберле, А. П. Руделл, Р. К. Кракко, К. С. Лай, М. Сомасундарум
принадлежность
- 1 Отделение неврологии, Медицинский научный центр SUNY, Бруклин 11203.

- PMID: 1710972
- DOI:
10.1016/0168-5597(91)
-а
PJ Maccabee et al. Электроэнцефалогр Клин Нейрофизиол. 1991 июня
. 1991 г., июнь; 81 (3): 224–37.
doi: 10.1016/0168-5597(91)
-а.
Авторы
П. Дж. Маккавей 1 , В. Э. Амассиан, Л. П. Эберле, А. П. Руделл, Р. К. Кракко, К. С. Лай, М. Сомасундарум
принадлежность
- 1 Отделение неврологии, Медицинский научный центр SUNY, Бруклин 11203.

- PMID: 1710972
- DOI:
10.1016/0168-5597(91)
-а
Абстрактный
Измерялись электрические поля, наводимые круглыми и восьмерками магнитными катушками (МК) в однородных и неоднородных объемных проводниках. В однородных средах круглый МК, расположенный тангенциально (т.е. плоско) к объемному проводнику, индуцировал кольцевое электрическое поле. При удерживании круглого МК на ребро (т. е. ортогонально) объемному проводнику индуцированное электрическое поле состояло из двух петель, в основном параллельных поверхности объемного проводника и сближающихся непосредственно под контактирующей кромкой МК. Тангенциально ориентированная восьмерка МК аналогичным образом индуцировала две петли электрического поля, которые максимально сближали друг друга под областью перехода по его длинной оси. В сложном неоднородном по объему проводнике, таком как сегмент шейно-грудного отдела позвоночника человека, расположенный эксцентрично внутри большого цилиндрического резервуара и погруженный в изотонический раствор, направление электрических полей внутри позвоночного канала и через межпозвонковые нейрофорамины было аналогично наблюдаемому. в однородном объемном проводнике. Однако в одном нейроотверстии и вблизи него электрическое поле и особенно его первая пространственная производная были заметно повышены по сравнению с полем, зарегистрированным в пределах длинной центральной оси позвоночного канала. Потенциалы действия моторных единиц и сложных мышц, вызванные в мышцах конечностей стимуляцией MC шейного отдела позвоночника человека, подтвердили предсказания, полученные на основе физической модели. Прогнозы включали: (1) отсутствие стимуляции спинного мозга по сравнению с относительной легкостью стимуляции нервных корешков током, который, скорее всего, концентрируется в нейрофораминах.
В сложном неоднородном по объему проводнике, таком как сегмент шейно-грудного отдела позвоночника человека, расположенный эксцентрично внутри большого цилиндрического резервуара и погруженный в изотонический раствор, направление электрических полей внутри позвоночного канала и через межпозвонковые нейрофорамины было аналогично наблюдаемому. в однородном объемном проводнике. Однако в одном нейроотверстии и вблизи него электрическое поле и особенно его первая пространственная производная были заметно повышены по сравнению с полем, зарегистрированным в пределах длинной центральной оси позвоночного канала. Потенциалы действия моторных единиц и сложных мышц, вызванные в мышцах конечностей стимуляцией MC шейного отдела позвоночника человека, подтвердили предсказания, полученные на основе физической модели. Прогнозы включали: (1) отсутствие стимуляции спинного мозга по сравнению с относительной легкостью стимуляции нервных корешков током, который, скорее всего, концентрируется в нейрофораминах.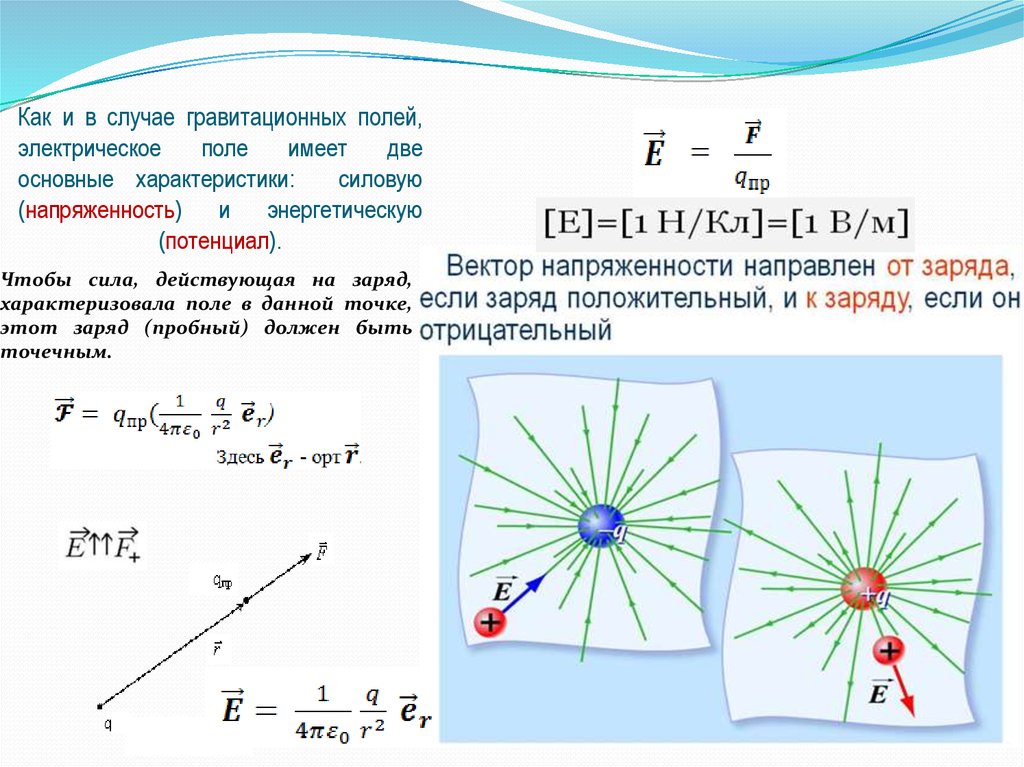 Когда стимулирующий ток направлен к периферии, предполагается, что наиболее вероятное место стимуляции с низким порогом находится дистальнее нейрофорамины. Подчеркивается, что при супрамаксимальной стимуляции могут возникать более дистальные участки возбуждения; 2) инвариантные латентные сдвиги пороговых интенсивностей при перемещении ТК вдоль рострокаудальной оси шейного отдела позвоночника; (3) существенное влияние (на пороги активации двигательных единиц) направления индуцированного тока, протекающего через нейрофорамины; (4) снижение стимуляции, когда целевые нервные корешки находятся близко к нулевой точке электрического поля, то есть между местами высокой напряженности электрического поля противоположной полярности; и (5) относительно очаговая стимуляция нервных корешков соединением поперечно ориентированной восьмерки MC, т.е. параллельно нервным корешкам.
Когда стимулирующий ток направлен к периферии, предполагается, что наиболее вероятное место стимуляции с низким порогом находится дистальнее нейрофорамины. Подчеркивается, что при супрамаксимальной стимуляции могут возникать более дистальные участки возбуждения; 2) инвариантные латентные сдвиги пороговых интенсивностей при перемещении ТК вдоль рострокаудальной оси шейного отдела позвоночника; (3) существенное влияние (на пороги активации двигательных единиц) направления индуцированного тока, протекающего через нейрофорамины; (4) снижение стимуляции, когда целевые нервные корешки находятся близко к нулевой точке электрического поля, то есть между местами высокой напряженности электрического поля противоположной полярности; и (5) относительно очаговая стимуляция нервных корешков соединением поперечно ориентированной восьмерки MC, т.е. параллельно нервным корешкам.
Похожие статьи
Механизмы стимуляции периферической нервной системы с помощью магнитной катушки.

Maccabee PJ, Amassian VE, Cracco RQ, Eberle LP, Rudell AP. Маккаби П.Дж. и др. Электроэнцефалог Clin Neurophysiol Suppl. 1991;43:344-61. Электроэнцефалог Clin Neurophysiol Suppl. 1991. PMID: 1773773
Пространственное распределение электрического поля, индуцируемого в объеме круглой и восьмеричной магнитными катушками: значение для активации сенсорных нервных волокон.
Maccabee PJ, Eberle L, Amassian VE, Cracco RQ, Rudell A, Jayachandra M. Маккаби П.Дж. и др. Электроэнцефалогр Клин Нейрофизиол. 1990 г., август; 76 (2): 131–41. doi: 10.1016/0013-4694(90)
-2. Электроэнцефалогр Клин Нейрофизиол. 1990. PMID: 1697241Анализ стимуляции периферических двигательных нервов у людей с помощью магнитной катушки.

Maccabee PJ, Amassian VE, Cracco RQ, Cadwell JA. Маккаби П.Дж. и др. Электроэнцефалогр Клин Нейрофизиол. 1988 декабрь; 70 (6): 524-33. doi: 10.1016/0013-4694(88)
-2. Электроэнцефалогр Клин Нейрофизиол. 1988 год. PMID: 2461286
Стимуляция нервной системы человека с помощью магнитной катушки.
Maccabee PJ, Amassian VE, Cracco RQ, Cracco JB, Eberle L, Rudell A. Маккаби П.Дж. и др. Дж. Клин Нейрофизиол. 1991 янв.; 8(1):38-55. doi: 10.1097/00004691-19
00-00006. Дж. Клин Нейрофизиол. 1991. PMID: 2019650 Обзор.Сопоставление фокальной и нефокальной стимуляции магнитной катушки со свойствами нервной системы человека: картирование полей двигательных единиц в моторной коре в отличие от изменения последовательных движений пальцев при стимуляции премоторной SMA.

Amassian VE, Cracco RQ, Maccabee PJ, Bigland-Ritchie B, Cracco JB. Амассиан В.Е. и соавт. Электроэнцефалог Clin Neurophysiol Suppl. 1991;43:3-28. Электроэнцефалог Clin Neurophysiol Suppl. 1991. PMID: 1773769 Обзор.
Посмотреть все похожие статьи
Цитируется
Противоречия и клиническое применение неинвазивной трансспинальной магнитной стимуляции: критический обзор и исследовательское исследование наследственной спастической параплегии.
Карра Р.Б., Сильва Г.Д., Парагвай IBB, Диниз де Лима Ф., Менезес Дж.Р., Пинеда А.М., Нуньес Г.А., Симоэнс Д.С., Франса М.К. мл., Кури Р.Г. Карра РБ и соавт. Дж. Клин Мед. 2022 14 августа; 11 (16): 4748. дои: 10.3390/jcm11164748. Дж. Клин Мед. 2022. PMID: 36012986 Бесплатная статья ЧВК.
Множественная регрессионная модель нормального времени центральной и периферической двигательной проводимости.

Джейсер С.Р., Барнс Д.Д., Бейкер С.Н., Бейкер М.Р. Джайсер С.Р. и др. Мышечный нерв. 2015 май; 51(5):706-12. doi: 10.1002/mus.24427. Epub 2015 14 марта. Мышечный нерв. 2015. PMID: 25154476 Бесплатная статья ЧВК.
Определение того, какие механизмы приводят к активации в моторной коре: исследование моделирования транскраниальной магнитной стимуляции с использованием реалистичных сигналов стимула и геометрии борозды.
Сальвадор Р., Сильва С., Бассер П.Дж., Миранда П.С. Сальвадор Р. и др. Клин Нейрофизиол. 2011 г., апрель; 122(4):748-58. doi: 10.1016/j.clinph.2010.09.022. Epub 2010 28 октября. Клин Нейрофизиол. 2011. PMID: 21035390 Бесплатная статья ЧВК.
Выяснение механизмов и локусов возбуждения нейронов транскраниальной магнитной стимуляцией с использованием конечно-элементной модели кортикальной борозды.

Сильва С., Бассер П.Дж., Миранда П.С. Сильва С. и др. Клин Нейрофизиол. 2008 г., октябрь; 119 (10): 2405-13. doi: 10.1016/j.clinph.2008.07.248. Epub 2008 9 сентября. Клин Нейрофизиол. 2008. PMID: 18783986 Бесплатная статья ЧВК.
Магнитная стимуляция неоднородных биологических структур.
Крастева В.Т., Папазов С.П., Даскалов И.К. Крастева В.Т. и соавт. Биомед Инж Онлайн. 2002, 17 сентября; 1:3. дои: 10.1186/1475-925x-1-3. Биомед Инж Онлайн. 2002. PMID: 12437784 Бесплатная статья ЧВК.
Просмотреть все статьи «Цитируется по»
термины MeSH
Неоднородное электрическое поле, индуцированное микрокатушками, вызывает нейронные реакции, подобные звуковым, в микросхемах слуховой коры мышей In Vivo
. 2018 10 февраля; 371: 346-370.
2018 10 февраля; 371: 346-370.
doi: 10.1016/j.neuroscience.2017.12.008. Epub 2017 12 декабря.
Хисаюки Осанай 1 , Сюнсуке Минуса 1 , Такаши Татено 2
Принадлежности
- 1 Биоинженерия и биоинформатика, Высшая школа информационных наук и технологий, Университет Хоккайдо, Кита 14, Ниси 9, Кита-ку, Саппоро 060-0814, Япония.
- 2 Биоинженерия и биоинформатика, Высшая школа информационных наук и технологий, Университет Хоккайдо, Кита 14, Ниси 9, Кита-ку, Саппоро 060-0814, Япония. Электронный адрес: [email protected].

- PMID: 284
- DOI: 10.1016/j.neuroscience.2017.12.008
Хисаюки Осанаи и др. Неврология. .
. 2018 10 февраля; 371: 346-370.
doi: 10.1016/j.neuroscience.2017.12.008. Epub 2017 12 декабря.
Авторы
Хисаюки Осанай 1 , Сюнсуке Минуса 1 , Такаши Татено 2
Принадлежности
- 1 Биоинженерия и биоинформатика, Высшая школа информационных наук и технологий, Университет Хоккайдо, Кита 14, Ниси 9, Кита-ку, Саппоро 060-0814, Япония.

- 2 Биоинженерия и биоинформатика, Высшая школа информационных наук и технологий, Университет Хоккайдо, Кита 14, Ниси 9, Кита-ку, Саппоро 060-0814, Япония. Электронный адрес: [email protected].
- PMID: 284
- DOI: 10.1016/j.neuroscience.2017.12.008
Абстрактный
Магнитная стимуляция широко используется в неврологических исследованиях и клиническом лечении. Несмотря на недавний прогресс в понимании механизма нейронной модуляции обычных методов магнитной стимуляции, физиологический механизм на уровне кортикальной микросхемы изучен недостаточно из-за плохой очаговости стимуляции и больших электрических артефактов при записи. Чтобы преодолеть эти проблемы, мы использовали субмиллиметровую катушку (микрокатушка) для стимуляции слуховой коры мыши в естественных условиях. Чтобы определить механизм, мы провели первую прямую электрофизиологическую запись управляемых микрокатушками нейронных ответов в нескольких местах на горизонтальной поверхности и ламинарных участках слуховой коры. Ламинарные ответы потенциалов локального поля (LFP) на магнитную стимуляцию достигали слоя 6, а пространственно-временные профили были очень похожи на таковые при акустической стимуляции, что свидетельствует об активации одной и той же кортикальной микросхемы. Горизонтальные ответы LFP на магнитную стимуляцию вызывались в пределах области шириной в миллиметр вокруг катушки стимуляции. Активированная область коры зависела от ориентации катушки, предоставляя полезную информацию об эффективном положении катушки относительно поверхности мозга для модуляции активности корковых цепей. Кроме того, численный расчет индуцированного электрического поля в мозге показал, что неоднородность горизонтального электрического поля по отношению к поверхности имеет решающее значение для активации коры, индуцированной микрокатушками.
Чтобы преодолеть эти проблемы, мы использовали субмиллиметровую катушку (микрокатушка) для стимуляции слуховой коры мыши в естественных условиях. Чтобы определить механизм, мы провели первую прямую электрофизиологическую запись управляемых микрокатушками нейронных ответов в нескольких местах на горизонтальной поверхности и ламинарных участках слуховой коры. Ламинарные ответы потенциалов локального поля (LFP) на магнитную стимуляцию достигали слоя 6, а пространственно-временные профили были очень похожи на таковые при акустической стимуляции, что свидетельствует об активации одной и той же кортикальной микросхемы. Горизонтальные ответы LFP на магнитную стимуляцию вызывались в пределах области шириной в миллиметр вокруг катушки стимуляции. Активированная область коры зависела от ориентации катушки, предоставляя полезную информацию об эффективном положении катушки относительно поверхности мозга для модуляции активности корковых цепей. Кроме того, численный расчет индуцированного электрического поля в мозге показал, что неоднородность горизонтального электрического поля по отношению к поверхности имеет решающее значение для активации коры, индуцированной микрокатушками. Результаты показывают, что наш метод микрокатушек может быть использован в качестве хронического, менее инвазивного и высокофокусного нейростимулятора и полезен для исследования реакции микросхем на магнитную стимуляцию для клинического лечения.
Результаты показывают, что наш метод микрокатушек может быть использован в качестве хронического, менее инвазивного и высокофокусного нейростимулятора и полезен для исследования реакции микросхем на магнитную стимуляцию для клинического лечения.
Ключевые слова: слуховая кора; электромагнитная микрокатушка; ламинарная структура; магнитная стимуляция; микросхема.
Copyright © 2017 ИБРО. Опубликовано Elsevier Ltd. Все права защищены.
Похожие статьи
Ламинарные профили, управляемые звуком и током, и метод их применения, имитирующий акустические реакции в слуховой коре мыши in vivo.
Мурамацу С., Тода М., Нисикава Дж., Татено Т. Мурамацу С. и др. Мозг Res. 2019 15 октября; 1721:146312. doi: 10.1016/j.brainres.2019.146312. Epub 2019 16 июля.
 Мозг Res. 2019.
PMID: 31323198
Мозг Res. 2019.
PMID: 31323198Многоканальная система магнитной стимуляции с использованием катушек субмиллиметрового размера: разработка системы и экспериментальное применение к мозгу грызунов in vivo.
Минуса С., Мурамацу С., Осанай Х., Татено Т. Минуса С. и др. Дж. Нейронная инженерия. 201923 октября; 16 (6): 066014. дои: 10.1088/1741-2552/ab3187. Дж. Нейронная инженерия. 2019. PMID: 31642445
Анализ профилей плотности источников тока, активированных локальной стимуляцией в слуховой коре мышей in vitro.
Ямамура Д., Сано А., Татено Т. Ямамура Д. и соавт. Мозг Res. 2017 15 марта; 1659:96-112. doi: 10.1016/j.brainres.2017.01.021. Epub 2017 21 января. Мозг Res. 2017. PMID: 28119054
Слуховые магнитные поля у пациентов с кохлеарными имплантами.

Пелиццоне М. Пелиццоне М. Физиол Изм. 1993 Ноябрь; 14 Дополнение 4A:A81-4. doi: 10.1088/0967-3334/14/4a/014. Физиол Изм. 1993. PMID: 8274990 Обзор.
Синаптические механизмы в работе слуховой коры.
Метерейт Р. Метерейт Р. Фронт биосай. 1998 г., 6 мая; 3: d494-501. дои: 10.2741/a296. Фронт биосай. 1998. PMID: 9569228 Обзор.
Посмотреть все похожие статьи
Цитируется
Магнитная стимуляция позволяет очаговой активации улитки мыши.
Ли Дж.И., Сейст Р., Макинтурф С., Ли Д.Дж., Браун М.С., Станкович К.М., Фрид С. Ли Джи и др. Элиф. 2022 24 мая; 11:e76682. doi: 10.7554/eLife.76682. Элиф. 2022. PMID: 35608242 Бесплатная статья ЧВК.

Пространственно ограниченные ответы зрительной коры мыши на внутрикортикальную магнитную стимуляцию микрокатушками.
Рю С.Б., Полк А.С., Ян Дж.С., Ганджи М., Дайех С.А., Кэш С.С., Фрид С.И., Ли С.В. Рю С.Б. и др. Дж. Нейронная инженерия. 2020 23 октября; 17 (5): 056036. doi: 10.1088/1741-2552/abbd22. Дж. Нейронная инженерия. 2020. PMID: 32998116 Бесплатная статья ЧВК.
Типы публикаций
термины MeSH
Влияние пространственно неоднородных внеклеточных электрических полей на нейроны
ПредыдущийСледующий
Статьи, Клеточные/Молекулярные
Костас А. Анастассиу, Шон М. Монтгомери, Маурисио Барахона, Дьёрдь Бужаки и Кристоф Кох
Journal of Neuroscience 3 февраля 2010 г. , 30 (5) 1925–1936; Doi: https://doi.org/10.1523/jneurosci.3635-09.2010
, 30 (5) 1925–1936; Doi: https://doi.org/10.1523/jneurosci.3635-09.2010
- Статья
- Рисунки и данные
- Info & Metrics
- Eletters
- ELETTERS
- ELETTS глия генерирует электрические поля, но их влияние на отдельные нейроны посредством эпаптических взаимодействий в основном неизвестно. Здесь мы анализируем влияние пространственно-неоднородных электрических полей на мембранный потенциал, индуцированное мембранное поле и плотность источника индуцированного тока одномерных кабелей, а также морфологически реалистичных нейронов и обсуждаем, как особенности внеклеточного поля влияют на эти величины. . С помощью моделирования мы показываем, что эндогенные поля, связанные с тета-волнами гиппокампа и острыми волнами, могут сильно влиять на время спайков. Эти результаты подразумевают, что локальные электрические поля, генерируемые совместными действиями клеток мозга, могут влиять на время нервной активности.
Введение
Нейроны погружены в электропроводящую среду, внеклеточную жидкость, что, в принципе, позволяет окружающим клеткам воспринимать внеклеточную активность одной клетки (Rall and Shepherd, 1968; Traub et al.
 , 1985). ; Tranchina and Nicholson, 1986; Holt and Koch, 1999; McIntyre and Grill, 1999; Bédard et al., 2004; Gold et al., 2006; Logothetis et al., 2007; Pettersen and Einevoll, 2008). Несмотря на обширные исследования, в основном в восстановленных препаратах, физиологическая роль таких внеклеточных токов в нейронах остается спорной (для обзора см. Jefferys, 19).95).
, 1985). ; Tranchina and Nicholson, 1986; Holt and Koch, 1999; McIntyre and Grill, 1999; Bédard et al., 2004; Gold et al., 2006; Logothetis et al., 2007; Pettersen and Einevoll, 2008). Несмотря на обширные исследования, в основном в восстановленных препаратах, физиологическая роль таких внеклеточных токов в нейронах остается спорной (для обзора см. Jefferys, 19).95).По внеклеточному потенциалу ( v e ) можно отслеживать быструю пиковую активность, а также более медленные v e колебания. Последние, обычно называемые локальными полевыми потенциалами (ЛПП), отражают суммарную электрическую активность нейронов и связанных с ними глиальных клеток и обеспечивают экспериментальный доступ к пространственно-временной активности афферентных, ассоциативных и локальных операций в конкретной структуре мозга (Buzsaki, 2004). ). Давний вопрос, касающийся LFP, заключался в том, являются ли LFP просто эпифеноменом передачи нейронных сигналов или они имеют функциональное значение.
 Ранний Эксперименты in vitro с препаратами СА1 гиппокампа показали, что в отсутствие синаптической связи внеклеточное поле вносит значительный вклад в синхронизацию популяций нейронов (Purpura and Malliani, 1966; Jefferys and Haas, 1982; Taylor and Dudek, 1982; Snow and Dudek). , 1984). Хотя LFP относительно малы по амплитуде, они охватывают более крупные области мозга (Katzner et al., 2009). Кроме того, учитывая относительно большое характерное время LFP (> 5 мс), на них гораздо меньше влияет низкочастотная фильтрация мембраны. Таким образом, было высказано предположение, что LFP могут выполнять функциональную роль в областях мозга, таких как гиппокамп, где ламинарная морфология (выравнивание нейронов) приводит к большим v e колебания (Buzsaki et al., 1983).
Ранний Эксперименты in vitro с препаратами СА1 гиппокампа показали, что в отсутствие синаптической связи внеклеточное поле вносит значительный вклад в синхронизацию популяций нейронов (Purpura and Malliani, 1966; Jefferys and Haas, 1982; Taylor and Dudek, 1982; Snow and Dudek). , 1984). Хотя LFP относительно малы по амплитуде, они охватывают более крупные области мозга (Katzner et al., 2009). Кроме того, учитывая относительно большое характерное время LFP (> 5 мс), на них гораздо меньше влияет низкочастотная фильтрация мембраны. Таким образом, было высказано предположение, что LFP могут выполнять функциональную роль в областях мозга, таких как гиппокамп, где ламинарная морфология (выравнивание нейронов) приводит к большим v e колебания (Buzsaki et al., 1983).В большинстве экспериментов, предназначенных для количественной оценки эффекта таких электростатических взаимодействий, использовалась либо фокальная стимуляция (Taylor and Dudek, 1982), либо, что чаще, расположение параллельных пластин (Jefferys and Haas, 1982; Chan and Nicholson, 1986; Chan et al.
 al., 1988; Radman et al., 2007), которые индуцируют ламинарное или (пространственно) постоянное электрическое поле соответственно. Тем не менее пространственно-диффузная стимуляция непредсказуемым образом воздействует на различные части нейронов и редко имитирует физиологическую ситуацию. Например, в гиппокампе активность LFP сильно зависит от времени и местоположения (Kamondi et al., 19).98; Хенце и Бужаки, 2001 г.; Клаусбергер и др., 2003, 2004). Хотя зависимость этих внеклеточных полей от времени рассматривалась в прошлом путем применения полей переменного тока вдоль нейронов (Deans et al., 2007; Radman et al., 2007), эффект пространственной неоднородности эндогенной электрической активности сохраняется. для изучения (Рубинштейн и Спелман, 1988; Рубинштейн, 1991).
al., 1988; Radman et al., 2007), которые индуцируют ламинарное или (пространственно) постоянное электрическое поле соответственно. Тем не менее пространственно-диффузная стимуляция непредсказуемым образом воздействует на различные части нейронов и редко имитирует физиологическую ситуацию. Например, в гиппокампе активность LFP сильно зависит от времени и местоположения (Kamondi et al., 19).98; Хенце и Бужаки, 2001 г.; Клаусбергер и др., 2003, 2004). Хотя зависимость этих внеклеточных полей от времени рассматривалась в прошлом путем применения полей переменного тока вдоль нейронов (Deans et al., 2007; Radman et al., 2007), эффект пространственной неоднородности эндогенной электрической активности сохраняется. для изучения (Рубинштейн и Спелман, 1988; Рубинштейн, 1991).В настоящей работе моделируется воздействие относительно малых (по амплитуде), неоднородных (в пространстве) и относительно медленных (во времени) внеклеточных электрических полей на пассивные кабели. Чтобы связать результаты моделирования с 9В ситуации 0322 in vivo мы также исследуем влияние активности LFP гиппокампа у ведущего себя животного (тета, острые волны) на морфологически реконструированный пассивный пирамидный нейрон.

Материалы и методы
Моделирование
Формулировка теории кабелей.
Безразмерное (правило обезразмеривания представлено ниже, а также в дополнительных материалах, доступных на сайте www.jneurosci.org) уравнение стационарного кабеля для внутриклеточного напряжения V i выглядит следующим образом (Rall, 1962):
где В e — безразмерный внеклеточный потенциал, а граничные условия при X = 0 и X = L формулируют ограничение, согласно которому ток не течет в осевом направлении на обоих концах кабеля (герметичный конец). граничное условие). В дополнительном разделе 2 (доступном на www.jneurosci.org в качестве дополнительного материала) мы решаем уравнение 1 в присутствии стационарного и пространственно гармонического (синусоидального) внеклеточного V e колебания вдоль кабеля.
Для того чтобы мембранный потенциал В м = В i − В e стал порядка 1, должны выполняться следующие два независимых условия (дополнительные разделы 2, 5, доступно на сайте www.
 jneurosci.org в качестве дополнительного материала):
jneurosci.org в качестве дополнительного материала):где Ω — нормированная радиальная частота пространственно-гармонических колебаний V e , а L длина кабеля.
Учет морфологического разнообразия кабеля.
Переформулировка условий (I) и (II) для морфологически неправильного кабеля, состоящего из M линейных взаимосвязанных сегментов в трех измерениях, приводит к следующему:
где ?0322 k и σ k — угловое смещение по азимуту и углу места, соответственно, между секцией кабеля k и базовой осью. В присутствии многомерного внеклеточного электрического поля E e его эффект можно объяснить в рамках настоящей схемы, определив уравнение 1 (а также уравнения 6, 7) для трехмерного вектора. Тогда условия (I) и (II) выполняются для каждого измерения.
Для стационарного моделирования вдоль реконструированного пирамидного нейрона СА1 крысы мы прикладываем внешний потенциал вдоль соматодендритного ( y -) оси (см.
 рис. 4 A ) следующим образом:
рис. 4 A ) следующим образом:где v e (в милливольтах) — внеклеточный потенциал (единичной амплитуды), который создает стационарное внеклеточное поле вдоль соматодендритной оси нейрона.
Анализ пространственно-временного поведения.
Зависимый от времени ответ на пространственно-временную v e флуктуацию рассматривали посредством приложения зависящего от времени и пространственно гармонического внеклеточного напряжения вдоль оси соматодендритов следующим образом:
где ω T = 2π F T и F T (в секундах — 1 ) — это временная частота, а F 3- ) — это временная частота, а F 3 — ) — это временная частота, причем F 3 — ) — это временная частота, а F 3 — ) — F 3 ). λ с = 1 мм.
 ϕ s определялась так, чтобы v e ( t , x , y , z ) находилась в центре исследуемого участка (височного) и одиночного моделировались колебания. Для количественной оценки временной фильтрации отклонение β индуцированного V m колебания из состояния покоя сравнивались со стационарным случаем со следующим: где P ( V m ) указывает диапазон (т. е. разницу между V m максимумом и V m минимумом) по сечению (максимальный диапазон среди всех внутренних узлов определенный участок) между нестационарным и стационарным (с.с.) случаем.
ϕ s определялась так, чтобы v e ( t , x , y , z ) находилась в центре исследуемого участка (височного) и одиночного моделировались колебания. Для количественной оценки временной фильтрации отклонение β индуцированного V m колебания из состояния покоя сравнивались со стационарным случаем со следующим: где P ( V m ) указывает диапазон (т. е. разницу между V m максимумом и V m минимумом) по сечению (максимальный диапазон среди всех внутренних узлов определенный участок) между нестационарным и стационарным (с.с.) случаем.Численные процедуры
Пакет программ NEURON (версия 6.1) (Hines and Carnevale, 1997) использовали для моделирования морфологически реконструированного пирамидного нейрона СА1 крысы (Gold et al., 2006). Во всех случаях для применения внеклеточного поля использовалась встроенная функция extracellular(x), а для численного решения модели кабеля применялся метод постоянного временного шага (Hines and Carnevale, 1997).
 Для морфологически детализированного нейрона были разработаны алгоритмы, которые отслеживают все внутренние узлы после сегментации и применяют поле. Для создания пространственно гладких профилей внеклеточного потенциала использовались кубические сплайны для интерполяции между местами записи (дополнительные рисунки S6, S7, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Сопротивление мембраны R m = 20 кОм см 2 , а внутриклеточное сопротивление R i = 20 Ом см (Koch, 1999). Для моделирования, зависящего от времени, емкость мембраны составляла Кл м = 1 мкФ см -2 , а ток мембраны определялся с использованием функции NEURON i_membrane(x) (Hines and Carnevale, 1997).
Для морфологически детализированного нейрона были разработаны алгоритмы, которые отслеживают все внутренние узлы после сегментации и применяют поле. Для создания пространственно гладких профилей внеклеточного потенциала использовались кубические сплайны для интерполяции между местами записи (дополнительные рисунки S6, S7, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Сопротивление мембраны R m = 20 кОм см 2 , а внутриклеточное сопротивление R i = 20 Ом см (Koch, 1999). Для моделирования, зависящего от времени, емкость мембраны составляла Кл м = 1 мкФ см -2 , а ток мембраны определялся с использованием функции NEURON i_membrane(x) (Hines and Carnevale, 1997).Экспериментальные процедуры
Экспериментальные процедуры были такими, как описано у Csicsvari et al. (1999) и Монтгомери и Бужаки (2007).
Результаты
Рассмотрим прямой и неразветвленный пассивный кабель длиной l (в миллиметрах), вдоль которого приложено стационарное и пространственно гармоническое (синусоидальное) внеклеточное напряжение, где v i и v e (в милливольтах) — внутриклеточное и внеклеточное напряжение соответственно, r i (в омах на миллиметр) — внутриклеточное сопротивление, r m (в омах миллиметрах) — сопротивление мембраны, v rest (в милливольтах) — потенциал покоя, λ el (в миллиметрах) — электротоническая длина кабеля, c m (в фарадах на миллиметр) — емкость мембраны (для все стационарные модели, c m игнорируются).
 Мембранный потенциал равен v m = v i − v e . Обратите внимание, что в большинстве исследований теории кабелей пренебрегают внеклеточными полевыми эффектами, устанавливая v e должны быть постоянными, обычно нулевыми (рис. 1). То есть они пренебрегают любым вкладом внеклеточного поля.
Мембранный потенциал равен v m = v i − v e . Обратите внимание, что в большинстве исследований теории кабелей пренебрегают внеклеточными полевыми эффектами, устанавливая v e должны быть постоянными, обычно нулевыми (рис. 1). То есть они пренебрегают любым вкладом внеклеточного поля.В настоящей работе все величины выражены в безразмерной форме (обозначены прописными буквами), если не указано иное. Более конкретно, v 0 (в милливольтах) представляет собой амплитуду гармонического колебания внеклеточного потенциала0325 x + ϕ s ), f s (в миллиметрах −1 ) — его пространственная частота, λ с = 1/ f 90 миллиметров с 90 миллиметров длина (или пространственная длина волны синусоиды), а ϕ s – ее фаза вдоль кабеля. Тогда внутриклеточное, внеклеточное и мембранное напряжение, нормированные на амплитуду внеклеточного потенциала, равны0324 i − v rest )/ v 0 , V e = v e / v 0 , and V m = v м / v 0 соответственно.
 Ω = 2π f s λ el – безразмерная угловая пространственная частота колебаний внеклеточного потенциала.
Ω = 2π f s λ el – безразмерная угловая пространственная частота колебаний внеклеточного потенциала.Из вышеизложенного следует, что при наличии стационарной и пространственно-неоднородной V e с V e ( X ) = sin(Ω X + ϕ s ) по кабелю длиной L 902 = l/4 эл. уравнение кабеля выглядит следующим образом:
Уравнение 5 дает индуцированный нормализованный мембранный потенциал, В м , связанный с наличием стационарного и пространственно неоднородного (гармонического) внеклеточного потенциала, В e . Подробный вывод уравнения 5, а также таблицу символов можно найти в дополнительных разделах 1 и 2 (доступны на сайте www.jneurosci.org в качестве дополнительного материала).
Уравнения 1 (и 5) подчеркивают общее заблуждение относительно влияния внеклеточных полей [т. е.
 отрицательная пространственная производная (параллельно кабелю) В e или E e = −Ω cos( Ом X + ϕ с )] на В м . Часто предполагается, что постоянные поля вдоль кабеля не влияют на В м . Из уравнения 1 видно, что, хотя уравнение кабеля остается неизменным при наличии постоянных полей, на границах кабеля появляются условия стока/источника, которые влияют на (стационарное) пространственное V m профиль (подробнее см. дополнительный раздел 2, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Следовательно, постоянные электрические поля воздействуют на В м с точным влиянием, зависящим от свойств кабеля и поля (Chan and Nicholson, 1986).
отрицательная пространственная производная (параллельно кабелю) В e или E e = −Ω cos( Ом X + ϕ с )] на В м . Часто предполагается, что постоянные поля вдоль кабеля не влияют на В м . Из уравнения 1 видно, что, хотя уравнение кабеля остается неизменным при наличии постоянных полей, на границах кабеля появляются условия стока/источника, которые влияют на (стационарное) пространственное V m профиль (подробнее см. дополнительный раздел 2, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Следовательно, постоянные электрические поля воздействуют на В м с точным влиянием, зависящим от свойств кабеля и поля (Chan and Nicholson, 1986).При наличии пространственно-гармонического внеклеточного напряжения вдоль кабеля результирующий профиль мембранного потенциала также зависит от характерной длины λ с (рис.
 2). При больших λ s (т.е. пространственно-однородных внешних полях) индуцированное V m остается малым, тогда как при малых λ s (т.е. пространственно более неоднородных внешних полях) V m сходится к − V e [ v i сходится к v остальные , как видно на рис. 2, третий столбец; последний вывод был также сделан Холтом и Кохом (1999)]. В общем, | В м | ≤ 1,25, хотя для большинства случаев | В м | ≤ 1 достаточно (дополнительный рисунок S1, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Для бесконечного кабеля В м всегда меньше единицы (Holt and Koch, 1999). Поляризация на краях кабеля приводит к | В м | ≥ 1 для внеклеточных полей, когда λ s аналогично L (рис. 2 B2 ), что связано с граничными условиями закрытого конца.
2). При больших λ s (т.е. пространственно-однородных внешних полях) индуцированное V m остается малым, тогда как при малых λ s (т.е. пространственно более неоднородных внешних полях) V m сходится к − V e [ v i сходится к v остальные , как видно на рис. 2, третий столбец; последний вывод был также сделан Холтом и Кохом (1999)]. В общем, | В м | ≤ 1,25, хотя для большинства случаев | В м | ≤ 1 достаточно (дополнительный рисунок S1, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Для бесконечного кабеля В м всегда меньше единицы (Holt and Koch, 1999). Поляризация на краях кабеля приводит к | В м | ≥ 1 для внеклеточных полей, когда λ s аналогично L (рис. 2 B2 ), что связано с граничными условиями закрытого конца. Следовательно, при наличии стационарного и пространственно гармонического внеклеточного потенциала амплитуда индуцированного мембранного потенциала не более чем в 1,25 раза превышает амплитуду внеклеточного потенциала.
Следовательно, при наличии стационарного и пространственно гармонического внеклеточного потенциала амплитуда индуцированного мембранного потенциала не более чем в 1,25 раза превышает амплитуду внеклеточного потенциала.Рисунок 1.
Схематичное изображение пассивной мембраны в точке x вдоль кабеля (Rall, 1962). Здесь мы анализируем влияние пространственно-временных вариаций внеклеточного напряжения В и на мембранное напряжение В м в терминах нормализованного мембранного потенциала В м ( м нормализовано по амплитуде v e ).
Рис. 2.
Влияние стационарного и пространственно изменяющегося внеклеточного напряжения В e вдоль пассивного кабеля на нормированный мембранный потенциал В m , мембранное поле E m и мембрану плотность источника тока, CSD m .
 Расстояние по кабелю нормировано на единицу. В верхнем ряду ( A1 , B1 , C1 ) V e колебания с пространственной частотой Ω показаны для Ω L /2π = 0,1 ( A1 ), 0,5 ( B1 ) и 3 ( C3 903 ), тогда как цветные линии 2 укажите ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Во второй строке ( A2 , B2 , C2 ) для этих трех случаев нанесен индуцированный мембранный потенциал (уравнение 5). Только пространственно-неоднородные поля с характерной длиной поля, сравнимой с длиной кабеля или меньшей, приводят к сильным В м отклонения. In the third ( A3 , B3 , C3 ) and the fourth ( A4 , B4 , C4 ) rows, the induced E Показаны м (уравнение 6) и CSD м (уравнение 7).
Расстояние по кабелю нормировано на единицу. В верхнем ряду ( A1 , B1 , C1 ) V e колебания с пространственной частотой Ω показаны для Ω L /2π = 0,1 ( A1 ), 0,5 ( B1 ) и 3 ( C3 903 ), тогда как цветные линии 2 укажите ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Во второй строке ( A2 , B2 , C2 ) для этих трех случаев нанесен индуцированный мембранный потенциал (уравнение 5). Только пространственно-неоднородные поля с характерной длиной поля, сравнимой с длиной кабеля или меньшей, приводят к сильным В м отклонения. In the third ( A3 , B3 , C3 ) and the fourth ( A4 , B4 , C4 ) rows, the induced E Показаны м (уравнение 6) и CSD м (уравнение 7). Серая область обозначает диапазон для всех пространственных фаз, тогда как пунктирные линии в двух нижних рядах указывают диапазон безразмерного внеклеточного поля E e и плотность источника тока CSD e соответственно. Для ϕ s ∈[0°, 360°) индуцированная | E м |/Ом- и |CSD м |/Ом 2 -диапазон равен единице. Как видно, CSD m аналогичен профилю V e (сравните отдельные профили V e и CSD m в верхнем и нижнем рядах) для больших Ω. Обратите внимание, что на этом и на всех остальных рисунках не моделируется подача постоянного тока или синаптический ввод. Все изменения в V m объясняются пространственно изменяющимся внеклеточным полем.
Серая область обозначает диапазон для всех пространственных фаз, тогда как пунктирные линии в двух нижних рядах указывают диапазон безразмерного внеклеточного поля E e и плотность источника тока CSD e соответственно. Для ϕ s ∈[0°, 360°) индуцированная | E м |/Ом- и |CSD м |/Ом 2 -диапазон равен единице. Как видно, CSD m аналогичен профилю V e (сравните отдельные профили V e и CSD m в верхнем и нижнем рядах) для больших Ω. Обратите внимание, что на этом и на всех остальных рисунках не моделируется подача постоянного тока или синаптический ввод. Все изменения в V m объясняются пространственно изменяющимся внеклеточным полем.Сдвиг фазы ϕ s внеклеточного напряжения от 0 до 2π эквивалентен полному колебанию пространственно-неоднородного V e квазистационарным образом, что происходит, когда постоянная времени (пространственно-временная) флуктуация внеклеточного напряжения намного больше, чем постоянная времени мембраны τ м = r м с м .
 В этих условиях влиянием емкостной фильтрации можно пренебречь. Более того, из уравнения 5 следует, что усреднение V m за один полный цикл внеклеточного потенциала [т.е. по всем ϕ s ∈[0, 2π)] приводит к 〈V m 〉 ϕ s =
В этих условиях влиянием емкостной фильтрации можно пренебречь. Более того, из уравнения 5 следует, что усреднение V m за один полный цикл внеклеточного потенциала [т.е. по всем ϕ s ∈[0, 2π)] приводит к 〈V m 〉 ϕ s =Таким образом, средние свойства, такие как 〈 V m 〉 ϕ s , недостаточны для количественной оценки эффекта пространственной гармоники В и .
Мерой воздействия внеклеточного поля на мембрану является индуцированное мембранное поле, E м , то есть отрицательный пространственный градиент индуцированного V м вдоль кабеля.
Большой | E м | указывает на наличие пространственно-неоднородных V m флуктуаций. На практике можно показать, что | E м | < Ω (рис.
 2, третья строка), так что внешний E e максимально наводит вдоль кабеля E м равной прочности.
2, третья строка), так что внешний E e максимально наводит вдоль кабеля E м равной прочности.Хотя индуцированное мембранное поле, E m , информативно для предсказания воздействия внешнего поля на мембрану, это плотность источника мембранного тока, CSD m (т.е. отрицательная вторая пространственная производная от В м вдоль кабеля), что напрямую переводится в токоподвод вдоль кабеля, обусловленное пространственно-неоднородным внешним полем (Николсон, 1973; Мицдорф, 1985) следующим образом:
Сила CSD m максимально равна силе плотности внеклеточного источника тока CSD e ( X ) = Ω 2 sin(Ω X + ϕ s ) (т.е. |CSD m | ≤ Ω 2 ) (рис. 2) (подробное описание связи между CSD m и CSD e см. в дополнительном разделе 3, доступном на сайте www.
 jneurosci.org в качестве дополнительного материала) . При малых λ s , CSD m ( X ) ≈ Ω 2 V m ( X ) so that for spatially inhomogeneous extracellular voltages the current source along the cable is analogous to the V м профиль. Однако, хотя | В м | ≤ 1,25, E m и CSD m являются линейной и квадратичной функциями Ω соответственно. Таким образом, тот факт, что малоамплитудный неоднородный V e приводит к малоамплитудным V m не переводится в малые наведенные E m или CSD m . Крайне неоднородные внеклеточные колебания напряжения могут привести к значительным мембранным полям и плотности источника тока вдоль кабеля с потенциально важными последствиями.
jneurosci.org в качестве дополнительного материала) . При малых λ s , CSD m ( X ) ≈ Ω 2 V m ( X ) so that for spatially inhomogeneous extracellular voltages the current source along the cable is analogous to the V м профиль. Однако, хотя | В м | ≤ 1,25, E m и CSD m являются линейной и квадратичной функциями Ω соответственно. Таким образом, тот факт, что малоамплитудный неоднородный V e приводит к малоамплитудным V m не переводится в малые наведенные E m или CSD m . Крайне неоднородные внеклеточные колебания напряжения могут привести к значительным мембранным полям и плотности источника тока вдоль кабеля с потенциально важными последствиями.Влияние свойств
V e на индуцированные V m , E m и CSD mКогда пространственно неоднородные внеклеточные колебания напряжения существенно влияют на V m и его первую и вторую пространственные производные, E m и CSD m соответственно? Чтобы индуцированная амплитуда В м стала порядка амплитуды В и , должны выполняться два независимых условия (уравнение 5): электротоническая длина должна быть больше характерной длины внешнего поле [Ом > 1; условие (I)], а длина кабеля должна быть больше характерной длины внешнего поля [Ом л > 1; условие (II)].
 Из этих двух условий следует, что воздействие на В м зависит от трех длин: характерной длины внеклеточного поля λ с , физической l и электротонической λ el длин. кабеля. Из сказанного выше следует, что для того, чтобы индуцированная амплитуда V m стала порядка амплитуды V e , λ el > λ s /2π [условие (I)] и l > λ s /2π [условие (II)].
Из этих двух условий следует, что воздействие на В м зависит от трех длин: характерной длины внеклеточного поля λ с , физической l и электротонической λ el длин. кабеля. Из сказанного выше следует, что для того, чтобы индуцированная амплитуда V m стала порядка амплитуды V e , λ el > λ s /2π [условие (I)] и l > λ s /2π [условие (II)].Практически, условие (I) утверждает, что чем больше λ el кабеля, тем сильнее влияние пространственно-неоднородного внешнего поля на В м за исключением случаев, когда оно уже насыщается из-за большого Ω ( Рис. 2 B2 , C2 ). Следовательно, увеличение мембранного сопротивления кабеля, r м , или его диаметра d (в микрометрах) или, как вариант, уменьшение внутриклеточного сопротивления, r i , увеличивает амплитуду индуцированного V m из-за меньшего тока, протекающего через мембрану, и большего распространения тока, соответственно.
 Это приводит к повышенной поляризации кабеля (дополнительный раздел 5 и рис. S1, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Более того, условие (II) требует, чтобы λ s было достаточно большим примерно для полугода.0322 V e -период в пределах длины кабеля. Таким образом, пространственно-однородные поля с большими λ s (малыми Ω) по сравнению с размером кабеля оказывают лишь незначительное влияние на V m (рис. 2, ср. A2 , C2 ).
Это приводит к повышенной поляризации кабеля (дополнительный раздел 5 и рис. S1, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Более того, условие (II) требует, чтобы λ s было достаточно большим примерно для полугода.0322 V e -период в пределах длины кабеля. Таким образом, пространственно-однородные поля с большими λ s (малыми Ω) по сравнению с размером кабеля оказывают лишь незначительное влияние на V m (рис. 2, ср. A2 , C2 ).При наличии определенного пространственно-неоднородного В е вдоль кабеля, каковы пространственные особенности индуцированного В м ? Хотя эффект V e на V m зависит от трех характерных длин, влияние на E m и CSD m является локальным (это означает, что оно не зависит от связь между λ s и λ el (уравнения 6, 7).
 Таким образом, влияние пространственно-неоднородного V e на E m и CSD m прогнозируется исключительно через условие (I). Пока λ s мал, дальность наведенного E m и CSD m меньше или равна E e и CSD e соответственно. Поэтому даже вдоль короткого кабеля, который на основании условия (II) приводит к малым В м , наведенные Е м и КСД м могут быть существенными (рис. 2 А3 , А4 ).
Таким образом, влияние пространственно-неоднородного V e на E m и CSD m прогнозируется исключительно через условие (I). Пока λ s мал, дальность наведенного E m и CSD m меньше или равна E e и CSD e соответственно. Поэтому даже вдоль короткого кабеля, который на основании условия (II) приводит к малым В м , наведенные Е м и КСД м могут быть существенными (рис. 2 А3 , А4 ).Обратите внимание, что, хотя представленные результаты описывают влияние пространственно гармонического внеклеточного напряжения на мембрану кабеля, для стационарных или квазистационарных случаев развитая здесь теория может быть расширена для учета произвольно сложных пространственных профилей V e с помощью преобразования Фурье (дополнительный раздел 4, доступен на сайте www.
 jneurosci.org в качестве дополнительного материала).
jneurosci.org в качестве дополнительного материала).Влияние морфологии на индуцированные
V m , E m и CSD mдр., 2007). Здесь мы рассматриваем вопрос об изменении ориентации кабеля относительно оси внешнего поля. Чтобы учесть морфологическую изменчивость, предположим, что кабель (родительский) разветвляется на два кабеля (дочерние), в которых все ответвления находятся в одной плоскости. В то время как родительский кабель выровнен по внеклеточному полю, две дочерние ветви образуют углы θ d ,1 и θ d ,2 к оси поля (рис. 3).
Рисунок 3.
Родительский кабель разветвляется на два дочерних кабеля (все ответвления находятся в одной плоскости) при наличии пространственно-неоднородного внеклеточного напряжения. Цветом обозначен внешний потенциал В и , изменяющийся за полупериод.
 Импедансы кабелей согласовываются по правилу 3/2 (Rall, 1962). Основной кабель выровнен по оси внешнего поля, тогда как угол между дочерними кабелями и осью поля следующий: θ d ,1 = 0° and θ d ,2 = −45° ( A ), θ d ,1 = 45° and θ D , 2 = –45 ° ( B ) и θ D , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = . ( С ). Ниже каждого корпуса результирующие В м (второй ряд), E m (третий ряд) и CSD m (четвертый ряд) показаны для ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Заметим, что для X > 0,5 L штриховые цветные линии иллюстрируют траекторию v м вдоль штриховой дочерней ветви (см.
Импедансы кабелей согласовываются по правилу 3/2 (Rall, 1962). Основной кабель выровнен по оси внешнего поля, тогда как угол между дочерними кабелями и осью поля следующий: θ d ,1 = 0° and θ d ,2 = −45° ( A ), θ d ,1 = 45° and θ D , 2 = –45 ° ( B ) и θ D , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = . ( С ). Ниже каждого корпуса результирующие В м (второй ряд), E m (третий ряд) и CSD m (четвертый ряд) показаны для ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Заметим, что для X > 0,5 L штриховые цветные линии иллюстрируют траекторию v м вдоль штриховой дочерней ветви (см. первую строку рисунка) для трех ϕ s , тогда как сплошные цветные линии показывают траекторию v m вдоль сплошной дочерней ветви. Дочерние ветви имеют такую же нормализованную длину, как и родительская ветвь, L родитель = L дочь = L /2. Диапазон V м , E м и CSD м вдоль всех ветвей обозначен серыми областями. Обратите внимание на возрастающее затухание в индуцированном E m — и CSD m -диапазонах, когда дочерний кабель становится перпендикулярным к оси внешнего поля.
первую строку рисунка) для трех ϕ s , тогда как сплошные цветные линии показывают траекторию v m вдоль сплошной дочерней ветви. Дочерние ветви имеют такую же нормализованную длину, как и родительская ветвь, L родитель = L дочь = L /2. Диапазон V м , E м и CSD м вдоль всех ветвей обозначен серыми областями. Обратите внимание на возрастающее затухание в индуцированном E m — и CSD m -диапазонах, когда дочерний кабель становится перпендикулярным к оси внешнего поля.Положим Ω = π/ L , так что этот случай аналогичен неразветвленному кабелю (рис. 2, средний столбец). При сравнении дальности и профилей индуцированных V м , E м , и CSD м между родительской ветвью, совпадающей с осью внешнего поля (рис. 3), и начальной половиной неразветвленного кабеля (рис.
 2 B2). –B4 ), становится очевидным, что они практически идентичны. Тем не менее, существуют значительные различия при сравнении второй части неразветвленного кабеля и второй дочерней ветви (θ d , 2 = -π/4) разветвленного кабеля. Они увеличиваются по мере того, как дочерний кабель становится перпендикулярным внеклеточному полю. Влияние угла θ d , j ( j = 1, 2) между двумя дочерьми и родителем можно учесть, определив прогнозируемую электротоническую длину λ эл, j 3 = 4 cos(θ d , j ) на оси внешнего поля. Отсюда следует, что малые углы мало влияют на V m . Но поскольку E m и CSD m являются линейной и квадратичной функциями Ω j = 2π F S λ EL, J , различия, вызванные θ D , D .
2 B2). –B4 ), становится очевидным, что они практически идентичны. Тем не менее, существуют значительные различия при сравнении второй части неразветвленного кабеля и второй дочерней ветви (θ d , 2 = -π/4) разветвленного кабеля. Они увеличиваются по мере того, как дочерний кабель становится перпендикулярным внеклеточному полю. Влияние угла θ d , j ( j = 1, 2) между двумя дочерьми и родителем можно учесть, определив прогнозируемую электротоническую длину λ эл, j 3 = 4 cos(θ d , j ) на оси внешнего поля. Отсюда следует, что малые углы мало влияют на V m . Но поскольку E m и CSD m являются линейной и квадратичной функциями Ω j = 2π F S λ EL, J , различия, вызванные θ D , D . Ряд рисунков 2 и 3. Следовательно, даже небольшие изменения ориентации кабеля (по отношению к оси внешнего поля) могут привести к значительным изменениям E m и CSD m .
Ряд рисунков 2 и 3. Следовательно, даже небольшие изменения ориентации кабеля (по отношению к оси внешнего поля) могут привести к значительным изменениям E m и CSD m .Обратите внимание, что между родительским и дочерним кабелями, показанными на рис. 3, действует закон Ралла 3/2, согласующий общий импеданс с эквивалентным цилиндром с характеристиками родительского кабеля с L родитель = L дочь = L /2 (Rall, 1962). Следовательно, в отсутствие внеклеточного поля возмущение В м в родительской секции индуцировало бы идентичные профили В м вдоль двух дочерних кабелей, которые, в свою очередь, были бы идентичны В м профиль вдоль прямого неразветвленного кабеля с теми же свойствами, что и основной кабель (Лондон и др., 1999). Любые различия между профилями V m двух дочерних кабелей объясняются наличием внеклеточного поля.
 Таким образом, при наличии пространственно-неоднородного внеклеточного напряжения изменение ориентации кабеля может привести к существенному различию профилей вдоль отрезков кабеля.
Таким образом, при наличии пространственно-неоднородного внеклеточного напряжения изменение ориентации кабеля может привести к существенному различию профилей вдоль отрезков кабеля.Мы предполагаем, что изменение ориентации кабеля происходит внезапно в точке разветвления. Даже если анатомически это не совсем верно, характерная длина поля обычно больше, чем длина, вдоль которой происходит изменение ориентации кабеля. Таким образом, воздействие остается локальным. Холт и Кох (1999) описал, как учитывать плавные изменения ориентации кабеля.
How does variability in r m , r i , and d manifest itself on V m , E m , and CSD m ? Действительно, изменения λ el приводят к изменениям Ω и L , тогда как произведение Ω L остается неизменным. Уменьшение λ эл приводит к увеличению λ с и, таким образом, к более слабым наведенным V m , E m , и CSD m колебаний вдоль кабеля.
 Для изучения этих эффектов мы провели анализ чувствительности, в котором Ω, L , θ d и расположение ветвления систематически варьировались. Установлено, что при выполнении условий (I) и (II) на участке кабеля изменение свойств кабеля ( r m , r i и d ), которые обычно встречаются в нейронах, не влияют на диапазон V m флуктуаций так, как они влияют на пространственный профиль E m и CSD m (Рис. 3; дополнительный раздел 5, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Кроме того, можно показать, что изменения ориентации кабеля эквивалентны изменениям λ el (дополнительные разделы 2, 5, доступные на сайте www.jneurosci.org в качестве дополнительного материала).
Для изучения этих эффектов мы провели анализ чувствительности, в котором Ω, L , θ d и расположение ветвления систематически варьировались. Установлено, что при выполнении условий (I) и (II) на участке кабеля изменение свойств кабеля ( r m , r i и d ), которые обычно встречаются в нейронах, не влияют на диапазон V m флуктуаций так, как они влияют на пространственный профиль E m и CSD m (Рис. 3; дополнительный раздел 5, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Кроме того, можно показать, что изменения ориентации кабеля эквивалентны изменениям λ el (дополнительные разделы 2, 5, доступные на сайте www.jneurosci.org в качестве дополнительного материала).Воздействие одномерного внеклеточного поля на морфологически реалистичный пирамидный нейрон СА1
Из-за линейности уравнения пассивного кабеля предыдущие результаты могут быть обобщены на морфологически нерегулярные пассивные кабели в присутствии одномерного электрического поля .
 Исходя из этих соображений, для морфологически неоднородного кабеля условия (I) и (II) необходимо лишь переформулировать в терминах проекций характерных длин вдоль оси внешнего поля (см. Материалы и методы). Для реконструированного пирамидного нейрона гиппокампа крысы СА1, показанного на рис. 4 A [нейрон d151 в исследовании Gold et al. (2006)], мы сосредоточили наш анализ на четырех разделах, в которых каждый раздел состоит из ряда взаимосвязанных линейных сегментов. К ним относятся: ( i ) срез базального дендрита, ( ii ) сома и проксимальный срез в апикальной области, соединенный непосредственно с сомой, ( iii ) медиальный срез в апикальной области и ( iv ) дистальный срез в апикальной области. Расположение этих секций показано на рисунке 4 A , а ориентация каждой секции показана на рисунке 4 B . Характеристические свойства каждой секции приведены в таблице 1 (т. е. длина l и средняя проекционная электротоническая длина 〈λ el,proj 〉, а также проекционная длина l̄ proj ) [обе длины проецируется на соматодендритную ось (рис.
Исходя из этих соображений, для морфологически неоднородного кабеля условия (I) и (II) необходимо лишь переформулировать в терминах проекций характерных длин вдоль оси внешнего поля (см. Материалы и методы). Для реконструированного пирамидного нейрона гиппокампа крысы СА1, показанного на рис. 4 A [нейрон d151 в исследовании Gold et al. (2006)], мы сосредоточили наш анализ на четырех разделах, в которых каждый раздел состоит из ряда взаимосвязанных линейных сегментов. К ним относятся: ( i ) срез базального дендрита, ( ii ) сома и проксимальный срез в апикальной области, соединенный непосредственно с сомой, ( iii ) медиальный срез в апикальной области и ( iv ) дистальный срез в апикальной области. Расположение этих секций показано на рисунке 4 A , а ориентация каждой секции показана на рисунке 4 B . Характеристические свойства каждой секции приведены в таблице 1 (т. е. длина l и средняя проекционная электротоническая длина 〈λ el,proj 〉, а также проекционная длина l̄ proj ) [обе длины проецируется на соматодендритную ось (рис. 4 A , y -оси)]. Как видно, хотя базальный отдел ( i ) почти в три раза длиннее, чем дистальный апикальный отдел ( iv ), его l̄ proj вдвое короче. Причина этого становится очевидной на рис. 4, А и В , на которых показано, что базальный разрез почти перпендикулярен оси соматодендритов. Следовательно, влияние пространственно-неоднородного напряжения вдоль оси y на V m базально-апикального отдела по сравнению с дистальным апикальным отделом будет минимальным. В самом деле, исходя из условия (II) и значения l̄ proj , при наличии пространственно-гармонического внешнего поля вдоль оси соматодендритов число пространственных V m колебаний вдоль базального отдела должно быть аналогично таковому вдоль проксимального верхушечного отдела и меньше, чем вдоль медиальный и дистальный апикальный отделы.
4 A , y -оси)]. Как видно, хотя базальный отдел ( i ) почти в три раза длиннее, чем дистальный апикальный отдел ( iv ), его l̄ proj вдвое короче. Причина этого становится очевидной на рис. 4, А и В , на которых показано, что базальный разрез почти перпендикулярен оси соматодендритов. Следовательно, влияние пространственно-неоднородного напряжения вдоль оси y на V m базально-апикального отдела по сравнению с дистальным апикальным отделом будет минимальным. В самом деле, исходя из условия (II) и значения l̄ proj , при наличии пространственно-гармонического внешнего поля вдоль оси соматодендритов число пространственных V m колебаний вдоль базального отдела должно быть аналогично таковому вдоль проксимального верхушечного отдела и меньше, чем вдоль медиальный и дистальный апикальный отделы.Рисунок 4.

Морфология реконструированного пирамидного нейрона СА1 крысы. A , Обозначенные участки представляют собой базальный дендрит (зеленый) ( i ), сома и связанный с ней проксимальный апикальный дендрит (синий) ( ii ), медиальный апикальный дендрит (голубой) ( iii ) и дистальный апогенный дендрит ) ( iv ). B , Ориентация cos(θ k )cos(σ k ) относительно оси соматодендритов (рис. 4 A , 9032 каждая) показана 2-3 вдоль оси , раздел ( i–iv ) в зависимости от нормированной длины дуги s / l : для базального отдела (зеленый), сомы и проксимального апикального отдела (синий; от s / l = от 0 до 0,25 сомы, а затем проксимальный апикальный дендрит), медиальный апикальный отдел (голубой) и дистальный апикальный отдел (пурпурный).
 Как видно, базальный дендрит почти перпендикулярен оси соматодендрита, тогда как остальные три секции относительно хорошо выровнены. Длина л каждой секции представлен в таблице 1.
Как видно, базальный дендрит почти перпендикулярен оси соматодендрита, тогда как остальные три секции относительно хорошо выровнены. Длина л каждой секции представлен в таблице 1.Таблица 1.
Характеристики участков, показанных на рис. 4 A , цветные линии
Применили три стационарных и пространственно-гармонических внеклеточных колебания напряжения вдоль соматодендритной оси нейрона и рассчитали индуцированные V m профили для трех характерных длин , λ с = 6,25, 1 и 0,2 мм (при ω = 2π f с и λ с = 1/ ф с ). Диапазон индуцированного В м отклонения вдоль каждого сечения можно предсказать из λ с < 2π l̄ proj [т.е. условие (II)], с проекцией каждого сечения на ось поля 1. Условие (II) выполняется только для самого сильного из наложенных полей (наименьшее λ с ) (рис.
 5, третий столбец) на медиальном апикальном и дистальном апикальном участках, а также (маргинально) на проксимальный апикальный отдел. Действительно, на рис. 5 Cii–iv видно, что в этих разрезах колебания V м значительны и гораздо сильнее, чем в базальном разрезе или соме. Мы заключаем, что условия (I) и (II) точно предсказывают влияние стационарного и пространственно-неоднородного внеклеточного потенциала на мембранный потенциал. В случае внешних полей с более чем одной доминирующей осью условия (I) и (II) выполняются для каждой оси.
5, третий столбец) на медиальном апикальном и дистальном апикальном участках, а также (маргинально) на проксимальный апикальный отдел. Действительно, на рис. 5 Cii–iv видно, что в этих разрезах колебания V м значительны и гораздо сильнее, чем в базальном разрезе или соме. Мы заключаем, что условия (I) и (II) точно предсказывают влияние стационарного и пространственно-неоднородного внеклеточного потенциала на мембранный потенциал. В случае внешних полей с более чем одной доминирующей осью условия (I) и (II) выполняются для каждой оси.Рисунок 5.
Влияние пространственно-гармонического одномерного электрического поля (вдоль оси соматодендритов) на V m реконструированного нейрона СА1 (верхний ряд; белыми линиями обозначены те же четыре сечения, что и на рис. 4 A ) для трех пространственных частот: λ с = 6,25 мм ( f с = 0,16 мм −1 ; A ), 1 мм (1 мм −1 ; B ) и 0,2 мМ (5 мм –1;
3 2222. 9032.9232.9232.9232.9232.9232. 9032. 9032.9232.9232. 9032. 9032.9232. 9032. . .9232.923. Цветовая карта иллюстрирует (пространственно) одномерный внеклеточный V e осцилляции вдоль оси соматодендритов для фазы ϕ y . Расстояние вдоль каждой секции показано как безразмерная длина дуги s / l . i – базальный; ii , сома и проксимальный верхушечный; iii медиальный апикальный; и iv , дистальный апикальный срез (рис. 4 A , таблица 1). Диапазон В м обозначено серым цветом, тогда как отдельные трассы имеют вид ϕ y = 0° (синий), 45° (красный) и 90° (зеленый). Условие (II) выполняется только для λ s = 0,2 мм (5 мм −1 ; C ) вдоль проксимального ( Cii ), медиального ( 2 Cii ) и дистальные апикальные ( Civ ) срезы (таблица 1), наблюдаемые в индуцированном диапазоне V м .
9032.9232.9232.9232.9232.9232. 9032. 9032.9232.9232. 9032. 9032.9232. 9032. . .9232.923. Цветовая карта иллюстрирует (пространственно) одномерный внеклеточный V e осцилляции вдоль оси соматодендритов для фазы ϕ y . Расстояние вдоль каждой секции показано как безразмерная длина дуги s / l . i – базальный; ii , сома и проксимальный верхушечный; iii медиальный апикальный; и iv , дистальный апикальный срез (рис. 4 A , таблица 1). Диапазон В м обозначено серым цветом, тогда как отдельные трассы имеют вид ϕ y = 0° (синий), 45° (красный) и 90° (зеленый). Условие (II) выполняется только для λ s = 0,2 мм (5 мм −1 ; C ) вдоль проксимального ( Cii ), медиального ( 2 Cii ) и дистальные апикальные ( Civ ) срезы (таблица 1), наблюдаемые в индуцированном диапазоне V м .
Из того же анализа мы обнаружили близкое соответствие между ориентацией вдоль каждого сечения (рис. 4 B ) и результирующий диапазон E m , а также отдельные профили E m (дополнительный раздел 6 и рис. S5, доступны на сайте www.jneurosci.org в качестве дополнительного материала). Поэтому, как уже было указано на рис. 3, особенности морфологии кабеля непосредственно проявляются в наведенном мембранном поле.
Воздействие медленно меняющихся пространственно-неоднородных внеклеточных полей
До сих пор мы продемонстрировали, что амплитуда пространственной флуктуации мембранного потенциала, индуцированная внеклеточно, может стать порядка амплитуды пространственной флуктуации внеклеточного напряжения. Сохраняются ли эти эффекты для зависящих от времени внеклеточных полей? Нейронная мембрана является емкостной, что приводит к временной фильтрации нижних частот. Воздействие пространственно-временного изменения внеклеточного поля намного медленнее, чем τ м будут минимально затронуты фильтрацией нижних частот.
 В этом случае применяется квазистационарность, и разработанная здесь методология может быть полностью принята. Но по мере того, как характерное время пространственно-временного неоднородного внешнего поля становится сравнимым с τ m , фильтрация нижних частот становится существенной.
В этом случае применяется квазистационарность, и разработанная здесь методология может быть полностью принята. Но по мере того, как характерное время пространственно-временного неоднородного внешнего поля становится сравнимым с τ m , фильтрация нижних частот становится существенной.Для оценки влияния пространственно-временных V e флуктуаций мы применяли зависящий от времени и пространственно гармоничный внеклеточный V e = sin(2π f t t ) sin(Ω X ) с Ω = π/ L и f t (в секундах 07 81090) пространственно-временного колебания V e . Этот случай подобен показанному на рис. 2, второй столбец, синие и красные линии, в том, что при увеличении t , V e колеблется около 0, тогда как наибольшее V e колебание вдоль кабель происходит в середине кабеля. На рисунке 6 A , показаны максимум V m и минимум V m наведенных V m колебаний вдоль кабеля для разных f t Цветные области обозначают амплитуду 90 322 В 90 323 90 324 м 90 325 вдоль кабеля, постоянный ток обозначен серым цветом, 100 с –1 зеленым и 200 с –1 красным.
 Примечательно, что для увеличения f t V м 9Амплитуда 0325 уменьшается (см. стрелки), так как V м не может следовать пространственно-временному колебанию V e . Таким образом, отношение β( V m ) между индуцированной амплитудой V m при определенном f t и V m обеспечивает измерение одного стационарного случая количественной оценки стационарной амплитуды. зависящее от времени воздействие на мембрану.
Примечательно, что для увеличения f t V м 9Амплитуда 0325 уменьшается (см. стрелки), так как V м не может следовать пространственно-временному колебанию V e . Таким образом, отношение β( V m ) между индуцированной амплитудой V m при определенном f t и V m обеспечивает измерение одного стационарного случая количественной оценки стационарной амплитуды. зависящее от времени воздействие на мембрану.Рисунок 6.
A , Максимум и минимум нормированного мембранного потенциала В м в присутствии пространственно неоднородного и колеблющегося внеклеточного поля В e . Цветные области обозначают амплитуду В м вдоль кабеля для постоянного тока (серая область) и f t = 100 (зеленая область) и 200 Гц (красная область).
) в черном цвете. Возбуждение было пространственно сосредоточено в середине каждой секции. Для типичного значения τ м = 20 мс (2π f t τ м ) 1/2 = 1 и 5 эквивалентны f t Гц, соответственно. Как и ожидалось для низкочастотной мембраны, при увеличении значений временной частоты f t (стрелки), V m все меньше и меньше следует за колебаниями V e . B , Влияние зависящего от времени гармонического возбуждения на В м , как описано через нормализованное отклонение β( В м ). Пока β( V m ) ≈ 0, отклик мембраны остается квазистационарным. Как только β отклоняется от нуля, фильтрация нижних частот влияет на весь процесс. Результаты показаны для базального дендрита (крестики), сомы (кружки), проксимального апикального дендрита (квадраты), медиального апикального дендрита (ромбы) и дистального апикального дендрита (9).0322 x
Как и ожидалось для низкочастотной мембраны, при увеличении значений временной частоты f t (стрелки), V m все меньше и меньше следует за колебаниями V e . B , Влияние зависящего от времени гармонического возбуждения на В м , как описано через нормализованное отклонение β( В м ). Пока β( V m ) ≈ 0, отклик мембраны остается квазистационарным. Как только β отклоняется от нуля, фильтрация нижних частот влияет на весь процесс. Результаты показаны для базального дендрита (крестики), сомы (кружки), проксимального апикального дендрита (квадраты), медиального апикального дендрита (ромбы) и дистального апикального дендрита (9).0322 x  β( В м ) также показано для случая неразветвленного кабеля (красная линия) для сравнения.
β( В м ) также показано для случая неразветвленного кабеля (красная линия) для сравнения.Те же самые принципы были применены для количественной оценки зависящих от времени эффектов на морфологически реалистичный нейрон. Мы применяли зависящее от времени и пространственно гармоничное внеклеточное поле вдоль оси соматодендритов с λ s = 1 мм и сравнили отклонение вынужденных V m колебаний со стационарным случаем. Было показано, что отклик V m на относительно медленно колеблющиеся (пространственно постоянные) поля параболически затухает с увеличением τ m (Svirskis et al., 1997; Deans et al., 2007). Так, β( V m ) (рис. 6 B ) показан как функция квадратного корня безразмерной постоянной времени мембраны (2π f t τ m ) 1/2 (определения см. в разделе «Материалы и методы»). Пока (2π f t τ m ) 1/2 ≤ 1, индуцированные колебания V m остаются незатронутыми емкостной фильтрацией.
 При увеличении (2π f t τ m ) 1/2 происходит линейный рост β( V m ). Когда (2π f t τ m ) 1/2 становится большим, отклонения от стационарности становятся зависимыми от локальной морфологии. Например, хотя общее снижение β( V m ) составляет примерно 40% в медиальном апикальном дендрите, оно достигает 75% в базальных дендритах. В целом эти результаты хорошо согласуются с теоретическими и экспериментальными исследованиями (Свирскис и др., 1997). Для сравнения, β( В м ) также показано для случая неразветвленного кабеля, описанного в предыдущем абзаце (красная линия). Для того же (2π f t τ m ) 1/2 , возникают секционные различия в β( V m ), которые объясняются, во-первых, морфологическими особенностями каждого разреза и, во-вторых, разность в размахе индуцированных В м — отклонение для стационарного случая по каждому сечению (рис.
При увеличении (2π f t τ m ) 1/2 происходит линейный рост β( V m ). Когда (2π f t τ m ) 1/2 становится большим, отклонения от стационарности становятся зависимыми от локальной морфологии. Например, хотя общее снижение β( V m ) составляет примерно 40% в медиальном апикальном дендрите, оно достигает 75% в базальных дендритах. В целом эти результаты хорошо согласуются с теоретическими и экспериментальными исследованиями (Свирскис и др., 1997). Для сравнения, β( В м ) также показано для случая неразветвленного кабеля, описанного в предыдущем абзаце (красная линия). Для того же (2π f t τ m ) 1/2 , возникают секционные различия в β( V m ), которые объясняются, во-первых, морфологическими особенностями каждого разреза и, во-вторых, разность в размахе индуцированных В м — отклонение для стационарного случая по каждому сечению (рис. 5, второй столбец). На проксимальных участках (толстые тросы, хорошее выравнивание) β( V m ) затухает меньше, чем на участках, в которых тросы тонкие (дистально-апикальные) или плохо ориентированные (базальные). Эти результаты показывают, что для типичного τ m значений [5 мс ≤ τ m ≤ 50 мс (Koch, 1999)], влияние внеклеточных полей сохраняется для относительно высоких временных частот [т.е. до (2π f t τ m ) 1/2 = 5, что для τ m = 20 мс соответствует f t до 200 Гц].
5, второй столбец). На проксимальных участках (толстые тросы, хорошее выравнивание) β( V m ) затухает меньше, чем на участках, в которых тросы тонкие (дистально-апикальные) или плохо ориентированные (базальные). Эти результаты показывают, что для типичного τ m значений [5 мс ≤ τ m ≤ 50 мс (Koch, 1999)], влияние внеклеточных полей сохраняется для относительно высоких временных частот [т.е. до (2π f t τ m ) 1/2 = 5, что для τ m = 20 мс соответствует f t до 200 Гц].Влияние ритмической эндогенной активности гиппокампа
Наконец, мы исследовали влияние эндогенных ритмов LFP гиппокампа на мембранный потенциал анатомически реконструированного (пассивного) пирамидного нейрона СА1. Для этого параллельные записи LFP из области СА1 крысы (ориентация: от молекулярного лакунозного слоя к ориентациям) были применены вдоль оси соматодендритов пассивного реконструированного нейрона СА1, показанного на рисунке 4-9.
и индуцированный профиль v м вдоль четырех обозначенных секций были рассчитаны численно (см. Материалы и методы) (дополнительные рисунки S6, S7, доступны на сайте www.jneurosci.org в качестве дополнительного материала). Мы сосредоточились на двух характерных примерах активности гиппокампа: тета-активности и острых волнах. 0322 A
0322 A Тета-активность
Тета-колебания гиппокампа (4–12 Гц), наиболее постоянно присутствующие при различных типах двигательной активности (Вандервольф, 1969) и сон с быстрыми движениями глаз (Jouvet, 1969), наиболее регулярны по частоте и наибольшей амплитуде в молекулярном лакунозном слое в СА1. Как амплитуда [приблизительно от 0,2 мВ в stratum oriens до 1 мВ в lacunosum mollele (Buzsaki et al., 1983; Bragin et al., 1995)], так и фаза тета-волн изменяются в зависимости от глубины (Bullock et al. , 1990). Ритмы с аналогичной временной частотой также присутствуют в неокортикальных структурах (Steriade, 2000). На рис. 7, левый столбец, индуцированные v m флуктуации в течение 1-секундной эпохи тета-активности показаны (рис.
 7 Ai–iv ; латинская нумерация соответствует секции нейронов, как определено на рис. 4 A и в таблице 1). Как и ожидалось, увлечение во внешнее поле зависит от глубины. Хотя в базальном отделе и соме | v m − v остальные | ≤ 0,3 мВ (| v e | ≤ 0,3 мВ) (дополнительный рисунок S6, доступный на www.jneurosci.org в качестве дополнительного материала), влияние внеклеточного поля увеличивается по направлению к дистальным апикальным отделам, что приводит к | v m − v остальные | ≤ 0,7 мВ (| v e | ≤ 0,8 мВ). Пространственные профили v м являются однородными, как и ожидалось, исходя из условия (II). Корзинчатые клетки, аксоаксоны и интернейрон-проксимальное торможение и опосредованное перфорантным путем дистальное возбуждение (Fox, 1989; Ylinen et al., 1995b; Klausberger et al., 2003) приводят к противофазному соотношению между и m в перисоматической области и дистальных отделах (ср.
7 Ai–iv ; латинская нумерация соответствует секции нейронов, как определено на рис. 4 A и в таблице 1). Как и ожидалось, увлечение во внешнее поле зависит от глубины. Хотя в базальном отделе и соме | v m − v остальные | ≤ 0,3 мВ (| v e | ≤ 0,3 мВ) (дополнительный рисунок S6, доступный на www.jneurosci.org в качестве дополнительного материала), влияние внеклеточного поля увеличивается по направлению к дистальным апикальным отделам, что приводит к | v m − v остальные | ≤ 0,7 мВ (| v e | ≤ 0,8 мВ). Пространственные профили v м являются однородными, как и ожидалось, исходя из условия (II). Корзинчатые клетки, аксоаксоны и интернейрон-проксимальное торможение и опосредованное перфорантным путем дистальное возбуждение (Fox, 1989; Ylinen et al., 1995b; Klausberger et al., 2003) приводят к противофазному соотношению между и m в перисоматической области и дистальных отделах (ср. фазу отдельных следов на рис. 7 Aii–iv ).
фазу отдельных следов на рис. 7 Aii–iv ).Рисунок 7.
Влияние активности внеклеточного поля тета (левая колонка) и SPW (правая колонка) на мембранный потенциал v m пирамидного нейрона СА1. A1 , B1 , Индивидуальные внеклеточные записи (черные кривые) с одинаково расположенных участков записи (показаны 8 из 16 электродов) (дополнительные рисунки S6, S7, доступные на www.jneurosci.org как дополнительный материал) показаны в течение двух 1-секундных эпох, начиная с лакунозного молекулярного слоя ( y = 0 мкм) по направлению к востоку от слоя ( y = 700 мкм). Цветная карта показывает текущую плотность источника csd e (единицы, милливольты на квадратный миллиметр) (Mitzdorf, 1985). Основываясь на экспериментальных данных, свидетельствующих о том, что эндогенное поле является наиболее сильным вдоль оси соматодендритов нейронов СА1, мы применили записи v e ( A1 , B1 ) вдоль оси -9032y.
 реалистичный нейрон (рис. 4 A ) и рассчитал результирующую пространственно-временную эволюцию v m (дополнительный раздел 7, доступен на www.jneurosci.org в качестве дополнительного материала). Ai–Aiv , LFP-индуцированные отклонения v м вдоль каждого сечения ( i–iv ) (табл. 1) во время тета. Серые области показывают диапазон, тогда как три отдельные трассы показывают v m − v остальные вдоль каждой секции для t = 0,13 с (черный), 0,22 с (синий) и 0,30 (голубой) и указаны стрелками в верхнем ряду. Периодические флуктуации внеклеточного потенциала индуцируют локализованные флуктуации мембранного потенциала, амплитуда которых увеличивается по направлению к молекулярному лакуновому слою. Противофазное соотношение между соматическими и апикальными дендритными флуктуациями v e приводит к противофазной v m флуктуации; то есть сравнить v m на пике тета (черная стрелка и линии) и впадине тета (синяя стрелка и линии) в соме ( Aii ) и дистальном апикальном отделе ( Aiv ) соответственно .
реалистичный нейрон (рис. 4 A ) и рассчитал результирующую пространственно-временную эволюцию v m (дополнительный раздел 7, доступен на www.jneurosci.org в качестве дополнительного материала). Ai–Aiv , LFP-индуцированные отклонения v м вдоль каждого сечения ( i–iv ) (табл. 1) во время тета. Серые области показывают диапазон, тогда как три отдельные трассы показывают v m − v остальные вдоль каждой секции для t = 0,13 с (черный), 0,22 с (синий) и 0,30 (голубой) и указаны стрелками в верхнем ряду. Периодические флуктуации внеклеточного потенциала индуцируют локализованные флуктуации мембранного потенциала, амплитуда которых увеличивается по направлению к молекулярному лакуновому слою. Противофазное соотношение между соматическими и апикальными дендритными флуктуациями v e приводит к противофазной v m флуктуации; то есть сравнить v m на пике тета (черная стрелка и линии) и впадине тета (синяя стрелка и линии) в соме ( Aii ) и дистальном апикальном отделе ( Aiv ) соответственно . Bi–Biv , LFP-индуцированные изменения v m во время SPW. Три отдельные трассы показывают v m − v rest вдоль каждой секции для t = 0,30 с (черный), 0,38 с (синий) и 0,48 (голубой). Обратите внимание на ярко выраженную противофазность в v m в отрицательности SPW (синяя стрелка и линии) между сомой ( Bii ) и медиальным апикальным отделом ( Biii ). В отличие от тета, потенциал соматической мембраны в значительной степени, но ненадолго, захватывается во время СПВ: сравните 90 322 v 90 323 90 324 м 90 325 отклонений непосредственно перед (черная стрелка и линии) и после (голубая стрелка и линии) СПВ (дополнительные фильмы, доступные на www.jneurosci.org в качестве дополнительного материала).
Bi–Biv , LFP-индуцированные изменения v m во время SPW. Три отдельные трассы показывают v m − v rest вдоль каждой секции для t = 0,30 с (черный), 0,38 с (синий) и 0,48 (голубой). Обратите внимание на ярко выраженную противофазность в v m в отрицательности SPW (синяя стрелка и линии) между сомой ( Bii ) и медиальным апикальным отделом ( Biii ). В отличие от тета, потенциал соматической мембраны в значительной степени, но ненадолго, захватывается во время СПВ: сравните 90 322 v 90 323 90 324 м 90 325 отклонений непосредственно перед (черная стрелка и линии) и после (голубая стрелка и линии) СПВ (дополнительные фильмы, доступные на www.jneurosci.org в качестве дополнительного материала).Острая волновая активность
Вторым рассматриваемым феноменом LFP является острая волна гиппокампа (SPW), нерегулярный, но очень синхронный паттерн, возникающий внутри цепи гиппокампа (Ylinen et al.
 , 1995a). В отсутствие тета нерегулярные SPW продолжительностью 40–120 мс наблюдаются во время завершающего поведения, неподвижности и медленного сна (Buzsaki et al., 1983, 1986; Suzuki and Smith, 1988). Непосредственной причиной СПВ в области СА1 является синхронный разряд большого количества пирамидных нейронов СА3 и последующая почти одновременная деполяризация пирамидных клеток СА1. Во время всплесков SPW диполи образуются в результате возбуждения дендритов и перисоматического торможения, что приводит к потенциалам в несколько милливольт (2–3 мВ в лучистом слое) (Ylinen et al., 19).95а). На рис. 7 B1 показано событие SPW при t = 0,4 с с многоэлектродной решеткой, расположенной в том же положении, что и на рис. 7 A1 . Здесь сток тока (синий цвет на карте; единицы в милливольтах на квадратный миллиметр) появляется в медиальной апикальной области ( y = 250 мкм; лучистый слой) и источник тока (красный цвет на карте) в перисоматической области ( y = 500 мкм, пирамидальный слой).
, 1995a). В отсутствие тета нерегулярные SPW продолжительностью 40–120 мс наблюдаются во время завершающего поведения, неподвижности и медленного сна (Buzsaki et al., 1983, 1986; Suzuki and Smith, 1988). Непосредственной причиной СПВ в области СА1 является синхронный разряд большого количества пирамидных нейронов СА3 и последующая почти одновременная деполяризация пирамидных клеток СА1. Во время всплесков SPW диполи образуются в результате возбуждения дендритов и перисоматического торможения, что приводит к потенциалам в несколько милливольт (2–3 мВ в лучистом слое) (Ylinen et al., 19).95а). На рис. 7 B1 показано событие SPW при t = 0,4 с с многоэлектродной решеткой, расположенной в том же положении, что и на рис. 7 A1 . Здесь сток тока (синий цвет на карте; единицы в милливольтах на квадратный миллиметр) появляется в медиальной апикальной области ( y = 250 мкм; лучистый слой) и источник тока (красный цвет на карте) в перисоматической области ( y = 500 мкм, пирамидальный слой). СПВ порождают гораздо большие v м колебаний (амплитуда ≤1,5 мВ), чем во время тета (рис. 7; дополнительный рисунок S6, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Хотя тета-индуцированные эффекты усиливаются по направлению к дистальным апикальным отделам, SPW индуцируют столь же выраженный эффект вдоль всего нейрона, при этом перисоматическая область и средние апикальные отделы особенно вовлечены. Обратите внимание, что во время повторяющейся ритмической активности (тета) максимальный диапазон 90 322 v 90 323 90 324 м 90 325 индуцируется в каждом цикле, в то время как переходное системное событие (SPW) лишь на мгновение вызывает большие v м отклонения. Лучше всего это видно в фильмах, предоставленных в качестве дополнительных материалов (доступных на сайте www.jneurosci.org), в которых ( v m − v rest ) показаны флуктуации вдоль всего нейрона во время тета-анализа.
СПВ порождают гораздо большие v м колебаний (амплитуда ≤1,5 мВ), чем во время тета (рис. 7; дополнительный рисунок S6, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Хотя тета-индуцированные эффекты усиливаются по направлению к дистальным апикальным отделам, SPW индуцируют столь же выраженный эффект вдоль всего нейрона, при этом перисоматическая область и средние апикальные отделы особенно вовлечены. Обратите внимание, что во время повторяющейся ритмической активности (тета) максимальный диапазон 90 322 v 90 323 90 324 м 90 325 индуцируется в каждом цикле, в то время как переходное системное событие (SPW) лишь на мгновение вызывает большие v м отклонения. Лучше всего это видно в фильмах, предоставленных в качестве дополнительных материалов (доступных на сайте www.jneurosci.org), в которых ( v m − v rest ) показаны флуктуации вдоль всего нейрона во время тета-анализа. и эпохи SPW.
и эпохи SPW.Такой же анализ был проведен для индуцируемого мембранного поля, и в соответствии с результатами анализов простых кабелей мы обнаружили, что индуцированное e m имеет равную силу с e e (сила e e обычно составляет 2-3 мВ мм -1 во время тета и 10-15 мВ мм -1 во время SPW) для срезов, которые выровнены по оси соматодендритов (дополнительный раздел 7, доступен на сайте www.jneurosci.org в качестве дополнительного материала).
Обсуждение
Как и следовало ожидать из теоретических соображений, пространственно-неоднородный потенциал локального поля действует как распределенный приемник/источник тока (Holt and Koch, 19).99) вдоль кабелей и может возмущать мембранный потенциал ( v m ) отдельных нейронов. Для постоянных полей влияние на v m определяется уравнением 5 для внешнего поля большой характерной длины вдоль кабеля (рис.
 2 A1 , 2 , синяя и красная линии) (Стен-Кнудсен , 1960; Ранк, 1963; Чан и Николсон, 1986). Для пространственно-неоднородных полей воздействие на v м более сложное и зависит от юстировки кабель-поля, а также от трех констант длины: характерной длины внешнего поля (λ s ), длина кабеля ( l ) и электротоническая длина (λ el ).
2 A1 , 2 , синяя и красная линии) (Стен-Кнудсен , 1960; Ранк, 1963; Чан и Николсон, 1986). Для пространственно-неоднородных полей воздействие на v м более сложное и зависит от юстировки кабель-поля, а также от трех констант длины: характерной длины внешнего поля (λ s ), длина кабеля ( l ) и электротоническая длина (λ el ).Влияние внеклеточного потенциала на простые кабели. индуцируемое пространственно-неоднородным внеклеточным полем, может стать порядка внеклеточного пространственного напряжения, поля (
e e ) и плотность источника тока (csd e ) соответственно. Например, профиль внешнего синусоидального потенциала с амплитудой v 0 = 0,5 мВ и пространственной частотой λ с = 0,5 мм, выровненный с кабелем, может привести к )-отклонения до 0,625 мВ и индуцируют мембранное поле до 6,3 мВ мм -1 и плотность источника мембранного тока до 78,9мВ мм −2 . Таким образом, малое λ s может локально привести к очень большим e m и csd m , даже если амплитуда v m остается относительно небольшой. Из теории также следует, что при увеличении диаметра кабеля (т.е. увеличении электротонической длины) влияние пространственно-неоднородных внеклеточных v e на v m возрастает [условие (I)] до тех пор, пока амплитуда ( v m − v rest ) — отклонение вдоль кабеля становится порядка амплитуды v e (дополнительный рис. S2, доступен на www.jneurosci.org в качестве дополнительного материала) и индуцированный мембранный потенциал достигает насыщения. И наоборот, для тонких волокон, таких как аксоны, индуцированный мембранный потенциал становится несущественным.
Таким образом, малое λ s может локально привести к очень большим e m и csd m , даже если амплитуда v m остается относительно небольшой. Из теории также следует, что при увеличении диаметра кабеля (т.е. увеличении электротонической длины) влияние пространственно-неоднородных внеклеточных v e на v m возрастает [условие (I)] до тех пор, пока амплитуда ( v m − v rest ) — отклонение вдоль кабеля становится порядка амплитуды v e (дополнительный рис. S2, доступен на www.jneurosci.org в качестве дополнительного материала) и индуцированный мембранный потенциал достигает насыщения. И наоборот, для тонких волокон, таких как аксоны, индуцированный мембранный потенциал становится несущественным.Влияние внеклеточного потенциала на морфологически реконструированные нейроны
Мы вывели простые условия, выполнение которых приводит к значительным v m и e m колебания внутри определенного участка нейрона.
 Хотя эти эффекты получены для стационарных случаев, моделирование пространственно-неоднородного внешнего потенциала в зависимости от времени ясно указывает на то, что эти события сохраняются для относительно высоких временных частот (<200 Гц; эффект ослабляется при увеличении временной частоты). Следовательно, наши результаты применимы к (пространственно) произвольно сложным внешним полям (и геометрии нейронов), даже когда эти поля меняются во времени. Таким образом, они имеют отношение ко всем нейронам, встроенным в электрически проводящую внеклеточную жидкость (Logothetis et al., 2007).
Хотя эти эффекты получены для стационарных случаев, моделирование пространственно-неоднородного внешнего потенциала в зависимости от времени ясно указывает на то, что эти события сохраняются для относительно высоких временных частот (<200 Гц; эффект ослабляется при увеличении временной частоты). Следовательно, наши результаты применимы к (пространственно) произвольно сложным внешним полям (и геометрии нейронов), даже когда эти поля меняются во времени. Таким образом, они имеют отношение ко всем нейронам, встроенным в электрически проводящую внеклеточную жидкость (Logothetis et al., 2007).Мы основывали наш анализ на предположении, что пространственно-неоднородные внешние электрические поля одномерны, вдоль оси соматодендритов. Ламинарная структура ЛФП в гиппокампе и неокортексе значительно упрощает трехмерное поле, поскольку очень низкие градиенты, параллельные клеточным слоям, означают, что плотности тангенциальных токов близки к нулю (Jefferys, 1979; Leung, 1979; Holsheimer, 1987; Лубенов, Сиапас, 2009).
 Активность LFP, представленная на рисунке 7, измеряется относительно редко (расстояние между электродами 100 мкм). Пространственно более плотные записи давали бы более точную информацию о флуктуациях поля вдоль оси мест регистрации (или, в идеале, в трех измерениях) и позволяли бы исследовать эндогенную внеклеточную активность <100 мкм. Несмотря на это, то, что ясно показано на рис. 7 (и на дополнительных рис. S6–S9)., доступный на www.jneurosci.org в качестве дополнительного материала), состоит в том, что профили, индуцированные v m во время тета- и SPW-активности in vivo , заметно отличаются от тех, которые обычно индуцируются вдоль параллельных пластин (как на постоянном, так и на переменном токе) (Chan и Николсон, 1986). Во время внутригиппокампальной активности диполи, индуцированные перисоматическим торможением и возбуждением дендритов, в сочетании с ламинарной структурой области СА1 приводят к пространственно неоднородному внеклеточному полю вдоль оси соматодендритов, что, в свою очередь, приводит к локализации специфичных v m колебания.
Активность LFP, представленная на рисунке 7, измеряется относительно редко (расстояние между электродами 100 мкм). Пространственно более плотные записи давали бы более точную информацию о флуктуациях поля вдоль оси мест регистрации (или, в идеале, в трех измерениях) и позволяли бы исследовать эндогенную внеклеточную активность <100 мкм. Несмотря на это, то, что ясно показано на рис. 7 (и на дополнительных рис. S6–S9)., доступный на www.jneurosci.org в качестве дополнительного материала), состоит в том, что профили, индуцированные v m во время тета- и SPW-активности in vivo , заметно отличаются от тех, которые обычно индуцируются вдоль параллельных пластин (как на постоянном, так и на переменном токе) (Chan и Николсон, 1986). Во время внутригиппокампальной активности диполи, индуцированные перисоматическим торможением и возбуждением дендритов, в сочетании с ламинарной структурой области СА1 приводят к пространственно неоднородному внеклеточному полю вдоль оси соматодендритов, что, в свою очередь, приводит к локализации специфичных v m колебания.
Хотя постоянные поля вдоль параллельных пластин хорошо определены (и, таким образом, их легче объяснить), тот факт, что их характерная длина обычно превышает размер нейрона, приводит к линейной поляризации (т. ) вдоль тросов (Chan, Nicholson, 1986), который нарушается только морфологической изменчивостью. Следовательно, чтобы понять влияние эндогенной активности на состояние и функцию отдельных нейронов посредством эпаптических взаимодействий, а не на очень локализованные компартменты, такие как сома, необходимо рассмотреть пространственную природу этих полей. Как мы показали здесь, эта пространственная изменчивость эндогенных полей вызывает v m колебания, решающим образом зависящие от характеристик поля, а также от морфологических (и мембранных) особенностей нейрона. Наиболее реалистичным экспериментом для проверки этих эффектов была бы внеклеточная стимуляция нейрона с помощью нескольких электродов, которые могут имитировать пространственно-временные характеристики эндогенных полей.

Эфаптическая связь между отдельными нейронами
Внеклеточное поле не только влияет на мембранный потенциал отдельных нейронов, но, в свою очередь, также может подвергаться влиянию трансмембранного тока отдельных нейронов. В то время как для пассивных мембран, рассматриваемых здесь, трансмембранные токи, возникающие в результате эфаптической связи, малы, мембраны с активными ионными каналами вызывают гораздо большие трансмембранные токи, особенно во время потенциалов действия (Koch, 19).99). Могут ли эти эффекты, в свою очередь, воздействовать на другой соседний нейрон? То есть могут ли два нейрона быть функционально связаны таким эпаптическим образом? Предыдущие теоретические исследования, согласующиеся с экспериментами in vivo , показали, что вклад любого данного нейрона во внеклеточный потенциал невелик и становится значимым лишь кратковременно (в течение примерно 0,5 мс) во время потенциала действия в перисоматической области (т. е., до 1 мВ в пределах 30–40 мкм от сомы) (Holt and Koch, 1999; Голд и др.
 , 2006, 2009). Тем не менее, численное моделирование показывает, что, в отличие от подпорогового и перипорогового диапазона (см. следующий раздел), внеклеточные электрические поля очень мало влияют на мембрану нейрона во время потенциала действия (Holt, 1997; Holt and Koch, 1999) (C.A. Anastassiou). , К. Сарма, К. Кох, неопубликованные наблюдения). Наконец, экспериментальные данные по коре ствола мыши показали, что, несмотря на когерентные колебания v m двух соседних нейронов и наличие эндогенного внеклеточного поля, активность потенциала действия была несопоставимой между двумя нейронами (Poulet and Petersen, 2008). ). Следовательно, близость и когерентность v m флуктуации не обязательно подразумевают когерентную пиковую активность в физиологических условиях. Однако во время сильно синхронизированной спайковой активности, такой как эпилептические разряды или сильные вызванные реакции, большие и локализованные внеклеточные токи, вызванные популяционным спайком, могут эффективно индуцировать спайки в подпороговых нейронах или даже в близлежащих окончаниях аксонов (Noebels and Prince, 1978).
, 2006, 2009). Тем не менее, численное моделирование показывает, что, в отличие от подпорогового и перипорогового диапазона (см. следующий раздел), внеклеточные электрические поля очень мало влияют на мембрану нейрона во время потенциала действия (Holt, 1997; Holt and Koch, 1999) (C.A. Anastassiou). , К. Сарма, К. Кох, неопубликованные наблюдения). Наконец, экспериментальные данные по коре ствола мыши показали, что, несмотря на когерентные колебания v m двух соседних нейронов и наличие эндогенного внеклеточного поля, активность потенциала действия была несопоставимой между двумя нейронами (Poulet and Petersen, 2008). ). Следовательно, близость и когерентность v m флуктуации не обязательно подразумевают когерентную пиковую активность в физиологических условиях. Однако во время сильно синхронизированной спайковой активности, такой как эпилептические разряды или сильные вызванные реакции, большие и локализованные внеклеточные токи, вызванные популяционным спайком, могут эффективно индуцировать спайки в подпороговых нейронах или даже в близлежащих окончаниях аксонов (Noebels and Prince, 1978).
Вышеизложенное также относится к эфаптической связи между аксонами. Поскольку эффекты внеклеточного поля наиболее сильны в подпороговых и перипороговых диапазонах напряжения, маловероятно, что такие эффекты будут инициировать выбросы в мембране в состоянии покоя, а также они не окажут существенного влияния на мембранный потенциал во время выброса.
Функциональные последствия эндогенных внеклеточных полей во время активности паттерна CA1
Для моделирования тета и SPW (рис. 7) используются свойства пассивной мембраны для изолированных нейронов. Учитывая, что средняя пирамидальная клетка гиппокампа получает входные данные примерно от 30 000 синапсов (Megías et al., 2001), эта фоновая синаптическая активность приводит к дополнительной проводимости мембраны. Бернандер и др. (1991) смоделировали электрическое поведение пирамидальной клетки коры 5 слоя и обнаружили, что при наличии фоновой синаптической активности электротоническая длина клетки уменьшается в 3 раза, тогда как τ м и соматическое сопротивление r в уменьшаются в 10 раз.
 Применяя эти значения к нашей модели, мы обнаружили лишь небольшие изменения в результатах рис. 7 (данные не показаны). Фактически диапазон отклонений v m и e m увеличился, хотя и незначительно. Таким образом, результаты этих симуляций показывают, что поведение, наблюдаемое на рисунке 7, ожидается в естественных условиях .
Применяя эти значения к нашей модели, мы обнаружили лишь небольшие изменения в результатах рис. 7 (данные не показаны). Фактически диапазон отклонений v m и e m увеличился, хотя и незначительно. Таким образом, результаты этих симуляций показывают, что поведение, наблюдаемое на рисунке 7, ожидается в естественных условиях .Учитывая эти наблюдения, каково влияние (эндогенных) внеклеточных полей на состояние и функцию нейронов? Чтобы нейрон гиппокампа возбудил потенциал действия в состоянии покоя, требуется деполяризация ~15 мВ (Henze and Buzsaki, 2001). Такие большие флуктуации напряжения трудно вызвать посредством эпаптического взаимодействия в состоянии покоя (даже СПВ, вызывающее сильнейшее физиологическое эндогенное поле, ∼15 мВ мм 9 ).0007 -1 , в гиппокампе крыс вызывает только v m отклонений порядка 2 мВ). Таким образом, в отсутствие другого входа эндогенные поля вряд ли сами по себе инициируют потенциал действия.

Однако было замечено, что даже небольшие поля могут влиять на синхронизацию спайков в присутствии фоновой синаптической активности (Bikson et al., 2004). Радман и др. (2007) использовали эксперименты с параллельными пластинами, чтобы продемонстрировать влияние постоянного и переменного электрических полей на синхронизацию спайков пирамидных нейронов СА1, получающих надпороговый синаптический вход. Они показали, что простая модель линейной амплификации с постоянным порогом возбуждения имитирует эффект возрастающей поляризации на мембранную активность. На основании этих экспериментов и некоторых дополнительных соображений (подробно представленных в дополнительном разделе 8, доступном на сайте www.jneurosci.org в качестве дополнительного материала) изменение временной фазы спайков Δψ, связанное с наличием внеклеточного поля, было аппроксимировано Radman et al. (2007) следующим образом:
где Δ v порог = v порог − v отдых (в милливольтах) – порог относительного потенциала действия, который мы установили равным 15 мВ (Henze and Buzsáki, 2001).
 ± = В ± — В REST > 0 — степень гиперполяризации (Δ В ± <0) или детекализация (Δ ± <0) или детекаларизация (Δ ± <0) (Δ depolarization ( ± <0) (Δ В ± <0) (Δ В ± <0). мембраны, связанной с фоновым синаптическим входом. Уравнение 8 является мерой влияния ( v m − v отдых ) — отклонения, связанные с наличием внеклеточного поля на активных мембранах в отношении времени потенциала действия. Для постоянных v m − v покоя и Δ v thresh влияние внеклеточных полей на пиковую фазу Δψ значительно возрастает по мере того, как мембрана деполяризуется синаптическим входом (дополнительный рис. 10). , доступный на www.jneurosci.org в качестве дополнительного материала; мы также показываем, что эта эмпирическая модель согласуется с численным моделированием пирамидных нейронов СА1 с потенциал-зависимой проводимостью, вызывающей потенциалы действия).
± = В ± — В REST > 0 — степень гиперполяризации (Δ В ± <0) или детекализация (Δ ± <0) или детекаларизация (Δ ± <0) (Δ depolarization ( ± <0) (Δ В ± <0) (Δ В ± <0). мембраны, связанной с фоновым синаптическим входом. Уравнение 8 является мерой влияния ( v m − v отдых ) — отклонения, связанные с наличием внеклеточного поля на активных мембранах в отношении времени потенциала действия. Для постоянных v m − v покоя и Δ v thresh влияние внеклеточных полей на пиковую фазу Δψ значительно возрастает по мере того, как мембрана деполяризуется синаптическим входом (дополнительный рис. 10). , доступный на www.jneurosci.org в качестве дополнительного материала; мы также показываем, что эта эмпирическая модель согласуется с численным моделированием пирамидных нейронов СА1 с потенциал-зависимой проводимостью, вызывающей потенциалы действия).
Измерения in vivo пирамидных нейронов СА1 крысы во время тета выявили тоническую гиперполяризацию 2-10 мВ в соматах пирамидных клеток (Kamondi et al., 1998; Fox, 1989; Ylinen et al., 1995b). Следовательно, для средней соматической гиперполяризации Δ v ± = v ± — v покоя = -6 мВ уравнение 8 предсказывает, что во впадине тета (пирамидный слой) (рис. 7) Aii , синяя линия), где v m − v отдых = 0,2 мВ, опережение времени соматических спайков, связанное с внешним полем, составляет приблизительно Δψ = 3,5°, тогда как для Δ v ± = −10 и −2 мВ, Δψ = 2,9 и 4,2° соответственно. Однако in vivo внутриклеточных записей в дистальных апикальных дендритах СА1 (> 200 мкм от сомы) выявили тоническую деполяризацию 2-12 мВ (Kamondi et al., 1998). Применяя те же соображения к дистальным апикальным дендритам, для средней деполяризации Δ v ± = 7 мВ и v m − v остальные = −0,5 мВ (рис.
 7 Aiv , синяя линия), тогда как предсказанная фазовая задержка Δψ = 2,5° =, 2,5° для Δ v ± = 2 и 12 мВ, Δψ = −14 и −60° соответственно. Следовательно, во время тета внеклеточное поле оказывает более заметное влияние на синхронизацию спайков в дистальной апикальной области (молекулярный лакунозный слой), чем в соме (пирамидный слой). Было высказано предположение, что наличие и время таких дендритных потенциалов действия во время тета важно для кодирования места (Kamondi et al., 19).98).
7 Aiv , синяя линия), тогда как предсказанная фазовая задержка Δψ = 2,5° =, 2,5° для Δ v ± = 2 и 12 мВ, Δψ = −14 и −60° соответственно. Следовательно, во время тета внеклеточное поле оказывает более заметное влияние на синхронизацию спайков в дистальной апикальной области (молекулярный лакунозный слой), чем в соме (пирамидный слой). Было высказано предположение, что наличие и время таких дендритных потенциалов действия во время тета важно для кодирования места (Kamondi et al., 19).98).Те же соображения можно использовать для прогнозирования изменения времени всплесков во время острых волн (SPW). СПВ связаны с высокочастотными (180–200 Гц) соматическими колебаниями, так называемыми «рябями» (Buzsaki et al., 1992). Потенциалы действия пирамидных клеток СА1, как группы, тесно связаны с отрицательными пиками волн ряби поля, зарегистрированными в пирамидном слое (Ylinen et al., 1995a). [Обратите внимание, что рябь вызывает LFP, амплитуда которого намного меньше, чем у SPW (Ylinen et al.
 , 19).95a), так что изменения в v m , показанные в правой колонке рис. 7, объясняются исключительно внеклеточным эффектом SPW.] Кроме того, внутриклеточные записи выявили деполяризацию ~ 5 мВ в соме во время SPW. из-за массивного коллатерального возбуждения Шаффера (Ylinen et al., 1995a). Следовательно, из уравнения 8 с v m — v отдых = -1 мВ (рис. 7 Bii ) и Δ v ± = 5 мВ изменение времени соматического спайка период пульсации становится Δψ = -36°. Одновременно массивный возбуждающий вход в апикальные дендриты вызывает еще большую локальную деполяризацию (Ylinen et al., 19).95а), что в сочетании с вызванной извне деполяризацией (∼1 мВ) (рис. 7 Aiii ) привело бы к дополнительному продвижению дендритного спайка. Например, для v m − v rest = 1 мВ (рис. 7 Biv , синяя линия) и Δ v ± = 10 мВ, 7 Δψ Эти прогнозы согласуются с предположением Гаспарини и Маги (2006) о том, что чрезвычайно своевременное появление потенциала действия, наблюдаемое во время SPW, требует задействования нелинейных интегративных свойств посредством возникновения дендритных потенциалов действия (Losonczy and Magee, 2006).
, 19).95a), так что изменения в v m , показанные в правой колонке рис. 7, объясняются исключительно внеклеточным эффектом SPW.] Кроме того, внутриклеточные записи выявили деполяризацию ~ 5 мВ в соме во время SPW. из-за массивного коллатерального возбуждения Шаффера (Ylinen et al., 1995a). Следовательно, из уравнения 8 с v m — v отдых = -1 мВ (рис. 7 Bii ) и Δ v ± = 5 мВ изменение времени соматического спайка период пульсации становится Δψ = -36°. Одновременно массивный возбуждающий вход в апикальные дендриты вызывает еще большую локальную деполяризацию (Ylinen et al., 19).95а), что в сочетании с вызванной извне деполяризацией (∼1 мВ) (рис. 7 Aiii ) привело бы к дополнительному продвижению дендритного спайка. Например, для v m − v rest = 1 мВ (рис. 7 Biv , синяя линия) и Δ v ± = 10 мВ, 7 Δψ Эти прогнозы согласуются с предположением Гаспарини и Маги (2006) о том, что чрезвычайно своевременное появление потенциала действия, наблюдаемое во время SPW, требует задействования нелинейных интегративных свойств посредством возникновения дендритных потенциалов действия (Losonczy and Magee, 2006). Примечательно, что предсказанное влияние внеклеточного поля на синхронизацию спайков может эффективно синхронизировать дендритные (и, как следствие, последующие соматические) потенциалы действия с LFP и, таким образом, привести к субмиллисекундной точности спайков, обычно наблюдаемой во время SPW. По сравнению с относительно скромными изменениями, вызванными синхронизацией соматических импульсов во время тета (которые могут только «точно настроить» осцилляторы), мы предполагаем, что поля, вызванные SPW, могут оказывать более заметное влияние на синхронизацию соматического и дендритного потенциалов действия.
Примечательно, что предсказанное влияние внеклеточного поля на синхронизацию спайков может эффективно синхронизировать дендритные (и, как следствие, последующие соматические) потенциалы действия с LFP и, таким образом, привести к субмиллисекундной точности спайков, обычно наблюдаемой во время SPW. По сравнению с относительно скромными изменениями, вызванными синхронизацией соматических импульсов во время тета (которые могут только «точно настроить» осцилляторы), мы предполагаем, что поля, вызванные SPW, могут оказывать более заметное влияние на синхронизацию соматического и дендритного потенциалов действия.Таким образом, LFP, коллективное проявление обработки нейронов в заданном объеме, может влиять на синхронизацию спайков отдельных клеток вблизи порога срабатывания посредством несинаптической, эпаптической связи.
Сноски
Эта работа была поддержана Исследовательским советом по инженерным и физическим наукам, Швейцарским национальным фондом и Национальным научным фондом (через совместный грант между G.
 B. и C.K.). Мы благодарим Simal Ozen, Joshua Milstein и Ueli Rutishauser за идеи и обсуждения, Ted Carnevale за обсуждение численной реализации и помощь с NEURON и Karthik Sarma за численные процедуры и фильмы.
B. и C.K.). Мы благодарим Simal Ozen, Joshua Milstein и Ueli Rutishauser за идеи и обсуждения, Ted Carnevale за обсуждение численной реализации и помощь с NEURON и Karthik Sarma за численные процедуры и фильмы.- Корреспонденцию следует направлять Костасу А. Анастассиу, Отделение биологии Калифорнийского технологического института, Пасадена, Калифорния . costas{at}caltech.edu
Ссылки
- ↵
- Bédard C,
- Kröger H,
- Destexhe A
(2004) Моделирование потенциалов внеклеточного поля и свойств частотной фильтрации внеклеточного пространства. Biophys J 86:1829–1842.
- ↵
- Bernander O,
- Douglas RJ,
- Martin KA,
- Koch C
(1991) Синаптическая фоновая активность влияет на пространственно-временную интеграцию в одиночных пирамидальных клетках. Proc Natl Acad Sci U S A 88:11569–11573.

- ↵
- Bikson M,
- Inoue M,
- Akiyama H,
- Deans JK,
- Fox JE,
- Miyakawa H,
- Jefferys JGR
(2004) Влияние однородных внеклеточных электрических полей постоянного тока на возбудимость срезов гиппокампа крыс in vitro. J Physiol 557:175–190.
- ↵
- Bragin A,
- Jandó G,
- Nádasdy Z,
- Hetke J,
- WISE K,
- BUZSáki G
(1995) Gamma Campoci g
(1995). ведет себя крыса. J Neurosci 15:47–60.
- ↵
- Bullock TH,
- Buzsaki G,
- McClune MC
(1990) Когерентность сложных полевых потенциалов выявляет разрывы в СА1-субикулуме гиппокампа у свободно движущихся крыс.
 Неврология 38:609–619.
Неврология 38:609–619. - ↵
- Buzsaki G
(2004) Крупномасштабная запись ансамблей нейронов. Nat Neurosci 7:446–451.
- ↵
- Buzsáki G,
- Leung L,
- Vanderwolf C
(1983) Клеточные основы гиппокампа ЭЭГ у крысы с поведением. Brain Res Rev 6:139–171.
- ↵
- Buzsaki G,
- Czopf J,
- Kondákor I,
- Kellényi L
(1986) Ламинарное распределение медленной ритмической активности гиппокампа (RSA) в поведении крысы, анализ плотности и плотности атропин. Brain Res 365: 125–137.
- ↵
- Buzsaki G,
- Horváth Z,
- Urioste R,
- Hetke J,
- Wise K
(1992) Колебания высокочастотных сетей в гиппокампе.
 Наука 256:1025–1027.
Наука 256:1025–1027. - ↵
- Chan CY,
- Nicholson C
(1986) Модуляция приложенными электрическими полями активности пуркинье и звездчатых клеток в мозжечке изолированной черепахи. J Physiol 371:89–114.
- ↵
- Chan CY,
- Hounsgaard J,
- Nicholson C
(1988) Влияние электрических полей на трансмембранный потенциал и возбудимость клеток Пуркинье мозжечка черепахи in vitro. J Physiol 402:751–771.
- ↵
- Csicsvari J,
- Hirase H,
- Czurkó A,
- Mamiya A,
- Buzsaki G
(1999) Колебательная связь пирамидных клеток гиппокампа и интернейронов у крыс с поведением. J Neurosci 19: 274–287.
- ↵
- Deans JK,
- Powell AD,
- Jefferys JGR
(2007) Чувствительность когерентных колебаний гиппокампа крысы к переменным электрическим полям.
 J Physiol 583:555–565.
J Physiol 583:555–565. - ↵
- Fox SE
(1989) Изменения мембранного потенциала и импеданса в пирамидных клетках гиппокампа во время тета-ритма. Exp Brain Res 77: 283–294.
- ↵
- Gasparini S,
- Magee JC
(2006) Зависящие от состояния дендритные вычисления в пирамидальных нейронах CA1 гиппокампа. J Neurosci 26:2088–2100.
- ↵
- Gold C,
- Henze DA,
- Koch C,
- Buzsaki G
(2006) О происхождении волны внеклеточного потенциала действия: моделирование. J Нейрофизиол 95:3113–3128.
- ↵
- Gold C,
- Girardin C,
- Martin K,
- Koch C
(2009) Высокоамплитудные положительные спайки, зарегистрированные внеклеточно в зрительной коре кошек.
 J Нейрофизиол 102:3340–3351.
J Нейрофизиол 102:3340–3351. - ↵
- Henze DA,
- Buzsáki G
(2001) Порог потенциала действия пирамидных клеток гиппокампа in vivo увеличивается за счет недавней пиковой активности. Неврология 105:121–130.
- ↵
- Hines ML,
- Carnevale NT
(1997) Среда моделирования нейронов. Нейронные вычисления 9:1179–1209.
- ↵
- Holsheimer J
(1987) Электропроводность слоев CA1 гиппокампа и применение к анализу плотности источника тока. Exp Brain Res 67: 402–410.
- ↵
- Holt GR
(1997) Критический пересмотр некоторых предположений и следствий кабельной теории в нейробиологии. Кандидатская диссертация, Калифорнийский технологический институт .

- ↵
- Holt GR,
- Koch C
(1999) Электрические взаимодействия через внеклеточный потенциал вблизи тел клеток. J Comp Neurosci 6:169–184.
- ↵
- Джефферис Дж. Г.
(1979) Инициация и распространение потенциалов действия в гранулярных клетках, поддерживаемых in vitro в срезах гиппокампа морской свинки. J Physiol 289:375–388.
- ↵
- Jefferys JG
(1995) Несинаптическая модуляция активности нейронов в головном мозге: электрические токи и внеклеточные ионы. Physiol Rev 75:689–723.
- ↵
- Jefferys JG,
- Haas HL
(1982) Синхронный разрыв пирамидных клеток СА1 при отсутствии синаптической передачи. Природа 300:448–450.

- ↵
- Jouvet M
(1969) Биогенные амины и состояние сна. Наука 163:32–41.
- ↵
- Kamondi A,
- Acsády L,
- Wang XJ,
- Buzsáki G
(1998) Тета-колебания в соматах и дендритах гиппокампа, зависимые от фазы потенциала-пирамидных клеток in vivo: активность-зависимая фаза потенциала-прецессия клеток гиппокампа. Гиппокамп 8: 244–261.
- ↵
- Katzner S,
- Nauhaus I,
- Benucci A,
- Bonin V,
- Ringach DL,
- Carandini M
- Нейрон 61:35–41.
- ↵
- Klausberger T,
- Magill PJ,
- Márton LF,
- Roberts JD,
- Cobden PM,
- Buzsáki G,
- Somogyi P
(2003) Запуск интернейронов гиппокампа в зависимости от состояния мозга и типа клеток in vivo.
 Природа 421:844–848.
Природа 421:844–848. - ↵
- Klausberger T,
- Márton LF,
- Baude A,
- Roberts JD,
- Magill PJ,
- Somogyi P
(2004) Spike timing of dendrite-targeting bistratified cells during hippocampal network oscillations in vivo . Nat Neurosci 7:41–47.
- ↵
- Koch C
(1999) Биофизика вычислений: обработка информации в отдельных нейронах (Оксфордский университет, Нью-Йорк).
- ↵
- Leung LW
(1979) Ортодромная активация области CA1 гиппокампа крысы. Мозг Res 176: 49–63.
- ↵
- Logothetis NK,
- Kayser C,
- Oeltermann A
(2007) Измерение спектра коркового импеданса у обезьян in vivo: влияние на распространение сигнала.
 Нейрон 55:809–823.
Нейрон 55:809–823. - ↵
- London M,
- Meunier C,
- Segev I
(1999) Передача сигнала в пассивных дендритах с неоднородной проводимостью мембраны. J Neurosci 19:8219–8233.
- ↵
- Лосончи А,
- Маги Дж. К.
(2006) Интегративные свойства радиальных косых дендритов пирамидных нейронов CA1 гиппокампа. Нейрон 20:291–307.
- ↵
- Лубенов Е.В.,
- Сиапас А.Г.
(2009) Тета-колебания гиппокампа – бегущие волны. Природа 459:534–539.
- ↵
- McIntyre CC,
- Grill WM
(1999) Возбуждение нейронов центральной нервной системы неоднородными электрическими полями. Biophys J 76:878–888.

- ↵
- Megías M,
- Emri Z,
- Freund TF,
- Gulyás AI
(2001) Общее количество и распределение тормозных и возбуждающих синапсов на пирамидных клетках CA1 гиппокампа. Неврология 102:527–540.
- ↵
- Mitzdorf U
(1985) Метод плотности источника тока и его применение в коре головного мозга кошек: исследование вызванных потенциалов и феноменов ЭЭГ. Physiol Rev 65:37–100.
- ↵
- Montgomery SM,
- Buzsaki G
(2007) Гамма-колебания динамически связывают области CA3 и CA1 гиппокампа во время выполнения задачи памяти. Proc Natl Acad Sci U S A 104:14495–14500.
- ↵
- Nicholson C
(1973) Теоретический анализ полевых потенциалов в анизотропных ансамблях нейронных элементов.
 IEEE Trans Biomed Eng 20: 278–288.
IEEE Trans Biomed Eng 20: 278–288. - ↵
- Noebels JL,
- Prince DA
(1978) Развитие фокальных припадков в коре головного мозга: роль терминального разрыва аксона. J Нейрофизиол 41:1267–1281.
- ↵
- Pettersen KH,
- Einevoll GT
(2008) Амплитудная изменчивость и внеклеточная низкочастотная фильтрация нейронных спайков. Biophys J 94:784–802.
- ↵
- Poulet JF,
- Petersen CC
(2008) Внутреннее состояние мозга регулирует синхронность мембранных потенциалов в стволовой коре головного мозга мышей. Природа 454:881–885.
- ↵
- Purpura DP,
- Malliani A
(1966) Генерация и распространение спайков инициируется в дендритах трансгиппокампальной поляризацией.
 Мозг Res 1: 403–406.
Мозг Res 1: 403–406. - ↵
- Radman T,
- Su Y,
- An JH,
- Parra LC,
- Bikson M
(2007) Время спайков усиливает влияние электрических полей на нейроны: последствия для нейронов. J Neurosci 27:3030–3036.
- ↵
- Rall W
(1962) Теория физиологических свойств дендритов. Ann NY Acad Sci 96:1071–1092.
- ↵
- Rall W,
- Shepherd GM
(1968) Теоретическая реконструкция полевых потенциалов и дендро-дендритных синаптических взаимодействий в обонятельной луковице. J Нейрофизиол 31:884–915.
- ↵
- Ranck JB Jr.
(1963) Анализ удельного импеданса коры головного мозга кролика.
 Exp Neurol 7: 153–174.
Exp Neurol 7: 153–174. - ↵
- Рубинштейн Дж. Т.
(1991) Аналитическая теория внеклеточной электрической стимуляции нерва фокальными электродами. II. Пассивный миелинизированный аксон. Biophys J 60:538–555.
- ↵
- Rubinstein JT,
- Spelman FA
(1988) Аналитическая теория внеклеточной стимуляции нерва фокальными электродами. Biophys J 54:975–981.
- ↵
- Снег RW,
- Дудек FE
(1984) Электрические поля непосредственно способствуют синхронизации потенциалов действия во время судорожных эпилептиформных вспышек. Brain Res 323:114–118.
- ↵
- Sten-Knudsen O
(1960) Инициируется ли сокращение мышц внутренним током? J Physiol 151:363–384.

- ↵
- Steriade M
(2000) Кортико-таламический резонанс, состояния бдительности и мышления. Неврология 101:243–276.
- ↵
- Stuart G,
- Spruston N,
- Häusser M
(2007) Дендриты (Oxford UP, Нью-Йорк).
- ↵
- Suzuki SS,
- Smith GK
(1988) Спонтанные спайки ЭЭГ в нормальном гиппокампе. III. Отношение к вызванным потенциалам. Электроэнцефалогр Клин Нейрофизиол 69:541–549.
- ↵
- Свирскис Г.,
- Багинскас А.,
- Хаунсгаард Дж.,
- Гутман А.
(1997) Электротонические измерения с помощью индуцированной электрическим полем поляризации в нейронах: теория и экспериментальная оценка. Biophys J 73:3004–3015.

- ↵
- Taylor CP,
- Dudek FE
(1982) Синхронные нейронные постразряды в срезах гиппокампа крыс без активных химических синапсов. Наука 218:810–812.
- ↵
- Tranchina D,
- Nicholson C
(1986) Модель поляризации нейронов внешними электрическими полями. Biophys J 50:1139–1156.
- ↵
- Traub RD,
- Dudek FE,
- Taylor CP,
- Knowles WD
(1985) Моделирование постразрядов гиппокампа, синхронизированных электрическими взаимодействиями. Неврология 14:1033–1038.
- ↵
- Vanderwolf CH
(1969) Электрическая активность гиппокампа и произвольные движения у крыс. Электроэнцефалогр Клин Нейрофизиол 26:407–418.

- ↵
- Ylinen A,
- BRAGIN A,
- Nádasdy Z,
- Jandó G,
- Szabó I,
- SIK A,
- Buzsáki G 44996 (
- Buzsáki G 44999186 (
- Buzsáki G 44444444996186 (
- (Buzsáki G 4444444444496186. 200 Гц) в интактном гиппокампе: сетевые и внутриклеточные механизмы. J Neurosci 15:30–46.
- ↵
- Ylinen A,
- Soltész I,
- Bragin A,
- Penttonen M,
- Sik A,
- Buzsáki G
(1995b) Intracellular correlates of hippocampal theta rhythm in identified pyramidal cells, granule cells and корзинчатые клетки. Гиппокамп 5:78–90.
- Контакт
- общие положения и условия
- Декларация о конфиденциальности
- Выходные данные
- Обзор Услуги
- Загрузки
- Каталоги
- Вебинары и видео
- Связаться со службой поддержки клиентов
- О нас
- Политика качества
- Безопасность в классе
- ID корпуса: 11
- 90
Наверх
Неоднородные электрические поля (дипольные поля)
Друкен
Lieferzeit:
Versandkostenfrei ab 300,- €
Nach oben
Legal
Служба
Компания
Обратите внимание:
* Цены указаны с учетом НДС.
Мы поставляем только компании, учреждения и учебные заведения. Нет продажи частным лицам.
Обратите внимание: в соответствии с регламентом ЕС 1272/2008 CLP компания PHYWE не продает химические вещества населению. Мы принимаем заказы только от реселлеров, профессиональных пользователей и исследовательских, учебных и образовательных учреждений.
Пожалуйста, введите имя, под которым ваша корзина должна быть сохранена.
Сохраненные корзины покупок можно найти в разделе Моя учетная запись .
Название корзины покупок
[PDF] Эффект Швингера в неоднородных электрических полях
@article{Hebenstreit2011SchwingerEI,
title={Эффект Швингера в неоднородных электрических полях},
автор = {F Hebenstreit},
journal={arXiv: Физика высоких энергий - Феноменология},
год = {2011}
} - F.
 Hebenstreit
Hebenstreit - Опубликовано 29 июня 2011 г.
- Physics
- arXiv: High Energy Physics — Phenomenology
поле, проявляющееся как рождение электрон-позитронных пар (эффект Швингера). Этот эффект был давним, но до сих пор не наблюдавшимся предсказанием, поскольку до сих пор невозможно было создать требуемую напряженность поля. Однако в связи с появлением нового поколения высокоинтенсивных лазерных систем, таких как European XFEL или Extreme Light…
Просмотр PDF на ARXIV
Электронно-позитронная производство пары в структурированных импульсах электрических полей
- Кристиан Колфурст
Физика
- 2012
СОЗВОДИТЕЛЬНОЙ Эффект SO-SCWINGER. сильные электрические поля, обсуждается уже почти восемьдесят лет, хотя экспериментальная проверка этого эффекта…
Динамический эффект Заутера-Швингера — непертурбативные и пертурбативные аспекты
- Г. Торгримссон, К. Шнайдер, Дж. Ортель, Р.
 Шютцхольд
Шютцхольд Физика
- 2017
Аннотация сильное и медленно меняющееся электрическое поле. Этому эффекту можно динамически способствовать…
Плотность тока в квантовой электродинамике в зависящих от времени внешних потенциалах и эффект Швингера
- Дж. Зан
Физика
- 2015
В рамках квантовой электродинамики (КЭД) во внешних потенциалах мы вводим метод вычисления временной зависимости математического ожидания плотности тока для зависящих от времени…
Тепловая зависимость производство пар Швингера с динамической поддержкой
- Г. Торгримссон
Физика
Physical Review D
- 2019
Мы изучаем образование пар электрон-позитрон в сочетании с сильным тепловым фоновым электрическим полем. Мы показываем, что этот процесс подобен Швингеру с динамическим содействием…
Рождение электрон-позитронных пар в неоднородных электромагнитных полях
- Кристиан Кольфурст
Физика
- 2015
Процесс рождения электрон-позитронных пар исследуется в рамках формализма фазового пространства Вигнера. Сходства между ионизацией атомов и рождением пар для однородных, но…
Сходства между ионизацией атомов и рождением пар для однородных, но…
Зависящие от пространства-времени эффекты электрического поля в вакууме и плазме с использованием формализма Вигнера
- Х. Аль-Насери, Дж. Заманян, Г. Бродин
Физика
- 2021
Выведем систему связанных дифференциальных уравнений в частных производных для одновременных функций Вигнера в произвольном сильном электромагнитном поле, используя Формализм Дирака-Гейзенберга-Вигнера. В…
Рождение электрон-позитронных пар в сильных электрических полях
- A. Blinne
Физика
- 2016
Работа посвящена рождению магнитных электрон-позитронных пар в пространственно-однородных электрических полях. Рассматриваются различные конфигурации поля для изучения различных явлений, включая… 9{-}$ рождение пар из сильных электрических полей
- Х. Тая, Х. Фуджи, К. Итакура
Физика
- 2014
Мы исследуем рождение электрон-позитронных пар из вакуума в импульсном электрическом фоне поле. Использование импульсного поля типа Заутера E ( t ) = E 0 sech 2 ( t / τ ) с высотой E 0 и шириной τ…
Использование импульсного поля типа Заутера E ( t ) = E 0 sech 2 ( t / τ ) с высотой E 0 и шириной τ…
Создание пар Швингера в постоянных и зависящих от времени полях
- A. Huet, Sang Pyo Ким, К. Шуберт
Физика
- 2014
Эффект рождения пар из вакуума в сильном электрическом поле, предсказанный Швингером в 1951 г., предположительно может быть подтвержден экспериментально с некоторыми сверхсильными лазерами, которые в настоящее время разрабатываются…
Производство частиц в Сильные поля, зависящие от времени
- Д. Блашке, С. Смолянский, А. Панферов, Л. Юхновски
Физика
- 2017
образуют вакуум в сильных, зависящих от времени внешних полях (динамический процесс Швингера). Мы первые…
ПОКАЗАНЫ 1-10 ИЗ 124 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные статьиНедавность
Рождение пар Швингера в пространственно- и времязависимых электрических полях: Связь формализма Вигнера с квантовой кинетической теорией Гис
Физика
Непертурбативное рождение электрон-позитронных пар (эффект Швингера) рассматривается для зависящих от пространства и времени электрических полей E-vector(x-vector,t). На основе теории Дирака-Гейзенберга-Вигнера…
На основе теории Дирака-Гейзенберга-Вигнера…
Рождение пар Швингера с помощью инстантонов в сильных электрических полях электрическое поле принимает вид не зависящего от времени уравнения Шредингера с потенциальным барьером. Мы предлагаем…
Рождение электрон-позитронных пар в пространственных или временных электрических полях
- H. Kleinert, R. Ruffini, S. Xue
Physics
- 2008
Рассматривая образование электронных и позитронных пар сильным электрическим полем из вакуума как процесс квантового туннелирования, мы получаем в полуклассическом приближении , общее выражение для…
Улучшенные приближения для рождения пар фермионов в неоднородных электрических полях
- Санг Пё Ким, Д. Страница
Физика
- 2007
Переформулируя инстантоны в комплексной плоскости для туннелирующих или передающих состояний, мы вычисляем скорость рождения пар заряженных фермионов в пространственно локализованном электрическом поле, иллюстрируемую…
Рождение пар фермионов в сильном электрическом поле.

- Клюгер, Айзенберг, Светицкий, Купер, Моттола
Физика
Физический обзор. D, Частицы и поля
- 1992
Метод адиабатической регуляризации к уравнению Дирака применяется для перенормировки среднего значения тока и получения конечной связанной системы обыкновенных дифференциальных уравнений для временной эволюции системы .
Временная эволюция вакуума КЭД в однородном электрическом поле: Полное аналитическое решение методом спинориального разложения эволюция плотности пар, создаваемых в вакууме КЭД не зависящим от времени однородным электрическим полем. Используемый здесь математический аппарат для…
Эффекты интерференции при производстве вакуумных пар Швингера для зависящих от времени лазерных импульсов
- Чесим К. Думлу, Г. Данн
Физика
- 2011
Мы представляем простые новые приближенные формулы как для скалярной, так и для спинорной КЭД для числа частиц, произведенных из вакуума зависящим от времени электрическим поле, включающее интерференционные эффекты…
Schwinger предел достижимости с помощью лазеров предельной мощности.

- Буланов С., Есиркепов Т., Томас А., Кога Дж., Буланов С.
Физика
Физический обзор писем
- 2010
Показано, что эффекты радиационного трения и развития электрон-позитронной лавины в вакууме зависят от поляризации электромагнитной волны, и имеется кажущаяся аналогия этих случаев с круговым и линейным электроном. ускорителей к соответствующей сдерживающей и уменьшенной роли потерь синхротронного излучения.
Неустойчивость вакуума во внешних полях.
- Гаврилов, Гитман
Физика
Физический обзор. D, Частицы и поля
- 1996
Показано, что распределения частиц, создаваемые квазипостоянными электрическими полями, могут быть записаны в виде, имеющем тепловой характер и кажущемся универсальным, т. е. справедливым для любой теории с квазипостоянными внешними полями.
Лагранжиан сильного электромагнитного поля и квантовая электродинамика на малых расстояниях
- В.
 И. Ритус
И. Ритус Физика. поля в пространстве и времени | Успехи теоретической физики
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Казуо Ямада
Казуо Ямада
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Прогресс теоретической физики , том 28, выпуск 2, август 1962 г.
 , страницы 299–314, https://doi.org/10.1143/PTP.28.299
, страницы 299–314, https://doi.org/10.1143/PTP.28.299Опубликовано:
01 августа 1962 г.
3 История статьи
Получено:
3 марта 1962 г.
Опубликовано:
01 августа 1962 г.
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Уравнение переноса электронов в проводниках под действием электрических полей, меняющихся как в пространстве, так и во времени, разработано квантово-механически.
 Случай упругого рассеяния электронов на статических примесных центрах и случай неупругого рассеяния на фононах рассматриваются отдельно. В полученном здесь уравнении появился новый дополнительный член, который представляет связанные эффекты столкновений электронов с примесями или фононами и движения электронов внешними осциллирующими полями. Этот член играет важную роль в области высоких частот, хотя и исчезает в статическом пределе. Проводимости в статическом пределе и в пределе высоких частот даются из специальных решений этого уравнения.
Случай упругого рассеяния электронов на статических примесных центрах и случай неупругого рассеяния на фононах рассматриваются отдельно. В полученном здесь уравнении появился новый дополнительный член, который представляет связанные эффекты столкновений электронов с примесями или фононами и движения электронов внешними осциллирующими полями. Этот член играет важную роль в области высоких частот, хотя и исчезает в статическом пределе. Проводимости в статическом пределе и в пределе высоких частот даются из специальных решений этого уравнения.Каталожные номера
1)
Кубо
Р.
. ,
J. Phys. соц. Япония
,
1957
, том.
12
10.1143/jpsj.12.570
2)
FAN
H.
 Y.
Y.,
Spitzer
W.
,
9000. J.,
9000. 9000. J.
. ,
Физ.
,
1956
, том.
101
10.1103/PhysRev.101.566
10.1103/PhysRev.112.298
10.1103/PhysRev.112.843
10.1103/PhysRev.120.376
10.1103/PhysRev.120.379
3)
Накано
Х.
. ,
Busseiron Kenkyu (на японском языке)
,
1960
, vol.

2-8
стр.
470
4)
Накадзима
С.
. ,
Проц. физ. соц.
,
1956
, том.
69
стр.
441
5)
Константинов
О.В.
,
Перель
В.И. ,
Сов. физ. JETP
,
1961
, том.
12
стр.
142
6)
Амбегаокар
В.
,
Кон
В.

. ,
Физ.
,
1960
, том.
117
10.1103/PhysRev.117.423
7)
Изуяма
Т.
. ,
Прог. Теор. физ.
,
1961
, том.
25
10.1143/PTP.25.964
8)
Kohn
W.
,
Luttinger
J. M.
. ,
Физ.
,
1957
, том.
108
10.1103/PhysRev.108.590
9)
Накадзима
С.

. ,
Прог. Теор. физ.
,
1960
, том.
23
10.1143/PTP.23.794
10)
Гуржи
Р. Н.
. ,
352; там же.
,
1958
, том.
6
стр.
506
11)
Гольштейн
Т.
. ,
Физ.
,
1954
, том.
96
10.1103/PhysRev.96.536
12)
Toyozawa
Y.



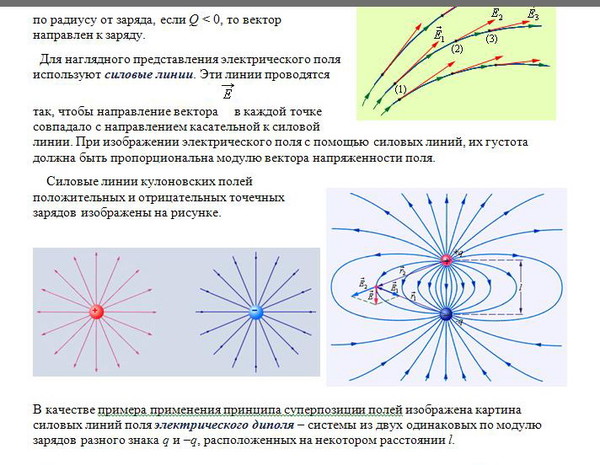
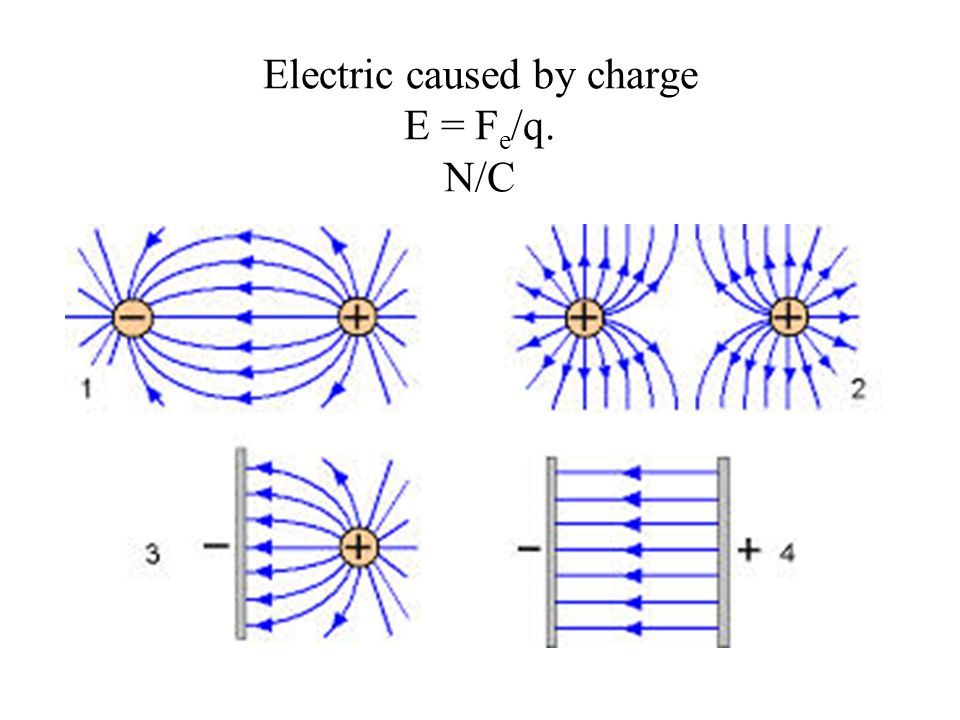 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 7)
7) 10)
10)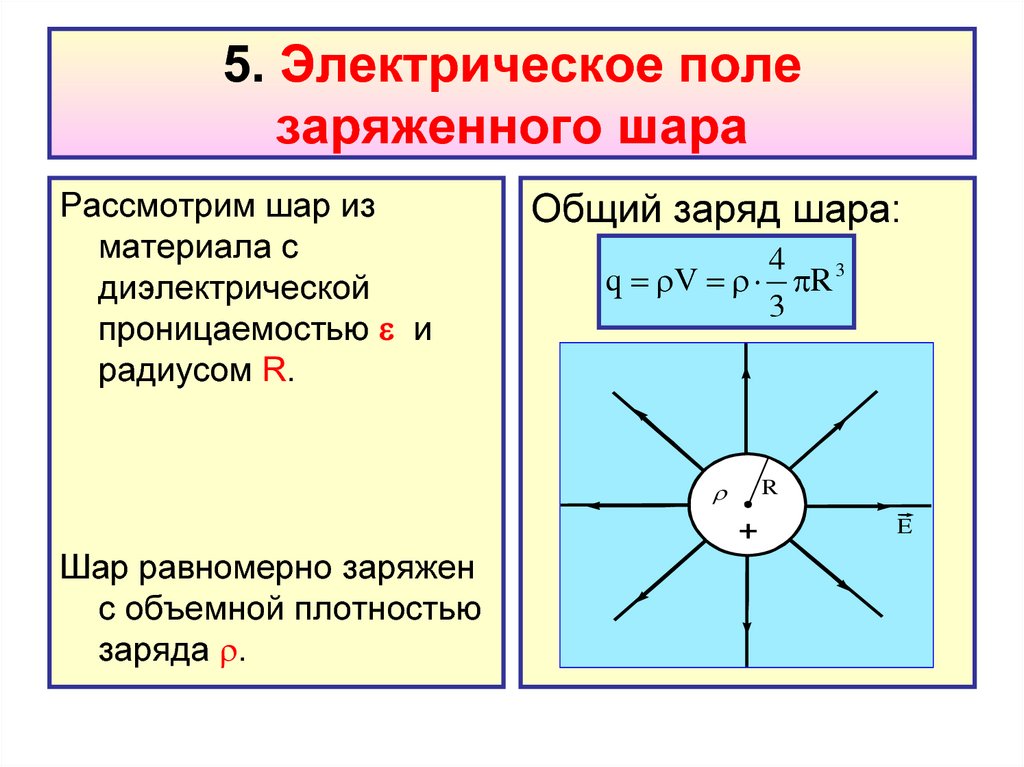 12)
12)


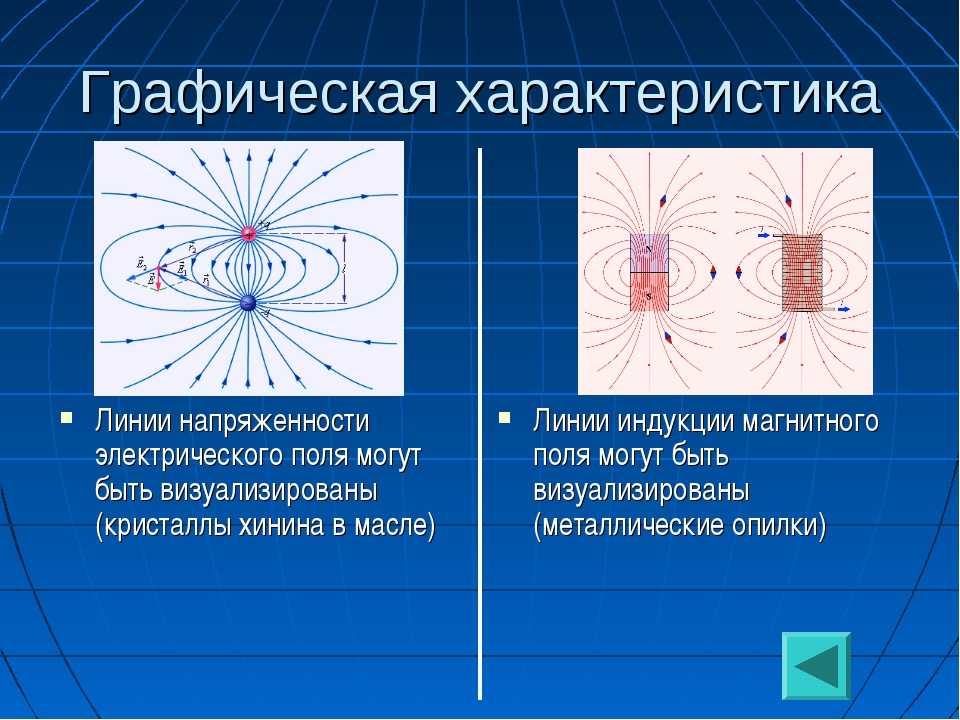
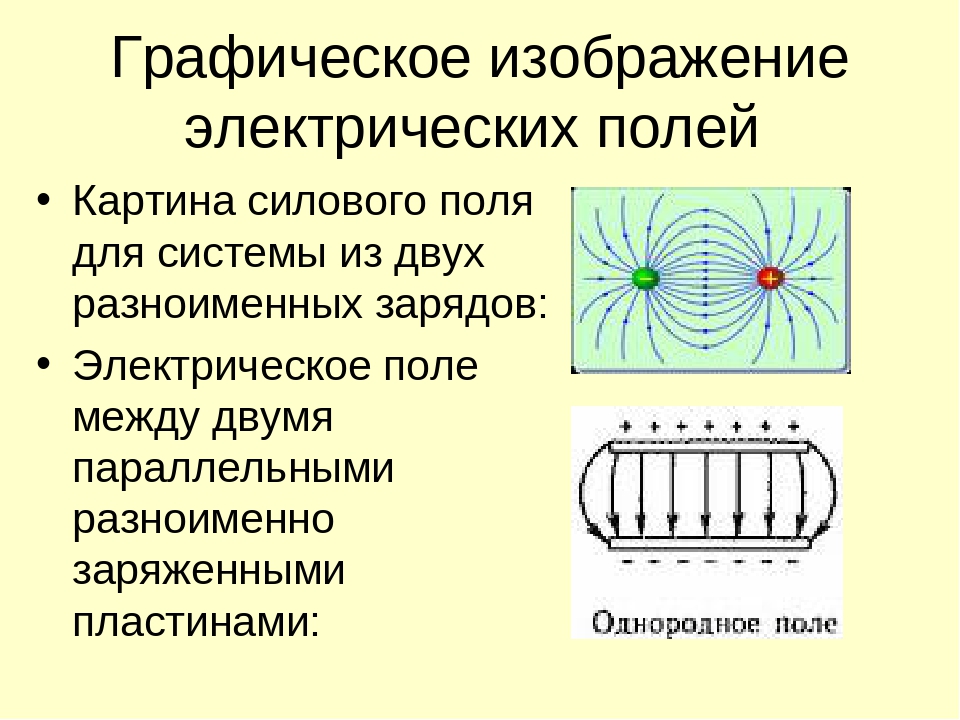

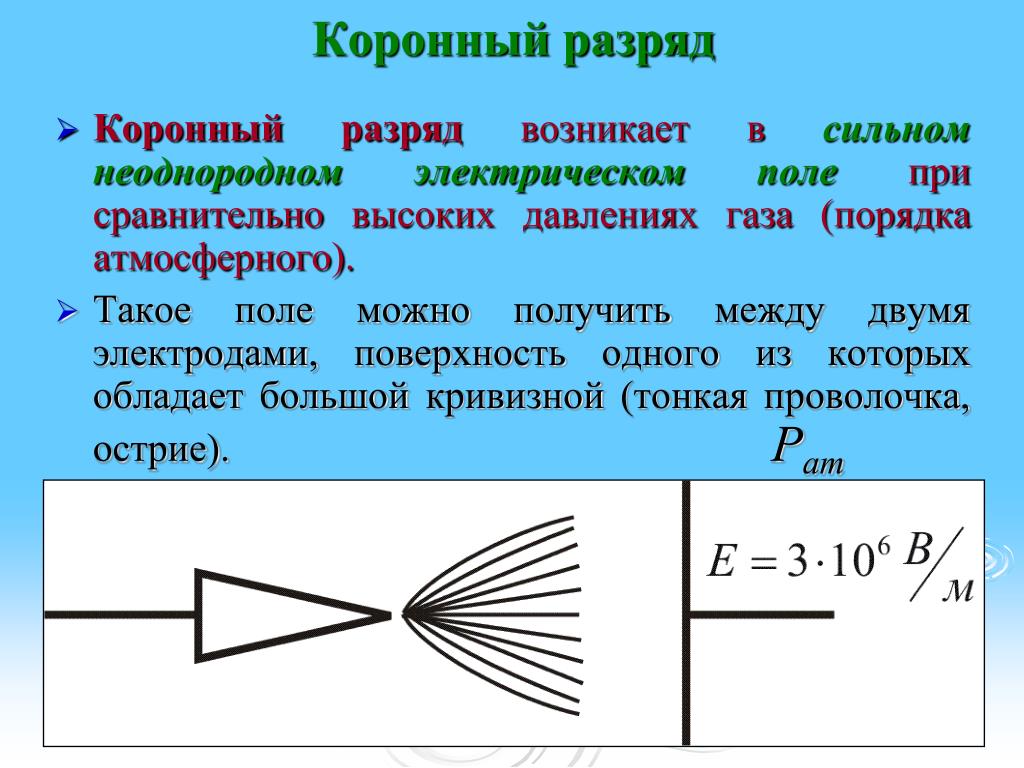

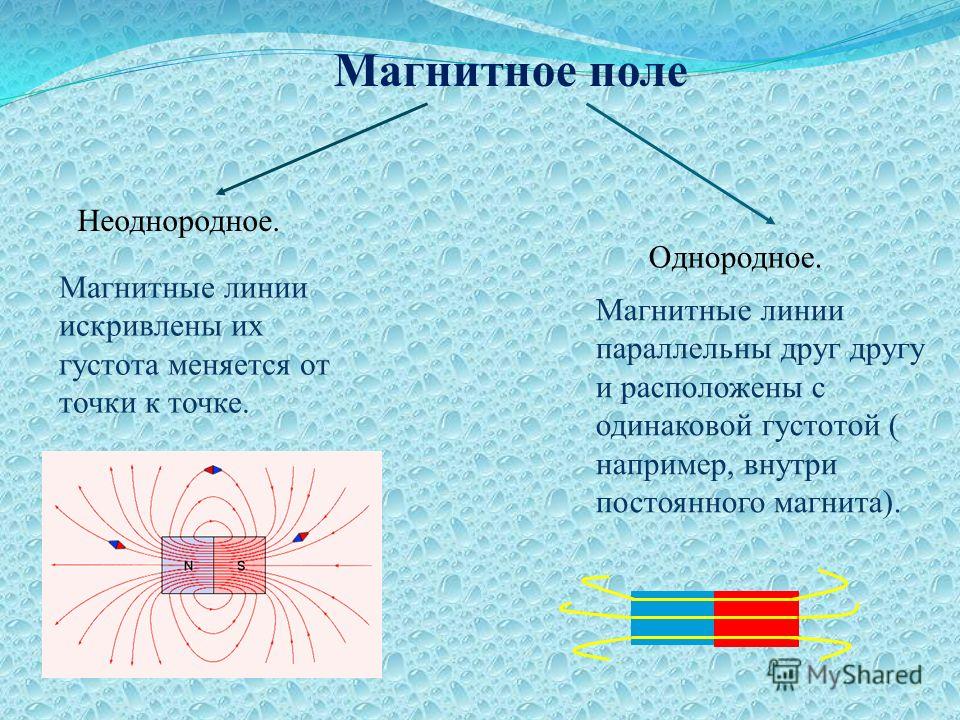
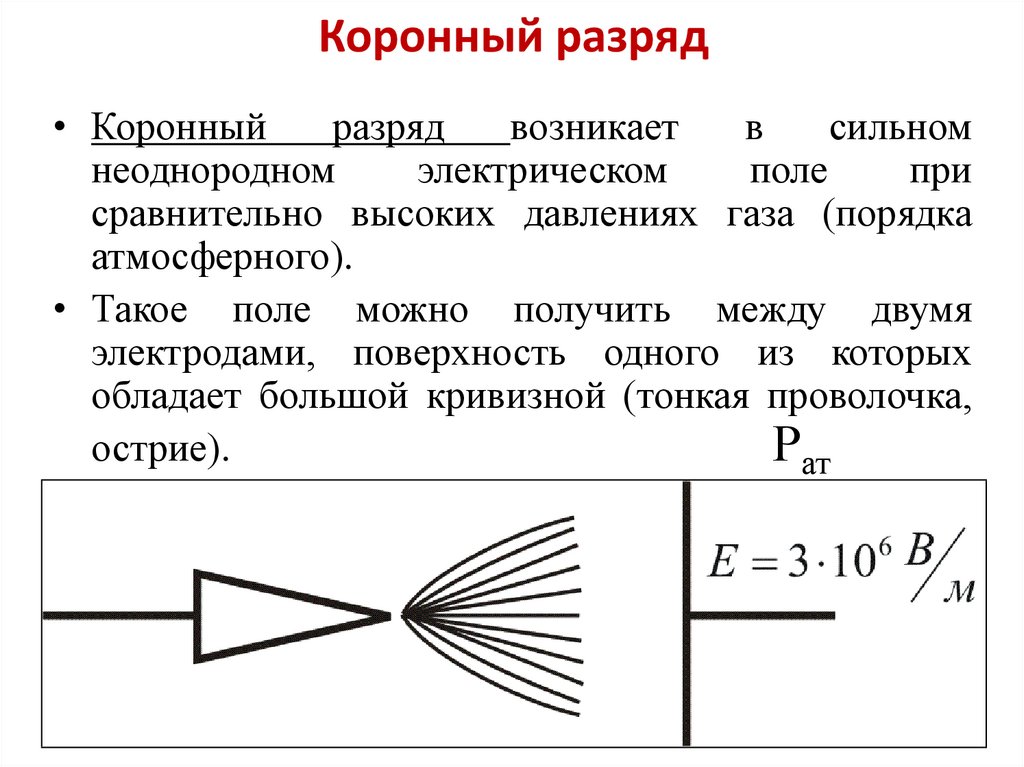 Мозг Res. 2019.
PMID: 31323198
Мозг Res. 2019.
PMID: 31323198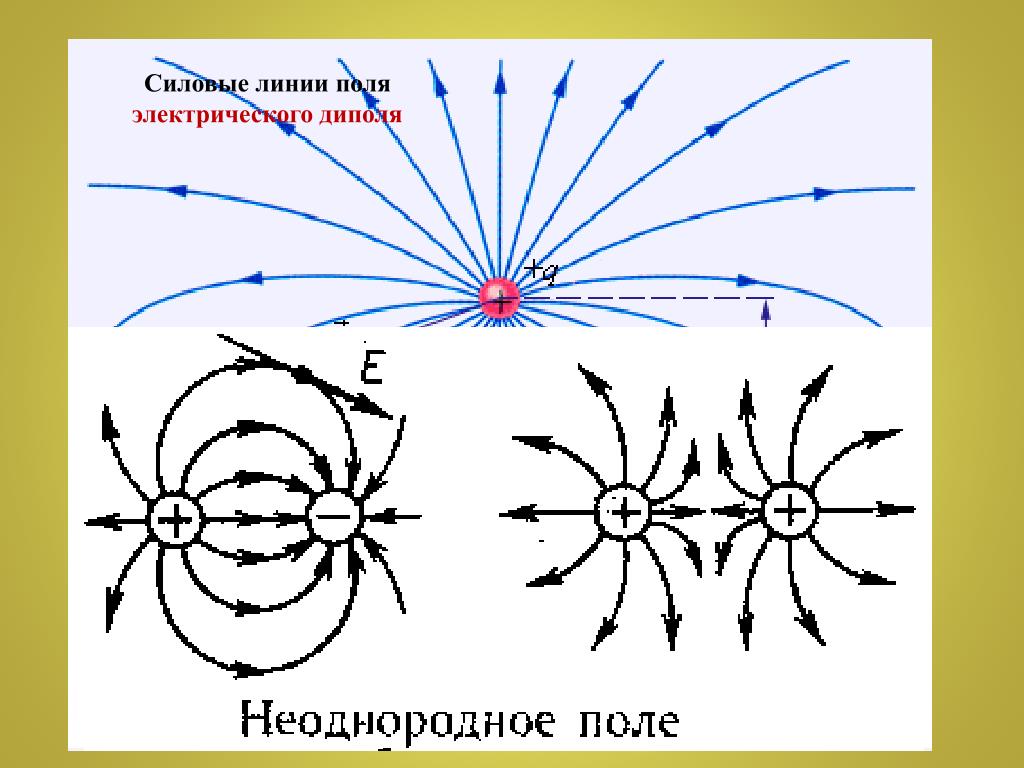
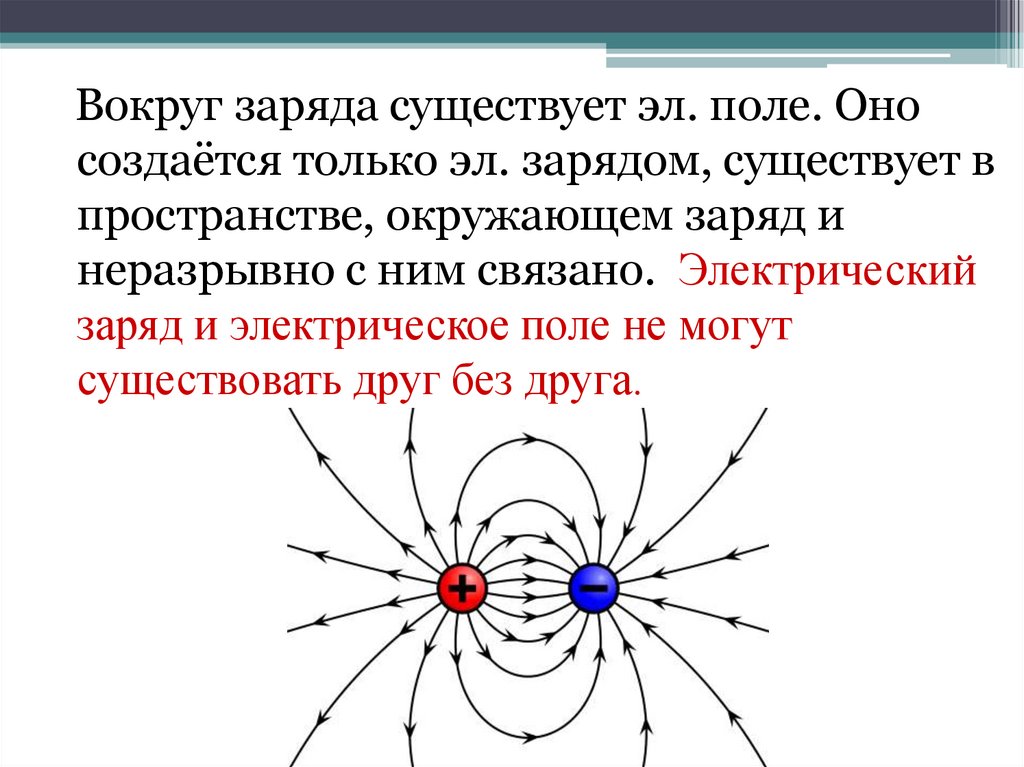
 , 1985). ; Tranchina and Nicholson, 1986; Holt and Koch, 1999; McIntyre and Grill, 1999; Bédard et al., 2004; Gold et al., 2006; Logothetis et al., 2007; Pettersen and Einevoll, 2008). Несмотря на обширные исследования, в основном в восстановленных препаратах, физиологическая роль таких внеклеточных токов в нейронах остается спорной (для обзора см. Jefferys, 19).95).
, 1985). ; Tranchina and Nicholson, 1986; Holt and Koch, 1999; McIntyre and Grill, 1999; Bédard et al., 2004; Gold et al., 2006; Logothetis et al., 2007; Pettersen and Einevoll, 2008). Несмотря на обширные исследования, в основном в восстановленных препаратах, физиологическая роль таких внеклеточных токов в нейронах остается спорной (для обзора см. Jefferys, 19).95).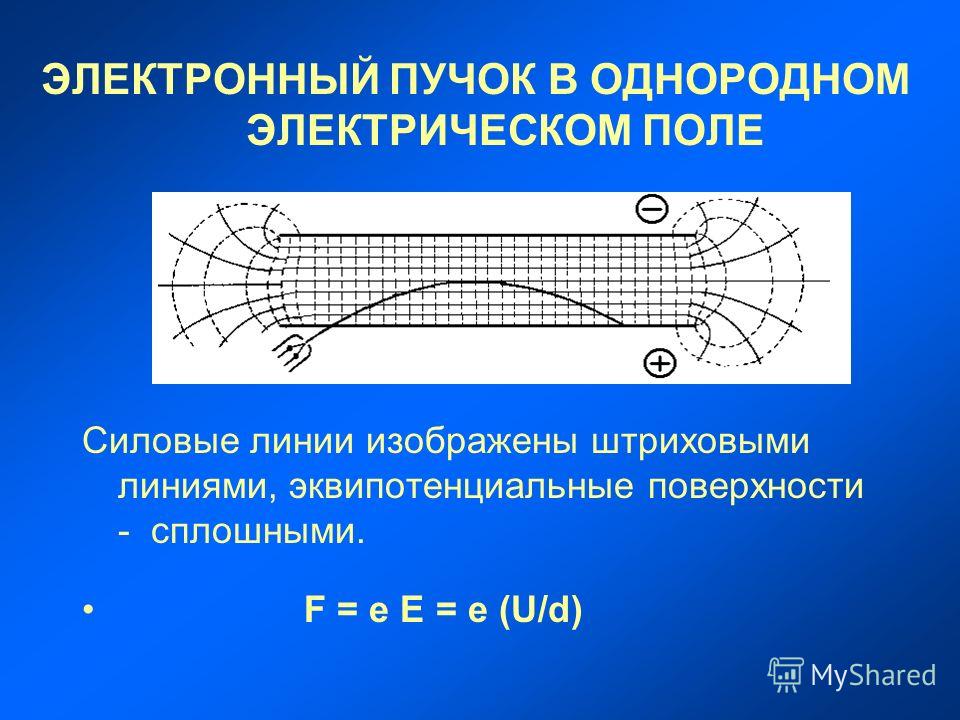 Ранний Эксперименты in vitro с препаратами СА1 гиппокампа показали, что в отсутствие синаптической связи внеклеточное поле вносит значительный вклад в синхронизацию популяций нейронов (Purpura and Malliani, 1966; Jefferys and Haas, 1982; Taylor and Dudek, 1982; Snow and Dudek). , 1984). Хотя LFP относительно малы по амплитуде, они охватывают более крупные области мозга (Katzner et al., 2009). Кроме того, учитывая относительно большое характерное время LFP (> 5 мс), на них гораздо меньше влияет низкочастотная фильтрация мембраны. Таким образом, было высказано предположение, что LFP могут выполнять функциональную роль в областях мозга, таких как гиппокамп, где ламинарная морфология (выравнивание нейронов) приводит к большим v e колебания (Buzsaki et al., 1983).
Ранний Эксперименты in vitro с препаратами СА1 гиппокампа показали, что в отсутствие синаптической связи внеклеточное поле вносит значительный вклад в синхронизацию популяций нейронов (Purpura and Malliani, 1966; Jefferys and Haas, 1982; Taylor and Dudek, 1982; Snow and Dudek). , 1984). Хотя LFP относительно малы по амплитуде, они охватывают более крупные области мозга (Katzner et al., 2009). Кроме того, учитывая относительно большое характерное время LFP (> 5 мс), на них гораздо меньше влияет низкочастотная фильтрация мембраны. Таким образом, было высказано предположение, что LFP могут выполнять функциональную роль в областях мозга, таких как гиппокамп, где ламинарная морфология (выравнивание нейронов) приводит к большим v e колебания (Buzsaki et al., 1983).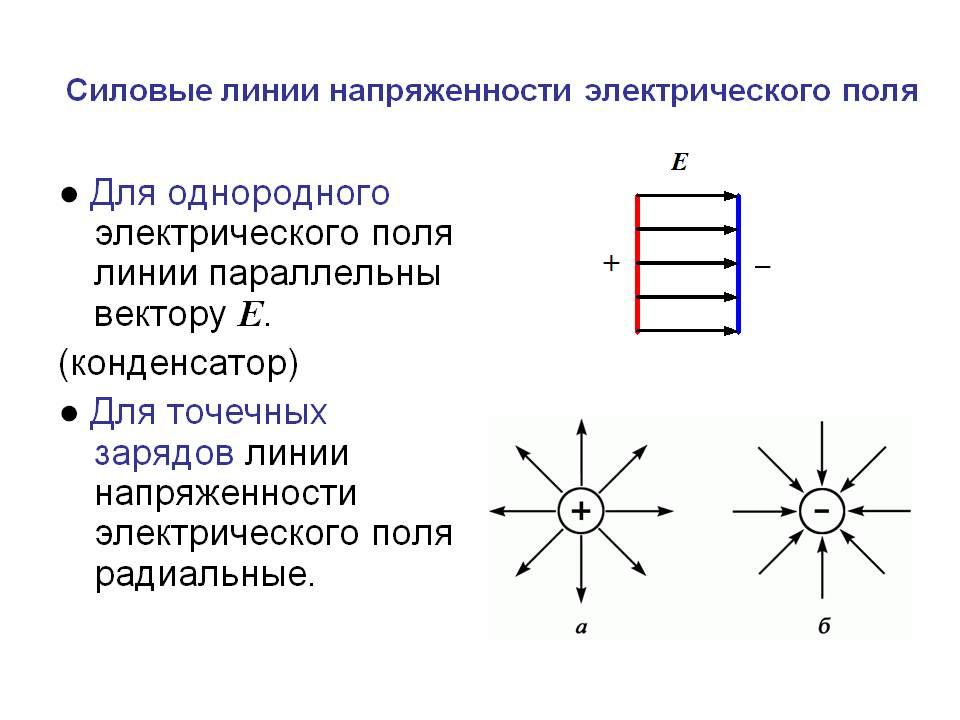 al., 1988; Radman et al., 2007), которые индуцируют ламинарное или (пространственно) постоянное электрическое поле соответственно. Тем не менее пространственно-диффузная стимуляция непредсказуемым образом воздействует на различные части нейронов и редко имитирует физиологическую ситуацию. Например, в гиппокампе активность LFP сильно зависит от времени и местоположения (Kamondi et al., 19).98; Хенце и Бужаки, 2001 г.; Клаусбергер и др., 2003, 2004). Хотя зависимость этих внеклеточных полей от времени рассматривалась в прошлом путем применения полей переменного тока вдоль нейронов (Deans et al., 2007; Radman et al., 2007), эффект пространственной неоднородности эндогенной электрической активности сохраняется. для изучения (Рубинштейн и Спелман, 1988; Рубинштейн, 1991).
al., 1988; Radman et al., 2007), которые индуцируют ламинарное или (пространственно) постоянное электрическое поле соответственно. Тем не менее пространственно-диффузная стимуляция непредсказуемым образом воздействует на различные части нейронов и редко имитирует физиологическую ситуацию. Например, в гиппокампе активность LFP сильно зависит от времени и местоположения (Kamondi et al., 19).98; Хенце и Бужаки, 2001 г.; Клаусбергер и др., 2003, 2004). Хотя зависимость этих внеклеточных полей от времени рассматривалась в прошлом путем применения полей переменного тока вдоль нейронов (Deans et al., 2007; Radman et al., 2007), эффект пространственной неоднородности эндогенной электрической активности сохраняется. для изучения (Рубинштейн и Спелман, 1988; Рубинштейн, 1991).
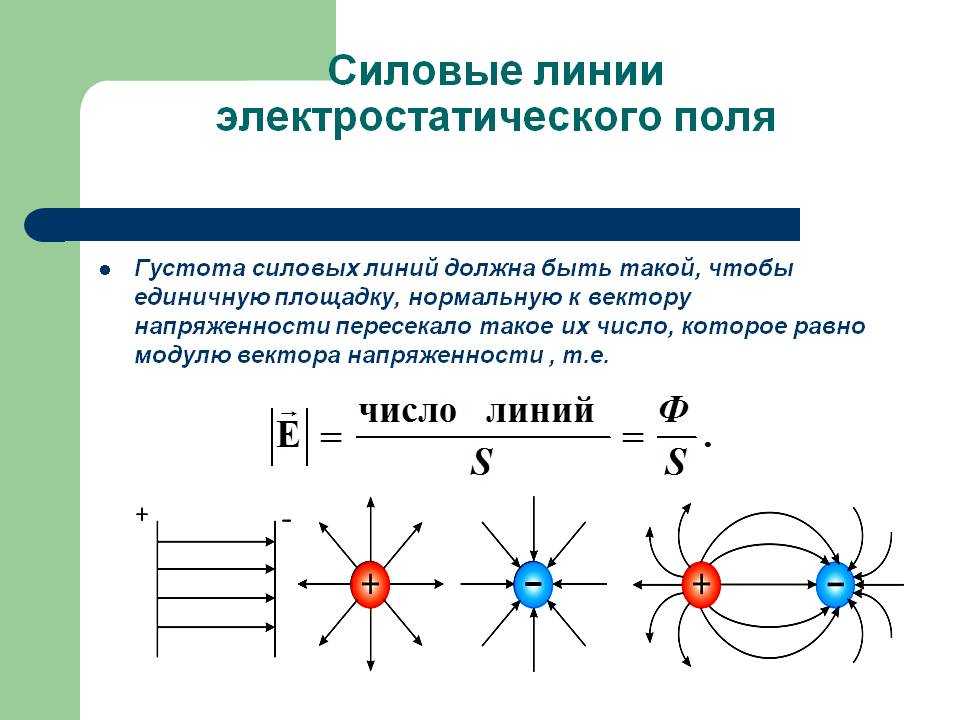 jneurosci.org в качестве дополнительного материала):
jneurosci.org в качестве дополнительного материала): рис. 4 A ) следующим образом:
рис. 4 A ) следующим образом: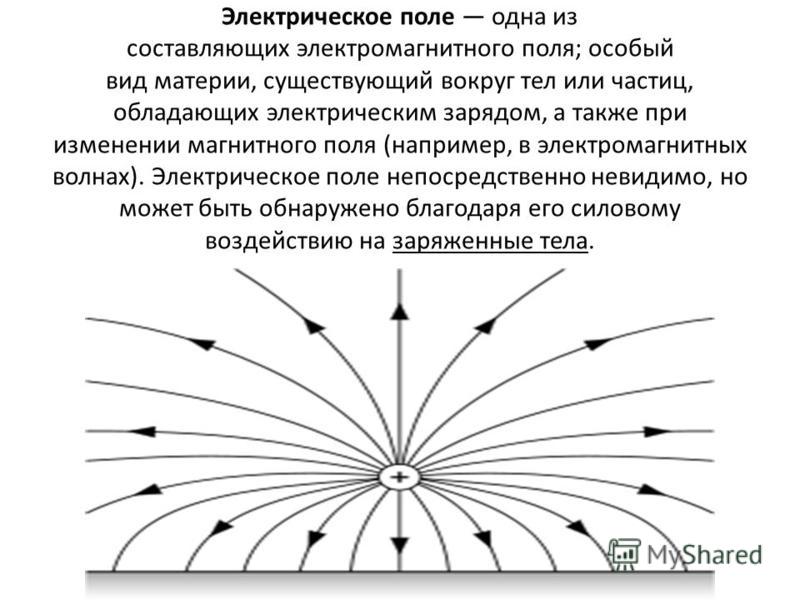 ϕ s определялась так, чтобы v e ( t , x , y , z ) находилась в центре исследуемого участка (височного) и одиночного моделировались колебания. Для количественной оценки временной фильтрации отклонение β индуцированного V m колебания из состояния покоя сравнивались со стационарным случаем со следующим: где P ( V m ) указывает диапазон (т. е. разницу между V m максимумом и V m минимумом) по сечению (максимальный диапазон среди всех внутренних узлов определенный участок) между нестационарным и стационарным (с.с.) случаем.
ϕ s определялась так, чтобы v e ( t , x , y , z ) находилась в центре исследуемого участка (височного) и одиночного моделировались колебания. Для количественной оценки временной фильтрации отклонение β индуцированного V m колебания из состояния покоя сравнивались со стационарным случаем со следующим: где P ( V m ) указывает диапазон (т. е. разницу между V m максимумом и V m минимумом) по сечению (максимальный диапазон среди всех внутренних узлов определенный участок) между нестационарным и стационарным (с.с.) случаем.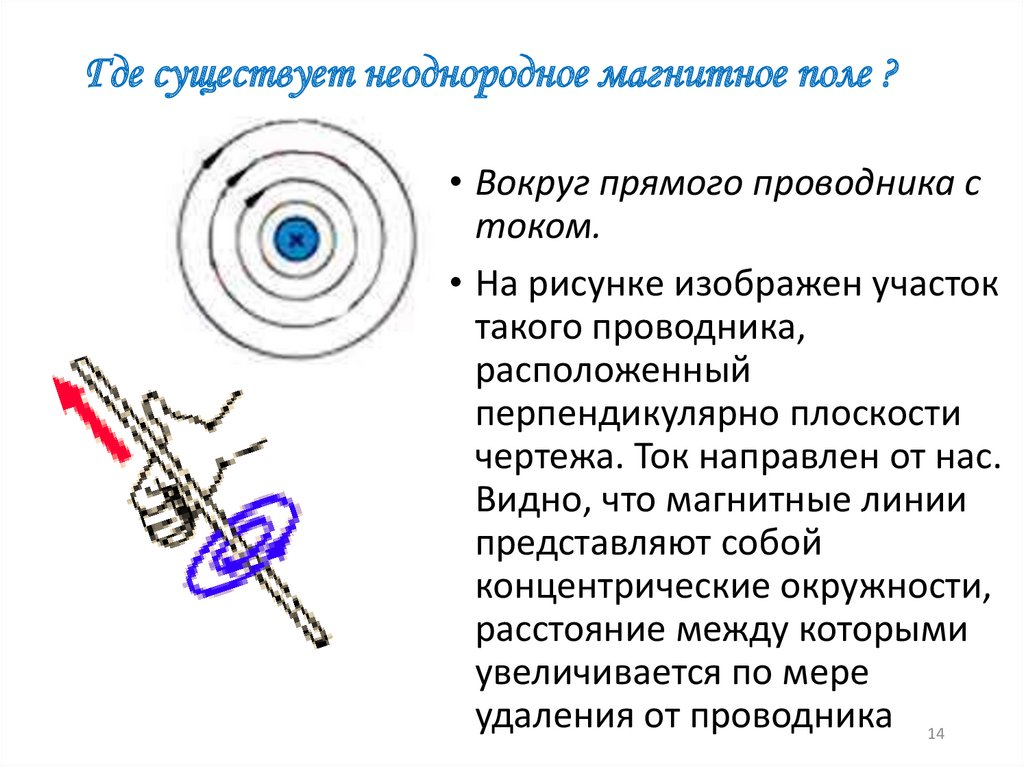 Для морфологически детализированного нейрона были разработаны алгоритмы, которые отслеживают все внутренние узлы после сегментации и применяют поле. Для создания пространственно гладких профилей внеклеточного потенциала использовались кубические сплайны для интерполяции между местами записи (дополнительные рисунки S6, S7, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Сопротивление мембраны R m = 20 кОм см 2 , а внутриклеточное сопротивление R i = 20 Ом см (Koch, 1999). Для моделирования, зависящего от времени, емкость мембраны составляла Кл м = 1 мкФ см -2 , а ток мембраны определялся с использованием функции NEURON i_membrane(x) (Hines and Carnevale, 1997).
Для морфологически детализированного нейрона были разработаны алгоритмы, которые отслеживают все внутренние узлы после сегментации и применяют поле. Для создания пространственно гладких профилей внеклеточного потенциала использовались кубические сплайны для интерполяции между местами записи (дополнительные рисунки S6, S7, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Сопротивление мембраны R m = 20 кОм см 2 , а внутриклеточное сопротивление R i = 20 Ом см (Koch, 1999). Для моделирования, зависящего от времени, емкость мембраны составляла Кл м = 1 мкФ см -2 , а ток мембраны определялся с использованием функции NEURON i_membrane(x) (Hines and Carnevale, 1997).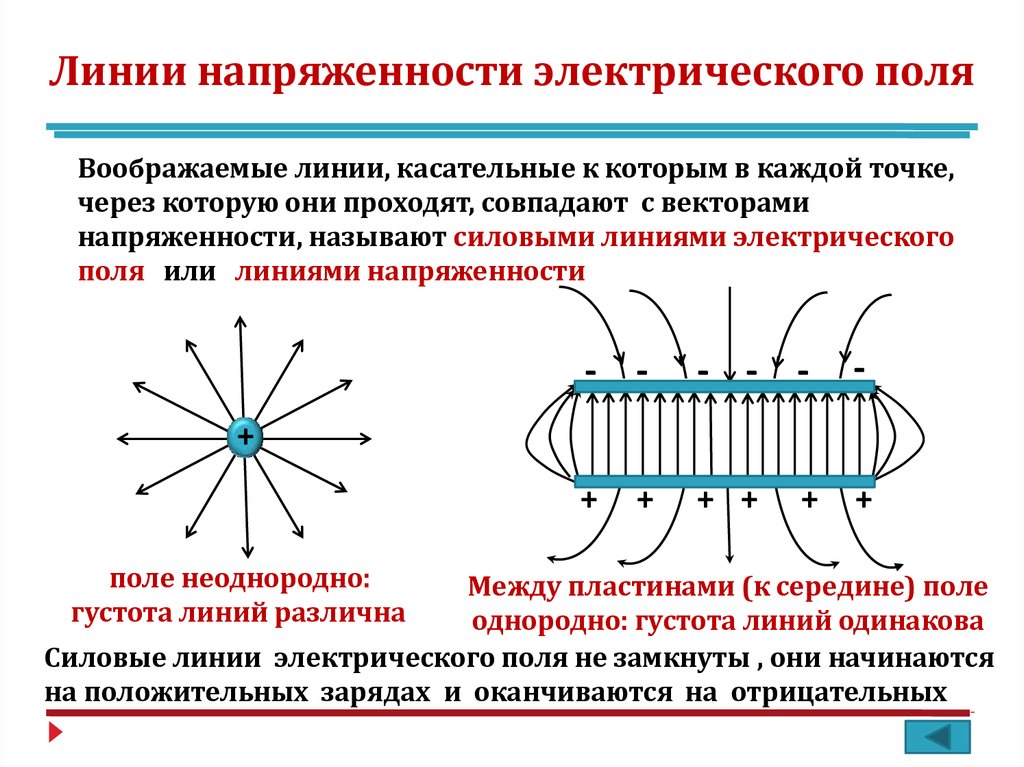 Мембранный потенциал равен v m = v i − v e . Обратите внимание, что в большинстве исследований теории кабелей пренебрегают внеклеточными полевыми эффектами, устанавливая v e должны быть постоянными, обычно нулевыми (рис. 1). То есть они пренебрегают любым вкладом внеклеточного поля.
Мембранный потенциал равен v m = v i − v e . Обратите внимание, что в большинстве исследований теории кабелей пренебрегают внеклеточными полевыми эффектами, устанавливая v e должны быть постоянными, обычно нулевыми (рис. 1). То есть они пренебрегают любым вкладом внеклеточного поля.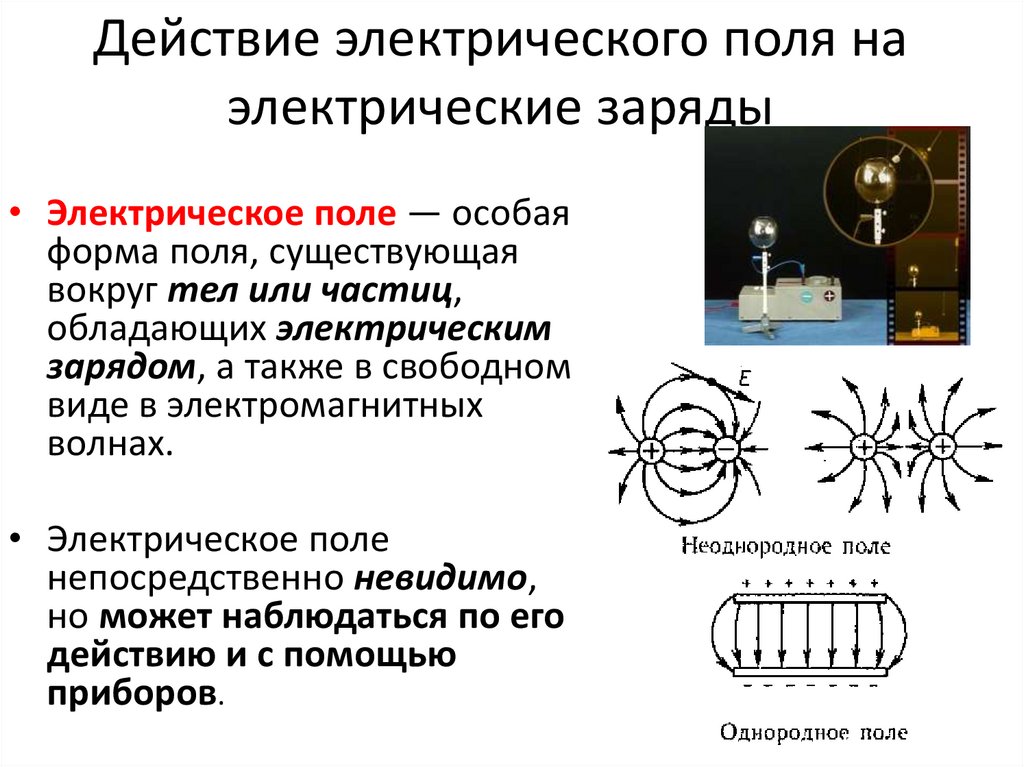 Ω = 2π f s λ el – безразмерная угловая пространственная частота колебаний внеклеточного потенциала.
Ω = 2π f s λ el – безразмерная угловая пространственная частота колебаний внеклеточного потенциала. отрицательная пространственная производная (параллельно кабелю) В e или E e = −Ω cos( Ом X + ϕ с )] на В м . Часто предполагается, что постоянные поля вдоль кабеля не влияют на В м . Из уравнения 1 видно, что, хотя уравнение кабеля остается неизменным при наличии постоянных полей, на границах кабеля появляются условия стока/источника, которые влияют на (стационарное) пространственное V m профиль (подробнее см. дополнительный раздел 2, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Следовательно, постоянные электрические поля воздействуют на В м с точным влиянием, зависящим от свойств кабеля и поля (Chan and Nicholson, 1986).
отрицательная пространственная производная (параллельно кабелю) В e или E e = −Ω cos( Ом X + ϕ с )] на В м . Часто предполагается, что постоянные поля вдоль кабеля не влияют на В м . Из уравнения 1 видно, что, хотя уравнение кабеля остается неизменным при наличии постоянных полей, на границах кабеля появляются условия стока/источника, которые влияют на (стационарное) пространственное V m профиль (подробнее см. дополнительный раздел 2, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Следовательно, постоянные электрические поля воздействуют на В м с точным влиянием, зависящим от свойств кабеля и поля (Chan and Nicholson, 1986). 2). При больших λ s (т.е. пространственно-однородных внешних полях) индуцированное V m остается малым, тогда как при малых λ s (т.е. пространственно более неоднородных внешних полях) V m сходится к − V e [ v i сходится к v остальные , как видно на рис. 2, третий столбец; последний вывод был также сделан Холтом и Кохом (1999)]. В общем, | В м | ≤ 1,25, хотя для большинства случаев | В м | ≤ 1 достаточно (дополнительный рисунок S1, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Для бесконечного кабеля В м всегда меньше единицы (Holt and Koch, 1999). Поляризация на краях кабеля приводит к | В м | ≥ 1 для внеклеточных полей, когда λ s аналогично L (рис. 2 B2 ), что связано с граничными условиями закрытого конца.
2). При больших λ s (т.е. пространственно-однородных внешних полях) индуцированное V m остается малым, тогда как при малых λ s (т.е. пространственно более неоднородных внешних полях) V m сходится к − V e [ v i сходится к v остальные , как видно на рис. 2, третий столбец; последний вывод был также сделан Холтом и Кохом (1999)]. В общем, | В м | ≤ 1,25, хотя для большинства случаев | В м | ≤ 1 достаточно (дополнительный рисунок S1, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Для бесконечного кабеля В м всегда меньше единицы (Holt and Koch, 1999). Поляризация на краях кабеля приводит к | В м | ≥ 1 для внеклеточных полей, когда λ s аналогично L (рис. 2 B2 ), что связано с граничными условиями закрытого конца.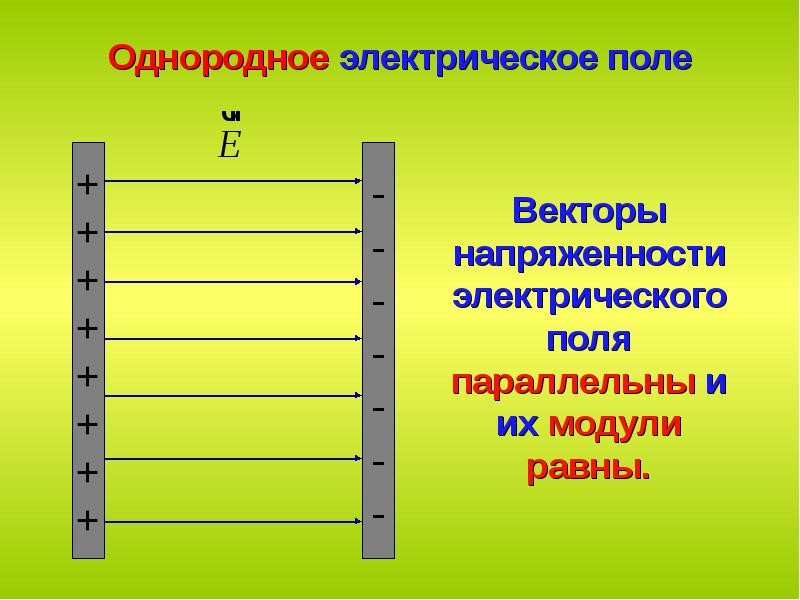 Следовательно, при наличии стационарного и пространственно гармонического внеклеточного потенциала амплитуда индуцированного мембранного потенциала не более чем в 1,25 раза превышает амплитуду внеклеточного потенциала.
Следовательно, при наличии стационарного и пространственно гармонического внеклеточного потенциала амплитуда индуцированного мембранного потенциала не более чем в 1,25 раза превышает амплитуду внеклеточного потенциала.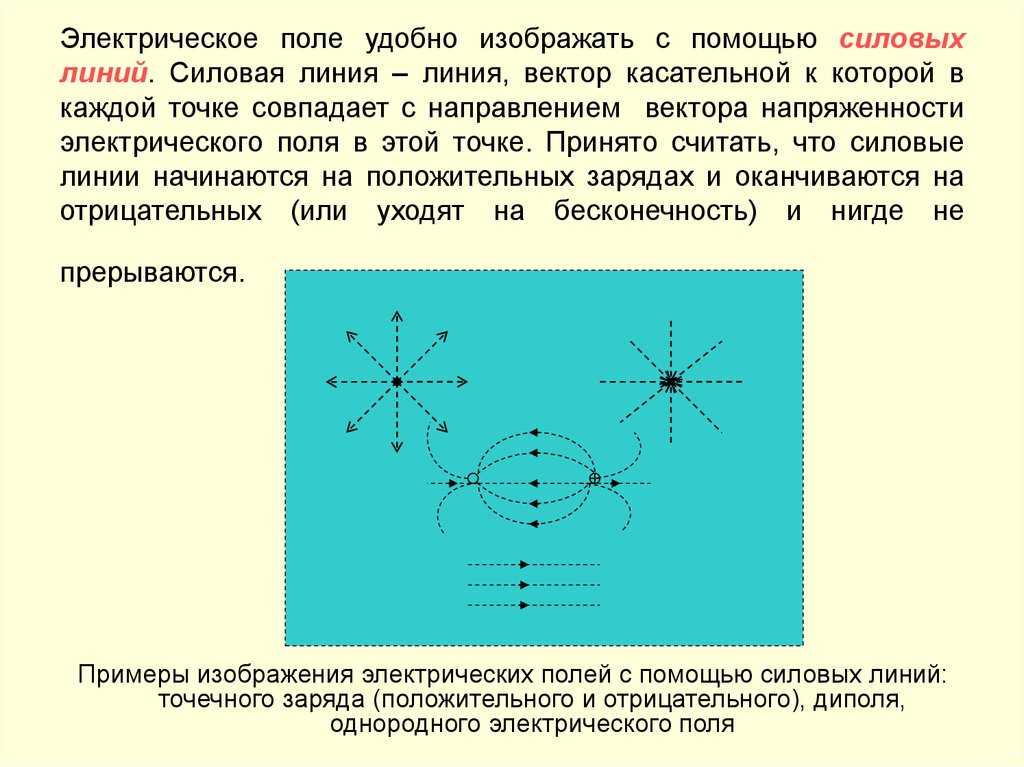 Расстояние по кабелю нормировано на единицу. В верхнем ряду ( A1 , B1 , C1 ) V e колебания с пространственной частотой Ω показаны для Ω L /2π = 0,1 ( A1 ), 0,5 ( B1 ) и 3 ( C3 903 ), тогда как цветные линии 2 укажите ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Во второй строке ( A2 , B2 , C2 ) для этих трех случаев нанесен индуцированный мембранный потенциал (уравнение 5). Только пространственно-неоднородные поля с характерной длиной поля, сравнимой с длиной кабеля или меньшей, приводят к сильным В м отклонения. In the third ( A3 , B3 , C3 ) and the fourth ( A4 , B4 , C4 ) rows, the induced E Показаны м (уравнение 6) и CSD м (уравнение 7).
Расстояние по кабелю нормировано на единицу. В верхнем ряду ( A1 , B1 , C1 ) V e колебания с пространственной частотой Ω показаны для Ω L /2π = 0,1 ( A1 ), 0,5 ( B1 ) и 3 ( C3 903 ), тогда как цветные линии 2 укажите ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Во второй строке ( A2 , B2 , C2 ) для этих трех случаев нанесен индуцированный мембранный потенциал (уравнение 5). Только пространственно-неоднородные поля с характерной длиной поля, сравнимой с длиной кабеля или меньшей, приводят к сильным В м отклонения. In the third ( A3 , B3 , C3 ) and the fourth ( A4 , B4 , C4 ) rows, the induced E Показаны м (уравнение 6) и CSD м (уравнение 7). Серая область обозначает диапазон для всех пространственных фаз, тогда как пунктирные линии в двух нижних рядах указывают диапазон безразмерного внеклеточного поля E e и плотность источника тока CSD e соответственно. Для ϕ s ∈[0°, 360°) индуцированная | E м |/Ом- и |CSD м |/Ом 2 -диапазон равен единице. Как видно, CSD m аналогичен профилю V e (сравните отдельные профили V e и CSD m в верхнем и нижнем рядах) для больших Ω. Обратите внимание, что на этом и на всех остальных рисунках не моделируется подача постоянного тока или синаптический ввод. Все изменения в V m объясняются пространственно изменяющимся внеклеточным полем.
Серая область обозначает диапазон для всех пространственных фаз, тогда как пунктирные линии в двух нижних рядах указывают диапазон безразмерного внеклеточного поля E e и плотность источника тока CSD e соответственно. Для ϕ s ∈[0°, 360°) индуцированная | E м |/Ом- и |CSD м |/Ом 2 -диапазон равен единице. Как видно, CSD m аналогичен профилю V e (сравните отдельные профили V e и CSD m в верхнем и нижнем рядах) для больших Ω. Обратите внимание, что на этом и на всех остальных рисунках не моделируется подача постоянного тока или синаптический ввод. Все изменения в V m объясняются пространственно изменяющимся внеклеточным полем. В этих условиях влиянием емкостной фильтрации можно пренебречь. Более того, из уравнения 5 следует, что усреднение V m за один полный цикл внеклеточного потенциала [т.е. по всем ϕ s ∈[0, 2π)] приводит к 〈V m 〉 ϕ s =
В этих условиях влиянием емкостной фильтрации можно пренебречь. Более того, из уравнения 5 следует, что усреднение V m за один полный цикл внеклеточного потенциала [т.е. по всем ϕ s ∈[0, 2π)] приводит к 〈V m 〉 ϕ s =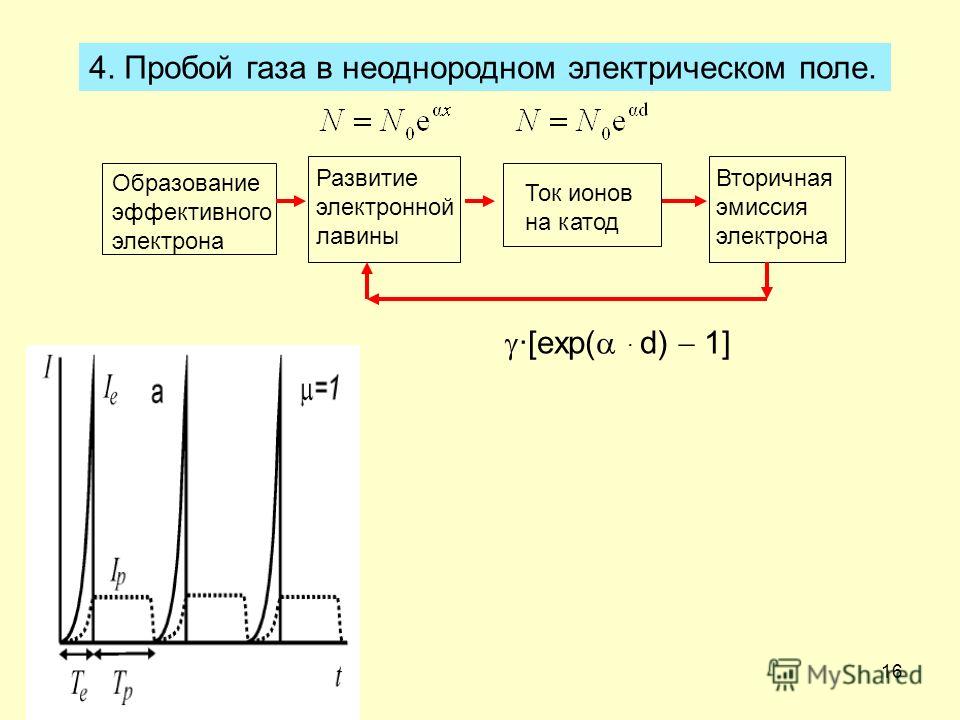 2, третья строка), так что внешний E e максимально наводит вдоль кабеля E м равной прочности.
2, третья строка), так что внешний E e максимально наводит вдоль кабеля E м равной прочности.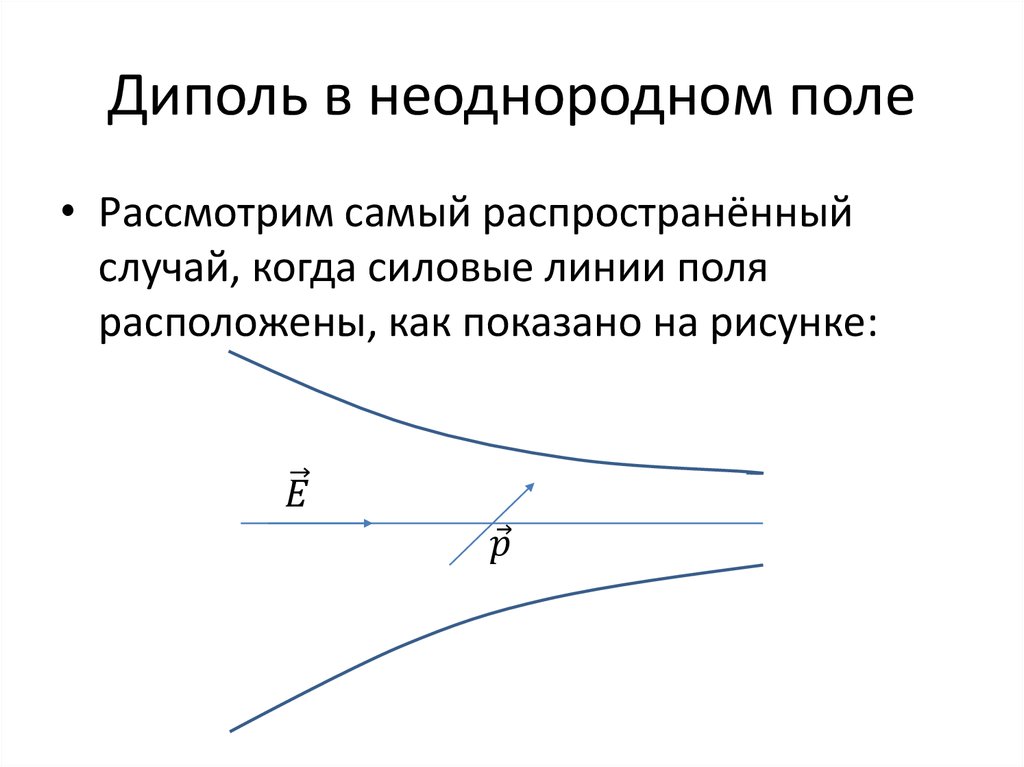 jneurosci.org в качестве дополнительного материала) . При малых λ s , CSD m ( X ) ≈ Ω 2 V m ( X ) so that for spatially inhomogeneous extracellular voltages the current source along the cable is analogous to the V м профиль. Однако, хотя | В м | ≤ 1,25, E m и CSD m являются линейной и квадратичной функциями Ω соответственно. Таким образом, тот факт, что малоамплитудный неоднородный V e приводит к малоамплитудным V m не переводится в малые наведенные E m или CSD m . Крайне неоднородные внеклеточные колебания напряжения могут привести к значительным мембранным полям и плотности источника тока вдоль кабеля с потенциально важными последствиями.
jneurosci.org в качестве дополнительного материала) . При малых λ s , CSD m ( X ) ≈ Ω 2 V m ( X ) so that for spatially inhomogeneous extracellular voltages the current source along the cable is analogous to the V м профиль. Однако, хотя | В м | ≤ 1,25, E m и CSD m являются линейной и квадратичной функциями Ω соответственно. Таким образом, тот факт, что малоамплитудный неоднородный V e приводит к малоамплитудным V m не переводится в малые наведенные E m или CSD m . Крайне неоднородные внеклеточные колебания напряжения могут привести к значительным мембранным полям и плотности источника тока вдоль кабеля с потенциально важными последствиями. Из этих двух условий следует, что воздействие на В м зависит от трех длин: характерной длины внеклеточного поля λ с , физической l и электротонической λ el длин. кабеля. Из сказанного выше следует, что для того, чтобы индуцированная амплитуда V m стала порядка амплитуды V e , λ el > λ s /2π [условие (I)] и l > λ s /2π [условие (II)].
Из этих двух условий следует, что воздействие на В м зависит от трех длин: характерной длины внеклеточного поля λ с , физической l и электротонической λ el длин. кабеля. Из сказанного выше следует, что для того, чтобы индуцированная амплитуда V m стала порядка амплитуды V e , λ el > λ s /2π [условие (I)] и l > λ s /2π [условие (II)]. Это приводит к повышенной поляризации кабеля (дополнительный раздел 5 и рис. S1, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Более того, условие (II) требует, чтобы λ s было достаточно большим примерно для полугода.0322 V e -период в пределах длины кабеля. Таким образом, пространственно-однородные поля с большими λ s (малыми Ω) по сравнению с размером кабеля оказывают лишь незначительное влияние на V m (рис. 2, ср. A2 , C2 ).
Это приводит к повышенной поляризации кабеля (дополнительный раздел 5 и рис. S1, доступные на сайте www.jneurosci.org в качестве дополнительного материала). Более того, условие (II) требует, чтобы λ s было достаточно большим примерно для полугода.0322 V e -период в пределах длины кабеля. Таким образом, пространственно-однородные поля с большими λ s (малыми Ω) по сравнению с размером кабеля оказывают лишь незначительное влияние на V m (рис. 2, ср. A2 , C2 ). Таким образом, влияние пространственно-неоднородного V e на E m и CSD m прогнозируется исключительно через условие (I). Пока λ s мал, дальность наведенного E m и CSD m меньше или равна E e и CSD e соответственно. Поэтому даже вдоль короткого кабеля, который на основании условия (II) приводит к малым В м , наведенные Е м и КСД м могут быть существенными (рис. 2 А3 , А4 ).
Таким образом, влияние пространственно-неоднородного V e на E m и CSD m прогнозируется исключительно через условие (I). Пока λ s мал, дальность наведенного E m и CSD m меньше или равна E e и CSD e соответственно. Поэтому даже вдоль короткого кабеля, который на основании условия (II) приводит к малым В м , наведенные Е м и КСД м могут быть существенными (рис. 2 А3 , А4 ). jneurosci.org в качестве дополнительного материала).
jneurosci.org в качестве дополнительного материала).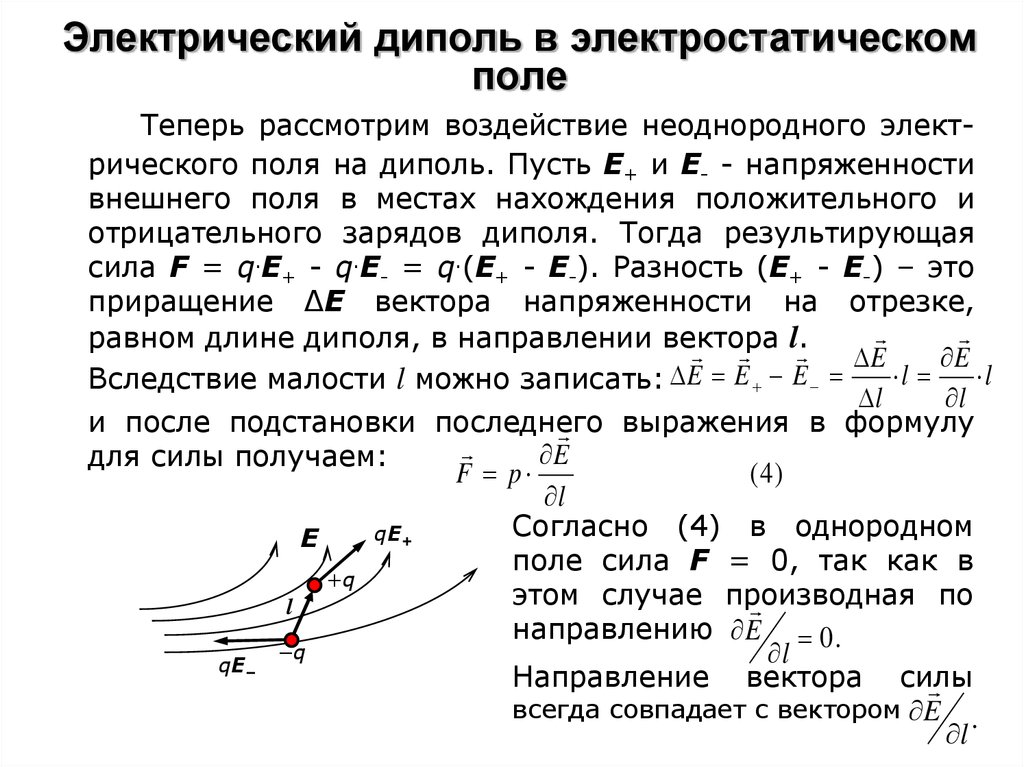 Импедансы кабелей согласовываются по правилу 3/2 (Rall, 1962). Основной кабель выровнен по оси внешнего поля, тогда как угол между дочерними кабелями и осью поля следующий: θ d ,1 = 0° and θ d ,2 = −45° ( A ), θ d ,1 = 45° and θ D , 2 = –45 ° ( B ) и θ D , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = . ( С ). Ниже каждого корпуса результирующие В м (второй ряд), E m (третий ряд) и CSD m (четвертый ряд) показаны для ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Заметим, что для X > 0,5 L штриховые цветные линии иллюстрируют траекторию v м вдоль штриховой дочерней ветви (см.
Импедансы кабелей согласовываются по правилу 3/2 (Rall, 1962). Основной кабель выровнен по оси внешнего поля, тогда как угол между дочерними кабелями и осью поля следующий: θ d ,1 = 0° and θ d ,2 = −45° ( A ), θ d ,1 = 45° and θ D , 2 = –45 ° ( B ) и θ D , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = , 1 = . ( С ). Ниже каждого корпуса результирующие В м (второй ряд), E m (третий ряд) и CSD m (четвертый ряд) показаны для ϕ s = 0° (синий), 90° (зеленый) и 180° (красный). Заметим, что для X > 0,5 L штриховые цветные линии иллюстрируют траекторию v м вдоль штриховой дочерней ветви (см. первую строку рисунка) для трех ϕ s , тогда как сплошные цветные линии показывают траекторию v m вдоль сплошной дочерней ветви. Дочерние ветви имеют такую же нормализованную длину, как и родительская ветвь, L родитель = L дочь = L /2. Диапазон V м , E м и CSD м вдоль всех ветвей обозначен серыми областями. Обратите внимание на возрастающее затухание в индуцированном E m — и CSD m -диапазонах, когда дочерний кабель становится перпендикулярным к оси внешнего поля.
первую строку рисунка) для трех ϕ s , тогда как сплошные цветные линии показывают траекторию v m вдоль сплошной дочерней ветви. Дочерние ветви имеют такую же нормализованную длину, как и родительская ветвь, L родитель = L дочь = L /2. Диапазон V м , E м и CSD м вдоль всех ветвей обозначен серыми областями. Обратите внимание на возрастающее затухание в индуцированном E m — и CSD m -диапазонах, когда дочерний кабель становится перпендикулярным к оси внешнего поля. 2 B2). –B4 ), становится очевидным, что они практически идентичны. Тем не менее, существуют значительные различия при сравнении второй части неразветвленного кабеля и второй дочерней ветви (θ d , 2 = -π/4) разветвленного кабеля. Они увеличиваются по мере того, как дочерний кабель становится перпендикулярным внеклеточному полю. Влияние угла θ d , j ( j = 1, 2) между двумя дочерьми и родителем можно учесть, определив прогнозируемую электротоническую длину λ эл, j 3 = 4 cos(θ d , j ) на оси внешнего поля. Отсюда следует, что малые углы мало влияют на V m . Но поскольку E m и CSD m являются линейной и квадратичной функциями Ω j = 2π F S λ EL, J , различия, вызванные θ D , D .
2 B2). –B4 ), становится очевидным, что они практически идентичны. Тем не менее, существуют значительные различия при сравнении второй части неразветвленного кабеля и второй дочерней ветви (θ d , 2 = -π/4) разветвленного кабеля. Они увеличиваются по мере того, как дочерний кабель становится перпендикулярным внеклеточному полю. Влияние угла θ d , j ( j = 1, 2) между двумя дочерьми и родителем можно учесть, определив прогнозируемую электротоническую длину λ эл, j 3 = 4 cos(θ d , j ) на оси внешнего поля. Отсюда следует, что малые углы мало влияют на V m . Но поскольку E m и CSD m являются линейной и квадратичной функциями Ω j = 2π F S λ EL, J , различия, вызванные θ D , D . Ряд рисунков 2 и 3. Следовательно, даже небольшие изменения ориентации кабеля (по отношению к оси внешнего поля) могут привести к значительным изменениям E m и CSD m .
Ряд рисунков 2 и 3. Следовательно, даже небольшие изменения ориентации кабеля (по отношению к оси внешнего поля) могут привести к значительным изменениям E m и CSD m . Таким образом, при наличии пространственно-неоднородного внеклеточного напряжения изменение ориентации кабеля может привести к существенному различию профилей вдоль отрезков кабеля.
Таким образом, при наличии пространственно-неоднородного внеклеточного напряжения изменение ориентации кабеля может привести к существенному различию профилей вдоль отрезков кабеля. Для изучения этих эффектов мы провели анализ чувствительности, в котором Ω, L , θ d и расположение ветвления систематически варьировались. Установлено, что при выполнении условий (I) и (II) на участке кабеля изменение свойств кабеля ( r m , r i и d ), которые обычно встречаются в нейронах, не влияют на диапазон V m флуктуаций так, как они влияют на пространственный профиль E m и CSD m (Рис. 3; дополнительный раздел 5, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Кроме того, можно показать, что изменения ориентации кабеля эквивалентны изменениям λ el (дополнительные разделы 2, 5, доступные на сайте www.jneurosci.org в качестве дополнительного материала).
Для изучения этих эффектов мы провели анализ чувствительности, в котором Ω, L , θ d и расположение ветвления систематически варьировались. Установлено, что при выполнении условий (I) и (II) на участке кабеля изменение свойств кабеля ( r m , r i и d ), которые обычно встречаются в нейронах, не влияют на диапазон V m флуктуаций так, как они влияют на пространственный профиль E m и CSD m (Рис. 3; дополнительный раздел 5, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Кроме того, можно показать, что изменения ориентации кабеля эквивалентны изменениям λ el (дополнительные разделы 2, 5, доступные на сайте www.jneurosci.org в качестве дополнительного материала).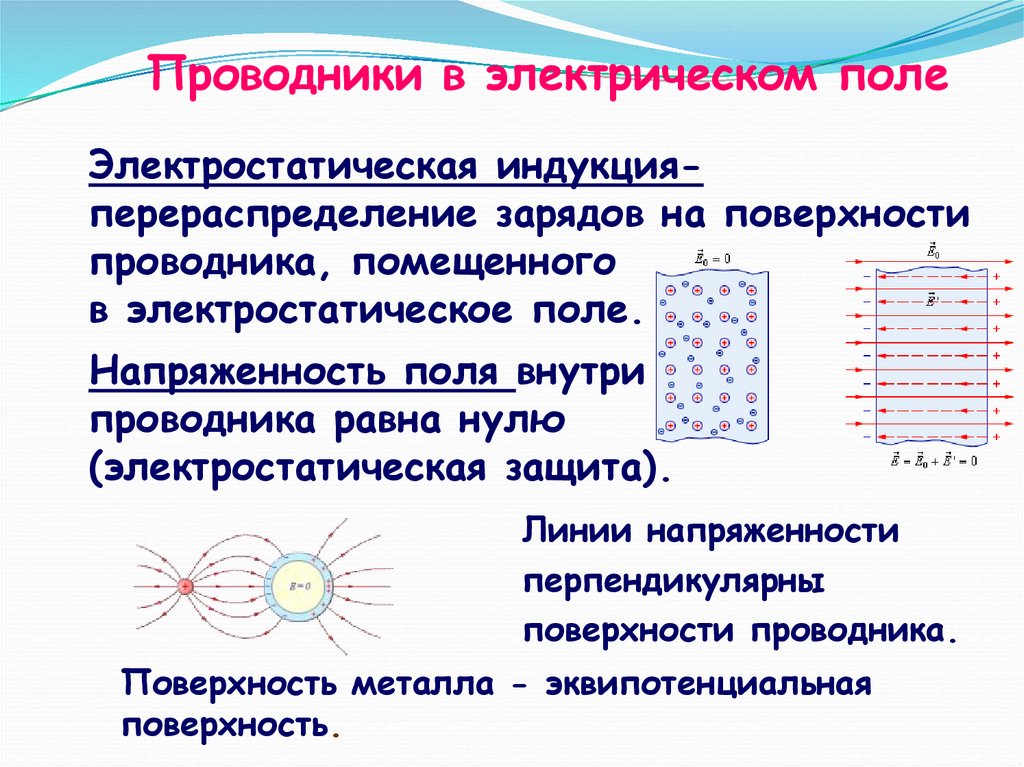 Исходя из этих соображений, для морфологически неоднородного кабеля условия (I) и (II) необходимо лишь переформулировать в терминах проекций характерных длин вдоль оси внешнего поля (см. Материалы и методы). Для реконструированного пирамидного нейрона гиппокампа крысы СА1, показанного на рис. 4 A [нейрон d151 в исследовании Gold et al. (2006)], мы сосредоточили наш анализ на четырех разделах, в которых каждый раздел состоит из ряда взаимосвязанных линейных сегментов. К ним относятся: ( i ) срез базального дендрита, ( ii ) сома и проксимальный срез в апикальной области, соединенный непосредственно с сомой, ( iii ) медиальный срез в апикальной области и ( iv ) дистальный срез в апикальной области. Расположение этих секций показано на рисунке 4 A , а ориентация каждой секции показана на рисунке 4 B . Характеристические свойства каждой секции приведены в таблице 1 (т. е. длина l и средняя проекционная электротоническая длина 〈λ el,proj 〉, а также проекционная длина l̄ proj ) [обе длины проецируется на соматодендритную ось (рис.
Исходя из этих соображений, для морфологически неоднородного кабеля условия (I) и (II) необходимо лишь переформулировать в терминах проекций характерных длин вдоль оси внешнего поля (см. Материалы и методы). Для реконструированного пирамидного нейрона гиппокампа крысы СА1, показанного на рис. 4 A [нейрон d151 в исследовании Gold et al. (2006)], мы сосредоточили наш анализ на четырех разделах, в которых каждый раздел состоит из ряда взаимосвязанных линейных сегментов. К ним относятся: ( i ) срез базального дендрита, ( ii ) сома и проксимальный срез в апикальной области, соединенный непосредственно с сомой, ( iii ) медиальный срез в апикальной области и ( iv ) дистальный срез в апикальной области. Расположение этих секций показано на рисунке 4 A , а ориентация каждой секции показана на рисунке 4 B . Характеристические свойства каждой секции приведены в таблице 1 (т. е. длина l и средняя проекционная электротоническая длина 〈λ el,proj 〉, а также проекционная длина l̄ proj ) [обе длины проецируется на соматодендритную ось (рис.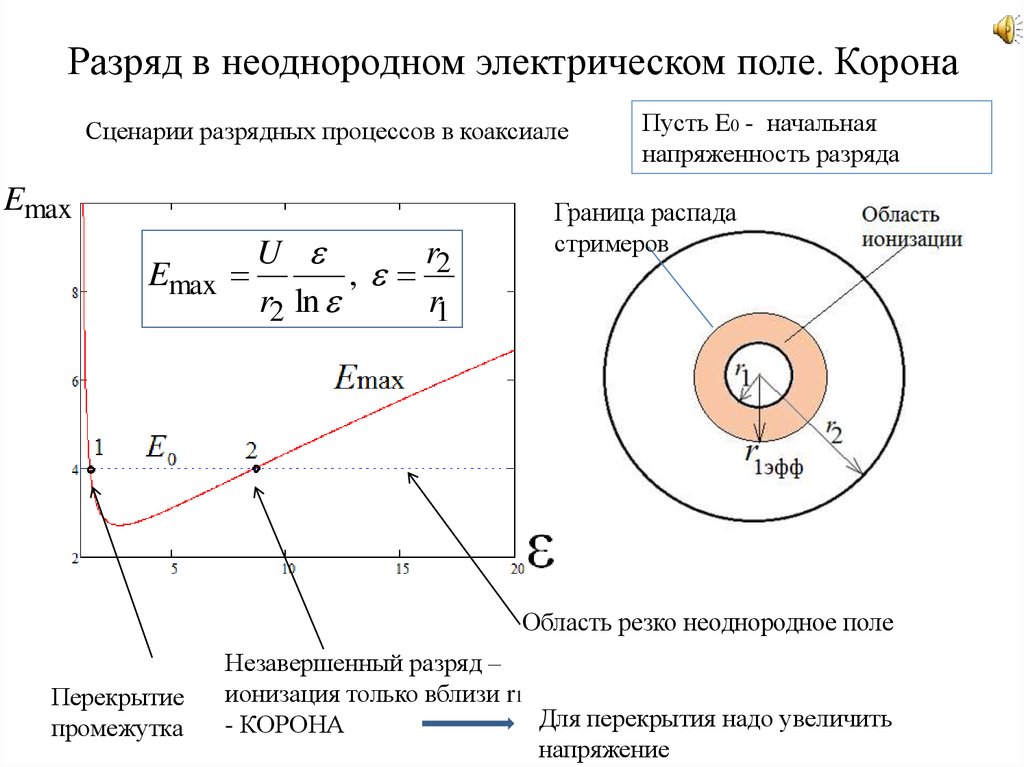 4 A , y -оси)]. Как видно, хотя базальный отдел ( i ) почти в три раза длиннее, чем дистальный апикальный отдел ( iv ), его l̄ proj вдвое короче. Причина этого становится очевидной на рис. 4, А и В , на которых показано, что базальный разрез почти перпендикулярен оси соматодендритов. Следовательно, влияние пространственно-неоднородного напряжения вдоль оси y на V m базально-апикального отдела по сравнению с дистальным апикальным отделом будет минимальным. В самом деле, исходя из условия (II) и значения l̄ proj , при наличии пространственно-гармонического внешнего поля вдоль оси соматодендритов число пространственных V m колебаний вдоль базального отдела должно быть аналогично таковому вдоль проксимального верхушечного отдела и меньше, чем вдоль медиальный и дистальный апикальный отделы.
4 A , y -оси)]. Как видно, хотя базальный отдел ( i ) почти в три раза длиннее, чем дистальный апикальный отдел ( iv ), его l̄ proj вдвое короче. Причина этого становится очевидной на рис. 4, А и В , на которых показано, что базальный разрез почти перпендикулярен оси соматодендритов. Следовательно, влияние пространственно-неоднородного напряжения вдоль оси y на V m базально-апикального отдела по сравнению с дистальным апикальным отделом будет минимальным. В самом деле, исходя из условия (II) и значения l̄ proj , при наличии пространственно-гармонического внешнего поля вдоль оси соматодендритов число пространственных V m колебаний вдоль базального отдела должно быть аналогично таковому вдоль проксимального верхушечного отдела и меньше, чем вдоль медиальный и дистальный апикальный отделы.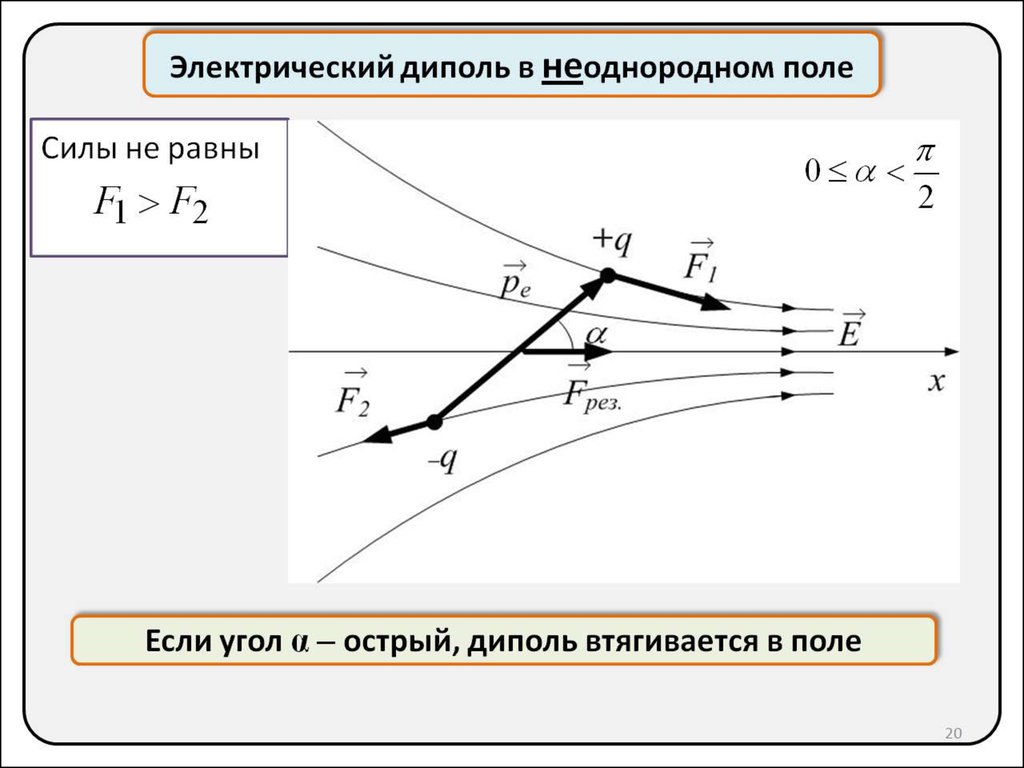
 Как видно, базальный дендрит почти перпендикулярен оси соматодендрита, тогда как остальные три секции относительно хорошо выровнены. Длина л каждой секции представлен в таблице 1.
Как видно, базальный дендрит почти перпендикулярен оси соматодендрита, тогда как остальные три секции относительно хорошо выровнены. Длина л каждой секции представлен в таблице 1. 5, третий столбец) на медиальном апикальном и дистальном апикальном участках, а также (маргинально) на проксимальный апикальный отдел. Действительно, на рис. 5 Cii–iv видно, что в этих разрезах колебания V м значительны и гораздо сильнее, чем в базальном разрезе или соме. Мы заключаем, что условия (I) и (II) точно предсказывают влияние стационарного и пространственно-неоднородного внеклеточного потенциала на мембранный потенциал. В случае внешних полей с более чем одной доминирующей осью условия (I) и (II) выполняются для каждой оси.
5, третий столбец) на медиальном апикальном и дистальном апикальном участках, а также (маргинально) на проксимальный апикальный отдел. Действительно, на рис. 5 Cii–iv видно, что в этих разрезах колебания V м значительны и гораздо сильнее, чем в базальном разрезе или соме. Мы заключаем, что условия (I) и (II) точно предсказывают влияние стационарного и пространственно-неоднородного внеклеточного потенциала на мембранный потенциал. В случае внешних полей с более чем одной доминирующей осью условия (I) и (II) выполняются для каждой оси.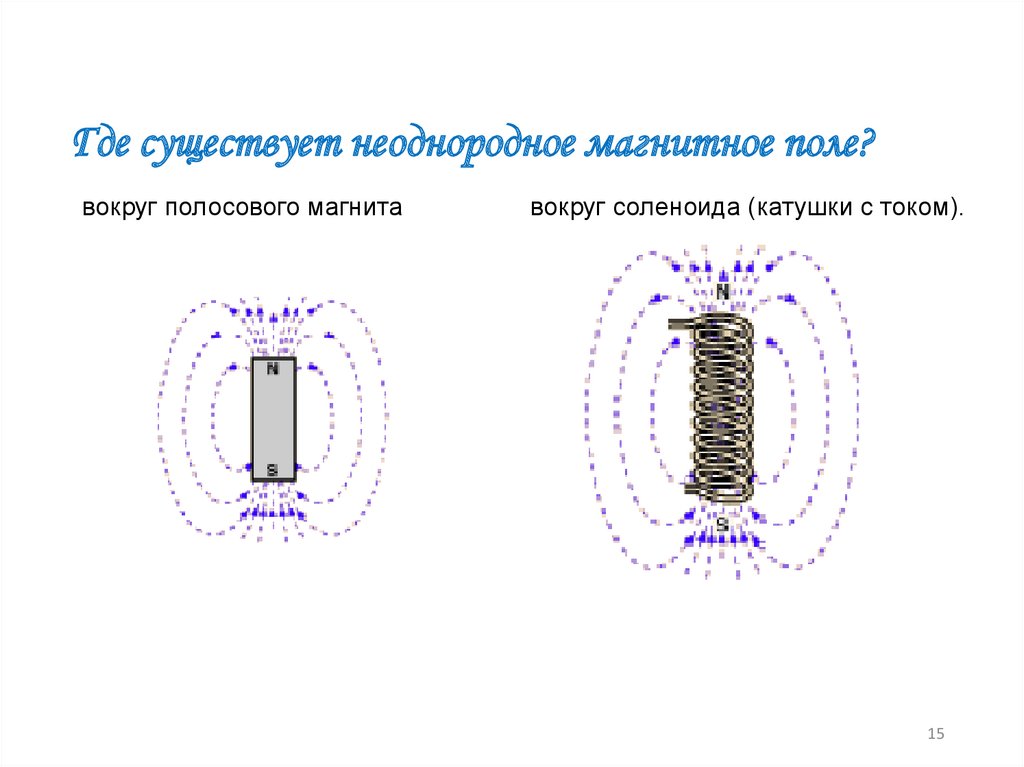 9032.9232.9232.9232.9232.9232. 9032. 9032.9232.9232. 9032. 9032.9232. 9032. . .9232.923. Цветовая карта иллюстрирует (пространственно) одномерный внеклеточный V e осцилляции вдоль оси соматодендритов для фазы ϕ y . Расстояние вдоль каждой секции показано как безразмерная длина дуги s / l . i – базальный; ii , сома и проксимальный верхушечный; iii медиальный апикальный; и iv , дистальный апикальный срез (рис. 4 A , таблица 1). Диапазон В м обозначено серым цветом, тогда как отдельные трассы имеют вид ϕ y = 0° (синий), 45° (красный) и 90° (зеленый). Условие (II) выполняется только для λ s = 0,2 мм (5 мм −1 ; C ) вдоль проксимального ( Cii ), медиального ( 2 Cii ) и дистальные апикальные ( Civ ) срезы (таблица 1), наблюдаемые в индуцированном диапазоне V м .
9032.9232.9232.9232.9232.9232. 9032. 9032.9232.9232. 9032. 9032.9232. 9032. . .9232.923. Цветовая карта иллюстрирует (пространственно) одномерный внеклеточный V e осцилляции вдоль оси соматодендритов для фазы ϕ y . Расстояние вдоль каждой секции показано как безразмерная длина дуги s / l . i – базальный; ii , сома и проксимальный верхушечный; iii медиальный апикальный; и iv , дистальный апикальный срез (рис. 4 A , таблица 1). Диапазон В м обозначено серым цветом, тогда как отдельные трассы имеют вид ϕ y = 0° (синий), 45° (красный) и 90° (зеленый). Условие (II) выполняется только для λ s = 0,2 мм (5 мм −1 ; C ) вдоль проксимального ( Cii ), медиального ( 2 Cii ) и дистальные апикальные ( Civ ) срезы (таблица 1), наблюдаемые в индуцированном диапазоне V м .
 В этом случае применяется квазистационарность, и разработанная здесь методология может быть полностью принята. Но по мере того, как характерное время пространственно-временного неоднородного внешнего поля становится сравнимым с τ m , фильтрация нижних частот становится существенной.
В этом случае применяется квазистационарность, и разработанная здесь методология может быть полностью принята. Но по мере того, как характерное время пространственно-временного неоднородного внешнего поля становится сравнимым с τ m , фильтрация нижних частот становится существенной. Примечательно, что для увеличения f t V м 9Амплитуда 0325 уменьшается (см. стрелки), так как V м не может следовать пространственно-временному колебанию V e . Таким образом, отношение β( V m ) между индуцированной амплитудой V m при определенном f t и V m обеспечивает измерение одного стационарного случая количественной оценки стационарной амплитуды. зависящее от времени воздействие на мембрану.
Примечательно, что для увеличения f t V м 9Амплитуда 0325 уменьшается (см. стрелки), так как V м не может следовать пространственно-временному колебанию V e . Таким образом, отношение β( V m ) между индуцированной амплитудой V m при определенном f t и V m обеспечивает измерение одного стационарного случая количественной оценки стационарной амплитуды. зависящее от времени воздействие на мембрану. Как и ожидалось для низкочастотной мембраны, при увеличении значений временной частоты f t (стрелки), V m все меньше и меньше следует за колебаниями V e . B , Влияние зависящего от времени гармонического возбуждения на В м , как описано через нормализованное отклонение β( В м ). Пока β( V m ) ≈ 0, отклик мембраны остается квазистационарным. Как только β отклоняется от нуля, фильтрация нижних частот влияет на весь процесс. Результаты показаны для базального дендрита (крестики), сомы (кружки), проксимального апикального дендрита (квадраты), медиального апикального дендрита (ромбы) и дистального апикального дендрита (9).0322 x
Как и ожидалось для низкочастотной мембраны, при увеличении значений временной частоты f t (стрелки), V m все меньше и меньше следует за колебаниями V e . B , Влияние зависящего от времени гармонического возбуждения на В м , как описано через нормализованное отклонение β( В м ). Пока β( V m ) ≈ 0, отклик мембраны остается квазистационарным. Как только β отклоняется от нуля, фильтрация нижних частот влияет на весь процесс. Результаты показаны для базального дендрита (крестики), сомы (кружки), проксимального апикального дендрита (квадраты), медиального апикального дендрита (ромбы) и дистального апикального дендрита (9).0322 x  β( В м ) также показано для случая неразветвленного кабеля (красная линия) для сравнения.
β( В м ) также показано для случая неразветвленного кабеля (красная линия) для сравнения. При увеличении (2π f t τ m ) 1/2 происходит линейный рост β( V m ). Когда (2π f t τ m ) 1/2 становится большим, отклонения от стационарности становятся зависимыми от локальной морфологии. Например, хотя общее снижение β( V m ) составляет примерно 40% в медиальном апикальном дендрите, оно достигает 75% в базальных дендритах. В целом эти результаты хорошо согласуются с теоретическими и экспериментальными исследованиями (Свирскис и др., 1997). Для сравнения, β( В м ) также показано для случая неразветвленного кабеля, описанного в предыдущем абзаце (красная линия). Для того же (2π f t τ m ) 1/2 , возникают секционные различия в β( V m ), которые объясняются, во-первых, морфологическими особенностями каждого разреза и, во-вторых, разность в размахе индуцированных В м — отклонение для стационарного случая по каждому сечению (рис.
При увеличении (2π f t τ m ) 1/2 происходит линейный рост β( V m ). Когда (2π f t τ m ) 1/2 становится большим, отклонения от стационарности становятся зависимыми от локальной морфологии. Например, хотя общее снижение β( V m ) составляет примерно 40% в медиальном апикальном дендрите, оно достигает 75% в базальных дендритах. В целом эти результаты хорошо согласуются с теоретическими и экспериментальными исследованиями (Свирскис и др., 1997). Для сравнения, β( В м ) также показано для случая неразветвленного кабеля, описанного в предыдущем абзаце (красная линия). Для того же (2π f t τ m ) 1/2 , возникают секционные различия в β( V m ), которые объясняются, во-первых, морфологическими особенностями каждого разреза и, во-вторых, разность в размахе индуцированных В м — отклонение для стационарного случая по каждому сечению (рис. 5, второй столбец). На проксимальных участках (толстые тросы, хорошее выравнивание) β( V m ) затухает меньше, чем на участках, в которых тросы тонкие (дистально-апикальные) или плохо ориентированные (базальные). Эти результаты показывают, что для типичного τ m значений [5 мс ≤ τ m ≤ 50 мс (Koch, 1999)], влияние внеклеточных полей сохраняется для относительно высоких временных частот [т.е. до (2π f t τ m ) 1/2 = 5, что для τ m = 20 мс соответствует f t до 200 Гц].
5, второй столбец). На проксимальных участках (толстые тросы, хорошее выравнивание) β( V m ) затухает меньше, чем на участках, в которых тросы тонкие (дистально-апикальные) или плохо ориентированные (базальные). Эти результаты показывают, что для типичного τ m значений [5 мс ≤ τ m ≤ 50 мс (Koch, 1999)], влияние внеклеточных полей сохраняется для относительно высоких временных частот [т.е. до (2π f t τ m ) 1/2 = 5, что для τ m = 20 мс соответствует f t до 200 Гц].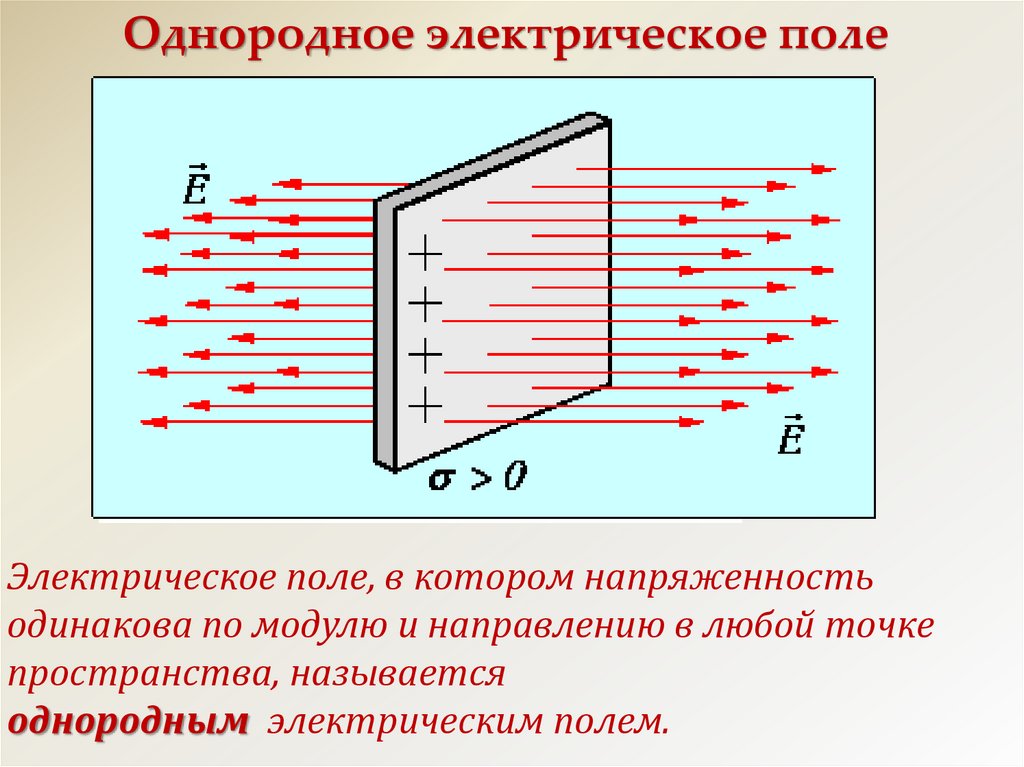 0322 A
0322 A  7 Ai–iv ; латинская нумерация соответствует секции нейронов, как определено на рис. 4 A и в таблице 1). Как и ожидалось, увлечение во внешнее поле зависит от глубины. Хотя в базальном отделе и соме | v m − v остальные | ≤ 0,3 мВ (| v e | ≤ 0,3 мВ) (дополнительный рисунок S6, доступный на www.jneurosci.org в качестве дополнительного материала), влияние внеклеточного поля увеличивается по направлению к дистальным апикальным отделам, что приводит к | v m − v остальные | ≤ 0,7 мВ (| v e | ≤ 0,8 мВ). Пространственные профили v м являются однородными, как и ожидалось, исходя из условия (II). Корзинчатые клетки, аксоаксоны и интернейрон-проксимальное торможение и опосредованное перфорантным путем дистальное возбуждение (Fox, 1989; Ylinen et al., 1995b; Klausberger et al., 2003) приводят к противофазному соотношению между и m в перисоматической области и дистальных отделах (ср.
7 Ai–iv ; латинская нумерация соответствует секции нейронов, как определено на рис. 4 A и в таблице 1). Как и ожидалось, увлечение во внешнее поле зависит от глубины. Хотя в базальном отделе и соме | v m − v остальные | ≤ 0,3 мВ (| v e | ≤ 0,3 мВ) (дополнительный рисунок S6, доступный на www.jneurosci.org в качестве дополнительного материала), влияние внеклеточного поля увеличивается по направлению к дистальным апикальным отделам, что приводит к | v m − v остальные | ≤ 0,7 мВ (| v e | ≤ 0,8 мВ). Пространственные профили v м являются однородными, как и ожидалось, исходя из условия (II). Корзинчатые клетки, аксоаксоны и интернейрон-проксимальное торможение и опосредованное перфорантным путем дистальное возбуждение (Fox, 1989; Ylinen et al., 1995b; Klausberger et al., 2003) приводят к противофазному соотношению между и m в перисоматической области и дистальных отделах (ср.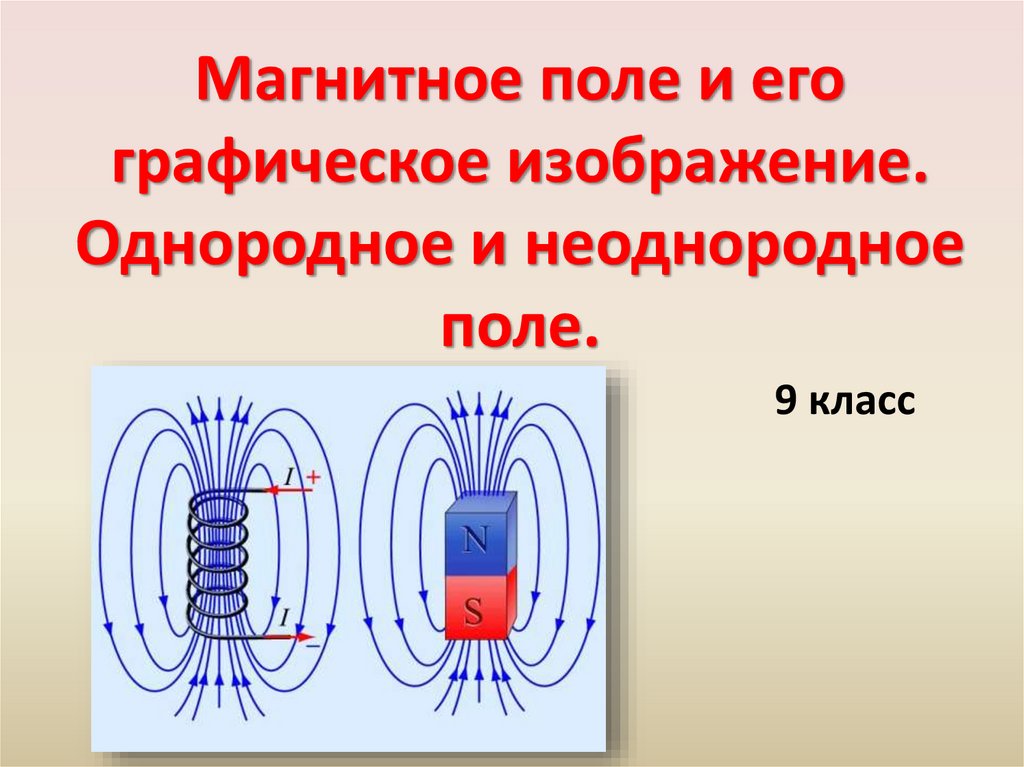 фазу отдельных следов на рис. 7 Aii–iv ).
фазу отдельных следов на рис. 7 Aii–iv ). реалистичный нейрон (рис. 4 A ) и рассчитал результирующую пространственно-временную эволюцию v m (дополнительный раздел 7, доступен на www.jneurosci.org в качестве дополнительного материала). Ai–Aiv , LFP-индуцированные отклонения v м вдоль каждого сечения ( i–iv ) (табл. 1) во время тета. Серые области показывают диапазон, тогда как три отдельные трассы показывают v m − v остальные вдоль каждой секции для t = 0,13 с (черный), 0,22 с (синий) и 0,30 (голубой) и указаны стрелками в верхнем ряду. Периодические флуктуации внеклеточного потенциала индуцируют локализованные флуктуации мембранного потенциала, амплитуда которых увеличивается по направлению к молекулярному лакуновому слою. Противофазное соотношение между соматическими и апикальными дендритными флуктуациями v e приводит к противофазной v m флуктуации; то есть сравнить v m на пике тета (черная стрелка и линии) и впадине тета (синяя стрелка и линии) в соме ( Aii ) и дистальном апикальном отделе ( Aiv ) соответственно .
реалистичный нейрон (рис. 4 A ) и рассчитал результирующую пространственно-временную эволюцию v m (дополнительный раздел 7, доступен на www.jneurosci.org в качестве дополнительного материала). Ai–Aiv , LFP-индуцированные отклонения v м вдоль каждого сечения ( i–iv ) (табл. 1) во время тета. Серые области показывают диапазон, тогда как три отдельные трассы показывают v m − v остальные вдоль каждой секции для t = 0,13 с (черный), 0,22 с (синий) и 0,30 (голубой) и указаны стрелками в верхнем ряду. Периодические флуктуации внеклеточного потенциала индуцируют локализованные флуктуации мембранного потенциала, амплитуда которых увеличивается по направлению к молекулярному лакуновому слою. Противофазное соотношение между соматическими и апикальными дендритными флуктуациями v e приводит к противофазной v m флуктуации; то есть сравнить v m на пике тета (черная стрелка и линии) и впадине тета (синяя стрелка и линии) в соме ( Aii ) и дистальном апикальном отделе ( Aiv ) соответственно .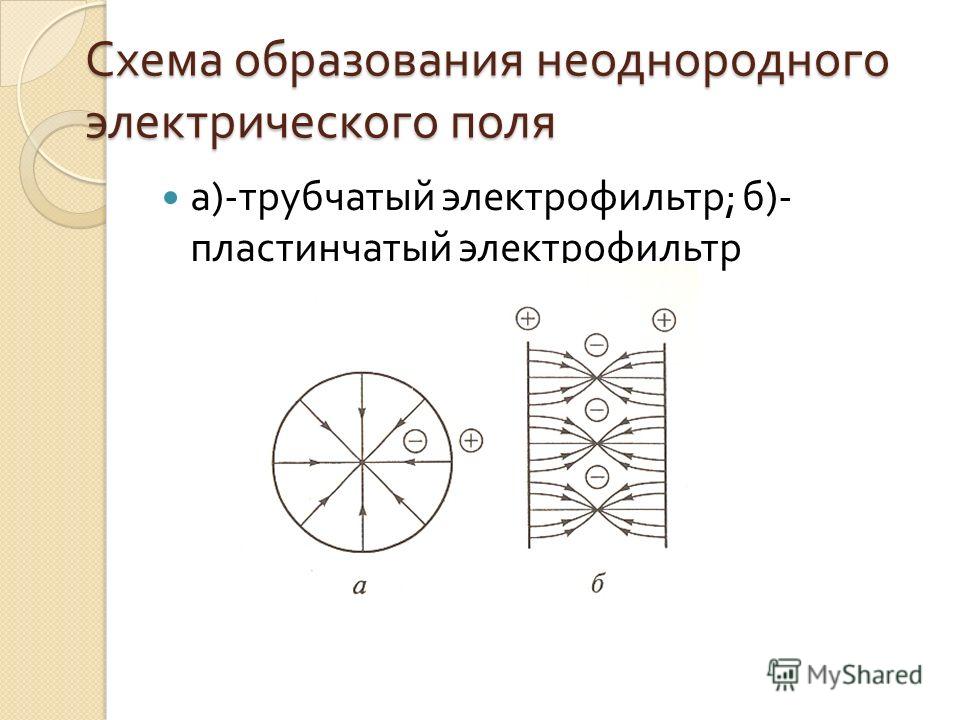 Bi–Biv , LFP-индуцированные изменения v m во время SPW. Три отдельные трассы показывают v m − v rest вдоль каждой секции для t = 0,30 с (черный), 0,38 с (синий) и 0,48 (голубой). Обратите внимание на ярко выраженную противофазность в v m в отрицательности SPW (синяя стрелка и линии) между сомой ( Bii ) и медиальным апикальным отделом ( Biii ). В отличие от тета, потенциал соматической мембраны в значительной степени, но ненадолго, захватывается во время СПВ: сравните 90 322 v 90 323 90 324 м 90 325 отклонений непосредственно перед (черная стрелка и линии) и после (голубая стрелка и линии) СПВ (дополнительные фильмы, доступные на www.jneurosci.org в качестве дополнительного материала).
Bi–Biv , LFP-индуцированные изменения v m во время SPW. Три отдельные трассы показывают v m − v rest вдоль каждой секции для t = 0,30 с (черный), 0,38 с (синий) и 0,48 (голубой). Обратите внимание на ярко выраженную противофазность в v m в отрицательности SPW (синяя стрелка и линии) между сомой ( Bii ) и медиальным апикальным отделом ( Biii ). В отличие от тета, потенциал соматической мембраны в значительной степени, но ненадолго, захватывается во время СПВ: сравните 90 322 v 90 323 90 324 м 90 325 отклонений непосредственно перед (черная стрелка и линии) и после (голубая стрелка и линии) СПВ (дополнительные фильмы, доступные на www.jneurosci.org в качестве дополнительного материала).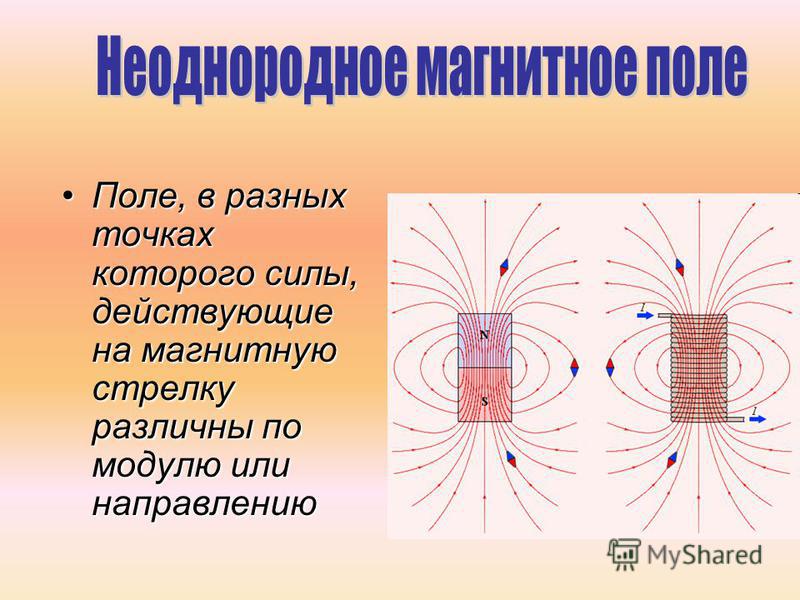 , 1995a). В отсутствие тета нерегулярные SPW продолжительностью 40–120 мс наблюдаются во время завершающего поведения, неподвижности и медленного сна (Buzsaki et al., 1983, 1986; Suzuki and Smith, 1988). Непосредственной причиной СПВ в области СА1 является синхронный разряд большого количества пирамидных нейронов СА3 и последующая почти одновременная деполяризация пирамидных клеток СА1. Во время всплесков SPW диполи образуются в результате возбуждения дендритов и перисоматического торможения, что приводит к потенциалам в несколько милливольт (2–3 мВ в лучистом слое) (Ylinen et al., 19).95а). На рис. 7 B1 показано событие SPW при t = 0,4 с с многоэлектродной решеткой, расположенной в том же положении, что и на рис. 7 A1 . Здесь сток тока (синий цвет на карте; единицы в милливольтах на квадратный миллиметр) появляется в медиальной апикальной области ( y = 250 мкм; лучистый слой) и источник тока (красный цвет на карте) в перисоматической области ( y = 500 мкм, пирамидальный слой).
, 1995a). В отсутствие тета нерегулярные SPW продолжительностью 40–120 мс наблюдаются во время завершающего поведения, неподвижности и медленного сна (Buzsaki et al., 1983, 1986; Suzuki and Smith, 1988). Непосредственной причиной СПВ в области СА1 является синхронный разряд большого количества пирамидных нейронов СА3 и последующая почти одновременная деполяризация пирамидных клеток СА1. Во время всплесков SPW диполи образуются в результате возбуждения дендритов и перисоматического торможения, что приводит к потенциалам в несколько милливольт (2–3 мВ в лучистом слое) (Ylinen et al., 19).95а). На рис. 7 B1 показано событие SPW при t = 0,4 с с многоэлектродной решеткой, расположенной в том же положении, что и на рис. 7 A1 . Здесь сток тока (синий цвет на карте; единицы в милливольтах на квадратный миллиметр) появляется в медиальной апикальной области ( y = 250 мкм; лучистый слой) и источник тока (красный цвет на карте) в перисоматической области ( y = 500 мкм, пирамидальный слой).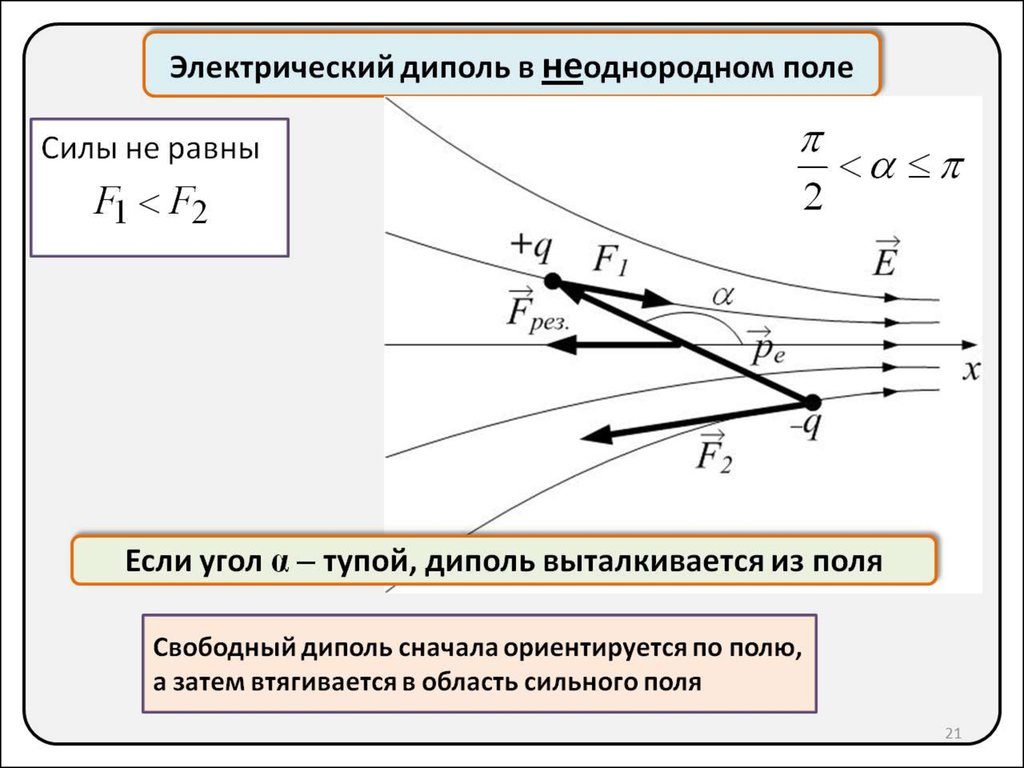 СПВ порождают гораздо большие v м колебаний (амплитуда ≤1,5 мВ), чем во время тета (рис. 7; дополнительный рисунок S6, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Хотя тета-индуцированные эффекты усиливаются по направлению к дистальным апикальным отделам, SPW индуцируют столь же выраженный эффект вдоль всего нейрона, при этом перисоматическая область и средние апикальные отделы особенно вовлечены. Обратите внимание, что во время повторяющейся ритмической активности (тета) максимальный диапазон 90 322 v 90 323 90 324 м 90 325 индуцируется в каждом цикле, в то время как переходное системное событие (SPW) лишь на мгновение вызывает большие v м отклонения. Лучше всего это видно в фильмах, предоставленных в качестве дополнительных материалов (доступных на сайте www.jneurosci.org), в которых ( v m − v rest ) показаны флуктуации вдоль всего нейрона во время тета-анализа.
СПВ порождают гораздо большие v м колебаний (амплитуда ≤1,5 мВ), чем во время тета (рис. 7; дополнительный рисунок S6, доступный на сайте www.jneurosci.org в качестве дополнительного материала). Хотя тета-индуцированные эффекты усиливаются по направлению к дистальным апикальным отделам, SPW индуцируют столь же выраженный эффект вдоль всего нейрона, при этом перисоматическая область и средние апикальные отделы особенно вовлечены. Обратите внимание, что во время повторяющейся ритмической активности (тета) максимальный диапазон 90 322 v 90 323 90 324 м 90 325 индуцируется в каждом цикле, в то время как переходное системное событие (SPW) лишь на мгновение вызывает большие v м отклонения. Лучше всего это видно в фильмах, предоставленных в качестве дополнительных материалов (доступных на сайте www.jneurosci.org), в которых ( v m − v rest ) показаны флуктуации вдоль всего нейрона во время тета-анализа. и эпохи SPW.
и эпохи SPW.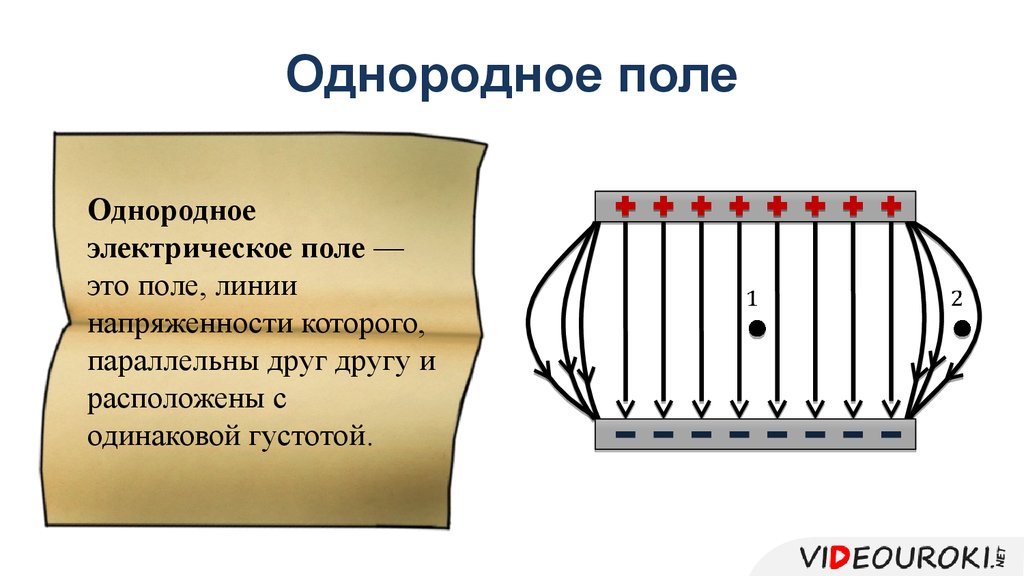 2 A1 , 2 , синяя и красная линии) (Стен-Кнудсен , 1960; Ранк, 1963; Чан и Николсон, 1986). Для пространственно-неоднородных полей воздействие на v м более сложное и зависит от юстировки кабель-поля, а также от трех констант длины: характерной длины внешнего поля (λ s ), длина кабеля ( l ) и электротоническая длина (λ el ).
2 A1 , 2 , синяя и красная линии) (Стен-Кнудсен , 1960; Ранк, 1963; Чан и Николсон, 1986). Для пространственно-неоднородных полей воздействие на v м более сложное и зависит от юстировки кабель-поля, а также от трех констант длины: характерной длины внешнего поля (λ s ), длина кабеля ( l ) и электротоническая длина (λ el ).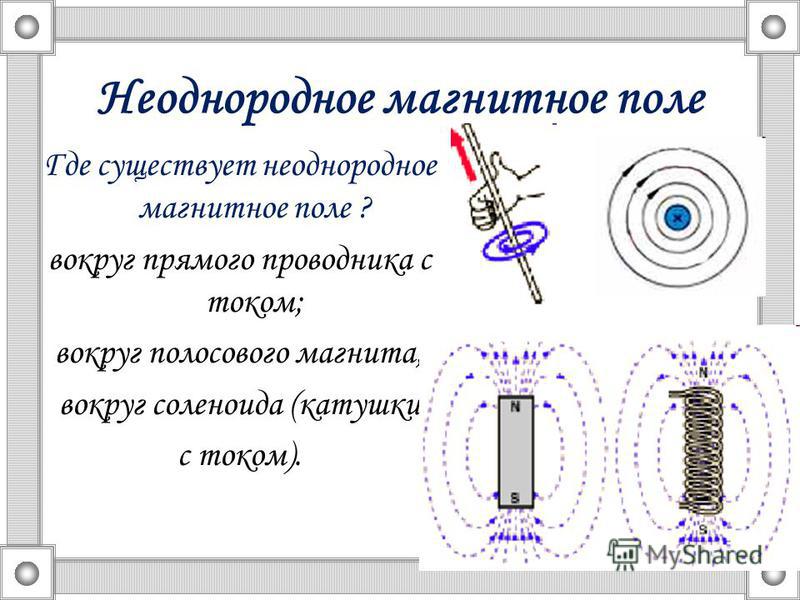 Таким образом, малое λ s может локально привести к очень большим e m и csd m , даже если амплитуда v m остается относительно небольшой. Из теории также следует, что при увеличении диаметра кабеля (т.е. увеличении электротонической длины) влияние пространственно-неоднородных внеклеточных v e на v m возрастает [условие (I)] до тех пор, пока амплитуда ( v m − v rest ) — отклонение вдоль кабеля становится порядка амплитуды v e (дополнительный рис. S2, доступен на www.jneurosci.org в качестве дополнительного материала) и индуцированный мембранный потенциал достигает насыщения. И наоборот, для тонких волокон, таких как аксоны, индуцированный мембранный потенциал становится несущественным.
Таким образом, малое λ s может локально привести к очень большим e m и csd m , даже если амплитуда v m остается относительно небольшой. Из теории также следует, что при увеличении диаметра кабеля (т.е. увеличении электротонической длины) влияние пространственно-неоднородных внеклеточных v e на v m возрастает [условие (I)] до тех пор, пока амплитуда ( v m − v rest ) — отклонение вдоль кабеля становится порядка амплитуды v e (дополнительный рис. S2, доступен на www.jneurosci.org в качестве дополнительного материала) и индуцированный мембранный потенциал достигает насыщения. И наоборот, для тонких волокон, таких как аксоны, индуцированный мембранный потенциал становится несущественным. Хотя эти эффекты получены для стационарных случаев, моделирование пространственно-неоднородного внешнего потенциала в зависимости от времени ясно указывает на то, что эти события сохраняются для относительно высоких временных частот (<200 Гц; эффект ослабляется при увеличении временной частоты). Следовательно, наши результаты применимы к (пространственно) произвольно сложным внешним полям (и геометрии нейронов), даже когда эти поля меняются во времени. Таким образом, они имеют отношение ко всем нейронам, встроенным в электрически проводящую внеклеточную жидкость (Logothetis et al., 2007).
Хотя эти эффекты получены для стационарных случаев, моделирование пространственно-неоднородного внешнего потенциала в зависимости от времени ясно указывает на то, что эти события сохраняются для относительно высоких временных частот (<200 Гц; эффект ослабляется при увеличении временной частоты). Следовательно, наши результаты применимы к (пространственно) произвольно сложным внешним полям (и геометрии нейронов), даже когда эти поля меняются во времени. Таким образом, они имеют отношение ко всем нейронам, встроенным в электрически проводящую внеклеточную жидкость (Logothetis et al., 2007). Активность LFP, представленная на рисунке 7, измеряется относительно редко (расстояние между электродами 100 мкм). Пространственно более плотные записи давали бы более точную информацию о флуктуациях поля вдоль оси мест регистрации (или, в идеале, в трех измерениях) и позволяли бы исследовать эндогенную внеклеточную активность <100 мкм. Несмотря на это, то, что ясно показано на рис. 7 (и на дополнительных рис. S6–S9)., доступный на www.jneurosci.org в качестве дополнительного материала), состоит в том, что профили, индуцированные v m во время тета- и SPW-активности in vivo , заметно отличаются от тех, которые обычно индуцируются вдоль параллельных пластин (как на постоянном, так и на переменном токе) (Chan и Николсон, 1986). Во время внутригиппокампальной активности диполи, индуцированные перисоматическим торможением и возбуждением дендритов, в сочетании с ламинарной структурой области СА1 приводят к пространственно неоднородному внеклеточному полю вдоль оси соматодендритов, что, в свою очередь, приводит к локализации специфичных v m колебания.
Активность LFP, представленная на рисунке 7, измеряется относительно редко (расстояние между электродами 100 мкм). Пространственно более плотные записи давали бы более точную информацию о флуктуациях поля вдоль оси мест регистрации (или, в идеале, в трех измерениях) и позволяли бы исследовать эндогенную внеклеточную активность <100 мкм. Несмотря на это, то, что ясно показано на рис. 7 (и на дополнительных рис. S6–S9)., доступный на www.jneurosci.org в качестве дополнительного материала), состоит в том, что профили, индуцированные v m во время тета- и SPW-активности in vivo , заметно отличаются от тех, которые обычно индуцируются вдоль параллельных пластин (как на постоянном, так и на переменном токе) (Chan и Николсон, 1986). Во время внутригиппокампальной активности диполи, индуцированные перисоматическим торможением и возбуждением дендритов, в сочетании с ламинарной структурой области СА1 приводят к пространственно неоднородному внеклеточному полю вдоль оси соматодендритов, что, в свою очередь, приводит к локализации специфичных v m колебания.
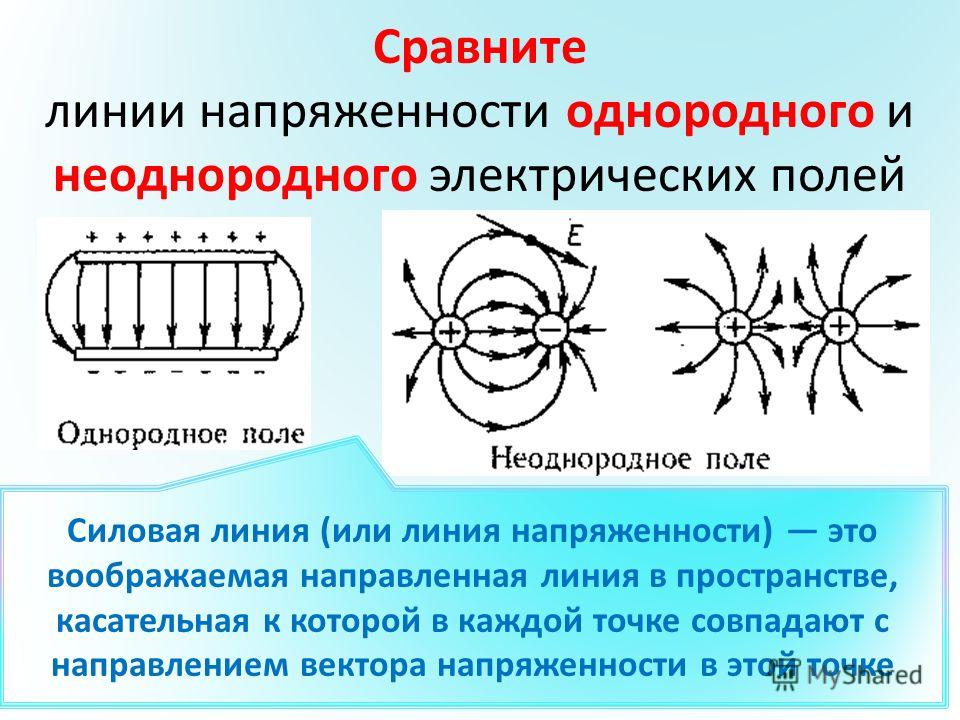
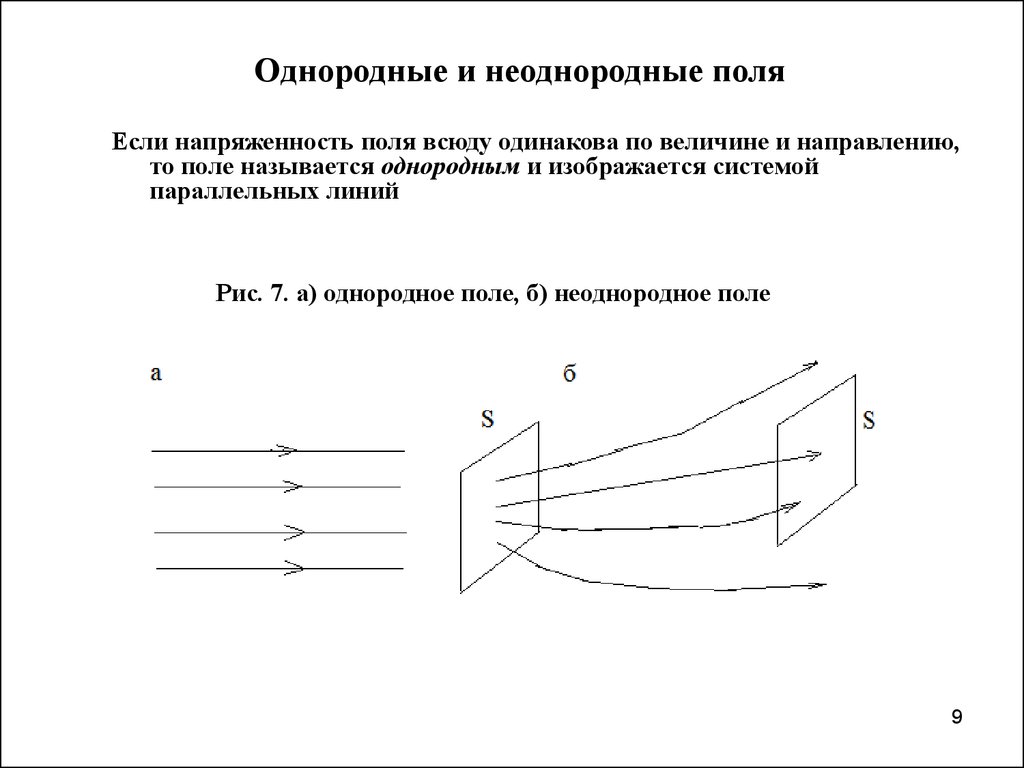 , 2006, 2009). Тем не менее, численное моделирование показывает, что, в отличие от подпорогового и перипорогового диапазона (см. следующий раздел), внеклеточные электрические поля очень мало влияют на мембрану нейрона во время потенциала действия (Holt, 1997; Holt and Koch, 1999) (C.A. Anastassiou). , К. Сарма, К. Кох, неопубликованные наблюдения). Наконец, экспериментальные данные по коре ствола мыши показали, что, несмотря на когерентные колебания v m двух соседних нейронов и наличие эндогенного внеклеточного поля, активность потенциала действия была несопоставимой между двумя нейронами (Poulet and Petersen, 2008). ). Следовательно, близость и когерентность v m флуктуации не обязательно подразумевают когерентную пиковую активность в физиологических условиях. Однако во время сильно синхронизированной спайковой активности, такой как эпилептические разряды или сильные вызванные реакции, большие и локализованные внеклеточные токи, вызванные популяционным спайком, могут эффективно индуцировать спайки в подпороговых нейронах или даже в близлежащих окончаниях аксонов (Noebels and Prince, 1978).
, 2006, 2009). Тем не менее, численное моделирование показывает, что, в отличие от подпорогового и перипорогового диапазона (см. следующий раздел), внеклеточные электрические поля очень мало влияют на мембрану нейрона во время потенциала действия (Holt, 1997; Holt and Koch, 1999) (C.A. Anastassiou). , К. Сарма, К. Кох, неопубликованные наблюдения). Наконец, экспериментальные данные по коре ствола мыши показали, что, несмотря на когерентные колебания v m двух соседних нейронов и наличие эндогенного внеклеточного поля, активность потенциала действия была несопоставимой между двумя нейронами (Poulet and Petersen, 2008). ). Следовательно, близость и когерентность v m флуктуации не обязательно подразумевают когерентную пиковую активность в физиологических условиях. Однако во время сильно синхронизированной спайковой активности, такой как эпилептические разряды или сильные вызванные реакции, большие и локализованные внеклеточные токи, вызванные популяционным спайком, могут эффективно индуцировать спайки в подпороговых нейронах или даже в близлежащих окончаниях аксонов (Noebels and Prince, 1978).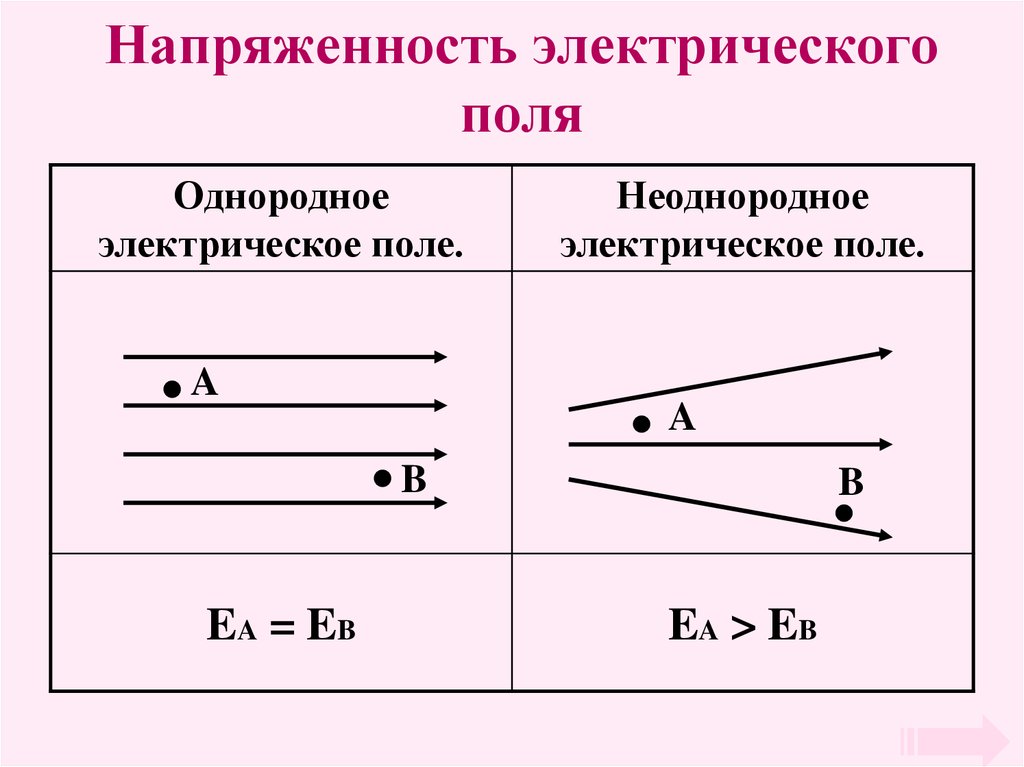
 Применяя эти значения к нашей модели, мы обнаружили лишь небольшие изменения в результатах рис. 7 (данные не показаны). Фактически диапазон отклонений v m и e m увеличился, хотя и незначительно. Таким образом, результаты этих симуляций показывают, что поведение, наблюдаемое на рисунке 7, ожидается в естественных условиях .
Применяя эти значения к нашей модели, мы обнаружили лишь небольшие изменения в результатах рис. 7 (данные не показаны). Фактически диапазон отклонений v m и e m увеличился, хотя и незначительно. Таким образом, результаты этих симуляций показывают, что поведение, наблюдаемое на рисунке 7, ожидается в естественных условиях .
 ± = В ± — В REST > 0 — степень гиперполяризации (Δ В ± <0) или детекализация (Δ ± <0) или детекаларизация (Δ ± <0) (Δ depolarization ( ± <0) (Δ В ± <0) (Δ В ± <0). мембраны, связанной с фоновым синаптическим входом. Уравнение 8 является мерой влияния ( v m − v отдых ) — отклонения, связанные с наличием внеклеточного поля на активных мембранах в отношении времени потенциала действия. Для постоянных v m − v покоя и Δ v thresh влияние внеклеточных полей на пиковую фазу Δψ значительно возрастает по мере того, как мембрана деполяризуется синаптическим входом (дополнительный рис. 10). , доступный на www.jneurosci.org в качестве дополнительного материала; мы также показываем, что эта эмпирическая модель согласуется с численным моделированием пирамидных нейронов СА1 с потенциал-зависимой проводимостью, вызывающей потенциалы действия).
± = В ± — В REST > 0 — степень гиперполяризации (Δ В ± <0) или детекализация (Δ ± <0) или детекаларизация (Δ ± <0) (Δ depolarization ( ± <0) (Δ В ± <0) (Δ В ± <0). мембраны, связанной с фоновым синаптическим входом. Уравнение 8 является мерой влияния ( v m − v отдых ) — отклонения, связанные с наличием внеклеточного поля на активных мембранах в отношении времени потенциала действия. Для постоянных v m − v покоя и Δ v thresh влияние внеклеточных полей на пиковую фазу Δψ значительно возрастает по мере того, как мембрана деполяризуется синаптическим входом (дополнительный рис. 10). , доступный на www.jneurosci.org в качестве дополнительного материала; мы также показываем, что эта эмпирическая модель согласуется с численным моделированием пирамидных нейронов СА1 с потенциал-зависимой проводимостью, вызывающей потенциалы действия).
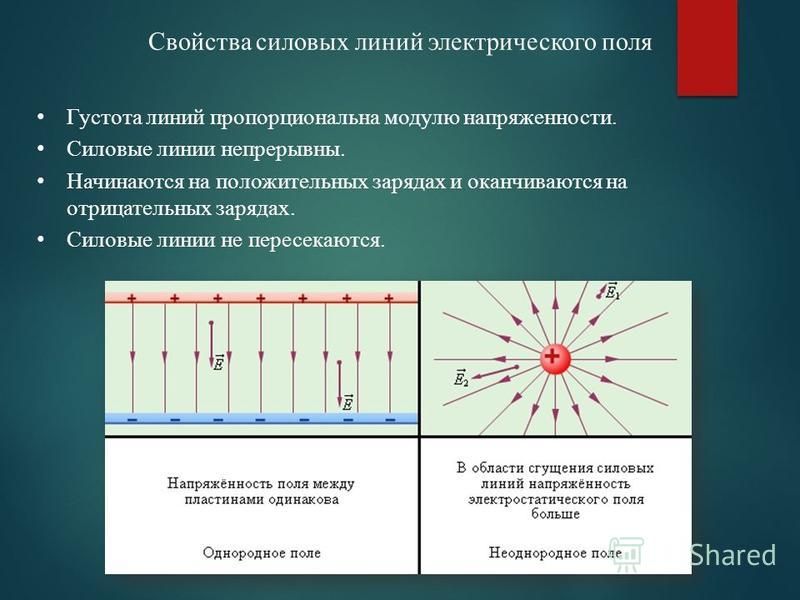 7 Aiv , синяя линия), тогда как предсказанная фазовая задержка Δψ = 2,5° =, 2,5° для Δ v ± = 2 и 12 мВ, Δψ = −14 и −60° соответственно. Следовательно, во время тета внеклеточное поле оказывает более заметное влияние на синхронизацию спайков в дистальной апикальной области (молекулярный лакунозный слой), чем в соме (пирамидный слой). Было высказано предположение, что наличие и время таких дендритных потенциалов действия во время тета важно для кодирования места (Kamondi et al., 19).98).
7 Aiv , синяя линия), тогда как предсказанная фазовая задержка Δψ = 2,5° =, 2,5° для Δ v ± = 2 и 12 мВ, Δψ = −14 и −60° соответственно. Следовательно, во время тета внеклеточное поле оказывает более заметное влияние на синхронизацию спайков в дистальной апикальной области (молекулярный лакунозный слой), чем в соме (пирамидный слой). Было высказано предположение, что наличие и время таких дендритных потенциалов действия во время тета важно для кодирования места (Kamondi et al., 19).98).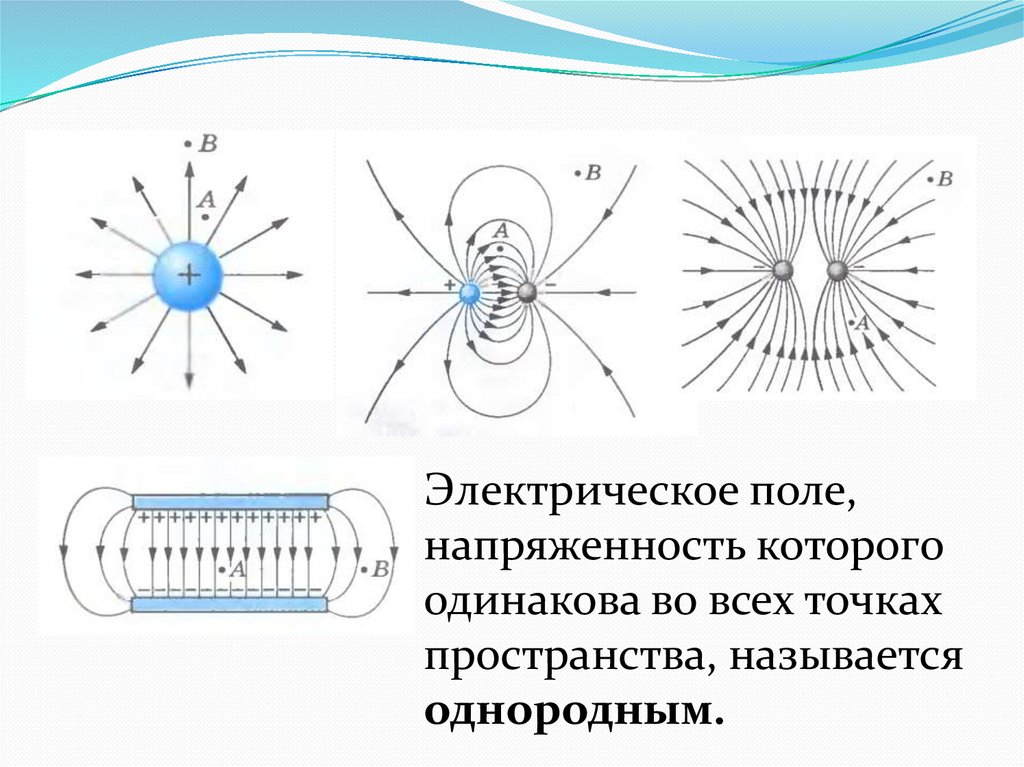 , 19).95a), так что изменения в v m , показанные в правой колонке рис. 7, объясняются исключительно внеклеточным эффектом SPW.] Кроме того, внутриклеточные записи выявили деполяризацию ~ 5 мВ в соме во время SPW. из-за массивного коллатерального возбуждения Шаффера (Ylinen et al., 1995a). Следовательно, из уравнения 8 с v m — v отдых = -1 мВ (рис. 7 Bii ) и Δ v ± = 5 мВ изменение времени соматического спайка период пульсации становится Δψ = -36°. Одновременно массивный возбуждающий вход в апикальные дендриты вызывает еще большую локальную деполяризацию (Ylinen et al., 19).95а), что в сочетании с вызванной извне деполяризацией (∼1 мВ) (рис. 7 Aiii ) привело бы к дополнительному продвижению дендритного спайка. Например, для v m − v rest = 1 мВ (рис. 7 Biv , синяя линия) и Δ v ± = 10 мВ, 7 Δψ Эти прогнозы согласуются с предположением Гаспарини и Маги (2006) о том, что чрезвычайно своевременное появление потенциала действия, наблюдаемое во время SPW, требует задействования нелинейных интегративных свойств посредством возникновения дендритных потенциалов действия (Losonczy and Magee, 2006).
, 19).95a), так что изменения в v m , показанные в правой колонке рис. 7, объясняются исключительно внеклеточным эффектом SPW.] Кроме того, внутриклеточные записи выявили деполяризацию ~ 5 мВ в соме во время SPW. из-за массивного коллатерального возбуждения Шаффера (Ylinen et al., 1995a). Следовательно, из уравнения 8 с v m — v отдых = -1 мВ (рис. 7 Bii ) и Δ v ± = 5 мВ изменение времени соматического спайка период пульсации становится Δψ = -36°. Одновременно массивный возбуждающий вход в апикальные дендриты вызывает еще большую локальную деполяризацию (Ylinen et al., 19).95а), что в сочетании с вызванной извне деполяризацией (∼1 мВ) (рис. 7 Aiii ) привело бы к дополнительному продвижению дендритного спайка. Например, для v m − v rest = 1 мВ (рис. 7 Biv , синяя линия) и Δ v ± = 10 мВ, 7 Δψ Эти прогнозы согласуются с предположением Гаспарини и Маги (2006) о том, что чрезвычайно своевременное появление потенциала действия, наблюдаемое во время SPW, требует задействования нелинейных интегративных свойств посредством возникновения дендритных потенциалов действия (Losonczy and Magee, 2006).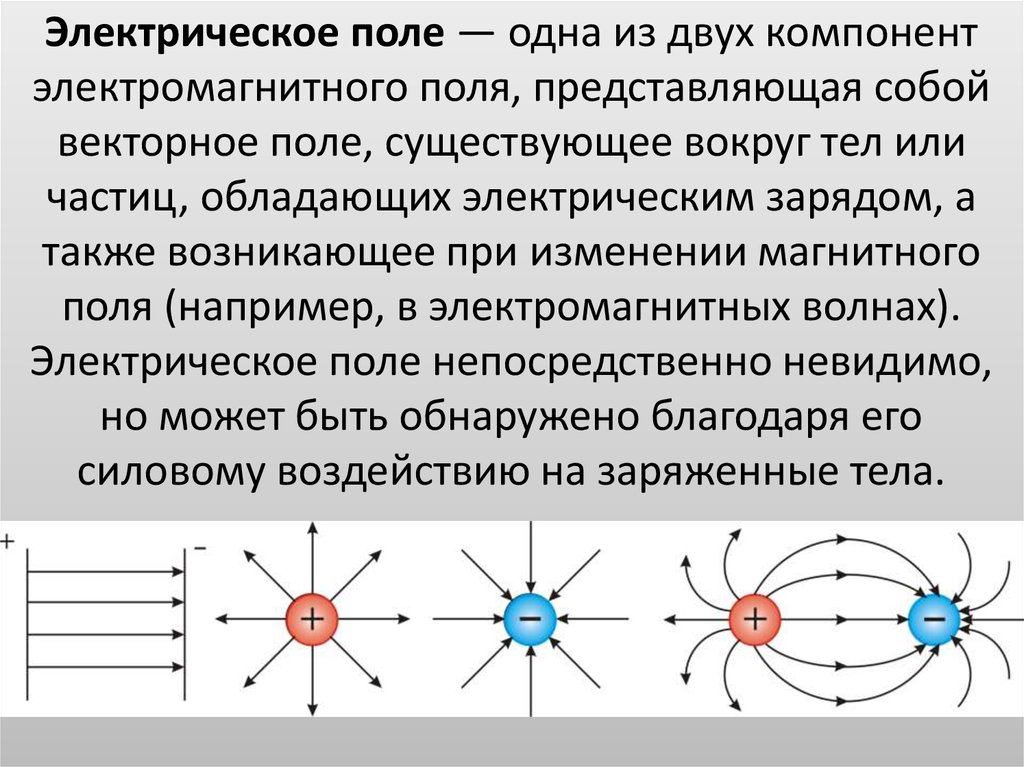 Примечательно, что предсказанное влияние внеклеточного поля на синхронизацию спайков может эффективно синхронизировать дендритные (и, как следствие, последующие соматические) потенциалы действия с LFP и, таким образом, привести к субмиллисекундной точности спайков, обычно наблюдаемой во время SPW. По сравнению с относительно скромными изменениями, вызванными синхронизацией соматических импульсов во время тета (которые могут только «точно настроить» осцилляторы), мы предполагаем, что поля, вызванные SPW, могут оказывать более заметное влияние на синхронизацию соматического и дендритного потенциалов действия.
Примечательно, что предсказанное влияние внеклеточного поля на синхронизацию спайков может эффективно синхронизировать дендритные (и, как следствие, последующие соматические) потенциалы действия с LFP и, таким образом, привести к субмиллисекундной точности спайков, обычно наблюдаемой во время SPW. По сравнению с относительно скромными изменениями, вызванными синхронизацией соматических импульсов во время тета (которые могут только «точно настроить» осцилляторы), мы предполагаем, что поля, вызванные SPW, могут оказывать более заметное влияние на синхронизацию соматического и дендритного потенциалов действия. B. и C.K.). Мы благодарим Simal Ozen, Joshua Milstein и Ueli Rutishauser за идеи и обсуждения, Ted Carnevale за обсуждение численной реализации и помощь с NEURON и Karthik Sarma за численные процедуры и фильмы.
B. и C.K.). Мы благодарим Simal Ozen, Joshua Milstein и Ueli Rutishauser за идеи и обсуждения, Ted Carnevale за обсуждение численной реализации и помощь с NEURON и Karthik Sarma за численные процедуры и фильмы.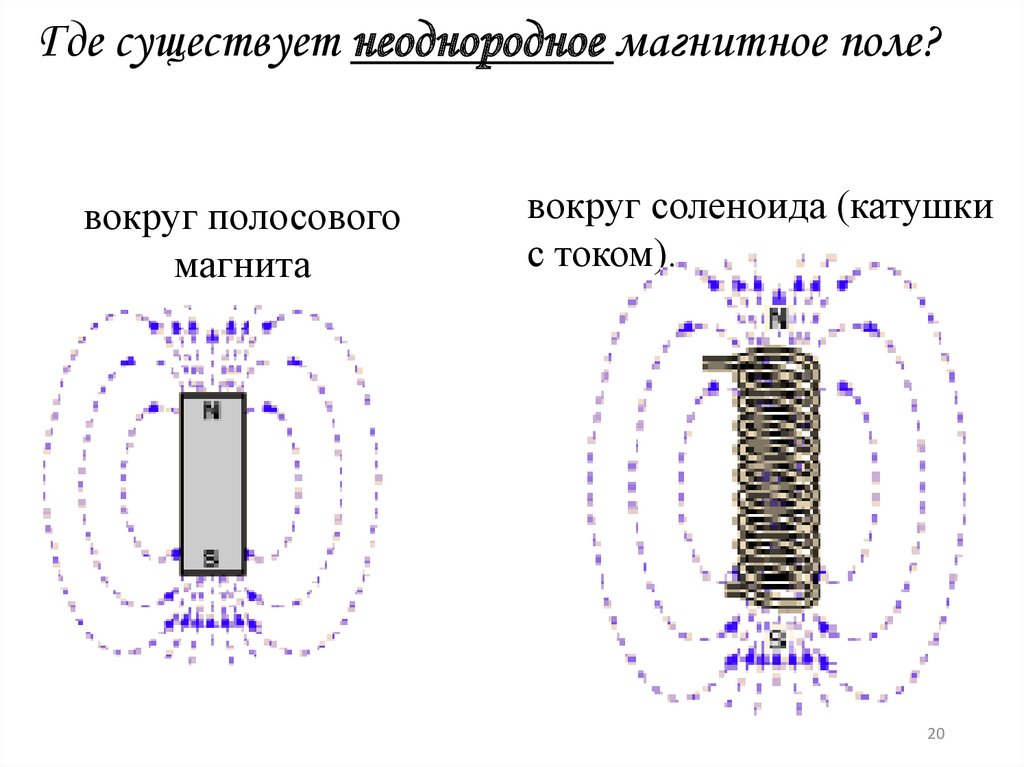
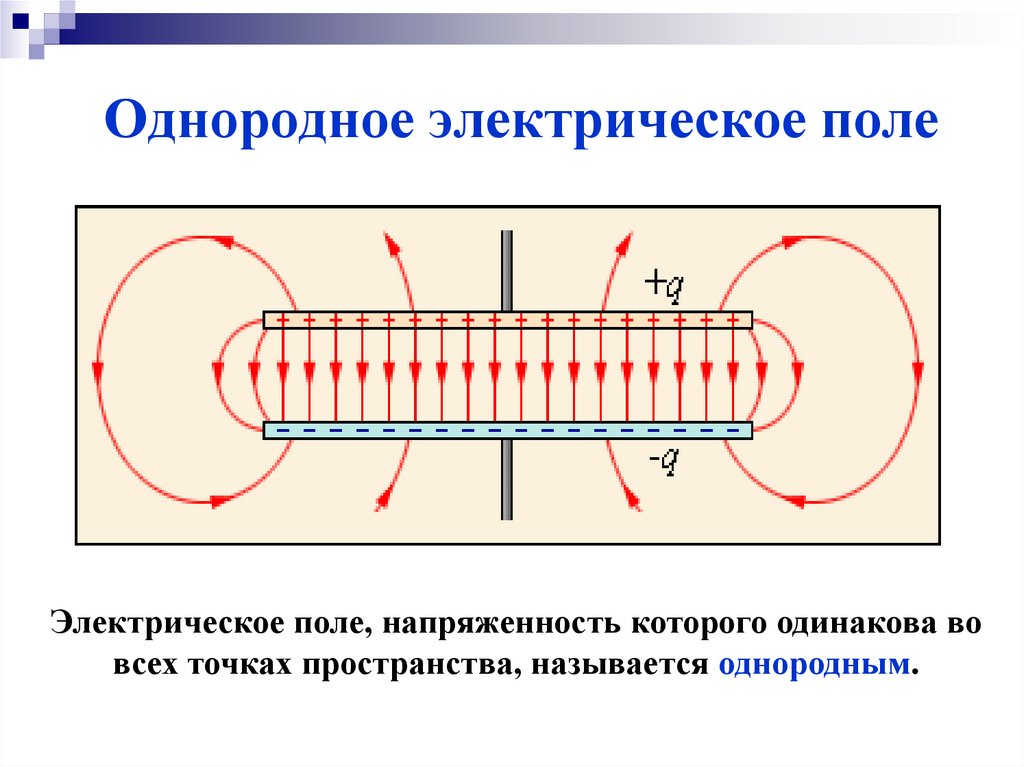 Неврология 38:609–619.
Неврология 38:609–619.  Наука 256:1025–1027.
Наука 256:1025–1027. 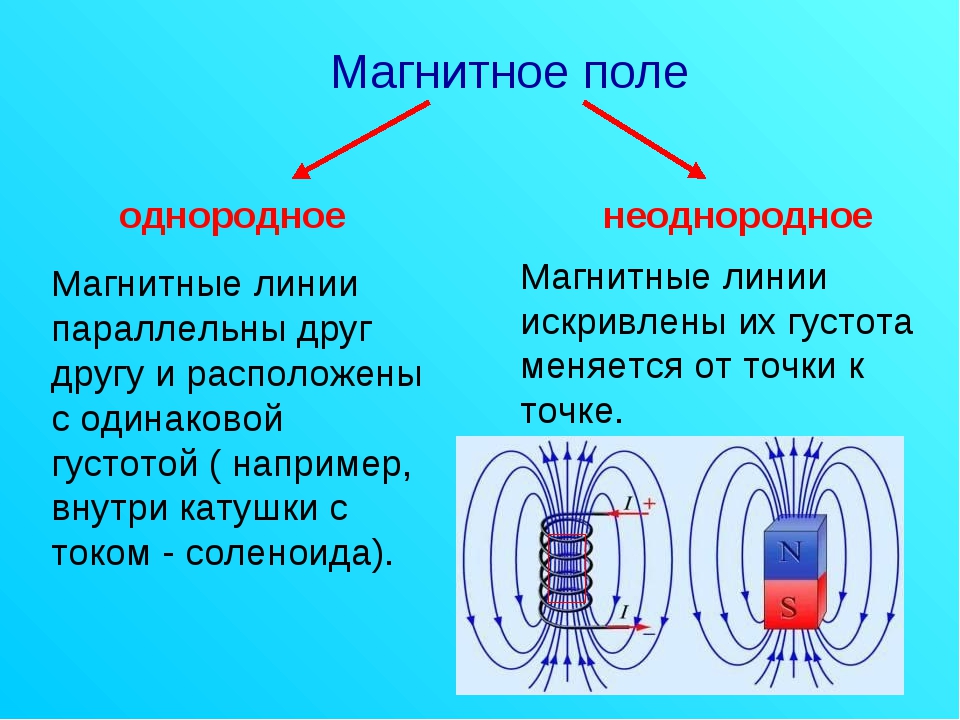 J Physiol 583:555–565.
J Physiol 583:555–565.