Электроемкость конденсатора: формулы и история
Электрический конденсатор является пассивным прибором, который способен накапливать и сохранять электрическую энергию. Он состоит из двух проводящих пластин, разделенных диэлектрическим материалом. Приложение электрических потенциалов различного знака к проводящим пластинам приводит к приобретению ими заряда, который на одной пластине является положительным, а на другой отрицательным. При этом суммарный заряд равен нулю.
В данной статье рассмотрены вопросы истории и определение электроемкости конденсатора.
История изобретения
В октябре 1745 года немецкий ученый Эвальд Георг фон Клейст заметил, что электрический заряд может быть запасен, если соединить с помощью кабеля электростатический генератор и некоторый объем воды, находящийся в стеклянном сосуде. В этом эксперименте рука фон Клейста и вода являлись проводниками, а стеклянный сосуд — электрическим изолятором. После того как ученый коснулся металлической проволоки рукой, произошел мощный разряд, который был намного сильнее, чем разряд электростатического генератора. В результате фон Клейст сделал вывод о существовании запасенной электрической энергии.
В результате фон Клейст сделал вывод о существовании запасенной электрической энергии.
В 1746 году голландский физик Питер ван Мушенбрук изобрел конденсатор, который назвал лейденской бутылкой в честь Лейденского университета, в котором работал ученый. Затем Даниэль Гралат увеличил электроемкость конденсатора, соединив несколько лейденских бутылок.
В 1749 году Бенджамин Франклин исследовал лейденский конденсатор и пришел к выводу, что электрический заряд запасается не в воде, как полагали до этого, а на границе воды и стекла. Благодаря открытию Франклина, лейденские бутылки стали изготавливать, покрывая внутреннюю и внешнюю поверхность стеклянных сосудов металлическими пластинами.
Развитие индустрии
Термин «конденсатор» ввел в употребление Алессандро Вольта в 1782 году. Изначально для изготовления изоляторов электрических конденсаторов использовали такие материалы, как стекло, фарфор, слюду и обычную бумагу. Так, радиотехник Гульельмо Маркони использовал для своих аппаратов-передатчиков фарфоровые конденсаторы, а для приемников — небольшие конденсаторы с изолятором слюды, которые были изобретены в 1909 году — до Второй мировой войны в США именно они были наиболее распространенными.
Первый электролитический конденсатор был изобретен в 1896 году и представлял собой электролит с алюминиевыми электродами. Бурное развитие электроники началось только после изобретения в 1950 году танталового миниатюрного конденсатора с твердым электролитом.
Во время Второй мировой войны в результате развития химии пластмасс стали появляться конденсаторы, в которых роль изолятора была отведена тонким полимерным пленкам.
Наконец, в 50-60 годах развивается индустрия суперконденсаторов, которые обладают несколькими рабочими проводящими поверхностями, благодаря чему электроемкость конденсаторов повышается на 3 порядка в сравнении с ее значением для обычных конденсаторов.
Понятие об электроемкости конденсатора
Электрический заряд, запасенный в пластине конденсатора, пропорционален напряжению электрического поля, которое существует между пластинами прибора. При этом коэффициент пропорциональности называется электроемкостью плоского конденсатора. В СИ (международная система единиц) электроемкость, как физическая величина, измеряется в фарадах. Один фарад — это такая электроемкость конденсатора, напряжение между пластинами которого равно 1 вольт при запасенном заряде в 1 кулон.
Один фарад — это такая электроемкость конденсатора, напряжение между пластинами которого равно 1 вольт при запасенном заряде в 1 кулон.
Электроемкость в 1 фарад является огромной, и на практике в электротехнике и электронике обычно пользуются конденсаторы с емкостями порядка пикофарада, нанофарада и микрофарада. Исключением являются только суперконденсаторы, которые состоят из активированного угля, благодаря чему увеличивается рабочая площадь прибора. Они могут достигать емкостей в тысячи фарадов и используются для питания прототипов электромобилей.
Таким образом, электроемкость конденсатора равна: C = Q1/(V1-V2). Здесь C — электроемкость, Q1 — электрический заряд, запасенный в одной пластине конденсатора, V1-V2 — разница между электрическими потенциалами пластин.
Формула для емкости плоского конденсатора имеет вид: C = e0eS/d. Здесь e0 и e — универсальная диэлектрическая постоянная и диэлектрическая постоянная материала изолятора S — площадь пластин, d — расстояние между пластинами. Эта формула позволяет понять, как изменится электроемкость конденсатора, если изменить материал изолятора, расстояние между пластинами или их площадь.
Эта формула позволяет понять, как изменится электроемкость конденсатора, если изменить материал изолятора, расстояние между пластинами или их площадь.
Виды используемых диэлектриков
Для изготовления конденсаторов используют различные типы диэлектриков. Наиболее популярными являются следующие:
- Воздух. Эти конденсаторы представляют собой две пластины из проводящего материала, которые разделены прослойкой воздуха и помещены в стеклянный корпус. Электроемкость воздушных конденсаторов невелика. Обычно они используются в радиотехнике.
- Слюда. Свойства слюды (способность разделяться на тонкие пластины и выдерживать высокие температуры) являются подходящими для ее использования в качестве изоляторов в конденсаторах.
- Бумага. Для защиты от намокания используют парафинированную или лакированную бумагу.
Запасенная энергия
По мере того, как увеличивается разность потенциалов между пластинами конденсатора, прибор запасает электрическую энергию благодаря присутствию внутри него электрического поля. Если разность потенциалов между пластинами уменьшается, то конденсатор разряжается, отдавая энергию в электрическую цепь.
Если разность потенциалов между пластинами уменьшается, то конденсатор разряжается, отдавая энергию в электрическую цепь.
Математически электрическую энергию, которая запасена в конденсаторе произвольного типа, можно выразить следующей формулой: E = ½C(V2-V1)2, где V2 и V1 — конечное и начальное напряжение между пластинами.
Заряд и разряд
Если конденсатор подсоединить в электрическую цепь с резистором и каким-либо источником электрического тока, тогда по цепи пойдет ток, и конденсатор начнет заряжаться. Как только он будет полностью заряжен, электрический ток в цепи прекратится.
Если заряженный конденсатор подсоединить параллельно резистору, то от одной пластины к другой через резистор потечет ток, который будет продолжаться до тех пор, пока прибор полностью не разрядится. В данном случае направление тока разряда будет противоположно направлению течения электрического тока, когда прибор заряжался.
Заряд и разряд конденсатора подчиняется экспоненциальной зависимости от времени. Например, напряжение между пластинами конденсатора при его разряде изменяется согласно следующей формуле: V(t) = Vie-t/(RC), где Vi — начальное напряжение на конденсаторе, R — электрическое сопротивление в цепи, t — время разряда.
Например, напряжение между пластинами конденсатора при его разряде изменяется согласно следующей формуле: V(t) = Vie-t/(RC), где Vi — начальное напряжение на конденсаторе, R — электрическое сопротивление в цепи, t — время разряда.
Объединение в электрической цепи
Чтобы определить электроемкость конденсаторов, которые имеются в электрической цепи, следует вспомнить, что они могут объединяться двумя различными способами:
- Последовательное соединение: 1/Cs = 1/C1+1/C2+…+1/Cn.
- Параллельное соединение: Cs = C1+C2+…+Cn.
Cs — суммарная емкость n конденсаторов. Суммарная электроемкость конденсаторов определяется по формулам, аналогичным математическим выражениям для суммарного электрического сопротивления, только формула для последовательного соединения приборов справедлива для параллельного соединения резисторов и наоборот.
Что такое электроемкость конденсатора? :: SYL.ru
Электроемкость конденсатора — это его способность накапливать электрический заряд. Формула электроемкости следующая.
C=q/U
Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах.
В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию.
Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся.
То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров.
Формула будет следующей
Только эти параметры влияют на реальную электроемкость конденсатора.
На любом конденсаторе есть маркировка с техническими параметрами.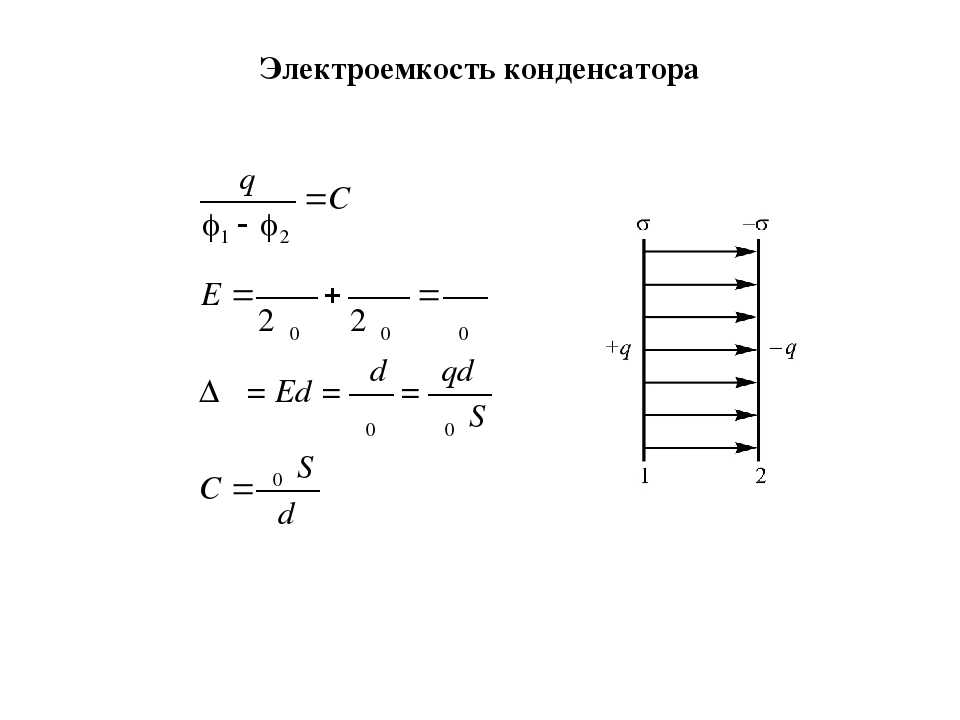
Разобраться несложно. Достаточно минимальных знаний по электричеству.
Соединение конденсаторов
Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения.
Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается.
При подключении последовательно заряд размещается равномерно. Он будет везде одинаков — как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.
Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде.
Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет.
Если емкость, то огромного напряжения не будет.
Виды конденсаторов
Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме.
Разумеется, емкость вычисляется у всех по-разному.
Электроемкость плоского конденсатора
Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других.
Здесь всё зависит от физических параметров и среды между пластинами.
Сферический конденсатор
Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса.
Цилиндрический конденсатор
В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра.
Повреждения в конденсаторах
Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов.
Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены.
Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу.
Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества.
Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого).
Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может.
Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали.
Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.
Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт.
Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи.
Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя.
Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным.
Меры предосторожности
Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут «вылиться» электроны в конденсаторе? Ведь он запечатан полностью!
Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет.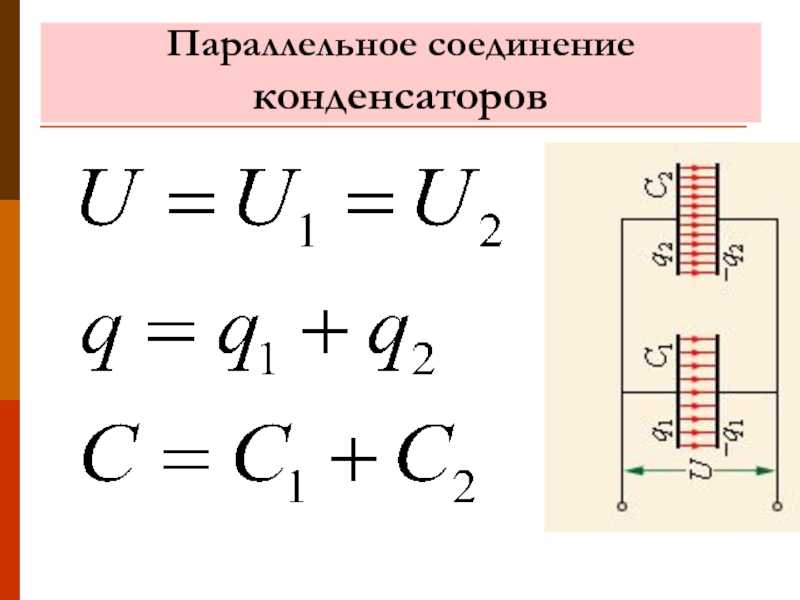 Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.
Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.
Будьте аккуратны!
31
Электроемкостью (емкостью) C уединенного изолированного проводника называется физическая величина, равная отношению изменения заряда проводника q к изменению его потенциала f: C = Dq/Df.
Электроемкость уединенного проводника зависит только от его формы и размеров, а также от окружающей его диэлектрической среды (e). Единица измерения емкости в системе СИ называется Фарадой. Фарада (Ф) — это емкость такого уединенного проводника, потенциал которого повышается на 1 Вольт при сообщении ему заряда в 1 Кулон. 1 Ф = 1 Кл/1 В.
Конденсатором
называют систему двух разноименно
заряженных проводников, разделенных
диэлектриком (например, воздухом).
Свойство
конденсаторов накапливать и сохранять
электрические заряды и связанное
с ними электрическое поле характеризуется
величиной, называемой электроемкостью
конденсатора.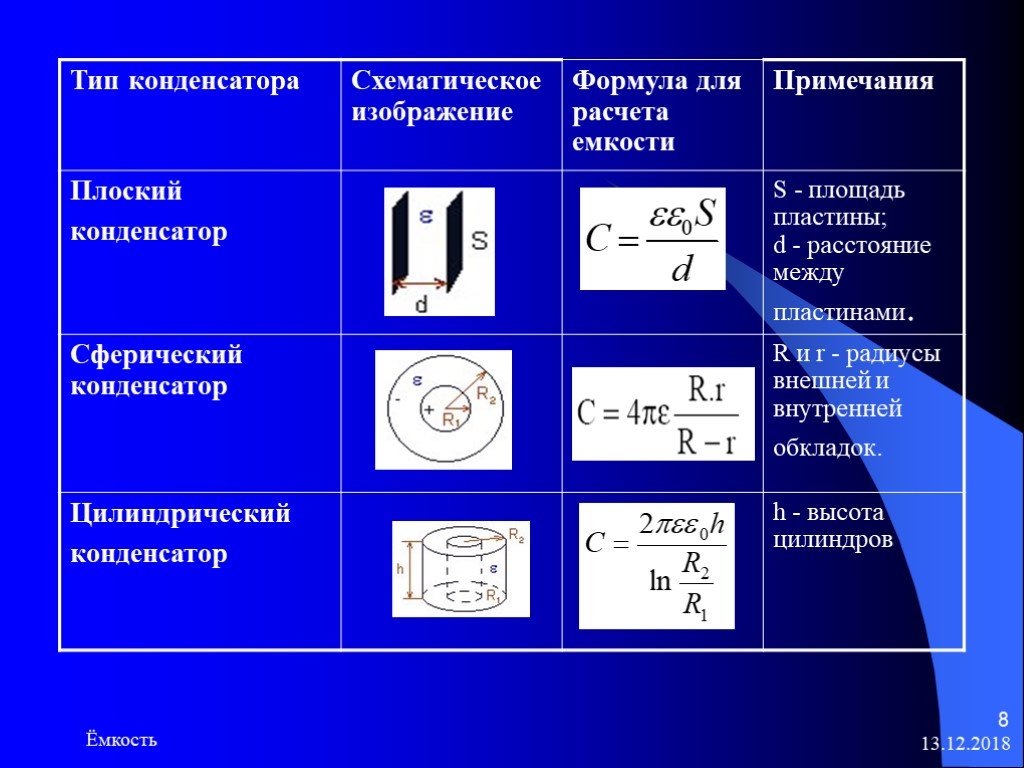 Электроемкость конденсатора
равна отношению заряда одной из пластин
Q к напряжению между ними U:
C =
Q/U.
Электроемкость конденсатора
равна отношению заряда одной из пластин
Q к напряжению между ними U:
C =
Q/U.
В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими и цилиндрическими. Формулы для расчета емкостей этих конденсаторов приведены в таблице.
Соединение конденсаторов в батареи. На практике конденсаторы часто соединяют в батареи — последовательно или параллельно.
При параллельном соединении напряжение на всех обкладках одинаковое U1 = U2 = U3 = U = e, а емкость батареи равняется сумме емкостей отдельных конденсаторов C = C1 + C2 + C3.
При последовательном соединении заряд на обкладках всех конденсаторов одинаков Q1 = Q2 = Q3, а напряжение батареи равняется сумме напряжений отдельных конденсаторов U = U1 + U2 + U3.
Емкость всей системы последовательно соединенных конденсаторов рассчитывается из соотношения: 1/C = U/Q = 1/C1 + 1/C2 + 1/C3.
Емкость
батареи последовательно соединенных
конденсаторов всегда меньше, чем емкость
каждого из этих конденсаторов
в отдельности.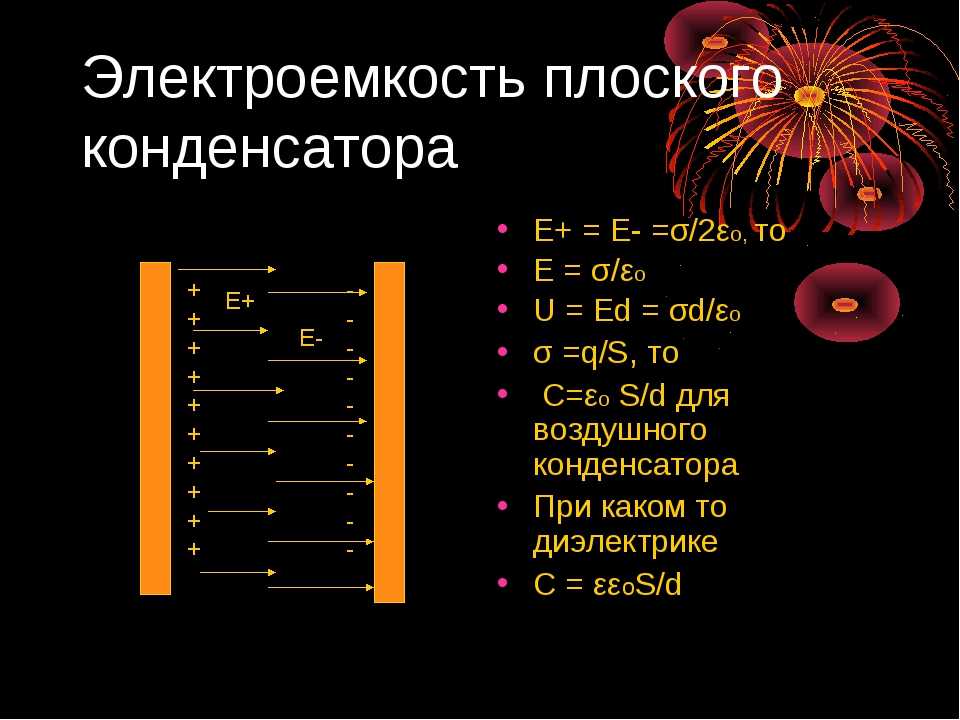 Энергия электростатического
поля.
Энергия заряженного плоского
конденсатора Eк равна работе A, которая
была затрачена при его зарядке, или
совершается при его разрядке.
A =
CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку
напряжение на конденсаторе может
быть рассчитано из соотношения:
U =
E*d,
где E — напряженность поля между
обкладками конденсатора,
d —
расстояние между пластинами
конденсатора,
то энергия заряженного
конденсатора равна:
Eк = CU2/2 =
ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2,
где V —
объем пространства между обкладками
конденсатора.
Энергия заряженного
конденсатора сосредоточена в его
электрическом поле.
Энергия электростатического
поля.
Энергия заряженного плоского
конденсатора Eк равна работе A, которая
была затрачена при его зарядке, или
совершается при его разрядке.
A =
CU2/2 = Q2/2С = QU/2 = Eк.
Поскольку
напряжение на конденсаторе может
быть рассчитано из соотношения:
U =
E*d,
где E — напряженность поля между
обкладками конденсатора,
d —
расстояние между пластинами
конденсатора,
то энергия заряженного
конденсатора равна:
Eк = CU2/2 =
ee0S/2d*E2*d2 = ee0S*d*E2/2 = ee0V*E2/2,
где V —
объем пространства между обкладками
конденсатора.
Энергия заряженного
конденсатора сосредоточена в его
электрическом поле.
Тип конденсатора | Формула для расчета емкости | Примечания | Схематическое изображение |
Плоский конденсатор | C = ee0S/d | S — площадь пластины;
d
— расстояние между пластинами. | |
Сферический конденсатор | C = 4pee0R1R2/(R2 — R1) | R2 и R1 — радиусы внешней и внутренней обкладок. | |
Цилиндрический конденсатор | C = 2pee0h/ln(R2/R1) | h — высота цилиндров. |
Как и любая система заряженных тел, конденсатор обладает энергией. Вычислить энергию заряженного плоского конденсатора с однородным полем внутри него несложно.
 14.37).
При разрядке конденсатора лампа
вспыхивает. Энергия конденсатора
превращается в тепло и энергию света.
14.37).
При разрядке конденсатора лампа
вспыхивает. Энергия конденсатора
превращается в тепло и энергию света.Выведем формулу для энергии плоского конденсатора. Напряженность поля, созданного зарядом одной из пластин, равна
W=qE/2d
где q — заряд конденсатора, а d — расстояние между пластинами. Так как Ed=U, где U — разность потенциалов между обкладками конденсатора, то его энергия равна:
W=qU/2
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин вплотную. Заменив в формуле (14.25) разность потенциалов или заряд с помощью выражения (14.22) для электроемкости конденсатора, получим:
W=qU/2=q^2/ 2C=CU^2/ 2
Можно
доказать, что эти формулы справедливы
для любого конденсатора, а не только
для плоского.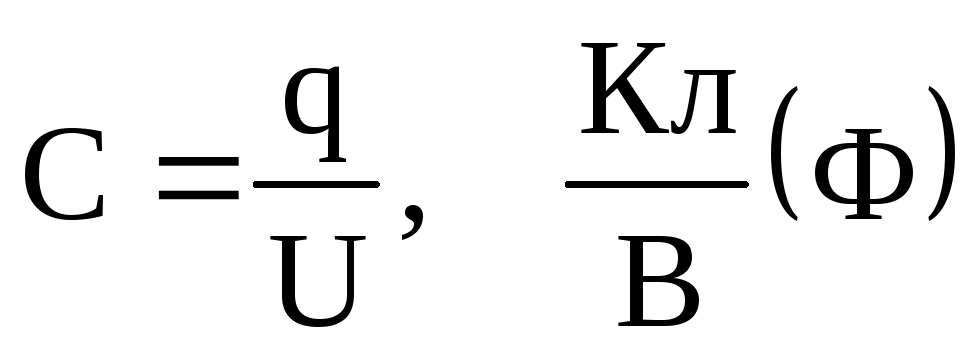 2
.
Применение
конденсаторов.
Зависимость электроемкости конденсатора
от расстояния между его пластинами
используется при создании одного из
типов клавиатур компьютера. На тыльной
стороне каждой клавиши располагается
одна пластина конденсатора, а на плате,
расположенной под клавишами, — другая.
Нажатие клавиши изменяет емкость
конденсатора. Электронная схема,
подключенная к этому конденсатору,
преобразует сигнал в соответствующий
код, передаваемый в компьютер.
Энергия конденсатора обычно не очень
велика — не более сотен джоулей. К тому
же она не сохраняется долго из-за
неизбежной утечки заряда. Поэтому
заряженные конденсаторы не могут
заменить, например, аккумуляторы в
качестве источников электрической энергии.
Но это совсем не означает, что конденсаторы
как накопители энергии не получили
практического применения. Они имеют
одно важное свойство: конденсаторы
могут накапливать энергию более или
менее длительное время, а при разрядке
через цепь с малым сопротивлением они
отдают энергию почти мгновенно.
2
.
Применение
конденсаторов.
Зависимость электроемкости конденсатора
от расстояния между его пластинами
используется при создании одного из
типов клавиатур компьютера. На тыльной
стороне каждой клавиши располагается
одна пластина конденсатора, а на плате,
расположенной под клавишами, — другая.
Нажатие клавиши изменяет емкость
конденсатора. Электронная схема,
подключенная к этому конденсатору,
преобразует сигнал в соответствующий
код, передаваемый в компьютер.
Энергия конденсатора обычно не очень
велика — не более сотен джоулей. К тому
же она не сохраняется долго из-за
неизбежной утечки заряда. Поэтому
заряженные конденсаторы не могут
заменить, например, аккумуляторы в
качестве источников электрической энергии.
Но это совсем не означает, что конденсаторы
как накопители энергии не получили
практического применения. Они имеют
одно важное свойство: конденсаторы
могут накапливать энергию более или
менее длительное время, а при разрядке
через цепь с малым сопротивлением они
отдают энергию почти мгновенно. Именно
это свойство широко используют на
практике.
Лампа-вспышка, применяемая в фотографии,
питается электрическим током разряда
конденсатора, заряжаемого предварительно
специальной батареей. Возбуждение
квантовых источников света — лазеров
осуществляется с помощью газоразрядной
трубки, вспышка которой происходит при
разрядке батареи конденсаторов большой
электроемкости.
Однако основное применение конденсаторы
находят в радиотехнике.
Энергия конденсатора пропорциональна
его электроемкости и квадрату напряжения
между пластинами. Вся эта энергия
сосредоточена в электрическом поле.
Энергия поля пропорциональна квадрату
напряженности поля.
Именно
это свойство широко используют на
практике.
Лампа-вспышка, применяемая в фотографии,
питается электрическим током разряда
конденсатора, заряжаемого предварительно
специальной батареей. Возбуждение
квантовых источников света — лазеров
осуществляется с помощью газоразрядной
трубки, вспышка которой происходит при
разрядке батареи конденсаторов большой
электроемкости.
Однако основное применение конденсаторы
находят в радиотехнике.
Энергия конденсатора пропорциональна
его электроемкости и квадрату напряжения
между пластинами. Вся эта энергия
сосредоточена в электрическом поле.
Энергия поля пропорциональна квадрату
напряженности поля.
Электроемкость конденсатора: формулы и история
Электрический конденсатор является пассивным прибором, который способен накапливать и сохранять электрическую энергию. Он состоит из двух проводящих пластин, разделенных диэлектрическим материалом. Приложение электрических потенциалов различного знака к проводящим пластинам приводит к приобретению ими заряда, который на одной пластине является положительным, а на другой отрицательным. При этом суммарный заряд равен нулю.
При этом суммарный заряд равен нулю.
В данной статье рассмотрены вопросы истории и определение электроемкости конденсатора.
История изобретения
В октябре 1745 года немецкий ученый Эвальд Георг фон Клейст заметил, что электрический заряд может быть запасен, если соединить с помощью кабеля электростатический генератор и некоторый объем воды, находящийся в стеклянном сосуде. В этом эксперименте рука фон Клейста и вода являлись проводниками, а стеклянный сосуд — электрическим изолятором. После того как ученый коснулся металлической проволоки рукой, произошел мощный разряд, который был намного сильнее, чем разряд электростатического генератора. В результате фон Клейст сделал вывод о существовании запасенной электрической энергии.
В 1746 году голландский физик Питер ван Мушенбрук изобрел конденсатор, который назвал лейденской бутылкой в честь Лейденского университета, в котором работал ученый. Затем Даниэль Гралат увеличил электроемкость конденсатора, соединив несколько лейденских бутылок.
В 1749 году Бенджамин Франклин исследовал лейденский конденсатор и пришел к выводу, что электрический заряд запасается не в воде, как полагали до этого, а на границе воды и стекла. Благодаря открытию Франклина, лейденские бутылки стали изготавливать, покрывая внутреннюю и внешнюю поверхность стеклянных сосудов металлическими пластинами.
Развитие индустрии
Термин «конденсатор» ввел в употребление Алессандро Вольта в 1782 году. Изначально для изготовления изоляторов электрических конденсаторов использовали такие материалы, как стекло, фарфор, слюду и обычную бумагу. Так, радиотехник Гульельмо Маркони использовал для своих аппаратов-передатчиков фарфоровые конденсаторы, а для приемников — небольшие конденсаторы с изолятором слюды, которые были изобретены в 1909 году — до Второй мировой войны в США именно они были наиболее распространенными.
Первый электролитический конденсатор был изобретен в 1896 году и представлял собой электролит с алюминиевыми электродами. Бурное развитие электроники началось только после изобретения в 1950 году танталового миниатюрного конденсатора с твердым электролитом.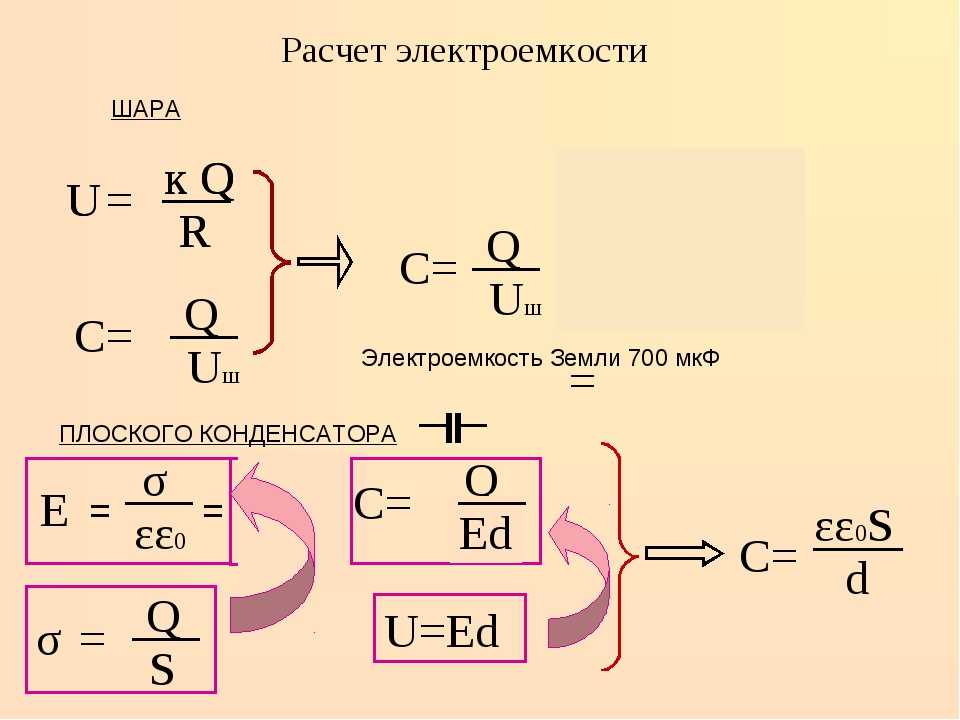
Во время Второй мировой войны в результате развития химии пластмасс стали появляться конденсаторы, в которых роль изолятора была отведена тонким полимерным пленкам.
Наконец, в 50-60 годах развивается индустрия суперконденсаторов, которые обладают несколькими рабочими проводящими поверхностями, благодаря чему электроемкость конденсаторов повышается на 3 порядка в сравнении с ее значением для обычных конденсаторов.
Понятие об электроемкости конденсатора
Электрический заряд, запасенный в пластине конденсатора, пропорционален напряжению электрического поля, которое существует между пластинами прибора. При этом коэффициент пропорциональности называется электроемкостью плоского конденсатора. В СИ (международная система единиц) электроемкость, как физическая величина, измеряется в фарадах. Один фарад — это такая электроемкость конденсатора, напряжение между пластинами которого равно 1 вольт при запасенном заряде в 1 кулон.
Электроемкость в 1 фарад является огромной, и на практике в электротехнике и электронике обычно пользуются конденсаторы с емкостями порядка пикофарада, нанофарада и микрофарада. Исключением являются только суперконденсаторы, которые состоят из активированного угля, благодаря чему увеличивается рабочая площадь прибора. Они могут достигать емкостей в тысячи фарадов и используются для питания прототипов электромобилей.
Исключением являются только суперконденсаторы, которые состоят из активированного угля, благодаря чему увеличивается рабочая площадь прибора. Они могут достигать емкостей в тысячи фарадов и используются для питания прототипов электромобилей.
Таким образом, электроемкость конденсатора равна: C = Q1/(V1-V2). Здесь C — электроемкость, Q1 — электрический заряд, запасенный в одной пластине конденсатора, V1-V2 — разница между электрическими потенциалами пластин.
Формула для емкости плоского конденсатора имеет вид: C = e0eS/d. Здесь e0 и e — универсальная диэлектрическая постоянная и диэлектрическая постоянная материала изолятора S — площадь пластин, d — расстояние между пластинами. Эта формула позволяет понять, как изменится электроемкость конденсатора, если изменить материал изолятора, расстояние между пластинами или их площадь.
Виды используемых диэлектриков
Для изготовления конденсаторов используют различные типы диэлектриков. Наиболее популярными являются следующие:
Наиболее популярными являются следующие:
- Воздух. Эти конденсаторы представляют собой две пластины из проводящего материала, которые разделены прослойкой воздуха и помещены в стеклянный корпус. Электроемкость воздушных конденсаторов невелика. Обычно они используются в радиотехнике.
- Слюда. Свойства слюды (способность разделяться на тонкие пластины и выдерживать высокие температуры) являются подходящими для ее использования в качестве изоляторов в конденсаторах.
- Бумага. Для защиты от намокания используют парафинированную или лакированную бумагу.
Запасенная энергия
По мере того, как увеличивается разность потенциалов между пластинами конденсатора, прибор запасает электрическую энергию благодаря присутствию внутри него электрического поля. Если разность потенциалов между пластинами уменьшается, то конденсатор разряжается, отдавая энергию в электрическую цепь.
Математически электрическую энергию, которая запасена в конденсаторе произвольного типа, можно выразить следующей формулой: E = ½C(V2-V1)2, где V2 и V1 — конечное и начальное напряжение между пластинами.
Заряд и разряд
Если конденсатор подсоединить в электрическую цепь с резистором и каким-либо источником электрического тока, тогда по цепи пойдет ток, и конденсатор начнет заряжаться. Как только он будет полностью заряжен, электрический ток в цепи прекратится.
Если заряженный конденсатор подсоединить параллельно резистору, то от одной пластины к другой через резистор потечет ток, который будет продолжаться до тех пор, пока прибор полностью не разрядится. В данном случае направление тока разряда будет противоположно направлению течения электрического тока, когда прибор заряжался.
Заряд и разряд конденсатора подчиняется экспоненциальной зависимости от времени. Например, напряжение между пластинами конденсатора при его разряде изменяется согласно следующей формуле: V(t) = Vie-t/(RC), где Vi — начальное напряжение на конденсаторе, R — электрическое сопротивление в цепи, t — время разряда.
Объединение в электрической цепи
Чтобы определить электроемкость конденсаторов, которые имеются в электрической цепи, следует вспомнить, что они могут объединяться двумя различными способами:
- Последовательное соединение: 1/Cs = 1/C1+1/C2+.
 ..+1/Cn.
..+1/Cn. - Параллельное соединение: Cs = C1+C2+…+Cn.
Cs — суммарная емкость n конденсаторов. Суммарная электроемкость конденсаторов определяется по формулам, аналогичным математическим выражениям для суммарного электрического сопротивления, только формула для последовательного соединения приборов справедлива для параллельного соединения резисторов и наоборот.
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 6 из 11Следующая ⇒ План ответа 1. Определение конденсатора. 2. Обозначение. 3. Электроемкость конденсатора. 4. Электроемкость плоского конденсатора. 5. Применение конденсаторов.
Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы. Конденсатор — это система двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные диэлектриком, образуют плоский конденсатор. Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность между пластинами будет в два раза больше, чем напряженность одной пластины. Вне пластин напряженность равна нулю. Обозначаются конденсаторы на схемах так: —1| конденсатор постоянной емкости; J^y — конденсатор переменной емкости. Электроемкостью конденсатора называют величину, равную отношению величины заряда одной из пластин к напряжению между ними. Электроемкость обозначается С. По определению С = q/U. Единицей электроемкости является фарад (Ф). 1 фарад — это электроемкость такого конденсатора, напряжение между обкладками которого равно 1 вольту при сообщении обкладкам разноименных зарядов по 1 кулону. Электроемкость плоского конденсатора (рис. 16) находится по формуле: где е0 — электрическая постоянная, е — диэлектрическая постоянная среды, S — площадь обкладки конденсатора, d — расстояние между обкладками (или толщина диэлектрика). В зависимости от типа диэлектрика конденсаторы бывают воздушные, бумажные, слюдяные. Конденсаторы применяются для накопления электрической энергии и использования ее при быстром разряде (фотовспышка), для разделения цепей постоянного и переменного тока, в выпрямителях, колебательных контурах и других радиоэлектронных устройствах. Билет № 20 Работа и мощность в цепи постоянного тока. Электродвижущая сила. Закон Ома для полной цепи План ответа 1. Работа тока. 2. Закон Джоуля—Ленца. 3. Электродвижущая сила. 4. Закон Ома для полной цепи.
Из формулы определения напряжения (U = A/q) легко получить выражение для расчета работы по переносу электрического заряда А = Uq; так как сила тока связана с зарядом соотношением q = It, то работа тока: А = UIt, или А = I2Rt = U2t/R. Мощность по определению N = А/T, следовательно, N = UI =I2R = U2t/R. Русский ученый X. Ленц и английский ученый Д. Джоуль опытным путем в середине XIX в. установили независимо друг от друга закон, который называется законом Джоуля—Ленца и читается так: при прохождении тока по проводнику количество теплоты, выделившееся в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока: Q = I2Rt. Полная замкнутая цепь представляет собой электрическую цепь, в состав которой входят внешние сопротивления и источник тока (рис. 17). Как один из участков цепи, источник тока обладает сопротивлением, которое называют внутренним, r. Для того чтобы ток проходил по замкнутой цепи, необходимо, чтобы в источнике тока зарядам сообщалась дополнительная энергия, она появляется за счет работы по перемещению зарядов, которую производят силы неэлектрического происхождения (сторонние силы) против сил электрического поля. Источник тока характеризуется энергетической характеристикой, которая называется ЭДС — электродвижущая сила источника. ЭДС измеряется отношением работы сторонних сил по перемещению вдоль замкнутой цепи положительного заряда к величине этого заряда £ = Acт/q. Пусть за время t через поперечное сечение проводника пройдет электрический заряд q. Тогда работу сторонних сил при перемещении заряда можно записать так: Аст = $q. Согласно определению силы тока, q = It, поэтому Аст = fIt. Билет № 21 ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Где возникла философия и почему? Относительная высота сжатой зоны бетона Сущность проекции Гаусса-Крюгера и использование ее в геодезии Тарифы на перевозку пассажиров |
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 555; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Электроемкость. Конденсаторы. Энергия заряженного конденсатора
1. Электроемкость. Конденсаторы. Энергия заряженного конденсатора.
Преподаватель физики: Бирюкова ТатьянаИвановна
ОГБПОУ г. Рязань
1 Курс
2. Цель урока
Познакомиться:с понятием «электроемкость», «конденсаторы»;
с типами конденсаторов
с формулой электроемкости и энергии
заряженного конденсатора
с практическим применением конденсаторов
3. Задачи урока
Сформировать умения:решать задачи на расчет различных
характеристик конденсаторов
выражать величину из формулы
производить математические расчеты
4. Повторение
1.2.
3.
4.
5.
6.
Характеристики электрического поля
Напряженность
Потенциал
Разность потенциалов
Формула связи напряженности с напряжением
(разностью потенциалов)
При каком условии можно накопить на
проводниках большой заряд?
5.
 Электроемкость – величина, характеризующая способность двух проводников накапливать электрический заряд.q
Электроемкость – величина, характеризующая способность двух проводников накапливать электрический заряд.qq
q
C
U
С – электроемкость, Ф
q – заряд одного из проводников, Кл
U – разность потенциалов между
проводниками, В
диэлектрик
на практике:
1 мкФ = 10-6 Ф
1 пФ = 10-12 Ф
R kC
ш
ш
Если емкость шара 1 фарад,
то радиус шара равен 9 млн.км.
проводник
Электроемкость зависит от:
1. геометрических размеров и формы проводников;
2. взаимного расположения проводников;
3. диэлектрической проницаемости
6. История создания конденсатора
В 1745 годув Лейдене немецкий физик
Эвальд Юрген фон Клейст
и голландский физик
Питер ван Мушенбрук
создали первый
конденсатор
«лейденскую банку».
1692-1761
7. Конденсатор – система двух разноименно заряженных проводников, разделенных диэлектриком
Типы конденсаторовпостоянной и переменной емкости и различаются по
роду диэлектрика между пластинами
бумажные, керамические, воздушные …
8.
 Плоский конденсатор — две заряженные параллельные пластины, находящиеся на малом расстоянии— — — — — — — — — — — d
Плоский конденсатор — две заряженные параллельные пластины, находящиеся на малом расстоянии— — — — — — — — — — — dдиэлектрик
+ + + + + + + + + +
C
S
0
С – электроемкость плоского
конденсатора, Ф
ε – диэлектрическая проницаемость
ε0 — электрическая постоянная, Ф/м
S — площадь пластины конденсатора, м2
d — расстояние между пластинами, м
d
Электроемкость плоского конденсатора прямо
пропорциональна площади пластины конденсатора и
обратно пропорциональна расстоянию между
пластинами
9. Шаровой конденсатор
R2_
_
+
R1
_
Электрическое поле
сосредоточено внутри
конденсатора
_
R
R
C 4
R R
1
2
0
2
1
10. Последовательное соединение
С1+
С2
_
+
U2
U1
+
_
C
_
q q q
1
2
U U U
q q1 q2
C C1 C 2
1
2
U
d↑ , следовательно , С↓
1 1 1
C C C
1
2
11.
 Параллельное соединениеС1 +
Параллельное соединениеС1 ++
q q q
_
q1
C
2
U U U
_
1
С2
+
1
2
q2
CU C U C U
_
1
1
2
q
S↑, следовательно, С↑
C C C
1
2
2
12. Соединение конденсаторов одноименными полюсами
+С1
—
Соединение конденсаторов
одноименными полюсами
q C1U 1 C 2U 2
+
С2
—
C C C
1
C U C U
q
U
C
C
C
1
1
2
1
2
2
2
13. Соединение конденсаторов разноименными полюсами
+С1
—
Соединение конденсаторов
разноименными полюсами
q C1U 1 C 2U 2
С2
+
C C C
1
C U C U
q
U
C
C
C
1
1
2
1
2
2
2
14. Энергия заряженного конденсатора
qUW
2
CU
2
2
2
q
2C
W – энергия заряженного конденсатора
(энергия электрического поля), Дж
q — заряд пластины конденсатора, Кл
U — разность потенциалов, В
С – электроемкость конденсатора, Ф
15.
 Плотность энергии конденсатораW
Плотность энергии конденсатораWV
E
2
0
2
ω – плотность энергии, Дж/м3
V – объем, м3
Е – напряженность, В/м
16. Применение конденсаторов
в радиотехнике, вавтоматизации
производственных
процессов, в
вычислительной
технике и т.д.
используется
свойство
накапливать и
сохранять заряд
17. Применение конденсаторов
Петличный микрофон.Микрофон конденсаторный.
Студийный
конденсаторный
направленный микрофон
широкого применения.
Применение конденсаторов
Лампа фотовспышки.
Батарея конденсаторов
Светильники с
разрядными лампами.
Металлопленочные конденсаторы
обладают неограниченной
возможностью
самовосстановления. Таким
образом, возможность короткого
замыкания практически
исключается. Конденсаторы
устойчивы к большим импульсным
токам и высокому уровню
пульсаций.
Применяются в мобильных
телефонах, персональных
компьютерах, телевизорах,
электронных балластах и
автомобильной электронике.

20. Применение конденсаторов
в компьютерной технике –клавиатура (зависимость емкости
от расстояния между пластинами)
На тыльной стороне клавиши одна
пластина конденсатора, а на
плате,- другая. Нажатие клавиши
изменяет емкость конденсатора.
21. Электролитические конденсаторы
Полимерные конденсаторыс твердым электролитом
на чипсете
Отличительными
чертами алюминиевых
электролитических
конденсаторов является большая
удельная емкость на единицу
объема (произведением CV) и
прекрасная работа при повышенных
токах. Поэтому они незаменимые
компоненты в цепях постоянного
тока тяговых устройств, в составе
преобразователей частоты, в схемах
электронных балластов, в ИБП
(источниках бесперебойного
питания) и импульсных
преобразователях напряжения, в
студийных лампах-вспышках и в
автомобильной электронике.
23. Решение задач
1. Определите толщину диэлектрикаконденсатора, электроемкость которого 1400
пФ, площадь пластин 1,4 ·10-3 м2.
 Диэлектрик –
Диэлектрик –слюда (ε=6).
2. Разность потенциалов 150 В между пластинами
плоского конденсатора. Площадь каждой
пластины 1,2·10-2 м2, заряд 5 нКл. На каком
расстоянии друг от друга находятся пластины?
Дано:
Решение:
С=1400 ·10-12Ф
S=1,4 ·10-3 м2
ε=6
ε0=8,85·10-12 Ф/м
C
S
d
S
0
d
0
C
d-?
6 8,85 10 Ф 1,4 10 м
м
0,0053 мм
d
1400 10 Ф
3
12
2
12
Ответ: d = 5,3 мкм
Дано:
U=150 В
S=1,2·10-2 м2
q=5·10-9 Кл
ε=1
ε0=8,85·10-12Ф/м
Решение:
C
S
0
d
d
S
0
C
5 10 Кл 0,33 10 Ф
150В
9
q
C
U
9
1 8,85 10 Ф 1,2 10 м
S
м
d
C
0,033 10 Ф
0,32 10 м 3,2 мм
12
d-?
0
9
2
Ответ: d=3,2 мм
2
2
26. Решение задач
3. Площадь пластинплоского воздушного
конденсатора равна
10-2 м2, расстояние
между ними 5 мм. До
какой разности
потенциалов был
заряжен конденсатор,
если при его разрядке
выделилось 4,2·10-3
Дж энергии?
Дано:
Решение:
CU
2
U
2W
C
W
S=10-2 м2
2
S
d=5 мм=5·10-3м
C
d
ε=1
ε0=8,85·10-12Ф/м
1 8,85 10 Фм 10 м
1,77 10 Ф
C
-3
W=4,2·10 Дж
5 10 м
0
12
2
2
11
3
U-?
2 4,2 10 Дж
1,77 10 Ф
3
U
Ответ:
11
2,2 10
4
U 2,2 10 В
4
В
29.
 Задача 4. Определите общую электроемкость куба, состоящего из 12 одинаковых конденсаторов емкостью С
Задача 4. Определите общую электроемкость куба, состоящего из 12 одинаковых конденсаторов емкостью С30. Эквивалентная схема
СС
С
С
С
С
С
С
С
С
С
С1 3С
С1
1
С
об
С
С2
С3
2
3
3
С 6С
2
1 1 1 1 1 1 5
С С С 3С 6С 3С 6С
1
С 3С
6
С С
5
об
31. Электроемкость плоского конденсатора с квадратными пластинами со стороной 10 см, расположенными на расстоянии 1 мм друг от
друга, в воздухе примерно равна10 пФ
2. 0,1 нФ
3. 1 мкФ
4. 0,1мФ
1.
32. Как изменится электроемкость плоского воздушного конденсатора, если расстояние между его пластинами увеличить в 2 раза?
1. Уменьшится в 2 раза2. Уменьшится в 4 раза
3. Увеличится в 4 раза
4. Увеличится в 2 раза
33. Как изменится электроемкость плоского воздушного конденсатора, если площадь его пластин увеличить в два раза, а расстояние
между ними уменьшить в 2 раза?1.
 Не изменится
Не изменится2. Уменьшится в 4 раза
3. Увеличится в 4 раза
4. Увеличится в 2 раза
34. Плоский конденсатор подключен к источнику постоянного тока. Как изменятся при увеличении зазора между обкладками конденсатора
три величины:— емкость конденсатора;
— величина заряда на обкладках
конденсатора;
— разность потенциалов между
ними.
1. увеличится; 2. уменьшится; 3. не изменится
35. Плоский воздушный конденсатор зарядили до некоторой разности потенциалов и отключили от источника тока. Для каждой величины —
заряд на обкладках конденсатора— электроемкость конденсатора
-энергия электрического поля
конденсатора
определите соответствующий характер
изменения:
1. увеличится; 2. уменьшится; 3. не изменится.
Плоский конденсатор отключили от
источника тока, а затем увеличили
расстояние между его пластинами. Что
произойдет при этом
— с зарядом конденсатора
— с электроемкостью конденсатора
— с напряжением на его обкладках?
Для каждой величины определите
соответствующий характер изменения:
1.
 увеличится; 2. уменьшится; 3. не изменится.
увеличится; 2. уменьшится; 3. не изменится.37. Определите электроемкость батареи состоящей из четырех одинаковых конденсаторов электроемкостью С.
1С
С
С
С
1.
2.
2
С
С
3.
4.
5.
6.
С
С
С/4
С
2С/5
4С/3
3С/5
3С/4
38. Домашнее задание
§ 99-101 прочитатьвопросы устно
Упр. № 18
Составить интелект-схему «Конденсатор»
Формула сферического конденсатора — GeeksforGeeks
Конденсатор — это просто электрическое устройство, состоящее из двух клемм, способных накапливать энергию в виде электрического заряда. Его можно сконструировать, просто разместив два электрических проводника на расстоянии друг от друга. Пустое пространство между проводниками может быть заполнено вакуумом (или воздухом) или изоляционным материалом, известным как диэлектрик. Способность конденсатора накапливать заряды называется емкостью.
В конденсаторе две клеммы с противоположными зарядами расположены на расстоянии друг от друга, что позволяет ему генерировать (хранить) энергию. Простейшая конструкция конденсатора представляет собой параллельную пластину, состоящую из двух металлических пластин с зазором между ними. Следует отметить, что конденсатор может быть любой формы или размера или быть изготовлен из любого материала, пока его клеммы не будут накапливать противоположные заряды и, таким образом, накапливать энергию.
Простейшая конструкция конденсатора представляет собой параллельную пластину, состоящую из двух металлических пластин с зазором между ними. Следует отметить, что конденсатор может быть любой формы или размера или быть изготовлен из любого материала, пока его клеммы не будут накапливать противоположные заряды и, таким образом, накапливать энергию.
Емкость конденсатора
Рассмотрим конденсатор, положительные и отрицательные пластины которого удерживают заряд +q и -q соответственно. На него подается источник постоянного напряжения, который создает разность потенциалов V на пластинах. Теперь, как мы знаем,
Q α V
Ввод константы C в это отношение.
Q=CV.
Примечание: Емкость каждого материала уникальна, и ее единицей СИ является Фарад (Ф).
Работа конденсатора
Предположим, что нам дана простейшая форма конденсатора, то есть конденсатор с параллельными пластинами. Он состоит из двух параллельных пластин, разделенных небольшим расстоянием, и этот зазор заполнен диэлектриком. Затем нам дан источник постоянного напряжения, подключенный через конденсатор, где одна пластина прикреплена к положительному концу (пластина I), а другая пластина подключена к отрицательному концу (пластина II). Когда потенциал батареи приложен к конденсатору, пластина I становится положительной по отношению к пластине II. В установившемся режиме ток пытается пройти через конденсатор от положительной пластины к отрицательной. Однако из-за зазора между ними с изолирующим слоем (диэлектриком) он не может течь.
Он состоит из двух параллельных пластин, разделенных небольшим расстоянием, и этот зазор заполнен диэлектриком. Затем нам дан источник постоянного напряжения, подключенный через конденсатор, где одна пластина прикреплена к положительному концу (пластина I), а другая пластина подключена к отрицательному концу (пластина II). Когда потенциал батареи приложен к конденсатору, пластина I становится положительной по отношению к пластине II. В установившемся режиме ток пытается пройти через конденсатор от положительной пластины к отрицательной. Однако из-за зазора между ними с изолирующим слоем (диэлектриком) он не может течь.
Структура простого конденсатора.
Некоторое время конденсатор продолжает заряжаться набегающим потоком тока. Но через некоторое время он достигает состояния, когда он удерживает максимально возможное количество заряда. Вот как конденсатор накапливает энергию. Время, необходимое для достижения этого состояния максимального заряда, называется временем зарядки конденсатора. Далее отключаем от цепи источник напряжения и вставляем в него нагрузочный резистор. Теперь ток начинает течь от положительно заряженного вывода конденсатора к отрицательно заряженному выводу и теряет при этом всю свою энергию. Этот период времени называется временем разрядки конденсатора.
Далее отключаем от цепи источник напряжения и вставляем в него нагрузочный резистор. Теперь ток начинает течь от положительно заряженного вывода конденсатора к отрицательно заряженному выводу и теряет при этом всю свою энергию. Этот период времени называется временем разрядки конденсатора.
Разряд конденсатора.
Формула сферического конденсатора
Как упоминалось ранее, емкость возникает, когда между двумя пластинами есть разделение. Итак, для изготовления сферического конденсатора возьмем полую сферу, у которой внутренняя поверхность заряжена положительно, а внешняя поверхность сферы заряжена отрицательно. Внутренний радиус сферы равен r, а внешний радиус равен R. Расстояние R-r между двумя противоположно заряженными поверхностями действует как диэлектрик. Предположим, что внутренняя сферическая поверхность имеет потенциал В 1 и V 2.
Сферический конденсатор
Далее, электрическое поле, создаваемое заряженной сферой (полой) радиусом r, имеющей заряд Q, определяется выражением
E= .
⇢ (1)
Кроме того, мы знаем, что генерируемое электрическое поле связано с разностью потенциалов как
E= . ⇢ (2)
Сравнивая (1) и (2),
Интегрируя в обе стороны в пределах V, V и r, R.
⇢ (3)
— это изменение потенциала при движении из сферы внутрь сферы наружу. Теперь емкость конденсатора определяется,
⇢ (4)
Сравнение (3) и (4),
Упрощение. t быть отрицательным, берется положительное значение. Это выражение для емкости сферического конденсатора.
Примеры вопросов
Вопрос 1. Сферический конденсатор имеет внутренний радиус 7 см и внешний радиус 10 см. Найдите емкость шара. Предположим, что диэлектриком между ними является воздух.
Решение:
емкость сферы определяется,
C =
здесь ∈ 0 = 8,85 × 10 -12 , r = 7, R = 10
C =.
С = 2,593 × 10 -12 F
Вопрос 2. В приведенной выше задаче найдите, какой заряд потребуется конденсатору, чтобы поднять его потенциал с 0 до 10 000 В.
Решение:
× 10 -12 F.
Требуемый заряд можно найти, используя Q = CV. где V — разность потенциалов.
Разность потенциалов V в этом случае равна 1000-0 = 1000В
Следовательно, Q = 3,7052 × 10 -12 × 1000
Q = 2,593 × 10 -9 C
Вопрос 3. Внутренний радиус сферического конденсатора равен x м, а его внешний радиус равен 5/4 x м, если внешний радиус увеличить до 3/2x м, найти, во сколько раз изменится его емкость.
Solution:
In this case
=
= 20 πε o x F
= 20 πε o x F
So the capacitance decreases as the внешний радиус увеличен.
9-8 C.
Solution:
C = 4 πε o x F
C = 4 × 3.14 × 8.85 × 10 −12 × 10 × 10 −2
C = 111.156 × 10 −13
C = 1,11 × 10 −11 F
Теперь Q = CV
Следовательно,
Следовательно V = 900,9 В
ВОПРОС 5: Верд радиус a ophericitor IS IS IS Sphericitor IS IS ophericitor IS IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS ophericitor IS IS IS ophericitor. на 10 % больше, чем его внутренний радиус. Емкость этого конденсатора 10 -8 F. Найдите значение его внутреннего и внешнего радиусов.
Ответ:
Здесь r = x, r = 1,1x и c = 10 -8 F
SO,
x = 0,009 M
So inner radius gradil. равен 0,09 см, а внешний радиус равен 0,099 см.
Вопрос 6: Внутренний и внешний радиусы сферического конденсатора равны 5см и 6см. Найдите энергию конденсатора, если к нему приложена разность потенциалов 1000 В.
Solution:
The capacitance of this capacitor is calculated as,
C = 3.3363 × 10 −12 F
U = 1/2 CV 2
U = 21 × 3,3363 × 10 −12 × (1000) 2
U = 1,66815 × 10 −9 Дж
см -8 Дж . Найдите его напряжение.
Решение:
Позвольте найти емкость первым,
C = 4,446 × 10 -9 F
U = 1/2 CV 2
9000 2 9000 2 9000 2 9000 29000 2
9000 2
9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000 2 9000.
12.
Определение, формула, единицы СИ, измерение
Конденсатор — это устройство, которое может накапливать электрические заряды, а также может использоваться для защиты цепей от нежелательных всплесков. Теперь вы можете подумать, что батарея также делает это.
Однако в этом случае разница заключается в том, что батарея хранит энергию в форме химического потенциала, тогда как конденсаторы хранят энергию в форме электрического потенциала. Кроме того, ток утечки у конденсаторов выше, чем у аккумуляторов, а это означает, что конденсаторы не могут удерживать заряд так же долго, как аккумуляторы.
Рис. 1. A Конденсатор. Источник: Эван-Амос, Wikimedia Commons (общественное достояние).
Быстрое движение электронов между двумя пластинами конденсатора делает его очень полезным в электронных приложениях.
Конденсатор
Внутри конденсатора находятся две металлические пластины из проводящего материала, например алюминия.
Эти пластины разделены изоляционным материалом, также известным как диэлектрик.
Прежде чем мы рассмотрим, как работает конденсатор, нам нужно понять концепцию поляризации.
Поляризация – это ориентация полярных молекул внутри диэлектрика по направлению к противоположным электродам.
Диэлектрик состоит из множества полярных молекул, которые имеют как положительный, так и отрицательный конец. Когда конденсатор не накапливает заряд, электрического поля нет, и эти молекулы случайным образом направлены в разные стороны.
Рис. 2. Случайные молекулы (вверху) и молекулы в электрическом поле (внизу). Источник: гиперфизика, Wikimedia Commons (общественное достояние).
При подаче напряжения на конденсатор создается электрическое поле. Положительные концы молекул притягиваются к отрицательно заряженной пластине и наоборот.
Поскольку диэлектрик является изолятором и молекулы не могут смещаться, поляризованные молекулы ориентируются таким образом, что противоположные заряды на молекулах и пластинах обращены друг к другу.
Рис. 3. Ориентация поляризованных молекул в электрическом поле. Источник: Brews ohare, Wikimedia Commons (CC BY-SA 3.0).
Поскольку электрическое поле поляризованных молекул противоположно направлению обкладок конденсатора, разность потенциалов уменьшается, а способность конденсатора накапливать заряд на единицу разности потенциалов увеличивается.
Возьмите батарейку и подсоедините отрицательный конец к отрицательному выводу конденсатора (обозначен полосой), а положительный конец к положительному выводу. Однако имейте в виду, что не все конденсаторы имеют маркировку полюсов. Если это так, они могут быть подключены в любом направлении в цепи.
Рисунок 4. Символ конденсатора. Источник: Wikimedia Commons (общественное достояние).
Заряды текут от батареи к отрицательной клемме конденсатора и от положительной пластины к положительной клемме батареи.
Рисунок 5. На диаграмме показано, как напряжение на пластинах и ток, протекающий через пластины, изменяются по мере заряда конденсатора.
Источник: jjbeard, Wikimedia Commons (общественное достояние).
После того, как заряды перетекли от положительной пластины к батарее и от батареи к отрицательной пластине, дальнейший поток электронов невозможен, и одна сторона конденсатора заряжена отрицательно, а другая сторона заряжена положительно. Конденсатор находится на том же уровне напряжения, что и батарея.
Поскольку электроны накапливаются на одной стороне конденсатора, мы говорим, что он накапливает энергию, которую можно высвобождать, когда это необходимо.
Между пластинами конденсатора создается разность потенциалов, так как существует разница в количестве зарядов на пластинах.
Применение конденсатора
Заряженный конденсатор можно использовать для обеспечения непрерывного заряда цепи.
Например, когда мы подключаем светодиод к полностью заряженному конденсатору, заряды от отрицательной пластины конденсатора текут через светодиод к положительной пластине конденсатора до тех пор, пока между двумя клеммами не исчезнет разность потенциалов.
В результате светодиод на короткое время мигнет.
Продолжительность вспышки будет очень короткой, так как поток электронов очень быстрый. Однако, если мы подключим батарею к конденсатору в этой цепи, конденсатор будет заряжаться и накапливать энергию и снова разряжаться, если в протекании тока возникнет какое-либо прерывание.
Измерение накопленной энергии
На конденсаторе есть два значения, одно показывает напряжение (В) и емкость в фарадах (Ф).
Рисунок 6. Конденсатор с показаниями напряжения и емкости. Источник: Jomegat, Wikimedia Commons (CC BY-SA 3.0).
Показание напряжения на конденсаторе указывает максимальное напряжение, которое он может выдержать. Если это значение превышено, есть вероятность, что конденсатор может сгореть, а иногда даже взорваться.
Емкость конденсатора
Каждый конденсатор имеет емкость, которая представляет собой его способность накапливать электрический заряд. Символом емкости является C, которая измеряется в фарадах.
Фарады — это количество кулонов, которые можно хранить на вольт:
Таким образом, емкость можно использовать для расчета заряда в кулонах:
- Q = электрический заряд.
- C = емкость.
- В = напряжение.
Формула емкости
Емкость можно рассчитать по следующей формуле:
- C = емкость, измеренная в кулонах на вольт (Ф).
- K = относительная диэлектрическая проницаемость, т. е. диэлектрическая проницаемость материала по отношению к диэлектрической проницаемости свободного пространства. Это выражается как εr/ε0, где εr — диэлектрическая проницаемость материала. Обычно указывается относительная диэлектрическая проницаемость. Например, воздух имеет диэлектрическую проницаемость 1,9.2 и разделены на 2,15 мм.
Поскольку K не указан, мы примем его равным 1. Сложение других значений дает:
Это может показаться очень маленькой емкостью, но на самом деле она огромна.
Емкость (только A2) — основные выводы
- Конденсатор — это проводник, который может накапливать заряд в электрической форме.
Каждый конденсатор имеет емкость, которая представляет собой количество заряда на единицу разности потенциалов.
Конденсатор используется для поддержания тока в цепи в случае прерывания.
Две проводящие пластины с диэлектрическим изолятором между ними образуют конденсатор.
Работа конденсатора заключается в накоплении отрицательных зарядов на одной пластине, что создает разность потенциалов между двумя пластинами.
Единицей измерения емкости являются фарады.
Преобразование емкости в импеданс и взаимосвязь между ними
Ключевые выводы
● Узнайте о формулах преобразования емкости в импеданс.
● Получите более полное представление о взаимодействии емкости и импеданса.
● Узнайте больше о важности импеданса при анализе цепей переменного тока.
Емкость и ее отношение к импедансу
Область электроники содержит различные параметры, которые измеряют, помогают и влияют на функциональность, а также производительность каждого электронного устройства. Эти параметры влияют на исходные и окончательные проектные решения.
Такие параметры, как емкость и импеданс, должны оставаться в допустимых проектных пределах, иначе даже самый точный проект не сможет обеспечить желаемый функциональный результат. Кроме того, бывают случаи, когда требуется преобразование одного параметра в эквивалент другого. Одно такое преобразование, такое как емкость в импеданс, требует детального анализа цепи переменного тока.
Конденсаторы и емкость
Компонентом, связанным с емкостью, является, конечно же, конденсатор, а способность системы накапливать электрический заряд называется емкостью.
В физике это отношение изменения электрического заряда в системе к изменению ее электрического потенциала. В любом случае стандартной единицей измерения емкости является фарад.
Эти пассивные электронные компоненты накапливают энергию в виде электростатического поля. В чистом виде конденсатор состоит из двух проводящих пластин, разделенных изолирующим материалом, называемым диэлектриком. Емкость конденсатора прямо пропорциональна площади поверхности его пластин и обратно пропорциональна расстоянию между этими пластинами. Однако чистая емкость также зависит от диэлектрической проницаемости вещества, разделяющего пластины.
При преобразовании импеданса конденсатора мы используем формулу Z = -jX. Имейте в виду, что реактивное сопротивление является более однозначным параметром и определяет, какое сопротивление будет иметь конденсатор на определенной частоте. Как указывалось ранее, знание импеданса необходимо для детального анализа цепи переменного тока.
Катушка индуктивности и импеданс
Понимание импеданса в цепи переменного тока
Импеданс — это активное сопротивление электрической цепи или компонента переменному току из-за комбинированного воздействия реактивного сопротивления и омического сопротивления. Другими словами, импеданс является расширением принципов сопротивления в цепях переменного тока. Мы также определяем импеданс как любое препятствие или меру сопротивления электрического тока потоку энергии при подаче напряжения.
Более техническое определение — это полное противодействие электрической цепи потоку переменного тока одной частоты. Таким образом, это комбинация реактивного сопротивления и сопротивления, которую мы измеряем в омах и обозначаем символом Z.
Реактивное сопротивление (X) выражает сопротивление компонента переменному току, тогда как импеданс (Z) указывает сопротивление компонента обоим переменного и постоянного тока.
Мы показываем его как комплексное число с помощью следующей формулы: Z = R + jX. В идеале импеданс резистора равен его сопротивлению. В этих условиях реальная или действительная часть импеданса представляет собой сопротивление, а мнимая часть равна нулю или нулю. Преобразование емкости в импеданс
Существуют калькуляторы емкостного реактивного сопротивления, которые позволяют определить полное сопротивление конденсатора при условии, что у вас есть значение его емкости (C) и частота сигнала, проходящего через него (f). Вы вводите емкость в фарадах, пикофарадах, микрофарадах или нанофарадах и частоту в единицах ГГц, МГц, кГц или Гц. Например, емкость в 2 фарад на частоте 100 герц даст импеданс 0,0008 Ом.
Следующая формула необходима для расчета вышеуказанных значений:
Теперь мы понимаем параметры идеального резистора, где его импеданс равен его сопротивлению.
Однако полное сопротивление идеального конденсатора равно величине его реактивного сопротивления, хотя эти два параметра не идентичны. Мы выражаем реактивное сопротивление как обычное число в омах, а полное сопротивление конденсатора представляет собой реактивное сопротивление, умноженное на -j. Это соответствует следующей формуле:
Z = -jX . В этом контексте термин -j представляет фазовый сдвиг на 90 градусов, который возникает между током и напряжением в чисто емкостной цепи. Используя уравнение преобразования
Используя приведенное выше уравнение (XC = 1/ωC = 1/2πƒC), вы можете получить реактивное сопротивление конденсатора, а для преобразования его в импеданс конденсатора вы можете использовать формулу Z = -jX . Помните, что реактивное сопротивление является более очевидным значением параметра, и оно определяет, какое сопротивление имеет конденсатор на определенной частоте.
Из приведенных выше уравнений видно, что реактивное сопротивление конденсатора обратно пропорционально емкости и частоте.
Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Эта обратная связь между частотой и реактивным сопротивлением облегчает использование конденсаторов для блокирования низкочастотных компонентов сигнала и одновременного пропускания высокочастотных компонентов.
Емкость в цепи переменного тока легко различима, но для тщательного анализа цепи переменного тока требуется импеданс. Логически это означает, что первостепенное значение имеет более глубокое понимание того, как взаимодействуют эти два параметра.
Обмотка индуктора из медного провода
Наличие функциональных и надежных схем зависит от наличия подходящего набора программного обеспечения для проектирования и анализа, помогающего создавать схемы, имитационные модели и посадочные места. Функции внешнего проектирования от Cadence интегрируются с мощным симулятором PSpice для создания идеальной программной системы для проектирования схем и моделирования.
Если вы хотите узнать больше о том, какое решение у Cadence есть для вас, обратитесь к нам и нашей команде экспертов. Вы также можете посетить наш канал YouTube и посмотреть видеоролики о моделировании и системном анализе, а также узнать, что нового в нашем наборе инструментов для проектирования и анализа.
Свяжитесь с нами
Решения Cadence PCB — это комплексный инструмент для проектирования от начала до конца, позволяющий быстро и эффективно создавать продукты. Cadence позволяет пользователям точно сократить циклы проектирования и передать их в производство с помощью современного отраслевого стандарта IPC-2581.
Подпишитесь на Linkedin Посетить сайт Больше контента от Cadence PCB Solutions
Загрузка, подождите
Ошибка — что-то пошло не так!
Хотите последние новости о печатных платах?
Подпишитесь на нашу ежемесячную рассылку новостейСпасибо!
Конденсаторы и диэлектрики | Физика II |
Цели обучения
К концу этого раздела вы сможете:
- Описывать действие конденсатора и определять емкость.
- Расскажите о конденсаторах с плоскими пластинами и их емкости.
- Обсудите процесс увеличения емкости диэлектрика.
- Определить емкость при данных заряде и напряжении.
Конденсатор представляет собой устройство, используемое для накопления электрического заряда. Применение конденсаторов варьируется от фильтрации статического электричества в радиоприеме до накопления энергии в сердечных дефибрилляторах. Как правило, коммерческие конденсаторы имеют две проводящие части, расположенные близко друг к другу, но не соприкасающиеся, как показано на рис. 1. (Большую часть времени между двумя пластинами используется изолятор для обеспечения разделения — см. обсуждение диэлектриков ниже.) Когда клеммы аккумулятора подключены к изначально незаряженному конденсатору, равному положительному и отрицательному заряду, + Q и – Q , разделены на две пластины. Конденсатор в целом остается нейтральным, но в этом случае мы называем его запасом заряда Q .
Рис. 1. Оба показанных здесь конденсатора были изначально разряжены перед подключением к аккумулятору. Теперь у них есть отдельные заряды + Q и – Q на две половинки. а) Конденсатор с плоскими пластинами. (b) Свернутый конденсатор с изоляционным материалом между двумя его проводящими листами.
Конденсатор
Конденсатор — это устройство, используемое для накопления электрического заряда.
Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Количество заряда
Q Конденсатор может хранитьКоличество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Рисунок 2. Линии электрического поля в этом плоском конденсаторе, как всегда, начинаются с положительных зарядов и заканчиваются с отрицательными зарядами. Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.
Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как показано на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для плоского конденсатора, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поле будет больше. линии, если есть больше заряда. (Рисовать одну силовую линию для каждого заряда — это только для удобства. Мы можем нарисовать много силовых линий для каждого заряда, но их общее число пропорционально количеству зарядов.
) Таким образом, напряженность электрического поля прямо пропорциональна В .
Поле пропорционально заряду:
E ∝ Q ,
где символ ∝ означает «пропорционально». Из обсуждения электрического потенциала в однородном электрическом поле мы знаем, что напряжение на параллельных пластинах равно
В = Эд .
Таким образом, V ∝ E . Отсюда следует, что V ∝ Q и, наоборот,
Q ∝ В .
В общем случае это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.
Различные конденсаторы сохраняют разное количество заряда при одном и том же приложенном напряжении в зависимости от их физических характеристик. Мы определяем их емкость C так, что заряд Q , хранящийся в конденсаторе, пропорционален C .
Заряд, хранящийся в конденсаторе, равен
Q = CV .
Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Преобразовывая уравнение, мы видим, что емкость C — это количество заряда, накопленного на вольт, или
C=QVC=\frac{Q}{V}\\C=VQ
.
Емкость
Емкость C — это количество заряда на вольт, или
C=QVC=\frac{Q}{V}\\C=VQ
Единицей измерения емкости является фарад (Ф), названный в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или
1 F=1 C1 V1\text{ F}=\frac{1\text{ C}}{1\text{ V }}\\1 F=1 V1 C
.
Конденсатор емкостью 1 фарад мог бы хранить 1 кулон (очень большое количество заряда) при приложении всего 1 вольта. Таким образом, один фарад — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарад (1 пФ = 10 −12 Ф) в миллифарад (1 мФ = 10 −3 Ф).
На рис. 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.
Рис. 3. Некоторые типовые конденсаторы. Размер и значение емкости не обязательно связаны. (кредит: Windell Oskay)
Конденсатор с параллельными пластинами
Рис. 4. Конденсатор с параллельными пластинами, пластины которого расположены на расстоянии d. Каждая пластина имеет площадь A.
Конденсатор с параллельными пластинами, показанный на рисунке 4, состоит из двух идентичных проводящих пластин, каждая из которых имеет площадь поверхности A , разделенных расстоянием d (без материала между пластинами).
Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость зависит от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом C должен быть больше для большего размера A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, C должно быть больше для меньшего d .
Можно показать, что для плоского конденсатора есть только два фактора ( A и d ), которые влияют на его емкость C . Емкость конденсатора с плоскими пластинами в виде уравнения определяется как
C=ϵoAdC=\epsilon_{o}\frac{A}{d}\\C=ϵodA
.
Емкость конденсатора с параллельными пластинами
C=ϵoAdC=\epsilon_{o}\frac{A}{d}\\C=ϵodA
A – площадь одной пластины в квадратных метрах, а d – расстояние между плитами в метрах. Постоянная ε 0 — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε 0 = 8,85 × 10 −12 Ф/м. Единицы Ф/м эквивалентны C 2 / Н · м 2 . Небольшое числовое значение ε 0 связано с большим размером фарад. Плоский конденсатор должен иметь большую площадь, чтобы иметь емкость, приближающуюся к фарадам. (Обратите внимание, что приведенное выше уравнение справедливо, когда параллельные пластины разделены воздухом или свободным пространством. Когда между пластинами помещается другой материал, уравнение модифицируется, как описано ниже.)
Пример 1. Емкость и накопленный заряд в Параллельный пластинчатый конденсатор
- Какова емкость плоского конденсатора с металлическими пластинами площадью 1,00 м 2 , каждая из которых расположена на расстоянии 1,00 мм друг от друга?
- Какой заряд накапливается в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 3 В ?
Стратегия
Нахождение емкости C является прямым применением уравнения
C=ϵoAdC=\epsilon_{o}\frac{A}{d}\\C=ϵodA
.
Как только C найдено, накопленный заряд можно найти с помощью уравнения 9.{-9}\text{ F}=8,85\text{ нФ}\end{массив}\\C ==ϵodA=(8,85×10−12 мФ)1,00×10−3 м1,00 м2 8,85×10−9 F=8,85 нФ
Обсуждение части 1
Это маленькое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу.
Решение для части 2
Заряд, хранящийся в любом конденсаторе, определяется уравнением Q = CV . Ввод известных значений в это уравнение дает 9{3}\text{ V}\right)\\\text{ }&=&26,6\mu\text{C}\end{массив}\\Q ==CV=(8,85×10−9 F )(3,00×103 В)26,6 мкКл
Обсуждение части 2
Этот заряд лишь немного больше, чем у типичного статического электричества. Поскольку воздух разрушается примерно при 3,00 × 10 6 В/м, на этом конденсаторе невозможно накопить больше заряда за счет увеличения напряжения.
Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в клеточной плазматической мембране. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам избирательно входить и выходить из клетки. Разность потенциалов на мембране около -70 мВ. Это связано с наличием в клетке в основном отрицательно заряженных ионов и преобладанием положительно заряженного натрия (Na 9{6}\text{ В/м}\\E=dV=8×10−9 м−70×10−3 В=−9×106 В/м
Этого электрического поля достаточно, чтобы вызвать пробой воздуха.
Диэлектрик
Предыдущий пример подчеркивает сложность хранения большого количества заряда в конденсаторах. Если d уменьшить для получения большей емкости, то максимальное напряжение должно быть пропорционально уменьшено, чтобы избежать пробоя (поскольку
E=VdE=\frac{V}{d}\\E=dV
).
Важным решением этой проблемы является размещение изоляционного материала, называемого 9.0391 диэлектрик , между пластинами конденсатора и пусть d будет как можно меньше. Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем пробиться.
Использование диэлектрика в конденсаторе имеет еще одно преимущество. В зависимости от используемого материала емкость больше, чем указанная в уравнении0003
на коэффициент κ , называемый диэлектрической проницаемостью . Емкость плоского конденсатора с диэлектриком между пластинами определяется выражением
C=κϵ0AdC=\kappa\epsilon_{0}\frac{A}{d}\\C=κϵ0dA
(конденсатор с параллельными пластинами с диэлектриком).
Значения диэлектрической проницаемости κ для различных материалов приведены в Таблице 1. Обратите внимание, что κ для вакуума точно равно 1, поэтому приведенное выше уравнение справедливо и в этом случае.
Если использовать диэлектрик, возможно, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в 9 раз.0391 κ , что для тефлона составляет 2,1.
Самостоятельный эксперимент: изготовление конденсатора
Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут алюминиевой фольгой, а перегородка (диэлектрик) между ними будет бумагой.
Таблица 1. Диэлектрическая проницаемость и электрическая прочность различных материалов при 20ºC Материал Диэлектрическая проницаемость κ Диэлектрическая прочность (В/м) Пылесос 1.00000 — Воздух 1.00059 3 × 10 6 Бакелит 4,9 24 × 10 6 Плавленый кварц 3,78 8 × 10 6 Неопреновый каучук 6,7 12 × 10 6 Нейлон 3,4 14 × 10 6 Бумага 3,7 16 × 10 6 Полистирол 2,56 24 × 10 6 Стекло пирекс 5,6 14 × 10 6 Силиконовое масло 2,5 15 × 10 6 Титанат стронция 233 8 × 10 6 Тефлон 2. 1
60 × 10 6 Вода 80 — Обратите также внимание на то, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют почти так же, как конденсаторы с вакуумом между пластинами , за исключением того, что воздух может стать проводящим, если напряженность электрического поля становится слишком большой. (Напомним, что
E=VdE=\frac{V}{d}\\E=dV
для плоского конденсатора.) В таблице 1 также показаны максимальные значения напряженности электрического поля в В/м, называемые диэлектрической прочностью , для нескольких материалов. Это поля, выше которых материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного разделения пластин. Например, в примере 1 расстояние составляет 1,00 мм, поэтому предел напряжения для воздуха составляет
9{-3}\text{ m}\right)\\\text{ }&=&3000\text{ V}\end{массив}\\V ===E⋅d(3×106 В/м) (1,00×10−3 м)3000 ВОднако предел для зазора в 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 6 В/м.
Так тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для заполненного воздухом конденсатора с плоскими пластинами, мы находим, что конденсатор с тефлоновым наполнением может хранить максимальный заряд 94\text{ V})\\\text{ }&=&1.1\text{ mC}\end{array}\\Q ====CVκCairV(2.1)(8,85 нФ)(6,0× 104 В)1,1 мКл
Это в 42 раза больше заряда того же конденсатора, наполненного воздухом.
Диэлектрическая прочность
Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется его диэлектрической прочностью.
С микроскопической точки зрения, как диэлектрик увеличивает емкость? В этом виновата поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .
Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рисунке 5 схематически показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии д прочь.
Рис. 5. (а) Молекулы изоляционного материала между пластинами конденсатора поляризуются заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость.
(b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.
Другой способ понять, как диэлектрик увеличивает емкость, — рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5(b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются на зарядах в диэлектрике, их меньшее количество проходит от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, хотя на пластинах находится тот же заряд. Напряжение между пластинами равно В = Эд , так что диэлектрик также уменьшает его. Таким образом, имеется меньшее напряжение В для того же заряда Q ; так как
C=QVC=\frac{Q}{V}\\C=VQ
, емкость C больше.
Диэлектрическая проницаемость обычно определяется как
κ=E0E\kappa=\frac{E_0}{E}\\κ=EE0
, или отношение электрического поля в вакууме к электрическому полю в диэлектрический материал и тесно связан с поляризуемостью материала.
Вещи большие и малые: субмикроскопическое происхождение поляризации
Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома изображает его как имеющее положительное ядро, вращающееся вокруг отрицательно заряженных электронов, подобно планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет усовершенствована в другом месте, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рис. 6.9.0003
Рис. 6. Представление художника о поляризованном атоме.
Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных положений и траекторий планет на их орбитах вокруг Земли). солнце). Это облако смещается кулоновской силой так, что атом в среднем имеет разделение заряда. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому их называют полярными молекулами. На рисунке 7 показано разделение заряда в молекуле воды, которая имеет два атома водорода и один атом кислорода (H 2 O).
Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Рис. 7. Представление художника о молекуле воды. Существует неотъемлемое разделение зарядов, поэтому вода является полярной молекулой. Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда вблизи двух ядер водорода. (Обратите внимание, что схема справа представляет собой грубую иллюстрацию распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)
PhET Explorations: Capacitor Lab
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость. Измените напряжение и увидите заряды на пластинах. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.
Резюме раздела
- Конденсатор — это устройство, используемое для накопления заряда.
- Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость C является количеством заряда, накопленного на вольт, или
C=QVC=\frac{Q}{V}\\C=VQ
.- Емкость плоского конденсатора составляет
C=ϵ0AdC={\epsilon }_{0}\frac{A}{d}\\C=ϵ0dA
, когда пластины разделены воздухом или свободным пространством .ϵ0{\epsilon }_{\text{0}}ϵ0
называется диэлектрической проницаемостью свободного пространства.- Емкость плоского конденсатора с диэлектриком между пластинами равна
C=κϵ0AdC=\kappa\epsilon_{0}\frac{A}{d}\\C=κϵ0dA
, где κ — диэлектрическая проницаемость материала.- Максимальная напряженность электрического поля, выше которой изоляционный материал начинает разрушаться и проводить ток, называется диэлектрической прочностью.
Концептуальные вопросы
- Зависит ли емкость устройства от приложенного напряжения? А заряд, хранящийся в нем?
- Используйте характеристики силы Кулона, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора.
Точно так же объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
- Объясните, почему диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора. Какова независимая причина того, что диэлектрический материал также позволяет прикладывать большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает большее В .)
- Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
- Искры будут возникать между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем при сухом. Объясните почему, учитывая полярность молекул воды.
- Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
- Мембраны живых клеток, в том числе клеток человека, характеризуются разделением заряда поперек мембраны.
Таким образом, мембраны представляют собой заряженные конденсаторы с важными функциями, связанными с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизация энергии пищи или какой-либо другой источник?
Рис. 8. Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K + (калий) и Cl – (хлорид) в указанных направлениях до тех пор, пока кулоновская сила не остановит дальнейший перенос. Это приводит к образованию слоя положительного заряда снаружи, слоя отрицательного заряда внутри и, таким образом, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na + (ионы натрия).
Задачи и упражнения
- Какой заряд накапливается в конденсаторе емкостью 180 мкФ при приложении к нему напряжения 120 В?
- Найдите заряд, накопленный при подаче 5,50 В на конденсатор емкостью 8,00 пФ.
- Какой заряд хранится в конденсаторе в примере 1?
- Рассчитайте напряжение, прикладываемое к конденсатору емкостью 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
- Какое напряжение необходимо приложить к конденсатору емкостью 8,00 нФ, чтобы накопить заряд 0,160 мКл?
- Какая емкость необходима для накопления заряда 3,00 мкКл при напряжении 120 В?
- Какова емкость вывода большого генератора Ван де Граафа, если он хранит 8,00 мКл заряда при напряжении 12,0 МВ?
- Найдите емкость плоского конденсатора с пластинами площадью 5,00 м 2 , разделенными тефлоновым слоем толщиной 0,100 мм.
- (a) Какова емкость плоского конденсатора с пластинами площадью 1,50 м 2 , разделенными 0,0200 мм неопреновой резины? б) Какой заряд он имеет, когда 9.00 В подается на него?
- Интегрированные концепции. Шутник подает напряжение 450 В на конденсатор емкостью 80,0 мкФ, а затем бросает его ничего не подозревающей жертве.
Палец пострадавшего обожжен разрядом конденсатора через 0,200 г плоти. Что такое повышение температуры тела? Разумно ли предположить отсутствие фазового перехода?
- Необоснованные результаты. (a) Некоторый конденсатор с параллельными пластинами имеет пластины площадью 4,00 м 2 , разделенные нейлоном толщиной 0,0100 мм, и сохраняет заряд 0,170 Кл. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие предположения ответственны или непоследовательны?
Глоссарий
Конденсатор: Устройство, которое хранит электрический заряд
емкость: Количество зарядов, хранящегося на единицу вольт
Dielectric: . изоляционный материал начинает разрушаться и проводить
конденсатор с плоскими пластинами: две одинаковые проводящие пластины, разделенные расстоянием
полярная молекула: молекула с присущим разделением зарядов
Избранные решения задач и упражнений
1.
21,6 мКл
3. 80,0 мКл
5. 20,0 кВ
7. 667 пФ
9. (а) 4,4 мкФ; (б) 4,0 × 10 −5 С
11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз превышает напряжение пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.
Лицензии и ссылки
Контент по лицензии CC, совместно используемый ранее
- College Physics. Автор : Колледж OpenStax. Расположен по адресу : https://openstax.org/books/college-physics/pages/1-introduction-to-science-and-the-realm-of-physics-physical-quantities-and-units. Лицензия : CC BY: Attribution . Условия лицензии : Лицензия
- Интерактивное моделирование PhET . Предоставлено : Университет Колорадо в Боулдере. Расположен по адресу : https://phet.colorado.edu/. Лицензия : CC BY: Атрибуция
Емкость, зарядка и разрядка конденсатора
Схема
Емкость
[adsense1] определяется как максимальная способность конденсатора сохранять емкость
3 900 электрический заряд (Q) в его теле.
Здесь заряд сохраняется в виде электростатической энергии. Емкость измеряется в основных единицах СИ, то есть в фарадах. Эти единицы измерения могут быть в микрофарадах, нанофарадах, пикофарадах или фарадах. Выражение для емкости дается выражением,
C = Q/V = εA/d = ε0 εr A/d
В уравнении выше A — площадь между пластинами,
d — расстояние между пластинами.
ε диэлектрическая проницаемость диэлектрика
ε0 диэлектрическая проницаемость свободного пространства
εr относительная диэлектрическая проницаемость свободного пространства
Собственная емкость
Свойство собственной емкости связано с конденсаторами, особенно с изолированными проводниками. Как следует из названия, емкость — это свойство изолированного проводника повышать разность потенциалов до одного вольта. Обычно нормальные проводники имеют взаимную емкость. Это также измеряется в единицах СИ, то есть в фарадах.
Самостоятельность проводящей сферы, которая имеет радиус ‘r’, дается,
C = 4 πɛ O R
приведен ниже.
- Для верхней пластины генератора Ван де Граффа радиусом 20 см собственная емкость составляет 22,24 пФ.
- Для планеты ЗЕМЛЯ собственная емкость составляет 710 мкФ.
[adsense2]
Паразитная емкость
Паразитная емкость — нежелательная емкость. Конденсаторы вносят некоторую емкость в цепь. Но такие компоненты, как резисторы, катушки индуктивности и даже провод, будут иметь некоторую емкость. Это называется паразитной емкостью. Как правило, на высоких частотах это вносит шум в схему. Эта нежелательная емкость невелика, если только проводники не расположены близко друг к другу на больших расстояниях или на большой площади.
Паразитную емкость нельзя полностью устранить, но ее можно уменьшить. Разработчики схем должны позаботиться о паразитной емкости при проектировании схемы. Разделение между компонентами и линиями должно быть сохранено, чтобы уменьшить нежелательную емкость.
Также измеряется в единицах СИ, т. е. в фарадах.
Примерами являются емкость между витками катушки, емкость между двумя соседними проводниками.
Емкость простых систем
Расчет емкости есть не что иное, как решение теоремы Лапласа ∇ 2 φ = 0 с постоянным потенциалом на поверхности конденсатора. Значения емкости и уравнения для некоторых простых систем приведены ниже.
Заряд конденсатора
Способность конденсатора накапливать максимальный заряд (Q) на своих металлических пластинах называется его емкостью (C). Полярность накопленного заряда может быть отрицательной или положительной. Например, положительный заряд (+ve) на одной пластине и отрицательный заряд (-ve) на другой пластине конденсатора. Выражения для заряда, емкости и напряжения приведены ниже.
C = Q/V, Q = CV, V = Q/C
Таким образом, заряд конденсатора прямо пропорционален его емкости и разности потенциалов между пластинами конденсатора. Заряд измеряется в кулонах.
Один кулон:Один кулон заряда конденсатора можно определить как емкость в один фарад между двумя проводниками, работающими под напряжением в один вольт.
С воздухом в качестве диэлектрика
Заряд ‘Q’, хранящийся в конденсаторе, имеющем емкость C, разность потенциалов ‘V’ и воздух в качестве его диэлектрика, определяется выражением,
Q =C V =(ε× (A ×V )) /d
С твердым диэлектриком
Заряд Q конденсатора, диэлектриком которого является твердое тело, определяется выражением
Q =C V =(ε0 ×εr× (A ×V)) /d
Здесь
ε0 — диэлектрическая проницаемость свободного пространства,
εr — относительная диэлектрическая проницаемость диэлектрического материала и
ε — диэлектрическая проницаемость диэлектрического материала.
Из приведенных выше двух случаев мы можем наблюдать
Заряд конденсатора прямо пропорционален площади пластин, диэлектрической проницаемости диэлектрического материала между пластинами и обратно пропорционален разделительному расстоянию между пластинами.
Таким образом, чем больше площадь пластин, тем больше заряд и чем больше расстояние между пластинами, тем меньше заряд на конденсаторе.
Конденсатор с параллельными пластинами
Рисунок 1. Схема конденсатора с параллельными пластинами.
На приведенном выше рисунке показана схема конденсатора с параллельными пластинами. Как известно, емкость прямо пропорциональна площади пластин (А) и обратно пропорциональна расстоянию (d) между двумя металлическими пластинами. Значение емкости плоского конденсатора определяется выражением
C = k ε0A/d
Здесь k — диэлектрическая проницаемость, а ε0 — диэлектрическая проницаемость свободного пространства и равна 8,854 X 10 -12 Ф/м. Диэлектрическая постоянная (k) — это параметр, относящийся к диэлектрическому материалу, который увеличивает емкость по сравнению с воздухом. Чем больше площадь поверхности пластин, тем больше значение емкости, а чем больше расстояние, тем меньше емкость. Еще один пример схемы конденсатора с параллельными пластинами показан на рисунке ниже.
Рисунок 2. Конденсатор с параллельными пластинами.
Емкость Пример №1
Теперь рассчитаем емкость плоского конденсатора в пикофарадах, имеющего площадь поверхности пластин 200 см2 и расстояние между ними 0,4 см, а воздух как его диэлектрический материал.
Мы знаем уравнение для емкости плоского конденсатора:0003
D = 0,4 см = 0,004 м
Теперь подставим эти значения в приведенное выше уравнение емкость конденсатора 44,27 пФ
Зарядка и разрядка конденсатора
Схема ниже используется для объяснения характеристик зарядки и разрядки конденсатора. Предположим, что конденсатор, изображенный на схеме, полностью разряжен. В этой схеме емкость конденсатора составляет 100 мкФ, а напряжение питания, подаваемое на эту цепь, составляет 12 В.
Теперь переключатель, который подключен к конденсатору в цепи, перемещается в точку A. Затем конденсатор начинает заряжаться зарядным током (i), и этот конденсатор также полностью заряжен. Зарядное напряжение на конденсаторе равно напряжению питания, когда конденсатор полностью заряжен, т.
е. VS = VC = 12 В. Когда конденсатор полностью заряжен, это означает, что конденсатор поддерживает заряд постоянного напряжения, даже если напряжение питания отключено от цепи.
В случае идеальных конденсаторов заряд на конденсаторе остается постоянным, но в случае обычных конденсаторов полностью заряженный конденсатор медленно разряжается из-за тока утечки.
Рисунок: Цепь зарядки и разрядки конденсатора
При переводе переключателя в положение B конденсатор медленно разряжается за счет включения лампы, включенной в цепь. Наконец он полностью разряжен в ноль. Лампа сначала ярко светится, когда конденсатор полностью заряжен, но яркость лампы уменьшается по мере уменьшения заряда в конденсаторе.
Пример заряда конденсатора №2
Теперь давайте рассчитаем заряд конденсатора в приведенной выше схеме, мы знаем, что уравнение для заряда конденсатора:
Q = CV
Здесь C = 100 мкФ = 12 В
Теперь подставим эти значения в приведенное выше уравнение:
Q = 100 мкФ * 12 В = 1,2 мКл
Следовательно, заряд конденсатора в приведенной выше схеме составляет 1,2 мКл.
Ток через конденсатор
Ток (i), протекающий через любую электрическую цепь, представляет собой скорость протекания заряда (Q) по отношению ко времени. Но заряд конденсатора прямо пропорционален приложенному к нему напряжению. Соотношение между зарядом, током и напряжением конденсатора приведено в приведенном ниже уравнении.
I (t) = d Q(t)/dt = C dV(t)/dt
Мы знаем, что
Q = CV
V = Q/C
V (t) = Q(t) /C
Q(t) =C V(t)
Отношение тока к напряжению определяется выражением I (t) = C dV(t)/dt
Из этого соотношения мы заметили, что ток, протекающий через конденсатор в цепи является произведением емкости и скорости изменения напряжения, приложенного к цепи. Ток, протекающий через конденсатор, прямо пропорционален емкости конденсатора и величине напряжения.
Чем больше ток, тем выше емкость цепи и выше приложенное напряжение, тем больше ток, протекающий через цепь. Если напряжение постоянно, то заряд тоже постоянный.
Таким образом, заряда нет. Следовательно, ток, протекающий по цепи, станет равным нулю.
Единица измерения емкости (Фарад)
Джозайя Латимер Кларк в 1861 году впервые использовал термин Фарад. Фарада – стандартная единица измерения емкости. Это чрезвычайно большая единица измерения емкости.
Емкость в один фарад определяется как емкость с зарядом в один кулон, работающая при напряжении в один вольт.
C = Q/V
1Farad = 1Columb/1Volt
Теперь доступны конденсаторы с большой емкостью в сотни фарад. Эти конденсаторы с высокими значениями емкости называются «суперконденсаторами». Эти конденсаторы используют большую площадь поверхности для передачи высокой энергии, потому что они имеют высокие значения емкости.
При низком напряжении суперконденсаторы обладают способностью накапливать большое количество энергии с высокими значениями емкости. Эти высокоэнергетические суперконденсаторы используются в ручных портативных устройствах для замены больших, тяжелых и дорогих конденсаторов литиевого типа, поскольку они накапливают большую энергию, как батареи.
Эти конденсаторы также используются в аудио- и видеосистемах автомобилей, заменяя аккумуляторы высокой емкости.
Единицы фарада
Стандартная единица измерения емкости — фарад. Но это вообще большая единица измерения емкости. Этот фарад имеет несколько субъединиц; это микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).
Соотношение между всеми этими единицами измерения и фарадами:
1 микрофарад (мкФ) = (1/1000000) Ф = 10-6 Ф
1 нано-Фарад (мкФ) = (1/1000000000) Ф = 10 -9 Ф
1 пико-Фарад (мкФ) = (1/1000000000000) Ф = 10-12 Ф
Теперь мы увидим некоторые преобразования между единицами измерения емкости,
(i) преобразование 33 пФ в нФ => 33 пФ = 0,033 нФ
(ii) преобразование 22 нФ в мкФ => 22 нФ = 0,022 мкФ
(iii) преобразование 11 мкФ в Ф => 11 мкФ = 0,11 Ф
Энергия в конденсаторе
Энергия – это количество работы против электростатического поля для полной зарядки конденсатора. В конденсаторе на начальной стадии заряда заряд Q переносится между обкладками с одной обкладки на другую.
Этот заряд либо +Q, либо -Q обменивается между двумя пластинами конденсатора. После преобразования некоторого заряда между пластинами образуется электрическое поле, в этом случае для полного заряда конденсатора потребуется дополнительная работа. Эта дополнительная работа называется энергией, запасенной в конденсаторе. Энергия измеряется в джоулях (Дж). Теперь мы видим уравнения для этой энергии и работы.
dW = V dQ
dW = (Q/C) dQ
После интегрирования приведенного выше уравнения будет W = CV 2 /2 Дж
В итоге мы получаем энергию, запасенную в конденсаторе:
Энергия (Вт) = CV 2 /2 Дж
Теперь рассчитаем энергию, запасенную в конденсаторе емкостью 200 мкФ. которые работают от напряжения 12В.
Вт = CV 2 /2
Вт = (200×10 -6 ×12 2 )/2 = 14,4 м Дж
- Разочаровывающий вопрос об энергии в конденсаторе
Калькулятор формулы емкости конденсатора: накопитель энергии конденсатора
Наиболее широко используемым электронным компонентом является конденсатор.
Конденсатор является пассивным элементом цепи, но он не поглощает электрическую энергию, а накапливает ее. Основное назначение конденсатора — хранить электрическую энергию в течение очень короткого промежутка времени. Запас энергии конденсатора зависит от емкости конденсатора. Емкость относится к различным параметрам по формуле емкости. Конденсатор также известен как конденсатор. Конденсаторы являются приложением статического электричества.
Конструкция конденсатора:
Конденсатор состоит из двух металлических пластин (проводящих пластин), удаленных от диэлектрика (непроводящего материала или изолятора). На рынке доступны различные типы конденсаторов, и все они имеют один и тот же основной принцип.
На практике проводящей пластиной может быть алюминиевый лист, а непроводящим материалом может быть воздух, керамика, бумага, слюда и т. д. В цепь можно включить конденсатор, как показано на схеме. Где напряжение $V$ обеспечивает заряд (электроны) пластины, подключенной к отрицательной клемме, и тот же источник получает заряд (электроны) от пластины, подключенной к положительной клемме.
Суммарный заряд $q$ на проводящих пластинах прямо пропорционален напряжению питания.
- Как услуги электрика помогают в обслуживании?
- Как работают микроволновые печи
$q\quad \propto \quad v$
$ q\quad =\quad Cv$Где «$q$» — заряд конденсатора, а «$v$ — напряжение, приложенное к конденсатору.
Что такое емкость?
Емкость – это способность конденсатора накапливать заряд. В приведенном выше уравнении буква «$C$» является константой пропорциональности и представляет емкость конденсатора 9.0017 . Единицей измерения емкости является фарад (названный в честь ученого Майкла Фарадея). Емкость – это свойство конденсатора, позволяющее оценить способность накапливать заряд.
Конденсатор будет иметь емкость в один Фарад тогда и только тогда, когда приложенное к нему напряжение равно одному вольту и он хранит заряд в один кулон.
Фарад — очень большая единица измерения емкости, наиболее часто используемые единицы измерения — микрофарад, нанофарад и пикофарад.
Формула емкости:
Емкость варьируется от конденсатора к конденсатору в зависимости от некоторых факторов, таких как площадь пластины, расстояние между ними и используемый материал.
По мере увеличения площади пластины увеличивается пространство для хранения заряда, поэтому оно имеет прямую связь с емкостью. Если пластины, расположенные далеко друг от друга, могут хранить меньше заряда по сравнению с пластинами, расположенными близко друг к другу, то это имеет косвенную связь. Математически
$C\quad \propto \quad A$
$C\quad \propto \quad \frac { 1 }{ d } $
$C\quad =\quad \varepsilon \frac { A }{ d } $
Выше приведена формула емкости конденсатора. Здесь A — площадь поверхности проводящих пластин (каждой пластины), d — расстояние между пластинами. Где $\varepsilon $ — диэлектрическая проницаемость непроводящего материала (диэлектрика). Он измеряет, насколько легко диэлектрик будет проходить линии электрического потока. Диэлектрическая проницаемость для вакуума представлена $\varepsilon _{o}$ и называется абсолютной диэлектрической проницаемостью.
9{-12}$F/м. Диэлектрическая проницаемость других материалов называется относительной диэлектрической проницаемостью и представлена в виде $\varepsilon_{r}=\frac{\varepsilon }{\varepsilon _{o}}$ по сравнению с абсолютной диэлектрической проницаемостью. Относительная диэлектрическая проницаемость также известна как диэлектрическая проницаемость. Для каждого материала существует порог, если приложенное к нему напряжение превышено. Диэлектрический материал разрушается, что свидетельствует о диэлектрической прочности и называется напряжением пробоя диэлектрика.
Калькулятор формулы емкости:
Калькулятор помогает определить емкость конденсатора по формуле емкости. Попробуйте определить площадь пластин конденсатора, относительную диэлектрическую проницаемость диэлектрика и расстояние между пластинами, чтобы найти емкость.
Площадь пластины A
Относительная диэлектрическая проницаемость ε r
Расстояние d
Емкость C
Конденсатор Запас энергии:
Энергия – это способность совершать работу путем приложения силы, когда работа заключается в перемещении массы.
В электротехнике энергия — это способность перемещать заряд под действием напряжения.
Конденсаторное накопление энергии означает перенос заряда с одной пластины на другую против действия электрического поля. Чтобы противодействовать электрической силе, создаваемой зарядом конденсатора, к конденсатору в обратном направлении подключается внешний источник, т. е. батарея. По мере накопления заряда на пластинах требуется все больше и больше силы для перемещения заряда в противоположном направлении. Напряжение на конденсаторе прямо пропорционально заряду на пластинах.
$V\quad=\quad \frac{q}{C}$ 9{2}$
Калькулятор запаса энергии конденсатора:
Чтобы рассчитать запас энергии конденсатора, попробуйте ввести заряд конденсатора, емкость и напряжение.
Заряд Q
Емкость C
Напряжение В
Запас энергии U
Ток утечки :
До сих пор мы предполагали, что проводящие пластины разделены изоляторами и ток не может проходить через них.



 ..+1/Cn.
..+1/Cn.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления



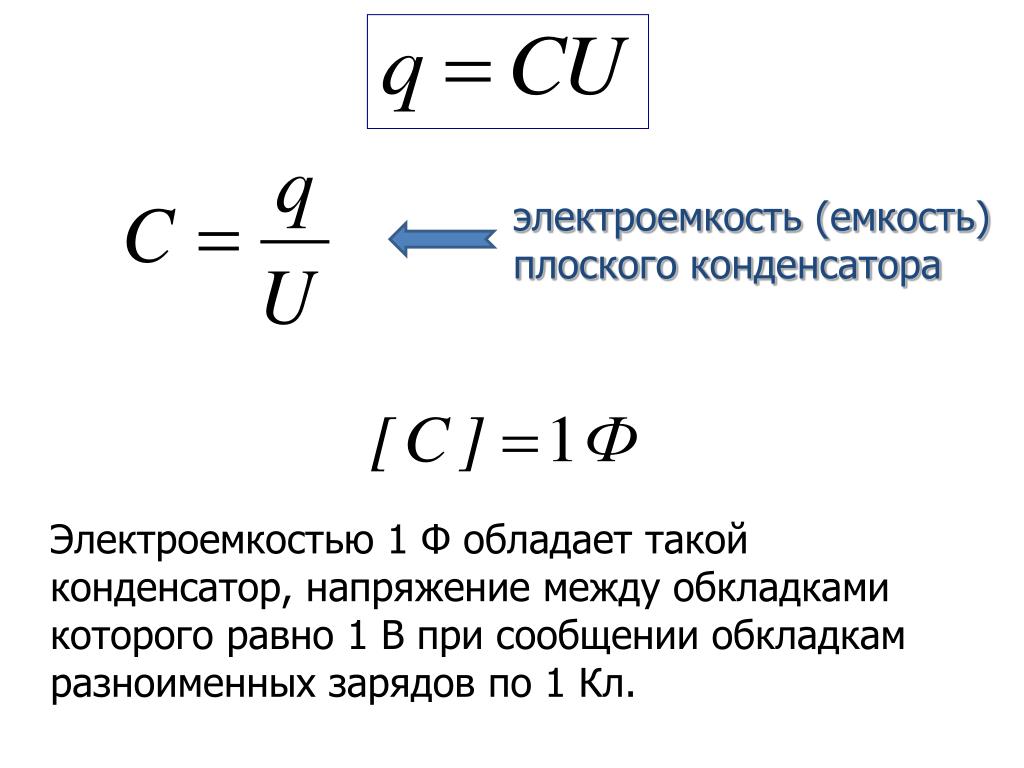 При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых R и r, выделяется некоторое количество теплоты. По закону Джоул—Ленца оно равно: Q = I2Rt + I2rt. Согласно закону сохранения энергии, А = Q. Следовательно, $ = IR + Ir. Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи. Обычно это выражение записывают так: I = @/(R + r). Эту зависимость опытным путем получил Георг Ом, называется она законом Ома для полной цепи и читается так: сила тока в полной цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи. При разомкнутой цепи ЭДС равна напряжению на зажимах источника и, следовательно, может быть измерена вольтметром.
При совершении этой работы на внутреннем и внешнем участках цепи, сопротивления которых R и r, выделяется некоторое количество теплоты. По закону Джоул—Ленца оно равно: Q = I2Rt + I2rt. Согласно закону сохранения энергии, А = Q. Следовательно, $ = IR + Ir. Произведение силы тока на сопротивление участка цепи часто называют падением напряжения на этом участке. Таким образом, ЭДС равна сумме падений напряжений на внутреннем и внешнем участках замкнутой цепи. Обычно это выражение записывают так: I = @/(R + r). Эту зависимость опытным путем получил Георг Ом, называется она законом Ома для полной цепи и читается так: сила тока в полной цепи прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению цепи. При разомкнутой цепи ЭДС равна напряжению на зажимах источника и, следовательно, может быть измерена вольтметром.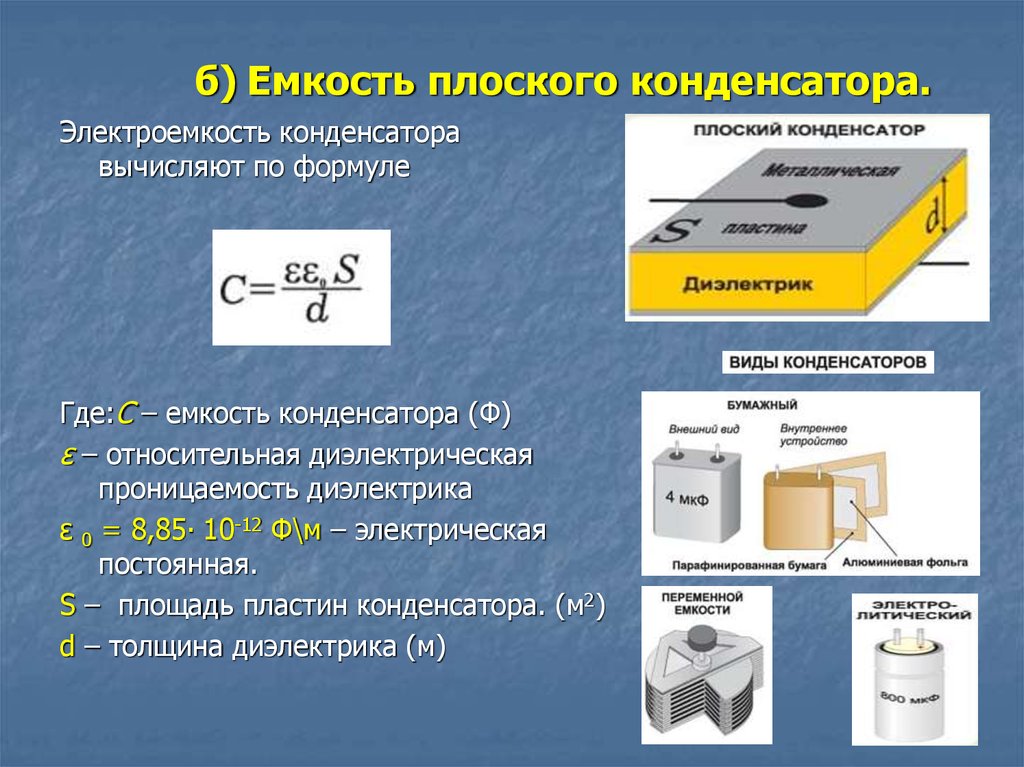 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.007 с.) ⇢ (1)
⇢ (1)
 9-8 C.
9-8 C. 
 12.
12. Эти пластины разделены изоляционным материалом, также известным как диэлектрик.
Эти пластины разделены изоляционным материалом, также известным как диэлектрик.
 Источник: jjbeard, Wikimedia Commons (общественное достояние).
Источник: jjbeard, Wikimedia Commons (общественное достояние). В результате светодиод на короткое время мигнет.
В результате светодиод на короткое время мигнет. Фарады — это количество кулонов, которые можно хранить на вольт:
Фарады — это количество кулонов, которые можно хранить на вольт: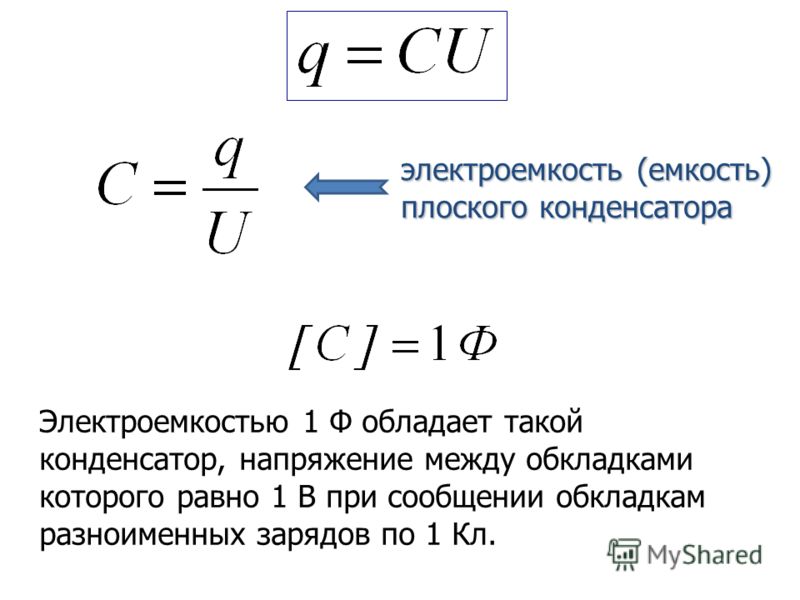

 В физике это отношение изменения электрического заряда в системе к изменению ее электрического потенциала. В любом случае стандартной единицей измерения емкости является фарад.
В физике это отношение изменения электрического заряда в системе к изменению ее электрического потенциала. В любом случае стандартной единицей измерения емкости является фарад.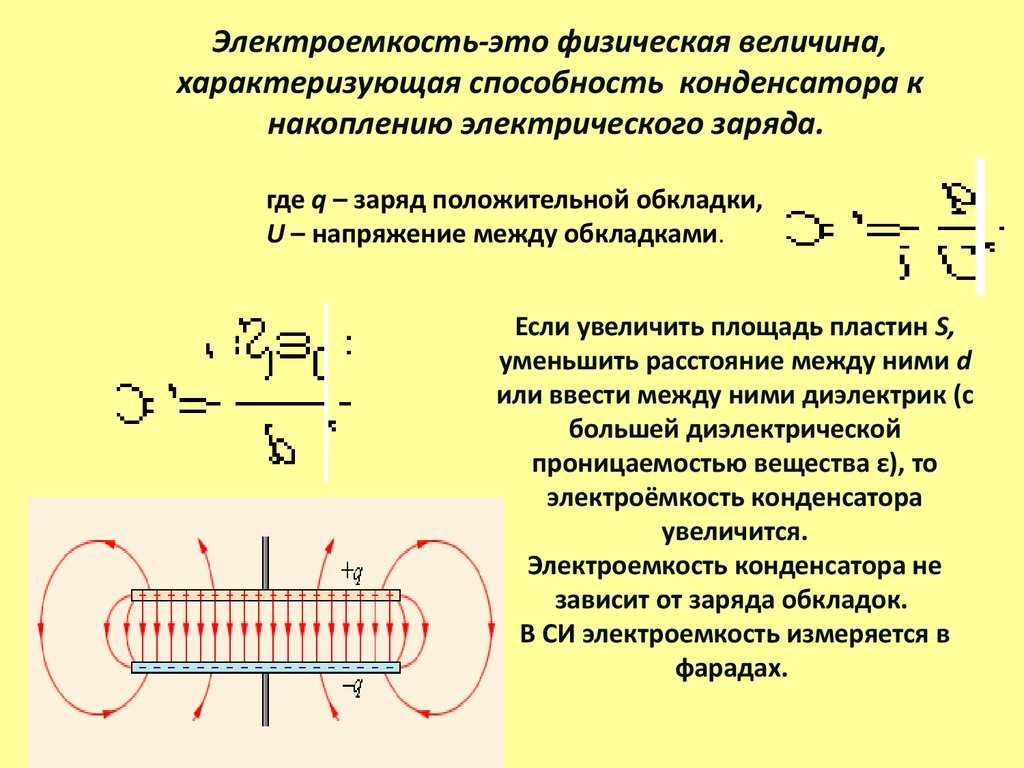

 Однако полное сопротивление идеального конденсатора равно величине его реактивного сопротивления, хотя эти два параметра не идентичны. Мы выражаем реактивное сопротивление как обычное число в омах, а полное сопротивление конденсатора представляет собой реактивное сопротивление, умноженное на -j. Это соответствует следующей формуле:
Однако полное сопротивление идеального конденсатора равно величине его реактивного сопротивления, хотя эти два параметра не идентичны. Мы выражаем реактивное сопротивление как обычное число в омах, а полное сопротивление конденсатора представляет собой реактивное сопротивление, умноженное на -j. Это соответствует следующей формуле:  Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Эта обратная связь между частотой и реактивным сопротивлением облегчает использование конденсаторов для блокирования низкочастотных компонентов сигнала и одновременного пропускания высокочастотных компонентов.
Следовательно, более высокая емкость и более высокая частота приводят к более низкому реактивному сопротивлению. Эта обратная связь между частотой и реактивным сопротивлением облегчает использование конденсаторов для блокирования низкочастотных компонентов сигнала и одновременного пропускания высокочастотных компонентов.


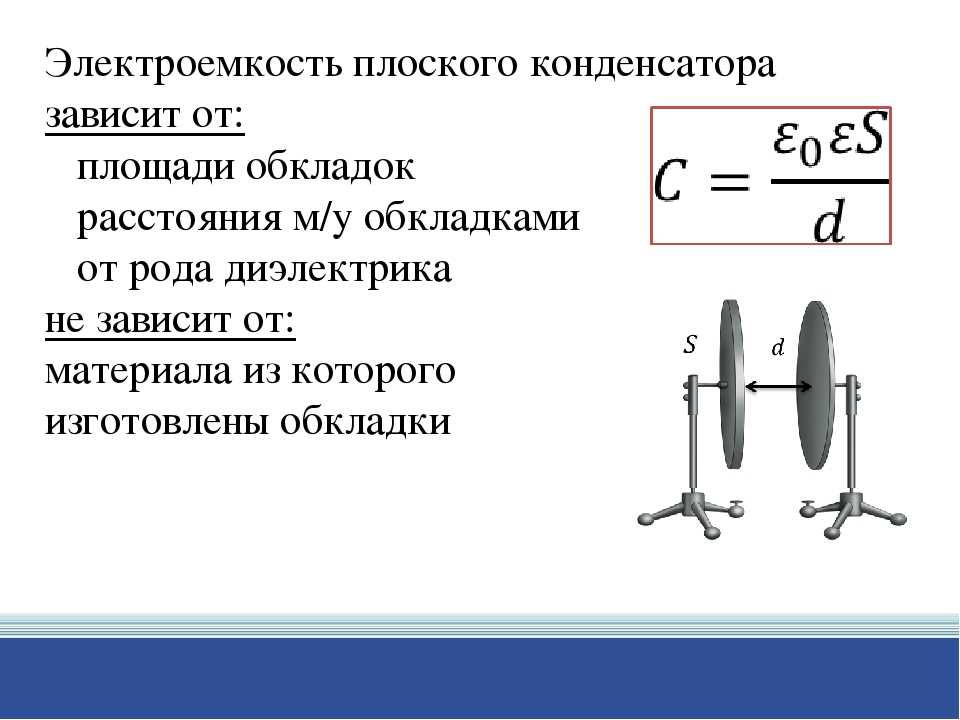
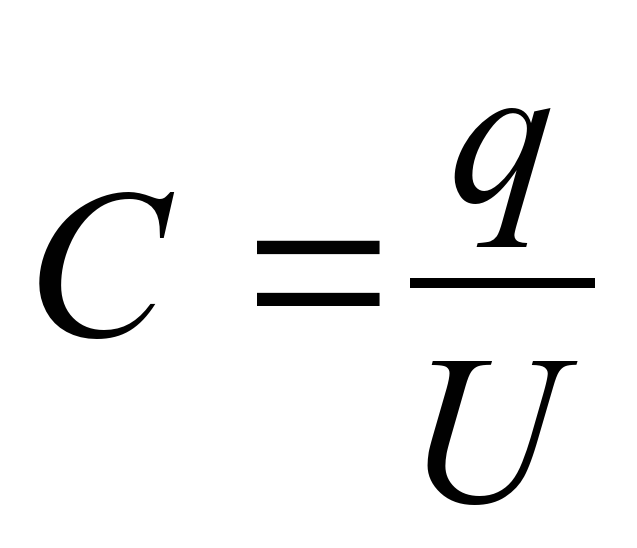 ) Таким образом, напряженность электрического поля прямо пропорциональна В .
) Таким образом, напряженность электрического поля прямо пропорциональна В . Заряд, хранящийся в конденсаторе, равен
Заряд, хранящийся в конденсаторе, равен Конденсатор емкостью 1 фарад мог бы хранить 1 кулон (очень большое количество заряда) при приложении всего 1 вольта. Таким образом, один фарад — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарад (1 пФ = 10 −12 Ф) в миллифарад (1 мФ = 10 −3 Ф).
Конденсатор емкостью 1 фарад мог бы хранить 1 кулон (очень большое количество заряда) при приложении всего 1 вольта. Таким образом, один фарад — это очень большая емкость. Типичные конденсаторы варьируются от долей пикофарад (1 пФ = 10 −12 Ф) в миллифарад (1 мФ = 10 −3 Ф). Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость зависит от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом C должен быть больше для большего размера A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, C должно быть больше для меньшего d .
Когда к конденсатору прикладывается напряжение В , он накапливает заряд Q , как показано на рисунке. Мы можем видеть, как его емкость зависит от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, разноименные притягиваются, а сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут распространяться дальше. Таким образом C должен быть больше для большего размера A . Точно так же, чем ближе пластины друг к другу, тем сильнее притяжение к ним противоположных зарядов. Таким образом, C должно быть больше для меньшего d .
 Как только C найдено, накопленный заряд можно найти с помощью уравнения 9.{-9}\text{ F}=8,85\text{ нФ}\end{массив}\\C ==ϵodA=(8,85×10−12 мФ)1,00×10−3 м1,00 м2 8,85×10−9 F=8,85 нФ
Как только C найдено, накопленный заряд можно найти с помощью уравнения 9.{-9}\text{ F}=8,85\text{ нФ}\end{массив}\\C ==ϵodA=(8,85×10−12 мФ)1,00×10−3 м1,00 м2 8,85×10−9 F=8,85 нФ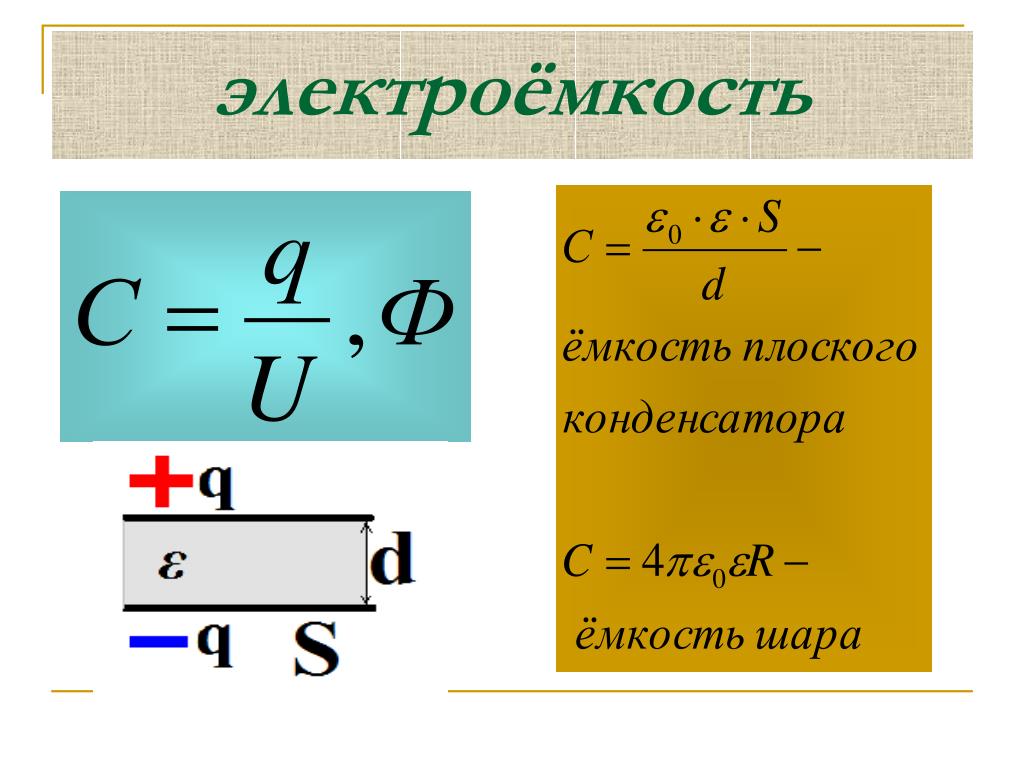
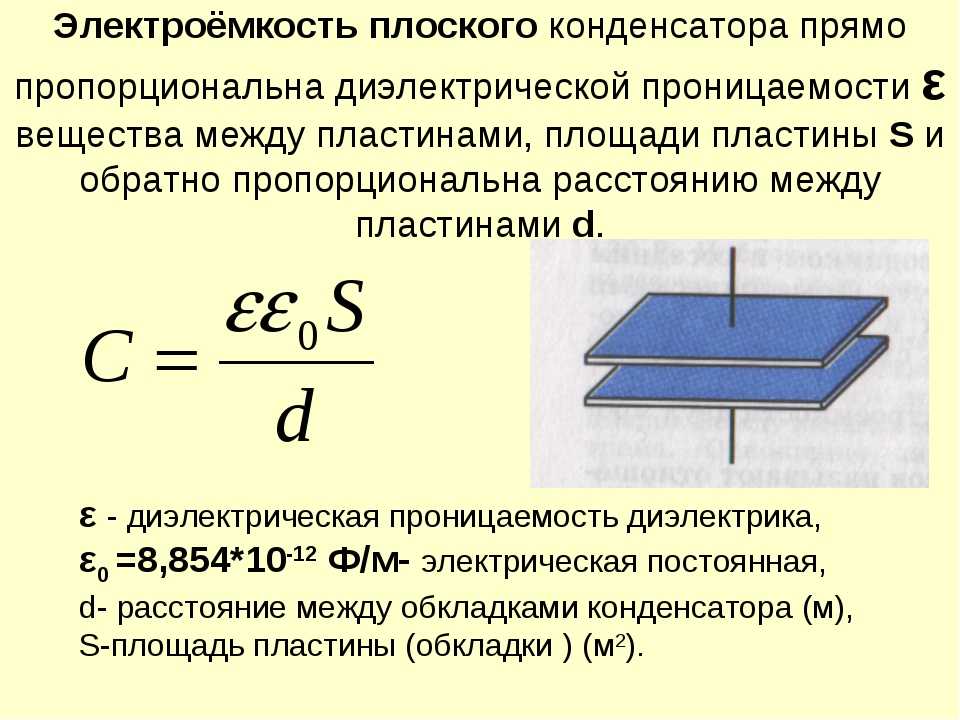 Важным решением этой проблемы является размещение изоляционного материала, называемого 9.0391 диэлектрик , между пластинами конденсатора и пусть d будет как можно меньше. Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем пробиться.
Важным решением этой проблемы является размещение изоляционного материала, называемого 9.0391 диэлектрик , между пластинами конденсатора и пусть d будет как можно меньше. Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем пробиться.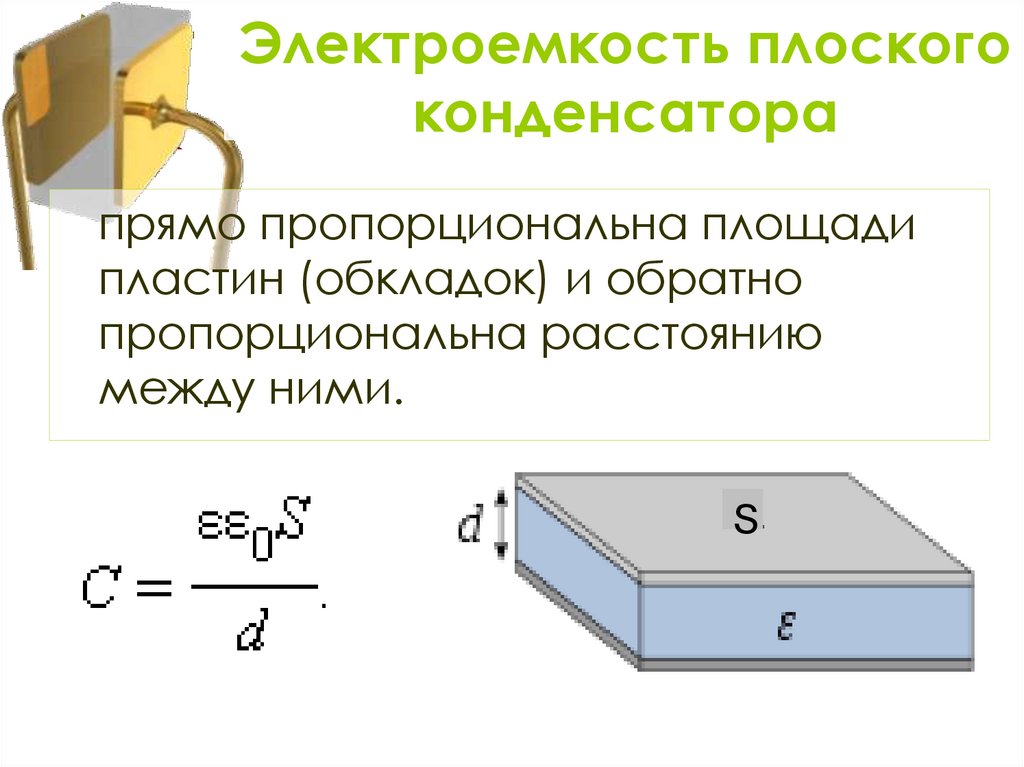 Если использовать диэлектрик, возможно, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в 9 раз.0391 κ , что для тефлона составляет 2,1.
Если использовать диэлектрик, возможно, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в 9 раз.0391 κ , что для тефлона составляет 2,1. 1
1 Так тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для заполненного воздухом конденсатора с плоскими пластинами, мы находим, что конденсатор с тефлоновым наполнением может хранить максимальный заряд 94\text{ V})\\\text{ }&=&1.1\text{ mC}\end{array}\\Q ====CVκCairV(2.1)(8,85 нФ)(6,0× 104 В)1,1 мКл
Так тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для заполненного воздухом конденсатора с плоскими пластинами, мы находим, что конденсатор с тефлоновым наполнением может хранить максимальный заряд 94\text{ V})\\\text{ }&=&1.1\text{ mC}\end{array}\\Q ====CVκCairV(2.1)(8,85 нФ)(6,0× 104 В)1,1 мКл Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рисунке 5 схематически показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии д прочь.
Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды приводит к тому, что она имеет относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации можно лучше всего объяснить с точки зрения характеристик кулоновской силы. На рисунке 5 схематически показано разделение заряда в молекулах диэлектрического материала, помещенного между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень велика, так как они очень близко друг к другу. Это притягивает к пластинам больше заряда, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии д прочь. (b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.
(b) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к меньшему напряжению между пластинами при том же заряде. Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.
 Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию.
Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны преувеличенно). Возникающее в результате разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что противоположный заряд теперь ближе к внешним зарядам, вызывая поляризацию. Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более сильно заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец оставляет слегка положительным. Присущее полярным молекулам разделение зарядов облегчает их согласование с внешними полями и зарядами. Поэтому полярные молекулы проявляют больший поляризационный эффект и имеют большую диэлектрическую проницаемость. Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды намного эффективнее собирают ионы, потому что они имеют электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

 Точно так же объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
Точно так же объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.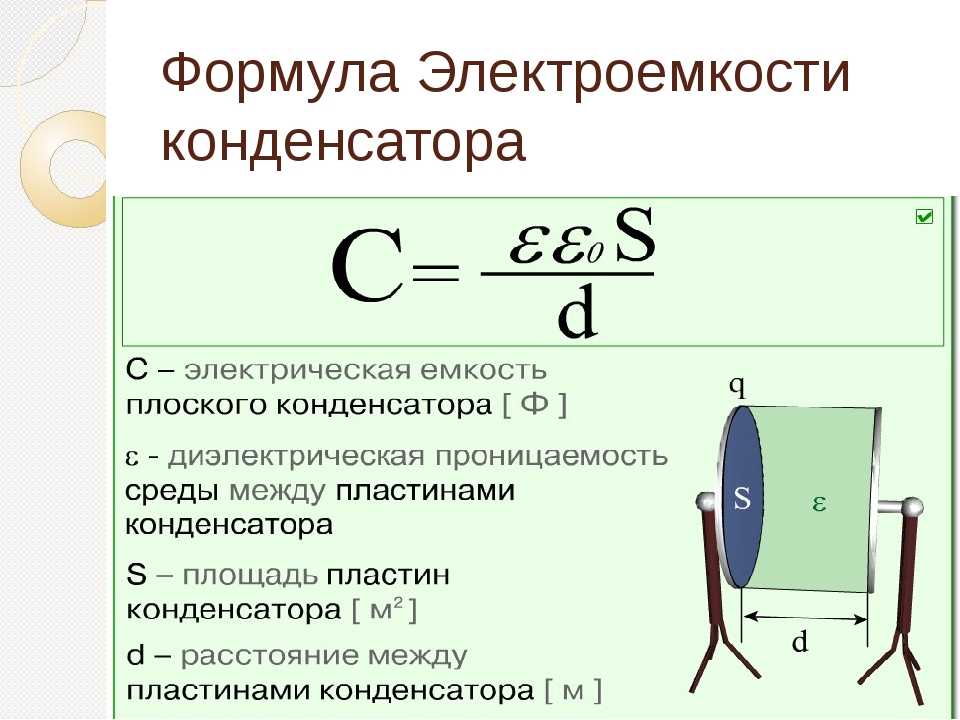 Таким образом, мембраны представляют собой заряженные конденсаторы с важными функциями, связанными с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизация энергии пищи или какой-либо другой источник?
Таким образом, мембраны представляют собой заряженные конденсаторы с важными функциями, связанными с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизация энергии пищи или какой-либо другой источник?
 Палец пострадавшего обожжен разрядом конденсатора через 0,200 г плоти. Что такое повышение температуры тела? Разумно ли предположить отсутствие фазового перехода?
Палец пострадавшего обожжен разрядом конденсатора через 0,200 г плоти. Что такое повышение температуры тела? Разумно ли предположить отсутствие фазового перехода? 21,6 мКл
21,6 мКл Здесь заряд сохраняется в виде электростатической энергии. Емкость измеряется в основных единицах СИ, то есть в фарадах. Эти единицы измерения могут быть в микрофарадах, нанофарадах, пикофарадах или фарадах. Выражение для емкости дается выражением,
Здесь заряд сохраняется в виде электростатической энергии. Емкость измеряется в основных единицах СИ, то есть в фарадах. Эти единицы измерения могут быть в микрофарадах, нанофарадах, пикофарадах или фарадах. Выражение для емкости дается выражением,

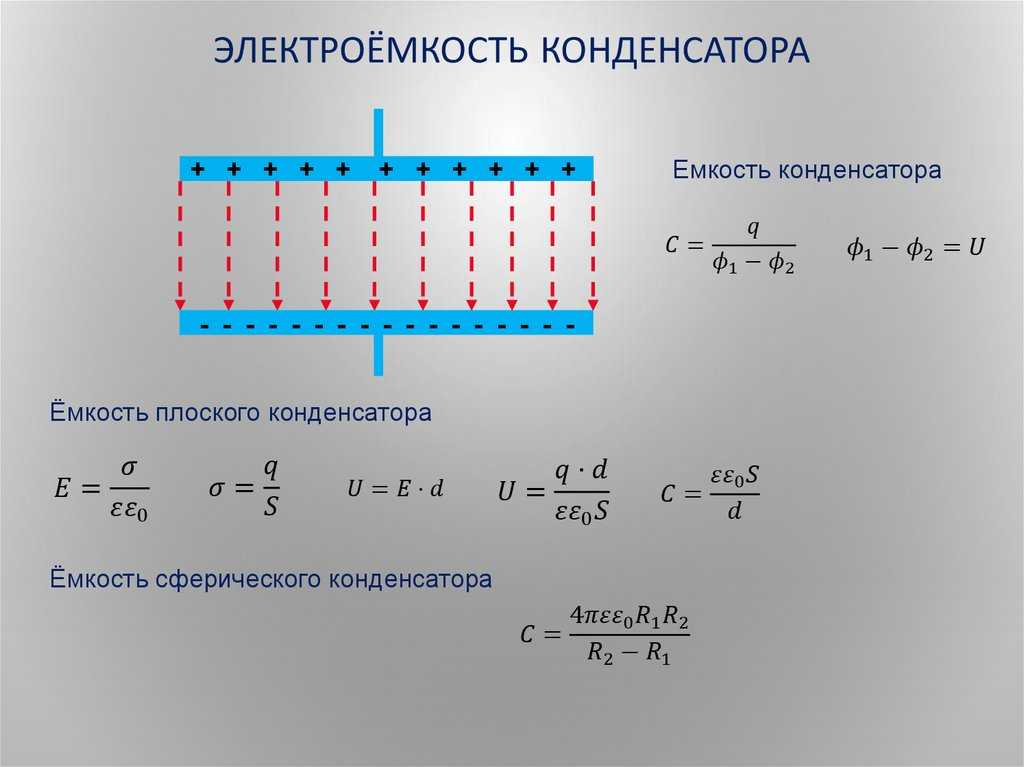


 е. VS = VC = 12 В. Когда конденсатор полностью заряжен, это означает, что конденсатор поддерживает заряд постоянного напряжения, даже если напряжение питания отключено от цепи.
е. VS = VC = 12 В. Когда конденсатор полностью заряжен, это означает, что конденсатор поддерживает заряд постоянного напряжения, даже если напряжение питания отключено от цепи.
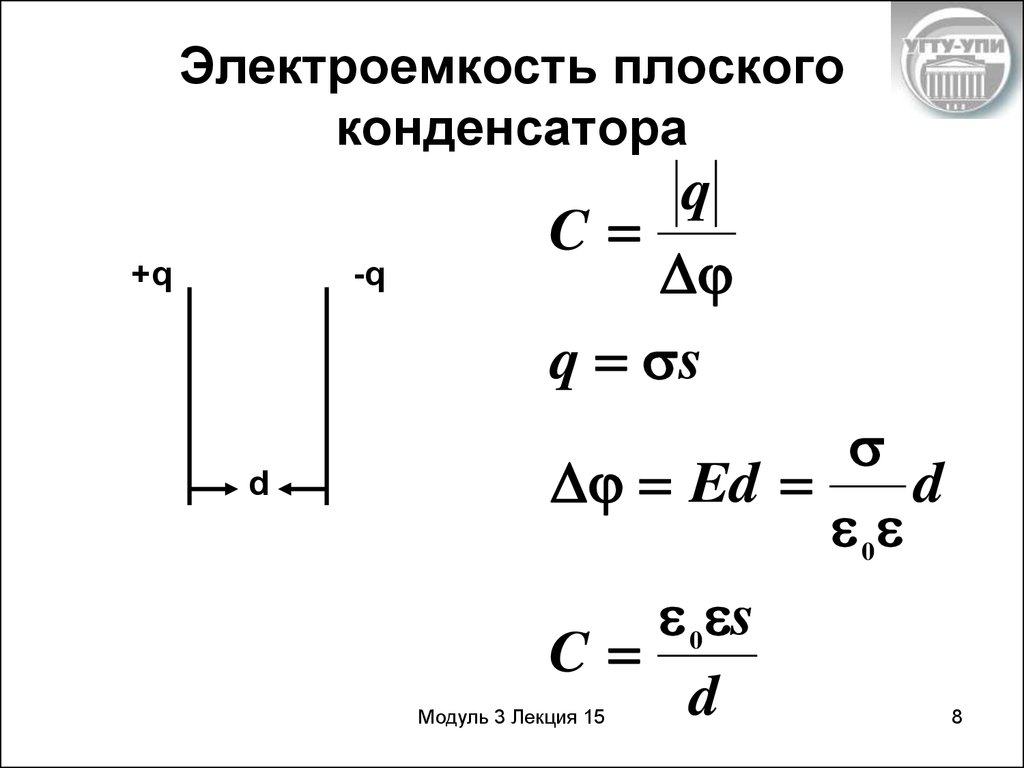 Таким образом, заряда нет. Следовательно, ток, протекающий по цепи, станет равным нулю.
Таким образом, заряда нет. Следовательно, ток, протекающий по цепи, станет равным нулю. Эти конденсаторы также используются в аудио- и видеосистемах автомобилей, заменяя аккумуляторы высокой емкости.
Эти конденсаторы также используются в аудио- и видеосистемах автомобилей, заменяя аккумуляторы высокой емкости.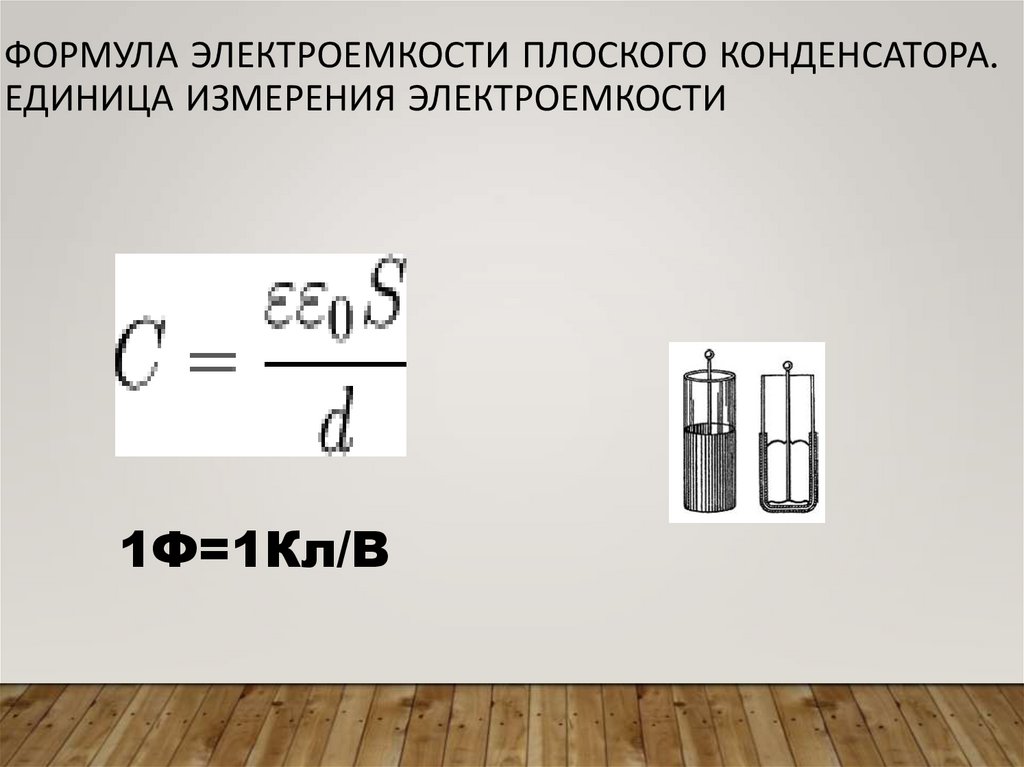 Этот заряд либо +Q, либо -Q обменивается между двумя пластинами конденсатора. После преобразования некоторого заряда между пластинами образуется электрическое поле, в этом случае для полного заряда конденсатора потребуется дополнительная работа. Эта дополнительная работа называется энергией, запасенной в конденсаторе. Энергия измеряется в джоулях (Дж). Теперь мы видим уравнения для этой энергии и работы.
Этот заряд либо +Q, либо -Q обменивается между двумя пластинами конденсатора. После преобразования некоторого заряда между пластинами образуется электрическое поле, в этом случае для полного заряда конденсатора потребуется дополнительная работа. Эта дополнительная работа называется энергией, запасенной в конденсаторе. Энергия измеряется в джоулях (Дж). Теперь мы видим уравнения для этой энергии и работы.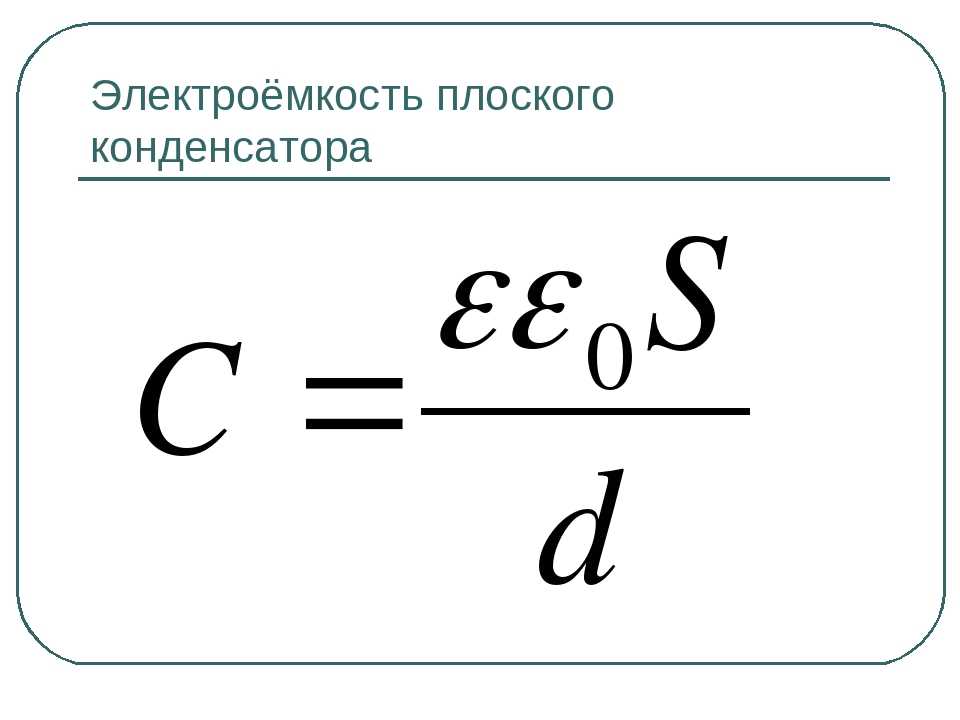 Конденсатор является пассивным элементом цепи, но он не поглощает электрическую энергию, а накапливает ее. Основное назначение конденсатора — хранить электрическую энергию в течение очень короткого промежутка времени. Запас энергии конденсатора зависит от емкости конденсатора. Емкость относится к различным параметрам по формуле емкости. Конденсатор также известен как конденсатор. Конденсаторы являются приложением статического электричества.
Конденсатор является пассивным элементом цепи, но он не поглощает электрическую энергию, а накапливает ее. Основное назначение конденсатора — хранить электрическую энергию в течение очень короткого промежутка времени. Запас энергии конденсатора зависит от емкости конденсатора. Емкость относится к различным параметрам по формуле емкости. Конденсатор также известен как конденсатор. Конденсаторы являются приложением статического электричества. Суммарный заряд $q$ на проводящих пластинах прямо пропорционален напряжению питания.
Суммарный заряд $q$ на проводящих пластинах прямо пропорционален напряжению питания.
 9{-12}$F/м. Диэлектрическая проницаемость других материалов называется относительной диэлектрической проницаемостью и представлена в виде $\varepsilon_{r}=\frac{\varepsilon }{\varepsilon _{o}}$ по сравнению с абсолютной диэлектрической проницаемостью. Относительная диэлектрическая проницаемость также известна как диэлектрическая проницаемость. Для каждого материала существует порог, если приложенное к нему напряжение превышено. Диэлектрический материал разрушается, что свидетельствует о диэлектрической прочности и называется напряжением пробоя диэлектрика.
9{-12}$F/м. Диэлектрическая проницаемость других материалов называется относительной диэлектрической проницаемостью и представлена в виде $\varepsilon_{r}=\frac{\varepsilon }{\varepsilon _{o}}$ по сравнению с абсолютной диэлектрической проницаемостью. Относительная диэлектрическая проницаемость также известна как диэлектрическая проницаемость. Для каждого материала существует порог, если приложенное к нему напряжение превышено. Диэлектрический материал разрушается, что свидетельствует о диэлектрической прочности и называется напряжением пробоя диэлектрика. В электротехнике энергия — это способность перемещать заряд под действием напряжения.
В электротехнике энергия — это способность перемещать заряд под действием напряжения.