Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости.  § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 11. Уравнение конического сечения в полярных координатах. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры.  § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии.  Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 9. Скалярное произведение векторов, заданных проекциями. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. Упражнения ГЛАВА III.  ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой. Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 9. Пересечение прямой с плоскостью. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка.  Конструкции В. Г. Шухова. Конструкции В. Г. Шухова.Упражнения Ответы |
Обоснуйте направления всех векторов на плане скоростей
Направление только вектора ра известно наперед, остальные мы получаем через план скоростей (это же векторное уравнение), мы через план узнаем направления движения точек как направление векторов. Стрелка показывает куда движется одна точка относительно другой. Например как на рисунке выше.
Как было определено направление угловой скорости какого-либо звена, указанного преподавателем
Для ползунного механизма все просто (смотрим на план скоростей) — вектор ab (или ас для Г -образного звена 2) показывает, куда поворачивается точка b (с) относительно А. Дальше надо мысленно приложить этот вектор к точке b (с) и понять, куда вращается конец шатуна 2 относительно А.
Для
рычажного механизма еще можно определить
направление вращения коромысла 3, берем
вектор (смотрим на план скоростей) из
полюса р до точки, в которой соединяются
звено 2 и 3 и мысленно прикладываем его
к этой точке на механизме, определяем
направление со3.
Для рычажных механизмов звено 3 иногда состоит из двух кусков, там значит две силы инерции, кроме ИЗ в индексе (верхнем) еще имена точек, определяющих про какой кусок идет речь.
Расскажите последовательность силового расчёта структурной группы.
Отбрасываем от механизма звено 1 и оставшуюся стойку (звено со штриховкой).
Для
ползунных механизмов: ну вот оторвали
края, теперь в точках где оторвали звено
1, вставляем по две силы — тангенциальную
и нормальную, первую перпендикулярно
звену 2 (помним про условности), вторую
— вдоль звена. Для звена три, если это
палка, вставляем силу перпендикулярную
звену в каждую из двух опор. Если ползун
— перпендикулярно его направляющей.
Составляем уравнение моментов относительно
точки соединения звеньев, оно равно
нулю и в нем неизвестная всего одна —
тангенциальная сила. Простеньким матаном
находим ее. Если не угадали с направлением,
то получим знак «-», похер, разворачиваем
ее, меняем знаки в уравнении, с
положительными числами работать как-то
проще, ИМХО.
Для рьгчажных механизмов расчет звена 3 такой же как для звена 2. Тангенциальную и нормальную силы строим из опоры перпендикулярно и параллельно куску звена 3. Через уравнение моментов находим тангенциальную силу, рисуем план и находим из него нормальные силы. Так что в силовом анализе группы 2-3 мы находим танг. силы (две) через матан, а нормальные через план.
Объясните, как были определены величина или направление какого- либо указанного преподавателем вектора на планах сил.

Силы тяжести G это масса звена, умноженная на ускорение свободного падения 9,81. Силы инерции это масса на ускорение своего центра масс S на плане ускорений. Момент инерции это геометрический момент инерции умноженный на угловое ускорение вращающегося звена. Смотрите расчеты. Силы инерции и моменты инерции направлены против ускорений и угловых ускорений соответственно.
Изменится ли, а если изменится, то как, величина уравновешивающей силы, если точку её приложения сместить ближе к центру вращения кривошипа?
Ясен, что изменится! Произведение этой силы на длину кривошипа есть крутящий момент на валу (смотреть первый рисунок в ПЗ), если сместить точку ближе приложения ближе к О, то плечо силы станет короче, а момент нам нужен тот же. Значит сила возрастет, причем пропорционально уменьшению длины ОА.
Изменится ли, а если изменится, то как, величина реакции стойки на входное звено силы, если точку приложения уравновешивающей силы сместить ближе к центру вращения кривошипа?
Смотрим
на план сил звена 1. Есть там какие-то
плечи? Нет. Вот и не изменится.
Есть там какие-то
плечи? Нет. Вот и не изменится.
Изменится ли при этом направление реакции стойки?
Да с чего бы ему меняться? План сил звена 1 строится только вектором ab, потом и его точек строим прямые вдоль звена 1 и перпендикулярно ему. Как тут не крути точки приложения силы, мы получим этот треугольник.
Обоснуйте правильность определения величины и направления реакции между звеньями, составляющими структурную группу.
План
сил специально строился так, что силы
для звена 2 идут в нем друг за другом. То
есть если взять вектор F21,
дорисовать после него G2
потом Fh3
, нарисовать из конца вектора Fh3
вектор к началу F21,
то получим замкнутый контур. Замкнутый
контур означает, что сумма сил, действующих
на звено 2 равна нулю, то есть звено
уравновешено. А равновесие звена это
единственное, что дает право считать
группу всякими моментами и планами.
Равновесие мы получили добавив инерционные
силы и моменты.
Направление векторного калькулятора
Если вы хотите рассчитать направление вектора , вы попали по адресу. Этот калькулятор находит угол направления вектора и вычисляет единичный вектор в этом направлении.
Векторы — это мощный инструмент для представления многих физических величин в нашем физическом мире. Они представляют собой силы, скорости и многие другие производные от них величины.
Помимо направления, также возможно найти величину вектора, если вы выберете расширенный режим калькулятора. Таким образом, с помощью этого инструмента вы можете найти величину и угол направления любого вектора.
Как рассчитать направление вектора?
Вы можете выразить или вычислить направление вектора v⃗ двумя способами:
- Вычисление угла направления вектора
v⃗. Направляющий угол — это угол, которыйv⃗образует с положительной осью x, считая против часовой стрелки.
- Вычисление единичного вектора в направлении того же вектора. Этот единичный вектор называется вектором направления .
Как найти угол направления вектора?
Чтобы вычислить угол θ\thetaθ, который двумерный вектор v⃗=(x,y)\vec{v} = (x, y)v=(x,y) образует с горизонтальной осью, используйте это уравнение:
θ=arctan(yx) \theta = \arctan\left(\frac{y}{x}\right)θ=arctan(xy)
Единственная проблема с этим уравнением заключается в том, что оно не дает нам угол относительно положительной оси x, но только относительно ближайшей горизонтальной оси. Если ваш вектор лежит в первом квадранте декартовой плоскости, как вектор, указывающий на P(3,5)P(3,5)P(3,5) на изображении, это не проблема. 9\circ — \gammaθ=180∘−γ. Мы можем распространить это рассуждение на другие случаи и составить следующие уравнения для вычисления направления вектора в каждом квадранте:
- В первом квадранте , } = \arctan(\frac{y}{x})θI=arctan(xy).

- Во втором квадранте , θII=180°-arctan(yx)\theta_\text{II} = 180° — \arctan(\frac{y}{x})θII=180°-arctan(xy ).
- В третьем квадранте , θIII=180°+arctan(yx)\theta_\text{III} = 180° + \arctan(\frac{y}{x})θIII=180°+arctan(xy ).
- В четвертом квадранте , θIV=360°−arctan(yx)\theta_\text{IV} = 360° — \arctan(\frac{y}{x})θIV=360°−arctan(xy ).
🙋 Термин arctan(yx)\arctan(\frac{y}{x})arctan(xy) дает угол в радианах, и вы должны преобразовать его в градусы, прежде чем использовать его во втором, третьем или уравнения четвертого квадранта. Посетите наш инструмент преобразования углов, чтобы узнать, как это сделать.
Как вычислить единичный вектор в направлении другого вектора?
Чтобы найти единичный вектор û в направлении другого вектора v⃗ = (x, y, z) , выполните следующие действия:
- Найдите модуль вектора
v⃗:
|v⃗| = √(x² + y² + z²) - Разделить каждый коэффициент вектора
v⃗на величинуv⃗:
û = v⃗/|v⃗| = (х/|v⃗|, у/|v⃗|, z/|v⃗|).
- Вот и все.
û— единичный вектор в направленииv⃗.
Как найти вектор одной величины в направлении другой?
Чтобы найти вектор определенной величины в направлении другого вектора v⃗ = (x, y, z) :
- Найти модуль вектора
v⃗:
|v⃗| = √(x² + y² + z²) - Найдите единичный вектор
ûв направленииv⃗. Для этого каждый коэффициент вектораv⃗разделим на модуль вектора:
û = v⃗/|v⃗| = (х/|v⃗|, у/|v⃗|, z/|v⃗|) - Умножить величину желаемого вектора на единичный вектор
х. Это приведет к желаемому вектору.
Как найти величину и направление двух векторов?
Чтобы найти величину и направление двух векторов, необходимо найти результирующий вектор (для этого можно использовать наш калькулятор сложения векторов) и применить к нему описанные выше действия.
Теперь, когда вы знаете, как найти величину и угол направления вектора, давайте рассмотрим некоторые числовые примеры и ответы на часто задаваемые вопросы.
FAQ
Как найти вектор величины 3 в направлении v = 12i — 5k?
Чтобы найти вектор величины 3 в направлении v⃗ = 12i − 5k :
- Найдите величину
v⃗:
|v⃗| = √(12² + (-5)²) = 13 - Найдите единичный вектор
ûв направленииv⃗. Для этого нужно разделитьv⃗на его величину:
û = v⃗/|v⃗| = (12/13)i - (5/13)k - Умножьте желаемую величину
3на единичный векторû. Получаем векторw⃗:
w⃗ = 3û = (36/13)i − (15/13)k
, которое имеет желаемое направление и величину.
Как вычислить единичный вектор в направлении v = i + j + 2k
Чтобы вычислить единичный вектор в направлении v⃗ = i + j + 2k :
- Найти модуль
v⃗:
|v⃗| = √(1² + 1² + 2²) = √6 ≈ 2,4495 - Разделить вектор
v⃗на его модуль:
û = v⃗/|v⃗| = (1/√6)i + (1/√6)j + (2/√6)k - Вот и все.

û— единичный вектор в направленииv⃗.
Является ли скалярное произведение двух векторов в одном направлении положительным или отрицательным?
Скалярное произведение двух векторов в одном направлении всегда положительно. Это потому, что скалярное произведение двух векторов в одном направлении равно произведению их величин, а их величины всегда положительны.
Как найти величину и направление суммы двух векторов?
Чтобы найти величину и направление суммы двух векторов:
- Найдите равнодействующую двух векторов.
- Просуммируйте квадрат каждого из компонентов результирующего вектора.
- Возьмите квадратный корень из предыдущего результата, и это будет величина суммы ваших двух векторов!
- Чтобы вычислить направление вектора
v⃗ = (x, y), используйте формулуθ = arctan(y/x), гдеθ— наименьший угол, который вектор образует с горизонтальной осью, а x и y компоненты результирующего вектора.
Описание направлений — доктора математики
Мы рассматриваем концепцию векторов на вводном уровне. На прошлой неделе мы рассмотрели, как они определяются в этом контексте (как величины с величиной и направлением) и как они складываются (что на самом деле является частью определения). Наша коллекция ответов от Ask Dr. Math на этот раз посвящена идеям единичных векторов, компонентов и «направленных косинусов», которые являются способами описания направления вектора.
Единичные векторы и коллинеарность
Первый вопрос из 2002:
Единичные векторы Я пытаюсь решить математическую задачу, которую я действительно не понимаю. Проблема гласит: «Найдите два единичных вектора , которые коллинеарны с каждым из следующих векторов. (a) вектор A = (3, -5)» Во всяком случае, это первый вопрос в этой задаче. Я не понимаю, что эта проблема даже просит меня сделать. Всегда ли единичный вектор равен 1? Я провел много исследований в своей книге и в Интернете, и я до сих пор не понимаю.Любая помощь, которую вы могли бы предоставить, будет БОЛЬШИМ образом оценена. Большое спасибо. 92}$$
Вот его три вектора, показывающие, что все они имеют длину 1: круг с центром в начале координат, радиус которого равен 1), вектор от начала до точки — единичный вектор (cos(a),sin(a)) , где a - угол от положительной оси x до точки.
Вот пример, где мой угол \(\theta\) равен 133°, поэтому его компоненты равны \((\cos(133°), \sin(133°)) = (-0,68, 0,73)\) : 92) и разделить оба компонента на это: 1/|(а,б)| * (а,б) = (а/|(а,б)|, б/|(а,б)|) Вы понимаете, почему он всегда будет коллинеарным исходному вектору и почему его длина всегда будет равна 1? (Обратите внимание, что единичный вектор, указывающий в _противоположном_ направлении, также коллинеарен.)
Деление обоих компонентов на \(|a|\) уменьшает длину до 1 без изменения направления. Умножение на минус 1 меняет направление. Вот наш вектор \(\mathbf{a} = (3, -5)\) и два единичных вектора \(\mathbf{u}_a = \left(\frac{3}{\sqrt{34}}, -\frac{5}{\sqrt{34}}\right)\) и \(-\mathbf{u}_a = \left(-\frac{3}{\sqrt{34}}, \frac{5 }{\sqrt{34}}\справа)\):
Единичные векторы, базисные векторы
Этот вопрос 1998 г. от студента, чьи цели выходят далеко за рамки основ, но которому нужна помощь в запуске:
от студента, чьи цели выходят далеко за рамки основ, но которому нужна помощь в запуске:
Единичные и базисные векторы в трех измерениях Пожалуйста, дайте мне простое объяснение: 1. Единичный вектор . Мои книги (например, «Векторный и тензорный анализ» Борисенко) неясны и предполагают, что я уже это понимаю. Кроме того, какая польза от единичного вектора? 2. Базисный вектор . Опять же, мои другие источники не ясны. P.S. Я изучаю теорию относительности самостоятельно, и поэтому я хотел бы понять основы, такие как тензорная алгебра.
Доктор Энтони ответил, дав основное определение векторов, которое мы обсуждали в прошлый раз, потому что оно применимо (с некоторыми небольшими изменениями) к физике:
величина и направление . Думайте о векторе как о прямой линии, указывающей в определенном направлении. Длина линии представляет собой звездную величину вектора. Таким образом, в случае единичного вектора , длина строки 1 единица.При работе над задачами удобно использовать единичные векторы. Если мы позволим u представлять вектор в определенном направлении и единицу величины, то 3u, 7u и -8u сразу же можно понять как векторы величин 3, 7 и -8, все в направлении от u (кроме -8u, поскольку отрицательный знак означает «в направлении, противоположном к +u»).
Так же, как выше мы начали с вектора a и нашли единичный вектор в том же направлении, здесь мы можем обратить процесс и описать вектор как единичный вектор справа направление , умноженное на его длину . При этом мы разбиваем вектор на его величину (число) и направление (единичный вектор). Вот единичный вектор u и упомянутые кратные:
Но мы можем сделать гораздо больше, выбрав стандартный набор единичных векторов, чтобы использовать его в качестве «основы» для описания любого вектора:
Это очень распространено использовать i, j и k как единичных вектора в направлениях осей x, y и z соответственно в трехмерном пространстве.Это означает, что КАЖДЫЙ вектор в пространстве может быть задан через его «компоненты», параллельные этим трем осям. Так, например, 5i + 2j - 6k — это вектор в пространстве, и его величина будет представлена длиной линии, соединяющей начало координат (0,0,0) с точкой (5,2,-6). Кстати, это отвечает на ваш второй вопрос: i, j, k называются «базовыми» векторами, потому что они используются в качестве основы для выражения всех других векторов. Любой другой вектор в трехмерном пространстве может быть задан через i, j и k.
Здесь я буду придерживаться двух измерений. Единичные базисные векторы i и j такие же, как u и v , которые мы использовали на первой иллюстрации выше:
Иногда удобно использовать другие векторы в качестве базовых векторов. Любые два непараллельных вектора можно использовать в качестве базовых векторов, чтобы задать любую точку на плоскости двух векторов. То есть любой другой вектор в этой плоскости может быть выражен через базовые векторы, точно так же, как мы говорим 6i + 4j, чтобы выразить вектор в плоскости xy.Точно так же любые три некомпланарных вектора могут использоваться в качестве базовых векторов, «охватывающих» трехмерное пространство. Опять же, наиболее распространенными базовыми векторами являются i, j, k, но бывают случаи, когда используется совершенно другой набор базовых векторов. Наконец, векторы не ограничиваются 1, 2 или 3 измерениями. Ты можешь имеют многомерные векторы, выраженные через 4, 5, 6 и высшие базовые векторы. Количество базовых векторов будет равно размер рассматриваемого пространства.
Вот наш вектор 6 i + 4 j , который также можно назвать (6, 4) с помощью его компонентов:
Направление в виде углов (2 измерения)
Следующий вопрос, из 1998 года, включает векторы, направление которых выражается как угол от положительной оси x :
Компоненты вектора, величина и направление Вектор M величиной 4,75 м находится под углом 58,0 градусов против часовой стрелки от положительной оси x.К вектору N 9 добавлено .0004 , а результирующее представляет собой вектор величиной 4,75 м, расположенный под углом 39 градусов против часовой стрелки от положительной оси x. Найдите: (а) компоненты N и (б) величину и направление N. Я нарисовал графическую иллюстрацию проблемы. Но я действительно не могу решить это, потому что я не знаю, как это сделать.
Здесь у нас складываются два вектора, и один из них и сумма описываются в терминах величины и направления. Мы хотим найти вектор n как по компонентам, так и по направлению (углу) и величине:
Доктор Рик ответил, предложив наиболее вероятный метод:
Привет, Кристин, Я помогу вам начать решение этой проблемы. Для этого вам понадобятся два инструмента: (1) преобразование между величиной/направлением и компонентами вектора и (2) добавление векторов. Первый требует некоторой тригонометрии, так что я надеюсь, что у вас есть некоторые. (1) Вам даны величина и направление векторов M и P (сумма M и N).Прежде чем вы сможете добавить их, вы должны найти их компоненты . Запомните эту схему: Мой+-------------* M | /| | / | | / | | / | | / | | л/ | | / | sin(a)|-----+ | | /| | | 1/ | | | / | | | /)а | | |/____|_______|__________ O cos(a) Mx Вектор длины 1 имеет компоненты (cos(a), sin(a)). По подобным треугольникам вектор M длины L имеет компоненты Mx = L*cos(a), My = L*sin(a). Сделайте это с обоими векторами M и P, чтобы получить их компоненты (Mx, My) и (Px, Py).
Как мы видели выше, мы можем думать о векторе м как о единичном векторе в заданном направлении, умноженном на его длину. Тригонометрические функции косинуса и синуса дают компоненты единичного вектора x и y , как мы видели в нашем первом ответе. Для нашего вектора m угол равен 58°, а длина равна 4,75, поэтому вектор $$(m_x, m_y) = (4,75\cos(58°), 4,75\sin(58°)) = (2,517 , 4. 028)$$
028)$$
Аналогично, для вектора p = m + n имеем угол 39° и длина 4,75, поэтому вектор равен $$(p_x, p_y) = (4,75\cos(39°), 4,75\sin(39°)) = (3,691, 2,989)$$
(2) Вы известно, что M + N = P. Чтобы сложить векторы, сложите их компоненты: Мх + Нх = Рх Мой + Ню = Ру Вы знаете Mx, My, Px и Py, поэтому должны быть в состоянии вычислить Nx и Ny. Это компоненты вектора N.
Чтобы найти компоненты n , мы просто вычитаем:{-1}(-0,885) = -41,5°$$
Вот инструменты, которые вам понадобятся. Посмотрим, сможешь ли ты выполнить эту работу сейчас. Напишите в ответ, если вы все еще запутались после того, как попробовали это.
Предположительно, Кристин сделала именно то, что мы сделали здесь.
Направление линии (3 измерения)
Этот вопрос 1997 года надеется найти способ указать направление трехмерного вектора, аналогичного углу или наклону в задаче предыдущего типа:
Формула для наклона 3- Линия D Спасибо, что ответили на наш вопрос о нахождении длины линии в трех измерениях.Теперь мы хотели бы знать формулу, чтобы найти наклон трехмерной линии . Мы просмотрели учебники и попытались адаптировать формулу, но безуспешно.
Доктор Роб ответил, сначала говоря о плоскостях, а не о линиях:
Не существует прямого аналога идеи наклона в двух измерениях . Предмет, который вы обсуждаете, — это аналитическая геометрия трех измерений. Следующие факты должны немного помочь. Линейное уравнение относительно x, y и z, такое как ax + by + cz = d, является уравнением 92). Результирующие коэффициенты x, y и z обладают тем свойством, что сумма их квадратов равна 1. Другая стандартная форма получается путем деления на d и записи уравнения в виде x/(d/a) + y/( d/b) + z/(d/c) = 1. Из этой формы вы можете прочитать точки пересечения с осями x, y и z: (d/a, 0, 0) является x- точка пересечения, (0, d/b, 0) — точка пересечения по оси y, а (0, 0, d/c) — точка пересечения по оси z (при условии, что все a, b, c и d отличны от нуля).Один из способов определения «наклона» плоскости состоит в том, чтобы записать единичный вектор, который перпендикулярен к ней, называемый 9.2), где I, J и K — единичные векторы в направлениях x, y и z. Коэффициенты I, J и K в этом выражении называются направляющими косинусами вектора, потому что они представляют собой косинусы углов между вектором и осями x, y и z соответственно.
Две стандартные формы, которые он упоминает для плоскости, суть $$a’x + b’y + c’z = d’$$, где вектор ( a ‘, b ‘, c ‘) — это единичный вектор, называемый единичным вектором нормали (это то, что мы увидим позже в этой серии или в последующих сериях), и $$\frac{x}{A} + \frac{y}{B} + \frac{z}{C} = 1$$, где A , B и C — точки пересечения трех осей. Вектор нормали представляет направление плоскости.
Но вопрос был о линии, и здесь также проявляются «направленные косинусы», только что упомянутые для единичного вектора нормали:
Линия определяется как пересечение двух непараллельных плоскостей.Это означает, что вам нужно два линейных уравнения относительно x, y и z, чтобы определить линию. Существует несколько стандартных форм уравнений прямой, но наиболее часто используемой является х - х0 у - у0 z - z0 ------ = ------ = ------ а б в Здесь (x0, y0, z0) — точка на прямой, а числа a, b и c определяют направление вдоль прямой: вектор a*I = b*J + c*K параллелен прямой. (Примечание: эта форма работает только тогда, когда линия не параллельна ни одной из плоскостей xy, xz или yz, т. е. когда ни a, ни b, ни c не равны нулю).
Обратите внимание, что эта форма представляет собой не одно уравнение, а пару уравнений, которые приравнивают три величины. В этой форме $$\frac{x – x_0}{a} = \frac{y – y_0}{b} = \frac{z – z_0}{c}$$ вектор ( a , b , c ) дает направление линии, которое является лучшим ответом на вопрос, подобно вектору нормали к плоскости.
В некотором смысле косинусы направления являются ближайшим аналогом наклона.В двух измерениях это просто косинус наклона, который представляет собой угол с осью x, и косинус его дополнения, который является синусом наклона. Наклон - это отношение этих двух, тангенс наклона. Точного аналога нет, потому что не существует «отношения» трех направляющих косинусов или любых трех чисел.
Мы могли бы, однако, сказать, что тройное отношение a : b : c является разумным аналогом наклона линии, хотя это и не число; направляющие косинусы, как мы увидим ниже, являются просто компонентами единичного вектора в направлении линии.
Как он предлагает, мы можем сделать все это в двух измерениях для сравнения, что весьма поучительно. Мы можем записать строку в виде $$\frac{x – x_0}{a} = \frac{y – y_0}{b}$$, которая (находя y ) можно переписать как $$y = \frac{b}{a}(x – x_0) + y_0$$ Наклон – это число \(\displaystyle\frac{b}{a} = \frac{ \cos(\theta_y)}{\cos(\theta_x)} = \frac{\sin(\theta_x)}{\cos(\theta_x)} = \tan(\theta)\), показывая, что отношение a : b тесно связано с наклоном, который представляет собой тангенс угла к оси x .






 Любая помощь, которую вы могли бы предоставить, будет БОЛЬШИМ образом оценена.
Большое спасибо. 92}$$
Любая помощь, которую вы могли бы предоставить, будет БОЛЬШИМ образом оценена.
Большое спасибо. 92}$$ 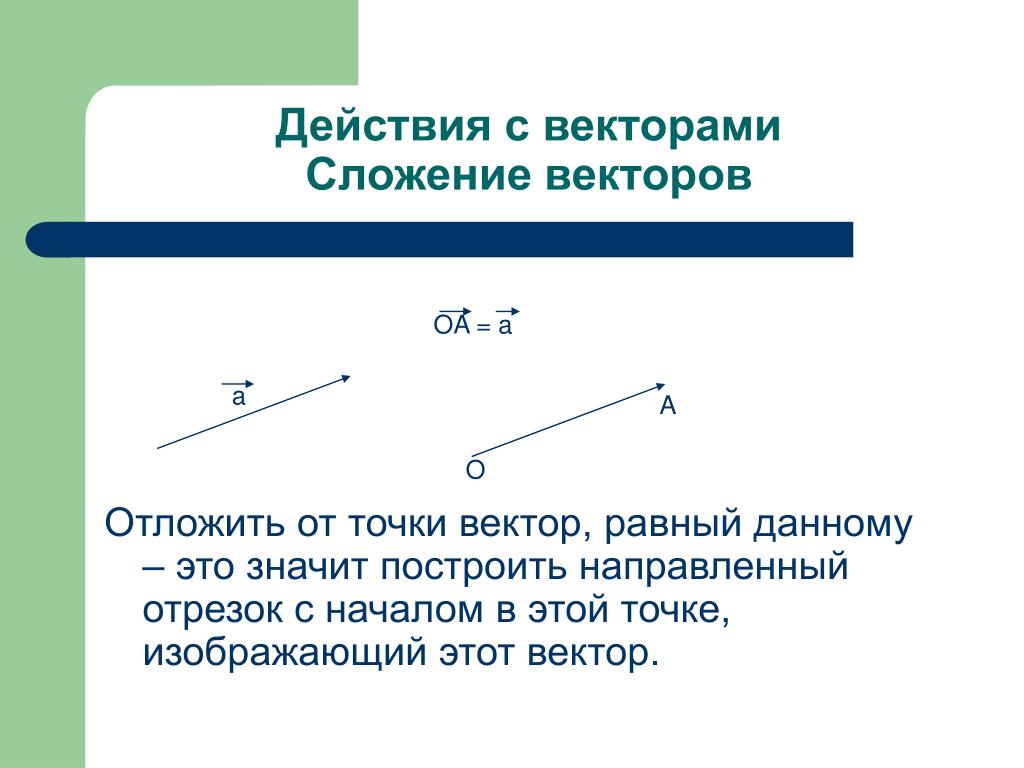 При работе над задачами удобно использовать единичные векторы. Если мы позволим u представлять вектор в определенном направлении и единицу величины, то 3u, 7u и -8u сразу же можно понять как векторы величин 3, 7 и -8, все в направлении от u (кроме -8u, поскольку отрицательный знак означает «в направлении, противоположном к +u»).
При работе над задачами удобно использовать единичные векторы. Если мы позволим u представлять вектор в определенном направлении и единицу величины, то 3u, 7u и -8u сразу же можно понять как векторы величин 3, 7 и -8, все в направлении от u (кроме -8u, поскольку отрицательный знак означает «в направлении, противоположном к +u»).  Это означает, что КАЖДЫЙ вектор в пространстве может быть задан через его «компоненты», параллельные этим трем осям. Так, например, 5i + 2j - 6k — это вектор в пространстве, и его величина будет представлена длиной линии, соединяющей начало координат (0,0,0) с точкой (5,2,-6).
Кстати, это отвечает на ваш второй вопрос: i, j, k называются «базовыми» векторами, потому что они используются в качестве основы для выражения всех других векторов. Любой другой вектор в трехмерном пространстве может быть задан через i, j и k.
Это означает, что КАЖДЫЙ вектор в пространстве может быть задан через его «компоненты», параллельные этим трем осям. Так, например, 5i + 2j - 6k — это вектор в пространстве, и его величина будет представлена длиной линии, соединяющей начало координат (0,0,0) с точкой (5,2,-6).
Кстати, это отвечает на ваш второй вопрос: i, j, k называются «базовыми» векторами, потому что они используются в качестве основы для выражения всех других векторов. Любой другой вектор в трехмерном пространстве может быть задан через i, j и k. 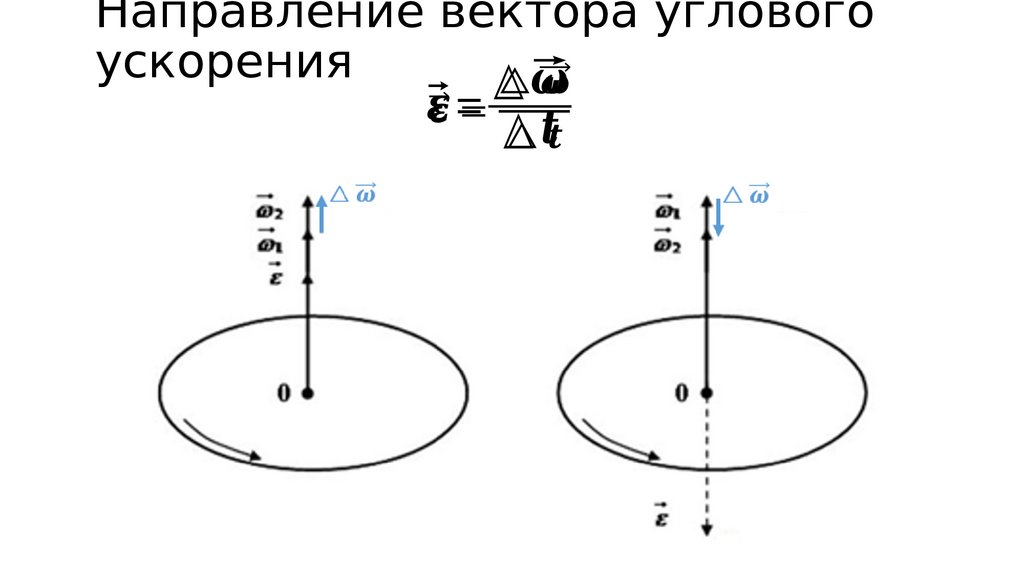 Точно так же любые три некомпланарных вектора могут использоваться в качестве базовых векторов, «охватывающих» трехмерное пространство. Опять же, наиболее распространенными базовыми векторами являются i, j, k, но бывают случаи, когда используется совершенно другой набор базовых векторов.
Наконец, векторы не ограничиваются 1, 2 или 3 измерениями. Ты можешь
имеют многомерные векторы, выраженные через 4, 5, 6 и
высшие базовые векторы. Количество базовых векторов будет равно
размер рассматриваемого пространства.
Точно так же любые три некомпланарных вектора могут использоваться в качестве базовых векторов, «охватывающих» трехмерное пространство. Опять же, наиболее распространенными базовыми векторами являются i, j, k, но бывают случаи, когда используется совершенно другой набор базовых векторов.
Наконец, векторы не ограничиваются 1, 2 или 3 измерениями. Ты можешь
имеют многомерные векторы, выраженные через 4, 5, 6 и
высшие базовые векторы. Количество базовых векторов будет равно
размер рассматриваемого пространства.  К вектору N 9 добавлено .0004 , а результирующее представляет собой вектор величиной 4,75 м, расположенный под углом 39 градусов против часовой стрелки от положительной оси x. Найдите: (а) компоненты N и (б) величину и направление N.
Я нарисовал графическую иллюстрацию проблемы. Но я действительно не могу решить это, потому что я не знаю, как это сделать.
К вектору N 9 добавлено .0004 , а результирующее представляет собой вектор величиной 4,75 м, расположенный под углом 39 градусов против часовой стрелки от положительной оси x. Найдите: (а) компоненты N и (б) величину и направление N.
Я нарисовал графическую иллюстрацию проблемы. Но я действительно не могу решить это, потому что я не знаю, как это сделать.  Прежде чем вы сможете добавить их, вы должны найти их компоненты . Запомните эту схему:
Мой+-------------* M
| /|
| / |
| / |
| / |
| / |
| л/ |
| / |
sin(a)|-----+ |
| /| |
| 1/ | |
| / | |
| /)а | |
|/____|_______|__________
O cos(a) Mx
Вектор длины 1 имеет компоненты (cos(a), sin(a)). По подобным треугольникам вектор M длины L имеет компоненты Mx = L*cos(a), My = L*sin(a). Сделайте это с обоими векторами M и P, чтобы получить их компоненты (Mx, My) и (Px, Py).
Прежде чем вы сможете добавить их, вы должны найти их компоненты . Запомните эту схему:
Мой+-------------* M
| /|
| / |
| / |
| / |
| / |
| л/ |
| / |
sin(a)|-----+ |
| /| |
| 1/ | |
| / | |
| /)а | |
|/____|_______|__________
O cos(a) Mx
Вектор длины 1 имеет компоненты (cos(a), sin(a)). По подобным треугольникам вектор M длины L имеет компоненты Mx = L*cos(a), My = L*sin(a). Сделайте это с обоими векторами M и P, чтобы получить их компоненты (Mx, My) и (Px, Py).  Теперь мы хотели бы знать формулу, чтобы найти наклон трехмерной линии . Мы просмотрели учебники и попытались адаптировать формулу, но безуспешно.
Теперь мы хотели бы знать формулу, чтобы найти наклон трехмерной линии . Мы просмотрели учебники и попытались адаптировать формулу, но безуспешно.  Один из способов определения «наклона» плоскости состоит в том, чтобы записать единичный вектор, который перпендикулярен к ней, называемый 9.2), где I, J и K — единичные векторы в направлениях x, y и z. Коэффициенты I, J и K в этом выражении называются направляющими косинусами вектора, потому что они представляют собой косинусы углов между вектором и осями x, y и z соответственно.
Один из способов определения «наклона» плоскости состоит в том, чтобы записать единичный вектор, который перпендикулярен к ней, называемый 9.2), где I, J и K — единичные векторы в направлениях x, y и z. Коэффициенты I, J и K в этом выражении называются направляющими косинусами вектора, потому что они представляют собой косинусы углов между вектором и осями x, y и z соответственно.  Это означает, что вам нужно два линейных уравнения относительно x, y и z, чтобы определить линию. Существует несколько стандартных форм уравнений прямой, но наиболее часто используемой является
х - х0 у - у0 z - z0
------ = ------ = ------
а б в
Здесь (x0, y0, z0) — точка на прямой, а числа a, b и c определяют направление вдоль прямой: вектор a*I = b*J + c*K параллелен прямой. (Примечание: эта форма работает только тогда, когда линия не параллельна ни одной из плоскостей xy, xz или yz, т. е. когда ни a, ни b, ни c не равны нулю).
Это означает, что вам нужно два линейных уравнения относительно x, y и z, чтобы определить линию. Существует несколько стандартных форм уравнений прямой, но наиболее часто используемой является
х - х0 у - у0 z - z0
------ = ------ = ------
а б в
Здесь (x0, y0, z0) — точка на прямой, а числа a, b и c определяют направление вдоль прямой: вектор a*I = b*J + c*K параллелен прямой. (Примечание: эта форма работает только тогда, когда линия не параллельна ни одной из плоскостей xy, xz или yz, т. е. когда ни a, ни b, ни c не равны нулю). 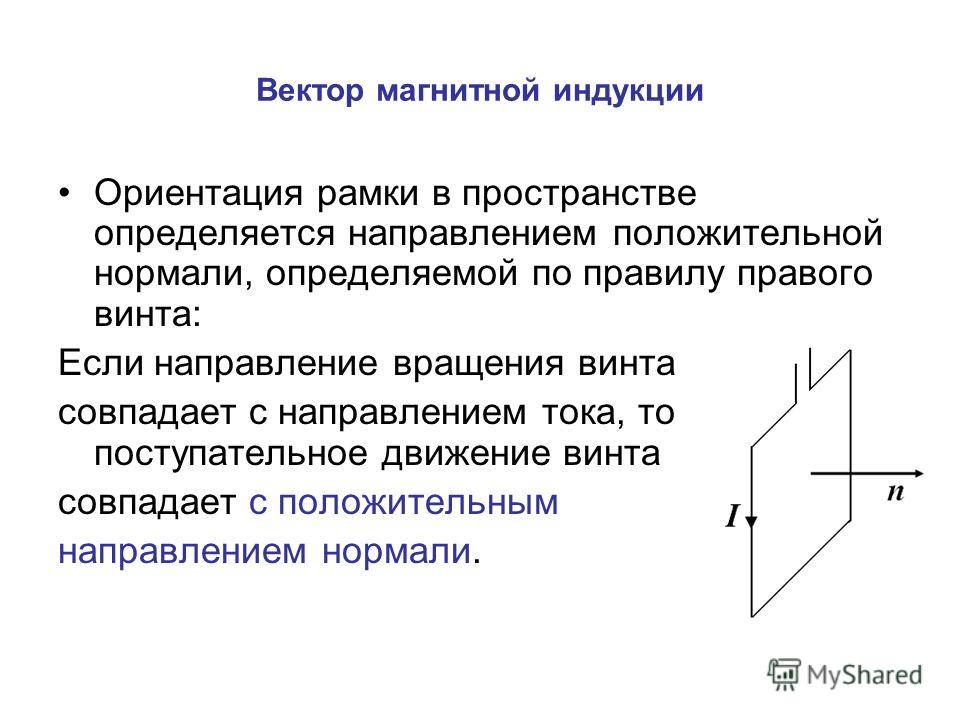 В двух измерениях это просто косинус наклона, который представляет собой угол с осью x, и косинус его дополнения, который является синусом наклона. Наклон - это отношение этих двух, тангенс наклона. Точного аналога нет, потому что не существует «отношения» трех направляющих косинусов или любых трех чисел.
В двух измерениях это просто косинус наклона, который представляет собой угол с осью x, и косинус его дополнения, который является синусом наклона. Наклон - это отношение этих двух, тангенс наклона. Точного аналога нет, потому что не существует «отношения» трех направляющих косинусов или любых трех чисел.