Страница не найдена

Поиск по сайту Авторизация Логин: Пароль: Запомнить меня Регистрация Забыли свой пароль? Войти как пользователь:

Главная  >  Образование  >  Кафедры  >  Кафедра теоретической механики Институт Сведения об Институте Институт Об Институте Реквизиты организации Противодействие коррупции Документы Наука Наука Научная деятельность ИГиЛ Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека Общая информация и правила пользования История библиотеки Новые поступления Информационные ресурсы Заказ литературы по МБА Каталог книг и продолжающихся изданий Каталог отечественной периодики Каталог иностранной периодики Каталог трудов сотрудников Совет научной молодежи Страница совета научной молодежи Института Новости Контакты Библиотека Технологии Технологии ИГиЛ Филиал ЦКП «Механика» Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека Вакансии Охрана труда Профсоюзный комитет Новости и объявления Организационно-финансовый сектор Социальное партнерство Охрана труда Социальные вопросы Жилищные вопросы Культурно-массовая работа Спортивно-оздоровительная работа Состав профкома Ссылки О нас пишут Отзывы Новости Контакты Совет научной молодежи Страница совета научной молодежи Института Библиотека Гражданская оборона Обучение сотрудников Института Институт Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека История Института Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека Филиал ЦКП «Механика» Структура Структура Института Структура Структура Института Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Семинары и конференции Семинары и конференции ИГиЛ Семинары и конференции Семинары и конференции ИГиЛ Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека Наука Научная деятельность ИГиЛ Технологии Технологии ИГиЛ Образование Образование в ИГиЛ Образование (основные сведения) Документы Кафедры Аспирантура Института Диссертационные советы Объявления Материально-техническое обеспечение НОЦ Клуб юных техников Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека Опытное производство филиала Опытное производство Продукция опытного производства Контакты опытного производства Конструкторский отдел Участок штамповки Взрывные камеры Новости Контакты Сотрудники Совет научной молодежи Страница совета научной молодежи Института Библиотека

Семинары Мар 29, 2023 Мемориальный семинар, посвященный памяти Швецова Геннадия Анатольевича 19 апреля 2023 15. 00, 2 этаж, Конференц-зал Института гидродинамики СО РАН Главный… Мар 27, 2023 Семинар «Прикладная гидродинамика» Семинар «Прикладная гидродинамика» 29 марта,   среда,   15-30 НСК,  … Оценка результативности ИГиЛ СО РАН 2013-2015 гг Программа развития ИГиЛ СО РАН Заключение РАН по Программе развития

Момент силы через момент инерции — Dudom

В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические вели­чины — момент сил и момент инерции, физический смысл которых рас­кроем ниже.

Пусть некоторое тело под действием силы , приложенной в точке А, приходит во вращение вокруг оси ОО’ (рисунок 5.1).

Рисунок 5.1 – К выводу понятия момента силы

Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, назы­вают плечом силы. Произведение силы на плечо определяет модуль мо­мента силы относительно точки О:

(5.1)

Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:

(5.2)

Единица момента силы — ньютон-метр (Н . м). Направление вектора момента силы находиться с помощью пра­вила правого винта.

Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, назы­ваемая моментом инерции тела относительно оси вращения.

Момент инерции материальной точки относительно оси враще­ния — произведение массы этой точки на квадрат расстояния от оси:

(5. 3)

Момент инерции тела относительно оси вращения — сумма мо­ментов инерции материальных точек, из которых состоит это тело:

(5.4)

В общем случае, если тело сплошное и представляет собой совокуп­ность точек с малыми массами dm, момент инерции определяется интег­рированием:

, (5.5)

где r — расстояние от оси вращения до элемента массой dm.

Если тело однородно и его плотность ρ = m/V, то момент инерции тела

(5.6)

Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.

Наиболее просто определяется момент инерции тел, имеющих пра­вильную геометрическую форму и равномерное распределение массы по объему.

Момент инерции однородного стержня относительно оси, прохо­дящей через центр инерции и перпендикулярной стержню,

(5.7)

Момент инерции однородного цилиндра относительно оси, перпен­дикулярной его основанию и проходящей через центр инерции,

(5. 8)

Момент инерции тонкостенного цилиндра или обруча относи­тельно оси, перпендикулярной плоскости его основания и проходящей через его центр,

(5.9)

Момент инерции шара относительно диаметра

(5.10)

Определим момент инерции диска относительно оси, проходящей че­рез центр инерции и перпендикулярной плоско­сти вращения. Пусть масса диска – m, а его радиус – R.

Площадь кольца (рисунок 5.2), заключенного между r и , равна .

Рисунок 5.2 – К выводу момента инерции диска

Площадь диска . При постоянной толщине кольца,

откуда или .

Тогда момент инерции диска,

(5.11)

Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.

Рисунок 5.3 – Моменты инерции I_C некоторых однородных твердых тел.

Теорема Штейнера

Приведенные выше формулы для моментов инерции тел даны при усло­вии, что ось вращения проходит через центр инерции.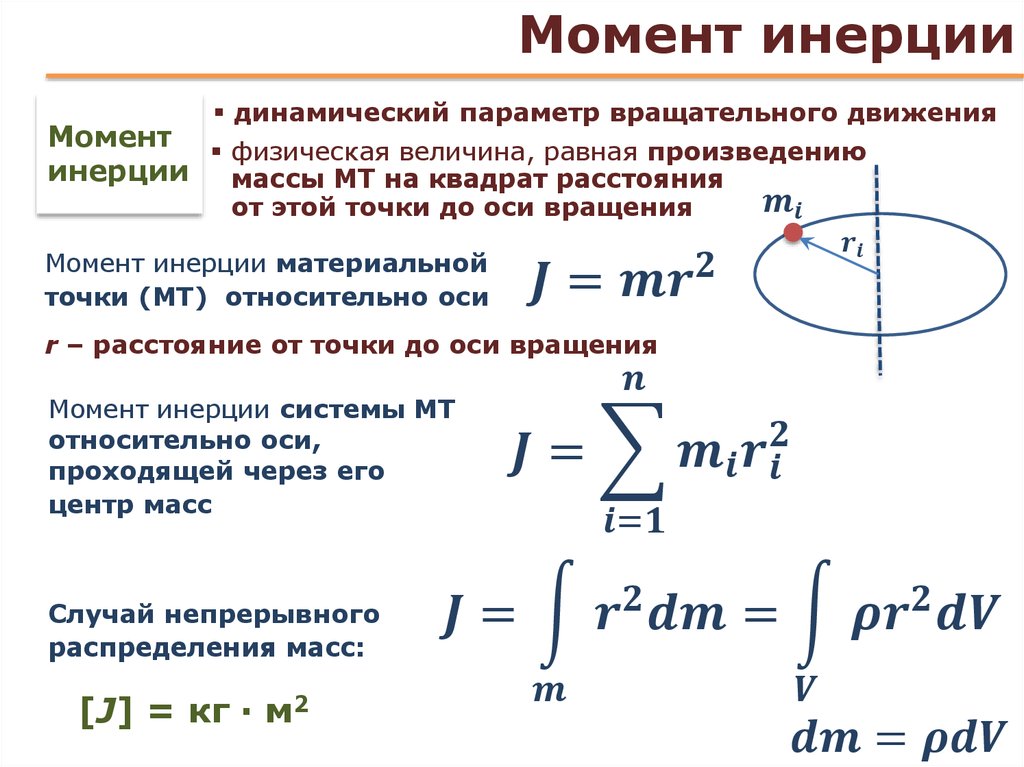 Чтобы определить моменты инерции тела относительно произвольной оси, следует восполь­зоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции J₀ отно­сительно оси, параллельной данной и проходящей через центр инер­ции тела, и величины md 2 :

(5.12)

где m — масса тела, d — расстояние от центра масс до выбранной оси вра­щения. Единица момента инерции — килограмм-метр в квадрате (кг . м 2 ).

Так, момент инерции однородного стержня длиной l относительно оси, про­ходящей через его конец, по теореме Штейнера равен

(5.13)

Дата добавления: 2017-01-08 ; просмотров: 24860 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружности и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения может быть подвижной и неподвижной.

Аналогия между параметрами кинематики и динамики:

S	ϕR	путь
V	ω	Скорость — угловая скорость
a	β	Ускорение – угловое ускорение
F	M=I*β	Сила – момент силы
m	I=km	Масса – момент инерции
P=mV	L=p*l	Импульс – момент импульса
A=F*S	A=M*ϕ	Работа
W=	W=	Энергия

Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

где: — масса i-й точки, — расстояние от i-й точки до оси.

Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.

Теорема Штейнера

Момент инерции твёрдого тела вокруг произвольной оси равен моменту инерции тела вокруг оси, проходящей через центр массы данного тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями.

Момент силы. Основной закон динамики вращательного движения.

Момент силы— векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр.

Основным законом динамики вращательного движения является связь момента силы М с моментом инерции и угловым ускорением β:

Работа при вращательном движении тела

— момент силы относительно оси вращения z.

— векторное произведение.

Кинетическая энергия при вращательном движении

— момент инерции твердого тела, относительно оси z.

Моментом инерции материальной точки называется величина:

Величина I зависит от положения оси вращения и от распределения масс в теле.

Момент импульса. Закон сохранения момента импульса.

Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется.

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

где — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:

Поскольку уравнение вращательного движения можно представить в виде:

Окончательно будем иметь:

Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.

Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:

ΔL = 0, если M = 0.

Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось

Неупругое вращательное столкновение двух дисков.

Закон сохранения момента импульса: = ( + )ω

Дата добавления: 2018-08-06 ; просмотров: 668 ; ЗАКАЗАТЬ РАБОТУ

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудахАрхимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

где — сила, действующая на частицу, а—радиус-вектор частицы.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется.

Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или JМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:

,

11. Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде: , если система находится в равновесии.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законымеханики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Определение момента инерции в физике.

(существительное)

Мера сопротивления тела изменению его угловой скорости вращения

• Момент инерции

  • Первый закон Ньютона, описывающий инерцию из тела в прямолинейном движении, можно распространить на инерцию из тела, вращающегося вокруг оси с использованием момента из инерции 900
  • Момент Инерция также зависит от оси, вокруг которой вы вращаете объект.
  • Основное соотношение между моментом инерцией и угловым ускорением состоит в том, что чем больше момент инерции , тем меньше угловое ускорение.
  • Краткое введение в момент инерция (вращательная инерция ) для студентов, изучающих физику.
  • Определить свойство из массы, описываемой моментом из инерцией

• Физический маятник

  • Период из физического маятника зависит от его момента из инерции относительно его точки вращения и расстояния от его центра из массы.
  • В этом случае период маятника зависит от его момент инерция вокруг точки вращения.
  • , где α — угловое ускорение, τ — крутящий момент, а I — момент из инерция .
  • момент из инерция из жесткий стержень относительно его центра равен:
  • Изменение формы, размера или распределения массы приведет к изменению момента инерции .

• Вращательная кинетическая энергия: работа, энергия и мощность

  • Рассмотрение энергии вращения отдельно вокруг оси объекта из вращения дает следующую зависимость от момента объекта из инерции :
  • где $\omega$ — угловая скорость, а $I$ — момент инерция вокруг оси вращения.
  • Во вращающейся системе момент из инерция играет роль из масса и угловая скорость играет роль из линейная скорость.
  • Земля имеет момент из инерция , I = 8,04×1037 кг·м2.
  • Отношение зависит от момента инерции объекта, который катится.

• Связь между крутящим моментом и угловым ускорением

  • Крутящий момент равен моменту инерции умноженному на угловое ускорение.
  • Крутящий момент и угловое ускорение связаны следующей формулой, где момент инерция инерция и $\alpha$ угловое ускорение.
  • Если вы замените крутящий момент на силу и вращательную инерцию на массу и угловое ускорение на линейное ускорение, вы получите второй закон Ньютона обратно.
  • Чистый крутящий момент вокруг оси вращения равен произведению инерции вращения вокруг этой оси и углового ускорения, как показано на рисунке 1.
  • Силы из двух пальцев отменили бы.

• Приложения кратных интегралов

  • Как и в случае с одной переменной, можно использовать множественный интеграл, чтобы найти среднее функции по заданному набору. 9n$ и интегрируемой функции $f$ по $D$, среднее значение из $f$ в ее области определения равно:
  • , где $m(D)$ — мера $D$.
  • В механике момент из инерция вычисляется как объемный интеграл (тройной интеграл) из плотность, взвешенная с квадратом из расстояние от оси:
  • В следующем примере электрическое поле, создаваемое распределением из зарядов, заданных объемной плотностью заряда $\rho (\vec r)$ , получается тройным интегралом из векторной функции:

• Вращательные столкновения

  • При столкновении из объектов в замкнутой системе импульс всегда сохраняется.
  • Что, если ввести вращательную составляющую движения ?
  • Как и следовало ожидать, объект, имеющий большой момент из инерция I, например Земля, имеет очень большой угловой момент.
  • Например, возьмем случай из : лучник решает выстрелить стрелой массой м1 в неподвижный цилиндр массой м2 и радиусом r, лежащий на боку.
  • Стрела попадает в край цилиндра, заставляя его катиться.

• Инерция вращения

  • Вращательная инерция тенденция из вращающийся объект остается вращающимся, если к нему не приложен крутящий момент.
  • Вращательная инерция , как показано на , является сопротивлением объектов изменениям их вращения.
  • Это уравнение является вращательным аналогом второго закона Ньютона (F=ma), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а mr2 аналогично массе (или инерция ).
  • Величина mr2 называется вращательной инерция или момент из инерция из масса точки m на расстоянии r от центра из вращения.
  • Различные формы из объектов имеют различную вращательную инерцию , которая зависит от распределения из их массы.

• Сохранение углового момента

  • Закон из сохранения из углового момента гласит, что когда на объект не действует внешний крутящий момент, никаких изменений 9Произойдет 0012 из моментов импульса.
  • Это выражение закона из сохранения из углового момента.
  • Когда она это делает, вращательная инерция уменьшается, а скорость вращения увеличивается, чтобы сохранить угловой момент $L = I \omega$ постоянным.
  • (I: вращение инерция , $\omega$: угловая скорость)
  • На следующем изображении ее скорость из вращений сильно увеличивается, когда она вытягивает руки, уменьшая ее момент из инерция .

• Сохранение энергии во вращательном движении

  • Искры летят, шум и вибрация возникают, когда слои из стали снимаются со столба.
  • Сила параллельна смещению, поэтому чистая работа (W) является произведением силы (F) и радиуса (r) диска (это иначе известно как крутящий момент (τ) ) умножить на угол (θ) из вращения:
  • Кинетическая энергия (К.Э.) при вращательном движении связана с моментом из вращательной инерцией (I) и угловой скоростью (ω):
  • Однако энергия никогда не уничтожается; он просто меняет форму от вращения из точильного камня к теплу, когда применяется трение.
  • Заключить взаимозаменяемость силы и радиуса с крутящим моментом и углом поворота при определении силы

• Первый закон: инерция

  • Первый закон Ньютона движения описывает инерцию .
  • Ускорение объекта параллельно и прямо пропорционально чистой силе, действующей на объект, направлено в направлении чистой силы и обратно пропорционально массе объекта.
  • Иногда этот первый закон движения называют законом из инерция .
  • Инерция есть свойство из тела оставаться в покое или двигаться с постоянной скоростью.
  • Некоторые объекты имеют большую инерцию , чем другие, потому что инерция объекта эквивалентна его массе.

Определение, формула, единица измерения, коэффициент, расчет

В этой статье вы узнаете полный обзор момента инерции , такие как его определение, формулы различных разделов, единицы измерения, коэффициенты зависимости, расчет и многое другое.

В физике и механике момент инерции играет важную роль при анализе вращательного движения тел.

Момент инерции, связанный с динамикой.

Используется для расчета крутящего момента, необходимого для вращения объекта вокруг заданной оси, а также углового ускорения объекта под действием заданного крутящего момента. Он также используется для определения устойчивости объекта при его вращении, а также для прогнозирования движения объектов под действием внешних сил или моментов.

Мы также обсуждали полярный момент инерции, момент инерции площади, первый момент площади в нашей предыдущей статье, здесь мы узнаем только о моменте инерции.

Что такое момент инерции?

Момент инерции, также известный как вращательная инерция, момент инерции массы, угловая масса и секундный момент массы, является мерой сопротивления объекта изменению его вращательного движения.

Определяется как сумма произведений массы каждой частицы в объекте и квадрата ее расстояния от оси вращения объекта.

Чем больше момент инерции, тем сложнее изменить скорость или направление вращения объекта.

Момент инерции объекта зависит от формы, размера и распределения массы объекта.

Например, сплошной цилиндр имеет другой момент инерции, чем полый цилиндр того же размера и массы. Как правило, объекты с большей массой, сосредоточенной в направлении их центра масс, имеют меньший момент инерции, чем объекты с более равномерно распределенной массой.

Обычно обозначается символом I.

Формула момента инерции

В выражениях для крутящего момента и углового момента для твердых тел (которые считаются объемными объектами) мы встретили термин Σmr².

Эта величина называется моментом инерции (I) массивного объекта. Для точки массой m на расстоянии r от фиксированной оси момент инерции определяется как mr².

Момент инерции точечной массы,

 I = mr²

Где,

m = масса тела

r = расстояние от оси вращения.

 Итак,

Момент инерции объемных объектов,

 I = Σmr²

При поступательном движении масса является мерой инерции; точно так же для вращательного движения момент инерции является мерой вращательной инерции.

В общем случае масса является неизменной величиной материи (за исключением движения, сравнимого со светом).

Но момент инерции тела не является постоянной величиной.

Зависит не только от массы тела, но и от того, как масса распределена вокруг оси вращения.

Найти момент инерции равномерно распределенной массы; мы должны рассматривать бесконечно малую массу (dm) как точечную массу и принимать ее положение (r) относительно оси.

Момент инерции этой точечной массы теперь можно записать как

 dI = (dm)r²

Мы получаем момент инерции всего объемного объекта путем интегрирования приведенного выше выражения.

I =  ∫ dI =  ∫(dm)r²

I =  ∫r²dm

Мы можем использовать приведенное выше выражение для определения момента инерции некоторых обычных объемных объектов, представляющих интерес, таких как стержни, кольца, диски,

Единица момента инерции

В системе СИ

Как известно, момент инерции

I = Σmr²

Итак,

I = кг-м²

I = кг-м² или кг-мм²

Аналогично в системе СГС будет

I = кг-см²

Итак, единица момента инерция, кг-м² или кг-мм² или кг-см² и его размер ML².

Факторы, от которых зависит момент инерции

Момент инерции тела зависит от нескольких факторов, в том числе:

• Форма тела
• Размер тела
• Распределение массы внутри тела
• Ориентация тела
• Ось вращения
• Свойства материала тела

Форма тела

Момент инерции обычно меньше для тела с более компактной и симметричной формой и больше для тела с более вытянутой или неправильной формы.

Размер тела 

Момент инерции, как правило, больше у более крупного тела, чем у меньшего тела той же формы и распределения массы.

Распределение массы внутри тела

Момент инерции обычно больше у тела с более централизованным распределением массы и меньше у тела с более равномерно распределенной массой.

Ориентация тела

Момент инерции тела может изменяться в зависимости от ориентации тела относительно оси вращения.

Ось вращения

Момент инерции тела зависит от расположения оси вращения относительно тела.

Например, момент инерции тела, вращающегося вокруг оси, проходящей через его центр масс, обычно меньше, чем момент инерции относительно оси, не проходящей через центр масс.

Свойства материала тела

На момент инерции тела могут влиять свойства материала тела, такие как плотность и жесткость материала.

Момент инерции для различных форм

Теперь шаг за шагом мы узнаем момент инерции различных сечений.

Момент инерции однородного стержня

Рассмотрим однородный стержень массы M и длины l, как показано на рисунке.

Найдем выражение для момента инерции этого стержня относительно оси, проходящей через центр масс и перпендикулярной стержню.

Сначала необходимо установить начало системы координат так, чтобы оно совпадало с центром масс, который также является геометрическим центром стержня.

Стержень теперь находится вдоль оси x. Возьмем бесконечно малую массу dm на расстоянии x от начала координат.

Момент инерции dl этой массы dm относительно оси равен,

dI = dm. x²

Поскольку масса распределена равномерно, масса на единицу длины стержня составляет, 

λ = M/L

Масса dm бесконечно малой длины M as, 

dm = λ.dx = (M/L).dx

Момент инерции I всего стержня можно найти путем интегрирования dI,

I = ∫ dI =   ∫dm.x² = ∫ {(M/L).dx}.x²

Поскольку масса распределена по обе стороны от начала координат, пределы интегрирования берутся от -L/2 до L/2.

Итак,

I = (M/L) ∫ x².dx      (от -L/2 до L/2)

Однородное кольцо

Рассмотрим однородное кольцо массой М и радиусом R. Чтобы найти момент инерции кольца относительно оси, проходящей через его центр и перпендикулярной плоскости, возьмем бесконечно малую массу (дм) длина (dx) кольца. Это (dm) расположено на расстоянии R, которое является радиусом кольца от оси, как показано на рисунке.

Момент инерции dl этой малой массы dm равен,

dl = dm.R²

Длина кольца равна его окружности (2πR).

Поскольку масса распределена равномерно, масса на единицу длины λ равна,

 λ =  масса/длина  = M/2πR

Масса (dm) бесконечно малой длины составляет, 

dm = λ. dx = (M/2πR).dx

Теперь момент инерции всего кольца равен

I = ∫ dI =   ∫dm.R² = ∫ {(M/2πr).dx}.R²

I = (MR/2π) ∫dx

Чтобы охватить всю длину кольца, пределы интегрирования берутся от 0 до 2πR.

I = (MR/2π) ∫dx      (от 0 до 2πR)

После интегрирования

I = M.R²

Момент инерции однородного диска

Рассмотрим диск массой M и радиусом R. Этот диск состоит из множества бесконечно малых колец, как показано на рисунке.

Рассмотрим одно такое кольцо массой dm, толщиной dr и радиусом r.

Момент инерции dl этого маленького кольца,

dI = (dm).r²

Поскольку масса распределена равномерно, масса на единицу площади

σ = масса/площадь = (M/π.R²)

Где,

σ = поверхностная плотность массы

Масса бесконечно малого кольца равна

dm = σ.2πrdr = (M/π.R²).2πrdr

Где член 2πrdr — площадь этого элементарного кольца, 2πr — длина, а dr — толщина .

dm = (2M/R²). rdr

Итак,

dI = (dm).r²

dI = (2M/R²).r³dr

Момент инерции всего диска равен,

I = ∫dI

Чтобы охватить всю длину диска, пределы интегрирования взяты от 0 до R.

I =  ∫(2M/R²) .r³dr       (От 0 до R)

После разрешения

I = 1/2(MR²)

Аналогичным образом можно найти

Момент инерции однородной сплошной сферы

I = (2MR²)/5

Момент инерции однородной полой сферы

I = (2MR²)/3

Момент инерции сплошного цилиндра

I = (1/2).m.r²

Момент инерции полого цилиндра

I = (1/2).m(R² + r²)

Момент инерции сплошной прямоугольной пластины

I = (1/12).M(h² + w²)

Момент инерции относительно осей x’ и y’

Иногда необходимо вычислить момент инерции тела относительно осей x’ и y’ оси.

Мы можем вычислить момент инерции для осей x’ и y’, используя две теоремы.

• Теорема о параллельных осях
• Теорема о перпендикулярной оси

Теорема о параллельной оси

Теорема о параллельной оси утверждает, что Момент инерции плоского сечения относительно любой оси, параллельной центральной оси, равен моменту инерции сечения относительно центральной оси плюс произведение площади сечения на квадрат расстояния между двумя осями.

Математически можно записать как

Iₓ, = Iₓ + Ad²

Где,

A = площадь тела

Iₓ = момент инерции относительно точки x

d = расстояние по перпендикуляру между двумя линиями x и x’.

Iₓ, = Момент инерции относительно точки x’

Аналогичный метод можно применить для расчета момента инерции относительно оси y’.

Теорема о перпендикулярной оси

Теорема утверждает, что момент инерции плоского ламинарного тела относительно оси, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух перпендикулярных осей, лежащих в плоскости тела, таких, что все три оси взаимно перпендикулярны и имеют общую точку.

Эту теорему также называют теоремой о полярной оси.

Математически,

Iz = Iₓ + Iᵧ

Где,

Iz = Момент инерции относительно оси Z

Iₓ = Момент инерции относительно оси X

4

4

Расчет момента инерции

Вопрос

Сплошной цилиндр имеет радиус 5 см и высоту 10 см.