Физика, 9 кл. (Буховерцев Б.Б.)
Физика, 9 кл. (Буховерцев Б.Б.)
ОглавлениеТЕПЛОВЫЕ ЯВЛЕНИЯ. МОЛЕКУЛЯРНАЯ ФИЗИКАГлава I. ОСНОВЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 1. ОСНОВНЫЕ ПОЛОЖЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ.  2. МАССА МОЛЕКУЛ. ПОСТОЯННАЯ АВОГАДРО 3. БРОУНОВСКОЕ ДВИЖЕНИЕ. 4. СИЛЫ ВЗАИМОДЕЙСТВИЯ МОЛЕКУЛ 5. СТРОЕНИЕ ГАЗООБРАЗНЫХ, ЖИДКИХ И ТВЕРДЫХ ТЕЛ 6. ИДЕАЛЬНЫЙ ГАЗ В МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ 7. ОСНОВНОЕ УРАВНЕНИЕ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ГАЗОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ I Глава II. ТЕМПЕРАТУРА. ЭНЕРГИЯ ТЕПЛОВОГО ДВИЖЕНИЯ МОЛЕКУЛ 8. ТЕПЛОВОЕ РАВНОВЕСИЕ. ТЕМПЕРАТУРА 9. ИЗМЕРЕНИЕ ТЕМПЕРАТУРЫ 10. АБСОЛЮТНАЯ ТЕМПЕРАТУРА. ТЕМПЕРАТУРА — МЕРА СРЕДНЕЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ МОЛЕКУЛ 11. ИЗМЕРЕНИЕ СКОРОСТЕЙ МОЛЕКУЛ ГАЗА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ II Глава III. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА. ГАЗОВЫЕ ЗАКОНЫ 13. ПРИМЕНЕНИЕ УРАВНЕНИЯ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА К РАЗЛИЧНЫМ ПРОЦЕССАМ 14. ПРИМЕНЕНИЕ ГАЗОВ В ТЕХНИКЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ III Глава IV. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 16. РАБОТА В ТЕРМОДИНАМИКЕ 17. 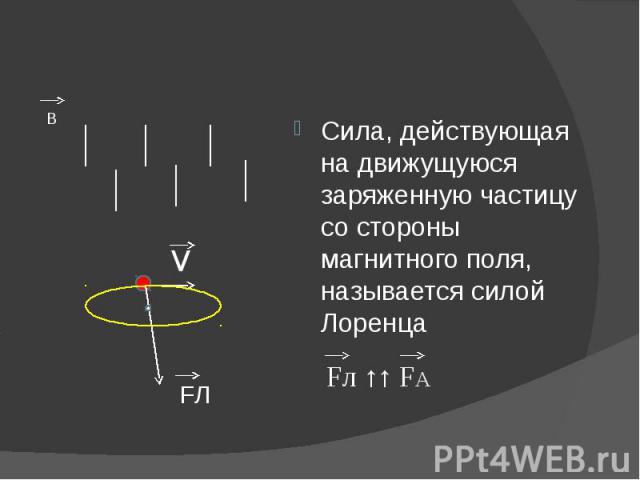 КОЛИЧЕСТВО ТЕПЛОТЫ18. ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ 19. ПРИМЕНЕНИЕ ПЕРВОГО ЗАКОНА ТЕРМОДИНАМИКИ К РАЗЛИЧНЫМ ПРОЦЕССАМ 20. НЕОБРАТИМОСТЬ ПРОЦЕССОВ В ПРИРОДЕ 21. ПРИНЦИПЫ ДЕЙСТВИЯ ТЕПЛОВЫХ ДВИГАТЕЛЕЙ 22. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ (КПД) ТЕПЛОВОГО ДВИГАТЕЛЯ. ТЕПЛОВЫЕ ДВИГАТЕЛИ И ОХРАНА ПРИРОДЫ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Глава V. ВЗАИМНЫЕ ПРЕВРАЩЕНИЯ ЖИДКОСТЕЙ И ГАЗОВ 23. НАСЫЩЕННЫЙ ПАР 24. ЗАВИСИМОСТЬ ДАВЛЕНИЯ НАСЫЩЕННОГО ПАРА ОТ ТЕМПЕРАТУРЫ. КИПЕНИЕ. КРИТИЧЕСКАЯ ТЕМПЕРАТУРА 25. ВЛАЖНОСТЬ ВОЗДУХА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ V Глава VI. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ ЖИДКОСТЕЙ 27. СИЛА ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ 28. КАПИЛЛЯРНЫЕ ЯВЛЕНИЯ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ VI Глава VII. ТВЕРДЫЕ ТЕЛА 29. КРИСТАЛЛИЧЕСКИЕ ТЕЛА 30. АМОРФНЫЕ ТЕЛА 31. ДЕФОРМАЦИЯ. ВИДЫ ДЕФОРМАЦИИ ТВЕРДЫХ ТЕЛ 32. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ. ДИАГРАММА РАСТЯЖЕНИЯ 33. ПЛАСТИЧНОСТЬ И ХРУПКОСТЬ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ОСНОВЫ ЭЛЕКТРОДИНАМИКИ 34. 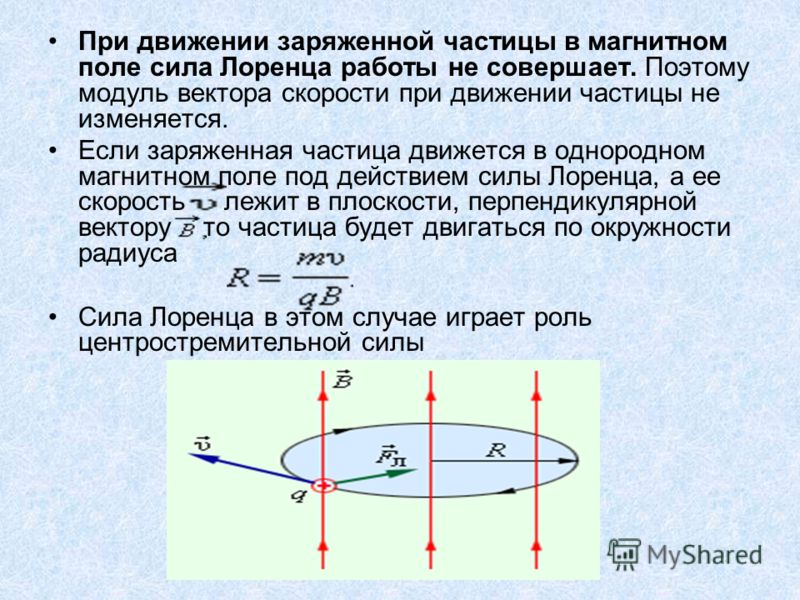 ЧТО ТАКОЕ ЭЛЕКТРОДИНАМИКА?Глава VIII. ЭЛЕКТРОСТАТИКА 35. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД И ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ 36. ЗАРЯЖЕННЫЕ ТЕЛА. ЭЛЕКТРИЗАЦИЯ ТЕЛ 37. ЗАКОН СОХРАНЕНИЯ ЭЛЕКТРИЧЕСКОГО ЗАРЯДА 38. ОСНОВНОЙ ЗАКОН ЭЛЕКТРОСТАТИКИ — ЗАКОН КУЛОНА 39. ЕДИНИЦА ЭЛЕКТРИЧЕСКОГО ЗАРЯДА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 40. БЛИЗКОДЕЙСТВИЕ И ДЕЙСТВИЕ НА РАССТОЯНИИ 41. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 42. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ 43. СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ 44. ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 45. НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ РАВНОМЕРНО ЗАРЯЖЕННОГО ПРОВОДЯЩЕГО ШАРА И БЕСКОНЕЧНОЙ ПЛОСКОСТИ 47. ПОЛЯРИЗАЦИЯ ДИЭЛЕКТРИКОВ. ДИЭЛЕКТРИЧЕСКАЯ ПРОНИЦАЕМОСТЬ 48. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ 49. ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ 50. ПОТЕНЦИАЛ ЭЛЕКТРИЧЕСКОГО ПОЛЯ ТОЧЕЧНОГО ЗАРЯДА 51. СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ЭЛЕКТРИЧЕСКОГО ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ. 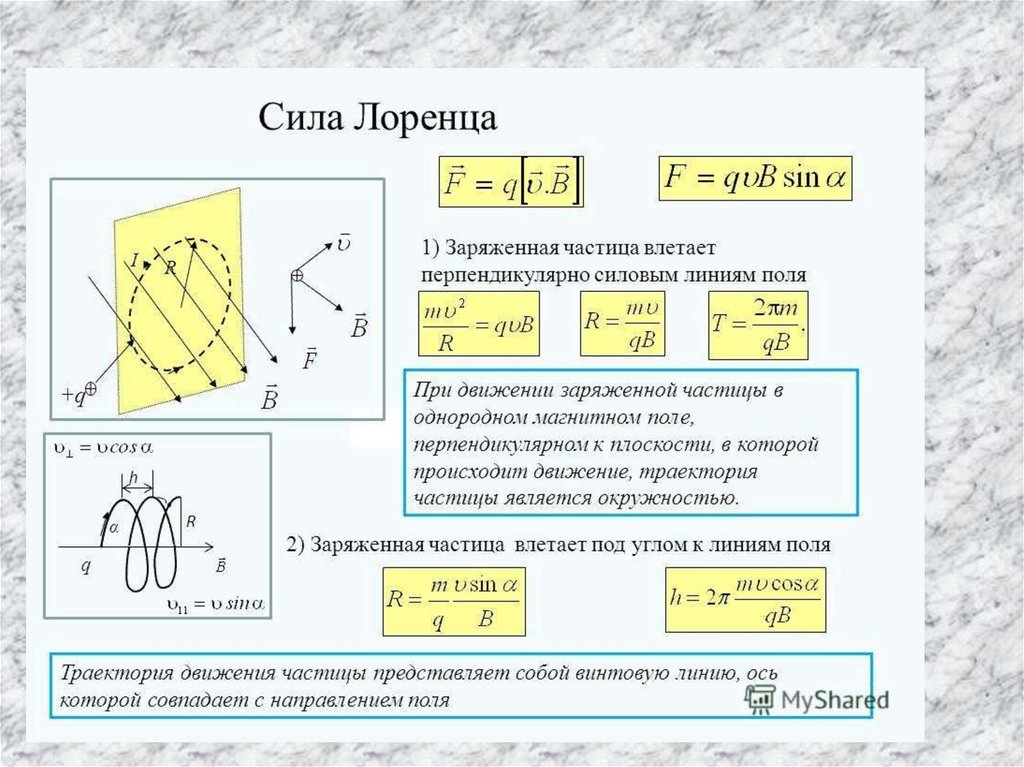 ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ52. ИЗМЕРЕНИЕ РАЗНОСТИ ПОТЕНЦИАЛОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 54. КОНДЕНСАТОРЫ. ЭЛЕКТРОЕМКОСТЬ ПЛОСКОГО КОНДЕНСАТОРА 55. ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА. ПРИМЕНЕНИЯ КОНДЕНСАТОРОВ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава IX. ПОСТОЯННЫЙ ЭЛЕКТРИЧЕСКИЙ ТОК 56. ЭЛЕКТРИЧЕСКИЙ ТОК. СИЛА ТОКА 57. УСЛОВИЯ, НЕОБХОДИМЫЕ ДЛЯ СУЩЕСТВОВАНИЯ ЭЛЕКТРИЧЕСКОГО ТОКА 58. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ. СОПРОТИВЛЕНИЕ 59. ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ПРОВОДНИКА ОТ ТЕМПЕРАТУРЫ 60. СВЕРХПРОВОДИМОСТЬ 61. ЭЛЕКТРИЧЕСКИЕ ЦЕПИ. ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЯ ПРОВОДНИКОВ 62. ИЗМЕРЕНИЕ СИЛЫ ТОКА И НАПРЯЖЕНИЯ 63. РАБОТА И МОЩНОСТЬ ПОСТОЯННОГО ТОКА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ 64. ЭЛЕКТРОДВИЖУЩАЯ СИЛА 65. ЗАКОН ОМА ДЛЯ ЗАМКНУТОЙ ЦЕПИ КРАТКИЕ ИТОГИ ГЛАВЫ IX Глава X. ЭЛЕКТРИЧЕСКИЙ ТОК В РАЗЛИЧНЫХ СРЕДАХ 66. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ РАЗЛИЧНЫХ ВЕЩЕСТВ 67.  ЭЛЕКТРОННАЯ ПРОВОДИМОСТЬ МЕТАЛЛОВ68. ЭЛЕКТРИЧЕСКИЙ ТОК В ЖИДКОСТЯХ 69. ЗАКОН ЭЛЕКТРОЛИЗА 70. ЭЛЕКТРИЧЕСКИЙ ТОК В ГАЗАХ 71. НЕСАМОСТОЯТЕЛЬНЫЙ И САМОСТОЯТЕЛЬНЫЙ РАЗРЯДЫ 72. РАЗЛИЧНЫЕ ТИПЫ САМОСТОЯТЕЛЬНОГО РАЗРЯДА И ИХ ТЕХНИЧЕСКИЕ ПРИМЕНЕНИЯ 73. ПЛАЗМА 74. ЭЛЕКТРИЧЕСКИЙ ТОК В ВАКУУМЕ 75. ДВУХЭЛЕКТРОДНАЯ ЭЛЕКТРОННАЯ ЛАМПА-ДИОД 76. ЭЛЕКТРОННЫЕ ПУЧКИ. ЭЛЕКТРОННОЛУЧЕВАЯ ТРУБКА 78. ЭЛЕКТРИЧЕСКАЯ ПРОВОДИМОСТЬ ПОЛУПРОВОДНИКОВ ПРИ НАЛИЧИИ ПРИМЕСЕЙ 79. ЭЛЕКТРИЧЕСКИЙ ТОК ЧЕРЕЗ КОНТАКТ ПОЛУПРОВОДНИКОВ p- И n- ТИПОВ 80. ПОЛУПРОВОДНИКОВЫЙ ДИОД 81. ТРАНЗИСТОР 82. ТЕРМИСТОРЫ И ФОТОРЕЗИСТОРЫ ПРИМЕР РЕШЕНИЯ ЗАДАЧИ КРАТКИЕ ИТОГИ ГЛАВЫ X Глава XI. МАГНИТНОЕ ПОЛЕ 83. ВЗАИМОДЕЙСТВИЕ ТОКОВ. МАГНИТНОЕ ПОЛЕ 84. ВЕКТОР МАГНИТНОЙ ИНДУКЦИИ 85. ЛИНИИ МАГНИТНОЙ ИНДУКЦИИ 86. ЭЛЕКТРОИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ 87. МОДУЛЬ ВЕКТОРА МАГНИТНОЙ ИНДУКЦИИ. МАГНИТНЫЙ ПОТОК 88. ЗАКОН АМПЕРА 89. ДЕЙСТВИЕ МАГНИТНОГО ПОЛЯ НА ДВИЖУЩИЙСЯ ЗАРЯД.  90. МАГНИТНЫЕ СВОЙСТВА ВЕЩЕСТВА ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XI Глава XII. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ 91. ОТКРЫТИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 92. НАПРАВЛЕНИЕ ИНДУКЦИОННОГО ТОКА. ПРАВИЛО ЛЕНЦА 93. ЗАКОН ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ 94. ВИХРЕВОЕ ЭЛЕКТРИЧЕСКОЕ ПОЛЕ 95. ЭДС ИНДУКЦИИ В ДВИЖУЩИХСЯ ПРОВОДНИКАХ 96. САМОИНДУКЦИЯ. ИНДУКТИВНОСТЬ 97. ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА 98. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРОДИНАМИКИ И ИХ ТЕХНИЧЕСКОЕ ПРИМЕНЕНИЕ ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ КРАТКИЕ ИТОГИ ГЛАВЫ XII ЗАКЛЮЧЕНИЕ ЛАБОРАТОРНЫЕ РАБОТЫ ОТВЕТЫ К УПРАЖНЕНИЯМ |
Сила Лоренца (эл. И магн. Часть). Закон Ампера. Действие магнитного поля на движущийся заряд. Сила Лоренца
Электрический
ток – это совокупность упорядоченно
движущихся заряженных частиц. Поэтому
действие магнитного поля на проводник
с током есть результат действия поля
на движущиеся заряженные частицы внутри
проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
Сила Ампера равна , сила тока равна(см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
где — угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так
как сила Лоренца перпендикулярна
скорости частицы, то она не совершает
работу. А, согласно теореме о кинетической
энергии, это означает, что сила Лоренца
не меняет кинетическую энергию частицы
и, следовательно модуль ее скорости.
Закон Ампера
Поместим
в магнитное поле проводник длинной l,
по которому течет ток I.
На проводник действует сила, прямо
пропорциональная силе тока, текущего
по проводнику, индукции магнитного
поля, длине проводника, и зависящая от
ориентации проводника в магнитном
поле. |F|=IBlsin,
где — угол между
направлением тока в проводнике и
направлением вектора магнитной индукции
B,
Направление силы Ампера определяется
по правилу
левой руки:
если левую руку расположить так, что
магнитные силовые линии входят в ладонь,
четыре вытянутых пальца направить по
току, то отогнутый большой палец укажет
направление силы. Очевидно, что сила
Ампера равна нулю, если проводник
расположен вдоль силовых линий поля и
максимальна, если проводник перпендикулярен
силовым линиям. Движение заряженных
частиц в магнитном поле. На проводник
с током в магнитном поле действует сила
Ампера F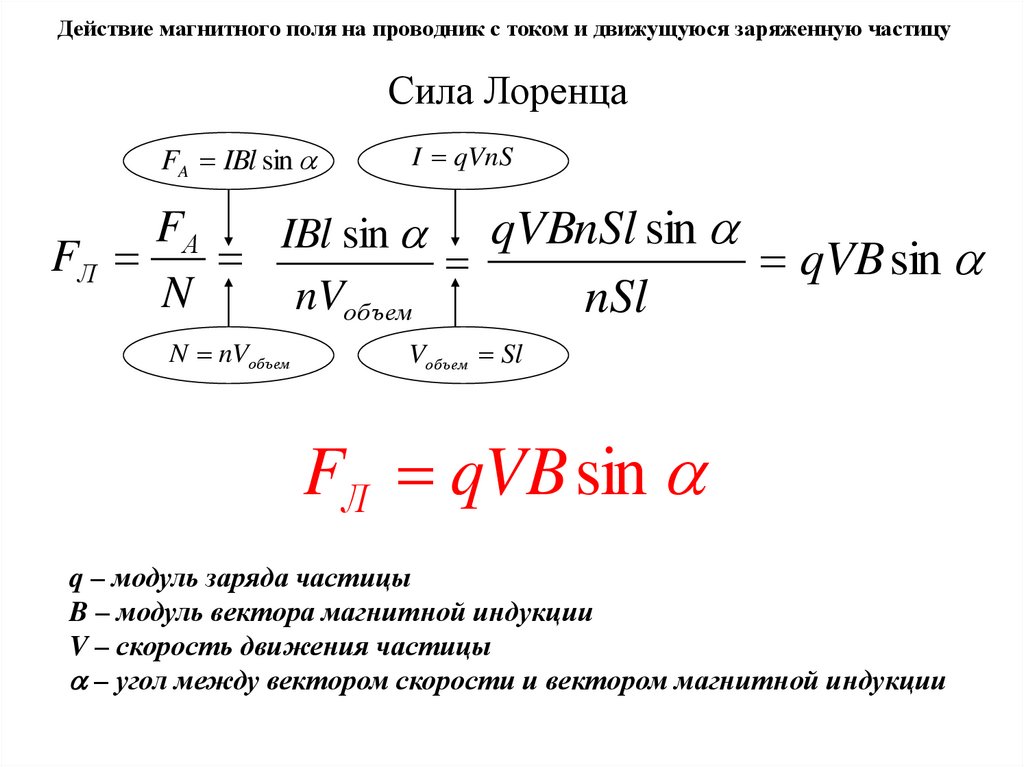
Ток,
в свою очередь, это направленное движение
заряженных частиц. Сила тока равна
I=qnvS,
где q
– заряд частицы, n-концентрация
движущихся заряженных частиц, v-средняя
скорость их направленного движения,
S-площадь
поперечного сечения проводника.
Подставив I
в выражение для FА,
получим FА= qnvSBlsin,
где nsl=N
– общее число частиц, создающих ток.
Тогда сила, действующая на отдельный
движущийся заряд – сила
Лоренца,
равна Fл=qvBsin.
где — угол между векторами скорости и
магнитной индукции. Направление силы
Лоренца определяется для положительно
заряженной частицы по правилу левой
руки.
Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное
изучение магнитного взаимодействия
показывает, что модуль силы Ампера
пропорционален длине проводника с
током, силе тока и зависит от ориентации
проводника в магнитном поле.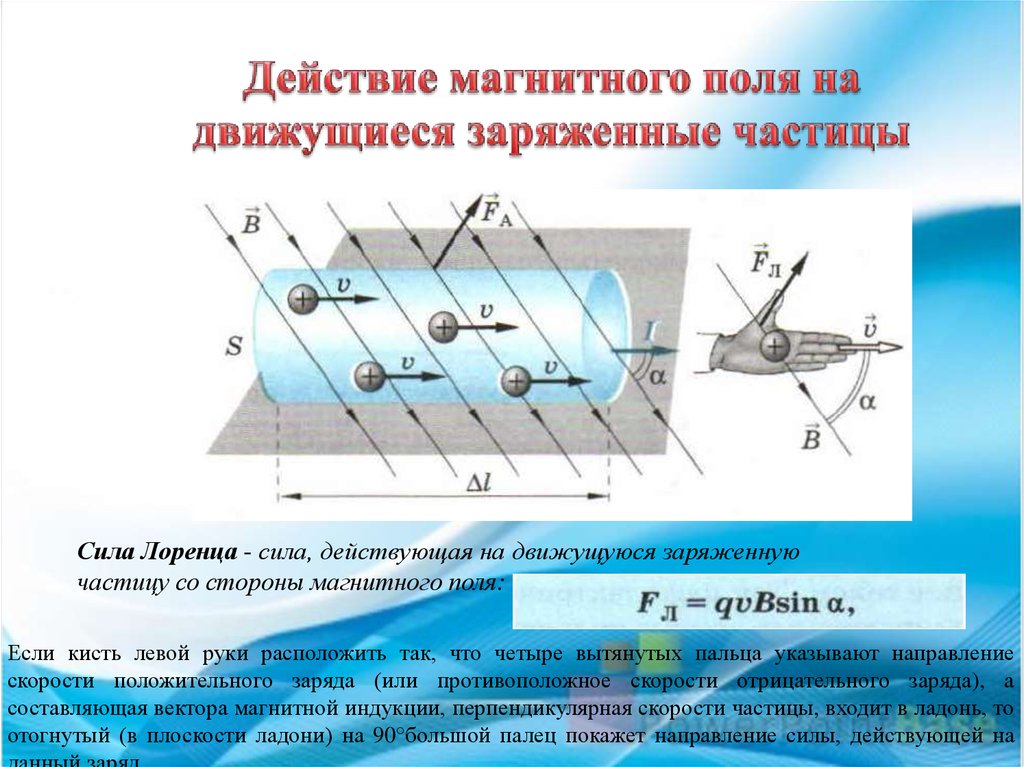
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное
взаимодействие проводников с током
используется в Международной системе
для определения единицы сила тока
–ампера.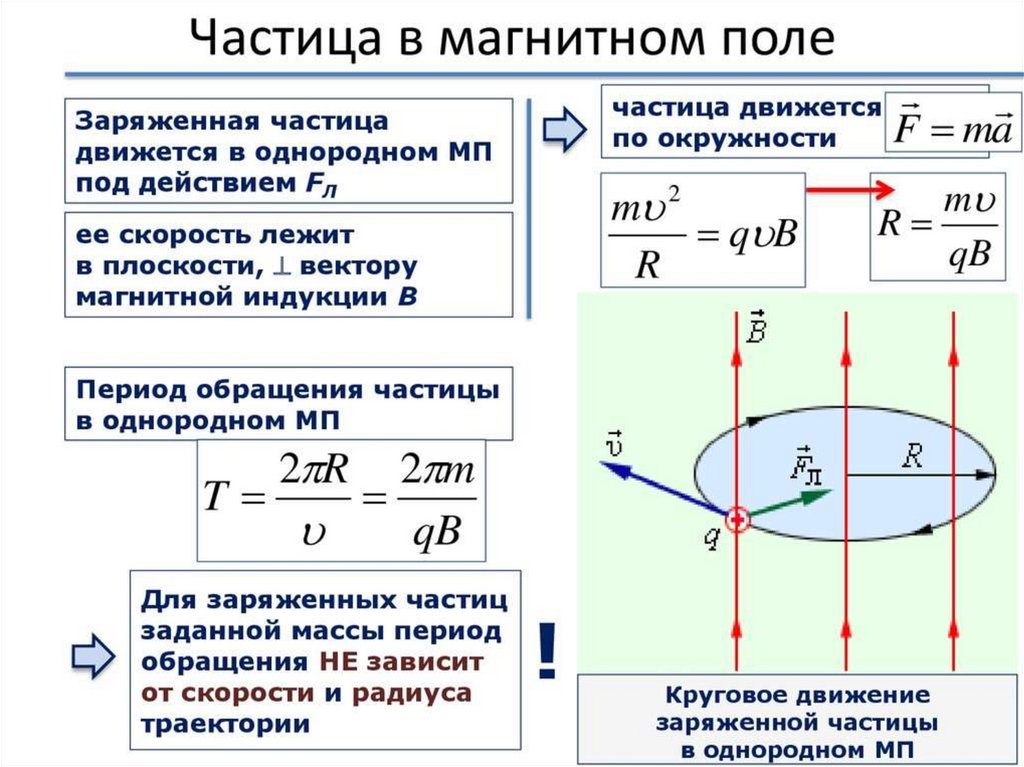
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
5.3 Напряженность магнитного поля: сила, действующая на движущийся заряд в магнитном поле
Цели обученияПравило правой руки 1
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать влияние магнитных полей на движущиеся заряды
- Используйте правило правой руки 1 для определения скорости заряда, направления магнитного поля и направления магнитной силы, действующей на движущийся заряд
- Расчет магнитной силы на движущийся заряд
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 2.
D.1.1 Учащийся может применять математические процедуры для выражения силы, действующей на движущийся заряженный объект магнитным полем. (П. 2.2) - 3.C.3.1 Учащийся может использовать правила правой руки для анализа ситуации, связанной с проводником с током и движущимся электрически заряженным объектом, чтобы определить направление магнитной силы, действующей на заряженный объект из-за магнитное поле, создаваемое проводником с током. (П. 1.4)
D.1.1 Учащийся может применять математические процедуры для выражения силы, действующей на движущийся заряженный объект магнитным полем. (П. 2.2) Каков механизм, с помощью которого один магнит воздействует на другой? Ответ связан с тем фактом, что весь магнетизм вызван током, потоком заряда. Магнитные поля воздействуют на движущиеся заряды , и поэтому они воздействуют на другие магниты, все из которых имеют движущиеся заряды.
Правило правой руки 1
Магнитная сила, действующая на движущийся заряд, является одной из самых фундаментальных известных.
Магнитная сила так же важна, как электростатическая или кулоновская сила. И все же магнитная сила более сложна как по количеству воздействующих на нее факторов, так и по своему направлению, чем относительно простая кулоновская сила. Величина магнитной силы FF размером 12{F} {} на заряд qq размером 12{q} {}, движущийся со скоростью vv размером 12{v} {} в магнитном поле напряженностью BB размером 12{B} { } задается
5.1 F=qvBsinθ,F=qvBsinθ, размер 12{F= ital «qvB»»sin»θ} {}
, где θθ размер 12{θ} {} — угол между направлениями vv и B.B. размер 12{B} {} Эту силу часто называют силой Лоренца. Фактически так мы определяем напряженность магнитного поля В—В—размер 12{В} {} через силу, действующую на заряженную частицу, движущуюся в магнитном поле. Единица СИ для напряженности магнитного поля BB размера 12{B} {} называется тесла (Т) в честь эксцентричного, но блестящего изобретателя Николы Теслы (1856–1819 гг.).43). Чтобы определить, как тесла соотносится с другими единицами СИ, мы решаем F=qvBsinθF=qvBsinθ size 12{F= ital «qvB»»sin»θ} {} для B.
B.size 12{B} {}
5.2 B=FqvsinθB=Fqvsinθ размер 12{B= {{F} над { ital «qv»»sin»θ} } } {}
Поскольку размер sinθsinθ 12{θ} {} безразмерен, тесла равен
5,3 1 T=1 NC⋅м/с=1 NA⋅м.1 T=1 NC⋅м/с=1 NA⋅м. size 12{«1 T»= {{«1 N»} над {C cdot «м/с»} } = {{1″ N»} над {A cdot m} } } {}
Обратите внимание, что C/s = A.
Еще одна меньшая единица, называемая гауссом (G), где 1G=10−4T, 1G=10−4T, размер 12{1`G=»10″ rSup { размер 8{ — 4} } `T} { } иногда используется. Самые сильные постоянные магниты имеют поля около 2 Тл; сверхпроводящие электромагниты могут достигать 10 Тл и более. Магнитное поле Земли на ее поверхности составляет всего около 5×10-5 Тл, 5×10-5 Тл, размер 12{5 умножить на «10» rSup { размер 8{ — 5} } `T} {} или 0,5 G.
Направление магнитной силы FF размера 12{F} {} перпендикулярно плоскости, образованной vv размером 12{v} {} и B, B, как определено правилом правой руки 1 (или RHR- 1), что показано на рис. 5.9.
RHR-1 утверждает, что для определения направления магнитной силы на положительный движущийся заряд вы указываете большим пальцем правой руки в направлении v, v, пальцами в направлении B, B и перпендикуляром к ладонь указывает в сторону Ф.Ф. Один из способов запомнить это состоит в том, что существует одна скорость, и поэтому ее представляет большой палец. Есть много линий поля, поэтому пальцы представляют их. Сила направлена в том направлении, куда вы бы толкнули ладонью. Сила, действующая на отрицательный заряд, направлена прямо противоположно силе на положительном заряде.
Рис. 5.9 Магнитные поля воздействуют на движущиеся заряды. Эта сила является одной из самых основных известных. Направление магнитной силы на движущийся заряд перпендикулярно плоскости, образованной vv и BB размером 12{B} {}, и следует правилу правой руки 1 (RHR-1), как показано. Величина силы пропорциональна q,q,size 12{q} {}v,v,size 12{v} {}B,B,size 12{B} {} и синусу угла между vv size 12{v} {} и B.
B.size 12{B} {}
Создание соединений: заряды и магниты
На статические заряды не действует магнитная сила. Однако на движущиеся заряды действует магнитная сила. Когда заряды неподвижны, их электрические поля не действуют на магниты. Но когда заряды движутся, они создают магнитные поля, которые воздействуют на другие магниты. При относительном движении возникает связь между электрическим и магнитным полями — одно влияет на другое.
Пример 5.1 Расчет магнитной силы: магнитное поле Земли на заряженном стеклянном стержне
За исключением компаса, вы редко видите или лично испытываете силы, связанные с небольшим магнитным полем Земли. Чтобы проиллюстрировать это, предположим, что в физической лаборатории вы натираете стеклянную палочку шелком, помещая на нее положительный заряд в 20 нКл. Вычислите силу, действующую на стержень со стороны магнитного поля Земли, если вы бросите его с горизонтальной скоростью 10 м/с строго на запад в месте, где поле Земли направлено строго на север параллельно земле.
(Направление силы определяется правилом правой руки 1 (RHR-1), как показано на рис. 5.10.)
Рис. 5.10. Положительно заряженный объект, движущийся строго на запад в области, где магнитное поле Земли направлено строго на север, подвергается воздействию силы, которая направлена прямо вниз, как показано на рисунке. Отрицательный заряд, движущийся в том же направлении, испытает силу прямо вверх.
Стратегия
Нам известны заряд, его скорость, напряженность и направление магнитного поля. Таким образом, мы можем использовать уравнение F=qvBsinθF=qvBsinθ size 12{F= ital «qvB»»sin»θ} {}, чтобы найти силу.
Решение
Магнитная сила равна
5,4 F=qvbsinθ.F=qvbsinθ. size 12{F= ital «qvb»»sin»θ} {}
Мы видим, что sinθ=1,sinθ=1,size 12{«sin»θ=1} {}, так как угол между скоростью и направлением поля 90º.90º.size 12{«90» rSup { size 8{ circ } } } {} Ввод других заданных величин дает
5,5 F=20×10–9C10 м/с5×10–5T=1 ×10–11C⋅м/sNC⋅м/с=1×10–11N.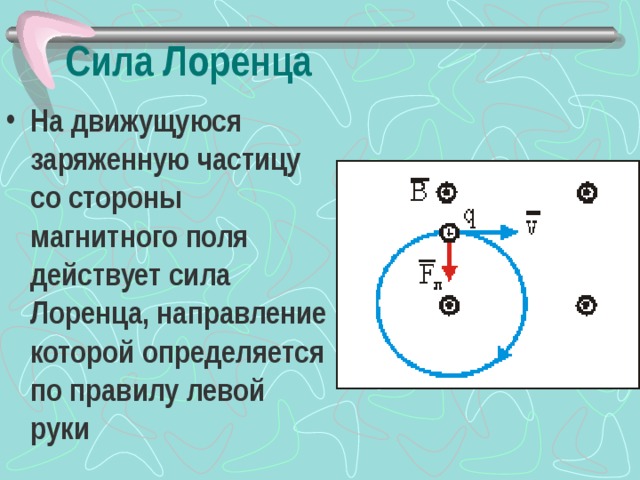
F=20×10–9C10 м/с5×10–5T=1×10–11C⋅м/sNC⋅м/с=1× 10–11N.alignl { стек { размер 12 {F = слева («20» умножить на «10» rSup { размер 8 { — 9} } `C вправо ) влево («10″`»м/с» вправо ) влево (5 раз «10» rSup { размер 8{- 5} } `T вправо )} {} # «»=1 раз «10 » rSup { размер 8{ — «11»} } ` влево (C cdot «м/с» вправо) влево ( { {N} над {C cdot «м/с»} } вправо )=1 раз «10» rSup {размер 8{-«11»} } `N «.» {} } } {}
Обсуждение
Этой силой можно пренебречь на любом макроскопическом объекте, что согласуется с опытом. Он рассчитывается только с одной цифрой, потому что поле Земли меняется в зависимости от местоположения и дается только с одной цифрой. Однако магнитное поле Земли оказывает очень важное воздействие, особенно на субмикроскопические частицы. Некоторые из них исследуются в книге «Сила движущегося заряда в магнитном поле: примеры и приложения».
- Печать
- Поделиться
Магнитное поле
Заряд в движении
Плазма на поверхности Солнца очерчивает огромные силовые линии магнитного поля.
Электромагнитное поле состоит из двух частей: электрического поля и магнитного поля (также называемого полем В). Мы можем начать понимать эти поля через их соответствующие силы.
Электрическая сила представляет собой взаимодействие между заряженными частицами.
Магнитная сила представляет собой взаимодействие между движущимися заряженными частицами.
Движущиеся заряженные частицы создают магнитное поле. Заряды, движущиеся через магнитное поле, испытывают силу. Движение через магнитное поле изменяет движение заряженных частиц. Сила, действующая на заряженную частицу со стороны магнитного поля, называется силой Лоренца.
Магнитное поле влияет на движение заряженных частиц, которое, в свою очередь, влияет на магнитное поле, который влияет на движение частиц, который влияет на поле, которое влияет на частицы…
Одиночная заряженная частица называется монополем и имеет радиальные линии электрического поля,
где пара противоположно заряженных частиц представляет собой диполь с силовыми линиями диполя Е.
Линии магнитного поля дают информацию о магнитном поле подобно линиям электрического поля. Линии поля в обоих случаях являются математическими конструкциями, иллюстрирующими свойства поля. Поле сильнее там, где линии ближе друг к другу, и линии помечены стрелками, чтобы указать направление векторного поля. Обратите внимание, что направление магнитного поля ферромагнетика, такого как этот стержневой магнит, указывает с севера на юг. вне магнита.
Железные опилки вокруг стержневого магнита показывают силовые линии магнитного поля. Компасы — это просто магниты, которые могут свободно вращаться, чтобы выровняться с магнитным полем.
Магнитных монополей не существует. Каждое магнитное поле имеет как минимум дипольную структуру.
Магнитное поле двух стержневых магнитов подобно двум электрическим диполям, расположенным рядом друг с другом.
Магнитное поле Земли возникает из-за вращения внешнего ядра из расплавленного металла.
Хотя на самом деле это очень сложно,
мы часто аппроксимируем его стержневым магнитом. Обратите внимание, что северный магнитный полюс на самом деле является южным полюсом «стержневого магнита».
Магнитное поле постоянного магнита, такого как стержневой магнит, вызвано магнитными доменами, в которых спины электронов выровнены.
Движущаяся заряженная частица создает магнитное поле, определяемое приведенным выше уравнением. Это уравнение называется законом Био-Савара.
Магнитное поле имеет единицы тесла, равные ньютонам на амперметр. Символ μ 0 называется константой проницаемости.
Закон Био-Савара представляет собой векторное уравнение. Мы можем найти направление магнитного поля, создаваемого движущейся заряженной частицей, используя правило правой руки.
Рассмотрим протон в начале координат с константой v
x = 1,0 x 10 7 м/с.
